d(ν) = max{n N : ν dmn p n } N. p d(ν) (ν) = ρ.
|
|
|
- Octavia Sherman
- 5 years ago
- Views:
Transcription
1 1. Trees; context free grammars Trees. Definition 1.1. By a tree we mean an ordered triple T = (N, ρ, p) (i) N is a finite set; (ii) ρ N ; (iii) p : N {ρ} N ; (iv) if n N + and ν dmn p n then p n (ν) ν. One can relax the condition that N be finite but we will have no use for infinite trees. Suppose T i = (N i, ρ i, p i ), i = 1, 2 are trees and ι : N 1 N 2. We say ι is an isomorphism from T 1 to T 2 if ι is univalent, rng ι = N 2, ι(ρ 1 ) = ρ 2 and p 2 (ι(ν)) = ι(p 1 (ν)) for ν N 1 {ρ 1 } Suppose (N, ρ, p) is a tree. Proposition 1.1. Suppose ν N. Then there is n N ν dmn p n. Proof. Suppose the Proposition were false. Let f = {(n, p n (ν)) : n N} and note that f : N N. Since N is finite and N is infinite there are m, n N with m < n and f(m) = f(n). But then p n m (p m (ν)) = p n (ν) = f(n) = f(m) = p m (ν) which contradicts (iii). Suppose ν N. In view of the preceding Proposition we may set Note that Set d(ν) = max{n N : ν dmn p n } N. p d(ν) (ν) = ρ. < ν >= (p d(ν) (ν), p d(ν) 1 (ν),..., p(ν), ν) N d(ν)+1. Note that (iii) implies < ν > is univalent. Note that For each δ N we let < ν > 0 = ρ and < ν > d(ν) = ν. N (δ) = {ν N : d(ν) = δ}. Note that N (0) = {ρ}. The members of N are called nodes. ρ is called the root node. If ν N {ρ} we call p(ν) the parent of ν. If ν N we let c(ν) = p 1 [{ν}] = {µ N {ρ} : p(µ) = ν} and call the members of this set the children of ν. A node which has children is called an interior node. A node which has no children is called a leaf node. 1
2 2 If µ, ν N we say µ is a descendant of ν if µ ν and ν is in the range of < µ > which amounts to saying that ν = p n (µ) for some n N +. If µ, ν N we say µ is an ancestor of ν if ν is a descendant of µ. We let i(t ) = {ν N : ν is an interior node} and we let l(t ) = {ν N : ν is a leaf node}. If ν is a node we call d(ν) the depth of ν. We d(t ) = max{d(ν) : ν N } and call this natural number the depth of T. Definition 1.2. We say the tree U = (O, σ, q) is a subtree of T = (N, ρ, p) if σ O N and q = p (O {σ}). Given ν N let N ν be the set whose members are ν and the descendants of ν, let p ν = p (N ν {ν}) and note that T ν = (N ν, ν, p ν ) is a subtree of T which we call the subtree associated to the node ν Ordered trees. Definition 1.3. By an ordered tree we mean an ordered quadruple O = (N, ρ, p, <) (N, ρ, p) is a tree; < is a linear ordering of N and (i) ρ < ν whenever ν N {ρ}; (ii) p(µ) < p(ν) µ < ν whenever µ, ν N {ρ}. Suppose O i = (N i, ρ i, p i ), i = 1, 2 are ordered trees and ι : N 1 N 2. We say ι is an isomorphism from O 1 to O 2 if ι is an isomorphism from (N 1, ρ 1, p 1 ) to (N 2, ρ 2, p 2 ) and µ, ξ N 1 and µ < 1 ξ ι(µ) < 2 ι(ξ). Suppose O = (N, ρ, p, <) is an ordered tree and U = (O, σ, q) is a subtree of T = (N, ρ, p). Let = {(µ, ξ) O O : µ < ξ} and note that (O, σ, q, ) is an ordered tree which we call the ordered tree associated to U. In particular, if ν N, O = N ν, σ = ν and q = q ν we call this ordered tree the ordered tree associated to ν Tree codes. We say a subset T of (N) is a tree code if (i) φ T ; (ii) if s T, j N and s (j) T then s T ; (iii) if s T then {j : s (j) T } = I(n) for some n N. Proposition 1.2. Suppose T is a tree code, p = {(s (j), s) : s T, j N and s (j) T } and < is the intersection with T T of the lexicographic ordering of (N). Then (T,, p, <) is an ordered tree. Definition 1.4. We call (T,, p, <) as in the preceding Proposition the tree associated to the tree code T.
3 Suppose T = (N, ρ, p) is a tree and, for each ν i(ν), < ν is a linear ordering of c(ν). We will show that there is one and only < (N, ρ, p, <) is an ordered tree and µ < ν ξ µ < ν whenever ν i(t ) and µ, ξ c(ν). Let D = d(t ). For each ν i(t ), let n ν = c(ν) and let be determined by the requirement that We define the functions c ν : I(n ν ) c(ν) i, j I(n ν ) and i < j c ν (i) < ν c ν (j). C d : N (d) N d, 0 D, by induction as follows. We let C 0 (ρ) = and, whenever 0 d < D we require that We let C d+1 (ν) = C d (p(ν)) (c p(ν) (ν)) whenever ν N (d+1). The following statements hold: C = D d=0 C d (i) C is a univalent function with domain N ; (ii) the range of C is a tree code; (iii) if < equals the set of (µ, ν) N N C(µ) precedes C(ν) in the lexicographic ordering on the rng C then (N, ρ, p, <) is an ordered tree; (iv) whenever ν i(t ) and µ, ξ c(ν) we have µ < ν ξ µ < ν. Evidently, C is a isomorphism from T to the tree code associated to the range of C. Proposition 1.3. Suppose T = (N, ρ, p) is a tree and (N, ρ, p, < i ), i = 1, 2 are ordered trees Then < 1 =< 2 µ < 1 ξ µ < 2 ξ whenever ν N and µ, ξ c(ν). Proof. Straightforward exercise for the reader. That is, the ordering in an ordered tree is determined by the ordering it induces on the sets c(ν) corresponding to interior nodes ν.
4 Growing trees. Suppose is a tree and satisfy the following conditions: T = (N, ρ, p) O and P (i) O and P are functions with domain the leaf nodes of T ; (ii) for each ν N, (O(ν), ν, P(ν)) is a tree; (iii) the family Let is disjointed. {i(t )} {O(ν) : ν l(t )} ( ) U = i(t ) {O(ν) : ν l(t )} and let ( ) q = p {P(ν) : ν l(t )}. We leave it as an exercise for the reader to verify that (U, ρ, q) is a tree; that N U; and that, for each ν l(t ), (O(ν), ν, P(ν)) is the subtree associated to the node ν of U. Now let us suppose that (N, ρ, p, <) is an ordered tree and that, for each ν l(t ), < ν is (O(ν), ν, P(ν), < ν ) is an ordered tree. We leave it to the reader to verify that there is one and only one (i) (U, ρ, q, ) is an ordered tree; (ii) if µ, ξ N and µ < ξ then µ ξ; (iii) if ν l(t ), µ, ξ O(ν) and µ < ν ξ then µ ξ. 2. Context free grammars. Definition 2.1. By a context free grammar ordered triple G = (T, N, s, P) (i) T is a set; (ii) N is a set, T N = and s N. (iii) P N (T N) ;
5 5 The members of T are called tokens or terminal symbols. The members of N are called nonterminals or nonterminal symbols. s is called the start symbol. The members of P are called productions. Instead of writing (r, s) P one often writes r := ɛ if s = 0 and r := s 0 s 1 s s 1 if s > 0. If r N, n N + and s 0,..., s n 1 (T N) one often writes instead of r := s 0 s 1 s n 1 (r, s i ) P, i I(n). Obviously, if (T, N, s, P) is a context free grammar then so is (T, N, t, P) if t N. Definition 2.2. A parse tree Q for the context free grammar G = (T, N, s, P) is an ordered quintuple (N, ρ, p, <, f) (i) (N, ρ, p, <) is an ordered tree; (ii) f : N T N; (a) if ν i(t ) then f(ν) N; (b) if ν l(t ) then f(ν) T ; (iii) if ν i(t ) and ν has m children then µ 0 < µ 2 <... < µ m 1 (f(ν), (f(µ 0 ),..., f(µ m 1 ))) P. Notice that the notion of parse tree is independent of s. We define < Q > (T ) as follows. Let and let If n = 0 we let and if n > 0 and are the members of L we let For each t N we let L = {ν l(t ) : f(ν) ɛ} n = L. < Q >= ɛ ν 0 < ν 1 < < ν n 1 < Q >= (f(ν 0 )) (f(ν 1 )) (f(ν n 1 )). L(G, t) be the set of < Q > as above where f(ρ) = t. We let L(G) = L(G, s) and we call this language on the alphabet T the language generated by G.
6 6 Definition 2.3. We say the context free grammar G is good if Q i = (N i, ρ i, p i, < i, f i ), i = 1, 2, are parse trees < Q 1 >=< Q 2 > then the ordered trees (N i, ρ i, p i, < i ) are isomorphic; recall that this is the case if and only if they have the same tree codes. We say G is bad if it is not good A bad grammar. Let B be the context free grammar defined as follows. Let T = N {, +, } and let N = { expr }. Let expr be the start symbol. Let the productions be given by expr := j for j N expr := expr expr := expr + expr expr := expr expr Note that there are an infinite number of productions. This grammar derives the string with two nonisomorphic parse trees so it is bad. There are a number of ways to deal with this problem. One is to introduce parentheses which we now do. As we shall see, there are other ways to deal with this problem.
Suppose h maps number and variables to ɛ, and opening parenthesis to 0 and closing parenthesis
 1 Introduction Parenthesis Matching Problem Describe the set of arithmetic expressions with correctly matched parenthesis. Arithmetic expressions with correctly matched parenthesis cannot be described
1 Introduction Parenthesis Matching Problem Describe the set of arithmetic expressions with correctly matched parenthesis. Arithmetic expressions with correctly matched parenthesis cannot be described
Comment: The induction is always on some parameter, and the basis case is always an integer or set of integers.
 1. For each of the following statements indicate whether it is true or false. For the false ones (if any), provide a counter example. For the true ones (if any) give a proof outline. (a) Union of two non-regular
1. For each of the following statements indicate whether it is true or false. For the false ones (if any), provide a counter example. For the true ones (if any) give a proof outline. (a) Union of two non-regular
Context-Free Grammars and Languages
 Context-Free Grammars and Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Context-Free Grammars and Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
3.10. TREE DOMAINS AND GORN TREES Tree Domains and Gorn Trees
 3.10. TREE DOMAINS AND GORN TREES 211 3.10 Tree Domains and Gorn Trees Derivation trees play a very important role in parsing theory and in the proof of a strong version of the pumping lemma for the context-free
3.10. TREE DOMAINS AND GORN TREES 211 3.10 Tree Domains and Gorn Trees Derivation trees play a very important role in parsing theory and in the proof of a strong version of the pumping lemma for the context-free
CHAPTER 1. Preliminaries. 1 Set Theory
 CHAPTER 1 Preliminaries 1 et Theory We assume that the reader is familiar with basic set theory. In this paragraph, we want to recall the relevant definitions and fix the notation. Our approach to set
CHAPTER 1 Preliminaries 1 et Theory We assume that the reader is familiar with basic set theory. In this paragraph, we want to recall the relevant definitions and fix the notation. Our approach to set
Languages. Languages. An Example Grammar. Grammars. Suppose we have an alphabet V. Then we can write:
 Languages A language is a set (usually infinite) of strings, also known as sentences Each string consists of a sequence of symbols taken from some alphabet An alphabet, V, is a finite set of symbols, e.g.
Languages A language is a set (usually infinite) of strings, also known as sentences Each string consists of a sequence of symbols taken from some alphabet An alphabet, V, is a finite set of symbols, e.g.
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
Context-Free Grammars (and Languages) Lecture 7
 Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
Context-Free Grammars (and Languages) Lecture 7 1 Today Beyond regular expressions: Context-Free Grammars (CFGs) What is a CFG? What is the language associated with a CFG? Creating CFGs. Reasoning about
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
MA/CSSE 474 Theory of Computation Bottom-up parsing Pumping Theorem for CFLs Recap: Going One Way Lemma: Each context-free language is accepted by some PDA. Proof (by construction): The idea: Let the stack
This lecture covers Chapter 5 of HMU: Context-free Grammars
 This lecture covers Chapter 5 of HMU: Context-free rammars (Context-free) rammars (Leftmost and Rightmost) Derivations Parse Trees An quivalence between Derivations and Parse Trees Ambiguity in rammars
This lecture covers Chapter 5 of HMU: Context-free rammars (Context-free) rammars (Leftmost and Rightmost) Derivations Parse Trees An quivalence between Derivations and Parse Trees Ambiguity in rammars
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Syntactical analysis. Syntactical analysis. Syntactical analysis. Syntactical analysis
 Context-free grammars Derivations Parse Trees Left-recursive grammars Top-down parsing non-recursive predictive parsers construction of parse tables Bottom-up parsing shift/reduce parsers LR parsers GLR
Context-free grammars Derivations Parse Trees Left-recursive grammars Top-down parsing non-recursive predictive parsers construction of parse tables Bottom-up parsing shift/reduce parsers LR parsers GLR
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Equivalence of Regular Expressions and FSMs
 Equivalence of Regular Expressions and FSMs Greg Plaxton Theory in Programming Practice, Spring 2005 Department of Computer Science University of Texas at Austin Regular Language Recall that a language
Equivalence of Regular Expressions and FSMs Greg Plaxton Theory in Programming Practice, Spring 2005 Department of Computer Science University of Texas at Austin Regular Language Recall that a language
5/10/16. Grammar. Automata and Languages. Today s Topics. Grammars Definition A grammar G is defined as G = (V, T, P, S) where:
 Grammar Automata and Languages Grammar Prof. Mohamed Hamada oftware Engineering Lab. The University of Aizu Japan Regular Grammar Context-free Grammar Context-sensitive Grammar Left-linear Grammar right-linear
Grammar Automata and Languages Grammar Prof. Mohamed Hamada oftware Engineering Lab. The University of Aizu Japan Regular Grammar Context-free Grammar Context-sensitive Grammar Left-linear Grammar right-linear
Context-Free Grammars and Languages. Reading: Chapter 5
 Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
Context-Free Grammars and Languages Reading: Chapter 5 1 Context-Free Languages The class of context-free languages generalizes the class of regular languages, i.e., every regular language is a context-free
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner. Tel Aviv University. November 28, 2016 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice Herlihy, Brown University.
6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs
 CSC4510/6510 AUTOMATA 6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs The Pumping Lemma for Context Free Languages One way to prove AnBn is not regular is to use the pumping lemma
CSC4510/6510 AUTOMATA 6.1 The Pumping Lemma for CFLs 6.2 Intersections and Complements of CFLs The Pumping Lemma for Context Free Languages One way to prove AnBn is not regular is to use the pumping lemma
Context-Free Languages
 CS:4330 Theory of Computation Spring 2018 Context-Free Languages Non-Context-Free Languages Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.3. Proving context-freeness
CS:4330 Theory of Computation Spring 2018 Context-Free Languages Non-Context-Free Languages Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.3. Proving context-freeness
302 CHAPTER 5. CONTEXT-FREE LANGUAGES AND PDA S. 5.6 Tree Domains and Gorn Trees
 302 CHAPTER 5. CONTEXT-FREE LANGUAGES AND PDA S 5.6 Tree Domains and Gorn Trees Derivation trees play a very important role in parsing theory and in the proof of a strong version of the pumping lemma for
302 CHAPTER 5. CONTEXT-FREE LANGUAGES AND PDA S 5.6 Tree Domains and Gorn Trees Derivation trees play a very important role in parsing theory and in the proof of a strong version of the pumping lemma for
2 Truth Tables, Equivalences and the Contrapositive
 2 Truth Tables, Equivalences and the Contrapositive 12 2 Truth Tables, Equivalences and the Contrapositive 2.1 Truth Tables In a mathematical system, true and false statements are the statements of the
2 Truth Tables, Equivalences and the Contrapositive 12 2 Truth Tables, Equivalences and the Contrapositive 2.1 Truth Tables In a mathematical system, true and false statements are the statements of the
Exam: Synchronous Grammars
 Exam: ynchronous Grammars Duration: 3 hours Written documents are allowed. The numbers in front of questions are indicative of hardness or duration. ynchronous grammars consist of pairs of grammars whose
Exam: ynchronous Grammars Duration: 3 hours Written documents are allowed. The numbers in front of questions are indicative of hardness or duration. ynchronous grammars consist of pairs of grammars whose
This lecture covers Chapter 7 of HMU: Properties of CFLs
 This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
This lecture covers Chapter 7 of HMU: Properties of CFLs Chomsky Normal Form Pumping Lemma for CFs Closure Properties of CFLs Decision Properties of CFLs Additional Reading: Chapter 7 of HMU. Chomsky Normal
EECS 229A Spring 2007 * * (a) By stationarity and the chain rule for entropy, we have
 EECS 229A Spring 2007 * * Solutions to Homework 3 1. Problem 4.11 on pg. 93 of the text. Stationary processes (a) By stationarity and the chain rule for entropy, we have H(X 0 ) + H(X n X 0 ) = H(X 0,
EECS 229A Spring 2007 * * Solutions to Homework 3 1. Problem 4.11 on pg. 93 of the text. Stationary processes (a) By stationarity and the chain rule for entropy, we have H(X 0 ) + H(X n X 0 ) = H(X 0,
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Assignment 5: Solutions
 Comp 21: Algorithms and Data Structures Assignment : Solutions 1. Heaps. (a) First we remove the minimum key 1 (which we know is located at the root of the heap). We then replace it by the key in the position
Comp 21: Algorithms and Data Structures Assignment : Solutions 1. Heaps. (a) First we remove the minimum key 1 (which we know is located at the root of the heap). We then replace it by the key in the position
1. Model existence theorem.
 We fix a first order logic F such that 1. Model existence theorem. C. We let S be the set of statements of F and we suppose Γ S. We let VFT be the set of variable free terms. For each s VFT we let [s]
We fix a first order logic F such that 1. Model existence theorem. C. We let S be the set of statements of F and we suppose Γ S. We let VFT be the set of variable free terms. For each s VFT we let [s]
Even More on Dynamic Programming
 Algorithms & Models of Computation CS/ECE 374, Fall 2017 Even More on Dynamic Programming Lecture 15 Thursday, October 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 26 Part I Longest Common Subsequence
Algorithms & Models of Computation CS/ECE 374, Fall 2017 Even More on Dynamic Programming Lecture 15 Thursday, October 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 26 Part I Longest Common Subsequence
Signed Measures and Complex Measures
 Chapter 8 Signed Measures Complex Measures As opposed to the measures we have considered so far, a signed measure is allowed to take on both positive negative values. To be precise, if M is a σ-algebra
Chapter 8 Signed Measures Complex Measures As opposed to the measures we have considered so far, a signed measure is allowed to take on both positive negative values. To be precise, if M is a σ-algebra
Theory of Computation
 Theory of Computation (Feodor F. Dragan) Department of Computer Science Kent State University Spring, 2018 Theory of Computation, Feodor F. Dragan, Kent State University 1 Before we go into details, what
Theory of Computation (Feodor F. Dragan) Department of Computer Science Kent State University Spring, 2018 Theory of Computation, Feodor F. Dragan, Kent State University 1 Before we go into details, what
Context-Free Languages (Pre Lecture)
 Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
Context-Free Languages (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Context-Free Languages (Pre Lecture) Fall 2017 1 / 34 Outline Pumping Lemma
CVO103: Programming Languages. Lecture 2 Inductive Definitions (2)
 CVO103: Programming Languages Lecture 2 Inductive Definitions (2) Hakjoo Oh 2018 Spring Hakjoo Oh CVO103 2018 Spring, Lecture 2 March 13, 2018 1 / 20 Contents More examples of inductive definitions natural
CVO103: Programming Languages Lecture 2 Inductive Definitions (2) Hakjoo Oh 2018 Spring Hakjoo Oh CVO103 2018 Spring, Lecture 2 March 13, 2018 1 / 20 Contents More examples of inductive definitions natural
Gap Embedding for Well-Quasi-Orderings 1
 WoLLIC 2003 Preliminary Version Gap Embedding for Well-Quasi-Orderings 1 Nachum Dershowitz 2 and Iddo Tzameret 3 School of Computer Science, Tel-Aviv University, Tel-Aviv 69978, Israel Abstract Given a
WoLLIC 2003 Preliminary Version Gap Embedding for Well-Quasi-Orderings 1 Nachum Dershowitz 2 and Iddo Tzameret 3 School of Computer Science, Tel-Aviv University, Tel-Aviv 69978, Israel Abstract Given a
Lecture 11 Context-Free Languages
 Lecture 11 Context-Free Languages COT 4420 Theory of Computation Chapter 5 Context-Free Languages n { a b : n n { ww } 0} R Regular Languages a *b* ( a + b) * Example 1 G = ({S}, {a, b}, S, P) Derivations:
Lecture 11 Context-Free Languages COT 4420 Theory of Computation Chapter 5 Context-Free Languages n { a b : n n { ww } 0} R Regular Languages a *b* ( a + b) * Example 1 G = ({S}, {a, b}, S, P) Derivations:
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Parikh s theorem. Håkan Lindqvist
 Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars formal properties Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2018 1 / 20 Normal forms (1) Hopcroft and Ullman (1979) A normal
Einführung in die Computerlinguistik Context-Free Grammars formal properties Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2018 1 / 20 Normal forms (1) Hopcroft and Ullman (1979) A normal
Chapter 6. Properties of Regular Languages
 Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
An Algebraic View of the Relation between Largest Common Subtrees and Smallest Common Supertrees
 An Algebraic View of the Relation between Largest Common Subtrees and Smallest Common Supertrees Francesc Rosselló 1, Gabriel Valiente 2 1 Department of Mathematics and Computer Science, Research Institute
An Algebraic View of the Relation between Largest Common Subtrees and Smallest Common Supertrees Francesc Rosselló 1, Gabriel Valiente 2 1 Department of Mathematics and Computer Science, Research Institute
Context-Free and Noncontext-Free Languages
 Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Examples: Context-Free and Noncontext-Free Languages a*b* is regular. A n B n = {a n b n : n 0} is context-free but not regular. A n B n C n = {a n b n c n : n 0} is not context-free The Regular and the
Introduction to Automata
 Introduction to Automata Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr 1 /
Introduction to Automata Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr 1 /
3. Only sequences that were formed by using finitely many applications of rules 1 and 2, are propositional formulas.
 1 Chapter 1 Propositional Logic Mathematical logic studies correct thinking, correct deductions of statements from other statements. Let us make it more precise. A fundamental property of a statement is
1 Chapter 1 Propositional Logic Mathematical logic studies correct thinking, correct deductions of statements from other statements. Let us make it more precise. A fundamental property of a statement is
PUSHDOWN AUTOMATA (PDA)
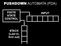 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
Properties of Context-Free Languages
 Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
Properties of Context-Free Languages Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr
CSC 4181Compiler Construction. Context-Free Grammars Using grammars in parsers. Parsing Process. Context-Free Grammar
 CSC 4181Compiler Construction Context-ree Grammars Using grammars in parsers CG 1 Parsing Process Call the scanner to get tokens Build a parse tree from the stream of tokens A parse tree shows the syntactic
CSC 4181Compiler Construction Context-ree Grammars Using grammars in parsers CG 1 Parsing Process Call the scanner to get tokens Build a parse tree from the stream of tokens A parse tree shows the syntactic
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL) Objectives Introduce Pumping Lemma for CFL Apply Pumping Lemma to show that some languages are non-cfl Pumping Lemma
The semantics of propositional logic
 The semantics of propositional logic Readings: Sections 1.3 and 1.4 of Huth and Ryan. In this module, we will nail down the formal definition of a logical formula, and describe the semantics of propositional
The semantics of propositional logic Readings: Sections 1.3 and 1.4 of Huth and Ryan. In this module, we will nail down the formal definition of a logical formula, and describe the semantics of propositional
CMSC 330: Organization of Programming Languages. Pushdown Automata Parsing
 CMSC 330: Organization of Programming Languages Pushdown Automata Parsing Chomsky Hierarchy Categorization of various languages and grammars Each is strictly more restrictive than the previous First described
CMSC 330: Organization of Programming Languages Pushdown Automata Parsing Chomsky Hierarchy Categorization of various languages and grammars Each is strictly more restrictive than the previous First described
Induced subgraphs of graphs with large chromatic number. VI. Banana trees
 Induced subgraphs of graphs with large chromatic number. VI. Banana trees Alex Scott Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK Paul Seymour 1 Princeton University, Princeton, NJ
Induced subgraphs of graphs with large chromatic number. VI. Banana trees Alex Scott Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK Paul Seymour 1 Princeton University, Princeton, NJ
Parsing. Context-Free Grammars (CFG) Laura Kallmeyer. Winter 2017/18. Heinrich-Heine-Universität Düsseldorf 1 / 26
 Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
Parsing Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Winter 2017/18 1 / 26 Table of contents 1 Context-Free Grammars 2 Simplifying CFGs Removing useless symbols Eliminating
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
Finite Universes. L is a fixed-length language if it has length n for some
 Finite Universes Finite Universes When the universe is finite (e.g., the interval 0, 2 1 ), all objects can be encoded by words of the same length. A language L has length n 0 if L =, or every word of
Finite Universes Finite Universes When the universe is finite (e.g., the interval 0, 2 1 ), all objects can be encoded by words of the same length. A language L has length n 0 if L =, or every word of
FLAC Context-Free Grammars
 FLAC Context-Free Grammars Klaus Sutner Carnegie Mellon Universality Fall 2017 1 Generating Languages Properties of CFLs Generation vs. Recognition 3 Turing machines can be used to check membership in
FLAC Context-Free Grammars Klaus Sutner Carnegie Mellon Universality Fall 2017 1 Generating Languages Properties of CFLs Generation vs. Recognition 3 Turing machines can be used to check membership in
Finite Automata and Formal Languages TMV026/DIT321 LP Useful, Useless, Generating and Reachable Symbols
 Finite Automata and Formal Languages TMV026/DIT321 LP4 2012 Lecture 13 Ana Bove May 7th 2012 Overview of today s lecture: Normal Forms for Context-Free Languages Pumping Lemma for Context-Free Languages
Finite Automata and Formal Languages TMV026/DIT321 LP4 2012 Lecture 13 Ana Bove May 7th 2012 Overview of today s lecture: Normal Forms for Context-Free Languages Pumping Lemma for Context-Free Languages
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
Isomorphisms between pattern classes
 Journal of Combinatorics olume 0, Number 0, 1 8, 0000 Isomorphisms between pattern classes M. H. Albert, M. D. Atkinson and Anders Claesson Isomorphisms φ : A B between pattern classes are considered.
Journal of Combinatorics olume 0, Number 0, 1 8, 0000 Isomorphisms between pattern classes M. H. Albert, M. D. Atkinson and Anders Claesson Isomorphisms φ : A B between pattern classes are considered.
Introduction. Chapter 1
 Chapter 1 Introduction Logic is concerned mainly with two concepts: truth and provability. These concepts have been investigated extensively for centuries, by philosophers, linguists, and mathematicians.
Chapter 1 Introduction Logic is concerned mainly with two concepts: truth and provability. These concepts have been investigated extensively for centuries, by philosophers, linguists, and mathematicians.
With Question/Answer Animations
 Chapter 5 With Question/Answer Animations Copyright McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education. Chapter Summary
Chapter 5 With Question/Answer Animations Copyright McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education. Chapter Summary
Lecture Notes on Inductive Definitions
 Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 28, 2003 These supplementary notes review the notion of an inductive definition and give
Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 28, 2003 These supplementary notes review the notion of an inductive definition and give
THEORY OF COMPUTATION
 THEORY OF COMPUTATION There are four sorts of men: He who knows not and knows not he knows not: he is a fool - shun him; He who knows not and knows he knows not: he is simple teach him; He who knows and
THEORY OF COMPUTATION There are four sorts of men: He who knows not and knows not he knows not: he is a fool - shun him; He who knows not and knows he knows not: he is simple teach him; He who knows and
Homework 1 (revised) Solutions
 Homework 1 (revised) Solutions 1. Textbook, 1.1.1, # 1.1.2 (p. 24) Let S be an ordered set. Let A be a non-empty finite subset. Then A is bounded and sup A, inf A A Solution. The hint was: Use induction,
Homework 1 (revised) Solutions 1. Textbook, 1.1.1, # 1.1.2 (p. 24) Let S be an ordered set. Let A be a non-empty finite subset. Then A is bounded and sup A, inf A A Solution. The hint was: Use induction,
Notes for Comp 497 (Comp 454) Week 10 4/5/05
 Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Notes for Comp 497 (Comp 454) Week 10 4/5/05 Today look at the last two chapters in Part II. Cohen presents some results concerning context-free languages (CFL) and regular languages (RL) also some decidability
Models of Computation. by Costas Busch, LSU
 Models of Computation by Costas Busch, LSU 1 Computation CPU memory 2 temporary memory input memory CPU output memory Program memory 3 Example: f ( x) x 3 temporary memory input memory Program memory compute
Models of Computation by Costas Busch, LSU 1 Computation CPU memory 2 temporary memory input memory CPU output memory Program memory 3 Example: f ( x) x 3 temporary memory input memory Program memory compute
Further discussion of Turing machines
 Further discussion of Turing machines In this lecture we will discuss various aspects of decidable and Turing-recognizable languages that were not mentioned in previous lectures. In particular, we will
Further discussion of Turing machines In this lecture we will discuss various aspects of decidable and Turing-recognizable languages that were not mentioned in previous lectures. In particular, we will
Pushdown Automata: Introduction (2)
 Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Induction and recursion. Chapter 5
 Induction and recursion Chapter 5 Chapter Summary Mathematical Induction Strong Induction Well-Ordering Recursive Definitions Structural Induction Recursive Algorithms Mathematical Induction Section 5.1
Induction and recursion Chapter 5 Chapter Summary Mathematical Induction Strong Induction Well-Ordering Recursive Definitions Structural Induction Recursive Algorithms Mathematical Induction Section 5.1
MATH 324 Summer 2011 Elementary Number Theory. Notes on Mathematical Induction. Recall the following axiom for the set of integers.
 MATH 4 Summer 011 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
MATH 4 Summer 011 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
Binary Decision Diagrams
 Binary Decision Diagrams Literature Some pointers: H.R. Andersen, An Introduction to Binary Decision Diagrams, Lecture notes, Department of Information Technology, IT University of Copenhagen Tools: URL:
Binary Decision Diagrams Literature Some pointers: H.R. Andersen, An Introduction to Binary Decision Diagrams, Lecture notes, Department of Information Technology, IT University of Copenhagen Tools: URL:
Propositional Logic: Part II - Syntax & Proofs 0-0
 Propositional Logic: Part II - Syntax & Proofs 0-0 Outline Syntax of Propositional Formulas Motivating Proofs Syntactic Entailment and Proofs Proof Rules for Natural Deduction Axioms, theories and theorems
Propositional Logic: Part II - Syntax & Proofs 0-0 Outline Syntax of Propositional Formulas Motivating Proofs Syntactic Entailment and Proofs Proof Rules for Natural Deduction Axioms, theories and theorems
Parsing Algorithms. CS 4447/CS Stephen Watt University of Western Ontario
 Parsing Algorithms CS 4447/CS 9545 -- Stephen Watt University of Western Ontario The Big Picture Develop parsers based on grammars Figure out properties of the grammars Make tables that drive parsing engines
Parsing Algorithms CS 4447/CS 9545 -- Stephen Watt University of Western Ontario The Big Picture Develop parsers based on grammars Figure out properties of the grammars Make tables that drive parsing engines
Lecture Notes on Inductive Definitions
 Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 September 2, 2004 These supplementary notes review the notion of an inductive definition and
Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 September 2, 2004 These supplementary notes review the notion of an inductive definition and
SMALL SUBSETS OF THE REALS AND TREE FORCING NOTIONS
 SMALL SUBSETS OF THE REALS AND TREE FORCING NOTIONS MARCIN KYSIAK AND TOMASZ WEISS Abstract. We discuss the question which properties of smallness in the sense of measure and category (e.g. being a universally
SMALL SUBSETS OF THE REALS AND TREE FORCING NOTIONS MARCIN KYSIAK AND TOMASZ WEISS Abstract. We discuss the question which properties of smallness in the sense of measure and category (e.g. being a universally
Context Free Language Properties
 Context Free Language Properties Knowing that the context free languages are exactly those sets accepted by nondeterministic pushdown automata provides us a bit of information about them. We know that
Context Free Language Properties Knowing that the context free languages are exactly those sets accepted by nondeterministic pushdown automata provides us a bit of information about them. We know that
Containment for XPath Fragments under DTD Constraints
 Containment for XPath Fragments under DTD Constraints Peter Wood School of Computer Science and Information Systems Birkbeck College University of London United Kingdom email: ptw@dcs.bbk.ac.uk 1 Outline
Containment for XPath Fragments under DTD Constraints Peter Wood School of Computer Science and Information Systems Birkbeck College University of London United Kingdom email: ptw@dcs.bbk.ac.uk 1 Outline
Math 324 Summer 2012 Elementary Number Theory Notes on Mathematical Induction
 Math 4 Summer 01 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
Math 4 Summer 01 Elementary Number Theory Notes on Mathematical Induction Principle of Mathematical Induction Recall the following axiom for the set of integers. Well-Ordering Axiom for the Integers If
arxiv: v1 [cs.pl] 19 May 2016
![arxiv: v1 [cs.pl] 19 May 2016 arxiv: v1 [cs.pl] 19 May 2016](/thumbs/73/68166465.jpg) arxiv:1605.05858v1 [cs.pl] 19 May 2016 Domain Theory: An Introduction Robert Cartwright Rice University Rebecca Parsons ThoughtWorks, Inc. Moez AbdelGawad SRTA-City Hunan University This monograph is an
arxiv:1605.05858v1 [cs.pl] 19 May 2016 Domain Theory: An Introduction Robert Cartwright Rice University Rebecca Parsons ThoughtWorks, Inc. Moez AbdelGawad SRTA-City Hunan University This monograph is an
Review CHAPTER. 2.1 Definitions in Chapter Sample Exam Questions. 2.1 Set; Element; Member; Universal Set Partition. 2.
 CHAPTER 2 Review 2.1 Definitions in Chapter 2 2.1 Set; Element; Member; Universal Set 2.2 Subset 2.3 Proper Subset 2.4 The Empty Set, 2.5 Set Equality 2.6 Cardinality; Infinite Set 2.7 Complement 2.8 Intersection
CHAPTER 2 Review 2.1 Definitions in Chapter 2 2.1 Set; Element; Member; Universal Set 2.2 Subset 2.3 Proper Subset 2.4 The Empty Set, 2.5 Set Equality 2.6 Cardinality; Infinite Set 2.7 Complement 2.8 Intersection
Realization Plans for Extensive Form Games without Perfect Recall
 Realization Plans for Extensive Form Games without Perfect Recall Richard E. Stearns Department of Computer Science University at Albany - SUNY Albany, NY 12222 April 13, 2015 Abstract Given a game in
Realization Plans for Extensive Form Games without Perfect Recall Richard E. Stearns Department of Computer Science University at Albany - SUNY Albany, NY 12222 April 13, 2015 Abstract Given a game in
Fall 1999 Formal Language Theory Dr. R. Boyer. Theorem. For any context free grammar G; if there is a derivation of w 2 from the
 Fall 1999 Formal Language Theory Dr. R. Boyer Week Seven: Chomsky Normal Form; Pumping Lemma 1. Universality of Leftmost Derivations. Theorem. For any context free grammar ; if there is a derivation of
Fall 1999 Formal Language Theory Dr. R. Boyer Week Seven: Chomsky Normal Form; Pumping Lemma 1. Universality of Leftmost Derivations. Theorem. For any context free grammar ; if there is a derivation of
Context Free Grammars
 Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Automata and Formal Languages Context Free Grammars Sipser pages 101-111 Lecture 11 Tim Sheard 1 Formal Languages 1. Context free languages provide a convenient notation for recursive description of languages.
Chapter 16: Non-Context-Free Languages
 Chapter 16: Non-Context-Free Languages Peter Cappello Department of Computer Science University of California, Santa Barbara Santa Barbara, CA 93106 cappello@cs.ucsb.edu Please read the corresponding chapter
Chapter 16: Non-Context-Free Languages Peter Cappello Department of Computer Science University of California, Santa Barbara Santa Barbara, CA 93106 cappello@cs.ucsb.edu Please read the corresponding chapter
FINAL EXAM CHEAT SHEET/STUDY GUIDE. You can use this as a study guide. You will also be able to use it on the Final Exam on
 FINAL EXAM CHEAT SHEET/STUDY GUIDE You can use this as a study guide. You will also be able to use it on the Final Exam on Tuesday. If there s anything else you feel should be on this, please send me email
FINAL EXAM CHEAT SHEET/STUDY GUIDE You can use this as a study guide. You will also be able to use it on the Final Exam on Tuesday. If there s anything else you feel should be on this, please send me email
Solution Scoring: SD Reg exp.: a(a
 MA/CSSE 474 Exam 3 Winter 2013-14 Name Solution_with explanations Section: 02(3 rd ) 03(4 th ) 1. (28 points) For each of the following statements, circle T or F to indicate whether it is True or False.
MA/CSSE 474 Exam 3 Winter 2013-14 Name Solution_with explanations Section: 02(3 rd ) 03(4 th ) 1. (28 points) For each of the following statements, circle T or F to indicate whether it is True or False.
Notes on the Catalan problem
 Notes on the Catalan problem Daniele Paolo Scarpazza Politecnico di Milano March 16th, 2004 Daniele Paolo Scarpazza Notes on the Catalan problem [1] An overview of Catalan problems
Notes on the Catalan problem Daniele Paolo Scarpazza Politecnico di Milano March 16th, 2004 Daniele Paolo Scarpazza Notes on the Catalan problem [1] An overview of Catalan problems
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES. 1. Compact Sets
 FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
Solutions to Problem Set 3
 V22.0453-001 Theory of Computation October 8, 2003 TA: Nelly Fazio Solutions to Problem Set 3 Problem 1 We have seen that a grammar where all productions are of the form: A ab, A c (where A, B non-terminals,
V22.0453-001 Theory of Computation October 8, 2003 TA: Nelly Fazio Solutions to Problem Set 3 Problem 1 We have seen that a grammar where all productions are of the form: A ab, A c (where A, B non-terminals,
Logic as a Tool Chapter 1: Understanding Propositional Logic 1.1 Propositions and logical connectives. Truth tables and tautologies
 Logic as a Tool Chapter 1: Understanding Propositional Logic 1.1 Propositions and logical connectives. Truth tables and tautologies Valentin Stockholm University September 2016 Propositions Proposition:
Logic as a Tool Chapter 1: Understanding Propositional Logic 1.1 Propositions and logical connectives. Truth tables and tautologies Valentin Stockholm University September 2016 Propositions Proposition:
Functions on languages:
 MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
MA/CSSE 474 Final Exam Notation and Formulas page Name (turn this in with your exam) Unless specified otherwise, r,s,t,u,v,w,x,y,z are strings over alphabet Σ; while a, b, c, d are individual alphabet
CPS 220 Theory of Computation
 CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
CPS 22 Theory of Computation Review - Regular Languages RL - a simple class of languages that can be represented in two ways: 1 Machine description: Finite Automata are machines with a finite number of
CS5371 Theory of Computation. Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA)
 CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
CS5371 Theory of Computation Lecture 9: Automata Theory VII (Pumping Lemma, Non-CFL, DPDA PDA) Objectives Introduce the Pumping Lemma for CFL Show that some languages are non- CFL Discuss the DPDA, which
Stat 451: Solutions to Assignment #1
 Stat 451: Solutions to Assignment #1 2.1) By definition, 2 Ω is the set of all subsets of Ω. Therefore, to show that 2 Ω is a σ-algebra we must show that the conditions of the definition σ-algebra are
Stat 451: Solutions to Assignment #1 2.1) By definition, 2 Ω is the set of all subsets of Ω. Therefore, to show that 2 Ω is a σ-algebra we must show that the conditions of the definition σ-algebra are
Tree Adjoining Grammars
 Tree Adjoining Grammars TAG: Parsing and formal properties Laura Kallmeyer & Benjamin Burkhardt HHU Düsseldorf WS 2017/2018 1 / 36 Outline 1 Parsing as deduction 2 CYK for TAG 3 Closure properties of TALs
Tree Adjoining Grammars TAG: Parsing and formal properties Laura Kallmeyer & Benjamin Burkhardt HHU Düsseldorf WS 2017/2018 1 / 36 Outline 1 Parsing as deduction 2 CYK for TAG 3 Closure properties of TALs
Madhavan Mukund Chennai Mathematical Institute
 AN INTRODUCTION TO LOGIC Madhavan Mukund Chennai Mathematical Institute E-mail: madhavan@cmiacin Abstract ese are lecture notes for an introductory course on logic aimed at graduate students in Computer
AN INTRODUCTION TO LOGIC Madhavan Mukund Chennai Mathematical Institute E-mail: madhavan@cmiacin Abstract ese are lecture notes for an introductory course on logic aimed at graduate students in Computer
An Extension of Newton s Method to ω-continuous Semirings
 An Extension of Newton s Method to ω-continuous Semirings Javier Esparza, Stefan Kiefer, and Michael Luttenberger Institute for Formal Methods in Computer Science Universität Stuttgart, Germany {esparza,kiefersn,luttenml}@informatik.uni-stuttgart.de
An Extension of Newton s Method to ω-continuous Semirings Javier Esparza, Stefan Kiefer, and Michael Luttenberger Institute for Formal Methods in Computer Science Universität Stuttgart, Germany {esparza,kiefersn,luttenml}@informatik.uni-stuttgart.de
Context Free Languages and Grammars
 Algorithms & Models of Computation CS/ECE 374, Fall 2017 Context Free Languages and Grammars Lecture 7 Tuesday, September 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 36 What stack got to do
Algorithms & Models of Computation CS/ECE 374, Fall 2017 Context Free Languages and Grammars Lecture 7 Tuesday, September 19, 2017 Sariel Har-Peled (UIUC) CS374 1 Fall 2017 1 / 36 What stack got to do
Chapter 4: Context-Free Grammars
 Chapter 4: Context-Free Grammars 4.1 Basics of Context-Free Grammars Definition A context-free grammars, or CFG, G is specified by a quadruple (N, Σ, P, S), where N is the nonterminal or variable alphabet;
Chapter 4: Context-Free Grammars 4.1 Basics of Context-Free Grammars Definition A context-free grammars, or CFG, G is specified by a quadruple (N, Σ, P, S), where N is the nonterminal or variable alphabet;
Grammars (part II) Prof. Dan A. Simovici UMB
 rammars (part II) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Length-Increasing vs. Context-Sensitive rammars Theorem The class L 1 equals the class of length-increasing languages. 3 / 1 Length-Increasing
rammars (part II) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Length-Increasing vs. Context-Sensitive rammars Theorem The class L 1 equals the class of length-increasing languages. 3 / 1 Length-Increasing
Notes for Comp 497 (454) Week 10
 Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Notes for Comp 497 (454) Week 10 Today we look at the last two chapters in Part II. Cohen presents some results concerning the two categories of language we have seen so far: Regular languages (RL). Context-free
Classes of Boolean Functions
 Classes of Boolean Functions Nader H. Bshouty Eyal Kushilevitz Abstract Here we give classes of Boolean functions that considered in COLT. Classes of Functions Here we introduce the basic classes of functions
Classes of Boolean Functions Nader H. Bshouty Eyal Kushilevitz Abstract Here we give classes of Boolean functions that considered in COLT. Classes of Functions Here we introduce the basic classes of functions
Probabilistic Context Free Grammars
 1 Defining PCFGs A PCFG G consists of Probabilistic Context Free Grammars 1. A set of terminals: {w k }, k = 1..., V 2. A set of non terminals: { i }, i = 1..., n 3. A designated Start symbol: 1 4. A set
1 Defining PCFGs A PCFG G consists of Probabilistic Context Free Grammars 1. A set of terminals: {w k }, k = 1..., V 2. A set of non terminals: { i }, i = 1..., n 3. A designated Start symbol: 1 4. A set
