Assignment 5: Solutions
|
|
|
- Ginger McKenzie
- 5 years ago
- Views:
Transcription
1 Comp 21: Algorithms and Data Structures Assignment : Solutions 1. Heaps. (a) First we remove the minimum key 1 (which we know is located at the root of the heap). We then replace it by the key in the position n of the heap. That is, we move key to the root. This gives the following tree: The heap property is now violated at the root. So we apply heapifydown from the root to reestablish the heap property. This process, showing how key moves down the tree, is illustrated below
2 (b) The set W of keys of value at most k can be found in O( W ) time. The reason for this is that the keys with low value are at the top of the heap and the keys with high value are near the bottom of the heap. In particular, the keys along ant path from the root to a leaf are increasing (or nondecreasing). This means we can find W using depth first search (or breadth first search) on the heap. We start at the root. If the key of the root node is at most k then we return the node and recurse on the children of the root. If the key is greater than k, then we do not need to recurse on the children (as their keys and the keys of their descendent must then also be larger than k). Now let s examine the running time. The DFS/BFS algorithm examines each node in W exactly once. In addition, it must examine the children of every node in W (to either find more nodes in W or to determine that the keys are now larger than k and we do not need to search in the corresponding subtree). Since we have a binary heap, each node in W has at most two children so the total number of nodes we examine in O( W ). 2
3 2. Heaps. (a) A heap with n vertices has depth Θ(log d n), so heapify-up takes time O(log d n). (b) heapify-down takes time O(d log d n) as, at each step, we need to compare the parent key to the keys of its d children. (c) Recall Dijkstra s algorithms may require n applications of extract-min and m applications of key-decrease. The former uses heapify-down and the latter uses heapify-up. Thus the total run time is O(n d log d n + m log d n) (d) The quickest implementation occurs if we equate n d log d n and m log d n. Thus we want n d = m. Since m = n 1+ɛ, we set d = n ɛ. Therefore n = d 1 ɛ. But then log d n = 1 ɛ. The total run time is then O( 1 ɛ m).
4 . Hash Tables. (a) We compute the hash function h(k) = k + 2 (mod ) for each value key k and insert it to the corresponding slot in the Hash table. h() = ( + 2) mod = 2 h() = ( + 2) mod = 2 h(2) = ( 2 + 2) mod = 1 h() = ( + 2) mod = 1 h() = ( + 2) mod = h(1) = ( 1 + 2) mod = h(20) = ( ) mod = 6 Each slot in the Hash table maintains a list (e.g. a linked list) of all the keys that hash to it. This is illustrated below: (b) Hash tables are not very useful if we want to keep keep track of the minimum key. In particular, the running time to find a minimum key is O(m + n) if the hash table has m slots and n keys. This is because we have to examine all m slots (even those that are empty) and we also have to go through each linked-list in every slot and thus examine all n keys.
5 . Binary Search Trees. (a) The binary search tree that we build is: (b) Suppose P = {k 1, k 2,..., k l } are the keys we find when searching for k. (In these examples the search was successful so k l = k.) Now let X = {x 1, x 2,..., x r } be those keys of P (in order) that are at most k and let Y = {y 1, y 2,..., y s } be those keys of P (in order) that are at least k. In a search on a BST, it must be the case that x 1 x 2 x r. Suppose not and that x i > x i+1. Since x i k, after we examine x i we then search its right subtree R i. But, by definition, every key in R i is larger than x i. In particular, as x i+1 R i we must have x i x i+1, a contradiction. A similar argument shows that y 1 y 2 y r. i. X = {2,,, 6, 1} and Y = {,,,, 0, 1}. This is not a valid BST search sequence as < in Y. ii. X = {1, 6, 6,, 1, 0,, 6,, 1} and Y = {6,, 1,, 6,, 1}. This is a valid BST search sequence. iii. X = {1, 1, 0, 1, 0, 6, 1} and Y = {0,, 2, 1}. This is not a valid BST search sequence as 0 < 1 in X.
6 . Binary Search Trees. Let P be the path from v 0 up to the root r. Define X = {x 0, x 1, x 2,..., x t } where x 0 = v 0 and, for i 0, x i+1 is the closest ancestor of x i on P whose right child is an ancestor of x i. (Possibly x t is the root, but it need not be.) It takes O(d) time to find all the vertices in X as the length of P is at most d = depth(t ). Let L i be the left subtree at x i, and let L i = λ i. Now every vertex that is not in X or one of its left subtrees has a key greater than v 0 = x 0. So to find the {v 1,..., v l } it suffices to consider just the nodes in X t i=0 L i. Observe that vertices in L i are in the right subtree of x i+1, thus they have larger keys than x i+1. It follows that the keys increase according to the order: {L t, x t, L t 1, x t 1,..., L 1, x 1, L 0, x 0 } So the nodes in L 0 are the immediate predecessors of x 0 = v 0, next comes x 1, then L 1, etc. Assume that {L s, x s, L s 1, x s 1,..., L 1, x 1, L 0 } l and that {L s 1, x s 1,..., L 1, x 1, L 0 } < l. We saw in class the we can sort L i (or any subtree of a BST) in linear time via in-order DFS. Thus we can sort all of L 0, L 1,..., L s 1 in time O( s 1 i=0 λ i) = O(l). The largest l {x s, L s 1, x s 1,..., L 1, x 1, L 0 } keys in L s are then required to complete the list {v l,..., v 2, v 1 }. If λ s = O(l) we can just sort L s. Otherwise, we find the maximum key in L s by following the rightmost path Q = {q 1, q 2,..., q d } we then recursively order their left subtrees ˆL d, ˆL d 1,... until we have found l {x s, L s 1, x s 1,..., L 1, x 1, L 0 } keys in L s. The total run time is O(d + l). 6
7 6. Data Structures for Disjoint Sets. The depth of the resulting tree T is again O(log T ). vertices the find(v) operation still takes O(log n) time. So for a tree with n We prove by induction that a tree with depth d has at least 2 d vertices. For the base cases, if d = 0 then T has at least 1 = 2 0 vertices as required; similarly if d = 1 then T has at least 2 = 2 1 vertices as required. Now consider a tree T with depth d + 1. Consider the time that T first had depth d+1. Assume this happened when we applied the operation merge(x, y) to merge two trees T x and T y. We may assume that x pointed to y because T x = ω(x) ω(y) = T y. Before the merge it must be the case that depth(t x ) was exactly d. Thus by induction T x 2 d. But by definition T x T y. So T 2 T x 2 d+1 as desired.
Priority queues implemented via heaps
 Priority queues implemented via heaps Comp Sci 1575 Data s Outline 1 2 3 Outline 1 2 3 Priority queue: most important first Recall: queue is FIFO A normal queue data structure will not implement a priority
Priority queues implemented via heaps Comp Sci 1575 Data s Outline 1 2 3 Outline 1 2 3 Priority queue: most important first Recall: queue is FIFO A normal queue data structure will not implement a priority
Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)
![Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts) Quiz 1 Solutions. Problem 2. Asymptotics & Recurrences [20 points] (3 parts)](/thumbs/87/95581149.jpg) Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Introduction to Algorithms October 13, 2010 Massachusetts Institute of Technology 6.006 Fall 2010 Professors Konstantinos Daskalakis and Patrick Jaillet Quiz 1 Solutions Quiz 1 Solutions Problem 1. We
Chapter 5 Data Structures Algorithm Theory WS 2017/18 Fabian Kuhn
 Chapter 5 Data Structures Algorithm Theory WS 2017/18 Fabian Kuhn Priority Queue / Heap Stores (key,data) pairs (like dictionary) But, different set of operations: Initialize-Heap: creates new empty heap
Chapter 5 Data Structures Algorithm Theory WS 2017/18 Fabian Kuhn Priority Queue / Heap Stores (key,data) pairs (like dictionary) But, different set of operations: Initialize-Heap: creates new empty heap
Divide-and-Conquer Algorithms Part Two
 Divide-and-Conquer Algorithms Part Two Recap from Last Time Divide-and-Conquer Algorithms A divide-and-conquer algorithm is one that works as follows: (Divide) Split the input apart into multiple smaller
Divide-and-Conquer Algorithms Part Two Recap from Last Time Divide-and-Conquer Algorithms A divide-and-conquer algorithm is one that works as follows: (Divide) Split the input apart into multiple smaller
Optimal Tree-decomposition Balancing and Reachability on Low Treewidth Graphs
 Optimal Tree-decomposition Balancing and Reachability on Low Treewidth Graphs Krishnendu Chatterjee Rasmus Ibsen-Jensen Andreas Pavlogiannis IST Austria Abstract. We consider graphs with n nodes together
Optimal Tree-decomposition Balancing and Reachability on Low Treewidth Graphs Krishnendu Chatterjee Rasmus Ibsen-Jensen Andreas Pavlogiannis IST Austria Abstract. We consider graphs with n nodes together
Randomized Sorting Algorithms Quick sort can be converted to a randomized algorithm by picking the pivot element randomly. In this case we can show th
 CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
CSE 3500 Algorithms and Complexity Fall 2016 Lecture 10: September 29, 2016 Quick sort: Average Run Time In the last lecture we started analyzing the expected run time of quick sort. Let X = k 1, k 2,...,
CS 151. Red Black Trees & Structural Induction. Thursday, November 1, 12
 CS 151 Red Black Trees & Structural Induction 1 Announcements Majors fair tonight 4:30-6:30pm in the Root Room in Carnegie. Come and find out about the CS major, or some other major. Winter Term in CS
CS 151 Red Black Trees & Structural Induction 1 Announcements Majors fair tonight 4:30-6:30pm in the Root Room in Carnegie. Come and find out about the CS major, or some other major. Winter Term in CS
8 Priority Queues. 8 Priority Queues. Prim s Minimum Spanning Tree Algorithm. Dijkstra s Shortest Path Algorithm
 8 Priority Queues 8 Priority Queues A Priority Queue S is a dynamic set data structure that supports the following operations: S. build(x 1,..., x n ): Creates a data-structure that contains just the elements
8 Priority Queues 8 Priority Queues A Priority Queue S is a dynamic set data structure that supports the following operations: S. build(x 1,..., x n ): Creates a data-structure that contains just the elements
Part IA Algorithms Notes
 Part IA Algorithms Notes 1 Sorting 1.1 Insertion Sort 1 d e f i n s e r t i o n S o r t ( a ) : 2 f o r i from 1 i n c l u d e d to l e n ( a ) excluded : 3 4 j = i 1 5 w h i l e j >= 0 and a [ i ] > a
Part IA Algorithms Notes 1 Sorting 1.1 Insertion Sort 1 d e f i n s e r t i o n S o r t ( a ) : 2 f o r i from 1 i n c l u d e d to l e n ( a ) excluded : 3 4 j = i 1 5 w h i l e j >= 0 and a [ i ] > a
ENS Lyon Camp. Day 2. Basic group. Cartesian Tree. 26 October
 ENS Lyon Camp. Day 2. Basic group. Cartesian Tree. 26 October Contents 1 Cartesian Tree. Definition. 1 2 Cartesian Tree. Construction 1 3 Cartesian Tree. Operations. 2 3.1 Split............................................
ENS Lyon Camp. Day 2. Basic group. Cartesian Tree. 26 October Contents 1 Cartesian Tree. Definition. 1 2 Cartesian Tree. Construction 1 3 Cartesian Tree. Operations. 2 3.1 Split............................................
Binary Search Trees. Dictionary Operations: Additional operations: find(key) insert(key, value) erase(key)
 Binary Search Trees Dictionary Operations: find(key) insert(key, value) erase(key) Additional operations: ascend() get(index) (indexed binary search tree) delete(index) (indexed binary search tree) Complexity
Binary Search Trees Dictionary Operations: find(key) insert(key, value) erase(key) Additional operations: ascend() get(index) (indexed binary search tree) delete(index) (indexed binary search tree) Complexity
Fundamental Algorithms
 Fundamental Algorithms Chapter 5: Searching Michael Bader Winter 2014/15 Chapter 5: Searching, Winter 2014/15 1 Searching Definition (Search Problem) Input: a sequence or set A of n elements (objects)
Fundamental Algorithms Chapter 5: Searching Michael Bader Winter 2014/15 Chapter 5: Searching, Winter 2014/15 1 Searching Definition (Search Problem) Input: a sequence or set A of n elements (objects)
CS Data Structures and Algorithm Analysis
 CS 483 - Data Structures and Algorithm Analysis Lecture VII: Chapter 6, part 2 R. Paul Wiegand George Mason University, Department of Computer Science March 22, 2006 Outline 1 Balanced Trees 2 Heaps &
CS 483 - Data Structures and Algorithm Analysis Lecture VII: Chapter 6, part 2 R. Paul Wiegand George Mason University, Department of Computer Science March 22, 2006 Outline 1 Balanced Trees 2 Heaps &
Binary Search Trees. Lecture 29 Section Robb T. Koether. Hampden-Sydney College. Fri, Apr 8, 2016
 Binary Search Trees Lecture 29 Section 19.2 Robb T. Koether Hampden-Sydney College Fri, Apr 8, 2016 Robb T. Koether (Hampden-Sydney College) Binary Search Trees Fri, Apr 8, 2016 1 / 40 1 Binary Search
Binary Search Trees Lecture 29 Section 19.2 Robb T. Koether Hampden-Sydney College Fri, Apr 8, 2016 Robb T. Koether (Hampden-Sydney College) Binary Search Trees Fri, Apr 8, 2016 1 / 40 1 Binary Search
Contents Lecture 4. Greedy graph algorithms Dijkstra s algorithm Prim s algorithm Kruskal s algorithm Union-find data structure with path compression
 Contents Lecture 4 Greedy graph algorithms Dijkstra s algorithm Prim s algorithm Kruskal s algorithm Union-find data structure with path compression Jonas Skeppstedt (jonasskeppstedt.net) Lecture 4 2018
Contents Lecture 4 Greedy graph algorithms Dijkstra s algorithm Prim s algorithm Kruskal s algorithm Union-find data structure with path compression Jonas Skeppstedt (jonasskeppstedt.net) Lecture 4 2018
25. Minimum Spanning Trees
 695 25. Minimum Spanning Trees Motivation, Greedy, Algorithm Kruskal, General Rules, ADT Union-Find, Algorithm Jarnik, Prim, Dijkstra, Fibonacci Heaps [Ottman/Widmayer, Kap. 9.6, 6.2, 6.1, Cormen et al,
695 25. Minimum Spanning Trees Motivation, Greedy, Algorithm Kruskal, General Rules, ADT Union-Find, Algorithm Jarnik, Prim, Dijkstra, Fibonacci Heaps [Ottman/Widmayer, Kap. 9.6, 6.2, 6.1, Cormen et al,
25. Minimum Spanning Trees
 Problem Given: Undirected, weighted, connected graph G = (V, E, c). 5. Minimum Spanning Trees Motivation, Greedy, Algorithm Kruskal, General Rules, ADT Union-Find, Algorithm Jarnik, Prim, Dijkstra, Fibonacci
Problem Given: Undirected, weighted, connected graph G = (V, E, c). 5. Minimum Spanning Trees Motivation, Greedy, Algorithm Kruskal, General Rules, ADT Union-Find, Algorithm Jarnik, Prim, Dijkstra, Fibonacci
Quiz 1 Solutions. (a) f 1 (n) = 8 n, f 2 (n) = , f 3 (n) = ( 3) lg n. f 2 (n), f 1 (n), f 3 (n) Solution: (b)
 Introduction to Algorithms October 14, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Srini Devadas and Constantinos (Costis) Daskalakis Quiz 1 Solutions Quiz 1 Solutions Problem
Introduction to Algorithms October 14, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Srini Devadas and Constantinos (Costis) Daskalakis Quiz 1 Solutions Quiz 1 Solutions Problem
Advanced Implementations of Tables: Balanced Search Trees and Hashing
 Advanced Implementations of Tables: Balanced Search Trees and Hashing Balanced Search Trees Binary search tree operations such as insert, delete, retrieve, etc. depend on the length of the path to the
Advanced Implementations of Tables: Balanced Search Trees and Hashing Balanced Search Trees Binary search tree operations such as insert, delete, retrieve, etc. depend on the length of the path to the
AVL Trees. Manolis Koubarakis. Data Structures and Programming Techniques
 AVL Trees Manolis Koubarakis 1 AVL Trees We will now introduce AVL trees that have the property that they are kept almost balanced but not completely balanced. In this way we have O(log n) search time
AVL Trees Manolis Koubarakis 1 AVL Trees We will now introduce AVL trees that have the property that they are kept almost balanced but not completely balanced. In this way we have O(log n) search time
4.8 Huffman Codes. These lecture slides are supplied by Mathijs de Weerd
 4.8 Huffman Codes These lecture slides are supplied by Mathijs de Weerd Data Compression Q. Given a text that uses 32 symbols (26 different letters, space, and some punctuation characters), how can we
4.8 Huffman Codes These lecture slides are supplied by Mathijs de Weerd Data Compression Q. Given a text that uses 32 symbols (26 different letters, space, and some punctuation characters), how can we
The Complexity of Constructing Evolutionary Trees Using Experiments
 The Complexity of Constructing Evolutionary Trees Using Experiments Gerth Stlting Brodal 1,, Rolf Fagerberg 1,, Christian N. S. Pedersen 1,, and Anna Östlin2, 1 BRICS, Department of Computer Science, University
The Complexity of Constructing Evolutionary Trees Using Experiments Gerth Stlting Brodal 1,, Rolf Fagerberg 1,, Christian N. S. Pedersen 1,, and Anna Östlin2, 1 BRICS, Department of Computer Science, University
16. Binary Search Trees. [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap ]
![16. Binary Search Trees. [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap ] 16. Binary Search Trees. [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap ]](/thumbs/72/67371940.jpg) 418 16. Binary Search Trees [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap. 12.1-12.3] 419 Dictionary implementation Hashing: implementation of dictionaries with expected very fast access times. Disadvantages
418 16. Binary Search Trees [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap. 12.1-12.3] 419 Dictionary implementation Hashing: implementation of dictionaries with expected very fast access times. Disadvantages
CSE 591 Foundations of Algorithms Homework 4 Sample Solution Outlines. Problem 1
 CSE 591 Foundations of Algorithms Homework 4 Sample Solution Outlines Problem 1 (a) Consider the situation in the figure, every edge has the same weight and V = n = 2k + 2. Easy to check, every simple
CSE 591 Foundations of Algorithms Homework 4 Sample Solution Outlines Problem 1 (a) Consider the situation in the figure, every edge has the same weight and V = n = 2k + 2. Easy to check, every simple
16. Binary Search Trees. [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap ]
![16. Binary Search Trees. [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap ] 16. Binary Search Trees. [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap ]](/thumbs/81/84624162.jpg) 423 16. Binary Search Trees [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap. 12.1-12.3] Dictionary implementation 424 Hashing: implementation of dictionaries with expected very fast access times. Disadvantages
423 16. Binary Search Trees [Ottman/Widmayer, Kap. 5.1, Cormen et al, Kap. 12.1-12.3] Dictionary implementation 424 Hashing: implementation of dictionaries with expected very fast access times. Disadvantages
The null-pointers in a binary search tree are replaced by pointers to special null-vertices, that do not carry any object-data
 Definition 1 A red black tree is a balanced binary search tree in which each internal node has two children. Each internal node has a color, such that 1. The root is black. 2. All leaf nodes are black.
Definition 1 A red black tree is a balanced binary search tree in which each internal node has two children. Each internal node has a color, such that 1. The root is black. 2. All leaf nodes are black.
CS 4407 Algorithms Lecture: Shortest Path Algorithms
 CS 440 Algorithms Lecture: Shortest Path Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Outline Shortest Path Problem General Lemmas and Theorems. Algorithms Bellman-Ford
CS 440 Algorithms Lecture: Shortest Path Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Outline Shortest Path Problem General Lemmas and Theorems. Algorithms Bellman-Ford
Outline. Computer Science 331. Cost of Binary Search Tree Operations. Bounds on Height: Worst- and Average-Case
 Outline Computer Science Average Case Analysis: Binary Search Trees Mike Jacobson Department of Computer Science University of Calgary Lecture #7 Motivation and Objective Definition 4 Mike Jacobson (University
Outline Computer Science Average Case Analysis: Binary Search Trees Mike Jacobson Department of Computer Science University of Calgary Lecture #7 Motivation and Objective Definition 4 Mike Jacobson (University
Fibonacci Heaps These lecture slides are adapted from CLRS, Chapter 20.
 Fibonacci Heaps These lecture slides are adapted from CLRS, Chapter 20. Princeton University COS 4 Theory of Algorithms Spring 2002 Kevin Wayne Priority Queues Operation mae-heap insert find- delete- union
Fibonacci Heaps These lecture slides are adapted from CLRS, Chapter 20. Princeton University COS 4 Theory of Algorithms Spring 2002 Kevin Wayne Priority Queues Operation mae-heap insert find- delete- union
Randomized Algorithms III Min Cut
 Chapter 11 Randomized Algorithms III Min Cut CS 57: Algorithms, Fall 01 October 1, 01 11.1 Min Cut 11.1.1 Problem Definition 11. Min cut 11..0.1 Min cut G = V, E): undirected graph, n vertices, m edges.
Chapter 11 Randomized Algorithms III Min Cut CS 57: Algorithms, Fall 01 October 1, 01 11.1 Min Cut 11.1.1 Problem Definition 11. Min cut 11..0.1 Min cut G = V, E): undirected graph, n vertices, m edges.
CMPUT 675: Approximation Algorithms Fall 2014
 CMPUT 675: Approximation Algorithms Fall 204 Lecture 25 (Nov 3 & 5): Group Steiner Tree Lecturer: Zachary Friggstad Scribe: Zachary Friggstad 25. Group Steiner Tree In this problem, we are given a graph
CMPUT 675: Approximation Algorithms Fall 204 Lecture 25 (Nov 3 & 5): Group Steiner Tree Lecturer: Zachary Friggstad Scribe: Zachary Friggstad 25. Group Steiner Tree In this problem, we are given a graph
CS 240 Data Structures and Data Management. Module 4: Dictionaries
 CS 24 Data Structures and Data Management Module 4: Dictionaries A. Biniaz A. Jamshidpey É. Schost Based on lecture notes by many previous cs24 instructors David R. Cheriton School of Computer Science,
CS 24 Data Structures and Data Management Module 4: Dictionaries A. Biniaz A. Jamshidpey É. Schost Based on lecture notes by many previous cs24 instructors David R. Cheriton School of Computer Science,
Dictionary: an abstract data type
 2-3 Trees 1 Dictionary: an abstract data type A container that maps keys to values Dictionary operations Insert Search Delete Several possible implementations Balanced search trees Hash tables 2 2-3 trees
2-3 Trees 1 Dictionary: an abstract data type A container that maps keys to values Dictionary operations Insert Search Delete Several possible implementations Balanced search trees Hash tables 2 2-3 trees
Binary Search Trees. Motivation
 Binary Search Trees Motivation Searching for a particular record in an unordered list takes O(n), too slow for large lists (databases) If the list is ordered, can use an array implementation and use binary
Binary Search Trees Motivation Searching for a particular record in an unordered list takes O(n), too slow for large lists (databases) If the list is ordered, can use an array implementation and use binary
Advanced Data Structures
 Simon Gog gog@kit.edu - Simon Gog: KIT University of the State of Baden-Wuerttemberg and National Research Center of the Helmholtz Association www.kit.edu Predecessor data structures We want to support
Simon Gog gog@kit.edu - Simon Gog: KIT University of the State of Baden-Wuerttemberg and National Research Center of the Helmholtz Association www.kit.edu Predecessor data structures We want to support
CSE 202: Design and Analysis of Algorithms Lecture 3
 CSE 202: Design and Analysis of Algorithms Lecture 3 Instructor: Kamalika Chaudhuri Announcement Homework 1 out Due on Tue Jan 24 in class No late homeworks will be accepted Greedy Algorithms Direct argument
CSE 202: Design and Analysis of Algorithms Lecture 3 Instructor: Kamalika Chaudhuri Announcement Homework 1 out Due on Tue Jan 24 in class No late homeworks will be accepted Greedy Algorithms Direct argument
Dictionary: an abstract data type
 2-3 Trees 1 Dictionary: an abstract data type A container that maps keys to values Dictionary operations Insert Search Delete Several possible implementations Balanced search trees Hash tables 2 2-3 trees
2-3 Trees 1 Dictionary: an abstract data type A container that maps keys to values Dictionary operations Insert Search Delete Several possible implementations Balanced search trees Hash tables 2 2-3 trees
Algorithm for exact evaluation of bivariate two-sample Kolmogorov-Smirnov statistics in O(nlogn) time.
 Algorithm for exact evaluation of bivariate two-sample Kolmogorov-Smirnov statistics in O(nlogn) time. Krystian Zawistowski January 3, 2019 Abstract We propose an O(nlogn) algorithm for evaluation of bivariate
Algorithm for exact evaluation of bivariate two-sample Kolmogorov-Smirnov statistics in O(nlogn) time. Krystian Zawistowski January 3, 2019 Abstract We propose an O(nlogn) algorithm for evaluation of bivariate
Sorting Algorithms. We have already seen: Selection-sort Insertion-sort Heap-sort. We will see: Bubble-sort Merge-sort Quick-sort
 Sorting Algorithms We have already seen: Selection-sort Insertion-sort Heap-sort We will see: Bubble-sort Merge-sort Quick-sort We will show that: O(n log n) is optimal for comparison based sorting. Bubble-Sort
Sorting Algorithms We have already seen: Selection-sort Insertion-sort Heap-sort We will see: Bubble-sort Merge-sort Quick-sort We will show that: O(n log n) is optimal for comparison based sorting. Bubble-Sort
Each internal node v with d(v) children stores d 1 keys. k i 1 < key in i-th sub-tree k i, where we use k 0 = and k d =.
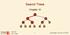
 7.5 (a, b)-trees 7.5 (a, b)-trees Definition For b a an (a, b)-tree is a search tree with the following properties. all leaves have the same distance to the root. every internal non-root vertex v has at
7.5 (a, b)-trees 7.5 (a, b)-trees Definition For b a an (a, b)-tree is a search tree with the following properties. all leaves have the same distance to the root. every internal non-root vertex v has at
Data Structures and Algorithms " Search Trees!!
 Data Structures and Algorithms " Search Trees!! Outline" Binary Search Trees! AVL Trees! (2,4) Trees! 2 Binary Search Trees! "! < 6 2 > 1 4 = 8 9 Ordered Dictionaries" Keys are assumed to come from a total
Data Structures and Algorithms " Search Trees!! Outline" Binary Search Trees! AVL Trees! (2,4) Trees! 2 Binary Search Trees! "! < 6 2 > 1 4 = 8 9 Ordered Dictionaries" Keys are assumed to come from a total
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 8 Greedy Algorithms V Huffman Codes Adam Smith Review Questions Let G be a connected undirected graph with distinct edge weights. Answer true or false: Let e be the
Algorithm Design and Analysis LECTURE 8 Greedy Algorithms V Huffman Codes Adam Smith Review Questions Let G be a connected undirected graph with distinct edge weights. Answer true or false: Let e be the
Binary Decision Diagrams. Graphs. Boolean Functions
 Binary Decision Diagrams Graphs Binary Decision Diagrams (BDDs) are a class of graphs that can be used as data structure for compactly representing boolean functions. BDDs were introduced by R. Bryant
Binary Decision Diagrams Graphs Binary Decision Diagrams (BDDs) are a class of graphs that can be used as data structure for compactly representing boolean functions. BDDs were introduced by R. Bryant
Data Structures 1 NTIN066
 Data Structures 1 NTIN066 Jiří Fink https://kam.mff.cuni.cz/ fink/ Department of Theoretical Computer Science and Mathematical Logic Faculty of Mathematics and Physics Charles University in Prague Winter
Data Structures 1 NTIN066 Jiří Fink https://kam.mff.cuni.cz/ fink/ Department of Theoretical Computer Science and Mathematical Logic Faculty of Mathematics and Physics Charles University in Prague Winter
Advanced Data Structures
 Simon Gog gog@kit.edu - Simon Gog: KIT The Research University in the Helmholtz Association www.kit.edu Predecessor data structures We want to support the following operations on a set of integers from
Simon Gog gog@kit.edu - Simon Gog: KIT The Research University in the Helmholtz Association www.kit.edu Predecessor data structures We want to support the following operations on a set of integers from
Insertion Sort. We take the first element: 34 is sorted
 Insertion Sort Idea: by Ex Given the following sequence to be sorted 34 8 64 51 32 21 When the elements 1, p are sorted, then the next element, p+1 is inserted within these to the right place after some
Insertion Sort Idea: by Ex Given the following sequence to be sorted 34 8 64 51 32 21 When the elements 1, p are sorted, then the next element, p+1 is inserted within these to the right place after some
IS 709/809: Computational Methods in IS Research Fall Exam Review
 IS 709/809: Computational Methods in IS Research Fall 2017 Exam Review Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Exam When: Tuesday (11/28) 7:10pm
IS 709/809: Computational Methods in IS Research Fall 2017 Exam Review Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Exam When: Tuesday (11/28) 7:10pm
Inge Li Gørtz. Thank you to Kevin Wayne for inspiration to slides
 02110 Inge Li Gørtz Thank you to Kevin Wayne for inspiration to slides Welcome Inge Li Gørtz. Reverse teaching and discussion of exercises: 3 teaching assistants 8.00-9.15 Group work 9.15-9.45 Discussions
02110 Inge Li Gørtz Thank you to Kevin Wayne for inspiration to slides Welcome Inge Li Gørtz. Reverse teaching and discussion of exercises: 3 teaching assistants 8.00-9.15 Group work 9.15-9.45 Discussions
Problem. Maintain the above set so as to support certain
 Randomized Data Structures Roussos Ioannis Fundamental Data-structuring Problem Collection {S 1,S 2, } of sets of items. Each item i is an arbitrary record, indexed by a key k(i). Each k(i) is drawn from
Randomized Data Structures Roussos Ioannis Fundamental Data-structuring Problem Collection {S 1,S 2, } of sets of items. Each item i is an arbitrary record, indexed by a key k(i). Each k(i) is drawn from
Programming Binary Search Tree. Virendra Singh Indian Institute of Science Bangalore Lecture 12
 SE-286: Data Structures and Programming g Binary Search Tree Virendra Singh Indian Institute of Science Bangalore Lecture 12 Courtesy: Prof. Sartaj Sahni 1 Binary Search Trees Dictionary Operations: get(key)
SE-286: Data Structures and Programming g Binary Search Tree Virendra Singh Indian Institute of Science Bangalore Lecture 12 Courtesy: Prof. Sartaj Sahni 1 Binary Search Trees Dictionary Operations: get(key)
CS361 Homework #3 Solutions
 CS6 Homework # Solutions. Suppose I have a hash table with 5 locations. I would like to know how many items I can store in it before it becomes fairly likely that I have a collision, i.e., that two items
CS6 Homework # Solutions. Suppose I have a hash table with 5 locations. I would like to know how many items I can store in it before it becomes fairly likely that I have a collision, i.e., that two items
d(ν) = max{n N : ν dmn p n } N. p d(ν) (ν) = ρ.
 1. Trees; context free grammars. 1.1. Trees. Definition 1.1. By a tree we mean an ordered triple T = (N, ρ, p) (i) N is a finite set; (ii) ρ N ; (iii) p : N {ρ} N ; (iv) if n N + and ν dmn p n then p n
1. Trees; context free grammars. 1.1. Trees. Definition 1.1. By a tree we mean an ordered triple T = (N, ρ, p) (i) N is a finite set; (ii) ρ N ; (iii) p : N {ρ} N ; (iv) if n N + and ν dmn p n then p n
Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018
 CS17 Integrated Introduction to Computer Science Klein Contents Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018 1 Tree definitions 1 2 Analysis of mergesort using a binary tree 1 3 Analysis of
CS17 Integrated Introduction to Computer Science Klein Contents Lecture 17: Trees and Merge Sort 10:00 AM, Oct 15, 2018 1 Tree definitions 1 2 Analysis of mergesort using a binary tree 1 3 Analysis of
CS 161: Design and Analysis of Algorithms
 CS 161: Design and Analysis of Algorithms Greedy Algorithms 3: Minimum Spanning Trees/Scheduling Disjoint Sets, continued Analysis of Kruskal s Algorithm Interval Scheduling Disjoint Sets, Continued Each
CS 161: Design and Analysis of Algorithms Greedy Algorithms 3: Minimum Spanning Trees/Scheduling Disjoint Sets, continued Analysis of Kruskal s Algorithm Interval Scheduling Disjoint Sets, Continued Each
Heaps and Priority Queues
 Heaps and Priority Queues Motivation Situations where one has to choose the next most important from a collection. Examples: patients in an emergency room, scheduling programs in a multi-tasking OS. Need
Heaps and Priority Queues Motivation Situations where one has to choose the next most important from a collection. Examples: patients in an emergency room, scheduling programs in a multi-tasking OS. Need
On improving matchings in trees, via bounded-length augmentations 1
 On improving matchings in trees, via bounded-length augmentations 1 Julien Bensmail a, Valentin Garnero a, Nicolas Nisse a a Université Côte d Azur, CNRS, Inria, I3S, France Abstract Due to a classical
On improving matchings in trees, via bounded-length augmentations 1 Julien Bensmail a, Valentin Garnero a, Nicolas Nisse a a Université Côte d Azur, CNRS, Inria, I3S, France Abstract Due to a classical
Functional Data Structures
 Functional Data Structures with Isabelle/HOL Tobias Nipkow Fakultät für Informatik Technische Universität München 2017-2-3 1 Part II Functional Data Structures 2 Chapter 1 Binary Trees 3 1 Binary Trees
Functional Data Structures with Isabelle/HOL Tobias Nipkow Fakultät für Informatik Technische Universität München 2017-2-3 1 Part II Functional Data Structures 2 Chapter 1 Binary Trees 3 1 Binary Trees
6.854 Advanced Algorithms
 6.854 Advanced Algorithms Homework Solutions Hashing Bashing. Solution:. O(log U ) for the first level and for each of the O(n) second level functions, giving a total of O(n log U ) 2. Suppose we are using
6.854 Advanced Algorithms Homework Solutions Hashing Bashing. Solution:. O(log U ) for the first level and for each of the O(n) second level functions, giving a total of O(n log U ) 2. Suppose we are using
7.3 AVL-Trees. Definition 15. Lemma 16. AVL-trees are binary search trees that fulfill the following balance condition.
 Definition 15 AVL-trees are binary search trees that fulfill the following balance condition. F eery node height(left sub-tree()) height(right sub-tree()) 1. Lemma 16 An AVL-tree of height h contains at
Definition 15 AVL-trees are binary search trees that fulfill the following balance condition. F eery node height(left sub-tree()) height(right sub-tree()) 1. Lemma 16 An AVL-tree of height h contains at
Partitions and Covers
 University of California, Los Angeles CS 289A Communication Complexity Instructor: Alexander Sherstov Scribe: Dong Wang Date: January 2, 2012 LECTURE 4 Partitions and Covers In previous lectures, we saw
University of California, Los Angeles CS 289A Communication Complexity Instructor: Alexander Sherstov Scribe: Dong Wang Date: January 2, 2012 LECTURE 4 Partitions and Covers In previous lectures, we saw
past balancing schemes require maintenance of balance info at all times, are aggresive use work of searches to pay for work of rebalancing
 1 Splay Trees Sleator and Tarjan, Self Adjusting Binary Search Trees JACM 32(3) 1985 The claim planning ahead. But matches previous idea of being lazy, letting potential build up, using it to pay for expensive
1 Splay Trees Sleator and Tarjan, Self Adjusting Binary Search Trees JACM 32(3) 1985 The claim planning ahead. But matches previous idea of being lazy, letting potential build up, using it to pay for expensive
Improved Submatrix Maximum Queries in Monge Matrices
 Improved Submatrix Maximum Queries in Monge Matrices Pawe l Gawrychowski 1, Shay Mozes 2, and Oren Weimann 3 1 MPII, gawry@mpi-inf.mpg.de 2 IDC Herzliya, smozes@idc.ac.il 3 University of Haifa, oren@cs.haifa.ac.il
Improved Submatrix Maximum Queries in Monge Matrices Pawe l Gawrychowski 1, Shay Mozes 2, and Oren Weimann 3 1 MPII, gawry@mpi-inf.mpg.de 2 IDC Herzliya, smozes@idc.ac.il 3 University of Haifa, oren@cs.haifa.ac.il
Search Trees. Chapter 10. CSE 2011 Prof. J. Elder Last Updated: :52 AM
 Search Trees Chapter 1 < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 3 - Binary Search Trees Ø A binary search
Search Trees Chapter 1 < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 3 - Binary Search Trees Ø A binary search
k-protected VERTICES IN BINARY SEARCH TREES
 k-protected VERTICES IN BINARY SEARCH TREES MIKLÓS BÓNA Abstract. We show that for every k, the probability that a randomly selected vertex of a random binary search tree on n nodes is at distance k from
k-protected VERTICES IN BINARY SEARCH TREES MIKLÓS BÓNA Abstract. We show that for every k, the probability that a randomly selected vertex of a random binary search tree on n nodes is at distance k from
Binary Decision Diagrams
 Binary Decision Diagrams Binary Decision Diagrams (BDDs) are a class of graphs that can be used as data structure for compactly representing boolean functions. BDDs were introduced by R. Bryant in 1986.
Binary Decision Diagrams Binary Decision Diagrams (BDDs) are a class of graphs that can be used as data structure for compactly representing boolean functions. BDDs were introduced by R. Bryant in 1986.
INF2220: algorithms and data structures Series 1
 Universitetet i Oslo Institutt for Informatikk I. Yu, D. Karabeg INF2220: algorithms and data structures Series 1 Topic Function growth & estimation of running time, trees (Exercises with hints for solution)
Universitetet i Oslo Institutt for Informatikk I. Yu, D. Karabeg INF2220: algorithms and data structures Series 1 Topic Function growth & estimation of running time, trees (Exercises with hints for solution)
7 Dictionary. 7.1 Binary Search Trees. Binary Search Trees: Searching. 7.1 Binary Search Trees
 7 Dictionary Dictionary: S.insert(): Insert an element. S.delete(): Delete the element pointed to by. 7.1 Binary Search Trees An (internal) binary search tree stores the elements in a binary tree. Each
7 Dictionary Dictionary: S.insert(): Insert an element. S.delete(): Delete the element pointed to by. 7.1 Binary Search Trees An (internal) binary search tree stores the elements in a binary tree. Each
7 Dictionary. EADS c Ernst Mayr, Harald Räcke 109
 7 Dictionary Dictionary: S.insert(x): Insert an element x. S.delete(x): Delete the element pointed to by x. S.search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise return
7 Dictionary Dictionary: S.insert(x): Insert an element x. S.delete(x): Delete the element pointed to by x. S.search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise return
Data Structures for Disjoint Sets
 Data Structures for Disjoint Sets Advanced Data Structures and Algorithms (CLRS, Chapter 2) James Worrell Oxford University Computing Laboratory, UK HT 200 Disjoint-set data structures Also known as union
Data Structures for Disjoint Sets Advanced Data Structures and Algorithms (CLRS, Chapter 2) James Worrell Oxford University Computing Laboratory, UK HT 200 Disjoint-set data structures Also known as union
Problem 5. Use mathematical induction to show that when n is an exact power of two, the solution of the recurrence
 A. V. Gerbessiotis CS 610-102 Spring 2014 PS 1 Jan 27, 2014 No points For the remainder of the course Give an algorithm means: describe an algorithm, show that it works as claimed, analyze its worst-case
A. V. Gerbessiotis CS 610-102 Spring 2014 PS 1 Jan 27, 2014 No points For the remainder of the course Give an algorithm means: describe an algorithm, show that it works as claimed, analyze its worst-case
Chapter 11. Min Cut Min Cut Problem Definition Some Definitions. By Sariel Har-Peled, December 10, Version: 1.
 Chapter 11 Min Cut By Sariel Har-Peled, December 10, 013 1 Version: 1.0 I built on the sand And it tumbled down, I built on a rock And it tumbled down. Now when I build, I shall begin With the smoke from
Chapter 11 Min Cut By Sariel Har-Peled, December 10, 013 1 Version: 1.0 I built on the sand And it tumbled down, I built on a rock And it tumbled down. Now when I build, I shall begin With the smoke from
NAOMI NISHIMURA Department of Computer Science, University of Waterloo, Waterloo, Ontario, N2L 3G1, Canada.
 International Journal of Foundations of Computer Science c World Scientific Publishing Company FINDING SMALLEST SUPERTREES UNDER MINOR CONTAINMENT NAOMI NISHIMURA Department of Computer Science, University
International Journal of Foundations of Computer Science c World Scientific Publishing Company FINDING SMALLEST SUPERTREES UNDER MINOR CONTAINMENT NAOMI NISHIMURA Department of Computer Science, University
Breadth First Search, Dijkstra s Algorithm for Shortest Paths
 CS 374: Algorithms & Models of Computation, Spring 2017 Breadth First Search, Dijkstra s Algorithm for Shortest Paths Lecture 17 March 1, 2017 Chandra Chekuri (UIUC) CS374 1 Spring 2017 1 / 42 Part I Breadth
CS 374: Algorithms & Models of Computation, Spring 2017 Breadth First Search, Dijkstra s Algorithm for Shortest Paths Lecture 17 March 1, 2017 Chandra Chekuri (UIUC) CS374 1 Spring 2017 1 / 42 Part I Breadth
Recitation 7. Treaps and Combining BSTs. 7.1 Announcements. FingerLab is due Friday afternoon. It s worth 125 points.
 Recitation 7 Treaps and Combining BSTs 7. Announcements FingerLab is due Friday afternoon. It s worth 25 points. RangeLab will be released on Friday. 39 40 RECITATION 7. TREAPS AND COMBINING BSTS 7.2 Deletion
Recitation 7 Treaps and Combining BSTs 7. Announcements FingerLab is due Friday afternoon. It s worth 25 points. RangeLab will be released on Friday. 39 40 RECITATION 7. TREAPS AND COMBINING BSTS 7.2 Deletion
arxiv: v1 [math.co] 22 Jan 2013
![arxiv: v1 [math.co] 22 Jan 2013 arxiv: v1 [math.co] 22 Jan 2013](/thumbs/85/92098505.jpg) NESTED RECURSIONS, SIMULTANEOUS PARAMETERS AND TREE SUPERPOSITIONS ABRAHAM ISGUR, VITALY KUZNETSOV, MUSTAZEE RAHMAN, AND STEPHEN TANNY arxiv:1301.5055v1 [math.co] 22 Jan 2013 Abstract. We apply a tree-based
NESTED RECURSIONS, SIMULTANEOUS PARAMETERS AND TREE SUPERPOSITIONS ABRAHAM ISGUR, VITALY KUZNETSOV, MUSTAZEE RAHMAN, AND STEPHEN TANNY arxiv:1301.5055v1 [math.co] 22 Jan 2013 Abstract. We apply a tree-based
An Algebraic View of the Relation between Largest Common Subtrees and Smallest Common Supertrees
 An Algebraic View of the Relation between Largest Common Subtrees and Smallest Common Supertrees Francesc Rosselló 1, Gabriel Valiente 2 1 Department of Mathematics and Computer Science, Research Institute
An Algebraic View of the Relation between Largest Common Subtrees and Smallest Common Supertrees Francesc Rosselló 1, Gabriel Valiente 2 1 Department of Mathematics and Computer Science, Research Institute
Notes on Logarithmic Lower Bounds in the Cell Probe Model
 Notes on Logarithmic Lower Bounds in the Cell Probe Model Kevin Zatloukal November 10, 2010 1 Overview Paper is by Mihai Pâtraşcu and Erik Demaine. Both were at MIT at the time. (Mihai is now at AT&T Labs.)
Notes on Logarithmic Lower Bounds in the Cell Probe Model Kevin Zatloukal November 10, 2010 1 Overview Paper is by Mihai Pâtraşcu and Erik Demaine. Both were at MIT at the time. (Mihai is now at AT&T Labs.)
Fundamental Algorithms
 Fundamental Algithms Chapter 4: AVL Trees Jan Křetínský Winter 2016/17 Chapter 4: AVL Trees, Winter 2016/17 1 Part I AVL Trees (Adelson-Velsky and Landis, 1962) Chapter 4: AVL Trees, Winter 2016/17 2 Binary
Fundamental Algithms Chapter 4: AVL Trees Jan Křetínský Winter 2016/17 Chapter 4: AVL Trees, Winter 2016/17 1 Part I AVL Trees (Adelson-Velsky and Landis, 1962) Chapter 4: AVL Trees, Winter 2016/17 2 Binary
CS 577 Introduction to Algorithms: Strassen s Algorithm and the Master Theorem
 CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
CS 577 Introduction to Algorithms: Jin-Yi Cai University of Wisconsin Madison In the last class, we described InsertionSort and showed that its worst-case running time is Θ(n 2 ). Check Figure 2.2 for
BFS Dijkstra. Oct abhi shelat
 4102 BFS Dijkstra Oct 22 2009 abhi shelat breadth first search bfs(g, a) 1 2 a b 1 2 d c e f g 2 h bfs theorem Theorem 1 (CLRS, p. 599) Let G =(V, E) be a graph and suppose that BFS is run on G from vertex
4102 BFS Dijkstra Oct 22 2009 abhi shelat breadth first search bfs(g, a) 1 2 a b 1 2 d c e f g 2 h bfs theorem Theorem 1 (CLRS, p. 599) Let G =(V, E) be a graph and suppose that BFS is run on G from vertex
Cographs; chordal graphs and tree decompositions
 Cographs; chordal graphs and tree decompositions Zdeněk Dvořák September 14, 2015 Let us now proceed with some more interesting graph classes closed on induced subgraphs. 1 Cographs The class of cographs
Cographs; chordal graphs and tree decompositions Zdeněk Dvořák September 14, 2015 Let us now proceed with some more interesting graph classes closed on induced subgraphs. 1 Cographs The class of cographs
Dynamic Ordered Sets with Exponential Search Trees
 Dynamic Ordered Sets with Exponential Search Trees Arne Andersson Computing Science Department Information Technology, Uppsala University Box 311, SE - 751 05 Uppsala, Sweden arnea@csd.uu.se http://www.csd.uu.se/
Dynamic Ordered Sets with Exponential Search Trees Arne Andersson Computing Science Department Information Technology, Uppsala University Box 311, SE - 751 05 Uppsala, Sweden arnea@csd.uu.se http://www.csd.uu.se/
Lecture 6 January 15, 2014
 Advanced Graph Algorithms Jan-Apr 2014 Lecture 6 January 15, 2014 Lecturer: Saket Sourah Scrie: Prafullkumar P Tale 1 Overview In the last lecture we defined simple tree decomposition and stated that for
Advanced Graph Algorithms Jan-Apr 2014 Lecture 6 January 15, 2014 Lecturer: Saket Sourah Scrie: Prafullkumar P Tale 1 Overview In the last lecture we defined simple tree decomposition and stated that for
Identifying an m-ary Partition Identity through an m-ary Tree
 Bridgewater State University Virtual Commons - Bridgewater State University Mathematics Faculty Publications Mathematics Department 06 Identifying an m-ary Partition Identity through an m-ary Tree Timothy
Bridgewater State University Virtual Commons - Bridgewater State University Mathematics Faculty Publications Mathematics Department 06 Identifying an m-ary Partition Identity through an m-ary Tree Timothy
CS60007 Algorithm Design and Analysis 2018 Assignment 1
 CS60007 Algorithm Design and Analysis 2018 Assignment 1 Palash Dey and Swagato Sanyal Indian Institute of Technology, Kharagpur Please submit the solutions of the problems 6, 11, 12 and 13 (written in
CS60007 Algorithm Design and Analysis 2018 Assignment 1 Palash Dey and Swagato Sanyal Indian Institute of Technology, Kharagpur Please submit the solutions of the problems 6, 11, 12 and 13 (written in
CS 161 Summer 2009 Homework #2 Sample Solutions
 CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
CS 161 Summer 2009 Homework #2 Sample Solutions Regrade Policy: If you believe an error has been made in the grading of your homework, you may resubmit it for a regrade. If the error consists of more than
Data Structure. Mohsen Arab. January 13, Yazd University. Mohsen Arab (Yazd University ) Data Structure January 13, / 86
 Data Structure Mohsen Arab Yazd University January 13, 2015 Mohsen Arab (Yazd University ) Data Structure January 13, 2015 1 / 86 Table of Content Binary Search Tree Treaps Skip Lists Hash Tables Mohsen
Data Structure Mohsen Arab Yazd University January 13, 2015 Mohsen Arab (Yazd University ) Data Structure January 13, 2015 1 / 86 Table of Content Binary Search Tree Treaps Skip Lists Hash Tables Mohsen
Optimal Color Range Reporting in One Dimension
 Optimal Color Range Reporting in One Dimension Yakov Nekrich 1 and Jeffrey Scott Vitter 1 The University of Kansas. yakov.nekrich@googlemail.com, jsv@ku.edu Abstract. Color (or categorical) range reporting
Optimal Color Range Reporting in One Dimension Yakov Nekrich 1 and Jeffrey Scott Vitter 1 The University of Kansas. yakov.nekrich@googlemail.com, jsv@ku.edu Abstract. Color (or categorical) range reporting
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Single Source Shortest Paths
 CMPS 00 Fall 015 Single Source Shortest Paths Carola Wenk Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk 1 Paths in graphs Consider a digraph G = (V, E) with an edge-weight
CMPS 00 Fall 015 Single Source Shortest Paths Carola Wenk Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk 1 Paths in graphs Consider a digraph G = (V, E) with an edge-weight
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort
 Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Analysis of Algorithms I: Asymptotic Notation, Induction, and MergeSort Xi Chen Columbia University We continue with two more asymptotic notation: o( ) and ω( ). Let f (n) and g(n) are functions that map
Average Case Analysis of QuickSort and Insertion Tree Height using Incompressibility
 Average Case Analysis of QuickSort and Insertion Tree Height using Incompressibility Tao Jiang, Ming Li, Brendan Lucier September 26, 2005 Abstract In this paper we study the Kolmogorov Complexity of a
Average Case Analysis of QuickSort and Insertion Tree Height using Incompressibility Tao Jiang, Ming Li, Brendan Lucier September 26, 2005 Abstract In this paper we study the Kolmogorov Complexity of a
Reckhow s Theorem. Yuval Filmus. November 2010
 Reckhow s Theorem Yuval Filmus November 2010 1 Introduction In 5.3.1 of his thesis [2], Reckhow showed that any two Frege systems p-simulate each other. One of the difficulties involves translation of
Reckhow s Theorem Yuval Filmus November 2010 1 Introduction In 5.3.1 of his thesis [2], Reckhow showed that any two Frege systems p-simulate each other. One of the difficulties involves translation of
Heapable subsequences and related concepts
 Supported by IDEI Grant PN-II-ID-PCE-2011-3-0981 Structure and computational difficulty in combinatorial optimization: an interdisciplinary approach. Heapable subsequences and related concepts Gabriel
Supported by IDEI Grant PN-II-ID-PCE-2011-3-0981 Structure and computational difficulty in combinatorial optimization: an interdisciplinary approach. Heapable subsequences and related concepts Gabriel
Breadth-First Search of Graphs
 Breadth-First Search of Graphs Analysis of Algorithms Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Applications of Breadth-First Search of Graphs a) Single Source
Breadth-First Search of Graphs Analysis of Algorithms Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Applications of Breadth-First Search of Graphs a) Single Source
Data Structures 1 NTIN066
 Data Structures 1 NTIN066 Jirka Fink Department of Theoretical Computer Science and Mathematical Logic Faculty of Mathematics and Physics Charles University in Prague Winter semester 2017/18 Last change
Data Structures 1 NTIN066 Jirka Fink Department of Theoretical Computer Science and Mathematical Logic Faculty of Mathematics and Physics Charles University in Prague Winter semester 2017/18 Last change
1. Prove: A full m- ary tree with i internal vertices contains n = mi + 1 vertices.
 1. Prove: A full m- ary tree with i internal vertices contains n = mi + 1 vertices. Proof: Every vertex, except the root, is the child of an internal vertex. Since there are i internal vertices, each of
1. Prove: A full m- ary tree with i internal vertices contains n = mi + 1 vertices. Proof: Every vertex, except the root, is the child of an internal vertex. Since there are i internal vertices, each of
Review Of Topics. Review: Induction
 Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
Review Of Topics Asymptotic notation Solving recurrences Sorting algorithms Insertion sort Merge sort Heap sort Quick sort Counting sort Radix sort Medians/order statistics Randomized algorithm Worst-case
7 Dictionary. Harald Räcke 125
 7 Dictionary Dictionary: S. insert(x): Insert an element x. S. delete(x): Delete the element pointed to by x. S. search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise
7 Dictionary Dictionary: S. insert(x): Insert an element x. S. delete(x): Delete the element pointed to by x. S. search(k): Return a pointer to an element e with key[e] = k in S if it exists; otherwise
Dominating Set Counting in Graph Classes
 Dominating Set Counting in Graph Classes Shuji Kijima 1, Yoshio Okamoto 2, and Takeaki Uno 3 1 Graduate School of Information Science and Electrical Engineering, Kyushu University, Japan kijima@inf.kyushu-u.ac.jp
Dominating Set Counting in Graph Classes Shuji Kijima 1, Yoshio Okamoto 2, and Takeaki Uno 3 1 Graduate School of Information Science and Electrical Engineering, Kyushu University, Japan kijima@inf.kyushu-u.ac.jp
