Multisoliton Interaction of Perturbed Manakov System: Effects of External Potentials
|
|
|
- Edmund William Webster
- 5 years ago
- Views:
Transcription
1 Multisoliton Interaction of Perturbed Manakov System: Effects of External Potentials Michail D. Todorov Faculty of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria (Work done in collaboration with V. S. Gerdjikov and A. Kyuldjiev from INRNE-BAS, Sofia) Seminar in Department of Physics University of New Orleans, LA, USA, April 5th, 2013
2 Outline Idea of Adiabatic Approximation Variational Approach and Perturbed CTC Non-perturbed and Perturbed CNSE. Manakov System. Choice of Initial Conditions and Potential Perturbations Effects of Polarization Vectors Conservative Numerical Method vs Variational Approach Main Results and Discussion References
3 Idea of Adiabatic Approximation The idea of the adiabatic approximation to the soliton interactions (Karpman&Solov ev (1981)) led to effective modeling of the N-soliton trains of the perturbed scalar NLS eq.: iu t u xx + u 2 u(x, t) = ir[u]. (1) By N-soliton train we mean a solution of the NLSE (1) with initial condition N u(x, t = 0) = u k (x, t = 0), (2) k=1 u k (x, t)=2ν k e iφ k sechz k, z k =2ν k (x ξ k (t)), ξ k (t)=2µ k t+ξ k,0, φ k = µ k ν k z k + δ k (t), δ k (t)=2(µ 2 k + ν2 k )t + δ k,0. Here µ k are the amplitudes, ν k the velocities, δ k the phase shifts, ξ k - the centers of solitons.
4 Idea of Adiabatic Approximation The adiabatic approximation holds if the soliton parameters satisfy the restrictions ν k ν 0 ν 0, µ k µ 0 µ 0, ν k ν 0 ξ k+1,0 ξ k,0 1, (3) where ν 0 and µ 0 are the average amplitude and velocity respectively. In fact we have two different scales: ν k ν 0 ε 1/2 0, µ k µ 0 ε 1/2 0, ξ k+1,0 ξ k,0 ε 1 0. In this approximation the dynamics of the N-soliton train is described by a dynamical system for the 4N soliton parameters. In our previous works we investigate it in presence of periodic and polynomial potentials. Now, we are interested in what follow perturbation(s) by external sech-potentials: ir[u] V (x)u(x, t), V (x) = s c s sech 2 (2ν 0 x y s ). (4) The latter allows us to realize the idea about localized potential wells(depressions) and humps.
5 Potential Perturbations Figure: 1. Sketch of potential sech-like wells and humps used.
6 Perturbed Vector Complex Toda Chain In the present paper we generalize the above results to the perturbed vector NLS i u t u xx + ( u, u) u(x, t) = ir[ u]. (5) The corresponding vector N-soliton train is determined by the initial condition N u(x, t = 0) = u k (x, t = 0), u k (x, t) = 2ν k e iφ k sechz k n k, (6) k=1 and the amplitudes, the velocities, the phase shifts, and the centers of solitons are as in Eq.(2). The phenomenology, however, is enriched by introducing a constant polarization vectors n k that are normalized by the conditions n ( n k, n k) = 1, arg n k;s = 0. s=1
7 Generalized Complex Toda Chain and CNSE More precisely after involving these vectors we derive a generalized version of the CTC (GCTC) model, which allows to have in mind the polarization effects in the N-soliton train of the vector NLS.
8 Perturbed Vector Complex Toda Chain Model. Initial Conditions The corresponding model is known as the perturbed CTC model which can be written down in the form dλ ( ) k = 4ν 0 e Q k+1 Q k e Q k Q k 1 + M k + in k, dt (7) dq k = 4ν 0 λ k + 2i(µ 0 + iν 0 )Ξ k ix k, dt where λ k = µ k + iν k and X k = 2µ k Ξ k + D k and Q k = 2ν 0 ξ k + k ln 4ν0 2 i(δ k + δ 0 + kπ 2µ 0 ξ k ), ν 0 = 1 N ν s, µ 0 = 1 N µ s, δ 0 = 1 N δ s. N N N s=1 s=1 s=1 (8)
9 Variational approach and PCTC We use the variational approach (Anderson and Lisak (1986)) and derive the GCTC model. Like the (unperturbed) CTC, GCTC is a finite dimensional completely integrable model allowing Lax representation. The Lagrangian of the vector NLS perturbed by external potential is: L[ u] = dt i [ ] ( u, u t ) ( u t, u) H, 2 [ H[ u] = dx 1 2 ( u x, u x ) + 1 ] (9) 2 ( u, u) 2 ( u, u)v (x). Then the Lagrange equations of motion: d dt δl δ u t δl = 0, (10) δ u coincide with the vector NLS with external potential V (x).
10 Variational approach and PCTC Next we insert u(x, t) = N k=1 u k(x, t) (see eq. (6)) and integrate over x neglecting all terms of order ɛ and higher. Thus after long calculations we obtain: L = N L k + k=1 N k=1 n=k±1 L k,n, L k,n = 16ν 3 0e k,n (R k,n + R k,n ), R k,n = e i( δ n δ k ) ( n k n n), δk = δ k 2µ 0 ξ k, k,n = 2s k,n ν 0 (ξ k ξ n ) 1, s k,k+1 = 1, s k,k 1 = 1. (11) where ) L k = 2iν k (( n k,t, n k) ( n k, n dξ k k,t) + 8µ k ν k dt dδ k 4ν k dt +... (12)
11 Variational approach and PCTC The equations of motion are given by: where p k = {δ k, ξ k, µ k, ν k, n k }. d δl δl = 0, (13) dt δp k,t δp k ν k t =N[u k], ξ k t = 1 Imh(ζ) + Ξ[u k ], 2ν k µ k t =M[u k], δ k t =2µ ξ k k t + Reh(ζ) + D[u k], (14)
12 Variational approach and PCTC where h(ζ) = 2ζ 2 and N k [u]= 1 2 Re R[u k ] sech z k e iφ k dz k, M k [u]= 1 2 Im R[u k ] tanh z k sech z k e iφ k dz k, Ξ k [u]= 1 4 Re R[u k ]z k sech z k e iφ k dz k, D k [u]= 1 2ν k Im R[u k ](1 z k tanh z k ) sech z k e iφ k dz k,
13 Variational approach and PCTC The corresponding system is a generalization of CTC: dλ ( ) k dt = 4ν 0 e Q k+1 Q k ( n k+1, n k) e Q k Q k 1 ( n k, n k 1) +M k +in k, dq k dt = 4ν d n k 0λ k + 2i(µ 0 + iν 0 )Ξ k ix k, = O(ɛ), dt (15) where again λ k = µ k + iν k and the other variables are given by (8). The explicit form of M k, N k, Ξ k and D k is given by M k = s 2c s ν k P( k,s ), N k = 0, Ξ k = 0, D k = s c s R( k,s ). (16) where k,s = 2ν 0 ξ k y s and the functions P( ) and R( ) are known explicitly.
14 Integrals Figure: 2. The integrals N( ), R( ), and P( ).
15 Variational approach and PCTC Now we have additional equations describing the evolution of the polarization vectors. But note, that their evolution is slow, and in addition the products ( n k+1, n k) multiply the exponents e Q k+1 Q k which are also of the order of ɛ. Since we are keeping only terms of the order of ɛ we can replace ( n k+1, n k) by their initial values ( n k+1, n k) = m0k 2 e2iφ 0k, k = 1,..., N 1 (17) t=0
16 Effects of the polarization vectors on the soliton interaction We formulate a condition on n s that is compatible with the adiabatic approximation. We also formulate the conditions on the initial vector soliton parameters responsible for the different asymptotic regimes. The CTC is completely integrable model; it allows Lax representation L t = [A.L], where: L = A = N (b s E ss + a s (E s,s+1 + E s+1,s )), s=1 N (a s (E s,s+1 E s+1,s )), s=1 (18) where a s = exp((q s+1 Q s )/2), b s = µ s,t + iν s,t and the matrices E ks are determined by (E ks ) pj = δ kp δ sj. The eigenvalues of L are integrals of motion and determine the asymptotic velocities.
17 Effects of the polarization vectors on the soliton interaction The GCTC is also a completely integrable model because it allows Lax representation L t = [Ã. L], where: L = Ã = N s=1 ( b s E ss + ã s (E s,s+1 + E s+1,s )), N (ã s (E s,s+1 E s+1,s )), s=1 (19) where ã s = m 2 0k e2iφ 0k a s, b s = µ s,t + iν s,t. Like for the scalar case, the eigenvalues of L are integrals of motion. If we denote by ζ s = κ s + iη s (resp. ζ s = κ + i η s ) the set of eigenvalues of L (resp. L) then their real parts κ s (resp. κ s ) determine the asymptotic velocities for the soliton train described by CTC (resp. GCTC).
18 RTC and CTC. Asymptotic regimes While for the RTC the set of eigenvalues ζ s of the Lax matrix are all real, for the CTC they generically take complex values, e.g., ζ s = κ s + iη s. Hence, the only possible asymptotic behavior in the RTC is an asymptotically separating, free motion of the solitons. In opposite, for the CTC the real parts κ s Reζ s of eigenvalues of the Lax matrix ζ s determines the asymptotic velocity of the sth soliton.
19 Effects of the polarization vectors on the soliton interaction Thus, starting from the set of initial soliton parameters we can calculate L t=0 (resp. L t=0 ), evaluate the real parts of their eigenvalues and thus determine the asymptotic regime of the soliton train. Regime (i) κ k κ j ( κ k κ j ) for k j asymptotically separating, free solitons; Regime (ii) κ 1 = κ 2 = = κ N = 0 ( κ 1 = κ 2 = = κ N = 0) a bound state; Regime (iii) group of particles move with the same mean asymptotic velocity and the rest of the particles will have free asymptotic motion. Varying only the polarization vectors one can change the asymptotic regime of the soliton train.
20 Effects of the external potentials on the GCTC. Numeric checks vs Variational approach The predictions and validity of the CTC and GCTC are compared and verified with the numerical solutions of the corresponding CNSE using fully explicit difference scheme of Crank-Nicolson type, which conserves the energy, the mass, and the pseudomomentum. The scheme is implemented in a complex arithmetics. Such comparison is conducted for all dynamical regimes considered. First we study the soliton interaction of the pure Manakov model (without perturbations, V (x) 0) and with vanishing cross-modulation α 2 = 0; 2-soliton configurations and transitions between different asymptotic regimes; 3-soliton configurations and transitions between different asymptotic regimes; 2- and 3-soliton configurations and transitions under the effect of well- and hump-like external potential.
21 Two-soliton configurations and transitions between different asymptotic regimes: free asymptotic regime Figure: 3. ν = ν 2 ν 1 < ν cr = ν cr = 2 2 cos(θ 1 θ 2 )ν 0 exp ( ν 0 r 0 ), µ k0 = 0.1, ν 10 = 0.49, ν 20 = 0.51, ξ 10,20 = ±4, δ 10 = 0, δ 20 = π + 2µ 0 r 0, θ 10 = 2π/10, θ 20 = θ 10 π/10.
22 Three-soliton configurations in mixed asymptotic regimes: two-bound state + free soliton Figure: 4. ν = 0.01 < ν cr. ν cr = 2 2 cos(θ 1 θ 2 )ν 0 exp ( ν 0 r 0 ), µ k0 = 0.03, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3.
23 Three-soliton configurations and transitions between different asymptotic regimes: free asymptotic regime Figure: 5. ν = 0.01 < ν cr. ν cr = 2 2 cos(θ 1 θ 2 )ν 0 exp ( ν 0 r 0 ), µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ k0 = 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3.
24 Three-soliton configurations and transitions in mixed regimes two-soliton bound state + free soliton Figure: 6. ν = 0.01 < ν cr = ν cr = 2 2 cos(θ 1 θ 2 )ν 0 exp ( ν 0 r 0 ), µ k0 = 0.03, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3.
25 Effects of the external potentials on the GCTC 3-soliton configurations Figure: 7. ν = 0.01, µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3, two potential wells y 1 = 12, y 2 = 4, c s =
26 Effects of the external potentials on the GCTC 3-soliton configurations Figure: 8. ν = 0.01, µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3, one potential hump at y = 12, c s = 0.01.
27 Effects of the external potentials on the GCTC 3-soliton configurations Figure: 9. ν = 0.01, µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3, one potential hump at y = 12, c s = 0.01.
28 Effects of the external potentials on the GCTC 3-soliton configurations Figure: 10. ν = 0.01, µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3, two potential humps at y = ±12, c s = 0.1.
29 Effects of the external potentials on the GCTC 3-soliton configurations Figure: 11. ν = 0.01, µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3, one potential well at y = 12, c s = 0.01.
30 Effects of the external potentials on the GCTC 3-soliton configurations Figure: 12. ν = 0.01, µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3, one potential well at y = 4, c s = 0.01.
31 Effects of the external potentials on the GCTC 3-soliton configurations Figure: 13. ν = 0.01, µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3, one potential well at y = 4, c s = 0.01.
32 Effects of the external potentials on the GCTC. Numeric checks vs Variational approach Figure: 14. ν = 0.01, µ k0 = 0, ν 20 = 0.5, ν 10,30 = ν 20 ± ν, ξ 20 = 0, ξ 10,30 = ±8, δ 10 = 0, δ 20,30 = ±π/2 + 2µ 0 r 0, θ 10 = 3π/10, θ k0 = θ k 1,0 π/10, k = 2, 3, two potential wells at y = ±12, c s = 0.01.
33 Effects of the external potentials on the GCTC 2-soliton configurations Figure: 15. ν = 0, µ k0 = 0.005, ν k0 = 0.5, ξ 10,20 = ±4, ξ 10,20 = ±4, δ 10 = 0, 20 = 2µ 0 r 0, θ 10 = 3π/10, θ 20 = θ 10 π/10, three potential humps at y = ±15, y = 0, c s =
34 Bibliography J. Moser. Finitely many mass points on the line under the influence of an exponential potential an integrable system. in Dynamical Systems, Theory and Applications. Lecture Notes in Physics, vol. 38, Springer, 1975, p V.I. Karpman, V.V. Solov ev. A perturbational approach to the two-soliton systems. Physica D 3: , T. R. Taha and M. J. Ablovitz. Analytical and numerical aspects of certain nonlinear evolution equations. ii. numerical, Schrödinger equation. J. Comp. Phys., 55: , C. I. Christov, S. Dost, and G. A. Maugin. Inelasticity of soliton collisions in system of coupled NLS equations. Physica Scripta, 50: , V.S. Gerdjikov, E.G. Dyankov, D.J. Kaup, G.L. Diankov, I.M. Uzunov. Stability and quasi-equidistant propagation of NLS soliton trains. Physics Letters A 241: , 1998.
35 Bibliography V. S. Gerdjikov. N-soliton interactions, the Complex Toda Chain and stability of NLS soliton trains. In E. Kriezis (Ed), Proceedings of the International Symposium on Electromagnetic Theory, vol. 1, pp , Aristotle University of Thessaloniki, Greece, V.S. Gerdjikov, E.V. Doktorov, N.P. Matsuka. N-soliton train and Generalized Complex Toda Chain for Manakov System. Theor. Math. Phys. 151: , M. D. Todorov and C. I. Christov. Conservative scheme in complex arithmetic for coupled nonlinear Schrödinger equations. Discrete and Continuous Dynamical Systems, Supplement: , 2007 M. D. Todorov and C. I. Christov. Impact of the Large Cross-Modulation Parameter on the Collision Dynamics of Quasi-Particles Governed by Vector NLSE. Journal of Mathematics and Computers in Simulation, 80: 46 55, 2009.
36 Bibliography R. Goodman. Hamiltonian Hopf bifurcations and dynamics of NLS/GP standing-wave modes. J. Phys. A: Math. Theor., 44: (28pp), V.S. Gerdjikov and M.D. Todorov. N-soliton Interactions for the Manakov system: Effects of external potentials, accepted in Physics of Wave Phenomena, 2012.
37 Thanks Thank you for your kind attention!
Modeling Interactions of Soliton Trains. Effects of External Potentials. Part II
 Modeling Interactions of Soliton Trains. Effects of External Potentials. Part II Michail Todorov Department of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria Work done
Modeling Interactions of Soliton Trains. Effects of External Potentials. Part II Michail Todorov Department of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria Work done
On N-soliton Interactions of Gross-Pitaevsky Equation in Two Space-time Dimensions
 On N-soliton Interactions of Gross-Pitaevsky Equation in Two Space-time Dimensions Michail D. Todorov Faculty of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria (Work done
On N-soliton Interactions of Gross-Pitaevsky Equation in Two Space-time Dimensions Michail D. Todorov Faculty of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria (Work done
Modeling Soliton Interactions of the Perturbed Vector Nonlinear Schrödinger Equation
 Bulg. J. Phys. 38 (2011) 274 283 Modeling Soliton Interactions of the Perturbed Vector Nonlinear Schrödinger Equation V.S. Gerdjikov Institute of Nuclear Research and Nuclear Energy, Bulgarian Academy
Bulg. J. Phys. 38 (2011) 274 283 Modeling Soliton Interactions of the Perturbed Vector Nonlinear Schrödinger Equation V.S. Gerdjikov Institute of Nuclear Research and Nuclear Energy, Bulgarian Academy
Michail D. Todorov. Faculty of Applied Mathematics and Informatics Technical University of Sofia, Bulgaria
 Wave Equations and Quasi-Particle Concept of Dynamics of Solitary Waves: Integrability vs. Consistency, Nonlinearity vs. Dispersion, Adiabatic Approximation Michail D. Todorov Faculty of Applied Mathematics
Wave Equations and Quasi-Particle Concept of Dynamics of Solitary Waves: Integrability vs. Consistency, Nonlinearity vs. Dispersion, Adiabatic Approximation Michail D. Todorov Faculty of Applied Mathematics
Quasi-Particle Dynamics of Linearly Coupled Systems of Nonlinear Schrödinger Equations
 Quasi-Particle Dynamics of Linearly Coupled Systems of Nonlinear Schrödinger Equations Michail D. Todorov Faculty of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria SS25
Quasi-Particle Dynamics of Linearly Coupled Systems of Nonlinear Schrödinger Equations Michail D. Todorov Faculty of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria SS25
Michail D. Todorov. Faculty of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria
 The Effect of the Initial Polarization on the Quasi-Particle Dynamics of Linearly and Nonlinearly Coupled Systems of Nonlinear Schroedinger Schroedinger Equations Michail D. Todorov Faculty of Applied
The Effect of the Initial Polarization on the Quasi-Particle Dynamics of Linearly and Nonlinearly Coupled Systems of Nonlinear Schroedinger Schroedinger Equations Michail D. Todorov Faculty of Applied
Vector Schroedinger Equation. Generalized Wave Equation. Boussinesq Paradigm. Nonintegrability and Conservativity of Soliton Solutions
 Vector Schroedinger Equation. Generalized Wave Equation. Boussinesq Paradigm. Nonintegrability and Conservativity of Soliton Solutions Michail D. Todorov Faculty of Applied Mathematics and Informatics
Vector Schroedinger Equation. Generalized Wave Equation. Boussinesq Paradigm. Nonintegrability and Conservativity of Soliton Solutions Michail D. Todorov Faculty of Applied Mathematics and Informatics
Relation between Periodic Soliton Resonance and Instability
 Proceedings of Institute of Mathematics of NAS of Ukraine 004 Vol. 50 Part 1 486 49 Relation between Periodic Soliton Resonance and Instability Masayoshi TAJIRI Graduate School of Engineering Osaka Prefecture
Proceedings of Institute of Mathematics of NAS of Ukraine 004 Vol. 50 Part 1 486 49 Relation between Periodic Soliton Resonance and Instability Masayoshi TAJIRI Graduate School of Engineering Osaka Prefecture
Exact analytical Helmholtz bright and dark solitons
 Exact analytical Helmholtz bright and dark solitons P. CHAMORRO POSADA Dpto. Teoría de la Señal y Comunicaciones e Ingeniería Telemática ETSI Telecomunicación Universidad de Valladolid, Spain G. S. McDONALD
Exact analytical Helmholtz bright and dark solitons P. CHAMORRO POSADA Dpto. Teoría de la Señal y Comunicaciones e Ingeniería Telemática ETSI Telecomunicación Universidad de Valladolid, Spain G. S. McDONALD
Perturbation theory for the defocusing nonlinear Schrödinger equation
 Perturbation theory for the defocusing nonlinear Schrödinger equation Theodoros P. Horikis University of Ioannina In collaboration with: M. J. Ablowitz, S. D. Nixon and D. J. Frantzeskakis Outline What
Perturbation theory for the defocusing nonlinear Schrödinger equation Theodoros P. Horikis University of Ioannina In collaboration with: M. J. Ablowitz, S. D. Nixon and D. J. Frantzeskakis Outline What
Systems of MKdV equations related to the affine Lie algebras
 Integrability and nonlinearity in field theory XVII International conference on Geometry, Integrability and Quantization 5 10 June 2015, Varna, Bulgaria Systems of MKdV equations related to the affine
Integrability and nonlinearity in field theory XVII International conference on Geometry, Integrability and Quantization 5 10 June 2015, Varna, Bulgaria Systems of MKdV equations related to the affine
Diagonalization of the Coupled-Mode System.
 Diagonalization of the Coupled-Mode System. Marina Chugunova joint work with Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Collaborators: Mason A. Porter, California Institute
Diagonalization of the Coupled-Mode System. Marina Chugunova joint work with Dmitry Pelinovsky Department of Mathematics, McMaster University, Canada Collaborators: Mason A. Porter, California Institute
Continuous limits and integrability for a semidiscrete system Zuo-nong Zhu Department of Mathematics, Shanghai Jiao Tong University, P R China
 Continuous limits and integrability for a semidiscrete system Zuo-nong Zhu Department of Mathematics, Shanghai Jiao Tong University, P R China the 3th GCOE International Symposium, Tohoku University, 17-19
Continuous limits and integrability for a semidiscrete system Zuo-nong Zhu Department of Mathematics, Shanghai Jiao Tong University, P R China the 3th GCOE International Symposium, Tohoku University, 17-19
Numerical Implementation of Fourier Integral-Transform Method for the Wave Equations
 Numerical Implementation of Fourier Integral-Transform Method for the Wave Equations Michail D. Todorov Faculty of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria (Work
Numerical Implementation of Fourier Integral-Transform Method for the Wave Equations Michail D. Todorov Faculty of Applied Mathematics and Computer Science Technical University of Sofia, Bulgaria (Work
Moving Weakly Relativistic Electromagnetic Solitons in Laser-Plasmas
 Moving Weakly Relativistic Electromagnetic Solitons in Laser-Plasmas Lj. Hadžievski, A. Mančić and M.M. Škorić Department of Physics, Faculty of Sciences and Mathematics, University of Niš, P.O. Box 4,
Moving Weakly Relativistic Electromagnetic Solitons in Laser-Plasmas Lj. Hadžievski, A. Mančić and M.M. Škorić Department of Physics, Faculty of Sciences and Mathematics, University of Niš, P.O. Box 4,
Hamiltonian partial differential equations and Painlevé transcendents
 The 6th TIMS-OCAMI-WASEDA Joint International Workshop on Integrable Systems and Mathematical Physics March 22-26, 2014 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN
The 6th TIMS-OCAMI-WASEDA Joint International Workshop on Integrable Systems and Mathematical Physics March 22-26, 2014 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN
Generalized Burgers equations and Miura Map in nonabelian ring. nonabelian rings as integrable systems.
 Generalized Burgers equations and Miura Map in nonabelian rings as integrable systems. Sergey Leble Gdansk University of Technology 05.07.2015 Table of contents 1 Introduction: general remarks 2 Remainders
Generalized Burgers equations and Miura Map in nonabelian rings as integrable systems. Sergey Leble Gdansk University of Technology 05.07.2015 Table of contents 1 Introduction: general remarks 2 Remainders
Generation of undular bores and solitary wave trains in fully nonlinear shallow water theory
 Generation of undular bores and solitary wave trains in fully nonlinear shallow water theory Gennady El 1, Roger Grimshaw 1 and Noel Smyth 2 1 Loughborough University, UK, 2 University of Edinburgh, UK
Generation of undular bores and solitary wave trains in fully nonlinear shallow water theory Gennady El 1, Roger Grimshaw 1 and Noel Smyth 2 1 Loughborough University, UK, 2 University of Edinburgh, UK
2 Soliton Perturbation Theory
 Revisiting Quasistationary Perturbation Theory for Equations in 1+1 Dimensions Russell L. Herman University of North Carolina at Wilmington, Wilmington, NC Abstract We revisit quasistationary perturbation
Revisiting Quasistationary Perturbation Theory for Equations in 1+1 Dimensions Russell L. Herman University of North Carolina at Wilmington, Wilmington, NC Abstract We revisit quasistationary perturbation
Weakly non-linear completely resonant hamiltonian PDEs and the problem of weak turbulence
 Sergei Kuksin Weakly non-linear completely resonant hamiltonian PDEs and the problem of weak turbulence (Toronto, 10 January, 2014 ) 1 1 Introduction: weak turbulence (WT) (One of) origines: Rudolf Peierls,
Sergei Kuksin Weakly non-linear completely resonant hamiltonian PDEs and the problem of weak turbulence (Toronto, 10 January, 2014 ) 1 1 Introduction: weak turbulence (WT) (One of) origines: Rudolf Peierls,
Hamiltonian partial differential equations and Painlevé transcendents
 Winter School on PDEs St Etienne de Tinée February 2-6, 2015 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN SISSA, Trieste Cauchy problem for evolutionary PDEs with
Winter School on PDEs St Etienne de Tinée February 2-6, 2015 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN SISSA, Trieste Cauchy problem for evolutionary PDEs with
A NEW APPROACH FOR SOLITON SOLUTIONS OF RLW EQUATION AND (1+2)-DIMENSIONAL NONLINEAR SCHRÖDINGER S EQUATION
 A NEW APPROACH FOR SOLITON SOLUTIONS OF RLW EQUATION AND (+2-DIMENSIONAL NONLINEAR SCHRÖDINGER S EQUATION ALI FILIZ ABDULLAH SONMEZOGLU MEHMET EKICI and DURGUN DURAN Communicated by Horia Cornean In this
A NEW APPROACH FOR SOLITON SOLUTIONS OF RLW EQUATION AND (+2-DIMENSIONAL NONLINEAR SCHRÖDINGER S EQUATION ALI FILIZ ABDULLAH SONMEZOGLU MEHMET EKICI and DURGUN DURAN Communicated by Horia Cornean In this
Internal Oscillations and Radiation Damping of Vector Solitons
 Internal Oscillations and Radiation Damping of Vector Solitons By Dmitry E. Pelinovsky and Jianke Yang Internal modes of vector solitons and their radiation-induced damping are studied analytically and
Internal Oscillations and Radiation Damping of Vector Solitons By Dmitry E. Pelinovsky and Jianke Yang Internal modes of vector solitons and their radiation-induced damping are studied analytically and
Integrable dynamics of soliton gases
 Integrable dynamics of soliton gases Gennady EL II Porto Meeting on Nonlinear Waves 2-22 June 213 Outline INTRODUCTION KINETIC EQUATION HYDRODYNAMIC REDUCTIONS CONCLUSIONS Motivation & Background Main
Integrable dynamics of soliton gases Gennady EL II Porto Meeting on Nonlinear Waves 2-22 June 213 Outline INTRODUCTION KINETIC EQUATION HYDRODYNAMIC REDUCTIONS CONCLUSIONS Motivation & Background Main
Lecture 11: Internal solitary waves in the ocean
 Lecture 11: Internal solitary waves in the ocean Lecturer: Roger Grimshaw. Write-up: Yiping Ma. June 19, 2009 1 Introduction In Lecture 6, we sketched a derivation of the KdV equation applicable to internal
Lecture 11: Internal solitary waves in the ocean Lecturer: Roger Grimshaw. Write-up: Yiping Ma. June 19, 2009 1 Introduction In Lecture 6, we sketched a derivation of the KdV equation applicable to internal
Vortex knots dynamics and momenta of a tangle:
 Lecture 2 Vortex knots dynamics and momenta of a tangle: - Localized Induction Approximation (LIA) and Non-Linear Schrödinger (NLS) equation - Integrable vortex dynamics and LIA hierarchy - Torus knot
Lecture 2 Vortex knots dynamics and momenta of a tangle: - Localized Induction Approximation (LIA) and Non-Linear Schrödinger (NLS) equation - Integrable vortex dynamics and LIA hierarchy - Torus knot
Exact Solutions to the Focusing Discrete Nonlinear Schrödinger Equation
 Exact Solutions to the Focusing Discrete Nonlinear Schrödinger Equation Francesco Demontis (based on a joint work with C. van der Mee) Università degli Studi di Cagliari Dipartimento di Matematica e Informatica
Exact Solutions to the Focusing Discrete Nonlinear Schrödinger Equation Francesco Demontis (based on a joint work with C. van der Mee) Università degli Studi di Cagliari Dipartimento di Matematica e Informatica
A Numerical Solution of the Lax s 7 th -order KdV Equation by Pseudospectral Method and Darvishi s Preconditioning
 Int. J. Contemp. Math. Sciences, Vol. 2, 2007, no. 22, 1097-1106 A Numerical Solution of the Lax s 7 th -order KdV Equation by Pseudospectral Method and Darvishi s Preconditioning M. T. Darvishi a,, S.
Int. J. Contemp. Math. Sciences, Vol. 2, 2007, no. 22, 1097-1106 A Numerical Solution of the Lax s 7 th -order KdV Equation by Pseudospectral Method and Darvishi s Preconditioning M. T. Darvishi a,, S.
Yair Zarmi Physics Department & Jacob Blaustein Institutes for Desert Research Ben-Gurion University of the Negev Midreshet Ben-Gurion, Israel
 PERTURBED NONLINEAR EVOLUTION EQUATIONS AND ASYMPTOTIC INTEGRABILITY Yair Zarmi Physics Department & Jacob Blaustein Institutes for Desert Research Ben-Gurion University of the Negev Midreshet Ben-Gurion,
PERTURBED NONLINEAR EVOLUTION EQUATIONS AND ASYMPTOTIC INTEGRABILITY Yair Zarmi Physics Department & Jacob Blaustein Institutes for Desert Research Ben-Gurion University of the Negev Midreshet Ben-Gurion,
Computational Solutions for the Korteweg devries Equation in Warm Plasma
 COMPUTATIONAL METHODS IN SCIENCE AND TECHNOLOGY 16(1, 13-18 (1 Computational Solutions for the Korteweg devries Equation in Warm Plasma E.K. El-Shewy*, H.G. Abdelwahed, H.M. Abd-El-Hamid. Theoretical Physics
COMPUTATIONAL METHODS IN SCIENCE AND TECHNOLOGY 16(1, 13-18 (1 Computational Solutions for the Korteweg devries Equation in Warm Plasma E.K. El-Shewy*, H.G. Abdelwahed, H.M. Abd-El-Hamid. Theoretical Physics
Stable One-Dimensional Dissipative Solitons in Complex Cubic-Quintic Ginzburg Landau Equation
 Vol. 112 (2007) ACTA PHYSICA POLONICA A No. 5 Proceedings of the International School and Conference on Optics and Optical Materials, ISCOM07, Belgrade, Serbia, September 3 7, 2007 Stable One-Dimensional
Vol. 112 (2007) ACTA PHYSICA POLONICA A No. 5 Proceedings of the International School and Conference on Optics and Optical Materials, ISCOM07, Belgrade, Serbia, September 3 7, 2007 Stable One-Dimensional
A Dimension-Breaking Phenomenon for Steady Water Waves with Weak Surface Tension
 A Dimension-Breaking Phenomenon for Steady Water Waves with Weak Surface Tension Erik Wahlén, Lund University, Sweden Joint with Mark Groves, Saarland University and Shu-Ming Sun, Virginia Tech Nonlinear
A Dimension-Breaking Phenomenon for Steady Water Waves with Weak Surface Tension Erik Wahlén, Lund University, Sweden Joint with Mark Groves, Saarland University and Shu-Ming Sun, Virginia Tech Nonlinear
Exact Solutions of The Regularized Long-Wave Equation: The Hirota Direct Method Approach to Partially Integrable Equations
 Thai Journal of Mathematics Volume 5(2007) Number 2 : 273 279 www.math.science.cmu.ac.th/thaijournal Exact Solutions of The Regularized Long-Wave Equation: The Hirota Direct Method Approach to Partially
Thai Journal of Mathematics Volume 5(2007) Number 2 : 273 279 www.math.science.cmu.ac.th/thaijournal Exact Solutions of The Regularized Long-Wave Equation: The Hirota Direct Method Approach to Partially
BIFURCATION TO TRAVELING WAVES IN THE CUBIC-QUINTIC COMPLEX GINZBURG LANDAU EQUATION
 BIFURCATION TO TRAVELING WAVES IN THE CUBIC-QUINTIC COMPLEX GINZBURG LANDAU EQUATION JUNGHO PARK AND PHILIP STRZELECKI Abstract. We consider the 1-dimensional complex Ginzburg Landau equation(cgle) which
BIFURCATION TO TRAVELING WAVES IN THE CUBIC-QUINTIC COMPLEX GINZBURG LANDAU EQUATION JUNGHO PARK AND PHILIP STRZELECKI Abstract. We consider the 1-dimensional complex Ginzburg Landau equation(cgle) which
Geometry and Exact Soliton Solutions of the Integrable su(3)-
 Geometry and Exact Soliton Solutions of the Integrable su(3)-spin Systems Eurasian national university, Astana, Kazakhstan Varna, Bulgaria 2018 Introduction The vector nonlinear Schrödinger equation is
Geometry and Exact Soliton Solutions of the Integrable su(3)-spin Systems Eurasian national university, Astana, Kazakhstan Varna, Bulgaria 2018 Introduction The vector nonlinear Schrödinger equation is
DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS
 DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS ADILBEK KAIRZHAN, DMITRY E. PELINOVSKY, AND ROY H. GOODMAN Abstract. When the coefficients of the cubic terms match the coefficients in the boundary
DRIFT OF SPECTRALLY STABLE SHIFTED STATES ON STAR GRAPHS ADILBEK KAIRZHAN, DMITRY E. PELINOVSKY, AND ROY H. GOODMAN Abstract. When the coefficients of the cubic terms match the coefficients in the boundary
Normal form for the non linear Schrödinger equation
 Normal form for the non linear Schrödinger equation joint work with Claudio Procesi and Nguyen Bich Van Universita di Roma La Sapienza S. Etienne de Tinee 4-9 Feb. 2013 Nonlinear Schrödinger equation Consider
Normal form for the non linear Schrödinger equation joint work with Claudio Procesi and Nguyen Bich Van Universita di Roma La Sapienza S. Etienne de Tinee 4-9 Feb. 2013 Nonlinear Schrödinger equation Consider
Dispersion relations, stability and linearization
 Dispersion relations, stability and linearization 1 Dispersion relations Suppose that u(x, t) is a function with domain { < x 0}, and it satisfies a linear, constant coefficient partial differential
Dispersion relations, stability and linearization 1 Dispersion relations Suppose that u(x, t) is a function with domain { < x 0}, and it satisfies a linear, constant coefficient partial differential
Semiclassical spin coherent state method in the weak spin-orbit coupling limit
 arxiv:nlin/847v1 [nlin.cd] 9 Aug Semiclassical spin coherent state method in the weak spin-orbit coupling limit Oleg Zaitsev Institut für Theoretische Physik, Universität Regensburg, D-934 Regensburg,
arxiv:nlin/847v1 [nlin.cd] 9 Aug Semiclassical spin coherent state method in the weak spin-orbit coupling limit Oleg Zaitsev Institut für Theoretische Physik, Universität Regensburg, D-934 Regensburg,
Recursion Systems and Recursion Operators for the Soliton Equations Related to Rational Linear Problem with Reductions
 GMV The s Systems and for the Soliton Equations Related to Rational Linear Problem with Reductions Department of Mathematics & Applied Mathematics University of Cape Town XIV th International Conference
GMV The s Systems and for the Soliton Equations Related to Rational Linear Problem with Reductions Department of Mathematics & Applied Mathematics University of Cape Town XIV th International Conference
Evolution of solitary waves for a perturbed nonlinear Schrödinger equation
 University of Wollongong Research Online Faculty of Informatics - Papers (Archive) Faculty of Engineering and Information Sciences 2010 Evolution of solitary waves for a perturbed nonlinear Schrödinger
University of Wollongong Research Online Faculty of Informatics - Papers (Archive) Faculty of Engineering and Information Sciences 2010 Evolution of solitary waves for a perturbed nonlinear Schrödinger
Chapter 3. Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons.
 Chapter 3 Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons. 73 3.1 Introduction The study of linear and nonlinear wave propagation
Chapter 3 Head-on collision of ion acoustic solitary waves in electron-positron-ion plasma with superthermal electrons and positrons. 73 3.1 Introduction The study of linear and nonlinear wave propagation
On Decompositions of KdV 2-Solitons
 On Decompositions of KdV 2-Solitons Alex Kasman College of Charleston Joint work with Nick Benes and Kevin Young Journal of Nonlinear Science, Volume 16 Number 2 (2006) pages 179-200 -5-2.50 2.5 0 2.5
On Decompositions of KdV 2-Solitons Alex Kasman College of Charleston Joint work with Nick Benes and Kevin Young Journal of Nonlinear Science, Volume 16 Number 2 (2006) pages 179-200 -5-2.50 2.5 0 2.5
On quasiperiodic boundary condition problem
 JOURNAL OF MATHEMATICAL PHYSICS 46, 03503 (005) On quasiperiodic boundary condition problem Y. Charles Li a) Department of Mathematics, University of Missouri, Columbia, Missouri 65 (Received 8 April 004;
JOURNAL OF MATHEMATICAL PHYSICS 46, 03503 (005) On quasiperiodic boundary condition problem Y. Charles Li a) Department of Mathematics, University of Missouri, Columbia, Missouri 65 (Received 8 April 004;
Soliton solutions of Hirota equation and Hirota-Maccari system
 NTMSCI 4, No. 3, 231-238 (2016) 231 New Trends in Mathematical Sciences http://dx.doi.org/10.20852/ntmsci.2016115853 Soliton solutions of Hirota equation and Hirota-Maccari system M. M. El-Borai 1, H.
NTMSCI 4, No. 3, 231-238 (2016) 231 New Trends in Mathematical Sciences http://dx.doi.org/10.20852/ntmsci.2016115853 Soliton solutions of Hirota equation and Hirota-Maccari system M. M. El-Borai 1, H.
Soliton solutions to the ABS list
 to the ABS list Department of Physics, University of Turku, FIN-20014 Turku, Finland in collaboration with James Atkinson, Frank Nijhoff and Da-jun Zhang DIS-INI, February 2009 The setting CAC The setting
to the ABS list Department of Physics, University of Turku, FIN-20014 Turku, Finland in collaboration with James Atkinson, Frank Nijhoff and Da-jun Zhang DIS-INI, February 2009 The setting CAC The setting
EXACT DARK SOLITON, PERIODIC SOLUTIONS AND CHAOTIC DYNAMICS IN A PERTURBED GENERALIZED NONLINEAR SCHRODINGER EQUATION
 CANADIAN APPLIED MATHEMATICS QUARTERLY Volume 17, Number 1, Spring 9 EXACT DARK SOLITON, PERIODIC SOLUTIONS AND CHAOTIC DYNAMICS IN A PERTURBED GENERALIZED NONLINEAR SCHRODINGER EQUATION JIBIN LI ABSTRACT.
CANADIAN APPLIED MATHEMATICS QUARTERLY Volume 17, Number 1, Spring 9 EXACT DARK SOLITON, PERIODIC SOLUTIONS AND CHAOTIC DYNAMICS IN A PERTURBED GENERALIZED NONLINEAR SCHRODINGER EQUATION JIBIN LI ABSTRACT.
IBVPs for linear and integrable nonlinear evolution PDEs
 IBVPs for linear and integrable nonlinear evolution PDEs Dionyssis Mantzavinos Department of Applied Mathematics and Theoretical Physics, University of Cambridge. Edinburgh, May 31, 212. Dionyssis Mantzavinos
IBVPs for linear and integrable nonlinear evolution PDEs Dionyssis Mantzavinos Department of Applied Mathematics and Theoretical Physics, University of Cambridge. Edinburgh, May 31, 212. Dionyssis Mantzavinos
13.1 Ion Acoustic Soliton and Shock Wave
 13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
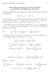 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Adaptive WENO Schemes for Singular in Space and Time Solutions of Nonlinear Degenerate Reaction-Diffusion Problems
 EPJ Web of Conferences 108, 0019 (016) DOI: 10.1051/ epjconf/ 0161080019 C Owned by the authors, published by EDP Sciences, 016 Adaptive WENO Schemes for Singular in Space and Time Solutions of Nonlinear
EPJ Web of Conferences 108, 0019 (016) DOI: 10.1051/ epjconf/ 0161080019 C Owned by the authors, published by EDP Sciences, 016 Adaptive WENO Schemes for Singular in Space and Time Solutions of Nonlinear
Numerical Study of Oscillatory Regimes in the KP equation
 Numerical Study of Oscillatory Regimes in the KP equation C. Klein, MPI for Mathematics in the Sciences, Leipzig, with C. Sparber, P. Markowich, Vienna, math-ph/"#"$"%& C. Sparber (generalized KP), personal-homepages.mis.mpg.de/klein/
Numerical Study of Oscillatory Regimes in the KP equation C. Klein, MPI for Mathematics in the Sciences, Leipzig, with C. Sparber, P. Markowich, Vienna, math-ph/"#"$"%& C. Sparber (generalized KP), personal-homepages.mis.mpg.de/klein/
Symbolic Computation of Conserved Densities and Symmetries of Nonlinear Evolution and Differential-Difference Equations WILLY HEREMAN
 . Symbolic Computation of Conserved Densities and Symmetries of Nonlinear Evolution and Differential-Difference Equations WILLY HEREMAN Joint work with ÜNAL GÖKTAŞ and Grant Erdmann Graduate Seminar Department
. Symbolic Computation of Conserved Densities and Symmetries of Nonlinear Evolution and Differential-Difference Equations WILLY HEREMAN Joint work with ÜNAL GÖKTAŞ and Grant Erdmann Graduate Seminar Department
The Sommerfeld Polynomial Method: Harmonic Oscillator Example
 Chemistry 460 Fall 2017 Dr. Jean M. Standard October 2, 2017 The Sommerfeld Polynomial Method: Harmonic Oscillator Example Scaling the Harmonic Oscillator Equation Recall the basic definitions of the harmonic
Chemistry 460 Fall 2017 Dr. Jean M. Standard October 2, 2017 The Sommerfeld Polynomial Method: Harmonic Oscillator Example Scaling the Harmonic Oscillator Equation Recall the basic definitions of the harmonic
A Low-Dimensional Model for the Maximal Amplification Factor of Bichromatic Wave Groups
 PROC. ITB Eng. Science Vol. 35 B, No., 3, 39-53 39 A Low-Dimensional Model for the Maximal Amplification Factor of Bichromatic Wave Groups W. N. Tan,* & Andonowati Fakulti Sains, Universiti Teknologi Malaysia
PROC. ITB Eng. Science Vol. 35 B, No., 3, 39-53 39 A Low-Dimensional Model for the Maximal Amplification Factor of Bichromatic Wave Groups W. N. Tan,* & Andonowati Fakulti Sains, Universiti Teknologi Malaysia
Reductions and New types of Integrable models in two and more dimensions
 0-0 XIV International conference Geometry Integrabiliy and Quantization Varna, 8-13 June 2012, Bulgaria Reductions and New types of Integrable models in two and more dimensions V. S. Gerdjikov Institute
0-0 XIV International conference Geometry Integrabiliy and Quantization Varna, 8-13 June 2012, Bulgaria Reductions and New types of Integrable models in two and more dimensions V. S. Gerdjikov Institute
Wave interactions and the analysis of the perturbed. Burgers equation
 Wave interactions and the analysis of the perturbed Burgers equation Alex Veksler 1 and Yair Zarmi 1,2 Ben-Gurion University of the Negev, Israel 1 Department of Physics, Beer-Sheva, 84105 2 Department
Wave interactions and the analysis of the perturbed Burgers equation Alex Veksler 1 and Yair Zarmi 1,2 Ben-Gurion University of the Negev, Israel 1 Department of Physics, Beer-Sheva, 84105 2 Department
New Homoclinic and Heteroclinic Solutions for Zakharov System
 Commun. Theor. Phys. 58 (2012) 749 753 Vol. 58, No. 5, November 15, 2012 New Homoclinic and Heteroclinic Solutions for Zakharov System WANG Chuan-Jian ( ), 1 DAI Zheng-De (à ), 2, and MU Gui (½ ) 3 1 Department
Commun. Theor. Phys. 58 (2012) 749 753 Vol. 58, No. 5, November 15, 2012 New Homoclinic and Heteroclinic Solutions for Zakharov System WANG Chuan-Jian ( ), 1 DAI Zheng-De (à ), 2, and MU Gui (½ ) 3 1 Department
Statistical Mechanics and Thermodynamics of Small Systems
 Statistical Mechanics and Thermodynamics of Small Systems Luca Cerino Advisors: A. Puglisi and A. Vulpiani Final Seminar of PhD course in Physics Cycle XXIX Rome, October, 26 2016 Outline of the talk 1.
Statistical Mechanics and Thermodynamics of Small Systems Luca Cerino Advisors: A. Puglisi and A. Vulpiani Final Seminar of PhD course in Physics Cycle XXIX Rome, October, 26 2016 Outline of the talk 1.
Solving the Generalized Kaup Kupershmidt Equation
 Adv Studies Theor Phys, Vol 6, 2012, no 18, 879-885 Solving the Generalized Kaup Kupershmidt Equation Alvaro H Salas Department of Mathematics Universidad de Caldas, Manizales, Colombia Universidad Nacional
Adv Studies Theor Phys, Vol 6, 2012, no 18, 879-885 Solving the Generalized Kaup Kupershmidt Equation Alvaro H Salas Department of Mathematics Universidad de Caldas, Manizales, Colombia Universidad Nacional
Hamiltonian partial differential equations and Painlevé transcendents
 The 6th TIMS-OCAMI-WASEDA Joint International Workshop on Integrable Systems and Mathematical Physics March 22-26, 2014 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN
The 6th TIMS-OCAMI-WASEDA Joint International Workshop on Integrable Systems and Mathematical Physics March 22-26, 2014 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN
QCD and Rescattering in Nuclear Targets Lecture 2
 QCD and Rescattering in Nuclear Targets Lecture Jianwei Qiu Iowa State University The 1 st Annual Hampton University Graduate Studies Program (HUGS 006) June 5-3, 006 Jefferson Lab, Newport News, Virginia
QCD and Rescattering in Nuclear Targets Lecture Jianwei Qiu Iowa State University The 1 st Annual Hampton University Graduate Studies Program (HUGS 006) June 5-3, 006 Jefferson Lab, Newport News, Virginia
On Certain Aspects of the Theory of Polynomial Bundle Lax Operators Related to Symmetric Spaces. Tihomir Valchev
 0-0 XIII th International Conference Geometry, Integrability and Quantization June 3 8, 2011, St. Constantin and Elena, Varna On Certain Aspects of the Theory of Polynomial Bundle Lax Operators Related
0-0 XIII th International Conference Geometry, Integrability and Quantization June 3 8, 2011, St. Constantin and Elena, Varna On Certain Aspects of the Theory of Polynomial Bundle Lax Operators Related
Decay profiles of a linear artificial viscosity system
 Decay profiles of a linear artificial viscosity system Gene Wayne, Ryan Goh and Roland Welter Boston University rwelter@bu.edu July 2, 2018 This research was supported by funding from the NSF. Roland Welter
Decay profiles of a linear artificial viscosity system Gene Wayne, Ryan Goh and Roland Welter Boston University rwelter@bu.edu July 2, 2018 This research was supported by funding from the NSF. Roland Welter
Long-wave Instability in Anisotropic Double-Diffusion
 Long-wave Instability in Anisotropic Double-Diffusion Jean-Luc Thiffeault Institute for Fusion Studies and Department of Physics University of Texas at Austin and Neil J. Balmforth Department of Theoretical
Long-wave Instability in Anisotropic Double-Diffusion Jean-Luc Thiffeault Institute for Fusion Studies and Department of Physics University of Texas at Austin and Neil J. Balmforth Department of Theoretical
The DKP equation in the Woods-Saxon potential well: Bound states
 arxiv:1601.0167v1 [quant-ph] 6 Jan 016 The DKP equation in the Woods-Saxon potential well: Bound states Boutheina Boutabia-Chéraitia Laboratoire de Probabilités et Statistiques (LaPS) Université Badji-Mokhtar.
arxiv:1601.0167v1 [quant-ph] 6 Jan 016 The DKP equation in the Woods-Saxon potential well: Bound states Boutheina Boutabia-Chéraitia Laboratoire de Probabilités et Statistiques (LaPS) Université Badji-Mokhtar.
Separatrix Map Analysis for Fractal Scatterings in Weak Interactions of Solitary Waves
 Separatrix Map Analysis for Fractal Scatterings in Weak Interactions of Solitary Waves By Yi Zhu, Richard Haberman, and Jianke Yang Previous studies have shown that fractal scatterings in weak interactions
Separatrix Map Analysis for Fractal Scatterings in Weak Interactions of Solitary Waves By Yi Zhu, Richard Haberman, and Jianke Yang Previous studies have shown that fractal scatterings in weak interactions
Dispersion-managed Solitons
 Proceedings of the Steklov Institute of Mathematics, Suppl., 3, pp. S98 S7. Translated from Trudy Instituta Matematiki i Mekhaniki UrO RAN, Vol. 9, No., 3. Original Russian Text Copyright c 3 by Kalisch,
Proceedings of the Steklov Institute of Mathematics, Suppl., 3, pp. S98 S7. Translated from Trudy Instituta Matematiki i Mekhaniki UrO RAN, Vol. 9, No., 3. Original Russian Text Copyright c 3 by Kalisch,
Symmetry Reductions of (2+1) dimensional Equal Width. Wave Equation
 Authors: Symmetry Reductions of (2+1) dimensional Equal Width 1. Dr. S. Padmasekaran Wave Equation Asst. Professor, Department of Mathematics Periyar University, Salem 2. M.G. RANI Periyar University,
Authors: Symmetry Reductions of (2+1) dimensional Equal Width 1. Dr. S. Padmasekaran Wave Equation Asst. Professor, Department of Mathematics Periyar University, Salem 2. M.G. RANI Periyar University,
MATH3383. Quantum Mechanics. Appendix D: Hermite Equation; Orthogonal Polynomials
 MATH3383. Quantum Mechanics. Appendix D: Hermite Equation; Orthogonal Polynomials. Hermite Equation In the study of the eigenvalue problem of the Hamiltonian for the quantum harmonic oscillator we have
MATH3383. Quantum Mechanics. Appendix D: Hermite Equation; Orthogonal Polynomials. Hermite Equation In the study of the eigenvalue problem of the Hamiltonian for the quantum harmonic oscillator we have
Rational Form Solitary Wave Solutions and Doubly Periodic Wave Solutions to (1+1)-Dimensional Dispersive Long Wave Equation
 Commun. Theor. Phys. (Beijing, China) 43 (005) pp. 975 98 c International Academic Publishers Vol. 43, No. 6, June 15, 005 Rational Form Solitary Wave Solutions and Doubly Periodic Wave Solutions to (1+1)-Dimensional
Commun. Theor. Phys. (Beijing, China) 43 (005) pp. 975 98 c International Academic Publishers Vol. 43, No. 6, June 15, 005 Rational Form Solitary Wave Solutions and Doubly Periodic Wave Solutions to (1+1)-Dimensional
Global stabilization of feedforward systems with exponentially unstable Jacobian linearization
 Global stabilization of feedforward systems with exponentially unstable Jacobian linearization F Grognard, R Sepulchre, G Bastin Center for Systems Engineering and Applied Mechanics Université catholique
Global stabilization of feedforward systems with exponentially unstable Jacobian linearization F Grognard, R Sepulchre, G Bastin Center for Systems Engineering and Applied Mechanics Université catholique
Some Elliptic Traveling Wave Solutions to the Novikov-Veselov Equation
 Progress In Electromagnetics Research Symposium 006, Cambridge, USA, March 6-9 59 Some Elliptic Traveling Wave Solutions to the Novikov-Veselov Equation J. Nickel, V. S. Serov, and H. W. Schürmann University
Progress In Electromagnetics Research Symposium 006, Cambridge, USA, March 6-9 59 Some Elliptic Traveling Wave Solutions to the Novikov-Veselov Equation J. Nickel, V. S. Serov, and H. W. Schürmann University
Today: 5 July 2008 ٢
 Anderson localization M. Reza Rahimi Tabar IPM 5 July 2008 ١ Today: 5 July 2008 ٢ Short History of Anderson Localization ٣ Publication 1) F. Shahbazi, etal. Phys. Rev. Lett. 94, 165505 (2005) 2) A. Esmailpour,
Anderson localization M. Reza Rahimi Tabar IPM 5 July 2008 ١ Today: 5 July 2008 ٢ Short History of Anderson Localization ٣ Publication 1) F. Shahbazi, etal. Phys. Rev. Lett. 94, 165505 (2005) 2) A. Esmailpour,
An Analytic Study of the (2 + 1)-Dimensional Potential Kadomtsev-Petviashvili Equation
 Adv. Theor. Appl. Mech., Vol. 3, 21, no. 11, 513-52 An Analytic Study of the (2 + 1)-Dimensional Potential Kadomtsev-Petviashvili Equation B. Batiha and K. Batiha Department of Mathematics, Faculty of
Adv. Theor. Appl. Mech., Vol. 3, 21, no. 11, 513-52 An Analytic Study of the (2 + 1)-Dimensional Potential Kadomtsev-Petviashvili Equation B. Batiha and K. Batiha Department of Mathematics, Faculty of
arxiv: v1 [quant-ph] 25 Apr 2008
![arxiv: v1 [quant-ph] 25 Apr 2008 arxiv: v1 [quant-ph] 25 Apr 2008](/thumbs/78/77126510.jpg) Generalized Geometrical Phase in the Case of Continuous Spectra M. Maamache and Y. Saadi Laboratoire de Physique Quantique et Systèmes Dynamiques, Faculté des Sciences,Université Ferhat Abbas de Sétif,
Generalized Geometrical Phase in the Case of Continuous Spectra M. Maamache and Y. Saadi Laboratoire de Physique Quantique et Systèmes Dynamiques, Faculté des Sciences,Université Ferhat Abbas de Sétif,
Lecture II Search Method for Lax Pairs of Nonlinear Partial Differential Equations
 Lecture II Search Method for Lax Pairs of Nonlinear Partial Differential Equations Usama Al Khawaja, Department of Physics, UAE University, 24 Jan. 2012 First International Winter School on Quantum Gases
Lecture II Search Method for Lax Pairs of Nonlinear Partial Differential Equations Usama Al Khawaja, Department of Physics, UAE University, 24 Jan. 2012 First International Winter School on Quantum Gases
Applicable Analysis. Dark-dark and dark-bright soliton interactions in the twocomponent
 Dark-dark and dark-bright soliton interactions in the twocomponent defocusing nonlinear Schr ödinger equation Journal: Manuscript ID: GAPA-0-0 Manuscript Type: Original Paper Date Submitted by the Author:
Dark-dark and dark-bright soliton interactions in the twocomponent defocusing nonlinear Schr ödinger equation Journal: Manuscript ID: GAPA-0-0 Manuscript Type: Original Paper Date Submitted by the Author:
This ODE arises in many physical systems that we shall investigate. + ( + 1)u = 0. (λ + s)x λ + s + ( + 1) a λ. (s + 1)(s + 2) a 0
 Legendre equation This ODE arises in many physical systems that we shall investigate We choose We then have Substitution gives ( x 2 ) d 2 u du 2x 2 dx dx + ( + )u u x s a λ x λ a du dx λ a λ (λ + s)x
Legendre equation This ODE arises in many physical systems that we shall investigate We choose We then have Substitution gives ( x 2 ) d 2 u du 2x 2 dx dx + ( + )u u x s a λ x λ a du dx λ a λ (λ + s)x
2. The Schrödinger equation for one-particle problems. 5. Atoms and the periodic table of chemical elements
 1 Historical introduction The Schrödinger equation for one-particle problems 3 Mathematical tools for quantum chemistry 4 The postulates of quantum mechanics 5 Atoms and the periodic table of chemical
1 Historical introduction The Schrödinger equation for one-particle problems 3 Mathematical tools for quantum chemistry 4 The postulates of quantum mechanics 5 Atoms and the periodic table of chemical
On Hamiltonian perturbations of hyperbolic PDEs
 Bologna, September 24, 2004 On Hamiltonian perturbations of hyperbolic PDEs Boris DUBROVIN SISSA (Trieste) Class of 1+1 evolutionary systems w i t +Ai j (w)wj x +ε (B i j (w)wj xx + 1 2 Ci jk (w)wj x wk
Bologna, September 24, 2004 On Hamiltonian perturbations of hyperbolic PDEs Boris DUBROVIN SISSA (Trieste) Class of 1+1 evolutionary systems w i t +Ai j (w)wj x +ε (B i j (w)wj xx + 1 2 Ci jk (w)wj x wk
A Short historical review Our goal The hierarchy and Lax... The Hamiltonian... The Dubrovin-type... Algebro-geometric... Home Page.
 Page 1 of 46 Department of Mathematics,Shanghai The Hamiltonian Structure and Algebro-geometric Solution of a 1 + 1-Dimensional Coupled Equations Xia Tiecheng and Pan Hongfei Page 2 of 46 Section One A
Page 1 of 46 Department of Mathematics,Shanghai The Hamiltonian Structure and Algebro-geometric Solution of a 1 + 1-Dimensional Coupled Equations Xia Tiecheng and Pan Hongfei Page 2 of 46 Section One A
Partition function of one matrix-models in the multi-cut case and Painlevé equations. Tamara Grava and Christian Klein
 Partition function of one matrix-models in the multi-cut case and Painlevé equations Tamara Grava and Christian Klein SISSA IMS, Singapore, March 2006 Main topics Large N limit beyond the one-cut case
Partition function of one matrix-models in the multi-cut case and Painlevé equations Tamara Grava and Christian Klein SISSA IMS, Singapore, March 2006 Main topics Large N limit beyond the one-cut case
221A Lecture Notes Convergence of Perturbation Theory
 A Lecture Notes Convergence of Perturbation Theory Asymptotic Series An asymptotic series in a parameter ɛ of a function is given in a power series f(ɛ) = f n ɛ n () n=0 where the series actually does
A Lecture Notes Convergence of Perturbation Theory Asymptotic Series An asymptotic series in a parameter ɛ of a function is given in a power series f(ɛ) = f n ɛ n () n=0 where the series actually does
University of Central Florida. Quantifying Variational Solutions
 University of Central Florida Institute for Simulation & Training and epartment of Mathematics and CREOL.J. Kaup and Thomas K. Vogel Quantifying Variational Solutions (Preprint available at http://gauss.math.ucf.edu/~kaup/)
University of Central Florida Institute for Simulation & Training and epartment of Mathematics and CREOL.J. Kaup and Thomas K. Vogel Quantifying Variational Solutions (Preprint available at http://gauss.math.ucf.edu/~kaup/)
On the Whitham Equation
 On the Whitham Equation Henrik Kalisch Department of Mathematics University of Bergen, Norway Joint work with: Handan Borluk, Denys Dutykh, Mats Ehrnström, Daulet Moldabayev, David Nicholls Research partially
On the Whitham Equation Henrik Kalisch Department of Mathematics University of Bergen, Norway Joint work with: Handan Borluk, Denys Dutykh, Mats Ehrnström, Daulet Moldabayev, David Nicholls Research partially
Numerical methods for a fractional diffusion/anti-diffusion equation
 Numerical methods for a fractional diffusion/anti-diffusion equation Afaf Bouharguane Institut de Mathématiques de Bordeaux (IMB), Université Bordeaux 1, France Berlin, November 2012 Afaf Bouharguane Numerical
Numerical methods for a fractional diffusion/anti-diffusion equation Afaf Bouharguane Institut de Mathématiques de Bordeaux (IMB), Université Bordeaux 1, France Berlin, November 2012 Afaf Bouharguane Numerical
Transient Phenomena in Quantum Bound States Subjected to a Sudden Perturbation
 Symmetry, Integrability and Geometry: Methods and Applications Vol. (5), Paper 3, 9 pages Transient Phenomena in Quantum Bound States Subjected to a Sudden Perturbation Marcos MOSHINSKY and Emerson SADURNÍ
Symmetry, Integrability and Geometry: Methods and Applications Vol. (5), Paper 3, 9 pages Transient Phenomena in Quantum Bound States Subjected to a Sudden Perturbation Marcos MOSHINSKY and Emerson SADURNÍ
Freedom in the Expansion and Obstacles to Integrability in Multiple-Soliton Solutions of the Perturbed KdV Equation
 Freedom in the Expansion and Obstacles to Integrability in Multiple-Soliton Solutions of the Perturbed KdV Equation Alex Veksler 1 and Yair Zarmi 1, Ben-Gurion University of the Negev, Israel 1 Department
Freedom in the Expansion and Obstacles to Integrability in Multiple-Soliton Solutions of the Perturbed KdV Equation Alex Veksler 1 and Yair Zarmi 1, Ben-Gurion University of the Negev, Israel 1 Department
Ultra-short pulse propagation in dispersion-managed birefringent optical fiber
 Chapter 3 Ultra-short pulse propagation in dispersion-managed birefringent optical fiber 3.1 Introduction This chapter deals with the real world physical systems, where the inhomogeneous parameters of
Chapter 3 Ultra-short pulse propagation in dispersion-managed birefringent optical fiber 3.1 Introduction This chapter deals with the real world physical systems, where the inhomogeneous parameters of
the renormalization group (RG) idea
 the renormalization group (RG) idea Block Spin Partition function Z =Tr s e H. block spin transformation (majority rule) T (s, if s i ; s,...,s 9 )= s i > 0; 0, otherwise. b Block Spin (block-)transformed
the renormalization group (RG) idea Block Spin Partition function Z =Tr s e H. block spin transformation (majority rule) T (s, if s i ; s,...,s 9 )= s i > 0; 0, otherwise. b Block Spin (block-)transformed
Vector Solitons and Their Internal Oscillations in Birefringent Nonlinear Optical Fibers
 Vector Solitons and Their Internal Oscillations in Birefringent Nonlinear Optical Fibers By Jianke Yang In this article, the vector solitons in birefringent nonlinear optical fibers are studied first.
Vector Solitons and Their Internal Oscillations in Birefringent Nonlinear Optical Fibers By Jianke Yang In this article, the vector solitons in birefringent nonlinear optical fibers are studied first.
Wave interactions. J. Vanneste. School of Mathematics University of Edinburgh, UK. vanneste < > - + Wave interactions p.
 Wave interactions J. Vanneste School of Mathematics University of Edinburgh, UK www.maths.ed.ac.uk/ vanneste Wave interactions p.1/50 Linear waves in conservative systems Small amplitude motion: linearize
Wave interactions J. Vanneste School of Mathematics University of Edinburgh, UK www.maths.ed.ac.uk/ vanneste Wave interactions p.1/50 Linear waves in conservative systems Small amplitude motion: linearize
A Novel Nonlinear Evolution Equation Integrable by the Inverse Scattering Method
 Proceedings of Institute of Mathematics of NAS of Ukraine 2002, Vol. 43, Part, 384 39 A Novel Nonlinear Evolution Equation Integrable by the Inverse Scattering Method Vyacheslav VAKHNENKO and John PARKES
Proceedings of Institute of Mathematics of NAS of Ukraine 2002, Vol. 43, Part, 384 39 A Novel Nonlinear Evolution Equation Integrable by the Inverse Scattering Method Vyacheslav VAKHNENKO and John PARKES
Lecture No 1 Introduction to Diffusion equations The heat equat
 Lecture No 1 Introduction to Diffusion equations The heat equation Columbia University IAS summer program June, 2009 Outline of the lectures We will discuss some basic models of diffusion equations and
Lecture No 1 Introduction to Diffusion equations The heat equation Columbia University IAS summer program June, 2009 Outline of the lectures We will discuss some basic models of diffusion equations and
Linear and Nonlinear Oscillators (Lecture 2)
 Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Prof. dr. A. Achterberg, Astronomical Dept., IMAPP, Radboud Universiteit
 Prof. dr. A. Achterberg, Astronomical Dept., IMAPP, Radboud Universiteit Central concepts: Phase velocity: velocity with which surfaces of constant phase move Group velocity: velocity with which slow
Prof. dr. A. Achterberg, Astronomical Dept., IMAPP, Radboud Universiteit Central concepts: Phase velocity: velocity with which surfaces of constant phase move Group velocity: velocity with which slow
Equations of linear stellar oscillations
 Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Propagation of Solitons Under Colored Noise
 Propagation of Solitons Under Colored Noise Dr. Russell Herman Departments of Mathematics & Statistics, Physics & Physical Oceanography UNC Wilmington, Wilmington, NC January 6, 2009 Outline of Talk 1
Propagation of Solitons Under Colored Noise Dr. Russell Herman Departments of Mathematics & Statistics, Physics & Physical Oceanography UNC Wilmington, Wilmington, NC January 6, 2009 Outline of Talk 1
Hamiltonian partial differential equations and Painlevé transcendents
 Winter School on PDEs St Etienne de Tinée February 2-6, 2015 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN SISSA, Trieste Lecture 2 Recall: the main goal is to compare
Winter School on PDEs St Etienne de Tinée February 2-6, 2015 Hamiltonian partial differential equations and Painlevé transcendents Boris DUBROVIN SISSA, Trieste Lecture 2 Recall: the main goal is to compare
