APPLICATIONS OF PARTIAL DIFFERENTIAL EQUATIONS. Classification of second order quasi linear partial. Solutions of one dimensional wave equation
|
|
|
- Jesse Preston
- 6 years ago
- Views:
Transcription
1 APPICATIONS OF PARTIA DIFFERENTIA EQUATIONS Cassifiaio of sod ordr quasi iar paria diffria quaios Souios of o dimsioa wav quaio O dimsioa ha quaio Sad sa souio of wo-dimsioa ha quaio Isuad dgs udd Fourir sris souios i Carsia oordias. I mahmais paria diffria quaios PDE ar a p of diffria quaio i.. a raio ivovig a ukow fuio or fuios of svra idpd variabs ad is or hir paria drivaivs wih rsp o hos variabs. Paria diffria quaios ar usd o formua ad hus aid h souio of probms ivovig fuios of svra variabs; suh as h propagaio of soud or ha rosais rodamis fuid fow ad asii. Smig disi phsia phoma ma hav idia mahmaia formuaios ad hus b govrd b h sam udrig dami.
2 I mahmais i h fid of diffria quaios a boudar vau probm is a diffria quaio oghr wih a s of addiioa rsrais ad h boudar odiios. A souio o a boudar vau probm is a souio o h diffria quaio whih aso saisfis h boudar odiios. Boudar vau probms aris i svra brahs of phsis as a phsia diffria quaio wi hav hm. Probms ivovig h wav quaio suh as h drmiaio of orma mods ar of sad as boudar vau probms. A arg ass of impora boudar vau probms ar h Surm-iouvi probms. Th aasis of hs probms ivovs h igfuios of a diffria opraor. To b usfu i appiaios a boudar vau probm shoud b w posd. This mas ha giv h ipu o h probm hr iss a uiqu souio whih dpds oiuous o h ipu. Muh horia work i h fid of paria diffria quaios is dvod o provig ha boudar vau probms arisig from siifi ad girig appiaios ar i fa w-posd. Amog h aris boudar vau probms o b sudid is h Dirih probm of fidig h harmoi fuios souios o apa's quaio; h souio was giv b h Dirih's priip.
3 Iiia vau probm A mor mahmaia wa o piur h diffr bw a iiia vau probm ad a boudar vau probm is ha a iiia vau probm has a of h odiios spifid a h sam vau of h idpd variab i h quaio ad ha vau is a h owr boudar of h domai hus h rm "iiia" vau. O h ohr had a boudar vau probm has odiios spifid a h rms of h idpd variab. For amp if h idpd variab is im ovr h domai [] a iiia vau probm woud spif a vau of ad ' a im whi a boudar vau probm woud spif vaus for a boh ad. If h probm is dpd o boh spa ad im h isad of spifig h vau of h probm a a giv poi for a im h daa oud b giv a a giv im for a spa. For amp h mpraur of a iro bar wih o d kp a absou zro ad h ohr d a h frzig poi of war woud b a boudar vau probm. Tps of boudar vau probms Th boudar vau probm for a idaisd D rod If h boudar givs a vau o h orma drivaiv of h probm h i is a Numa boudar odiio. For amp if hr is a har a o d of a iro rod h rg woud b addd a a osa ra bu h aua mpraur woud o b kow. If h boudar givs a vau o h probm h i is a Dirih boudar odiio. For amp if o d of a iro rod is hd a absou zro h h vau of h probm woud b kow a ha poi i spa. If h boudar has h form of a urv or surfa ha givs a vau o h orma drivaiv ad h probm isf h i is a Cauh boudar odiio. Asid from h boudar odiio boudar vau probms ar aso assifid aordig o h p of diffria opraor ivovd. For a ipi opraor o disusss ipi boudar vau probms. For a hprboi opraor o disusss hprboi boudar
4 vau probms. Ths agoris ar furhr subdividd io iar ad various oiar ps. Rad mahmais: Phsia appiaios: Numria agorihms: iiia vau probm diffria quaios Gr's fuios Sohasi prosss ad boudar vau probms Eamps of boudar vau probms Surm-iouvi hor Dirih boudar odiio Numa boudar odiio Sommrfd radiaio odiio Cauh boudar odiio wavs orma mods rosais apa's quaio poia hor shooig mhod dir muip shooig mhod CASSIFICATION OF PARTIA DIFFERENTIA EQUATIONS OF THE SECOND ORDER a sod ordr paria diffria quaio i h fuio u of h wo idpd variab b of h form. u u u A B C u u f u
5 Eq is assifid as ipi paraboi or hprboi a h pois of a giv rgio R dpdig o whhr B -AC < B -AC < B -AC < [ ipi quaio] [ Paraboi quaio] [ hprboi quaio] CASSIFY THE FOOWING EQUATIONS :- f f > >. So : - Hr A ; C B - A - - v wh > > Th quaio is ipi. f - f > > So :- Hr A; B - B A - v Th quaio is hprboi u -u u Hr A; B - B - AC - Th quaio is paraboi f f f > > Hr AB C 5
6 B -AC v Th quaio is ipi 5 f - f for - << << Hr A ; B ; C- B -AC is awas v i -<< - is gaiv i -<< B -AC - v Th quaio is ipi If B -AC Th quaio is paraboi. ONE DIMENSIONA WAVE EQUATION i Probms o Vibraig srig wih zro voi ii Probms o vibraig srig wih o zro voi O dimsioa wav quaio is 6
7 a Th various souios of h wav quaio is [ C p C -p ] [C pa C -pa ] [ C 5 osp C 6 sip] [ C 7 ospa C 8 sipa] [ C 9 C ] [ C C ] No: I probms of vibraio of srigs w awas ak h foowig as h orr souio; [ C osp C sip] [C ospa C sipa ] i Probms o Vibraig srig wih zro iiia voi A srig is srhd ad fasd o wo pois ad aspr. Moio is sard b dispaig h srig io h form k- from whih i is rasd a im o. Fid h dispam of a poi o h srig a a disa of from o d a im. So:- Hr w hav o sov h wav quaio a wih giv boudar odiios i Ths wo odiios ar fid odiios i wav Eq ii iii iiia voi is o giv i probm. So w ak i as. iv K iiia dispam is giv i probm i sf. Th orr souio of is 7
8 [C osp C sip] [C ospa C sipa] App odiio i i w g C [C ospa C sipa] >C ospa C sipa C Sub C i w g h souio C sip [ C ospa C sipa] App odiio ii i w g C sip [C ospa C sipa] > C ad C ospa C sipa sip i. p si - i. p i. p Sub p i w g h souio a C si [ C os C a si 8
9 9 `P.Diff w.r.o w g App odiio iii i I w g Sub C i w g h souio Bu suprposiio priip w g h souio App odiio iv i 5 w g This show ha his is h haf rag F.S.sris of K-. Usig Fourir offii formua a a C a a C C os si si si & & si si C aso a C a C C a C C os si ] os si ] C C whrc a C a C C a C os si 5 Si b K Si C I
10 b V si u V -os u V - si u V os C K os - -si os Sub C i 5 w g whih is h rquird so d k si C K d K si os K [ ] K K a K os si
11 A igh srhd srig wih fid d pois ad is iiia i a posiio giv b si p/.if i is rasd from rs from his posiio. Fid h dispam a a disa from d a a im. So : - Hr w hav o sov h wav quaio a Wih boudar odiios i ii iii iv Th orr souio of is si si si osp sip ospa sipa App odiio i i w g [ ospa sipa] > ospa sipa sub i w g sip ospa sipa App odiio ii i w g sip ospa sipa > o ad ospa sipa sip i. p
12 sub p i w g Paia diff w.r. w g a a a a os si si App odiio iii i w g B suprposiio priip w g App odiio iv i 5 w g p si a a si os os si os si si si si whr a a wg i sub ad a a a a > a os si o si si si 5
13 o si si si si o si si... si si Equaig h offi w g ; ; ; 5... Subsiu hs vaus i 5 w g o a o a si os si os whih is h rquird so A srig is igh srhd ad is ds ar fasd a wo pois ad. Th mid poi of h srig is dispad rasvrs hrough a sma disa b ad h srig is rasd from rs i ha posiio. Fid a prssio for h rasvrs dispam of h srig a a im durig h subsqu moio. So Hr firs w hav o fid iiia dispam i[o ] of h srig i giv probm. D /b b / / A C B
14 Now w fid Equaio of h srig i is iiia posiio ADB Th quaio of h srigor i AD is. Th quaio of h srig or i DB is / / / b b b < < [ ] b b b b b b b b b b b b b b b b b b b b b < <
15 H iiia h dispam of h srig is i h form. b X b / o < < < < / Now w hav o sov h wav quaio a wih boudar odiios i ii Th orr souio of is iii b iv < < / b / < < os p si p os pa si pa App odiio i i w g [ ospa sipa] > ospa sipa Sub i w g si p[ ospa si pa] 5
16 6 App odiio ii i w g Y sip[ ospa ospa] > ad ospa sipa sip i p Sub Paria diff w.r.o w g si App odiio iii i w g si si si > ad a a a p wg i p si a a si os a a a a os si
17 7 Sub i w g C C si a os C si os whr a B supr posiio priip w g App odiio iv i 5 w g whr b a os si < < < < b b b si / si / / si si d d b si si d b d b 5
18 8 / / si os si os X X X b u vsi u- u v -os u - v - si Sub i 5 w g whih is h rquird so A au srig of gh has is ds fid. Th poi whr / is draw asid a sma disa h h dispam saisfis a.drmi a a im. si os si os b si b si 8 b os si si 8 a b
19 So Hr firs w hav o fid B/h h iiia dispam of h srig i h i. o fid q of OBA / Eq. of h srig or i OB is A - - -/ -h i. - - /h i. h i <</ Eq of h srig or i BA is -/ -h / h- -h - h - -h h- - h- h - h- h h- h - i / << Th iiia dispam of h srig is h <</ h- / << 9
20 Now w hav o sov h wav q a wih boudar odiios i ii iii iv h <</ h- /<< h prod his probm sov as prvious probm. 5 Th pois of risio of a srig ar pad asid hrough a disa b o opposi sids of h posiio of quiibrium ad h srig is rasd from rs. Fid h dispam of h srig a a subsqu im. So : - Hr firs w hav o fid a iiia dispam of h srig.
21 B /a a B A -a C /-a Hr B & C b h pois of h risio of h srig OA. Iiia h srig is hd i h form OB C A whr BB CC a Eq of OB is - - -/ -a > a i / Eq of B is -/ /-/ -a aa > -/ -/ -a a > a- - -a > a- a > a-6aa
22 a-6a a- i // Eq of C A is -/ a / -a - a -a -a- - a a- - a a-a-a a-a a- i / H hr iiia dispam of h srig is a </ a- / </ a- / </ Now w hav o sov h wav q a
23 wih boudar odiios i ii iii iv - a </ a- / </ a- / </ h prod his probm sam as prvious probms Probms o vibraig srig wih o-zro voi A igh srhd srig wih fid d pois ad is iiia a rs i is quiibrium posiio ad ah of is pois is giv h voi. Drmi h dispam fuio V si << So : - Hr w hav o sov h wav quaio a wih boudar odiios i ii iii iv V si V / si -/ si Th orr so of is [C osp C sip ] [C ospa C sipa]
24 App odiio i i w g [ ospa _ sipa] > ospa C sipa Sub i w g [ sip [ Cospa sipa] App odiio ii i w g sip [ ospa sipa] sip i. psi - p p sub p i w g si os a si a App odiio i w g si si & si
25 5 Sub i w g si si a si si a si si a B suprposiio priip w g Paria w.r.o ; w g App odiio iv w g Equa h offiis w g C si si a 5 a a os si V a si si si > V V a a a si si... si si si V a a V o V a
26 Vo a & 5.. Sub hs vaus of s i 5 w g V a Vo a si si si si a a A srig is srhd bw wo fid pois a a disa apar & h pois of h srig ar giv iiia voiis V whr V is << / - i < < big h disa from a d poi.. fid h dispam of h srig as a im Souio:- Hr w hav o sov h wav quaio a Whr for ovi Wih boudar odiios i ii iii iv <</ 6
27 - / < < Th orr So of is osp sip ospa sipa App odiio i is w g ospa sipa > ospa sipa sub i w g sip ospa sipa App odiio ii i w g sip ospa sipa > ospa sipa & sip psi - p p Sub p i w g 7
28 si os a si a App odiio iii i w g si > si > & si sub i w g si si a si si a B suprposiio priip w g si si a 5 Paria w. r. o w g a si si a App odiio iv w g 8
29 9 <</ a si b si - /<< / whr a b si d - si d / u v si u- u v -os u - v -si / si si d d / si os si os
30 > Sub i 5 w g Rpa b w g si os. si os si si 8 si 8 si 8 a a C 8 si / a si si si 8 a a si si si 6 a a
31 whih is h rquird so Fid h dispam of a igh srhd srig of gh 7 ms vibraig bw fid d pois if iiia dispam is si So ad iiia voi is 5 si Hr w hav o sov h wav quaio u u Hr 7 m wih boudar odiios w g i ii hr boh iiia voi iii si & iiia dispam ar giv. iv 5 si Th orr so of is [ osp sip] [ ospa sipa] App odiio i i w g [ ospa sipa]
32 > ospa sipa Sub i w g App odiio ii i w g sip [ ospa sipa] > ospa sipa & sip p si - p Sub p i w g sip ospa sipa p a a si os si > > a d a a a si si os si si si os si
33 B supr posiio priip w g si osa d si si a sia d si a si App odiio iii i. w g si si N si si si. si Equa ik offiis w g &. A From w g a -sia d aos a si App odiio iv w g d a si 5 si 9 d 9 9a 5 [Equa ik offiis] d 9 5 & d d.d 8 d B 9a sub A & Bi w g
34 a 5 9a 9 si si si si 9a whr 7 ONE DIMENSIONA HEAT FOW EQUATION O dimsioa ha quaio is u α u Th various souios of h ha quaios is u [ ] p p [ ] α p u 5 [ os p si p] α p u No Th orr so of o dimsioa ha fow q as u α p [ Aos p B si p] Probms. Sov h quaio u α u subj o h boudar odiios u u u. So:- Hr w hav o sov h ha fow quaio u α u
35 wih giv boudar odiios i u ii u iii u Th orr so of is u A osp B sip α p App odiio i i w g u A α p > α p A Sub A i w g u B sip α p App odiio ii is w g u Bsip α p > B α p > sip p p 5
36 Sub p i w g u Bsi I gra u α α B si B suprposiio priip w g u B si α App odiio iii is w g u B si b si - whr B b / si u v si u v - os v si B - os si / / / -- / 6
37 B - Sub B i w g α u - si - STEADY STATE CONDITIONS AND ZERO BOUNDARY CONDITIONS Probms: A rod of gh has is ds A ad B kp a of ui sad sa odiio prvai. if h mpraur a B is rdud sudd o & kp so whi ha of A is maiaid fid h mpraur u a a disa from A ad im. SOUTION: Sad sa A B I giv probm Wh sad sa prvais h d A is a ad h d B is a Now w hav o fid h mpraur wh sad sa odiio prvais i. o fid u bfor h d B is rdud o H wh sad sa odiios prvais h ha fow quaio boms u > d u d 7
38 > uab wih boudar odiios i u ii u App i i w g u b > b Sub b is w g u a App ii i w g u a >a/ Sub a is w g u I sad sa h mpraur disribuio is u Now h mpraur disribuio rahd a h sad sa boms h iiia disribuio for h usad sa i u is << 8
39 Usad sa A B h d A is a C & B is a C H wh usad sa odiio prvais u u wih boudar odiios i u ii u iii u i << Th orr so of 5 is u A osp Bsip α p 6 App odiio i is 6 w g u A α p > α p A Sub A is 6 w g u Bsip α p 7 9
40 App odiio ii is 7 w g u B sip α p > B & sip p p Sub p i u Bsi I gra 7 α p w g α u B si α B suprposiio priip w g u α B si 8 App odiio iii i 8 w g u B si b si Whr B b / si d u u v si v -os /
41 v si B os si B - Sub B i 8 w g u α si STEDY STATE CONDITIONS AND NON-ZERO BOUNDARY CONDITIONS Probms : A bar m og wih isuad sids has is ds A&B kp a C ad C rspiv ui sad sa odiios prvai. Th mpraur a A is h sudd raisd o 5 C & a h somim ha a B is rdud a C.Fid h mpraur a a poi of h bar a a im So: - I sad sa odiio h ha fow quaio boms Sad sa d u d m uab A B C C wih boudar odiios i u ii u App i i w g
42 ub > b Sub b i w g ua App ii i w g ua >a >a sub a i w g u I sad sa h mpraur disribuio is u Now h mpraur a A & B ar hagd A his sag h sad sa is hagd io usad sa. From his sag h iiia mpraur disribuio is u i << H wh usad sa odiio prvais h ha fow quaio is u α u 5 wih boudar odiios i u5 m ii u5 A B iiiu 5 Th orr souios of 5 is uaosp Bsip α p 6
43 App i i 6 w g ua α p 5 7 App ii i 6 w g uaosp Bsip α p 8 From & i is o possib o fid h osas A & B. 7 8 I his as w spi h souio u io wo pars. i. uu s u 9 whr u s is a souio of h u α u ad is a fuio of ao ad saisfig h odiios u s 5 & u s ad u is a rasi souio saisfig To fid u s u s a b 9 whih drass as irass. wih boudar odiios i u s 5 ii u s App i is u s b 5 w g > b 5 Sub b i w g u s a 5
44 App ii i w g u s a 5 a 5 a -5 a - sub a i w g u s - 5 To fid u > u u-u s 9 is a rasi souio of u α u Now w hav o fid h boudar odiios for u i u u-u s 5-5 ii u u-u s - iii u u-u s Th orr souio of is u Aosp Bsip α p 5 App odiio i w g u A α p > α P A Sub A i 5 w g u B p α p si 6
45 App ii i 6 w g u Bsi p α P > B & si p p p α P Sub p i 6 wg u B si I gra u B si α α B suprposiio priips w g u B si α 7 App odiio iii i 7 w g u B si 6 si d 5 b si WhrBu- b 6 si v si d u v os 5
46 v si B 5 os si 5 5 X B -6 - Sub B i 7 w g u 6 si α Bu u u s u > u 5 6 si α whih is h rquird so :- Thrma isuad ds: - If hr wi b o ha fow passs hrough h ds of h bar h ha wo ds ar said o b hrma isuad. No : If h d sa is hrma isuad h w hav 6
47 Probms : ad if h d sa is hrma isuad h w hav Th mpraur a o d of a bar 5 m og wih isuad sids is kp a C ad ha a h ohr d is kp a C ui sad sa odiios prvai. Th wo ds ar h sudd isuad so ha h mpraur gradi is zro a ah d hrafr. Fid h mpraur disribuio. So :- A 5m B Wh sad sa odiio prvais C C Th ha fow quaio boms d u d > u ab wih boudar odiios i u ii u5 App i i w g u b > b sub b i i w g u a App ii i w g u5 a[5] a 7
48 > Sub a i w g u B I sad sa h mpraur disribuio u Now h mpraur a A & B ar hagd. A his sag h sad sa is hagd io usad sa. From his sag h iiia mpraur disribuio is u Whr usad sa odiios prvais h ha fow quaio is u α u 5 wih boudar odiios i u h wo ds ar hrma isuad ii u5 iii u <<5 Th orr souio of 5 is u A os p B si p α p 6 Diff. Paraia w. r.o. w g u α p [ Ap si p Bp os p] App odiio i w g 8
49 > α p & p u α p Bp & p Sub B i 6 w g u A os p α p 7 Paria diff w.r.o w g u α p A si p App odiio ii w g u5 Asi 5 p α p si 5P α p > A & > 5 p p 5 Sub p 5 i 7 w g u Aos 5 α 5 B suprposiio priip w g 9
50 u A os 5 α 5 8 App odiio iii w g u A os 5 A A os 5 a a os 5 Now Whr A a & A a a d 5 5 a A 5 a os os 5 5 d d u v os 5 si 5 5 5
51 u v v os si 5 5 os X 5 [ ] a A Sub A & A i 8 w g u 5 α 5 os 5 whih is h rquird so TRY YOURSEF: 9Th mpraur a o d of a bar m og & wih isuad sids is kp a C & ha a h ohr d is kp a 6 C ui sad sa odiios prvai. Th wo ds ar h sudd isuad so ha h mpraur is C a ah d hr afr. Fid h mpraur disribuio of h bar. 5
52 A isuad ma rod of gh m has o d A kp a C & h ohr d B a C ui sad sa odiios prvai. A im h d B is sudd isuad whi h mpraur a A is maiaid a C. Fid h mpraur a poi of h rod a a subsqu im. So Wh sad sa odiios prvai i h rod h mp disribuio is giv b d d h orrspodig boudar odiios ar u u soig w g u usig & i w g & u 5 O d B is isuad hough h mpraur a A is o ard h ha fow udr usad sa odiios & h subsqu mpraur disribuio is giv b u u α 6 wih boudar odiios i u for a o ii u for a iii u for o<< Th orr souio is u Aos p Bsi p α p 5
53 App odiio i i 7 w g > p u A α α p A sub A i 7 w g u Bsi p α p 8 Paria diff 8 w.r.o w g App odiio u u pb os p pb os p α p α p ii 8 w g α p > p ; ; B osp > p os - a odd muip of / or - / p whr... sub p i 8 w g u B si α 5
54 h mos gra souio is u B si α 9 App odiio iii i 9 w g u B si This is of h Fourir fi sris form whrb b si d si os si 8 B 8 Sub i 9 w g 5
55 8 u si α Whih is h rquird souio PROBEMS WITH NON ZERO BOUNDARY VAUES & STEADY STATE CONDITIONS. A bar m og wih isuad sids has is ds A & B kp a C & C rsp. ui sad sa. Codiios prvai. Th mpraur a A is h sudd raisd o 5 C & a h sam im ha a B is rdud a C.Fid h mpraur a a poi of h bar a a im. C C So I sad sa odiios h ha fow quaio boms d d A B 5 C C > u a b wih boudar odiios i uo ii u App i i w g u b > b sub b i w g 55
56 u a App ii i w g u a >a > a Sub a i w g u I sad sa h mpraur disribuio is u Now h mpraur a A & B ar hagd. A his sag h sad sa is hagd io usad sa. From his sag h iiia mpraur disribuio is u i < < H wh usad sa odiio prvais h ha fow quaio is u u α 5 m wih boudar odiios A B i u 5 5 C C ii u iii u Th orr so of 5 is u α p Aos p Bsi p 6 56
57 App i i 6 w g u o A App ii i 6 w g α p 7 5 u Aos p Bsi p α p 8 From 7 & 8 i is o possib o fid h osas A & B. I his as w spi h so u io wo pars. i. u u s u 9 Whr u s is a so of h q u u α & is a fuio of ao u [ i d u i d ] & saisfig h odiios u s 5 & u s ad u is a rasi souio saisfig 9 whih drass as irass To fid u s u s a b wih boudar odiios i u s 5 ii u s App i i w g 57
58 u s b 5 > b 5 sub b i w g u s a 5 App ii i w g u s a 5 a 5 a -5 a - sub a i w g u s - 5 To fid u 9 > u u u s u u is a rasi souio of α Now w hav o fid h boudar odiios for u i u u u s 5-5 ii u u u s - iii u u u s Th orr so of is u α p Aos p B si p 5 App odiios i w g 58
59 u o A α p > α p A Sub A i 5 w g u Bsi p α p 6 App ii i 6 w g u B si p α p > B & α p si p p Sub p p i 6 wg u Bsi u B si α α I gra B suprposiio priip w g u α B si 6 59
60 App odiios iii i 6 w g u B si 6 b si whrb b 6 si d si d u - v si u v v os si B os si B 6 Sub B i 6 w g u 6 si α 6
61 Bu u u s u > u 5 6 si α whih is h rquird so TWO DIMENSIONA HEAT FOW EQUATION Th wo dimsioa ha fow quaio or apa quaio is u u α Th various souios of quaio is i u p p os p si p ii u 5 os p 6 si p 7 p 8 p iii u 9 Probms A squar pa is boudd b h is o &. Is fas isuad. Th mpraur aog h uppr horizoa dg is giv b u -wh << whi h ohr hr dgs ar kp a C. Fid h sad sa mpraur i h pa. So 6
62 us ak h sids of h pa b for ovi Th mpraur disribuio is giv b u u Y wih boudar odiios i u u- ii u iii u C C iv u - << Th orr souio of q is X u osp sip p -p App odiios i i w g u p -p > p -p Sub i w g u sip p -p App odiio ii i w g u sip p -p > & p -p sip p si - p p 6
63 6 sub p i w g App odiio iii i w g > - Sub - i w g Th mos gra souio is App odiio iv i 6 w g u ρ si si u & si > u si si sih si sih si u sih si sih si u 6
64 6 whih is of h form of F.S. sris whr i. u - u - u - sih si f u si b f d b si sih d si sih os si os si v v v v [ ] os si os sih sih
65 os h Sub i 6 w g u osh sih si Rpa b w g u osh sih si u 6 osh sih si Fid h sad sa mpraur a a poi of a squar pa whos wo adja dgs ar kp a C & h ohr wo dgs ar kp a h osa mp C. So h sid of h squar pa b Th mpraur u is giv b u u wih boudar odiios Y C C C i u for << ii u for << iii u for << iv u for << u u u whr u & u ar saisfig h foowig boudar odiios. 65
66 a u a u b u b u u u d u d u To fid u Th orr souio is u osp sip p -p App odiio a i w g u p -p > p -p Sub i w g u sip p -p App odiio b i w g u sip p -p Sub p i w g > & p -p sip p si - p u si App odiio i w g 66
67 67 > & si > - Sub - i w g Th mos gra souio is App odiio d i 6 w g whih is of h form of Fourir si sris f b si whr si o u u si si sih si sih si sih si sih si u 6 sih si u d b si sih
68 os sih > Sub i 6 w g osh u osh sih sih To fid u Th orr souio is u osp sip p -p Appig h boudar odiios a b & d w g u osh sih sih Th souio of is u u u 68
69 osh sih sih si sih Tr oursf: A raguar pa is boudd b h is a & b h dg mpraur ar u ua ub u si a fid h mpraur disribuio. A raguar pa is boudd b h is a & b & h mpraurs a h dgs ar giv b. u i <<b/ b- i b/ <<b ; ua ; ub & pa. u 5si si a a. Fid h sad sa mpraur disribuio isid h Ifii pas A ifii og raguar pa has is surfas isuad & h wo sids as w as o of h shor sids ar maiaid a C. fid a prssio for h sad sa mp u if h shor sid is m og & is kp a u C. So :- Th mpraur disribuio is giv b u u wih boudar odiios i u ii u iii u iv uo u Th orr so is u osp sip p -p C C C u C 69
70 App odiio i i w g u p -p Hr p -p Sub i w g u sip p -p App odiio ii i w g u sip p -p Hr p -p & sip p si - p > p sub p i w g u si - App odiio iii i w g u si > ; si & Sub i w g u si - u - si u - si 7
71 7 Th mos gra souio is App odiio iv i 5 w g This is of h form of Fourir si sris whr Sub i 5 w g u si 5 si u o u b f si d f b si u si d u u u o o o os u u si u u si
72 A ifii og raguar pa wih isuad surfa is m.th wo og dgs & o shor dg ar kp a C. whi h ohr dg is kp a u for < < 5 - for 5<< Fid h sad sa mpraur disribuio i h pa. So Th mpraur disribuio is giv b u u wih boudar odiios C i u ii u iii u iv u < < / - / << for h ovi f O C C Th orr souio is u p -p osp sip App odiio i i w g uo p -p > sub i w g u p -p sip 7
73 7 App odiio ii i w g u p -p sip Hr sip i p > Sub p i w g App odiio iii i w g u - si > Sub i w g Th mos gra so is p u si si & si u si si si
74 7 App odiio iv i 5 w g whr f < </ - /< < This is form of h F.S.Sris u si 5 si f u si b f d f b si } si os si os si os si os si si ` d d si
75 8 si 6 Sub 6 i 5 w g u 8 si si Rpaig b w g whih is h rquird souio. si 8 u si Objiv Qusios Th suiab souio of ODWE is a A p B -p C pa D -pa b A p B -p C os pa D si pa A os pa B si pa C os pa D si pa d A B CD I o dimsioa wav quaio u a u a sads for a b d No of hs [T-Tsiom-Mass pr ui gh] I ODWE mass of h srig pr ui gh is a a b Cosa dvariab Amog h hr possib souio i ODWE h suiab souio is ak baus a Dispam is priodi i aur b I oais rigoomri rms Boh a & b d No of hs 75
76 5 Whih boudar odiio i ODWE shoud b ak as o ad usd afr fidig mos gra souio a. boudar odiio wih zro vau b. boudar odiio wih o zro vau. boh a ad b d. o of hs 6 Th sad sa mpraur of a rod of gh whos ds ar kp a ad is b d 7 Th gra souio of vibraor moio of a srig of gh wih fid d pois ad zro iiia voi is a b si л/ si лa/ b b os л/ os лa/ b os л/ si лa/ d b si л/ os лa/ 8 Two dimsioa sad sa ha oduio quaio is a U U bu a U U a U d No of hs. 9 Th quai of ha rquird o produ a giv mpraur hag i a bod is proporioa o h mass of h bod ad o h Chag atmpraur bdisa Tim dno of hs I o dimsioa ha fow quaio if h mpraur fuio u is idpd of im h h souio is acosa bsad Usad dno of Ths O of h possib souio o wo dimsioa ha fow quaio i Carsia ssm of oordias is au C C C C b u C C C C u C C C C dno of hs I wo dimsioa ha fow h ra of ha fow aross a ara is proporioa o a Ara ad h mpraur gradi para o h ara b Ara ad h mpraur orma o h ara Ara ad h mpraur gradi orma o h ara d Ara ad h mpraur para o h ara I D ha fow h mpraur a a poi is idpd of a Tim b X-Coordia Y-Coordia d Z-Coordia 76
77 I o dimsioa ha fow quaio u α u α sads for a Diffusivi of h maria b Thrma oduivi of h maria Spifi ha of h maria d Dsi of h maria 5 Wh h ds of a rod i o zro for o dimsioa ha fow quaio. Th mpraur fuio u is modifid as h sum of h sad sa ad rasi sa mpraur. Th rasi par of h souio whih a Iras wih iras of im b Dras wih iras of im Dras wih dras of im d Iras wih iras of im 6Th O Dimsioa Wav Equaio is au U bu a U U a U dno of hs. 7Th O Dimsioa Ha Equaio is au U bu a U U a U dno of hs. 8A Sod ordr Paria Diffria quaio is said o b ipi if ab -AC< bb -AC B -AC> dno of hs 9 A Sod ordr Paria Diffria quaio is said o b hprboi if ab -AC< bb -AC B -AC> dno of hs A Sod ordr Paria Diffria quaio is said o b paraboi if ab -AC< bb -AC B -AC> dno of hs I drivig O Dimsioa Wav Equaio w assum ha moio aks pa ir i pa. ao bwo hr dno of hs I drivig O Dimsioa Wav Equaio w assum ha h Tsio T is a a pois & a a im of h dfd srig. acosa bvaris Zro do of hs. I drivig O Dimsioa Ha Equaio w assum ha ha fows from o mpraur. ahigh o ow bow o high high o high dno of hs. W rquir umbr of boudar odiios o sov O Dimsioa Ha Equaio a b d 5 W rquir umbr of boudar odiios o sov O Dimsioa wav Equaio a b d 77
78 6Th suiab souio of h O Dimsioa Ha Equaio is auaos p B si p b UAos p B si p UAos p B si p dno of hs. PART-A. Cassif h paria diffria quaio z p z z z z si :. Wri dow a possib souios of o dimsioa wav quaio.. A au srig of gh 5 m fasd a boh ds is disurbd from is posiio of quiibrium b imparig o ah of is pois a iiia voi of magiud k for < < 5. Formua h probm mahmaia..wri dow a possib souios of h o dimsioa ha ow quaio. 5. If h mpraur a o d of a bar 5 m og ad wih isuad sids is kp a ±C ad ha h ohr d is kp a ±C ui sad sa odiios prvai d h sad sa mpraur i h rod. PART-B. A au srig of gh is fasd a boh ds. Th midpoi of his srig is ak o a high of b ad h rasd from rs i his posiio. Fid h dispam of h srig a a im.. A au srig of gh is fasd a boh ds. Th midpoi of h srig is ak o a high b ad h rasd from rs i ha posiio. Fid h dispam of a poi of h srig a a subsqu im.. A igh srhd srig wih fid d pois ad is iiia a rs i is quiibrium posiio. If i is s vibraig b givig ah poi a voi λ. fid h dispam of h srig a a disa from o d a a im.. Th d A ad B of a rod m og hav h mpraurs ad 9 a ui sad sa prvais. Th mpraur a A is sudd raisd o 9 ad a h sam im ha a B is owrd o.fid h mpraur disribuio i h rod a im.aso show ha h 78
79 mpraur a h mid poi of h rod rmais uard for a im rgardss of h marias of h rod. 5. A ma bar m og wih isuad sids has is ds A ad B kp a o ad o rspiv ui sad sa odiios prvai. Th mpraur a A is h sudd raisd o 5 o ad a h sam isa ha a B is owrd o o. Fid h subsqu mpraur a a poi a h bar a a im. 6. A raguar pa wih isuad surfa is m wid ad so og ompard o is widh ha i ma b osidrd ifii gh. If h mpraur aog shor dg is giv b Π u 8 si whr <<whi h wo og dgs ad as w as h ohr shor dg ar kp a.fid h sad sa mpraur fuio u. 79
Practice papers A and B, produced by Edexcel in 2009, with mark schemes. Practice Paper A. 5 cosh x 2 sinh x = 11,
 Prai paprs A ad B, produd by Edl i 9, wih mark shms Prai Papr A. Fid h valus of for whih 5 osh sih =, givig your aswrs as aural logarihms. (Toal 6 marks) k. A = k, whr k is a ral osa. 9 (a) Fid valus of
Prai paprs A ad B, produd by Edl i 9, wih mark shms Prai Papr A. Fid h valus of for whih 5 osh sih =, givig your aswrs as aural logarihms. (Toal 6 marks) k. A = k, whr k is a ral osa. 9 (a) Fid valus of
Chapter 3 Linear Equations of Higher Order (Page # 144)
 Ma Modr Dirial Equaios Lcur wk 4 Jul 4-8 Dr Firozzama Darm o Mahmaics ad Saisics Arizoa Sa Uivrsi This wk s lcur will covr har ad har 4 Scios 4 har Liar Equaios o Highr Ordr Pag # 44 Scio Iroducio: Scod
Ma Modr Dirial Equaios Lcur wk 4 Jul 4-8 Dr Firozzama Darm o Mahmaics ad Saisics Arizoa Sa Uivrsi This wk s lcur will covr har ad har 4 Scios 4 har Liar Equaios o Highr Ordr Pag # 44 Scio Iroducio: Scod
1973 AP Calculus BC: Section I
 97 AP Calculus BC: Scio I 9 Mius No Calculaor No: I his amiaio, l dos h aural logarihm of (ha is, logarihm o h bas ).. If f ( ) =, h f ( ) = ( ). ( ) + d = 7 6. If f( ) = +, h h s of valus for which f
97 AP Calculus BC: Scio I 9 Mius No Calculaor No: I his amiaio, l dos h aural logarihm of (ha is, logarihm o h bas ).. If f ( ) =, h f ( ) = ( ). ( ) + d = 7 6. If f( ) = +, h h s of valus for which f
UNIT I FOURIER SERIES T
 UNIT I FOURIER SERIES PROBLEM : Th urig mom T o h crkh o m gi i giv or ri o vu o h crk g dgr 6 9 5 8 T 5 897 785 599 66 Epd T i ri o i. Souio: L T = i + i + i +, Sic h ir d vu o T r rpd gc o T T i T i
UNIT I FOURIER SERIES PROBLEM : Th urig mom T o h crkh o m gi i giv or ri o vu o h crk g dgr 6 9 5 8 T 5 897 785 599 66 Epd T i ri o i. Souio: L T = i + i + i +, Sic h ir d vu o T r rpd gc o T T i T i
( A) ( B) ( C) ( D) ( E)
 d Smsr Fial Exam Worksh x 5x.( NC)If f ( ) d + 7, h 4 f ( ) d is 9x + x 5 6 ( B) ( C) 0 7 ( E) divrg +. (NC) Th ifii sris ak has h parial sum S ( ) for. k Wha is h sum of h sris a? ( B) 0 ( C) ( E) divrgs
d Smsr Fial Exam Worksh x 5x.( NC)If f ( ) d + 7, h 4 f ( ) d is 9x + x 5 6 ( B) ( C) 0 7 ( E) divrg +. (NC) Th ifii sris ak has h parial sum S ( ) for. k Wha is h sum of h sris a? ( B) 0 ( C) ( E) divrgs
Response of LTI Systems to Complex Exponentials
 3 Fourir sris coiuous-im Rspos of LI Sysms o Complx Expoials Ouli Cosidr a LI sysm wih h ui impuls rspos Suppos h ipu sigal is a complx xpoial s x s is a complx umbr, xz zis a complx umbr h or h h w will
3 Fourir sris coiuous-im Rspos of LI Sysms o Complx Expoials Ouli Cosidr a LI sysm wih h ui impuls rspos Suppos h ipu sigal is a complx xpoial s x s is a complx umbr, xz zis a complx umbr h or h h w will
MAT3700. Tutorial Letter 201/2/2016. Mathematics III (Engineering) Semester 2. Department of Mathematical sciences MAT3700/201/2/2016
 MAT3700/0//06 Tuorial Lr 0//06 Mahmaics III (Egirig) MAT3700 Smsr Dparm of Mahmaical scics This uorial lr coais soluios ad aswrs o assigms. BARCODE CONTENTS Pag SOLUTIONS ASSIGNMENT... 3 SOLUTIONS ASSIGNMENT...
MAT3700/0//06 Tuorial Lr 0//06 Mahmaics III (Egirig) MAT3700 Smsr Dparm of Mahmaical scics This uorial lr coais soluios ad aswrs o assigms. BARCODE CONTENTS Pag SOLUTIONS ASSIGNMENT... 3 SOLUTIONS ASSIGNMENT...
82A Engineering Mathematics
 Class Nos 5: Sod Ordr Diffrial Eqaio No Homoos 8A Eiri Mahmais Sod Ordr Liar Diffrial Eqaios Homoos & No Homoos v q Homoos No-homoos q ar iv oios fios o h o irval I Sod Ordr Liar Diffrial Eqaios Homoos
Class Nos 5: Sod Ordr Diffrial Eqaio No Homoos 8A Eiri Mahmais Sod Ordr Liar Diffrial Eqaios Homoos & No Homoos v q Homoos No-homoos q ar iv oios fios o h o irval I Sod Ordr Liar Diffrial Eqaios Homoos
Part B: Transform Methods. Professor E. Ambikairajah UNSW, Australia
 Par B: rasform Mhods Profssor E. Ambikairaah UNSW, Ausralia Chapr : Fourir Rprsaio of Sigal. Fourir Sris. Fourir rasform.3 Ivrs Fourir rasform.4 Propris.4. Frqucy Shif.4. im Shif.4.3 Scalig.4.4 Diffriaio
Par B: rasform Mhods Profssor E. Ambikairaah UNSW, Ausralia Chapr : Fourir Rprsaio of Sigal. Fourir Sris. Fourir rasform.3 Ivrs Fourir rasform.4 Propris.4. Frqucy Shif.4. im Shif.4.3 Scalig.4.4 Diffriaio
Fourier Series: main points
 BIOEN 3 Lcur 6 Fourir rasforms Novmbr 9, Fourir Sris: mai pois Ifii sum of sis, cosis, or boh + a a cos( + b si( All frqucis ar igr mulipls of a fudamal frqucy, o F.S. ca rprs ay priodic fucio ha w ca
BIOEN 3 Lcur 6 Fourir rasforms Novmbr 9, Fourir Sris: mai pois Ifii sum of sis, cosis, or boh + a a cos( + b si( All frqucis ar igr mulipls of a fudamal frqucy, o F.S. ca rprs ay priodic fucio ha w ca
Intrinsic formulation for elastic line deformed on a surface by an external field in the pseudo-galilean space 3. Nevin Gürbüz
 risic formuaio for asic i form o a surfac by a xra fi i h psuo-aia spac Nvi ürbüz Eskişhir Osmaazi Uivrsiy Mahmaics a Compur Scics Dparm urbuz@ouur Absrac: his papr w riv irisic formuaio for asic i form
risic formuaio for asic i form o a surfac by a xra fi i h psuo-aia spac Nvi ürbüz Eskişhir Osmaazi Uivrsiy Mahmaics a Compur Scics Dparm urbuz@ouur Absrac: his papr w riv irisic formuaio for asic i form
Numerical Simulation for the 2-D Heat Equation with Derivative Boundary Conditions
 IOSR Joural of Applid Chmisr IOSR-JAC -ISSN: 78-576.Volum 9 Issu 8 Vr. I Aug. 6 PP 4-8 www.iosrjourals.org Numrical Simulaio for h - Ha Equaio wih rivaiv Boudar Codiios Ima. I. Gorial parm of Mahmaics
IOSR Joural of Applid Chmisr IOSR-JAC -ISSN: 78-576.Volum 9 Issu 8 Vr. I Aug. 6 PP 4-8 www.iosrjourals.org Numrical Simulaio for h - Ha Equaio wih rivaiv Boudar Codiios Ima. I. Gorial parm of Mahmaics
Right Angle Trigonometry
 Righ gl Trigoomry I. si Fs d Dfiiios. Righ gl gl msurig 90. Srigh gl gl msurig 80. u gl gl msurig w 0 d 90 4. omplmry gls wo gls whos sum is 90 5. Supplmry gls wo gls whos sum is 80 6. Righ rigl rigl wih
Righ gl Trigoomry I. si Fs d Dfiiios. Righ gl gl msurig 90. Srigh gl gl msurig 80. u gl gl msurig w 0 d 90 4. omplmry gls wo gls whos sum is 90 5. Supplmry gls wo gls whos sum is 80 6. Righ rigl rigl wih
LINEAR 2 nd ORDER DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS
 Diol Bgyoko (0) I.INTRODUCTION LINEAR d ORDER DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS I. Dfiiio All suh diffril quios s i h sdrd or oil form: y + y + y Q( x) dy d y wih y d y d dx dx whr,, d
Diol Bgyoko (0) I.INTRODUCTION LINEAR d ORDER DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS I. Dfiiio All suh diffril quios s i h sdrd or oil form: y + y + y Q( x) dy d y wih y d y d dx dx whr,, d
Continous system: differential equations
 /6/008 Coious sysm: diffrial quaios Drmiisic modls drivaivs isad of (+)-( r( compar ( + ) R( + r ( (0) ( R ( 0 ) ( Dcid wha hav a ffc o h sysm Drmi whhr h paramrs ar posiiv or gaiv, i.. giv growh or rducio
/6/008 Coious sysm: diffrial quaios Drmiisic modls drivaivs isad of (+)-( r( compar ( + ) R( + r ( (0) ( R ( 0 ) ( Dcid wha hav a ffc o h sysm Drmi whhr h paramrs ar posiiv or gaiv, i.. giv growh or rducio
DIFFERENTIAL EQUATIONS MTH401
 DIFFERENTIAL EQUATIONS MTH Virual Uivrsi of Pakisa Kowldg bod h boudaris Tabl of Cos Iroduio... Fudamals.... Elms of h Thor.... Spifi Eampls of ODE s.... Th ordr of a quaio.... Ordiar Diffrial Equaio....5
DIFFERENTIAL EQUATIONS MTH Virual Uivrsi of Pakisa Kowldg bod h boudaris Tabl of Cos Iroduio... Fudamals.... Elms of h Thor.... Spifi Eampls of ODE s.... Th ordr of a quaio.... Ordiar Diffrial Equaio....5
BMM3553 Mechanical Vibrations
 BMM3553 Mhaial Vibraio Chapr 3: Damp Vibraio of Sigl Dgr of From Sym (Par ) by Ch Ku Ey Nizwa Bi Ch Ku Hui Fauly of Mhaial Egirig mail: y@ump.u.my Chapr Dripio Ep Ouom Su will b abl o: Drmi h aural frquy
BMM3553 Mhaial Vibraio Chapr 3: Damp Vibraio of Sigl Dgr of From Sym (Par ) by Ch Ku Ey Nizwa Bi Ch Ku Hui Fauly of Mhaial Egirig mail: y@ump.u.my Chapr Dripio Ep Ouom Su will b abl o: Drmi h aural frquy
Poisson Arrival Process
 1 Poisso Arrival Procss Arrivals occur i) i a mmorylss mar ii) [ o arrival durig Δ ] = λδ + ( Δ ) P o [ o arrival durig Δ ] = 1 λδ + ( Δ ) P o P j arrivals durig Δ = o Δ for j = 2,3, ( ) o Δ whr lim =
1 Poisso Arrival Procss Arrivals occur i) i a mmorylss mar ii) [ o arrival durig Δ ] = λδ + ( Δ ) P o [ o arrival durig Δ ] = 1 λδ + ( Δ ) P o P j arrivals durig Δ = o Δ for j = 2,3, ( ) o Δ whr lim =
Overview. Review Elliptic and Parabolic. Review General and Hyperbolic. Review Multidimensional II. Review Multidimensional
 Mlil idd variabls March 9 Mlidisioal Parial Dirial Eaios arr aro Mchaical Egirig 5B iar i Egirig Aalsis March 9 Ovrviw Rviw las class haracrisics ad classiicaio o arial dirial aios Probls i or ha wo idd
Mlil idd variabls March 9 Mlidisioal Parial Dirial Eaios arr aro Mchaical Egirig 5B iar i Egirig Aalsis March 9 Ovrviw Rviw las class haracrisics ad classiicaio o arial dirial aios Probls i or ha wo idd
Poisson Arrival Process
 Poisso Arrival Procss Arrivals occur i) i a mmylss mar ii) [ o arrival durig Δ ] = λδ + ( Δ ) P o [ o arrival durig Δ ] = λδ + ( Δ ) P o P j arrivals durig Δ = o Δ f j = 2,3, o Δ whr lim =. Δ Δ C C 2 C
Poisso Arrival Procss Arrivals occur i) i a mmylss mar ii) [ o arrival durig Δ ] = λδ + ( Δ ) P o [ o arrival durig Δ ] = λδ + ( Δ ) P o P j arrivals durig Δ = o Δ f j = 2,3, o Δ whr lim =. Δ Δ C C 2 C
x, x, e are not periodic. Properties of periodic function: 1. For any integer n,
 Chpr Fourir Sri, Igrl, d Tror. Fourir Sri A uio i lld priodi i hr i o poiiv ur p uh h p, p i lld priod o R i,, r priodi uio.,, r o priodi. Propri o priodi uio:. For y igr, p. I d g hv priod p, h h g lo
Chpr Fourir Sri, Igrl, d Tror. Fourir Sri A uio i lld priodi i hr i o poiiv ur p uh h p, p i lld priod o R i,, r priodi uio.,, r o priodi. Propri o priodi uio:. For y igr, p. I d g hv priod p, h h g lo
Lecture 14. Time Harmonic Fields
 Lcu 4 Tim amic Filds I his lcu u will la: Cmpl mahmaics f im-hamic filds Mawll s quais f im-hamic filds Cmpl Pig vc C 303 Fall 007 Faha aa Cll Uivsi Tim-amic Filds ad -filds f a pla wav a (fm las lcu:
Lcu 4 Tim amic Filds I his lcu u will la: Cmpl mahmaics f im-hamic filds Mawll s quais f im-hamic filds Cmpl Pig vc C 303 Fall 007 Faha aa Cll Uivsi Tim-amic Filds ad -filds f a pla wav a (fm las lcu:
Boyce/DiPrima/Meade 11 th ed, Ch 4.1: Higher Order Linear ODEs: General Theory
 Bo/DiPima/Mad h d Ch.: High Od Lia ODEs: Gal Tho Elma Diffial Eqaios ad Boda Val Poblms h diio b William E. Bo Rihad C. DiPima ad Dog Mad 7 b Joh Wil & Sos I. A h od ODE has h gal fom d d P P P d d W assm
Bo/DiPima/Mad h d Ch.: High Od Lia ODEs: Gal Tho Elma Diffial Eqaios ad Boda Val Poblms h diio b William E. Bo Rihad C. DiPima ad Dog Mad 7 b Joh Wil & Sos I. A h od ODE has h gal fom d d P P P d d W assm
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
Decline Curves. Exponential decline (constant fractional decline) Harmonic decline, and Hyperbolic decline.
 Dlin Curvs Dlin Curvs ha lo flow ra vs. im ar h mos ommon ools for forasing roduion and monioring wll rforman in h fild. Ths urvs uikly show by grahi mans whih wlls or filds ar roduing as xd or undr roduing.
Dlin Curvs Dlin Curvs ha lo flow ra vs. im ar h mos ommon ools for forasing roduion and monioring wll rforman in h fild. Ths urvs uikly show by grahi mans whih wlls or filds ar roduing as xd or undr roduing.
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Spectral Simulation of Turbulence. and Tracking of Small Particles
 Specra Siuaio of Turbuece ad Trackig of Sa Parices Hoogeeous Turbuece Saisica ie average properies RMS veociy fucuaios dissipaio rae are idepede of posiio. Hoogeeous urbuece ca be odeed wih radoy sirred
Specra Siuaio of Turbuece ad Trackig of Sa Parices Hoogeeous Turbuece Saisica ie average properies RMS veociy fucuaios dissipaio rae are idepede of posiio. Hoogeeous urbuece ca be odeed wih radoy sirred
(A) 1 (B) 1 + (sin 1) (C) 1 (sin 1) (D) (sin 1) 1 (C) and g be the inverse of f. Then the value of g'(0) is. (C) a. dx (a > 0) is
 [STRAIGHT OBJECTIVE TYPE] l Q. Th vlu of h dfii igrl, cos d is + (si ) (si ) (si ) Q. Th vlu of h dfii igrl si d whr [, ] cos cos Q. Vlu of h dfii igrl ( si Q. L f () = d ( ) cos 7 ( ) )d d g b h ivrs
[STRAIGHT OBJECTIVE TYPE] l Q. Th vlu of h dfii igrl, cos d is + (si ) (si ) (si ) Q. Th vlu of h dfii igrl si d whr [, ] cos cos Q. Vlu of h dfii igrl ( si Q. L f () = d ( ) cos 7 ( ) )d d g b h ivrs
Linear Systems Analysis in the Time Domain
 Liar Sysms Aalysis i h Tim Domai Firs Ordr Sysms di vl = L, vr = Ri, d di L + Ri = () d R x= i, x& = x+ ( ) L L X() s I() s = = = U() s E() s Ls+ R R L s + R u () = () =, i() = L i () = R R Firs Ordr Sysms
Liar Sysms Aalysis i h Tim Domai Firs Ordr Sysms di vl = L, vr = Ri, d di L + Ri = () d R x= i, x& = x+ ( ) L L X() s I() s = = = U() s E() s Ls+ R R L s + R u () = () =, i() = L i () = R R Firs Ordr Sysms
Lecture 4: Laplace Transforms
 Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
Mixing time with Coupling
 Mixig im wih Couplig Jihui Li Mig Zhg Saisics Dparm May 7 Goal Iroducio o boudig h mixig im for MCMC wih couplig ad pah couplig Prsig a simpl xampl o illusra h basic ida Noaio M is a Markov chai o fii
Mixig im wih Couplig Jihui Li Mig Zhg Saisics Dparm May 7 Goal Iroducio o boudig h mixig im for MCMC wih couplig ad pah couplig Prsig a simpl xampl o illusra h basic ida Noaio M is a Markov chai o fii
The convection-diffusion equation for a finite domain with time varying boundaries 1,2,3
 Th covcio-diffusio quaio for a fii domai wih im varyig boudaris 1,,3 W. J. GOLZ parm of Civi ad Eviroma Egirig, Louisiaa Sa Uivrsiy Bao oug, Louisiaa 783, USA J.. OOH parm of Mahmaics, Louisiaa Sa Uivrsiy
Th covcio-diffusio quaio for a fii domai wih im varyig boudaris 1,,3 W. J. GOLZ parm of Civi ad Eviroma Egirig, Louisiaa Sa Uivrsiy Bao oug, Louisiaa 783, USA J.. OOH parm of Mahmaics, Louisiaa Sa Uivrsiy
Note 6 Frequency Response
 No 6 Frqucy Rpo Dparm of Mchaical Egirig, Uivriy Of Sakachwa, 57 Campu Driv, Sakaoo, S S7N 59, Caada Dparm of Mchaical Egirig, Uivriy Of Sakachwa, 57 Campu Driv, Sakaoo, S S7N 59, Caada. alyical Exprio
No 6 Frqucy Rpo Dparm of Mchaical Egirig, Uivriy Of Sakachwa, 57 Campu Driv, Sakaoo, S S7N 59, Caada Dparm of Mchaical Egirig, Uivriy Of Sakachwa, 57 Campu Driv, Sakaoo, S S7N 59, Caada. alyical Exprio
Boyce/DiPrima 9 th ed, Ch 7.9: Nonhomogeneous Linear Systems
 BoDiPrima 9 h d Ch 7.9: Nohomogou Liar Sm Elmar Diffrial Equaio ad Boudar Valu Prolm 9 h diio William E. Bo ad Rihard C. DiPrima 9 Joh Wil & So I. Th gral hor of a ohomogou m of quaio g g aralll ha of
BoDiPrima 9 h d Ch 7.9: Nohomogou Liar Sm Elmar Diffrial Equaio ad Boudar Valu Prolm 9 h diio William E. Bo ad Rihard C. DiPrima 9 Joh Wil & So I. Th gral hor of a ohomogou m of quaio g g aralll ha of
Pupil / Class Record We can assume a word has been learned when it has been either tested or used correctly at least three times.
 2 Pupi / Css Rr W ssum wr hs b r wh i hs b ihr s r us rry s hr ims. Nm: D Bu: fr i bus brhr u firs hf hp hm s uh i iv iv my my mr muh m w ih w Tik r pp push pu sh shu sisr s sm h h hir hr hs im k w vry
2 Pupi / Css Rr W ssum wr hs b r wh i hs b ihr s r us rry s hr ims. Nm: D Bu: fr i bus brhr u firs hf hp hm s uh i iv iv my my mr muh m w ih w Tik r pp push pu sh shu sisr s sm h h hir hr hs im k w vry
EEE 303: Signals and Linear Systems
 33: Sigls d Lir Sysms Orhogoliy bw wo sigls L us pproim fucio f () by fucio () ovr irvl : f ( ) = c( ); h rror i pproimio is, () = f() c () h rgy of rror sigl ovr h irvl [, ] is, { }{ } = f () c () d =
33: Sigls d Lir Sysms Orhogoliy bw wo sigls L us pproim fucio f () by fucio () ovr irvl : f ( ) = c( ); h rror i pproimio is, () = f() c () h rgy of rror sigl ovr h irvl [, ] is, { }{ } = f () c () d =
) and furthermore all X. The definition of the term stationary requires that the distribution fulfills the condition:
 Assigm Thomas Aam, Spha Brumm, Haik Lor May 6 h, 3 8 h smsr, 357, 7544, 757 oblm For R b X a raom variabl havig ormal isribuio wih ma µ a variac σ (his is wri as ~ (,) X. by: R a. Is X ) a urhrmor all
Assigm Thomas Aam, Spha Brumm, Haik Lor May 6 h, 3 8 h smsr, 357, 7544, 757 oblm For R b X a raom variabl havig ormal isribuio wih ma µ a variac σ (his is wri as ~ (,) X. by: R a. Is X ) a urhrmor all
Control Systems. Transient and Steady State Response.
 Corol Sym Trai a Say Sa Ro chibum@oulch.ac.kr Ouli Tim Domai Aalyi orr ym Ui ro Ui ram ro Ui imul ro Chibum L -Soulch Corol Sym Tim Domai Aalyi Afr h mahmaical mol of h ym i obai, aalyi of ym rformac i.
Corol Sym Trai a Say Sa Ro chibum@oulch.ac.kr Ouli Tim Domai Aalyi orr ym Ui ro Ui ram ro Ui imul ro Chibum L -Soulch Corol Sym Tim Domai Aalyi Afr h mahmaical mol of h ym i obai, aalyi of ym rformac i.
Lecture contents Macroscopic Electrodynamics Propagation of EM Waves in dielectrics and metals
 Leure oes Marosopi lerodyamis Propagaio of M Waves i dieleris ad meals NNS 58 M Leure #4 Maxwell quaios Maxwell equaios desribig he ouplig of eleri ad magei fields D q ev B D J [SI] [CGS] D 4 B D 4 J B
Leure oes Marosopi lerodyamis Propagaio of M Waves i dieleris ad meals NNS 58 M Leure #4 Maxwell quaios Maxwell equaios desribig he ouplig of eleri ad magei fields D q ev B D J [SI] [CGS] D 4 B D 4 J B
EXERCISE - 01 CHECK YOUR GRASP
 DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
Improved Exponential Estimator for Population Variance Using Two Auxiliary Variables
 Improvd Epoal Emaor for Populao Varac Ug Two Aular Varabl Rajh gh Dparm of ac,baara Hdu Uvr(U.P., Ida (rgha@ahoo.com Pakaj Chauha ad rmala awa chool of ac, DAVV, Idor (M.P., Ida Flor maradach Dparm of
Improvd Epoal Emaor for Populao Varac Ug Two Aular Varabl Rajh gh Dparm of ac,baara Hdu Uvr(U.P., Ida (rgha@ahoo.com Pakaj Chauha ad rmala awa chool of ac, DAVV, Idor (M.P., Ida Flor maradach Dparm of
Final Exam : Solutions
 Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b
Comp : Algorihm and Daa Srucur Final Exam : Soluion. Rcuriv Algorihm. (a) To bgin ind h mdian o {x, x,... x n }. Sinc vry numbr xcp on in h inrval [0, n] appar xacly onc in h li, w hav ha h mdian mu b
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
 I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
Math 3301 Homework Set 6 Solutions 10 Points. = +. The guess for the particular P ( ) ( ) ( ) ( ) ( ) ( ) ( ) cos 2 t : 4D= 2
 Mah 0 Homwork S 6 Soluions 0 oins. ( ps) I ll lav i o you o vrify ha y os sin = +. Th guss for h pariular soluion and is drivaivs is blow. Noi ha w ndd o add s ono h las wo rms sin hos ar xaly h omplimnary
Mah 0 Homwork S 6 Soluions 0 oins. ( ps) I ll lav i o you o vrify ha y os sin = +. Th guss for h pariular soluion and is drivaivs is blow. Noi ha w ndd o add s ono h las wo rms sin hos ar xaly h omplimnary
ECEN620: Network Theory Broadband Circuit Design Fall 2014
 ECE60: work Thory Broadbad Circui Dig Fall 04 Lcur 6: PLL Trai Bhavior Sam Palrmo Aalog & Mixd-Sigal Cr Txa A&M Uivriy Aoucm, Agda, & Rfrc HW i du oday by 5PM PLL Trackig Rpo Pha Dcor Modl PLL Hold Rag
ECE60: work Thory Broadbad Circui Dig Fall 04 Lcur 6: PLL Trai Bhavior Sam Palrmo Aalog & Mixd-Sigal Cr Txa A&M Uivriy Aoucm, Agda, & Rfrc HW i du oday by 5PM PLL Trackig Rpo Pha Dcor Modl PLL Hold Rag
Boyce/DiPrima 9 th ed, Ch 7.8: Repeated Eigenvalues
 Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
AR(1) Process. The first-order autoregressive process, AR(1) is. where e t is WN(0, σ 2 )
 AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
FOR MORE PAPERS LOGON TO
 IT430 - E-Commerce Quesion No: 1 ( Marks: 1 )- Please choose one MAC sand for M d a A ss Conro a M d a A ss Consor M r of As an Co n on of s Quesion No: 2 ( Marks: 1 )- Please choose one C oos orr HTML
IT430 - E-Commerce Quesion No: 1 ( Marks: 1 )- Please choose one MAC sand for M d a A ss Conro a M d a A ss Consor M r of As an Co n on of s Quesion No: 2 ( Marks: 1 )- Please choose one C oos orr HTML
Erlkönig. t t.! t t. t t t tj "tt. tj t tj ttt!t t. e t Jt e t t t e t Jt
 Gsng Po 1 Agio " " lkö (Compl by Rhol Bckr, s Moifi by Mrk S. Zimmr)!! J "! J # " c c " Luwig vn Bhovn WoO 131 (177) I Wr Who!! " J J! 5 ri ris hro' h spä h, I urch J J Nch rk un W Es n wil A J J is f
Gsng Po 1 Agio " " lkö (Compl by Rhol Bckr, s Moifi by Mrk S. Zimmr)!! J "! J # " c c " Luwig vn Bhovn WoO 131 (177) I Wr Who!! " J J! 5 ri ris hro' h spä h, I urch J J Nch rk un W Es n wil A J J is f
EE415/515 Fundamentals of Semiconductor Devices Fall 2012
 3 EE4555 Fudmls of Smicoducor vics Fll cur 8: PN ucio iod hr 8 Forwrd & rvrs bis Moriy crrir diffusio Brrir lowrd blcd by iffusio rducd iffusio icrsd mioriy crrir drif rif hcd 3 EE 4555. E. Morris 3 3
3 EE4555 Fudmls of Smicoducor vics Fll cur 8: PN ucio iod hr 8 Forwrd & rvrs bis Moriy crrir diffusio Brrir lowrd blcd by iffusio rducd iffusio icrsd mioriy crrir drif rif hcd 3 EE 4555. E. Morris 3 3
+ x. x 2x. 12. dx. 24. dx + 1)
 INTEGRATION of FUNCTION of ONE VARIABLE INDEFINITE INTEGRAL Fidig th idfiit itgrals Rductio to basic itgrals, usig th rul f ( ) f ( ) d =... ( ). ( )d. d. d ( ). d. d. d 7. d 8. d 9. d. d. d. d 9. d 9.
INTEGRATION of FUNCTION of ONE VARIABLE INDEFINITE INTEGRAL Fidig th idfiit itgrals Rductio to basic itgrals, usig th rul f ( ) f ( ) d =... ( ). ( )d. d. d ( ). d. d. d 7. d 8. d 9. d. d. d. d 9. d 9.
Worksheet: Taylor Series, Lagrange Error Bound ilearnmath.net
 Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
Chapter Taylor Theorem Revisited
 Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
Infinite Continued Fraction (CF) representations. of the exponential integral function, Bessel functions and Lommel polynomials
 Ifii Coiu Fraio CF rraio of h oial igral fuio l fuio a Lol olyoial Coiu Fraio CF rraio a orhogoal olyoial I hi io w rall h rlaio bw ifi rurry rlaio of olyoial orroig orhogoaliy a aroria ifii oiu fraio
Ifii Coiu Fraio CF rraio of h oial igral fuio l fuio a Lol olyoial Coiu Fraio CF rraio a orhogoal olyoial I hi io w rall h rlaio bw ifi rurry rlaio of olyoial orroig orhogoaliy a aroria ifii oiu fraio
Lecture 2: Current in RC circuit D.K.Pandey
 Lcur 2: urrn in circui harging of apacior hrough Rsisr L us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R and a ky K in sris. Whn h ky K is swichd on, h charging
Lcur 2: urrn in circui harging of apacior hrough Rsisr L us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R and a ky K in sris. Whn h ky K is swichd on, h charging
Probability & Statistics,
 Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
Problems and Solutions for Section 3.2 (3.15 through 3.25)
 3-7 Problems ad Soluios for Secio 3 35 hrough 35 35 Calculae he respose of a overdamped sigle-degree-of-freedom sysem o a arbirary o-periodic exciaio Soluio: From Equaio 3: x = # F! h "! d! For a overdamped
3-7 Problems ad Soluios for Secio 3 35 hrough 35 35 Calculae he respose of a overdamped sigle-degree-of-freedom sysem o a arbirary o-periodic exciaio Soluio: From Equaio 3: x = # F! h "! d! For a overdamped
Transverse Wave Motion
 Trasverse Wave Moio Defiiio of Waves wave is a disurbae ha moves hrough a medium wihou givig he medium, as a whole, a permae displaeme. The geeral ame for hese waves is progressive wave. If he disurbae
Trasverse Wave Moio Defiiio of Waves wave is a disurbae ha moves hrough a medium wihou givig he medium, as a whole, a permae displaeme. The geeral ame for hese waves is progressive wave. If he disurbae
Ordinary Differential Equations
 Basi Nomlatur MAE 0 all 005 Egirig Aalsis Ltur Nots o: Ordiar Diffrtial Equatios Author: Profssor Albrt Y. Tog Tpist: Sakurako Takahashi Cosidr a gral O. D. E. with t as th idpdt variabl, ad th dpdt variabl.
Basi Nomlatur MAE 0 all 005 Egirig Aalsis Ltur Nots o: Ordiar Diffrtial Equatios Author: Profssor Albrt Y. Tog Tpist: Sakurako Takahashi Cosidr a gral O. D. E. with t as th idpdt variabl, ad th dpdt variabl.
FOURIER ANALYSIS Signals and System Analysis
 FOURIER ANALYSIS Isc Nwo Whi ligh cosiss of sv compos J Bpis Josph Fourir Bor: Mrch 768 i Auxrr, Bourgog, Frc Did: 6 My 83 i Pris, Frc Fourir Sris A priodic sigl of priod T sisfis ft f for ll f f for ll
FOURIER ANALYSIS Isc Nwo Whi ligh cosiss of sv compos J Bpis Josph Fourir Bor: Mrch 768 i Auxrr, Bourgog, Frc Did: 6 My 83 i Pris, Frc Fourir Sris A priodic sigl of priod T sisfis ft f for ll f f for ll
2.1. Differential Equations and Solutions #3, 4, 17, 20, 24, 35
 MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
Transfer function and the Laplace transformation
 Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
1.7 Vector Calculus 2 - Integration
 cio.7.7 cor alculus - Igraio.7. Ordiary Igrals o a cor A vcor ca b igrad i h ordiary way o roduc aohr vcor or aml 5 5 d 6.7. Li Igrals Discussd hr is h oio o a dii igral ivolvig a vcor ucio ha gras a scalar.
cio.7.7 cor alculus - Igraio.7. Ordiary Igrals o a cor A vcor ca b igrad i h ordiary way o roduc aohr vcor or aml 5 5 d 6.7. Li Igrals Discussd hr is h oio o a dii igral ivolvig a vcor ucio ha gras a scalar.
S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]
![S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15] S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]](/thumbs/92/108666103.jpg) S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
Time : 1 hr. Test Paper 08 Date 04/01/15 Batch - R Marks : 120
 Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
( ) ( ) + = ( ) + ( )
 Mah 0 Homwork S 6 Soluions 0 oins. ( ps I ll lav i o you vrify ha h omplimnary soluion is : y ( os( sin ( Th guss for h pariular soluion and is drivaivs ar, +. ( os( sin ( ( os( ( sin ( Y ( D 6B os( +
Mah 0 Homwork S 6 Soluions 0 oins. ( ps I ll lav i o you vrify ha h omplimnary soluion is : y ( os( sin ( Th guss for h pariular soluion and is drivaivs ar, +. ( os( sin ( ( os( ( sin ( Y ( D 6B os( +
Chemistry 342 Spring, The Hydrogen Atom.
 Th Hyrogn Ato. Th quation. Th first quation w want to sov is φ This quation is of faiiar for; rca that for th fr partic, w ha ψ x for which th soution is Sinc k ψ ψ(x) a cos kx a / k sin kx ± ix cos x
Th Hyrogn Ato. Th quation. Th first quation w want to sov is φ This quation is of faiiar for; rca that for th fr partic, w ha ψ x for which th soution is Sinc k ψ ψ(x) a cos kx a / k sin kx ± ix cos x
On the Derivatives of Bessel and Modified Bessel Functions with Respect to the Order and the Argument
 Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn
Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn
( ) ( ) ( ) ( ) (b) (a) sin. (c) sin sin 0. 2 π = + (d) k l k l (e) if x = 3 is a solution of the equation x 5x+ 12=
 Eesio Mahemaics Soluios HSC Quesio Oe (a) d 6 si 4 6 si si (b) (c) 7 4 ( si ).si +. ( si ) si + 56 (d) k + l ky + ly P is, k l k l + + + 5 + 7, + + 5 9, ( 5,9) if is a soluio of he equaio 5+ Therefore
Eesio Mahemaics Soluios HSC Quesio Oe (a) d 6 si 4 6 si si (b) (c) 7 4 ( si ).si +. ( si ) si + 56 (d) k + l ky + ly P is, k l k l + + + 5 + 7, + + 5 9, ( 5,9) if is a soluio of he equaio 5+ Therefore
Physics 302 Exam Find the curve that passes through endpoints (0,0) and (1,1) and minimizes 1
 Physis Exam 6. Fid th urv that passs through dpoits (, ad (, ad miimizs J [ y' y ]dx Solutio: Si th itgrad f dos ot dpd upo th variabl of itgratio x, w will us th sod form of Eulr s quatio: f f y' y' y
Physis Exam 6. Fid th urv that passs through dpoits (, ad (, ad miimizs J [ y' y ]dx Solutio: Si th itgrad f dos ot dpd upo th variabl of itgratio x, w will us th sod form of Eulr s quatio: f f y' y' y
19 Fourier Series and Practical Harmonic Analysis
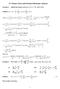 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
A Simple Representation of the Weighted Non-Central Chi-Square Distribution
 SSN: 9-875 raoa Joura o ovav Rarch Scc grg a Tchoogy (A S 97: 7 Cr rgaao) Vo u 9 Sbr A S Rrao o h Wgh No-Cra Ch-Squar Drbuo Dr ay A hry Dr Sahar A brah Dr Ya Y Aba Proor D o Mahaca Sac u o Saca Su a Rarch
SSN: 9-875 raoa Joura o ovav Rarch Scc grg a Tchoogy (A S 97: 7 Cr rgaao) Vo u 9 Sbr A S Rrao o h Wgh No-Cra Ch-Squar Drbuo Dr ay A hry Dr Sahar A brah Dr Ya Y Aba Proor D o Mahaca Sac u o Saca Su a Rarch
dt d Chapter 30: 1-Faraday s Law of induction (induced EMF) Chapter 30: 1-Faraday s Law of induction (induced Electromotive Force)
 Chaptr 3: 1-Faraday s aw of induction (inducd ctromotiv Forc) Variab (incrasing) Constant Variab (dcrasing) whn a magnt is movd nar a wir oop of ara A, currnt fows through that wir without any battris!
Chaptr 3: 1-Faraday s aw of induction (inducd ctromotiv Forc) Variab (incrasing) Constant Variab (dcrasing) whn a magnt is movd nar a wir oop of ara A, currnt fows through that wir without any battris!
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Boyce/DiPrima 9 th ed, Ch 2.1: Linear Equations; Method of Integrating Factors
 Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Further Results on Pair Sum Graphs
 Applid Mathmatis, 0,, 67-75 http://dx.doi.org/0.46/am.0.04 Publishd Oli Marh 0 (http://www.sirp.org/joural/am) Furthr Rsults o Pair Sum Graphs Raja Poraj, Jyaraj Vijaya Xavir Parthipa, Rukhmoi Kala Dpartmt
Applid Mathmatis, 0,, 67-75 http://dx.doi.org/0.46/am.0.04 Publishd Oli Marh 0 (http://www.sirp.org/joural/am) Furthr Rsults o Pair Sum Graphs Raja Poraj, Jyaraj Vijaya Xavir Parthipa, Rukhmoi Kala Dpartmt
MA 201: Partial Differential Equations Lecture - 11
 MA 201: Partia Differentia Equations Lecture - 11 Heat Equation Heat conduction in a thin rod The IBVP under consideration consists of: The governing equation: u t = αu xx, (1) where α is the therma diffusivity.
MA 201: Partia Differentia Equations Lecture - 11 Heat Equation Heat conduction in a thin rod The IBVP under consideration consists of: The governing equation: u t = αu xx, (1) where α is the therma diffusivity.
Department of Mathematics. Birla Institute of Technology, Mesra, Ranchi MA 2201(Advanced Engg. Mathematics) Session: Tutorial Sheet No.
 Dpm o Mhmics Bi Isi o Tchoog Ms Rchi MA Advcd gg. Mhmics Sssio: 7---- MODUL IV Toi Sh No. --. Rdc h oowig i homogos dii qios io h Sm Liovi om: i. ii. iii. iv. Fid h ig-vs d ig-cios o h oowig Sm Liovi bod
Dpm o Mhmics Bi Isi o Tchoog Ms Rchi MA Advcd gg. Mhmics Sssio: 7---- MODUL IV Toi Sh No. --. Rdc h oowig i homogos dii qios io h Sm Liovi om: i. ii. iii. iv. Fid h ig-vs d ig-cios o h oowig Sm Liovi bod
Fourier series. Part - A
 Fourier series Part - A 1.Define Dirichet s conditions Ans: A function defined in c x c + can be expanded as an infinite trigonometric series of the form a + a n cos nx n 1 + b n sin nx, provided i) f
Fourier series Part - A 1.Define Dirichet s conditions Ans: A function defined in c x c + can be expanded as an infinite trigonometric series of the form a + a n cos nx n 1 + b n sin nx, provided i) f
What is a Communications System?
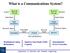 Wha is a ommuiaios Sysem? Aual Real Life Messae Real Life Messae Replia Ipu Sial Oupu Sial Ipu rasduer Oupu rasduer Eleroi Sial rasmier rasmied Sial hael Reeived Sial Reeiver Eleroi Sial Noise ad Disorio
Wha is a ommuiaios Sysem? Aual Real Life Messae Real Life Messae Replia Ipu Sial Oupu Sial Ipu rasduer Oupu rasduer Eleroi Sial rasmier rasmied Sial hael Reeived Sial Reeiver Eleroi Sial Noise ad Disorio
Adomian Decomposition Method for Dispersion. Phenomena Arising in Longitudinal Dispersion of. Miscible Fluid Flow through Porous Media
 dv. Thor. ppl. Mch. Vol. 3 o. 5 - domia Dcomposiio Mhod for Disprsio Phoma risig i ogiudial Disprsio of Miscibl Fluid Flow hrough Porous Mdia Ramakaa Mhr ad M.N. Mha Dparm of Mahmaics S.V. Naioal Isiu
dv. Thor. ppl. Mch. Vol. 3 o. 5 - domia Dcomposiio Mhod for Disprsio Phoma risig i ogiudial Disprsio of Miscibl Fluid Flow hrough Porous Mdia Ramakaa Mhr ad M.N. Mha Dparm of Mahmaics S.V. Naioal Isiu
2. The Laplace Transform
 Th aac Tranorm Inroucion Th aac ranorm i a unamna an vry uu oo or uying many nginring robm To in h aac ranorm w conir a comx variab σ, whr σ i h ra ar an i h imaginary ar or ix vau o σ an w viw a a oin
Th aac Tranorm Inroucion Th aac ranorm i a unamna an vry uu oo or uying many nginring robm To in h aac ranorm w conir a comx variab σ, whr σ i h ra ar an i h imaginary ar or ix vau o σ an w viw a a oin
2 Dirac delta function, modeling of impulse processes. 3 Sine integral function. Exponential integral function
 Chapr VII Spcial Fucios Ocobr 7, 7 479 CHAPTER VII SPECIAL FUNCTIONS Cos: Havisid sp fucio, filr fucio Dirac dla fucio, modlig of impuls procsss 3 Si igral fucio 4 Error fucio 5 Gamma fucio E Epoial igral
Chapr VII Spcial Fucios Ocobr 7, 7 479 CHAPTER VII SPECIAL FUNCTIONS Cos: Havisid sp fucio, filr fucio Dirac dla fucio, modlig of impuls procsss 3 Si igral fucio 4 Error fucio 5 Gamma fucio E Epoial igral
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
ELECTROMAGNETIC COMPATIBILITY HANDBOOK 1. Chapter 12: Spectra of Periodic and Aperiodic Signals
 ELECTOMAGNETIC COMPATIBILITY HANDBOOK Chapr : Spcra of Priodic ad Apriodic Sigals. Drmi whhr ach of h followig fucios ar priodic. If hy ar priodic, provid hir fudamal frqucy ad priod. a) x 4cos( 5 ) si(
ELECTOMAGNETIC COMPATIBILITY HANDBOOK Chapr : Spcra of Priodic ad Apriodic Sigals. Drmi whhr ach of h followig fucios ar priodic. If hy ar priodic, provid hir fudamal frqucy ad priod. a) x 4cos( 5 ) si(
CSE 245: Computer Aided Circuit Simulation and Verification
 CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
 www.vidrhipu.com TRANSFORMS & PDE MA65 Quio Bk wih Awr UNIT I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Oi pri diffri quio imiig rirr co d from z A.U M/Ju Souio: Giv z ----- Diff Pri w.r. d p > - p/ q > q/
www.vidrhipu.com TRANSFORMS & PDE MA65 Quio Bk wih Awr UNIT I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Oi pri diffri quio imiig rirr co d from z A.U M/Ju Souio: Giv z ----- Diff Pri w.r. d p > - p/ q > q/
F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics
![F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mathematics](/thumbs/89/97771684.jpg) F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mahemaics Prelim Quesio Paper Soluio Q. Aemp ay FIVE of he followig : [0] Q.(a) Defie Eve ad odd fucios. [] As.: A fucio f() is said o be eve fucio if
F.Y. Diploma : Sem. II [AE/CH/FG/ME/PT/PG] Applied Mahemaics Prelim Quesio Paper Soluio Q. Aemp ay FIVE of he followig : [0] Q.(a) Defie Eve ad odd fucios. [] As.: A fucio f() is said o be eve fucio if
Integrated Optical Waveguides
 Su Opls Faha Raa Cll Uvs Chap 8 Ia Opal Wavus 7 Dl Slab Wavus 7 Iu: A va f ff a pal wavus a us f a u lh a hp Th s bas pal wavu s a slab wavus shw blw Th suu s uf h - Lh s u s h b al al fl a h -la fas Cla
Su Opls Faha Raa Cll Uvs Chap 8 Ia Opal Wavus 7 Dl Slab Wavus 7 Iu: A va f ff a pal wavus a us f a u lh a hp Th s bas pal wavu s a slab wavus shw blw Th suu s uf h - Lh s u s h b al al fl a h -la fas Cla
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
ECE351: Signals and Systems I. Thinh Nguyen
 ECE35: Sigals ad Sysms I Thih Nguy FudamalsofSigalsadSysms x Fudamals of Sigals ad Sysms co. Fudamals of Sigals ad Sysms co. x x] Classificaio of sigals Classificaio of sigals co. x] x x] =xt s =x
ECE35: Sigals ad Sysms I Thih Nguy FudamalsofSigalsadSysms x Fudamals of Sigals ad Sysms co. Fudamals of Sigals ad Sysms co. x x] Classificaio of sigals Classificaio of sigals co. x] x x] =xt s =x
Copyright 2012 Pearson Education, Inc. Publishing as Prentice Hall.
 Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
CHAPTER 9 Compressible Flow
 CHPTER 9 Corssibl Flow Inrouion 9. v R. kv. R or R k k Rk k Char 9 / Corssibl Flow S of Soun 9.4 Subsiu Eq. 4.5.8 ino Eq. 4.5.7 an ngl onial nrgy hang: Q WS u~ u~. Enhaly is fin in Throynais as h u~ v
CHPTER 9 Corssibl Flow Inrouion 9. v R. kv. R or R k k Rk k Char 9 / Corssibl Flow S of Soun 9.4 Subsiu Eq. 4.5.8 ino Eq. 4.5.7 an ngl onial nrgy hang: Q WS u~ u~. Enhaly is fin in Throynais as h u~ v
, then the old equilibrium biomass was greater than the new B e. and we want to determine how long it takes for B(t) to reach the value B e.
 SURPLUS PRODUCTION (coiud) Trasiio o a Nw Equilibrium Th followig marials ar adapd from lchr (978), o h Rcommdd Radig lis caus () approachs h w quilibrium valu asympoically, i aks a ifii amou of im o acually
SURPLUS PRODUCTION (coiud) Trasiio o a Nw Equilibrium Th followig marials ar adapd from lchr (978), o h Rcommdd Radig lis caus () approachs h w quilibrium valu asympoically, i aks a ifii amou of im o acually
UNIT #5 EXPONENTIAL AND LOGARITHMIC FUNCTIONS
 Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
MA 1201 Engineering Mathematics MO/2017 Tutorial Sheet No. 2
 BIRLA INSTITUTE OF TECHNOLOGY, MESRA, RANCHI DEPARTMENT OF MATHEMATICS MA Egieeig Matheatis MO/7 Tutoia Sheet No. Modue IV:. Defie Beta futio ad Gaa futio.. Pove that,,,. Pove that, d. Pove that. & whee
BIRLA INSTITUTE OF TECHNOLOGY, MESRA, RANCHI DEPARTMENT OF MATHEMATICS MA Egieeig Matheatis MO/7 Tutoia Sheet No. Modue IV:. Defie Beta futio ad Gaa futio.. Pove that,,,. Pove that, d. Pove that. & whee
Elementary Differential Equations and Boundary Value Problems
 Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
T ansmission Line Theory Smith Chart
 Tranmiion Thory Smih har Tranmiion Thory Wir conncion Anao / Diia circui: No voa rop on wir conncion Tranmiion Microwav circui: wav on ranmiion Fi anayi: E H EM wav Tranmiion Thory Fiur. p. 5 oa an currn
Tranmiion Thory Smih har Tranmiion Thory Wir conncion Anao / Diia circui: No voa rop on wir conncion Tranmiion Microwav circui: wav on ranmiion Fi anayi: E H EM wav Tranmiion Thory Fiur. p. 5 oa an currn
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at

 +
+