Chapter Thirteen: Traveling Waves and the Wave Equation in Air, Water and the Ether
|
|
|
- Samson Dylan Tucker
- 6 years ago
- Views:
Transcription
1 Chapter Thirteen: Traveling Waves and the Wave Equation in Air, Water and the Ether We have been discussing the waves that are found in the string of a guitar or violin and how they are the physical reality that underlies music. But there are other kinds of waves: there are water waves and non-musical sound waves, such as the sound of hands clapping. These are not confined to a string but propagate over large distances in air and water. Some waves of this kind are easy to create yourself. Take a piece of rope, a jump rope for example and stretch it between 2 people. If one person gives it a shake, you will see the shake in the form of a bump in the rope moving from one person to the other. Slinkies will do the same. These are called traveling waves as are the waves of the ocean or the sound wave of clapping than to music: they can travel large distances without changing their shape very much. Their mathematical basis is even simpler than the sines and cosines we have worked with above. Their explanation was discovered by the French mathematician Jean Le Rond D Alembert in 1747 ( Recherches sur la Courbe que Forme une Corde Tendue mise en Vibration Studies of the Curve Formed by a String set in Vibration published by Royal Academy of Berlin). His quite simple but fundamental observation was that you can start with any function f(x) which is to be the shape of the string at time 0, then define the position of the string at all later times by yxt (, ) = f( x t) and this will satisfy the vibrating string equation: 2 2 y y = 2 2 If f& and && f are the first and second derivatives of f, then we can compute all the derivatives of y and check that y(x,t) satisfies the equation like this: = f& ( x t), = f& ( x t), so ( ) y y y = && f( x t), = && f( x t) = && f( x t) =, It s easy to visualize this solution too. At any fixed t=a>0, y(x,t) is the same function f, but shifted; this means that the value f(0) occurs not at x=t=0, but at x=t=a. We can see an example in the figure below:
2 These are half the traveling wave solutions. After all, why should the wave always travel to the right? The ones which travel to the left are given by yxt (, ) = gx ( + t) It s easy to check that this solves the vibrating string equation also. In fact, we can add these two waves and have one wave going right, one going left t the same time: yxt (, ) = f( x t) + gx ( + t) It can look really neat if 2 people shake a rope at the same time, producing short waves, one going right, one going left. They collide in the middle of the rope but, after a short time, they reappear having passed each other and recovering the same shape they had before the collision. This is all a consequence of linearity, that the sum of 2 solutions of the vibrating string equation is also a solution. D Alembert also claimed that all solutions of the vibrating string equation could be expressed this way. This result not needed for the our discussion but maybe it s interesting to see what he said. Suppose y(x,t) is some function of x and t that solves the equation. He then looked at the 2 auxiliary functions: pxt (, ) =, and qxt (, ) = + He then calculates the derivative with respect to s of p(x+s,t+s) by using the chain rule: d p p y y y y ( px ( + st, + s) ) = ( x+ st, + s) + ( x+ st, + s) = = ds Thus p( x+ s, t+ s) does not change when s changes. So it must be equal to some function of x-t, i.e. p( xt, ) = hx ( t) for some function h. Let f be the indefinite integral of h. Now the same argument shows that qxt (, ) = kx ( + t). Let g be the indefinite integral of k. The final step is to check that yxt (, ) f( x t) + gx ( t) 2 = a constant ( ) We get this by showing that the derivatives of the left hand side with respect to both x and t are zero, so it must be a constant. We have ignored one small thing: we are pretending the string or rope is infinite so we don t have to think about its 2 ends. For the correct vibrating string, we have to add in one complication: that it never moves at its 2 ends, say at x=0 and x=l. This what D Alembert looked at next. Start with the assumptions: yxt (, ) = f( x t) + gx ( + t), y(0, t) 0, y( L, t) 0 Then vanishing at the first end works out to mean:
3 0 = y(0, t) = f( t) + g( t) implies f( t) = g( t), or yxt (, ) = gt ( + x) gt ( x). This implies that y( x, t) = y( x, t) which means that there is always a negative version of wave to the left of 0 of exactly the same shape as the wave to the right of 0. This is what gives us the cancellation at 0. Vanishing at the second end works out like this: 0 = ylt (, ) = gt ( + L) gt ( L) or g is periodic of period 2 L: g( t+ 2 L) g( t) The conclusion is that the 2 travelling waves manage to cancel each other out at the two endpoints and create a periodic wave which repeats when time is advanced by the interval 2L. Here s an example which should help make these formulas clearer. In the example, there is a positive bump, shown in blue, traveling from right to left, and a negative bump, also shown in blue, traveling from left to right. The two vertical lines represent the two ends of the string where the wave will always have value 0. At t=0, the negative wave has just separated from the positive one and is moving across [0,1]. The movie proceeds by reading down until the waves meet at x=1. Then, for a split second, they cancel, as seen in the bottom panel. On the right, the movie proceeds, now with the positive wave going left from 1 to 0. Note also how we need to have a train of positive and negative waves spaced every 2 units to keep the whole thing going. This is what our equations showed us.
4 Now we have two ways of producing solutions of the vibrating string equation: by superposition of the sine waves, as in Chapter 10, or by traveling waves. The question is: are they the same? This got the 3 mathematicians D Alembert, Bernouilli and Euler quite excited. In the polite discourse of the Enlightenment, Bernouilli wrote in the 1753 paper quoted above, that these new solutions were improper though strictly speaking correct solutions! With traveling waves we are able to write down solutions in which the string starts in any position at all. To see this, suppose f(x) is any initial position of the string, which we assume tied down at x=0 and x=1. Then first we imagine an infinite string which extends the one which is tied down and now goes all the way from - on the left to + on the right. We need to set an initial position of the rest of the string. What we do is place the string in the inverted position on [-1,0]: f( x) = f( x), if 1 x 0 and then we make the string repeat its position every 2 units of x: f ( x+ 2) f( x) (See figure.) Then all we need to do is break up the initial position of the string into 2 waves of half the size of f(x), one travelling left and one travelling right: 1 yxt (, ) = ( f( x+ t) + f( x t) ) 2 This is just the general story behind the example given above.
5 So we can start the string in any position at all, release it and let it vibrate. What bothered Bernouilli and then became a big issue between him, Euler and D Alembert is whther we get more solutions of the vibrating string equation this way. What this means is: can we expand any function f(x) as a sum of sines: f( x) = a1sin(2 πx) + a2sin(4 πx) + a3sin(6 πx) +L in which case the two versions of the solution (D Alembert s on the left, Bernouilli s on the right) are the same: 1 ( ( ) ( )) 1 sin(2 ) cos(2 ) 2 sin(4 ) cos(4 ) 3 sin(6 ) cos(6 ) 2 f x+ t + f x t = a πx πt + a πx πt + a πx πt +L Can any initial position can be written as a sum of sine waves at the basic frequency and all its harmonics. [MUST REARRANGE MATERIAL: DISCUSSION OF FOURIER EXPANSION OF ARBITRARY FUNCTIONS SHOULD BE HERE.] All this has been about the waves which can be produced in a string under tension. But waves are something that occurs in a myriad of other settings. For example the head of a drum vibrates when hit, also in a periodic fashion with the membrane of the drum head going up and down in a definite pattern. The surface of water, in a glass or the ocean, supports many types of waves, some regular, some chaotic. Sound is a wave in the air, caused by alternating compression and rarefaction of the air, oscillating at many possible speeds. And, most important for our technology, radio waves, radar and light are all waves, but remarkably, waves without an underlying medium like air or water. They are waves of rapidly varying electric and magnetic fields. The Reason we have lingered so long on the vibrating string is because all the basic ideas are present in this simple example. The mathematics appears in its simplest form in this case and we can simulate it most simply on the computer. To go further, we need more than 1 space variable. Instead of describing the wave by y(x,t), with one space variable x (as well as one time variable t and one variable y which carries the wave), we need [FUTURE MATERIAL: Emphasize superposition and linearity. Computer demos. (Visual illusions: plaids.) Show circularly symmetric solutions of 2D wave equations, as per demo. (Aside on computing Laplacian of 1/sqrt(t^2- x ^2).) Sound and pressure waves. Euler s equations with advection term and its linear version. Simplest Example, as in Newton. Non-linear term in equation. Hmm: Eulerian or Lagrangian version? Maxwell s equations must not get bogged down in details here light and EM waves and the speed of light. Maybe doing the vector potential is easiest? Easiest 1D wave with X_x, H_y and motion along z-axis. Cable equation and story of the trans-atlantic cable.
6 The simplest approx to water waves (pics of this). Newton s discussion of water waves and anlogy with pendulum. Modern version with Hilbert transform easy to do numerically. (Comments on shallow water?, Pego s derivation of KdV)
Chapter 15. Mechanical Waves
 Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
PHYSICS 149: Lecture 24
 PHYSICS 149: Lecture 24 Chapter 11: Waves 11.8 Reflection and Refraction 11.10 Standing Waves Chapter 12: Sound 12.1 Sound Waves 12.4 Standing Sound Waves Lecture 24 Purdue University, Physics 149 1 ILQ
PHYSICS 149: Lecture 24 Chapter 11: Waves 11.8 Reflection and Refraction 11.10 Standing Waves Chapter 12: Sound 12.1 Sound Waves 12.4 Standing Sound Waves Lecture 24 Purdue University, Physics 149 1 ILQ
MITOCW 6. Standing Waves Part I
 MITOCW 6. Standing Waves Part I The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
MITOCW 6. Standing Waves Part I The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
Boundary value problems for partial differential equations
 Boundary value problems for partial differential equations Henrik Schlichtkrull March 11, 213 1 Boundary value problem 2 1 Introduction This note contains a brief introduction to linear partial differential
Boundary value problems for partial differential equations Henrik Schlichtkrull March 11, 213 1 Boundary value problem 2 1 Introduction This note contains a brief introduction to linear partial differential
Lecture 6: Differential Equations Describing Vibrations
 Lecture 6: Differential Equations Describing Vibrations In Chapter 3 of the Benson textbook, we will look at how various types of musical instruments produce sound, focusing on issues like how the construction
Lecture 6: Differential Equations Describing Vibrations In Chapter 3 of the Benson textbook, we will look at how various types of musical instruments produce sound, focusing on issues like how the construction
Complex Number Review:
 Complex Numbers and Waves Review 1 of 14 Complex Number Review: Wave functions Ψ are in general complex functions. So it's worth a quick review of complex numbers, since we'll be dealing with this all
Complex Numbers and Waves Review 1 of 14 Complex Number Review: Wave functions Ψ are in general complex functions. So it's worth a quick review of complex numbers, since we'll be dealing with this all
Born of the Wave Equation
 Corso di Laurea in Fisica - UNITS ISTITUZIONI DI FISICA PER IL SISTEMA TERRA Born of the Wave Equation FABIO ROMANELLI Department of Mathematics & Geosciences Universit of Trieste romanel@units.it http://moodle.units.it/course/view.php?id=887
Corso di Laurea in Fisica - UNITS ISTITUZIONI DI FISICA PER IL SISTEMA TERRA Born of the Wave Equation FABIO ROMANELLI Department of Mathematics & Geosciences Universit of Trieste romanel@units.it http://moodle.units.it/course/view.php?id=887
Chapter 9. Electromagnetic Waves
 Chapter 9. Electromagnetic Waves 9.1 Waves in One Dimension 9.1.1 The Wave Equation What is a "wave?" Let's start with the simple case: fixed shape, constant speed: How would you represent such a string
Chapter 9. Electromagnetic Waves 9.1 Waves in One Dimension 9.1.1 The Wave Equation What is a "wave?" Let's start with the simple case: fixed shape, constant speed: How would you represent such a string
Chapter 13, Vibrations and Waves. 1. A large spring requires a force of 150 N to compress it only m. What is the spring constant of the spring?
 CHAPTER 13 1. A large spring requires a force of 150 N to compress it only 0.010 m. What is the spring constant of the spring? a. 125 000 N/m b. 15 000 N/m c. 15 N/m d. 1.5 N/m 2. A 0.20-kg object is attached
CHAPTER 13 1. A large spring requires a force of 150 N to compress it only 0.010 m. What is the spring constant of the spring? a. 125 000 N/m b. 15 000 N/m c. 15 N/m d. 1.5 N/m 2. A 0.20-kg object is attached
Waves 2006 Physics 23. Armen Kocharian Lecture 3: Sep
 Waves 2006 Physics 23 Armen Kocharian Lecture 3: Sep 12. 2006 Last Time What is a wave? A "disturbance" that moves through space. Mechanical waves through a medium. Transverse vs. Longitudinal e.g., string
Waves 2006 Physics 23 Armen Kocharian Lecture 3: Sep 12. 2006 Last Time What is a wave? A "disturbance" that moves through space. Mechanical waves through a medium. Transverse vs. Longitudinal e.g., string
Chapter 17: Fourier Series
 Section A Introduction to Fourier Series By the end of this section you will be able to recognise periodic functions sketch periodic functions determine the period of the given function Why are Fourier
Section A Introduction to Fourier Series By the end of this section you will be able to recognise periodic functions sketch periodic functions determine the period of the given function Why are Fourier
Light as a Transverse Wave.
 Waves and Superposition (Keating Chapter 21) The ray model for light (i.e. light travels in straight lines) can be used to explain a lot of phenomena (like basic object and image formation and even aberrations)
Waves and Superposition (Keating Chapter 21) The ray model for light (i.e. light travels in straight lines) can be used to explain a lot of phenomena (like basic object and image formation and even aberrations)
Mathématiques appliquées (MATH0504-1) B. Dewals, Ch. Geuzaine
 Lecture 2 The wave equation Mathématiques appliquées (MATH0504-1) B. Dewals, Ch. Geuzaine V1.0 28/09/2018 1 Learning objectives of this lecture Understand the fundamental properties of the wave equation
Lecture 2 The wave equation Mathématiques appliquées (MATH0504-1) B. Dewals, Ch. Geuzaine V1.0 28/09/2018 1 Learning objectives of this lecture Understand the fundamental properties of the wave equation
Chapter 12 Partial Differential Equations
 Chapter 12 Partial Differential Equations Advanced Engineering Mathematics Wei-Ta Chu National Chung Cheng University wtchu@cs.ccu.edu.tw 1 2 12.1 Basic Concepts of PDEs Partial Differential Equation A
Chapter 12 Partial Differential Equations Advanced Engineering Mathematics Wei-Ta Chu National Chung Cheng University wtchu@cs.ccu.edu.tw 1 2 12.1 Basic Concepts of PDEs Partial Differential Equation A
A Guided Tour of the Wave Equation
 A Guided Tour of the Wave Equation Background: In order to solve this problem we need to review some facts about ordinary differential equations: Some Common ODEs and their solutions: f (x) = 0 f(x) =
A Guided Tour of the Wave Equation Background: In order to solve this problem we need to review some facts about ordinary differential equations: Some Common ODEs and their solutions: f (x) = 0 f(x) =
MATH 308 COURSE SUMMARY
 MATH 308 COURSE SUMMARY Approximately a third of the exam cover the material from the first two midterms, that is, chapter 6 and the first six sections of chapter 7. The rest of the exam will cover the
MATH 308 COURSE SUMMARY Approximately a third of the exam cover the material from the first two midterms, that is, chapter 6 and the first six sections of chapter 7. The rest of the exam will cover the
Vibrations and Eigenvalues
 Vibrations and Eigenvalues Rajendra Bhatia President s Address at the 45th Annual Conference of the Association of Mathematics Teachers of India, Kolkata, December 27, 2010 The vibrating string problem
Vibrations and Eigenvalues Rajendra Bhatia President s Address at the 45th Annual Conference of the Association of Mathematics Teachers of India, Kolkata, December 27, 2010 The vibrating string problem
1 f. result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by
 result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by amplitude (how far do the bits move from their equilibrium positions? Amplitude of MEDIUM)
result from periodic disturbance same period (frequency) as source Longitudinal or Transverse Waves Characterized by amplitude (how far do the bits move from their equilibrium positions? Amplitude of MEDIUM)
AP physics B - Webreview ch 13 Waves
 Name: Class: _ Date: _ AP physics B - Webreview ch 13 Waves Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A large spring requires a force of 150 N to
Name: Class: _ Date: _ AP physics B - Webreview ch 13 Waves Multiple Choice Identify the choice that best completes the statement or answers the question. 1. A large spring requires a force of 150 N to
Physics 342 Lecture 23. Radial Separation. Lecture 23. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
Continuum Limit and Fourier Series
 Chapter 6 Continuum Limit and Fourier Series Continuous is in the eye of the beholder Most systems that we think of as continuous are actually made up of discrete pieces In this chapter, we show that a
Chapter 6 Continuum Limit and Fourier Series Continuous is in the eye of the beholder Most systems that we think of as continuous are actually made up of discrete pieces In this chapter, we show that a
Important because SHM is a good model to describe vibrations of a guitar string, vibrations of atoms in molecules, etc.
 Simple Harmonic Motion Oscillatory motion under a restoring force proportional to the amount of displacement from equilibrium A restoring force is a force that tries to move the system back to equilibrium
Simple Harmonic Motion Oscillatory motion under a restoring force proportional to the amount of displacement from equilibrium A restoring force is a force that tries to move the system back to equilibrium
Chapter 15 Mechanical Waves
 Chapter 15 Mechanical Waves 1 Types of Mechanical Waves This chapter and the next are about mechanical waves waves that travel within some material called a medium. Waves play an important role in how
Chapter 15 Mechanical Waves 1 Types of Mechanical Waves This chapter and the next are about mechanical waves waves that travel within some material called a medium. Waves play an important role in how
Differential Equations
 Electricity and Magnetism I (P331) M. R. Shepherd October 14, 2008 Differential Equations The purpose of this note is to provide some supplementary background on differential equations. The problems discussed
Electricity and Magnetism I (P331) M. R. Shepherd October 14, 2008 Differential Equations The purpose of this note is to provide some supplementary background on differential equations. The problems discussed
Physics 101 Lecture 18 Vibrations, SHM, Waves (II)
 Physics 101 Lecture 18 Vibrations, SHM, Waves (II) Reminder: simple harmonic motion is the result if we have a restoring force that is linear with the displacement: F = -k x What would happen if you could
Physics 101 Lecture 18 Vibrations, SHM, Waves (II) Reminder: simple harmonic motion is the result if we have a restoring force that is linear with the displacement: F = -k x What would happen if you could
Lecture 17. Mechanical waves. Transverse waves. Sound waves. Standing Waves.
 Lecture 17 Mechanical waves. Transverse waves. Sound waves. Standing Waves. What is a wave? A wave is a traveling disturbance that transports energy but not matter. Examples: Sound waves (air moves back
Lecture 17 Mechanical waves. Transverse waves. Sound waves. Standing Waves. What is a wave? A wave is a traveling disturbance that transports energy but not matter. Examples: Sound waves (air moves back
Mechanical Waves. 3: Mechanical Waves (Chapter 16) Waves: Space and Time
 3: Mechanical Waves (Chapter 6) Phys3, A Dr. Robert MacDonald Mechanical Waves A mechanical wave is a travelling disturbance in a medium (like water, string, earth, Slinky, etc). Move some part of the
3: Mechanical Waves (Chapter 6) Phys3, A Dr. Robert MacDonald Mechanical Waves A mechanical wave is a travelling disturbance in a medium (like water, string, earth, Slinky, etc). Move some part of the
MITOCW MITRES18_005S10_DiffEqnsMotion_300k_512kb-mp4
 MITOCW MITRES18_005S10_DiffEqnsMotion_300k_512kb-mp4 PROFESSOR: OK, this lecture, this day, is differential equations day. I just feel even though these are not on the BC exams, that we've got everything
MITOCW MITRES18_005S10_DiffEqnsMotion_300k_512kb-mp4 PROFESSOR: OK, this lecture, this day, is differential equations day. I just feel even though these are not on the BC exams, that we've got everything
3/9/2011. Outline Chapter 7 Waves Water Waves Water Waves. Water waves are really circular. They are an example of Mechanical waves.
 Outline Chapter 7 Waves 7-1. Water Waves 7-2. Transverse and Longitudinal Waves 7-3. Describing Waves 7-4. Standing Waves 7-5. Sound 7-6. Doppler Effect 7-7. Musical Sounds 7-8. Electromagnetic Waves 7-9.
Outline Chapter 7 Waves 7-1. Water Waves 7-2. Transverse and Longitudinal Waves 7-3. Describing Waves 7-4. Standing Waves 7-5. Sound 7-6. Doppler Effect 7-7. Musical Sounds 7-8. Electromagnetic Waves 7-9.
Waves Part 3A: Standing Waves
 Waves Part 3A: Standing Waves Last modified: 24/01/2018 Contents Links Contents Superposition Standing Waves Definition Nodes Anti-Nodes Standing Waves Summary Standing Waves on a String Standing Waves
Waves Part 3A: Standing Waves Last modified: 24/01/2018 Contents Links Contents Superposition Standing Waves Definition Nodes Anti-Nodes Standing Waves Summary Standing Waves on a String Standing Waves
is a What you Hear The Pressure Wave sets the Ear Drum into Vibration.
 is a What you Hear The ear converts sound energy to mechanical energy to a nerve impulse which is transmitted to the brain. The Pressure Wave sets the Ear Drum into Vibration. electroencephalogram v S
is a What you Hear The ear converts sound energy to mechanical energy to a nerve impulse which is transmitted to the brain. The Pressure Wave sets the Ear Drum into Vibration. electroencephalogram v S
THE WAVE EQUATION. F = T (x, t) j + T (x + x, t) j = T (sin(θ(x, t)) + sin(θ(x + x, t)))
 THE WAVE EQUATION The aim is to derive a mathematical model that describes small vibrations of a tightly stretched flexible string for the one-dimensional case, or of a tightly stretched membrane for the
THE WAVE EQUATION The aim is to derive a mathematical model that describes small vibrations of a tightly stretched flexible string for the one-dimensional case, or of a tightly stretched membrane for the
u tt = a 2 u xx u tt = a 2 (u xx + u yy )
 10.7 The wave equation 10.7 The wave equation O. Costin: 10.7 1 This equation describes the propagation of waves through a medium: in one dimension, such as a vibrating string u tt = a 2 u xx 1 This equation
10.7 The wave equation 10.7 The wave equation O. Costin: 10.7 1 This equation describes the propagation of waves through a medium: in one dimension, such as a vibrating string u tt = a 2 u xx 1 This equation
d 1 µ 2 Θ = 0. (4.1) consider first the case of m = 0 where there is no azimuthal dependence on the angle φ.
 4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
4 Legendre Functions In order to investigate the solutions of Legendre s differential equation d ( µ ) dθ ] ] + l(l + ) m dµ dµ µ Θ = 0. (4.) consider first the case of m = 0 where there is no azimuthal
PHY 103: Standing Waves and Harmonics. Segev BenZvi Department of Physics and Astronomy University of Rochester
 PHY 103: Standing Waves and Harmonics Segev BenZvi Department of Physics and Astronomy University of Rochester Sounds of the Universe NASA/JPL, September 2016 2 Properties of Waves Wavelength: λ, length
PHY 103: Standing Waves and Harmonics Segev BenZvi Department of Physics and Astronomy University of Rochester Sounds of the Universe NASA/JPL, September 2016 2 Properties of Waves Wavelength: λ, length
Physics 121H Fall Homework #15 23-November-2015 Due Date : 2-December-2015
 Reading : Chapters 16 and 17 Note: Reminder: Physics 121H Fall 2015 Homework #15 23-November-2015 Due Date : 2-December-2015 This is a two-week homework assignment that will be worth 2 homework grades
Reading : Chapters 16 and 17 Note: Reminder: Physics 121H Fall 2015 Homework #15 23-November-2015 Due Date : 2-December-2015 This is a two-week homework assignment that will be worth 2 homework grades
Partial Differential Equations
 Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives with respect to those variables. Most (but
Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives with respect to those variables. Most (but
Electromagnetic Waves
 Electromagnetic Waves As the chart shows, the electromagnetic spectrum covers an extremely wide range of wavelengths and frequencies. Though the names indicate that these waves have a number of sources,
Electromagnetic Waves As the chart shows, the electromagnetic spectrum covers an extremely wide range of wavelengths and frequencies. Though the names indicate that these waves have a number of sources,
Partial Differential Equations (PDEs)
 C H A P T E R Partial Differential Equations (PDEs) 5 A PDE is an equation that contains one or more partial derivatives of an unknown function that depends on at least two variables. Usually one of these
C H A P T E R Partial Differential Equations (PDEs) 5 A PDE is an equation that contains one or more partial derivatives of an unknown function that depends on at least two variables. Usually one of these
Physics 1C. Lecture 12C
 Physics 1C Lecture 12C Simple Pendulum The simple pendulum is another example of simple harmonic motion. Making a quick force diagram of the situation, we find:! The tension in the string cancels out with
Physics 1C Lecture 12C Simple Pendulum The simple pendulum is another example of simple harmonic motion. Making a quick force diagram of the situation, we find:! The tension in the string cancels out with
x(t+ δt) - x(t) = slope δt t+δt
 Techniques of Physics Worksheet 2 Classical Vibrations and Waves Introduction You will have encountered many different examples of wave phenomena in your courses and should be familiar with most of the
Techniques of Physics Worksheet 2 Classical Vibrations and Waves Introduction You will have encountered many different examples of wave phenomena in your courses and should be familiar with most of the
Partial Differential Equations Summary
 Partial Differential Equations Summary 1. The heat equation Many physical processes are governed by partial differential equations. temperature of a rod. In this chapter, we will examine exactly that.
Partial Differential Equations Summary 1. The heat equation Many physical processes are governed by partial differential equations. temperature of a rod. In this chapter, we will examine exactly that.
ENGI 9420 Lecture Notes 8 - PDEs Page 8.01
 ENGI 940 ecture Notes 8 - PDEs Page 8.0 8. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
ENGI 940 ecture Notes 8 - PDEs Page 8.0 8. Partial Differential Equations Partial differential equations (PDEs) are equations involving functions of more than one variable and their partial derivatives
Physics 142 Mechanical Waves Page 1. Mechanical Waves
 Physics 142 Mechanical Waves Page 1 Mechanical Waves This set of notes contains a review of wave motion in mechanics, emphasizing the mathematical formulation that will be used in our discussion of electromagnetic
Physics 142 Mechanical Waves Page 1 Mechanical Waves This set of notes contains a review of wave motion in mechanics, emphasizing the mathematical formulation that will be used in our discussion of electromagnetic
Physics 123 Unit #3 Review
 Physics 123 Unit #3 Review I. Definitions and Facts longitudinal wave transverse wave traveling wave standing wave wave front wavelength wave number frequency angular frequency period crest trough node
Physics 123 Unit #3 Review I. Definitions and Facts longitudinal wave transverse wave traveling wave standing wave wave front wavelength wave number frequency angular frequency period crest trough node
MATH 320, WEEK 2: Slope Fields, Uniqueness of Solutions, Initial Value Problems, Separable Equations
 MATH 320, WEEK 2: Slope Fields, Uniqueness of Solutions, Initial Value Problems, Separable Equations 1 Slope Fields We have seen what a differential equation is (relationship with a function and its derivatives),
MATH 320, WEEK 2: Slope Fields, Uniqueness of Solutions, Initial Value Problems, Separable Equations 1 Slope Fields We have seen what a differential equation is (relationship with a function and its derivatives),
1. Partial differential equations. Chapter 12: Partial Differential Equations. Examples. 2. The one-dimensional wave equation
 1. Partial differential equations Definitions Examples A partial differential equation PDE is an equation giving a relation between a function of two or more variables u and its partial derivatives. The
1. Partial differential equations Definitions Examples A partial differential equation PDE is an equation giving a relation between a function of two or more variables u and its partial derivatives. The
Lecture #4: The Classical Wave Equation and Separation of Variables
 5.61 Fall 013 Lecture #4 page 1 Lecture #4: The Classical Wave Equation and Separation of Variables Last time: Two-slit experiment paths to same point on screen paths differ by nλ-constructive interference
5.61 Fall 013 Lecture #4 page 1 Lecture #4: The Classical Wave Equation and Separation of Variables Last time: Two-slit experiment paths to same point on screen paths differ by nλ-constructive interference
Figure 1: Doing work on a block by pushing it across the floor.
 Work Let s imagine I have a block which I m pushing across the floor, shown in Figure 1. If I m moving the block at constant velocity, then I know that I have to apply a force to compensate the effects
Work Let s imagine I have a block which I m pushing across the floor, shown in Figure 1. If I m moving the block at constant velocity, then I know that I have to apply a force to compensate the effects
A. Incorrect! Frequency and wavelength are not directly proportional to each other.
 MCAT Physics Problem Solving Drill 1: Waves and Periodic Motion Question No. 1 of 10 Question 1. Two waves on identical strings have frequencies in a ratio of 3 to. If their wave speeds are the same, then
MCAT Physics Problem Solving Drill 1: Waves and Periodic Motion Question No. 1 of 10 Question 1. Two waves on identical strings have frequencies in a ratio of 3 to. If their wave speeds are the same, then
FROM NEWTON S MECHANICS TO EULER S EQUATIONS
 1 EE250 FROM NEWTON S MECHANICS TO EULER S EQUATIONS How the equation of fluid dynamics were born 250 years ago Olivier Darrigol and Uriel Frisch CNRS : Rehseis, Paris, France Laboratoire Cassiopée, UNSA,
1 EE250 FROM NEWTON S MECHANICS TO EULER S EQUATIONS How the equation of fluid dynamics were born 250 years ago Olivier Darrigol and Uriel Frisch CNRS : Rehseis, Paris, France Laboratoire Cassiopée, UNSA,
Mathematics 102 Fall 1999 The formal rules of calculus The three basic rules The sum rule. The product rule. The composition rule.
 Mathematics 02 Fall 999 The formal rules of calculus So far we have calculated the derivative of each function we have looked at all over again from scratch, applying what is essentially the definition
Mathematics 02 Fall 999 The formal rules of calculus So far we have calculated the derivative of each function we have looked at all over again from scratch, applying what is essentially the definition
Fourier and Partial Differential Equations
 Chapter 5 Fourier and Partial Differential Equations 5.1 Fourier MATH 294 SPRING 1982 FINAL # 5 5.1.1 Consider the function 2x, 0 x 1. a) Sketch the odd extension of this function on 1 x 1. b) Expand the
Chapter 5 Fourier and Partial Differential Equations 5.1 Fourier MATH 294 SPRING 1982 FINAL # 5 5.1.1 Consider the function 2x, 0 x 1. a) Sketch the odd extension of this function on 1 x 1. b) Expand the
10.2-3: Fourier Series.
 10.2-3: Fourier Series. 10.2-3: Fourier Series. O. Costin: Fourier Series, 10.2-3 1 Fourier series are very useful in representing periodic functions. Examples of periodic functions. A function is periodic
10.2-3: Fourier Series. 10.2-3: Fourier Series. O. Costin: Fourier Series, 10.2-3 1 Fourier series are very useful in representing periodic functions. Examples of periodic functions. A function is periodic
Normal modes. where. and. On the other hand, all such systems, if started in just the right way, will move in a simple way.
 Chapter 9. Dynamics in 1D 9.4. Coupled motions in 1D 491 only the forces from the outside; the interaction forces cancel because they come in equal and opposite (action and reaction) pairs. So we get:
Chapter 9. Dynamics in 1D 9.4. Coupled motions in 1D 491 only the forces from the outside; the interaction forces cancel because they come in equal and opposite (action and reaction) pairs. So we get:
PEER REVIEW. ... Your future in science will be largely controlled by anonymous letters from your peers. peers. Matt. Corinne
 PEER REVIEW 1... Your future in science will be largely controlled by anonymous letters from your peers. Matt peers Corinne 2 3 4 5 6 MULTIPLE DRIVNG FREQUENCIES LRC circuit L I = (1/Z)V ext Z must have
PEER REVIEW 1... Your future in science will be largely controlled by anonymous letters from your peers. Matt peers Corinne 2 3 4 5 6 MULTIPLE DRIVNG FREQUENCIES LRC circuit L I = (1/Z)V ext Z must have
Topic 4: Waves 4.3 Wave characteristics
 Guidance: Students will be expected to calculate the resultant of two waves or pulses both graphically and algebraically Methods of polarization will be restricted to the use of polarizing filters and
Guidance: Students will be expected to calculate the resultant of two waves or pulses both graphically and algebraically Methods of polarization will be restricted to the use of polarizing filters and
Electromagnetic waves in free space
 Waveguide notes 018 Electromagnetic waves in free space We start with Maxwell s equations for an LIH medum in the case that the source terms are both zero. = =0 =0 = = Take the curl of Faraday s law, then
Waveguide notes 018 Electromagnetic waves in free space We start with Maxwell s equations for an LIH medum in the case that the source terms are both zero. = =0 =0 = = Take the curl of Faraday s law, then
Oscillations and Waves
 Oscillations and Waves Periodic Motion Simple Harmonic Motion Connections between Uniform Circular Motion and Simple Harmonic Motion The Period of a Mass on a Spring Energy Conservation in Oscillatory
Oscillations and Waves Periodic Motion Simple Harmonic Motion Connections between Uniform Circular Motion and Simple Harmonic Motion The Period of a Mass on a Spring Energy Conservation in Oscillatory
Topic 5 Notes Jeremy Orloff. 5 Homogeneous, linear, constant coefficient differential equations
 Topic 5 Notes Jeremy Orloff 5 Homogeneous, linear, constant coefficient differential equations 5.1 Goals 1. Be able to solve homogeneous constant coefficient linear differential equations using the method
Topic 5 Notes Jeremy Orloff 5 Homogeneous, linear, constant coefficient differential equations 5.1 Goals 1. Be able to solve homogeneous constant coefficient linear differential equations using the method
Lab 10: Harmonic Motion and the Pendulum
 Lab 10 Harmonic Motion and the Pendulum 119 Name Date Partners Lab 10: Harmonic Motion and the Pendulum OVERVIEW A body is said to be in a position of stable equilibrium if, after displacement in any direction,
Lab 10 Harmonic Motion and the Pendulum 119 Name Date Partners Lab 10: Harmonic Motion and the Pendulum OVERVIEW A body is said to be in a position of stable equilibrium if, after displacement in any direction,
AP Physics 1. April 11, Simple Harmonic Motion. Table of Contents. Period. SHM and Circular Motion
 AP Physics 1 2016-07-20 www.njctl.org Table of Contents Click on the topic to go to that section Period and Frequency SHM and UCM Spring Pendulum Simple Pendulum Sinusoidal Nature of SHM Period and Frequency
AP Physics 1 2016-07-20 www.njctl.org Table of Contents Click on the topic to go to that section Period and Frequency SHM and UCM Spring Pendulum Simple Pendulum Sinusoidal Nature of SHM Period and Frequency
Advection, Conservation, Conserved Physical Quantities, Wave Equations
 EP711 Supplementary Material Thursday, September 4, 2014 Advection, Conservation, Conserved Physical Quantities, Wave Equations Jonathan B. Snively!Embry-Riddle Aeronautical University Contents EP711 Supplementary
EP711 Supplementary Material Thursday, September 4, 2014 Advection, Conservation, Conserved Physical Quantities, Wave Equations Jonathan B. Snively!Embry-Riddle Aeronautical University Contents EP711 Supplementary
What is a Wave. Why are Waves Important? Power PHYSICS 220. Lecture 19. Waves
 PHYSICS 220 Lecture 19 Waves What is a Wave A wave is a disturbance that travels away from its source and carries energy. A wave can transmit energy from one point to another without transporting any matter
PHYSICS 220 Lecture 19 Waves What is a Wave A wave is a disturbance that travels away from its source and carries energy. A wave can transmit energy from one point to another without transporting any matter
Notes on Fourier Series and Integrals Fourier Series
 Notes on Fourier Series and Integrals Fourier Series et f(x) be a piecewise linear function on [, ] (This means that f(x) may possess a finite number of finite discontinuities on the interval). Then f(x)
Notes on Fourier Series and Integrals Fourier Series et f(x) be a piecewise linear function on [, ] (This means that f(x) may possess a finite number of finite discontinuities on the interval). Then f(x)
Wave Phenomena Physics 15c. Lecture 9 Wave Reflection Standing Waves
 Wave Phenomena Physics 15c Lecture 9 Wave Reflection Standing Waves What We Did Last Time Energy and momentum in LC transmission lines Transfer rates for normal modes: and The energy is carried by the
Wave Phenomena Physics 15c Lecture 9 Wave Reflection Standing Waves What We Did Last Time Energy and momentum in LC transmission lines Transfer rates for normal modes: and The energy is carried by the
I WAVES (ENGEL & REID, 13.2, 13.3 AND 12.6)
 I WAVES (ENGEL & REID, 13., 13.3 AND 1.6) I.1 Introduction A significant part of the lecture From Quantum to Matter is devoted to developing the basic concepts of quantum mechanics. This is not possible
I WAVES (ENGEL & REID, 13., 13.3 AND 1.6) I.1 Introduction A significant part of the lecture From Quantum to Matter is devoted to developing the basic concepts of quantum mechanics. This is not possible
Waves Part 1: Travelling Waves
 Waves Part 1: Travelling Waves Last modified: 15/05/2018 Links Contents Travelling Waves Harmonic Waves Wavelength Period & Frequency Summary Example 1 Example 2 Example 3 Example 4 Transverse & Longitudinal
Waves Part 1: Travelling Waves Last modified: 15/05/2018 Links Contents Travelling Waves Harmonic Waves Wavelength Period & Frequency Summary Example 1 Example 2 Example 3 Example 4 Transverse & Longitudinal
How to Use Calculus Like a Physicist
 How to Use Calculus Like a Physicist Physics A300 Fall 2004 The purpose of these notes is to make contact between the abstract descriptions you may have seen in your calculus classes and the applications
How to Use Calculus Like a Physicist Physics A300 Fall 2004 The purpose of these notes is to make contact between the abstract descriptions you may have seen in your calculus classes and the applications
Schedule for the remainder of class
 Schedule for the remainder of class 04/25 (today): Regular class - Sound and the Doppler Effect 04/27: Cover any remaining new material, then Problem Solving/Review (ALL chapters) 04/29: Problem Solving/Review
Schedule for the remainder of class 04/25 (today): Regular class - Sound and the Doppler Effect 04/27: Cover any remaining new material, then Problem Solving/Review (ALL chapters) 04/29: Problem Solving/Review
Bell s spaceship paradox
 Bell s spaceship paradox If the two ships start accelerating at the same time, I always see them travelling at the same velocity, and keeping a constant distance... But I said the objects get shorter when
Bell s spaceship paradox If the two ships start accelerating at the same time, I always see them travelling at the same velocity, and keeping a constant distance... But I said the objects get shorter when
Raymond A. Serway Chris Vuille. Chapter Thirteen. Vibrations and Waves
 Raymond A. Serway Chris Vuille Chapter Thirteen Vibrations and Waves Periodic Motion and Waves Periodic motion is one of the most important kinds of physical behavior Will include a closer look at Hooke
Raymond A. Serway Chris Vuille Chapter Thirteen Vibrations and Waves Periodic Motion and Waves Periodic motion is one of the most important kinds of physical behavior Will include a closer look at Hooke
Special Classical Physical Systems
 Chapter 6 Special Classical Physical Systems 6.1 Introduction In order to understand the ideas of modern physics, it is essential to understand the operations of some special classical systems. Not only
Chapter 6 Special Classical Physical Systems 6.1 Introduction In order to understand the ideas of modern physics, it is essential to understand the operations of some special classical systems. Not only
Lecture 5: Function Approximation: Taylor Series
 1 / 10 Lecture 5: Function Approximation: Taylor Series MAR514 Geoffrey Cowles Department of Fisheries Oceanography School for Marine Science and Technology University of Massachusetts-Dartmouth Better
1 / 10 Lecture 5: Function Approximation: Taylor Series MAR514 Geoffrey Cowles Department of Fisheries Oceanography School for Marine Science and Technology University of Massachusetts-Dartmouth Better
0.1 Infinite Limits 2 = (2 1) =. Finally, we conclude that
 0. Infinite Limits The concept of infinity (or symbolically, ) plays an important role in calculus. This concept is related to the boundedness of a function. Definition 0.. (Bounded Function). A function
0. Infinite Limits The concept of infinity (or symbolically, ) plays an important role in calculus. This concept is related to the boundedness of a function. Definition 0.. (Bounded Function). A function
PHY2048 Final Exam Review, Spring 2017
 1. A 4kg block is at rest on a frictionless horizontal track. A constant horizontal force acts on the block at t = 0s. A graph of the position of the block at 1 second time intervals is shown in the figure.
1. A 4kg block is at rest on a frictionless horizontal track. A constant horizontal force acts on the block at t = 0s. A graph of the position of the block at 1 second time intervals is shown in the figure.
What is a wave? Waves
 What is a wave? Waves Waves What is a wave? A wave is a disturbance that carries energy from one place to another. Classifying waves 1. Mechanical Waves - e.g., water waves, sound waves, and waves on strings.
What is a wave? Waves Waves What is a wave? A wave is a disturbance that carries energy from one place to another. Classifying waves 1. Mechanical Waves - e.g., water waves, sound waves, and waves on strings.
(The) Three Linear Partial Differential Equations
 (The) Three Linear Partial Differential Equations 1 Introduction A partial differential equation (PDE) is an equation of a function of 2 or more variables, involving 2 or more partial derivatives in different
(The) Three Linear Partial Differential Equations 1 Introduction A partial differential equation (PDE) is an equation of a function of 2 or more variables, involving 2 or more partial derivatives in different
Lecture 9 - Rotational Dynamics
 Lecture 9 - Rotational Dynamics A Puzzle... Angular momentum is a 3D vector, and changing its direction produces a torque τ = dl. An important application in our daily lives is that bicycles don t fall
Lecture 9 - Rotational Dynamics A Puzzle... Angular momentum is a 3D vector, and changing its direction produces a torque τ = dl. An important application in our daily lives is that bicycles don t fall
The wave equation in one dimension
 The wave equation in one dimension Prof. Joyner 1 The theory of the vibrating string touches on musical theory and the theory of oscillating waves, so has likely been a concern of scholars since ancient
The wave equation in one dimension Prof. Joyner 1 The theory of the vibrating string touches on musical theory and the theory of oscillating waves, so has likely been a concern of scholars since ancient
Question 01. A. Incorrect! The speed of sound is not the same in all medium; it is dependent on the properties of the material.
 High School Physics - Problem Drill 15: Sound 1. Which of these is not a true statement about sound waves? Question 01 (A) Sound waves are travel at different speeds in different mediums. (B) Sound waves
High School Physics - Problem Drill 15: Sound 1. Which of these is not a true statement about sound waves? Question 01 (A) Sound waves are travel at different speeds in different mediums. (B) Sound waves
= k, (2) p = h λ. x o = f1/2 o a. +vt (4)
 Traveling Functions, Traveling Waves, and the Uncertainty Principle R.M. Suter Department of Physics, Carnegie Mellon University Experimental observations have indicated that all quanta have a wave-like
Traveling Functions, Traveling Waves, and the Uncertainty Principle R.M. Suter Department of Physics, Carnegie Mellon University Experimental observations have indicated that all quanta have a wave-like
Content of the course 3NAB0 (see study guide)
 Content of the course 3NAB0 (see study guide) 17 November diagnostic test! Week 1 : 14 November Week 2 : 21 November Introduction, units (Ch1), Circuits (Ch25,26) Heat (Ch17), Kinematics (Ch2 3) Week 3:
Content of the course 3NAB0 (see study guide) 17 November diagnostic test! Week 1 : 14 November Week 2 : 21 November Introduction, units (Ch1), Circuits (Ch25,26) Heat (Ch17), Kinematics (Ch2 3) Week 3:
In this section we extend the idea of Fourier analysis to multivariate functions: that is, functions of more than one independent variable.
 7in x 1in Felder c9_online.tex V - January 24, 215 2: P.M. Page 9 9.8 Multivariate Fourier Series 9.8 Multivariate Fourier Series 9 In this section we extend the idea of Fourier analysis to multivariate
7in x 1in Felder c9_online.tex V - January 24, 215 2: P.M. Page 9 9.8 Multivariate Fourier Series 9.8 Multivariate Fourier Series 9 In this section we extend the idea of Fourier analysis to multivariate
Chapter Nine: Music, Chords and Harmony
 1 Chapter Nine: Music, Chords and Harmony If the stars and planets are the gears of the universe, revolving in intricate ways in the skies, then music came to be seen from ancient times as a subtle reflection
1 Chapter Nine: Music, Chords and Harmony If the stars and planets are the gears of the universe, revolving in intricate ways in the skies, then music came to be seen from ancient times as a subtle reflection
Lecture 21: The one dimensional Wave Equation: D Alembert s Solution
 Introductory lecture notes on Partial Differential Equations - c Anthony Peirce. Not to be copied, used, or revised without explicit written permission from the copyright owner. 1 Lecture 21: The one dimensional
Introductory lecture notes on Partial Differential Equations - c Anthony Peirce. Not to be copied, used, or revised without explicit written permission from the copyright owner. 1 Lecture 21: The one dimensional
Work. Work and Energy Examples. Energy. To move an object we must do work Work is calculated as the force applied to the object through a distance or:
 Work To move an object we must do work Work is calculated as the force applied to the object through a distance or: W F( d) Work has the units Newton meters (N m) or Joules 1 Joule = 1 N m Energy Work
Work To move an object we must do work Work is calculated as the force applied to the object through a distance or: W F( d) Work has the units Newton meters (N m) or Joules 1 Joule = 1 N m Energy Work
Subject: Mathematics III Subject Code: Branch: B. Tech. all branches Semester: (3rd SEM) i) Dr. G. Pradhan (Coordinator) ii) Ms.
 Subject: Mathematics III Subject Code: BSCM1205 Branch: B. Tech. all branches Semester: (3 rd SEM) Lecture notes prepared by: i) Dr. G. Pradhan (Coordinator) Asst. Prof. in Mathematics College of Engineering
Subject: Mathematics III Subject Code: BSCM1205 Branch: B. Tech. all branches Semester: (3 rd SEM) Lecture notes prepared by: i) Dr. G. Pradhan (Coordinator) Asst. Prof. in Mathematics College of Engineering
Homework #4 Reminder Due Wed. 10/6
 Homework #4 Reminder Chap. 6 Concept: 36 Problems 14, 18 Chap. 8 Concept: 8, 12, 30, 34 Problems 2, 10 Due Wed. 10/6 Chapter 8: Wave Motion A wave is a sort of motion But unlike motion of particles A propagating
Homework #4 Reminder Chap. 6 Concept: 36 Problems 14, 18 Chap. 8 Concept: 8, 12, 30, 34 Problems 2, 10 Due Wed. 10/6 Chapter 8: Wave Motion A wave is a sort of motion But unlike motion of particles A propagating
Week 01 : Introduction. A usually formal statement of the equality or equivalence of mathematical or logical expressions
 1. What are partial differential equations. An equation: Week 01 : Introduction Marriam-Webster Online: A usually formal statement of the equality or equivalence of mathematical or logical expressions
1. What are partial differential equations. An equation: Week 01 : Introduction Marriam-Webster Online: A usually formal statement of the equality or equivalence of mathematical or logical expressions
The Particle in a Box
 Page 324 Lecture 17: Relation of Particle in a Box Eigenstates to Position and Momentum Eigenstates General Considerations on Bound States and Quantization Continuity Equation for Probability Date Given:
Page 324 Lecture 17: Relation of Particle in a Box Eigenstates to Position and Momentum Eigenstates General Considerations on Bound States and Quantization Continuity Equation for Probability Date Given:
Chapter 7: Trigonometric Equations and Identities
 Section 7. Solving Trigonometric Equations and Identities 5 Chapter 7: Trigonometric Equations and Identities In the last two chapters we have used basic definitions and relationships to simplify trigonometric
Section 7. Solving Trigonometric Equations and Identities 5 Chapter 7: Trigonometric Equations and Identities In the last two chapters we have used basic definitions and relationships to simplify trigonometric
Chapter 7: Trigonometric Equations and Identities
 Chapter 7: Trigonometric Equations and Identities In the last two chapters we have used basic definitions and relationships to simplify trigonometric expressions and equations. In this chapter we will
Chapter 7: Trigonometric Equations and Identities In the last two chapters we have used basic definitions and relationships to simplify trigonometric expressions and equations. In this chapter we will
COMP 546, Winter 2018 lecture 19 - sound 2
 Sound waves Last lecture we considered sound to be a pressure function I(X, Y, Z, t). However, sound is not just any function of those four variables. Rather, sound obeys the wave equation: 2 I(X, Y, Z,
Sound waves Last lecture we considered sound to be a pressure function I(X, Y, Z, t). However, sound is not just any function of those four variables. Rather, sound obeys the wave equation: 2 I(X, Y, Z,
Chapter 7: Trigonometric Equations and Identities
 Chapter 7: Trigonometric Equations and Identities In the last two chapters we have used basic definitions and relationships to simplify trigonometric expressions and equations. In this chapter we will
Chapter 7: Trigonometric Equations and Identities In the last two chapters we have used basic definitions and relationships to simplify trigonometric expressions and equations. In this chapter we will
f 1/ T T 1/ f Formulas Fs kx m T s 2 k l T p 2 g v f
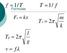 f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
f 1/T Formulas T 1/ f Fs kx Ts 2 m k Tp 2 l g v f What do the following all have in common? Swing, pendulum, vibrating string They all exhibit forms of periodic motion. Periodic Motion: When a vibration
Chapter 16 Waves in One Dimension
 Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
Chapter 16 Waves in One Dimension Slide 16-1 Reading Quiz 16.05 f = c Slide 16-2 Reading Quiz 16.06 Slide 16-3 Reading Quiz 16.07 Heavier portion looks like a fixed end, pulse is inverted on reflection.
LEARNING STATION III: WHAT OSCILLATES WITH LIGHT? 27
 LEARNING STATION III: WHAT OSCILLATES WITH LIGHT? 27 1 Mechanical waves 27 1.a Source of mechanical waves 27 1.b Medium needed? 27 1.c Propagation and displacement in the same direction or in a different
LEARNING STATION III: WHAT OSCILLATES WITH LIGHT? 27 1 Mechanical waves 27 1.a Source of mechanical waves 27 1.b Medium needed? 27 1.c Propagation and displacement in the same direction or in a different
PHYSICS 149: Lecture 22
 PHYSICS 149: Lecture 22 Chapter 11: Waves 11.1 Waves and Energy Transport 11.2 Transverse and Longitudinal Waves 11.3 Speed of Transverse Waves on a String 11.4 Periodic Waves Lecture 22 Purdue University,
PHYSICS 149: Lecture 22 Chapter 11: Waves 11.1 Waves and Energy Transport 11.2 Transverse and Longitudinal Waves 11.3 Speed of Transverse Waves on a String 11.4 Periodic Waves Lecture 22 Purdue University,
Lab 1: Damped, Driven Harmonic Oscillator
 1 Introduction Lab 1: Damped, Driven Harmonic Oscillator The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
1 Introduction Lab 1: Damped, Driven Harmonic Oscillator The purpose of this experiment is to study the resonant properties of a driven, damped harmonic oscillator. This type of motion is characteristic
