( ) :. : - 1. : - 2. : - 3. : - 4., - :. - :1 -.,M /M/1. :2 -. :* - 3.,M /M/ M, /M/c/, K M/M/c :4 - :. : - 1. : - 2.
|
|
|
- Oscar Francis
- 6 years ago
- Views:
Transcription
1 75 35
2 75 8 ' / ' ' * / 3 4 * 5 I 6 II 3 ' 4 5 * 6 7 / 8 * Hazard * 7 *8 *9
3 M/M/ *3 4 M/M/c/K M/M/c M/M/ 3
4 75 ' 8 4
5 75 / [] D ' D ' D T ' T T T [ T T T S { } D D T S T 8 5
6 75 / = = = Excel =3 3 % /3 7 7 =E E S S S S S E {95} S S E ~ 8 6
7 75 U r d Uform E ~ Uform 59 =3 U r /3 + S U U r r Excel 3 8 7
8 75 S
9 75 9 8? T T ' 8 9 /
10 75 8 ' ' ' 35 ' ' ' ' ' '
11 75 8 a b a b a a a a a a 3 A A A A 4 exx! x x e a b! c d
12 75? a a a f 7 f f f f f 3 f 3 f 3 f xf x dx d f x dx x f x ddx f x dxd x x x f lm g! f Srlg! e g 8 F x x { w w x} 8
13 75 lm F x x lm F x F x x F x x f x x x F x xf x x x x x F x f d x E xf x dx E x x x g Y=g Y Y Z Gamma/ / Z Y Y EY Eg g x f x dx E =3 g x x 8 3
14 75 Var E E E E? / / E F x dx E F E ' ' ' F ' ' ' E xf x dx f x dxd F d x M Ee = ' ' /!!! 8 4
15 75 = s L s Ee ' G E ' ' Y Y F Y x y x Y y F x x Y lm F x y y Y Y x y x Y y 8 5
16 75 Ideede ad decally dsrbued d d ' d F x x F x F x x F x F x d { S } S S S S S a b { b } a { a } b c a b a b a b Y Y c Z=+Y 8 6
17 75 [ Y ] Y [ Y ] [ Y ] Y Z Y [ Y ] Y Y Y Y ' / 3 Berull < > = q q = q = q = = = = = ~ B 4 osso osso? Z 8 7
18 75 Z e e e!!!!!!! e!?? Y M Ee Ee e Ee Ee M M Y Y Y Y Y / '? Z 5 M e 8 8
19 75 Z M M M e e e ' d S S lm E / S lm E S lm E S d lm F x F x S E Z Var Z 8 9
20 75 log! e osso d Var S Var S osso { } S E ES S S S S S / x / e dx / S e! e! d 8
21 75 m arg m m arg m m arg m m max arg m arg max F x x x x x x x F x F x x x x F x x x! C f x x f x I 8
22 75 C C { x x x x x } = ~ Uform A { } { }! A ' C { x x x x x} ' A ' A C A C A C A C A C A C ' A A C! A C! f x dx! f x I dx x A C A C 8
23 75 3 B A A B AB B AB=AB A B=A B A AB B A AB A B B A AB= AB { B } A A B B B B A B B A B A B A A B B A A B B '' ' ' ' ' ' '?'' ' ' ' ' ' ' ' ' B ' ' 5 T R 8 3
24 75 T R R T T R T T R T T ' 3 ' ' 3 ' 3 ' ' ' ' A 3 A E A 3 E A E A E A 3 E E A A E A A E A3 A3 * * * A E A E 3 * E A A 3 E 3 * E A3 A3 3 E 3 AB A B B 8 4
25 75 B B B B B B B B B B B B B B B B B B B B B B B B x y x Y y Y Y x y x Y y Y x y x Y x y y Y f Y x y f Y Y x y f y x y y x x x y Y y y x f Y x y x y f Y x y x fy y y x x x y Y y y x Y x x f Y x y f x 8 osso osso 8 5
26 75 e e e!!! B B B r r r r r r r r r r r r r r r r r Hyerg r r 8 6
27 75 = r x f x e I{[ } x I{[]} [] [ ] f x f x f f x I{[]} e dx I{[]} Uform f x x f x e I{[ } x f E[ Y y] x x y x Y E[ Y y] xf x y dx Y E[ Y] Y ' E[ Y]? m m d m E[ ] 8 7
28 75 m m E[ ] E[ ] E[ ] m E[ ] m E[ E[ Y ]] E[ ] E[ Y] Y f Y x y E[ E[ Y ]] E[ xf Y x y dx] E[ x dx] f y f x y Y x dxfy y dy xf Y x y dxdy xf x dx E fy y Var E[ ] E[ ] EE[[ Y ]] E[ E[ Y ]] Y 8 8
29 75 4 ' ' Y Y ' ' ' ' T Y ET E[ E[ T Y ]] E[ T Y ] Y E[ T Y ] Y E[ T ] q ET ET qet q ET q q ET d 8 9
30 75 S E[S] E[ S] E[ ] E[ E[ ]] E[ ] E[ ] E E E[ S] E[ E ] E E VarS Var S E[ S ] E[ S ] E[ S ] E[ ] E[ ] E[ S ] S [ ] [ ] [ [ ]] E S E E E [ ] [ ] [ ] E E E E[ 3 3 ] E[ ] E[ ] E[ ] E[ ] E[ ] E[ ] E[ ] E[ ]? E[ ] E[ ] E[ ] E[ ] E[ ] E[ ] E[ ] 8 3
31 75 [ ] [ [ ]] [ [ ] [ ] [ ] ] E S E E E E E E E[ ] E[ ] E[ ] E[ ] E[ ] E[ ] E[ ] Var E[ ] E[ ] Var S E[ S ] E[ ] E[ ] E[ ] Var E[ ] E[ ] E[ ] E[ ] E[ ] Var Var E[ ] S S M M S [ [ ]] M Ee E E e [ ] E e Ee Ee M M E M E e M M log [ ] [ M S ] log x x quc sor x C quc sor x x x x = = > S x S x S x S /
32 75 S S 58 7 S S = S 7 S S ' 5 S ' 8 S ' S ' S ' = S ' S 4 S ' 7 S ' 4578 ~ S M S M quc sor M M M M M = M M M M M M M M M M M M 8 3
33 75 M M + M M M M M M M M M M M M M M M M log log quc sor 8 33
34 75 q= I { } { } A A 5 [] E I A d d { } d d { } bs E Var q * d d d d d d d d d 8 34
35 75? E E E[ ] E E?Var Var Var Var Var q q A { } A = { } q { } lm q 8 35
36 75 q ' ' q q q q q q q q q q q q 3 q 3q 3 q 3q 3 3 q q q 8 36
37 q q q q q q q 4 q 6 q 4 q q ~ B m m m m m m 8 37
38 75 m l l m m l m { Z } Z Z Z Z m l m l Z Z Z Z { Z }?
39 q q q !!! 3 E[ 35] E[ 35] E3E E[ ] E[ ] E[ ] E E E 3E 5 3 E E 3E E q 3 5 3q m l m l l m l m
40 q q q ? m m l 8 4
41 75 { } d II { } 5 { } { T } d { } {} T T T T T T T { T } T { } { T } T m{ } 5 T 3 { 3 } 3 T3 m{ 3 }? { 3 } {567893} T 3 5? T 8 4
42 d? { T } 75 d T B { T } T Geom B T ~ T { } { } { } d { T } { } { T } ' { } ' { T } d { T } { T } { T } { } { T } { } { } { } { } T { } { T } { } { } { T } { T } { } { T } T 8 4
43 ' 75 FT T q F ' + { T } { } T q q { T } { } { Z } d Z { Y } Y Y { Z } d Z Y Z Y T Geom d { T } B B Geom B B ' T T ~ Geom { T } 8 43
44 75 ET E[ T T T T T ] ET E[ T T ] E[ T T ] [ ] E T Var T q q +r ' c Ec ce c c 5 c r ' c 5 c r c r c c 5 r 5 c ce T E c T c E T B T G E T T T T T T T T T T T T T T G E E E T E E E E E E E E T T T T T T T T T T ~ Geom G E q q q T T ' E T q G T q q c E T 8 44
45 75 T q c E c GT c G T c G T c c q q c c c q q q q r c r r 8 45
46 75 ' 8 46
47 75 E E ] E ] V VxV { } a b c d V V={3} E={33} =/ =/ 3=/ =/ 3= a 3 / / / /
48 75 E V V E ] E / / / / b c x 4 5 V { } '? = + E ] ½ ½ 3 3 ½
49 75 ½ 3 ' ' ½ ' ' 3 ' Geom/ ' 3 ' 3 ' ' ' Geom/ { } { }
50 75 / 3 {3} ? 5 3?3 V V ab 3 9 c { 3} V bc { } a b ab d d { } 8 5
51 75 { z z } d 3 b d a {} b a a b? 4 { } 5 8 5
52 75 q q q 6 d q q q q? 7 { } { } q= q { } I{ } q q 8 5
53 75 Ehrefes 8 { } { } { } = = { } = ? 9 Y ss ss 8 53
54 75 { D } S d Y s {s+ S} { s S } a a a a max a / D S D? D s S S D s D D s S Z d D Z f Z Z Brachg 8 54
55 75 d + Z {3} Z Z = I{} b d Z ~ B Z Z ~ B b b b b b b b b? ' {34} mod Y { Y } Y mod5 {34} Y Clar Z Z Z 8 55
56 75 Z { Z } { 3 45} 4 4? 5? 3 4 {34567} 8 56
57 Reflecg Radom Wal {3} 5 {3} 6 { 3} / / 8 57
58 75 ' 3 x 3 x x x x x a a a ab a a b a ba b b b m m m m m m m m m m 8 58
59 75 I I{ } AB x S S S S AB a b ChamaKolmogorov m m ' m m S? > ' = ' m m m S 8 59
60 75 m m m m m m m m m m m m m m m m m m m m m m m m S S S S S S l l l 3 b a a b 8 6
61 75 a b a b b a b b a b b a b b a b b a b b a b b a b b a a b a b b a b a b a b b a b a b b a b a b a b b b a b a b a b b b a b a b a b a b a b a b a b a b a b a b a b a a a b a b a b a b b a b a lm a b a b!!! 8 6
62 75 b b a b a b a b a b a b a b a b a b a a a b a b a b a b a b a b b a a b a b a b b b a b a b a b b a a a a b a b b a b b 8 6
63 75 4 E V V E R V V V V V V a b a V b V R V V V V={3} { } V 3 V R a b a V b V V 5 4 R 4 R a b a b a V b V E V V E a a E a V b a E a b E a b E b E a E E V E { a b a b V ame a ame b} / 3 [ a] V a V E [ a] { b V a b E} a b E b V a b c / a b / a b c 3 4 V V V E 8 63
64 75 I R l l m l l m m m S l m m m l l S l l ' l A A S A S A S \ A 8 64
65 a b a b a b 5 3 {}{34}{5} Iroduco o Algorhms by T H Corma C E Leserso ad R L Rves MIT ress ad McGrawHll 994 S
66 75 Or Ad +=+=+=+= f f m m ' 3 ½ f f f f f f Geomerc f f f f 8 66
67 75 I { } E[ ] E[ I ] E[ I ] { } { } m++ m I m m m m m m m 8 67
68 75 / T T { } T max{ T T T } {34567} {476} {5} {}{3} { } { } 7 {}{} 8 68
69 75 / 6 3!!!! e /! e 4 / /!! e e 4 QQQQ /? 4 / / 4 [/ / / =/ 8 69
70 75 / hg me T m{ } d f f T f T T T T? T m{ } osve recurre osve recurre { } E[ T ] E[ T ] 3 8 7
71 75 S S S S S S S S S S? E[ T ] 5 8 7
72 75? = = = = = 8 7
73 75 / / / =/ / 3 6 I { } Greaes Commo Dvsor I {46} 6 =5 Ehrefes
74 75 I { 46} I I QQQQ 6 I C C C d S C C Cd C 8 74
75
76 75 5 T m{ } f T f f T f E[ T ] f f f Geomerc f f f f I f f f f f f f f S \{ } f 7 { } 8 76
77 75 q q { } A A / T f m m f f + +? f f f? { } f f f qf f A A A f qf f A q f f qf f qf f qf q f f f f = = =q=/ q f f f f? f f f f f f 8 77
78 75 =q=/ f f c f f f f f f f f c f f c f f f f f f f f 5 5 5= =q=/ 5? f q f f f f d f f q d d? d d f f f q q q q q f f f d d d d f 8 78
79 75 q q q q f f f f f f f f q q q q q f f f f f q q q q q q q q q q f $ 5? $ $ f q 5 8 q m{ { } E[ ] 8 79
80 75 + q { } q q * 3 * 4 { } 8 8
81 75 = =5 q q q q 8 8
82 75 6 { T} '? lm E T T [ T ] T E T T E T lm E T w T T T T { } { } T T E T d T T T E lm T T T 8 8
83 75 r x { x x } S r S S r I { } r x x x x 3 r I {} c c r c 9 {5} {}{3} {476} 4 {476} {5} 8 83
84 75 r y {5} f {476} f{476} f{5} I {} x x x y y m m m f {5} m z {476} {5} x x xm zm z m m m {476} {476} {476} {5} {5} {5} {476}? 8 84
85 75 ' m { } m m d? S S S 8 85
86 75 / 7 S S S S S? S lm lm T m{ } E[ T ] 3 { x x } r S 4 r x 8 86
87 75 r I { } lm r r S lm I{ } e e
88 MATLAB >> =[ ] = >> ^ as = >> ^3 as = >> ^4 as = >> ^5 as = >> ^6 as = 8 88
89 >> ^7 as = >> ^8 as = >> ^9 as = lm ' r I {} r =3 {34} ? 8 89
90 { 3 4} 3 3 dealed balace codo S S S S S S S 4 S { 3 4}
91 MATLAB = = >> * as = >> sum as = 8 9
92
93 75 S lm QQQQ S r r lm r r S 4 QQQQ QQQQ E[ T ] 8 93
94
95 75 8 a b 3 b a a b 3 b a a a a b a b b a b b b a? a b b a a a b a lm a b b a b b a b b a b a a b a b a a b b 8 95
96 75 a a a b b a a b b=3 75% a=9 b a b ? 3 5? ' 3 S { 33 3} ' 8 96
97 ' /
98 A S A c A S \ A S { } QQQQ
99 75 Mea Tme Bewee Falures MTBF 5 6 QQQQ A c A a b Y I Y c A A b a c A 3 a c A A 4 b A c A
100 75 5 b c A A a = A c A c A {3 4} A {} c S A A
101 75 QQQQ QQQQ {34} S S S S T S S S S 5 S S S 5 S Reflecg Radom Wal 5 8
102 /
103 75 ' Z F Z 3 Z F Z 3 4 Z 3 F Z F Z Z F Z F Z 8 3
104 75 F Z EZ EZ F Z EZ F Z Z EZ F Z Z ~ Geom Z Z Z EZ Z 8 4
105 75 4 Hazard 8 5
106 75 ex x x f x e I x [ [ [ x x x F x e I x dx I x e x x F x F x e I x I x [ s s s s s / e e s s e s s Y s Y Y s Y s Y Y Y s F Y s F Y s F Y F Y x e Cx C g y Cy ' g s g s g F Y l l F Y s l F Y s l F Y l F Y y Cy C ' F Y Cx F Y x e C 8 6
107 75 / = G ~ ex G ] x x x e e dx e e x e e e e q e G x x x M Ee e e dx e d x x e x lm e x x E ~ ex x x x x x lm x x x e E x e dx x e e dx x E F x dx e dx dm E ' d x e 8 7
108 75 CV ' d M E '' ' d 3 Var E E Var CV E ' ' F x M x x x F x M ~ x F x F x e e M x ' ex Y MY Y M Y Y Y Y ~ ex ~ ex Y Y Y 8 8
109 75 f x y e I x e I y x Y y Y [ Y [ x<y xy Y ' x Y y f x y dydx e e dydx Y Y x y x x y x e e dydx e F Y x dx x Y y x Y x y x x e e dx e dx x Y x Y x Y x Y x Y Y ' Y Y x f x dx F x f x dx e e dx e dx Y x x Y x Y Y x x Y x Y x ~ ex U M U M U ~ ex U U U x e x x K x dx Kx ' ' 8 9
110 75 '! ' e d ' ~ gamma f x x e I x ~ gamma x [ ~ gamma ' f x x x I[] x ~ Bea u=s/x f x f x f x f s f x s ds f s f x s ds s s x s s x s s e x s e ds x x x x s x s e ds e s x s ds s x e ux x ux xdu u x x x xe u u du u x x e u u du u x s x e x ' ' ~ gamma s s s M e s e ds s e ds s s 8
111 75 M M M gamma ' T ~ gamma Erlag gamma ex ~ ex gamma d erlag x T [ f x x e I x! ET Var T 8
112 75 Hazard x G F x F x f x x M G f x Hazard Hazard r x f F x x Hazard ex r x e e x x ' x Hazard >x x x x x x x x x x x x x x x x x x x x x x x F x x x x x x f x x rx x F x x 8
113 75 x x x? r x ~ Uform f x F x x r x F F ' x x log g' g ' g x r x log F x' r s ds log F x F x e x r s ds x 8 3
114 75 / / QQQQ r x x Webull Webull = x 8 4
115 75 3 / { } / / h s] { } s s< 3 s s< 4 = 5 5 { } / { } { T } / { T } 8 5
116 75 su{ T } T T f{ } { } { T } { } { T } { } { } { } { } { } { } { }\{ } { } { T }\{ T } [ ] 8 6
117 75!!!! lm e!? ' +s +s
118 75 ] s s s / / oh f h lm h h oh f oh oh f h h lm lm lm h h h h h h f h h lm lm lm h h h h h oh oh oh f x f x f x x x x oh oh oh g x c f x c f x oh f f c f h f h lm c lm c h h h h oh c f f h g h f h f h lm lm lm h h h h h h oh oh oh ' 8 8
119 { [ } { [ } h h o h h o h s { [ } osso s s 3 3 ex T d 4 T su{ T } su{ T } h ' 8 9
120 75 s { [ } 3 osso s 4 E Cov s s s ~ oso s< h h o h o h h h o h ex ex erlag 3 34 s= 4 5 a osso a 6 covarace a osso a 7 Cov Cov Cov Cov s s s s s s s s Var s s h o h o h h h h h o h h o h d h QQQQ 8
121 h h h h h h h h h f f ' af f Ce a f f a c e e e a log f a c log f ' a f Ce C a f ' f a 3 f ' af g a e a e f ' a ae f a e g e a f ' a e g f as e g s ds a e QQQQ 8
122 75 h h h o h h h h o h h h o h lm h h h oh ' e e [+h [ [+h [ [+h [ { } h +h { h } { h } { h h } h 3 ' = c s e ce s e e c e ce s e! e! QQQQ s e s ds e e s s e e ds! e s ds e c e!! c 8
123 75 ~ oso T d ~ oso T { } { } T F e ss+] A s A A e ~ ex s A s A ex d T T ~ erlag F T e T! 8 3
124 75 d d f e e e e T d!! d! e e e e!!! '! ' ' e! 8 4
125 75 5 T T T T s s T s s s s s s s e e s s!! s e! <s T s s< T s T ~ Uform ' ' s s s T T ' s s T s T s f s s T T lm f s s lm su T T su T [ s s T [ s s T s T s s s s s A s s A 8 5
126 75 A s s s s!! e! e e e!! d d s s s s s s emal s s s T s T s T T cles Uform emal emal T C E T E T E T E E[ T ] U U T T Uform d E U EU 8 6
127 75 C E E ' Q QQQ M/G/ M/G/ QQQQ E d F x ' s s s F s [ ] QQQQ s] [s] s s s s s s ~ B 8 7
128 75 e s s s s s s s s s s e!!! s s s s!! e! s s 8 8
129 75 6 QQQQ osso Ex Erlag B Uform B Geom B HG DscreeUform s T T T T m T T 8 9
130 75 7 B s s s s B s s! e! e!!! e e!! 8 3
131 s s s s ' ' [ s s s s ~ osso s s ~ osso 4 s s s s ~ osso 3 7? QQQQ QQQQ 8 3
132 75 QQQQ QQQQ? 4 r 6 g Durre age 4 QQQQ 8 3
133 75 8 { } d { Y } { } Y { Y } 5 Y Y y oher Y S d Y { Y } E[ S] E[ Y ] E[ ] 8 33
134 75 Var S E[ ] Var Y Var E[ Y ] M S s M log MY s ' ~ oso E Var M s e s e E EY Var Var Y E[ Y ] E[ Y ] E[ Y ] E[ Y ] E[ Y ] Y log M s e M s e e M s y I Y y {} E[ Y ] E[ Y ] M s Ee e e ' sy s s Y Clar age 9 QQQQ 8 34
135 75 9 / ' { } h o h h o h h 3 h h +h oh m s ds ~ osso m m s m m s m s e! ~ osso m s m s m d { d } b 8 35
136 75 f x xe d= / d x ' d xe / d x e / d x / / d xe d x dx / d x x d d A / d d Ade Ade A e d f x e xe d / d x f e d e I b e / d e I[ d 3 / d b d 57 d 583 d 93/
137 M/G/ QQQQ Record Values QQQQ QQQQ 8 37
138
139 75 QQQQ s s s S { } s s u u s s s s s s s { } { } s { s } s { u u s} s+ s s u u s s {} e 8 39
140 75 e e e e ' Q Q q Q Geeraor Marx S S S S q S \{ } q Q? q 8 4
141 75 h o h h h q h o h h= q h o h q h h h lm h h q q h lm q h h h h h S \{ } h h S \{ } h lm lm lm h h h h h S \{ } h S \{ } q q q q s { H s} H? H? H s H s { H s } H s H s H H 8 4
142 75? H q H S Q { } q q < ' q ' 8 4
143 75 Q Q? q q S \{ } q q q q ' q q ' / / q S 8 43
144 75 T f{ } ' 8 44
145 75 ' ' ' ' ' ' Q S {} Q 8 45
146 75 QQQQ 3 QQQQQ + ' ' 4 ' ' 5 3 / S {3} Q 6 q
147 75! ex lm E[ T ] T E[ T T ] / / E[ T T ] E[ T ] E[ T ] E[ T ] E[ T ] E[ T ] E[ T T ] lm E[ T T ] lm E[ T ] lm E[ T ] QQQQ 7 QQQQ hase ye 8 QQQQ 8 47
148 75 Q ' 3 Q ' ' S s s s s s s S S S S s s s s s s s s s s s S s S ' h h S h h S 8 48
149 75 h h h S \{ } h h h S \{ } h lm h h S \{ } h lm h q h h h ' h h lm h h h S \{ } lm q h h S \{ } h lm h h ' q q S \{ } q ' q S ' Q S ' q S ' Q QQQQ ' 8 49
150 75 h h h S ' h h h h h S S \{ } S \{ } h h h h ' q q S \{ } ' q S ' Q S ' q S ' Q Durre boom age 66 QQQQ ex 8% ex %? 55 Q 8 5
151 ' q S * ' ' ' ' * c ' s ' s c ** ' *** ' h h' ' *** h ' h h' h log' h log' h s [] log h c 8 5
152 75 h Ke Ke? K K e *** e e 55 e! ' q S ' q q ' e ' e e!!! 8 5
153 75 e ' e e e e e e q Yule * e Yule e e ' q q q S ' * e e e e &&& e e e * e e e e &&&& e e e &&&& = &&& I!!! I e e 8 53
154 75 4 e lm { } r { } lm r s ds r S e? Q Q e S \{ } S q q 8 54
155 75 ' Q ' q S ' q S S S S S d d S d d d d q S S q S S S q S S ' 8 55
156 75 d ' d S S S q ' Q ' q S d q d S S S d q d S S S d d S S S S 8 56
157 75 3 Q / 3 / 3 S={3} / 3 / 3 / 4 / 4 / 4 / 4 3 3/ 8 4 / 8 / 8 Q S q q q q S \{ } q q S \{ } S \{ } q S \{ } S \{ } q q q S q 8 57
158 75 Q 7 Gray Code Gray Gray Dec Gray Bary Gray 5 Gray Gray 7 Gray Q Gray S { }
159 75 ' ' ' 3 ' ' ' ' 3 '
160 75 8 6
161 75 {} { } { } { } Q
162 75 ' Yule ex G Yule ' E[ ] e M E[ ] M M M e M M T M E[ ] E[ T s] f s ds T f s e T s 8 6
163 75 M E[ T s] f s ds E[ T s] f s ds T T s E[ T s] s s s< s s< M s M s s T M M s e ds f s ds? M s e ds e s M M s s e e e ds e e s e e ds e e [ e s e e e e e e e 8 63
164 75 { } lm / / 8 64
165 75 + R E[ T ] + R R R R + I I I + E[ T I ] E[ T I ] R R 8 65
166 75 R I R + + I I R E[ T ] EE[ T I ] E[ T I ] I E[ T I ] I R R R R R R R R R R R R R R 8 66
167 M/M/? hoss rouers ace Frs Come Frs Serve FCFS + +
168 75 Kc B A c B Kc K? c K / c B A AB A/B/c/K/ FCFS + Kedall oao A B c K A B { M D G} / M D M D G 8 68
169 75 d ex B= M A= M ' Kc x raffc esy ulzao q s s q s q q s s W q W Wq W W W x W W q q 8 69
170 75 d M/M/ ex M/M/ osso exµ M /M/? M/M/ M/M/ ~ erlag 8 7
171 75 d ex d ex x d M/M/ s q s q q s q s 8 7
172 75 s q s Wq W W q W q W W q W q M/M/ FIFO QQQQ 8 7
173 75 M/M/ QQQQ 3 x { } { x } { } D D/D/ / { } { } { x }? ' I [ \{}] d M/M/ ' ' ' A D s A max{ } D { s } 8 73
174 75 /?{ s } D D D { D D } x s x x x D max{ s x } D/D/ D D D A A D D A AD A D G G/G/ D/D/ { } { 435 4} { x } {3 } 8 74
175 75 { } { 435 4} { } { } QQQQ AD W W { s } lm s ds lm D lm lm W A W W 8 75
176 75 q W q + QQQQ W QQQQ 8 76
177 75 M/M/ M/M/c/K M/M/c 4 M/M/c c? c c c c c c max c max c QQQQ M/M/ M/M/c QQQQ QQQQ M/M/c/K K K max c 8 77
178 75 QQQQ QQQQ c! c c K c! c mgf QQQQ M/M/c/K M/M/c/c K=c c /! /! QQQQ c r / c c r=7 r ErlagCalc 6 loss c c c r c r / c! /! 8 78
179 75 /h//wwwcerscom 8 79
180
181 75 arcs ' 3 Tme Reversal Sho ose Uformzao QQQQ hasetye G / M / M / G / Jacso 8 8
182 75 3 Durre R Esseals of Sochasc rocesses Srger ew Yor 999 Taylor H ad Karl S Iroduco o Sochasc Modelg Academc ress ew Yor 984 Ross S Iroduco o robably Models Fourh Edo Academc ress Boso 989 Kular VG Modelg Aalyss Desg ad Corol of Sochasc Sysems Srger ew Yor 999 Clar E Iroduco o Sochasc rocesses recehall Eglewood Clffs ew Jersey 975 Ross S Sochasc rocesses Wley ew Yor 983 Karl S ad Taylor H A Frs Course Sochasc rocesses Secod Edo Academc ress ew Yor 975 orrs JR Marov Chas Cambrdge Uversy ress ew Yor 997 Resc S Adveures Sochasc rocesses Brhauser Boso 99 Kleroc L Queug Sysems Vol Theory Wley ew Yor 975 Gross D ad Harrs C Fudameals of Queug Theory Thrd Edo Wley
183 Ths docume was creaed wh WDF avalable a h//wwwwdfcom The uregsered verso of WDF s for evaluao or ocommercal use oly
8. Queueing systems lect08.ppt S Introduction to Teletraffic Theory - Fall
8. Queueg sysems lec8. S-38.45 - Iroduco o Teleraffc Theory - Fall 8. Queueg sysems Coes Refresher: Smle eleraffc model M/M/ server wag laces M/M/ servers wag laces 8. Queueg sysems Smle eleraffc model
Fault Tolerant Computing. Fault Tolerant Computing CS 530 Probabilistic methods: overview
Probably 1/19/ CS 53 Probablsc mehods: overvew Yashwa K. Malaya Colorado Sae Uversy 1 Probablsc Mehods: Overvew Cocree umbers presece of uceray Probably Dsjo eves Sascal depedece Radom varables ad dsrbuos
Parts Manual. EPIC II Critical Care Bed REF 2031
EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
6.041/6.431 Fall 2010 Quiz 2 Solutions
6.04/6.43: Probabilistic Systems Analysis (Fall 200) 6.04/6.43 Fall 200 Quiz 2 Solutions Problem. (80 points) In this problem: (i) X is a (continuous) uniform random variable on [0, 4]. (ii) Y is an exponential
1 Expectation of a continuously distributed random variable
OCTOBER 3, 204 LECTURE 9 EXPECTATION OF A CONTINUOUSLY DISTRIBUTED RANDOM VARIABLE, DISTRIBUTION FUNCTION AND CHANGE-OF-VARIABLE TECHNIQUES Expectation of a continuously distributed random variable Recall
Stat 366 A1 (Fall 2006) Midterm Solutions (October 23) page 1
Stat 366 A1 Fall 6) Midterm Solutions October 3) page 1 1. The opening prices per share Y 1 and Y measured in dollars) of two similar stocks are independent random variables, each with a density function
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Moment Generating Function
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
APPLIED MATHEMATICS. Introduction to Differential Equations APM2A10. Supplementary Test 1: 23/03/2016
APPLIED MATHEMATICS Introduction to Differential Equations APMA0 Supplementary Test : 3/03/06 Duration: 70 minutes Marks: 30 Assessor: Mr KD Anderson Moderator: Prof M Khumalo Instructions:. Answer all
EP2200 Queuing theory and teletraffic systems. 3rd lecture Markov chains Birth-death process - Poisson process. Viktoria Fodor KTH EES
EP Queung heory and eleraffc sysems 3rd lecure Marov chans Brh-deah rocess - Posson rocess Vora Fodor KTH EES Oulne for oday Marov rocesses Connuous-me Marov-chans Grah and marx reresenaon Transen and
Continuous r.v practice problems
Continuous r.v practice problems SDS 321 Intro to Probability and Statistics 1. (2+2+1+1 6 pts) The annual rainfall (in inches) in a certain region is normally distributed with mean 4 and standard deviation
HW4 : Bivariate Distributions (1) Solutions
STAT/MATH 395 A - PROBABILITY II UW Winter Quarter 7 Néhémy Lim HW4 : Bivariate Distributions () Solutions Problem. The joint probability mass function of X and Y is given by the following table : X Y
Properties of Random Variables
Properties of Random Variables 1 Definitions A discrete random variable is defined by a probability distribution that lists each possible outcome and the probability of obtaining that outcome If the random
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA
THE ROYAL STATISTICAL SOCIETY 4 EXAINATIONS SOLUTIONS GRADUATE DIPLOA PAPER I STATISTICAL THEORY & ETHODS The Societ provides these solutions to assist candidates preparing for the examinations in future
Random Variables (Continuous Case)
Chapter 6 Random Variables (Continuous Case) Thus far, we have purposely limited our consideration to random variables whose ranges are countable, or discrete. The reason for that is that distributions
Random Signals and Systems. Chapter 3. Jitendra K Tugnait. Department of Electrical & Computer Engineering. Auburn University.
Random Signals and Systems Chapter 3 Jitendra K Tugnait Professor Department of Electrical & Computer Engineering Auburn University Two Random Variables Previously, we only dealt with one random variable
Outline. Computer Networks: Theory, Modeling, and Analysis. Delay Models. Queuing Theory Framework. Delay Models. Little s Theorem
Oule Couer Newors: Theory, Modelg, ad Aalyss Guevara Noubr COM35, lecure 3 Delay Models Lle s Theore The M/M/ queug syse The M/G/ queug syse F, COM35 Couer Newors Lecure 3, F, COM35 Couer Newors Lecure
and ALiTO SOLO LOWELL, MICHIGAN, THURSDAY, AUGUST 9, 1928 First Results of the 1928 Nationwide Presidential Poll
E E XXX E Y! D 22 5 Q G Y G Y D G G q - YEE 24-? G Y E x - E Q- E 7// < D D D G E G D - 2 ; - j E ; (z ; 4 2 z 5 q z: G $7 z: $5 z: $3 E G DY G 9 928 54 Y! 8! GEG : : ; j: D - DY DY G z D zz!!!-! G E DDED
Outline. Queuing Theory Framework. Delay Models. Fundamentals of Computer Networking: Introduction to Queuing Theory. Delay Models.
Oule Fudaeals of Couer Neworg: Iroduco o ueug Theory eadg: Texboo chaer 3. Guevara Noubr CSG5, lecure 3 Delay Models Lle s Theore The M/M/ queug syse The M/G/ queug syse F3, CSG5 Fudaeals of Couer Neworg
P a g e 3 6 of R e p o r t P B 4 / 0 9
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
MATHEMATICS FOR ENGINEERS & SCIENTISTS 23
MATHEMATICS FOR ENGINEERS & SCIENTISTS 3.5. Second order linear O.D.E.s: non-homogeneous case.. We ll now consider non-homogeneous second order linear O.D.E.s. These are of the form a + by + c rx) for
Chapter 4 Multiple Random Variables
Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Model structure. Lecture Note #3 (Chap.6) Identification of time series model. ARMAX Models and Difference Equations
System Modeling and Identification Lecture ote #3 (Chap.6) CHBE 70 Korea University Prof. Dae Ryoo Yang Model structure ime series Multivariable time series x [ ] x x xm Multidimensional time series (temporal+spatial)
Joint Distributions. (a) Scalar multiplication: k = c d. (b) Product of two matrices: c d. (c) The transpose of a matrix:
Joint Distributions Joint Distributions A bivariate normal distribution generalizes the concept of normal distribution to bivariate random variables It requires a matrix formulation of quadratic forms,
THE ROYAL STATISTICAL SOCIETY 2016 EXAMINATIONS SOLUTIONS HIGHER CERTIFICATE MODULE 5
THE ROAL STATISTICAL SOCIET 6 EAMINATIONS SOLUTIONS HIGHER CERTIFICATE MODULE The Society is providing these solutions to assist candidates preparing for the examinations in 7. The solutions are intended
DIFFERENTIAL EQUATIONS
DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
Multivariate distributions
CHAPTER Multivariate distributions.. Introduction We want to discuss collections of random variables (X, X,..., X n ), which are known as random vectors. In the discrete case, we can define the density
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
EXAM. Exam #1. Math 3350 Summer II, July 21, 2000 ANSWERS
EXAM Exam #1 Math 3350 Summer II, 2000 July 21, 2000 ANSWERS i 100 pts. Problem 1. 1. In each part, find the general solution of the differential equation. dx = x2 e y We use the following sequence of
Ex. 1. Find the general solution for each of the following differential equations:
MATH 261.007 Instr. K. Ciesielski Spring 2010 NAME (print): SAMPLE TEST # 2 Solve the following exercises. Show your work. (No credit will be given for an answer with no supporting work shown.) Ex. 1.
Brownian Motion and Stochastic Calculus. Brownian Motion and Stochastic Calculus
Browa Moo Sochasc Calculus Xogzh Che Uversy of Hawa a Maoa earme of Mahemacs Seember, 8 Absrac Ths oe s abou oob decomoso he bascs of Suare egrable margales Coes oob-meyer ecomoso Suare Iegrable Margales
ECE 302 Division 2 Exam 2 Solutions, 11/4/2009.
NAME: ECE 32 Division 2 Exam 2 Solutions, /4/29. You will be required to show your student ID during the exam. This is a closed-book exam. A formula sheet is provided. No calculators are allowed. Total
Ordinary Differential Equations (ODEs)
Chapter 13 Ordinary Differential Equations (ODEs) We briefly review how to solve some of the most standard ODEs. 13.1 First Order Equations 13.1.1 Separable Equations A first-order ordinary differential
1 Solution to Problem 2.1
Solution to Problem 2. I incorrectly worked this exercise instead of 2.2, so I decided to include the solution anyway. a) We have X Y /3, which is a - function. It maps the interval, ) where X lives) onto
electronic reserve R regular reserve: required background reading for those without background in early China Course introduction 1/20
PHILOSOPHICAL MASTERS OF ANCIENT CHINA P T A W O: KJ 128 O : M 4-5; W 2-3 Hy 333 Spg 2004 C : TR 10:30-11:45 C : CUPR 203 Rq x p: T A C A Wy (Vg Bk 1938; Rp ) M DC L (Pg C Vkg P; Rp ) T C Wy V: T g Lz
Mathematics 426 Robert Gross Homework 9 Answers
Mathematics 4 Robert Gross Homework 9 Answers. Suppose that X is a normal random variable with mean µ and standard deviation σ. Suppose that PX > 9 PX
35H MPa Hydraulic Cylinder 3.5 MPa Hydraulic Cylinder 35H-3
- - - - ff ff - - - - - - B B BB f f f f f f f 6 96 f f f f f f f 6 f LF LZ f 6 MM f 9 P D RR DD M6 M6 M6 M. M. M. M. M. SL. E 6 6 9 ZB Z EE RC/ RC/ RC/ RC/ RC/ ZM 6 F FP 6 K KK M. M. M. M. M M M M f f
Lesson 3: Linear differential equations of the first order Solve each of the following differential equations by two methods.
Lesson 3: Linear differential equations of the first der Solve each of the following differential equations by two methods. Exercise 3.1. Solution. Method 1. It is clear that y + y = 3 e dx = e x is an
T h e C S E T I P r o j e c t
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
STAT 515 MIDTERM 2 EXAM November 14, 2018
STAT 55 MIDTERM 2 EXAM November 4, 28 NAME: Section Number: Instructor: In problems that require reasoning, algebraic calculation, or the use of your graphing calculator, it is not sufficient just to write
8. Queueing systems. Contents. Simple teletraffic model. Pure queueing system
8. Quug sysms Cos 8. Quug sysms Rfrshr: Sml lraffc modl Quug dscl M/M/ srvr wag lacs Alcao o ack lvl modllg of daa raffc M/M/ srvrs wag lacs lc8. S-38.45 Iroduco o Tlraffc Thory Srg 5 8. Quug sysms 8.
Chapter 2. Some Basic Probability Concepts. 2.1 Experiments, Outcomes and Random Variables
Chapter 2 Some Basic Probability Concepts 2.1 Experiments, Outcomes and Random Variables A random variable is a variable whose value is unknown until it is observed. The value of a random variable results
Ma 221 Final Exam Solutions 5/14/13
Ma 221 Final Exam Solutions 5/14/13 1. Solve (a) (8 pts) Solution: The equation is separable. dy dx exy y 1 y0 0 y 1e y dy e x dx y 1e y dy e x dx ye y e y dy e x dx ye y e y e y e x c The last step comes
Exercise: concepts from chapter 3
Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
Partial Solutions for h4/2014s: Sampling Distributions
27 Partial Solutions for h4/24s: Sampling Distributions ( Let X and X 2 be two independent random variables, each with the same probability distribution given as follows. f(x 2 e x/2, x (a Compute the
17.2 Nonhomogeneous Linear Equations. 27 September 2007
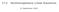17.2 Nonhomogeneous Linear Equations 27 September 2007 Nonhomogeneous Linear Equations The differential equation to be studied is of the form ay (x) + by (x) + cy(x) = G(x) (1) where a 0, b, c are given
14. Poisson Processes
4. Posso Processes I Lecure 4 we roduced Posso arrvals as he lmg behavor of Bomal radom varables. Refer o Posso approxmao of Bomal radom varables. From he dscusso here see 4-6-4-8 Lecure 4 " arrvals occur
Section 3.1 Homework Solutions. 1. y = 5, so dy dx = y = 3x, so dy dx = y = x 12, so dy. dx = 12x11. dx = 12x 13
Math 122 1. y = 5, so dx = 0 2. y = 3x, so dx = 3 3. y = x 12, so dx = 12x11 4. y = x 12, so dx = 12x 13 5. y = x 4/3, so dx = 4 3 x1/3 6. y = 8t 3, so = 24t2 7. y = 3t 4 2t 2, so = 12t3 4t 8. y = 5x +
trawhmmry ffimmf,f;wnt
r nsr rwry fff,f;wn My 26, $51 Swe, k "Te Srwberry Cp f e Vr,, c) [ re ers 6 (, r " * f rn ff e # s S,r,* )er*,3n*,.\ ) x 8 2 n v c e 6 r D r, } e ;s 1 :n..< Z r : 66 3 X f; 1r_ X r { j r Z r 1r 3r B s
DIFFERENTIAL EQUATIONS
DIFFERENTIAL EQUATIONS Basic Terminology A differential equation is an equation that contains an unknown function together with one or more of its derivatives. 1 Examples: 1. y = 2x + cos x 2. dy dt =
IS 709/809: Computational Methods in IS Research. Simple Markovian Queueing Model
IS 79/89: Comutatoal Methods IS Research Smle Marova Queueg Model Nrmalya Roy Deartmet of Iformato Systems Uversty of Marylad Baltmore Couty www.umbc.edu Queueg Theory Software QtsPlus software The software
1 Basic continuous random variable problems
Name M362K Final Here are problems concerning material from Chapters 5 and 6. To review the other chapters, look over previous practice sheets for the two exams, previous quizzes, previous homeworks and
180B Lecture Notes, W2011
Bruce K. Driver 180B Lecture Notes, W2011 January 11, 2011 File:180Lec.tex Contents Part 180B Notes 0 Course Notation List......................................................................................................................
Section 2 Notes. Elizabeth Stone and Charles Wang. January 15, Expectation and Conditional Expectation of a Random Variable.
Secto Notes Elzabeth Stoe ad Charles Wag Jauar 5, 9 Jot, Margal, ad Codtoal Probablt Useful Rules/Propertes. P ( x) P P ( x; ) or R f (x; ) d. P ( xj ) P (x; ) P ( ) 3. P ( x; ) P ( xj ) P ( ) 4. Baes
A L A BA M A L A W R E V IE W
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
MATH2715: Statistical Methods
MATH2715: Statistical Methods Exercises IV (based on lectures 7-8, work week 5, hand in lecture Mon 30 Oct) ALL questions count towards the continuous assessment for this module. Q1. If a random variable
2 (Statistics) Random variables
2 (Statistics) Random variables References: DeGroot and Schervish, chapters 3, 4 and 5; Stirzaker, chapters 4, 5 and 6 We will now study the main tools use for modeling experiments with unknown outcomes
Notes for Math 324, Part 19
48 Notes for Math 324, Part 9 Chapter 9 Multivariate distributions, covariance Often, we need to consider several random variables at the same time. We have a sample space S and r.v. s X, Y,..., which
18.01 Single Variable Calculus Fall 2006
MIT OpenCourseWare http://ocw.mit.edu 18.01 Single Variable Calculus Fall 2006 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Exam 4 Review 1. Trig substitution
The Mean Residual Lifetime of (n k + 1)-out-of-n Systems in Discrete Setting
Appled Mahemacs 4 5 466-477 Publshed Ole February 4 (hp//wwwscrporg/oural/am hp//dxdoorg/436/am45346 The Mea Resdual Lfeme of ( + -ou-of- Sysems Dscree Seg Maryam Torab Sahboom Deparme of Sascs Scece ad
ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA Errata
ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
Department of Mathematics UNIVERSITY OF OSLO. FORMULAS FOR STK4040 (version 1, September 12th, 2011) A - Vectors and matrices
Deartet of Matheatcs UNIVERSITY OF OSLO FORMULAS FOR STK4040 (verso Seteber th 0) A - Vectors ad atrces A) For a x atrx A ad a x atrx B we have ( AB) BA A) For osgular square atrces A ad B we have ( )
APPLICATIONS OF FD APPROXIMATIONS FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS
LECTURE 10 APPLICATIONS OF FD APPROXIMATIONS FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS Ordinary Differential Equations Initial Value Problems For Initial Value problems (IVP s), conditions are specified
dy dx dx = 7 1 x dx dy = 7 1 x dx e u du = 1 C = 0
1. = 6x = 6x = 6 x = 6 x x 2 y = 6 2 + C = 3x2 + C General solution: y = 3x 2 + C 3. = 7 x = 7 1 x = 7 1 x General solution: y = 7 ln x + C. = e.2x = e.2x = e.2x (u =.2x, du =.2) y = e u 1.2 du = 1 e u
Local Chapter. Mr raised the que stion of what is ad't. deliver the s, nnun. You are cor- c Mr 1 n d. "P**"' iropiie.
D D D? M G D Y M 2 99 M «4 \ & M? x q M M GM M \ M! 94 - G? \ M M q > G -? Y - M - - - z - > M Z >? - M» > M M - > G! /? - «\- - < x - M-! z - M M M \- - x 7 x GG q M _ ~ > M > # > > M - -
STA 256: Statistics and Probability I
Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. There are situations where one might be interested
Exam 1 Review: Questions and Answers. Part I. Finding solutions of a given differential equation.
Exam 1 Review: Questions and Answers Part I. Finding solutions of a given differential equation. 1. Find the real numbers r such that y = e x is a solution of y y 30y = 0. Answer: r = 6, 5 2. Find the
Math Spring Practice for the final Exam.
Math 4 - Spring 8 - Practice for the final Exam.. Let X, Y, Z be three independnet random variables uniformly distributed on [, ]. Let W := X + Y. Compute P(W t) for t. Honors: Compute the CDF function
STA 4321/5325 Solution to Homework 5 March 3, 2017
STA 4/55 Solution to Homework 5 March, 7. Suppose X is a RV with E(X and V (X 4. Find E(X +. By the formula, V (X E(X E (X E(X V (X + E (X. Therefore, in the current setting, E(X V (X + E (X 4 + 4 8. Therefore,
Chapter 4 Multiple Random Variables
Review for the previous lecture Definition: n-dimensional random vector, joint pmf (pdf), marginal pmf (pdf) Theorem: How to calculate marginal pmf (pdf) given joint pmf (pdf) Example: How to calculate
Introduction to First Order Equations Sections
A B I L E N E C H R I S T I A N U N I V E R S I T Y Department of Mathematics Introduction to First Order Equations Sections 2.1-2.3 Dr. John Ehrke Department of Mathematics Fall 2012 Course Goals The
MAS223 Statistical Inference and Modelling Exercises
MAS223 Statistical Inference and Modelling Exercises The exercises are grouped into sections, corresponding to chapters of the lecture notes Within each section exercises are divided into warm-up questions,
Problem Y is an exponential random variable with parameter λ = 0.2. Given the event A = {Y < 2},
ECE32 Spring 25 HW Solutions April 6, 25 Solutions to HW Note: Most of these solutions were generated by R. D. Yates and D. J. Goodman, the authors of our textbook. I have added comments in italics where
For a stochastic process {Y t : t = 0, ±1, ±2, ±3, }, the mean function is defined by (2.2.1) ± 2..., γ t,
CHAPTER 2 FUNDAMENTAL CONCEPTS This chapter describes the fundamental concepts in the theory of time series models. In particular, we introduce the concepts of stochastic processes, mean and covariance
Variance reduction. Michel Bierlaire. Transport and Mobility Laboratory. Variance reduction p. 1/18
Variance reduction p. 1/18 Variance reduction Michel Bierlaire michel.bierlaire@epfl.ch Transport and Mobility Laboratory Variance reduction p. 2/18 Example Use simulation to compute I = 1 0 e x dx We
FLAP M6.1 Introducing differential equations COPYRIGHT 1998 THE OPEN UNIVERSITY S570 V1.1
F1 (a) This equation is of first order and of first degree. It is a linear equation, since the dependent variable y and its derivative only appear raised to the first power, and there are no products of
th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)
![th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)](/thumbs/80/81319353.jpg "th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)")
1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
UCSD ECE153 Handout #27 Prof. Young-Han Kim Tuesday, May 6, Solutions to Homework Set #5 (Prepared by TA Fatemeh Arbabjolfaei)
UCSD ECE53 Handout #7 Prof. Young-Han Kim Tuesday, May 6, 4 Solutions to Homework Set #5 (Prepared by TA Fatemeh Arbabjolfaei). Neural net. Let Y = X + Z, where the signal X U[,] and noise Z N(,) are independent.
3 Operations on One R.V. - Expectation
0402344 Engineering Dept.-JUST. EE360 Signal Analysis-Electrical - Electrical Engineering Department. EE360-Random Signal Analysis-Electrical Engineering Dept.-JUST. EE360-Random Signal Analysis-Electrical
(a) x cos 3x dx We apply integration by parts. Take u = x, so that dv = cos 3x dx, v = 1 sin 3x, du = dx. Thus
Math 128 Midterm Examination 2 October 21, 28 Name 6 problems, 112 (oops) points. Instructions: Show all work partial credit will be given, and Answers without work are worth credit without points. You
AP Calculus BC - Problem Solving Drill 19: Parametric Functions and Polar Functions
AP Calculus BC - Problem Solving Drill 19: Parametric Functions and Polar Functions Question No. 1 of 10 Instructions: (1) Read the problem and answer choices carefully () Work the problems on paper as
Massachusetts Institute of Technology
6.4/6.43: Probabilistic Systems Analysis (Fall ) Recitation Solutions October 9,. cov(ax + b,y ) ρ(ax + b,y ) var(ax + b)(var(y )) E[(aX + b E[aX + b])(y E[Y ])] a var(x)var(y ) E[(aX + b ae[x] b)(y E[Y
MATH Topics in Applied Mathematics Lecture 2-6: Isomorphism. Linear independence (revisited).
MATH 311-504 Topics in Applied Mathematics Lecture 2-6: Isomorphism. Linear independence (revisited). Definition. A mapping f : V 1 V 2 is one-to-one if it maps different elements from V 1 to different
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
". :'=: "t',.4 :; :::-':7'- --,r. "c:"" --; : I :. \ 1 :;,'I ~,:-._._'.:.:1... ~~ \..,i ... ~.. ~--~ ( L ;...3L-. ' f.':... I. -.1;':'.
= 47 \ \ L 3L f \ / \ L \ \ j \ \ 6! \ j \ / w j / \ \ 4 / N L5 Dm94 O6zq 9 qmn j!!! j 3DLLE N f 3LLE Of ADL!N RALROAD ORAL OR AL AOAON N 5 5 D D 9 94 4 E ROL 2LL RLLAY RL AY 3 ER OLLL 832 876 8 76 L A
Chapter 4 Multiple Random Variables
Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
Upper Bounds of Dynamic Chromatic Number
Upper Bounds of Dynamic Chromatic Number Hong-Jian Lai, Bruce Montgomery and Hoifung Poon Department of Mathematics West Virginia University, Morgantown, WV 26506-6310 June 22, 2000 Abstract A proper vertex
Some Basic Probability Concepts. 2.1 Experiments, Outcomes and Random Variables
Some Basic Probability Cocepts 2. Experimets, Outcomes ad Radom Variables A radom variable is a variable whose value is ukow util it is observed. The value of a radom variable results from a experimet;
HW Solution 12 Due: Dec 2, 9:19 AM
ECS 315: Probability and Random Processes 2015/1 HW Solution 12 Due: Dec 2, 9:19 AM Lecturer: Prapun Suksompong, Ph.D. Problem 1. Let X E(3). (a) For each of the following function g(x). Indicate whether
Solving First Order PDEs
Solving Ryan C. Trinity University Partial Differential Equations Lecture 2 Solving the transport equation Goal: Determine every function u(x, t) that solves u t +v u x = 0, where v is a fixed constant.
Differential Equations, Math 315 Midterm 2 Solutions
Name: Section: Differential Equations, Math 35 Midterm 2 Solutions. A mass of 5 kg stretches a spring 0. m (meters). The mass is acted on by an external force of 0 sin(t/2)n (newtons) and moves in a medium
ENGI 4421 Joint Probability Distributions Page Joint Probability Distributions [Navidi sections 2.5 and 2.6; Devore sections
ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
Math 510 midterm 3 answers
Math 51 midterm 3 answers Problem 1 (1 pts) Suppose X and Y are independent exponential random variables both with parameter λ 1. Find the probability that Y < 7X. P (Y < 7X) 7x 7x f(x, y) dy dx e x e
106 70/140H-8 70/140H-8
7/H- 6 H 7/H- 7 H ffffff ff ff ff ff ff ff ff ff f f f f f f f f f f f ff f f f H 7/H- 7/H- H φφ φφ φφ φφ! H 1 7/H- 7/H- H 1 f f f f f f f f f f f f f f f f f f f f f f f f f f f f f ff ff ff ff φ φ φ
2. The volume of the solid of revolution generated by revolving the area bounded by the
IIT JAM Mathematical Statistics (MS) Solved Paper. A eigevector of the matrix M= ( ) is (a) ( ) (b) ( ) (c) ( ) (d) ( ) Solutio: (a) Eigevalue of M = ( ) is. x So, let x = ( y) be the eigevector. z (M
THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA
THE ROYAL STATISTICAL SOCIETY 3 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA PAPER I STATISTICAL THEORY & METHODS The Socety provdes these solutos to assst caddates preparg for the examatos future years ad
Solutions to Assignment #8 Math 501 1, Spring 2006 University of Utah
Solutions to Assignment #8 Math 5, Spring 26 University of Utah Problems:. A man and a woman agree to meet at a certain location at about 2:3 p.m. If the man arrives at a time uniformly distributed between
Real-Time Systems. Example: scheduling using EDF. Feasibility analysis for EDF. Example: scheduling using EDF
EDA/DIT6 Real-Tme Sysems, Chalmers/GU, 0/0 ecure # Updaed February, 0 Real-Tme Sysems Specfcao Problem: Assume a sysem wh asks accordg o he fgure below The mg properes of he asks are gve he able Ivesgae
MATH 2250 Final Exam Solutions
MATH 225 Final Exam Solutions Tuesday, April 29, 28, 6: 8:PM Write your name and ID number at the top of this page. Show all your work. You may refer to one double-sided sheet of notes during the exam