Dynamic Systems and Applications 13 (2004) PARTIAL DIFFERENTIATION ON TIME SCALES
|
|
|
- Drusilla Naomi Rice
- 6 years ago
- Views:
Transcription
1 Dynamic Systems and Applications 13 (2004) PARTIAL DIFFERENTIATION ON TIME SCALES MARTIN BOHNER AND GUSEIN SH GUSEINOV University of Missouri Rolla, Department of Mathematics and Statistics, Rolla, Missouri 65401, USA Atilim University, Department of Mathematics, Incek, Ankara, Turkey ABSTRACT In this paper a differential calculus for multivariable functions on time scales is presented Such a calculus can be used to develop a theory of partial dynamic equations on time scales in order to unify and extend the usual partial differential and partial difference equations AMS (MOS) Subject Classification 26B05, 39A10, 26B10 1 INTRODUCTION A time scale is an arbitrary nonempty closed subset of the real numbers The calculus of time scales was initiated by B Aulbach and S Hilger 4, 9] in order to create a theory that can unify discrete and continuous analysis For a treatment of the single variable calculus of time scales see 5,6,11] and the references given therein The present paper deals with the differential calculus for multivariable functions on time scales and intends to prepare an instrument for introducing and investigating partial dynamic equations on time scales Note that already two papers related to this subject appeared 2, 10] An integral calculus of multivariable functions on time scales will be given in forthcoming papers of the authors There are a number of differences between the calculus of one and of two variables The calculus of functions of three or more variables differs only slightly from that of two variables The study in this paper will be therefore limited largely to functions of two variables Also we mainly consider partial delta derivatives Partial nabla derivatives and combinations of partial delta and nabla derivatives can be investigated in a similar manner The paper is organized as follows In Section 2 we introduce partial delta and nabla derivatives for multivariable functions on time scales and offer several new concepts related to differentiability Section 3 deals with a geometric interpretation of delta differentiability Section 4 contains several useful mean value theorems for derivatives In Section 5 sufficient conditions to ensure differentiability of functions Received August 15, $1500 c Dynamic Publishers, Inc
2 352 MARTIN BOHNER AND GUSEIN SH GUSEINOV are provided In Section 6 we present sufficient conditions for equality of mixed partial delta derivatives Section 7 is devoted to the chain rule for multivariable functions on time scales, while Section 8 treats the concept of the directional derivative Finally, in Section 9, we study implicit functions on time scales 2 PARTIAL DERIVATIVES AND DIFFERENTIABILITY Let n N be fixed Further, for each i {1,, n} let T i denote a time scale, that is, T i is a nonempty closed subset of the real numbers R Let us set Λ n = T 1 T n = {t = (t 1,, t n ) : t i T i for all i {1,, n}} We call Λ n an n-dimensional time scale The set Λ n is a complete metric space with the metric d defined by ( n ) 1/2 d(t, s) = t i s i 2 for t, s Λ n i=1 Consequently, according to the well-known theory of general metric spaces, we have for Λ n the fundamental concepts such as open balls, neighbourhoods of points, open sets, closed sets, compact sets, and so on In particular, for a given number δ > 0, the δ-neigbourhood U δ (t 0 ) of a given point t 0 Λ n is the set of all points t Λ n such that d(t 0, t) < δ By a neigbourhood of a point t 0 Λ n is meant an arbitrary set in Λ n containing a δ-neighbourhood of the point t 0 Also we have for functions f : Λ n R the concepts of the limit, continuity, and properties of continuous functions on general complete metric spaces Our main task in this section is to introduce and investigate partial derivatives for functions f : Λ n R This proves to be possible due to the special structure of the metric space Λ n Let σ i and ρ i denote, respectively, the forward and backward jump operators in T i Remember that for u T i the forward jump operator σ i : T i T i is defined by σ i (u) = inf {v T i : v > u} and the backward jump operator ρ i : T i T i is defined by ρ i (u) = sup {v T i : v < u} In this definition we put σ i (max T i ) = max T i if T i has a finite maximum, and ρ i (min T i ) = min T i if T i has a finite minimum If σ i (u) > u, then we say that u is right-scattered (in T i ), while any u with ρ i (u) < u is called left-scattered (in T i ) Also, if u < max T i and σ i (u) = u, then u is called right-dense (in T i ), and if u > min T i and ρ i (u) = u, then u is called left-dense (in T i ) If T i has a leftscattered maximum M, then we define T κ i = T i \ {M}, otherwise T κ i = T i If T i has a right-scattered minimum m, then we define (T i ) κ = T i \ {m}, otherwise (T i ) κ = T i
3 t i T κ i PARTIAL DIFFERENTIATION ON TIME SCALES 353 Let f : Λ n R be a function The partial delta derivative of f with respect to is defined as the limit f(t 1,, t i 1, σ i (t i ), t i+1,, t n ) f(t 1,, t i 1, s i, t i+1,, t n ) lim s i t i σ i (t i ) s i s i σ i (t i ) provided that this limit exists as a finite number, and is denoted by any of the following symbols: f(t 1,, t n ) i t i, f(t) i t i, f i t i (t), f i t i (t) If f has partial derivatives f(t) 1,, f(t) nt n, then we can also consider their partial delta derivatives These are called second order partial delta derivatives We write 2 f(t) i t 2 i and 2 f(t) or f i i j t j i t i ] t i t i (t) and f i j (t) for the partial delta derivatives of f(t) i t i with respect to t i and with respect to t j, respectively Thus 2 f(t) i t 2 i = i t i ( ) f(t) i t i and 2 f(t) j t j i t i = j t j t i t j ( f(t) Higher order partial delta derivatives are similarly defined The partial nabla derivative of f with respect to t i (T i ) κ is defined as the limit i t i f(t 1,, t i 1, ρ i (t i ), t i+1,, t n ) f(t 1,, t i 1, s i, t i+1,, t n ) lim s i t i ρ i (t i ) s i s i ρ i (t i ) and denoted by f(t) i t i, provided that this limit exists as a finite number In an obvious way we can define higher order partial nabla derivatives and also mixed derivatives obtained by combining both delta and nabla differentiations such as, for instance, 2 f(t) i t i j t j or 3 f(t) i t 2 i jt j Definition 21 We say that a function f : Λ n R is completely delta differentiable at a point t 0 = (t 0 1,, t 0 n) T κ 1 T κ n if there exist numbers A 1,, A n independent of t = (t 1,, t n ) Λ n (but, in general, dependent on t 0 ) such that for all t U δ (t 0 ), (21) f(t 0 1,, t 0 n) f(t 1,, t n ) = n A i (t 0 i t i ) + i=1 and, for each j {1,, n} and all t U δ (t 0 ), ) n α i (t 0 i t i ) (22) f(t 0 1,, t 0 j 1, σ j (t 0 j), t 0 j+1,, t 0 n) f(t 1,, t j 1, t j, t j+1,, t n ) ] n ] n = A j σj (t 0 j) t j + A i (t 0 i t i ) + β jj σj (t 0 j) t j + β ij (t 0 i t i ), i=1 i j i=1 i=1 i j
4 354 MARTIN BOHNER AND GUSEIN SH GUSEINOV where δ is a sufficiently small positive number, U δ (t 0 ) is the δ-neighbourhood of t 0 in Λ n, α i = α i (t 0, t) and β ij = β ij (t 0, t) are defined on U δ (t 0 ) such that they are equal to zero at t = t 0 and such that lim α i(t 0, t) = 0 and lim β ij(t 0, t) = 0 for all i, j {1,, n} t t 0 t t 0 In the case T 1 = = T n = R, this definition coincides with the classical (total) differentiability of functions of n real variables (see, for example, 3, 12]) In the one-variable case, Definition 21 becomes the following: A function f : T R is called completely delta differentiable at a point t 0 T κ if there exists a number A such that (23) f(t 0 ) f(t) = A(t 0 t) + α(t 0 t) for all t U δ (t 0 ) and (24) f(σ(t 0 )) f(t) = A σ(t 0 ) t ] + β σ(t 0 ) t ] for all t U δ (t 0 ), where α = α(t 0, t) and β = β(t 0, t) are equal to zero at t = t 0 and lim α(t0, t) = 0 and lim β(t0, t) = 0 t t 0 t t 0 If t 0 is right-dense, then the conditions (23) and (24) coincide and are equivalent to the existence of a usual derivative of f at t 0, being equal to A If t 0 is right-scattered and left-dense, then (23) and (24) mean, respectively, that the function f has at t 0 a usual left-sided derivative and a delta derivative and that these derivatives coincide and are equal to A In this place we see a difference between the completely delta differentiability and delta differentiability, where the latter means, simply, the existence of a delta derivative This is why we use the term completely delta differentiable rather than delta differentiable Finally, if t 0 is right-scattered and left-scattered at the same time (ie, an isolated point), then the condition (23) disappears because both of its sides are zero independent of A and α (for sufficiently small δ, the neighbourhood U δ (t 0 ) consists of the single point t 0 ), and (24) means the existence (which holds, in this case) of a delta derivative of f at t 0, being equal to A In the two-variable case, Definition 21 becomes the following: A function f : T 1 T 2 R is completely delta differentiable at a point (t 0, s 0 ) T κ 1 T κ 2 if there exist numbers A 1 and A 2 such that (25) f(t 0, s 0 ) f(t, s) = A 1 (t 0 t) + A 2 (s 0 s) + α 1 (t 0 t) + α 2 (s 0 s) and (26) f(σ 1 (t 0 ), s 0 ) f(t, s) = A 1 σ1 (t 0 ) t ] + A 2 (s 0 s) + β 11 σ1 (t 0 ) t ] + β 12 (s 0 s),
5 PARTIAL DIFFERENTIATION ON TIME SCALES 355 (27) f(t 0, σ 2 (s 0 )) f(t, s) = A 1 (t 0 t) + A 2 σ2 (s 0 ) s ] + β 21 (t 0 t) + β 22 σ2 (s 0 ) s ] for all (t, s) U δ (t 0, s 0 ), where α i = α i (t 0, s 0 ; t, s) and β ij = β ij (t 0, s 0 ; t, s) are equal to zero at (t, s) = (t 0, s 0 ) and for i, j {1, 2} lim α i (t 0, s 0 ; t, s) = 0 and lim β ij (t 0, s 0 ; t, s) = 0 (t,s) (t 0,s 0 ) (t,s) (t 0,s 0 ) Note that in the case T 1 = T 2 = Z, the neighbourhood U δ (t 0, s 0 ) contains the single point (t 0, s 0 ) for δ < 1 Therefore in this case the condition (25) disappears while the conditions (26) and (27) hold with β ij = 0 and with and A 1 = f(t 0 + 1, s 0 ) f(t 0, s 0 ) = f(t0, s 0 ) A 2 = f(t 0, s 0 + 1) f(t 0, s 0 ) = f(t0, s 0 ) This shows that each function f : Z Z R is completely delta differentiable at every point It follows from Definition 21 that if the function f : Λ n R is completely delta differentiable at the point t 0 T κ 1 T κ n, then it is continuous at that point and has at t 0 the first order partial delta derivatives equal, respectively, to A 1,, A n : f(t 0 ) 1 = A 1,, f(t 0 ) n t n = A n The continuity of f at t 0 follows, in fact, from any one of (21) and (22) for some j {1,, n} Indeed, (21) obviously yields the continuity of f at t 0 Let now (22) hold for some j {1,, n} In the case σ j (t 0 j) = t 0 j, (22) immediately gives the continuity of f at t 0 Consider the case σ j (t 0 j) > t 0 j Except of f(t), each term in (22) has a limit as t t 0 Therefore f(t) also has a limit as t t 0, and passing to the limit we get f(t 0 1,, t 0 j 1, σ j (t 0 j), t 0 j+1,, t 0 n) lim t t 0 f(t) = A j Further, letting t = t 0 in (22), we obtain ] σj (t 0 j) t 0 j f(t 0 1,, t 0 j 1, σ j (t 0 j), t 0 j+1,, t 0 n) f(t 0 ) = A j σj (t 0 j) t 0 j] Comparing the last two relations gives lim f(t) = f(t0 ) t t 0 so that the continuity of f at t 0 is shown Next, setting in (22) t i = t 0 i for all i j and then dividing both sides by σ j (t 0 j) t j and passing to the limit as t j t 0 j, we arrive at f(t0 ) j t j = A j This also shows the uniqueness of the numbers A 1,, A n
6 356 MARTIN BOHNER AND GUSEIN SH GUSEINOV presented in (21), (22) Note also that due to the continuity of f at t 0 we get from (22) in the case σ j (t 0 j) > t 0 j the formula f(t 0 ) = f(t0 1,, t 0 j 1, σ j (t 0 j), t 0 j+1,, t 0 n) f(t 0 ) j t j σ j (t 0 j ) t0 j Remark 22 The conditions of the form (26) and (27) can be considered as natural in order to be able to prove the formulas A 1 = f(t0,s 0 ) and A t 2 = f(t0,s 0 ) 2 If we s assume f to be not dependent on t or on s, then we can see from (26) and (27) that the condition (23) for one-variable functions is necessary along with condition (24) Similarly we can see the necessity of condition (25) for two-variable functions by considering analogues of the conditions (26) and (27) for three variable functions Definition 23 We say that a function f : T 1 T 2 R is σ 1 -completely delta differentiable at a point (t 0, s 0 ) T κ 1 T κ 2 if it is completely delta differentiable at that point in the sense of conditions (25) (27) and moreover, along with the numbers A 1 and A 2 presented in (25) (27) there exists also a number B independent of (t, s) T 1 T 2 (but, generally, dependent on (t 0, s 0 )) such that (28) f(σ 1 (t 0 ), σ 2 (s 0 )) f(t, s) = A 1 σ1 (t 0 ) t ] + B σ 2 (s 0 ) s ] + γ 1 σ1 (t 0 ) t ] + γ 2 σ2 (s 0 ) s ] for all (t, s) V σ 1 (t 0, s 0 ), where V σ 1 (t 0, s 0 ) is a union of some neighbourhoods of the points (t 0, s 0 ) and (σ 1 (t 0 ), s 0 ), and the functions γ 1 = γ 1 (t 0, s 0 ; t, s) and γ 2 = γ 2 (t 0, s 0 ; s) are equal to zero for (t, s) = (t 0, s 0 ) and lim γ 1 (t 0, s 0 ; t, s) = 0 and lim γ 2(t 0, s 0 ; s) = 0 (t,s) (t 0,s 0 ) s s 0 Note that in (28) the function γ 2 depends only on the variable s Setting t = σ 1 (t 0 ) in (28) yields (here it is essential that γ 2 does not depend on t) B = f(σ 1(t 0 ), s 0 ) Definition 24 We say that a function f : T 1 T 2 R is σ 2 -completely delta differentiable at a point (t 0, s 0 ) T κ 1 T κ 2 if it is completely delta differentiable at that point in the sense of conditions (25) (27) and moreover, along with the numbers A 1 and A 2 presented in (25) (27) there exists also a number D independent of (t, s) T 1 T 2 (but, generally, dependent on (t 0, s 0 )) such that (29) f(σ 1 (t 0 ), σ 2 (s 0 )) f(t, s) = D σ 1 (t 0 ) t ] + A 2 σ2 (s 0 ) s ] + η 1 σ1 (t 0 ) t ] + η 2 σ2 (s 0 ) s ] for all (t, s) V σ 2 (t 0, s 0 ), where V σ 2 (t 0, s 0 ) is a union of some neighbourhoods of the points (t 0, s 0 ) and (t 0, σ 2 (s 0 )), and the functions η 1 = η 1 (t 0, s 0 ; t) and η 2 =
7 PARTIAL DIFFERENTIATION ON TIME SCALES 357 η 2 (t 0, s 0 ; t, s) are equal to zero for (t, s) = (t 0, s 0 ) and lim η 1(t 0, s 0 ; t) = 0 and lim η 2 (t 0, s 0 ; t, s) = 0 t t 0 (t,s) (t 0,s 0 ) Note that in (29) the function η 1 depends only on the variable t Setting s = σ 2 (s 0 ) in (29) yields D = f(t0, σ 2 (s 0 )) Concluding this section, let us give two simple examples Example 25 Let T = 0, 1] {2}, where 0, 1] is the real number interval Define the function f : T R by f(t) = t 2 for t 0, 1] and f(2) = 2 Then f (t) = 2t for t 0, 1) and f (1) = 1 We see that f (1 ) = 2 1 = f (1), and therefore the function f is not completely delta differentiable at the point t = 1 However, if we set f(2) = 3, then we have f (1) = 2 and f becomes completely delta differentiable at t = 1 Example 26 Let T 1 = 0, 1] {2} and T 2 = 0, 1], where 0, 1] is the real number interval Define the function f : T 1 T 2 R by f(t, s) = t 2 +s 2 for (t, s) 0, 1] 0, 1] and f(2, s) = 3 + s for s 0, 1] Then we have and f(t, s) f(t, s) = 2t for (t, s) 0, 1) 0, 1], = 2s for (t, s) 0, 1] 0, 1), f(1, s) f(2, s) = 2 + s s 2 for s 0, 1] = 1 2 s for s (0, 1) This function f is completely delta differentiable at the point (1, 0), but it is not σ 1 -completely delta differentiable at that point However, if we set f(2, s) = 3 + s for s 0, 1], say, then f becomes σ 1 -completely delta differentiable at the point (1, 0) 3 GEOMETRIC SENSE OF DIFFERENTIABILITY First we consider the geometric sense of complete delta differentiability in the case of single variable functions on time scales (see also 8]) Let T be a time scale with the forward jump operator σ and the delta differentiation operator Consider a real-valued continuous function (31) u = f(t) for t T Let Γ be the curve represented by the function (31), that is, the set of points {(t, f(t)) : t T} in the xy-plane Let t 0 be a fixed point in T κ Then P 0 = (t 0, f(t 0 )) is a point on Γ Definition 31 A line L 0 passing through the point P 0 is called the delta tangent line to the curve Γ at the point P 0 if
8 358 MARTIN BOHNER AND GUSEIN SH GUSEINOV (i) L 0 passes also through the point P σ 0 = (σ(t 0 ), f(σ(t 0 ))); (ii) if P 0 is not an isolated point of the curve Γ, then d(p, L 0 ) (32) lim P P 0 d(p, P 0 ) = 0, P P 0 where P is the moving point of the curve Γ, d(p, L 0 ) is the distance from the point P to the line L 0, and d(p, P σ 0 ) is the distance from the point P to the point P σ 0 Figure 31 T consists of two separate real number intervals Accordingly, the (time scale) curve Γ consists of two arcs of usual curves In order the curve Γ to have a delta tangent line L 0 at the point P 0, there must exist the usual left-sided tangent line to Γ at P 0 and, moreover, that line must pass through the point P0 σ u P P 0 P σ 0 0 t0 σ(t 0 ) Ḷ 0 t Theorem 32 If the function f is completely delta differentiable at the point t 0, then the curve represented by this function has the uniquely determined delta tangent line at the point P 0 = (t 0, f(t 0 )) specified by the equation (33) y f(t 0 ) = f (t 0 )(x t 0 ), where (x, y) is the current point of the line Proof Let f be a completely delta differentiable function at a point t 0 T κ, Γ be the curve represented by this function, and L 0 be the line described by equation (33) Let us show that L 0 passes also through the point P0 σ Indeed, if σ(t 0 ) = t 0, then
9 P σ 0 PARTIAL DIFFERENTIATION ON TIME SCALES 359 = P 0 and the statement is true Let now σ(t 0 ) > t 0 Substituting the coordinates (σ(t 0 ), f(σ(t 0 ))) of the point P σ 0 into equation (33), we get f(σ(t 0 )) f(t 0 ) = f (t 0 ) σ(t 0 ) t 0], which is obviously true by virtue of the continuity of f at t 0 Now we check condition (32) Assume that P 0 is not an isolated point of the curve Γ (note that if P 0 is an isolated point of Γ, then from P P 0 we get P = P 0 and the left-hand side of (32) becomes meaningless) The variable point P Γ has the coordinates (t, f(t)) As is known from analytic geometry, the distance of the point P from the line L 0 with equation (33) is expressed by the formula d(p, L 0 ) = 1 M f(t) f(t 0 ) f (t 0 ) ( t t 0), where M = 1 + f (t 0 )] 2 Hence, by the differentiability condition (23) in which we have A = f (t 0 ) due to the other differentiability condition (24), Next, Therefore d(p, L 0 ) = 1 M d(p, P 0 ) = α(t t 0 ) = 1 M α t t 0 (t t 0 ) 2 + f(t) f(t 0 )] 2 t t 0 d(p, L 0 ) d(p, P 0 ) 1 M α 0 as P P 0 Thus we have proved that the line specified by equation (33) is the delta tangent line to Γ at the point P 0 Now we must show that there are no other delta tangent lines to Γ at the point P 0 distinct from L 0 If P 0 P σ 0, then the delta tangent line (provided it exists) is unique as it passes through the distinct points P 0 and P σ 0 Let now P 0 = P σ 0 so that P 0 is nonisolated Suppose that there is a delta tangent line L to Γ at the point P 0 described by an equation (34) a(x t 0 ) b y f(t 0 ) ] = 0 with a 2 + b 2 = 1 Let P = (t, f(t)) be a variable point on Γ Using equation (34), we have d(p, L) = a ( t t 0 ) b f(t) f(t 0 ) ] Hence, by the differentiability condition (23) with A = f (t 0 ), the latter being a result of the condition (24), d(p, L) = a b f (t 0 ) + α ] t t 0
10 360 MARTIN BOHNER AND GUSEIN SH GUSEINOV Next, by the same differentiability condition, d(p, P 0 ) = (t t 0 ) 2 + f(t) f(t 0 )] 2 = (t t 0 ) 2 + f (t 0 ) + α] 2 (t t 0 ) 2 = 1 + f (t 0 ) + α] 2 t t 0 So we have d(p, L) d(p, P 0 ) = a b f (t 0 ) + α ] 1 + f (t 0 ) + α] 2 Passing here to the limit as t t 0 and taking into account that the left-hand side (by the definition of delta tangent line) and α tend to zero, we obtain a bf (t 0 ) = 0 We now see that b 0 for if otherwise, we would have a = b = 0 Hence the line L is described by equation (33) Remark 33 If P 0 is an isolated point of the curve Γ (hence P 0 P σ 0 ), then there exists a delta tangent line at the point P 0 to the curve Γ that coincides with the unique line through the points P 0 and P σ 0 Remark 34 If P 0 is not an isolated point of the curve Γ and if Γ has a delta tangent line at the point P 0, then the line P P 0, where P Γ (and P P 0 ), approaches this tangent line as P P 0 Conversely, if the line P P 0 approaches as P P 0 some line L 0 passing through the point P σ 0, then this limiting line is a delta tangent line at P 0 For the proof it is sufficient to note that if ϕ is the angle between the lines L 0 and P P 0, then (see Figure 31) d(p, L 0 ) d(p, P 0 ) = sin ϕ Passing now to the two-variable case, let us consider the surface S represented by a real-valued continuous function u = f(t, s) defined on T 1 T 2, that is, the set of points {(t, s, f(t, s)) : (t, s) T 1 T 2 } in the xyz-space Let (t 0, s 0 ) be a fixed point in T κ 1 T κ 2 Definition 35 A plane Ω 0 passing through the point P 0 = (t 0, s 0, f(t 0, s 0 )) is called the delta tangent plane to the surface S at the point P 0 if (i) Ω 0 passes also through the points P σ 1 0 = (σ 1 (t 0 ), s 0, f(σ 1 (t 0 ), s 0 )) and P σ 2 0 = (t 0, σ 2 (s 0 ), f(t 0, σ 2 (s 0 ))); (ii) if P 0 is not an isolated point of the surface S, then d(p, Ω 0 ) (35) lim P P 0 d(p, P 0 ) = 0, P P 0
11 PARTIAL DIFFERENTIATION ON TIME SCALES 361 where P is the moving point of the surface S, d(p, Ω 0 ) is the distance from the point P to the plane Ω 0, and d(p, P 0 ) is the distance of the point P from the point P 0 Figure 32 Each of T 1 and T 2 consists of a real number interval and a separate point Accordingly, the (time scale) surface S consists of one piece of a usual surface, two arcs of usual curves and one separate point In order the surface S to have a delta tangent plane Ω 0 at the point P 0, there must exist the usual left-sided tangent plane to S at P 0 and, moreover, that plane must pass through both points P σ 1 0 and P σ 2 0 u P Ω 0 P 0 P σ 2 P σ t 0 σ 1 (t 0 ) t s0 σ 2(s 0 ) s Theorem 36 If the function f is completely delta differentiable at the point (t 0, s 0 ), then the surface represented by this function has the uniquely determined delta tangent plane at the point P 0 = (t 0, s 0, f(t 0, s 0 )) specified by the equation (36) z f(t 0, s 0 ) = f(t0, s 0 ) where (x, y, z) is the current point of the plane (x t 0 ) + f(t0, s 0 ) (y s 0 ),
12 362 MARTIN BOHNER AND GUSEIN SH GUSEINOV Proof Let f be a completely delta differentiable function at a point (t 0, s 0 ) T κ 1 T κ 2, S be the surface represented by this function, and Ω 0 be the plane described by equation (36) Let us show that Ω 0 passes also through the point P σ 1 0 Indeed, if σ 1 (t 0 ) = t 0, then P σ 1 0 = P 0 and the statement is true Let now σ 1 (t 0 ) > t 0 Substituting the coordinates (σ 1 (t 0 ), s 0, f(σ 1 (t 0 ), s 0 )) of the point P σ 1 0 into equation (36), we get f(σ 1 (t 0 ), s 0 ) f(t 0, s 0 ) = f(t0, s 0 ) σ1 (t 0 ) t 0], which is obviously true due to the continuity of f at (t 0, s 0 ) Similarly we can see that Ω 0 passes also through the point P σ 2 0 Now we check (35) Assume that P 0 is not an isolated point of the surface S The variable point P S has the coordinates (t, s, f(t, s)) As is known from analytic geometry, the distance between P and Ω 0 with equation (36) is expressed by the formula d(p, Ω 0 ) = 1 N f(t, s) f(t0, s 0 ) f(t0, s 0 ) (t t 0 ) f(t0, s 0 ) (s s 0 ), where ] f(t0, s N = ] ) f(t0, s ) Hence, by the differentiability condition (25) in which A 1 = f(t0,s 0 ) and A t 2 = f(t0,s 0 ) due to the other differentiability conditions (26) and (27), d(p, Ω 0 ) = 1 α1 (t t 0 ) + α 2 (s s 0 ) N 1 α1 2 + α 2 N 2 (t t0 ) 2 + (s s 0 ) 2 Next, d(p, P 0 ) = (t t 0 ) 2 + (s s 0 ) 2 + f(t, s) f(t 0, s 0 )] 2 (t t 0 ) 2 + (s s 0 ) 2 Therefore d(p, Ω 0 ) d(p, P 0 ) 1 α1 2 + α2 2 0 as P P 0 N Thus we have proved that the plane specified by equation (36) is the delta tangent plane to S at the point P 0 Now we must show that there are no other delta tangent planes to S at the point P 0 distinct from Ω 0 If σ 1 (t 0 ) > t 0 and σ 2 (s 0 ) > s 0 at the same time, the points P 0, P σ 1 0, and P σ 2 0 are pairwise distinct In this case the delta tangent plane (provided it exists) is unique as it passes through the three distinct points P 0, P σ 1 0, and P σ 2 0 Further we have to consider the remaining possible cases Suppose that there is a delta tangent plane Ω to S at the point P 0 described by an equation (37) a(x t 0 ) + b(y s 0 ) c z f(t 0, s 0 ) ] = 0 with a 2 + b 2 + c 2 = 1
13 PARTIAL DIFFERENTIATION ON TIME SCALES 363 Let P = (t, s, f(t, s)) be a variable point on S Using equation (37), we have d(p, Ω) = a ( t t 0 ) + b(s s 0 ) c f(t, s) f(t 0, s 0 ) ] Hence, by the differentiability condition (26) in which A 1 = f(t0,s 0 ) and A 2 = f(t0,s 0 ), the latter being a result of the conditions (26) and (27), d(p, Ω) = a c(a1 + α 1 )] (t t 0 ) + b c(a 2 + α 2 )] (s s 0 ) Next, by the same differentiability condition, d(p, P 0 ) = (t t 0 ) 2 + (s s 0 ) 2 + f(t, s) f(t 0, s 0 )] 2 = (t t 0 ) 2 + (s s 0 ) 2 + (A 1 + α 1 )(t t 0 ) + (A 2 + α 2 )(s s 0 )] 2 So we have (38) d(p, Ω) d(p, P 0 ) = a c(a 1 + α 1 )] (t t 0 ) + b c(a 2 + α 2 )] (s s 0 ) (t t 0 ) 2 + (s s 0 ) 2 + (A 1 + α 1 )(t t 0 ) + (A 2 + α 2 )(s s 0 )] 2 Now we discuss the remaining possible cases (a) Let σ 1 (t 0 ) = t 0 and σ 2 (s 0 ) = s 0 By our assumption, the left-hand side of (38) tends to zero as (t, s) (t 0, s 0 ), that is, as P P 0 On putting s = s 0 in (38), dividing in the right-hand side the numerator and denominator by t t 0, and passing then to the limit as t t 0, we get (39) a ca 1 = 0, that is, a c f(t0, s 0 ) Similarly, putting t = t 0 in (38), cancelling s s 0, and passing then to the limit as s s 0, we obtain (310) b ca 2 = 0, that is, b c f(t0, s 0 ) We see that c 0 because, if otherwise, we would have a = b = c = 0 Hence the plane Ω is described by equation (36) = 0 = 0 (b) Let now σ 1 (t 0 ) = t 0 and σ 2 (s 0 ) > s 0 In this case we obtain (39) from (38) as in case (a) However, now we can, in general, not get (310) from (38) as in case (a) because the point s 0 may be isolated in T 2, and therefore for all points (t, s) in a sufficiently small neighbourhood of (t 0, s 0 ) we may have s = s 0 (and hence we cannot divide by s s 0 in order to pass then to the limit as s s 0 ) We proceed as follows Since by definition of the delta tangent plane, the plane Ω must also pass through the point P σ 2 0, we also have the equation a(x t 0 ) + b y σ 2 (s 0 ) ] c z f(t 0, σ 2 (s 0 )) ] = 0 for the same plane Ω Using this equation, we obtain d(p, Ω) = a(t t 0 ) + b s σ 2 (s 0 ) ] c f(t, s) f(t 0, σ 2 (s 0 )) ]
14 364 MARTIN BOHNER AND GUSEIN SH GUSEINOV Hence, by the differentiability condition (27), we get Therefore d(p, Ω) d(p, P 0 ) = d(p, Ω) = a c(a1 + β 21 )] (t t 0 ) + b c(a 2 + β 22 )] σ 2 (s 0 ) s ] a c(a 1 + β 21 )] (t t 0 ) + b c(a 2 + β 22 )] σ 2 (s 0 ) s] (t t 0 ) 2 + (s s 0 ) 2 + (A 1 + α 1 )(t t 0 ) + (A 2 + α 2 )(s s 0 )] 2 Setting here s = s 0 and taking into account (39) proved in the considered case, we obtain d(p, Ω) d(p, P 0 ) s=s 0 Passing here to the limit as t t 0, we see that = cβ 21(t t 0 ) + b c(a 2 + β 22 )] σ 2 (s 0 ) s 0 ] t t (A 1 + α 1 ) 2 b ca 2 = 0, that is, b c f(t0, s 0 ) because, if otherwise, the right-hand side would tend to infinity Further, the proof is completed as in case (a) (c) Finally, suppose σ 1 (t 0 ) > t 0 and σ 2 (s 0 ) = s 0 In this case the proof is analogous to that in case (b) and uses the equation (Ω also passes through P σ 1 0 ) = 0 a x σ 1 (t 0 ) ] + b(y s 0 ) c z f(σ 1 (t 0 ), s 0 ) ] = 0 and the differentiability condition (26) Remark 37 If P σ 1 0 P 0 and P σ 2 0 P 0 (hence also P σ 1 0 P σ 2 0 ) at the same time and if there is a delta tangent plane at the point P 0 to the surface S, then it coincides with the unique plane through the three points P 0, P σ 1 0, and P σ MEAN VALUE THEOREMS First we present mean value results in the single variable case (see 7] or 6, Chapter 1]) that will be used to obtain mean value results in the multivariable case They will also be used below in Sections 5, 6, and 9 Let T be a time scale and a, b T with a < b Further, let f : T R be a function Below all intervals are time scales intervals Theorem 41 Suppose that f is continuous on a, b] and has a delta derivative at each point of a, b) If f(a) = f(b), then there exist points ξ, ξ a, b) such that f (ξ ) 0 f (ξ) Proof Since the function f is continuous on the compact set a, b], f assumes its minimum m and its maximum M Therefore there exist ξ, ξ a, b] such that m = f(ξ) and M = f(ξ ) Since f(a) = f(b), we may assume that ξ, ξ a, b) It is not difficult to see that f (ξ ) 0 and f (ξ) 0
15 PARTIAL DIFFERENTIATION ON TIME SCALES 365 Theorem 42 (Mean Value Theorem) Suppose that f is a continuous function on a, b] and has a delta derivative at each point of a, b) Then there exist ξ, ξ a, b) such that (41) f (ξ )(b a) f(b) f(a) f (ξ)(b a) Proof Consider the function ϕ defined on a, b] by ϕ(t) = f(t) f(a) f(b) f(a) (t a) b a Clearly ϕ is continuous on a, b] and has a delta derivative at each point of a, b) Also ϕ(a) = ϕ(b) = 0 Therefore by Theorem 41 there exist ξ, ξ a, b) such that Hence, taking into account that ϕ (ξ ) 0 ϕ (ξ) ϕ (t) = f (t) we arrive at the statement of the theorem f(b) f(a), b a Corollary 43 Let f be a continuous function on a, b] that has a delta derivative at each point of a, b) If f (t) = 0 for all t a, b), then f is a constant function on a, b] Corollary 44 Let f be a continuous function on a, b] that has a delta derivative at each point of a, b) Then f is increasing, decreasing, nondecreasing, and nonincreasing on a, b] if f (t) > 0, f (t) < 0, f (t) 0, and f (t) 0 for all t a, b), respectively Above in Theorem 42 we assumed that a < b We can remove that restriction as follows If a = b, then we may assume that (41) is true as all three parts of the inequalities (41) become zero in this case independent of ξ and ξ Further, we always can rewrite (41), multiplying it by 1, in the form f (ξ)(a b) f(a) f(b) f (ξ )(a b) These considerations allow us to state the following result Theorem 45 Let a and b be two arbitrary points in T and let us set α = min{a, b} and β = max{a, b} Let, further, f be a continuous function on α, β] that has a delta derivative at each point of α, β) Then there exist ξ, ξ α, β) such that f (ξ )(a b) f(a) f(b) f (ξ)(a b) Passing now to the two-variable case, we consider functions f : T 1 T 2 R of the variables (t, s) T 1 T 2
16 366 MARTIN BOHNER AND GUSEIN SH GUSEINOV Theorem 46 (Mean Value Theorem) Let (a 1, a 2 ) and (b 1, b 2 ) be any two points in T 1 T 2 and let us set α i = min{a i, b i } and β i = max{a i, b i } for i {1, 2} Let, further, f be a continuous function on α 1, β 1 ] α 2, β 2 ] T 1 T 2 that has first order partial delta derivatives f(t,a 2) for each t α t 1, β 1 ) and f(b 1,s) 2 for each s s α 2, β 2 ) Then there exist ξ, ξ α 1, β 1 ) and η, η α 2, β 2 ) such that (42) f(ξ, a 2 ) (a 1 b 1 ) + f(b 1, η ) (a 2 b 2 ) f(a 1, a 2 ) f(b 1, b 2 ) f(ξ, a 2) (a 1 b 1 ) + f(b 1, η) (a 2 b 2 ) Also, if f has first order partial derivatives f(t,b 2) for each t α t 1, β 1 ) and f(a 1,s) for each s α 2, β 2 ), then there exist τ, τ α 1, β 1 ) and θ, θ α 2, β 2 ) such that (43) f(τ, b 2 ) (a 1 b 1 ) + f(b 1, θ ) (a 2 b 2 ) f(a 1, a 2 ) f(b 1, b 2 ) f(τ, b 2) (a 1 b 1 ) + f(a 1, θ) (a 2 b 2 ) Proof To prove (42) we consider the difference (44) f(a 1, a 2 ) f(b 1, b 2 ) = f(a 1, a 2 ) f(b 1, a 2 )] + f(b 1, a 2 ) f(b 1, b 2 )] By Theorem 45 there exist ξ, ξ α 1, β 1 ) and η, η α 2, β 2 ) such that and f(ξ, a 2 ) f(b 1, η ) (a 1 b 1 ) f(a 1, a 2 ) f(b 1, a 2 ) f(ξ, a 2) (a 1 b 1 ) (a 2 b 2 ) f(b 1, a 2 ) f(b 1, b 2 ) f(b 1, η) (a 2 b 2 ) Adding these inequalities side by side and taking into account (44), we obtain (42) Using the relation f(a 1, a 2 ) f(b 1, b 2 ) = f(a 1, b 2 ) f(b 1, b 2 )] + f(a 1, a 2 ) f(a 1, b 2 )], the inequalities (43) can be proved similarly From Theorem 46 we get the following corollary Corollary 47 Let f be a continuous function on T 1 T 2 that has first order partial derivatives f(t,s) and f(t,s) t 2 for (t, s) T κ s 1 T 2 and (t, s) T 1 T κ 2, respectively If these derivatives are identically zero, then f is a constant function on T 1 T 2 Note that the statement of Corollary 47 can be obtained also from Corollary 43
17 PARTIAL DIFFERENTIATION ON TIME SCALES SUFFICIENT CONDITIONS FOR DIFFERENTIABILITY The existence of all partial delta derivatives (even in the single variable time scales case) is in general not sufficient for the completely delta differentiability The next theorem gives sufficient conditions for the completely delta differentiability Theorem 51 Let a function f : T 1 T 2 R be continuous and have first order partial delta derivatives f(t,s) and f(t,s) t 2 in some δ-neighbourhood U s δ (t 0, s 0 ) of the point (t 0, s 0 ) T κ 1 T κ 2 If these derivatives are continuous at the point (t 0, s 0 ), then f is completely delta differentiable at (t 0, s 0 ) Proof For better clearness of the proof we first consider the single variable case So, let f : T R be a function that has a delta derivative f (t) in some δ-neighbourhood U δ (t 0 ) of the point t 0 T κ (note that, in contrast to the multivariable case, in the single variable case existence of the derivative at a point implies continuity of the function at that point) The relation (24) with A = f (t 0 ) follows immediately from the definition of the delta derivative (51) f(σ(t 0 )) f(t) = f (t 0 ) σ(t 0 ) t ] + β σ(t 0 ) t ], where β = β(t 0, t) and β 0 as t t 0 In order to prove (23), we consider all possible cases separately (i) If the point t 0 is isolated in T, then (23) is satisfied independent of A and α, since in this case U δ (t 0 ) consists of the single point t 0 for sufficiently small δ > 0 (ii) Let t 0 be right-dense Regardless whether t 0 is left-scattered or left-dense, we have in this case σ(t 0 ) = t 0 and (51) coincides with (23) (iii) Finally, let t 0 be left-dense and right-scattered Then for sufficiently small δ > 0, any point t U δ (t 0 ) \ {t 0 } must satisfy t < t 0 Applying Theorem 45, we obtain f (ξ )(t 0 t) f(t 0 ) f(t) f (ξ)(t 0 t), where ξ, ξ t, t 0 ) Since ξ t 0 and ξ t 0 as t t 0, we get from the latter inequalities by the assumed continuity of the delta derivative Therefore f(t 0 ) f(t) lim t t 0 t 0 t f(t 0 ) f(t) t 0 t = f (t 0 ) = f (t 0 ) + α, where α = α(t 0, t) and α 0 as t t 0 Consequently, in the considered case we obtain (23) with A = f (t 0 ) as well
18 368 MARTIN BOHNER AND GUSEIN SH GUSEINOV Now we consider the two-variable case as it is stated in the theorem To prove (25), we take the difference (52) f(t 0, s 0 ) f(t, s) = f(t 0, s 0 ) f(t, s 0 ) ] + f(t, s 0 ) f(t, s) ] By the one-variable case considered above, we have (53) f(t 0, s 0 ) f(t, s 0 ) = f(t0, s 0 ) (t 0 t) + α 1 (t 0 t) for (t, s 0 ) U δ (t 0, s 0 ), where α 1 = α 1 (t 0, s 0 ; t) and α 1 0 as t t 0 Further, applying the one-variable mean value result, Theorem 45, for fixed t and variable s, we have (54) f(t, ξ ) (s 0 s) f(t, s 0 ) f(t, s) f(t, ξ) (s0 s), where ξ, ξ α, β) and α = min{s 0, s}, β = max{s 0, s} Since ξ s 0 and ξ s 0 as s s 0, by the assumed continuity of the partial delta derivatives at (t 0, s 0 ) we have f(t, ξ ) lim (t,s) (t 0,s 0 ) Therefore from (54) we obtain f(t, ξ) = lim (t,s) (t 0,s 0 ) = f(t0, s 0 ) (55) f(t, s 0 ) f(t, s) = f(t0, s 0 ) (s 0 s) + α 2 (s 0 s), where α 2 = α 2 (t 0, s 0 ; t, s) and α 2 0 as (t, s) (t 0, s 0 ) Substituting (53) and (55) in (52), we get a relation of the form (25) with A 1 = f(t0,s 0 ) and A t 2 = f(t0,s 0 ) 2 To s prove (26) we take the difference (56) f(σ 1 (t 0 ), s 0 ) f(t, s) = f(σ 1 (t 0 ), s 0 ) f(t, s 0 ) ] + f(t, s 0 ) f(t, s) ] By the definition of the partial delta derivative we have (57) f(σ 1 (t 0 ), s 0 ) f(t, s 0 ) = f(t0, s 0 ) σ1 (t 0 ) t ] + β 11 σ1 (t 0 ) t ], where β 11 = β 11 (t 0, s 0 ; t) and β 11 0 as t t 0 Now substituting (57) and (55) into (56), we obtain a relation of the form (26) with A 1 = f(t0,s 0 ) and A t 2 = f(t0,s 0 ) 2 s The equality (27) can be proved similarly by considering the difference f(t 0, σ 2 (s 0 )) f(t, s) = f(t 0, s) f(t, s) ] + f(t 0, σ 2 (s 0 )) f(t 0, s) ] The proof is complete The next theorem presents sufficient conditions for σ 1 -completely delta differentiability Theorem 52 Let f : T 1 T 2 R be a continuous function that has the partial derivatives f(t,s) and f(t,s) t 2 in a union of some neighbourhoods of the points s (t 0, s 0 ) T κ 1 T κ 2 and (σ 1 (t 0 ), s 0 ) If these derivatives are continuous at the point (t 0, s 0 ) and, moreover, f(σ 1(t 0 ),s) 2 is continuous at s = s 0, then f is σ s 1 -completely delta differentiable at (t 0, s 0 )
19 PARTIAL DIFFERENTIATION ON TIME SCALES 369 Proof It follows from Theorem 51 that f is completely delta differentiable at (t 0, s 0 ) It remains to prove (28) To this end consider the difference (58) f(σ 1 (t 0 ), σ 2 (s 0 )) f(t, s) = f(σ 1 (t 0 ), s) f(t, s) ] + f(σ 1 (t 0 ), σ 2 (s 0 )) f(σ 1 (t 0 ), s) ] Applying the one-variable mean value theorem, Theorem 45, for fixed s and variable t, we have f(ξ, s) σ1 (t 0 ) t ] f(σ 1 (t 0 ), s) f(t, s) f(ξ, s) σ1 (t 0 ) t ], where ξ, ξ α, β) and α = min{σ 1 (t 0 ), t}, β = max{σ 1 (t 0 ), t} Hence, since ξ t 0 and ξ t 0 as t t 0, by the assumed continuity of the partial delta derivative f(t,s) at (t 0, s 0 ), we obtain (59) f(σ 1 (t 0 ), s) f(t, s) = f(t0, s 0 ) σ1 (t 0 ) t ] + γ 1 σ1 (t 0 ) t ], where γ 1 = γ 1 (t 0, s 0 ; t, s) and γ 1 0 as (t, s) (t 0, s 0 ) Further, by the definition of the partial delta derivative, we have (510) f(σ 1 (t 0 ), σ 2 (s 0 )) f(σ 1 (t 0 ), s) = f(σ 1(t 0 ), s) σ2 (s 0 ) s ] + γ 2 σ2 (s 0 ) s ], where γ 2 = γ 2 (t 0, s 0 ; s) and γ 2 0 as s s 0 Now substituting (59) and (510) into (58) and taking into account the continuity of f(σ 1(t 0 ),s) 2 at s = s 0, we get a relation s of the form (28) with A 1 = f(t0,s 0 ) and B = f(σ 1(t 0 ),s 0 ) t 2 s The next theorem can be proved similarly as Theorem 52 by considering the difference f(σ 1 (t 0 ), σ 2 (s 0 )) f(t, s) = f(σ 1 (t 0 ), σ 2 (s 0 )) f(t, σ 2 (s 0 )) ] + f(t, σ 2 (s 0 )) f(t, s) ] Theorem 53 Let f : T 1 T 2 R be a continuous function that has the partial derivatives f(t,s) and f(t,s) t 2 in a union of some neighbourhoods of the points (t 0, s 0 ) s T κ 1 T κ 2 and (t 0, σ 2 (s 0 )) If these derivatives are continuous at the point (t 0, s 0 ), and, moreover, f(t,σ 2(s 0 )) is continuous at t = t 0, then f is σ t 2 -completely delta differentiable at (t 0, s 0 ) 6 EQUALITY OF MIXED PARTIAL DERIVATIVES The next theorem gives us a sufficient condition for the independence of mixed partial delta derivatives of the order of differentiation
20 370 MARTIN BOHNER AND GUSEIN SH GUSEINOV Theorem 61 Let a function f : T 1 T 2 R have the mixed partial delta derivatives 2 f(t,s) and 2 f(t,s) in some neighbourhood of the point (t 0, s 0 ) T κ t 1 T κ 2 If these derivatives are continuous at the point (t 0, s 0 ), then Proof Consider the function 2 f(t 0, s 0 ) = 2 f(t 0, s 0 ) Φ(t, s) = f(σ 1 (t 0 ), σ 2 (s 0 )) f(σ 1 (t 0 ), s) f(t, σ 2 (s 0 )) + f(t, s), where (t, s) T 1 T 2 Setting we can write ϕ(t) = f(t, σ 2 (s 0 )) f(t, s), Φ(t, s) = ϕ(σ 1 (t 0 )) ϕ(t) Therefore, applying the mean value theorem, Theorem 45, we have ϕ (ξ ) σ 1 (t 0 ) t ] Φ(t, s) ϕ (ξ) σ 1 (t 0 ) t ], where ξ, ξ α, β) and α = min{t, σ 1 (t 0 )}, β = max{t, σ 1 (t 0 )} That is, ] f(ξ, σ 2 (s 0 )) f(ξ, s) σ1 (t 0 ) t ] Φ(t, s) ] f(ξ, σ2 (s 0 )) f(ξ, s) σ1 (t 0 ) t ] Hence and f(ξ, σ 2 (s 0 )) f(ξ, σ 2 (s 0 )) f(ξ, s) f(ξ, s) Φ(t, s) σ 1 (t 0 ) t f(ξ, σ 2(s 0 )) f(ξ, s) Φ(t, s) σ 1 (t 0 ) t f(ξ, σ 2 (s 0 )) f(ξ, s) if t < σ 1 (t 0 ) if t > σ 1 (t 0 ) Further, again by the same mean value result, Theorem 45, there exist η, η and θ, θ in the interval γ, δ), where γ = min{s, σ 2 (s 0 )}, δ = max{s, σ 2 (s 0 )}, such that and 2 f(ξ, η ) 2 f(ξ, θ ) σ2 (s 0 ) s ] f(ξ, σ 2(s 0 )) σ2 (s 0 ) s ] f(ξ, σ 2 (s 0 )) f(ξ, s) f(ξ, s) 2 f(ξ, η) 2 f(ξ, θ) σ2 (s 0 ) s ] σ2 (s 0 ) s ] From the above four inequalities, by the assumed continuity of 2 f(t,s), we conclude t that Φ(t, s) (61) lim (t,s) (t 0,s 0 ) σ 1 (t 0 ) t] σ 2 (s 0 ) s] = 2 f(t 0, s 0 ) t σ 1 (t 0 ), s σ 2 (s 0 )
21 PARTIAL DIFFERENTIATION ON TIME SCALES 371 Similarly, using the expression of Φ(t, s) in the form Φ(t, s) = ψ(σ 2 (s 0 )) ψ(s), where ψ(s) = f(σ 1 (t 0 ), s) f(t, s), and the continuity of 2 f(t,s) 2, we can prove the equality s Φ(t, s) (62) lim (t,s) (t 0,s 0 ) σ 1 (t 0 ) t] σ 2 (s 0 ) s] = 2 f(t 0, s 0 ) t σ 1 (t 0 ), s σ 2 (s 0 ) Now, the left-hand sides of (61) and (62) are the same Consequently, their righthand sides must be equal to each other This completes the proof 7 THE CHAIN RULE The chain rule for one-variable functions on time scales has been presented in 1] and 5, Chapter 1] To get an extension to two-variable functions on time scales we start with a time scale T Denote its forward jump operator by σ and its delta differentiation operator by Let, further, two functions be given Let us set ϕ : T R and ψ : T R ϕ(t) = T 1 and ψ(t) = T 2 We will assume that T 1 and T 2 are time scales Denote by σ 1, and σ 2, 2 the forward jump operators and delta operators for T 1 and T 2, respectively Take a point ξ 0 T κ and put We will also assume that t 0 = ϕ(ξ 0 ) and s 0 = ψ(ξ 0 ) (71) ϕ(σ(ξ 0 )) = σ 1 (ϕ(ξ 0 )) and ψ(σ(ξ 0 )) = σ 2 (ψ(ξ 0 )) Under the above assumptions let a function f : T 1 T 2 R be given Theorem 71 Let the function f be σ 1 -completely delta differentiable at the point (t 0, s 0 ) If the functions ϕ and ψ have delta derivatives at the point ξ 0, then the composite function (72) F (ξ) = f(ϕ(ξ), ψ(ξ)) for ξ T has a delta derivative at that point which is expressed by the formula (73) F (ξ 0 ) = f(t0, s 0 ) ϕ (ξ 0 ) + f(σ 1(t 0 ), s 0 ) ψ (ξ 0 )
22 372 MARTIN BOHNER AND GUSEIN SH GUSEINOV Proof Using (71) and (28) with A 1 = f(t0,s 0 ) and B = f(σ 1(t 0 ),s 0 ) t 2, we have s F (σ(ξ 0 )) F (ξ) = f(ϕ(σ(ξ 0 )), ψ(σ(ξ 0 ))) f(ϕ(ξ), ψ(ξ)) = f(σ 1 (ϕ(ξ 0 )), σ 2 (ψ(ξ 0 ))) f(ϕ(ξ), ψ(ξ)) = f(ϕ(ξ0 ), ψ(ξ 0 )) σ1 (ϕ(ξ 0 )) ϕ(ξ) ] + f(σ 1(ϕ(ξ 0 )), ψ(ξ 0 )) +γ 1 σ1 (ϕ(ξ 0 )) ϕ(ξ) ] + γ 2 σ2 (ψ(ξ 0 )) ψ(ξ) ] = f(t0, s 0 ) ϕ(σ(ξ 0 )) ϕ(ξ) ] + f(σ 1(t 0 ), s 0 ) +γ 1 ϕ(σ(ξ 0 )) ϕ(ξ) ] + γ 2 ψ(σ(ξ 0 )) ψ(ξ) ] ψ(σ(ξ 0 )) ψ(ξ) ] σ2 (ψ(ξ 0 )) ψ(ξ) ] Dividing both sides of this equality by σ(ξ 0 ) ξ and passing then to the limit as ξ ξ 0, we get the formula (73) because ξ ξ 0 implies γ 1 0 and γ 2 0 The next theorem can be proved similarly to Theorem 71 by using (29) Theorem 72 Let the function f be σ 2 -completely delta differentiable at the point (t 0, s 0 ) If the functions ϕ and ψ have delta derivatives at the point ξ 0, then the composite function F defined by (72) has the delta derivative F (ξ 0 ) which is expressed by the formula F (ξ 0 ) = f(t0, σ 2 (s 0 )) ϕ (ξ 0 ) + f(t0, s 0 ) ψ (ξ 0 ) Remark 73 One or both of the functions ϕ and ψ may be constant In that case one or both of T 1 and T 2 will be a single point time scale For a single point time scale T 1 = {t 1 } we assume that σ 1 (t 1 ) = t 1 and for each function g : T 1 R we assume that g (t 1 ) = 0 Let now two time scales T (1) and T (2) be given Denote their forward jump operators and delta differentiation operators by σ (1), (1) and σ (2), (2), respectively Let, further, two functions ϕ : T (1) T (2) R and ψ : T (1) T (2) R of two variables (ξ, η) T (1) T (2), and a fixed point (ξ 0, η 0 ) T κ (1) Tκ (2) Let us set be given T 1 = T 1 (η 0 ) = ϕ(t (1), η 0 ) and T 2 = T 2 (ξ 0 ) = ψ(ξ 0, T (2) ) and t 0 = ϕ(ξ 0, η 0 ) and s 0 = ψ(ξ 0, η 0 ) We will assume that T 1 and T 2 are time scales Denote their forward jump operators and delta differentiation operators by σ 1, and σ 2, 2, respectively We will also assume (74) ϕ(σ (1) (ξ 0 ), η 0 ) = σ 1 (ϕ(ξ 0, η 0 )), ψ(σ (1) (ξ 0 ), η 0 ) = σ 2 (ψ(ξ 0, η 0 ))
23 PARTIAL DIFFERENTIATION ON TIME SCALES 373 and (75) ϕ(ξ 0, σ (2) (η 0 )) = σ 1 (ϕ(ξ 0, η 0 )), ψ(ξ 0, σ (2) (η 0 )) = σ 2 (ψ(ξ 0, η 0 )) Under the above conditions let a function f : T 1 T 2 R of two variables (t, s) T 1 T 2 be given Theorem 74 Let the function f be σ 1 -completely delta differentiable at the point (t 0, s 0 ) If the functions ϕ and ψ have first order partial delta derivatives at the point (ξ 0, η 0 ), then the composite function (76) F (ξ, η) = f(ϕ(ξ, η), ψ(ξ, η)) for (ξ, η) T (1) T (2) has first order partial delta derivatives at (ξ 0, η 0 ) which are expressed by the formulas (77) and (78) F (ξ 0, η 0 ) (1) ξ F (ξ 0, η 0 ) (2) η = f(t0, s 0 ) ϕ(ξ 0, η 0 ) (1) ξ = f(t0, s 0 ) ϕ(ξ 0, η 0 ) (2) η + f(σ 1(t 0 ), s 0 ) ψ(ξ 0, η 0 ) (1) ξ + f(σ 1(t 0 ), s 0 ) ψ(ξ 0, η 0 ) (2) η Proof Using (74) and (28) with A 1 = f(t0,s 0 ) and B = f(σ 1(t 0 ),s 0 ) t 2, we have s F (σ (1) (ξ 0 ), η 0 ) F (ξ, η 0 ) = f(ϕ(σ (1) (ξ 0 ), η 0 ), ψ(σ (1) (ξ 0 ), η 0 )) f(ϕ(ξ, η 0 ), ψ(ξ, η 0 )) = f(σ 1 (ϕ(ξ 0, η 0 )), σ 2 (ψ(ξ 0, η 0 ))) f(ϕ(ξ, η 0 ), ψ(ξ, η 0 )) = f(ϕ(ξ0, η 0 ), ψ(ξ 0, η 0 )) σ1 (ϕ(ξ 0, η 0 )) ϕ(ξ, η 0 ) ] + f(σ 1(ϕ(ξ 0, η 0 )), ψ(ξ 0, η 0 )) σ2 (ψ(ξ 0, η 0 )) ψ(ξ, η 0 ) ] +γ 1 σ1 (ϕ(ξ 0, η 0 )) ϕ(ξ, η 0 ) ] + γ 2 σ2 (ψ(ξ 0, η 0 )) ψ(ξ, η 0 ) ] = f(t0, s 0 ) + f(σ 1(t 0 ), s 0 ) ϕ(σ(1) (ξ 0 ), η 0 ) ϕ(ξ, η 0 ) ] ψ(σ(1) (ξ 0 ), η 0 ) ψ(ξ, η 0 ) ] +γ 1 ϕ(σ(1) (ξ 0 ), η 0 ) ϕ(ξ, η 0 ) ] + γ 2 ψ(σ(1) (ξ 0 ), η 0 ) ψ(ξ, η 0 ) ] On dividing both sides of this equality by σ (1) (ξ 0 ) ξ and passing to the limit as ξ ξ 0, we get the formula (77) because ξ ξ 0 implies γ 1 0 and γ 2 0
24 374 MARTIN BOHNER AND GUSEIN SH GUSEINOV Similarly, using (75) and (28), we obtain F (ξ 0, σ (2) (η 0 )) F (ξ 0, η) = f(ϕ(ξ 0, σ (2) (η 0 )), ψ(ξ 0, σ (2) (η 0 ))) f(ϕ(ξ 0, η), ψ(ξ 0, η)) = f(σ 1 (ϕ(ξ 0, η 0 )), σ 2 (ψ(ξ 0, η 0 ))) f(ϕ(ξ 0, η), ψ(ξ 0, η)) = f(ϕ(ξ0, η 0 ), ψ(ξ 0, η 0 )) σ1 (ϕ(ξ 0, η 0 )) ϕ(ξ 0, η) ] + f(σ 1(ϕ(ξ 0, η 0 )), ψ(ξ 0, η 0 )) σ2 (ψ(ξ 0, η 0 )) ψ(ξ 0, η) ] +γ 1 σ1 (ϕ(ξ 0, η 0 )) ϕ(ξ 0, η) ] + γ 2 σ2 (ψ(ξ 0, η 0 )) ψ(ξ 0, η) ] = f(t0, s 0 ) + f(σ 1(t 0 ), s 0 ) ϕ(ξ 0, σ (2) (η 0 )) ϕ(ξ 0, η) ] ψ(ξ 0, σ (2) (η 0 )) ψ(ξ 0, η) ] +γ 1 ϕ(ξ 0, σ (2) (η 0 )) ϕ(ξ 0, η) ] + γ 2 ψ(ξ 0, σ (2) (η 0 )) ψ(ξ 0, η) ] On dividing both sides of this equality by σ (2) (η 0 ) η and passing to the limit as η η 0, we get the formula (78) because η η 0 implies γ 1 0 and γ 2 0 The theorem is proved The next theorem can be proved in a similar way by using (74), (75), and (29) Theorem 75 Let the function f be σ 2 -completely delta differentiable at the point (t 0, s 0 ) If the functions ϕ and ψ have first order partial delta derivatives at the point (ξ 0, η 0 ), then the composite function F (ξ, η) defined by (76) has first order partial delta derivatives at (ξ 0, η 0 ) which are expressed by the formulas and F (ξ 0, η 0 ) (1) ξ F (ξ 0, η 0 ) (2) η = f(t0, σ 2 (s 0 )) ϕ(ξ 0, η 0 ) (1) ξ = f(t0, σ 2 (s 0 )) ϕ(ξ 0, η 0 ) (2) η + f(t0, s 0 ) ψ(ξ 0, η 0 ) (1) ξ + f(t0, s 0 ) ψ(ξ 0, η 0 ) (2) η 8 THE DIRECTIONAL DERIVATIVE Let T be a time scale with the forward jump operator σ and the delta operator We will assume that 0 T Further, let ω = ( ω 1 ω 2 ) R 2 be a unit vector and let (t 0, s 0 ) be a fixed point in R 2 Let us set T 1 = { t = t 0 + ξω 1 : ξ T } and T 2 = { s = s 0 + ξω 2 : ξ T } Then T 1 and T 2 are time scales and t 0 T 1, s 0 T 2 Denote the forward jump operators of T 1 and T 2 by σ 1 and σ 2, the delta operators by and 2, respectively
25 PARTIAL DIFFERENTIATION ON TIME SCALES 375 Definition 81 Let a function f : T 1 T 2 R be given The directional delta derivative of the function f at the point (t 0, s 0 ) in the direction of the vector ω (along ω) is defined as the number (81) provided it exists, where f(t 0, s 0 ) ω = F (0), (82) F (ξ) = f(t 0 + ξω 1, s 0 + ξω 2 ) for ξ T Theorem 82 Suppose that the function f is σ 1 -completely delta differentiable at the point (t 0, s 0 ) Then the directional delta derivative of f at (t 0, s 0 ) in the direction of the vector ω exists and is expressed by the formula (83) f(t 0, s 0 ) ω = f(t0, s 0 ) ω 1 + f(σ 1(t 0 ), s 0 ) ω 2 Proof The proof is obtained from the definitions (81) and (82) by applying Theorem 71 The next theorem follows similarly by applying Theorem 72 Theorem 83 Suppose that the function f is σ 2 -completely delta differentiable at the point (t 0, s 0 ) Then the directional delta derivative of f at (t 0, s 0 ) in the direction of the vector ω exists and is expressed by the formula f(t 0, s 0 ) ω = f(t0, σ 2 (s 0 )) ω 1 + f(t0, s 0 ) ω 2 Remark 84 For ω 1 = 1 and ω 2 = 0, (83) coincides with f(t0,s 0 ), while for ω 1 = 0 and ω 2 = 1 it coincides with f(t0,s 0 ) because then T 1 = {t 0 } and hence σ 1 (t 0 ) = t 0 (see Remark 73) 9 IMPLICIT FUNCTIONS Let T be a time scale with the forward jump operator σ and the delta differentiation Take an arbitrary real-valued function f defined on T R and consider the equation (91) f(t, y) = 0 for (t, y) T R Let M denote the set of all points (t, y) T R for which equation (91) is fulfilled and let (t 0, y 0 ) be a point belonging to this set, that is, f(t 0, y 0 ) = 0 If no additional conditions are imposed on the function f, then the set M can be of an arbitrary structure We also often encounter the case when, at least in a sufficiently small neighbourhood of (t 0, y 0 ), the set M is a curve described by a continuous (single-valued) function (92) y = ψ(t)
26 376 MARTIN BOHNER AND GUSEIN SH GUSEINOV The problem is to decide whether the equation (91) determines y as a function of t If so, we have (92) for some function ψ We say that ψ is defined implicitly by (91) The implicit function theorems give a description of conditions under which there exists the function ψ as well as some conclusions about this function Theorem 91 Let an equation (91) satisfy the following conditions: (i) The function f is defined in a neigbourhood U of the point (t 0, y 0 ) T κ R and is continuous in U together with its partial derivatives f(t,y) and f(t,y) ; t y (ii) f(t 0, y 0 ) = 0; (iii) f(t0,y 0 ) 0 y Then the following statements are true: (a) There is a rectangle (a neighbourhood of the point (t 0, y 0 ) in T R) (93) N = { (t, y) T R : t t 0 < δ, y y 0 < δ } belonging to U such that the set M N is described by a (uniquely determined) single-valued function (94) y = ψ(t) for t N 0, where M = {(t, y) T R : f(t, y) = 0} and N 0 = { t T : t t 0 < δ } ; (b) y 0 = ψ(t 0 ); (c) the function ψ(t) is continuous in N 0 ; (d) the function ψ(t) has a delta derivative ψ (t) on N 0 Proof Without loss of generality we can suppose that U is an open rectangle of the form U = { (t, y) T R : t t 0 < a, y y 0 < b }, and also for the definiteness we can suppose that f(t0,y 0 ) y on U we then also have of f(t,y) y (95) f(t, y) y > 0 in a small neighbourhood U 1 U of the point (t 0, y 0 ) of the form U 1 = { (t, y) T R : t t 0 < a 1, y y 0 < b 1 } > 0 From the continuity Then the function f(t 0, y) of the single variable y is continuous on the closed interval y 0 b 1, y 0 +b 1 ], is strictly increasing on that interval, and turns into zero at the point y = y 0 (f(t 0, y 0 ) = 0) It follows that f(t 0, y 0 b 1 ) < 0 and f(t 0, y 0 + b 1 ) > 0
Tangent Space and Derivative Mapping on Time Scale
 International J.Math. Combin. Vol.2 (2009, 01-10 Tangent Space and Derivative Mapping on Time Scale Emin ÖZYILMAZ (Department of Mathematics,University of Ege, 35100, İzmir, Turkey E-mail: emin.ozyilmaz@ege.edu.tr
International J.Math. Combin. Vol.2 (2009, 01-10 Tangent Space and Derivative Mapping on Time Scale Emin ÖZYILMAZ (Department of Mathematics,University of Ege, 35100, İzmir, Turkey E-mail: emin.ozyilmaz@ege.edu.tr
Dynamic Systems and Applications xx (2005) pp-pp MULTIPLE INTEGRATION ON TIME SCALES
 Dynamic Systems and Applications xx (2005) pp-pp MULTIPL INTGATION ON TIM SCALS MATIN BOHN AND GUSIN SH. GUSINOV University of Missouri olla, Department of Mathematics and Statistics, olla, Missouri 65401,
Dynamic Systems and Applications xx (2005) pp-pp MULTIPL INTGATION ON TIM SCALS MATIN BOHN AND GUSIN SH. GUSINOV University of Missouri olla, Department of Mathematics and Statistics, olla, Missouri 65401,
Submitted Version to CAMWA, September 30, 2009 THE LAPLACE TRANSFORM ON ISOLATED TIME SCALES
 Submitted Version to CAMWA, September 30, 2009 THE LAPLACE TRANSFORM ON ISOLATED TIME SCALES MARTIN BOHNER AND GUSEIN SH. GUSEINOV Missouri University of Science and Technology, Department of Mathematics
Submitted Version to CAMWA, September 30, 2009 THE LAPLACE TRANSFORM ON ISOLATED TIME SCALES MARTIN BOHNER AND GUSEIN SH. GUSEINOV Missouri University of Science and Technology, Department of Mathematics
A Mean Value Theorem for the Conformable Fractional Calculus on Arbitrary Time Scales
 Progr. Fract. Differ. Appl. 2, No. 4, 287-291 (2016) 287 Progress in Fractional Differentiation and Applications An International Journal http://dx.doi.org/10.18576/pfda/020406 A Mean Value Theorem for
Progr. Fract. Differ. Appl. 2, No. 4, 287-291 (2016) 287 Progress in Fractional Differentiation and Applications An International Journal http://dx.doi.org/10.18576/pfda/020406 A Mean Value Theorem for
Boundary Value Problems For A Differential Equation On A Measure Chain
 Boundary Value Problems For A Differential Equation On A Measure Chain Elvan Akin Department of Mathematics and Statistics, University of Nebraska-Lincoln Lincoln, NE 68588-0323 eakin@math.unl.edu Abstract
Boundary Value Problems For A Differential Equation On A Measure Chain Elvan Akin Department of Mathematics and Statistics, University of Nebraska-Lincoln Lincoln, NE 68588-0323 eakin@math.unl.edu Abstract
Research Article Normal and Osculating Planes of Δ-Regular Curves
 Abstract and Applied Analysis Volume 2010, Article ID 923916, 8 pages doi:10.1155/2010/923916 Research Article Normal and Osculating Planes of Δ-Regular Curves Sibel Paşalı Atmaca Matematik Bölümü, Fen-Edebiyat
Abstract and Applied Analysis Volume 2010, Article ID 923916, 8 pages doi:10.1155/2010/923916 Research Article Normal and Osculating Planes of Δ-Regular Curves Sibel Paşalı Atmaca Matematik Bölümü, Fen-Edebiyat
Equations with Separated Variables on Time Scales
 International Journal of Difference Equations ISSN 973-669, Volume 12, Number 1, pp. 1 11 (217) http://campus.mst.edu/ijde Equations with Separated Variables on Time Scales Antoni Augustynowicz Institute
International Journal of Difference Equations ISSN 973-669, Volume 12, Number 1, pp. 1 11 (217) http://campus.mst.edu/ijde Equations with Separated Variables on Time Scales Antoni Augustynowicz Institute
COMPLETENESS THEOREM FOR THE DISSIPATIVE STURM-LIOUVILLE OPERATOR ON BOUNDED TIME SCALES. Hüseyin Tuna
 Indian J. Pure Appl. Math., 47(3): 535-544, September 2016 c Indian National Science Academy DOI: 10.1007/s13226-016-0196-1 COMPLETENESS THEOREM FOR THE DISSIPATIVE STURM-LIOUVILLE OPERATOR ON BOUNDED
Indian J. Pure Appl. Math., 47(3): 535-544, September 2016 c Indian National Science Academy DOI: 10.1007/s13226-016-0196-1 COMPLETENESS THEOREM FOR THE DISSIPATIVE STURM-LIOUVILLE OPERATOR ON BOUNDED
Exercises from other sources REAL NUMBERS 2,...,
 Exercises from other sources REAL NUMBERS 1. Find the supremum and infimum of the following sets: a) {1, b) c) 12, 13, 14, }, { 1 3, 4 9, 13 27, 40 } 81,, { 2, 2 + 2, 2 + 2 + } 2,..., d) {n N : n 2 < 10},
Exercises from other sources REAL NUMBERS 1. Find the supremum and infimum of the following sets: a) {1, b) c) 12, 13, 14, }, { 1 3, 4 9, 13 27, 40 } 81,, { 2, 2 + 2, 2 + 2 + } 2,..., d) {n N : n 2 < 10},
MULTIPLE POSITIVE SOLUTIONS FOR DYNAMIC m-point BOUNDARY VALUE PROBLEMS
 Dynamic Systems and Applications 17 (2008) 25-42 MULTIPLE POSITIVE SOLUTIONS FOR DYNAMIC m-point BOUNDARY VALUE PROBLEMS ILKAY YASLAN KARACA Department of Mathematics Ege University, 35100 Bornova, Izmir,
Dynamic Systems and Applications 17 (2008) 25-42 MULTIPLE POSITIVE SOLUTIONS FOR DYNAMIC m-point BOUNDARY VALUE PROBLEMS ILKAY YASLAN KARACA Department of Mathematics Ege University, 35100 Bornova, Izmir,
arxiv: v1 [math.ap] 4 Sep 2007
![arxiv: v1 [math.ap] 4 Sep 2007 arxiv: v1 [math.ap] 4 Sep 2007](/thumbs/83/88184350.jpg) EXISENCE OF POSIIVE SOLUIONS FOR NON LOCAL p-laplacian HERMISOR PROBLEMS ON IME SCALES MOULAY RCHID SIDI AMMI AND DELFIM F. M. ORRES Abstract. We make use of the Guo-Krasnoselskii fixed point theorem on
EXISENCE OF POSIIVE SOLUIONS FOR NON LOCAL p-laplacian HERMISOR PROBLEMS ON IME SCALES MOULAY RCHID SIDI AMMI AND DELFIM F. M. ORRES Abstract. We make use of the Guo-Krasnoselskii fixed point theorem on
Proof. We indicate by α, β (finite or not) the end-points of I and call
 C.6 Continuous functions Pag. 111 Proof of Corollary 4.25 Corollary 4.25 Let f be continuous on the interval I and suppose it admits non-zero its (finite or infinite) that are different in sign for x tending
C.6 Continuous functions Pag. 111 Proof of Corollary 4.25 Corollary 4.25 Let f be continuous on the interval I and suppose it admits non-zero its (finite or infinite) that are different in sign for x tending
Stability and Instability for Dynamic Equations on Time Scales
 PERGAMON Computers and Mathematics with Applications 0 (2005) 1 0 www.elsevier.com/locate/camwa Stability and Instability for Dynamic Equations on Time Scales J. Hoffacker Department of Mathematical Sciences,
PERGAMON Computers and Mathematics with Applications 0 (2005) 1 0 www.elsevier.com/locate/camwa Stability and Instability for Dynamic Equations on Time Scales J. Hoffacker Department of Mathematical Sciences,
Solving Third Order Three-Point Boundary Value Problem on Time Scales by Solution Matching Using Differential Inequalities
 Global Journal of Science Frontier Research Mathematics & Decision Sciences Volume 12 Issue 3 Version 1.0 Type : Double Blind Peer Reviewed International Research Journal Publisher: Global Journals Inc.
Global Journal of Science Frontier Research Mathematics & Decision Sciences Volume 12 Issue 3 Version 1.0 Type : Double Blind Peer Reviewed International Research Journal Publisher: Global Journals Inc.
ANALYTIC FUNCTIONS ON TIME SCALES
 ANALYTIC FUNCTIONS ON TIME SCALES A Thesis Submitted to the Graduate School of Engineering Sciences of İzmir Institute of Technology in Partial Fulfillment of the Requirements for the Degree of MASTER
ANALYTIC FUNCTIONS ON TIME SCALES A Thesis Submitted to the Graduate School of Engineering Sciences of İzmir Institute of Technology in Partial Fulfillment of the Requirements for the Degree of MASTER
International Publications (USA) PanAmerican Mathematical Journal
 International Publications (USA) PanAmerican Mathematical Journal Volume 6(2006), Number 2, 6 73 Exponential Stability of Dynamic Equations on Time Scales M. Rashford, J. Siloti, and J. Wrolstad University
International Publications (USA) PanAmerican Mathematical Journal Volume 6(2006), Number 2, 6 73 Exponential Stability of Dynamic Equations on Time Scales M. Rashford, J. Siloti, and J. Wrolstad University
(x k ) sequence in F, lim x k = x x F. If F : R n R is a function, level sets and sublevel sets of F are any sets of the form (respectively);
 STABILITY OF EQUILIBRIA AND LIAPUNOV FUNCTIONS. By topological properties in general we mean qualitative geometric properties (of subsets of R n or of functions in R n ), that is, those that don t depend
STABILITY OF EQUILIBRIA AND LIAPUNOV FUNCTIONS. By topological properties in general we mean qualitative geometric properties (of subsets of R n or of functions in R n ), that is, those that don t depend
EXISTENCE OF POSITIVE SOLUTIONS FOR NON LOCAL p-laplacian THERMISTOR PROBLEMS ON TIME SCALES
 Volume 8 27, Issue 3, Article 69, 1 pp. EXISENCE OF POSIIVE SOLUIONS FOR NON LOCAL p-laplacian HERMISOR PROBLEMS ON IME SCALES MOULAY RCHID SIDI AMMI AND DELFIM F. M. ORRES DEPARMEN OF MAHEMAICS UNIVERSIY
Volume 8 27, Issue 3, Article 69, 1 pp. EXISENCE OF POSIIVE SOLUIONS FOR NON LOCAL p-laplacian HERMISOR PROBLEMS ON IME SCALES MOULAY RCHID SIDI AMMI AND DELFIM F. M. ORRES DEPARMEN OF MAHEMAICS UNIVERSIY
Course 212: Academic Year Section 1: Metric Spaces
 Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
The Frenet Serret formulas
 The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
Chapter 1. Measure Spaces. 1.1 Algebras and σ algebras of sets Notation and preliminaries
 Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Contents. 1. Introduction
 FUNDAMENTAL THEOREM OF THE LOCAL THEORY OF CURVES KAIXIN WANG Abstract. In this expository paper, we present the fundamental theorem of the local theory of curves along with a detailed proof. We first
FUNDAMENTAL THEOREM OF THE LOCAL THEORY OF CURVES KAIXIN WANG Abstract. In this expository paper, we present the fundamental theorem of the local theory of curves along with a detailed proof. We first
THEOREMS, ETC., FOR MATH 515
 THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
4th Preparation Sheet - Solutions
 Prof. Dr. Rainer Dahlhaus Probability Theory Summer term 017 4th Preparation Sheet - Solutions Remark: Throughout the exercise sheet we use the two equivalent definitions of separability of a metric space
Prof. Dr. Rainer Dahlhaus Probability Theory Summer term 017 4th Preparation Sheet - Solutions Remark: Throughout the exercise sheet we use the two equivalent definitions of separability of a metric space
CHAPTER 7. Connectedness
 CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
CHAPTER 7 Connectedness 7.1. Connected topological spaces Definition 7.1. A topological space (X, T X ) is said to be connected if there is no continuous surjection f : X {0, 1} where the two point set
March 25, 2010 CHAPTER 2: LIMITS AND CONTINUITY OF FUNCTIONS IN EUCLIDEAN SPACE
 March 25, 2010 CHAPTER 2: LIMIT AND CONTINUITY OF FUNCTION IN EUCLIDEAN PACE 1. calar product in R n Definition 1.1. Given x = (x 1,..., x n ), y = (y 1,..., y n ) R n,we define their scalar product as
March 25, 2010 CHAPTER 2: LIMIT AND CONTINUITY OF FUNCTION IN EUCLIDEAN PACE 1. calar product in R n Definition 1.1. Given x = (x 1,..., x n ), y = (y 1,..., y n ) R n,we define their scalar product as
BOUNDEDNESS AND EXPONENTIAL STABILITY OF SOLUTIONS TO DYNAMIC EQUATIONS ON TIME SCALES
 Electronic Journal of Differential Equations, Vol. 20062006, No. 12, pp. 1 14. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu login: ftp BOUNDEDNESS
Electronic Journal of Differential Equations, Vol. 20062006, No. 12, pp. 1 14. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu login: ftp BOUNDEDNESS
25. Chain Rule. Now, f is a function of t only. Expand by multiplication:
 25. Chain Rule The Chain Rule is present in all differentiation. If z = f(x, y) represents a two-variable function, then it is plausible to consider the cases when x and y may be functions of other variable(s).
25. Chain Rule The Chain Rule is present in all differentiation. If z = f(x, y) represents a two-variable function, then it is plausible to consider the cases when x and y may be functions of other variable(s).
Notes on Complex Analysis
 Michael Papadimitrakis Notes on Complex Analysis Department of Mathematics University of Crete Contents The complex plane.. The complex plane...................................2 Argument and polar representation.........................
Michael Papadimitrakis Notes on Complex Analysis Department of Mathematics University of Crete Contents The complex plane.. The complex plane...................................2 Argument and polar representation.........................
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Definition 3 (Continuity). A function f is continuous at c if lim x c f(x) = f(c).
 Functions of Several Variables A function of several variables is just what it sounds like. It may be viewed in at least three different ways. We will use a function of two variables as an example. z =
Functions of Several Variables A function of several variables is just what it sounds like. It may be viewed in at least three different ways. We will use a function of two variables as an example. z =
Some Applications to Lebesgue Points in Variable Exponent Lebesgue Spaces
 Çankaya University Journal of Science and Engineering Volume 7 (200), No. 2, 05 3 Some Applications to Lebesgue Points in Variable Exponent Lebesgue Spaces Rabil A. Mashiyev Dicle University, Department
Çankaya University Journal of Science and Engineering Volume 7 (200), No. 2, 05 3 Some Applications to Lebesgue Points in Variable Exponent Lebesgue Spaces Rabil A. Mashiyev Dicle University, Department
UNIQUENESS OF SOLUTIONS TO MATRIX EQUATIONS ON TIME SCALES
 Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 50, pp. 1 13. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu UNIQUENESS OF
Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 50, pp. 1 13. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu UNIQUENESS OF
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
Periodic Solutions in Shifts δ ± for a Dynamic Equation on Time Scales
 Advances in Dynamical Systems and Applications ISSN 0973-5321, Volume 9, Number 1, pp. 97 108 (2014) http://campus.mst.edu/adsa Periodic Solutions in Shifts δ ± for a Dynamic Equation on Time Scales Erbil
Advances in Dynamical Systems and Applications ISSN 0973-5321, Volume 9, Number 1, pp. 97 108 (2014) http://campus.mst.edu/adsa Periodic Solutions in Shifts δ ± for a Dynamic Equation on Time Scales Erbil
TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES
 TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES DOUGLAS R. ANDERSON Abtract. We are concerned with the repreentation of polynomial for nabla dynamic equation on time cale. Once etablihed,
TAYLOR POLYNOMIALS FOR NABLA DYNAMIC EQUATIONS ON TIME SCALES DOUGLAS R. ANDERSON Abtract. We are concerned with the repreentation of polynomial for nabla dynamic equation on time cale. Once etablihed,
Set theory and topology
 arxiv:1306.6926v1 [math.ho] 28 Jun 2013 Set theory and topology An introduction to the foundations of analysis 1 Part II: Topology Fundamental Felix Nagel Abstract We provide a formal introduction into
arxiv:1306.6926v1 [math.ho] 28 Jun 2013 Set theory and topology An introduction to the foundations of analysis 1 Part II: Topology Fundamental Felix Nagel Abstract We provide a formal introduction into
Introduction to Topology
 Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Research Article On the Existence of Solutions for Dynamic Boundary Value Problems under Barrier Strips Condition
 Hindawi Publishing Corporation Advances in Difference Equations Volume 2011, Article ID 378686, 9 pages doi:10.1155/2011/378686 Research Article On the Existence of Solutions for Dynamic Boundary Value
Hindawi Publishing Corporation Advances in Difference Equations Volume 2011, Article ID 378686, 9 pages doi:10.1155/2011/378686 Research Article On the Existence of Solutions for Dynamic Boundary Value
PERTURBATION THEORY FOR NONLINEAR DIRICHLET PROBLEMS
 Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 28, 2003, 207 222 PERTURBATION THEORY FOR NONLINEAR DIRICHLET PROBLEMS Fumi-Yuki Maeda and Takayori Ono Hiroshima Institute of Technology, Miyake,
Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 28, 2003, 207 222 PERTURBATION THEORY FOR NONLINEAR DIRICHLET PROBLEMS Fumi-Yuki Maeda and Takayori Ono Hiroshima Institute of Technology, Miyake,
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY. (τ + arg z) + 1
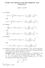 NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
AN EFFECTIVE METRIC ON C(H, K) WITH NORMAL STRUCTURE. Mona Nabiei (Received 23 June, 2015)
 NEW ZEALAND JOURNAL OF MATHEMATICS Volume 46 (2016), 53-64 AN EFFECTIVE METRIC ON C(H, K) WITH NORMAL STRUCTURE Mona Nabiei (Received 23 June, 2015) Abstract. This study first defines a new metric with
NEW ZEALAND JOURNAL OF MATHEMATICS Volume 46 (2016), 53-64 AN EFFECTIVE METRIC ON C(H, K) WITH NORMAL STRUCTURE Mona Nabiei (Received 23 June, 2015) Abstract. This study first defines a new metric with
Chapter 4. Inverse Function Theorem. 4.1 The Inverse Function Theorem
 Chapter 4 Inverse Function Theorem d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d dd d d d d This chapter
Chapter 4 Inverse Function Theorem d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d dd d d d d This chapter
An introduction to Mathematical Theory of Control
 An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
An introduction to Mathematical Theory of Control Vasile Staicu University of Aveiro UNICA, May 2018 Vasile Staicu (University of Aveiro) An introduction to Mathematical Theory of Control UNICA, May 2018
Metric Spaces. Exercises Fall 2017 Lecturer: Viveka Erlandsson. Written by M.van den Berg
 Metric Spaces Exercises Fall 2017 Lecturer: Viveka Erlandsson Written by M.van den Berg School of Mathematics University of Bristol BS8 1TW Bristol, UK 1 Exercises. 1. Let X be a non-empty set, and suppose
Metric Spaces Exercises Fall 2017 Lecturer: Viveka Erlandsson Written by M.van den Berg School of Mathematics University of Bristol BS8 1TW Bristol, UK 1 Exercises. 1. Let X be a non-empty set, and suppose
POINT SET TOPOLOGY. Definition 2 A set with a topological structure is a topological space (X, O)
 POINT SET TOPOLOGY Definition 1 A topological structure on a set X is a family O P(X) called open sets and satisfying (O 1 ) O is closed for arbitrary unions (O 2 ) O is closed for finite intersections.
POINT SET TOPOLOGY Definition 1 A topological structure on a set X is a family O P(X) called open sets and satisfying (O 1 ) O is closed for arbitrary unions (O 2 ) O is closed for finite intersections.
Problem Set 4. f(a + h) = P k (h) + o( h k ). (3)
 Analysis 2 Antti Knowles Problem Set 4 1. Let f C k+1 in a neighborhood of a R n. In class we saw that f can be expressed using its Taylor series as f(a + h) = P k (h) + R k (h) (1) where P k (h).= k r=0
Analysis 2 Antti Knowles Problem Set 4 1. Let f C k+1 in a neighborhood of a R n. In class we saw that f can be expressed using its Taylor series as f(a + h) = P k (h) + R k (h) (1) where P k (h).= k r=0
Some nonlinear dynamic inequalities on time scales
 Proc. Indian Acad. Sci. Math. Sci.) Vol. 117, No. 4, November 2007,. 545 554. Printed in India Some nonlinear dynamic inequalities on time scales WEI NIAN LI 1,2 and WEIHONG SHENG 1 1 Deartment of Mathematics,
Proc. Indian Acad. Sci. Math. Sci.) Vol. 117, No. 4, November 2007,. 545 554. Printed in India Some nonlinear dynamic inequalities on time scales WEI NIAN LI 1,2 and WEIHONG SHENG 1 1 Deartment of Mathematics,
Analysis Finite and Infinite Sets The Real Numbers The Cantor Set
 Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
Analysis Finite and Infinite Sets Definition. An initial segment is {n N n n 0 }. Definition. A finite set can be put into one-to-one correspondence with an initial segment. The empty set is also considered
Jensen s inequality for multivariate medians
 Jensen s inequality for multivariate medians Milan Merkle University of Belgrade, Serbia emerkle@etf.rs Given a probability measure µ on Borel sigma-field of R d, and a function f : R d R, the main issue
Jensen s inequality for multivariate medians Milan Merkle University of Belgrade, Serbia emerkle@etf.rs Given a probability measure µ on Borel sigma-field of R d, and a function f : R d R, the main issue
2 Statement of the problem and assumptions
 Mathematical Notes, 25, vol. 78, no. 4, pp. 466 48. Existence Theorem for Optimal Control Problems on an Infinite Time Interval A.V. Dmitruk and N.V. Kuz kina We consider an optimal control problem on
Mathematical Notes, 25, vol. 78, no. 4, pp. 466 48. Existence Theorem for Optimal Control Problems on an Infinite Time Interval A.V. Dmitruk and N.V. Kuz kina We consider an optimal control problem on
1 Directional Derivatives and Differentiability
 Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
Wednesday, January 18, 2012 1 Directional Derivatives and Differentiability Let E R N, let f : E R and let x 0 E. Given a direction v R N, let L be the line through x 0 in the direction v, that is, L :=
A NOTE ON ALMOST PERIODIC VARIATIONAL EQUATIONS
 A NOTE ON ALMOST PERIODIC VARIATIONAL EQUATIONS PETER GIESL AND MARTIN RASMUSSEN Abstract. The variational equation of a nonautonomous differential equation ẋ = F t, x) along a solution µ is given by ẋ
A NOTE ON ALMOST PERIODIC VARIATIONAL EQUATIONS PETER GIESL AND MARTIN RASMUSSEN Abstract. The variational equation of a nonautonomous differential equation ẋ = F t, x) along a solution µ is given by ẋ
DIEUDONNE AGBOR AND JAN BOMAN
 ON THE MODULUS OF CONTINUITY OF MAPPINGS BETWEEN EUCLIDEAN SPACES DIEUDONNE AGBOR AND JAN BOMAN Abstract Let f be a function from R p to R q and let Λ be a finite set of pairs (θ, η) R p R q. Assume that
ON THE MODULUS OF CONTINUITY OF MAPPINGS BETWEEN EUCLIDEAN SPACES DIEUDONNE AGBOR AND JAN BOMAN Abstract Let f be a function from R p to R q and let Λ be a finite set of pairs (θ, η) R p R q. Assume that
The Skorokhod problem in a time-dependent interval
 The Skorokhod problem in a time-dependent interval Krzysztof Burdzy, Weining Kang and Kavita Ramanan University of Washington and Carnegie Mellon University Abstract: We consider the Skorokhod problem
The Skorokhod problem in a time-dependent interval Krzysztof Burdzy, Weining Kang and Kavita Ramanan University of Washington and Carnegie Mellon University Abstract: We consider the Skorokhod problem
3 (Due ). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MODULUS OF CONTINUITY OF THE DIRICHLET SOLUTIONS
 MODULUS OF CONTINUITY OF THE DIRICHLET SOLUTIONS HIROAKI AIKAWA Abstract. Let D be a bounded domain in R n with n 2. For a function f on D we denote by H D f the Dirichlet solution, for the Laplacian,
MODULUS OF CONTINUITY OF THE DIRICHLET SOLUTIONS HIROAKI AIKAWA Abstract. Let D be a bounded domain in R n with n 2. For a function f on D we denote by H D f the Dirichlet solution, for the Laplacian,
Math Advanced Calculus II
 Math 452 - Advanced Calculus II Manifolds and Lagrange Multipliers In this section, we will investigate the structure of critical points of differentiable functions. In practice, one often is trying to
Math 452 - Advanced Calculus II Manifolds and Lagrange Multipliers In this section, we will investigate the structure of critical points of differentiable functions. In practice, one often is trying to
EXISTENCE OF POSITIVE SOLUTIONS FOR p-laplacian THREE-POINT BOUNDARY-VALUE PROBLEMS ON TIME SCALES
 Electronic Journal of Differential Equations, Vol. 28(28, No. 92, pp. 1 14. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp EXISTENCE
Electronic Journal of Differential Equations, Vol. 28(28, No. 92, pp. 1 14. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp EXISTENCE
2. Dual space is essential for the concept of gradient which, in turn, leads to the variational analysis of Lagrange multipliers.
 Chapter 3 Duality in Banach Space Modern optimization theory largely centers around the interplay of a normed vector space and its corresponding dual. The notion of duality is important for the following
Chapter 3 Duality in Banach Space Modern optimization theory largely centers around the interplay of a normed vector space and its corresponding dual. The notion of duality is important for the following
A Concise Course on Stochastic Partial Differential Equations
 A Concise Course on Stochastic Partial Differential Equations Michael Röckner Reference: C. Prevot, M. Röckner: Springer LN in Math. 1905, Berlin (2007) And see the references therein for the original
A Concise Course on Stochastic Partial Differential Equations Michael Röckner Reference: C. Prevot, M. Röckner: Springer LN in Math. 1905, Berlin (2007) And see the references therein for the original
LECTURE 15: COMPLETENESS AND CONVEXITY
 LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
MAPPINGS BETWEEN INVERSE LIMITS OF CONTINUA WITH MULTIVALUED BONDING FUNCTIONS
 MAPPINGS BETWEEN INVERSE LIMITS OF CONTINUA WITH MULTIVALUED BONDING FUNCTIONS W LODZIMIERZ J. CHARATONIK AND ROBERT P. ROE Abstract. We investigate the limit mappings between inverse limits of continua
MAPPINGS BETWEEN INVERSE LIMITS OF CONTINUA WITH MULTIVALUED BONDING FUNCTIONS W LODZIMIERZ J. CHARATONIK AND ROBERT P. ROE Abstract. We investigate the limit mappings between inverse limits of continua
arxiv: v1 [math.ca] 12 Feb 2010
![arxiv: v1 [math.ca] 12 Feb 2010 arxiv: v1 [math.ca] 12 Feb 2010](/thumbs/93/114127631.jpg) YOUNG S INTEGRAL INEQUALITY WITH UPPER AND LOWER BOUNDS DOUGLAS R. ANDERSON, STEVEN NOREN, AND BRENT PERREAULT arxiv:12.2463v1 [math.ca] 12 Feb 21 Abstract. Young s integral inequality is reformulated
YOUNG S INTEGRAL INEQUALITY WITH UPPER AND LOWER BOUNDS DOUGLAS R. ANDERSON, STEVEN NOREN, AND BRENT PERREAULT arxiv:12.2463v1 [math.ca] 12 Feb 21 Abstract. Young s integral inequality is reformulated
Course 224: Geometry - Continuity and Differentiability
 Course 224: Geometry - Continuity and Differentiability Lecture Notes by Prof. David Simms L A TEXed by Chris Blair 1 Continuity Consider M, N finite dimensional real or complex vector spaces. What does
Course 224: Geometry - Continuity and Differentiability Lecture Notes by Prof. David Simms L A TEXed by Chris Blair 1 Continuity Consider M, N finite dimensional real or complex vector spaces. What does
M311 Functions of Several Variables. CHAPTER 1. Continuity CHAPTER 2. The Bolzano Weierstrass Theorem and Compact Sets CHAPTER 3.
 M311 Functions of Several Variables 2006 CHAPTER 1. Continuity CHAPTER 2. The Bolzano Weierstrass Theorem and Compact Sets CHAPTER 3. Differentiability 1 2 CHAPTER 1. Continuity If (a, b) R 2 then we write
M311 Functions of Several Variables 2006 CHAPTER 1. Continuity CHAPTER 2. The Bolzano Weierstrass Theorem and Compact Sets CHAPTER 3. Differentiability 1 2 CHAPTER 1. Continuity If (a, b) R 2 then we write
EXPOSITORY NOTES ON DISTRIBUTION THEORY, FALL 2018
 EXPOSITORY NOTES ON DISTRIBUTION THEORY, FALL 2018 While these notes are under construction, I expect there will be many typos. The main reference for this is volume 1 of Hörmander, The analysis of liner
EXPOSITORY NOTES ON DISTRIBUTION THEORY, FALL 2018 While these notes are under construction, I expect there will be many typos. The main reference for this is volume 1 of Hörmander, The analysis of liner
Segment Description of Turbulence
 Dynamics of PDE, Vol.4, No.3, 283-291, 2007 Segment Description of Turbulence Y. Charles Li Communicated by Y. Charles Li, received August 25, 2007. Abstract. We propose a segment description for turbulent
Dynamics of PDE, Vol.4, No.3, 283-291, 2007 Segment Description of Turbulence Y. Charles Li Communicated by Y. Charles Li, received August 25, 2007. Abstract. We propose a segment description for turbulent
Lie-point symmetries of the Lagrangian system on time scales
 ie-point symmetries of the agrangian system on time scales Cai Ping-Ping Song-Duan Fu Jing-i Fang-Yu Hong Institute of Mathematical Physics Zhejiang Sci-Tech University Hangzhou 008 China Eastern iaodong
ie-point symmetries of the agrangian system on time scales Cai Ping-Ping Song-Duan Fu Jing-i Fang-Yu Hong Institute of Mathematical Physics Zhejiang Sci-Tech University Hangzhou 008 China Eastern iaodong
Metric Spaces Lecture 17
 Metric Spaces Lecture 17 Homeomorphisms At the end of last lecture an example was given of a bijective continuous function f such that f 1 is not continuous. For another example, consider the sets T =
Metric Spaces Lecture 17 Homeomorphisms At the end of last lecture an example was given of a bijective continuous function f such that f 1 is not continuous. For another example, consider the sets T =
ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY
 ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY AND ω-limit SETS CHRIS GOOD AND JONATHAN MEDDAUGH Abstract. Let f : X X be a continuous map on a compact metric space, let ω f be the collection of ω-limit
ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY AND ω-limit SETS CHRIS GOOD AND JONATHAN MEDDAUGH Abstract. Let f : X X be a continuous map on a compact metric space, let ω f be the collection of ω-limit
Math 361: Homework 1 Solutions
 January 3, 4 Math 36: Homework Solutions. We say that two norms and on a vector space V are equivalent or comparable if the topology they define on V are the same, i.e., for any sequence of vectors {x
January 3, 4 Math 36: Homework Solutions. We say that two norms and on a vector space V are equivalent or comparable if the topology they define on V are the same, i.e., for any sequence of vectors {x
On a general definition of transition waves and their properties
 On a general definition of transition waves and their properties Henri Berestycki a and François Hamel b a EHESS, CAMS, 54 Boulevard Raspail, F-75006 Paris, France b Université Aix-Marseille III, LATP,
On a general definition of transition waves and their properties Henri Berestycki a and François Hamel b a EHESS, CAMS, 54 Boulevard Raspail, F-75006 Paris, France b Université Aix-Marseille III, LATP,
Advances in Difference Equations 2012, 2012:7
 Advances in Difference Equations This Provisional PDF corresponds to the article as it appeared upon acceptance. Fully formatted PDF and full text (HTML) versions will be made available soon. Extremal
Advances in Difference Equations This Provisional PDF corresponds to the article as it appeared upon acceptance. Fully formatted PDF and full text (HTML) versions will be made available soon. Extremal
Research Article Quasilinearization Technique for Φ-Laplacian Type Equations
 International Mathematics and Mathematical Sciences Volume 0, Article ID 975760, pages doi:0.55/0/975760 Research Article Quasilinearization Technique for Φ-Laplacian Type Equations Inara Yermachenko and
International Mathematics and Mathematical Sciences Volume 0, Article ID 975760, pages doi:0.55/0/975760 Research Article Quasilinearization Technique for Φ-Laplacian Type Equations Inara Yermachenko and
APPLICATIONS OF DIFFERENTIABILITY IN R n.
 APPLICATIONS OF DIFFERENTIABILITY IN R n. MATANIA BEN-ARTZI April 2015 Functions here are defined on a subset T R n and take values in R m, where m can be smaller, equal or greater than n. The (open) ball
APPLICATIONS OF DIFFERENTIABILITY IN R n. MATANIA BEN-ARTZI April 2015 Functions here are defined on a subset T R n and take values in R m, where m can be smaller, equal or greater than n. The (open) ball
Introduction. Itaï Ben-Yaacov C. Ward Henson. September American Institute of Mathematics Workshop. Continuous logic Continuous model theory
 Itaï Ben-Yaacov C. Ward Henson American Institute of Mathematics Workshop September 2006 Outline Continuous logic 1 Continuous logic 2 The metric on S n (T ) Origins Continuous logic Many classes of (complete)
Itaï Ben-Yaacov C. Ward Henson American Institute of Mathematics Workshop September 2006 Outline Continuous logic 1 Continuous logic 2 The metric on S n (T ) Origins Continuous logic Many classes of (complete)
Rectifiability of sets and measures
 Rectifiability of sets and measures Tatiana Toro University of Washington IMPA February 7, 206 Tatiana Toro (University of Washington) Structure of n-uniform measure in R m February 7, 206 / 23 State of
Rectifiability of sets and measures Tatiana Toro University of Washington IMPA February 7, 206 Tatiana Toro (University of Washington) Structure of n-uniform measure in R m February 7, 206 / 23 State of
Journal of Complexity. New general convergence theory for iterative processes and its applications to Newton Kantorovich type theorems
 Journal of Complexity 26 (2010) 3 42 Contents lists available at ScienceDirect Journal of Complexity journal homepage: www.elsevier.com/locate/jco New general convergence theory for iterative processes
Journal of Complexity 26 (2010) 3 42 Contents lists available at ScienceDirect Journal of Complexity journal homepage: www.elsevier.com/locate/jco New general convergence theory for iterative processes
2 Sequences, Continuity, and Limits
 2 Sequences, Continuity, and Limits In this chapter, we introduce the fundamental notions of continuity and limit of a real-valued function of two variables. As in ACICARA, the definitions as well as proofs
2 Sequences, Continuity, and Limits In this chapter, we introduce the fundamental notions of continuity and limit of a real-valued function of two variables. As in ACICARA, the definitions as well as proofs
2tdt 1 y = t2 + C y = which implies C = 1 and the solution is y = 1
 Lectures - Week 11 General First Order ODEs & Numerical Methods for IVPs In general, nonlinear problems are much more difficult to solve than linear ones. Unfortunately many phenomena exhibit nonlinear
Lectures - Week 11 General First Order ODEs & Numerical Methods for IVPs In general, nonlinear problems are much more difficult to solve than linear ones. Unfortunately many phenomena exhibit nonlinear
8 Change of variables
 Tel Aviv University, 2013/14 Analysis-III,IV 111 8 Change of variables 8a What is the problem................ 111 8b Examples and exercises............... 113 8c Differentiating set functions............
Tel Aviv University, 2013/14 Analysis-III,IV 111 8 Change of variables 8a What is the problem................ 111 8b Examples and exercises............... 113 8c Differentiating set functions............
= ϕ r cos θ. 0 cos ξ sin ξ and sin ξ cos ξ. sin ξ 0 cos ξ
 8. The Banach-Tarski paradox May, 2012 The Banach-Tarski paradox is that a unit ball in Euclidean -space can be decomposed into finitely many parts which can then be reassembled to form two unit balls
8. The Banach-Tarski paradox May, 2012 The Banach-Tarski paradox is that a unit ball in Euclidean -space can be decomposed into finitely many parts which can then be reassembled to form two unit balls
Limits and Continuity
 Limits and Continuity Notes by Walter Noll, 1991 1 Real Sequences, Convergence Let an index set I be given. The set R I of all real families indexed on I has the natural structure of a commutative ring
Limits and Continuity Notes by Walter Noll, 1991 1 Real Sequences, Convergence Let an index set I be given. The set R I of all real families indexed on I has the natural structure of a commutative ring
On Characterizations of Meir-Keeler Contractive Maps
 On Characterizations of Meir-Keeler Contractive Maps Teck-Cheong Lim Department of Mathematical Sciences George Mason University 4400, University Drive Fairfax, VA 030 U.S.A. e-mail address: tlim@gmu.edu
On Characterizations of Meir-Keeler Contractive Maps Teck-Cheong Lim Department of Mathematical Sciences George Mason University 4400, University Drive Fairfax, VA 030 U.S.A. e-mail address: tlim@gmu.edu
Lecture 4: Numerical solution of ordinary differential equations
 Lecture 4: Numerical solution of ordinary differential equations Department of Mathematics, ETH Zürich General explicit one-step method: Consistency; Stability; Convergence. High-order methods: Taylor
Lecture 4: Numerical solution of ordinary differential equations Department of Mathematics, ETH Zürich General explicit one-step method: Consistency; Stability; Convergence. High-order methods: Taylor
1 The Existence and Uniqueness Theorem for First-Order Differential Equations
 1 The Existence and Uniqueness Theorem for First-Order Differential Equations Let I R be an open interval and G R n, n 1, be a domain. Definition 1.1 Let us consider a function f : I G R n. The general
1 The Existence and Uniqueness Theorem for First-Order Differential Equations Let I R be an open interval and G R n, n 1, be a domain. Definition 1.1 Let us consider a function f : I G R n. The general
Lecture 12. F o s, (1.1) F t := s>t
 Lecture 12 1 Brownian motion: the Markov property Let C := C(0, ), R) be the space of continuous functions mapping from 0, ) to R, in which a Brownian motion (B t ) t 0 almost surely takes its value. Let
Lecture 12 1 Brownian motion: the Markov property Let C := C(0, ), R) be the space of continuous functions mapping from 0, ) to R, in which a Brownian motion (B t ) t 0 almost surely takes its value. Let
Mathematics for Engineers II. lectures. Differential Equations
 Differential Equations Examples for differential equations Newton s second law for a point mass Consider a particle of mass m subject to net force a F. Newton s second law states that the vector acceleration
Differential Equations Examples for differential equations Newton s second law for a point mass Consider a particle of mass m subject to net force a F. Newton s second law states that the vector acceleration
OPTIMAL SOLUTIONS TO STOCHASTIC DIFFERENTIAL INCLUSIONS
 APPLICATIONES MATHEMATICAE 29,4 (22), pp. 387 398 Mariusz Michta (Zielona Góra) OPTIMAL SOLUTIONS TO STOCHASTIC DIFFERENTIAL INCLUSIONS Abstract. A martingale problem approach is used first to analyze
APPLICATIONES MATHEMATICAE 29,4 (22), pp. 387 398 Mariusz Michta (Zielona Góra) OPTIMAL SOLUTIONS TO STOCHASTIC DIFFERENTIAL INCLUSIONS Abstract. A martingale problem approach is used first to analyze
Archivum Mathematicum
 Archivum Mathematicum Deepak B. Pachpatte Some dynamic inequalities applicable to partial integrodifferential equations on time scales Archivum Mathematicum, Vol. 51 2015, No. 3, 143 152 Persistent URL:
Archivum Mathematicum Deepak B. Pachpatte Some dynamic inequalities applicable to partial integrodifferential equations on time scales Archivum Mathematicum, Vol. 51 2015, No. 3, 143 152 Persistent URL:
P-adic Functions - Part 1
 P-adic Functions - Part 1 Nicolae Ciocan 22.11.2011 1 Locally constant functions Motivation: Another big difference between p-adic analysis and real analysis is the existence of nontrivial locally constant
P-adic Functions - Part 1 Nicolae Ciocan 22.11.2011 1 Locally constant functions Motivation: Another big difference between p-adic analysis and real analysis is the existence of nontrivial locally constant
Lecture Note 13:Continuous Time Switched Optimal Control: Embedding Principle and Numerical Algorithms
 ECE785: Hybrid Systems:Theory and Applications Lecture Note 13:Continuous Time Switched Optimal Control: Embedding Principle and Numerical Algorithms Wei Zhang Assistant Professor Department of Electrical
ECE785: Hybrid Systems:Theory and Applications Lecture Note 13:Continuous Time Switched Optimal Control: Embedding Principle and Numerical Algorithms Wei Zhang Assistant Professor Department of Electrical
Exercise 1 (Formula for connection 1-forms) Using the first structure equation, show that
 1 Stokes s Theorem Let D R 2 be a connected compact smooth domain, so that D is a smooth embedded circle. Given a smooth function f : D R, define fdx dy fdxdy, D where the left-hand side is the integral
1 Stokes s Theorem Let D R 2 be a connected compact smooth domain, so that D is a smooth embedded circle. Given a smooth function f : D R, define fdx dy fdxdy, D where the left-hand side is the integral
MATH & MATH INTRODUCTION TO ANALYSIS EXERCISES FALL 2016 & SPRING Scientia Imperii Decus et Tutamen 1
 MATH 5110.001 & MATH 5120.001 INTRODUCTION TO ANALYSIS EXERCISES FALL 2016 & SPRING 2017 Scientia Imperii Decus et Tutamen 1 Robert R. Kallman University of North Texas Department of Mathematics 1155 Union
MATH 5110.001 & MATH 5120.001 INTRODUCTION TO ANALYSIS EXERCISES FALL 2016 & SPRING 2017 Scientia Imperii Decus et Tutamen 1 Robert R. Kallman University of North Texas Department of Mathematics 1155 Union
Georgian Mathematical Journal 1(94), No. 4, ON THE INITIAL VALUE PROBLEM FOR FUNCTIONAL DIFFERENTIAL SYSTEMS
 Georgian Mathematical Journal 1(94), No. 4, 419-427 ON THE INITIAL VALUE PROBLEM FOR FUNCTIONAL DIFFERENTIAL SYSTEMS V. ŠEDA AND J. ELIAŠ Astract. For a system of functional differential equations of an
Georgian Mathematical Journal 1(94), No. 4, 419-427 ON THE INITIAL VALUE PROBLEM FOR FUNCTIONAL DIFFERENTIAL SYSTEMS V. ŠEDA AND J. ELIAŠ Astract. For a system of functional differential equations of an
Chapter 8: Taylor s theorem and L Hospital s rule
 Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
Maths 212: Homework Solutions
 Maths 212: Homework Solutions 1. The definition of A ensures that x π for all x A, so π is an upper bound of A. To show it is the least upper bound, suppose x < π and consider two cases. If x < 1, then
Maths 212: Homework Solutions 1. The definition of A ensures that x π for all x A, so π is an upper bound of A. To show it is the least upper bound, suppose x < π and consider two cases. If x < 1, then
Math 67. Rumbos Fall Solutions to Review Problems for Final Exam. (a) Use the triangle inequality to derive the inequality
 Math 67. umbos Fall 8 Solutions to eview Problems for Final Exam. In this problem, u and v denote vectors in n. (a) Use the triangle inequality to derive the inequality Solution: Write v u v u for all
Math 67. umbos Fall 8 Solutions to eview Problems for Final Exam. In this problem, u and v denote vectors in n. (a) Use the triangle inequality to derive the inequality Solution: Write v u v u for all
