x x 1 x 2 + x 2 1 > 0. HW5. Text defines:
|
|
|
- Mildred Chandler
- 6 years ago
- Views:
Transcription
1 Lecture 15: Last time: MVT. Special case: Rolle s Theorem (when f(a) = f(b)). Recall: Defn: Let f be defined on an interval I. f is increasing (or strictly increasing) if whenever x 1, x 2 I and x 2 > x 1, then f(x 2 ) > f(x 1 ). Note: I could be open, closed, half-open, half-closed, infinite, R. Another application of MVT: Theorem 12, p. 140: If f is cts. on [a, b] and diffble. on (a, b) and f (x) > 0 for all x (a, b), then f is increasing on [a, b]. Recall Proof: Let a x 1 < x 2 b. By MVT, there exists c s.t. x 1 < c < x 2 and f(x 2 ) f(x 1 ) x 2 x 1 = f (c) > 0. Since x 2 x 1 > 0, we have f(x 2 ) f(x 1 ) > 0. Note: in above, we applied MVT to a = x 1, b = x 2. Theorem 12 is stated more generally in text: can replace [a, b] by any interval J := (a, b) S where S {a, b}. Require f to be diffble. on (a, b) and cts. on J. In particular, if f is diffble. on an open interval I and f (x) > 0 for all x I then f is increasing on I. Q: If f is differentiable and increasing on an open interval I, is f (x) > 0 for all x in the interval? No. 1
2 f(x) = x 3 : (problem 21, p. 143): f (x) = 3x 2 and so f (0) = 0. Claim: f is increasing on R. Proof: Since f (x) > 0 on (0, ) it is increasing on (0, ). Similarly it is increasing on (, 0). Finally, if x 2 > 0 > x 1, then x 3 2 > 0 > x 3 1. Another proof: x 3 2 x 3 1 = (x 2 x 1 )(x x 1 x 2 + x 2 1) Suffices to show: for all x 1, x 2 s.t. (x 1, x 2 ) (0, 0), HW5. Text defines: x x 1 x 2 + x 2 1 > 0. decreasing (strictly decreasing): if whenever x 1, x 2 I and x 2 > x 1, then f(x 1 ) > f(x 2 ). non-decreasing: if whenever x 1, x 2 I and x 2 > x 1, then f(x 2 ) f(x 1 ). non-increasing: if whenever x 1, x 2 I and x 2 > x 1, then f(x 2 ) f(x 1 ). and the proof of Theorem 12 carries over to analogues of these. if f (x) < 0, then decreasing; if f (x) 0, then non-decreasing; if f (x) 0, then non-increasing; Examples: of a non-decreasing diffble function : { } x f(x) = 2 x 0 0 x < 0 2
3 (diffble. because f + (0) = 0 = f (0)). As pointed out by a student: Proposition: If f is non-decreasing and differentiable on an open interval I, then f (x) 0 for all x I. Proof: For x I, f f(x + h) f(x) (x) = lim 0 h 0 + h Since for sufficiently small h > 0, x + h I and since f is nondecreasing, f(x + h) f(x) 0. Implicit Differentiation A curve in the xy-plane is usually described as the set of all points (x, y) that satisfy a given equation F (x, y) = 0. Examples: 1. y x 2 = 0, 2. x 2 + y 2 4 = 0. Often the equation F (x, y) = 0 determines y implicitly as a function y = f(x), ie., F (x, f(x)) = 0. The function f is found by solving for y in terms of x. Sometimes there is more than one function f that works. Examples: 1. y = f(x) = x y = f 1 (x) = 4 x 2, y = f 2 (x) = 4 x 2. In order for this to work so that the implicit function f is differentiable, the two-variable function F must satisfy a two-variable differentiability property that we will not delve into. In implicit differentiation,, goal is to find f (x) without explicitly finding f(x). Namely, differentiate both sides of F (x, y) = 0 with respect to x and then solve for y = dy dx in terms of x and y. This should give y for all functions f determined implicitly by F (x, y) = 0. 3
4 Example 1: y x 2 = 0. y 2x = 0 and so y = 2x. Example 2: x 2 + y 2 4 = 0. 2x + 2yy = 0 and so y = x y. Here, we have used the chain rule: y 2 = (f(x)) 2 for some unknown function f; by the chain rule (y 2 ) = ((f(x)) 2 ) = 2f(x)f (x) = 2yy Verify in terms of derivatives of explicit functions: y = f 1 (x) = 4 x 2 : y 1 = (1/2)( 2x) = x 4 x 2 y and the same holds for y = f 2 (x) = 4 x 2. Note that the implicit function may not be differentiable when y = 0, which is indeed the case for f 1 and f 2. 4
5 Lecture 16: In some examples, the curve is defined by G(x, y) = H(x, y), which is equivalent to F ((x, y) = 0, where F (x, y) = G(x, y) H(x, y): Example 3: x sin(xy y) = x 2 1. sin(xy y) + x(cos(xy y))(y + xy y ) = 2x y (x 1)x(cos(xy y)) = 2x sin(xy y) x(cos(xy y))(y) y 2x sin(xy y) x(cos(xy y))(y) = (x 1)x(cos(xy y)) Higher Order Implicit Differentiation: Differentiate again: Example 2: x 2 + y 2 4 = 0. Recall that y = x y. So, y = y + xy y 2 = y + x x y y 2 = y x2 y y 2 = x2 + y 2 y 3 = 4 y 3 Power rule for rational exponents: recall that we proved the power rule only for integer exponents (although we have been using it for rational exponents). Proposition: Let m and n be integers with n 0. Let f(x) = x m/n. Then f (x) = (m/n)x (m/n) 1. The function y = f(x) = x m/n is an implicit function of y n x m = 0. Then So ny n 1 y = mx m 1 y = mxm 1 ny n 1 = m n x m 1 y n 1 5
6 = m n x m 1 (x m/n ) n 1 = m n xm 1+(m(1 n)/n) = m n x(m/n) 1 Recall that we will later define and prove the power rule for f(x) = x r for all real r. So far, we have shown this only for rational r. One-to-One functions and increasing/decreasing functions: Proposition: Let I be an interval. Let f be increasing on I or decreasing I. Then f is one-to-one on I. Proof: Case 1: f is increasing. If x 1 x 2, then one is larger than the other. WLOG x 2 > x 1. Then f(x 2 ) > f(x 1 ) and so f(x 2 ) f(x 1 ). Thus, f is one-to-one. Case 2: f is decreasing. Then g(x) := f(x) is increasing and so g is one-to-one. Then f is one-to-one: if x 1 x 2, then g(x 2 ) g(x 1 ) and so f(x 2 ) f(x 1 ). The kettle. Q: If f is one-to-one on an interval I, must it be increasing on I or decreasing I? A: No Example: f(x) = { x 0 x 1 x 1 < x 2 f is one-to-one because its graph passes the horizontal line test. } 6
7 But f is neither increasing nor decreasing. Proposition: If f is one-to-one and continuous on an interval I, it must be increasing on I or decreasing on I. Outline of Proof: Special case: I is a closed interval: I = [a, b]. Since f is one-to-one, f(a) f(b). Case 1: f(b) > f(a). Show that f is increasing on I. Proof by contradiction: if f is not increasing, then there exist c, d s.t. a c < d b and f(c) > f(d). By intermediate value theorem, f is not one-to-one on [a, b]. Case 2: f(b) < f(a). Show that f is decreasing on I. Apply Case 1 to g(x) := f(x). Then f is increasing and so f is decreasing. Can extend proof from closed intervals to arbitrary intervals: f is increasing on an interval iff it is increasing on all closed sub-intervals. 7
8 Lecture 17: Inverse functions Defn. Let f be one-to-one on an interval I. We define the inverse function f 1 by f 1 (y) is the (unique) x in the domain of f s.t. y = f(x). x = f 1 (y) iff y = f(x) i.e., you solve for x in terms of y from the equation y = f(x) Examples: 1. f(x) = 3x is 1-1 on R. So, the inverse function is obtained by solving for x in terms of y in the eqn. y = 3x; so x = (1/3)y is the inverse function. 2. f(x) = x 2 is 1-1 on [0, ). So, the inverse function is obtained by solving for x in terms of y in the eqn. y = x 2 ; so x = y is the inverse function. 3. f(x) = tan(x) is 1-1 on ( π/2, π/2): since f (x) = sec 2 (x) > 0 on ( π/2, π/2), by Theorem 12 f is increasing on ( π/2, π/2), and so is 1-1 on ( π/2, π/2). The inverse function is x = arctan(y). Usually, we write use the letter x for the domain variable and y for the range variable. So, if f(x) = 3x on R then f 1 (y) = (1/3)y, but we write f 1 (x) = (1/3)x, i.e., we find the inverse function x = f 1 (y) and then reverse the roles of x and y and write y = f 1 (x). Similarly, if f(x) = x 2 on [0, ), we write f 1 (x) = x. And if f(x) = tan(x) on (π/2, π/2), we write f 1 (x) = arctan x. Note that the domain of f 1 is the range of f and the range of f 1 is the domain of f. In terms of graphs, the graph of f 1 is obtained from the graph of f by reflecting across the line y = x, i.e., interchanging the x and 8
9 y coordinates: Graph of f = {(x, f(x)) : x Dom(f)} = {(f 1 (y), y) : y Ran(f)} Reflect across x = y and we get: {(y, f 1 (y)) : y Ran(f)} = {(x, f 1 (x)) : x Dom(f 1 )} = Graph of f 1 Draw graphs of 3x, (1/3)x, x 2, x, tan(x), arctan(x). Caution: Do not confuse f 1 (x) with 1 f(x). Properties: (f 1 ) 1 = f. f 1 (f(x)) = x = f(f 1 (x)) If f and f 1 are differentiable, then 1 = f (f 1 (x))((f 1 ) (x)) So (f 1 ) (x) = Example: f(x) = x 2 and f 1 (x) = x. 1 f (f 1 (x)) (1) (f 1 ) (x) = 1 f (f 1 (x)) = 1 2f 1 (x) = 1 2 x But this assumes that f 1 is diffble at x and f (f 1 (x)) 0. Inverse function theorem: If f is diffble. on an open interval I and either f (x) > 0 for all x I or f (x) < 0 for all x I, then f 1 is diffble. on the range of f I and (??) holds. Proof is a bit involved. Another example: Let f(x) = x 3 + x. Find (f 1 ) (10). 9
10 ((f 1 ) (x) = 1 f (f 1 (x)) = 1 3(f 1 (x)) (f 1 )(10) = 2 (f 1 ) (10) = 1/13 Recall f(x) = x r can be defined for all real r. Similarly, g(x) = a x can be defined for all a > 0. Consider the difference between f(x) = x 2 and g(x) = 2 x. f(10) = 100, g(10) 1000, f(20) = 400, g(20) 1, 000, 000. f(x) is a polynomial and g(x) is an exponential function. Exponential functions grow much faster than polynomials. Example: f(x) = 2 x ; then f 1 (x) = log 2 (x): y = 2 x x = log 2 (y); the switch the roles of x and y. Draw graphs. Brief review of laws of exponents and laws of logarithms and limits at infinity for exponential functions and logarithmic functions. For a > 1, For 0 < a < 1, For a > 1, For 0 < a < 1, lim x ax =, lim x ax = 0 lim x ax = 0, lim x ax = lim log a(x) =, lim log a(x) = x x 0 + lim log a(x) =, lim log a(x) = x x
11 Lecture 18: Will not cover antiderivatives and integrals until later. Defn: For x > 0, let A x be the area of the region in the yt-plane bounded by the curve y = 1/t, the t-axis, and the vertical lines t = 1 and t = x. Define { } Ax x 1 ln(x) = A x 0 < x < 1 Note that the domain of ln is (0, ), f(x) > 0 for x > 1, f(x) < 0 for 0 < x < 1, and f(1) = 0. Note that these properties all hold for f(x) = log a (x) when a > 1. Theorem 1 (p. 175): Let f(x) = ln(x). Then f (x) = 1 x This is a special case of the Fundamental Theorem of Calculus (chapter 5). Proof: Let x > 0. Apply the definition: d ln(x + h) ln(x) ln(x) = lim dx h 0 h From the picture, we see that for h > 0, h x + h < ln(x + h) ln(x) < h x ; this clear if x > 1, but in fact it is true for all x. Thus, 1 x + h < ln(x + h) ln(x) h By the squeeze theorem, f +(x) = 1 x. 11 < 1 x
12 So, A similar picture shows that for h < 0 and x + h > 0, h x > ln(x + h) ln(x) > h x + h 1 ln(x + h) ln(x) < < 1 x h x + h Thus, f (x) = 1 x. Thus, f (x) = 1 x. Corollary: ln(x) is an increasing function. Theorem 2: Properties of ln(x): 1. ln(xy) = ln(x) + ln(y) 2. ln(1/x) = ln(x). 3. ln(x/y) = ln(x) ln(y) 4. ln(x r ) = r ln(x) (for now, only for rational r) Deja vu from log a (x)? Lemma (Theorem 13, p.141, an application of MVT): If f is continuous on an interval I and f (x) = 0 for all interior points x of I, then f is constant on I. Proof: Let x 0, x 1 I s.t. x 0 < x 1. By MVT, there exists c s.t. x 0 < c < x 1 and f(x 1 ) f(x 0 ) = f (c) = 0. x 1 x 0 So, f(x 1 ) = f(x 0 ). So, f is constant. Proof of Theorem 2: (i) Fix y > 0, and let g(y) = ln(xy) ln(x). By the Chain Rule, g (y) = d y (ln(xy) ln(x)) = dx xy 1 x = 0. 12
13 By the Lemma, ln(xy) ln(x) is a constant (as a function of x). But for x = 1, we have ln(xy) ln(x) = ln(y) ln(1) = ln(y). Thus, for all x > 0, ln(xy) ln(x) = ln(y). (ii) By (i), ln(x) + ln(1/x) = ln(x(1/x)) = ln(1) = 0. (iii) By (i), ln(y)+ln(x/y) = ln(x). Thus, ln(x/y) = ln(x) ln(y). (iv) By (i), this holds for all positive integers r. It then follows from (ii) that this holds for all negative integers r. And ln(x 0 ) = ln(1), which we have already noted is 0. So, (iv) holds for all integers. For a rational m/n, we have (x m/n ) n = x m. Thus, since (iv) holds for integers, we have n ln(x m/n ) = ln((x m/n ) n ) = ln(x m ) = m ln(x). Thus, ln(x m/n ) = (m/n) ln(x). Corollary: 1) lim x ln(x) = and 2) lim x 0 + ln(x) = Proof: 1): For a positive integer n, log(2 n ) = n log(2) can be made arbitrarily large (by choosing n large). If x > 2 n, then, since ln(x) is increasing, ln(x) > n log(2) can be made arbitrarily large. Rigorous proof: Let N > 0. Let K be any integer N/ ln(2). Let M := 2 K. If x > M, then since ln(x) is increasing, ln(x) > ln(m) = K ln(2) (N/ ln(2)) ln(2) = N. 2): As x 0 +, 1/x and so ln(x) = ln(1/x). 13
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
7.1. Calculus of inverse functions. Text Section 7.1 Exercise:
 Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
Contents 7. Inverse functions 1 7.1. Calculus of inverse functions 2 7.2. Derivatives of exponential function 4 7.3. Logarithmic function 6 7.4. Derivatives of logarithmic functions 7 7.5. Exponential
Induction, sequences, limits and continuity
 Induction, sequences, limits and continuity Material covered: eclass notes on induction, Chapter 11, Section 1 and Chapter 2, Sections 2.2-2.5 Induction Principle of mathematical induction: Let P(n) be
Induction, sequences, limits and continuity Material covered: eclass notes on induction, Chapter 11, Section 1 and Chapter 2, Sections 2.2-2.5 Induction Principle of mathematical induction: Let P(n) be
Composition of Functions
 Math 120 Intermediate Algebra Sec 9.1: Composite and Inverse Functions Composition of Functions The composite function f g, the composition of f and g, is defined as (f g)(x) = f(g(x)). Recall that a function
Math 120 Intermediate Algebra Sec 9.1: Composite and Inverse Functions Composition of Functions The composite function f g, the composition of f and g, is defined as (f g)(x) = f(g(x)). Recall that a function
Section 3.5: Implicit Differentiation
 Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
Section 3.5: Implicit Differentiation In the previous sections, we considered the problem of finding the slopes of the tangent line to a given function y = f(x). The idea of a tangent line however is not
7.4* General logarithmic and exponential functions
 7.4* General logarithmic and exponential functions Mark Woodard Furman U Fall 2010 Mark Woodard (Furman U) 7.4* General logarithmic and exponential functions Fall 2010 1 / 9 Outline 1 General exponential
7.4* General logarithmic and exponential functions Mark Woodard Furman U Fall 2010 Mark Woodard (Furman U) 7.4* General logarithmic and exponential functions Fall 2010 1 / 9 Outline 1 General exponential
4. We accept without proofs that the following functions are differentiable: (e x ) = e x, sin x = cos x, cos x = sin x, log (x) = 1 sin x
 4 We accept without proofs that the following functions are differentiable: (e x ) = e x, sin x = cos x, cos x = sin x, log (x) = 1 sin x x, x > 0 Since tan x = cos x, from the quotient rule, tan x = sin
4 We accept without proofs that the following functions are differentiable: (e x ) = e x, sin x = cos x, cos x = sin x, log (x) = 1 sin x x, x > 0 Since tan x = cos x, from the quotient rule, tan x = sin
Lecture 5 - Logarithms, Slope of a Function, Derivatives
 Lecture 5 - Logarithms, Slope of a Function, Derivatives 5. Logarithms Note the graph of e x This graph passes the horizontal line test, so f(x) = e x is one-to-one and therefore has an inverse function.
Lecture 5 - Logarithms, Slope of a Function, Derivatives 5. Logarithms Note the graph of e x This graph passes the horizontal line test, so f(x) = e x is one-to-one and therefore has an inverse function.
3 Algebraic Methods. we can differentiate both sides implicitly to obtain a differential equation involving x and y:
 3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
3 Algebraic Methods b The first appearance of the equation E Mc 2 in Einstein s handwritten notes. So far, the only general class of differential equations that we know how to solve are directly integrable
Chapter 3: Transcendental Functions
 Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
Chapter 3: Transcendental Functions Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 32 Except for the power functions, the other basic elementary functions are also called the transcendental
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Fall 2018, WEEK 3 JoungDong Kim Week 3 Section 2.3, 2.5, 2.6, Calculating Limits Using the Limit Laws, Continuity, Limits at Infinity; Horizontal Asymptotes. Section
MATH 151 Engineering Mathematics I Fall 2018, WEEK 3 JoungDong Kim Week 3 Section 2.3, 2.5, 2.6, Calculating Limits Using the Limit Laws, Continuity, Limits at Infinity; Horizontal Asymptotes. Section
Calculus I Review Solutions
 Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Week 1: need to know. November 14, / 20
 Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
Week 1: need to know How to find domains and ranges, operations on functions (addition, subtraction, multiplication, division, composition), behaviors of functions (even/odd/ increasing/decreasing), library
Section 6.1: Composite Functions
 Section 6.1: Composite Functions Def: Given two function f and g, the composite function, which we denote by f g and read as f composed with g, is defined by (f g)(x) = f(g(x)). In other words, the function
Section 6.1: Composite Functions Def: Given two function f and g, the composite function, which we denote by f g and read as f composed with g, is defined by (f g)(x) = f(g(x)). In other words, the function
Solutions to Math 41 First Exam October 15, 2013
 Solutions to Math 41 First Exam October 15, 2013 1. (16 points) Find each of the following its, with justification. If the it does not exist, explain why. If there is an infinite it, then explain whether
Solutions to Math 41 First Exam October 15, 2013 1. (16 points) Find each of the following its, with justification. If the it does not exist, explain why. If there is an infinite it, then explain whether
Sec 4.1 Limits, Informally. When we calculated f (x), we first started with the difference quotient. f(x + h) f(x) h
 1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
2.6 Logarithmic Functions. Inverse Functions. Question: What is the relationship between f(x) = x 2 and g(x) = x?
 Inverse Functions Question: What is the relationship between f(x) = x 3 and g(x) = 3 x? Question: What is the relationship between f(x) = x 2 and g(x) = x? Definition (One-to-One Function) A function f
Inverse Functions Question: What is the relationship between f(x) = x 3 and g(x) = 3 x? Question: What is the relationship between f(x) = x 2 and g(x) = x? Definition (One-to-One Function) A function f
(e) 2 (f) 2. (c) + (d). Limits at Infinity. 2.5) 9-14,25-34,41-43,46-47,56-57, (c) (d) 2
 Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
Math 150A. Final Review Answers, Spring 2018. Limits. 2.2) 7-10, 21-24, 28-1, 6-8, 4-44. 1. Find the values, or state they do not exist. (a) (b) 1 (c) DNE (d) 1 (e) 2 (f) 2 (g) 2 (h) 4 2. lim f(x) = 2,
Section 4.2: The Mean Value Theorem
 Section 4.2: The Mean Value Theorem Before we continue with the problem of describing graphs using calculus we shall briefly pause to examine some interesting applications of the derivative. In previous
Section 4.2: The Mean Value Theorem Before we continue with the problem of describing graphs using calculus we shall briefly pause to examine some interesting applications of the derivative. In previous
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
2 Limits 2.1 The Tangent Problems The word tangent is derived from the Latin word tangens, which means touching. A tangent line to a curve is a line that touches the curve and a secant line is a line that
MAT137 Calculus! Lecture 9
 MAT137 Calculus! Lecture 9 Today we will study: Limits at infinity. L Hôpital s Rule. Mean Value Theorem. (11.5,11.6, 4.1) PS3 is due this Friday June 16. Next class: Applications of the Mean Value Theorem.
MAT137 Calculus! Lecture 9 Today we will study: Limits at infinity. L Hôpital s Rule. Mean Value Theorem. (11.5,11.6, 4.1) PS3 is due this Friday June 16. Next class: Applications of the Mean Value Theorem.
f(x) f(z) c x z > 0 1
 INVERSE AND IMPLICIT FUNCTION THEOREMS I use df x for the linear transformation that is the differential of f at x.. INVERSE FUNCTION THEOREM Definition. Suppose S R n is open, a S, and f : S R n is a
INVERSE AND IMPLICIT FUNCTION THEOREMS I use df x for the linear transformation that is the differential of f at x.. INVERSE FUNCTION THEOREM Definition. Suppose S R n is open, a S, and f : S R n is a
Learning Objectives for Math 165
 Learning Objectives for Math 165 Chapter 2 Limits Section 2.1: Average Rate of Change. State the definition of average rate of change Describe what the rate of change does and does not tell us in a given
Learning Objectives for Math 165 Chapter 2 Limits Section 2.1: Average Rate of Change. State the definition of average rate of change Describe what the rate of change does and does not tell us in a given
2.1 The Tangent and Velocity Problems
 2.1 The Tangent and Velocity Problems Tangents What is a tangent? Tangent lines and Secant lines Estimating slopes from discrete data: Example: 1. A tank holds 1000 gallons of water, which drains from
2.1 The Tangent and Velocity Problems Tangents What is a tangent? Tangent lines and Secant lines Estimating slopes from discrete data: Example: 1. A tank holds 1000 gallons of water, which drains from
MATH 151 Engineering Mathematics I
 MATH 151 Engineering Mathematics I Spring 2018, WEEK 3 JoungDong Kim Week 3 Section 2.5, 2.6, 2.7, Continuity, Limits at Infinity; Horizontal Asymptotes, Derivatives and Rates of Change. Section 2.5 Continuity
MATH 151 Engineering Mathematics I Spring 2018, WEEK 3 JoungDong Kim Week 3 Section 2.5, 2.6, 2.7, Continuity, Limits at Infinity; Horizontal Asymptotes, Derivatives and Rates of Change. Section 2.5 Continuity
10/9/10. The line x = a is a vertical asymptote of the graph of a function y = f(x) if either. Definitions and Theorems.
 Definitions and Theorems Introduction Unit 2 Limits and Continuity Definition - Vertical Asymptote Definition - Horizontal Asymptote Definition Continuity Unit 3 Derivatives Definition - Derivative Definition
Definitions and Theorems Introduction Unit 2 Limits and Continuity Definition - Vertical Asymptote Definition - Horizontal Asymptote Definition Continuity Unit 3 Derivatives Definition - Derivative Definition
1 Functions, Graphs and Limits
 1 Functions, Graphs and Limits 1.1 The Cartesian Plane In this course we will be dealing a lot with the Cartesian plane (also called the xy-plane), so this section should serve as a review of it and its
1 Functions, Graphs and Limits 1.1 The Cartesian Plane In this course we will be dealing a lot with the Cartesian plane (also called the xy-plane), so this section should serve as a review of it and its
Differentiation. Table of contents Definition Arithmetics Composite and inverse functions... 5
 Differentiation Table of contents. Derivatives................................................. 2.. Definition................................................ 2.2. Arithmetics...............................................
Differentiation Table of contents. Derivatives................................................. 2.. Definition................................................ 2.2. Arithmetics...............................................
Honors Calculus Quiz 9 Solutions 12/2/5
 Honors Calculus Quiz Solutions //5 Question Find the centroid of the region R bounded by the curves 0y y + x and y 0y + 50 x Also determine the volumes of revolution of the region R about the coordinate
Honors Calculus Quiz Solutions //5 Question Find the centroid of the region R bounded by the curves 0y y + x and y 0y + 50 x Also determine the volumes of revolution of the region R about the coordinate
MA4001 Engineering Mathematics 1 Lecture 15 Mean Value Theorem Increasing and Decreasing Functions Higher Order Derivatives Implicit Differentiation
 MA4001 Engineering Mathematics 1 Lecture 15 Mean Value Theorem Increasing and Decreasing Functions Higher Order Derivatives Implicit Differentiation Dr. Sarah Mitchell Autumn 2014 Rolle s Theorem Theorem
MA4001 Engineering Mathematics 1 Lecture 15 Mean Value Theorem Increasing and Decreasing Functions Higher Order Derivatives Implicit Differentiation Dr. Sarah Mitchell Autumn 2014 Rolle s Theorem Theorem
2. Theory of the Derivative
 2. Theory of the Derivative 2.1 Tangent Lines 2.2 Definition of Derivative 2.3 Rates of Change 2.4 Derivative Rules 2.5 Higher Order Derivatives 2.6 Implicit Differentiation 2.7 L Hôpital s Rule 2.8 Some
2. Theory of the Derivative 2.1 Tangent Lines 2.2 Definition of Derivative 2.3 Rates of Change 2.4 Derivative Rules 2.5 Higher Order Derivatives 2.6 Implicit Differentiation 2.7 L Hôpital s Rule 2.8 Some
Definitions & Theorems
 Definitions & Theorems Math 147, Fall 2009 December 19, 2010 Contents 1 Logic 2 1.1 Sets.................................................. 2 1.2 The Peano axioms..........................................
Definitions & Theorems Math 147, Fall 2009 December 19, 2010 Contents 1 Logic 2 1.1 Sets.................................................. 2 1.2 The Peano axioms..........................................
Section 3.7. Rolle s Theorem and the Mean Value Theorem
 Section.7 Rolle s Theorem and the Mean Value Theorem The two theorems which are at the heart of this section draw connections between the instantaneous rate of change and the average rate of change of
Section.7 Rolle s Theorem and the Mean Value Theorem The two theorems which are at the heart of this section draw connections between the instantaneous rate of change and the average rate of change of
Section 3.1 Extreme Values
 Math 132 Extreme Values Section 3.1 Section 3.1 Extreme Values Example 1: Given the following is the graph of f(x) Where is the maximum (x-value)? What is the maximum (y-value)? Where is the minimum (x-value)?
Math 132 Extreme Values Section 3.1 Section 3.1 Extreme Values Example 1: Given the following is the graph of f(x) Where is the maximum (x-value)? What is the maximum (y-value)? Where is the minimum (x-value)?
CH 2: Limits and Derivatives
 2 The tangent and velocity problems CH 2: Limits and Derivatives the tangent line to a curve at a point P, is the line that has the same slope as the curve at that point P, ie the slope of the tangent
2 The tangent and velocity problems CH 2: Limits and Derivatives the tangent line to a curve at a point P, is the line that has the same slope as the curve at that point P, ie the slope of the tangent
Math 117: Honours Calculus I Fall, 2002 List of Theorems. a n k b k. k. Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
 Math 117: Honours Calculus I Fall, 2002 List of Theorems Theorem 1.1 (Binomial Theorem) For all n N, (a + b) n = n k=0 ( ) n a n k b k. k Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
Math 117: Honours Calculus I Fall, 2002 List of Theorems Theorem 1.1 (Binomial Theorem) For all n N, (a + b) n = n k=0 ( ) n a n k b k. k Theorem 2.1 (Convergent Bounded) A convergent sequence is bounded.
3.9 Derivatives of Exponential and Logarithmic Functions
 322 Chapter 3 Derivatives 3.9 Derivatives of Exponential and Logarithmic Functions Learning Objectives 3.9.1 Find the derivative of exponential functions. 3.9.2 Find the derivative of logarithmic functions.
322 Chapter 3 Derivatives 3.9 Derivatives of Exponential and Logarithmic Functions Learning Objectives 3.9.1 Find the derivative of exponential functions. 3.9.2 Find the derivative of logarithmic functions.
Name (print): Question 4. exercise 1.24 (compute the union, then the intersection of two sets)
 MTH299 - Homework 1 Question 1. exercise 1.10 (compute the cardinality of a handful of finite sets) Solution. Write your answer here. Question 2. exercise 1.20 (compute the union of two sets) Question
MTH299 - Homework 1 Question 1. exercise 1.10 (compute the cardinality of a handful of finite sets) Solution. Write your answer here. Question 2. exercise 1.20 (compute the union of two sets) Question
2.1 The derivative. Rates of change. m sec = y f (a + h) f (a)
 2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
2.1 The derivative Rates of change 1 The slope of a secant line is m sec = y f (b) f (a) = x b a and represents the average rate of change over [a, b]. Letting b = a + h, we can express the slope of the
Final Exam Study Guide
 Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
MATH 409 Advanced Calculus I Lecture 10: Continuity. Properties of continuous functions.
 MATH 409 Advanced Calculus I Lecture 10: Continuity. Properties of continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if
MATH 409 Advanced Calculus I Lecture 10: Continuity. Properties of continuous functions. Continuity Definition. Given a set E R, a function f : E R, and a point c E, the function f is continuous at c if
Part 2 Continuous functions and their properties
 Part 2 Continuous functions and their properties 2.1 Definition Definition A function f is continuous at a R if, and only if, that is lim f (x) = f (a), x a ε > 0, δ > 0, x, x a < δ f (x) f (a) < ε. Notice
Part 2 Continuous functions and their properties 2.1 Definition Definition A function f is continuous at a R if, and only if, that is lim f (x) = f (a), x a ε > 0, δ > 0, x, x a < δ f (x) f (a) < ε. Notice
Wed. Sept 28th: 1.3 New Functions from Old Functions: o vertical and horizontal shifts o vertical and horizontal stretching and reflecting o
 Homework: Appendix A: 1, 2, 3, 5, 6, 7, 8, 11, 13-33(odd), 34, 37, 38, 44, 45, 49, 51, 56. Appendix B: 3, 6, 7, 9, 11, 14, 16-21, 24, 29, 33, 36, 37, 42. Appendix D: 1, 2, 4, 9, 11-20, 23, 26, 28, 29,
Homework: Appendix A: 1, 2, 3, 5, 6, 7, 8, 11, 13-33(odd), 34, 37, 38, 44, 45, 49, 51, 56. Appendix B: 3, 6, 7, 9, 11, 14, 16-21, 24, 29, 33, 36, 37, 42. Appendix D: 1, 2, 4, 9, 11-20, 23, 26, 28, 29,
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Calculus I - Homework Chapter 2 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether the graph is the graph of a function. 1) 1)
Calculus I - Homework Chapter 2 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Determine whether the graph is the graph of a function. 1) 1)
MATH 2053 Calculus I Review for the Final Exam
 MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
Continuity, Intermediate Value Theorem (2.4)
 Continuity, Intermediate Value Theorem (2.4) Xiannan Li Kansas State University January 29th, 2017 Intuitive Definition: A function f(x) is continuous at a if you can draw the graph of y = f(x) without
Continuity, Intermediate Value Theorem (2.4) Xiannan Li Kansas State University January 29th, 2017 Intuitive Definition: A function f(x) is continuous at a if you can draw the graph of y = f(x) without
b n x n + b n 1 x n b 1 x + b 0
 Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Math Partial Fractions Stewart 7.4 Integrating basic rational functions. For a function f(x), we have examined several algebraic methods for finding its indefinite integral (antiderivative) F (x) = f(x)
Limits at Infinity. Horizontal Asymptotes. Definition (Limits at Infinity) Horizontal Asymptotes
 Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
2.4 The Precise Definition of a Limit
 2.4 The Precise Definition of a Limit Reminders/Remarks: x 4 < 3 means that the distance between x and 4 is less than 3. In other words, x lies strictly between 1 and 7. So, x a < δ means that the distance
2.4 The Precise Definition of a Limit Reminders/Remarks: x 4 < 3 means that the distance between x and 4 is less than 3. In other words, x lies strictly between 1 and 7. So, x a < δ means that the distance
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Chapter 2: Differentiation
 Chapter 2: Differentiation Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 82 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Chapter 2: Differentiation Spring 2018 Department of Mathematics Hong Kong Baptist University 1 / 82 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
What is on today. 1 Linear approximation. MA 123 (Calculus I) Lecture 17: November 2, 2017 Section A2. Professor Jennifer Balakrishnan,
 Professor Jennifer Balakrishnan, jbala@bu.edu What is on today 1 Linear approximation 1 1.1 Linear approximation and concavity....................... 2 1.2 Change in y....................................
Professor Jennifer Balakrishnan, jbala@bu.edu What is on today 1 Linear approximation 1 1.1 Linear approximation and concavity....................... 2 1.2 Change in y....................................
MATH 409 Advanced Calculus I Lecture 12: Uniform continuity. Exponential functions.
 MATH 409 Advanced Calculus I Lecture 12: Uniform continuity. Exponential functions. Uniform continuity Definition. A function f : E R defined on a set E R is called uniformly continuous on E if for every
MATH 409 Advanced Calculus I Lecture 12: Uniform continuity. Exponential functions. Uniform continuity Definition. A function f : E R defined on a set E R is called uniformly continuous on E if for every
Final Exam Review Exercise Set A, Math 1551, Fall 2017
 Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Mean Value Theorem. MATH 161 Calculus I. J. Robert Buchanan. Summer Department of Mathematics
 Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem. MATH 161 Calculus I. J. Robert Buchanan. Summer Department of Mathematics
 Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
University of Toronto Solutions to MAT186H1F TERM TEST of Tuesday, October 15, 2013 Duration: 100 minutes
 University of Toronto Solutions to MAT186H1F TERM TEST of Tuesday, October 15, 2013 Duration: 100 minutes Only aids permitted: Casio FX-991 or Sharp EL-520 calculator. Instructions: Answer all questions.
University of Toronto Solutions to MAT186H1F TERM TEST of Tuesday, October 15, 2013 Duration: 100 minutes Only aids permitted: Casio FX-991 or Sharp EL-520 calculator. Instructions: Answer all questions.
Topics and Concepts. 1. Limits
 Topics and Concepts 1. Limits (a) Evaluating its (Know: it exists if and only if the it from the left is the same as the it from the right) (b) Infinite its (give rise to vertical asymptotes) (c) Limits
Topics and Concepts 1. Limits (a) Evaluating its (Know: it exists if and only if the it from the left is the same as the it from the right) (b) Infinite its (give rise to vertical asymptotes) (c) Limits
Caculus 221. Possible questions for Exam II. March 19, 2002
 Caculus 221 Possible questions for Exam II March 19, 2002 These notes cover the recent material in a style more like the lecture than the book. The proofs in the book are in section 1-11. At the end there
Caculus 221 Possible questions for Exam II March 19, 2002 These notes cover the recent material in a style more like the lecture than the book. The proofs in the book are in section 1-11. At the end there
Final Exam. Math 3 December 7, 2010
 Final Exam Math 3 December 7, 200 Name: On this final examination for Math 3 in Fall 200, I will work individually, neither giving nor receiving help, guided by the Dartmouth Academic Honor Principle.
Final Exam Math 3 December 7, 200 Name: On this final examination for Math 3 in Fall 200, I will work individually, neither giving nor receiving help, guided by the Dartmouth Academic Honor Principle.
Chapter 2: Functions, Limits and Continuity
 Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Chapter 2: Functions, Limits and Continuity Functions Limits Continuity Chapter 2: Functions, Limits and Continuity 1 Functions Functions are the major tools for describing the real world in mathematical
Math 180, Final Exam, Fall 2007 Problem 1 Solution
 Problem Solution. Differentiate with respect to x. Write your answers showing the use of the appropriate techniques. Do not simplify. (a) x 27 x 2/3 (b) (x 2 2x + 2)e x (c) ln(x 2 + 4) (a) Use the Power
Problem Solution. Differentiate with respect to x. Write your answers showing the use of the appropriate techniques. Do not simplify. (a) x 27 x 2/3 (b) (x 2 2x + 2)e x (c) ln(x 2 + 4) (a) Use the Power
V. Graph Sketching and Max-Min Problems
 V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information.
V. Graph Sketching and Max-Min Problems The signs of the first and second derivatives of a function tell us something about the shape of its graph. In this chapter we learn how to find that information.
Math 1 Lecture 23. Dartmouth College. Wednesday
 Math 1 Lecture 23 Dartmouth College Wednesday 11-02-16 Contents Reminders/Announcements Last Time Derivatives of Logarithmic and Exponential Functions Examish Exercises Reminders/Announcements WebWork
Math 1 Lecture 23 Dartmouth College Wednesday 11-02-16 Contents Reminders/Announcements Last Time Derivatives of Logarithmic and Exponential Functions Examish Exercises Reminders/Announcements WebWork
Chapter 2: Differentiation
 Chapter 2: Differentiation Winter 2016 Department of Mathematics Hong Kong Baptist University 1 / 75 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Chapter 2: Differentiation Winter 2016 Department of Mathematics Hong Kong Baptist University 1 / 75 2.1 Tangent Lines and Their Slopes This section deals with the problem of finding a straight line L
Lectures. Section Theoretical (Definitions & Theorem) Examples Exercises HW
 King Abdul-Aziz University Academic year 1437-1438 Department of Mathematics 2016-2017 Math 110 (S & E) Syllabus / Term (1) Book: Calculus Early Transcendentals by James Stewart 7 th edition Lectures Chapter
King Abdul-Aziz University Academic year 1437-1438 Department of Mathematics 2016-2017 Math 110 (S & E) Syllabus / Term (1) Book: Calculus Early Transcendentals by James Stewart 7 th edition Lectures Chapter
QF101: Quantitative Finance August 22, Week 1: Functions. Facilitator: Christopher Ting AY 2017/2018
 QF101: Quantitative Finance August 22, 2017 Week 1: Functions Facilitator: Christopher Ting AY 2017/2018 The chief function of the body is to carry the brain around. Thomas A. Edison 1.1 What is a function?
QF101: Quantitative Finance August 22, 2017 Week 1: Functions Facilitator: Christopher Ting AY 2017/2018 The chief function of the body is to carry the brain around. Thomas A. Edison 1.1 What is a function?
MATH 1A, Complete Lecture Notes. Fedor Duzhin
 MATH 1A, Complete Lecture Notes Fedor Duzhin 2007 Contents I Limit 6 1 Sets and Functions 7 1.1 Sets................................. 7 1.2 Functions.............................. 8 1.3 How to define a
MATH 1A, Complete Lecture Notes Fedor Duzhin 2007 Contents I Limit 6 1 Sets and Functions 7 1.1 Sets................................. 7 1.2 Functions.............................. 8 1.3 How to define a
2210 fall 2002 Exponential and log functions Positive Integer exponents Negative integer exponents Fractional exponents
 220 fall 2002 Exponential and log functions Exponential functions, even simple ones like 0 x, or 2 x, are relatively difficult to describe and to calculate because they involve taking high roots of integers,
220 fall 2002 Exponential and log functions Exponential functions, even simple ones like 0 x, or 2 x, are relatively difficult to describe and to calculate because they involve taking high roots of integers,
Solutions Definition 2: a solution
 Solutions As was stated before, one of the goals in this course is to solve, or find solutions of differential equations. In the next definition we consider the concept of a solution of an ordinary differential
Solutions As was stated before, one of the goals in this course is to solve, or find solutions of differential equations. In the next definition we consider the concept of a solution of an ordinary differential
Iowa State University. Instructor: Alex Roitershtein Summer Homework #5. Solutions
 Math 50 Iowa State University Introduction to Real Analysis Department of Mathematics Instructor: Alex Roitershtein Summer 205 Homework #5 Solutions. Let α and c be real numbers, c > 0, and f is defined
Math 50 Iowa State University Introduction to Real Analysis Department of Mathematics Instructor: Alex Roitershtein Summer 205 Homework #5 Solutions. Let α and c be real numbers, c > 0, and f is defined
Functions. Remark 1.2 The objective of our course Calculus is to study functions.
 Functions 1.1 Functions and their Graphs Definition 1.1 A function f is a rule assigning a number to each of the numbers. The number assigned to the number x via the rule f is usually denoted by f(x).
Functions 1.1 Functions and their Graphs Definition 1.1 A function f is a rule assigning a number to each of the numbers. The number assigned to the number x via the rule f is usually denoted by f(x).
MATH 1A - FINAL EXAM DELUXE - SOLUTIONS. x x x x x 2. = lim = 1 =0. 2) Then ln(y) = x 2 ln(x) 3) ln(x)
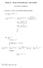 MATH A - FINAL EXAM DELUXE - SOLUTIONS PEYAM RYAN TABRIZIAN. ( points, 5 points each) Find the following limits (a) lim x x2 + x ( ) x lim x2 + x x2 + x 2 + + x x x x2 + + x x 2 + x 2 x x2 + + x x x2 +
MATH A - FINAL EXAM DELUXE - SOLUTIONS PEYAM RYAN TABRIZIAN. ( points, 5 points each) Find the following limits (a) lim x x2 + x ( ) x lim x2 + x x2 + x 2 + + x x x x2 + + x x 2 + x 2 x x2 + + x x x2 +
Engg. Math. I. Unit-I. Differential Calculus
 Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Calculus. Weijiu Liu. Department of Mathematics University of Central Arkansas 201 Donaghey Avenue, Conway, AR 72035, USA
 Calculus Weijiu Liu Department of Mathematics University of Central Arkansas 201 Donaghey Avenue, Conway, AR 72035, USA 1 Opening Welcome to your Calculus I class! My name is Weijiu Liu. I will guide you
Calculus Weijiu Liu Department of Mathematics University of Central Arkansas 201 Donaghey Avenue, Conway, AR 72035, USA 1 Opening Welcome to your Calculus I class! My name is Weijiu Liu. I will guide you
2.3 The Chain Rule and Inverse Functions
 2.3 The Chain Rule and Inverse Functions 2.3. The Chain Rule and its Applications Theorem 2.3. (Chain Rule). If f(x) and g(x) are differentiable, then the derivative of the composite function (f g)(x)
2.3 The Chain Rule and Inverse Functions 2.3. The Chain Rule and its Applications Theorem 2.3. (Chain Rule). If f(x) and g(x) are differentiable, then the derivative of the composite function (f g)(x)
Solutions to Math 41 Final Exam December 10, 2012
 Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
1.5 Inverse Trigonometric Functions
 1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
1.5 Inverse Trigonometric Functions Remember that only one-to-one functions have inverses. So, in order to find the inverse functions for sine, cosine, and tangent, we must restrict their domains to intervals
Math 117: Honours Calculus I Fall, 2012 List of Theorems. a n k b k. k. Theorem 2.1 (Convergent Bounded): A convergent sequence is bounded.
 Math 117: Honours Calculus I Fall, 2012 List of Theorems Theorem 1.1 (Binomial Theorem): For all n N, (a+b) n = n k=0 ( ) n a n k b k. k Theorem 2.1 (Convergent Bounded): A convergent sequence is bounded.
Math 117: Honours Calculus I Fall, 2012 List of Theorems Theorem 1.1 (Binomial Theorem): For all n N, (a+b) n = n k=0 ( ) n a n k b k. k Theorem 2.1 (Convergent Bounded): A convergent sequence is bounded.
Math 131 Exam 2 Spring 2016
 Math 3 Exam Spring 06 Name: ID: 7 multiple choice questions worth 4.7 points each. hand graded questions worth 0 points each. 0. free points (so the total will be 00). Exam covers sections.7 through 3.0
Math 3 Exam Spring 06 Name: ID: 7 multiple choice questions worth 4.7 points each. hand graded questions worth 0 points each. 0. free points (so the total will be 00). Exam covers sections.7 through 3.0
2.12: Derivatives of Exp/Log (cont d) and 2.15: Antiderivatives and Initial Value Problems
 2.12: Derivatives of Exp/Log (cont d) and 2.15: Antiderivatives and Initial Value Problems Mathematics 3 Lecture 14 Dartmouth College February 03, 2010 Derivatives of the Exponential and Logarithmic Functions
2.12: Derivatives of Exp/Log (cont d) and 2.15: Antiderivatives and Initial Value Problems Mathematics 3 Lecture 14 Dartmouth College February 03, 2010 Derivatives of the Exponential and Logarithmic Functions
Mathematic 108, Fall 2015: Solutions to assignment #7
 Mathematic 08, Fall 05: Solutions to assignment #7 Problem # Suppose f is a function with f continuous on the open interval I and so that f has a local maximum at both x = a and x = b for a, b I with a
Mathematic 08, Fall 05: Solutions to assignment #7 Problem # Suppose f is a function with f continuous on the open interval I and so that f has a local maximum at both x = a and x = b for a, b I with a
x 2 + y 2 = 1. dx 2y and we conclude that, whichever function we chose, dx y2 = 2x + dy dx x2 + d dy dx = 2x = x y sinh(x) = ex e x 2
 Implicit differentiation Suppose we know some relation between x and y, e.g. x + y =. Here, y isn t a function of x. But if we restrict attention to y, then y is a function of x; similarly for y. These
Implicit differentiation Suppose we know some relation between x and y, e.g. x + y =. Here, y isn t a function of x. But if we restrict attention to y, then y is a function of x; similarly for y. These
Calculus & Analytic Geometry I
 TQS 124 Autumn 2008 Quinn Calculus & Analytic Geometry I The Derivative: Analytic Viewpoint Derivative of a Constant Function. For c a constant, the derivative of f(x) = c equals f (x) = Derivative of
TQS 124 Autumn 2008 Quinn Calculus & Analytic Geometry I The Derivative: Analytic Viewpoint Derivative of a Constant Function. For c a constant, the derivative of f(x) = c equals f (x) = Derivative of
2. Which of the following is an equation of the line tangent to the graph of f(x) = x 4 + 2x 2 at the point where
 AP Review Chapter Name: Date: Per: 1. The radius of a circle is decreasing at a constant rate of 0.1 centimeter per second. In terms of the circumference C, what is the rate of change of the area of the
AP Review Chapter Name: Date: Per: 1. The radius of a circle is decreasing at a constant rate of 0.1 centimeter per second. In terms of the circumference C, what is the rate of change of the area of the
Calculus I Exam 1 Review Fall 2016
 Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Calculus. Central role in much of modern science Physics, especially kinematics and electrodynamics Economics, engineering, medicine, chemistry, etc.
 Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
1 Functions of Several Variables 2019 v2
 1 Functions of Several Variables 2019 v2 11 Notation The subject of this course is the study of functions f : R n R m The elements of R n, for n 2, will be called vectors so, if m > 1, f will be said to
1 Functions of Several Variables 2019 v2 11 Notation The subject of this course is the study of functions f : R n R m The elements of R n, for n 2, will be called vectors so, if m > 1, f will be said to
Chapter 4. Section Derivatives of Exponential and Logarithmic Functions
 Chapter 4 Section 4.2 - Derivatives of Exponential and Logarithmic Functions Objectives: The student will be able to calculate the derivative of e x and of lnx. The student will be able to compute the
Chapter 4 Section 4.2 - Derivatives of Exponential and Logarithmic Functions Objectives: The student will be able to calculate the derivative of e x and of lnx. The student will be able to compute the
Math Calculus II Material for Exam II
 Lecture /9. Definition of a function A function f : R(the omain) R(the coomain), where R is the collection(set) of real numbers, assigns to every number in the omain, a unique number in the coomain...
Lecture /9. Definition of a function A function f : R(the omain) R(the coomain), where R is the collection(set) of real numbers, assigns to every number in the omain, a unique number in the coomain...
Chapter 8: Taylor s theorem and L Hospital s rule
 Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
Chapter 8: Taylor s theorem and L Hospital s rule Theorem: [Inverse Mapping Theorem] Suppose that a < b and f : [a, b] R. Given that f (x) > 0 for all x (a, b) then f 1 is differentiable on (f(a), f(b))
3.4 The Chain Rule. F (x) = f (g(x))g (x) Alternate way of thinking about it: If y = f(u) and u = g(x) where both are differentiable functions, then
 3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
3.4 The Chain Rule To find the derivative of a function that is the composition of two functions for which we already know the derivatives, we can use the Chain Rule. The Chain Rule: Suppose F (x) = f(g(x)).
Math LM (24543) Lectures 02
 Math 32300 LM (24543) Lectures 02 Ethan Akin Office: NAC 6/287 Phone: 650-5136 Email: ethanakin@earthlink.net Spring, 2018 Contents Continuity, Ross Chapter 3 Uniform Continuity and Compactness Connectedness
Math 32300 LM (24543) Lectures 02 Ethan Akin Office: NAC 6/287 Phone: 650-5136 Email: ethanakin@earthlink.net Spring, 2018 Contents Continuity, Ross Chapter 3 Uniform Continuity and Compactness Connectedness
Workbook for Calculus I
 Workbook for Calculus I By Hüseyin Yüce New York 2007 1 Functions 1.1 Four Ways to Represent a Function 1. Find the domain and range of the function f(x) = 1 + x + 1 and sketch its graph. y 3 2 1-3 -2-1
Workbook for Calculus I By Hüseyin Yüce New York 2007 1 Functions 1.1 Four Ways to Represent a Function 1. Find the domain and range of the function f(x) = 1 + x + 1 and sketch its graph. y 3 2 1-3 -2-1
MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS
 MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT100 is a fast-paced and thorough tour of precalculus mathematics, where the choice of topics is primarily motivated by the conceptual and technical knowledge
MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT100 is a fast-paced and thorough tour of precalculus mathematics, where the choice of topics is primarily motivated by the conceptual and technical knowledge
University of Toronto MAT137Y1 Calculus! Test 2 1 December 2017 Time: 110 minutes
 University of Toronto MAT137Y1 Calculus! Test 2 1 December 2017 Time: 110 minutes Please complete this cover page with ALL CAPITAL LETTERS. Last name......................................................................................
University of Toronto MAT137Y1 Calculus! Test 2 1 December 2017 Time: 110 minutes Please complete this cover page with ALL CAPITAL LETTERS. Last name......................................................................................
Limit. Chapter Introduction
 Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
Chapter 9 Limit Limit is the foundation of calculus that it is so useful to understand more complicating chapters of calculus. Besides, Mathematics has black hole scenarios (dividing by zero, going to
MATH 408N PRACTICE FINAL
 2/03/20 Bormashenko MATH 408N PRACTICE FINAL Show your work for all the problems. Good luck! () Let f(x) = ex e x. (a) [5 pts] State the domain and range of f(x). Name: TA session: Since e x is defined
2/03/20 Bormashenko MATH 408N PRACTICE FINAL Show your work for all the problems. Good luck! () Let f(x) = ex e x. (a) [5 pts] State the domain and range of f(x). Name: TA session: Since e x is defined
Math 1000 Final Exam Review Solutions. (x + 3)(x 2) = lim. = lim x 2 = 3 2 = 5. (x + 1) 1 x( x ) = lim. = lim. f f(1 + h) f(1) (1) = lim
 Math Final Eam Review Solutions { + 3 if < Consider f() Find the following limits: (a) lim f() + + (b) lim f() + 3 3 (c) lim f() does not eist Find each of the following limits: + 6 (a) lim 3 + 3 (b) lim
Math Final Eam Review Solutions { + 3 if < Consider f() Find the following limits: (a) lim f() + + (b) lim f() + 3 3 (c) lim f() does not eist Find each of the following limits: + 6 (a) lim 3 + 3 (b) lim
