Inferences about a Mean Vector
|
|
|
- Juliana Barnett
- 6 years ago
- Views:
Transcription
1 Inferences about a Mean Vector Edps/Soc 584, Psych 594 Carolyn J. Anderson Department of Educational Psychology I L L I N O I S university of illinois at urbana-champaign c Board of Trustees, University of Illinois Spring 2017
2 Overview Goal Univariate Case Multivariate Case Hotelling T 2 Likelihood Ratio test Comparison/relationship IF Reject H o... Confidence regions Simultaneous comparisons (univariate/one-at-a-time) T 2 intervals Bonferroni intervals Comparison Large sample inferences about a population mean vector. Reading: Johnson & Wichern pages C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
3 Goal Inference: To make a valid conclusion about the means of a population based on a sample (information about the population). When we have p correlated variables, they must be analyzed jointly. Simultaneous analysis yields stronger tests, with better error control. The tests covered in this set of notes are all of the form: H o :µ = µ o where µ p 1 vector of populations means and µ o,p 1 is the some specified values under the null hypothesis. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
4 Univariate Case We re interested in the mean of a population and we have a random sample of n observations from the population, where (i.e., Assumptions): X 1,X 2,...,X n Observations are independent (i.e., X j is independent from X j for j j ). Observations are from the same population; that is, E(X j ) = µ for all j If the sample size is small, we ll also assume that X j N(µ,σ 2 ) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
5 Hypothesis & Test Hypothesis: H o : µ = µ o versus H 1 : µ µ o where µ o is some specified value. In this case, H 1 is 2 sided alternative. Test Statistic: t = X µ o s/ n where X = (1/n) n j=1 X j and s = (1/(n 1)) n j 1 (X j X) 2 Sampling Distribution: If H o and assumptions are true, then the sampling distribution of t is Student s - t distribution with df = n 1. Decision: Reject H o when t is large (i.e., small p value). C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
6 Picture of Decision Each green area = α/2 = C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
7 Confidence Interval Confidence Interval: A region or range of plausible µ s (given observations/data). The set of all µ s such that x µ o s/ n t n 1,(α/2) where t n 1,(α/2) is the upper (α/2)100% percentile of Student s t-distribution with df = n 1....OR { } s s µ o such that x t n 1,(α/2) µ o x +t n 1,(α/2) n n A 100(1 α) th ( confidence interval or region for µ is ) s s x t n 1,(α/2), x +t n 1,(α/2) n n Before for sample is selected, the ends of the interval depend on random variables X s and s; this is a random interval. 100(1 α) th percent of the time such intervals with contain the true mean µ. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
8 Prepare for Jump to p Dimensions Square the test statistic t: t 2 = ( x µ o) 2 s 2 /n = n( x µ o )(s 2 ) 1 ( x µ o ) So t 2 is a squared statistical distance between the sample mean x and the hypothesized value µ o. Remember that t 2 df = F 1,df? That is, the sampling distribution of t 2 = n( x µ o )(s 2 ) 1 ( x µ o ) F 1,n 1. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
9 Multivariate Case: Hotelling s T 2 For the extension from the univariate to multivariate case, replace scalars with vectors and matrices: T 2 = n( X µ o ) S 1 ( X µ o ) Xp 1 = (1/n) n j=1 X j µ o,(p 1) = (µ 1o,µ 2o,...,µ po ) S p p = 1 n n 1 j=1 (X j X)(X j X) T 2 is Hotelling s T 2 The sample distribution of T 2 T 2 (n 1)p n p F p,(n p) We can use this to test H o : µ = µ o...assuming that observations are a random sample from N p (µ,σ) i.i.d. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
10 Since Hotelling s T 2 T 2 (n 1)p n p F p,(n p) We can compute T 2 and compare it to OR use the fact that Compute T 2 as and the (n 1)p n p F p,(n p)(α) n p (n 1)p T2 F p,(n p) T 2 = n( x µ o )S 1 ( x µ o ) { p value = Prob F p,(n p) (n p) } (n 1)p T2 Reject H o when p-value is small (i.e., when T 2 is large). C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
11 A Really Little Example n = 3 and p = 2 H o : µ = Data: X = ( ) ւ x = (8,6) տ Ho : µ = (9,5) Assuming data come from a multivariate normal distribution and independent observations, ( ) ( ) x = S = S 1 = ( ) ( ) /3 1/9 = 4(9) ( 3)( 3) 3 4 1/9 4/27 C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
12 Simple Example continued T 2 = n( x µ o ) S 1 ( x µ o ) ( )( 1/3 1/9 (8 9) = 3((8 9),(6 5)) 1/9 4/27 (6 5) ( )( ) 1/3 1/9 1 = 3( 1,1) 1/9 4/27 1 = 3(7/27) = 7/9 ) Value we need for α =.05 is F 2,1 (.05) = (3 1) = 4(199.51) = Since T 2 (n 1)p (n p) F p,n p, we can compare our T 2 to Alternatively, we could compute p-value: compare.25(7/9) = to F 2,1 and we get p-value =.85. Do not reject H o. ( x and µ are close in the figure). C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
13 Example: WAIS and n = 101 elderly subjects From Morrison (1990), Multivariate Statistical Methods, pp : There are two variables, verbal and performance scores for n = 101 elderly subjects aged on the Wechsler Adult Intelligence test (WAIS). Assume that the data are from a bivariate normal distribution with unknown mean vector µ and unknown covariance matrix Σ. H o : µ = ( ) versus H o : µ ( Sample mean vector and covariance matrix: ( ) ( x = and S = C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59 ) )
14 Under the null hypothesis, this is distributed as F p,(n p). Since F 2,99 (α =.05) = 3.11, we reject the null hypothesis. Big question: was the null hypothesis rejected because of the verbal score, performance score, or both? C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59 Univariate Hotelling s T 2 Likelihood Ratio Confidence Regions One-at-a-Time T 2 Bonferroni Comparison Large-Samples We need T 2 for WAIS example Compute test statistic: ( ) S = T 2 =n( x µ) S 1 ( x µ) ( =101(( ),( )) = )( ) So to test the hypothesis, compute (n p) (n 1)p T2 = (101 2) = (101 1)2
15 Back to the Univariate Case Recall that for the univariate case t = X µ o s/ n or t 2 = ( X µ o ) 2 s 2 /n = n( X µ o )(s 2 ) 1 ( X µ o ) Since X N(µ,(1/n)σ 2 ), n( X µo ) N( n(µ µ o ),σ 2 ) This is is a linear function of X, which is a random variable. We also know that (n 1)s 2 = n (X j X) 2 σ 2 χ 2 (n 1) j=1 because n j=1 (X j X) 2 σ 2 = j=1 C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59 n Z 2 j χ 2 (n 1)
16 Back to the Univariate Case continued So s 2 = n j=1 (X j X) 2 n 1 = Putting this all together, we find t 2 = normal random variable chi-square random variable degrees of freedom chi-square random varible degress of freedom 1 normal random variable Now we ll go through the same thing but with the multivariate case... C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
17 The Multivariate Case T 2 = n( X µ o ) (S) 1 n( X µ o ) Since X N p (µ,(1/n)σ) and n( X µ o ) is a linear combination of X, n( X µo ) N p ( n(µ µ o ),Σ) Also S = = = n j=1 (X j X)(X j X) (n 1) n j=1 Z jz j (n 1) Wishart random matrix with df = n 1 degrees of freedom where Z j N p (0,Σ) i.i.d... if H o is true. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
18 The Multivariate Case continued Recall that a Wishart distribution is a matrix generalization of the chi-square distribution. The sampling distribution of (n 1)S is Wishart where W m ( Σ) = m Z j Z j j=1 where Z j N p (0,Σ) i.i.d.. So, multiavirate T 2 = normal Wishart random matrix random degress of freedom vector 1 multiavirate normal random vector C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
19 Invariance of T 2 T 2 is invariant with respect to change of location (i.e., mean) or scale (i.e. covariance matrix); that is, a T 2 is invariant by linear transformation. Rather than X p 1, we may want to consider Y p 1 = C p p }{{} scale X p 1 + d p 1 }{{} location where C is non-singular (or equivalently C > 0, or C has p linearly independent rows (columns), or C 1 exists). vµ y = Cµ x +d and Σ y = CΣ x C The T 2 for the Y data is exactly the same as the T 2 for the X data (see text for proof). This result it true for the univariate t-test. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
20 Likelihood Ratio Another approach to testing null hypothesis about mean vector µ (as well as other multivariate tests in general). It s equivalent to Hotelling s T 2 for H o : µ = µ o or H o : µ 1 = µ 2. It s more general than T 2 in that it can be used to test other hypotheses (e.g., those regarding Σ) and in different circumstances. Foreshadow: When testing more than 1 or 2 mean vectors, there are lots of different test statistics (about 5 common ones). T 2 and likelihood ratio tests are based on different underlying principles. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
21 Underlying Principles T 2 is based on the union-intersection principle, which takes a multivariate hypothesis and turns it into a univariate problem by considering linear combinations of variables. i.e., is a linear combination. T 2 = a ( X µ o ) We select the combination vector a that lead to the largest possible value of T 2. (We ll talk more about this later). The emphasis is on the direction of maximal difference. The likelihood ratio test the emphasis is on overall difference. Plan: First talk about the basic idea behind Likelihood ratio tests and then we ll apply it to the specific problem of testing µ = µ o. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
22 Basic idea of Likelihood Ratio Tests Θ o = a set of unknown parameters under H o (e.g., Σ). Θ = the set of unknown parameters under the alternative hypothesis (model), which is more general (e.g., µ and Σ). L( ) is the likelihood function. It is a function of parameters that indicates how likely Θ (or Θ o ) is given the data. L(Θ) L(Θ o ). The more general model/hypothesis is always more (or equally) likely than the more restrictive model/hypothesis. The Likelihood Ratio Statistic is Λ = maxl(θ o) max L(Θ) X = ˆµ MLE of mean S n = ˆΣ MLE of covariance matrix If Λ is small, then the data are not likely to have occurred under H o Reject H o. If Λ is large, then the data are likely to have occurred under H o Retain H o. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
23 Likelihood Ratio Test for Mean Vector Let X j N p (µ,σ) and i.i.d. where Λ = max Σ[L(µ o,σ)] maxµ,σ[l(µ, Σ)] max Σ = the maximum of L( ) over all possible Σ s. maxµ,σ = the maximum of L( ) over all possible µ s & Σ s. where ( ˆΣ Λ = ˆΣ o ) n/2 ˆΣ = MLE of Σ = (1/n) n j=1 (X j X)(X j X) = S n ˆΣ o = MLE of Σ assuming that µ = µ o = (1/n) n j=1 (X j µ o )(X j µ o ) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
24 Likelihood Ratio Test for Mean Vector ( ˆΣ Λ = ˆΣ o ) n/2 Λ = (ratio of two generalized sample variances) n/2 If µ o is really far from µ, then ˆΣ o will be much larger than ˆΣ, which uses a good estimator of µ (i.e., X). The likelihood ratio statistic Λ is called Wilk s Lambda for the special case of testing hypotheses about mean vectors. For large samples (i.e., large n), 2ln(Λ) χ 2 p, which can be used to test H o : µ = µ o C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
25 Degrees of Freedom for LR Test We need to consider the number of parameter estimates under each hypothesis: The alternative hypothesis ( full model ), Θ = {µ,σ} p means + The null hypothesis, Θ o = {Σ} p(p 1) 2 p(p 1) 2 covariances covariances degrees of freedom = df = difference between number of parameters = p estimated under each hypothesis If the H o is true and all assumptions valid, then for large samples, 2ln(Λ) χ 2 p. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
26 Example: 4 Psychological Tests n = 64, p = 4, x = (14.15,14.91,21.92,22.34), S = & det(s) = Test: H o : µ = (20,20,20,20) versus H o : µ (20,20,20,20) Σ o = 1 n (X 1µ o ) (X 1µ o ) = det(σ o ) = Wilk s Lambda is Λ = ( / ) 64/2 = 3.047E 30, and Comparing 2ln(Λ) = to a χ 2 4 gives p value <<.01. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
27 Comparison of T 2 & Likelihood Ratio Hotelling s T 2 and Wilk s Lambda are functionally related. Let X 1,X 2,...,X n be a random sample from a N p (µ,σ) population, then the test of H o : µ = µ o versus H A : µ µ o based on T 2 is equivalent to the test based on Λ. The relationship is given by So, Λ = (Λ) 2/n = ) 1 (1+ T2 (n 1) ) n/2 (1+ T2 and T 2 = (n 1)Λ 2/n (n 1) (n 1) Since they are inversely related, We reject H o for large T 2 We reject H o for small Λ. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
28 Example: Comparison of T 2 & Likelihood Ratio Using our 4 psychological test data, we found that (Λ) = 3.047E 30 If we compute Hotelling s T 2 for these data we ld find that T 2 = and Λ = ( ) 64/2 = 3.047E 30 (64 1) T 2 = (64 1)(3.047E 30) 2/64 (64 1) Note: I did this in SAS. The SAS/IML code is on the web-site if you want to check this for yourself. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
29 After Rejection: Confidence Regions Our goal is to make inferences about populations from samples. In univariate statistics, we form confidence intervals; we ll generalization this to multivariate confidence region. General definition: A confidence region is a region of likely values of parameters θ which is determined by data: where R(X) = confidence region X = (X 1,X 2,...X n ); that is, data. R(X) is a 100(1 α)% confidence region if before the sample was selected Prob[R(X) contains the trueθ] = 1 α C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
30 Confidence Region for µ For µ p 1 of a p-dimensional multivariate normal distribution, [ Prob n( X µ) S 1 ( X µ) (n 1)p ] n p F p,n p(α) = 1 α...before we have data (observations). i.e., X is within (n 1)p n p F p,n p(α) of µ with probability 1 α (where distance is measured or defined in terms of ns 1 ). For a typical sample, (1) Calculate x and S. (2) Find (n 1)p/(n p)f p,n p (α). (3) Consider all µ s that satisfy the equation n( X µ) S 1 ( X µ) (n 1)p n p F p,n p(α) This is the confidence region, which is an equation of an ellipsoid. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
31 Confidence Region for µ continued To determine whether a particular µ falls within in a confidence region, compute the squared statistical distance of X to µ and see if it s less than or greater than (n 1)p n p F p,n p(α). The confidence region consists of all vectors µ o that lead to retaining the H o : µ = µ o using Hotelling s T 2 (or equivalently Wilk s lambda). These regions are ellipsoids where their shapes are determined by S (the eigenvalues and eigenvectors of S). We ll continue our WAIS example of n = 101 elderly and the verbal and performance sub-tests of WAIS (p = 2). Recall that H o : µ = (60,50) But first a closer look at the ellipsoid... C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
32 The Shape of the Ellipsoid The ellipsoid is centered at x. The direction of the axes are given by the eigenvectors e i of S. The (half) length of the axes equal p(n 1) λi n(n p) F λi p,n p(α) = c n So, from the center, which is at x, the axes are x± p(n 1) λ i n(n p) F p,n p(α) e i where Se i = λ i e i for i = 1,2,...,p. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
33 WAIS Example Equation for the (1 α)100% confidence region: n( x µ) S 1 ( x µ) or (n 1)p (n p) F p,n p(α) T 2 (n 1)p (n p) F p,n p(α) The confidence region is an ellipse (ellipsoid for p > 2) centered at x with axses x± p(n 1) λ i n(n p) F p,n p(α) e i where λ i and e i are the eigenvalues and eigenvectors, respectively, of S (λ i is not Wilk s lambda). For the WAIS data, λ 1 = , e 1 = (.818,.576) λ 2 = , e 2 = (.576,.818) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
34 WAIS Example: Finding Major and Minor ( x± λ i p(n 1) n(n p) F p,n p(α) e i The major axis: ) ± (101 1) 101(101 2) 3.11 which gives us (51.71, 32.48) and (58.77, 37.46). The minor axis: ( ) ± ( ( 2(101 1) (101 2) which gives us (56.03, 33.85) and (54.45, 36.09). C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59 ) )
35 Graph of 95% Confidence Region Performance Length of major = 8.64 (half-length= 4.32) Length of minor = 2.74 (half-length= 1.37) (56.03, 33.85) (51.71, 32.48) (58.77,37.46) x = (55.24,34.97) (54.45, 36.09) 30 Verbal C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
36 Example continued We note that µ o = (60,50) is not in the confidence region. Using the equation for the ellipse, we find T 2 = > (100(2)/99)(3.11) = 6.283, so (60,50) is not in the 95% confidence region. What about µ = (60,40)? T 2 = 101(( ),( )) ( )( ) = Since is greater than 6.28, (60,40) also in not in 95% confidence region. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
37 Alternatives to Confidence Regions The confidence regions consider all the components of µ jointly. We often desire a confidence statement (i.e, confidence interval) about individual components of µ or a linear combination of the µ i s. We want all such statements to hold simultaneously with some specified large probability; that is, want to make sure that the probability that any one of the confidence statements is incorrect is small. Three ways of forming simultaneous confidence intervals considered: one-at-a-time intervals T 2 intervals Bonferroni C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
38 One-at-a-Time Intervals (they re related to the confidence region). Let X N p (µ,σ), where X = (X 1,X 2,...,X p ) and consider the linear combination Z = a 1 X 1 +a 2 X 2 + +a p X p = a X From what we know about linear combinations of random vectors and multivariate normal distribution, we know E(Z) = µ z = a µ var(z) = σ 2 Z = a Σa Z N 1 (a µ,a Σa) Estimate µ Z by a X and estimate var(z) = a Σa by a Sa. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
39 Univariate Intervals A Simultaneous 100(1 α)% confidence interval for µ Z where Z = a X with unknown Σ (but known a) is z ±t n 1,(α/2) a Sa n where t n 1,(α/2) is the upper 100(α/2) percentile of Student s t-distribution with df = n 1 Can put intervals around any element of µ by choice of a s: a = (0,0,..., }{{} 1,0,...0) i th element So a µ = µ i a x = x i and a Sa = s ii and the one-at-a-time interval for µ i is sii x i ±t n 1,(α/2) n C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
40 WAIS Example: One-at-a-time Intervals Univariate Confidence Intervals x i ±t n 1,(α/2) sii /n We ll let α =.05 (for a 95% confidence interval), so t 100,(.025) = For verbal score: For performance score: 55.24± / ± 2.87 (52.37, 58.11) 34.97± /101 = ± 2.17 (32.80, 37.14) For our hypothesized values µ o1 = 60 and µ o2 = 50, neither are in the respective intervals. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
41 Graph of one-at-a time intervals Performance 40 Multivariate versus Univariate: 95% Confidence region (ellipse) 95% one-at-a-time intervals Verbal C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
42 Problem with Univariate Intervals Problem with the Global coverage rate: If the rate is 100(1 α)% for one interval, then the overall experimentwise coverage rate could be much less that 100(1 α)%. If you want the overall coverage rate to be 100(1 α)%, then we have to consider simultaneously all possible choices for the vector a such that the coverage rate over all of them is 100(1 α)% How? What a gives the maximum possible test-statistic? Using this a, consider the distribution for the maximum. If we achieve (1 α) for the maximum, then the remainder (all others) have > (1 α). We use the distribution of the maximum for our fudge-factor. The largest value is proportional to S 1 ( x µ o ) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
43 T 2 Intervals Let X 1,X 2,...,X n be a random sample from N p (µ,σ) population with det(σ) > 0, then simultaneously for all a, the interval a x± p(n 1) a (n p) F p,n p(α) Sa n will contain a µ with coverage rate 100(1 α)%. These are called T 2 intervals because the fudge-factor (p(n 1)/(n p))f p,n p is the distribution of Hotelling s T 2. Set a i = (0,0,..., 1,0,...0) i = 1,...,p. & compute a }{{} i x ± x i }{{} i th element p(n 1) a (n p) F p,n p(α) Sa, i = 1,...,p. }{{ n } s ii /n C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
44 T 2 Intervals a i x± p(n 1) a (n p) F p,n p(α) Sa n, i = 1,...,p. are Component T 2 Intervals and are useful for data snooping because the coverage rate remains fixed at 100(1 α)% regardless of The number of intervals you construct Whether or not the a s are chosen a priori C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
45 WAIS Example For the verbal score: 100(2) 55.24± 99 (3.11) /101 = 55.24±3.62 (51.62,58.86) For the performance score: 100(2) 34.97± 99 (3.11) /101 = 34.97±2.73 (32.24,37.70) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
46 Performance WAIS: Comparison 40 ellipse Confidence region T 2 intervals Univariate intervals Verbal C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
47 Summary of Comparison One-at-a-Time Narrower (more precise) More powerful Liberal Coverage rate < 100(1 α) Coverage rate depends on number of intervals and S. Accuracy may be OK provided if reject H o : µ = µ o. T 2 Intervals Wider (less precise) Less powerful Conservative Coverage rate 100(1 α) Coverage rate does not depend on number of intervals. Good if do a lot of intervals (e.g., > p) Compromise: Bonferroni C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
48 Bonferroni Intervals This method will Give narrower (more precise) intervals than T 2, but not as narrow are the univariate ones. Good if The intervals that you construct are decided upon a priori. You only construct p intervals. Suppose that we want to make m confidence statements about m linear combinations a 1µ, a 2µ,..., a mµ It uses a form of the Bonferroni inequality. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
49 Bonferroni Inequality Prob{all intervals are valid} = 1 Prob{at least 1 false} m 1 Prob{i th interval is false} = 1 = 1 i=1 m 1 Prob{i th interval is true} i=1 m i=1 This is a form of the Bonferroni inequality: Prob{all intervals are ture} 1 (α 1 +α 2 + +α m ) We set α i = α/m using a pre-determined α level, then Prob{all intervals are ture} 1 (α/m +α/m + +α/m) = 1 α }{{} m of these α i C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
50 Bonferroni Confidence Statements Use α/m for each of the m intervals (both α and specific intervals pre-determined) a x±t n 1,(α/2m) }{{} We just replace the fudge-factor a Sa WAIS example: We ll only consider a 1 = (1,0) and a 2 = (0,1) (i.e., the component means). df = n 1 = = 100 n α =.05 α/2 =.025 t 100,(.025/2) = You can get t s from the pvalue.exe program on course web-site (under handy programs and links), or from SAS using, for example... C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
51 WAIS & Bonferroni Intervals data tvalue; df= 100; p = 1.05/(2 2); t= quantile( t,p,100); proc print; run; Verbal Scores: Performance Scores: α/(p m); ± /101 ± (1.4438) ± (51.95, 58.53) ± /101 ± ( ) ± (32.49, 37.45) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
52 WAIS: All four Confidence Methods Performance 40 ellipse Confidence region T 2 intervals Bonferroni Univariate intervals Verbal C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
53 Interval Methods Comparisons Performance 40 ellipse Confidence region T 2 intervals Bonferroni Univariate intervals Points are some possible places for µ o Verbal C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
54 Few last statements on Confidence Statements Hypothesis testing of H o : µ = µ o may lead to some seemingly inconsistent results. For example, The multivariate tests may reject Ho, but the component means are within their respective confidence intervals for them (regardless of how intervals are computed, e.g., the red dot). Separate t-tests for component means may not be rejected, but you do reject for multivariate (e.g., orange dot). The confidence region, which contains all values of µ o for which the null hypothesis would not be rejected, is the only one that takes into consideration the covariances, as well as variances. Multivariate approach is most powerful. In higher dimensions, we can t see what s going on, but concepts are same. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
55 In the Face of Inconsistencies or to get a better idea of what s going on... Recall that T 2 is based on the union intersection principle: T 2 = na ( X µ o ) where a is the one that gives the largest value for T 2 among all possible vectors a. This vector is a = ( X µ o ) S 1 Examining a can lead to insight into why H o : µ = µ o was rejected. For the WAIS example when H o : µ = (60,50), ( X µ o ) S 1 = ( ) Note: ( X µ o ) = ( 4.76, 15.03) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
56 Large-Sample Inferences about a population mean vector µ So far, we ve assumed that X j N p (µ,σ). But what if the data are not multivariate normal? We can still make inferences (hypothesis testing & make confidence statements) about population means IF we have Large samples relative to p (i.e., n p is large). Let X 1,X 2,...,X n be a random sample from a population with µ and Σ (Σ is positive definite) T 2 = n( x µ o ) S 1 ( x µ o ) χ 2 p means approximately. Prob(n( x µ o ) S 1 ( x µ o )) χ 2 p (α) 1 α. As n gets large, F p,n p and χ 2 p(α) become closer in value: As n, (n 1)p n p F p,n p χ 2 p (Show this) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
57 Large-Sample Inferences continued For large n p, Hypothesis test: H o : µ = µ o Reject H o if T 2 > χ 2 p (α) where χ2 p (α) is the upper αth percentile of the chi-square distribution with df = p. Simultaneous T 2 intervals: a x± a χ 2 p(α) Sa n Confidence region for µ: ( x µ) S 1 ( x µ) χ2 p (α) n C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
58 WAIS: Large-Sample WAIS example with n = 101, F p,n p (α) = F 2,99 (.05) = 3.11 (n 1)p n p F p,n p = 100(2) (3.11) = χ 2 2(.05) = 5.99 The value 6.28 is fairly close to It s generally true that the more you assume, the more powerful your test (more precise estimates). The larger n, the more power...this is generally true. C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
59 Show How to Do Tests, etc.... SAS PROC IML and tests Use Psychological test scores (on course web-site) C.J. Anderson (Illinois) Inferences about a Mean Vector Spring / 59
I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
 Comparisons of Two Means Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J. Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN c
Comparisons of Two Means Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J. Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN c
Sample Geometry. Edps/Soc 584, Psych 594. Carolyn J. Anderson
 Sample Geometry Edps/Soc 584, Psych 594 Carolyn J. Anderson Department of Educational Psychology I L L I N O I S university of illinois at urbana-champaign c Board of Trustees, University of Illinois Spring
Sample Geometry Edps/Soc 584, Psych 594 Carolyn J. Anderson Department of Educational Psychology I L L I N O I S university of illinois at urbana-champaign c Board of Trustees, University of Illinois Spring
5 Inferences about a Mean Vector
 5 Inferences about a Mean Vector In this chapter we use the results from Chapter 2 through Chapter 4 to develop techniques for analyzing data. A large part of any analysis is concerned with inference that
5 Inferences about a Mean Vector In this chapter we use the results from Chapter 2 through Chapter 4 to develop techniques for analyzing data. A large part of any analysis is concerned with inference that
Comparisons of Several Multivariate Populations
 Comparisons of Several Multivariate Populations Edps/Soc 584, Psych 594 Carolyn J Anderson Department of Educational Psychology I L L I N O I S university of illinois at urbana-champaign c Board of Trustees,
Comparisons of Several Multivariate Populations Edps/Soc 584, Psych 594 Carolyn J Anderson Department of Educational Psychology I L L I N O I S university of illinois at urbana-champaign c Board of Trustees,
I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
 Comparisons of Several Multivariate Populations Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS
Comparisons of Several Multivariate Populations Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS
More Linear Algebra. Edps/Soc 584, Psych 594. Carolyn J. Anderson
 More Linear Algebra Edps/Soc 584, Psych 594 Carolyn J. Anderson Department of Educational Psychology I L L I N O I S university of illinois at urbana-champaign c Board of Trustees, University of Illinois
More Linear Algebra Edps/Soc 584, Psych 594 Carolyn J. Anderson Department of Educational Psychology I L L I N O I S university of illinois at urbana-champaign c Board of Trustees, University of Illinois
Applied Multivariate and Longitudinal Data Analysis
 Applied Multivariate and Longitudinal Data Analysis Chapter 2: Inference about the mean vector(s) Ana-Maria Staicu SAS Hall 5220; 919-515-0644; astaicu@ncsu.edu 1 In this chapter we will discuss inference
Applied Multivariate and Longitudinal Data Analysis Chapter 2: Inference about the mean vector(s) Ana-Maria Staicu SAS Hall 5220; 919-515-0644; astaicu@ncsu.edu 1 In this chapter we will discuss inference
1. Density and properties Brief outline 2. Sampling from multivariate normal and MLE 3. Sampling distribution and large sample behavior of X and S 4.
 Multivariate normal distribution Reading: AMSA: pages 149-200 Multivariate Analysis, Spring 2016 Institute of Statistics, National Chiao Tung University March 1, 2016 1. Density and properties Brief outline
Multivariate normal distribution Reading: AMSA: pages 149-200 Multivariate Analysis, Spring 2016 Institute of Statistics, National Chiao Tung University March 1, 2016 1. Density and properties Brief outline
I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
 Canonical Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J. Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN Canonical Slide
Canonical Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J. Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN Canonical Slide
Multivariate Statistical Analysis
 Multivariate Statistical Analysis Fall 2011 C. L. Williams, Ph.D. Lecture 9 for Applied Multivariate Analysis Outline Addressing ourliers 1 Addressing ourliers 2 Outliers in Multivariate samples (1) For
Multivariate Statistical Analysis Fall 2011 C. L. Williams, Ph.D. Lecture 9 for Applied Multivariate Analysis Outline Addressing ourliers 1 Addressing ourliers 2 Outliers in Multivariate samples (1) For
Multivariate Statistical Analysis
 Multivariate Statistical Analysis Fall 2011 C. L. Williams, Ph.D. Lecture 9 for Applied Multivariate Analysis Outline Two sample T 2 test 1 Two sample T 2 test 2 Analogous to the univariate context, we
Multivariate Statistical Analysis Fall 2011 C. L. Williams, Ph.D. Lecture 9 for Applied Multivariate Analysis Outline Two sample T 2 test 1 Two sample T 2 test 2 Analogous to the univariate context, we
I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
 Principal Analysis Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J. Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN c Board
Principal Analysis Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J. Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN c Board
Mean Vector Inferences
 Mean Vector Inferences Lecture 5 September 21, 2005 Multivariate Analysis Lecture #5-9/21/2005 Slide 1 of 34 Today s Lecture Inferences about a Mean Vector (Chapter 5). Univariate versions of mean vector
Mean Vector Inferences Lecture 5 September 21, 2005 Multivariate Analysis Lecture #5-9/21/2005 Slide 1 of 34 Today s Lecture Inferences about a Mean Vector (Chapter 5). Univariate versions of mean vector
Rejection regions for the bivariate case
 Rejection regions for the bivariate case The rejection region for the T 2 test (and similarly for Z 2 when Σ is known) is the region outside of an ellipse, for which there is a (1-α)% chance that the test
Rejection regions for the bivariate case The rejection region for the T 2 test (and similarly for Z 2 when Σ is known) is the region outside of an ellipse, for which there is a (1-α)% chance that the test
You can compute the maximum likelihood estimate for the correlation
 Stat 50 Solutions Comments on Assignment Spring 005. (a) _ 37.6 X = 6.5 5.8 97.84 Σ = 9.70 4.9 9.70 75.05 7.80 4.9 7.80 4.96 (b) 08.7 0 S = Σ = 03 9 6.58 03 305.6 30.89 6.58 30.89 5.5 (c) You can compute
Stat 50 Solutions Comments on Assignment Spring 005. (a) _ 37.6 X = 6.5 5.8 97.84 Σ = 9.70 4.9 9.70 75.05 7.80 4.9 7.80 4.96 (b) 08.7 0 S = Σ = 03 9 6.58 03 305.6 30.89 6.58 30.89 5.5 (c) You can compute
Statistical Inference
 Statistical Inference Classical and Bayesian Methods Revision Class for Midterm Exam AMS-UCSC Th Feb 9, 2012 Winter 2012. Session 1 (Revision Class) AMS-132/206 Th Feb 9, 2012 1 / 23 Topics Topics We will
Statistical Inference Classical and Bayesian Methods Revision Class for Midterm Exam AMS-UCSC Th Feb 9, 2012 Winter 2012. Session 1 (Revision Class) AMS-132/206 Th Feb 9, 2012 1 / 23 Topics Topics We will
I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
 Introduction Edps/Psych/Stat/ 584 Applied Multivariate Statistics Carolyn J Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN c Board of Trustees,
Introduction Edps/Psych/Stat/ 584 Applied Multivariate Statistics Carolyn J Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN c Board of Trustees,
Lecture 3. Inference about multivariate normal distribution
 Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X 1,..., X n be i.i.d. N p (µ, Σ). We are interested in evaluation of the maximum likelihood estimates
Lecture 3. Inference about multivariate normal distribution 3.1 Point and Interval Estimation Let X 1,..., X n be i.i.d. N p (µ, Σ). We are interested in evaluation of the maximum likelihood estimates
STT 843 Key to Homework 1 Spring 2018
 STT 843 Key to Homework Spring 208 Due date: Feb 4, 208 42 (a Because σ = 2, σ 22 = and ρ 2 = 05, we have σ 2 = ρ 2 σ σ22 = 2/2 Then, the mean and covariance of the bivariate normal is µ = ( 0 2 and Σ
STT 843 Key to Homework Spring 208 Due date: Feb 4, 208 42 (a Because σ = 2, σ 22 = and ρ 2 = 05, we have σ 2 = ρ 2 σ σ22 = 2/2 Then, the mean and covariance of the bivariate normal is µ = ( 0 2 and Σ
Statistical Inference: Estimation and Confidence Intervals Hypothesis Testing
 Statistical Inference: Estimation and Confidence Intervals Hypothesis Testing 1 In most statistics problems, we assume that the data have been generated from some unknown probability distribution. We desire
Statistical Inference: Estimation and Confidence Intervals Hypothesis Testing 1 In most statistics problems, we assume that the data have been generated from some unknown probability distribution. We desire
Exam 2. Jeremy Morris. March 23, 2006
 Exam Jeremy Morris March 3, 006 4. Consider a bivariate normal population with µ 0, µ, σ, σ and ρ.5. a Write out the bivariate normal density. The multivariate normal density is defined by the following
Exam Jeremy Morris March 3, 006 4. Consider a bivariate normal population with µ 0, µ, σ, σ and ρ.5. a Write out the bivariate normal density. The multivariate normal density is defined by the following
simple if it completely specifies the density of x
 3. Hypothesis Testing Pure significance tests Data x = (x 1,..., x n ) from f(x, θ) Hypothesis H 0 : restricts f(x, θ) Are the data consistent with H 0? H 0 is called the null hypothesis simple if it completely
3. Hypothesis Testing Pure significance tests Data x = (x 1,..., x n ) from f(x, θ) Hypothesis H 0 : restricts f(x, θ) Are the data consistent with H 0? H 0 is called the null hypothesis simple if it completely
STAT 501 Assignment 2 NAME Spring Chapter 5, and Sections in Johnson & Wichern.
 STAT 01 Assignment NAME Spring 00 Reading Assignment: Written Assignment: Chapter, and Sections 6.1-6.3 in Johnson & Wichern. Due Monday, February 1, in class. You should be able to do the first four problems
STAT 01 Assignment NAME Spring 00 Reading Assignment: Written Assignment: Chapter, and Sections 6.1-6.3 in Johnson & Wichern. Due Monday, February 1, in class. You should be able to do the first four problems
z = β βσβ Statistical Analysis of MV Data Example : µ=0 (Σ known) consider Y = β X~ N 1 (β µ, β Σβ) test statistic for H 0β is
 Example X~N p (µ,σ); H 0 : µ=0 (Σ known) consider Y = β X~ N 1 (β µ, β Σβ) H 0β : β µ = 0 test statistic for H 0β is y z = β βσβ /n And reject H 0β if z β > c [suitable critical value] 301 Reject H 0 if
Example X~N p (µ,σ); H 0 : µ=0 (Σ known) consider Y = β X~ N 1 (β µ, β Σβ) H 0β : β µ = 0 test statistic for H 0β is y z = β βσβ /n And reject H 0β if z β > c [suitable critical value] 301 Reject H 0 if
Lecture 2: Basic Concepts and Simple Comparative Experiments Montgomery: Chapter 2
 Lecture 2: Basic Concepts and Simple Comparative Experiments Montgomery: Chapter 2 Fall, 2013 Page 1 Random Variable and Probability Distribution Discrete random variable Y : Finite possible values {y
Lecture 2: Basic Concepts and Simple Comparative Experiments Montgomery: Chapter 2 Fall, 2013 Page 1 Random Variable and Probability Distribution Discrete random variable Y : Finite possible values {y
STAT 501 EXAM I NAME Spring 1999
 STAT 501 EXAM I NAME Spring 1999 Instructions: You may use only your calculator and the attached tables and formula sheet. You can detach the tables and formula sheet from the rest of this exam. Show your
STAT 501 EXAM I NAME Spring 1999 Instructions: You may use only your calculator and the attached tables and formula sheet. You can detach the tables and formula sheet from the rest of this exam. Show your
I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
 Linear Combinations of Variables Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
Linear Combinations of Variables Edps/Soc 584 and Psych 594 Applied Multivariate Statistics Carolyn J Anderson Department of Educational Psychology I L L I N O I S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN
THE UNIVERSITY OF CHICAGO Booth School of Business Business 41912, Spring Quarter 2012, Mr. Ruey S. Tsay
 THE UNIVERSITY OF CHICAGO Booth School of Business Business 41912, Spring Quarter 2012, Mr. Ruey S. Tsay Lecture 3: Comparisons between several multivariate means Key concepts: 1. Paired comparison & repeated
THE UNIVERSITY OF CHICAGO Booth School of Business Business 41912, Spring Quarter 2012, Mr. Ruey S. Tsay Lecture 3: Comparisons between several multivariate means Key concepts: 1. Paired comparison & repeated
STA 437: Applied Multivariate Statistics
 Al Nosedal. University of Toronto. Winter 2015 1 Chapter 5. Tests on One or Two Mean Vectors If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition Chapter 5. Tests
Al Nosedal. University of Toronto. Winter 2015 1 Chapter 5. Tests on One or Two Mean Vectors If you can t explain it simply, you don t understand it well enough Albert Einstein. Definition Chapter 5. Tests
Multivariate Time Series: VAR(p) Processes and Models
 Multivariate Time Series: VAR(p) Processes and Models A VAR(p) model, for p > 0 is X t = φ 0 + Φ 1 X t 1 + + Φ p X t p + A t, where X t, φ 0, and X t i are k-vectors, Φ 1,..., Φ p are k k matrices, with
Multivariate Time Series: VAR(p) Processes and Models A VAR(p) model, for p > 0 is X t = φ 0 + Φ 1 X t 1 + + Φ p X t p + A t, where X t, φ 0, and X t i are k-vectors, Φ 1,..., Φ p are k k matrices, with
Multivariate Analysis Homework 1
 Multivariate Analysis Homework A490970 Yi-Chen Zhang March 6, 08 4.. Consider a bivariate normal population with µ = 0, µ =, σ =, σ =, and ρ = 0.5. a Write out the bivariate normal density. b Write out
Multivariate Analysis Homework A490970 Yi-Chen Zhang March 6, 08 4.. Consider a bivariate normal population with µ = 0, µ =, σ =, σ =, and ρ = 0.5. a Write out the bivariate normal density. b Write out
COMPARISON OF FIVE TESTS FOR THE COMMON MEAN OF SEVERAL MULTIVARIATE NORMAL POPULATIONS
 Communications in Statistics - Simulation and Computation 33 (2004) 431-446 COMPARISON OF FIVE TESTS FOR THE COMMON MEAN OF SEVERAL MULTIVARIATE NORMAL POPULATIONS K. Krishnamoorthy and Yong Lu Department
Communications in Statistics - Simulation and Computation 33 (2004) 431-446 COMPARISON OF FIVE TESTS FOR THE COMMON MEAN OF SEVERAL MULTIVARIATE NORMAL POPULATIONS K. Krishnamoorthy and Yong Lu Department
STA 2201/442 Assignment 2
 STA 2201/442 Assignment 2 1. This is about how to simulate from a continuous univariate distribution. Let the random variable X have a continuous distribution with density f X (x) and cumulative distribution
STA 2201/442 Assignment 2 1. This is about how to simulate from a continuous univariate distribution. Let the random variable X have a continuous distribution with density f X (x) and cumulative distribution
3. (a) (8 points) There is more than one way to correctly express the null hypothesis in matrix form. One way to state the null hypothesis is
 Stat 501 Solutions and Comments on Exam 1 Spring 005-4 0-4 1. (a) (5 points) Y ~ N, -1-4 34 (b) (5 points) X (X,X ) = (5,8) ~ N ( 11.5, 0.9375 ) 3 1 (c) (10 points, for each part) (i), (ii), and (v) are
Stat 501 Solutions and Comments on Exam 1 Spring 005-4 0-4 1. (a) (5 points) Y ~ N, -1-4 34 (b) (5 points) X (X,X ) = (5,8) ~ N ( 11.5, 0.9375 ) 3 1 (c) (10 points, for each part) (i), (ii), and (v) are
Lecture 5: Hypothesis tests for more than one sample
 1/23 Lecture 5: Hypothesis tests for more than one sample Måns Thulin Department of Mathematics, Uppsala University thulin@math.uu.se Multivariate Methods 8/4 2011 2/23 Outline Paired comparisons Repeated
1/23 Lecture 5: Hypothesis tests for more than one sample Måns Thulin Department of Mathematics, Uppsala University thulin@math.uu.se Multivariate Methods 8/4 2011 2/23 Outline Paired comparisons Repeated
401 Review. 6. Power analysis for one/two-sample hypothesis tests and for correlation analysis.
 401 Review Major topics of the course 1. Univariate analysis 2. Bivariate analysis 3. Simple linear regression 4. Linear algebra 5. Multiple regression analysis Major analysis methods 1. Graphical analysis
401 Review Major topics of the course 1. Univariate analysis 2. Bivariate analysis 3. Simple linear regression 4. Linear algebra 5. Multiple regression analysis Major analysis methods 1. Graphical analysis
Multilevel Models in Matrix Form. Lecture 7 July 27, 2011 Advanced Multivariate Statistical Methods ICPSR Summer Session #2
 Multilevel Models in Matrix Form Lecture 7 July 27, 2011 Advanced Multivariate Statistical Methods ICPSR Summer Session #2 Today s Lecture Linear models from a matrix perspective An example of how to do
Multilevel Models in Matrix Form Lecture 7 July 27, 2011 Advanced Multivariate Statistical Methods ICPSR Summer Session #2 Today s Lecture Linear models from a matrix perspective An example of how to do
Fall 2017 STAT 532 Homework Peter Hoff. 1. Let P be a probability measure on a collection of sets A.
 1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
1. Let P be a probability measure on a collection of sets A. (a) For each n N, let H n be a set in A such that H n H n+1. Show that P (H n ) monotonically converges to P ( k=1 H k) as n. (b) For each n
MATH5745 Multivariate Methods Lecture 07
 MATH5745 Multivariate Methods Lecture 07 Tests of hypothesis on covariance matrix March 16, 2018 MATH5745 Multivariate Methods Lecture 07 March 16, 2018 1 / 39 Test on covariance matrices: Introduction
MATH5745 Multivariate Methods Lecture 07 Tests of hypothesis on covariance matrix March 16, 2018 MATH5745 Multivariate Methods Lecture 07 March 16, 2018 1 / 39 Test on covariance matrices: Introduction
Serial Correlation. Edps/Psych/Stat 587. Carolyn J. Anderson. Fall Department of Educational Psychology
 Serial Correlation Edps/Psych/Stat 587 Carolyn J. Anderson Department of Educational Psychology c Board of Trustees, University of Illinois Fall 017 Model for Level 1 Residuals There are three sources
Serial Correlation Edps/Psych/Stat 587 Carolyn J. Anderson Department of Educational Psychology c Board of Trustees, University of Illinois Fall 017 Model for Level 1 Residuals There are three sources
CH.9 Tests of Hypotheses for a Single Sample
 CH.9 Tests of Hypotheses for a Single Sample Hypotheses testing Tests on the mean of a normal distributionvariance known Tests on the mean of a normal distributionvariance unknown Tests on the variance
CH.9 Tests of Hypotheses for a Single Sample Hypotheses testing Tests on the mean of a normal distributionvariance known Tests on the mean of a normal distributionvariance unknown Tests on the variance
Stat 206: Estimation and testing for a mean vector,
 Stat 206: Estimation and testing for a mean vector, Part II James Johndrow 2016-12-03 Comparing components of the mean vector In the last part, we talked about testing the hypothesis H 0 : µ 1 = µ 2 where
Stat 206: Estimation and testing for a mean vector, Part II James Johndrow 2016-12-03 Comparing components of the mean vector In the last part, we talked about testing the hypothesis H 0 : µ 1 = µ 2 where
Testing Hypothesis. Maura Mezzetti. Department of Economics and Finance Università Tor Vergata
 Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
Maura Department of Economics and Finance Università Tor Vergata Hypothesis Testing Outline It is a mistake to confound strangeness with mystery Sherlock Holmes A Study in Scarlet Outline 1 The Power Function
STAT 730 Chapter 5: Hypothesis Testing
 STAT 730 Chapter 5: Hypothesis Testing Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 28 Likelihood ratio test def n: Data X depend on θ. The
STAT 730 Chapter 5: Hypothesis Testing Timothy Hanson Department of Statistics, University of South Carolina Stat 730: Multivariate Analysis 1 / 28 Likelihood ratio test def n: Data X depend on θ. The
Political Science 236 Hypothesis Testing: Review and Bootstrapping
 Political Science 236 Hypothesis Testing: Review and Bootstrapping Rocío Titiunik Fall 2007 1 Hypothesis Testing Definition 1.1 Hypothesis. A hypothesis is a statement about a population parameter The
Political Science 236 Hypothesis Testing: Review and Bootstrapping Rocío Titiunik Fall 2007 1 Hypothesis Testing Definition 1.1 Hypothesis. A hypothesis is a statement about a population parameter The
Analysis of variance, multivariate (MANOVA)
 Analysis of variance, multivariate (MANOVA) Abstract: A designed experiment is set up in which the system studied is under the control of an investigator. The individuals, the treatments, the variables
Analysis of variance, multivariate (MANOVA) Abstract: A designed experiment is set up in which the system studied is under the control of an investigator. The individuals, the treatments, the variables
Introduction to the Analysis of Variance (ANOVA) Computing One-Way Independent Measures (Between Subjects) ANOVAs
 Introduction to the Analysis of Variance (ANOVA) Computing One-Way Independent Measures (Between Subjects) ANOVAs The Analysis of Variance (ANOVA) The analysis of variance (ANOVA) is a statistical technique
Introduction to the Analysis of Variance (ANOVA) Computing One-Way Independent Measures (Between Subjects) ANOVAs The Analysis of Variance (ANOVA) The analysis of variance (ANOVA) is a statistical technique
Hypothesis Testing. Robert L. Wolpert Department of Statistical Science Duke University, Durham, NC, USA
 Hypothesis Testing Robert L. Wolpert Department of Statistical Science Duke University, Durham, NC, USA An Example Mardia et al. (979, p. ) reprint data from Frets (9) giving the length and breadth (in
Hypothesis Testing Robert L. Wolpert Department of Statistical Science Duke University, Durham, NC, USA An Example Mardia et al. (979, p. ) reprint data from Frets (9) giving the length and breadth (in
The t-distribution. Patrick Breheny. October 13. z tests The χ 2 -distribution The t-distribution Summary
 Patrick Breheny October 13 Patrick Breheny Biostatistical Methods I (BIOS 5710) 1/25 Introduction Introduction What s wrong with z-tests? So far we ve (thoroughly!) discussed how to carry out hypothesis
Patrick Breheny October 13 Patrick Breheny Biostatistical Methods I (BIOS 5710) 1/25 Introduction Introduction What s wrong with z-tests? So far we ve (thoroughly!) discussed how to carry out hypothesis
Comparing two independent samples
 In many applications it is necessary to compare two competing methods (for example, to compare treatment effects of a standard drug and an experimental drug). To compare two methods from statistical point
In many applications it is necessary to compare two competing methods (for example, to compare treatment effects of a standard drug and an experimental drug). To compare two methods from statistical point
MANOVA is an extension of the univariate ANOVA as it involves more than one Dependent Variable (DV). The following are assumptions for using MANOVA:
 MULTIVARIATE ANALYSIS OF VARIANCE MANOVA is an extension of the univariate ANOVA as it involves more than one Dependent Variable (DV). The following are assumptions for using MANOVA: 1. Cell sizes : o
MULTIVARIATE ANALYSIS OF VARIANCE MANOVA is an extension of the univariate ANOVA as it involves more than one Dependent Variable (DV). The following are assumptions for using MANOVA: 1. Cell sizes : o
STAT 135 Lab 5 Bootstrapping and Hypothesis Testing
 STAT 135 Lab 5 Bootstrapping and Hypothesis Testing Rebecca Barter March 2, 2015 The Bootstrap Bootstrap Suppose that we are interested in estimating a parameter θ from some population with members x 1,...,
STAT 135 Lab 5 Bootstrapping and Hypothesis Testing Rebecca Barter March 2, 2015 The Bootstrap Bootstrap Suppose that we are interested in estimating a parameter θ from some population with members x 1,...,
Testing equality of two mean vectors with unequal sample sizes for populations with correlation
 Testing equality of two mean vectors with unequal sample sizes for populations with correlation Aya Shinozaki Naoya Okamoto 2 and Takashi Seo Department of Mathematical Information Science Tokyo University
Testing equality of two mean vectors with unequal sample sizes for populations with correlation Aya Shinozaki Naoya Okamoto 2 and Takashi Seo Department of Mathematical Information Science Tokyo University
Statistical Data Analysis Stat 3: p-values, parameter estimation
 Statistical Data Analysis Stat 3: p-values, parameter estimation London Postgraduate Lectures on Particle Physics; University of London MSci course PH4515 Glen Cowan Physics Department Royal Holloway,
Statistical Data Analysis Stat 3: p-values, parameter estimation London Postgraduate Lectures on Particle Physics; University of London MSci course PH4515 Glen Cowan Physics Department Royal Holloway,
Lecture 15. Hypothesis testing in the linear model
 14. Lecture 15. Hypothesis testing in the linear model Lecture 15. Hypothesis testing in the linear model 1 (1 1) Preliminary lemma 15. Hypothesis testing in the linear model 15.1. Preliminary lemma Lemma
14. Lecture 15. Hypothesis testing in the linear model Lecture 15. Hypothesis testing in the linear model 1 (1 1) Preliminary lemma 15. Hypothesis testing in the linear model 15.1. Preliminary lemma Lemma
Vectors and Matrices Statistics with Vectors and Matrices
 Vectors and Matrices Statistics with Vectors and Matrices Lecture 3 September 7, 005 Analysis Lecture #3-9/7/005 Slide 1 of 55 Today s Lecture Vectors and Matrices (Supplement A - augmented with SAS proc
Vectors and Matrices Statistics with Vectors and Matrices Lecture 3 September 7, 005 Analysis Lecture #3-9/7/005 Slide 1 of 55 Today s Lecture Vectors and Matrices (Supplement A - augmented with SAS proc
Multivariate Capability Analysis Using Statgraphics. Presented by Dr. Neil W. Polhemus
 Multivariate Capability Analysis Using Statgraphics Presented by Dr. Neil W. Polhemus Multivariate Capability Analysis Used to demonstrate conformance of a process to requirements or specifications that
Multivariate Capability Analysis Using Statgraphics Presented by Dr. Neil W. Polhemus Multivariate Capability Analysis Used to demonstrate conformance of a process to requirements or specifications that
Introduction to the Analysis of Variance (ANOVA)
 Introduction to the Analysis of Variance (ANOVA) The Analysis of Variance (ANOVA) The analysis of variance (ANOVA) is a statistical technique for testing for differences between the means of multiple (more
Introduction to the Analysis of Variance (ANOVA) The Analysis of Variance (ANOVA) The analysis of variance (ANOVA) is a statistical technique for testing for differences between the means of multiple (more
INTERVAL ESTIMATION AND HYPOTHESES TESTING
 INTERVAL ESTIMATION AND HYPOTHESES TESTING 1. IDEA An interval rather than a point estimate is often of interest. Confidence intervals are thus important in empirical work. To construct interval estimates,
INTERVAL ESTIMATION AND HYPOTHESES TESTING 1. IDEA An interval rather than a point estimate is often of interest. Confidence intervals are thus important in empirical work. To construct interval estimates,
Notes on the Multivariate Normal and Related Topics
 Version: July 10, 2013 Notes on the Multivariate Normal and Related Topics Let me refresh your memory about the distinctions between population and sample; parameters and statistics; population distributions
Version: July 10, 2013 Notes on the Multivariate Normal and Related Topics Let me refresh your memory about the distinctions between population and sample; parameters and statistics; population distributions
Chapter 2 Multivariate Normal Distribution
 Chapter Multivariate Normal Distribution In this chapter, we define the univariate and multivariate normal distribution density functions and then we discuss the tests of differences of means for multiple
Chapter Multivariate Normal Distribution In this chapter, we define the univariate and multivariate normal distribution density functions and then we discuss the tests of differences of means for multiple
Institute of Actuaries of India
 Institute of Actuaries of India Subject CT3 Probability & Mathematical Statistics May 2011 Examinations INDICATIVE SOLUTION Introduction The indicative solution has been written by the Examiners with the
Institute of Actuaries of India Subject CT3 Probability & Mathematical Statistics May 2011 Examinations INDICATIVE SOLUTION Introduction The indicative solution has been written by the Examiners with the
Multiple Linear Regression
 Multiple Linear Regression Simple linear regression tries to fit a simple line between two variables Y and X. If X is linearly related to Y this explains some of the variability in Y. In most cases, there
Multiple Linear Regression Simple linear regression tries to fit a simple line between two variables Y and X. If X is linearly related to Y this explains some of the variability in Y. In most cases, there
Chapter 7, continued: MANOVA
 Chapter 7, continued: MANOVA The Multivariate Analysis of Variance (MANOVA) technique extends Hotelling T 2 test that compares two mean vectors to the setting in which there are m 2 groups. We wish to
Chapter 7, continued: MANOVA The Multivariate Analysis of Variance (MANOVA) technique extends Hotelling T 2 test that compares two mean vectors to the setting in which there are m 2 groups. We wish to
Quantitative Methods for Economics, Finance and Management (A86050 F86050)
 Quantitative Methods for Economics, Finance and Management (A86050 F86050) Matteo Manera matteo.manera@unimib.it Marzio Galeotti marzio.galeotti@unimi.it 1 This material is taken and adapted from Guy Judge
Quantitative Methods for Economics, Finance and Management (A86050 F86050) Matteo Manera matteo.manera@unimib.it Marzio Galeotti marzio.galeotti@unimi.it 1 This material is taken and adapted from Guy Judge
Multivariate Distributions
 Copyright Cosma Rohilla Shalizi; do not distribute without permission updates at http://www.stat.cmu.edu/~cshalizi/adafaepov/ Appendix E Multivariate Distributions E.1 Review of Definitions Let s review
Copyright Cosma Rohilla Shalizi; do not distribute without permission updates at http://www.stat.cmu.edu/~cshalizi/adafaepov/ Appendix E Multivariate Distributions E.1 Review of Definitions Let s review
Applied Multivariate Statistical Analysis Richard Johnson Dean Wichern Sixth Edition
 Applied Multivariate Statistical Analysis Richard Johnson Dean Wichern Sixth Edition Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE England and Associated Companies throughout the world
Applied Multivariate Statistical Analysis Richard Johnson Dean Wichern Sixth Edition Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE England and Associated Companies throughout the world
Least Squares Estimation
 Least Squares Estimation Using the least squares estimator for β we can obtain predicted values and compute residuals: Ŷ = Z ˆβ = Z(Z Z) 1 Z Y ˆɛ = Y Ŷ = Y Z(Z Z) 1 Z Y = [I Z(Z Z) 1 Z ]Y. The usual decomposition
Least Squares Estimation Using the least squares estimator for β we can obtain predicted values and compute residuals: Ŷ = Z ˆβ = Z(Z Z) 1 Z Y ˆɛ = Y Ŷ = Y Z(Z Z) 1 Z Y = [I Z(Z Z) 1 Z ]Y. The usual decomposition
Lecture 10: Generalized likelihood ratio test
 Stat 200: Introduction to Statistical Inference Autumn 2018/19 Lecture 10: Generalized likelihood ratio test Lecturer: Art B. Owen October 25 Disclaimer: These notes have not been subjected to the usual
Stat 200: Introduction to Statistical Inference Autumn 2018/19 Lecture 10: Generalized likelihood ratio test Lecturer: Art B. Owen October 25 Disclaimer: These notes have not been subjected to the usual
Multivariate Linear Models
 Multivariate Linear Models Stanley Sawyer Washington University November 7, 2001 1. Introduction. Suppose that we have n observations, each of which has d components. For example, we may have d measurements
Multivariate Linear Models Stanley Sawyer Washington University November 7, 2001 1. Introduction. Suppose that we have n observations, each of which has d components. For example, we may have d measurements
Loglikelihood and Confidence Intervals
 Stat 504, Lecture 2 1 Loglikelihood and Confidence Intervals The loglikelihood function is defined to be the natural logarithm of the likelihood function, l(θ ; x) = log L(θ ; x). For a variety of reasons,
Stat 504, Lecture 2 1 Loglikelihood and Confidence Intervals The loglikelihood function is defined to be the natural logarithm of the likelihood function, l(θ ; x) = log L(θ ; x). For a variety of reasons,
STA442/2101: Assignment 5
 STA442/2101: Assignment 5 Craig Burkett Quiz on: Oct 23 rd, 2015 The questions are practice for the quiz next week, and are not to be handed in. I would like you to bring in all of the code you used to
STA442/2101: Assignment 5 Craig Burkett Quiz on: Oct 23 rd, 2015 The questions are practice for the quiz next week, and are not to be handed in. I would like you to bring in all of the code you used to
Random Matrices and Multivariate Statistical Analysis
 Random Matrices and Multivariate Statistical Analysis Iain Johnstone, Statistics, Stanford imj@stanford.edu SEA 06@MIT p.1 Agenda Classical multivariate techniques Principal Component Analysis Canonical
Random Matrices and Multivariate Statistical Analysis Iain Johnstone, Statistics, Stanford imj@stanford.edu SEA 06@MIT p.1 Agenda Classical multivariate techniques Principal Component Analysis Canonical
Practice Problems Section Problems
 Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
Practice Problems Section 4-4-3 4-4 4-5 4-6 4-7 4-8 4-10 Supplemental Problems 4-1 to 4-9 4-13, 14, 15, 17, 19, 0 4-3, 34, 36, 38 4-47, 49, 5, 54, 55 4-59, 60, 63 4-66, 68, 69, 70, 74 4-79, 81, 84 4-85,
y ˆ i = ˆ " T u i ( i th fitted value or i th fit)
 1 2 INFERENCE FOR MULTIPLE LINEAR REGRESSION Recall Terminology: p predictors x 1, x 2,, x p Some might be indicator variables for categorical variables) k-1 non-constant terms u 1, u 2,, u k-1 Each u
1 2 INFERENCE FOR MULTIPLE LINEAR REGRESSION Recall Terminology: p predictors x 1, x 2,, x p Some might be indicator variables for categorical variables) k-1 non-constant terms u 1, u 2,, u k-1 Each u
Chapter 9. Hotelling s T 2 Test. 9.1 One Sample. The one sample Hotelling s T 2 test is used to test H 0 : µ = µ 0 versus
 Chapter 9 Hotelling s T 2 Test 9.1 One Sample The one sample Hotelling s T 2 test is used to test H 0 : µ = µ 0 versus H A : µ µ 0. The test rejects H 0 if T 2 H = n(x µ 0 ) T S 1 (x µ 0 ) > n p F p,n
Chapter 9 Hotelling s T 2 Test 9.1 One Sample The one sample Hotelling s T 2 test is used to test H 0 : µ = µ 0 versus H A : µ µ 0. The test rejects H 0 if T 2 H = n(x µ 0 ) T S 1 (x µ 0 ) > n p F p,n
Lecture 32: Asymptotic confidence sets and likelihoods
 Lecture 32: Asymptotic confidence sets and likelihoods Asymptotic criterion In some problems, especially in nonparametric problems, it is difficult to find a reasonable confidence set with a given confidence
Lecture 32: Asymptotic confidence sets and likelihoods Asymptotic criterion In some problems, especially in nonparametric problems, it is difficult to find a reasonable confidence set with a given confidence
Multivariate Analysis and Likelihood Inference
 Multivariate Analysis and Likelihood Inference Outline 1 Joint Distribution of Random Variables 2 Principal Component Analysis (PCA) 3 Multivariate Normal Distribution 4 Likelihood Inference Joint density
Multivariate Analysis and Likelihood Inference Outline 1 Joint Distribution of Random Variables 2 Principal Component Analysis (PCA) 3 Multivariate Normal Distribution 4 Likelihood Inference Joint density
STAT 135 Lab 6 Duality of Hypothesis Testing and Confidence Intervals, GLRT, Pearson χ 2 Tests and Q-Q plots. March 8, 2015
 STAT 135 Lab 6 Duality of Hypothesis Testing and Confidence Intervals, GLRT, Pearson χ 2 Tests and Q-Q plots March 8, 2015 The duality between CI and hypothesis testing The duality between CI and hypothesis
STAT 135 Lab 6 Duality of Hypothesis Testing and Confidence Intervals, GLRT, Pearson χ 2 Tests and Q-Q plots March 8, 2015 The duality between CI and hypothesis testing The duality between CI and hypothesis
Likelihood Ratio tests
 Likelihood Ratio tests For general composite hypotheses optimality theory is not usually successful in producing an optimal test. instead we look for heuristics to guide our choices. The simplest approach
Likelihood Ratio tests For general composite hypotheses optimality theory is not usually successful in producing an optimal test. instead we look for heuristics to guide our choices. The simplest approach
STAT 461/561- Assignments, Year 2015
 STAT 461/561- Assignments, Year 2015 This is the second set of assignment problems. When you hand in any problem, include the problem itself and its number. pdf are welcome. If so, use large fonts and
STAT 461/561- Assignments, Year 2015 This is the second set of assignment problems. When you hand in any problem, include the problem itself and its number. pdf are welcome. If so, use large fonts and
Maximum Likelihood. F θ, θ Θ. X 1,..., X n. L(θ) = f(x i ; θ) l(θ) = ln L(θ) = i.i.d. i=1. n ln f(x i ; θ) Sometimes
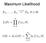 Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
Maximum Likelihood X 1,..., X n i.i.d. F θ, θ Θ L(θ) = n i=1 f(x i ; θ) l(θ) = ln L(θ) = Sometimes n i=1 ln f(x i ; θ) Close your eyes and differentiate? Let X 1,..., X n be a random sample from a Gamma
THE UNIVERSITY OF CHICAGO Booth School of Business Business 41912, Spring Quarter 2016, Mr. Ruey S. Tsay
 THE UNIVERSITY OF CHICAGO Booth School of Business Business 41912, Spring Quarter 2016, Mr. Ruey S. Tsay Lecture 5: Multivariate Multiple Linear Regression The model is Y n m = Z n (r+1) β (r+1) m + ɛ
THE UNIVERSITY OF CHICAGO Booth School of Business Business 41912, Spring Quarter 2016, Mr. Ruey S. Tsay Lecture 5: Multivariate Multiple Linear Regression The model is Y n m = Z n (r+1) β (r+1) m + ɛ
Multivariate Linear Regression Models
 Multivariate Linear Regression Models Regression analysis is used to predict the value of one or more responses from a set of predictors. It can also be used to estimate the linear association between
Multivariate Linear Regression Models Regression analysis is used to predict the value of one or more responses from a set of predictors. It can also be used to estimate the linear association between
The Multivariate Normal Distribution 1
 The Multivariate Normal Distribution 1 STA 302 Fall 2014 1 See last slide for copyright information. 1 / 37 Overview 1 Moment-generating Functions 2 Definition 3 Properties 4 χ 2 and t distributions 2
The Multivariate Normal Distribution 1 STA 302 Fall 2014 1 See last slide for copyright information. 1 / 37 Overview 1 Moment-generating Functions 2 Definition 3 Properties 4 χ 2 and t distributions 2
Group comparison test for independent samples
 Group comparison test for independent samples The purpose of the Analysis of Variance (ANOVA) is to test for significant differences between means. Supposing that: samples come from normal populations
Group comparison test for independent samples The purpose of the Analysis of Variance (ANOVA) is to test for significant differences between means. Supposing that: samples come from normal populations
14.30 Introduction to Statistical Methods in Economics Spring 2009
 MIT OpenCourseWare http://ocw.mit.edu 4.0 Introduction to Statistical Methods in Economics Spring 009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
MIT OpenCourseWare http://ocw.mit.edu 4.0 Introduction to Statistical Methods in Economics Spring 009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
An Introduction to Multivariate Statistical Analysis
 An Introduction to Multivariate Statistical Analysis Third Edition T. W. ANDERSON Stanford University Department of Statistics Stanford, CA WILEY- INTERSCIENCE A JOHN WILEY & SONS, INC., PUBLICATION Contents
An Introduction to Multivariate Statistical Analysis Third Edition T. W. ANDERSON Stanford University Department of Statistics Stanford, CA WILEY- INTERSCIENCE A JOHN WILEY & SONS, INC., PUBLICATION Contents
4.5.1 The use of 2 log Λ when θ is scalar
 4.5. ASYMPTOTIC FORM OF THE G.L.R.T. 97 4.5.1 The use of 2 log Λ when θ is scalar Suppose we wish to test the hypothesis NH : θ = θ where θ is a given value against the alternative AH : θ θ on the basis
4.5. ASYMPTOTIC FORM OF THE G.L.R.T. 97 4.5.1 The use of 2 log Λ when θ is scalar Suppose we wish to test the hypothesis NH : θ = θ where θ is a given value against the alternative AH : θ θ on the basis
POLI 443 Applied Political Research
 POLI 443 Applied Political Research Session 6: Tests of Hypotheses Contingency Analysis Lecturer: Prof. A. Essuman-Johnson, Dept. of Political Science Contact Information: aessuman-johnson@ug.edu.gh College
POLI 443 Applied Political Research Session 6: Tests of Hypotheses Contingency Analysis Lecturer: Prof. A. Essuman-Johnson, Dept. of Political Science Contact Information: aessuman-johnson@ug.edu.gh College
Harvard University. Rigorous Research in Engineering Education
 Statistical Inference Kari Lock Harvard University Department of Statistics Rigorous Research in Engineering Education 12/3/09 Statistical Inference You have a sample and want to use the data collected
Statistical Inference Kari Lock Harvard University Department of Statistics Rigorous Research in Engineering Education 12/3/09 Statistical Inference You have a sample and want to use the data collected
HYPOTHESIS TESTING. Hypothesis Testing
 MBA 605 Business Analytics Don Conant, PhD. HYPOTHESIS TESTING Hypothesis testing involves making inferences about the nature of the population on the basis of observations of a sample drawn from the population.
MBA 605 Business Analytics Don Conant, PhD. HYPOTHESIS TESTING Hypothesis testing involves making inferences about the nature of the population on the basis of observations of a sample drawn from the population.
Statistical Foundations:
 Statistical Foundations: t distributions, t-tests tests Psychology 790 Lecture #12 10/03/2006 Today sclass The t-distribution t ib ti in its full glory. Why we use it for nearly everything. Confidence
Statistical Foundations: t distributions, t-tests tests Psychology 790 Lecture #12 10/03/2006 Today sclass The t-distribution t ib ti in its full glory. Why we use it for nearly everything. Confidence
Stat 427/527: Advanced Data Analysis I
 Stat 427/527: Advanced Data Analysis I Review of Chapters 1-4 Sep, 2017 1 / 18 Concepts you need to know/interpret Numerical summaries: measures of center (mean, median, mode) measures of spread (sample
Stat 427/527: Advanced Data Analysis I Review of Chapters 1-4 Sep, 2017 1 / 18 Concepts you need to know/interpret Numerical summaries: measures of center (mean, median, mode) measures of spread (sample
Some General Types of Tests
 Some General Types of Tests We may not be able to find a UMP or UMPU test in a given situation. In that case, we may use test of some general class of tests that often have good asymptotic properties.
Some General Types of Tests We may not be able to find a UMP or UMPU test in a given situation. In that case, we may use test of some general class of tests that often have good asymptotic properties.
Applied Multivariate and Longitudinal Data Analysis
 Applied Multivariate and Longitudinal Data Analysis Chapter 2: Inference about the mean vector(s) II Ana-Maria Staicu SAS Hall 5220; 919-515-0644; astaicu@ncsu.edu 1 1 Compare Means from More Than Two
Applied Multivariate and Longitudinal Data Analysis Chapter 2: Inference about the mean vector(s) II Ana-Maria Staicu SAS Hall 5220; 919-515-0644; astaicu@ncsu.edu 1 1 Compare Means from More Than Two
Basic Concepts of Inference
 Basic Concepts of Inference Corresponds to Chapter 6 of Tamhane and Dunlop Slides prepared by Elizabeth Newton (MIT) with some slides by Jacqueline Telford (Johns Hopkins University) and Roy Welsch (MIT).
Basic Concepts of Inference Corresponds to Chapter 6 of Tamhane and Dunlop Slides prepared by Elizabeth Newton (MIT) with some slides by Jacqueline Telford (Johns Hopkins University) and Roy Welsch (MIT).
Introduction to Normal Distribution
 Introduction to Normal Distribution Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 17-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Introduction
Introduction to Normal Distribution Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 17-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Introduction
Let us first identify some classes of hypotheses. simple versus simple. H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided
 Let us first identify some classes of hypotheses. simple versus simple H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided H 0 : θ θ 0 versus H 1 : θ > θ 0. (2) two-sided; null on extremes H 0 : θ θ 1 or
Let us first identify some classes of hypotheses. simple versus simple H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided H 0 : θ θ 0 versus H 1 : θ > θ 0. (2) two-sided; null on extremes H 0 : θ θ 1 or
Section 4.6 Simple Linear Regression
 Section 4.6 Simple Linear Regression Objectives ˆ Basic philosophy of SLR and the regression assumptions ˆ Point & interval estimation of the model parameters, and how to make predictions ˆ Point and interval
Section 4.6 Simple Linear Regression Objectives ˆ Basic philosophy of SLR and the regression assumptions ˆ Point & interval estimation of the model parameters, and how to make predictions ˆ Point and interval
