Payo Function Decomposition by Fabrice Douglas Rouah
|
|
|
- Albert Lambert
- 6 years ago
- Views:
Transcription
1 Payo Fnction Decomposition by Fabrice Doglas Roah For any twice- The following identify is often sed in option pricing. di erentiable fnction f() de ned on R we can write f() = f() + f ()( ) + () f (K)(K ) + dk + f (K)( K) + dk for some threshold. I have seen three proofs of this.. Uses the Dirac delta fnction. Fond in papers by Carr and Madan. 2. Uses the Fndamental Theorem of Calcls. Fond in a paper by John Crosby at Glasgow University. 3. Uses the Taylor eries expansion of f(): Fond in a paper by Attilio Mecci. In this Note these three proofs are each presented in detail. We rst present some fnctions that will be needed. Dirac Delta and Other Fnctions De nition of the Dirac delta fnction (K) (K) = for K = elsewhere and (K)dK = : The sifting property of the Dirac delta fnction is f(a) = a+" a " f(k) (a K) dk for " > : The Heaviside fnction H(K) is de ned as for K > H(K) = for K < = (K>): The derivative of H(K) is easy to chec d H(K) = (K): dk
2 The derivative of (K) + = max(; K) is also easy to chec d dk (K)+ = H(K): The de nitions and derivatives needed for the proofs in this Note are presented in the following table. For ( K) For (K ) ( K) = for K = elsewhere (K ) = for = K elsewhere H( K) = (>K) H(K ) = (K>) d dk H( K) = ( K) d dk H(K ) = (K ) d dk ( K)+ d = (>K) dk (K )+ = (K>) 2 Proof Using the Dirac Delta Fnction Carr and Madan consider > in eqation (), since they se it for an nderlying price : f() = f() + f ()( ) + (2) f (K)(K ) + dk + f (K)( K) + dk: Apply the sifting property of the Dirac delta fnction to f() and choose some threshold > f() = = = = I + I 2 : f(k)( K)dK (3) f(k)( K)dK + f(k)(k )dk + 2. First Integration by Parts f(k)( f(k)( K)dK K)dK Apply integration by parts to each of the two integrals I and I 2. 2
3 2.. Evalating I For I choose = f(k); v = (K ). Hence = f (K); v = (K>). I = 2..2 Evalating I 2 f(k)(k )dk (4) = f(k) (K>) = f() (>) f (K) (K>) dk: f (K) (K>) dk (5) For I 2 choose = f(k); v = ( K) so that = f (K); v = (K>) : I 2 = f(k)( K)dK (6) = f(k) (>K) + f (K) (K<) dk (7) = f() (>) + f (K) (K<) dk: bstitte I and I 2 from eqations (4) and (6) into eqation (3) to obtain f() = f() = f() I 3 + I 4 : f (K) (K>) dk econd Integration by Parts f (K) (K<) dk (8) Apply integration by parts again, to each of the two integrals I 3 and I Evalating I 3 For I 3 choose = f (K); v = (K>) ; = f (K); v = (K ) +. Hence I 3 = f (K) (K>) dk (9) = f (K)(K ) + f (K)(K ) + dk () = f ()( ) + f (K)(K ) + dk: 3
4 2.2.2 Evalating I 4 Finally, for I 4 choose = f (K); v = (>K) ; = f (K); v = ( K) + : I 4 = f (K) (K<) dk () = f (K)( K) + + f (K)( K) + dk (2) = f ()( ) + + f (K)( 2.3 Obtaining the Payo Decomposition K) + dk: bstitte I 3 and I 4 from eqations (9) and () into eqation (8) to btain f() = f() + f () ( ) + ( ) + (3) + f (K)(K ) + dk + f (K)( K) + dk: Eqivalently, since [( ) + ( ) + ] = (which can be veri ed by considering the cases > and < separately), eqation (3) can be written f() = f() + f ()( ) + which is eqation (2). f (K)(K ) + dk + 3 Proof Using the FTC f (K)( K) + This proof ses the Fndamental Theorem of Calcls (FTC) Hence we can write f() as f() f() = f() = f() + f ()d: f ()d: (4) We will focs on the integral R f ()d in eqation (4). Note that the integral can be broen into two parts: when > and when < f ()d = (>) f ()d + (<) f ()d (5) = (>) f ()d 4 (<) f ()d:
5 In R eqation (5) apply the FTC to the rst integral so that f () f () = f (v)dv and to the second integral so that f () f () = R f (v)dv f ()d = (>) f () + f (v)dv d (6) (<) f () f (v)dv d: Re-arrange the integrals to obtain f ()d = (>) f ()d (>) (<) f ()d + (7) f (v)dvd + (<) Consider each of these for integrals in eqation (7) in pairs. f (v)dvd: 3. First Pair of Integrals The rst two integrals in eqation (7) are (>) f ()d (<) f ()d (8) = (>) f ()d + (<) f ()d = f ()d = f () 3.2 econd Pair of Integrals d = f ()( The last two integrals in eqation () can be evalated sing Fbini s theorem changing the order of integration, maing sre to preserve the same domain of integration. The integral has domain of integration <v< << can write the integral (9) as imilarly, the integral f (v)dvd = ): f (v)dvd (9), which is eqivalent to v<< <v< v f (v)ddv = f (v)(. Hence we v)dv: f (v)dvd (2) 5
6 has domain of integration <v< << can write the integral (2) as f (v)dvd = v 3.3 Recombing the Integrals, which is eqivalent to <<v <v< f (v)ddv = f (v)(v. Hence we )dv: We pt these two integrals bac into eqation (7), and sbstitte into eqation (4). We obtain f() = f() + (>) f (v)( v)dv + (<) f (v)(v )dv: (2) ince (>) = only when >, and since (<) = only when <, these can be replaced by the () + fnction on the linear parts of each integrand in eqation (2). Hence we have the desired reslt f() = f() + f ()( ) + which, again, is eqation (). f (v)( v) + dv + 4 Proof Using Taylor eries De ne the fnction g(x) as g(x) = f()+f ()(x )+ f ()(x f (v)(v ) + dv ) + d+ f ()( x) + d: (22) The proof involves demonstrating that g(x) = f(x). This is done by showing that g() = f() and that the derivatives of g and f evalated at any point x are the same, i.e. g (n) (x) = f (n) (x). The Taylor series expansion of f and g will therefore be identical, and conseqently, so will f and g themselves, at all vales of x. First note that for x =, eqation (22) becomes g() = f()+f ()( )+ f ()( ) + d+ f ()( ) + d: (23) In eqation (23), the rst integral is zero since ( ) + = for >, and the second integral is zero since ( ) + = for <. Hence g() = f(). 4. First Derivative Tae the rst derivative of g(x) in eqation (22) g (x) = f () + = f () + f () d dx (x )+ d + f ()H(x 6 )d f () d dx ( f ()H( x)d: x)+ d(24)
7 Consider the second line of eqation (24). In the rst integral, H(x ) = only when < x. Hence the pper limit can be replaced with x. Moreover, H(x ) = only when x >, in which case the integral is R x f ()d. This can be accomplished by inclding the term H(x ) otside the integral. imilarly, for the second integral, H( x) = only when > x so the lower limit can be replaced with x, and H( x) = only when x <, so we pt H( x) otside the integral. This means that eqation () can be written as g (x) = f () + H(x ) x f ()d H( x) x f ()d: (25) To evalate eqation (25) we consider the cases x > and x < separately. 4.. Case For x > we have H( x) = and H(x ) x f ()d = x f ()d = f (x) f () Hence eqation (25) becomes 4..2 Case 2 g (x) = f () + [f (x) f ()] = f (x): For x < we have H(x ) = and H( x) x f ()d = f () f(x): Hence eqation (25) becomes g (x) = f () + [f () f (x)] = f (x): o for both cases we have g (x) = f (x): 4.2 econd Derivative Tae the second derivative of g(x) in eqation (22) g (x) = = f () d2 dx 2 (x )+ d + f ()(x )d + f ()( f () d2 dx 2 ( x)+ d (26) x)d: Consider the second line of eqation (26). The sifting property of the Dirac delta fnction implies that the rst integral is f (x), bt only when x >, 7
8 since this ensres that the domain of integral is s ciently wide for the sifting property to hold. Otherwise, the integral is zero. This can be accomplished by mltiplying the integral by H(x ): imilarly, the second integral is f (x) only when x <, so we mltiply the integral by H( x). This implies that we can write g (x) as g (x) = H(x ) f ()(x )d + H( x) f ()( = H(x )f (x) + H( x)f (x) = f (x) x)d where the second line follows by the sifting property of the Dirac delta fnction. 4.3 Higher Order Derivatives The nth derivative of g(x) is " d n dn g(x) = dxn dx n f() + f ()(x ) + " = dn 2 dx n 2 f ()(x ) + d + f ()( # f () d2 dx 2 (x )+ d + f () d2 dx 2 ( x)+ d : x) + d # From eqation (26) in the preceding section we now that the term inside the sqare bracets is simply d2 dx f(x). Hence we can write 2 d n dx n g(x) = dn 2 d 2 dx n 2 dx 2 f(x) = dn dx n f(x): Apply the Taylor theorem to g(x) g(x) = g() + = f() + = f(x): X n= X n= n! g(n) (x ) n n! f (n) (x ) n ince the fnctions f and g are identical, eqation (22) becomes eqation () and the proof is complete. 8
Section 7.4: Integration of Rational Functions by Partial Fractions
 Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
Mean Value Formulae for Laplace and Heat Equation
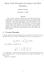 Mean Vale Formlae for Laplace and Heat Eqation Abhinav Parihar December 7, 03 Abstract Here I discss a method to constrct the mean vale theorem for the heat eqation. To constrct sch a formla ab initio,
Mean Vale Formlae for Laplace and Heat Eqation Abhinav Parihar December 7, 03 Abstract Here I discss a method to constrct the mean vale theorem for the heat eqation. To constrct sch a formla ab initio,
Second-Order Wave Equation
 Second-Order Wave Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 3 December 016 1 Introdction The classical wave eqation is a second-order
Second-Order Wave Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 3 December 016 1 Introdction The classical wave eqation is a second-order
STEP Support Programme. STEP III Hyperbolic Functions: Solutions
 STEP Spport Programme STEP III Hyperbolic Fnctions: Soltions Start by sing the sbstittion t cosh x. This gives: sinh x cosh a cosh x cosh a sinh x t sinh x dt t dt t + ln t ln t + ln cosh a ln ln cosh
STEP Spport Programme STEP III Hyperbolic Fnctions: Soltions Start by sing the sbstittion t cosh x. This gives: sinh x cosh a cosh x cosh a sinh x t sinh x dt t dt t + ln t ln t + ln cosh a ln ln cosh
Optimization via the Hamilton-Jacobi-Bellman Method: Theory and Applications
 Optimization via the Hamilton-Jacobi-Bellman Method: Theory and Applications Navin Khaneja lectre notes taken by Christiane Koch Jne 24, 29 1 Variation yields a classical Hamiltonian system Sppose that
Optimization via the Hamilton-Jacobi-Bellman Method: Theory and Applications Navin Khaneja lectre notes taken by Christiane Koch Jne 24, 29 1 Variation yields a classical Hamiltonian system Sppose that
Calculations involving a single random variable (SRV)
 Calclations involving a single random variable (SRV) Example of Bearing Capacity q φ = 0 µ σ c c = 100kN/m = 50kN/m ndrained shear strength parameters What is the relationship between the Factor of Safety
Calclations involving a single random variable (SRV) Example of Bearing Capacity q φ = 0 µ σ c c = 100kN/m = 50kN/m ndrained shear strength parameters What is the relationship between the Factor of Safety
Math 116 First Midterm October 14, 2009
 Math 116 First Midterm October 14, 9 Name: EXAM SOLUTIONS Instrctor: Section: 1. Do not open this exam ntil yo are told to do so.. This exam has 1 pages inclding this cover. There are 9 problems. Note
Math 116 First Midterm October 14, 9 Name: EXAM SOLUTIONS Instrctor: Section: 1. Do not open this exam ntil yo are told to do so.. This exam has 1 pages inclding this cover. There are 9 problems. Note
Chem 4501 Introduction to Thermodynamics, 3 Credits Kinetics, and Statistical Mechanics. Fall Semester Homework Problem Set Number 10 Solutions
 Chem 4501 Introdction to Thermodynamics, 3 Credits Kinetics, and Statistical Mechanics Fall Semester 2017 Homework Problem Set Nmber 10 Soltions 1. McQarrie and Simon, 10-4. Paraphrase: Apply Eler s theorem
Chem 4501 Introdction to Thermodynamics, 3 Credits Kinetics, and Statistical Mechanics Fall Semester 2017 Homework Problem Set Nmber 10 Soltions 1. McQarrie and Simon, 10-4. Paraphrase: Apply Eler s theorem
Figure 1 Probability density function of Wedge copula for c = (best fit to Nominal skew of DRAM case study).
 Wedge Copla This docment explains the constrction and properties o a particlar geometrical copla sed to it dependency data rom the edram case stdy done at Portland State University. The probability density
Wedge Copla This docment explains the constrction and properties o a particlar geometrical copla sed to it dependency data rom the edram case stdy done at Portland State University. The probability density
ECON3120/4120 Mathematics 2, spring 2009
 University of Oslo Department of Economics Arne Strøm ECON3/4 Mathematics, spring 9 Problem soltions for Seminar 4, 6 Febrary 9 (For practical reasons some of the soltions may inclde problem parts that
University of Oslo Department of Economics Arne Strøm ECON3/4 Mathematics, spring 9 Problem soltions for Seminar 4, 6 Febrary 9 (For practical reasons some of the soltions may inclde problem parts that
PhysicsAndMathsTutor.com
 C Integration - By sbstittion PhysicsAndMathsTtor.com. Using the sbstittion cos +, or otherwise, show that e cos + sin d e(e ) (Total marks). (a) Using the sbstittion cos, or otherwise, find the eact vale
C Integration - By sbstittion PhysicsAndMathsTtor.com. Using the sbstittion cos +, or otherwise, show that e cos + sin d e(e ) (Total marks). (a) Using the sbstittion cos, or otherwise, find the eact vale
sin xdx = cos x + c We also run into antiderivatives for tan x, cot x, sec x and csc x in the section on Log integrals. They are: cos ax sec ax a
 Trig Integrals We already know antiderivatives for sin x, cos x, sec x tan x, csc x, sec x and csc x cot x. They are cos xdx = sin x sin xdx = cos x sec x tan xdx = sec x csc xdx = cot x sec xdx = tan
Trig Integrals We already know antiderivatives for sin x, cos x, sec x tan x, csc x, sec x and csc x cot x. They are cos xdx = sin x sin xdx = cos x sec x tan xdx = sec x csc xdx = cot x sec xdx = tan
Uncertainties of measurement
 Uncertainties of measrement Laboratory tas A temperatre sensor is connected as a voltage divider according to the schematic diagram on Fig.. The temperatre sensor is a thermistor type B5764K [] with nominal
Uncertainties of measrement Laboratory tas A temperatre sensor is connected as a voltage divider according to the schematic diagram on Fig.. The temperatre sensor is a thermistor type B5764K [] with nominal
Oxford Scholarship Online
 University Press Scholarship Online Oxford Scholarship Online Methods in Theoretical Quantum Optics Stephen Barnett and Paul Radmore Print publication date: 2002 Print ISBN-13: 9780198563617 Published
University Press Scholarship Online Oxford Scholarship Online Methods in Theoretical Quantum Optics Stephen Barnett and Paul Radmore Print publication date: 2002 Print ISBN-13: 9780198563617 Published
The Linear Quadratic Regulator
 10 The Linear Qadratic Reglator 10.1 Problem formlation This chapter concerns optimal control of dynamical systems. Most of this development concerns linear models with a particlarly simple notion of optimality.
10 The Linear Qadratic Reglator 10.1 Problem formlation This chapter concerns optimal control of dynamical systems. Most of this development concerns linear models with a particlarly simple notion of optimality.
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain.
 Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
Lecture 32: Taylor Series and McLaurin series We saw last day that some functions are equal to a power series on part of their domain. For example f(x) = 1 1 x = 1 + x + x2 + x 3 + = ln(1 + x) = x x2 2
ON THE SHAPES OF BILATERAL GAMMA DENSITIES
 ON THE SHAPES OF BILATERAL GAMMA DENSITIES UWE KÜCHLER, STEFAN TAPPE Abstract. We investigate the for parameter family of bilateral Gamma distribtions. The goal of this paper is to provide a thorogh treatment
ON THE SHAPES OF BILATERAL GAMMA DENSITIES UWE KÜCHLER, STEFAN TAPPE Abstract. We investigate the for parameter family of bilateral Gamma distribtions. The goal of this paper is to provide a thorogh treatment
Setting The K Value And Polarization Mode Of The Delta Undulator
 LCLS-TN-4- Setting The Vale And Polarization Mode Of The Delta Undlator Zachary Wolf, Heinz-Dieter Nhn SLAC September 4, 04 Abstract This note provides the details for setting the longitdinal positions
LCLS-TN-4- Setting The Vale And Polarization Mode Of The Delta Undlator Zachary Wolf, Heinz-Dieter Nhn SLAC September 4, 04 Abstract This note provides the details for setting the longitdinal positions
CHARACTERIZATIONS OF EXPONENTIAL DISTRIBUTION VIA CONDITIONAL EXPECTATIONS OF RECORD VALUES. George P. Yanev
 Pliska Std. Math. Blgar. 2 (211), 233 242 STUDIA MATHEMATICA BULGARICA CHARACTERIZATIONS OF EXPONENTIAL DISTRIBUTION VIA CONDITIONAL EXPECTATIONS OF RECORD VALUES George P. Yanev We prove that the exponential
Pliska Std. Math. Blgar. 2 (211), 233 242 STUDIA MATHEMATICA BULGARICA CHARACTERIZATIONS OF EXPONENTIAL DISTRIBUTION VIA CONDITIONAL EXPECTATIONS OF RECORD VALUES George P. Yanev We prove that the exponential
Discussion of The Forward Search: Theory and Data Analysis by Anthony C. Atkinson, Marco Riani, and Andrea Ceroli
 1 Introdction Discssion of The Forward Search: Theory and Data Analysis by Anthony C. Atkinson, Marco Riani, and Andrea Ceroli Søren Johansen Department of Economics, University of Copenhagen and CREATES,
1 Introdction Discssion of The Forward Search: Theory and Data Analysis by Anthony C. Atkinson, Marco Riani, and Andrea Ceroli Søren Johansen Department of Economics, University of Copenhagen and CREATES,
Garret Sobczyk s 2x2 Matrix Derivation
 Garret Sobczyk s x Matrix Derivation Krt Nalty May, 05 Abstract Using matrices to represent geometric algebras is known, bt not necessarily the best practice. While I have sed small compter programs to
Garret Sobczyk s x Matrix Derivation Krt Nalty May, 05 Abstract Using matrices to represent geometric algebras is known, bt not necessarily the best practice. While I have sed small compter programs to
Elements of Coordinate System Transformations
 B Elements of Coordinate System Transformations Coordinate system transformation is a powerfl tool for solving many geometrical and kinematic problems that pertain to the design of gear ctting tools and
B Elements of Coordinate System Transformations Coordinate system transformation is a powerfl tool for solving many geometrical and kinematic problems that pertain to the design of gear ctting tools and
FEA Solution Procedure
 EA Soltion Procedre (demonstrated with a -D bar element problem) EA Procedre for Static Analysis. Prepare the E model a. discretize (mesh) the strctre b. prescribe loads c. prescribe spports. Perform calclations
EA Soltion Procedre (demonstrated with a -D bar element problem) EA Procedre for Static Analysis. Prepare the E model a. discretize (mesh) the strctre b. prescribe loads c. prescribe spports. Perform calclations
1 Undiscounted Problem (Deterministic)
 Lectre 9: Linear Qadratic Control Problems 1 Undisconted Problem (Deterministic) Choose ( t ) 0 to Minimize (x trx t + tq t ) t=0 sbject to x t+1 = Ax t + B t, x 0 given. x t is an n-vector state, t a
Lectre 9: Linear Qadratic Control Problems 1 Undisconted Problem (Deterministic) Choose ( t ) 0 to Minimize (x trx t + tq t ) t=0 sbject to x t+1 = Ax t + B t, x 0 given. x t is an n-vector state, t a
Chapter 2 Introduction to the Stiffness (Displacement) Method. The Stiffness (Displacement) Method
 CIVL 7/87 Chater - The Stiffness Method / Chater Introdction to the Stiffness (Dislacement) Method Learning Objectives To define the stiffness matrix To derive the stiffness matrix for a sring element
CIVL 7/87 Chater - The Stiffness Method / Chater Introdction to the Stiffness (Dislacement) Method Learning Objectives To define the stiffness matrix To derive the stiffness matrix for a sring element
11.10a Taylor and Maclaurin Series
 11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
11.10a 1 11.10a Taylor and Maclaurin Series Let y = f(x) be a differentiable function at x = a. In first semester calculus we saw that (1) f(x) f(a)+f (a)(x a), for all x near a The right-hand side of
1 The space of linear transformations from R n to R m :
 Math 540 Spring 20 Notes #4 Higher deriaties, Taylor s theorem The space of linear transformations from R n to R m We hae discssed linear transformations mapping R n to R m We can add sch linear transformations
Math 540 Spring 20 Notes #4 Higher deriaties, Taylor s theorem The space of linear transformations from R n to R m We hae discssed linear transformations mapping R n to R m We can add sch linear transformations
An Investigation into Estimating Type B Degrees of Freedom
 An Investigation into Estimating Type B Degrees of H. Castrp President, Integrated Sciences Grop Jne, 00 Backgrond The degrees of freedom associated with an ncertainty estimate qantifies the amont of information
An Investigation into Estimating Type B Degrees of H. Castrp President, Integrated Sciences Grop Jne, 00 Backgrond The degrees of freedom associated with an ncertainty estimate qantifies the amont of information
Discussion Papers Department of Economics University of Copenhagen
 Discssion Papers Department of Economics University of Copenhagen No. 10-06 Discssion of The Forward Search: Theory and Data Analysis, by Anthony C. Atkinson, Marco Riani, and Andrea Ceroli Søren Johansen,
Discssion Papers Department of Economics University of Copenhagen No. 10-06 Discssion of The Forward Search: Theory and Data Analysis, by Anthony C. Atkinson, Marco Riani, and Andrea Ceroli Søren Johansen,
ECON2285: Mathematical Economics
 ECON2285: Mathematical Economics Yulei Luo Economics, HKU September 17, 2018 Luo, Y. (Economics, HKU) ME September 17, 2018 1 / 46 Static Optimization and Extreme Values In this topic, we will study goal
ECON2285: Mathematical Economics Yulei Luo Economics, HKU September 17, 2018 Luo, Y. (Economics, HKU) ME September 17, 2018 1 / 46 Static Optimization and Extreme Values In this topic, we will study goal
Assignment Fall 2014
 Assignment 5.086 Fall 04 De: Wednesday, 0 December at 5 PM. Upload yor soltion to corse website as a zip file YOURNAME_ASSIGNMENT_5 which incldes the script for each qestion as well as all Matlab fnctions
Assignment 5.086 Fall 04 De: Wednesday, 0 December at 5 PM. Upload yor soltion to corse website as a zip file YOURNAME_ASSIGNMENT_5 which incldes the script for each qestion as well as all Matlab fnctions
Prandl established a universal velocity profile for flow parallel to the bed given by
 EM 0--00 (Part VI) (g) The nderlayers shold be at least three thicknesses of the W 50 stone, bt never less than 0.3 m (Ahrens 98b). The thickness can be calclated sing Eqation VI-5-9 with a coefficient
EM 0--00 (Part VI) (g) The nderlayers shold be at least three thicknesses of the W 50 stone, bt never less than 0.3 m (Ahrens 98b). The thickness can be calclated sing Eqation VI-5-9 with a coefficient
Lecture 6: Contraction mapping, inverse and implicit function theorems
 Lecture 6: Contraction mapping, inverse and implicit function theorems 1 The contraction mapping theorem De nition 11 Let X be a metric space, with metric d If f : X! X and if there is a number 2 (0; 1)
Lecture 6: Contraction mapping, inverse and implicit function theorems 1 The contraction mapping theorem De nition 11 Let X be a metric space, with metric d If f : X! X and if there is a number 2 (0; 1)
(1.1) g(x) = f'ek(xy)fy)dy,
 THE G-FÜNCTIONS AS UNSYMMETRICAL FOURIER KERNELS. Ill ROOP NARAIN 1. The fnctions k(x) and h(x) are said to form a pair of Forier kernels if the reciprocal eqations (1.1) g(x) = f'ek(xy)fy)dy, J o (1.1')
THE G-FÜNCTIONS AS UNSYMMETRICAL FOURIER KERNELS. Ill ROOP NARAIN 1. The fnctions k(x) and h(x) are said to form a pair of Forier kernels if the reciprocal eqations (1.1) g(x) = f'ek(xy)fy)dy, J o (1.1')
Integration of Basic Functions. Session 7 : 9/23 1
 Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Integration o Basic Fnctions Session 7 : 9/3 Antiderivation Integration Deinition: Taking the antiderivative, or integral, o some nction F(), reslts in the nction () i ()F() Pt simply: i yo take the integral
Transition Density Function and Partial Di erential Equations
 Transition Density Function and Partial Di erential Equations In this lecture Generalised Functions - Dirac delta and heaviside Transition Density Function - Forward and Backward Kolmogorov Equation Similarity
Transition Density Function and Partial Di erential Equations In this lecture Generalised Functions - Dirac delta and heaviside Transition Density Function - Forward and Backward Kolmogorov Equation Similarity
1 Review of di erential calculus
 Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
BLOOM S TAXONOMY. Following Bloom s Taxonomy to Assess Students
 BLOOM S TAXONOMY Topic Following Bloom s Taonomy to Assess Stdents Smmary A handot for stdents to eplain Bloom s taonomy that is sed for item writing and test constrction to test stdents to see if they
BLOOM S TAXONOMY Topic Following Bloom s Taonomy to Assess Stdents Smmary A handot for stdents to eplain Bloom s taonomy that is sed for item writing and test constrction to test stdents to see if they
i=1 y i 1fd i = dg= P N i=1 1fd i = dg.
 ECOOMETRICS II (ECO 240S) University of Toronto. Department of Economics. Winter 208 Instrctor: Victor Agirregabiria SOLUTIO TO FIAL EXAM Tesday, April 0, 208. From 9:00am-2:00pm (3 hors) ISTRUCTIOS: -
ECOOMETRICS II (ECO 240S) University of Toronto. Department of Economics. Winter 208 Instrctor: Victor Agirregabiria SOLUTIO TO FIAL EXAM Tesday, April 0, 208. From 9:00am-2:00pm (3 hors) ISTRUCTIOS: -
Lecture: Corporate Income Tax - Unlevered firms
 Lectre: Corporate Income Tax - Unlevered firms Ltz Krschwitz & Andreas Löffler Disconted Cash Flow, Section 2.1, Otline 2.1 Unlevered firms Similar companies Notation 2.1.1 Valation eqation 2.1.2 Weak
Lectre: Corporate Income Tax - Unlevered firms Ltz Krschwitz & Andreas Löffler Disconted Cash Flow, Section 2.1, Otline 2.1 Unlevered firms Similar companies Notation 2.1.1 Valation eqation 2.1.2 Weak
Pulses on a Struck String
 8.03 at ESG Spplemental Notes Plses on a Strck String These notes investigate specific eamples of transverse motion on a stretched string in cases where the string is at some time ndisplaced, bt with a
8.03 at ESG Spplemental Notes Plses on a Strck String These notes investigate specific eamples of transverse motion on a stretched string in cases where the string is at some time ndisplaced, bt with a
Control Systems
 6.5 Control Systems Last Time: Introdction Motivation Corse Overview Project Math. Descriptions of Systems ~ Review Classification of Systems Linear Systems LTI Systems The notion of state and state variables
6.5 Control Systems Last Time: Introdction Motivation Corse Overview Project Math. Descriptions of Systems ~ Review Classification of Systems Linear Systems LTI Systems The notion of state and state variables
3. Several Random Variables
 . Several Random Variables. To Random Variables. Conditional Probabilit--Revisited. Statistical Independence.4 Correlation beteen Random Variables Standardied (or ero mean normalied) random variables.5
. Several Random Variables. To Random Variables. Conditional Probabilit--Revisited. Statistical Independence.4 Correlation beteen Random Variables Standardied (or ero mean normalied) random variables.5
A fundamental inverse problem in geosciences
 A fndamental inverse problem in geosciences Predict the vales of a spatial random field (SRF) sing a set of observed vales of the same and/or other SRFs. y i L i ( ) + v, i,..., n i ( P)? L i () : linear
A fndamental inverse problem in geosciences Predict the vales of a spatial random field (SRF) sing a set of observed vales of the same and/or other SRFs. y i L i ( ) + v, i,..., n i ( P)? L i () : linear
3.4-Miscellaneous Equations
 .-Miscellaneos Eqations Factoring Higher Degree Polynomials: Many higher degree polynomials can be solved by factoring. Of particlar vale is the method of factoring by groping, however all types of factoring
.-Miscellaneos Eqations Factoring Higher Degree Polynomials: Many higher degree polynomials can be solved by factoring. Of particlar vale is the method of factoring by groping, however all types of factoring
, applyingl Hospital s Rule again x 0 2 cos(x) xsinx
 Lecture 3 We give a couple examples of using L Hospital s Rule: Example 3.. [ (a) Compute x 0 sin(x) x. To put this into a form for L Hospital s Rule we first put it over a common denominator [ x 0 sin(x)
Lecture 3 We give a couple examples of using L Hospital s Rule: Example 3.. [ (a) Compute x 0 sin(x) x. To put this into a form for L Hospital s Rule we first put it over a common denominator [ x 0 sin(x)
Approximate Solution for the System of Non-linear Volterra Integral Equations of the Second Kind by using Block-by-block Method
 Astralian Jornal of Basic and Applied Sciences, (1): 114-14, 008 ISSN 1991-8178 Approximate Soltion for the System of Non-linear Volterra Integral Eqations of the Second Kind by sing Block-by-block Method
Astralian Jornal of Basic and Applied Sciences, (1): 114-14, 008 ISSN 1991-8178 Approximate Soltion for the System of Non-linear Volterra Integral Eqations of the Second Kind by sing Block-by-block Method
Classify by number of ports and examine the possible structures that result. Using only one-port elements, no more than two elements can be assembled.
 Jnction elements in network models. Classify by nmber of ports and examine the possible strctres that reslt. Using only one-port elements, no more than two elements can be assembled. Combining two two-ports
Jnction elements in network models. Classify by nmber of ports and examine the possible strctres that reslt. Using only one-port elements, no more than two elements can be assembled. Combining two two-ports
Lecture: Corporate Income Tax
 Lectre: Corporate Income Tax Ltz Krschwitz & Andreas Löffler Disconted Cash Flow, Section 2.1, Otline 2.1 Unlevered firms Similar companies Notation 2.1.1 Valation eqation 2.1.2 Weak atoregressive cash
Lectre: Corporate Income Tax Ltz Krschwitz & Andreas Löffler Disconted Cash Flow, Section 2.1, Otline 2.1 Unlevered firms Similar companies Notation 2.1.1 Valation eqation 2.1.2 Weak atoregressive cash
Study of the diffusion operator by the SPH method
 IOSR Jornal of Mechanical and Civil Engineering (IOSR-JMCE) e-issn: 2278-684,p-ISSN: 2320-334X, Volme, Isse 5 Ver. I (Sep- Oct. 204), PP 96-0 Stdy of the diffsion operator by the SPH method Abdelabbar.Nait
IOSR Jornal of Mechanical and Civil Engineering (IOSR-JMCE) e-issn: 2278-684,p-ISSN: 2320-334X, Volme, Isse 5 Ver. I (Sep- Oct. 204), PP 96-0 Stdy of the diffsion operator by the SPH method Abdelabbar.Nait
Generalized Jinc functions and their application to focusing and diffraction of circular apertures
 Qing Cao Vol. 20, No. 4/April 2003/J. Opt. Soc. Am. A 66 Generalized Jinc fnctions and their application to focsing and diffraction of circlar apertres Qing Cao Optische Nachrichtentechnik, FernUniversität
Qing Cao Vol. 20, No. 4/April 2003/J. Opt. Soc. Am. A 66 Generalized Jinc fnctions and their application to focsing and diffraction of circlar apertres Qing Cao Optische Nachrichtentechnik, FernUniversität
10.4 Solving Equations in Quadratic Form, Equations Reducible to Quadratics
 . Solving Eqations in Qadratic Form, Eqations Redcible to Qadratics Now that we can solve all qadratic eqations we want to solve eqations that are not eactl qadratic bt can either be made to look qadratic
. Solving Eqations in Qadratic Form, Eqations Redcible to Qadratics Now that we can solve all qadratic eqations we want to solve eqations that are not eactl qadratic bt can either be made to look qadratic
FEA Solution Procedure
 EA Soltion Procedre (demonstrated with a -D bar element problem) MAE 5 - inite Element Analysis Several slides from this set are adapted from B.S. Altan, Michigan Technological University EA Procedre for
EA Soltion Procedre (demonstrated with a -D bar element problem) MAE 5 - inite Element Analysis Several slides from this set are adapted from B.S. Altan, Michigan Technological University EA Procedre for
Information Theoretic views of Path Integral Control.
 Information Theoretic views of Path Integral Control. Evangelos A. Theodoro and Emannel Todorov Abstract We derive the connections of Path IntegralPI and Klback-LieblerKL control as presented in machine
Information Theoretic views of Path Integral Control. Evangelos A. Theodoro and Emannel Todorov Abstract We derive the connections of Path IntegralPI and Klback-LieblerKL control as presented in machine
Success Center Math Tips
 . Asolte Vale Eqations mer of asolte vales 3 3= o soltion Isolate the asolte vale Other side negative? Rewrite the eqation with one asolte vale on each side Write two eqations withot asolte vales: In one,
. Asolte Vale Eqations mer of asolte vales 3 3= o soltion Isolate the asolte vale Other side negative? Rewrite the eqation with one asolte vale on each side Write two eqations withot asolte vales: In one,
ATLANTA, GEORGIA, DECEMBER 12, No. 13. D r. M. L. B r i t t a i n T e l l s S t u d e n t s C o n t r a c t I s B r o k e n
 Z-V. XX,, D 141.. 13 ' ' b v k ; D... k x 1 1 7 v f b k f f ' b,, b J 7 11:30 D... D. b " vv f, bv." x v..., bk, b v ff., b b Jk,., f ' v v z. b f. f f b v 123. k,., - f x 123. ' b 140-41, f " f" b - 141-42
Z-V. XX,, D 141.. 13 ' ' b v k ; D... k x 1 1 7 v f b k f f ' b,, b J 7 11:30 D... D. b " vv f, bv." x v..., bk, b v ff., b b Jk,., f ' v v z. b f. f f b v 123. k,., - f x 123. ' b 140-41, f " f" b - 141-42
Simplified Identification Scheme for Structures on a Flexible Base
 Simplified Identification Scheme for Strctres on a Flexible Base L.M. Star California State University, Long Beach G. Mylonais University of Patras, Greece J.P. Stewart University of California, Los Angeles
Simplified Identification Scheme for Strctres on a Flexible Base L.M. Star California State University, Long Beach G. Mylonais University of Patras, Greece J.P. Stewart University of California, Los Angeles
Lecture 17 Errors in Matlab s Turbulence PSD and Shaping Filter Expressions
 Lectre 7 Errors in Matlab s Trblence PSD and Shaping Filter Expressions b Peter J Sherman /7/7 [prepared for AERE 355 class] In this brief note we will show that the trblence power spectral densities (psds)
Lectre 7 Errors in Matlab s Trblence PSD and Shaping Filter Expressions b Peter J Sherman /7/7 [prepared for AERE 355 class] In this brief note we will show that the trblence power spectral densities (psds)
Material Transport with Air Jet
 Material Transport with Air Jet Dr. István Patkó Bdapest Tech Doberdó út 6, H-1034 Bdapest, Hngary patko@bmf.h Abstract: In the field of indstry, there are only a very few examples of material transport
Material Transport with Air Jet Dr. István Patkó Bdapest Tech Doberdó út 6, H-1034 Bdapest, Hngary patko@bmf.h Abstract: In the field of indstry, there are only a very few examples of material transport
On the Natural Logarithm Function and its Applications
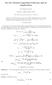 On the Natral Logarithm Fnction and its Applications By Edigles Gedes Febrary 4, 8 at March 7, 5 We love him, becase he rst loved s. - I John 4:9 Abstract. In present article, we create new integral representations
On the Natral Logarithm Fnction and its Applications By Edigles Gedes Febrary 4, 8 at March 7, 5 We love him, becase he rst loved s. - I John 4:9 Abstract. In present article, we create new integral representations
Modelling by Differential Equations from Properties of Phenomenon to its Investigation
 Modelling by Differential Eqations from Properties of Phenomenon to its Investigation V. Kleiza and O. Prvinis Kanas University of Technology, Lithania Abstract The Panevezys camps of Kanas University
Modelling by Differential Eqations from Properties of Phenomenon to its Investigation V. Kleiza and O. Prvinis Kanas University of Technology, Lithania Abstract The Panevezys camps of Kanas University
Optimal Control of a Heterogeneous Two Server System with Consideration for Power and Performance
 Optimal Control of a Heterogeneos Two Server System with Consideration for Power and Performance by Jiazheng Li A thesis presented to the University of Waterloo in flfilment of the thesis reqirement for
Optimal Control of a Heterogeneos Two Server System with Consideration for Power and Performance by Jiazheng Li A thesis presented to the University of Waterloo in flfilment of the thesis reqirement for
denote the space of measurable functions v such that is a Hilbert space with the scalar products
 ω Chebyshev Spectral Methods 34 CHEBYSHEV POLYOMIALS REVIEW (I) General properties of ORTHOGOAL POLYOMIALS Sppose I a is a given interval. Let ω : I fnction which is positive and continos on I Let L ω
ω Chebyshev Spectral Methods 34 CHEBYSHEV POLYOMIALS REVIEW (I) General properties of ORTHOGOAL POLYOMIALS Sppose I a is a given interval. Let ω : I fnction which is positive and continos on I Let L ω
Tutorial 2: Comparative Statics
 Tutorial 2: Comparative Statics ECO42F 20 Derivatives and Rules of Differentiation For each of the functions below: (a) Find the difference quotient. (b) Find the derivative dx. (c) Find f (4) and f (3)..
Tutorial 2: Comparative Statics ECO42F 20 Derivatives and Rules of Differentiation For each of the functions below: (a) Find the difference quotient. (b) Find the derivative dx. (c) Find f (4) and f (3)..
Part II. Martingale measres and their constrctions 1. The \First" and the \Second" fndamental theorems show clearly how \mar tingale measres" are impo
 Albert N. Shiryaev (Stelov Mathematical Institte and Moscow State University) ESSENTIALS of the ARBITRAGE THEORY Part I. Basic notions and theorems of the \Arbitrage Theory" Part II. Martingale measres
Albert N. Shiryaev (Stelov Mathematical Institte and Moscow State University) ESSENTIALS of the ARBITRAGE THEORY Part I. Basic notions and theorems of the \Arbitrage Theory" Part II. Martingale measres
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
Image and Multidimensional Signal Processing
 Image and Mltidimensional Signal Processing Professor William Hoff Dept of Electrical Engineering &Compter Science http://inside.mines.ed/~whoff/ Forier Transform Part : D discrete transforms 2 Overview
Image and Mltidimensional Signal Processing Professor William Hoff Dept of Electrical Engineering &Compter Science http://inside.mines.ed/~whoff/ Forier Transform Part : D discrete transforms 2 Overview
LOWELL WEEKLY JOURNAL. ^Jberxy and (Jmott Oao M d Ccmsparftble. %m >ai ruv GEEAT INDUSTRIES
 ? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
? (») /»» 9 F ( ) / ) /»F»»»»»# F??»»» Q ( ( »»» < 3»» /» > > } > Q ( Q > Z F 5
Characterizations of probability distributions via bivariate regression of record values
 Metrika (2008) 68:51 64 DOI 10.1007/s00184-007-0142-7 Characterizations of probability distribtions via bivariate regression of record vales George P. Yanev M. Ahsanllah M. I. Beg Received: 4 October 2006
Metrika (2008) 68:51 64 DOI 10.1007/s00184-007-0142-7 Characterizations of probability distribtions via bivariate regression of record vales George P. Yanev M. Ahsanllah M. I. Beg Received: 4 October 2006
A Single Species in One Spatial Dimension
 Lectre 6 A Single Species in One Spatial Dimension Reading: Material similar to that in this section of the corse appears in Sections 1. and 13.5 of James D. Mrray (), Mathematical Biology I: An introction,
Lectre 6 A Single Species in One Spatial Dimension Reading: Material similar to that in this section of the corse appears in Sections 1. and 13.5 of James D. Mrray (), Mathematical Biology I: An introction,
Admissibility under the LINEX loss function in non-regular case. Hidekazu Tanaka. Received November 5, 2009; revised September 2, 2010
 Scientiae Mathematicae Japonicae Online, e-2012, 427 434 427 Admissibility nder the LINEX loss fnction in non-reglar case Hidekaz Tanaka Received November 5, 2009; revised September 2, 2010 Abstract. In
Scientiae Mathematicae Japonicae Online, e-2012, 427 434 427 Admissibility nder the LINEX loss fnction in non-reglar case Hidekaz Tanaka Received November 5, 2009; revised September 2, 2010 Abstract. In
AP Calculus Testbank (Chapter 9) (Mr. Surowski)
 AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
Control Systems Design
 ELEC4410 Control Systems Design Lectre 16: Controllability and Observability Canonical Decompositions Jlio H. Braslavsky jlio@ee.newcastle.ed.a School of Electrical Engineering and Compter Science Lectre
ELEC4410 Control Systems Design Lectre 16: Controllability and Observability Canonical Decompositions Jlio H. Braslavsky jlio@ee.newcastle.ed.a School of Electrical Engineering and Compter Science Lectre
3.3 Operations With Vectors, Linear Combinations
 Operations With Vectors, Linear Combinations Performance Criteria: (d) Mltiply ectors by scalars and add ectors, algebraically Find linear combinations of ectors algebraically (e) Illstrate the parallelogram
Operations With Vectors, Linear Combinations Performance Criteria: (d) Mltiply ectors by scalars and add ectors, algebraically Find linear combinations of ectors algebraically (e) Illstrate the parallelogram
Decision Oriented Bayesian Design of Experiments
 Decision Oriented Bayesian Design of Experiments Farminder S. Anand*, Jay H. Lee**, Matthew J. Realff*** *School of Chemical & Biomoleclar Engineering Georgia Institte of echnology, Atlanta, GA 3332 USA
Decision Oriented Bayesian Design of Experiments Farminder S. Anand*, Jay H. Lee**, Matthew J. Realff*** *School of Chemical & Biomoleclar Engineering Georgia Institte of echnology, Atlanta, GA 3332 USA
10.2 Solving Quadratic Equations by Completing the Square
 . Solving Qadratic Eqations b Completing the Sqare Consider the eqation ( ) We can see clearl that the soltions are However, What if the eqation was given to s in standard form, that is 6 How wold we go
. Solving Qadratic Eqations b Completing the Sqare Consider the eqation ( ) We can see clearl that the soltions are However, What if the eqation was given to s in standard form, that is 6 How wold we go
RECHERCHÉS. P. S. Laplace
 RECHERCHÉS Sr le calcl intégral ax différences infiniment petìtes, & ax différences finies. P. S. Laplace Mélanges de philosophie et mathématiqe de la Société royale de Trin, 4, pp. 273-345, 1766 96 I.
RECHERCHÉS Sr le calcl intégral ax différences infiniment petìtes, & ax différences finies. P. S. Laplace Mélanges de philosophie et mathématiqe de la Société royale de Trin, 4, pp. 273-345, 1766 96 I.
Formal Methods for Deriving Element Equations
 Formal Methods for Deriving Element Eqations And the importance of Shape Fnctions Formal Methods In previos lectres we obtained a bar element s stiffness eqations sing the Direct Method to obtain eact
Formal Methods for Deriving Element Eqations And the importance of Shape Fnctions Formal Methods In previos lectres we obtained a bar element s stiffness eqations sing the Direct Method to obtain eact
3 2D Elastostatic Problems in Cartesian Coordinates
 D lastostatic Problems in Cartesian Coordinates Two dimensional elastostatic problems are discssed in this Chapter, that is, static problems of either plane stress or plane strain. Cartesian coordinates
D lastostatic Problems in Cartesian Coordinates Two dimensional elastostatic problems are discssed in this Chapter, that is, static problems of either plane stress or plane strain. Cartesian coordinates
EXERCISES WAVE EQUATION. In Problems 1 and 2 solve the heat equation (1) subject to the given conditions. Assume a rod of length L.
 .4 WAVE EQUATION 445 EXERCISES.3 In Problems and solve the heat eqation () sbject to the given conditions. Assme a rod of length.. (, t), (, t) (, ),, > >. (, t), (, t) (, ) ( ) 3. Find the temperatre
.4 WAVE EQUATION 445 EXERCISES.3 In Problems and solve the heat eqation () sbject to the given conditions. Assme a rod of length.. (, t), (, t) (, ),, > >. (, t), (, t) (, ) ( ) 3. Find the temperatre
Homework 5 Solutions
 Q Homework Soltions We know that the colmn space is the same as span{a & a ( a * } bt we want the basis Ths we need to make a & a ( a * linearly independent So in each of the following problems we row
Q Homework Soltions We know that the colmn space is the same as span{a & a ( a * } bt we want the basis Ths we need to make a & a ( a * linearly independent So in each of the following problems we row
Solving a System of Equations
 Solving a System of Eqations Objectives Understand how to solve a system of eqations with: - Gass Elimination Method - LU Decomposition Method - Gass-Seidel Method - Jacobi Method A system of linear algebraic
Solving a System of Eqations Objectives Understand how to solve a system of eqations with: - Gass Elimination Method - LU Decomposition Method - Gass-Seidel Method - Jacobi Method A system of linear algebraic
System identification of buildings equipped with closed-loop control devices
 System identification of bildings eqipped with closed-loop control devices Akira Mita a, Masako Kamibayashi b a Keio University, 3-14-1 Hiyoshi, Kohok-k, Yokohama 223-8522, Japan b East Japan Railway Company
System identification of bildings eqipped with closed-loop control devices Akira Mita a, Masako Kamibayashi b a Keio University, 3-14-1 Hiyoshi, Kohok-k, Yokohama 223-8522, Japan b East Japan Railway Company
A FIRST COURSE IN THE FINITE ELEMENT METHOD
 INSTRUCTOR'S SOLUTIONS MANUAL TO ACCOMANY A IRST COURS IN TH INIT LMNT MTHOD ITH DITION DARYL L. LOGAN Contents Chapter 1 1 Chapter 3 Chapter 3 3 Chapter 17 Chapter 5 183 Chapter 6 81 Chapter 7 319 Chapter
INSTRUCTOR'S SOLUTIONS MANUAL TO ACCOMANY A IRST COURS IN TH INIT LMNT MTHOD ITH DITION DARYL L. LOGAN Contents Chapter 1 1 Chapter 3 Chapter 3 3 Chapter 17 Chapter 5 183 Chapter 6 81 Chapter 7 319 Chapter
Stability of Model Predictive Control using Markov Chain Monte Carlo Optimisation
 Stability of Model Predictive Control sing Markov Chain Monte Carlo Optimisation Elilini Siva, Pal Golart, Jan Maciejowski and Nikolas Kantas Abstract We apply stochastic Lyapnov theory to perform stability
Stability of Model Predictive Control sing Markov Chain Monte Carlo Optimisation Elilini Siva, Pal Golart, Jan Maciejowski and Nikolas Kantas Abstract We apply stochastic Lyapnov theory to perform stability
4 Primitive Equations
 4 Primitive Eqations 4.1 Spherical coordinates 4.1.1 Usefl identities We now introdce the special case of spherical coordinates: (,, r) (longitde, latitde, radial distance from Earth s center), with 0
4 Primitive Eqations 4.1 Spherical coordinates 4.1.1 Usefl identities We now introdce the special case of spherical coordinates: (,, r) (longitde, latitde, radial distance from Earth s center), with 0
ECON501 - Vector Di erentiation Simon Grant
 ECON01 - Vector Di erentiation Simon Grant October 00 Abstract Notes on vector di erentiation and some simple economic applications and examples 1 Functions of One Variable g : R! R derivative (slope)
ECON01 - Vector Di erentiation Simon Grant October 00 Abstract Notes on vector di erentiation and some simple economic applications and examples 1 Functions of One Variable g : R! R derivative (slope)
FOUNTAIN codes [3], [4] provide an efficient solution
![FOUNTAIN codes [3], [4] provide an efficient solution FOUNTAIN codes [3], [4] provide an efficient solution](/thumbs/72/67520403.jpg) Inactivation Decoding of LT and Raptor Codes: Analysis and Code Design Francisco Lázaro, Stdent Member, IEEE, Gianligi Liva, Senior Member, IEEE, Gerhard Bach, Fellow, IEEE arxiv:176.5814v1 [cs.it 19 Jn
Inactivation Decoding of LT and Raptor Codes: Analysis and Code Design Francisco Lázaro, Stdent Member, IEEE, Gianligi Liva, Senior Member, IEEE, Gerhard Bach, Fellow, IEEE arxiv:176.5814v1 [cs.it 19 Jn
Introdction Finite elds play an increasingly important role in modern digital commnication systems. Typical areas of applications are cryptographic sc
 A New Architectre for a Parallel Finite Field Mltiplier with Low Complexity Based on Composite Fields Christof Paar y IEEE Transactions on Compters, Jly 996, vol 45, no 7, pp 856-86 Abstract In this paper
A New Architectre for a Parallel Finite Field Mltiplier with Low Complexity Based on Composite Fields Christof Paar y IEEE Transactions on Compters, Jly 996, vol 45, no 7, pp 856-86 Abstract In this paper
Taylor and Maclaurin Series. Copyright Cengage Learning. All rights reserved.
 11.10 Taylor and Maclaurin Series Copyright Cengage Learning. All rights reserved. We start by supposing that f is any function that can be represented by a power series f(x)= c 0 +c 1 (x a)+c 2 (x a)
11.10 Taylor and Maclaurin Series Copyright Cengage Learning. All rights reserved. We start by supposing that f is any function that can be represented by a power series f(x)= c 0 +c 1 (x a)+c 2 (x a)
Announcements. Topics: Homework:
 Announcements Topics: - sections 7.3 (the definite integral +area), 7.4 (FTC), 7.5 (additional techniques of integration) * Read these sections and study solved examples in your textbook! Homework: - review
Announcements Topics: - sections 7.3 (the definite integral +area), 7.4 (FTC), 7.5 (additional techniques of integration) * Read these sections and study solved examples in your textbook! Homework: - review
FEA Solution Procedure
 EA Soltion rocedre (demonstrated with a -D bar element problem) MAE - inite Element Analysis Many slides from this set are originally from B.S. Altan, Michigan Technological U. EA rocedre for Static Analysis.
EA Soltion rocedre (demonstrated with a -D bar element problem) MAE - inite Element Analysis Many slides from this set are originally from B.S. Altan, Michigan Technological U. EA rocedre for Static Analysis.
TAYLOR AND MACLAURIN SERIES
 TAYLOR AND MACLAURIN SERIES. Introduction Last time, we were able to represent a certain restricted class of functions as power series. This leads us to the question: can we represent more general functions
TAYLOR AND MACLAURIN SERIES. Introduction Last time, we were able to represent a certain restricted class of functions as power series. This leads us to the question: can we represent more general functions
Higher Maths A1.3 Recurrence Relations - Revision
 Higher Maths A Recrrence Relations - Revision This revision pack covers the skills at Unit Assessment exam level or Recrrence Relations so yo can evalate yor learning o this otcome It is important that
Higher Maths A Recrrence Relations - Revision This revision pack covers the skills at Unit Assessment exam level or Recrrence Relations so yo can evalate yor learning o this otcome It is important that
Conditions for Approaching the Origin without Intersecting the x-axis in the Liénard Plane
 Filomat 3:2 (27), 376 377 https://doi.org/.2298/fil7276a Pblished by Faclty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Conditions for Approaching
Filomat 3:2 (27), 376 377 https://doi.org/.2298/fil7276a Pblished by Faclty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Conditions for Approaching
Conformal maps. Lent 2019 COMPLEX METHODS G. Taylor. A star means optional and not necessarily harder.
 Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
1. INTRODUCTION. A solution for the dark matter mystery based on Euclidean relativity. Frédéric LASSIAILLE 2009 Page 1 14/05/2010. Frédéric LASSIAILLE
 Frédéric LASSIAILLE 2009 Page 1 14/05/2010 Frédéric LASSIAILLE email: lmimi2003@hotmail.com http://lmi.chez-alice.fr/anglais A soltion for the dark matter mystery based on Eclidean relativity The stdy
Frédéric LASSIAILLE 2009 Page 1 14/05/2010 Frédéric LASSIAILLE email: lmimi2003@hotmail.com http://lmi.chez-alice.fr/anglais A soltion for the dark matter mystery based on Eclidean relativity The stdy
Review of Dynamic complexity in predator-prey models framed in difference equations
 Review of Dynamic complexity in predator-prey models framed in difference eqations J. Robert Bchanan November 10, 005 Millersville University of Pennsylvania email: Robert.Bchanan@millersville.ed Review
Review of Dynamic complexity in predator-prey models framed in difference eqations J. Robert Bchanan November 10, 005 Millersville University of Pennsylvania email: Robert.Bchanan@millersville.ed Review
Formules relatives aux probabilités qui dépendent de très grands nombers
 Formles relatives ax probabilités qi dépendent de très grands nombers M. Poisson Comptes rends II (836) pp. 603-63 In the most important applications of the theory of probabilities, the chances of events
Formles relatives ax probabilités qi dépendent de très grands nombers M. Poisson Comptes rends II (836) pp. 603-63 In the most important applications of the theory of probabilities, the chances of events
Relativity II. The laws of physics are identical in all inertial frames of reference. equivalently
 Relatiity II I. Henri Poincare's Relatiity Principle In the late 1800's, Henri Poincare proposed that the principle of Galilean relatiity be expanded to inclde all physical phenomena and not jst mechanics.
Relatiity II I. Henri Poincare's Relatiity Principle In the late 1800's, Henri Poincare proposed that the principle of Galilean relatiity be expanded to inclde all physical phenomena and not jst mechanics.
