arxiv: v1 [quant-ph] 11 Jul 2014
|
|
|
- Betty Barton
- 6 years ago
- Views:
Transcription
1 The quantum pigeonhole principle and the nature of quantum correlations Y. Aharonov 1,2,3, F. Colombo 3,4, S. Popescu 3,5, I. Sabadini 3,4, D.C.Struppa 2,3, and J. Tollaksen 2,3 1 School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel 2 Schmid College for Science and Technology, Chapman University, 1 University Dr, Orange, CA, USA 3 Institute for Quantum Studies, Chapman University, 1 University Dr, Orange, CA, USA 4 Politecnico di ilano, Dipartimento di atematica, Via E. Bonardi, ilano, Italy and 5 H.H.Wills Physics Laboratory, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, U.K. (Dated:) arxiv: v1 [quant-ph] 11 Jul 2014 The pigeonhole principle: If you put three pigeons in two pigeonholes at least two of the pigeons end up in the same hole is an obvious yet fundamental principle of Nature as it captures the very essence of counting. Here however we show that in quantum mechanics this is not true! We find instances when three quantum particles are put in two boxes, yet no two particles are in the same box. Furthermore, we show that the above quantum pigeonhole principle is only one of a host of related quantum effects, and points to a very interesting structure of quantum mechanics that was hitherto unnoticed. Our results shed new light on the very notions of separability and correlations in quantum mechanics and on the nature of interactions. It also presents a new role for entanglement, complementary to the usual one. Finally, interferometric experiments that illustrate our effects are proposed. THE QUANTU PIGEONHOLE PRINCIPLE Arguably the most important lesson of quantum mechanics is that we need to critically revisit our most basic assumptions about Nature. It all started with challenging the idea that particles can have, at the same time, both a well-defined position and a well-defined momentum, and went on and on to similar paradoxical facts. But the pigeon-hole principle that is the subject of our paper seems far less likely to be challenged. Indeed, while on one hand it relates to physical properties of objects - it deals, say, with actual pigeons and pigeon-holes - it also encapsulates abstract mathematical notions that go to the core of what numbers and counting are so it underlies, implicitly or explicitly, virtually the whole of mathematics. (In its explicit form the principle was first stated by Dirichlet in 1834 [1] and even in its simplest form its uses in mathematics are numerous and highly non-trivial [2].) It seems therefore to be an abstract and immutable truth, beyond any doubt. Yet, as we show here, for quantum particles the principle does not hold. Consider three particles and two boxes, denoted L (left) and R (right). To start our experiment, we prepare each particle in a superposition of being in the two boxes, + = 1 ) ( L + R. (1) 2 The overall state of the three particles is therefore Ψ = (2) Now, it is obvious that in this state any two particles have non-zero probability to be found in the same box. We want however to show that there are instances in which we can guarantee that no two particles are together; we cannot arrange that to happen in every instance, but, crucially, there are instances like that. To find those instances we subject each particle to a second measurement: we measure whether ) each particle is in the ) state + i = 1 2 ( L + i R or i = 1 2 ( L i R (these are two orthogonal states, so there is an operator whose eigenstates they are - we measure that operator). The cases we are interested in are those in which all particles are found in + i, i.e. the final state Φ = + i 1 + i 2 + i 3. (3) Importantly, neither the initial state nor the finally selected state contain any correlations between the position of the particles. Furthermore, both the preparation and the post-selection are done independently, acting on each particle separately. Let us now check whether two of the particles are in the same box. Since the state is symmetric, we could focus on particles 1 and 2 without any loss of generality - any result obtained for this pair applies to every other pair. Particles 1 and 2 being in the same box means the state being in the subspace spanned by L 1 L 2 and R 1 R 2 ; being in different boxes corresponds to the complementary subspace, spanned by L 1 R 2 and R 1 L 2. The projectors corresponding to these subspaces are 1,2 = Π LL 1,2 + Π RR 1,2 Π diff 1,2 = Π LR 1,2 + Π RL 1,2 (4)
2 2 where GENERALIZING THE QUANTU PIGEONHOLE PRINCIPLE Π LL 1,2 = L 1 L 2 1 L 2 L, Π RR 1,2 = R 1 R 2 1 R 2 R, Π LR 1,2 = L 1 R 2 1 R 2 L, Π RL On the initial state alone, the probabilities to find particles 1 and 2 in the same box and in different boxes are both 50%. On the other hand, given the results of the final measurements, we always find particles 1 and 2 in different boxes. Indeed, suppose that at the intermediate time we find the particles in the same box. The wavefunction then collapses (up to normalisation) to Ψ = 1,2 Ψ = 1 2( L 1 L 2 + R 1 R 2 ) + 3 (6) which is orthogonal to the post-selected state (3), i.e. 1,2 = R 1 L 2 1 L 2 R. (5) The above effect is but one of a multitude of similar effects. For example, in the case of N particles in < N boxes we can guarantee that no two particles are in the same box when we prepare each particle in the state 0 = 1 k (8) and we find, in a final measurement, each particle in the state π = 1 e i πk k (9) (see supplementary information). Φ 1,2 Ψ = 0. (7) Hence in this case the final measurements cannot find the particles in the state Φ. Therefore the only cases in which the final measurement can find the particles in the state Φ are those in which the intermediate measurement found that particles 1 and 2 are in different boxes. Crucially, as noted before, the state is symmetric under permutation, hence what is true for particles 1 and 2 is true for all pairs. In other words, given the above preand post-selection, we have three particles in two boxes, yet no two particles can be found in the same box - our quantum pigeonhole principle. A RELATED EFFECT FOR EVERY FINAL OUTCOE In the previous section we focused on what happens when at the final measurement all particles are found in the state + i. It is in this case that the intermediate measurements exhibit the quantum pigeon-hole effect. However this is only one of the eight possible outcomes of the final measurement - indeed, each particle can be found either in + i or in i. It is important to note that in each of these cases an interesting effect occurs: In the case when the final state is i 1 i 2 i 3 the intermediate measurements exhibit once again the quantum pigeon-hole effect, i.e. no two particles can be found in the same box. For the final state i 1 + i 2 + i 3 intermediate measurements find that particle 2 is in the same box as 1, particle 3 is in the same box as 1 but particles 2 and 3 are not in the same box (see supplementary information). Similar patterns occur in all other cases. THE NATURE OF QUANTU CORRELATIONS Before analyzing our paradox in more detail, we would like to comment more on the nature of quantum correlations. The first thing to notice is that neither the pre-selected state nor the post-selected state are correlated (they are both direct products and each particle is prepared and post-selected individually) yet the particles are correlated. The second thing to notice is that if we measure the location of each particle individually, they appear to be completely uncorrelated. Indeed, suppose we measure separately the location of particle 1 and 2. There are four possible outcomes of this measurement: LL, LR, RL RR and, as one can easily show, they all occur with equal probabilities. It is only when we ask solely about the correlation, and no other information, (i.e whether the two particles are in the same box or not, without asking in which box they are), that we find them correlated. The above shows a fundamental difference in the way in which the probabilities work in the standard, preselected only experiment and in a pre- and postselected one (i.e. when we only consider the cases in which a final measurement gave a particular answer). Indeed, consider first the standard situation, that is, consider that the particles are prepared in the state Ψ and we do not perform a final measurement and selection according to its result. Suppose first that we measure separately the location of each particle. The probabilities to find LL and RR are given, respectively by
3 3 P (LL) = Ψ Π LL 1,2 Ψ P (RR) = Ψ Π RR 1,2 Ψ. (10) Hence, the probability to find the particles in the same box by using this measurement is P (LL or RR) = P (LL) + P (RR) = Ψ Π LL 1,2 Ψ + Ψ Π RR 1,2 Ψ = Ψ Π LL 1,2 + Π RR 1,2 Ψ. (11) Suppose however that we measure an operator that only tells us whether or not the particles are in the same box, without indicating in which box they are. This operator has only two eigenvalues, corresponding to same and different and the corresponding projectors Π diff 1,2 1,2 and. The probability to find the two particles in the same box by this measurement is then P (same) = Ψ 1,2 Ψ = Ψ Π LL 1,2 + Π LL 1,2 Ψ (12) which is identical to the probability of finding the particles in the same box when we measure their position individually. Hence for a standard, pre-selected only situation, the course-grained measurement that asks only about correlations but no other information gives the same probabilities as the more detailed measurement. On the other hand, suppose we compare the above two measurement methods but in the case of a pre- and postselected ensemble. In full generality, when one measures an arbitrary operator A on a pre and post selected ensemble, the probability to obtain the eigenvalue a i is given by P (a i ) = Φ Π i Ψ Φ Π j Ψ 2 (13) j where Π i are the corresponding projectors [4]. Using this result, in the case of separate measurements on each particle we find P (LL) = 1 Φ Π LL N with N = 1,2 Ψ 2, kl=l,r 2 P (RR) = 1 Φ Π RR N 1,2 Ψ 2 (14) Φ Π kl 1,2 Ψ 2 (15) Obviously P (LL or RR) = P (LL) + P (RR) is now different from Φ 1,2 Ψ 2 P (same) = Φ 2 + Φ Π diff 1,2 Ψ 2. (16) 1,2 Ψ What the above discussion shows is that there is a significant difference between correlations that can be observed when we measure particles separately and when we measure them jointly. This difference can be observed only when we consider pre- and post-selected ensembles, but it is always there, as an intrinsic part of quantum mechanics. Indeed, one may not be familiar with the idea of preand post-selection but it fact it is something that we encounter routinely: Every time when we have a sequence of measurements we can split the original ensemble into a number of different pre and post-selected sub-ensembles according to the result of the final measurement, and in each such sub-ensemble we can observe a similar effect. The third thing to notice is that the global measurement which only asks about correlations but no other detailed information is, in some sense, better than the detailed measurement as it delivers the information about correlations while minimizing the disturbance that it produces to the state. Indeed, suppose two particles are in an arbitrary superposition α L 1 R 2 + β R 1 L 2. The global measurement will tell us that the particles are in different boxes and will not disturb the state at all, since it is an eigenstate of the measured operator. On the other hand, if we measure each particle separately, we disturb the state, collapsing it on either L 1 R 2 or R 1 L 2. In the case of a pre-selected only ensemble, what happens to the state after the measurement doesn t matter, but if we are interested in following this measurement with a subsequent measurement and look at the different preand post-selected ensembles, how much the intermediate time measurement disturbed the state is essential. This is the reason why post-selection is essential in order to see the effect. Finally, and most importantly, we note that the global measurement is a measurement of an operator with entangled eigenstates and it requires either to put the particles in interaction or consume some entanglement resources to perform it. The quantum pigeonhole effect is thus an example of a new aspect of entanglement: entanglement in the measurement is needed to reveal correlations existing in a direct product state. THE NATURE OF QUANTU INTERACTIONS. A FIRST EXPERIENT. The quantum pigeonhole effect has major implications for the understanding of the very nature of quantum interactions. Consider again three particles and two boxes. Let the particles interact with each other by bipartite short-range interactions, i.e. any two particles interact when they are in the same box and do not interact otherwise. Then, as there are three particles and only two
4 4 boxes we expect that always at least two of the particles should interact. But, due to our pigeonhole effect, this is not so, as shown in the following experiments. Consider a ach-zender interferometer for electrons, as depicted in Fig. 1. It consists of two beam-splitters BS1 and BS2 a phase shifter PS that introduces a phase-shift of π and two detectors, D 1 and D 2. The detectors have spatial resolution, so they can tell exactly where each particle landed. When an electron is injected from the left side, the ) first beam-splitter generates the state + = 1 2 ( L + R. The phase shifter, final beam-splitter and the detectors in effect implement) a measurement with eigenstates ± i = 1 2 ( L ± R. Indeed, if the state before PS is + i the electron ends, with certainty at D 1 while if it is i it ends with certainty at D 2. Suppose now that we inject simultaneously three electrons in the interferometer from the left side, such that they travel in parallel beams. The beams are arranged, as shown in Fig 1a, in an equilateral triangle configuration. When two electrons go through the same arm of the interferometer they repel each other and their trajectories are deflected. Indeed, the force that one electron exerts on the other produces a change in momentum and this in turn leads to the deflection of the beams by an amount depending on the original separation of the beams, the length of the interferometer and the speed of the electrons. When the electrons go through different arms they effectively do not interact (since the arms are separated by a large distance). Since we have three electrons and only two arms, we expect to always have interactions, regardless of which detectors the electrons end up at after traversing the interferometer. We are interested in what happens in the cases when all three electrons end up at D 1 and when the interaction between the electrons is not too strong. Ending up at D 1 is our desired post-selection. The requirement that the interaction should not be too strong (which can be arranged, for example, by spacing the parallel beams further away or making the arms shorter) is more subtle. The point is the following. We know that when considering three non-interacting particles in two boxes, given the appropriate pre and post-selection, no two particles are in the same box. We certified this by showing that whichever pair of particles we measured we always find them in different boxes. But if we were to try to measure two or all pairs in the same experiment, the measurements would disturb one another and we would not see the effect. Indeed, suppose we first measure if particles 1 and 2 are in the same box, then particles 1 and 3 and then we make the post-selection. Now it is actually possible to find 1 and 2, or 1 and 3 or both 1 and 2 and FIG. 1: A ach-zender interferometer for electrons. BS 1 and BS 2 are beam-splitters, P S is a π phase shifter and D 1 and D 2 are detectors with spatial resolution. Three electrons are simultaneously injected on parallel trajectories. The cross section shows the spatial arrangement of the beams. The image at the detector is obtained by superposing the results of many runs, but only keeping those runs in which all three electrons arrived at D 1. FIG. 2: (a) The observed distribution shows no displacement of the beams, while naively we would expect the beam to be moved and deformed, due to to a combination of different cases depicted in (b), which depend on which particles are in the same arm and repel each other. 1 and 3 in the same box. Indeed, for example starting with the initial state (2) we can find particles 1 and 2 in the same box. In this case the state collapses to Ψ = 1,2 Ψ. This state is orthogonal to the postselected state (3), so if we were to make the post-selection now this even would not be selected - this was our main proof of the quantum pigeon-hole effect. However, suppose that instead of making the post-selection at this point we now make a measurement of the pair 1,3. We can also find 1 and 3 in the same box. The state now collapses to Ψ = 1,3 1,2 Ψ. But now, crucially, Ψ is not orthogonal to the post-selected state (3) hence these events are not eliminated from the post-selected ensemble. To be able to see the effect we need to limit the mutual disturbance of the measurements. In our interferometer case, the interaction between the
5 5 electrons leads to the deflection of the beams whenever two electrons are in the same arm. The deflection of the beams is therefore effectively like a measurement of whether or not two electrons are in the same arm. To limit the disturbance produced by the simultaneous existence of the interaction between all three pairs, we just need to reduce the strength of the effect of the interaction. Technically, we want to ensure that the change in the momentum of an electron due to the force produced by the other electrons is smaller than the spread in its momentum. Due to this, the deflection of a beam - if it occurs - is smaller than it s spatial spread, hence, by seing where one electron landed on D 1 we cannot tell if its trajectory was deflected or not. However, by collecting the results of multiple runs we can easily identify if the electrons were deflected or not (see Fig. 2). Naively, we would expect to see the three beams deflected outwards and deformed, - each electron should move radially outwards when all three are present in the same arm, and sideways when only two electrons are present. We expect the deviation to be by less than the cross section but nevertheless by a noticeable amount. Instead (see supplementary information) what we find is that the beams are completely un-deflected and undisturbed (up to second order perturbations), indicating that indeed there was no interaction whatsoever between the electrons. is smaller than the spread of the spectral line, so that the three pairwise interactions should not disturb each other. Again, due to this, one single photon observation cannot tell us whether the frequency was shifted or not, but accumulating the statistics we can detect the shift. Since there are three atoms but only two arms, similarly to the previous experiment, we expect that in each run of the experiment at least two atoms will be in the same arm, so the photons they emit will be frequency shifted, no matter which detector the atoms end up in. Yet, according to our quantum pigeonhole effect, when we look at the cases in which all three atoms end up at D 1, we see that the spectral lines are unshifted. CONCLUSIONS In conclusion we presented a new quantum effect that requires us to revisit some of the most basic notions of quantum physics - the notions of separability, of correlations and of interactions. It is still very early to say what the implications of this revision are, but we feel one should expect them to be major since we are dealing with such fundamental concepts. A SECOND EXPERIENT A second experiment uses a similar interferometer as described in the first experiment, but instead of electrons we now inject atoms. Let all the atoms start in an excited state and arrange the setting in such way that there is a very significant probability for the atoms to spontaneously emit photons while traversing the interferometer. We surround the interferometer with photon detectors that could detect the emitted photons. Importantly, we chose the energy separation between the ground and excited state such that the wave-length of the emitted photons is much larger than the separation between the arms,so that by detecting a photon we cannot tell whether the atom that emitted it went through the left or right arm. Again, we inject all three atoms from the left and are interested only in the cases in which all three end up at detector D 1. When two atoms are close to each other (being in the same arm) they interact with each other (for example by dipole-dipole interactions) and the energy levels are shifted. Observing the wavelength of the emitted photons we can then tell if the atoms were in the same arm or not. Following the same reasoning as used in the previous experiment, we also arrange that the frequency shift [1] P.G.L. Dirichlet and R. Dedekind, Vorlesungen ber Zahlentheorie 1863; English translation: P.G.L. Dirichlet and R. Dedekind, Lectures on Number Theory, American athematical Society, 1999 ISBN [2] R.B.J.T. Allenby and A.B. Slomson, How to count: An introduction to combinatorics, 2nd ed. CRC Press (2011). [3]. Nielsen and I. Chuang, Quantum Computation and Quantum Information, Cambridge University Press (2000). [4] Y. Aharonov, P. Bergmann, and J. Lebowitz, Phys. Rev. 134, B 1410 (1964). SUPPLEENTARY INFORATION GENERALIZING THE PIGEONHOLE EFFECT Consider N particles in < N boxes. Let the initial state of each particle be 0 = 1 k. (17) Suppose that finally we perform on each particle a measurement of an operator that has the state π = 1 e i πk k (18)
6 6 as one of its eigenstates, and suppose we find each particle in this state. In other words, let the initial state be Ψ = N (19) and the final measurement finds the overall state Φ = π 1 π 2... π N. (20) Suppose now that at the intermediate time we measure whether or not particles 1 and 2 are in the same box. The projector corresponding to the particles being in the same box is 1,2 = j 1 j 22 j 1 j. (21) j=1 Suppose now that at the intermediate measurement we do find particles 1 and 2 in the same box. The initial state then collapses to 1,2 Ψ which is orthogonal to Φ. Indeed Φ 1,2 Ψ = 2πk = 0. (22) Therefore if at the intermediate time we do find particles 1 and 2 in the same box, we couldn t find Φ at the final measurement, which means that if we did find Φ at the final measurement, the intermediate measurement found particles 1 and 2 to be in different boxes. Again, since both the initial and the final states are symmetric under permutation, the same conclusion holds for any pair of particles. In other words, we have a situation where N particles are in < N boxes, but no two particles are in the same box. THE INTERFEROETRIC EXPERIENT To describe our interferometric experiment it is useful to separate he degrees of freedom into a which arm degree of freedom and the relative positions r ij of the electrons when they are in the same arm. Using this decomposition, the initial wavefunction inside the interferometer is Ψ ϕ where Ψ = and ϕ describes the relative degrees of freedom. The interaction Hamiltonian between the electrons can be approximated by H int = 3 i,j=1 i,j V (r i,j ) (23) where V is the interaction potential. The projector i,j describes the fact that the electrons interact only when they are in the same arm. Furthermore, the which arm degree of freedom is a constant of motion (i.e. the electrons do not go from one arm to the other). The time evolution of the state, in the interaction picture is then given by e ihintt Ψ ϕ (24) where T is the total time of the interaction (the time taken for the electrons to go through the interferometer) and where for simplicity, we set = 1. We are interested in the relative degrees of freedom (the detailed positions of the beams) given the post-selection, i.e. in Φ e ihintt Ψ ϕ (25) where Φ = + i 1 + i 2 + i 3 is the post-selected state. Given that we take the interaction to be relatively weak, we could approximate it by the first order perturbation Φ (1 ih int T ) Ψ ϕ = Φ Ψ ϕ it Φ H int Ψ ϕ. (26) But Φ H int Ψ = Φ = 3 i,j=1 Φ 3 i,j=1 i,j V (r i,j ) Ψ i,j Ψ V (r i,j ) = 0 (27) where the last equality follows from the fact that Φ i,j Ψ = 0 which is the basis for the pigeonh0le effect. Hence, in the first order of approximation, given the success of the post-selection, there is effectively no interaction between the electrons.
Even quantum pigeons may thrive together
 1 LUTP 14-39 Even quantum pigeons may thrive together A note on the quantum pigeonhole principle B. E. Y. Svensson Theoretical High Energy Physics, Department of Astronomy and Theoretical Physics, Lund
1 LUTP 14-39 Even quantum pigeons may thrive together A note on the quantum pigeonhole principle B. E. Y. Svensson Theoretical High Energy Physics, Department of Astronomy and Theoretical Physics, Lund
arxiv: v2 [quant-ph] 4 Dec 2014
![arxiv: v2 [quant-ph] 4 Dec 2014 arxiv: v2 [quant-ph] 4 Dec 2014](/thumbs/88/115693883.jpg) On the implications of the Quantum-Pigeonhole Effect Alastair Rae and Ted Forgan School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK. arxiv:1412.1333v2 [quant-ph]
On the implications of the Quantum-Pigeonhole Effect Alastair Rae and Ted Forgan School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK. arxiv:1412.1333v2 [quant-ph]
The Two-State Vector Formalism
 arxiv:0706.1347v1 [quant-ph] 10 Jun 007 The Two-State Vector Formalism February 1, 013 The two-state vector formalism (TSVF) [1] is a time-symmetric description of the standard quantum mechanics originated
arxiv:0706.1347v1 [quant-ph] 10 Jun 007 The Two-State Vector Formalism February 1, 013 The two-state vector formalism (TSVF) [1] is a time-symmetric description of the standard quantum mechanics originated
Delayed Choice Paradox
 Chapter 20 Delayed Choice Paradox 20.1 Statement of the Paradox Consider the Mach-Zehnder interferometer shown in Fig. 20.1. The second beam splitter can either be at its regular position B in where the
Chapter 20 Delayed Choice Paradox 20.1 Statement of the Paradox Consider the Mach-Zehnder interferometer shown in Fig. 20.1. The second beam splitter can either be at its regular position B in where the
Quantum Measurements: some technical background
 Quantum Measurements: some technical background [From the projection postulate to density matrices & (introduction to) von Neumann measurements] (AKA: the boring lecture) First: One more example I wanted
Quantum Measurements: some technical background [From the projection postulate to density matrices & (introduction to) von Neumann measurements] (AKA: the boring lecture) First: One more example I wanted
arxiv:quant-ph/ v1 11 Apr 2001
 Revisiting Hardy s Paradox: Counterfactual Statements, Real Measurements, Entanglement and Weak Values Yakir Aharonov (a,b,c), Alonso Botero (c,d), Sandu Popescu (e,f), Benni Reznik a, Jeff Tollaksen g
Revisiting Hardy s Paradox: Counterfactual Statements, Real Measurements, Entanglement and Weak Values Yakir Aharonov (a,b,c), Alonso Botero (c,d), Sandu Popescu (e,f), Benni Reznik a, Jeff Tollaksen g
Multiple-Time States and Multiple-Time Measurements In Quantum Mechanics
 Chapman University Chapman University Digital Commons Mathematics, Physics, and Computer Science Faculty Articles and Research Science and Technology Faculty Articles and Research 009 Multiple-Time States
Chapman University Chapman University Digital Commons Mathematics, Physics, and Computer Science Faculty Articles and Research Science and Technology Faculty Articles and Research 009 Multiple-Time States
arxiv:quant-ph/ v3 18 May 2004
 Shutters, Boxes, But No Paradoxes: Time Symmetry Puzzles in Quantum Theory RUTH E. KASTNER Department of Philosophy arxiv:quant-ph/277v3 8 May 24 University of Maryland College Park, MD 2742 USA. Abstract.
Shutters, Boxes, But No Paradoxes: Time Symmetry Puzzles in Quantum Theory RUTH E. KASTNER Department of Philosophy arxiv:quant-ph/277v3 8 May 24 University of Maryland College Park, MD 2742 USA. Abstract.
Introduction. Introductory Remarks
 Introductory Remarks This is probably your first real course in quantum mechanics. To be sure, it is understood that you have encountered an introduction to some of the basic concepts, phenomenology, history,
Introductory Remarks This is probably your first real course in quantum mechanics. To be sure, it is understood that you have encountered an introduction to some of the basic concepts, phenomenology, history,
How to use the simulator
 How to use the simulator Overview The application allows for the exploration of four quantum circuits in all. Each simulator grants the user a large amount of freedom in experments they wish to conduct.
How to use the simulator Overview The application allows for the exploration of four quantum circuits in all. Each simulator grants the user a large amount of freedom in experments they wish to conduct.
Analysis by Stephen Parrott Version 2
 Comment on The quantum pigeonhole principle and the nature of quantum correlations by Y. Aharonov, F. Colombe, S. Popescu, I. Sabadini, D. C. Struppa, and J. Tollaksen Analysis by Stephen Parrott Version
Comment on The quantum pigeonhole principle and the nature of quantum correlations by Y. Aharonov, F. Colombe, S. Popescu, I. Sabadini, D. C. Struppa, and J. Tollaksen Analysis by Stephen Parrott Version
Logical inconsistency in quantum mechanics
 1 LU TP 18-05 ver 2 April 2018 Logical inconsistency in quantum mechanics B. E. Y. Svensson Theoretical High Energy Physics, Department of Astronomy and Theoretical Physics, Lund University, Sölvegatan
1 LU TP 18-05 ver 2 April 2018 Logical inconsistency in quantum mechanics B. E. Y. Svensson Theoretical High Energy Physics, Department of Astronomy and Theoretical Physics, Lund University, Sölvegatan
Two-State Vector Formalism
 802 Two-State Vector Formalism Secondary Literature 9. E. Merzbacher: Quantum Mechanics, 2nd ed. (Wiley, New York 1970) 10. S. Gasiorowicz: Quantum Physics (Wiley, New York 1996) 11. A. Sommerfeld: Lectures
802 Two-State Vector Formalism Secondary Literature 9. E. Merzbacher: Quantum Mechanics, 2nd ed. (Wiley, New York 1970) 10. S. Gasiorowicz: Quantum Physics (Wiley, New York 1996) 11. A. Sommerfeld: Lectures
Continuous quantum states, Particle on a line and Uncertainty relations
 Continuous quantum states, Particle on a line and Uncertainty relations So far we have considered k-level (discrete) quantum systems. Now we turn our attention to continuous quantum systems, such as a
Continuous quantum states, Particle on a line and Uncertainty relations So far we have considered k-level (discrete) quantum systems. Now we turn our attention to continuous quantum systems, such as a
3. Quantum Mechanics in 3D
 3. Quantum Mechanics in 3D 3.1 Introduction Last time, we derived the time dependent Schrödinger equation, starting from three basic postulates: 1) The time evolution of a state can be expressed as a unitary
3. Quantum Mechanics in 3D 3.1 Introduction Last time, we derived the time dependent Schrödinger equation, starting from three basic postulates: 1) The time evolution of a state can be expressed as a unitary
PHY305: Notes on Entanglement and the Density Matrix
 PHY305: Notes on Entanglement and the Density Matrix Here follows a short summary of the definitions of qubits, EPR states, entanglement, the density matrix, pure states, mixed states, measurement, and
PHY305: Notes on Entanglement and the Density Matrix Here follows a short summary of the definitions of qubits, EPR states, entanglement, the density matrix, pure states, mixed states, measurement, and
Chemistry 271 Quantum Mechanics
 Chemistry 271 Quantum Mechanics Professor Michael D. Fayer Email: fayer@stanford.edu Room: 113 Keck Phone: 650 723-4446 TAs DJ Hoffman John Breen djhoff@stanford.edu jpbreen@stanford.edu Material on CourseWork
Chemistry 271 Quantum Mechanics Professor Michael D. Fayer Email: fayer@stanford.edu Room: 113 Keck Phone: 650 723-4446 TAs DJ Hoffman John Breen djhoff@stanford.edu jpbreen@stanford.edu Material on CourseWork
A time-symmetric formulation of quantum mechanics
 pt_aharonov1110 article 11/1/2010 1:24 PM Page 27 feature A time-symmetric formulation of quantum mechanics Yakir Aharonov, Sandu Popescu, and Jeff Tollaksen Quantum mechanics allows one to independently
pt_aharonov1110 article 11/1/2010 1:24 PM Page 27 feature A time-symmetric formulation of quantum mechanics Yakir Aharonov, Sandu Popescu, and Jeff Tollaksen Quantum mechanics allows one to independently
Introduction. Introductory Remarks
 Introductory Remarks This is probably your first real course in quantum mechanics. To be sure, it is understood that you have encountered an introduction to some of the basic concepts, phenomenology, history,
Introductory Remarks This is probably your first real course in quantum mechanics. To be sure, it is understood that you have encountered an introduction to some of the basic concepts, phenomenology, history,
Erwin Schrödinger and his cat
 Erwin Schrödinger and his cat How to relate discrete energy levels with Hamiltonian described in terms of continгous coordinate x and momentum p? Erwin Schrödinger (887-96) Acoustics: set of frequencies
Erwin Schrödinger and his cat How to relate discrete energy levels with Hamiltonian described in terms of continгous coordinate x and momentum p? Erwin Schrödinger (887-96) Acoustics: set of frequencies
Incompatibility Paradoxes
 Chapter 22 Incompatibility Paradoxes 22.1 Simultaneous Values There is never any difficulty in supposing that a classical mechanical system possesses, at a particular instant of time, precise values of
Chapter 22 Incompatibility Paradoxes 22.1 Simultaneous Values There is never any difficulty in supposing that a classical mechanical system possesses, at a particular instant of time, precise values of
Introduction to Quantum Computing
 Introduction to Quantum Computing Petros Wallden Lecture 3: Basic Quantum Mechanics 26th September 2016 School of Informatics, University of Edinburgh Resources 1. Quantum Computation and Quantum Information
Introduction to Quantum Computing Petros Wallden Lecture 3: Basic Quantum Mechanics 26th September 2016 School of Informatics, University of Edinburgh Resources 1. Quantum Computation and Quantum Information
ECE 501b Homework #4 Due: 10/22/2012
 1. Game Strategy: Consider a multiplayer boardgame that takes place on the following board and with the following rules: 7 8 9 10 6 11 5 12 4 3 2 1 The board contains six squares that are property (the
1. Game Strategy: Consider a multiplayer boardgame that takes place on the following board and with the following rules: 7 8 9 10 6 11 5 12 4 3 2 1 The board contains six squares that are property (the
Hardy s Paradox. Chapter Introduction
 Chapter 25 Hardy s Paradox 25.1 Introduction Hardy s paradox resembles the Bohm version of the Einstein-Podolsky-Rosen paradox, discussed in Chs. 23 and 24, in that it involves two correlated particles,
Chapter 25 Hardy s Paradox 25.1 Introduction Hardy s paradox resembles the Bohm version of the Einstein-Podolsky-Rosen paradox, discussed in Chs. 23 and 24, in that it involves two correlated particles,
Time Symmetry and the Many-Worlds Interpretation
 Time Symmetry and the Many-Worlds Interpretation Lev Vaidman Abstract An attempt to solve the collapse problem in the framework of a time-symmetric quantum formalism is reviewed. Although the proposal
Time Symmetry and the Many-Worlds Interpretation Lev Vaidman Abstract An attempt to solve the collapse problem in the framework of a time-symmetric quantum formalism is reviewed. Although the proposal
1 Mach-Zehder Interferometer 1. 2 Elitzur-Vaidman Bombs 6
 Chapter : Experiments with photons B. Zwiebach February 9, 6 Contents Mach-Zehder Interferometer Elitzur-Vaidman Bombs 6 Mach-Zehder Interferometer We have discussed before the Mach-Zehnder interferometer,
Chapter : Experiments with photons B. Zwiebach February 9, 6 Contents Mach-Zehder Interferometer Elitzur-Vaidman Bombs 6 Mach-Zehder Interferometer We have discussed before the Mach-Zehnder interferometer,
WEAK-VALUES AMPLIFICATION: WHEN PRECISION MEASUREMENTS BECOME EASY
 WEAK-VALUES AMPLIFICATION: WHEN PRECISION MEASUREMENTS BECOME EASY Julián Martínez-Rincón Department of Physics & Astronomy University of Rochester 03/05/14 OUTLINE A quick review on QM: Strong/projective
WEAK-VALUES AMPLIFICATION: WHEN PRECISION MEASUREMENTS BECOME EASY Julián Martínez-Rincón Department of Physics & Astronomy University of Rochester 03/05/14 OUTLINE A quick review on QM: Strong/projective
ECE 487 Lecture 6 : Time-Dependent Quantum Mechanics I Class Outline:
 ECE 487 Lecture 6 : Time-Dependent Quantum Mechanics I Class Outline: Time-Dependent Schrödinger Equation Solutions to thetime-dependent Schrödinger Equation Expansion of Energy Eigenstates Things you
ECE 487 Lecture 6 : Time-Dependent Quantum Mechanics I Class Outline: Time-Dependent Schrödinger Equation Solutions to thetime-dependent Schrödinger Equation Expansion of Energy Eigenstates Things you
Quantum Images and the Measurement Process
 EJTP 4, No. 14 (2007) 121 128 Electronic Journal of Theoretical Physics Quantum Images and the Measurement Process Fariel Shafee Department of Physics Princeton University Princeton, NJ 08540 USA Received
EJTP 4, No. 14 (2007) 121 128 Electronic Journal of Theoretical Physics Quantum Images and the Measurement Process Fariel Shafee Department of Physics Princeton University Princeton, NJ 08540 USA Received
Paradoxes of the Aharonov-Bohm and the Aharonov-Casher effects.
 Paradoxes of the Aharonov-Bohm and the Aharonov-Casher effects. L. Vaidman Raymond and Beverly Sackler School of Physics and Astronomy Tel-Aviv University, Tel-Aviv 69978, Israel For a believer in locality
Paradoxes of the Aharonov-Bohm and the Aharonov-Casher effects. L. Vaidman Raymond and Beverly Sackler School of Physics and Astronomy Tel-Aviv University, Tel-Aviv 69978, Israel For a believer in locality
C/CS/Phys C191 Amplitude Amplification, Quantum Zeno, Vaidman s bomb 11/10/09 Fall 2009 Lecture 22
 C/CS/Phys C191 Amplitude Amplification, Quantum Zeno, Vaidman s bomb 11/10/09 Fall 2009 Lecture 22 1 Readings Kaye et al, Ch 83 Nielsen and Chuang: Ch 63-65 Grover s algorithm and amplitude amplification:
C/CS/Phys C191 Amplitude Amplification, Quantum Zeno, Vaidman s bomb 11/10/09 Fall 2009 Lecture 22 1 Readings Kaye et al, Ch 83 Nielsen and Chuang: Ch 63-65 Grover s algorithm and amplitude amplification:
Weak measurements: subensembles from tunneling to Let s Make a Quantum Deal to Hardy s Paradox
 Weak measurements: subensembles from tunneling to Let s Make a Quantum Deal to Hardy s Paradox First: some more on tunneling times, by way of motivation... How does one discuss subensembles in quantum
Weak measurements: subensembles from tunneling to Let s Make a Quantum Deal to Hardy s Paradox First: some more on tunneling times, by way of motivation... How does one discuss subensembles in quantum
The Stern-Gerlach experiment and spin
 The Stern-Gerlach experiment and spin Experiments in the early 1920s discovered a new aspect of nature, and at the same time found the simplest quantum system in existence. In the Stern-Gerlach experiment,
The Stern-Gerlach experiment and spin Experiments in the early 1920s discovered a new aspect of nature, and at the same time found the simplest quantum system in existence. In the Stern-Gerlach experiment,
Coherent states, beam splitters and photons
 Coherent states, beam splitters and photons S.J. van Enk 1. Each mode of the electromagnetic (radiation) field with frequency ω is described mathematically by a 1D harmonic oscillator with frequency ω.
Coherent states, beam splitters and photons S.J. van Enk 1. Each mode of the electromagnetic (radiation) field with frequency ω is described mathematically by a 1D harmonic oscillator with frequency ω.
arxiv:quant-ph/ v3 8 Sep 2005
 Why the Afshar Experiment Does Not Refute Complementarity arxiv:quant-ph/0500v3 8 Sep 005 R. E. Kastner Department of Philosophy University of Maryland College Park, MD 074 Version of April 6, 005 ABSTRACT.
Why the Afshar Experiment Does Not Refute Complementarity arxiv:quant-ph/0500v3 8 Sep 005 R. E. Kastner Department of Philosophy University of Maryland College Park, MD 074 Version of April 6, 005 ABSTRACT.
Quantum Weak Values and Logic: An Uneasy Couple
 Found Phys (2017) 47:430 452 DOI 10.1007/s10701-017-0068-5 Quantum Weak Values and Logic: An Uneasy Couple Bengt E. Y. Svensson 1 Received: 20 May 2016 / Accepted: 24 January 2017 / Published online: 6
Found Phys (2017) 47:430 452 DOI 10.1007/s10701-017-0068-5 Quantum Weak Values and Logic: An Uneasy Couple Bengt E. Y. Svensson 1 Received: 20 May 2016 / Accepted: 24 January 2017 / Published online: 6
arxiv: v3 [quant-ph] 9 Feb 2018
![arxiv: v3 [quant-ph] 9 Feb 2018 arxiv: v3 [quant-ph] 9 Feb 2018](/thumbs/92/107758363.jpg) Comment on Particle Path Through a Nested Mach-Zehnder Interferometer arxiv:1608.01640v3 [quant-ph] 9 Feb 2018 Hatim Salih 1, 1 epartment of Mathematics, University of York, Heslington, York YO10 5, UK
Comment on Particle Path Through a Nested Mach-Zehnder Interferometer arxiv:1608.01640v3 [quant-ph] 9 Feb 2018 Hatim Salih 1, 1 epartment of Mathematics, University of York, Heslington, York YO10 5, UK
Bloch Wilson Hamiltonian and a Generalization of the Gell-Mann Low Theorem 1
 Bloch Wilson Hamiltonian and a Generalization of the Gell-Mann Low Theorem 1 Axel Weber 2 arxiv:hep-th/9911198v1 25 Nov 1999 Instituto de Física y Matemáticas, Universidad Michoacana de San Nicolás de
Bloch Wilson Hamiltonian and a Generalization of the Gell-Mann Low Theorem 1 Axel Weber 2 arxiv:hep-th/9911198v1 25 Nov 1999 Instituto de Física y Matemáticas, Universidad Michoacana de San Nicolás de
Asymptotic Pure State Transformations
 Asymptotic Pure State Transformations PHYS 500 - Southern Illinois University April 18, 2017 PHYS 500 - Southern Illinois University Asymptotic Pure State Transformations April 18, 2017 1 / 15 Entanglement
Asymptotic Pure State Transformations PHYS 500 - Southern Illinois University April 18, 2017 PHYS 500 - Southern Illinois University Asymptotic Pure State Transformations April 18, 2017 1 / 15 Entanglement
Solutions Final exam 633
 Solutions Final exam 633 S.J. van Enk (Dated: June 9, 2008) (1) [25 points] You have a source that produces pairs of spin-1/2 particles. With probability p they are in the singlet state, ( )/ 2, and with
Solutions Final exam 633 S.J. van Enk (Dated: June 9, 2008) (1) [25 points] You have a source that produces pairs of spin-1/2 particles. With probability p they are in the singlet state, ( )/ 2, and with
Nonlocality of single fermions branches that borrow particles
 1 Nonlocality of single fermions branches that borrow particles Sofia Wechsler Computers Engineering Center, Nahariya, P.O.B. 2004, 22265, Israel Abstract An experiment performed in 2002 by Sciarrino et
1 Nonlocality of single fermions branches that borrow particles Sofia Wechsler Computers Engineering Center, Nahariya, P.O.B. 2004, 22265, Israel Abstract An experiment performed in 2002 by Sciarrino et
A Note Concerning von Neumann Projector Measurement Pointer States, Weak Values, and Interference. Abstract
 A Note Concerning von Neumann Projector Measurement Pointer States, Weak Values, and Interference A. D. Parks and J. E. Gray Electromagnetic and Sensor Systems Department Naval Surface Warfare Center Dahlgren,
A Note Concerning von Neumann Projector Measurement Pointer States, Weak Values, and Interference A. D. Parks and J. E. Gray Electromagnetic and Sensor Systems Department Naval Surface Warfare Center Dahlgren,
arxiv:quant-ph/ v2 6 Sep 1995
 DTP/95/5 quant-ph/9505017 arxiv:quant-ph/9505017v 6 Sep 1995 Realism and Time Symmetry in Quantum Mechanics Benedikt Bläsi and Lucien Hardy Department of Mathematical Sciences University of Durham South
DTP/95/5 quant-ph/9505017 arxiv:quant-ph/9505017v 6 Sep 1995 Realism and Time Symmetry in Quantum Mechanics Benedikt Bläsi and Lucien Hardy Department of Mathematical Sciences University of Durham South
Unusual Interactions of Pre-and-Post-Selected Particles
 EP J Web of Conferences 70, 00053 (04) DOI: 0.05 ep jconf 047000053 C Owned by the authors, published by EDP Sciences, 04 Unusual Interactions of Pre-and-Post-Selected Particles Y. Aharonov, E.Cohen, S.Ben-Moshe
EP J Web of Conferences 70, 00053 (04) DOI: 0.05 ep jconf 047000053 C Owned by the authors, published by EDP Sciences, 04 Unusual Interactions of Pre-and-Post-Selected Particles Y. Aharonov, E.Cohen, S.Ben-Moshe
Generators for Continuous Coordinate Transformations
 Page 636 Lecture 37: Coordinate Transformations: Continuous Passive Coordinate Transformations Active Coordinate Transformations Date Revised: 2009/01/28 Date Given: 2009/01/26 Generators for Continuous
Page 636 Lecture 37: Coordinate Transformations: Continuous Passive Coordinate Transformations Active Coordinate Transformations Date Revised: 2009/01/28 Date Given: 2009/01/26 Generators for Continuous
The Framework of Quantum Mechanics
 The Framework of Quantum Mechanics We now use the mathematical formalism covered in the last lecture to describe the theory of quantum mechanics. In the first section we outline four axioms that lie at
The Framework of Quantum Mechanics We now use the mathematical formalism covered in the last lecture to describe the theory of quantum mechanics. In the first section we outline four axioms that lie at
Quantum Mechanical Interaction-Free Measurements
 Eoundations of Physics, Vol. 23, No. 7, 1993 Quantum Mechanical Interaction-Free Measurements Avshalom C. Elitzur 1'2 and Lev Vaidman ~ Received August 17, 1992; revised January 2, 1993 A novel manifestation
Eoundations of Physics, Vol. 23, No. 7, 1993 Quantum Mechanical Interaction-Free Measurements Avshalom C. Elitzur 1'2 and Lev Vaidman ~ Received August 17, 1992; revised January 2, 1993 A novel manifestation
The reality of de Broglie s pilot wave
 The reality of de Broglie s pilot wave António Cardoso Centro de Filosofia das Ciências da Universidade de Lisboa, Faculdade de Ciências da Universidade de Lisboa, Campo Grande, Edifício C4, 1749-016 Lisboa,
The reality of de Broglie s pilot wave António Cardoso Centro de Filosofia das Ciências da Universidade de Lisboa, Faculdade de Ciências da Universidade de Lisboa, Campo Grande, Edifício C4, 1749-016 Lisboa,
A Simple Model of Quantum Trajectories. Todd A. Brun University of Southern California
 A Simple Model of Quantum Trajectories Todd A. Brun University of Southern California Outline 1. Review projective and generalized measurements. 2. A simple model of indirect measurement. 3. Weak measurements--jump-like
A Simple Model of Quantum Trajectories Todd A. Brun University of Southern California Outline 1. Review projective and generalized measurements. 2. A simple model of indirect measurement. 3. Weak measurements--jump-like
arxiv: v2 [quant-ph] 14 Sep 2015
![arxiv: v2 [quant-ph] 14 Sep 2015 arxiv: v2 [quant-ph] 14 Sep 2015](/thumbs/88/115694016.jpg) arxiv:1505.00098v2 [quant-ph] 14 Sep 2015 Contextuality, Pigeonholes, Cheshire Cats, Mean Kings, and Weak Values Mordecai Waegell, Jeff Tollaksen Institute for Quantum Studies, Chapman University Orange,
arxiv:1505.00098v2 [quant-ph] 14 Sep 2015 Contextuality, Pigeonholes, Cheshire Cats, Mean Kings, and Weak Values Mordecai Waegell, Jeff Tollaksen Institute for Quantum Studies, Chapman University Orange,
PHYS 508 (2015-1) Final Exam January 27, Wednesday.
 PHYS 508 (2015-1) Final Exam January 27, Wednesday. Q1. Scattering with identical particles The quantum statistics have some interesting consequences for the scattering of identical particles. This is
PHYS 508 (2015-1) Final Exam January 27, Wednesday. Q1. Scattering with identical particles The quantum statistics have some interesting consequences for the scattering of identical particles. This is
Weak measurement and quantum interference
 Weak measurement and quantum interference from a geometrical point of view Masao Kitano Department of Electronic Science and Engineering, Kyoto University February 13-15, 2012 GCOE Symposium, Links among
Weak measurement and quantum interference from a geometrical point of view Masao Kitano Department of Electronic Science and Engineering, Kyoto University February 13-15, 2012 GCOE Symposium, Links among
Simple scheme for efficient linear optics quantum gates
 PHYSICAL REVIEW A, VOLUME 65, 012314 Simple scheme for efficient linear optics quantum gates T. C. Ralph,* A. G. White, W. J. Munro, and G. J. Milburn Centre for Quantum Computer Technology, University
PHYSICAL REVIEW A, VOLUME 65, 012314 Simple scheme for efficient linear optics quantum gates T. C. Ralph,* A. G. White, W. J. Munro, and G. J. Milburn Centre for Quantum Computer Technology, University
The Particle in a Box
 Page 324 Lecture 17: Relation of Particle in a Box Eigenstates to Position and Momentum Eigenstates General Considerations on Bound States and Quantization Continuity Equation for Probability Date Given:
Page 324 Lecture 17: Relation of Particle in a Box Eigenstates to Position and Momentum Eigenstates General Considerations on Bound States and Quantization Continuity Equation for Probability Date Given:
Decoherence and the Classical Limit
 Chapter 26 Decoherence and the Classical Limit 26.1 Introduction Classical mechanics deals with objects which have a precise location and move in a deterministic way as a function of time. By contrast,
Chapter 26 Decoherence and the Classical Limit 26.1 Introduction Classical mechanics deals with objects which have a precise location and move in a deterministic way as a function of time. By contrast,
Lecture 13B: Supplementary Notes on Advanced Topics. 1 Inner Products and Outer Products for Single Particle States
 Lecture 13B: Supplementary Notes on Advanced Topics Outer Products, Operators, Density Matrices In order to explore the complexity of many particle systems a different way to represent multiparticle states
Lecture 13B: Supplementary Notes on Advanced Topics Outer Products, Operators, Density Matrices In order to explore the complexity of many particle systems a different way to represent multiparticle states
Page 684. Lecture 40: Coordinate Transformations: Time Transformations Date Revised: 2009/02/02 Date Given: 2009/02/02
 Page 684 Lecture 40: Coordinate Transformations: Time Transformations Date Revised: 2009/02/02 Date Given: 2009/02/02 Time Transformations Section 12.5 Symmetries: Time Transformations Page 685 Time Translation
Page 684 Lecture 40: Coordinate Transformations: Time Transformations Date Revised: 2009/02/02 Date Given: 2009/02/02 Time Transformations Section 12.5 Symmetries: Time Transformations Page 685 Time Translation
Joint measurement of interference and path observables in optics and neutron interferometry 1
 Joint measurement of interference and path observables in optics and neutron interferometry W.M. de Muynck W.W. Stoffels and H. Martens Department of Theoretical Physics Eindhoven University of Technology
Joint measurement of interference and path observables in optics and neutron interferometry W.M. de Muynck W.W. Stoffels and H. Martens Department of Theoretical Physics Eindhoven University of Technology
1. Griffiths Suppose two spin-1/2 particles are known to be in the singlet configuration.
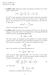 Physics 443 HW #7 Due March 12, 2008 1. Griffiths 4.50. Suppose two spin-1/2 particles are known to be in the singlet configuration. ( 00 = 1 2 ( + 1 2 1 2 1 2 +1 2 ) Let S a (1) be the component of the
Physics 443 HW #7 Due March 12, 2008 1. Griffiths 4.50. Suppose two spin-1/2 particles are known to be in the singlet configuration. ( 00 = 1 2 ( + 1 2 1 2 1 2 +1 2 ) Let S a (1) be the component of the
Time Independent Perturbation Theory Contd.
 Time Independent Perturbation Theory Contd. A summary of the machinery for the Perturbation theory: H = H o + H p ; H 0 n >= E n n >; H Ψ n >= E n Ψ n > E n = E n + E n ; E n = < n H p n > + < m H p n
Time Independent Perturbation Theory Contd. A summary of the machinery for the Perturbation theory: H = H o + H p ; H 0 n >= E n n >; H Ψ n >= E n Ψ n > E n = E n + E n ; E n = < n H p n > + < m H p n
Counterfactual quantum protocols
 Counterfactual quantum protocols L. Vaidman Raymond and Beverly Sackler School of Physics and Astronomy Tel-Aviv University, Tel-Aviv 69978, Israel The counterfactuality of recently proposed protocols
Counterfactual quantum protocols L. Vaidman Raymond and Beverly Sackler School of Physics and Astronomy Tel-Aviv University, Tel-Aviv 69978, Israel The counterfactuality of recently proposed protocols
Ensembles and incomplete information
 p. 1/32 Ensembles and incomplete information So far in this course, we have described quantum systems by states that are normalized vectors in a complex Hilbert space. This works so long as (a) the system
p. 1/32 Ensembles and incomplete information So far in this course, we have described quantum systems by states that are normalized vectors in a complex Hilbert space. This works so long as (a) the system
Quantum Entanglement. Chapter Introduction. 8.2 Entangled Two-Particle States
 Chapter 8 Quantum Entanglement 8.1 Introduction In our final chapter on quantum mechanics we introduce the concept of entanglement. This is a feature of two-particle states (or multi-particle states) in
Chapter 8 Quantum Entanglement 8.1 Introduction In our final chapter on quantum mechanics we introduce the concept of entanglement. This is a feature of two-particle states (or multi-particle states) in
The Postulates of Quantum Mechanics Common operators in QM: Potential Energy. Often depends on position operator: Kinetic Energy 1-D case: 3-D case
 The Postulates of Quantum Mechanics Common operators in QM: Potential Energy Often depends on position operator: Kinetic Energy 1-D case: 3-D case Time Total energy = Hamiltonian To find out about the
The Postulates of Quantum Mechanics Common operators in QM: Potential Energy Often depends on position operator: Kinetic Energy 1-D case: 3-D case Time Total energy = Hamiltonian To find out about the
How the Result of a Measurement of a Component of the Spin of a Spin- 1 2 Particle Can Turn Out to be 100
 How the Result of a Measurement of a Component of the Spin of a Spin- 1 2 Particle Can Turn Out to be 100 Aharonov, Albert and Vaidman April 4, 1988 PRL Abstract We have found that the usual measuring
How the Result of a Measurement of a Component of the Spin of a Spin- 1 2 Particle Can Turn Out to be 100 Aharonov, Albert and Vaidman April 4, 1988 PRL Abstract We have found that the usual measuring
Why Kastner analysis does not apply to a modified Afshar experiment. Eduardo Flores and Ernst Knoesel
 Why Kastner analysis does not apply to a modified Afshar experiment Eduardo Flores and Ernst Knoesel Department of Physics & Astronomy, Rowan University, Glassboro, NJ 08028 In an analysis of the Afshar
Why Kastner analysis does not apply to a modified Afshar experiment Eduardo Flores and Ernst Knoesel Department of Physics & Astronomy, Rowan University, Glassboro, NJ 08028 In an analysis of the Afshar
Dependent (Contextual) Events
 Chapter 14 Dependent (Contextual) Events 14.1 n Example Consider two spin-half particles a and b, and suppose that the corresponding oolean algebra L of properties on the tensor product space is generated
Chapter 14 Dependent (Contextual) Events 14.1 n Example Consider two spin-half particles a and b, and suppose that the corresponding oolean algebra L of properties on the tensor product space is generated
Lecture 4 (Sep. 18, 2017)
 Lecture 4 8.3 Quantum Theory I, Fall 07 Lecture 4 (Sep. 8, 07) 4. Measurement 4.. Spin- Systems Last time, we said that a general state in a spin- system can be written as ψ = c + + + c, (4.) where +,
Lecture 4 8.3 Quantum Theory I, Fall 07 Lecture 4 (Sep. 8, 07) 4. Measurement 4.. Spin- Systems Last time, we said that a general state in a spin- system can be written as ψ = c + + + c, (4.) where +,
LS coupling. 2 2 n + H s o + H h f + H B. (1) 2m
 LS coupling 1 The big picture We start from the Hamiltonian of an atomic system: H = [ ] 2 2 n Ze2 1 + 1 e 2 1 + H s o + H h f + H B. (1) 2m n e 4πɛ 0 r n 2 4πɛ 0 r nm n,m Here n runs pver the electrons,
LS coupling 1 The big picture We start from the Hamiltonian of an atomic system: H = [ ] 2 2 n Ze2 1 + 1 e 2 1 + H s o + H h f + H B. (1) 2m n e 4πɛ 0 r n 2 4πɛ 0 r nm n,m Here n runs pver the electrons,
Quantum control of dissipative systems. 1 Density operators and mixed quantum states
 Quantum control of dissipative systems S. G. Schirmer and A. I. Solomon Quantum Processes Group, The Open University Milton Keynes, MK7 6AA, United Kingdom S.G.Schirmer@open.ac.uk, A.I.Solomon@open.ac.uk
Quantum control of dissipative systems S. G. Schirmer and A. I. Solomon Quantum Processes Group, The Open University Milton Keynes, MK7 6AA, United Kingdom S.G.Schirmer@open.ac.uk, A.I.Solomon@open.ac.uk
Lecture 8: Wave-Particle Duality. Lecture 8, p 2
 We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery.
We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery.
Atomic Systems (PART I)
 Atomic Systems (PART I) Lecturer: Location: Recommended Text: Dr. D.J. Miller Room 535, Kelvin Building d.miller@physics.gla.ac.uk Joseph Black C407 (except 15/1/10 which is in Kelvin 312) Physics of Atoms
Atomic Systems (PART I) Lecturer: Location: Recommended Text: Dr. D.J. Miller Room 535, Kelvin Building d.miller@physics.gla.ac.uk Joseph Black C407 (except 15/1/10 which is in Kelvin 312) Physics of Atoms
Interference Between Distinguishable States. Thomas Alexander Meyer
 Interference Between Distinguishable States Thomas Alexander Meyer Interference effects are known to have a dependence upon indistinguishability of path. For this reason, it is accepted that different
Interference Between Distinguishable States Thomas Alexander Meyer Interference effects are known to have a dependence upon indistinguishability of path. For this reason, it is accepted that different
1.1.1 Bell Inequality - Spin correlation
 January 8, 015 Lecture IV 1.1.1 Bell Inequality - Spin correlation Consider the final spin singlet state of the decay η 0 µ + µ We suppose that the η 0 decays and the muon and µ + travel in opposite directions,
January 8, 015 Lecture IV 1.1.1 Bell Inequality - Spin correlation Consider the final spin singlet state of the decay η 0 µ + µ We suppose that the η 0 decays and the muon and µ + travel in opposite directions,
Weak measurement criteria for the past of a quantum particle
 1 LU-TP 14-29 ver 2 July 2014 Weak measurement criteria for the past of a quantum particle B. E. Y. Svensson Theoretical High Energy Physics, Department of Astronomy and Theoretical Physics, Lund University,
1 LU-TP 14-29 ver 2 July 2014 Weak measurement criteria for the past of a quantum particle B. E. Y. Svensson Theoretical High Energy Physics, Department of Astronomy and Theoretical Physics, Lund University,
M.L. Dalla Chiara, R. Giuntini, R. Leporini, G. Sergioli. Qudit Spaces and a Many-valued Approach to Quantum Comp
 Qudit Spaces and a Many-valued Approach to Quantum Computational Logics Quantum computational logics are special examples of quantum logic based on the following semantic idea: linguistic formulas are
Qudit Spaces and a Many-valued Approach to Quantum Computational Logics Quantum computational logics are special examples of quantum logic based on the following semantic idea: linguistic formulas are
1 Mathematical preliminaries
 1 Mathematical preliminaries The mathematical language of quantum mechanics is that of vector spaces and linear algebra. In this preliminary section, we will collect the various definitions and mathematical
1 Mathematical preliminaries The mathematical language of quantum mechanics is that of vector spaces and linear algebra. In this preliminary section, we will collect the various definitions and mathematical
Illustrating the Superposition Principle with Single Photon Interference. Frank Rioux. Department of Chemistry. St.
 Illustrating the Superposition Principle with Single Photon Interference Frank Rioux Department of Chemistry St. John s University College of St. Benedict St. Joseph, MN 56374 Abstract Single-photon interference
Illustrating the Superposition Principle with Single Photon Interference Frank Rioux Department of Chemistry St. John s University College of St. Benedict St. Joseph, MN 56374 Abstract Single-photon interference
Physics 486 Discussion 5 Piecewise Potentials
 Physics 486 Discussion 5 Piecewise Potentials Problem 1 : Infinite Potential Well Checkpoints 1 Consider the infinite well potential V(x) = 0 for 0 < x < 1 elsewhere. (a) First, think classically. Potential
Physics 486 Discussion 5 Piecewise Potentials Problem 1 : Infinite Potential Well Checkpoints 1 Consider the infinite well potential V(x) = 0 for 0 < x < 1 elsewhere. (a) First, think classically. Potential
4. Two-level systems. 4.1 Generalities
 4. Two-level systems 4.1 Generalities 4. Rotations and angular momentum 4..1 Classical rotations 4.. QM angular momentum as generator of rotations 4..3 Example of Two-Level System: Neutron Interferometry
4. Two-level systems 4.1 Generalities 4. Rotations and angular momentum 4..1 Classical rotations 4.. QM angular momentum as generator of rotations 4..3 Example of Two-Level System: Neutron Interferometry
The quantum way to diagonalize hermitean matrices
 Fortschr. Phys. 51, No. 2 3, 249 254 (2003) / DOI 10.1002/prop.200310035 The quantum way to diagonalize hermitean matrices Stefan Weigert HuMP Hull Mathematical Physics, Department of Mathematics University
Fortschr. Phys. 51, No. 2 3, 249 254 (2003) / DOI 10.1002/prop.200310035 The quantum way to diagonalize hermitean matrices Stefan Weigert HuMP Hull Mathematical Physics, Department of Mathematics University
Lecture #13 1. Incorporating a vector potential into the Hamiltonian 2. Spin postulates 3. Description of spin states 4. Identical particles in
 Lecture #3. Incorporating a vector potential into the Hamiltonian. Spin postulates 3. Description of spin states 4. Identical particles in classical and QM 5. Exchange degeneracy - the fundamental problem
Lecture #3. Incorporating a vector potential into the Hamiltonian. Spin postulates 3. Description of spin states 4. Identical particles in classical and QM 5. Exchange degeneracy - the fundamental problem
Proposal of Michelson-Morley experiment via single photon. interferometer: Interpretation of Michelson-Morley
 Proposal of Michelson-Morley experiment via single photon interferometer: Interpretation of Michelson-Morley experimental results using de Broglie-Bohm picture Masanori Sato Honda Electronics Co., Ltd.,
Proposal of Michelson-Morley experiment via single photon interferometer: Interpretation of Michelson-Morley experimental results using de Broglie-Bohm picture Masanori Sato Honda Electronics Co., Ltd.,
Advanced Optical Communications Prof. R. K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay
 Advanced Optical Communications Prof. R. K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture No. # 15 Laser - I In the last lecture, we discussed various
Advanced Optical Communications Prof. R. K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture No. # 15 Laser - I In the last lecture, we discussed various
arxiv:quant-ph/ v1 19 Mar 2006
 On the simulation of quantum circuits Richard Jozsa Department of Computer Science, University of Bristol, Merchant Venturers Building, Bristol BS8 1UB U.K. Abstract arxiv:quant-ph/0603163v1 19 Mar 2006
On the simulation of quantum circuits Richard Jozsa Department of Computer Science, University of Bristol, Merchant Venturers Building, Bristol BS8 1UB U.K. Abstract arxiv:quant-ph/0603163v1 19 Mar 2006
Chapter 5. Density matrix formalism
 Chapter 5 Density matrix formalism In chap we formulated quantum mechanics for isolated systems. In practice systems interect with their environnement and we need a description that takes this feature
Chapter 5 Density matrix formalism In chap we formulated quantum mechanics for isolated systems. In practice systems interect with their environnement and we need a description that takes this feature
FIG. 16: A Mach Zehnder interferometer consists of two symmetric beam splitters BS1 and BS2
 Lecture 11: Application: The Mach Zehnder interferometer Coherent-state input Squeezed-state input Mach-Zehnder interferometer with coherent-state input: Now we apply our knowledge about quantum-state
Lecture 11: Application: The Mach Zehnder interferometer Coherent-state input Squeezed-state input Mach-Zehnder interferometer with coherent-state input: Now we apply our knowledge about quantum-state
Coins and Counterfactuals
 Chapter 19 Coins and Counterfactuals 19.1 Quantum Paradoxes The next few chapters are devoted to resolving a number of quantum paradoxes in the sense of giving a reasonable explanation of a seemingly paradoxical
Chapter 19 Coins and Counterfactuals 19.1 Quantum Paradoxes The next few chapters are devoted to resolving a number of quantum paradoxes in the sense of giving a reasonable explanation of a seemingly paradoxical
IDLER DCC SIGNAL SHUTTER
 1 Interaction-Free Measurements Lev Vaidman School of Physics and Astronomy, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel 1 The Penrose bomb testing
1 Interaction-Free Measurements Lev Vaidman School of Physics and Astronomy, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel 1 The Penrose bomb testing
Lecture 12c: The range of classical and quantum correlations
 Pre-Collegiate Institutes Quantum Mechanics 015 ecture 1c: The range of classical and quantum correlations The simplest entangled case: Consider a setup where two photons are emitted from a central source
Pre-Collegiate Institutes Quantum Mechanics 015 ecture 1c: The range of classical and quantum correlations The simplest entangled case: Consider a setup where two photons are emitted from a central source
Singlet State Correlations
 Chapter 23 Singlet State Correlations 23.1 Introduction This and the following chapter can be thought of as a single unit devoted to discussing various issues raised by a famous paper published by Einstein,
Chapter 23 Singlet State Correlations 23.1 Introduction This and the following chapter can be thought of as a single unit devoted to discussing various issues raised by a famous paper published by Einstein,
Topic 2: The mathematical formalism and the standard way of thin
 The mathematical formalism and the standard way of thinking about it http://www.wuthrich.net/ MA Seminar: Philosophy of Physics Vectors and vector spaces Vectors and vector spaces Operators Albert, Quantum
The mathematical formalism and the standard way of thinking about it http://www.wuthrich.net/ MA Seminar: Philosophy of Physics Vectors and vector spaces Vectors and vector spaces Operators Albert, Quantum
Quantum Field Theory. Chapter Introduction. 8.2 The Many Particle State
 Chapter 8 Quantum Field Theory?? 8.1 Introduction We have studied the properties of photons primarily as single particles. It was Einstein s great discovery to realize that particulate basis of light.
Chapter 8 Quantum Field Theory?? 8.1 Introduction We have studied the properties of photons primarily as single particles. It was Einstein s great discovery to realize that particulate basis of light.
37-6 Watching the electrons (matter waves)
 37-6 Watching the electrons (matter waves) 1 testing our proposition: the electrons go either through hole 1 or hole 2 add a very strong light source behind walls between two holes, electrons will scatter
37-6 Watching the electrons (matter waves) 1 testing our proposition: the electrons go either through hole 1 or hole 2 add a very strong light source behind walls between two holes, electrons will scatter
We can't solve problems by using the same kind of thinking we used when we created them.!
 PuNng Local Realism to the Test We can't solve problems by using the same kind of thinking we used when we created them.! - Albert Einstein! Day 39: Ques1ons? Revisit EPR-Argument Tes1ng Local Realism
PuNng Local Realism to the Test We can't solve problems by using the same kind of thinking we used when we created them.! - Albert Einstein! Day 39: Ques1ons? Revisit EPR-Argument Tes1ng Local Realism
Quantum Mechanics II: Examples
 Quantum Mechanics II: Examples Michael A. Nielsen University of Queensland Goals: 1. To apply the principles introduced in the last lecture to some illustrative examples: superdense coding, and quantum
Quantum Mechanics II: Examples Michael A. Nielsen University of Queensland Goals: 1. To apply the principles introduced in the last lecture to some illustrative examples: superdense coding, and quantum
QUANTUM INFORMATION -THE NO-HIDING THEOREM p.1/36
 QUANTUM INFORMATION - THE NO-HIDING THEOREM Arun K Pati akpati@iopb.res.in Instititute of Physics, Bhubaneswar-751005, Orissa, INDIA and Th. P. D, BARC, Mumbai-400085, India QUANTUM INFORMATION -THE NO-HIDING
QUANTUM INFORMATION - THE NO-HIDING THEOREM Arun K Pati akpati@iopb.res.in Instititute of Physics, Bhubaneswar-751005, Orissa, INDIA and Th. P. D, BARC, Mumbai-400085, India QUANTUM INFORMATION -THE NO-HIDING
arxiv:quant-ph/ v2 10 Jun 2007
 The Two-State Vector Formalism: an Updated Review Yakir Aharonov 1,2 and Lev Vaidman 1 arxiv:quant-ph/0105101v2 10 Jun 2007 1 School of Physics and Astronomy Raymond and Beverly Sackler Faculty of Exact
The Two-State Vector Formalism: an Updated Review Yakir Aharonov 1,2 and Lev Vaidman 1 arxiv:quant-ph/0105101v2 10 Jun 2007 1 School of Physics and Astronomy Raymond and Beverly Sackler Faculty of Exact
THE OBJECTIVE PAST OF
 THE OBJECTIVE PAST OF A QUANTUM UNIVERSE: REDUNDANT RECORDS OF CONSISTENT HISTORIES C. Jess Riedel with Charles Bennett, Wojciech Zurek, and Michael Zwolak arxiv:1312.0331 IBM Watson Research Lab arxiv:1310.4473
THE OBJECTIVE PAST OF A QUANTUM UNIVERSE: REDUNDANT RECORDS OF CONSISTENT HISTORIES C. Jess Riedel with Charles Bennett, Wojciech Zurek, and Michael Zwolak arxiv:1312.0331 IBM Watson Research Lab arxiv:1310.4473
Combinatorics. But there are some standard techniques. That s what we ll be studying.
 Combinatorics Problem: How to count without counting. How do you figure out how many things there are with a certain property without actually enumerating all of them. Sometimes this requires a lot of
Combinatorics Problem: How to count without counting. How do you figure out how many things there are with a certain property without actually enumerating all of them. Sometimes this requires a lot of
