Gamma and Normal Distribuions
|
|
|
- Abigayle Tate
- 6 years ago
- Views:
Transcription
1 Gamma and Normal Distribuions Sections 5.4 & 5.5 Cathy Poliak, Ph.D. Office in Fleming 11c Department of Mathematics University of Houston Lecture Cathy Poliak, Ph.D. Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
2 Outline 1 Exponential Distribution 2 Gamma Distribution 3 Normal Distribution 4 The Empirical Rule 5 The Standard Normal Distribution 6 Using the z-table Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
3 Definition of a Density Function A density function is a nonnegative function f defined of the set of real numbers such that: f (x)dx = 1. If f is a density function, then its integral F(x) = x f (u)du is a continuous cumulative distribution function (cdf), that is P(X x) = F(x). If X is a random variable with this density function, then for any two real numbers, a and b P(a X b) = b a f (x)dx. Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
4 Using the cdf F (X) to Compute Probabilities Let X be a continuous random variable with pdf f (x) and cdf F(x). Then for any number a, P(X > a) = 1 F(a) and for any two numbers a and b with a < b, P(a X b) = F (b) F(a) Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
5 Popper 06 Questions The waiting time, in hours, between succesive speeders spotted by a radar unit is a continuous random variable with cdf { 0 x < 0 F(x) = 1 e 8x, x 0 1. Find the probability of waiting less than 15 minutes. between successive speeders. a) b) c) 0 d) 1 2. Give the pdf of this distribution. a) f (x) = b) f (x) = { 1 e 8x x 0 0 otherwise { e 8x x 0 0 otherwise c) f (x) = d) f (x) = { 8e 8x x 0 0 otherwise { 8e 8x x 0 0 otherwise Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
6 The Exponential Distribution X is said to have an exponential distribution with parameter λ (λ > 0) if the pdf of X is: { λe λx x 0 f (x) = 0 otherwise Where λ is a rate parameter, we write X Exp(λ). The cdf of a exponential random variable is: { 0 x < 0 F(x) = 1 e λx x 0 The mean of the exponential distribution is µ x = E(X) = 1 λ the standard deviation is also 1 λ. Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
7 The Gamma Function The gamma function Γ(α) is defined by: Γ(α) = 0 x α 1 e x dx Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
8 Properties of the Gamma Function The most important properties of the gamma function are the following: 1. For any α > 1, Γ(α) = (α 1)Γ(α 1) 2. For any positive integer, n, Γ(n) = (n 1)! 3. Γ( 1 2 ) = π Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
9 The PDF of a Gamma Distribution A continuous random variable X is said to have a gamma distribution if the pdf of X is { 1 β f (x; α, β) = α Γ(α) x α 1 e x/β x 0 0 otherwise where parameters α and β satisfy α > 0, β > 0. Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Sections (Department 5.4 & 5.5of Mathematics University of Lecture Houston 15 ) / 43
10 Gamma Distribution Related to the Poisson Gamma distribution is a distribution that arises naturally in processes for which the waiting times between events are relevant. It can be thought of as a waiting time between Poisson distributed events, unitl k arrivals. Thus the scale parameter can also be thought of as the inverse of the rate parameter (µ), 1 µ. Then α = k and β = 1 µ In R, P(X x) = pgamma(x, α, 1 β ) / 43
11 Gamma Density Curve Gamma Density Curve alpha = 2, beta = 1/3 alpa = 1, beta = 1 alpha = 2, beta = 2 alpha = 2, beta = / 43
12 Applications of the Gamma Distribution The gamma distribution can be used a range of disciplines including queuing models, climatology, and financial services. Examples of events that may be modeled by gamma distribution include: The amount of rainfall accumulated in a reservoir The size of loan defaults or aggregate insurance claims The flow of items through manufacturing and distribution processes The load on web servers The many and varied forms of telecom exchange / 43
13 Example Suppose that the telephone calls arriving at a prticular switchboard follow a Poisson process with an average of 5 calls coming per minute. What is the probability that up to a minute will elapse until 2 calls have come in to the switchboard? Average of 5 calls coming per minute means that β = 1 5. Until 2 calls have come into the switchboard means that α = / 43
14 Mean and Variance of the Gamma Distribution The mean and variance of a random variable X having the gamma distribution are: E(X) = µ = αβ Var(X) = σ 2 = αβ / 43
15 Example of Gamma Distribution Suppose that a transistor of a certain type is subjected to an accelerated life test, the lifetime Y (in weeks) has a gamma distribution with a mean of 24 and a standard deviation of Find the values of α and β. 2. Find P(Y 24) / 43
16 The Normal distributions Common type of probability distributions for continuous random variables. The highest probability is where the values are centered around the mean. Then the probability declines the further from the mean a value gets. These curves are symmetric, single-peaked, and bell-shaped. The mean µ is located at the center of the curve and is the same as the median. The standard deviation σ controls the spread of the curve. If σ is small then the curve is tall and slim. If σ is large then the curve is short and fat / 43
17 Normal distributions important to statistics? Normal distributions are good descriptions for some distributions of real data. Normal distributions are good approximations to the results of many kinds of chance outcomes. Many statistical inference procedures based on Normal distributions work well for other roughly symmetric distributions / 43
18 Facts about the Normal distribution The curve is symmetric about the mean. That is, 50% of the area under the curve is below the mean. 50% of the area under the curve is above the mean. The spread of the curve is determined by the standard deviation. The area under the curve is with respect to the number of standard deviations a value is from the mean. Total area under the curve is 1. Area under the curve is the same a probability within a range of values. If X is a Normal distribution with mean µ and standard deviation σ we would write it as N(µ, σ) / 43
19 Density Function This is the graph of the density function. Density Curves for Normal Distributions mean = 0, sd = 1 mean = 0, sd = 2 mean = 2, sd = 1 mean = 2, sd = / 43
20 PDF of a Normal Distribution A continuous random variable X is said to have a Normal distribution with parameters µ and σ (or µ and σ 2 ), where < µ < and 0 < σ, if the pdf of X is: f (x) = 1 2πσ e (x µ)2 /2σ 2 For all < x < / 43
21 The Empirical Rule or Rule Unfortunately to find the area under this density curve is not as easy to compute. Thus we can use the following approximate rule for the area under the Normal density curve. In the Normal Distribution with mean µ and standard deviation σ: 68% of the observations fall within 1 standard deviation σ of the mean µ. 95% of the observations fall within 2 standard deviations 2σ of the mean µ. 99.7% of the observations fall within 3 standard deviations 3σ of the mean µ / 43
22 The rule for Normal distributions / 43
23 MPG of Prius The MPG of Prius has a Normal distribution with mean µ = 49 mpg and standard deviation σ = 3.5 mpg. 49-3(3.5) 49-2(3.5) (3.5) (3.5) / 43
24 MPG of Prius About what percent have between 42 and 52.5 mpg? 49-3(3.5) 49-2(3.5) (3.5) (3.5) / 43
25 MPG of Prius About what percent have between 42 and 45.5 mpg? 49-3(3.5) 49-2(3.5) (3.5) (3.5) / 43
26 MPG of Prius About what percent have less than 42 mpg? 49-3(3.5) 49-2(3.5) (3.5) (3.5) / 43
27 Orange Juice An orange juice producer buys all his oranges from a large orange grove. The amount of juice squeezed from each of these oranges is approximately normally distributed, with a mean of 4.70 ounces and a standard deviation of 0.40 ounce. 1. What is the probability that an orange from this orange grove has between 3.9 and 5.5 ounces of juice? 2. What is the probability that an orange from this orange grove has less than 4.7 ounces of juice? 3. Approximately 95% of the oranges have juice between what two middle values? / 43
28 Not 1, 2 or 3 Standard Deviations An orange juice producer buys all his oranges from a large orange grove. The amount of juice squeezed from each of these oranges is approximately normally distributed, with a mean of 4.70 ounces and a standard deviation of 0.40 ounce. The random variable is X = the amount of juice squeezed from one orange. What is the probability that an orange will have less than 4 ounces of juice? P(X < 4). There are a couple of ways to answer this question. R: pnorm(x,mean,sd), pnorm(4,4.7,0.4) = Z-Table: In your textbook. This table is for Standard Normal Distribution / 43
29 Determine the probabilities? X = amount of juice squeezed with N(4.7, 0.4). 1. What is the probability that more than four ounces of juice will be squeezed? 2. What is the probability that between 3.5 and 4.5 ounces of juice will be squeezed? 3. What is the probability that beyond 3 or beyond 5 ounces of juice will be squeezed? / 43
30 Standard Normal Distribution To compute P(a X b) when X is a Normal random variable with parameters µ and σ, we must evaluate: b a 1 2πσ e (x µ)2 /2σ 2 dx None of the standard integration techniques can be used to evaluate this, thus we "standardize" the values by: Z = X µ σ where µ Z = 0 and σ Z = 1 to get the pdf: f (z) = 1 2π e z2 /2 The cdf of Z is P(Z z) = z f (y)dy which we denote by Φ(z) / 43
31 Key concepts for z-scores The z-score is the number of standard deviations a value is from the mean. Z -scores have no units They measure the distance an observation is from the mean in standard deviations. Positive z-scores indicate that the observation is above the mean. Negative z-scores indicate that the observation is below the mean. Z -scores usually are between 3 and 3. Anything beyond these two values indicates that the observation is extreme / 43
32 Example of Z-scores A certain town has a mean monthly high temperature in January of 35 F and a standard deviation of 8 F. This town also has a mean monthly high temperature in July of 75 F with a standard deviation of 10 F. In which month is it more unusual to have a day with a high temperature of 55 degrees? / 43
33 Another Example The score on a test has a mean of 75 with standard deviation 15. If I said your standard score (z-score) is 2.25, what is your actual test score? / 43
34 Normal Distribution Calculations Area under a Normal curve represent proportions (probability) of observations within a range of values. There is no easy way to find the area under a Normal curve. We use a table or software that calculates the desired areas. The table we use is Z-table It uses a cumulative proportion. A cumulative proportion is the proportion (probability) of observations in a distribution that lie at or below a given value. This is Φ(z). When the distribution is given by a density curve, the cumulative proportion is the area under the curve to the left of a given value / 43
35 Using The Z-table The vertical margin are the left most digits of a z-score. The top margin is the hundredths place of a z-score. The numbers inside the table represents the area from to that z-score. Remember that the standard Normal density curve is symmetric and the total area is equal to 1. Note: R can calculate these probabilities and also some calculators. Without having to convert to z-scores / 43
36 P(Z 1.52) P(Z -1.52) / 43
37 P(Z 1.52) = R: pnorm(-1.52) = Table A: P(Z < z) z P(Z -1.52) / 43
38 P(Z 0.95) P(Z 0.95) / 43
39 P(Z 0.95) = R: 1 - pnorm(0.95) = Table A: P(Z < z) z P(Z 0.95)= 1 P( Z < 0.95) = = / 43
40 P(1.3 < Z < 1.72) P(1.3 < Z < 1.72) / 43
41 P(1.3 < Z < 1.72) = R: pnorm(1.72) - pnorm(1.3) = z P(1.3 < Z < 1.72) = = / 43
42 Determine the probabilities? X = amount of juice squeezed with N(4.7, 0.4). Using the z-table 1. What is the probability that more than four ounces of juice will be squeezed? 2. What is the probability that between 3.5 and 4.5 ounces of juice will be squeezed? 3. What is the probability that beyond 3 or beyond 5 ounces of juice will be squeezed? / 43
43
44 Popper 06 Questions 3. D 4. C 5. B / 43
The Normal Distribuions
 The Normal Distribuions Sections 5.4 & 5.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 15-3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
The Normal Distribuions Sections 5.4 & 5.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 15-3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
Exponential, Gamma and Normal Distribuions
 Exponential, Gamma and Normal Distribuions Sections 5.4, 5.5 & 6.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy Poliak,
Exponential, Gamma and Normal Distribuions Sections 5.4, 5.5 & 6.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy Poliak,
Expected Values, Exponential and Gamma Distributions
 Expected Values, Exponential and Gamma Distributions Sections 5.2-5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 14-3339 Cathy Poliak,
Expected Values, Exponential and Gamma Distributions Sections 5.2-5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 14-3339 Cathy Poliak,
Standard Normal Calculations
 Standard Normal Calculations Section 4.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 10-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Standard Normal Calculations Section 4.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 10-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Density Curves & Normal Distributions
 Density Curves & Normal Distributions Sections 4.1 & 4.2 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Density Curves & Normal Distributions Sections 4.1 & 4.2 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Expected Values, Exponential and Gamma Distributions
 Expected Values, Exponential and Gamma Distributions Sections 5.2 & 5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13-3339 Cathy
Expected Values, Exponential and Gamma Distributions Sections 5.2 & 5.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 13-3339 Cathy
Inverse Normal Distribution and Sampling Distributions
 Inverse Normal Distribution and Sampling Distributions Section 4.3 & 4.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Department of Mathematics University of Houston Lecture 11-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Inverse Normal Distribution and Sampling Distributions Section 4.3 & 4.4 Cathy Poliak, Ph.D. cathy@math.uh.edu Department of Mathematics University of Houston Lecture 11-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Chapter 4: Continuous Probability Distributions
 Chapter 4: Continuous Probability Distributions Seungchul Baek Department of Statistics, University of South Carolina STAT 509: Statistics for Engineers 1 / 57 Continuous Random Variable A continuous random
Chapter 4: Continuous Probability Distributions Seungchul Baek Department of Statistics, University of South Carolina STAT 509: Statistics for Engineers 1 / 57 Continuous Random Variable A continuous random
Continuous Random Variables and Continuous Distributions
 Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
Continuous Random Variables and Continuous Distributions Continuous Random Variables and Continuous Distributions Expectation & Variance of Continuous Random Variables ( 5.2) The Uniform Random Variable
1 Probability and Random Variables
 1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
1 Probability and Random Variables The models that you have seen thus far are deterministic models. For any time t, there is a unique solution X(t). On the other hand, stochastic models will result in
STAT Chapter 5 Continuous Distributions
 STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
STAT 270 - Chapter 5 Continuous Distributions June 27, 2012 Shirin Golchi () STAT270 June 27, 2012 1 / 59 Continuous rv s Definition: X is a continuous rv if it takes values in an interval, i.e., range
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
Chapter 3 sections Chapter 3 - continued 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions
STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution
 STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution Pengyuan (Penelope) Wang June 15, 2011 Review Discussed Uniform Distribution and Normal Distribution Normal Approximation
STAT 430/510 Probability Lecture 12: Central Limit Theorem and Exponential Distribution Pengyuan (Penelope) Wang June 15, 2011 Review Discussed Uniform Distribution and Normal Distribution Normal Approximation
STAT509: Continuous Random Variable
 University of South Carolina September 23, 2014 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite or infinite) of real numbers for its range.
University of South Carolina September 23, 2014 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite or infinite) of real numbers for its range.
Chapter 4: Continuous Random Variable
 Chapter 4: Continuous Random Variable Shiwen Shen University of South Carolina 2017 Summer 1 / 57 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite
Chapter 4: Continuous Random Variable Shiwen Shen University of South Carolina 2017 Summer 1 / 57 Continuous Random Variable A continuous random variable is a random variable with an interval (either finite
3 Continuous Random Variables
 Jinguo Lian Math437 Notes January 15, 016 3 Continuous Random Variables Remember that discrete random variables can take only a countable number of possible values. On the other hand, a continuous random
Jinguo Lian Math437 Notes January 15, 016 3 Continuous Random Variables Remember that discrete random variables can take only a countable number of possible values. On the other hand, a continuous random
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models
 System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 20, 2012 Introduction Introduction The world of the model-builder
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 20, 2012 Introduction Introduction The world of the model-builder
Probability Density Functions
 Probability Density Functions Probability Density Functions Definition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that
Probability Density Functions Probability Density Functions Definition Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f (x) such that
Common ontinuous random variables
 Common ontinuous random variables CE 311S Earlier, we saw a number of distribution families Binomial Negative binomial Hypergeometric Poisson These were useful because they represented common situations:
Common ontinuous random variables CE 311S Earlier, we saw a number of distribution families Binomial Negative binomial Hypergeometric Poisson These were useful because they represented common situations:
Experimental Design and Statistics - AGA47A
 Experimental Design and Statistics - AGA47A Czech University of Life Sciences in Prague Department of Genetics and Breeding Fall/Winter 2014/2015 Matúš Maciak (@ A 211) Office Hours: M 14:00 15:30 W 15:30
Experimental Design and Statistics - AGA47A Czech University of Life Sciences in Prague Department of Genetics and Breeding Fall/Winter 2014/2015 Matúš Maciak (@ A 211) Office Hours: M 14:00 15:30 W 15:30
Chapter 3 sections. SKIP: 3.10 Markov Chains. SKIP: pages Chapter 3 - continued
 Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Chapter 3 sections 3.1 Random Variables and Discrete Distributions 3.2 Continuous Distributions 3.3 The Cumulative Distribution Function 3.4 Bivariate Distributions 3.5 Marginal Distributions 3.6 Conditional
Brief Review of Probability
 Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Maura Department of Economics and Finance Università Tor Vergata Outline 1 Distribution Functions Quantiles and Modes of a Distribution 2 Example 3 Example 4 Distributions Outline Distribution Functions
Applied Statistics and Probability for Engineers. Sixth Edition. Chapter 4 Continuous Random Variables and Probability Distributions.
 Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE Random
Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE Random
Chapter 4 Continuous Random Variables and Probability Distributions
 Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE 4-1
Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 4 Continuous Random Variables and Probability Distributions 4 Continuous CHAPTER OUTLINE 4-1
Introduction to Statistical Data Analysis Lecture 3: Probability Distributions
 Introduction to Statistical Data Analysis Lecture 3: Probability Distributions James V. Lambers Department of Mathematics The University of Southern Mississippi James V. Lambers Statistical Data Analysis
Introduction to Statistical Data Analysis Lecture 3: Probability Distributions James V. Lambers Department of Mathematics The University of Southern Mississippi James V. Lambers Statistical Data Analysis
15 Discrete Distributions
 Lecture Note 6 Special Distributions (Discrete and Continuous) MIT 4.30 Spring 006 Herman Bennett 5 Discrete Distributions We have already seen the binomial distribution and the uniform distribution. 5.
Lecture Note 6 Special Distributions (Discrete and Continuous) MIT 4.30 Spring 006 Herman Bennett 5 Discrete Distributions We have already seen the binomial distribution and the uniform distribution. 5.
STA 256: Statistics and Probability I
 Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. Exercise 4.1 Let X be a random variable with p(x)
Al Nosedal. University of Toronto. Fall 2017 My momma always said: Life was like a box of chocolates. You never know what you re gonna get. Forrest Gump. Exercise 4.1 Let X be a random variable with p(x)
Slides 8: Statistical Models in Simulation
 Slides 8: Statistical Models in Simulation Purpose and Overview The world the model-builder sees is probabilistic rather than deterministic: Some statistical model might well describe the variations. An
Slides 8: Statistical Models in Simulation Purpose and Overview The world the model-builder sees is probabilistic rather than deterministic: Some statistical model might well describe the variations. An
Stat410 Probability and Statistics II (F16)
 Stat4 Probability and Statistics II (F6 Exponential, Poisson and Gamma Suppose on average every /λ hours, a Stochastic train arrives at the Random station. Further we assume the waiting time between two
Stat4 Probability and Statistics II (F6 Exponential, Poisson and Gamma Suppose on average every /λ hours, a Stochastic train arrives at the Random station. Further we assume the waiting time between two
Continuous random variables
 Continuous random variables Can take on an uncountably infinite number of values Any value within an interval over which the variable is definied has some probability of occuring This is different from
Continuous random variables Can take on an uncountably infinite number of values Any value within an interval over which the variable is definied has some probability of occuring This is different from
Continuous Random Variables
 Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability. Often, there is interest in random variables
CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS. 6.2 Normal Distribution. 6.1 Continuous Uniform Distribution
 CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS Recall that a continuous random variable X is a random variable that takes all values in an interval or a set of intervals. The distribution of a continuous
CHAPTER 6 SOME CONTINUOUS PROBABILITY DISTRIBUTIONS Recall that a continuous random variable X is a random variable that takes all values in an interval or a set of intervals. The distribution of a continuous
CIVL Continuous Distributions
 CIVL 3103 Continuous Distributions Learning Objectives - Continuous Distributions Define continuous distributions, and identify common distributions applicable to engineering problems. Identify the appropriate
CIVL 3103 Continuous Distributions Learning Objectives - Continuous Distributions Define continuous distributions, and identify common distributions applicable to engineering problems. Identify the appropriate
SDS 321: Introduction to Probability and Statistics
 SDS 321: Introduction to Probability and Statistics Lecture 14: Continuous random variables Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin www.cs.cmu.edu/
SDS 321: Introduction to Probability and Statistics Lecture 14: Continuous random variables Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin www.cs.cmu.edu/
Bernoulli Trials, Binomial and Cumulative Distributions
 Bernoulli Trials, Binomial and Cumulative Distributions Sec 4.4-4.6 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy Poliak,
Bernoulli Trials, Binomial and Cumulative Distributions Sec 4.4-4.6 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy Poliak,
Continuous random variables
 Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Continuous random variables Continuous r.v. s take an uncountably infinite number of possible values. Examples: Heights of people Weights of apples Diameters of bolts Life lengths of light-bulbs We cannot
Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R
 Random Variables Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R As such, a random variable summarizes the outcome of an experiment
Random Variables Definition: A random variable X is a real valued function that maps a sample space S into the space of real numbers R. X : S R As such, a random variable summarizes the outcome of an experiment
Moments. Raw moment: February 25, 2014 Normalized / Standardized moment:
 Moments Lecture 10: Central Limit Theorem and CDFs Sta230 / Mth 230 Colin Rundel Raw moment: Central moment: µ n = EX n ) µ n = E[X µ) 2 ] February 25, 2014 Normalized / Standardized moment: µ n σ n Sta230
Moments Lecture 10: Central Limit Theorem and CDFs Sta230 / Mth 230 Colin Rundel Raw moment: Central moment: µ n = EX n ) µ n = E[X µ) 2 ] February 25, 2014 Normalized / Standardized moment: µ n σ n Sta230
Probability and Distributions
 Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Probability and Distributions What is a statistical model? A statistical model is a set of assumptions by which the hypothetical population distribution of data is inferred. It is typically postulated
Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is
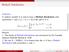 Weibull Distribution Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is { α β x α 1 e f (x; α, β) = α (x/β)α x 0 0 x < 0 Remark:
Weibull Distribution Definition A random variable X is said to have a Weibull distribution with parameters α and β (α > 0, β > 0) if the pdf of X is { α β x α 1 e f (x; α, β) = α (x/β)α x 0 0 x < 0 Remark:
Probability Distributions for Continuous Variables. Probability Distributions for Continuous Variables
 Probability Distributions for Continuous Variables Probability Distributions for Continuous Variables Let X = lake depth at a randomly chosen point on lake surface If we draw the histogram so that the
Probability Distributions for Continuous Variables Probability Distributions for Continuous Variables Let X = lake depth at a randomly chosen point on lake surface If we draw the histogram so that the
Continuous Distributions
 A normal distribution and other density functions involving exponential forms play the most important role in probability and statistics. They are related in a certain way, as summarized in a diagram later
A normal distribution and other density functions involving exponential forms play the most important role in probability and statistics. They are related in a certain way, as summarized in a diagram later
Inference for Proportions, Variance and Standard Deviation
 Inference for Proportions, Variance and Standard Deviation Sections 7.10 & 7.6 Cathy Poliak, Ph.D. cathy@math.uh.edu Office Fleming 11c Department of Mathematics University of Houston Lecture 12 Cathy
Inference for Proportions, Variance and Standard Deviation Sections 7.10 & 7.6 Cathy Poliak, Ph.D. cathy@math.uh.edu Office Fleming 11c Department of Mathematics University of Houston Lecture 12 Cathy
Estimation and Confidence Intervals
 Estimation and Confidence Intervals Sections 7.1-7.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 17-3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
Estimation and Confidence Intervals Sections 7.1-7.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 17-3339 Cathy Poliak, Ph.D. cathy@math.uh.edu
Random Variables and Their Distributions
 Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Chapter 3 Random Variables and Their Distributions A random variable (r.v.) is a function that assigns one and only one numerical value to each simple event in an experiment. We will denote r.vs by capital
Let X be a continuous random variable, < X < f(x) is the so called probability density function (pdf) if
 University of California, Los Angeles Department of Statistics Statistics 1A Instructor: Nicolas Christou Continuous probability distributions Let X be a continuous random variable, < X < f(x) is the so
University of California, Los Angeles Department of Statistics Statistics 1A Instructor: Nicolas Christou Continuous probability distributions Let X be a continuous random variable, < X < f(x) is the so
A Probability Primer. A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes.
 A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
Exponential & Gamma Distributions
 Exponential & Gamma Distributions Engineering Statistics Section 4.4 Josh Engwer TTU 7 March 26 Josh Engwer (TTU) Exponential & Gamma Distributions 7 March 26 / 2 PART I PART I: EXPONENTIAL DISTRIBUTION
Exponential & Gamma Distributions Engineering Statistics Section 4.4 Josh Engwer TTU 7 March 26 Josh Engwer (TTU) Exponential & Gamma Distributions 7 March 26 / 2 PART I PART I: EXPONENTIAL DISTRIBUTION
Lecture 4. Continuous Random Variables and Transformations of Random Variables
 Math 408 - Mathematical Statistics Lecture 4. Continuous Random Variables and Transformations of Random Variables January 25, 2013 Konstantin Zuev (USC) Math 408, Lecture 4 January 25, 2013 1 / 13 Agenda
Math 408 - Mathematical Statistics Lecture 4. Continuous Random Variables and Transformations of Random Variables January 25, 2013 Konstantin Zuev (USC) Math 408, Lecture 4 January 25, 2013 1 / 13 Agenda
Chapter 2. Continuous random variables
 Chapter 2 Continuous random variables Outline Review of probability: events and probability Random variable Probability and Cumulative distribution function Review of discrete random variable Introduction
Chapter 2 Continuous random variables Outline Review of probability: events and probability Random variable Probability and Cumulative distribution function Review of discrete random variable Introduction
SDS 321: Introduction to Probability and Statistics
 SDS 321: Introduction to Probability and Statistics Lecture 17: Continuous random variables: conditional PDF Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin
SDS 321: Introduction to Probability and Statistics Lecture 17: Continuous random variables: conditional PDF Purnamrita Sarkar Department of Statistics and Data Science The University of Texas at Austin
Math438 Actuarial Probability
 Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
Math438 Actuarial Probability Jinguo Lian Department of Math and Stats Jan. 22, 2016 Continuous Random Variables-Part I: Definition A random variable X is continuous if its set of possible values is an
BMIR Lecture Series on Probability and Statistics Fall, 2015 Uniform Distribution
 Lecture #5 BMIR Lecture Series on Probability and Statistics Fall, 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University s 5.1 Definition ( ) A continuous random
Lecture #5 BMIR Lecture Series on Probability and Statistics Fall, 2015 Department of Biomedical Engineering and Environmental Sciences National Tsing Hua University s 5.1 Definition ( ) A continuous random
Chapter 1: Revie of Calculus and Probability
 Chapter 1: Revie of Calculus and Probability Refer to Text Book: Operations Research: Applications and Algorithms By Wayne L. Winston,Ch. 12 Operations Research: An Introduction By Hamdi Taha, Ch. 12 OR441-Dr.Khalid
Chapter 1: Revie of Calculus and Probability Refer to Text Book: Operations Research: Applications and Algorithms By Wayne L. Winston,Ch. 12 Operations Research: An Introduction By Hamdi Taha, Ch. 12 OR441-Dr.Khalid
Topic 4: Continuous random variables
 Topic 4: Continuous random variables Course 003, 2018 Page 0 Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative
Topic 4: Continuous random variables Course 003, 2018 Page 0 Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative
Topic 4: Continuous random variables
 Topic 4: Continuous random variables Course 3, 216 Page Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative function
Topic 4: Continuous random variables Course 3, 216 Page Continuous random variables Definition (Continuous random variable): An r.v. X has a continuous distribution if there exists a non-negative function
Chapter 5. Chapter 5 sections
 1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Ching-Han Hsu, BMES, National Tsing Hua University c 2015 by Ching-Han Hsu, Ph.D., BMIR Lab. = a + b 2. b a. x a b a = 12
 Lecture 5 Continuous Random Variables BMIR Lecture Series in Probability and Statistics Ching-Han Hsu, BMES, National Tsing Hua University c 215 by Ching-Han Hsu, Ph.D., BMIR Lab 5.1 1 Uniform Distribution
Lecture 5 Continuous Random Variables BMIR Lecture Series in Probability and Statistics Ching-Han Hsu, BMES, National Tsing Hua University c 215 by Ching-Han Hsu, Ph.D., BMIR Lab 5.1 1 Uniform Distribution
Chapter 4 - Lecture 3 The Normal Distribution
 Chapter 4 - Lecture 3 The October 28th, 2009 Chapter 4 - Lecture 3 The Standard Chapter 4 - Lecture 3 The Standard Normal distribution is a statistical unicorn It is the most important distribution in
Chapter 4 - Lecture 3 The October 28th, 2009 Chapter 4 - Lecture 3 The Standard Chapter 4 - Lecture 3 The Standard Normal distribution is a statistical unicorn It is the most important distribution in
Continuous Random Variables and Probability Distributions
 Continuous Random Variables and Probability Distributions Instructor: Lingsong Zhang 1 4.1 Probability Density Functions Probability Density Functions Recall from Chapter 3 that a random variable X is
Continuous Random Variables and Probability Distributions Instructor: Lingsong Zhang 1 4.1 Probability Density Functions Probability Density Functions Recall from Chapter 3 that a random variable X is
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models
 System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 29, 2014 Introduction Introduction The world of the model-builder
System Simulation Part II: Mathematical and Statistical Models Chapter 5: Statistical Models Fatih Cavdur fatihcavdur@uludag.edu.tr March 29, 2014 Introduction Introduction The world of the model-builder
Determining the Spread of a Distribution Variance & Standard Deviation
 Determining the Spread of a Distribution Variance & Standard Deviation 1.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Department of Mathematics University of Houston Lecture 3 Lecture 3 1 / 32 Outline 1 Describing
Determining the Spread of a Distribution Variance & Standard Deviation 1.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Department of Mathematics University of Houston Lecture 3 Lecture 3 1 / 32 Outline 1 Describing
Determining the Spread of a Distribution
 Determining the Spread of a Distribution 1.3-1.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Department of Mathematics University of Houston Lecture 3-2311 Lecture 3-2311 1 / 58 Outline 1 Describing Quantitative
Determining the Spread of a Distribution 1.3-1.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Department of Mathematics University of Houston Lecture 3-2311 Lecture 3-2311 1 / 58 Outline 1 Describing Quantitative
Probability and Statistics Concepts
 University of Central Florida Computer Science Division COT 5611 - Operating Systems. Spring 014 - dcm Probability and Statistics Concepts Random Variable: a rule that assigns a numerical value to each
University of Central Florida Computer Science Division COT 5611 - Operating Systems. Spring 014 - dcm Probability and Statistics Concepts Random Variable: a rule that assigns a numerical value to each
Mathematical statistics
 October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
October 1 st, 2018 Lecture 11: Sufficient statistic Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation
Chapter 2 Continuous Distributions
 Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
Chapter Continuous Distributions Continuous random variables For a continuous random variable X the probability distribution is described by the probability density function f(x), which has the following
Basics of Stochastic Modeling: Part II
 Basics of Stochastic Modeling: Part II Continuous Random Variables 1 Sandip Chakraborty Department of Computer Science and Engineering, INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR August 10, 2016 1 Reference
Basics of Stochastic Modeling: Part II Continuous Random Variables 1 Sandip Chakraborty Department of Computer Science and Engineering, INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR August 10, 2016 1 Reference
Determining the Spread of a Distribution
 Determining the Spread of a Distribution 1.3-1.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Department of Mathematics University of Houston Lecture 3-2311 Lecture 3-2311 1 / 58 Outline 1 Describing Quantitative
Determining the Spread of a Distribution 1.3-1.5 Cathy Poliak, Ph.D. cathy@math.uh.edu Department of Mathematics University of Houston Lecture 3-2311 Lecture 3-2311 1 / 58 Outline 1 Describing Quantitative
Probability Midterm Exam 2:15-3:30 pm Thursday, 21 October 1999
 Name: 2:15-3:30 pm Thursday, 21 October 1999 You may use a calculator and your own notes but may not consult your books or neighbors. Please show your work for partial credit, and circle your answers.
Name: 2:15-3:30 pm Thursday, 21 October 1999 You may use a calculator and your own notes but may not consult your books or neighbors. Please show your work for partial credit, and circle your answers.
Math Review Sheet, Fall 2008
 1 Descriptive Statistics Math 3070-5 Review Sheet, Fall 2008 First we need to know about the relationship among Population Samples Objects The distribution of the population can be given in one of the
1 Descriptive Statistics Math 3070-5 Review Sheet, Fall 2008 First we need to know about the relationship among Population Samples Objects The distribution of the population can be given in one of the
Chapter 4: Continuous Random Variables and Probability Distributions
 Chapter 4: and Probability Distributions Walid Sharabati Purdue University February 14, 2014 Professor Sharabati (Purdue University) Spring 2014 (Slide 1 of 37) Chapter Overview Continuous random variables
Chapter 4: and Probability Distributions Walid Sharabati Purdue University February 14, 2014 Professor Sharabati (Purdue University) Spring 2014 (Slide 1 of 37) Chapter Overview Continuous random variables
Chapter 3 Common Families of Distributions
 Lecture 9 on BST 631: Statistical Theory I Kui Zhang, 9/3/8 and 9/5/8 Review for the previous lecture Definition: Several commonly used discrete distributions, including discrete uniform, hypergeometric,
Lecture 9 on BST 631: Statistical Theory I Kui Zhang, 9/3/8 and 9/5/8 Review for the previous lecture Definition: Several commonly used discrete distributions, including discrete uniform, hypergeometric,
Part IA Probability. Definitions. Based on lectures by R. Weber Notes taken by Dexter Chua. Lent 2015
 Part IA Probability Definitions Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Part IA Probability Definitions Based on lectures by R. Weber Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures.
Continuous random variables and probability distributions
 and probability distributions Sta. 113 Chapter 4 of Devore March 12, 2010 Table of contents 1 2 Mathematical definition Definition A random variable X is continuous if its set of possible values is an
and probability distributions Sta. 113 Chapter 4 of Devore March 12, 2010 Table of contents 1 2 Mathematical definition Definition A random variable X is continuous if its set of possible values is an
1.1 Review of Probability Theory
 1.1 Review of Probability Theory Angela Peace Biomathemtics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
1.1 Review of Probability Theory Angela Peace Biomathemtics II MATH 5355 Spring 2017 Lecture notes follow: Allen, Linda JS. An introduction to stochastic processes with applications to biology. CRC Press,
IE 230 Probability & Statistics in Engineering I. Closed book and notes. 60 minutes.
 Closed book and notes. 60 minutes. A summary table of some univariate continuous distributions is provided. Four Pages. In this version of the Key, I try to be more complete than necessary to receive full
Closed book and notes. 60 minutes. A summary table of some univariate continuous distributions is provided. Four Pages. In this version of the Key, I try to be more complete than necessary to receive full
HW7 Solutions. f(x) = 0 otherwise. 0 otherwise. The density function looks like this: = 20 if x [10, 90) if x [90, 100]
![HW7 Solutions. f(x) = 0 otherwise. 0 otherwise. The density function looks like this: = 20 if x [10, 90) if x [90, 100] HW7 Solutions. f(x) = 0 otherwise. 0 otherwise. The density function looks like this: = 20 if x [10, 90) if x [90, 100]](/thumbs/76/73074579.jpg) HW7 Solutions. 5 pts.) James Bond James Bond, my favorite hero, has again jumped off a plane. The plane is traveling from from base A to base B, distance km apart. Now suppose the plane takes off from
HW7 Solutions. 5 pts.) James Bond James Bond, my favorite hero, has again jumped off a plane. The plane is traveling from from base A to base B, distance km apart. Now suppose the plane takes off from
18.440: Lecture 28 Lectures Review
 18.440: Lecture 28 Lectures 18-27 Review Scott Sheffield MIT Outline Outline It s the coins, stupid Much of what we have done in this course can be motivated by the i.i.d. sequence X i where each X i is
18.440: Lecture 28 Lectures 18-27 Review Scott Sheffield MIT Outline Outline It s the coins, stupid Much of what we have done in this course can be motivated by the i.i.d. sequence X i where each X i is
Continuous Distributions
 Chapter 3 Continuous Distributions 3.1 Continuous-Type Data In Chapter 2, we discuss random variables whose space S contains a countable number of outcomes (i.e. of discrete type). In Chapter 3, we study
Chapter 3 Continuous Distributions 3.1 Continuous-Type Data In Chapter 2, we discuss random variables whose space S contains a countable number of outcomes (i.e. of discrete type). In Chapter 3, we study
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Data Modeling & Analysis Techniques. Probability & Statistics. Manfred Huber
 Data Modeling & Analysis Techniques Probability & Statistics Manfred Huber 2017 1 Probability and Statistics Probability and statistics are often used interchangeably but are different, related fields
Data Modeling & Analysis Techniques Probability & Statistics Manfred Huber 2017 1 Probability and Statistics Probability and statistics are often used interchangeably but are different, related fields
Continuous Random Variables
 MATH 38 Continuous Random Variables Dr. Neal, WKU Throughout, let Ω be a sample space with a defined probability measure P. Definition. A continuous random variable is a real-valued function X defined
MATH 38 Continuous Random Variables Dr. Neal, WKU Throughout, let Ω be a sample space with a defined probability measure P. Definition. A continuous random variable is a real-valued function X defined
Chapter 4 Multiple Random Variables
 Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
Review for the previous lecture Theorems and Examples: How to obtain the pmf (pdf) of U = g ( X Y 1 ) and V = g ( X Y) Chapter 4 Multiple Random Variables Chapter 43 Bivariate Transformations Continuous
Exponential Distribution and Poisson Process
 Exponential Distribution and Poisson Process Stochastic Processes - Lecture Notes Fatih Cavdur to accompany Introduction to Probability Models by Sheldon M. Ross Fall 215 Outline Introduction Exponential
Exponential Distribution and Poisson Process Stochastic Processes - Lecture Notes Fatih Cavdur to accompany Introduction to Probability Models by Sheldon M. Ross Fall 215 Outline Introduction Exponential
Why study probability? Set theory. ECE 6010 Lecture 1 Introduction; Review of Random Variables
 ECE 6010 Lecture 1 Introduction; Review of Random Variables Readings from G&S: Chapter 1. Section 2.1, Section 2.3, Section 2.4, Section 3.1, Section 3.2, Section 3.5, Section 4.1, Section 4.2, Section
ECE 6010 Lecture 1 Introduction; Review of Random Variables Readings from G&S: Chapter 1. Section 2.1, Section 2.3, Section 2.4, Section 3.1, Section 3.2, Section 3.5, Section 4.1, Section 4.2, Section
p. 6-1 Continuous Random Variables p. 6-2
 Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability (>). Often, there is interest in random variables
Continuous Random Variables Recall: For discrete random variables, only a finite or countably infinite number of possible values with positive probability (>). Often, there is interest in random variables
Special distributions
 Special distributions August 22, 2017 STAT 101 Class 4 Slide 1 Outline of Topics 1 Motivation 2 Bernoulli and binomial 3 Poisson 4 Uniform 5 Exponential 6 Normal STAT 101 Class 4 Slide 2 What distributions
Special distributions August 22, 2017 STAT 101 Class 4 Slide 1 Outline of Topics 1 Motivation 2 Bernoulli and binomial 3 Poisson 4 Uniform 5 Exponential 6 Normal STAT 101 Class 4 Slide 2 What distributions
MATH : EXAM 2 INFO/LOGISTICS/ADVICE
 MATH 3342-004: EXAM 2 INFO/LOGISTICS/ADVICE INFO: WHEN: Friday (03/11) at 10:00am DURATION: 50 mins PROBLEM COUNT: Appropriate for a 50-min exam BONUS COUNT: At least one TOPICS CANDIDATE FOR THE EXAM:
MATH 3342-004: EXAM 2 INFO/LOGISTICS/ADVICE INFO: WHEN: Friday (03/11) at 10:00am DURATION: 50 mins PROBLEM COUNT: Appropriate for a 50-min exam BONUS COUNT: At least one TOPICS CANDIDATE FOR THE EXAM:
CSE 312, 2017 Winter, W.L. Ruzzo. 7. continuous random variables
 CSE 312, 2017 Winter, W.L. Ruzzo 7. continuous random variables The new bit continuous random variables Discrete random variable: values in a finite or countable set, e.g. X {1,2,..., 6} with equal probability
CSE 312, 2017 Winter, W.L. Ruzzo 7. continuous random variables The new bit continuous random variables Discrete random variable: values in a finite or countable set, e.g. X {1,2,..., 6} with equal probability
Sampling Distributions
 Sampling Distributions In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of
Sampling Distributions In statistics, a random sample is a collection of independent and identically distributed (iid) random variables, and a sampling distribution is the distribution of a function of
Probability Review. Yutian Li. January 18, Stanford University. Yutian Li (Stanford University) Probability Review January 18, / 27
 Probability Review Yutian Li Stanford University January 18, 2018 Yutian Li (Stanford University) Probability Review January 18, 2018 1 / 27 Outline 1 Elements of probability 2 Random variables 3 Multiple
Probability Review Yutian Li Stanford University January 18, 2018 Yutian Li (Stanford University) Probability Review January 18, 2018 1 / 27 Outline 1 Elements of probability 2 Random variables 3 Multiple
Continuous Random Variables. and Probability Distributions. Continuous Random Variables and Probability Distributions ( ) ( ) Chapter 4 4.
 UCLA STAT 11 A Applied Probability & Statistics for Engineers Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Christopher Barr University of California, Los Angeles,
UCLA STAT 11 A Applied Probability & Statistics for Engineers Instructor: Ivo Dinov, Asst. Prof. In Statistics and Neurology Teaching Assistant: Christopher Barr University of California, Los Angeles,
MAS1302 Computational Probability and Statistics
 MAS1302 Computational Probability and Statistics April 23, 2008 3. Simulating continuous random behaviour 3.1 The Continuous Uniform U(0,1) Distribution We have already used this random variable a great
MAS1302 Computational Probability and Statistics April 23, 2008 3. Simulating continuous random behaviour 3.1 The Continuous Uniform U(0,1) Distribution We have already used this random variable a great
Hypergeometric, Poisson & Joint Distributions
 Hypergeometric, Poisson & Joint Distributions Sec 4.7-4.9 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 6-3339 Cathy Poliak, Ph.D.
Hypergeometric, Poisson & Joint Distributions Sec 4.7-4.9 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 6-3339 Cathy Poliak, Ph.D.
Review for the previous lecture
 Lecture 1 and 13 on BST 631: Statistical Theory I Kui Zhang, 09/8/006 Review for the previous lecture Definition: Several discrete distributions, including discrete uniform, hypergeometric, Bernoulli,
Lecture 1 and 13 on BST 631: Statistical Theory I Kui Zhang, 09/8/006 Review for the previous lecture Definition: Several discrete distributions, including discrete uniform, hypergeometric, Bernoulli,
Chapter 4. Continuous Random Variables
 Chapter 4. Continuous Random Variables Review Continuous random variable: A random variable that can take any value on an interval of R. Distribution: A density function f : R R + such that 1. non-negative,
Chapter 4. Continuous Random Variables Review Continuous random variable: A random variable that can take any value on an interval of R. Distribution: A density function f : R R + such that 1. non-negative,
Math 2311 Sections 4.1, 4.2 and 4.3
 Math 2311 Sections 4.1, 4.2 and 4.3 4.1 - Density Curves What do we know about density curves? Example: Suppose we have a density curve defined for defined by the line y = x. Sketch: What percent of observations
Math 2311 Sections 4.1, 4.2 and 4.3 4.1 - Density Curves What do we know about density curves? Example: Suppose we have a density curve defined for defined by the line y = x. Sketch: What percent of observations
Test 1 Review. Review. Cathy Poliak, Ph.D. Office in Fleming 11c (Department Reveiw of Mathematics University of Houston Exam 1)
 Test 1 Review Review Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Exam 1 Review Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c
Test 1 Review Review Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Exam 1 Review Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c
Distributions of Functions of Random Variables. 5.1 Functions of One Random Variable
 Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Distributions of Functions of Random Variables 5.1 Functions of One Random Variable 5.2 Transformations of Two Random Variables 5.3 Several Random Variables 5.4 The Moment-Generating Function Technique
Continuous random variables
 Continuous random variables CE 311S What was the difference between discrete and continuous random variables? The possible outcomes of a discrete random variable (finite or infinite) can be listed out;
Continuous random variables CE 311S What was the difference between discrete and continuous random variables? The possible outcomes of a discrete random variable (finite or infinite) can be listed out;
