Some Applications of the Mellin Transform to Asymptotics of Series P. A. Martin
|
|
|
- Penelope Davidson
- 6 years ago
- Views:
Transcription
1 In: Inverse Scattering and Potential Problems in Mathematical Physics (ed. R. E. Kleinman, R. Kress and E. Martensen), Peter Lang, Frankfurt, 1995, pp Some Applications of the Mellin Transform to Asymptotics of Series P. A. Martin Department of Mathematics, University of Manchester Manchester M13 9PL, England Abstract Mellin transforms are used to find asymptotic approximations for functions defined by series. Such approximations were needed in the analysis of a water-wave problem, namely, the trapping of waves by submerged plates. The method seems to have wider applicability. 1 Introduction It is well known that asymptotic approximations for functions defined by integrals can often be found using Mellin transforms [2], [8]. Analogous results can also be sought for functions defined by series, f(x) = c n u(µ n x), (1) where c n and µ n are known constants and u(y) is defined for all y >. We assume that the series is convergent for all x >, and seek the asymptotic behaviour of f(x) as x +. Ramanujan [1, Ch. 15] considered some problems of this type, such as µ n = n p and u(x) = e x, using the Euler- Maclaurin formula. In (1), u(y) is sampled at points y = µ n x; we describe such points, and the series (1), as separable. Separable series can often be analysed using Mellin transforms; this method was used to confirm some of Ramanujan s results [1]. More generally, we study non-separable series f(x) = c n u(λ n (x)), (2)
2 2 P. A. Martin where u(y) is sampled at non-separable points, y = λ n (x). We find asymptotic approximations to such series by first finding suitable separable approximations to λ n (x), and then use Mellin transforms. Both separable and non-separable series arise in waveguide problems. In this context, the limit 1/h is of interest, where the walls are at y = and y = h. A typical problem in acoustics concerns an infinite bifurcated waveguide, with a semi-infinite plate (the septum) along y = d, x < (closed geometry). A waveguide mode is incident from x = in the region < y < d; it is partially reflected at the end of the septum and partially transmitted into the rest of the guide. The same problem can be considered when h =. This corresponds to an open-ended waveguide (open geometry). The connection between open-geometry and related closed-geometry problems is of interest because the latter are often easier to solve. The same closed geometry has been used by Linton & Evans [4] in the context of linear water waves. The governing equation is the modified Helmholtz equation ( 2 l 2 )φ =, where l is the positive wavenumber in a direction perpendicular to the xy-plane. The septum and the bottom (y = h) are hard, whereas the boundary condition on the free surface y = is Kφ + φ/ y =, where K is another positive wavenumber. Two more wavenumbers, k and k, are defined to be the unique positive real roots of K = k tanh kd and K = k tanh k h, (3) respectively, and then l is chosen to satisfy K < k < l < k. Hence, a surface wave incident from x = will be totally reflected by the end of the plate. Linton & Evans [4] gave an explicit formula for the argument of the (complex) reflection coefficient, which they used to estimate the frequencies of waves trapped above a long horizontal submerged plate. We examine their formula below, and extract the limiting formula for deep water (h ). Indeed, it was a study of the limiting problem that originally motivated the present analysis. 2 Mellin transforms To find asymptotic approximations for separable series (1), we use the Mellin transform. The Mellin transform of a function f, and its inverse, are f(z) = f(x)x z 1 dx and f(x) = 1 2πi c+i c i f(z)x z dz, respectively. Typically, f(z) will be an analytic function of z within a strip, a < σ < b, say, where z = σ + iτ; within this strip, f(z) as τ ; and a < c < b. We can obtain an asymptotic expansion of f(x) for small
3 Asymptotic Approximations 3 x by moving the inversion contour to the left; each term arises as a residue contribution from an appropriate pole in the analytic continuation of f(z) into σ a. Specifically, we have the following result. Theorem 1 ([6, p. 7]) Suppose that f(z) is analytic in a left-hand plane, σ a, apart from poles at z = a m, m =, 1, 2,...; let the principal part of the Laurent expansion of f(z) about z = a m be given by N(m) n= A mn ( 1) n n! (z + a m ) n+1. Assume that f(σ +iτ) as τ for a σ a, and that f(a +iτ) is integrable for τ <. Then, if a can be chosen so that Re (a M+1 ) < a < Re (a M ) for some M, f(x) has the asymptotic expansion f(x) N(m) m= n= A mn x am (log x) n as x +. For more information on Mellin transforms, see [2, Ch. 4], [5], [8, Ch. 3]. 3 Separable series: a problem of Ramanujan Example 1. Let ν be a real parameter. Find the behaviour of f ν (x) = n ν 1 e nx as x +. We can take c n = n ν 1, µ n = n and u(x) = e x. Hence f ν (z) = ζ(z ν + 1)Γ(z), (4) where Γ(z) is the the gamma function and ζ(z) is the Riemann zeta function. It is known that Γ(z) is an analytic function of z, apart from simple poles at z = N with residue ( 1) N /N!, for N =, 1, 2,.... It is also known that ζ(z) is analytic for all z, apart from a simple pole at z = 1; near z = 1, ζ(z) (z 1) 1 + γ, where γ = is Euler s constant. Let us suppose that < ν < 1. Then, fν (z) is analytic for σ > ν. We choose the inversion contour along σ = c, with c > ν. Moving the contour to the left, we pick up a residue contribution from the simple pole at z = ν: this gives the leading contribution as f ν (x) x ν Γ(ν) as x +. If we move
4 4 P. A. Martin the inversion contour further to the left, we formally obtain Ramanujan s expansion [1, p. 36], f ν (x) x ν Γ(ν) + ( x) m ζ(1 ν m) as x. (5) m! m= The fact that this is an asymptotic expansion follows from Theorem 1 and the known properties of ζ(z) and Γ(z) as τ. Actually, (5) is valid for all values of ν, apart from ν = N. In these cases, there is a double pole at z = N, giving a term proportional to x N log x. 4 Non-separable series: a model problem Let us consider some non-separable series involving the roots of the transcendental equation (3) 2. This has real roots ±k and an infinite number of pure imaginary roots, ±ik n, n = 1, 2,...; thus, k n are the positive real roots of K + k n tan k n h =, n = 1, 2,... ; (6) they are ordered so that (n 1 2 )π < k nh < nπ. In the context of water-wave problems, h is the constant water depth and K is the positive real wavenumber. We are interested in the deep-water limit, h. In dimensionless variables, we define x = (Kh) 1 and λ n (x) = k n h, so that cos λ n (x) + xλ n (x) sin λ n (x) = with (7) (n 1 2 )π < λ n(x) < nπ, n = 1, 2,.... (8) It is straightforward to show that λ n (x) behaves as follows: as n for fixed x, and λ n (x) nπ (nπx) 1 (x 1 3 )(nπx) 3 (9) λ n (x) (n 1 2 )π(1 + x + x2 ) (1) as x for fixed n. It is this non-uniform behaviour that causes difficulties. To find some uniform approximations, we rewrite the definition (7) as sin ν n (x) x{µ n + ν n (x)} cos ν n (x) =, where (11) λ n (x) = µ n + ν n (x), (12) µ n = (n 1 2 )π and < ν n < π/2. Discarding the second term inside the braces in (11) (this is certainly reasonable for large n), we obtain ν n (x) tan 1 (µ n x) = ν (1) n (x), (13)
5 Asymptotic Approximations 5 say, which is a separable approximation to ν n (x). The approximation λ n (x) µ n + ν n (1) (x) agrees with the first two terms in (9) and with the first two terms in (1). This approximation can be improved by iteration: replace ν n (x) by ν n (1) (x) inside the braces in (11) to give ν n (x) tan 1 {µ n x + x tan 1 (µ n x)} = ν (2) n (x), (14) say. Then, the approximation λ n (x) µ n + ν n (2) (x) agrees with the threeterm asymptotics in (9) and in (1). Example 2. Find the behaviour of ( 1 f(x) = π λ n (x) 1 ) as x +. nπ The series converges for all x ; in fact, using the bounds (8), we have < f(x) < 2 log 2 for x >. As λ n () = (n 1 2 )π = µ n, for all n, write S(x) = π f(x) = 2 log 2 + S(x), where (15) s n (x) and s n (x) = 1 λ n (x) 1 µ n. We have S(x) as x and S(x) is bounded as x, whence S(z) is analytic in a strip δ < σ <, where δ >. In fact, we note that s n (x) = O(x) as x and is bounded as x, whence s n (z) is analytic for 1 < σ < ; thus, we expect that δ = 1. We shall treat S(x) using our separable approximations for ν n (x). Since the latter may not be appropriate for small values of n, we split the sum: S(x) = π s n (x) + π n=m+1 say, where M is fixed. For S M, we can use (1) to give S M (x) π µ 1 n {(1 + x + x 2 ) 1 1} = πx s n (x) = S M (x) + S M (x), (16) µ 1 n + O(x 3 ) (17) as x. For SM, we start with s n(x) µ 2 n (ν n νn/µ 2 n ), since ν n /µ n is small. Next, we approximate ν n by ν n (2) and νn 2 by (ν n (1) ) 2. Finally, since ν n (1) /µ n is small, we can approximate ν n (2) using the Taylor approximation tan 1 (X + H) tan 1 X + H(1 + X 2 ) 1 (18)
6 6 P. A. Martin for small H; the result is s n (x) µ 2 n {ν (1) n (x)+xν n (1) (x) [1+(µ n x) 2 ] 1 µ 1 n [ν (1) n (x)] 2 } = s (1) n (x), say. This is our final separable approximation for s n (x). We find that the error, s n s (1) n is O(n 4 ) as n for fixed x, and is O(x 3 ) as x for fixed n. The Mellin transform of s (1) n (x) is given by s (1) n ũ 1 (z) = ũ 2 (z) = (z) = µ z 2 n ũ 1 (z) + µ z 3 n ũ 2 (z), where (19) x z 1 tan 1 x dx = π 2z sin [π(z 1)/2], (2) x z 1 {tan 1 x x(1 + x 2 ) 1 } tan 1 x dx. (21) ũ 1 (z) is analytic for 1 < σ < and ũ 2 (z) is analytic for 4 < σ <. Summing over n, using (16) and (19), gives where, by definition, S M (z) ψ M (z + 2)ũ 1 (z) + ψ M (z + 3)ũ 2 (z), (22) ψ M (z) = π n=m+1 µ z n = π 1 z (2 z 1)ζ(z) π ψ M (z) is analytic for all z, apart from a simple pole at z = 1; ψ M (z) (z 1) 1 + γ + log (4/π) π µ z n. (23) µ 1 n near z = 1. (24) To invert S M (z), we start with the inversion contour to the left of z =, and then move it further to the left; thus, we are interested in singularities in σ <. Consider the first term on the right-hand side of (22). From (2), we see that ũ 1 (z) has simple poles at z = 1, 3,...; near z = 1, we have ũ 1 (z) (z + 1) Hence, ψ M (z + 2)ũ 1 (z) has a double pole at z = 1, giving terms proportional to x log x and x in SM (x). The next singularity at z = 3 gives a term in x 3, but we have already made errors of this order when we replaced s n (x) by s (1) n (x). The second term on the right-hand side of (22) is analytic for 4 < σ <, apart from a simple pole at z = 2: this gives a term in x 2. Combining these results gives { } SM (x) = x log x x 1 + γ + log (4/π) π + O(x 2 ) µ 1 n
7 Asymptotic Approximations 7 as x. Finally, using (16) and (17), we obtain S(x) = x log x x{1 + γ + log (4/π)} + O(x 2 ), as x ; (25) f(x) is given by (15). Note that this result does not depend on M; see (16). 5 A problem of Linton and Evans In this section, we consider a water-wave problem described in 1 and solved by Linton & Evans [4]. They calculate a certain complex reflection coefficient; its argument is proportional to E(h) = tan 1 ( α 1 l 2 k 2 ) tan 1 (l/α) 1 2 π (α/π)l + T, (26) where L = c log (h/c) + d log (h/d) and T is the sum { } tan 1 α l2 + n 2 π 2 /c α 2 tan 1 + tan 1 α. l2 + kn 2 l2 + κ 2 n The parameters d, l, K and κ n (n = 1, 2,...) are fixed. k is defined by (3) 2 and α = k 2 l 2, where k is defined by (3) 1. We have c = h d > and K < k < l < k. Example 3. Find lim E(h) = E, (27) h say. This corresponds, physically, to solving the problem of Linton & Evans [4] when the water is infinitely deep. Note that, as h varies, so too do k, k n and c; all other parameters remain unchanged. To begin with, (3) 2 shows that k h Kh(1 + 2e 2Kh ) as Kh, so we can replace k by K in the first term of E(h), as h. It is elementary to show that L = d(log h + 1 log d) + o(1) as h. For T, we note that the arguments of the three inverse tangents behave like αc/(nπ), αh/(nπ) and αd/(nπ), respectively, as n, and so we can write T = T 1 T 2 + T 3, where ( ) } T 1 = {tan 1 α αc, (28) l2 + n 2 π 2 /c 2 nπ ( ) } T 2 = {tan 1 α αh, (29) l2 + kn 2 nπ ( ) } T 3 = {tan 1 α αd, (3) l2 + κ 2 nπ n
8 8 P. A. Martin using c h + d =. Note that T 1 is a separable series, T 2 is a non-separable series and T 3 is independent of h. So, at this stage, we have E(h) = tan 1 [α(l 2 K 2 ) 1/2 ] tan 1 (l/α) (αd/π)(log h + 1 log d) + T 1 T 2 + T 3 + o(1) as h. Deep-water behaviour of T 1. From (28), we have T 1 = f(π/c), where f(x) is defined by (1) with c n = 1, ( ) u(x) = tan 1 α α (31) l2 + x 2 x and µ n = n. Proceeding as in 3, we obtain f(z) = ζ(z)ũ(z), where ũ(z) is analytic for 1 < σ < 3. We must find the singularities of ũ(z) in σ 1. For 1 < σ < 3, we integrate by parts to give f(z) = (α/z)ζ(z)ũ 1 (z), (32) where ũ 1 (z) = { x z x x2 + l 2 (x 2 + k 2 ) 1 } x 2 dx. (33) is analytic for 1 < σ < 3. It turns out that ũ 1 can be continued analytically into 2 < σ < 3, apart from a simple pole at z = 1; near z = 1, we find that ũ 1 (z) (z 1) 1 + Q, where Q = log (2/l) + (k/α) log [(k α)/l]. (34) Hence, (32), shows that f(z) has a double pole at z = 1, a simple pole at z =, and is otherwise analytic in 2 < σ < 3; near z = 1, f(z) α(1 + w) 1 (w 1 + γ)( w 1 + Q) α{ w 2 + w 1 (Q γ + 1)}, where w = z 1, whereas near z =, f(z) (α/z)ζ()ũ 1 () = 1 2 z 1 tan 1 (α/l). We can then move the inversion contour to the left of z =, giving f(x) = (α/x) log x + (α/x)(q γ + 1) 1 2 tan 1 (α/l) + o(1) as x. Replacing x by π/c, and expanding for large h gives T 1 = (αh/π){ log h + log π + Q γ + 1} 1 2 tan 1 (α/l) + (αd/π){log (h/π) Q γ} + o(1) as h. (35)
9 Asymptotic Approximations 9 Deep-water behaviour of T 2. As in Example 2, we expect the leading behaviour of the non-separable series T 2 to be given by (29) with k n h replaced by µ n = (n 1 2 )π. So, consider ( ) } T (1/h) = {tan 1 α αh. (36) l2 + µ 2 n/h 2 nπ We have T (x) = ( {tan 1 ) α l2 + µ 2 nx 2 } α + α µ n x x ( 1 1 ) ; µ n nπ the second sum is (2/π) log 2. Hence, T (x) = (2α/(πx)) log 2+f(x), where f(x) is the separable series (1), with c n = 1, µ n = (n 1 2 )π and u(x) is again given by (31). We obtain f(z) = π z (2 z 1)ζ(z)ũ(z) = (α/z)π z (2 z 1)ζ(z)ũ 1 (z), where ũ 1 (z) is defined by (33). Note that, unlike the function defined by (32), here, f(z) does not have a pole at z =. However, it does have a double pole at z = 1; near z = 1, f(z) (α/π){ (z 1) 2 + (z 1) 1 (Q γ log π 2 log 2)}. Hence T (x) = (α/π){x 1 log x + x 1 (Q γ log π)} + o(1) as x, and so, as h, we obtain T (1/h) = (α/π)h log h + (α/π)h(q γ log π) + o(1). (37) We now examine the difference between T 2 and T (1/h). Let T 4 = T 2 T (1/h) = t n, where (38) ( ) ( ) t n = tan 1 α tan 1 α. l2 + kn 2 l2 + µ 2 n/h 2 Clearly, t n = o(1) as h, for fixed n, so we have T 4 = t n + o(1) as h, n=m+1 where M is fixed (cf. (16)). Writing k n h = µ n + ν n, as in (12), we have l 2 + k 2 n 2 n + 2ν n µ n /h 2 as ν n /µ n is small, where 2 n = l 2 + µ 2 n/h 2. Hence, using the Taylor approximation (18), we find that t n αν n µ n h 2 n ( 2 n + α 2 ).
10 1 P. A. Martin Finally, we use the approximation (13), ν n ν n (1) giving t n (α/h)t (1) n (1/h), where = tan 1 (µ n /(Kh)), t (1) n (y) = µ ny tan 1 (µ n y/k) l2 + µ 2 ny 2 (k 2 + µ 2 ny 2 ), (39) using k 2 = α 2 + l 2. So, we have approximated T 4 by a separable series: T 4 = (α/h)t M (1/h) + o(1) as h, where (4) T M (x) = n=m+1 t (1) n (x) and t (1) n (x) is defined by (39). As t (1) n (x) 1 2 π(µ nx) 2 as x, we see that T M (z) is analytic in a strip β < σ < 2, for some β, so we can take the inversion contour just to the left of σ = 2. We have T M (z) = π 1 ψ M (z)ũ(z), where ψ M (z) is defined by (23) and ũ(z) = y z tan 1 (y/k) y2 + l 2 (y 2 + k 2 ) dy is analytic for 2 < σ < 2. Hence, T M (z) is analytic for 2 < σ < 2, apart from a simple pole at z = 1; using (24), we have T M (z) Lπ 1 (z 1) 1 near z = 1, where L = ũ(1) = y tan 1 (y/k) dy. (41) y2 + l 2 (y 2 + k 2 ) Hence, as the conditions of Theorem 1 are satisfied, we obtain T M (x) = L/(πx) + o(1) as x, whence (4) gives T 4 = (α/π)l + o(1) as h. Finally, we combine this result with (37) and (38) to give T 2 = (α/π){ h log h + h(q γ log π) L} + o(1) as h. (42) The integral defining L, (41), is not elementary. expressed in terms of dilogarithms [3]; we find that However, it can be αl = 1 4 π2 1 2 A log(k + K) A log(k K) δ tan 1 (ψ/α) L (43) where ψ = l 2 K 2, A = log((k α)/l), δ = tan 1 (ψ/k) and L = Li 2 (e A, δ) Li 2 (e A, π + δ). (44)
11 Asymptotic Approximations 11 Here, the dilogarithm is defined by Li 2 (z) = z log(1 w) dw w (45) for complex z, and Li 2 (r, θ) = Re { Li 2 (re iθ ) }. Synthesis. From (35) and (42), we have T 1 T 2 = (α/π){l + d(log h log π Q + γ)} 1 2 tan 1 (α/l) + o(1), (46) as h, so that the terms involving h and h log h in (35) and (42) cancel. Moreover, when (46) is substituted into (31), we see that the terms in log h cancel, leaving only bounded terms as h. Finally, substituting for Q and L, we obtain E = αd π { log ld 2π + γ 1 } + T 3 1 π L + 1 2π log k α l kd π log k α tan 1 α l ψ 1 l 2 tan 1 α log k + K k K 1 π tan 1 ψ K tan 1 ψ α. (47) This expression for E bears little resemblance to E(h); indeed, it is perhaps surprising to see terms involving products of logarithms and products of inverse tangents. Nevertheless, the result can be checked by solving the deep-water problem directly. This has been done by Parsons [7], using the Wiener-Hopf technique; the two approaches yield the same result. References [1] B.C. Berndt, Ramanujan s Notebooks, Part II, Springer, [2] N. Bleistein & R.A. Handelsman, Asymptotic Expansions of Integrals, Holt, Rinehart & Winston, New York, [3] L. Lewin, Dilogarithms & Associated Functions, Macdonald, [4] C.M. Linton & D.V. Evans, Quart. J. Mech. Appl. Math. 44 (1991), [5] P.A. Martin, Proc. Roy. Soc. A 432 (1991), [6] F. Oberhettinger, Tables of Mellin Transforms, Springer, [7] N.F. Parsons, Ph.D. thesis, University of Manchester, in preparation. [8] R. Wong, Asymptotic Approximations of Integrals, Academic, 1989.
Mathematics 324 Riemann Zeta Function August 5, 2005
 Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Some Fun with Divergent Series
 Some Fun with Divergent Series 1. Preliminary Results We begin by examining the (divergent) infinite series S 1 = 1 + 2 + 3 + 4 + 5 + 6 + = k=1 k S 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + = k=1 k 2 (i)
Some Fun with Divergent Series 1. Preliminary Results We begin by examining the (divergent) infinite series S 1 = 1 + 2 + 3 + 4 + 5 + 6 + = k=1 k S 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + = k=1 k 2 (i)
Conformal maps. Lent 2019 COMPLEX METHODS G. Taylor. A star means optional and not necessarily harder.
 Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS
 MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS ABDUL HASSEN AND HIEU D. NGUYEN Abstract. This paper investigates a generalization the classical Hurwitz zeta function. It is shown that many of the properties
MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS ABDUL HASSEN AND HIEU D. NGUYEN Abstract. This paper investigates a generalization the classical Hurwitz zeta function. It is shown that many of the properties
2 Write down the range of values of α (real) or β (complex) for which the following integrals converge. (i) e z2 dz where {γ : z = se iα, < s < }
 Mathematical Tripos Part II Michaelmas term 2007 Further Complex Methods, Examples sheet Dr S.T.C. Siklos Comments and corrections: e-mail to stcs@cam. Sheet with commentary available for supervisors.
Mathematical Tripos Part II Michaelmas term 2007 Further Complex Methods, Examples sheet Dr S.T.C. Siklos Comments and corrections: e-mail to stcs@cam. Sheet with commentary available for supervisors.
THERMAL GROOVING BY SURFACE DIFFUSION: MULLINS REVISITED AND EXTENDED TO MULTIPLE GROOVES
 THERMAL GROOVING BY SURFACE DIFFUSION: MULLINS REVISITED AND EXTENDED TO MULTIPLE GROOVES P. A. MARTIN Department of Mathematical and Computer Sciences Colorado School of Mines, Golden, CO 841-1887, USA
THERMAL GROOVING BY SURFACE DIFFUSION: MULLINS REVISITED AND EXTENDED TO MULTIPLE GROOVES P. A. MARTIN Department of Mathematical and Computer Sciences Colorado School of Mines, Golden, CO 841-1887, USA
Math 185 Fall 2015, Sample Final Exam Solutions
 Math 185 Fall 2015, Sample Final Exam Solutions Nikhil Srivastava December 12, 2015 1. True or false: (a) If f is analytic in the annulus A = {z : 1 < z < 2} then there exist functions g and h such that
Math 185 Fall 2015, Sample Final Exam Solutions Nikhil Srivastava December 12, 2015 1. True or false: (a) If f is analytic in the annulus A = {z : 1 < z < 2} then there exist functions g and h such that
Problems for MATH-6300 Complex Analysis
 Problems for MATH-63 Complex Analysis Gregor Kovačič December, 7 This list will change as the semester goes on. Please make sure you always have the newest version of it.. Prove the following Theorem For
Problems for MATH-63 Complex Analysis Gregor Kovačič December, 7 This list will change as the semester goes on. Please make sure you always have the newest version of it.. Prove the following Theorem For
Synopsis of Complex Analysis. Ryan D. Reece
 Synopsis of Complex Analysis Ryan D. Reece December 7, 2006 Chapter Complex Numbers. The Parts of a Complex Number A complex number, z, is an ordered pair of real numbers similar to the points in the real
Synopsis of Complex Analysis Ryan D. Reece December 7, 2006 Chapter Complex Numbers. The Parts of a Complex Number A complex number, z, is an ordered pair of real numbers similar to the points in the real
Hypergeometric series and the Riemann zeta function
 ACTA ARITHMETICA LXXXII.2 (997) Hypergeometric series and the Riemann zeta function by Wenchang Chu (Roma) For infinite series related to the Riemann zeta function, De Doelder [4] established numerous
ACTA ARITHMETICA LXXXII.2 (997) Hypergeometric series and the Riemann zeta function by Wenchang Chu (Roma) For infinite series related to the Riemann zeta function, De Doelder [4] established numerous
1. The COMPLEX PLANE AND ELEMENTARY FUNCTIONS: Complex numbers; stereographic projection; simple and multiple connectivity, elementary functions.
 Complex Analysis Qualifying Examination 1 The COMPLEX PLANE AND ELEMENTARY FUNCTIONS: Complex numbers; stereographic projection; simple and multiple connectivity, elementary functions 2 ANALYTIC FUNCTIONS:
Complex Analysis Qualifying Examination 1 The COMPLEX PLANE AND ELEMENTARY FUNCTIONS: Complex numbers; stereographic projection; simple and multiple connectivity, elementary functions 2 ANALYTIC FUNCTIONS:
Second Midterm Exam Name: Practice Problems March 10, 2015
 Math 160 1. Treibergs Second Midterm Exam Name: Practice Problems March 10, 015 1. Determine the singular points of the function and state why the function is analytic everywhere else: z 1 fz) = z + 1)z
Math 160 1. Treibergs Second Midterm Exam Name: Practice Problems March 10, 015 1. Determine the singular points of the function and state why the function is analytic everywhere else: z 1 fz) = z + 1)z
Math Final Exam.
 Math 106 - Final Exam. This is a closed book exam. No calculators are allowed. The exam consists of 8 questions worth 100 points. Good luck! Name: Acknowledgment and acceptance of honor code: Signature:
Math 106 - Final Exam. This is a closed book exam. No calculators are allowed. The exam consists of 8 questions worth 100 points. Good luck! Name: Acknowledgment and acceptance of honor code: Signature:
Complex Homework Summer 2014
 omplex Homework Summer 24 Based on Brown hurchill 7th Edition June 2, 24 ontents hw, omplex Arithmetic, onjugates, Polar Form 2 2 hw2 nth roots, Domains, Functions 2 3 hw3 Images, Transformations 3 4 hw4
omplex Homework Summer 24 Based on Brown hurchill 7th Edition June 2, 24 ontents hw, omplex Arithmetic, onjugates, Polar Form 2 2 hw2 nth roots, Domains, Functions 2 3 hw3 Images, Transformations 3 4 hw4
MATH5685 Assignment 3
 MATH5685 Assignment 3 Due: Wednesday 3 October 1. The open unit disk is denoted D. Q1. Suppose that a n for all n. Show that (1 + a n) converges if and only if a n converges. [Hint: prove that ( N (1 +
MATH5685 Assignment 3 Due: Wednesday 3 October 1. The open unit disk is denoted D. Q1. Suppose that a n for all n. Show that (1 + a n) converges if and only if a n converges. [Hint: prove that ( N (1 +
Complex Variables. Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit.
 Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit. 1. The TI-89 calculator says, reasonably enough, that x 1) 1/3 1 ) 3 = 8. lim
Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit. 1. The TI-89 calculator says, reasonably enough, that x 1) 1/3 1 ) 3 = 8. lim
Exercises for Part 1
 MATH200 Complex Analysis. Exercises for Part Exercises for Part The following exercises are provided for you to revise complex numbers. Exercise. Write the following expressions in the form x + iy, x,y
MATH200 Complex Analysis. Exercises for Part Exercises for Part The following exercises are provided for you to revise complex numbers. Exercise. Write the following expressions in the form x + iy, x,y
CHAPTER 3 ELEMENTARY FUNCTIONS 28. THE EXPONENTIAL FUNCTION. Definition: The exponential function: The exponential function e z by writing
 CHAPTER 3 ELEMENTARY FUNCTIONS We consider here various elementary functions studied in calculus and define corresponding functions of a complex variable. To be specific, we define analytic functions of
CHAPTER 3 ELEMENTARY FUNCTIONS We consider here various elementary functions studied in calculus and define corresponding functions of a complex variable. To be specific, we define analytic functions of
Divergent Series: why = 1/12. Bryden Cais
 Divergent Series: why + + 3 + = /. Bryden Cais Divergent series are the invention of the devil, and it is shameful to base on them any demonstration whatsoever.. H. Abel. Introduction The notion of convergence
Divergent Series: why + + 3 + = /. Bryden Cais Divergent series are the invention of the devil, and it is shameful to base on them any demonstration whatsoever.. H. Abel. Introduction The notion of convergence
Chapter 30 MSMYP1 Further Complex Variable Theory
 Chapter 30 MSMYP Further Complex Variable Theory (30.) Multifunctions A multifunction is a function that may take many values at the same point. Clearly such functions are problematic for an analytic study,
Chapter 30 MSMYP Further Complex Variable Theory (30.) Multifunctions A multifunction is a function that may take many values at the same point. Clearly such functions are problematic for an analytic study,
ARGUMENT INVERSION FOR MODIFIED THETA FUNCTIONS. Introduction
 ARGUMENT INVERION FOR MODIFIED THETA FUNCTION MAURICE CRAIG The standard theta function has the inversion property Introduction θ(x) = exp( πxn 2 ), (n Z, Re(x) > ) θ(1/x) = θ(x) x. This formula is proved
ARGUMENT INVERION FOR MODIFIED THETA FUNCTION MAURICE CRAIG The standard theta function has the inversion property Introduction θ(x) = exp( πxn 2 ), (n Z, Re(x) > ) θ(1/x) = θ(x) x. This formula is proved
A class of trees and its Wiener index.
 A class of trees and its Wiener index. Stephan G. Wagner Department of Mathematics Graz University of Technology Steyrergasse 3, A-81 Graz, Austria wagner@finanz.math.tu-graz.ac.at Abstract In this paper,
A class of trees and its Wiener index. Stephan G. Wagner Department of Mathematics Graz University of Technology Steyrergasse 3, A-81 Graz, Austria wagner@finanz.math.tu-graz.ac.at Abstract In this paper,
Math Homework 2
 Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
III. Consequences of Cauchy s Theorem
 MTH6 Complex Analysis 2009-0 Lecture Notes c Shaun Bullett 2009 III. Consequences of Cauchy s Theorem. Cauchy s formulae. Cauchy s Integral Formula Let f be holomorphic on and everywhere inside a simple
MTH6 Complex Analysis 2009-0 Lecture Notes c Shaun Bullett 2009 III. Consequences of Cauchy s Theorem. Cauchy s formulae. Cauchy s Integral Formula Let f be holomorphic on and everywhere inside a simple
MATH COMPLEX ANALYSIS. Contents
 MATH 3964 - OMPLEX ANALYSIS ANDREW TULLOH AND GILES GARDAM ontents 1. ontour Integration and auchy s Theorem 2 1.1. Analytic functions 2 1.2. ontour integration 3 1.3. auchy s theorem and extensions 3
MATH 3964 - OMPLEX ANALYSIS ANDREW TULLOH AND GILES GARDAM ontents 1. ontour Integration and auchy s Theorem 2 1.1. Analytic functions 2 1.2. ontour integration 3 1.3. auchy s theorem and extensions 3
Bessel Functions Michael Taylor. Lecture Notes for Math 524
 Bessel Functions Michael Taylor Lecture Notes for Math 54 Contents 1. Introduction. Conversion to first order systems 3. The Bessel functions J ν 4. The Bessel functions Y ν 5. Relations between J ν and
Bessel Functions Michael Taylor Lecture Notes for Math 54 Contents 1. Introduction. Conversion to first order systems 3. The Bessel functions J ν 4. The Bessel functions Y ν 5. Relations between J ν and
EXTENDED RECIPROCAL ZETA FUNCTION AND AN ALTERNATE FORMULATION OF THE RIEMANN HYPOTHESIS. M. Aslam Chaudhry. Received May 18, 2007
 Scientiae Mathematicae Japonicae Online, e-2009, 05 05 EXTENDED RECIPROCAL ZETA FUNCTION AND AN ALTERNATE FORMULATION OF THE RIEMANN HYPOTHESIS M. Aslam Chaudhry Received May 8, 2007 Abstract. We define
Scientiae Mathematicae Japonicae Online, e-2009, 05 05 EXTENDED RECIPROCAL ZETA FUNCTION AND AN ALTERNATE FORMULATION OF THE RIEMANN HYPOTHESIS M. Aslam Chaudhry Received May 8, 2007 Abstract. We define
Evaluating multiloop Feynman integrals by Mellin-Barnes representation
 April 7, 004 Loops&Legs 04 Evaluating multiloop Feynman integrals by Mellin-Barnes representation V.A. Smirnov Nuclear Physics Institute of Moscow State University Mellin-Barnes representation as a tool
April 7, 004 Loops&Legs 04 Evaluating multiloop Feynman integrals by Mellin-Barnes representation V.A. Smirnov Nuclear Physics Institute of Moscow State University Mellin-Barnes representation as a tool
EXISTENCE OF GUIDED MODES ON PERIODIC SLABS
 SUBMITTED FOR: PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS June 16 19, 2004, Pomona, CA, USA pp. 1 8 EXISTENCE OF GUIDED MODES ON PERIODIC SLABS Stephen
SUBMITTED FOR: PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON DYNAMICAL SYSTEMS AND DIFFERENTIAL EQUATIONS June 16 19, 2004, Pomona, CA, USA pp. 1 8 EXISTENCE OF GUIDED MODES ON PERIODIC SLABS Stephen
Part IB. Complex Analysis. Year
 Part IB Complex Analysis Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 Paper 1, Section I 2A Complex Analysis or Complex Methods 7 (a) Show that w = log(z) is a conformal
Part IB Complex Analysis Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 Paper 1, Section I 2A Complex Analysis or Complex Methods 7 (a) Show that w = log(z) is a conformal
Complex Analysis Math 185A, Winter 2010 Final: Solutions
 Complex Analysis Math 85A, Winter 200 Final: Solutions. [25 pts] The Jacobian of two real-valued functions u(x, y), v(x, y) of (x, y) is defined by the determinant (u, v) J = (x, y) = u x u y v x v y.
Complex Analysis Math 85A, Winter 200 Final: Solutions. [25 pts] The Jacobian of two real-valued functions u(x, y), v(x, y) of (x, y) is defined by the determinant (u, v) J = (x, y) = u x u y v x v y.
Here are brief notes about topics covered in class on complex numbers, focusing on what is not covered in the textbook.
 Phys374, Spring 2008, Prof. Ted Jacobson Department of Physics, University of Maryland Complex numbers version 5/21/08 Here are brief notes about topics covered in class on complex numbers, focusing on
Phys374, Spring 2008, Prof. Ted Jacobson Department of Physics, University of Maryland Complex numbers version 5/21/08 Here are brief notes about topics covered in class on complex numbers, focusing on
Precise error estimate of the Brent-McMillan algorithm for the computation of Euler s constant
 Precise error estimate of the Brent-McMillan algorithm for the computation of Euler s constant Jean-Pierre Demailly Université de Grenoble Alpes, Institut Fourier Abstract Brent and McMillan introduced
Precise error estimate of the Brent-McMillan algorithm for the computation of Euler s constant Jean-Pierre Demailly Université de Grenoble Alpes, Institut Fourier Abstract Brent and McMillan introduced
Quadratic Transformations of Hypergeometric Function and Series with Harmonic Numbers
 Quadratic Transformations of Hypergeometric Function and Series with Harmonic Numbers Martin Nicholson In this brief note, we show how to apply Kummer s and other quadratic transformation formulas for
Quadratic Transformations of Hypergeometric Function and Series with Harmonic Numbers Martin Nicholson In this brief note, we show how to apply Kummer s and other quadratic transformation formulas for
MATH 452. SAMPLE 3 SOLUTIONS May 3, (10 pts) Let f(x + iy) = u(x, y) + iv(x, y) be an analytic function. Show that u(x, y) is harmonic.
 MATH 45 SAMPLE 3 SOLUTIONS May 3, 06. (0 pts) Let f(x + iy) = u(x, y) + iv(x, y) be an analytic function. Show that u(x, y) is harmonic. Because f is holomorphic, u and v satisfy the Cauchy-Riemann equations:
MATH 45 SAMPLE 3 SOLUTIONS May 3, 06. (0 pts) Let f(x + iy) = u(x, y) + iv(x, y) be an analytic function. Show that u(x, y) is harmonic. Because f is holomorphic, u and v satisfy the Cauchy-Riemann equations:
Complex Series (3A) Young Won Lim 8/17/13
 Complex Series (3A) 8/7/3 Copyright (c) 202, 203 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or
Complex Series (3A) 8/7/3 Copyright (c) 202, 203 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or
Considering our result for the sum and product of analytic functions, this means that for (a 0, a 1,..., a N ) C N+1, the polynomial.
 Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
A FEW REMARKS ON THE SUPREMUM OF STABLE PROCESSES P. PATIE
 A FEW REMARKS ON THE SUPREMUM OF STABLE PROCESSES P. PATIE Abstract. In [1], Bernyk et al. offer a power series and an integral representation for the density of S 1, the maximum up to time 1, of a regular
A FEW REMARKS ON THE SUPREMUM OF STABLE PROCESSES P. PATIE Abstract. In [1], Bernyk et al. offer a power series and an integral representation for the density of S 1, the maximum up to time 1, of a regular
Appendix A Vector Analysis
 Appendix A Vector Analysis A.1 Orthogonal Coordinate Systems A.1.1 Cartesian (Rectangular Coordinate System The unit vectors are denoted by x, ŷ, ẑ in the Cartesian system. By convention, ( x, ŷ, ẑ triplet
Appendix A Vector Analysis A.1 Orthogonal Coordinate Systems A.1.1 Cartesian (Rectangular Coordinate System The unit vectors are denoted by x, ŷ, ẑ in the Cartesian system. By convention, ( x, ŷ, ẑ triplet
INTRODUCTION TO COMPLEX ANALYSIS W W L CHEN
 INTRODUTION TO OMPLEX ANALYSIS W W L HEN c W W L hen, 986, 2008. This chapter originates from material used by the author at Imperial ollege, University of London, between 98 and 990. It is available free
INTRODUTION TO OMPLEX ANALYSIS W W L HEN c W W L hen, 986, 2008. This chapter originates from material used by the author at Imperial ollege, University of London, between 98 and 990. It is available free
MATH 311: COMPLEX ANALYSIS CONTOUR INTEGRALS LECTURE
 MATH 3: COMPLEX ANALYSIS CONTOUR INTEGRALS LECTURE Recall the Residue Theorem: Let be a simple closed loop, traversed counterclockwise. Let f be a function that is analytic on and meromorphic inside. Then
MATH 3: COMPLEX ANALYSIS CONTOUR INTEGRALS LECTURE Recall the Residue Theorem: Let be a simple closed loop, traversed counterclockwise. Let f be a function that is analytic on and meromorphic inside. Then
PRIME NUMBER THEOREM
 PRIME NUMBER THEOREM RYAN LIU Abstract. Prime numbers have always been seen as the building blocks of all integers, but their behavior and distribution are often puzzling. The prime number theorem gives
PRIME NUMBER THEOREM RYAN LIU Abstract. Prime numbers have always been seen as the building blocks of all integers, but their behavior and distribution are often puzzling. The prime number theorem gives
(z + n) 2. n=0. 2 (z + 2) (z + n). 2 We d like to compute this as an integral. To this end, we d like a function with residues
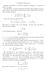 8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
1 Discussion on multi-valued functions
 Week 3 notes, Math 7651 1 Discussion on multi-valued functions Log function : Note that if z is written in its polar representation: z = r e iθ, where r = z and θ = arg z, then log z log r + i θ + 2inπ
Week 3 notes, Math 7651 1 Discussion on multi-valued functions Log function : Note that if z is written in its polar representation: z = r e iθ, where r = z and θ = arg z, then log z log r + i θ + 2inπ
Week 2 Notes, Math 865, Tanveer
 Week 2 Notes, Math 865, Tanveer 1. Incompressible constant density equations in different forms Recall we derived the Navier-Stokes equation for incompressible constant density, i.e. homogeneous flows:
Week 2 Notes, Math 865, Tanveer 1. Incompressible constant density equations in different forms Recall we derived the Navier-Stokes equation for incompressible constant density, i.e. homogeneous flows:
July 21 Math 2254 sec 001 Summer 2015
 July 21 Math 2254 sec 001 Summer 2015 Section 8.8: Power Series Theorem: Let a n (x c) n have positive radius of convergence R, and let the function f be defined by this power series f (x) = a n (x c)
July 21 Math 2254 sec 001 Summer 2015 Section 8.8: Power Series Theorem: Let a n (x c) n have positive radius of convergence R, and let the function f be defined by this power series f (x) = a n (x c)
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Complex Variables & Integral Transforms
 Complex Variables & Integral Transforms Notes taken by J.Pearson, from a S4 course at the U.Manchester. Lecture delivered by Dr.W.Parnell July 9, 007 Contents 1 Complex Variables 3 1.1 General Relations
Complex Variables & Integral Transforms Notes taken by J.Pearson, from a S4 course at the U.Manchester. Lecture delivered by Dr.W.Parnell July 9, 007 Contents 1 Complex Variables 3 1.1 General Relations
(a) To show f(z) is analytic, explicitly evaluate partials,, etc. and show. = 0. To find v, integrate u = v to get v = dy u =
 Homework -5 Solutions Problems (a) z = + 0i, (b) z = 7 + 24i 2 f(z) = u(x, y) + iv(x, y) with u(x, y) = e 2y cos(2x) and v(x, y) = e 2y sin(2x) u (a) To show f(z) is analytic, explicitly evaluate partials,,
Homework -5 Solutions Problems (a) z = + 0i, (b) z = 7 + 24i 2 f(z) = u(x, y) + iv(x, y) with u(x, y) = e 2y cos(2x) and v(x, y) = e 2y sin(2x) u (a) To show f(z) is analytic, explicitly evaluate partials,,
A Note on the Differential Equations with Distributional Coefficients
 MATEMATIKA, 24, Jilid 2, Bil. 2, hlm. 115 124 c Jabatan Matematik, UTM. A Note on the Differential Equations with Distributional Coefficients Adem Kilicman Department of Mathematics, Institute for Mathematical
MATEMATIKA, 24, Jilid 2, Bil. 2, hlm. 115 124 c Jabatan Matematik, UTM. A Note on the Differential Equations with Distributional Coefficients Adem Kilicman Department of Mathematics, Institute for Mathematical
Qualifying Exam Complex Analysis (Math 530) January 2019
 Qualifying Exam Complex Analysis (Math 53) January 219 1. Let D be a domain. A function f : D C is antiholomorphic if for every z D the limit f(z + h) f(z) lim h h exists. Write f(z) = f(x + iy) = u(x,
Qualifying Exam Complex Analysis (Math 53) January 219 1. Let D be a domain. A function f : D C is antiholomorphic if for every z D the limit f(z + h) f(z) lim h h exists. Write f(z) = f(x + iy) = u(x,
Math 259: Introduction to Analytic Number Theory More about the Gamma function
 Math 59: Introduction to Analytic Number Theory More about the Gamma function We collect some more facts about Γs as a function of a complex variable that will figure in our treatment of ζs and Ls, χ.
Math 59: Introduction to Analytic Number Theory More about the Gamma function We collect some more facts about Γs as a function of a complex variable that will figure in our treatment of ζs and Ls, χ.
1 Introduction. or equivalently f(z) =
 Introduction In this unit on elliptic functions, we ll see how two very natural lines of questions interact. The first, as we have met several times in Berndt s book, involves elliptic integrals. In particular,
Introduction In this unit on elliptic functions, we ll see how two very natural lines of questions interact. The first, as we have met several times in Berndt s book, involves elliptic integrals. In particular,
AP Calculus Testbank (Chapter 9) (Mr. Surowski)
 AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
Surface Tension Effect on a Two Dimensional. Channel Flow against an Inclined Wall
 Applied Mathematical Sciences, Vol. 1, 007, no. 7, 313-36 Surface Tension Effect on a Two Dimensional Channel Flow against an Inclined Wall A. Merzougui *, H. Mekias ** and F. Guechi ** * Département de
Applied Mathematical Sciences, Vol. 1, 007, no. 7, 313-36 Surface Tension Effect on a Two Dimensional Channel Flow against an Inclined Wall A. Merzougui *, H. Mekias ** and F. Guechi ** * Département de
Asymptotics of integrals
 December 9, Asymptotics o integrals Paul Garrett garrett@math.umn.e http://www.math.umn.e/ garrett/ [This document is http://www.math.umn.e/ garrett/m/v/basic asymptotics.pd]. Heuristic or the main term
December 9, Asymptotics o integrals Paul Garrett garrett@math.umn.e http://www.math.umn.e/ garrett/ [This document is http://www.math.umn.e/ garrett/m/v/basic asymptotics.pd]. Heuristic or the main term
UNIFORM BOUNDS FOR BESSEL FUNCTIONS
 Journal of Applied Analysis Vol. 1, No. 1 (006), pp. 83 91 UNIFORM BOUNDS FOR BESSEL FUNCTIONS I. KRASIKOV Received October 8, 001 and, in revised form, July 6, 004 Abstract. For ν > 1/ and x real we shall
Journal of Applied Analysis Vol. 1, No. 1 (006), pp. 83 91 UNIFORM BOUNDS FOR BESSEL FUNCTIONS I. KRASIKOV Received October 8, 001 and, in revised form, July 6, 004 Abstract. For ν > 1/ and x real we shall
THE LAPLACE TRANSFORM OF THE FOURTH MOMENT OF THE ZETA-FUNCTION. Aleksandar Ivić
 THE LAPLACE TRANSFORM OF THE FOURTH MOMENT OF THE ZETA-FUNCTION Aleksandar Ivić Univ. Beograd. Publ. Elektrotehn. Fak. Ser. Mat. (2), 4 48. Abstract. The Laplace transform of ζ( 2 +ix) 4 is investigated,
THE LAPLACE TRANSFORM OF THE FOURTH MOMENT OF THE ZETA-FUNCTION Aleksandar Ivić Univ. Beograd. Publ. Elektrotehn. Fak. Ser. Mat. (2), 4 48. Abstract. The Laplace transform of ζ( 2 +ix) 4 is investigated,
2. Complex Analytic Functions
 2. Complex Analytic Functions John Douglas Moore July 6, 2011 Recall that if A and B are sets, a function f : A B is a rule which assigns to each element a A a unique element f(a) B. In this course, we
2. Complex Analytic Functions John Douglas Moore July 6, 2011 Recall that if A and B are sets, a function f : A B is a rule which assigns to each element a A a unique element f(a) B. In this course, we
Riemann s zeta function, Newton s method, and holomorphic index
 Riemann s zeta function, Newton s method, and holomorphic index Tomoki Kawahira Nagoya University, Nagoya, JAPAN URL: http://math.nagoya-u.ac.jp/ kawahira Abstract. We apply some root finding algorithms
Riemann s zeta function, Newton s method, and holomorphic index Tomoki Kawahira Nagoya University, Nagoya, JAPAN URL: http://math.nagoya-u.ac.jp/ kawahira Abstract. We apply some root finding algorithms
Complex Analysis Qualifying Exam Solutions
 Complex Analysis Qualifying Exam Solutions May, 04 Part.. Let log z be the principal branch of the logarithm defined on G = {z C z (, 0]}. Show that if t > 0, then the equation log z = t has exactly one
Complex Analysis Qualifying Exam Solutions May, 04 Part.. Let log z be the principal branch of the logarithm defined on G = {z C z (, 0]}. Show that if t > 0, then the equation log z = t has exactly one
arxiv: v1 [physics.class-ph] 14 Mar 2014
![arxiv: v1 [physics.class-ph] 14 Mar 2014 arxiv: v1 [physics.class-ph] 14 Mar 2014](/thumbs/77/75715778.jpg) Alberta Thy 5-14 Current distribution in an infinite plate Andrzej Czarnecki Department of Physics, University of Alberta, Edmonton, Alberta, Canada T6G 2E1 arxiv:1403.3468v1 [physics.class-ph] 14 Mar
Alberta Thy 5-14 Current distribution in an infinite plate Andrzej Czarnecki Department of Physics, University of Alberta, Edmonton, Alberta, Canada T6G 2E1 arxiv:1403.3468v1 [physics.class-ph] 14 Mar
Chapter 2 Non-linear Equations
 Chapter 2 Non-linear Equations 2.1 First Examples of Non-linear Ordinary Differential Equations Before describing some general properties of non-linear equations, we find it useful to present some well-known
Chapter 2 Non-linear Equations 2.1 First Examples of Non-linear Ordinary Differential Equations Before describing some general properties of non-linear equations, we find it useful to present some well-known
INTEGRATION WORKSHOP 2003 COMPLEX ANALYSIS EXERCISES
 INTEGRATION WORKSHOP 23 COMPLEX ANALYSIS EXERCISES DOUGLAS ULMER 1. Meromorphic functions on the Riemann sphere It s often useful to allow functions to take the value. This exercise outlines one way to
INTEGRATION WORKSHOP 23 COMPLEX ANALYSIS EXERCISES DOUGLAS ULMER 1. Meromorphic functions on the Riemann sphere It s often useful to allow functions to take the value. This exercise outlines one way to
Solutions to practice problems for the final
 Solutions to practice problems for the final Holomorphicity, Cauchy-Riemann equations, and Cauchy-Goursat theorem 1. (a) Show that there is a holomorphic function on Ω = {z z > 2} whose derivative is z
Solutions to practice problems for the final Holomorphicity, Cauchy-Riemann equations, and Cauchy-Goursat theorem 1. (a) Show that there is a holomorphic function on Ω = {z z > 2} whose derivative is z
Additional material: Linear Differential Equations
 Chapter 5 Additional material: Linear Differential Equations 5.1 Introduction The material in this chapter is not formally part of the LTCC course. It is included for completeness as it contains proofs
Chapter 5 Additional material: Linear Differential Equations 5.1 Introduction The material in this chapter is not formally part of the LTCC course. It is included for completeness as it contains proofs
Assignment 2 - Complex Analysis
 Assignment 2 - Complex Analysis MATH 440/508 M.P. Lamoureux Sketch of solutions. Γ z dz = Γ (x iy)(dx + idy) = (xdx + ydy) + i Γ Γ ( ydx + xdy) = (/2)(x 2 + y 2 ) endpoints + i [( / y) y ( / x)x]dxdy interiorγ
Assignment 2 - Complex Analysis MATH 440/508 M.P. Lamoureux Sketch of solutions. Γ z dz = Γ (x iy)(dx + idy) = (xdx + ydy) + i Γ Γ ( ydx + xdy) = (/2)(x 2 + y 2 ) endpoints + i [( / y) y ( / x)x]dxdy interiorγ
The generalized Euler-Maclaurin formula for the numerical solution of Abel-type integral equations.
 The generalized Euler-Maclaurin formula for the numerical solution of Abel-type integral equations. Johannes Tausch Abstract An extension of the Euler-Maclaurin formula to singular integrals was introduced
The generalized Euler-Maclaurin formula for the numerical solution of Abel-type integral equations. Johannes Tausch Abstract An extension of the Euler-Maclaurin formula to singular integrals was introduced
In this chapter we study elliptical PDEs. That is, PDEs of the form. 2 u = lots,
 Chapter 8 Elliptic PDEs In this chapter we study elliptical PDEs. That is, PDEs of the form 2 u = lots, where lots means lower-order terms (u x, u y,..., u, f). Here are some ways to think about the physical
Chapter 8 Elliptic PDEs In this chapter we study elliptical PDEs. That is, PDEs of the form 2 u = lots, where lots means lower-order terms (u x, u y,..., u, f). Here are some ways to think about the physical
Complex Variables...Review Problems (Residue Calculus Comments)...Fall Initial Draft
 Complex Variables........Review Problems Residue Calculus Comments)........Fall 22 Initial Draft ) Show that the singular point of fz) is a pole; determine its order m and its residue B: a) e 2z )/z 4,
Complex Variables........Review Problems Residue Calculus Comments)........Fall 22 Initial Draft ) Show that the singular point of fz) is a pole; determine its order m and its residue B: a) e 2z )/z 4,
1. Introduction Interest in this project began with curiosity about the Laplace transform of the Digamma function, e as ψ(s + 1)ds,
 ON THE LAPLACE TRANSFORM OF THE PSI FUNCTION M. LAWRENCE GLASSER AND DANTE MANNA Abstract. Guided by numerical experimentation, we have been able to prove that Z 8 / x x + ln dx = γ + ln) [cosx)] and to
ON THE LAPLACE TRANSFORM OF THE PSI FUNCTION M. LAWRENCE GLASSER AND DANTE MANNA Abstract. Guided by numerical experimentation, we have been able to prove that Z 8 / x x + ln dx = γ + ln) [cosx)] and to
Sample Final Questions: Solutions Math 21B, Winter y ( y 1)(1 + y)) = A y + B
 Sample Final Questions: Solutions Math 2B, Winter 23. Evaluate the following integrals: tan a) y y dy; b) x dx; c) 3 x 2 + x dx. a) We use partial fractions: y y 3 = y y ) + y)) = A y + B y + C y +. Putting
Sample Final Questions: Solutions Math 2B, Winter 23. Evaluate the following integrals: tan a) y y dy; b) x dx; c) 3 x 2 + x dx. a) We use partial fractions: y y 3 = y y ) + y)) = A y + B y + C y +. Putting
MT3503 Complex Analysis MRQ
 MT353 Complex Analysis MRQ November 22, 26 Contents Introduction 3 Structure of the lecture course............................... 5 Prerequisites......................................... 5 Recommended
MT353 Complex Analysis MRQ November 22, 26 Contents Introduction 3 Structure of the lecture course............................... 5 Prerequisites......................................... 5 Recommended
Math 115 HW #5 Solutions
 Math 5 HW #5 Solutions From 29 4 Find the power series representation for the function and determine the interval of convergence Answer: Using the geometric series formula, f(x) = 3 x 4 3 x 4 = 3(x 4 )
Math 5 HW #5 Solutions From 29 4 Find the power series representation for the function and determine the interval of convergence Answer: Using the geometric series formula, f(x) = 3 x 4 3 x 4 = 3(x 4 )
Complex Analysis MATH 6300 Fall 2013 Homework 4
 Complex Analysis MATH 6300 Fall 2013 Homework 4 Due Wednesday, December 11 at 5 PM Note that to get full credit on any problem in this class, you must solve the problems in an efficient and elegant manner,
Complex Analysis MATH 6300 Fall 2013 Homework 4 Due Wednesday, December 11 at 5 PM Note that to get full credit on any problem in this class, you must solve the problems in an efficient and elegant manner,
CERTAIN INTEGRALS ARISING FROM RAMANUJAN S NOTEBOOKS
 CERTAIN INTEGRALS ARISING FROM RAMANUJAN S NOTEBOOKS BRUCE C. BERNDT AND ARMIN STRAUB Abstract. In his third noteboo, Ramanujan claims that log x dx + π 2 x 2 dx. + 1 In a following cryptic line, which
CERTAIN INTEGRALS ARISING FROM RAMANUJAN S NOTEBOOKS BRUCE C. BERNDT AND ARMIN STRAUB Abstract. In his third noteboo, Ramanujan claims that log x dx + π 2 x 2 dx. + 1 In a following cryptic line, which
BTL What is the value of m if the vector is solenoidal. BTL What is the value of a, b, c if the vector may be irrotational.
 VALLIAMMAI ENGINEERING OLLEGE SRM NAGAR, KATTANDKULATHUR Department of Mathematics MA65 - MATHEMATIS II QUESTION BANK - 6 UNIT - I VETOR ALULUS Part - A. Find, if at (, -, ). BTL-. Find the Directional
VALLIAMMAI ENGINEERING OLLEGE SRM NAGAR, KATTANDKULATHUR Department of Mathematics MA65 - MATHEMATIS II QUESTION BANK - 6 UNIT - I VETOR ALULUS Part - A. Find, if at (, -, ). BTL-. Find the Directional
MA3111S COMPLEX ANALYSIS I
 MA3111S COMPLEX ANALYSIS I 1. The Algebra of Complex Numbers A complex number is an expression of the form a + ib, where a and b are real numbers. a is called the real part of a + ib and b the imaginary
MA3111S COMPLEX ANALYSIS I 1. The Algebra of Complex Numbers A complex number is an expression of the form a + ib, where a and b are real numbers. a is called the real part of a + ib and b the imaginary
Infinite Series. 1 Introduction. 2 General discussion on convergence
 Infinite Series 1 Introduction I will only cover a few topics in this lecture, choosing to discuss those which I have used over the years. The text covers substantially more material and is available for
Infinite Series 1 Introduction I will only cover a few topics in this lecture, choosing to discuss those which I have used over the years. The text covers substantially more material and is available for
Complex Inversion Formula for Stieltjes and Widder Transforms with Applications
 Int. J. Contemp. Math. Sciences, Vol. 3, 8, no. 16, 761-77 Complex Inversion Formula for Stieltjes and Widder Transforms with Applications A. Aghili and A. Ansari Department of Mathematics, Faculty of
Int. J. Contemp. Math. Sciences, Vol. 3, 8, no. 16, 761-77 Complex Inversion Formula for Stieltjes and Widder Transforms with Applications A. Aghili and A. Ansari Department of Mathematics, Faculty of
FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS
 FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS HUNDUMA LEGESSE GELETA, ABDULKADIR HASSEN Both authors would like to dedicate this in fond memory of Marvin Knopp. Knop was the most humble and exemplary teacher
FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS HUNDUMA LEGESSE GELETA, ABDULKADIR HASSEN Both authors would like to dedicate this in fond memory of Marvin Knopp. Knop was the most humble and exemplary teacher
The result above is known as the Riemann mapping theorem. We will prove it using basic theory of normal families. We start this lecture with that.
 Lecture 15 The Riemann mapping theorem Variables MATH-GA 2451.1 Complex The point of this lecture is to prove that the unit disk can be mapped conformally onto any simply connected open set in the plane,
Lecture 15 The Riemann mapping theorem Variables MATH-GA 2451.1 Complex The point of this lecture is to prove that the unit disk can be mapped conformally onto any simply connected open set in the plane,
Exercises for Part 1
 MATH200 Complex Analysis. Exercises for Part Exercises for Part The following exercises are provided for you to revise complex numbers. Exercise. Write the following expressions in the form x+iy, x,y R:
MATH200 Complex Analysis. Exercises for Part Exercises for Part The following exercises are provided for you to revise complex numbers. Exercise. Write the following expressions in the form x+iy, x,y R:
On spherical-wave scattering by a spherical scatterer and related near-field inverse problems
 IMA Journal of Applied Mathematics (2001) 66, 539 549 On spherical-wave scattering by a spherical scatterer and related near-field inverse problems C. ATHANASIADIS Department of Mathematics, University
IMA Journal of Applied Mathematics (2001) 66, 539 549 On spherical-wave scattering by a spherical scatterer and related near-field inverse problems C. ATHANASIADIS Department of Mathematics, University
Chapter 6: Residue Theory. Introduction. The Residue Theorem. 6.1 The Residue Theorem. 6.2 Trigonometric Integrals Over (0, 2π) Li, Yongzhao
 Outline Chapter 6: Residue Theory Li, Yongzhao State Key Laboratory of Integrated Services Networks, Xidian University June 7, 2009 Introduction The Residue Theorem In the previous chapters, we have seen
Outline Chapter 6: Residue Theory Li, Yongzhao State Key Laboratory of Integrated Services Networks, Xidian University June 7, 2009 Introduction The Residue Theorem In the previous chapters, we have seen
13 Definite integrals
 3 Definite integrals Read: Boas h. 4. 3. Laurent series: Def.: Laurent series (LS). If f() is analytic in a region R, then converges in R, with a n = πi f() = a n ( ) n + n= n= f() ; b ( ) n+ n = πi b
3 Definite integrals Read: Boas h. 4. 3. Laurent series: Def.: Laurent series (LS). If f() is analytic in a region R, then converges in R, with a n = πi f() = a n ( ) n + n= n= f() ; b ( ) n+ n = πi b
ON THE TAYLOR COEFFICIENTS OF THE HURWITZ ZETA FUNCTION
 ON THE TAYLOR COEFFICIENTS OF THE HURWITZ ZETA FUNCTION Khristo N. Boyadzhiev Department of Mathematics, Ohio Northern University, Ada, Ohio, 45810 k-boyadzhiev@onu.edu Abstract. We find a representation
ON THE TAYLOR COEFFICIENTS OF THE HURWITZ ZETA FUNCTION Khristo N. Boyadzhiev Department of Mathematics, Ohio Northern University, Ada, Ohio, 45810 k-boyadzhiev@onu.edu Abstract. We find a representation
Polyexponentials. Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH
 Polyexponentials Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH 45810 k-boyadzhiev@onu.edu 1. Introduction. The polylogarithmic function [15] (1.1) and the more general
Polyexponentials Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH 45810 k-boyadzhiev@onu.edu 1. Introduction. The polylogarithmic function [15] (1.1) and the more general
Physics 216 Problem Set 4 Spring 2010 DUE: MAY 25, 2010
 Physics 216 Problem Set 4 Spring 2010 DUE: MAY 25, 2010 1. (a) Consider the Born approximation as the first term of the Born series. Show that: (i) the Born approximation for the forward scattering amplitude
Physics 216 Problem Set 4 Spring 2010 DUE: MAY 25, 2010 1. (a) Consider the Born approximation as the first term of the Born series. Show that: (i) the Born approximation for the forward scattering amplitude
Self-similar solutions for the diffraction of weak shocks
 Self-similar solutions for the diffraction of weak shocks Allen M. Tesdall John K. Hunter Abstract. We numerically solve a problem for the unsteady transonic small disturbance equations that describes
Self-similar solutions for the diffraction of weak shocks Allen M. Tesdall John K. Hunter Abstract. We numerically solve a problem for the unsteady transonic small disturbance equations that describes
Theorem [Mean Value Theorem for Harmonic Functions] Let u be harmonic on D(z 0, R). Then for any r (0, R), u(z 0 ) = 1 z z 0 r
![Theorem [Mean Value Theorem for Harmonic Functions] Let u be harmonic on D(z 0, R). Then for any r (0, R), u(z 0 ) = 1 z z 0 r Theorem [Mean Value Theorem for Harmonic Functions] Let u be harmonic on D(z 0, R). Then for any r (0, R), u(z 0 ) = 1 z z 0 r](/thumbs/77/75527144.jpg) 2. A harmonic conjugate always exists locally: if u is a harmonic function in an open set U, then for any disk D(z 0, r) U, there is f, which is analytic in D(z 0, r) and satisfies that Re f u. Since such
2. A harmonic conjugate always exists locally: if u is a harmonic function in an open set U, then for any disk D(z 0, r) U, there is f, which is analytic in D(z 0, r) and satisfies that Re f u. Since such
FINAL EXAM MATH 220A, UCSD, AUTUMN 14. You have three hours.
 FINAL EXAM MATH 220A, UCSD, AUTUMN 4 You have three hours. Problem Points Score There are 6 problems, and the total number of points is 00. Show all your work. Please make your work as clear and easy to
FINAL EXAM MATH 220A, UCSD, AUTUMN 4 You have three hours. Problem Points Score There are 6 problems, and the total number of points is 00. Show all your work. Please make your work as clear and easy to
ODD MAGNE OGREID AND PER OSLAND
 DESY 97-45 hep-th/9868 December 997 SUMMING ONE- AND TWO-DIMENSIONAL SERIES RELATED TO THE EULER SERIES arxiv:hep-th/9868v 6 Jan 998 ODD MAGNE OGREID AND PER OSLAND Abstract We present results for some
DESY 97-45 hep-th/9868 December 997 SUMMING ONE- AND TWO-DIMENSIONAL SERIES RELATED TO THE EULER SERIES arxiv:hep-th/9868v 6 Jan 998 ODD MAGNE OGREID AND PER OSLAND Abstract We present results for some
Reciprocity formulae for general Dedekind Rademacher sums
 ACTA ARITHMETICA LXXIII4 1995 Reciprocity formulae for general Dedekind Rademacher sums by R R Hall York, J C Wilson York and D Zagier Bonn 1 Introduction Let B 1 x = { x [x] 1/2 x R \ Z, 0 x Z If b and
ACTA ARITHMETICA LXXIII4 1995 Reciprocity formulae for general Dedekind Rademacher sums by R R Hall York, J C Wilson York and D Zagier Bonn 1 Introduction Let B 1 x = { x [x] 1/2 x R \ Z, 0 x Z If b and
Complex Analysis Qual Sheet
 Complex Analysis Qual Sheet Robert Won Tricks and traps. traps. Basically all complex analysis qualifying exams are collections of tricks and - Jim Agler Useful facts. e z = 2. sin z = n=0 3. cos z = z
Complex Analysis Qual Sheet Robert Won Tricks and traps. traps. Basically all complex analysis qualifying exams are collections of tricks and - Jim Agler Useful facts. e z = 2. sin z = n=0 3. cos z = z
18.04 Practice problems exam 2, Spring 2018 Solutions
 8.04 Practice problems exam, Spring 08 Solutions Problem. Harmonic functions (a) Show u(x, y) = x 3 3xy + 3x 3y is harmonic and find a harmonic conjugate. It s easy to compute: u x = 3x 3y + 6x, u xx =
8.04 Practice problems exam, Spring 08 Solutions Problem. Harmonic functions (a) Show u(x, y) = x 3 3xy + 3x 3y is harmonic and find a harmonic conjugate. It s easy to compute: u x = 3x 3y + 6x, u xx =
Analyse 3 NA, FINAL EXAM. * Monday, January 8, 2018, *
 Analyse 3 NA, FINAL EXAM * Monday, January 8, 08, 4.00 7.00 * Motivate each answer with a computation or explanation. The maximum amount of points for this exam is 00. No calculators!. (Holomorphic functions)
Analyse 3 NA, FINAL EXAM * Monday, January 8, 08, 4.00 7.00 * Motivate each answer with a computation or explanation. The maximum amount of points for this exam is 00. No calculators!. (Holomorphic functions)
This ODE arises in many physical systems that we shall investigate. + ( + 1)u = 0. (λ + s)x λ + s + ( + 1) a λ. (s + 1)(s + 2) a 0
 Legendre equation This ODE arises in many physical systems that we shall investigate We choose We then have Substitution gives ( x 2 ) d 2 u du 2x 2 dx dx + ( + )u u x s a λ x λ a du dx λ a λ (λ + s)x
Legendre equation This ODE arises in many physical systems that we shall investigate We choose We then have Substitution gives ( x 2 ) d 2 u du 2x 2 dx dx + ( + )u u x s a λ x λ a du dx λ a λ (λ + s)x
Dirichlet s Theorem. Martin Orr. August 21, The aim of this article is to prove Dirichlet s theorem on primes in arithmetic progressions:
 Dirichlet s Theorem Martin Orr August 1, 009 1 Introduction The aim of this article is to prove Dirichlet s theorem on primes in arithmetic progressions: Theorem 1.1. If m, a N are coprime, then there
Dirichlet s Theorem Martin Orr August 1, 009 1 Introduction The aim of this article is to prove Dirichlet s theorem on primes in arithmetic progressions: Theorem 1.1. If m, a N are coprime, then there
NOTES ON RIEMANN S ZETA FUNCTION. Γ(z) = t z 1 e t dt
 NOTES ON RIEMANN S ZETA FUNCTION DRAGAN MILIČIĆ. Gamma function.. Definition of the Gamma function. The integral Γz = t z e t dt is well-defined and defines a holomorphic function in the right half-plane
NOTES ON RIEMANN S ZETA FUNCTION DRAGAN MILIČIĆ. Gamma function.. Definition of the Gamma function. The integral Γz = t z e t dt is well-defined and defines a holomorphic function in the right half-plane
