Complex Homework Summer 2014
|
|
|
- Cornelius Matthews
- 6 years ago
- Views:
Transcription
1 omplex Homework Summer 24 Based on Brown hurchill 7th Edition June 2, 24 ontents hw, omplex Arithmetic, onjugates, Polar Form 2 2 hw2 nth roots, Domains, Functions 2 3 hw3 Images, Transformations 3 4 hw4 Limits 3 5 hw5 Unbounded 4 6 hw6 Derivatives, auchy-riemann 4 7 hw7 Exp Log 5 8 hw8 Log log 5 9 hw9 Principal values, Integrals over a Real Variable 6 hw ontour Integrals 6 hw More on ontour Integrals 7 2 hw2 Path independence 7 3 hw3 auchy Goursat 8 4 hw4 Applications of auchy Integral Formula 8 5 hw5 Liouville 9 6 hw6 Series 9 7 hw7 Taylor Series 8 hw8 Laurent Series 9 hw9 Derivative of Series, Substituting, Poles, Residues 2 hw2 Singular points 2 2 hw2 Residues, Poles, Order of a Pole 2
2 22 hw22 omputing Integrals 3 23 hw23 Poles Zeros 3 24 hw24 ool Integrals 3 These are problems will be due both daily at the end of classes. This PDF file was created on June 2, 24. hw, omplex Arithmetic, onjugates, Polar Form. (B3.) Reduce each of these 3 expressions to a real number + 2i 3 4i + 2 i 5i 5i ( i)(2 i)(3 i) ( i) 4 2. (B4.) In each case locate vectorially = 2i, 2 = 2 3 i = ( 3, ), 2 = ( 3, ) = ( 3, ), 2 = (, 4) = x + iy, 2 = x iy 3. (B4.4) Sketch the set of points determined by each equation + i = + i 3 + 4i 4 4. (B5.3,4) Verify 2 = 2, 2 = 2, 2 3 = = (B5.5) Verify 2 = 2 ( 2 ) 6. (B5.5) Show that the hyperbola x 2 y 2 = can be written = 2 7. (B7.) Find the principal argument Arg for both = 8. (B7.2) Show e iθ = e iθ = e iθ i 2 2i = ( 3 i) 6 9. (B7.5) Use de Moivre s formula to derive the following trig identities. cos 3θ = cos 3 θ 3 cos θ sin 2 θ = 4 cos 3 θ 3 cos θ sin 3θ = 3 cos 2 θ sin θ sin 3 θ = 3 sin θ 4 sin 3 θ 2 hw2 nth roots, Domains, Functions. (B7.7) Show if R > R 2 > then Arg( 2 ) = Arg + Arg 2 2. (B9.) Find the square roots of 2i i 3 expressed in rectangular form 3. (B9.3) Find all of the roots in rectangle coordinates of ( ) /3 8 /6. 2
3 4. (B9.6) Find the 4 roots of p() = = use them to factor p() into quadratic factors with real coefficients. 5. (B.-3) Sketch the 6 sets determine which are domains, which are bounded, which are neither open nor closed: 2 + i > 4 I > I = arg π/4 ( ) 4 6. (B.4) Find the closure of the 4 sets: π < arg < π ( ) R < R( ) 2 R( 2 ) > 7. (B.) For each function, describe the domain that is understood: f() = 2 + f() = Arg( ) f() = + f() = 2 8. (B.2) Write as u(x, y) + iv(x, y) 9. (B.3) Write simplify f() = x 2 y 2 2y + i(2x 2xy) in terms of using x = ( + )/2 y = ( )/2i. (B.4) Write f() = + / ( ) in the form u(r, θ) + iv(r, θ) 3 hw3 Images, Transformations. (B3.) Find a domain in the -plane whose image under the transformation w = 2 is the square domain in the w-plane bounded by the lines u =, u = 2, v =, v = 2 2. (B3.3) Sketch the region onto which the sector r, θ π/4 is mapped by the 3 transformations w = 2, w = 3, w = 4 3. (B3.4) Show that lines ay = x (a ) are mapped onto the spirals ρ = exp(aθ) under the transformation w = exp, where w = ρ exp(iφ) 4. (B3.7) Find the image of the semi-infinite strip x, y π under the transformation w = exp. Label the corresponding portions of the boundaries. 5. (B3.8) Graphically indicate the vector fields represented by w = i w = / 4 hw4 Limits. (B7.3) Find the limits. n is a positive integer, P () Q() are polynomials with Q( ) lim n ( ) i 3 lim i + i P () lim Q() 2. (B7.5) Show that the following limit does not exist lim ( )2 3
4 3. (B7.) Use a theorem to show: lim 4 2 ( ) 2 = 4 lim 4. (B7.) Suppose ad bc let: Use a theorem to show 2 + = lim ( ) 3 = T () = a + b c + d lim T () = (if c = ) lim T () = a (if c ) lim T () = (if c ) c d/c 5 hw5 Unbounded. (B7.3)( Show that a set S is unbounded if only if every neighborhood of the point at infinity contains at least one point of S. 6 hw6 Derivatives, auchy-riemann. (B9.) Find f () when f() = f() = ( 4 2 ) 3 f() = 2 + ( 2 ) f() = ( + 2 ) 4 2 ( ) 2. (B9.2) Show if P () = a + a + a a n n then P () = a + 2a na n hence a = P (), a = P ()!, a 2 = P (),... a n = P (n) () 2! n! 3. (B9.9) Let f denote the function whose values are { f() = 2 / when when = Show that if =, then w/ = at each nonero point on the real imaginary axes in the or x y-plane. Then show then w/ = at each nonero point along the line y = x. onclude that f () does not exist. 4. (B22.6) Let f denote the function above. Show that the auchy-riemann equations are satisfied at the origin = (, ) 5. (B22.) Use a theorem to show that f () does not exist at any point for each function: f() = f() = f() = 2x + ixy 2 f(x) = e x e iy 6. (B22.2) Use a theorem to show that f () its derivative f () exist everywhere find f (). f() = i + 2 f() = e x e iy f() = 3 f() = cos x cosh y i sin x sinh y 4
5 7. Extra redit (B22.) Recall = x + iy implies x = ( + )/2 y = ( )/2i. Use the formal chain rule to show F = F x x + F y y = 2 ( F x + i F y ) Define the operator = 2 ( x + i y ) apply it to u(x, y)+iv(x, y) to obtain the complex form of the auchy-reimann equations f/ =. 7 hw7 Exp Log. (B28.) Show that exp(2 ± 3πi) = e 2, exp((2 + πi)/4) = ( + i) e/2 exp( + πi) = exp. 2. (B28.2) State why the function e + e is entire. 3. (B28.3) Show f() = exp is not analytic anywhere. 4. (B28.7) Prove exp( 2) < if only if R >. 5. (B28.8) Find all values of such that e = 2, or e = + 3i or exp(2 ) = 6. (B28.) Show that if e is real, then I = nπ (n =, ±, ±2,... ). If e is pure imaginary, what restriction is placed on? 7. (B3.) Show that Log( ei) = π 2 i Log( i) = 2 ln 2 π 4 i. 8 hw8 Log log. (B3.2) Verify for n =, ±, ±2,...:. log e = + 2nπi log i = (2n + 2 )πi log( + 3i) = ln 2 + 2(n + 3 )πi 2. (B3.3) Show that Log( + i) 2 = 2 Log( + i) Log( + i) 2 2 Log( + i). 3. (B3.5) Show that the set of values of log(i /2 ) is {(n + 4 )πi : n =, ±, ±2,... } that the same is true of (/2) log i. 4. (B3.6) Given that the branch log = ln r + iθ (r >, α < θ < α + 2π) of the logarithmic function is analytic at each point in the stated domain, obtain its derivative by differentiating each side of the identity exp(log ) = using the chain rule. 5. (B3.7) Find all the roots of the equation log = iπ/2. 6. (B3.9) Show that Log( i) is analytic everywhere except on the half line y = (x ). Show Log( + 4) 2 + i is analytic everywhere except at the points ±( i)/ 2 on the portion x 4 of the real axis. 5
6 9 hw9 Principal values, Integrals over a Real Variable. (B3.) Show if R > R 2 > then Log( 2 ) = Log + Log (B3.2) Show that for any two complex numbers 2, Log( 2 ) = Log + Log 2 + 2Nπi where N has one of the values, ±. 3. (B32.) Show that when n =, ±, ±2... ( + i) i = exp( π 4 + 2nπ) exp( i 2 ln 2) ( )/π = e (2n+)i 4. (B32.2) Find the principal values of each expression: i i [ e 2 ( 3i)] 3πi ( i) 4i 5. (B32.5) Show that the principal n-th root of a nonero complex number is the same as the principal value of /n that was previously defined. 6. (B32.8) Let c, d, be complex numbers with. Prove that if all the powers involved are principal values, then c = c ( c ) n = cn (n =, 2,... ) c d = c+d 7. (B37.2) Evaluate c d = c d. 2 ( t i)2 dt π/6 e i2t dt e t dt (R > ) 8. (B37.5) Let w(t) be a continuous complex-valued funtion of t defined on an interval a t b. By considering the special case w(t) = e it on the interval t 2π, show that it is not always true that there is a number c in the interval a < t < b such that hw ontour Integrals b a w(t) dt = w(c)(b a). (B38.2) Let denote the right-h half of the circle = 2, in the counterclockwise direction note that two parametric representations for are Verify that Z(y) = [φ(y)], where = (θ) = 2e iθ ( π 2 θ π 2 ) = Z(y) = 4 y 2 + iy ( 2 y 2) φ(y) = arctan y 4 y 2 ( π 2 arctan t π 2 ) Also, show that this function φ has a positive derivative, as required in the conditions following (9) Sec 38. 6
7 2. (B4.,2,3,5,6) Evaluate for the given f() contour f() = ( + 2)/ is = 2e iθ ( θ π) f() = ( + 2)/ is = 2e iθ (π θ 2π) f() = ( + 2)/ is = 2e iθ ( θ 2π) f() = + is = + e iθ (π θ 2π) f() = + is = t ( t 2) f() = π exp(π) is square from,, + i, i f() d f() = is arbitrary curve from to 2 f() = +i is = positively oriented use branch exp[( + i) log ] ( >, < arg < 2π) 3. (B4.) Let denote the circle = R taken counterclockwise. Use the parametric representation = + Re iθ ( π θ π) for to derive the following integration formula s: d = 2πi ( ) n d = (n = ±, ±2,... ) hw More on ontour Integrals. (B4.4) Let R denote the upper half of the circle = R (R > 2), taken in the counterclockwise direction. Show that 2 2 R d πr(2r2 + ) (R 2 )(R 2 4) 2. (B43.) Use an antiderivative to show that, for every contour extending from a point to a point 2, n d = n + (n+ 2 n+ ) (n =,,... ) 3. (B43.2) By finding an antiderivative, evaluate each of these integrals, where the path is any contour between the indicated limits of integration. i/2 i e π d π+2i cos( 3 2 ) d ( 2) 3 d 2 hw2 Path independence. (B43.3) Use a theorem to show ( ) n d = (n = ±, ±2,... ) when is any closed contour which does not pass through the point. 2. (B43.4) Let, (resp. 2 ), be any contour from = 3 to = 3 that except for its end points, lies above (resp. below) the x-axis. Find an antiderivative F 2 () of the branch f 2 () of /2 = re iθ/2 (r >, π 2 < θ < 5π 2 ) 7
8 to show that the integral 2 /2 d has value 2 3( + i). Note that the value of the integral of the function /2 = re iθ/2 around the closed contour 2 in that example is, therefore 4 3 given that /2 d = 2 3( + i). (Lots of parts from example 43.4.) 3 hw3 auchy Goursat. (B46.) Apply the auchy-goursat theorem to show that f() d = when the contour is the circle =, in either direction when f() = 2 3 f() = e f() = f() = sech f() = tan f() = Log( + 2) 2. (B46.2) Let be the positively oriented circle = 4 let 2 be the positively oriented boundary of the square whose sides lie along the lines x = ±, y = ±. Point out why f() d = f() d 2 when f() = f() = + 2 sin(/2) f() = e 3. (B46.3) If is the boundary of the rectangle x 3, y 2, described in the positive sense, then ( 2 i) n = 2πi when n = when n = ±, ±2, (B46.4) Extra redit???? 4 hw4 Applications of auchy Integral Formula. (B48.abc) Let denote the positively oriented boundary of the square whose sides lie along the lines x = ±2, y = ±2. Evaluate the integrals e d (πi/2) cos d ( 2 + 8) d 2 + 8
9 2. (B48.2) Find the integral of g() around the circle i = 2 in the positive sense when g() = /( 2 + 4) when g() = /( 2 + 4) (B48.3) Let be the circle = 3 decribed in the positive sense. Show that if g(w) = d ( w 3) w then g(2) = 8πi. What is the value of g(w) when w > 3? 4. (B48.7) Let be the unit circle = e iθ ( π θ π). First show that for any real constant a, e a d = 2πi Then write this integral in terms of θ to derive the integration formula π e a cos θ cos(a sin θ) dθ = π 5. (B48.6) Extra redit???? Let f denote a function that is continuous on a simple closed contour. Prove the function g() = f(ξ) dξ 2πi ξ is analytic as each point interior to that g () = 2πi at such a point. 5 hw5 Liouville f(ξ) dξ (ξ ) 2. (B5.) Let f be an entire function such that f() A for all, where A is a fixed positive number. Show that f() = a, where a is a complex constant. [Hint: use auchy s inequality to show f () is ero.] 2. (B5.) Suppose f() is entire that the harmonic function u(x, y) = Rf() has an upper bound u : that is, u(x, y) u for all points (x, y) in the xy-plane. Show that u(x, y) must be constant throughout the plane. [Hint: use Liouville s theorem on exp(f()).] 3. (B5.4,5) Let a function f be continuous in a closed bounded region R, let it be analytic not constant throughout the interior of R. Assuming f() anywhere in R, prove that f() has a minimum value m in R which occurs on the boundary of R never in the interior. [Hint: look at /f().] Use the function f() = to show that the condition f() anywhere is necessary for this conclusion. 6 hw6 Series. (B52.6) Show if n= n = S, then n= n = S. 2. (B52.7) Show for any complex number c Show if n= n = S, then n= c n = cs. 3. (B52.8) Show if n= n = S n= w n = T, then n= ( n + w n ) = S + T. 9
10 7 hw7 Taylor Series. (B54.2) Obtain the Taylor e = e ( ) n two ways. First using f (n) () second by using e = ee. 2. (B54.3) Find the Maclaurin series expansion for the function f() = n! ( < ) = /9 3. (B54.5) Derive the Maclaurin series for cos by showing f (2n) () = ( ) n f (2n+) () = by using cos = (e i + e i )/2. 4. (B54.) Show when, 5. (B54.3) Show that when < < 4, 8 hw8 Laurent Series e 2 = ! + 3! + 2 4! + sin( 2 ) 4 = 2 2 3! + 6 5! + 7! 4 2 = 4 + n 4 n+2. (B56.) Find the Laurent series that represents the function f() = 2 sin(/ 2 ) in the domain < <. 2. (B56.2) Derive the Laurent series representation [ e ( + ) 2 = ] ( + ) n e (n + 2)! ( + ) 2 3. (B56.3) Find a representation for the function f() = + = + (/) in negative powers of that is valid for < <. 4. (B56.4) Give two Laurent series expansions in powers of for the function f() = /[ 2 ( )] specify the regions in which the expansions are valid. [Hint: about ] 5. (B56.5) Represent the function f() = + by both its Maclaurin series (stating where it is valid) by a Laurent series in the domain < < 6. (B56.6) Show that when < < 2, ( )( 3) = 3 ( ) n 2 n+2 2( )
11 9 hw9 Derivative of Series, Substituting, Poles, Residues. (B6.) By differentiating the Maclaurin series representation obtain the expressions = n ( < ) ( ) 2 = (n + ) n ( < ) 2 ( ) 3 = (n + )(n + 2) n ( < ) 2. (B6.2) By substituting /( ) for in the expansion ( ) 2 = (n + ) n ( < ) found above, derive the Laurent series representation 2 = n=2 3. (B6.3) Find the Taylor series for the function ( ) n (n ) ( ) n ( < < ) = 2 + ( 2) = 2 + ( 2)/2 about the point = 2. Then by differentiating that series term by term, show that 2 = ( ) n (n + )( )n ( 2 < 2) 4. (B6.) Use multiplication of series to show that e ( 2 + ) = ( < < ) 5. (B6.3) Use division to obtain the Laurent series representation e = ( < < 2π) 6. (B64.) Find the residue at = of the functions + 2 cos( ) sin cot 4 sinh 4 ( 2 ) 7. (B64.2) Use auchy s residue theorem to evaluate the integral of each of these functions around the circle = 3 in the positive sense: exp( ) 2 exp( ) ( ) 2 2 exp( ) (B64.3) Use a theorem involving a single residue to evaluate the integral of each of these functions around the circle = 2 in the positive sense
12 2 hw2 Singular points. (B65.) In each case, write the principal part of the function at its isolated singular point determine whether that point is a pole, a removable singular point or an essential singular pont. exp( ) 2 + sin cos (2 ) 3 2. (B65.2) Show that the singular point of each of the following functions is a pole. Determine the order m of the pole the corresponding residue B. cosh 3 exp(2) 4 exp(2) ( ) 2 3. (B65.3) Suppose f is analytic at write g() = f()/( ). Show that: (a) If f( ), then is a simple pole of g, with residue f( ). (b) Iff( ) =, then is a removable singular point of g. 2 hw2 Residues, Poles, Order of a Pole. (B65.4) Write the function as f() = f() = 8a3 2 ( 2 + a 2 ) 3 (a > ) φ() ( ai) 3 where φ() = 8a3 2 ( + ai) 3 Point out why φ() has a Taylor series representation about = ai, then use it to show that the principal part of f at that point is φ (ai)/2 ai + φ (ai) ( ai) 2 + φ(ai) ( ai) 3 = i/2 ai a/2 ( ai) 2 a 2 i ( ai) 3 2. (B67.) In each case, show that any singular point of the function is a pole. Determine the order m of the pole find the corresponding residue B ( 2 + )3 exp 2 + π 2 3. (B67.2) Show that Res = Res =i /4 + = + i 2 ( >, < arg < 2π) Res =i /2 ( 2 + ) 2 = i (B67.3) Find the value of the integral Log ( 2 + ) 2 = π + 2i 8 ( >, < arg < 2π) ( )( 2 + 9) d taken counterclockwise around both circles 2 = 2 = 4 2
13 22 hw22 omputing Integrals. (B67.4) Find the value of the integral d 3 ( + 4) taken counterclockwise around both circles = = 3 2. (B69.) Show that the point = is a simple pole of the function f() = csc = / sin by a theorem by computing the Laurent series. 3. (B69.3a) Show that Res ( sec ) = ( ) n+ n, where n = π + nπ (n =, ±, ±2,... = n 2 4. (B69.4a) Let denote the positively oriented circle = 2 evaluate the integral tan d 5. (B69.5) Let N denote the positive oriented boundary of the square whose edges lie along the lines where N is a positive integer. Show that x = ±(N + 2 )π y = ±(N + 2 )π N [ d 2 sin = 2πi N n= ] ( ) n n 2 π 2 then using the fact that the value of this integral tends to ero as N tends to infinity, point out how it follows that ( ) n n 2 = π hw23 Poles Zeros n=. (B69.9) Let p q denote functions that are analytic at a point where p( ) q( ) =. Show that if the quotient p()/q() has a pole of order m at, then is a ero of order m of q. 24 hw24 ool Integrals. (B72.,2,4) Use residues to evaluate the following integrals dx x 2 + dx (x 2 + ) 2 x 2 dx (x 2 + )(x 2 + 4) 2. (B74.,2) Use residues to evaluate the following integrals cos x dx (x 2 + a 2 )(x 2 + b 2 ) (a > b > ) cos ax dx x 2 + (a > ) 3
Second Midterm Exam Name: Practice Problems March 10, 2015
 Math 160 1. Treibergs Second Midterm Exam Name: Practice Problems March 10, 015 1. Determine the singular points of the function and state why the function is analytic everywhere else: z 1 fz) = z + 1)z
Math 160 1. Treibergs Second Midterm Exam Name: Practice Problems March 10, 015 1. Determine the singular points of the function and state why the function is analytic everywhere else: z 1 fz) = z + 1)z
Lecture Notes Complex Analysis. Complex Variables and Applications 7th Edition Brown and Churchhill
 Lecture Notes omplex Analysis based on omplex Variables and Applications 7th Edition Brown and hurchhill Yvette Fajardo-Lim, Ph.D. Department of Mathematics De La Salle University - Manila 2 ontents THE
Lecture Notes omplex Analysis based on omplex Variables and Applications 7th Edition Brown and hurchhill Yvette Fajardo-Lim, Ph.D. Department of Mathematics De La Salle University - Manila 2 ontents THE
= 2πi Res. z=0 z (1 z) z 5. z=0. = 2πi 4 5z
 MTH30 Spring 07 HW Assignment 7: From [B4]: hap. 6: Sec. 77, #3, 7; Sec. 79, #, (a); Sec. 8, #, 3, 5, Sec. 83, #5,,. The due date for this assignment is 04/5/7. Sec. 77, #3. In the example in Sec. 76,
MTH30 Spring 07 HW Assignment 7: From [B4]: hap. 6: Sec. 77, #3, 7; Sec. 79, #, (a); Sec. 8, #, 3, 5, Sec. 83, #5,,. The due date for this assignment is 04/5/7. Sec. 77, #3. In the example in Sec. 76,
MTH 3102 Complex Variables Final Exam May 1, :30pm-5:30pm, Skurla Hall, Room 106
 Name (Last name, First name): MTH 32 Complex Variables Final Exam May, 27 3:3pm-5:3pm, Skurla Hall, Room 6 Exam Instructions: You have hour & 5 minutes to complete the exam. There are a total of problems.
Name (Last name, First name): MTH 32 Complex Variables Final Exam May, 27 3:3pm-5:3pm, Skurla Hall, Room 6 Exam Instructions: You have hour & 5 minutes to complete the exam. There are a total of problems.
MTH3101 Spring 2017 HW Assignment 4: Sec. 26: #6,7; Sec. 33: #5,7; Sec. 38: #8; Sec. 40: #2 The due date for this assignment is 2/23/17.
 MTH0 Spring 07 HW Assignment : Sec. 6: #6,7; Sec. : #5,7; Sec. 8: #8; Sec. 0: # The due date for this assignment is //7. Sec. 6: #6. Use results in Sec. to verify that the function g z = ln r + iθ r >
MTH0 Spring 07 HW Assignment : Sec. 6: #6,7; Sec. : #5,7; Sec. 8: #8; Sec. 0: # The due date for this assignment is //7. Sec. 6: #6. Use results in Sec. to verify that the function g z = ln r + iθ r >
Syllabus: for Complex variables
 EE-2020, Spring 2009 p. 1/42 Syllabus: for omplex variables 1. Midterm, (4/27). 2. Introduction to Numerical PDE (4/30): [Ref.num]. 3. omplex variables: [Textbook]h.13-h.18. omplex numbers and functions,
EE-2020, Spring 2009 p. 1/42 Syllabus: for omplex variables 1. Midterm, (4/27). 2. Introduction to Numerical PDE (4/30): [Ref.num]. 3. omplex variables: [Textbook]h.13-h.18. omplex numbers and functions,
CHAPTER 3 ELEMENTARY FUNCTIONS 28. THE EXPONENTIAL FUNCTION. Definition: The exponential function: The exponential function e z by writing
 CHAPTER 3 ELEMENTARY FUNCTIONS We consider here various elementary functions studied in calculus and define corresponding functions of a complex variable. To be specific, we define analytic functions of
CHAPTER 3 ELEMENTARY FUNCTIONS We consider here various elementary functions studied in calculus and define corresponding functions of a complex variable. To be specific, we define analytic functions of
Math 185 Homework Exercises II
 Math 185 Homework Exercises II Instructor: Andrés E. Caicedo Due: July 10, 2002 1. Verify that if f H(Ω) C 2 (Ω) is never zero, then ln f is harmonic in Ω. 2. Let f = u+iv H(Ω) C 2 (Ω). Let p 2 be an integer.
Math 185 Homework Exercises II Instructor: Andrés E. Caicedo Due: July 10, 2002 1. Verify that if f H(Ω) C 2 (Ω) is never zero, then ln f is harmonic in Ω. 2. Let f = u+iv H(Ω) C 2 (Ω). Let p 2 be an integer.
1 z n = 1. 9.(Problem) Evaluate each of the following, that is, express each in standard Cartesian form x + iy. (2 i) 3. ( 1 + i. 2 i.
 . 5(b). (Problem) Show that z n = z n and z n = z n for n =,,... (b) Use polar form, i.e. let z = re iθ, then z n = r n = z n. Note e iθ = cos θ + i sin θ =. 9.(Problem) Evaluate each of the following,
. 5(b). (Problem) Show that z n = z n and z n = z n for n =,,... (b) Use polar form, i.e. let z = re iθ, then z n = r n = z n. Note e iθ = cos θ + i sin θ =. 9.(Problem) Evaluate each of the following,
EE2007: Engineering Mathematics II Complex Analysis
 EE2007: Engineering Mathematics II omplex Analysis Ling KV School of EEE, NTU ekvling@ntu.edu.sg V4.2: Ling KV, August 6, 2006 V4.1: Ling KV, Jul 2005 EE2007 V4.0: Ling KV, Jan 2005, EE2007 V3.1: Ling
EE2007: Engineering Mathematics II omplex Analysis Ling KV School of EEE, NTU ekvling@ntu.edu.sg V4.2: Ling KV, August 6, 2006 V4.1: Ling KV, Jul 2005 EE2007 V4.0: Ling KV, Jan 2005, EE2007 V3.1: Ling
MA 412 Complex Analysis Final Exam
 MA 4 Complex Analysis Final Exam Summer II Session, August 9, 00.. Find all the values of ( 8i) /3. Sketch the solutions. Answer: We start by writing 8i in polar form and then we ll compute the cubic root:
MA 4 Complex Analysis Final Exam Summer II Session, August 9, 00.. Find all the values of ( 8i) /3. Sketch the solutions. Answer: We start by writing 8i in polar form and then we ll compute the cubic root:
MTH4101 CALCULUS II REVISION NOTES. 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) ax 2 + bx + c = 0. x = b ± b 2 4ac 2a. i = 1.
 MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
MTH4101 CALCULUS II REVISION NOTES 1. COMPLEX NUMBERS (Thomas Appendix 7 + lecture notes) 1.1 Introduction Types of numbers (natural, integers, rationals, reals) The need to solve quadratic equations:
Math 312 Fall 2013 Final Exam Solutions (2 + i)(i + 1) = (i 1)(i + 1) = 2i i2 + i. i 2 1
 . (a) We have 2 + i i Math 32 Fall 203 Final Exam Solutions (2 + i)(i + ) (i )(i + ) 2i + 2 + i2 + i i 2 3i + 2 2 3 2 i.. (b) Note that + i 2e iπ/4 so that Arg( + i) π/4. This implies 2 log 2 + π 4 i..
. (a) We have 2 + i i Math 32 Fall 203 Final Exam Solutions (2 + i)(i + ) (i )(i + ) 2i + 2 + i2 + i i 2 3i + 2 2 3 2 i.. (b) Note that + i 2e iπ/4 so that Arg( + i) π/4. This implies 2 log 2 + π 4 i..
MTH 3102 Complex Variables Solutions: Practice Exam 2 Mar. 26, 2017
 Name Last name, First name): MTH 31 omplex Variables Solutions: Practice Exam Mar. 6, 17 Exam Instructions: You have 1 hour & 1 minutes to complete the exam. There are a total of 7 problems. You must show
Name Last name, First name): MTH 31 omplex Variables Solutions: Practice Exam Mar. 6, 17 Exam Instructions: You have 1 hour & 1 minutes to complete the exam. There are a total of 7 problems. You must show
lim when the limit on the right exists, the improper integral is said to converge to that limit.
 hapter 7 Applications of esidues - evaluation of definite and improper integrals occurring in real analysis and applied math - finding inverse Laplace transform by the methods of summing residues. 6. Evaluation
hapter 7 Applications of esidues - evaluation of definite and improper integrals occurring in real analysis and applied math - finding inverse Laplace transform by the methods of summing residues. 6. Evaluation
Math Spring 2014 Solutions to Assignment # 8 Completion Date: Friday May 30, 2014
 Math 3 - Spring 4 Solutions to Assignment # 8 ompletion Date: Friday May 3, 4 Question. [p 49, #] By finding an antiderivative, evaluate each of these integrals, where the path is any contour between the
Math 3 - Spring 4 Solutions to Assignment # 8 ompletion Date: Friday May 3, 4 Question. [p 49, #] By finding an antiderivative, evaluate each of these integrals, where the path is any contour between the
MTH 3102 Complex Variables Final Exam May 1, :30pm-5:30pm, Skurla Hall, Room 106
 Name (Last name, First name): MTH 02 omplex Variables Final Exam May, 207 :0pm-5:0pm, Skurla Hall, Room 06 Exam Instructions: You have hour & 50 minutes to complete the exam. There are a total of problems.
Name (Last name, First name): MTH 02 omplex Variables Final Exam May, 207 :0pm-5:0pm, Skurla Hall, Room 06 Exam Instructions: You have hour & 50 minutes to complete the exam. There are a total of problems.
Complex Analysis Homework 1: Solutions
 Complex Analysis Fall 007 Homework 1: Solutions 1.1.. a) + i)4 + i) 8 ) + 1 + )i 5 + 14i b) 8 + 6i) 64 6) + 48 + 48)i 8 + 96i c) 1 + ) 1 + i 1 + 1 i) 1 + i)1 i) 1 + i ) 5 ) i 5 4 9 ) + 4 4 15 i ) 15 4
Complex Analysis Fall 007 Homework 1: Solutions 1.1.. a) + i)4 + i) 8 ) + 1 + )i 5 + 14i b) 8 + 6i) 64 6) + 48 + 48)i 8 + 96i c) 1 + ) 1 + i 1 + 1 i) 1 + i)1 i) 1 + i ) 5 ) i 5 4 9 ) + 4 4 15 i ) 15 4
Math 417 Midterm Exam Solutions Friday, July 9, 2010
 Math 417 Midterm Exam Solutions Friday, July 9, 010 Solve any 4 of Problems 1 6 and 1 of Problems 7 8. Write your solutions in the booklet provided. If you attempt more than 5 problems, you must clearly
Math 417 Midterm Exam Solutions Friday, July 9, 010 Solve any 4 of Problems 1 6 and 1 of Problems 7 8. Write your solutions in the booklet provided. If you attempt more than 5 problems, you must clearly
Part IB. Complex Analysis. Year
 Part IB Complex Analysis Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 Paper 1, Section I 2A Complex Analysis or Complex Methods 7 (a) Show that w = log(z) is a conformal
Part IB Complex Analysis Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 Paper 1, Section I 2A Complex Analysis or Complex Methods 7 (a) Show that w = log(z) is a conformal
1 Res z k+1 (z c), 0 =
 32. COMPLEX ANALYSIS FOR APPLICATIONS Mock Final examination. (Monday June 7..am 2.pm) You may consult your handwritten notes, the book by Gamelin, and the solutions and handouts provided during the Quarter.
32. COMPLEX ANALYSIS FOR APPLICATIONS Mock Final examination. (Monday June 7..am 2.pm) You may consult your handwritten notes, the book by Gamelin, and the solutions and handouts provided during the Quarter.
18.04 Practice problems exam 1, Spring 2018 Solutions
 8.4 Practice problems exam, Spring 8 Solutions Problem. omplex arithmetic (a) Find the real and imaginary part of z + z. (b) Solve z 4 i =. (c) Find all possible values of i. (d) Express cos(4x) in terms
8.4 Practice problems exam, Spring 8 Solutions Problem. omplex arithmetic (a) Find the real and imaginary part of z + z. (b) Solve z 4 i =. (c) Find all possible values of i. (d) Express cos(4x) in terms
Conformal maps. Lent 2019 COMPLEX METHODS G. Taylor. A star means optional and not necessarily harder.
 Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
BTL What is the value of m if the vector is solenoidal. BTL What is the value of a, b, c if the vector may be irrotational.
 VALLIAMMAI ENGINEERING OLLEGE SRM NAGAR, KATTANDKULATHUR Department of Mathematics MA65 - MATHEMATIS II QUESTION BANK - 6 UNIT - I VETOR ALULUS Part - A. Find, if at (, -, ). BTL-. Find the Directional
VALLIAMMAI ENGINEERING OLLEGE SRM NAGAR, KATTANDKULATHUR Department of Mathematics MA65 - MATHEMATIS II QUESTION BANK - 6 UNIT - I VETOR ALULUS Part - A. Find, if at (, -, ). BTL-. Find the Directional
MATH 452. SAMPLE 3 SOLUTIONS May 3, (10 pts) Let f(x + iy) = u(x, y) + iv(x, y) be an analytic function. Show that u(x, y) is harmonic.
 MATH 45 SAMPLE 3 SOLUTIONS May 3, 06. (0 pts) Let f(x + iy) = u(x, y) + iv(x, y) be an analytic function. Show that u(x, y) is harmonic. Because f is holomorphic, u and v satisfy the Cauchy-Riemann equations:
MATH 45 SAMPLE 3 SOLUTIONS May 3, 06. (0 pts) Let f(x + iy) = u(x, y) + iv(x, y) be an analytic function. Show that u(x, y) is harmonic. Because f is holomorphic, u and v satisfy the Cauchy-Riemann equations:
1 Discussion on multi-valued functions
 Week 3 notes, Math 7651 1 Discussion on multi-valued functions Log function : Note that if z is written in its polar representation: z = r e iθ, where r = z and θ = arg z, then log z log r + i θ + 2inπ
Week 3 notes, Math 7651 1 Discussion on multi-valued functions Log function : Note that if z is written in its polar representation: z = r e iθ, where r = z and θ = arg z, then log z log r + i θ + 2inπ
13 Definite integrals
 3 Definite integrals Read: Boas h. 4. 3. Laurent series: Def.: Laurent series (LS). If f() is analytic in a region R, then converges in R, with a n = πi f() = a n ( ) n + n= n= f() ; b ( ) n+ n = πi b
3 Definite integrals Read: Boas h. 4. 3. Laurent series: Def.: Laurent series (LS). If f() is analytic in a region R, then converges in R, with a n = πi f() = a n ( ) n + n= n= f() ; b ( ) n+ n = πi b
Topic 4 Notes Jeremy Orloff
 Topic 4 Notes Jeremy Orloff 4 auchy s integral formula 4. Introduction auchy s theorem is a big theorem which we will use almost daily from here on out. Right away it will reveal a number of interesting
Topic 4 Notes Jeremy Orloff 4 auchy s integral formula 4. Introduction auchy s theorem is a big theorem which we will use almost daily from here on out. Right away it will reveal a number of interesting
Final Exam - MATH 630: Solutions
 Final Exam - MATH 630: Solutions Problem. Find all x R satisfying e xeix e ix. Solution. Comparing the moduli of both parts, we obtain e x cos x, and therefore, x cos x 0, which is possible only if x 0
Final Exam - MATH 630: Solutions Problem. Find all x R satisfying e xeix e ix. Solution. Comparing the moduli of both parts, we obtain e x cos x, and therefore, x cos x 0, which is possible only if x 0
North MaharashtraUniversity ; Jalgaon.
 North MaharashtraUniversity ; Jalgaon. Question Bank S.Y.B.Sc. Mathematics (Sem II) MTH. Functions of a omplex Variable. Authors ; Prof. M.D.Suryawanshi (o-ordinator) Head, Department of Mathematics, S.S.V.P.S.
North MaharashtraUniversity ; Jalgaon. Question Bank S.Y.B.Sc. Mathematics (Sem II) MTH. Functions of a omplex Variable. Authors ; Prof. M.D.Suryawanshi (o-ordinator) Head, Department of Mathematics, S.S.V.P.S.
1. The COMPLEX PLANE AND ELEMENTARY FUNCTIONS: Complex numbers; stereographic projection; simple and multiple connectivity, elementary functions.
 Complex Analysis Qualifying Examination 1 The COMPLEX PLANE AND ELEMENTARY FUNCTIONS: Complex numbers; stereographic projection; simple and multiple connectivity, elementary functions 2 ANALYTIC FUNCTIONS:
Complex Analysis Qualifying Examination 1 The COMPLEX PLANE AND ELEMENTARY FUNCTIONS: Complex numbers; stereographic projection; simple and multiple connectivity, elementary functions 2 ANALYTIC FUNCTIONS:
EE2007 Tutorial 7 Complex Numbers, Complex Functions, Limits and Continuity
 EE27 Tutorial 7 omplex Numbers, omplex Functions, Limits and ontinuity Exercise 1. These are elementary exercises designed as a self-test for you to determine if you if have the necessary pre-requisite
EE27 Tutorial 7 omplex Numbers, omplex Functions, Limits and ontinuity Exercise 1. These are elementary exercises designed as a self-test for you to determine if you if have the necessary pre-requisite
Exercises for Part 1
 MATH200 Complex Analysis. Exercises for Part Exercises for Part The following exercises are provided for you to revise complex numbers. Exercise. Write the following expressions in the form x + iy, x,y
MATH200 Complex Analysis. Exercises for Part Exercises for Part The following exercises are provided for you to revise complex numbers. Exercise. Write the following expressions in the form x + iy, x,y
Physics 307. Mathematical Physics. Luis Anchordoqui. Wednesday, August 31, 16
 Physics 307 Mathematical Physics Luis Anchordoqui 1 Bibliography L. A. Anchordoqui and T. C. Paul, ``Mathematical Models of Physics Problems (Nova Publishers, 2013) G. F. D. Duff and D. Naylor, ``Differential
Physics 307 Mathematical Physics Luis Anchordoqui 1 Bibliography L. A. Anchordoqui and T. C. Paul, ``Mathematical Models of Physics Problems (Nova Publishers, 2013) G. F. D. Duff and D. Naylor, ``Differential
Math Final Exam.
 Math 106 - Final Exam. This is a closed book exam. No calculators are allowed. The exam consists of 8 questions worth 100 points. Good luck! Name: Acknowledgment and acceptance of honor code: Signature:
Math 106 - Final Exam. This is a closed book exam. No calculators are allowed. The exam consists of 8 questions worth 100 points. Good luck! Name: Acknowledgment and acceptance of honor code: Signature:
Complex Variables. Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit.
 Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit. 1. The TI-89 calculator says, reasonably enough, that x 1) 1/3 1 ) 3 = 8. lim
Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit. 1. The TI-89 calculator says, reasonably enough, that x 1) 1/3 1 ) 3 = 8. lim
Complex Analysis for Applications, Math 132/1, Home Work Solutions-II Masamichi Takesaki
 Page 48, Problem. Complex Analysis for Applications, Math 3/, Home Work Solutions-II Masamichi Takesaki Γ Γ Γ 0 Page 9, Problem. If two contours Γ 0 and Γ are respectively shrunkable to single points in
Page 48, Problem. Complex Analysis for Applications, Math 3/, Home Work Solutions-II Masamichi Takesaki Γ Γ Γ 0 Page 9, Problem. If two contours Γ 0 and Γ are respectively shrunkable to single points in
Midterm Examination #2
 Anthony Austin MATH 47 April, 9 AMDG Midterm Examination #. The integrand has poles of order whenever 4, which occurs when is equal to i, i,, or. Since a R, a >, the only one of these poles that lies inside
Anthony Austin MATH 47 April, 9 AMDG Midterm Examination #. The integrand has poles of order whenever 4, which occurs when is equal to i, i,, or. Since a R, a >, the only one of these poles that lies inside
Homework #11 Solutions
 Homework # Solutions Math 8, Fall 03 Instructor: Dr. Doreen De Leon HW #a Find the singularities and determine if they are isolated for. f cos cos has one singularity, 0 0. and g is entire. cos is analytic
Homework # Solutions Math 8, Fall 03 Instructor: Dr. Doreen De Leon HW #a Find the singularities and determine if they are isolated for. f cos cos has one singularity, 0 0. and g is entire. cos is analytic
Solutions to practice problems for the final
 Solutions to practice problems for the final Holomorphicity, Cauchy-Riemann equations, and Cauchy-Goursat theorem 1. (a) Show that there is a holomorphic function on Ω = {z z > 2} whose derivative is z
Solutions to practice problems for the final Holomorphicity, Cauchy-Riemann equations, and Cauchy-Goursat theorem 1. (a) Show that there is a holomorphic function on Ω = {z z > 2} whose derivative is z
Chapter II. Complex Variables
 hapter II. omplex Variables Dates: October 2, 4, 7, 2002. These three lectures will cover the following sections of the text book by Keener. 6.1. omplex valued functions and branch cuts; 6.2.1. Differentiation
hapter II. omplex Variables Dates: October 2, 4, 7, 2002. These three lectures will cover the following sections of the text book by Keener. 6.1. omplex valued functions and branch cuts; 6.2.1. Differentiation
MA 201 Complex Analysis Lecture 6: Elementary functions
 MA 201 Complex Analysis : The Exponential Function Recall: Euler s Formula: For y R, e iy = cos y + i sin y and for any x, y R, e x+y = e x e y. Definition: If z = x + iy, then e z or exp(z) is defined
MA 201 Complex Analysis : The Exponential Function Recall: Euler s Formula: For y R, e iy = cos y + i sin y and for any x, y R, e x+y = e x e y. Definition: If z = x + iy, then e z or exp(z) is defined
Solution for Final Review Problems 1
 Solution for Final Review Problems Final time and location: Dec. Gymnasium, Rows 23, 25 5, 2, Wednesday, 9-2am, Main ) Let fz) be the principal branch of z i. a) Find f + i). b) Show that fz )fz 2 ) λfz
Solution for Final Review Problems Final time and location: Dec. Gymnasium, Rows 23, 25 5, 2, Wednesday, 9-2am, Main ) Let fz) be the principal branch of z i. a) Find f + i). b) Show that fz )fz 2 ) λfz
MA3111S COMPLEX ANALYSIS I
 MA3111S COMPLEX ANALYSIS I 1. The Algebra of Complex Numbers A complex number is an expression of the form a + ib, where a and b are real numbers. a is called the real part of a + ib and b the imaginary
MA3111S COMPLEX ANALYSIS I 1. The Algebra of Complex Numbers A complex number is an expression of the form a + ib, where a and b are real numbers. a is called the real part of a + ib and b the imaginary
3 Elementary Functions
 3 Elementary Functions 3.1 The Exponential Function For z = x + iy we have where Euler s formula gives The note: e z = e x e iy iy = cos y + i sin y When y = 0 we have e x the usual exponential. When z
3 Elementary Functions 3.1 The Exponential Function For z = x + iy we have where Euler s formula gives The note: e z = e x e iy iy = cos y + i sin y When y = 0 we have e x the usual exponential. When z
Taylor and Laurent Series
 Chapter 4 Taylor and Laurent Series 4.. Taylor Series 4... Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function f : R R is given by: f (x + f (x (x x + f (x
Chapter 4 Taylor and Laurent Series 4.. Taylor Series 4... Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function f : R R is given by: f (x + f (x (x x + f (x
Functions of a Complex Variable and Integral Transforms
 Functions of a Complex Variable and Integral Transforms Department of Mathematics Zhou Lingjun Textbook Functions of Complex Analysis with Applications to Engineering and Science, 3rd Edition. A. D. Snider
Functions of a Complex Variable and Integral Transforms Department of Mathematics Zhou Lingjun Textbook Functions of Complex Analysis with Applications to Engineering and Science, 3rd Edition. A. D. Snider
Integration in the Complex Plane (Zill & Wright Chapter 18)
 Integration in the omplex Plane Zill & Wright hapter 18) 116-4-: omplex Variables Fall 11 ontents 1 ontour Integrals 1.1 Definition and Properties............................. 1. Evaluation.....................................
Integration in the omplex Plane Zill & Wright hapter 18) 116-4-: omplex Variables Fall 11 ontents 1 ontour Integrals 1.1 Definition and Properties............................. 1. Evaluation.....................................
Math 421 Midterm 2 review questions
 Math 42 Midterm 2 review questions Paul Hacking November 7, 205 () Let U be an open set and f : U a continuous function. Let be a smooth curve contained in U, with endpoints α and β, oriented from α to
Math 42 Midterm 2 review questions Paul Hacking November 7, 205 () Let U be an open set and f : U a continuous function. Let be a smooth curve contained in U, with endpoints α and β, oriented from α to
Math 185 Fall 2015, Sample Final Exam Solutions
 Math 185 Fall 2015, Sample Final Exam Solutions Nikhil Srivastava December 12, 2015 1. True or false: (a) If f is analytic in the annulus A = {z : 1 < z < 2} then there exist functions g and h such that
Math 185 Fall 2015, Sample Final Exam Solutions Nikhil Srivastava December 12, 2015 1. True or false: (a) If f is analytic in the annulus A = {z : 1 < z < 2} then there exist functions g and h such that
Complex Analysis. Travis Dirle. December 4, 2016
 Complex Analysis 2 Complex Analysis Travis Dirle December 4, 2016 2 Contents 1 Complex Numbers and Functions 1 2 Power Series 3 3 Analytic Functions 7 4 Logarithms and Branches 13 5 Complex Integration
Complex Analysis 2 Complex Analysis Travis Dirle December 4, 2016 2 Contents 1 Complex Numbers and Functions 1 2 Power Series 3 3 Analytic Functions 7 4 Logarithms and Branches 13 5 Complex Integration
Suggested Homework Solutions
 Suggested Homework Solutions Chapter Fourteen Section #9: Real and Imaginary parts of /z: z = x + iy = x + iy x iy ( ) x iy = x #9: Real and Imaginary parts of ln z: + i ( y ) ln z = ln(re iθ ) = ln r
Suggested Homework Solutions Chapter Fourteen Section #9: Real and Imaginary parts of /z: z = x + iy = x + iy x iy ( ) x iy = x #9: Real and Imaginary parts of ln z: + i ( y ) ln z = ln(re iθ ) = ln r
Math 460: Complex Analysis MWF 11am, Fulton Hall 425 Homework 8 Solutions Please write neatly, and in complete sentences when possible.
 Math 460: Complex Analysis MWF am, Fulton Hall 45 Homework 8 Solutions Please write neatly, and in complete sentences when possible. Do the following problems from the book:.4.,.4.0,.4.-.4.6, 4.., 4..,
Math 460: Complex Analysis MWF am, Fulton Hall 45 Homework 8 Solutions Please write neatly, and in complete sentences when possible. Do the following problems from the book:.4.,.4.0,.4.-.4.6, 4.., 4..,
Complex Integration Line Integral in the Complex Plane CHAPTER 14
 HAPTER 14 omplex Integration hapter 13 laid the groundwork for the study of complex analysis, covered complex numbers in the complex plane, limits, and differentiation, and introduced the most important
HAPTER 14 omplex Integration hapter 13 laid the groundwork for the study of complex analysis, covered complex numbers in the complex plane, limits, and differentiation, and introduced the most important
EE2012 ~ Page 9 / Part 2. ben m chen, nus ece
 omplex Analysis EE ~ Page 9 / Part Flow hart of Material in omplex Analysis x iy t () xt () iyt () f( ) uivu( x, y) iv( x, y) Starting omplex function of a real variable ~ define a curve on a complex plane
omplex Analysis EE ~ Page 9 / Part Flow hart of Material in omplex Analysis x iy t () xt () iyt () f( ) uivu( x, y) iv( x, y) Starting omplex function of a real variable ~ define a curve on a complex plane
Considering our result for the sum and product of analytic functions, this means that for (a 0, a 1,..., a N ) C N+1, the polynomial.
 Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Math 715 Homework 1 Solutions
 . [arrier, Krook and Pearson Section 2- Exercise ] Show that no purely real function can be analytic, unless it is a constant. onsider a function f(z) = u(x, y) + iv(x, y) where z = x + iy and where u
. [arrier, Krook and Pearson Section 2- Exercise ] Show that no purely real function can be analytic, unless it is a constant. onsider a function f(z) = u(x, y) + iv(x, y) where z = x + iy and where u
Completion Date: Monday February 11, 2008
 MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
Residues and Contour Integration Problems
 Residues and ontour Integration Problems lassify the singularity of fz at the indicated point.. fz = cotz at z =. Ans. Simple pole. Solution. The test for a simple pole at z = is that lim z z cotz exists
Residues and ontour Integration Problems lassify the singularity of fz at the indicated point.. fz = cotz at z =. Ans. Simple pole. Solution. The test for a simple pole at z = is that lim z z cotz exists
The Calculus of Residues
 hapter 7 The alculus of Residues If fz) has a pole of order m at z = z, it can be written as Eq. 6.7), or fz) = φz) = a z z ) + a z z ) +... + a m z z ) m, 7.) where φz) is analytic in the neighborhood
hapter 7 The alculus of Residues If fz) has a pole of order m at z = z, it can be written as Eq. 6.7), or fz) = φz) = a z z ) + a z z ) +... + a m z z ) m, 7.) where φz) is analytic in the neighborhood
(z + n) 2. n=0. 2 (z + 2) (z + n). 2 We d like to compute this as an integral. To this end, we d like a function with residues
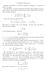 8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
Math 411, Complex Analysis Definitions, Formulas and Theorems Winter y = sinα
 Math 411, Complex Analysis Definitions, Formulas and Theorems Winter 014 Trigonometric Functions of Special Angles α, degrees α, radians sin α cos α tan α 0 0 0 1 0 30 π 6 45 π 4 1 3 1 3 1 y = sinα π 90,
Math 411, Complex Analysis Definitions, Formulas and Theorems Winter 014 Trigonometric Functions of Special Angles α, degrees α, radians sin α cos α tan α 0 0 0 1 0 30 π 6 45 π 4 1 3 1 3 1 y = sinα π 90,
July 21 Math 2254 sec 001 Summer 2015
 July 21 Math 2254 sec 001 Summer 2015 Section 8.8: Power Series Theorem: Let a n (x c) n have positive radius of convergence R, and let the function f be defined by this power series f (x) = a n (x c)
July 21 Math 2254 sec 001 Summer 2015 Section 8.8: Power Series Theorem: Let a n (x c) n have positive radius of convergence R, and let the function f be defined by this power series f (x) = a n (x c)
Math 120 A Midterm 2 Solutions
 Math 2 A Midterm 2 Solutions Jim Agler. Find all solutions to the equations tan z = and tan z = i. Solution. Let α be a complex number. Since the equation tan z = α becomes tan z = sin z eiz e iz cos z
Math 2 A Midterm 2 Solutions Jim Agler. Find all solutions to the equations tan z = and tan z = i. Solution. Let α be a complex number. Since the equation tan z = α becomes tan z = sin z eiz e iz cos z
MATH 106 HOMEWORK 4 SOLUTIONS. sin(2z) = 2 sin z cos z. (e zi + e zi ) 2. = 2 (ezi e zi )
 MATH 16 HOMEWORK 4 SOLUTIONS 1 Show directly from the definition that sin(z) = ezi e zi i sin(z) = sin z cos z = (ezi e zi ) i (e zi + e zi ) = sin z cos z Write the following complex numbers in standard
MATH 16 HOMEWORK 4 SOLUTIONS 1 Show directly from the definition that sin(z) = ezi e zi i sin(z) = sin z cos z = (ezi e zi ) i (e zi + e zi ) = sin z cos z Write the following complex numbers in standard
Qualifying Exam Complex Analysis (Math 530) January 2019
 Qualifying Exam Complex Analysis (Math 53) January 219 1. Let D be a domain. A function f : D C is antiholomorphic if for every z D the limit f(z + h) f(z) lim h h exists. Write f(z) = f(x + iy) = u(x,
Qualifying Exam Complex Analysis (Math 53) January 219 1. Let D be a domain. A function f : D C is antiholomorphic if for every z D the limit f(z + h) f(z) lim h h exists. Write f(z) = f(x + iy) = u(x,
2.5 (x + iy)(a + ib) = xa yb + i(xb + ya) = (az by) + i(bx + ay) = (a + ib)(x + iy). The middle = uses commutativity of real numbers.
 Complex Analysis Sketches of Solutions to Selected Exercises Homework 2..a ( 2 i) i( 2i) = 2 i i + i 2 2 = 2 i i 2 = 2i 2..b (2, 3)( 2, ) = (2( 2) ( 3), 2() + ( 3)( 2)) = (, 8) 2.2.a Re(iz) = Re(i(x +
Complex Analysis Sketches of Solutions to Selected Exercises Homework 2..a ( 2 i) i( 2i) = 2 i i + i 2 2 = 2 i i 2 = 2i 2..b (2, 3)( 2, ) = (2( 2) ( 3), 2() + ( 3)( 2)) = (, 8) 2.2.a Re(iz) = Re(i(x +
Types of Real Integrals
 Math B: Complex Variables Types of Real Integrals p(x) I. Integrals of the form P.V. dx where p(x) and q(x) are polynomials and q(x) q(x) has no eros (for < x < ) and evaluate its integral along the fol-
Math B: Complex Variables Types of Real Integrals p(x) I. Integrals of the form P.V. dx where p(x) and q(x) are polynomials and q(x) q(x) has no eros (for < x < ) and evaluate its integral along the fol-
CHAPTER 4. Elementary Functions. Dr. Pulak Sahoo
 CHAPTER 4 Elementary Functions BY Dr. Pulak Sahoo Assistant Professor Department of Mathematics University Of Kalyani West Bengal, India E-mail : sahoopulak1@gmail.com 1 Module-4: Multivalued Functions-II
CHAPTER 4 Elementary Functions BY Dr. Pulak Sahoo Assistant Professor Department of Mathematics University Of Kalyani West Bengal, India E-mail : sahoopulak1@gmail.com 1 Module-4: Multivalued Functions-II
Here are brief notes about topics covered in class on complex numbers, focusing on what is not covered in the textbook.
 Phys374, Spring 2008, Prof. Ted Jacobson Department of Physics, University of Maryland Complex numbers version 5/21/08 Here are brief notes about topics covered in class on complex numbers, focusing on
Phys374, Spring 2008, Prof. Ted Jacobson Department of Physics, University of Maryland Complex numbers version 5/21/08 Here are brief notes about topics covered in class on complex numbers, focusing on
Complex Variables & Integral Transforms
 Complex Variables & Integral Transforms Notes taken by J.Pearson, from a S4 course at the U.Manchester. Lecture delivered by Dr.W.Parnell July 9, 007 Contents 1 Complex Variables 3 1.1 General Relations
Complex Variables & Integral Transforms Notes taken by J.Pearson, from a S4 course at the U.Manchester. Lecture delivered by Dr.W.Parnell July 9, 007 Contents 1 Complex Variables 3 1.1 General Relations
* Problems may be difficult. (2) Given three distinct complex numbers α, β, γ. Show that they are collinear iff Im(αβ + βγ + γα) =0.
 Practice Exercise Set I * Problems may be difficult. ( Describe the sets whose points satisfy the following relations (a + = (b + < (c = (d arg + i = π 3 ( Given three distinct complex numbers α, β, γ.
Practice Exercise Set I * Problems may be difficult. ( Describe the sets whose points satisfy the following relations (a + = (b + < (c = (d arg + i = π 3 ( Given three distinct complex numbers α, β, γ.
Math Homework 2
 Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
Math 73 Homework Due: September 8, 6 Suppose that f is holomorphic in a region Ω, ie an open connected set Prove that in any of the following cases (a) R(f) is constant; (b) I(f) is constant; (c) f is
Complex Series. Chapter 20
 hapter 20 omplex Series As in the real case, representation of functions by infinite series of simpler functions is an endeavor worthy of our serious consideration. We start with an examination of the
hapter 20 omplex Series As in the real case, representation of functions by infinite series of simpler functions is an endeavor worthy of our serious consideration. We start with an examination of the
Complex Practice Exam 1
 Complex Practice Exam This practice exam contains sample questions. The actual exam will have fewer questions, and may contain questions not listed here.. Be prepared to explain the following concepts,
Complex Practice Exam This practice exam contains sample questions. The actual exam will have fewer questions, and may contain questions not listed here.. Be prepared to explain the following concepts,
Summary: Primer on Integral Calculus:
 Physics 2460 Electricity and Magnetism I, Fall 2006, Primer on Integration: Part I 1 Summary: Primer on Integral Calculus: Part I 1. Integrating over a single variable: Area under a curve Properties of
Physics 2460 Electricity and Magnetism I, Fall 2006, Primer on Integration: Part I 1 Summary: Primer on Integral Calculus: Part I 1. Integrating over a single variable: Area under a curve Properties of
EE2 Mathematics : Complex Variables
 EE Mathematics : omplex Variables J. D. Gibbon (Professor J. D Gibbon 1, Dept of Mathematics) j.d.gibbon@ic.ac.uk http://www.imperial.ac.uk/ jdg These notes are not identical word-for-word with my lectures
EE Mathematics : omplex Variables J. D. Gibbon (Professor J. D Gibbon 1, Dept of Mathematics) j.d.gibbon@ic.ac.uk http://www.imperial.ac.uk/ jdg These notes are not identical word-for-word with my lectures
4 Uniform convergence
 4 Uniform convergence In the last few sections we have seen several functions which have been defined via series or integrals. We now want to develop tools that will allow us to show that these functions
4 Uniform convergence In the last few sections we have seen several functions which have been defined via series or integrals. We now want to develop tools that will allow us to show that these functions
Tutorial 1, B. Tech. Sem III, 24 July, (Root Findings and Linear System of Equations)
 Tutorial, B. Tech. Sem III, 24 July, 206 (Root Findings and Linear System of Equations). Find the root of the equation e x = 3x lying in [0,] correct to three decimal places using Bisection, Regula-Falsi
Tutorial, B. Tech. Sem III, 24 July, 206 (Root Findings and Linear System of Equations). Find the root of the equation e x = 3x lying in [0,] correct to three decimal places using Bisection, Regula-Falsi
Complex Variables, Summer 2016 Homework Assignments
 Complex Variables, Summer 2016 Homework Assignments Homeworks 1-4, due Thursday July 14th Do twenty-four of the following problems. Question 1 Let a = 2 + i and b = 1 i. Sketch the complex numbers a, b,
Complex Variables, Summer 2016 Homework Assignments Homeworks 1-4, due Thursday July 14th Do twenty-four of the following problems. Question 1 Let a = 2 + i and b = 1 i. Sketch the complex numbers a, b,
MATH 417 Homework 4 Instructor: D. Cabrera Due July 7. z c = e c log z (1 i) i = e i log(1 i) i log(1 i) = 4 + 2kπ + i ln ) cosz = eiz + e iz
 MATH 47 Homework 4 Instructor: D. abrera Due July 7. Find all values of each expression below. a) i) i b) cos i) c) sin ) Solution: a) Here we use the formula z c = e c log z i) i = e i log i) The modulus
MATH 47 Homework 4 Instructor: D. abrera Due July 7. Find all values of each expression below. a) i) i b) cos i) c) sin ) Solution: a) Here we use the formula z c = e c log z i) i = e i log i) The modulus
MATH243 First Semester 2013/14. Exercises 1
 Complex Functions Dr Anna Pratoussevitch MATH43 First Semester 013/14 Exercises 1 Submit your solutions to questions marked with [HW] in the lecture on Monday 30/09/013 Questions or parts of questions
Complex Functions Dr Anna Pratoussevitch MATH43 First Semester 013/14 Exercises 1 Submit your solutions to questions marked with [HW] in the lecture on Monday 30/09/013 Questions or parts of questions
Topic 7 Notes Jeremy Orloff
 Topic 7 Notes Jeremy Orloff 7 Taylor and Laurent series 7. Introduction We originally defined an analytic function as one where the derivative, defined as a limit of ratios, existed. We went on to prove
Topic 7 Notes Jeremy Orloff 7 Taylor and Laurent series 7. Introduction We originally defined an analytic function as one where the derivative, defined as a limit of ratios, existed. We went on to prove
Chapter 9. Analytic Continuation. 9.1 Analytic Continuation. For every complex problem, there is a solution that is simple, neat, and wrong.
 Chapter 9 Analytic Continuation For every complex problem, there is a solution that is simple, neat, and wrong. - H. L. Mencken 9.1 Analytic Continuation Suppose there is a function, f 1 (z) that is analytic
Chapter 9 Analytic Continuation For every complex problem, there is a solution that is simple, neat, and wrong. - H. L. Mencken 9.1 Analytic Continuation Suppose there is a function, f 1 (z) that is analytic
NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Complex Analysis II Lecture Notes Part I
 NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Comple Analsis II Lecture Notes Part I Chapter 1 Preliminar results/review of Comple Analsis I These are more detailed notes for the results
NATIONAL UNIVERSITY OF SINGAPORE Department of Mathematics MA4247 Comple Analsis II Lecture Notes Part I Chapter 1 Preliminar results/review of Comple Analsis I These are more detailed notes for the results
Advanced Mathematics Support Programme Edexcel Year 2 Core Pure Suggested Scheme of Work ( )
 Edexcel Year 2 Core Pure Suggested Scheme of Work (2018-2019) This template shows how Integral Resources and AMSP FM videos can be used to support Further Mathematics students and teachers. This template
Edexcel Year 2 Core Pure Suggested Scheme of Work (2018-2019) This template shows how Integral Resources and AMSP FM videos can be used to support Further Mathematics students and teachers. This template
MATH COMPLEX ANALYSIS. Contents
 MATH 3964 - OMPLEX ANALYSIS ANDREW TULLOH AND GILES GARDAM ontents 1. ontour Integration and auchy s Theorem 2 1.1. Analytic functions 2 1.2. ontour integration 3 1.3. auchy s theorem and extensions 3
MATH 3964 - OMPLEX ANALYSIS ANDREW TULLOH AND GILES GARDAM ontents 1. ontour Integration and auchy s Theorem 2 1.1. Analytic functions 2 1.2. ontour integration 3 1.3. auchy s theorem and extensions 3
INDIAN INSTITUTE OF TECHNOLOGY BOMBAY MA205 Complex Analysis Autumn 2012
 INDIAN INSTITUTE OF TECHNOLOGY BOMBAY MA205 Complex Analysis Autumn 2012 September 5, 2012 Mapping Properties Lecture 13 We shall once again return to the study of general behaviour of holomorphic functions
INDIAN INSTITUTE OF TECHNOLOGY BOMBAY MA205 Complex Analysis Autumn 2012 September 5, 2012 Mapping Properties Lecture 13 We shall once again return to the study of general behaviour of holomorphic functions
cosh 2 x sinh 2 x = 1 sin 2 x = 1 2 cos 2 x = 1 2 dx = dt r 2 = x 2 + y 2 L =
 Integrals Volume: Suppose A(x) is the cross-sectional area of the solid S perpendicular to the x-axis, then the volume of S is given by V = b a A(x) dx Work: Suppose f(x) is a force function. The work
Integrals Volume: Suppose A(x) is the cross-sectional area of the solid S perpendicular to the x-axis, then the volume of S is given by V = b a A(x) dx Work: Suppose f(x) is a force function. The work
NOTES FOR 18.04, Spring 2017
 NOTES FOR 8.04, Spring 207 0 8.04 course introduction 0. Brief course description Jeremy Orloff omplex analysis is a beautiful, tightly integrated subject. It revolves around complex analytic functions.
NOTES FOR 8.04, Spring 207 0 8.04 course introduction 0. Brief course description Jeremy Orloff omplex analysis is a beautiful, tightly integrated subject. It revolves around complex analytic functions.
) z r θ ( ) ( ) ( ) = then. Complete Solutions to Examination Questions Complete Solutions to Examination Questions 10.
 Complete Solutions to Examination Questions 0 Complete Solutions to Examination Questions 0. (i We need to determine + given + j, j: + + j + j (ii The product ( ( + j6 + 6 j 8 + j is given by ( + j( j
Complete Solutions to Examination Questions 0 Complete Solutions to Examination Questions 0. (i We need to determine + given + j, j: + + j + j (ii The product ( ( + j6 + 6 j 8 + j is given by ( + j( j
Theorem [Mean Value Theorem for Harmonic Functions] Let u be harmonic on D(z 0, R). Then for any r (0, R), u(z 0 ) = 1 z z 0 r
![Theorem [Mean Value Theorem for Harmonic Functions] Let u be harmonic on D(z 0, R). Then for any r (0, R), u(z 0 ) = 1 z z 0 r Theorem [Mean Value Theorem for Harmonic Functions] Let u be harmonic on D(z 0, R). Then for any r (0, R), u(z 0 ) = 1 z z 0 r](/thumbs/77/75527144.jpg) 2. A harmonic conjugate always exists locally: if u is a harmonic function in an open set U, then for any disk D(z 0, r) U, there is f, which is analytic in D(z 0, r) and satisfies that Re f u. Since such
2. A harmonic conjugate always exists locally: if u is a harmonic function in an open set U, then for any disk D(z 0, r) U, there is f, which is analytic in D(z 0, r) and satisfies that Re f u. Since such
Synopsis of Complex Analysis. Ryan D. Reece
 Synopsis of Complex Analysis Ryan D. Reece December 7, 2006 Chapter Complex Numbers. The Parts of a Complex Number A complex number, z, is an ordered pair of real numbers similar to the points in the real
Synopsis of Complex Analysis Ryan D. Reece December 7, 2006 Chapter Complex Numbers. The Parts of a Complex Number A complex number, z, is an ordered pair of real numbers similar to the points in the real
4.1 Exponential and Logarithmic Functions
 . Exponential and Logarithmic Functions Joseph Heavner Honors Complex Analysis Continued) Chapter July, 05 3.) Find the derivative of f ) e i e i. d d e i e i) d d ei ) d d e i ) e i d d i) e i d d i)
. Exponential and Logarithmic Functions Joseph Heavner Honors Complex Analysis Continued) Chapter July, 05 3.) Find the derivative of f ) e i e i. d d e i e i) d d ei ) d d e i ) e i d d i) e i d d i)
Complex Variables...Review Problems (Residue Calculus Comments)...Fall Initial Draft
 Complex Variables........Review Problems Residue Calculus Comments)........Fall 22 Initial Draft ) Show that the singular point of fz) is a pole; determine its order m and its residue B: a) e 2z )/z 4,
Complex Variables........Review Problems Residue Calculus Comments)........Fall 22 Initial Draft ) Show that the singular point of fz) is a pole; determine its order m and its residue B: a) e 2z )/z 4,
Lecture 9. = 1+z + 2! + z3. 1 = 0, it follows that the radius of convergence of (1) is.
 The Exponential Function Lecture 9 The exponential function 1 plays a central role in analysis, more so in the case of complex analysis and is going to be our first example using the power series method.
The Exponential Function Lecture 9 The exponential function 1 plays a central role in analysis, more so in the case of complex analysis and is going to be our first example using the power series method.
Math 220A Fall 2007 Homework #7. Will Garner A
 Math A Fall 7 Homework #7 Will Garner Pg 74 #13: Find the power series expansion of about ero and determine its radius of convergence Consider f( ) = and let ak f ( ) = k! k = k be its power series expansion
Math A Fall 7 Homework #7 Will Garner Pg 74 #13: Find the power series expansion of about ero and determine its radius of convergence Consider f( ) = and let ak f ( ) = k! k = k be its power series expansion
Selected Solutions To Problems in Complex Analysis
 Selected Solutions To Problems in Complex Analysis E. Chernysh November 3, 6 Contents Page 8 Problem................................... Problem 4................................... Problem 5...................................
Selected Solutions To Problems in Complex Analysis E. Chernysh November 3, 6 Contents Page 8 Problem................................... Problem 4................................... Problem 5...................................
B Elements of Complex Analysis
 Fourier Transform Methods in Finance By Umberto Cherubini Giovanni Della Lunga Sabrina Mulinacci Pietro Rossi Copyright 21 John Wiley & Sons Ltd B Elements of Complex Analysis B.1 COMPLEX NUMBERS The purpose
Fourier Transform Methods in Finance By Umberto Cherubini Giovanni Della Lunga Sabrina Mulinacci Pietro Rossi Copyright 21 John Wiley & Sons Ltd B Elements of Complex Analysis B.1 COMPLEX NUMBERS The purpose
FINAL EXAM { SOLUTION
 United Arab Emirates University ollege of Sciences Department of Mathematical Sciences FINAL EXAM { SOLUTION omplex Analysis I MATH 5 SETION 0 RN 56 9:0 { 0:45 on Monday & Wednesday Date: Wednesday, January
United Arab Emirates University ollege of Sciences Department of Mathematical Sciences FINAL EXAM { SOLUTION omplex Analysis I MATH 5 SETION 0 RN 56 9:0 { 0:45 on Monday & Wednesday Date: Wednesday, January
