Hankel determinants, continued fractions, orthgonal polynomials, and hypergeometric series
|
|
|
- Rolf Hodges
- 6 years ago
- Views:
Transcription
1 Hankel determinants, continued fractions, orthgonal polynomials, and hypergeometric series Ira M. Gessel with Jiang Zeng and Guoce Xin LaBRI June 8, 2007
2 Continued fractions and Hankel determinants There is a close relationship between continued fractions, Hankel determinants, and orthogonal polynomials.
3 Continued fractions and Hankel determinants There is a close relationship between continued fractions, Hankel determinants, and orthogonal polynomials. Why are we interested in these things?
4 Continued fractions and Hankel determinants There is a close relationship between continued fractions, Hankel determinants, and orthogonal polynomials. Why are we interested in these things? Continued fractions count certain weighted Motzkin paths which encode objects of enumerative interest such as partitions and permutations. Flajolet)
5 Continued fractions and Hankel determinants There is a close relationship between continued fractions, Hankel determinants, and orthogonal polynomials. Why are we interested in these things? Continued fractions count certain weighted Motzkin paths which encode objects of enumerative interest such as partitions and permutations. Flajolet) Hankel determinants arise in some enumeration problems, for example, counting certain kinds of tilings or alternating sign matrices.
6 Orthogonal polynomials A sequence of polynomials p n x) ) n 0, where p nx) has degree n, is orthogonal if there is a linear functional L on polynomials such that L p m x)p n x) ) = 0 for m n, but L p m x) 2) 0. We will assume that L1) = 1.
7 Orthogonal polynomials A sequence of polynomials p n x) ) n 0, where p nx) has degree n, is orthogonal if there is a linear functional L on polynomials such that L p m x)p n x) ) = 0 for m n, but L p m x) 2) 0. We will assume that L1) = 1. The moments of the sequence p n x) ) are µ n = Lx n ).
8 Orthogonal polynomials A sequence of polynomials p n x) ) n 0, where p nx) has degree n, is orthogonal if there is a linear functional L on polynomials such that L p m x)p n x) ) = 0 for m n, but L p m x) 2) 0. We will assume that L1) = 1. The moments of the sequence p n x) ) are µ n = Lx n ). So µ 0 = 1.
9 Orthogonal polynomials A sequence of polynomials p n x) ) n 0, where p nx) has degree n, is orthogonal if there is a linear functional L on polynomials such that L p m x)p n x) ) = 0 for m n, but L p m x) 2) 0. We will assume that L1) = 1. The moments of the sequence p n x) ) are µ n = Lx n ). So µ 0 = 1. Theorem. The sequence p n x) ) of monic polynomials is orthogonal if and only if there exist numbers a n )n 0 and bn ) n 1, with b n 0 for all n 1 such that xp n x) = p n+1 x) + a n p n x) + b n p n 1 x), n 1 with p 0 x) = 1 and p 1 x) = x a 0.
10 The connection We then have the continued fraction µ k x k = k=0 1 b 1 x 2 1 a 0 x b 2 x 2 1 a 1 x 1 a 2 x and the Hankel determinant detµ i+j ) 0 i,j<n is equal to b n 1 1 b n 2 2 bn 2 2 b 1.
11 If we re interested in Hankel determinants or continued fractions, what good are the orthogonal polynomials?
12 If we re interested in Hankel determinants or continued fractions, what good are the orthogonal polynomials? There is a systematic treatment of all the classical orthogonal polynomials, that have explicit expressions as hypergeometric series, called the Askey scheme. In a comprehensive paper or web site) by Koekoek and Swarttouw, you can look up all of these orthogonal polynomials and find out everything you might want to know about them...
13 If we re interested in Hankel determinants or continued fractions, what good are the orthogonal polynomials? There is a systematic treatment of all the classical orthogonal polynomials, that have explicit expressions as hypergeometric series, called the Askey scheme. In a comprehensive paper or web site) by Koekoek and Swarttouw, you can look up all of these orthogonal polynomials and find out everything you might want to know about them... except the moments.
14 If we re interested in Hankel determinants or continued fractions, what good are the orthogonal polynomials? There is a systematic treatment of all the classical orthogonal polynomials, that have explicit expressions as hypergeometric series, called the Askey scheme. In a comprehensive paper or web site) by Koekoek and Swarttouw, you can look up all of these orthogonal polynomials and find out everything you might want to know about them... except the moments. What are the moments of the classical orthogonal polynomials?
15 If we re interested in Hankel determinants or continued fractions, what good are the orthogonal polynomials? There is a systematic treatment of all the classical orthogonal polynomials, that have explicit expressions as hypergeometric series, called the Askey scheme. In a comprehensive paper or web site) by Koekoek and Swarttouw, you can look up all of these orthogonal polynomials and find out everything you might want to know about them... except the moments. What are the moments of the classical orthogonal polynomials? What are their generating functions?
16 If we re interested in Hankel determinants or continued fractions, what good are the orthogonal polynomials? There is a systematic treatment of all the classical orthogonal polynomials, that have explicit expressions as hypergeometric series, called the Askey scheme. In a comprehensive paper or web site) by Koekoek and Swarttouw, you can look up all of these orthogonal polynomials and find out everything you might want to know about them... except the moments. What are the moments of the classical orthogonal polynomials? What are their generating functions? Why do some, but not all of them, have nice exponential generating functions?
17 If we re interested in Hankel determinants or continued fractions, what good are the orthogonal polynomials? There is a systematic treatment of all the classical orthogonal polynomials, that have explicit expressions as hypergeometric series, called the Askey scheme. In a comprehensive paper or web site) by Koekoek and Swarttouw, you can look up all of these orthogonal polynomials and find out everything you might want to know about them... except the moments. What are the moments of the classical orthogonal polynomials? What are their generating functions? Why do some, but not all of them, have nice exponential generating functions? What are the orthogonal polynomials whose moments are the Genocchi numbers?
18 How do we find the moments of a sequence of orthogonal polynomials? The key is to find numbers α 0, α 1, α 2,... such that we can evaluate L x + α 0 )x + α 1 ) x + α k ) ) for each k. Usually this isn t too hard to do.)
19 How do we find the moments of a sequence of orthogonal polynomials? The key is to find numbers α 0, α 1, α 2,... such that we can evaluate L x + α 0 )x + α 1 ) x + α k ) ) for each k. Usually this isn t too hard to do.) We then apply the following Lemma: t n x+α 0 )x+α 1 ) x+α n 1 ) 1 + α 0 t) 1 + α n t) = 1 1 xt. Proof. We have the indefinite sum m t n x + α 0 ) x + α n 1 ) 1 + α 0 t) 1 + α n t) = 1 [ t m+1 ] 1 x + α 0 ) x + α n ), 1 xt 1 + α 0 t) 1 + α n t) which is easily proved by induction. The lemma follows by taking m.
20 Now suppose that L x + α 0 )x + α 1 ) x + α n 1 ) ) = M n. We apply L to t n x+α 0 )x+α 1 ) x+α n 1 ) 1 + α 0 t) 1 + α n t) = 1 1 xt. to get M n t n 1 + α 0 t) 1 + α n t) = L = 1 ) 1 xt Lx k )t k = k=0 µ k t k. k=0
21 Let s look at an example. First, the standard notation: α) n = αα + 1) α + n 1) ) a1,..., a p pf q b 1,..., b p z a 1 ) n a p ) n = z n n! b 1 ) n b q ) n The Hahn polynomials are defined by Q n x; α, β, N) = 3 F 2 n, n + α + β + 1, x α + 1, N ) 1 They are orthogonal with respect to the linear functional L given by L px) ) N ) ) α + x β + N x = px), x N x x=0 By applying Vandermonde s theorem we find that L x + α + 1) k ) = α + β + 2) N N! α + 1) k α + β N) k α + β + 2) k.
22 Since we want L1) to be 1, we normalize this by dividing L by α + β + 2) N /N!. This is independent of k.) Then with our new normalization, L x + α + 1) k ) = α + 1) k α + β N) k α + β + 2) k. Since the right side is a rational function of α, β, and N, we don t need N to be a nonnegative integer and we can therefore make a change of variables, α = A 1, β = C A 1, N = B C. Then L x +A) n ) = L x +A)x +A+n) x +A+n 1) ) = A) n B) n C) n. Now we can apply our lemma to get the ordinary generating function for the moments µ n of the Hahn polynomials: µ n t n = A) n B) n C) n t n n j=0 1 + A + j)t).
23 This can be written as a rather strange-looking hypergeometric series 1 A) n B n ) 1 + At C) n 1 + A + t 1 = 1 ) A, B, 1 ) n 1 + At 3 F 2 C, 1 + A + t 1 1.
24 This can be written as a rather strange-looking hypergeometric series 1 A) n B n ) 1 + At C) n 1 + A + t 1 = 1 ) A, B, 1 ) n 1 + At 3 F 2 C, 1 + A + t 1 1. How do we get an exponential generating function for the moments?
25 This can be written as a rather strange-looking hypergeometric series 1 A) n B n ) 1 + At C) n 1 + A + t 1 = 1 ) A, B, 1 ) n 1 + At 3 F 2 C, 1 + A + t 1 1. How do we get an exponential generating function for the moments? We define a linear operator ε on formal power series by ) ε u n t n = u n t n n!.
26 This can be written as a rather strange-looking hypergeometric series 1 A) n B n ) 1 + At C) n 1 + A + t 1 = 1 ) A, B, 1 ) n 1 + At 3 F 2 C, 1 + A + t 1 1. How do we get an exponential generating function for the moments? We define a linear operator ε on formal power series by ) ε u n t n = Then we apply ε to µ nt n. u n t n n!.
27 Lemma. t n ) ε = e At 1 e t ) n. 1 + At)1 + A + 1)t) 1 + A + n)t) n! Proof #1. Expand the left side by partial fractions and the right side by the binomial theorem. Proof #2. Without explicitly computing the partial fraction on the left, we can see that it will be a linear combination of e At, e A+1)t,..., e A+n)t and the first nonzero term is t n /n!. The right side is the only possibility.
28 Lemma. t n ) ε = e At 1 e t ) n. 1 + At)1 + A + 1)t) 1 + A + n)t) n! Proof #1. Expand the left side by partial fractions and the right side by the binomial theorem. Proof #2. Without explicitly computing the partial fraction on the left, we can see that it will be a linear combination of e At, e A+1)t,..., e A+n)t and the first nonzero term is t n /n!. The right side is the only possibility. Now we apply the lemma to µ n t n = A) n B) n C) n t n n j=0 1 + A + j)t).
29 We have µ n t n n! = A) n B) n e At 1 e t ) n C) n n! ) 1 e t. = e At 2F 1 A, B C Let s look at a few examples. First let s see how this generalizes the Meixner polynomials, which are the most general Sheffer orthogonal polynomials. To get one form of) the Meixner polynomials, we take B = uc and then take the limit as C, getting as the exponential generating function for the moments 1 u)e t + u ) A
30 We have µ n t n n! = A) n B) n e At 1 e t ) n C) n n! ) 1 e t. = e At 2F 1 A, B C As another example, if we take A = B = 1, C = 2, we get the Bernoulli numbers: so µ n = B n. µ n t n n! = t e t 1,
31 We have µ n t n n! = A) n B) n e At 1 e t ) n C) n n! ) 1 e t. = e At 2F 1 A, B C Similarly, if we take A = 1, B = 2, C = 3, we get the Bernoulli numbers shifted by 1: so µ n = 2B n+1. t n µ n n! = 2d t dt e t 1,
32 We can use the same approach on the Wilson polynomials, which are the most general classical orthogonal polynomials with q = 1). They are defined by W n x 2 ) = 4 F 3 n, n + a + c + d 1, a + ix, a ix a + b, a + c, a + d ) 1, in this form they are not monic). The corresponding linear functional is L px) ) = 1 Γa + ix)γb + ix)γc + ix)γd + ix) 2 2π Γ2ix) px 2 ) dx 0
33 It follows easily from known facts that L x + a 2 )x + a + 1) 2 ) x + a + n 1) 2 ) ) = a + b) na + c) n a + d) n a + b + c + d) n so from our first lemma, µ n t n a + b) n a + c) n a + d) n t n = a + b + c + d) n n j=0 1 + a + j) 2 t )
34 It follows easily from known facts that L x + a 2 )x + a + 1) 2 ) x + a + n 1) 2 ) ) = a + b) na + c) n a + d) n a + b + c + d) n so from our first lemma, µ n t n a + b) n a + c) n a + d) n t n = a + b + c + d) n n j=0 1 + a + j) 2 t ) What about an exponential generating function?
35 It follows easily from known facts that L x + a 2 )x + a + 1) 2 ) x + a + n 1) 2 ) ) = a + b) na + c) n a + d) n a + b + c + d) n so from our first lemma, µ n t n a + b) n a + c) n a + d) n t n = a + b + c + d) n n j=0 1 + a + j) 2 t ) What about an exponential generating function? If we replace t with t 2, then the denominator factors into linear factors: n 1 a + j) 2 t 2) = ) ) ) 1 a + n)t 1 a + 1)t 1 at j=0 1 + at ) 1 + a + 1 ) t 1 + a + n)t ).
36 We want to apply our lemma t m ) ε = e At 1 e t ) m. 1 + At)1 + A + 1)t) 1 + A + m)t) m! to t 2n 1 a + n)t ) 1 a + 1)t ) 1 at ) 1 + at ) 1 + a + 1 ) t 1 + a + n)t ).
37 We want to apply our lemma t m ) ε = e At 1 e t ) m. 1 + At)1 + A + 1)t) 1 + A + m)t) m! to t 2n 1 a + n)t ) 1 a + 1)t ) 1 at ) 1 + at ) 1 + a + 1 ) t 1 + a + n)t ). We can do this if a = 0 or if a = 1/2. If a = 1/2, we must multiply by t.) Our conclusion is
38 For a = 0, and for a = 1/2, t 2n µ n 2n)! = 3F 2 µ n t 2n+1 2n + 1)! = 2 sin t 2 3 F 2 b, c, d t ) b + c + d, 1 sin2 2 2 b + 1 2, c + 1 2, d b + c + d + 1 2, 3 2 ) t sin2 2
39 If we take the limit as d in the Wilson polynomials ) n, n + a + c + d 1, a + ix, a ix W n x 2 ) = 4 F 3 a + b, a + c, a + d 1, we get the continuous dual Hahn polynomials ) n, a + ix, a ix p n x 2 ) = 3 F 2 a + b, a + c 1. The generating function for the moments of the continuous dual Hahn polynomials is µ n a, b, c)t n = a + b) n a + c) n t n n j=0 1 + a + j) 2 t ) Then it is clear that the moments µ n a, b, c) are polynomials in a, b, and c, and they have nonnegative coefficients, as is clear from the corresponding continued fraction.
40 In fact µ n 1, 1, 1) = G 2n+4 and µ n 0, 1, 1) = G 2n+2, where the Genocchi numbers are given by x tan 1 2 x = n=2 G nx n /n!, and the polynomials µ n a, b, c) are polynomials studied by Dumont and Foata as refinements of the Genocchi numbers.
41 In fact µ n 1, 1, 1) = G 2n+4 and µ n 0, 1, 1) = G 2n+2, where the Genocchi numbers are given by x tan 1 2 x = n=2 G nx n /n!, and the polynomials µ n a, b, c) are polynomials studied by Dumont and Foata as refinements of the Genocchi numbers. For a = 0 we have the generating function µ n 0, b, c) t2n 2n)! = 2F 1 b, c 1 2 t sin2 2 ),
42 In fact µ n 1, 1, 1) = G 2n+4 and µ n 0, 1, 1) = G 2n+2, where the Genocchi numbers are given by x tan 1 2 x = n=2 G nx n /n!, and the polynomials µ n a, b, c) are polynomials studied by Dumont and Foata as refinements of the Genocchi numbers. For a = 0 we have the generating function µ n 0, b, c) t2n 2n)! = 2F 1 and it s not hard to check that indeed, 2F 1 1, t ) sin2 = 2 b, c 1 2 t sin2 2 ), G n+2 x n n! = d 2 dx 2 x tan x 2 using 2F 1 1, ) y 2 = 1 y 2 + y sin 1 y 1 y 2 ) 3/2.
43 Another application of the continuous dual Hahn polynomials We have µ n 1 2, 1 2 γ, 1 t2n 2γ) 2n)! = 2F 1 = sin 1 2 γt γ sin 1 2 t γ), ) γ) t sin2 2 In the case γ = 1/3, the corresponding Hankel determinant counts alternating sign matrices Colomo and Pronko). 3 2
44 Hankel Determinants and Ternary Tree Numbers Let a n = ) 1 3n, 2n + 1 n so that a n is the number of trees with n vertices. Michael Somos conjectured that deta i+j ) 0 i,j n 1 is the number of cyclically symmetric transpose complement plane partitions whose Ferrers diagrams fit in an n n n box. This number is known to be n 3i + 1) 6i)! 2i)!. 4i + 1)! 4i)! i=1 Somos had similar conjectures for the Hankel determinants deta i+j ) 0 i,j n 1 and deta i+j+1)/2 ) 0 i,j n 1, relating them to alternating sign matrices invariant under vertical reflection and alternating sign matrices invariant under both vertical and horizontal reflection.
45 Let gx) = Then gx) satisfies ) 1 3n x n = 2n + 1 n gx) = 1 + xgx) 3. a n x n. If we compute the continued fraction for gx), we find empirically that it has a simple formula, which implies the determinant evaluation. I found a complicated) proof of this continued fraction. Then Guoce Xin found a much nicer proof, using Gauss s continued fraction.
46 Let gx) = Then gx) satisfies ) 1 3n x n = 2n + 1 n gx) = 1 + xgx) 3. a n x n. If we compute the continued fraction for gx), we find empirically that it has a simple formula, which implies the determinant evaluation. I found a complicated) proof of this continued fraction. Then Guoce Xin found a much nicer proof, using Gauss s continued fraction. However, the same method had already been used by Ulrich Tamm to evaluate these determinants, before Somos stated his conjectures. But there is no known combinatorial connection between these Hankel determinants and plane partitions or alternating sign matrices.)
47 The key fact is that the continued fraction for gx) is a special case of Gauss s continued fraction: where 2F 1 a, b + 1 c + 1 ) / x 2F 1 a, b c ) x = Sx; λ 1, λ 2,...), 1) a + n 1)c b + n 1) λ 2n 1 =, c + 2n 2)c + 2n 1) n = 1, 2,..., b + n)c a + n) λ 2n =, c + 2n 1)c + 2n) n = 1, 2,..., and Sx; λ 1, λ 2, λ 3,...) denotes the continued fraction 1 Sx; λ 1, λ 2, λ 3,...) = λ 1 x 1 1 λ 2x 1 λ 3x... 2)
48 In fact we have g = 2 F 1 2 3, 4 3 ; x ) /2F 1 2 3, 1 3 ; x ). and this isn t too hard to prove; if we set f = g 1 by Lagrange inversion one can show that the numerator is 1 + f ) 2 /1 2f ) and the denominator is 1 + f )/1 2f ). Xin and I tried to find all related cases where an instance of Gauss s continued fraction is a polynomial in f and thus the coefficients have an explicit formula).
49 In fact we have g = 2 F 1 2 3, 4 3 ; x ) /2F 1 2 3, 1 3 ; x ). and this isn t too hard to prove; if we set f = g 1 by Lagrange inversion one can show that the numerator is 1 + f ) 2 /1 2f ) and the denominator is 1 + f )/1 2f ). Xin and I tried to find all related cases where an instance of Gauss s continued fraction is a polynomial in f and thus the coefficients have an explicit formula). We found exactly 10, but we couldn t prove that there aren t any more.
50 Five of them are 1 + f = 2 F 1 2 3, 4 3 ; f ) 2 = 2 F 1 4 3, 5 3 ; f ) f ) = 2F 1 5 3, 7 3 ; f )1 1 2 f ) = 2F 1 5 3, 7 3 ; f ) f ) = 2F 1 2 3, 4 3 ; 5 2 Why do they factor? ) ) 27 4 /2F x 2 1 3, 1 3 ; x ) ) 27 4 /2F x 4 1 3, 2 3 ; x ) ) 27 4 /2F x 5 1 3, 4 3 ; x ) ) 27 4 /2F x 5 1 3, 4 3 ; x ) ) 27 4 /2F x 2 1 3, 1 3 ; x
51 Five of them are 1 + f = 2 F 1 2 3, 4 3 ; f ) 2 = 2 F 1 4 3, 5 3 ; f ) f ) = 2F 1 5 3, 7 3 ; f )1 1 2 f ) = 2F 1 5 3, 7 3 ; f ) f ) = 2F 1 2 3, 4 3 ; 5 2 Why do they factor? We don t know. ) ) 27 4 /2F x 2 1 3, 1 3 ; x ) ) 27 4 /2F x 4 1 3, 2 3 ; x ) ) 27 4 /2F x 5 1 3, 4 3 ; x ) ) 27 4 /2F x 5 1 3, 4 3 ; x ) ) 27 4 /2F x 2 1 3, 1 3 ; x
52 Five of them are 1 + f = 2 F 1 2 3, 4 3 ; f ) 2 = 2 F 1 4 3, 5 3 ; f ) f ) = 2F 1 5 3, 7 3 ; f )1 1 2 f ) = 2F 1 5 3, 7 3 ; f ) f ) = 2F 1 2 3, 4 3 ; 5 2 Why do they factor? We don t know. ) ) 27 4 /2F x 2 1 3, 1 3 ; x ) ) 27 4 /2F x 4 1 3, 2 3 ; x ) ) 27 4 /2F x 5 1 3, 4 3 ; x ) ) 27 4 /2F x 5 1 3, 4 3 ; x ) ) 27 4 /2F x 2 1 3, 1 3 ; x The other five are the same as these, but with different constant terms.
Symmetric Inclusion-Exclusion
 Symmetric Inclusion-Exclusion Ira M. Gessel Brandeis University Institut Mittag-Leffler Séminaire Lotharingien de Combinatoire, April 4, 2005 Maison Saint-Bernard, Lucelle, France Inclusion-exclusion Suppose
Symmetric Inclusion-Exclusion Ira M. Gessel Brandeis University Institut Mittag-Leffler Séminaire Lotharingien de Combinatoire, April 4, 2005 Maison Saint-Bernard, Lucelle, France Inclusion-exclusion Suppose
Combinatorial Enumeration. Jason Z. Gao Carleton University, Ottawa, Canada
 Combinatorial Enumeration Jason Z. Gao Carleton University, Ottawa, Canada Counting Combinatorial Structures We are interested in counting combinatorial (discrete) structures of a given size. For example,
Combinatorial Enumeration Jason Z. Gao Carleton University, Ottawa, Canada Counting Combinatorial Structures We are interested in counting combinatorial (discrete) structures of a given size. For example,
Is Analysis Necessary?
 Is Analysis Necessary? Ira M. Gessel Brandeis University Waltham, MA gessel@brandeis.edu Special Session on Algebraic and Analytic Combinatorics AMS Fall Eastern Meeting University of Connecticut, Storrs
Is Analysis Necessary? Ira M. Gessel Brandeis University Waltham, MA gessel@brandeis.edu Special Session on Algebraic and Analytic Combinatorics AMS Fall Eastern Meeting University of Connecticut, Storrs
Chapter Generating Functions
 Chapter 8.1.1-8.1.2. Generating Functions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 8. Generating Functions Math 184A / Fall 2017 1 / 63 Ordinary Generating Functions (OGF) Let a n (n = 0, 1,...)
Chapter 8.1.1-8.1.2. Generating Functions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 8. Generating Functions Math 184A / Fall 2017 1 / 63 Ordinary Generating Functions (OGF) Let a n (n = 0, 1,...)
Generating Functions
 8.30 lecture notes March, 0 Generating Functions Lecturer: Michel Goemans We are going to discuss enumeration problems, and how to solve them using a powerful tool: generating functions. What is an enumeration
8.30 lecture notes March, 0 Generating Functions Lecturer: Michel Goemans We are going to discuss enumeration problems, and how to solve them using a powerful tool: generating functions. What is an enumeration
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
Generating Function Notes , Fall 2005, Prof. Peter Shor
 Counting Change Generating Function Notes 80, Fall 00, Prof Peter Shor In this lecture, I m going to talk about generating functions We ve already seen an example of generating functions Recall when we
Counting Change Generating Function Notes 80, Fall 00, Prof Peter Shor In this lecture, I m going to talk about generating functions We ve already seen an example of generating functions Recall when we
Ira M. Gessel Department of Mathematics, Brandeis University, P.O. Box 9110, Waltham, MA Revised September 30, 1988
 GENERALIZED ROOK POLYNOMIALS AND ORTHOGONAL POLYNOMIALS Ira M. Gessel Department of Mathematics, Brandeis University, P.O. Box 9110, Waltham, MA 02254-9110 Revised September 30, 1988 Abstract. We consider
GENERALIZED ROOK POLYNOMIALS AND ORTHOGONAL POLYNOMIALS Ira M. Gessel Department of Mathematics, Brandeis University, P.O. Box 9110, Waltham, MA 02254-9110 Revised September 30, 1988 Abstract. We consider
A Combinatorial Interpretation of the Numbers 6 (2n)! /n! (n + 2)!
 1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 8 (2005), Article 05.2.3 A Combinatorial Interpretation of the Numbers 6 (2n)! /n! (n + 2)! Ira M. Gessel 1 and Guoce Xin Department of Mathematics Brandeis
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 8 (2005), Article 05.2.3 A Combinatorial Interpretation of the Numbers 6 (2n)! /n! (n + 2)! Ira M. Gessel 1 and Guoce Xin Department of Mathematics Brandeis
(part 3) Algèbres d opérateurs et Physique combinatoire. Xavier Viennot CNRS, LaBRI, Bordeaux
 Algèbres d opérateurs et Physique combinatoire (part 3) 12 Avril 2012 colloquium de l IMJ Institut mathématiques de Jussieu Xavier Viennot CNRS, LaBRI, Bordeaux quadratic algebra operators data structures
Algèbres d opérateurs et Physique combinatoire (part 3) 12 Avril 2012 colloquium de l IMJ Institut mathématiques de Jussieu Xavier Viennot CNRS, LaBRI, Bordeaux quadratic algebra operators data structures
2.2 Separable Equations
 2.2 Separable Equations Definition A first-order differential equation that can be written in the form Is said to be separable. Note: the variables of a separable equation can be written as Examples Solve
2.2 Separable Equations Definition A first-order differential equation that can be written in the form Is said to be separable. Note: the variables of a separable equation can be written as Examples Solve
2 J. ZENG THEOREM 1. In the ring of formal power series of x the following identities hold : (1:4) 1 + X n1 =1 S q [n; ]a x n = 1 ax? aq x 2 b x? +1 x
![2 J. ZENG THEOREM 1. In the ring of formal power series of x the following identities hold : (1:4) 1 + X n1 =1 S q [n; ]a x n = 1 ax? aq x 2 b x? +1 x 2 J. ZENG THEOREM 1. In the ring of formal power series of x the following identities hold : (1:4) 1 + X n1 =1 S q [n; ]a x n = 1 ax? aq x 2 b x? +1 x](/thumbs/81/83785321.jpg) THE q-stirling NUMBERS CONTINUED FRACTIONS AND THE q-charlier AND q-laguerre POLYNOMIALS By Jiang ZENG Abstract. We give a simple proof of the continued fraction expansions of the ordinary generating functions
THE q-stirling NUMBERS CONTINUED FRACTIONS AND THE q-charlier AND q-laguerre POLYNOMIALS By Jiang ZENG Abstract. We give a simple proof of the continued fraction expansions of the ordinary generating functions
MY PUTNAM PROBLEMS. log(1 + x) dx = π2
 MY PUTNAM PROBLEMS These are the problems I proposed when I was on the Putnam Problem Committee for the 984 86 Putnam Exams. Problems intended to be A or B (and therefore relatively easy) are marked accordingly.
MY PUTNAM PROBLEMS These are the problems I proposed when I was on the Putnam Problem Committee for the 984 86 Putnam Exams. Problems intended to be A or B (and therefore relatively easy) are marked accordingly.
arxiv:math-ph/ v2 22 Dec 2004
 Square ice, alternating sign matrices, and classical orthogonal polynomials arxiv:math-ph/0411076v2 22 Dec 2004 F. Colomo and A. G. Pronko 1 I..F.., Sezione di Firenze, and Dipartimento di Fisica, Università
Square ice, alternating sign matrices, and classical orthogonal polynomials arxiv:math-ph/0411076v2 22 Dec 2004 F. Colomo and A. G. Pronko 1 I..F.., Sezione di Firenze, and Dipartimento di Fisica, Università
Limits at Infinity. Horizontal Asymptotes. Definition (Limits at Infinity) Horizontal Asymptotes
 Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Sec 4.1 Limits, Informally. When we calculated f (x), we first started with the difference quotient. f(x + h) f(x) h
 1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
1 Sec 4.1 Limits, Informally When we calculated f (x), we first started with the difference quotient f(x + h) f(x) h and made h small. In other words, f (x) is the number f(x+h) f(x) approaches as h gets
Generating Functions
 Semester 1, 2004 Generating functions Another means of organising enumeration. Two examples we have seen already. Example 1. Binomial coefficients. Let X = {1, 2,..., n} c k = # k-element subsets of X
Semester 1, 2004 Generating functions Another means of organising enumeration. Two examples we have seen already. Example 1. Binomial coefficients. Let X = {1, 2,..., n} c k = # k-element subsets of X
arxiv: v1 [math.ca] 7 Mar 2013
![arxiv: v1 [math.ca] 7 Mar 2013 arxiv: v1 [math.ca] 7 Mar 2013](/thumbs/72/66360420.jpg) A SIMPLE PROOF OF ANDREWS S 5 F 4 EVALUATION IRA M. GESSEL arxiv:1303.1757v1 [math.ca] 7 Mar 2013 Department of Mathematics Brandeis University Waltham, MA 02453 gessel@brandeis.edu Abstract. We give a
A SIMPLE PROOF OF ANDREWS S 5 F 4 EVALUATION IRA M. GESSEL arxiv:1303.1757v1 [math.ca] 7 Mar 2013 Department of Mathematics Brandeis University Waltham, MA 02453 gessel@brandeis.edu Abstract. We give a
Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) a n z n. n=0
 Lecture 22 Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) Recall a few facts about power series: a n z n This series in z is centered at z 0. Here z can
Lecture 22 Power series solutions for 2nd order linear ODE s (not necessarily with constant coefficients) Recall a few facts about power series: a n z n This series in z is centered at z 0. Here z can
Integration of Rational Functions by Partial Fractions
 Title Integration of Rational Functions by MATH 1700 MATH 1700 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 2 / 11 Rational functions A rational function is one of the form where P and Q are
Title Integration of Rational Functions by MATH 1700 MATH 1700 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 2 / 11 Rational functions A rational function is one of the form where P and Q are
Evaluating a Determinant
 Evaluating a Determinant Thotsaporn Thanatipanonda Joint Work with Christoph Koutschan Research Institute for Symbolic Computation, Johannes Kepler University of Linz, Austria June 15th, 2011 Outline of
Evaluating a Determinant Thotsaporn Thanatipanonda Joint Work with Christoph Koutschan Research Institute for Symbolic Computation, Johannes Kepler University of Linz, Austria June 15th, 2011 Outline of
Generating Functions
 Generating Functions Karen Ge May, 07 Abstract Generating functions gives us a global perspective when we need to study a local property. We define generating functions and present its applications in
Generating Functions Karen Ge May, 07 Abstract Generating functions gives us a global perspective when we need to study a local property. We define generating functions and present its applications in
Integration of Rational Functions by Partial Fractions
 Title Integration of Rational Functions by Partial Fractions MATH 1700 December 6, 2016 MATH 1700 Partial Fractions December 6, 2016 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 Partial Fractions
Title Integration of Rational Functions by Partial Fractions MATH 1700 December 6, 2016 MATH 1700 Partial Fractions December 6, 2016 1 / 11 Readings Readings Readings: Section 7.4 MATH 1700 Partial Fractions
Applications. More Counting Problems. Complexity of Algorithms
 Recurrences Applications More Counting Problems Complexity of Algorithms Part I Recurrences and Binomial Coefficients Paths in a Triangle P(0, 0) P(1, 0) P(1,1) P(2, 0) P(2,1) P(2, 2) P(3, 0) P(3,1) P(3,
Recurrences Applications More Counting Problems Complexity of Algorithms Part I Recurrences and Binomial Coefficients Paths in a Triangle P(0, 0) P(1, 0) P(1,1) P(2, 0) P(2,1) P(2, 2) P(3, 0) P(3,1) P(3,
e x = 1 + x + x2 2! + x3 If the function f(x) can be written as a power series on an interval I, then the power series is of the form
 Taylor Series Given a function f(x), we would like to be able to find a power series that represents the function. For example, in the last section we noted that we can represent e x by the power series
Taylor Series Given a function f(x), we would like to be able to find a power series that represents the function. For example, in the last section we noted that we can represent e x by the power series
A Catalan-Hankel Determinant Evaluation
 A Catalan-Hankel Determinant Evaluation Ömer Eğecioğlu Department of Computer Science, University of California, Santa Barbara CA 93106 (omer@cs.ucsb.edu) Abstract Let C k = ( ) 2k k /(k +1) denote the
A Catalan-Hankel Determinant Evaluation Ömer Eğecioğlu Department of Computer Science, University of California, Santa Barbara CA 93106 (omer@cs.ucsb.edu) Abstract Let C k = ( ) 2k k /(k +1) denote the
Free Meixner distributions and random matrices
 Free Meixner distributions and random matrices Michael Anshelevich July 13, 2006 Some common distributions first... 1 Gaussian Negative binomial Gamma Pascal chi-square geometric exponential 1 2πt e x2
Free Meixner distributions and random matrices Michael Anshelevich July 13, 2006 Some common distributions first... 1 Gaussian Negative binomial Gamma Pascal chi-square geometric exponential 1 2πt e x2
CALCULUS JIA-MING (FRANK) LIOU
 CALCULUS JIA-MING (FRANK) LIOU Abstract. Contents. Power Series.. Polynomials and Formal Power Series.2. Radius of Convergence 2.3. Derivative and Antiderivative of Power Series 4.4. Power Series Expansion
CALCULUS JIA-MING (FRANK) LIOU Abstract. Contents. Power Series.. Polynomials and Formal Power Series.2. Radius of Convergence 2.3. Derivative and Antiderivative of Power Series 4.4. Power Series Expansion
Scientific Computing
 2301678 Scientific Computing Chapter 2 Interpolation and Approximation Paisan Nakmahachalasint Paisan.N@chula.ac.th Chapter 2 Interpolation and Approximation p. 1/66 Contents 1. Polynomial interpolation
2301678 Scientific Computing Chapter 2 Interpolation and Approximation Paisan Nakmahachalasint Paisan.N@chula.ac.th Chapter 2 Interpolation and Approximation p. 1/66 Contents 1. Polynomial interpolation
Introduction to orthogonal polynomials. Michael Anshelevich
 Introduction to orthogonal polynomials Michael Anshelevich November 6, 2003 µ = probability measure on R with finite moments m n (µ) = R xn dµ(x)
Introduction to orthogonal polynomials Michael Anshelevich November 6, 2003 µ = probability measure on R with finite moments m n (µ) = R xn dµ(x)
Measures, orthogonal polynomials, and continued fractions. Michael Anshelevich
 Measures, orthogonal polynomials, and continued fractions Michael Anshelevich November 7, 2008 MEASURES AND ORTHOGONAL POLYNOMIALS. µ a positive measure on R. A linear functional µ[p ] = P (x) dµ(x), µ
Measures, orthogonal polynomials, and continued fractions Michael Anshelevich November 7, 2008 MEASURES AND ORTHOGONAL POLYNOMIALS. µ a positive measure on R. A linear functional µ[p ] = P (x) dµ(x), µ
18.06 Problem Set 8 - Solutions Due Wednesday, 14 November 2007 at 4 pm in
 806 Problem Set 8 - Solutions Due Wednesday, 4 November 2007 at 4 pm in 2-06 08 03 Problem : 205+5+5+5 Consider the matrix A 02 07 a Check that A is a positive Markov matrix, and find its steady state
806 Problem Set 8 - Solutions Due Wednesday, 4 November 2007 at 4 pm in 2-06 08 03 Problem : 205+5+5+5 Consider the matrix A 02 07 a Check that A is a positive Markov matrix, and find its steady state
Linearization coefficients for orthogonal polynomials. Michael Anshelevich
 Linearization coefficients for orthogonal polynomials Michael Anshelevich February 26, 2003 P n = monic polynomials of degree n = 0, 1,.... {P n } = basis for the polynomials in 1 variable. Linearization
Linearization coefficients for orthogonal polynomials Michael Anshelevich February 26, 2003 P n = monic polynomials of degree n = 0, 1,.... {P n } = basis for the polynomials in 1 variable. Linearization
Algebra 2 (2006) Correlation of the ALEKS Course Algebra 2 to the California Content Standards for Algebra 2
 Algebra 2 (2006) Correlation of the ALEKS Course Algebra 2 to the California Content Standards for Algebra 2 Algebra II - This discipline complements and expands the mathematical content and concepts of
Algebra 2 (2006) Correlation of the ALEKS Course Algebra 2 to the California Content Standards for Algebra 2 Algebra II - This discipline complements and expands the mathematical content and concepts of
Review session Midterm 1
 AS.110.109: Calculus II (Eng) Review session Midterm 1 Yi Wang, Johns Hopkins University Fall 2018 7.1: Integration by parts Basic integration method: u-sub, integration table Integration By Parts formula
AS.110.109: Calculus II (Eng) Review session Midterm 1 Yi Wang, Johns Hopkins University Fall 2018 7.1: Integration by parts Basic integration method: u-sub, integration table Integration By Parts formula
The WZ method and zeta function identities
 The WZ method and zeta function identities Ira M. Gessel Department of Mathematics Brandeis University American Mathematical Society 2010 Fall Eastern Sectional Meeting Syracuse University October 3, 2010
The WZ method and zeta function identities Ira M. Gessel Department of Mathematics Brandeis University American Mathematical Society 2010 Fall Eastern Sectional Meeting Syracuse University October 3, 2010
Taylor and Maclaurin Series. Copyright Cengage Learning. All rights reserved.
 11.10 Taylor and Maclaurin Series Copyright Cengage Learning. All rights reserved. We start by supposing that f is any function that can be represented by a power series f(x)= c 0 +c 1 (x a)+c 2 (x a)
11.10 Taylor and Maclaurin Series Copyright Cengage Learning. All rights reserved. We start by supposing that f is any function that can be represented by a power series f(x)= c 0 +c 1 (x a)+c 2 (x a)
Rook theory and simplicial complexes
 Rook theory and simplicial complexes Ira M. Gessel Department of Mathematics Brandeis University A Conference to Celebrate The Mathematics of Michelle Wachs University of Miami, Coral Gables, Florida January
Rook theory and simplicial complexes Ira M. Gessel Department of Mathematics Brandeis University A Conference to Celebrate The Mathematics of Michelle Wachs University of Miami, Coral Gables, Florida January
Measures, orthogonal polynomials, and continued fractions. Michael Anshelevich
 Measures, orthogonal polynomials, and continued fractions Michael Anshelevich November 7, 2008 MEASURES AND ORTHOGONAL POLYNOMIALS. MEASURES AND ORTHOGONAL POLYNOMIALS. µ a positive measure on R. 2 MEASURES
Measures, orthogonal polynomials, and continued fractions Michael Anshelevich November 7, 2008 MEASURES AND ORTHOGONAL POLYNOMIALS. MEASURES AND ORTHOGONAL POLYNOMIALS. µ a positive measure on R. 2 MEASURES
Almost Product Evaluation of Hankel Determinants
 Almost Product Evaluation of Hankel Determinants Ömer Eğecioğlu Department of Computer Science University of California, Santa Barbara CA 93106 omer@csucsbedu Timothy Redmond Stanford Medical Informatics,
Almost Product Evaluation of Hankel Determinants Ömer Eğecioğlu Department of Computer Science University of California, Santa Barbara CA 93106 omer@csucsbedu Timothy Redmond Stanford Medical Informatics,
Lucas Polynomials and Power Sums
 Lucas Polynomials and Power Sums Ulrich Tamm Abstract The three term recurrence x n + y n = (x + y (x n + y n xy (x n + y n allows to express x n + y n as a polynomial in the two variables x + y and xy.
Lucas Polynomials and Power Sums Ulrich Tamm Abstract The three term recurrence x n + y n = (x + y (x n + y n xy (x n + y n allows to express x n + y n as a polynomial in the two variables x + y and xy.
Introduction to Orthogonal Polynomials: Definition and basic properties
 Introduction to Orthogonal Polynomials: Definition and basic properties Prof. Dr. Mama Foupouagnigni African Institute for Mathematical Sciences, Limbe, Cameroon and Department of Mathematics, Higher Teachers
Introduction to Orthogonal Polynomials: Definition and basic properties Prof. Dr. Mama Foupouagnigni African Institute for Mathematical Sciences, Limbe, Cameroon and Department of Mathematics, Higher Teachers
Prentice Hall: Algebra 2 with Trigonometry 2006 Correlated to: California Mathematics Content Standards for Algebra II (Grades 9-12)
 California Mathematics Content Standards for Algebra II (Grades 9-12) This discipline complements and expands the mathematical content and concepts of algebra I and geometry. Students who master algebra
California Mathematics Content Standards for Algebra II (Grades 9-12) This discipline complements and expands the mathematical content and concepts of algebra I and geometry. Students who master algebra
Series Solution of Linear Ordinary Differential Equations
 Series Solution of Linear Ordinary Differential Equations Department of Mathematics IIT Guwahati Aim: To study methods for determining series expansions for solutions to linear ODE with variable coefficients.
Series Solution of Linear Ordinary Differential Equations Department of Mathematics IIT Guwahati Aim: To study methods for determining series expansions for solutions to linear ODE with variable coefficients.
Numerical Analysis: Interpolation Part 1
 Numerical Analysis: Interpolation Part 1 Computer Science, Ben-Gurion University (slides based mostly on Prof. Ben-Shahar s notes) 2018/2019, Fall Semester BGU CS Interpolation (ver. 1.00) AY 2018/2019,
Numerical Analysis: Interpolation Part 1 Computer Science, Ben-Gurion University (slides based mostly on Prof. Ben-Shahar s notes) 2018/2019, Fall Semester BGU CS Interpolation (ver. 1.00) AY 2018/2019,
NOTES ON LINEAR ALGEBRA. 1. Determinants
 NOTES ON LINEAR ALGEBRA 1 Determinants In this section, we study determinants of matrices We study their properties, methods of computation and some applications We are familiar with the following formulas
NOTES ON LINEAR ALGEBRA 1 Determinants In this section, we study determinants of matrices We study their properties, methods of computation and some applications We are familiar with the following formulas
where c R and the content of f is one. 1
 9. Gauss Lemma Obviously it would be nice to have some more general methods of proving that a given polynomial is irreducible. The first is rather beautiful and due to Gauss. The basic idea is as follows.
9. Gauss Lemma Obviously it would be nice to have some more general methods of proving that a given polynomial is irreducible. The first is rather beautiful and due to Gauss. The basic idea is as follows.
Combinatorial proofs of addition formulas
 Combinatorial proofs of addition formulas Xiang-Ke Chang Xing-Biao Hu LSEC, ICMSEC, Academy of Mathematics and Systems Science Chinese Academy of Sciences Beijing, China Hongchuan Lei College of Science
Combinatorial proofs of addition formulas Xiang-Ke Chang Xing-Biao Hu LSEC, ICMSEC, Academy of Mathematics and Systems Science Chinese Academy of Sciences Beijing, China Hongchuan Lei College of Science
Notes on the Matrix-Tree theorem and Cayley s tree enumerator
 Notes on the Matrix-Tree theorem and Cayley s tree enumerator 1 Cayley s tree enumerator Recall that the degree of a vertex in a tree (or in any graph) is the number of edges emanating from it We will
Notes on the Matrix-Tree theorem and Cayley s tree enumerator 1 Cayley s tree enumerator Recall that the degree of a vertex in a tree (or in any graph) is the number of edges emanating from it We will
On certain combinatorial expansions of the Legendre-Stirling numbers
 On certain combinatorial expansions of the Legendre-Stirling numbers Shi-Mei Ma School of Mathematics and Statistics Northeastern University at Qinhuangdao Hebei, P.R. China shimeimapapers@163.com Yeong-Nan
On certain combinatorial expansions of the Legendre-Stirling numbers Shi-Mei Ma School of Mathematics and Statistics Northeastern University at Qinhuangdao Hebei, P.R. China shimeimapapers@163.com Yeong-Nan
Quadrant marked mesh patterns in alternating permutations
 Quadrant marked mesh patterns in alternating permutations arxiv:1205.0570v1 [math.co] 2 May 2012 Sergey Kitaev School of Computer and Information Sciences University of Strathclyde Glasgow G1 1XH, United
Quadrant marked mesh patterns in alternating permutations arxiv:1205.0570v1 [math.co] 2 May 2012 Sergey Kitaev School of Computer and Information Sciences University of Strathclyde Glasgow G1 1XH, United
Combinatorial Analysis of the Geometric Series
 Combinatorial Analysis of the Geometric Series David P. Little April 7, 205 www.math.psu.edu/dlittle Analytic Convergence of a Series The series converges analytically if and only if the sequence of partial
Combinatorial Analysis of the Geometric Series David P. Little April 7, 205 www.math.psu.edu/dlittle Analytic Convergence of a Series The series converges analytically if and only if the sequence of partial
+ i sin. + i sin. = 2 cos
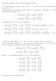 Math 11 Lesieutre); Exam review I; December 4, 017 1. a) Find all complex numbers z for which z = 8. Write your answers in rectangular non-polar) form. We are going to use de Moivre s theorem. For 1, r
Math 11 Lesieutre); Exam review I; December 4, 017 1. a) Find all complex numbers z for which z = 8. Write your answers in rectangular non-polar) form. We are going to use de Moivre s theorem. For 1, r
q xk y n k. , provided k < n. (This does not hold for k n.) Give a combinatorial proof of this recurrence by means of a bijective transformation.
 Math 880 Alternative Challenge Problems Fall 2016 A1. Given, n 1, show that: m1 m 2 m = ( ) n+ 1 2 1, where the sum ranges over all positive integer solutions (m 1,..., m ) of m 1 + + m = n. Give both
Math 880 Alternative Challenge Problems Fall 2016 A1. Given, n 1, show that: m1 m 2 m = ( ) n+ 1 2 1, where the sum ranges over all positive integer solutions (m 1,..., m ) of m 1 + + m = n. Give both
Quadratic forms. Here. Thus symmetric matrices are diagonalizable, and the diagonalization can be performed by means of an orthogonal matrix.
 Quadratic forms 1. Symmetric matrices An n n matrix (a ij ) n ij=1 with entries on R is called symmetric if A T, that is, if a ij = a ji for all 1 i, j n. We denote by S n (R) the set of all n n symmetric
Quadratic forms 1. Symmetric matrices An n n matrix (a ij ) n ij=1 with entries on R is called symmetric if A T, that is, if a ij = a ji for all 1 i, j n. We denote by S n (R) the set of all n n symmetric
Chapter 11 - Sequences and Series
 Calculus and Analytic Geometry II Chapter - Sequences and Series. Sequences Definition. A sequence is a list of numbers written in a definite order, We call a n the general term of the sequence. {a, a
Calculus and Analytic Geometry II Chapter - Sequences and Series. Sequences Definition. A sequence is a list of numbers written in a definite order, We call a n the general term of the sequence. {a, a
Counting points on hyperelliptic curves
 University of New South Wales 9th November 202, CARMA, University of Newcastle Elliptic curves Let p be a prime. Let X be an elliptic curve over F p. Want to compute #X (F p ), the number of F p -rational
University of New South Wales 9th November 202, CARMA, University of Newcastle Elliptic curves Let p be a prime. Let X be an elliptic curve over F p. Want to compute #X (F p ), the number of F p -rational
Some Review Problems for Exam 3: Solutions
 Math 3355 Spring 017 Some Review Problems for Exam 3: Solutions I thought I d start by reviewing some counting formulas. Counting the Complement: Given a set U (the universe for the problem), if you want
Math 3355 Spring 017 Some Review Problems for Exam 3: Solutions I thought I d start by reviewing some counting formulas. Counting the Complement: Given a set U (the universe for the problem), if you want
Partition of Integers into Distinct Summands with Upper Bounds. Partition of Integers into Even Summands. An Example
 Partition of Integers into Even Summands We ask for the number of partitions of m Z + into positive even integers The desired number is the coefficient of x m in + x + x 4 + ) + x 4 + x 8 + ) + x 6 + x
Partition of Integers into Even Summands We ask for the number of partitions of m Z + into positive even integers The desired number is the coefficient of x m in + x + x 4 + ) + x 4 + x 8 + ) + x 6 + x
Finite-dimensional spaces. C n is the space of n-tuples x = (x 1,..., x n ) of complex numbers. It is a Hilbert space with the inner product
 Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Chapter 4 Hilbert Spaces 4.1 Inner Product Spaces Inner Product Space. A complex vector space E is called an inner product space (or a pre-hilbert space, or a unitary space) if there is a mapping (, )
Inverses. Stephen Boyd. EE103 Stanford University. October 28, 2017
 Inverses Stephen Boyd EE103 Stanford University October 28, 2017 Outline Left and right inverses Inverse Solving linear equations Examples Pseudo-inverse Left and right inverses 2 Left inverses a number
Inverses Stephen Boyd EE103 Stanford University October 28, 2017 Outline Left and right inverses Inverse Solving linear equations Examples Pseudo-inverse Left and right inverses 2 Left inverses a number
TEST CODE: MMA (Objective type) 2015 SYLLABUS
 TEST CODE: MMA (Objective type) 2015 SYLLABUS Analytical Reasoning Algebra Arithmetic, geometric and harmonic progression. Continued fractions. Elementary combinatorics: Permutations and combinations,
TEST CODE: MMA (Objective type) 2015 SYLLABUS Analytical Reasoning Algebra Arithmetic, geometric and harmonic progression. Continued fractions. Elementary combinatorics: Permutations and combinations,
An Introduction to Combinatorial Species
 An Introduction to Combinatorial Species Ira M. Gessel Department of Mathematics Brandeis University Summer School on Algebraic Combinatorics Korea Institute for Advanced Study Seoul, Korea June 14, 2016
An Introduction to Combinatorial Species Ira M. Gessel Department of Mathematics Brandeis University Summer School on Algebraic Combinatorics Korea Institute for Advanced Study Seoul, Korea June 14, 2016
Ir O D = D = ( ) Section 2.6 Example 1. (Bottom of page 119) dim(v ) = dim(l(v, W )) = dim(v ) dim(f ) = dim(v )
 Section 3.2 Theorem 3.6. Let A be an m n matrix of rank r. Then r m, r n, and, by means of a finite number of elementary row and column operations, A can be transformed into the matrix ( ) Ir O D = 1 O
Section 3.2 Theorem 3.6. Let A be an m n matrix of rank r. Then r m, r n, and, by means of a finite number of elementary row and column operations, A can be transformed into the matrix ( ) Ir O D = 1 O
Applied Calculus I. Lecture 29
 Applied Calculus I Lecture 29 Integrals of trigonometric functions We shall continue learning substitutions by considering integrals involving trigonometric functions. Integrals of trigonometric functions
Applied Calculus I Lecture 29 Integrals of trigonometric functions We shall continue learning substitutions by considering integrals involving trigonometric functions. Integrals of trigonometric functions
Section 33 Finite fields
 Section 33 Finite fields Instructor: Yifan Yang Spring 2007 Review Corollary (23.6) Let G be a finite subgroup of the multiplicative group of nonzero elements in a field F, then G is cyclic. Theorem (27.19)
Section 33 Finite fields Instructor: Yifan Yang Spring 2007 Review Corollary (23.6) Let G be a finite subgroup of the multiplicative group of nonzero elements in a field F, then G is cyclic. Theorem (27.19)
Legendre s Equation. PHYS Southern Illinois University. October 18, 2016
 Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
Matrices. Chapter What is a Matrix? We review the basic matrix operations. An array of numbers a a 1n A = a m1...
 Chapter Matrices We review the basic matrix operations What is a Matrix? An array of numbers a a n A = a m a mn with m rows and n columns is a m n matrix Element a ij in located in position (i, j The elements
Chapter Matrices We review the basic matrix operations What is a Matrix? An array of numbers a a n A = a m a mn with m rows and n columns is a m n matrix Element a ij in located in position (i, j The elements
and the compositional inverse when it exists is A.
 Lecture B jacques@ucsd.edu Notation: R denotes a ring, N denotes the set of sequences of natural numbers with finite support, is a generic element of N, is the infinite zero sequence, n 0 R[[ X]] denotes
Lecture B jacques@ucsd.edu Notation: R denotes a ring, N denotes the set of sequences of natural numbers with finite support, is a generic element of N, is the infinite zero sequence, n 0 R[[ X]] denotes
18. Cyclotomic polynomials II
 18. Cyclotomic polynomials II 18.1 Cyclotomic polynomials over Z 18.2 Worked examples Now that we have Gauss lemma in hand we can look at cyclotomic polynomials again, not as polynomials with coefficients
18. Cyclotomic polynomials II 18.1 Cyclotomic polynomials over Z 18.2 Worked examples Now that we have Gauss lemma in hand we can look at cyclotomic polynomials again, not as polynomials with coefficients
Ma 530 Power Series II
 Ma 530 Power Series II Please note that there is material on power series at Visual Calculus. Some of this material was used as part of the presentation of the topics that follow. Operations on Power Series
Ma 530 Power Series II Please note that there is material on power series at Visual Calculus. Some of this material was used as part of the presentation of the topics that follow. Operations on Power Series
Exponential tail inequalities for eigenvalues of random matrices
 Exponential tail inequalities for eigenvalues of random matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify
Exponential tail inequalities for eigenvalues of random matrices M. Ledoux Institut de Mathématiques de Toulouse, France exponential tail inequalities classical theme in probability and statistics quantify
0.1 Rational Canonical Forms
 We have already seen that it is useful and simpler to study linear systems using matrices. But matrices are themselves cumbersome, as they are stuffed with many entries, and it turns out that it s best
We have already seen that it is useful and simpler to study linear systems using matrices. But matrices are themselves cumbersome, as they are stuffed with many entries, and it turns out that it s best
Linear Transformations: Standard Matrix
 Linear Transformations: Standard Matrix Linear Algebra Josh Engwer TTU November 5 Josh Engwer (TTU) Linear Transformations: Standard Matrix November 5 / 9 PART I PART I: STANDARD MATRIX (THE EASY CASE)
Linear Transformations: Standard Matrix Linear Algebra Josh Engwer TTU November 5 Josh Engwer (TTU) Linear Transformations: Standard Matrix November 5 / 9 PART I PART I: STANDARD MATRIX (THE EASY CASE)
Algebra and Trigonometry 2006 (Foerster) Correlated to: Washington Mathematics Standards, Algebra 2 (2008)
 A2.1. Core Content: Solving problems The first core content area highlights the type of problems students will be able to solve by the end of, as they extend their ability to solve problems with additional
A2.1. Core Content: Solving problems The first core content area highlights the type of problems students will be able to solve by the end of, as they extend their ability to solve problems with additional
QUADRANT MARKED MESH PATTERNS IN 132-AVOIDING PERMUTATIONS III
 #A39 INTEGERS 5 (05) QUADRANT MARKED MESH PATTERNS IN 3-AVOIDING PERMUTATIONS III Sergey Kitaev Department of Computer and Information Sciences, University of Strathclyde, Glasgow, United Kingdom sergey.kitaev@cis.strath.ac.uk
#A39 INTEGERS 5 (05) QUADRANT MARKED MESH PATTERNS IN 3-AVOIDING PERMUTATIONS III Sergey Kitaev Department of Computer and Information Sciences, University of Strathclyde, Glasgow, United Kingdom sergey.kitaev@cis.strath.ac.uk
CROSSINGS, MOTZKIN PATHS AND MOMENTS
 CROSSINGS, MOTZKIN PATHS AND MOMENTS MATTHIEU JOSUAT-VERGÈS AND MARTIN RUBEY Dedicated to Jean-Guy Penaud Abstract. Kasraoui, Stanton and Zeng, and Kim, Stanton and Zeng introduced certain q-analogues
CROSSINGS, MOTZKIN PATHS AND MOMENTS MATTHIEU JOSUAT-VERGÈS AND MARTIN RUBEY Dedicated to Jean-Guy Penaud Abstract. Kasraoui, Stanton and Zeng, and Kim, Stanton and Zeng introduced certain q-analogues
Power series and Taylor series
 Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
q-binomial coefficient congruences
 CARMA Analysis and Number Theory Seminar University of Newcastle August 23, 2011 Tulane University, New Orleans 1 / 35 Our first -analogs The natural number n has the -analog: [n] = n 1 1 = 1 + +... n
CARMA Analysis and Number Theory Seminar University of Newcastle August 23, 2011 Tulane University, New Orleans 1 / 35 Our first -analogs The natural number n has the -analog: [n] = n 1 1 = 1 + +... n
Functions, Graphs, Equations and Inequalities
 CAEM DPP Learning Outcomes per Module Module Functions, Graphs, Equations and Inequalities Learning Outcomes 1. Functions, inverse functions and composite functions 1.1. concepts of function, domain and
CAEM DPP Learning Outcomes per Module Module Functions, Graphs, Equations and Inequalities Learning Outcomes 1. Functions, inverse functions and composite functions 1.1. concepts of function, domain and
Homework 8 Solutions to Selected Problems
 Homework 8 Solutions to Selected Problems June 7, 01 1 Chapter 17, Problem Let f(x D[x] and suppose f(x is reducible in D[x]. That is, there exist polynomials g(x and h(x in D[x] such that g(x and h(x
Homework 8 Solutions to Selected Problems June 7, 01 1 Chapter 17, Problem Let f(x D[x] and suppose f(x is reducible in D[x]. That is, there exist polynomials g(x and h(x in D[x] such that g(x and h(x
Lecture 22: Jordan canonical form of upper-triangular matrices (1)
 Lecture 22: Jordan canonical form of upper-triangular matrices (1) Travis Schedler Tue, Dec 6, 2011 (version: Tue, Dec 6, 1:00 PM) Goals (2) Definition, existence, and uniqueness of Jordan canonical form
Lecture 22: Jordan canonical form of upper-triangular matrices (1) Travis Schedler Tue, Dec 6, 2011 (version: Tue, Dec 6, 1:00 PM) Goals (2) Definition, existence, and uniqueness of Jordan canonical form
FINITE-DIMENSIONAL LINEAR ALGEBRA
 DISCRETE MATHEMATICS AND ITS APPLICATIONS Series Editor KENNETH H ROSEN FINITE-DIMENSIONAL LINEAR ALGEBRA Mark S Gockenbach Michigan Technological University Houghton, USA CRC Press Taylor & Francis Croup
DISCRETE MATHEMATICS AND ITS APPLICATIONS Series Editor KENNETH H ROSEN FINITE-DIMENSIONAL LINEAR ALGEBRA Mark S Gockenbach Michigan Technological University Houghton, USA CRC Press Taylor & Francis Croup
Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008
 Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008 Exam 2 will be held on Tuesday, April 8, 7-8pm in 117 MacMillan What will be covered The exam will cover material from the lectures
Math 520 Exam 2 Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008 Exam 2 will be held on Tuesday, April 8, 7-8pm in 117 MacMillan What will be covered The exam will cover material from the lectures
A description of a math circle set of activities around polynomials, especially interpolation.
 A description of a math circle set of activities around polynomials, especially interpolation. Bob Sachs Department of Mathematical Sciences George Mason University Fairfax, Virginia 22030 rsachs@gmu.edu
A description of a math circle set of activities around polynomials, especially interpolation. Bob Sachs Department of Mathematical Sciences George Mason University Fairfax, Virginia 22030 rsachs@gmu.edu
BMT 2016 Orthogonal Polynomials 12 March Welcome to the power round! This year s topic is the theory of orthogonal polynomials.
 Power Round Welcome to the power round! This year s topic is the theory of orthogonal polynomials. I. You should order your papers with the answer sheet on top, and you should number papers addressing
Power Round Welcome to the power round! This year s topic is the theory of orthogonal polynomials. I. You should order your papers with the answer sheet on top, and you should number papers addressing
Simplifying Rational Expressions and Functions
 Department of Mathematics Grossmont College October 15, 2012 Recall: The Number Types Definition The set of whole numbers, ={0, 1, 2, 3, 4,...} is the set of natural numbers unioned with zero, written
Department of Mathematics Grossmont College October 15, 2012 Recall: The Number Types Definition The set of whole numbers, ={0, 1, 2, 3, 4,...} is the set of natural numbers unioned with zero, written
For more information visit
 If the integrand is a derivative of a known function, then the corresponding indefinite integral can be directly evaluated. If the integrand is not a derivative of a known function, the integral may be
If the integrand is a derivative of a known function, then the corresponding indefinite integral can be directly evaluated. If the integrand is not a derivative of a known function, the integral may be
1 The distributive law
 THINGS TO KNOW BEFORE GOING INTO DISCRETE MATHEMATICS The distributive law The distributive law is this: a(b + c) = ab + bc This can be generalized to any number of terms between parenthesis; for instance:
THINGS TO KNOW BEFORE GOING INTO DISCRETE MATHEMATICS The distributive law The distributive law is this: a(b + c) = ab + bc This can be generalized to any number of terms between parenthesis; for instance:
MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION
 MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION 1. Polynomial rings (review) Definition 1. A polynomial f(x) with coefficients in a ring R is n f(x) = a i x i = a 0 + a 1 x + a 2 x 2 + + a n x n i=0
MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION 1. Polynomial rings (review) Definition 1. A polynomial f(x) with coefficients in a ring R is n f(x) = a i x i = a 0 + a 1 x + a 2 x 2 + + a n x n i=0
MA22S3 Summary Sheet: Ordinary Differential Equations
 MA22S3 Summary Sheet: Ordinary Differential Equations December 14, 2017 Kreyszig s textbook is a suitable guide for this part of the module. Contents 1 Terminology 1 2 First order separable 2 2.1 Separable
MA22S3 Summary Sheet: Ordinary Differential Equations December 14, 2017 Kreyszig s textbook is a suitable guide for this part of the module. Contents 1 Terminology 1 2 First order separable 2 2.1 Separable
Cyclic Derangements. Sami H. Assaf. Department of Mathematics MIT, Cambridge, MA 02139, USA
 Cyclic Derangements Sami H. Assaf Department of Mathematics MIT, Cambridge, MA 02139, USA sassaf@math.mit.edu Submitted: Apr 16, 2010; Accepted: Oct 26, 2010; Published: Dec 3, 2010 Mathematics Subject
Cyclic Derangements Sami H. Assaf Department of Mathematics MIT, Cambridge, MA 02139, USA sassaf@math.mit.edu Submitted: Apr 16, 2010; Accepted: Oct 26, 2010; Published: Dec 3, 2010 Mathematics Subject
1. General Vector Spaces
 1.1. Vector space axioms. 1. General Vector Spaces Definition 1.1. Let V be a nonempty set of objects on which the operations of addition and scalar multiplication are defined. By addition we mean a rule
1.1. Vector space axioms. 1. General Vector Spaces Definition 1.1. Let V be a nonempty set of objects on which the operations of addition and scalar multiplication are defined. By addition we mean a rule
Congruences for algebraic sequences
 Congruences for algebraic sequences Eric Rowland 1 Reem Yassawi 2 1 Université du Québec à Montréal 2 Trent University 2013 September 27 Eric Rowland (UQAM) Congruences for algebraic sequences 2013 September
Congruences for algebraic sequences Eric Rowland 1 Reem Yassawi 2 1 Université du Québec à Montréal 2 Trent University 2013 September 27 Eric Rowland (UQAM) Congruences for algebraic sequences 2013 September
BOOK REVIEWS 297 WILLIAM D. SUDDERTH American Mathematical Society /85 $ $.25 per page
 BOOK REVIEWS 297 4. S. Geisser, A predictivistic primer, Bayesian Analysis in Econometrics and Statistics, North-Holland, Amsterdam, 1980. 5. D. Heath and W. Sudderth, On finitely additive priors, coherence,
BOOK REVIEWS 297 4. S. Geisser, A predictivistic primer, Bayesian Analysis in Econometrics and Statistics, North-Holland, Amsterdam, 1980. 5. D. Heath and W. Sudderth, On finitely additive priors, coherence,
Math review. Math review
 Math review 1 Math review 3 1 series approximations 3 Taylor s Theorem 3 Binomial approximation 3 sin(x), for x in radians and x close to zero 4 cos(x), for x in radians and x close to zero 5 2 some geometry
Math review 1 Math review 3 1 series approximations 3 Taylor s Theorem 3 Binomial approximation 3 sin(x), for x in radians and x close to zero 4 cos(x), for x in radians and x close to zero 5 2 some geometry
Two-boundary lattice paths and parking functions
 Two-boundary lattice paths and parking functions Joseph PS Kung 1, Xinyu Sun 2, and Catherine Yan 3,4 1 Department of Mathematics, University of North Texas, Denton, TX 76203 2,3 Department of Mathematics
Two-boundary lattice paths and parking functions Joseph PS Kung 1, Xinyu Sun 2, and Catherine Yan 3,4 1 Department of Mathematics, University of North Texas, Denton, TX 76203 2,3 Department of Mathematics
There are two things that are particularly nice about the first basis
 Orthogonality and the Gram-Schmidt Process In Chapter 4, we spent a great deal of time studying the problem of finding a basis for a vector space We know that a basis for a vector space can potentially
Orthogonality and the Gram-Schmidt Process In Chapter 4, we spent a great deal of time studying the problem of finding a basis for a vector space We know that a basis for a vector space can potentially
ENUMERATION BY KERNEL POSITIONS
 ENUMERATION BY KERNEL POSITIONS Abstract. We introduce a class of two-player games on posets with a rank function, in which each move of the winning strategy is unique. This allows to enumerate the kernel
ENUMERATION BY KERNEL POSITIONS Abstract. We introduce a class of two-player games on posets with a rank function, in which each move of the winning strategy is unique. This allows to enumerate the kernel
