A first order divided difference
|
|
|
- Kristian Fitzgerald
- 5 years ago
- Views:
Transcription
1 A first order divided difference For a given function f (x) and two distinct points x 0 and x 1, define f [x 0, x 1 ] = f (x 1) f (x 0 ) x 1 x 0 This is called the first order divided difference of f (x). By the Mean-value theorem, f (x 1 ) f (x 0 ) = f (c)(x 1 x 0 ) for some c between x 0 and x 1. Thus f [x 0, x 1 ] = f (c) and the divided difference is very much like the derivative, especially if x 0 and x 1 are quite close together. In fact, ( ) f x1 + x 0 f [x 0, x 1 ] 2 is quite an accurate approximation of the derivative.
2 Second order divided difference Given three distinct points x 0, x 1, and x 2, define f [x 0, x 1, x 2 ] = f [x 1, x 2 ] f [x 0, x 1 ] x 2 x 0 This is called the second order divided difference of f (x). We can show that f [x 0, x 1, x 2 ] = 1 2 f (c) for some c intermediate to x 0, x 1, and 2. In fact, f (x 1 ) 2f [x 0, x 1, x 2 ] in the case when nodes are evenly spaced, x 1 x 0 = x 2 x 1.
3 Example Consider the table x cos x Let x 0 = 1, x 1 = 1.1, and x 2 = 1.2. Then f [x 0, x 1 ] = = f [x 1, x 2 ] = = f [x 0, x 1, x 2 ] = f [x 1, x 2 ] f [x 0, x1] x 2 x ( ) = = ( ) For comparison, f x1 + x 0 = sin(1.05) =
4 General divided differences Given n + 1 distinct points x 0,..., x n, with n 2, define f [x 0,..., x n ] = f [x 1,..., x n ] f [x 0,..., x n 1 ] x n x 0 This is a recursive definition of the n-th order divided difference of f (x), using divided differences of order n. We can also relate this to the derivative as follows: f [x 0,..., x n ] = 1 n! f (n) (c) for some c intermediate to the points {x 0,..., x n }.
5 Order of nodes We see that f [x 0, x 1 ] = f (x 1) f (x 0 ) x 1 x 0 = f (x 0) f (x 1 ) x 0 x 1 = f [x 1, x 0 ] The order of x 0 and x 1 does not matter. We have for 2nd order divided difference: f [x 0, x 1, x 2 ] = f [x 1, x 2 ] f [x 0, x 1 ] x 2 x 0 f (x 0 ) = (x 0 x 1 )(x 0 x 2 ) f (x 1 ) + (x 1 x 0 )(x 1 x 2 ) f (x 2 ) + (x 2 x 0 )(x 2 x 1 )
6 Order of nodes Using this formula, we can show that f [x 0, x 1, x 2 ] = f [x 0, x 2, x 1 ] Mathematically, f [x 0, x 1, x 2 ] = f [x i0, x i1, x i2 ] for any permutation (i 0, i 1, i 2 ) of (0, 1, 2).
7 Newton s interpolating polynomial Recall that the general interpolation problem: find a polynomial P n (x) of degree n for which P n (x i ) = y i, i = 0, 1,..., n with given data points (x 0, y 0 ), (x 1, y 1 ),..., (x n, y n ), where {x 0,..., x n } distinct points.
8 Newton s interpolating polynomial Let the data values be generated from a function f (x): y i = f (x i ), i = 0, 1,..., n Using divided differences f [x 0, x 1 ], f [x 0, x 1, x 2 ],..., f [x 0,..., x n ] we can write the interpolation polynomials P 1 (x), P 2 (x),..., P n (x) in a way that is simple to compute. P 1 (x) = f (x 0 ) + f [x 0, x 1 ](x x 0 ) P 2 (x) = f (x 0 ) + f [x 0, x 1 ](x x 0 ) +f [x 0, x 1, x 2 ](x x 0 )(x x 1 ) = P 1 (x) + f [x 0, x 1, x 2 ](x x 0 )(x x 1 )
9 Newton s interpolating polynomial For the case of general n-th degree polynomial, we have P n (x) = f (x 0 ) + f [x 0, x 1 ](x x 0 ) +f [x 0, x 1, x 2 ](x x 0 )(x x 1 ) f [x 0,..., x n ](x x 0 )... (x x n 1 ) Therefore P n (x) = P n 1 (x) + f [x 0,..., x n ](x x 0 )... (x x n 1 ) in which P n 1 (x) interpolates f (x) at points in {x 0,..., x n 1 }
10 Example Consider the table Define x cos x D k f (x i ) = f [x i,..., x i+k ] i x i f (x i ) D 1 f (x i ) D 2 f (x i ) D 3 f (x i ) D 4 f (x i ) These were computed using the recursive definition f [x 0,..., x n ] = f [x 1,..., x n ] f [x 0,..., x n 1 ] x n x 0
11 Then P 1 (x) = (x 1) P 2 (x) = P 1 (x) (x 1)(x 1.1) P 3 (x) = P 2 (x) (x 1)(x 1.1)(x 1.2) P 4 (x) = P 3 (x) (x 1)(x 1.1)(x 1.2)(x 1.3) We can now estimate cos(1.05) using various order polynomials and the results are tabulated below: n P n (1.05) Error
12 Error of interpolation Let P n (x) be a n-th degree interpolating polynomial that agree with f (x) on n + 1 distinct points. Let the error E(x) be defined as E(x) = f (x) P n (x) Since E(x i ) = 0 for i = 0,..., n, we can write E(x) = (x x 0 )(x x 1 )... (x x n )g(x), where the function g(x) has to be determined. We see that f (x) P n (x) (x x 0 )(x x 1 )... (x x n )g(x) = 0
13 Error of interpolation Let us introduce a new function W (t) = f (t) P n (t) (t x 0 )(t x 1 )... (t x n )g(x) Note that W (t) = 0 at t = x, x 0, x 1,..., x n. Therefore, W (t) has n + 2 zeros. We assume that W (t) is continuous and differentiable and use mean value theorem. Therefore, W (c) = 0 if c is a number intermediate in {x 0, x 1,..., x n, x}.
14 Error of interpolation Using mean value theorem repeatedly, we get W n+1 (c) = 0 = f (n+1) (c) (n + 1)!g(x) for c intermediate in {x 0, x n, x}. Thus Hence g(x) = f (n+1) (c) (n + 1)! E(x) = (x x 0 )(x x 1 )... (x x n ) f (n+1) (c) (n + 1)!
15 Error of interpolation Example: If the function f (x) = sin x is approximated by a polynomial of degree 9 that interpolates f (x) at ten points in the interval [0, 1], estimate the interpolation error.
INTERPOLATION. and y i = cos x i, i = 0, 1, 2 This gives us the three points. Now find a quadratic polynomial. p(x) = a 0 + a 1 x + a 2 x 2.
 INTERPOLATION Interpolation is a process of finding a formula (often a polynomial) whose graph will pass through a given set of points (x, y). As an example, consider defining and x 0 = 0, x 1 = π/4, x
INTERPOLATION Interpolation is a process of finding a formula (often a polynomial) whose graph will pass through a given set of points (x, y). As an example, consider defining and x 0 = 0, x 1 = π/4, x
NUMERICAL METHODS. x n+1 = 2x n x 2 n. In particular: which of them gives faster convergence, and why? [Work to four decimal places.
 NUMERICAL METHODS 1. Rearranging the equation x 3 =.5 gives the iterative formula x n+1 = g(x n ), where g(x) = (2x 2 ) 1. (a) Starting with x = 1, compute the x n up to n = 6, and describe what is happening.
NUMERICAL METHODS 1. Rearranging the equation x 3 =.5 gives the iterative formula x n+1 = g(x n ), where g(x) = (2x 2 ) 1. (a) Starting with x = 1, compute the x n up to n = 6, and describe what is happening.
Jim Lambers MAT 460/560 Fall Semester Practice Final Exam
 Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
Interpolating Accuracy without underlying f (x)
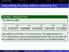 Example: Tabulated Data The following table x 1.0 1.3 1.6 1.9 2.2 f (x) 0.7651977 0.6200860 0.4554022 0.2818186 0.1103623 lists values of a function f at various points. The approximations to f (1.5) obtained
Example: Tabulated Data The following table x 1.0 1.3 1.6 1.9 2.2 f (x) 0.7651977 0.6200860 0.4554022 0.2818186 0.1103623 lists values of a function f at various points. The approximations to f (1.5) obtained
3.1 Interpolation and the Lagrange Polynomial
 MATH 4073 Chapter 3 Interpolation and Polynomial Approximation Fall 2003 1 Consider a sample x x 0 x 1 x n y y 0 y 1 y n. Can we get a function out of discrete data above that gives a reasonable estimate
MATH 4073 Chapter 3 Interpolation and Polynomial Approximation Fall 2003 1 Consider a sample x x 0 x 1 x n y y 0 y 1 y n. Can we get a function out of discrete data above that gives a reasonable estimate
Numerical Mathematics & Computing, 7 Ed. 4.1 Interpolation
 Numerical Mathematics & Computing, 7 Ed. 4.1 Interpolation Ward Cheney/David Kincaid c UT Austin Engage Learning: Thomson-Brooks/Cole www.engage.com www.ma.utexas.edu/cna/nmc6 November 7, 2011 2011 1 /
Numerical Mathematics & Computing, 7 Ed. 4.1 Interpolation Ward Cheney/David Kincaid c UT Austin Engage Learning: Thomson-Brooks/Cole www.engage.com www.ma.utexas.edu/cna/nmc6 November 7, 2011 2011 1 /
Scientific Computing
 2301678 Scientific Computing Chapter 2 Interpolation and Approximation Paisan Nakmahachalasint Paisan.N@chula.ac.th Chapter 2 Interpolation and Approximation p. 1/66 Contents 1. Polynomial interpolation
2301678 Scientific Computing Chapter 2 Interpolation and Approximation Paisan Nakmahachalasint Paisan.N@chula.ac.th Chapter 2 Interpolation and Approximation p. 1/66 Contents 1. Polynomial interpolation
Interpolation and Approximation
 Interpolation and Approximation The Basic Problem: Approximate a continuous function f(x), by a polynomial p(x), over [a, b]. f(x) may only be known in tabular form. f(x) may be expensive to compute. Definition:
Interpolation and Approximation The Basic Problem: Approximate a continuous function f(x), by a polynomial p(x), over [a, b]. f(x) may only be known in tabular form. f(x) may be expensive to compute. Definition:
Chapter 4: Interpolation and Approximation. October 28, 2005
 Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Section Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence.
 Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. f n (0)x n Recall from
Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. f n (0)x n Recall from
1 Solutions to selected problems
 Solutions to selected problems Section., #a,c,d. a. p x = n for i = n : 0 p x = xp x + i end b. z = x, y = x for i = : n y = y + x i z = zy end c. y = (t x ), p t = a for i = : n y = y(t x i ) p t = p
Solutions to selected problems Section., #a,c,d. a. p x = n for i = n : 0 p x = xp x + i end b. z = x, y = x for i = : n y = y + x i z = zy end c. y = (t x ), p t = a for i = : n y = y(t x i ) p t = p
Math 651 Introduction to Numerical Analysis I Fall SOLUTIONS: Homework Set 1
 ath 651 Introduction to Numerical Analysis I Fall 2010 SOLUTIONS: Homework Set 1 1. Consider the polynomial f(x) = x 2 x 2. (a) Find P 1 (x), P 2 (x) and P 3 (x) for f(x) about x 0 = 0. What is the relation
ath 651 Introduction to Numerical Analysis I Fall 2010 SOLUTIONS: Homework Set 1 1. Consider the polynomial f(x) = x 2 x 2. (a) Find P 1 (x), P 2 (x) and P 3 (x) for f(x) about x 0 = 0. What is the relation
We consider the problem of finding a polynomial that interpolates a given set of values:
 Chapter 5 Interpolation 5. Polynomial Interpolation We consider the problem of finding a polynomial that interpolates a given set of values: x x 0 x... x n y y 0 y... y n where the x i are all distinct.
Chapter 5 Interpolation 5. Polynomial Interpolation We consider the problem of finding a polynomial that interpolates a given set of values: x x 0 x... x n y y 0 y... y n where the x i are all distinct.
Polynomial Interpolation with n + 1 nodes
 Polynomial Interpolation with n + 1 nodes Given n + 1 distinct points (x 0, f (x 0 )), (x 1, f (x 1 )),, (x n, f (x n )), Interpolating polynomial of degree n P(x) = f (x 0 )L 0 (x) + f (x 1 )L 1 (x) +
Polynomial Interpolation with n + 1 nodes Given n + 1 distinct points (x 0, f (x 0 )), (x 1, f (x 1 )),, (x n, f (x n )), Interpolating polynomial of degree n P(x) = f (x 0 )L 0 (x) + f (x 1 )L 1 (x) +
Computational Physics
 Interpolation, Extrapolation & Polynomial Approximation Lectures based on course notes by Pablo Laguna and Kostas Kokkotas revamped by Deirdre Shoemaker Spring 2014 Introduction In many cases, a function
Interpolation, Extrapolation & Polynomial Approximation Lectures based on course notes by Pablo Laguna and Kostas Kokkotas revamped by Deirdre Shoemaker Spring 2014 Introduction In many cases, a function
Introduction Linear system Nonlinear equation Interpolation
 Interpolation Interpolation is the process of estimating an intermediate value from a set of discrete or tabulated values. Suppose we have the following tabulated values: y y 0 y 1 y 2?? y 3 y 4 y 5 x
Interpolation Interpolation is the process of estimating an intermediate value from a set of discrete or tabulated values. Suppose we have the following tabulated values: y y 0 y 1 y 2?? y 3 y 4 y 5 x
(0, 0), (1, ), (2, ), (3, ), (4, ), (5, ), (6, ).
 1 Interpolation: The method of constructing new data points within the range of a finite set of known data points That is if (x i, y i ), i = 1, N are known, with y i the dependent variable and x i [x
1 Interpolation: The method of constructing new data points within the range of a finite set of known data points That is if (x i, y i ), i = 1, N are known, with y i the dependent variable and x i [x
Suppose that f is continuous on [a, b] and differentiable on (a, b). Then
![Suppose that f is continuous on [a, b] and differentiable on (a, b). Then Suppose that f is continuous on [a, b] and differentiable on (a, b). Then](/thumbs/74/71325034.jpg) Lectures 1/18 Derivatives and Graphs When we have a picture of the graph of a function f(x), we can make a picture of the derivative f (x) using the slopes of the tangents to the graph of f. In this section
Lectures 1/18 Derivatives and Graphs When we have a picture of the graph of a function f(x), we can make a picture of the derivative f (x) using the slopes of the tangents to the graph of f. In this section
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS
 LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
Interpolation. s(s 1)(s 2) Δ 3 f ! s(s 1) Δ 2 f 0 + 2! f(x s )=f 0 + sδf 0 +
 Interpolation For equally spaced sample points, the Newton-Gregory formula can be used effectively in two ways: (1) Use for derivation of well-known intepolation formulas. (2) Use directy for numerical
Interpolation For equally spaced sample points, the Newton-Gregory formula can be used effectively in two ways: (1) Use for derivation of well-known intepolation formulas. (2) Use directy for numerical
Section 5.6. Integration By Parts. MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10
 Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
Section 5.6 Integration By Parts MATH 126 (Section 5.6) Integration By Parts The University of Kansas 1 / 10 Integration By Parts Manipulating the Product Rule d dx (f (x) g(x)) = f (x) g (x) + f (x) g(x)
Math 2: Algebra 2, Geometry and Statistics Ms. Sheppard-Brick Chapter 4 Test Review
 Chapter 4 Test Review Students will be able to (SWBAT): Write an explicit and a recursive function rule for a linear table of values. Write an explicit function rule for a quadratic table of values. Determine
Chapter 4 Test Review Students will be able to (SWBAT): Write an explicit and a recursive function rule for a linear table of values. Write an explicit function rule for a quadratic table of values. Determine
Interpolation and the Lagrange Polynomial
 Interpolation and the Lagrange Polynomial MATH 375 J. Robert Buchanan Department of Mathematics Fall 2013 Introduction We often choose polynomials to approximate other classes of functions. Theorem (Weierstrass
Interpolation and the Lagrange Polynomial MATH 375 J. Robert Buchanan Department of Mathematics Fall 2013 Introduction We often choose polynomials to approximate other classes of functions. Theorem (Weierstrass
Section 10.7 Taylor series
 Section 10.7 Taylor series 1. Common Maclaurin series 2. s and approximations with Taylor polynomials 3. Multiplication and division of power series Math 126 Enhanced 10.7 Taylor Series The University
Section 10.7 Taylor series 1. Common Maclaurin series 2. s and approximations with Taylor polynomials 3. Multiplication and division of power series Math 126 Enhanced 10.7 Taylor Series The University
Interpolation & Polynomial Approximation. Hermite Interpolation I
 Interpolation & Polynomial Approximation Hermite Interpolation I Numerical Analysis (th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011
Interpolation & Polynomial Approximation Hermite Interpolation I Numerical Analysis (th Edition) R L Burden & J D Faires Beamer Presentation Slides prepared by John Carroll Dublin City University c 2011
BSM510 Numerical Analysis
 BSM510 Numerical Analysis Polynomial Interpolation Prof. Manar Mohaisen Department of EEC Engineering Review of Precedent Lecture Polynomial Regression Multiple Linear Regression Nonlinear Regression Lecture
BSM510 Numerical Analysis Polynomial Interpolation Prof. Manar Mohaisen Department of EEC Engineering Review of Precedent Lecture Polynomial Regression Multiple Linear Regression Nonlinear Regression Lecture
10.1 Sequences. Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1.
 10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
Chapter 3: Root Finding. September 26, 2005
 Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
Lecture 10 Polynomial interpolation
 Lecture 10 Polynomial interpolation Weinan E 1,2 and Tiejun Li 2 1 Department of Mathematics, Princeton University, weinan@princeton.edu 2 School of Mathematical Sciences, Peking University, tieli@pku.edu.cn
Lecture 10 Polynomial interpolation Weinan E 1,2 and Tiejun Li 2 1 Department of Mathematics, Princeton University, weinan@princeton.edu 2 School of Mathematical Sciences, Peking University, tieli@pku.edu.cn
1 Solutions to selected problems
 Solutions to selected problems Section., #a,c,d. a. p x = n for i = n : 0 p x = xp x + i end b. z = x, y = x for i = : n y = y + x i z = zy end c. y = (t x ), p t = a for i = : n y = y(t x i ) p t = p
Solutions to selected problems Section., #a,c,d. a. p x = n for i = n : 0 p x = xp x + i end b. z = x, y = x for i = : n y = y + x i z = zy end c. y = (t x ), p t = a for i = : n y = y(t x i ) p t = p
Lecture Note 3: Polynomial Interpolation. Xiaoqun Zhang Shanghai Jiao Tong University
 Lecture Note 3: Polynomial Interpolation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 24, 2013 1.1 Introduction We first look at some examples. Lookup table for f(x) = 2 π x 0 e x2
Lecture Note 3: Polynomial Interpolation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 24, 2013 1.1 Introduction We first look at some examples. Lookup table for f(x) = 2 π x 0 e x2
Chapter 1 Divide and Conquer Algorithm Theory WS 2016/17 Fabian Kuhn
 Chapter 1 Divide and Conquer Algorithm Theory WS 2016/17 Fabian Kuhn Formulation of the D&C principle Divide-and-conquer method for solving a problem instance of size n: 1. Divide n c: Solve the problem
Chapter 1 Divide and Conquer Algorithm Theory WS 2016/17 Fabian Kuhn Formulation of the D&C principle Divide-and-conquer method for solving a problem instance of size n: 1. Divide n c: Solve the problem
MA2501 Numerical Methods Spring 2015
 Norwegian University of Science and Technology Department of Mathematics MA2501 Numerical Methods Spring 2015 Solutions to exercise set 7 1 Cf. Cheney and Kincaid, Exercise 4.1.9 Consider the data points
Norwegian University of Science and Technology Department of Mathematics MA2501 Numerical Methods Spring 2015 Solutions to exercise set 7 1 Cf. Cheney and Kincaid, Exercise 4.1.9 Consider the data points
LECTURE 16 GAUSS QUADRATURE In general for Newton-Cotes (equispaced interpolation points/ data points/ integration points/ nodes).
 CE 025 - Lecture 6 LECTURE 6 GAUSS QUADRATURE In general for ewton-cotes (equispaced interpolation points/ data points/ integration points/ nodes). x E x S fx dx hw' o f o + w' f + + w' f + E 84 f 0 f
CE 025 - Lecture 6 LECTURE 6 GAUSS QUADRATURE In general for ewton-cotes (equispaced interpolation points/ data points/ integration points/ nodes). x E x S fx dx hw' o f o + w' f + + w' f + E 84 f 0 f
Root Finding (and Optimisation)
 Root Finding (and Optimisation) M.Sc. in Mathematical Modelling & Scientific Computing, Practical Numerical Analysis Michaelmas Term 2018, Lecture 4 Root Finding The idea of root finding is simple we want
Root Finding (and Optimisation) M.Sc. in Mathematical Modelling & Scientific Computing, Practical Numerical Analysis Michaelmas Term 2018, Lecture 4 Root Finding The idea of root finding is simple we want
Fixed point iteration Numerical Analysis Math 465/565
 Fixed point iteration Numerical Analysis Math 465/565 1 Fixed Point Iteration Suppose we wanted to solve : f(x) = cos(x) x =0 or cos(x) =x We might consider a iteration of this type : x k+1 = cos(x k )
Fixed point iteration Numerical Analysis Math 465/565 1 Fixed Point Iteration Suppose we wanted to solve : f(x) = cos(x) x =0 or cos(x) =x We might consider a iteration of this type : x k+1 = cos(x k )
Vector Spaces - Definition
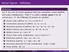 Vector Spaces - Definition Definition Let V be a set of vectors equipped with two operations: vector addition and scalar multiplication. Then V is called a vector space if for all vectors u,v V, the following
Vector Spaces - Definition Definition Let V be a set of vectors equipped with two operations: vector addition and scalar multiplication. Then V is called a vector space if for all vectors u,v V, the following
SOLVED PROBLEMS ON TAYLOR AND MACLAURIN SERIES
 SOLVED PROBLEMS ON TAYLOR AND MACLAURIN SERIES TAYLOR AND MACLAURIN SERIES Taylor Series of a function f at x = a is ( f k )( a) ( x a) k k! It is a Power Series centered at a. Maclaurin Series of a function
SOLVED PROBLEMS ON TAYLOR AND MACLAURIN SERIES TAYLOR AND MACLAURIN SERIES Taylor Series of a function f at x = a is ( f k )( a) ( x a) k k! It is a Power Series centered at a. Maclaurin Series of a function
Chapter 3 Interpolation and Polynomial Approximation
 Chapter 3 Interpolation and Polynomial Approximation Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 128A Numerical Analysis Polynomial Interpolation
Chapter 3 Interpolation and Polynomial Approximation Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 128A Numerical Analysis Polynomial Interpolation
Mean Value Theorem. MATH 161 Calculus I. J. Robert Buchanan. Summer Department of Mathematics
 Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
11.5. The Chain Rule. Introduction. Prerequisites. Learning Outcomes
 The Chain Rule 11.5 Introduction In this Section we will see how to obtain the derivative of a composite function (often referred to as a function of a function ). To do this we use the chain rule. This
The Chain Rule 11.5 Introduction In this Section we will see how to obtain the derivative of a composite function (often referred to as a function of a function ). To do this we use the chain rule. This
UNIT-II INTERPOLATION & APPROXIMATION
 UNIT-II INTERPOLATION & APPROXIMATION LAGRANGE POLYNAMIAL 1. Find the polynomial by using Lagrange s formula and hence find for : 0 1 2 5 : 2 3 12 147 : 0 1 2 5 : 0 3 12 147 Lagrange s interpolation formula,
UNIT-II INTERPOLATION & APPROXIMATION LAGRANGE POLYNAMIAL 1. Find the polynomial by using Lagrange s formula and hence find for : 0 1 2 5 : 2 3 12 147 : 0 1 2 5 : 0 3 12 147 Lagrange s interpolation formula,
Chapter Generating Functions
 Chapter 8.1.1-8.1.2. Generating Functions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 8. Generating Functions Math 184A / Fall 2017 1 / 63 Ordinary Generating Functions (OGF) Let a n (n = 0, 1,...)
Chapter 8.1.1-8.1.2. Generating Functions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 8. Generating Functions Math 184A / Fall 2017 1 / 63 Ordinary Generating Functions (OGF) Let a n (n = 0, 1,...)
Lecture Note 3: Interpolation and Polynomial Approximation. Xiaoqun Zhang Shanghai Jiao Tong University
 Lecture Note 3: Interpolation and Polynomial Approximation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 10, 2015 2 Contents 1.1 Introduction................................ 3 1.1.1
Lecture Note 3: Interpolation and Polynomial Approximation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 10, 2015 2 Contents 1.1 Introduction................................ 3 1.1.1
Numerical Methods. King Saud University
 Numerical Methods King Saud University Aims In this lecture, we will... find the approximate solutions of derivative (first- and second-order) and antiderivative (definite integral only). Numerical Differentiation
Numerical Methods King Saud University Aims In this lecture, we will... find the approximate solutions of derivative (first- and second-order) and antiderivative (definite integral only). Numerical Differentiation
Mean Value Theorem. MATH 161 Calculus I. J. Robert Buchanan. Summer Department of Mathematics
 Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
ERROR IN LINEAR INTERPOLATION
 ERROR IN LINEAR INTERPOLATION Let P 1 (x) be the linear polynomial interpolating f (x) at x 0 and x 1. Assume f (x) is twice continuously differentiable on an interval [a, b] which contains the points
ERROR IN LINEAR INTERPOLATION Let P 1 (x) be the linear polynomial interpolating f (x) at x 0 and x 1. Assume f (x) is twice continuously differentiable on an interval [a, b] which contains the points
Review of Integration Techniques
 A P P E N D I X D Brief Review of Integration Techniques u-substitution The basic idea underlying u-substitution is to perform a simple substitution that converts the intergral into a recognizable form
A P P E N D I X D Brief Review of Integration Techniques u-substitution The basic idea underlying u-substitution is to perform a simple substitution that converts the intergral into a recognizable form
Interpolation. Escuela de Ingeniería Informática de Oviedo. (Dpto. de Matemáticas-UniOvi) Numerical Computation Interpolation 1 / 34
 Interpolation Escuela de Ingeniería Informática de Oviedo (Dpto. de Matemáticas-UniOvi) Numerical Computation Interpolation 1 / 34 Outline 1 Introduction 2 Lagrange interpolation 3 Piecewise polynomial
Interpolation Escuela de Ingeniería Informática de Oviedo (Dpto. de Matemáticas-UniOvi) Numerical Computation Interpolation 1 / 34 Outline 1 Introduction 2 Lagrange interpolation 3 Piecewise polynomial
MAT 300 Midterm Exam Summer 2017
 MAT Midterm Exam Summer 7 Note: For True-False questions, a statement is only True if it must always be True under the given assumptions, otherwise it is False.. The control points of a Bezier curve γ(t)
MAT Midterm Exam Summer 7 Note: For True-False questions, a statement is only True if it must always be True under the given assumptions, otherwise it is False.. The control points of a Bezier curve γ(t)
MAT137 Calculus! Lecture 45
 official website http://uoft.me/mat137 MAT137 Calculus! Lecture 45 Today: Taylor Polynomials Taylor Series Next: Taylor Series Power Series Definition (Power Series) A power series is a series of the form
official website http://uoft.me/mat137 MAT137 Calculus! Lecture 45 Today: Taylor Polynomials Taylor Series Next: Taylor Series Power Series Definition (Power Series) A power series is a series of the form
Convergence rates of derivatives of a family of barycentric rational interpolants
 Convergence rates of derivatives of a family of barycentric rational interpolants J.-P. Berrut, M. S. Floater and G. Klein University of Fribourg (Switzerland) CMA / IFI, University of Oslo jean-paul.berrut@unifr.ch
Convergence rates of derivatives of a family of barycentric rational interpolants J.-P. Berrut, M. S. Floater and G. Klein University of Fribourg (Switzerland) CMA / IFI, University of Oslo jean-paul.berrut@unifr.ch
Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error. 2- Fixed point
 Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error In this method we assume initial value of x, and substitute in the equation. Then modify x and continue till we
Numerical Analysis Solution of Algebraic Equation (non-linear equation) 1- Trial and Error In this method we assume initial value of x, and substitute in the equation. Then modify x and continue till we
Numerical Methods-Lecture VIII: Interpolation
 Numerical Methods-Lecture VIII: Interpolation (See Judd Chapter 6) Trevor Gallen Fall, 2015 1 / 113 Motivation Most solutions are functions Many functions are (potentially) high-dimensional Want a way
Numerical Methods-Lecture VIII: Interpolation (See Judd Chapter 6) Trevor Gallen Fall, 2015 1 / 113 Motivation Most solutions are functions Many functions are (potentially) high-dimensional Want a way
Jim Lambers MAT 460 Fall Semester Lecture 2 Notes
 Jim Lambers MAT 460 Fall Semester 2009-10 Lecture 2 Notes These notes correspond to Section 1.1 in the text. Review of Calculus Among the mathematical problems that can be solved using techniques from
Jim Lambers MAT 460 Fall Semester 2009-10 Lecture 2 Notes These notes correspond to Section 1.1 in the text. Review of Calculus Among the mathematical problems that can be solved using techniques from
Chapter 6: Rational Expr., Eq., and Functions Lecture notes Math 1010
 Section 6.1: Rational Expressions and Functions Definition of a rational expression Let u and v be polynomials. The algebraic expression u v is a rational expression. The domain of this rational expression
Section 6.1: Rational Expressions and Functions Definition of a rational expression Let u and v be polynomials. The algebraic expression u v is a rational expression. The domain of this rational expression
1.1 Introduction to Limits
 Chapter 1 LIMITS 1.1 Introduction to Limits Why Limit? Suppose that an object steadily moves forward, with s(t) denotes the position at time t. The average speed over the interval [1,2] is The average
Chapter 1 LIMITS 1.1 Introduction to Limits Why Limit? Suppose that an object steadily moves forward, with s(t) denotes the position at time t. The average speed over the interval [1,2] is The average
MATH 312 Section 4.5: Undetermined Coefficients
 MATH 312 Section 4.5: Undetermined Coefficients Prof. Jonathan Duncan Walla Walla College Spring Quarter, 2007 Outline 1 Differential Operators 2 Annihilators 3 Undetermined Coefficients 4 Conclusion ODEs
MATH 312 Section 4.5: Undetermined Coefficients Prof. Jonathan Duncan Walla Walla College Spring Quarter, 2007 Outline 1 Differential Operators 2 Annihilators 3 Undetermined Coefficients 4 Conclusion ODEs
Mathematical Olympiad Training Polynomials
 Mathematical Olympiad Training Polynomials Definition A polynomial over a ring R(Z, Q, R, C) in x is an expression of the form p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, a i R, for 0 i n. If a n 0,
Mathematical Olympiad Training Polynomials Definition A polynomial over a ring R(Z, Q, R, C) in x is an expression of the form p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, a i R, for 0 i n. If a n 0,
Cubic Splines; Bézier Curves
 Cubic Splines; Bézier Curves 1 Cubic Splines piecewise approximation with cubic polynomials conditions on the coefficients of the splines 2 Bézier Curves computer-aided design and manufacturing MCS 471
Cubic Splines; Bézier Curves 1 Cubic Splines piecewise approximation with cubic polynomials conditions on the coefficients of the splines 2 Bézier Curves computer-aided design and manufacturing MCS 471
Neville s Method. MATH 375 Numerical Analysis. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan Neville s Method
 Neville s Method MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation We have learned how to approximate a function using Lagrange polynomials and how to estimate
Neville s Method MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation We have learned how to approximate a function using Lagrange polynomials and how to estimate
Calculus. Central role in much of modern science Physics, especially kinematics and electrodynamics Economics, engineering, medicine, chemistry, etc.
 Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
Calculus Calculus - the study of change, as related to functions Formally co-developed around the 1660 s by Newton and Leibniz Two main branches - differential and integral Central role in much of modern
November 20, Interpolation, Extrapolation & Polynomial Approximation
 Interpolation, Extrapolation & Polynomial Approximation November 20, 2016 Introduction In many cases we know the values of a function f (x) at a set of points x 1, x 2,..., x N, but we don t have the analytic
Interpolation, Extrapolation & Polynomial Approximation November 20, 2016 Introduction In many cases we know the values of a function f (x) at a set of points x 1, x 2,..., x N, but we don t have the analytic
BEKG 2452 NUMERICAL METHODS Solution of Nonlinear Equations
 BEKG 2452 NUMERICAL METHODS Solution of Nonlinear Equations Ser Lee Loh a, Wei Sen Loi a a Fakulti Kejuruteraan Elektrik Universiti Teknikal Malaysia Melaka Lesson Outcome Upon completion of this lesson,
BEKG 2452 NUMERICAL METHODS Solution of Nonlinear Equations Ser Lee Loh a, Wei Sen Loi a a Fakulti Kejuruteraan Elektrik Universiti Teknikal Malaysia Melaka Lesson Outcome Upon completion of this lesson,
ROOT FINDING REVIEW MICHELLE FENG
 ROOT FINDING REVIEW MICHELLE FENG 1.1. Bisection Method. 1. Root Finding Methods (1) Very naive approach based on the Intermediate Value Theorem (2) You need to be looking in an interval with only one
ROOT FINDING REVIEW MICHELLE FENG 1.1. Bisection Method. 1. Root Finding Methods (1) Very naive approach based on the Intermediate Value Theorem (2) You need to be looking in an interval with only one
Order of convergence
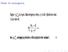 Order of convergence Linear and Quadratic Order of convergence Computing square root with Newton s Method Given a > 0, p def = a is positive root of equation Newton s Method p k+1 = p k p2 k a 2p k = 1
Order of convergence Linear and Quadratic Order of convergence Computing square root with Newton s Method Given a > 0, p def = a is positive root of equation Newton s Method p k+1 = p k p2 k a 2p k = 1
Preliminary Examination in Numerical Analysis
 Department of Applied Mathematics Preliminary Examination in Numerical Analysis August 7, 06, 0 am pm. Submit solutions to four (and no more) of the following six problems. Show all your work, and justify
Department of Applied Mathematics Preliminary Examination in Numerical Analysis August 7, 06, 0 am pm. Submit solutions to four (and no more) of the following six problems. Show all your work, and justify
Section 3.1: Derivatives of Polynomials and Exponential Functions
 Section 3.1: Derivatives of Polynomials and Exponential Functions In previous sections we developed te concept of te derivative and derivative function. Te only issue wit our definition owever is tat it
Section 3.1: Derivatives of Polynomials and Exponential Functions In previous sections we developed te concept of te derivative and derivative function. Te only issue wit our definition owever is tat it
Hermite Interpolation
 Jim Lambers MAT 77 Fall Semester 010-11 Lecture Notes These notes correspond to Sections 4 and 5 in the text Hermite Interpolation Suppose that the interpolation points are perturbed so that two neighboring
Jim Lambers MAT 77 Fall Semester 010-11 Lecture Notes These notes correspond to Sections 4 and 5 in the text Hermite Interpolation Suppose that the interpolation points are perturbed so that two neighboring
Lagrange Interpolation and Neville s Algorithm. Ron Goldman Department of Computer Science Rice University
 Lagrange Interpolation and Neville s Algorithm Ron Goldman Department of Computer Science Rice University Tension between Mathematics and Engineering 1. How do Mathematicians actually represent curves
Lagrange Interpolation and Neville s Algorithm Ron Goldman Department of Computer Science Rice University Tension between Mathematics and Engineering 1. How do Mathematicians actually represent curves
EVALUATING A POLYNOMIAL
 EVALUATING A POLYNOMIAL Consider having a polynomial p(x) = a + a 1 x + a 2 x 2 + + a n x n which you need to evaluate for many values of x. How do you evaluate it? This may seem a strange question, but
EVALUATING A POLYNOMIAL Consider having a polynomial p(x) = a + a 1 x + a 2 x 2 + + a n x n which you need to evaluate for many values of x. How do you evaluate it? This may seem a strange question, but
Then, Lagrange s interpolation formula is. 2. What is the Lagrange s interpolation formula to find, if three sets of values. are given.
 SRI RAMAKRISHNA INSTITUTE OF TECHNOLOGY, COIMBATORE- 10 DEPARTMENT OF SCIENCE AND HUMANITIES SUBJECT NUMERICAL METHODS & LINEAR PROGRAMMING ( SEMESTER IV ) IV- INTERPOLATION, NUMERICAL DIFFERENTIATION
SRI RAMAKRISHNA INSTITUTE OF TECHNOLOGY, COIMBATORE- 10 DEPARTMENT OF SCIENCE AND HUMANITIES SUBJECT NUMERICAL METHODS & LINEAR PROGRAMMING ( SEMESTER IV ) IV- INTERPOLATION, NUMERICAL DIFFERENTIATION
( ) y 2! 4. ( )( y! 2)
 1. Dividing: 4x3! 8x 2 + 6x 2x 5.7 Division of Polynomials = 4x3 2x! 8x2 2x + 6x 2x = 2x2! 4 3. Dividing: 1x4 + 15x 3! 2x 2!5x 2 = 1x4!5x 2 + 15x3!5x 2! 2x2!5x 2 =!2x2! 3x + 4 5. Dividing: 8y5 + 1y 3!
1. Dividing: 4x3! 8x 2 + 6x 2x 5.7 Division of Polynomials = 4x3 2x! 8x2 2x + 6x 2x = 2x2! 4 3. Dividing: 1x4 + 15x 3! 2x 2!5x 2 = 1x4!5x 2 + 15x3!5x 2! 2x2!5x 2 =!2x2! 3x + 4 5. Dividing: 8y5 + 1y 3!
CS 323: Numerical Analysis and Computing
 CS 323: Numerical Analysis and Computing MIDTERM #2 Instructions: This is an open notes exam, i.e., you are allowed to consult any textbook, your class notes, homeworks, or any of the handouts from us.
CS 323: Numerical Analysis and Computing MIDTERM #2 Instructions: This is an open notes exam, i.e., you are allowed to consult any textbook, your class notes, homeworks, or any of the handouts from us.
LECTURE 14 NUMERICAL INTEGRATION. Find
 LECTURE 14 NUMERCAL NTEGRATON Find b a fxdx or b a vx ux fx ydy dx Often integration is required. However te form of fx may be suc tat analytical integration would be very difficult or impossible. Use
LECTURE 14 NUMERCAL NTEGRATON Find b a fxdx or b a vx ux fx ydy dx Often integration is required. However te form of fx may be suc tat analytical integration would be very difficult or impossible. Use
Lecture 1: Interpolation and approximation
 ecture notes on Variational and Approximate Methods in Applied Mathematics - A Peirce UBC ecture : Interpolation and approximation (Compiled 6 August 207 In this lecture we introduce the concept of approximation
ecture notes on Variational and Approximate Methods in Applied Mathematics - A Peirce UBC ecture : Interpolation and approximation (Compiled 6 August 207 In this lecture we introduce the concept of approximation
Department of Applied Mathematics and Theoretical Physics. AMA 204 Numerical analysis. Exam Winter 2004
 Department of Applied Mathematics and Theoretical Physics AMA 204 Numerical analysis Exam Winter 2004 The best six answers will be credited All questions carry equal marks Answer all parts of each question
Department of Applied Mathematics and Theoretical Physics AMA 204 Numerical analysis Exam Winter 2004 The best six answers will be credited All questions carry equal marks Answer all parts of each question
Polynomial Interpolation Part II
 Polynomial Interpolation Part II Prof. Dr. Florian Rupp German University of Technology in Oman (GUtech) Introduction to Numerical Methods for ENG & CS (Mathematics IV) Spring Term 2016 Exercise Session
Polynomial Interpolation Part II Prof. Dr. Florian Rupp German University of Technology in Oman (GUtech) Introduction to Numerical Methods for ENG & CS (Mathematics IV) Spring Term 2016 Exercise Session
Interpolation APPLIED PROBLEMS. Reading Between the Lines FLY ROCKET FLY, FLY ROCKET FLY WHAT IS INTERPOLATION? Figure Interpolation of discrete data.
 WHAT IS INTERPOLATION? Given (x 0,y 0 ), (x,y ), (x n,y n ), find the value of y at a value of x that is not given. Interpolation Reading Between the Lines Figure Interpolation of discrete data. FLY ROCKET
WHAT IS INTERPOLATION? Given (x 0,y 0 ), (x,y ), (x n,y n ), find the value of y at a value of x that is not given. Interpolation Reading Between the Lines Figure Interpolation of discrete data. FLY ROCKET
Functions. Chapter Continuous Functions
 Chapter 3 Functions 3.1 Continuous Functions A function f is determined by the domain of f: dom(f) R, the set on which f is defined, and the rule specifying the value f(x) of f at each x dom(f). If f is
Chapter 3 Functions 3.1 Continuous Functions A function f is determined by the domain of f: dom(f) R, the set on which f is defined, and the rule specifying the value f(x) of f at each x dom(f). If f is
COURSE Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method
 COURSE 7 3. Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method The presence of derivatives in the remainder difficulties in applicability to practical problems
COURSE 7 3. Numerical integration of functions (continuation) 3.3. The Romberg s iterative generation method The presence of derivatives in the remainder difficulties in applicability to practical problems
Numerical Methods. Lecture Notes #08 Discrete Least Square Approximation
 Numerical Methods Discrete Least Square Approximation Pavel Ludvík, March 30, 2016 Department of Mathematics and Descriptive Geometry VŠB-TUO http://homen.vsb.cz/ lud0016/ 1 / 23
Numerical Methods Discrete Least Square Approximation Pavel Ludvík, March 30, 2016 Department of Mathematics and Descriptive Geometry VŠB-TUO http://homen.vsb.cz/ lud0016/ 1 / 23
and lim lim 6. The Squeeze Theorem
 Limits (day 3) Things we ll go over today 1. Limits of the form 0 0 (continued) 2. Limits of piecewise functions 3. Limits involving absolute values 4. Limits of compositions of functions 5. Limits similar
Limits (day 3) Things we ll go over today 1. Limits of the form 0 0 (continued) 2. Limits of piecewise functions 3. Limits involving absolute values 4. Limits of compositions of functions 5. Limits similar
Romberg Integration and Gaussian Quadrature
 Romberg Integration and Gaussian Quadrature P. Sam Johnson October 17, 014 P. Sam Johnson (NITK) Romberg Integration and Gaussian Quadrature October 17, 014 1 / 19 Overview We discuss two methods for integration.
Romberg Integration and Gaussian Quadrature P. Sam Johnson October 17, 014 P. Sam Johnson (NITK) Romberg Integration and Gaussian Quadrature October 17, 014 1 / 19 Overview We discuss two methods for integration.
Fixed point iteration and root finding
 Fixed point iteration and root finding The sign function is defined as x > 0 sign(x) = 0 x = 0 x < 0. It can be evaluated via an iteration which is useful for some problems. One such iteration is given
Fixed point iteration and root finding The sign function is defined as x > 0 sign(x) = 0 x = 0 x < 0. It can be evaluated via an iteration which is useful for some problems. One such iteration is given
Problems in Algebra. 2 4ac. 2a
 Problems in Algebra Section Polynomial Equations For a polynomial equation P (x) = c 0 x n + c 1 x n 1 + + c n = 0, where c 0, c 1,, c n are complex numbers, we know from the Fundamental Theorem of Algebra
Problems in Algebra Section Polynomial Equations For a polynomial equation P (x) = c 0 x n + c 1 x n 1 + + c n = 0, where c 0, c 1,, c n are complex numbers, we know from the Fundamental Theorem of Algebra
Calculus I Exam 1 Review Fall 2016
 Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Problem 1: Decide whether the following statements are true or false: (a) If f, g are differentiable, then d d x (f g) = f g. (b) If a function is continuous, then it is differentiable. (c) If a function
Taylor and Maclaurin Series
 Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Differential Equations DIRECT INTEGRATION. Graham S McDonald
 Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
Midterm for Introduction to Numerical Analysis I, AMSC/CMSC 466, on 10/29/2015
 Midterm for Introduction to Numerical Analysis I, AMSC/CMSC 466, on 10/29/2015 The test lasts 1 hour and 15 minutes. No documents are allowed. The use of a calculator, cell phone or other equivalent electronic
Midterm for Introduction to Numerical Analysis I, AMSC/CMSC 466, on 10/29/2015 The test lasts 1 hour and 15 minutes. No documents are allowed. The use of a calculator, cell phone or other equivalent electronic
Math 141: Lecture 11
 Math 141: Lecture 11 The Fundamental Theorem of Calculus and integration methods Bob Hough October 12, 2016 Bob Hough Math 141: Lecture 11 October 12, 2016 1 / 36 First Fundamental Theorem of Calculus
Math 141: Lecture 11 The Fundamental Theorem of Calculus and integration methods Bob Hough October 12, 2016 Bob Hough Math 141: Lecture 11 October 12, 2016 1 / 36 First Fundamental Theorem of Calculus
Some notes on Chapter 8: Polynomial and Piecewise-polynomial Interpolation
 Some notes on Chapter 8: Polynomial and Piecewise-polynomial Interpolation See your notes. 1. Lagrange Interpolation (8.2) 1 2. Newton Interpolation (8.3) different form of the same polynomial as Lagrange
Some notes on Chapter 8: Polynomial and Piecewise-polynomial Interpolation See your notes. 1. Lagrange Interpolation (8.2) 1 2. Newton Interpolation (8.3) different form of the same polynomial as Lagrange
Interpolation Theory
 Numerical Analysis Massoud Malek Interpolation Theory The concept of interpolation is to select a function P (x) from a given class of functions in such a way that the graph of y P (x) passes through the
Numerical Analysis Massoud Malek Interpolation Theory The concept of interpolation is to select a function P (x) from a given class of functions in such a way that the graph of y P (x) passes through the
1.4 CONTINUITY AND ITS CONSEQUENCES
 Continuity: Informal Idea We say that a function is continuous on an interval if its graph on that t interval can be drawn without t interruption, ti that is, without lifting the pencil from the paper.
Continuity: Informal Idea We say that a function is continuous on an interval if its graph on that t interval can be drawn without t interruption, ti that is, without lifting the pencil from the paper.
Math 106 Calculus 1 Topics for first exam
 Chapter 2: Limits and Continuity Rates of change and its: Math 06 Calculus Topics for first exam Limit of a function f at a point a = the value the function should take at the point = the value that the
Chapter 2: Limits and Continuity Rates of change and its: Math 06 Calculus Topics for first exam Limit of a function f at a point a = the value the function should take at the point = the value that the
Series Solutions of Differential Equations
 Chapter 6 Series Solutions of Differential Equations In this chapter we consider methods for solving differential equations using power series. Sequences and infinite series are also involved in this treatment.
Chapter 6 Series Solutions of Differential Equations In this chapter we consider methods for solving differential equations using power series. Sequences and infinite series are also involved in this treatment.
k-protected VERTICES IN BINARY SEARCH TREES
 k-protected VERTICES IN BINARY SEARCH TREES MIKLÓS BÓNA Abstract. We show that for every k, the probability that a randomly selected vertex of a random binary search tree on n nodes is at distance k from
k-protected VERTICES IN BINARY SEARCH TREES MIKLÓS BÓNA Abstract. We show that for every k, the probability that a randomly selected vertex of a random binary search tree on n nodes is at distance k from
X. Numerical Methods
 X. Numerical Methods. Taylor Approximation Suppose that f is a function defined in a neighborhood of a point c, and suppose that f has derivatives of all orders near c. In section 5 of chapter 9 we introduced
X. Numerical Methods. Taylor Approximation Suppose that f is a function defined in a neighborhood of a point c, and suppose that f has derivatives of all orders near c. In section 5 of chapter 9 we introduced
Lecture 12: November 6, 2017
 Information and Coding Theory Autumn 017 Lecturer: Madhur Tulsiani Lecture 1: November 6, 017 Recall: We were looking at codes of the form C : F k p F n p, where p is prime, k is the message length, and
Information and Coding Theory Autumn 017 Lecturer: Madhur Tulsiani Lecture 1: November 6, 017 Recall: We were looking at codes of the form C : F k p F n p, where p is prime, k is the message length, and
3 Interpolation and Polynomial Approximation
 CHAPTER 3 Interpolation and Polynomial Approximation Introduction A census of the population of the United States is taken every 10 years. The following table lists the population, in thousands of people,
CHAPTER 3 Interpolation and Polynomial Approximation Introduction A census of the population of the United States is taken every 10 years. The following table lists the population, in thousands of people,
