Interpolation and the Lagrange Polynomial
|
|
|
- Diana Nelson
- 6 years ago
- Views:
Transcription
1 Interpolation and the Lagrange Polynomial MATH 375 J. Robert Buchanan Department of Mathematics Fall 2013
2 Introduction We often choose polynomials to approximate other classes of functions. Theorem (Weierstrass Approximation Theorem) If f C[a, b] and ɛ > 0 then there exists a polynomial P such that f (x) P(x) < ɛ, for all x [a, b].
3 Introduction We often choose polynomials to approximate other classes of functions. Theorem (Weierstrass Approximation Theorem) If f C[a, b] and ɛ > 0 then there exists a polynomial P such that f (x) P(x) < ɛ, for all x [a, b]. We have used Taylor polynomials to approximate functions. n f (k) (x 0 ) P(x) = (x x 0 ) k k! k=0 Away from x 0 the approximation may be very poor.
4 Linear Approximation (1 of 2) y 1 f x 1 y 0 f x 0 x 1 x Using the two-point formula for a line we determine the equation of the line to be ( ) f (x1 ) f (x 0 ) y = f (x 0 ) + (x x 0 ). x 1 x 0
5 Linear Approximation (2 of 2) We can take another approach to finding the linear approximation. Define L 0 (x) = x x 1 x 0 x 1, L 1 (x) = x x 0 x 1 x 0,
6 Linear Approximation (2 of 2) We can take another approach to finding the linear approximation. Define L 0 (x) = x x 1 x 0 x 1, then L 0 (x 0 ) = 1 and L 0 (x 1 ) = 0. L 1 (x) = x x 0 x 1 x 0,
7 Linear Approximation (2 of 2) We can take another approach to finding the linear approximation. Define L 0 (x) = x x 1 x 0 x 1, then L 0 (x 0 ) = 1 and L 0 (x 1 ) = 0. L 1 (x) = x x 0 x 1 x 0, then L 1 (x 0 ) = 0 and L 1 (x 1 ) = 1.
8 Linear Approximation (2 of 2) We can take another approach to finding the linear approximation. Define L 0 (x) = x x 1 x 0 x 1, then L 0 (x 0 ) = 1 and L 0 (x 1 ) = 0. L 1 (x) = x x 0 x 1 x 0, then L 1 (x 0 ) = 0 and L 1 (x 1 ) = 1. If f (x) is any function then P(x) = f (x 0 ) L 0 (x) + f (x 1 ) L 1 (x) is a linear function which matches f (x) at x = x 0 and x = x 1.
9 Linear Approximation (2 of 2) We can take another approach to finding the linear approximation. Define L 0 (x) = x x 1 x 0 x 1, then L 0 (x 0 ) = 1 and L 0 (x 1 ) = 0. L 1 (x) = x x 0 x 1 x 0, then L 1 (x 0 ) = 0 and L 1 (x 1 ) = 1. If f (x) is any function then P(x) = f (x 0 ) L 0 (x) + f (x 1 ) L 1 (x) is a linear function which matches f (x) at x = x 0 and x = x 1. We want to extend this idea to higher order polynomials.
10 Construction of Polynomials Challenge: given a function f (x), construct a polynomial P(x) of degree at most n which matches f (x) at n + 1 distinct points. {(x 0, f (x 0 )), (x 1, f (x 1 )),..., (x n, f (x n ))}
11 Construction of Polynomials Challenge: given a function f (x), construct a polynomial P(x) of degree at most n which matches f (x) at n + 1 distinct points. {(x 0, f (x 0 )), (x 1, f (x 1 )),..., (x n, f (x n ))} Strategy: construct n + 1 polynomials L n,k (x) of degree n with the property that { 0 if k i, L n,k (x i ) = 1 if k = i for k = 0, 1, 2,..., n.
12 Lagrange Basis Polynomials Definition Suppose {x 0, x 1,..., x n } is a set of n + 1 distinct points. A Lagrange Basis Polynomial is a polynomial of degree n having the form L n,k (x) = n i=0, i k x x i x k x i.
13 Lagrange Basis Polynomials Definition Suppose {x 0, x 1,..., x n } is a set of n + 1 distinct points. A Lagrange Basis Polynomial is a polynomial of degree n having the form Remarks: L n,k (x) = We will let k = 0, 1, 2,..., n. L n,k (x i ) = 1 for i = k. L n,k (x i ) = 0 for i k. n i=0, i k x x i x k x i.
14 Example If x i = i for i = 0, 1, 2 then we can create three different Lagrange Basis Polynomials. L 2,0 (x) = L 2,1 (x) = L 2,2 (x) =
15 Example If x i = i for i = 0, 1, 2 then we can create three different Lagrange Basis Polynomials. L 2,0 (x) = x x = 1 (x 1)(x 2) 2 L 2,1 (x) = L 2,2 (x) =
16 Example If x i = i for i = 0, 1, 2 then we can create three different Lagrange Basis Polynomials. L 2,0 (x) = x x = 1 (x 1)(x 2) 2 L 2,1 (x) = x x 2 = x(2 x) 1 2 L 2,2 (x) =
17 Example If x i = i for i = 0, 1, 2 then we can create three different Lagrange Basis Polynomials. L 2,0 (x) = x x = 1 (x 1)(x 2) 2 L 2,1 (x) = x x 2 = x(2 x) 1 2 L 2,2 (x) = x x = 1 x(x 1) 2
18 Graph L 2,0 (x) = 1 (x 1)(x 2) 2 L 2,1 (x) = x(2 x) L 2,2 (x) = 1 2 x(x 1) x 1
19 Lagrange Interpolating Polynomials Definition Let {x 0, x 1,..., x n } be a set of n + 1 distinct points at which the function f (x) is defined. The (unique) Lagrange Interpolating Polynomial of f (x) of degree n is the polynomial having the form n P(x) = f (x k )L n,k (x). Properties: L n,k (x i ) = 0 for all i k. L n,k (x k ) = 1. k=0 P(x k ) = f (x k ) for k = 0, 1,..., n.
20 Example If n = 9 and the nodes are {0, 1,..., 9} then L 9,4 (x) has a graph resembling the following x 2 4
21 Example (1 of 3) Let f (x) = sin x, n = 3, and x k = kπ/3 for k = 0, 1, 2, 3. The four Lagrange Basis Polynomials are listed below. L 3,0 (x) = x π 3 0 π 3 x 2π 3 0 2π 3 x π 0 π = 1 (π 3x)(2π 3x)(π x) 2π3 L 3,1 (x) = 9 x(2π 3x)(π x) 2π3 L 3,2 (x) = 9 x(π 3x)(π x) 2π3 L 3,3 (x) = 1 x(π 3x)(2π 3x) 2π3
22 Example (2 of 3) The Lagrange Interpolating Polynomial of degree 3 for f (x) = sin x and x k = kπ/3 for k = 0, 1, 2, 3 is ( P(x) = (sin 0) L 3,0 (x) + sin π ) ( L 3,1 (x) + sin 2π ) L 3,2 (x) 3 3 = + (sin π) L 3,3 (x) 3 2 = 9 3 x(π x) 4π2 9 x(2π 3x)(π x) 2π x(π 3x)(π x) 2π3
23 Example (3 of 3) The graphs of P(x), f (x), and the absolute error are shown below. 1.0 Abs. Err Π x x
24 Lagrange Polynomial with Error Term Theorem Suppose x 0, x 1,..., x n are distinct numbers in the interval [a, b] and suppose f C n+1 [a, b]. Then for each x [a, b] there exists a number z(x) (a, b) for which f (x) = P(x) + f (n+1) (z(x)) (x x 0 )(x x 1 ) (x x n ), (n + 1)! where P(x) is the Lagrange Interpolating Polynomial.
25 Comments Compare the error terms of the Lagrange polynomial and the Taylor polynomial. Taylor: f (n+1) (z(x)) (x x 0 ) n+1 (n + 1)! f (n+1) (z(x)) Lagrange: (x x 0 )(x x 1 ) (x x n ) (n + 1)! Lagrange polynomials form the basis of many numerical approximations to derivatives and integrals, and thus the error term is important to understanding the errors present in those approximations.
26 Application Example Suppose we are preparing a table of values for cos x on [0, π]. The entries in the table will have eight accurate decimal places and we will linearly interpolate between adjacent entries to determine intermediate values. What should the spacing between adjacent x-values be to preserve the eight-decimal-place accuracy in the interpolation?
27 Solution cos x P(x) = cos z 2 x x j x x j+1 for some 0 z π 1 2 max 0 z π cos z max x x j x x j+1 x j x x j+1 = 1 2 = h2 8 max (x jh)(x (j + 1)h jh x (j+1)h Thus if h 2 /8 < 10 8 then h <
28 Error in sin x Earlier we found the Lagrange interpolating polynomial of degree 3 for f (x) = sin x using nodes x k = kπ/3 for k = 0, 1, 2, 3 was P(x) = 9 3 x(π x). 4π2 What is an error bound for this approximation?
29 Error in sin x Earlier we found the Lagrange interpolating polynomial of degree 3 for f (x) = sin x using nodes x k = kπ/3 for k = 0, 1, 2, 3 was P(x) = 9 3 x(π x). 4π2 What is an error bound for this approximation? R(x) = sin z ( (x 0) x π ) ( x 2π 4! 3 3 ) (x π)
30 Error Bound vs. Actual Error Π x
31 Homework Read Section 3.1 Exercises: 1, 3, 5a, 7a, 13, 17
Computer Arithmetic. MATH 375 Numerical Analysis. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan Computer Arithmetic
 Computer Arithmetic MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Machine Numbers When performing arithmetic on a computer (laptop, desktop, mainframe, cell phone,
Computer Arithmetic MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Machine Numbers When performing arithmetic on a computer (laptop, desktop, mainframe, cell phone,
Romberg Integration. MATH 375 Numerical Analysis. J. Robert Buchanan. Spring Department of Mathematics
 Romberg Integration MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Spring 019 Objectives and Background In this lesson we will learn to obtain high accuracy approximations to
Romberg Integration MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Spring 019 Objectives and Background In this lesson we will learn to obtain high accuracy approximations to
3.1 Interpolation and the Lagrange Polynomial
 MATH 4073 Chapter 3 Interpolation and Polynomial Approximation Fall 2003 1 Consider a sample x x 0 x 1 x n y y 0 y 1 y n. Can we get a function out of discrete data above that gives a reasonable estimate
MATH 4073 Chapter 3 Interpolation and Polynomial Approximation Fall 2003 1 Consider a sample x x 0 x 1 x n y y 0 y 1 y n. Can we get a function out of discrete data above that gives a reasonable estimate
Cubic Splines MATH 375. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan Cubic Splines
 Cubic Splines MATH 375 J. Robert Buchanan Department of Mathematics Fall 2006 Introduction Given data {(x 0, f(x 0 )), (x 1, f(x 1 )),...,(x n, f(x n ))} which we wish to interpolate using a polynomial...
Cubic Splines MATH 375 J. Robert Buchanan Department of Mathematics Fall 2006 Introduction Given data {(x 0, f(x 0 )), (x 1, f(x 1 )),...,(x n, f(x n ))} which we wish to interpolate using a polynomial...
Review of Power Series
 Review of Power Series MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Introduction In addition to the techniques we have studied so far, we may use power
Review of Power Series MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Introduction In addition to the techniques we have studied so far, we may use power
INTERPOLATION. and y i = cos x i, i = 0, 1, 2 This gives us the three points. Now find a quadratic polynomial. p(x) = a 0 + a 1 x + a 2 x 2.
 INTERPOLATION Interpolation is a process of finding a formula (often a polynomial) whose graph will pass through a given set of points (x, y). As an example, consider defining and x 0 = 0, x 1 = π/4, x
INTERPOLATION Interpolation is a process of finding a formula (often a polynomial) whose graph will pass through a given set of points (x, y). As an example, consider defining and x 0 = 0, x 1 = π/4, x
Neville s Method. MATH 375 Numerical Analysis. J. Robert Buchanan. Fall Department of Mathematics. J. Robert Buchanan Neville s Method
 Neville s Method MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation We have learned how to approximate a function using Lagrange polynomials and how to estimate
Neville s Method MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation We have learned how to approximate a function using Lagrange polynomials and how to estimate
Linear Independence. MATH 322, Linear Algebra I. J. Robert Buchanan. Spring Department of Mathematics
 Linear Independence MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Given a set of vectors {v 1, v 2,..., v r } and another vector v span{v 1, v 2,...,
Linear Independence MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Given a set of vectors {v 1, v 2,..., v r } and another vector v span{v 1, v 2,...,
Series Solutions Near a Regular Singular Point
 Series Solutions Near a Regular Singular Point MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Background We will find a power series solution to the equation:
Series Solutions Near a Regular Singular Point MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Background We will find a power series solution to the equation:
Exponential Functions
 Exponential Functions MATH 160, Precalculus J. Robert Buchanan Department of Mathematics Fall 2011 Objectives In this lesson we will learn to: recognize and evaluate exponential functions with base a,
Exponential Functions MATH 160, Precalculus J. Robert Buchanan Department of Mathematics Fall 2011 Objectives In this lesson we will learn to: recognize and evaluate exponential functions with base a,
Accelerating Convergence
 Accelerating Convergence MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation We have seen that most fixed-point methods for root finding converge only linearly
Accelerating Convergence MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation We have seen that most fixed-point methods for root finding converge only linearly
Mean Value Theorem. MATH 161 Calculus I. J. Robert Buchanan. Summer Department of Mathematics
 Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem. MATH 161 Calculus I. J. Robert Buchanan. Summer Department of Mathematics
 Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Mean Value Theorem MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Background: Corollary to the Intermediate Value Theorem Corollary Suppose f is continuous on the closed interval
Continuity. MATH 161 Calculus I. J. Robert Buchanan. Fall Department of Mathematics
 Continuity MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Fall 2017 Intuitive Idea A process or an item can be described as continuous if it exists without interruption. The mathematical
Continuity MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Fall 2017 Intuitive Idea A process or an item can be described as continuous if it exists without interruption. The mathematical
Jim Lambers MAT 460/560 Fall Semester Practice Final Exam
 Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
Jim Lambers MAT 460/560 Fall Semester 2009-10 Practice Final Exam 1. Let f(x) = sin 2x + cos 2x. (a) Write down the 2nd Taylor polynomial P 2 (x) of f(x) centered around x 0 = 0. (b) Write down the corresponding
NUMERICAL METHODS. x n+1 = 2x n x 2 n. In particular: which of them gives faster convergence, and why? [Work to four decimal places.
 NUMERICAL METHODS 1. Rearranging the equation x 3 =.5 gives the iterative formula x n+1 = g(x n ), where g(x) = (2x 2 ) 1. (a) Starting with x = 1, compute the x n up to n = 6, and describe what is happening.
NUMERICAL METHODS 1. Rearranging the equation x 3 =.5 gives the iterative formula x n+1 = g(x n ), where g(x) = (2x 2 ) 1. (a) Starting with x = 1, compute the x n up to n = 6, and describe what is happening.
Advanced Math Quiz Review Name: Dec Use Synthetic Division to divide the first polynomial by the second polynomial.
 Advanced Math Quiz 3.1-3.2 Review Name: Dec. 2014 Use Synthetic Division to divide the first polynomial by the second polynomial. 1. 5x 3 + 6x 2 8 x + 1, x 5 1. Quotient: 2. x 5 10x 3 + 5 x 1, x + 4 2.
Advanced Math Quiz 3.1-3.2 Review Name: Dec. 2014 Use Synthetic Division to divide the first polynomial by the second polynomial. 1. 5x 3 + 6x 2 8 x + 1, x 5 1. Quotient: 2. x 5 10x 3 + 5 x 1, x + 4 2.
Section 8.7. Taylor and MacLaurin Series. (1) Definitions, (2) Common Maclaurin Series, (3) Taylor Polynomials, (4) Applications.
 Section 8.7 Taylor and MacLaurin Series (1) Definitions, (2) Common Maclaurin Series, (3) Taylor Polynomials, (4) Applications. MATH 126 (Section 8.7) Taylor and MacLaurin Series The University of Kansas
Section 8.7 Taylor and MacLaurin Series (1) Definitions, (2) Common Maclaurin Series, (3) Taylor Polynomials, (4) Applications. MATH 126 (Section 8.7) Taylor and MacLaurin Series The University of Kansas
Diagonalization. MATH 322, Linear Algebra I. J. Robert Buchanan. Spring Department of Mathematics
 Diagonalization MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Motivation Today we consider two fundamental questions: Given an n n matrix A, does there exist a basis
Diagonalization MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Motivation Today we consider two fundamental questions: Given an n n matrix A, does there exist a basis
Midterm Review. Igor Yanovsky (Math 151A TA)
 Midterm Review Igor Yanovsky (Math 5A TA) Root-Finding Methods Rootfinding methods are designed to find a zero of a function f, that is, to find a value of x such that f(x) =0 Bisection Method To apply
Midterm Review Igor Yanovsky (Math 5A TA) Root-Finding Methods Rootfinding methods are designed to find a zero of a function f, that is, to find a value of x such that f(x) =0 Bisection Method To apply
Approximation theory
 Approximation theory Xiaojing Ye, Math & Stat, Georgia State University Spring 2019 Numerical Analysis II Xiaojing Ye, Math & Stat, Georgia State University 1 1 1.3 6 8.8 2 3.5 7 10.1 Least 3squares 4.2
Approximation theory Xiaojing Ye, Math & Stat, Georgia State University Spring 2019 Numerical Analysis II Xiaojing Ye, Math & Stat, Georgia State University 1 1 1.3 6 8.8 2 3.5 7 10.1 Least 3squares 4.2
INTERPOLATION Background Polynomial Approximation Problem:
 INTERPOLATION Background Polynomial Approximation Problem: given f(x) C[a, b], find P n (x) = a 0 + a 1 x + a 2 x 2 + + a n x n with P n (x) close to f(x) for x [a, b]. Motivations: f(x) might be difficult
INTERPOLATION Background Polynomial Approximation Problem: given f(x) C[a, b], find P n (x) = a 0 + a 1 x + a 2 x 2 + + a n x n with P n (x) close to f(x) for x [a, b]. Motivations: f(x) might be difficult
Limit Theorems. MATH 464/506, Real Analysis. J. Robert Buchanan. Summer Department of Mathematics. J. Robert Buchanan Limit Theorems
 Limit s MATH 464/506, Real Analysis J. Robert Buchanan Department of Mathematics Summer 2007 Bounded Functions Definition Let A R, let f : A R, and let c R be a cluster point of A. We say that f is bounded
Limit s MATH 464/506, Real Analysis J. Robert Buchanan Department of Mathematics Summer 2007 Bounded Functions Definition Let A R, let f : A R, and let c R be a cluster point of A. We say that f is bounded
Extrema and the First-Derivative Test
 Extrema and the First-Derivative Test MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2018 Why Maximize or Minimize? In almost all quantitative fields there are objective
Extrema and the First-Derivative Test MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics 2018 Why Maximize or Minimize? In almost all quantitative fields there are objective
A first order divided difference
 A first order divided difference For a given function f (x) and two distinct points x 0 and x 1, define f [x 0, x 1 ] = f (x 1) f (x 0 ) x 1 x 0 This is called the first order divided difference of f (x).
A first order divided difference For a given function f (x) and two distinct points x 0 and x 1, define f [x 0, x 1 ] = f (x 1) f (x 0 ) x 1 x 0 This is called the first order divided difference of f (x).
Interpolation Theory
 Numerical Analysis Massoud Malek Interpolation Theory The concept of interpolation is to select a function P (x) from a given class of functions in such a way that the graph of y P (x) passes through the
Numerical Analysis Massoud Malek Interpolation Theory The concept of interpolation is to select a function P (x) from a given class of functions in such a way that the graph of y P (x) passes through the
Taylor and Maclaurin Series. Approximating functions using Polynomials.
 Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Row Space, Column Space, and Nullspace
 Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
Row Space, Column Space, and Nullspace MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Introduction Every matrix has associated with it three vector spaces: row space
MAT137 Calculus! Lecture 45
 official website http://uoft.me/mat137 MAT137 Calculus! Lecture 45 Today: Taylor Polynomials Taylor Series Next: Taylor Series Power Series Definition (Power Series) A power series is a series of the form
official website http://uoft.me/mat137 MAT137 Calculus! Lecture 45 Today: Taylor Polynomials Taylor Series Next: Taylor Series Power Series Definition (Power Series) A power series is a series of the form
Chapter 3 Interpolation and Polynomial Approximation
 Chapter 3 Interpolation and Polynomial Approximation Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 128A Numerical Analysis Polynomial Interpolation
Chapter 3 Interpolation and Polynomial Approximation Per-Olof Persson persson@berkeley.edu Department of Mathematics University of California, Berkeley Math 128A Numerical Analysis Polynomial Interpolation
Infinite Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Infinite Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background Consider the repeating decimal form of 2/3. 2 3 = 0.666666 = 0.6 + 0.06 + 0.006 + 0.0006 + = 6(0.1)
Infinite Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background Consider the repeating decimal form of 2/3. 2 3 = 0.666666 = 0.6 + 0.06 + 0.006 + 0.0006 + = 6(0.1)
3 Interpolation and Polynomial Approximation
 CHAPTER 3 Interpolation and Polynomial Approximation Introduction A census of the population of the United States is taken every 10 years. The following table lists the population, in thousands of people,
CHAPTER 3 Interpolation and Polynomial Approximation Introduction A census of the population of the United States is taken every 10 years. The following table lists the population, in thousands of people,
Taylor and Maclaurin Series. Approximating functions using Polynomials.
 Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Taylor and Maclaurin Series Approximating functions using Polynomials. Approximating f x = e x near x = 0 In order to approximate the function f x = e x near x = 0, we can use the tangent line (The Linear
Lecture Note 3: Interpolation and Polynomial Approximation. Xiaoqun Zhang Shanghai Jiao Tong University
 Lecture Note 3: Interpolation and Polynomial Approximation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 10, 2015 2 Contents 1.1 Introduction................................ 3 1.1.1
Lecture Note 3: Interpolation and Polynomial Approximation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 10, 2015 2 Contents 1.1 Introduction................................ 3 1.1.1
1 Solutions to selected problems
 Solutions to selected problems Section., #a,c,d. a. p x = n for i = n : 0 p x = xp x + i end b. z = x, y = x for i = : n y = y + x i z = zy end c. y = (t x ), p t = a for i = : n y = y(t x i ) p t = p
Solutions to selected problems Section., #a,c,d. a. p x = n for i = n : 0 p x = xp x + i end b. z = x, y = x for i = : n y = y + x i z = zy end c. y = (t x ), p t = a for i = : n y = y(t x i ) p t = p
1) The line has a slope of ) The line passes through (2, 11) and. 6) r(x) = x + 4. From memory match each equation with its graph.
 Review Test 2 Math 1314 Name Write an equation of the line satisfying the given conditions. Write the answer in standard form. 1) The line has a slope of - 2 7 and contains the point (3, 1). Use the point-slope
Review Test 2 Math 1314 Name Write an equation of the line satisfying the given conditions. Write the answer in standard form. 1) The line has a slope of - 2 7 and contains the point (3, 1). Use the point-slope
Fixed-Point Iteration
 Fixed-Point Iteration MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation Several root-finding algorithms operate by repeatedly evaluating a function until its
Fixed-Point Iteration MATH 375 Numerical Analysis J. Robert Buchanan Department of Mathematics Fall 2013 Motivation Several root-finding algorithms operate by repeatedly evaluating a function until its
6.2 Deeper Properties of Continuous Functions
 6.2. DEEPER PROPERTIES OF CONTINUOUS FUNCTIONS 69 6.2 Deeper Properties of Continuous Functions 6.2. Intermediate Value Theorem and Consequences When one studies a function, one is usually interested in
6.2. DEEPER PROPERTIES OF CONTINUOUS FUNCTIONS 69 6.2 Deeper Properties of Continuous Functions 6.2. Intermediate Value Theorem and Consequences When one studies a function, one is usually interested in
The Normal Equations. For A R m n with m > n, A T A is singular if and only if A is rank-deficient. 1 Proof:
 Applied Math 205 Homework 1 now posted. Due 5 PM on September 26. Last time: piecewise polynomial interpolation, least-squares fitting Today: least-squares, nonlinear least-squares The Normal Equations
Applied Math 205 Homework 1 now posted. Due 5 PM on September 26. Last time: piecewise polynomial interpolation, least-squares fitting Today: least-squares, nonlinear least-squares The Normal Equations
Bessel s Equation. MATH 365 Ordinary Differential Equations. J. Robert Buchanan. Fall Department of Mathematics
 Bessel s Equation MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Background Bessel s equation of order ν has the form where ν is a constant. x 2 y + xy
Bessel s Equation MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Background Bessel s equation of order ν has the form where ν is a constant. x 2 y + xy
The answer in each case is the error in evaluating the taylor series for ln(1 x) for x = which is 6.9.
 Brad Nelson Math 26 Homework #2 /23/2. a MATLAB outputs: >> a=(+3.4e-6)-.e-6;a- ans = 4.449e-6 >> a=+(3.4e-6-.e-6);a- ans = 2.224e-6 And the exact answer for both operations is 2.3e-6. The reason why way
Brad Nelson Math 26 Homework #2 /23/2. a MATLAB outputs: >> a=(+3.4e-6)-.e-6;a- ans = 4.449e-6 >> a=+(3.4e-6-.e-6);a- ans = 2.224e-6 And the exact answer for both operations is 2.3e-6. The reason why way
MA 3021: Numerical Analysis I Numerical Differentiation and Integration
 MA 3021: Numerical Analysis I Numerical Differentiation and Integration Suh-Yuh Yang ( 楊肅煜 ) Department of Mathematics, National Central University Jhongli District, Taoyuan City 32001, Taiwan syyang@math.ncu.edu.tw
MA 3021: Numerical Analysis I Numerical Differentiation and Integration Suh-Yuh Yang ( 楊肅煜 ) Department of Mathematics, National Central University Jhongli District, Taoyuan City 32001, Taiwan syyang@math.ncu.edu.tw
Taylor and Maclaurin Series
 Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Taylor and Maclaurin Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Background We have seen that some power series converge. When they do, we can think of them as
Series Solutions Near an Ordinary Point
 Series Solutions Near an Ordinary Point MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 Ordinary Points (1 of 2) Consider the second order linear homogeneous
Series Solutions Near an Ordinary Point MATH 365 Ordinary Differential Equations J. Robert Buchanan Department of Mathematics Spring 2018 Ordinary Points (1 of 2) Consider the second order linear homogeneous
Introduction Linear system Nonlinear equation Interpolation
 Interpolation Interpolation is the process of estimating an intermediate value from a set of discrete or tabulated values. Suppose we have the following tabulated values: y y 0 y 1 y 2?? y 3 y 4 y 5 x
Interpolation Interpolation is the process of estimating an intermediate value from a set of discrete or tabulated values. Suppose we have the following tabulated values: y y 0 y 1 y 2?? y 3 y 4 y 5 x
Interpolating Accuracy without underlying f (x)
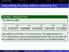 Example: Tabulated Data The following table x 1.0 1.3 1.6 1.9 2.2 f (x) 0.7651977 0.6200860 0.4554022 0.2818186 0.1103623 lists values of a function f at various points. The approximations to f (1.5) obtained
Example: Tabulated Data The following table x 1.0 1.3 1.6 1.9 2.2 f (x) 0.7651977 0.6200860 0.4554022 0.2818186 0.1103623 lists values of a function f at various points. The approximations to f (1.5) obtained
5.5 Deeper Properties of Continuous Functions
 5.5. DEEPER PROPERTIES OF CONTINUOUS FUNCTIONS 195 5.5 Deeper Properties of Continuous Functions 5.5.1 Intermediate Value Theorem and Consequences When one studies a function, one is usually interested
5.5. DEEPER PROPERTIES OF CONTINUOUS FUNCTIONS 195 5.5 Deeper Properties of Continuous Functions 5.5.1 Intermediate Value Theorem and Consequences When one studies a function, one is usually interested
Mathematics 206 Solutions for HWK 23 Section 6.3 p358
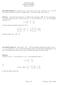 Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Downloaded from
 Question 1: Exercise 2.1 The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x), in each case. (i) (ii) (iii) Page 1 of 24 (iv) (v) (v) Page
Question 1: Exercise 2.1 The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x), in each case. (i) (ii) (iii) Page 1 of 24 (iv) (v) (v) Page
Functions: Polynomial, Rational, Exponential
 Functions: Polynomial, Rational, Exponential MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Spring 2014 Objectives In this lesson we will learn to: identify polynomial expressions,
Functions: Polynomial, Rational, Exponential MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Spring 2014 Objectives In this lesson we will learn to: identify polynomial expressions,
Review all the activities leading to Midterm 3. Review all the problems in the previous online homework sets (8+9+10).
 MA109, Activity 34: Review (Sections 3.6+3.7+4.1+4.2+4.3) Date: Objective: Additional Assignments: To prepare for Midterm 3, make sure that you can solve the types of problems listed in Activities 33 and
MA109, Activity 34: Review (Sections 3.6+3.7+4.1+4.2+4.3) Date: Objective: Additional Assignments: To prepare for Midterm 3, make sure that you can solve the types of problems listed in Activities 33 and
Interpolation and Approximation
 Interpolation and Approximation The Basic Problem: Approximate a continuous function f(x), by a polynomial p(x), over [a, b]. f(x) may only be known in tabular form. f(x) may be expensive to compute. Definition:
Interpolation and Approximation The Basic Problem: Approximate a continuous function f(x), by a polynomial p(x), over [a, b]. f(x) may only be known in tabular form. f(x) may be expensive to compute. Definition:
2.3 Some Properties of Continuous Functions
 2.3 Some Properties of Continuous Functions In this section we look at some properties, some quite deep, shared by all continuous functions. They are known as the following: 1. Preservation of sign property
2.3 Some Properties of Continuous Functions In this section we look at some properties, some quite deep, shared by all continuous functions. They are known as the following: 1. Preservation of sign property
1 Solutions to selected problems
 Solutions to selected problems Section., #a,c,d. a. p x = n for i = n : 0 p x = xp x + i end b. z = x, y = x for i = : n y = y + x i z = zy end c. y = (t x ), p t = a for i = : n y = y(t x i ) p t = p
Solutions to selected problems Section., #a,c,d. a. p x = n for i = n : 0 p x = xp x + i end b. z = x, y = x for i = : n y = y + x i z = zy end c. y = (t x ), p t = a for i = : n y = y(t x i ) p t = p
MATH 1014 Tutorial Notes 8
 MATH4 Calculus II (8 Spring) Topics covered in tutorial 8:. Numerical integration. Approximation integration What you need to know: Midpoint rule & its error Trapezoid rule & its error Simpson s rule &
MATH4 Calculus II (8 Spring) Topics covered in tutorial 8:. Numerical integration. Approximation integration What you need to know: Midpoint rule & its error Trapezoid rule & its error Simpson s rule &
Calculus and Parametric Equations
 Calculus and Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Given a pair a parametric equations x = f (t) y = g(t) for a t b we know how
Calculus and Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Given a pair a parametric equations x = f (t) y = g(t) for a t b we know how
Math 601 Solutions to Homework 3
 Math 601 Solutions to Homework 3 1 Use Cramer s Rule to solve the following system of linear equations (Solve for x 1, x 2, and x 3 in terms of a, b, and c 2x 1 x 2 + 7x 3 = a 5x 1 2x 2 x 3 = b 3x 1 x
Math 601 Solutions to Homework 3 1 Use Cramer s Rule to solve the following system of linear equations (Solve for x 1, x 2, and x 3 in terms of a, b, and c 2x 1 x 2 + 7x 3 = a 5x 1 2x 2 x 3 = b 3x 1 x
Math 334 A1 Homework 3 (Due Nov. 5 5pm)
 Math 334 A1 Homework 3 Due Nov. 5 5pm No Advanced or Challenge problems will appear in homeworks. Basic Problems Problem 1. 4.1 11 Verify that the given functions are solutions of the differential equation,
Math 334 A1 Homework 3 Due Nov. 5 5pm No Advanced or Challenge problems will appear in homeworks. Basic Problems Problem 1. 4.1 11 Verify that the given functions are solutions of the differential equation,
Numerical Methods of Approximation
 Contents 31 Numerical Methods of Approximation 31.1 Polynomial Approximations 2 31.2 Numerical Integration 28 31.3 Numerical Differentiation 58 31.4 Nonlinear Equations 67 Learning outcomes In this Workbook
Contents 31 Numerical Methods of Approximation 31.1 Polynomial Approximations 2 31.2 Numerical Integration 28 31.3 Numerical Differentiation 58 31.4 Nonlinear Equations 67 Learning outcomes In this Workbook
Homework #6 Solutions
 Problems Section.1: 6, 4, 40, 46 Section.:, 8, 10, 14, 18, 4, 0 Homework #6 Solutions.1.6. Determine whether the functions f (x) = cos x + sin x and g(x) = cos x sin x are linearly dependent or linearly
Problems Section.1: 6, 4, 40, 46 Section.:, 8, 10, 14, 18, 4, 0 Homework #6 Solutions.1.6. Determine whether the functions f (x) = cos x + sin x and g(x) = cos x sin x are linearly dependent or linearly
Extrema of Functions of Several Variables
 Extrema of Functions of Several Variables MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Background (1 of 3) In single-variable calculus there are three important results
Extrema of Functions of Several Variables MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Background (1 of 3) In single-variable calculus there are three important results
MEMORIAL UNIVERSITY OF NEWFOUNDLAND
 MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Section 5. Math 090 Fall 009 SOLUTIONS. a) Using long division of polynomials, we have x + x x x + ) x 4 4x + x + 0x x 4 6x
MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Section 5. Math 090 Fall 009 SOLUTIONS. a) Using long division of polynomials, we have x + x x x + ) x 4 4x + x + 0x x 4 6x
8.2 Discrete Least Squares Approximation
 Chapter 8 Approximation Theory 8.1 Introduction Approximation theory involves two types of problems. One arises when a function is given explicitly, but we wish to find a simpler type of function, such
Chapter 8 Approximation Theory 8.1 Introduction Approximation theory involves two types of problems. One arises when a function is given explicitly, but we wish to find a simpler type of function, such
1 Lecture 8: Interpolating polynomials.
 1 Lecture 8: Interpolating polynomials. 1.1 Horner s method Before turning to the main idea of this part of the course, we consider how to evaluate a polynomial. Recall that a polynomial is an expression
1 Lecture 8: Interpolating polynomials. 1.1 Horner s method Before turning to the main idea of this part of the course, we consider how to evaluate a polynomial. Recall that a polynomial is an expression
Lagrange s polynomial
 Lagrange s polynomial Nguyen Trung Tuan November 13, 2016 Abstract...In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x j and numbers
Lagrange s polynomial Nguyen Trung Tuan November 13, 2016 Abstract...In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x j and numbers
Numerical Methods. King Saud University
 Numerical Methods King Saud University Aims In this lecture, we will... find the approximate solutions of derivative (first- and second-order) and antiderivative (definite integral only). Numerical Differentiation
Numerical Methods King Saud University Aims In this lecture, we will... find the approximate solutions of derivative (first- and second-order) and antiderivative (definite integral only). Numerical Differentiation
Inverses. Stephen Boyd. EE103 Stanford University. October 28, 2017
 Inverses Stephen Boyd EE103 Stanford University October 28, 2017 Outline Left and right inverses Inverse Solving linear equations Examples Pseudo-inverse Left and right inverses 2 Left inverses a number
Inverses Stephen Boyd EE103 Stanford University October 28, 2017 Outline Left and right inverses Inverse Solving linear equations Examples Pseudo-inverse Left and right inverses 2 Left inverses a number
Fundamental Theorem of Calculus
 Fundamental Theorem of Calculus MATH 6 Calculus I J. Robert Buchanan Department of Mathematics Summer 208 Remarks The Fundamental Theorem of Calculus (FTC) will make the evaluation of definite integrals
Fundamental Theorem of Calculus MATH 6 Calculus I J. Robert Buchanan Department of Mathematics Summer 208 Remarks The Fundamental Theorem of Calculus (FTC) will make the evaluation of definite integrals
Secondary Math 3 Honors - Polynomial and Polynomial Functions Test Review
 Name: Class: Date: Secondary Math 3 Honors - Polynomial and Polynomial Functions Test Review 1 Write 3x 2 ( 2x 2 5x 3 ) in standard form State whether the function is even, odd, or neither Show your work
Name: Class: Date: Secondary Math 3 Honors - Polynomial and Polynomial Functions Test Review 1 Write 3x 2 ( 2x 2 5x 3 ) in standard form State whether the function is even, odd, or neither Show your work
Chapter 4: Interpolation and Approximation. October 28, 2005
 Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
Chapter 4: Interpolation and Approximation October 28, 2005 Outline 1 2.4 Linear Interpolation 2 4.1 Lagrange Interpolation 3 4.2 Newton Interpolation and Divided Differences 4 4.3 Interpolation Error
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS
 LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
' Liberty and Umou Ono and Inseparablo "
 3 5? #< q 8 2 / / ) 9 ) 2 ) > < _ / ] > ) 2 ) ) 5 > x > [ < > < ) > _ ] ]? <
3 5? #< q 8 2 / / ) 9 ) 2 ) > < _ / ] > ) 2 ) ) 5 > x > [ < > < ) > _ ] ]? <
Chain Rule. MATH 311, Calculus III. J. Robert Buchanan. Spring Department of Mathematics
 3.33pt Chain Rule MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Spring 2019 Single Variable Chain Rule Suppose y = g(x) and z = f (y) then dz dx = d (f (g(x))) dx = f (g(x))g (x)
3.33pt Chain Rule MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Spring 2019 Single Variable Chain Rule Suppose y = g(x) and z = f (y) then dz dx = d (f (g(x))) dx = f (g(x))g (x)
Completion Date: Monday February 11, 2008
 MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
Evaluating Determinants by Row Reduction
 Evaluating Determinants by Row Reduction MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Objectives Reduce a matrix to row echelon form and evaluate its determinant.
Evaluating Determinants by Row Reduction MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Objectives Reduce a matrix to row echelon form and evaluate its determinant.
Lecture Note 3: Polynomial Interpolation. Xiaoqun Zhang Shanghai Jiao Tong University
 Lecture Note 3: Polynomial Interpolation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 24, 2013 1.1 Introduction We first look at some examples. Lookup table for f(x) = 2 π x 0 e x2
Lecture Note 3: Polynomial Interpolation Xiaoqun Zhang Shanghai Jiao Tong University Last updated: October 24, 2013 1.1 Introduction We first look at some examples. Lookup table for f(x) = 2 π x 0 e x2
Skills Practice Skills Practice for Lesson 10.1
 Skills Practice Skills Practice for Lesson.1 Name Date Higher Order Polynomials and Factoring Roots of Polynomial Equations Problem Set Solve each polynomial equation using factoring. Then check your solution(s).
Skills Practice Skills Practice for Lesson.1 Name Date Higher Order Polynomials and Factoring Roots of Polynomial Equations Problem Set Solve each polynomial equation using factoring. Then check your solution(s).
Two hours. To be provided by Examinations Office: Mathematical Formula Tables. THE UNIVERSITY OF MANCHESTER. 29 May :45 11:45
 Two hours MATH20602 To be provided by Examinations Office: Mathematical Formula Tables. THE UNIVERSITY OF MANCHESTER NUMERICAL ANALYSIS 1 29 May 2015 9:45 11:45 Answer THREE of the FOUR questions. If more
Two hours MATH20602 To be provided by Examinations Office: Mathematical Formula Tables. THE UNIVERSITY OF MANCHESTER NUMERICAL ANALYSIS 1 29 May 2015 9:45 11:45 Answer THREE of the FOUR questions. If more
MATH ASSIGNMENT 07 SOLUTIONS. 8.1 Following is census data showing the population of the US between 1900 and 2000:
 MATH4414.01 ASSIGNMENT 07 SOLUTIONS 8.1 Following is census data showing the population of the US between 1900 and 2000: Years after 1900 Population in millions 0 76.0 20 105.7 40 131.7 60 179.3 80 226.5
MATH4414.01 ASSIGNMENT 07 SOLUTIONS 8.1 Following is census data showing the population of the US between 1900 and 2000: Years after 1900 Population in millions 0 76.0 20 105.7 40 131.7 60 179.3 80 226.5
MA2501 Numerical Methods Spring 2015
 Norwegian University of Science and Technology Department of Mathematics MA5 Numerical Methods Spring 5 Solutions to exercise set 9 Find approximate values of the following integrals using the adaptive
Norwegian University of Science and Technology Department of Mathematics MA5 Numerical Methods Spring 5 Solutions to exercise set 9 Find approximate values of the following integrals using the adaptive
PRACTICE PROBLEM SET
 PRACTICE PROBLEM SET NOTE: On the exam, you will have to show all your work (unless told otherwise), so write down all your steps and justify them. Exercise. Solve the following inequalities: () x < 3
PRACTICE PROBLEM SET NOTE: On the exam, you will have to show all your work (unless told otherwise), so write down all your steps and justify them. Exercise. Solve the following inequalities: () x < 3
BSM510 Numerical Analysis
 BSM510 Numerical Analysis Polynomial Interpolation Prof. Manar Mohaisen Department of EEC Engineering Review of Precedent Lecture Polynomial Regression Multiple Linear Regression Nonlinear Regression Lecture
BSM510 Numerical Analysis Polynomial Interpolation Prof. Manar Mohaisen Department of EEC Engineering Review of Precedent Lecture Polynomial Regression Multiple Linear Regression Nonlinear Regression Lecture
Section 10.7 Taylor series
 Section 10.7 Taylor series 1. Common Maclaurin series 2. s and approximations with Taylor polynomials 3. Multiplication and division of power series Math 126 Enhanced 10.7 Taylor Series The University
Section 10.7 Taylor series 1. Common Maclaurin series 2. s and approximations with Taylor polynomials 3. Multiplication and division of power series Math 126 Enhanced 10.7 Taylor Series The University
AP Calculus (BC) Chapter 9 Test No Calculator Section Name: Date: Period:
 WORKSHEET: Series, Taylor Series AP Calculus (BC) Chapter 9 Test No Calculator Section Name: Date: Period: 1 Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.) 1. The
WORKSHEET: Series, Taylor Series AP Calculus (BC) Chapter 9 Test No Calculator Section Name: Date: Period: 1 Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.) 1. The
Numerical Mathematics & Computing, 7 Ed. 4.1 Interpolation
 Numerical Mathematics & Computing, 7 Ed. 4.1 Interpolation Ward Cheney/David Kincaid c UT Austin Engage Learning: Thomson-Brooks/Cole www.engage.com www.ma.utexas.edu/cna/nmc6 November 7, 2011 2011 1 /
Numerical Mathematics & Computing, 7 Ed. 4.1 Interpolation Ward Cheney/David Kincaid c UT Austin Engage Learning: Thomson-Brooks/Cole www.engage.com www.ma.utexas.edu/cna/nmc6 November 7, 2011 2011 1 /
CHAPTER 2 POLYNOMIALS KEY POINTS
 CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
Solutions 2. January 23, x x
 Solutions 2 January 23, 2016 1 Exercise 3.1.1 (a), p. 149 Let us compute Lagrange polynomials first for our case x 1 = 0, x 2 = 2, x 3 = 3: In [14]: from sympy import * init_printing(use_latex=true) x=symbols(
Solutions 2 January 23, 2016 1 Exercise 3.1.1 (a), p. 149 Let us compute Lagrange polynomials first for our case x 1 = 0, x 2 = 2, x 3 = 3: In [14]: from sympy import * init_printing(use_latex=true) x=symbols(
Lagrange s polynomial
 Lagrange s polynomial Nguyen Trung Tuan November 16, 2016 Abstract In this article, I will use Lagrange polynomial to solve some problems from Mathematical Olympiads. Contents 1 Lagrange s interpolation
Lagrange s polynomial Nguyen Trung Tuan November 16, 2016 Abstract In this article, I will use Lagrange polynomial to solve some problems from Mathematical Olympiads. Contents 1 Lagrange s interpolation
Exam 2. Average: 85.6 Median: 87.0 Maximum: Minimum: 55.0 Standard Deviation: Numerical Methods Fall 2011 Lecture 20
 Exam 2 Average: 85.6 Median: 87.0 Maximum: 100.0 Minimum: 55.0 Standard Deviation: 10.42 Fall 2011 1 Today s class Multiple Variable Linear Regression Polynomial Interpolation Lagrange Interpolation Newton
Exam 2 Average: 85.6 Median: 87.0 Maximum: 100.0 Minimum: 55.0 Standard Deviation: 10.42 Fall 2011 1 Today s class Multiple Variable Linear Regression Polynomial Interpolation Lagrange Interpolation Newton
Review 1 Math 321: Linear Algebra Spring 2010
 Department of Mathematics and Statistics University of New Mexico Review 1 Math 321: Linear Algebra Spring 2010 This is a review for Midterm 1 that will be on Thursday March 11th, 2010. The main topics
Department of Mathematics and Statistics University of New Mexico Review 1 Math 321: Linear Algebra Spring 2010 This is a review for Midterm 1 that will be on Thursday March 11th, 2010. The main topics
Properties of Linear Transformations from R n to R m
 Properties of Linear Transformations from R n to R m MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Topic Overview Relationship between the properties of a matrix transformation
Properties of Linear Transformations from R n to R m MATH 322, Linear Algebra I J. Robert Buchanan Department of Mathematics Spring 2015 Topic Overview Relationship between the properties of a matrix transformation
We consider the problem of finding a polynomial that interpolates a given set of values:
 Chapter 5 Interpolation 5. Polynomial Interpolation We consider the problem of finding a polynomial that interpolates a given set of values: x x 0 x... x n y y 0 y... y n where the x i are all distinct.
Chapter 5 Interpolation 5. Polynomial Interpolation We consider the problem of finding a polynomial that interpolates a given set of values: x x 0 x... x n y y 0 y... y n where the x i are all distinct.
Vectors in the Plane
 Vectors in the Plane MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Vectors vs. Scalars scalar quantity having only a magnitude (e.g. temperature, volume, length, area) and
Vectors in the Plane MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Vectors vs. Scalars scalar quantity having only a magnitude (e.g. temperature, volume, length, area) and
Lecture 10 Polynomial interpolation
 Lecture 10 Polynomial interpolation Weinan E 1,2 and Tiejun Li 2 1 Department of Mathematics, Princeton University, weinan@princeton.edu 2 School of Mathematical Sciences, Peking University, tieli@pku.edu.cn
Lecture 10 Polynomial interpolation Weinan E 1,2 and Tiejun Li 2 1 Department of Mathematics, Princeton University, weinan@princeton.edu 2 School of Mathematical Sciences, Peking University, tieli@pku.edu.cn
Limits and Continuity
 Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
Limits and Continuity MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After this lesson we will be able to: Determine the left-hand and right-hand limits
6.1 Polynomial Functions
 6.1 Polynomial Functions Definition. A polynomial function is any function p(x) of the form p(x) = p n x n + p n 1 x n 1 + + p 2 x 2 + p 1 x + p 0 where all of the exponents are non-negative integers and
6.1 Polynomial Functions Definition. A polynomial function is any function p(x) of the form p(x) = p n x n + p n 1 x n 1 + + p 2 x 2 + p 1 x + p 0 where all of the exponents are non-negative integers and
. Get closed expressions for the following subsequences and decide if they converge. (1) a n+1 = (2) a 2n = (3) a 2n+1 = (4) a n 2 = (5) b n+1 =
 Math 316, Intro to Analysis subsequences. Recall one of our arguments about why a n = ( 1) n diverges. Consider the subsequences a n = ( 1) n = +1. It converges to 1. On the other hand, the subsequences
Math 316, Intro to Analysis subsequences. Recall one of our arguments about why a n = ( 1) n diverges. Consider the subsequences a n = ( 1) n = +1. It converges to 1. On the other hand, the subsequences
Question 1: The graphs of y = p(x) are given in following figure, for some Polynomials p(x). Find the number of zeroes of p(x), in each case.
 Class X - NCERT Maths EXERCISE NO:.1 Question 1: The graphs of y = p(x) are given in following figure, for some Polynomials p(x). Find the number of zeroes of p(x), in each case. (i) (ii) (iii) (iv) (v)
Class X - NCERT Maths EXERCISE NO:.1 Question 1: The graphs of y = p(x) are given in following figure, for some Polynomials p(x). Find the number of zeroes of p(x), in each case. (i) (ii) (iii) (iv) (v)
AP Calculus Testbank (Chapter 9) (Mr. Surowski)
 AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
AP Calculus Testbank (Chapter 9) (Mr. Surowski) Part I. Multiple-Choice Questions n 1 1. The series will converge, provided that n 1+p + n + 1 (A) p > 1 (B) p > 2 (C) p >.5 (D) p 0 2. The series
a. Do you think the function is linear or non-linear? Explain using what you know about powers of variables.
 8.5.8 Lesson Date: Graphs of Non-Linear Functions Student Objectives I can examine the average rate of change for non-linear functions and learn that they do not have a constant rate of change. I can determine
8.5.8 Lesson Date: Graphs of Non-Linear Functions Student Objectives I can examine the average rate of change for non-linear functions and learn that they do not have a constant rate of change. I can determine
