A RUIN FUNCTION APPROXIMATION JOHN A. BEEKMAN*
|
|
|
- Owen Allen
- 5 years ago
- Views:
Transcription
1 TRANSACTIONS OF SOCIETY OF ACTUARIES 1969 VOL. 21 PT. 1 NO. 59 AB A RUIN FUNCTION APPROXIMATION JOHN A. BEEKMAN* ABSTRACT This paper derives a formula for approximating the ruin function of collective risk theory. This formula is simple to calculate and is based on the distribution of claims and the security loading. It is partially based on several papers in the Transactions dealing with approximating the distribution of total claims in collective risk theory. The derivations for the formula are given in the Appendix. Use of the ruin function in setting retention limits is explained. The following questions are answered, for example. If the retention level is set at $X, what fund is needed in order that the adverse fluctuation will stay below its value with high probability, say, 0.99? Various retention levels and funds are compared for practical distributions. If the upper limit on adverse fluctuation is $Y, what is the corresponding retention level? Use of the ruin function in deciding the amount of initial capital for a new line of business is discussed. INTRODUCTION I N" COLLECTIVE risk theory the ruin function is of great importance. We will emphasize this briefly with several examples. But, if we grant its importance, it is necessary to know how to calculate it. My recent paper [3] contains some new ways in which to calculate it. These and earlier methods, however, are hard to perform in most cases and impossible to perform in many practical cases. It is therefore very worthwhile to study approximation methods. We will derive an approximation to the ruin function, using some recent results of Mr. D. K. Bartlett [1] and Dr. Newton L. Bowers [4], We will then compare values obtained through the approximation method with the exact values in one well-known example and then give several values of the ruin function for a practical example. Let us consider two examples in which the ruin function can be used. Assume that you work for a company that is contemplating entering a * This research was partially supported by the National Science Foundation through Grant NSF GP
2 4:2 A RUIN FUNCTION APPROXIMATION new line of insurance, say, accident and health insurance. Your company would like to set aside some capital for this venture. How much is needed in order that there is a 99 per cent chance that you will not have to dip into your other funds? Provided you are willing to make several assumptions, this question can be answered by using the ruin function. As a second example, assume that you are involved in setting a retention limit and are interested in the following questions. If the retention level is set at SX, what fund is needed in order that the adverse fluctuation will stay below its value with high probability, say, 0.99? Or, if the upper limit on adverse fluctuation is SY, what is the corresponding retention level? Again the fundamental tool for answering these questions is the ruin function. Let us now describe the ruin function in words and symbols. The ruin function computes the chance that the initial reserve plus premiums minus claims ever turns negative. I. THE RUIN ~FUNCTION We will repeat part of the description in my recent paper [3]. Let P(z) be the distribution for a claim; that is, P(z) is the probability that, if a claim occurs, it will be less than or equal to z. We will assume that P(0) = 0, which rules out nonpositive claims. Such claims occur when a life annuity terminates and a reserve is released. We will let the Variable t be operational time. This means, for example, that if past records indicate thirty claims per year, then t = 30 will correspond to one calendar year. N(t) is the random number of claims in time t. We will assume that claims occur in such a way that N(t) has a Poisson distribution with mean t. The reader can consult Dr. Paul Kahn's paper [6] relative to this assumption. If pl is the average claim amount, then in time t the insurance company would charge p~t as the aggregale net risk premium, plus an aggregate security loading of Xt. We also assume that the insurance company begins with a risk reserve of size u. At time t, the risk reserve U(t) is given by N(t) u(t) = u + (p, + x)t - ~x,, (1) i*1 where the X~'s are independent random variables, representing the claims. Each X~ has the distribution P(z). The symbol N(t) ~x, represents the aggregate claims up to time t. The expression m,mmum U(t) o<~<r
3 A RUIN FUNCTION APPROXIMATION 43 will refer to the smallest value of U(t) over the time range 0 < t < T. The ruin function is #(u) = hm P[minimum U(t) < 0]. Z--* 0_< t_< T This represents the probability that the risk reserve eventually becomes negative. Let us explain the use of ~(u) in the two examples. In the first example, the capital set aside is u. It is determined by setting the expression for ~k(u) = 0.01 and solving for u. In the second example, the retention level equals the upper limit of.p(z). The adverse fluctuation equals the excess of total claims over total gross premiums. It will exceed a level u with probability #(u). Holding u fixed, one can vary the retention level so that #(u) stays below an appropriate level, say, #(u) is not a probability distribution function (see Hoel [5], pp. 23, 37), but it is simply related to one, namely, ~'(u) tl-~(u)' o, u u> 0 < 0. (2) As a distribution function, #'(u) involves the random variable Z defined by Z rn(0 "i = mammum[ ~_,X, -- t(p, + X)[. (3) 0<t<~ L i.1 J The proof of this is in the Appendix. Roughly speaking, Z is the maximum excess of claims over income examined at each time point of very long time periods. We will now quote the formulas for the mean and variance of ~*(u). ii. ~om~nts of ~'(u) The introduction has revealed how ~b(u) depends on P(z) and ),. It is therefore to be expecte.d that the mean value of ~k'(u) does too. The proofs of the following theorems are in the Appendix. Theorem L--If E(X 2) is the second moment about the origin of the claim distribution and X is the security loading, the mean of ~k*(u) is denoted and given by the formula E(Z) = E(X~) (4) 2X One would expect the variance of Z to depend on higher moments of the claim distribution. This is the case.
4 44 A RUIN FUNCTION APPROXIMATION Theorem 2.--If E(X") is the third moment about the origin of the claim distribution, and X is the security loading, E(x") Var (Z) = 3k + [E(Z)]~" (5) As the first example of these calculations, assume that P(z) = 1 -- e--', z _> 0. Then E[X k] = k!. Assume k = 0.3. Then E(Z)= 3.333, and Var (Z) = (We are using $1,000 units.) As the second example, assume that P(z) = 0 for z< 2 = 0.3 for 2<z<5 = 0.5 for 5<z< 10 = 0.8 for 10 < z < 20 = 1.0 for 20 < z. Then E(Z) = 22.4 and Var (Z) = These figures are based on X = 0.3E(X) = 2.6, E(X 2) = 116.2, and E(X 8) = As a third example, assume that P(z) =0 for z< 2 = 0.3 for 2<z< 5 = 0.5 for 5<z < 10 = 0.8 for 10 < z < 20 = 0.85 for 20 < z < 30 = 0.90 for 30 _< z < 40 = 0.95 for 40 < z < 50 = 1.00 for 50 _< z. Here )~ = 0.3E(X) = 3.5, E(X *) = 306.2, and E(X a) = 11, Using these figures, we obtain E(Z) = 43.7 and Var (Z) = 3, m. A P OX ArION OF,'(U) The papers by Bartlett and Bowers tell how to approximate a density function in terms of gamma densities. We will now apply the preceding results to such an approximation. Since Bowers' paper refers to the approximation of any density (not just to that of aggregate losses, as Bartlett's paper does), we will refer to Bowers' paper throughout. We assume, as Bowers does [4, p. 127], that ~*(u) has a density function. Theorem 3.--The distribution function ~'(u) has a jump of 1- t)1/(l)1 n t- k) at u = 0, and for u > 0 has the approximate form where/3 -- E(Z)/Var (Z) and, Bu 2va_le_ w V(-) = = of r(.---t- dw, (6) = [E(Z)]VVar (Z),
5 A RUIN FUNCTION APPROXIMATION 45 We will now illustrate this with Example 1. There /3 = 0.187, a = To compare with the known values of 0.99, 0.95, and 0.90 from reference [3], we will let u = , , and thousand dollar units, respectively. To find #*(18.8) = 1"(3.516, 0.625), one can use the references to incomplete gamma functions cited by Bowers. We used reference [8]. Some explanation of that table is appropriate. By the use of the letters of that reference, several transformations reveal that the "areas" are values of r(~ +2t,±'~ Since 4~as ~ will always be too large for us, we repeatedly used a recursion relation of Bowers: r(x, a - 3) = r(x, ~ + 1) :~ae--= xa--le--z Xa-2e- :g.a-se-a: + r(. + 1) + - r(~) - + r(~ - i) + F~(= - 2) Thus, setting 4/a, * = 4.625, we obtained a8 = 0.93, and, setting 4/an 2 + (2/a3)t = 3.516, we obtained l = Using these values of an and t produced r(3.516, 4.625) = We next computed (3.516)8.n25 -t.516/ r(4.625), using the fact that r(4.625) = 3.625(2.625)(1.625)D(1.625) and that F(1.625) = (reference [7]). The quotient value obtained was The other terms had values of , , and and were easy to calculate. Thus (3.516)2.n"se'-3.516/I'(3.625) = 3.625/3.516 (0.2042) = Adding these five numbers gave #*(18.8) = 1"(3.516, 0.625) = , remarkably close to the exact value. Similarly, # (11.833) = , and #*(8.831) = This provides a rough check on the accuracy of the approximation and implies that this method is probably quite accurate. We will now compare the initial capitals needed to hold #(u) in Examples 2 ~/nd 3. This will illustrate the effect of raising the retention limit. For Example 2, /~ = 0.03, a = 0.67, and #*(125)= For Example 3,/~ = 0.015, a = 0.635, and #*(250) = Thus, increasing the retention level from $20,000 to $50,000 requires $125,000 additional initial capital to hold the probability of ruin to The approach to 0.99 probability becomes quite slow. For example, with a fund of $200,000, one already has a probability of If we felt that $200,000 was an appropriate upper bound on adverse fluctuation, we could have solved for the retention level, by trying distribufions with upper limits varying from $20,000 to $50,000, until we
6 46 A RUIN FUNCTION APPROXIMATION found one such that ~k(200) ~ By using the previous distributions as guides, we are led to the following distribution: P(z) =0 for z<2 = 0.3 for 2_<z<5 = 0.5 for 5_<z< 10 = 0.8 for 10_< z < 20 = 0.87 for 20 < z < 30 = 0.94 for 30 _< z < 40 = 1.00 for 40 _< z. Again, we assume X = 0.3p~, or If the reader consults the author's earlier paper [3], the asymptotic formula (3) for if(u) produced much lower values for the u's necessary to hold ~k(u) in Examples 2 and 3, namely, $91,429 and $180,857. One reason for these differences will now be given. The u's probably were not large enough to use the asymptotic formula with great accuracy, and the results were too low. This statement is based on a study of Table VII on page 45 of Harald Cram~r's paper "Collective Risk Theory," the 1955 Jubilee Volume of F~rs~krlngsaktiebolaget Skandia. That table shows 98 per cent accuracy for the asymptotic formula only for a u value 40 times pt. This emphasizes the advantage of this paper's approximation method, since it applies for all u >_ 0. APPENDIX We will now give the proofs of the three theorems and of equation (3). Assume thatu >_ 0: PROOP O~ EQUATION 3 But ~'(u) = 1 - ~(u) = 1 -- lim P[minimum U(t) < 0]. 1 = lira P[minlmum U(t) < 0] +rlim P[mimmum U(t) > 0]. T-~,- 0_<t_< r 0<t< T -- Hence ~k*(u) = lira P[minlmum U(t) > 0] T--* =0 0_<I_<T -- N(O -~ = lira Ptminimum [u + (p,'+ k)t- )-~.xil > 0 l O<J_<T i=t a -- by the definition of U(t)
7 A RUIN FUNCTION APPROXIMATION 47 rn(o = rl~m P lmaximum / )-'~X, -- t(pt + X)] < u t t O<J<r,- i=t by inspection of the sample graphs rn(0 =.Plmaximum I )'~X,- t(px + k)] < u t O<It < m L. i--1 (See Wilks [10], p. 13.) by the monotonicity of the sets. Since Z > O, PROOF OF THEORE~ i E(Z) = ud,,pz(u) = f ud,,~k'(u). 0 0 (As in reference [3], the Stieltjes integral reduces to f ud~ez(u) 0.~up(u) du, 0 ff Pz(u) has a derivative p(u) for all u values, and to if Pz(u) is a pure step function.) By corollary 3 of reference [2], ~,,xpz(u3, of e-"ud~*(u) = ax/[/e-*~dp(x)--1 + a(pt + k)]. (7) Using the Stieltjes version of Theorem 14 of Widder [9], p. 358, E[Z] = _A da ~ e-:'d'+*(u) la- = fe-':-d: (-) I..o 0 Differentiating the right-hand side of equation (7) produces the form 0/0 when a We then apply L'H6pital's rule (see reference [9], p. 250) twice to obtain equation (4).
8 48 A RUIN FUNCTION APPROXIMATION PROOF O]~ THEOREM 2 Car (z) = E(z0 - [~(z)] 2. E(z 2) = a~,,2d~'(u) o d 2,~ = --d~2 fe-'"d.+'(u). [o.0. Differentiating the right-hand side of equation (7) twice produces the form 0/0 when a = 0. We then apply L'H6pital's rule three times and do much elementary algebra to obtain equation (5). PaooF o~ ~ o ~ 3 The first part is well known since ~b(0)= pt/(p, + X). Following Bowers [4, p. 127], if X = flz, with E(X) = Var (X), then BE(Z) = /~2 Var (Z) or B = E(Z)/Var (Z). In Bowers' notation, a = E(X) = fie(z) = [E(Z)]2/Var (Z). We also have P [z < u] = 2 ~ [~z < t~u] = f/(x)dx, o where we assume ~b*(u) has a densityf(x). Using the first term of series (2) in reference [4], f(x) = x~-xe--*/f(a), for a as above. This completes the proof. BIBLIOGRAPHY 1. BARTLET% D. K. "Excess Ratio Distribution in Risk Theory," TSA, XVli (1965), BEXK~'q, JOHN A. "Research on the Collective Risk Stochastic Process," Skandinavisk Aktuarletidskrifl, XLIX (1966), "Collective Risk Results," TSA, XX (1968), BOWERS, NEWTON L., JR. "Expansion of Probability Density Functions as a Sum of Gamma Densities with Applications in Risk Theory," TSA, XVIII (1966), ttoel, P. G. Introduction to Mathematical Statistics (NewYork: John Wiley & Sons, 1962). 6. Kmizq, P. M. "An Introduction to Collective Risk Theory and Its Applications to Stop-Loss Reinsurance," TSA, XIV (1962), Mathematical Tables from Handbook of Chemistry and Physics (Cleveland: Chemical Rubber Publishing Co., 1962). 8. SALVOSA, L. R. "Tables of Pearson's Type III Function," Annals of Mathematical Statistics, I (1930), WINDER, D. V. Advanced Calculus (Englewood Cliffs, N.J.: Prentice-Hall, 1961). 10. WILKS, S. S. Mathematical Statistic~ (New York: John Wiley & Sons, 1962). #u
Some Approximations on the Probability of Ruin and the Inverse Ruin Function
 MATIMYÁS MATEMATIKA Journal of the Mathematical Society of the Philippines ISSN 115-6926 Vol. 38 Nos. 1-2 (215) pp. 43-5 Some Approximations on the Probability of Ruin and the Inverse Ruin Function Lu
MATIMYÁS MATEMATIKA Journal of the Mathematical Society of the Philippines ISSN 115-6926 Vol. 38 Nos. 1-2 (215) pp. 43-5 Some Approximations on the Probability of Ruin and the Inverse Ruin Function Lu
Ruin Theory. A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science at George Mason University
 Ruin Theory A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science at George Mason University by Ashley Fehr Bachelor of Science West Virginia University, Spring
Ruin Theory A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science at George Mason University by Ashley Fehr Bachelor of Science West Virginia University, Spring
Analysis of the ruin probability using Laplace transforms and Karamata Tauberian theorems
 Analysis of the ruin probability using Laplace transforms and Karamata Tauberian theorems Corina Constantinescu and Enrique Thomann Abstract The classical result of Cramer-Lundberg states that if the rate
Analysis of the ruin probability using Laplace transforms and Karamata Tauberian theorems Corina Constantinescu and Enrique Thomann Abstract The classical result of Cramer-Lundberg states that if the rate
Optimal Reinsurance Strategy with Bivariate Pareto Risks
 University of Wisconsin Milwaukee UWM Digital Commons Theses and Dissertations May 2014 Optimal Reinsurance Strategy with Bivariate Pareto Risks Evelyn Susanne Gaus University of Wisconsin-Milwaukee Follow
University of Wisconsin Milwaukee UWM Digital Commons Theses and Dissertations May 2014 Optimal Reinsurance Strategy with Bivariate Pareto Risks Evelyn Susanne Gaus University of Wisconsin-Milwaukee Follow
University Of Calgary Department of Mathematics and Statistics
 University Of Calgary Department of Mathematics and Statistics Hawkes Seminar May 23, 2018 1 / 46 Some Problems in Insurance and Reinsurance Mohamed Badaoui Department of Electrical Engineering National
University Of Calgary Department of Mathematics and Statistics Hawkes Seminar May 23, 2018 1 / 46 Some Problems in Insurance and Reinsurance Mohamed Badaoui Department of Electrical Engineering National
Discrete Distributions Chapter 6
 Discrete Distributions Chapter 6 Negative Binomial Distribution section 6.3 Consider k r, r +,... independent Bernoulli trials with probability of success in one trial being p. Let the random variable
Discrete Distributions Chapter 6 Negative Binomial Distribution section 6.3 Consider k r, r +,... independent Bernoulli trials with probability of success in one trial being p. Let the random variable
Mixture distributions in Exams MLC/3L and C/4
 Making sense of... Mixture distributions in Exams MLC/3L and C/4 James W. Daniel Jim Daniel s Actuarial Seminars www.actuarialseminars.com February 1, 2012 c Copyright 2012 by James W. Daniel; reproduction
Making sense of... Mixture distributions in Exams MLC/3L and C/4 James W. Daniel Jim Daniel s Actuarial Seminars www.actuarialseminars.com February 1, 2012 c Copyright 2012 by James W. Daniel; reproduction
Reinsurance and ruin problem: asymptotics in the case of heavy-tailed claims
 Reinsurance and ruin problem: asymptotics in the case of heavy-tailed claims Serguei Foss Heriot-Watt University, Edinburgh Karlovasi, Samos 3 June, 2010 (Joint work with Tomasz Rolski and Stan Zachary
Reinsurance and ruin problem: asymptotics in the case of heavy-tailed claims Serguei Foss Heriot-Watt University, Edinburgh Karlovasi, Samos 3 June, 2010 (Joint work with Tomasz Rolski and Stan Zachary
Worst-Case-Optimal Dynamic Reinsurance for Large Claims
 Worst-Case-Optimal Dynamic Reinsurance for Large Claims by Olaf Menkens School of Mathematical Sciences Dublin City University (joint work with Ralf Korn and Mogens Steffensen) LUH-Kolloquium Versicherungs-
Worst-Case-Optimal Dynamic Reinsurance for Large Claims by Olaf Menkens School of Mathematical Sciences Dublin City University (joint work with Ralf Korn and Mogens Steffensen) LUH-Kolloquium Versicherungs-
1.3 Algebraic Expressions. Copyright Cengage Learning. All rights reserved.
 1.3 Algebraic Expressions Copyright Cengage Learning. All rights reserved. Objectives Adding and Subtracting Polynomials Multiplying Algebraic Expressions Special Product Formulas Factoring Common Factors
1.3 Algebraic Expressions Copyright Cengage Learning. All rights reserved. Objectives Adding and Subtracting Polynomials Multiplying Algebraic Expressions Special Product Formulas Factoring Common Factors
ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA Errata
 ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
1 Basic concepts from probability theory
 Basic concepts from probability theory This chapter is devoted to some basic concepts from probability theory.. Random variable Random variables are denoted by capitals, X, Y, etc. The expected value or
Basic concepts from probability theory This chapter is devoted to some basic concepts from probability theory.. Random variable Random variables are denoted by capitals, X, Y, etc. The expected value or
Tail Conditional Expectations for. Extended Exponential Dispersion Models
 Tail Conditional Expectations for Extended Exponential Dispersion Models A Thesis Presented to the Faculty of the Department of Mathematical Sciences Middle Tennessee State University In Partial Fulfillment
Tail Conditional Expectations for Extended Exponential Dispersion Models A Thesis Presented to the Faculty of the Department of Mathematical Sciences Middle Tennessee State University In Partial Fulfillment
x C) y = - A) $20000; 14 years B) $28,000; 14 years C) $28,000; 28 years D) $30,000; 15 years
 Dr. Lee - Math 35 - Calculus for Business - Review of 3 - Show Complete Work for Each Problem MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find
Dr. Lee - Math 35 - Calculus for Business - Review of 3 - Show Complete Work for Each Problem MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find
Course 1 Solutions November 2001 Exams
 Course Solutions November Exams . A For i =,, let R = event that a red ball is drawn form urn i i B = event that a blue ball is drawn from urn i. i Then if x is the number of blue balls in urn, ( R R)
Course Solutions November Exams . A For i =,, let R = event that a red ball is drawn form urn i i B = event that a blue ball is drawn from urn i. i Then if x is the number of blue balls in urn, ( R R)
Multivariate Risk Processes with Interacting Intensities
 Multivariate Risk Processes with Interacting Intensities Nicole Bäuerle (joint work with Rudolf Grübel) Luminy, April 2010 Outline Multivariate pure birth processes Multivariate Risk Processes Fluid Limits
Multivariate Risk Processes with Interacting Intensities Nicole Bäuerle (joint work with Rudolf Grübel) Luminy, April 2010 Outline Multivariate pure birth processes Multivariate Risk Processes Fluid Limits
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.262 Discrete Stochastic Processes Midterm Quiz April 6, 2010 There are 5 questions, each with several parts.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.262 Discrete Stochastic Processes Midterm Quiz April 6, 2010 There are 5 questions, each with several parts.
Practice Exam #1 CAS Exam 3L
 Practice Exam #1 CAS Exam 3L These practice exams should be used during the last month prior to your exam. This practice exam contains 25 questions, of equal value, corresponding to an exam of about 2.5
Practice Exam #1 CAS Exam 3L These practice exams should be used during the last month prior to your exam. This practice exam contains 25 questions, of equal value, corresponding to an exam of about 2.5
Reserving for multiple excess layers
 Reserving for multiple excess layers Ben Zehnwirth and Glen Barnett Abstract Patterns and changing trends among several excess-type layers on the same business tend to be closely related. The changes in
Reserving for multiple excess layers Ben Zehnwirth and Glen Barnett Abstract Patterns and changing trends among several excess-type layers on the same business tend to be closely related. The changes in
Lycka till!
 Avd. Matematisk statistik TENTAMEN I SF294 SANNOLIKHETSTEORI/EXAM IN SF294 PROBABILITY THE- ORY MONDAY THE 14 T H OF JANUARY 28 14. p.m. 19. p.m. Examinator : Timo Koski, tel. 79 71 34, e-post: timo@math.kth.se
Avd. Matematisk statistik TENTAMEN I SF294 SANNOLIKHETSTEORI/EXAM IN SF294 PROBABILITY THE- ORY MONDAY THE 14 T H OF JANUARY 28 14. p.m. 19. p.m. Examinator : Timo Koski, tel. 79 71 34, e-post: timo@math.kth.se
Figure 10.1: Recording when the event E occurs
 10 Poisson Processes Let T R be an interval. A family of random variables {X(t) ; t T} is called a continuous time stochastic process. We often consider T = [0, 1] and T = [0, ). As X(t) is a random variable
10 Poisson Processes Let T R be an interval. A family of random variables {X(t) ; t T} is called a continuous time stochastic process. We often consider T = [0, 1] and T = [0, ). As X(t) is a random variable
Errata for the ASM Study Manual for Exam P, Fourth Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA
 Errata for the ASM Study Manual for Exam P, Fourth Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Effective July 5, 3, only the latest edition of this manual will have its
Errata for the ASM Study Manual for Exam P, Fourth Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Effective July 5, 3, only the latest edition of this manual will have its
Lecture Notes on Risk Theory
 Lecture Notes on Risk Theory February 2, 21 Contents 1 Introduction and basic definitions 1 2 Accumulated claims in a fixed time interval 3 3 Reinsurance 7 4 Risk processes in discrete time 1 5 The Adjustment
Lecture Notes on Risk Theory February 2, 21 Contents 1 Introduction and basic definitions 1 2 Accumulated claims in a fixed time interval 3 3 Reinsurance 7 4 Risk processes in discrete time 1 5 The Adjustment
Chapter 3: Root Finding. September 26, 2005
 Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
Chapter 3: Root Finding September 26, 2005 Outline 1 Root Finding 2 3.1 The Bisection Method 3 3.2 Newton s Method: Derivation and Examples 4 3.3 How To Stop Newton s Method 5 3.4 Application: Division
MONOTONICITY OF RATIOS INVOLVING INCOMPLETE GAMMA FUNCTIONS WITH ACTUARIAL APPLICATIONS
 MONOTONICITY OF RATIOS INVOLVING INCOMPLETE GAMMA FUNCTIONS WITH ACTUARIAL APPLICATIONS EDWARD FURMAN Department of Mathematics and Statistics York University Toronto, Ontario M3J 1P3, Canada EMail: efurman@mathstat.yorku.ca
MONOTONICITY OF RATIOS INVOLVING INCOMPLETE GAMMA FUNCTIONS WITH ACTUARIAL APPLICATIONS EDWARD FURMAN Department of Mathematics and Statistics York University Toronto, Ontario M3J 1P3, Canada EMail: efurman@mathstat.yorku.ca
Business and Life Calculus
 Business and Life Calculus George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 2 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 203 / 55
Business and Life Calculus George Voutsadakis Mathematics and Computer Science Lake Superior State University LSSU Math 2 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 203 / 55
Measuring the effects of reinsurance by the adjustment coefficient in the Sparre Anderson model
 Measuring the effects of reinsurance by the adjustment coefficient in the Sparre Anderson model Centeno, Maria de Lourdes CEMAPRE, ISEG, Technical University of Lisbon and Centre for Actuarial Studies,
Measuring the effects of reinsurance by the adjustment coefficient in the Sparre Anderson model Centeno, Maria de Lourdes CEMAPRE, ISEG, Technical University of Lisbon and Centre for Actuarial Studies,
Stability of the Defect Renewal Volterra Integral Equations
 19th International Congress on Modelling and Simulation, Perth, Australia, 12 16 December 211 http://mssanz.org.au/modsim211 Stability of the Defect Renewal Volterra Integral Equations R. S. Anderssen,
19th International Congress on Modelling and Simulation, Perth, Australia, 12 16 December 211 http://mssanz.org.au/modsim211 Stability of the Defect Renewal Volterra Integral Equations R. S. Anderssen,
The finite-time Gerber-Shiu penalty function for two classes of risk processes
 The finite-time Gerber-Shiu penalty function for two classes of risk processes July 10, 2014 49 th Actuarial Research Conference University of California, Santa Barbara, July 13 July 16, 2014 The finite
The finite-time Gerber-Shiu penalty function for two classes of risk processes July 10, 2014 49 th Actuarial Research Conference University of California, Santa Barbara, July 13 July 16, 2014 The finite
Ruin Probabilities of a Discrete-time Multi-risk Model
 Ruin Probabilities of a Discrete-time Multi-risk Model Andrius Grigutis, Agneška Korvel, Jonas Šiaulys Faculty of Mathematics and Informatics, Vilnius University, Naugarduko 4, Vilnius LT-035, Lithuania
Ruin Probabilities of a Discrete-time Multi-risk Model Andrius Grigutis, Agneška Korvel, Jonas Šiaulys Faculty of Mathematics and Informatics, Vilnius University, Naugarduko 4, Vilnius LT-035, Lithuania
Math RE - Calculus II Antiderivatives and the Indefinite Integral Page 1 of 5
 Math 201-203-RE - Calculus II Antiderivatives and the Indefinite Integral Page 1 of 5 What is the Antiderivative? In a derivative problem, a function f(x) is given and you find the derivative f (x) using
Math 201-203-RE - Calculus II Antiderivatives and the Indefinite Integral Page 1 of 5 What is the Antiderivative? In a derivative problem, a function f(x) is given and you find the derivative f (x) using
LUNG CHEUNG GOVERNMENT SECONDARY SCHOOL Mock Examination 2006 / 2007 Mathematics and Statistics
 S.7 LUNG CHEUNG GOVERNMENT SECONDARY SCHOOL Mock Examination 006 / 007 Mathematics and Statistics Maximum Mark: 100 Date: 1 007 Time: 8 30 11 30 1. This paper consists of Section A and Section B.. Answer
S.7 LUNG CHEUNG GOVERNMENT SECONDARY SCHOOL Mock Examination 006 / 007 Mathematics and Statistics Maximum Mark: 100 Date: 1 007 Time: 8 30 11 30 1. This paper consists of Section A and Section B.. Answer
Review. The derivative of y = f(x) has four levels of meaning: Physical: If y is a quantity depending on x, the derivative dy
 Math 132 Area and Distance Stewart 4.1/I Review. The derivative of y = f(x) has four levels of meaning: Physical: If y is a quantity depending on x, the derivative dy dx x=a is the rate of change of y
Math 132 Area and Distance Stewart 4.1/I Review. The derivative of y = f(x) has four levels of meaning: Physical: If y is a quantity depending on x, the derivative dy dx x=a is the rate of change of y
Upper Bounds for the Ruin Probability in a Risk Model With Interest WhosePremiumsDependonthe Backward Recurrence Time Process
 Λ4flΛ4» ν ff ff χ Vol.4, No.4 211 8fl ADVANCES IN MATHEMATICS Aug., 211 Upper Bounds for the Ruin Probability in a Risk Model With Interest WhosePremiumsDependonthe Backward Recurrence Time Process HE
Λ4flΛ4» ν ff ff χ Vol.4, No.4 211 8fl ADVANCES IN MATHEMATICS Aug., 211 Upper Bounds for the Ruin Probability in a Risk Model With Interest WhosePremiumsDependonthe Backward Recurrence Time Process HE
Solutions to Math 41 Final Exam December 10, 2012
 Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
Solutions to Math 4 Final Exam December,. ( points) Find each of the following limits, with justification. If there is an infinite limit, then explain whether it is or. x ln(t + ) dt (a) lim x x (5 points)
APPROXIMATIONS OF RUIN PROBABILITY BY DI-ATOMIC OR DI-EXPONENTIAL CLAIMS. University of Toronto, Canada
 APPROXIMATIONS OF RUIN PROBABILITY BY DI-ATOMIC OR DI-EXPONENTIAL CLAIMS BY JOSHUA BABIER AND BEDA CHAN University of Toronto, Canada A BSTRACT The sensitivity of the ruin probability depending on the
APPROXIMATIONS OF RUIN PROBABILITY BY DI-ATOMIC OR DI-EXPONENTIAL CLAIMS BY JOSHUA BABIER AND BEDA CHAN University of Toronto, Canada A BSTRACT The sensitivity of the ruin probability depending on the
MATH 1325 Business Calculus Guided Notes
 MATH 135 Business Calculus Guided Notes LSC North Harris By Isabella Fisher Section.1 Functions and Theirs Graphs A is a rule that assigns to each element in one and only one element in. Set A Set B Set
MATH 135 Business Calculus Guided Notes LSC North Harris By Isabella Fisher Section.1 Functions and Theirs Graphs A is a rule that assigns to each element in one and only one element in. Set A Set B Set
1. If X has density. cx 3 e x ), 0 x < 0, otherwise. Find the value of c that makes f a probability density. f(x) =
 1. If X has density f(x) = { cx 3 e x ), 0 x < 0, otherwise. Find the value of c that makes f a probability density. 2. Let X have density f(x) = { xe x, 0 < x < 0, otherwise. (a) Find P (X > 2). (b) Find
1. If X has density f(x) = { cx 3 e x ), 0 x < 0, otherwise. Find the value of c that makes f a probability density. 2. Let X have density f(x) = { xe x, 0 < x < 0, otherwise. (a) Find P (X > 2). (b) Find
ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA Errata
 ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
Ruin probabilities of the Parisian type for small claims
 Ruin probabilities of the Parisian type for small claims Angelos Dassios, Shanle Wu October 6, 28 Abstract In this paper, we extend the concept of ruin in risk theory to the Parisian type of ruin. For
Ruin probabilities of the Parisian type for small claims Angelos Dassios, Shanle Wu October 6, 28 Abstract In this paper, we extend the concept of ruin in risk theory to the Parisian type of ruin. For
I. Setting the problem
 APPROXATONS OF THE GENERALSED POSSON FUNCTON LAUR (AUPP and PERTT OJANTAKANEN Helsinki. Setting the problem One of the basic functions of risk theory is the so-called generalised Poisson function F(x),
APPROXATONS OF THE GENERALSED POSSON FUNCTON LAUR (AUPP and PERTT OJANTAKANEN Helsinki. Setting the problem One of the basic functions of risk theory is the so-called generalised Poisson function F(x),
Algebra 1 S1 Lesson Summaries. Lesson Goal: Mastery 70% or higher
 Algebra 1 S1 Lesson Summaries For every lesson, you need to: Read through the LESSON REVIEW which is located below or on the last page of the lesson and 3-hole punch into your MATH BINDER. Read and work
Algebra 1 S1 Lesson Summaries For every lesson, you need to: Read through the LESSON REVIEW which is located below or on the last page of the lesson and 3-hole punch into your MATH BINDER. Read and work
Stochastic integral. Introduction. Ito integral. References. Appendices Stochastic Calculus I. Geneviève Gauthier.
 Ito 8-646-8 Calculus I Geneviève Gauthier HEC Montréal Riemann Ito The Ito The theories of stochastic and stochastic di erential equations have initially been developed by Kiyosi Ito around 194 (one of
Ito 8-646-8 Calculus I Geneviève Gauthier HEC Montréal Riemann Ito The Ito The theories of stochastic and stochastic di erential equations have initially been developed by Kiyosi Ito around 194 (one of
Chapter 1: Fundamentals of Algebra Lecture notes Math 1010
 Section 1.1: The Real Number System Definition of set and subset A set is a collection of objects and its objects are called members. If all the members of a set A are also members of a set B, then A is
Section 1.1: The Real Number System Definition of set and subset A set is a collection of objects and its objects are called members. If all the members of a set A are also members of a set B, then A is
MATH150-E01 Test #2 Summer 2016 Show all work. Name 1. Find an equation in slope-intercept form for the line through (4, 2) and (1, 3).
 1. Find an equation in slope-intercept form for the line through (4, 2) and (1, 3). 2. Let the supply and demand functions for sugar be given by p = S(q) = 1.4q 0.6 and p = D(q) = 2q + 3.2 where p is the
1. Find an equation in slope-intercept form for the line through (4, 2) and (1, 3). 2. Let the supply and demand functions for sugar be given by p = S(q) = 1.4q 0.6 and p = D(q) = 2q + 3.2 where p is the
Lecture 6: Finite Fields
 CCS Discrete Math I Professor: Padraic Bartlett Lecture 6: Finite Fields Week 6 UCSB 2014 It ain t what they call you, it s what you answer to. W. C. Fields 1 Fields In the next two weeks, we re going
CCS Discrete Math I Professor: Padraic Bartlett Lecture 6: Finite Fields Week 6 UCSB 2014 It ain t what they call you, it s what you answer to. W. C. Fields 1 Fields In the next two weeks, we re going
THREE METHODS TO CALCULATE THE PROBABILITY OF RUIN. University of Lausanne, Switzerland
 THREE METHODS TO CALCULATE THE PROBABILITY OF RUIN BY FRANCOIS DUFRESNE AND HANS U. GERBER University of Lausanne, Switzerland ABSTRACT The first method, essentially due to GOOVAERTS and DE VYLDER, uses
THREE METHODS TO CALCULATE THE PROBABILITY OF RUIN BY FRANCOIS DUFRESNE AND HANS U. GERBER University of Lausanne, Switzerland ABSTRACT The first method, essentially due to GOOVAERTS and DE VYLDER, uses
Math Essentials of Calculus by James Stewart Prepared by Jason Gaddis
 Math 231 - Essentials of Calculus by James Stewart Prepared by Jason Gaddis Chapter 3 - Applications of Differentiation 3.1 - Maximum and Minimum Values Note We continue our study of functions using derivatives.
Math 231 - Essentials of Calculus by James Stewart Prepared by Jason Gaddis Chapter 3 - Applications of Differentiation 3.1 - Maximum and Minimum Values Note We continue our study of functions using derivatives.
A polynomial expansion to approximate ruin probabilities
 A polynomial expansion to approximate ruin probabilities P.O. Goffard 1 X. Guerrault 2 S. Loisel 3 D. Pommerêt 4 1 Axa France - Institut de mathématiques de Luminy Université de Aix-Marseille 2 Axa France
A polynomial expansion to approximate ruin probabilities P.O. Goffard 1 X. Guerrault 2 S. Loisel 3 D. Pommerêt 4 1 Axa France - Institut de mathématiques de Luminy Université de Aix-Marseille 2 Axa France
An Introduction to Probability Theory and Its Applications
 An Introduction to Probability Theory and Its Applications WILLIAM FELLER (1906-1970) Eugene Higgins Professor of Mathematics Princeton University VOLUME II SECOND EDITION JOHN WILEY & SONS Contents I
An Introduction to Probability Theory and Its Applications WILLIAM FELLER (1906-1970) Eugene Higgins Professor of Mathematics Princeton University VOLUME II SECOND EDITION JOHN WILEY & SONS Contents I
Solutions to the Spring 2015 CAS Exam ST
 Solutions to the Spring 2015 CAS Exam ST (updated to include the CAS Final Answer Key of July 15) There were 25 questions in total, of equal value, on this 2.5 hour exam. There was a 10 minute reading
Solutions to the Spring 2015 CAS Exam ST (updated to include the CAS Final Answer Key of July 15) There were 25 questions in total, of equal value, on this 2.5 hour exam. There was a 10 minute reading
EXPERIENCE-BASED LONGEVITY ASSESSMENT
 EXPERIENCE-BASED LONGEVITY ASSESSMENT ERMANNO PITACCO Università di Trieste ermanno.pitacco@econ.units.it p. 1/55 Agenda Introduction Stochastic modeling: the process risk Uncertainty in future mortality
EXPERIENCE-BASED LONGEVITY ASSESSMENT ERMANNO PITACCO Università di Trieste ermanno.pitacco@econ.units.it p. 1/55 Agenda Introduction Stochastic modeling: the process risk Uncertainty in future mortality
Mathematics for Economics ECON MA/MSSc in Economics-2017/2018. Dr. W. M. Semasinghe Senior Lecturer Department of Economics
 Mathematics for Economics ECON 53035 MA/MSSc in Economics-2017/2018 Dr. W. M. Semasinghe Senior Lecturer Department of Economics MATHEMATICS AND STATISTICS LERNING OUTCOMES: By the end of this course unit
Mathematics for Economics ECON 53035 MA/MSSc in Economics-2017/2018 Dr. W. M. Semasinghe Senior Lecturer Department of Economics MATHEMATICS AND STATISTICS LERNING OUTCOMES: By the end of this course unit
STA2603/205/1/2014 /2014. ry II. Tutorial letter 205/1/
 STA263/25//24 Tutorial letter 25// /24 Distribution Theor ry II STA263 Semester Department of Statistics CONTENTS: Examination preparation tutorial letterr Solutions to Assignment 6 2 Dear Student, This
STA263/25//24 Tutorial letter 25// /24 Distribution Theor ry II STA263 Semester Department of Statistics CONTENTS: Examination preparation tutorial letterr Solutions to Assignment 6 2 Dear Student, This
INTERNET MAT 117. Solution for the Review Problems. (1) Let us consider the circle with equation. x 2 + 2x + y 2 + 3y = 3 4. (x + 1) 2 + (y + 3 2
 INTERNET MAT 117 Solution for the Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (i) Group
INTERNET MAT 117 Solution for the Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (i) Group
1 Gambler s Ruin Problem
 1 Gambler s Ruin Problem Consider a gambler who starts with an initial fortune of $1 and then on each successive gamble either wins $1 or loses $1 independent of the past with probabilities p and q = 1
1 Gambler s Ruin Problem Consider a gambler who starts with an initial fortune of $1 and then on each successive gamble either wins $1 or loses $1 independent of the past with probabilities p and q = 1
UNIVERSITY OF KWA-ZULU NATAL
 UNIVERSITY OF KWA-ZULU NATAL EXAMINATIONS: June 006 Solutions Subject, course and code: Mathematics 34 MATH34P Multiple Choice Answers. B. B 3. E 4. E 5. C 6. A 7. A 8. C 9. A 0. D. C. A 3. D 4. E 5. B
UNIVERSITY OF KWA-ZULU NATAL EXAMINATIONS: June 006 Solutions Subject, course and code: Mathematics 34 MATH34P Multiple Choice Answers. B. B 3. E 4. E 5. C 6. A 7. A 8. C 9. A 0. D. C. A 3. D 4. E 5. B
On Finite-Time Ruin Probabilities in a Risk Model Under Quota Share Reinsurance
 Applied Mathematical Sciences, Vol. 11, 217, no. 53, 269-2629 HIKARI Ltd, www.m-hikari.com https://doi.org/1.12988/ams.217.7824 On Finite-Time Ruin Probabilities in a Risk Model Under Quota Share Reinsurance
Applied Mathematical Sciences, Vol. 11, 217, no. 53, 269-2629 HIKARI Ltd, www.m-hikari.com https://doi.org/1.12988/ams.217.7824 On Finite-Time Ruin Probabilities in a Risk Model Under Quota Share Reinsurance
MATH1190 CALCULUS 1 - NOTES AND AFTERNOTES
 MATH90 CALCULUS - NOTES AND AFTERNOTES DR. JOSIP DERADO. Historical background Newton approach - from physics to calculus. Instantaneous velocity. Leibniz approach - from geometry to calculus Calculus
MATH90 CALCULUS - NOTES AND AFTERNOTES DR. JOSIP DERADO. Historical background Newton approach - from physics to calculus. Instantaneous velocity. Leibniz approach - from geometry to calculus Calculus
MA Lesson 12 Notes Section 3.4 of Calculus part of textbook
 MA 15910 Lesson 1 Notes Section 3.4 of Calculus part of textbook Tangent Line to a curve: To understand the tangent line, we must first discuss a secant line. A secant line will intersect a curve at more
MA 15910 Lesson 1 Notes Section 3.4 of Calculus part of textbook Tangent Line to a curve: To understand the tangent line, we must first discuss a secant line. A secant line will intersect a curve at more
ABC methods for phase-type distributions with applications in insurance risk problems
 ABC methods for phase-type with applications problems Concepcion Ausin, Department of Statistics, Universidad Carlos III de Madrid Joint work with: Pedro Galeano, Universidad Carlos III de Madrid Simon
ABC methods for phase-type with applications problems Concepcion Ausin, Department of Statistics, Universidad Carlos III de Madrid Joint work with: Pedro Galeano, Universidad Carlos III de Madrid Simon
Math 211 Business Calculus TEST 3. Question 1. Section 2.2. Second Derivative Test.
 Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. p. 1/?? Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. Question 2. Section 2.3. Graph
Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. p. 1/?? Math 211 Business Calculus TEST 3 Question 1. Section 2.2. Second Derivative Test. Question 2. Section 2.3. Graph
IEOR 3106: Introduction to Operations Research: Stochastic Models. Professor Whitt. SOLUTIONS to Homework Assignment 2
 IEOR 316: Introduction to Operations Research: Stochastic Models Professor Whitt SOLUTIONS to Homework Assignment 2 More Probability Review: In the Ross textbook, Introduction to Probability Models, read
IEOR 316: Introduction to Operations Research: Stochastic Models Professor Whitt SOLUTIONS to Homework Assignment 2 More Probability Review: In the Ross textbook, Introduction to Probability Models, read
THE LINDEBERG-FELLER CENTRAL LIMIT THEOREM VIA ZERO BIAS TRANSFORMATION
 THE LINDEBERG-FELLER CENTRAL LIMIT THEOREM VIA ZERO BIAS TRANSFORMATION JAINUL VAGHASIA Contents. Introduction. Notations 3. Background in Probability Theory 3.. Expectation and Variance 3.. Convergence
THE LINDEBERG-FELLER CENTRAL LIMIT THEOREM VIA ZERO BIAS TRANSFORMATION JAINUL VAGHASIA Contents. Introduction. Notations 3. Background in Probability Theory 3.. Expectation and Variance 3.. Convergence
LIMITS AND DERIVATIVES
 2 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES 2.2 The Limit of a Function In this section, we will learn: About limits in general and about numerical and graphical methods for computing them. THE LIMIT
2 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES 2.2 The Limit of a Function In this section, we will learn: About limits in general and about numerical and graphical methods for computing them. THE LIMIT
Functions. A function is a rule that gives exactly one output number to each input number.
 Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us? The set of all input numbers to which the rule applies is called the domain of the function.
Functions A function is a rule that gives exactly one output number to each input number. Why it is important to us? The set of all input numbers to which the rule applies is called the domain of the function.
RMSC 2001 Introduction to Risk Management
 RMSC 2001 Introduction to Risk Management Tutorial 4 (2011/12) 1 February 20, 2012 Outline: 1. Failure Time 2. Loss Frequency 3. Loss Severity 4. Aggregate Claim ====================================================
RMSC 2001 Introduction to Risk Management Tutorial 4 (2011/12) 1 February 20, 2012 Outline: 1. Failure Time 2. Loss Frequency 3. Loss Severity 4. Aggregate Claim ====================================================
INTERNET MAT 117 Review Problems. (1) Let us consider the circle with equation. (b) Find the center and the radius of the circle given above.
 INTERNET MAT 117 Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (b) Find the center and
INTERNET MAT 117 Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (b) Find the center and
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics Unit 2 Limits and Continuity
 Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Advanced Mathematics 3208 Unit 2 Limits and Continuity NEED TO KNOW Expanding Expanding Expand the following: A) (a + b) 2 B) (a + b) 3 C) (a + b)4 Pascals Triangle: D) (x + 2) 4 E) (2x -3) 5 Random Factoring
Math 106 Answers to Exam 1a Fall 2015
 Math 06 Answers to Exam a Fall 05.. Find the derivative of the following functions. Do not simplify your answers. (a) f(x) = ex cos x x + (b) g(z) = [ sin(z ) + e z] 5 Using the quotient rule on f(x) and
Math 06 Answers to Exam a Fall 05.. Find the derivative of the following functions. Do not simplify your answers. (a) f(x) = ex cos x x + (b) g(z) = [ sin(z ) + e z] 5 Using the quotient rule on f(x) and
Math 261 Calculus I. Test 1 Study Guide. Name. Decide whether the limit exists. If it exists, find its value. 1) lim x 1. f(x) 2) lim x -1/2 f(x)
 Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
Math 261 Calculus I Test 1 Study Guide Name Decide whether the it exists. If it exists, find its value. 1) x 1 f(x) 2) x -1/2 f(x) Complete the table and use the result to find the indicated it. 3) If
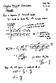 121 Section 3.1 Example 3.6.9 (Higher-order Poisson moments) g(x) = x2 and use (3.6.5): For X '" Poisson{A), take E(AX2 ) = E (X(X - 1) 2 ) E(X3-2X2 + X). Therefore, the third moment of a Poisson( ). )
121 Section 3.1 Example 3.6.9 (Higher-order Poisson moments) g(x) = x2 and use (3.6.5): For X '" Poisson{A), take E(AX2 ) = E (X(X - 1) 2 ) E(X3-2X2 + X). Therefore, the third moment of a Poisson( ). )
2.2. Limits Involving Infinity. Copyright 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall
 2.2 Limits Involving Infinity Copyright 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Finite Limits as x ± What you ll learn about Sandwich Theorem Revisited Infinite Limits as x a End
2.2 Limits Involving Infinity Copyright 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Finite Limits as x ± What you ll learn about Sandwich Theorem Revisited Infinite Limits as x a End
SPRING 2005 EXAM M SOLUTIONS. = When (as given in the problem), (x) dies in the second year from issue, the curtate future lifetime x + 1 is 0, so
 SPRING 005 EXAM M SOLUTIONS Question # Key: B Let K be the curtate future lifetime of (x + k) K + k L 000v 000Px :3 ak + When (as given in the problem), (x) dies in the second year from issue, the curtate
SPRING 005 EXAM M SOLUTIONS Question # Key: B Let K be the curtate future lifetime of (x + k) K + k L 000v 000Px :3 ak + When (as given in the problem), (x) dies in the second year from issue, the curtate
Sequences and series UNCORRECTED PAGE PROOFS
 3 Sequences and series 3.1 Kick off with CAS 3. Describing sequences 3.3 Arithmetic sequences 3.4 Arithmetic series 3.5 Geometric sequences 3.6 Geometric series 3.7 Applications of sequences and series
3 Sequences and series 3.1 Kick off with CAS 3. Describing sequences 3.3 Arithmetic sequences 3.4 Arithmetic series 3.5 Geometric sequences 3.6 Geometric series 3.7 Applications of sequences and series
M(t) = 1 t. (1 t), 6 M (0) = 20 P (95. X i 110) i=1
 Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
Math 66/566 - Midterm Solutions NOTE: These solutions are for both the 66 and 566 exam. The problems are the same until questions and 5. 1. The moment generating function of a random variable X is M(t)
2. (12 points) Find an equation for the line tangent to the graph of f(x) =
 November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
Errata and Updates for ASM Exam LTAM (First Edition Second Printing) Sorted by Page
 Errata for ASM Exam LTAM Study Manual (First Edition Second Printing) Sorted by Page Errata and Updates for ASM Exam LTAM (First Edition Second Printing) Sorted by Page Practice Exam 0:A7, 2:A7, and 2:A8
Errata for ASM Exam LTAM Study Manual (First Edition Second Printing) Sorted by Page Errata and Updates for ASM Exam LTAM (First Edition Second Printing) Sorted by Page Practice Exam 0:A7, 2:A7, and 2:A8
Errata and Updates for ASM Exam LTAM (First Edition Second Printing) Sorted by Date
 Errata for ASM Exam LTAM Study Manual (First Edition Second Printing) Sorted by Date Errata and Updates for ASM Exam LTAM (First Edition Second Printing) Sorted by Date Practice Exam 0:A7, 2:A7, and 2:A8
Errata for ASM Exam LTAM Study Manual (First Edition Second Printing) Sorted by Date Errata and Updates for ASM Exam LTAM (First Edition Second Printing) Sorted by Date Practice Exam 0:A7, 2:A7, and 2:A8
Arithmetic Operations. The real numbers have the following properties: In particular, putting a 1 in the Distributive Law, we get
 MCA AP Calculus AB Summer Assignment The following packet is a review of many of the skills needed as we begin the study of Calculus. There two major sections to this review. Pages 2-9 are review examples
MCA AP Calculus AB Summer Assignment The following packet is a review of many of the skills needed as we begin the study of Calculus. There two major sections to this review. Pages 2-9 are review examples
The Growth of Functions. A Practical Introduction with as Little Theory as possible
 The Growth of Functions A Practical Introduction with as Little Theory as possible Complexity of Algorithms (1) Before we talk about the growth of functions and the concept of order, let s discuss why
The Growth of Functions A Practical Introduction with as Little Theory as possible Complexity of Algorithms (1) Before we talk about the growth of functions and the concept of order, let s discuss why
A NOTE ON THE RUIN PROBLEM FOR A CLASS OF STOCHASTIC PROCESSES WITH INTERCHANGEABLE INCREMENTS
 A NOTE ON THE RUIN PROBLEM FOR A CLASS OF STOCHASTIC PROCESSES WITH INTERCHANGEABLE INCREMENTS,JAN GRANDELL and LARS PEIRAM University of Stockholm SUMMARY Models for the risk business of an insurance
A NOTE ON THE RUIN PROBLEM FOR A CLASS OF STOCHASTIC PROCESSES WITH INTERCHANGEABLE INCREMENTS,JAN GRANDELL and LARS PEIRAM University of Stockholm SUMMARY Models for the risk business of an insurance
f X (x) = λe λx, , x 0, k 0, λ > 0 Γ (k) f X (u)f X (z u)du
 11 COLLECTED PROBLEMS Do the following problems for coursework 1. Problems 11.4 and 11.5 constitute one exercise leading you through the basic ruin arguments. 2. Problems 11.1 through to 11.13 but excluding
11 COLLECTED PROBLEMS Do the following problems for coursework 1. Problems 11.4 and 11.5 constitute one exercise leading you through the basic ruin arguments. 2. Problems 11.1 through to 11.13 but excluding
MATH 115 FIRST MIDTERM EXAM SOLUTIONS
 MATH 5 FIRST MIDTERM EXAM SOLUTIONS. ( points each) Circle or False for each of the following problems. Circle only is the statement is always true. No explanation is necessary. (a) log( A ) = log(a).
MATH 5 FIRST MIDTERM EXAM SOLUTIONS. ( points each) Circle or False for each of the following problems. Circle only is the statement is always true. No explanation is necessary. (a) log( A ) = log(a).
November 2000 Course 1. Society of Actuaries/Casualty Actuarial Society
 November 2000 Course 1 Society of Actuaries/Casualty Actuarial Society 1. A recent study indicates that the annual cost of maintaining and repairing a car in a town in Ontario averages 200 with a variance
November 2000 Course 1 Society of Actuaries/Casualty Actuarial Society 1. A recent study indicates that the annual cost of maintaining and repairing a car in a town in Ontario averages 200 with a variance
MTH4100 Calculus I. Bill Jackson School of Mathematical Sciences QMUL. Week 9, Semester 1, 2013
 MTH4100 School of Mathematical Sciences QMUL Week 9, Semester 1, 2013 Concavity Concavity In the literature concave up is often referred to as convex, and concave down is simply called concave. The second
MTH4100 School of Mathematical Sciences QMUL Week 9, Semester 1, 2013 Concavity Concavity In the literature concave up is often referred to as convex, and concave down is simply called concave. The second
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY
 EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 2015 MODULE 1 : Probability distributions Time allowed: Three hours Candidates should answer FIVE questions. All questions carry equal marks.
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 2015 MODULE 1 : Probability distributions Time allowed: Three hours Candidates should answer FIVE questions. All questions carry equal marks.
Arkansas Tech University MATH 3513: Applied Statistics I Dr. Marcel B. Finan
 2.4 Random Variables Arkansas Tech University MATH 3513: Applied Statistics I Dr. Marcel B. Finan By definition, a random variable X is a function with domain the sample space and range a subset of the
2.4 Random Variables Arkansas Tech University MATH 3513: Applied Statistics I Dr. Marcel B. Finan By definition, a random variable X is a function with domain the sample space and range a subset of the
THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA
 THE ROYAL STATISTICAL SOCIETY 4 EXAINATIONS SOLUTIONS GRADUATE DIPLOA PAPER I STATISTICAL THEORY & ETHODS The Societ provides these solutions to assist candidates preparing for the examinations in future
THE ROYAL STATISTICAL SOCIETY 4 EXAINATIONS SOLUTIONS GRADUATE DIPLOA PAPER I STATISTICAL THEORY & ETHODS The Societ provides these solutions to assist candidates preparing for the examinations in future
Actuarial Science Exam 1/P
 Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
Actuarial Science Exam /P Ville A. Satopää December 5, 2009 Contents Review of Algebra and Calculus 2 2 Basic Probability Concepts 3 3 Conditional Probability and Independence 4 4 Combinatorial Principles,
Math 3338, Homework 4. f(u)du. (Note that f is discontinuous, whereas F is continuous everywhere.)
 Math 3338, Homework 4. Define a function f by f(x) = { if x < if x < if x. Calculate an explicit formula for F(x) x f(u)du. (Note that f is discontinuous, whereas F is continuous everywhere.) 2. Define
Math 3338, Homework 4. Define a function f by f(x) = { if x < if x < if x. Calculate an explicit formula for F(x) x f(u)du. (Note that f is discontinuous, whereas F is continuous everywhere.) 2. Define
1 (t + 4)(t 1) dt. Solution: The denominator of the integrand is already factored with the factors being distinct, so 1 (t + 4)(t 1) = A
 Calculus Topic: Integration of Rational Functions Section 8. # 0: Evaluate the integral (t + )(t ) Solution: The denominator of the integrand is already factored with the factors being distinct, so (t
Calculus Topic: Integration of Rational Functions Section 8. # 0: Evaluate the integral (t + )(t ) Solution: The denominator of the integrand is already factored with the factors being distinct, so (t
FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 2016 MAT 133Y1Y Calculus and Linear Algebra for Commerce
 FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 206 MAT YY Calculus and Linear Algebra for Commerce Duration: Examiners: hours N. Hoell A. Igelfeld D. Reiss L. Shorser J. Tate
FACULTY OF ARTS AND SCIENCE University of Toronto FINAL EXAMINATIONS, APRIL 206 MAT YY Calculus and Linear Algebra for Commerce Duration: Examiners: hours N. Hoell A. Igelfeld D. Reiss L. Shorser J. Tate
Notes for Math 324, Part 17
 126 Notes for Math 324, Part 17 Chapter 17 Common discrete distributions 17.1 Binomial Consider an experiment consisting by a series of trials. The only possible outcomes of the trials are success and
126 Notes for Math 324, Part 17 Chapter 17 Common discrete distributions 17.1 Binomial Consider an experiment consisting by a series of trials. The only possible outcomes of the trials are success and
Experience Rating in General Insurance by Credibility Estimation
 Experience Rating in General Insurance by Credibility Estimation Xian Zhou Department of Applied Finance and Actuarial Studies Macquarie University, Sydney, Australia Abstract This work presents a new
Experience Rating in General Insurance by Credibility Estimation Xian Zhou Department of Applied Finance and Actuarial Studies Macquarie University, Sydney, Australia Abstract This work presents a new
Introduction to Rare Event Simulation
 Introduction to Rare Event Simulation Brown University: Summer School on Rare Event Simulation Jose Blanchet Columbia University. Department of Statistics, Department of IEOR. Blanchet (Columbia) 1 / 31
Introduction to Rare Event Simulation Brown University: Summer School on Rare Event Simulation Jose Blanchet Columbia University. Department of Statistics, Department of IEOR. Blanchet (Columbia) 1 / 31
AP Calculus Chapter 3 Testbank (Mr. Surowski)
 AP Calculus Chapter 3 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.). If f(x) = 0x 4 3 + x, then f (8) = (A) (B) 4 3 (C) 83 3 (D) 2 3 (E) 2
AP Calculus Chapter 3 Testbank (Mr. Surowski) Part I. Multiple-Choice Questions (5 points each; please circle the correct answer.). If f(x) = 0x 4 3 + x, then f (8) = (A) (B) 4 3 (C) 83 3 (D) 2 3 (E) 2
DELTA METHOD and RESERVING
 XXXVI th ASTIN COLLOQUIUM Zurich, 4 6 September 2005 DELTA METHOD and RESERVING C.PARTRAT, Lyon 1 university (ISFA) N.PEY, AXA Canada J.SCHILLING, GIE AXA Introduction Presentation of methods based on
XXXVI th ASTIN COLLOQUIUM Zurich, 4 6 September 2005 DELTA METHOD and RESERVING C.PARTRAT, Lyon 1 university (ISFA) N.PEY, AXA Canada J.SCHILLING, GIE AXA Introduction Presentation of methods based on
Bridging the Gap between Center and Tail for Multiscale Processes
 Bridging the Gap between Center and Tail for Multiscale Processes Matthew R. Morse Department of Mathematics and Statistics Boston University BU-Keio 2016, August 16 Matthew R. Morse (BU) Moderate Deviations
Bridging the Gap between Center and Tail for Multiscale Processes Matthew R. Morse Department of Mathematics and Statistics Boston University BU-Keio 2016, August 16 Matthew R. Morse (BU) Moderate Deviations
