Reachability in Petri nets with Inhibitor arcs
|
|
|
- Violet Hannah Shelton
- 5 years ago
- Views:
Transcription
1 Reachability in Petri nets with Inhibitor arcs Klaus Reinhardt Universität Tübingen
2 Overview Multisets, New operators Q and Q on multisets, Semilinearity Petri nets, Inhibitor arcs The reachability relation for Petri nets with one inhibitor arc Nested Petri Nets as normal form for expressions new Overview: Decision algorithm, Logic, Automata
3 Multisets We write a multiset f N B as a set {b f (b) b B}, as a table [ b1 or as an n-ary vector A B N A N B f(b 1 ) f(b ). f(b n ). f N A g N B (f + g) N A B f (b 1 ), b f (b n ) f (b ),..., b n ] /0 with /0(x) = 0 for all x is neutral element for +. N A N B = N A B
4 sgn(f) := {a f(a) > 0}, sgn(m) := f M sgn(f). Restriction: f A := {b f(b) b A} f A := {b f(b) b A}, thus f = f A +f A. A set M = {m 1,...,m k } N A of multi-sets generate linear combinations: M := {a 1 m a k m k i k a i N} More generally, by M 0 := {/0} and M i+1 := M i + M, we can define M := i M i. Linear set: m c + M. Semilinear set: finite union of linear sets. Semilinear sets: Smallest class of sets of multisets containing all finite sets of multisets and being closed under,+ and. [GS65],[ES69]: The semilinear sets are also closed under.
5 New operators Q and Q on multisets For an unambiguous and injective binary relation Q and two sets of Multisets M and N we define { } N Q M := n π1 (Q) +m π (Q) n N,m M, (a,b) Q n(a) = m(b). For example, or { {, , } 5 {(b1,b )} } { {(b3,b 3 )} {, ,, 7 5 3, } 5 3 = } { 8 6 =, { ( , ) (, )} }
6 For π 1 (Q) and π (Q) disjoint, we define Id Q := {{a 1,b 1} (a,b) Q} which is the neutral element for Q. Obviously, it holds N /0 M = N+M which makes + with the neutral element Id /0 = {/0} a special case of the Q operator. Furthermore, for Q with π 1 (Q) and π (Q) disjoint, we define Q (M) as the closure of M Id Q under Q and the addition /0. In other words, 0 Q (M) := Id Q, i+1 Q (M) := i Q (M) QM + Id Q and Q (M) := i i Q (M). Again, /0(M) = M is a special case.
7 Properties: N Q M = M Q 1N For N,M N A we get N M = N Q L Q M with Q := {(a,a ) a A}, Q := {(a,a) a A} and L := {{a 1,a 1,a 1} a A}. In general, N Q L Q M can only be written without brackets because π 1 (Q ) (sgn(m) \ π (Q )) and π (Q ) (sgn(n) \ π 1 (Q )) are disjoint. If, additionally, π (Q ) and sgn(n) are disjoint and sgn(m) and π 1 (Q )) are disjoint, then N Q L Q M = L Q 1 Q (M + N).
8 Semilinearity Q preserves semilinearity: Assume N and M are semilinear sets over A. N semilinear set over A \ π 1 (Q) π 1 (Q). M semilinear set over A \ π (Q) π (Q). E Q := {{a 1,b 1},{c 1} (a,b) Q,c A} = {f (a,b) Q f(a ) = f(b )} semilinear sets over the set A π 1 (Q) π 1 (Q). Thus, N Q M = ((N + M ) E Q ) π 1 (Q) π 1 (Q) is semilinear. Q does not preserve semilinearity: Let M := {, then {(b3,b )} (M) = a b c } c ba not semilinear.
9 Petri net We describe a Petri net as the triple N = (P,T,W) with the places P, the transitions T and the weight function W N P T T P. A transition t T can fire from a marking m N P to a marking m N P, denoted by m[t m, if m W(.,t) = m W(t,.) N P. A firing sequence w = t 1...t n T can fire from m 0 to m n, denoted by m 0 [w m n, if m 1,...m n 1 exist with m 0 [t 1 m 1 [t...[t n m n. Reachability problem: given net N with start- and end markings m 0,m e N P, decide if there is a w T with m 0 [w m e. [May84][Kos84][Lam9]: decidable.
10 Let P + := {p + p P} and P := {p p P} be copies of the places and ˆP := {(p +, p ) p P}. For m define the corresponding copies m := {p m(p) p P} and m + := {p + m(p) p P}. Reachability relation for a transition t: R(t) := {m + m + } m[t m { = r N P+ P } p P r(p ) W(p,t) = r(p + ) W(t, p) N Reachability relation for a set of transitions T as R(T ) := R(t). Monotonicity: Whenever m[w m, then also (m + n)[w (m + n) for any n N P. t T This corresponds to adding Id P := Id ˆP and R(t) = c t + Id P is a linear set using c t with c t (p ) = W(p,t) and c t (p + ) = W(t, p) for all p P.
11 Concatenation of two firing sequences described by the operator P := ˆP iteration described by P := ˆP. The reachability relation of the petri net N is R(N) := R(T ) := P (R(T )). The reachability problem: (m 0 + m+ e ) R(N). Corollary 1 There is a firing sequence w T with m 0 [w m e in N if and only if m + 0 PR(N) P m e = (m 0 + m+ e ) A R(N) = {/0} for A := {(p, p ),(p +, p + ) p P}. In the other case (m 0 + m+ e ) A R(N) = /0.
12 Inhibitor arcs We describe such a Petri net as the 6-tuple (P,T,W,I,m 0,m e ) with the places P, the transitions T, the weight function W N P T T P, the inhibitor arcs I P T and, the start and end markings m 0,m e N P. We will denote an inhibitor arc in the pictures by. m[t m only if p P (p,t) I m(p) = 0. Lemma 1 Each Petri net (P,T,W,I,m 0,m e ) can be changed in such a way that the condition p P,t T (p,t) I W(t, p) = 0 holds without changing the inhibitor arcs or the reachability problem. p x t
13 x t p p p t t a Lemma Each Petri net (P,T,W,I,m 0,m e ) can be changed in a way such that the condition p P,t T (p,t) I m 0 (p) = m e (p) = 0 holds by changing neither the inhibitor arcs, the condition in Lemma 1 nor the reachability problem.
14 The reachability relation for Petri nets with one inhibitor arc Given a Petri-net (P,T,W,{(p 1, ˆt)},m 0,m e ).w (T \ {ˆt}). R 1 = R((P,T \ {ˆt},W)) = P (R(T \ {ˆt})) R = R 1 {r N P,P + r(p 1 ) = r(p+ 1 ) = 0} R 3 = R R(ˆt) R 4 = P\{p1 } (R 3)
15 Lemma 3 Given a Petri-net (P,T,W,{(p 1, ˆt)},m 0,m e ) with only one inhibitor arc (p 1, ˆt) having the property of lemmata 1 and, then there is a firing sequence w T with m 0 [w m e if and only if m + 0 P\{p 1 } R 4 P\{p1 } m e = (m 0 + m+ e ) A R 4 = {/0} A := {(p, p ),(p +, p + ) p P \ {p 1 }}. In the other case (m 0 + m+ e ) A R 4 = /0
16 t 7 p 3 1 t 8 Example: p ˆt 5 7 p 3 with the start marking {p 4, p 3 } and the end marking {p 4, p 3 3}. We have R(t 7 ) = {p 1, p+ 1 3} + Id P, R(t 8 ) = {p 1, p+ 3 1} + Id P and R(ˆt) = {p 3 7, p+ 5} + Id P\{p 1 }. This yields ({[ = p ] R 1 = R((P,{t 7,t 8 })) P, p , [ p 1, p+ 31 ]}) = {[ ] [ ] [ ] [ ] [ ] [ ]} p, 1 p+ p, 13, 1 p+ p, 31, 1 p+, 11 p+ p, 31, 1 p, 11 p+ p, 3, p+, 1 p+ p, 3, p Id P
17 and R = R 1 {(p 1,x),(p + 1,y)}{/0} = {[ p, p+ 3 3 ]} + Id {p,p 3 }. We can cut the firing sequences in (t 7 + t 8 + ˆt) = ((t 7 + t 8 ) + ˆt) into parts in (t 7 + t 8 ) and ˆt all starting and ending with no token on p 1. This yields R 3 = R R(ˆt) and R 4 = {p,p 3 } (R 3) = {[ p, p+ 33 ], [ p 37, p+ 5 ], [ p, p 34, p+ 5 ], [ p 4, p 31, p+ 5 ], [ ] [ ] p, 37 p+, 3 p+ p, 33, 37 p+, 1 p+,..., 36 [ ] [ ] [ ] [ ]} p, 4 p, 3 p+ p, 38, 5 p, 31 p+, 1 p+ p, 37, 36 p+, 4 p+ p, 33, 4 p, 3 p+, 4 p Id {p,p 3 }.
18 Nested Petri Nets as normal form for expressions For every expression e, there is a carrier set C(e) sgn(r(e))}. R(e) N C(e). R is the evaluation function for an expression defined in a way such that is always commutes with the expression operators P, Q, and +, and the additional operator. Expression for an elementary transition: t = L t is an expression for the linear set L t = R(L t ) = c t + Γ t. Example: Γ t = {{p 1, p + 1} p P} leading to Γ t = Id P. C(t) := P P + sgn({c t } Γ t ).
19 Expression for sets of transitions: T = t 1 t... t l for expressions t i T. Expression for a sub-net: N = PT (T ) for N consisting of P T and T. Let C(N) := C(T ) := t T C(t). Expression for a generalized transition: t = L t QA K t, where L t again expresses a linear set, and K t is a set of sub-nets and interpreted as expression K t = N i where the C(N i ) are pairwise disjoint. Ni K t Using Q A := {(a,a) a A} with A = N i K t C(N i ), we define C(t) := {a (c t + g Γ t g)(a) > 0} \ A. This means that the behavior of t is mainly described by the linear set c t +Γ t but it is additionally controlled by the reachability in the sub-nets N i.
20 Example (continued): We identify t 7 = { ˆp 1, ˆp+ 1 3} + Id { ˆp 1, ˆp, ˆp 3 }, t 8 = { ˆp 1, ˆp+ 3 1} + Id { ˆp 1, ˆp, ˆp 3 } and ˆt = {p 3 7, p+ 5} + Id {p,p 3 }. This yields = the expressions T 1 = t 7 t 8 and N 1 { ˆp1, ˆp, ˆp 3 } (T 1). On the next level, we get the generalized transition t = ( /0 + {[ p 1, ˆp 1 ], [ p 31, ˆp 31 ], [ p + 1, ˆp+ 1 ], [ ]} ) p +, 31 ˆp+ 31 {( ˆp, ˆp ),( ˆp 3, ˆp 3 ),( ˆp+, ˆp+ ),( ˆp+ 3, ˆp+ 3 )}N 1, which we visualize as t = t 7 ˆp 1 ˆp 3 t 8 ˆp 3
21 = T = t ˆt and N {p,p 3 } (T ). On the top level, we get [ ] p T 3 = t 3 =, 4 p, 3 p+, 4 p+ 33 {(p,p ),(p 3,p 3 )}N, which we visualize as 3 7 y 4 4 t p 3 p z 5 ˆt
22 Expression T T.1.b t T {c t } Γ t N N i K t T i T.1.b t T i {c t } Γ t N Carrier set C(T ) = C(t) = P T P+ T {w c t,w g,...} C(N i ) = C(T i ) = C(t ) = P T i P + T i {w ct,w g,...}...
23 new Overview The property T The size of an expression Additional operators working on expressions, Logic with mtc The main algorithm establishing property T The reachability relation for Petri nets with inhibitor arcs Priority-Multicounter-Automata Restricted Priority- Multipushdown- Automata
24 The property T Definition 1 An expression T has the property T if t T, N i = PTi (T i ) K t the following 5 conditions hold: 1. In recursive manner, T i has (a) the property T, and (b) For all t T i it holds g {c t } Γ t w g C(t ) g(w g ) = 1, g t T i {c t } Γ t \ {g} g (w g ) = 0.
25 . g {c t } Γ t, p P Ti g(p ) ind(g)(p ) = g(p + ) ind(g)(p + ), where ind(g) := g(w g )g t T i,g {c t } Γ t 3. w C(N i ) \ (P + T i P T i ) Σ g Γt g(w) > There are multisets m +,m R(N i ) with p P Ti m + P Ti (c t + Γ t ) P Ti (( g Γ t g(p ) = 0) m + (p + ) > m + (p )) m P + Ti (c t + Γ t ) P + Ti (( g Γ t g(p + ) = 0) m (p ) > m (p + )).
26 5. c t C(t) R(t). Theorem 1 For every expression T, we can effectively construct a T with R(T ) = R(T ) such that T has property T. Corollary The reachability problem for a Petri net with one inhibitor arc is decidable.
27 The size of an expression m :< m if there is an e with m(e) < m (e) and m(e ) = m (e ) for all e > e. [DM79]: Noetherian order on e s Noetherian order on m s. S(T ) := t T {S(t) 1}. S(t) := (S(K t ),b,b 5 + Γ t ). Here, b i = 0 if Condition T.i is fulfilled, and b i = 1 otherwise. S(K t ) = {S(N i ) 1}. Ni K t
28 S(N i ) := (s m + { P Ti 1},S(T i ),b 1b, C(N i ) ) with s m := max{s s s ((s,.,.,.)) > 0,S(T i )((s,.,.)) > 0}. Example (continued): S(t 7 ) = S(t 8 ) = (/0,0,3), S(T 1 ) = {(/0,0,3) }, S(N 1 ) = ({3 1},{(/0,0,3) },1,6), S(t ) = ({S(N 1 ) 1},1,4), S(T ) = {S(t ) 1,(/0,0,) 1}, S(N ) = ({3 1, 1},S(T ),1,4). Lemma 4 The ordering on S defined above is Noetherian
29 Additional operators working on expressions Lemma 5 Let t = L t Q K t be an expressions for a transition and L be (an expression for) a semi linear set. Then, we can construct an expression T := t L (with R(T ) = (R(L t ) R(L)) Q R(K t )) where the occurring sizes S(t ) with t T increase relatively to S(t) only in the last position in the triple. Lemma 6 Let T and T be expressions for sets of transitions, and Q be a relation. Then, we can construct an expression T := T Q T (with R(T ) = R(T ) Q R(T )) where the occurring sizes S(t) increase only in the last position in the triple and sum up in the first position. Lemma 7 Let N be an expression for a subnet. Then, we can construct an equivalent expression for a transition t(n) with R(t(N)) = R(N) and t P (N) with R(t P (N)) = {m R(N) p P m(p ) = m(p + ) = 0}.
30 Logic Given a formula φ(x 1,...,x k,x 1,...,x k ), then mtc(φ) denotes the smallest set S N k containing all of the following: (x 1,...,x k,x 1,...,x k ) for (x 1,...,x k ) N k (this stands for the identity), (x 1,...,x k,x 1,...,x k ) for φ(x 1,...,x k,x 1,...,x k ) (x 1,...,x k,x 1,...,x k ) for (x 1,...,x k,x 1,...,x k ),(x 1,...,x k,x 1,...,x k ) S, and (x 1 +x 1,...,x k+x N k. k,x 1 +x 1,...,x k +x k ) for a (x 1,...,x k,x 1,...,x k ) S and (x 1,...,x k )
31 Corollary 3 The emptiness and satisfiability is decidable for formulas with an FO+PLUS-formula inside and,, and mtc operators outside. corresponds to expressible with Q Lemma 6 corresponds to expressible since T is already a union remove the element mtc is done by using Lemma 7.
32 The main algorithm establishing property T function reacheq(t ): begin repeat i:= 1 while i 5 and t T, N K t Condition T.i fulfilled do i:=i+1 od if i=6 then return T else T :=T for T according to treatment of Condition T.i until i=6 end reacheq
33 in each step S(T ) decreases (S(reacheq(T )) < S(T ) if T reacheq(t )); due to Lemma 4 the algorithm terminates. Change of size S(t) during the treatment of Condition T.i: S(t) S(N i ) S(t ) for t T i s m + { P Ti 1} S(K t ) b b 5 + Γ t b 1b C(N i ) b b 5 + Γ t T T T T.4 T
34 Condition 1 Recursion and introducing witnesses Let Condition 1 be not fulfilled by T i ; let T i := reacheq(t i ), which terminates by induction since S(T i ) < S(T ). Construct T from T by adding witnesses inside as for T = T = T ˆt in following continued example: Replace t 7 and t 8 by t 7 = { ˆp 1, ˆp+ 1 3,w c t 7 1} + Id ˆp1, ˆp, ˆp 3 and t 8 = { ˆp 1, ˆp + 3 1,w c t 8 1} + Id ˆp1, ˆp, ˆp 3 T 1 = t 7 t 8 and N = 1 { ˆp 1, ˆp, ˆp 3 }(T 1 ). t = (/0 + {{p 1, ˆp 1},{p 3 1, ˆp 3 1},{p+ 1, ˆp+ 1},{p+ 3 1, ˆp+ 3 1},{w ct 1},{w ct 1}} ), 7 8 {( ˆp, ˆp ),( ˆp 3, ˆp 3 ),( ˆp+, ˆp+ ),( ˆp+ 3, ˆp+ 3 )}N 1 and T = t ˆt.
35 The new sizes are now S(t 7 ) = S(t 8 ) = (/0,0,3) = S(t 7), S(T 1 ) = {(/0,0,3) } = S(T 1), S(N 1 ) = ({3 1},{(/0,0,3) },0,8) < S(N 1), S(t ) = ({S(N 1 ) 1},1,6) < S(t ), S(T ) = {S(t ) 1,(/0,0,) 1} < S(T ).
36 Condition Quantitative consistency Let Condition be not fulfilled by T i. The set L := g NC L p P Ti g(p ) ind(g)(p ) = g(p + ) ind(g)(p + ) N i K t is a Presburger set. Construct T := T \ {t} t L using Lemma 5. In the example L is characterized by the following three equations: g(w ct 8 ) = 3g(w ct 7 ), g( ˆp ) g(w c t 7 ) = g( ˆp + ), g( ˆp 3 ) = g( ˆp+ 3 ) g(w c t 8 ). Their solutions are described by the linear set L t = L t L = {[ p ] [ /0 +, 1 ˆp, 1 p+, 1 ˆp+ p, 1 ] [, 31 ˆp, 31 p+, 31 ˆp+ wct, 7 31, w c t 8 3, p, ˆp, p 3, ˆp ]}
37 t = L t {(a,a) a { ˆp, ˆp+, ˆp 3, ˆp+ 3 }}N 1 with S(t ) = ({S(N 1 ) 1},0,3) < S(t ). Adding the witnesses leads to L t {[ p /0 + 1, ˆp 1, p+ 1, ˆp+ 1, w 1 1 ], = [ p 3 1, ˆp 3 1, p+ 3 1, ˆp+ 3 1, w 1 ], [ wct 7, w ]} c t 8, p 3, ˆp, p 3 3, ˆp 3 3, w 3 1 (we omit the witness for /0.) with S(t ) = S(t ) = ({S(N 1 ) 1},0,3). Defining T = t ˆt with S(T ) = S(T ) and N = { ˆp 1, ˆp, ˆp 3 }(T ) with S(N ) = ({3 1, 1},S(T ),0,8) < S(N ) = ({3 1, 1},S(T ),1,4) we get ([ ] t 3 = p { 4, p 3, p+ 4, p+ [w1 ] [ , w ] [ 1, w3 ] [ ]} ) 1, wcˆt 1 {(a,a) a {p,p +,p 3,p+ 3 }}N.
38 Condition 3 Elimination of witnesses Let Condition 3 be not fulfilled by witness w C(N i ) \ (P + T i P T i ). Replace N i by some expression ˆT with R( ˆT ) = R(N i ) (w,w) c t w since for all m L t, we have m(w) = c t (w). Then, we can replace in T := T \ {t} (L t {w} Q\QC(Ni ) (K t \ {N i })) QC(Ni )\{w} ˆT [ ] Example: Consider t with c t = w, p 4, p+ { 5, g Γ t g(w) = 0, K t = {p} (v t j )}, [ ] and c t j = w1, p 6, p+ 7, q 8, q+ { 9, K t j = {q} (u)}.
39 v [ p 04, p+ 06, q 18, q+ 19, p 17, p+ 16, q 8, q+ 9, p 7, p+ 5 ], further- Then t is defined such that c t = [ ] [ ] p more,, 11 p+ p, 01, 1 p+ Γ 11 t and q 8 9 u 6 7 p 4 5 K t = { {p0 } (v 0), {q1 } (u 1), {p1 } (v 1), {q } (u ), {p } (v )}, where p i,q i,v i and u i are replacements caused by disjointness condition in Lemma 6.
40 p 0 q 1 p 1 q p 4 6+x x 6+y y 5 v 0 u 1 v 1 u v The variables x and y illustrate the effect of the periods in Γ t which originate from the (omitted) periods of t j.
41 Condition 4 Elimination of bounded places Condition 4 is decidable by two covering graph constructions for every i: Every node in the covering graph CG (i,+) (CG (i, ), respectively ) has a marking from (N {ω}) P T i ((N {ω}) P+ T i, respectively ). The root of the covering graph CG (i,+) has the marking c t P Ti +ω {p g Γg(p )>0}. For a node in CG (i,+) marked with m, we construct T i with R(T i ) = {g R(T i) g P m} using Lemma 5 as T Ti i := {t {g Lt g P m} t T i }. Compute T i := Ti reacheq(t i ) recursively. For every t T i, add to the covering graph CG (i,+) m := m c t P Ti +{p (c t (p + ) + ω a new node Σ (p + )) p P Ti } g Γ t
42 If m > m for an m on the path from the root to m, then we set m := m +ω(m m ). If for all i a node marked with ω P T i is in CG (i,+) and, analogously, a node marked with ω P+ T i is in CG (i, ), then the Condition 4 is fulfilled. Otherwise, we calculate k := min σ {+, } max min path CG (i,σ) p P Ti max m path m(pσ ) and construct T := T \ {t} U(p) (restrict place p to k). p P Ti Tj,h l 1 U(p) = (L t {p,p + } Q\Q C(Ni ) (K t \ {N i })) QC(Ni )\{p,p + } T k c t (p ),c t (p + ) describes firing sequences in N i with the following property: They start with a marking m 0 with m 0 (p) = j, end with a marking m 1 with m 1 (p) = h, and meanwhile the number tokens on p is always less than l.
43 Example: Let t = (c + Γ ) {p} P {p} P (N i }) with c(p ) = 1, N i = v w t j and t j = (c j + Γ j ) {q} Q {q} Q (u) with c j (p + ) = 1, c j (q ) = 8 and c j (q + ) = 9 q v 8 9 u p w
44 k = 1 firing sequences are restricted to the regular expression ((wv t j ) + v) wv. T0,0 1 and T 1 1,1 a copy of t j. only consist of a copy of v, T 1 1,0 only of a copy of w and T 1 0,1 only of T 0 0,0 = t( P(T 1 0,0 )) correponds to v, T 0 1,1 = T 1 1,0 PT 0 0,0 PT 1 0,1 T 1 1,1 corresponds to wv t j + v and T 1 1,0 = T 1 1,1 PT 0 1,0 = t( P(T 0 1,1 )) PT 1 1,0 PT 0 0,0 Every t in (c + Γ ) {p,p + } Q C(Ni )\{p,p + } T 1 1,0 looks like
45 T 1 1,0 T 1 0,0 q 8 9 u T 1 1,0 T 1 0,0 T 1 1,1
46 Corollary 4 If the conditions 1-4 hold for t, then it holds f g Γ t g + Γ t k (c t + kf) C(t) R(t) This immediately follows from: Lemma 8 If the conditions 1-4 hold for t, then it holds } f g + Γt e (Γ t Γ t ) k {(c t + kf) C(t),(c t + kf + e) C(t) R(t) g Γ t
47 Condition 5 Making the constant firing If Condition 5 is not fulfilled for t then, according to Corollary 4, for f = g, there g Γ exists a (smallest) k such that (c + kf) C(t) R(t). So we decompose L t such that R(L t ) = R(L t + kf) R(c t + jg + (Γ t \ {g}) ). Set g Γ j k T := T \ {t} {t K t = K t,γ t = Γ t c t = c t + kf)} {t j k,g Γ Γ t = Γ t \ {g}) c t = c t + jg)}. The size S(t ) is smaller than S(t) since b 5 is now zero or Γ \ {g} < Γ.
48 The reachability relation for Petri nets with inhibitor arcs Theorem In a Petri-net (P,T,W,I,m 0,m e ) with g N P + p, p P g(p) g(p ) ( t T (p,t) I (p,t) I), we can construct an expression T g such that there is a firing sequence w T with m 0 [w m e if and only if R(T g ) is (= {/0} and) not empty. With Theorem 1 we derive the following: Corollary 5 The reachability problem for a Petri net (P,T,W,I,m 0,m e ) with is decidable. g N P + p, p P g(p) g(p ) ( t T (p,t) I (p,t) I),
49 Example: Start marking: {p 3 3, p 4 }, end marking {p 4 7} t 6 p 3 t 7 3 p 4 3 p 5 t 9 5 p 1 t 8 We find g with{[ g(p 1 ) = 1, g(p ] [) = and g(p 3 )]} = g(p 4 ) = 3 and construct T 1 = {t 6,t 7 } p with R(T 1 ) =, 43 p+, 1 p+ p, 31, 11 p, 31 p+, p+ + Id 41 P, as innermost net of
50 7 p 4 5 t 9 3 p 3 p 5 t 8 p 3 p 4 t 6 3 p 4 p 3 p 1 t7 p This enables the firing sequence w = t 6 t 7 t 7 from [ p 3 1, p ] [ 4 3 to p 4, p ] 4 on the innermost level as, 31 p, 43 p+, 4 p+ R( 4 PT1 (T 1 )) = R(t ) R(T ). Together [ ] p with
51 [ ] p, 5 p+ R(T 3 ) for t 8, we get the firing sequence w = (w)(w)t 8 (w)t 8 (w)t 8 (w)t 8 from [ [ ] p 3, p ] [ 4 7 to p3 5, p ] 4 p on the next level as 3, p 4 7, p+ 3 5, p+ 4 R( PT (T )) = [ ] p R(t 3 ) R(T 3 ). Together with, 31 p+ R(T 45 3 ) for t 9, this enables the firing sequence w = t 9 (w )t9 5 from [ [ ] p 3 3, p ] [ 4 to p4 ] p 7 on the following level as 3 3, p 4, p+ 4 7 R( PT3 (T 3 )) = R(t 4 ) = R(T 4 ).
52 Priority-Multicounter-Automata A priority-multicounter-automaton is a one-way automaton described by the 6- tuple A = (k,z,σ,δ,z 0,E) with the set of states Z, the input alphabet Σ, the transition relation δ (Z (Σ {λ}) {0...k}) (Z { 1,0,1} k ), initial state z 0, the accepting states E Z, the set of configurations C A = Z Σ N k, the initial configuration σ A (x) = z 0,x,0,...,0 }{{} and configuration transition k relation z,ax,n 1,...,n k A z,x,n 1 + i 1,...,n k + i k
53 if and only if z,z Z,a Σ {λ}, (z,a, j),(z,i 1,...i k ) δ, i j n i = 0. Recognized language: L(A) = {w z e E n 1,...,n k N z 0,w,0,...,0 A z e,λ,n 1,...,n k. Alternatively L(A) = {w z 0,w,0,...,0 A z e,λ,0,...,0 }. Using Theorem, we get: Theorem 3 The emptiness problem for priority-multicounter-automata is decidable. The same holds for the halting problem by constructing an automaton which contains its input in the states.
54 Restricted Priority- Multipushdown- Automata Different treatment of one of the two pushdown symbols {0, 1}: A 0 can be pushed to and popped from every pushdown store independently, but a 1 can only be pushed to or popped from a pushdown store if all pushdown stores with a lower order are empty. Restriction: If a 1 is popped from a pushdown store, then a 1 cannot be pushed anymore to this store until it is empty. Theorem 4 The emptiness problem for restricted priority-multipushdown-automata is decidable.
55 This generalizes the result in [JKLP90] that LIN%D 1 (the class of languages generated by linear grammar and deletion of semi Dyck words) is recursive. Conjecture: Decidability still holds in the unrestricted case. Open problem: Pushdown automaton with additional weak counters (without zero-test).
The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets
 The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets Georg Zetzsche Technische Universität Kaiserslautern Reachability Problems 2015 Georg Zetzsche (TU KL) Emptiness
The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets Georg Zetzsche Technische Universität Kaiserslautern Reachability Problems 2015 Georg Zetzsche (TU KL) Emptiness
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Chapter 6. Properties of Regular Languages
 Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Chapter 6 Properties of Regular Languages Regular Sets and Languages Claim(1). The family of languages accepted by FSAs consists of precisely the regular sets over a given alphabet. Every regular set is
Pushdown Automata (2015/11/23)
 Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
Analyzing Asynchronous Programs with Preemption
 Foundations of Software Technology and Theoretical Computer Science (Bangalore) 2008. Editors: R. Hariharan, M. Mukund, V. Vinay; pp 37-48 Analyzing Asynchronous Programs with Preemption Mohamed Faouzi
Foundations of Software Technology and Theoretical Computer Science (Bangalore) 2008. Editors: R. Hariharan, M. Mukund, V. Vinay; pp 37-48 Analyzing Asynchronous Programs with Preemption Mohamed Faouzi
Advanced Automata Theory 10 Transducers and Rational Relations
 Advanced Automata Theory 10 Transducers and Rational Relations Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Advanced
Advanced Automata Theory 10 Transducers and Rational Relations Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Advanced
Dense-Timed Pushdown Automata
 Dense-Timed Pushdown Automata Parosh Aziz Abdulla Uppsala University Sweden Mohamed Faouzi Atig Uppsala University Sweden Jari Stenman Uppsala University Sweden Abstract We propose a model that captures
Dense-Timed Pushdown Automata Parosh Aziz Abdulla Uppsala University Sweden Mohamed Faouzi Atig Uppsala University Sweden Jari Stenman Uppsala University Sweden Abstract We propose a model that captures
UNIT-VI PUSHDOWN AUTOMATA
 Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
DES. 4. Petri Nets. Introduction. Different Classes of Petri Net. Petri net properties. Analysis of Petri net models
 4. Petri Nets Introduction Different Classes of Petri Net Petri net properties Analysis of Petri net models 1 Petri Nets C.A Petri, TU Darmstadt, 1962 A mathematical and graphical modeling method. Describe
4. Petri Nets Introduction Different Classes of Petri Net Petri net properties Analysis of Petri net models 1 Petri Nets C.A Petri, TU Darmstadt, 1962 A mathematical and graphical modeling method. Describe
Introduction to Formal Languages, Automata and Computability p.1/42
 Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Some techniques and results in deciding bisimilarity
 Some techniques and results in deciding bisimilarity Petr Jančar Dept of Computer Science Technical University Ostrava (FEI VŠB-TU) Czech Republic www.cs.vsb.cz/jancar Talk at the Verification Seminar,
Some techniques and results in deciding bisimilarity Petr Jančar Dept of Computer Science Technical University Ostrava (FEI VŠB-TU) Czech Republic www.cs.vsb.cz/jancar Talk at the Verification Seminar,
Petri nets. s 1 s 2. s 3 s 4. directed arcs.
 Petri nets Petri nets Petri nets are a basic model of parallel and distributed systems (named after Carl Adam Petri). The basic idea is to describe state changes in a system with transitions. @ @R s 1
Petri nets Petri nets Petri nets are a basic model of parallel and distributed systems (named after Carl Adam Petri). The basic idea is to describe state changes in a system with transitions. @ @R s 1
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
Theory of Computation
 Theory of Computation (Feodor F. Dragan) Department of Computer Science Kent State University Spring, 2018 Theory of Computation, Feodor F. Dragan, Kent State University 1 Before we go into details, what
Theory of Computation (Feodor F. Dragan) Department of Computer Science Kent State University Spring, 2018 Theory of Computation, Feodor F. Dragan, Kent State University 1 Before we go into details, what
How to Pop a Deep PDA Matters
 How to Pop a Deep PDA Matters Peter Leupold Department of Mathematics, Faculty of Science Kyoto Sangyo University Kyoto 603-8555, Japan email:leupold@cc.kyoto-su.ac.jp Abstract Deep PDA are push-down automata
How to Pop a Deep PDA Matters Peter Leupold Department of Mathematics, Faculty of Science Kyoto Sangyo University Kyoto 603-8555, Japan email:leupold@cc.kyoto-su.ac.jp Abstract Deep PDA are push-down automata
The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets
 The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets Georg Zetzsche Concurrency Theory Group Fachbereich Informatik Technische Universität Kaiserslautern zetzsche@cs.uni-kl.de
The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets Georg Zetzsche Concurrency Theory Group Fachbereich Informatik Technische Universität Kaiserslautern zetzsche@cs.uni-kl.de
Fundamenta Informaticae 30 (1997) 23{41 1. Petri Nets, Commutative Context-Free Grammars,
 Fundamenta Informaticae 30 (1997) 23{41 1 IOS Press Petri Nets, Commutative Context-Free Grammars, and Basic Parallel Processes Javier Esparza Institut fur Informatik Technische Universitat Munchen Munchen,
Fundamenta Informaticae 30 (1997) 23{41 1 IOS Press Petri Nets, Commutative Context-Free Grammars, and Basic Parallel Processes Javier Esparza Institut fur Informatik Technische Universitat Munchen Munchen,
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Automata Theory (2A) Young Won Lim 5/31/18
 Automata Theory (2A) Copyright (c) 2018 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Automata Theory (2A) Copyright (c) 2018 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Valence automata as a generalization of automata with storage
 Valence automata as a generalization of automata with storage Georg Zetzsche Technische Universität Kaiserslautern D-CON 2013 Georg Zetzsche (TU KL) Valence automata D-CON 2013 1 / 23 Example (Pushdown
Valence automata as a generalization of automata with storage Georg Zetzsche Technische Universität Kaiserslautern D-CON 2013 Georg Zetzsche (TU KL) Valence automata D-CON 2013 1 / 23 Example (Pushdown
The Downward-Closure of Petri Net Languages
 The Downward-Closure of Petri Net Languages Peter Habermehl 1, Roland Meyer 1, and Harro Wimmel 2 1 LIAFA, Paris Diderot University & CNRS e-mail: {peter.habermehl,roland.meyer}@liafa.jussieu.fr 2 Department
The Downward-Closure of Petri Net Languages Peter Habermehl 1, Roland Meyer 1, and Harro Wimmel 2 1 LIAFA, Paris Diderot University & CNRS e-mail: {peter.habermehl,roland.meyer}@liafa.jussieu.fr 2 Department
An Alternative Construction in Symbolic Reachability Analysis of Second Order Pushdown Systems
 An Alternative Construction in Symbolic Reachability Analysis of Second Order Pushdown Systems Anil Seth CSE Department, I.I.T. Kanpur, Kanpur 208016, INDIA. seth@cse.iitk.ac.in Abstract. Recently, it
An Alternative Construction in Symbolic Reachability Analysis of Second Order Pushdown Systems Anil Seth CSE Department, I.I.T. Kanpur, Kanpur 208016, INDIA. seth@cse.iitk.ac.in Abstract. Recently, it
Some hierarchies for the communication complexity measures of cooperating grammar systems
 Some hierarchies for the communication complexity measures of cooperating grammar systems Juraj Hromkovic 1, Jarkko Kari 2, Lila Kari 2 June 14, 2010 Abstract We investigate here the descriptional and
Some hierarchies for the communication complexity measures of cooperating grammar systems Juraj Hromkovic 1, Jarkko Kari 2, Lila Kari 2 June 14, 2010 Abstract We investigate here the descriptional and
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
Closure Properties of Regular Languages. Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism
 Closure Properties of Regular Languages Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism Closure Properties Recall a closure property is a statement
Closure Properties of Regular Languages Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism Closure Properties Recall a closure property is a statement
Final exam study sheet for CS3719 Turing machines and decidability.
 Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Final exam study sheet for CS3719 Turing machines and decidability. A Turing machine is a finite automaton with an infinite memory (tape). Formally, a Turing machine is a 6-tuple M = (Q, Σ, Γ, δ, q 0,
Sri vidya college of engineering and technology
 Unit I FINITE AUTOMATA 1. Define hypothesis. The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order
Unit I FINITE AUTOMATA 1. Define hypothesis. The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 3: Finite State Automata Motivation In the previous lecture we learned how to formalize
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
COM364 Automata Theory Lecture Note 2 - Nondeterminism
 COM364 Automata Theory Lecture Note 2 - Nondeterminism Kurtuluş Küllü March 2018 The FA we saw until now were deterministic FA (DFA) in the sense that for each state and input symbol there was exactly
COM364 Automata Theory Lecture Note 2 - Nondeterminism Kurtuluş Küllü March 2018 The FA we saw until now were deterministic FA (DFA) in the sense that for each state and input symbol there was exactly
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
ACS2: Decidability Decidability
 Decidability Bernhard Nebel and Christian Becker-Asano 1 Overview An investigation into the solvable/decidable Decidable languages The halting problem (undecidable) 2 Decidable problems? Acceptance problem
Decidability Bernhard Nebel and Christian Becker-Asano 1 Overview An investigation into the solvable/decidable Decidable languages The halting problem (undecidable) 2 Decidable problems? Acceptance problem
September 11, Second Part of Regular Expressions Equivalence with Finite Aut
 Second Part of Regular Expressions Equivalence with Finite Automata September 11, 2013 Lemma 1.60 If a language is regular then it is specified by a regular expression Proof idea: For a given regular language
Second Part of Regular Expressions Equivalence with Finite Automata September 11, 2013 Lemma 1.60 If a language is regular then it is specified by a regular expression Proof idea: For a given regular language
Chapter 5. Finite Automata
 Chapter 5 Finite Automata 5.1 Finite State Automata Capable of recognizing numerous symbol patterns, the class of regular languages Suitable for pattern-recognition type applications, such as the lexical
Chapter 5 Finite Automata 5.1 Finite State Automata Capable of recognizing numerous symbol patterns, the class of regular languages Suitable for pattern-recognition type applications, such as the lexical
Reversal-Bounded Counter Machines Revisited
 Reversal-Bounded Counter Machines Revisited Alain Finkel 1 and Arnaud Sangnier 1,2 1 LSV, ENS Cachan, CNRS & 2 EDF R&D 61 av. du pdt Wilson 94230 Cachan. France {finkel,sangnier}@lsv.ens-cachan.fr Abstract.
Reversal-Bounded Counter Machines Revisited Alain Finkel 1 and Arnaud Sangnier 1,2 1 LSV, ENS Cachan, CNRS & 2 EDF R&D 61 av. du pdt Wilson 94230 Cachan. France {finkel,sangnier}@lsv.ens-cachan.fr Abstract.
Computability and Complexity
 Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Discrete Event Systems Exam
 Computer Engineering and Networks Laboratory TEC, NSG, DISCO HS 2016 Prof. L. Thiele, Prof. L. Vanbever, Prof. R. Wattenhofer Discrete Event Systems Exam Friday, 3 rd February 2017, 14:00 16:00. Do not
Computer Engineering and Networks Laboratory TEC, NSG, DISCO HS 2016 Prof. L. Thiele, Prof. L. Vanbever, Prof. R. Wattenhofer Discrete Event Systems Exam Friday, 3 rd February 2017, 14:00 16:00. Do not
C6.2 Push-Down Automata
 Theory of Computer Science April 5, 2017 C6. Context-free Languages: Push-down Automata Theory of Computer Science C6. Context-free Languages: Push-down Automata Malte Helmert University of Basel April
Theory of Computer Science April 5, 2017 C6. Context-free Languages: Push-down Automata Theory of Computer Science C6. Context-free Languages: Push-down Automata Malte Helmert University of Basel April
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
UNIT II REGULAR LANGUAGES
 1 UNIT II REGULAR LANGUAGES Introduction: A regular expression is a way of describing a regular language. The various operations are closure, union and concatenation. We can also find the equivalent regular
1 UNIT II REGULAR LANGUAGES Introduction: A regular expression is a way of describing a regular language. The various operations are closure, union and concatenation. We can also find the equivalent regular
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
The Parikh image of languages and linear constraints
 The Parikh image of languages and linear constraints Peter.Habermehl@liafa.univ-paris-diderot.fr 1 1 LIAFA, Université Paris Diderot, Sorbonne Paris Cité, CNRS CP meets CAV, Turunç June 28th, 2012 Peter
The Parikh image of languages and linear constraints Peter.Habermehl@liafa.univ-paris-diderot.fr 1 1 LIAFA, Université Paris Diderot, Sorbonne Paris Cité, CNRS CP meets CAV, Turunç June 28th, 2012 Peter
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Part I: Definitions and Properties
 Turing Machines Part I: Definitions and Properties Finite State Automata Deterministic Automata (DFSA) M = {Q, Σ, δ, q 0, F} -- Σ = Symbols -- Q = States -- q 0 = Initial State -- F = Accepting States
Turing Machines Part I: Definitions and Properties Finite State Automata Deterministic Automata (DFSA) M = {Q, Σ, δ, q 0, F} -- Σ = Symbols -- Q = States -- q 0 = Initial State -- F = Accepting States
Pushdown Automata: Introduction (2)
 Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
SYLLABUS. Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 3 : REGULAR EXPRESSIONS AND LANGUAGES
 Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
MPRI 1-22 Introduction to Verification January 4, TD 6: Petri Nets
 TD 6: Petri Nets 1 Modeling Using Petri Nets Exercise 1 (Traffic Lights). Consider again the traffic lights example from the lecture notes: r r ry y r y ry g g y g 1. How can you correct this Petri net
TD 6: Petri Nets 1 Modeling Using Petri Nets Exercise 1 (Traffic Lights). Consider again the traffic lights example from the lecture notes: r r ry y r y ry g g y g 1. How can you correct this Petri net
Regular Expressions and Language Properties
 Regular Expressions and Language Properties Mridul Aanjaneya Stanford University July 3, 2012 Mridul Aanjaneya Automata Theory 1/ 47 Tentative Schedule HW #1: Out (07/03), Due (07/11) HW #2: Out (07/10),
Regular Expressions and Language Properties Mridul Aanjaneya Stanford University July 3, 2012 Mridul Aanjaneya Automata Theory 1/ 47 Tentative Schedule HW #1: Out (07/03), Due (07/11) HW #2: Out (07/10),
New Complexity Results for Some Linear Counting Problems Using Minimal Solutions to Linear Diophantine Equations
 New Complexity Results for Some Linear Counting Problems Using Minimal Solutions to Linear Diophantine Equations (Extended Abstract) Gaoyan Xie, Cheng Li and Zhe Dang School of Electrical Engineering and
New Complexity Results for Some Linear Counting Problems Using Minimal Solutions to Linear Diophantine Equations (Extended Abstract) Gaoyan Xie, Cheng Li and Zhe Dang School of Electrical Engineering and
CPS 220 Theory of Computation Pushdown Automata (PDA)
 CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
Theory of Computation
 Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
Fall 2002 (YEN) Theory of Computation Midterm Exam. Name:... I.D.#:... 1. (30 pts) True or false (mark O for true ; X for false ). (Score=Max{0, Right- 1 2 Wrong}.) (1) X... If L 1 is regular and L 2 L
A shrinking lemma for random forbidding context languages
 Theoretical Computer Science 237 (2000) 149 158 www.elsevier.com/locate/tcs A shrinking lemma for random forbidding context languages Andries van der Walt a, Sigrid Ewert b; a Department of Mathematics,
Theoretical Computer Science 237 (2000) 149 158 www.elsevier.com/locate/tcs A shrinking lemma for random forbidding context languages Andries van der Walt a, Sigrid Ewert b; a Department of Mathematics,
CMSC 330: Organization of Programming Languages. Theory of Regular Expressions Finite Automata
 : Organization of Programming Languages Theory of Regular Expressions Finite Automata Previous Course Review {s s defined} means the set of string s such that s is chosen or defined as given s A means
: Organization of Programming Languages Theory of Regular Expressions Finite Automata Previous Course Review {s s defined} means the set of string s such that s is chosen or defined as given s A means
UNIT-II. NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: SIGNIFICANCE. Use of ε-transitions. s t a r t. ε r. e g u l a r
 Syllabus R9 Regulation UNIT-II NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: In the automata theory, a nondeterministic finite automaton (NFA) or nondeterministic finite state machine is a finite
Syllabus R9 Regulation UNIT-II NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: In the automata theory, a nondeterministic finite automaton (NFA) or nondeterministic finite state machine is a finite
CS243, Logic and Computation Nondeterministic finite automata
 CS243, Prof. Alvarez NONDETERMINISTIC FINITE AUTOMATA (NFA) Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ Maloney Hall, room 569 alvarez@cs.bc.edu Computer Science Department voice: (67) 552-4333
CS243, Prof. Alvarez NONDETERMINISTIC FINITE AUTOMATA (NFA) Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ Maloney Hall, room 569 alvarez@cs.bc.edu Computer Science Department voice: (67) 552-4333
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Chapter 3. Regular grammars
 Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
PUSHDOWN AUTOMATA (PDA)
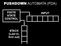 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
ECS 120 Lesson 15 Turing Machines, Pt. 1
 ECS 120 Lesson 15 Turing Machines, Pt. 1 Oliver Kreylos Wednesday, May 2nd, 2001 Before we can start investigating the really interesting problems in theoretical computer science, we have to introduce
ECS 120 Lesson 15 Turing Machines, Pt. 1 Oliver Kreylos Wednesday, May 2nd, 2001 Before we can start investigating the really interesting problems in theoretical computer science, we have to introduce
Jumping Petri Nets. Specific Properties
 Fundamenta Informaticae, vol 32, issue 3-4, 373-392, 1997 Jumping Petri Nets. Specific Properties Ferucio Laurenţiu ŢIPLEA (1 and Erkki MÄKINEN (2 (1 Faculty of Informatics Al. I. Cuza University of Iaşi
Fundamenta Informaticae, vol 32, issue 3-4, 373-392, 1997 Jumping Petri Nets. Specific Properties Ferucio Laurenţiu ŢIPLEA (1 and Erkki MÄKINEN (2 (1 Faculty of Informatics Al. I. Cuza University of Iaşi
Push-down Automata = FA + Stack
 Push-down Automata = FA + Stack PDA Definition A push-down automaton M is a tuple M = (Q,, Γ, δ, q0, F) where Q is a finite set of states is the input alphabet (of terminal symbols, terminals) Γ is the
Push-down Automata = FA + Stack PDA Definition A push-down automaton M is a tuple M = (Q,, Γ, δ, q0, F) where Q is a finite set of states is the input alphabet (of terminal symbols, terminals) Γ is the
Büchi Automata and their closure properties. - Ajith S and Ankit Kumar
 Büchi Automata and their closure properties - Ajith S and Ankit Kumar Motivation Conventional programs accept input, compute, output result, then terminate Reactive program : not expected to terminate
Büchi Automata and their closure properties - Ajith S and Ankit Kumar Motivation Conventional programs accept input, compute, output result, then terminate Reactive program : not expected to terminate
Chapter 2: Finite Automata
 Chapter 2: Finite Automata 2.1 States, State Diagrams, and Transitions Finite automaton is the simplest acceptor or recognizer for language specification. It is also the simplest model of a computer. A
Chapter 2: Finite Automata 2.1 States, State Diagrams, and Transitions Finite automaton is the simplest acceptor or recognizer for language specification. It is also the simplest model of a computer. A
THEORY OF COMPUTATION
 THEORY OF COMPUTATION There are four sorts of men: He who knows not and knows not he knows not: he is a fool - shun him; He who knows not and knows he knows not: he is simple teach him; He who knows and
THEORY OF COMPUTATION There are four sorts of men: He who knows not and knows not he knows not: he is a fool - shun him; He who knows not and knows he knows not: he is simple teach him; He who knows and
VTU QUESTION BANK. Unit 1. Introduction to Finite Automata. 1. Obtain DFAs to accept strings of a s and b s having exactly one a.
 VTU QUESTION BANK Unit 1 Introduction to Finite Automata 1. Obtain DFAs to accept strings of a s and b s having exactly one a.(5m )( Dec-2014) 2. Obtain a DFA to accept strings of a s and b s having even
VTU QUESTION BANK Unit 1 Introduction to Finite Automata 1. Obtain DFAs to accept strings of a s and b s having exactly one a.(5m )( Dec-2014) 2. Obtain a DFA to accept strings of a s and b s having even
HENNING FERNAU Fachbereich IV, Abteilung Informatik, Universität Trier, D Trier, Germany
 International Journal of Foundations of Computer Science c World Scientific Publishing Company PROGRAMMMED GRAMMARS WITH RULE QUEUES HENNING FERNAU Fachbereich IV, Abteilung Informatik, Universität Trier,
International Journal of Foundations of Computer Science c World Scientific Publishing Company PROGRAMMMED GRAMMARS WITH RULE QUEUES HENNING FERNAU Fachbereich IV, Abteilung Informatik, Universität Trier,
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Languages, regular languages, finite automata
 Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Outline. Complexity Theory. Example. Sketch of a log-space TM for palindromes. Log-space computations. Example VU , SS 2018
 Complexity Theory Complexity Theory Outline Complexity Theory VU 181.142, SS 2018 3. Logarithmic Space Reinhard Pichler Institute of Logic and Computation DBAI Group TU Wien 3. Logarithmic Space 3.1 Computational
Complexity Theory Complexity Theory Outline Complexity Theory VU 181.142, SS 2018 3. Logarithmic Space Reinhard Pichler Institute of Logic and Computation DBAI Group TU Wien 3. Logarithmic Space 3.1 Computational
Closure under the Regular Operations
 Closure under the Regular Operations Application of NFA Now we use the NFA to show that collection of regular languages is closed under regular operations union, concatenation, and star Earlier we have
Closure under the Regular Operations Application of NFA Now we use the NFA to show that collection of regular languages is closed under regular operations union, concatenation, and star Earlier we have
CSE 211. Pushdown Automata. CSE 211 (Theory of Computation) Atif Hasan Rahman
 CSE 211 Pushdown Automata CSE 211 (Theory of Computation) Atif Hasan Rahman Lecturer Department of Computer Science and Engineering Bangladesh University of Engineering & Technology Adapted from slides
CSE 211 Pushdown Automata CSE 211 (Theory of Computation) Atif Hasan Rahman Lecturer Department of Computer Science and Engineering Bangladesh University of Engineering & Technology Adapted from slides
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 1 Course Web Page www3.cs.stonybrook.edu/ cse303 The webpage contains: lectures notes slides; very detailed solutions to
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 1 Course Web Page www3.cs.stonybrook.edu/ cse303 The webpage contains: lectures notes slides; very detailed solutions to
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 5 CHAPTER 2 FINITE AUTOMATA 1. Deterministic Finite Automata DFA 2. Nondeterministic Finite Automata NDFA 3. Finite Automata
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 5 CHAPTER 2 FINITE AUTOMATA 1. Deterministic Finite Automata DFA 2. Nondeterministic Finite Automata NDFA 3. Finite Automata
REGular and Context-Free Grammars
 REGular and Context-Free Grammars Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it March 26, 2018 1 Partly Based on Alessandro Barenghi s
REGular and Context-Free Grammars Nicholas Mainardi 1 Dipartimento di Elettronica e Informazione Politecnico di Milano nicholas.mainardi@polimi.it March 26, 2018 1 Partly Based on Alessandro Barenghi s
CS Pushdown Automata
 Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
P Systems with Symport/Antiport of Rules
 P Systems with Symport/Antiport of Rules Matteo CAVALIERE Research Group on Mathematical Linguistics Rovira i Virgili University Pl. Imperial Tárraco 1, 43005 Tarragona, Spain E-mail: matteo.cavaliere@estudiants.urv.es
P Systems with Symport/Antiport of Rules Matteo CAVALIERE Research Group on Mathematical Linguistics Rovira i Virgili University Pl. Imperial Tárraco 1, 43005 Tarragona, Spain E-mail: matteo.cavaliere@estudiants.urv.es
arxiv: v1 [cs.fl] 8 Jan 2019
![arxiv: v1 [cs.fl] 8 Jan 2019 arxiv: v1 [cs.fl] 8 Jan 2019](/thumbs/93/112539658.jpg) Languages ordered by the subword order Dietrich Kuske TU Ilmenau, Germany dietrich.kuske@tu-ilmenau.de Georg Zetzsche MPI-SWS, Germany georg@mpi-sws.org arxiv:1901.02194v1 [cs.fl] 8 Jan 2019 Abstract We
Languages ordered by the subword order Dietrich Kuske TU Ilmenau, Germany dietrich.kuske@tu-ilmenau.de Georg Zetzsche MPI-SWS, Germany georg@mpi-sws.org arxiv:1901.02194v1 [cs.fl] 8 Jan 2019 Abstract We
Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer.
 Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer. Language Generator: Context free grammars are language generators,
Context Free Languages (CFL) Language Recognizer A device that accepts valid strings. The FA are formalized types of language recognizer. Language Generator: Context free grammars are language generators,
Non-context-Free Languages. CS215, Lecture 5 c
 Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
Non-context-Free Languages CS215, Lecture 5 c 2007 1 The Pumping Lemma Theorem. (Pumping Lemma) Let be context-free. There exists a positive integer divided into five pieces, Proof for for each, and..
ON STATELESS AUTOMATA AND P SYSTEMS
 ON STATELESS AUTOMATA AND P SYSTEMS Linmin Yang School of Electrical Engineering and Computer Science Washington State University, Pullman, Washington 99164, USA lyang1@eecs.wsu.edu Zhe Dang School of
ON STATELESS AUTOMATA AND P SYSTEMS Linmin Yang School of Electrical Engineering and Computer Science Washington State University, Pullman, Washington 99164, USA lyang1@eecs.wsu.edu Zhe Dang School of
Automata and Computability. Solutions to Exercises
 Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
Automata and Computability Solutions to Exercises Fall 28 Alexis Maciel Department of Computer Science Clarkson University Copyright c 28 Alexis Maciel ii Contents Preface vii Introduction 2 Finite Automata
TWO-VARIABLE LOGIC WITH COUNTING AND A LINEAR ORDER
 Logical Methods in Computer Science Vol. 12(2:8)2016, pp. 1 31 www.lmcs-online.org Submitted Nov. 2, 2015 Published Jun. 23, 2016 TWO-VARIABLE LOGIC WITH COUNTING AND A LINEAR ORDER WITOLD CHARATONIK AND
Logical Methods in Computer Science Vol. 12(2:8)2016, pp. 1 31 www.lmcs-online.org Submitted Nov. 2, 2015 Published Jun. 23, 2016 TWO-VARIABLE LOGIC WITH COUNTING AND A LINEAR ORDER WITOLD CHARATONIK AND
Petri Nets (for Planners)
 Petri (for Planners) B. Bonet, P. Haslum... from various places... ICAPS 2011 & Motivation Petri (PNs) is formalism for modelling discrete event systems Developed by (and named after) C.A. Petri in 1960s
Petri (for Planners) B. Bonet, P. Haslum... from various places... ICAPS 2011 & Motivation Petri (PNs) is formalism for modelling discrete event systems Developed by (and named after) C.A. Petri in 1960s
Counter Automata and Classical Logics for Data Words
 Counter Automata and Classical Logics for Data Words Amal Dev Manuel amal@imsc.res.in Institute of Mathematical Sciences, Taramani, Chennai, India. January 31, 2012 Data Words Definition (Data Words) A
Counter Automata and Classical Logics for Data Words Amal Dev Manuel amal@imsc.res.in Institute of Mathematical Sciences, Taramani, Chennai, India. January 31, 2012 Data Words Definition (Data Words) A
Reverse mathematics of some topics from algorithmic graph theory
 F U N D A M E N T A MATHEMATICAE 157 (1998) Reverse mathematics of some topics from algorithmic graph theory by Peter G. C l o t e (Chestnut Hill, Mass.) and Jeffry L. H i r s t (Boone, N.C.) Abstract.
F U N D A M E N T A MATHEMATICAE 157 (1998) Reverse mathematics of some topics from algorithmic graph theory by Peter G. C l o t e (Chestnut Hill, Mass.) and Jeffry L. H i r s t (Boone, N.C.) Abstract.
Binary Decision Diagrams
 Binary Decision Diagrams Literature Some pointers: H.R. Andersen, An Introduction to Binary Decision Diagrams, Lecture notes, Department of Information Technology, IT University of Copenhagen Tools: URL:
Binary Decision Diagrams Literature Some pointers: H.R. Andersen, An Introduction to Binary Decision Diagrams, Lecture notes, Department of Information Technology, IT University of Copenhagen Tools: URL:
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Grammars (part II) Prof. Dan A. Simovici UMB
 rammars (part II) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Length-Increasing vs. Context-Sensitive rammars Theorem The class L 1 equals the class of length-increasing languages. 3 / 1 Length-Increasing
rammars (part II) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Length-Increasing vs. Context-Sensitive rammars Theorem The class L 1 equals the class of length-increasing languages. 3 / 1 Length-Increasing
CSE 200 Lecture Notes Turing machine vs. RAM machine vs. circuits
 CSE 200 Lecture Notes Turing machine vs. RAM machine vs. circuits Chris Calabro January 13, 2016 1 RAM model There are many possible, roughly equivalent RAM models. Below we will define one in the fashion
CSE 200 Lecture Notes Turing machine vs. RAM machine vs. circuits Chris Calabro January 13, 2016 1 RAM model There are many possible, roughly equivalent RAM models. Below we will define one in the fashion
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION
 FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
FORMAL LANGUAGES, AUTOMATA AND COMPUTATION DECIDABILITY ( LECTURE 15) SLIDES FOR 15-453 SPRING 2011 1 / 34 TURING MACHINES-SYNOPSIS The most general model of computation Computations of a TM are described
Flat counter automata almost everywhere!
 Flat counter automata almost everywhere! Jérôme Leroux and Grégoire Sutre Projet Vertecs, IRISA / INRIA Rennes, FRANCE Équipe MVTsi, CNRS / LABRI, FRANCE Counter-automata verification A simple counter-automata:
Flat counter automata almost everywhere! Jérôme Leroux and Grégoire Sutre Projet Vertecs, IRISA / INRIA Rennes, FRANCE Équipe MVTsi, CNRS / LABRI, FRANCE Counter-automata verification A simple counter-automata:
Automata on linear orderings
 Automata on linear orderings Véronique Bruyère Institut d Informatique Université de Mons-Hainaut Olivier Carton LIAFA Université Paris 7 September 25, 2006 Abstract We consider words indexed by linear
Automata on linear orderings Véronique Bruyère Institut d Informatique Université de Mons-Hainaut Olivier Carton LIAFA Université Paris 7 September 25, 2006 Abstract We consider words indexed by linear
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
AC68 FINITE AUTOMATA & FORMULA LANGUAGES DEC 2013
 Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Q.2 a. Prove by mathematical induction n 4 4n 2 is divisible by 3 for n 0. Basic step: For n = 0, n 3 n = 0 which is divisible by 3. Induction hypothesis: Let p(n) = n 3 n is divisible by 3. Induction
Chapter 1. Automata over infinite alphabets
 Chapter 1 Automata over infinite alphabets Amaldev Manuel and R. Ramanujam Institute of Mathematical Sciences, C.I.T campus, Taramani, Chennai - 600113. In many contexts such as validation of XML data,
Chapter 1 Automata over infinite alphabets Amaldev Manuel and R. Ramanujam Institute of Mathematical Sciences, C.I.T campus, Taramani, Chennai - 600113. In many contexts such as validation of XML data,
Pushdown Automata (Pre Lecture)
 Pushdown Automata (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Pushdown Automata (Pre Lecture) Fall 2017 1 / 41 Outline Pushdown Automata Pushdown
Pushdown Automata (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Pushdown Automata (Pre Lecture) Fall 2017 1 / 41 Outline Pushdown Automata Pushdown
MTH401A Theory of Computation. Lecture 17
 MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Automata Theory and Formal Grammars: Lecture 1
 Automata Theory and Formal Grammars: Lecture 1 Sets, Languages, Logic Automata Theory and Formal Grammars: Lecture 1 p.1/72 Sets, Languages, Logic Today Course Overview Administrivia Sets Theory (Review?)
Automata Theory and Formal Grammars: Lecture 1 Sets, Languages, Logic Automata Theory and Formal Grammars: Lecture 1 p.1/72 Sets, Languages, Logic Today Course Overview Administrivia Sets Theory (Review?)
