A Study of Solving Linear System of Equations by GAUSS-JORDAN Matrix Method-An Algorithmic Approach
|
|
|
- Kathlyn Fisher
- 5 years ago
- Views:
Transcription
1 A Study of Solving Linear System of Equations by GAUSS-JORDAN Matrix Method-An Algorithmic Approach ABSTRACT Dr. YOGEESH N Assistant professor in Mathematics Government First Grade College BH Road, Tumkur Government of Karnataka, INDIA yogeesh.r@gmail.com This paper shows how to solve any system of linear equations over an arbitrary field, using the Gauss- Jordan algorithm. For this, we need to define some concepts called row echelon form, elementary row operations, row equivalence and with other knowledge like linear equation, matrices and determinants also. By knowing all the above information here, we designed the Gauss-Jordan Algorithm to solve linear equations with some examples this will be useful to write the computational program to solve the system of equations using Gauss-Jordon method. KEYWORDS Row-echelon form, reduced row-echelon form, Elementary row operations, Row equivalence, augmented matrix, Gauss-Jordan Algorithm. INTRODUCTION The Gauss-Jordon method is one of the methods to solve system of linear equations using matrix method. Now a days these methods are incorporated in the computational field to solve these type of equations using the program code to compute the solutions. Therefore, by knowing the basic knowledge about the process one can easily write the computational codes in the relevant computer language. GAUSS-JORDAN Method of solving linear equations. We show how to solve any system of linear equations over an arbitrary field, using the GAUSS- JORDAN algorithm. We first need to define some terms. Definition (Row-echelon form) A matrix is in row-echelon form if a. All zero rows (if any) are at the bottom of the matrix and b. If two successive rows are non-zero, the second row starts with more zeros than the first (moving from left to right). For example, the matrix JETIR Journal of Emerging Technologies and Innovative Research (JETIR) 314
2 [ ] Is in row-echelon form, Whereas the matrix [ ] is not in row-echelon form The zero matrix of any size is always in row-echelon form. Definition (Reduced row-echelon form) A matrix is in reduced row-echelon form if 1. It is in row-echelon form, 2. The leading (leftmost non-zero) entry in each non-zero row is 1, 3. All other elements of the column in which the leading entry 1 occurs are zeros. For example the matrices [ ] and [ ] are in reduced row-echelon form, whereas the matrices form [ 0 1 0] and [ 0 1 0] are not in reduced row-echelon form, but are in row-echelon The zero matrix of any size is always in reduced row-echelon form. Notation: If a matrix is in reduced row-echelon form, it is useful to denote the column numbers in which the leading entries 1 occur, by c1, c2,....cr, with the remaining column numbers being denoted by cr+1,.... cn, where r is the number of non-zero rows. For example, in the 4 x 6 matrix above, we have r = 3, c1=2, c2=4, c3=5, c4=1, c5=3, c6=6. The following operations are the ones used on systems of linear equations and do not change the solutions. Definition (Elementary row operations) There are three types of elementary row operations that can be performed on matrices. 1. Interchanging two rows: Ri Rj interchanges rows i and j. 2. Multiplying a row by a non-zero scalar: JETIR Journal of Emerging Technologies and Innovative Research (JETIR) 315
3 Ri tri multiplies row i by the non-zero scalar t. 3. Adding a multiple of one row to another row: Rj Rj + tri adds t times row i to row j. Definition (Row equivalence) Matrix A is row-equivalent to matrix B, if B is obtained from A by a sequence of elementary row operations. Example. Working from left to right A = [ 2 1 1] R2 R2+2R3 [ 4 1 5] R2 R3 [ 1 1 2] R1 2R1 [ 1 1 2] = B Thus A is row-equivalent to B. clearly B is also row-equivalent to A, by performing the inverse rowoperations R1 ½ R1, R2 R3, R2 R2-2R3 on B. It is not difficult to prove that if A and B are row-equivalent augmented matrices of two systems of linear equations, then the two systems have the same solution sets a solution of the one system is a solution of the other. For example, the systems whose augmented matrices are A and B in the above example are respectively x + 2y = 0 { 2x + y = 1 x y = 2 2x + 4y = 0 and { x y = 2 4x y = 5 and these systems have precisely the same solutions. The Gauss-Jordan algorithm We now describe the GAUSS-JORDAN ALGORITHM. This is a process, which starts with a given matrix A and produces a matrix B in reduced row-echelon form, which is row-equivalent to A. If A is the augmented matrix of a system of linear equations, then B will be a much simpler matrix than A from which the consistency or inconsistency of the corresponding system is immediately apparent and in fact, the complete solution of the system can be follow. STEP 1 Find the first non-zero column moving from left to right, (column c1) and select a non-zero entry from this column. By interchanging rows, if necessary, ensure that the first entry in this column is non-zero. Multiply row 1 by the multiplicative inverse of a1c1 thereby converting a1c1 to 1. For each non-zero element aic1, i > 1, (if any) in column c1, add aic1 times row 1 to row i, thereby ensuring that all elements in column c1, apart from the first, are zero. JETIR Journal of Emerging Technologies and Innovative Research (JETIR) 316
4 STEP 2 If the matrix obtained at Step 1 has its 2 nd,...., m th rows all zero, the matrix is in reduced row-echelon form. Otherwise, suppose that the first column, which has a non-zero element in the rows below the first, is column c2. Then c1 < c2. By interchanging rows below the first, if necessary, ensure that a2c2 is non-zero. Then convert a2c2 to 1 and by adding suitable multiples of row 2 to the remaining rows, where necessary, ensure that all remaining elements in column c2 are zero. The process is repeated and will eventually stop after r steps, either because we run out of rows, or because we run out of non-zero columns. In general, the final matrix will be in reduced rowechelon form and will have r non-zero rows, with leading entries 1 in columns c1,....cr, respectively Example. [ ] R1 R2 [ ] / /2 R1 ½ R1 [ ] R3 R3-5R1 [ ] / /2 R2 ¼ R2 [ ] { R /2 1 R 1 + R 2 [ ] R /2 3 R 3 4R /2 R / R3 [ ] R1 R1-5 2 R3 [ ] The last matrix is in reduced row-echelon form. REMARK: It is possible to show that a given matrix over an arbitrary field is row-equivalent to precisely one matrix, which is in reduced row-echelon form. A flow-chart for the Gauss-Jordan algorithm, is presented in figure below. Systematic solution of linear systems Suppose a system of m linear equations in n unknowns x1,....xn has augmented matrix A and that A is row-equivalent to a matrix B which is in reduced row-echelon form, via the Gauss-Jordan algorithm. Then A and B are m x (n+1). Suppose that B has r non-zero rows and that the leading entry 1 in row i occurs in column number ci, for 1 i r. Then 1 c1 < c2 <..., <cr n+1 JETIR Journal of Emerging Technologies and Innovative Research (JETIR) 317
5 START Input A, m, n i=1, j=1 Are the elements in the j th column on and below the i th row all zero? J = j + 1 Let apj be the first non-zero element in column j on or below the i th row Is j = n? Is p=i? Interchange the p th and i th rows Divide the i th row by aij Subtract aqj times the i th row from the q th row for q=1,...., m(q i) Set c i = j i = i+1 j = j+1 Is i = m? Print A, C1,...ci Is j = n? STOP Figure 1: Diagram showing Gauss-Jordan Algorithm Also assume that the remaining column numbers are cr+1,..., cn+1, Where 1 cr+1 < Cr+2 <.... < cn n+1 Case 1: cr = n+1. The system is inconsistent. For the last non-zero row of B is corresponding equation is 0x1 + 0x xn = 1. [0, 0,..., 1] and the Which has no solutions. Consequently, the original system has no solutions. JETIR Journal of Emerging Technologies and Innovative Research (JETIR) 318
6 Case 2: cr n. The system of equations corresponding to the non-zero rows of B is inconsistent. First, notice that r n here. If r = n, then c1 = 1, c2 = 2,..., cn = n and There is a unique solution x1 = d1, x2 = d2,..., xn = dn d d 2.. B = d n [ ] If r < n, there will be more than one solution (infinitely many if the field is infinite). For all solutions are obtained by taking the unknownsx c1,..., x cr as dependent unknowns and using the r equations corresponding to the non-zero rows of B to express these unknowns in terms of the remaining independent unknowns x cr+1,..., x cn, which can take on arbitrary values: x c1 = b1n+1 b 1cr+1 x cr+1,... b 1cn x cn x cr = brn+1 b rcr+1 x cr+1,... b rcn x cn. In particular, taking x cr+1 = 0,, x cn 1 = 0 and x cn = 0, 1 respectively, produces at least two solutions. Theoretical Examples to solve this type of system of equations 1. Example. Solve the system x + y = 0; x y = 1; 4x + 2y = 1 Solution: The augmented matrix of the system is ½ A = [ 1 1 1] which is row equivalent to B = [ 0 1 ½] We read off the unique solution x = ½, y = -½ (Here n = 2, r = 2, c1 = 1, c2 = 2. Also cr = c2 = 2 < 3 = n+1 and r = n) 2. Example. Solve the system 2x1 + 2x2 2x3 = 5; 7x1 + 7x2 + x3 = 10; 5x1 + 5x2 x3 = 5. Solution: The augmented matrix is A = [ ] which is row equivalent to B = [ ] We read off inconsistency for the original system. (Here n = 3, r = 3, c1 = 1, c2= 3. Also cr = c3 = 4 = n+1) 3. Example. Solve the system x1 x2 + x3 = 1; x1 + x2 x3 = 2. JETIR Journal of Emerging Technologies and Innovative Research (JETIR) 319
7 Solution: The augmented matrix is A = [ /2 ] which is row equivalent to B = [1 1 ] The complete solution is x1 = 3/2, x2 = ½ +x3, with x3 arbitrary. (Here n = 3, r = 2, c1 = 1, c2 = 2. Also cr = c2 = 2 < 4 = n+1 and r < n) Example. Solve the system 6x3 + 2x4 4x5 8x6 = 8; 3x3 + x4 2x5 4x6 = 4; 2x1 3x2 + x3 + 4x4 7x5 + x6 = 2; 6x1 9x2 + 11x4 19x5 + 3x6 = 1. Solution: The augmented matrix is A = [ ] which is row equivalent to /2 0 11/6 19/6 0 1/ /3 2/3 0 5/3 B = [ ] / The complete solution is, x1 = x x x 6 5, x3 = 5 1 x x 3 5, x6 = ¼, with x2, x4, x5 arbitrary. (Here n = 6, r = 3, c1 = 1, c2 = 3, c3 = 6; cr = c3 = 6 < 7 = n+1; r < n) CONCLUSION Here by making use of this, Gauss-Jordan algorithm one can easily write the program code in different platforms to get desired solutions for the system of linear equations. This paper allows the program writers in different computer languages in easy and quick glimpse of idea regarding this type problem solving. Therefore, the Gauss-Jordan Algorithm to solve linear equations with some examples this will be useful to write the computational program to solve the system of equations using Gauss-Jordon method. REFERENCES 1. Howard Anton -Elementary Linear Algebra : John Wiley & sons(1987) 2. Charles G. Cullen -Matrices and linear Transformations : Second Edition, Dover (1990) 3. Daniel T. Finkbeiner III - Introduction to Matrices and Linear Transformations: Third Edition W.H. Freeman and company (1978) 4. R.J.Goult, R.F. Hoskins, J.A.Milner, M.J. Pratt-Computational Methods in linear Algebra: Wiley (1975) 5. Kanneth Hoffman, Ray Kunze -Linear Algebra -Second edition Prertice-Hall(1971) 6. Donald E. Knuth -The art of computer programming :Addison Wesley (1988) 7. Serge Lang -Linear Algebra :Addison-Wesley (1966) 8. James R. Munkres -Elementary linear Algebra : Addison-Wesley(1964) JETIR Journal of Emerging Technologies and Innovative Research (JETIR) 320
8 9. Evar D. Nering - Linear Algebra and matrix theory :Second edition-john Willey (1970) 10. A. Edelman - The distribution and moments of the smallest Eigenvalue of a random matrix of wishart type-linear Algebra :Appl(1991) 11. L. Arnold - On the asymptotic distribution of the eigenvalues of random matrices: J. Math Asar(1967) 12. D. Bau and L. Trefethem- Numerical linear algebra :Society for Industrial and applied mathematics (SIAM) Philodelphia PA (1997) 13. J. Komlos - On the determinant of (0.1) Matrice : Studia Sci math Hungar-2 (1967). 14. T. Tao and V. Vu -On random ±1 matrices: Singularity and Determinant Random structures algorithms (2006) 15. P. Wigner -On the distribution of the roots of certain symmetric matrices : The annuals of mathematics (1958) 16. John R. Rice- Numerical methods, Software and Analysis : Second edition Academic press (1993.) 17. Lary Smith -Linear Algebra : Second edition Springer Verlag (1984) 18. Gilbert Strang -The fundamental Theorem of linear Algebra :American Mathematical Month (1993) 19. D. Hearn and M.P. Baker -Computer Graphics: Scott, Forsman and company, Glenview, iilinois (1988) 20. R.E. Larson and B.H. Edwards -Elementary Linear Algebra :D.C. Heath and company, Lexington Massachusetts Toronto (1988) 21. P.J. Antsaklis and A.N. Michel -Linear Systems :Mc Graw Hill (1997) JETIR Journal of Emerging Technologies and Innovative Research (JETIR) 321
MAC Module 1 Systems of Linear Equations and Matrices I
 MAC 2103 Module 1 Systems of Linear Equations and Matrices I 1 Learning Objectives Upon completing this module, you should be able to: 1. Represent a system of linear equations as an augmented matrix.
MAC 2103 Module 1 Systems of Linear Equations and Matrices I 1 Learning Objectives Upon completing this module, you should be able to: 1. Represent a system of linear equations as an augmented matrix.
Math "Matrix Approach to Solving Systems" Bibiana Lopez. November Crafton Hills College. (CHC) 6.3 November / 25
 Math 102 6.3 "Matrix Approach to Solving Systems" Bibiana Lopez Crafton Hills College November 2010 (CHC) 6.3 November 2010 1 / 25 Objectives: * Define a matrix and determine its order. * Write the augmented
Math 102 6.3 "Matrix Approach to Solving Systems" Bibiana Lopez Crafton Hills College November 2010 (CHC) 6.3 November 2010 1 / 25 Objectives: * Define a matrix and determine its order. * Write the augmented
Matrix Solutions to Linear Equations
 Matrix Solutions to Linear Equations Augmented matrices can be used as a simplified way of writing a system of linear equations. In an augmented matrix, a vertical line is placed inside the matrix to represent
Matrix Solutions to Linear Equations Augmented matrices can be used as a simplified way of writing a system of linear equations. In an augmented matrix, a vertical line is placed inside the matrix to represent
Chapter 1. Vectors, Matrices, and Linear Spaces
 1.4 Solving Systems of Linear Equations 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.4. Solving Systems of Linear Equations Note. We give an algorithm for solving a system of linear equations (called
1.4 Solving Systems of Linear Equations 1 Chapter 1. Vectors, Matrices, and Linear Spaces 1.4. Solving Systems of Linear Equations Note. We give an algorithm for solving a system of linear equations (called
Linear Algebra Practice Problems
 Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
Math 7, Professor Ramras Linear Algebra Practice Problems () Consider the following system of linear equations in the variables x, y, and z, in which the constants a and b are real numbers. x y + z = a
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Corrected Version, 7th April 013 Comments to the author at keithmatt@gmail.com Chapter 1 LINEAR EQUATIONS 1.1
ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Corrected Version, 7th April 013 Comments to the author at keithmatt@gmail.com Chapter 1 LINEAR EQUATIONS 1.1
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2.
 Chapter 1 LINEAR EQUATIONS 11 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,, a n, b are given real
Chapter 1 LINEAR EQUATIONS 11 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,, a n, b are given real
Definition of Equality of Matrices. Example 1: Equality of Matrices. Consider the four matrices
 IT 131: Mathematics for Science Lecture Notes 3 Source: Larson, Edwards, Falvo (2009): Elementary Linear Algebra, Sixth Edition. Matrices 2.1 Operations with Matrices This section and the next introduce
IT 131: Mathematics for Science Lecture Notes 3 Source: Larson, Edwards, Falvo (2009): Elementary Linear Algebra, Sixth Edition. Matrices 2.1 Operations with Matrices This section and the next introduce
9.1 - Systems of Linear Equations: Two Variables
 9.1 - Systems of Linear Equations: Two Variables Recall that a system of equations consists of two or more equations each with two or more variables. A solution to a system in two variables is an ordered
9.1 - Systems of Linear Equations: Two Variables Recall that a system of equations consists of two or more equations each with two or more variables. A solution to a system in two variables is an ordered
Section 6.2 Larger Systems of Linear Equations
 Section 6.2 Larger Systems of Linear Equations Gaussian Elimination In general, to solve a system of linear equations using its augmented matrix, we use elementary row operations to arrive at a matrix
Section 6.2 Larger Systems of Linear Equations Gaussian Elimination In general, to solve a system of linear equations using its augmented matrix, we use elementary row operations to arrive at a matrix
Gauss-Jordan Row Reduction and Reduced Row Echelon Form
 Gauss-Jordan Row Reduction and Reduced Row Echelon Form If we put the augmented matrix of a linear system in reduced row-echelon form, then we don t need to back-substitute to solve the system. To put
Gauss-Jordan Row Reduction and Reduced Row Echelon Form If we put the augmented matrix of a linear system in reduced row-echelon form, then we don t need to back-substitute to solve the system. To put
Chapter 2. Systems of Equations and Augmented Matrices. Creighton University
 Chapter Section - Systems of Equations and Augmented Matrices D.S. Malik Creighton University Systems of Linear Equations Common ways to solve a system of equations: Eliminationi Substitution Elimination
Chapter Section - Systems of Equations and Augmented Matrices D.S. Malik Creighton University Systems of Linear Equations Common ways to solve a system of equations: Eliminationi Substitution Elimination
5x 2 = 10. x 1 + 7(2) = 4. x 1 3x 2 = 4. 3x 1 + 9x 2 = 8
 1 To solve the system x 1 + x 2 = 4 2x 1 9x 2 = 2 we find an (easier to solve) equivalent system as follows: Replace equation 2 with (2 times equation 1 + equation 2): x 1 + x 2 = 4 Solve equation 2 for
1 To solve the system x 1 + x 2 = 4 2x 1 9x 2 = 2 we find an (easier to solve) equivalent system as follows: Replace equation 2 with (2 times equation 1 + equation 2): x 1 + x 2 = 4 Solve equation 2 for
3. Replace any row by the sum of that row and a constant multiple of any other row.
 Section. Solution of Linear Systems by Gauss-Jordan Method A matrix is an ordered rectangular array of numbers, letters, symbols or algebraic expressions. A matrix with m rows and n columns has size or
Section. Solution of Linear Systems by Gauss-Jordan Method A matrix is an ordered rectangular array of numbers, letters, symbols or algebraic expressions. A matrix with m rows and n columns has size or
Lesson 3. Inverse of Matrices by Determinants and Gauss-Jordan Method
 Module 1: Matrices and Linear Algebra Lesson 3 Inverse of Matrices by Determinants and Gauss-Jordan Method 3.1 Introduction In lecture 1 we have seen addition and multiplication of matrices. Here we shall
Module 1: Matrices and Linear Algebra Lesson 3 Inverse of Matrices by Determinants and Gauss-Jordan Method 3.1 Introduction In lecture 1 we have seen addition and multiplication of matrices. Here we shall
Syllabus For II nd Semester Courses in MATHEMATICS
 St. Xavier s College Autonomous Mumbai Syllabus For II nd Semester Courses in MATHEMATICS Contents: (November 2016 onwards) Theory Syllabus for Courses: S.MAT.2.01 : Calculus II. S.MAT.2.02 : Linear Algebra.
St. Xavier s College Autonomous Mumbai Syllabus For II nd Semester Courses in MATHEMATICS Contents: (November 2016 onwards) Theory Syllabus for Courses: S.MAT.2.01 : Calculus II. S.MAT.2.02 : Linear Algebra.
Linear Algebra I Lecture 10
 Linear Algebra I Lecture 10 Xi Chen 1 1 University of Alberta January 30, 2019 Outline 1 Gauss-Jordan Algorithm ] Let A = [a ij m n be an m n matrix. To reduce A to a reduced row echelon form using elementary
Linear Algebra I Lecture 10 Xi Chen 1 1 University of Alberta January 30, 2019 Outline 1 Gauss-Jordan Algorithm ] Let A = [a ij m n be an m n matrix. To reduce A to a reduced row echelon form using elementary
MAC Module 2 Systems of Linear Equations and Matrices II. Learning Objectives. Upon completing this module, you should be able to :
 MAC 0 Module Systems of Linear Equations and Matrices II Learning Objectives Upon completing this module, you should be able to :. Find the inverse of a square matrix.. Determine whether a matrix is invertible..
MAC 0 Module Systems of Linear Equations and Matrices II Learning Objectives Upon completing this module, you should be able to :. Find the inverse of a square matrix.. Determine whether a matrix is invertible..
Chapter 6 Page 1 of 10. Lecture Guide. Math College Algebra Chapter 6. to accompany. College Algebra by Julie Miller
 Chapter 6 Page 1 of 10 Lecture Guide Math 105 - College Algebra Chapter 6 to accompany College Algebra by Julie Miller Corresponding Lecture Videos can be found at Prepared by Stephen Toner & Nichole DuBal
Chapter 6 Page 1 of 10 Lecture Guide Math 105 - College Algebra Chapter 6 to accompany College Algebra by Julie Miller Corresponding Lecture Videos can be found at Prepared by Stephen Toner & Nichole DuBal
Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination
 Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination Winfried Just, Ohio University September 22, 2017 Review: The coefficient matrix Consider a system of m linear equations in n variables.
Lecture 12: Solving Systems of Linear Equations by Gaussian Elimination Winfried Just, Ohio University September 22, 2017 Review: The coefficient matrix Consider a system of m linear equations in n variables.
Notes on Row Reduction
 Notes on Row Reduction Francis J. Narcowich Department of Mathematics Texas A&M University September The Row-Reduction Algorithm The row-reduced form of a matrix contains a great deal of information, both
Notes on Row Reduction Francis J. Narcowich Department of Mathematics Texas A&M University September The Row-Reduction Algorithm The row-reduced form of a matrix contains a great deal of information, both
Methods for Solving Linear Systems Part 2
 Methods for Solving Linear Systems Part 2 We have studied the properties of matrices and found out that there are more ways that we can solve Linear Systems. In Section 7.3, we learned that we can use
Methods for Solving Linear Systems Part 2 We have studied the properties of matrices and found out that there are more ways that we can solve Linear Systems. In Section 7.3, we learned that we can use
Elementary matrices, continued. To summarize, we have identified 3 types of row operations and their corresponding
 Elementary matrices, continued To summarize, we have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices
Elementary matrices, continued To summarize, we have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices
Linear Algebra I Lecture 8
 Linear Algebra I Lecture 8 Xi Chen 1 1 University of Alberta January 25, 2019 Outline 1 2 Gauss-Jordan Elimination Given a system of linear equations f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n
Linear Algebra I Lecture 8 Xi Chen 1 1 University of Alberta January 25, 2019 Outline 1 2 Gauss-Jordan Elimination Given a system of linear equations f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 998 Comments to the author at krm@mathsuqeduau All contents copyright c 99 Keith
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 998 Comments to the author at krm@mathsuqeduau All contents copyright c 99 Keith
7.6 The Inverse of a Square Matrix
 7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
7.6 The Inverse of a Square Matrix Copyright Cengage Learning. All rights reserved. What You Should Learn Verify that two matrices are inverses of each other. Use Gauss-Jordan elimination to find inverses
Lecture 2 Systems of Linear Equations and Matrices, Continued
 Lecture 2 Systems of Linear Equations and Matrices, Continued Math 19620 Outline of Lecture Algorithm for putting a matrix in row reduced echelon form - i.e. Gauss-Jordan Elimination Number of Solutions
Lecture 2 Systems of Linear Equations and Matrices, Continued Math 19620 Outline of Lecture Algorithm for putting a matrix in row reduced echelon form - i.e. Gauss-Jordan Elimination Number of Solutions
MAC1105-College Algebra. Chapter 5-Systems of Equations & Matrices
 MAC05-College Algebra Chapter 5-Systems of Equations & Matrices 5. Systems of Equations in Two Variables Solving Systems of Two Linear Equations/ Two-Variable Linear Equations A system of equations is
MAC05-College Algebra Chapter 5-Systems of Equations & Matrices 5. Systems of Equations in Two Variables Solving Systems of Two Linear Equations/ Two-Variable Linear Equations A system of equations is
4.3 Row operations. As we have seen in Section 4.1 we can simplify a system of equations by either:
 4.3 Row operations As we have seen in Section 4.1 we can simplify a system of equations by either: 1. Swapping the order of the equations around. For example: can become 3x 1 + 7x 2 = 9 x 1 2x 1 = 2 x
4.3 Row operations As we have seen in Section 4.1 we can simplify a system of equations by either: 1. Swapping the order of the equations around. For example: can become 3x 1 + 7x 2 = 9 x 1 2x 1 = 2 x
Section 5.6. LU and LDU Factorizations
 5.6. LU and LDU Factorizations Section 5.6. LU and LDU Factorizations Note. We largely follow Fraleigh and Beauregard s approach to this topic from Linear Algebra, 3rd Edition, Addison-Wesley (995). See
5.6. LU and LDU Factorizations Section 5.6. LU and LDU Factorizations Note. We largely follow Fraleigh and Beauregard s approach to this topic from Linear Algebra, 3rd Edition, Addison-Wesley (995). See
Section 1.1 System of Linear Equations. Dr. Abdulla Eid. College of Science. MATHS 211: Linear Algebra
 Section 1.1 System of Linear Equations College of Science MATHS 211: Linear Algebra (University of Bahrain) Linear System 1 / 33 Goals:. 1 Define system of linear equations and their solutions. 2 To represent
Section 1.1 System of Linear Equations College of Science MATHS 211: Linear Algebra (University of Bahrain) Linear System 1 / 33 Goals:. 1 Define system of linear equations and their solutions. 2 To represent
Row Reduced Echelon Form
 Math 40 Row Reduced Echelon Form Solving systems of linear equations lies at the heart of linear algebra. In high school we learn to solve systems in or variables using elimination and substitution of
Math 40 Row Reduced Echelon Form Solving systems of linear equations lies at the heart of linear algebra. In high school we learn to solve systems in or variables using elimination and substitution of
Linear Equations in Linear Algebra
 1 Linear Equations in Linear Algebra 1.1 SYSTEMS OF LINEAR EQUATIONS LINEAR EQUATION x 1,, x n A linear equation in the variables equation that can be written in the form a 1 x 1 + a 2 x 2 + + a n x n
1 Linear Equations in Linear Algebra 1.1 SYSTEMS OF LINEAR EQUATIONS LINEAR EQUATION x 1,, x n A linear equation in the variables equation that can be written in the form a 1 x 1 + a 2 x 2 + + a n x n
SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON 1.2]
![SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON 1.2] SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON 1.2]](/thumbs/91/104518447.jpg) SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON.2 EQUIVALENT LINEAR SYSTEMS: Two m n linear systems are equivalent both systems have the exact same solution sets. When solving a linear system Ax = b,
SOLVING Ax = b: GAUSS-JORDAN ELIMINATION [LARSON.2 EQUIVALENT LINEAR SYSTEMS: Two m n linear systems are equivalent both systems have the exact same solution sets. When solving a linear system Ax = b,
Midterm 1 Review. Written by Victoria Kala SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015
 Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
Midterm 1 Review Written by Victoria Kala vtkala@math.ucsb.edu SH 6432u Office Hours: R 12:30 1:30 pm Last updated 10/10/2015 Summary This Midterm Review contains notes on sections 1.1 1.5 and 1.7 in your
4 Elementary matrices, continued
 4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices are constructed
4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. If you check the previous examples, you ll find that these matrices are constructed
1 - Systems of Linear Equations
 1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
Row Reduction and Echelon Forms
 Row Reduction and Echelon Forms 1 / 29 Key Concepts row echelon form, reduced row echelon form pivot position, pivot, pivot column basic variable, free variable general solution, parametric solution existence
Row Reduction and Echelon Forms 1 / 29 Key Concepts row echelon form, reduced row echelon form pivot position, pivot, pivot column basic variable, free variable general solution, parametric solution existence
Chapter 4. Solving Systems of Equations. Chapter 4
 Solving Systems of Equations 3 Scenarios for Solutions There are three general situations we may find ourselves in when attempting to solve systems of equations: 1 The system could have one unique solution.
Solving Systems of Equations 3 Scenarios for Solutions There are three general situations we may find ourselves in when attempting to solve systems of equations: 1 The system could have one unique solution.
Solving Systems of Linear Equations Using Matrices
 Solving Systems of Linear Equations Using Matrices What is a Matrix? A matrix is a compact grid or array of numbers. It can be created from a system of equations and used to solve the system of equations.
Solving Systems of Linear Equations Using Matrices What is a Matrix? A matrix is a compact grid or array of numbers. It can be created from a system of equations and used to solve the system of equations.
4 Elementary matrices, continued
 4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. To repeat the recipe: These matrices are constructed by performing the given row
4 Elementary matrices, continued We have identified 3 types of row operations and their corresponding elementary matrices. To repeat the recipe: These matrices are constructed by performing the given row
Chapter 1: Systems of linear equations and matrices. Section 1.1: Introduction to systems of linear equations
 Chapter 1: Systems of linear equations and matrices Section 1.1: Introduction to systems of linear equations Definition: A linear equation in n variables can be expressed in the form a 1 x 1 + a 2 x 2
Chapter 1: Systems of linear equations and matrices Section 1.1: Introduction to systems of linear equations Definition: A linear equation in n variables can be expressed in the form a 1 x 1 + a 2 x 2
Lecture 3: Gaussian Elimination, continued. Lecture 3: Gaussian Elimination, continued
 Definition The process of solving a system of linear equations by converting the system to an augmented matrix is called Gaussian Elimination. The general strategy is as follows: Convert the system of
Definition The process of solving a system of linear equations by converting the system to an augmented matrix is called Gaussian Elimination. The general strategy is as follows: Convert the system of
Solving Linear Systems Using Gaussian Elimination
 Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
Solving Linear Systems Using Gaussian Elimination DEFINITION: A linear equation in the variables x 1,..., x n is an equation that can be written in the form a 1 x 1 +...+a n x n = b, where a 1,...,a n
PH1105 Lecture Notes on Linear Algebra.
 PH05 Lecture Notes on Linear Algebra Joe Ó hógáin E-mail: johog@mathstcdie Main Text: Calculus for the Life Sciences by Bittenger, Brand and Quintanilla Other Text: Linear Algebra by Anton and Rorres Matrices
PH05 Lecture Notes on Linear Algebra Joe Ó hógáin E-mail: johog@mathstcdie Main Text: Calculus for the Life Sciences by Bittenger, Brand and Quintanilla Other Text: Linear Algebra by Anton and Rorres Matrices
Example: 2x y + 3z = 1 5y 6z = 0 x + 4z = 7. Definition: Elementary Row Operations. Example: Type I swap rows 1 and 3
 Math 0 Row Reduced Echelon Form Techniques for solving systems of linear equations lie at the heart of linear algebra. In high school we learn to solve systems with or variables using elimination and substitution
Math 0 Row Reduced Echelon Form Techniques for solving systems of linear equations lie at the heart of linear algebra. In high school we learn to solve systems with or variables using elimination and substitution
3.4 Elementary Matrices and Matrix Inverse
 Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Math 220: Summer 2015 3.4 Elementary Matrices and Matrix Inverse A n n elementary matrix is a matrix which is obtained from the n n identity matrix I n n by a single elementary row operation. Elementary
Math 1314 Week #14 Notes
 Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
Math 3 Week # Notes Section 5.: A system of equations consists of two or more equations. A solution to a system of equations is a point that satisfies all the equations in the system. In this chapter,
Matrices and RRE Form
 Matrices and RRE Form Notation R is the real numbers, C is the complex numbers (we will only consider complex numbers towards the end of the course) is read as an element of For instance, x R means that
Matrices and RRE Form Notation R is the real numbers, C is the complex numbers (we will only consider complex numbers towards the end of the course) is read as an element of For instance, x R means that
MATH 2331 Linear Algebra. Section 1.1 Systems of Linear Equations. Finding the solution to a set of two equations in two variables: Example 1: Solve:
 MATH 2331 Linear Algebra Section 1.1 Systems of Linear Equations Finding the solution to a set of two equations in two variables: Example 1: Solve: x x = 3 1 2 2x + 4x = 12 1 2 Geometric meaning: Do these
MATH 2331 Linear Algebra Section 1.1 Systems of Linear Equations Finding the solution to a set of two equations in two variables: Example 1: Solve: x x = 3 1 2 2x + 4x = 12 1 2 Geometric meaning: Do these
Pre-Calculus I. For example, the system. x y 2 z. may be represented by the augmented matrix
 Pre-Calculus I 8.1 Matrix Solutions to Linear Systems A matrix is a rectangular array of elements. o An array is a systematic arrangement of numbers or symbols in rows and columns. Matrices (the plural
Pre-Calculus I 8.1 Matrix Solutions to Linear Systems A matrix is a rectangular array of elements. o An array is a systematic arrangement of numbers or symbols in rows and columns. Matrices (the plural
March 19 - Solving Linear Systems
 March 19 - Solving Linear Systems Welcome to linear algebra! Linear algebra is the study of vectors, vector spaces, and maps between vector spaces. It has applications across data analysis, computer graphics,
March 19 - Solving Linear Systems Welcome to linear algebra! Linear algebra is the study of vectors, vector spaces, and maps between vector spaces. It has applications across data analysis, computer graphics,
Chapter 9: Systems of Equations and Inequalities
 Chapter 9: Systems of Equations and Inequalities 9. Systems of Equations Solve the system of equations below. By this we mean, find pair(s) of numbers (x, y) (if possible) that satisfy both equations.
Chapter 9: Systems of Equations and Inequalities 9. Systems of Equations Solve the system of equations below. By this we mean, find pair(s) of numbers (x, y) (if possible) that satisfy both equations.
Math 313 Chapter 1 Review
 Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Math 313 Chapter 1 Review Howard Anton, 9th Edition May 2010 Do NOT write on me! Contents 1 1.1 Introduction to Systems of Linear Equations 2 2 1.2 Gaussian Elimination 3 3 1.3 Matrices and Matrix Operations
Finite Mathematics Chapter 2. where a, b, c, d, h, and k are real numbers and neither a and b nor c and d are both zero.
 Finite Mathematics Chapter 2 Section 2.1 Systems of Linear Equations: An Introduction Systems of Equations Recall that a system of two linear equations in two variables may be written in the general form
Finite Mathematics Chapter 2 Section 2.1 Systems of Linear Equations: An Introduction Systems of Equations Recall that a system of two linear equations in two variables may be written in the general form
7.5 Operations with Matrices. Copyright Cengage Learning. All rights reserved.
 7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
7.5 Operations with Matrices Copyright Cengage Learning. All rights reserved. What You Should Learn Decide whether two matrices are equal. Add and subtract matrices and multiply matrices by scalars. Multiply
Lectures on Linear Algebra for IT
 Lectures on Linear Algebra for IT by Mgr. Tereza Kovářová, Ph.D. following content of lectures by Ing. Petr Beremlijski, Ph.D. Department of Applied Mathematics, VSB - TU Ostrava Czech Republic 2. Systems
Lectures on Linear Algebra for IT by Mgr. Tereza Kovářová, Ph.D. following content of lectures by Ing. Petr Beremlijski, Ph.D. Department of Applied Mathematics, VSB - TU Ostrava Czech Republic 2. Systems
Lecture 1 Systems of Linear Equations and Matrices
 Lecture 1 Systems of Linear Equations and Matrices Math 19620 Outline of Course Linear Equations and Matrices Linear Transformations, Inverses Bases, Linear Independence, Subspaces Abstract Vector Spaces
Lecture 1 Systems of Linear Equations and Matrices Math 19620 Outline of Course Linear Equations and Matrices Linear Transformations, Inverses Bases, Linear Independence, Subspaces Abstract Vector Spaces
Lecture 4: Gaussian Elimination and Homogeneous Equations
 Lecture 4: Gaussian Elimination and Homogeneous Equations Reduced Row Echelon Form An augmented matrix associated to a system of linear equations is said to be in Reduced Row Echelon Form (RREF) if the
Lecture 4: Gaussian Elimination and Homogeneous Equations Reduced Row Echelon Form An augmented matrix associated to a system of linear equations is said to be in Reduced Row Echelon Form (RREF) if the
10.3 Matrices and Systems Of
 10.3 Matrices and Systems Of Linear Equations Copyright Cengage Learning. All rights reserved. Objectives Matrices The Augmented Matrix of a Linear System Elementary Row Operations Gaussian Elimination
10.3 Matrices and Systems Of Linear Equations Copyright Cengage Learning. All rights reserved. Objectives Matrices The Augmented Matrix of a Linear System Elementary Row Operations Gaussian Elimination
The matrix will only be consistent if the last entry of row three is 0, meaning 2b 3 + b 2 b 1 = 0.
 ) Find all solutions of the linear system. Express the answer in vector form. x + 2x + x + x 5 = 2 2x 2 + 2x + 2x + x 5 = 8 x + 2x + x + 9x 5 = 2 2 Solution: Reduce the augmented matrix [ 2 2 2 8 ] to
) Find all solutions of the linear system. Express the answer in vector form. x + 2x + x + x 5 = 2 2x 2 + 2x + 2x + x 5 = 8 x + 2x + x + 9x 5 = 2 2 Solution: Reduce the augmented matrix [ 2 2 2 8 ] to
System of Linear Equations
 Math 20F Linear Algebra Lecture 2 1 System of Linear Equations Slide 1 Definition 1 Fix a set of numbers a ij, b i, where i = 1,, m and j = 1,, n A system of m linear equations in n variables x j, is given
Math 20F Linear Algebra Lecture 2 1 System of Linear Equations Slide 1 Definition 1 Fix a set of numbers a ij, b i, where i = 1,, m and j = 1,, n A system of m linear equations in n variables x j, is given
Math 2331 Linear Algebra
 1.1 Linear System Math 2331 Linear Algebra 1.1 Systems of Linear Equations Shang-Huan Chiu Department of Mathematics, University of Houston schiu@math.uh.edu math.uh.edu/ schiu/ Shang-Huan Chiu, University
1.1 Linear System Math 2331 Linear Algebra 1.1 Systems of Linear Equations Shang-Huan Chiu Department of Mathematics, University of Houston schiu@math.uh.edu math.uh.edu/ schiu/ Shang-Huan Chiu, University
COURSE: MATRIX ALGEBRA (2 credit) CODE: MT 304
 COURSE: MATRIX ALGEBRA (2 credit) CODE: MT 304 Description: The purpose of this course is to improve students ability in understanding basic concepts of Matrix Algebra As provisions for teaching school
COURSE: MATRIX ALGEBRA (2 credit) CODE: MT 304 Description: The purpose of this course is to improve students ability in understanding basic concepts of Matrix Algebra As provisions for teaching school
Exercise Sketch these lines and find their intersection.
 These are brief notes for the lecture on Friday August 21, 2009: they are not complete, but they are a guide to what I want to say today. They are not guaranteed to be correct. 1. Solving systems of linear
These are brief notes for the lecture on Friday August 21, 2009: they are not complete, but they are a guide to what I want to say today. They are not guaranteed to be correct. 1. Solving systems of linear
Gauss-Jordan elimination ( used in the videos below) stops when the augmented coefficient
 To review these matrix methods for solving systems of linear equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering all the basic
To review these matrix methods for solving systems of linear equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering all the basic
Elementary Linear Algebra
 Elementary Linear Algebra Linear algebra is the study of; linear sets of equations and their transformation properties. Linear algebra allows the analysis of; rotations in space, least squares fitting,
Elementary Linear Algebra Linear algebra is the study of; linear sets of equations and their transformation properties. Linear algebra allows the analysis of; rotations in space, least squares fitting,
Lecture Notes: Solving Linear Systems with Gauss Elimination
 Lecture Notes: Solving Linear Systems with Gauss Elimination Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Echelon Form and Elementary
Lecture Notes: Solving Linear Systems with Gauss Elimination Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk 1 Echelon Form and Elementary
Matrix Algebra Lecture Notes. 1 What is Matrix Algebra? Last change: 18 July Linear forms
 Matrix Algebra Lecture Notes Last change: 18 July 2017 1 What is Matrix Algebra? 1.1 Linear forms It is well-known that the total cost of a purchase of amounts (in kilograms) g 1, g 2, g 3 of some goods
Matrix Algebra Lecture Notes Last change: 18 July 2017 1 What is Matrix Algebra? 1.1 Linear forms It is well-known that the total cost of a purchase of amounts (in kilograms) g 1, g 2, g 3 of some goods
Math x + 3y 5z = 14 3x 2y + 3z = 17 4x + 3y 2z = 1
 Math 210 1. Solve the system: x + y + z = 1 2x + 3y + 4z = 5 (a z = 2, y = 1 and x = 0 (b z =any value, y = 3 2z and x = z 2 (c z =any value, y = 3 2z and x = z + 2 (d z =any value, y = 3 + 2z and x =
Math 210 1. Solve the system: x + y + z = 1 2x + 3y + 4z = 5 (a z = 2, y = 1 and x = 0 (b z =any value, y = 3 2z and x = z 2 (c z =any value, y = 3 2z and x = z + 2 (d z =any value, y = 3 + 2z and x =
Linear System Equations
 King Saud University September 24, 2018 Table of contents 1 2 3 4 Definition A linear system of equations with m equations and n unknowns is defined as follows: a 1,1 x 1 + a 1,2 x 2 + + a 1,n x n = b
King Saud University September 24, 2018 Table of contents 1 2 3 4 Definition A linear system of equations with m equations and n unknowns is defined as follows: a 1,1 x 1 + a 1,2 x 2 + + a 1,n x n = b
MAC Module 3 Determinants. Learning Objectives. Upon completing this module, you should be able to:
 MAC 2 Module Determinants Learning Objectives Upon completing this module, you should be able to:. Determine the minor, cofactor, and adjoint of a matrix. 2. Evaluate the determinant of a matrix by cofactor
MAC 2 Module Determinants Learning Objectives Upon completing this module, you should be able to:. Determine the minor, cofactor, and adjoint of a matrix. 2. Evaluate the determinant of a matrix by cofactor
Solving Systems of Linear Equations
 LECTURE 5 Solving Systems of Linear Equations Recall that we introduced the notion of matrices as a way of standardizing the expression of systems of linear equations In today s lecture I shall show how
LECTURE 5 Solving Systems of Linear Equations Recall that we introduced the notion of matrices as a way of standardizing the expression of systems of linear equations In today s lecture I shall show how
Chapter Contents. A 1.6 Further Results on Systems of Equations and Invertibility 1.7 Diagonal, Triangular, and Symmetric Matrices
 Chapter Contents. Introduction to System of Linear Equations. Gaussian Elimination.3 Matrices and Matri Operations.4 Inverses; Rules of Matri Arithmetic.5 Elementary Matrices and a Method for Finding A.6
Chapter Contents. Introduction to System of Linear Equations. Gaussian Elimination.3 Matrices and Matri Operations.4 Inverses; Rules of Matri Arithmetic.5 Elementary Matrices and a Method for Finding A.6
LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS
 LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1 Linear equations We now switch gears to discuss the topic of solving linear equations, and more interestingly, systems
LECTURES 4/5: SYSTEMS OF LINEAR EQUATIONS MA1111: LINEAR ALGEBRA I, MICHAELMAS 2016 1 Linear equations We now switch gears to discuss the topic of solving linear equations, and more interestingly, systems
Linear Equations in Linear Algebra
 1 Linear Equations in Linear Algebra 1.1 SYSTEMS OF LINEAR EQUATIONS LINEAR EQUATION,, 1 n A linear equation in the variables equation that can be written in the form a a a b 1 1 2 2 n n a a is an where
1 Linear Equations in Linear Algebra 1.1 SYSTEMS OF LINEAR EQUATIONS LINEAR EQUATION,, 1 n A linear equation in the variables equation that can be written in the form a a a b 1 1 2 2 n n a a is an where
MATH 54 - WORKSHEET 1 MONDAY 6/22
 MATH 54 - WORKSHEET 1 MONDAY 6/22 Row Operations: (1 (Replacement Add a multiple of one row to another row. (2 (Interchange Swap two rows. (3 (Scaling Multiply an entire row by a nonzero constant. A matrix
MATH 54 - WORKSHEET 1 MONDAY 6/22 Row Operations: (1 (Replacement Add a multiple of one row to another row. (2 (Interchange Swap two rows. (3 (Scaling Multiply an entire row by a nonzero constant. A matrix
Topics. Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij
 Topics Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij or a ij lives in row i and column j Definition of a matrix
Topics Vectors (column matrices): Vector addition and scalar multiplication The matrix of a linear function y Ax The elements of a matrix A : A ij or a ij lives in row i and column j Definition of a matrix
DM559 Linear and Integer Programming. Lecture 2 Systems of Linear Equations. Marco Chiarandini
 DM559 Linear and Integer Programming Lecture Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. Outline 1. 3 A Motivating Example You are organizing
DM559 Linear and Integer Programming Lecture Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. Outline 1. 3 A Motivating Example You are organizing
SYLLABUS UNDER AUTONOMY MATHEMATICS
 SYLLABUS UNDER AUTONOMY SEMESTER III Calculus and Analysis MATHEMATICS COURSE: A.MAT.3.01 [45 LECTURES] LEARNING OBJECTIVES : To learn about i) lub axiom of R and its consequences ii) Convergence of sequences
SYLLABUS UNDER AUTONOMY SEMESTER III Calculus and Analysis MATHEMATICS COURSE: A.MAT.3.01 [45 LECTURES] LEARNING OBJECTIVES : To learn about i) lub axiom of R and its consequences ii) Convergence of sequences
Lecture Notes in Mathematics. Arkansas Tech University Department of Mathematics. The Basics of Linear Algebra
 Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics The Basics of Linear Algebra Marcel B. Finan c All Rights Reserved Last Updated November 30, 2015 2 Preface Linear algebra
Lecture Notes in Mathematics Arkansas Tech University Department of Mathematics The Basics of Linear Algebra Marcel B. Finan c All Rights Reserved Last Updated November 30, 2015 2 Preface Linear algebra
CHAPTER 9: Systems of Equations and Matrices
 MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 9: Systems of Equations and Matrices 9.1 Systems of Equations in Two Variables 9.2 Systems of Equations in Three Variables
MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 9: Systems of Equations and Matrices 9.1 Systems of Equations in Two Variables 9.2 Systems of Equations in Three Variables
Linear Algebra 1 Exam 1 Solutions 6/12/3
 Linear Algebra 1 Exam 1 Solutions 6/12/3 Question 1 Consider the linear system in the variables (x, y, z, t, u), given by the following matrix, in echelon form: 1 2 1 3 1 2 0 1 1 3 1 4 0 0 0 1 2 3 Reduce
Linear Algebra 1 Exam 1 Solutions 6/12/3 Question 1 Consider the linear system in the variables (x, y, z, t, u), given by the following matrix, in echelon form: 1 2 1 3 1 2 0 1 1 3 1 4 0 0 0 1 2 3 Reduce
1. (7pts) Find the points of intersection, if any, of the following planes. 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1
 Math 125 Exam 1 Version 1 February 20, 2006 1. (a) (7pts) Find the points of intersection, if any, of the following planes. Solution: augmented R 1 R 3 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1 3 9
Math 125 Exam 1 Version 1 February 20, 2006 1. (a) (7pts) Find the points of intersection, if any, of the following planes. Solution: augmented R 1 R 3 3x + 9y + 6z = 3 2x 6y 4z = 2 x + 3y + 2z = 1 3 9
Using MATLAB. Linear Algebra
 Using MATLAB in Linear Algebra Edward Neuman Department of Mathematics Southern Illinois University at Carbondale One of the nice features of MATLAB is its ease of computations with vectors and matrices.
Using MATLAB in Linear Algebra Edward Neuman Department of Mathematics Southern Illinois University at Carbondale One of the nice features of MATLAB is its ease of computations with vectors and matrices.
Elementary Row Operations on Matrices
 King Saud University September 17, 018 Table of contents 1 Definition A real matrix is a rectangular array whose entries are real numbers. These numbers are organized on rows and columns. An m n matrix
King Saud University September 17, 018 Table of contents 1 Definition A real matrix is a rectangular array whose entries are real numbers. These numbers are organized on rows and columns. An m n matrix
Math 200 A and B: Linear Algebra Spring Term 2007 Course Description
 Math 200 A and B: Linear Algebra Spring Term 2007 Course Description February 25, 2007 Instructor: John Schmitt Warner 311, Ext. 5952 jschmitt@middlebury.edu Office Hours: Monday, Wednesday 11am-12pm,
Math 200 A and B: Linear Algebra Spring Term 2007 Course Description February 25, 2007 Instructor: John Schmitt Warner 311, Ext. 5952 jschmitt@middlebury.edu Office Hours: Monday, Wednesday 11am-12pm,
Problem Sheet 1 with Solutions GRA 6035 Mathematics
 Problem Sheet 1 with Solutions GRA 6035 Mathematics BI Norwegian Business School 2 Problems 1. From linear system to augmented matrix Write down the coefficient matrix and the augmented matrix of the following
Problem Sheet 1 with Solutions GRA 6035 Mathematics BI Norwegian Business School 2 Problems 1. From linear system to augmented matrix Write down the coefficient matrix and the augmented matrix of the following
ICT Tool: - C Language Program for Gauss Elimination Method
 ICT Tool: - C Language Program for Gauss Elimination Method Sanjay C. Gawande 1, Pradip P. Kolhe 2 and Prakash R. Kolhe 3 1 Assistant Professor, College of Agriculture, Dr. PDKV, Akola 2 Assistant Professor,
ICT Tool: - C Language Program for Gauss Elimination Method Sanjay C. Gawande 1, Pradip P. Kolhe 2 and Prakash R. Kolhe 3 1 Assistant Professor, College of Agriculture, Dr. PDKV, Akola 2 Assistant Professor,
Homework 1.1 and 1.2 WITH SOLUTIONS
 Math 220 Linear Algebra (Spring 2018) Homework 1.1 and 1.2 WITH SOLUTIONS Due Thursday January 25 These will be graded in detail and will count as two (TA graded) homeworks. Be sure to start each of these
Math 220 Linear Algebra (Spring 2018) Homework 1.1 and 1.2 WITH SOLUTIONS Due Thursday January 25 These will be graded in detail and will count as two (TA graded) homeworks. Be sure to start each of these
Chapter 1: Systems of Linear Equations
 Chapter : Systems of Linear Equations February, 9 Systems of linear equations Linear systems Lecture A linear equation in variables x, x,, x n is an equation of the form a x + a x + + a n x n = b, where
Chapter : Systems of Linear Equations February, 9 Systems of linear equations Linear systems Lecture A linear equation in variables x, x,, x n is an equation of the form a x + a x + + a n x n = b, where
Fundamentals of Linear Algebra. Marcel B. Finan Arkansas Tech University c All Rights Reserved
 Fundamentals of Linear Algebra Marcel B. Finan Arkansas Tech University c All Rights Reserved 2 PREFACE Linear algebra has evolved as a branch of mathematics with wide range of applications to the natural
Fundamentals of Linear Algebra Marcel B. Finan Arkansas Tech University c All Rights Reserved 2 PREFACE Linear algebra has evolved as a branch of mathematics with wide range of applications to the natural
Recall, we solved the system below in a previous section. Here, we learn another method. x + 4y = 14 5x + 3y = 2
 We will learn how to use a matrix to solve a system of equations. College algebra Class notes Matrices and Systems of Equations (section 6.) Recall, we solved the system below in a previous section. Here,
We will learn how to use a matrix to solve a system of equations. College algebra Class notes Matrices and Systems of Equations (section 6.) Recall, we solved the system below in a previous section. Here,
CHAPTER 9: Systems of Equations and Matrices
 MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 9: Systems of Equations and Matrices 9.1 Systems of Equations in Two Variables 9.2 Systems of Equations in Three Variables
MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 9: Systems of Equations and Matrices 9.1 Systems of Equations in Two Variables 9.2 Systems of Equations in Three Variables
Ack: 1. LD Garcia, MTH 199, Sam Houston State University 2. Linear Algebra and Its Applications - Gilbert Strang
 Gaussian Elimination CS6015 : Linear Algebra Ack: 1. LD Garcia, MTH 199, Sam Houston State University 2. Linear Algebra and Its Applications - Gilbert Strang The Gaussian Elimination Method The Gaussian
Gaussian Elimination CS6015 : Linear Algebra Ack: 1. LD Garcia, MTH 199, Sam Houston State University 2. Linear Algebra and Its Applications - Gilbert Strang The Gaussian Elimination Method The Gaussian
If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined
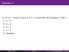 Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
Question 1 If A is a 4 6 matrix and B is a 6 3 matrix then the dimension of AB is A. 4 6 B. 6 6 C. 4 3 D. 3 4 E. Undefined Quang T. Bach Math 18 October 18, 2017 1 / 17 Question 2 1 2 Let A = 3 4 1 2 3
System of Linear Equations. Slide for MA1203 Business Mathematics II Week 1 & 2
 System of Linear Equations Slide for MA1203 Business Mathematics II Week 1 & 2 Function A manufacturer would like to know how his company s profit is related to its production level. How does one quantity
System of Linear Equations Slide for MA1203 Business Mathematics II Week 1 & 2 Function A manufacturer would like to know how his company s profit is related to its production level. How does one quantity
Solutions of Linear system, vector and matrix equation
 Goals: Solutions of Linear system, vector and matrix equation Solutions of linear system. Vectors, vector equation. Matrix equation. Math 112, Week 2 Suggested Textbook Readings: Sections 1.3, 1.4, 1.5
Goals: Solutions of Linear system, vector and matrix equation Solutions of linear system. Vectors, vector equation. Matrix equation. Math 112, Week 2 Suggested Textbook Readings: Sections 1.3, 1.4, 1.5
