Organization of Receptive Fields in Networks with. Hebbian Learning: The Connection Between. Box 1843, Brown University.
|
|
|
- Ella Atkins
- 5 years ago
- Views:
Transcription
1 Organization of Receptive Fields in Networks with Hebbian Learning: The Connection Between Synaptic and Phenomenological Models Harel Shouval and Leon N Cooper Department of Physics, The Department of Neuroscience and The Institute for Brain and Neural Systems Box 1843, Brown University Providence, R. I., hzs@cns.brown.edu May 28, 1996 Abstract In this paper we address the question of how does the lateral interaction aæect the formation and organization of receptive æelds in a network composed of interacting neurons with Hebbian type learning. We will show how to partially decouple the single cell eæects from the network eæects, and how some phenomenological models can be seen as approximations to these learning networks. We show that the interaction eæects the structure of receptive æelds. We also demonstrate how the organization of diæerent receptive æelds across the cortex is inæuenced by the interaction term, and that the type of singularities depend on the symmetries of the receptive æelds. 1 Introduction: Synaptic Plasticity and the structure of the Visual Cortex Recently Erwin et. al. è94è performed a comparison between predictions of many models, which attempt to explain organization of receptive æelds in the visual cortex, and cortical maps obtained by optical imageing è?;?è. In this paper we will consider two classes of such models; detailed synaptic models è?;?;?è, and iterative phenomenological models è?;?è. Erwin et. al. è94è have examined these classes of models claim that the phenomenological models æt the experimental observations much better than the synaptic models. Detailed synaptic models are fairly complex systems, with a large number of parameters. The experience of the last couple of decades in physics of complex systems has shown that phenomenological models are extremely important in explaining properties of complex systems. For complex systems of many interacting particles it is typically hopeless to try and solve the exact microscopic theory of these interacting systems, however in many cases coarse grained phenomenological models, that do not take into account most of the microscopic detail, do manage to predict the properties of such systems. It seems that if this is the case for the relatively simple complex systems of the physical sciences, then it might also be the case for the much more complex systems of neurobiology. 1
2 In this paper we show how the detailed synaptic models can be approximated by much simpler models that are related to some of the phenomenological models. These simpler models can be used in order to gain a better understanding of the properties of the complex synaptic models and possibly to understand where reported the diæerences in their properties è?è arise from. We analyze a cortical network of learning neurons, each of the neurons in this network forms plastic bonds with the sensory projections, and æxed bonds with other cortical neurons. The learning rule assumed herein is a normalized Hebbian ruleè?;?è. The type of network architecture assumed here is similar to that used in many other synaptic models of cortical plasticity è?;?;?;?;?, etc.è. Rather then presenting a new model we have attempted, in this paper, to analyze the behavior of these existing models, and map them onto much simpler models which we might be able to understand better When this analysis is be performed, it becomes clear that in order to understand the behavior of such networks, it is ærst necessary to understand how single neurons using the same learning rule behave. The purpose of this paper is to start giving answers to two related questions about such networks. èaè How do the lateral interactions aæect the receptive æelds of single cortical neurons, and in particular can cortical interactions produce oriented receptive æelds, where the single cell model produces radially symmetric receptive æelds. èbè How do the cortical interactions aæect the organization of diæerent receptive æelds across the cortex. A similar analysis has been used by Rubinstein è94è in order to answer the second question. His analysis diæerences form our in that it concentrates on a periodic homogenous network, and does not examine the eæect of the lateral interactions on receptive æeld formation. 2 A self organizing network model We assume a network of interconnected neurons, which are connected with modiæable synapses to the input layer. The learning rule examined is a normalized Hebbian rule which is sensitive only to the second order statistics. The output cèrè, of each neuron, in this model is deæned as cèrè= Ièr, xèaèç, æèxèèdèçèmèx;çè: x;ç where æ is the center of the symmetric arbor function A, and is a function of x. I is the cortical interaction function, m are the weights, d the input vectors, ç denotes points in input space, r and x in output space. The energy function H, we will try to minimize is now H =, r =, c 2 èrè, æèmè Ièr, xèièr, x 0 è r;x;x 0 ç;ç 0 Aèç, æèxèèaèç 0, æèx 0 èèmèx;çèmèx 0 ;ç 0 èdèçèdèç 0 è,æèmè è1è 2
3 where æ is an abstract constraint on the allowed values of m. We now perform the standard procedure, of turning this into a correlational model, by taking the ensemble average over the input environment, and also taking the sum over r. Thus H =, x;x 0 ~ Ièx, x0 è è2è ç;ç 0 Aèç, æèxèèaèç 0, æèx 0 èèmèx;çèmèx 0 ;ç 0 èqèç,ç 0 è,æèmè: Where ~ Ièx, x 0 è= P r Ièr,xèIèr,x0 è is the new eæective interaction term, and Qèç, ç 0 è=édèçèdèç 0 èéis the correlation function. From now on, in order to simplify matters, we assume a step arbor function of the form, Aèxè=è 1 for jxj ççmax 0 for jxj éç max è3è Using this function is justiæed since it can produce oriented receptive æelds in both network models è?è and single cell models è?è. The gradient descent dynamics implied by this Hamiltonian are now dmèx;çè = dt 8 é é: x 0 jç 0,æèx 0 èjéçmax ~Ièx, x 0 èmèx 0 ;ç 0 èqèç,ç 0 è for jx, æèxèj éç max 0 for jx, æèxèj éç max è4è This equation is the same as Millers è1994è synaptic plasticity equations for the step arbor function. The method we use now, is to represent the weights m in terms of the complete set, i.e mèç; xè= P ln a ln èxèm ln èç; xè. We havechosen this complete set to be a solution of the non interacting eigenvalue problem. jç 0,æj m ln èç 0 ; xèqèjç, ç 0 jè=ç ln m ln èç, æ; xè; In a radially symmetric environment the eigenfunctions will take the form m ln èç; xè =m ln èç; ç ln èxèè = e ilç ln èxè U ln èçè where ç ln èxè is an arbitrary phase which is undetermined, due to the radially symmetric nature of the correlation function. Using this expansion, and taking sum over ç the Hamiltonian takes the form, è5è H =, x;x 0 lnl 0 n 0 ~ Ièx, x0 èç ln a ln èxèa l 0 n 0èx0 è O æ l; n; l 0 ;n 0 ;ç ln èxè;ç ln èx 0 è;æèxè;æèx 0 è æ,æèaè è6è 3
4 Where O the overlap between two receptive æelds, is O æ l; n; l 0 ;n 0 ;ç ln èxè;ç ln èx 0 è;æèxè;æèx 0 è æ = ç 0 m ln, ç 0, æèxè;ç ln èxè æ m l 0 n 0, ç 0, æèx 0 è;ç l 0 n 0èx0 è æ : è7è It is important to notice that in general, O depends on the distance between the two arbor functions, as well as on the shapes and phases of the two eigen-states. 3 Analysis of the Common Input model: We will now make the simpliæcation that æ = æ = 0 that is that all neurons have an arbor function with the same center point, this simpliæcation makes analysis simpler, and is a good approximation when the number of output neurons is much greater than the dimensionality of the input. It is important to notice though that the conclusions which we deduce from this Common input model, may not be applicable to more complex models. In particular it is important to notice that in other models, O may change signs as a function of jx, x 0 j and thus turn an excitatory model, i.e: one in which I ç 0 to one in which there is eæectively an inhibitory portion to the interaction. For this choice of arbor function the overlap O takes a very simple form, æ æ O l; n; l 0 ;n 0 ;ç ln èxè;ç ln èx 0 è = æ ll 0æ nn 0 exp ilëç ln èxè,ç ln èx0 èë : Thus for the common input model the Hamiltonian takes the form H =, xx 0 lm ~Ièx, x 0 èç ln a ln èxèa ln èx 0 èe ilëç ln èxè,ç ln èx0 èë, æèaè: è8è When observing equation 8 it is easy to see that the eigenvalues of the correlation function, play a major role in the resulting Hamiltonian. They could serve as an importance parameter by which approximations can be made. Hence the approximation proposed here is to neglect all terms except those multiplying the largest eigenvalues, these approximations will be termed herein simpliæed models. In order to make things concrete, we assume that ç 01 = ç 0, and ç 11 = ç 1 are the largest eigenvalues and considerably larger then the other eigen-values. This is not an artiæcial choice, since in many circumstances this indeed seems to be the case è?;?;?è, although in other regimes other eigen-states will dominate. Under this approximation the Hamiltonian will take the form. H =, rr 0 ~ Ièr, r0 è æ ç 0 aèrèaè r 0 è+ç 1 bèrèbèr 0 ècosëçèrè, çèr 0 èë æ, æèa; bè Where a = a 01 and b = a 11. Diæerent types of constraints can be considered. Given the constraint that the weights are square normalized, i.e that P ç mèç; xè 2 =1, 1 which for the approximate model takes the form a 2 èrè+b 2 èrè = 1, the model is equivalent to the non isotropic Heisenberg spin model embedded in two dimensions. This can be made more evident when this is rewritten in two 1 This is the constraint to which the Oja è82è rule converges 4
5 equivalent forms. If we set aèrè =S z èrè=cosèçèrèè; bèrè =sinèçèrèè, S x èrè =bèrècosèçèrèè and S y èrè=bèrèsinèçèrèè: then the Hamiltonian takes the form, H =, rr 0 ~ Ièr, r0 è æ ç 0 S z èrès z èr 0 è+ç 1 ës x èrès x èr 0 è+s y èrès y èr 0 èë æ è9è Subject to the constraint that S 2 x + S 2 y + S 2 z =1. This can also be put in the closed form, H = r;r 0 Ièr, r 0 èfç 0 cosèçèrèè cosèçèèr 0 èè + ç 1 sinèçèrèè sinèçèr 0 èèëcosèçèrèè cosèçèr 0 èè + sinèçèrèè sinèçèr 0 èèëg: è10è Which is exactly the nonisotropic Heisenberg model of Statistical Mechanics. Thus it can be seen that each neuron is associated with only two dynamical variables ç and ç, thus this approximation has resulted in a major simpliæcation in the complexity of the model. If ç 1 éé ç 0 and we can discard of the terms multiplying the ç 0 this becomes an Y model and is equivalent to the phenomenological model proposed by Cowan and Friedmann è?è. Thus in this case the Hamiltonian takes the simple form H =, rr 0 Ièr, r 0 è cos, çèrè, çèr 0 è æ ; è11è and the dynamics are _çèrè =ç, æ Ièr,r 0 è sin çèrè, çèr 0 è : è12è r 0 Another, well known, phenomenological models is the Swindale model è82è for the development of orientation selectivity, we will show that it is similar to the Cowan Friedmann model. Swindale deænes the complex variable Zèrè =S x èrè+is y èrè orzèrè=bèrè expèiçèrèè 2. For which he deænes the dynamics _Zèrè= r 0 Ièr,r 0 èzèr 0 èè1,jzèrèjè: è13è Thus for the variables çèrè =tg,1 ès x =S y è and bèrè=jzèrèj, the dynamics are _çèrè =çè1, bèrèè r 0 Ièr, r 0 è sin, çèrè, çèr 0 è æ è14è and _bèrè =çè1, bèrèè bèrè r 0 Ièr, r 0 è cos, çèrè, çèr 0 è æ è15è 2 This angle is diæerent than the one Swindale chooses for the orientation angle, He deænes the orientation angle çs as çs = 1 2 ç: 5
6 Comparing equations 12 and 14 we see that for bèrè é 1 the dynamics of the angle ç in the Swindale model are parallel to those in the Cowan model. However, when bèrè = 1 the Swindale dynamics terminate, and when bèrè é 1 they are anti parallel to the Cowan and Friedmann dynamics. The dynamics for bèrè when bèrè é 1 are such that if hèrè = P r 0Ièr,r0 è sinèçèrè, çèr 0 èè é 0 then bèrè! 1, this would be the common case since the dynamics for çèrè try to maximize hèrè however in some cases, such as near orientation singularities this may not be possible and in these cases bèrè! 0. Thus it can be expected that if the Swindale simulations are started at small values of bèrè and the learning rate is slow enough, then the æxed points of the orientation maps would be similar to the Cowan and Friedmann æxed points. In synaptic space the constraint imposed in the Swindale model is equivalent to stopping the update of each neuron once it's synaptic weight becomes normalized. This seems a non local constraint, although it could possibly be made local by a procedure similar to the one Oja has used to attain square normalization. The ænal state of a Swindale type model can depend on the initial conditions, and on the learning rate ç, thus the Swindale model has extra èspuriousè æxed points, which the Cowan and Friedmann model does not possess. Another possible choice for the normalization, is to set a+b=1, then the approximate Hamiltonian takes the form H =, rr 0 Ièr, r 0 è æ ç 0 aèrèaè r 0 è+ç 1 ë1, aèrèëë1, aèr 0 èëcosëçèrè, çèr 0 èë æ It is important to note that this Hamiltonian is not bounded, as may be the case when the van der Malsburg è73è type of normalization is used. This choice of normalization is therefore not valid for our purpose. In the following sections we will use the simpliæed model, as deæned in equations 9 to 10 to answer the questions posed in the introduction. 4 The Excitatory case I ç 0 In the Excitatory case, we know that the global minimum of the common input energy function èeq:8è as well as in the approximation èeq:10è, occurs when all receptive æelds are equivalent to the principal component, and have the same orientation. Since we know what the global minim is, it is interesting to see how simulations of the simpliæed model manage to reach this minimum. Doing this is a test of our procedures, but it also has interesting implications for simulations of detailed synaptic models of the Miller, Linsker type. In Figures:1 and 2 we show the time evolution of the excitatory simpliæed model, when ç 1 =ç 0 = 1:3, i.e: the oriented solution has a higher eigenvalue. In these simulations we used a Gaussian interaction function, with a standard deviation ç = 2:5. We have deæned one iteration in this network as the number of random updates, required for updating each neuron on average once. We can see that the global minimum is indeed reached, however it takes several hundred iterations to reach the global minimum for the parameters we have used, which wehave tried to optimize. The neurons attain their maximal selectivity quickly, most of them after 30 iterations, however it takes a very long time in comparison for the neurons to become parallel. 6
7 Figure 1: Time evolution of receptive æelds in an excitatory network, in each iteration each neuron is updated on average one time. The images show the receptive æelds in a 30 by 30 network of neurons, which were run for 5,30,100 and 600 iterations, displayed from left to right, top to bottom. The learning rate ç was reduced during learning from :1 to :02, inorder to speed up the convergence. Simulations of the detailed synaptic models which are much more complex, were typically run with a smaller number of iteration è?è. In the Miller model the learning rule used was unstable, therefore saturation limits were set on the synapses. When synapses reached these limits they were frozen, these type of bounds we term sticky bounds. When a high fraction of the synapses become saturated, the simulations are terminated. Since in our simulations neurons their maximal degree of orientation selectivity long before they became parallel, it implies that if the sticky bounds were not used by Miller è?è and if simulations were run for more iterations, then the resulting orientation maps may be quite diæerent. Thus sticky boundaries are more than a computational convenience. and they should either have biological motivation, or be omited from simulations. Another diæerence in the way these simulations, and the detailed synaptic simulations have been performed is that we used random sequential dynamics, whereas parallel dynamics have been used in the simulations of the complete synaptic models è?;?è. This implies that all synapses in the network are updated synchronously, i.e: at once. This assumption does not seem biologically plausible, furthermore although parallel dynamics are computationally convenient, they may alter 7
8 Figure 2: Time evolution of orientation in an excitatory network. These simulations are the same as in the previous ægure but here we have only displayed the optimal orientation and added some intermediate time steps. The images show the orientations in a 30 by 30 network of neurons, which were run for 5,15,30,100,400 and 600 iterations, displayed from left to right, top to bottom. The direction of the line codes orientation, and it's intensity codes for the degree of orientation selectivity. A great majority of the cells have already attained a high degree of selectivity, at 100 iterations, but it takes several hundred more iterations for them to become completely parallel. the ænal state the network will reach and in particular they can prevent the model from obtaining the real energy minima. These types of continuous spin models, even with only excitatory connections, can attain vortex states as well, if a ænite amount of noise is introduced into the dynamics è?è. These vortex states however are æuctuations in the statistical mechanics sense, therefore they will move in time and in this sense they are quite diæerent from the vortex states we will show can be attained with models which include inhibition. 5 Interactions with Inhibition In the case where there is some inhibition in the network, the situation is more complex, and more interesting. In this case we do not know what the global minimum is, we will therefore use simulations of the simpliæed models in order to examine numerically what these minima are. Using the simpliæed model has the great advantage of being much less complex, and therefore requiring much less computation, furthermore deænitions such as orientation selectivity, and orientation angle have a transparent deænition. On the other hand it runs the risk of not being a 8
9 valid approximation. This would happen if when running the full model, the ænal receptive æelds would have strong components of the less prominent eigenfunctions which are not represented in the approximation. In order to examine the amount of single cell symmetry breaking, we deæne an order parameter, rmsèaè, which is deæned as rmsèaè = p éa 2 éwhere the average is taken over all network sites, this order parameter shows how much the single cell receptive æelds in the network deviate from non interacting single cells. Since in the all excitatory case the values of rmsèaè should be like those in the non interacting case, we can asses the eæect of the interaction by comparing the values of rmsèaè for interactions with inhibition, to those which have only excitation. Strong eæects of the interaction may also imply that the approximation may break down. In our simulations, we used an interaction function of the form, ~Ièrè = expë,èr 2 =2ç 2 èë, IN æ expë,èr 2 =2è2çè 2 èë; where we have æxed ç = 2:5. Hence for simplicity we have varied only the value of IN. Cross sections of the diæerent interaction terms used are shown in ægure: 3. The cases we have examined are Excitatory IN = 0:0, Balanced IN = :25, where the integral of the interaction function is zero, Net Inhibitory IN = :5 in which the is more inhibition then excitation, and Net Excitatory IN = :125 where there is more excitation then inhibition. We have run all of our simulations for at least 1500 iterations and tested the stability of the ænal state, in order to make sure that we have indeed reached a stable æxed point. The Lateral Interaction I(r) Excitatory Balanced Net Inhibitory Net Excitatory r Figure 3: This image presents the diæerent types of interaction functions of the form Ièrè = expè,r 2 =ç 2 è,inæexpè,r 2 =è2çè 2 è. Excitatory IN =0:0, i.e there is only excitation, Balanced IN = :25 i.e the inhibition and excitation are balanced, Net Inhibitory IN = :5 more excitation then inhibition, and Net Excitatory IN = :125 more excitation then inhibition. As can be seen ægure 4 the interaction can indeed break the symmetry, although only mildly since under the most conditions investigated most receptive æelds remain dominated by the ærst principal component. In ægure 5, we chose to display the network, in an extreme case of symmetry breaking, even here most receptive æelds have a strong, radially symmetric component. The eæect of the interaction on the global ordering is more pronounced. In ægure 6, we can see that when the radially symmetric principal component is dominant, the eæect of the interaction would be a staggered type of ænal state. When the oriented solution dominates, the emerging structure has bands with similar orientations, and some orientation singularities as can be seen in ægure: 7. 9
10 rmsèaè The eæect of the lateral interaction on Symmetry breaking Excitatory Balanced 3 Net Inhibitory + Net Excitatory ç 1 =ç 0 Figure 4: This image presents the rms value of a as a function of ç 1 =ç 0 for the diæerent types of interactions as deæned above. Inhibitory interactions can create orientation selective cells in regions in which single cells are radially symmetric. The diæerent types of interaction we have used have the form Ièrè = expè,r 2 =ç 2 è, IN æ expè,r 2 =è2çè 2 è. and diæer in the value of IN, Excitatory IN = 0:0, i.e there is only excitation, Balanced IN = :25 i.e the inhibition and excitation are balanced, Net Inhibitory IN = :5 more excitation then inhibition, and Net Excitatory IN = :125 more excitation then inhibition. These singularities however, are of the S = 1type which means that, around a singularity, the orientation angle changes by 360 deg. It has been claimed è?è that in the cortex and in many models such as in the Swindale è92è model and in the Miller è94è model, the singularities are of the S = 1 type. i.e the orientation angle changes by 180 deg, examples of such singularities are 2 illustrated in ægure 8. This stands in contradiction to the results in the simpliæed model, which therefore raises the question of what is the source of these diæerences? In the Swindale model the orientations angles are deæned to be half of the angle of the complex variable z, i.e ç s = 1 ç, and thus when ç has a S = 1 singularity ç 2 s has a S = 1 singularity. 2 The diæerences between the simpliæed model and the Swindale model actually arise from a similar reason. We claim that when the dominant single cell solution has the angular component cosèmçè, or in general when a rotation of è360=nè deg leaves the receptive æeld as it was, then the resulting singularities will be of the type S = 1. The heuristic reasoning for this claim is the following; m suppose that we divide the interaction function into two terms, an inhibitory term and an excitatory term, I = I E + I I such that I E é 0 and I I é 0. It is usually assumed that the excitatory term dominates the short range interactions. The excitatory term attempts to enforce continuity, and low curvature, i.e: a small as possible change between neighboring orientations. Thus a closed path around a singularity should exhibit the minimal curvature which retains continuity which for receptive æelds with an angular dependence cosèmçè, it is a rotation around the curve by 360=m 10
11 Figure 5: Simulations results for ç 1 =ç 0 =0:95 and a balanced interaction. The receptive æelds èleftè and the orientation directions èrightè. The single cell solution is radially symmetric, but here some symmetry breaking does occur although many of the cells are still dominated by the radially symmetric component èshown by the short length of many of bars representing orientationè. In order to represent the single receptive æelds we have chosen an arbitrary normalized functions, one radially symmetric and one with an angular dependence of ècosèçè degrees, i.e a singularity oftype S = 1. More explicitly we predict that when the single cell solution m has a cosè2çè angular dependence, then the singularities exhibited will be of the type S = 1. In 2 ægure 9 we have displayed what the simpliæed model produces when we make this assumption. The receptive æelds obtained in the cosè2çè model look far from plausible biologically, ina previous paper è?è it had been shown that this can be corrected by the asymmetric portion of the correlation function, which we did not take into account here, however when we simulate the degenerate case èç 2 = ç 0 èasshown in ægure 10 we obtain more plausible receptive æelds even in the absence of the non symmetric portion of the correlation function. However, all the receptive æelds obtained under the assumptions we have made in this paper have a broader tuning curve than typically found in the cortex. We believe that the type of singularities exhibited in synaptic types of models, depend critically on the dominant eigen function of the single cell in the same parameter regime. Our belief is based on the simpliæcations obtained by the analysis performed in this paper, and this is but one example of the power and usefulness of such analysis. Therefore claims about synaptic models è?è should be restricted to the parameters examined. 6 Related Models When we do not make the common input assumption, the overlap function O takes on a diæerent form. The other extreme from the common input case, is the case where inputs to neighboring cells have no spatial overlap. In this case the overlap function takes the simple form 11
12 Figure 6: Simulations results for ç 1 =ç 0 =0:3Balanced interaction. The single cell solution is radially symmetric, and so are the network solutions. The eæect of the inhibitory term in the lateral interaction has been to form staggered ordering. O ë1; 1; 1; 1; x; èx 0 è;æèxè;æèx 0 èë = æèx, x 0 èæ ll 0æ mm 0 H = x ln In which case, the Hamiltonian takes the form ~Iè0èç ln a 2 ln, æèaè: Thus the Hamiltonian becomes a a non interacting Hamiltonian, and no eæective interaction exists between neighboring neurons. Therefore the ænal state will be such that each neuron will settle in the single cell receptive æelds, and the orientations will not be coupled. For this model no continuity of the orientation æeld should be expected. It should be noted that the outputs of the neurons Cèrè are correlated due to the interactions, just the angels of the feed forward component ofthe receptive æelds become uncorrelated in this case. A more complex case is the one which is examined in the Linsker and Miller models, in which æèxè =x, in this case the overlap function is complex, and depends on the exact details of the receptive æelds, however we can obtain some understanding by looking qualitatively at the form of the overlap function. When æèxè = const an overlap exists only between same type receptive æelds, when the inputs are shifted, interactions exists between diæerent types of receptive æelds as well, e.g between cosèçè and cosè2çè receptive æelds. The interaction between same type receptive æelds is also a function of the distance of their centers in the input plane, and in particular it can change signs as a function of jx, x 0 j. Some such abstract examples are shown in ægure 11. When this happens, a model which is purely excitatory can behave like a model with inhibition. To understand this lets assume for simplicity that ç 11 éç ij for every i and j, and that the cross term overlaps are very small as well. In such a case the Hamiltonian will take the form, H ç xx 0 ~ Ièx, x0 èo æ çèxè;çèx 0 è;æèxè;æèx 0 è æ : è16è Where we have omitted the l = l 0 = 1 and n = n 0 = 1 indexes for simplicity. In a purely excitatory case, ~ I é 0, the aim will be to minimize the overlap functions O, as a function of the angles 12
13 Figure 7: When ç 1 =ç 0 =1:3the ænal state shows a banded structure, and structures sometimes described in the biological literature as pinwheels, The map displayed here shows singularities of the S =1type. ç. When observing ægure 11, it is obvious that for Y = æèxè, æèx 0 è small the two receptive æelds would preferentially have the same phase angle ç, where as at larger distances it would be minimized when çèxè =çèx 0 è+ç. This observation enables us to understand that the common input approximation is sensible, If the width of the interaction term ~ I is smaller that the ærst zero crossing of the overlap term O. 7 Discussion We haveinvestigated models of interacting Hebbian neurons and have shown that learning in such a network is equivalent to minimizing an energy function. We have further shown that under certain conditions this network can be approximated by continuous spin models, and is similar to some of the proposed phenomenological models è?;?è. In the common input case we have shown that for excitatory interactions there is no symmetry breaking, and that all receptive æelds have the same orientation. We have also used this case to make the point that sticky boundary assumptions can drastically change the organization of receptive æelds in the model, so that reported results are heavily dependent on when simulations are terminated. We have also shown that inhibition eæect both the structure of the receptive æelds and the organization of diæerent receptive æelds across the cortex. In extreme cases we have shown that inhibition can create oriented receptive æelds, where the single cell receptive æelds are radially symmetric. The global organization produced by models with inhibition, shows Iso-orientation patches, and pinwheel type of singularities. We demonstrated that the type of singularities depend critically on the on the symmetry of the receptive æelds. 13
14 S=1 S=0.5 Figure 8: A schematic drawing of diæerent types of singularities, S =1are drawn above, S = 1 2 below. The major qualitative diæerence between the common input model, and shifted input models, is that even in the absence of inhibition, shifted input models can behave like models with inhibition. We have qualitatively demonstrated why this is the case. 8 Acknowledgments The authors thank Yong Liu, Igor Bukharev, Bob Pelcovits and all the members of Institute for Brain and Neural Systems for many helpful discussions. Research was supported by grants from ONR and ARO. References Blasdel, G. G. è1992è. Orientation selectivity,preference, and continuity in monkey striate cortex. The Journal of Neuroscience, 12è8è:3139í3161. Bonhoeæer, T. and Gringald, A. è1991è. Iso-orientation domains in cat visual cortex are arranged in pinwheel-like patterns. Nature, 353:429í431. Cowan, J. D. and Friedman, A. E. è1991è. Simple spin models for the development of ocular dominance columns and iso-orientation patches. In J. D. Cowan, G. T. and Alspector, J., editors, Advances in Neural Information Processing Systems 3. Erwin, E., Obermayer, K., and Schulten, K. è1994è. A simple network model of unsupervised learning. Technical report, University of Illinois. 14
15 Figure 9: When the dominant eigenfunction has a cosè2çè angular form, and respectively ç 2 =ç 0 = 1:3 the ænal state shows S = 1 type singularities. 2 Kosterlitz, M. J. and Thouless, D. J. è73è. Ordering, metastability and phase transitions in twodimensional systerms. J. Phys., C6:1181. Linsker, R. è1986aè. From basic network principles to neural architecture. Proc. Natl. Acad. Sci. USA, 83:8779í83. Linsker, R. è1986bè. From basic network principles to neural architecture. Proc. Natl. Acad. Sci. USA, 83:7508í12, 8390í4, 8779í83. Liu, Y. è1994è. Synaptic Plasticity: From Single Cell to Cortical Network. PhD thesis, Brown University. Liu, Y. and Shouval, H. è1994è. Localized principal components of natural images - an analytic solution. Network., 5.2:317í325. MacKay, D. J. and Miller, K. D. è1990è. Analysis of linsker's simulations of hebbian rules to linear networks. Network, 1:257í297. Miller, K. D. è1992è. Development of orientation columns via competition between on- anf oæ-center inputs. NeuroReprot, 3:73í76. Miller, K. D. è1994è. A model for the development of simple cell receptive æelds and the ordered arrangement of orientation columns through activity-dependent competition between on- and oæ-center inputs. J. of Neurosci., 14:409í441. Miller, K. D., Keller, J. B., and Striker, M. P. è1989è. Ocular dominance column development: Analysis and simulation. Science, 245:605í
16 Figure 10: In the degenerate case, when the eigen value of the radially symmetric, center surround, solution ç 0 is equal to that of the cosè2çè solution, the resulting receptive æeld structure seems biologically plausible, and the ænal state shows S = 1 2 type singularities. Miller, K. D. and MacKay, D. J. C. è1994è. The role of constraints in Hebbian learning. Neural Computation, 6:98í124. Nass, M. N. and Cooper, L. N. è1975è. A theory for the development of feature detecting cells in visual cortex. Biol. Cyb., 19:1í18. Oja, E. è1982è. A simpliæed neuron model as a principal component analyzer. Journal of Mathematical Biology, 15:267í273. Rubinstien, J. è1994è. Pattern formation in associative neural networks with weak lateral interaction. Biological Cybernetics, 70. Shouval, H. and Liu, Y. è1996è. Principal component neurons in a realistic visual environment. Network. In Press. Swindale, N. è1982è. A model for the formation of orientation columns. Proc. R. Soc. London, B208:243. von der Malsburg, C. è1973è. Self-organization of orientation sensitive cells in striate cortex. Kybernetik, 14:85í
17 Y Y O O 1 1 Y Y Y Y o Y Y Figure 11: A schematic drawing of some aspects of the overlap functions for shifted inputs. We have deæned Y = æèxè,æèx 0 è.above cases of overlaps between diæerent types of RF's are displayed, below between same kinds of RF's 17
The Hebb rule Neurons that fire together wire together.
 Unsupervised learning The Hebb rule Neurons that fire together wire together. PCA RF development with PCA Classical Conditioning and Hebbʼs rule Ear A Nose B Tongue When an axon in cell A is near enough
Unsupervised learning The Hebb rule Neurons that fire together wire together. PCA RF development with PCA Classical Conditioning and Hebbʼs rule Ear A Nose B Tongue When an axon in cell A is near enough
Hierarchy. Will Penny. 24th March Hierarchy. Will Penny. Linear Models. Convergence. Nonlinear Models. References
 24th March 2011 Update Hierarchical Model Rao and Ballard (1999) presented a hierarchical model of visual cortex to show how classical and extra-classical Receptive Field (RF) effects could be explained
24th March 2011 Update Hierarchical Model Rao and Ballard (1999) presented a hierarchical model of visual cortex to show how classical and extra-classical Receptive Field (RF) effects could be explained
A MEAN FIELD THEORY OF LAYER IV OF VISUAL CORTEX AND ITS APPLICATION TO ARTIFICIAL NEURAL NETWORKS*
 683 A MEAN FIELD THEORY OF LAYER IV OF VISUAL CORTEX AND ITS APPLICATION TO ARTIFICIAL NEURAL NETWORKS* Christopher L. Scofield Center for Neural Science and Physics Department Brown University Providence,
683 A MEAN FIELD THEORY OF LAYER IV OF VISUAL CORTEX AND ITS APPLICATION TO ARTIFICIAL NEURAL NETWORKS* Christopher L. Scofield Center for Neural Science and Physics Department Brown University Providence,
Auto-correlation of retinal ganglion cell mosaics shows hexagonal structure
 Supplementary Discussion Auto-correlation of retinal ganglion cell mosaics shows hexagonal structure Wässle and colleagues first observed that the local structure of cell mosaics was approximately hexagonal
Supplementary Discussion Auto-correlation of retinal ganglion cell mosaics shows hexagonal structure Wässle and colleagues first observed that the local structure of cell mosaics was approximately hexagonal
Neuroinformatics. Marcus Kaiser. Week 10: Cortical maps and competitive population coding (textbook chapter 7)!
 0 Neuroinformatics Marcus Kaiser Week 10: Cortical maps and competitive population coding (textbook chapter 7)! Outline Topographic maps Self-organizing maps Willshaw & von der Malsburg Kohonen Dynamic
0 Neuroinformatics Marcus Kaiser Week 10: Cortical maps and competitive population coding (textbook chapter 7)! Outline Topographic maps Self-organizing maps Willshaw & von der Malsburg Kohonen Dynamic
Outline. NIP: Hebbian Learning. Overview. Types of Learning. Neural Information Processing. Amos Storkey
 Outline NIP: Hebbian Learning Neural Information Processing Amos Storkey 1/36 Overview 2/36 Types of Learning Types of learning, learning strategies Neurophysiology, LTP/LTD Basic Hebb rule, covariance
Outline NIP: Hebbian Learning Neural Information Processing Amos Storkey 1/36 Overview 2/36 Types of Learning Types of learning, learning strategies Neurophysiology, LTP/LTD Basic Hebb rule, covariance
leading to a ænal state with missing energy. The rate for such processes is strongly dependent on the number of extra dimensions as well as the exact
 SLAC-PUB-8204 July 1999 TESTS OF LOW SCALE QUANTUM GRAVITY IN e, e, AND ææ COLLISIONS a T.G. RIZZO b Stanford Linear Accelerator Center, Stanford University, Stanford, CA 94309, USA Arkani-Hamed, Dimopoulos
SLAC-PUB-8204 July 1999 TESTS OF LOW SCALE QUANTUM GRAVITY IN e, e, AND ææ COLLISIONS a T.G. RIZZO b Stanford Linear Accelerator Center, Stanford University, Stanford, CA 94309, USA Arkani-Hamed, Dimopoulos
problem of detection naturally arises in technical diagnostics, where one is interested in detecting cracks, corrosion, or any other defect in a sampl
 In: Structural and Multidisciplinary Optimization, N. Olhoæ and G. I. N. Rozvany eds, Pergamon, 1995, 543í548. BOUNDS FOR DETECTABILITY OF MATERIAL'S DAMAGE BY NOISY ELECTRICAL MEASUREMENTS Elena CHERKAEVA
In: Structural and Multidisciplinary Optimization, N. Olhoæ and G. I. N. Rozvany eds, Pergamon, 1995, 543í548. BOUNDS FOR DETECTABILITY OF MATERIAL'S DAMAGE BY NOISY ELECTRICAL MEASUREMENTS Elena CHERKAEVA
Effects of Interactive Function Forms in a Self-Organized Critical Model Based on Neural Networks
 Commun. Theor. Phys. (Beijing, China) 40 (2003) pp. 607 613 c International Academic Publishers Vol. 40, No. 5, November 15, 2003 Effects of Interactive Function Forms in a Self-Organized Critical Model
Commun. Theor. Phys. (Beijing, China) 40 (2003) pp. 607 613 c International Academic Publishers Vol. 40, No. 5, November 15, 2003 Effects of Interactive Function Forms in a Self-Organized Critical Model
Synaptic Plasticity. Introduction. Biophysics of Synaptic Plasticity. Functional Modes of Synaptic Plasticity. Activity-dependent synaptic plasticity:
 Synaptic Plasticity Introduction Dayan and Abbott (2001) Chapter 8 Instructor: Yoonsuck Choe; CPSC 644 Cortical Networks Activity-dependent synaptic plasticity: underlies learning and memory, and plays
Synaptic Plasticity Introduction Dayan and Abbott (2001) Chapter 8 Instructor: Yoonsuck Choe; CPSC 644 Cortical Networks Activity-dependent synaptic plasticity: underlies learning and memory, and plays
Effects of Interactive Function Forms and Refractoryperiod in a Self-Organized Critical Model Based on Neural Networks
 Commun. Theor. Phys. (Beijing, China) 42 (2004) pp. 121 125 c International Academic Publishers Vol. 42, No. 1, July 15, 2004 Effects of Interactive Function Forms and Refractoryperiod in a Self-Organized
Commun. Theor. Phys. (Beijing, China) 42 (2004) pp. 121 125 c International Academic Publishers Vol. 42, No. 1, July 15, 2004 Effects of Interactive Function Forms and Refractoryperiod in a Self-Organized
7 Recurrent Networks of Threshold (Binary) Neurons: Basis for Associative Memory
 Physics 178/278 - David Kleinfeld - Winter 2019 7 Recurrent etworks of Threshold (Binary) eurons: Basis for Associative Memory 7.1 The network The basic challenge in associative networks, also referred
Physics 178/278 - David Kleinfeld - Winter 2019 7 Recurrent etworks of Threshold (Binary) eurons: Basis for Associative Memory 7.1 The network The basic challenge in associative networks, also referred
Radial Basis Functions for Process Control Lyle H. Ungar Tom Johnson Richard D. De Veaux University ofpennsylvania Voice Processing Corp. Princeton Un
 Radial Basis Functions for Process Control Lyle H. Ungar Tom Johnson Richard D. De Veaux University ofpennsylvania Voice Processing Corp. Princeton University Abstract Radial basis function èrbfsè neural
Radial Basis Functions for Process Control Lyle H. Ungar Tom Johnson Richard D. De Veaux University ofpennsylvania Voice Processing Corp. Princeton University Abstract Radial basis function èrbfsè neural
Introduction to Neural Networks
 Introduction to Neural Networks What are (Artificial) Neural Networks? Models of the brain and nervous system Highly parallel Process information much more like the brain than a serial computer Learning
Introduction to Neural Networks What are (Artificial) Neural Networks? Models of the brain and nervous system Highly parallel Process information much more like the brain than a serial computer Learning
Ângelo Cardoso 27 May, Symbolic and Sub-Symbolic Learning Course Instituto Superior Técnico
 BIOLOGICALLY INSPIRED COMPUTER MODELS FOR VISUAL RECOGNITION Ângelo Cardoso 27 May, 2010 Symbolic and Sub-Symbolic Learning Course Instituto Superior Técnico Index Human Vision Retinal Ganglion Cells Simple
BIOLOGICALLY INSPIRED COMPUTER MODELS FOR VISUAL RECOGNITION Ângelo Cardoso 27 May, 2010 Symbolic and Sub-Symbolic Learning Course Instituto Superior Técnico Index Human Vision Retinal Ganglion Cells Simple
0 b ject ive Functions for Neural Map Format ion
 242 4th Joint Symposium on Neural Computation Proceedings 1997 0 b ject ive Functions for Neural Map Format ion Laurenz Wiskottl and Terrence Sejn~wskil~~ lcomputational Neurobiology Laboratory 2Howard
242 4th Joint Symposium on Neural Computation Proceedings 1997 0 b ject ive Functions for Neural Map Format ion Laurenz Wiskottl and Terrence Sejn~wskil~~ lcomputational Neurobiology Laboratory 2Howard
A Three-dimensional Physiologically Realistic Model of the Retina
 A Three-dimensional Physiologically Realistic Model of the Retina Michael Tadross, Cameron Whitehouse, Melissa Hornstein, Vicky Eng and Evangelia Micheli-Tzanakou Department of Biomedical Engineering 617
A Three-dimensional Physiologically Realistic Model of the Retina Michael Tadross, Cameron Whitehouse, Melissa Hornstein, Vicky Eng and Evangelia Micheli-Tzanakou Department of Biomedical Engineering 617
Self-organized Criticality and Synchronization in a Pulse-coupled Integrate-and-Fire Neuron Model Based on Small World Networks
 Commun. Theor. Phys. (Beijing, China) 43 (2005) pp. 466 470 c International Academic Publishers Vol. 43, No. 3, March 15, 2005 Self-organized Criticality and Synchronization in a Pulse-coupled Integrate-and-Fire
Commun. Theor. Phys. (Beijing, China) 43 (2005) pp. 466 470 c International Academic Publishers Vol. 43, No. 3, March 15, 2005 Self-organized Criticality and Synchronization in a Pulse-coupled Integrate-and-Fire
Information maximization in a network of linear neurons
 Information maximization in a network of linear neurons Holger Arnold May 30, 005 1 Introduction It is known since the work of Hubel and Wiesel [3], that many cells in the early visual areas of mammals
Information maximization in a network of linear neurons Holger Arnold May 30, 005 1 Introduction It is known since the work of Hubel and Wiesel [3], that many cells in the early visual areas of mammals
CS 294-2, Visual Grouping and Recognition èprof. Jitendra Malikè Sept. 8, 1999
 CS 294-2, Visual Grouping and Recognition èprof. Jitendra Malikè Sept. 8, 999 Lecture è6 èbayesian estimation and MRFè DRAFT Note by Xunlei Wu æ Bayesian Philosophy æ Markov Random Fields Introduction
CS 294-2, Visual Grouping and Recognition èprof. Jitendra Malikè Sept. 8, 999 Lecture è6 èbayesian estimation and MRFè DRAFT Note by Xunlei Wu æ Bayesian Philosophy æ Markov Random Fields Introduction
(Feed-Forward) Neural Networks Dr. Hajira Jabeen, Prof. Jens Lehmann
 (Feed-Forward) Neural Networks 2016-12-06 Dr. Hajira Jabeen, Prof. Jens Lehmann Outline In the previous lectures we have learned about tensors and factorization methods. RESCAL is a bilinear model for
(Feed-Forward) Neural Networks 2016-12-06 Dr. Hajira Jabeen, Prof. Jens Lehmann Outline In the previous lectures we have learned about tensors and factorization methods. RESCAL is a bilinear model for
Probabilistic Models in Theoretical Neuroscience
 Probabilistic Models in Theoretical Neuroscience visible unit Boltzmann machine semi-restricted Boltzmann machine restricted Boltzmann machine hidden unit Neural models of probabilistic sampling: introduction
Probabilistic Models in Theoretical Neuroscience visible unit Boltzmann machine semi-restricted Boltzmann machine restricted Boltzmann machine hidden unit Neural models of probabilistic sampling: introduction
7 Rate-Based Recurrent Networks of Threshold Neurons: Basis for Associative Memory
 Physics 178/278 - David Kleinfeld - Fall 2005; Revised for Winter 2017 7 Rate-Based Recurrent etworks of Threshold eurons: Basis for Associative Memory 7.1 A recurrent network with threshold elements The
Physics 178/278 - David Kleinfeld - Fall 2005; Revised for Winter 2017 7 Rate-Based Recurrent etworks of Threshold eurons: Basis for Associative Memory 7.1 A recurrent network with threshold elements The
pairs. Such a system is a reinforcement learning system. In this paper we consider the case where we have a distribution of rewarded pairs of input an
 Learning Canonical Correlations Hans Knutsson Magnus Borga Tomas Landelius knutte@isy.liu.se magnus@isy.liu.se tc@isy.liu.se Computer Vision Laboratory Department of Electrical Engineering Linkíoping University,
Learning Canonical Correlations Hans Knutsson Magnus Borga Tomas Landelius knutte@isy.liu.se magnus@isy.liu.se tc@isy.liu.se Computer Vision Laboratory Department of Electrical Engineering Linkíoping University,
The functional organization of the visual cortex in primates
 The functional organization of the visual cortex in primates Dominated by LGN M-cell input Drosal stream for motion perception & spatial localization V5 LIP/7a V2 V4 IT Ventral stream for object recognition
The functional organization of the visual cortex in primates Dominated by LGN M-cell input Drosal stream for motion perception & spatial localization V5 LIP/7a V2 V4 IT Ventral stream for object recognition
Equivalence of Backpropagation and Contrastive Hebbian Learning in a Layered Network
 LETTER Communicated by Geoffrey Hinton Equivalence of Backpropagation and Contrastive Hebbian Learning in a Layered Network Xiaohui Xie xhx@ai.mit.edu Department of Brain and Cognitive Sciences, Massachusetts
LETTER Communicated by Geoffrey Hinton Equivalence of Backpropagation and Contrastive Hebbian Learning in a Layered Network Xiaohui Xie xhx@ai.mit.edu Department of Brain and Cognitive Sciences, Massachusetts
Analysis of Neural Networks with Chaotic Dynamics
 Chaos, Solitonr & Fructals Vol. 3, No. 2, pp. 133-139, 1993 Printed in Great Britain @60-0779/93$6.00 + 40 0 1993 Pergamon Press Ltd Analysis of Neural Networks with Chaotic Dynamics FRANCOIS CHAPEAU-BLONDEAU
Chaos, Solitonr & Fructals Vol. 3, No. 2, pp. 133-139, 1993 Printed in Great Britain @60-0779/93$6.00 + 40 0 1993 Pergamon Press Ltd Analysis of Neural Networks with Chaotic Dynamics FRANCOIS CHAPEAU-BLONDEAU
Technical Report No AN APPLICATION OF PARALLEL COMPUTATION TO DYNAMICAL SYSTEMS æ Selim G. Akl and Weiguang Yao School of Computing Queen's
 Technical Report No. 2003-466 AN APPLICATION OF PARALLEL COMPUTATION TO DYNAMICAL SYSTEMS æ Selim G. Akl and Weiguang Yao School of Computing Queen's University Kingston, Ontario, Canada K7L 3N6 June 27,
Technical Report No. 2003-466 AN APPLICATION OF PARALLEL COMPUTATION TO DYNAMICAL SYSTEMS æ Selim G. Akl and Weiguang Yao School of Computing Queen's University Kingston, Ontario, Canada K7L 3N6 June 27,
High-conductance states in a mean-eld cortical network model
 Neurocomputing 58 60 (2004) 935 940 www.elsevier.com/locate/neucom High-conductance states in a mean-eld cortical network model Alexander Lerchner a;, Mandana Ahmadi b, John Hertz b a Oersted-DTU, Technical
Neurocomputing 58 60 (2004) 935 940 www.elsevier.com/locate/neucom High-conductance states in a mean-eld cortical network model Alexander Lerchner a;, Mandana Ahmadi b, John Hertz b a Oersted-DTU, Technical
Emergence of Phase- and Shift-Invariant Features by Decomposition of Natural Images into Independent Feature Subspaces
 LETTER Communicated by Bartlett Mel Emergence of Phase- and Shift-Invariant Features by Decomposition of Natural Images into Independent Feature Subspaces Aapo Hyvärinen Patrik Hoyer Helsinki University
LETTER Communicated by Bartlett Mel Emergence of Phase- and Shift-Invariant Features by Decomposition of Natural Images into Independent Feature Subspaces Aapo Hyvärinen Patrik Hoyer Helsinki University
Hopfield Neural Network and Associative Memory. Typical Myelinated Vertebrate Motoneuron (Wikipedia) Topic 3 Polymers and Neurons Lecture 5
 Hopfield Neural Network and Associative Memory Typical Myelinated Vertebrate Motoneuron (Wikipedia) PHY 411-506 Computational Physics 2 1 Wednesday, March 5 1906 Nobel Prize in Physiology or Medicine.
Hopfield Neural Network and Associative Memory Typical Myelinated Vertebrate Motoneuron (Wikipedia) PHY 411-506 Computational Physics 2 1 Wednesday, March 5 1906 Nobel Prize in Physiology or Medicine.
Supporting Online Material for
 www.sciencemag.org/cgi/content/full/319/5869/1543/dc1 Supporting Online Material for Synaptic Theory of Working Memory Gianluigi Mongillo, Omri Barak, Misha Tsodyks* *To whom correspondence should be addressed.
www.sciencemag.org/cgi/content/full/319/5869/1543/dc1 Supporting Online Material for Synaptic Theory of Working Memory Gianluigi Mongillo, Omri Barak, Misha Tsodyks* *To whom correspondence should be addressed.
transitions in matter. This gives us the beauty of color and is the reason why our eyes
 8 CHAPTER 1. FOUNDATIONS OF NANO-OPTICS 1.3 Macroscopic Electrodynamics Light embraces the most fascinating spectrum of electromagnetic radiation. This is mainly due to the fact that the energy of light
8 CHAPTER 1. FOUNDATIONS OF NANO-OPTICS 1.3 Macroscopic Electrodynamics Light embraces the most fascinating spectrum of electromagnetic radiation. This is mainly due to the fact that the energy of light
(a) (b) (c) Time Time. Time
 Baltzer Journals Stochastic Neurodynamics and the System Size Expansion Toru Ohira and Jack D. Cowan 2 Sony Computer Science Laboratory 3-4-3 Higashi-gotanda, Shinagawa, Tokyo 4, Japan E-mail: ohiracsl.sony.co.jp
Baltzer Journals Stochastic Neurodynamics and the System Size Expansion Toru Ohira and Jack D. Cowan 2 Sony Computer Science Laboratory 3-4-3 Higashi-gotanda, Shinagawa, Tokyo 4, Japan E-mail: ohiracsl.sony.co.jp
Logic Learning in Hopfield Networks
 Logic Learning in Hopfield Networks Saratha Sathasivam (Corresponding author) School of Mathematical Sciences, University of Science Malaysia, Penang, Malaysia E-mail: saratha@cs.usm.my Wan Ahmad Tajuddin
Logic Learning in Hopfield Networks Saratha Sathasivam (Corresponding author) School of Mathematical Sciences, University of Science Malaysia, Penang, Malaysia E-mail: saratha@cs.usm.my Wan Ahmad Tajuddin
Renormalization Group analysis of 2D Ising model
 Renormalization Group analysis of D Ising model Amir Bar January 7, 013 1 Introduction In this tutorial we will see explicitly how RG can be used to probe the phase diagram of d > 1 systems, focusing as
Renormalization Group analysis of D Ising model Amir Bar January 7, 013 1 Introduction In this tutorial we will see explicitly how RG can be used to probe the phase diagram of d > 1 systems, focusing as
Data Mining Part 5. Prediction
 Data Mining Part 5. Prediction 5.5. Spring 2010 Instructor: Dr. Masoud Yaghini Outline How the Brain Works Artificial Neural Networks Simple Computing Elements Feed-Forward Networks Perceptrons (Single-layer,
Data Mining Part 5. Prediction 5.5. Spring 2010 Instructor: Dr. Masoud Yaghini Outline How the Brain Works Artificial Neural Networks Simple Computing Elements Feed-Forward Networks Perceptrons (Single-layer,
ADAPTIVE LATERAL INHIBITION FOR NON-NEGATIVE ICA. Mark Plumbley
 Submitteed to the International Conference on Independent Component Analysis and Blind Signal Separation (ICA2) ADAPTIVE LATERAL INHIBITION FOR NON-NEGATIVE ICA Mark Plumbley Audio & Music Lab Department
Submitteed to the International Conference on Independent Component Analysis and Blind Signal Separation (ICA2) ADAPTIVE LATERAL INHIBITION FOR NON-NEGATIVE ICA Mark Plumbley Audio & Music Lab Department
Causality and communities in neural networks
 Causality and communities in neural networks Leonardo Angelini, Daniele Marinazzo, Mario Pellicoro, Sebastiano Stramaglia TIRES-Center for Signal Detection and Processing - Università di Bari, Bari, Italy
Causality and communities in neural networks Leonardo Angelini, Daniele Marinazzo, Mario Pellicoro, Sebastiano Stramaglia TIRES-Center for Signal Detection and Processing - Università di Bari, Bari, Italy
Synaptic Rewiring for Topographic Map Formation
 Synaptic Rewiring for Topographic Map Formation Simeon A. Bamford 1, Alan F. Murray 2, and David J. Willshaw 3 1 Doctoral Training Centre in Neuroinformatics, sim.bamford@ed.ac.uk, 2 Institute of Integrated
Synaptic Rewiring for Topographic Map Formation Simeon A. Bamford 1, Alan F. Murray 2, and David J. Willshaw 3 1 Doctoral Training Centre in Neuroinformatics, sim.bamford@ed.ac.uk, 2 Institute of Integrated
Laboratory for Astronomy & Solar Physics, Code 681, NASAèGSFC, Greenbelt MD
 1997 HST Calibration Workshop Space Telescope Science Institute, 1997 S. Casertano, et al., eds. Correction for the STIS Echelle Blaze Function Sara R. Heap and Thomas M. Brown 1 Laboratory for Astronomy
1997 HST Calibration Workshop Space Telescope Science Institute, 1997 S. Casertano, et al., eds. Correction for the STIS Echelle Blaze Function Sara R. Heap and Thomas M. Brown 1 Laboratory for Astronomy
1 Receptive Fields and Maps in the Visual Cortex: Models of Ocular Dominance and Orientation Columns Kenneth D. Miller 1 Published in: Models of Neura
 1 Receptive Fields and Maps in the Visual Cortex: Models of Ocular Dominance and Orientation Columns Kenneth D. Miller 1 Published in: Models of Neural Networks III, E. Domany,J.L. vanhemmen, and K. Schulten,
1 Receptive Fields and Maps in the Visual Cortex: Models of Ocular Dominance and Orientation Columns Kenneth D. Miller 1 Published in: Models of Neural Networks III, E. Domany,J.L. vanhemmen, and K. Schulten,
Optimal In-Place Self-Organization for Cortical Development: Limited Cells, Sparse Coding and Cortical Topography
 Optimal In-Place Self-Organization for Cortical Development: Limited Cells, Sparse Coding and Cortical Topography Juyang Weng and Matthew D. Luciw Department of Computer Science and Engineering Michigan
Optimal In-Place Self-Organization for Cortical Development: Limited Cells, Sparse Coding and Cortical Topography Juyang Weng and Matthew D. Luciw Department of Computer Science and Engineering Michigan
SUPPLEMENTARY INFORMATION
 Supplementary discussion 1: Most excitatory and suppressive stimuli for model neurons The model allows us to determine, for each model neuron, the set of most excitatory and suppresive features. First,
Supplementary discussion 1: Most excitatory and suppressive stimuli for model neurons The model allows us to determine, for each model neuron, the set of most excitatory and suppresive features. First,
Fast neural network simulations with population density methods
 Fast neural network simulations with population density methods Duane Q. Nykamp a,1 Daniel Tranchina b,a,c,2 a Courant Institute of Mathematical Science b Department of Biology c Center for Neural Science
Fast neural network simulations with population density methods Duane Q. Nykamp a,1 Daniel Tranchina b,a,c,2 a Courant Institute of Mathematical Science b Department of Biology c Center for Neural Science
How to do backpropagation in a brain
 How to do backpropagation in a brain Geoffrey Hinton Canadian Institute for Advanced Research & University of Toronto & Google Inc. Prelude I will start with three slides explaining a popular type of deep
How to do backpropagation in a brain Geoffrey Hinton Canadian Institute for Advanced Research & University of Toronto & Google Inc. Prelude I will start with three slides explaining a popular type of deep
Natural Image Statistics
 Natural Image Statistics A probabilistic approach to modelling early visual processing in the cortex Dept of Computer Science Early visual processing LGN V1 retina From the eye to the primary visual cortex
Natural Image Statistics A probabilistic approach to modelling early visual processing in the cortex Dept of Computer Science Early visual processing LGN V1 retina From the eye to the primary visual cortex
Leo Kadanoff and 2d XY Models with Symmetry-Breaking Fields. renormalization group study of higher order gradients, cosines and vortices
 Leo Kadanoff and d XY Models with Symmetry-Breaking Fields renormalization group study of higher order gradients, cosines and vortices Leo Kadanoff and Random Matrix Theory Non-Hermitian Localization in
Leo Kadanoff and d XY Models with Symmetry-Breaking Fields renormalization group study of higher order gradients, cosines and vortices Leo Kadanoff and Random Matrix Theory Non-Hermitian Localization in
also has x æ as a local imizer. Of course, æ is typically not known, but an algorithm can approximate æ as it approximates x æ èas the augmented Lagra
 Introduction to sequential quadratic programg Mark S. Gockenbach Introduction Sequential quadratic programg èsqpè methods attempt to solve a nonlinear program directly rather than convert it to a sequence
Introduction to sequential quadratic programg Mark S. Gockenbach Introduction Sequential quadratic programg èsqpè methods attempt to solve a nonlinear program directly rather than convert it to a sequence
CMSC 421: Neural Computation. Applications of Neural Networks
 CMSC 42: Neural Computation definition synonyms neural networks artificial neural networks neural modeling connectionist models parallel distributed processing AI perspective Applications of Neural Networks
CMSC 42: Neural Computation definition synonyms neural networks artificial neural networks neural modeling connectionist models parallel distributed processing AI perspective Applications of Neural Networks
Pattern Recognition Prof. P. S. Sastry Department of Electronics and Communication Engineering Indian Institute of Science, Bangalore
 Pattern Recognition Prof. P. S. Sastry Department of Electronics and Communication Engineering Indian Institute of Science, Bangalore Lecture - 27 Multilayer Feedforward Neural networks with Sigmoidal
Pattern Recognition Prof. P. S. Sastry Department of Electronics and Communication Engineering Indian Institute of Science, Bangalore Lecture - 27 Multilayer Feedforward Neural networks with Sigmoidal
CS-184: Computer Graphics
 CS-184: Computer Graphics Lecture #25: Rigid Body Simulations Tobias Pfaff 537 Soda (Visual Computing Lab) tpfaff@berkeley.edu Reminder Final project presentations next week! Game Physics Types of Materials
CS-184: Computer Graphics Lecture #25: Rigid Body Simulations Tobias Pfaff 537 Soda (Visual Computing Lab) tpfaff@berkeley.edu Reminder Final project presentations next week! Game Physics Types of Materials
the x's and the y's unlike the standard k-means clustering on the x's ë8ë. We then present results comparing EMRBF with standard RBF estimation method
 EMRBF: A Statistical Basis for Using Radial Basis Functions for Process Control Lyle H. Ungar Department of Chemical Engineering University ofpennsylvania ungar@cis.upenn.edu Richard D. De Veaux Mathematics
EMRBF: A Statistical Basis for Using Radial Basis Functions for Process Control Lyle H. Ungar Department of Chemical Engineering University ofpennsylvania ungar@cis.upenn.edu Richard D. De Veaux Mathematics
Balance of Electric and Diffusion Forces
 Balance of Electric and Diffusion Forces Ions flow into and out of the neuron under the forces of electricity and concentration gradients (diffusion). The net result is a electric potential difference
Balance of Electric and Diffusion Forces Ions flow into and out of the neuron under the forces of electricity and concentration gradients (diffusion). The net result is a electric potential difference
Artificial Neural Networks. Edward Gatt
 Artificial Neural Networks Edward Gatt What are Neural Networks? Models of the brain and nervous system Highly parallel Process information much more like the brain than a serial computer Learning Very
Artificial Neural Networks Edward Gatt What are Neural Networks? Models of the brain and nervous system Highly parallel Process information much more like the brain than a serial computer Learning Very
Biological Modeling of Neural Networks:
 Week 14 Dynamics and Plasticity 14.1 Reservoir computing - Review:Random Networks - Computing with rich dynamics Biological Modeling of Neural Networks: 14.2 Random Networks - stationary state - chaos
Week 14 Dynamics and Plasticity 14.1 Reservoir computing - Review:Random Networks - Computing with rich dynamics Biological Modeling of Neural Networks: 14.2 Random Networks - stationary state - chaos
An objective function for self-limiting neural plasticity rules.
 ESANN 5 proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. Bruges (Belgium), -4 April 5, i6doc.com publ., ISBN 978-875874-8. An objective function
ESANN 5 proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. Bruges (Belgium), -4 April 5, i6doc.com publ., ISBN 978-875874-8. An objective function
256 Facta Universitatis ser.: Elect. and Energ. vol. 11, No.2 è1998è primarily concerned with narrow range of frequencies near ærst resonance èwhere s
 FACTA UNIVERSITATIS èni ç Sè Series: Electronics and Energetics vol. 11, No.2 è1998è, 255-261 EFFICIENT CALCULATION OF RADAR CROSS SECTION FOR FINITE STRIP ARRAY ON DIELECTRIC SLAB Borislav Popovski and
FACTA UNIVERSITATIS èni ç Sè Series: Electronics and Energetics vol. 11, No.2 è1998è, 255-261 EFFICIENT CALCULATION OF RADAR CROSS SECTION FOR FINITE STRIP ARRAY ON DIELECTRIC SLAB Borislav Popovski and
November 9, Abstract. properties change in response to the application of a magnetic æeld. These æuids typically
 On the Eæective Magnetic Properties of Magnetorheological Fluids æ November 9, 998 Tammy M. Simon, F. Reitich, M.R. Jolly, K. Ito, H.T. Banks Abstract Magnetorheological èmrè æuids represent a class of
On the Eæective Magnetic Properties of Magnetorheological Fluids æ November 9, 998 Tammy M. Simon, F. Reitich, M.R. Jolly, K. Ito, H.T. Banks Abstract Magnetorheological èmrè æuids represent a class of
Sparse Coding as a Generative Model
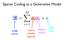 Sparse Coding as a Generative Model image vector neural activity (sparse) feature vector other stuff Find activations by descending E Coefficients via gradient descent Driving input (excitation) Lateral
Sparse Coding as a Generative Model image vector neural activity (sparse) feature vector other stuff Find activations by descending E Coefficients via gradient descent Driving input (excitation) Lateral
Neuron. Detector Model. Understanding Neural Components in Detector Model. Detector vs. Computer. Detector. Neuron. output. axon
 Neuron Detector Model 1 The detector model. 2 Biological properties of the neuron. 3 The computational unit. Each neuron is detecting some set of conditions (e.g., smoke detector). Representation is what
Neuron Detector Model 1 The detector model. 2 Biological properties of the neuron. 3 The computational unit. Each neuron is detecting some set of conditions (e.g., smoke detector). Representation is what
Analysis of an Attractor Neural Network s Response to Conflicting External Inputs
 Journal of Mathematical Neuroscience (2018) 8:6 https://doi.org/10.1186/s13408-018-0061-0 RESEARCH OpenAccess Analysis of an Attractor Neural Network s Response to Conflicting External Inputs Kathryn Hedrick
Journal of Mathematical Neuroscience (2018) 8:6 https://doi.org/10.1186/s13408-018-0061-0 RESEARCH OpenAccess Analysis of an Attractor Neural Network s Response to Conflicting External Inputs Kathryn Hedrick
Artificial Neural Networks. Q550: Models in Cognitive Science Lecture 5
 Artificial Neural Networks Q550: Models in Cognitive Science Lecture 5 "Intelligence is 10 million rules." --Doug Lenat The human brain has about 100 billion neurons. With an estimated average of one thousand
Artificial Neural Networks Q550: Models in Cognitive Science Lecture 5 "Intelligence is 10 million rules." --Doug Lenat The human brain has about 100 billion neurons. With an estimated average of one thousand
Artificial Neural Network and Fuzzy Logic
 Artificial Neural Network and Fuzzy Logic 1 Syllabus 2 Syllabus 3 Books 1. Artificial Neural Networks by B. Yagnanarayan, PHI - (Cover Topologies part of unit 1 and All part of Unit 2) 2. Neural Networks
Artificial Neural Network and Fuzzy Logic 1 Syllabus 2 Syllabus 3 Books 1. Artificial Neural Networks by B. Yagnanarayan, PHI - (Cover Topologies part of unit 1 and All part of Unit 2) 2. Neural Networks
Synthesis of Reinforcement Learning, Neural Networks, and PI Control Applied to a Simulated Heating Coil
 Synthesis of Reinforcement Learning, Neural Networks, and PI Control Applied to a Simulated Heating Coil Charles W. Anderson 1, Douglas C. Hittle 2, Alon D. Katz 2, and R. Matt Kretchmar 1 1 Department
Synthesis of Reinforcement Learning, Neural Networks, and PI Control Applied to a Simulated Heating Coil Charles W. Anderson 1, Douglas C. Hittle 2, Alon D. Katz 2, and R. Matt Kretchmar 1 1 Department
Processing of Time Series by Neural Circuits with Biologically Realistic Synaptic Dynamics
 Processing of Time Series by Neural Circuits with iologically Realistic Synaptic Dynamics Thomas Natschläger & Wolfgang Maass Institute for Theoretical Computer Science Technische Universität Graz, ustria
Processing of Time Series by Neural Circuits with iologically Realistic Synaptic Dynamics Thomas Natschläger & Wolfgang Maass Institute for Theoretical Computer Science Technische Universität Graz, ustria
Iterative face image feature extraction with Generalized Hebbian Algorithm and a Sanger-like BCM rule
 Iterative face image feature extraction with Generalized Hebbian Algorithm and a Sanger-like BCM rule Clayton Aldern (Clayton_Aldern@brown.edu) Tyler Benster (Tyler_Benster@brown.edu) Carl Olsson (Carl_Olsson@brown.edu)
Iterative face image feature extraction with Generalized Hebbian Algorithm and a Sanger-like BCM rule Clayton Aldern (Clayton_Aldern@brown.edu) Tyler Benster (Tyler_Benster@brown.edu) Carl Olsson (Carl_Olsson@brown.edu)
RESEARCH STATEMENT. Nora Youngs, University of Nebraska - Lincoln
 RESEARCH STATEMENT Nora Youngs, University of Nebraska - Lincoln 1. Introduction Understanding how the brain encodes information is a major part of neuroscience research. In the field of neural coding,
RESEARCH STATEMENT Nora Youngs, University of Nebraska - Lincoln 1. Introduction Understanding how the brain encodes information is a major part of neuroscience research. In the field of neural coding,
Memory capacity of networks with stochastic binary synapses
 Memory capacity of networks with stochastic binary synapses Alexis M. Dubreuil 1,, Yali Amit 3 and Nicolas Brunel 1, 1 UMR 8118, CNRS, Université Paris Descartes, Paris, France Departments of Statistics
Memory capacity of networks with stochastic binary synapses Alexis M. Dubreuil 1,, Yali Amit 3 and Nicolas Brunel 1, 1 UMR 8118, CNRS, Université Paris Descartes, Paris, France Departments of Statistics
Influence of Criticality on 1/f α Spectral Characteristics of Cortical Neuron Populations
 Influence of Criticality on 1/f α Spectral Characteristics of Cortical Neuron Populations Robert Kozma rkozma@memphis.edu Computational Neurodynamics Laboratory, Department of Computer Science 373 Dunn
Influence of Criticality on 1/f α Spectral Characteristics of Cortical Neuron Populations Robert Kozma rkozma@memphis.edu Computational Neurodynamics Laboratory, Department of Computer Science 373 Dunn
Statistics and geometry of orientation selectivity in primary visual cortex
 Biol Cybern (2014) 108:631 653 DOI 10.1007/s00422-013-0576-0 ORIGINAL PAPER Statistics and geometry of orientation selectivity in primary visual cortex Sadra Sadeh Stefan Rotter Received: 7 June 2013 /
Biol Cybern (2014) 108:631 653 DOI 10.1007/s00422-013-0576-0 ORIGINAL PAPER Statistics and geometry of orientation selectivity in primary visual cortex Sadra Sadeh Stefan Rotter Received: 7 June 2013 /
Department of Technical Physics, Helsinki University of Technology, FIN Espoo, Finland
 Local Density of States in a Dirty Normal Metal Connected to a Superconductor W. Belzig, C. Bruder, and Gerd Schíon ; Institut fíur Theoretische Festkíorperphysik, Universitíat Karlsruhe, D-768 Karlsruhe,
Local Density of States in a Dirty Normal Metal Connected to a Superconductor W. Belzig, C. Bruder, and Gerd Schíon ; Institut fíur Theoretische Festkíorperphysik, Universitíat Karlsruhe, D-768 Karlsruhe,
TWO METHODS FOR ESTIMATING OVERCOMPLETE INDEPENDENT COMPONENT BASES. Mika Inki and Aapo Hyvärinen
 TWO METHODS FOR ESTIMATING OVERCOMPLETE INDEPENDENT COMPONENT BASES Mika Inki and Aapo Hyvärinen Neural Networks Research Centre Helsinki University of Technology P.O. Box 54, FIN-215 HUT, Finland ABSTRACT
TWO METHODS FOR ESTIMATING OVERCOMPLETE INDEPENDENT COMPONENT BASES Mika Inki and Aapo Hyvärinen Neural Networks Research Centre Helsinki University of Technology P.O. Box 54, FIN-215 HUT, Finland ABSTRACT
A New Invariance Property of Lyapunov Characteristic Directions S. Bharadwaj and K.D. Mease Mechanical and Aerospace Engineering University of Califor
 A New Invariance Property of Lyapunov Characteristic Directions S. Bharadwaj and K.D. Mease Mechanical and Aerospace Engineering University of California, Irvine, California, 92697-3975 Email: sanjay@eng.uci.edu,
A New Invariance Property of Lyapunov Characteristic Directions S. Bharadwaj and K.D. Mease Mechanical and Aerospace Engineering University of California, Irvine, California, 92697-3975 Email: sanjay@eng.uci.edu,
Artificial Neural Network
 Artificial Neural Network Contents 2 What is ANN? Biological Neuron Structure of Neuron Types of Neuron Models of Neuron Analogy with human NN Perceptron OCR Multilayer Neural Network Back propagation
Artificial Neural Network Contents 2 What is ANN? Biological Neuron Structure of Neuron Types of Neuron Models of Neuron Analogy with human NN Perceptron OCR Multilayer Neural Network Back propagation
Potts And XY, Together At Last
 Potts And XY, Together At Last Daniel Kolodrubetz Massachusetts Institute of Technology, Center for Theoretical Physics (Dated: May 16, 212) We investigate the behavior of an XY model coupled multiplicatively
Potts And XY, Together At Last Daniel Kolodrubetz Massachusetts Institute of Technology, Center for Theoretical Physics (Dated: May 16, 212) We investigate the behavior of an XY model coupled multiplicatively
TIME-SEQUENTIAL SELF-ORGANIZATION OF HIERARCHICAL NEURAL NETWORKS. Ronald H. Silverman Cornell University Medical College, New York, NY 10021
 709 TIME-SEQUENTIAL SELF-ORGANIZATION OF HIERARCHICAL NEURAL NETWORKS Ronald H. Silverman Cornell University Medical College, New York, NY 10021 Andrew S. Noetzel polytechnic University, Brooklyn, NY 11201
709 TIME-SEQUENTIAL SELF-ORGANIZATION OF HIERARCHICAL NEURAL NETWORKS Ronald H. Silverman Cornell University Medical College, New York, NY 10021 Andrew S. Noetzel polytechnic University, Brooklyn, NY 11201
Spontaneous origin of topological complexity in self-organizing neural networks
 Network: Comput. Neural Syst. 8 (1997) 185 194. Printed in the UK PII: S0954-898X(97)78402-1 Spontaneous origin of topological complexity in self-organizing neural networks George Chapline Lawrence Livermore
Network: Comput. Neural Syst. 8 (1997) 185 194. Printed in the UK PII: S0954-898X(97)78402-1 Spontaneous origin of topological complexity in self-organizing neural networks George Chapline Lawrence Livermore
Abstract. subplans to arrive at a more eæcient implementation. Our algorithm improves upon the
 An OèT 3 è algorithm for the economic lot-sizing problem with constant capacities C.P.M. van Hoesel æ A.P.M. Wagelmans y Revised June 1994 Abstract We develop an algorithm that solves the constant capacities
An OèT 3 è algorithm for the economic lot-sizing problem with constant capacities C.P.M. van Hoesel æ A.P.M. Wagelmans y Revised June 1994 Abstract We develop an algorithm that solves the constant capacities
Recursive Least Squares for an Entropy Regularized MSE Cost Function
 Recursive Least Squares for an Entropy Regularized MSE Cost Function Deniz Erdogmus, Yadunandana N. Rao, Jose C. Principe Oscar Fontenla-Romero, Amparo Alonso-Betanzos Electrical Eng. Dept., University
Recursive Least Squares for an Entropy Regularized MSE Cost Function Deniz Erdogmus, Yadunandana N. Rao, Jose C. Principe Oscar Fontenla-Romero, Amparo Alonso-Betanzos Electrical Eng. Dept., University
Neuron, Volume 63. Supplemental Data. Generating Coherent Patterns of Activity. from Chaotic Neural Networks. David Sussillo and L.F.
 Neuron, Volume 63 Supplemental Data Generating Coherent Patterns of Activity from Chaotic Neural Networks David Sussillo and L.F. Abbott Supplementary Material FORCE Learning without RLS It is possible
Neuron, Volume 63 Supplemental Data Generating Coherent Patterns of Activity from Chaotic Neural Networks David Sussillo and L.F. Abbott Supplementary Material FORCE Learning without RLS It is possible
Introduction Biologically Motivated Crude Model Backpropagation
 Introduction Biologically Motivated Crude Model Backpropagation 1 McCulloch-Pitts Neurons In 1943 Warren S. McCulloch, a neuroscientist, and Walter Pitts, a logician, published A logical calculus of the
Introduction Biologically Motivated Crude Model Backpropagation 1 McCulloch-Pitts Neurons In 1943 Warren S. McCulloch, a neuroscientist, and Walter Pitts, a logician, published A logical calculus of the
Hebb rule book: 'The Organization of Behavior' Theory about the neural bases of learning
 PCA by neurons Hebb rule 1949 book: 'The Organization of Behavior' Theory about the neural bases of learning Learning takes place in synapses. Synapses get modified, they get stronger when the pre- and
PCA by neurons Hebb rule 1949 book: 'The Organization of Behavior' Theory about the neural bases of learning Learning takes place in synapses. Synapses get modified, they get stronger when the pre- and
Ways to make neural networks generalize better
 Ways to make neural networks generalize better Seminar in Deep Learning University of Tartu 04 / 10 / 2014 Pihel Saatmann Topics Overview of ways to improve generalization Limiting the size of the weights
Ways to make neural networks generalize better Seminar in Deep Learning University of Tartu 04 / 10 / 2014 Pihel Saatmann Topics Overview of ways to improve generalization Limiting the size of the weights
Neural Networks and Fuzzy Logic Rajendra Dept.of CSE ASCET
 Unit-. Definition Neural network is a massively parallel distributed processing system, made of highly inter-connected neural computing elements that have the ability to learn and thereby acquire knowledge
Unit-. Definition Neural network is a massively parallel distributed processing system, made of highly inter-connected neural computing elements that have the ability to learn and thereby acquire knowledge
-2q. +3q. +6q. +2q. -3q. -2q. -3q. +2q. +3q. +6q
 Name: Sectè èor TA nameè: Student Id è Please æll in your name, student id number, section number and FORM on your test scan forms. PHYSICS 22 FALL 1997 FIRST MIDTERM EXAM, FORM A 1. You are given two
Name: Sectè èor TA nameè: Student Id è Please æll in your name, student id number, section number and FORM on your test scan forms. PHYSICS 22 FALL 1997 FIRST MIDTERM EXAM, FORM A 1. You are given two
An Adaptive Bayesian Network for Low-Level Image Processing
 An Adaptive Bayesian Network for Low-Level Image Processing S P Luttrell Defence Research Agency, Malvern, Worcs, WR14 3PS, UK. I. INTRODUCTION Probability calculus, based on the axioms of inference, Cox
An Adaptive Bayesian Network for Low-Level Image Processing S P Luttrell Defence Research Agency, Malvern, Worcs, WR14 3PS, UK. I. INTRODUCTION Probability calculus, based on the axioms of inference, Cox
Outline Introduction OLS Design of experiments Regression. Metamodeling. ME598/494 Lecture. Max Yi Ren
 1 / 34 Metamodeling ME598/494 Lecture Max Yi Ren Department of Mechanical Engineering, Arizona State University March 1, 2015 2 / 34 1. preliminaries 1.1 motivation 1.2 ordinary least square 1.3 information
1 / 34 Metamodeling ME598/494 Lecture Max Yi Ren Department of Mechanical Engineering, Arizona State University March 1, 2015 2 / 34 1. preliminaries 1.1 motivation 1.2 ordinary least square 1.3 information
Computational Explorations in Cognitive Neuroscience Chapter 2
 Computational Explorations in Cognitive Neuroscience Chapter 2 2.4 The Electrophysiology of the Neuron Some basic principles of electricity are useful for understanding the function of neurons. This is
Computational Explorations in Cognitive Neuroscience Chapter 2 2.4 The Electrophysiology of the Neuron Some basic principles of electricity are useful for understanding the function of neurons. This is
The Role of Weight Normalization in Competitive Learning
 Communicated by Todd Leen The Role of Weight Normalization in Competitive Learning Geoffrey J. Goodhill University of Edinburgh, Centre for Cognitive Science, 2 Buccleiich Place, Edinburgh EH8 9LW, United
Communicated by Todd Leen The Role of Weight Normalization in Competitive Learning Geoffrey J. Goodhill University of Edinburgh, Centre for Cognitive Science, 2 Buccleiich Place, Edinburgh EH8 9LW, United
Stable Adaptive Momentum for Rapid Online Learning in Nonlinear Systems
 Stable Adaptive Momentum for Rapid Online Learning in Nonlinear Systems Thore Graepel and Nicol N. Schraudolph Institute of Computational Science ETH Zürich, Switzerland {graepel,schraudo}@inf.ethz.ch
Stable Adaptive Momentum for Rapid Online Learning in Nonlinear Systems Thore Graepel and Nicol N. Schraudolph Institute of Computational Science ETH Zürich, Switzerland {graepel,schraudo}@inf.ethz.ch
Adaptation in the Neural Code of the Retina
 Adaptation in the Neural Code of the Retina Lens Retina Fovea Optic Nerve Optic Nerve Bottleneck Neurons Information Receptors: 108 95% Optic Nerve 106 5% After Polyak 1941 Visual Cortex ~1010 Mean Intensity
Adaptation in the Neural Code of the Retina Lens Retina Fovea Optic Nerve Optic Nerve Bottleneck Neurons Information Receptors: 108 95% Optic Nerve 106 5% After Polyak 1941 Visual Cortex ~1010 Mean Intensity
Discrete and Indiscrete Models of Biological Networks
 Discrete and Indiscrete Models of Biological Networks Winfried Just Ohio University November 17, 2010 Who are we? What are we doing here? Who are we? What are we doing here? A population of interacting
Discrete and Indiscrete Models of Biological Networks Winfried Just Ohio University November 17, 2010 Who are we? What are we doing here? Who are we? What are we doing here? A population of interacting
Deænition 1 A set S is ænite if there exists a number N such that the number of elements in S èdenoted jsjè is less than N. If no such N exists, then
 Morphology of Proof An introduction to rigorous proof techniques Craig Silverstein September 26, 1998 1 Methodology of Proof an example Deep down, all theorems are of the form if A then B. They may be
Morphology of Proof An introduction to rigorous proof techniques Craig Silverstein September 26, 1998 1 Methodology of Proof an example Deep down, all theorems are of the form if A then B. They may be
Brains and Computation
 15-883: Computational Models of Neural Systems Lecture 1.1: Brains and Computation David S. Touretzky Computer Science Department Carnegie Mellon University 1 Models of the Nervous System Hydraulic network
15-883: Computational Models of Neural Systems Lecture 1.1: Brains and Computation David S. Touretzky Computer Science Department Carnegie Mellon University 1 Models of the Nervous System Hydraulic network
APPENDIX E., where the boundary values on the sector are given by = 0. n=1. a 00 n + 1 r a0 n, n2
 APPENDIX E Solutions to Problem Set 5. èproblem 4.5.4 in textè èaè Use a series expansion to nd èèr;è satisfying èe.è è rr + r è r + r 2 è =, r 2 cosèè in the sector éré3, 0 éé 2, where the boundary values
APPENDIX E Solutions to Problem Set 5. èproblem 4.5.4 in textè èaè Use a series expansion to nd èèr;è satisfying èe.è è rr + r è r + r 2 è =, r 2 cosèè in the sector éré3, 0 éé 2, where the boundary values
A spherical model for orientation and spatial-frequency tuning in a cortical hypercolumn
 FirstCite e-publishing Received 13 December 1 Accepted 9 April Published online A spherical model for orientation spatial-frequency tuning in a cortical hypercolumn Paul C. Bressloff 1 Jack D. Cowan *
FirstCite e-publishing Received 13 December 1 Accepted 9 April Published online A spherical model for orientation spatial-frequency tuning in a cortical hypercolumn Paul C. Bressloff 1 Jack D. Cowan *
90 CHAPTER 15. AXISYMMETRIC & TRIAXIAL MODELS the resulting model, or work backwards from a model towards a distribution function. From fèe;j z è to ç
 Chapter 15 Axisymmetric & Triaxial Models Dynamical models are useful in èaè constraining the true shapes of elliptical galaxies and èbè searching for dark matter andèor nuclear black holes. Two-integral
Chapter 15 Axisymmetric & Triaxial Models Dynamical models are useful in èaè constraining the true shapes of elliptical galaxies and èbè searching for dark matter andèor nuclear black holes. Two-integral
action statements, which are called classiæers, and a corresponding list of real numbers, called the strengths of the classiæers. Classiæers bid their
 Reinforcement learning and dynamic optimization Erdem Baçsçcç and Mehmet Orhan 1 Department of Economics, Bilkent University, 06533, Bilkent, Ankara, Turkey Abstract This paper is about learning in dynamic
Reinforcement learning and dynamic optimization Erdem Baçsçcç and Mehmet Orhan 1 Department of Economics, Bilkent University, 06533, Bilkent, Ankara, Turkey Abstract This paper is about learning in dynamic
Using a Hopfield Network: A Nuts and Bolts Approach
 Using a Hopfield Network: A Nuts and Bolts Approach November 4, 2013 Gershon Wolfe, Ph.D. Hopfield Model as Applied to Classification Hopfield network Training the network Updating nodes Sequencing of
Using a Hopfield Network: A Nuts and Bolts Approach November 4, 2013 Gershon Wolfe, Ph.D. Hopfield Model as Applied to Classification Hopfield network Training the network Updating nodes Sequencing of
