Substituting back this result into the original Einstein equations we realize that they can be written as
|
|
|
- Sabina Pitts
- 5 years ago
- Views:
Transcription
1 CHAPTER 8 THE CHWARZCHILD-DROTE OLUTION As you see, the wa teated me kindly enough, in spite of the heavy gunfie, to allow me to get away fom it all and take this walk in the land of you ideas chwazschild s lette to Einstein duing Wold Wa I Most of the wok done till now has been elated to weak-field solutions of the Einstein equations. In this Chapte, we go a step fowad an look fo exact solutions. Given the non-lineaity of the field equations and the associated difficulty in finding analytical solutions fo abitay matte distibutions, we will estict ouselves to vacuum solutions. To detemine ou stating point, let me ewite the Einstein equations G µν + Λg µν = κ 2 T M µν in a much moe convenient fom. Multiplying by the invese metic and taking the tace we obtain a elation between the Ricci scala, the cosmological constant and the tace T M g µν T M µν of the locally conseved enegy-momentum tenso T M µν, namely R µ µ 1 2 Rδµ µ + Λδ µ µ = κ 2 T M R = κ 2 T M + 4Λ. 8.1) ubstituting back this esult into the oiginal Einstein equations we ealize that they can be witten as R µν = κ T 2 µν 1 ) 2 g µνt + Λg µν. 8.2) Vacuum solutions T M µν = Λ = 0) coespond then to solutions of the equation athe that to solutions of G µν =0. R µν = 0, 8.3) Vacuum solutions ae not necessaily flat Eq. 8.3) does not imply the vanishing of the Riemann tenso R µ νρσ, which contains exta components.
2 8.1 A spheically symmetic ansatz 110 The poblem of finding a solution of this equation is futhe simplified in those cases in which the poblem is highly symmetic. In what follows, we will look fo spheically symmetic solutions. 8.1 A spheically symmetic ansatz Conside the spacetime outside a spheically symmetic mass distibution, which can be static o not. A spacetime is said to posses a paticula symmety if the functional fom of the metic unde the action of such a symmety is maintained. In paticula, a spheically symmetic spacetime is a spacetime whose line element is invaiant unde otations o, if you want. a spacetime with the symmeties of the sphee ). The only otational invaiants of the spacelike coodinates x = x i and thei diffeential ae x x 2, dx dx, x dx. 8.4) The most geneal spatially isotopic metic that can be constucted with these elements takes the fom ds 2 = at, )dt 2 2bt, )dt x dx) + ct, ) x dx) 2 + dt, )dx dx, 8.5) with a, b, c and d some abitay functions of t and. The equied invaiance unde otations suggests the use of spheical coodinates {, θ, φ}. Pefoming the change of vaiables we ealize that all the angula dependence in 8.5) is isolated in the dx dx pat x x = 2, x dx = d, dx dx = d dθ sin 2 θdφ ) ubstituting these expessions into 8.5) we aive to the equivalent fom ds 2 = at, )dt 2 2bt, )dtd + ct, ) 2 d 2 + dt, ) d dω 2), 8.7) whee we have defined dω 2 abitay, functions = dθ 2 + sin 2 θdφ 2. Collecting tems togethe and defining some, still At, ) at, ), Bt, ) bt, ), Ct, ) 2 ct, ) + dt, ), Dt, ) 2 dt, ), to take into account the exta factos of in Eq. 8.7), we ae left with ds 2 = At, )dt 2 2Bt, )dtd + Ct, )d 2 + Dt, )dω ) The esulting metic can be futhe simplified by using the feedom in the choice of coodinates. Fo instance, we can define a new adial coodinate 2 Dt, ) and eliminate and d in tems of, t, d and dt. This gives ise to a big mess that changes the explicit fom of the coefficients A, B, C to some new, but still abitay, coefficients A, B, C ds 2 = A t, )dt 2 2B t, )dtd + C t, )d dω ) The next thing we can do is to find some new coodinate time tt, ) to get id of the nasty tem dtd. To do that, let me define this new time as d t = µt, ) [A t, )dt + B t, )d ] = t Ψt, )dt + Ψt, )d, 8.10) whee the new unknown integating facto µ is detemined by the condition that the second equality holds fo some Ψ. In othe wods, we equie µt, ) [A t, )dt + B t, )d ] to be a total diffeential, so that the fist equality makes sense. quaing Eq.8.10) d t 2 = µ 2 A 2 dt 2 + 2A B dtd + B 2 d 2) 8.11)
3 8.2 pheical symmety and staticity 111 and isolating the tems elated to dt 2 and dtd, we get A dt 2 + 2B dtd = 1 A µ 2 d t 2 B 2 A d ) In tems of the new tempoal coodinate t the coss tem disappeas and the antsatz 8.9) becomes diagonal ds 2 = 1 ) A µ 2 d t 2 + C + B 2 d dω ) A ince the functions of t and in this expession ae abitay we can collect them into some abitay new functions 1 e 2α 1 A µ 2, e2β C + B 2 A, 8.14) and wite ds 2 = e 2α t, ) d t 2 + e 2β t, ) d dω ) Dopping the bas to maintain the notation as light as possible, we aive to ou fist impotant esult ds 2 = e 2αt,) dt 2 + e 2βt,) d dω ) Just by using spheical symmety and ou feedom to change coodinates, we have been able to educe the 10 functions in g µν to two functions of only two vaiables! Rathe impessive. 8.2 pheical symmety and staticity The unknown functions α and β can be detemined by inseting the antsatz 8.16) into the vacuum Einstein equations 8.3). The fist step in this pocedue is to compute the metic connection Γ µ νσ. The job is conceptually staightfowad but athe tedious. Whateve the way you do it 2, you should obtain 12 non-vanishing components out of 40, namely Γ t tt = t α, Γ t t = Γ t t = α, Γ t = e 2β α) t β, Γ tt = e 2α β) α, Γ t = Γ t = t β, Γ = β, Γ θθ = e 2β, Γ φφ = sin 2 θ Γ θθ, Γθ θ = Γ θ θ = 1/, 8.17) Γ θ φφ = sin θ cos θ, Γ φ θφ = Γ φ θφ = cot θ, Γφ φ = Γ φ φ = 1/. The non-vanishing components of the Riemann tenso associated to these Chistoffel symbols ae given by R t t = e 2β α) [ 2 t β + t β) 2 t α t β] + [ α β 2 α α) 2], R t θtθ = e 2β α, R t φtφ = e 2β sin 2 θ α, R t θθ = e 2α t β, R t φφ = e 2α sin 2 θ t β, R θθ = e 2β β, R φφ = e 2β sin 2 θ β, 8.18) R θ φθφ = 1 e 2β ) sin 2 θ.. 1 This exponential fom is specially useful fo witing compact expessions fo the components of the metic connections and the Riemann tenso. 2 The quicke way to get Γ µ νσ is by using the Lagangian pocedue fo geodesics, but you can also use the bute foce method and compute them via Eq. 4.62).
4 8.2 pheical symmety and staticity 112 which, contacted, povide us with the non-vanishing components of the Ricci tenso R tt = [ 2 t β + t β) 2 t α t β ] + [ 2 α + α) 2 α β + 2 α ] e 2α β), R = [ 2 t β + t β) 2 t α t β ] e 2β α) [ 2 α + α) 2 α β 2 β ], 8.19) R t = 2 tβ, R θθ = 1 + e 2β [ β α) 1], R φφ = R θθ sin 2 θ. Undestanding the esult The esult 8.19) can be easily undestood fom simple symmety consideations. Conside fo instance the R θ component and note that the metic 8.16) is invaiant unde eflections in the θ and φ coodinates, i.e. θ θ and φ φ. When θ θ, the sign of R θ changes and we ae foce to have R θ = 0. The same kind of agument can be applied to many components to get R θ = R φ = R tθ = R tφ = R θφ = ) The elation between R φφ and R θθ can be also deived without pefoming the explicit computation. To see this, conside the coodinate tansfomation θ, φ) θ, φ) and wite the expession fo the angula pat of the line element in both coodinate systems [ ) 2 ) ] 2 θ φ dθ 2 + sin 2 θdφ 2 = θ + sin 2 θ θ dθ ) The invaiance of the line element unde otations implies the equality ) 2 ) 2 θ φ θ + sin 2 θ θ = ) ubstituting this into the tansfomation law fo the R θθ component ) 2 ) 2 θ φ R θ θ = θ R θθ + θ R φφ R θθ = 1 sin 2 θ ) ) 2 φ θ + and demanding R θ θ = R θθ, we get the sought-fo elation R φφ = sin 2 R θθ. ) 2 φ θ R φφ The empty-space field equations ae obtained by setting each of the components 8.19) equal to zeo. These gives ise to 5 equations among which only 4 ae useful since the R φφ component simply epeats the infomation of the R θθ component. Among these 4 equations, the simplest one is that associated to R t. A simple inspection of this equation eveals a vey inteesting popety: the function β must be independent of time R t = 0 t β = 0 β = β). 8.23) Taking into account this esult and pefoming the time deivative of the vacuum equation R θθ = 0, we get t R θθ = 0 t α = 0 α = γ) + κt). 8.24) The coefficient e 2α,t) can be then splited into two pieces e 2α,t) = e 2γ) e 2κt). This allows us to pefom an exta coodinate edefinition dt e κt) dt, γ) α), 8.25)
5 8.3 The chwazschild-doste solution 113 in Eq. 8.16) to obtain a much simple line element ds 2 = e 2α) dt 2 + e 2β) d dω 2, 8.26) specified by only two time-independent functions α) and β). The esulting metic is static 3 even though we did not impose any equiement on the souce apat fom being spheically symmetic. The souce could be as dynamical as a collapsing o a pulsating sta and the metic outside the matte distibution would still take the fom 8.26), as long as the collapse is symmetic. This esult is in pefect ageement with ou discussion on gavitational waves: if a spheically symmetic body undegoes pue adial pulsations, thee is no quadupole and thee is no emission of gavitational waves. All vacuum solutions of the Einstein equations with O3) symmety ae necessaily static. 8.3 The chwazschild-doste solution Thanks to symmety, we ae left with 3 equations of a single vaiable fo two unknows α and β. Let me ewite them as ) R tt = + α + α 2 α β + 2α e 2α β) = 0, 8.27) ) R = α + α 2 α β 2β = 0, 8.28) R θθ = 1 e 2β 1 + α β ) = 0, 8.29) with the pime denoting deivatives with espect to. Note that the fist two equations ae athe simila. Multiplying the fist one by e 2α β) and adding it to the second we get e 2β α) R tt + R = 2 α + β ) = 0 α + β = 0 α) + β) = constant. 8.30) The integation constant appeaing in the pevious expession can be always set to zeo by simply pefoming a coodinate edefinition, allowing us to set α = β. Inseting this esult into Eq. 8.29) we get R θθ = α ) e 2α = 1 e 2α) = 1, 8.31) which can be easily integated to obtain e 2α = + C e 2α = e 2β = 1 + C, 8.32) o equivalently ds 2 = 1 + C ) dt C ) 1 d dω ) 3 A static spacetime is one in which i) The components of g µν ae independent of the timelike component x 0. ii) The line element is invaiant unde the tansfomation x 0 x 0. If the second condition is not satisfied the spacetime is athe said to be stationay. A paticula example of stationay metic is the one geneated by a otating sta, whee the change x 0 x 0 changes the sense of otation.
6 8.3 The chwazschild-doste solution 114 The obtained metic is asymptotically flat: it tends to the Minkowski metic when. Bikhoff s theoem Any solution of the vacuum Einstein equations with O3) symmety must be static and asymptotically flat. The only thing left is to associate the constant C to some physical paamete. The most impotant use of a spheically symmetic vacuum solution is to epesent the spacetime outside stas o planets. In that case, we would expect to ecove the Newtonian limit g 00 = 1 2GM ), g = 1 + 2GM ), 8.34) at lage values. Compaing 8.34) with the limit of the metic 8.32) g 00 = 1 + C ), g = 1 C ), 8.35) we get C = 2GM, which allows us to wite the final and taditional expession fo the so-called chwazchild-doste metic 4 ds 2 = 1 R ) dt R ) 1 d dω ) with the chwazschild adius 5. R 2GM c 2 ) M 3km, 8.37) M Execise Veify that 8.36) satisfies Eq. 8.29). Explain why this is guaanteed to happen even though we initially had thee equations fo two unknowns. how that the chwazschild metic can be witten in a fom that makes explicit its isotopic chaacte, namely ) 2 1 R ds 2 4ρ = ) 2 dt R 4ρ 1 + R ) 4 dx 2 + dy 2 + dz 2), 8.38) 4ρ with ρ = 1 2 GM + ) 2 2GM. 8.39) 4 Kal chwazschild found this exact solution in 1915 while seving in the Geman amy on the Russian font duing the Wold Wa I and died a yea late fom pemphigus, a painful autoimmune disease. An altenative deivation of this solution based on the Weyl method was pesented by Doste aound the same time but fo some eason the physics community completely ignoed it. 5 We have momentaily estoed the factos of c.
7 8.4 Measuing distances and times Measuing distances and times Which is the physical meaning of the coodinates t,, θ, φ) appeaing in the chwazschild-doste solution? Although they povide a global efeence fame fo an obseve making measuements at an infinite distance fom the souce asymptotic flatness), not all of them epesent physical quantities measued by abitay obseves. While θ and φ have the same intepetation than the spheical angula coodinates in flat spacetime, the coodinate adius and the coodinate time t cannot be geneically intepeted as the physical adius o the physical time measued by a clock. Physical quantities must be computed fom the metic. The physical inteval in the adial diection measued by an abitay local obseve is given by the pope distance dt = dθ = dφ) ds = 1 R ) 1/2 d, 8.40) while the time measued by an stationay clock at d = dθ = dφ = 0) is given by the pope time inteval dτ = 1 R ) 1/2 dt. 8.41) Undestanding the esult In the chwazschild metic, space is foliated by sphees 2 of aea 4π 2 sepaated by a pope distance 1 R ) 1/2 d. 8.5 Visualizing chwazschild spacetime A mental image of the chwazschild-doste spacetime can be obtained by embedding a subset of it into a highe dimensional spacetime 6. ince ou solution is static and spheically symmetic, we can, without loss of geneality, fix t =constant and θ = π/2. This leaves us with a 2-dimensional suface dx 2 = 1 R ) 1 d dφ 2 = f) 1 d dφ 2, 8.42) which can be easily embeded into the odinay 3-dimensional Euclidean space [ ) ] 2 dz) dx 2 = dz 2 + d 2 + dφ 2 = 1 + d dφ ) d The function z) can be obtained by simply compaing 8.42) and 8.43) ) 2 dz) 1 + = f) 1, 8.44) d and pefoming a tivial integation z) = 0 d 1 f ) f = 2 R R ) + constant. 8.45) ) The esulting embedding diagam is the Flamm s paaboloid shown in Fig The distances between cicles on this suface ae lage than just, in clea ageement with the discussion pesented in the pevious section. 6 Remembe that such embedding diagams can be misleading. Fo instance, a 2-dimensional cylinde embedded in 3-dimensional Euclidean space can seem to be cuved even though it is intinsically flat, K = κ 1 κ 2 = 0.
8 8.6 Appaent singulaity 116 Figue 8.1: Embedding diagam fo the chwazschild φ) plane: Flamm s paaboloid 8.6 Appaent singulaity The line element 8.36) appeas to contain two singulaities, one at = 0 coming fom the g tt component blue dashed line) and anothe at = R coming fom g ed line). Is this a poblem? Not necessaily. In most of the astophysical applications the typical size R of the souce is much lage than the chwazschild adius 8.37) R R 10 9 R, R 10 6 R, R ) N This fact makes the singulaities at = 0 and = R s completely ielevant in most of the cases, since they lie in the inteio of objects whee the exteio chwazschild solution does not apply. Indeed, the poblem disappeas when one conside ealistic inteio solutions of the Einstein equations ds 2 = 1 2GM) ) dt GM) ) 1 d dω 2, 8.47) since the function M) deceases faste than and effectively kills all the above singulaities.
9 8.7 Geodesics in chwazschild metic 117 We should woy and speculate about the singulaities only in those cases in which the size of the object is such that the chwazschild-doste solution applies all the way down to = R. This kind of objects ae called black holes. Even in that case the two singulaities descibed above ae not on equal footing. The metic coefficients in the line element 8.36) depend on the choice of a paticula coodinate system and you should not extact any conclusion fom them alone. Let me pesent an illustative example. A woked-out examples: Coodinates should not be tusted Conside the completely egula and singulaity-fee Euclidean space in two dimensions dx 2 = dx 2 + dy 2, 8.48) and pefom a geneal coodinate tansfomation to a new vaiable ρ defined though x = 2 ρ to get ds 2 = 1 ρ 2 dρ2 + dy ) The metic appeas to blow up at ρ = 0 even though we know that ou space is, by constuction, flat and fee of singulaities. The appaent singulaity is a beakdown of ou coodinate system at the point in which ρ becomes negative. It has nothing to do with a beakdown of the undelaying manifold! In ode to detemine if we ae dealing with some atifice of ou coodinate system o with a tue physical singulaity, we cannot neithe look to the cuvatue tensos alone, since thei components ae coodinate-dependent 7. We should athe constuct scalas out of the cuvatue tensos. If any the scala blows up in a paticula coodinate system, it will do in all of them. The simplest possibility would be to conside the Ricci scala, R but we can also constuct highe ode scalas such as R µν R µν R µνρσ R µνρσ. Fo the paticula case of the chwazschild-doste metic, the fist two quantities ae not useful since ae identically equal to zeo. We ae foced then to conside the squae of the Riemann tenso, the so-called Ketschmann scala. Taking into account the non-vanishing components of the Riemann tenso 8.18), we obtain K = R µνρσ R µνρσ = 12R2 6, 8.50) which is a pefectly egula quantity at the chwazschild adius, but becomes infinity at = 0. This last point is a eal physical singulaity! The singulaity at = R is, on the othe hand, just a pathology of the specific coodinate system used. 8.7 Geodesics in chwazschild metic Let us study the motion of pointlike objects in ou ecently found chwazschild solution. To do that, let me conside the epaametization invaiant action 3.27) = L dσ = 1 dσ e 1 dx µ dx ν ) σ)g µν 2 dσ dσ m2 eσ), 8.51) 7 They can catch singulaities when going fom one coodinate system to anothe though the tansfomation matices x µ / x ν.
10 8.7 Geodesics in chwazschild metic 118 in the massive eσ) = 1/m) and massless eσ) = 1, m 0) cases 8 massive = 1 2 m dx dσ g µ dx ν ) µν dσ dσ 1, massless = 1 2 dx dσ g µ µν dσ dx ν ). 8.52) dσ The geodesic equations fo both actions can be diectly witten by taking into account the nonvanishing Chistoffel symbols 8.17). Let s denote the deivatives with espect to the affine paamete σ by a dot. The explicit fom 9 obtained by following this pocedue tuns out to be not vey useful since the esulting equations ae coupled R ẗ = R )ṙṫ, 8.53) = R R ) 2 3 ṫ 2 R + R ) θ + sin 2 θ 2 R, 8.54) θ = 2 θṙ + sin θ cos θ φ 2, 8.55) φ = 2 φṙ 2 cot θ θ φ. 8.56) Fotunately, ou task can be geatly simplified by consideing the symmeties of the chwazschild- Doste metic. ince 8.36) does not depend on the coodinates t and θ they ae cyclic coodinates in 8.52)), we have two consevation laws t L = 0 E = 1 R ) ṫ = constant, 8.57) φ L = 0 h = 2 sin 2 θ φ = constant, 8.58) with a clea physical intepetation. In the massless case, E and h ae the elativistic enegy and angula momentum that the paticle would have at =. In the massive case, they ae the elativistic enegy and angula momentum pe unit mass. Execise Check this by taking the non-elativistic limit of 8.57) and 8.58) at the equatoial plane θ = π/2. Consevation of angula momentum means that the paticle moves in a plane, which we can set to be the equatoial plane θ = π 2 without loss of geneality. Indeed, a simple inspection of Eq. 8.55) shows that if we conside a geodesic passing though a point on the equato θ = π 2 and tangent to the equatoial plane θ = 0, we will always have θ = 0 and θ = 0. On top of the above symmeties, we have still a geneic consevation law associated to the invaiance of the action 8.51) unde epaametizations of the path σ σ = fσ) cf. ection 3.5.1). This eads d gµν u µ u ν) = 0 g µν u µ u ν = ɛ, 8.59) dσ with ɛ = 1 and 0 fo massive and massless paticles espectively. Expanding this equation 10 8 Remembe that σ = τ in the massive case. 9 Up to a global facto m in the massive case. 10 Remembe that θ = π/2. 1 R ) ṫ R ) 1 ṙ φ2 = ɛ 8.60)
11 8.7 Geodesics in chwazschild metic 119 and plugging 8.57) and 8.58) we obtain a single equation fo σ) with V ) ɛ GM playing the ole of an exact effective potential and 1 2 ) 2 d + V ) = E, 8.61) dσ E h2 2 2 GMh ) E 2 ɛ ). 8.63) Eq. 8.61) is stuctually equivalent to that of a paticle of unit mass and enegy 11 E moving in an effective potential V ). It is inteesting to compae the obtained potential with the Newtonian esult V N ) = GM + h ) The fist two tems in Eq. 8.62) ae just the univesal gavitational attaction and the centifugal baie that wee aleady pesent in Newton s theoy of gavity. The thid tem is new. At sufficiently long distances, the exta contibution is athe small and does not significantly modify the Newtonian effective potential 12 cf. Fig. 8.4). The situation is completely diffeent at shot distances. The new tem eventually dominates ove the centifugal baie fo small and dives the potential to 13. Let me analyze the massive and massless case sepaately. Massive paticles, ɛ = 1, σ = τ: We can distinguish two cases: If h 2 > 3R 2, the potential displays both a maximum and a minimum at dv ) d = 0 max,min = h2 1 ± 1 3 ɛ=1 h R R ) 2, 8.65) We have then fou possibilities depending of the elation between the effective enegy of the paticle and the potential cf. Fig.??): 1. Cicula obits: If E = V max ) o E = V min ) the paticle descibes an unstable o stable obit espectively. 2. Bound pecessing obits: If 0 > E > V min ) the paticle is tapped into the potential and descibes an elliptical obit with shifting peihelion see below). 3. catteing obits: If V max ) > E > 0 the paticle bumps in the potential and eteats back to infinity. 4. Plunging obits: If E > V max ) the paticle sails ove the top of the potential to finally spial into the black hole. 11 The tue enegy pe unit mass in E but the effective potential fo athe esponds to E. 12 The small coection will play howeve a cental ole! ee next section. 13 Note that the potential is always zeo at = R.
12 8.7 Geodesics in chwazschild metic VN V Figue 8.2: Effective potentials in Newtonian gavity and Geneal Relativity fo massive paticles. Diffeent lines coespond to h 2 /R 2 = 0, 1, 3, 5, 7, 9 fom bown to blue). Note the change in the potential at the citical value h 2 /R 2 = 3. Figue 8.3: Obits fo massive paticles in chwazschild-doste geomety
13 8.7 Geodesics in chwazschild metic 121 Execise What happens with max and min when h 0? And when h deceases? Which is the minimal value of h and allowing fo a stable cicula obit? If h 2 < 3R 2 the centifugal baie disappeas and the paticle has no othe option but to spial into the singulaity. Conside fo claity the limiting case h = 0 in which the paticle follows a adial tajectoy. In this case, the adial equation of motion 8.61) becomes 14 d dτ = ± R ) 1/2 Integating the pevious equation we get d 1/2 = R dτ. 8.66) τ) = 2 3 R 3/2 0 3/2), 8.67) with 0 > an integation constant fixing the initial value of the pope time to zeo. The paticle eaches the chwazschild adius in a finite pope time τ. The inteval measued by an obseve at est at spatial infinite is howeve quite diffeent. Indeed, it is infinite, as can be easily seen by evaluating d dt = dτ d dt dτ = 1 R ) ) 1/2 R dt = R 1/2 3/2 d R 8.68) at = R. Fo the obseve at infinite the paticle appeas to appoach but neve quite coss the hoizon! This is just anothe indication that the chwazschild coodinates ae flawed nea R = R. Execise What happens with t when the obseve cosses the hoizon? Massless paticles, ɛ = 0: The potential 8.62) with ɛ = 0 displays a unique maximum fo all values of h at Thus, the motion of massless paticles can be divided into thee cases: max = 3 2 R. 8.69) 1. Cicula obit: If E = V max ) the paticle descibes an unstable cicula obit. 2. catteing obits: If V max ) > E the paticle bumps in the potential and eteats back to infinity deflection of light). 3. Plunging obits: If E > V max ) the paticle sails ove the top of the potential to finally spial into the black hole. 14 Among the two signs in the squae oot we take the negative one, in such a way that we fall towad 0
14 8.7 Geodesics in chwazschild metic VN V Figue 8.4: Effective potentials in Newtonian gavity and Geneal Relativity fo massless paticles. Diffeent lines coespond to h 2 /R 2 = 0, 1, 3, 5, 7, 9 fom bown to blue). Figue 8.5: Obits fo massless paticles in chwazschild-doste geomety
15 8.8 olving the adial equation olving the adial equation Let us detemine the equation fo the obits descibed in the pevious section. Fo doing that, we make use of Eq. 8.58) with θ = π/2 and change the deivatives with espect to the affine paamete in Eq. 8.61) to deivatives with espect the angula vaiable φ to obtain d dσ = d dφ dφ dτ = h d 2 dφ, 8.70) ) 2 h d 2 + h2 dφ 2 = ɛ2gm + 2GMh E. 8.71) The ticks to solve this kind of equation ae well known. Let s pefom a change of vaiable u 1/ in 8.71) ) 2 du + u 2 = ɛ 2GMu dφ h 2 + 2GMu 3 + 2E h 2, 8.72) and deive the esult with espect to φ. This gives ise to a second ode diffeential equation of the fom d 2 u dφ 2 + u = ɛgm h 2 + 3GMu ) The massive case: Peihelion advance of Mecuy In the massive case ɛ = 1 and 8.73) becomes d 2 u dφ 2 + u = GM h 2 + 3GMu ) The esulting equation is extemely simila to the Newtonian equation of motion of a paticle of mass m in the equatoial plane d 2 u 0 dφ 2 + u 0 = GM h ) even though the intepetation of the adial vaiable is completely diffeent 15. As you pobably emembe fom you Classical Mechanics couse, the geneal solution of 8.75) is a conic u 0 = GM h e cos φ) 0 = a1 e2 ) 1 + e cos φ) 8.76) with a1 e 2 ) = h2 GM. 8.77) 15 In Newtonian gavity is the adial distance fom the mass while in the elativistic it is just a adial coodinate that can be only elated to a distance though the metic.
16 8.8 olving the adial equation 124 Obital Mumbo Jumbo a=semi-majo axis: 1/2 of the long axis of the ellipse. b=semi-mino axis: 1/2 of the shot axis of the ellipse. e=eccenticity : It chaacteizes the deviation of the ellipse fom cicula. When e = 0 the ellipse is a cicle, when e = 1 the ellipse is a paabola. It is defined in tems of the semi majo and semi mino axes a and b as e = 1 ) 2 b. 8.78) a f=focus: The point ove the semi-majo axis at a distance f = ae fom the geometic cente of the ellipse. l=semi-latus ectum: The distance l = b2 a paallel to the semi-mino axis. fom the focus to the ellipse along a line p =peiapsis: The distance p = a1 e) fom the focus to the neaest point of appoach of the ellipse. a =apoapsis: The distance a = a1+e) fom the focus to the futhest point of appoach of the ellipse. The equation of the obit: It gives the distance to the obiting body fom the focus of the obit as a function of the pola angle θ θ) = a1 e2 ) 1 + e cos θ. 8.79) If the gavitational field is sufficiently weak, Newtonian gavity alone is expected to povide a good appoximation to the motion of massive paticles in Geneal Relativity. This suggest to teat to exta tem 3GMu 2 as a petubation of top of the solution of Eq. 8.75). The petubative solution of Eq. 8.74) can be detemined by consideing the antsatz u = u 0 + u, 8.80)
17 8.8 olving the adial equation 125 with u 0 given by 8.76). Inseting this into 8.74) we get d 2 ) u [1 dφ 2 + u = A + e2 + 2e cos φ + 1 ] 2 2 e2 cos 2φ with 8.81) A = 3 GM)3 h ) a tiny paamete. To solve this equation let me notice two identities d 2 φ φ sin φ) + φ sin φ = 2 cos φ, 8.83) dφ2 d 2 cos 2φ) + cos 2φ = 3 cos 2φ. 8.84) dφ2 A diect compaison of 8.83) and 8.84) with 8.81) suggests the solution ) u = A [1 + e2 16 ] 2 cos 2φ + eφ sin φ, 8.85) which can be checked by diect diffeentiation. The thee tems in the squae backet ae athe diffeent. The fist and the second one ae just a constant and an oscillatoy tem aound zeo, both of them vey small due to the constant A in font. The thid one is diffeent since it accumulates ove successive obits and gadually gows with time. Retaining only this last tem we get which can be witten in a moe enlightening way by taking into account that fo u = GM [1 + e cos φ + αφ sin φ)] 8.86) h2 u GM [1 + e cos 1 α) φ] 8.87) h2 cos [φ 1 α)] = cos φ cos αφ + sin φ sin αφ cos φ + αφ sin φ 8.88) α 3 GM)2 h ) The solution 8.87) shows that the obit is still peiodic, but with a peiod that is not longe 2π, but athe 2π1 α). The values of epeats on cycles lage than 2π and the obit pecesses.
18 8.8 olving the adial equation 126 The advance of the peihelion in one evolution is φ = 2π 1 α 2π 2φα = 6πG2 M 2 h 2, 8.90) which taking into account 8.77) can be witten as 16 note that we estoe the c factos) φ = 6G2 M 2 h 2 c 2 = 6πGM a1 e 2 )c ) Because it is a small effect, let s accumulate this ove 100 yeas to get the obsevable quantity φ 100 φ T 100 yeas centuy, 8.92) with T the peiod of the obit in yeas. In tems of obsevable obits within the sola system, Mecuy is the closest planet to the un, and so it should have the lagest pecession. Object Mass Mean Equatoial Radius Peiod emimajo axis Eccenticity kg) 10 3 km) days) 10 8 km) Mecuy Venus Eath Mas Jupite atun Uanus Neptune Taking into account the values fo Mecuy s obit, we obtain φ ) The majo axis of Mecuy pecesses at a ate of 43 acsecs pe centuy. The obsevational esults ae in excellent ageement with Geneal Relativity Planet Obseved esidual GR pediction Mecuy ± 0.45) Venus 8.4 ± 4.8) 8.6 Eath 5.0 ± 1.2) The use of the expessions fo the unpetubed solution is justified by the fact that we ae looking to a vey small quantity.
19 8.9 The massless case: Gavitational deflection of light acseconds and the end of the Newtonian empie Newton s theoy had been a vey successful theoy, extensively used by astonomes fo centuies. It had pedicted the etun of comet Halley 1758) with an eo of 33 days, the elliptical chaacte of the ecently discoveed Uanus 1781) and even moe supisingly the location, mass and obit paametes of Neptune, even befoe it was diectly obseved 1846). Leveie discoveed it just with the point of his pen! a ; clealy an amazing poof of the univesality of the gavitational inteaction. Nevetheless, at the end of the 19th centuy thee wee still some caveats elated to Mecuy s obit. As you should know the 1/ 2 dependence of the Newton s foce gives ise to elliptical tajectoies on a plane, and the coesponding peihelion is a pioi a fixed point b. Howeve, diffeent petubations due fo instance to the pesence of othe massive objects in the ola system, such as Jupite, o to the quadupole moment of the un), give ise to a peihelion advance, and theefoe to an ellipse tuning on the plane. Even when all those effects wee taken into account thee was a esidual contibution to the shift. As pointed out by Leveie and Newcomb at the end of the 19th, Mecuy s peihelion pecesses at a ate of 575 pe centuy, but only 532 can be explained by the petubations associated to the othe planets. The emaining 43 pe centuy could not be accounted fo by the Newtonian theoy even when eos wee taken into account. The obsevational poblem was basically closed fo eveyone apat fom Leveie c ), but the theoetical poblem would emain open till the intoduction of Geneal Relativity in a Fancois Aago b The Laplace-Runge-Lenz vecto is conseved. c He died believing that the histoy of the discovey of Neptune would epeat and a new planet with a mass enough to account fo the 43 pe centuy would be encounteed between the un and Mecuy. 8.9 The massless case: Gavitational deflection of light Let us conside now the massless case whee ɛ = 0 and 8.61) becomes d 2 u dφ 2 + u = 3GMu ) In the absence of the tem 3GMu 2, the pevious solution educes to the simple hamonic oscillato equation d 2 u 0 dφ 2 + u 0 = 0, 8.95) whose solutions u 0 = sin φ, 8.96) b can be intepeted as staight lines passing at a distance b fom the oigin. Following a simila pocedue to the one used in the pevious section, we look fo petubative solutions of the fom u = u 0 + u = sin φ b + u 8.97) with u 0 given by 8.96). ubstituting 8.97) into 8.94) we get a linea equation in u whose solution is given by d 2 u dφ 2 u = 3GM 2b 2 3GM + u = b 2 sin 2 φ, 8.98) ) cos 2φ). 8.99)
20 8.10 The post-newtonian fomalism 128 Adding this to the unpetubed solution we get u = sin φ b + 3GM 2b 2 which in the limit, u 0 and fo small φ gives ise to The total deflection angle is twice this value ) cos 2φ), 8.100) φ 2GM bc ) φ = 2R s b Fo ays coming fom a distant stas and gazing the suface of the un 17 we get = 4GM bc ) b R = km M = Kg 8.103) φ = 4GM c 2 R = ) Light paths so close to the un ae of couse not visible by day, but they become visible at the time of a total eclipse. Thei position elative to the othe backgound stas duing the total eclipse appeas shifted elative to the position in the usual night sky. This pediction of Geneal Relativity was veified in 1919 just a few yeas late the fomulation of the theoy. Two sepaate goups led by Athu Eddington and Andew Commelin moved to Guinea and Bazil to obseve the total eclipse of May 29, They epoted deflections of 1.61 ± 0.40) and 1.98 ± 0.16), in easonable ageement with Einstein s pediction 8.104) The post-newtonian fomalism Nowdays, the ageement between theoy and obsevation is at the level of a few pats in a thousand. The deviations fom the Geneal Relativity ae usually paametized in tems of the so-called post- Newtonian paametes β and γ measuing espectively the non-lineaity in the supeposition law fo gavity and the spatial cuvatue poduced by unit est mass ds 2 = 1 2GM + 2 β γ) G2 M 2 ) 2 dt γGM ) 1 d dω ) When this paametes ae taken into account Eqs. 8.91) and 8.102) become espectively ) ) 2 β + 2γ 6πGM 1 + γ 4GM φ = 3 a1 e 2 )c 2, φ = 2 bc ) The Geneal Relativity limit coesponds to γ = β = 1. Recent measuements povide values γ = ± and 2γ β 2 < , in excellent ageement with GR. 17 In this case, the effect is maximized and easie to obseve.
The Schwartzchild Geometry
 UNIVERSITY OF ROCHESTER The Schwatzchild Geomety Byon Osteweil Decembe 21, 2018 1 INTRODUCTION In ou study of geneal elativity, we ae inteested in the geomety of cuved spacetime in cetain special cases
UNIVERSITY OF ROCHESTER The Schwatzchild Geomety Byon Osteweil Decembe 21, 2018 1 INTRODUCTION In ou study of geneal elativity, we ae inteested in the geomety of cuved spacetime in cetain special cases
GENERAL RELATIVITY: THE GEODESICS OF THE SCHWARZSCHILD METRIC
 GENERAL RELATIVITY: THE GEODESICS OF THE SCHWARZSCHILD METRIC GILBERT WEINSTEIN 1. Intoduction Recall that the exteio Schwazschild metic g defined on the 4-manifold M = R R 3 \B 2m ) = {t,, θ, φ): > 2m}
GENERAL RELATIVITY: THE GEODESICS OF THE SCHWARZSCHILD METRIC GILBERT WEINSTEIN 1. Intoduction Recall that the exteio Schwazschild metic g defined on the 4-manifold M = R R 3 \B 2m ) = {t,, θ, φ): > 2m}
The Precession of Mercury s Perihelion
 The Pecession of Mecuy s Peihelion Owen Biesel Januay 25, 2008 Contents 1 Intoduction 2 2 The Classical olution 2 3 Classical Calculation of the Peiod 4 4 The Relativistic olution 5 5 Remaks 9 1 1 Intoduction
The Pecession of Mecuy s Peihelion Owen Biesel Januay 25, 2008 Contents 1 Intoduction 2 2 The Classical olution 2 3 Classical Calculation of the Peiod 4 4 The Relativistic olution 5 5 Remaks 9 1 1 Intoduction
A New Approach to General Relativity
 Apeion, Vol. 14, No. 3, July 7 7 A New Appoach to Geneal Relativity Ali Rıza Şahin Gaziosmanpaşa, Istanbul Tukey E-mail: aizasahin@gmail.com Hee we pesent a new point of view fo geneal elativity and/o
Apeion, Vol. 14, No. 3, July 7 7 A New Appoach to Geneal Relativity Ali Rıza Şahin Gaziosmanpaşa, Istanbul Tukey E-mail: aizasahin@gmail.com Hee we pesent a new point of view fo geneal elativity and/o
d 2 x 0a d d =0. Relative to an arbitrary (accelerating frame) specified by x a = x a (x 0b ), the latter becomes: d 2 x a d 2 + a dx b dx c
 Chapte 6 Geneal Relativity 6.1 Towads the Einstein equations Thee ae seveal ways of motivating the Einstein equations. The most natual is pehaps though consideations involving the Equivalence Pinciple.
Chapte 6 Geneal Relativity 6.1 Towads the Einstein equations Thee ae seveal ways of motivating the Einstein equations. The most natual is pehaps though consideations involving the Equivalence Pinciple.
AST 121S: The origin and evolution of the Universe. Introduction to Mathematical Handout 1
 Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
Please ead this fist... AST S: The oigin and evolution of the Univese Intoduction to Mathematical Handout This is an unusually long hand-out and one which uses in places mathematics that you may not be
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department. Problem Set 10 Solutions. r s
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.033 Decembe 5, 003 Poblem Set 10 Solutions Poblem 1 M s y x test paticle The figue above depicts the geomety of the poblem. The position
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.033 Decembe 5, 003 Poblem Set 10 Solutions Poblem 1 M s y x test paticle The figue above depicts the geomety of the poblem. The position
Conformal transformations + Schwarzschild
 Intoduction to Geneal Relativity Solutions of homewok assignments 5 Confomal tansfomations + Schwazschild 1. To pove the identity, let s conside the fom of the Chistoffel symbols in tems of the metic tenso
Intoduction to Geneal Relativity Solutions of homewok assignments 5 Confomal tansfomations + Schwazschild 1. To pove the identity, let s conside the fom of the Chistoffel symbols in tems of the metic tenso
Homework 7 Solutions
 Homewok 7 olutions Phys 4 Octobe 3, 208. Let s talk about a space monkey. As the space monkey is oiginally obiting in a cicula obit and is massive, its tajectoy satisfies m mon 2 G m mon + L 2 2m mon 2
Homewok 7 olutions Phys 4 Octobe 3, 208. Let s talk about a space monkey. As the space monkey is oiginally obiting in a cicula obit and is massive, its tajectoy satisfies m mon 2 G m mon + L 2 2m mon 2
Physics 235 Chapter 5. Chapter 5 Gravitation
 Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
Chapte 5 Gavitation In this Chapte we will eview the popeties of the gavitational foce. The gavitational foce has been discussed in geat detail in you intoductoy physics couses, and we will pimaily focus
Classical Mechanics Homework set 7, due Nov 8th: Solutions
 Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Classical Mechanics Homewok set 7, due Nov 8th: Solutions 1. Do deivation 8.. It has been asked what effect does a total deivative as a function of q i, t have on the Hamiltonian. Thus, lets us begin with
Geometry of the homogeneous and isotropic spaces
 Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
Geomety of the homogeneous and isotopic spaces H. Sonoda Septembe 2000; last evised Octobe 2009 Abstact We summaize the aspects of the geomety of the homogeneous and isotopic spaces which ae most elevant
KEPLER S LAWS OF PLANETARY MOTION
 EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
EPER S AWS OF PANETARY MOTION 1. Intoduction We ae now in a position to apply what we have leaned about the coss poduct and vecto valued functions to deive eple s aws of planetay motion. These laws wee
The Schwarzschild Solution
 The Schwazschild Solution Johannes Schmude 1 Depatment of Physics Swansea Univesity, Swansea, SA2 8PP, United Kingdom Decembe 6, 2007 1 pyjs@swansea.ac.uk Intoduction We use the following conventions:
The Schwazschild Solution Johannes Schmude 1 Depatment of Physics Swansea Univesity, Swansea, SA2 8PP, United Kingdom Decembe 6, 2007 1 pyjs@swansea.ac.uk Intoduction We use the following conventions:
Chapter 13 Gravitation
 Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
Chapte 13 Gavitation In this chapte we will exploe the following topics: -Newton s law of gavitation, which descibes the attactive foce between two point masses and its application to extended objects
Homework # 3 Solution Key
 PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
PHYSICS 631: Geneal Relativity Homewok # 3 Solution Key 1. You e on you hono not to do this one by hand. I ealize you can use a compute o simply look it up. Please don t. In a flat space, the metic in
Physics 181. Assignment 4
 Physics 181 Assignment 4 Solutions 1. A sphee has within it a gavitational field given by g = g, whee g is constant and is the position vecto of the field point elative to the cente of the sphee. This
Physics 181 Assignment 4 Solutions 1. A sphee has within it a gavitational field given by g = g, whee g is constant and is the position vecto of the field point elative to the cente of the sphee. This
From Gravitational Collapse to Black Holes
 Fom Gavitational Collapse to Black Holes T. Nguyen PHY 391 Independent Study Tem Pape Pof. S.G. Rajeev Univesity of Rocheste Decembe 0, 018 1 Intoduction The pupose of this independent study is to familiaize
Fom Gavitational Collapse to Black Holes T. Nguyen PHY 391 Independent Study Tem Pape Pof. S.G. Rajeev Univesity of Rocheste Decembe 0, 018 1 Intoduction The pupose of this independent study is to familiaize
OSCILLATIONS AND GRAVITATION
 1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
1. SIMPLE HARMONIC MOTION Simple hamonic motion is any motion that is equivalent to a single component of unifom cicula motion. In this situation the velocity is always geatest in the middle of the motion,
Physics 161 Fall 2011 Extra Credit 2 Investigating Black Holes - Solutions The Following is Worth 50 Points!!!
 Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
Physics 161 Fall 011 Exta Cedit Investigating Black Holes - olutions The Following is Woth 50 Points!!! This exta cedit assignment will investigate vaious popeties of black holes that we didn t have time
MODULE 5 ADVANCED MECHANICS GRAVITATIONAL FIELD: MOTION OF PLANETS AND SATELLITES VISUAL PHYSICS ONLINE
 VISUAL PHYSICS ONLIN MODUL 5 ADVANCD MCHANICS GRAVITATIONAL FILD: MOTION OF PLANTS AND SATLLITS SATLLITS: Obital motion of object of mass m about a massive object of mass M (m
VISUAL PHYSICS ONLIN MODUL 5 ADVANCD MCHANICS GRAVITATIONAL FILD: MOTION OF PLANTS AND SATLLITS SATLLITS: Obital motion of object of mass m about a massive object of mass M (m
Newton s Laws, Kepler s Laws, and Planetary Orbits
 Newton s Laws, Keple s Laws, and Planetay Obits PROBLEM SET 4 DUE TUESDAY AT START OF LECTURE 28 Septembe 2017 ASTRONOMY 111 FALL 2017 1 Newton s & Keple s laws and planetay obits Unifom cicula motion
Newton s Laws, Keple s Laws, and Planetay Obits PROBLEM SET 4 DUE TUESDAY AT START OF LECTURE 28 Septembe 2017 ASTRONOMY 111 FALL 2017 1 Newton s & Keple s laws and planetay obits Unifom cicula motion
Physics: Work & Energy Beyond Earth Guided Inquiry
 Physics: Wok & Enegy Beyond Eath Guided Inquiy Elliptical Obits Keple s Fist Law states that all planets move in an elliptical path aound the Sun. This concept can be extended to celestial bodies beyond
Physics: Wok & Enegy Beyond Eath Guided Inquiy Elliptical Obits Keple s Fist Law states that all planets move in an elliptical path aound the Sun. This concept can be extended to celestial bodies beyond
Central Force Motion
 Cental Foce Motion Cental Foce Poblem Find the motion of two bodies inteacting via a cental foce. Examples: Gavitational foce (Keple poblem): m1m F 1, ( ) =! G ˆ Linea estoing foce: F 1, ( ) =! k ˆ Two
Cental Foce Motion Cental Foce Poblem Find the motion of two bodies inteacting via a cental foce. Examples: Gavitational foce (Keple poblem): m1m F 1, ( ) =! G ˆ Linea estoing foce: F 1, ( ) =! k ˆ Two
Tutorial Exercises: Central Forces
 Tutoial Execises: Cental Foces. Tuning Points fo the Keple potential (a) Wite down the two fist integals fo cental motion in the Keple potential V () = µm/ using J fo the angula momentum and E fo the total
Tutoial Execises: Cental Foces. Tuning Points fo the Keple potential (a) Wite down the two fist integals fo cental motion in the Keple potential V () = µm/ using J fo the angula momentum and E fo the total
Physics 2B Chapter 22 Notes - Magnetic Field Spring 2018
 Physics B Chapte Notes - Magnetic Field Sping 018 Magnetic Field fom a Long Staight Cuent-Caying Wie In Chapte 11 we looked at Isaac Newton s Law of Gavitation, which established that a gavitational field
Physics B Chapte Notes - Magnetic Field Sping 018 Magnetic Field fom a Long Staight Cuent-Caying Wie In Chapte 11 we looked at Isaac Newton s Law of Gavitation, which established that a gavitational field
Mechanics Physics 151
 Mechanics Physics 151 Lectue 5 Cental Foce Poblem (Chapte 3) What We Did Last Time Intoduced Hamilton s Pinciple Action integal is stationay fo the actual path Deived Lagange s Equations Used calculus
Mechanics Physics 151 Lectue 5 Cental Foce Poblem (Chapte 3) What We Did Last Time Intoduced Hamilton s Pinciple Action integal is stationay fo the actual path Deived Lagange s Equations Used calculus
= 1. For a hyperbolic orbit with an attractive inverse square force, the polar equation with origin at the center of attraction is
 15. Kepleian Obits Michael Fowle Peliminay: Pola Equations fo Conic Section Cuves As we shall find, Newton s equations fo paticle motion in an invese-squae cental foce give obits that ae conic section
15. Kepleian Obits Michael Fowle Peliminay: Pola Equations fo Conic Section Cuves As we shall find, Newton s equations fo paticle motion in an invese-squae cental foce give obits that ae conic section
= 4 3 π( m) 3 (5480 kg m 3 ) = kg.
 CHAPTER 11 THE GRAVITATIONAL FIELD Newton s Law of Gavitation m 1 m A foce of attaction occus between two masses given by Newton s Law of Gavitation Inetial mass and gavitational mass Gavitational potential
CHAPTER 11 THE GRAVITATIONAL FIELD Newton s Law of Gavitation m 1 m A foce of attaction occus between two masses given by Newton s Law of Gavitation Inetial mass and gavitational mass Gavitational potential
SIO 229 Gravity and Geomagnetism. Lecture 6. J 2 for Earth. J 2 in the solar system. A first look at the geoid.
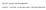 SIO 229 Gavity and Geomagnetism Lectue 6. J 2 fo Eath. J 2 in the sola system. A fist look at the geoid. The Thee Big Themes of the Gavity Lectues 1.) An ellipsoidal otating Eath Refeence body (mass +
SIO 229 Gavity and Geomagnetism Lectue 6. J 2 fo Eath. J 2 in the sola system. A fist look at the geoid. The Thee Big Themes of the Gavity Lectues 1.) An ellipsoidal otating Eath Refeence body (mass +
4. Kruskal Coordinates and Penrose Diagrams.
 4. Kuskal Coodinates and Penose Diagams. 4.1. Removing a coodinate ingulaity at the chwazschild Radius. The chwazschild metic has a singulaity at = whee g 0 and g. Howeve, 00 we have aleady seen that a
4. Kuskal Coodinates and Penose Diagams. 4.1. Removing a coodinate ingulaity at the chwazschild Radius. The chwazschild metic has a singulaity at = whee g 0 and g. Howeve, 00 we have aleady seen that a
Appendix B The Relativistic Transformation of Forces
 Appendix B The Relativistic Tansfomation of oces B. The ou-foce We intoduced the idea of foces in Chapte 3 whee we saw that the change in the fou-momentum pe unit time is given by the expession d d w x
Appendix B The Relativistic Tansfomation of oces B. The ou-foce We intoduced the idea of foces in Chapte 3 whee we saw that the change in the fou-momentum pe unit time is given by the expession d d w x
ASTR415: Problem Set #6
 ASTR45: Poblem Set #6 Cuan D. Muhlbege Univesity of Mayland (Dated: May 7, 27) Using existing implementations of the leapfog and Runge-Kutta methods fo solving coupled odinay diffeential equations, seveal
ASTR45: Poblem Set #6 Cuan D. Muhlbege Univesity of Mayland (Dated: May 7, 27) Using existing implementations of the leapfog and Runge-Kutta methods fo solving coupled odinay diffeential equations, seveal
Determining solar characteristics using planetary data
 Detemining sola chaacteistics using planetay data Intoduction The Sun is a G-type main sequence sta at the cente of the Sola System aound which the planets, including ou Eath, obit. In this investigation
Detemining sola chaacteistics using planetay data Intoduction The Sun is a G-type main sequence sta at the cente of the Sola System aound which the planets, including ou Eath, obit. In this investigation
Is there a magnification paradox in gravitational lensing?
 Is thee a magnification paadox in gavitational ing? Olaf Wucknitz wucknitz@asto.uni-bonn.de Astophysics semina/colloquium, Potsdam, 6 Novembe 7 Is thee a magnification paadox in gavitational ing? gavitational
Is thee a magnification paadox in gavitational ing? Olaf Wucknitz wucknitz@asto.uni-bonn.de Astophysics semina/colloquium, Potsdam, 6 Novembe 7 Is thee a magnification paadox in gavitational ing? gavitational
Between any two masses, there exists a mutual attractive force.
 YEAR 12 PHYSICS: GRAVITATION PAST EXAM QUESTIONS Name: QUESTION 1 (1995 EXAM) (a) State Newton s Univesal Law of Gavitation in wods Between any two masses, thee exists a mutual attactive foce. This foce
YEAR 12 PHYSICS: GRAVITATION PAST EXAM QUESTIONS Name: QUESTION 1 (1995 EXAM) (a) State Newton s Univesal Law of Gavitation in wods Between any two masses, thee exists a mutual attactive foce. This foce
B. Spherical Wave Propagation
 11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
11/8/007 Spheical Wave Popagation notes 1/1 B. Spheical Wave Popagation Evey antenna launches a spheical wave, thus its powe density educes as a function of 1, whee is the distance fom the antenna. We
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department. Problem Set 9
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.033 Novembe 17, 2006 Poblem Set 9 Due: Decembe 8, at 4:00PM. Please deposit the poblem set in the appopiate 8.033 bin, labeled with name
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.033 Novembe 17, 2006 Poblem Set 9 Due: Decembe 8, at 4:00PM. Please deposit the poblem set in the appopiate 8.033 bin, labeled with name
Paths of planet Mars in sky
 Section 4 Gavity and the Sola System The oldest common-sense view is that the eath is stationay (and flat?) and the stas, sun and planets evolve aound it. This GEOCENTRIC MODEL was poposed explicitly by
Section 4 Gavity and the Sola System The oldest common-sense view is that the eath is stationay (and flat?) and the stas, sun and planets evolve aound it. This GEOCENTRIC MODEL was poposed explicitly by
Such objects are called black holes, and there is extremely strong circumstantial evidence that they exist.
 Chapte 11 Spheical black holes One of the most spectacula consequences of geneal elativity is the pediction that gavitational fields can become so stong that they can effectively tap even light. Space
Chapte 11 Spheical black holes One of the most spectacula consequences of geneal elativity is the pediction that gavitational fields can become so stong that they can effectively tap even light. Space
Universal Gravitation
 Chapte 1 Univesal Gavitation Pactice Poblem Solutions Student Textbook page 580 1. Conceptualize the Poblem - The law of univesal gavitation applies to this poblem. The gavitational foce, F g, between
Chapte 1 Univesal Gavitation Pactice Poblem Solutions Student Textbook page 580 1. Conceptualize the Poblem - The law of univesal gavitation applies to this poblem. The gavitational foce, F g, between
F 12. = G m m 1 2 F 21 = F 12. = G m 1m 2. Review. Physics 201, Lecture 22. Newton s Law Of Universal Gravitation
 Physics 201, Lectue 22 Review Today s Topics n Univesal Gavitation (Chapte 13.1-13.3) n Newton s Law of Univesal Gavitation n Popeties of Gavitational Foce n Planet Obits; Keple s Laws by Newton s Law
Physics 201, Lectue 22 Review Today s Topics n Univesal Gavitation (Chapte 13.1-13.3) n Newton s Law of Univesal Gavitation n Popeties of Gavitational Foce n Planet Obits; Keple s Laws by Newton s Law
But for simplicity, we ll define significant as the time it takes a star to lose all memory of its original trajectory, i.e.,
 Stella elaxation Time [Chandasekha 1960, Pinciples of Stella Dynamics, Chap II] [Ostike & Davidson 1968, Ap.J., 151, 679] Do stas eve collide? Ae inteactions between stas (as opposed to the geneal system
Stella elaxation Time [Chandasekha 1960, Pinciples of Stella Dynamics, Chap II] [Ostike & Davidson 1968, Ap.J., 151, 679] Do stas eve collide? Ae inteactions between stas (as opposed to the geneal system
AY 7A - Fall 2010 Section Worksheet 2 - Solutions Energy and Kepler s Law
 AY 7A - Fall 00 Section Woksheet - Solutions Enegy and Keple s Law. Escape Velocity (a) A planet is obiting aound a sta. What is the total obital enegy of the planet? (i.e. Total Enegy = Potential Enegy
AY 7A - Fall 00 Section Woksheet - Solutions Enegy and Keple s Law. Escape Velocity (a) A planet is obiting aound a sta. What is the total obital enegy of the planet? (i.e. Total Enegy = Potential Enegy
Physics 161: Black Holes: Lecture 5: 22 Jan 2013
 Physics 161: Black Holes: Lectue 5: 22 Jan 2013 Pofesso: Kim Giest 5 Equivalence Pinciple, Gavitational Redshift and Geodesics of the Schwazschild Metic 5.1 Gavitational Redshift fom the Schwazschild metic
Physics 161: Black Holes: Lectue 5: 22 Jan 2013 Pofesso: Kim Giest 5 Equivalence Pinciple, Gavitational Redshift and Geodesics of the Schwazschild Metic 5.1 Gavitational Redshift fom the Schwazschild metic
EM Boundary Value Problems
 EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
EM Bounday Value Poblems 10/ 9 11/ By Ilekta chistidi & Lee, Seung-Hyun A. Geneal Desciption : Maxwell Equations & Loentz Foce We want to find the equations of motion of chaged paticles. The way to do
The Strain Compatibility Equations in Polar Coordinates RAWB, Last Update 27/12/07
 The Stain Compatibility Equations in Pola Coodinates RAWB Last Update 7//7 In D thee is just one compatibility equation. In D polas it is (Equ.) whee denotes the enineein shea (twice the tensoial shea)
The Stain Compatibility Equations in Pola Coodinates RAWB Last Update 7//7 In D thee is just one compatibility equation. In D polas it is (Equ.) whee denotes the enineein shea (twice the tensoial shea)
Problems with Mannheim s conformal gravity program
 Poblems with Mannheim s confomal gavity pogam Abstact We show that Mannheim s confomal gavity pogam, whose potential has a tem popotional to 1/ and anothe tem popotional to, does not educe to Newtonian
Poblems with Mannheim s confomal gavity pogam Abstact We show that Mannheim s confomal gavity pogam, whose potential has a tem popotional to 1/ and anothe tem popotional to, does not educe to Newtonian
Solving Problems of Advance of Mercury s Perihelion and Deflection of. Photon Around the Sun with New Newton s Formula of Gravity
 Solving Poblems of Advance of Mecuy s Peihelion and Deflection of Photon Aound the Sun with New Newton s Fomula of Gavity Fu Yuhua (CNOOC Reseach Institute, E-mail:fuyh945@sina.com) Abstact: Accoding to
Solving Poblems of Advance of Mecuy s Peihelion and Deflection of Photon Aound the Sun with New Newton s Fomula of Gavity Fu Yuhua (CNOOC Reseach Institute, E-mail:fuyh945@sina.com) Abstact: Accoding to
Math 124B February 02, 2012
 Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Math 24B Febuay 02, 202 Vikto Gigoyan 8 Laplace s equation: popeties We have aleady encounteed Laplace s equation in the context of stationay heat conduction and wave phenomena. Recall that in two spatial
Scattering in Three Dimensions
 Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Scatteing in Thee Dimensions Scatteing expeiments ae an impotant souce of infomation about quantum systems, anging in enegy fom vey low enegy chemical eactions to the highest possible enegies at the LHC.
Lecture 8 - Gauss s Law
 Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Lectue 8 - Gauss s Law A Puzzle... Example Calculate the potential enegy, pe ion, fo an infinite 1D ionic cystal with sepaation a; that is, a ow of equally spaced chages of magnitude e and altenating sign.
Geodesic motion in Kerr spacetime
 Chapte 20 Geodesic motion in Ke spacetime Let us conside a geodesic with affine paamete λ and tangent vecto u µ = dxµ dλ ẋµ. (20.1) In this section we shall use Boye-Lindquist s coodinates, and the dot
Chapte 20 Geodesic motion in Ke spacetime Let us conside a geodesic with affine paamete λ and tangent vecto u µ = dxµ dλ ẋµ. (20.1) In this section we shall use Boye-Lindquist s coodinates, and the dot
Projection Gravitation, a Projection Force from 5-dimensional Space-time into 4-dimensional Space-time
 Intenational Jounal of Physics, 17, Vol. 5, No. 5, 181-196 Available online at http://pubs.sciepub.com/ijp/5/5/6 Science and ducation Publishing DOI:1.1691/ijp-5-5-6 Pojection Gavitation, a Pojection Foce
Intenational Jounal of Physics, 17, Vol. 5, No. 5, 181-196 Available online at http://pubs.sciepub.com/ijp/5/5/6 Science and ducation Publishing DOI:1.1691/ijp-5-5-6 Pojection Gavitation, a Pojection Foce
Chapter 12. Kinetics of Particles: Newton s Second Law
 Chapte 1. Kinetics of Paticles: Newton s Second Law Intoduction Newton s Second Law of Motion Linea Momentum of a Paticle Systems of Units Equations of Motion Dynamic Equilibium Angula Momentum of a Paticle
Chapte 1. Kinetics of Paticles: Newton s Second Law Intoduction Newton s Second Law of Motion Linea Momentum of a Paticle Systems of Units Equations of Motion Dynamic Equilibium Angula Momentum of a Paticle
AH Mechanics Checklist (Unit 2) AH Mechanics Checklist (Unit 2) Circular Motion
 AH Mechanics Checklist (Unit ) AH Mechanics Checklist (Unit ) Cicula Motion No. kill Done 1 Know that cicula motion efes to motion in a cicle of constant adius Know that cicula motion is conveniently descibed
AH Mechanics Checklist (Unit ) AH Mechanics Checklist (Unit ) Cicula Motion No. kill Done 1 Know that cicula motion efes to motion in a cicle of constant adius Know that cicula motion is conveniently descibed
Introduction to General Relativity 2
 Intoduction to Geneal Relativity 2 Geneal Relativity Diffeential geomety Paallel tanspot How to compute metic? Deviation of geodesics Einstein equations Consequences Tests of Geneal Relativity Sola system
Intoduction to Geneal Relativity 2 Geneal Relativity Diffeential geomety Paallel tanspot How to compute metic? Deviation of geodesics Einstein equations Consequences Tests of Geneal Relativity Sola system
Physics 411 Lecture 34. Sourced Radiation. Lecture 34. Physics 411 Classical Mechanics II
 Physics 411 Lectue 34 Souced Radiation Lectue 34 Physics 411 Classical Mechanics II Novembe 21st, 2007 We ae eady to move on to the souce side of lineaized waves. The point of this whole section has been
Physics 411 Lectue 34 Souced Radiation Lectue 34 Physics 411 Classical Mechanics II Novembe 21st, 2007 We ae eady to move on to the souce side of lineaized waves. The point of this whole section has been
TAMPINES JUNIOR COLLEGE 2009 JC1 H2 PHYSICS GRAVITATIONAL FIELD
 TAMPINES JUNIOR COLLEGE 009 JC1 H PHYSICS GRAVITATIONAL FIELD OBJECTIVES Candidates should be able to: (a) show an undestanding of the concept of a gavitational field as an example of field of foce and
TAMPINES JUNIOR COLLEGE 009 JC1 H PHYSICS GRAVITATIONAL FIELD OBJECTIVES Candidates should be able to: (a) show an undestanding of the concept of a gavitational field as an example of field of foce and
PHYS 705: Classical Mechanics. Small Oscillations
 PHYS 705: Classical Mechanics Small Oscillations Fomulation of the Poblem Assumptions: V q - A consevative system with depending on position only - The tansfomation equation defining does not dep on time
PHYS 705: Classical Mechanics Small Oscillations Fomulation of the Poblem Assumptions: V q - A consevative system with depending on position only - The tansfomation equation defining does not dep on time
I. CONSTRUCTION OF THE GREEN S FUNCTION
 I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
I. CONSTRUCTION OF THE GREEN S FUNCTION The Helmohltz equation in 4 dimensions is 4 + k G 4 x, x = δ 4 x x. In this equation, G is the Geen s function and 4 efes to the dimensionality. In the vey end,
( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx.
![( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx. ( ) [ ] [ ] [ ] δf φ = F φ+δφ F. xdx.](/thumbs/90/103689049.jpg) 9. LAGRANGIAN OF THE ELECTROMAGNETIC FIELD In the pevious section the Lagangian and Hamiltonian of an ensemble of point paticles was developed. This appoach is based on a qt. This discete fomulation can
9. LAGRANGIAN OF THE ELECTROMAGNETIC FIELD In the pevious section the Lagangian and Hamiltonian of an ensemble of point paticles was developed. This appoach is based on a qt. This discete fomulation can
PHYS 110B - HW #7 Spring 2004, Solutions by David Pace Any referenced equations are from Griffiths Problem statements are paraphrased
 PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
PHYS 0B - HW #7 Sping 2004, Solutions by David Pace Any efeenced euations ae fom Giffiths Poblem statements ae paaphased. Poblem 0.3 fom Giffiths A point chage,, moves in a loop of adius a. At time t 0
KEPLER S LAWS AND PLANETARY ORBITS
 KEPE S AWS AND PANETAY OBITS 1. Selected popeties of pola coodinates and ellipses Pola coodinates: I take a some what extended view of pola coodinates in that I allow fo a z diection (cylindical coodinates
KEPE S AWS AND PANETAY OBITS 1. Selected popeties of pola coodinates and ellipses Pola coodinates: I take a some what extended view of pola coodinates in that I allow fo a z diection (cylindical coodinates
10. Universal Gravitation
 10. Univesal Gavitation Hee it is folks, the end of the echanics section of the couse! This is an appopiate place to complete the study of mechanics, because with his Law of Univesal Gavitation, Newton
10. Univesal Gavitation Hee it is folks, the end of the echanics section of the couse! This is an appopiate place to complete the study of mechanics, because with his Law of Univesal Gavitation, Newton
Gravitation. AP/Honors Physics 1 Mr. Velazquez
 Gavitation AP/Honos Physics 1 M. Velazquez Newton s Law of Gavitation Newton was the fist to make the connection between objects falling on Eath and the motion of the planets To illustate this connection
Gavitation AP/Honos Physics 1 M. Velazquez Newton s Law of Gavitation Newton was the fist to make the connection between objects falling on Eath and the motion of the planets To illustate this connection
Math 2263 Solutions for Spring 2003 Final Exam
 Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
Math 6 Solutions fo Sping Final Exam ) A staightfowad appoach to finding the tangent plane to a suface at a point ( x, y, z ) would be to expess the cuve as an explicit function z = f ( x, y ), calculate
University Physics Volume I Unit 1: Mechanics Chapter 13: Gravitation Conceptual Questions
 OpenStax Univesity Physics Volume I Univesity Physics Volume I Conceptual Questions 1. Action at a distance, such as is the case fo gavity, was once thought to be illogical and theefoe untue. What is the
OpenStax Univesity Physics Volume I Univesity Physics Volume I Conceptual Questions 1. Action at a distance, such as is the case fo gavity, was once thought to be illogical and theefoe untue. What is the
History of Astronomy - Part II. Tycho Brahe - An Observer. Johannes Kepler - A Theorist
 Histoy of Astonomy - Pat II Afte the Copenican Revolution, astonomes stived fo moe obsevations to help bette explain the univese aound them Duing this time (600-750) many majo advances in science and astonomy
Histoy of Astonomy - Pat II Afte the Copenican Revolution, astonomes stived fo moe obsevations to help bette explain the univese aound them Duing this time (600-750) many majo advances in science and astonomy
Physics 506 Winter 2006 Homework Assignment #9 Solutions
 Physics 506 Winte 2006 Homewok Assignment #9 Solutions Textbook poblems: Ch. 12: 12.2, 12.9, 12.13, 12.14 12.2 a) Show fom Hamilton s pinciple that Lagangians that diffe only by a total time deivative
Physics 506 Winte 2006 Homewok Assignment #9 Solutions Textbook poblems: Ch. 12: 12.2, 12.9, 12.13, 12.14 12.2 a) Show fom Hamilton s pinciple that Lagangians that diffe only by a total time deivative
j i i,i j The second term on the right vanishes by Newton s third law. If we define N and Figure 1: Definition of relative coordinates r j.
 Cental Foces We owe the development of Newtonian mechanics to the poblem of celestial mechanics and Newton s claim to Edmund Halley that the motion of a body to a foce that vaies invesely with the squae
Cental Foces We owe the development of Newtonian mechanics to the poblem of celestial mechanics and Newton s claim to Edmund Halley that the motion of a body to a foce that vaies invesely with the squae
Central Force Problem. Central Force Motion. Two Body Problem: Center of Mass Coordinates. Reduction of Two Body Problem 8.01 W14D1. + m 2. m 2.
 Cental oce Poblem ind the motion of two bodies inteacting via a cental foce. Cental oce Motion 8.01 W14D1 Examples: Gavitational foce (Keple poblem): 1 1, ( ) G mm Linea estoing foce: ( ) k 1, Two Body
Cental oce Poblem ind the motion of two bodies inteacting via a cental foce. Cental oce Motion 8.01 W14D1 Examples: Gavitational foce (Keple poblem): 1 1, ( ) G mm Linea estoing foce: ( ) k 1, Two Body
Spherical Solutions due to the Exterior Geometry of a Charged Weyl Black Hole
 Spheical Solutions due to the Exteio Geomety of a Chaged Weyl Black Hole Fain Payandeh 1, Mohsen Fathi Novembe 7, 018 axiv:10.415v [g-qc] 10 Oct 01 1 Depatment of Physics, Payame Noo Univesity, PO BOX
Spheical Solutions due to the Exteio Geomety of a Chaged Weyl Black Hole Fain Payandeh 1, Mohsen Fathi Novembe 7, 018 axiv:10.415v [g-qc] 10 Oct 01 1 Depatment of Physics, Payame Noo Univesity, PO BOX
m 1 r = r 1 - r 2 m 2 r 2 m1 r1
 Topic 4: Two-Body Cental Foce Motion Reading Assignment: Hand & Finch Chap. 4 This will be the last topic coveed on the midtem exam. I will pass out homewok this week but not next week.. Eliminating the
Topic 4: Two-Body Cental Foce Motion Reading Assignment: Hand & Finch Chap. 4 This will be the last topic coveed on the midtem exam. I will pass out homewok this week but not next week.. Eliminating the
Pressure Calculation of a Constant Density Star in the Dynamic Theory of Gravity
 Pessue Calculation of a Constant Density Sta in the Dynamic Theoy of Gavity Ioannis Iaklis Haanas Depatment of Physics and Astonomy Yok Univesity A Petie Science Building Yok Univesity Toonto Ontaio CANADA
Pessue Calculation of a Constant Density Sta in the Dynamic Theoy of Gavity Ioannis Iaklis Haanas Depatment of Physics and Astonomy Yok Univesity A Petie Science Building Yok Univesity Toonto Ontaio CANADA
arxiv: v1 [physics.pop-ph] 3 Jun 2013
![arxiv: v1 [physics.pop-ph] 3 Jun 2013 arxiv: v1 [physics.pop-ph] 3 Jun 2013](/thumbs/89/100795062.jpg) A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
A note on the electostatic enegy of two point chages axiv:1306.0401v1 [physics.pop-ph] 3 Jun 013 A C Tot Instituto de Física Univesidade Fedeal do io de Janeio Caixa Postal 68.58; CEP 1941-97 io de Janeio,
2. Electrostatics. Dr. Rakhesh Singh Kshetrimayum 8/11/ Electromagnetic Field Theory by R. S. Kshetrimayum
 2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
2. Electostatics D. Rakhesh Singh Kshetimayum 1 2.1 Intoduction In this chapte, we will study how to find the electostatic fields fo vaious cases? fo symmetic known chage distibution fo un-symmetic known
15 Solving the Laplace equation by Fourier method
 5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
5 Solving the Laplace equation by Fouie method I aleady intoduced two o thee dimensional heat equation, when I deived it, ecall that it taes the fom u t = α 2 u + F, (5.) whee u: [0, ) D R, D R is the
Physics 2212 GH Quiz #2 Solutions Spring 2016
 Physics 2212 GH Quiz #2 Solutions Sping 216 I. 17 points) Thee point chages, each caying a chage Q = +6. nc, ae placed on an equilateal tiangle of side length = 3. mm. An additional point chage, caying
Physics 2212 GH Quiz #2 Solutions Sping 216 I. 17 points) Thee point chages, each caying a chage Q = +6. nc, ae placed on an equilateal tiangle of side length = 3. mm. An additional point chage, caying
working pages for Paul Richards class notes; do not copy or circulate without permission from PGR 2004/11/3 10:50
 woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
woking pages fo Paul Richads class notes; do not copy o ciculate without pemission fom PGR 2004/11/3 10:50 CHAPTER7 Solid angle, 3D integals, Gauss s Theoem, and a Delta Function We define the solid angle,
Right-handed screw dislocation in an isotropic solid
 Dislocation Mechanics Elastic Popeties of Isolated Dislocations Ou study of dislocations to this point has focused on thei geomety and thei ole in accommodating plastic defomation though thei motion. We
Dislocation Mechanics Elastic Popeties of Isolated Dislocations Ou study of dislocations to this point has focused on thei geomety and thei ole in accommodating plastic defomation though thei motion. We
Chapter 5 Force and Motion
 Chapte 5 Foce and Motion In Chaptes 2 and 4 we have studied kinematics, i.e., we descibed the motion of objects using paametes such as the position vecto, velocity, and acceleation without any insights
Chapte 5 Foce and Motion In Chaptes 2 and 4 we have studied kinematics, i.e., we descibed the motion of objects using paametes such as the position vecto, velocity, and acceleation without any insights
Chapter 5 Force and Motion
 Chapte 5 Foce and Motion In chaptes 2 and 4 we have studied kinematics i.e. descibed the motion of objects using paametes such as the position vecto, velocity and acceleation without any insights as to
Chapte 5 Foce and Motion In chaptes 2 and 4 we have studied kinematics i.e. descibed the motion of objects using paametes such as the position vecto, velocity and acceleation without any insights as to
Derivation of the Gravitational Red Shift from the Theorem of Orbits
 1 Deivation of the Gavitational Red Shift fom the Theoem of Obits by Myon W. Evans, Alpha Institute fo Advanced Study, Civil List Scientist. emyone@aol.com and www.aias.us Abstact The expeimentally obsevable
1 Deivation of the Gavitational Red Shift fom the Theoem of Obits by Myon W. Evans, Alpha Institute fo Advanced Study, Civil List Scientist. emyone@aol.com and www.aias.us Abstact The expeimentally obsevable
7.2. Coulomb s Law. The Electric Force
 Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
Coulomb s aw Recall that chaged objects attact some objects and epel othes at a distance, without making any contact with those objects Electic foce,, o the foce acting between two chaged objects, is somewhat
13. Adiabatic Invariants and Action-Angle Variables Michael Fowler
 3 Adiabatic Invaiants and Action-Angle Vaiables Michael Fowle Adiabatic Invaiants Imagine a paticle in one dimension oscillating back and foth in some potential he potential doesn t have to be hamonic,
3 Adiabatic Invaiants and Action-Angle Vaiables Michael Fowle Adiabatic Invaiants Imagine a paticle in one dimension oscillating back and foth in some potential he potential doesn t have to be hamonic,
2. Plane Elasticity Problems
 S0 Solid Mechanics Fall 009. Plane lasticity Poblems Main Refeence: Theoy of lasticity by S.P. Timoshenko and J.N. Goodie McGaw-Hill New Yok. Chaptes 3..1 The plane-stess poblem A thin sheet of an isotopic
S0 Solid Mechanics Fall 009. Plane lasticity Poblems Main Refeence: Theoy of lasticity by S.P. Timoshenko and J.N. Goodie McGaw-Hill New Yok. Chaptes 3..1 The plane-stess poblem A thin sheet of an isotopic
Astro 250: Solutions to Problem Set 1. by Eugene Chiang
 Asto 250: Solutions to Poblem Set 1 by Eugene Chiang Poblem 1. Apsidal Line Pecession A satellite moves on an elliptical obit in its planet s equatoial plane. The planet s gavitational potential has the
Asto 250: Solutions to Poblem Set 1 by Eugene Chiang Poblem 1. Apsidal Line Pecession A satellite moves on an elliptical obit in its planet s equatoial plane. The planet s gavitational potential has the
arxiv: v2 [gr-qc] 18 Aug 2014
![arxiv: v2 [gr-qc] 18 Aug 2014 arxiv: v2 [gr-qc] 18 Aug 2014](/thumbs/74/71355709.jpg) Self-Consistent, Self-Coupled Scala Gavity J. Fanklin Depatment of Physics, Reed College, Potland, Oegon 970, USA Abstact A scala theoy of gavity extending Newtonian gavity to include field enegy as its
Self-Consistent, Self-Coupled Scala Gavity J. Fanklin Depatment of Physics, Reed College, Potland, Oegon 970, USA Abstact A scala theoy of gavity extending Newtonian gavity to include field enegy as its
! E da = 4πkQ enc, has E under the integral sign, so it is not ordinarily an
 Physics 142 Electostatics 2 Page 1 Electostatics 2 Electicity is just oganized lightning. Geoge Calin A tick that sometimes woks: calculating E fom Gauss s law Gauss s law,! E da = 4πkQ enc, has E unde
Physics 142 Electostatics 2 Page 1 Electostatics 2 Electicity is just oganized lightning. Geoge Calin A tick that sometimes woks: calculating E fom Gauss s law Gauss s law,! E da = 4πkQ enc, has E unde
Chapter 2: Basic Physics and Math Supplements
 Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
Chapte 2: Basic Physics and Math Supplements Decembe 1, 215 1 Supplement 2.1: Centipetal Acceleation This supplement expands on a topic addessed on page 19 of the textbook. Ou task hee is to calculate
PHYSICS NOTES GRAVITATION
 GRAVITATION Newton s law of gavitation The law states that evey paticle of matte in the univese attacts evey othe paticle with a foce which is diectly popotional to the poduct of thei masses and invesely
GRAVITATION Newton s law of gavitation The law states that evey paticle of matte in the univese attacts evey othe paticle with a foce which is diectly popotional to the poduct of thei masses and invesely
As is natural, our Aerospace Structures will be described in a Euclidean three-dimensional space R 3.
 Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
Appendix A Vecto Algeba As is natual, ou Aeospace Stuctues will be descibed in a Euclidean thee-dimensional space R 3. A.1 Vectos A vecto is used to epesent quantities that have both magnitude and diection.
AST2000 Lecture Notes
 AST000 Lectue Notes Pat C Geneal Relativity: Basic pinciples Questions to ponde befoe the lectue 1. What is a black hole? how would you define it?). If you, situated in a safe place fa away fom the black
AST000 Lectue Notes Pat C Geneal Relativity: Basic pinciples Questions to ponde befoe the lectue 1. What is a black hole? how would you define it?). If you, situated in a safe place fa away fom the black
Problems with Mannheim s conformal gravity program
 Poblems with Mannheim s confomal gavity pogam June 4, 18 Youngsub Yoon axiv:135.163v6 [g-qc] 7 Jul 13 Depatment of Physics and Astonomy Seoul National Univesity, Seoul 151-747, Koea Abstact We show that
Poblems with Mannheim s confomal gavity pogam June 4, 18 Youngsub Yoon axiv:135.163v6 [g-qc] 7 Jul 13 Depatment of Physics and Astonomy Seoul National Univesity, Seoul 151-747, Koea Abstact We show that
DEVIL PHYSICS THE BADDEST CLASS ON CAMPUS IB PHYSICS
 DEVIL PHYSICS THE BADDEST CLASS ON CAMPUS IB PHYSICS LSN 10-: MOTION IN A GRAVITATIONAL FIELD Questions Fom Reading Activity? Gavity Waves? Essential Idea: Simila appoaches can be taken in analyzing electical
DEVIL PHYSICS THE BADDEST CLASS ON CAMPUS IB PHYSICS LSN 10-: MOTION IN A GRAVITATIONAL FIELD Questions Fom Reading Activity? Gavity Waves? Essential Idea: Simila appoaches can be taken in analyzing electical
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Electromagnetism II September 15, 2012 Prof. Alan Guth PROBLEM SET 2
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.07: Electomagnetism II Septembe 5, 202 Pof. Alan Guth PROBLEM SET 2 DUE DATE: Monday, Septembe 24, 202. Eithe hand it in at the lectue,
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Depatment Physics 8.07: Electomagnetism II Septembe 5, 202 Pof. Alan Guth PROBLEM SET 2 DUE DATE: Monday, Septembe 24, 202. Eithe hand it in at the lectue,
Review: Electrostatics and Magnetostatics
 Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
Review: Electostatics and Magnetostatics In the static egime, electomagnetic quantities do not vay as a function of time. We have two main cases: ELECTROSTATICS The electic chages do not change postion
Hawking Radiation. Alex Fontana
 Hawking Radiation Alex Fontana In this epot the aim is to undestand the behaviou of a Schwazshild Black Hole in a context whee quantum field fluctuations ae taken into account. We ae going to see how to
Hawking Radiation Alex Fontana In this epot the aim is to undestand the behaviou of a Schwazshild Black Hole in a context whee quantum field fluctuations ae taken into account. We ae going to see how to
Physics 121 Hour Exam #5 Solution
 Physics 2 Hou xam # Solution This exam consists of a five poblems on five pages. Point values ae given with each poblem. They add up to 99 points; you will get fee point to make a total of. In any given
Physics 2 Hou xam # Solution This exam consists of a five poblems on five pages. Point values ae given with each poblem. They add up to 99 points; you will get fee point to make a total of. In any given
