m 1 m 2 π/2 θ NATURAL SCIENCES TRIPOS Wednesday 16 January 2013 THEORETICAL PHYSICS I Answers
|
|
|
- Jasper Elvin Sherman
- 5 years ago
- Views:
Transcription
1 NTURL SCIENCES TRIPOS Part II Wednesday 16 January 013 THEORETICL PHYSICS I nswers 1 Consider a double pendulum composed of two masses m 1 and m attached to two rigid massless rods of equal length l as illustrated in the figure. The two rods are connected by a frictionless hinge at point B and the other end of the first rod is pinned by a frictionless hinge to rotate about point. massless spring of elastic constant κ connects the ends points and C. π/ θ θ B m 1 φ C m (a) [book work] Consider the case m 1 = m = m. The angle between the two rods is π/ θ+π/+φ = π+φ θ and thus the distance between points and C is lsin[π/+(φ θ)/] = lcos[(φ θ)/]. The positions of mass m 1 and m are given by r 1 = l(sinθ, cosθ) r = r 1 +l(sinφ, cosφ). Therefore, the kinetic and potential energies of the system can be written as T = ml θ +ml θ 1 φcos(θ φ)+ ml φ V = mglcosθ mglcosφ+κl cos ( ) θ φ,
2 where we used the trigonometric relation cos(θ)cos(φ)+sin(θ)sin(φ) = cos(θ φ). Expanding to second order in θ, φ, θ, and φ, after a few lines of algebra, we obtain T = ml [ θ + θ φ+ 1 φ ] V = mglθ + 1 mglφ 1 κl (φ θ), where we ignored irrelevant constants in V(θ,φ). These in turn give the expected Lagrangian [9] ( θ L = ml + θ φ+ 1 φ ) mgl (θ + 1 ) φ + 1 κl (θ φ). (b) [part book work, part new] In order to write the Euler-Lagrange equations, we compute = θ mglθ+κl (θ φ) = φ mglφ κl (θ φ) = ml( θ+ φ) θ = ml( φ+ θ), φ to obtain { ml ( θ+ φ) = mglθ+κl (θ φ) ml ( φ+ θ) = mglφ κl (θ φ). For convenience, we introduce the two frequencies ω0 = g/l and ω 1 = κ/m and re-write the equations of motion as { θ+ φ+ω 0 θ ω1 (θ φ) = 0 φ+ θ+ω 0 φ+ω 1 (θ φ) = 0. n oscillatory solution where θ and φ have the same frequency and satisfy the initial conditions θ(0) = φ(0) = ξ and θ(0) = φ = 0 takes the form θ(t) = ξcos(ωt) φ(t) = ξcos(ωt). Substituting into the equations of motion and cancelling out the common factor of cos(ωt), { ω +ω 0 ω 1 = 0 ω 0 +ω 1 = 0 we immediately see that a solution exists only if ω0 = ω 1 (i.e., if g/l = κ/m), in which case ω = ω1 = ω 0. The initial conditions correspond to the two masses at rest with the first rod at an angle ξ, say, to the right of the vertical and the second rod at an opposite angle. Since the two rods have the same length, this means that the mass m lies exactly underneath the hinge at. The latter condition holds
3 3 throughout the motion of the pendulum, where the mass m 1 swings from side to side whereas the mass m only moves up and down. [7] (c) [book work] If m 1 = 0,m = m, the Lagrangian of the system can be obtained in a similar manner, T = ml ( 1 θ + θ φ+ 1 φ ) V = 1 mglθ + 1 mglφ 1 κl (φ θ) L = 1 ml( θ+ φ) 1 mgl(θ +φ )+ 1 κl (θ φ). The Euler-Lagrange equations of motion are { ml ( θ + φ)+mglθ κl (θ φ) = 0 ml ( θ + φ)+mglφ+κl (θ φ) = 0, which can be readily re-written in terms of η = θ +φ and ν = θ φ by taking the sum and difference of the two equations, { η+ω 0 η = 0 (ω 0 ω 1 )ν = 0, where this time we defined ω0 = g/l and ω 1 = κ/m. [Note the factor of in the new definition of ω 0 with respect to the definition used in part (b) above]. In the new variables, the two equations are decoupled since each variable appears in one and only one of them. The variable η follows simple harmonic motion whereas ν = 0. If we set ω 0 = ω 1, the variable ν is undetermined by the equations of motion. Had we made the change of variables θ,φ η,ν at the Lagrangian level, we would have indeed noticed that L is then independent of ν. This is of course an artefact of the second order expansion. [5] (d) [part book work, part new] Let us consider the Fourier transform of the equation in the paper, η +γ η +ω 0 η = { 0 t < 0 e αt t 0, where is a constant of dimensions (time) : ω ˆη +iωγˆη +ω0ˆη = dte αt e iωt Θ(t) = i ω iα, (using the chosen definition of Fourier transform). The Green s function of the left hand side is nothing but 1 ω iωγ ω 0 = 1 (ω iγ/ ω)(ω iγ/+ω),
4 4 where ω = ω0 γ /4 (which is a real number as we are working under the assumption that ω 0 > γ/). solution to the equation of motion is thus given in reciprocal space by ˆη(k) = i (ω iγ/ ω)(ω iγ/+ω)(ω iα). In order to obtain η(t) we need to compute the inverse Fourier transform η(t) = dω ie iωt π (ω iγ/ ω)(ω iγ/+ω)(ω iα), which can be done via Cauchy integration of the three simple poles at ω 1 = iγ/+ω ω = iγ/ ω ω 3 = iα. Notice that all the poles are above the real axis. For t < 0 we ought to close the contour in the lower half plane; the path encircles no poles and the integral vanishes: η(t) = 0 for t < 0. For t > 0, the path is in the upper half plane and it encloses all three poles, leading to the solution: η(t) = { e iωt γt/ ω(ω +iγ/ iα) + e iωt γt/ ω( ω +iγ/ iα) e αt } (ω +iγ/ iα)( ω +iγ/ iα) = ( ω +iγ/ iα)eiωt γt/ (ω +iγ/ iα)e iωt γt/ +ωe αt ω[ω +(α γ/) ] = ωcos(ωt)e γt/ (γ/ α)sin(ωt)e γt/ +ωe αt ω[ω +(α γ/) ] general solution of the differential equation we are interested in can alternatively be produced by summing the solution of the relative homogeneous problem ( η +γ η+ω 0η = 0) to a specific solution of the full equation (which can be guessed of the form Ce αt and C = /(α γα+ω0 ) is readily obtained): e αt η(t) = C 1 cos(ωt)e γt/ +C sin(ωt)e γt/ +. α γα+ω0 Observing that ω +(α γ/) = α γα+ω0, the last term in the solution obtained via the Green s function is clearly the same as the one in the general solution. The remaining two terms are of the same form in both solutions. quick calculation shows that the solution obtained via Green s function satisfies η(0) = 0 and η(0) = 0. [1]
5 5 Consider two charged particles of mass m 1 and m and of charge e 1 = e = e constrained to move in the x y plane in presence of a magnetic field perpendicular to the plane, B = Bẑ. The two particles interact via the Coulomb potential V(r) = e /r, r = r 1 r. (a) [part book work, part new] Using the inverse relations r 1, = R m,1 r/m, the kinetic energy of the system can be written as T = 1 m 1ṙ m ṙ = M Ṙ + µ ṙ, where R = (m 1 r 1 +m r )/M, M = m 1 +m, r = r r 1, and µ = m 1 m /M. With the suggested gauge choice (r) = (B r)/, the potential energy of the system is = e r e ) m (Ṙ M ṙ = e r + e = e r + e e V = r 1 r er 1 (r 1 )+er (r ) [ B ( R m M r )]+ e ) [ ( m 1 (Ṙ+ M ṙ B R+ m )] 1 M r m 1 m M ṙ (B r)+ Ṙ (B e r)+ e (B R) ṙ m 1 m M ṙ (B r)+ Ṙ (B e r) e R (B ṙ) = e r + e m 1 m M ṙ (B r)+eṙ (B r) Ṙ (B e r) e R (B ṙ), where we used the cyclic property of (B C). Notice that the last two terms can be neglected as they are proportional to the total time derivative of R (B r) and thus contribute only vanishing boundary terms. The Lagrangian can be written as L = M Ṙ + µ ṙ + e r e m 1 m ṙ (B r) eṙ (B r), M as expected. [10] (b) [book work] In order to obtain the Hamiltonian of the system we need to evaluate H = p ṙ +P Ṙ L as a function of p, P, r, and R, using the relations and p = dl dṙ = µṙ e B r P = dl = MṘ eb r. dṙ
6 Substituting into the expression for H one gets 6 H = p P 1 µ (p+e B r)+ +eb r) M (P M (P +eb r) 1 µ (p+e B r) e r + e µ (p+e B r) (B r)+ e (P +eb r) (B r), M which gives, after some algebra, H = [P +e(b r)] M + [p+e (B r)] µ e r. The Hamiltonian does not depend directly on time and therefore the energy of the system is conserved. Moreover, the Hamiltonian does not depend on R and thus P is conserved. [6] (c) [part book work, part new] If we set P = 0 and observe that B r = Br, the Hamiltonian reduces to H = p µ + e e p (B r) µ r + e B r M + (e ) B r µ = p µ + e e p (B r) µ r + e B r 8µ. Hamilton s equations of motion are therefore ṗ x = dh dx = e µ p yb e e B x r 3x 4µ ṗ y = dh dy = e µ p xb e r 3y e B y 4µ ẋ = dh dp x = p x µ e µ By ẏ = dh dp y = p y µ + e µ Bx, where r = (x,y). [6] (d) [part book work, part new] From the last two equations of motion we can obtain an expression for p x and p y, respectively, as a function of x,y and their time derivatives. Taking the time derivative of the same expressions, we obtain similarly the dependence of ṗ x and ṗ y. Substituting these expressions into the first two equations of motion, we obtain µẍ+e Bẏ = e B e x x e B (µẏ 4µ r 3 µ e Bx) µÿ e Bẋ = e B y e y + e B 4µ r 3 µ (µẋ+e By),
7 7 and with a few simplifications, { µẍ+e Bẏ = e B M e x x r 3 µÿ e Bẋ = e B M y e r 3 y. Using the solutions for x and y suggested in the paper, { x = Rcos(ωt) y = Rsin(ωt), with R, ω constant, the two equations above reduce to the same equation µω e Bω e B M e R 3 = 0 which always admits real-valued solutions for ω (recall that M, R, and µ are positive). This demonstrates that the suggested time dependence of r, whereby one particle moves in a perfect circle at constant angular velocity in the reference frame of the other particle, is indeed a solution of the equations of motion. This solution is consistent with the expectation that charged particles moving in the x y plane subject to a magnetic field perpendicular to the plane follow circular trajectories. It is also consistent with the centrosymmetric Coulomb potential between two charged particles, which admits solutions in the form of circular orbits. The values of ω for which the suggested time dependence is a solution of the equations of motion are given by e B ± (e ) B +µ ( e B + ) e M R ω = 3. µ [11] 3 dynamical system with Hamiltonian H is described by independent coordinates q i (i = 1,...,n) and corresponding generalised (canonical) momenta p i. (a) [book work] The Poisson Bracket (PB) {f,g} of two functions f(q i,p i,t) and g(q i,p i,t) that depend on the generalised coordinates and on time is defined by ( n f g {f,g} = f ) g, q i p i p i q i i=1 where in the partial derivatives all the other coordinates, canonical momenta and time are held fixed. From now on we use the summation convention and introduce a shorthand notation qi f = f/ q i etc. Suppose that g = q j, then qi g = δ ij and pi g = 0 and similarly for g = p j. Hence {f,q j } = f p j, {f,p j } = + f q j,
8 and using the second of these relationships with f = q i gives {q i,p j } = δ ij, as expected. This can also of course be obtained directly from the PB definition. Hamilton s equations of motion are Hence dp i dt = H q i, 8 dq i dt = H p i. df dt = f t + f dq i q i dt + f dp i p i dt and substituting for the coordinate time derivatives immediately gives the required result: df dt = f t +{f,h}. Substituting h = H in the Jacobi Identity: {H,{f,g}} = {f,{g,h}} {g,{h,f} = {f, g f } {g, t t } = t {f,g} and therefore h = {f,g} satisfies the same equation as f and g. (b) new set of coordinates and momenta (Q i,p i ) is defined by Q i = Q i (q j,p j ), P i = P i (q j,p j ), i = 1,...,n. necessary and sufficient condition for this transformation to be canonical is {Q i,p j } = δ ij, {Q i,q j } = 0, {P i,p j } = 0, where as before the partial derivatives are with respect to the q i and p i. For a system with two degrees of freedom, two new coordinates are defined by Then Q 1 = q 1, Q = q 1 +q. 0 = {Q 1,P } = q 1 p1 P p1 P = 0 0 = {Q,P 1 } = p1 P 1 + p P 1 1 = {Q 1,P 1 } = q 1 p1 P 1 1 = {Q,P } = p1 P + p P = p P. The first of these implies P = F(q 1,q,p ) and the fourth then implies P = p +f(q 1,q ). The third implies P 1 = p 1 /(q 1 )+G(q 1,q,p ) and then the second implies P 1 = (p 1 p )/(q 1 )+g(q 1,q ). We further need to impose 0 = {Q 1,Q } (trivially satisfied) 0 = {P 1,P } = q g 1 q1 q1f + 1 q1 qf.
9 to is evidently particular choice that reduces the Hamiltonian H = 9 ( ) p1 p +p +(q 1 +q ) q 1 H = P 1 +P P 1 = (p 1 p )/(q 1 ), P = p +(q 1 +q ), which corresponds to g = 0 and f = (q 1 +q ) (one can immediately verify that it satisfied all the conditions above). 4 (a) [book work] The Lagrangian density for a triplet of real scalar fields in 3+1 space-time dimensions, ϕ a (t,x 1,x,x 3 ) with a = 1,,3, is L = 1 ( µϕ a )( µ ϕ a ) 1 λϕ aϕ a, where µ = ( / t, / x 1, / x, / x 3 ). We use the Euler-Lagrange equations in the form (see lectures) = ( ) ϕ a t ( ϕ a / t) + 3 i=1 to obtain the field equations of motion ( ), (a = 1,,3), x i ( ϕ a / x i ) µ µ ϕ a ϕ a ϕ a ϕ a ϕ a +λϕ t x 1 x x a = 0, (a = 1,,3). 3 (b) To show that L is invariant under the infinitesimal SO(3) rotation by an angle θ ϕ a ϕ a +θǫ abc n b ϕ c where n a is an arbitrary unit vector and ǫ abc is the three-dimensional Levi-Civita symbol, we consider δl = 1 ( µδϕ a )( µ ϕ a )+ 1 ( µϕ a )( µ δϕ a ) λϕ a δϕ a, where we have kept only first-order terms in δϕ a. Now using δϕ a = θǫ abc n b ϕ c, we note that ϕ a δϕ a = θǫ abc n b ϕ a ϕ c = 0 because the product of the ϕ fields is symmetric in indices a,c, while the Levi-Civita tensor is antisymmetric. Similarly µ ϕ a µ δϕ a = θǫ abc n b µ ϕ a µ ϕ c = 0
10 10 for the same reason. Hence δl = 0 under this particular transformation. (c) [book work] From lectures, the Noether current J µ corresponding to a symmetry of the Lagrangian density is derived as follows. Suppose that the Lagrangian is invariant under the transformation symmetry under a transformation of the form ϕ a ϕ a +δϕ a where δϕ a is infinitesimal. Symmetry means that L does not change: 0 = δl = δϕ a + ϕ a ( ϕ a / x i ) δ( ϕ a/ x i )+ δ ϕ a, ϕ a where summation over i and a is understood. The Euler-Lagrange equations of motion (see above) then imply that δl = ( ) δϕ a + (δϕ a ) x i ( ϕ a / x i ) ( ϕ a / x i ) x i + ( ) δϕ a + t ϕ a ϕ a t (δϕ a) = 0 ( ) x i ( ϕ a / x i ) δϕ a + ( ) δϕ a = 0 t ϕ a ( ) x µ ( ϕ a / x µ ) δϕ a = 0. This then implies the existence of a conserved Noether current, µ J µ = 0, where J µ j ( µ ϕ a ) δϕ a. By substituting for the δϕ a given above, keeping only linear terms in θ, and dropping the overall factor of θ, we obtain the Noether current in this case, J µ = ǫ abc n b ( µ ϕ a )ϕ c, which satisfies µ J µ = 0. The corresponding continuity equation is with ρ t + J = 0, ρ = ǫ abc n b ϕ a ϕ c, J = ǫ abc n b ( ϕ a )ϕ c. Now take d 3 x (over all space) of the continuity equation. The term d 3 x J = S ds J vanishes by the assumed vanishing of the fields as
11 x. Hence 0 = d 3 x ρ t 11 = d d 3 xǫ abc n b ϕ a ϕ c dt d = n b d 3 xǫ abc ϕ a ϕ c dt dq b = n b where Q b = d 3 xǫ bac ϕ a ϕ c dt Now n a is an arbitrary unit vector, and hence n a X a = 0 X a = 0. Hence the three quantities Q a = d 3 ϕ b x ǫ abc t ϕ c are all conserved. To verify this directly using the field equations, we take dq a dt = = = d 3 x ǫ abc t ( ϕ bϕ c ) d 3 x ǫ abc ( ϕ b ϕ c + ϕ b ϕ c ) d 3 x ǫ abc ϕ b ϕ c. where we have used the antisymmetry/symmetry of the tensors to drop the second term in the penultimate line. Substituting for ϕ b from the field equations, and again noting that the term proportional to ϕ b ϕ c vanishes by antisymmetry/symmetry, we have dq a dt = = d 3 x ǫ abc ( ϕ b )ϕ c d 3 x ǫ abc [ (( ϕ b )ϕ c ) ( ϕ b ) ( ϕ c )] Now the first term inside the integral vanishes because, by the Divergence Theorem, it corresponds to a surface integral at infinity, under the assumption that the fields vanish there, and the second term vanishes by antisymmetry/symmetry on the indices b,c. Thus we have verified directly that the quantities Q a are indeed conserved. 5 The non-linear version of the Klein-Gordon Lagrangian density for a scalar field φ(x,t) is given by L = 1 ( ) φ 1 t ( ) φ +F(φ), x where F(φ) is a differentiable function of its argument.
12 (a) The Euler-Lagrange equations for the fields φ are φ ( ) ( ) x φ t φ = 0, where and denote partial derivatives with respect to x and t respectively. Substituting for L then gives 1 f(φ)+ φ x φ t = 0, where f(φ) = F (φ). This is the result to be proved. Define φ 1 = φ(xcoshβ +tsinhβ,tcoshβ +xsinhβ). Then φ 1 x = coshβφ +sinhβ φ, φ 1 t = sinhβφ +coshβ φ. and φ 1 x = cosh βφ +sinh β φ+coshβsinhβ φ φ 1 = sinh βφ +cosh β φ+coshβsinhβ t φ. Subtracting these equations and using cosh β sinh β = 1 then gives φ 1 x φ 1 t = φ φ = f(φ) = f(φ 1 ), and so φ 1 satisfies the same partial differential equation as φ. (b) Consider the particular case f(φ) = aφ+bφ n, for positive constants a,b and integer n > 1, and the function w(x) = [ cosh (Bx) ] 1 1 n. To show that this is indeed a static solution of the equation we need to prove w aw +bw n = 0, where w = dw/dx. Write p = /(1 n) < 0, then w = p/ pbcosh (p 1) (Bx)sinh(Bx) and w = p/ pb [ (p 1)cosh (p ) (Bx)sinh (Bx)+cosh p (Bx) ] = p/ pb [ pcosh p (Bx) (p 1)cosh (p ) (Bx) ]. Therefore w aw +bw n = p/[ (p B a)cosh p (Bx) p(p 1)B cosh (p ) (Bx) + p(n 1)/ bcosh pn (Bx) ].
13 Now pn = n/(1 n) = p. Therefore to obtain a solution we require the coefficients of cosh p (Bx) and cosh (p ) (Bx) to vanish, i.e. a B = ± p = ±1 a(n 1) i.e. 13 b p(n 1)/ = b 1 = p(p 1)B = a(p 1)/p = a(1+n)/ = b a(n+1), B = ± a(n 1)/. The function w(x) has a maximum value of w(0) = 1/(1 n) at x = 0 and w 0 as x ±. s n, w(0) 1. By the first part of the question, the function φ(x,t) = w(xcoshβ tsinhβ), is a solution of the full equation for any constant β. This has a maximum at xcoshβ tsinhβ = 0, i.e. x = vt where v = tanhβ > 0, since β is a positive constant. This therefore corresponds to a travelling-wave solution moving with the same shape in x and travelling in the positive x direction with uniform velocity v. 6 The Landau free energy expansion for a uniaxial ferromagnet in a magnetic field can be written as F = F 0 hm+ a m + b 4 m4. (a) [book work] Phase transitions occur when a new state (ordered) state develops from the disordered (high temperature) phase. The appearance of the new state is typically described using an order parameter, say the magnetisation in an Ising moded. Ginzburg-Landau theory provides a phenomenological description of critical phenomena based on an appropriately coarse grained order parameter m. It is constructed on the basis of symmetries rather than precise knowledge of the microscopic properties of the system. Near the transition temperature, where the order parameter vanishes, one can expand the Ginzburg-Landau free energy in powers of m and its derivatives. The latter often penalise spatial variations of the parameter m and thus one can further simplify the free energy expansion by considering the case of uniform m, as in this example. In an expansion of the form F = F 0 hm+ a m + b 4 m4 we require that b > 0 for the free energy to be bounded from below (b = 0 is acceptable if a > 0); we also recognise the second term on the right hand side as an
14 14 externally applied magnetic field; finally, we also know that a transition in this free energy occurs when a changes sign (and therefore a(t c ) = 0). [4] (b) [book work] The magnetisation of the system scales like a power law of the applied field along the critical isotherm (for small fields), and the exponent is 1/δ. long the critical isotherm T = T c, a(t c ) = 0 and F(T c ) = F 0 hm+ b 4 m4. The equilibrium value of m can be obtained from the equation F/ m = 0, F(T c ) h m = h+bm3 = 0 m = 3 b and therefore δ = 1/3. [6] (c) [part book work, part new] The dependence of the magnetisation on the applied field and temperature can be obtained as above, F(T) m = h+a(t)m+b(t)m3 = 0. However, rather than solving for m, it is convenient to take a further derivative with respect to h: F(T) h m = 1+a(T)χ+3b(T)m χ = 0 χ = 1 a(t)+3b(t)m. For t > 0 (T > T c ), we know that m = 0 and therefore χ = a(t) 1. For t < 0, m 0 and we can re-write the first equation as b(t)m = h a(t)m. m Substituting into the expression for χ, one obtains χ = 1 = a(t)+3(h/m a(t)) h=0 1 a(t) = 1 a(t), where we used the fact that a(t) is negative for T < T c. Finally, it is straightforwad to combine these results and show that χ(t) lim t 0 + χ( t) = a( t) a(t) where we used knoweldge of the fact that a(t) (T T c )/T c for T close to T c. [8] =,
15 (d) [new] Once we add dm 3 /3 to the free energy F and set h = 0, 15 F = F 0 + a m + d 3 m3 + b 4 m4, the equilibrium value of the magnetisation is given by which admits solutions of the form F m = 0 = am+dm +bm 3, m = 0 and m = d± d 4ab. b The latter of course are acceptable only if d > 4ab. By looking at the form of the second derivative with respect to m, F m = a+dm+3bm, we see immediately that the sign at m = 0 is controlled solely by the parameter a: if a > 0 then m = 0 is a minimum; if a < 0, it is a maximum. If a < 0, the other two solutions of F/ m = 0 are acceptable (d > 4ab) and therefore they both have to be minima (observe that in this case the two solutions lie on opposite sides of m = 0, and that F(m) + for m ± ). If a > 0, then the other two solutions (if they exist) are either both positive or both negative. They are thereofore a maximum and a minimum, respectively. So long as d is sufficiently small however, the global minimum remains at m = 0 (one can check that this is indeed the case for d < 9ab/). The case of larger values of d can well be studied using this very same approach but it is more involved and beyond the scope of the question. Similarly to the case d = 0 considered in the lectures, it is the sign of a that drives a transition from a state with m = 0 to a state with m 0. However, the cubic term introduces two major changes: (i) the symmetry in the ordered phase is broken explicitely, since m = ( d d 4ab)/(b) has a lower free energy than m = ( d+ d 4ab)/(b); (ii) the change in the order parameter across the critical point a = 0 is discontinuous, hence the transition has become first order. [15] END OF PPER
Part II. Classical Dynamics. Year
 Part II Year 28 27 26 25 24 23 22 21 20 2009 2008 2007 2006 2005 28 Paper 1, Section I 8B Derive Hamilton s equations from an action principle. 22 Consider a two-dimensional phase space with the Hamiltonian
Part II Year 28 27 26 25 24 23 22 21 20 2009 2008 2007 2006 2005 28 Paper 1, Section I 8B Derive Hamilton s equations from an action principle. 22 Consider a two-dimensional phase space with the Hamiltonian
Hamilton s principle and Symmetries
 Hamilton s principle and Symmetries Sourendu Gupta TIFR, Mumbai, India Classical Mechanics 2011 August 18, 2011 The Hamiltonian The change in the Lagrangian due to a virtual change of coordinates is dl
Hamilton s principle and Symmetries Sourendu Gupta TIFR, Mumbai, India Classical Mechanics 2011 August 18, 2011 The Hamiltonian The change in the Lagrangian due to a virtual change of coordinates is dl
Curves in the configuration space Q or in the velocity phase space Ω satisfying the Euler-Lagrange (EL) equations,
 Physics 6010, Fall 2010 Hamiltonian Formalism: Hamilton s equations. Conservation laws. Reduction. Poisson Brackets. Relevant Sections in Text: 8.1 8.3, 9.5 The Hamiltonian Formalism We now return to formal
Physics 6010, Fall 2010 Hamiltonian Formalism: Hamilton s equations. Conservation laws. Reduction. Poisson Brackets. Relevant Sections in Text: 8.1 8.3, 9.5 The Hamiltonian Formalism We now return to formal
Physics 5153 Classical Mechanics. Canonical Transformations-1
 1 Introduction Physics 5153 Classical Mechanics Canonical Transformations The choice of generalized coordinates used to describe a physical system is completely arbitrary, but the Lagrangian is invariant
1 Introduction Physics 5153 Classical Mechanics Canonical Transformations The choice of generalized coordinates used to describe a physical system is completely arbitrary, but the Lagrangian is invariant
M2A2 Problem Sheet 3 - Hamiltonian Mechanics
 MA Problem Sheet 3 - Hamiltonian Mechanics. The particle in a cone. A particle slides under gravity, inside a smooth circular cone with a vertical axis, z = k x + y. Write down its Lagrangian in a) Cartesian,
MA Problem Sheet 3 - Hamiltonian Mechanics. The particle in a cone. A particle slides under gravity, inside a smooth circular cone with a vertical axis, z = k x + y. Write down its Lagrangian in a) Cartesian,
Physical Dynamics (PHY-304)
 Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS. Prof. N. Harnew University of Oxford TT 2017
 CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS Prof. N. Harnew University of Oxford TT 2017 1 OUTLINE : CP1 REVISION LECTURE 3 : INTRODUCTION TO CLASSICAL MECHANICS 1. Angular velocity and
CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS Prof. N. Harnew University of Oxford TT 2017 1 OUTLINE : CP1 REVISION LECTURE 3 : INTRODUCTION TO CLASSICAL MECHANICS 1. Angular velocity and
Physical Dynamics (SPA5304) Lecture Plan 2018
 Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
COMPLETE ALL ROUGH WORKINGS IN THE ANSWER BOOK AND CROSS THROUGH ANY WORK WHICH IS NOT TO BE ASSESSED.
 BSc/MSci EXAMINATION PHY-304 Time Allowed: Physical Dynamics 2 hours 30 minutes Date: 28 th May 2009 Time: 10:00 Instructions: Answer ALL questions in section A. Answer ONLY TWO questions from section
BSc/MSci EXAMINATION PHY-304 Time Allowed: Physical Dynamics 2 hours 30 minutes Date: 28 th May 2009 Time: 10:00 Instructions: Answer ALL questions in section A. Answer ONLY TWO questions from section
Homework 3. 1 Goldstein Part (a) Theoretical Dynamics September 24, The Hamiltonian is given by
 Theoretical Dynamics September 4, 010 Instructor: Dr. Thomas Cohen Homework 3 Submitted by: Vivek Saxena 1 Goldstein 8.1 1.1 Part (a) The Hamiltonian is given by H(q i, p i, t) = p i q i L(q i, q i, t)
Theoretical Dynamics September 4, 010 Instructor: Dr. Thomas Cohen Homework 3 Submitted by: Vivek Saxena 1 Goldstein 8.1 1.1 Part (a) The Hamiltonian is given by H(q i, p i, t) = p i q i L(q i, q i, t)
NIU PHYS 500, Fall 2006 Classical Mechanics Solutions for HW6. Solutions
 NIU PHYS 500, Fall 006 Classical Mechanics Solutions for HW6 Assignment: HW6 [40 points] Assigned: 006/11/10 Due: 006/11/17 Solutions P6.1 [4 + 3 + 3 = 10 points] Consider a particle of mass m moving in
NIU PHYS 500, Fall 006 Classical Mechanics Solutions for HW6 Assignment: HW6 [40 points] Assigned: 006/11/10 Due: 006/11/17 Solutions P6.1 [4 + 3 + 3 = 10 points] Consider a particle of mass m moving in
SOLUTIONS, PROBLEM SET 11
 SOLUTIONS, PROBLEM SET 11 1 In this problem we investigate the Lagrangian formulation of dynamics in a rotating frame. Consider a frame of reference which we will consider to be inertial. Suppose that
SOLUTIONS, PROBLEM SET 11 1 In this problem we investigate the Lagrangian formulation of dynamics in a rotating frame. Consider a frame of reference which we will consider to be inertial. Suppose that
Hamiltonian Field Theory
 Hamiltonian Field Theory August 31, 016 1 Introduction So far we have treated classical field theory using Lagrangian and an action principle for Lagrangian. This approach is called Lagrangian field theory
Hamiltonian Field Theory August 31, 016 1 Introduction So far we have treated classical field theory using Lagrangian and an action principle for Lagrangian. This approach is called Lagrangian field theory
Quantum Field Theory Notes. Ryan D. Reece
 Quantum Field Theory Notes Ryan D. Reece November 27, 2007 Chapter 1 Preliminaries 1.1 Overview of Special Relativity 1.1.1 Lorentz Boosts Searches in the later part 19th century for the coordinate transformation
Quantum Field Theory Notes Ryan D. Reece November 27, 2007 Chapter 1 Preliminaries 1.1 Overview of Special Relativity 1.1.1 Lorentz Boosts Searches in the later part 19th century for the coordinate transformation
for changing independent variables. Most simply for a function f(x) the Legendre transformation f(x) B(s) takes the form B(s) = xs f(x) with s = df
 Physics 106a, Caltech 1 November, 2018 Lecture 10: Hamiltonian Mechanics I The Hamiltonian In the Hamiltonian formulation of dynamics each second order ODE given by the Euler- Lagrange equation in terms
Physics 106a, Caltech 1 November, 2018 Lecture 10: Hamiltonian Mechanics I The Hamiltonian In the Hamiltonian formulation of dynamics each second order ODE given by the Euler- Lagrange equation in terms
Classical Mechanics Comprehensive Exam Solution
 Classical Mechanics Comprehensive Exam Solution January 31, 011, 1:00 pm 5:pm Solve the following six problems. In the following problems, e x, e y, and e z are unit vectors in the x, y, and z directions,
Classical Mechanics Comprehensive Exam Solution January 31, 011, 1:00 pm 5:pm Solve the following six problems. In the following problems, e x, e y, and e z are unit vectors in the x, y, and z directions,
P321(b), Assignement 1
 P31(b), Assignement 1 1 Exercise 3.1 (Fetter and Walecka) a) The problem is that of a point mass rotating along a circle of radius a, rotating with a constant angular velocity Ω. Generally, 3 coordinates
P31(b), Assignement 1 1 Exercise 3.1 (Fetter and Walecka) a) The problem is that of a point mass rotating along a circle of radius a, rotating with a constant angular velocity Ω. Generally, 3 coordinates
Course 241: Advanced Mechanics. Scholarship Questions
 Course 41: Advanced echanics Scholarship Questions This covers the first sixteen questions from part I up to the end of rigid bodies, and a selection of the questions from part II. I wouldn t be too bothered
Course 41: Advanced echanics Scholarship Questions This covers the first sixteen questions from part I up to the end of rigid bodies, and a selection of the questions from part II. I wouldn t be too bothered
The Geometry of Euler s equation. Introduction
 The Geometry of Euler s equation Introduction Part 1 Mechanical systems with constraints, symmetries flexible joint fixed length In principle can be dealt with by applying F=ma, but this can become complicated
The Geometry of Euler s equation Introduction Part 1 Mechanical systems with constraints, symmetries flexible joint fixed length In principle can be dealt with by applying F=ma, but this can become complicated
4.1 Important Notes on Notation
 Chapter 4. Lagrangian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 4.1 Important Notes on Notation In this chapter, unless otherwise stated, the
Chapter 4. Lagrangian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 4.1 Important Notes on Notation In this chapter, unless otherwise stated, the
Lecture 4. Alexey Boyarsky. October 6, 2015
 Lecture 4 Alexey Boyarsky October 6, 2015 1 Conservation laws and symmetries 1.1 Ignorable Coordinates During the motion of a mechanical system, the 2s quantities q i and q i, (i = 1, 2,..., s) which specify
Lecture 4 Alexey Boyarsky October 6, 2015 1 Conservation laws and symmetries 1.1 Ignorable Coordinates During the motion of a mechanical system, the 2s quantities q i and q i, (i = 1, 2,..., s) which specify
Physics 235 Chapter 7. Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics
 Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics Many interesting physics systems describe systems of particles on which many forces are acting. Some of these forces are immediately
Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics Many interesting physics systems describe systems of particles on which many forces are acting. Some of these forces are immediately
Phys 7221 Homework # 8
 Phys 71 Homework # 8 Gabriela González November 15, 6 Derivation 5-6: Torque free symmetric top In a torque free, symmetric top, with I x = I y = I, the angular velocity vector ω in body coordinates with
Phys 71 Homework # 8 Gabriela González November 15, 6 Derivation 5-6: Torque free symmetric top In a torque free, symmetric top, with I x = I y = I, the angular velocity vector ω in body coordinates with
ANALYTISK MEKANIK I HT 2016
 Karlstads Universitet Fysik ANALYTISK MEKANIK I HT 2016 Kursens kod: FYGB08 Kursansvarig lärare: Jürgen Fuchs rum 21F 316 tel. 054-700 1817 el.mail: juerfuch@kau.se FYGB08 HT 2016 Exercises 1 2016-12-14
Karlstads Universitet Fysik ANALYTISK MEKANIK I HT 2016 Kursens kod: FYGB08 Kursansvarig lärare: Jürgen Fuchs rum 21F 316 tel. 054-700 1817 el.mail: juerfuch@kau.se FYGB08 HT 2016 Exercises 1 2016-12-14
PHY411 Lecture notes Part 2
 PHY411 Lecture notes Part 2 Alice Quillen April 6, 2017 Contents 1 Canonical Transformations 2 1.1 Poisson Brackets................................. 2 1.2 Canonical transformations............................
PHY411 Lecture notes Part 2 Alice Quillen April 6, 2017 Contents 1 Canonical Transformations 2 1.1 Poisson Brackets................................. 2 1.2 Canonical transformations............................
Physics 212: Statistical mechanics II Lecture XI
 Physics 212: Statistical mechanics II Lecture XI The main result of the last lecture was a calculation of the averaged magnetization in mean-field theory in Fourier space when the spin at the origin is
Physics 212: Statistical mechanics II Lecture XI The main result of the last lecture was a calculation of the averaged magnetization in mean-field theory in Fourier space when the spin at the origin is
Analytical Dynamics: Lagrange s Equation and its Application A Brief Introduction
 Analytical Dynamics: Lagrange s Equation and its Application A Brief Introduction D. S. Stutts, Ph.D. Associate Professor of Mechanical Engineering Missouri University of Science and Technology Rolla,
Analytical Dynamics: Lagrange s Equation and its Application A Brief Introduction D. S. Stutts, Ph.D. Associate Professor of Mechanical Engineering Missouri University of Science and Technology Rolla,
Chapter 1. Principles of Motion in Invariantive Mechanics
 Chapter 1 Principles of Motion in Invariantive Mechanics 1.1. The Euler-Lagrange and Hamilton s equations obtained by means of exterior forms Let L = L(q 1,q 2,...,q n, q 1, q 2,..., q n,t) L(q, q,t) (1.1)
Chapter 1 Principles of Motion in Invariantive Mechanics 1.1. The Euler-Lagrange and Hamilton s equations obtained by means of exterior forms Let L = L(q 1,q 2,...,q n, q 1, q 2,..., q n,t) L(q, q,t) (1.1)
Complex Numbers. The set of complex numbers can be defined as the set of pairs of real numbers, {(x, y)}, with two operations: (i) addition,
 Complex Numbers Complex Algebra The set of complex numbers can be defined as the set of pairs of real numbers, {(x, y)}, with two operations: (i) addition, and (ii) complex multiplication, (x 1, y 1 )
Complex Numbers Complex Algebra The set of complex numbers can be defined as the set of pairs of real numbers, {(x, y)}, with two operations: (i) addition, and (ii) complex multiplication, (x 1, y 1 )
is conserved, calculating E both at θ = 0 and θ = π/2 we find that this happens for a value ω = ω given by: 2g
 UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mechanics Theory 2016 fall Set 5 for 23. September 2016 Problem 27: A string can only support
UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mechanics Theory 2016 fall Set 5 for 23. September 2016 Problem 27: A string can only support
Lecture 2. Contents. 1 Fermi s Method 2. 2 Lattice Oscillators 3. 3 The Sine-Gordon Equation 8. Wednesday, August 28
 Lecture 2 Wednesday, August 28 Contents 1 Fermi s Method 2 2 Lattice Oscillators 3 3 The Sine-Gordon Equation 8 1 1 Fermi s Method Feynman s Quantum Electrodynamics refers on the first page of the first
Lecture 2 Wednesday, August 28 Contents 1 Fermi s Method 2 2 Lattice Oscillators 3 3 The Sine-Gordon Equation 8 1 1 Fermi s Method Feynman s Quantum Electrodynamics refers on the first page of the first
The Particle-Field Hamiltonian
 The Particle-Field Hamiltonian For a fundamental understanding of the interaction of a particle with the electromagnetic field we need to know the total energy of the system consisting of particle and
The Particle-Field Hamiltonian For a fundamental understanding of the interaction of a particle with the electromagnetic field we need to know the total energy of the system consisting of particle and
FINAL EXAM GROUND RULES
 PHYSICS 507 Fall 2011 FINAL EXAM Room: ARC-108 Time: Wednesday, December 21, 10am-1pm GROUND RULES There are four problems based on the above-listed material. Closed book Closed notes Partial credit will
PHYSICS 507 Fall 2011 FINAL EXAM Room: ARC-108 Time: Wednesday, December 21, 10am-1pm GROUND RULES There are four problems based on the above-listed material. Closed book Closed notes Partial credit will
06. Lagrangian Mechanics II
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 06. Lagrangian Mechanics II Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 06. Lagrangian Mechanics II Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
Selected Topics in Physics a lecture course for 1st year students by W.B. von Schlippe Spring Semester 2007
 Selected Topics in Physics a lecture course for st year students by W.B. von Schlippe Spring Semester 7 Lecture : Oscillations simple harmonic oscillations; coupled oscillations; beats; damped oscillations;
Selected Topics in Physics a lecture course for st year students by W.B. von Schlippe Spring Semester 7 Lecture : Oscillations simple harmonic oscillations; coupled oscillations; beats; damped oscillations;
28. Pendulum phase portrait Draw the phase portrait for the pendulum (supported by an inextensible rod)
 28. Pendulum phase portrait Draw the phase portrait for the pendulum (supported by an inextensible rod) θ + ω 2 sin θ = 0. Indicate the stable equilibrium points as well as the unstable equilibrium points.
28. Pendulum phase portrait Draw the phase portrait for the pendulum (supported by an inextensible rod) θ + ω 2 sin θ = 0. Indicate the stable equilibrium points as well as the unstable equilibrium points.
HAMILTON S PRINCIPLE
 HAMILTON S PRINCIPLE In our previous derivation of Lagrange s equations we started from the Newtonian vector equations of motion and via D Alembert s Principle changed coordinates to generalised coordinates
HAMILTON S PRINCIPLE In our previous derivation of Lagrange s equations we started from the Newtonian vector equations of motion and via D Alembert s Principle changed coordinates to generalised coordinates
Linear and Nonlinear Oscillators (Lecture 2)
 Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
Linear and Nonlinear Oscillators (Lecture 2) January 25, 2016 7/441 Lecture outline A simple model of a linear oscillator lies in the foundation of many physical phenomena in accelerator dynamics. A typical
PHY 5246: Theoretical Dynamics, Fall November 16 th, 2015 Assignment # 11, Solutions. p θ = L θ = mr2 θ, p φ = L θ = mr2 sin 2 θ φ.
 PHY 5246: Theoretical Dynamics, Fall 215 November 16 th, 215 Assignment # 11, Solutions 1 Graded problems Problem 1 1.a) The Lagrangian is L = 1 2 m(ṙ2 +r 2 θ2 +r 2 sin 2 θ φ 2 ) V(r), (1) and the conjugate
PHY 5246: Theoretical Dynamics, Fall 215 November 16 th, 215 Assignment # 11, Solutions 1 Graded problems Problem 1 1.a) The Lagrangian is L = 1 2 m(ṙ2 +r 2 θ2 +r 2 sin 2 θ φ 2 ) V(r), (1) and the conjugate
The Hamiltonian formulation of gauge theories
 The Hamiltonian formulation of gauge theories I [p, q] = dt p i q i H(p, q) " # q i = @H @p i =[q i, H] ṗ i = @H =[p @q i i, H] 1. Symplectic geometry, Hamilton-Jacobi theory,... 2. The first (general)
The Hamiltonian formulation of gauge theories I [p, q] = dt p i q i H(p, q) " # q i = @H @p i =[q i, H] ṗ i = @H =[p @q i i, H] 1. Symplectic geometry, Hamilton-Jacobi theory,... 2. The first (general)
Attempts at relativistic QM
 Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Attempts at relativistic QM based on S-1 A proper description of particle physics should incorporate both quantum mechanics and special relativity. However historically combining quantum mechanics and
Lecture 5. Alexey Boyarsky. October 21, Legendre transformation and the Hamilton equations of motion
 Lecture 5 Alexey Boyarsky October 1, 015 1 The Hamilton equations of motion 1.1 Legendre transformation and the Hamilton equations of motion First-order equations of motion. In the Lagrangian formulation,
Lecture 5 Alexey Boyarsky October 1, 015 1 The Hamilton equations of motion 1.1 Legendre transformation and the Hamilton equations of motion First-order equations of motion. In the Lagrangian formulation,
3 Space curvilinear motion, motion in non-inertial frames
 3 Space curvilinear motion, motion in non-inertial frames 3.1 In-class problem A rocket of initial mass m i is fired vertically up from earth and accelerates until its fuel is exhausted. The residual mass
3 Space curvilinear motion, motion in non-inertial frames 3.1 In-class problem A rocket of initial mass m i is fired vertically up from earth and accelerates until its fuel is exhausted. The residual mass
Classical mechanics of particles and fields
 Classical mechanics of particles and fields D.V. Skryabin Department of Physics, University of Bath PACS numbers: The concise and transparent exposition of many topics covered in this unit can be found
Classical mechanics of particles and fields D.V. Skryabin Department of Physics, University of Bath PACS numbers: The concise and transparent exposition of many topics covered in this unit can be found
Two-Body Problem. Central Potential. 1D Motion
 Two-Body Problem. Central Potential. D Motion The simplest non-trivial dynamical problem is the problem of two particles. The equations of motion read. m r = F 2, () We already know that the center of
Two-Body Problem. Central Potential. D Motion The simplest non-trivial dynamical problem is the problem of two particles. The equations of motion read. m r = F 2, () We already know that the center of
Quantum Field Theory I Examination questions will be composed from those below and from questions in the textbook and previous exams
 Quantum Field Theory I Examination questions will be composed from those below and from questions in the textbook and previous exams III. Quantization of constrained systems and Maxwell s theory 1. The
Quantum Field Theory I Examination questions will be composed from those below and from questions in the textbook and previous exams III. Quantization of constrained systems and Maxwell s theory 1. The
Seminar 6: COUPLED HARMONIC OSCILLATORS
 Seminar 6: COUPLED HARMONIC OSCILLATORS 1. Lagrangian Equations of Motion Let consider a system consisting of two harmonic oscillators that are coupled together. As a model, we will use two particles attached
Seminar 6: COUPLED HARMONIC OSCILLATORS 1. Lagrangian Equations of Motion Let consider a system consisting of two harmonic oscillators that are coupled together. As a model, we will use two particles attached
Physics 351, Spring 2017, Homework #4. Due at start of class, Friday, February 10, 2017
 Physics 351, Spring 2017, Homework #4. Due at start of class, Friday, February 10, 2017 Course info is at positron.hep.upenn.edu/p351 When you finish this homework, remember to visit the feedback page
Physics 351, Spring 2017, Homework #4. Due at start of class, Friday, February 10, 2017 Course info is at positron.hep.upenn.edu/p351 When you finish this homework, remember to visit the feedback page
HW 6 Mathematics 503, Mathematical Modeling, CSUF, June 24, 2007
 HW 6 Mathematics 503, Mathematical Modeling, CSUF, June 24, 2007 Nasser M. Abbasi June 15, 2014 Contents 1 Problem 1 (section 3.5,#9, page 197 1 2 Problem 1 (section 3.5,#9, page 197 7 1 Problem 1 (section
HW 6 Mathematics 503, Mathematical Modeling, CSUF, June 24, 2007 Nasser M. Abbasi June 15, 2014 Contents 1 Problem 1 (section 3.5,#9, page 197 1 2 Problem 1 (section 3.5,#9, page 197 7 1 Problem 1 (section
PHY 5246: Theoretical Dynamics, Fall September 28 th, 2015 Midterm Exam # 1
 Name: SOLUTIONS PHY 5246: Theoretical Dynamics, Fall 2015 September 28 th, 2015 Mierm Exam # 1 Always remember to write full work for what you do. This will help your grade in case of incomplete or wrong
Name: SOLUTIONS PHY 5246: Theoretical Dynamics, Fall 2015 September 28 th, 2015 Mierm Exam # 1 Always remember to write full work for what you do. This will help your grade in case of incomplete or wrong
HANDOUT #12: THE HAMILTONIAN APPROACH TO MECHANICS
 MATHEMATICS 7302 (Analytical Dynamics) YEAR 2016 2017, TERM 2 HANDOUT #12: THE HAMILTONIAN APPROACH TO MECHANICS These notes are intended to be read as a supplement to the handout from Gregory, Classical
MATHEMATICS 7302 (Analytical Dynamics) YEAR 2016 2017, TERM 2 HANDOUT #12: THE HAMILTONIAN APPROACH TO MECHANICS These notes are intended to be read as a supplement to the handout from Gregory, Classical
NTNU Trondheim, Institutt for fysikk
 NTNU Trondheim, Institutt for fysikk Examination for FY3464 Quantum Field Theory I Contact: Michael Kachelrieß, tel. 99890701 Allowed tools: mathematical tables Some formulas can be found on p.2. 1. Concepts.
NTNU Trondheim, Institutt for fysikk Examination for FY3464 Quantum Field Theory I Contact: Michael Kachelrieß, tel. 99890701 Allowed tools: mathematical tables Some formulas can be found on p.2. 1. Concepts.
L = 1 2 a(q) q2 V (q).
 Physics 3550, Fall 2011 Motion near equilibrium - Small Oscillations Relevant Sections in Text: 5.1 5.6 Motion near equilibrium 1 degree of freedom One of the most important situations in physics is motion
Physics 3550, Fall 2011 Motion near equilibrium - Small Oscillations Relevant Sections in Text: 5.1 5.6 Motion near equilibrium 1 degree of freedom One of the most important situations in physics is motion
In which we count degrees of freedom and find the normal modes of a mess o masses and springs, which is a lovely model of a solid.
 Coupled Oscillators Wednesday, 26 October 2011 In which we count degrees of freedom and find the normal modes of a mess o masses and springs, which is a lovely model of a solid. Physics 111 θ 1 l k θ 2
Coupled Oscillators Wednesday, 26 October 2011 In which we count degrees of freedom and find the normal modes of a mess o masses and springs, which is a lovely model of a solid. Physics 111 θ 1 l k θ 2
Canonical transformations (Lecture 4)
 Canonical transformations (Lecture 4) January 26, 2016 61/441 Lecture outline We will introduce and discuss canonical transformations that conserve the Hamiltonian structure of equations of motion. Poisson
Canonical transformations (Lecture 4) January 26, 2016 61/441 Lecture outline We will introduce and discuss canonical transformations that conserve the Hamiltonian structure of equations of motion. Poisson
Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be.
 Chapter 4 Energy and Stability 4.1 Energy in 1D Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be T = 1 2 mẋ2 and the potential energy
Chapter 4 Energy and Stability 4.1 Energy in 1D Consider a particle in 1D at position x(t), subject to a force F (x), so that mẍ = F (x). Define the kinetic energy to be T = 1 2 mẋ2 and the potential energy
8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS
 8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS Lecturer: McGreevy Scribe: Francesco D Eramo October 16, 2008 Today: 1. the boundary of AdS 2. Poincaré patch 3. motivate boundary
8.821 F2008 Lecture 12: Boundary of AdS; Poincaré patch; wave equation in AdS Lecturer: McGreevy Scribe: Francesco D Eramo October 16, 2008 Today: 1. the boundary of AdS 2. Poincaré patch 3. motivate boundary
Linear Differential Equations. Problems
 Chapter 1 Linear Differential Equations. Problems 1.1 Introduction 1.1.1 Show that the function ϕ : R R, given by the expression ϕ(t) = 2e 3t for all t R, is a solution of the Initial Value Problem x =
Chapter 1 Linear Differential Equations. Problems 1.1 Introduction 1.1.1 Show that the function ϕ : R R, given by the expression ϕ(t) = 2e 3t for all t R, is a solution of the Initial Value Problem x =
Solution Set Two. 1 Problem #1: Projectile Motion Cartesian Coordinates Polar Coordinates... 3
 : Solution Set Two Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein October 7, 2015 Contents 1 Problem #1: Projectile Motion. 2 1.1 Cartesian Coordinates....................................
: Solution Set Two Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein October 7, 2015 Contents 1 Problem #1: Projectile Motion. 2 1.1 Cartesian Coordinates....................................
Coupled Oscillators Monday, 29 October 2012 normal mode Figure 1:
 Coupled Oscillators Monday, 29 October 2012 In which we count degrees of freedom and find the normal modes of a mess o masses and springs, which is a lovely model of a solid. Physics 111 θ 1 l m k θ 2
Coupled Oscillators Monday, 29 October 2012 In which we count degrees of freedom and find the normal modes of a mess o masses and springs, which is a lovely model of a solid. Physics 111 θ 1 l m k θ 2
Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th)
 Chapter 5 Magnetostatics Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th) 5.1 Biot-Savart Law So far we were concerned with static configuration of charges known as electrostatics. We now switch to
Chapter 5 Magnetostatics Problem Set #5: 5.7,5.9,5.13 (Due Monday, April 8th) 5.1 Biot-Savart Law So far we were concerned with static configuration of charges known as electrostatics. We now switch to
[#1] R 3 bracket for the spherical pendulum
![[#1] R 3 bracket for the spherical pendulum [#1] R 3 bracket for the spherical pendulum](/thumbs/92/108356856.jpg) .. Holm Tuesday 11 January 2011 Solutions to MSc Enhanced Coursework for MA16 1 M3/4A16 MSc Enhanced Coursework arryl Holm Solutions Tuesday 11 January 2011 [#1] R 3 bracket for the spherical pendulum
.. Holm Tuesday 11 January 2011 Solutions to MSc Enhanced Coursework for MA16 1 M3/4A16 MSc Enhanced Coursework arryl Holm Solutions Tuesday 11 January 2011 [#1] R 3 bracket for the spherical pendulum
Hamiltonian. March 30, 2013
 Hamiltonian March 3, 213 Contents 1 Variational problem as a constrained problem 1 1.1 Differential constaint......................... 1 1.2 Canonic form............................. 2 1.3 Hamiltonian..............................
Hamiltonian March 3, 213 Contents 1 Variational problem as a constrained problem 1 1.1 Differential constaint......................... 1 1.2 Canonic form............................. 2 1.3 Hamiltonian..............................
15. Hamiltonian Mechanics
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 15. Hamiltonian Mechanics Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 15. Hamiltonian Mechanics Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
Fourier transforms, Generalised functions and Greens functions
 Fourier transforms, Generalised functions and Greens functions T. Johnson 2015-01-23 Electromagnetic Processes In Dispersive Media, Lecture 2 - T. Johnson 1 Motivation A big part of this course concerns
Fourier transforms, Generalised functions and Greens functions T. Johnson 2015-01-23 Electromagnetic Processes In Dispersive Media, Lecture 2 - T. Johnson 1 Motivation A big part of this course concerns
arxiv:gr-qc/ v1 22 Jul 1994
 A COMPARISON OF TWO QUANTIZATION PROCEDURES FOR LINEAL GRAVITY Eric Benedict arxiv:gr-qc/9407035v1 22 Jul 1994 Department of Physics Boston University 590 Commonwealth Avenue Boston, Massachusets 02215
A COMPARISON OF TWO QUANTIZATION PROCEDURES FOR LINEAL GRAVITY Eric Benedict arxiv:gr-qc/9407035v1 22 Jul 1994 Department of Physics Boston University 590 Commonwealth Avenue Boston, Massachusets 02215
Department of Physics
 Department of Physics PHYS101-051 FINAL EXAM Test Code: 100 Tuesday, 4 January 006 in Building 54 Exam Duration: 3 hrs (from 1:30pm to 3:30pm) Name: Student Number: Section Number: Page 1 1. A car starts
Department of Physics PHYS101-051 FINAL EXAM Test Code: 100 Tuesday, 4 January 006 in Building 54 Exam Duration: 3 hrs (from 1:30pm to 3:30pm) Name: Student Number: Section Number: Page 1 1. A car starts
Physics 127b: Statistical Mechanics. Landau Theory of Second Order Phase Transitions. Order Parameter
 Physics 127b: Statistical Mechanics Landau Theory of Second Order Phase Transitions Order Parameter Second order phase transitions occur when a new state of reduced symmetry develops continuously from
Physics 127b: Statistical Mechanics Landau Theory of Second Order Phase Transitions Order Parameter Second order phase transitions occur when a new state of reduced symmetry develops continuously from
Chaotic motion. Phys 420/580 Lecture 10
 Chaotic motion Phys 420/580 Lecture 10 Finite-difference equations Finite difference equation approximates a differential equation as an iterative map (x n+1,v n+1 )=M[(x n,v n )] Evolution from time t
Chaotic motion Phys 420/580 Lecture 10 Finite-difference equations Finite difference equation approximates a differential equation as an iterative map (x n+1,v n+1 )=M[(x n,v n )] Evolution from time t
THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS
 THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS ALEXANDER TOLISH Abstract. Newton s Laws of Motion, which equate forces with the timerates of change of momenta, are a convenient way to describe mechanical
THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS ALEXANDER TOLISH Abstract. Newton s Laws of Motion, which equate forces with the timerates of change of momenta, are a convenient way to describe mechanical
Symmetries 2 - Rotations in Space
 Symmetries 2 - Rotations in Space This symmetry is about the isotropy of space, i.e. space is the same in all orientations. Thus, if we continuously rotated an entire system in space, we expect the system
Symmetries 2 - Rotations in Space This symmetry is about the isotropy of space, i.e. space is the same in all orientations. Thus, if we continuously rotated an entire system in space, we expect the system
ANALYTISK MEKANIK I HT 2014
 Karlstads Universitet Fysik ANALYTISK MEKANIK I HT 2014 Kursens kod: FYGB08 Undervisande lärare: Jürgen Fuchs rum 21F 316 tel. 054-700 1817 el.mail: jfuchs@fuchs.tekn.kau.se FYGB08 HT 2014 Exercises 1
Karlstads Universitet Fysik ANALYTISK MEKANIK I HT 2014 Kursens kod: FYGB08 Undervisande lärare: Jürgen Fuchs rum 21F 316 tel. 054-700 1817 el.mail: jfuchs@fuchs.tekn.kau.se FYGB08 HT 2014 Exercises 1
7 Pendulum. Part II: More complicated situations
 MATH 35, by T. Lakoba, University of Vermont 60 7 Pendulum. Part II: More complicated situations In this Lecture, we will pursue two main goals. First, we will take a glimpse at a method of Classical Mechanics
MATH 35, by T. Lakoba, University of Vermont 60 7 Pendulum. Part II: More complicated situations In this Lecture, we will pursue two main goals. First, we will take a glimpse at a method of Classical Mechanics
Hamilton-Jacobi Formulation of A Non-Abelian Yang-Mills Theories
 EJTP 5, No. 17 (2008) 65 72 Electronic Journal of Theoretical Physics Hamilton-Jacobi Formulation of A Non-Abelian Yang-Mills Theories W. I. Eshraim and N. I. Farahat Department of Physics Islamic University
EJTP 5, No. 17 (2008) 65 72 Electronic Journal of Theoretical Physics Hamilton-Jacobi Formulation of A Non-Abelian Yang-Mills Theories W. I. Eshraim and N. I. Farahat Department of Physics Islamic University
Quantum Field Theory II
 Quantum Field Theory II T. Nguyen PHY 391 Independent Study Term Paper Prof. S.G. Rajeev University of Rochester April 2, 218 1 Introduction The purpose of this independent study is to familiarize ourselves
Quantum Field Theory II T. Nguyen PHY 391 Independent Study Term Paper Prof. S.G. Rajeev University of Rochester April 2, 218 1 Introduction The purpose of this independent study is to familiarize ourselves
Physics 106a, Caltech 4 December, Lecture 18: Examples on Rigid Body Dynamics. Rotating rectangle. Heavy symmetric top
 Physics 106a, Caltech 4 December, 2018 Lecture 18: Examples on Rigid Body Dynamics I go through a number of examples illustrating the methods of solving rigid body dynamics. In most cases, the problem
Physics 106a, Caltech 4 December, 2018 Lecture 18: Examples on Rigid Body Dynamics I go through a number of examples illustrating the methods of solving rigid body dynamics. In most cases, the problem
Quantization of Scalar Field
 Quantization of Scalar Field Wei Wang 2017.10.12 Wei Wang(SJTU) Lectures on QFT 2017.10.12 1 / 41 Contents 1 From classical theory to quantum theory 2 Quantization of real scalar field 3 Quantization of
Quantization of Scalar Field Wei Wang 2017.10.12 Wei Wang(SJTU) Lectures on QFT 2017.10.12 1 / 41 Contents 1 From classical theory to quantum theory 2 Quantization of real scalar field 3 Quantization of
1 Hamiltonian formalism
 1 Hamiltonian formalism 1.1 Hamilton s principle of stationary action A dynamical system with a finite number n degrees of freedom can be described by real functions of time q i (t) (i =1, 2,..., n) which,
1 Hamiltonian formalism 1.1 Hamilton s principle of stationary action A dynamical system with a finite number n degrees of freedom can be described by real functions of time q i (t) (i =1, 2,..., n) which,
Linear Response and Onsager Reciprocal Relations
 Linear Response and Onsager Reciprocal Relations Amir Bar January 1, 013 Based on Kittel, Elementary statistical physics, chapters 33-34; Kubo,Toda and Hashitsume, Statistical Physics II, chapter 1; and
Linear Response and Onsager Reciprocal Relations Amir Bar January 1, 013 Based on Kittel, Elementary statistical physics, chapters 33-34; Kubo,Toda and Hashitsume, Statistical Physics II, chapter 1; and
Phase transitions and critical phenomena
 Phase transitions and critical phenomena Classification of phase transitions. Discontinous (st order) transitions Summary week -5 st derivatives of thermodynamic potentials jump discontinously, e.g. (
Phase transitions and critical phenomena Classification of phase transitions. Discontinous (st order) transitions Summary week -5 st derivatives of thermodynamic potentials jump discontinously, e.g. (
Principles of Dynamics. Tom Charnock
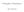 Principles of Dynamics Tom Charnock Contents 1 Coordinates, Vectors and Matrices 4 1.1 Cartesian Coordinates...................................... 4 1. Polar Coordinates........................................
Principles of Dynamics Tom Charnock Contents 1 Coordinates, Vectors and Matrices 4 1.1 Cartesian Coordinates...................................... 4 1. Polar Coordinates........................................
An Exactly Solvable 3 Body Problem
 An Exactly Solvable 3 Body Problem The most famous n-body problem is one where particles interact by an inverse square-law force. However, there is a class of exactly solvable n-body problems in which
An Exactly Solvable 3 Body Problem The most famous n-body problem is one where particles interact by an inverse square-law force. However, there is a class of exactly solvable n-body problems in which
Exercise 1 Classical Bosonic String
 Exercise 1 Classical Bosonic String 1. The Relativistic Particle The action describing a free relativistic point particle of mass m moving in a D- dimensional Minkowski spacetime is described by ) 1 S
Exercise 1 Classical Bosonic String 1. The Relativistic Particle The action describing a free relativistic point particle of mass m moving in a D- dimensional Minkowski spacetime is described by ) 1 S
Massachusetts Institute of Technology Department of Physics. Final Examination December 17, 2004
 Massachusetts Institute of Technology Department of Physics Course: 8.09 Classical Mechanics Term: Fall 004 Final Examination December 17, 004 Instructions Do not start until you are told to do so. Solve
Massachusetts Institute of Technology Department of Physics Course: 8.09 Classical Mechanics Term: Fall 004 Final Examination December 17, 004 Instructions Do not start until you are told to do so. Solve
Lecture 9 - Rotational Dynamics
 Lecture 9 - Rotational Dynamics A Puzzle... Angular momentum is a 3D vector, and changing its direction produces a torque τ = dl. An important application in our daily lives is that bicycles don t fall
Lecture 9 - Rotational Dynamics A Puzzle... Angular momentum is a 3D vector, and changing its direction produces a torque τ = dl. An important application in our daily lives is that bicycles don t fall
Mechanics IV: Oscillations
 Mechanics IV: Oscillations Chapter 4 of Morin covers oscillations, including damped and driven oscillators in detail. Also see chapter 10 of Kleppner and Kolenkow. For more on normal modes, see any book
Mechanics IV: Oscillations Chapter 4 of Morin covers oscillations, including damped and driven oscillators in detail. Also see chapter 10 of Kleppner and Kolenkow. For more on normal modes, see any book
Model building using Lie-point symmetries
 Model building using Lie-point symmetries Damien P. George Nikhef theory group Amsterdam, The Netherlands CERN LPCC Summer Institute 18 th August 2011 (arxiv:1105.4604) The Lie point symmetry method Want
Model building using Lie-point symmetries Damien P. George Nikhef theory group Amsterdam, The Netherlands CERN LPCC Summer Institute 18 th August 2011 (arxiv:1105.4604) The Lie point symmetry method Want
Dynamics of Relativistic Particles and EM Fields
 October 7, 2008 1 1 J.D.Jackson, Classical Electrodynamics, 3rd Edition, Chapter 12 Lagrangian Hamiltonian for a Relativistic Charged Particle The equations of motion [ d p dt = e E + u ] c B de dt = e
October 7, 2008 1 1 J.D.Jackson, Classical Electrodynamics, 3rd Edition, Chapter 12 Lagrangian Hamiltonian for a Relativistic Charged Particle The equations of motion [ d p dt = e E + u ] c B de dt = e
Classical Mechanics and Electrodynamics
 Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo December 2009 2 Preface These notes are prepared for the physics course FYS 3120,
Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo December 2009 2 Preface These notes are prepared for the physics course FYS 3120,
Special and General Relativity (PHZ 4601/5606) Fall 2018 Classwork and Homework. Every exercise counts 10 points unless stated differently.
 1 Special and General Relativity (PHZ 4601/5606) Fall 2018 Classwork and Homework Every exercise counts 10 points unless stated differently. Set 1: (1) Homework, due ( F ) 8/31/2018 before ( ) class. Consider
1 Special and General Relativity (PHZ 4601/5606) Fall 2018 Classwork and Homework Every exercise counts 10 points unless stated differently. Set 1: (1) Homework, due ( F ) 8/31/2018 before ( ) class. Consider
Physics GRE: Classical Mechanics. G. J. Loges 1. University of Rochester Dept. of Physics & Astronomy. xkcd.com/815/
 Physics GRE: Classical Mechanics G. J. Loges University of Rochester Dept. of Physics & Astronomy xkcd.com/85/ c Gregory Loges, 206 Contents Newtonian Mechanics. Kinematics..........................................2
Physics GRE: Classical Mechanics G. J. Loges University of Rochester Dept. of Physics & Astronomy xkcd.com/85/ c Gregory Loges, 206 Contents Newtonian Mechanics. Kinematics..........................................2
NATURAL SCIENCES TRIPOS. Past questions. EXPERIMENTAL AND THEORETICAL PHYSICS Minor Topics. (27 February 2010)
 NATURAL SCIENCES TRIPOS Part III Past questions EXPERIMENTAL AND THEORETICAL PHYSICS Minor Topics (27 February 21) 1 In one-dimension, the q-state Potts model is defined by the lattice Hamiltonian βh =
NATURAL SCIENCES TRIPOS Part III Past questions EXPERIMENTAL AND THEORETICAL PHYSICS Minor Topics (27 February 21) 1 In one-dimension, the q-state Potts model is defined by the lattice Hamiltonian βh =
Week 1, solution to exercise 2
 Week 1, solution to exercise 2 I. THE ACTION FOR CLASSICAL ELECTRODYNAMICS A. Maxwell s equations in relativistic form Maxwell s equations in vacuum and in natural units (c = 1) are, E=ρ, B t E=j (inhomogeneous),
Week 1, solution to exercise 2 I. THE ACTION FOR CLASSICAL ELECTRODYNAMICS A. Maxwell s equations in relativistic form Maxwell s equations in vacuum and in natural units (c = 1) are, E=ρ, B t E=j (inhomogeneous),
Gauge Fixing and Constrained Dynamics in Numerical Relativity
 Gauge Fixing and Constrained Dynamics in Numerical Relativity Jon Allen The Dirac formalism for dealing with constraints in a canonical Hamiltonian formulation is reviewed. Gauge freedom is discussed and
Gauge Fixing and Constrained Dynamics in Numerical Relativity Jon Allen The Dirac formalism for dealing with constraints in a canonical Hamiltonian formulation is reviewed. Gauge freedom is discussed and
Nonlinear Single-Particle Dynamics in High Energy Accelerators
 Nonlinear Single-Particle Dynamics in High Energy Accelerators Part 2: Basic tools and concepts Nonlinear Single-Particle Dynamics in High Energy Accelerators This course consists of eight lectures: 1.
Nonlinear Single-Particle Dynamics in High Energy Accelerators Part 2: Basic tools and concepts Nonlinear Single-Particle Dynamics in High Energy Accelerators This course consists of eight lectures: 1.
8.821 String Theory Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 8.81 String Theory Fall 008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 8.81 F008 Lecture 1: Boundary of AdS;
MIT OpenCourseWare http://ocw.mit.edu 8.81 String Theory Fall 008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 8.81 F008 Lecture 1: Boundary of AdS;
Lagrangian and Hamiltonian Mechanics (Symon Chapter Nine)
 Lagrangian and Hamiltonian Mechanics (Symon Chapter Nine Physics A301 Spring 2005 Contents 1 Lagrangian Mechanics 3 1.1 Derivation of the Lagrange Equations...................... 3 1.1.1 Newton s Second
Lagrangian and Hamiltonian Mechanics (Symon Chapter Nine Physics A301 Spring 2005 Contents 1 Lagrangian Mechanics 3 1.1 Derivation of the Lagrange Equations...................... 3 1.1.1 Newton s Second
Preliminaries: what you need to know
 January 7, 2014 Preliminaries: what you need to know Asaf Pe er 1 Quantum field theory (QFT) is the theoretical framework that forms the basis for the modern description of sub-atomic particles and their
January 7, 2014 Preliminaries: what you need to know Asaf Pe er 1 Quantum field theory (QFT) is the theoretical framework that forms the basis for the modern description of sub-atomic particles and their
Small oscillations and normal modes
 Chapter 4 Small oscillations and normal modes 4.1 Linear oscillations Discuss a generalization of the harmonic oscillator problem: oscillations of a system of several degrees of freedom near the position
Chapter 4 Small oscillations and normal modes 4.1 Linear oscillations Discuss a generalization of the harmonic oscillator problem: oscillations of a system of several degrees of freedom near the position
Assignment 6. Using the result for the Lagrangian for a double pendulum in Problem 1.22, we get
 Assignment 6 Goldstein 6.4 Obtain the normal modes of vibration for the double pendulum shown in Figure.4, assuming equal lengths, but not equal masses. Show that when the lower mass is small compared
Assignment 6 Goldstein 6.4 Obtain the normal modes of vibration for the double pendulum shown in Figure.4, assuming equal lengths, but not equal masses. Show that when the lower mass is small compared
