H =Π Φ L= Φ Φ L. [Φ( x, t ), Φ( y, t )] = 0 = Φ( x, t ), Φ( y, t )

Transcription

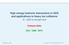
1 2.2 THE SPIN ZERO SCALAR FIELD We now turn to applying our quantization procedure to various free fields. As we will see all goes smoothly for spin zero fields but we will require some change in the CCR when we apply the rules to spin 1/2 fields; we will need CAR. Further modification will be required when we try to quantize spin 1 fields in a manifestly Lorentz covariant manner due to gauge invariance. First let s consider the case of a free scalar, spin zero, mass m, Hermitian field. As we have seen earlier it is described by the Lagrangian L = 1 2 µφ µ Φ 1 2 m2 Φ 2 (2.2.1) with the Euler-Lagrange equation ( 2 + m 2 )Φ(x) = 0. The canonical quantization rules state Π= L Φ = Φ and Π µ = L µ Φ = µ Φ. (2.2.2) So that the Hamiltonian density becomes H =Π Φ L= Φ Φ L H = 1 2 Φ Φ Φ+ 1 2 m2 Φ 2, (2.2.3) The equal time commutation relations are ] Π( x, t ), Φ( y, t )] = Φ( x, t ), Φ( y, t ) = iδ 3 ( x y ) ] Φ( x, t ), Φ( y, t )] = 0 = Φ( x, t ), Φ( y, t ) (2.2.4) The Euler-Lagrange equations are then equivalent to the Heisenberg equations of motion H, Φ(x)] = i Φ(x) H, Φ(x) ] = i Φ(x). (2.2.5) We can construct the energy-momentum tensor and angular momentum tensor as defined earlier according to our classical Noether s theorem ( T µν ν Φ ) L g µν L µ Φ 106

2 T µν = 1 2 ( µ Φ ν Φ+ ν Φ µ Φ) g µν L, (2.2.6) where we have written T µν in symmetric form. We can check explicitly that T µν is conserved by using the Euler-Lagrange equations of Φ µ T µν = Φ ν Φ+ 1 2 µ Φ µ ν Φ µ ν Φ µ Φ+ 1 2 ν Φ 2 Φ ν L = m2 2 Φ ν Φ m2 2 ν ΦΦ + 1. (2.2.7) 2 ν ( µ Φ µ Φ) ν L ( 1 = ν 2 µφ µ Φ 1 ) 2 m2 Φ 2 ν L =0 Even though T µν = T νµ there are still Belinfante improvement terms that one can add G ρµν = b (g µν ρ g ρν µ )Φ 2. (2.2.8) So and G ρµν = G µρν (2.2.9) ρ G ρµν = b ( g µν 2 µ ν) Φ 2 (2.2.10) Now the improved energy momentum tensor is given by Θ µν I = T µν + ρ G ρµν. (2.2.11) Usually b is chosen so that Θ λ Iλ = m2 Φ 2 but this is useful only when one considers conformal symmetries in addition to Poincare symmetries. The additional current for scale transformations is defined by D µ = x ν Θ µν I Now Θ λ Iλ = T λ λ +3b 2 Φ 2 = λ Φ λ Φ 2 λ Φ λ Φ+2m 2 Φ 2 +3b 2 Φ 2 µ D µ =Θ λ Iλ. (2.2.12) ( =2m 2 Φ 2 λ Φ λ Φ ) +Φ 2 Φ+3b 2 Φ 2 = Φ 2 +3b 2 Φ 2 + m 2 Φ 2 +Φ ( 2 + m 2) Φ 1. (2.2.13) 2 λ λ Φ, Φ] =(3b 1 2 ) 2 Φ 2 + m 2 Φ 2 107

3 Hence we choose So we have b = 1 6. (2.2.14) Θ µν I = T µν + 1 ( g µν 2 µ ν) Φ 2 6 µ Θ µν I =0 Θ µν I =Θ νµ I Θ λ Iλ = m 2 Φ 2. (2.2.15) The energy momentum operator is given by either T µν or Θ µν as P µ = d 3 xt 0µ 1 ( Φ) ] = d 3 x Φ ν Φ+ ν Φ g 0µ L 2 P µ = Now using the ETCR equations (2.2.4) we find d 3 x H, 1 ( Π i Φ+ i ΦΠ )]. (2.2.16) 2 T 0ν ( y, t ), Φ( x, t ) ] 1 ( = Φ( y, t ) ν Φ( y, t )+ ν Φ( y, t ) 2 Φ( y, t )) g 0ν 1 ] 2 Φ( y, t ) 2, Φ( x, t ) = i Φ(x)δ 3 ( x y ), ν =0 = i i Φ(x)δ 3 ( x y ), ν =1, 2, 3. that is So δ(x 0 y 0 ) T 0ν (y), Φ(x) ] = i ν Φ(x)δ 4 (x y). (2.2.17) P µ, Φ(x)] = i µ Φ(x) (2.2.18) as desired. Further the angular momentum tensor is M µνρ = x ν T µρ x ρ T µν 108

4 µ M µνρ =0 (2.2.19) since T µν = T νµ. The angular momentum operator is then M µν = d 3 xm 0µν = d 3 x ( x µ T 0ν x ν T 0µ). ( ) So we have using (2.2.17) M µν, Φ(x)] = i (x µ ν x ν µ )Φ(x). (2.2.20) Given these quantum field theoretic properties for the field operators we would like to further interpret the physical system being described by them. To do this let s go over to momentum space and expand the field operator Φ(x) = d 4 k (2π) 4 e ikx Φ(k). (2.2.21) Φ(x) obeys the Klein-Gordon equation ( 2 + m 2 )Φ(x) = 0 thus we should be expanding Φ(x) in terms of solutions to the K.G. equation ( 2 m 2 )Φ(x) =0= d 4 k (2π) 4 e ikx ( k 2 + m 2 ) Φ(k) (2.2.22) this implies Φ(k) =(2π)δ(k 2 m 2 )a( k,k 0 ) (2.2.23) with a( k,k 0 ) an operator coefficient, and hence As before we use Φ(x) = d 4 k (2π) 3 δ(k2 m 2 )a( k,k 0 )e ikx. (2.2.24) δ(k 2 m 2 )= 1 2ω k θ(k 0 )δ(k 0 ω k )+θ( k 0 )δ(k 0 + ω k ) ] (2.2.25) 109

5 with so that Φ(x) = = ω k =+ k 2 + m 2 (2.2.26) a( (2π) 3 2ω k,+ω k )e iω kx 0 +i k x + a( ] k, ω k )e +iω kx 0 +i k x k, (2.2.27) a( (2π) 3 2ω k,+ω k )e ikx + a( k, ω k )e +ikx] k where the second equality was obtained by letting k k in the second integral. But the field is Hermitian, Φ(x) =Φ (x), implying a ( k,+ω k )=a( k, ω k ), thus defining the operators a( k) a( k,+ω k ) a ( k)=a ( k,+ω k )=a( k, ω k ) (2.2.28) we have the hermitian form for the Fourier transform Φ(x) = a( (2π) 3 2ω k)e ikx + a ( ] k)e ikx k (2.2.29) where it is understood that k 2 = m 2 here, that is k 0 = ω k. We have expanded Φ(x) in terms of the positive frequency u k (x) =e ikx and negative frequency solutions v k (x) =u k (x) =e ikx of the Klein-Gordon equation ( 2 + m 2 )u k (x) =0 ( 2 + m 2 )v k (x) =0. (2.2.30) These have the orthogonality property (u k,u k )=i d 3 xu k (x) 0 u l (x) = d 3 x(ω l + ω k )e i(ω l ω k )x 0 e i( l k) x (2.2.31) =(2π) 3 2ω k where f µ g = f( µ g) ( µ f)g (2.2.32) 110

6 and the completeness relation d 3 k u (2π) 3 k (x)u 2ω k (y) = k (2π) 3 2ω k e ik(x y) = i + (x y) (2.2.33) which will be discussed in further detail later. Thus where Φ(x) =Φ + (x)+φ (x) (2.2.34) Φ + (x) Φ (x) (2π) 3 2ω k a( k)e ikx (2.2.35) (2π) 3 2ω k a ( k)e ikx (2.2.36) are the positive and negative frequency components respectively. Inverting the Fourier transform we find a( k)=i d 3 xe ikx 0 Φ(x) (2.2.37) a ( k)=i d 3 xφ(x) 0 e ikx. (2.2.38) So writing out the time derivatives, we have a( k)=i ] d 3 xe ikx Φ(x) iωk Φ(x) (2.2.39) a ( k)=i d 3 xe ikx iω k Φ(x) Φ(x) ]. (2.2.40) Note, since k 2 = m 2 the above integrals are indeed independent of time ȧ( k)=i = i = i = i ] d 3 xe iω ikx k Φ+ωkΦ+ Φ 2 iω k Φ ] d 3 xe ikx k 2 Φ+m 2 Φ+ Φ ]. (2.2.41) d 3 xe ikx 2 Φ+ Φ+m 2 Φ d 3 xe ikx ( 2 + m 2) Φ=0 111

7 We can evaluate the commutators for a( k) and a ( k) by using the equal time commutation relations equation (2.2.4) for Φ(x) and Φ(x). We secure a( k),a ( ] l ) =(2π) 3 2ω k δ 3 ( k l ) a( k),a( ] l ) =0= a ( k),a ( ] l ). (2.2.42) We obtain the harmonic oscillator creation operator a ( k) and annihilation operator a( k) commutation relations. We can also apply the energy-momentum commutation relation P µ, Φ(x)] = i µ Φ(x) (2.2.43) to a( k)and a ( k) to find P µ,a( ] k) = k µ a( k) P µ,a ( ] k) =+k µ a ( k). (2.2.44) Thus, if p >is an eigenstate of energy and momentum P µ p>= p µ p>, (2.2.45) then P µ a( k) p >= P µ,a( ] k) p >+a( k)p µ p> =( k µ + p µ )a(. (2.2.46) k) p > Hence P a( µ ] k) p > =(p µ k µ ) a( ] k) p > (2.2.47) and similarly P a µ ( ] k) p > =(p µ + k µ ) a ( ] k) p >, (2.2.48) thus a( k) p >is an eigenstate of P µ with energy-momentum (p k) µ and a ( k) p > is an eigenstate of P µ with energy-momentum (p + k) µ. Now we could keep acting on p >with annihilation operators, then ( P µ a( k 1 ) a( k N ) p >= p ) µ N k i a( k 1 ) a( k N ) p >. (2.2.49) i=1 112

8 Eventually P 0 = H will go negative!! However, H = d 3 x 1 Φ 2 + Φ 2 Φ+m ] 2 Φ 2 (2.2.50) is a positive operator. This implies that there is a lowest energy state so that, for some number N, we must have a( k) a( k 1 ) a( ] k N ) p > =0. (2.2.51) Denoting this lowest energy state, called the ground state or vacuum, by 0 > and its energy by E 0 and noting that its momentum is 0, we have for equation (2.2.51) a( k) 0 >= 0 (2.2.52) for all k. a ( k) 0 > then has the energy and momentum of a single particle relative to that of 0 >, H a ( ] k) 0 > =(E 0 + ω k ) a ( ] k) 0 > P a ( ] k) 0 > = k a ( ] k) 0 > (2.2.53) with ωk 2 = k 2 + m 2, the relativistic relation. Thus we interpret the state k> a ( ] k) 0 > as a single particle state with momentum k and mass m, hence energy ω k. Continuing, k 1, k 2 >= a (k 1 )a (k 2 ) 0 > (2.2.54) has energy and momentum H k 1, k 2 >=(E 0 + ω k1 + ω k2 ) k 1, k 2 > (2.2.55) P k 1, k 2 >=( k 1 + k 2 ) k 1, k 2 > (2.2.56) and represents states with two noninteracting particles each with momentum k i and energy ω ki. Continuing further, the N-particle states are given by k 1,, k N >= a ( k 1 ) a ( k N ) 0 > (2.2.57) with ( ) H k 1,, N k N >= E 0 + ω ki k 1,, k N > (2.2.58) i=1 113

9 ( N ) P k 1,, k N >= ki k 1,, k N >. (2.2.59) i=1 Thus, we can define the number density operator as N ( k)= 1 (2π) 3 2ω k a ( k)a( k) (2.2.60) with N ( k),a( ] k ) = δ 3 ( k k )a( k) (2.2.61) N ( k),a ( ] k ) =+δ( k k )a ( k). (2.2.62) So operating on the N-particle state gives N ( k) k 1,, k N >= δ 3 ( k k 1 )+ + δ 3 ( k ] k N ) k 1,, k N >, (2.2.63) N ( k) equals the number of particles per unit volume in momentum space with momentum k. Therefore, N ( k) (2.2.64) is equal to the number of particles with momentum differentially close to k. Hence, the total number operator is given by N = N ( k)= (2π) 3 2ω k a ( k)a( k) (2.2.65) and N k 1,, k N >= N k 1,, k N >. (2.2.66) So a ( k) increases the number of particles by creating a particle with momentum k and energy ωk while a( k) decreases the number of particles by annihilating a particle with momentum k and energy ω k. For further insight into the vacuum energy E 0 let s Fourier transform our expression for the energy momentum operator P µ P 0 = H = 1 d 3 x 2 Φ Φ 2 Φ+ 1 ] 2 m2 Φ 2 114

10 P = d 3 x 1 2 Φ Φ+ Φ Φ]. (2.2.67) First the momentum operator P = d 3 d 3 l 1 x iωk (2π) 3 2ω k (2π) 3 a( 2ω l 2 k)e ikx + iω k a ( k)e +ikx] i la( l )e ilx i la ( l )e ilx] + interchange d 3 l = (2π) 3 2ω k (2π) 3 d 3 x 1 ωk la( k)a( l )e i(k+l ) x 2ω l 2 + ω k la( k)a ( l )e i(k l )x + ω k la ( k)a( i(k l )x l )e ω k la ( k)a ( l )e i(k+l )x]. (2.2.68) + interchange d 3 l 1 = (2π) 3 δ 3 ( (2π) 3 2ω k (2π) 3 2ω l 2 k + l )e i2ω kx 0 (+ω k k)a( k)a( k) +(2π) 3 δ 3 ( k + l )e i2ω kx 0 (ω k k)a ( k)a ( k) +(2π) 3 δ 3 ( k l ) ω k ka( k)a (+ k)+ω k ka ( k)a( k) ]] + interchange Thus we find P = + 1 (2π) 3 2ω k 2 k a( k)a ( k)+a ( k)a( ] k) 1 (2π) 3 2ω k 4 ( k e i2ω kx 0 a( k)a( k)+a( k)a( k) )] +e i2ω kx 0 ( a ( k)a ( k)+a ( k)a ( k) ). (2.2.69) The integrand of the second integral on the right hand side is odd in k and hence vanishes, yielding d P 3 k 1 = (2π) 3 2ω k 2 k a ( k)a( k)+a( k)a ( ] k). (2.2.70) Similarly, in this integral we can rearrange a( k)a ( k) since the commutator is even in k 1 ka( k)a ( 2 (2π) 3 2ω k)= 1 ka ( k 2 (2π) 3 2ω k)a( k) k + 1 k a( 2 (2π) 3 2ω k),a ( ] k) k 115

11 = 1 d 3 k ka ( 2 (2π) 3 2ω k)a( k)+ k(2π) 3 2ω k (2π) 3 k δ 3 ( 2ω k k) k = 1 ka ( 2 (2π) 3 2ω k)a( k). (2.2.71) k Consequently, we find the usual expression for the number operator of particles with momentum k times the momentum k d P 3 k = ka (2π) 3 ( 2ω k)a( k). (2.2.72) k Thus we find P 0 >= 0 since a( k) 0 >= 0, as previously stated. Next consider the Hamiltonian, after an integration by parts with vanishing surface term, 1 H = d 3 x 2 Φ 2 1 ] 2 Φ( 2 Φ m 2 Φ) (2.2.73) but Φ 2 Φ+m 2 Φ = 0, so 1 H = d 3 x 2 Φ 2 1 ] 2 Φ Φ. (2.2.74) Expanding the fields, we have H = 1 d 3 d 3 l x ωk 2 (2π) 3 2ω k (2π) 3 ω l a( 2ω k)a( i(k+l )x l )e k + ω k ω l a( k)a ( l )e i(k l )x + ω k ω l a ( k)a( l )e i(k l )x ω k ω l a ( k)a ( i(k+l )x l )e (a( k)e ikx + a ( k)e )( ω ikx l 2 a( l )e ilx ωl 2 a ( ) ] l )e ilx = 1 d 3 l { (2π) 3 δ 3 ( 2 (2π) 3 2ω k (2π) 3 2ω k + ( l )( ωk) 2 e i2ω kx 0 a( k)a( k) l +e i2ω kx 0 a ( k)a ( ) k) + ωkδ 2 3 ( k ( l ) a( k)a ( k)+a ( k)a( ). k) + ωk 2 δ 3 ( k + l ) (a( k)a( k)e 2iω kx 0 + a ( k)a ( k)e +i2ω kx 0) +δ( k ( l ) a( k)a ( k)+a ( k)a(+ )]} k) = = 1 (2π) 3 2ω k 2 ω k a( k)a ( k)+a ( k)a( ] k) (2π) 3 2ω k ω k a ( k)a( k)+ (2π) 3 2ω k 1 2 ω k(2π) 3 2ω k δ 3 (0) 116 (2.2.75)

12 That is we finally find H = d 3 k ω (2π) 3 k a ( 2ω k)a( k)+ k 1 2 ω kδ 3 (0). (2.2.76) Thus when acting on the lowest energy state 0 > defined by a( k) 0 >= 0, we have ( H 0 >= 1 ) 2 ω kδ 3 (0) 0 >= E 0 0 >, (2.2.77) hence E 0 = 1 2 ω kδ 3 (0) = = constant. (2.2.78) One way to look at this is that the vacuum contains an infinite zero point energy from the infinite number of harmonic oscillators in the Hamiltonian and that all measurements are made relative to this vacuum state i.e. only differences in energy are measured so that the infinite constant does not matter. Alternatively, the Hamiltonian is defined only up to a constant, the zero of energy being arbitrary. Thus, we can define another Hamiltonian as Ĥ H E 0, the lowest energy state, defined by a( k) 0 >= 0, having zero energy Ĥ 0 >= 0. Physically it is reasonable to define the no particle state, the vacuum, 0 >, which is the lowest energy state as having zero as its energy and momentum a( k) 0 >= 0 (2.2.79) and Ĥ 0 >= 0 (2.2.80) P 0 >= 0 (2.2.81) so that the vacuum is space-time translation invariant U(a, 1) 0 >= 0 >. Mathematically what we are finding is that the formal manipulations of writing a Lagrangian and a Hamiltonian for quantum fields in analogy to classical fields or even quantum mechanical systems with a finite number of degrees of freedom must be modified. The problem arises from the products of field operators at the same space-time point as in the Lagrangian or the Hamiltonian (this follows from the equal time commutation relations Φ( x, t ), Φ( y, t )] = iδ 3 ( x y ) 117

13 for x y ). For noninteracting fields we can easily eliminate these difficulties by defining the products of the fields more carefully. In the interacting case it is more difficult but possible and comprises the subject of renormalization theory. A well defined product of free fields is given by the normal ordering or Wick ordering of the fields. For example, the normal product denoted NΦ 2 (x)] or : Φ 2 (x) : (or NΦ(x)Φ(y)] for that matter) is defined so that all annihilation operators in the product are to the right of all the creation operators, hence, NΦ 2 (x)] = Φ + (x)φ + (x)+φ (x)φ (x) +2Φ (x)φ + (x) (2.2.81) so that the vacuum expectation value of a normal product vanishes On the other hand < 0 NΦ 2 (x)] 0 >= 0. (2.2.82) Φ 2 (x) =Φ + (x)φ + (x)+φ (x)φ (x) +Φ (x)φ + (x) +Φ + (x)φ (x). (2.2.83) Thus, we can relate the two products NΦ 2 (x)] = Φ 2 (x) +Φ (x), Φ + (x)]. (2.2.84) In terms of the Fourier transform creation and annihilation operators we have Na( k)a ( k)] = a ( k)a( k)=na ( k)a( k)]. (2.2.85) So for the product at zero momentum we have d 3 xnφ 2 (x)] = d 3 x ( Φ 2 (x)+φ (x), Φ + (x)] ). (2.2.86) But d 3 xφ (x), Φ + (x)] = d 3 x (2π) 3 2ω k = (2π) 3 2ω k = d 3 l (2π) 3 2ω l e i(k l )x a ( k),a( l )] d 3 l (2π) 3 2ω l (2π) 3 δ 3 ( k l )a ( k),a( l )] (2π) 3 2ω k (2π) 3 δ 3 (0) 118 (2.2.87)

14 which is just the type of singularity we are finding in the Hamiltonian and this normal ordering can be used to eliminate the singularity in H! Thus, the well defined product of field operators making up the Hamiltonian is Ĥ = NH]. (2.2.88) Similarly, the Lagrangian should be defined with normal ordering ˆL = NL] (2.2.89) as well as all other composite operators ˆT µν = NT µν ] (2.2.90) ˆM µνρ = NM µνρ ]. (2.2.91) The field equations in the free field case stay the same since this normal ordering of H just corresponds, as we have seen, to the addition of an infinite constant to the naive Hamiltonian. So ( 2 + m 2) Φ(x) =0 (2.2.92) still holds. Fourier transforming we now obtain directly that Ĥ = ˆ P = P = (2π) 3 2ω k ω k a ( k)a( k) (2.2.93) (2π) 3 2ω k ka ( k)a( k) (2.2.94) and Ĥ 0 >= 0 and ˆ P 0 >= 0. All conservation equations stay intact and ˆPµ = NP µ ] still generates the space-time translations. Following our quantization rules for free fields we must Wick or normal order all products of field operators to make them well defined in the limit of coincident points. (Of course we could have started in momentum space as in the introduction then this would have been the natural order to appear!) The general definition of NΦ(x 1 ) Φ(x N )] is to rearrange all creation operators to the left and all annihilation operators to the right (the order among creation operators is irrelevant since they commute and similarly for the annihilation operators). To summarize 119

15 the free scalar field case then, we define the dynamics through the normal product of a formal Lagrangian L = L(Φ r, µ Φ r ), (2.2.95) with the normal ordered Lagrangian given by ˆL = NL]. (2.2.96) The Euler-Lagrange equations are the same in the free field case ˆL ˆL µ = L L µ =0 (2.2.97) Φ r µ Φ r Φ r µ Φ r and so is the momentum Π r L Φ. (2.2.98) r The canonical commutation relations are Π r ( x, t ), Φ s ( y, t )] = iδ rs δ 3 ( x y ) Π r ( x, t ), Π s ( y, t )] = 0 = Φ r ( x, t ), Φ s ( y, t )]. (2.2.99) The Hamiltonian density becomes the normal product of the classical formal Hamiltonian Ĥ = NH] =NΠ r Φ r ] ˆL H =Π r Φ r L ( ) and Ĥ = d 3 xnh]. ( ) The quantum action principle and quantum Noether s theorem have the same form except N-products appear on all operator products (note that operator ordering does not matter in a normal product since the N operator normal orders all products) ˆT µν = NT µν ] T µν = L µ Φ ν Φ g µν L. ( ) 120

16 One can prove that µ ˆT µν = 0 since T µν and ˆT µν differ by a constant (the only change is E 0 from H) and since the operators are normal ordered ˆT µν = ˆT νµ. Further the energy-momentum operator is given by ˆP µ = d 3 x ˆT 0µ ( ) with ˆP µ, Φ(x)] = i µ Φ(x). ( ) Similarly, the angular momentum tensor is defined by ˆM µνρ = x ν ˆT µρ x ρ ˆT µν ( ) with µ ˆM µνρ =0 ( ) and the angular momentum operator is ˆM µν = d 3 x ˆM 0µν ( ) with ˆM µν, Φ(x)] = i(x µ ν x ν µ )Φ(x). ( ) The particle states of the system are given by the vacuum state 0 > defined as the no particle state a( k) 0 >= 0 with Ĥ 0 >= 0= ˆP 0 >.The N-particle state is given by k 1,, k N >= a ( k 1 ) a ( k N ) 0 >.The inner product is given in terms of the one particle subspace and < 0 0 >= 1 so that < k k >=(2π) 3 2ω k δ 3 ( k k ). ( ) Finally, we can see that the spin of the particle is zero by considering the action of the angular momentum operator (the generator of rotations in coordinate space) on the one particle state k>. Recall from the review of relativity and quantum mechanics that ˆMµν, Φ(x)] = i(x µ ν x ν µ )Φ(x) M µν Φ(x). ( ) 121

17 The angular momentum operator is given by J i 1 2 ɛ ijk ˆM jk ( ) and is represented on the fields as space-time differential operators The operators obey the angular momentum algebra J i 1 2 ɛ ijkm jk = i( x ) i. ( ) J i, J j ]=iɛ ijk J k ( ) and J generates spatial rotations on the states and field as represented by the unitary operator U r ( θ)=e i θ J. ( ) Fourier transforming the field we find ˆM ij, Φ(x)] = i(x i j x j i ) = So for the creation operator this yields e ikx a( (2π) 3 2ω k)+e +ikx a ( ] k) k (2π) 3 2ω k ( i)e ikx (k j i k ki j k )a( k) +e ikx (k j i k k i j k )a ( k)]. ( ) ˆM ij,a ( k)] = +i(k i j k kj i k)a ( k). ( ) Hence, for rotations or in vector notation J i,a ( k)] = iɛ ijl k j l ka ( k) ( ) J,a ( k)] = i k k a ( k). ( ) For a particle at rest, i.e. in the particle s rest frame, k = 0. So J,a (0)] = 0 ( ) 122

18 and since J 0 >= 0 J k =0>= 0. ( ) The angular momentum as measured in the rest frame is zero and hence the spin is zero, therefore, in general the totat angular momentum J k>= i k k k> ( ) is just the orbital angular momentum L = r p, the spin is equal to zero. Thus, the free hermitian, scalar field Φ(x) describes a system of non-interacting, mass m, spinless particles. Let s return to the equal time quantization conditions and show that our quantization procedure, although it singles out time, is Lorentz invariant due to the scalar nature of the field and the invariance of the field equations. (Although we have chosen an equal time surface on which to specify these initial conditions, the quantization conditions can be specified in terms of general space-like surfaces and hence be made to appear explicitly covariant.) The fact that the field is a scalar under restricted Poincare transformations implies P µ, Φ(x)] = i µ Φ(x) M µν, Φ(x)] = i(x µ ν x ν µ )Φ(x). ( ) Thus, finite transformations are given by the action of the unitary operator and according to ( ) implies U(a, Λ) = e ip µa µ e i 2 ω µν (Λ)M µν ( ) e i 2 ω µν M µν Φ(x)e i 2 ω µνm µν = Φ(Λx) e ip µa µ Φ(y)e ip µa µ =Φ(y + a) ( ) that is U (a, Λ)Φ(Λx + a)u(a, Λ) = Φ(x). ( ) As we have seen the field equation leads to the momentum decomposition Φ(x) = a( (2π) 3 2ω k)e ikx + a ( ] k)e +ikx k 123

19 =Φ + (x) +Φ (x) ( ) which can be used to calculate the all-time commutator of Φ(x) and Φ(y) Φ(x), Φ(y)] = Φ + (x), Φ (y) ] + Φ (x), Φ + (y) ] ( ) since a( k),a( l)] = 0 or Φ + (x), Φ + (y)] = 0 = Φ (x), Φ (y)]. Now Φ + (x), Φ d 3 l (y)] = e ikx e +ily a( (2π) 3 2ω k (2π) 3 2ω k),a ( l )], ( ) l but the creation and annihilation operator commutation relation a( k),a ( k)] = (2π) 3 2ω k δ 3 ( k l ) ( ) may be used to obtain Φ + (x), Φ (y)] = d 3 x (2π) 3 2ω k e ik(x y) i + (x y). ( ) This function appears often and so we have given it a special symbol i + (x y) e ik(x y). ( ) (2π) 3 2ω k Using δ(k 2 m 2 )= 1 2ω k δ(k 0 ω k )+δ(k 0 + ω k )] we have i + (x y) = d 4 k (2π) 4 2πδ(k2 m 2 )θ(k 0 )e ik(x y). ( ) Note that under restricted Poincare transformations this is invariant since k 0 does not change sign under such transformations and all other terms are manifestly invariant. We also need Φ (x), Φ + (y)] = i + (y x) = = (2π) 3 2ω k e +ik(x y) d 4 k (2π) 4 (2π)δ(k2 m 2 )θ( k 0 )e ik(x y) +i (x y). ( ) 124

20 As seen from above the function is given by (x y) = + (y x) ( ) and is also P + invariant. The all time field commutator is given by the sum of + and and is just a c-number Φ(x), Φ(y)] = i + (x y)+i (x y) = i( + (x y)+ (x y)). ( ) i (x y) Thus, (x y) is restricted Poincare (P +) invariant. This also follows directly from Φ(x) being a scalar field and (x y) being a c-number U(a, Λ) Φ(x), Φ(y)] U (a, Λ) = Φ(Λx + a), Φ(Λy + a)] = i (Λ(x y)) = U(a, Λ)i (x y)u (a, Λ). = i (x y) ( ) So adding and subtracting a µ,wehave (x y) = (Λx + a] Λy + a]), ( ) hence (x y) isp + invariant. We can now represent (x y) in several ways which will be useful later on, for instance (x y) = i = 2 = 2 ] e ik(x y) e +ik(x y) (2π) 3 2ω k (2π) 3 2ω k sin k(x y) (2π) 3 2ω k e +i k ( x y ) sin ω k (x 0 y 0 ) Alternately we can express as an energy-momentum integral i (x y) =. ( ) d 4 k (2π) 4 2πδ(k2 m 2 )e ik(x y) θ(k 0 ) θ( k 0 ) ]. ( ) 125

21

22 It satisfies the initial conditions ( x, 0) = ( 0, 0) = 0 ( ) since Further Φ( x, t ), Φ(0, t)] = 0. ( ) 1 ( x, t )= ω x0 (2π) 3 k e +i k x cos ω k t, ( ) ω k so at time t = 0, multiplying by i, we find t i ( x, t ) t=0 = i (2π) 3 e +i k x = iδ 3 ( x ). ( ) This is just the initial condition i ( x, 0) = Φ( x, t ), Φ( 0,t)] = iδ 3 ( x ), ( ) and of course ( x ], t ) t=0 = 0 since Φ( x, t ), Φ(0,t) = 0. Furthermore, we note that since (x y) = (Λ(x y)), ( ) and, for any space-like separation (x y) 2 transformation such that x 0 = y 0,wehave < 0, we can always find a Lorentz (x y) = ( x y, 0). ( ) From equation ( ) ( x, 0) = 0, thus (x y) = 0 for (x y) 2 < 0 ( ) and consequently Φ(x), Φ(y)] = 0 for (x y) 2 < 0. ( ) This space-like commutivity property is known as the principle of microcausality. For observables depending on Φ(x), two observations performed at space-like separations cannot interfere with each other. This is a statement of relativistic invariance since the theory of special relativity forbids signals with v > c from being sent 127

23

24

25 where k 0 = ω k is understood in the final integral. In addition to these covariant commutators we can also evaluate the vacuum expectation values of the fields and time ordered products of the fields. These play a fundamental role in quantum field theory since they are related to matrix elements of observables as we will see. First the vacuum expectation value of Φ(x)Φ(y), is simply related to + < 0 Φ(x)Φ(y) 0 >, ( ) < 0 Φ(x)Φ(y) 0 >=< 0 (Φ + (x)+φ (x))(φ + (y)+φ (y)) 0 > =< 0 Φ + (x)φ (y) 0 > ( ) since Φ + 0 >= 0 and < 0 Φ =0. Then since Φ + (x) 0 >= 0 we can replace Φ + Φ with the commutator < 0 Φ(x)Φ(y) 0 >=< 0 Φ + (x), Φ (y)] 0 >. ( ) Thus < 0 Φ(x)Φ(y) 0 >= Φ + (x), Φ (y)] = i + (x y) ( ) since < 0 0 >= 1 and the commutator is a c-number. This VEV of two fields is called the two point Wightman function, and is denoted W (2) (x, y). In general the n-point Wightman function is W (n) (x 1,,x n ) < 0 Φ(x 1 ) Φ(x n ) 0 >. ( ) We can evaluate this product by using the creation and annihiltion properties of Φ. Hence, using < 0 Φ (x 1 )=0andΦ + (x 1 ) 0 >= 0 and the fact that the commutator is a c-number, we have < 0 Φ(x 1 )Φ(x 2 ) Φ(x n ) 0 > =< 0 Φ + (x 1 )Φ(x 2 ) Φ(x n ) 0 >=< 0 Φ + (x 1 ), Φ(x 2 ) Φ(x n ) ] 0 > =< 0 Φ + (x 1 ), Φ(x 2 ) ] Φ(x 3 ) Φ(x n ) 0 > 130

26 = + < 0 Φ(x 2 ) Φ + (x 1 ), Φ(x 3 ) ] Φ(x 4 ) Φ(x n ) 0 > + + < 0 Φ(x 2 ) Φ(x i 1 ) Φ + (x 1 ), Φ(x i ) ] Φ(x i+1 ) Φ(x n ) 0 > + n Φ + (x 1 ), Φ (x i ) ] < 0 Φ(x 2 ) Φ(x i 1 )Φ(x i+1 ) Φ(x n ) 0 >. ( ) i=2 Thus, we have reduced W (n) (x 1,,x n )to + times W (n 2) (x i1,,x in 2 ). Proceeding until no fields are left we find { W (n) (x 1,,x n )= P W (2) (x i1,x j1 ) W (2) (x i n2,x j n2 ), n even ( ) 0,nodd where P is a sum over all permutations P of (1,,n) into n 2 pairs (i 1,j 1 ) (i n,j n ) with i <j 1,,in <j n and i <i 2 < <in. For example, the 4-point 2 Wightman function is W (4) (x 1,x 2,x 3,x 4 )= Φ + (x 1 ), Φ (x 2 ) ] < 0 Φ(x 3 )Φ(x 4 ) 0 > + Φ + (x 1 ), Φ (x 3 ) ] < 0 Φ(x 3 )Φ(x 4 ) 0 > + Φ + (x 1 ), Φ (x 4 ) ] < 0 Φ(x 2 )Φ(x 3 ) 0 > = W (2) (x 1,x 2 )W (2) (x 3,x 4 ) + W (2) (x 1,x 3 )W (2) (x 2,x 4 ) + W (2) (x 1,x 4 )W (2) (x 2,x 3 ). ( ) These product formulae for the Wightman functions are just special cases of the general reduction of a product of free fields in terms of Wick or Normal products of the free fields. The reduction formula is known as Wick s Theorem and is given by (here we have generalized to possibly different free fields denoted by subscript i, Φ i ) Wick s Theorem: + Φ 1 (x 1 )Φ 2 (x 2 ) Φ n (x n )=N Φ 1 (x 1 ) Φ n (x n )] + Φ1 (x 1 ) Φ n (x n ) < 0 Φ i (x i )Φ j (x j ) 0 >N Φ i (x i )Φ j (x j ) 1 pairing 1 i<j n < 0 Φ i1(x i1)φ j1(x j1) 0 >< 0 Φ i2(x i2)φ j2(x j2) 0 > 2 pairings i 1 <i 2,i 1 <j 1,i 2 <j ]

27

28

29

30

31 The proof is as in the pure field product case, the only difference being we now no longer have pairings between fields in the same normal product since their internal order is already normal (thus we have no self-pairings ). We only have pairings between fields in different normal products. Besides Wightman functions we can also evaluate the time ordered functions for free fields, that is, the vacuum expectation value of the time ordered products of the fields, which, as we recall, will be relevant when we consider the perturbative expansion of the S-matrix. Recall the definition of the time ordering operator for one and two operators T Φ(x) =Φ(x) T Φ(x 1 )Φ(x 2 )=θ(x 0 1 x 0 2)Φ(x 1 )Φ(x 2 )+θ(x 0 2 x 0 1)Φ(x 2 )Φ(x 1 ), ( ) and in general = (1,,n) (i 1,,i n ) T Φ(x 1 ) Φ(x n ) θ(x 0 i 1 x 0 i 2 )θ(x 0 i 2 x 0 i 3 ) θ(x 0 i (n 1) x 0 i n )Φ(x i1 ) Φ(x in ). ( ) The vacuum expectation values of the time ordered product of operators are called the time ordered functions, the Green functions, the τ-functions, or the n-point functions and are denoted G (n) (x 1,,x n ) < 0 T Φ(x 1 ) Φ(x n ) 0 >. ( ) Since G (n) is expressible in terms of Wightman functions we see that G (2n+1) =0. Also as with the Wightman functions, we will express the n-point function for free fields in terms of products of the free field 2-point functions. Hence we start by evaluating the 2-point function, also known as the Feynman propagator < 0 T Φ(x 1 )Φ(x 2 ) 0 > = θ(x 0 1 x0 2 ) < 0 Φ(x 1)Φ(x 2 ) 0 > + θ(x 0 2 x 0 1) < 0 Φ(x 2 )Φ(x 1 ) 0 > = θ(x 0 1 x 0 2)i + (x 1 x 2 )+θ(x 0 2 x 0 1)i + (x 2 x 1 ) = i θ(x 0 1 x 0 2) + (x 1 x 2 ) θ(x 0 2 x 0 1) (x 1 x 2 ) ] F (x 1 x 2 ). 136 ( )

32

33

34

35

36

37

38 each chronological ordering. Thus we obtain the Wick Theorem expansion for the time ordered product of free fields. Similar to the product of normal products, we can derive a Wick expansion for the chronological product of normal products T (N Φ 1 (x) Φ a (x)] N Φ a+1 (y) Φ a+b (y)] N Φ a+b+ +1 (z) Φ n (z)]). ( ) Wick s Theorem has just the same form as for the time ordered products of the fields themselves except now there are no contractions between fields from the same normal product allowed on the right hand side of the Wick expansion. Our theorem for Green functions follows directly from Wick s Theorem by taking the VEV of equation ( ). The VEV of all normal products on the right hand side vanish and hence we are left with < 0 T Φ(x 1 ) Φ(x n ) 0 > { 0,nodd = P < 0 T Φ(x i 1 )Φ(x j1 ) 0 > < 0 T Φ(x i n )Φ(x j n ) 0 >, n even ( ) 2 2 where P is a sum over all permutations P of (1,,n) into n 2 pairs (i 1,j 1 ) (i n,j n ) with i 1 <j 2 2 1,,in <j n and i 1 <i < <in. 2 Finally let s see why these time ordered functions are called Green functions. They are the Green functions of the Klein-Gordon equation, that is, ( 2 x + m 2) < 0 T Φ(x)Φ(y) 0 >= ( x 2 + m 2 ) F (x y) d 4 k = (2π) 4 ( k2 + m 2 )e ik(x y) i k 2 m 2 + iɛ d 4 k = (2π) 4 ( i)e ik(x y) = iδ 4 (x y). ( ) This also follows directly from the definition of the time ordered operators and the equal time commutation relations. Consider the time derivative of T Φ(x)Φ(y) =θ(x 0 y 0 )Φ(x)Φ(y) +θ(y 0 x 0 )Φ(y)Φ(x), 0 x T Φ(x)Φ(y) =θ(x 0 y 0 ) Φ(x)Φ(y) +θ(y 0 x 0 )Φ(y) Φ(x) + 0 x θ(x0 y 0 ) ] Φ(x)Φ(y) + 0 x θ(y0 x 0 ) ] Φ(y)Φ(x). ( ) 143

39

40

41 For infinitesimal rotations, that is, infinitesimal α, U = 1 + iαq and thus, ( ) ( )( ) ( ) Φ1 1 α Φ1 Φ1 + αφ (1 iαq) (1 + iαq) = = 2. ( ) Φ 2 α 1 Φ 2 Φ 2 αφ 1 This implies or alternatively, iα Q, Φ 1 ]=αφ 2 iα Q, Φ 2 ]= αφ 1 ( ) Q, Φ 1 ]=iφ 2 iδφ 1 Q, Φ 2 ]= iφ 1 iδφ 2. ( ) We may express these relations in the notation discussed in section 2.1 on Noether s Theorem Q, Φ r ] id rs Φ s ( ) where r = s =1, 2 and ( ) 0 1 D rs =. ( ) +1 0 Now we check if the Lagrangian is invariant under such rotations. It is sufficient to consider infinitesimal rotations. So δl = δl = i Q, L] ( ) and performing the variations of the Lagrangian we find (note, we have no operator ordering problems since δφ 1, Φ 1 ]=0=δΦ 2, Φ 2 ]) δl = L Φ r δφ r + L µ Φ r µ δφ r = µ Φ 1 ( µ δφ 1 )+ µ Φ 2 ( µ δφ 2 ) m 2 1Φ 1 δφ 1 m 2 2Φ 2 δφ 2 = µ Φ 1 ( µ Φ 2 )+ µ Φ 2 ( µ Φ 1 )+m 2 1 Φ 1Φ 2 m 2 2 Φ 2Φ 1 = ( m 2 1 m 2 2) Φ1 Φ 2. ( ) If the masses of the particles are equal, m 1 = m 2 m, then δl = 0 and internal rotational symmetry is a good symmetry of the system. By Noether s theorem we have a conserved current J µ L µ Φ 1 δφ 1 + L µ Φ 2 δφ 2 = µ Φ 1 ( Φ 2 )+ µ Φ 2 (Φ 1 ) =Φ 1 µ Φ ( )

42 (Again note that Ĵ µ = NJ µ ] = J µ since Φ 1 and Φ 2 commute.) Let s check explicitly that this current is conserved µ J µ = ( 2 Φ 1 ) Φ2 +Φ 1 2 Φ 2 ( ) where the cross terms cancel. However, each field obeys the Klein-Gordon equation L L µ =0= ( ) 2 + m 2 r Φr ( ) Φ r µ Φ r where r=1,2. Thus, and µ J µ = m 2 1 Φ 1Φ 2 m 2 2 Φ 1Φ 2 = ( ) m 2 1 m 2 2 Φ1 Φ 2 ( ) δl = µ J µ ( ) as Noether s Theorem required. Hence for equal masses, m 1 = m 2 = m, we have an invariant Lagrangian and a conserved current δl =0 µ J µ =0. ( ) The charge Q is given by Noether s Theorem accordingly Q = d 3 xj 0 = d 3 x Φ 1 Π 2 Φ 2 Π 1 ] ( ) which is independent of time, that is, Q = 0. So we check using the ETCR that this is indeed Q Q, Φ 1 ]= d 3 y Φ 2 Π 1, Φ 1 ] = i d 3 yδ 3 (x y)φ 2 = iφ 2 Q, Φ 2 ]= d 3 y Φ 1 Π 2, Φ 2 ] = iφ 1. ( ) 147

43 The group multiplication law that U(α) obeys is U(α 1 )U(α 2 )=e iα 1Q e iα 2Q = e i(α 1+α 2 )Q ( ) = U(α 1 + α 2 ). This is just the product law for the Abelian group O(2) or more generally called U(1), the Abelian group of phase transformations. To make this explicit consider defining the non-hermitian (that is, complex) fields Φ and Φ in terms of the two real fields in the following manner Φ 1 2 (Φ 1 iφ 2 ) Φ 1 2 (Φ 1 + iφ 2 ). ( ) Under these O(2) or U(1) rotations we find Q, Φ] = 1 2 (Q, Φ 1 ] i Q, Φ 2 ]) = 1 2 (iφ 2 i ( i)φ 1 ) = 1 2 (Φ 1 iφ 2 ) Q, Φ] = Φ, ( ) and similarly Q, Φ ] =+Φ. ( ) So calculating the multiple commutators trivially, we have for finite phase transformations U (α)φu(α) =e iαq Φe iαq = e iα Φ ( ) and U (α)φ U(α) =e iα Φ. ( ) The O(2) rotation transformation of the real fields is just the U(1) phase symmetry transformation for the complex fields. Futhermore, all the quantities we have can be rewritten in terms of Φ and Φ since Φ 1 = 1 ( ) Φ+Φ ( ) 2 148

44 and Hence, Φ 2 = i 2 ( Φ Φ ). ( ) ˆL = NL] L = µ Φ µ Φ m 2 Φ Φ ( ) where the factors of 1 2 disappear and as expected Φ e+iα Φ;Φ e iα Φ is a symmetry of this Langrangian. The Euler-Lagrange equations and commutation relations can now be formulated in terms of Φ and Φ. We obtain the results directly by treating Φ and Φ as independent fields L Φ L µ µ Φ =0= ( 2 + m 2) Φ L Φ L µ µ Φ =0= ( 2 + m 2) Φ. ( ) The canonical momenta for the complex fields are Π and Π.So Π L Φ = Φ Π L Φ = Φ. ( ) and the equal time commutation relations become Φ ( x, t ), Φ( y, t )] = iδ 3 ( x y ) ( ) or conjugating Φ( x, t ), Φ ( y, t )] = iδ 3 ( x y ) ( ) while Φ( x, t ), Φ( y, t )] = 0 Φ( x, t ), Φ ( y, t ) ] =0 Φ( x, t ), Φ( y, t ) ] =0 149

45 Φ( x, t ), Φ ( y, t )] =0. ( ) In addition, we have the current and associated charge in terms of the complex fields ] J µ = in Φ µ Φ Q = i d 3 xn Φ Π ΠΦ ]. ( ) To further physically interpret this complex scalar field let s Fourier transform to momentum space. As previously derived we have the momentum decomposition for the two Hermitian fields Φ 1 (x) = a (2π) 3 1 ( 2ω ] k)e ikx + a 1 ( k)e +ikx k ( ) and Φ 2 (x) = a (2π) 3 2 ( 2ω ] k)e ikx + a 2 ( k)e +ikx. ( ) k The operator a r( k) creates particles of type r with momentum k, mass m, spin zero and energy ω k. Since H, Q] = 0, the Q eigenvalues will also label the states. As a consequence of the fact that Φ and Φ diagonalize the rotation matrix, the states created by them will have a definite charge, that is Φ= 1 (Φ 1 iφ 2 ) 2 d 3 k 1 = (2π) 3 2ω k 2 ( a 1 ( k) ia 2 ( ) k) e ikx + 1 ) ] (a 1 ( k) ia 2 ( k) e +ikx 2 where the complex creation and annihilation operators are given by a( k) 1 a 1 ( k) ia 2 ( ] k) 2 ( ) b ( k) 1 ] a 1 ( k) ia 2 ( k). ( ) 2 Note that a ( k) and b ( k) are independent, that is, a ( k)= 1 ] a 1 ( k)+ia 2 ( k) b ( k). ( ) 2 150

46 So we have the momentum decomposition of the complex fields Φ(x) = a( (2π) 3 2ω k)e ikx + b ( ] k)e +ikx k ( ) and Φ (x) = Hence, by inverting our Fourier transform we have a( k)=i d 3 xe ikx 0 Φ(x)] b( (2π) 3 2ω k)e ikx + a ( ] k)e +ikx. ( ) k a ( k)=i b( k)=i b ( k)=i d 3 xφ (x) 0 e ikx ] d 3 xe ikx 0 Φ (x)] d 3 xφ(x) 0 e ikx ]. ( ) The CCR for a and b follow as usual from the Φ and Π ETCR a( k),a ( ] l ) =(2π) 3 2ω k δ 3 ( x l ) b( k),b ( ] l ) =(2π) 3 2ω k δ 3 ( x l ) ( ) all other commutators vanish. As before Ĥ = (2π) 3 ω k a ( 2ω k)a( k)+b ( k)b( ] k) k and P = Q = k a ( (2π) 3 2ω k)a( k)+b ( k)b( ] k) k ( ) a ( (2π) 3 2ω k)a( k) b ( k)b( ] k). ( ) k Thus, we again have two types of particles a and b type. In addition note that Q, a( ] k) = a( k) 151

47 Q, a ( ] k) =+a ( k) Q, b( ] k) =+b( k) Q, b ( ] k) = b ( k). ( ) Since P µ,q] = 0 we label the one particle states with k, m 2, and the eigenvalues of Q which are ±1 on this subspace. So the Hilbert space of states is built up from the vacuum state, 0 >, which is defined as the no particle state, a( k) 0 >= 0 and b( k) 0 >= 0. As a result, Ĥ 0 >= P 0 >= Q 0 >= 0. The one particle states are constructed by k, + > a ( k) 0 > k, > b ( k) 0 >. ( ) So using the charge commutation relations Q, a( ] k) = a( k), etc., we find Q k, + > = Qa ( k) 0 >= Q, a ( ] k) 0 > =+a ( k) 0 >= + k,+ > ( ) and similarly Q k, >= k, >. Thus, a particles have a U(1) charge of +1 unit and b particles have a unit of negative charge, 1. This could be electric charge or hypercharge. As we have done previously we can introduce a positively charged particle number operator N + (2π) 3 2ω k a ( k)a( k) ( ) and a negatively charged particle number operator N b ( (2π) 3 2ω k)b( k). ( ) k The total number operator is given by N = N + + N while the charge operator is Q = N + N. Thus, the many particle state is n +,n > ( k 1, +); ( k 2, +); ;( k n+, +); ( l 1, ); ( l 2, ); ;( l n, ) > = a ( k 1 ) a ( k n+ )b ( l 1 ) b ( l n ) 0 > ( ) 152

48 and as usual Ĥ n +,n >= P n +,n >= n + i=1 n + i=1 ω ki + ki + n j=1 n j=1 ω lj n +,n > lj n +,n > Q n +,n >=(n + n ) n +,n > N n +,n >=(n + + n ) n +,n >. ( ) The particles are identical except for their charge. This pairing of oppositely charged particles has a deep reason associated with CPT invariance and the a and b particles are called particle and antiparticle (which is which is convention). Finally, the CCR imply the (all time) covariant commutation relations Φ(x), Φ(y)] = 0 ( ) and Φ(x), Φ (y) ] = i (x y). ( ) Furthermore, and while < 0 Φ(x)Φ (y) 0 >= i + (x y) ( ) < 0 T Φ(x)Φ (y) 0 >= i F (x y) ( ) < 0 T Φ(x)Φ(y) 0 >=< 0 T Φ (x)φ (y) 0 >= 0. ( ) Wick s theorem has an analogous form to that previously obtained. We are now ready to consider particles with spin