Logistic regression and linear classifiers COMS 4771
|
|
|
- Sherman Douglas
- 5 years ago
- Views:
Transcription
1 Logistic regression and linear classifiers COMS 4771
2 1. Prediction functions (again)
3 Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random pairs (i.e., labeled examples). 1 / 33
4 Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random pairs (i.e., labeled examples). X takes values in X. E.g., X = R d. Y takes values in Y. E.g., (regression problems) Y = R; (classification problems) Y = {1,..., K} or Y = {0, 1} or Y = { 1, +1}. 1 / 33
5 Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random pairs (i.e., labeled examples). X takes values in X. E.g., X = R d. Y takes values in Y. E.g., (regression problems) Y = R; (classification problems) Y = {1,..., K} or Y = {0, 1} or Y = { 1, +1}. 1. We observe (X 1, Y 1),..., (X n, Y n), and the choose a prediction function (i.e., predictor) ˆf : X Y, This is called learning or training. 1 / 33
6 Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random pairs (i.e., labeled examples). X takes values in X. E.g., X = R d. Y takes values in Y. E.g., (regression problems) Y = R; (classification problems) Y = {1,..., K} or Y = {0, 1} or Y = { 1, +1}. 1. We observe (X 1, Y 1),..., (X n, Y n), and the choose a prediction function (i.e., predictor) ˆf : X Y, This is called learning or training. 2. At prediction time, observe X, and form prediction ˆf(X). 1 / 33
7 Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random pairs (i.e., labeled examples). X takes values in X. E.g., X = R d. Y takes values in Y. E.g., (regression problems) Y = R; (classification problems) Y = {1,..., K} or Y = {0, 1} or Y = { 1, +1}. 1. We observe (X 1, Y 1),..., (X n, Y n), and the choose a prediction function (i.e., predictor) ˆf : X Y, This is called learning or training. 2. At prediction time, observe X, and form prediction ˆf(X). 3. Outcome is Y, and squared loss is ( ˆf(X) Y ) 2 (regression problems). zero-one loss is 1{ ˆf(X) Y } (classification problems). 1 / 33
8 Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random pairs (i.e., labeled examples). X takes values in X. E.g., X = R d. Y takes values in Y. E.g., (regression problems) Y = R; (classification problems) Y = {1,..., K} or Y = {0, 1} or Y = { 1, +1}. 1. We observe (X 1, Y 1),..., (X n, Y n), and the choose a prediction function (i.e., predictor) ˆf : X Y, This is called learning or training. 2. At prediction time, observe X, and form prediction ˆf(X). 3. Outcome is Y, and squared loss is ( ˆf(X) Y ) 2 (regression problems). zero-one loss is 1{ ˆf(X) Y } (classification problems). Note: expected zero-one loss is which we also call error rate. E[1{ ˆf(X) Y }] = P( ˆf(X) Y ), 1 / 33
9 Distributions over labeled examples X : space of possible side-information (feature space). Y: space of possible outcomes (label space or output space). 2 / 33
10 Distributions over labeled examples X : space of possible side-information (feature space). Y: space of possible outcomes (label space or output space). Distribution P of random pair (X, Y ) taking values in X Y can be thought of in two parts: 2 / 33
11 Distributions over labeled examples X : space of possible side-information (feature space). Y: space of possible outcomes (label space or output space). Distribution P of random pair (X, Y ) taking values in X Y can be thought of in two parts: 1. Marginal distribution P X of X: P X is a probability distribution on X. 2 / 33
12 Distributions over labeled examples X : space of possible side-information (feature space). Y: space of possible outcomes (label space or output space). Distribution P of random pair (X, Y ) taking values in X Y can be thought of in two parts: 1. Marginal distribution P X of X: P X is a probability distribution on X. 2. Conditional distribution P Y X=x of Y given X = x, for each x X : P Y X=x is a probability distribution on Y. 2 / 33
13 Optimal classifier For binary classification, what function f : X {0, 1} has smallest risk (i.e., error rate) R(f) := P(f(X) Y )? 3 / 33
14 Optimal classifier For binary classification, what function f : X {0, 1} has smallest risk (i.e., error rate) R(f) := P(f(X) Y )? Conditional on X = x, the minimizer of conditional risk ŷ P(ŷ Y X = x) is ŷ := { 1 if P(Y = 1 X = x) > 1/2, 0 if P(Y = 1 X = x) 1/2. 3 / 33
15 Optimal classifier For binary classification, what function f : X {0, 1} has smallest risk (i.e., error rate) R(f) := P(f(X) Y )? Conditional on X = x, the minimizer of conditional risk is ŷ := ŷ P(ŷ Y X = x) { 1 if P(Y = 1 X = x) > 1/2, 0 if P(Y = 1 X = x) 1/2. Therefore, the function f : X {0, 1} where { f 1 if P(Y = 1 X = x) > 1/2, (x) = 0 if P(Y = 1 X = x) 1/2, has the smallest risk. x X, 3 / 33
16 Optimal classifier For binary classification, what function f : X {0, 1} has smallest risk (i.e., error rate) R(f) := P(f(X) Y )? Conditional on X = x, the minimizer of conditional risk is ŷ := ŷ P(ŷ Y X = x) { 1 if P(Y = 1 X = x) > 1/2, 0 if P(Y = 1 X = x) 1/2. Therefore, the function f : X {0, 1} where { f 1 if P(Y = 1 X = x) > 1/2, (x) = 0 if P(Y = 1 X = x) 1/2, has the smallest risk. f is called the Bayes (optimal) classifier. x X, 3 / 33
17 Optimal classifier For binary classification, what function f : X {0, 1} has smallest risk (i.e., error rate) R(f) := P(f(X) Y )? Conditional on X = x, the minimizer of conditional risk is ŷ := ŷ P(ŷ Y X = x) { 1 if P(Y = 1 X = x) > 1/2, 0 if P(Y = 1 X = x) 1/2. Therefore, the function f : X {0, 1} where { f 1 if P(Y = 1 X = x) > 1/2, (x) = 0 if P(Y = 1 X = x) 1/2, has the smallest risk. f is called the Bayes (optimal) classifier. For Y = {1,..., K}, f (x) = arg max P(Y = y X = x), x X. y Y x X, 3 / 33
18 2. Logistic regression
19 Logistic regression Suppose X = R d and Y = {0, 1}. A logistic regression model is a statistical model where the conditional probability function has a particular form: Y X = x Bern(η β (x)), x R d, with and η β (x) := logistic(x T β), x R d, logistic(z) := 1 ez = 1 + e z 1 + e, z R. z 4 / 33
20 Logistic regression Suppose X = R d and Y = {0, 1}. A logistic regression model is a statistical model where the conditional probability function has a particular form: Y X = x Bern(η β (x)), x R d, with and η β (x) := logistic(x T β), x R d, logistic(z) := 1 ez = 1 + e z 1 + e, z R. z / 33
21 Logistic regression Suppose X = R d and Y = {0, 1}. A logistic regression model is a statistical model where the conditional probability function has a particular form: Y X = x Bern(η β (x)), x R d, with and η β (x) := logistic(x T β), x R d, logistic(z) := 1 ez = 1 + e z 1 + e, z R. z Parameters: β = (β 1,..., β d ) R d. 4 / 33
22 Logistic regression Suppose X = R d and Y = {0, 1}. A logistic regression model is a statistical model where the conditional probability function has a particular form: Y X = x Bern(η β (x)), x R d, with and η β (x) := logistic(x T β), x R d, logistic(z) := 1 ez = 1 + e z 1 + e, z R. z Parameters: β = (β 1,..., β d ) R d. Conditional distribution of Y given X is Bernoulli; marginal distribution of X not specified. 4 / 33
23 MLE for logistic regression Log-likelihood of β in iid logistic regression model, given data (X i, Y i) = (x i, y i) for i = 1,..., n: ln n η β (x i) y ( i 1 η β (x ) 1 y i i) = i=1 n y i ln η β (x i) + (1 y i) ln(1 η β (x i)). i=1 5 / 33
24 MLE for logistic regression Log-likelihood of β in iid logistic regression model, given data (X i, Y i) = (x i, y i) for i = 1,..., n: ln n η β (x i) y ( i 1 η β (x ) 1 y i i) = i=1 No closed-form formula for MLE. n y i ln η β (x i) + (1 y i) ln(1 η β (x i)). i=1 5 / 33
25 MLE for logistic regression Log-likelihood of β in iid logistic regression model, given data (X i, Y i) = (x i, y i) for i = 1,..., n: ln n η β (x i) y ( i 1 η β (x ) 1 y i i) = i=1 No closed-form formula for MLE. n y i ln η β (x i) + (1 y i) ln(1 η β (x i)). i=1 Nevertheless, there are efficient algorithms that obtain an approximate maximizer of the log-likelihood function. E.g., Newton s method. 5 / 33
26 Log-odds function and classifier Equivalent way to characterize logistic regression model: The log-odds function, given by e xt β η β (x) log-odds β (x) = ln 1 η β (x) = ln 1 + e xt β 1 = xt β, 1 + e xt β is a linear function 1, parameterized by β R d. 1 Some authors allow affine function; we can get this using affine expansion. 6 / 33
27 Log-odds function and classifier Equivalent way to characterize logistic regression model: The log-odds function, given by e xt β η β (x) log-odds β (x) = ln 1 η β (x) = ln 1 + e xt β 1 = xt β, 1 + e xt β is a linear function 1, parameterized by β R d. Bayes optimal classifier f β : R d {0, 1} in logistic regression model: { 0 if x T β 0, f β (x) = 1 if x T β > 0. 1 Some authors allow affine function; we can get this using affine expansion. 6 / 33
28 Log-odds function and classifier Equivalent way to characterize logistic regression model: The log-odds function, given by e xt β η β (x) log-odds β (x) = ln 1 η β (x) = ln 1 + e xt β 1 = xt β, 1 + e xt β is a linear function 1, parameterized by β R d. Bayes optimal classifier f β : R d {0, 1} in logistic regression model: { 0 if x T β 0, f β (x) = 1 if x T β > 0. Such classifiers are called linear classifiers. 1 Some authors allow affine function; we can get this using affine expansion. 6 / 33
29 3. Origin story for logistic regression
30 Where does the logistic regression model come from? The following is one way the logistic regression model comes about (but not the only way). 7 / 33
31 Where does the logistic regression model come from? The following is one way the logistic regression model comes about (but not the only way). Consider the following generative model for (X, Y ) where Y Bern(π), X Y = y N(µ y, Σ). 7 / 33
32 Where does the logistic regression model come from? The following is one way the logistic regression model comes about (but not the only way). Consider the following generative model for (X, Y ) where Y Bern(π), X Y = y N(µ y, Σ). Parameters: π [0, 1], µ 0, µ 1 R d, Σ R d d sym. & pos. def. 7 / 33
33 Where does the logistic regression model come from? The following is one way the logistic regression model comes about (but not the only way). Consider the following generative model for (X, Y ) where Y Bern(π), X Y = y N(µ y, Σ). Parameters: π [0, 1], µ 0, µ 1 R d, Σ R d d sym. & pos. def x Figure shows (unconditional) probability density function for X. P(ω 2)=.5 P(ω 1)=.5 R1 R / 33
34 Statistical model for conditional distribution Suppose we are given the following. p Y : probability mass function for Y. p X Y =y : conditional probability density function for X given Y = y. 8 / 33
35 Statistical model for conditional distribution Suppose we are given the following. p Y : probability mass function for Y. p X Y =y : conditional probability density function for X given Y = y. What is the conditional distribution of Y given X? 8 / 33
36 Statistical model for conditional distribution Suppose we are given the following. p Y : probability mass function for Y. p X Y =y : conditional probability density function for X given Y = y. What is the conditional distribution of Y given X? By Bayes rule: for any x R d, P(Y = y X = x) = py (y) p X Y =y(x) p X (x) (where p X is unconditional density for X). 8 / 33
37 Statistical model for conditional distribution Suppose we are given the following. p Y : probability mass function for Y. p X Y =y : conditional probability density function for X given Y = y. What is the conditional distribution of Y given X? By Bayes rule: for any x R d, P(Y = y X = x) = py (y) p X Y =y(x) p X (x) (where p X is unconditional density for X). Therefore, log-odds function is log-odds(x) = ln ( ) p Y (1) p Y (0) px Y =1(x). p X Y =0 (x) 8 / 33
38 Log-odds function for our toy model Log-odds function: log-odds(x) = ln ( ) ( ) py (1) px Y =1 (x) + ln. p Y (0) p X Y =0 (x) 9 / 33
39 Log-odds function for our toy model Log-odds function: log-odds(x) = ln ( ) ( ) py (1) px Y =1 (x) + ln. p Y (0) p X Y =0 (x) In our toy model, we have Y Bern(π) and X Y = y N(µ y, AA T ), so: 1 π log-odds(x) = ln 1 π + ln e 2 A 1 (x µ 1 ) 2 2 e 1 2 A 1 (x µ 0 ) 2 2 π = ln 1 π 1 2 A 1 (x µ 1 ) A 1 (x µ 0 ) 2 2 π = ln 1 π 1 2 ( A 1 µ A 1 µ 0 2 2) + (µ 1 µ 0 ) T (AA T ) 1 x. }{{}}{{} linear function of x constant doesn t depend on x 9 / 33
40 Log-odds function for our toy model Log-odds function: log-odds(x) = ln ( ) ( ) py (1) px Y =1 (x) + ln. p Y (0) p X Y =0 (x) In our toy model, we have Y Bern(π) and X Y = y N(µ y, AA T ), so: 1 π log-odds(x) = ln 1 π + ln e 2 A 1 (x µ 1 ) 2 2 e 1 2 A 1 (x µ 0 ) 2 2 π = ln 1 π 1 2 A 1 (x µ 1 ) A 1 (x µ 0 ) 2 2 π = ln 1 π 1 2 ( A 1 µ A 1 µ 0 2 2) + (µ 1 µ 0 ) T (AA T ) 1 x. }{{}}{{} linear function of x constant doesn t depend on x This is an affine function of x. 9 / 33
41 Log-odds function for our toy model Log-odds function: log-odds(x) = ln ( ) ( ) py (1) px Y =1 (x) + ln. p Y (0) p X Y =0 (x) In our toy model, we have Y Bern(π) and X Y = y N(µ y, AA T ), so: 1 π log-odds(x) = ln 1 π + ln e 2 A 1 (x µ 1 ) 2 2 e 1 2 A 1 (x µ 0 ) 2 2 π = ln 1 π 1 2 A 1 (x µ 1 ) A 1 (x µ 0 ) 2 2 π = ln 1 π 1 2 ( A 1 µ A 1 µ 0 2 2) + (µ 1 µ 0 ) T (AA T ) 1 x. }{{}}{{} linear function of x constant doesn t depend on x This is an affine function of x. Hence, the statistical model for Y X is a logistic regression model (with affine feature expansion). 9 / 33
42 Log-odds function for our toy model Log-odds function: log-odds(x) = ln ( ) ( ) py (1) px Y =1 (x) + ln. p Y (0) p X Y =0 (x) In our toy model, we have Y Bern(π) and X Y = y N(µ y, AA T ), so: 1 π log-odds(x) = ln 1 π + ln e 2 A 1 (x µ 1 ) 2 2 e 1 2 A 1 (x µ 0 ) 2 2 π = ln 1 π 1 2 A 1 (x µ 1 ) A 1 (x µ 0 ) 2 2 π = ln 1 π 1 2 ( A 1 µ A 1 µ 0 2 2) + (µ 1 µ 0 ) T (AA T ) 1 x. }{{}}{{} linear function of x constant doesn t depend on x This is an affine function of x. Hence, the statistical model for Y X is a logistic regression model (with affine feature expansion). Important: Logistic regression model forgets about p X Y =y! 9 / 33
43 4. Linear classifiers
44 Linear classifiers A linear classifier is specified by a weight vector w R d : { 1 if x T w 0, f w(x) := +1 if x T w > 0. (Will be notationally simpler to use { 1, +1} instead of {0, 1}.) 10 / 33
45 Linear classifiers A linear classifier is specified by a weight vector w R d : { 1 if x T w 0, f w(x) := +1 if x T w > 0. (Will be notationally simpler to use { 1, +1} instead of {0, 1}.) Interpretation: does a linear combination of input features exceed 0? For w = (w 1,..., w d ) and x = (x 1,..., x d ), x T w = d? w ix i > 0. i=1 10 / 33
46 Geometry of linear classifiers H x 2 w A hyperplane in R d is a linear subspace of dimension d 1. A R 2 -hyperplane is a line. A R 3 -hyperplane is a plane. As a linear subspace, a hyperplane always contains the origin. x 1 A hyperplane H can be specified by a (non-zero) normal vector w R d. The hyperplane with normal vector w is the set of points orthogonal to w: { } H = x R d : x T w = / 33
47 Classification with a hyperplane H w span{w} 12 / 33
48 Classification with a hyperplane H span{w} x w θ x 2 cos θ Projection of x onto span{w} (a line) has coordinate x 2 cos(θ) where xt w cos θ =. w 2 x 2 (Distance to hyperplane is x 2 cos(θ).) 12 / 33
49 Classification with a hyperplane H span{w} x w θ x 2 cos θ Projection of x onto span{w} (a line) has coordinate x 2 cos(θ) where xt w cos θ =. w 2 x 2 (Distance to hyperplane is x 2 cos(θ).) Decision boundary is hyperplane (oriented by w): x T w > 0 x 2 cos(θ) > 0 x on same side of H as w 12 / 33
50 Classification with a hyperplane H span{w} x w θ x 2 cos θ Projection of x onto span{w} (a line) has coordinate x 2 cos(θ) where xt w cos θ =. w 2 x 2 (Distance to hyperplane is x 2 cos(θ).) Decision boundary is hyperplane (oriented by w): x T w > 0 x 2 cos(θ) > 0 x on same side of H as w What should we do if we want hyperplane decision boundary that doesn t (necessarily) go through origin? 12 / 33
51 Decision boundary with quadratic feature expansion elliptical decision boundary hyperbolic decision boundary 13 / 33
52 Decision boundary with quadratic feature expansion elliptical decision boundary hyperbolic decision boundary Same feature expansions we saw for linear regression models can also be used here to upgrade linear classifiers. 13 / 33
53 Text features How can we get features for text? 14 / 33
54 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } 14 / 33
55 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy } 14 / 33
56 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) 14 / 33
57 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) x length 3 = 1{length 3} 14 / 33
58 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) x length 3 = 1{length 3} x length 4 = 1{length 4} 14 / 33
59 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) x length 3 = 1{length 3} x length 4 = 1{length 4}... (same for all positive integers up to 20) 14 / 33
60 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) x length 3 = 1{length 3} x length 4 = 1{length 4}... (same for all positive integers up to 20) Classifying documents (input = a sequence of words) 14 / 33
61 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) x length 3 = 1{length 3} x length 4 = 1{length 4}... (same for all positive integers up to 20) Classifying documents (input = a sequence of words) x contains aardvark = 1{contains aardvark } 14 / 33
62 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) x length 3 = 1{length 3} x length 4 = 1{length 4}... (same for all positive integers up to 20) Classifying documents (input = a sequence of words) x contains aardvark = 1{contains aardvark }... (same for all words in dictionary) 14 / 33
63 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) x length 3 = 1{length 3} x length 4 = 1{length 4}... (same for all positive integers up to 20) Classifying documents (input = a sequence of words) x contains aardvark = 1{contains aardvark }... (same for all words in dictionary) x contains each day = 1{contains each day } 14 / 33
64 Text features How can we get features for text? Classifying words (input = a sequence of characters) x starts with anti = 1{starts with anti } x ends with logy = 1{ends with logy }... (same for all four-letter prefixes/suffixes) x length 3 = 1{length 3} x length 4 = 1{length 4}... (same for all positive integers up to 20) Classifying documents (input = a sequence of words) x contains aardvark = 1{contains aardvark }... (same for all words in dictionary) x contains each day = 1{contains each day }... (same for all bi-grams of words in dictionary) Etc. Typically end up with lots of features! 14 / 33
65 Sparse representations If x has few non-zero entries, then better to use sparse representation: 15 / 33
66 Sparse representations If x has few non-zero entries, then better to use sparse representation: E.g., see spot run. Sparse representation (e.g., using hash table): x = { "contains_see":1, "contains_spot":1, "contains_run":1, "contains_see_spot":1, "contains_spot_run":1 } 15 / 33
67 Sparse representations If x has few non-zero entries, then better to use sparse representation: E.g., see spot run. Sparse representation (e.g., using hash table): x = { "contains_see":1, "contains_spot":1, "contains_run":1, "contains_see_spot":1, "contains_spot_run":1 } Compare to dense representation (using array): x = [ 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,... ] 15 / 33
68 Sparse representations If x has few non-zero entries, then better to use sparse representation: E.g., see spot run. Sparse representation (e.g., using hash table): x = { "contains_see":1, "contains_spot":1, "contains_run":1, "contains_see_spot":1, "contains_spot_run":1 } Compare to dense representation (using array): x = [ 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,... ] To compute inner product w T x: sum = 0. for feature in x: sum = sum + w[feature] * x[feature] Running time number of non-zero entries of x. 15 / 33
69 Sparse representations If x has few non-zero entries, then better to use sparse representation: E.g., see spot run. Sparse representation (e.g., using hash table): x = { "contains_see":1, "contains_spot":1, "contains_run":1, "contains_see_spot":1, "contains_spot_run":1 } Compare to dense representation (using array): x = [ 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,... ] To compute inner product w T x: sum = 0. for feature in x: sum = sum + w[feature] * x[feature] Running time number of non-zero entries of x. If x s are sparse, would you expect there to be a good sparse linear classifier? 15 / 33
70 5. Learning linear classifiers
71 Learning linear classifiers Even if Bayes optimal classifier is not linear (in our chosen feature space), we can hope that it has a good linear approximation. 16 / 33
72 Learning linear classifiers Even if Bayes optimal classifier is not linear (in our chosen feature space), we can hope that it has a good linear approximation. Goal: learn ŵ R d using iid sample (X 1, Y 1),..., (X n, Y n) such that Excess risk(fŵ) := R(fŵ) }{{} risk of your classifier min R(fw) w R } d {{} risk of best linear classifier is as small as possible, where the loss function is zero-one loss. 16 / 33
73 Learning linear classifiers Even if Bayes optimal classifier is not linear (in our chosen feature space), we can hope that it has a good linear approximation. Goal: learn ŵ R d using iid sample (X 1, Y 1),..., (X n, Y n) such that Excess risk(fŵ) := R(fŵ) }{{} risk of your classifier min R(fw) w R } d {{} risk of best linear classifier is as small as possible, where the loss function is zero-one loss. Empirical risk minimization (ERM): find f w with minimum empirical risk R(f w) := 1 n n 1{f w(x i) Y i}. i=1 16 / 33
74 Learning linear classifiers Even if Bayes optimal classifier is not linear (in our chosen feature space), we can hope that it has a good linear approximation. Goal: learn ŵ R d using iid sample (X 1, Y 1),..., (X n, Y n) such that Excess risk(fŵ) := R(fŵ) }{{} risk of your classifier min R(fw) w R } d {{} risk of best linear classifier is as small as possible, where the loss function is zero-one loss. Empirical risk minimization (ERM): find f w with minimum empirical risk R(f w) := 1 n Theorem: ERM solution fŵ satisfies as n at rate n 1{f w(x i) Y i}. i=1 E R(fŵ) min R(fw) w R d d n (and sometimes even faster!). 16 / 33
75 ERM for zero-one loss Unforunately, cannot compute (zero-one loss) ERM in general. 17 / 33
76 ERM for zero-one loss Unforunately, cannot compute (zero-one loss) ERM in general. The following problem is NP-hard (i.e., computationally intractable ): input n labeled examples from R d {0, 1} with promise that there is a linear classifier with empirical risk output a linear classifier with empirical risk (Zero-one loss is very different from squared loss!) 17 / 33
77 ERM for zero-one loss Unforunately, cannot compute (zero-one loss) ERM in general. The following problem is NP-hard (i.e., computationally intractable ): input n labeled examples from R d {0, 1} with promise that there is a linear classifier with empirical risk output a linear classifier with empirical risk (Zero-one loss is very different from squared loss!) Potential saving grace: Real-world problems we need to solve do not look like the encodings of difficult 3-SAT instances. 17 / 33
78 6. Linearly separable data and Perceptron
79 Linearly separable data Suppose there is a linear classifier that perfectly classifies the training examples S := ( (x 1, y 1),..., (x n, y n) ), i.e., for some w R d, f w (x) = y, for all (x, y) S. In this case, we say the training data is linearly separable. w 18 / 33
80 Finding a linear separator Problem: given training examples S from R d { 1, 1}, determine whether or not there exists w R d such that (and find such a vector if one exists). f w(x) = y, for all (x, y) S; 19 / 33
81 Finding a linear separator Problem: given training examples S from R d { 1, 1}, determine whether or not there exists w R d such that (and find such a vector if one exists). d variables: w R d S inequalities: for (x, y) S, f w(x) = y, for all (x, y) S; if y = 1: x T w 0, if y = +1: x T w > 0. Can be solved in polynomial time using algorithms for linear programming. 19 / 33
82 Finding a linear separator Problem: given training examples S from R d { 1, 1}, determine whether or not there exists w R d such that (and find such a vector if one exists). d variables: w R d S inequalities: for (x, y) S, f w(x) = y, for all (x, y) S; if y = 1: x T w 0, if y = +1: x T w > 0. Can be solved in polynomial time using algorithms for linear programming. If one exists, and the inequalities can be satisfied with some non-negligible wiggle room, then there is a very simple algorithm that finds a solution. 19 / 33
83 Perceptron (Rosenblatt, 1958) Perceptron input Labeled examples S from R d { 1, +1}. 1: initialize ŵ 1 := 0. 2: for t = 1, 2,..., do 3: if there is an example in S misclassified by fŵt then 4: Let (x t, y t ) be any such misclassified example from S. 5: Update: ŵ t+1 := ŵ t + y t x t. 6: else 7: return ŵ t. 8: end if 9: end for 20 / 33
84 Perceptron (Rosenblatt, 1958) Perceptron input Labeled examples S from R d { 1, +1}. 1: initialize ŵ 1 := 0. 2: for t = 1, 2,..., do 3: if there is an example in S misclassified by fŵt then 4: Let (x t, y t ) be any such misclassified example from S. 5: Update: ŵ t+1 := ŵ t + y t x t. 6: else 7: return ŵ t. 8: end if 9: end for Note 1: An example (x, y) is misclassified by f w if yx T w / 33
85 Perceptron (Rosenblatt, 1958) Perceptron input Labeled examples S from R d { 1, +1}. 1: initialize ŵ 1 := 0. 2: for t = 1, 2,..., do 3: if there is an example in S misclassified by fŵt then 4: Let (x t, y t ) be any such misclassified example from S. 5: Update: ŵ t+1 := ŵ t + y t x t. 6: else 7: return ŵ t. 8: end if 9: end for Note 1: An example (x, y) is misclassified by f w if yx T w 0. Note 2: If Perceptron terminates, then fŵt perfectly classifies the data! 20 / 33
86 Perceptron demo Scenario 1 x t ŵ t y t = 1 x T tŵt 0 Current vector ŵ t comparble to x t in length. 21 / 33
87 Perceptron demo Scenario 1 ŵ t+1 x t ŵ t y t = 1 x T tŵt 0 Updated vector ŵ t+1 now correctly classifies (x t, y t). 21 / 33
88 Perceptron demo Scenario 2 ŵ t x t y t = 1 x T tŵt 0 Current vector ŵ t much longer than x t. 21 / 33
89 Perceptron demo Scenario 2 ŵ t+1 ŵ t x y t = 1 t x T tŵt 0 Updated vector ŵ t+1 does not correctly classify (x t, y t). 21 / 33
90 Perceptron demo Scenario 2 ŵ t+1 ŵ t x y t = 1 t x T tŵt 0 Updated vector ŵ t+1 does not correctly classify (x t, y t). Not obvious that Perceptron will eventually terminate! 21 / 33
91 When is there a lot of wiggle room? Suppose w R d satisfies min yx T w > 0. (x,y) S 22 / 33
92 When is there a lot of wiggle room? Suppose w R d satisfies Then so does, e.g., w/100. min yx T w > 0. (x,y) S 22 / 33
93 When is there a lot of wiggle room? Suppose w R d satisfies min yx T w > 0. (x,y) S Then so does, e.g., w/100. Let s fix a particular scaling of w. 22 / 33
94 When is there a lot of wiggle room? Suppose w R d satisfies min yx T w > 0. (x,y) S Then so does, e.g., w/100. Let s fix a particular scaling of w. Let ( x, ỹ) be any example in S that achieves the minimum. 22 / 33
95 When is there a lot of wiggle room? Suppose w R d satisfies min yx T w > 0. (x,y) S Then so does, e.g., w/100. Let s fix a particular scaling of w. Let ( x, ỹ) be any example in S that achieves the minimum. H ỹ x T w w 2 ỹ x w 22 / 33
96 When is there a lot of wiggle room? Suppose w R d satisfies min yx T w > 0. (x,y) S Then so does, e.g., w/100. Let s fix a particular scaling of w. Let ( x, ỹ) be any example in S that achieves the minimum. Rescale w so that ỹ x T w = 1. H ỹ x T w w 2 ỹ x (Now scaling is fixed.) w 22 / 33
97 When is there a lot of wiggle room? Suppose w R d satisfies min yx T w > 0. (x,y) S Then so does, e.g., w/100. Let s fix a particular scaling of w. Let ( x, ỹ) be any example in S that achieves the minimum. Rescale w so that ỹ x T w = 1. H ỹ x T w w 2 ỹ x w (Now scaling is fixed.) 1 Now distance from ỹ x to H is. w 2 This distance is called the margin. 22 / 33
98 When is there a lot of wiggle room? Suppose w R d satisfies min yx T w > 0. (x,y) S Then so does, e.g., w/100. Let s fix a particular scaling of w. Let ( x, ỹ) be any example in S that achieves the minimum. Rescale w so that ỹ x T w = 1. H ỹ x T w w 2 ỹ x w (Now scaling is fixed.) 1 Now distance from ỹ x to H is. w 2 This distance is called the margin. Therefore, if w is a short vector satisfying min (x,y) S yxt w = 1, then it corresponds to a linear separator with large margin on examples in S. 22 / 33
99 When is there a lot of wiggle room? Suppose w R d satisfies min yx T w > 0. (x,y) S Then so does, e.g., w/100. Let s fix a particular scaling of w. Let ( x, ỹ) be any example in S that achieves the minimum. Rescale w so that ỹ x T w = 1. H ỹ x T w w 2 ỹ x w (Now scaling is fixed.) 1 Now distance from ỹ x to H is. w 2 This distance is called the margin. Therefore, if w is a short vector satisfying min (x,y) S yxt w = 1, then it corresponds to a linear separator with large margin on examples in S. Theorem : Perceptron converges quickly when there short w with min (x,y) S yx T w = / 33
100 Perceptron convergence theorem Theorem. Assume there exists w R d such that min (x,y) S yxt w = 1. Let L := max (x,y) S x 2. Then Perceptron halts after w 2 2L 2 iterations. 23 / 33
101 Perceptron convergence theorem Theorem. Assume there exists w R d such that min (x,y) S yxt w = 1. Let L := max (x,y) S x 2. Then Perceptron halts after w 2 2L 2 iterations. Proof: Suppose Perceptron does not exit the for-loop in iteration t. 23 / 33
102 Perceptron convergence theorem Theorem. Assume there exists w R d such that min (x,y) S yxt w = 1. Let L := max (x,y) S x 2. Then Perceptron halts after w 2 2L 2 iterations. Proof: Suppose Perceptron does not exit the for-loop in iteration t. Then there is a labeled example in S which we call (x t, y t) such that: y tw T x t 1 (by definition of w ) y tŵ T t x t 0 (since fŵt misclassifies the example) ŵ t+1 = ŵ t + y tx t (since an update is made) 23 / 33
103 Perceptron convergence theorem Theorem. Assume there exists w R d such that min (x,y) S yxt w = 1. Let L := max (x,y) S x 2. Then Perceptron halts after w 2 2L 2 iterations. Proof: Suppose Perceptron does not exit the for-loop in iteration t. Then there is a labeled example in S which we call (x t, y t) such that: y tw T x t 1 (by definition of w ) y tŵ T t x t 0 (since fŵt misclassifies the example) ŵ t+1 = ŵ t + y tx t (since an update is made) Use this information to (inductively) lower-bound cos (angle between w and ŵ t+1) = w T ŵ t+1 w 2 ŵ t / 33
104 Proof of Perceptron convergence theorem Goal: lower-bound w T ŵ t+1 w 2 ŵ t / 33
105 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) 24 / 33
106 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t 24 / 33
107 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t / 33
108 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t + 1. Therefore, by induction (with ŵ 1 = 0), w T ŵ t+1 t. 24 / 33
109 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t + 1. Therefore, by induction (with ŵ 1 = 0), w T ŵ t+1 t. Denominator: ŵ t = ŵt + ytxt / 33
110 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t + 1. Therefore, by induction (with ŵ 1 = 0), w T ŵ t+1 t. Denominator: ŵ t = ŵt + ytxt 2 2 = ŵt ytŵT t x t + x t / 33
111 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t + 1. Therefore, by induction (with ŵ 1 = 0), w T ŵ t+1 t. Denominator: ŵ t = ŵt + ytxt 2 2 = ŵt ytŵT t x t + x t 2 2 ŵt L2. 24 / 33
112 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t + 1. Therefore, by induction (with ŵ 1 = 0), w T ŵ t+1 t. Denominator: ŵ t = ŵt + ytxt 2 2 = ŵt ytŵT t x t + x t 2 2 ŵt L2. Therefore, by induction (with ŵ 1 = 0), ŵ t L2 t. 24 / 33
113 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t + 1. Therefore, by induction (with ŵ 1 = 0), w T ŵ t+1 t. Denominator: ŵ t = ŵt + ytxt 2 2 = ŵt ytŵT t x t + x t 2 2 ŵt L2. Therefore, by induction (with ŵ 1 = 0), ŵ t L2 t. w T cos (angle between w and ŵ t+1) = ŵ t+1 w 2 ŵ t / 33
114 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t + 1. Therefore, by induction (with ŵ 1 = 0), w T ŵ t+1 t. Denominator: ŵ t = ŵt + ytxt 2 2 = ŵt ytŵT t x t + x t 2 2 ŵt L2. Therefore, by induction (with ŵ 1 = 0), ŵ t L2 t. cos (angle between w and ŵ t+1) = w T ŵ t+1 t w 2 ŵ t+1 2 w 2 L t. 24 / 33
115 Proof of Perceptron convergence theorem Goal: lower-bound Numerator: w T ŵ t+1 w 2 ŵ t+1 2. w T ŵ t+1 = w T (ŵ t + y tx t) = w T ŵ t + y tw T x t w T ŵ t + 1. Therefore, by induction (with ŵ 1 = 0), w T ŵ t+1 t. Denominator: ŵ t = ŵt + ytxt 2 2 = ŵt ytŵT t x t + x t 2 2 ŵt L2. Therefore, by induction (with ŵ 1 = 0), ŵ t L2 t. cos (angle between w and ŵ t+1) = w T ŵ t+1 t w 2 ŵ t+1 2 w 2 L t. Since cosine is at most one, we conclude t w 2 2 L2. 24 / 33
116 Sneak peek: maximum margin linear classifier We can obtain the linear separator with the largest margin by finding the shortest vector w such that min yx T w = 1. (x,y) S largest margin smaller margin 25 / 33
117 Sneak peek: maximum margin linear classifier We can obtain the linear separator with the largest margin by finding the shortest vector w such that min yx T w = 1. (x,y) S largest margin smaller margin This can be expressed as a mathematical optimization problem that is the basis of support vector machines. (More on this later.) 25 / 33
118 7. Online Perceptron
119 Online Perceptron If data is not linearly separable, Perceptron runs forever! 26 / 33
120 Online Perceptron If data is not linearly separable, Perceptron runs forever! Alternative: consider each example once, then stop. Online Perceptron input Labeled examples ((x i, y i )) n i=1 from Rd { 1, +1}. 1: initialize ŵ 1 := 0. 2: for t = 1, 2,..., n do 3: if y t x T tŵt 0 then 4: ŵ t+1 := ŵ t + y t x t. 5: else 6: ŵ t+1 := ŵ t 7: end if 8: end for 9: return ŵ n / 33
121 Online Perceptron If data is not linearly separable, Perceptron runs forever! Alternative: consider each example once, then stop. Online Perceptron input Labeled examples ((x i, y i )) n i=1 from Rd { 1, +1}. 1: initialize ŵ 1 := 0. 2: for t = 1, 2,..., n do 3: if y t x T tŵt 0 then 4: ŵ t+1 := ŵ t + y t x t. 5: else 6: ŵ t+1 := ŵ t 7: end if 8: end for 9: return ŵ n+1. Final classifier fŵn+1 is not necessarily a linear separator (even if one exists!). 26 / 33
122 Online learning Online learning algorithms: Go through examples (x 1, y 1), (x 2, y 2),... one-by-one. 27 / 33
123 Online learning Online learning algorithms: Go through examples (x 1, y 1), (x 2, y 2),... one-by-one. Before seeing (x t, y t), learner has a current classifier ˆf t in hand. 27 / 33
124 Online learning Online learning algorithms: Go through examples (x 1, y 1), (x 2, y 2),... one-by-one. Before seeing (x t, y t), learner has a current classifier ˆf t in hand. Upon seeing x t, learner makes a prediction: ŷ t := ˆf t(x t). 27 / 33
125 Online learning Online learning algorithms: Go through examples (x 1, y 1), (x 2, y 2),... one-by-one. Before seeing (x t, y t), learner has a current classifier ˆf t in hand. Upon seeing x t, learner makes a prediction: ŷ t := ˆf t(x t). If ŷ t y t, then the prediction was a mistake. 27 / 33
126 Online learning Online learning algorithms: Go through examples (x 1, y 1), (x 2, y 2),... one-by-one. Before seeing (x t, y t), learner has a current classifier ˆf t in hand. Upon seeing x t, learner makes a prediction: ŷ t := ˆf t(x t). If ŷ t y t, then the prediction was a mistake. See correct label y t; update ˆf t to get ˆf t+1. Typically, update is very computationally cheap to compute. 27 / 33
127 Online learning Online learning algorithms: Go through examples (x 1, y 1), (x 2, y 2),... one-by-one. Before seeing (x t, y t), learner has a current classifier ˆf t in hand. Upon seeing x t, learner makes a prediction: ŷ t := ˆf t(x t). If ŷ t y t, then the prediction was a mistake. See correct label y t; update ˆf t to get ˆf t+1. Typically, update is very computationally cheap to compute. Theorem : If there is a short w with min y t tx T t w 1, then Online Perceptron makes a small number of mistakes. 27 / 33
128 Online learning Online learning algorithms: Go through examples (x 1, y 1), (x 2, y 2),... one-by-one. Before seeing (x t, y t), learner has a current classifier ˆf t in hand. Upon seeing x t, learner makes a prediction: ŷ t := ˆf t(x t). If ŷ t y t, then the prediction was a mistake. See correct label y t; update ˆf t to get ˆf t+1. Typically, update is very computationally cheap to compute. Theorem : If there is a short w with min y t tx T t w 1, then Online Perceptron makes a small number of mistakes. Theorem : If there is a short w that makes a small number of hinge loss mistakes, then Online Perceptron makes a small number of mistakes. (See reading assignment we ll discuss hinge loss in an upcoming lecture.) 27 / 33
129 What good is a small mistake bound? Sequence of classifiers ˆf 1, ˆf 2,... is accurate (on average) in predicting labels of iid sequence (X 1, Y 1), (X 2, Y 2),... X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 ˆf 1 ˆf2 ˆf3 ˆf4 ˆf5 ˆf6 ˆf7 ˆf8 ˆf9 ˆf10 ŷ 1 ŷ 2 ŷ 3 ŷ 4 ŷ 5 ŷ 6 ŷ 7 ŷ 8 ŷ 9 ŷ 10 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 Y 8 Y 9 Y / 33
130 What good is a small mistake bound? Sequence of classifiers ˆf 1, ˆf 2,... is accurate (on average) in predicting labels of iid sequence (X 1, Y 1), (X 2, Y 2),... Combine classifiers ˆf 1, ˆf 2,... into a single, accurate classifier ˆf. X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 ˆf 1 ˆf2 ˆf3 ˆf4 ˆf5 ˆf6 ˆf7 ˆf8 ˆf9 ˆf10 ŷ 1 ŷ 2 ŷ 3 ŷ 4 ŷ 5 ŷ 6 ŷ 7 ŷ 8 ŷ 9 ŷ 10 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 Y 8 Y 9 Y 10 ˆf 28 / 33
131 What good is a small mistake bound? Sequence of classifiers ˆf 1, ˆf 2,... is accurate (on average) in predicting labels of iid sequence (X 1, Y 1), (X 2, Y 2),... Combine classifiers ˆf 1, ˆf 2,... into a single, accurate classifier ˆf. X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 ˆf 1 ˆf2 ˆf3 ˆf4 ˆf5 ˆf6 ˆf7 ˆf8 ˆf9 ˆf10 ŷ 1 ŷ 2 ŷ 3 ŷ 4 ŷ 5 ŷ 6 ŷ 7 ŷ 8 ŷ 9 ŷ 10 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 Y 8 Y 9 Y 10 ˆf This is achieved via online-to-batch conversion. 28 / 33
132 Online-to-batch conversion Run online learning algorithm on sequence of examples (x 1, y 1),..., (x n, y n) (in random order) to produce sequence of binary classifiers ˆf 1,..., ˆf n+1, ( ˆf i : X {±1}). 29 / 33
133 Online-to-batch conversion Run online learning algorithm on sequence of examples (x 1, y 1),..., (x n, y n) (in random order) to produce sequence of binary classifiers ( ˆf i : X {±1}). ˆf 1,..., ˆf n+1, Final classifier: majority vote over the ˆf i s { 1 if n+1 i=1 ˆf(x) := ˆf i(x) 0, +1 if n+1 ˆf i=1 i(x) > / 33
134 Online-to-batch conversion Run online learning algorithm on sequence of examples (x 1, y 1),..., (x n, y n) (in random order) to produce sequence of binary classifiers ( ˆf i : X {±1}). ˆf 1,..., ˆf n+1, Final classifier: majority vote over the ˆf i s { 1 if n+1 i=1 ˆf(x) := ˆf i(x) 0, +1 if n+1 ˆf i=1 i(x) > 0. There are many variants of online-to-batch conversions that make sense! 29 / 33
135 Practical suggestions for online-to-batch variant 30 / 33
136 Practical suggestions for online-to-batch variant Run online learning algorithm to make a few (e.g., two) passes over training examples, each time in a different random order. Pass 1: (x 2, y 2 ), (x 9, y 9 ), (x 6, y 6 ), (x 1, y 1 ), (x 3, y 3 ), (x 4, y 4 ), (x 10, y 10 ), (x 8, y 8 ), (x 7, y 7 ), (x 5, y 5 ) Pass 2: (x 4, y 4 ), (x 5, y 5 ), (x 1, y 1 ), (x 2, y 2 ), (x 3, y 3 ), (x 10, y 10 ), (x 7, y 7 ), (x 9, y 9 ), (x 6, y 6 ), (x 8, y 8 ) (Total of 2n rounds) 30 / 33
137 Practical suggestions for online-to-batch variant Run online learning algorithm to make a few (e.g., two) passes over training examples, each time in a different random order. Pass 1: (x 2, y 2 ), (x 9, y 9 ), (x 6, y 6 ), (x 1, y 1 ), (x 3, y 3 ), (x 4, y 4 ), (x 10, y 10 ), (x 8, y 8 ), (x 7, y 7 ), (x 5, y 5 ) Pass 2: (x 4, y 4 ), (x 5, y 5 ), (x 1, y 1 ), (x 2, y 2 ), (x 3, y 3 ), (x 10, y 10 ), (x 7, y 7 ), (x 9, y 9 ), (x 6, y 6 ), (x 8, y 8 ) (Total of 2n rounds) For linear classifiers, instead of using majority vote to combine, just average weight vectors. ŵ := 2n+1 1 ŵ i. 2n + 1 i=1 30 / 33
138 Practical suggestions for online-to-batch variant Run online learning algorithm to make a few (e.g., two) passes over training examples, each time in a different random order. Pass 1: (x 2, y 2 ), (x 9, y 9 ), (x 6, y 6 ), (x 1, y 1 ), (x 3, y 3 ), (x 4, y 4 ), (x 10, y 10 ), (x 8, y 8 ), (x 7, y 7 ), (x 5, y 5 ) Pass 2: (x 4, y 4 ), (x 5, y 5 ), (x 1, y 1 ), (x 2, y 2 ), (x 3, y 3 ), (x 10, y 10 ), (x 7, y 7 ), (x 9, y 9 ), (x 6, y 6 ), (x 8, y 8 ) (Total of 2n rounds) For linear classifiers, instead of using majority vote to combine, just average weight vectors. ŵ := 2n+1 1 ŵ i. 2n + 1 i=1 Don t use weight vectors from first pass through data. ŵ := 1 n + 1 2n+1 i=n+1 (Weight vectors at start are rubbish anyway.) ŵ i. 30 / 33
139 Example: restaurant review classification Data: 1M reviews of Pittsburgh restaruants (from Yelp). Y = {at least 4 stars, below 4 stars} (66.2% have at least 4 (out of 5) stars.) Reviews represented as bags-of-words: e.g., x great = # times great appears in review. (d unique words.) 31 / 33
140 Example: restaurant review classification Data: 1M reviews of Pittsburgh restaruants (from Yelp). Y = {at least 4 stars, below 4 stars} (66.2% have at least 4 (out of 5) stars.) Reviews represented as bags-of-words: e.g., x great = # times great appears in review. (d unique words.) Results Online Perceptron + affine expansion + online-to-batch variant: Training risk: 10.1%. Test risk (on held-out test examples): 10.5%. Running time: 1.5 minutes on single Intel Xeon 2.30GHz CPU. (This omits time to load data, which was another 4 minutes from the raw text.) 31 / 33
141 Other approaches for learning linear (or affine) classifiers Naïve Bayes generative model MLE Gaussian generative model MLE (sometimes) Methods for linear regression (+ thresholding) 32 / 33
142 Other approaches for learning linear (or affine) classifiers Naïve Bayes generative model MLE Gaussian generative model MLE (sometimes) Methods for linear regression (+ thresholding) Logistic regression, linear programming, Perceptron, Online Perceptron 32 / 33
143 Other approaches for learning linear (or affine) classifiers Naïve Bayes generative model MLE Gaussian generative model MLE (sometimes) Methods for linear regression (+ thresholding) Logistic regression, linear programming, Perceptron, Online Perceptron Support vector machines, etc. (Next lecture.) 32 / 33
144 Key takeaways 1. Logistic regression model. 2. Structure/geometry of linear classifiers. 3. Empirical risk minimization for linear classifiers and intractability. 4. Linear separability; two approaches to find a linear separator. 5. Online Perceptron; online-to-batch conversion. 33 / 33
Decision trees COMS 4771
 Decision trees COMS 4771 1. Prediction functions (again) Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random pairs (i.e., labeled examples).
Decision trees COMS 4771 1. Prediction functions (again) Learning prediction functions IID model for supervised learning: (X 1, Y 1),..., (X n, Y n), (X, Y ) are iid random pairs (i.e., labeled examples).
Machine Learning. Linear Models. Fabio Vandin October 10, 2017
 Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Linear regression COMS 4771
 Linear regression COMS 4771 1. Old Faithful and prediction functions Prediction problem: Old Faithful geyser (Yellowstone) Task: Predict time of next eruption. 1 / 40 Statistical model for time between
Linear regression COMS 4771 1. Old Faithful and prediction functions Prediction problem: Old Faithful geyser (Yellowstone) Task: Predict time of next eruption. 1 / 40 Statistical model for time between
The Perceptron algorithm
 The Perceptron algorithm Tirgul 3 November 2016 Agnostic PAC Learnability A hypothesis class H is agnostic PAC learnable if there exists a function m H : 0,1 2 N and a learning algorithm with the following
The Perceptron algorithm Tirgul 3 November 2016 Agnostic PAC Learnability A hypothesis class H is agnostic PAC learnable if there exists a function m H : 0,1 2 N and a learning algorithm with the following
Minimax risk bounds for linear threshold functions
 CS281B/Stat241B (Spring 2008) Statistical Learning Theory Lecture: 3 Minimax risk bounds for linear threshold functions Lecturer: Peter Bartlett Scribe: Hao Zhang 1 Review We assume that there is a probability
CS281B/Stat241B (Spring 2008) Statistical Learning Theory Lecture: 3 Minimax risk bounds for linear threshold functions Lecturer: Peter Bartlett Scribe: Hao Zhang 1 Review We assume that there is a probability
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1394 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1394 1 / 34 Table
Linear Classifiers and the Perceptron
 Linear Classifiers and the Perceptron William Cohen February 4, 2008 1 Linear classifiers Let s assume that every instance is an n-dimensional vector of real numbers x R n, and there are only two possible
Linear Classifiers and the Perceptron William Cohen February 4, 2008 1 Linear classifiers Let s assume that every instance is an n-dimensional vector of real numbers x R n, and there are only two possible
1 Machine Learning Concepts (16 points)
 CSCI 567 Fall 2018 Midterm Exam DO NOT OPEN EXAM UNTIL INSTRUCTED TO DO SO PLEASE TURN OFF ALL CELL PHONES Problem 1 2 3 4 5 6 Total Max 16 10 16 42 24 12 120 Points Please read the following instructions
CSCI 567 Fall 2018 Midterm Exam DO NOT OPEN EXAM UNTIL INSTRUCTED TO DO SO PLEASE TURN OFF ALL CELL PHONES Problem 1 2 3 4 5 6 Total Max 16 10 16 42 24 12 120 Points Please read the following instructions
Machine Learning 2017
 Machine Learning 2017 Volker Roth Department of Mathematics & Computer Science University of Basel 21st March 2017 Volker Roth (University of Basel) Machine Learning 2017 21st March 2017 1 / 41 Section
Machine Learning 2017 Volker Roth Department of Mathematics & Computer Science University of Basel 21st March 2017 Volker Roth (University of Basel) Machine Learning 2017 21st March 2017 1 / 41 Section
COMS F18 Homework 3 (due October 29, 2018)
 COMS 477-2 F8 Homework 3 (due October 29, 208) Instructions Submit your write-up on Gradescope as a neatly typeset (not scanned nor handwritten) PDF document by :59 PM of the due date. On Gradescope, be
COMS 477-2 F8 Homework 3 (due October 29, 208) Instructions Submit your write-up on Gradescope as a neatly typeset (not scanned nor handwritten) PDF document by :59 PM of the due date. On Gradescope, be
COMS 4721: Machine Learning for Data Science Lecture 10, 2/21/2017
 COMS 4721: Machine Learning for Data Science Lecture 10, 2/21/2017 Prof. John Paisley Department of Electrical Engineering & Data Science Institute Columbia University FEATURE EXPANSIONS FEATURE EXPANSIONS
COMS 4721: Machine Learning for Data Science Lecture 10, 2/21/2017 Prof. John Paisley Department of Electrical Engineering & Data Science Institute Columbia University FEATURE EXPANSIONS FEATURE EXPANSIONS
Machine Learning. Linear Models. Fabio Vandin October 10, 2017
 Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Machine Learning Linear Models Fabio Vandin October 10, 2017 1 Linear Predictors and Affine Functions Consider X = R d Affine functions: L d = {h w,b : w R d, b R} where ( d ) h w,b (x) = w, x + b = w
Overfitting, Bias / Variance Analysis
 Overfitting, Bias / Variance Analysis Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 8, 207 / 40 Outline Administration 2 Review of last lecture 3 Basic
Overfitting, Bias / Variance Analysis Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 8, 207 / 40 Outline Administration 2 Review of last lecture 3 Basic
CMU-Q Lecture 24:
 CMU-Q 15-381 Lecture 24: Supervised Learning 2 Teacher: Gianni A. Di Caro SUPERVISED LEARNING Hypotheses space Hypothesis function Labeled Given Errors Performance criteria Given a collection of input
CMU-Q 15-381 Lecture 24: Supervised Learning 2 Teacher: Gianni A. Di Caro SUPERVISED LEARNING Hypotheses space Hypothesis function Labeled Given Errors Performance criteria Given a collection of input
Logistic Regression. Machine Learning Fall 2018
 Logistic Regression Machine Learning Fall 2018 1 Where are e? We have seen the folloing ideas Linear models Learning as loss minimization Bayesian learning criteria (MAP and MLE estimation) The Naïve Bayes
Logistic Regression Machine Learning Fall 2018 1 Where are e? We have seen the folloing ideas Linear models Learning as loss minimization Bayesian learning criteria (MAP and MLE estimation) The Naïve Bayes
Regression with Numerical Optimization. Logistic
 CSG220 Machine Learning Fall 2008 Regression with Numerical Optimization. Logistic regression Regression with Numerical Optimization. Logistic regression based on a document by Andrew Ng October 3, 204
CSG220 Machine Learning Fall 2008 Regression with Numerical Optimization. Logistic regression Regression with Numerical Optimization. Logistic regression based on a document by Andrew Ng October 3, 204
MIDTERM SOLUTIONS: FALL 2012 CS 6375 INSTRUCTOR: VIBHAV GOGATE
 MIDTERM SOLUTIONS: FALL 2012 CS 6375 INSTRUCTOR: VIBHAV GOGATE March 28, 2012 The exam is closed book. You are allowed a double sided one page cheat sheet. Answer the questions in the spaces provided on
MIDTERM SOLUTIONS: FALL 2012 CS 6375 INSTRUCTOR: VIBHAV GOGATE March 28, 2012 The exam is closed book. You are allowed a double sided one page cheat sheet. Answer the questions in the spaces provided on
Linear Classifiers. Michael Collins. January 18, 2012
 Linear Classifiers Michael Collins January 18, 2012 Today s Lecture Binary classification problems Linear classifiers The perceptron algorithm Classification Problems: An Example Goal: build a system that
Linear Classifiers Michael Collins January 18, 2012 Today s Lecture Binary classification problems Linear classifiers The perceptron algorithm Classification Problems: An Example Goal: build a system that
Warm up: risk prediction with logistic regression
 Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Warm up: risk prediction with logistic regression Boss gives you a bunch of data on loans defaulting or not: {(x i,y i )} n i= x i 2 R d, y i 2 {, } You model the data as: P (Y = y x, w) = + exp( yw T
Recap from previous lecture
 Recap from previous lecture Learning is using past experience to improve future performance. Different types of learning: supervised unsupervised reinforcement active online... For a machine, experience
Recap from previous lecture Learning is using past experience to improve future performance. Different types of learning: supervised unsupervised reinforcement active online... For a machine, experience
Classification objectives COMS 4771
 Classification objectives COMS 4771 1. Recap: binary classification Scoring functions Consider binary classification problems with Y = { 1, +1}. 1 / 22 Scoring functions Consider binary classification
Classification objectives COMS 4771 1. Recap: binary classification Scoring functions Consider binary classification problems with Y = { 1, +1}. 1 / 22 Scoring functions Consider binary classification
Training the linear classifier
 215, Training the linear classifier A natural way to train the classifier is to minimize the number of classification errors on the training data, i.e. choosing w so that the training error is minimized.
215, Training the linear classifier A natural way to train the classifier is to minimize the number of classification errors on the training data, i.e. choosing w so that the training error is minimized.
Statistical Data Mining and Machine Learning Hilary Term 2016
 Statistical Data Mining and Machine Learning Hilary Term 2016 Dino Sejdinovic Department of Statistics Oxford Slides and other materials available at: http://www.stats.ox.ac.uk/~sejdinov/sdmml Naïve Bayes
Statistical Data Mining and Machine Learning Hilary Term 2016 Dino Sejdinovic Department of Statistics Oxford Slides and other materials available at: http://www.stats.ox.ac.uk/~sejdinov/sdmml Naïve Bayes
Gaussian and Linear Discriminant Analysis; Multiclass Classification
 Gaussian and Linear Discriminant Analysis; Multiclass Classification Professor Ameet Talwalkar Slide Credit: Professor Fei Sha Professor Ameet Talwalkar CS260 Machine Learning Algorithms October 13, 2015
Gaussian and Linear Discriminant Analysis; Multiclass Classification Professor Ameet Talwalkar Slide Credit: Professor Fei Sha Professor Ameet Talwalkar CS260 Machine Learning Algorithms October 13, 2015
Linear Models for Classification
 Linear Models for Classification Oliver Schulte - CMPT 726 Bishop PRML Ch. 4 Classification: Hand-written Digit Recognition CHINE INTELLIGENCE, VOL. 24, NO. 24, APRIL 2002 x i = t i = (0, 0, 0, 1, 0, 0,
Linear Models for Classification Oliver Schulte - CMPT 726 Bishop PRML Ch. 4 Classification: Hand-written Digit Recognition CHINE INTELLIGENCE, VOL. 24, NO. 24, APRIL 2002 x i = t i = (0, 0, 0, 1, 0, 0,
Cheng Soon Ong & Christian Walder. Canberra February June 2018
 Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
CSE 151 Machine Learning. Instructor: Kamalika Chaudhuri
 CSE 151 Machine Learning Instructor: Kamalika Chaudhuri Linear Classification Given labeled data: (xi, feature vector yi) label i=1,..,n where y is 1 or 1, find a hyperplane to separate from Linear Classification
CSE 151 Machine Learning Instructor: Kamalika Chaudhuri Linear Classification Given labeled data: (xi, feature vector yi) label i=1,..,n where y is 1 or 1, find a hyperplane to separate from Linear Classification
Machine Learning for NLP
 Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Machine Learning for NLP Linear Models Joakim Nivre Uppsala University Department of Linguistics and Philology Slides adapted from Ryan McDonald, Google Research Machine Learning for NLP 1(26) Outline
Bias-Variance Tradeoff
 What s learning, revisited Overfitting Generative versus Discriminative Logistic Regression Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University September 19 th, 2007 Bias-Variance Tradeoff
What s learning, revisited Overfitting Generative versus Discriminative Logistic Regression Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University September 19 th, 2007 Bias-Variance Tradeoff
Machine Learning for NLP
 Machine Learning for NLP Uppsala University Department of Linguistics and Philology Slides borrowed from Ryan McDonald, Google Research Machine Learning for NLP 1(50) Introduction Linear Classifiers Classifiers
Machine Learning for NLP Uppsala University Department of Linguistics and Philology Slides borrowed from Ryan McDonald, Google Research Machine Learning for NLP 1(50) Introduction Linear Classifiers Classifiers
Mark your answers ON THE EXAM ITSELF. If you are not sure of your answer you may wish to provide a brief explanation.
 CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
CS 189 Spring 2015 Introduction to Machine Learning Midterm You have 80 minutes for the exam. The exam is closed book, closed notes except your one-page crib sheet. No calculators or electronic items.
Generative Learning algorithms
 CS9 Lecture notes Andrew Ng Part IV Generative Learning algorithms So far, we ve mainly been talking about learning algorithms that model p(y x; θ), the conditional distribution of y given x. For instance,
CS9 Lecture notes Andrew Ng Part IV Generative Learning algorithms So far, we ve mainly been talking about learning algorithms that model p(y x; θ), the conditional distribution of y given x. For instance,
1 Learning Linear Separators
 10-601 Machine Learning Maria-Florina Balcan Spring 2015 Plan: Perceptron algorithm for learning linear separators. 1 Learning Linear Separators Here we can think of examples as being from {0, 1} n or
10-601 Machine Learning Maria-Florina Balcan Spring 2015 Plan: Perceptron algorithm for learning linear separators. 1 Learning Linear Separators Here we can think of examples as being from {0, 1} n or
Warm up. Regrade requests submitted directly in Gradescope, do not instructors.
 Warm up Regrade requests submitted directly in Gradescope, do not email instructors. 1 float in NumPy = 8 bytes 10 6 2 20 bytes = 1 MB 10 9 2 30 bytes = 1 GB For each block compute the memory required
Warm up Regrade requests submitted directly in Gradescope, do not email instructors. 1 float in NumPy = 8 bytes 10 6 2 20 bytes = 1 MB 10 9 2 30 bytes = 1 GB For each block compute the memory required
CS229 Supplemental Lecture notes
 CS229 Supplemental Lecture notes John Duchi Binary classification In binary classification problems, the target y can take on at only two values. In this set of notes, we show how to model this problem
CS229 Supplemental Lecture notes John Duchi Binary classification In binary classification problems, the target y can take on at only two values. In this set of notes, we show how to model this problem
Linear models: the perceptron and closest centroid algorithms. D = {(x i,y i )} n i=1. x i 2 R d 9/3/13. Preliminaries. Chapter 1, 7.
 Preliminaries Linear models: the perceptron and closest centroid algorithms Chapter 1, 7 Definition: The Euclidean dot product beteen to vectors is the expression d T x = i x i The dot product is also
Preliminaries Linear models: the perceptron and closest centroid algorithms Chapter 1, 7 Definition: The Euclidean dot product beteen to vectors is the expression d T x = i x i The dot product is also
Support vector machines Lecture 4
 Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
Support vector machines Lecture 4 David Sontag New York University Slides adapted from Luke Zettlemoyer, Vibhav Gogate, and Carlos Guestrin Q: What does the Perceptron mistake bound tell us? Theorem: The
Machine Learning, Fall 2012 Homework 2
 0-60 Machine Learning, Fall 202 Homework 2 Instructors: Tom Mitchell, Ziv Bar-Joseph TA in charge: Selen Uguroglu email: sugurogl@cs.cmu.edu SOLUTIONS Naive Bayes, 20 points Problem. Basic concepts, 0
0-60 Machine Learning, Fall 202 Homework 2 Instructors: Tom Mitchell, Ziv Bar-Joseph TA in charge: Selen Uguroglu email: sugurogl@cs.cmu.edu SOLUTIONS Naive Bayes, 20 points Problem. Basic concepts, 0
The Perceptron Algorithm 1
 CS 64: Machine Learning Spring 5 College of Computer and Information Science Northeastern University Lecture 5 March, 6 Instructor: Bilal Ahmed Scribe: Bilal Ahmed & Virgil Pavlu Introduction The Perceptron
CS 64: Machine Learning Spring 5 College of Computer and Information Science Northeastern University Lecture 5 March, 6 Instructor: Bilal Ahmed Scribe: Bilal Ahmed & Virgil Pavlu Introduction The Perceptron
Empirical Risk Minimization Algorithms
 Empirical Risk Minimization Algorithms Tirgul 2 Part I November 2016 Reminder Domain set, X : the set of objects that we wish to label. Label set, Y : the set of possible labels. A prediction rule, h:
Empirical Risk Minimization Algorithms Tirgul 2 Part I November 2016 Reminder Domain set, X : the set of objects that we wish to label. Label set, Y : the set of possible labels. A prediction rule, h:
1 Learning Linear Separators
 8803 Machine Learning Theory Maria-Florina Balcan Lecture 3: August 30, 2011 Plan: Perceptron algorithm for learning linear separators. 1 Learning Linear Separators Here we can think of examples as being
8803 Machine Learning Theory Maria-Florina Balcan Lecture 3: August 30, 2011 Plan: Perceptron algorithm for learning linear separators. 1 Learning Linear Separators Here we can think of examples as being
Max Margin-Classifier
 Max Margin-Classifier Oliver Schulte - CMPT 726 Bishop PRML Ch. 7 Outline Maximum Margin Criterion Math Maximizing the Margin Non-Separable Data Kernels and Non-linear Mappings Where does the maximization
Max Margin-Classifier Oliver Schulte - CMPT 726 Bishop PRML Ch. 7 Outline Maximum Margin Criterion Math Maximizing the Margin Non-Separable Data Kernels and Non-linear Mappings Where does the maximization
Generative v. Discriminative classifiers Intuition
 Logistic Regression (Continued) Generative v. Discriminative Decision rees Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University January 31 st, 2007 2005-2007 Carlos Guestrin 1 Generative
Logistic Regression (Continued) Generative v. Discriminative Decision rees Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University January 31 st, 2007 2005-2007 Carlos Guestrin 1 Generative
Ad Placement Strategies
 Case Study 1: Estimating Click Probabilities Tackling an Unknown Number of Features with Sketching Machine Learning for Big Data CSE547/STAT548, University of Washington Emily Fox 2014 Emily Fox January
Case Study 1: Estimating Click Probabilities Tackling an Unknown Number of Features with Sketching Machine Learning for Big Data CSE547/STAT548, University of Washington Emily Fox 2014 Emily Fox January
Least Squares Regression
 CIS 50: Machine Learning Spring 08: Lecture 4 Least Squares Regression Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may not cover all the
CIS 50: Machine Learning Spring 08: Lecture 4 Least Squares Regression Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the lecture. They may or may not cover all the
Is the test error unbiased for these programs?
 Is the test error unbiased for these programs? Xtrain avg N o Preprocessing by de meaning using whole TEST set 2017 Kevin Jamieson 1 Is the test error unbiased for this program? e Stott see non for f x
Is the test error unbiased for these programs? Xtrain avg N o Preprocessing by de meaning using whole TEST set 2017 Kevin Jamieson 1 Is the test error unbiased for this program? e Stott see non for f x
Machine Learning Practice Page 2 of 2 10/28/13
 Machine Learning 10-701 Practice Page 2 of 2 10/28/13 1. True or False Please give an explanation for your answer, this is worth 1 pt/question. (a) (2 points) No classifier can do better than a naive Bayes
Machine Learning 10-701 Practice Page 2 of 2 10/28/13 1. True or False Please give an explanation for your answer, this is worth 1 pt/question. (a) (2 points) No classifier can do better than a naive Bayes
Support Vector Machines
 Support Vector Machines Le Song Machine Learning I CSE 6740, Fall 2013 Naïve Bayes classifier Still use Bayes decision rule for classification P y x = P x y P y P x But assume p x y = 1 is fully factorized
Support Vector Machines Le Song Machine Learning I CSE 6740, Fall 2013 Naïve Bayes classifier Still use Bayes decision rule for classification P y x = P x y P y P x But assume p x y = 1 is fully factorized
More about the Perceptron
 More about the Perceptron CMSC 422 MARINE CARPUAT marine@cs.umd.edu Credit: figures by Piyush Rai and Hal Daume III Recap: Perceptron for binary classification Classifier = hyperplane that separates positive
More about the Perceptron CMSC 422 MARINE CARPUAT marine@cs.umd.edu Credit: figures by Piyush Rai and Hal Daume III Recap: Perceptron for binary classification Classifier = hyperplane that separates positive
Classification CE-717: Machine Learning Sharif University of Technology. M. Soleymani Fall 2012
 Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Classification CE-717: Machine Learning Sharif University of Technology M. Soleymani Fall 2012 Topics Discriminant functions Logistic regression Perceptron Generative models Generative vs. discriminative
Introduction to Machine Learning
 1, DATA11002 Introduction to Machine Learning Lecturer: Teemu Roos TAs: Ville Hyvönen and Janne Leppä-aho Department of Computer Science University of Helsinki (based in part on material by Patrik Hoyer
1, DATA11002 Introduction to Machine Learning Lecturer: Teemu Roos TAs: Ville Hyvönen and Janne Leppä-aho Department of Computer Science University of Helsinki (based in part on material by Patrik Hoyer
Linear discriminant functions
 Andrea Passerini passerini@disi.unitn.it Machine Learning Discriminative learning Discriminative vs generative Generative learning assumes knowledge of the distribution governing the data Discriminative
Andrea Passerini passerini@disi.unitn.it Machine Learning Discriminative learning Discriminative vs generative Generative learning assumes knowledge of the distribution governing the data Discriminative
> DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE GRAVIS 2016 BASEL. Logistic Regression. Pattern Recognition 2016 Sandro Schönborn University of Basel
 Logistic Regression Pattern Recognition 2016 Sandro Schönborn University of Basel Two Worlds: Probabilistic & Algorithmic We have seen two conceptual approaches to classification: data class density estimation
Logistic Regression Pattern Recognition 2016 Sandro Schönborn University of Basel Two Worlds: Probabilistic & Algorithmic We have seen two conceptual approaches to classification: data class density estimation
Lecture 4: Linear predictors and the Perceptron
 Lecture 4: Linear predictors and the Perceptron Introduction to Learning and Analysis of Big Data Kontorovich and Sabato (BGU) Lecture 4 1 / 34 Inductive Bias Inductive bias is critical to prevent overfitting.
Lecture 4: Linear predictors and the Perceptron Introduction to Learning and Analysis of Big Data Kontorovich and Sabato (BGU) Lecture 4 1 / 34 Inductive Bias Inductive bias is critical to prevent overfitting.
Linear & nonlinear classifiers
 Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Linear & nonlinear classifiers Machine Learning Hamid Beigy Sharif University of Technology Fall 1396 Hamid Beigy (Sharif University of Technology) Linear & nonlinear classifiers Fall 1396 1 / 44 Table
Linear Methods for Prediction
 Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Chapter 5 Linear Methods for Prediction 5.1 Introduction We now revisit the classification problem and focus on linear methods. Since our prediction Ĝ(x) will always take values in the discrete set G we
Linear Discrimination Functions
 Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari November 4, 2009 Outline Linear models Gradient descent Perceptron Minimum square error approach
Laurea Magistrale in Informatica Nicola Fanizzi Dipartimento di Informatica Università degli Studi di Bari November 4, 2009 Outline Linear models Gradient descent Perceptron Minimum square error approach
Statistical Machine Learning Hilary Term 2018
 Statistical Machine Learning Hilary Term 2018 Pier Francesco Palamara Department of Statistics University of Oxford Slide credits and other course material can be found at: http://www.stats.ox.ac.uk/~palamara/sml18.html
Statistical Machine Learning Hilary Term 2018 Pier Francesco Palamara Department of Statistics University of Oxford Slide credits and other course material can be found at: http://www.stats.ox.ac.uk/~palamara/sml18.html
Bayesian Methods: Naïve Bayes
 Bayesian Methods: aïve Bayes icholas Ruozzi University of Texas at Dallas based on the slides of Vibhav Gogate Last Time Parameter learning Learning the parameter of a simple coin flipping model Prior
Bayesian Methods: aïve Bayes icholas Ruozzi University of Texas at Dallas based on the slides of Vibhav Gogate Last Time Parameter learning Learning the parameter of a simple coin flipping model Prior
Linear Models in Machine Learning
 CS540 Intro to AI Linear Models in Machine Learning Lecturer: Xiaojin Zhu jerryzhu@cs.wisc.edu We briefly go over two linear models frequently used in machine learning: linear regression for, well, regression,
CS540 Intro to AI Linear Models in Machine Learning Lecturer: Xiaojin Zhu jerryzhu@cs.wisc.edu We briefly go over two linear models frequently used in machine learning: linear regression for, well, regression,
Machine Learning Basics Lecture 7: Multiclass Classification. Princeton University COS 495 Instructor: Yingyu Liang
 Machine Learning Basics Lecture 7: Multiclass Classification Princeton University COS 495 Instructor: Yingyu Liang Example: image classification indoor Indoor outdoor Example: image classification (multiclass)
Machine Learning Basics Lecture 7: Multiclass Classification Princeton University COS 495 Instructor: Yingyu Liang Example: image classification indoor Indoor outdoor Example: image classification (multiclass)
Linear Regression (continued)
 Linear Regression (continued) Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 6, 2017 1 / 39 Outline 1 Administration 2 Review of last lecture 3 Linear regression
Linear Regression (continued) Professor Ameet Talwalkar Professor Ameet Talwalkar CS260 Machine Learning Algorithms February 6, 2017 1 / 39 Outline 1 Administration 2 Review of last lecture 3 Linear regression
Least Squares Regression
 E0 70 Machine Learning Lecture 4 Jan 7, 03) Least Squares Regression Lecturer: Shivani Agarwal Disclaimer: These notes are a brief summary of the topics covered in the lecture. They are not a substitute
E0 70 Machine Learning Lecture 4 Jan 7, 03) Least Squares Regression Lecturer: Shivani Agarwal Disclaimer: These notes are a brief summary of the topics covered in the lecture. They are not a substitute
Empirical Risk Minimization
 Empirical Risk Minimization Fabrice Rossi SAMM Université Paris 1 Panthéon Sorbonne 2018 Outline Introduction PAC learning ERM in practice 2 General setting Data X the input space and Y the output space
Empirical Risk Minimization Fabrice Rossi SAMM Université Paris 1 Panthéon Sorbonne 2018 Outline Introduction PAC learning ERM in practice 2 General setting Data X the input space and Y the output space
Last Time. Today. Bayesian Learning. The Distributions We Love. CSE 446 Gaussian Naïve Bayes & Logistic Regression
 CSE 446 Gaussian Naïve Bayes & Logistic Regression Winter 22 Dan Weld Learning Gaussians Naïve Bayes Last Time Gaussians Naïve Bayes Logistic Regression Today Some slides from Carlos Guestrin, Luke Zettlemoyer
CSE 446 Gaussian Naïve Bayes & Logistic Regression Winter 22 Dan Weld Learning Gaussians Naïve Bayes Last Time Gaussians Naïve Bayes Logistic Regression Today Some slides from Carlos Guestrin, Luke Zettlemoyer
COMS 4771 Introduction to Machine Learning. Nakul Verma
 COMS 4771 Introduction to Machine Learning Nakul Verma Announcements HW1 due next lecture Project details are available decide on the group and topic by Thursday Last time Generative vs. Discriminative
COMS 4771 Introduction to Machine Learning Nakul Verma Announcements HW1 due next lecture Project details are available decide on the group and topic by Thursday Last time Generative vs. Discriminative
Last updated: Oct 22, 2012 LINEAR CLASSIFIERS. J. Elder CSE 4404/5327 Introduction to Machine Learning and Pattern Recognition
 Last updated: Oct 22, 2012 LINEAR CLASSIFIERS Problems 2 Please do Problem 8.3 in the textbook. We will discuss this in class. Classification: Problem Statement 3 In regression, we are modeling the relationship
Last updated: Oct 22, 2012 LINEAR CLASSIFIERS Problems 2 Please do Problem 8.3 in the textbook. We will discuss this in class. Classification: Problem Statement 3 In regression, we are modeling the relationship
Linear smoother. ŷ = S y. where s ij = s ij (x) e.g. s ij = diag(l i (x))
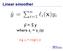 Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Linear smoother ŷ = S y where s ij = s ij (x) e.g. s ij = diag(l i (x)) 2 Online Learning: LMS and Perceptrons Partially adapted from slides by Ryan Gabbard and Mitch Marcus (and lots original slides by
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
EE 511 Online Learning Perceptron
 Slides adapted from Ali Farhadi, Mari Ostendorf, Pedro Domingos, Carlos Guestrin, and Luke Zettelmoyer, Kevin Jamison EE 511 Online Learning Perceptron Instructor: Hanna Hajishirzi hannaneh@washington.edu
Slides adapted from Ali Farhadi, Mari Ostendorf, Pedro Domingos, Carlos Guestrin, and Luke Zettelmoyer, Kevin Jamison EE 511 Online Learning Perceptron Instructor: Hanna Hajishirzi hannaneh@washington.edu
Final Exam. December 11 th, This exam booklet contains five problems, out of which you are expected to answer four problems of your choice.
 CS446: Machine Learning Fall 2012 Final Exam December 11 th, 2012 This is a closed book exam. Everything you need in order to solve the problems is supplied in the body of this exam. Note that there is
CS446: Machine Learning Fall 2012 Final Exam December 11 th, 2012 This is a closed book exam. Everything you need in order to solve the problems is supplied in the body of this exam. Note that there is
Neural networks COMS 4771
 Neural networks COMS 4771 1. Logistic regression Logistic regression Suppose X = R d and Y = {0, 1}. A logistic regression model is a statistical model where the conditional probability function has a
Neural networks COMS 4771 1. Logistic regression Logistic regression Suppose X = R d and Y = {0, 1}. A logistic regression model is a statistical model where the conditional probability function has a
Machine Learning Lecture 7
 Course Outline Machine Learning Lecture 7 Fundamentals (2 weeks) Bayes Decision Theory Probability Density Estimation Statistical Learning Theory 23.05.2016 Discriminative Approaches (5 weeks) Linear Discriminant
Course Outline Machine Learning Lecture 7 Fundamentals (2 weeks) Bayes Decision Theory Probability Density Estimation Statistical Learning Theory 23.05.2016 Discriminative Approaches (5 weeks) Linear Discriminant
CSCI-567: Machine Learning (Spring 2019)
 CSCI-567: Machine Learning (Spring 2019) Prof. Victor Adamchik U of Southern California Mar. 19, 2019 March 19, 2019 1 / 43 Administration March 19, 2019 2 / 43 Administration TA3 is due this week March
CSCI-567: Machine Learning (Spring 2019) Prof. Victor Adamchik U of Southern California Mar. 19, 2019 March 19, 2019 1 / 43 Administration March 19, 2019 2 / 43 Administration TA3 is due this week March
Logistic Regression Review Fall 2012 Recitation. September 25, 2012 TA: Selen Uguroglu
 Logistic Regression Review 10-601 Fall 2012 Recitation September 25, 2012 TA: Selen Uguroglu!1 Outline Decision Theory Logistic regression Goal Loss function Inference Gradient Descent!2 Training Data
Logistic Regression Review 10-601 Fall 2012 Recitation September 25, 2012 TA: Selen Uguroglu!1 Outline Decision Theory Logistic regression Goal Loss function Inference Gradient Descent!2 Training Data
Introduction to Machine Learning
 1, DATA11002 Introduction to Machine Learning Lecturer: Antti Ukkonen TAs: Saska Dönges and Janne Leppä-aho Department of Computer Science University of Helsinki (based in part on material by Patrik Hoyer,
1, DATA11002 Introduction to Machine Learning Lecturer: Antti Ukkonen TAs: Saska Dönges and Janne Leppä-aho Department of Computer Science University of Helsinki (based in part on material by Patrik Hoyer,
Engineering Part IIB: Module 4F10 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers
 Engineering Part IIB: Module 4F0 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers Phil Woodland: pcw@eng.cam.ac.uk Michaelmas 202 Engineering Part IIB:
Engineering Part IIB: Module 4F0 Statistical Pattern Processing Lecture 5: Single Layer Perceptrons & Estimating Linear Classifiers Phil Woodland: pcw@eng.cam.ac.uk Michaelmas 202 Engineering Part IIB:
Universität Potsdam Institut für Informatik Lehrstuhl Maschinelles Lernen. Linear Classifiers. Blaine Nelson, Tobias Scheffer
 Universität Potsdam Institut für Informatik Lehrstuhl Linear Classifiers Blaine Nelson, Tobias Scheffer Contents Classification Problem Bayesian Classifier Decision Linear Classifiers, MAP Models Logistic
Universität Potsdam Institut für Informatik Lehrstuhl Linear Classifiers Blaine Nelson, Tobias Scheffer Contents Classification Problem Bayesian Classifier Decision Linear Classifiers, MAP Models Logistic
a b = a T b = a i b i (1) i=1 (Geometric definition) The dot product of two Euclidean vectors a and b is defined by a b = a b cos(θ a,b ) (2)
 This is my preperation notes for teaching in sections during the winter 2018 quarter for course CSE 446. Useful for myself to review the concepts as well. More Linear Algebra Definition 1.1 (Dot Product).
This is my preperation notes for teaching in sections during the winter 2018 quarter for course CSE 446. Useful for myself to review the concepts as well. More Linear Algebra Definition 1.1 (Dot Product).
Convex optimization COMS 4771
 Convex optimization COMS 4771 1. Recap: learning via optimization Soft-margin SVMs Soft-margin SVM optimization problem defined by training data: w R d λ 2 w 2 2 + 1 n n [ ] 1 y ix T i w. + 1 / 15 Soft-margin
Convex optimization COMS 4771 1. Recap: learning via optimization Soft-margin SVMs Soft-margin SVM optimization problem defined by training data: w R d λ 2 w 2 2 + 1 n n [ ] 1 y ix T i w. + 1 / 15 Soft-margin
10-701/ Machine Learning - Midterm Exam, Fall 2010
 10-701/15-781 Machine Learning - Midterm Exam, Fall 2010 Aarti Singh Carnegie Mellon University 1. Personal info: Name: Andrew account: E-mail address: 2. There should be 15 numbered pages in this exam
10-701/15-781 Machine Learning - Midterm Exam, Fall 2010 Aarti Singh Carnegie Mellon University 1. Personal info: Name: Andrew account: E-mail address: 2. There should be 15 numbered pages in this exam
LINEAR CLASSIFICATION, PERCEPTRON, LOGISTIC REGRESSION, SVC, NAÏVE BAYES. Supervised Learning
 LINEAR CLASSIFICATION, PERCEPTRON, LOGISTIC REGRESSION, SVC, NAÏVE BAYES Supervised Learning Linear vs non linear classifiers In K-NN we saw an example of a non-linear classifier: the decision boundary
LINEAR CLASSIFICATION, PERCEPTRON, LOGISTIC REGRESSION, SVC, NAÏVE BAYES Supervised Learning Linear vs non linear classifiers In K-NN we saw an example of a non-linear classifier: the decision boundary
Discriminative Models
 No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
No.5 Discriminative Models Hui Jiang Department of Electrical Engineering and Computer Science Lassonde School of Engineering York University, Toronto, Canada Outline Generative vs. Discriminative models
Probabilistic modeling. The slides are closely adapted from Subhransu Maji s slides
 Probabilistic modeling The slides are closely adapted from Subhransu Maji s slides Overview So far the models and algorithms you have learned about are relatively disconnected Probabilistic modeling framework
Probabilistic modeling The slides are closely adapted from Subhransu Maji s slides Overview So far the models and algorithms you have learned about are relatively disconnected Probabilistic modeling framework
Notes on Discriminant Functions and Optimal Classification
 Notes on Discriminant Functions and Optimal Classification Padhraic Smyth, Department of Computer Science University of California, Irvine c 2017 1 Discriminant Functions Consider a classification problem
Notes on Discriminant Functions and Optimal Classification Padhraic Smyth, Department of Computer Science University of California, Irvine c 2017 1 Discriminant Functions Consider a classification problem
Generative v. Discriminative classifiers Intuition
 Logistic Regression Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University September 24 th, 2007 1 Generative v. Discriminative classifiers Intuition Want to Learn: h:x a Y X features
Logistic Regression Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University September 24 th, 2007 1 Generative v. Discriminative classifiers Intuition Want to Learn: h:x a Y X features
Machine Learning and Data Mining. Linear classification. Kalev Kask
 Machine Learning and Data Mining Linear classification Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ = f(x ; q) Parameters q Program ( Learner ) Learning algorithm Change q
Machine Learning and Data Mining Linear classification Kalev Kask Supervised learning Notation Features x Targets y Predictions ŷ = f(x ; q) Parameters q Program ( Learner ) Learning algorithm Change q
6.867 Machine learning: lecture 2. Tommi S. Jaakkola MIT CSAIL
 6.867 Machine learning: lecture 2 Tommi S. Jaakkola MIT CSAIL tommi@csail.mit.edu Topics The learning problem hypothesis class, estimation algorithm loss and estimation criterion sampling, empirical and
6.867 Machine learning: lecture 2 Tommi S. Jaakkola MIT CSAIL tommi@csail.mit.edu Topics The learning problem hypothesis class, estimation algorithm loss and estimation criterion sampling, empirical and
Gaussian discriminant analysis Naive Bayes
 DM825 Introduction to Machine Learning Lecture 7 Gaussian discriminant analysis Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. is 2. Multi-variate
DM825 Introduction to Machine Learning Lecture 7 Gaussian discriminant analysis Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. is 2. Multi-variate
Logistic Regression Logistic
 Case Study 1: Estimating Click Probabilities L2 Regularization for Logistic Regression Machine Learning/Statistics for Big Data CSE599C1/STAT592, University of Washington Carlos Guestrin January 10 th,
Case Study 1: Estimating Click Probabilities L2 Regularization for Logistic Regression Machine Learning/Statistics for Big Data CSE599C1/STAT592, University of Washington Carlos Guestrin January 10 th,
The Perceptron Algorithm, Margins
 The Perceptron Algorithm, Margins MariaFlorina Balcan 08/29/2018 The Perceptron Algorithm Simple learning algorithm for supervised classification analyzed via geometric margins in the 50 s [Rosenblatt
The Perceptron Algorithm, Margins MariaFlorina Balcan 08/29/2018 The Perceptron Algorithm Simple learning algorithm for supervised classification analyzed via geometric margins in the 50 s [Rosenblatt
Pattern Recognition and Machine Learning. Perceptrons and Support Vector machines
 Pattern Recognition and Machine Learning James L. Crowley ENSIMAG 3 - MMIS Fall Semester 2016 Lessons 6 10 Jan 2017 Outline Perceptrons and Support Vector machines Notation... 2 Perceptrons... 3 History...3
Pattern Recognition and Machine Learning James L. Crowley ENSIMAG 3 - MMIS Fall Semester 2016 Lessons 6 10 Jan 2017 Outline Perceptrons and Support Vector machines Notation... 2 Perceptrons... 3 History...3
Lecture 16: Modern Classification (I) - Separating Hyperplanes
 Lecture 16: Modern Classification (I) - Separating Hyperplanes Outline 1 2 Separating Hyperplane Binary SVM for Separable Case Bayes Rule for Binary Problems Consider the simplest case: two classes are
Lecture 16: Modern Classification (I) - Separating Hyperplanes Outline 1 2 Separating Hyperplane Binary SVM for Separable Case Bayes Rule for Binary Problems Consider the simplest case: two classes are
Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods.
 Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods. Linear models for classification Logistic regression Gradient descent and second-order methods
Lecture 5: Linear models for classification. Logistic regression. Gradient Descent. Second-order methods. Linear models for classification Logistic regression Gradient descent and second-order methods
Advanced Introduction to Machine Learning CMU-10715
 Advanced Introduction to Machine Learning CMU-10715 Risk Minimization Barnabás Póczos What have we seen so far? Several classification & regression algorithms seem to work fine on training datasets: Linear
Advanced Introduction to Machine Learning CMU-10715 Risk Minimization Barnabás Póczos What have we seen so far? Several classification & regression algorithms seem to work fine on training datasets: Linear
NONLINEAR CLASSIFICATION AND REGRESSION. J. Elder CSE 4404/5327 Introduction to Machine Learning and Pattern Recognition
 NONLINEAR CLASSIFICATION AND REGRESSION Nonlinear Classification and Regression: Outline 2 Multi-Layer Perceptrons The Back-Propagation Learning Algorithm Generalized Linear Models Radial Basis Function
NONLINEAR CLASSIFICATION AND REGRESSION Nonlinear Classification and Regression: Outline 2 Multi-Layer Perceptrons The Back-Propagation Learning Algorithm Generalized Linear Models Radial Basis Function
Ch 4. Linear Models for Classification
 Ch 4. Linear Models for Classification Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Department of Computer Science and Engineering Pohang University of Science and echnology 77 Cheongam-ro,
Ch 4. Linear Models for Classification Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Department of Computer Science and Engineering Pohang University of Science and echnology 77 Cheongam-ro,
Linear Methods for Classification
 Linear Methods for Classification Department of Statistics The Pennsylvania State University Email: jiali@stat.psu.edu Classification Supervised learning Training data: {(x 1, g 1 ), (x 2, g 2 ),..., (x
Linear Methods for Classification Department of Statistics The Pennsylvania State University Email: jiali@stat.psu.edu Classification Supervised learning Training data: {(x 1, g 1 ), (x 2, g 2 ),..., (x
Machine Learning: Chenhao Tan University of Colorado Boulder LECTURE 9
 Machine Learning: Chenhao Tan University of Colorado Boulder LECTURE 9 Slides adapted from Jordan Boyd-Graber Machine Learning: Chenhao Tan Boulder 1 of 39 Recap Supervised learning Previously: KNN, naïve
Machine Learning: Chenhao Tan University of Colorado Boulder LECTURE 9 Slides adapted from Jordan Boyd-Graber Machine Learning: Chenhao Tan Boulder 1 of 39 Recap Supervised learning Previously: KNN, naïve
Learning Methods for Linear Detectors
 Intelligent Systems: Reasoning and Recognition James L. Crowley ENSIMAG 2 / MoSIG M1 Second Semester 2011/2012 Lesson 20 27 April 2012 Contents Learning Methods for Linear Detectors Learning Linear Detectors...2
Intelligent Systems: Reasoning and Recognition James L. Crowley ENSIMAG 2 / MoSIG M1 Second Semester 2011/2012 Lesson 20 27 April 2012 Contents Learning Methods for Linear Detectors Learning Linear Detectors...2
