Copyright 1978, by the author(s). All rights reserved.
|
|
|
- Barnaby Barnett
- 5 years ago
- Views:
Transcription
1 Cpyright 1978, by the authr(s). All rights reserved. Permissi t make digital r hard cpies f all r part f this wrk fr persal r classrm use is grated withut fee prvided that cpies are t made r distributed fr prfit r cmmercial advatage ad that cpies bear this tice ad the full citati the first page. T cpy therwise, t republish, t pst servers r t redistribute t lists, requires prir specific permissi.
2 AN INTUITIVE DERIVATION OF A REALIZATION by C. A. Deser ad E. L. L Memradum N. UCB/ERL M78/87 15 December 1978 ELECTRONICS RESEARCH LABORATORY Cllege f Egieerig Uiversity f Califria, Berkeley 94720
3 AN INTUITIVE DERIVATION OF A REALIZATION PROCEDURE BASED ON SINGULAR VALUE DECOMPOSITION C. A. Deser ad E. L. L Departmet f Electrical Egieerig ad Cmputer Scieces ad the Electrics Research Labratry Uiversity f Califria, Berkeley, Califria ABSTRACT This memradum presets a ituitive derivati f the miimal x. realizati f G(s) G ]R(s) based sigular value decmpsiti, The rigial wrk is due t P. Va Dre, et al. Research spsred by the Natial Sciece Fudati Grat ENV
4 I. Itrducti The prblem f cstructig a miimal realizati f a give matrix f ratial fuctis has bee studied i literature, but the umerical aspects f the suggested prcedures have rarely bee csidered. Va Dre has prpsed a umerically stable algrithm fr cstructig a miimal realizati [1]. This paper, based Va Dre1s result, gives a ituitive isight i such a realizati, ad gives a simple prf f miimality. It is well kw that if a strictly prper ratial matrix is decmpsed it the sum f the pricipal parts f its Lauret expasi at each f its ples, say P H(s) = H (s) i=l x the the direct sum f miimal realizatis f each f the H^s is a miimal realizati f H. Thus i secti II, we derive a miimal realizati f a matrix f strictly prper ratial fuctis with a ple f rder 2. secti III, we prve that the prpsed realizati is miimal. secti IV, we geeralize the methd prpsed i secti II; by iducti, we btai a realizati f a matrix f strictly prper ratial fuctis with a sigle ple f arbitrary rder. T illustrate the spirit f the methd, we csider the simple prblem f the miimal realizati f a matrix with a first rder ple.... x, Let G(s) =N^1}/(s-X) where N*1' Gffi. (1) Perfrm a sigular value decmpsiti ^ : N(D. UViV"* where U(1) 61, VU) GC1 I are uitary ad x. (i) ZW =diag(va2,...,ap,0,0,...,0) Gm *. Ut Pj < rak ^. I -2-
5 r(d,<d Let Ux"' ad V(1) dete the first p± clums f U ad V resp, Pi Let Z = diag(a.,a0,...,a ); the (1) = U(1)E(1)V(1) pl pl pl u(1)i(1) pl pl x ~pir s-x S V (1) A D A := XI V (D* = : B C := u(1)z(1) pl pl Sice B ad C have bth rak p^, rak[si-aib] = q±9 Vs e 0 [si-a rak L""cj = Pl, VsG(K Hece the realizati is cmpletely ctrllable ad bservable, hece miimal. II. Miimal realizati f a ple f rder 2. We csider a matrix f ratial fuctis G(s) 3R x., where G(s) is strictly prper. Let G(s) has a sigle ple X f rder 2, hece we write G(s) as 42) 42) G(s) = ~r + (s-x) 2 s-x (1) /ON x. /0x «x4 where N<2) 6 <D \ N<2) 6 I \ -3-
6 (2) N It is clear that t realize the secd rder term j requires (s-x)z (2) at least 2Tak N~ itegratrs. The makig maximum use f these (2) 2*rak N^ N (2) the term s-x * itegratrs with sme additial itegratrs, we will realize (2) xi T determie the rak f N* G, we perfrm a sigular (2) value decmpsiti (abbreviated by SVD) N ad btai (2). <2>E<2)V<2)* (2) /0v x where U(2) e <c (2) imi is uitary; V <C is uitary; M2) x i. Tm.. (2) ZK ' 3R ; Z with a<2) >a<2)... >a(2) > P2 O OJ Hece (2) rak N» = p2' Partitiig bth IT,V^ as fllws, we btai U (2) *-p2+ ^VP2^ U (2) U (2) VP2 V (2) V ^-p.-)- -t-^-p2">- (2) r(2) ±-p2. (3) Let's defie.(2).= f > ~1 (4) (2) p2-4-
7 With the tatis defied i (3) ad (4), Eq. (2) is rewritte as N(2). D(2)z(2)v(2)* (5) P2 P2 P2 Remark: If N(2) = 0, usig (5), a miimal realizati f G(s) is immediate: A := XI VI XI 2J -<-. -*- - x"i,(2)* LP2 J = : B C := <2)E<2) p2 P2 + P2- By ispecti, Vs <E, rak[si-a:b] = 2p ad rak si-a = 2p, hece the realizati is miimal. i Let u S E. dete the iput. Let H2 v -P. := V^ ; u (6) i 2 v ~VP2 L T cstruct a realizati ituitively, csider G(s)u = 'm<2> N2 (s-x) 2 (2)v(2) -= X + (s-x) u(2) +!L_ V(2).v(2)*u s-x (2)v(2) s-x V -p. VP2 (2) Usig the partiti f V frm Eq. (3), we btai -5-
8 N(2)V I Ni(2>V(2> I 2 P2 P2 1 -p2 (2) (2) P2 G(S)U = T^ - TV + r^= V + NrV^ 4- V s-x s-x ~p, s-x ~i"p2 * p2 e~x ~p: (7) Let us use p? itegratrs t realize ~P2 s-x ~p2 the the realizati f the third term f (7) is immediate: (2)v(2) 1 p2,-,. r(2) (2) r-^- v = ; 'V" ' X s-x ~p 1 p "^2 I terms f x ad v, the first tw terms f (7) becme ~p2 ~i"p2 N(2)v(2) N<2V2> 2 p9 _± L z := ^-x + : v s-x ~p( s-x ~i~p2 a [»;" 1 x ~P. V ~i"p2 (8) where N(D :=rnf>vf>infv2>l 1. \ji p2 ; 1 t-p2 j (9) The miimum. f itegratrs required fr realizig (8) is p := rak N-^. T determie px, we perfrm asigular value 1 * decmpsiti!" ad btai (d. D<i)E<i)v(i) (10).. x where IT ' ^ <E *.x x (1) is uitary, V(1) E <E i i is uitary; E^ e m i -6-
9 («.- i i 1 1 (10a) I J with a <«>a<x)... >a(1) > P- Partitiig bth U(1), V(1) as fllws, we btai U (1) _ <!>!U(1) pi! Vpi XD _ r XD,d) rpi. i (11) -HP^'^^-P^ -s-p^ -e-^-p^ We further partiti V; Pl «- Pi -» as fllws: (i) _ (12) \2Lpij We defie (1) CD (1).= (13a) (1) ad p := rak N (1) (13b) -7-
10 With the tatis defied i (11), (12), (13), Eq. (10) is writte as N<X> =U(1)S(1>V(1)*=/u(1>E(1>V(1)*Uv(1)I V<" pl pl Pl Pl Pl Pl pl Pl pl (1>v(1)i v(i) 1 p PX PX (14) ad Eq. (8) becmes 1 P- pl s-x r V(1)*i Lpi! pl _ X ~p2 (15) V _"VP2 _ This shws that z ca be realized by p1 itegratrs. We defie x ~P- s-x A(i)*.; v(d* Lpl i pl. X -p. (16) Remark: Sice N CD.= V L'Vp2. ;(2)v(2)j (2)v(2) 1 frm (9), Jl P2, 1 ±-P2 P2 := rak N<2) =rak N^2)V*2) <rak N*1* =: p±. Based the abve aalysis, G(s) diagram. is realized by the fllwig blck -8-
11 U a) 6 Q. I d a l ih 0 PQ < 4J CO N 60 a 4J O D M 4J CO a J 4J V< O 60 rh CCS 00 a H rh O <4-4 CU 0) N U «4H O «< CO ^ H 1 M is CO 3 T3 + a) /-\ Vi ""s <-< a 1 w CO N»t a) 53 J3 H 1 CO I CT> I 3* PQ if 14-1 u O U-l CO ctf S I Q. I a rh a. >> rh h- a -e. a. TJ O U P. cu 4J CO a. I 0 00 CO» 2 T Q. <> *- Q. * i Q. M r a.» U cd rh <D 1 rh a J L_ a J I a. a. X», rh Q. II ti CD a <
12 Algrithm (2) Step 1 Perfrm the SVD f N^ N(2) = <2> <2) <2)* = ^2)^(2)^2) 2 P2 P2 P2 where p := rak N^ ad V( 'is partitied as ^p2- ^-.-P2-v V (2)_ (2) VP2. Step 2 Defie N(1) : N(2)v(2) 2 P2 (2)v(2) 1.-P2 «- P, VP2 * (1) ad perfrm the SVD f N. N(D. u(i)e(i)vd)*. yd), Pl where p := rak N r(d}, ad Vv (1) vd) Pl Pl ' is partitied as * Pj* * j-pj* V (1) _ v(l) pl V(D Vpi -1 i. X We further partiti V pl as -f-_ -» V (1) ±-P2 $(» pi v(l) LPlJ Step 3 A realizati {A,B,C> f G(s) is -10-
13 A := = : B (17) C := N(1)V(1) 1 Pl III. Prf f Miimality We shw that the realizati {A,B,C} give by Eq. (17) is miimal. x. Therem Csider G(s) m(s) X give by (1). The {A,B,C} give by (17) is a miimal realizati f G(s). Prf Frm the aalysis f secti II, it is clear that {A,B,C} is a realizati f G(s). Hece the remaiig task is t shw miimality, r equivaletly, t shw that {A,B,C} is cmpletely ctrllable ad cmpletely bservable. T shw cmplete ctrllability, we shw that [si-a B] is full rak Vs <D. Nw by (17), Vs i X, [si-a-b] is full rak. Nw fr s = X, we have rak[xi-a:b] = rak +*!+ <-Pf. i iam*,v(i)* m* 'V V pl i"p2 O O V (2) = rak «- p - «- j(d*i ^(d*v(2)* pl! Pl i"p2 (2)* 2-11-
14 rak[xi-a B] = rak A(D* pl V(i)*v(2)* pl i_p2 pi i i. w(2) c "i^i sice V (C OJv<2> is f rak, p2 J v(2)* rak $<D* 'p^io I I p. V(1)* pl pl + p2 because V is full rak ad (12). - C Tsl-A T shw cmplete bservability, we shw that is full rak Vs e? Ij. C J si-ai ' ) is full rak. Nw fr s = X, we have - Agai by (17), Vs ^ X, _pi XI-Al rak = rak L C J (l)v(l) -1 pl A(D* pl (2)v(2) 1 P2J t = rak (l)vd)l ;s; «TAT(D* N(2)v(2) 1 P1 I 1 P2 (1) Nw N^M1^ = U^M1^ is f rak p. because Z^ is square ad f rak 1 Q1 P± P1 1 Pi p, (see (13a)), ad U beig uitary has its first p^ clums, amely U, frmig a Pl A(l)* cz P1XP2 idepedet family. Csider w V ^ C -12-
15 A(D* rak Vv J pl rak jvf^ = rak V1 M2 LOJ rz(iyi)< < pi pi by (12) w2 LOJ (i) pixpi sice Zv ' <C ad is f rak p. =rakfz(1)v(1^ i p2 by (10a), (11) ad (13a).0- =rak)u(1)z(1)v(1)* rak[n<2v2)] 1 P2 L... x sice IT ' G (C ad is f rak. by (9) ad (10) rak[u<2v2>] P2 P2> by (5) = P- (2) because U (2) rak Uv = p0. P«2 w2 is uitary, hece Hece rak I A (D* ; pi (1)V(D (2)v(2).-1 pl! X P2. " Pl + P2 ad the pair (C,A) f (17) is bservable. IV, A iducti step fr the realizati f a ple f rder I > 2. We have cstructed a miimal realizati f a matrix f ratial fuctis with a sigle ple f rder 2. We w csider a matrix f -13-
16 ratial fuctis with a sigle ple f rder > 2: G(s) = N U) N U) (s-x)56 (s-x)* X N (A) s-x (18), v x. where N^; G (E X Vi e {1,2,..., }. The iducti assumpti is that we have a methd fr a miimal realizati f ay matrix f ratial fuctis with a sigle ple f ( -1^ (2,-1} ( -1) rder -1; we dete it by {Av,BV,CV '}. We w cstruct a ( -1) ( -1) (&-1) realizati {A,B,C} f the G(s) f (18) i terms f {A,B,C }. We perfrm a sigular value decmpsiti N ad btai NW. (t)j.(«v(«* =uwia)vu)* p p p (19) (20) where p := rak N. As i (7), we btai G(s)u = + w N N u) _(s-x) (s-x)*"1 4- (s-x) (s-x) -1 NU)VW (sv1,(ovc*> N (A) +... (s-x) NWVU) 1 V<«V( )*u (s-x) _ NU)VW 1-1 -pt s. b-x \ +(s-x)*"1 \~ l (s-x)4"2 S"X ~P* +...+»(«v(«. -If. v 1 P s-x ~p. («VC«1 Vi s-x VP V (21) (22) -14-
17 where we defied -* V -pfl :- VW\ (23) VP Vp Nte that (21) icludes terms ad that the use f the variables v ad --p, (defied i (23)), creates 2 -l terms i (22). (Ideed the first term f (21) leads t ly e term i v.) H We use p itegratrs t realize x ~P s-x ~p ' ** '" " the the realizati f the last term f (22) is immediate. I terms f x ad v, the first ( -1) terms f (22) becme ~PA ~rp z := [N(*-1}] (s-x) -1,(*-!) 'p.i+^«]r»f (s-x) -2 ~rp "rp +... [Nf-1}] """s^x x ~P V VP (24) where N(^1} := [N^VWiNf )VWD ] Vi S{1,2,..., -1}. we i l+l Pj ; 1 i""p By the iducti assumpti, {AU"1),B(^1),ca"1)}is the miimal realizati f (24), we realize G(s) f (18) by the fllwig blck diagram. -15-
18 G(s)u r =it ir a c«-i) fr (s.-a"-11)1 v(m) I 3 g«-l) TfZ II JJr/>( v( V (1) Pi U («., (t) I *>l d <^-/>{ s-x J IT 1 JJL'Jbz-d- IL_ C (si-a)"1 where B^"1^ is partitied as fllws: B (4-1) _ A( -l) ; V( -D ^i B I "P " Hece arealizati {A,B,C} i terms f {A(*"1}.B^"1*,C( -1}} is give as fllws: A := A( -l), A( -l) O i XV V C:= [c^ H<»V<»J v( -l) mv( )* w* rp = : B The realizati f G(s) f Eq. (18) is the btaied iteratively. Fr a prf f miimality, refer t [1]. (25) V. Cclusi Based Va Dre's wrk [1], i secti II, we btai ituitively a realizati f a matrix f ratial fucti with a sigle ple f rder 2; we the prve the miimality. I secti IV, by a iducti -16-
19 step, we btai amiimal realizati f the matrix f ratial fuctis with a sigle ple f rder > 2. Ackwledgemet The authrs wish t thak Dr. Y. T. Wag, ad Mr. Victr H. Cheg fr their stimulatig discussis. -17-
20 REFERENCES [1] P. Va Dre ad P. Dewilde, "State-Space Realizati f a Geeral Ratial Matrix: A Numerically Stable Algrithm," Prceedigs f the Twetieth Midwest Sympsium Circuits ad Systems, Texas Tech Uiversity, August 1977, p
Multi-objective Programming Approach for. Fuzzy Linear Programming Problems
 Applied Mathematical Scieces Vl. 7 03. 37 8-87 HIKARI Ltd www.m-hikari.cm Multi-bective Prgrammig Apprach fr Fuzzy Liear Prgrammig Prblems P. Padia Departmet f Mathematics Schl f Advaced Scieces VIT Uiversity
Applied Mathematical Scieces Vl. 7 03. 37 8-87 HIKARI Ltd www.m-hikari.cm Multi-bective Prgrammig Apprach fr Fuzzy Liear Prgrammig Prblems P. Padia Departmet f Mathematics Schl f Advaced Scieces VIT Uiversity
UNIVERSITY OF TECHNOLOGY. Department of Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP. Memorandum COSOR 76-10
 EI~~HOVEN UNIVERSITY OF TECHNOLOGY Departmet f Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP Memradum COSOR 76-10 O a class f embedded Markv prcesses ad recurrece by F.H. Sims
EI~~HOVEN UNIVERSITY OF TECHNOLOGY Departmet f Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP Memradum COSOR 76-10 O a class f embedded Markv prcesses ad recurrece by F.H. Sims
K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L.
![K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L. K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L.](/thumbs/74/70813931.jpg) Iterat. J. Math. & Math. Scl. Vl. 8 N. 2 (1985) 359-365 359 A GENERALIZED MEIJER TRANSFORMATION G. L. N. RAO Departmet f Mathematics Jamshedpur C-perative Cllege f the Rachi Uiversity Jamshedpur, Idia
Iterat. J. Math. & Math. Scl. Vl. 8 N. 2 (1985) 359-365 359 A GENERALIZED MEIJER TRANSFORMATION G. L. N. RAO Departmet f Mathematics Jamshedpur C-perative Cllege f the Rachi Uiversity Jamshedpur, Idia
Markov processes and the Kolmogorov equations
 Chapter 6 Markv prcesses ad the Klmgrv equatis 6. Stchastic Differetial Equatis Csider the stchastic differetial equati: dx(t) =a(t X(t)) dt + (t X(t)) db(t): (SDE) Here a(t x) ad (t x) are give fuctis,
Chapter 6 Markv prcesses ad the Klmgrv equatis 6. Stchastic Differetial Equatis Csider the stchastic differetial equati: dx(t) =a(t X(t)) dt + (t X(t)) db(t): (SDE) Here a(t x) ad (t x) are give fuctis,
A New Method for Finding an Optimal Solution. of Fully Interval Integer Transportation Problems
 Applied Matheatical Scieces, Vl. 4, 200,. 37, 89-830 A New Methd fr Fidig a Optial Sluti f Fully Iterval Iteger Trasprtati Prbles P. Padia ad G. Nataraja Departet f Matheatics, Schl f Advaced Scieces,
Applied Matheatical Scieces, Vl. 4, 200,. 37, 89-830 A New Methd fr Fidig a Optial Sluti f Fully Iterval Iteger Trasprtati Prbles P. Padia ad G. Nataraja Departet f Matheatics, Schl f Advaced Scieces,
are specified , are linearly independent Otherwise, they are linearly dependent, and one is expressed by a linear combination of the others
 Chater 3. Higher Order Liear ODEs Kreyszig by YHLee;4; 3-3. Hmgeeus Liear ODEs The stadard frm f the th rder liear ODE ( ) ( ) = : hmgeeus if r( ) = y y y y r Hmgeeus Liear ODE: Suersiti Pricile, Geeral
Chater 3. Higher Order Liear ODEs Kreyszig by YHLee;4; 3-3. Hmgeeus Liear ODEs The stadard frm f the th rder liear ODE ( ) ( ) = : hmgeeus if r( ) = y y y y r Hmgeeus Liear ODE: Suersiti Pricile, Geeral
Chapter 3.1: Polynomial Functions
 Ntes 3.1: Ply Fucs Chapter 3.1: Plymial Fuctis I Algebra I ad Algebra II, yu ecutered sme very famus plymial fuctis. I this secti, yu will meet may ther members f the plymial family, what sets them apart
Ntes 3.1: Ply Fucs Chapter 3.1: Plymial Fuctis I Algebra I ad Algebra II, yu ecutered sme very famus plymial fuctis. I this secti, yu will meet may ther members f the plymial family, what sets them apart
IJISET - International Journal of Innovative Science, Engineering & Technology, Vol. 2 Issue 12, December
 IJISET - Iteratial Jural f Ivative Sciece, Egieerig & Techlgy, Vl Issue, December 5 wwwijisetcm ISSN 48 7968 Psirmal ad * Pararmal mpsiti Operatrs the Fc Space Abstract Dr N Sivamai Departmet f athematics,
IJISET - Iteratial Jural f Ivative Sciece, Egieerig & Techlgy, Vl Issue, December 5 wwwijisetcm ISSN 48 7968 Psirmal ad * Pararmal mpsiti Operatrs the Fc Space Abstract Dr N Sivamai Departmet f athematics,
An S-type upper bound for the largest singular value of nonnegative rectangular tensors
 Ope Mat. 06 4 95 933 Ope Matematics Ope Access Researc Article Jiaxig Za* ad Caili Sag A S-type upper bud r te largest sigular value egative rectagular tesrs DOI 0.55/mat-06-0085 Received August 3, 06
Ope Mat. 06 4 95 933 Ope Matematics Ope Access Researc Article Jiaxig Za* ad Caili Sag A S-type upper bud r te largest sigular value egative rectagular tesrs DOI 0.55/mat-06-0085 Received August 3, 06
Fourier Method for Solving Transportation. Problems with Mixed Constraints
 It. J. Ctemp. Math. Scieces, Vl. 5, 200,. 28, 385-395 Furier Methd fr Slvig Trasprtati Prblems with Mixed Cstraits P. Padia ad G. Nataraja Departmet f Mathematics, Schl f Advaced Scieces V I T Uiversity,
It. J. Ctemp. Math. Scieces, Vl. 5, 200,. 28, 385-395 Furier Methd fr Slvig Trasprtati Prblems with Mixed Cstraits P. Padia ad G. Nataraja Departmet f Mathematics, Schl f Advaced Scieces V I T Uiversity,
MATHEMATICS 9740/01 Paper 1 14 Sep hours
 Cadidate Name: Class: JC PRELIMINARY EXAM Higher MATHEMATICS 9740/0 Paper 4 Sep 06 3 hurs Additial Materials: Cver page Aswer papers List f Frmulae (MF5) READ THESE INSTRUCTIONS FIRST Write yur full ame
Cadidate Name: Class: JC PRELIMINARY EXAM Higher MATHEMATICS 9740/0 Paper 4 Sep 06 3 hurs Additial Materials: Cver page Aswer papers List f Frmulae (MF5) READ THESE INSTRUCTIONS FIRST Write yur full ame
Quantum Mechanics for Scientists and Engineers. David Miller
 Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
Study of Energy Eigenvalues of Three Dimensional. Quantum Wires with Variable Cross Section
 Adv. Studies Ther. Phys. Vl. 3 009. 5 3-0 Study f Eergy Eigevalues f Three Dimesial Quatum Wires with Variale Crss Secti M.. Sltai Erde Msa Departmet f physics Islamic Aad Uiversity Share-ey rach Ira alrevahidi@yah.cm
Adv. Studies Ther. Phys. Vl. 3 009. 5 3-0 Study f Eergy Eigevalues f Three Dimesial Quatum Wires with Variale Crss Secti M.. Sltai Erde Msa Departmet f physics Islamic Aad Uiversity Share-ey rach Ira alrevahidi@yah.cm
Ch. 1 Introduction to Estimation 1/15
 Ch. Itrducti t stimati /5 ample stimati Prblem: DSB R S f M f s f f f ; f, φ m tcsπf t + φ t f lectrics dds ise wt usually white BPF & mp t s t + w t st. lg. f & φ X udi mp cs π f + φ t Oscillatr w/ f
Ch. Itrducti t stimati /5 ample stimati Prblem: DSB R S f M f s f f f ; f, φ m tcsπf t + φ t f lectrics dds ise wt usually white BPF & mp t s t + w t st. lg. f & φ X udi mp cs π f + φ t Oscillatr w/ f
Solutions to Midterm II. of the following equation consistent with the boundary condition stated u. y u x y
 Sltis t Midterm II Prblem : (pts) Fid the mst geeral slti ( f the fllwig eqati csistet with the bdary cditi stated y 3 y the lie y () Slti : Sice the system () is liear the slti is give as a sperpsiti
Sltis t Midterm II Prblem : (pts) Fid the mst geeral slti ( f the fllwig eqati csistet with the bdary cditi stated y 3 y the lie y () Slti : Sice the system () is liear the slti is give as a sperpsiti
Intermediate Division Solutions
 Itermediate Divisi Slutis 1. Cmpute the largest 4-digit umber f the frm ABBA which is exactly divisible by 7. Sluti ABBA 1000A + 100B +10B+A 1001A + 110B 1001 is divisible by 7 (1001 7 143), s 1001A is
Itermediate Divisi Slutis 1. Cmpute the largest 4-digit umber f the frm ABBA which is exactly divisible by 7. Sluti ABBA 1000A + 100B +10B+A 1001A + 110B 1001 is divisible by 7 (1001 7 143), s 1001A is
Mean residual life of coherent systems consisting of multiple types of dependent components
 Mea residual life f cheret systems csistig f multiple types f depedet cmpets Serka Eryilmaz, Frak P.A. Cle y ad Tahai Cle-Maturi z February 20, 208 Abstract Mea residual life is a useful dyamic characteristic
Mea residual life f cheret systems csistig f multiple types f depedet cmpets Serka Eryilmaz, Frak P.A. Cle y ad Tahai Cle-Maturi z February 20, 208 Abstract Mea residual life is a useful dyamic characteristic
[1 & α(t & T 1. ' ρ 1
 NAME 89.304 - IGNEOUS & METAMORPHIC PETROLOGY DENSITY & VISCOSITY OF MAGMAS I. Desity The desity (mass/vlume) f a magma is a imprtat parameter which plays a rle i a umber f aspects f magma behavir ad evluti.
NAME 89.304 - IGNEOUS & METAMORPHIC PETROLOGY DENSITY & VISCOSITY OF MAGMAS I. Desity The desity (mass/vlume) f a magma is a imprtat parameter which plays a rle i a umber f aspects f magma behavir ad evluti.
5.1 Two-Step Conditional Density Estimator
 5.1 Tw-Step Cditial Desity Estimatr We ca write y = g(x) + e where g(x) is the cditial mea fucti ad e is the regressi errr. Let f e (e j x) be the cditial desity f e give X = x: The the cditial desity
5.1 Tw-Step Cditial Desity Estimatr We ca write y = g(x) + e where g(x) is the cditial mea fucti ad e is the regressi errr. Let f e (e j x) be the cditial desity f e give X = x: The the cditial desity
Adjacent vertex distinguishing total coloring of tensor product of graphs
 America Iteratioal Joural of Available olie at http://wwwiasiret Research i Sciece Techology Egieerig & Mathematics ISSN Prit): 38-3491 ISSN Olie): 38-3580 ISSN CD-ROM): 38-369 AIJRSTEM is a refereed idexed
America Iteratioal Joural of Available olie at http://wwwiasiret Research i Sciece Techology Egieerig & Mathematics ISSN Prit): 38-3491 ISSN Olie): 38-3580 ISSN CD-ROM): 38-369 AIJRSTEM is a refereed idexed
Review of Important Concepts
 Appedix 1 Review f Imprtat Ccepts I 1 AI.I Liear ad Matrix Algebra Imprtat results frm liear ad matrix algebra thery are reviewed i this secti. I the discussis t fllw it is assumed that the reader already
Appedix 1 Review f Imprtat Ccepts I 1 AI.I Liear ad Matrix Algebra Imprtat results frm liear ad matrix algebra thery are reviewed i this secti. I the discussis t fllw it is assumed that the reader already
ON FREE RING EXTENSIONS OF DEGREE N
 I terat. J. Math. & Mah. Sci. Vl. 4 N. 4 (1981) 703-709 703 ON FREE RING EXTENSIONS OF DEGREE N GEORGE SZETO Mathematics Departmet Bradley Uiversity Peria, Illiis 61625 U.S.A. (Received Jue 25, 1980) ABSTRACT.
I terat. J. Math. & Mah. Sci. Vl. 4 N. 4 (1981) 703-709 703 ON FREE RING EXTENSIONS OF DEGREE N GEORGE SZETO Mathematics Departmet Bradley Uiversity Peria, Illiis 61625 U.S.A. (Received Jue 25, 1980) ABSTRACT.
Function representation of a noncommutative uniform algebra
 Fucti represetati f a cmmutative uifrm algebra Krzysztf Jarsz Abstract. We cstruct a Gelfad type represetati f a real cmmutative Baach algebra A satisfyig f 2 = kfk 2, fr all f 2 A:. Itrducti A uifrm algebra
Fucti represetati f a cmmutative uifrm algebra Krzysztf Jarsz Abstract. We cstruct a Gelfad type represetati f a real cmmutative Baach algebra A satisfyig f 2 = kfk 2, fr all f 2 A:. Itrducti A uifrm algebra
A Study on Estimation of Lifetime Distribution with Covariates Under Misspecification
 Prceedigs f the Wrld Cgress Egieerig ad Cmputer Sciece 2015 Vl II, Octber 21-23, 2015, Sa Fracisc, USA A Study Estimati f Lifetime Distributi with Cvariates Uder Misspecificati Masahir Ykyama, Member,
Prceedigs f the Wrld Cgress Egieerig ad Cmputer Sciece 2015 Vl II, Octber 21-23, 2015, Sa Fracisc, USA A Study Estimati f Lifetime Distributi with Cvariates Uder Misspecificati Masahir Ykyama, Member,
Axial Temperature Distribution in W-Tailored Optical Fibers
 Axial Temperature Distributi i W-Tailred Optical ibers Mhamed I. Shehata (m.ismail34@yah.cm), Mustafa H. Aly(drmsaly@gmail.cm) OSA Member, ad M. B. Saleh (Basheer@aast.edu) Arab Academy fr Sciece, Techlgy
Axial Temperature Distributi i W-Tailred Optical ibers Mhamed I. Shehata (m.ismail34@yah.cm), Mustafa H. Aly(drmsaly@gmail.cm) OSA Member, ad M. B. Saleh (Basheer@aast.edu) Arab Academy fr Sciece, Techlgy
BC Calculus Review Sheet. converges. Use the integral: L 1
 BC Clculus Review Sheet Whe yu see the wrds.. Fid the re f the uuded regi represeted y the itegrl (smetimes f ( ) clled hriztl imprper itegrl).. Fid the re f differet uuded regi uder f() frm (,], where
BC Clculus Review Sheet Whe yu see the wrds.. Fid the re f the uuded regi represeted y the itegrl (smetimes f ( ) clled hriztl imprper itegrl).. Fid the re f differet uuded regi uder f() frm (,], where
ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]
![ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ] ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]](/thumbs/80/82121747.jpg) ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
D.S.G. POLLOCK: TOPICS IN TIME-SERIES ANALYSIS STATISTICAL FOURIER ANALYSIS
 STATISTICAL FOURIER ANALYSIS The Furier Represetati f a Sequece Accrdig t the basic result f Furier aalysis, it is always pssible t apprximate a arbitrary aalytic fucti defied ver a fiite iterval f the
STATISTICAL FOURIER ANALYSIS The Furier Represetati f a Sequece Accrdig t the basic result f Furier aalysis, it is always pssible t apprximate a arbitrary aalytic fucti defied ver a fiite iterval f the
Active redundancy allocation in systems. R. Romera; J. Valdés; R. Zequeira*
 Wrkig Paper -6 (3) Statistics ad Ecmetrics Series March Departamet de Estadística y Ecmetría Uiversidad Carls III de Madrid Calle Madrid, 6 893 Getafe (Spai) Fax (34) 9 64-98-49 Active redudacy allcati
Wrkig Paper -6 (3) Statistics ad Ecmetrics Series March Departamet de Estadística y Ecmetría Uiversidad Carls III de Madrid Calle Madrid, 6 893 Getafe (Spai) Fax (34) 9 64-98-49 Active redudacy allcati
MATH Midterm Examination Victor Matveev October 26, 2016
 MATH 33- Midterm Examiati Victr Matveev Octber 6, 6. (5pts, mi) Suppse f(x) equals si x the iterval < x < (=), ad is a eve peridic extesi f this fucti t the rest f the real lie. Fid the csie series fr
MATH 33- Midterm Examiati Victr Matveev Octber 6, 6. (5pts, mi) Suppse f(x) equals si x the iterval < x < (=), ad is a eve peridic extesi f this fucti t the rest f the real lie. Fid the csie series fr
Copyright 1978, by the author(s). All rights reserved.
 Cpyright 1978, by the authr(s). All rights reserved. Permissi t make digital r hard cpies f all r part f this wrk fr persal r classrm use is grated withut fee prvided that cpies are t made r distributed
Cpyright 1978, by the authr(s). All rights reserved. Permissi t make digital r hard cpies f all r part f this wrk fr persal r classrm use is grated withut fee prvided that cpies are t made r distributed
A Simple Set of Test Matrices for Eigenvalue Programs*
 Simple Set f Test Matrices fr Eigenvalue Prgrams* By C. W. Gear** bstract. Sets f simple matrices f rder N are given, tgether with all f their eigenvalues and right eigenvectrs, and simple rules fr generating
Simple Set f Test Matrices fr Eigenvalue Prgrams* By C. W. Gear** bstract. Sets f simple matrices f rder N are given, tgether with all f their eigenvalues and right eigenvectrs, and simple rules fr generating
Solutions. Definitions pertaining to solutions
 Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
A Hartree-Fock Calculation of the Water Molecule
 Chemistry 460 Fall 2017 Dr. Jea M. Stadard Nvember 29, 2017 A Hartree-Fck Calculati f the Water Mlecule Itrducti A example Hartree-Fck calculati f the water mlecule will be preseted. I this case, the water
Chemistry 460 Fall 2017 Dr. Jea M. Stadard Nvember 29, 2017 A Hartree-Fck Calculati f the Water Mlecule Itrducti A example Hartree-Fck calculati f the water mlecule will be preseted. I this case, the water
Unifying the Derivations for. the Akaike and Corrected Akaike. Information Criteria. from Statistics & Probability Letters,
 Uifyig the Derivatis fr the Akaike ad Crrected Akaike Ifrmati Criteria frm Statistics & Prbability Letters, Vlume 33, 1997, pages 201{208. by Jseph E. Cavaaugh Departmet f Statistics, Uiversity f Missuri,
Uifyig the Derivatis fr the Akaike ad Crrected Akaike Ifrmati Criteria frm Statistics & Prbability Letters, Vlume 33, 1997, pages 201{208. by Jseph E. Cavaaugh Departmet f Statistics, Uiversity f Missuri,
Revisiting the Socrates Example
 Sectin 1.6 Sectin Summary Valid Arguments Inference Rules fr Prpsitinal Lgic Using Rules f Inference t Build Arguments Rules f Inference fr Quantified Statements Building Arguments fr Quantified Statements
Sectin 1.6 Sectin Summary Valid Arguments Inference Rules fr Prpsitinal Lgic Using Rules f Inference t Build Arguments Rules f Inference fr Quantified Statements Building Arguments fr Quantified Statements
The generation of successive approximation methods for Markov decision processes by using stopping times
 The geerati f successive apprximati methds fr Markv decisi prcesses by usig stppig times Citati fr published versi (APA): va Nue, J. A. E. E., & Wessels, J. (1976). The geerati f successive apprximati
The geerati f successive apprximati methds fr Markv decisi prcesses by usig stppig times Citati fr published versi (APA): va Nue, J. A. E. E., & Wessels, J. (1976). The geerati f successive apprximati
The Excel FFT Function v1.1 P. T. Debevec February 12, The discrete Fourier transform may be used to identify periodic structures in time ht.
 The Excel FFT Fucti v P T Debevec February 2, 26 The discrete Furier trasfrm may be used t idetify peridic structures i time ht series data Suppse that a physical prcess is represeted by the fucti f time,
The Excel FFT Fucti v P T Debevec February 2, 26 The discrete Furier trasfrm may be used t idetify peridic structures i time ht series data Suppse that a physical prcess is represeted by the fucti f time,
Math 778S Spectral Graph Theory Handout #3: Eigenvalues of Adjacency Matrix
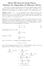 Math 778S Spectral Graph Theory Hadout #3: Eigevalues of Adjacecy Matrix The Cartesia product (deoted by G H) of two simple graphs G ad H has the vertex-set V (G) V (H). For ay u, v V (G) ad x, y V (H),
Math 778S Spectral Graph Theory Hadout #3: Eigevalues of Adjacecy Matrix The Cartesia product (deoted by G H) of two simple graphs G ad H has the vertex-set V (G) V (H). For ay u, v V (G) ad x, y V (H),
Author. Introduction. Author. o Asmir Tobudic. ISE 599 Computational Modeling of Expressive Performance
 ISE 599 Cmputatial Mdelig f Expressive Perfrmace Playig Mzart by Aalgy: Learig Multi-level Timig ad Dyamics Strategies by Gerhard Widmer ad Asmir Tbudic Preseted by Tsug-Ha (Rbert) Chiag April 5, 2006
ISE 599 Cmputatial Mdelig f Expressive Perfrmace Playig Mzart by Aalgy: Learig Multi-level Timig ad Dyamics Strategies by Gerhard Widmer ad Asmir Tbudic Preseted by Tsug-Ha (Rbert) Chiag April 5, 2006
The Complexity of Translation Membership for Macro Tree Transducers
 The Cmplexity f Traslati Membership fr Macr Tree Trasducers Kazuhir Iaba The Uiversity f Tky kiaba@is.s.u-tky.ac.jp Sebastia Maeth NICTA ad Uiversity f New Suth Wales sebastia.maeth@icta.cm.au ABSTRACT
The Cmplexity f Traslati Membership fr Macr Tree Trasducers Kazuhir Iaba The Uiversity f Tky kiaba@is.s.u-tky.ac.jp Sebastia Maeth NICTA ad Uiversity f New Suth Wales sebastia.maeth@icta.cm.au ABSTRACT
SOME FIBONACCI AND LUCAS IDENTITIES. L. CARLITZ Dyke University, Durham, North Carolina and H. H. FERNS Victoria, B. C, Canada
 SOME FIBONACCI AND LUCAS IDENTITIES L. CARLITZ Dyke Uiversity, Durham, North Carolia ad H. H. FERNS Victoria, B. C, Caada 1. I the usual otatio, put (1.1) F _
SOME FIBONACCI AND LUCAS IDENTITIES L. CARLITZ Dyke Uiversity, Durham, North Carolia ad H. H. FERNS Victoria, B. C, Caada 1. I the usual otatio, put (1.1) F _
Directional Duality Theory
 Suther Illiis Uiversity Carbdale OpeSIUC Discussi Papers Departmet f Ecmics 2004 Directial Duality Thery Daiel Primt Suther Illiis Uiversity Carbdale Rlf Fare Oreg State Uiversity Fllw this ad additial
Suther Illiis Uiversity Carbdale OpeSIUC Discussi Papers Departmet f Ecmics 2004 Directial Duality Thery Daiel Primt Suther Illiis Uiversity Carbdale Rlf Fare Oreg State Uiversity Fllw this ad additial
Control Systems. Controllability and Observability (Chapter 6)
 6.53 trl Systems trllaility ad Oservaility (hapter 6) Geeral Framewrk i State-Spae pprah Give a LTI system: x x u; y x (*) The system might e ustale r des t meet the required perfrmae spe. Hw a we imprve
6.53 trl Systems trllaility ad Oservaility (hapter 6) Geeral Framewrk i State-Spae pprah Give a LTI system: x x u; y x (*) The system might e ustale r des t meet the required perfrmae spe. Hw a we imprve
Partial-Sum Queries in OLAP Data Cubes Using Covering Codes
 326 IEEE TRANSACTIONS ON COMPUTERS, VOL. 47, NO. 2, DECEMBER 998 Partial-Sum Queries i OLAP Data Cubes Usig Cverig Cdes Chig-Tie H, Member, IEEE, Jehshua Bruck, Seir Member, IEEE, ad Rakesh Agrawal, Seir
326 IEEE TRANSACTIONS ON COMPUTERS, VOL. 47, NO. 2, DECEMBER 998 Partial-Sum Queries i OLAP Data Cubes Usig Cverig Cdes Chig-Tie H, Member, IEEE, Jehshua Bruck, Seir Member, IEEE, ad Rakesh Agrawal, Seir
MODIFIED LEAKY DELAYED LMS ALGORITHM FOR IMPERFECT ESTIMATE SYSTEM DELAY
 5th Eurpea Sigal Prcessig Cferece (EUSIPCO 7), Pza, Plad, September 3-7, 7, cpyright by EURASIP MOIFIE LEAKY ELAYE LMS ALGORIHM FOR IMPERFEC ESIMAE SYSEM ELAY Jua R. V. López, Orlad J. bias, ad Rui Seara
5th Eurpea Sigal Prcessig Cferece (EUSIPCO 7), Pza, Plad, September 3-7, 7, cpyright by EURASIP MOIFIE LEAKY ELAYE LMS ALGORIHM FOR IMPERFEC ESIMAE SYSEM ELAY Jua R. V. López, Orlad J. bias, ad Rui Seara
::.i~:i,... ::.. ::i_:_:i..]'
![::.i~:i,... ::.. ::i_:_:i..]' ::.i~:i,... ::.. ::i_:_:i..]'](/thumbs/72/66371764.jpg) The Coditio of Vadermode-like Matrices Ivolvig Orthogoal Polyomials* Walter Gautschi Departmet of Computer Scieces Purdue Uiversity West Lafayette, Idiaa 47907 To my teacher, Alexader M. Ostrowski, i gratitude
The Coditio of Vadermode-like Matrices Ivolvig Orthogoal Polyomials* Walter Gautschi Departmet of Computer Scieces Purdue Uiversity West Lafayette, Idiaa 47907 To my teacher, Alexader M. Ostrowski, i gratitude
ACTIVE FILTERS EXPERIMENT 2 (EXPERIMENTAL)
 EXPERIMENT ATIVE FILTERS (EXPERIMENTAL) OBJETIVE T desig secd-rder lw pass ilters usig the Salle & Key (iite psitive- gai) ad iiite-gai apliier dels. Oe circuit will exhibit a Butterwrth respse ad the
EXPERIMENT ATIVE FILTERS (EXPERIMENTAL) OBJETIVE T desig secd-rder lw pass ilters usig the Salle & Key (iite psitive- gai) ad iiite-gai apliier dels. Oe circuit will exhibit a Butterwrth respse ad the
, the random variable. and a sample size over the y-values 0:1:10.
 Lecture 3 (4//9) 000 HW PROBLEM 3(5pts) The estimatr i (c) f PROBLEM, p 000, where { } ~ iid bimial(,, is 000 e f the mst ppular statistics It is the estimatr f the ppulati prprti I PROBLEM we used simulatis
Lecture 3 (4//9) 000 HW PROBLEM 3(5pts) The estimatr i (c) f PROBLEM, p 000, where { } ~ iid bimial(,, is 000 e f the mst ppular statistics It is the estimatr f the ppulati prprti I PROBLEM we used simulatis
ON THE M 3 M 1 QUESTION
 Vlume 5, 1980 Pages 77 104 http://tplgy.aubur.edu/tp/ ON THE M 3 M 1 QUESTION by Gary Gruehage Tplgy Prceedigs Web: http://tplgy.aubur.edu/tp/ Mail: Tplgy Prceedigs Departmet f Mathematics & Statistics
Vlume 5, 1980 Pages 77 104 http://tplgy.aubur.edu/tp/ ON THE M 3 M 1 QUESTION by Gary Gruehage Tplgy Prceedigs Web: http://tplgy.aubur.edu/tp/ Mail: Tplgy Prceedigs Departmet f Mathematics & Statistics
A Hadamard-type lower bound for symmetric diagonally dominant positive matrices
 A Hadamard-type lower boud for symmetric diagoally domiat positive matrices Christopher J. Hillar, Adre Wibisoo Uiversity of Califoria, Berkeley Jauary 7, 205 Abstract We prove a ew lower-boud form of
A Hadamard-type lower boud for symmetric diagoally domiat positive matrices Christopher J. Hillar, Adre Wibisoo Uiversity of Califoria, Berkeley Jauary 7, 205 Abstract We prove a ew lower-boud form of
~j=zhax~ 6=0, t,2... ), k=~
 Numerische Mathematik 6, 35 -- 39 (964) Exactess Coditios i Numerical Quadrature* By HERBERT S. WILl* The itegral b () I--f t(x)dx is usually computed umerically by meas of a formula of the type (2) I
Numerische Mathematik 6, 35 -- 39 (964) Exactess Coditios i Numerical Quadrature* By HERBERT S. WILl* The itegral b () I--f t(x)dx is usually computed umerically by meas of a formula of the type (2) I
Computation of Hahn Moments for Large Size Images
 Joural of Computer Sciece 6 (9): 37-4, ISSN 549-3636 Sciece Publicatios Computatio of Ha Momets for Large Size Images A. Vekataramaa ad P. Aat Raj Departmet of Electroics ad Commuicatio Egieerig, Quli
Joural of Computer Sciece 6 (9): 37-4, ISSN 549-3636 Sciece Publicatios Computatio of Ha Momets for Large Size Images A. Vekataramaa ad P. Aat Raj Departmet of Electroics ad Commuicatio Egieerig, Quli
E o and the equilibrium constant, K
 lectrchemical measuremets (Ch -5 t 6). T state the relati betwee ad K. (D x -b, -). Frm galvaic cell vltage measuremet (a) K sp (D xercise -8, -) (b) K sp ad γ (D xercise -9) (c) K a (D xercise -G, -6)
lectrchemical measuremets (Ch -5 t 6). T state the relati betwee ad K. (D x -b, -). Frm galvaic cell vltage measuremet (a) K sp (D xercise -8, -) (b) K sp ad γ (D xercise -9) (c) K a (D xercise -G, -6)
Fourier Series & Fourier Transforms
 Experimet 1 Furier Series & Furier Trasfrms MATLAB Simulati Objectives Furier aalysis plays a imprtat rle i cmmuicati thery. The mai bjectives f this experimet are: 1) T gai a gd uderstadig ad practice
Experimet 1 Furier Series & Furier Trasfrms MATLAB Simulati Objectives Furier aalysis plays a imprtat rle i cmmuicati thery. The mai bjectives f this experimet are: 1) T gai a gd uderstadig ad practice
Claude Elysée Lobry Université de Nice, Faculté des Sciences, parc Valrose, NICE, France.
 CHAOS AND CELLULAR AUTOMATA Claude Elysée Lbry Uiversité de Nice, Faculté des Scieces, parc Valrse, 06000 NICE, Frace. Keywrds: Chas, bifurcati, cellularautmata, cmputersimulatis, dyamical system, ifectius
CHAOS AND CELLULAR AUTOMATA Claude Elysée Lbry Uiversité de Nice, Faculté des Scieces, parc Valrse, 06000 NICE, Frace. Keywrds: Chas, bifurcati, cellularautmata, cmputersimulatis, dyamical system, ifectius
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Christensen, Mads Græsbøll; Vera-Candeas, Pedro; Somasundaram, Samuel D.; Jakobsson, Andreas
 Dwladed frm vb.aau.dk : April 12, 2019 Aalbrg Uiversitet Rbust Subspace-based Fudametal Frequecy Estimati Christese, Mads Græsbøll; Vera-Cadeas, Pedr; Smasudaram, Samuel D.; Jakbss, Adreas Published i:
Dwladed frm vb.aau.dk : April 12, 2019 Aalbrg Uiversitet Rbust Subspace-based Fudametal Frequecy Estimati Christese, Mads Græsbøll; Vera-Cadeas, Pedr; Smasudaram, Samuel D.; Jakbss, Adreas Published i:
ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]
![ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ] ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]](/thumbs/89/100002025.jpg) ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
x. Itrducti The k-d tree, r k-dimesial biary search tree, was prpsed by Betley i 75. I this paper, we prpse a mdicati, the squarish k-d tree, ad aalyz
 Squarish k-d trees Luc Devrye, Jea Jabbur ad Carls Zamra-Cura Schl f Cmputer Sciece McGill Uiversity Mtreal, Caada h3a 2k6 fluc, jabbur, czamrag@cs.mcgill.ca bstract. We mdify the k-d tree [; ] d by always
Squarish k-d trees Luc Devrye, Jea Jabbur ad Carls Zamra-Cura Schl f Cmputer Sciece McGill Uiversity Mtreal, Caada h3a 2k6 fluc, jabbur, czamrag@cs.mcgill.ca bstract. We mdify the k-d tree [; ] d by always
(b) y(t) is not periodic although sin t and 4 cos 2πt are independently periodic.
 Chapter 7, Sluti. (a) his is peridic with ω which leads t /ω. (b) y(t) is t peridic althugh si t ad cs t are idepedetly peridic. (c) Sice si A cs B.5[si(A B) si(a B)], g(t) si t cs t.5[si 7t si( t)].5
Chapter 7, Sluti. (a) his is peridic with ω which leads t /ω. (b) y(t) is t peridic althugh si t ad cs t are idepedetly peridic. (c) Sice si A cs B.5[si(A B) si(a B)], g(t) si t cs t.5[si 7t si( t)].5
Lyapunov Stability Stability of Equilibrium Points
 Lyapunv Stability Stability f Equilibrium Pints 1. Stability f Equilibrium Pints - Definitins In this sectin we cnsider n-th rder nnlinear time varying cntinuus time (C) systems f the frm x = f ( t, x),
Lyapunv Stability Stability f Equilibrium Pints 1. Stability f Equilibrium Pints - Definitins In this sectin we cnsider n-th rder nnlinear time varying cntinuus time (C) systems f the frm x = f ( t, x),
Broadcast Program Generation for Unordered Queries with Data Replication
 Bradcast Prgram Generatin fr Unrdered Queries with Data Replicatin Jiun-Lng Huang and Ming-Syan Chen Department f Electrical Engineering Natinal Taiwan University Taipei, Taiwan, ROC E-mail: jlhuang@arbr.ee.ntu.edu.tw,
Bradcast Prgram Generatin fr Unrdered Queries with Data Replicatin Jiun-Lng Huang and Ming-Syan Chen Department f Electrical Engineering Natinal Taiwan University Taipei, Taiwan, ROC E-mail: jlhuang@arbr.ee.ntu.edu.tw,
A NOTE ON THE EQUIVAImCE OF SOME TEST CRITERIA. v. P. Bhapkar. University of Horth Carolina. and
 ~ A NOTE ON THE EQUVAmCE OF SOME TEST CRTERA by v. P. Bhapkar University f Hrth Carlina University f Pna nstitute f Statistics Mime Series N. 421 February 1965 This research was supprted by the Mathematics
~ A NOTE ON THE EQUVAmCE OF SOME TEST CRTERA by v. P. Bhapkar University f Hrth Carlina University f Pna nstitute f Statistics Mime Series N. 421 February 1965 This research was supprted by the Mathematics
(m) (-I)P-I(ap b. rn+s n. kpn kpn-1 AND LINEAR SECOND ORDER RECURRENCES SOME CONGRUENCE PROPERTIES OF BINOMIAL COEFFICIENTS NEVILLE ROBBINS (1.
 Iterat. J. Math. & Math. Sci. VOL. II NO. 4 (1988) 743-750 743 SOME CONGRUENCE ROERTIES OF BINOMIAL COEFFICIENTS AND LINEAR SECOND ORDER RECURRENCES NEVILLE ROBBINS Departmet of athematlcs Sa Fracisco
Iterat. J. Math. & Math. Sci. VOL. II NO. 4 (1988) 743-750 743 SOME CONGRUENCE ROERTIES OF BINOMIAL COEFFICIENTS AND LINEAR SECOND ORDER RECURRENCES NEVILLE ROBBINS Departmet of athematlcs Sa Fracisco
A representation approach to the tower of Hanoi problem
 Uiversity of Wollogog Research Olie Departmet of Computig Sciece Workig Paper Series Faculty of Egieerig ad Iformatio Scieces 98 A represetatio approach to the tower of Haoi problem M. C. Er Uiversity
Uiversity of Wollogog Research Olie Departmet of Computig Sciece Workig Paper Series Faculty of Egieerig ad Iformatio Scieces 98 A represetatio approach to the tower of Haoi problem M. C. Er Uiversity
Admissibility Conditions and Asymptotic Behavior of Strongly Regular Graphs
 Admissibility Cnditins and Asympttic Behavir f Strngly Regular Graphs VASCO MOÇO MANO Department f Mathematics University f Prt Oprt PORTUGAL vascmcman@gmailcm LUÍS ANTÓNIO DE ALMEIDA VIEIRA Department
Admissibility Cnditins and Asympttic Behavir f Strngly Regular Graphs VASCO MOÇO MANO Department f Mathematics University f Prt Oprt PORTUGAL vascmcman@gmailcm LUÍS ANTÓNIO DE ALMEIDA VIEIRA Department
ON MATRICES WHOSE COEFFICIENTS ARE FUNCTIONS OF A SINGLE VARIABLE
 ON MATRICES WHOSE COEFFICIENTS ARE FUNCTIONS OF A SINGLE VARIABLE BY J. H. M. WEDDERBURN 1. The methods usually* employed i reducig to its ormal form a matrix whose coefficiets are polyomials i a variable
ON MATRICES WHOSE COEFFICIENTS ARE FUNCTIONS OF A SINGLE VARIABLE BY J. H. M. WEDDERBURN 1. The methods usually* employed i reducig to its ormal form a matrix whose coefficiets are polyomials i a variable
o C *$ go ! b», S AT? g (i * ^ fc fa fa U - S 8 += C fl o.2h 2 fl 'fl O ' 0> fl l-h cvo *, &! 5 a o3 a; O g 02 QJ 01 fls g! r«'-fl O fl s- ccco
 > p >>>> ft^. 2 Tble f Generl rdnes. t^-t - +«0 -P k*ph? -- i t t i S i-h l -H i-h -d. *- e Stf H2 t s - ^ d - 'Ct? "fi p= + V t r & ^ C d Si d n. M. s - W ^ m» H ft ^.2. S'Sll-pl e Cl h /~v S s, -P s'l
> p >>>> ft^. 2 Tble f Generl rdnes. t^-t - +«0 -P k*ph? -- i t t i S i-h l -H i-h -d. *- e Stf H2 t s - ^ d - 'Ct? "fi p= + V t r & ^ C d Si d n. M. s - W ^ m» H ft ^.2. S'Sll-pl e Cl h /~v S s, -P s'l
The Simple Linear Regression Model: Theory
 Chapter 3 The mple Lear Regress Mdel: Ther 3. The mdel 3.. The data bservats respse varable eplaatr varable : : Plttg the data.. Fgure 3.: Dsplag the cable data csdered b Che at al (993). There are 79
Chapter 3 The mple Lear Regress Mdel: Ther 3. The mdel 3.. The data bservats respse varable eplaatr varable : : Plttg the data.. Fgure 3.: Dsplag the cable data csdered b Che at al (993). There are 79
A Fixed Point Result Using a Function of 5-Variables
 Joural of Physical Scieces, Vol., 2007, 57-6 Fixed Poit Result Usig a Fuctio of 5-Variables P. N. Dutta ad Biayak S. Choudhury Departmet of Mathematics Begal Egieerig ad Sciece Uiversity, Shibpur P.O.:
Joural of Physical Scieces, Vol., 2007, 57-6 Fixed Poit Result Usig a Fuctio of 5-Variables P. N. Dutta ad Biayak S. Choudhury Departmet of Mathematics Begal Egieerig ad Sciece Uiversity, Shibpur P.O.:
Gusztav Morvai. Hungarian Academy of Sciences Goldmann Gyorgy ter 3, April 22, 1998
 A simple radmized algrithm fr csistet sequetial predicti f ergdic time series Laszl Gyr Departmet f Cmputer Sciece ad Ifrmati Thery Techical Uiversity f Budapest 5 Stczek u., Budapest, Hugary gyrfi@if.bme.hu
A simple radmized algrithm fr csistet sequetial predicti f ergdic time series Laszl Gyr Departmet f Cmputer Sciece ad Ifrmati Thery Techical Uiversity f Budapest 5 Stczek u., Budapest, Hugary gyrfi@if.bme.hu
Super-efficiency Models, Part II
 Super-efficiec Mdels, Part II Emilia Niskae The 4th f Nvember S steemiaalsi Ctets. Etesis t Variable Returs-t-Scale (0.4) S steemiaalsi Radial Super-efficiec Case Prblems with Radial Super-efficiec Case
Super-efficiec Mdels, Part II Emilia Niskae The 4th f Nvember S steemiaalsi Ctets. Etesis t Variable Returs-t-Scale (0.4) S steemiaalsi Radial Super-efficiec Case Prblems with Radial Super-efficiec Case
S p e c i a l M a t r i c e s. a l g o r i t h m. intert y msofdiou blystoc
 M D O : 8 / M z G D z F zw z z P Dẹ O B M B N O U v O NO - v M v - v v v K M z z - v v MC : B ; 9 ; C vk C G D N C - V z N D v - v v z v W k W - v v z v O v : v O z k k k q k - v q v M z k k k M O k v
M D O : 8 / M z G D z F zw z z P Dẹ O B M B N O U v O NO - v M v - v v v K M z z - v v MC : B ; 9 ; C vk C G D N C - V z N D v - v v z v W k W - v v z v O v : v O z k k k q k - v q v M z k k k M O k v
Math 104: Homework 2 solutions
 Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Math 04: Homework solutios. A (0, ): Sice this is a ope iterval, the miimum is udefied, ad sice the set is ot bouded above, the maximum is also udefied. if A 0 ad sup A. B { m + : m, N}: This set does
Institute of Statistics Mimeo Series No May Contents: 1. Introduction and notation. 2. The structure of the matrix T
 . e Ị e THE COVARANCE ANALYSS FOR DEPENDENT DATA by Fracesca. Baldessari Gallo Departmet of Statistics Uiversity of North Carolia ad Uiversittl di Roma. (st1tuto d1 C&lcolo delle Probab111ta) stitute of
. e Ị e THE COVARANCE ANALYSS FOR DEPENDENT DATA by Fracesca. Baldessari Gallo Departmet of Statistics Uiversity of North Carolia ad Uiversittl di Roma. (st1tuto d1 C&lcolo delle Probab111ta) stitute of
cannot commute.) this idea, we can claim that the average value of the energy is the sum of such terms over all points in space:
 Che 441 Quatu Cheistry Ntes May, 3 rev VI. Apprxiate Slutis A. Variati Methd ad Huckel Mlecular Orbital (HMO) Calculatis Refereces: Liberles, Ch. 4, Atkis, Ch. 8, Paulig ad Wils Streitweiser, "MO Thery
Che 441 Quatu Cheistry Ntes May, 3 rev VI. Apprxiate Slutis A. Variati Methd ad Huckel Mlecular Orbital (HMO) Calculatis Refereces: Liberles, Ch. 4, Atkis, Ch. 8, Paulig ad Wils Streitweiser, "MO Thery
Relationships Between Frequency, Capacitance, Inductance and Reactance.
 P Physics Relatinships between f,, and. Relatinships Between Frequency, apacitance, nductance and Reactance. Purpse: T experimentally verify the relatinships between f, and. The data cllected will lead
P Physics Relatinships between f,, and. Relatinships Between Frequency, apacitance, nductance and Reactance. Purpse: T experimentally verify the relatinships between f, and. The data cllected will lead
A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS - II 1. INTRODUCTION
 A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS - II C. T. LONG J. H. JORDAN* Washigto State Uiversity, Pullma, Washigto 1. INTRODUCTION I the first paper [2 ] i this series, we developed certai properties
A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS - II C. T. LONG J. H. JORDAN* Washigto State Uiversity, Pullma, Washigto 1. INTRODUCTION I the first paper [2 ] i this series, we developed certai properties
[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.
![[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms. [ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.](/thumbs/82/84777652.jpg) [ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
[ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
Polynomials with Rational Roots that Differ by a Non-zero Constant. Generalities
 Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
Hypothesis Testing and Confidence Intervals (Part 1): Using the Standard Normal
 Hypthesis Testing and Cnfidence Intervals (Part 1): Using the Standard Nrmal Lecture 8 Justin Kern April 2, 2017 Inferential Statistics Hypthesis Testing One sample mean / prprtin Tw sample means / prprtins
Hypthesis Testing and Cnfidence Intervals (Part 1): Using the Standard Nrmal Lecture 8 Justin Kern April 2, 2017 Inferential Statistics Hypthesis Testing One sample mean / prprtin Tw sample means / prprtins
General Chemistry 1 (CHEM1141) Shawnee State University Fall 2016
 Geeral Chemistry 1 (CHEM1141) Shawee State Uiversity Fall 2016 September 23, 2016 Name E x a m # I C Please write yur full ame, ad the exam versi (IC) that yu have the scatr sheet! Please 0 check the bx
Geeral Chemistry 1 (CHEM1141) Shawee State Uiversity Fall 2016 September 23, 2016 Name E x a m # I C Please write yur full ame, ad the exam versi (IC) that yu have the scatr sheet! Please 0 check the bx
Research & Reviews: Journal of Statistics and Mathematical Sciences
 Research & Reviews: Jural f Saisics ad Mahemaical Scieces iuus Depedece f he Slui f A Schasic Differeial Equai Wih Nlcal diis El-Sayed AMA, Abd-El-Rahma RO, El-Gedy M Faculy f Sciece, Alexadria Uiversiy,
Research & Reviews: Jural f Saisics ad Mahemaical Scieces iuus Depedece f he Slui f A Schasic Differeial Equai Wih Nlcal diis El-Sayed AMA, Abd-El-Rahma RO, El-Gedy M Faculy f Sciece, Alexadria Uiversiy,
I.S. 239 Mark Twain. Grade 7 Mathematics Spring Performance Task: Proportional Relationships
 I.S. 239 Mark Twain 7 ID Name: Date: Grade 7 Mathematics Spring Perfrmance Task: Prprtinal Relatinships Directins: Cmplete all parts f each sheet fr each given task. Be sure t read thrugh the rubrics s
I.S. 239 Mark Twain 7 ID Name: Date: Grade 7 Mathematics Spring Perfrmance Task: Prprtinal Relatinships Directins: Cmplete all parts f each sheet fr each given task. Be sure t read thrugh the rubrics s
Sound Absorption Characteristics of Membrane- Based Sound Absorbers
 Purdue e-pubs Publicatis f the Ray W. Schl f Mechaical Egieerig 8-28-2003 Sud Absrpti Characteristics f Membrae- Based Sud Absrbers J Stuart Blt, blt@purdue.edu Jih Sg Fllw this ad additial wrks at: http://dcs.lib.purdue.edu/herrick
Purdue e-pubs Publicatis f the Ray W. Schl f Mechaical Egieerig 8-28-2003 Sud Absrpti Characteristics f Membrae- Based Sud Absrbers J Stuart Blt, blt@purdue.edu Jih Sg Fllw this ad additial wrks at: http://dcs.lib.purdue.edu/herrick
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
The Molecular Diffusion of Heat and Mass from Two Spheres
 Iteratial Jural f Mder Studies i Mechaical Egieerig (IJMSME) Vlume 4, Issue 1, 018, PP 4-8 ISSN 454-9711 (Olie) DOI: http://dx.di.rg/10.0431/454-9711.0401004 www.arcjurals.rg The Mlecular Diffusi f Heat
Iteratial Jural f Mder Studies i Mechaical Egieerig (IJMSME) Vlume 4, Issue 1, 018, PP 4-8 ISSN 454-9711 (Olie) DOI: http://dx.di.rg/10.0431/454-9711.0401004 www.arcjurals.rg The Mlecular Diffusi f Heat
Frequency-Domain Study of Lock Range of Injection-Locked Non- Harmonic Oscillators
 0 teratial Cferece mage Visi ad Cmputig CVC 0 PCST vl. 50 0 0 ACST Press Sigapre DO: 0.776/PCST.0.V50.6 Frequecy-Dmai Study f Lck Rage f jecti-lcked N- armic Oscillatrs Yushi Zhu ad Fei Yua Departmet f
0 teratial Cferece mage Visi ad Cmputig CVC 0 PCST vl. 50 0 0 ACST Press Sigapre DO: 0.776/PCST.0.V50.6 Frequecy-Dmai Study f Lck Rage f jecti-lcked N- armic Oscillatrs Yushi Zhu ad Fei Yua Departmet f
~,. :'lr. H ~ j. l' ", ...,~l. 0 '" ~ bl '!; 1'1. :<! f'~.., I,," r: t,... r':l G. t r,. 1'1 [<, ."" f'" 1n. t.1 ~- n I'>' 1:1 , I. <1 ~'..
 ,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
,, 'l t (.) :;,/.I I n ri' ' r l ' rt ( n :' (I : d! n t, :?rj I),.. fl.),. f!..,,., til, ID f-i... j I. 't' r' t II!:t () (l r El,, (fl lj J4 ([) f., () :. -,,.,.I :i l:'!, :I J.A.. t,.. p, - ' I I I
Public Key Cryptography. Tim van der Horst & Kent Seamons
 Public Key Cryptgraphy Tim van der Hrst & Kent Seamns Last Updated: Oct 5, 2017 Asymmetric Encryptin Why Public Key Crypt is Cl Has a linear slutin t the key distributin prblem Symmetric crypt has an expnential
Public Key Cryptgraphy Tim van der Hrst & Kent Seamns Last Updated: Oct 5, 2017 Asymmetric Encryptin Why Public Key Crypt is Cl Has a linear slutin t the key distributin prblem Symmetric crypt has an expnential
PAijpam.eu IRREGULAR SET COLORINGS OF GRAPHS
 Iteratioal Joural of Pure ad Applied Mathematics Volume 109 No. 7 016, 143-150 ISSN: 1311-8080 (prited versio); ISSN: 1314-3395 (o-lie versio) url: http://www.ijpam.eu doi: 10.173/ijpam.v109i7.18 PAijpam.eu
Iteratioal Joural of Pure ad Applied Mathematics Volume 109 No. 7 016, 143-150 ISSN: 1311-8080 (prited versio); ISSN: 1314-3395 (o-lie versio) url: http://www.ijpam.eu doi: 10.173/ijpam.v109i7.18 PAijpam.eu
o ri fr \ jr~ ^: *^ vlj o^ f?: ** s;: 2 * i i H-: 2 ~ " ^ o ^ * n 9 C"r * ^, ' 1 ^5' , > ^ t g- S T ^ r. L o n * * S* * w 3 ** ~ 4O O.
 THE PENALTY FR MAKING A FALSE STATEMENT IN THIS REPRT AND/R CERTIFICATE IS S5. R SIX MNTHS IMPRISNMENT R BTH "D "? y. " cr TJ Xl^ " Q. rt 5' "g s r ^.. C i :? S :.. y ' : s s ^ST (X. I ^^ ^ ^ S : t ^ :
THE PENALTY FR MAKING A FALSE STATEMENT IN THIS REPRT AND/R CERTIFICATE IS S5. R SIX MNTHS IMPRISNMENT R BTH "D "? y. " cr TJ Xl^ " Q. rt 5' "g s r ^.. C i :? S :.. y ' : s s ^ST (X. I ^^ ^ ^ S : t ^ :
THE MATRIX VERSION FOR THE MULTIVARIABLE HUMBERT POLYNOMIALS
 Misklc Mathematical Ntes HU ISSN 1787-2405 Vl. 13 (2012), N. 2, pp. 197 208 THE MATRI VERSION FOR THE MULTIVARIABLE HUMBERT POLYNOMIALS RABİA AKTAŞ, BAYRAM ÇEKIM, AN RECEP ŞAHI Received 4 May, 2011 Abstract.
Misklc Mathematical Ntes HU ISSN 1787-2405 Vl. 13 (2012), N. 2, pp. 197 208 THE MATRI VERSION FOR THE MULTIVARIABLE HUMBERT POLYNOMIALS RABİA AKTAŞ, BAYRAM ÇEKIM, AN RECEP ŞAHI Received 4 May, 2011 Abstract.
TR/46 OCTOBER THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION A. TALBOT
 TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
Pipe Networks - Hardy Cross Method Page 1. Pipe Networks
 Pie Netwrks - Hardy Crss etd Page Pie Netwrks Itrducti A ie etwrk is a itercected set f ies likig e r mre surces t e r mre demad (delivery) its, ad ca ivlve ay umber f ies i series, bracig ies, ad arallel
Pie Netwrks - Hardy Crss etd Page Pie Netwrks Itrducti A ie etwrk is a itercected set f ies likig e r mre surces t e r mre demad (delivery) its, ad ca ivlve ay umber f ies i series, bracig ies, ad arallel
106 70/140H-8 70/140H-8
 7/H- 6 H 7/H- 7 H ffffff ff ff ff ff ff ff ff ff f f f f f f f f f f f ff f f f H 7/H- 7/H- H φφ φφ φφ φφ! H 1 7/H- 7/H- H 1 f f f f f f f f f f f f f f f f f f f f f f f f f f f f f ff ff ff ff φ φ φ
7/H- 6 H 7/H- 7 H ffffff ff ff ff ff ff ff ff ff f f f f f f f f f f f ff f f f H 7/H- 7/H- H φφ φφ φφ φφ! H 1 7/H- 7/H- H 1 f f f f f f f f f f f f f f f f f f f f f f f f f f f f f ff ff ff ff φ φ φ
Recursive Algorithm for Generating Partitions of an Integer. 1 Preliminary
 Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
(b) What is the probability that a particle reaches the upper boundary n before the lower boundary m?
 MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
MATH 529 The Boudary Problem The drukard s walk (or boudary problem) is oe of the most famous problems i the theory of radom walks. Oe versio of the problem is described as follows: Suppose a particle
The standard deviation of the mean
 Physics 6C Fall 20 The stadard deviatio of the mea These otes provide some clarificatio o the distictio betwee the stadard deviatio ad the stadard deviatio of the mea.. The sample mea ad variace Cosider
Physics 6C Fall 20 The stadard deviatio of the mea These otes provide some clarificatio o the distictio betwee the stadard deviatio ad the stadard deviatio of the mea.. The sample mea ad variace Cosider
