Introductions to InverseErfc
|
|
|
- Owen Bailey
- 5 years ago
- Views:
Transcription
1 Introductions to InverseErfc Introduction to the probability integrals and inverses General The probability integral (error function) erf has a long history beginning with the articles of A. de Moivre (78 733) and P.-S. Laplace (774) where it was expressed through the following integral: t t. Later C. Kramp (799) used this integral for the definition of the complementary error function erfc. P.-S. Laplace (8) derived an asymptotic expansion of the error function. The probability integrals were so named because they are widely applied in the theory of probability, in both normal and limit distributions. To obtain, say, a normal distributed random variable from a uniformly distributed random variable, the inverse of the error function, namely erf is needed. The inverse was systematically investigated in the second half of the twentieth century, especially by J. R. Philip (960) and A. J. Strecok (968). Definitions of probability integrals and inverses The probability integral (error function) erf, the generalied error function erf,, the complementary error function erfc, the imaginary error function erfi, the inverse error function erf, the inverse of the generalied error function erf,, and the inverse complementary error function erfc are defined through the following formulas: erf 0 t t erf, erf erf erfc t t erfi 0 t t erfw ; w erf erf, w ; w erf, erfcw ; w erfc. These seven functions are typically called probability integrals and their inverses.
2 Instead of using definite integrals, the three univariate error functions can be defined through the following infinite series. erf k k k k erfc k k k k erfi k k. k A quick look at the probability integrals and inverses Here is a quick look at the graphics for the probability integrals and inverses along the real axis. erf x erfcx erfix In[0]:= (* set text style options *) Off[General::spell]; Off[General::spell]; SetOptions[#, TextStyle -> {FontFamily -> "Helvetica", FontSlant -> "Italic", FontSie -> 0}]& /@ {Graphics, Graphics3D, Plot3D, ListPlot3D, GraphicsArray, Plot, ListPlot, ContourPlot, DensityPlot, ParametricPlot, ParametricPlot3D, ListContourPlot, ListDensityPlot}; Module[{funs, tab, triggraphic, legend, ε = 0^-8}, funs = {InverseErf, InverseErfc}; tab = Table[ Plot[Evaluate[funs[[k]][x]], {x, x0-4, x0 + }, Frame -> True, Axes -> True, PlotPoints -> 0, DisplayFunction -> Identity, PlotStyle -> {{Hue[0.8 (k - )/Length[funs]], Thickness[0.00]}}, FrameTicks -> {Automatic, Automatic, None, None}, FrameLabel -> {x, f}, AspectRatio -> /, PlotRange -> {All,.0 {-5, 5}}], {k, Length[funs]}, {x0, 0, 0}]; triggraphic = Show[tab]; legend = Graphics[ Table[{Hue[0.8 (k - )/Length[funs]], Line[{{0, -0k + 5}, {, -0k + 5}}], Text[TraditionalForm[funs[[k]][x]], {.3, -0k + 5}]}, {k,, Length[funs]}], Frame -> True, FrameTicks -> None, PlotRange -> {{0,.5}, {0, }}]; Show[GraphicsArray[{trigGraphic, legend}]]];
3 3 erf 0, x erf, x Connections within the group of probability integrals and inverses and with other function groups Representations through more general functions The probability integrals erf, erf,, erfc, and erfi are the particular cases of two more general functions: hypergeometric and Meijer G functions. For example, they can be represented through the confluent hypergeometric functions F and U: erf F ; 3 ; erf U,, erf, F ; 3 ; F ; 3 ; erf, U,, U,, erfc F ; 3 ; erfc U,, erfi F ; 3 ; erfi U,,. Representations of the probability integrals erf, erf,, erfc, and erfi through classical Meijer G functions are rather simple:
4 4 erf G,, 0, erf, G,, G,, 0, 0, erfc G,, 0, erfi G,, 0,. The factor in the last four formulas can be removed by changing the classical Meijer G functions to the generalied one: erf G,,,, 0 erf, G,,,, 0 G,,,, 0 erfc G,0,, 0, erfi G,,,, 0. The probability integrals erf, erf,, erfc, and erfi are the particular cases of the incomplete gamma function, regularied incomplete gamma function, and exponential integral E: erf, erf Q, erf E erf,,, erf, Q, Q,
5 5 erf, E E erfc, erfc Q, erfc E erfi, erfi Q, erfi E. Representations through related equivalent functions The probability integrals erf, erfc, and erfi can be represented through Fresnel integrals by the following formulas: erf C S erfc C S erfi C S. Representations through other probability integrals and inverses The probability integrals and their inverses erf, erf,, erfc, erfi, erf, erf,, and erfc are interconnected by the following formulas: erf erf0, erf erfc erf erfi erferf
6 6 erferf 0, erf, erf, erferfc erfc erf, erfc erf erfc erfi erfcerf erfcerf, erfcerfc erfi erf, 0 erfi erfc erfi erf erfi erf erfi erf 0, erfi erfc erf erf 0, erf erfc erfc erf, erfc erf. The best-known properties and formulas for probability integrals and inverses Real values for real arguments For real values of argument, the values of the probability integrals erf, erf,, erfc, and erfi are real. For real arguments, the values of the inverse error function erf are real; for real arguments,, the values of the inverse of the generalied error function erf, are real; and for real arguments 0, the values of the inverse complementary error function erfc are real. Simple values at ero and one The probability integrals erf, erf,, erfc, and erfi, and their inverses erf, erf,, and erfc have simple values for ero or unit arguments:
7 7 erf0 0 erf0, 0 0 erfc0 erfi0 0 erf 0 0 erf erf 0, 0 0 erf 0, erf, 0 erfc 0 erfc 0. Simple values at infinity The probability integrals erf, erfc, and erfi have simple values at infinity: erf erfc 0 erfi. Specific values for specialied arguments In cases when or is equal to 0 or, the generalied error function erf, and its inverse erf, can be expressed through the probability integrals erf, erfc, or their inverses by the following formulas: erf, 0 erf erf0, erf erf, erfc erf, erf erf 0, erf erf, erfc. Analyticity The probability integrals erf, erfc, and erfi, and their inverses erf, and erfc are defined for all complex values of, and they are analytical functions of over the whole complex -plane. The probability integrals erf, erfc, and erfi are entire functions with an essential singular point at, and they do not have branch cuts or branch points.
8 8 The generalied error function erf, is an analytical function of and, which is defined in. For fixed, it is an entire function of. For fixed, it is an entire function of. It does not have branch cuts or branch points. The inverse of the generalied error function erf, is an analytical function of and, which is defined in. Poles and essential singularities The probability integrals erf, erfc, and erfi have only one singular point at. It is an essential singular point. The generalied error function erf, has singular points at and. They are essential singular points. Periodicity The probability integrals erf, erf,, erfc, and erfi, and their inverses erf, erf,, and erfc do not have periodicity. Parity and symmetry The probability integrals erf, erf,, and erfi are odd functions and have mirror symmetry: erf erf erf erf erf, erf, erf, erf, erfi erfi erfi erfi. The generalied error function erf, has permutation symmetry: erf, erf,. The complementary error function erfc has mirror symmetry: erfc erfc. Series representations The probability integrals erf, erf,, erfc, and erfi, and their inverses erf and erfc have the following series expansions: erf ; 0 0 erf k k k k erf, ; 0 0
9 9 erf, k k k k k erfc ; 0 0 erfc k k k k erfi ; 0 0 erfi k k k erf 3 O5 erf k c k k k c m c km ; c 0 c k m m m 0 erf, erf erf erf erf O 3 erf, 4 O 3 erfc 3 O 5 erfc k c k k k c m c km ; c 0 c k m m. m 0 The series for functions erf, erf,, erfc, and erfi converge for all complex values of their arguments. Interestingly, closed-form expressions for the truncated version of the Taylor series at the origin can be expressed through generalied hypergeometric function F, for example: erf F ; F n n k k erf n k k n3 F, n 3 n 3 n ; n, n 5 ; n. Asymptotic series expansions The asymptotic behavior of the probability integrals erf, erfc, and erfi can be described by the following formulas (only the main terms of the asymptotic expansion are given): erf O ;
10 0 erfc O ; erfi O ;. The previous formulas are valid in any direction approaching infinity ( can be simplified to the following relations: ). In particular cases, these formulas erf O ; Re 0 erfc O ; Re 0 erfi O ; Im 0. Integral representations The probability integrals erf, erf,, erfc, and erfi can also be represented through the following equivalent integrals: erfx t sin x t t ; x 0 t erf, t t erfcx t sin x t t ; x 0 t erfix x 0 t sin x tt ; x erfix t x t ; x. t x The symbol in the preceding integral means that the integral evaluates as the Cauchy principal value: b f t a tx t lim xε f t Ε0 a tx t xε Transformations b f t tx t ; a x b. If the arguments of the probability integrals erf, erfc, and erfi contain square roots, the arguments can sometimes be simplified: erf erf
11 erfc erf erfi erfi. Representations of derivatives The derivative of the probability integrals erf, erf,, erfc, and erfi, and their inverses erf, erf,, and erfc have simple representations through elementary functions: erf erf, erf, erfc erfi erf erf erf, erf, erf, erf, erfc erfc. The symbolic n th -order derivatives from the probability integrals erf, erf,, erfc, and erfi have the following simple representations through the regularied generalied hypergeometric function F : n erf n n n F n erf, n n F n, ; n, 3 n ; ; n, ; n, 3 n ; 3 ; n
12 n erf, n n F n n erfc n n n F n erfi n n n F, ; n, 3 n ; 3 ; n, ; n, 3 n ; ; n, ; n, 3 n ; ; n. But the symbolic n th -order derivatives from the inverse probability integrals erf, erf,, and erfc have very complicated structures in which the regularied generalied hypergeometric function F appears in the multidimensional sums, for example: n erf erf n n n erf n n n j 0 n j n 0 n i n i j i,n i j i n n j i i n j i i i erf i erf i j i F, ; i, 3 i ; erf j i ; n. Differential equations The probability integrals erf, erf,, erfc, and erfi satisfy the following second-order linear differential equations: w w 0 ; w erf w0 0 w 0 w w 0 ; w c erf, c w w 0 ; w c erf, c w w 0 ; w erfc w0 w 0 w w 0 ; w erfi w0 0 w 0, where c and c are arbitrary constants. The inverses of the probability integrals erf, erf,, and erfc satisfy the following ordinary secondorder nonlinear differential equations: w w w 0 ; w erf w w w 0 ; w erf, w w w 0 ; w erfc. Applications of probability integrals and inverses
13 3 Applications of probability integrals include solutions of linear partial differential equations, probability theory, Monte Carlo simulations, and the Ewald method for calculating electrostatic lattice constants.
14 4 Copyright This document was downloaded from functions.wolfram.com, a comprehensive online compendium of formulas involving the special functions of mathematics. For a key to the notations used here, see Please cite this document by referring to the functions.wolfram.com page from which it was downloaded, for example: To refer to a particular formula, cite functions.wolfram.com followed by the citation number. e.g.: This document is currently in a preliminary form. If you have comments or suggestions, please comments@functions.wolfram.com , Wolfram Research, Inc.
Introductions to ExpIntegralEi
 Introductions to ExpIntegralEi Introduction to the exponential integrals General The exponential-type integrals have a long history. After the early developments of differential calculus, mathematicians
Introductions to ExpIntegralEi Introduction to the exponential integrals General The exponential-type integrals have a long history. After the early developments of differential calculus, mathematicians
Factorial2. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
 Factorial Notations Traditional name Double factorial Traditional notation n Mathematica StandardForm notation Factorialn Primary definition n 06.0.0.000.0 cos n 4 n n Specific values Specialized values
Factorial Notations Traditional name Double factorial Traditional notation n Mathematica StandardForm notation Factorialn Primary definition n 06.0.0.000.0 cos n 4 n n Specific values Specialized values
EllipticK. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
 EllipticK Notations Traditional name Complete elliptic integral of the first kind Traditional notation K Mathematica StandardForm notation EllipticK Primary definition 08.0.0.000.0 K F Specific values
EllipticK Notations Traditional name Complete elliptic integral of the first kind Traditional notation K Mathematica StandardForm notation EllipticK Primary definition 08.0.0.000.0 K F Specific values
Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation. Specialized values
 KleinInvariant Notations Traditional name Klein invariant modular function Traditional notation z Mathematica StandardForm notation KleinInvariant z Primary definition 09.50.0.0001.01 ϑ 0, Π z 8 ϑ 3 0,
KleinInvariant Notations Traditional name Klein invariant modular function Traditional notation z Mathematica StandardForm notation KleinInvariant z Primary definition 09.50.0.0001.01 ϑ 0, Π z 8 ϑ 3 0,
Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation. Specialized values
 PolyLog Notations Traditional name Diarithm Traditional notation Li Mathematica StandardForm notation PolyLog, Primary definition Li 0.07.0.000.0 k k ; k Specific values Specialied values Π p Li q 0.07.03.000.0
PolyLog Notations Traditional name Diarithm Traditional notation Li Mathematica StandardForm notation PolyLog, Primary definition Li 0.07.0.000.0 k k ; k Specific values Specialied values Π p Li q 0.07.03.000.0
InverseBetaRegularized
 InverseBetaRegularized Notations Traditional name Inverse of the regularized incomplete beta function Traditional notation I z 1 a, b Mathematica StandardForm notation InverseBetaRegularizedz, a, b Primary
InverseBetaRegularized Notations Traditional name Inverse of the regularized incomplete beta function Traditional notation I z 1 a, b Mathematica StandardForm notation InverseBetaRegularizedz, a, b Primary
Round. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation. Specialized values
 Round Notations Traditional name Nearest integer function Traditional notation z Mathematica StandardForm notation Roundz Primary definition 0.03.0.0001.01 x n ; x n x n 1 0.03.0.000.01 z Rez Imz 0.03.0.0003.01
Round Notations Traditional name Nearest integer function Traditional notation z Mathematica StandardForm notation Roundz Primary definition 0.03.0.0001.01 x n ; x n x n 1 0.03.0.000.01 z Rez Imz 0.03.0.0003.01
EllipticTheta2. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
 EllipticTheta Notations Traditional name Jacobi theta function ϑ Traditional notation ϑ z, Mathematica StandardForm notation EllipticTheta, z, Primary definition 09.0.0.0001.01 ϑ z, cos k 1 z ; 1 Specific
EllipticTheta Notations Traditional name Jacobi theta function ϑ Traditional notation ϑ z, Mathematica StandardForm notation EllipticTheta, z, Primary definition 09.0.0.0001.01 ϑ z, cos k 1 z ; 1 Specific
Ceiling. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation. Specialized values
 Ceiling Notations Traditional name Ceiling function Traditional notation z Mathematica StandardForm notation Ceilingz Primary definition 04.0.0.0001.01 x n ; x n n 1 x n 04.0.0.000.01 z Rez Imz For real
Ceiling Notations Traditional name Ceiling function Traditional notation z Mathematica StandardForm notation Ceilingz Primary definition 04.0.0.0001.01 x n ; x n n 1 x n 04.0.0.000.01 z Rez Imz For real
JacobiDS Notations Traditional name Traditional notation Mathematica StandardForm notation Primary definition
 JacobiDS Notations Traditional name Jacobi elliptic function ds Traditional notation dsz m Mathematica StandardForm notation JacobiDSz, m Primary definition 09.30.02.0001.01 dnz m snz m Specific values
JacobiDS Notations Traditional name Jacobi elliptic function ds Traditional notation dsz m Mathematica StandardForm notation JacobiDSz, m Primary definition 09.30.02.0001.01 dnz m snz m Specific values
GammaRegularized. Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation
 GmmRegulrized Nottions Trditionl nme Regulrized incomplete gmm function Trditionl nottion Q, z Mthemtic StndrdForm nottion GmmRegulrized, z Primry definition 06.08.0.000.0, z Q, z Specific vlues Specilized
GmmRegulrized Nottions Trditionl nme Regulrized incomplete gmm function Trditionl nottion Q, z Mthemtic StndrdForm nottion GmmRegulrized, z Primry definition 06.08.0.000.0, z Q, z Specific vlues Specilized
Continued Fractions for Special Functions: Handbook and Software
 Continued Fractions for Special Functions: Handbook and Software Team: A. Cuyt, V.B. Petersen, J. Van Deun, H. Waadeland, F. Backeljauw, S. Becuwe, M. Colman, W.B. Jones Universiteit Antwerpen Sør-Trøndelag
Continued Fractions for Special Functions: Handbook and Software Team: A. Cuyt, V.B. Petersen, J. Van Deun, H. Waadeland, F. Backeljauw, S. Becuwe, M. Colman, W.B. Jones Universiteit Antwerpen Sør-Trøndelag
Mathematica for Calculus II (Version 9.0)
 Mathematica for Calculus II (Version 9.0) C. G. Melles Mathematics Department United States Naval Academy December 31, 013 Contents 1. Introduction. Volumes of revolution 3. Solving systems of equations
Mathematica for Calculus II (Version 9.0) C. G. Melles Mathematics Department United States Naval Academy December 31, 013 Contents 1. Introduction. Volumes of revolution 3. Solving systems of equations
MATHEMATICAL FORMULAS AND INTEGRALS
 MATHEMATICAL FORMULAS AND INTEGRALS ALAN JEFFREY Department of Engineering Mathematics University of Newcastle upon Tyne Newcastle upon Tyne United Kingdom Academic Press San Diego New York Boston London
MATHEMATICAL FORMULAS AND INTEGRALS ALAN JEFFREY Department of Engineering Mathematics University of Newcastle upon Tyne Newcastle upon Tyne United Kingdom Academic Press San Diego New York Boston London
Notations. Primary definition. Specific values. Traditional name. Traditional notation. Mathematica StandardForm notation. Specialized values
 InverseJacobiCS Notations Traditional nae Inverse of the Jacobi elliptic function cs Traditional notation cs Matheatica StandardFor notation InverseJacobiCS, Priary definition 09.39.0.000.0 csw ; w cs
InverseJacobiCS Notations Traditional nae Inverse of the Jacobi elliptic function cs Traditional notation cs Matheatica StandardFor notation InverseJacobiCS, Priary definition 09.39.0.000.0 csw ; w cs
COMPLEX VARIABLES. Principles and Problem Sessions YJ? A K KAPOOR. University of Hyderabad, India. World Scientific NEW JERSEY LONDON
 COMPLEX VARIABLES Principles and Problem Sessions A K KAPOOR University of Hyderabad, India NEW JERSEY LONDON YJ? World Scientific SINGAPORE BEIJING SHANGHAI HONG KONG TAIPEI CHENNAI CONTENTS Preface vii
COMPLEX VARIABLES Principles and Problem Sessions A K KAPOOR University of Hyderabad, India NEW JERSEY LONDON YJ? World Scientific SINGAPORE BEIJING SHANGHAI HONG KONG TAIPEI CHENNAI CONTENTS Preface vii
Class 4: More Pendulum results
 Class 4: More Pendulum results The pendulum is a mechanical problem with a long and interesting history, from Galileo s first ansatz that the period was independent of the amplitude based on watching priests
Class 4: More Pendulum results The pendulum is a mechanical problem with a long and interesting history, from Galileo s first ansatz that the period was independent of the amplitude based on watching priests
MATHEMATICAL FORMULAS AND INTEGRALS
 HANDBOOK OF MATHEMATICAL FORMULAS AND INTEGRALS Second Edition ALAN JEFFREY Department of Engineering Mathematics University of Newcastle upon Tyne Newcastle upon Tyne United Kingdom ACADEMIC PRESS A Harcourt
HANDBOOK OF MATHEMATICAL FORMULAS AND INTEGRALS Second Edition ALAN JEFFREY Department of Engineering Mathematics University of Newcastle upon Tyne Newcastle upon Tyne United Kingdom ACADEMIC PRESS A Harcourt
SPECIAL FUNCTIONS OF MATHEMATICS FOR ENGINEERS
 SPECIAL FUNCTIONS OF MATHEMATICS FOR ENGINEERS Second Edition LARRY C. ANDREWS OXFORD UNIVERSITY PRESS OXFORD TOKYO MELBOURNE SPIE OPTICAL ENGINEERING PRESS A Publication of SPIE The International Society
SPECIAL FUNCTIONS OF MATHEMATICS FOR ENGINEERS Second Edition LARRY C. ANDREWS OXFORD UNIVERSITY PRESS OXFORD TOKYO MELBOURNE SPIE OPTICAL ENGINEERING PRESS A Publication of SPIE The International Society
Notes on Ewald summation techniques
 February 3, 011 Notes on Ewald summation techniques Adapted from similar presentation in PHY 71 he total electrostatic potential energy of interaction between point charges {q i } at the positions {r i
February 3, 011 Notes on Ewald summation techniques Adapted from similar presentation in PHY 71 he total electrostatic potential energy of interaction between point charges {q i } at the positions {r i
Notes on the Unicycle Puzzle (PoW 1248)
 Notes on the Unicycle Puzzle (PoW 248) Stan Wagon, wagon@macalester.edu, Sept. 207. The basic idea here is due to David Finn. Here are papers on the subject. D. Finn, Can a bicycle create a unicycle track,
Notes on the Unicycle Puzzle (PoW 248) Stan Wagon, wagon@macalester.edu, Sept. 207. The basic idea here is due to David Finn. Here are papers on the subject. D. Finn, Can a bicycle create a unicycle track,
Math 4263 Homework Set 1
 Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Homework Set 1 1. Solve the following PDE/BVP 2. Solve the following PDE/BVP 2u t + 3u x = 0 u (x, 0) = sin (x) u x + e x u y = 0 u (0, y) = y 2 3. (a) Find the curves γ : t (x (t), y (t)) such that that
Mathematica Project, Math21b Spring 2008
 Mathematica Project, Math21b Spring 2008 Oliver Knill, Harvard University, Spring 2008 Support Welcome to the Mathematica computer project! In case problems with this assignment, please email Oliver at
Mathematica Project, Math21b Spring 2008 Oliver Knill, Harvard University, Spring 2008 Support Welcome to the Mathematica computer project! In case problems with this assignment, please email Oliver at
Contents. I Basic Methods 13
 Preface xiii 1 Introduction 1 I Basic Methods 13 2 Convergent and Divergent Series 15 2.1 Introduction... 15 2.1.1 Power series: First steps... 15 2.1.2 Further practical aspects... 17 2.2 Differential
Preface xiii 1 Introduction 1 I Basic Methods 13 2 Convergent and Divergent Series 15 2.1 Introduction... 15 2.1.1 Power series: First steps... 15 2.1.2 Further practical aspects... 17 2.2 Differential
FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS
 FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS HUNDUMA LEGESSE GELETA, ABDULKADIR HASSEN Both authors would like to dedicate this in fond memory of Marvin Knopp. Knop was the most humble and exemplary teacher
FRACTIONAL HYPERGEOMETRIC ZETA FUNCTIONS HUNDUMA LEGESSE GELETA, ABDULKADIR HASSEN Both authors would like to dedicate this in fond memory of Marvin Knopp. Knop was the most humble and exemplary teacher
Concepts of Approximate Error: Approximate Error, Absolute Approximate Error, Relative Approximate Error, and Absolute Relative Approximate Error
 Concepts of Approximate Error: Approximate Error, Absolute Approximate Error, Relative Approximate Error, and Absolute Relative Approximate Error Sean Rodby, Luke Snyder, Autar Kaw University of South
Concepts of Approximate Error: Approximate Error, Absolute Approximate Error, Relative Approximate Error, and Absolute Relative Approximate Error Sean Rodby, Luke Snyder, Autar Kaw University of South
Taylor and Maclaurin Series. Copyright Cengage Learning. All rights reserved.
 11.10 Taylor and Maclaurin Series Copyright Cengage Learning. All rights reserved. We start by supposing that f is any function that can be represented by a power series f(x)= c 0 +c 1 (x a)+c 2 (x a)
11.10 Taylor and Maclaurin Series Copyright Cengage Learning. All rights reserved. We start by supposing that f is any function that can be represented by a power series f(x)= c 0 +c 1 (x a)+c 2 (x a)
Stability of critical points in Linear Systems of Ordinary Differential Equations (SODE)
 Stability of critical points in Linear Systems of Ordinary Differential Equations (SODE) In this chapter Mathematica will be used to study the stability of the critical points of twin equation linear SODE.
Stability of critical points in Linear Systems of Ordinary Differential Equations (SODE) In this chapter Mathematica will be used to study the stability of the critical points of twin equation linear SODE.
A Summary of Contour Integration
 A Summary of Contour Integration vs 0., 5//08 ' Niels Walet, University of Manchester In this document I will summarise some very simple results of contour integration. The Basics The key word linked to
A Summary of Contour Integration vs 0., 5//08 ' Niels Walet, University of Manchester In this document I will summarise some very simple results of contour integration. The Basics The key word linked to
(z + n) 2. n=0. 2 (z + 2) (z + n). 2 We d like to compute this as an integral. To this end, we d like a function with residues
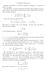 8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
8. Stirling Formula Stirling s Formula is a classical formula to compute n! accurately when n is large. We will derive a version of Stirling s formula using complex analysis and residues. Recall the formula
Special Functions of Mathematical Physics
 Arnold F. Nikiforov Vasilii B. Uvarov Special Functions of Mathematical Physics A Unified Introduction with Applications Translated from the Russian by Ralph P. Boas 1988 Birkhäuser Basel Boston Table
Arnold F. Nikiforov Vasilii B. Uvarov Special Functions of Mathematical Physics A Unified Introduction with Applications Translated from the Russian by Ralph P. Boas 1988 Birkhäuser Basel Boston Table
Computation of the error functions erf and erfc in arbitrary precision with correct rounding
 Computation of the error functions erf and erfc in arbitrary precision with correct rounding Sylvain Chevillard Arenaire, LIP, ENS-Lyon, France Sylvain.Chevillard@ens-lyon.fr Nathalie Revol INRIA, Arenaire,
Computation of the error functions erf and erfc in arbitrary precision with correct rounding Sylvain Chevillard Arenaire, LIP, ENS-Lyon, France Sylvain.Chevillard@ens-lyon.fr Nathalie Revol INRIA, Arenaire,
JPEG BMP. jpeg1.nb 1 JPEG. [Reference] /10/ /10/21 Takuichi Hirano (Tokyo Institute of Technology)
![JPEG BMP. jpeg1.nb 1 JPEG. [Reference] /10/ /10/21 Takuichi Hirano (Tokyo Institute of Technology) JPEG BMP. jpeg1.nb 1 JPEG. [Reference] /10/ /10/21 Takuichi Hirano (Tokyo Institute of Technology)](/thumbs/95/124822432.jpg) peg1.nb 1 JPEG JPEG [Reference] http://en.wikipedia.org/wiki/jpeg 2006/10/21 2006/10/21 Takuichi Hirano (Tokyo Institute of Technology) BMP In[1]:= Out[1]= SetDirectory@"d:êhira2êpublic_htmlêhobbyêeduêpeg"D
peg1.nb 1 JPEG JPEG [Reference] http://en.wikipedia.org/wiki/jpeg 2006/10/21 2006/10/21 Takuichi Hirano (Tokyo Institute of Technology) BMP In[1]:= Out[1]= SetDirectory@"d:êhira2êpublic_htmlêhobbyêeduêpeg"D
Chapter 11 Parametric Equations, Polar Curves, and Conic Sections
 Chapter 11 Parametric Equations, Polar Curves, and Conic Sections ü 11.1 Parametric Equations Students should read Sections 11.1-11. of Rogawski's Calculus [1] for a detailed discussion of the material
Chapter 11 Parametric Equations, Polar Curves, and Conic Sections ü 11.1 Parametric Equations Students should read Sections 11.1-11. of Rogawski's Calculus [1] for a detailed discussion of the material
MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS
 MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS ABDUL HASSEN AND HIEU D. NGUYEN Abstract. This paper investigates a generalization the classical Hurwitz zeta function. It is shown that many of the properties
MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS ABDUL HASSEN AND HIEU D. NGUYEN Abstract. This paper investigates a generalization the classical Hurwitz zeta function. It is shown that many of the properties
Notes on Complex Analysis
 Michael Papadimitrakis Notes on Complex Analysis Department of Mathematics University of Crete Contents The complex plane.. The complex plane...................................2 Argument and polar representation.........................
Michael Papadimitrakis Notes on Complex Analysis Department of Mathematics University of Crete Contents The complex plane.. The complex plane...................................2 Argument and polar representation.........................
Asymptotic Expansions
 Asymptotic Expansions V 1.5.4 217/1/3 Suppose we have a function f(x) of single real parameter x and we are interested in an approximation to f(x) for x close to x. The approximation might depend on whether
Asymptotic Expansions V 1.5.4 217/1/3 Suppose we have a function f(x) of single real parameter x and we are interested in an approximation to f(x) for x close to x. The approximation might depend on whether
NATIONAL BOARD FOR HIGHER MATHEMATICS. M. A. and M.Sc. Scholarship Test. September 22, Time Allowed: 150 Minutes Maximum Marks: 30
 NATIONAL BOARD FOR HIGHER MATHEMATICS M A and MSc Scholarship Test September 22, 2018 Time Allowed: 150 Minutes Maximum Marks: 30 Please read, carefully, the instructions that follow INSTRUCTIONS TO CANDIDATES
NATIONAL BOARD FOR HIGHER MATHEMATICS M A and MSc Scholarship Test September 22, 2018 Time Allowed: 150 Minutes Maximum Marks: 30 Please read, carefully, the instructions that follow INSTRUCTIONS TO CANDIDATES
Calculus from Graphical, Numerical, and Symbolic Points of View Overview of 2nd Edition
 Calculus from Graphical, Numerical, and Symbolic Points of View Overview of 2nd Edition General notes. These informal notes briefly overview plans for the 2nd edition (2/e) of the Ostebee/Zorn text. This
Calculus from Graphical, Numerical, and Symbolic Points of View Overview of 2nd Edition General notes. These informal notes briefly overview plans for the 2nd edition (2/e) of the Ostebee/Zorn text. This
COMPUTATIONAL EXPLORATIONS IN MAGNETRON SPUTTERING
 COMPUTATIONAL EXPLORATIONS IN MAGNETRON SPUTTERING E. J. McInerney Basic Numerics Press 4. ELECTRON MOTION With the groundwork laid in the last two chapters, we can now simulate the motion of electrons
COMPUTATIONAL EXPLORATIONS IN MAGNETRON SPUTTERING E. J. McInerney Basic Numerics Press 4. ELECTRON MOTION With the groundwork laid in the last two chapters, we can now simulate the motion of electrons
AN INTRODUCTION TO THE FRACTIONAL CALCULUS AND FRACTIONAL DIFFERENTIAL EQUATIONS
 AN INTRODUCTION TO THE FRACTIONAL CALCULUS AND FRACTIONAL DIFFERENTIAL EQUATIONS KENNETH S. MILLER Mathematical Consultant Formerly Professor of Mathematics New York University BERTRAM ROSS University
AN INTRODUCTION TO THE FRACTIONAL CALCULUS AND FRACTIONAL DIFFERENTIAL EQUATIONS KENNETH S. MILLER Mathematical Consultant Formerly Professor of Mathematics New York University BERTRAM ROSS University
GENERAL CONSIDERATIONS 1 What functions are. Organization of the Atlas. Notational conventions. Rules of the calculus.
 Every chapter has sections devoted to: notation, behavior, definitions, special cases, intrarelationships, expansions, particular values, numerical values, limits and approximations, operations of the
Every chapter has sections devoted to: notation, behavior, definitions, special cases, intrarelationships, expansions, particular values, numerical values, limits and approximations, operations of the
Series Solutions of Differential Equations
 Chapter 6 Series Solutions of Differential Equations In this chapter we consider methods for solving differential equations using power series. Sequences and infinite series are also involved in this treatment.
Chapter 6 Series Solutions of Differential Equations In this chapter we consider methods for solving differential equations using power series. Sequences and infinite series are also involved in this treatment.
The closed-form resolution of integrals is one of the
 Construction of Generalized Integral Formulas By Means of Laplace Transformations Adam C. Buss, Department of Physics, Indiana University - Northwest Faculty Mentor: Dr. Axel Schulze-Halberg ABSTRACT We
Construction of Generalized Integral Formulas By Means of Laplace Transformations Adam C. Buss, Department of Physics, Indiana University - Northwest Faculty Mentor: Dr. Axel Schulze-Halberg ABSTRACT We
Advanced Mathematical Methods for Scientists and Engineers I
 Carl M. Bender Steven A. Orszag Advanced Mathematical Methods for Scientists and Engineers I Asymptotic Methods and Perturbation Theory With 148 Figures Springer CONTENTS! Preface xiii PART I FUNDAMENTALS
Carl M. Bender Steven A. Orszag Advanced Mathematical Methods for Scientists and Engineers I Asymptotic Methods and Perturbation Theory With 148 Figures Springer CONTENTS! Preface xiii PART I FUNDAMENTALS
2.2. Limits Involving Infinity. Copyright 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall
 2.2 Limits Involving Infinity Copyright 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Finite Limits as x ± What you ll learn about Sandwich Theorem Revisited Infinite Limits as x a End
2.2 Limits Involving Infinity Copyright 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Finite Limits as x ± What you ll learn about Sandwich Theorem Revisited Infinite Limits as x a End
Using Mathematica to study series (part II)
 Using Mathematica to study series (part II) Truncation errors Example of exponential; first consider x>0 Remainder if use only first 3 terms in power series for exponential: PlotExpx1xx ^,x, 0,, PlotStyleThick,
Using Mathematica to study series (part II) Truncation errors Example of exponential; first consider x>0 Remainder if use only first 3 terms in power series for exponential: PlotExpx1xx ^,x, 0,, PlotStyleThick,
1 Solutions in cylindrical coordinates: Bessel functions
 1 Solutions in cylindrical coordinates: Bessel functions 1.1 Bessel functions Bessel functions arise as solutions of potential problems in cylindrical coordinates. Laplace s equation in cylindrical coordinates
1 Solutions in cylindrical coordinates: Bessel functions 1.1 Bessel functions Bessel functions arise as solutions of potential problems in cylindrical coordinates. Laplace s equation in cylindrical coordinates
Topic 5: The Difference Equation
 Topic 5: The Difference Equation Yulei Luo Economics, HKU October 30, 2017 Luo, Y. (Economics, HKU) ME October 30, 2017 1 / 42 Discrete-time, Differences, and Difference Equations When time is taken to
Topic 5: The Difference Equation Yulei Luo Economics, HKU October 30, 2017 Luo, Y. (Economics, HKU) ME October 30, 2017 1 / 42 Discrete-time, Differences, and Difference Equations When time is taken to
EQ: What are limits, and how do we find them? Finite limits as x ± Horizontal Asymptote. Example Horizontal Asymptote
 Finite limits as x ± The symbol for infinity ( ) does not represent a real number. We use to describe the behavior of a function when the values in its domain or range outgrow all finite bounds. For example,
Finite limits as x ± The symbol for infinity ( ) does not represent a real number. We use to describe the behavior of a function when the values in its domain or range outgrow all finite bounds. For example,
Index. B beats, 508 Bessel equation, 505 binomial coefficients, 45, 141, 153 binomial formula, 44 biorthogonal basis, 34
 Index A Abel theorems on power series, 442 Abel s formula, 469 absolute convergence, 429 absolute value estimate for integral, 188 adiabatic compressibility, 293 air resistance, 513 algebra, 14 alternating
Index A Abel theorems on power series, 442 Abel s formula, 469 absolute convergence, 429 absolute value estimate for integral, 188 adiabatic compressibility, 293 air resistance, 513 algebra, 14 alternating
Advanced. Engineering Mathematics
 Advanced Engineering Mathematics A new edition of Further Engineering Mathematics K. A. Stroud Formerly Principal Lecturer Department of Mathematics, Coventry University with additions by Dexter j. Booth
Advanced Engineering Mathematics A new edition of Further Engineering Mathematics K. A. Stroud Formerly Principal Lecturer Department of Mathematics, Coventry University with additions by Dexter j. Booth
MSE 310/ECE 340. Instructor: Bill Knowlton. Initialize data Clear somedata, someplot. Place data in list somedata
 MSE 3/ECE 340 Instructor: Bill Knowlton Examples of Plotting Functions ü Example 1: Using the command ListPlot[ ] to plot data in a scatter plot In[1]:= Initialize data Clear somedata someplot Place data
MSE 3/ECE 340 Instructor: Bill Knowlton Examples of Plotting Functions ü Example 1: Using the command ListPlot[ ] to plot data in a scatter plot In[1]:= Initialize data Clear somedata someplot Place data
Section 5.2 Series Solution Near Ordinary Point
 DE Section 5.2 Series Solution Near Ordinary Point Page 1 of 5 Section 5.2 Series Solution Near Ordinary Point We are interested in second order homogeneous linear differential equations with variable
DE Section 5.2 Series Solution Near Ordinary Point Page 1 of 5 Section 5.2 Series Solution Near Ordinary Point We are interested in second order homogeneous linear differential equations with variable
Theory and Practice of Symbolic Integration in Maple
 Theory and Practice of Symbolic Integration in Maple John May Senior Developer Mathematical Software September 2010 Introduction When the talking version of a popular doll said Math is Hard!, she was almost
Theory and Practice of Symbolic Integration in Maple John May Senior Developer Mathematical Software September 2010 Introduction When the talking version of a popular doll said Math is Hard!, she was almost
1.2. Functions and Their Properties. Copyright 2011 Pearson, Inc.
 1.2 Functions and Their Properties Copyright 2011 Pearson, Inc. What you ll learn about Function Definition and Notation Domain and Range Continuity Increasing and Decreasing Functions Boundedness Local
1.2 Functions and Their Properties Copyright 2011 Pearson, Inc. What you ll learn about Function Definition and Notation Domain and Range Continuity Increasing and Decreasing Functions Boundedness Local
MTH 3102 Complex Variables Final Exam May 1, :30pm-5:30pm, Skurla Hall, Room 106
 Name (Last name, First name): MTH 32 Complex Variables Final Exam May, 27 3:3pm-5:3pm, Skurla Hall, Room 6 Exam Instructions: You have hour & 5 minutes to complete the exam. There are a total of problems.
Name (Last name, First name): MTH 32 Complex Variables Final Exam May, 27 3:3pm-5:3pm, Skurla Hall, Room 6 Exam Instructions: You have hour & 5 minutes to complete the exam. There are a total of problems.
Point Charge Between Two Parallel Conducting Plates
 Point Charge Between Two Parallel Conducting Plates PROBLEM: A point charge Q is located between two infinite grounded parallel conducting sheets at a distance of d y from the plate passing through the
Point Charge Between Two Parallel Conducting Plates PROBLEM: A point charge Q is located between two infinite grounded parallel conducting sheets at a distance of d y from the plate passing through the
Control Systems I. Lecture 7: Feedback and the Root Locus method. Readings: Jacopo Tani. Institute for Dynamic Systems and Control D-MAVT ETH Zürich
 Control Systems I Lecture 7: Feedback and the Root Locus method Readings: Jacopo Tani Institute for Dynamic Systems and Control D-MAVT ETH Zürich November 2, 2018 J. Tani, E. Frazzoli (ETH) Lecture 7:
Control Systems I Lecture 7: Feedback and the Root Locus method Readings: Jacopo Tani Institute for Dynamic Systems and Control D-MAVT ETH Zürich November 2, 2018 J. Tani, E. Frazzoli (ETH) Lecture 7:
Two special equations: Bessel s and Legendre s equations. p Fourier-Bessel and Fourier-Legendre series. p
 LECTURE 1 Table of Contents Two special equations: Bessel s and Legendre s equations. p. 259-268. Fourier-Bessel and Fourier-Legendre series. p. 453-460. Boundary value problems in other coordinate system.
LECTURE 1 Table of Contents Two special equations: Bessel s and Legendre s equations. p. 259-268. Fourier-Bessel and Fourier-Legendre series. p. 453-460. Boundary value problems in other coordinate system.
SPECIAL FUNCTIONS AN INTRODUCTION TO THE CLASSICAL FUNCTIONS OF MATHEMATICAL PHYSICS
 SPECIAL FUNCTIONS AN INTRODUCTION TO THE CLASSICAL FUNCTIONS OF MATHEMATICAL PHYSICS SPECIAL FUNCTIONS AN INTRODUCTION TO THE CLASSICAL FUNCTIONS OF MATHEMATICAL PHYSICS NICO M.TEMME Centrum voor Wiskunde
SPECIAL FUNCTIONS AN INTRODUCTION TO THE CLASSICAL FUNCTIONS OF MATHEMATICAL PHYSICS SPECIAL FUNCTIONS AN INTRODUCTION TO THE CLASSICAL FUNCTIONS OF MATHEMATICAL PHYSICS NICO M.TEMME Centrum voor Wiskunde
The degree of a function is the highest exponent in the expression
 L1 1.1 Power Functions Lesson MHF4U Jensen Things to Remember About Functions A relation is a function if for every x-value there is only 1 corresponding y-value. The graph of a relation represents a function
L1 1.1 Power Functions Lesson MHF4U Jensen Things to Remember About Functions A relation is a function if for every x-value there is only 1 corresponding y-value. The graph of a relation represents a function
13 Definite integrals
 3 Definite integrals Read: Boas h. 4. 3. Laurent series: Def.: Laurent series (LS). If f() is analytic in a region R, then converges in R, with a n = πi f() = a n ( ) n + n= n= f() ; b ( ) n+ n = πi b
3 Definite integrals Read: Boas h. 4. 3. Laurent series: Def.: Laurent series (LS). If f() is analytic in a region R, then converges in R, with a n = πi f() = a n ( ) n + n= n= f() ; b ( ) n+ n = πi b
FINAL EXAM MATH 220A, UCSD, AUTUMN 14. You have three hours.
 FINAL EXAM MATH 220A, UCSD, AUTUMN 4 You have three hours. Problem Points Score There are 6 problems, and the total number of points is 00. Show all your work. Please make your work as clear and easy to
FINAL EXAM MATH 220A, UCSD, AUTUMN 4 You have three hours. Problem Points Score There are 6 problems, and the total number of points is 00. Show all your work. Please make your work as clear and easy to
1954] BOOK REVIEWS 185
![1954] BOOK REVIEWS 185 1954] BOOK REVIEWS 185](/thumbs/76/73433431.jpg) 1954] BOOK REVIEWS 185 = i*(7r w +i(i n )) where i:k n ~*K n+l is the identity map. When, in addition, ir n +i(k)=0 and n>3, T n + 2 (K) is computed to be H n {K)/2H n {K). This is equivalent to the statement
1954] BOOK REVIEWS 185 = i*(7r w +i(i n )) where i:k n ~*K n+l is the identity map. When, in addition, ir n +i(k)=0 and n>3, T n + 2 (K) is computed to be H n {K)/2H n {K). This is equivalent to the statement
Final Exam - MATH 630: Solutions
 Final Exam - MATH 630: Solutions Problem. Find all x R satisfying e xeix e ix. Solution. Comparing the moduli of both parts, we obtain e x cos x, and therefore, x cos x 0, which is possible only if x 0
Final Exam - MATH 630: Solutions Problem. Find all x R satisfying e xeix e ix. Solution. Comparing the moduli of both parts, we obtain e x cos x, and therefore, x cos x 0, which is possible only if x 0
Curriculum Map for Mathematics HL (DP1)
 Curriculum Map for Mathematics HL (DP1) Unit Title (Time frame) Sequences and Series (8 teaching hours or 2 weeks) Permutations & Combinations (4 teaching hours or 1 week) Standards IB Objectives Knowledge/Content
Curriculum Map for Mathematics HL (DP1) Unit Title (Time frame) Sequences and Series (8 teaching hours or 2 weeks) Permutations & Combinations (4 teaching hours or 1 week) Standards IB Objectives Knowledge/Content
Complex Variables. Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit.
 Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit. 1. The TI-89 calculator says, reasonably enough, that x 1) 1/3 1 ) 3 = 8. lim
Instructions Solve any eight of the following ten problems. Explain your reasoning in complete sentences to maximize credit. 1. The TI-89 calculator says, reasonably enough, that x 1) 1/3 1 ) 3 = 8. lim
Taylor and Laurent Series
 Chapter 4 Taylor and Laurent Series 4.. Taylor Series 4... Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function f : R R is given by: f (x + f (x (x x + f (x
Chapter 4 Taylor and Laurent Series 4.. Taylor Series 4... Taylor Series for Holomorphic Functions. In Real Analysis, the Taylor series of a given function f : R R is given by: f (x + f (x (x x + f (x
Complex Homework Summer 2014
 omplex Homework Summer 24 Based on Brown hurchill 7th Edition June 2, 24 ontents hw, omplex Arithmetic, onjugates, Polar Form 2 2 hw2 nth roots, Domains, Functions 2 3 hw3 Images, Transformations 3 4 hw4
omplex Homework Summer 24 Based on Brown hurchill 7th Edition June 2, 24 ontents hw, omplex Arithmetic, onjugates, Polar Form 2 2 hw2 nth roots, Domains, Functions 2 3 hw3 Images, Transformations 3 4 hw4
Bessel function - Wikipedia, the free encyclopedia
 Bessel function - Wikipedia, the free encyclopedia Bessel function Page 1 of 9 From Wikipedia, the free encyclopedia In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli
Bessel function - Wikipedia, the free encyclopedia Bessel function Page 1 of 9 From Wikipedia, the free encyclopedia In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli
Conformal maps. Lent 2019 COMPLEX METHODS G. Taylor. A star means optional and not necessarily harder.
 Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
Lent 29 COMPLEX METHODS G. Taylor A star means optional and not necessarily harder. Conformal maps. (i) Let f(z) = az + b, with ad bc. Where in C is f conformal? cz + d (ii) Let f(z) = z +. What are the
Notes 14 The Steepest-Descent Method
 ECE 638 Fall 17 David R. Jackson Notes 14 The Steepest-Descent Method Notes are adapted from ECE 6341 1 Steepest-Descent Method Complex Integral: Ω g z I f z e dz Ω = C The method was published by Peter
ECE 638 Fall 17 David R. Jackson Notes 14 The Steepest-Descent Method Notes are adapted from ECE 6341 1 Steepest-Descent Method Complex Integral: Ω g z I f z e dz Ω = C The method was published by Peter
Optical Fiber Intro - Part 1 Waveguide concepts
 Optical Fiber Intro - Part 1 Waveguide concepts Copy Right HQL Overview and study guide Loading package 1. Introduction waveguide concept 1.1 Discussion If we let a light beam freely propagates in free
Optical Fiber Intro - Part 1 Waveguide concepts Copy Right HQL Overview and study guide Loading package 1. Introduction waveguide concept 1.1 Discussion If we let a light beam freely propagates in free
Last Update: March 1 2, 201 0
 M ath 2 0 1 E S 1 W inter 2 0 1 0 Last Update: March 1 2, 201 0 S eries S olutions of Differential Equations Disclaimer: This lecture note tries to provide an alternative approach to the material in Sections
M ath 2 0 1 E S 1 W inter 2 0 1 0 Last Update: March 1 2, 201 0 S eries S olutions of Differential Equations Disclaimer: This lecture note tries to provide an alternative approach to the material in Sections
THE RADIUS OF CONVERGENCE FORMULA. a n (z c) n, f(z) =
 THE RADIUS OF CONVERGENCE FORMULA Every complex power series, f(z) = (z c) n, n=0 has a radius of convergence, nonnegative-real or infinite, R = R(f) [0, + ], that describes the convergence of the series,
THE RADIUS OF CONVERGENCE FORMULA Every complex power series, f(z) = (z c) n, n=0 has a radius of convergence, nonnegative-real or infinite, R = R(f) [0, + ], that describes the convergence of the series,
Nelinearna regresija. SetOptions Plot, ImageSize 6 72, Frame True, GridLinesStyle Directive Gray, Dashed, Method "GridLinesInFront" True,
 Nelinearna regresija In[1]:= SetOptions ListPlot, ImageSize 6 72, Frame True, GridLinesStyle Directive Gray, Dashed, Method "GridLinesInFront" True, PlotStyle Directive Thickness Medium, PointSize Large,
Nelinearna regresija In[1]:= SetOptions ListPlot, ImageSize 6 72, Frame True, GridLinesStyle Directive Gray, Dashed, Method "GridLinesInFront" True, PlotStyle Directive Thickness Medium, PointSize Large,
An Introduction to Complex Function Theory
 Bruce P. Palka An Introduction to Complex Function Theory With 138 luustrations Springer 1 Contents Preface vü I The Complex Number System 1 1 The Algebra and Geometry of Complex Numbers 1 1.1 The Field
Bruce P. Palka An Introduction to Complex Function Theory With 138 luustrations Springer 1 Contents Preface vü I The Complex Number System 1 1 The Algebra and Geometry of Complex Numbers 1 1.1 The Field
Analytic Continuation of the Theodorus Spiral
 Analytic Continuation of the Theodorus Spiral Jörg Waldvogel Seminar für Angewandte Mathematik, ETH Zürich E-mail: waldvogel@math.ethz.ch October 9, 8 to February 9 Abstract The remarkable classical pattern
Analytic Continuation of the Theodorus Spiral Jörg Waldvogel Seminar für Angewandte Mathematik, ETH Zürich E-mail: waldvogel@math.ethz.ch October 9, 8 to February 9 Abstract The remarkable classical pattern
Asymptotic Methods of ODEs: Exploring Singularities of the Second Kind
 The Mathematica Journal Asymptotic Methods of ODEs: Exploring Singularities of the Second Kind Christopher J. Winfield Madison Area Science and Technology We develop symbolic methods of asymptotic approximations
The Mathematica Journal Asymptotic Methods of ODEs: Exploring Singularities of the Second Kind Christopher J. Winfield Madison Area Science and Technology We develop symbolic methods of asymptotic approximations
Contents. Preface. Notation
 Contents Preface Notation xi xv 1 The fractional Laplacian in one dimension 1 1.1 Random walkers with constant steps.............. 1 1.1.1 Particle number density distribution.......... 2 1.1.2 Numerical
Contents Preface Notation xi xv 1 The fractional Laplacian in one dimension 1 1.1 Random walkers with constant steps.............. 1 1.1.1 Particle number density distribution.......... 2 1.1.2 Numerical
Spring 2010 Exam 2. You may not use your books, notes, or any calculator on this exam.
 MTH 282 final Spring 2010 Exam 2 Time Limit: 110 Minutes Name (Print): Instructor: Prof. Houhong Fan This exam contains 6 pages (including this cover page) and 5 problems. Check to see if any pages are
MTH 282 final Spring 2010 Exam 2 Time Limit: 110 Minutes Name (Print): Instructor: Prof. Houhong Fan This exam contains 6 pages (including this cover page) and 5 problems. Check to see if any pages are
1. If 1, ω, ω 2, -----, ω 9 are the 10 th roots of unity, then (1 + ω) (1 + ω 2 ) (1 + ω 9 ) is A) 1 B) 1 C) 10 D) 0
 4 INUTES. If, ω, ω, -----, ω 9 are the th roots of unity, then ( + ω) ( + ω ) ----- ( + ω 9 ) is B) D) 5. i If - i = a + ib, then a =, b = B) a =, b = a =, b = D) a =, b= 3. Find the integral values for
4 INUTES. If, ω, ω, -----, ω 9 are the th roots of unity, then ( + ω) ( + ω ) ----- ( + ω 9 ) is B) D) 5. i If - i = a + ib, then a =, b = B) a =, b = a =, b = D) a =, b= 3. Find the integral values for
BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES
 1 BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES 1.1 Separable Partial Differential Equations 1. Classical PDEs and Boundary-Value Problems 1.3 Heat Equation 1.4 Wave Equation 1.5 Laplace s Equation
1 BOUNDARY-VALUE PROBLEMS IN RECTANGULAR COORDINATES 1.1 Separable Partial Differential Equations 1. Classical PDEs and Boundary-Value Problems 1.3 Heat Equation 1.4 Wave Equation 1.5 Laplace s Equation
Calculus I Homework: The Derivatives of Polynomials and Exponential Functions Page 1
 Calculus I Homework: The Derivatives of Polynomials and Exponential Functions Page 1 Questions Example Differentiate the function y = ae v + b v + c v 2. Example Differentiate the function y = A + B x
Calculus I Homework: The Derivatives of Polynomials and Exponential Functions Page 1 Questions Example Differentiate the function y = ae v + b v + c v 2. Example Differentiate the function y = A + B x
Indeterminate Forms and L Hospital s Rule
 APPLICATIONS OF DIFFERENTIATION Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at certain points. INDETERMINATE FORM TYPE
APPLICATIONS OF DIFFERENTIATION Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at certain points. INDETERMINATE FORM TYPE
Considering our result for the sum and product of analytic functions, this means that for (a 0, a 1,..., a N ) C N+1, the polynomial.
 Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Lecture 3 Usual complex functions MATH-GA 245.00 Complex Variables Polynomials. Construction f : z z is analytic on all of C since its real and imaginary parts satisfy the Cauchy-Riemann relations and
Introduction to the Mathematical and Statistical Foundations of Econometrics Herman J. Bierens Pennsylvania State University
 Introduction to the Mathematical and Statistical Foundations of Econometrics 1 Herman J. Bierens Pennsylvania State University November 13, 2003 Revised: March 15, 2004 2 Contents Preface Chapter 1: Probability
Introduction to the Mathematical and Statistical Foundations of Econometrics 1 Herman J. Bierens Pennsylvania State University November 13, 2003 Revised: March 15, 2004 2 Contents Preface Chapter 1: Probability
arxiv: v3 [math.ca] 26 Jul 2013
![arxiv: v3 [math.ca] 26 Jul 2013 arxiv: v3 [math.ca] 26 Jul 2013](/thumbs/81/83861101.jpg) Symmetry, Integrability and Geometry: Methods and Applications A Connection Formula for the -Conf luent Hypergeometric Function Takeshi MORITA SIGMA 9 2013, 050, 13 pages arxiv:11055770v3 [mathca] 26 Jul
Symmetry, Integrability and Geometry: Methods and Applications A Connection Formula for the -Conf luent Hypergeometric Function Takeshi MORITA SIGMA 9 2013, 050, 13 pages arxiv:11055770v3 [mathca] 26 Jul
Activity 8: Eigenvectors and Linear Transformations
 Activity 8: Eigenvectors and Linear Transformations MATH 20, Fall 2010 November 1, 2010 Names: In this activity, we will explore the effects of matrix diagonalization on the associated linear transformation.
Activity 8: Eigenvectors and Linear Transformations MATH 20, Fall 2010 November 1, 2010 Names: In this activity, we will explore the effects of matrix diagonalization on the associated linear transformation.
MA22S3 Summary Sheet: Ordinary Differential Equations
 MA22S3 Summary Sheet: Ordinary Differential Equations December 14, 2017 Kreyszig s textbook is a suitable guide for this part of the module. Contents 1 Terminology 1 2 First order separable 2 2.1 Separable
MA22S3 Summary Sheet: Ordinary Differential Equations December 14, 2017 Kreyszig s textbook is a suitable guide for this part of the module. Contents 1 Terminology 1 2 First order separable 2 2.1 Separable
ENGIN 211, Engineering Math. Complex Numbers
 ENGIN 211, Engineering Math Complex Numbers 1 Imaginary Number and the Symbol J Consider the solutions for this quadratic equation: x 2 + 1 = 0 x = ± 1 1 is called the imaginary number, and we use the
ENGIN 211, Engineering Math Complex Numbers 1 Imaginary Number and the Symbol J Consider the solutions for this quadratic equation: x 2 + 1 = 0 x = ± 1 1 is called the imaginary number, and we use the
Complex Functions (1A) Young Won Lim 2/22/14
 Complex Functions (1A) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Complex Functions (1A) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Mathematical Methods for Engineers and Scientists 1
 K.T. Tang Mathematical Methods for Engineers and Scientists 1 Complex Analysis, Determinants and Matrices With 49 Figures and 2 Tables fyj Springer Part I Complex Analysis 1 Complex Numbers 3 1.1 Our Number
K.T. Tang Mathematical Methods for Engineers and Scientists 1 Complex Analysis, Determinants and Matrices With 49 Figures and 2 Tables fyj Springer Part I Complex Analysis 1 Complex Numbers 3 1.1 Our Number
Mathematica tools for uncertainty analysis
 Journal of Physics: Conference Series OPEN ACCESS Mathematica tools for uncertainty analysis To cite this article: M D Mikhailov and V Y Aibe 015 J. Phys.: Conf. Ser. 575 0104 View the article online for
Journal of Physics: Conference Series OPEN ACCESS Mathematica tools for uncertainty analysis To cite this article: M D Mikhailov and V Y Aibe 015 J. Phys.: Conf. Ser. 575 0104 View the article online for
West Windsor-Plainsboro Regional School District Pre-Calculus Grades 11-12
 West Windsor-Plainsboro Regional School District Pre-Calculus Grades 11-12 Unit 1: Solving Equations and Inequalities Algebraically and Graphically Content Area: Mathematics Course & Grade Level: Pre Calculus,
West Windsor-Plainsboro Regional School District Pre-Calculus Grades 11-12 Unit 1: Solving Equations and Inequalities Algebraically and Graphically Content Area: Mathematics Course & Grade Level: Pre Calculus,
MORE CONSEQUENCES OF CAUCHY S THEOREM
 MOE CONSEQUENCES OF CAUCHY S THEOEM Contents. The Mean Value Property and the Maximum-Modulus Principle 2. Morera s Theorem and some applications 3 3. The Schwarz eflection Principle 6 We have stated Cauchy
MOE CONSEQUENCES OF CAUCHY S THEOEM Contents. The Mean Value Property and the Maximum-Modulus Principle 2. Morera s Theorem and some applications 3 3. The Schwarz eflection Principle 6 We have stated Cauchy
Semester University of Sheffield. School of Mathematics and Statistics
 University of Sheffield School of Mathematics and Statistics MAS140: Mathematics (Chemical) MAS15: Civil Engineering Mathematics MAS15: Essential Mathematical Skills & Techniques MAS156: Mathematics (Electrical
University of Sheffield School of Mathematics and Statistics MAS140: Mathematics (Chemical) MAS15: Civil Engineering Mathematics MAS15: Essential Mathematical Skills & Techniques MAS156: Mathematics (Electrical
PURE MATHEMATICS AM 27
 AM SYLLABUS (2020) PURE MATHEMATICS AM 27 SYLLABUS 1 Pure Mathematics AM 27 (Available in September ) Syllabus Paper I(3hrs)+Paper II(3hrs) 1. AIMS To prepare students for further studies in Mathematics
AM SYLLABUS (2020) PURE MATHEMATICS AM 27 SYLLABUS 1 Pure Mathematics AM 27 (Available in September ) Syllabus Paper I(3hrs)+Paper II(3hrs) 1. AIMS To prepare students for further studies in Mathematics
Integrals, Series, Eighth Edition. Table of. and Products USA. Daniel Zwillinger, Editor Rensselaer Polytechnic Institute,
 Table of Integrals, Series, and Products Eighth Edition I S Gradshteyn and I M Ryzhik Daniel Zwillinger, Editor Rensselaer Polytechnic Institute, USA Victor Moll (Scientific Editor) Tulane University,
Table of Integrals, Series, and Products Eighth Edition I S Gradshteyn and I M Ryzhik Daniel Zwillinger, Editor Rensselaer Polytechnic Institute, USA Victor Moll (Scientific Editor) Tulane University,
