Section 3.7 Optimization Problems 1. (a)
|
|
|
- Ronald Hensley
- 5 years ago
- Views:
Transcription
1 Section 3.7 Optimization Problems 303 Section 3.7 Optimization Problems 1. (a) First Number, x Second Number Product, P (110-10)= (110-0)= (110-30)= (110-40) = 800 5O (110-50)= (110-60) = 3000 (b) First Number, x Second Number Product, P (110-10)= (110-0)= (110-30)= (110-40) = (110-50)= (110-60) = (110-70)= (110-80)= (110-90)= ( )= 1000 The maximum is attained near x = 50 and 60. (c) P = x(ll0-x) = ll0x-x (d) asoo o The solution appears to be x = 55. (e)--dp = llo-x = O when x = 55. dx dp --=- <0 dx P is a maximum when x = x = 55. The two numbers are 55 and 55.
2 304 Chapter 3 Applications of Differentiation. (a) Height, x Length & Width Volume 1 4-(1) 114- (1)] = () [4 - ()1 = (3) 3[4 - (3)] = (4) 4[4- (4)1= (5) 5[4 - (5)1 = (6) 6[4 - (6)1 = 864 The maximum is attained near x = 4. (b) V = x(z4-x),0 < x 1 < (c) d~v = x(4 - x)(-) + (4 - x) = (4 - x)(4-6x) = 1(1 - x)(4 - x) = 0 when x = 1, 4 (1 is not in the domain). dv - 1(x- 16) dv -- < 0whenx = 4. dx (d) 100 When x = 4, V = 104 is maximum. o The maximum volume seems to be Let x and y be two positive numbers such that x+y=s. P = xy = x(s-x) = Sx-x dp S -- = S-x = 0whenx =--. dx dp S - < Owhenx =--. dx P is a maximum when x = y = S/. 4. Let x and y be two positive numbers such that xy = 185. S=x+y=x ds when x = 1,,/i-~. dx x ds > 0 when x = ~ dx X 3 S is a minimum when x = y = 1-x/]-~. X 5. Let x and y be two positive, numbers such that xy = S = x+3y =--+3y Y -- ds = wheny = 7. dy y ds 94 > Owheny = 7. dy y3 S is minimum when y = 7 and x = 1. Let x be a positive number. 1 S=x+x ds 1 1 dx 7f 0 when x 1. ds > 0whenx = 1. dx x 3 The sum is a minimum when x = 1 and 1Ix = 1.
3 Section 3.7 Optimization Problems Let x and y be two positive numbers such that x + y = 108. P = xy = y(108- y) = 108y- y dp -- = 108-4y = 0wheny = 7. dp --4 < 0wheny = 7. P is a maximum when x = 54 and y = 7. Let x and y be two positive numbers such that X -F y = 54. P = xy = x(54-x ) = 54x-x 3 dp dx 54-3x = 0 when x 3~/~. dp - dx 6x < 0 when x = 3~r~. The product is a maximum when x = 3~/~ and y = Let x be the length and y the width of the rectangle. x + y = 80 y = 40-x A = xy = x(40-x) = 40x-x da -- = 40-x = 0whenx = 0. da -- =- < 0whenx = Let x be the length and y the width of the rectangle. xy = 3 3 P = x+y = x+ = x+-- x dp 64 dr -~- 0 when x = 4~/~. dp 18 ~ =-- > 0whenx = 4.f~. dr X 3 P is minimum when x = y = 4~/~ ft. 1. Let x be the length and y the width of the rectangle. xy=a A P= x+y=x+(---a~= x+-- A ~,x) dp A 0 when x = ~t-~. dr x dp 4A dr - x 3 > 0 when P is minimum when x = y = ~ cm. (A square!) A is maximum when x = y = 0 m. 10. Let x be the length and y the width of the rectangle. x + y = P P - x P y- - X A = xy = x -x =--x- da P P - x = 0whenx =--. dr 4 da p - - < 0whenx =--. dr 4 A is maximum when x = y = P/4 units. (A square!) = x/(x- = 4x 4-4x * (17/4) Because d is smallest when the expression inside the radical is smallest, you need only find the critical numbers of 17 f(x) = x 4-4x + 7 f (x) = 4x 3-4 = 0 x=l By the First Derivative Test, the point nearest to (, ½)is y
4 306 Chapter 3 Applications of Differentiation d= (. - 1)~, (-5, 3) + I(x_,)_ = ~(x~+10x+ 5)+(x 4.4x~+8x+4) = ~x 4-4x ~ +x ~ +18x+9 Because dis smallest when the expression inside ~e radical is smallest, you need to find the critical n~bers of g(x) = X X 3 + X + 18x + 9 g (x) = 4x 3-1x a + x + 18 : ~(~ + 1)(~x ~- 8x + 9): 0 x = -1 By the First Derivative Test, x = -1 yields a minimum. so, (-1, 4) is olosest to (-S, 3). = x/x -7x+16 Because d is smallest when the expression inside the radical is smallest, you need only find the critical numbers of f(x) = x ~ -7x+16. f (x) = x-7 = 0 X ~ -- 7 By the First Derivative Test, the point nearest to (4, 0) is (x,,/) 16. f(x) : ~x - 8, (1, 0) = 4X -- 4x x - 8 = x/x ~ - 3x Because d is smallest when the expression inside the radical is smallest, you need to find the critical numbers of g(x) = x ~ - 3x g (x),, : x-3 : 0whenx :-- 3 g"(x),, = > 0atx =-- The point nearest to (1, 0) is 3O 17. xy = 30 ~ y =-- x A = (x + )(3--~ + 3 (see figure) x ~0 / - 0 when x = By the First Derivative Test, the dimensions (x + ) by (y + )are ( + ~)by ( + ~)(approximately by 7.477). These dimensions yield a minimum area. ~x+~ (4, 0)
5 18. xy=36~ y=-- 36 x 108 = x+9 x da -108 dx -- x +3 = 0 ~ 3x = 108 ~ x = 6, y = 6 Dimensions: 9 9 Section 3.7 Optimization Problems x + 3y = 400 is the perimeter. (see figure) 4oo-4x) ~ = loox - x da _ 8_(100 _ x]/ = 0 when x da < Owhenx = 50. dx 3 00 A is a maximum when x = 50 ft and y = -- ft. 3 y dq = kx(qo - x) = kqox - kx ~ dx dzq - kqo - kx = k(qo - x) = 0 when x = -~-. d3q -.k < 0 when x = --. dx 3 dq/dx is maximum when x = Qo/. F= + 0.0v df - O.0v ~ dv ( + 0.0v) = 0 when v = wiilo0 ~ By the First Derivative Test, the flow rate on the road is maximized when v ~ 33 mi/h. 3. (a) A = 4(area ofside) + (area of Top) (1).4 = 4(3)(11) + (3)(3) = 150in. ().4 = 4(5)(5) + (5)(5) = 150 in. (3).4 = 4(3.5)(6) + (6)(6) = 150 in. (b) V = (length)(width)(height) (1) V = (3)(3)(11) = 99in 3. () V = (5)(5)(5) = 15 in 3. (3) V = (6)(6)(3.5) = 117 in a x (c) S = 4xy + x = 150 ~ y - 4x Z = x~y = x~i-150- x~l 75 lx3 ~x ") = T x- V x = 0 ~ x = +5 x 1. xy = 45,000 (see figure) S =x+y where S is the length of fence needed. ds 490, = 0whenx = 700. dx x das 980,000. > 0 when x = 700. dx ~ x 3 S is a minimum when x = 700 m and y = 350 m. x By the First Derivative Test, x = 5 yields the maximum volume. Dimensions: 5 5 x 5 in. (A cube!)
6 308 Chapter 3 Applications of Differentiation 4 S = x + 4xy = = x - -x 3 dv x = 0 =:, x 56.5 => x = 7.5 and y 7.5. dx dv --3x < 0forx = 7.5. dx The maximum value occurs when x = y = 7.5 cm = 4y+x+~rx 3 - x - rex y= 4 A = xy + ~-\-~j.3 - x4 - xx. x + = --8x - l-x - x + x 4 8 da =8-x---x+ =8-xl+ dx 4 dx =- 1+ < 0whenx- 4+~r 3-13/(4 + r)~- ~re3/(4 + n )~ 16 _ y= 4 4+~ 16 3 The area is maximum when y = ~ ft and x - ft. 4+~ 4+~ 6. You can see from the figure that A = xy and y = ~ 8 3 when x = ( r/4] 4 + y da _ 1(6_x), = 0whenx = 3. da --1 < 0whenx = 3. dx A is a maximum when x = 3 and y = 3/.
7 Section 3.7 Optimization Problems (a) y x-1 y=+-- x-1!;=,,/x+y = x+ +~ = x x>l (b) lo ol [ (.587,4.16) o L is minimum when x =.587 and L ~ ~xy= x+ =x+~ X (x-1)-x 1 A (x) = 1 + = (x -1) ~ (x - 1) (X -- 1) = 1 x-1 =_+1 x = 0, (select x = ) Theyy = 4and A = 4. Vertices: (0, 0), (, 0), (0, 4) 8. (a) A= lbasexheight = ~(x/36-h~)(6+ h)= x/36-h(6+ h) da:l(dh,36 - h)-l/(-h)(6 + h) + (36 - h) 1/ = (36 - h)-l/~[-h(6 + h)+ (36 - h~)] = -(h + 3h -18) = -(h + 6)(h - 3) ~36 - h ~ ~36- h da = 0 when h = 3, which is a maximum by the First Derivative Test. So, the sides are ~/36 - h = 6w/ ~, an dh equilateral triangle. Area = 7w/~ sq. units.
8 310 Chapter 3 Applications of Differentiation (b) cos cr = ",J36 - h tan c~ - 6+h Area= (½/(~J36-h )(6+h) = (6+ h) tan~z = 144cos 4atana A (o 0 = 144[cos4 o~ sec~ ~z + 4 cos~(-sin a)tan c~] = 0 :~ COS 40~ sec o~ = 1= 1 4 sin o~ = 4 cos ~ a sin a tan a 4 cos o~ sin a tan c~ sin z c~ 1 - ~ ~z = 30 and A = 7~r~. (c) Equilateral triangle 9. A = xy = x,,/5- x ~ (see figure) g = ~-~--~.) = Owhenx = y =~ da x(l ]( -x 1 + "j5 - x = ( 5-x / By the First Derivative Test, the inscribed rectangle of maximum area has vertices Width: 5"v/~; Length: 5w/-~ , >--x 30. A = xy = x,jr - x (see figure) da ( r - x ) 45r -- = - 0 when x - dx 4r _ x Bythe First Derivative Test, A is maximum when the rectangle has dimensions ~/~r by (45r)/. (-r, O) (r, O)
9 Section 3.7 Optimization Problems (a) P = x+rcr = x+ n-y = 00 (b) Length, x Width, y Area, xy 10 ~(100-10) (10)-~(100-10) = ~(100-0) (0)-~(100-0) ~ ~(100-30) (30)~(100-30) ~ oo - 4ot (40)-~(100-40) ~ 158 5O ~(100-50) (50)~(100-50) ~ 159 6O ~(100-60) (60)(100-60) ~ 158 The maximum area of the rectangle is approximately 159 m. (c) A= xy= x~(100-x)--~(100x-x ) (d) A = --(100 - x). A = 0 when x = Maximum value is approximately 159 when length = 50 m and width - (e) 000 o Maximum area is approximately m (x = 50 m).
10 31 Chapter 3 Applications of Differentiation 3. V = zrh = cubic inches or h = ~ ]/-r (a) Radius, r Height Surface Area 0. z(0.) z(0.)0. + z(0.) z(0.4) z(0.4)0.4 + ~ z(0.4) ~ z(0.6) z(0.6)0.6 + z(0.6) z( ~ 59.0 (b) Radius, r Height Surface Area 0. z(0.) (o.) 0. + z(o.1_ z(0.4) z(0.4)0.4 + z(0.4) ~ z(0.6) z(0.6) z(o~ z(0.8) / (0.8) 7/ (0.8) z(1.o) z(1.0)1.0 + z(1.0) z(1.) z(1.)1. + z(1.) _ z(1.4) z(1.4) 1.4+~ z(1.6) z(1.6) z(1.6) z(1.8) z(1.8) z(1.8) z(.0) z( ~ 47.1 The minimum seems to the about 43.6 for r = 1.6. (c) S = zr + zrh zr(r + h) = rcr + = zr + m r
11 Section 3.7 Optimization Problems 313 (d) loo (1.5, 43.46) -10 The minimum seems to be for r ~ 1.5. ds = 4n-r (e) -~r r = 0 when r = 3~l/n- ~, 1.5 in. h = ~ = 3.04 in. n-r Note: Notice that h - (111/3"~ n-r n-(llln-)/3 - ~-~-~-)= r. 33. Let x be the sides of the square ends and y the length of the package. P = 4x+y = 108 ~ y = 108-4x V = xy = x(108-4x) = 108x - 4x 3 dv -- = 16x-1x = 1x(18 -x) = 0 when x = 18. dv x = -16 < 0 when x = 18. The volume is maximum when x = 18 in. and Y = 108-4(18) = 36 in. 34. V = n-rx x + n-r = 108 => x = n-r (see figure) V = n-r(108- n-r)= n-(lo8r - n-r 3) dv _ a (16r - 6n-r ) = 6n-r(36 - n-r) dr 36 = Owhenr =--andx = 36. dv 36 - n-(16-1n-r) < 0 when r = -- dr Volume is maximum when x = 36 in. and r = 36/n" ~ in. 35. V = ln-xh = ln-x(r + ~/r - x)(see figure) n x r + ~/r - x dx 3.,Jr _ x n-x (r+rx/r_x_3x)= _ 0 3.,Jr _ x ~ r + rx/tgr ~ - x - 3x = 0 (0, r) rx/-~r ~ _ x = 3x _ r 4r(r - x ) ~- 9x 4 _ 1xr + 4r 4 0 = 9x 4-8xr = x(9x - 8r ) xi~r 3 By the First Derivative Test, the volume is a maximum when ~/~r x - and h = r + x/r _ x = 4r Thus, the maximum volume is V= ln-(8r1 4rl = 3n-r3 cubicunits
12 314 Chapter 3 Applications of Differentiation 36. V = rcxh = n x(~)= rcx~r ~ -x (see figure) dx = x/ r~ - x ~ -r - 3x- = O when x = O and x 3 ~ -f~r and h = r By the First Derivative Test, the volume is a maximum when x = -- /-;. 3 Thus, the maximum volume is V = 37. No. The volume will change because the shape of the container changes when squeezed. 38. No, there is no minimum area. If the sides arex andy, then x + y = 0 ~ y = 10 - x. The area is A(x) = x(10 - x) = 10x - x. This can be made arbitrarily small by selecting x ~ V = 14 = 4~r3 + ~crh (4/3)~cr h ~ -- r n-r ;rr 3 S = 4/rr + urh = 4~r + ur(14~r 4~) as a /al ~r-~ = Owhenr =r~ ~ 1.495cm. dr 3 r~ ~~ d~s 8 56 /1 - ~+ > Owhenr = 8 8 8~r = 4~r +-- r 3 3 r The surface area is minimum when r =,3/~ cm and h = 0. The resulting solid is a sphere of radius r = cm. h
13 Section 3.7 Optimization Problems 315 A 40. V = 4000 = Z~rr 3 + rcrh r ~r 3 Let k = cost per square foot of the surface area of the sides, then k = cost per square foot of the hemispherical ends. By the Second Derivative Test, you have d~c = k n" + [~ > 0 when r = 3~7~ -. 0 The cost is minimum when r = 3~ ff and h ~ ft. 41. Let x be the length of a side of the square and y the length of a side of the triangle. 4x + 3y = 10 (10-3y) ~ ~ ~ y + 4~/-~y=0 3O y- 9 +4x/~ daa 9 + 4Vr~ -- dy ~ 8 (10-3y)(-3) + --~-y = 0 >0 30 lo~r~ A is minimum when y = and x ~"~ (a) Let x be the side of the triangle andy the side of the square. A = ~(c t-~)x: + ~(c t-~)y: where 3x + 4y = 0 When x = 0, A= 5, when x = 60/(4-,/~ + 9),A, , andwhen x = 0/3, A = Area is maximum when all 0 feet are used on the square.
14 316 Chapter 3 Applications of Differentiation (b) Let x be the side of the square andy the side of the pentagon. A = ~lcot-~lx +~(cot-~)ywhere4x + 5y= 0 = x x,0 < x_< 5. A = x / ~x = 0 x ~.6 When x = 0, A ~ 7.58, when x ~.6, A ~ 13.10, and when x = 5, A ~ 5.Area is maximum when all0 feet are used on the pentagon. (c) Let x be the side of the pentagon andy the side of the hexagon. A = ~(cot-~)x + ~(cot-~ly where 5x + 6y = 0 = cot x + 6 0_<x_<4. A = cot x = 0 x ~ When x = 0, A ~ 8.868, when x ~.0475, A ~ , and when x = 4, A ~ Area is maximum when all 0 feet are used on the hexagon (d) Let x be the side of the hexagon and r the radius of the circle. A =-~@ot~)x +~rrwhere6x+~rr =0 10 = x+~ - 0NxN~. 3 x ~ When x = 0, A ~ , when x ~ 1.748, A ~ , andwhen x = 10/3, A ~ ~ea is maximum when all 0 feet are used on the circle. In general, using all of the wire for the figure with more sides will enclose the most area. 43. Let Sbe the strength and kthe constant of proportionality. Given h + w --- 0, h = 0 - w, S = kwh S = kw(400 - w ) m k(400w - w 3) ds - k[400" - 3w " = 0 when w 0./-~ - in. and h = ~ dw \ j 0-~/-~. 3 3 ds -- =-6kw < 0whenwdw 0x/-~ 3 These values yield a maximum. in.
15 Section 3.7 Optimization Problems LetA be the amount of the power line. A = h-y+x/x +y da y x -- =-1+ = 0wheny - dy ~/x ~ + y.~-~ d~a x ~ x - > 0fory = ~-. dy ~ (x + y) 3/ The amount of power line is minimum when y = x/~f~. (0, h) h - y /(-x, o) (x, O) 45. R = Vo sin 0 g dr Vo ~ x 3n" cos 0 = 0when0- do g 4 4 dr 4v ~ sin 0 < 0 when 0 = --. do ~ g 4 By the Second Derivative Test, R is maximum when 0 = ~r/4. : 1 1 [0, 4] 46. f(x) -~x g(x) = 1-!gx 4 - -~x on (a) -1 4 (c) +/ -- z( t x 3 if(x) = x--~x = O ~ gx = ~ x = 0, xi~(in [0, 4]) The maximum distance is d = 4 when x = f (x) = x, Tangent line at (~/~, 4)is y - 4 = x/~(x - ~,/~) y = ~/~x - 4. g (x) : ¼x 3 - x, Tangent line at ("xi ~, O)is y- 0 = (¼("xi~) 3 - "x/~)(x - -xi~) y = ~,J~x - 8. The tangent lines are parallel and 4 vertical units apart. (d) The tangent lines will be parallel. Ifd(x) = f(x) - g(x), then d (x) = 0 = f (x) - g (x) implies that f (x) = g (x) at the point x where the distance is maximum.
16 318 Chapter 3 Applications of Differentiation h h ~r 47. sina =- ~ s -,0 < a <-- s sin a h tan a tana =- ~ h = tana ~ s - sin a - seca I - ksina _ ksina _ ksinacos: s: 4 sec a 4 di = _~Esin a(- sin a cos a)+ cos: a(cos a)~ da k aecos a sin a ] = ~ COS -- 4 k ae1 3 sin: a~ = -- COS -- 4 zr 3z 1 = 0 when - a, or when sin a = +_-~. 1 Because a is acute, you have sina -~ ~ h = tana = = ~/~ ft. Because (di)/(da ) = (k/4)sin a(9 sina - 7) < 0when sin a = 1/x/~, this yields a maximum. 48. Let F be the illumination at point P which is x units from source 1. ki1 ki F =-~-+ (d_ x) df -ki~ ki + dx x3 (d- x)~ X - 0 when k/~ x 3 -- k/ (d - df 6kI1 --._~ -- 6ki dx x4 (d- x)4 This is the minimum point. > 0 when x =
17 Section 3.7 Optimization Problems s -- 4yx~ + ~, ~ = ~/~ + (~ _ x/~ ~x +4 ~x -6x+10 Time = T dt x x-3 + dx ~x + 4 4~/x =0-6x + 10 x You need to find the roots of this equation in the interval [0, 3]. By using a computer or graphing utility you can determine that this equation has only one root in this interval (x = 1). Testing at this value and at the endpoints, you see that x = 1 yields the minimum time. So, the man should row to a point 1 mile from the nearest point on the coast. 50. (a) ~~~,~ I ~ 3-tanot h tanet ""~ \ Q sec a 3 - tan a 3 - tan a T - + = sec a dt 1 (b) -- = seea tan a --see a = 0 da 1 tana =-seca 1 sin a = - 7 r(o) = ~ Endpoint /arot n( Endpoint l) Minimum time: xi~ ~ hours 4
18 30 Chapter 3 Applications of Differentiation sec a 3 - tan o~ (c) r dt - sec a tan a - -- sec o~ = 0 da vl v tan o~ V 1 -- seca V depends on (d) Cost = ( sec o~)c 1 + (3 - tan a)c - sec a (3 - tan a) From above part (c), minimum cost when sin 1/Cl a = _ C ~_ ~ - /c Cl 51. x/x +4 qx T= + -6x+10 V1 11 dt -,~ x + x-3 =0 dx hx/x + 4 va/x - 6x + 10 Because x x-3 - sin 01 and = -sin ~x +4 ~x -6x+10 you have sin 01 sin 0 sin0~ sin0 _ 0 ~ V Because dt >0 dx v~(x + 4) 3/ 11(X - 6X + 10) 3/ this condition yields a minimum time. 5. r _,,Jx + d1 + x/d~_~- + (a- x) 11 dt x x-a dx 1114 X + dl v4d + (a - x) =0 Because x - sin 01 and x - a = -sin 0 ~/x + dl 4d + (a - x) you have sino~ sino _ 0 ~--- sin O~ sin VZ Because dt d~ d + dx 111(X + d1) 3/ 11[d + (a- x)] 3/ this condition yields a minimum time. >0
19 Section 3.7 Optimization Problems 31 g3. f(x) = -sinx 55. Fcos0 = k(w-fsino) y ~x I 4 (a) Distance from origin to y-intercept is. Distance from origin to x-intercept is a / ~ (b) d = ~/x +y = 4x +(_sinx) 3 (0.7967, ) Minimum distance = at x = (c) Let f(x) = d(x) = x q- ( - sin X). f (x) = X + (- sin X)(-- COS X) Setting f (x) = 0, you obtain x ~ , which corresponds to d = C(x) = k~x +4 +k(4-x) xk C (x)- ~x+ 4 k=o x = ~x +4 4X = X + 4 3X = 4 x-x/~ Or, use Exercise 50(d): -sin 0 - C 1~ 0 = 30. So, x - W/~ ~ 4-x 56. kw F= cos 0 + k sin 0 df = -kw(k cos 0 - sin 0) = 0 do (cos 0 + k sin 0) kcos0 = sin0 ~ k = tan0 ~ 0 = arctank Because cos 0 + k sin 0 1 k v/~5 + 1, the minimum force is kw kw F = - cos 0 + k sin 0 %/k + 1 V = l~rrh = 1~rr-,/144 - r ~r r r ~) + - dr 3 _ ln.i88r 7_.3r3 3 L.]144-rl F r(96 - r ) x/144 - r 0 when r O, 4x/-~. = ~ k... = = By the First Derivative Test, V is maximum when r = 4x/-~ and h = 4x/-~. Area of circle: A = at(1) = 144n" Lateral surface area of cone: S = ~(4-,,/-~)~(4~~) + 4W/-~ ( ) = 48"~n" Area of sector: 144n ,j-~a = lot = 70 0= 144a ,f~a" 7 = -~-~ ~r (3 - w/-~) ~ radians or 66
20 3 Chapter 3 Applications of Differentiation 57. (a) (b) Base 1 Base Altitude Area cos 10 8 sin cos 0 8 sin cos 30 8 sin cos 40 8 sin cos 50 8 sin cos 60 8 sin Base 1 Base Altitude Area cos 10 8 sin cos 0 8 sin cos 30 8 sin cos 40 8 sin cos 50 8 sin cos 60 8 sin cos 70 8 sin cos 80 8 sin cos 90 8 sin The maximum cross-sectional area is approximately 83.1 ft. (c) A = (a+b)~ = [-8 + ( cos 0)~ 8 sin 0 = 64(1+ cos0) sin0,0 < 0 < 90 da = 64(1 + cos 0)cos 0 + (-64 sin 0)sin 0 (d) d--~ (e) loo = 64(cos (9 + cos (9 - sin O) = 64(cos :0+ coso-1) = 64( cos 0-1)(cos 0 + 1) = 0 when 0 = 60, 180, 300. The maximum occurs when 0 = 60. (60, 83.1) Let d be the amount deposited in the bank, i be the interest rate paid by the bank, and P be the profit. P = (0.1)d -id d = ki(because d is proportional to fl) p =,(0.1)(ki)_ i(ki ) = k(0.1i _ i3) dp k(0.4i - 3i z ) = 0 when i di ~ " 3 d~p- = k(0.4-6i) < 0 when i= 0.08 (Note: k > 0). dfl The profit is a maximum when i = 8%. C= ~,--~-- 100(00 +) l<xx x -~ 30" - C =100(-400~ x3 +-~-~(x 30 Approximation: x ~ hundred units, or 4045 units P = -- ~--~-S 3 q- 6S ~ dp 3 (a) - s ~ + 1s ds 10 (b) = --~os(s - 40) = 0whenx = 0, s = 40. dp 3 -,s + 1 ds 5 ~ {0) > 0 ~ s = 0 yields a minimum. dp-~s(40) < 0 ~ s = 40 yields a maximum. The maximum profit occurs when s = 40, which corresponds to $40,000 (P = $3,600,000). d~p 3 s+1 = 0whens = 0. ds 5 The point of diminishing returns occurs when s = 0, which corresponds to $0,000 being spent on advertising. o
21 Section 3.7 Optimization Problems S~ = (4m-1) +(5m-6) +(10m-3) ds1 - (4m - 1)(4) + (5m - 6)(5) + (10m - 3)(10) dm 64 = 8m-18 = 0whenm Line: y =--x $ = 4m m m - 3 Using a graphing utility, you can see that the minimum occurs when m = 0.3. Line y = 0.3x $ = 4(0.3) (0.3) (0.3) - 31 = 4.7 mi. S, 63. $ m m I10m - 3 x/~m~ + 1 xi-~m~ + 1 x/~m~ + 1 Using a graphing utility, you can see that the minimum occurs when x ~ 0.3. Line: y ~ 0.3x $3 = 14(0 3) (0.3) (0.3) - 3 = 4.5 mi. N/(0.3) mi = 1-~ i~-- = 14--i- 0- lo-~ (0. / 4.7) (a) Label the figure so that r = x + h. Then, the areaa is 8 times the area of the region given by OPQR: h h 8x r -- X A (x) 8.,/r x 8x = - +8x=0 = 8x+8~r -x~ r _ X x - r = X4F -- X 4x 4-4xr + r 4 = x(r - x ) 5x 4-5xr + r 4 = 0 Quadratic in x. X = 5r ± 45r4 -- 0r4 = F5 - wi~ L Take positive value. x = r + 10 ~ r Critical number
22 34 Chapter 3 Applications of Differentiation [9 x (b) Note that sin--0 = _h and cos -- = -. The area A of the cross equals the sum of two large rectangles minus the common r r square in the middle. A= (x)(h) - 4h = 8xh - 4h = 8rZsin--0 cos 0 A (O) =4r( c s O - sin -- COS O = 0 ~) cos 0 = sin -- cos -- = - sin 0 tan 0 = 0 = arctan() ~ or 63.4 (c) Note that x = --[5 + ~-~], and r - x = ---[5 - w/-~). 10 x 10 x A~x)" " =~ /~x,,/ r ~ - x ~ + 4x -4r :8 (5+ ~/-~)~0(5- ~/~) + 4~0(5 + ~/~) - 4r LlO ] 5 =~r~_r + ~r 5 5 : r=[~-~ ] : r(~/-~ - 1) Using the angle approach, note that tan 0 =, sin 0 = ~5-5 and sin (~) = ~(1 - cos 0) = ~(1 - ~5]. So, A(0) = 4r sin0-sin ~ = 4r - 1--~ = 65. f(x) = x 3-3x; X < 13x X x + 36 = (x - 9)(x - 4) = (x-3)(x-)(x+)(x+3) < 0 So,-3 _< x_<-or _< x_< 3. f (x) = 3x - 3 = 3(x + 1)(x- 1) fis increasing on (-m,-1) and (1, m). So, f is increasing on [-3,-] and [, 3]. f(-) = -, f(3) = 18. The maximum value off is 18.
23 Section 3.8 Newton s Method Let a = x + and b = X 3 -- X > O. X 3 Let f(x) : / (x l/x) 6- (x 6 1Ix 6 ) /x + v4~+ (~ + ~/~) a _ b -a-b a+b = x 3 +3x x 3 + x =3x+--=3x+. x 1 1 Let g(x) : x +-,x g (x) : 1--~ = 0 :=> x : 1. g"(x) = =and g"(1): > 0. So g is a minimum at x = 1: g(1)=. x J Finally, f is a minimum of 3() = 6. Section 3.8 Newton s Method The following solutions may vary depending on the software or calculator used, and on rounding. 1. y(x) : x- 5 f (x) : x n Xl =. f(x,,) f (x.) x. f (x.) f(x) = x 3-3 f (x) : 3x Xl = 1.4 f(x,) f(x.) f(x.) n X n x. f (x,)
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 78 Section. Rolle s Theorem and the Mean Value Theorem. 8 Section. Increasing and Decreasing Functions and the First
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
Introduction to Differentials
 Introduction to Differentials David G Radcliffe 13 March 2007 1 Increments Let y be a function of x, say y = f(x). The symbol x denotes a change or increment in the value of x. Note that a change in the
Introduction to Differentials David G Radcliffe 13 March 2007 1 Increments Let y be a function of x, say y = f(x). The symbol x denotes a change or increment in the value of x. Note that a change in the
Math 2413 General Review for Calculus Last Updated 02/23/2016
 Math 243 General Review for Calculus Last Updated 02/23/206 Find the average velocity of the function over the given interval.. y = 6x 3-5x 2-8, [-8, ] Find the slope of the curve for the given value of
Math 243 General Review for Calculus Last Updated 02/23/206 Find the average velocity of the function over the given interval.. y = 6x 3-5x 2-8, [-8, ] Find the slope of the curve for the given value of
Solutions to O Level Add Math paper
 Solutions to O Level Add Math paper 04. Find the value of k for which the coefficient of x in the expansion of 6 kx x is 860. [] The question is looking for the x term in the expansion of kx and x 6 r
Solutions to O Level Add Math paper 04. Find the value of k for which the coefficient of x in the expansion of 6 kx x is 860. [] The question is looking for the x term in the expansion of kx and x 6 r
Math 147 Exam II Practice Problems
 Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 147 Exam II Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Calculus I (Math 241) (In Progress)
 Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
Calculus I (Math 241) (In Progress) The following is a collection of Calculus I (Math 241) problems. Students may expect that their final exam is comprised, more or less, of one problem from each section,
Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3)
 Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed.
 Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed. Part A: (SHORT ANSWER QUESTIONS) Do the following problems. Write the answer in the space provided. Only the answers
Sample Questions Exam II, FS2009 Paulette Saab Calculators are neither needed nor allowed. Part A: (SHORT ANSWER QUESTIONS) Do the following problems. Write the answer in the space provided. Only the answers
/ =0. (c) Section P.3 Functions and Their Graphs. (c) g(-2) = 5-(-2) 2 = 5-4 = 1. (e) g(x) = 0 for x = -I, 1 and 2. 2.
 Section P,3 Functions and Their Graphs 3 Section P.3 Functions and Their Graphs. (a) Domain off." -4 < x < 4 ~ [-4, 4] Range off:-3 < y < 5 ~ [-3, 5] Domain of g: -3 < x < 3 ~ [-3, 3] Range of g: -4
Section P,3 Functions and Their Graphs 3 Section P.3 Functions and Their Graphs. (a) Domain off." -4 < x < 4 ~ [-4, 4] Range off:-3 < y < 5 ~ [-3, 5] Domain of g: -3 < x < 3 ~ [-3, 3] Range of g: -4
MATH 2053 Calculus I Review for the Final Exam
 MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
Chapter 2: Rocket Launch
 Chapter 2: Rocket Launch Lesson 2.1.1. 2-1. Domain:!" # x # " Range: 2! y! " y-intercept! y = 2 no x-intercepts 2-2. a. Time Hours sitting Amount Earned 8PM 1 $4 9PM 2 $4*2hrs = $8 10PM 3 $4*3hrs = $12
Chapter 2: Rocket Launch Lesson 2.1.1. 2-1. Domain:!" # x # " Range: 2! y! " y-intercept! y = 2 no x-intercepts 2-2. a. Time Hours sitting Amount Earned 8PM 1 $4 9PM 2 $4*2hrs = $8 10PM 3 $4*3hrs = $12
AP Calculus Free-Response Questions 1969-present AB
 AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
AP Calculus Free-Response Questions 1969-present AB 1969 1. Consider the following functions defined for all x: f 1 (x) = x, f (x) = xcos x, f 3 (x) = 3e x, f 4 (x) = x - x. Answer the following questions
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
 Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
1 + x 2 d dx (sec 1 x) =
 Page This exam has: 8 multiple choice questions worth 4 points each. hand graded questions worth 4 points each. Important: No graphing calculators! Any non-graphing, non-differentiating, non-integrating
Page This exam has: 8 multiple choice questions worth 4 points each. hand graded questions worth 4 points each. Important: No graphing calculators! Any non-graphing, non-differentiating, non-integrating
See animations and interactive applets of some of these at. Fall_2009/Math123/Notes
 MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
MA123, Chapter 7 Word Problems (pp. 125-153) Chapter s Goal: In this chapter we study the two main types of word problems in Calculus. Optimization Problems. i.e., max - min problems Related Rates See
ANSWERS, Homework Problems, Fall 2014: Lectures Now You Try It, Supplemental problems in written homework, Even Answers. 24x + 72 (x 2 6x + 4) 4
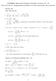 ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
2.8 Linear Approximation and Differentials
 2.8 Linear Approximation Contemporary Calculus 1 2.8 Linear Approximation and Differentials Newton's method used tangent lines to "point toward" a root of the function. In this section we examine and use
2.8 Linear Approximation Contemporary Calculus 1 2.8 Linear Approximation and Differentials Newton's method used tangent lines to "point toward" a root of the function. In this section we examine and use
Second Midterm Exam Name: Practice Problems Septmber 28, 2015
 Math 110 4. Treibergs Second Midterm Exam Name: Practice Problems Septmber 8, 015 1. Use the limit definition of derivative to compute the derivative of f(x = 1 at x = a. 1 + x Inserting the function into
Math 110 4. Treibergs Second Midterm Exam Name: Practice Problems Septmber 8, 015 1. Use the limit definition of derivative to compute the derivative of f(x = 1 at x = a. 1 + x Inserting the function into
Summer Review for Students Entering AP Calculus AB
 Summer Review for Students Entering AP Calculus AB Class: Date: AP Calculus AB Summer Packet Please show all work in the spaces provided The answers are provided at the end of the packet Algebraic Manipulation
Summer Review for Students Entering AP Calculus AB Class: Date: AP Calculus AB Summer Packet Please show all work in the spaces provided The answers are provided at the end of the packet Algebraic Manipulation
Free Response Questions Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom
 Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
MAC Find the x-value that maximizes the area of the shaded rectangle inscribed in a right triangle below.
 MAC 23. Find the x-value that maximizes the area of the shaded rectangle inscribed in a right triangle below. (x, y) y = 3 x + 4 a. x = 6 b. x = 4 c. x = 2 d. x = 5 e. x = 3 2. Consider the area of the
MAC 23. Find the x-value that maximizes the area of the shaded rectangle inscribed in a right triangle below. (x, y) y = 3 x + 4 a. x = 6 b. x = 4 c. x = 2 d. x = 5 e. x = 3 2. Consider the area of the
ENGI Partial Differentiation Page y f x
 ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
ENGI 3424 4 Partial Differentiation Page 4-01 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
CALCULUS ASSESSMENT REVIEW
 CALCULUS ASSESSMENT REVIEW DEPARTMENT OF MATHEMATICS CHRISTOPHER NEWPORT UNIVERSITY 1. Introduction and Topics The purpose of these notes is to give an idea of what to expect on the Calculus Readiness
CALCULUS ASSESSMENT REVIEW DEPARTMENT OF MATHEMATICS CHRISTOPHER NEWPORT UNIVERSITY 1. Introduction and Topics The purpose of these notes is to give an idea of what to expect on the Calculus Readiness
Linearization and Extreme Values of Functions
 Linearization and Extreme Values of Functions 3.10 Linearization and Differentials Linear or Tangent Line Approximations of function values Equation of tangent to y = f(x) at (a, f(a)): Tangent line approximation
Linearization and Extreme Values of Functions 3.10 Linearization and Differentials Linear or Tangent Line Approximations of function values Equation of tangent to y = f(x) at (a, f(a)): Tangent line approximation
OPTIMATIZATION - MAXIMUM/MINIMUM PROBLEMS BC CALCULUS
 1 OPTIMATIZATION - MAXIMUM/MINIMUM PROBLEMS BC CALCULUS 1. Read each problem slowly and carefully. Read the problem at least three times before trying to solve it. Sometimes words can be ambiguous. It
1 OPTIMATIZATION - MAXIMUM/MINIMUM PROBLEMS BC CALCULUS 1. Read each problem slowly and carefully. Read the problem at least three times before trying to solve it. Sometimes words can be ambiguous. It
Math 131 Exam 2 Spring 2016
 Math 3 Exam Spring 06 Name: ID: 7 multiple choice questions worth 4.7 points each. hand graded questions worth 0 points each. 0. free points (so the total will be 00). Exam covers sections.7 through 3.0
Math 3 Exam Spring 06 Name: ID: 7 multiple choice questions worth 4.7 points each. hand graded questions worth 0 points each. 0. free points (so the total will be 00). Exam covers sections.7 through 3.0
1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is
 1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr
![or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr or - CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~2[0- (x :2-6x)] dr=-~2(x 2-6x) dr](/thumbs/89/98001178.jpg) CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~[0- (x : 6x)] dr=-~(x 6x) dr 6~ 1356 or - 6. A: ~[(x- 1) 3 -(x-1)]dx 11. [~/3 ( - see x) dx 5- - 3 - I 1 3 5
CHAPTER 7 Applications of Integration Section 7.1 Area of a Region Between Two Curves 1. A= ~[0- (x : 6x)] dr=-~(x 6x) dr 6~ 1356 or - 6. A: ~[(x- 1) 3 -(x-1)]dx 11. [~/3 ( - see x) dx 5- - 3 - I 1 3 5
Log1 Contest Round 2 Theta Geometry
 008 009 Log Contest Round Theta Geometry Name: Leave answers in terms of π. Non-integer rational numbers should be given as a reduced fraction. Units are not needed. 4 points each What is the perimeter
008 009 Log Contest Round Theta Geometry Name: Leave answers in terms of π. Non-integer rational numbers should be given as a reduced fraction. Units are not needed. 4 points each What is the perimeter
MAC 2311 Calculus I Spring 2004
 MAC 2 Calculus I Spring 2004 Homework # Some Solutions.#. Since f (x) = d dx (ln x) =, the linearization at a = is x L(x) = f() + f ()(x ) = ln + (x ) = x. The answer is L(x) = x..#4. Since e 0 =, and
MAC 2 Calculus I Spring 2004 Homework # Some Solutions.#. Since f (x) = d dx (ln x) =, the linearization at a = is x L(x) = f() + f ()(x ) = ln + (x ) = x. The answer is L(x) = x..#4. Since e 0 =, and
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. 2) h(x) = x2-5x + 5
 Assignment 7 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Using the derivative of f(x) given below, determine the critical points of f(x).
Assignment 7 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Using the derivative of f(x) given below, determine the critical points of f(x).
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
APPLICATIONS OF DERIVATIVES
 9 APPLICATIONS OF DERIVATIVES In the previous lesson, we have learnt that the slope of a line is the tangent of the angle which the line makes with the positive direction of x-axis. It is denoted by the
9 APPLICATIONS OF DERIVATIVES In the previous lesson, we have learnt that the slope of a line is the tangent of the angle which the line makes with the positive direction of x-axis. It is denoted by the
y2 + 4y - 5 c a + b 27 i C) ) (16, ) B) (16 3 3, )
 MAT 107 Final, Version A, Spring 2008 1) If (4, 4) is the endpoint of a line segment, and (2, 1) is its midpoint, find the other endpoint. A) (0, 7) B) (-2, 0) C) (8, 10) D) (0, -2) 2) Solve for x: A)
MAT 107 Final, Version A, Spring 2008 1) If (4, 4) is the endpoint of a line segment, and (2, 1) is its midpoint, find the other endpoint. A) (0, 7) B) (-2, 0) C) (8, 10) D) (0, -2) 2) Solve for x: A)
Final Examination 201-NYA-05 May 18, 2018
 . ( points) Evaluate each of the following limits. 3x x + (a) lim x x 3 8 x + sin(5x) (b) lim x sin(x) (c) lim x π/3 + sec x ( (d) x x + 5x ) (e) lim x 5 x lim x 5 + x 6. (3 points) What value of c makes
. ( points) Evaluate each of the following limits. 3x x + (a) lim x x 3 8 x + sin(5x) (b) lim x sin(x) (c) lim x π/3 + sec x ( (d) x x + 5x ) (e) lim x 5 x lim x 5 + x 6. (3 points) What value of c makes
Math 180, Lowman, Summer 2008, Old Exam Problems 1 Limit Problems
 Math 180, Lowman, Summer 2008, Old Exam Problems 1 Limit Problems 1. Find the limit of f(x) = (sin x) x x 3 as x 0. 2. Use L Hopital s Rule to calculate lim x 2 x 3 2x 2 x+2 x 2 4. 3. Given the function
Math 180, Lowman, Summer 2008, Old Exam Problems 1 Limit Problems 1. Find the limit of f(x) = (sin x) x x 3 as x 0. 2. Use L Hopital s Rule to calculate lim x 2 x 3 2x 2 x+2 x 2 4. 3. Given the function
APPLICATION OF DERIVATIVES
 94 APPLICATION OF DERIVATIVES Chapter 6 With the Calculus as a key, Mathematics can be successfully applied to the explanation of the course of Nature. WHITEHEAD 6. Introduction In Chapter 5, we have learnt
94 APPLICATION OF DERIVATIVES Chapter 6 With the Calculus as a key, Mathematics can be successfully applied to the explanation of the course of Nature. WHITEHEAD 6. Introduction In Chapter 5, we have learnt
Find all points where the function is discontinuous. 1) Find all vertical asymptotes of the given function. x(x - 1) 2) f(x) =
 Math 90 Final Review Find all points where the function is discontinuous. ) Find all vertical asymptotes of the given function. x(x - ) 2) f(x) = x3 + 4x Provide an appropriate response. 3) If x 3 f(x)
Math 90 Final Review Find all points where the function is discontinuous. ) Find all vertical asymptotes of the given function. x(x - ) 2) f(x) = x3 + 4x Provide an appropriate response. 3) If x 3 f(x)
Math 611b Assignment #6 Name. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Math 611b Assignment #6 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find a formula for the function graphed. 1) 1) A) f(x) = 5 + x, x < -
Math 611b Assignment #6 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find a formula for the function graphed. 1) 1) A) f(x) = 5 + x, x < -
MLC Practice Final Exam
 Name: Section: Recitation/Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through. Show all your work on the standard response
Name: Section: Recitation/Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages through. Show all your work on the standard response
AP Calculus Summer Assignment - Part 1
 2017-2018 AP CALCULUS SUMMER ASSIGNMENT Linear Functions AP Calculus Summer Assignment - Part 1 Determine the equation of the line that passes through the given points 1. (0,-1) and (5,9) 2. (-2,-1) and
2017-2018 AP CALCULUS SUMMER ASSIGNMENT Linear Functions AP Calculus Summer Assignment - Part 1 Determine the equation of the line that passes through the given points 1. (0,-1) and (5,9) 2. (-2,-1) and
Test 3 Review. fx ( ) ( x 2) 4/5 at the indicated extremum. y x 2 3x 2. Name: Class: Date: Short Answer
 Name: Class: Date: ID: A Test 3 Review Short Answer 1. Find the value of the derivative (if it exists) of fx ( ) ( x 2) 4/5 at the indicated extremum. 7. A rectangle is bounded by the x- and y-axes and
Name: Class: Date: ID: A Test 3 Review Short Answer 1. Find the value of the derivative (if it exists) of fx ( ) ( x 2) 4/5 at the indicated extremum. 7. A rectangle is bounded by the x- and y-axes and
3. On the grid below, sketch and label graphs of the following functions: y = sin x, y = cos x, and y = sin(x π/2). π/2 π 3π/2 2π 5π/2
 AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test
 UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test NAME: SCHOOL: 1. Let f be some function for which you know only that if 0 < x < 1, then f(x) 5 < 0.1. Which of the following
UNIVERSITY OF HOUSTON HIGH SCHOOL MATHEMATICS CONTEST Spring 2018 Calculus Test NAME: SCHOOL: 1. Let f be some function for which you know only that if 0 < x < 1, then f(x) 5 < 0.1. Which of the following
Chapter 1: Packing your Suitcase
 Chapter : Packing your Suitcase Lesson.. -. a. Independent variable = distance from end of tube to the wall. Dependent variable = width of field of view. e. The equation depends on the length and diameter
Chapter : Packing your Suitcase Lesson.. -. a. Independent variable = distance from end of tube to the wall. Dependent variable = width of field of view. e. The equation depends on the length and diameter
Math Fall 08 Final Exam Review
 Math 173.7 Fall 08 Final Exam Review 1. Graph the function f(x) = x 2 3x by applying a transformation to the graph of a standard function. 2.a. Express the function F(x) = 3 ln(x + 2) in the form F = f
Math 173.7 Fall 08 Final Exam Review 1. Graph the function f(x) = x 2 3x by applying a transformation to the graph of a standard function. 2.a. Express the function F(x) = 3 ln(x + 2) in the form F = f
Optimization: Other Applications
 Optimization: Other Applications MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After completing this section, we will be able to: use the concepts of
Optimization: Other Applications MATH 151 Calculus for Management J. Robert Buchanan Department of Mathematics Fall 2018 Objectives After completing this section, we will be able to: use the concepts of
( ) 7 ( 5x 5 + 3) 9 b) y = x x
 New York City College of Technology, CUNY Mathematics Department Fall 0 MAT 75 Final Eam Review Problems Revised by Professor Kostadinov, Fall 0, Fall 0, Fall 00. Evaluate the following its, if they eist:
New York City College of Technology, CUNY Mathematics Department Fall 0 MAT 75 Final Eam Review Problems Revised by Professor Kostadinov, Fall 0, Fall 0, Fall 00. Evaluate the following its, if they eist:
Practice Exam 1 Solutions
 Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
AP Calculus AB Semester 1 Practice Final
 Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
Class: Date: AP Calculus AB Semester 1 Practice Final Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the limit (if it exists). lim x x + 4 x a. 6
REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS
 REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS The Department of Applied Mathematics administers a Math Placement test to assess fundamental skills in mathematics that are necessary to begin the study
REQUIRED MATHEMATICAL SKILLS FOR ENTERING CADETS The Department of Applied Mathematics administers a Math Placement test to assess fundamental skills in mathematics that are necessary to begin the study
SOLUTIONS FOR PRACTICE FINAL EXAM
 SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
Mu Alpha Theta State 2007 Euclidean Circles
 Mu Alpha Theta State 2007 Euclidean Circles 1. Joe had a bet with Mr. Federer saying that if Federer can solve the following problem in one minute, Joe would be his slave for a whole month. The problem
Mu Alpha Theta State 2007 Euclidean Circles 1. Joe had a bet with Mr. Federer saying that if Federer can solve the following problem in one minute, Joe would be his slave for a whole month. The problem
Final Exam SOLUTIONS MAT 131 Fall 2011
 1. Compute the following its. (a) Final Exam SOLUTIONS MAT 131 Fall 11 x + 1 x 1 x 1 The numerator is always positive, whereas the denominator is negative for numbers slightly smaller than 1. Also, as
1. Compute the following its. (a) Final Exam SOLUTIONS MAT 131 Fall 11 x + 1 x 1 x 1 The numerator is always positive, whereas the denominator is negative for numbers slightly smaller than 1. Also, as
Old Math 220 Exams. David M. McClendon. Department of Mathematics Ferris State University
 Old Math 0 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Spring 05 Contents Contents General information about these exams 4 Exams from 0
Old Math 0 Exams David M. McClendon Department of Mathematics Ferris State University Last updated to include exams from Spring 05 Contents Contents General information about these exams 4 Exams from 0
(a) The best linear approximation of f at x = 2 is given by the formula. L(x) = f(2) + f (2)(x 2). f(2) = ln(2/2) = ln(1) = 0, f (2) = 1 2.
 Math 180 Written Homework Assignment #8 Due Tuesday, November 11th at the beginning of your discussion class. Directions. You are welcome to work on the following problems with other MATH 180 students,
Math 180 Written Homework Assignment #8 Due Tuesday, November 11th at the beginning of your discussion class. Directions. You are welcome to work on the following problems with other MATH 180 students,
Ch2 practice test. for the following functions. f (x) = 6x 2 + 2, Find the domain of the function using interval notation:
 Ch2 practice test Find for the following functions. f (x) = 6x 2 + 2, Find the domain of the function using interval notation: A hotel chain charges $75 each night for the first two nights and $55 for
Ch2 practice test Find for the following functions. f (x) = 6x 2 + 2, Find the domain of the function using interval notation: A hotel chain charges $75 each night for the first two nights and $55 for
MULTIVARIABLE CALCULUS
 MULTIVARIABLE CALCULUS Summer Assignment Welcome to Multivariable Calculus, Multivariable Calculus is a course commonly taken by second and third year college students. The general concept is to take the
MULTIVARIABLE CALCULUS Summer Assignment Welcome to Multivariable Calculus, Multivariable Calculus is a course commonly taken by second and third year college students. The general concept is to take the
MAXIMA AND MINIMA - 2
 MAXIMA AND MINIMA - GREATEST AND LEAST VALUES Definition: Let f be a function defined on a set A and l f( A ). Then l is said to be (i) the maimum value or the greatest value of f in A if f( ) l A. (ii)
MAXIMA AND MINIMA - GREATEST AND LEAST VALUES Definition: Let f be a function defined on a set A and l f( A ). Then l is said to be (i) the maimum value or the greatest value of f in A if f( ) l A. (ii)
Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note
 Math 001 - Term 171 Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note x A x belongs to A,x is in A Between an element and a set. A B A is a subset of B Between two sets. φ
Math 001 - Term 171 Reading Mathematical Expressions & Arithmetic Operations Expression Reads Note x A x belongs to A,x is in A Between an element and a set. A B A is a subset of B Between two sets. φ
Calculus 1: A Large and In Charge Review Solutions
 Calculus : A Large and n Charge Review Solutions use the symbol which is shorthand for the phrase there eists.. We use the formula that Average Rate of Change is given by f(b) f(a) b a (a) (b) 5 = 3 =
Calculus : A Large and n Charge Review Solutions use the symbol which is shorthand for the phrase there eists.. We use the formula that Average Rate of Change is given by f(b) f(a) b a (a) (b) 5 = 3 =
( ) 9 b) y = x x c) y = (sin x) 7 x d) y = ( x ) cos x
 NYC College of Technology, CUNY Mathematics Department Spring 05 MAT 75 Final Eam Review Problems Revised by Professor Africk Spring 05, Prof. Kostadinov, Fall 0, Fall 0, Fall 0, Fall 0, Fall 00 # Evaluate
NYC College of Technology, CUNY Mathematics Department Spring 05 MAT 75 Final Eam Review Problems Revised by Professor Africk Spring 05, Prof. Kostadinov, Fall 0, Fall 0, Fall 0, Fall 0, Fall 00 # Evaluate
Calculus I Review Solutions
 Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Calculus I Review Solutions. Compare and contrast the three Value Theorems of the course. When you would typically use each. The three value theorems are the Intermediate, Mean and Extreme value theorems.
Review for the Final Exam
 Calculus Lia Vas. Integrals. Evaluate the following integrals. (a) ( x 4 x 2 ) dx (b) (2 3 x + x2 4 ) dx (c) (3x + 5) 6 dx (d) x 2 dx x 3 + (e) x 9x 2 dx (f) x dx x 2 (g) xe x2 + dx (h) 2 3x+ dx (i) x
Calculus Lia Vas. Integrals. Evaluate the following integrals. (a) ( x 4 x 2 ) dx (b) (2 3 x + x2 4 ) dx (c) (3x + 5) 6 dx (d) x 2 dx x 3 + (e) x 9x 2 dx (f) x dx x 2 (g) xe x2 + dx (h) 2 3x+ dx (i) x
Final Exam Review Exercise Set A, Math 1551, Fall 2017
 Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Final Exam Review Exercise Set A, Math 1551, Fall 2017 This review set gives a list of topics that we explored throughout this course, as well as a few practice problems at the end of the document. A complete
Question. [The volume of a cone of radius r and height h is 1 3 πr2 h and the curved surface area is πrl where l is the slant height of the cone.
 Q1 An experiment is conducted using the conical filter which is held with its axis vertical as shown. The filter has a radius of 10cm and semi-vertical angle 30. Chemical solution flows from the filter
Q1 An experiment is conducted using the conical filter which is held with its axis vertical as shown. The filter has a radius of 10cm and semi-vertical angle 30. Chemical solution flows from the filter
1 The Derivative and Differrentiability
 1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
1 The Derivative and Differrentiability 1.1 Derivatives and rate of change Exercise 1 Find the equation of the tangent line to f (x) = x 2 at the point (1, 1). Exercise 2 Suppose that a ball is dropped
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS
 APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
APPLICATIONS OF DERIVATIVES UNIT PROBLEM SETS PROBLEM SET #1 Related Rates ***Calculators Allowed*** 1. An oil tanker spills oil that spreads in a circular pattern whose radius increases at the rate of
DRAFT - Math 101 Lecture Note - Dr. Said Algarni
 3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
3 Differentiation Rules 3.1 The Derivative of Polynomial and Exponential Functions In this section we learn how to differentiate constant functions, power functions, polynomials, and exponential functions.
(b) x = (d) x = (b) x = e (d) x = e4 2 ln(3) 2 x x. is. (b) 2 x, x 0. (d) x 2, x 0
 1. Solve the equation 3 4x+5 = 6 for x. ln(6)/ ln(3) 5 (a) x = 4 ln(3) ln(6)/ ln(3) 5 (c) x = 4 ln(3)/ ln(6) 5 (e) x = 4. Solve the equation e x 1 = 1 for x. (b) x = (d) x = ln(5)/ ln(3) 6 4 ln(6) 5/ ln(3)
1. Solve the equation 3 4x+5 = 6 for x. ln(6)/ ln(3) 5 (a) x = 4 ln(3) ln(6)/ ln(3) 5 (c) x = 4 ln(3)/ ln(6) 5 (e) x = 4. Solve the equation e x 1 = 1 for x. (b) x = (d) x = ln(5)/ ln(3) 6 4 ln(6) 5/ ln(3)
Problem Worth Score Total 14
 MATH 241, Fall 14 Extra Credit Preparation for Final Name: INSTRUCTIONS: Write legibly. Indicate your answer clearly. Revise and clean up solutions. Do not cross anything out. Rewrite the page, I will
MATH 241, Fall 14 Extra Credit Preparation for Final Name: INSTRUCTIONS: Write legibly. Indicate your answer clearly. Revise and clean up solutions. Do not cross anything out. Rewrite the page, I will
a Write down the coordinates of the point on the curve where t = 2. b Find the value of t at the point on the curve with coordinates ( 5 4, 8).
 Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Worksheet A 1 A curve is given by the parametric equations x = t + 1, y = 4 t. a Write down the coordinates of the point on the curve where t =. b Find the value of t at the point on the curve with coordinates
Math Exam 03 Review
 Math 10350 Exam 03 Review 1. The statement: f(x) is increasing on a < x < b. is the same as: 1a. f (x) is on a < x < b. 2. The statement: f (x) is negative on a < x < b. is the same as: 2a. f(x) is on
Math 10350 Exam 03 Review 1. The statement: f(x) is increasing on a < x < b. is the same as: 1a. f (x) is on a < x < b. 2. The statement: f (x) is negative on a < x < b. is the same as: 2a. f(x) is on
Practice Test Geometry 1. Which of the following points is the greatest distance from the y-axis? A. (1,10) B. (2,7) C. (3,5) D. (4,3) E.
 April 9, 01 Standards: MM1Ga, MM1G1b Practice Test Geometry 1. Which of the following points is the greatest distance from the y-axis? (1,10) B. (,7) C. (,) (,) (,1). Points P, Q, R, and S lie on a line
April 9, 01 Standards: MM1Ga, MM1G1b Practice Test Geometry 1. Which of the following points is the greatest distance from the y-axis? (1,10) B. (,7) C. (,) (,) (,1). Points P, Q, R, and S lie on a line
S(x) Section 1.5 infinite Limits. lim f(x)=-m x --," -3 + Jkx) - x ~
 8 Chapter Limits and Their Properties Section.5 infinite Limits -. f(x)- (x-) As x approaches from the left, x - is a small negative number. So, lim f(x) : -m As x approaches from the right, x - is a small
8 Chapter Limits and Their Properties Section.5 infinite Limits -. f(x)- (x-) As x approaches from the left, x - is a small negative number. So, lim f(x) : -m As x approaches from the right, x - is a small
H I G H E R S T I L L. Extended Unit Tests Higher Still Higher Mathematics. (more demanding tests covering all levels)
 M A T H E M A T I C S H I G H E R S T I L L Higher Still Higher Mathematics Extended Unit Tests 00-0 (more demanding tests covering all levels) Contents Unit Tests (at levels A, B and C) Detailed marking
M A T H E M A T I C S H I G H E R S T I L L Higher Still Higher Mathematics Extended Unit Tests 00-0 (more demanding tests covering all levels) Contents Unit Tests (at levels A, B and C) Detailed marking
Mathematics, Algebra, and Geometry
 Mathematics, Algebra, and Geometry by Satya http://www.thesatya.com/ Contents 1 Algebra 1 1.1 Logarithms............................................ 1. Complex numbers........................................
Mathematics, Algebra, and Geometry by Satya http://www.thesatya.com/ Contents 1 Algebra 1 1.1 Logarithms............................................ 1. Complex numbers........................................
SOLUTIONS TO THE FINAL EXAM. December 14, 2010, 9:00am-12:00 (3 hours)
 SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
SOLUTIONS TO THE 18.02 FINAL EXAM BJORN POONEN December 14, 2010, 9:00am-12:00 (3 hours) 1) For each of (a)-(e) below: If the statement is true, write TRUE. If the statement is false, write FALSE. (Please
High School Math Contest
 High School Math Contest University of South Carolina February 4th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) 4 (e) 48 Problem. Suppose the function g(x) = f(x)
High School Math Contest University of South Carolina February 4th, 017 Problem 1. If (x y) = 11 and (x + y) = 169, what is xy? (a) 11 (b) 1 (c) 1 (d) 4 (e) 48 Problem. Suppose the function g(x) = f(x)
Copyright 2012 Pearson Education, Inc. Publishing as Prentice Hall.
 Chapter 5 Review 95 (c) f( ) f ( 7) ( 7) 7 6 + ( 6 7) 7 6. 96 Chapter 5 Review Eercises (pp. 60 6). y y ( ) + ( )( ) + ( ) The first derivative has a zero at. 6 Critical point value: y 9 Endpoint values:
Chapter 5 Review 95 (c) f( ) f ( 7) ( 7) 7 6 + ( 6 7) 7 6. 96 Chapter 5 Review Eercises (pp. 60 6). y y ( ) + ( )( ) + ( ) The first derivative has a zero at. 6 Critical point value: y 9 Endpoint values:
Days 3 & 4 Notes: Related Rates
 AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
AP Calculus Unit 4 Applications of the Derivative Part 1 Days 3 & 4 Notes: Related Rates Implicitly differentiate the following formulas with respect to time. State what each rate in the differential equation
3.8 Exponential Growth and Decay
 3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
3.8 Exponential Growth and Decay Suppose the rate of change of y with respect to t is proportional to y itself. So there is some constant k such that dy dt = ky The only solution to this equation is an
Exam VI Section I Part A - No Calculators
 No Calculators SOLUTONS-Exam V Section Part A 81 Exam V Section Part A - No Calculators 1. A p.121 Using the product rule we obtain the first and second derivatives of y = xe x. X X Y = e + xe X X x y=e+e+xe
No Calculators SOLUTONS-Exam V Section Part A 81 Exam V Section Part A - No Calculators 1. A p.121 Using the product rule we obtain the first and second derivatives of y = xe x. X X Y = e + xe X X x y=e+e+xe
Semester 1 Review. Name. Period
 P A (Calculus )dx Semester Review Name Period Directions: Solve the following problems. Show work when necessary. Put the best answer in the blank provided, if appropriate.. Let y = g(x) be a function
P A (Calculus )dx Semester Review Name Period Directions: Solve the following problems. Show work when necessary. Put the best answer in the blank provided, if appropriate.. Let y = g(x) be a function
Math 131 Final Exam Spring 2016
 Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
Math 3 Final Exam Spring 06 Name: ID: multiple choice questions worth 5 points each. Exam is only out of 00 (so there is the possibility of getting more than 00%) Exam covers sections. through 5.4 No graphing
(D) (A) Q.3 To which of the following circles, the line y x + 3 = 0 is normal at the point ? 2 (A) 2
 CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
CIRCLE [STRAIGHT OBJECTIVE TYPE] Q. The line x y + = 0 is tangent to the circle at the point (, 5) and the centre of the circles lies on x y = 4. The radius of the circle is (A) 3 5 (B) 5 3 (C) 5 (D) 5
More Differentiation Page 1
 More Differentiation Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one problem. Note:
More Differentiation Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one problem. Note:
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Differential Calculus 2 Contents Limits..5 Gradients, Tangents and Derivatives.6 Differentiation from First Principles.8 Rules for Differentiation..10 Chain Rule.12
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Differential Calculus 2 Contents Limits..5 Gradients, Tangents and Derivatives.6 Differentiation from First Principles.8 Rules for Differentiation..10 Chain Rule.12
Academic Challenge 2009 Regional Mathematics Solution Set. #2 Ans. C. Let a be the side of the cube. Then its surface area equals 6a = 10, so
 Academic Challenge 009 Regional Mathematics Solution Set #1 Ans. C: x 4 = x 9 = -5 # Ans. C. Let a be the side of the cube. Then its surface area equals 6a = 10, so a = 10 / 6 and volume V = a = ( 10 /
Academic Challenge 009 Regional Mathematics Solution Set #1 Ans. C: x 4 = x 9 = -5 # Ans. C. Let a be the side of the cube. Then its surface area equals 6a = 10, so a = 10 / 6 and volume V = a = ( 10 /
AP Calculus BC Chapter 4 AP Exam Problems A) 4 B) 2 C) 1 D) 0 E) 2 A) 9 B) 12 C) 14 D) 21 E) 40
 Extreme Values in an Interval AP Calculus BC 1. The absolute maximum value of x = f ( x) x x 1 on the closed interval, 4 occurs at A) 4 B) C) 1 D) 0 E). The maximum acceleration attained on the interval
Extreme Values in an Interval AP Calculus BC 1. The absolute maximum value of x = f ( x) x x 1 on the closed interval, 4 occurs at A) 4 B) C) 1 D) 0 E). The maximum acceleration attained on the interval
MATH1910Chapter2TestReview
 Class: Date: MATH1910Chapter2TestReview Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the slope m of the line tangent to the graph of the function
Class: Date: MATH1910Chapter2TestReview Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the slope m of the line tangent to the graph of the function
Calculus I 5. Applications of differentiation
 2301107 Calculus I 5. Applications of differentiation Chapter 5:Applications of differentiation C05-2 Outline 5.1. Extreme values 5.2. Curvature and Inflection point 5.3. Curve sketching 5.4. Related rate
2301107 Calculus I 5. Applications of differentiation Chapter 5:Applications of differentiation C05-2 Outline 5.1. Extreme values 5.2. Curvature and Inflection point 5.3. Curve sketching 5.4. Related rate
Math 23b Practice Final Summer 2011
 Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
Math 2b Practice Final Summer 211 1. (1 points) Sketch or describe the region of integration for 1 x y and interchange the order to dy dx dz. f(x, y, z) dz dy dx Solution. 1 1 x z z f(x, y, z) dy dx dz
2. to-2.52+l (3x + 7) + 5{x - 1") 5. 2x2 +5y x-4y L.32-5(6+4)+Z. a. 3(x - 8y) Unit 2; Unit 4: Unit 1: 1Can...
 Name Date Period Math 8 EOST Review for Units 1-4 Review the "l Can" statement list for the main concepts of each unit (1-4) covered this semester. Unit 1: 1Can.... use order of operations to simplify
Name Date Period Math 8 EOST Review for Units 1-4 Review the "l Can" statement list for the main concepts of each unit (1-4) covered this semester. Unit 1: 1Can.... use order of operations to simplify
CHAPTER 9. Trigonometry. The concept upon which differentiation of trigonometric functions depends is based
 49 CHAPTER 9 Trigonometry The concept upon which differentiation of trigonometric functions depends is based on the fact that sin = 1. " 0 It should be remembered that, at the Calculus level, when we talk
49 CHAPTER 9 Trigonometry The concept upon which differentiation of trigonometric functions depends is based on the fact that sin = 1. " 0 It should be remembered that, at the Calculus level, when we talk
dollars for a week of sales t weeks after January 1. What is the total revenue (to the nearest hundred dollars) earned from t = 10 to t = 16?
 MATH 7 RIOHONDO SPRING 7 TEST (TAKE HOME) DUE 5//7 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. ) A department store has revenue from the sale
MATH 7 RIOHONDO SPRING 7 TEST (TAKE HOME) DUE 5//7 NAME: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. ) A department store has revenue from the sale
AP Calculus AB Unit 3 Assessment
 Class: Date: 2013-2014 AP Calculus AB Unit 3 Assessment Multiple Choice Identify the choice that best completes the statement or answers the question. A calculator may NOT be used on this part of the exam.
Class: Date: 2013-2014 AP Calculus AB Unit 3 Assessment Multiple Choice Identify the choice that best completes the statement or answers the question. A calculator may NOT be used on this part of the exam.
