Section 5.1 Logarithms and Their Properties
|
|
|
- Ruth Rogers
- 5 years ago
- Views:
Transcription
1 Section 5.1 Logarithms and Their Properties Definition. If x is a positive number, then 1. logx is the power of 10 that gives x. 2. lnx is the power of e that gives x. In other words, y = logx means that 10 y = x. y = lnx means that e y = x. Example 1. Calculate the following, exactly if possible. (a) log100 = 2 (since 10 2 = 100) (b) log0.1 = 1 (since 10 1 = 0.1) (c) lne = 1 (since e 1 = e) (d) ln(e 2 ) = 2 (e) log (using a calculator) Facts about Logarithms. 1. (a) log(10 x ) = x ln(e x ) = x (b) 10 logx = x e lnx = x 2. (a) log(ab) = loga+logb ln(ab) = lna+lnb (b) log( a b ) = loga logb (c) log(b t ) = t logb ln(a b ) = lna lnb ln(b t ) = t lnb 3. (a) log1 = 0 ln1 = 0 (b) log10 = 1 lne = 1 **Caution!! log(ab t ) does not equal tlog(ab). Example 2. Solve each of the following equations for x. (a) 5 4 x = 25 (b) 5x 4 = 25 (a) 5 4 x = 25 = 4 x = 5 = ln(4 x ) = ln5 = xln4 = ln5, so our answer is x = ln5 ln (b) 5x 4 = 25 = x 4 = 5 = (x 4 ) 1/4 = 25 1/4 = x = 4 25, so our answer is x = Activities to accompany Functions Modeling Change, Connally et al, Wiley,
2 Examples and Exercises 1. Solve each of the following equations for x. (a) 5 3 x = 2 7 x 5 3 x = 2 7 x = ln(5 3 x ) = ln(2 7 x ) = ln5+ln3 x = ln2+ln7 x = ln5+xln3 = ln2+xln7 = xln3 xln7 = ln2 ln5 = x(ln3 ln7) = ln2 ln5, so our answer is ln2 ln5 ln3 ln7. (b) 10e 4x+1 = 20 10e 4x+1 = 20 = e 4x+1 = 2 = ln(e 4x+1 ) = ln2 = 4x+1 = ln2 = 4x = ln2 1, so our answer is x = ln (c) a b t = c d 2t a b t = c d 2t = ln(a b t ) = ln(c d 2t ) = lna+ln(b t ) = lnc+ln(d 2t ) = lna+tlnb = lnc+2tlnd = tlnb 2tlnd = lnc lna = t(lnb 2lnd) = lnc lna, (d) 5x 9 = 10 5x 9 = 10 = x 9 = 2 = (x 9 ) 1/9 = 2 1/9 = x = 2 1/9, so our answer is x = 2 1/9, or 9 2. (e) e 2x +e 2x = 1 e 2x +e 2x = 1 = 2e 2x = 1 = e 2x = 1 2 ( ) 1 = ln(e 2x ) = ln 2 ( ) 1 = 2x = ln, 2 so our answer is x = ln(1/2). 2 (f) ln(x+5) = 10 ln(x+5) = 10 = e ln(x+5) = e 10 so our answer is x = e = x+5 = e 10 = x = e 10 5, so our answer is t = lnc lna lnb 2lnd. 2 Developed by Jerry Morris
3 2. Simplify each of the following expressions. (a) log(2a)+log(b) log(ab) (b) ln(ab t ) ln((ab) t ) lna (a) log(2a)+log(b) log(ab) = log(2ab) log(ab) = log ( ) 2AB AB = log 2, so our final answer is log2. (b) ln(ab t ) ln((ab) t ) lna = lna+ln(b t ) tln(ab) lna = ln(b t ) t(lna+lnb) = tlnb tlna tlnb = tlna, so our final answer is tlna. 3. Decide whether each of the following statements are true or false. (a) ln(x+y) = lnx+lny False. To illustrate this, let x = 1 and y = 1. Then ln(x+y) = ln(1+1) = ln2 lnx+lny = ln1+ln1 = 0, so the statement is therefore false because ln2 0. (b) ln(x+y) = (lnx)(lny) False. To illustrate this, let x = 1 and y = 1. Then ln(x+y) = ln(1+1) = ln2 (lnx)(lny) = (ln1)(ln1) = 0, so the statement is false because ln2 0. (c) ln(ab 2 ) = lna+2lnb This statement is true because, using properties of logs, we have ln(ab 2 ) = lna+ln(b 2 ) = lna+2lnb. (d) ln(ab x ) = lna+xlnb This statement is true because, using properties of logs, we have ln(ab x ) = lna+ln(b x ) = lna+xlnb. (e) ln(1/a) = lna This statement is true, because, using properties of logs, we have ln(1/a) = ln1 lna = 0 lna = lna. Activities to accompany Functions Modeling Change, Connally et al, Wiley,
4 Section 5.2 Logarithms and Exponential Models Review: Two ways of writing exponential functions: (1) Q = ab t (2) Q = ae kt a = initial amount b = 1+r, where r = growth or decay rate k = continuous growth or decay rate Example 1. Fill in the gaps in the chart below, assuming that t is measured in years: Formula Growth or Decay Rate Q = ab t Q = ae kt Per Year Continuous Per Year Q = 6(0.9608) t Q = 6e 0.04t 3.92% 4% Q = 5(1.2) t Q = 5e t 20% 18.23% Q = 10(0.91) t Q = 10e t 9% 9.43% (A) Q = 6e 0.04t = 6(e 0.04 ) t (k = 0.04) 6(0.9608) t (since e ) Thus, 1+r = b = , so r = = (B) so k = (C) Q = 5(1.2) t (1+r = 1.2 = r = 0.2) = 5(e ln1.2 ) t 5e t, Q = 10(0.91) t = 10(e ln0.91 ) t 10e t, (1+r = 0.91 = r = 0.09) so k = Developed by Jerry Morris
5 Example 2. The population of a bacteria colony starts at 100 and grows by 30% per hour. (a) Find a formula for the number of bacteria, P, after t hours. Since P is an exponential function of t, we know that P = ab t. We are also given that the starting number of bacteria is a = 30, and the hourly growth rate is 30%, which means that r = 0.3. Therefore, and our final answer is P = 100(1.3) t. b = 1+r = 1.3, (b) What is the doubling time for this population; that is, how long does it take the population to double in size? Here, we are being asked to solve for t when P = 200, which is double the starting population. P = 200 = 200 = 100(1.3) t = 2 = (1.3) t so the doubling time is t = (ln 2)/(ln 1.3) 2.64 hours. = ln2 = tln1.3 = ln2 ln1.3 = t, (c) What is the continuous growth rate of the colony? P = 100(1.3) t = P = 100(e ln1.3 ) t = P 100e t, so k = Therefore, the continuous growth rate of the colony is 26.24%. Activities to accompany Functions Modeling Change, Connally et al, Wiley,
6 Definition. The half-life of a radioactive substance is the amount of time that it takes for half of a given sample to decay. Example 3. The half-life of a Twinkie is 14 days. (a) Find a formula for the amount of Twinkie left after t days. Let Q be the amount of Twinkie left, in grams, and note that since Q is an exponential function of t, we have Q = ab t. Since the half-life is 14 days, and the initial amount of Twinkie is given by the constant a, we know that Q = (1/2)a when t = 14. Substituting these two values into the above equation, we obtain Q = ab t = 1 2 a = ab14 = 1 2 = b14 (after dividing both sides by a) = (0.5) 1/14 = b, so b = (0.5) 1/ Therefore, our final answer is Q = a((0.5) 1/14 ) t = a(0.5) t/14, or Q a(0.9517) t. (b) Find the daily decay rate of the Twinkie. Since Q a(0.9514) t from part (a), we see have so the daily decay rate is 4.83%. 1+r = b = = r = = , 6 Developed by Jerry Morris
7 Examples and Exercises 1. Scientists observing owl and hawk populations collect the following data. Their initial count for the owl population is 245 owls, and the population grows by 3% per year. They initially observe 63 hawks, and this population doubles every 10 years. (a) Find formulas for the size of the population of owls and hawks as functions of time. Let P 1 = ab t represent the owl population after t years. Since we are given that the starting population of owls is a = 245 and that the annual growth rate is r = 0.03, we have b = 1 + r = Therefore, our formula for the owl population is P 1 = 245(1.03) t. Now, let P 2 = cd t represent the hawk population after t years. This time, the initial population is c = 63, and since the population doubles every 10 years, we know that P 2 = 126 when t = 10. Therefore, we have P 2 = cd t = 126 = 63 d 10 = 2 = d 10 so our formula for the hawk population is = 2 1/10 = d, P 2 = 63(2 1/10 ) t = 63 2 t/10, or P 2 = 63(1.0718) t. (b) When will the populations be equal? P 1 = P 2 = 245(1.03) t = 63 2 t/10 = ln(245(1.03) t ) = ln(63 2 t/10 ) = ln245+tln1.03 = ln63+(t/10)ln2 = tln tln2 = ln63 ln245 = t(ln ln2) = ln63 ln245, so t = ln63 ln Therefore, the populations will be equal after about 34.2 ln ln2 years. Activities to accompany Functions Modeling Change, Connally et al, Wiley,
8 2. Find the half-lives of each of the following substances. (a) Tritium, which decays at an annual rate of 5.471% per year. Since we are given that r = , we have b = 1 + r = Therefore, Q = a( ) t is the amount of Tritium left after t years, where a is the initial amount present. We want to find t when Q = 0.5a (half the starting amount), so we have 0.5a = a( ) t = 0.5 = ( ) t = ln0.5 = tln , so the half life is t = (ln 0.5)/(ln ) years. (b) Vikinium, which decays at a continuous rate of 10% per week. Since we are given that k = 0.10, we have Q = ae 0.1t, where Q is the amount of Vikinium left after t weeks, and a is the starting amount. Again, we want to find t when Q = 0.5a, so we have 0.5a = ae 0.1t = 0.5 = e 0.1t so the half life is t = (ln0.5)/( 0.1) 6.93 weeks. = ln0.5 = 0.1t, 3. If 17% of a radioactive substance decays in 5 hours, how long will it take until only 10% of a given sample of the substance remains? Let Q represent the amount of the substance remaining after t hours, so that Q = ab t. Since 17% of the substance decays in 5 hours, this means that 83% of it will remain after 5 hours; that is, Q is 83% of the starting amount after 5 hours. In other words, we know that when t = 5, Q = 0.83a. Therefore, we have Q = ab t = 0.83a = ab 5 = 0.83 = b 5 = (0.83) 1/5 = b, so our formula becomes Q = a((0.83) 1/5 ) t = a(0.83) t/5. We are being asked to find t when Q is 10% of the starting amount; that is, Q = 0.1a. Substituting into the above formula, we have 0.1a = a(0.83) t/5 = 0.1 = (0.83) t/5 = ln0.1 = ln((0.83) t/5 ) = ln0.1 = (t/5)ln0.83 = 5ln0.1 = tln0.83, so t = (5ln0.1)/ln Therefore, it takes about hours until only 10% of the sample remains. 8 Developed by Jerry Morris
9 Section 5.3 The Logarithmic Function 1. Consider the functions f(x) = lnx and g(x) = logx. (a) Complete the table below. x ln x log x (b) Plug a few very small numbers x into lnx and logx (like 0.01, 0.001, etc.) What happens to the output values of each function? ln(0.01) = ln(0.001) = ln(0.0001) = log(0.01) = 2 log(0.001) = 3 log(0.0001) = 4 It appears that the output values are becoming more and more negative for both functions. It is clear from the pattern that logx approaches as x gets closer and closer to 0. In fact, the same behavior is true for lnx since ln(e 1 ) = 1, ln(e 2 ) = 2, ln(e 3 ) = 3, etc. (c) If you plug in x = 0 or negative numbers for x, are lnx and logx defined? Explain. No, because there is no power of 10 (or of e) that gives 0 or a negative number. (d) What is the domain of f(x) = lnx? What is the domain of g(x) = logx? The domain of both functions is {x : x > 0}. (e) Sketch a graph of f(x) = lnx below, choosing a reasonable scale on the x and y axes. Does f(x) have any vertical asymptotes? Any horizontal asymptotes? 10 y f has a vertical asymptote at x = 0 but no horizontal asymptote. Note that it does not have a horizontal asymptote because 8 lnx approaches as x approaches : ln(e) = 1, ln(e 2 ) = 2, ln(e 3 ) = 3, etc x 2 4 Activities to accompany Functions Modeling Change, Connally et al, Wiley,
10 2. What is the domain of the following four functions? (a) y = ln(x 2 ) (b) y = (lnx) 2 (c) y = ln(lnx) (d) y = ln(x 3) (a) In order for ln(x 2 ) to be defined, we need x 2 > 0. Since any number squared is positive (except 0), the domain is {x : x 0}; that is, all real numbers except 0. (b) Here, the variable x is being substituted into lnx, so we must have x > 0. Next, since any number can be squared, there are no further restrictions on x, so the domain is {x : x > 0}. (c) In order for lnx, the inside function, to be defined, we need x > 0. On the other hand, in order for ln(lnx) to be defined, we need lnx > 0. Therefore, since lnx is the power of e needed to get x, lnx > 0 means that x > 1. Thus, we need x > 0 and x > 1 to both be true, so the domain is {x : x > 1}. (d) In order for ln(x 3) to be defined, we need x 3 > 0, which means that x > 3. Therefore, the domain is {x : x > 3}. 3. Consider the exponential functions f(x) = e x and g(x) = e x. What are the domains of these two functions? Do they have any horizontal asymptotes? any vertical asymptotes? Since e x and e x can be calculated for any value of x, the domain of both f and g is all real numbers. Both functions have a horizontal asymptote at y = 0 but no vertical asymptote. 10 Developed by Jerry Morris
Unit #1 - Transformation of Functions; Exponential and Logarithms Section 1.4
 Unit #1 - Transformation of Functions; Exponential and Logarithms Section 1.4 Some material from Calculus, Single and MultiVariable by Hughes-Hallett, Gleason, McCallum et. al. Copyright 005 by John Wiley
Unit #1 - Transformation of Functions; Exponential and Logarithms Section 1.4 Some material from Calculus, Single and MultiVariable by Hughes-Hallett, Gleason, McCallum et. al. Copyright 005 by John Wiley
Skill 6 Exponential and Logarithmic Functions
 Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Internet Mat117 Formulas and Concepts. d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. ( x 1 + x 2 2., y 1 + y 2. (x h) 2 + (y k) 2 = r 2. m = y 2 y 1 x 2 x 1
 Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
CHAPTER FIVE. Solutions for Section 5.1. Skill Refresher. Exercises
 CHAPTER FIVE 5.1 SOLUTIONS 265 Solutions for Section 5.1 Skill Refresher S1. Since 1,000,000 = 10 6, we have x = 6. S2. Since 0.01 = 10 2, we have t = 2. S3. Since e 3 = ( e 3) 1/2 = e 3/2, we have z =
CHAPTER FIVE 5.1 SOLUTIONS 265 Solutions for Section 5.1 Skill Refresher S1. Since 1,000,000 = 10 6, we have x = 6. S2. Since 0.01 = 10 2, we have t = 2. S3. Since e 3 = ( e 3) 1/2 = e 3/2, we have z =
Internet Mat117 Formulas and Concepts. d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2., y 1 + y 2. ( x 1 + x 2 2
 Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Internet Mat117 Formulas and Concepts 1. The distance between the points A(x 1, y 1 ) and B(x 2, y 2 ) in the plane is d(a, B) = (x 2 x 1 ) 2 + (y 2 y 1 ) 2. 2. The midpoint of the line segment from A(x
Skill 6 Exponential and Logarithmic Functions
 Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Skill 6 Exponential and Logarithmic Functions Skill 6a: Graphs of Exponential Functions Skill 6b: Solving Exponential Equations (not requiring logarithms) Skill 6c: Definition of Logarithms Skill 6d: Graphs
Logarithms Dr. Laura J. Pyzdrowski
 1 Names: (8 communication points) About this Laboratory An exponential function of the form f(x) = a x, where a is a positive real number not equal to 1, is an example of a one-to-one function. This means
1 Names: (8 communication points) About this Laboratory An exponential function of the form f(x) = a x, where a is a positive real number not equal to 1, is an example of a one-to-one function. This means
7.1 Exponential Functions
 7.1 Exponential Functions 1. What is 16 3/2? Definition of Exponential Functions Question. What is 2 2? Theorem. To evaluate a b, when b is irrational (so b is not a fraction of integers), we approximate
7.1 Exponential Functions 1. What is 16 3/2? Definition of Exponential Functions Question. What is 2 2? Theorem. To evaluate a b, when b is irrational (so b is not a fraction of integers), we approximate
TEST 150 points Write neatly. Show all work. Write all responses on separate paper. Clearly label the exercises.
 Math 130 Fall 007 Name: TEST # @ 150 points Write neatly. Show all work. Write all responses on separate paper. Clearly label the exercises. 1. Consider the polynomial function 4 3 f ( x) = x 19x + 57x
Math 130 Fall 007 Name: TEST # @ 150 points Write neatly. Show all work. Write all responses on separate paper. Clearly label the exercises. 1. Consider the polynomial function 4 3 f ( x) = x 19x + 57x
Logarithmic Functions
 Metropolitan Community College The Natural Logarithmic Function The natural logarithmic function is defined on (0, ) as ln x = x 1 1 t dt. Example 1. Evaluate ln 1. Example 1. Evaluate ln 1. Solution.
Metropolitan Community College The Natural Logarithmic Function The natural logarithmic function is defined on (0, ) as ln x = x 1 1 t dt. Example 1. Evaluate ln 1. Example 1. Evaluate ln 1. Solution.
If a function has an inverse then we can determine the input if we know the output. For example if the function
 1 Inverse Functions We know what it means for a relation to be a function. Every input maps to only one output, it passes the vertical line test. But not every function has an inverse. A function has no
1 Inverse Functions We know what it means for a relation to be a function. Every input maps to only one output, it passes the vertical line test. But not every function has an inverse. A function has no
weebly.com/ Core Mathematics 3 Exponentials and Natural Logarithms
 http://kumarmaths. weebly.com/ Core Mathematics 3 Exponentials and Natural Logarithms Core Maths 3 Exponentials and natural Logarithms Page 1 Ln and Exponentials C3 Content By the end of this unit you
http://kumarmaths. weebly.com/ Core Mathematics 3 Exponentials and Natural Logarithms Core Maths 3 Exponentials and natural Logarithms Page 1 Ln and Exponentials C3 Content By the end of this unit you
Intermediate Algebra Chapter 12 Review
 Intermediate Algebra Chapter 1 Review Set up a Table of Coordinates and graph the given functions. Find the y-intercept. Label at least three points on the graph. Your graph must have the correct shape.
Intermediate Algebra Chapter 1 Review Set up a Table of Coordinates and graph the given functions. Find the y-intercept. Label at least three points on the graph. Your graph must have the correct shape.
MA 109 College Algebra EXAM 3 - REVIEW
 MA 109 College Algebra EXAM - REVIEW Name: Sec.: 1. In the picture below, the graph of y = f(x) is the solid graph, and the graph of y = g(x) is the dashed graph. Find a formula for g(x). y (a) g(x) =f(2x)
MA 109 College Algebra EXAM - REVIEW Name: Sec.: 1. In the picture below, the graph of y = f(x) is the solid graph, and the graph of y = g(x) is the dashed graph. Find a formula for g(x). y (a) g(x) =f(2x)
4.1 Solutions to Exercises
 4.1 Solutions to Exercises 1. Linear, because the average rate of change between any pair of points is constant. 3. Exponential, because the difference of consecutive inputs is constant and the ratio of
4.1 Solutions to Exercises 1. Linear, because the average rate of change between any pair of points is constant. 3. Exponential, because the difference of consecutive inputs is constant and the ratio of
4 Exponential and Logarithmic Functions
 4 Exponential and Logarithmic Functions 4.1 Exponential Functions Definition 4.1 If a > 0 and a 1, then the exponential function with base a is given by fx) = a x. Examples: fx) = x, gx) = 10 x, hx) =
4 Exponential and Logarithmic Functions 4.1 Exponential Functions Definition 4.1 If a > 0 and a 1, then the exponential function with base a is given by fx) = a x. Examples: fx) = x, gx) = 10 x, hx) =
2. (12 points) Find an equation for the line tangent to the graph of f(x) =
 November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
November 23, 2010 Name The total number of points available is 153 Throughout this test, show your work Throughout this test, you are expected to use calculus to solve problems Graphing calculator solutions
Chapter 11 Logarithms
 Chapter 11 Logarithms Lesson 1: Introduction to Logs Lesson 2: Graphs of Logs Lesson 3: The Natural Log Lesson 4: Log Laws Lesson 5: Equations of Logs using Log Laws Lesson 6: Exponential Equations using
Chapter 11 Logarithms Lesson 1: Introduction to Logs Lesson 2: Graphs of Logs Lesson 3: The Natural Log Lesson 4: Log Laws Lesson 5: Equations of Logs using Log Laws Lesson 6: Exponential Equations using
Topics from Algebra and Pre-Calculus. (Key contains solved problems)
 Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
Topics from Algebra and Pre-Calculus (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the calculator, except on p. (8) and
Chapter 6: Exponential and Logarithmic Functions
 Section 6.1: Algebra and Composition of Functions #1-9: Let f(x) = 2x + 3 and g(x) = 3 x. Find each function. 1) (f + g)(x) 2) (g f)(x) 3) (f/g)(x) 4) ( )( ) 5) ( g/f)(x) 6) ( )( ) 7) ( )( ) 8) (g+f)(x)
Section 6.1: Algebra and Composition of Functions #1-9: Let f(x) = 2x + 3 and g(x) = 3 x. Find each function. 1) (f + g)(x) 2) (g f)(x) 3) (f/g)(x) 4) ( )( ) 5) ( g/f)(x) 6) ( )( ) 7) ( )( ) 8) (g+f)(x)
Name: Partners: PreCalculus. Review 5 Version A
 Name: Partners: PreCalculus Date: Review 5 Version A [A] Circle whether each statement is true or false. 1. 3 log 3 5x = 5x 2. log 2 16 x+3 = 4x + 3 3. ln x 6 + ln x 5 = ln x 30 4. If ln x = 4, then e
Name: Partners: PreCalculus Date: Review 5 Version A [A] Circle whether each statement is true or false. 1. 3 log 3 5x = 5x 2. log 2 16 x+3 = 4x + 3 3. ln x 6 + ln x 5 = ln x 30 4. If ln x = 4, then e
Core Mathematics 3 Exponentials and Natural Logarithms
 Edexcel past paper questions Core Mathematics 3 Exponentials and Natural Logarithms Edited by: K V kumaran Email: kvkumaran@gmail.com Core Maths 3 Exponentials and natural Logarithms Page Ln and Exponentials
Edexcel past paper questions Core Mathematics 3 Exponentials and Natural Logarithms Edited by: K V kumaran Email: kvkumaran@gmail.com Core Maths 3 Exponentials and natural Logarithms Page Ln and Exponentials
INTERNET MAT 117 Review Problems. (1) Let us consider the circle with equation. (b) Find the center and the radius of the circle given above.
 INTERNET MAT 117 Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (b) Find the center and
INTERNET MAT 117 Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (b) Find the center and
Lesson 18: Problem Set Sample Solutions
 Problem Set Sample Solutions Problems 5 7 serve to review the process of computing f(g(x)) for given functions f and g in preparation for work with inverses of functions in Lesson 19. 1. Sketch the graphs
Problem Set Sample Solutions Problems 5 7 serve to review the process of computing f(g(x)) for given functions f and g in preparation for work with inverses of functions in Lesson 19. 1. Sketch the graphs
SOLUTIONS. Math 110 Quiz 5 (Sections )
 SOLUTIONS Name: Section (circle one): LSA (001) Engin (002) Math 110 Quiz 5 (Sections 5.1 5.3) Available: Wednesday, November 8 Friday, November 10 1. You have 30 minutes to complete this quiz. Keeping
SOLUTIONS Name: Section (circle one): LSA (001) Engin (002) Math 110 Quiz 5 (Sections 5.1 5.3) Available: Wednesday, November 8 Friday, November 10 1. You have 30 minutes to complete this quiz. Keeping
Exponential and Logarithmic Functions
 Graduate T.A. Department of Mathematics Dynamical Systems and Chaos San Diego State University April 9, 11 Definition (Exponential Function) An exponential function with base a is a function of the form
Graduate T.A. Department of Mathematics Dynamical Systems and Chaos San Diego State University April 9, 11 Definition (Exponential Function) An exponential function with base a is a function of the form
GOOD LUCK! 2. a b c d e 12. a b c d e. 3. a b c d e 13. a b c d e. 4. a b c d e 14. a b c d e. 5. a b c d e 15. a b c d e. 6. a b c d e 16.
 MA109 College Algebra Fall 2018 Practice Final Exam 2018-12-12 Name: Sec.: Do not remove this answer page you will turn in the entire exam. You have two hours to do this exam. No books or notes may be
MA109 College Algebra Fall 2018 Practice Final Exam 2018-12-12 Name: Sec.: Do not remove this answer page you will turn in the entire exam. You have two hours to do this exam. No books or notes may be
Exponential and Logarithmic Functions
 Exponential and Logarithmic Functions Learning Targets 1. I can evaluate, analyze, and graph exponential functions. 2. I can solve problems involving exponential growth & decay. 3. I can evaluate expressions
Exponential and Logarithmic Functions Learning Targets 1. I can evaluate, analyze, and graph exponential functions. 2. I can solve problems involving exponential growth & decay. 3. I can evaluate expressions
( ) ( ) x. The exponential function f(x) with base b is denoted by x
 Page of 7 Eponential and Logarithmic Functions Eponential Functions and Their Graphs: Section Objectives: Students will know how to recognize, graph, and evaluate eponential functions. The eponential function
Page of 7 Eponential and Logarithmic Functions Eponential Functions and Their Graphs: Section Objectives: Students will know how to recognize, graph, and evaluate eponential functions. The eponential function
Section 4.2 Logarithmic Functions & Applications
 34 Section 4.2 Logarithmic Functions & Applications Recall that exponential functions are one-to-one since every horizontal line passes through at most one point on the graph of y = b x. So, an exponential
34 Section 4.2 Logarithmic Functions & Applications Recall that exponential functions are one-to-one since every horizontal line passes through at most one point on the graph of y = b x. So, an exponential
Homework 3. (33-40) The graph of an exponential function is given. Match each graph to one of the following functions.
 Homework Section 4. (-40) The graph of an exponential function is given. Match each graph to one of the following functions. (a)y = x (b)y = x (c)y = x (d)y = x (e)y = x (f)y = x (g)y = x (h)y = x (46,
Homework Section 4. (-40) The graph of an exponential function is given. Match each graph to one of the following functions. (a)y = x (b)y = x (c)y = x (d)y = x (e)y = x (f)y = x (g)y = x (h)y = x (46,
Inverse Functions. Definition 1. The exponential function f with base a is denoted by. f(x) = a x
 Inverse Functions Definition 1. The exponential function f with base a is denoted by f(x) = a x where a > 0, a 1, and x is any real number. Example 1. In the same coordinate plane, sketch the graph of
Inverse Functions Definition 1. The exponential function f with base a is denoted by f(x) = a x where a > 0, a 1, and x is any real number. Example 1. In the same coordinate plane, sketch the graph of
Practice Questions for Final Exam - Math 1060Q - Fall 2014
 Practice Questions for Final Exam - Math 1060Q - Fall 01 Before anyone asks, the final exam is cumulative. It will consist of about 50% problems on exponential and logarithmic functions, 5% problems on
Practice Questions for Final Exam - Math 1060Q - Fall 01 Before anyone asks, the final exam is cumulative. It will consist of about 50% problems on exponential and logarithmic functions, 5% problems on
AP Calculus Summer Prep
 AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
AP Calculus Summer Prep Topics from Algebra and Pre-Calculus (Solutions are on the Answer Key on the Last Pages) The purpose of this packet is to give you a review of basic skills. You are asked to have
Logarithms. Professor Richard Blecksmith Dept. of Mathematical Sciences Northern Illinois University
 Logarithms Professor Richard Blecksmith richard@math.niu.edu Dept. of Mathematical Sciences Northern Illinois University http://math.niu.edu/ richard/math211 1. Definition of Logarithm For a > 0, a 1,
Logarithms Professor Richard Blecksmith richard@math.niu.edu Dept. of Mathematical Sciences Northern Illinois University http://math.niu.edu/ richard/math211 1. Definition of Logarithm For a > 0, a 1,
The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts.
 Math 141 Review for Final The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts. Part 1 (no calculator) graphing (polynomial, rational, linear, exponential, and logarithmic
Math 141 Review for Final The final is cumulative, but with more emphasis on chapters 3 and 4. There will be two parts. Part 1 (no calculator) graphing (polynomial, rational, linear, exponential, and logarithmic
April 9, 2009 Name The problems count as marked. The total number of points available is 160. Throughout this test, show your work.
 April 9, 009 Name The problems count as marked The total number of points available is 160 Throughout this test, show your work 1 (15 points) Consider the cubic curve f(x) = x 3 + 3x 36x + 17 (a) Build
April 9, 009 Name The problems count as marked The total number of points available is 160 Throughout this test, show your work 1 (15 points) Consider the cubic curve f(x) = x 3 + 3x 36x + 17 (a) Build
HW#1. Unit 4B Logarithmic Functions HW #1. 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7
 HW#1 Name Unit 4B Logarithmic Functions HW #1 Algebra II Mrs. Dailey 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7 2) If the graph of y =6 x is reflected
HW#1 Name Unit 4B Logarithmic Functions HW #1 Algebra II Mrs. Dailey 1) Which of the following is equivalent to y=log7 x? (1) y =x 7 (3) x = 7 y (2) x =y 7 (4) y =x 1/7 2) If the graph of y =6 x is reflected
True/False Problems from Old 115 Exam 1 s
 Douglass Houghton Workshop, September 2012 True/False Problems from Old 115 Exam 1 s Standard instructions: Answer true only if a statement MUST be true. No explanations are necessary. 1. Winter, 2001
Douglass Houghton Workshop, September 2012 True/False Problems from Old 115 Exam 1 s Standard instructions: Answer true only if a statement MUST be true. No explanations are necessary. 1. Winter, 2001
Module 6 Lecture Notes
 Module 6 Lecture Notes Contents 6. An Introduction to Logarithms....................... 6. Evaluating Logarithmic Expressions.................... 4 6.3 Graphs of Logarithmic Functions......................
Module 6 Lecture Notes Contents 6. An Introduction to Logarithms....................... 6. Evaluating Logarithmic Expressions.................... 4 6.3 Graphs of Logarithmic Functions......................
Exponential Growth (Doubling Time)
 Exponential Growth (Doubling Time) 4 Exponential Growth (Doubling Time) Suppose we start with a single bacterium, which divides every hour. After one hour we have 2 bacteria, after two hours we have 2
Exponential Growth (Doubling Time) 4 Exponential Growth (Doubling Time) Suppose we start with a single bacterium, which divides every hour. After one hour we have 2 bacteria, after two hours we have 2
Example. Determine the inverse of the given function (if it exists). f(x) = 3
 Example. Determine the inverse of the given function (if it exists). f(x) = g(x) = p x + x We know want to look at two di erent types of functions, called logarithmic functions and exponential functions.
Example. Determine the inverse of the given function (if it exists). f(x) = g(x) = p x + x We know want to look at two di erent types of functions, called logarithmic functions and exponential functions.
Chapter 3. Exponential and Logarithmic Functions. 3.2 Logarithmic Functions
 Chapter 3 Exponential and Logarithmic Functions 3.2 Logarithmic Functions 1/23 Chapter 3 Exponential and Logarithmic Functions 3.2 4, 8, 14, 16, 18, 20, 22, 30, 31, 32, 33, 34, 39, 42, 54, 56, 62, 68,
Chapter 3 Exponential and Logarithmic Functions 3.2 Logarithmic Functions 1/23 Chapter 3 Exponential and Logarithmic Functions 3.2 4, 8, 14, 16, 18, 20, 22, 30, 31, 32, 33, 34, 39, 42, 54, 56, 62, 68,
GUIDED NOTES 6.4 GRAPHS OF LOGARITHMIC FUNCTIONS
 GUIDED NOTES 6.4 GRAPHS OF LOGARITHMIC FUNCTIONS LEARNING OBJECTIVES In this section, you will: Identify the domain of a logarithmic function. Graph logarithmic functions. FINDING THE DOMAIN OF A LOGARITHMIC
GUIDED NOTES 6.4 GRAPHS OF LOGARITHMIC FUNCTIONS LEARNING OBJECTIVES In this section, you will: Identify the domain of a logarithmic function. Graph logarithmic functions. FINDING THE DOMAIN OF A LOGARITHMIC
INTERNET MAT 117. Solution for the Review Problems. (1) Let us consider the circle with equation. x 2 + 2x + y 2 + 3y = 3 4. (x + 1) 2 + (y + 3 2
 INTERNET MAT 117 Solution for the Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (i) Group
INTERNET MAT 117 Solution for the Review Problems (1) Let us consider the circle with equation x 2 + y 2 + 2x + 3y + 3 4 = 0. (a) Find the standard form of the equation of the circle given above. (i) Group
Exponential Functions
 10.1 Unlimited growth and doubling Bunnies A pair of bunnies makes 4 babies in 1 generation. Suppose a bunny weighs 1 kg, and the earth weighs 6 10 24 kg. When will the bunnies weigh as much as the earth,
10.1 Unlimited growth and doubling Bunnies A pair of bunnies makes 4 babies in 1 generation. Suppose a bunny weighs 1 kg, and the earth weighs 6 10 24 kg. When will the bunnies weigh as much as the earth,
in terms of p, q and r.
 Logarithms and Exponents 1. Let ln a = p, ln b = q. Write the following expressions in terms of p and q. ln a 3 b ln a b 2. Let log 10 P = x, log 10 Q = y and log 10 R = z. Express P log 10 QR 3 2 in terms
Logarithms and Exponents 1. Let ln a = p, ln b = q. Write the following expressions in terms of p and q. ln a 3 b ln a b 2. Let log 10 P = x, log 10 Q = y and log 10 R = z. Express P log 10 QR 3 2 in terms
, identify what the letters P, r, n and t stand for.
 1.In the formula At p 1 r n nt, identify what the letters P, r, n and t stand for. 2. Find the exponential function whose graph is given f(x) = a x 3. State the domain and range of the function (Enter
1.In the formula At p 1 r n nt, identify what the letters P, r, n and t stand for. 2. Find the exponential function whose graph is given f(x) = a x 3. State the domain and range of the function (Enter
Logarithmic Functions
 Logarithmic Functions Definition 1. For x > 0, a > 0, and a 1, y = log a x if and only if x = a y. The function f(x) = log a x is called the logarithmic function with base a. Example 1. Evaluate the following
Logarithmic Functions Definition 1. For x > 0, a > 0, and a 1, y = log a x if and only if x = a y. The function f(x) = log a x is called the logarithmic function with base a. Example 1. Evaluate the following
4. Sketch the graph of the function. Ans: A 9. Sketch the graph of the function. Ans B. Version 1 Page 1
 Name: Online ECh5 Prep Date: Scientific Calc ONLY! 4. Sketch the graph of the function. A) 9. Sketch the graph of the function. B) Ans B Version 1 Page 1 _ 10. Use a graphing utility to determine which
Name: Online ECh5 Prep Date: Scientific Calc ONLY! 4. Sketch the graph of the function. A) 9. Sketch the graph of the function. B) Ans B Version 1 Page 1 _ 10. Use a graphing utility to determine which
Exponential Functions Concept Summary See pages Vocabulary and Concept Check.
 Vocabulary and Concept Check Change of Base Formula (p. 548) common logarithm (p. 547) exponential decay (p. 524) exponential equation (p. 526) exponential function (p. 524) exponential growth (p. 524)
Vocabulary and Concept Check Change of Base Formula (p. 548) common logarithm (p. 547) exponential decay (p. 524) exponential equation (p. 526) exponential function (p. 524) exponential growth (p. 524)
Exponential and logarithmic functions (pp ) () Supplement October 14, / 1. a and b positive real numbers and x and y real numbers.
 MA123, Supplement Exponential and logaritmic functions pp. 315-319) Capter s Goal: Review te properties of exponential and logaritmic functions. Learn ow to differentiate exponential and logaritmic functions.
MA123, Supplement Exponential and logaritmic functions pp. 315-319) Capter s Goal: Review te properties of exponential and logaritmic functions. Learn ow to differentiate exponential and logaritmic functions.
Composition of Functions
 Math 120 Intermediate Algebra Sec 9.1: Composite and Inverse Functions Composition of Functions The composite function f g, the composition of f and g, is defined as (f g)(x) = f(g(x)). Recall that a function
Math 120 Intermediate Algebra Sec 9.1: Composite and Inverse Functions Composition of Functions The composite function f g, the composition of f and g, is defined as (f g)(x) = f(g(x)). Recall that a function
Section 6.8 Exponential Models; Newton's Law of Cooling; Logistic Models
 Section 6.8 Exponential Models; Newton's Law of Cooling; Logistic Models 197 Objective #1: Find Equations of Populations that Obey the Law of Uninhibited Growth. In the last section, we saw that when interest
Section 6.8 Exponential Models; Newton's Law of Cooling; Logistic Models 197 Objective #1: Find Equations of Populations that Obey the Law of Uninhibited Growth. In the last section, we saw that when interest
Section 5.1 Determine if a function is a polynomial function. State the degree of a polynomial function.
 Test Instructions Objectives Section 5.1 Section 5.1 Determine if a function is a polynomial function. State the degree of a polynomial function. Form a polynomial whose zeros and degree are given. Graph
Test Instructions Objectives Section 5.1 Section 5.1 Determine if a function is a polynomial function. State the degree of a polynomial function. Form a polynomial whose zeros and degree are given. Graph
Exponential and Logarithmic Functions. By Lauren Bae and Yamini Ramadurai
 Exponential and Logarithmic Functions By Lauren Bae and Yamini Ramadurai What is an Exponential Function? An exponential function any function where the variable is now the power, rather than the base.
Exponential and Logarithmic Functions By Lauren Bae and Yamini Ramadurai What is an Exponential Function? An exponential function any function where the variable is now the power, rather than the base.
SHORT ANSWER. Answer the question, including units in your answer if needed. Show work and circle your final answer.
 Math 131 Group Review Assignment (5.5, 5.6) Print Name SHORT ANSWER. Answer the question, including units in your answer if needed. Show work and circle your final answer. Solve the logarithmic equation.
Math 131 Group Review Assignment (5.5, 5.6) Print Name SHORT ANSWER. Answer the question, including units in your answer if needed. Show work and circle your final answer. Solve the logarithmic equation.
The Exponential function f with base b is f (x) = b x where b > 0, b 1, x a real number
 Chapter 4: 4.1: Exponential Functions Definition: Graphs of y = b x Exponential and Logarithmic Functions The Exponential function f with base b is f (x) = b x where b > 0, b 1, x a real number Graph:
Chapter 4: 4.1: Exponential Functions Definition: Graphs of y = b x Exponential and Logarithmic Functions The Exponential function f with base b is f (x) = b x where b > 0, b 1, x a real number Graph:
Logarithmic Properties
 Logarithmic Properties By: OpenStaxCollege The ph of hydrochloric acid is tested with litmus paper. (credit: David Berardan) In chemistry, ph is used as a measure of the acidity or alkalinity of a substance.
Logarithmic Properties By: OpenStaxCollege The ph of hydrochloric acid is tested with litmus paper. (credit: David Berardan) In chemistry, ph is used as a measure of the acidity or alkalinity of a substance.
Limits at Infinity. Use algebraic techniques to help with indeterminate forms of ± Use substitutions to evaluate limits of compositions of functions.
 SUGGESTED REFERENCE MATERIAL: Limits at Infinity As you work through the problems listed below, you should reference Chapter. of the recommended textbook (or the equivalent chapter in your alternative
SUGGESTED REFERENCE MATERIAL: Limits at Infinity As you work through the problems listed below, you should reference Chapter. of the recommended textbook (or the equivalent chapter in your alternative
5.6 Logarithmic and Exponential Equations
 SECTION 5.6 Logarithmic and Exponential Equations 305 5.6 Logarithmic and Exponential Equations PREPARING FOR THIS SECTION Before getting started, review the following: Solving Equations Using a Graphing
SECTION 5.6 Logarithmic and Exponential Equations 305 5.6 Logarithmic and Exponential Equations PREPARING FOR THIS SECTION Before getting started, review the following: Solving Equations Using a Graphing
A factor times a logarithm can be re-written as the argument of the logarithm raised to the power of that factor
 In this section we will be working with Properties of Logarithms in an attempt to take equations with more than one logarithm and condense them down into just a single logarithm. Properties of Logarithms:
In this section we will be working with Properties of Logarithms in an attempt to take equations with more than one logarithm and condense them down into just a single logarithm. Properties of Logarithms:
+ i sin. + i sin. = 2 cos
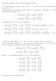 Math 11 Lesieutre); Exam review I; December 4, 017 1. a) Find all complex numbers z for which z = 8. Write your answers in rectangular non-polar) form. We are going to use de Moivre s theorem. For 1, r
Math 11 Lesieutre); Exam review I; December 4, 017 1. a) Find all complex numbers z for which z = 8. Write your answers in rectangular non-polar) form. We are going to use de Moivre s theorem. For 1, r
Notes for exponential functions The week of March 6. Math 140
 Notes for exponential functions The week of March 6 Math 140 Exponential functions: formulas An exponential function has the formula f (t) = ab t, where b is a positive constant; a is the initial value
Notes for exponential functions The week of March 6 Math 140 Exponential functions: formulas An exponential function has the formula f (t) = ab t, where b is a positive constant; a is the initial value
Section 2.3: Logarithmic Functions Lecture 3 MTH 124
 Procedural Skills Learning Objectives 1. Build an exponential function using the correct compounding identifiers (annually, monthly, continuously etc...) 2. Manipulate exponents algebraically. e.g. Solving
Procedural Skills Learning Objectives 1. Build an exponential function using the correct compounding identifiers (annually, monthly, continuously etc...) 2. Manipulate exponents algebraically. e.g. Solving
Math 137 Exam #3 Review Guide
 Math 7 Exam # Review Guide The third exam will cover Sections.-.6, 4.-4.7. The problems on this review guide are representative of the type of problems worked on homework and during class time. Do not
Math 7 Exam # Review Guide The third exam will cover Sections.-.6, 4.-4.7. The problems on this review guide are representative of the type of problems worked on homework and during class time. Do not
Section 6.1: Composite Functions
 Section 6.1: Composite Functions Def: Given two function f and g, the composite function, which we denote by f g and read as f composed with g, is defined by (f g)(x) = f(g(x)). In other words, the function
Section 6.1: Composite Functions Def: Given two function f and g, the composite function, which we denote by f g and read as f composed with g, is defined by (f g)(x) = f(g(x)). In other words, the function
Unit 5: Exponential and Logarithmic Functions
 71 Rational eponents Unit 5: Eponential and Logarithmic Functions If b is a real number and n and m are positive and have no common factors, then n m m b = b ( b ) m n n Laws of eponents a) b) c) d) e)
71 Rational eponents Unit 5: Eponential and Logarithmic Functions If b is a real number and n and m are positive and have no common factors, then n m m b = b ( b ) m n n Laws of eponents a) b) c) d) e)
Business and Life Calculus
 Business and Life Calculus George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 112 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 2013
Business and Life Calculus George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 112 George Voutsadakis (LSSU) Calculus For Business and Life Sciences Fall 2013
Graphing Exponentials 6.0 Topic: Graphing Growth and Decay Functions
 Graphing Exponentials 6.0 Topic: Graphing Growth and Decay Functions Date: Objectives: SWBAT (Graph Exponential Functions) Main Ideas: Mother Function Exponential Assignment: Parent Function: f(x) = b
Graphing Exponentials 6.0 Topic: Graphing Growth and Decay Functions Date: Objectives: SWBAT (Graph Exponential Functions) Main Ideas: Mother Function Exponential Assignment: Parent Function: f(x) = b
Applications of Exponential Functions Group Activity 7 STEM Project Week #10
 Applications of Exponential Functions Group Activity 7 STEM Project Week #10 In the last activity we looked at exponential functions. We looked at an example of a population growing at a certain rate.
Applications of Exponential Functions Group Activity 7 STEM Project Week #10 In the last activity we looked at exponential functions. We looked at an example of a population growing at a certain rate.
4.4 Graphs of Logarithmic Functions
 590 Chapter 4 Exponential and Logarithmic Functions 4.4 Graphs of Logarithmic Functions In this section, you will: Learning Objectives 4.4.1 Identify the domain of a logarithmic function. 4.4.2 Graph logarithmic
590 Chapter 4 Exponential and Logarithmic Functions 4.4 Graphs of Logarithmic Functions In this section, you will: Learning Objectives 4.4.1 Identify the domain of a logarithmic function. 4.4.2 Graph logarithmic
1.3 Exponential Functions
 22 Chapter 1 Prerequisites for Calculus 1.3 Exponential Functions What you will learn about... Exponential Growth Exponential Decay Applications The Number e and why... Exponential functions model many
22 Chapter 1 Prerequisites for Calculus 1.3 Exponential Functions What you will learn about... Exponential Growth Exponential Decay Applications The Number e and why... Exponential functions model many
Math 111: Final Review
 Math 111: Final Review Suggested Directions: Start by reviewing the new material with the first portion of the review sheet. Then take every quiz again as if it were a test. No book. No notes. Limit yourself
Math 111: Final Review Suggested Directions: Start by reviewing the new material with the first portion of the review sheet. Then take every quiz again as if it were a test. No book. No notes. Limit yourself
for every x in the gomain of g
 Section.7 Definition of Inverse Function Let f and g be two functions such that f(g(x)) = x for every x in the gomain of g and g(f(x)) = x for every x in the gomain of f Under these conditions, the function
Section.7 Definition of Inverse Function Let f and g be two functions such that f(g(x)) = x for every x in the gomain of g and g(f(x)) = x for every x in the gomain of f Under these conditions, the function
Section 3.1 Exercises
 Section Exponential and Logistic Functions Chapter Exponential, Logistic, and Logarithmic Functions Section Exponential and Logistic Functions Exploration The point (0, ) is common to all four graphs,
Section Exponential and Logistic Functions Chapter Exponential, Logistic, and Logarithmic Functions Section Exponential and Logistic Functions Exploration The point (0, ) is common to all four graphs,
x y
 (a) The curve y = ax n, where a and n are constants, passes through the points (2.25, 27), (4, 64) and (6.25, p). Calculate the value of a, of n and of p. [5] (b) The mass, m grams, of a radioactive substance
(a) The curve y = ax n, where a and n are constants, passes through the points (2.25, 27), (4, 64) and (6.25, p). Calculate the value of a, of n and of p. [5] (b) The mass, m grams, of a radioactive substance
Objectives. Use the number e to write and graph exponential functions representing realworld
 Objectives Use the number e to write and graph exponential functions representing realworld situations. Solve equations and problems involving e or natural logarithms. natural logarithm Vocabulary natural
Objectives Use the number e to write and graph exponential functions representing realworld situations. Solve equations and problems involving e or natural logarithms. natural logarithm Vocabulary natural
MAC Module 8. Exponential and Logarithmic Functions I. Learning Objectives. - Exponential Functions - Logarithmic Functions
 MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
MAC Module 8 Exponential and Logarithmic Functions I. Rev.S08
 MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
MAC 1105 Module 8 Exponential and Logarithmic Functions I Learning Objectives Upon completing this module, you should be able to: 1. Distinguish between linear and exponential growth. 2. Model data with
1. Find the real solutions, if any, of a. x 2 + 3x + 9 = 0 Discriminant: b 2 4ac = = 24 > 0, so 2 real solutions. Use the quadratic formula,
 Math 110, Winter 008, Sec, Instructor Whitehead P. 1 of 8 1. Find the real solutions, if any, of a. x + 3x + 9 = 0 Discriminant: b 4ac = 3 3 4 1 9 = 7 < 0, so NO real solutions b. x 4x = 0 Discriminant:
Math 110, Winter 008, Sec, Instructor Whitehead P. 1 of 8 1. Find the real solutions, if any, of a. x + 3x + 9 = 0 Discriminant: b 4ac = 3 3 4 1 9 = 7 < 0, so NO real solutions b. x 4x = 0 Discriminant:
10 Exponential and Logarithmic Functions
 10 Exponential and Logarithmic Functions Concepts: Rules of Exponents Exponential Functions Power Functions vs. Exponential Functions The Definition of an Exponential Function Graphing Exponential Functions
10 Exponential and Logarithmic Functions Concepts: Rules of Exponents Exponential Functions Power Functions vs. Exponential Functions The Definition of an Exponential Function Graphing Exponential Functions
Evaluate the expression using the values given in the table. 1) (f g)(6) x f(x) x g(x)
 M60 (Precalculus) ch5 practice test Evaluate the expression using the values given in the table. 1) (f g)(6) 1) x 1 4 8 1 f(x) -4 8 0 15 x -5-4 1 6 g(x) 1-5 4 8 For the given functions f and g, find the
M60 (Precalculus) ch5 practice test Evaluate the expression using the values given in the table. 1) (f g)(6) 1) x 1 4 8 1 f(x) -4 8 0 15 x -5-4 1 6 g(x) 1-5 4 8 For the given functions f and g, find the
Exp, Log, Poly Functions Quarter 3 Review Name
 Exp, Log, Poly Functions Quarter 3 Review Name Textbook problems for practice: p. 285-293; p. 293 #9-14, p. 294-5 #1-34, 49-52, 55,56, 57; p. 297-321 logs; p. 280-1 #11-84 *Blood Alcohol, Bungee-from binder
Exp, Log, Poly Functions Quarter 3 Review Name Textbook problems for practice: p. 285-293; p. 293 #9-14, p. 294-5 #1-34, 49-52, 55,56, 57; p. 297-321 logs; p. 280-1 #11-84 *Blood Alcohol, Bungee-from binder
4. Find x, log 4 32 = x. 5. ln e ln ln e. 8. log log log 3 243
 Session #5 Logarithms What is a log? it is the inverse of an exponential equation. When you take the inverse of an exponential equation with a base of e, you have a natural logarithm, written as ln. 1.
Session #5 Logarithms What is a log? it is the inverse of an exponential equation. When you take the inverse of an exponential equation with a base of e, you have a natural logarithm, written as ln. 1.
Functions Modeling Change A Preparation for Calculus Third Edition
 Powerpoint slides copied from or based upon: Functions Modeling Change A Preparation for Calculus Third Edition Connally, Hughes-Hallett, Gleason, Et Al. Copyright 2007 John Wiley & Sons, Inc. 1 Chapter
Powerpoint slides copied from or based upon: Functions Modeling Change A Preparation for Calculus Third Edition Connally, Hughes-Hallett, Gleason, Et Al. Copyright 2007 John Wiley & Sons, Inc. 1 Chapter
Name Math 125 Exam 3 Review. SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Name Math 125 Exam 3 Review SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. All of the values of functions g and f are shown in the given table. 1) Find
Name Math 125 Exam 3 Review SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. All of the values of functions g and f are shown in the given table. 1) Find
Math M110: Lecture Notes For Chapter 12 Section 12.1: Inverse and Composite Functions
 Math M110: Lecture Notes For Chapter 12 Section 12.1: Inverse and Composite Functions Inverse function (interchange x and y): Find the equation of the inverses for: y = 2x + 5 ; y = x 2 + 4 Function: (Vertical
Math M110: Lecture Notes For Chapter 12 Section 12.1: Inverse and Composite Functions Inverse function (interchange x and y): Find the equation of the inverses for: y = 2x + 5 ; y = x 2 + 4 Function: (Vertical
Lecture 5 - Logarithms, Slope of a Function, Derivatives
 Lecture 5 - Logarithms, Slope of a Function, Derivatives 5. Logarithms Note the graph of e x This graph passes the horizontal line test, so f(x) = e x is one-to-one and therefore has an inverse function.
Lecture 5 - Logarithms, Slope of a Function, Derivatives 5. Logarithms Note the graph of e x This graph passes the horizontal line test, so f(x) = e x is one-to-one and therefore has an inverse function.
Algebra II Honors Final Exam Review
 Class: Date: Algebra II Honors Final Exam Review Short Answer. Evaluate the series 5n. 8 n =. Evaluate the series (n + ). n = What is the sum of the finite arithmetic series?. 9+ + 5+ 8+ + + 59. 6 + 9
Class: Date: Algebra II Honors Final Exam Review Short Answer. Evaluate the series 5n. 8 n =. Evaluate the series (n + ). n = What is the sum of the finite arithmetic series?. 9+ + 5+ 8+ + + 59. 6 + 9
MAC Learning Objectives. Logarithmic Functions. Module 8 Logarithmic Functions
 MAC 1140 Module 8 Logarithmic Functions Learning Objectives Upon completing this module, you should be able to 1. evaluate the common logarithmic function. 2. solve basic exponential and logarithmic equations.
MAC 1140 Module 8 Logarithmic Functions Learning Objectives Upon completing this module, you should be able to 1. evaluate the common logarithmic function. 2. solve basic exponential and logarithmic equations.
Exponential and Logarithmic Functions
 Exponential and Logarithmic Functions Philippe B. Laval Kennesaw State University October 30, 2000 Abstract In this handout, exponential and logarithmic functions are first defined. Then, their properties
Exponential and Logarithmic Functions Philippe B. Laval Kennesaw State University October 30, 2000 Abstract In this handout, exponential and logarithmic functions are first defined. Then, their properties
What You Need to Know for the Chapter 7 Test
 Score: /46 Name: Date: / / Hr: Alg 2C Chapter 7 Review - WYNTK CH 7 What You Need to Know for the Chapter 7 Test 7.1 Write & evaluate exponential expressions to model growth and decay situations. Determine
Score: /46 Name: Date: / / Hr: Alg 2C Chapter 7 Review - WYNTK CH 7 What You Need to Know for the Chapter 7 Test 7.1 Write & evaluate exponential expressions to model growth and decay situations. Determine
Chapter 3 Exponential, Logistic, and Logarithmic Functions
 Chapter Exponential, Logistic, and Logarithmic Functions Section. Exponential and Logistic Functions 75 Section. Exponential and Logistic Functions Exploration. The point (0, ) is common to all four graphs,
Chapter Exponential, Logistic, and Logarithmic Functions Section. Exponential and Logistic Functions 75 Section. Exponential and Logistic Functions Exploration. The point (0, ) is common to all four graphs,
With topics from Algebra and Pre-Calculus to
 With topics from Algebra and Pre-Calculus to get you ready to the AP! (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the
With topics from Algebra and Pre-Calculus to get you ready to the AP! (Key contains solved problems) Note: The purpose of this packet is to give you a review of basic skills. You are asked not to use the
Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions. Recall that a power function has the form f(x) = x r where r is a real number.
 L7-1 Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions Recall that a power function has the form f(x) = x r where r is a real number. f(x) = x 1/2 f(x) = x 1/3 ex. Sketch the graph of
L7-1 Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions Recall that a power function has the form f(x) = x r where r is a real number. f(x) = x 1/2 f(x) = x 1/3 ex. Sketch the graph of
1 Functions, Graphs and Limits
 1 Functions, Graphs and Limits 1.1 The Cartesian Plane In this course we will be dealing a lot with the Cartesian plane (also called the xy-plane), so this section should serve as a review of it and its
1 Functions, Graphs and Limits 1.1 The Cartesian Plane In this course we will be dealing a lot with the Cartesian plane (also called the xy-plane), so this section should serve as a review of it and its
1 /30. APPM 1235 Final Exam Fall 2014 December 17, /30 3 /25
 Name Section # Page Score 1 /30 APPM 1235 Final Exam Fall 2014 December 17, 2014 AT THE TOP OF THE PAGE write your name and your section number. Textbooks, class notes and electronic devices of any kind
Name Section # Page Score 1 /30 APPM 1235 Final Exam Fall 2014 December 17, 2014 AT THE TOP OF THE PAGE write your name and your section number. Textbooks, class notes and electronic devices of any kind
FINAL REVIEW FALL 2017
 FINAL REVIEW FALL 7 Solutions to the following problems are found in the notes on my website. Lesson & : Integration by Substitution Ex. Evaluate 3x (x 3 + 6) 6 dx. Ex. Evaluate dt. + 4t Ex 3. Evaluate
FINAL REVIEW FALL 7 Solutions to the following problems are found in the notes on my website. Lesson & : Integration by Substitution Ex. Evaluate 3x (x 3 + 6) 6 dx. Ex. Evaluate dt. + 4t Ex 3. Evaluate
The above statement is the false product rule! The correct product rule gives g (x) = 3x 4 cos x+ 12x 3 sin x. for all angles θ.
 Math 7A Practice Midterm III Solutions Ch. 6-8 (Ebersole,.7-.4 (Stewart DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You
Math 7A Practice Midterm III Solutions Ch. 6-8 (Ebersole,.7-.4 (Stewart DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You
