Lecture 16 : Definitions, theorems, proofs. MTH299 Transition to Formal Mathematics Michigan State University 1 / 8
|
|
|
- Pearl Harvey
- 5 years ago
- Views:
Transcription
1 Lecture 16 : Definitions, theorems, proofs MTH299 Transition to Formal Mathematics Michigan State University 1 / 8
2 Meanings Definition : an explanation of the mathematical meaning of a word. Theorem : A statement that has been proven to be true. Proposition : A less important but nonetheless interesting true statement. Lemma: A true statement used in proving other true statements (that is, a less important theorem that is helpful in the proof of other results). Corollary: A true statment that is a simple deduction from a theorem or proposition. Proof: The explanation of why a statement is true. Conjecture: A statement believed to be true, but for which we have no proof. (a statement that is being proposed to be a true statement). Axiom: A basic assumption about a mathematical situation. (a statement we assume to be true). MTH299 Transition to Formal Mathematics Michigan State University 2 / 8
3 Group Axioms Definition A Group is a set G together with an operation #, for which the following axioms are satisfied. A 1. Closure: a, b G, a#b G A 2. Associativity: a, b, c G, (a#b)#c = a#(b#c) A 3. Identity element: e G such that a G, a#e = e#a = a A 4. Inverse element: a G, b G such that a#b = b#a = e 1 Is N with + a group? MTH299 Transition to Formal Mathematics Michigan State University 3 / 8
4 Group Axioms Definition A Group is a set G together with an operation #, for which the following axioms are satisfied. A 1. Closure: a, b G, a#b G A 2. Associativity: a, b, c G, (a#b)#c = a#(b#c) A 3. Identity element: e G such that a G, a#e = e#a = a A 4. Inverse element: a G, b G such that a#b = b#a = e 1 Is N with + a group? 2 Is Z with + a group? MTH299 Transition to Formal Mathematics Michigan State University 3 / 8
5 Group Axioms Definition A Group is a set G together with an operation #, for which the following axioms are satisfied. A 1. Closure: a, b G, a#b G A 2. Associativity: a, b, c G, (a#b)#c = a#(b#c) A 3. Identity element: e G such that a G, a#e = e#a = a A 4. Inverse element: a G, b G such that a#b = b#a = e 1 Is N with + a group? 2 Is Z with + a group? 3 Do the axioms imply that if G is a group and a, b G then a#b = b#a? MTH299 Transition to Formal Mathematics Michigan State University 3 / 8
6 Group Axioms Definition A Group is a set G together with an operation #, for which the following axioms are satisfied. A 1. Closure: a, b G, a#b G A 2. Associativity: a, b, c G, (a#b)#c = a#(b#c) A 3. Identity element: e G such that a G, a#e = e#a = a A 4. Inverse element: a G, b G such that a#b = b#a = e 1 Is N with + a group? 2 Is Z with + a group? 3 Do the axioms imply that if G is a group and a, b G then a#b = b#a? 4 Can you give an example of a group (all axioms A 1 A 4 are satisfied) whose elements do not commute with each other? MTH299 Transition to Formal Mathematics Michigan State University 3 / 8
7 Group Theorems Definition A Group is a set G together with an operation #, for which the following axioms are satisfied. A 1. Closure: a, b G, a#b G A 2. Associativity: a, b, c G, (a#b)#c = a#(b#c) A 3. Identity element: e G such that a G, a#e = e#a = a A 4. Inverse element: a G, b G such that a#b = b#a = e Theorem The identity element is unique. proof: Theorem For every element a G there exists a unique inverse. proof: MTH299 Transition to Formal Mathematics Michigan State University 4 / 8
8 Axiomatic Systems Axiomatic system 1: Definition Undefined terms: member, committee A 1. Every committee is a collection of at least two members. A 2. Every member is on at least one committee. 1 Find two different models for this set of axioms. MTH299 Transition to Formal Mathematics Michigan State University 5 / 8
9 Axiomatic Systems Axiomatic system 1: Definition Undefined terms: member, committee A 1. Every committee is a collection of at least two members. A 2. Every member is on at least one committee. 1 Find two different models for this set of axioms. 2 Discuss how it can be made categorical (there is a one-to-one correspondence between the elements in the model that preserves their relationship). MTH299 Transition to Formal Mathematics Michigan State University 5 / 8
10 Axiomatic Systems Axiomatic system 2: Definition Undefined terms: point, line A 1. Every line is a set of at least two points. A 2. Each two lines intersect in a unique point. A 3. There are precisely three lines. Find two different models for this set of axioms. MTH299 Transition to Formal Mathematics Michigan State University 6 / 8
11 Provide a definition of a circle. MTH299 Transition to Formal Mathematics Michigan State University 7 / 8
12 Provide a definition of a circle. Provide a definition of a sphere. MTH299 Transition to Formal Mathematics Michigan State University 7 / 8
13 Provide a definition of a circle. Provide a definition of a sphere. Provide a definition of a ball. MTH299 Transition to Formal Mathematics Michigan State University 7 / 8
14 Is the subset of a group also a group? Provide examples to support your claim. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
15 Is the subset of a group also a group? Provide examples to support your claim. Provide a formal definition of a subroup. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
16 Is the subset of a group also a group? Provide examples to support your claim. Provide a formal definition of a subroup. Provide a definition of a triangle. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
17 Is the subset of a group also a group? Provide examples to support your claim. Provide a formal definition of a subroup. Provide a definition of a triangle. Provide a definition of a quadrilateral. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
18 Is the subset of a group also a group? Provide examples to support your claim. Provide a formal definition of a subroup. Provide a definition of a triangle. Provide a definition of a quadrilateral. Provide a definition of a trapezoid. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
19 Is the subset of a group also a group? Provide examples to support your claim. Provide a formal definition of a subroup. Provide a definition of a triangle. Provide a definition of a quadrilateral. Provide a definition of a trapezoid. Provide a definition of a parallelogram. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
20 Is the subset of a group also a group? Provide examples to support your claim. Provide a formal definition of a subroup. Provide a definition of a triangle. Provide a definition of a quadrilateral. Provide a definition of a trapezoid. Provide a definition of a parallelogram. Provide a definition of a rectangle. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
21 Is the subset of a group also a group? Provide examples to support your claim. Provide a formal definition of a subroup. Provide a definition of a triangle. Provide a definition of a quadrilateral. Provide a definition of a trapezoid. Provide a definition of a parallelogram. Provide a definition of a rectangle. Provide a definition of a square. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
22 Is the subset of a group also a group? Provide examples to support your claim. Provide a formal definition of a subroup. Provide a definition of a triangle. Provide a definition of a quadrilateral. Provide a definition of a trapezoid. Provide a definition of a parallelogram. Provide a definition of a rectangle. Provide a definition of a square. Formulate conjectures involving the above figures, and their diagonals. Example: A parallelogram is a rectangle if and only if its diagonals have equal lengths. MTH299 Transition to Formal Mathematics Michigan State University 8 / 8
4 Arithmetic of Segments Hilbert s Road from Geometry
4 Arithmetic of Segments Hilbert s Road from Geometry to Algebra In this section, we explain Hilbert s procedure to construct an arithmetic of segments, also called Streckenrechnung. Hilbert constructs
Axioms of Probability
Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg Undefined Terms: Point, Line, Incident, Between, Congruent. Incidence Axioms:
Course 212: Academic Year Section 1: Metric Spaces
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Definition 2.1. A metric (or distance function) defined on a non-empty set X is a function d: X X R that satisfies: For all x, y, and z in X :
MATH 337 Metric Spaces Dr. Neal, WKU Let X be a non-empty set. The elements of X shall be called points. We shall define the general means of determining the distance between two points. Throughout we
Mathematics (Core - Level: 08) Pre-Algebra Course Outline
Crossings Christian School Academic Guide Middle School Division Grades 5-8 Mathematics (Core - Level: 08) Course Outline Exponents and Exponential Functions s will simplify expressions with zero and negative
Homework 1/Solutions. Graded Exercises
MTH 310-3 Abstract Algebra I and Number Theory S18 Homework 1/Solutions Graded Exercises Exercise 1. Below are parts of the addition table and parts of the multiplication table of a ring. Complete both
Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1
Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1 ALGEBRA I A.1 Mathematical process standards. The student
Test Corrections for Unit 1 Test
MUST READ DIRECTIONS: Read the directions located on www.koltymath.weebly.com to understand how to properly do test corrections. Ask for clarification from your teacher if there are parts that you are
Virginia Unit-Specific Learning Pathways. Grades 6-Algebra I: Standards of Learning
BUI L T F O VIR R G INIA 2014 2015 Virginia -Specific Learning Pathways Grades 6-Algebra I: Standards of Learning Table of Contents Grade 6...3 Grade 7...6 Grade 8...9 Algebra I... 11 Grade 6 Virginia
Homework 3/ Solutions
MTH 310-3 Abstract Algebra I and Number Theory S17 Homework 3/ Solutions Exercise 1. Prove the following Theorem: Theorem Let R and S be rings. Define an addition and multiplication on R S by for all r,
Math 1230, Notes 2. Aug. 28, Math 1230, Notes 2 Aug. 28, / 17
Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
Your quiz in recitation on Tuesday will cover 3.1: Arguments and inference. Your also have an online quiz, covering 3.1, due by 11:59 p.m., Tuesday.
Friday, February 15 Today we will begin Course Notes 3.2: Methods of Proof. Your quiz in recitation on Tuesday will cover 3.1: Arguments and inference. Your also have an online quiz, covering 3.1, due
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2009-03-26) Logic Rule 0 No unstated assumptions may be used in a proof.
0114ge. Geometry Regents Exam 0114
0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg ( )
Definitions, Axioms, Postulates, Propositions, and Theorems from Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg (2005-02-16) Logic Rules (Greenberg): Logic Rule 1 Allowable justifications.
Use this space for computations. 1 In trapezoid RSTV below with bases RS and VT, diagonals RT and SV intersect at Q.
Part I Answer all 28 questions in this part. Each correct answer will receive 2 credits. For each statement or question, choose the word or expression that, of those given, best completes the statement
Contact. Emina. Office: East Hall 1825 Phone:
to Contact Emina Email: eminaa@umich.edu Office: East Hall 1825 Phone: 734 647 5518 About me Born in Bosnia: Real home Utah Family Your turn Please fill out the questionnaire Back to business Class website
Lecture 2: A crash course in Real Analysis
EE5110: Probability Foundations for Electrical Engineers July-November 2015 Lecture 2: A crash course in Real Analysis Lecturer: Dr. Krishna Jagannathan Scribe: Sudharsan Parthasarathy This lecture is
Chapter 2 Preliminaries
Chapter 2 Preliminaries Where there is matter, there is geometry. Johannes Kepler (1571 1630) 2.1 Logic 2.1.1 Basic Concepts of Logic Let us consider A to be a non-empty set of mathematical objects. One
- 1 - Items related to expected use of technology appear in bold italics.
- 1 - Items related to expected use of technology appear in bold italics. Operating with Geometric and Cartesian Vectors Determining Intersections of Lines and Planes in Three- Space Similar content as
Math 309 Notes and Homework for Days 4-6
Math 309 Notes and Homework for Days 4-6 Day 4 Read Section 1.2 and the notes below. The following is the main definition of the course. Definition. A vector space is a set V (whose elements are called
Neutral Geometry. October 25, c 2009 Charles Delman
Neutral Geometry October 25, 2009 c 2009 Charles Delman Taking Stock: where we have been; where we are going Set Theory & Logic Terms of Geometry: points, lines, incidence, betweenness, congruence. Incidence
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Part (1) Second : Trigonometry. Tan
Part (1) Second : Trigonometry (1) Complete the following table : The angle Ratio 42 12 \ Sin 0.3214 Cas 0.5321 Tan 2.0625 (2) Complete the following : 1) 46 36 \ 24 \\ =. In degrees. 2) 44.125 = in degrees,
Quasiconformal Maps and Circle Packings
Quasiconformal Maps and Circle Packings Brett Leroux June 11, 2018 1 Introduction Recall the statement of the Riemann mapping theorem: Theorem 1 (Riemann Mapping). If R is a simply connected region in
Write down all the 3-digit positive integers that are squares and whose individual digits are non-zero squares. Answer: Relay
A Write down all the 3-digit positive integers that are squares and whose individual digits are non-zero squares. A2 What is the sum of all positive fractions that are less than and have denominator 73?
STAAR STANDARDS ALGEBRA I ALGEBRA II GEOMETRY
STANDARDS ALGEBRA I ALGEBRA II GEOMETRY STANDARDS ALGEBRA I TEKS Snapshot Algebra I (New TEKS 2015-16) Mathematical Process Standards A.1 Mathematical process standards. The student uses mathematical processes
2. Associative Law: A binary operator * on a set S is said to be associated whenever (A*B)*C = A*(B*C) for all A,B,C S.
BOOLEAN ALGEBRA 2.1 Introduction Binary logic deals with variables that have two discrete values: 1 for TRUE and 0 for FALSE. A simple switching circuit containing active elements such as a diode and transistor
Exercises for Unit V (Introduction to non Euclidean geometry)
Exercises for Unit V (Introduction to non Euclidean geometry) V.1 : Facts from spherical geometry Ryan : pp. 84 123 [ Note : Hints for the first two exercises are given in math133f07update08.pdf. ] 1.
Ohio Department of Education Academic Content Standards Mathematics Detailed Checklist ~Grade 9~
Ohio Department of Education Academic Content Standards Mathematics Detailed Checklist ~Grade 9~ Number, Number Sense and Operations Standard Students demonstrate number sense, including an understanding
NCERT Solutions for Class 7 Maths Chapter 14
NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Class 7 Chapter 14 Symmetry Exercise 14.1, 14.2, 14.3 Solutions Exercise 14.1 : Solutions of Questions on Page Number : 268 Q1 : Copy the figures with
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS
ADVANCED CALCULUS - MTH433 LECTURE 4 - FINITE AND INFINITE SETS 1. Cardinal number of a set The cardinal number (or simply cardinal) of a set is a generalization of the concept of the number of elements
The following techniques for methods of proofs are discussed in our text: - Vacuous proof - Trivial proof
Ch. 1.6 Introduction to Proofs The following techniques for methods of proofs are discussed in our text - Vacuous proof - Trivial proof - Direct proof - Indirect proof (our book calls this by contraposition)
Algebra 1 Math Year at a Glance
Real Operations Equations/Inequalities Relations/Graphing Systems Exponents/Polynomials Quadratics ISTEP+ Radicals Algebra 1 Math Year at a Glance KEY According to the Indiana Department of Education +
A. 180 B. 108 C. 360 D. 540
Part I - Multiple Choice - Circle your answer: 1. Find the area of the shaded sector. Q O 8 P A. 2 π B. 4 π C. 8 π D. 16 π 2. An octagon has sides. A. five B. six C. eight D. ten 3. The sum of the interior
chapter 1 vector geometry solutions V Consider the parallelogram shown alongside. Which of the following statements are true?
chapter vector geometry solutions V. Exercise A. For the shape shown, find a single vector which is equal to a)!!! " AB + BC AC b)! AD!!! " + DB AB c)! AC + CD AD d)! BC + CD!!! " + DA BA e) CD!!! " "
Transversals. What is a proof? A proof is logical argument in which each statement you make is backed up by a statement that is accepted true.
Chapter 2: Angles, Parallel Lines and Transversals Lesson 2.1: Writing a Proof Getting Ready: Your math teacher asked you to solve the equation: 4x 3 = 2x + 25. What is a proof? A proof is logical argument
Richard DiSalvo. Dr. Elmer. Mathematical Foundations of Economics. Fall/Spring,
The Finite Dimensional Normed Linear Space Theorem Richard DiSalvo Dr. Elmer Mathematical Foundations of Economics Fall/Spring, 20-202 The claim that follows, which I have called the nite-dimensional normed
ECE353: Probability and Random Processes. Lecture 2 - Set Theory
ECE353: Probability and Random Processes Lecture 2 - Set Theory Xiao Fu School of Electrical Engineering and Computer Science Oregon State University E-mail: xiao.fu@oregonstate.edu January 10, 2018 Set
Geometry EOC Review. ALIGNED TO GEOMETRY CROSSWALK P.E.s. Compiled By Stanwood Camano School District Teachers
Geometry EOC Review ALIGNED TO GEOMETRY CROSSWALK P.E.s Compiled By Stanwood Camano School District Teachers March, 2011 G.1 CORE CONTENT: Logical Arguments & Proofs G.I.C. Use deductive reasoning to prove
Chapter 3. Betweenness (ordering) A system satisfying the incidence and betweenness axioms is an ordered incidence plane (p. 118).
Chapter 3 Betweenness (ordering) Point B is between point A and point C is a fundamental, undefined concept. It is abbreviated A B C. A system satisfying the incidence and betweenness axioms is an ordered
G.GPE.B.4: Quadrilaterals in the Coordinate Plane 2
Regents Exam Questions www.jmap.org Name: 1 In square GEOM, the coordinates of G are (2, 2) and the coordinates of O are ( 4,2). Determine and state the coordinates of vertices E and M. [The use of the
Exercise 2.1. Identify the error or errors in the proof that all triangles are isosceles.
Exercises for Chapter Two He is unworthy of the name of man who is ignorant of the fact that the diagonal of a square is incommensurable with its side. Plato (429 347 B.C.) Exercise 2.1. Identify the error
Commutative laws for addition and multiplication: If a and b are arbitrary real numbers then
Appendix C Prerequisites C.1 Properties of Real Numbers Algebraic Laws Commutative laws for addition and multiplication: If a and b are arbitrary real numbers then a + b = b + a, (C.1) ab = ba. (C.2) Associative
LAMC Beginners Circle November 10, Oleg Gleizer. Warm-up
LAMC Beginners Circle November 10, 2013 Oleg Gleizer oleg1140@gmail.com Warm-up Problem 1 Can a power of two (a number of the form 2 n ) have all the decimal digits 0, 1,..., 9 the same number of times?
First selection test
First selection test Problem 1. Let ABC be a triangle right at C and consider points D, E on the sides BC, CA, respectively such that BD = AE = k. Lines BE and AC CD AD intersect at point O. Show that
11. Prove that the Missing Strip Plane is an. 12. Prove the above proposition.
10 Pasch Geometries Definition (Pasch s Postulate (PP)) A metric geometry satisfies Pasch s Postulate (PP) if for any line l, any triangle ABC, and any point D l such that A D B, then either l AC or l
Quads. 4. In the accompanying figure, ABCD is a parallelogram, m A = 2x + 35, and m C = 5x 22. Find the value of x.
Name: Date: 1. In the accompanying diagram of rhombus ACD, the lengths of the sides A and C are represented by 3x 4 and 2x + 1, respectively. Find the value of x. 4. In the accompanying figure, ACD is
Integrated Math III. IM3.1.2 Use a graph to find the solution set of a pair of linear inequalities in two variables.
Standard 1: Algebra and Functions Students solve inequalities, quadratic equations, and systems of equations. They graph polynomial, rational, algebraic, and piece-wise defined functions. They graph and
JANE LONG ACADEMY HIGH SCHOOL MATH SUMMER PREVIEW PACKET SCHOOL YEAR. Geometry
JANE LONG ACADEMY HIGH SCHOOL MATH SUMMER PREVIEW PACKET 2015-2016 SCHOOL YEAR Geometry STUDENT NAME: THE PARTS BELOW WILL BE COMPLETED ON THE FIRST DAY OF SCHOOL: DUE DATE: MATH TEACHER: PERIOD: Algebra
13 th Annual Harvard-MIT Mathematics Tournament Saturday 20 February 2010
13 th Annual Harvard-MIT Mathematics Tournament Saturday 0 February 010 1. [3] Suppose that x and y are positive reals such that Find x. x y = 3, x + y = 13. 3+ Answer: 17 Squaring both sides of x y =
MA651 Topology. Lecture 10. Metric Spaces.
MA65 Topology. Lecture 0. Metric Spaces. This text is based on the following books: Topology by James Dugundgji Fundamental concepts of topology by Peter O Neil Linear Algebra and Analysis by Marc Zamansky
In case (1) 1 = 0. Then using and from Friday,
Math 316, Intro to Analysis The order of the real numbers. The field axioms are not enough to give R, as an extra credit problem will show. Definition 1. An ordered field F is a field together with a nonempty
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES. 1. Compact Sets
FUNCTIONAL ANALYSIS LECTURE NOTES: COMPACT SETS AND FINITE-DIMENSIONAL SPACES CHRISTOPHER HEIL 1. Compact Sets Definition 1.1 (Compact and Totally Bounded Sets). Let X be a metric space, and let E X be
7. Homotopy and the Fundamental Group
7. Homotopy and the Fundamental Group The group G will be called the fundamental group of the manifold V. J. Henri Poincaré, 895 The properties of a topological space that we have developed so far have
WORKSHEET MATH 215, FALL 15, WHYTE. We begin our course with the natural numbers:
WORKSHEET MATH 215, FALL 15, WHYTE We begin our course with the natural numbers: N = {1, 2, 3,...} which are a subset of the integers: Z = {..., 2, 1, 0, 1, 2, 3,... } We will assume familiarity with their
In case (1) 1 = 0. Then using and from the previous lecture,
Math 316, Intro to Analysis The order of the real numbers. The field axioms are not enough to give R, as an extra credit problem will show. Definition 1. An ordered field F is a field together with a nonempty
Boolean Algebra and Propositional Logic
Boolean Algebra and Propositional Logic Takahiro Kato September 10, 2015 ABSTRACT. This article provides yet another characterization of Boolean algebras and, using this characterization, establishes a
Isometries. Chapter Transformations of the Plane
Chapter 1 Isometries The first three chapters of this book are dedicated to the study of isometries and their properties. Isometries, which are distance-preserving transformations from the plane to itself,
Boolean Algebra and Propositional Logic
Boolean Algebra and Propositional Logic Takahiro Kato June 23, 2015 This article provides yet another characterization of Boolean algebras and, using this characterization, establishes a more direct connection
Proof of the Equivalent Area of a Circle and a Right Triangle with Leg Lengths of the Radius and Circumference
Proof of the Equivalent Area of a ircle and a Right Triangle with Leg Lengths of the Radius and ircumference Brennan ain July 22, 2018 Abstract In this paper I seek to prove Archimedes Theorem that a circle
Warm-Up Exercises. Use the figure to answer the questions. 1. What are the values of x and y? ANSWER 125, 125
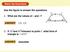Warm-Up Exercises Use the figure to answer the questions. 1. What are the values of x and y? 125, 125 2. If AX and BY intersect at point P, what kind of triangle is XPY? isosceles EXAMPLE Warm-Up 1Exercises
Chapter 1 Line and Angle Relationships
Chapter 1 Line and Angle Relationships SECTION 1.1: Sets, Statements, and Reasoning 1. a. Not a statement. b. Statement; true c. Statement; true d. Statement; false 5. Conditional 9. Simple 13. H: The
Problem Set 2: Solutions Math 201A: Fall 2016
Problem Set 2: s Math 201A: Fall 2016 Problem 1. (a) Prove that a closed subset of a complete metric space is complete. (b) Prove that a closed subset of a compact metric space is compact. (c) Prove that
Math 152: Affine Geometry
Math 152: Affine Geometry Christopher Eur October 21, 2014 This document summarizes results in Bennett s Affine and Projective Geometry by more or less following and rephrasing Faculty Senate Affine Geometry
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear.
Problems 01 - POINT Page 1 ( 1 ) Show that P ( a, b + c ), Q ( b, c + a ) and R ( c, a + b ) are collinear. ( ) Prove that the two lines joining the mid-points of the pairs of opposite sides and the line
Outline. 1 Overview. 2 From Geometry to Numbers. 4 Interlude on Circles. 5 An Area function. 6 Side-splitter. 7 Pythagorean Theorem
December 14, 2012 Outline 1 2 3 4 5 6 7 8 Agenda 1 G-SRT4 Context. orems about similarity 2 Proving that there is a field 3 Areas of parallelograms and triangles 4 lunch/discussion: Is it rational to fixate
Discrete Mathematics
Slides for Part IA CST 2015/16 Discrete Mathematics Prof Marcelo Fiore Marcelo.Fiore@cl.cam.ac.uk What are we up to? Learn to read and write, and also work with,
8. Quadrilaterals. If AC = 21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
8. Quadrilaterals Q 1 Name a quadrilateral whose each pair of opposite sides is equal. Mark (1) Q 2 What is the sum of two consecutive angles in a parallelogram? Mark (1) Q 3 The angles of quadrilateral
Strand 1: Statistics and Probability
Strand 1: Statistics and Probability Topic 1.1 Counting Listing outcomes of experiments in a systematic way, such as in a table, using sample spaces, tree diagrams. 1.2 C oncepts of The probability of
BENCHMARKS GRADE LEVEL INDICATORS STRATEGIES/RESOURCES
GRADE OHIO ACADEMIC CONTENT STANDARDS MATHEMATICS CURRICULUM GUIDE Tenth Grade Number, Number Sense and Operations Standard Students demonstrate number sense, including an understanding of number systems
Geometry Problem Solving Drill 13: Parallelograms
Geometry Problem Solving Drill 13: Parallelograms Question No. 1 of 10 Question 1. Mr. Smith s garden has 4 equal sides. It has 2 pairs of parallel sides. There are no right angles. Choose the most precise
Name Geometry Common Core Regents Review Packet - 3. Topic 1 : Equation of a circle
Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Real Analysis Notes. Thomas Goller
Real Analysis Notes Thomas Goller September 4, 2011 Contents 1 Abstract Measure Spaces 2 1.1 Basic Definitions........................... 2 1.2 Measurable Functions........................ 2 1.3 Integration..............................
12 Rigid Transformations
www.ck12.org CHAPTER 12 Rigid Transformations Chapter Outline 12.1 EXPLORING SYMMETRY 12.2 TRANSLATIONS AND VECTORS 12.3 REFLECTIONS 12.4 ROTATIONS 12.5 COMPOSITION OF TRANSFORMATIONS 12.6 EXTENSION: TESSELLATIONS
DEPARTMENT OF MATHEMATIC EDUCATION MATHEMATIC AND NATURAL SCIENCE FACULTY
HANDOUT ABSTRACT ALGEBRA MUSTHOFA DEPARTMENT OF MATHEMATIC EDUCATION MATHEMATIC AND NATURAL SCIENCE FACULTY 2012 BINARY OPERATION We are all familiar with addition and multiplication of two numbers. Both
Symmetry Groups 11/19/2017. Problem 1. Let S n be the set of all possible shuffles of n cards. 2. How many ways can we shuffle n cards?
Symmetry Groups 11/19/2017 1 Shuffles Problem 1 Let S n be the set of all possible shuffles of n cards. 1. How many ways can we shuffle 6 cards? 2. How many ways can we shuffle n cards? Problem 2 Given
Dr Prya Mathew SJCE Mysore
1 2 3 The word Mathematics derived from two Greek words Manthanein means learning Techne means an art or technique So Mathematics means the art of learning related to disciplines or faculties disciplines
Grade Eight (All Disciplines) Mathematics Standards Map Basic Program
1 Publisher Instructions. 1. In the header of this document, please fill in the program s identifying information. A basic program in mathematics for grade eight must address the standards for one of the
Reasoning and Proof Unit
Reasoning and Proof Unit 1 2 2 Conditional Statements Conditional Statement if, then statement the if part is hypothesis the then part is conclusion Conditional Statement How? if, then Example If an angle
586 Index. vertex, 369 disjoint, 236 pairwise, 272, 395 disjoint sets, 236 disjunction, 33, 36 distributive laws
Index absolute value, 135 141 additive identity, 254 additive inverse, 254 aleph, 465 algebra of sets, 245, 278 antisymmetric relation, 387 arcsine function, 349 arithmetic sequence, 208 arrow diagram,
2 Homework. Dr. Franz Rothe February 21, 2015 All3181\3181_spr15h2.tex
Math 3181 Dr. Franz Rothe February 21, 2015 All3181\3181_spr15h2.tex Name: Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
An adventitious angle problem concerning
n adventitious angle problem concerning and 7 / Darij Grinberg The purpose of this note is to give two solutions of the following problem (Fig 1): Let be an isosceles triangle with and 1 Let be a point
Areas of Polygons and Circles
Chapter 8 Areas of Polygons and Circles Copyright Cengage Learning. All rights reserved. 8.1 Area and Initial Postulates Copyright Cengage Learning. All rights reserved. Area and Initial Postulates Because
1 Topology Definition of a topology Basis (Base) of a topology The subspace topology & the product topology on X Y 3
Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
Correlation of Moving with Math Grade 7 to HSEE Mathematics Blueprint
Correlation of Moving with Math Grade 7 to HSEE Mathematics Blueprint Number Sense 1.0 Students know the properties of, and compute with, rational numbers expressed n a variety of forms: 1.1 Read, write
Logic, Proof, Axiom Systems
Logic, Proof, Axiom Systems MA 341 Topics in Geometry Lecture 03 29-Aug-2011 MA 341 001 2 Rules of Reasoning A tautology is a sentence which is true no matter what the truth value of its constituent parts.
Chapter 3 Cumulative Review Answers
Chapter 3 Cumulative Review Answers 1a. The triangle inequality is violated. 1b. The sum of the angles is not 180º. 1c. Two angles are equal, but the sides opposite those angles are not equal. 1d. The
SECONDARY MATHEMATICS I
SECONDARY MATHEMATICS I THE FUNDAMENTAL PURPOSE OF SECONDARY MATHEMATICS I is to formalize and extend the mathematics that students learned in the middle grades. The critical areas, organized into units,
1. Groups Definitions
1. Groups Definitions 1 1. Groups Definitions A group is a set S of elements between which there is defined a binary operation, usually called multiplication. For the moment, the operation will be denoted
4.! ABC ~ DEF,! AC = 6 ft, CB = 3 ft, AB = 7 ft, DF = 9 ft.! What is the measure of EF?
Name:!!!!!!!!!!!!! Geo(2) GEOMETRY (2) REVIEW FOR FINAL EXAM #2 1. If ABC is similar to ADE, then AB AD =? AE. Which replaces the? to make the statement true? A. AC!! B. AE!! C. DE!! D. BC 2. In ABC,
Foundations of Neutral Geometry
C H A P T E R 12 Foundations of Neutral Geometry The play is independent of the pages on which it is printed, and pure geometries are independent of lecture rooms, or of any other detail of the physical
Lecture 2: Isometries of R 2
Chapter 1 Lecture 2: Isometries of R 2 1.1 The synthetic vs. analytic approach; axiomatics We discussed briefly what an axiomatic system is: a collection of undefined terms related by axioms. Further terms
Section 2-1. Chapter 2. Make Conjectures. Example 1. Reasoning and Proof. Inductive Reasoning and Conjecture
Chapter 2 Reasoning and Proof Section 2-1 Inductive Reasoning and Conjecture Make Conjectures Inductive reasoning - reasoning that uses a number of specific examples to arrive at a conclusion Conjecture
Seul Lee, Dong-Soo Kim and Hyeon Park
Honam Mathematical J. 39 (2017), No. 2, pp. 247 258 https://doi.org/10.5831/hmj.2017.39.2.247 VARIOUS CENTROIDS OF QUADRILATERALS Seul Lee, Dong-Soo Kim and Hyeon Park Abstract. For a quadrilateral P,
Common Core State Standards for Mathematics Integrated Pathway: Mathematics I
A CORRELATION OF TO THE Standards for Mathematics A Correlation of Table of Contents Unit 1: Relationships between Quantities... 1 Unit 2: Linear and Exponential Relationships... 4 Unit 3: Reasoning with
Geometry Note Cards EXAMPLE:
Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
Additional Mathematics Lines and circles
Additional Mathematics Lines and circles Topic assessment 1 The points A and B have coordinates ( ) and (4 respectively. Calculate (i) The gradient of the line AB [1] The length of the line AB [] (iii)