G.GPE.B.4: Quadrilaterals in the Coordinate Plane 2
|
|
|
- Anna McCormick
- 5 years ago
- Views:
Transcription
1 Regents Exam Questions Name: 1 In square GEOM, the coordinates of G are (2, 2) and the coordinates of O are ( 4,2). Determine and state the coordinates of vertices E and M. [The use of the set of axes below is optional.] 2 The coordinates of quadrilateral ABCD are A( 1, 5), B(8,2), C(11,13), and D(2,6). Using coordinate geometry, prove that quadrilateral ABCD is a rhombus. [The use of the grid is optional.] 1
2 Regents Exam Questions 3 Jim is experimenting with a new drawing program on his computer. He created quadrilateral TEAM with coordinates T( 2,3), E( 5, 4), A(2, 1), and M(5,6). Jim believes that he has created a rhombus but not a square. Prove that Jim is correct. [The use of the grid is optional.] Name: 4 Quadrilateral PQRS has vertices P( 2,3), Q(3,8), R(4,1), and S( 1, 4). Prove that PQRS is a rhombus. Prove that PQRS is not a square. [The use of the set of axes below is optional.] 2
3 Regents Exam Questions 5 The vertices of quadrilateral MATH have coordinates M( 4,2), A( 1, 3), T(9,3), and H(6,8). Prove that quadrilateral MATH is a parallelogram. Prove that quadrilateral MATH is a rectangle. [The use of the set of axes below is optional.] Name: 7 The vertices of quadrilateral JKLM have coordinates J( 3,1), K(1, 5), L(7, 2), and M(3,4). Prove that JKLM is a parallelogram. Prove that JKLM is not a rhombus. [The use of the set of axes below is optional.] 6 Given: A( 2,2), B(6,5), C(4,0), D( 4, 3) Prove: ABCD is a parallelogram but not a rectangle. [The use of the grid is optional.] 8 Quadrilateral MATH has coordinates M(1,1), A( 2,5), T(3,5), and H(6,1). Prove that quadrilateral MATH is a rhombus and prove that it is not a square. [The use of the grid is optional.] 3
4 Regents Exam Questions 9 Quadrilateral ABCD has vertices A(2,3), B(7,10), C(9,4), and D(4, 3). Prove that ABCD is a parallelogram but not a rhombus. [The use of the grid is optional.] Name: 11 In rhombus MATH, the coordinates of the endpoints of the diagonal MT are M(0, 1) and T(4,6). Write an equation of the line that contains diagonal AH. [Use of the set of axes below is optional.] Using the given information, explain how you know that your line contains diagonal AH. 10 Given: Quadrilateral ABCD has vertices A( 5,6), B(6,6), C(8, 3), and D( 3, 3). Prove: Quadrilateral ABCD is a parallelogram but is neither a rhombus nor a rectangle. [The use of the grid below is optional.] 4
5 Regents Exam Questions 12 In the coordinate plane, the vertices of RST are R(6, 1), S(1, 4), and T( 5,6). Prove that RST is a right triangle. State the coordinates of point P such that quadrilateral RSTP is a rectangle. Prove that your quadrilateral RSTP is a rectangle. [The use of the set of axes below is optional.] Name: 13 Ashanti is surveying for a new parking lot shaped like a parallelogram. She knows that three of the vertices of parallelogram ABCD are A(0,0), B(5,2), and C(6,5). Find the coordinates of point D and sketch parallelogram ABCD on the accompanying set of axes. Justify mathematically that the figure you have drawn is a parallelogram. 14 Given: ABC with vertices A( 6, 2), B(2,8), and C(6, 2). AB has midpoint D, BC has midpoint E, and AC has midpoint F. Prove: ADEF is a parallelogram ADEF is not a rhombus [The use of the grid is optional.] 5
6 Regents Exam Questions 15 Quadrilateral ABCD with vertices A( 7,4), B( 3,6),C(3,0), and D(1, 8) is graphed on the set of axes below. Quadrilateral MNPQ is formed by joining M, N, P, and Q, the midpoints of AB, BC, CD, and AD, respectively. Prove that quadrilateral MNPQ is a parallelogram. Prove that quadrilateral MNPQ is not a rhombus. Name: 17 Quadrilateral KATE has vertices K(1,5), A(4,7), T(7,3), and E(1, 1). a Prove that KATE is a trapezoid. [The use of the grid is optional.] b Prove that KATE is not an isosceles trapezoid. 16 Given: A(1,6), B(7, 9), C(13,6), and D(3,1) Prove: ABCD is a trapezoid. [The use of the accompanying grid is optional.] 18 The coordinates of quadrilateral JKLM are J(1, 2), K(13,4), L(6,8), and M( 2,4). Prove that quadrilateral JKLM is a trapezoid but not an isosceles trapezoid. [The use of the grid is optional.] 6
7 Regents Exam Questions 19 Given: T( 1,1), R(3,4), A(7,2), and P( 1, 4) Prove: TRAP is a trapezoid. TRAP is not an isosceles trapezoid. [The use of the grid is optional.] Name: 20 In the coordinate plane, the vertices of triangle PAT are P( 1, 6), A( 4,5), and T(5, 2). Prove that PAT is an isosceles triangle. [The use of the set of axes below is optional.] State the coordinates of R so that quadrilateral PART is a parallelogram. Prove that quadrilateral PART is a parallelogram. 21 In the accompanying diagram of ABCD, where a b, prove ABCD is an isosceles trapezoid. 7
8 Answer Section 1 ANS: REF: geo 2 ANS:. To prove that ABCD is a rhombus, show that all sides are congruent using the distance formula: d AB = (8 ( 1)) 2 + (2 ( 5)) 2 = 130. d BC = (11 8) 2 + (13 2) 2 = 130 d CD = (11 2) 2 + (13 6) 2 = 130 d AD = (2 ( 1)) 2 + (6 ( 5)) 2 = 130 REF: b 1
9 3 ANS:. To prove that TEAM is a rhombus, show that all sides are congruent using the distance formula: d ET = ( 2 ( 5)) 2 + (3 ( 4)) 2 = 58. A square has four right angles. If TEAM is a square, then ET AE, d AM = (2 5) 2 + (( 1) 6) 2 = 58 d AE = ( 5 2) 2 + ( 4 ( 1)) 2 = 58 d MT = ( 2 5) 2 + (3 6) 2 = 58 AE AM, AM AT and MT ET. Lines that are perpendicular have slopes that are opposite reciprocals of each other. The slopes of sides of TEAM are: m ET = ( 2) = 7 4 ( 1) m 3 AE = 5 2 = 3 Because and 3 are not 7 m AM = 6 ( 1) 5 2 = 7 m MT = = 3 7 opposite reciprocals, consecutive sides of TEAM are not perpendicular, and TEAM is not a square. REF: b 4 ANS: PQ (8 3) 2 + (3 2) 2 = 50 QR (1 8) 2 + (4 3) 2 = 50 RS ( 4 1) 2 + ( 1 4) 2 = 50 PS ( 4 3) 2 + ( 1 2) 2 = 50 PQRS is a rhombus because all sides are congruent. m PQ = = 5 5 = 1 m QR = 1 8 = 7 Because the slopes of adjacent sides are not opposite reciprocals, they are not perpendicular 4 3 and do not form a right angle. Therefore PQRS is not a square. REF: geo 2
10 5 ANS: m MH = 6 10 = 3 5, m = 6 AT 10 = 3 5, m = 5 MA 3, m = 5 HT ; MH AT and MA HT. 3 MATH is a parallelogram since both sides of opposite sides are parallel. m MA = 5 3, m AT = 3. Since the slopes 5 are negative reciprocals, MA AT and A is a right angle. MATH is a rectangle because it is a parallelogram with a right angle. REF: geo 6 ANS: To prove that ABCD is a parallelogram, show that both pairs of opposite sides of the parallelogram are parallel by showing the opposite sides have the same slope: m AB = ( 2) = 3 8 m CD = = 3 8 m AD = ( 2) = 5 2 m BC = = 5 2 A rectangle has four right angles. If ABCD is a rectangle, then AB BC, BC CD, CD AD, and AD AB. Lines that are perpendicular have slopes that are the opposite and reciprocal of each other. Because 3 8 and 5 2 are not opposite reciprocals, the consecutive sides of ABCD are not perpendicular, and ABCD is not a rectangle. REF: b 3
11 7 ANS: m JM = = 3 6 = 1 2 m = ML = = 6 4 = m LK = 7 1 = 3 6 = 1 2 m KJ = = 6 4 = 3 2 Since both opposite sides have equal slopes and are parallel, JKLM is a parallelogram. JM = ( 3 3) 2 + (1 4) 2 = 45. JM is not congruent to ML, so JKLM is not a rhombus since not all sides ML= (7 3) 2 + ( 2 4) 2 = 52 are congruent. REF: ge 8 ANS: The length of each side of quadrilateral is 5. Since each side is congruent, quadrilateral MATH is a rhombus. The slope of MH is 0 and the slope of HT is 4. Since the slopes are not negative 3 reciprocals, the sides are not perpendicular and do not form rights angles. Since adjacent sides are not perpendicular, quadrilateral MATH is not a square. REF: ge 9 ANS: m AB = = 7 5, m = 4 ( 3) CD 9 4 = 7 5, m = 3 ( 3) AD 2 4 = 6 2 = 3, m = 10 4 BC 7 9 = 6 = 3 (Definition of 2 slope). AB CD, AD BC (Parallel lines have equal slope). Quadrilateral ABCD is a parallelogram (Definition of parallelogram). d AD = (2 4) 2 + (3 ( 3)) 2 = 40, d AB = (7 2) 2 + (10 3) 2 = 74 (Definition of distance). AD is not congruent to AB (Congruent lines have equal distance). ABCD is not a rhombus (A rhombus has four equal sides). REF: b 4
12 10 ANS: AB CD and AD CB because their slopes are equal. ABCD is a parallelogram because opposite side are parallel. AB BC. ABCD is not a rhombus because all sides are not equal. AB BC because their slopes are not opposite reciprocals. ABCD is not a rectangle because ABC is not a right angle. REF: ge 11 ANS: M , = M 2, 5 2 m = = 7 4 m = 4 7 y 2.5 = 4 (x 2) The diagonals, MT and AH, of 7 rhombus MATH are perpendicular bisectors of each other. REF: fall1411geo 12 ANS: m TS = 10 6 = 5 3 m SR = 3 5 Since the slopes of TS and SR are opposite reciprocals, they are perpendicular and form a right angle. RST is a right triangle because S is a right angle. P(0,9) m RP = 10 6 = 5 3 m = 3 PT 5 Since the slopes of all four adjacent sides (TS and SR, SR and RP, PT and TS, RP and PT ) are opposite reciprocals, they are perpendicular and form right angles. Quadrilateral RSTP is a rectangle because it has four right angles. REF: geo 5
13 13 ANS: Both pairs of opposite sides of a parallelogram are parallel. Parallel lines have the same slope. The slope of side BC is 3. For side AD to have a slope of 3, the coordinates of point D must be (1,3). m AB = = 2 5 m CD = = 2 5 m AD = = 3 m BC = = 3 REF: a 14 ANS: m AB = 6 + 2, = D(2,3) m = BC 2, = E(4,3) F(0, 2). To prove that ADEF is a 2 parallelogram, show that both pairs of opposite sides of the parallelogram are parallel by showing the opposite sides have the same slope: m AD = = 5 AF DE because all horizontal lines have the same slope. ADEF 4 m FE = = 5 4 is not a rhombus because not all sides are congruent. AD = = 41 AF = 6 REF: ge 6
14 15 ANS: M, = M( 5,5) N 3 + 3, = N(0,3) P , = P(2, 4) Q 7 + 1, = Q( 3, 2). m MN = = 2 5 m PQ = = 2 5 m NA = = 7 2 m QM = = 7 2. Since both opposite sides have equal slopes and are parallel, MNPQ is a parallelogram. MN = ( 5 0) 2 + (5 3) 2 = 29. MN is not congruent to NP, so MNPQ NA = (0 2) 2 + (3 4) 2 = 53 is not a rhombus since not all sides are congruent. REF: ge 16 ANS:. To prove that ABCD is a trapezoid, show that one pair of opposite sides of the figure is parallel by showing they have the same slope and that the other pair of opposite sides is not parallel by showing they do not have the same slope: m AB = = 3 6 = 1 2 REF: b m CD = = 5 10 = 1 2 m AD = = 5 2 m BC = = 3 6 = 1 2 7
15 17 ANS:. To prove that KATE is a trapezoid, show that one pair of opposite sides of the figure is parallel by showing they have the same slope and that the other pair of opposite sides is not parallel by showing they do not have the same slope: m AK = = 2 3 m EK = = undefined m ET = 3 ( 1) 7 1 = 4 6 = 2 m 3 AT = = 4 3 To prove that a trapezoid is not an isosceles trapezoid, show that the opposite sides that are not parallel are also not congruent using the distance formula: d EK = (1 1) 2 + (5 ( 1)) 2 = 6 REF: b 18 ANS: d AT = (4 7) 2 + (7 3) 2 = 5. To prove that JKLM is a trapezoid, show that one pair of opposite sides of the figure is parallel by showing they have the same slope and that the other pair of opposite sides is not parallel by showing they do not have the same slope: m JK = 4 ( 2) 13 1 = 1 2 m JM = ( 2) = 2 m LM = ( 2) = 1 2 m KL = = 4 7 To prove that a trapezoid is not an isosceles trapezoid, show that the opposite sides that are not parallel are also not congruent using the distance formula: d JM = (1 ( 2)) 2 + ( 2 4) 2 = 45 REF: b d KL = (13 6) 2 + (4 8) 2 = 65 8
16 19 ANS:. To prove that TRAP is a trapezoid, show that one pair of opposite sides of the figure is parallel by showing they have the same slope and that the other pair of opposite sides is not parallel by showing they do not have the same slope: m TR = = 3 4 m TP = 1 ( 4) 1 ( 1) = undefined m PA = = 3 4 m RA = = 1 2 To prove that a trapezoid is not an isosceles trapezoid, show that the opposite sides that are not parallel are also not congruent using the distance formula: d TP = ( 1 ( 1)) 2 + (1 ( 4)) 2 = 5 d RA = (3 7) 2 + (4 2) 2 = 20 = 2 5 REF: b 20 ANS: PAT is an isosceles triangle because sides AP and AT are congruent ( = = 130). R(2,9). Quadrilateral PART is a parallelogram because the opposite sides are parallel (m AR = 4 6 = 2 3 ; m PT = 4 6 = 2 3 ; m PA = 11 3 ; m RT = 11 3 ) REF: geo 9
17 21 ANS: To prove that ABCD is a trapezoid, show that one pair of opposite sides of the figure is parallel by showing they have the same slope and that the other pair of opposite sides is not parallel by showing they do not have the same slope: m AB = 0 0 a a = 0 2a = 0 m CD = c c b b = 0 2b = 0 m AD = c 0 b ( a) = m BC = c 0 b a = c b a c b + a If AD and BC are parallel, then: c b + a = c b a c(b a) = c( b + a) b a = b + a 2a = 2b a = b But the facts of the problem indicate a b, so AD and BC are not parallel. To prove that a trapezoid is an isosceles trapezoid, show that the opposite sides that are not parallel are congruent using the distance formula: d BC = (b a) 2 + (c 0) 2 d AD = ( b ( a)) 2 + (c 0) 2 = b 2 2ab + a 2 + c 2 = a 2 + b 2 2ab + c 2 = (a b) 2 + c 2 = a 2 2ab + b 2 + c 2 = a 2 + b 2 2ab + c 2 REF: b 10
0112ge. Geometry Regents Exam Line n intersects lines l and m, forming the angles shown in the diagram below.
 Geometry Regents Exam 011 011ge 1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would
Geometry Regents Exam 011 011ge 1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would
0612ge. Geometry Regents Exam
 0612ge 1 Triangle ABC is graphed on the set of axes below. 3 As shown in the diagram below, EF intersects planes P, Q, and R. Which transformation produces an image that is similar to, but not congruent
0612ge 1 Triangle ABC is graphed on the set of axes below. 3 As shown in the diagram below, EF intersects planes P, Q, and R. Which transformation produces an image that is similar to, but not congruent
Test Corrections for Unit 1 Test
 MUST READ DIRECTIONS: Read the directions located on www.koltymath.weebly.com to understand how to properly do test corrections. Ask for clarification from your teacher if there are parts that you are
MUST READ DIRECTIONS: Read the directions located on www.koltymath.weebly.com to understand how to properly do test corrections. Ask for clarification from your teacher if there are parts that you are
0811ge. Geometry Regents Exam
 0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 ) 8 3) 3 4) 6 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 ) 8 3) 3 4) 6 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0114ge. Geometry Regents Exam 0114
 0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT.
 1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would prove l m? 1) 2.5 2) 4.5 3)
1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would prove l m? 1) 2.5 2) 4.5 3)
0811ge. Geometry Regents Exam BC, AT = 5, TB = 7, and AV = 10.
 0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 2) 8 3) 3 4) 6 2 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 2) 8 3) 3 4) 6 2 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0610ge. Geometry Regents Exam The diagram below shows a right pentagonal prism.
 0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
1 What is the solution of the system of equations graphed below? y = 2x + 1
 1 What is the solution of the system of equations graphed below? y = 2x + 1 3 As shown in the diagram below, when hexagon ABCDEF is reflected over line m, the image is hexagon A'B'C'D'E'F'. y = x 2 + 2x
1 What is the solution of the system of equations graphed below? y = 2x + 1 3 As shown in the diagram below, when hexagon ABCDEF is reflected over line m, the image is hexagon A'B'C'D'E'F'. y = x 2 + 2x
0110ge. Geometry Regents Exam Which expression best describes the transformation shown in the diagram below?
 0110ge 1 In the diagram below of trapezoid RSUT, RS TU, X is the midpoint of RT, and V is the midpoint of SU. 3 Which expression best describes the transformation shown in the diagram below? If RS = 30
0110ge 1 In the diagram below of trapezoid RSUT, RS TU, X is the midpoint of RT, and V is the midpoint of SU. 3 Which expression best describes the transformation shown in the diagram below? If RS = 30
0809ge. Geometry Regents Exam Based on the diagram below, which statement is true?
 0809ge 1 Based on the diagram below, which statement is true? 3 In the diagram of ABC below, AB AC. The measure of B is 40. 1) a b ) a c 3) b c 4) d e What is the measure of A? 1) 40 ) 50 3) 70 4) 100
0809ge 1 Based on the diagram below, which statement is true? 3 In the diagram of ABC below, AB AC. The measure of B is 40. 1) a b ) a c 3) b c 4) d e What is the measure of A? 1) 40 ) 50 3) 70 4) 100
0113ge. Geometry Regents Exam In the diagram below, under which transformation is A B C the image of ABC?
 0113ge 1 If MNP VWX and PM is the shortest side of MNP, what is the shortest side of VWX? 1) XV ) WX 3) VW 4) NP 4 In the diagram below, under which transformation is A B C the image of ABC? In circle
0113ge 1 If MNP VWX and PM is the shortest side of MNP, what is the shortest side of VWX? 1) XV ) WX 3) VW 4) NP 4 In the diagram below, under which transformation is A B C the image of ABC? In circle
MEP Pupil Text 13-19, Additional Material. Gradients of Perpendicular Lines
 Graphs MEP Pupil Text -9, Additional Material.B Gradients of Perpendicular Lines In this section we explore the relationship between the gradients of perpendicular lines and line segments. Worked Example
Graphs MEP Pupil Text -9, Additional Material.B Gradients of Perpendicular Lines In this section we explore the relationship between the gradients of perpendicular lines and line segments. Worked Example
Warm-Up Exercises. Use the figure to answer the questions. 1. What are the values of x and y? ANSWER 125, 125
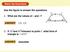 Warm-Up Exercises Use the figure to answer the questions. 1. What are the values of x and y? 125, 125 2. If AX and BY intersect at point P, what kind of triangle is XPY? isosceles EXAMPLE Warm-Up 1Exercises
Warm-Up Exercises Use the figure to answer the questions. 1. What are the values of x and y? 125, 125 2. If AX and BY intersect at point P, what kind of triangle is XPY? isosceles EXAMPLE Warm-Up 1Exercises
Name: Class: Date: 5. If the diagonals of a rhombus have lengths 6 and 8, then the perimeter of the rhombus is 28. a. True b.
 Indicate whether the statement is true or false. 1. If the diagonals of a quadrilateral are perpendicular, the quadrilateral must be a square. 2. If M and N are midpoints of sides and of, then. 3. The
Indicate whether the statement is true or false. 1. If the diagonals of a quadrilateral are perpendicular, the quadrilateral must be a square. 2. If M and N are midpoints of sides and of, then. 3. The
+2 u, 2s ) [D] ( r+ t + u, 2s )
![+2 u, 2s ) [D] ( r+ t + u, 2s ) +2 u, 2s ) [D] ( r+ t + u, 2s )](/thumbs/74/70220114.jpg) 1. Isosceles trapezoid JKLM has legs JK and LM, and base KL. If JK = 3x + 6, KL = 9x 3, and LM = 7x 9. Find the value of x. [A] 15 4 [] 3 4 [] 3 [] 3 4. Which best describes the relationship between the
1. Isosceles trapezoid JKLM has legs JK and LM, and base KL. If JK = 3x + 6, KL = 9x 3, and LM = 7x 9. Find the value of x. [A] 15 4 [] 3 4 [] 3 [] 3 4. Which best describes the relationship between the
Chapter 3 Summary 3.1. Determining the Perimeter and Area of Rectangles and Squares on the Coordinate Plane. Example
 Chapter Summar Ke Terms bases of a trapezoid (.) legs of a trapezoid (.) composite figure (.5).1 Determining the Perimeter and Area of Rectangles and Squares on the Coordinate Plane The perimeter or area
Chapter Summar Ke Terms bases of a trapezoid (.) legs of a trapezoid (.) composite figure (.5).1 Determining the Perimeter and Area of Rectangles and Squares on the Coordinate Plane The perimeter or area
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, August 17, 2011 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, August 17, 2011 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of
0611ge. Geometry Regents Exam Line segment AB is shown in the diagram below.
 0611ge 1 Line segment AB is shown in the diagram below. In the diagram below, A B C is a transformation of ABC, and A B C is a transformation of A B C. Which two sets of construction marks, labeled I,
0611ge 1 Line segment AB is shown in the diagram below. In the diagram below, A B C is a transformation of ABC, and A B C is a transformation of A B C. Which two sets of construction marks, labeled I,
Geometry. Midterm Review
 Geometry Midterm Review Class: Date: Geometry Midterm Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1 A plumber knows that if you shut off the water
Geometry Midterm Review Class: Date: Geometry Midterm Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1 A plumber knows that if you shut off the water
4.! ABC ~ DEF,! AC = 6 ft, CB = 3 ft, AB = 7 ft, DF = 9 ft.! What is the measure of EF?
 Name:!!!!!!!!!!!!! Geo(2) GEOMETRY (2) REVIEW FOR FINAL EXAM #2 1. If ABC is similar to ADE, then AB AD =? AE. Which replaces the? to make the statement true? A. AC!! B. AE!! C. DE!! D. BC 2. In ABC,
Name:!!!!!!!!!!!!! Geo(2) GEOMETRY (2) REVIEW FOR FINAL EXAM #2 1. If ABC is similar to ADE, then AB AD =? AE. Which replaces the? to make the statement true? A. AC!! B. AE!! C. DE!! D. BC 2. In ABC,
Downloaded from
 Triangles 1.In ABC right angled at C, AD is median. Then AB 2 = AC 2 - AD 2 AD 2 - AC 2 3AC 2-4AD 2 (D) 4AD 2-3AC 2 2.Which of the following statement is true? Any two right triangles are similar
Triangles 1.In ABC right angled at C, AD is median. Then AB 2 = AC 2 - AD 2 AD 2 - AC 2 3AC 2-4AD 2 (D) 4AD 2-3AC 2 2.Which of the following statement is true? Any two right triangles are similar
Use this space for computations. 1 In trapezoid RSTV below with bases RS and VT, diagonals RT and SV intersect at Q.
 Part I Answer all 28 questions in this part. Each correct answer will receive 2 credits. For each statement or question, choose the word or expression that, of those given, best completes the statement
Part I Answer all 28 questions in this part. Each correct answer will receive 2 credits. For each statement or question, choose the word or expression that, of those given, best completes the statement
A plane can be names using a capital cursive letter OR using three points, which are not collinear (not on a straight line)
 Geometry - Semester 1 Final Review Quadrilaterals (Including some corrections of typos in the original packet) 1. Consider the plane in the diagram. Which are proper names for the plane? Mark all that
Geometry - Semester 1 Final Review Quadrilaterals (Including some corrections of typos in the original packet) 1. Consider the plane in the diagram. Which are proper names for the plane? Mark all that
Distance. Warm Ups. Learning Objectives I can find the distance between two points. Football Problem: Bailey. Watson
 Distance Warm Ups Learning Objectives I can find the distance between two points. Football Problem: Bailey Watson. Find the distance between the points (, ) and (4, 5). + 4 = c 9 + 6 = c 5 = c 5 = c. Using
Distance Warm Ups Learning Objectives I can find the distance between two points. Football Problem: Bailey Watson. Find the distance between the points (, ) and (4, 5). + 4 = c 9 + 6 = c 5 = c 5 = c. Using
Skills Practice Skills Practice for Lesson 9.1
 Skills Practice Skills Practice for Lesson.1 Name Date Meeting Friends The Distance Formula Vocabular Define the term in our own words. 1. Distance Formula Problem Set Archaeologists map the location of
Skills Practice Skills Practice for Lesson.1 Name Date Meeting Friends The Distance Formula Vocabular Define the term in our own words. 1. Distance Formula Problem Set Archaeologists map the location of
Geometry Honors: Midterm Exam Review January 2018
 Name: Period: The midterm will cover Chapters 1-6. Geometry Honors: Midterm Exam Review January 2018 You WILL NOT receive a formula sheet, but you need to know the following formulas Make sure you memorize
Name: Period: The midterm will cover Chapters 1-6. Geometry Honors: Midterm Exam Review January 2018 You WILL NOT receive a formula sheet, but you need to know the following formulas Make sure you memorize
(b) the equation of the perpendicular bisector of AB. [3]
![(b) the equation of the perpendicular bisector of AB. [3] (b) the equation of the perpendicular bisector of AB. [3]](/thumbs/95/126119012.jpg) HORIZON EDUCATION SINGAPORE Additional Mathematics Practice Questions: Coordinate Geometr 1 Set 1 1 In the figure, ABCD is a rhombus with coordinates A(2, 9) and C(8, 1). The diagonals AC and BD cut at
HORIZON EDUCATION SINGAPORE Additional Mathematics Practice Questions: Coordinate Geometr 1 Set 1 1 In the figure, ABCD is a rhombus with coordinates A(2, 9) and C(8, 1). The diagonals AC and BD cut at
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 27, 2011 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 27, 2011 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
Geometry - Semester 1 Final Review Quadrilaterals
 Geometry - Semester 1 Final Review Quadrilaterals 1. Consider the plane in the diagram. Which are proper names for the plane? Mark all that apply. a. Plane L b. Plane ABC c. Plane DBC d. Plane E e. Plane
Geometry - Semester 1 Final Review Quadrilaterals 1. Consider the plane in the diagram. Which are proper names for the plane? Mark all that apply. a. Plane L b. Plane ABC c. Plane DBC d. Plane E e. Plane
Which statement is true about parallelogram FGHJ and parallelogram F ''G''H''J ''?
 Unit 2 Review 1. Parallelogram FGHJ was translated 3 units down to form parallelogram F 'G'H'J '. Parallelogram F 'G'H'J ' was then rotated 90 counterclockwise about point G' to obtain parallelogram F
Unit 2 Review 1. Parallelogram FGHJ was translated 3 units down to form parallelogram F 'G'H'J '. Parallelogram F 'G'H'J ' was then rotated 90 counterclockwise about point G' to obtain parallelogram F
8. Quadrilaterals. If AC = 21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
 8. Quadrilaterals Q 1 Name a quadrilateral whose each pair of opposite sides is equal. Mark (1) Q 2 What is the sum of two consecutive angles in a parallelogram? Mark (1) Q 3 The angles of quadrilateral
8. Quadrilaterals Q 1 Name a quadrilateral whose each pair of opposite sides is equal. Mark (1) Q 2 What is the sum of two consecutive angles in a parallelogram? Mark (1) Q 3 The angles of quadrilateral
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II
 The University of the State of New York REGENTS HGH SCHOOL EXAMNATON THREE-YEAR SEQUENCE FOR HGH SCHOOL MATHEMATCS COURSE Thursday, June 17, 1993-9:1.5 a.m. to 12:15 p.m., only Notice... Calculators must
The University of the State of New York REGENTS HGH SCHOOL EXAMNATON THREE-YEAR SEQUENCE FOR HGH SCHOOL MATHEMATCS COURSE Thursday, June 17, 1993-9:1.5 a.m. to 12:15 p.m., only Notice... Calculators must
2. A diagonal of a parallelogram divides it into two congruent triangles. 5. Diagonals of a rectangle bisect each other and are equal and vice-versa.
 QURILTERLS 1. Sum of the angles of a quadrilateral is 360. 2. diagonal of a parallelogram divides it into two congruent triangles. 3. In a parallelogram, (i) opposite sides are equal (ii) opposite angles
QURILTERLS 1. Sum of the angles of a quadrilateral is 360. 2. diagonal of a parallelogram divides it into two congruent triangles. 3. In a parallelogram, (i) opposite sides are equal (ii) opposite angles
9. AD = 7; By the Parallelogram Opposite Sides Theorem (Thm. 7.3), AD = BC. 10. AE = 7; By the Parallelogram Diagonals Theorem (Thm. 7.6), AE = EC.
 3. Sample answer: Solve 5x = 3x + 1; opposite sides of a parallelogram are congruent; es; You could start b setting the two parts of either diagonal equal to each other b the Parallelogram Diagonals Theorem
3. Sample answer: Solve 5x = 3x + 1; opposite sides of a parallelogram are congruent; es; You could start b setting the two parts of either diagonal equal to each other b the Parallelogram Diagonals Theorem
Applications. 12 The Shapes of Algebra. 1. a. Write an equation that relates the coordinates x and y for points on the circle.
 Applications 1. a. Write an equation that relates the coordinates and for points on the circle. 1 8 (, ) 1 8 O 8 1 8 1 (13, 0) b. Find the missing coordinates for each of these points on the circle. If
Applications 1. a. Write an equation that relates the coordinates and for points on the circle. 1 8 (, ) 1 8 O 8 1 8 1 (13, 0) b. Find the missing coordinates for each of these points on the circle. If
Geometry M1: Unit 3 Practice Exam
 Class: Date: Geometry M1: Unit 3 Practice Exam Short Answer 1. What is the value of x? 2. What is the value of x? 3. What is the value of x? 1 4. Find the value of x. The diagram is not to scale. Given:
Class: Date: Geometry M1: Unit 3 Practice Exam Short Answer 1. What is the value of x? 2. What is the value of x? 3. What is the value of x? 1 4. Find the value of x. The diagram is not to scale. Given:
+ 10 then give the value
 1. Match each vocabulary word to the picture. A. Linear Pair B. Vertical Angles P1 C. Angle Bisector D. Parallel Lines E. Orthocenter F. Centroid For questions 3 4 use the diagram below. Y Z X U W V A
1. Match each vocabulary word to the picture. A. Linear Pair B. Vertical Angles P1 C. Angle Bisector D. Parallel Lines E. Orthocenter F. Centroid For questions 3 4 use the diagram below. Y Z X U W V A
Name: Class: Date: c. WZ XY and XW YZ. b. WZ ZY and XW YZ. d. WN NZ and YN NX
 Class: Date: 2nd Semester Exam Review - Geometry CP 1. Complete this statement: A polygon with all sides the same length is said to be. a. regular b. equilateral c. equiangular d. convex 3. Which statement
Class: Date: 2nd Semester Exam Review - Geometry CP 1. Complete this statement: A polygon with all sides the same length is said to be. a. regular b. equilateral c. equiangular d. convex 3. Which statement
Properties of Quadrilaterals
 Properties of Quadrilaterals 1 Proving Properties of Parallelograms Given: ABC is a parallelogram Prove: AB C and A BC A B C Statements Reasons 1. 1. Given 2. AB C and A BC 2. 3. AB CB and CB AB 3. 4.
Properties of Quadrilaterals 1 Proving Properties of Parallelograms Given: ABC is a parallelogram Prove: AB C and A BC A B C Statements Reasons 1. 1. Given 2. AB C and A BC 2. 3. AB CB and CB AB 3. 4.
0609ge. Geometry Regents Exam AB DE, A D, and B E.
 0609ge 1 Juliann plans on drawing ABC, where the measure of A can range from 50 to 60 and the measure of B can range from 90 to 100. Given these conditions, what is the correct range of measures possible
0609ge 1 Juliann plans on drawing ABC, where the measure of A can range from 50 to 60 and the measure of B can range from 90 to 100. Given these conditions, what is the correct range of measures possible
0116ge. Geometry Regents Exam RT and SU intersect at O.
 Geometry Regents Exam 06 06ge What is the equation of a circle with its center at (5, ) and a radius of 3? ) (x 5) + (y + ) = 3 ) (x 5) + (y + ) = 9 3) (x + 5) + (y ) = 3 4) (x + 5) + (y ) = 9 In the diagram
Geometry Regents Exam 06 06ge What is the equation of a circle with its center at (5, ) and a radius of 3? ) (x 5) + (y + ) = 3 ) (x 5) + (y + ) = 9 3) (x + 5) + (y ) = 3 4) (x + 5) + (y ) = 9 In the diagram
MHR Principles of Mathematics 10 Solutions 1
 Course Review Note: Length and angle measures may vary slightly due to rounding. Course Review Question Page 8 a) Let l represent the length and w represent the width, then l + w 0. n+ q b) If n represents
Course Review Note: Length and angle measures may vary slightly due to rounding. Course Review Question Page 8 a) Let l represent the length and w represent the width, then l + w 0. n+ q b) If n represents
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXMINTION GEOMETRY Thursday, January 26, 2012 9:15 a.m. to 12:15 p.m., only Student Name: Notice School Name: Print your name and the
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXMINTION GEOMETRY Thursday, January 26, 2012 9:15 a.m. to 12:15 p.m., only Student Name: Notice School Name: Print your name and the
Geometry Honors Review for Midterm Exam
 Geometry Honors Review for Midterm Exam Format of Midterm Exam: Scantron Sheet: Always/Sometimes/Never and Multiple Choice 40 Questions @ 1 point each = 40 pts. Free Response: Show all work and write answers
Geometry Honors Review for Midterm Exam Format of Midterm Exam: Scantron Sheet: Always/Sometimes/Never and Multiple Choice 40 Questions @ 1 point each = 40 pts. Free Response: Show all work and write answers
Q.2 A, B and C are points in the xy plane such that A(1, 2) ; B (5, 6) and AC = 3BC. Then. (C) 1 1 or
 STRAIGHT LINE [STRAIGHT OBJECTIVE TYPE] Q. A variable rectangle PQRS has its sides parallel to fied directions. Q and S lie respectivel on the lines = a, = a and P lies on the ais. Then the locus of R
STRAIGHT LINE [STRAIGHT OBJECTIVE TYPE] Q. A variable rectangle PQRS has its sides parallel to fied directions. Q and S lie respectivel on the lines = a, = a and P lies on the ais. Then the locus of R
9. Areas of Parallelograms and Triangles
 9. Areas of Parallelograms and Triangles Q 1 State true or false : A diagonal of a parallelogram divides it into two parts of equal areas. Mark (1) Q 2 State true or false: Parallelograms on the same base
9. Areas of Parallelograms and Triangles Q 1 State true or false : A diagonal of a parallelogram divides it into two parts of equal areas. Mark (1) Q 2 State true or false: Parallelograms on the same base
Geometry Regents Practice Midterm
 Class: Date: Geometry Regents Practice Midterm Multiple Choice Identify the choice that best completes the statement or answers the question. 1. ( points) What is the equation of a line that is parallel
Class: Date: Geometry Regents Practice Midterm Multiple Choice Identify the choice that best completes the statement or answers the question. 1. ( points) What is the equation of a line that is parallel
VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER)
 BY:Prof. RAHUL MISHRA Class :- X QNo. VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER) CIRCLES Subject :- Maths General Instructions Questions M:9999907099,9818932244 1 In the adjoining figures, PQ
BY:Prof. RAHUL MISHRA Class :- X QNo. VAISHALI EDUCATION POINT (QUALITY EDUCATION PROVIDER) CIRCLES Subject :- Maths General Instructions Questions M:9999907099,9818932244 1 In the adjoining figures, PQ
Verifying Properties of Quadrilaterals
 Verifing roperties of uadrilaterals We can use the tools we have developed to find, classif, or verif properties of various shapes made b plotting coordinates on a Cartesian plane. Depending on the problem,
Verifing roperties of uadrilaterals We can use the tools we have developed to find, classif, or verif properties of various shapes made b plotting coordinates on a Cartesian plane. Depending on the problem,
Geometry Essentials ( ) Midterm Review. Chapter 1 For numbers 1 4, use the diagram below. 1. Classify as acute, obtuse, right or straight.
 Geometry Essentials (2015-2016) Midterm Review Name: Chapter 1 For numbers 1 4, use the diagram below. 1. Classify as acute, obtuse, right or straight. 2. is a linear pair with what other angle? 3. Name
Geometry Essentials (2015-2016) Midterm Review Name: Chapter 1 For numbers 1 4, use the diagram below. 1. Classify as acute, obtuse, right or straight. 2. is a linear pair with what other angle? 3. Name
Geometry CP Semester 1 Review Packet. answers_december_2012.pdf
 Geometry CP Semester 1 Review Packet Name: *If you lose this packet, you may print off your teacher s webpage. If you can t find it on their webpage, you can find one here: http://www.hfhighschool.org/assets/1/7/sem_1_review_packet
Geometry CP Semester 1 Review Packet Name: *If you lose this packet, you may print off your teacher s webpage. If you can t find it on their webpage, you can find one here: http://www.hfhighschool.org/assets/1/7/sem_1_review_packet
Geometry S1 (#2211) Foundations in Geometry S1 (#7771)
 Instructional Materials for WCSD Math Common Finals The Instructional Materials are for student and teacher use and are aligned to the Course Guides for the following courses: Geometry S1 (#2211) Foundations
Instructional Materials for WCSD Math Common Finals The Instructional Materials are for student and teacher use and are aligned to the Course Guides for the following courses: Geometry S1 (#2211) Foundations
Geometry Chapter 3 & 4 Test
 Class: Date: Geometry Chapter 3 & 4 Test Use the diagram to find the following. 1. What are three pairs of corresponding angles? A. angles 1 & 2, 3 & 8, and 4 & 7 C. angles 1 & 7, 8 & 6, and 2 & 4 B. angles
Class: Date: Geometry Chapter 3 & 4 Test Use the diagram to find the following. 1. What are three pairs of corresponding angles? A. angles 1 & 2, 3 & 8, and 4 & 7 C. angles 1 & 7, 8 & 6, and 2 & 4 B. angles
Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Ismailia Road Branch
 Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Sheet Ismailia Road Branch Sheet ( 1) 1-Complete 1. in the parallelogram, each two opposite
Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Sheet Ismailia Road Branch Sheet ( 1) 1-Complete 1. in the parallelogram, each two opposite
Q4. In ABC, AC = AB and B = 50. Find the value of C. SECTION B. Q5. Find two rational numbers between 1 2 and.
 SUMMATIVE ASSESSMENT 1 (2013 2014) CLASS IX (SET I) SUBJECT : MATHEMATICS Time: 3 hours M.M. : 90 General Instructions : (i) All questions are compulsory. (ii) The question paper consists of 31 questions
SUMMATIVE ASSESSMENT 1 (2013 2014) CLASS IX (SET I) SUBJECT : MATHEMATICS Time: 3 hours M.M. : 90 General Instructions : (i) All questions are compulsory. (ii) The question paper consists of 31 questions
PREPARED BY: ER. VINEET LOOMBA (B.TECH. IIT ROORKEE) 60 Best JEE Main and Advanced Level Problems (IIT-JEE). Prepared by IITians.
 www. Class XI TARGET : JEE Main/Adv PREPARED BY: ER. VINEET LOOMBA (B.TECH. IIT ROORKEE) ALP ADVANCED LEVEL PROBLEMS Straight Lines 60 Best JEE Main and Advanced Level Problems (IIT-JEE). Prepared b IITians.
www. Class XI TARGET : JEE Main/Adv PREPARED BY: ER. VINEET LOOMBA (B.TECH. IIT ROORKEE) ALP ADVANCED LEVEL PROBLEMS Straight Lines 60 Best JEE Main and Advanced Level Problems (IIT-JEE). Prepared b IITians.
Quads. 4. In the accompanying figure, ABCD is a parallelogram, m A = 2x + 35, and m C = 5x 22. Find the value of x.
 Name: Date: 1. In the accompanying diagram of rhombus ACD, the lengths of the sides A and C are represented by 3x 4 and 2x + 1, respectively. Find the value of x. 4. In the accompanying figure, ACD is
Name: Date: 1. In the accompanying diagram of rhombus ACD, the lengths of the sides A and C are represented by 3x 4 and 2x + 1, respectively. Find the value of x. 4. In the accompanying figure, ACD is
Geometry Final Exam REVIEW
 Name: Class: _ Date: _ Geometry Final Exam 09-10 - REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the perimeter and area of the parallelogram.
Name: Class: _ Date: _ Geometry Final Exam 09-10 - REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the perimeter and area of the parallelogram.
1) Use the figure below to name the following figures: 2) Identify the plane containing D, E, and C. 3) Two lines cross at. 4) Two planes cross at
 Geometry Semester 1 Final Exam Mixed Review Name: 1) Use the figure below to name the following figures: 2) Identify the plane containing D, E, and C. a) line b) ray c) Opposite rays d) Only adjacent angles
Geometry Semester 1 Final Exam Mixed Review Name: 1) Use the figure below to name the following figures: 2) Identify the plane containing D, E, and C. a) line b) ray c) Opposite rays d) Only adjacent angles
0616geo. Geometry CCSS Regents Exam x 2 + 4x = (y 2 20)
 0616geo 1 A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object below is generated by this rotation?
0616geo 1 A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object below is generated by this rotation?
The Coordinate Plane. Circles and Polygons on the Coordinate Plane. LESSON 13.1 Skills Practice. Problem Set
 LESSON.1 Skills Practice Name Date The Coordinate Plane Circles and Polgons on the Coordinate Plane Problem Set Use the given information to show that each statement is true. Justif our answers b using
LESSON.1 Skills Practice Name Date The Coordinate Plane Circles and Polgons on the Coordinate Plane Problem Set Use the given information to show that each statement is true. Justif our answers b using
PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES
 PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES 1. Find the value of k, if x =, y = 1 is a solution of the equation x + 3y = k.. Find the points where the graph of the equation
PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES 1. Find the value of k, if x =, y = 1 is a solution of the equation x + 3y = k.. Find the points where the graph of the equation
COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE. To find the length of a line segment joining two points A(x 1, y 1 ) and B(x 2, y 2 ), use
 COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE I. Length of a Line Segment: The distance between two points A ( x1, 1 ) B ( x, ) is given b A B = ( x x1) ( 1) To find the length of a line segment joining
COORDINATE GEOMETRY BASIC CONCEPTS AND FORMULAE I. Length of a Line Segment: The distance between two points A ( x1, 1 ) B ( x, ) is given b A B = ( x x1) ( 1) To find the length of a line segment joining
KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD 32
 KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD 3 SAMPLE PAPER 01 FOR PERIODIC TEST II EXAM (018-19) SUBJECT: MATHEMATICS(041) BLUE PRINT FOR PERIODIC TEST II EXAM: CLASS IX Chapter VSA (1 mark) SA I (
KENDRIYA VIDYALAYA GACHIBOWLI, GPRA CAMPUS, HYD 3 SAMPLE PAPER 01 FOR PERIODIC TEST II EXAM (018-19) SUBJECT: MATHEMATICS(041) BLUE PRINT FOR PERIODIC TEST II EXAM: CLASS IX Chapter VSA (1 mark) SA I (
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION COURSE II. Wednesday, August 16, :30 to 11:30 a.m.
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Wednesday, August 16, 000 8:30 to 11:30 a.m., only Notice... Scientific
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Wednesday, August 16, 000 8:30 to 11:30 a.m., only Notice... Scientific
2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain.
 1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain. 3) Explain why a four-legged
1) Explain what it means to bisect a segment. Why is it impossible to bisect a line? 2) Are all linear pairs supplementary angles? Are all supplementary angles linear pairs? Explain. 3) Explain why a four-legged
Rhombi, Rectangles and Squares
 Rhombi, Rectangles and Squares Math Practice Return to the Table of Contents 1 Three Special Parallelograms All the same properties of a parallelogram apply to the rhombus, rectangle, and square. Rhombus
Rhombi, Rectangles and Squares Math Practice Return to the Table of Contents 1 Three Special Parallelograms All the same properties of a parallelogram apply to the rhombus, rectangle, and square. Rhombus
Name: GEOMETRY: EXAM (A) A B C D E F G H D E. 1. How many non collinear points determine a plane?
 GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
NCERT SOLUTIONS OF Mensuration Exercise 2
 NCERT SOLUTIONS OF Mensuration Exercise 2 1 Question 1 The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them
NCERT SOLUTIONS OF Mensuration Exercise 2 1 Question 1 The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them
6. COORDINATE GEOMETRY
 6. CRDINATE GEMETRY Unit 6. : To Find the distance between two points A(, ) and B(, ) : AB = Eg. Given two points A(,3) and B(4,7) ( ) ( ). [BACK T BASICS] E. P(4,5) and Q(3,) Distance of AB = (4 ) (7
6. CRDINATE GEMETRY Unit 6. : To Find the distance between two points A(, ) and B(, ) : AB = Eg. Given two points A(,3) and B(4,7) ( ) ( ). [BACK T BASICS] E. P(4,5) and Q(3,) Distance of AB = (4 ) (7
TRIANGLES CHAPTER 7. (A) Main Concepts and Results. (B) Multiple Choice Questions
 CHAPTER 7 TRIANGLES (A) Main Concepts and Results Triangles and their parts, Congruence of triangles, Congruence and correspondence of vertices, Criteria for Congruence of triangles: (i) SAS (ii) ASA (iii)
CHAPTER 7 TRIANGLES (A) Main Concepts and Results Triangles and their parts, Congruence of triangles, Congruence and correspondence of vertices, Criteria for Congruence of triangles: (i) SAS (ii) ASA (iii)
Ch 5 Practice Exam. Name: Class: Date: Multiple Choice Identify the choice that best completes the statement or answers the question.
 Name: Class: Date: Ch 5 Practice Exam Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the value of x. The diagram is not to scale. a. 32 b. 50 c.
Name: Class: Date: Ch 5 Practice Exam Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the value of x. The diagram is not to scale. a. 32 b. 50 c.
Geometry Midterm Exam Review 3. Square BERT is transformed to create the image B E R T, as shown.
 1. Reflect FOXY across line y = x. 3. Square BERT is transformed to create the image B E R T, as shown. 2. Parallelogram SHAQ is shown. Point E is the midpoint of segment SH. Point F is the midpoint of
1. Reflect FOXY across line y = x. 3. Square BERT is transformed to create the image B E R T, as shown. 2. Parallelogram SHAQ is shown. Point E is the midpoint of segment SH. Point F is the midpoint of
Wahkiakum School District, Pre-EOC Geometry 2012
 Pre-EOC Assesment Geometry #1 Wahkiakum School District GEOM Page 1 1. What is the converse of If there are clouds in the sky, then it is raining? 2-2 A If it is raining, then there are clouds in the sky.
Pre-EOC Assesment Geometry #1 Wahkiakum School District GEOM Page 1 1. What is the converse of If there are clouds in the sky, then it is raining? 2-2 A If it is raining, then there are clouds in the sky.
AREAS OF PARALLELOGRAMS AND TRIANGLES
 AREAS OF PARALLELOGRAMS AND TRIANGLES Main Concepts and Results: The area of a closed plane figure is the measure of the region inside the figure: Fig.1 The shaded parts (Fig.1) represent the regions whose
AREAS OF PARALLELOGRAMS AND TRIANGLES Main Concepts and Results: The area of a closed plane figure is the measure of the region inside the figure: Fig.1 The shaded parts (Fig.1) represent the regions whose
H. Math 2 Benchmark 1 Review
 H. Math 2 enchmark 1 Review Name: ate: 1. Parallelogram C was translated to parallelogram C. 2. Which of the following is a model of a scalene triangle?.. How many units and in which direction were the
H. Math 2 enchmark 1 Review Name: ate: 1. Parallelogram C was translated to parallelogram C. 2. Which of the following is a model of a scalene triangle?.. How many units and in which direction were the
5. Using a compass and straightedge, construct a bisector of the angle shown below. [Leave all construction marks.]
![5. Using a compass and straightedge, construct a bisector of the angle shown below. [Leave all construction marks.] 5. Using a compass and straightedge, construct a bisector of the angle shown below. [Leave all construction marks.]](/thumbs/88/116790473.jpg) Name: Regents Review Session Two Date: Common Core Geometry 1. The diagram below shows AB and DE. Which transformation will move AB onto DE such that point D is the image of point A and point E is the
Name: Regents Review Session Two Date: Common Core Geometry 1. The diagram below shows AB and DE. Which transformation will move AB onto DE such that point D is the image of point A and point E is the
Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths
![Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths Topic 2 [312 marks] The rectangle ABCD is inscribed in a circle. Sides [AD] and [AB] have lengths](/thumbs/86/93150791.jpg) Topic 2 [312 marks] 1 The rectangle ABCD is inscribed in a circle Sides [AD] and [AB] have lengths [12 marks] 3 cm and (\9\) cm respectively E is a point on side [AB] such that AE is 3 cm Side [DE] is
Topic 2 [312 marks] 1 The rectangle ABCD is inscribed in a circle Sides [AD] and [AB] have lengths [12 marks] 3 cm and (\9\) cm respectively E is a point on side [AB] such that AE is 3 cm Side [DE] is
1. How many planes can be drawn through any three noncollinear points? a. 0 b. 1 c. 2 d. 3. a cm b cm c cm d. 21.
 FALL SEMESTER EXAM REVIEW (Chapters 1-6) CHAPTER 1 1. How many planes can be drawn through any three noncollinear points? a. 0 b. 1 c. 2 d. 3 2. Find the length of PQ. a. 50.9 cm b. 46.3 cm c. 25.7 cm
FALL SEMESTER EXAM REVIEW (Chapters 1-6) CHAPTER 1 1. How many planes can be drawn through any three noncollinear points? a. 0 b. 1 c. 2 d. 3 2. Find the length of PQ. a. 50.9 cm b. 46.3 cm c. 25.7 cm
JEFFERSON MATH PROJECT REGENTS AT RANDOM
 JEFFERSON MATH PROJECT REGENTS AT RANDOM The NY Geometry Regents Exams Fall 2008-August 2009 Dear Sir I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished
JEFFERSON MATH PROJECT REGENTS AT RANDOM The NY Geometry Regents Exams Fall 2008-August 2009 Dear Sir I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished
Chapter 1 Line and Angle Relationships
 Chapter 1 Line and Angle Relationships SECTION 1.1: Sets, Statements, and Reasoning 1. a. Not a statement. b. Statement; true c. Statement; true d. Statement; false 5. Conditional 9. Simple 13. H: The
Chapter 1 Line and Angle Relationships SECTION 1.1: Sets, Statements, and Reasoning 1. a. Not a statement. b. Statement; true c. Statement; true d. Statement; false 5. Conditional 9. Simple 13. H: The
Part (1) Second : Trigonometry. Tan
 Part (1) Second : Trigonometry (1) Complete the following table : The angle Ratio 42 12 \ Sin 0.3214 Cas 0.5321 Tan 2.0625 (2) Complete the following : 1) 46 36 \ 24 \\ =. In degrees. 2) 44.125 = in degrees,
Part (1) Second : Trigonometry (1) Complete the following table : The angle Ratio 42 12 \ Sin 0.3214 Cas 0.5321 Tan 2.0625 (2) Complete the following : 1) 46 36 \ 24 \\ =. In degrees. 2) 44.125 = in degrees,
Alg. (( Sheet 1 )) [1] Complete : 1) =.. 3) =. 4) 3 a 3 =.. 5) X 3 = 64 then X =. 6) 3 X 6 =... 7) 3
![Alg. (( Sheet 1 )) [1] Complete : 1) =.. 3) =. 4) 3 a 3 =.. 5) X 3 = 64 then X =. 6) 3 X 6 =... 7) 3 Alg. (( Sheet 1 )) [1] Complete : 1) =.. 3) =. 4) 3 a 3 =.. 5) X 3 = 64 then X =. 6) 3 X 6 =... 7) 3](/thumbs/88/117811617.jpg) Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Sheet Ismailia Road Branch [1] Complete : 1) 3 216 =.. Alg. (( Sheet 1 )) 1 8 2) 3 ( ) 2 =..
Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Sheet Ismailia Road Branch [1] Complete : 1) 3 216 =.. Alg. (( Sheet 1 )) 1 8 2) 3 ( ) 2 =..
2015 Canadian Team Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING cemc.uwaterloo.ca 205 Canadian Team Mathematics Contest April 205 Solutions 205 University of Waterloo 205 CTMC Solutions Page 2 Individual Problems.
TENTH YEAR MATHEMATICS
 ---------- The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION TENTH YEAR MATHEMATICS Monday, June 17, 1985 1:15 to 4:15 p.m., only The last page of the booklet is the answer sheet.
---------- The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION TENTH YEAR MATHEMATICS Monday, June 17, 1985 1:15 to 4:15 p.m., only The last page of the booklet is the answer sheet.
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION COURSE II. Friday, January 26, :15 a.m. to 12:15 p.m.
 The University of the State of New York REGENTS HIGH SCHOOL EXMINTION THREE-YER SEQUENCE FOR HIGH SCHOOL MTHEMTICS COURSE II Friday, January 26, 2001 9:15 a.m. to 12:15 p.m., only Notice... Scientific
The University of the State of New York REGENTS HIGH SCHOOL EXMINTION THREE-YER SEQUENCE FOR HIGH SCHOOL MTHEMTICS COURSE II Friday, January 26, 2001 9:15 a.m. to 12:15 p.m., only Notice... Scientific
Visit: ImperialStudy.com For More Study Materials Class IX Chapter 12 Heron s Formula Maths
 Exercise 1.1 1. Find the area of a triangle whose sides are respectively 150 cm, 10 cm and 00 cm. The triangle whose sides are a = 150 cm b = 10 cm c = 00 cm The area of a triangle = s(s a)(s b)(s c) Here
Exercise 1.1 1. Find the area of a triangle whose sides are respectively 150 cm, 10 cm and 00 cm. The triangle whose sides are a = 150 cm b = 10 cm c = 00 cm The area of a triangle = s(s a)(s b)(s c) Here
3D GEOMETRY. 3D-Geometry. If α, β, γ are angle made by a line with positive directions of x, y and z. axes respectively show that = 2.
 D GEOMETRY ) If α β γ are angle made by a line with positive directions of x y and z axes respectively show that i) sin α + sin β + sin γ ii) cos α + cos β + cos γ + 0 Solution:- i) are angle made by a
D GEOMETRY ) If α β γ are angle made by a line with positive directions of x y and z axes respectively show that i) sin α + sin β + sin γ ii) cos α + cos β + cos γ + 0 Solution:- i) are angle made by a
Answer ALL the questions in the SPECIAL ANSWER BOOK provided.
 Mathematics/P DBE/November 04 INSTRUCTIONS AND INFORMATION Read the following instructions carefully before answering the questions... 3. 4. 5. 6. 7. This question paper consists of 0 questions. Answer
Mathematics/P DBE/November 04 INSTRUCTIONS AND INFORMATION Read the following instructions carefully before answering the questions... 3. 4. 5. 6. 7. This question paper consists of 0 questions. Answer
JEFFERSON MATH PROJECT REGENTS AT RANDOM
 JEFFERSON MATH PROJECT REGENTS AT RANDOM The NY Geometry Regents Exams Fall 2008-January 2010 Dear Sir I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished
JEFFERSON MATH PROJECT REGENTS AT RANDOM The NY Geometry Regents Exams Fall 2008-January 2010 Dear Sir I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished
 1. Number a. Using a calculator or otherwise 1 3 1 5 i. 3 1 4 18 5 ii. 0.1014 5.47 1.5 5.47 0.6 5.1 b. Bus tour tickets . Algebra a. Write as a single fraction 3 4 11 3 4 1 b. 1 5 c. Factorize completely
1. Number a. Using a calculator or otherwise 1 3 1 5 i. 3 1 4 18 5 ii. 0.1014 5.47 1.5 5.47 0.6 5.1 b. Bus tour tickets . Algebra a. Write as a single fraction 3 4 11 3 4 1 b. 1 5 c. Factorize completely
Maharashtra State Board Class X Mathematics Geometry Board Paper 2015 Solution. Time: 2 hours Total Marks: 40
 Maharashtra State Board Class X Mathematics Geometry Board Paper 05 Solution Time: hours Total Marks: 40 Note:- () Solve all questions. Draw diagrams wherever necessary. ()Use of calculator is not allowed.
Maharashtra State Board Class X Mathematics Geometry Board Paper 05 Solution Time: hours Total Marks: 40 Note:- () Solve all questions. Draw diagrams wherever necessary. ()Use of calculator is not allowed.
G.CO.6-9 ONLY COMMON CORE QUESTIONS
 Class: Date: G.CO.6-9 ONLY COMMON CORE QUESTIONS Multiple Choice Identify the choice that best completes the statement or answers the question. 1 The image of ABC after a rotation of 90º clockwise about
Class: Date: G.CO.6-9 ONLY COMMON CORE QUESTIONS Multiple Choice Identify the choice that best completes the statement or answers the question. 1 The image of ABC after a rotation of 90º clockwise about
KENDRIYA VIDYALAYA SANGATHAN, HYDERABAD REGION
 KENDRIYA VIDYALAYA SANGATHAN, HYDERABAD REGION SAMPLE PAPER 01 FOR HALF YEARLY EXAM (017-18) SUBJECT: MATHEMATICS(041) BLUE PRINT FOR HALF YEARLY EXAM: CLASS IX Chapter VSA (1 mark) SA I ( marks) SA II
KENDRIYA VIDYALAYA SANGATHAN, HYDERABAD REGION SAMPLE PAPER 01 FOR HALF YEARLY EXAM (017-18) SUBJECT: MATHEMATICS(041) BLUE PRINT FOR HALF YEARLY EXAM: CLASS IX Chapter VSA (1 mark) SA I ( marks) SA II
CAREER POINT PRE FOUNDATION DIVISON CLASS-9. IMO Stage-II Exam MATHEMATICS Date :
 CAREER POINT PRE FOUNDATION DIVISON IMO Stage-II Exam.-07 CLASS-9 MATHEMATICS Date : -0-07 Q. In the given figure, PQR is a right angled triangle, right angled at Q. If QRST is a square on side QR and
CAREER POINT PRE FOUNDATION DIVISON IMO Stage-II Exam.-07 CLASS-9 MATHEMATICS Date : -0-07 Q. In the given figure, PQR is a right angled triangle, right angled at Q. If QRST is a square on side QR and
End of Course Review
 End of Course Review Geometry AIR Test Mar 14 3:07 PM Test blueprint with important areas: Congruence and Proof 33 39% Transformations, triangles (including ASA, SAS, SSS and CPCTC), proofs, coordinate/algebraic
End of Course Review Geometry AIR Test Mar 14 3:07 PM Test blueprint with important areas: Congruence and Proof 33 39% Transformations, triangles (including ASA, SAS, SSS and CPCTC), proofs, coordinate/algebraic
Class 9 Quadrilaterals
 ID : in-9-quadrilaterals [1] Class 9 Quadrilaterals For more such worksheets visit www.edugain.com Answer t he quest ions (1) The diameter of circumcircle of a rectangle is 13 cm and rectangle's width
ID : in-9-quadrilaterals [1] Class 9 Quadrilaterals For more such worksheets visit www.edugain.com Answer t he quest ions (1) The diameter of circumcircle of a rectangle is 13 cm and rectangle's width
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Wednesday, June 19, 00 1:15 to 4:15 p.m., only Notice... Scientific calculators
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Wednesday, June 19, 00 1:15 to 4:15 p.m., only Notice... Scientific calculators
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION COURSE II. Friday, January 26, :15 a.m. to 12:15 p.m.
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Friday, January 26, 2001 9:15 a.m. to 12:15 p.m., only Notice... Scientific
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Friday, January 26, 2001 9:15 a.m. to 12:15 p.m., only Notice... Scientific
