Fractals at infinity and SPDEs (Large scale random fractals)

Size: px

Start display at page:

Download "Fractals at infinity and SPDEs (Large scale random fractals)"

Blaze Leonard
5 years ago
Views:

1 Fractals at infinity and SPDEs (Large scale random fractals) Kunwoo Kim (joint with Davar Khoshnevisan and Yimin Xiao) Department of Mathematics University of Utah May 18, 2014 Frontier Probability Days 1 / 12

2 (local) Hausdorff dimension Let E R d. For every α 0 and δ > 0, define Hδ α (E) := inf Ei α ; E E i, E i < δ and then i 1 H α (E) := lim δ 0 H α δ. Then the (local) Hausdorff dimension of the set E is defined as dim H (E) := supα; H α (E) = } = infα; H α (E) < }. the Cantor set, the range of Brownian motion, the zero set of the Brownian motion, the set of fast times (t [0, 1]; lim sup h 0 B(t + h) B(t) / 2h log(1/h) γ}, and so on. Q) sets on Z d?? Q) sets at infinity, e.g. t R + ; B(t) 2γt log log t} (the set of points of peaks)?? 2 / 12

3 (local) Hausdorff dimension Let E R d. For every α 0 and δ > 0, define Hδ α (E) := inf Ei α ; E E i, E i < δ and then i 1 H α (E) := lim δ 0 H α δ. Then the (local) Hausdorff dimension of the set E is defined as dim H (E) := supα; H α (E) = } = infα; H α (E) < }. the Cantor set, the range of Brownian motion, the zero set of the Brownian motion, the set of fast times (t [0, 1]; lim sup h 0 B(t + h) B(t) / 2h log(1/h) γ}, and so on. Q) sets on Z d?? Q) sets at infinity, e.g. t R + ; B(t) 2γt log log t} (the set of points of peaks)?? 2 / 12

4 (local) Hausdorff dimension Let E R d. For every α 0 and δ > 0, define Hδ α (E) := inf Ei α ; E E i, E i < δ and then i 1 H α (E) := lim δ 0 H α δ. Then the (local) Hausdorff dimension of the set E is defined as dim H (E) := supα; H α (E) = } = infα; H α (E) < }. the Cantor set, the range of Brownian motion, the zero set of the Brownian motion, the set of fast times (t [0, 1]; lim sup h 0 B(t + h) B(t) / 2h log(1/h) γ}, and so on. Q) sets on Z d?? Q) sets at infinity, e.g. t R + ; B(t) 2γt log log t} (the set of points of peaks)?? 2 / 12

5 (local) Hausdorff dimension Let E R d. For every α 0 and δ > 0, define Hδ α (E) := inf Ei α ; E E i, E i < δ and then i 1 H α (E) := lim δ 0 H α δ. Then the (local) Hausdorff dimension of the set E is defined as dim H (E) := supα; H α (E) = } = infα; H α (E) < }. the Cantor set, the range of Brownian motion, the zero set of the Brownian motion, the set of fast times (t [0, 1]; lim sup h 0 B(t + h) B(t) / 2h log(1/h) γ}, and so on. Q) sets on Z d?? Q) sets at infinity, e.g. t R + ; B(t) 2γt log log t} (the set of points of peaks)?? 2 / 12

6 (local) Hausdorff dimension Let E R d. For every α 0 and δ > 0, define Hδ α (E) := inf Ei α ; E E i, E i < δ and then i 1 H α (E) := lim δ 0 H α δ. Then the (local) Hausdorff dimension of the set E is defined as dim H (E) := supα; H α (E) = } = infα; H α (E) < }. the Cantor set, the range of Brownian motion, the zero set of the Brownian motion, the set of fast times (t [0, 1]; lim sup h 0 B(t + h) B(t) / 2h log(1/h) γ}, and so on. Q) sets on Z d?? Q) sets at infinity, e.g. t R + ; B(t) 2γt log log t} (the set of points of peaks)?? 2 / 12

7 Large scale Hausdorff dimension by Barlow and Taylor ( 88 and 91) Let V n := [ e n 1, e n 1 ) d, S 1 := V 1, S n+1 := V n+1 \ V n for all n 1. For every α > 0, define να n on each S n as m ( ) } α να(e, n Qi m S n) := inf ; E S n Q i, 1 Q i e n. i=1 e n Then the large scale Hausdorff dimension of the set E is defined as } } Dim H (E) := sup α ; να(e, n S n) = = inf α ; να(e, n S n) <. i=1 n=1 n=1 If A B, then Dim H (A) Dim H (B). Dim H (Z k ) = k. Dim H (the range of the simple random walk on Z d ) = d 2. Dim H (a Bounded set) = 0 Fractal behavior at infinity. 3 / 12

8 Large scale Hausdorff dimension by Barlow and Taylor ( 88 and 91) Let V n := [ e n 1, e n 1 ) d, S 1 := V 1, S n+1 := V n+1 \ V n for all n 1. For every α > 0, define να n on each S n as m ( ) } α να(e, n Qi m S n) := inf ; E S n Q i, 1 Q i e n. i=1 e n Then the large scale Hausdorff dimension of the set E is defined as } } Dim H (E) := sup α ; να(e, n S n) = = inf α ; να(e, n S n) <. i=1 n=1 n=1 If A B, then Dim H (A) Dim H (B). Dim H (Z k ) = k. Dim H (the range of the simple random walk on Z d ) = d 2. Dim H (a Bounded set) = 0 Fractal behavior at infinity. 3 / 12

9 Large scale Hausdorff dimension by Barlow and Taylor ( 88 and 91) Let V n := [ e n 1, e n 1 ) d, S 1 := V 1, S n+1 := V n+1 \ V n for all n 1. For every α > 0, define να n on each S n as m ( ) } α να(e, n Qi m S n) := inf ; E S n Q i, 1 Q i e n. i=1 e n Then the large scale Hausdorff dimension of the set E is defined as } } Dim H (E) := sup α ; να(e, n S n) = = inf α ; να(e, n S n) <. i=1 n=1 n=1 If A B, then Dim H (A) Dim H (B). Dim H (Z k ) = k. Dim H (the range of the simple random walk on Z d ) = d 2. Dim H (a Bounded set) = 0 Fractal behavior at infinity. 3 / 12

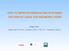
10 Peaks of Brownian motion Let B(t) be the standard Brownian motion on R. Consider the following set of exceedance times (peaks): for γ > 0 L B (γ) := t e e : B(t) } 2γt log log t y = 2.2t loglogt 60 y = t loglogt Figure : the red line shows L B (1.1) and the blue line shows L B (0.5). [Law of the Iterated Logarithm] L B (γ) is unbounded a.s. when γ 1; L B (γ) is bounded a.s. when γ > 1. 4 / 12

11 Peaks of Brownian motion Let B(t) be the standard Brownian motion on R. Consider the following set of exceedance times (peaks): for γ > 0 L B (γ) := t e e : B(t) } 2γt log log t y = 2.2t loglogt 60 y = t loglogt Figure : the red line shows L B (1.1) and the blue line shows L B (0.5). [Law of the Iterated Logarithm] L B (γ) is unbounded a.s. when γ 1; L B (γ) is bounded a.s. when γ > 1. 4 / 12

12 Peaks of Brownian motion Let B(t) be the standard Brownian motion on R. Consider the following set of exceedance times (peaks): for γ > 0 L B (γ) := t e e : B(t) } 2γt log log t y = 2.2t loglogt 60 y = t loglogt Figure : the red line shows L B (1.1) and the blue line shows L B (0.5). [Law of the Iterated Logarithm] L B (γ) is unbounded a.s. when γ 1; L B (γ) is bounded a.s. when γ > 1. 4 / 12

13 Peaks of Brownian motion Definition 1 (Asymptotic Density) Den(E) := lim sup t E [0, t]. t Theorem 2 (Strassen 64) For γ (0, 1), ( ) Den (L B (γ)) = 1 exp 4(γ 1 1). Theorem 3 (Khoshnevisan K Xiao) Almost surely, 1, if 0 < γ 1 Dim H (L B (γ)) = 0, if γ > 1. Dim H (L B (γ)) is always 0 or 1. Dim H L B (1) = 1 but Den(L B (1)) = 0. 5 / 12

14 Peaks of Brownian motion Definition 1 (Asymptotic Density) Den(E) := lim sup t E [0, t]. t Theorem 2 (Strassen 64) For γ (0, 1), ( ) Den (L B (γ)) = 1 exp 4(γ 1 1). Theorem 3 (Khoshnevisan K Xiao) Almost surely, 1, if 0 < γ 1 Dim H (L B (γ)) = 0, if γ > 1. Dim H (L B (γ)) is always 0 or 1. Dim H L B (1) = 1 but Den(L B (1)) = 0. 5 / 12

15 Peaks of Brownian motion Definition 1 (Asymptotic Density) Den(E) := lim sup t E [0, t]. t Theorem 2 (Strassen 64) For γ (0, 1), ( ) Den (L B (γ)) = 1 exp 4(γ 1 1). Theorem 3 (Khoshnevisan K Xiao) Almost surely, 1, if 0 < γ 1 Dim H (L B (γ)) = 0, if γ > 1. Dim H (L B (γ)) is always 0 or 1. Dim H L B (1) = 1 but Den(L B (1)) = 0. 5 / 12

16 Peaks of the Ornstein-Uhlenbeck process Let B(t) be the standard Brownian motion on R. Define U(t) := B(et ) e, t/2 L U (γ) := t e : U(t) (2γ log t) 1/2} (γ > 0). U(t) is centered Gaussian with E[U(t)U(s)] = exp ( t s /2) (O-U process). (LIL) lim sup t U(t) = 1, 2 log t a.s. L U (γ) = log L B (γ), thus L U (γ) is unbounded a.s. iff γ 1. Theorem 4 (Khoshnevisan K Xiao) If γ (0, 1], then Dim H (L U (γ)) = 1 γ a.s. Recall, for a Brownian motion, Dim H (L B (γ)) = 1 for 0 < γ 1. Brownian motion is mono-fractal whereas the Ornstein-Uhlenbeck process is multi-fractal. Dim H L U (1) = 0 but Dim H exp (L U (1)) (= L B (1)) = 1. (cf. Dim H (N) = 1 but Dim H (exp(n)) = 0.) 6 / 12

17 Peaks of the Ornstein-Uhlenbeck process Let B(t) be the standard Brownian motion on R. Define U(t) := B(et ) e, t/2 L U (γ) := t e : U(t) (2γ log t) 1/2} (γ > 0). U(t) is centered Gaussian with E[U(t)U(s)] = exp ( t s /2) (O-U process). (LIL) lim sup t U(t) = 1, 2 log t a.s. L U (γ) = log L B (γ), thus L U (γ) is unbounded a.s. iff γ 1. Theorem 4 (Khoshnevisan K Xiao) If γ (0, 1], then Dim H (L U (γ)) = 1 γ a.s. Recall, for a Brownian motion, Dim H (L B (γ)) = 1 for 0 < γ 1. Brownian motion is mono-fractal whereas the Ornstein-Uhlenbeck process is multi-fractal. Dim H L U (1) = 0 but Dim H exp (L U (1)) (= L B (1)) = 1. (cf. Dim H (N) = 1 but Dim H (exp(n)) = 0.) 6 / 12

18 Peaks of the Ornstein-Uhlenbeck process Let B(t) be the standard Brownian motion on R. Define U(t) := B(et ) e, t/2 L U (γ) := t e : U(t) (2γ log t) 1/2} (γ > 0). U(t) is centered Gaussian with E[U(t)U(s)] = exp ( t s /2) (O-U process). (LIL) lim sup t U(t) = 1, 2 log t a.s. L U (γ) = log L B (γ), thus L U (γ) is unbounded a.s. iff γ 1. Theorem 4 (Khoshnevisan K Xiao) If γ (0, 1], then Dim H (L U (γ)) = 1 γ a.s. Recall, for a Brownian motion, Dim H (L B (γ)) = 1 for 0 < γ 1. Brownian motion is mono-fractal whereas the Ornstein-Uhlenbeck process is multi-fractal. Dim H L U (1) = 0 but Dim H exp (L U (1)) (= L B (1)) = 1. (cf. Dim H (N) = 1 but Dim H (exp(n)) = 0.) 6 / 12

19 High peaks in SPDEs (space-time white noise) Linear stochastic heat equation ż t(x) = 1 2 z t (x) + ξ t(x) x R, t > 0, and z 0 (x) = 0. z t(x) is centered Gaussian. lim sup x z t(x)/ 2 log x = (t/π) 1/4 a.s. Let L zt (γ) := x e : z t(x) ( ) t 1/4 } π 2γ log x (t, γ > 0). No intermittency (Ez 2 t (x) = t/π, i.e. the moment Lyapunov exponent is 0) Stochastic parabolic anderson model u t(x) = 1 2 u t (x) + u t(x)ξ t(x) x R, t > 0, and u 0 (x) = 1. Let h t(x) := log u t(x). This h t(x) is the Hopf-Cole solution of the KPZ equation. 0 < lim sup x h t(x)/(log x) 2/3 < a.s. (Conus-Joseph-Khoshnevisan 13) } Let L ht (γ) := x e : h t(x) γ t 1/3 (log x) 2/3. Intermittency (E[u t(x)] k e ctk3, i.e. the moment Lyapunov exponent is like k 3 ). 7 / 12

20 High peaks in SPDEs (space-time white noise) Linear stochastic heat equation ż t(x) = 1 2 z t (x) + ξ t(x) x R, t > 0, and z 0 (x) = 0. z t(x) is centered Gaussian. lim sup x z t(x)/ 2 log x = (t/π) 1/4 a.s. Let L zt (γ) := x e : z t(x) ( ) t 1/4 } π 2γ log x (t, γ > 0). No intermittency (Ez 2 t (x) = t/π, i.e. the moment Lyapunov exponent is 0) Stochastic parabolic anderson model u t(x) = 1 2 u t (x) + u t(x)ξ t(x) x R, t > 0, and u 0 (x) = 1. Let h t(x) := log u t(x). This h t(x) is the Hopf-Cole solution of the KPZ equation. 0 < lim sup x h t(x)/(log x) 2/3 < a.s. (Conus-Joseph-Khoshnevisan 13) } Let L ht (γ) := x e : h t(x) γ t 1/3 (log x) 2/3. Intermittency (E[u t(x)] k e ctk3, i.e. the moment Lyapunov exponent is like k 3 ). 7 / 12

21 Simulations 4 3 x (a) Linear stochastic heat equaiton (b) Parabolic Anderson model Q) How about the large scale dimensions of the exceedance sets L zt (γ) and L ht (γ)? 8 / 12

22 Large scale dimension of High peaks in SPDEs Recall L zt (γ) := x e : z t(x) ( ) t 1/4 } π 2γ log x (t, γ > 0). Theorem 5 (Khoshnevisan K. Xiao) Choose and fix t > 0. The set L zt (γ) is almost surely unbounded if γ 1; else, if γ > 1 then L zt (γ) is almost surely bounded. Furthermore, a.s. for all t > 0 and γ (0, 1]. Recall L ht (γ) := Dim L zt (γ) = 1 γ, x e : h t(x) γ t 1/3 (log x) 2/3 } and h t(x) = log u t(x). Theorem 6 (Khoshnevisan K. Xiao) For every t and γ > 0, there exist two constants 0 < α β < such that 1 βγ 3/2 Dim L ht (γ) 1 αγ 3/2 a.s. 9 / 12

23 Large scale dimension of High peaks in SPDEs Recall L zt (γ) := x e : z t(x) ( ) t 1/4 } π 2γ log x (t, γ > 0). Theorem 5 (Khoshnevisan K. Xiao) Choose and fix t > 0. The set L zt (γ) is almost surely unbounded if γ 1; else, if γ > 1 then L zt (γ) is almost surely bounded. Furthermore, a.s. for all t > 0 and γ (0, 1]. Recall L ht (γ) := Dim L zt (γ) = 1 γ, x e : h t(x) γ t 1/3 (log x) 2/3 } and h t(x) = log u t(x). Theorem 6 (Khoshnevisan K. Xiao) For every t and γ > 0, there exist two constants 0 < α β < such that 1 βγ 3/2 Dim L ht (γ) 1 αγ 3/2 a.s. 9 / 12

24 General Bound (Upper bound) Let X := X t} t 0 be a stochastic process with values in R. Define c(b) := lim sup z C(b) := lim inf z z b inf t 0 z b sup log P X t > z}, t 0 log P Xt > z}. Theorem 7 (Upper bound) Suppose that there exists b (0, ) such that c(b) > 0 and for all γ (0, 1), ( ) } 1/b γ sup P sup X t > w 0 t [w,w+1] c(b) log s s γ+o(1) as s. Then, lim sup t (log t) 1/b X t [c(b)] 1/b a.s. Furthermore, for all γ (0, 1). Dim H t > e : X t ( ) } 1/b γ c(b) log t 1 γ, 10 / 12

25 General Bound (Lower bound) Definition 8 For every n 1 and δ (0, 1), let G n(δ) denote the collection of all finite sequences e n t 1 < t 2 <... < t m < e n+1 in S n such that t i+1 t i exp(δn) for all 1 i m. Definition 9 Let I denote the collection of all independent finite sequences of independent random variables. Theorem 10 (Lower bound) Suppose there exists b (0, ) such that C(b) <. n 1 max max inf log P X tj Y j > 1}, t i } m i=1 Gn(δ) 1 j m Y i } m i=1 I as n. Then, lim sup t (log t) 1/b X t [C(b)] 1/b a.s. Moreover, if γ (0, 1) then ( ) } 1/b γ Dim t > e : X t C(b) log t 1 γ a.s. 11 / 12

26 Thank You! 12 / 12

The Chaotic Character of the Stochastic Heat Equation

The Chaotic Character of the Stochastic Heat Equation March 11, 2011 Intermittency The Stochastic Heat Equation Blowup of the solution Intermittency-Example ξ j, j = 1, 2,, 10 i.i.d. random variables Taking