Probability. 25 th September lecture based on Hogg Tanis Zimmerman: Probability and Statistical Inference (9th ed.)
|
|
|
- Junior Black
- 5 years ago
- Views:
Transcription
1 Probability 25 th September 2017 lecture based on Hogg Tanis Zimmerman: Probability and Statistical Inference (9th ed.)
2 Properties of Probability Methods of Enumeration Conditional Probability Independent Events Bayes Theorem
3 Properties of Probability Methods of Enumeration Conditional Probability Independent Events Bayes Theorem
4 what statisticians do: problem/situation that needs to be considered (measurement problem) collect data through observations summarize the results (descriptive statistics, graphical methods) analyze the situation (statistical inferences) report with recommendations
5 statistics deals with the data collection and analysis of data variability in results statisticians try to find a pattern in data and deal with errors decision makers can decide upon confidence in the analyzed data
6 variability is a fact of life (variability is inherent) decisions have to involve uncertainties examples meteorology seismology medical research state legislature economy (weather forecast) (seismic hazard analysis) (drug/vaccine testing) (speed limit vs. no. of accidents) (estimation of unemployment rate)
7 how to make sense to the observations? sometimes the answers are obvious however, in many investigations appropriate probability and statistical models are needed
8 random experiments experiments for which the outcome cannot be predicted with certainty although the specific outcome of a r.e. cannot be predicted before the experiment is performed, the collection of all possible outcomes is known (can be described) outcome space S the collection of all possible outcomes event A A is a part of the collection of outcomes in S, A S
9 words set and event are interchangeable algebra of sets A B A B A B null or empty set A is subset of B union of A and B intersection of A and B A complement of A (all elements in S that are not in A) Venn diagrams
10 A 1, A 2, A k are mutually exclusive events A i A j =, i j that is, A 1, A 2, A k are disjoint sets A 1, A 2, A k are exhaustive events A 1 A 2 A k = S if A 1, A 2, A k are mutually exclusive and exhaustive events A i A j =, i j and A 1 A 2 A k = S
11 Commutative Laws Associative Laws Distributive Laws De Morgan s Laws A B = B A A B = B A (A B) C = A (B C ) (A B) C = A (B C ) A (B C) = (A B) (A C) A (B C) = (A B) (A C) (A B) = A B (A B) = A B
12 P(A) probability of event A (the chance of A occuring) consider repeating the experiment n times N(A) number of times that event A occurred throughout n performances ratio N(A) n is the relative frequency of event A in n repetitions relative frequency is usually very unstable for small values of n
13 number p number about which the relative frequency tends to stabilize (number that the relative frequency will be in future performances) although we cannot predict the outcome of a random experiment with certainty, if we know p (for a large number of n), we can predict fairly accurately the relative frequency of event A p is called probability of event A P(A) proportion of outcomes of a random experiment that terminate in the event A
14 set function a function such as P(A) that is evaluated for a set A PROPERTIES N(A)/n is always nonnegative if A = S, the outcome of the experiment will always belong to S N(A)/n = 1 if A and B are mutually exclusive events N(A B)/n = N(A)/n + N(B)/n
15 DEFINITION Probability is a real-valued set function P that assign, to each event A in the sample space S, a number P(A) called the probability of the event A, such that the following properties are satisfied (a) P(A) 0 (b) P(S) = 1 (c) A 1, A 2, A k are events and A i A j =, i j, then P(A 1 A 2 A k ) = P(A 1 ) + P(A 2 ) + + P(A k ) for each positive integer k P(A 1 A 2 ) = P(A 1 ) + P(A 2 ) + for an infinite, but countable, number of events
16 THEOREMS 1. For each event A, 2. P( ) = 0. P(A) = 1 P(A ). 3. If events A and B are such that A B, then P(A) P(B). 4. For each event A, P(A) If events A and B are two events, then P(A B) = P(A) + P(B) - P(A B). 6. If A, B and C are any three events, then P(A B C) = P(A) + P(B) + P(C) - P(A B) - P(A C) - P(B C) + P(A B C).
17 PROOF 1. For each event A, P(A) = 1 P(A ). from Venn diagrams, we have S = A A and A A = from properties (b) and (c) for probability, it follows than 1 = P(A) + P(A ) then P(A) = 1 P(A )
18 PROOF 2. P( ) = 0. in the previous theorem P(A) = 1 P(A ), take A = so that A = S then P( ) = 1 P(S) = 1-1 = 0
19 PROOF 3. If events A and B are such that A B, then P(A) P(B). we have B = A (B A ) and A (B A ) = from properties (b) and (c) for probability, it follows than P(B) = P(A) + P(B A ) P(A) because, from property (a) for probability, we have P(B A ) 0
20 PROOF 4. For each event A, P(A) 1. since A S, we have by theorem (1) and property (b) for probability P(A) P(S) = 1 which gives the desired result
21 PROOF 5. If events A and B are two events, then P(A B) = P(A) + P(B) - P(A B). from Venn diagrams, the event A and B can be represented as a union of mutually exclusive events, A A = A (A B) from property (c) for probability P(A B) = P(A) + P(A B) however B = (A B) (A B), which is a union of mutually exclusive events thus P(B) = P(A B) + P(A B) if we substitute P(A B) to the right-hand side of the second equation, we obtain the desired result
22 let S = e 1, e 2,, e m, e i is a possible outcome of the experiment integer m is called the total number of ways in which the random experiment can terminate if each of these outcomes has the same probability of occurring, we say that the m outcomes are equally likely P ( e i ) = 1/m, i = 1, 2, m if the number of outcomes in an event A is h, then the integer h is called the number of ways that are favorable to the event A P A = h m = N(A) N(S)
23 Properties of Probability Methods of Enumeration Conditional Probability Independent Events Bayes Theorem
24 Multiplication principle Suppose that the experiment E i has n i, i = 1,2, m possible outcomes after previous experiments have been performed. Then the composite experiment E 1 E 2 E m that consists of performing E 1, then E 2 and finally E m has n 1 n 2 n m possible outcomes.
25 Permutation Suppose that n positions are to be filled with n different objects. There are n choices for filling the first position, n - 1 for the second, and 1 choice for the last position. By multiplication principle, the are n (n - 1) (2) (1) = n! possible arrangements Each of the n! arrangements (in a row) of n different objects is called a permutation of n objects.
26 Permutation If only r positions are to be filled with objects selected from n different objects, r n, then the number of possible ordered arrangements is np r = n (n - 1) (n - 2) (n - r + 1) Each of the n P r arrangements is called a permutation of n objects taken r at a time. np r = n n 1 n r+1 n r 3 (2)(1) n r (3)(2)(1) = n! n r!
27 a set contains n objects consider a problem drawing r objects from the set the order in which the objects are drawn may/may not be important a drawn object is/is not replaced before the next object is drawn If r objects are selected from a set of n objects, and if the order of selection is noted, then the selected set of r objects is called an order sample of size r. Sampling with replacement occurs when an object is selected and then replaced before the next object is selected. The number of possible ordered samples of size r taken from a set of n objects is n r. (multiplication principle)
28 sampling without replacement occurs when an object is not replaced after it has been selected By the multiplication principle, the number of possible ordered samples of size r taken from a set of n objects without replacement is n n 1 (n r + 1) = n! n r! = np r
29 often the order of selection is not important and interest centers only on the selected set of r objects we are interested in a number of subsets of size r that can be selected from a set of n different objects each of the n C r unordered subsets is called a combination of n objects taken r at a time, where nc r = n r = n! r! n r! numbers n r are called binomial coefficients (a + b) n = n r=0 n r br a n r
30 suppose that in a set of n objects, n 1 are similar, n 2 are similar, n s are similar, where n 1 + n n s = n the number of distinguishable permutations of the n objects is n n! n 1, n 2, n = s n 1! n 2! n s! the coefficients are sometimes called multinomial coefficients expansion (a 1 + a a s ) n
31 Properties of Probability Methods of Enumeration Conditional Probability Independent Events Bayes Theorem
32 we are interested only in those outcomes which are elements of a subset B of the sample space S we are confronted with the problem of defining a probability set function with B as the new sample space for a given event A we want to define P(A B) the probability of A, considering only those outcomes of the random experiment that are elements of sample space B P A B = N(A B) N(B) = N(A B) N(S) N(B) N(S) = P(A B) P(B)
33 DEFINITION The conditional probability of an event A, given that event B has occurred, is defined by P A B = P(A B) P(B), provided that P(B) 0.
34 Conditional probability satisfies the axioms for a probability function, with P(B) 0 : 1. P(A B) 0 2. P(B B) = 1 3. if A 1, A 2, A k are mutually exclusive events, then P(A 1 A 2 A k B) = P(A 1 B) + P(A 2 B) + + P(A k B) for each positive integer k P(A 1 A 2 B) = P(A 1 B) + P(A 2 B) + for an infinite, but countable, number of events
35 once we know the conditional probability P(B A), we can determine the probability of the intersection of two events DEFINITION The probability that two events, A and B, both occur is given by the multiplication rule, P(A B) = P(A) P(B A), provided P(A) > 0 or by P(A B) = P(B) P(A B), provided P(B) > 0
36 the multiplication rule can be extended to three or more events P(A B C) = P[(A B) C] = P(A B) P(C A B) P(A B) = P(A) P(B A) P(A B C) = P(A) P(B A) P(C A B)
37 Properties of Probability Methods of Enumeration Conditional Probability Independent Events Bayes Theorem
38 for certain pair of events, the occurrence of one of them may/may not change the probability of the occurrence of the other DEFINITION Events A and B are independent if and only if P(A B) = P(A) P(B). Otherwise, A and B are called dependent events. statistically independent stochastically independent independent in a probabilistic sense
39 THEOREM DEFINITION If A and B are independent events, then the following pairs of events are also independent: A and B A and B A and B Events A, B and C are mutually independent if and only if the following two conditions hold: 1. A, B, and C are pairwise independent, that is P(A B) = P(A) P(B), P(A C) = P(A) P(C), P(B C) = P(B) P(C) 2. P(A B C) = P(A) P(B) P(C)
40 Properties of Probability Methods of Enumeration Conditional Probability Independent Events Bayes Theorem
41 let B 1, B 2 B m constitute a partition of the sample space S S = B 1 B 2 B m and B i B j =, i j events B 1, B 2, B m are mutually exclusive and exhaustive suppose that the prior probability of the event B i is positive, P(B i ) > 0, i = 1, m if A is an event, then A is the union of m mutually exclusive events A = (B 1 A) (B 2 A) (B m A) P A = m i=1 P B i A = m i=1 P B i P A B i law of total probability
42 If P(A) > 0, then P B k A = P(B k A) P(A), k = 1,2, m Bayes theorem P B k A = P B k P A B k m, k = 1,2,... m P B i P A B i i=1 the conditional probability P B k A is often called the posterior probability of B k
43 EXAMPLE Compute the probability that building X collapses during the next earthquake in the region. We do not know exactly if the next earthquake will be strong, medium or weak, but we estimated the following probabilities: P(strong) = 0,01, P(medium) = 0,1, P(weak) = 0,89 Additionally, structural engineers have performed analyses and estimated following: P(collapse strong) = 0,9, P(collapse medium) = 0,2, P(collapse weak) = 0,01 law of total probability P(collapse) = P(collapse strong) P(strong) + P(collapse medium) P(medium) + P(collapse weak) P(weak) P(collapse) = 0,9. 0,01 + 0, ,01. 0,89 = 0,0379 l.o.t.p. allows us to break the problem into 2 parts (size of an earthquake, capacity of the building)
44 EXAMPLE Suppose that an earthquake occurred and building X collapsed. Bayes theorem P(strong collapse) = P(collapse strong)p(strong) P(collapse) = 0,9.0,01 0,0379 = 0.24 B.t. provides a valuable calculation approach for combining pieces of information to compute a probability that may be difficult to determine directly
Statistical Inference
 Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
Elements of probability theory
 The role of probability theory in statistics We collect data so as to provide evidentiary support for answers we give to our many questions about the world (and in our particular case, about the business
The role of probability theory in statistics We collect data so as to provide evidentiary support for answers we give to our many questions about the world (and in our particular case, about the business
MATH 556: PROBABILITY PRIMER
 MATH 6: PROBABILITY PRIMER 1 DEFINITIONS, TERMINOLOGY, NOTATION 1.1 EVENTS AND THE SAMPLE SPACE Definition 1.1 An experiment is a one-off or repeatable process or procedure for which (a there is a well-defined
MATH 6: PROBABILITY PRIMER 1 DEFINITIONS, TERMINOLOGY, NOTATION 1.1 EVENTS AND THE SAMPLE SPACE Definition 1.1 An experiment is a one-off or repeatable process or procedure for which (a there is a well-defined
tossing a coin selecting a card from a deck measuring the commuting time on a particular morning
 2 Probability Experiment An experiment or random variable is any activity whose outcome is unknown or random upfront: tossing a coin selecting a card from a deck measuring the commuting time on a particular
2 Probability Experiment An experiment or random variable is any activity whose outcome is unknown or random upfront: tossing a coin selecting a card from a deck measuring the commuting time on a particular
LECTURE 1. 1 Introduction. 1.1 Sample spaces and events
 LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
LECTURE 1 1 Introduction The first part of our adventure is a highly selective review of probability theory, focusing especially on things that are most useful in statistics. 1.1 Sample spaces and events
CMPSCI 240: Reasoning about Uncertainty
 CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
CMPSCI 240: Reasoning about Uncertainty Lecture 2: Sets and Events Andrew McGregor University of Massachusetts Last Compiled: January 27, 2017 Outline 1 Recap 2 Experiments and Events 3 Probabilistic Models
Lecture Notes 1 Basic Probability. Elements of Probability. Conditional probability. Sequential Calculation of Probability
 Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Lecture Notes 1 Basic Probability Set Theory Elements of Probability Conditional probability Sequential Calculation of Probability Total Probability and Bayes Rule Independence Counting EE 178/278A: Basic
Week 2: Probability: Counting, Sets, and Bayes
 Statistical Methods APPM 4570/5570, STAT 4000/5000 21 Probability Introduction to EDA Week 2: Probability: Counting, Sets, and Bayes Random variable Random variable is a measurable quantity whose outcome
Statistical Methods APPM 4570/5570, STAT 4000/5000 21 Probability Introduction to EDA Week 2: Probability: Counting, Sets, and Bayes Random variable Random variable is a measurable quantity whose outcome
Properties of Probability
 Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
Econ 325 Notes on Probability 1 By Hiro Kasahara Properties of Probability In statistics, we consider random experiments, experiments for which the outcome is random, i.e., cannot be predicted with certainty.
Origins of Probability Theory
 1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
1 16.584: INTRODUCTION Theory and Tools of Probability required to analyze and design systems subject to uncertain outcomes/unpredictability/randomness. Such systems more generally referred to as Experiments.
Lecture 1. Chapter 1. (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 ( ). 1. What is Statistics?
 Lecture 1 (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 (2.1 --- 2.6). Chapter 1 1. What is Statistics? 2. Two definitions. (1). Population (2). Sample 3. The objective of statistics.
Lecture 1 (Part I) Material Covered in This Lecture: Chapter 1, Chapter 2 (2.1 --- 2.6). Chapter 1 1. What is Statistics? 2. Two definitions. (1). Population (2). Sample 3. The objective of statistics.
Review Basic Probability Concept
 Economic Risk and Decision Analysis for Oil and Gas Industry CE81.9008 School of Engineering and Technology Asian Institute of Technology January Semester Presented by Dr. Thitisak Boonpramote Department
Economic Risk and Decision Analysis for Oil and Gas Industry CE81.9008 School of Engineering and Technology Asian Institute of Technology January Semester Presented by Dr. Thitisak Boonpramote Department
Basic Probabilistic Reasoning SEG
 Basic Probabilistic Reasoning SEG 7450 1 Introduction Reasoning under uncertainty using probability theory Dealing with uncertainty is one of the main advantages of an expert system over a simple decision
Basic Probabilistic Reasoning SEG 7450 1 Introduction Reasoning under uncertainty using probability theory Dealing with uncertainty is one of the main advantages of an expert system over a simple decision
Probability- describes the pattern of chance outcomes
 Chapter 6 Probability the study of randomness Probability- describes the pattern of chance outcomes Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long
Chapter 6 Probability the study of randomness Probability- describes the pattern of chance outcomes Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long
Probability Theory and Applications
 Probability Theory and Applications Videos of the topics covered in this manual are available at the following links: Lesson 4 Probability I http://faculty.citadel.edu/silver/ba205/online course/lesson
Probability Theory and Applications Videos of the topics covered in this manual are available at the following links: Lesson 4 Probability I http://faculty.citadel.edu/silver/ba205/online course/lesson
Chapter 1 (Basic Probability)
 Chapter 1 (Basic Probability) What is probability? Consider the following experiments: 1. Count the number of arrival requests to a web server in a day. 2. Determine the execution time of a program. 3.
Chapter 1 (Basic Probability) What is probability? Consider the following experiments: 1. Count the number of arrival requests to a web server in a day. 2. Determine the execution time of a program. 3.
Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com
 1 School of Oriental and African Studies September 2015 Department of Economics Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com Gujarati D. Basic Econometrics, Appendix
1 School of Oriental and African Studies September 2015 Department of Economics Preliminary Statistics Lecture 2: Probability Theory (Outline) prelimsoas.webs.com Gujarati D. Basic Econometrics, Appendix
Axioms of Probability
 Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
Sample Space (denoted by S) The set of all possible outcomes of a random experiment is called the Sample Space of the experiment, and is denoted by S. Example 1.10 If the experiment consists of tossing
Lecture 6. Probability events. Definition 1. The sample space, S, of a. probability experiment is the collection of all
 Lecture 6 1 Lecture 6 Probability events Definition 1. The sample space, S, of a probability experiment is the collection of all possible outcomes of an experiment. One such outcome is called a simple
Lecture 6 1 Lecture 6 Probability events Definition 1. The sample space, S, of a probability experiment is the collection of all possible outcomes of an experiment. One such outcome is called a simple
Module 1. Probability
 Module 1 Probability 1. Introduction In our daily life we come across many processes whose nature cannot be predicted in advance. Such processes are referred to as random processes. The only way to derive
Module 1 Probability 1. Introduction In our daily life we come across many processes whose nature cannot be predicted in advance. Such processes are referred to as random processes. The only way to derive
Axiomatic Foundations of Probability. Definition: Probability Function
 Chapter 1 sections We will SKIP a number of sections Set theory SKIP Real number uncountability Definition of probability Finite sample spaces Counting methods Combinatorial methods SKIP tennis tournament
Chapter 1 sections We will SKIP a number of sections Set theory SKIP Real number uncountability Definition of probability Finite sample spaces Counting methods Combinatorial methods SKIP tennis tournament
CIVL 7012/8012. Basic Laws and Axioms of Probability
 CIVL 7012/8012 Basic Laws and Axioms of Probability Why are we studying probability and statistics? How can we quantify risks of decisions based on samples from a population? How should samples be selected
CIVL 7012/8012 Basic Laws and Axioms of Probability Why are we studying probability and statistics? How can we quantify risks of decisions based on samples from a population? How should samples be selected
Lecture 1 : The Mathematical Theory of Probability
 Lecture 1 : The Mathematical Theory of Probability 0/ 30 1. Introduction Today we will do 2.1 and 2.2. We will skip Chapter 1. We all have an intuitive notion of probability. Let s see. What is the probability
Lecture 1 : The Mathematical Theory of Probability 0/ 30 1. Introduction Today we will do 2.1 and 2.2. We will skip Chapter 1. We all have an intuitive notion of probability. Let s see. What is the probability
Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006
 Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006 Topics What is a set? Notations for sets Empty set Inclusion/containment and subsets Sample spaces and events Operations
Statistics for Financial Engineering Session 2: Basic Set Theory March 19 th, 2006 Topics What is a set? Notations for sets Empty set Inclusion/containment and subsets Sample spaces and events Operations
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR. NPTEL National Programme on Technology Enhanced Learning. Probability Methods in Civil Engineering
 INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR NPTEL National Programme on Technology Enhanced Learning Probability Methods in Civil Engineering Prof. Rajib Maity Department of Civil Engineering IIT Kharagpur
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR NPTEL National Programme on Technology Enhanced Learning Probability Methods in Civil Engineering Prof. Rajib Maity Department of Civil Engineering IIT Kharagpur
Sample Space: Specify all possible outcomes from an experiment. Event: Specify a particular outcome or combination of outcomes.
 Chapter 2 Introduction to Probability 2.1 Probability Model Probability concerns about the chance of observing certain outcome resulting from an experiment. However, since chance is an abstraction of something
Chapter 2 Introduction to Probability 2.1 Probability Model Probability concerns about the chance of observing certain outcome resulting from an experiment. However, since chance is an abstraction of something
Notes Week 2 Chapter 3 Probability WEEK 2 page 1
 Notes Week 2 Chapter 3 Probability WEEK 2 page 1 The sample space of an experiment, sometimes denoted S or in probability theory, is the set that consists of all possible elementary outcomes of that experiment
Notes Week 2 Chapter 3 Probability WEEK 2 page 1 The sample space of an experiment, sometimes denoted S or in probability theory, is the set that consists of all possible elementary outcomes of that experiment
Math 3338: Probability (Fall 2006)
 Math 3338: Probability (Fall 2006) Jiwen He Section Number: 10853 http://math.uh.edu/ jiwenhe/math3338fall06.html Probability p.1/8 Chapter Two: Probability (I) Probability p.2/8 2.1 Sample Spaces and
Math 3338: Probability (Fall 2006) Jiwen He Section Number: 10853 http://math.uh.edu/ jiwenhe/math3338fall06.html Probability p.1/8 Chapter Two: Probability (I) Probability p.2/8 2.1 Sample Spaces and
ECE353: Probability and Random Processes. Lecture 2 - Set Theory
 ECE353: Probability and Random Processes Lecture 2 - Set Theory Xiao Fu School of Electrical Engineering and Computer Science Oregon State University E-mail: xiao.fu@oregonstate.edu January 10, 2018 Set
ECE353: Probability and Random Processes Lecture 2 - Set Theory Xiao Fu School of Electrical Engineering and Computer Science Oregon State University E-mail: xiao.fu@oregonstate.edu January 10, 2018 Set
2. AXIOMATIC PROBABILITY
 IA Probability Lent Term 2. AXIOMATIC PROBABILITY 2. The axioms The formulation for classical probability in which all outcomes or points in the sample space are equally likely is too restrictive to develop
IA Probability Lent Term 2. AXIOMATIC PROBABILITY 2. The axioms The formulation for classical probability in which all outcomes or points in the sample space are equally likely is too restrictive to develop
Probability and distributions. Francesco Corona
 Probability Probability and distributions Francesco Corona Department of Computer Science Federal University of Ceará, Fortaleza Probability Many kinds of studies can be characterised as (repeated) experiments
Probability Probability and distributions Francesco Corona Department of Computer Science Federal University of Ceará, Fortaleza Probability Many kinds of studies can be characterised as (repeated) experiments
Probability. Lecture Notes. Adolfo J. Rumbos
 Probability Lecture Notes Adolfo J. Rumbos October 20, 204 2 Contents Introduction 5. An example from statistical inference................ 5 2 Probability Spaces 9 2. Sample Spaces and σ fields.....................
Probability Lecture Notes Adolfo J. Rumbos October 20, 204 2 Contents Introduction 5. An example from statistical inference................ 5 2 Probability Spaces 9 2. Sample Spaces and σ fields.....................
CIVL Why are we studying probability and statistics? Learning Objectives. Basic Laws and Axioms of Probability
 CIVL 3103 Basic Laws and Axioms of Probability Why are we studying probability and statistics? How can we quantify risks of decisions based on samples from a population? How should samples be selected
CIVL 3103 Basic Laws and Axioms of Probability Why are we studying probability and statistics? How can we quantify risks of decisions based on samples from a population? How should samples be selected
Chapter 2 Class Notes
 Chapter 2 Class Notes Probability can be thought of in many ways, for example as a relative frequency of a long series of trials (e.g. flips of a coin or die) Another approach is to let an expert (such
Chapter 2 Class Notes Probability can be thought of in many ways, for example as a relative frequency of a long series of trials (e.g. flips of a coin or die) Another approach is to let an expert (such
UNIT Explain about the partition of a sampling space theorem?
 UNIT -1 1. Explain about the partition of a sampling space theorem? PARTITIONS OF A SAMPLE SPACE The events B1, B2. B K represent a partition of the sample space 'S" if (a) So, when the experiment E is
UNIT -1 1. Explain about the partition of a sampling space theorem? PARTITIONS OF A SAMPLE SPACE The events B1, B2. B K represent a partition of the sample space 'S" if (a) So, when the experiment E is
2.6 Tools for Counting sample points
 2.6 Tools for Counting sample points When the number of simple events in S is too large, manual enumeration of every sample point in S is tedious or even impossible. (Example) If S contains N equiprobable
2.6 Tools for Counting sample points When the number of simple events in S is too large, manual enumeration of every sample point in S is tedious or even impossible. (Example) If S contains N equiprobable
Fundamentals of Probability CE 311S
 Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
Fundamentals of Probability CE 311S OUTLINE Review Elementary set theory Probability fundamentals: outcomes, sample spaces, events Outline ELEMENTARY SET THEORY Basic probability concepts can be cast in
Statistical Theory 1
 Statistical Theory 1 Set Theory and Probability Paolo Bautista September 12, 2017 Set Theory We start by defining terms in Set Theory which will be used in the following sections. Definition 1 A set is
Statistical Theory 1 Set Theory and Probability Paolo Bautista September 12, 2017 Set Theory We start by defining terms in Set Theory which will be used in the following sections. Definition 1 A set is
2) There should be uncertainty as to which outcome will occur before the procedure takes place.
 robability Numbers For many statisticians the concept of the probability that an event occurs is ultimately rooted in the interpretation of an event as an outcome of an experiment, others would interpret
robability Numbers For many statisticians the concept of the probability that an event occurs is ultimately rooted in the interpretation of an event as an outcome of an experiment, others would interpret
Conditional Probability
 Chapter 3 Conditional Probability 3.1 Definition of conditional probability In spite of our misgivings, let us persist with the frequency definition of probability. Consider an experiment conducted N times
Chapter 3 Conditional Probability 3.1 Definition of conditional probability In spite of our misgivings, let us persist with the frequency definition of probability. Consider an experiment conducted N times
Announcements. Topics: To Do:
 Announcements Topics: In the Probability and Statistics module: - Sections 1 + 2: Introduction to Stochastic Models - Section 3: Basics of Probability Theory - Section 4: Conditional Probability; Law of
Announcements Topics: In the Probability and Statistics module: - Sections 1 + 2: Introduction to Stochastic Models - Section 3: Basics of Probability Theory - Section 4: Conditional Probability; Law of
Stat 451: Solutions to Assignment #1
 Stat 451: Solutions to Assignment #1 2.1) By definition, 2 Ω is the set of all subsets of Ω. Therefore, to show that 2 Ω is a σ-algebra we must show that the conditions of the definition σ-algebra are
Stat 451: Solutions to Assignment #1 2.1) By definition, 2 Ω is the set of all subsets of Ω. Therefore, to show that 2 Ω is a σ-algebra we must show that the conditions of the definition σ-algebra are
Probabilistic models
 Probabilistic models Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became
Probabilistic models Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became
Probability and Statistics Notes
 Probability and Statistics Notes Chapter One Jesse Crawford Department of Mathematics Tarleton State University (Tarleton State University) Chapter One Notes 1 / 71 Outline 1 A Sketch of Probability and
Probability and Statistics Notes Chapter One Jesse Crawford Department of Mathematics Tarleton State University (Tarleton State University) Chapter One Notes 1 / 71 Outline 1 A Sketch of Probability and
Basic Statistics and Probability Chapter 3: Probability
 Basic Statistics and Probability Chapter 3: Probability Events, Sample Spaces and Probability Unions and Intersections Complementary Events Additive Rule. Mutually Exclusive Events Conditional Probability
Basic Statistics and Probability Chapter 3: Probability Events, Sample Spaces and Probability Unions and Intersections Complementary Events Additive Rule. Mutually Exclusive Events Conditional Probability
4. Probability of an event A for equally likely outcomes:
 University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Probability Probability: A measure of the chance that something will occur. 1. Random experiment:
University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Probability Probability: A measure of the chance that something will occur. 1. Random experiment:
STAT 302 Introduction to Probability Learning Outcomes. Textbook: A First Course in Probability by Sheldon Ross, 8 th ed.
 STAT 302 Introduction to Probability Learning Outcomes Textbook: A First Course in Probability by Sheldon Ross, 8 th ed. Chapter 1: Combinatorial Analysis Demonstrate the ability to solve combinatorial
STAT 302 Introduction to Probability Learning Outcomes Textbook: A First Course in Probability by Sheldon Ross, 8 th ed. Chapter 1: Combinatorial Analysis Demonstrate the ability to solve combinatorial
Sixth Edition. Chapter 2 Probability. Copyright 2014 John Wiley & Sons, Inc. All rights reserved. Probability
 Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 2 Probability 2 Probability CHAPTER OUTLINE 2-1 Sample Spaces and Events 2-1.1 Random Experiments
Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger Chapter 2 Probability 2 Probability CHAPTER OUTLINE 2-1 Sample Spaces and Events 2-1.1 Random Experiments
Venn Diagrams; Probability Laws. Notes. Set Operations and Relations. Venn Diagram 2.1. Venn Diagrams; Probability Laws. Notes
 Lecture 2 s; Text: A Course in Probability by Weiss 2.4 STAT 225 Introduction to Probability Models January 8, 2014 s; Whitney Huang Purdue University 2.1 Agenda s; 1 2 2.2 Intersection: the intersection
Lecture 2 s; Text: A Course in Probability by Weiss 2.4 STAT 225 Introduction to Probability Models January 8, 2014 s; Whitney Huang Purdue University 2.1 Agenda s; 1 2 2.2 Intersection: the intersection
Probability Theory. Fourier Series and Fourier Transform are widely used techniques to model deterministic signals.
 Probability Theory Introduction Fourier Series Fourier Transform are widely used techniques to model deterministic signals. In a typical communication system, the output of an information source (e.g.
Probability Theory Introduction Fourier Series Fourier Transform are widely used techniques to model deterministic signals. In a typical communication system, the output of an information source (e.g.
2011 Pearson Education, Inc
 Statistics for Business and Economics Chapter 3 Probability Contents 1. Events, Sample Spaces, and Probability 2. Unions and Intersections 3. Complementary Events 4. The Additive Rule and Mutually Exclusive
Statistics for Business and Economics Chapter 3 Probability Contents 1. Events, Sample Spaces, and Probability 2. Unions and Intersections 3. Complementary Events 4. The Additive Rule and Mutually Exclusive
1 The Basic Counting Principles
 1 The Basic Counting Principles The Multiplication Rule If an operation consists of k steps and the first step can be performed in n 1 ways, the second step can be performed in n ways [regardless of how
1 The Basic Counting Principles The Multiplication Rule If an operation consists of k steps and the first step can be performed in n 1 ways, the second step can be performed in n ways [regardless of how
Probability, Random Processes and Inference
 INSTITUTO POLITÉCNICO NACIONAL CENTRO DE INVESTIGACION EN COMPUTACION Laboratorio de Ciberseguridad Probability, Random Processes and Inference Dr. Ponciano Jorge Escamilla Ambrosio pescamilla@cic.ipn.mx
INSTITUTO POLITÉCNICO NACIONAL CENTRO DE INVESTIGACION EN COMPUTACION Laboratorio de Ciberseguridad Probability, Random Processes and Inference Dr. Ponciano Jorge Escamilla Ambrosio pescamilla@cic.ipn.mx
Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails.
 Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails. (In Mathematical language, the result of our toss is a random variable,
Example: Suppose we toss a quarter and observe whether it falls heads or tails, recording the result as 1 for heads and 0 for tails. (In Mathematical language, the result of our toss is a random variable,
F71SM STATISTICAL METHODS
 F71SM STATISTICAL METHODS RJG SUMMARY NOTES 2 PROBABILITY 2.1 Introduction A random experiment is an experiment which is repeatable under identical conditions, and for which, at each repetition, the outcome
F71SM STATISTICAL METHODS RJG SUMMARY NOTES 2 PROBABILITY 2.1 Introduction A random experiment is an experiment which is repeatable under identical conditions, and for which, at each repetition, the outcome
ICS141: Discrete Mathematics for Computer Science I
 ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
Chapter 6: Probability The Study of Randomness
 Chapter 6: Probability The Study of Randomness 6.1 The Idea of Probability 6.2 Probability Models 6.3 General Probability Rules 1 Simple Question: If tossing a coin, what is the probability of the coin
Chapter 6: Probability The Study of Randomness 6.1 The Idea of Probability 6.2 Probability Models 6.3 General Probability Rules 1 Simple Question: If tossing a coin, what is the probability of the coin
ECE 340 Probabilistic Methods in Engineering M/W 3-4:15. Lecture 2: Random Experiments. Prof. Vince Calhoun
 ECE 340 Probabilistic Methods in Engineering M/W 3-4:15 Lecture 2: Random Experiments Prof. Vince Calhoun Reading This class: Section 2.1-2.2 Next class: Section 2.3-2.4 Homework: Assignment 1: From the
ECE 340 Probabilistic Methods in Engineering M/W 3-4:15 Lecture 2: Random Experiments Prof. Vince Calhoun Reading This class: Section 2.1-2.2 Next class: Section 2.3-2.4 Homework: Assignment 1: From the
STAT 509: Statistics for Engineers Dr. Dewei Wang. Copyright 2014 John Wiley & Sons, Inc. All rights reserved.
 STAT 509: Statistics for Engineers Dr. Dewei Wang Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger 2 Probability CHAPTER OUTLINE 2-1 Sample Spaces and
STAT 509: Statistics for Engineers Dr. Dewei Wang Applied Statistics and Probability for Engineers Sixth Edition Douglas C. Montgomery George C. Runger 2 Probability CHAPTER OUTLINE 2-1 Sample Spaces and
Why study probability? Set theory. ECE 6010 Lecture 1 Introduction; Review of Random Variables
 ECE 6010 Lecture 1 Introduction; Review of Random Variables Readings from G&S: Chapter 1. Section 2.1, Section 2.3, Section 2.4, Section 3.1, Section 3.2, Section 3.5, Section 4.1, Section 4.2, Section
ECE 6010 Lecture 1 Introduction; Review of Random Variables Readings from G&S: Chapter 1. Section 2.1, Section 2.3, Section 2.4, Section 3.1, Section 3.2, Section 3.5, Section 4.1, Section 4.2, Section
CS626 Data Analysis and Simulation
 CS626 Data Analysis and Simulation Instructor: Peter Kemper R 104A, phone 221-3462, email:kemper@cs.wm.edu Today: Probability Primer Quick Reference: Sheldon Ross: Introduction to Probability Models 9th
CS626 Data Analysis and Simulation Instructor: Peter Kemper R 104A, phone 221-3462, email:kemper@cs.wm.edu Today: Probability Primer Quick Reference: Sheldon Ross: Introduction to Probability Models 9th
SETS. Chapter Overview
 Chapter 1 SETS 1.1 Overview This chapter deals with the concept of a set, operations on sets.concept of sets will be useful in studying the relations and functions. 1.1.1 Set and their representations
Chapter 1 SETS 1.1 Overview This chapter deals with the concept of a set, operations on sets.concept of sets will be useful in studying the relations and functions. 1.1.1 Set and their representations
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page α 2 θ 1 u 3. wear coat. θ 2 = warm u 2 = sweaty! θ 1 = cold u 3 = brrr!
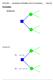 ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
God doesn t play dice. - Albert Einstein
 ECE 450 Lecture 1 God doesn t play dice. - Albert Einstein As far as the laws of mathematics refer to reality, they are not certain; as far as they are certain, they do not refer to reality. Lecture Overview
ECE 450 Lecture 1 God doesn t play dice. - Albert Einstein As far as the laws of mathematics refer to reality, they are not certain; as far as they are certain, they do not refer to reality. Lecture Overview
AIM HIGH SCHOOL. Curriculum Map W. 12 Mile Road Farmington Hills, MI (248)
 AIM HIGH SCHOOL Curriculum Map 2923 W. 12 Mile Road Farmington Hills, MI 48334 (248) 702-6922 www.aimhighschool.com COURSE TITLE: Statistics DESCRIPTION OF COURSE: PREREQUISITES: Algebra 2 Students will
AIM HIGH SCHOOL Curriculum Map 2923 W. 12 Mile Road Farmington Hills, MI 48334 (248) 702-6922 www.aimhighschool.com COURSE TITLE: Statistics DESCRIPTION OF COURSE: PREREQUISITES: Algebra 2 Students will
the time it takes until a radioactive substance undergoes a decay
 1 Probabilities 1.1 Experiments with randomness Wewillusethetermexperimentinaverygeneralwaytorefertosomeprocess that produces a random outcome. Examples: (Ask class for some first) Here are some discrete
1 Probabilities 1.1 Experiments with randomness Wewillusethetermexperimentinaverygeneralwaytorefertosomeprocess that produces a random outcome. Examples: (Ask class for some first) Here are some discrete
STT When trying to evaluate the likelihood of random events we are using following wording.
 Introduction to Chapter 2. Probability. When trying to evaluate the likelihood of random events we are using following wording. Provide your own corresponding examples. Subjective probability. An individual
Introduction to Chapter 2. Probability. When trying to evaluate the likelihood of random events we are using following wording. Provide your own corresponding examples. Subjective probability. An individual
Econ 325: Introduction to Empirical Economics
 Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
Econ 325: Introduction to Empirical Economics Lecture 2 Probability Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 3-1 3.1 Definition Random Experiment a process leading to an uncertain
MA : Introductory Probability
 MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
MA 320-001: Introductory Probability David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma320/ Spring 2017 David Murrugarra (University of Kentucky) MA 320:
A B is shaded A B A B
 NION: Let and be subsets of a universal set. The union of sets and is the set of all elements in that belong to or to or to both, and is denoted. Symbolically: = {x x or x } EMMPLE: Let = {a, b, c, d,
NION: Let and be subsets of a universal set. The union of sets and is the set of all elements in that belong to or to or to both, and is denoted. Symbolically: = {x x or x } EMMPLE: Let = {a, b, c, d,
Probabilistic models
 Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became the definitive formulation
Kolmogorov (Andrei Nikolaevich, 1903 1987) put forward an axiomatic system for probability theory. Foundations of the Calculus of Probabilities, published in 1933, immediately became the definitive formulation
STAT Chapter 3: Probability
 Basic Definitions STAT 515 --- Chapter 3: Probability Experiment: A process which leads to a single outcome (called a sample point) that cannot be predicted with certainty. Sample Space (of an experiment):
Basic Definitions STAT 515 --- Chapter 3: Probability Experiment: A process which leads to a single outcome (called a sample point) that cannot be predicted with certainty. Sample Space (of an experiment):
Probability and Applications
 Chapter 5 Probability and Applications 5.2 SOME USEFUL DEFINITIONS Random experiment: a process that has an unknown outcome or outcomes that are known only after the process is completed. Event: an outcome
Chapter 5 Probability and Applications 5.2 SOME USEFUL DEFINITIONS Random experiment: a process that has an unknown outcome or outcomes that are known only after the process is completed. Event: an outcome
Probability 1 (MATH 11300) lecture slides
 Probability 1 (MATH 11300) lecture slides Márton Balázs School of Mathematics University of Bristol Autumn, 2015 December 16, 2015 To know... http://www.maths.bris.ac.uk/ mb13434/prob1/ m.balazs@bristol.ac.uk
Probability 1 (MATH 11300) lecture slides Márton Balázs School of Mathematics University of Bristol Autumn, 2015 December 16, 2015 To know... http://www.maths.bris.ac.uk/ mb13434/prob1/ m.balazs@bristol.ac.uk
STAT:5100 (22S:193) Statistical Inference I
 STAT:5100 (22S:193) Statistical Inference I Week 3 Luke Tierney University of Iowa Fall 2015 Luke Tierney (U Iowa) STAT:5100 (22S:193) Statistical Inference I Fall 2015 1 Recap Matching problem Generalized
STAT:5100 (22S:193) Statistical Inference I Week 3 Luke Tierney University of Iowa Fall 2015 Luke Tierney (U Iowa) STAT:5100 (22S:193) Statistical Inference I Fall 2015 1 Recap Matching problem Generalized
Probability. Part 1 - Basic Counting Principles. 1. References. (1) R. Durrett, The Essentials of Probability, Duxbury.
 Probability Part 1 - Basic Counting Principles 1. References (1) R. Durrett, The Essentials of Probability, Duxbury. (2) L.L. Helms, Probability Theory with Contemporary Applications, Freeman. (3) J.J.
Probability Part 1 - Basic Counting Principles 1. References (1) R. Durrett, The Essentials of Probability, Duxbury. (2) L.L. Helms, Probability Theory with Contemporary Applications, Freeman. (3) J.J.
A Probability Primer. A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes.
 A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
BOOLEAN ALGEBRA INTRODUCTION SUBSETS
 BOOLEAN ALGEBRA M. Ragheb 1/294/2018 INTRODUCTION Modern algebra is centered around the concept of an algebraic system: A, consisting of a set of elements: ai, i=1, 2,, which are combined by a set of operations
BOOLEAN ALGEBRA M. Ragheb 1/294/2018 INTRODUCTION Modern algebra is centered around the concept of an algebraic system: A, consisting of a set of elements: ai, i=1, 2,, which are combined by a set of operations
Probability Dr. Manjula Gunarathna 1
 Probability Dr. Manjula Gunarathna Probability Dr. Manjula Gunarathna 1 Introduction Probability theory was originated from gambling theory Probability Dr. Manjula Gunarathna 2 History of Probability Galileo
Probability Dr. Manjula Gunarathna Probability Dr. Manjula Gunarathna 1 Introduction Probability theory was originated from gambling theory Probability Dr. Manjula Gunarathna 2 History of Probability Galileo
Lecture notes for probability. Math 124
 Lecture notes for probability Math 124 What is probability? Probabilities are ratios, expressed as fractions, decimals, or percents, determined by considering results or outcomes of experiments whose result
Lecture notes for probability Math 124 What is probability? Probabilities are ratios, expressed as fractions, decimals, or percents, determined by considering results or outcomes of experiments whose result
Review of Probabilities and Basic Statistics
 Alex Smola Barnabas Poczos TA: Ina Fiterau 4 th year PhD student MLD Review of Probabilities and Basic Statistics 10-701 Recitations 1/25/2013 Recitation 1: Statistics Intro 1 Overview Introduction to
Alex Smola Barnabas Poczos TA: Ina Fiterau 4 th year PhD student MLD Review of Probabilities and Basic Statistics 10-701 Recitations 1/25/2013 Recitation 1: Statistics Intro 1 Overview Introduction to
Probability Theory Review
 Cogsci 118A: Natural Computation I Lecture 2 (01/07/10) Lecturer: Angela Yu Probability Theory Review Scribe: Joseph Schilz Lecture Summary 1. Set theory: terms and operators In this section, we provide
Cogsci 118A: Natural Computation I Lecture 2 (01/07/10) Lecturer: Angela Yu Probability Theory Review Scribe: Joseph Schilz Lecture Summary 1. Set theory: terms and operators In this section, we provide
Information Science 2
 Information Science 2 Probability Theory: An Overview Week 12 College of Information Science and Engineering Ritsumeikan University Agenda Terms and concepts from Week 11 Basic concepts of probability
Information Science 2 Probability Theory: An Overview Week 12 College of Information Science and Engineering Ritsumeikan University Agenda Terms and concepts from Week 11 Basic concepts of probability
Set Theory. CPT Section D Quantitative Aptitude Chapter 7 Brijeshwar Prasad Gupta
 Set Theory CPT Section D Quantitative Aptitude Chapter 7 Brijeshwar Prasad Gupta Learning Objectives Number system Set Theory Set operations Product of Sets MCQ Number system Natural numbers:- N N = {1,2,3..}
Set Theory CPT Section D Quantitative Aptitude Chapter 7 Brijeshwar Prasad Gupta Learning Objectives Number system Set Theory Set operations Product of Sets MCQ Number system Natural numbers:- N N = {1,2,3..}
Mean, Median and Mode. Lecture 3 - Axioms of Probability. Where do they come from? Graphically. We start with a set of 21 numbers, Sta102 / BME102
 Mean, Median and Mode Lecture 3 - Axioms of Probability Sta102 / BME102 Colin Rundel September 1, 2014 We start with a set of 21 numbers, ## [1] -2.2-1.6-1.0-0.5-0.4-0.3-0.2 0.1 0.1 0.2 0.4 ## [12] 0.4
Mean, Median and Mode Lecture 3 - Axioms of Probability Sta102 / BME102 Colin Rundel September 1, 2014 We start with a set of 21 numbers, ## [1] -2.2-1.6-1.0-0.5-0.4-0.3-0.2 0.1 0.1 0.2 0.4 ## [12] 0.4
A new Approach to Drawing Conclusions from Data A Rough Set Perspective
 Motto: Let the data speak for themselves R.A. Fisher A new Approach to Drawing Conclusions from Data A Rough et Perspective Zdzisław Pawlak Institute for Theoretical and Applied Informatics Polish Academy
Motto: Let the data speak for themselves R.A. Fisher A new Approach to Drawing Conclusions from Data A Rough et Perspective Zdzisław Pawlak Institute for Theoretical and Applied Informatics Polish Academy
Lecture 4. Selected material from: Ch. 6 Probability
 Lecture 4 Selected material from: Ch. 6 Probability Example: Music preferences F M Suppose you want to know what types of CD s males and females are more likely to buy. The CD s are classified as Classical,
Lecture 4 Selected material from: Ch. 6 Probability Example: Music preferences F M Suppose you want to know what types of CD s males and females are more likely to buy. The CD s are classified as Classical,
CHAPTER 1 SETS AND EVENTS
 CHPTER 1 SETS ND EVENTS 1.1 Universal Set and Subsets DEFINITION: set is a well-defined collection of distinct elements in the universal set. This is denoted by capital latin letters, B, C, If an element
CHPTER 1 SETS ND EVENTS 1.1 Universal Set and Subsets DEFINITION: set is a well-defined collection of distinct elements in the universal set. This is denoted by capital latin letters, B, C, If an element
EE 178 Lecture Notes 0 Course Introduction. About EE178. About Probability. Course Goals. Course Topics. Lecture Notes EE 178
 EE 178 Lecture Notes 0 Course Introduction About EE178 About Probability Course Goals Course Topics Lecture Notes EE 178: Course Introduction Page 0 1 EE 178 EE 178 provides an introduction to probabilistic
EE 178 Lecture Notes 0 Course Introduction About EE178 About Probability Course Goals Course Topics Lecture Notes EE 178: Course Introduction Page 0 1 EE 178 EE 178 provides an introduction to probabilistic
Making Hard Decision. Probability Basics. ENCE 627 Decision Analysis for Engineering
 CHAPTER Duxbury Thomson Learning Making Hard Decision Probability asics Third Edition A. J. Clark School of Engineering Department of Civil and Environmental Engineering 7b FALL 003 y Dr. Ibrahim. Assakkaf
CHAPTER Duxbury Thomson Learning Making Hard Decision Probability asics Third Edition A. J. Clark School of Engineering Department of Civil and Environmental Engineering 7b FALL 003 y Dr. Ibrahim. Assakkaf
Probability. Chapter 1 Probability. A Simple Example. Sample Space and Probability. Sample Space and Event. Sample Space (Two Dice) Probability
 Probability Chapter 1 Probability 1.1 asic Concepts researcher claims that 10% of a large population have disease H. random sample of 100 people is taken from this population and examined. If 20 people
Probability Chapter 1 Probability 1.1 asic Concepts researcher claims that 10% of a large population have disease H. random sample of 100 people is taken from this population and examined. If 20 people
Section 2: Classes of Sets
 Section 2: Classes of Sets Notation: If A, B are subsets of X, then A \ B denotes the set difference, A \ B = {x A : x B}. A B denotes the symmetric difference. A B = (A \ B) (B \ A) = (A B) \ (A B). Remarks
Section 2: Classes of Sets Notation: If A, B are subsets of X, then A \ B denotes the set difference, A \ B = {x A : x B}. A B denotes the symmetric difference. A B = (A \ B) (B \ A) = (A B) \ (A B). Remarks
Probability - Lecture 4
 1 Introduction Probability - Lecture 4 Many methods of computation physics and the comparison of data to a mathematical representation, apply stochastic methods. These ideas were first introduced in the
1 Introduction Probability - Lecture 4 Many methods of computation physics and the comparison of data to a mathematical representation, apply stochastic methods. These ideas were first introduced in the
Introduction to Probability and Sample Spaces
 2.2 2.3 Introduction to Probability and Sample Spaces Prof. Tesler Math 186 Winter 2019 Prof. Tesler Ch. 2.3-2.4 Intro to Probability Math 186 / Winter 2019 1 / 26 Course overview Probability: Determine
2.2 2.3 Introduction to Probability and Sample Spaces Prof. Tesler Math 186 Winter 2019 Prof. Tesler Ch. 2.3-2.4 Intro to Probability Math 186 / Winter 2019 1 / 26 Course overview Probability: Determine
CPSC340. Probability. Nando de Freitas September, 2012 University of British Columbia
 CPSC340 Probability Nando de Freitas September, 2012 University of British Columbia Outline of the lecture This lecture is intended at revising probabilistic concepts that play an important role in the
CPSC340 Probability Nando de Freitas September, 2012 University of British Columbia Outline of the lecture This lecture is intended at revising probabilistic concepts that play an important role in the
PROBABILITY THEORY 1. Basics
 PROILITY THEORY. asics Probability theory deals with the study of random phenomena, which under repeated experiments yield different outcomes that have certain underlying patterns about them. The notion
PROILITY THEORY. asics Probability theory deals with the study of random phenomena, which under repeated experiments yield different outcomes that have certain underlying patterns about them. The notion
Notes 1 Autumn Sample space, events. S is the number of elements in the set S.)
 MAS 108 Probability I Notes 1 Autumn 2005 Sample space, events The general setting is: We perform an experiment which can have a number of different outcomes. The sample space is the set of all possible
MAS 108 Probability I Notes 1 Autumn 2005 Sample space, events The general setting is: We perform an experiment which can have a number of different outcomes. The sample space is the set of all possible
Lecture 8: Probability
 Lecture 8: Probability The idea of probability is well-known The flipping of a balanced coin can produce one of two outcomes: T (tail) and H (head) and the symmetry between the two outcomes means, of course,
Lecture 8: Probability The idea of probability is well-known The flipping of a balanced coin can produce one of two outcomes: T (tail) and H (head) and the symmetry between the two outcomes means, of course,
Topic 3: Introduction to Probability
 Topic 3: Introduction to Probability 1 Contents 1. Introduction 2. Simple Definitions 3. Types of Probability 4. Theorems of Probability 5. Probabilities under conditions of statistically independent events
Topic 3: Introduction to Probability 1 Contents 1. Introduction 2. Simple Definitions 3. Types of Probability 4. Theorems of Probability 5. Probabilities under conditions of statistically independent events
Probability: Sets, Sample Spaces, Events
 Probability: Sets, Sample Spaces, Events Engineering Statistics Section 2.1 Josh Engwer TTU 01 February 2016 Josh Engwer (TTU) Probability: Sets, Sample Spaces, Events 01 February 2016 1 / 29 The Need
Probability: Sets, Sample Spaces, Events Engineering Statistics Section 2.1 Josh Engwer TTU 01 February 2016 Josh Engwer (TTU) Probability: Sets, Sample Spaces, Events 01 February 2016 1 / 29 The Need
