MAT SYS 5120 (Winter 2012) Assignment 5 (not to be submitted) There are 4 questions.
|
|
|
- Hubert Lamb
- 5 years ago
- Views:
Transcription
1 MAT SYS 5120 (Winter 2012) Assignment 5 (not to be submitted) There are 4 questions. Question 1: Consider the following generator for a continuous time Markov chain Q = (a) Give the probability transition matrix P for the corresponding embedded Markov chain. (b) Based on the following output from R, give the stationary distribution φ for the embedded Markov chain. > P<-matrix(nrow=3,c(0,2/5,5/7,1/4,0,2/7,3/4,3/5,0)) > P [1,] [2,] [3,] > # the transpose of P > Pt<-t(P) > Pt [1,] [2,] [3,] > # the eigenvalues and vectors of P transpose > v<-eigen(pt) > v$values [1] > v$vectors [1,] [2,] [3,] (c) Use returns to state 1 of the continuous time Markov chain to define cycles for a renewal process. Define X n as the length of the nth cycle and R n 1
2 as the time in state 1 during the n cycle. Define N(t) as the renewal counting process, i.e. it counts the number cycles by time t. In words, what do R(t) = N(t) n=1 R n and R(t)/t represent within the context of this problem? (d) Refer to part (c). Find the expected reward of a cycle, i.e. E[R], and the expected length of a cycle, i.e. E[X]. (e) Let π 1 be the long run proportion of time in 1. Use parts (c) and (d) to find π 1. Using similar arguments, give π 2 and π 3. (f) Let π be the long-run probability vector from part (e). Show that π is the stationary distribution of the continuous time Markov chain by showing that it satisfies the general balance equations (or equilibrium equations). solution: (a) The elements of Q are the transition rates. For example, q ij is the transition rate from state i to state j. The state transition probabilities of the embedded chain are { qij /q p ij = ii, i j 0, i = j. Thus, P = 0 1/4 3/4 2/5 0 3/5 5/7 2/7 0 (b) The vector v = [ , , ] is a left eigenvector to P with corresponding eigenvalue 1. Normalizing v to get a distribution gives the stationary distribution for the embedded chain. We get φ = 1 [ , , ] ( ) + ( ) = [0.3779, , ]. (c) R(t) is the total amount of time that the CTMC is in state i up to time t. Thus, R(t)/t is the proportion of time that the CTMC is in state i. (d) R is the sojourn time in state 1. It has an exponential distribution with rate j:j 1 q 1j. Thus, 1 E[R] = j:j 1 q = 1 1j 4 =
3 Between visits to state 1, the following visit ratios give the mean number of visits to state 2 and state 3 for the embedded chain, respectively, ν 12 = φ 2 φ 1 = = , ν 13 = φ 3 φ 1 = = By Wald s identity, the expected length of a cycle is E[X] = µ 1 + ν 12 µ 2 + ν 13 µ 3, where µ i represents a mean sojourn time in state i. We get E[X] = 1 ( ) ( ) ( ) ( ) = (e) From the law of large numbers for reward renewal processes, we have R(t) t E[R] E[X] almost surely as t. Therefore, the long-run proportion of time in state 1 is π 1 = = Similarly, and π 2 = π 3 = φ 2 µ 2 (0.2117)(1/5) 3 i=1 φ = i µ i (0.3779)(1/4) + (0.2117)(1/5) + (0.4104)(1/7) = φ 3 µ 3 (0.4104)(1/7) 3 i=1 φ = i µ i (0.3779)(1/4) + (0.2117)(1/5) + (0.4104)(1/7) = (f) We need to show that π Q = 0. Here is a verification with R: > Q<-matrix(nrow=3,c(-4,2,5,1,-5,2,3,3,-7)) > Q [1,] [2,] [3,] > pi<-matrix(nrow=1,c(0.4834, , )) > pi [1,] > pi %*% Q [1,] -4e-04 4e e-16 3
4 Taking rounding under consideration, we have π Q = 0. Question 2: In a two-bay car wash, where cars arrive at the rate of λ = 9 cars per hour and the average duration of a car wash is twelve minutes, what is the probability that an arriving customer will find at least one of the bays occupied? Solution: We can model the car wash as an M/M/2 queueing model. The arrival rate is λ = 9 cars per hour. The mean time to service a car is 12 minutes, which is equivalent to 0.2 hour. So the service rate for a bay is µ = 1/0.2 = 5 cars per hour. We want the probability that the system is not empty, that is 1 π 0 = 1 1 ρ 1 + ρ = = 0.947, where the traffic intensity is ρ = λ/(2 µ) = 9/(2 (5)) = 0.9. So the probability that an arriving customer will find at least one of the bays occupied is 94.7%. Question 3: At a particular exit ramp on the highway, there is a single tollbooth. It was originally thought that there would be insufficient traffic at this point to justify more than one booth, but the traffic has increased recently. There are now (during rush hour, which is the period of concern) an average of 210 cars per hours, and the average service time is fifteen seconds. Two proposals have been made. The first is to add another toll booth identical to the first (assume the traffic would split evenly and at random between the two). The second is to add an automatic (that is, no human operator) booth that accepts exact change only. That booth would have an average service time of only five seconds, but only a third of the arrivals (selected at random) would have exact change. The performance measure of concern is the average delay incurred by the people who exit at this ramp. Using an appropriate queuing model, estimate the delay under the present system, the first proposal, and the second proposal. solution: Consider the case where we add a second booth. We have two M/M/1 queues, each as an arrival rate of λ = 210/2 = 105 cars per hour. The service rate at a booth is 1 customer per 15 seconds, which is equivalent to 4 customers per minute or µ = 240 customers per hour. The traffic intensity for each M/M/1 queue is ρ = λ/µ = 105/240 = The mean waiting time to go through such a system (i.e. queueing time plus 4
5 service time) is W = 1 λ L = = hours (or seconds). Remark: We used the fact that the mean number of customers in the system for an M/M/1 queue is L = and Little s Law that L = λ W. ρ 1 ρ = = Now let us consider the scenario with an automatic booth. Again we have 2 M/M/1 queues, but the traffic intensity of the first queue (with the human operators) is ρ = λ (2/3) (210) = = µ 240 The mean waiting time to go through such a system (i.e. queueing time plus service time) is where W = 1 λ L = = hours (or 36 seconds), (2/3)(210) L = ρ 1 ρ = = The traffic intensity of the second queue (with the automatic operator) is ρ = λ µ = (1/3) (210) (3600)/5 = The mean waiting time to go through such a system (i.e. queueing time plus service time) is where W = 1 λ L = = hours (or 5.54 seconds), (1/3)(210) L = ρ 1 ρ = = Thus, one third of the customers have a mean delay of 5.54 seconds, while the others have a mean delay of 36 seconds. So the expected delay time for the second scenario is (1/3) (2/3) 36 = seconds. The mean delay for the first option is seconds. Using an automatic booth will only improve the mean delay overall customers. However, the majority of 5
6 the drivers in the latter case would see their mean delay go up to 36 seconds. The first scenario is probably the best choice. Question 4: Consider an M/M/2/4 queue. (a) Set up the state transition rate diagram. (b) What are the equilibrium equations? (c) Solve the equilibrium equations to obtain the stationary distribution. solution: (a) (b) From equation 0, we get Substitute into equation 1, we get state flow in = flow out 0 π 1 µ = π 0 λ 1 π 0 λ + π 2 (2 µ) = π 1 (λ + µ) 2 π 1 λ + π 3 (2 µ) = π 2 (λ + 2 µ) 3 π 2 λ + π 4 (2 µ) = π 3 (λ + 2 µ) 4 π 3 λ = π 4 (2 µ) π 1 = π 0 λ/µ. π 2 = π 0 λ/µ(λ + µ) 2 µ Substitute into equation 2, we get π 3 = π 0 (λ 2 /(2µ 2 ))(λ + µ) 2 µ Substitute into equation 3, we get Using 1 = 4 i=0 π i, gives π 0 = λ 2 π 0 λ 2 µ = π 0 2 µ 2. π 1 λ 2 µ = π 0 (λ 2 /(2µ 2 ))(λ + µ) π 0 λ 2 2 µ 2 µ 2 = π 0 λ 3 4 µ 3. π 4 = π 0 λ 4 8 µ 4. [ 1 + λ µ + λ ] 1 2 µ 2 + λ3 4µ 3 + λ4 8µ 4. 6
7 Note that equation 4 is also satisfied. Therefore, π 1 = π 0 λ/µ, π 2 = π 0 λ 2 2 µ 2, π 3 = π 0 λ 3 4 µ 3, π 4 = π 0 λ 4 8 µ 4, and π 0 = [ 1 + λ µ + λ ] 1 2 µ 2 + λ3 4µ 3 + λ4 8µ 4. 7
The Transition Probability Function P ij (t)
 The Transition Probability Function P ij (t) Consider a continuous time Markov chain {X(t), t 0}. We are interested in the probability that in t time units the process will be in state j, given that it
The Transition Probability Function P ij (t) Consider a continuous time Markov chain {X(t), t 0}. We are interested in the probability that in t time units the process will be in state j, given that it
IEOR 6711: Stochastic Models I, Fall 2003, Professor Whitt. Solutions to Final Exam: Thursday, December 18.
 IEOR 6711: Stochastic Models I, Fall 23, Professor Whitt Solutions to Final Exam: Thursday, December 18. Below are six questions with several parts. Do as much as you can. Show your work. 1. Two-Pump Gas
IEOR 6711: Stochastic Models I, Fall 23, Professor Whitt Solutions to Final Exam: Thursday, December 18. Below are six questions with several parts. Do as much as you can. Show your work. 1. Two-Pump Gas
Introduction to Queuing Networks Solutions to Problem Sheet 3
 Introduction to Queuing Networks Solutions to Problem Sheet 3 1. (a) The state space is the whole numbers {, 1, 2,...}. The transition rates are q i,i+1 λ for all i and q i, for all i 1 since, when a bus
Introduction to Queuing Networks Solutions to Problem Sheet 3 1. (a) The state space is the whole numbers {, 1, 2,...}. The transition rates are q i,i+1 λ for all i and q i, for all i 1 since, when a bus
Performance Evaluation of Queuing Systems
 Performance Evaluation of Queuing Systems Introduction to Queuing Systems System Performance Measures & Little s Law Equilibrium Solution of Birth-Death Processes Analysis of Single-Station Queuing Systems
Performance Evaluation of Queuing Systems Introduction to Queuing Systems System Performance Measures & Little s Law Equilibrium Solution of Birth-Death Processes Analysis of Single-Station Queuing Systems
Markov Chains. X(t) is a Markov Process if, for arbitrary times t 1 < t 2 <... < t k < t k+1. If X(t) is discrete-valued. If X(t) is continuous-valued
 Markov Chains X(t) is a Markov Process if, for arbitrary times t 1 < t 2
Markov Chains X(t) is a Markov Process if, for arbitrary times t 1 < t 2
Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem. Wade Trappe
 Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem Wade Trappe Lecture Overview Network of Queues Introduction Queues in Tandem roduct Form Solutions Burke s Theorem What
Queuing Networks: Burke s Theorem, Kleinrock s Approximation, and Jackson s Theorem Wade Trappe Lecture Overview Network of Queues Introduction Queues in Tandem roduct Form Solutions Burke s Theorem What
Part I Stochastic variables and Markov chains
 Part I Stochastic variables and Markov chains Random variables describe the behaviour of a phenomenon independent of any specific sample space Distribution function (cdf, cumulative distribution function)
Part I Stochastic variables and Markov chains Random variables describe the behaviour of a phenomenon independent of any specific sample space Distribution function (cdf, cumulative distribution function)
QUEUING MODELS AND MARKOV PROCESSES
 QUEUING MODELS AND MARKOV ROCESSES Queues form when customer demand for a service cannot be met immediately. They occur because of fluctuations in demand levels so that models of queuing are intrinsically
QUEUING MODELS AND MARKOV ROCESSES Queues form when customer demand for a service cannot be met immediately. They occur because of fluctuations in demand levels so that models of queuing are intrinsically
CPSC 531: System Modeling and Simulation. Carey Williamson Department of Computer Science University of Calgary Fall 2017
 CPSC 531: System Modeling and Simulation Carey Williamson Department of Computer Science University of Calgary Fall 2017 Motivating Quote for Queueing Models Good things come to those who wait - poet/writer
CPSC 531: System Modeling and Simulation Carey Williamson Department of Computer Science University of Calgary Fall 2017 Motivating Quote for Queueing Models Good things come to those who wait - poet/writer
Non Markovian Queues (contd.)
 MODULE 7: RENEWAL PROCESSES 29 Lecture 5 Non Markovian Queues (contd) For the case where the service time is constant, V ar(b) = 0, then the P-K formula for M/D/ queue reduces to L s = ρ + ρ 2 2( ρ) where
MODULE 7: RENEWAL PROCESSES 29 Lecture 5 Non Markovian Queues (contd) For the case where the service time is constant, V ar(b) = 0, then the P-K formula for M/D/ queue reduces to L s = ρ + ρ 2 2( ρ) where
Solutions to Homework Discrete Stochastic Processes MIT, Spring 2011
 Exercise 6.5: Solutions to Homework 0 6.262 Discrete Stochastic Processes MIT, Spring 20 Consider the Markov process illustrated below. The transitions are labelled by the rate q ij at which those transitions
Exercise 6.5: Solutions to Homework 0 6.262 Discrete Stochastic Processes MIT, Spring 20 Consider the Markov process illustrated below. The transitions are labelled by the rate q ij at which those transitions
Continuous-Time Markov Chain
 Continuous-Time Markov Chain Consider the process {X(t),t 0} with state space {0, 1, 2,...}. The process {X(t),t 0} is a continuous-time Markov chain if for all s, t 0 and nonnegative integers i, j, x(u),
Continuous-Time Markov Chain Consider the process {X(t),t 0} with state space {0, 1, 2,...}. The process {X(t),t 0} is a continuous-time Markov chain if for all s, t 0 and nonnegative integers i, j, x(u),
Lecture 20: Reversible Processes and Queues
 Lecture 20: Reversible Processes and Queues 1 Examples of reversible processes 11 Birth-death processes We define two non-negative sequences birth and death rates denoted by {λ n : n N 0 } and {µ n : n
Lecture 20: Reversible Processes and Queues 1 Examples of reversible processes 11 Birth-death processes We define two non-negative sequences birth and death rates denoted by {λ n : n N 0 } and {µ n : n
Figure 10.1: Recording when the event E occurs
 10 Poisson Processes Let T R be an interval. A family of random variables {X(t) ; t T} is called a continuous time stochastic process. We often consider T = [0, 1] and T = [0, ). As X(t) is a random variable
10 Poisson Processes Let T R be an interval. A family of random variables {X(t) ; t T} is called a continuous time stochastic process. We often consider T = [0, 1] and T = [0, ). As X(t) is a random variable
Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis.
 Service Engineering Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis. G/G/1 Queue: Virtual Waiting Time (Unfinished Work). GI/GI/1: Lindley s Equations
Service Engineering Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis. G/G/1 Queue: Virtual Waiting Time (Unfinished Work). GI/GI/1: Lindley s Equations
(b) What is the variance of the time until the second customer arrives, starting empty, assuming that we measure time in minutes?
 IEOR 3106: Introduction to Operations Research: Stochastic Models Fall 2006, Professor Whitt SOLUTIONS to Final Exam Chapters 4-7 and 10 in Ross, Tuesday, December 19, 4:10pm-7:00pm Open Book: but only
IEOR 3106: Introduction to Operations Research: Stochastic Models Fall 2006, Professor Whitt SOLUTIONS to Final Exam Chapters 4-7 and 10 in Ross, Tuesday, December 19, 4:10pm-7:00pm Open Book: but only
Chapter 2 SOME ANALYTICAL TOOLS USED IN THE THESIS
 Chapter 2 SOME ANALYTICAL TOOLS USED IN THE THESIS 63 2.1 Introduction In this chapter we describe the analytical tools used in this thesis. They are Markov Decision Processes(MDP), Markov Renewal process
Chapter 2 SOME ANALYTICAL TOOLS USED IN THE THESIS 63 2.1 Introduction In this chapter we describe the analytical tools used in this thesis. They are Markov Decision Processes(MDP), Markov Renewal process
BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS
 BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS Andrea Bobbio Anno Accademico 999-2000 Queueing Systems 2 Notation for Queueing Systems /λ mean time between arrivals S = /µ ρ = λ/µ N mean service time traffic
BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS Andrea Bobbio Anno Accademico 999-2000 Queueing Systems 2 Notation for Queueing Systems /λ mean time between arrivals S = /µ ρ = λ/µ N mean service time traffic
Statistics 150: Spring 2007
 Statistics 150: Spring 2007 April 23, 2008 0-1 1 Limiting Probabilities If the discrete-time Markov chain with transition probabilities p ij is irreducible and positive recurrent; then the limiting probabilities
Statistics 150: Spring 2007 April 23, 2008 0-1 1 Limiting Probabilities If the discrete-time Markov chain with transition probabilities p ij is irreducible and positive recurrent; then the limiting probabilities
Homework 1 - SOLUTION
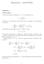 Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Introduction to Markov Chains, Queuing Theory, and Network Performance
 Introduction to Markov Chains, Queuing Theory, and Network Performance Marceau Coupechoux Telecom ParisTech, departement Informatique et Réseaux marceau.coupechoux@telecom-paristech.fr IT.2403 Modélisation
Introduction to Markov Chains, Queuing Theory, and Network Performance Marceau Coupechoux Telecom ParisTech, departement Informatique et Réseaux marceau.coupechoux@telecom-paristech.fr IT.2403 Modélisation
Queueing Theory I Summary! Little s Law! Queueing System Notation! Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K "
 Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION MH4702/MAS446/MTH437 Probabilistic Methods in OR
 NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION 2013-201 MH702/MAS6/MTH37 Probabilistic Methods in OR December 2013 TIME ALLOWED: 2 HOURS INSTRUCTIONS TO CANDIDATES 1. This examination paper contains
NANYANG TECHNOLOGICAL UNIVERSITY SEMESTER I EXAMINATION 2013-201 MH702/MAS6/MTH37 Probabilistic Methods in OR December 2013 TIME ALLOWED: 2 HOURS INSTRUCTIONS TO CANDIDATES 1. This examination paper contains
Random Walk on a Graph
 IOR 67: Stochastic Models I Second Midterm xam, hapters 3 & 4, November 2, 200 SOLUTIONS Justify your answers; show your work.. Random Walk on a raph (25 points) Random Walk on a raph 2 5 F B 3 3 2 Figure
IOR 67: Stochastic Models I Second Midterm xam, hapters 3 & 4, November 2, 200 SOLUTIONS Justify your answers; show your work.. Random Walk on a raph (25 points) Random Walk on a raph 2 5 F B 3 3 2 Figure
Data analysis and stochastic modeling
 Data analysis and stochastic modeling Lecture 7 An introduction to queueing theory Guillaume Gravier guillaume.gravier@irisa.fr with a lot of help from Paul Jensen s course http://www.me.utexas.edu/ jensen/ormm/instruction/powerpoint/or_models_09/14_queuing.ppt
Data analysis and stochastic modeling Lecture 7 An introduction to queueing theory Guillaume Gravier guillaume.gravier@irisa.fr with a lot of help from Paul Jensen s course http://www.me.utexas.edu/ jensen/ormm/instruction/powerpoint/or_models_09/14_queuing.ppt
HITTING TIME IN AN ERLANG LOSS SYSTEM
 Probability in the Engineering and Informational Sciences, 16, 2002, 167 184+ Printed in the U+S+A+ HITTING TIME IN AN ERLANG LOSS SYSTEM SHELDON M. ROSS Department of Industrial Engineering and Operations
Probability in the Engineering and Informational Sciences, 16, 2002, 167 184+ Printed in the U+S+A+ HITTING TIME IN AN ERLANG LOSS SYSTEM SHELDON M. ROSS Department of Industrial Engineering and Operations
Dynamic Control of a Tandem Queueing System with Abandonments
 Dynamic Control of a Tandem Queueing System with Abandonments Gabriel Zayas-Cabán 1 Jungui Xie 2 Linda V. Green 3 Mark E. Lewis 1 1 Cornell University Ithaca, NY 2 University of Science and Technology
Dynamic Control of a Tandem Queueing System with Abandonments Gabriel Zayas-Cabán 1 Jungui Xie 2 Linda V. Green 3 Mark E. Lewis 1 1 Cornell University Ithaca, NY 2 University of Science and Technology
L = λ W time average number in Line or system arrival rate W average Waiting time per customer
 IEOR 4615, Lecture 3, January 27, 2015 L λ Little s Law* L = λ W time average number in Line or system arrival rate W average Waiting time per customer *J. D. C. Little, A proof of the queueing formula:
IEOR 4615, Lecture 3, January 27, 2015 L λ Little s Law* L = λ W time average number in Line or system arrival rate W average Waiting time per customer *J. D. C. Little, A proof of the queueing formula:
Examination paper for TMA4265 Stochastic Processes
 Department of Mathematical Sciences Examination paper for TMA4265 Stochastic Processes Academic contact during examination: Andrea Riebler Phone: 456 89 592 Examination date: December 14th, 2015 Examination
Department of Mathematical Sciences Examination paper for TMA4265 Stochastic Processes Academic contact during examination: Andrea Riebler Phone: 456 89 592 Examination date: December 14th, 2015 Examination
Exercises Stochastic Performance Modelling. Hamilton Institute, Summer 2010
 Exercises Stochastic Performance Modelling Hamilton Institute, Summer Instruction Exercise Let X be a non-negative random variable with E[X ]
Exercises Stochastic Performance Modelling Hamilton Institute, Summer Instruction Exercise Let X be a non-negative random variable with E[X ]
IEOR 6711, HMWK 5, Professor Sigman
 IEOR 6711, HMWK 5, Professor Sigman 1. Semi-Markov processes: Consider an irreducible positive recurrent discrete-time Markov chain {X n } with transition matrix P (P i,j ), i, j S, and finite state space.
IEOR 6711, HMWK 5, Professor Sigman 1. Semi-Markov processes: Consider an irreducible positive recurrent discrete-time Markov chain {X n } with transition matrix P (P i,j ), i, j S, and finite state space.
Statistics 253/317 Introduction to Probability Models. Winter Midterm Exam Friday, Feb 8, 2013
 Statistics 253/317 Introduction to Probability Models Winter 2014 - Midterm Exam Friday, Feb 8, 2013 Student Name (print): (a) Do not sit directly next to another student. (b) This is a closed-book, closed-note
Statistics 253/317 Introduction to Probability Models Winter 2014 - Midterm Exam Friday, Feb 8, 2013 Student Name (print): (a) Do not sit directly next to another student. (b) This is a closed-book, closed-note
2905 Queueing Theory and Simulation PART III: HIGHER DIMENSIONAL AND NON-MARKOVIAN QUEUES
 295 Queueing Theory and Simulation PART III: HIGHER DIMENSIONAL AND NON-MARKOVIAN QUEUES 16 Queueing Systems with Two Types of Customers In this section, we discuss queueing systems with two types of customers.
295 Queueing Theory and Simulation PART III: HIGHER DIMENSIONAL AND NON-MARKOVIAN QUEUES 16 Queueing Systems with Two Types of Customers In this section, we discuss queueing systems with two types of customers.
GI/M/1 and GI/M/m queuing systems
 GI/M/1 and GI/M/m queuing systems Dmitri A. Moltchanov moltchan@cs.tut.fi http://www.cs.tut.fi/kurssit/tlt-2716/ OUTLINE: GI/M/1 queuing system; Methods of analysis; Imbedded Markov chain approach; Waiting
GI/M/1 and GI/M/m queuing systems Dmitri A. Moltchanov moltchan@cs.tut.fi http://www.cs.tut.fi/kurssit/tlt-2716/ OUTLINE: GI/M/1 queuing system; Methods of analysis; Imbedded Markov chain approach; Waiting
P (L d k = n). P (L(t) = n),
 4 M/G/1 queue In the M/G/1 queue customers arrive according to a Poisson process with rate λ and they are treated in order of arrival The service times are independent and identically distributed with
4 M/G/1 queue In the M/G/1 queue customers arrive according to a Poisson process with rate λ and they are treated in order of arrival The service times are independent and identically distributed with
EXAM IN COURSE TMA4265 STOCHASTIC PROCESSES Wednesday 7. August, 2013 Time: 9:00 13:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Page 1 of 7 English Contact: Håkon Tjelmeland 48 22 18 96 EXAM IN COURSE TMA4265 STOCHASTIC PROCESSES Wednesday 7. August, 2013
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Page 1 of 7 English Contact: Håkon Tjelmeland 48 22 18 96 EXAM IN COURSE TMA4265 STOCHASTIC PROCESSES Wednesday 7. August, 2013
Lecture 10: Semi-Markov Type Processes
 Lecture 1: Semi-Markov Type Processes 1. Semi-Markov processes (SMP) 1.1 Definition of SMP 1.2 Transition probabilities for SMP 1.3 Hitting times and semi-markov renewal equations 2. Processes with semi-markov
Lecture 1: Semi-Markov Type Processes 1. Semi-Markov processes (SMP) 1.1 Definition of SMP 1.2 Transition probabilities for SMP 1.3 Hitting times and semi-markov renewal equations 2. Processes with semi-markov
Chapter 5: Special Types of Queuing Models
 Chapter 5: Special Types of Queuing Models Some General Queueing Models Discouraged Arrivals Impatient Arrivals Bulk Service and Bulk Arrivals OR37-Dr.Khalid Al-Nowibet 1 5.1 General Queueing Models 1.
Chapter 5: Special Types of Queuing Models Some General Queueing Models Discouraged Arrivals Impatient Arrivals Bulk Service and Bulk Arrivals OR37-Dr.Khalid Al-Nowibet 1 5.1 General Queueing Models 1.
Link Models for Circuit Switching
 Link Models for Circuit Switching The basis of traffic engineering for telecommunication networks is the Erlang loss function. It basically allows us to determine the amount of telephone traffic that can
Link Models for Circuit Switching The basis of traffic engineering for telecommunication networks is the Erlang loss function. It basically allows us to determine the amount of telephone traffic that can
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours)
 1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
UNIVERSITY OF YORK. MSc Examinations 2004 MATHEMATICS Networks. Time Allowed: 3 hours.
 UNIVERSITY OF YORK MSc Examinations 2004 MATHEMATICS Networks Time Allowed: 3 hours. Answer 4 questions. Standard calculators will be provided but should be unnecessary. 1 Turn over 2 continued on next
UNIVERSITY OF YORK MSc Examinations 2004 MATHEMATICS Networks Time Allowed: 3 hours. Answer 4 questions. Standard calculators will be provided but should be unnecessary. 1 Turn over 2 continued on next
Stochastic Processes. Theory for Applications. Robert G. Gallager CAMBRIDGE UNIVERSITY PRESS
 Stochastic Processes Theory for Applications Robert G. Gallager CAMBRIDGE UNIVERSITY PRESS Contents Preface page xv Swgg&sfzoMj ybr zmjfr%cforj owf fmdy xix Acknowledgements xxi 1 Introduction and review
Stochastic Processes Theory for Applications Robert G. Gallager CAMBRIDGE UNIVERSITY PRESS Contents Preface page xv Swgg&sfzoMj ybr zmjfr%cforj owf fmdy xix Acknowledgements xxi 1 Introduction and review
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.262 Discrete Stochastic Processes Midterm Quiz April 6, 2010 There are 5 questions, each with several parts.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Electrical Engineering and Computer Science 6.262 Discrete Stochastic Processes Midterm Quiz April 6, 2010 There are 5 questions, each with several parts.
Stochastic process. X, a series of random variables indexed by t
 Stochastic process X, a series of random variables indexed by t X={X(t), t 0} is a continuous time stochastic process X={X(t), t=0,1, } is a discrete time stochastic process X(t) is the state at time t,
Stochastic process X, a series of random variables indexed by t X={X(t), t 0} is a continuous time stochastic process X={X(t), t=0,1, } is a discrete time stochastic process X(t) is the state at time t,
2.2t t 3 =1.2t+0.035' t= D, = f ? t 3 dt f ' 2 dt
 5.5 Queuing Theory and Traffic Flow Analysis 159 EXAMPLE 5.8 After observing arrivals and departures at a highway toll booth over a 60-minute tim e period, an observer notes that the arrival and departure
5.5 Queuing Theory and Traffic Flow Analysis 159 EXAMPLE 5.8 After observing arrivals and departures at a highway toll booth over a 60-minute tim e period, an observer notes that the arrival and departure
Since D has an exponential distribution, E[D] = 0.09 years. Since {A(t) : t 0} is a Poisson process with rate λ = 10, 000, A(0.
![Since D has an exponential distribution, E[D] = 0.09 years. Since {A(t) : t 0} is a Poisson process with rate λ = 10, 000, A(0. Since D has an exponential distribution, E[D] = 0.09 years. Since {A(t) : t 0} is a Poisson process with rate λ = 10, 000, A(0.](/thumbs/95/124116804.jpg) IEOR 46: Introduction to Operations Research: Stochastic Models Chapters 5-6 in Ross, Thursday, April, 4:5-5:35pm SOLUTIONS to Second Midterm Exam, Spring 9, Open Book: but only the Ross textbook, the
IEOR 46: Introduction to Operations Research: Stochastic Models Chapters 5-6 in Ross, Thursday, April, 4:5-5:35pm SOLUTIONS to Second Midterm Exam, Spring 9, Open Book: but only the Ross textbook, the
Name of the Student:
 SUBJECT NAME : Probability & Queueing Theory SUBJECT CODE : MA 6453 MATERIAL NAME : Part A questions REGULATION : R2013 UPDATED ON : November 2017 (Upto N/D 2017 QP) (Scan the above QR code for the direct
SUBJECT NAME : Probability & Queueing Theory SUBJECT CODE : MA 6453 MATERIAL NAME : Part A questions REGULATION : R2013 UPDATED ON : November 2017 (Upto N/D 2017 QP) (Scan the above QR code for the direct
Solutions to Homework Discrete Stochastic Processes MIT, Spring 2011
 Exercise 1 Solutions to Homework 6 6.262 Discrete Stochastic Processes MIT, Spring 2011 Let {Y n ; n 1} be a sequence of rv s and assume that lim n E[ Y n ] = 0. Show that {Y n ; n 1} converges to 0 in
Exercise 1 Solutions to Homework 6 6.262 Discrete Stochastic Processes MIT, Spring 2011 Let {Y n ; n 1} be a sequence of rv s and assume that lim n E[ Y n ] = 0. Show that {Y n ; n 1} converges to 0 in
IE 5112 Final Exam 2010
 IE 5112 Final Exam 2010 1. There are six cities in Kilroy County. The county must decide where to build fire stations. The county wants to build as few fire stations as possible while ensuring that there
IE 5112 Final Exam 2010 1. There are six cities in Kilroy County. The county must decide where to build fire stations. The county wants to build as few fire stations as possible while ensuring that there
Continuous-time Markov Chains
 Continuous-time Markov Chains Gonzalo Mateos Dept. of ECE and Goergen Institute for Data Science University of Rochester gmateosb@ece.rochester.edu http://www.ece.rochester.edu/~gmateosb/ October 23, 2017
Continuous-time Markov Chains Gonzalo Mateos Dept. of ECE and Goergen Institute for Data Science University of Rochester gmateosb@ece.rochester.edu http://www.ece.rochester.edu/~gmateosb/ October 23, 2017
T. Liggett Mathematics 171 Final Exam June 8, 2011
 T. Liggett Mathematics 171 Final Exam June 8, 2011 1. The continuous time renewal chain X t has state space S = {0, 1, 2,...} and transition rates (i.e., Q matrix) given by q(n, n 1) = δ n and q(0, n)
T. Liggett Mathematics 171 Final Exam June 8, 2011 1. The continuous time renewal chain X t has state space S = {0, 1, 2,...} and transition rates (i.e., Q matrix) given by q(n, n 1) = δ n and q(0, n)
Chapter 6 Queueing Models. Banks, Carson, Nelson & Nicol Discrete-Event System Simulation
 Chapter 6 Queueing Models Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Purpose Simulation is often used in the analysis of queueing models. A simple but typical queueing model: Queueing
Chapter 6 Queueing Models Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Purpose Simulation is often used in the analysis of queueing models. A simple but typical queueing model: Queueing
Queuing Theory. Richard Lockhart. Simon Fraser University. STAT 870 Summer 2011
 Queuing Theory Richard Lockhart Simon Fraser University STAT 870 Summer 2011 Richard Lockhart (Simon Fraser University) Queuing Theory STAT 870 Summer 2011 1 / 15 Purposes of Today s Lecture Describe general
Queuing Theory Richard Lockhart Simon Fraser University STAT 870 Summer 2011 Richard Lockhart (Simon Fraser University) Queuing Theory STAT 870 Summer 2011 1 / 15 Purposes of Today s Lecture Describe general
Queueing systems. Renato Lo Cigno. Simulation and Performance Evaluation Queueing systems - Renato Lo Cigno 1
 Queueing systems Renato Lo Cigno Simulation and Performance Evaluation 2014-15 Queueing systems - Renato Lo Cigno 1 Queues A Birth-Death process is well modeled by a queue Indeed queues can be used to
Queueing systems Renato Lo Cigno Simulation and Performance Evaluation 2014-15 Queueing systems - Renato Lo Cigno 1 Queues A Birth-Death process is well modeled by a queue Indeed queues can be used to
Introduction to queuing theory
 Introduction to queuing theory Queu(e)ing theory Queu(e)ing theory is the branch of mathematics devoted to how objects (packets in a network, people in a bank, processes in a CPU etc etc) join and leave
Introduction to queuing theory Queu(e)ing theory Queu(e)ing theory is the branch of mathematics devoted to how objects (packets in a network, people in a bank, processes in a CPU etc etc) join and leave
SOLUTIONS IEOR 3106: Second Midterm Exam, Chapters 5-6, November 8, 2012
 SOLUTIONS IEOR 3106: Second Midterm Exam, Chapters 5-6, November 8, 2012 This exam is closed book. YOU NEED TO SHOW YOUR WORK. Honor Code: Students are expected to behave honorably, following the accepted
SOLUTIONS IEOR 3106: Second Midterm Exam, Chapters 5-6, November 8, 2012 This exam is closed book. YOU NEED TO SHOW YOUR WORK. Honor Code: Students are expected to behave honorably, following the accepted
Networking = Plumbing. Queueing Analysis: I. Last Lecture. Lecture Outline. Jeremiah Deng. 29 July 2013
 Networking = Plumbing TELE302 Lecture 7 Queueing Analysis: I Jeremiah Deng University of Otago 29 July 2013 Jeremiah Deng (University of Otago) TELE302 Lecture 7 29 July 2013 1 / 33 Lecture Outline Jeremiah
Networking = Plumbing TELE302 Lecture 7 Queueing Analysis: I Jeremiah Deng University of Otago 29 July 2013 Jeremiah Deng (University of Otago) TELE302 Lecture 7 29 July 2013 1 / 33 Lecture Outline Jeremiah
Q = (c) Assuming that Ricoh has been working continuously for 7 days, what is the probability that it will remain working at least 8 more days?
 IEOR 4106: Introduction to Operations Research: Stochastic Models Spring 2005, Professor Whitt, Second Midterm Exam Chapters 5-6 in Ross, Thursday, March 31, 11:00am-1:00pm Open Book: but only the Ross
IEOR 4106: Introduction to Operations Research: Stochastic Models Spring 2005, Professor Whitt, Second Midterm Exam Chapters 5-6 in Ross, Thursday, March 31, 11:00am-1:00pm Open Book: but only the Ross
Queueing Theory II. Summary. ! M/M/1 Output process. ! Networks of Queue! Method of Stages. ! General Distributions
 Queueing Theory II Summary! M/M/1 Output process! Networks of Queue! Method of Stages " Erlang Distribution " Hyperexponential Distribution! General Distributions " Embedded Markov Chains M/M/1 Output
Queueing Theory II Summary! M/M/1 Output process! Networks of Queue! Method of Stages " Erlang Distribution " Hyperexponential Distribution! General Distributions " Embedded Markov Chains M/M/1 Output
Little s result. T = average sojourn time (time spent) in the system N = average number of customers in the system. Little s result says that
 J. Virtamo 38.143 Queueing Theory / Little s result 1 Little s result The result Little s result or Little s theorem is a very simple (but fundamental) relation between the arrival rate of customers, average
J. Virtamo 38.143 Queueing Theory / Little s result 1 Little s result The result Little s result or Little s theorem is a very simple (but fundamental) relation between the arrival rate of customers, average
Irreducibility. Irreducible. every state can be reached from every other state For any i,j, exist an m 0, such that. Absorbing state: p jj =1
 Irreducibility Irreducible every state can be reached from every other state For any i,j, exist an m 0, such that i,j are communicate, if the above condition is valid Irreducible: all states are communicate
Irreducibility Irreducible every state can be reached from every other state For any i,j, exist an m 0, such that i,j are communicate, if the above condition is valid Irreducible: all states are communicate
Queues and Queueing Networks
 Queues and Queueing Networks Sanjay K. Bose Dept. of EEE, IITG Copyright 2015, Sanjay K. Bose 1 Introduction to Queueing Models and Queueing Analysis Copyright 2015, Sanjay K. Bose 2 Model of a Queue Arrivals
Queues and Queueing Networks Sanjay K. Bose Dept. of EEE, IITG Copyright 2015, Sanjay K. Bose 1 Introduction to Queueing Models and Queueing Analysis Copyright 2015, Sanjay K. Bose 2 Model of a Queue Arrivals
Queuing Analysis. Chapter Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall
 Queuing Analysis Chapter 13 13-1 Chapter Topics Elements of Waiting Line Analysis The Single-Server Waiting Line System Undefined and Constant Service Times Finite Queue Length Finite Calling Problem The
Queuing Analysis Chapter 13 13-1 Chapter Topics Elements of Waiting Line Analysis The Single-Server Waiting Line System Undefined and Constant Service Times Finite Queue Length Finite Calling Problem The
16:330:543 Communication Networks I Midterm Exam November 7, 2005
 l l l l l l l l 1 3 np n = ρ 1 ρ = λ µ λ. n= T = E[N] = 1 λ µ λ = 1 µ 1. 16:33:543 Communication Networks I Midterm Exam November 7, 5 You have 16 minutes to complete this four problem exam. If you know
l l l l l l l l 1 3 np n = ρ 1 ρ = λ µ λ. n= T = E[N] = 1 λ µ λ = 1 µ 1. 16:33:543 Communication Networks I Midterm Exam November 7, 5 You have 16 minutes to complete this four problem exam. If you know
STAT 380 Continuous Time Markov Chains
 STAT 380 Continuous Time Markov Chains Richard Lockhart Simon Fraser University Spring 2018 Richard Lockhart (Simon Fraser University)STAT 380 Continuous Time Markov Chains Spring 2018 1 / 35 Continuous
STAT 380 Continuous Time Markov Chains Richard Lockhart Simon Fraser University Spring 2018 Richard Lockhart (Simon Fraser University)STAT 380 Continuous Time Markov Chains Spring 2018 1 / 35 Continuous
THE ROYAL STATISTICAL SOCIETY 2009 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULAR FORMAT MODULE 3 STOCHASTIC PROCESSES AND TIME SERIES
 THE ROYAL STATISTICAL SOCIETY 9 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULAR FORMAT MODULE 3 STOCHASTIC PROCESSES AND TIME SERIES The Society provides these solutions to assist candidates preparing
THE ROYAL STATISTICAL SOCIETY 9 EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA MODULAR FORMAT MODULE 3 STOCHASTIC PROCESSES AND TIME SERIES The Society provides these solutions to assist candidates preparing
Introduction to Queueing Theory with Applications to Air Transportation Systems
 Introduction to Queueing Theory with Applications to Air Transportation Systems John Shortle George Mason University February 28, 2018 Outline Why stochastic models matter M/M/1 queue Little s law Priority
Introduction to Queueing Theory with Applications to Air Transportation Systems John Shortle George Mason University February 28, 2018 Outline Why stochastic models matter M/M/1 queue Little s law Priority
Course Outline Introduction to Transportation Highway Users and their Performance Geometric Design Pavement Design
 Course Outline Introduction to Transportation Highway Users and their Performance Geometric Design Pavement Design Speed Studies - Project Traffic Queuing Intersections Level of Service in Highways and
Course Outline Introduction to Transportation Highway Users and their Performance Geometric Design Pavement Design Speed Studies - Project Traffic Queuing Intersections Level of Service in Highways and
Slides 9: Queuing Models
 Slides 9: Queuing Models Purpose Simulation is often used in the analysis of queuing models. A simple but typical queuing model is: Queuing models provide the analyst with a powerful tool for designing
Slides 9: Queuing Models Purpose Simulation is often used in the analysis of queuing models. A simple but typical queuing model is: Queuing models provide the analyst with a powerful tool for designing
Computer Systems Modelling
 Computer Systems Modelling Computer Laboratory Computer Science Tripos, Part II Lent Term 2010/11 R. J. Gibbens Problem sheet William Gates Building 15 JJ Thomson Avenue Cambridge CB3 0FD http://www.cl.cam.ac.uk/
Computer Systems Modelling Computer Laboratory Computer Science Tripos, Part II Lent Term 2010/11 R. J. Gibbens Problem sheet William Gates Building 15 JJ Thomson Avenue Cambridge CB3 0FD http://www.cl.cam.ac.uk/
Statistics 433 Practice Final Exam: Cover Sheet and Marking Sheet
 Statistics 433 Practice Final Exam: Cover Sheet and Marking Sheet YOUR NAME INSTRUCTIONS: No notes, no calculators, and no communications devices are permitted. Please keep all materials away from your
Statistics 433 Practice Final Exam: Cover Sheet and Marking Sheet YOUR NAME INSTRUCTIONS: No notes, no calculators, and no communications devices are permitted. Please keep all materials away from your
Chapter 5. Continuous-Time Markov Chains. Prof. Shun-Ren Yang Department of Computer Science, National Tsing Hua University, Taiwan
 Chapter 5. Continuous-Time Markov Chains Prof. Shun-Ren Yang Department of Computer Science, National Tsing Hua University, Taiwan Continuous-Time Markov Chains Consider a continuous-time stochastic process
Chapter 5. Continuous-Time Markov Chains Prof. Shun-Ren Yang Department of Computer Science, National Tsing Hua University, Taiwan Continuous-Time Markov Chains Consider a continuous-time stochastic process
The shortest queue problem
 The shortest queue problem Ivo Adan March 19, 2002 1/40 queue 1 join the shortest queue queue 2 Where: Poisson arrivals with rate Exponential service times with mean 1/ 2/40 queue 1 queue 2 randomly assign
The shortest queue problem Ivo Adan March 19, 2002 1/40 queue 1 join the shortest queue queue 2 Where: Poisson arrivals with rate Exponential service times with mean 1/ 2/40 queue 1 queue 2 randomly assign
MATH 56A: STOCHASTIC PROCESSES CHAPTER 6
 MATH 56A: STOCHASTIC PROCESSES CHAPTER 6 6. Renewal Mathematically, renewal refers to a continuous time stochastic process with states,, 2,. N t {,, 2, 3, } so that you only have jumps from x to x + and
MATH 56A: STOCHASTIC PROCESSES CHAPTER 6 6. Renewal Mathematically, renewal refers to a continuous time stochastic process with states,, 2,. N t {,, 2, 3, } so that you only have jumps from x to x + and
Continuous time Markov chains
 Continuous time Markov chains Alejandro Ribeiro Dept. of Electrical and Systems Engineering University of Pennsylvania aribeiro@seas.upenn.edu http://www.seas.upenn.edu/users/~aribeiro/ October 16, 2017
Continuous time Markov chains Alejandro Ribeiro Dept. of Electrical and Systems Engineering University of Pennsylvania aribeiro@seas.upenn.edu http://www.seas.upenn.edu/users/~aribeiro/ October 16, 2017
Session-Based Queueing Systems
 Session-Based Queueing Systems Modelling, Simulation, and Approximation Jeroen Horters Supervisor VU: Sandjai Bhulai Executive Summary Companies often offer services that require multiple steps on the
Session-Based Queueing Systems Modelling, Simulation, and Approximation Jeroen Horters Supervisor VU: Sandjai Bhulai Executive Summary Companies often offer services that require multiple steps on the
DISCRETE STOCHASTIC PROCESSES Draft of 2nd Edition
 DISCRETE STOCHASTIC PROCESSES Draft of 2nd Edition R. G. Gallager January 31, 2011 i ii Preface These notes are a draft of a major rewrite of a text [9] of the same name. The notes and the text are outgrowths
DISCRETE STOCHASTIC PROCESSES Draft of 2nd Edition R. G. Gallager January 31, 2011 i ii Preface These notes are a draft of a major rewrite of a text [9] of the same name. The notes and the text are outgrowths
Markov Processes and Queues
 MIT 2.853/2.854 Introduction to Manufacturing Systems Markov Processes and Queues Stanley B. Gershwin Laboratory for Manufacturing and Productivity Massachusetts Institute of Technology Markov Processes
MIT 2.853/2.854 Introduction to Manufacturing Systems Markov Processes and Queues Stanley B. Gershwin Laboratory for Manufacturing and Productivity Massachusetts Institute of Technology Markov Processes
Time Reversibility and Burke s Theorem
 Queuing Analysis: Time Reversibility and Burke s Theorem Hongwei Zhang http://www.cs.wayne.edu/~hzhang Acknowledgement: this lecture is partially based on the slides of Dr. Yannis A. Korilis. Outline Time-Reversal
Queuing Analysis: Time Reversibility and Burke s Theorem Hongwei Zhang http://www.cs.wayne.edu/~hzhang Acknowledgement: this lecture is partially based on the slides of Dr. Yannis A. Korilis. Outline Time-Reversal
5/15/18. Operations Research: An Introduction Hamdy A. Taha. Copyright 2011, 2007 by Pearson Education, Inc. All rights reserved.
 The objective of queuing analysis is to offer a reasonably satisfactory service to waiting customers. Unlike the other tools of OR, queuing theory is not an optimization technique. Rather, it determines
The objective of queuing analysis is to offer a reasonably satisfactory service to waiting customers. Unlike the other tools of OR, queuing theory is not an optimization technique. Rather, it determines
Queuing Theory. Using the Math. Management Science
 Queuing Theory Using the Math 1 Markov Processes (Chains) A process consisting of a countable sequence of stages, that can be judged at each stage to fall into future states independent of how the process
Queuing Theory Using the Math 1 Markov Processes (Chains) A process consisting of a countable sequence of stages, that can be judged at each stage to fall into future states independent of how the process
TCOM 501: Networking Theory & Fundamentals. Lecture 6 February 19, 2003 Prof. Yannis A. Korilis
 TCOM 50: Networking Theory & Fundamentals Lecture 6 February 9, 003 Prof. Yannis A. Korilis 6- Topics Time-Reversal of Markov Chains Reversibility Truncating a Reversible Markov Chain Burke s Theorem Queues
TCOM 50: Networking Theory & Fundamentals Lecture 6 February 9, 003 Prof. Yannis A. Korilis 6- Topics Time-Reversal of Markov Chains Reversibility Truncating a Reversible Markov Chain Burke s Theorem Queues
Renewal theory and its applications
 Renewal theory and its applications Stella Kapodistria and Jacques Resing September 11th, 212 ISP Definition of a Renewal process Renewal theory and its applications If we substitute the Exponentially
Renewal theory and its applications Stella Kapodistria and Jacques Resing September 11th, 212 ISP Definition of a Renewal process Renewal theory and its applications If we substitute the Exponentially
Stationary remaining service time conditional on queue length
 Stationary remaining service time conditional on queue length Karl Sigman Uri Yechiali October 7, 2006 Abstract In Mandelbaum and Yechiali (1979) a simple formula is derived for the expected stationary
Stationary remaining service time conditional on queue length Karl Sigman Uri Yechiali October 7, 2006 Abstract In Mandelbaum and Yechiali (1979) a simple formula is derived for the expected stationary
Queuing Theory. 3. Birth-Death Process. Law of Motion Flow balance equations Steady-state probabilities: , if
 1 Queuing Theory 3. Birth-Death Process Law of Motion Flow balance equations Steady-state probabilities: c j = λ 0λ 1...λ j 1 µ 1 µ 2...µ j π 0 = 1 1+ j=1 c j, if j=1 c j is finite. π j = c j π 0 Example
1 Queuing Theory 3. Birth-Death Process Law of Motion Flow balance equations Steady-state probabilities: c j = λ 0λ 1...λ j 1 µ 1 µ 2...µ j π 0 = 1 1+ j=1 c j, if j=1 c j is finite. π j = c j π 0 Example
A TANDEM QUEUEING SYSTEM WITH APPLICATIONS TO PRICING STRATEGY. Wai-Ki Ching. Tang Li. Sin-Man Choi. Issic K.C. Leung
 Manuscript submitted to AIMS Journals Volume X, Number 0X, XX 00X Website: http://aimsciences.org pp. X XX A TANDEM QUEUEING SYSTEM WITH APPLICATIONS TO PRICING STRATEGY WAI-KI CHING SIN-MAN CHOI TANG
Manuscript submitted to AIMS Journals Volume X, Number 0X, XX 00X Website: http://aimsciences.org pp. X XX A TANDEM QUEUEING SYSTEM WITH APPLICATIONS TO PRICING STRATEGY WAI-KI CHING SIN-MAN CHOI TANG
1 IEOR 4701: Continuous-Time Markov Chains
 Copyright c 2006 by Karl Sigman 1 IEOR 4701: Continuous-Time Markov Chains A Markov chain in discrete time, {X n : n 0}, remains in any state for exactly one unit of time before making a transition (change
Copyright c 2006 by Karl Sigman 1 IEOR 4701: Continuous-Time Markov Chains A Markov chain in discrete time, {X n : n 0}, remains in any state for exactly one unit of time before making a transition (change
Discrete Event Systems Exam
 Computer Engineering and Networks Laboratory TEC, NSG, DISCO HS 2016 Prof. L. Thiele, Prof. L. Vanbever, Prof. R. Wattenhofer Discrete Event Systems Exam Friday, 3 rd February 2017, 14:00 16:00. Do not
Computer Engineering and Networks Laboratory TEC, NSG, DISCO HS 2016 Prof. L. Thiele, Prof. L. Vanbever, Prof. R. Wattenhofer Discrete Event Systems Exam Friday, 3 rd February 2017, 14:00 16:00. Do not
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY
 EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 011 MODULE 3 : Stochastic processes and time series Time allowed: Three Hours Candidates should answer FIVE questions. All questions carry
EXAMINATIONS OF THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA, 011 MODULE 3 : Stochastic processes and time series Time allowed: Three Hours Candidates should answer FIVE questions. All questions carry
QueueTraffic and queuing theory
 QueueTraffic and queuing theory + Queues in everyday life You have certainly been in a queue somewhere. Where? How were they different? At ticket vending machines, cash desks, at the doctors, at printers,
QueueTraffic and queuing theory + Queues in everyday life You have certainly been in a queue somewhere. Where? How were they different? At ticket vending machines, cash desks, at the doctors, at printers,
Continuous Time Processes
 page 102 Chapter 7 Continuous Time Processes 7.1 Introduction In a continuous time stochastic process (with discrete state space), a change of state can occur at any time instant. The associated point
page 102 Chapter 7 Continuous Time Processes 7.1 Introduction In a continuous time stochastic process (with discrete state space), a change of state can occur at any time instant. The associated point
IEOR 6711: Stochastic Models I Fall 2012, Professor Whitt, Thursday, October 4 Renewal Theory: Renewal Reward Processes
 IEOR 67: Stochastic Models I Fall 202, Professor Whitt, Thursday, October 4 Renewal Theory: Renewal Reward Processes Simple Renewal-Reward Theory Suppose that we have a sequence of i.i.d. random vectors
IEOR 67: Stochastic Models I Fall 202, Professor Whitt, Thursday, October 4 Renewal Theory: Renewal Reward Processes Simple Renewal-Reward Theory Suppose that we have a sequence of i.i.d. random vectors
PBW 654 Applied Statistics - I Urban Operations Research
 PBW 654 Applied Statistics - I Urban Operations Research Lecture 2.I Queuing Systems An Introduction Operations Research Models Deterministic Models Linear Programming Integer Programming Network Optimization
PBW 654 Applied Statistics - I Urban Operations Research Lecture 2.I Queuing Systems An Introduction Operations Research Models Deterministic Models Linear Programming Integer Programming Network Optimization
Introduction to queuing theory
 Introduction to queuing theory Claude Rigault ENST claude.rigault@enst.fr Introduction to Queuing theory 1 Outline The problem The number of clients in a system The client process Delay processes Loss
Introduction to queuing theory Claude Rigault ENST claude.rigault@enst.fr Introduction to Queuing theory 1 Outline The problem The number of clients in a system The client process Delay processes Loss
Intro Refresher Reversibility Open networks Closed networks Multiclass networks Other networks. Queuing Networks. Florence Perronnin
 Queuing Networks Florence Perronnin Polytech Grenoble - UGA March 23, 27 F. Perronnin (UGA) Queuing Networks March 23, 27 / 46 Outline Introduction to Queuing Networks 2 Refresher: M/M/ queue 3 Reversibility
Queuing Networks Florence Perronnin Polytech Grenoble - UGA March 23, 27 F. Perronnin (UGA) Queuing Networks March 23, 27 / 46 Outline Introduction to Queuing Networks 2 Refresher: M/M/ queue 3 Reversibility
Readings: Finish Section 5.2
 LECTURE 19 Readings: Finish Section 5.2 Lecture outline Markov Processes I Checkout counter example. Markov process: definition. -step transition probabilities. Classification of states. Example: Checkout
LECTURE 19 Readings: Finish Section 5.2 Lecture outline Markov Processes I Checkout counter example. Markov process: definition. -step transition probabilities. Classification of states. Example: Checkout
Classification of Queuing Models
 Classification of Queuing Models Generally Queuing models may be completely specified in the following symbol form:(a/b/c):(d/e)where a = Probability law for the arrival(or inter arrival)time, b = Probability
Classification of Queuing Models Generally Queuing models may be completely specified in the following symbol form:(a/b/c):(d/e)where a = Probability law for the arrival(or inter arrival)time, b = Probability
Lecture 7: Simulation of Markov Processes. Pasi Lassila Department of Communications and Networking
 Lecture 7: Simulation of Markov Processes Pasi Lassila Department of Communications and Networking Contents Markov processes theory recap Elementary queuing models for data networks Simulation of Markov
Lecture 7: Simulation of Markov Processes Pasi Lassila Department of Communications and Networking Contents Markov processes theory recap Elementary queuing models for data networks Simulation of Markov
QUEUING SYSTEM. Yetunde Folajimi, PhD
 QUEUING SYSTEM Yetunde Folajimi, PhD Part 2 Queuing Models Queueing models are constructed so that queue lengths and waiting times can be predicted They help us to understand and quantify the effect of
QUEUING SYSTEM Yetunde Folajimi, PhD Part 2 Queuing Models Queueing models are constructed so that queue lengths and waiting times can be predicted They help us to understand and quantify the effect of
Modelling data networks stochastic processes and Markov chains
 Modelling data networks stochastic processes and Markov chains a 1, 3 1, 2 2, 2 b 0, 3 2, 3 u 1, 3 α 1, 6 c 0, 3 v 2, 2 β 1, 1 Richard G. Clegg (richard@richardclegg.org) December 2011 Available online
Modelling data networks stochastic processes and Markov chains a 1, 3 1, 2 2, 2 b 0, 3 2, 3 u 1, 3 α 1, 6 c 0, 3 v 2, 2 β 1, 1 Richard G. Clegg (richard@richardclegg.org) December 2011 Available online
