arxiv: v2 [math.ds] 9 Jun 2013

Transcription

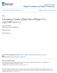
1 SHAPES OF POLYNOMIAL JULIA SETS KATHRYN A. LINDSEY arxiv: v2 [math.ds] 9 Jun 203 Abstract. Any Jordan curve in the complex plane can be approximated arbitrarily well in the Hausdorff topology by Julia sets of polynomials. Finite collections of disjoint Jordan domains can be approximated by the basins of attraction of rational maps. Figure. A filled Julia set in the shape of a cat. The polynomial which generates this Julia set has degree 30. For any complex-valued rational function f on the Riemann sphere Ĉ such that the point is an attracting fixed point of f, define the following notation: Date: June, 203.

2 2 KATHRYN A. LINDSEY L(f) = the basin of attraction of for the map f, K(f) = Ĉ \ L(f), J (f) = (K(f)), where (X) denotes the boundary of a set X. If f is a a polynomial then J (f) is the Julia set of f, K(f) is the filled Julia set of f, and K(f) is given by K(f) = {z Ĉ f n (z) as n }. Theorem.6 gives a constructive proof that for any open bounded annulus A in the complex plane, there exists a polynomial P such that J (P ) contains an essential closed curve of the closure Ā, the bounded connected component of Ĉ\Ā is contained in K(P ), and the unbounded connected component of Ĉ\ Ā is contained in L(P ). Theorem 2.2 reformulates this result in terms of the Hausdorff metric, showing that any Jordan curve in the complex plane can be approximated arbitrarily well in the Hausdorff topology by Julia sets of polynomials. Theorems 3.2, 3.3 and 3.4 combine these polynomials to form rational maps whose basins of attraction approximate more complicated sets. Acknowledgments. This project was initially a joint undertaking with William P. Thurston, who conjectured that Theorem 2.2 should be true and guided the author toward the approach presented in this paper. Sadly, William Thurston passed away in August 202, before this project reached fruition. The author wishes to express her gratitude to the anonymous referee, whose numerous helpful suggestions greatly improved the paper. She also thanks John Smillie, John Hamal Hubbard and Sarah Koch for many helpful conversations during the development of this paper. Kathryn Lindsey was supported by the Department of Defense through a National Defense Science and Engineering Graduate Fellowship and by the National Science Foundation through a Graduate Research Fellowship.. Annular decompositions and polynomial Julia sets Define A to be the collection of all subsets of Ĉ which can be written as the closure of an open, bounded (i.e. has empty intersection with some ball about ) annulus in Ĉ. For any A A, Ĉ \ A consists of two topological disks; let A denote the unbounded connected component of Ĉ \ A and let A 0 denote the bounded connected component of Ĉ\A. Thus for each A A, Ĉ = A A A 0. For each A A, let γ A be a fixed Jordan curve in C contained in the interior of A such that π (γ A ) injects into π (A) under the map induced by inclusion (i.e. γ A is an essential core curve of the annulus A). Define U A to be the unbounded connected component of Ĉ \ γ A, which is a topological disk. Let ϕ A denote a fixed inverse Riemann map ϕ A : {z Ĉ < z } U A

3 SHAPES OF POLYNOMIAL JULIA SETS 3 such that the points at infinity correspond. For some sufficiently small ɛ = ɛ(a) > 0, the set ϕ A ({z Ĉ z = + ɛ} is contained in the interior of A. Define C A to be this set, i.e. C A = ϕ A ({z Ĉ z = + ɛ}). We will now rescale the conformal map ϕ A so that the unit circle maps to C A. Specifically, define the map ϕ A : {z Ĉ +ɛ < z } Ĉ by ϕ A (z) = ϕ A (( + ɛ)(z)). Lemma.. For each A A, (i) The set C A is a Jordan curve contained in the interior of A such that π (C A ) injects into π (A) under the map induced by inclusion. (ii) C A is rectifiable with respect to the Euclidean metric on C. (iii) ϕ A is non-vanishing and of bounded variation on the unit circle. Proof. The set C A is a conformal image of S and hence a Jordan curve. It is homotopic to γ A, whose fundamental group injects nontrivially by assumption, proving (i). Since ϕ A is a conformal map, ϕ is everywhere nonzero. By the maximum modulus principle, ϕ A is bounded on S, which is itself of finite Euclidean arc length, implying (ii) and (iii). For each A A, the set Ĉ \ C A consists of two topological disks; let O A denote the unbounded connected component of Ĉ \ C A and let I A denote the bounded connected component of Ĉ\C A. Thus for each A A, we have a decomposition Ĉ = O A C A I A. Because ϕ A is injective, the coefficients for all the terms of degree greater than in the Laurent series centered at 0 for ϕ A must be zero. Hence any such Laurent series has the form ϕ A (z) = c A z + c (A,0) + c (A,) + c (A,2) z z , z, with c A, c (A,0), c (A,),... C. For each pair of natural numbers (k, n) with k n and for each A A, set r (k,n) A = ϕ A (e k2πi/n ). For each n N and A A, define ω A,n : Ĉ Ĉ by ω A,n (z) = c n A n (z r (k,n) A ). For each n N and A A, define the polynomial P A,n : Ĉ Ĉ by j= P A,n (z) = z(ω A,n (z) + ). The definitions of the map ϕ and the polynomials ω n use only the Jordan curve C A, and not the fact that C A came from the annulus A. Thus any Jordan curve C in C determines both a conformal map ϕ C and a family of polynomials ω C,n, n N; these polynomials are called fundamental polynomials of Lagrange interpolation. Curtiss proved the following two theorems about the uniform convergence of such polynomials in [Cur4] (we transcribe them here using our notation):

4 4 KATHRYN A. LINDSEY Theorem.2. [Cur4] If C is a rectifiable Jordan curve in C, then () lim n ω C,n(z) = uniformly for z on any closed subset of the region interior to C, and ω C,n (z) (2) lim n w n =, where z = ϕ C(w), uniformly for z on any closed subset of the region exterior to C. Theorem.3. [Cur4] If ϕ C (w) is non-vanishing and of bounded variation for w = then limit (2) in Theorem.2 converges uniformly for z in the closed region C C, where C denotes the unbounded connected component of Ĉ \ C. The reason for choosing the curve C A as we did was to use Curtiss theorems to guarantee that the polynomials ω A,n converge uniformly not only on bounded subsets of O A (as in Theorem.2) but also on unbounded compact subsets of O A Ĉ. Lemma. together with Theorems.2 and.3 immediately yield: Corollary.4. For any A A and any compact set I I A uniformly for z on I and ω A,n (z) lim n w n =, uniformly for z on C A O A. lim ω A,n(z) = n where z = ϕ A(w) Lemma.5. Fix a real number r > 0 and any A A such that 0 A 0. Then there exists a real number K such that for any real number κ > K there exists N N such that n N implies (i) P A,n (z) < r for all z A 0, (ii) P A,n (z) > κ z for all z A, and (iii) κ z > sup{ x : x Ĉ \ A } for all z A. Proof. Without loss of generality, we will assume that r is small enough that B r (0) A 0, where B r (0) denotes the open ball of radius r about 0. Set α = sup{ x : x A 0 }, β = sup{ x : x A 0 A} γ = inf{ x : x A } δ = inf{ x : x ϕ A (A )}. Notice that α, β, and γ are all at least r, and, in particular, are nonzero. Notice also that δ >. This is because the distance function from a point in the unit circle to the set ϕ A ( A ) {w : w > } is continuous on the unit circle, and hence attains its minimum, which is nonzero. Hence inf{ x : x ϕ A (A )} >. Let K = max{, β γ }. Fix κ > K; then κ > and κ γ > β. Pick ɛ 2 > 0 such that ɛ 2 < r/α. Since lim n ω A,n (z) (ϕ A (z))n =

5 SHAPES OF POLYNOMIAL JULIA SETS 5 uniformly for z A by Corollary.4, and ϕ A (z) > on A, we also have that ω A,n (z) + lim n (ϕ A (z))n = uniformly on A. Hence there exists N N such that n N implies ω A,n (z) + > ( ɛ 2 ) w n for all z A, with z = ϕ A (w). Pick N 2 N such that n N 2 implies δ n > + κ. ɛ 2 Since ω A,n (z) converges uniformly to on A 0 by Corollary.4, there exists N 3 N such that n N 3 implies ω A,n (z) + < ɛ 2 for all z A 0. Let N = max{n, N 2, N 3 }. Now consider P A,n for n N. For z A 0, For z A, P A,n (z) = z ω A,n (z) + α ɛ 2 < r. P A,n (z) = z ω A,n (z) + z ( ɛ 2 ) w n + z ( ɛ 2 ) w n z ( ɛ 2 ) (δ n κ ) > z ( ɛ 2 )( ) = z κ ɛ 2 Theorem.6. Fix A A and any point t A 0. Let τ : Ĉ Ĉ denote the translation z z t. Then there exists N N such that n N implies (i) A 0 K(τ P τ(a),n τ), (ii) A L(τ P τ(a),n τ), (iii) J (τ P τ(a),n τ) A, and (iv) any path from a point in A to a point in A 0 has nonempty intersection with J (τ P τ(a),n τ). Proof. To start, we will consider only the case that 0 A 0 and τ is the identity map. So pick r > 0 such that B r (0) A 0. Pick a real number κ > and N N as in the statement of Lemma.5. Let n N, n N. Since A 0 contains the disk B r (0), the property P A,n (z) < r for all z A 0 implies A 0 K(P A,n ). The property P A,n (z) > κ z > sup{ w : w Ĉ \ A } for all z A implies that P A,n (A ) A, and thus that P m A,n (z) > κ m z for all m N and z A. Hence, A L(P A,n ). The partition of the Riemann sphere as Ĉ = A A A 0 together with the facts A 0 K(P A,n ) and A L(P A,n ) imply that K(P A,n ) A. Any path connecting a point in K(P A,n ) and a point in (K(P A,n )) c = L(P A,n ) must have nonempty intersection with K(P A,n ). This proves the theorem in the case that 0 A 0 and τ is the identity. Now consider the general case, in which τ is any fixed map z z t for some t A 0. The translated annulus τ(a) is an element of A and its interior region, τ(a) 0, contains the point 0. Hence the conclusion of the theorem holds for the annulus τ(a) and the identity translation. The composition τ P τ(a),n τ is a polynomial and K(τ P τ(a),n τ) = τ (K(P τ(a),n )).

6 6 KATHRYN A. LINDSEY Therefore K(τ P τ(a),n τ) τ (τ(a) 0 ) = A 0 ; statements (ii), (iii) and (iv) follow similarly. 2. Hausdorff distance and annular approximations Figure 2. A filled Julia set in the shape of a butterfly. The polynomial which generates this Julia set has degree 30. The purpose of this section is to carry out the technical arguments necessary to reformulate the conclusion of Theorem.6 in terms of the Hausdorff topology and Jordan curves (Theorem 2.2). For any two non-empty subsets X and Y of C, we denote by d H (X, Y ) the Hausdorff distance between X and Y, defined by where d H (X, Y ) = inf{ɛ > 0 X N ɛ (Y ) and Y N ɛ (X)}, N ɛ (X) = {z Ĉ d(z, x) ɛ}. x X We will also consider the Hausdorff distance d H (X, Y ) in the case where X, Y Ĉ and both X and Y contain an open ball, say B, about the point. In this case, we define d H (X, Y ) to be the Hausdorff distance d H (X \ B, Y \ B), which is well-defined and finite. We will denote by C the collection of Jordan curves in the complex plane C Ĉ. The Jordan-Schoenflies Theorem says that for each Jordan curve

7 SHAPES OF POLYNOMIAL JULIA SETS 7 J C, there exists a homeomorphism f J : C C such that f J (J) = S and such that f maps the bounded component of J c to the unit disk. For each real number ɛ with > ɛ > 0, define J ɛ = f ({z C ɛ z + ɛ}). J The set Ĉ \ J ɛ consists of two connected components; let J0 ɛ denote the bounded component and let J ɛ denote the unbounded component. Thus for each J C and ɛ > 0 we have a decomposition Ĉ = J 0 ɛ J ɛ J. ɛ Lemma 2.. Fix a Jordan curve J C and a real number δ > 0. Then there exists a real number ρ > 0 such that ρ > ɛ > 0 implies (i) J ɛ N δ (J), (ii) For every point j J, B δ (j) J ɛ 0 and B δ(j) J ɛ. Proof. Define a function w δ : S R by w δ (s) = sup{r > 0 B r (s) f J (N δ (J))}. Since f J (N δ (J)) is an open set which contains S, w δ (s) is well-defined and positive for each s S. Since w δ is continuous on S and S is compact, there exists a real number ρ > 0 such that w δ (s) ρ for all s S. Then for any real number ɛ with 0 < ɛ < ρ and for any s S, we have B ɛ (s) f J (N δ (J)), and thus N ɛ (S ) = s S B ɛ (s) f J (N δ (J)). Therefore 0 < ɛ < ρ implies J ɛ N δ (J). Define a function y δ : J R by y δ (j) = sup{ɛ > 0 B δ (j) J ɛ and B δ (j) J ɛ 0 }. Notice that y δ (j) is well-defined and positive for each point j J. Since y δ is continuous on J and J is compact (J is the image of S under f ), there exists a real number ρ 2 > 0 such that y δ (j) > ρ 2 for all j J. Then ρ 2 > ɛ > 0 implies B δ (j) J ɛ and B δ (j) J0 ɛ for all j J. Let ρ = min{ρ, ρ 2 }. Then ρ > ɛ > 0 implies properties (i) and (ii). Theorem 2.2. Let J be a Jordan curve in C and fix a real number δ > 0. Denote by I the bounded component of Ĉ\J and denote by O the unbounded component of Ĉ \ J. There exists a polynomial P : Ĉ Ĉ such that (i) d H (I, K(P )) < δ, (ii) d H (J, J (P )) < δ, and (iii) d H (O, L(P )) < δ. Proof. Pick a real number δ such that 0 < δ < δ/3. Apply Lemma 2. using the parameter δ to obtain ρ > 0 such that ρ > ɛ > 0 implies (a) J ɛ N δ (J) and (b) B δ (j) J ɛ 0 and B δ (j) J ɛ for all j J. Fix a real number ɛ with ρ > ɛ > 0. Apply Theorem.6 to the annulus J ɛ A to obtain a polynomial P n such that J ɛ 0 K(P n), J ɛ L(P n ),

8 8 KATHRYN A. LINDSEY J (P n ) J ɛ, any path from a point in J ɛ to a point in J0 ɛ has nonempty intersection with J (P n ). We know J0 ɛ K(P n) J ɛ J0 ɛ and J 0 ɛ I J ɛ J0 ɛ. Consequently the symmetric difference K(P n ) I is contained in J ɛ. By (a) any point x J ɛ is within distance at most δ of some point j J, and by (b), the point j is within distance at most δ of a point in J0 ɛ I K(P n). Hence d H (I, K(P n )) 2δ < δ. Similarly, J ɛ L(P n ) J ɛ J ɛ and J ɛ O J ɛ J, ɛ implying L(P n ) O J ɛ and thus d H (L(P n ), O) < δ. Let j be a point in J. By (b), pick points p B δ (j) J0 ɛ and p 2 B δ (j) J ɛ and let γ be the path consisting of the two line segments p j and p 2 j. By construction, the length of γ is at most 2δ. Since γ connects K(P n ) with L(P n ) = (K(P n )) c, γ contains a point in (K(P n )) = J (P n ). Hence d H (j, J (P n )) 2δ. The containments J (P n ) J ɛ N δ (J) imply d H (a, J) δ for any point a J (P n ). Therefore d H (J (P n ), J) < δ. 3. Rational Maps Let A denote a finite collection {A,..., A m } of annuli in A. For each i, let A i,0 and A i, denote the bounded component and unbounded component, respectively, of Ĉ \ A i. Let A denote the number of elements of A. We will say that the elements of A are mutually exterior if A j (A i A i,0 ) = for all i j. For any finite collection A of mutually exterior annuli in A and any n N, define a rational function Ω A,n : Ĉ Ĉ by A (3) Ω A,n (z) = (ω Aj,n(z) + ). j= Also define for each n N the rational function R A,n : Ĉ Ĉ by Define also R A,n (z) = z Ω A,n (z). A + = A j= A j, A 0 = A j= A j,0, A = A j= A j,. Thus we have a decomposition Ĉ = A 0 A + A. Lemma 3.. Let A be a finite collection of mutually exterior annuli in A and fix real numbers B > b > 0. Then there exists N N such that for all integers n N, (i) Ω A,n (z) < b for all z A 0, and (ii) Ω A,n (z) > B for all z A.

9 SHAPES OF POLYNOMIAL JULIA SETS 9 Figure 3. K(ρ) for a rational map ρ constructed as in Theorem 3.2. Proof. Pick positive real numbers d and D with d small enough and D large enough that d A D D < b and A > B. As a consequence of Corollary.4, there exists N N such that for all n N and all j A, ω Aj,n(z) + < d for all z A j,0 and ω Aj,n(z) + > D for all z A j,. Fix n N. For z A i,0, A A ω Aj,n(z) + ω Ai,n(z) + ω j,n (z) + d A D. j= j=,j i Hence Ω A,n (z) < b for all z A 0. For z A, A A ω Aj,n(z) + ω Aj,n(z) + A D. j= Hence Ω A,n (z) > B for all z A. j=

10 0 KATHRYN A. LINDSEY Theorem 3.2. Let A = {A,..., A m } be a finite collection of mutually exterior annuli in A. Fix any point t A 0 and let τ : Ĉ Ĉ be the translation z z t. Then there exists N N such that for any integer n N, (i) A 0 K(τ R τ(a),n τ) (ii) A L(τ R τ(a),n τ) (iii) J (τ R τ(a),n τ) A + (iv) For any A i A, any path connecting A i, and A i,0 has nonempty intersection with J (τ R τ(a),n τ). Proof. To begin, we will consider the case that 0 A 0 and τ is the identity map. So assume 0 A 0 and let ρ be the radius of a small ball centered at 0 and contained in A 0. Fix a real number b > 0 small enough that b sup{ z z A 0 } < ρ. Fix a real number B > large enough that B inf{ z z A } > sup{ z z A + A 0 }. Let N be the integer guaranteed by Lemma 3., and fix an integer n N. Then for any z A 0 R A,n (z) = z Ω A,n (z) z b < ρ. Hence R A,n (z) A 0 for any z A 0. For any z A R A,n (z) = z Ω A,n (z) z B. Hence for any z A, we have R A,n (z) A and so RA,n m (z) > Bm z for all m N. Therefore, the basin of attraction of for the map R A,n contains all of A and has empty intersection with A 0. This proves the theorem in the case that 0 A 0 and τ is the identity map. For the general case, in which τ is any fixed map z z t for some t A 0, it suffices to observe that K(τ R τ(a),n τ) = τ (K(R A,n )). For any finite collection J = {J,..., J m } of mutually exterior bounded Jordan curves in Ĉ, define the sets J +, J 0, and J as follows. Let J + = i J i. Let J 0 denote the union of the bounded connected components of Ĉ \ J i. Let J = Ĉ \ (J + J 0 ). Thus Ĉ = J 0 J + J. Theorem 3.3. Let J = {J,..., J m } be a finite collection of mutually exterior bounded Jordan curves in Ĉ and fix a real number δ > 0. Then there exists a rational map Q : Ĉ Ĉ for which is an attracting fixed point and (i) d H (J 0, K(Q)) < δ, (ii) d H (J +, J (Q)) < δ, and (iii) d H (J, L(Q)) < δ. Proof. Let η = 2 inf{d(x, y) x J i,0, y J j,0, i j}. Because the curves in J are mutually exterior, η > 0. Let δ = min{δ/3, η}. For each i, let ρ i be the positive real number guaranteed by Lemma 2. using the parameter δ. Let ρ = min{ρ 0, ρ,..., ρ m }.

11 SHAPES OF POLYNOMIAL JULIA SETS Fix a real number ɛ such that ρ > ɛ > 0. Let A denote the collection of annulus J ɛ,..., J m ɛ (the notation J ɛ is as defined at the beginning of Section 2). The condition that δ < η implies that the annuli in A are all pairwise disjoint and thus mutually exterior. Apply Theorem 3.3 using the finite collection of mutually exterior annuli A to obtain a rational map Q : Ĉ Ĉ such that (i) A 0 K, (ii) A L(Q), (iii) J (Q) A +, and (iv) every path between a point in A 0 and a point in A has nonempty intersection with J (Q). The Hausdorff distance estimates can then be proved in the same way as in the proof of Theorem 2.2. Theorem 3.4. Let A be an annulus in A and fix a real number δ > 0. Then there exists a rational function S : Ĉ Ĉ for which is an attracting fixed point and (i) d H (A, K(S)) < δ, (ii) d H (A A 0, L(S)) < δ, (iii) d H ( A, J (S)) < δ. Proof. The boundary of A is composed of two Jordan curves; let C denote the outer curve and C 2 denote the inner curve. Set ξ = inf{d(x, y) x C, y C 2 }. Notice the compactness of the Jordan curves C and C 2 implies ξ > 0. Let E and F be the annuli guaranteed by Lemma 2. using C and C 2, respectively, and the parameter δ = 3 min{δ, ξ}. By construction, E and F are disjoint. Thus Ĉ\(E F ) consists of three connected components; denote the outside component (which contains ) by O, denote the middle component by M, and denote the inside component by I. Thus Ĉ = O E M F I. Assume for now that 0 M. Fix real numbers R > r > 0 such that B r (0) M and (Ĉ \ O) B R(0). Set η = inf{ z : z O}. Fix a real number κ such that κ > max {, η( + r 2 ), η(r + r } 2 ). By Lemma.5, there exists N E N such that n > N E implies P E,n (z) < r 2 for all z M F I and Notice that P E,n (z) > κ z for all z O. κ z > η(r + r 2 ) z R + r 2

12 2 KATHRYN A. LINDSEY for all z O. Notice also that (4) κ z r 2 > (2 + r 2 η) z r 2 = 2 z + r (η z ) 2 z 2 for all z O. By Corollary.4, there exists N F N such that for any integer m > N F, ω F,m (z) + > R + r for all z I 2 and ω F,m (z) + < r for all z M E O. 2 For each n N, define a rational map S n : Ĉ Ĉ by S n (z) = P E,n (z) + ω F,n (z) +. Set N = max{n E, N F }. Fix any integer n > N. The inequalities above imply that S n (z) > R for all z O I and S n (z) < r for all z M. Consequently, S n (z) O for all z O I and S n (z) M for all z M. Furthermore, for any z O the inequality (4) implies S n (z) P E,n(z) ω F,n (z) + κ z r 2 > 2 z. Hence S t n(z) > 2 t z for all z O and t N. Consequently, O I L(S n ) and M K(S n ). The Hausdorff distance estimates may then be obtained in a way similar to that in the proof of Theorem Discussion Theorem 2.2 extends the analogy between the dynamics of rational maps and Kleinian groups. The discussion of inversive two-manifolds in [ST83] examines Kleinian groups generated by inversions through circles arranged in a chain along a Jordan curve. The approach in [ST83] leads to the following theorem: Theorem 4.. Any simple closed curve C can be approximated in the Hausdorff topology by limits sets of finitely-generated quasi-fuchsian groups. This result above is stated in [Hub]. The maps constructed in this paper and in Theorem 4. all use a set of special points strung along the curve in the first case it is the roots of the polynomials, and in the second case it is the centers of the circles which define the inversions. Question. Characterize those sets S C such that for any ɛ > 0 there exists a polynomial (or rational map) P such that d Haus (S, K(P )) < ɛ and d Haus (Ĉ S, Ĉ K(P )) < ɛ. The theme of this paper has been to first fix the shape we wish to approximate, and then vary the degree of the polynomials whose Julia sets approximate the shape. However, the reverse approach first fix a degree

13 SHAPES OF POLYNOMIAL JULIA SETS 3 d, and then analyze the set of Julia sets for polynomials of degree d also warrants investigation. Question. Find a method to determine {P : P is a polynomial of degree d and d Haus (J (P ), S) ɛ} for any given d N, ɛ 0, and S C. References [Cur4] J. H. Curtiss, Riemann sums and the fundamental polynomials of lagrange interpolation, Duke Math. J. 8 (94), [Hub] John Hamal Hubbard, Teichmüller theory, volume II, in progress. [ST83] Dennis Sullivan and William Thurston, Manifolds with canonical coordinate charts: some examples, Enseign. Math. 29 (983), (Kathryn Lindsey) Department of Mathematics, Cornell University, Ithaca, NY 4853, USA address: klindsey@math.cornell.edu