PHYS 705: Classical Mechanics. Hamiltonian Formulation & Canonical Transformation
|
|
|
- Hugh Hamilton
- 5 years ago
- Views:
Transcription
1 1 PHYS 705: Classical Mechanics Hamiltonian Formulation & Canonical Transformation
2 Legendre Transform Let consider the simple case with ust a real value function: F x F x expresses a relationship between an independent variable x and its dependent value F This relation is encoded in the functional form of We will denote this encoding in general by: F, x F x As one has learned in math and physics, it is sometime useful to encode the information contained in a function in different ways e.g., Fourier Transform, Laplace Transform, etc.
3 3 Legendre Transform 1 F k e F x dx As in the Fourier Transform: ˆ ikx and its inverse transform: F x The original information of for a given x value is encoded in terms ˆF k of the Fourier components and a new set of variables k. In our new encoding scheme, we will say that 1 ikx Fx e Fˆ kdk Fk ˆ, encodes the SAME information as F, x
4 4 Legendre Transform The Legendre Transform is yet another (convenient) encoding scheme F x for when the following two conditions are true: 1. The function is strictly convex (concave), i.e, nd derivative always positive (negative) and smooth df dx. It is easier to measure, control, or think about than x itself df dx Since never changes sign (condition 1), there is a one-to-one df dx correspondence between and x Legendre Transform gives us a new encoding scheme with s df dx being a function of instead of x Gs, Gs
5 5 Legendre Transform Here is the definition of the Legendre Transform for F x G s G s sx s F x s Note that is a function of s and we have to express in df x terms of s by inverting the function: to get s dx F x s xs
6 6 Legendre Transform Geometric Construction of the Legendre Transform: G sxf F x slope = s F F G sx G G sx y-intercept of slope x
7 7 Legendre Transform Important Properties of the Legendre Transform: 1. The Legendre Transform is its own inverse transform: G s - Suppose we have and define s y H y ys y G s y y s dg s - Using the inverted relation, the Legendre Transform of is G syh ds G s - This can be rewritten as and comparing to our original H, y F, x G sx F transform, we can immediate see that F xsg and is F s own inverse transform.
8 8 Legendre Transform - The two independent variables are two conugate pair of variables related to each other through x s dg s ds or x, s - Note that there is only ONE independent variable (either x or s) in: F x G s x s x x s s s s F x G x s x df x dx
9 9 Legendre Transform. Properties of the Minima [note: is convex, an extrema is a minimum] F x F x At the minimum of we have the slope F min F x s df dx 0 F min So, we have Gs ( 0) x0f F min G 0 min
10 10 Legendre Transform. Properties of the Minima Similarly, at a minimum G min of We again have correspondingly Gs y-intercept coincides with tangent pt F x dg slope for G ds x 0 So, we have G min F 0 F 0 G min
11 11 Legendre Transform. Reciprocal Relation of F & G s curvature Start with the two reciprocal definitions x s dg s ds and s x df x Now take derivatives with respective to their independent variables, dx ds F x dg s ds ds dx dx d F x dx dx ds dx ds d F x d G s ds dx 1 G s So, if is with curvature, then will have curvature 1
12 1 Review of Lagrangian Formulation Recall Lagrangian Formulation of Mechanics -Pick n proper (independent) generalized coordinates to describe the state of the system this defines a n-dim Configuration Space. - Apply the Hamilton s Principle: The motion of the system from t 1 to t in config. space is such that the Action (I) has a stationary value, i.e., 1 I L q, q, t dt 0 - Using Variational Calculus, this implies the Euler-Lagrange Eq: L d L 0, 1,, n q dtq
13 13 Review of Lagrangian Formulation L d L 0, 1,, n q dtq Solving this gives the Equations of Motion Notes: -We have n independent generalized coordinates. q 1 n - The n are time derivatives of the. n q 1 -We have n nd -order ODEs for the equations of motion - We need n initial conditions to completely specify the motion. n q 1
14 14 Hamiltonian Formulation -Instead of n nd -order ODEs as EOM with n independent generalized coordinates in configuration space. - Seek n 1 nd -order ODEs as EOM with n independent generalized coordinates in phase space. (Note: In Hamiltonian Formulation, we need to start with a set of independent generalized coordinates. If they are not proper, a reduced set of m < n proper coordinates must be chosen first.) - The most natural choice for this set of n variables in phase space is: n q 1 generalized coordinates n p 1 where p L q generalized conugate momenta
15 15 Hamiltonian Formulation Notes: - As we will see this is NOT the only choice - Coordinates in this n-dim phase space are call canonical variables (In Landau & Lifshitz: they are called canonical since the EOM resulted from them has the simplicity and symmetry in form.) - Later, we will investigate invariant ways to transform the system to other n canonical variables using canonical transformations
16 16 Configuration Space vs. Phase Space 1 q q A given point in configuration space prescribes fully the 1,, n configuration of the system at a given time t. However, the specification of a point in this space does NOT specify the time evolution of the system completely! (a unique soln for a n-dim nd order ODE needs n ICs) Many different paths can go thru a given point in config space q P Different paths crossing P will have n n q 1 q 1 the same set of but diff q 1
17 17 Configuration Space vs. Phase Space To specify the state AND time evolution of a system uniquely at a given time, one needs to specify BOTH AND q, p or equivalently, The n-dim space where both and are independent variables is called phase space. q q q p Thru any given point in phase space, there can only be ONE unique path! p GOAL: to find the EOM that applies to points in phase space. q
18 18 Hamiltonian Formulation - Instead of using the Lagrangian,, we will introduce a new function that depends on,, and t: L Lq, q, t q p H H q, p, t - This new function is call the Hamiltonian and it is defined by: L H q L q - Plugging in the definition for the generalized momenta: H p q L One can think of this as a coordinate transformation from to To be more specific, is the Legendre Transform of. H is defined similarly to the Jacobi (energy) function h BUT h is a q, q q, p (Einstein s Convention: function of and H is a function of. Repeated indices are summed) ( sum) p L q Hq, p Lqq, q, q q, p
19 19 L and H are a Legendre Transform Pair Consider a simple Lagrangian for a single particle m under the influence of a conservative potential Then, we have mq V q L p mq dq, L qq V q Inverting the above relation and arriving at Then, the Legendre Transform of is: L qq,,, H q p pq p L q q p q p p m L, q H, p p m p p p V q V q m m m xq sl q p F L G H G sxf H pq L (q is an irrelevant variable in this L-Trans)
20 0 Hamiltonian Formulation - Taking the differential of our definition for, we have - Now, we require that so that we should have - To be consistent, let try to resolve this by expanding dl: p - Plug in : dh p dq q dp dl H H q, p, t H H H dh dq dp dt q p t L L L dl dq dq dt ( sum) q q t L q L L dl dq p dq dt ( sum) q t H pq L ( sum) ( sum)
21 1 Hamiltonian Formulation - Now, since the system satisfies the Euler-Lagrange Equation, we have L d L q dt q - Substituting this into our previous equation, we have: L dl p dq p dq dt t - Now, plug this into our equation for dh: p (** this is an important step if we want our formalism to describe the same dynamic.) ( sum) dh q q dq p dq dp pd p L dh qdp p dq dt ( sum) t L dt t
22 Hamiltonian Formulation -If H describes the same dynamics as is given by the EL equation, the two expressions must equal to each other: L H H H dh p dq qdp dt dh dq dp dt t q p t - Comparing gives the condition: H q H p p q and H t L t These are called the Hamilton s Equations of Motion and they are the desired set of equations describing the EOM in phase space.
23 3 Hamiltonian Formulation Summary of Steps: 1. Pick a proper set of and form the Lagrangian L. Obtain the conugate momenta by calculating 3. Form 4. Eliminate from H using the inverse of so as to have 5. Apply the Hamilton s Equation of Motion: q H pq L q H H( q, p, t) H q H p and q p p L q As you will see, this formulation does not necessary simplify practical calculations but it forms a theoretical bridge to QM and SM. p L q
24 4 Hamilton Equations in Matrix (Symplectic) Notation The pair of Hamilton equations look almost symmetric (except the - sign). The following is an elegant way to write the Hamilton equations into a single matrix equation: For a system with n dofs, we group all of our q i s and p i s into a n-dim vector η: q, p ; 1,, n n Similarly, we will define another n-dimensional column vector : H H H H, ; 1,, n η q η p n H η
25 5 Hamilton Equations in Matrix (Symplectic) Notation n n Now, we define a anti-symmetric matrix, 0 I J I 0 Note that the transpose of J is its own inverse (orthogonal): J T 0 I I 0 and In summary, we have the following properties for J: T 1, J J J J n n where I is a identity matrix 0 is a n n zero matrix T T I 0 JJJJ 0 I J I, J det 1
26 6 Hamilton Equations in Matrix (Symplectic) Notation The Hamilton equation can then be written in a compact form: H η J η As an example, with only dofs, this matrix equation expands into: q H q p1 q H q p p H p q 1 p H p q This is typically referred to as the matrix or symplectic notation for the Hamilton equations.
27 7 Example: Spherical Pendulum Thus, ds U T mv mb mb E-L equations gives two nd order ODEs: Pick Generalized Coordinates:, b dsbd θˆ bsin dˆ m ds v b θˆ bsin ˆ dt sin 1 1 cos L T U mb mb sin mgb g sincos sin 0 b sin sincos 0 U mgbcos
28 8 Example: Spherical Pendulum U 0 Practically, we can do one integration immediately b through the two constants of motion: ds m Conservation of E: 1 1 E mb mb sin mgbcos d L 0 dt L p mb sin const is cyclic, i.e : These two 1 st order ODEs can be solved easily by substitute from the equation into the E equation. p
29 9 Example: Spherical Pendulum U cos L mb mb sin mgb Now, let consider the Hamiltonian Formalism. b ds m We first need to calculate the conugate momenta: L p p mb mb L p mb sin mb p sin The boxed equations are the desired transformation from the config. space to the canonical variables in phase space.
30 30 Example: Spherical Pendulum Construct the Hamiltonian: H q p L sum H p p L p p 1 1 mb mb sin mb mb sin mgb cos p p p p mgb cos mb mb sin mb mb sin p p mb mb sin mgbcos U 0 b ds m (H is properly expressed in terms of the canonical variables.),, p, p, t
31 31 Example: Spherical Pendulum H p p mb mb sin mgbcos U 0 Apply Hamilton s Equations to get four 1 st order ODEs: H p 3 p sin cos mgbsin p mb p cos p mgbsin 3 mb sin H p p 0 H p H p p mb mb p sin Just repeated what we had b ds Since is cyclic, P is a constant and can be integrated to get (t). We will exploit this later. m
32 3 Symmetry and Conservation Theorem Again - Consider the full-time derivative of H, dh H H H q p dt q p t Using the Hamilton s Equations: dh dt pq q p H t dh dt H t (so if time does not explicitly appears in H (time is cyclic), H is conserved!) Note: H = E if 1. U does not depend on the generalized velocities. Transformation defining does not depend on t explicitly. q
33 33 Subtle Difference between h and H Recall that the Jacobi integral h is a function of instead of q, q, t q, p, t L hq, q, t q L q Also, from the E-L Eq, we know that Thus, we can rewrite the above equation as, h L L q t tq t L dh t dt h L q t t q dh dt Thus, unless the red term is explicitly zero, h t 0 dh dt 0
34 34 Subtle Difference between h and H Example: 1 L mq t q L hq L q L mq qt V q 1 1 mq qt So, hqmqt mq qt V q mq 1 tq h mq V q V q
35 35 Subtle Difference between h and H 1 L mq qt V q 1 h mq V q So, L q t 0 h t but 0 From our previous calculations, we have the following relationship, h L dh q t tq dt 0 So, the LHS is zero and we can also explicitly check that the RHS=0 too dh 0 dt but with.
36 36 Subtle Difference between h and H h t q t L q dh dt L dh d 1 q q tmq t q mq t dt dt q V mqq q L dh V q qmq 0 tq dt q Thus, we have, h t 0 V q q This has to be zero since and indeed, it does. From EL Eq, we have d L L dt q q 0 d dt V q tmq 0 V mq 0 q
37 37 Subtle Difference between h and H 1 L mq qt V q So, for this specific example, we have 1 h mq V q h t 0 but L t 0 q One can also calculate using H H q, p, t 0 dh and 0 dt V mqq q q L p tmq q pt H dh V q 0 m t dt 0
38 38 Symmetry and Conservation Theorem Again - Other cyclic coordinates: q n missing Lagrangian Formalism q n If is cyclic, the Lagrangian is L q n const L L( q,, q,, q,, q, t) 1 n1 1 The n-th EOM is then given by: q n is still here (The LHS is usually a complicated function of q & q and much efforts still needed to solve for q () n t.) n Hamiltonian q n In contrast, if is cyclic in the Hamiltonian Formalism, H q n 0 pn p const (conserved) (This equation is immediately solved from IC n p n is gone from the prob.) (The Hamiltonian Formalism has a much nicer structure for cyclic coords)
39 39 Routh s Procedure Goal: Transform only the cyclic coordinates to take advantage of simplicity in phase space for the cyclic variables (missing) L L( q,, q,, q,, q, t) Let say we have: 1 s 1 n s1 n Define the Routhian, R q p R pq L s1 where R depends on where q,, q are cyclic q, 1, qs d R R 0 for 1,, s dt q q q,, s1 q R p 0 and q for s 1,, n p const similar to Hamiltonian q,, q, q,, q, p,, p, t 1 s 1 s s1 n Then, apply the EL equation to non-cyclic variables, And, apply the Hamilton s equation to cyclic variables, n n
40 40 Routh s Procedure: example A single particle in a central potential: V() r k r n From previous chapter, we have: is cyclic and r is not, so we define m m k L r r r p L mr n p mr The Routhian is: R pq L n p m m p k p m k R r r r mr mr r mr r n Depends on rrp,, only as advertised
41 41 Routh s Procedure: example p m k R r n mr r Applying the EL equation to the non-cyclic variable r : d R R d p 1 k 0 mr 3 1 n 0 n dt r r dt m r r p nk mr mr r 0 3 n1 And, the Hamilton s Equation for : R p 0 p const l R p p mr l mr
42 4 Cyclic Variables: Action-Angle Coordinates - Note that a given system can be described by several different sets of generalized coordinates Generalized coordinates are not unique! - Recall also that the # of cyclic variables can depend on the choice of the generalized coordinates e.g., in the previous central force problem: Rect coord (x, y): both x, y are not cyclic polar coord (r, ): is cyclic
43 43 Cyclic Variables: Action-Angle Coordinates - Although one might not be able to pick a set of generalized coordinates (from a given physical system) to have ALL q being cyclic, one can imagine transforming them to an ideal set such that they are all cyclic. Canonical Transformation (next Chapter) - If possible, then, all the conugate momenta are constant: additionally, if H is a constant of motion, then p const H H,, 1 n cannot depend on t and q explicitly! constant in time cyclic
44 44 Cyclic Variables: Action-Angle Coordinates consequently, the EOM for the are simple: q q H H func of consts, 1 n p q () t t are integration constants depending on IC - Recall that the natural choice of the n-dim phase space variables is with q being the regular generalized coordinates and being their conugate momenta. BUT, this is NOT the only choice! The Hamiltonian Formalism can be extended to other possibilities:,,,, Q Q q p t and P P q p t p (indices for q, p are suppressed here)
45 45 Cyclic Variables: Action-Angle Coordinates Q Q, P, P,,,, Q Q q p t and P P q p t are the canonically transformed variables from the original ones needs to satisfy the corresponding Hamilton s Equations in the transformed coordinates. There are no preference between the transformation above for & P The canonical transformation treats both equally. Q Q & P Q & P are on the same theoretical footing in the Hamiltonian Formalism! The Hamiltonian Formalism is the starting point in analyzing QM systems.
46 46 Connection to Statistical Mechanics - The Hamilton s Equations describe motion in phase space q, - a point in phase space uniquely determines the state of the system p AND its future evolution. - nearby points represent system states with similar but slightly different initial conditions. - One can imagine a cloud of points bounded by a closed surface S with nearly identical initial conditions moving in time. q0, p0 q', p' S t q, p q', p' t t
47 47 Connection to Statistical Mechanics -Let say at time t, a small subset of these points crosses a differential area da on S in a given outward normal direction ˆn such that da daˆ n S da ˆn t t - Let v q, p be the mean velocity for points in da - Then, after a given time dt, this small subset of points will trace out a differential volume in phase space given by vdt da v vdt da
48 48 Connection to Statistical Mechanics - Summing up all points in the cloud bounded by S, we have, or, dv v d a dt S dv dt v d a S surface integral of the velocity field v for the points in the cloud rate of change of phase-space volume due to the motion of the points - Then, by Gauss s Law, we have dv dt v d a v S V dv V enclosed by S
49 49 Liouville s Theorem dv dt v d a v - In phase space, we have -So that, V S V dv v qqˆ q qˆ p pˆ p pˆ q q 1 1 n n 1 1 n n k k v dv dv (*) V p p k k k - Using the Hamilton s Equations, we have: q k H H q q p q p k k k k k p k H H pk pk q p q k k k
50 50 Liouville s Theorem - Substituting into Eq (*), we have, dv H dt k qkp V k p k H q k dv (H is a smooth function) dv dt 0! This is the Liouville s Theorem: collection of phase-space points move as an incompressible fluid. Phase space volume occupied by a set of points in phase space is constant in time.
51 51 Liouville s Theorem This is the starting point for statistical mechanics - Imagine many (N) identical mechanical systems but with different initial conditions (ensemble of systems). - Each is a different point in phase space with q, p - Statistical properties can be specified by a density of states function per unit volume in phase space q, p, t dv # system points in phase space volume dv q, located at at time t. p
52 5 Liouville s Theorem At statistical equilibrium, The # of points in the ensemble (N) does not change Then, since N is fixed, V stays constant, = N/V = constant as well! Thus, Liouville s Thm implies: density in a neighborhood of any system state = const as the system evolutes in phase space. Thus, equilibrium is uniform along the flow lines of the system points. (SM s Master Eq. or Fokker-Planck Eq.) This condition is typically used to solve for the equilibrium distribution eq for a statistical mechanical problem in phase space with which various statistical averages, P, T, U, S, can be calculated.
Housekeeping. No announcement HW #7: 3.19
 1 Housekeeping No announcement HW #7: 3.19 2 Configuration Space vs. Phase Space 1 A given point in configuration space q q prescribes fully the 1,, n configuration of the system at a given time t. The
1 Housekeeping No announcement HW #7: 3.19 2 Configuration Space vs. Phase Space 1 A given point in configuration space q q prescribes fully the 1,, n configuration of the system at a given time t. The
for changing independent variables. Most simply for a function f(x) the Legendre transformation f(x) B(s) takes the form B(s) = xs f(x) with s = df
 Physics 106a, Caltech 1 November, 2018 Lecture 10: Hamiltonian Mechanics I The Hamiltonian In the Hamiltonian formulation of dynamics each second order ODE given by the Euler- Lagrange equation in terms
Physics 106a, Caltech 1 November, 2018 Lecture 10: Hamiltonian Mechanics I The Hamiltonian In the Hamiltonian formulation of dynamics each second order ODE given by the Euler- Lagrange equation in terms
HAMILTON S PRINCIPLE
 HAMILTON S PRINCIPLE In our previous derivation of Lagrange s equations we started from the Newtonian vector equations of motion and via D Alembert s Principle changed coordinates to generalised coordinates
HAMILTON S PRINCIPLE In our previous derivation of Lagrange s equations we started from the Newtonian vector equations of motion and via D Alembert s Principle changed coordinates to generalised coordinates
Curves in the configuration space Q or in the velocity phase space Ω satisfying the Euler-Lagrange (EL) equations,
 Physics 6010, Fall 2010 Hamiltonian Formalism: Hamilton s equations. Conservation laws. Reduction. Poisson Brackets. Relevant Sections in Text: 8.1 8.3, 9.5 The Hamiltonian Formalism We now return to formal
Physics 6010, Fall 2010 Hamiltonian Formalism: Hamilton s equations. Conservation laws. Reduction. Poisson Brackets. Relevant Sections in Text: 8.1 8.3, 9.5 The Hamiltonian Formalism We now return to formal
REVIEW. Hamilton s principle. based on FW-18. Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws!
 Hamilton s principle Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws! based on FW-18 REVIEW the particle takes the path that minimizes the integrated difference
Hamilton s principle Variational statement of mechanics: (for conservative forces) action Equivalent to Newton s laws! based on FW-18 REVIEW the particle takes the path that minimizes the integrated difference
(Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) p j . (5.1) !q j. " d dt = 0 (5.2) !p j . (5.
 Chapter 5. Hamiltonian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 5.1 The Canonical Equations of Motion As we saw in section 4.7.4, the generalized
Chapter 5. Hamiltonian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 5.1 The Canonical Equations of Motion As we saw in section 4.7.4, the generalized
Physics 235 Chapter 7. Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics
 Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics Many interesting physics systems describe systems of particles on which many forces are acting. Some of these forces are immediately
Chapter 7 Hamilton's Principle - Lagrangian and Hamiltonian Dynamics Many interesting physics systems describe systems of particles on which many forces are acting. Some of these forces are immediately
Canonical transformations (Lecture 4)
 Canonical transformations (Lecture 4) January 26, 2016 61/441 Lecture outline We will introduce and discuss canonical transformations that conserve the Hamiltonian structure of equations of motion. Poisson
Canonical transformations (Lecture 4) January 26, 2016 61/441 Lecture outline We will introduce and discuss canonical transformations that conserve the Hamiltonian structure of equations of motion. Poisson
Lecture 5. Alexey Boyarsky. October 21, Legendre transformation and the Hamilton equations of motion
 Lecture 5 Alexey Boyarsky October 1, 015 1 The Hamilton equations of motion 1.1 Legendre transformation and the Hamilton equations of motion First-order equations of motion. In the Lagrangian formulation,
Lecture 5 Alexey Boyarsky October 1, 015 1 The Hamilton equations of motion 1.1 Legendre transformation and the Hamilton equations of motion First-order equations of motion. In the Lagrangian formulation,
Hamiltonian Systems of Negative Curvature are Hyperbolic
 Hamiltonian Systems of Negative Curvature are Hyperbolic A. A. Agrachev N. N. Chtcherbakova Abstract The curvature and the reduced curvature are basic differential invariants of the pair: Hamiltonian system,
Hamiltonian Systems of Negative Curvature are Hyperbolic A. A. Agrachev N. N. Chtcherbakova Abstract The curvature and the reduced curvature are basic differential invariants of the pair: Hamiltonian system,
Liouville Equation. q s = H p s
 Liouville Equation In this section we will build a bridge from Classical Mechanics to Statistical Physics. The bridge is Liouville equation. We start with the Hamiltonian formalism of the Classical Mechanics,
Liouville Equation In this section we will build a bridge from Classical Mechanics to Statistical Physics. The bridge is Liouville equation. We start with the Hamiltonian formalism of the Classical Mechanics,
8.044 Lecture Notes Chapter 5: Thermodynamcs, Part 2
 8.044 Lecture Notes Chapter 5: hermodynamcs, Part 2 Lecturer: McGreevy 5.1 Entropy is a state function............................ 5-2 5.2 Efficiency of heat engines............................. 5-6 5.3
8.044 Lecture Notes Chapter 5: hermodynamcs, Part 2 Lecturer: McGreevy 5.1 Entropy is a state function............................ 5-2 5.2 Efficiency of heat engines............................. 5-6 5.3
15. Hamiltonian Mechanics
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 15. Hamiltonian Mechanics Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 15. Hamiltonian Mechanics Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
Maxima/minima with constraints
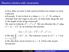 Maxima/minima with constraints Very often we want to find maxima/minima but subject to some constraint Example: A wire is bent to a shape y = 1 x 2. If a string is stretched from the origin to the wire,
Maxima/minima with constraints Very often we want to find maxima/minima but subject to some constraint Example: A wire is bent to a shape y = 1 x 2. If a string is stretched from the origin to the wire,
The Geometry of Euler s equation. Introduction
 The Geometry of Euler s equation Introduction Part 1 Mechanical systems with constraints, symmetries flexible joint fixed length In principle can be dealt with by applying F=ma, but this can become complicated
The Geometry of Euler s equation Introduction Part 1 Mechanical systems with constraints, symmetries flexible joint fixed length In principle can be dealt with by applying F=ma, but this can become complicated
Physics 5153 Classical Mechanics. Canonical Transformations-1
 1 Introduction Physics 5153 Classical Mechanics Canonical Transformations The choice of generalized coordinates used to describe a physical system is completely arbitrary, but the Lagrangian is invariant
1 Introduction Physics 5153 Classical Mechanics Canonical Transformations The choice of generalized coordinates used to describe a physical system is completely arbitrary, but the Lagrangian is invariant
Sketchy Notes on Lagrangian and Hamiltonian Mechanics
 Sketchy Notes on Lagrangian and Hamiltonian Mechanics Robert Jones Generalized Coordinates Suppose we have some physical system, like a free particle, a pendulum suspended from another pendulum, or a field
Sketchy Notes on Lagrangian and Hamiltonian Mechanics Robert Jones Generalized Coordinates Suppose we have some physical system, like a free particle, a pendulum suspended from another pendulum, or a field
Part of the advantage : Constraint forces do no virtual. work under a set of virtual displacements compatible
 FORCES OF CONSTRAINT Lagrangian formalism : Generalized coordinate Minimum set of Eqns Part of the advantage : Constraint forces do no virtual work under a set of virtual displacements compatible with
FORCES OF CONSTRAINT Lagrangian formalism : Generalized coordinate Minimum set of Eqns Part of the advantage : Constraint forces do no virtual work under a set of virtual displacements compatible with
AN INTRODUCTION TO CURVILINEAR ORTHOGONAL COORDINATES
 AN INTRODUCTION TO CURVILINEAR ORTHOGONAL COORDINATES Overview Throughout the first few weeks of the semester, we have studied vector calculus using almost exclusively the familiar Cartesian x,y,z coordinate
AN INTRODUCTION TO CURVILINEAR ORTHOGONAL COORDINATES Overview Throughout the first few weeks of the semester, we have studied vector calculus using almost exclusively the familiar Cartesian x,y,z coordinate
M. van Berkel DCT
 Explicit solution of the ODEs describing the 3 DOF Control Moment Gyroscope M. van Berkel DCT 28.14 Traineeship report Coach(es): Supervisor: dr. N. Sakamoto Prof. dr. H. Nijmeijer Technische Universiteit
Explicit solution of the ODEs describing the 3 DOF Control Moment Gyroscope M. van Berkel DCT 28.14 Traineeship report Coach(es): Supervisor: dr. N. Sakamoto Prof. dr. H. Nijmeijer Technische Universiteit
The first order formalism and the transition to the
 Problem 1. Hamiltonian The first order formalism and the transition to the This problem uses the notion of Lagrange multipliers and Legendre transforms to understand the action in the Hamiltonian formalism.
Problem 1. Hamiltonian The first order formalism and the transition to the This problem uses the notion of Lagrange multipliers and Legendre transforms to understand the action in the Hamiltonian formalism.
Dirac Structures and the Legendre Transformation for Implicit Lagrangian and Hamiltonian Systems
 Dirac Structures and the Legendre Transformation for Implicit Lagrangian and Hamiltonian Systems Hiroaki Yoshimura Mechanical Engineering, Waseda University Tokyo, Japan Joint Work with Jerrold E. Marsden
Dirac Structures and the Legendre Transformation for Implicit Lagrangian and Hamiltonian Systems Hiroaki Yoshimura Mechanical Engineering, Waseda University Tokyo, Japan Joint Work with Jerrold E. Marsden
Hamiltonian Mechanics
 Chapter 3 Hamiltonian Mechanics 3.1 Convex functions As background to discuss Hamiltonian mechanics we discuss convexity and convex functions. We will also give some applications to thermodynamics. We
Chapter 3 Hamiltonian Mechanics 3.1 Convex functions As background to discuss Hamiltonian mechanics we discuss convexity and convex functions. We will also give some applications to thermodynamics. We
FINAL EXAM GROUND RULES
 PHYSICS 507 Fall 2011 FINAL EXAM Room: ARC-108 Time: Wednesday, December 21, 10am-1pm GROUND RULES There are four problems based on the above-listed material. Closed book Closed notes Partial credit will
PHYSICS 507 Fall 2011 FINAL EXAM Room: ARC-108 Time: Wednesday, December 21, 10am-1pm GROUND RULES There are four problems based on the above-listed material. Closed book Closed notes Partial credit will
Euler-Lagrange Cohomology, Discrete Versions and Applications
 November, 2002 Euler-Lagrange Cohomology, Discrete Versions and Applications Han-Ying Guo In collaboration with J.Z. Pan, S.K. Wang, S.Y. Wu, K. Wu and B. Zhou et al. Contents 1 Introduction 2 2 ELCGs
November, 2002 Euler-Lagrange Cohomology, Discrete Versions and Applications Han-Ying Guo In collaboration with J.Z. Pan, S.K. Wang, S.Y. Wu, K. Wu and B. Zhou et al. Contents 1 Introduction 2 2 ELCGs
PHYS 705: Classical Mechanics. Calculus of Variations I
 1 PHYS 705: Classical Mechanics Calculus of Variations I Calculus of Variations: The Problem Determine the function y() such that the following integral is min(ma)imized. Comments: I F y( ), y'( ); d 1.
1 PHYS 705: Classical Mechanics Calculus of Variations I Calculus of Variations: The Problem Determine the function y() such that the following integral is min(ma)imized. Comments: I F y( ), y'( ); d 1.
Introduction. Statistical physics: microscopic foundation of thermodynamics degrees of freedom 2 3 state variables!
 Introduction Thermodynamics: phenomenological description of equilibrium bulk properties of matter in terms of only a few state variables and thermodynamical laws. Statistical physics: microscopic foundation
Introduction Thermodynamics: phenomenological description of equilibrium bulk properties of matter in terms of only a few state variables and thermodynamical laws. Statistical physics: microscopic foundation
G : Statistical Mechanics
 G25.2651: Statistical Mechanics Notes for Lecture 1 Defining statistical mechanics: Statistical Mechanics provies the connection between microscopic motion of individual atoms of matter and macroscopically
G25.2651: Statistical Mechanics Notes for Lecture 1 Defining statistical mechanics: Statistical Mechanics provies the connection between microscopic motion of individual atoms of matter and macroscopically
CE 530 Molecular Simulation
 CE 530 Molecular Simulation Lecture Molecular Dynamics Simulation David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu MD of hard disks intuitive Review and Preview collision
CE 530 Molecular Simulation Lecture Molecular Dynamics Simulation David A. Kofke Department of Chemical Engineering SUNY Buffalo kofke@eng.buffalo.edu MD of hard disks intuitive Review and Preview collision
Caltech Ph106 Fall 2001
 Caltech h106 Fall 2001 ath for physicists: differential forms Disclaimer: this is a first draft, so a few signs might be off. 1 Basic properties Differential forms come up in various parts of theoretical
Caltech h106 Fall 2001 ath for physicists: differential forms Disclaimer: this is a first draft, so a few signs might be off. 1 Basic properties Differential forms come up in various parts of theoretical
Hamiltonian formulation: water waves Lecture 3
 Hamiltonian formulation: water waves Lecture 3 Wm.. Hamilton V.E. Zakharov Hamiltonian formulation: water waves This lecture: A. apid review of Hamiltonian machinery (see also extra notes) B. Hamiltonian
Hamiltonian formulation: water waves Lecture 3 Wm.. Hamilton V.E. Zakharov Hamiltonian formulation: water waves This lecture: A. apid review of Hamiltonian machinery (see also extra notes) B. Hamiltonian
Supplement on Lagrangian, Hamiltonian Mechanics
 Supplement on Lagrangian, Hamiltonian Mechanics Robert B. Griffiths Version of 28 October 2008 Reference: TM = Thornton and Marion, Classical Dynamics, 5th edition Courant = R. Courant, Differential and
Supplement on Lagrangian, Hamiltonian Mechanics Robert B. Griffiths Version of 28 October 2008 Reference: TM = Thornton and Marion, Classical Dynamics, 5th edition Courant = R. Courant, Differential and
THEODORE VORONOV DIFFERENTIABLE MANIFOLDS. Fall Last updated: November 26, (Under construction.)
 4 Vector fields Last updated: November 26, 2009. (Under construction.) 4.1 Tangent vectors as derivations After we have introduced topological notions, we can come back to analysis on manifolds. Let M
4 Vector fields Last updated: November 26, 2009. (Under construction.) 4.1 Tangent vectors as derivations After we have introduced topological notions, we can come back to analysis on manifolds. Let M
THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS
 THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS ALEXANDER TOLISH Abstract. Newton s Laws of Motion, which equate forces with the timerates of change of momenta, are a convenient way to describe mechanical
THE LAGRANGIAN AND HAMILTONIAN MECHANICAL SYSTEMS ALEXANDER TOLISH Abstract. Newton s Laws of Motion, which equate forces with the timerates of change of momenta, are a convenient way to describe mechanical
PHYS 705: Classical Mechanics. Examples: Lagrange Equations and Constraints
 1 PHYS 705: Classical Mechanics Examples: Lagrange Equations and Constraints x R Note: an object rolls because of friction but static friction does no work this is different from our previous case with
1 PHYS 705: Classical Mechanics Examples: Lagrange Equations and Constraints x R Note: an object rolls because of friction but static friction does no work this is different from our previous case with
Hamiltonian Mechanics
 Alain J. Brizard Saint Michael's College Hamiltonian Mechanics 1 Hamiltonian The k second-order Euler-Lagrange equations on con guration space q =(q 1 ; :::; q k ) d @ _q j = @q j ; (1) can be written
Alain J. Brizard Saint Michael's College Hamiltonian Mechanics 1 Hamiltonian The k second-order Euler-Lagrange equations on con guration space q =(q 1 ; :::; q k ) d @ _q j = @q j ; (1) can be written
[S R (U 0 ɛ 1 ) S R (U 0 ɛ 2 ]. (0.1) k B
![[S R (U 0 ɛ 1 ) S R (U 0 ɛ 2 ]. (0.1) k B [S R (U 0 ɛ 1 ) S R (U 0 ɛ 2 ]. (0.1) k B](/thumbs/72/67524544.jpg) Canonical ensemble (Two derivations) Determine the probability that a system S in contact with a reservoir 1 R to be in one particular microstate s with energy ɛ s. (If there is degeneracy we are picking
Canonical ensemble (Two derivations) Determine the probability that a system S in contact with a reservoir 1 R to be in one particular microstate s with energy ɛ s. (If there is degeneracy we are picking
The kinetic equation (Lecture 11)
 The kinetic equation (Lecture 11) January 29, 2016 190/441 Lecture outline In the preceding lectures we focused our attention on a single particle motion. In this lecture, we will introduce formalism for
The kinetic equation (Lecture 11) January 29, 2016 190/441 Lecture outline In the preceding lectures we focused our attention on a single particle motion. In this lecture, we will introduce formalism for
A variational formulation for dissipative systems
 International/Interdisciplinary Seminar on Nonlinear Science The University of Tokyo, komaba Campus March 22, 2017 ------------------------------------------------------------------------------- A variational
International/Interdisciplinary Seminar on Nonlinear Science The University of Tokyo, komaba Campus March 22, 2017 ------------------------------------------------------------------------------- A variational
Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations
![Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations](/thumbs/87/96222240.jpg) D. D. Holm Solutions to M3-4A16 Assessed Problems # 3 15 Dec 2010 1 Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations Vector notation for differential basis elements:
D. D. Holm Solutions to M3-4A16 Assessed Problems # 3 15 Dec 2010 1 Solutions of M3-4A16 Assessed Problems # 3 [#1] Exercises in exterior calculus operations Vector notation for differential basis elements:
Hamiltonian flow in phase space and Liouville s theorem (Lecture 5)
 Hamiltonian flow in phase space and Liouville s theorem (Lecture 5) January 26, 2016 90/441 Lecture outline We will discuss the Hamiltonian flow in the phase space. This flow represents a time dependent
Hamiltonian flow in phase space and Liouville s theorem (Lecture 5) January 26, 2016 90/441 Lecture outline We will discuss the Hamiltonian flow in the phase space. This flow represents a time dependent
Gauge Fixing and Constrained Dynamics in Numerical Relativity
 Gauge Fixing and Constrained Dynamics in Numerical Relativity Jon Allen The Dirac formalism for dealing with constraints in a canonical Hamiltonian formulation is reviewed. Gauge freedom is discussed and
Gauge Fixing and Constrained Dynamics in Numerical Relativity Jon Allen The Dirac formalism for dealing with constraints in a canonical Hamiltonian formulation is reviewed. Gauge freedom is discussed and
New Identities for Weak KAM Theory
 New Identities for Weak KAM Theory Lawrence C. Evans Department of Mathematics University of California, Berkeley Abstract This paper records for the Hamiltonian H = p + W (x) some old and new identities
New Identities for Weak KAM Theory Lawrence C. Evans Department of Mathematics University of California, Berkeley Abstract This paper records for the Hamiltonian H = p + W (x) some old and new identities
Under evolution for a small time δt the area A(t) = q p evolves into an area
 Physics 106a, Caltech 6 November, 2018 Lecture 11: Hamiltonian Mechanics II Towards statistical mechanics Phase space volumes are conserved by Hamiltonian dynamics We can use many nearby initial conditions
Physics 106a, Caltech 6 November, 2018 Lecture 11: Hamiltonian Mechanics II Towards statistical mechanics Phase space volumes are conserved by Hamiltonian dynamics We can use many nearby initial conditions
CANONICAL EQUATIONS. Application to the study of the equilibrium of flexible filaments and brachistochrone curves. By A.
 Équations canoniques. Application a la recherche de l équilibre des fils flexibles et des courbes brachystochrones, Mem. Acad. Sci de Toulouse (8) 7 (885), 545-570. CANONICAL EQUATIONS Application to the
Équations canoniques. Application a la recherche de l équilibre des fils flexibles et des courbes brachystochrones, Mem. Acad. Sci de Toulouse (8) 7 (885), 545-570. CANONICAL EQUATIONS Application to the
Distributions of statistical mechanics
 CHAPTER II Distributions of statistical mechanics The purpose of Statistical Mechanics is to explain the thermodynamic properties of macroscopic systems starting from underlying microscopic models possibly
CHAPTER II Distributions of statistical mechanics The purpose of Statistical Mechanics is to explain the thermodynamic properties of macroscopic systems starting from underlying microscopic models possibly
Ostrogradsky theorem (from 1850)
 Ostrogradsky theorem (from 1850) Marián Fecko Department of Theoretical Physics Comenius University Bratislava fecko@fmph.uniba.sk Student Colloqium and School on Mathematical Physics, Stará Lesná, Slovakia,
Ostrogradsky theorem (from 1850) Marián Fecko Department of Theoretical Physics Comenius University Bratislava fecko@fmph.uniba.sk Student Colloqium and School on Mathematical Physics, Stará Lesná, Slovakia,
The inverse problem for Lagrangian systems with certain non-conservative forces
 The inverse problem for Lagrangian systems with certain non-conservative forces Tom Mestdag Ghent University (Belgium) http://users.ugent.be/ tmestdag Joint work with Mike Crampin and Willy Sarlet Example
The inverse problem for Lagrangian systems with certain non-conservative forces Tom Mestdag Ghent University (Belgium) http://users.ugent.be/ tmestdag Joint work with Mike Crampin and Willy Sarlet Example
Homework 4. Goldstein 9.7. Part (a) Theoretical Dynamics October 01, 2010 (1) P i = F 1. Q i. p i = F 1 (3) q i (5) P i (6)
 Theoretical Dynamics October 01, 2010 Instructor: Dr. Thomas Cohen Homework 4 Submitted by: Vivek Saxena Goldstein 9.7 Part (a) F 1 (q, Q, t) F 2 (q, P, t) P i F 1 Q i (1) F 2 (q, P, t) F 1 (q, Q, t) +
Theoretical Dynamics October 01, 2010 Instructor: Dr. Thomas Cohen Homework 4 Submitted by: Vivek Saxena Goldstein 9.7 Part (a) F 1 (q, Q, t) F 2 (q, P, t) P i F 1 Q i (1) F 2 (q, P, t) F 1 (q, Q, t) +
Legendre Transforms, Calculus of Varations, and Mechanics Principles
 page 437 Appendix C Legendre Transforms, Calculus of Varations, and Mechanics Principles C.1 Legendre Transforms Legendre transforms map functions in a vector space to functions in the dual space. From
page 437 Appendix C Legendre Transforms, Calculus of Varations, and Mechanics Principles C.1 Legendre Transforms Legendre transforms map functions in a vector space to functions in the dual space. From
The linear equations can be classificed into the following cases, from easier to more difficult: 1. Linear: u y. u x
 Week 02 : Method of C haracteristics From now on we will stu one by one classical techniques of obtaining solution formulas for PDEs. The first one is the method of characteristics, which is particularly
Week 02 : Method of C haracteristics From now on we will stu one by one classical techniques of obtaining solution formulas for PDEs. The first one is the method of characteristics, which is particularly
Variation Principle in Mechanics
 Section 2 Variation Principle in Mechanics Hamilton s Principle: Every mechanical system is characterized by a Lagrangian, L(q i, q i, t) or L(q, q, t) in brief, and the motion of he system is such that
Section 2 Variation Principle in Mechanics Hamilton s Principle: Every mechanical system is characterized by a Lagrangian, L(q i, q i, t) or L(q, q, t) in brief, and the motion of he system is such that
Review for Final. elementary mechanics. Lagrangian and Hamiltonian Dynamics. oscillations
 Review for Final elementary mechanics Newtonian mechanics gravitation dynamics of systems of particles Lagrangian and Hamiltonian Dynamics Lagrangian mechanics Variational dynamics Hamiltonian dynamics
Review for Final elementary mechanics Newtonian mechanics gravitation dynamics of systems of particles Lagrangian and Hamiltonian Dynamics Lagrangian mechanics Variational dynamics Hamiltonian dynamics
4.1 Important Notes on Notation
 Chapter 4. Lagrangian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 4.1 Important Notes on Notation In this chapter, unless otherwise stated, the
Chapter 4. Lagrangian Dynamics (Most of the material presented in this chapter is taken from Thornton and Marion, Chap. 7) 4.1 Important Notes on Notation In this chapter, unless otherwise stated, the
ENGI Partial Differentiation Page y f x
 ENGI 344 4 Partial Differentiation Page 4-0 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
ENGI 344 4 Partial Differentiation Page 4-0 4. Partial Differentiation For functions of one variable, be found unambiguously by differentiation: y f x, the rate of change of the dependent variable can
L(q, q) = m 2 q2 V (q) 2 m + V (q)
 Lecture 7 Phase Space, Part 1 MATH-GA 71.1 Mechanics 1 Phase portraits 1.1 One dimensional system Consider the generic one dimensional case of a point mass m described by a generalized coordinate q and
Lecture 7 Phase Space, Part 1 MATH-GA 71.1 Mechanics 1 Phase portraits 1.1 One dimensional system Consider the generic one dimensional case of a point mass m described by a generalized coordinate q and
Surfaces JWR. February 13, 2014
 Surfaces JWR February 13, 214 These notes summarize the key points in the second chapter of Differential Geometry of Curves and Surfaces by Manfredo P. do Carmo. I wrote them to assure that the terminology
Surfaces JWR February 13, 214 These notes summarize the key points in the second chapter of Differential Geometry of Curves and Surfaces by Manfredo P. do Carmo. I wrote them to assure that the terminology
Mechanics Physics 151
 Mechanics Physics 151 Lecture 4 Continuous Systems and Fields (Chapter 13) What We Did Last Time Built Lagrangian formalism for continuous system Lagrangian L Lagrange s equation = L dxdydz Derived simple
Mechanics Physics 151 Lecture 4 Continuous Systems and Fields (Chapter 13) What We Did Last Time Built Lagrangian formalism for continuous system Lagrangian L Lagrange s equation = L dxdydz Derived simple
Chapter 1. Principles of Motion in Invariantive Mechanics
 Chapter 1 Principles of Motion in Invariantive Mechanics 1.1. The Euler-Lagrange and Hamilton s equations obtained by means of exterior forms Let L = L(q 1,q 2,...,q n, q 1, q 2,..., q n,t) L(q, q,t) (1.1)
Chapter 1 Principles of Motion in Invariantive Mechanics 1.1. The Euler-Lagrange and Hamilton s equations obtained by means of exterior forms Let L = L(q 1,q 2,...,q n, q 1, q 2,..., q n,t) L(q, q,t) (1.1)
Discrete Dirac Mechanics and Discrete Dirac Geometry
 Discrete Dirac Mechanics and Discrete Dirac Geometry Melvin Leok Mathematics, University of California, San Diego Joint work with Anthony Bloch and Tomoki Ohsawa Geometric Numerical Integration Workshop,
Discrete Dirac Mechanics and Discrete Dirac Geometry Melvin Leok Mathematics, University of California, San Diego Joint work with Anthony Bloch and Tomoki Ohsawa Geometric Numerical Integration Workshop,
MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES
 MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES J. WONG (FALL 2017) What did we cover this week? Basic definitions: DEs, linear operators, homogeneous (linear) ODEs. Solution techniques for some classes
MATH 353 LECTURE NOTES: WEEK 1 FIRST ORDER ODES J. WONG (FALL 2017) What did we cover this week? Basic definitions: DEs, linear operators, homogeneous (linear) ODEs. Solution techniques for some classes
Physics 106a, Caltech 13 November, Lecture 13: Action, Hamilton-Jacobi Theory. Action-Angle Variables
 Physics 06a, Caltech 3 November, 08 Lecture 3: Action, Hamilton-Jacobi Theory Starred sections are advanced topics for interest and future reference. The unstarred material will not be tested on the final
Physics 06a, Caltech 3 November, 08 Lecture 3: Action, Hamilton-Jacobi Theory Starred sections are advanced topics for interest and future reference. The unstarred material will not be tested on the final
Lecture 4. Alexey Boyarsky. October 6, 2015
 Lecture 4 Alexey Boyarsky October 6, 2015 1 Conservation laws and symmetries 1.1 Ignorable Coordinates During the motion of a mechanical system, the 2s quantities q i and q i, (i = 1, 2,..., s) which specify
Lecture 4 Alexey Boyarsky October 6, 2015 1 Conservation laws and symmetries 1.1 Ignorable Coordinates During the motion of a mechanical system, the 2s quantities q i and q i, (i = 1, 2,..., s) which specify
Nonlinear Single-Particle Dynamics in High Energy Accelerators
 Nonlinear Single-Particle Dynamics in High Energy Accelerators Part 2: Basic tools and concepts Nonlinear Single-Particle Dynamics in High Energy Accelerators This course consists of eight lectures: 1.
Nonlinear Single-Particle Dynamics in High Energy Accelerators Part 2: Basic tools and concepts Nonlinear Single-Particle Dynamics in High Energy Accelerators This course consists of eight lectures: 1.
where (E) is the partition function of the uniform ensemble. Recalling that we have (E) = E (E) (E) i = ij x (E) j E = ij ln (E) E = k ij ~ S E = kt i
 G25.265: Statistical Mechanics Notes for Lecture 4 I. THE CLASSICAL VIRIAL THEOREM (MICROCANONICAL DERIVATION) Consider a system with Hamiltonian H(x). Let x i and x j be specic components of the phase
G25.265: Statistical Mechanics Notes for Lecture 4 I. THE CLASSICAL VIRIAL THEOREM (MICROCANONICAL DERIVATION) Consider a system with Hamiltonian H(x). Let x i and x j be specic components of the phase
EULER-LAGRANGE TO HAMILTON. The goal of these notes is to give one way of getting from the Euler-Lagrange equations to Hamilton s equations.
 EULER-LAGRANGE TO HAMILTON LANCE D. DRAGER The goal of these notes is to give one way of getting from the Euler-Lagrange equations to Hamilton s equations. 1. Euler-Lagrange to Hamilton We will often write
EULER-LAGRANGE TO HAMILTON LANCE D. DRAGER The goal of these notes is to give one way of getting from the Euler-Lagrange equations to Hamilton s equations. 1. Euler-Lagrange to Hamilton We will often write
1 Hamiltonian formalism
 1 Hamiltonian formalism 1.1 Hamilton s principle of stationary action A dynamical system with a finite number n degrees of freedom can be described by real functions of time q i (t) (i =1, 2,..., n) which,
1 Hamiltonian formalism 1.1 Hamilton s principle of stationary action A dynamical system with a finite number n degrees of freedom can be described by real functions of time q i (t) (i =1, 2,..., n) which,
Half of Final Exam Name: Practice Problems October 28, 2014
 Math 54. Treibergs Half of Final Exam Name: Practice Problems October 28, 24 Half of the final will be over material since the last midterm exam, such as the practice problems given here. The other half
Math 54. Treibergs Half of Final Exam Name: Practice Problems October 28, 24 Half of the final will be over material since the last midterm exam, such as the practice problems given here. The other half
arxiv: v1 [quant-ph] 4 Nov 2008
![arxiv: v1 [quant-ph] 4 Nov 2008 arxiv: v1 [quant-ph] 4 Nov 2008](/thumbs/72/66818329.jpg) International Journal of Modern Physics E c World Scientific Publishing Company arxiv:0811.0496v1 [quant-ph] 4 Nov 2008 Extended Hamilton-Lagrange formalism and its application to Feynman s path integral
International Journal of Modern Physics E c World Scientific Publishing Company arxiv:0811.0496v1 [quant-ph] 4 Nov 2008 Extended Hamilton-Lagrange formalism and its application to Feynman s path integral
Hamilton-Jacobi theory
 Hamilton-Jacobi theory November 9, 04 We conclude with the crowning theorem of Hamiltonian dynamics: a proof that for any Hamiltonian dynamical system there exists a canonical transformation to a set of
Hamilton-Jacobi theory November 9, 04 We conclude with the crowning theorem of Hamiltonian dynamics: a proof that for any Hamiltonian dynamical system there exists a canonical transformation to a set of
Hierarchical Modeling of Complicated Systems
 Hierarchical Modeling of Complicated Systems C. David Levermore Department of Mathematics and Institute for Physical Science and Technology University of Maryland, College Park, MD lvrmr@math.umd.edu presented
Hierarchical Modeling of Complicated Systems C. David Levermore Department of Mathematics and Institute for Physical Science and Technology University of Maryland, College Park, MD lvrmr@math.umd.edu presented
Classical mechanics of particles and fields
 Classical mechanics of particles and fields D.V. Skryabin Department of Physics, University of Bath PACS numbers: The concise and transparent exposition of many topics covered in this unit can be found
Classical mechanics of particles and fields D.V. Skryabin Department of Physics, University of Bath PACS numbers: The concise and transparent exposition of many topics covered in this unit can be found
Dynamics and Stability application to submerged bodies, vortex streets and vortex-body systems
 Dynamics and Stability application to submerged bodies, vortex streets and vortex-body systems Eva Kanso University of Southern California CDS 140B Introduction to Dynamics February 5 and 7, 2008 Fish
Dynamics and Stability application to submerged bodies, vortex streets and vortex-body systems Eva Kanso University of Southern California CDS 140B Introduction to Dynamics February 5 and 7, 2008 Fish
Physics 5153 Classical Mechanics. Solution by Quadrature-1
 October 14, 003 11:47:49 1 Introduction Physics 5153 Classical Mechanics Solution by Quadrature In the previous lectures, we have reduced the number o eective degrees o reedom that are needed to solve
October 14, 003 11:47:49 1 Introduction Physics 5153 Classical Mechanics Solution by Quadrature In the previous lectures, we have reduced the number o eective degrees o reedom that are needed to solve
III. Kinetic Theory of Gases
 III. Kinetic Theory of Gases III.A General Definitions Kinetic theory studies the macroscopic properties of large numbers of particles, starting from their (classical) equations of motion. Thermodynamics
III. Kinetic Theory of Gases III.A General Definitions Kinetic theory studies the macroscopic properties of large numbers of particles, starting from their (classical) equations of motion. Thermodynamics
Lecture I: Constrained Hamiltonian systems
 Lecture I: Constrained Hamiltonian systems (Courses in canonical gravity) Yaser Tavakoli December 15, 2014 1 Introduction In canonical formulation of general relativity, geometry of space-time is given
Lecture I: Constrained Hamiltonian systems (Courses in canonical gravity) Yaser Tavakoli December 15, 2014 1 Introduction In canonical formulation of general relativity, geometry of space-time is given
Euler-Lagrange's equations in several variables
 Euler-Lagrange's equations in several variables So far we have studied one variable and its derivative Let us now consider L2:1 More:1 Taylor: 226-227 (This proof is slightly more general than Taylor's.)
Euler-Lagrange's equations in several variables So far we have studied one variable and its derivative Let us now consider L2:1 More:1 Taylor: 226-227 (This proof is slightly more general than Taylor's.)
A Very General Hamilton Jacobi Theorem
 University of Salerno 9th AIMS ICDSDEA Orlando (Florida) USA, July 1 5, 2012 Introduction: Generalized Hamilton-Jacobi Theorem Hamilton-Jacobi (HJ) Theorem: Consider a Hamiltonian system with Hamiltonian
University of Salerno 9th AIMS ICDSDEA Orlando (Florida) USA, July 1 5, 2012 Introduction: Generalized Hamilton-Jacobi Theorem Hamilton-Jacobi (HJ) Theorem: Consider a Hamiltonian system with Hamiltonian
Multibody simulation
 Multibody simulation Dynamics of a multibody system (Euler-Lagrange formulation) Dimitar Dimitrov Örebro University June 16, 2012 Main points covered Euler-Lagrange formulation manipulator inertia matrix
Multibody simulation Dynamics of a multibody system (Euler-Lagrange formulation) Dimitar Dimitrov Örebro University June 16, 2012 Main points covered Euler-Lagrange formulation manipulator inertia matrix
Dynamical Systems & Lyapunov Stability
 Dynamical Systems & Lyapunov Stability Harry G. Kwatny Department of Mechanical Engineering & Mechanics Drexel University Outline Ordinary Differential Equations Existence & uniqueness Continuous dependence
Dynamical Systems & Lyapunov Stability Harry G. Kwatny Department of Mechanical Engineering & Mechanics Drexel University Outline Ordinary Differential Equations Existence & uniqueness Continuous dependence
Lecture: Lorentz Invariant Dynamics
 Chapter 5 Lecture: Lorentz Invariant Dynamics In the preceding chapter we introduced the Minkowski metric and covariance with respect to Lorentz transformations between inertial systems. This was shown
Chapter 5 Lecture: Lorentz Invariant Dynamics In the preceding chapter we introduced the Minkowski metric and covariance with respect to Lorentz transformations between inertial systems. This was shown
Thermodynamics of phase transitions
 Thermodynamics of phase transitions Katarzyna Sznajd-Weron Department of Theoretical of Physics Wroc law University of Science and Technology, Poland March 12, 2017 Katarzyna Sznajd-Weron (WUST) Thermodynamics
Thermodynamics of phase transitions Katarzyna Sznajd-Weron Department of Theoretical of Physics Wroc law University of Science and Technology, Poland March 12, 2017 Katarzyna Sznajd-Weron (WUST) Thermodynamics
Canonical transformations and exact invariants for time-dependent Hamiltonian systems
 Ann. Phys. Leipzig 11 00 1, 15 38 Canonical transformations and exact invariants for time-dependent Hamiltonian systems Jürgen Struckmeier a and Claus Riedel Gesellschaft für Schwerionenforschung GSI,
Ann. Phys. Leipzig 11 00 1, 15 38 Canonical transformations and exact invariants for time-dependent Hamiltonian systems Jürgen Struckmeier a and Claus Riedel Gesellschaft für Schwerionenforschung GSI,
Hamiltonian Field Theory
 Hamiltonian Field Theory August 31, 016 1 Introduction So far we have treated classical field theory using Lagrangian and an action principle for Lagrangian. This approach is called Lagrangian field theory
Hamiltonian Field Theory August 31, 016 1 Introduction So far we have treated classical field theory using Lagrangian and an action principle for Lagrangian. This approach is called Lagrangian field theory
M3/4A16. GEOMETRICAL MECHANICS, Part 1
 M3/4A16 GEOMETRICAL MECHANICS, Part 1 (2009) Page 1 of 5 UNIVERSITY OF LONDON Course: M3/4A16 Setter: Holm Checker: Gibbons Editor: Chen External: Date: January 27, 2008 BSc and MSci EXAMINATIONS (MATHEMATICS)
M3/4A16 GEOMETRICAL MECHANICS, Part 1 (2009) Page 1 of 5 UNIVERSITY OF LONDON Course: M3/4A16 Setter: Holm Checker: Gibbons Editor: Chen External: Date: January 27, 2008 BSc and MSci EXAMINATIONS (MATHEMATICS)
Review for the Final Exam
 Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Math 171 Review for the Final Exam 1 Find the limits (4 points each) (a) lim 4x 2 3; x x (b) lim ( x 2 x x 1 )x ; (c) lim( 1 1 ); x 1 ln x x 1 sin (x 2) (d) lim x 2 x 2 4 Solutions (a) The limit lim 4x
Two simple ideas from calculus applied to Riemannian geometry
 Calibrated Geometries and Special Holonomy p. 1/29 Two simple ideas from calculus applied to Riemannian geometry Spiro Karigiannis karigiannis@math.uwaterloo.ca Department of Pure Mathematics, University
Calibrated Geometries and Special Holonomy p. 1/29 Two simple ideas from calculus applied to Riemannian geometry Spiro Karigiannis karigiannis@math.uwaterloo.ca Department of Pure Mathematics, University
Borel Summability in PDE initial value problems
 Borel Summability in PDE initial value problems Saleh Tanveer (Ohio State University) Collaborator Ovidiu Costin & Guo Luo Research supported in part by Institute for Math Sciences (IC), EPSRC & NSF. Main
Borel Summability in PDE initial value problems Saleh Tanveer (Ohio State University) Collaborator Ovidiu Costin & Guo Luo Research supported in part by Institute for Math Sciences (IC), EPSRC & NSF. Main
September Math Course: First Order Derivative
 September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
September Math Course: First Order Derivative Arina Nikandrova Functions Function y = f (x), where x is either be a scalar or a vector of several variables (x,..., x n ), can be thought of as a rule which
16. Working with the Langevin and Fokker-Planck equations
 16. Working with the Langevin and Fokker-Planck equations In the preceding Lecture, we have shown that given a Langevin equation (LE), it is possible to write down an equivalent Fokker-Planck equation
16. Working with the Langevin and Fokker-Planck equations In the preceding Lecture, we have shown that given a Langevin equation (LE), it is possible to write down an equivalent Fokker-Planck equation
Definition 5.1. A vector field v on a manifold M is map M T M such that for all x M, v(x) T x M.
 5 Vector fields Last updated: March 12, 2012. 5.1 Definition and general properties We first need to define what a vector field is. Definition 5.1. A vector field v on a manifold M is map M T M such that
5 Vector fields Last updated: March 12, 2012. 5.1 Definition and general properties We first need to define what a vector field is. Definition 5.1. A vector field v on a manifold M is map M T M such that
Numerical Algorithms as Dynamical Systems
 A Study on Numerical Algorithms as Dynamical Systems Moody Chu North Carolina State University What This Study Is About? To recast many numerical algorithms as special dynamical systems, whence to derive
A Study on Numerical Algorithms as Dynamical Systems Moody Chu North Carolina State University What This Study Is About? To recast many numerical algorithms as special dynamical systems, whence to derive
G : Statistical Mechanics Notes for Lecture 3 I. MICROCANONICAL ENSEMBLE: CONDITIONS FOR THERMAL EQUILIBRIUM Consider bringing two systems into
 G25.2651: Statistical Mechanics Notes for Lecture 3 I. MICROCANONICAL ENSEMBLE: CONDITIONS FOR THERMAL EQUILIBRIUM Consider bringing two systems into thermal contact. By thermal contact, we mean that the
G25.2651: Statistical Mechanics Notes for Lecture 3 I. MICROCANONICAL ENSEMBLE: CONDITIONS FOR THERMAL EQUILIBRIUM Consider bringing two systems into thermal contact. By thermal contact, we mean that the
Noether Symmetries and Conserved Momenta of Dirac Equation in Presymplectic Dynamics
 International Mathematical Forum, 2, 2007, no. 45, 2207-2220 Noether Symmetries and Conserved Momenta of Dirac Equation in Presymplectic Dynamics Renato Grassini Department of Mathematics and Applications
International Mathematical Forum, 2, 2007, no. 45, 2207-2220 Noether Symmetries and Conserved Momenta of Dirac Equation in Presymplectic Dynamics Renato Grassini Department of Mathematics and Applications
Physics 351 Wednesday, February 14, 2018
 Physics 351 Wednesday, February 14, 2018 HW4 due Friday. For HW help, Bill is in DRL 3N6 Wed 4 7pm. Grace is in DRL 2C2 Thu 5:30 8:30pm. Respond at pollev.com/phys351 or text PHYS351 to 37607 once to join,
Physics 351 Wednesday, February 14, 2018 HW4 due Friday. For HW help, Bill is in DRL 3N6 Wed 4 7pm. Grace is in DRL 2C2 Thu 5:30 8:30pm. Respond at pollev.com/phys351 or text PHYS351 to 37607 once to join,
CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS. Prof. N. Harnew University of Oxford TT 2017
 CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS Prof. N. Harnew University of Oxford TT 2017 1 OUTLINE : CP1 REVISION LECTURE 3 : INTRODUCTION TO CLASSICAL MECHANICS 1. Angular velocity and
CP1 REVISION LECTURE 3 INTRODUCTION TO CLASSICAL MECHANICS Prof. N. Harnew University of Oxford TT 2017 1 OUTLINE : CP1 REVISION LECTURE 3 : INTRODUCTION TO CLASSICAL MECHANICS 1. Angular velocity and
Symplectic critical surfaces in Kähler surfaces
 Symplectic critical surfaces in Kähler surfaces Jiayu Li ( Joint work with X. Han) ICTP-UNESCO and AMSS-CAS November, 2008 Symplectic surfaces Let M be a compact Kähler surface, let ω be the Kähler form.
Symplectic critical surfaces in Kähler surfaces Jiayu Li ( Joint work with X. Han) ICTP-UNESCO and AMSS-CAS November, 2008 Symplectic surfaces Let M be a compact Kähler surface, let ω be the Kähler form.
2 Equations of Motion
 2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
2 Equations of Motion system. In this section, we will derive the six full equations of motion in a non-rotating, Cartesian coordinate 2.1 Six equations of motion (non-rotating, Cartesian coordinates)
Tulczyjew triples: from statics to field theory
 Tulczyjew triples: from statics to field theory Janusz Grabowski Polish Academy of Sciences 3rd Iberoamerican Meetings on Geometry, Mechanics and Control Salamanca, Sept. 3, 2012 J.Grabowski (IMPAN) Tulczyjew
Tulczyjew triples: from statics to field theory Janusz Grabowski Polish Academy of Sciences 3rd Iberoamerican Meetings on Geometry, Mechanics and Control Salamanca, Sept. 3, 2012 J.Grabowski (IMPAN) Tulczyjew
The Simple Double Pendulum
 The Simple Double Pendulum Austin Graf December 13, 2013 Abstract The double pendulum is a dynamic system that exhibits sensitive dependence upon initial conditions. This project explores the motion of
The Simple Double Pendulum Austin Graf December 13, 2013 Abstract The double pendulum is a dynamic system that exhibits sensitive dependence upon initial conditions. This project explores the motion of
