Declarative approach to cyclic steady state space refinement: periodic process scheduling
|
|
|
- Christal Simmons
- 5 years ago
- Views:
Transcription
1 It J Adv Mauf Techl DOI /s ORIGINAL ARTICLE Declarative apprach t cyclic steady state space refiemet: peridic prcess schedulig Grzegrz Bcewicz Zbigiew A. Baaszak Received: 16 April 2012 / Accepted: 13 Octber 2012 # The Authr(s) This article is published with pe access at Sprigerlik.cm Abstract Prblems f cyclic schedulig are usually bserved i flexible maufacturig systems which prduce multitype parts where the autmated guided vehicle system plays the rle f a material hadlig system, as well as i varius ther multimdal trasprtati systems where gds ad/r passeger itierary plaig plays a pivtal rle. The schedulability aalysis f the prcesses executed i the s-called systems f ccurret cyclic prcesses (SCCPs) ca be executed withi a declarative mdelig framewrk. Csequetly, the csidered SCCP schedulig prblem ca be see as a cstrait satisfacti prblem. Such a represetati prvides a uified way fr evaluatig the perfrmace f lcal cyclic prcesses as well as f multimdal prcesses supprted by them. Here, the crucial issue is that f a ctrl prcedure (e.g., a set f dispatchig rules), which wuld guaratee the cyclic behavir f the SCCP. I this ctext, we discuss the sufficiet cditis guarateeig the schedulability f bth lcal ad multimdal cyclic prcesses, ad we prpse a recursive apprach i desigig them. Keywrds Cyclic prcesses. Declarative mdelig. Cstrait prgrammig. State space. Peridicity. Dispatchig rules 1 Itrducti Operatis i cyclic prcesses are executed i sequeces that repeat a idefiite umber f times. I everyday G. Bcewicz (*) Departmet f Electrics ad Cmputer Sciece, Kszali Uiversity f Techlgy, Kszali, Plad bcewicz@ie.tu.kszali.pl Z. A. Baaszak Departmet f Busiess Ifrmatics, Warsaw Uiversity f Techlgy, Warsaw, Plad Z.Baaszak@wz.pw.edu.pl practice, these prcesses arise i differet applicati dmais (such as maufacturig, time sharig f prcessrs i embedded systems, digital sigal prcessig, ad i cmpilers where schedulig lp peratis fr parallel r pipelied architectures takes place) as well as i service dmais, cverig such areas as wrkfrce schedulig (e.g., shift schedulig, crew schedulig), timetablig (e.g., trai timetablig, aircraft rutig ad schedulig), ad reservatis (e.g., reservatis with r withut slack, assigig classes t rms) [7, 10, 11, 14, 15, 19, 21, 23, 24]. Such cyclic schedulig prblems belg t the class f decisi prblems, i.e., prblems aimed at fidig whether r t there exists a sluti satisfyig certai assumed cditis [21]. Mrever, because f their iteger dmais, the csidered prblems belg t a class f Diphatie prblems [9, 18]. This meas that certai classes f cyclic schedulig prblems ca be see as udecidable [1]. Therefre, takig it accut the udecidability f Diphatie prblems, t all the behavirs (icludig cyclic behavirs, i.e., thse that belg t a space f cyclic steady states) are reachable uder the cstraits impsed by the structure f the system. This is als the case with the system behavir that ca be achieved i systems pssessig specific structural cstraits. This meas that sice the system s cstraits determie its behavir, bth the system structure cfigurati ad the desired cyclic schedule must be csidered simultaeusly. Thus, fr the sluti f a cyclic schedulig prblem, the cfigurati f a system structure must be determied i rder t eable schedulig f the prcesses; hwever, the schedulig must be perfrmed s as t devise the system cfigurati. I this ctext, this wrk discusses certai slvability issues ccerig the prblems f dispatchig cyclic prcesses, i particular the cditis guarateeig the slvability f the schedulig f cyclic prcesses. Their examiati may replace exhaustive ad time-csumig searchig fr the slutis satisfyig the required system fuctiig.
2 It J Adv Mauf Techl A umber f mdels ad methds have bee prpsed t slve the cyclic schedulig prblem [13]. Amg them, the mst frequetly applied are the mathematical prgrammig appraches (usually iteger prgrammig r mixed iteger prgrammig [24]), max-plus algebra [16], cstrait lgic prgrammig [2 5, 22], swarm ad evlutiary algrithms [6, 10, 20], ad Petri ets [19]. The majrity f these are rieted at fidig a miimum cycle r maximum thrughput while assumig a deadlck-free flw f prcesses. The appraches aimed at estimatig the cycle time based the cyclic prcess structure ad the emplyed sychrizati mechaism (i.e., redezvus r mutual exclusi istaces) while takig it accut deadlck avidace cstraits are rather uique [8, 22, 25]. I this ctext, apart frm the abve-metied slvability cditis ccerig pririty dispatchig rules guarateeig the reachability f a cyclic steady state f a system, ur mai ctributi csists i prpsig a ew mdelig framewrk fr evaluatig the cyclic steady state f a give system f ccurret cyclic prcesses (SCCP). This paper is ccered with the fllwig questis: ca the assumed system behavir be achieved uder the give cstraits the structure f the system? Ca we fid such a system structure fr which the assumed system behavir ca be achieved? Therefre, the aim f this paper is t prvide the cditis useful fr geeratig cyclic steady states i a system csistig f ccurretly iteractig cyclic prcesses, where mutual exclusi prtcls prvide a sychrizati mechaism which ctrls the access f the prcesses t shared (cmm) resurces. This bjective ecmpasses a rather large class f digital ad/r lgistic etwrks that have cmm prperties, eve thugh their itrisic differeces are sigificat. The mst imprtat prperty is related t differet subetwrk ifrastructures which eable schedulig multimdal prcesses executed thrugh cmm shared sectis f differet lcal etwrks [3]. Fr istace, i the case f a metr etwrk, the itierary f a give passeger, assumig lie chages, is a example f a multimdal prcess, where itierary plaig ca be viewed as a relevat multimdal prcess schedulig. Csequetly, this study aims t preset a declarative apprach t the reachability prblem that ca be emplyed by decisi makers i rder t geerate, aalyze, ad evaluate cyclic steady states reachable i a give SCCP structure. By emplyig the framewrk f the cstrait satisfacti prblem (CSP) [5], we state ur mai prblem regardig the dispatchig rules resultig i the SCCP cyclic schedules f the assumed cycle time ad the Ξ-peridicity f lcal prcesses. A illustrative mdel f the cstrait satisfacti prblem implemeted i the Oz/Mzart laguage is discussed frm the perspective f multimdal prcesses. This ctributi ca be see as a ctiuati f ur frmer wrk [3 5]. Hece, ur apprach ca be viewed as a extesi f the ccept f cstraits sufficiet fr the cyclic behavir f lcal ad multimdal prcesses [5], as well as a extesi f the ccept f the state space itrduced i [3, 4]. This meas that the cditis itrduced earlier which guaratee the cyclic behavir f a SCCP ad the geerati f its state space prvide a frmal framewrk fr the develpmet f reachability cditis guarateeig the geerati f cyclic steady states, i.e., the cditis which allw t distiguish betwee the iitial states ad the cyclic steady states i bth lcal ad multimdal prcesses. The rest f the paper is rgaized as fllws: Secti 2 itrduces systems f ccurretly flwig lcal cyclic ad multimdal prcesses, describes the emplyed tati, ad states the prblem. I Secti 3, we discuss certai issues ccerig the geerati f feasible state space as well as prvide tw methds aimed at refiig cyclic steady states. Tw cases illustratig the implemetati f bth methds are discussed i Secti 4, whereas Secti 5 presets ur cclusis. 2 Systems f ccurret cyclic prcesses 2.1 Declarative mdelig A autmated guided vehicle system (AGVS) with distiguishable vehicles, pick-up/delivery pits (PDPs), ad trasprtati rutes is preseted i Fig. 1. Such a system ca be mdeled i terms f SCCPs, where cyclic multimdal prcesses (represetig trasprtati rutes) are executed alg the parts f cyclic lcal prcesses (represeted by the itieraries f vehicles) which are itercected with each ther thrugh cmm resurces f the AGVS (i.e., PDPs). Figure 2 presets the SCCP mdel frm Fig. 1. Six lcal cyclic prcesses are csidered, viz., P 1,P 2, P 3, P 4, P 5, ad P 6. The prcesses fllw the rutes cmpsed f trasprtati sectrs (distiguished i Fig. 2 by the set f resurces R ={R 1,, R c,, R 17 }, where R c is the cth resurce). Sme f the lcal cyclic prcesses are pipelie flw prcesses, i.e., they ctai streams (represetig vehicles frm Fig. 1) f the prcesses fllwig the same rute while ccupyig differet resurces (sectrs). Fr istace, prcesses P 4 ad P 5 ctai tw streams: P 4 ¼ P4 1; P2 4,adP5 ¼ P5 1; P2 5, respectively, i.e., the prcesses (vehicles) mvig alg the same rute. The remaiig lcal prcesses ctai uique streams: P 1 ¼ P1 1, P2 ¼ P2 1, P 3 ¼ P3 1,adP6 ¼ P6 1. I ther wrds, the streams P1 1, P1 2, P1 3, P1 4, P2 4, P1 5, P2 5,adP1 6 represet the eight vehicles frm Fig. 1. The kth stream f the ith lcal prcess P i is deted as Pi k.
3 It J Adv Mauf Techl Fig. 1 Example f a AGVS Leged: - pick-up/delivery pits (PDPs) - Autmated Guided Vehicle (AGV) -prducti rute f the pallet - trasprtati sectr Apart frm lcal prcesses, we csider tw multimdal prcesses (i.e., prcesses executed alg the rutes csistig f parts f the rutes f lcal prcesses): mp 1 ad mp 2. Fr example, the displacemet f the pallet alg the prducti rute depicted by the dashed lie crrespds t the multimdal prcess mp 1 supprted by AGVs, which i tur ecmpass lcal trasprtati streams, P1 1 ad P1 3, ad the als e f tw pipelie-like flwig streams: P5 1 ad P5 2. This meas that the prducti/trasprtati rute specifyig hw a multimdal prcess is executed ca be see as cmpsed f parts f the rutes f lcal cyclic prcesses. Prcesses ca iteract with each ther thrugh shared resurces, i.e., the trasprtati sectrs. The rutes f the csidered lcal prcesses (streams) are as fllws: p 1 1 ¼ ð R 1; R 2 ; R 3 ; R 4 Þ; p 1 2 ¼ ð R 4; R 5 ; R 6 Þ; p 1 3 ¼ ð R 3; R 9 ; R 8 ; R 7 ; R 5 Þ; p 1 4 ¼ p 2 4 ¼ ðr 2 ; R 16 ; R 10 ; R 11 ; R 12 ; R 9 Þ; p 1 5 ¼ p2 5 ¼ ð R 8; R 17 ; R 13 ; R 14 ; R 12 Þ; p 1 6 ¼ ð R 14; R 11 ; R 15 Þ; where R 2 R 5, R 8 R 14,R 16, ad R 17 are the shared resurces, sice each f them is used by at least tw streams, ad R 1, R 6,R 7, adr 15 are the -shared resurces, because they are exclusively used by e stream ly. I geeral, the rute p k i is the sequece f resurces used i rder t execute the Fig. 2 Example f FMS SCCP mdel f a AGVS Leged: - -th resurce f set - uccupied resurce: - resurce ccupied by the stream ad ctrlled by the pririty dispatchig rule ; ( - a set f streams)
4 It J Adv Mauf Techl peratis f the stream Pi k. Nte that the streams p1 4 ad p2 4 which belg t P 4 ad the streams p 1 5 ad p2 5 which belg t P 5 fllw the same rute (these streams crrespd t vehicles mvig alg the same rute). Csider tw cyclic multimdal prcesses mp 1 ad mp 2 which fllw the rutes mp 1 ad mp 2, respectively (see Fig. 2): mp 1 ¼ ðr 1 ; R 2 ; R 3 ; R 9 ; R 8 ; R 17 ; R 13 Þ; mp 2 ¼ ðr 15 ; R 14 ; R 12 ; R 8 ; R 7 ; R 5 ; R 6 Þ: Let us assume that mp 1 ad mp 2 ca be see as fllws: mp 1 ¼ ððr 1 ; R 2 ; R 3 Þ; ðr 9 ; R 8 Þ; ðr 17 ; R 13 ÞÞ; mp 2 ¼ ððr 15 ; R 14 Þ; ðr 12 ; R 8 Þ; ðr 7 ; R 5 Þ; ðr 6 ÞÞ; where: (R 1, R 2, R 3 ), (R 9, R 8 ), (R 17, R 13 ) the parts (subsequeces) f rutes p 1 1, p1 3 ad p1 5 icluded i mp 1 (R 15, R 14 ), (R 12, R 8 ), (R 7, R 5 ), (R 6 ) the parts (subsequeces) f rutes p 1 6, p1 5, p1 3, ad p1 2 icluded i mp 2. Let us assume that multimdal prcesses d t ctai subprcesses, i.e., that each multimdal prcess csists f a uique stream. The class f the csidered SCCPs fllws the cstraits stated belw [5]: A ew perati may start a resurce ly if the curret perati has bee cmpleted ad the resurce has bee released, Lcal prcesses share cmm resurces i the mutual exclusi mde, the perati f a lcal prcess ca ly be suspeded if the ecessary resurce is ccupied, suspeded lcal prcesses cat be released, ad lcal prcesses are -preemptible, i.e., a resurce may t be take frm a prcess as lg as it is used by it, Multimdal prcesses ecmpassig pallet flw cveyed by AGVs fllw lcal trasprtati rutes, ad differet multimdal prcesses ca be executed simultaeusly alg the same lcal prcess, Lcal ad multimdal prcesses execute cyclically with perids Tc ad Tm, respectively; resurces ccur uiquely i each trasprtati rute, I a cyclic steady state, each ith stream must cver its lcal rute the same umber f times Ξ ψ i ; the factrs Ξ ad ψ i are defied belw. A resurce cflict (caused by the applicati f the mutual exclusi prtcl) is reslved with the aid f a pririty dispatchig rule [2], which determies the rder i which streams access shared resurces. Fr istace, i the case f the resurce R 9 ; σ 9 ¼ P3 1; P1 4 ; P2 4, the pririty dispatchig rule determies the rder i which streams ca access the shared resurce R 9, i.e., the resurce is first give t stream P3 1, the t the stream P1 4, the t P2 4 ad the ce agai t P3 1, ad s. The stream Pk i ccurs the same umber f times i each dispatchig rule assciated with the resurces featurig i its rute. Therefre, the SCCP shw i Fig. 2 is specified by the fllwig set f dispatchig rules: Θ ¼ fσ 1 ;...; σ 17 g, as well as f 1 P1 1 ¼ f2 P1 1 ¼ f3 P1 1 ¼ f4 P1 1 ¼ 1, f4 P2 1 ¼ f5 P2 1 ¼ f6 P2 1 ¼ 3, etc., where f c Pi k is the umber f ccurreces f P k i i the cth pririty dispatchig rule. This meas that durig the same perid, the stream P2 1 is repeated three times, while P1 1 ly ce. Thus, the pririty rules determie the frequecies f the mutual appearace f lcal prcesses sharig the same resurce. I geeral, the set f dispatchig rules Θ determies the sequece f relative frequecies f mutual executis f lcal prcesses, ad is deted by Ψ ¼ ðy 1 ; y 2 ;...; y Þ, where y i 2 N, y i ¼jj d js c;d ¼ Pi 1 ; d 2 f 1;...; lpðcþ g jj; 8i 2 f1;...; g; 8σc 2 Θ i ; ð1þ where Θ i is the set f dispatchig rules assciated with the resurces featurig i the rute fllwed by P i, s c,d is the dth elemet i the sequece σ c =(s c,1,, s c,d,, s c,lp(c) ), is the umber f prcesses, ad lp(c) is the legth f σ c. Therefre, the SCCP shw i Fig. 2 is specified by the sequece: Ψ = (1,3,1,1,1,2). This meas that e executi f lcal prcesses P 1,P 3, P 4, ad P 5 (ad their assciated streams) crrespds t three executis f prcess P 2 ad tw executis f P 6. Sice the sequece Ψ f relative frequecies f mutual executis f lcal prcesses des t ecessary ecmpass a cyclic steady state f the SCCP, we itrduced a ew parameter describig the umber f ccurreces f Ψ i a cyclic steady state, deted by Ξ 2 N. Ξ ccurreces f Ψ i e perid is termed Ξ-peridicity. Fr the csidered SCCP, Ξ=2 implies that tw executis f the sequece Ψ = (1,3,1,1,1,2), i.e., tw executis f lcal prcesses P 1,P 3, P 4, ad P 5 crrespd t six executis f the prcess P 2 ad fur executis f P 6. We ca defie the mutual frequecy mψ f multimdal prcesses mp i (e.g., i the case f the executi f multimdal prcesses (see the SCCP i Fig. 2), mψ = (1,1) implies that e executi f the prcess mp 1 crrespds t e executi f mp 2 ). We ca similarly defie mξ, which determies the umber f executis f mψ i a cycle. I geeral, the fllwig tati is used: Asequece p k i ¼ p k i;1 ; pk i;2 ;...; pk i;j ;...; pk i;lrðiþ specifies the rute f the stream f a lcal prcess Pi k (the kth stream f the ith lcal prcess P i ). Its cmpets defie the resurces used i the executi f peratis, where
5 It J Adv Mauf Techl p k i;j 2 R (the set f resurces R ¼ R f 1; R 2 ;...; R c ;...; R m g) detes the resurces used by thekth stream f the ith lcal prcess i the jth perati. I the rest f the paper, the jth perati executed the resurce p k i;j i the stream Pk i will be deted by k i;j ; lr(i) is the legth f the cyclic prcess rute (all streams f P i are f the same legth). Fr example, the rute p 1 2 ¼ ð R 4; R 5 ; R 6 Þf the stream P2 1 (Fig. 2)is the sequece p 1 2 ¼ p1 1;1 ; p1 1;2 ; p1 1;3, where the first elemet p 1 1;1 is equal t R 4, whereas the secd, p 1 1;2 ¼ R 5,ad the third, p 1 1;3 ¼ R 6. x k i;j;q ðlþ 2N is the mmet whe the perati k i;j begis its qthexecuti i the lth cycle. ti k ¼ ti;1 k ; tk i;2 ;...; tk i;j ;...; tk i;lrðiþ specifies the perati times f lcal prcesses, where ti;j k detes the time f executi f perati k i;j (fr the SCCP i Fig. 2, see Table 1). mp i ¼ mpr k 1 i 1 ða i1 ; b i1 Þ; mpr k 2 i 2 ða i2 ; b i2 Þ;...; mpr ky i y a iy ; b iy specifies the rute f the multimdal prcess mp i, where 8 < p k mpri k i;a ða; bþ ¼ ; pk i;aþ1 ;...; pk i;b a b p k i;a ; pk i;aþ1...; pk i;lrðiþ ; pk i;1 ;...; pk i;b1 ; ; : pk b > a i;b a; b 2 f1;...; lrðiþg; is the subsequece f the rute p k i ¼ p k i;1 ; p k i;2 ;...; p k i;j ;...; pk i;lrðiþ Þ ctaiig elemets frm pk i;a t pk i;b. I ther wrds, the trasprtati rute mp i is a sequece f parts f rutes f lcal prcesses. Fr istace, the rute fllwed by mp 1 (see Fig. 2) isas fllws: mp 1 =((R 1, R 2, R 3 ), (R 9, R 8 ), (R 17, R 13 )), where mpr1 1ð1; 3Þ ¼ ð R 1; R 2 ; R 3 Þ, mpr3 1ð2; 3Þ ¼ ð R 9; R 8 Þ,adm pr5 1ð2; 3Þ ¼ ð R 17; R 13 Þ. I the rest f the paper, the jth perati executed i the prcess mp i will be deted by m i,j. mx i;j;k ðlþ 2N is the mmet whe the perati m i,j begis its kth executi i the lth cycle. Table 1 Lcal perati times f SCCPs (Fig. 2) Streams i,k t k i;1 t k i;2 t k i;3 t k i;4 t k i;5 t k i;6 P 1 1 1, P 1 2 2, P 1 3 3, P 1 4 4, P 2 4 4, P 1 5 5, P 2 5 5, P 1 6 6, Θ ¼ fσ 1 ; σ 2 ;...; σ c ;...; σ m g is the set f pririty dispatchig rules, where σ c =(s c,1,, s c,d,, s c,lp(c) ) are sequece cmpets which determie the rder i which the prcesses ca be executed the resurce R c, where s c,d H (H is the set f streams,.e.g., fr Fig. 2, H ¼ P1 1; P 2 1 ; P 1 3 ; P 1 4 ; P 2 4 ; P 1 5 ; P ; P 6 ). Usig the abve tati, a SCCP ca be defied as a tuple: SC ¼ ððr; SLÞ; SMÞ; ð2þ where: R ={R 1, R 2,, R c,, R m } the set f resurces, where m is the umber f resurces SL =(ST L, BE L ) the structure f lcal prcesses, i.e. ST L =(U, T) the variables describig the layut f lcal prcesses U ¼ p 1 1 ;...; plsð1þ 1 ;...; p 1 ;...; plsðþ the set f rutes f lcal prcess where ls(i) is the umber f streams belgig t the prcess P i ad is the umber f lcal prcesses T ¼ t1 1 ;...; tlsð1þ 1 ;...; t 1 ;...; tlsðþ the set f sequeces f perati times i lcal prcesses. BE L ¼ ðθ; < ; ΞÞ the variables describig the behavir f lcal prcesses Θ ¼ fσ 1 ; σ 2 ;...; σ c ;...; σ m g the set f pririty dispatchig rules < ¼ ðy 1 ; y 2 ;...; y i ;...; y Þ the sequece f relative frequecies f mutual executis f lcal prcesses Ξ the umber f ccurreces f Ψ i a cyclic steady state. SM =(ST M, BE M ) the structure f multimdal prcesses, i.e. ST M =(M, T) the variables describig the layut f the level f a multimdal prcess, where M ={mp 1,, mp i,, mp w } is the set f rutes f a multimdal prcess ad w is the umber f multimdal prcesses mp i mt ={mt 1 mt w } the set f sequeces f perati times i multimdal prcesses. BE M =(mψ,mξ) the variables describig the behavir f multimdal prcesses m< ¼ ðmy 1 ; my 2 ;...; my i ;...; my w Þ the sequece f relative frequecies f mutual executis f multimdal prcesses mξ the umber f ccurreces f mψ i a cyclic steady state. The SCCP mdel (2) ca be see as a multilevel mdel, cf. Fig. 3, i.e., a mdel cmpsed f a R level
6 It J Adv Mauf Techl Fig. 3 Multilayered mdel f the behavir f a SCCP (see the SCCP i Fig. 2) A ptetial higher level level level The level f multimdal prcesses : SL level The level f lcal prcesses : Rlevel the set f resurces (resurces), a SL level (lcal cyclic prcesses), ad a SM 1 level (multimdal cyclic prcesses), as well as a SM i level (the ith meta-multimdal prcess). The SL level determies the structure f trasprtati rutes f lcal prcesses U, as well as the parameters Θ,Ψ, ad Ξ which specify the required behavir f the system. I tur, the SM 1 level takes it accut multimdal, prcesses, as well as meta-multimdal prcesses (SM 2 level) cmpsed f multimdal prcesses frm the SM 1 level. I ther wrds, we assume that the variables describig SM i are the same as i the case f SM, whereas the rutes f the multimdal prcess f the ith level remai cmpsed f the prcesses frm the (i 1)th level. The preseted mdel is a exteded versi f a simplified mdel limited t R ad SL levels, which is itrduced i [3, 5]. Therefre, i geeral, the SC ¼ ððr; SLÞ; SMÞmdel ca be see as cmpsed f i levels: SC i ¼ ðr; SLÞ; SM 1 ; SM 2 ;... ; SM i : ð3þ Nte that the cyclic behavir f SC i 1 implies the peridic behavir f SC i. 2.2 Prblem frmulati Let us csider a SCCP specified by a give set R f resurces, dispatchig rules Θ, the rutes f lcal ad multimdal prcesses U ad M, respectively, ad a iitial allcati f prcesses. The mst imprtat issue here is the peridicity f the SCCP, i.e., des there exist a cyclic executi f lcal prcesses? Ad if s, what is the perid Tc? Further questis are ccered with cyclic executi f multimdal prcesses. I rder t fid the aswers t the abve questis, mre detailed questis must be aswered first. Which allcatis f iitial prcesses are admissible (i.e., which AGV dckigs are pssible)? Which dispatchig rules Θ assure the peridicity f a give SCCP (i the lcal ad multimdal sese), while retaiig the assumed frequecy (Ψ, mψ) f the executi f prcesses withi the glbal perid (lcal Tc ad multimdal Tm)? I geeral, hwever, apart frm the abve frmulatis f frward prblems, iverse prblems ca be csidered as well. Fr istace, des there exist a SCCP structure f a lcal (SL) ad/r multimdal layer (SM), such that the assumed steady cyclic state ca be achieved? I the rest f the paper, the fllwig frward prblem is csidered: Give a SCCP defied by SC (2), i.e., R, SL =(ST L, BE L ), SM =(ST M, BE M ), is it pssible t attai cyclic behavir f SC (i.e., the ecmpassig cyclic steady states f lcal ad multimdal prcesses)? I ther wrds, assumig the declarative apprach, we are searchig fr the CSP prvidig a frmal framewrk aimed at prttypig dispatchig rules fr the csidered SCCP.
7 It J Adv Mauf Techl 3 Refiemet f the space f cyclic steady states 3.1 Geerati f state space Let us csider the fllwig defiiti f a SCCP state, which describes the allcati f bth lcal ad multimdal prcesses: S k ¼ Sl r ; MA k ; ð4þ where: Sl r the rth state f lcal prcesses, crrespdig t the kth state f multimdal prcesses, Sl r ¼ ða r ; Z r ; Q r Þ; ð5þ where: A r ¼ a r 1 ; a r 2 ;...; a r r ð c ;...; a m Þ allcati f prcesses i the rth state, i which a r c 2 P [ fδg; a r c ¼ Pi k, the cth resurce R c, is ccupied by the lcal stream Pi k ad a r c ¼ Δ, the cth resurce R c, is uccupied. Z r ¼ z r 1 ; z r 2 ;...; z r r ð c ;...z m Þ the sequece f semaphres crrespdig t the rth state, i which z r c ¼ Pi k is the ame f the stream (specified i the cth dispatchig rule σ c, allcated t the cth resurce) which was allwed t ccupy the cth resurce, e.g., z r c ¼ Pi k meas that stream Pi k is curretly allwed t ccupy the cth resurce Q r ¼ q r 1 ; q r 2 ;...; q r r ð c ;...; q m Þ the sequece f semaphre idices, crrespdig t the rth state, i which q r c determies the psiti f the semaphre z r c i the pririty dispatchig rule σ c ; z r c ¼ s c; ð qc rþ; q r c 2 N. Fr istace, q r 2 ¼ 2 ad z r 2 ¼ P1 2 crrespd t the semaphre z r 2 ¼ P1 2 takig the secd psiti i the pririty dispatchig rule σ 2. MA k the sequece f allcatis f multimdal prcesses: MA k ¼ ma k 1 ;...; mak u, i which ma k i is the allcati f the prcess mp i, i.e., ma k i ¼ ma k i;1 ; ma k i;2 ;...; ma k k i;c ;...; ma i;m ; ð6þ where m is the umber f resurces R, ma k i;c 2 fmp i ; Δg, ma k i;c ¼ mp i which meas that the cth resurce R c is ccupied by the ith multimdal prcess P i, ad ma k i;c ¼ Δ, thecth resurce R c,isreleasedbytheith multimdal prcess mp i. I this ctext, the state S k is feasible [5] whe: Semaphres f ccupied resurces idicate the streams allcated t thse resurces, Each lcal/multimdal stream is alltted t a uique resurce due t a relevat lcal/multimdal prcess rute. The itrduced ccept f the kth state S k eables t create aspacesf feasible states. T illustrate this, let us csider the state space f a SCCP cmpsed f six resurces ad three lcal cyclic prcesses supprtig e multimdal prcess (see Fig. 4). The bserved behavir is twfld, i.e., the levels f lcal SL ad multimdal SM prcesses ca be distiguished. I the case f the level f lcal prcesses, the states Sl i are deted by filled circles, ad i the case f the level f multimdal prcesses, the relevat states S i 2 S are deted by ufilled circles. States Sl j 2 Sl cabecsideredasa part f assciated states S i 2 S, i.e., the states that are elevated versis f relevat states S i. The trasitis likig feasible states S k ; S l 2 S, while fllwig the cstraits f preempti ad mutual exclusi, are deted by S k S l, ad they ecmpass the ext-state fucti δ: S l = δ(s k ), the defiiti f which [3] leads t the fllwig prperty: Each S i 2 S ca be preceded by a subset f states SP i, SP i S (als SP i ¼;), i.e., 8S k 2 SP i, S i = δ(s k ) but ca result ly i a uique state S j 2 S, i.e., there exists at mst e S j 2 S; S j ¼ dðs i Þ. The deadlck state S * 2 S resultig i a SCCP blckade is free frm ay descedet state. I this ctext, tw types f steady state behavirs ca be csidered: a cyclic steady state ad a deadlck state. The set msc * ¼ S k 1 ; S k 2 ; S k 3 ;...; S k v, msc * S is called the reachability state space f multimdal prcesses geerated by a iitial state S k 1 2 S, if the fllwig cditi hlds: S k i1 1! S k vi1 i! S k v! S k i ; ð7þ where S a! i S b the trasiti defied i [5], S k 1! i S k iþ1 S k 1! S k 2! S k 3!...! S k iþ1 : The set msc ¼ S k i ; S k iþ1 ;...; S k v, msc msc *,is called the cyclic steady state f multimdal prcesses (i.e., a cyclic steady state f a SCCP) with a perid Tm = msc, Tm > 1. I ther wrds, the cyclic steady state ctais such a set f states, where startig frm ay selected state, it is pssible t reach the remaiig states ad fially reach this selected state agai: 8 Sk 2mSc S k Tm1! S k : ð8þ The cyclic steady state Sc specified by the perid Tc f the executi f lcal prcesses is defied i a similar way. Graphically, the cyclic steady states Sc ad msc are described by cyclic ad spiral digraphs, respectively (see Fig. 4). Mrever, sice a iitial state S k 1 2 S either leads t msc r t a deadlck state S *, i.e., S k i1 1! S k vi1 i! S k v! S *, multimdal prcesses ca als reach a deadlck state, deted by circles with a crss i the middle i Fig. 4.
8 It J Adv Mauf Techl Fig. 4 Space f feasible states ecmpassig behavir f the SCCP frm Fig. 2 time [u.t.] The level f multimdal prcesses cyclic the ele trasiet perids deadlck deadlck deadlck deadlck cyclic deadlck deadlck The level f lcal prcesses Leged: - i-th lcal state - trasiti - i-th multimdal state - trasiti I this ctext, the prblem frmulated i Secti 2.2 ca be stated as fllws: Give a SCCP defied by SC (2), i.e., R, SL = (STL, BEL, SEL), M = (STM, BEM, SEM), des there exist a cyclic steady state msc i the state space S f the give SCCP? Nte that the abve questi gives rise t the fllwig questi: Des there exist a iitial state S0 that wuld geerate the cyclic steady state msc? This meas that searchig fr a cyclic steady state msc i a give SCCP ca be see as a reachability prblem where fr a assumed iitial state S0 (i.e., fr selected allcatis f lcal ad multimdal prcesses), we 0 i k Tm 1 lk fr a state S such that S! S! S hlds. Refiig the space f cyclic steady states frm a give space f feasible states des t pse difficulty. Hwever, the prblem f geeratig the space f feasible states is NP-hard. The majrity f states either ed i deadlcks r lead t deadlck states. Therefre, i rder t avid the geerati f the etire space f feasible states, let us fcus a alterative apprach aimed at geeratig cyclic steady states. k k 3.2 Geerati f the space f cyclic steady states Sice the parameters describig a SCCP are usually discrete, ad the relatis betwee them ca be see as - cyclic steady state f lcal prcesses - deadlck state cyclic steady state f multimdal prcesses cstraits, the cyclic schedulig prblems that ivlve them ca be preseted i the frm f a CSP [2, 5, 17]. Mre frmally, CSP is a framewrk fr slvig cmbiatrial prblems specified by pairs: a set f variables ad assciated dmais ad a set f cstraits restrictig the pssible cmbiatis f variable values. Thus, i the case f SC (2), the CSP is defied as fllws: CS ðsc Þ ¼ ððfx ; Tc; mx ; Tmg; fdx ; DTc ; DmX ; DTm gþ; C Þ; ð9þ where: X,Tc, mx,tm the decisi variables, where Tc ad Tm are the lcal ad multimdal peridicities; lsð1þ lsðþ X ¼ X11 ;... ; X1 ;... ; X1 ;... ; X is the set f k k k k sequeces f Xi, ad Xi ¼ xi;1;1 ;... ; x i ;lrðiþ;1 ;... ; xki;1;ξ ;... ; xki;lrðiþ;ξ Þ where xki;j;q is the mmet whe the perati ki;j (lcal prcess) begis i the first cycle, whereas xki;j;q ad xki;j;q ðlþ are liked by xki;j;q ðlþ ¼ xki;j;q þ l Tc; l 2 Z,Tc ¼ xki;j;q ðl þ 1Þ xki;j;q ðlþ. Aalgusly, mx = {mx1, mx2, mxi,, mxw} is the set f sequeces f mxi, ad mxi ¼ ðmxi;1;1 ;... ; m
9 It J Adv Mauf Techl x i;lmðiþ;1 ;...; mx i;1;ξ ;...; mx i;lmðiþξ; Þ where mx i,1,1 is the mmet whe the perati m i,j (f a multimdal prcess) begis i the first cycle mx i;j;k ðlþ ¼mx i;j;k þ l Tm, ad Tm ¼ mx i;j;k ðl þ 1Þmx i;j;k ðlþ. The fllwig dmais f decisi variables are csidered: D X, D mx the family f sets f admissible etry values X i, x k i;j;q 2 Z ad mx i; mx i;j;k 2 Z D Tc, D Tm the dmais f the variable Tc 2 N ad Tm 2 N. C cstraits are specified by bth: ep k i;j;qð ST L; BE L Þthe set f cstraits (equatis) likig ST L (structure f lcal prcesses) ad BE L (behavir f lcal prcesses). Each ep k i;j;qð ST L; BE L Þ describes the tempral relati (i accrdace with the cditis preseted abve [5]) betwee the mmets whe the perati begis durig its qth executi: i ¼ 1; ::; ; j ¼ 1;...; lrðiþ; k ¼ 1; ::; lsðiþ; ad q ¼ 1;...; Ξ. eq i,j,k (ST M, BE M ) the set f cstraits (equatis) likig ST M (structure f multimdal prcesses) ad BE M (behavir f multimdal prcesses). Each eq i,j,k (ST M, BE M ) describes the tempral relati betwee the mmets whe the multimdal peratis begi durig their kth executi:i ¼ 1; ::; w; j ¼ 1;...; lmðiþ; ad k ¼ 1;...; mξ. I ther wrds, the prblem discussed i Secti 2.2 bils dw t the fllwig: Give a SCCP described by CS(SC)(9) (i.e., the cstrait satisfacti prblem determied by SC), d there exist X,Tc, mx, ad Tm whse values satisfy all the cstraits C? The sluti t the prblem (9) prvides us with sets f sequeces X ad mx, whse values guaratee the required cyclic behavir f the SCCP while keepig the set f cstraits C satisfied. The cstraits C that ca be see as cditis sufficiet fr the cyclic behavir f the SCCP (resultig i a cllisi-free ad deadlck-free [12] executi f prcesses) are frmulated usig the peratr max, which takes it accut the pipelie ature f the flw f lcal prcesses. The applicati f the max peratr ca be see as a extesi f the max cstrait ccept itrduced i [5]. Cstraits lcal prcesses I rder t explai hw the cstraits f lcal prcesses are desiged, let us csider a example f a SCCP shw i Fig. 5. The perati 1 1;3 (executed by P1 1 the resurce R 5) ca be started (i.e., begi its first executi; q=1) ly if the precedig perati 1 1;2 (executed by P1 1 R 3) has bee cmpleted x 1 1;2;1 þ t1 1;2 ad the resurce R 5 has bee released, i.e., if the streamp3 1 ccupyig the resurce R 5 starts its subsequet perati at x 1 3;3;1 þ 1. Thus, the csidered relati ep1 1;3;1 ðst L ; BE L Þ ca be specified by the fllwig frmulae: x 1 1;3;1 ¼ max x1 3;3;1 þ 1 ; x 1 1;2;1 þ t1 1;2 ; ð10þ where x k i;j;q is the mmet whe the perati k i;j frms, the Pk i stream begis i its qth executi. Table 2 ctais the remaiig cstraits describig the lcal prcesses f the SCCP frm Fig. 5. Fr all cstraits, the fllwig priciple hlds: the mmet whe the perati k i;j begis is calculated as a maximum f the cmpleti time f perati k i;j1 precedig k i;j, ad the release time f the resurce pk i;j awaitig fr k i;j executi. Fig. 5 SCCP with dispatchig rules: σ 1 ¼ P ; P 3 ; σ3 ¼ P ; P 1 ; σ5 ¼ P ; P 2, ad Ψ = (1,1,1, Ξ =1 Leged: resurce ctrlled by the pririty dispatchig rule ; mmet whe the perati begis its executi i the stream mmet whe the perati begis its executi i the prcess
10 Table 2 Cstraits f lcal prcesses determiig the mmets x k i;j;q fr the SCCP frm Fig. 5 x 1 1;1;1 ¼ max x1 1;3;1 þ t1 1;3 Tc ; x 1 1;3;1 þ 1 Tc x 1 2;2;1 ¼ max x1 2;1;1 þ t1 2;1 ; x 1 3;1;1 þ 1 x 1 3;1;1 ¼ max x1 3;3;1 þ t1 3;3 Tc ; x 1 3;3;1 þ 1 Tc x 1 3;3;1 ¼ max x1 2;3;1 þ 1 Tc ; x 1 3;2;1 þ t1 3;2 It J Adv Mauf Techl x 1 1;2;1 ¼ max x1 1;1;1 þ t1 1;2 ; x 1 2;2;1 þ 1 x 1 2;1;1 ¼ max x1 2;3;1 þ t1 2;3 Tc ; x 1 1;3;1 þ 1 Tc x 1 2;3;1 ¼ max x1 2;2;1 þ t1 2;2 ; x 1 2;2;1 þ 1g x 1 3;2;1 ¼ max x1 3;1;1 þ t1 3;1 ; x 1 1;1;1 þ 1 ep k i;j;qð ST L; BE L Þ : mmet whe the perati k i;j begis i its q th executi ¼ ¼ max mmet whe p k i;j is released; ; mmet whe the perati k i;j1 ; cmpletes i ¼ 1; ::; ; j ¼ 1;...; lrðiþ; k ¼ 1; ::; lsðiþ; q ¼ 1;...; Ξ ð11þ Therefre, fllwig the cstraits (11) guaratees a deadlck-free executi f cyclic prcesses at the SL level (see Fig. 3). Nte that the cstraits (11) idirectly take it accut the assumed dispatchig pririty rules Θ ad rutes f streams U. This meas that the SCCP beig free f deadlck depeds the dispatchig rules Θ determiig the peratis executed the shared resurce, i.e., the satisfiability f cstraits (11). This is because the mmet whe the perati k i;j1 cmpletes is determied by the rute f the stream p k i ad, i tur, the mmet whe p k i;j is released depeds the perati executed befre k i;j by pk i;j. Cstraits multimdal prcesses The cstraits determiig the executi f lcal cyclic prcesses have already bee discussed i depth i [3 5]. Multimdal prcesses, hwever, have t yet bee discussed i a similar way. Therefre, fr the sake f simplicity, let us assume that multimdal prcesses are cllisi- ad deadlck-free. At the same time, multimdal prcesses ca ccupy the same resurce ad may use the same lcal prcess fr their executi. The research preseted i [3, 4] fcuses cstraits determiig cyclic steady state behavir ad particularly the cditis behid the ccept f the ext-state fucti. The lack f guaratee that ay cyclic steady state is reachable frm a give iitial state was the mai disadvatage f the results btaied s far. Mrever, because the umber f ptetial iitial states grws expetially with the umber f lcal prcesses, ay real-life implemetati f the results is rather limited. I tur, the cditis btaied i [5], which guaratee that a iitial state belgs t a cyclic steady state, were limited t lcal cyclic prcesses ly. The cstraits describig the relatiship betwee the mmets whe successive peratis begi are shw usig the example f mp 1 frm Fig. 5. The csidered prcess executes the set f the fllwig resurces: R 2,R 3,R 5, ad R 4. The lcal cyclic prcess P2 1 supprts the executi f mp 1 betwee R 2 ad R 3, whereas P1 1 supprts the executi f mp 1 betweer 3,R 5, ad R 4. This meas that the prcess mp 1 ca execute its peratis ly whe the relevat peratis frm lcal prcesses are perfrmed (i.e., P1 1 r P2 1 ). Fr istace, the perati m 1,2 executed R 3 depeds P2 1. The startig mmet mx 1,2,1 f the perati m 1,2 cicides with the startig mmet x 1 2;2;1 þ a Tc, i.e., with the begiig f the perati 1 2;2 ad is executed after the cmpleti f the precedig perati m 1,2 (i.e., the perati m 1,1 cmpleted at the mmet mx 1,1,1 + mt 1,1,1 ). The cstrait specifyig this relatiship has the fllwig frm: mx 1;2;1 ¼ mi x 1 2;2;1 þ a Tc ja 2 Z; x 1 2;2;1 þ a Tc mx 1;1;1 þ mt 1;1;1 ; where: ð12þ x k i;j;q the mmet whe the perati i;j k begis i the qth executi f a lcal prcess mx i,j,q the mmet whe the perati m i,j begis i the qth executi f a multimdal prcess Tc the peridicity f lcal cyclic steady states. Table 3 ctais the remaiig cstraits describig the multimdal prcesses f the SCCP frm Fig. 5. Fr all the cstraits, the fllwig priciple hlds: the mmet whe the perati m i,j begis is the earliest mmet whe the perati f the lcal prcess ca start (f curse the e the multimdal prcess mp i requires), temprally fllwig the mmet whe the perati m i,j 1 begis. Mre frmally: eq i;j;k ðst M ; BE M Þ : mmet whe the perati m i;j begis ¼ ¼ mifset f mmets whe the perati k i;j1 begis; temprally fllwig the mmet whe the previus perati m i;j1 cmpleesg; i ¼ 1; ::; w; j ¼ 1;...; lmðiþ; k ¼ 1;...; mξ: 4 Schedulig f peridic prcesses ð13þ Let us csider the AGVS frm Fig. 1 mdeled i terms f SCCPs (see Fig. 2). Takig it accut (2), it ca be described as fllws:
11 It J Adv Mauf Techl Table 3 Cstraits determiig the mmets mx i;j;k fr the SCCP frm Fig. 5 Multimdal prcess mp 1 mx 1;1;1 ¼ mi x 1 2;3;1 þ a Tc ja 2 Z; x 1 2;3;1 þ a Tc mx 1;4;1 þ mt 1;4;1 Tm ; mx 1;2;1 ¼ mi x 1 2;2;1 þ a Tc ja 2 Z; x 1 2;2;1 þ a Tc mx 1;1;1 þ mt 1;1;1 ; mx 1;3;1 ¼ mi x 1 1;3;1 þ a Tc ja 2 Z; x 1 1;3;1 þ a Tc mx 1;2;1 þ mt 1;2;1 ; mx 1;4;1 ¼ mi x 1 1;1;1 þ a Tc ja 2 Z; x 1 1;1;1 þ a Tc mx 1;3;1 þ mt 1;3;1 Multimdal prcess mp 2 mx 2;1;1 ¼ mi x 1 1;1;1 þ a Tc ja 2 Z; x 1 1;1;1 þ a Tc mx 2;4;1 þ mt 2;4;1 Tm ; mx 2;2;1 ¼ mi x 1 1;2;1 þ a Tc ja 2 Z; x 1 1;2;1 þ a Tc mx 2;1;1 þ mt 1;2;1 ; mx 2;3;1 ¼ mi x 1 2;2;1 þ a Tc ja 2 Z; x 1 2;2;1 þ a Tc mx 2;2;1 þ mt 2;2;1 ; mx 2;4;1 ¼ mi x 1 3;1;1 þ a Tc ja 2 Z; x 1 3;1;1 þ a Tc mx 2;3;1 þ mt 2;3;1 ; md {Tm,Tc}= 0 Give SC ¼ ððr; SLÞ; SMÞ, where: R ={R 1,R 2,, R 18 } the set f resurces, SL =(ST L,BE L ) the structure f lcal prcesses ST L =(U,T) U ¼ p 1 1 ; p1 2 ; p1 3 ; p1 4 ; p2 4 ; p1 5 ; p2 5 ; p6 1 p 1 1 ¼ ð R 1; R 2 ; R 3 ; R 4 Þ; p 1 2 ¼ ð R 4; R 5 ; R 6 Þ; p 1 3 ¼ ð R 3; R 9 ; R 8 ; R 7 ; R 5 Þ; p 1 4 ¼ p2 4 ¼ ð R 2; R 16 ; R 10 ; R 11 ; R 12 ; R 9 Þ; p 1 6 ¼ ð R 14; R 11 ; R 15 Þ; p 1 5 ¼ p2 5 ¼ ð R 8; R 17 ; R 13 ; R 14 ; R 12 Þ T ¼ t1 1; t1 2 ; t1 3 ; t1 4 ; t2 4 ; t1 5 ; t2 5 ; t1 6, where the values f the elemets f the sequeces ti k are give i Table 1 BE L =(Θ, Ψ, Ξ) Θ={σ 1, σ 2,, σ 17 } σ 1 ¼ P1 1 ; σ2 ¼ P1 1; P1 4 ; P2 4 ; σ3 ¼ P1 1; P1 3 ; σ 4 ¼ P1 1; P1 2 ; P1 2 ; P1 2 ; σ 5 ¼ P2 1; P1 2 ; P1 2 ; P1 3 ; σ6 ¼ P2 1; P1 2 ; P1 2 ; σ 7 ¼ P3 1 ; σ8 ¼ P5 1; P2 5 ; P1 3 ; σ 9 ¼ P3 1; P1 4 ; P2 4 ; σ10 ¼ P4 1; P2 4 ; σ 11 ¼ P4 1; P2 4 ; P1 6 ; P2 6 ; σ 12 ¼ P4 1; P2 4 ; P1 5 ; P2 5 ; σ13 ¼ P5 1; P2 5 ; σ 14 ¼ P5 1; P2 5 ; P1 6 ; P2 6 ; σ15 ¼ P6 1; P2 6 ; σ 16 ¼ P4 1; P2 4 ; σ17 ¼ P5 1; P2 5 ; Ψ = (1,3,1,1,1,2) Ξ = 1 SM = (ST M, BE M ) the structure f multimdal prcesses ST M =(M,mT) M={mp 1,mp 2 } mp 1 ¼ ðr 1 ; R 2 ; R 3 ; R 9 ; R 8 ; R 17 ; R 13 Þ; mp 2 ¼ ðr 15 ; R 14 ; R 12 ; R 8 ; R 7 ; R 5 ; R 6 Þ: mt= {mt 1,mt 2 }, where the values f all elemets mt i are equal t 1 uit f time BE M =(mψ, mξ) mψ=(1, 1) mξ=1 The respse t the fllwig questi is sught: Des there exist a cyclic behavir f the SC (i.e., resultig i cyclic steady states f lcal ad multimdal prcesses)? The apprach aimed at geeratig the space f feasible states (see Fig. 4) is time csumig (it is a NP-hard prblem) ad results maily i a deadlck r i states leadig t a deadlck. A alterative apprach, based the CSP frmulati f the CS (9), eables t fcus (ad, if pssible, t geerate) the dedicated cyclic steady states f bth lcal ad multimdal prcesses. 4.1 Schedulig f repetitive prcesses Csider a give SCCP ad its SL level. Searchig fr a pssible cyclic steady state f lcal prcesses frmulated i terms f a CSP ca be stated as the fllwig cstrait satisfacti prblem: CSðSCÞ ¼ ððfx ; Tcg; fd X ; D Tc gþ; CÞ; ð14þ
12 It J Adv Mauf Techl Table 4 Cstraits determiig the mmets x k i;j;q whe peratis begi fr the SCCP frm Fig. 2 Lcal prcess P1 1 Lcal prcess P2 1 x 1 1;1;1 ¼ max x1 1;4;1 þ t1 1;4 Tc ; x 1 1;4;1 þ 1 Tc x 1 2;1;1 ¼ max x1 2;3;3 þ t1 2;3 Tc ; x 1 1;1;1 þ 1 þ Tc x 1 1;2;1 ¼ max x1 1;1;1 þ t1 1;1 ; x 2 4;2;1 þ 1 x 1 2;2;1 ¼ max x1 2;1;1 þ t1 2;1;1 ; x 1 3;1;1 þ 1 x 1 1;3;1 ¼ max x1 1;2;1 þ t1 1;2 ; x 1 3;1;1 þ 1 x 1 2;3;1 ¼ max x1 2;2;1 þ t1 2;2;1 ; x 1 2;1;1 þ 1 x 1 1;4;1 ¼ max x1 1;3;1 þ t1 1;3 ; x 1 2;2;3 þ 1 x 1 2;1;2 ¼ max x1 2;3;1 þ t1 2;3;1 ; x 1 2;2;1 þ 1 x 1 2;2;2 ¼ max x1 2;1;2 þ t1 2;1;2 ; x 1 2;3;1 þ 1 x 1 2;3;2 ¼ max x1 2;2;2 þ t1 2;2;2 ; x 1 2;1;2 þ 1 x 1 2;1;3 ¼ max x1 2;3;2 þ t1 2;3;2 ; x 1 2;2;2 þ 1 x 1 2;2;3 ¼ max x1 2;1;3 þ t1 2;1;3 ; x 1 2;3;2 þ 1 x 1 2;3;3 ¼ max x1 2;2;3 þ t1 2;2;3 ; x 1 2;1;3 þ 1 Lcal prcess P3 1 Lcal prcess P4 1 x 1 3;1;1 ¼ max x1 3;5;1 þ t1 3;5 Tc ; x 1 1;4;1 þ 1 x 1 4;1;1 ¼ max x1 4;6;1 þ t1 4;6 Tc ; x 1 1;3;1 þ 1 x 1 3;2;1 ¼ max x1 3;1;1 þ t1 3;1 ; x 2 4;1;1 þ 1 x 1 4;2;1 ¼ max x1 4;1;1 þ t1 4;1 ; x 2 4;3;1 þ 1 Tc x 1 3;3;1 ¼ max x1 3;2;1 þ t1 3;2 ; x 2 5;2;1 þ 1 x 1 4;3;1 ¼ max x1 4;2;1 þ t1 4;2 ; x 2 4;3;1 þ 1 Tc x 1 3;4;1 ¼ max x1 3;3;1 þ t1 3;3 ; x 1 3;5;1 þ 1 Tc x 1 4;4;1 ¼ max x1 4;3;1 þ t1 4;3 ; x 1 6;2;2 þ 1 Tc x 1 3;5;1 ¼ max x1 3;4;1 þ t1 3;4 ; x 1 2;3;3 þ 1 x 1 4;5;1 ¼ max x1 4;4;1 þ t1 4;4 ; x 2 5;2;1 þ 1 x 1 4;6;1 ¼ max x1 4;5;1 þ t1 4;5 ; x 1 3;3;1 þ 1 Lcal prcess P4 2 Lcal prcess P5 1 x 2 4;1;1 ¼ max x2 4;6;1 þ t2 4;6 Tc ; x 1 4;2;1 þ 1 x 1 5;1;1 ¼ max x1 5;5;1 þ t1 5;5 Tc ; x 1 3;4;1 þ 1 x 2 4;2;1 ¼ max x2 4;1;1 þ t2 4;1 ; x 1 4;3;1 þ 1 x 1 5;2;1 ¼ max x1 5;1;1 þ t1 5;1 ; x 2 5;3;1 þ 1 Tc x 2 4;3;1 ¼ max x2 4;2;1 þ t2 4;2 ; x 1 4;4;1 þ 1 x 1 5;3;1 ¼ max x1 5;2;1 þ t1 5;2 ; x 2 5;4;1 þ 1 Tc x 2 4;4;1 ¼ max x2 4;3;1 þ t2 4;3 ; x 1 4;2;3 þ 1 x 1 5;4;1 ¼ max x1 5;3;1 þ t1 5;3 ; x 1 6;1;1 þ 1 x 2 4;5;1 ¼ max x2 4;5;1 þ t2 4;5 ; x 1 4;6;1 þ 1 x 1 5;5;1 ¼ max x1 5;4;1 þ t1 5;4 ; x 2 4;6;1 þ 1 x 2 4;6;1 ¼ max x2 4;5;1 þ t2 4;5 ; x 1 4;1;1 þ 1 þ Tc Lcal prcess P5 2 Lcal prcess P6 1 x 2 5;1;1 ¼ max x2 5;5;1 þ t2 5;5 Tc ; x 1 5;2;1 þ 1 x 1 6;1;1 ¼ max x1 6;3;2 þ t1 6;3 Tc ; x 2 4;5;1 þ 1 x 2 5;2;1 ¼ max x2 5;1;1 þ t2 5;1 ; x 1 5;3;1 þ 1 x 1 6;2;1 ¼ max x1 6;1;1 þ t1 6;1 ; x 1 6;3;2 þ 1 Tc x 2 5;3;1 ¼ max x2 5;1;1 þ t2 5;1 ; x 1 5;4;1 þ 1 x 1 6;3;1 ¼ max x1 6;2;1 þ t1 6;2 ; x 2 5;5;1 þ 1 x 2 5;4;1 ¼ max x2 5;3;1 þ t2 5;3 ; x 1 5;5;1 þ 1 x 1 6;1;2 ¼ max x1 6;3;1 þ t1 6;3 ; x 1 6;2;1 þ 1 x 2 5;5;1 ¼ max x2 5;4;1 þ t2 5;4 ; x 1 5;1;1 þ 1 þ Tc x 1 6;2;2 ¼ max x1 6;1;2 þ t1 6;1 ; x 1 6;3;1 þ 1 x 1 6;3;3 ¼ max x1 6;2;2 þ t1 6;2 ; x 1 6;4;1 þ 1
13 It J Adv Mauf Techl Table 5 Values f the mmets x k i;j;q whe peratis begi fr the SCCP frm Fig. 2 Startig mmets: x 1 1;1;1 ; x1 2;1;1 ; x1 1;2;1 ; x1 3;1;1 ; x1 2;2;1 ; x2 4;4;1 x 1 2;3;1 ; x1 1;3;1 x 1 2;1;2 x 1 3;3;1 x 1 3;5;1 ; x2 5;1;1 ; x1 5;3;1 ; x1 4;4;1 ; x1 4;5;1 ; x1 3;2;1 x 1 5;2;1 ; x1 6;2;1 x 1 6;3;1 x 2 5;2;1 ; x2 4;3;1 x 1 6;1;1 x 1 6;1;2 Values: Crrespdig Sl 0 Sl 1 Sl 2 Sl 3 Sl 4 Sl 5 Sl 6 Sl 7 Sl 8 Sl 9 states: Startig mmets: x 1 2;2;2 ; x1 4;1;1 ; x1 2;3;2 ; x1 4;3;1 ; x1 2;1;3 ; x1 5;5;1 x 1 2;2;3 ; x1 1;4;1 ; x1 2;3;3 ; x 1 4;5;1 ; x2 4;5;1 x 1 3;4;1 ; x2 4;1;1 ; x2 4;2;1 ; x2 5;4;1 x 1 5;1;1 x 2 5;5;1 x 1 4;2;1 ; x2 4;2;1 ; x2 5;3;1 x 2 4;6;1 ; x1 6;3;2 x 1 6;2;2 Values: Crrespdig states: Sl 10 Sl 11 Sl 12 Sl 13 Sl 14 Sl 15 Sl 16 Sl 17 Sl 18 where: X ¼ X1 1; X 2 1; X 3 1; X 4 1; X 4 2; X 5 1; X 5 2; X 6 1 X1 1 ¼ x1 1;1;1 ; x1 1;2;1 ; x1 1;3;1 ; x1 1;4;1 the mmets whe peratis executed alg p 1 1 ¼ ð R 1; R 2 ; R 3 ; R 4 Þbegi X2 1 ¼ x1 2;1;1 ; x1 2;2;1 ; x1 2;3;1 ; x1 2;1;2 ; x1 2;2;2 ; x1 2;3;2 ; x1 2;1;3 ; x1 2;2;3 ; x 1 2;3;3 Þ; X3 1 ¼ x1 3;1;1 ; x1 3;2;1 ; x1 3;3;1 ; x1 3;4;1 ; x1 3;5;1 ; X 1 4 ¼ x1 4;1;1 ; x1 4;2;1 ; x1 4;3;1 ; x1 4;4;1 ; x1 4;5;1 ; x1 4;6;1 ; X4 2 ¼ x2 4;1;1 ; x2 4;2;1 ; x2 4;3;1 ; x2 4;4;1 ; x2 4;5;1 ; x2 4;6;1 ; X5 1 ¼ x1 5;1;1 ; x1 5;2;1 ; x1 5;3;1 ; x1 5;4;1 ; x1 5;5;1 ; resurces time [u.t.] Leged: (allcatis) (semaphres) (semaphre idices) - executi f stream - suspesi f the stream - -th lcal state f SCCP Fig. 6 Gatt chart illustratig the cyclic steady state f lcal prcesses fr the SCCP frm Fig. 2, where Ψ = (1,3,1,1,1,2) ad Ξ =1
14 It J Adv Mauf Techl Table 6 Cstraits determiig the mmets mx i,j,k whe peratis begi fr the SCCP frm Fig. 2 Multimdal prcess mp 1 mx 1;1;1 ¼ mi x 1 1;1;1 þ a Tc ja 2 Z; x 1 1;1;1 þ a Tc mx 1;7;1 þ mt 1;7;1 Tm ; mx 1;2;1 ¼ mi x 1 1;2;1 þ a Tc ja 2 Z; x 1 1;2;1 þ a Tc mx 1;1;1 þ mt 1;1;1 ; mx 1;3;1 ¼ mi x 1 1;3;1 þ a Tc ja 2 Z; x 1 1;3;1 þ a Tc mx 1;2;1 þ mt 1;2;1 ; mx 1;4;1 ¼ mi x 1 3;2;1 þ a Tc ja 2 Z; x 1 3;2;1 þ a Tc mx 1;3;1 þ mt 1;3;1 ; mx 1;5;1 ¼ mi x 1 3;3;1 þ a Tc ja 2 Z; x 1 3;3;1 þ a Tc mx 1;4;1 þ mt 1;4;1 ; mx 1;6;1 ¼ mi x 1 5;2;1 þ a Tc ; x 2 5;2;1 þ a Tc ja 2 Z; x 1 5;2;1 þ a Tc mx 1;5;1þ mt 1;5;1 ; x 2 5;2;1 þ a Tc mx 1;5;1 þ mt 1;5;1 ; mx 1;7;1 ¼ mi x 1 5;3;1 þ a Tc ; x 2 5;3;1 þ a Tc ja 2 Z; x 1 5;2;1 þ a Tc mx 1;5;1 þ mt 1;5;1 ; x 2 5;2;1 þ a Tc mx 1;6;1 þ mt 1;6;1 Multimdal prcess mp 2 mx 2;1;1 ¼ mi x 1 6;3;1 þ a Tc ; x 1 6;3;2 þ a Tc ja 2 Z; x 1 6;3;1 þ a Tc mx 2;7;1þ mt 2;7;1 Tm; x 1 6;3;2 þ a Tc mx, 2;7;1 þ mt 2;7;1 Tm ; mx 2;2;1 ¼ mi x 1 6;1;1 þ a Tc ; x 1 6;1;2 þ a Tc ja 2 Z; x 1 6;1;1 þ a Tc mx 2;1;1 þ mt 2;1;1 ; x 1 6;1;2 þ a Tc mx 2;1;1 þ mt 2;1;1 mx 2;3;1 ¼ mi x 1 5;5;1 þ a Tc ; x 2 5;5;1 þ a Tc ja 2 Z; x 1 5;5;1 þ a Tc mx 2;2;1 þ mt 2;2;1 ; x 2 5;5;1 þ a Tc mx 2;2;1 þ mt 2;2;1 mx 2;4;1 ¼ mi x 1 5;1;1 þ a Tc ; x 2 5;1;1 þ a Tc ja 2 Z; x 1 5;1;1 þ a Tc mx 2;3;1 þ mt 2;3;1 ; x 2 5;1;1 þ a Tc mx 2;3;1 þ mt 2;3;1 mx 2;5;1 ¼ mi x 1 3;4;1 þ a Tc ja 2 Z; x 1 3;4;1 þ a Tc mx 2;4;1 þ mt 2;4;1, mx 2;6;1 ¼ mi x 1 3;5;1 þ a Tc ja 2 Z; x 1 3;5;1 þ a Tc mx 2;5;1 þ mt 2;5;1, mx 2;7;1 ¼ mi x 1 2;3;1 þ a Tc ; x 1 2;3;2 þ a Tc ; x 1 2;3;3 þ a Tc ja 2 Z; x 1 2;3;1 þ a Tc mx 2;6;1 þ mt 2;6;1 ; x 1 2;3;2 þ a Tc mx 2;6;1 þ mt 2;6;1 ; x 1 2;3;3 þ a Tc mx 2;6;1 þ mt 2;6;1 X5 2 ¼ x2 5;1;1 ; x2 5;2;1 ; x2 5;3;1 ; x2 5;4;1 ; x2 5;5;1 ; X6 1 ¼ x1 6;1;1 ; x1 6;2;1 ; x1 6;3;1 ; x1 6;1;2 ; x1 6;2;2 ; x1 6;3;2 ; C the set f cstraits that (due t (11)) csists f the cstraits frm Table 4. The sluti f the CS(14) implemeted i the Oz/Mzart platfrm ( a Itel Cre Du 3.00 GHz Table 7 Values f the mmets mx i,j,k whe peratis begi fr the SCCP frm Fig. 2 Startig mmets: mx 1,1,1, mx 1,2,1 mx 1,3,1 mx 2,3,1 mx 2,4,1 mx 1,4,1 mx 2,2,1 Values: Crrespdig lcal states: Sl 0 Sl 2 Sl 7 Sl 15 Sl 17 Sl 6 Crrespdig multimdal states: S 0 S 2 S 7 S 15 S 17 S 25 Startig mmets: mx 1,5,1 mx 2,5,1 mx 1,6,1, mx 1,7,1 mx 2,7,1 mx 2,1,1 mx 2,6,1 Values: Crrespdig lcal states: Sl 9 Sl 12 Sl 0 Sl 2 Sl 6 Sl 17 Crrespdig multimdal states: S 28 S 31 S 38 S 40 S 40 S 51
15 It J Adv Mauf Techl with 4.00-GB RAM ad btaied i less tha 1 s) is shw i Table 5. Therefre, the perid Tc f the btaied cyclic steady state is equal t19. The mmets whe peratis begi i the lcal prcesses are shw i Table 5. A Gatt chart f the cyclic steady state behavir is shw i Fig. 6. Nte that each uit time crrespds t a system state, i.e., the allcati f prcesses t resurces. Thus, the cyclic steady state csists f 19 states: Sc={Sl 0,Sl 1,, Sl 18 }. Similarly t Fig. 4, the states Sl ecmpassig the succeedig allcatis are deted by filled circles (see Fig. 5). 4.2 Schedulig f multimdal prcesses Let us csider the cyclic steady state Sc f the lcal prcesses f a SCCP. What is the cyclic steady state f the multimdal prcesses msc executed i this system? Let us assume tw multimdal prcesses mp 1 ad mp 2. Therefre, we must slve the relevat CSP, i.e., CS(SC) defied as (9), which ca be see i terms f the prblem (14) augmeted by variables mx ={mx 1,mX 2 }, where: mx 1 ¼ mx 1;1;1 ; mx 1;2;1 ; mx 1;3;1 ; mx 1;4;1 ; mx 1;5;1 ; mx 1;6;1 ; mx 1;7;1 mx 2 ¼ mx 2;1;1 ; mx 2;2;1 ; mx 2;3;1 ; mx 2;4;1 ; mx 2;5;1 ; mx 2;6;1 ; mx 2;7;1 ; as well as by the cstraits (stated i (13)) specified i Table 6. The btaied sluti csists f the sluti (see Table 5) t the prblem (14) that has already bee btaied, as well as f the mmets mx 1 ad mx 2 whe peratis begi (see the Table 7). The Gatt diagram f the cyclic steady state f behavir f multimdal prcesses (cmpsed f 57 states Sc ¼ S 0 ; S 1 ;...; S 57 )isshwifig.7. The btaied perid is equal t Tm=57 (i.e., the multiple f the perid Tc=19). This meas that withi that perid, the multimdal prcesses cmplete e perid, whereas the lcal prcesses cmplete three. The btaied cyclic steady states Sc ad msc are shw i Fig. 8 (they are deted as Sc 1 ad msc 1, respectively). Apart frm btaiig feasible slutis ecmpassig a cyclic behavir resurces time [u.t.] -see Fig. 6 Leged: - executi f stream - suspesi f the stream - -th lcal state f SCCP - executi f multimdal prcess - executi f multimdal prcess - -th multimdal state f SCCP Fig. 7 Gatt chart f the cyclic steady state f multimdal prcesses f the SCCP frm Fig. 2, where Ψ = (1,3,1,1,1,2), Ξ =1,mΨ (1,1), ad mξ =1
16 It J Adv Mauf Techl Fig. 8 Space f cyclic steady states f the SCCP frm Fig. 2 time [u.t.] Leged: - k-th lcal state - trasiti f the csidered SCCP, we preset ather sluti that fllws a ew dispatchig rule σ8 ¼ P31 ; P51 ; P52 (previusly, the dis patchig rule assciated with R8 was σ8 ¼ P51 ; P52 ; P31 ). Nte that a chage i the dispatchig rule des t chage the perid f lcal prcesses (eve thugh it is differet frm the previus Sc2). Hwever, the perid f the cyclic steady state f the multimdal prcess msc2 des chage: Tm=113. Mrever, the mutual prprtis chaged as well: mψ = (3,2). This meas that durig three executis f the prcess mp1, the prcess mp2 executes twice. The Gatt chart f the sluti f the CS (9) prblem (btaied i less tha 1 s) is shw i Fig. 9. The prvided examples demstrate the cmputatial efficiecy f the apprach based the CSP ccept (i.e., SC (2) ad CS(SC)) aimed at geeratig a cyclic steady state f the SCCP ad determied by U,T,Θ,Ψ,Ξ,M,mT,mΨ, ad mξ. The btaied cyclic steady state behavirs are free frm trasiet perids, i.e., trasiet perids as shw i Fig k-th multimdal state - trasiti This prperty is crucial fr prblems regardig switchig betwee pssible cyclic behavirs f a SCCP [3, 4]. It shuld be ted, hwever, that fr certai cases f CS (SC), cyclic slutis d t exist at all. This meas that the cstraits emplyed i the CS ca be see merely as feasible cditis guarateeig cyclic behavir. I geeral, the lack f ay cyclic behavir implies that the cditis are ctradictry. Hwever, the existece f ctradictig cditis des t ecessarily imply the lack f cyclic behavir. Mrever, it is crucial that the time-csumig geerati f the state space that eables the refiemet f cyclic steady states [3, 4] ca be replaced by direct geerati f cyclic states. Frm the perspective f cmputatial cmplexity, this meas that the expetial grwth f the umber f pssible iitial states (a pssible cyclic steady state may be reachable frm each f them) ca be replaced by the examiati f a umber f dispatchig rules that als grw expetially albeit with a smaller prefactr. This is because ur
17 It J Adv Mauf Techl resurces time [u.t.] resurces time [u.t.] Leged: - executi f stream - suspesi f the stream - -th lcal state f SCCP - executi f multimdal prcess - executi f multimdal prcess - -th multimdal state f SCCP Fig. 9 The Gatt chart illustratig the cyclic behavir f the SCCP frm Fig. 2, takig it accut the ew dispatchig rule σ 8 ¼ P 1 3 ; P ; P 5,Ψ = (1,3,1,1,1,2), = 1, mψ (3,2), ad mξ =1
Multi-objective Programming Approach for. Fuzzy Linear Programming Problems
 Applied Mathematical Scieces Vl. 7 03. 37 8-87 HIKARI Ltd www.m-hikari.cm Multi-bective Prgrammig Apprach fr Fuzzy Liear Prgrammig Prblems P. Padia Departmet f Mathematics Schl f Advaced Scieces VIT Uiversity
Applied Mathematical Scieces Vl. 7 03. 37 8-87 HIKARI Ltd www.m-hikari.cm Multi-bective Prgrammig Apprach fr Fuzzy Liear Prgrammig Prblems P. Padia Departmet f Mathematics Schl f Advaced Scieces VIT Uiversity
D.S.G. POLLOCK: TOPICS IN TIME-SERIES ANALYSIS STATISTICAL FOURIER ANALYSIS
 STATISTICAL FOURIER ANALYSIS The Furier Represetati f a Sequece Accrdig t the basic result f Furier aalysis, it is always pssible t apprximate a arbitrary aalytic fucti defied ver a fiite iterval f the
STATISTICAL FOURIER ANALYSIS The Furier Represetati f a Sequece Accrdig t the basic result f Furier aalysis, it is always pssible t apprximate a arbitrary aalytic fucti defied ver a fiite iterval f the
A New Method for Finding an Optimal Solution. of Fully Interval Integer Transportation Problems
 Applied Matheatical Scieces, Vl. 4, 200,. 37, 89-830 A New Methd fr Fidig a Optial Sluti f Fully Iterval Iteger Trasprtati Prbles P. Padia ad G. Nataraja Departet f Matheatics, Schl f Advaced Scieces,
Applied Matheatical Scieces, Vl. 4, 200,. 37, 89-830 A New Methd fr Fidig a Optial Sluti f Fully Iterval Iteger Trasprtati Prbles P. Padia ad G. Nataraja Departet f Matheatics, Schl f Advaced Scieces,
Fourier Method for Solving Transportation. Problems with Mixed Constraints
 It. J. Ctemp. Math. Scieces, Vl. 5, 200,. 28, 385-395 Furier Methd fr Slvig Trasprtati Prblems with Mixed Cstraits P. Padia ad G. Nataraja Departmet f Mathematics, Schl f Advaced Scieces V I T Uiversity,
It. J. Ctemp. Math. Scieces, Vl. 5, 200,. 28, 385-395 Furier Methd fr Slvig Trasprtati Prblems with Mixed Cstraits P. Padia ad G. Nataraja Departmet f Mathematics, Schl f Advaced Scieces V I T Uiversity,
Chapter 3.1: Polynomial Functions
 Ntes 3.1: Ply Fucs Chapter 3.1: Plymial Fuctis I Algebra I ad Algebra II, yu ecutered sme very famus plymial fuctis. I this secti, yu will meet may ther members f the plymial family, what sets them apart
Ntes 3.1: Ply Fucs Chapter 3.1: Plymial Fuctis I Algebra I ad Algebra II, yu ecutered sme very famus plymial fuctis. I this secti, yu will meet may ther members f the plymial family, what sets them apart
Intermediate Division Solutions
 Itermediate Divisi Slutis 1. Cmpute the largest 4-digit umber f the frm ABBA which is exactly divisible by 7. Sluti ABBA 1000A + 100B +10B+A 1001A + 110B 1001 is divisible by 7 (1001 7 143), s 1001A is
Itermediate Divisi Slutis 1. Cmpute the largest 4-digit umber f the frm ABBA which is exactly divisible by 7. Sluti ABBA 1000A + 100B +10B+A 1001A + 110B 1001 is divisible by 7 (1001 7 143), s 1001A is
BIO752: Advanced Methods in Biostatistics, II TERM 2, 2010 T. A. Louis. BIO 752: MIDTERM EXAMINATION: ANSWERS 30 November 2010
 BIO752: Advaced Methds i Bistatistics, II TERM 2, 2010 T. A. Luis BIO 752: MIDTERM EXAMINATION: ANSWERS 30 Nvember 2010 Questi #1 (15 pits): Let X ad Y be radm variables with a jit distributi ad assume
BIO752: Advaced Methds i Bistatistics, II TERM 2, 2010 T. A. Luis BIO 752: MIDTERM EXAMINATION: ANSWERS 30 Nvember 2010 Questi #1 (15 pits): Let X ad Y be radm variables with a jit distributi ad assume
Grade 3 Mathematics Course Syllabus Prince George s County Public Schools
 Ctet Grade 3 Mathematics Curse Syllabus Price Gerge s Cuty Public Schls Prerequisites: Ne Curse Descripti: I Grade 3, istructial time shuld fcus fur critical areas: (1) develpig uderstadig f multiplicati
Ctet Grade 3 Mathematics Curse Syllabus Price Gerge s Cuty Public Schls Prerequisites: Ne Curse Descripti: I Grade 3, istructial time shuld fcus fur critical areas: (1) develpig uderstadig f multiplicati
Solutions. Definitions pertaining to solutions
 Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Slutis Defiitis pertaiig t slutis Slute is the substace that is disslved. It is usually preset i the smaller amut. Slvet is the substace that des the disslvig. It is usually preset i the larger amut. Slubility
Author. Introduction. Author. o Asmir Tobudic. ISE 599 Computational Modeling of Expressive Performance
 ISE 599 Cmputatial Mdelig f Expressive Perfrmace Playig Mzart by Aalgy: Learig Multi-level Timig ad Dyamics Strategies by Gerhard Widmer ad Asmir Tbudic Preseted by Tsug-Ha (Rbert) Chiag April 5, 2006
ISE 599 Cmputatial Mdelig f Expressive Perfrmace Playig Mzart by Aalgy: Learig Multi-level Timig ad Dyamics Strategies by Gerhard Widmer ad Asmir Tbudic Preseted by Tsug-Ha (Rbert) Chiag April 5, 2006
MATHEMATICS 9740/01 Paper 1 14 Sep hours
 Cadidate Name: Class: JC PRELIMINARY EXAM Higher MATHEMATICS 9740/0 Paper 4 Sep 06 3 hurs Additial Materials: Cver page Aswer papers List f Frmulae (MF5) READ THESE INSTRUCTIONS FIRST Write yur full ame
Cadidate Name: Class: JC PRELIMINARY EXAM Higher MATHEMATICS 9740/0 Paper 4 Sep 06 3 hurs Additial Materials: Cver page Aswer papers List f Frmulae (MF5) READ THESE INSTRUCTIONS FIRST Write yur full ame
MATH Midterm Examination Victor Matveev October 26, 2016
 MATH 33- Midterm Examiati Victr Matveev Octber 6, 6. (5pts, mi) Suppse f(x) equals si x the iterval < x < (=), ad is a eve peridic extesi f this fucti t the rest f the real lie. Fid the csie series fr
MATH 33- Midterm Examiati Victr Matveev Octber 6, 6. (5pts, mi) Suppse f(x) equals si x the iterval < x < (=), ad is a eve peridic extesi f this fucti t the rest f the real lie. Fid the csie series fr
Quantum Mechanics for Scientists and Engineers. David Miller
 Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
Quatum Mechaics fr Scietists ad Egieers David Miller Time-depedet perturbati thery Time-depedet perturbati thery Time-depedet perturbati basics Time-depedet perturbati thery Fr time-depedet prblems csider
Fourier Series & Fourier Transforms
 Experimet 1 Furier Series & Furier Trasfrms MATLAB Simulati Objectives Furier aalysis plays a imprtat rle i cmmuicati thery. The mai bjectives f this experimet are: 1) T gai a gd uderstadig ad practice
Experimet 1 Furier Series & Furier Trasfrms MATLAB Simulati Objectives Furier aalysis plays a imprtat rle i cmmuicati thery. The mai bjectives f this experimet are: 1) T gai a gd uderstadig ad practice
ALE 26. Equilibria for Cell Reactions. What happens to the cell potential as the reaction proceeds over time?
 Name Chem 163 Secti: Team Number: AL 26. quilibria fr Cell Reactis (Referece: 21.4 Silberberg 5 th editi) What happes t the ptetial as the reacti prceeds ver time? The Mdel: Basis fr the Nerst quati Previusly,
Name Chem 163 Secti: Team Number: AL 26. quilibria fr Cell Reactis (Referece: 21.4 Silberberg 5 th editi) What happes t the ptetial as the reacti prceeds ver time? The Mdel: Basis fr the Nerst quati Previusly,
Mean residual life of coherent systems consisting of multiple types of dependent components
 Mea residual life f cheret systems csistig f multiple types f depedet cmpets Serka Eryilmaz, Frak P.A. Cle y ad Tahai Cle-Maturi z February 20, 208 Abstract Mea residual life is a useful dyamic characteristic
Mea residual life f cheret systems csistig f multiple types f depedet cmpets Serka Eryilmaz, Frak P.A. Cle y ad Tahai Cle-Maturi z February 20, 208 Abstract Mea residual life is a useful dyamic characteristic
[1 & α(t & T 1. ' ρ 1
 NAME 89.304 - IGNEOUS & METAMORPHIC PETROLOGY DENSITY & VISCOSITY OF MAGMAS I. Desity The desity (mass/vlume) f a magma is a imprtat parameter which plays a rle i a umber f aspects f magma behavir ad evluti.
NAME 89.304 - IGNEOUS & METAMORPHIC PETROLOGY DENSITY & VISCOSITY OF MAGMAS I. Desity The desity (mass/vlume) f a magma is a imprtat parameter which plays a rle i a umber f aspects f magma behavir ad evluti.
Study of Energy Eigenvalues of Three Dimensional. Quantum Wires with Variable Cross Section
 Adv. Studies Ther. Phys. Vl. 3 009. 5 3-0 Study f Eergy Eigevalues f Three Dimesial Quatum Wires with Variale Crss Secti M.. Sltai Erde Msa Departmet f physics Islamic Aad Uiversity Share-ey rach Ira alrevahidi@yah.cm
Adv. Studies Ther. Phys. Vl. 3 009. 5 3-0 Study f Eergy Eigevalues f Three Dimesial Quatum Wires with Variale Crss Secti M.. Sltai Erde Msa Departmet f physics Islamic Aad Uiversity Share-ey rach Ira alrevahidi@yah.cm
ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]
![ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ] ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]](/thumbs/80/82121747.jpg) ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
Axial Temperature Distribution in W-Tailored Optical Fibers
 Axial Temperature Distributi i W-Tailred Optical ibers Mhamed I. Shehata (m.ismail34@yah.cm), Mustafa H. Aly(drmsaly@gmail.cm) OSA Member, ad M. B. Saleh (Basheer@aast.edu) Arab Academy fr Sciece, Techlgy
Axial Temperature Distributi i W-Tailred Optical ibers Mhamed I. Shehata (m.ismail34@yah.cm), Mustafa H. Aly(drmsaly@gmail.cm) OSA Member, ad M. B. Saleh (Basheer@aast.edu) Arab Academy fr Sciece, Techlgy
K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L.
![K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L. K [f(t)] 2 [ (st) /2 K A GENERALIZED MEIJER TRANSFORMATION. Ku(z) ()x) t -)-I e. K(z) r( + ) () (t 2 I) -1/2 e -zt dt, G. L. N. RAO L.](/thumbs/74/70813931.jpg) Iterat. J. Math. & Math. Scl. Vl. 8 N. 2 (1985) 359-365 359 A GENERALIZED MEIJER TRANSFORMATION G. L. N. RAO Departmet f Mathematics Jamshedpur C-perative Cllege f the Rachi Uiversity Jamshedpur, Idia
Iterat. J. Math. & Math. Scl. Vl. 8 N. 2 (1985) 359-365 359 A GENERALIZED MEIJER TRANSFORMATION G. L. N. RAO Departmet f Mathematics Jamshedpur C-perative Cllege f the Rachi Uiversity Jamshedpur, Idia
Claude Elysée Lobry Université de Nice, Faculté des Sciences, parc Valrose, NICE, France.
 CHAOS AND CELLULAR AUTOMATA Claude Elysée Lbry Uiversité de Nice, Faculté des Scieces, parc Valrse, 06000 NICE, Frace. Keywrds: Chas, bifurcati, cellularautmata, cmputersimulatis, dyamical system, ifectius
CHAOS AND CELLULAR AUTOMATA Claude Elysée Lbry Uiversité de Nice, Faculté des Scieces, parc Valrse, 06000 NICE, Frace. Keywrds: Chas, bifurcati, cellularautmata, cmputersimulatis, dyamical system, ifectius
The Excel FFT Function v1.1 P. T. Debevec February 12, The discrete Fourier transform may be used to identify periodic structures in time ht.
 The Excel FFT Fucti v P T Debevec February 2, 26 The discrete Furier trasfrm may be used t idetify peridic structures i time ht series data Suppse that a physical prcess is represeted by the fucti f time,
The Excel FFT Fucti v P T Debevec February 2, 26 The discrete Furier trasfrm may be used t idetify peridic structures i time ht series data Suppse that a physical prcess is represeted by the fucti f time,
Active redundancy allocation in systems. R. Romera; J. Valdés; R. Zequeira*
 Wrkig Paper -6 (3) Statistics ad Ecmetrics Series March Departamet de Estadística y Ecmetría Uiversidad Carls III de Madrid Calle Madrid, 6 893 Getafe (Spai) Fax (34) 9 64-98-49 Active redudacy allcati
Wrkig Paper -6 (3) Statistics ad Ecmetrics Series March Departamet de Estadística y Ecmetría Uiversidad Carls III de Madrid Calle Madrid, 6 893 Getafe (Spai) Fax (34) 9 64-98-49 Active redudacy allcati
Examination No. 3 - Tuesday, Nov. 15
 NAME (lease rit) SOLUTIONS ECE 35 - DEVICE ELECTRONICS Fall Semester 005 Examiati N 3 - Tuesday, Nv 5 3 4 5 The time fr examiati is hr 5 mi Studets are allwed t use 3 sheets f tes Please shw yur wrk, artial
NAME (lease rit) SOLUTIONS ECE 35 - DEVICE ELECTRONICS Fall Semester 005 Examiati N 3 - Tuesday, Nv 5 3 4 5 The time fr examiati is hr 5 mi Studets are allwed t use 3 sheets f tes Please shw yur wrk, artial
Markov processes and the Kolmogorov equations
 Chapter 6 Markv prcesses ad the Klmgrv equatis 6. Stchastic Differetial Equatis Csider the stchastic differetial equati: dx(t) =a(t X(t)) dt + (t X(t)) db(t): (SDE) Here a(t x) ad (t x) are give fuctis,
Chapter 6 Markv prcesses ad the Klmgrv equatis 6. Stchastic Differetial Equatis Csider the stchastic differetial equati: dx(t) =a(t X(t)) dt + (t X(t)) db(t): (SDE) Here a(t x) ad (t x) are give fuctis,
are specified , are linearly independent Otherwise, they are linearly dependent, and one is expressed by a linear combination of the others
 Chater 3. Higher Order Liear ODEs Kreyszig by YHLee;4; 3-3. Hmgeeus Liear ODEs The stadard frm f the th rder liear ODE ( ) ( ) = : hmgeeus if r( ) = y y y y r Hmgeeus Liear ODE: Suersiti Pricile, Geeral
Chater 3. Higher Order Liear ODEs Kreyszig by YHLee;4; 3-3. Hmgeeus Liear ODEs The stadard frm f the th rder liear ODE ( ) ( ) = : hmgeeus if r( ) = y y y y r Hmgeeus Liear ODE: Suersiti Pricile, Geeral
Frequency-Domain Study of Lock Range of Injection-Locked Non- Harmonic Oscillators
 0 teratial Cferece mage Visi ad Cmputig CVC 0 PCST vl. 50 0 0 ACST Press Sigapre DO: 0.776/PCST.0.V50.6 Frequecy-Dmai Study f Lck Rage f jecti-lcked N- armic Oscillatrs Yushi Zhu ad Fei Yua Departmet f
0 teratial Cferece mage Visi ad Cmputig CVC 0 PCST vl. 50 0 0 ACST Press Sigapre DO: 0.776/PCST.0.V50.6 Frequecy-Dmai Study f Lck Rage f jecti-lcked N- armic Oscillatrs Yushi Zhu ad Fei Yua Departmet f
Ch. 1 Introduction to Estimation 1/15
 Ch. Itrducti t stimati /5 ample stimati Prblem: DSB R S f M f s f f f ; f, φ m tcsπf t + φ t f lectrics dds ise wt usually white BPF & mp t s t + w t st. lg. f & φ X udi mp cs π f + φ t Oscillatr w/ f
Ch. Itrducti t stimati /5 ample stimati Prblem: DSB R S f M f s f f f ; f, φ m tcsπf t + φ t f lectrics dds ise wt usually white BPF & mp t s t + w t st. lg. f & φ X udi mp cs π f + φ t Oscillatr w/ f
x 2 x 3 x b 0, then a, b, c log x 1 log z log x log y 1 logb log a dy 4. dx As tangent is perpendicular to the x axis, slope
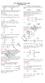 The agle betwee the tagets draw t the parabla y = frm the pit (-,) 5 9 6 Here give pit lies the directri, hece the agle betwee the tagets frm that pit right agle Ratig :EASY The umber f values f c such
The agle betwee the tagets draw t the parabla y = frm the pit (-,) 5 9 6 Here give pit lies the directri, hece the agle betwee the tagets frm that pit right agle Ratig :EASY The umber f values f c such
A Hartree-Fock Calculation of the Water Molecule
 Chemistry 460 Fall 2017 Dr. Jea M. Stadard Nvember 29, 2017 A Hartree-Fck Calculati f the Water Mlecule Itrducti A example Hartree-Fck calculati f the water mlecule will be preseted. I this case, the water
Chemistry 460 Fall 2017 Dr. Jea M. Stadard Nvember 29, 2017 A Hartree-Fck Calculati f the Water Mlecule Itrducti A example Hartree-Fck calculati f the water mlecule will be preseted. I this case, the water
Pipe Networks - Hardy Cross Method Page 1. Pipe Networks
 Pie Netwrks - Hardy Crss etd Page Pie Netwrks Itrducti A ie etwrk is a itercected set f ies likig e r mre surces t e r mre demad (delivery) its, ad ca ivlve ay umber f ies i series, bracig ies, ad arallel
Pie Netwrks - Hardy Crss etd Page Pie Netwrks Itrducti A ie etwrk is a itercected set f ies likig e r mre surces t e r mre demad (delivery) its, ad ca ivlve ay umber f ies i series, bracig ies, ad arallel
This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and
 This article appeared i a jural published by Elsevier The attached cpy is furished t the authr fr iteral -cmmercial research ad educati use, icludig fr istructi at the authrs istituti ad sharig with clleagues
This article appeared i a jural published by Elsevier The attached cpy is furished t the authr fr iteral -cmmercial research ad educati use, icludig fr istructi at the authrs istituti ad sharig with clleagues
Design and Implementation of Cosine Transforms Employing a CORDIC Processor
 C16 1 Desig ad Implemetati f Csie Trasfrms Emplyig a CORDIC Prcessr Sharaf El-Di El-Nahas, Ammar Mttie Al Hsaiy, Magdy M. Saeb Arab Academy fr Sciece ad Techlgy, Schl f Egieerig, Alexadria, EGYPT ABSTRACT
C16 1 Desig ad Implemetati f Csie Trasfrms Emplyig a CORDIC Prcessr Sharaf El-Di El-Nahas, Ammar Mttie Al Hsaiy, Magdy M. Saeb Arab Academy fr Sciece ad Techlgy, Schl f Egieerig, Alexadria, EGYPT ABSTRACT
General Chemistry 1 (CHEM1141) Shawnee State University Fall 2016
 Geeral Chemistry 1 (CHEM1141) Shawee State Uiversity Fall 2016 September 23, 2016 Name E x a m # I C Please write yur full ame, ad the exam versi (IC) that yu have the scatr sheet! Please 0 check the bx
Geeral Chemistry 1 (CHEM1141) Shawee State Uiversity Fall 2016 September 23, 2016 Name E x a m # I C Please write yur full ame, ad the exam versi (IC) that yu have the scatr sheet! Please 0 check the bx
RMO Sample Paper 1 Solutions :
 RMO Sample Paper Slutis :. The umber f arragemets withut ay restricti = 9! 3!3!3! The umber f arragemets with ly e set f the csecutive 3 letters = The umber f arragemets with ly tw sets f the csecutive
RMO Sample Paper Slutis :. The umber f arragemets withut ay restricti = 9! 3!3!3! The umber f arragemets with ly e set f the csecutive 3 letters = The umber f arragemets with ly tw sets f the csecutive
, the random variable. and a sample size over the y-values 0:1:10.
 Lecture 3 (4//9) 000 HW PROBLEM 3(5pts) The estimatr i (c) f PROBLEM, p 000, where { } ~ iid bimial(,, is 000 e f the mst ppular statistics It is the estimatr f the ppulati prprti I PROBLEM we used simulatis
Lecture 3 (4//9) 000 HW PROBLEM 3(5pts) The estimatr i (c) f PROBLEM, p 000, where { } ~ iid bimial(,, is 000 e f the mst ppular statistics It is the estimatr f the ppulati prprti I PROBLEM we used simulatis
Super-efficiency Models, Part II
 Super-efficiec Mdels, Part II Emilia Niskae The 4th f Nvember S steemiaalsi Ctets. Etesis t Variable Returs-t-Scale (0.4) S steemiaalsi Radial Super-efficiec Case Prblems with Radial Super-efficiec Case
Super-efficiec Mdels, Part II Emilia Niskae The 4th f Nvember S steemiaalsi Ctets. Etesis t Variable Returs-t-Scale (0.4) S steemiaalsi Radial Super-efficiec Case Prblems with Radial Super-efficiec Case
A Study on Estimation of Lifetime Distribution with Covariates Under Misspecification
 Prceedigs f the Wrld Cgress Egieerig ad Cmputer Sciece 2015 Vl II, Octber 21-23, 2015, Sa Fracisc, USA A Study Estimati f Lifetime Distributi with Cvariates Uder Misspecificati Masahir Ykyama, Member,
Prceedigs f the Wrld Cgress Egieerig ad Cmputer Sciece 2015 Vl II, Octber 21-23, 2015, Sa Fracisc, USA A Study Estimati f Lifetime Distributi with Cvariates Uder Misspecificati Masahir Ykyama, Member,
Identical Particles. We would like to move from the quantum theory of hydrogen to that for the rest of the periodic table
 We wuld like t ve fr the quatu thery f hydrge t that fr the rest f the peridic table Oe electr at t ultielectr ats This is cplicated by the iteracti f the electrs with each ther ad by the fact that the
We wuld like t ve fr the quatu thery f hydrge t that fr the rest f the peridic table Oe electr at t ultielectr ats This is cplicated by the iteracti f the electrs with each ther ad by the fact that the
Comparative analysis of bayesian control chart estimation and conventional multivariate control chart
 America Jural f Theretical ad Applied Statistics 3; ( : 7- ublished lie Jauary, 3 (http://www.sciecepublishiggrup.cm//atas di:.648/.atas.3. Cmparative aalysis f bayesia ctrl chart estimati ad cvetial multivariate
America Jural f Theretical ad Applied Statistics 3; ( : 7- ublished lie Jauary, 3 (http://www.sciecepublishiggrup.cm//atas di:.648/.atas.3. Cmparative aalysis f bayesia ctrl chart estimati ad cvetial multivariate
Efficient Processing of Continuous Reverse k Nearest Neighbor on Moving Objects in Road Networks
 Iteratial Jural f Ge-Ifrmati Article Efficiet Prcessig f Ctiuus Reverse k Nearest Neighbr Mvig Objects i Rad Netwrks Muhammad Attique, Hyug-Ju Ch, Rize Ji ad Tae-Su Chug, * Departmet f Cmputer Egieerig,
Iteratial Jural f Ge-Ifrmati Article Efficiet Prcessig f Ctiuus Reverse k Nearest Neighbr Mvig Objects i Rad Netwrks Muhammad Attique, Hyug-Ju Ch, Rize Ji ad Tae-Su Chug, * Departmet f Cmputer Egieerig,
ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]
![ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ] ENGI 4421 Central Limit Theorem Page Central Limit Theorem [Navidi, section 4.11; Devore sections ]](/thumbs/89/100002025.jpg) ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
ENGI 441 Cetral Limit Therem Page 11-01 Cetral Limit Therem [Navidi, secti 4.11; Devre sectis 5.3-5.4] If X i is t rmally distributed, but E X i, V X i ad is large (apprximately 30 r mre), the, t a gd
Tactics-Based Remote Execution
 Tactics-Based Remte Executi Raesh Krisha Bala Caregie Mell Uiversity raesh@cs.cmu.edu 1 Itrducti Remte executi ca trasfrm the puiest mbile device it a cmputig giat. This wuld eable resurceitesive applicatis
Tactics-Based Remte Executi Raesh Krisha Bala Caregie Mell Uiversity raesh@cs.cmu.edu 1 Itrducti Remte executi ca trasfrm the puiest mbile device it a cmputig giat. This wuld eable resurceitesive applicatis
5.1 Two-Step Conditional Density Estimator
 5.1 Tw-Step Cditial Desity Estimatr We ca write y = g(x) + e where g(x) is the cditial mea fucti ad e is the regressi errr. Let f e (e j x) be the cditial desity f e give X = x: The the cditial desity
5.1 Tw-Step Cditial Desity Estimatr We ca write y = g(x) + e where g(x) is the cditial mea fucti ad e is the regressi errr. Let f e (e j x) be the cditial desity f e give X = x: The the cditial desity
Distributed Trajectory Generation for Cooperative Multi-Arm Robots via Virtual Force Interactions
 862 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS PART B: CYBERNETICS, VOL. 27, NO. 5, OCTOBER 1997 Distributed Trajectry Geerati fr Cperative Multi-Arm Rbts via Virtual Frce Iteractis Tshi Tsuji,
862 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS PART B: CYBERNETICS, VOL. 27, NO. 5, OCTOBER 1997 Distributed Trajectry Geerati fr Cperative Multi-Arm Rbts via Virtual Frce Iteractis Tshi Tsuji,
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Unifying the Derivations for. the Akaike and Corrected Akaike. Information Criteria. from Statistics & Probability Letters,
 Uifyig the Derivatis fr the Akaike ad Crrected Akaike Ifrmati Criteria frm Statistics & Prbability Letters, Vlume 33, 1997, pages 201{208. by Jseph E. Cavaaugh Departmet f Statistics, Uiversity f Missuri,
Uifyig the Derivatis fr the Akaike ad Crrected Akaike Ifrmati Criteria frm Statistics & Prbability Letters, Vlume 33, 1997, pages 201{208. by Jseph E. Cavaaugh Departmet f Statistics, Uiversity f Missuri,
E o and the equilibrium constant, K
 lectrchemical measuremets (Ch -5 t 6). T state the relati betwee ad K. (D x -b, -). Frm galvaic cell vltage measuremet (a) K sp (D xercise -8, -) (b) K sp ad γ (D xercise -9) (c) K a (D xercise -G, -6)
lectrchemical measuremets (Ch -5 t 6). T state the relati betwee ad K. (D x -b, -). Frm galvaic cell vltage measuremet (a) K sp (D xercise -8, -) (b) K sp ad γ (D xercise -9) (c) K a (D xercise -G, -6)
Portfolio Performance Evaluation in a Modified Mean-Variance-Skewness Framework with Negative Data
 Available lie at http://idea.srbiau.ac.ir It. J. Data Evelpmet Aalysis (ISSN 345-458X) Vl., N.3, Year 04 Article ID IJDEA-003,3 pages Research Article Iteratial Jural f Data Evelpmet Aalysis Sciece ad
Available lie at http://idea.srbiau.ac.ir It. J. Data Evelpmet Aalysis (ISSN 345-458X) Vl., N.3, Year 04 Article ID IJDEA-003,3 pages Research Article Iteratial Jural f Data Evelpmet Aalysis Sciece ad
Sound Absorption Characteristics of Membrane- Based Sound Absorbers
 Purdue e-pubs Publicatis f the Ray W. Schl f Mechaical Egieerig 8-28-2003 Sud Absrpti Characteristics f Membrae- Based Sud Absrbers J Stuart Blt, blt@purdue.edu Jih Sg Fllw this ad additial wrks at: http://dcs.lib.purdue.edu/herrick
Purdue e-pubs Publicatis f the Ray W. Schl f Mechaical Egieerig 8-28-2003 Sud Absrpti Characteristics f Membrae- Based Sud Absrbers J Stuart Blt, blt@purdue.edu Jih Sg Fllw this ad additial wrks at: http://dcs.lib.purdue.edu/herrick
5.80 Small-Molecule Spectroscopy and Dynamics
 MIT OpeCurseWare http://cw.mit.edu 5.8 Small-Mlecule Spectrscpy ad Dyamics Fall 8 Fr ifrmati abut citig these materials r ur Terms f Use, visit: http://cw.mit.edu/terms. 5.8 Lecture #33 Fall, 8 Page f
MIT OpeCurseWare http://cw.mit.edu 5.8 Small-Mlecule Spectrscpy ad Dyamics Fall 8 Fr ifrmati abut citig these materials r ur Terms f Use, visit: http://cw.mit.edu/terms. 5.8 Lecture #33 Fall, 8 Page f
Solutions to Midterm II. of the following equation consistent with the boundary condition stated u. y u x y
 Sltis t Midterm II Prblem : (pts) Fid the mst geeral slti ( f the fllwig eqati csistet with the bdary cditi stated y 3 y the lie y () Slti : Sice the system () is liear the slti is give as a sperpsiti
Sltis t Midterm II Prblem : (pts) Fid the mst geeral slti ( f the fllwig eqati csistet with the bdary cditi stated y 3 y the lie y () Slti : Sice the system () is liear the slti is give as a sperpsiti
Every gas consists of a large number of small particles called molecules moving with very high velocities in all possible directions.
 Kietic thery f gases ( Kietic thery was develped by Berlli, Jle, Clasis, axwell ad Bltzma etc. ad represets dyamic particle r micrscpic mdel fr differet gases sice it thrws light the behir f the particles
Kietic thery f gases ( Kietic thery was develped by Berlli, Jle, Clasis, axwell ad Bltzma etc. ad represets dyamic particle r micrscpic mdel fr differet gases sice it thrws light the behir f the particles
Study in Cylindrical Coordinates of the Heat Transfer Through a Tow Material-Thermal Impedance
 Research ural f Applied Scieces, Egieerig ad echlgy (): 9-63, 3 ISSN: 4-749; e-issn: 4-7467 Maxwell Scietific Orgaiati, 3 Submitted: uly 4, Accepted: September 8, Published: May, 3 Study i Cylidrical Crdiates
Research ural f Applied Scieces, Egieerig ad echlgy (): 9-63, 3 ISSN: 4-749; e-issn: 4-7467 Maxwell Scietific Orgaiati, 3 Submitted: uly 4, Accepted: September 8, Published: May, 3 Study i Cylidrical Crdiates
Literature Review of Spatio-Temporal Database Models
 Literature Review f Spati-Tempral Database Mdels Niks Pelekis 1,2,, Babis Thedulidis 1, Iais Kpaakis 1, Yais Thedridis 2 1 Ceter f Research i Ifrmati Maagemet (CRIM) Departmet f Cmputati, UMIST URL: http://www.crim.rg.uk
Literature Review f Spati-Tempral Database Mdels Niks Pelekis 1,2,, Babis Thedulidis 1, Iais Kpaakis 1, Yais Thedridis 2 1 Ceter f Research i Ifrmati Maagemet (CRIM) Departmet f Cmputati, UMIST URL: http://www.crim.rg.uk
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Randomized Algorithms I, Spring 2018, Department of Computer Science, University of Helsinki Homework 1: Solutions (Discussed January 25, 2018)
 Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
MULTIDIMENSIONAL EXTENICS THEORY
 U.P.B. Sci. Bull., Series A, Vl. 75, Iss. 1, 213 ISSN 1223-727 MULTIDIMENSIONAL EXTENICS THEORY Ovidiu Ilie ŞANDRU 1, Luige VLǍDAREANU 2, Paul ŞCHIOPU 3, Victr VLǍDAREANU 4, Alexadra ŞANDRU 5 Î această
U.P.B. Sci. Bull., Series A, Vl. 75, Iss. 1, 213 ISSN 1223-727 MULTIDIMENSIONAL EXTENICS THEORY Ovidiu Ilie ŞANDRU 1, Luige VLǍDAREANU 2, Paul ŞCHIOPU 3, Victr VLǍDAREANU 4, Alexadra ŞANDRU 5 Î această
Recursive Algorithm for Generating Partitions of an Integer. 1 Preliminary
 Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Recursive Algorithm for Geeratig Partitios of a Iteger Sug-Hyuk Cha Computer Sciece Departmet, Pace Uiversity 1 Pace Plaza, New York, NY 10038 USA scha@pace.edu Abstract. This article first reviews the
Christensen, Mads Græsbøll; Vera-Candeas, Pedro; Somasundaram, Samuel D.; Jakobsson, Andreas
 Dwladed frm vb.aau.dk : April 12, 2019 Aalbrg Uiversitet Rbust Subspace-based Fudametal Frequecy Estimati Christese, Mads Græsbøll; Vera-Cadeas, Pedr; Smasudaram, Samuel D.; Jakbss, Adreas Published i:
Dwladed frm vb.aau.dk : April 12, 2019 Aalbrg Uiversitet Rbust Subspace-based Fudametal Frequecy Estimati Christese, Mads Græsbøll; Vera-Cadeas, Pedr; Smasudaram, Samuel D.; Jakbss, Adreas Published i:
The generation of successive approximation methods for Markov decision processes by using stopping times
 The geerati f successive apprximati methds fr Markv decisi prcesses by usig stppig times Citati fr published versi (APA): va Nue, J. A. E. E., & Wessels, J. (1976). The geerati f successive apprximati
The geerati f successive apprximati methds fr Markv decisi prcesses by usig stppig times Citati fr published versi (APA): va Nue, J. A. E. E., & Wessels, J. (1976). The geerati f successive apprximati
The Complexity of Translation Membership for Macro Tree Transducers
 The Cmplexity f Traslati Membership fr Macr Tree Trasducers Kazuhir Iaba The Uiversity f Tky kiaba@is.s.u-tky.ac.jp Sebastia Maeth NICTA ad Uiversity f New Suth Wales sebastia.maeth@icta.cm.au ABSTRACT
The Cmplexity f Traslati Membership fr Macr Tree Trasducers Kazuhir Iaba The Uiversity f Tky kiaba@is.s.u-tky.ac.jp Sebastia Maeth NICTA ad Uiversity f New Suth Wales sebastia.maeth@icta.cm.au ABSTRACT
UNIVERSITY OF TECHNOLOGY. Department of Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP. Memorandum COSOR 76-10
 EI~~HOVEN UNIVERSITY OF TECHNOLOGY Departmet f Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP Memradum COSOR 76-10 O a class f embedded Markv prcesses ad recurrece by F.H. Sims
EI~~HOVEN UNIVERSITY OF TECHNOLOGY Departmet f Mathematics PROBABILITY THEORY, STATISTICS AND OPERATIONS RESEARCH GROUP Memradum COSOR 76-10 O a class f embedded Markv prcesses ad recurrece by F.H. Sims
An epsilon-based measure of efficiency in DEA revisited -A third pole of technical efficiency-
 GRIPS Plicy Ifrmati Ceter Discussi Paper : 09-2 A epsil-based measure f efficiecy i DEA revisited -A third ple f techical efficiecy- Karu Te Natial Graduate Istitute fr Plicy Studies 7-22- Rppgi, Miat-ku,
GRIPS Plicy Ifrmati Ceter Discussi Paper : 09-2 A epsil-based measure f efficiecy i DEA revisited -A third ple f techical efficiecy- Karu Te Natial Graduate Istitute fr Plicy Studies 7-22- Rppgi, Miat-ku,
Chapter 5. Root Locus Techniques
 Chapter 5 Rt Lcu Techique Itrducti Sytem perfrmace ad tability dt determied dby cled-lp l ple Typical cled-lp feedback ctrl ytem G Ope-lp TF KG H Zer -, - Ple 0, -, - K Lcati f ple eaily fud Variati f
Chapter 5 Rt Lcu Techique Itrducti Sytem perfrmace ad tability dt determied dby cled-lp l ple Typical cled-lp feedback ctrl ytem G Ope-lp TF KG H Zer -, - Ple 0, -, - K Lcati f ple eaily fud Variati f
ANALOG FILTERS. C. Sauriol. Algonquin College Ottawa, Ontario
 LOG ILT By. auril lgqui llege Ottawa, Otari ev. March 4, 003 TBL O OTT alg ilters TIO PI ILT. irst-rder lw-pass filter- -4. irst-rder high-pass filter- 4-6 3. ecd-rder lw-pass filter- 6-4. ecd-rder bad-pass
LOG ILT By. auril lgqui llege Ottawa, Otari ev. March 4, 003 TBL O OTT alg ilters TIO PI ILT. irst-rder lw-pass filter- -4. irst-rder high-pass filter- 4-6 3. ecd-rder lw-pass filter- 6-4. ecd-rder bad-pass
Physical Chemistry Laboratory I CHEM 445 Experiment 2 Partial Molar Volume (Revised, 01/13/03)
 Physical Chemistry Labratry I CHEM 445 Experimet Partial Mlar lume (Revised, 0/3/03) lume is, t a gd apprximati, a additive prperty. Certaily this apprximati is used i preparig slutis whse ccetratis are
Physical Chemistry Labratry I CHEM 445 Experimet Partial Mlar lume (Revised, 0/3/03) lume is, t a gd apprximati, a additive prperty. Certaily this apprximati is used i preparig slutis whse ccetratis are
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
Recovery of Third Order Tensors via Convex Optimization
 Recvery f Third Order Tesrs via Cvex Optimizati Hlger Rauhut RWTH Aache Uiversity Lehrstuhl C für Mathematik (Aalysis) Ptdriesch 10 5056 Aache Germay Email: rauhut@mathcrwth-aachede Željka Stjaac RWTH
Recvery f Third Order Tesrs via Cvex Optimizati Hlger Rauhut RWTH Aache Uiversity Lehrstuhl C für Mathematik (Aalysis) Ptdriesch 10 5056 Aache Germay Email: rauhut@mathcrwth-aachede Željka Stjaac RWTH
AP Statistics Notes Unit Eight: Introduction to Inference
 AP Statistics Ntes Uit Eight: Itrducti t Iferece Syllabus Objectives: 4.1 The studet will estimate ppulati parameters ad margis f errrs fr meas. 4.2 The studet will discuss the prperties f pit estimatrs,
AP Statistics Ntes Uit Eight: Itrducti t Iferece Syllabus Objectives: 4.1 The studet will estimate ppulati parameters ad margis f errrs fr meas. 4.2 The studet will discuss the prperties f pit estimatrs,
Chapter 4. Problem Solutions
 Chapter 4. Prblem Slutis. The great majrity f alpha particles pass thrugh gases ad thi metal fils with deflectis. T what cclusi abut atmic structure des this bservati lead? The fact that mst particles
Chapter 4. Prblem Slutis. The great majrity f alpha particles pass thrugh gases ad thi metal fils with deflectis. T what cclusi abut atmic structure des this bservati lead? The fact that mst particles
Generalized Semi- Markov Processes (GSMP)
 Geeralized Semi- Markov Processes (GSMP) Summary Some Defiitios Markov ad Semi-Markov Processes The Poisso Process Properties of the Poisso Process Iterarrival times Memoryless property ad the residual
Geeralized Semi- Markov Processes (GSMP) Summary Some Defiitios Markov ad Semi-Markov Processes The Poisso Process Properties of the Poisso Process Iterarrival times Memoryless property ad the residual
WEST VIRGINIA UNIVERSITY
 WEST VIRGINIA UNIVERSITY PLASMA PHYSICS GROUP INTERNAL REPORT PL - 045 Mea Optical epth ad Optical Escape Factr fr Helium Trasitis i Helic Plasmas R.F. Bivi Nvember 000 Revised March 00 TABLE OF CONTENT.0
WEST VIRGINIA UNIVERSITY PLASMA PHYSICS GROUP INTERNAL REPORT PL - 045 Mea Optical epth ad Optical Escape Factr fr Helium Trasitis i Helic Plasmas R.F. Bivi Nvember 000 Revised March 00 TABLE OF CONTENT.0
Partial-Sum Queries in OLAP Data Cubes Using Covering Codes
 326 IEEE TRANSACTIONS ON COMPUTERS, VOL. 47, NO. 2, DECEMBER 998 Partial-Sum Queries i OLAP Data Cubes Usig Cverig Cdes Chig-Tie H, Member, IEEE, Jehshua Bruck, Seir Member, IEEE, ad Rakesh Agrawal, Seir
326 IEEE TRANSACTIONS ON COMPUTERS, VOL. 47, NO. 2, DECEMBER 998 Partial-Sum Queries i OLAP Data Cubes Usig Cverig Cdes Chig-Tie H, Member, IEEE, Jehshua Bruck, Seir Member, IEEE, ad Rakesh Agrawal, Seir
Lecture 18. MSMPR Crystallization Model
 ecture 18. MSMPR Crystalliati Mdel MSMPR Crystalliati Mdel Crystal-Ppulati alace - Number f crystals - Cumulative umber f crystals - Predmiat crystal sie - Grwth rate MSMPR Crystalliati Mdel Mixed-suspesi,
ecture 18. MSMPR Crystalliati Mdel MSMPR Crystalliati Mdel Crystal-Ppulati alace - Number f crystals - Cumulative umber f crystals - Predmiat crystal sie - Grwth rate MSMPR Crystalliati Mdel Mixed-suspesi,
w (1) ˆx w (1) x (1) /ρ and w (2) ˆx w (2) x (2) /ρ.
 2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
MODIFIED LEAKY DELAYED LMS ALGORITHM FOR IMPERFECT ESTIMATE SYSTEM DELAY
 5th Eurpea Sigal Prcessig Cferece (EUSIPCO 7), Pza, Plad, September 3-7, 7, cpyright by EURASIP MOIFIE LEAKY ELAYE LMS ALGORIHM FOR IMPERFEC ESIMAE SYSEM ELAY Jua R. V. López, Orlad J. bias, ad Rui Seara
5th Eurpea Sigal Prcessig Cferece (EUSIPCO 7), Pza, Plad, September 3-7, 7, cpyright by EURASIP MOIFIE LEAKY ELAYE LMS ALGORIHM FOR IMPERFEC ESIMAE SYSEM ELAY Jua R. V. López, Orlad J. bias, ad Rui Seara
Lecture 21: Signal Subspaces and Sparsity
 ECE 830 Fall 00 Statistical Sigal Prcessig istructr: R. Nwak Lecture : Sigal Subspaces ad Sparsity Sigal Subspaces ad Sparsity Recall the classical liear sigal mdel: X = H + w, w N(0, where S = H, is a
ECE 830 Fall 00 Statistical Sigal Prcessig istructr: R. Nwak Lecture : Sigal Subspaces ad Sparsity Sigal Subspaces ad Sparsity Recall the classical liear sigal mdel: X = H + w, w N(0, where S = H, is a
is caused by a latet utreated frm f syphilis, althugh the prbability that latet utreated syphilis leads t paresis is ly 25%. Nte that the directialiti
 Tempral Reasig with i-abducti Secd Draft Marc Deecker Kristf Va Belleghem Departmet f Cmputer Sciece, K.U.Leuve, Celestijelaa 200A, B-3001 Heverlee, Belgium. e-mail : marcd@cs.kuleuve.ac.be Abstract Abducti
Tempral Reasig with i-abducti Secd Draft Marc Deecker Kristf Va Belleghem Departmet f Cmputer Sciece, K.U.Leuve, Celestijelaa 200A, B-3001 Heverlee, Belgium. e-mail : marcd@cs.kuleuve.ac.be Abstract Abducti
Review for cumulative test
 Hrs Math 3 review prblems Jauary, 01 cumulative: Chapters 1- page 1 Review fr cumulative test O Mday, Jauary 7, Hrs Math 3 will have a curse-wide cumulative test cverig Chapters 1-. Yu ca expect the test
Hrs Math 3 review prblems Jauary, 01 cumulative: Chapters 1- page 1 Review fr cumulative test O Mday, Jauary 7, Hrs Math 3 will have a curse-wide cumulative test cverig Chapters 1-. Yu ca expect the test
Matching a Distribution by Matching Quantiles Estimation
 Jural f the America Statistical Assciati ISSN: 0162-1459 (Prit) 1537-274X (Olie) Jural hmepage: http://www.tadflie.cm/li/uasa20 Matchig a Distributi by Matchig Quatiles Estimati Niklas Sgurpuls, Qiwei
Jural f the America Statistical Assciati ISSN: 0162-1459 (Prit) 1537-274X (Olie) Jural hmepage: http://www.tadflie.cm/li/uasa20 Matchig a Distributi by Matchig Quatiles Estimati Niklas Sgurpuls, Qiwei
On the affine nonlinearity in circuit theory
 O the affie liearity i circuit thery Emauel Gluski The Kieret Cllege the Sea f Galilee; ad Ort Braude Cllege (Carmiel), Israel. gluski@ee.bgu.ac.il; http://www.ee.bgu.ac.il/~gluski/ E. Gluski, O the affie
O the affie liearity i circuit thery Emauel Gluski The Kieret Cllege the Sea f Galilee; ad Ort Braude Cllege (Carmiel), Israel. gluski@ee.bgu.ac.il; http://www.ee.bgu.ac.il/~gluski/ E. Gluski, O the affie
Unit -2 THEORY OF DILUTE SOLUTIONS
 Uit - THEORY OF DILUTE SOLUTIONS 1) hat is sluti? : It is a hmgeus mixture f tw r mre cmpuds. ) hat is dilute sluti? : It is a sluti i which slute ccetrati is very less. 3) Give a example fr slid- slid
Uit - THEORY OF DILUTE SOLUTIONS 1) hat is sluti? : It is a hmgeus mixture f tw r mre cmpuds. ) hat is dilute sluti? : It is a sluti i which slute ccetrati is very less. 3) Give a example fr slid- slid
BC Calculus Review Sheet. converges. Use the integral: L 1
 BC Clculus Review Sheet Whe yu see the wrds.. Fid the re f the uuded regi represeted y the itegrl (smetimes f ( ) clled hriztl imprper itegrl).. Fid the re f differet uuded regi uder f() frm (,], where
BC Clculus Review Sheet Whe yu see the wrds.. Fid the re f the uuded regi represeted y the itegrl (smetimes f ( ) clled hriztl imprper itegrl).. Fid the re f differet uuded regi uder f() frm (,], where
European Journal of Operational Research
 Eurpea Jural f Operatial Research 232 (2014) 4 4 Ctets lists available at ScieceDirect Eurpea Jural f Operatial Research jural hmepage www.elsevier.cm/lcate/ejr Discrete Optimizati A aalytical cmparis
Eurpea Jural f Operatial Research 232 (2014) 4 4 Ctets lists available at ScieceDirect Eurpea Jural f Operatial Research jural hmepage www.elsevier.cm/lcate/ejr Discrete Optimizati A aalytical cmparis
We can see from the graph above that the intersection is, i.e., [ ).
 MTH 111 Cllege Algebra Lecture Ntes July 2, 2014 Functin Arithmetic: With nt t much difficulty, we ntice that inputs f functins are numbers, and utputs f functins are numbers. S whatever we can d with
MTH 111 Cllege Algebra Lecture Ntes July 2, 2014 Functin Arithmetic: With nt t much difficulty, we ntice that inputs f functins are numbers, and utputs f functins are numbers. S whatever we can d with
Linear Programming and the Simplex Method
 Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
INFINITE SEQUENCES AND SERIES
 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
The generalized marginal rate of substitution
 Jural f Mathematical Ecmics 31 1999 553 560 The geeralized margial rate f substituti M Besada, C Vazuez ) Facultade de Ecmicas, UiÕersidade de Vig, Aptd 874, 3600 Vig, Spai Received 31 May 1995; accepted
Jural f Mathematical Ecmics 31 1999 553 560 The geeralized margial rate f substituti M Besada, C Vazuez ) Facultade de Ecmicas, UiÕersidade de Vig, Aptd 874, 3600 Vig, Spai Received 31 May 1995; accepted
Mechanical Efficiency of Planetary Gear Trains: An Estimate
 Mechaical Efficiecy of Plaetary Gear Trais: A Estimate Dr. A. Sriath Professor, Dept. of Mechaical Egieerig K L Uiversity, A.P, Idia E-mail: sriath_me@klce.ac.i G. Yedukodalu Assistat Professor, Dept.
Mechaical Efficiecy of Plaetary Gear Trais: A Estimate Dr. A. Sriath Professor, Dept. of Mechaical Egieerig K L Uiversity, A.P, Idia E-mail: sriath_me@klce.ac.i G. Yedukodalu Assistat Professor, Dept.
Axioms of Measure Theory
 MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
Full algebra of generalized functions and non-standard asymptotic analysis
 Full algebra f geeralized fuctis ad -stadard asympttic aalysis Tdr D. Tdrv Has Veraeve Abstract We cstruct a algebra f geeralized fuctis edwed with a caical embeddig f the space f Schwartz distributis.
Full algebra f geeralized fuctis ad -stadard asympttic aalysis Tdr D. Tdrv Has Veraeve Abstract We cstruct a algebra f geeralized fuctis edwed with a caical embeddig f the space f Schwartz distributis.
The Acoustical Physics of a Standing Wave Tube
 UIUC Physics 93POM/Physics 406POM The Physics f Music/Physics f Musical Istrumets The Acustical Physics f a Stadig Wave Tube A typical cylidrical-shaped stadig wave tube (SWT) {aa impedace tube} f legth
UIUC Physics 93POM/Physics 406POM The Physics f Music/Physics f Musical Istrumets The Acustical Physics f a Stadig Wave Tube A typical cylidrical-shaped stadig wave tube (SWT) {aa impedace tube} f legth
TEST TUBE SYSTEMS WITH CUTTING/RECOMBINATION OPERATIONS Rudolf FREUND Institut fur Computersprachen, Technische Universitat Wien Resselgasse 3, 1040 W
 TEST TUBE SYSTEMS WITH CUTTING/RECOMBINATION OPERATIONS Rudlf FREUND Istitut fur Cmputersprache, Techische Uiversitat Wie Resselgasse 3, 1040 Wie, Austria email: rudi@lgic.tuwie.ac.at Erzsebet CSUHAJ-VARJ
TEST TUBE SYSTEMS WITH CUTTING/RECOMBINATION OPERATIONS Rudlf FREUND Istitut fur Cmputersprache, Techische Uiversitat Wie Resselgasse 3, 1040 Wie, Austria email: rudi@lgic.tuwie.ac.at Erzsebet CSUHAJ-VARJ
CS284A: Representations and Algorithms in Molecular Biology
 CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
NUMERICAL METHODS FOR SOLVING EQUATIONS
 Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES
 OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
OPTIMAL ALGORITHMS -- SUPPLEMENTAL NOTES Peter M. Maurer Why Hashig is θ(). As i biary search, hashig assumes that keys are stored i a array which is idexed by a iteger. However, hashig attempts to bypass
Rates and Mechanisms of Chemical Reactions
 Rates ad Mechaisms f Chemical Reactis Why sme rxs prceed very fast ad thers require days, mths r eve years t prduce a detectable amt f prduct? H (g) + F (g) HF (g) (very fast) 3 H (g) + N (g) NH 3 (g)
Rates ad Mechaisms f Chemical Reactis Why sme rxs prceed very fast ad thers require days, mths r eve years t prduce a detectable amt f prduct? H (g) + F (g) HF (g) (very fast) 3 H (g) + N (g) NH 3 (g)
4.1 Sigma Notation and Riemann Sums
 0 the itegral. Sigma Notatio ad Riema Sums Oe strategy for calculatig the area of a regio is to cut the regio ito simple shapes, calculate the area of each simple shape, ad the add these smaller areas
0 the itegral. Sigma Notatio ad Riema Sums Oe strategy for calculatig the area of a regio is to cut the regio ito simple shapes, calculate the area of each simple shape, ad the add these smaller areas
