Learning from positive and unlabeled examples
|
|
|
- Brett Crawford
- 6 years ago
- Views:
Transcription
1 Theoretical Computer Science 348 (2005) Learning from positive and unlabeled examples François Denis a,, Rémi Gilleron b, Fabien Letouzey b a Équipe BDAA, LIF, UMR 6166 CNRS, Université de Provence, Marseille, France b Équipe Grappa, LIFL, UPRESA 8022 CNRS, Université de Lille 1 and Université Charles de Gaulle, Lille 3, France Abstract In many machine learning settings, labeled examples are difficult to collect while unlabeled data are abundant. Also, for some binary classification problems, positive examples which are elements of the target concept are available. Can these additional data be used to improve accuracy of supervised learning algorithms? We investigate in this paper the design of learning algorithms from positive and unlabeled data only. Many machine learning and data mining algorithms, such as decision tree induction algorithms and naive Bayes algorithms, use examples only to evaluate statistical queries (SQ-like algorithms). Kearns designed the statistical query learning model in order to describe these algorithms. Here, we design an algorithm scheme which transforms any SQ-like algorithm into an algorithm based on positive statistical queries (estimate for probabilities over the set of positive instances) and instance statistical queries (estimate for probabilities over the instance space). We prove that any class learnable in the statistical query learning model is learnable from positive statistical queries and instance statistical queries only if a lower bound on the weight of any target concept f can be estimated in polynomial time. Then, we design a decision tree induction algorithm POSC4.5, based on C4.5, that uses only positive and unlabeled examples and we give experimental results for this algorithm. In the case of imbalanced classes in the sense that one of the two classes (say the positive class) is heavily underrepresented compared to the other class, the learning problem remains open. This problem is challenging because it is encountered in many real-world applications Elsevier B.V. All rights reserved. Keywords: PAC learning; Statistical query model; Semi-supervised learning; Data mining 1. Introduction The field of data mining (sometimes referred to knowledge discovery in databases) addresses the question of how best to use various sets of data to discover regularities and to improve decisions. The learning step is central in the data mining process. A first generation of supervised machine learning algorithms (e.g. decision tree induction algorithms, neural network learning methods, Bayesian learning methods, logistic regression,...) have been demonstrated to be of significant value in a data mining perspective and they are now widely used and available in commercial products. But these machine learning methods are issued from nonparametric statistics and suppose that the input sample is a quite large set of independently and identically distributed (i.i.d.) labeled data described by numeric or symbolic features. But, in a data mining or a text mining perspective, one has to use historical data that have been collected from various This research was partially supported by: CPER , Contrat de Planétat, région Nord/Pas-de-Calais: axe TACT, projet TIC ; fonds européens FEDER TIC, Fouille Intelligente de données, Traitement Intelligent des Connaissances OBJ 2-phasing out, 2001/ n3. Corresponding author. Tel.: ; fax: addresses: fdenis@cmi.univ-mrs.fr (F. Denis), gilleron@lifl.fr (R. Gilleron), letouzey@lifl.fr (F. Letouzey) /$ - see front matter 2005 Elsevier B.V. All rights reserved. doi: /j.tcs
2 F. Denis et al. / Theoretical Computer Science 348 (2005) origins and moreover, i.i.d. labeled data may be expensive to collect or even unavailable. On the other hand, unlabeled data providing information about the underlying distribution or examples of one particular class (that we shall call the positive class) may be easily available. Can this additional information help to learn? Here, we address the issue of designing classification algorithms that are able to utilize data from diverse data sources: labeled data (if available), unlabeled data, and positive data. Along this line of research, there has recently been significant interest in semi-supervised learning, that is the design of learning algorithms from both labeled and unlabeled data. In the semi-supervised setting, one of the questions is: can unlabeled data be used to improve accuracy of supervised learning algorithms? Intuitively, the answer is positive because unlabeled data must provide some information about the hidden distribution. Nevertheless, it seems that the question is challenging from a theoretical perspective as well as a practical one. A promising line of research is the co-training setting first defined in [3]. Supposing that the features are naturally divided into two disjoint sets, the cotraining algorithm builds two classifiers, and each one of these two is used to label unlabeled data for the other. In [3], theoretical results are proved, learning situations for which the assumption is true are described in [14], experimental results may be found in [3,15]. See also [8] for another approach of the co-training setting. Other approaches include using the EM algorithm [16], and using transductive inference [11]. A NIPS 99 workshop and a NIPS 00 competition were also organized on using unlabeled data for supervised learning. In this paper, we consider binary classification problems. One of the two classes is called the positive class. We are interested in the following questions: How can unlabeled data and positive data be used to improve the accuracy of supervised learning algorithms? How can learning algorithms from unlabeled data and positive data be designed from previously known supervised learning algorithms? First, let us justify that the problem is relevant for applications. We argue that, in many practical situations, elements of the target concept may be abundant and cheap to collect. For instance, consider one diagnosis of diseases: in order to obtain an i.i.d. sample of labeled examples, it is necessary to systematically detect the disease on a representative sample of patients and this task may be quite expensive (or impossible). On the other hand, it may be easy to collect the medical files of patients who have the disease. Also, unlabeled data are any pool of patients possibly having the disease. Second, let us note that many machine learning algorithms as decision tree learning algorithms and Bayesian learning algorithms only use examples to estimate statistics. In other words, many machine learning algorithms may be considered as statistical query (SQ) learning algorithms. Thus, we are interested in general schemes which transform supervised SQ-like learning algorithms into learning algorithms from both unlabeled data and positive data. In a preliminary paper [6], we have given evidence with both theoretical and empirical arguments that positive data and unlabeled data can boost accuracy of SQ-like learning algorithms. It was noted that learning with positive and unlabeled data is possible as soon as the weight of the target concept (i.e. the ratio of positive examples) is known by the learner. An estimate of the weight can be obtained either by an extra-oracle (say for a similar problem) or from a small set of labeled examples. In the present paper, we consider the more general problem where only positive data and unlabeled data are available. We present a general scheme which transforms any SQ-like supervised learning algorithm L into an algorithm PL using only positive data and unlabeled data. We prove that PL is a learning algorithm as soon as the learner is given access to a lower bound on the weight of the target concept. It remains open whether it is possible to design an algorithm from positive data and unlabeled data from any SQ learning algorithm in the general case. The theoretical framework is presented in Section 2. Our learning algorithm is defined and proved in Section 3, some consequences about the equivalence of models are also given. It is applied to tree induction and experimental results are given in Section Learning models 2.1. Learning models from labeled data For each n 1, X n denotes an instance space on n attributes. A concept f is a subset of some instance space X n or equivalently a {0, 1}-valued function defined on X n. For each n 1, let C n 2 X n be a set of concepts. Then C = n 1 C n denotes a concept class over X = n 1 X n. The size of a concept f is the size of a smallest representation
3 72 F. Denis et al. / Theoretical Computer Science 348 (2005) of f for a given representation scheme. An example of a concept f is a pair x,f(x), which is positive if f(x)= 1 and negative otherwise. Let D be a distribution over the instance space X n, for a subset A of X n, we denote by D(A) the probability of the event [x A]. For a subset A of X n such that D(A) = 0, we denote by D A the induced distribution over A. For instance, for a concept f over X n such that D(f ) = 0 and for any x X n, D f (x) = D(x)/D(f ) when f(x)= 1 and D f (x) = 0 otherwise. Let f and g be concepts over the instance space X n, we denote by f the complement of the set f in X n and by f Δg the set f Δg ={x X n f(x) = g(x)}. Let f be a target concept over X in some concept class C. Let D be the hidden distribution defined over X. In the PAC model [18], the learner is given access to an example oracle EX(f, D) which returns an example x,f(x) drawn randomly according to D at each call. A concept class C is PAC learnable if there exist a learning algorithm L and a polynomial p(.,.,.,.) with the following property: for any n and any f C n, for any distribution D on X n, and for any 0 < ε < 1 and 0 < δ < 1, if L is given access to EX(f, D) and to inputs ε and δ, then with probability at least 1 δ, L outputs a hypothesis concept h satisfying error(h) = D(f Δh) ε in time bounded by p(1/ε, 1/δ,n,size(f )). In this paper, we always suppose that the value of size(f ) is known by the learner. Recall that if size(f ) is not given then the halting criterion of the algorithm is probabilistic [9]. Also, for many concept classes the natural definition of size(f ) is already bounded by a polynomial in n. One criticism of the PAC model is that it is a noise-free model. Therefore, extensions in which the label provided with each random example may be corrupted with random noise were studied. The classification noise model (CN model for short) was first defined by Angluin and Laird [1]. A variant of the CN model, namely the constant-partition classification noise model (CPCN model for short) has been defined by Decatur [5]. In this model, the labeled example space is partitioned into a constant number of regions, each of which may have a different noise rate. An interesting example is the case where the rate of false-positive examples differs from the rate of false-negative examples. We only define this restricted variant of the CPCN model. The noisy oracle EX η +,η (f, D) is a procedure which, at each call, draws an element x of X n according to D and returns (i) (x, 1) with probability 1 η + and (x, 0) with probability η + if x f, (ii) (x, 0) with probability 1 η and (x, 1) with probability η if x f. Let C be a concept class over X. We say that C is CPCN learnable if there exist a learning algorithm L and a polynomial p(.,.,.,.,.) with the following property: for any n and any f C n, for any distribution D on X n, and for any 0 η +, η < 2 1 and 0 < ε, δ < 1, if L is given access to EX η +,η (f, D) and to inputs ε and δ, then with probability at least 1 δ, L outputs a hypothesis concept h C satisfying D(f Δh) ε in time bounded by p(1/ε, 1/δ, 1/γ, size(f ), n) where γ = min{1/2 η +, 1/2 η }. Many machine learning algorithms only use examples in order to estimate probabilities. This is the case for induction tree algorithms such as C4.5 [17] and CART [4]. This is also the case for highly practical Bayesian learning method as the naive Bayes classifier. Kearns defined the statistical query model (SQ model for short) in [12]. The SQ model is a specialization of the PAC model in which the learner forms its hypothesis solely on the basis of estimates of probabilities. A statistical query over X n is a mapping χ : X n {0, 1} {0, 1} associated with a tolerance parameter 0 < τ 1. In the SQ model the learner is given access to a statistical oracle STAT(f, D) which, at each query (χ, τ), returns an estimate of D({x χ( x,f(x) ) = 1}) within accuracy τ. Let C be a concept class over X. We say that C is SQ learnable if there exist a learning algorithm L and polynomials p(.,.,.), q(.,.,.) and r(.,.,.) with the following property: for any f C, for any distribution D over X, and for any 0 < ε < 1, if L is given access to STAT(f, D) and to input ε, then, for every query (χ, τ) made by L, the predicate χ can be evaluated in time q(1/ε,n,size(f )), and 1/τ is bounded by r(1/ε,n,size(f )), L halts in time bounded by p(1/ε,n,size(f )) and L outputs a hypothesis h C satisfying D(f Δh) ε. We slightly modify the statistical oracle STAT(f, D). Let f be the target concept and let us consider a statistical query χ made by a statistical query learning algorithm L. The statistical oracle STAT(f, D) returns an estimate D χ of D χ = D({x χ( x,f(x) ) = 1}) within some given accuracy. We may write: D χ = D({x χ( x,1 ) = 1 f(x)= 1}) + D({x χ( x,0 ) = 1 f(x)= 0}) = D({x χ( x,1 ) = 1} f)+ D({x χ( x,0 ) = 1} f) = D(B f)+ D(C f), where the sets B and C are defined by B ={x χ( x,1 ) = 1} and C ={x χ( x,0 ) = 1}.
4 F. Denis et al. / Theoretical Computer Science 348 (2005) Therefore, we consider a statistical oracle which, at each query (A, τ), returns estimates for probabilities D(f A) and D(f A) within accuracy τ, where f is the target concept, f its complement and A any subset for which membership is decidable in polynomial time of the instance space. It should be clear for the reader that this technical modification does not change the SQ learnable classes. It is clear that access to the example oracle EX(f, D) being given, it is easy to simulate the statistical oracle STAT(f, D) by drawing a sufficiently large set of labeled examples. Moreover, there is a general scheme which transforms any SQ learning algorithm into a PAC learning algorithm. It is also proved in [12] that the class of parity functions is learnable in the PAC model but cannot be learned from statistical queries. It has been shown by Kearns that any class learnable from statistical query is also learnable in the presence of classification noise [12]. Following the results by Kearns, it has been proved by Decatur [5] that any class learnable from statistical queries is also learnable in the presence of CPCN. The proof uses the hypothesis testing property: a hypothesis with small error can be selected from a set of hypotheses by selecting the one with the fewest errors on a set of CPCN corrupted examples. If we confuse, in the notations, the name of the model and the set of learnable classes, we can write the following inclusions: SQ CPCN CN PAC, SQ PAC. (1) (2) To our knowledge, the equivalences between the models CN and SQ or between the models CN and PAC remain open despite recent insights [2,10] Learning models from positive and unlabeled data The learning model from positive examples (POSEX for short) was first defined in [7]. The model differs from the PAC model in the following way: the learner gets information about the target function and the hidden distribution from two oracles, namely a positive example oracle POS(f, D) and an instance oracle INST(D) instead of an example oracle EX(f, D). At each request by the learner, the instance oracle INST(D) returns an element of the instance space X, i.e. an unlabeled example, according to the hidden distribution D. At each request by the learner, the positive example oracle POS(f, D) returns a positive example according to the hidden distribution D f. We have the following result: Proposition 1 (Denis [7]). Any class learnable in the CPCN model is learnable in the POSEX model. Proof. The proof is simple and as it may help to understand the proof of the main algorithm of the present paper, we sketch it below. Let C be a CPCN learnable concept class, let L be a learning algorithm for C in the CPCN model, let f be the target concept, let D be a distribution over the instance space and let us suppose that D(f ) = 0. We must show how L can be used to learn from the oracles POS(f, D) and INST(D). Run L. At each call of the noisy oracle: with probability 2 3, call POS(f, D) and keep the positive label, with probability 1 3, call INST(D) and label the example as negative. It can easily be shown that this is strictly equivalent calling the noisy oracle EX η +,η (f, D ) where: D(x) if f(x)= 0, D (x) = 3 D(x) + 2D f (x) if f(x)= 1, 3 η + = D(f ) 2 + D(f ), η = 0.
5 74 F. Denis et al. / Theoretical Computer Science 348 (2005) Note that η < 2 1. And as for any subset A of the instance space, we have D(A) 3D (A), it is sufficient to run the algorithm L with input accuracy ε/3 and input confidence δ to output with confidence greater than 1 δ a hypothesis whose error rate is less than ε. The learning model from positive queries (POSQ for short) was also defined in [7]. In the POSQ model, there are a positive statistical oracle PSTAT(f, D) which provides estimates for probabilities D f (A) for any subset A of the instance space within a given tolerance and an instance statistical oracle ISTAT(D) which provides estimates for probabilities D(A) for any subset A of the instance space within a given tolerance. The definition of a POSQ learnable class is similar to the definition of a SQ learnable class: the oracle STAT(f, D) is replaced by the two oracles PSTAT(f, D) and ISTAT(D). The POSQ model is weaker than the SQ model as there is no direct way to obtain an estimate of the weight D(f ) of the target concept. However, if we can get such an estimate, both models become equivalent. Indeed, statistical queries can be computed from instance queries and positive statistical queries as soon as the weight of the target concept is known because of the following equations: ˆD(f A) = Dˆ f (A) ˆD(f ), ˆD(f A) = ˆD(A) ˆD(f A). (3) So, any class learnable in the SQ model is learnable in the POSQ model as soon as the learner is given access to the weight of the target concept or can compute it from the positive statistical oracle and the instance statistical oracle. This is formalized in the following result: Proposition 2 (Denis [7]). Let C be a concept class such that the weight of any target concept can be estimated in polynomial time within any given tolerance. If C is SQ learnable then C is POSQ learnable. We can summarize all the results with the following inclusions: POSQ SQ CPCN POSEX PAC, (4) CPCN CN PAC, SQ POSEX. (5) (6) The inequality between SQ and POSEX holds because the class of parity functions is POSEX learnable but not SQ learnable. Equivalences between POSQ and SQ and between POSEX and PAC remain open. 3. Learning algorithms from positive and unlabeled examples We have already noticed that in practical data mining and text mining situations, statistical query-like algorithms, such as C4.5 or naive Bayes, are widely used. It is straightforward to see how a statistical query can be evaluated from labeled data. In a similar way, positive and instance statistical queries can easily be evaluated from positive and unlabeled data. So, in order to adapt classical learning algorithms to positive and unlabeled examples, we can show how SQ learning algorithms can be modified into POSQ learning algorithms. In [6], we have studied the case where the weight of the target concept is either given by an oracle or evaluated from a small set of labeled examples. In this case, Eqs. (3) and Proposition 2 show how the transformation of the SQ algorithm can be achieved. We now consider the more general problem where no information on the weight of the target concept is given to the learner A generic learning algorithm from positive statistical queries and instance statistical queries In this section, we provide a general scheme which transforms any SQ-like algorithm into a POSQ-like algorithm. Let us consider a concept class C learnable in the SQ model by a learning algorithm L, and let γ be a positive real number. Let us recall that we suppose that size(f ) is known by the learner. Also note that for most concept classes C learnable from statistical queries, the size of every target concept f C n is bounded by a polynomial in n. We design
6 F. Denis et al. / Theoretical Computer Science 348 (2005) Fig. 1. Learning algorithm from positive and unlabeled queries. a POSQ learning algorithm PL based on the algorithm L which learns any target concept f in C such that D(f ) γ. A consequence of this result is that whenever a lower bound on the weight of the target concept is known a priori, every SQ learnable class is POSQ learnable. First, we give some comments on the algorithm PL which is described in Fig. 1 and second, we prove its correctness in Section 3.2. The algorithm PL is based on a SQ learning algorithm L and is given access to a lower bound γ on the weight of the target concept. PL is composed of two stages: in the first stage, a set of hypotheses is constructed; in the second stage, a hypothesis is selected in the hypothesis set. In the first stage, the algorithm PL iterates over larger guesses for D(f ). At each guess, the SQ learning algorithm is called. But only positive and instance queries are available, thus when L makes a SQ, Eqs. (3) are used with the current estimate ˆp i of D(f ) together with the estimates returned by the oracles PSTAT(f, D) and ISTAT(D): at each statistical query (A, τ), return ˆD(f A) = Dˆ f (A) ˆp i and ˆD(f A) = ˆD(A) ˆD(f A) where Dˆ f (A) is the estimate given by the positive statistical oracle PSTAT(f, D) with set A within tolerance τ min /4 and where ˆD(A) is the estimate given by the instance statistical oracle with set A within tolerance τ min /4. Note that the simulation of STAT(f, D) may produce erroneous results when the estimate ˆp i of D(f ) is poor. In this case, the behavior of the algorithm L is not known. Thus, we bound the running time of L and output a default hypothesis. In the second stage, the algorithm PL selects the hypothesis h which minimizes the quantity ê(h). Minimizing ê(h) is equivalent to minimizing an estimate of the error rate according to the noisy oracle defined in the proof of Proposition 1: with probability 2 3 draw a positive example and label it as positive and with probability 1 3 draw an unlabeled example and label it as negative. Indeed, if an unlabeled example is drawn, the probability of error is equal to D(h). And if a positive example is drawn, the probability of error is equal to D f (h). That is, the error rate using the noisy oracle is (2D f (h) + D(h))/3. Minimizing ê(h) can also be seen as: choosing a hypothesis h approximately consistent with positive data when minimizing the first term of the sum 2 ˆD f (h i ) while avoiding over-generalization when minimizing the second term ˆD(h i ). Note that as the statistical oracles PSTAT(f, D) and ISTAT(D) can be simulated by using positive and unlabeled examples. Consequently, the previous scheme allows to transform any SQ-like learning algorithm into an algorithm using positive and unlabeled examples only.
7 76 F. Denis et al. / Theoretical Computer Science 348 (2005) Proof of the algorithm Lemma 3. There exists i {1,...,N} such that error(h i ) ε. Proof. There exists i such that D(f ) [ˆp i α, ˆp i + α] since, by definition of ˆp i, i [ˆp i α, ˆp i + α] =[0, 1]. For that value, ˆp i is an estimate of D(f ) within tolerance τ min /4 since α τ min /4. For all queries made by L, the oracles PSTAT and ISTAT are called with tolerance τ min /4 and Eqs. (3) are used. It is easy to prove that estimates for algorithm L are made within tolerance τ min. Consequently, by hypothesis on L, L outputs some h i such that error(h i ) ε. Lemma 4. Let f be the target concept, let g be some hypothesis and let β 2D(f ). We have ( ) β D(f ) error(g) e β (g) D(f ) error(g), D(f ) where error(g) = D(f Δg) is the (classical) error and e β (g) = βd f (g) + D(g). Proof. We have error(g) = D(f g) + D(g f) = D(g) D(f ) + 2D(f g) = e β (g) D(f ) + 2D(f g) βd f (g) ( = e β (g) D(f ) + D(f g) 2 β ) D(f ) e β (g) D(f ) = error(g) + D(f g) β 2D(f ). D(f ) As β 2D(f ) and D(f g) error(g),wehave [ error(g) e β (g) D(f ) error(g) 1 + β 2D(f ) ] D(f ) = error(g) β D(f ). D(f ) Note that the learner is not given access to an upper bound on D(f ). The previous lemma holds if β 2D(f ), thus we set β to 2 and we simply denote e 2 (h) by e(h). That is we have: e(g) = 2D f (g) + D(g) and the reader should note that in the hypothesis testing stage of the algorithm PL we use an estimate ê(h) of e(h) where h is a hypothesis in the hypothesis set. Lemma 5. Let h and h be two hypotheses such that error(h) 1 2 γ/(2 γ) ε and error(h ) > ε, then e(h ) e(h) > ε/2. Proof. Using the previous lemma with β = 2,wehave ( ) 2 D(f ) e(h ) e(h) error(h ) error(h). D(f ) As the function r(x) = (2 x)/x is decreasing and D(f ) γ, wehave ( ) 2 γ e(h ) e(h) error(h ) error(h). γ By hypothesis on h and h, error(h) < 1 ( ) γ error(h ), 2 2 γ
8 F. Denis et al. / Theoretical Computer Science 348 (2005) so e(h ) e(h) > error(h ) 2 > ε/2. Proposition 6. The output hypothesis satisfies error(h) ε and the running time is polynomial in 1/ε, n, l and 1/γ. Proof. All estimates ê(h i ) of e(h i ) are done within tolerance ε/4 and Lemmas 3 and 5 ensure that the output hypothesis satisfies error(h) ε. The number of hypotheses is N which is linear in 1/τ min. We have supposed for sake of clarity in the definition of the algorithm that τ min was fixed and known by the learner. Actually, τ min is polynomial in the input accuracy of L, therefore τ min is polynomial in ε that is also polynomial in ε and γ. It is easy to verify that all queries are made within a tolerance polynomial in ε and γ Equivalence of the SQ and POSQ models Whether or not any SQ algorithm can be transformed into a POSQ algorithm remains an open question. It has been proved in [7] that this transformation is possible when the weight of the target concept can be estimated from the oracles PSTAT(f, D) and ISTAT(D) in polynomial time. In this paper, we improve this result by showing that any SQ algorithm can be transformed into a POSQ algorithm when a lower bound on the weight of the target concept is given to the learner. However, the running time of the algorithm is polynomial in the inverse of this lower bound. Let us consider a concept class C which is SQ learnable. We say that C satisfies the property Lowerbound if there exists an algorithm W which, for any f in C, for any distribution D on X, with input ε and given access to PSTAT(f, D) and ISTAT(D) yes if D(f ) < ε 2, outputs no if D(f ) > ε,? if ε D(f ) ε 2 in time polynomial in 1/ε. Then we have the following result: Proposition 7. Any SQ learnable class which satisfies Lowerbound is POSQ learnable. Proof. Consider the following algorithm: input: ε if W outputs yes output function 0 else run the POSQ learning algorithm with parameter γ = ε/2 and input ε It is easy to prove that this algorithm is a learning algorithm from positive and instance statistical queries using Proposition 6 and the definition of the property Lowerbound. Note that proving the property Lowerbound for every SQ learnable concept class would imply the equality between SQ and POSQ. 4. Decision tree learning algorithms from positive and unlabeled examples Induction tree algorithms are widely used for data mining purposes. These algorithms are SQ like since they only use examples in order to estimate probabilities. In the first part of this section, we recall the notions of entropy and information gain on which C4.5 is based. In the second part, we introduce C4.5POSUNL, a learning algorithm based
9 78 F. Denis et al. / Theoretical Computer Science 348 (2005) on C4.5 first defined in [6], where the statistical queries required by C4.5 are estimated with the help of Eqs. (3), an estimate of the weight of the target concept being given as input. In the third part of this section, we present POSC4.5 an induction tree learning algorithm from positive data and unlabeled data only. In the last part of this section, we give experimental results for POSC4.5 both on artificial problems and on two benchmarks chosen from the UCI Machine Learning Database Top down decision tree algorithms Most algorithms for tree induction use a top-down, greedy search through the space of decision trees. The splitting criterion used by C4.5 [17] is based on a statistical property, called information gain, itself based on a measure from information theory, called entropy. We only consider binary problems. Given a sample S of some target concept, the entropy of S is Entropy(S) = p 0 log 2 p 0 p 1 log 2 p 1, (7) where p i is the proportion of examples in S belonging to the class i. The information gain is the expected reduction in entropy by partitioning the sample according to an attribute test t. It is defined as Gain(S, t) = Entropy(S) v Values(t) N v N Entropy(S v), (8) where Values(t) is the set of every possible value for the attribute test t, N v is the cardinality of the set S v of examples in S for which t has value v and N is the cardinality of S. As the information gain criterion has a strong bias in favor of tests with many outcomes, the criterion used in C4.5 is the Gain ratio defined by where GainRatio(S, t) = SplitInfo(S, t) = Gain(S, t) SplitInfo(S, t), v Values(t) N v N log N v N. Let D be the hidden distribution defined over the set of instances. Let n be the current node, let D n be the filtered distribution, that is the hidden distribution D restricted to instances reaching the node n. Let S be the set of training examples associated with the current node n and let p 1 be the proportion of positive examples in S: p 1 is an estimate of D n (f ) and p 0 is an estimate of D n (f) C4.5POSUNL: a top-down induction tree algorithm from positive and unlabeled examples with the help of an estimate of the weight of the target concept Roughly speaking, C4.5POSUNL is a version of C4.5 in which the statistical queries are estimated from positive examples and unlabeled examples by using Eqs. (3), an estimate of the weight of the target concept being given. The differences between C4.5POSUNL and C4.5 are the following: C4.5POSUNL takes as input: a set POS of positive examples, together with a set UNL of unlabeled examples, together with an estimate ˆD(f ) of D(f ) which is the weight of the target concept. For the current node, entropy and gain are calculated using Eqs. (7) and (8) where, based on Eqs. (3), the ratios p 0 and p 1 are given by the equations: { POS n p 1 = inf ˆD(f ) UNL } POS UNL n, 1, p 0 = 1 p 1, (9)
10 F. Denis et al. / Theoretical Computer Science 348 (2005) Fig. 2. POSC4.5: induction tree algorithm from positive and unlabeled examples. where POS n is the set of positive examples associated with the node n and UNL n is the set of unlabeled examples associated with the node n. When the gain ratio is used instead of the information gain, split information SplitInfo is calculated from unlabeled examples. The majority class is chosen as 0 or 1 according to the values of p 0 and p 1 calculated with Eqs. (9). Halting criteria during the top-down tree generation are evaluated from unlabeled data. When pruning trees, classification errors are estimated with the help of ratios p 0 and p 1 from (9) POSC4.5: a top-down induction tree algorithm from positive and unlabeled examples only The learning algorithm POSC4.5 is given in Fig. 2. It is based on the theoretical result proved in Section 3. We intend to use the algorithm scheme PL to transform C4.5. But as C4.5POSUNL can already be viewed as a variant of C4.5 which uses positive and unlabeled examples together with an estimate of the target weight, we have directly incorporated C4.5POSUNL in the PL algorithm. Another difference between PL and POSC4.5 is that the lower bound γ is not given as input to POSC4.5. Instead, it is implicitly supposed that the weight of the target concept is not too small. The algorithm takes as input a set POS of examples of the target class together with a set UNL of unlabeled examples. The algorithm splits the set POS (respectively UNL) into two sets POS L and POS T (respectively UNL L and UNL T ) using the usual values 2 3 and 1 3. The sets POS L and UNL L are used for the construction of the hypothesis set. More precisely, these sets are used to simulate the positive statistical oracle and the instance statistical oracle. In this stage, we run nine times C4.5POSUNL with input POS L, UNL L and an estimate ˆD(f ) of D(f ) taking the successive values 0.1,...,0.9. In the second stage of POSC4.5, i.e. the hypothesis testing algorithm, the sets POS T and UNL T are used to simulate the positive statistical oracle and the instance statistical oracle. In our implementation, we select in POSC4.5 the best estimate ˆD(f ) of D(f ) according to the minimal estimate ê(h) of e(h) instead of selecting the best hypothesis like in PL. The output of POSC4.5 is the output of C4.5POSUNL with input POS, UNL together with the best estimate ˆD(f ) of D(f ) Experiments with decision lists A decision list over x 1,...,x n is an ordered sequence L = (m 1,b 1 ),...,(m p,b p ) of terms, in which each m j is a monomial over x 1,...,x n, and each b j {0, 1}. The last monomial is always m p = 1. For any input a {0, 1} n, the
11 80 F. Denis et al. / Theoretical Computer Science 348 (2005) value L(a) is defined as b j, where j is the smallest index satisfying m j (a) = 1. We only consider 1-decision list where each monomial is a variable x i or its negation x i.wesetp to 11 and n to 20. The choice of a target decision list f, the choice of the weight D(f ) and the choice of the distribution D are done as follows: a target decision list f is chosen randomly; for any a {0, 1} n, a weight w a is chosen randomly in [0, 1); a normalization procedure is applied to the two sets of weights {w a f(a)= 1} and {w a f(a)= 0}. Thus, we get two distributions D 1 on f and D 2 on f ; a weight D(f ) for the target concept is chosen using a procedure that depends on the experiment; D is defined by: a {0, 1} n, D(a) = D(f ) D 1 (a) + (1 D(f )) D 2 (a). In the experiments, we compare C4.5POSUNL and POSC4.5. The algorithm C4.5POSUNL takes as input a set POS of positive examples, a set UNL of unlabeled examples and an estimate ˆD(f ) of D(f ). The experimental results for C4.5POSUNL depend on the accuracy of the estimate ˆD(f ) of D(f ). Thus, we consider two cases: the exact value of D(f ) is given as input of the learning algorithm. In the following and in the figures, we denote by C4.5POSUNL(D(f )) this variant of C4.5POSUNL; the estimate ˆD(f ) is set to the ratio of positive examples in a (small) set LAB of labeled examples given as input. We denote by C4.5POSUNL(LAB) this variant of C4.5POSUNL. The set LAB is only used for the calculation of ˆD(f ). In the experimental results and in the plots, the error rates and target weights are expressed in percent. The size of a set is its cardinality. Experiment 1. In order to obtain experimental results on the relative value of examples, we let the number of positive examples vary and we compare POSC4.5, C4.5POSUNL(LAB) and C4.5POSUNL(D(f )). We set D(f ) to 0.5, the size of POS is equal to the size of UNL and ranges from 50 to 1000 by step 50, the size of LAB is fixed to 25. For a given size of POS, we iterate 100 times the experiment: a target f is drawn, a distribution D is chosen, sets LAB, POS and UNL are drawn randomly, we run the three algorithms and calculate the error rate of the output hypothesis on a large test set of examples. We average the error rates over the 100 experiments. The results are given in Fig. A.1. The learning algorithm POSC4.5 performs as well as C4.5POSUNL(D(f )) where the exact value of D(f ) is given to the learner. Thus for this artificial problem, the results of POSC4.5 which is based on a hypothesis testing algorithm are convincing. The reader should also note that the two algorithms POSC4.5 and C4.5POSUNL(D(f )) outperform C4.5POSUNL(LAB) which uses a rough estimate of D(f ) (solely based on 25 labeled examples). In this first set of experiments, the weight of the target concept is set equal to 0.5. An equal ratio between positive and negative examples is the most favorable to POSC4.5. Therefore, in a second set of experiments, we consider different values for D(f ). Experiment 2. The weight D(f ) of the target concept ranges from 0 to 1 by step The size of POS is equal to the size of UNL and is set to The size of LAB is fixed to 25. For a given value of D(f ), we average the error rates over 100 experiments. The results are given in Fig. A.2. The results are similar: POSC4.5 performs as well as C4.5POSUNL(D(f )); POSC4.5 and C4.5POSUNL(D(f )) outperform C4.5POSUNL(LAB). For this set of experiments, POSC4.5 is robust to the value of the weight of the target concept. Note that the plots for D(f ) = 0.05 and 0.95 are not significant because POSC4.5 makes its guesses from 0.1 to Experiments with UCI problems We consider two data sets from the UCI Machine Learning Database [13]: kr-vs-kp and adult. The majority class is chosen as positive. In the experiments, we compare C4.5POSUNL and POSC4.5 with C4.5.
12 F. Denis et al. / Theoretical Computer Science 348 (2005) Experiment 3. In order to obtain experimental results for the relative value of examples, we compare C4.5 and C4.5POSUNL(LAB). For kr-vs-kp, the size of POS and the size of UNL are set equal to 600; the error rate is estimated on a hold-out test set of 1000 labeled examples. For adult, the size of POS and the size of UNL are set equal to ; the error rate is estimated on a hold-out test set of labeled examples. We let the number of labeled examples vary, and compare the error rate of C4.5 and C4.5POSUNL(LAB). For a given size of LAB, we iterate 100 times the following: all sets are selected randomly, we compute the error rate for C4.5 with input LAB and the error rate for C4.5POSUNL with input POS, UNL and an estimate of the weight of the target concept which is the ratio of positive examples in the set LAB. The reader should note that C4.5POSUNL(LAB) only uses labeled examples to compute a rough estimate of the weight of the target concept. Then, we average the error rates over the 1000 experiments.the results can be seen in Fig. A.3. For the two datasets, C4.5POSUNL(LAB) outperforms C4.5 when the number of labeled examples is small until a limit which is about 100 for kr-vs-kp recall that there are 600 positive examples and 600 unlabeled examples and about 500 for adult recall that there are positive examples and unlabeled examples. One could also note that, when the estimate of the weight of the target concept is precise enough, the error rate for is C4.5POSUNL constant. Also note that C4.5POSUNL trees are consistently larger than C4.5 ones because of the pruning procedure in C4.5POSUNL which is not optimized. Experiment 4. In this second set of experiments, we fix the size of LAB and we let the number of positive and unlabeled examples vary, and compare the error rate of C4.5POSUNL(LAB), C4.5POSUNL(D(f )) and OSC4.5. The results can be seen in Fig. A.4. For kr-vs-kp, the plots are similar, the least good results are obtained by POSC4.5. This seems natural because it uses less information. Surprisingly, POSC4.5 obtains the best results for the data set adult. 5. Conclusion We have given evidence in the present paper that the weight of the target concept is a key parameter for learning from positive data and unlabeled data. In the co-training framework [3], it seems that the weight of the target concept is implicitly known by the learner. The ratio of positive examples in the labeled training sample is set to the weight of the target concept and this ratio is preserved throughout the learning process. It is unclear whether the results depend on this implicit hypothesis. In this paper, we have shown that knowledge of a lower bound of the target weight is sufficient when learning from positive and unlabeled data. Nevertheless the equivalence between SQ and POSQ remains open. In the semi-supervised setting as in our setting of learning from positive and unlabeled examples, it should be interesting to investigate the relative value of examples (labeled examples vs positive examples vs unlabeled examples). Also it should be clear that more experimental results are needed. We are currently applying the results of the present paper to real-world text mining problems using the naive Bayes algorithm. Lastly, it is now a challenging problem to find algorithms from positive data and unlabeled data when the weight of the target concept is quite small because many applications fall in this case. For imbalanced classes the classifier s performance cannot be expressed in terms of the accuracy: if only 1% examples are positive the default hypothesis achieves an accuracy of 99%. Thus, another criterion of success for the learning algorithm should be used, say for example the geometric mean of accuracies observed separately on positive examples, and on negative examples. We also plan to investigate this problem, but it is known to be difficult even when learning from labeled data. Appendix A. Experimental results The experimental results are summarized in Figs A.1 A.4.
13 82 F. Denis et al. / Theoretical Computer Science 348 (2005) C4.5POSUNL(LAB) C4.5POSUNL(D(f)) POSC4.5 8 error rate size(pos)=size(unl) Fig. A.1. We consider decision lists where D(f ) = 0.5. We compare C4.5POSUNL(LAB) where the estimate of D(f ) is done on a small random set of 25 labeled examples, C4.5POSUNL(D(f )) where the exact value of D(f ) is given as input and POSC4.5. The three algorithms take as input a set POS and a set UNL where size(p OS) = size(unl) ranges from 50 to 1000 by step C4.5POSUNL(LAB) C4.5POSUNL(D(f)) POSC4.5 8 error rate Fig. A.2. We consider decision lists where D(f ) ranges from 0 to 1 by step We compare C4.5POSUNL(LAB) where the estimate of D(f ) is done on a small random set of 25 labeled examples, C4.5POSUNL(D(f )) where the exact value of D(f ) is given as input and POSC4.5. The three algorithms take as input a set POS and a set UNL where size(pos) = size(unl) = D(f) error rate LAB only LAB + fixed number of POS and UNL examples error rate LAB only LAB + fixed number of POS and UNL examples LAB size LAB size Fig. A.3. Error rate of C4.5 and C4.5POSUNL(LAB) averaged over 100 trials on the kr-vs-kp data set (left plot) and on the adult data sets (right plot).
14 F. Denis et al. / Theoretical Computer Science 348 (2005) error rate size(pos)=size(unl) C4.5POSUNL(LAB) C4.5POSUNL(D(f)) POSC4.5 error rate C4.5POSUNL(LAB) C4.5POSUNL(D(f)) POSC4.5 majority rule C4.5 with labeled examples size(pos)=size(unl) Fig. A.4. The kr-vs-kp data set corresponds to the left plot where size(lab) = 25, size(pos) = size(unl) ranges from 50 to 700 by step 50 and D(f ) 0.5; the adult data set corresponds to the right plot where size(lab) = 25, size(pos) = size(unl) ranges from 500 to by step 500 and D(f ) References [1] D. Angluin, P. Laird, Learning from noisy examples, Machine Learning 2 (4) (1988) [2] A. Blum, A. Kalai, H. Wasserman, Noise-tolerant learning, the parity problem, and the statistical query model, in: Proc. 32nd Annu. ACM Symp. on Theory of Computing, 2000, pp [3] A. Blum, T. Mitchell, Combining labeled and unlabeled data with co-training, in: Proc. 11th Annu. Conf. on Computational Learning Theory, 1998, pp [4] L. Breiman, J.H. Friedman, R.A. Olshen, C.J. Stone, Classification and regression trees, Technical Report, Wadsworth International, Monterey, CA, [5] S.E. Decatur, Pac learning with constant-partition classification noise and applications to decision tree induction, in: Proc. 14th Internat. Conf. on Machine Learning, 1997, pp [6] F. DeComité, F. Denis, R. Gilleron, F. Letouzey, Positive and unlabeled examples help learning, in: Proc. 10th Internat. Conf. on Algorithmic Learning Theory, 1999, pp [7] F. Denis, PAC learning from positive statistical queries, in: Proc. 9th Internat. Conf. on Algorithmic Learning Theory, 1998, pp [8] S. Goldman, Y. Zhou, Enhancing supervised learning with unlabeled data, in: Proc. 17th Internat. Conf. on Machine Learning, 2000, pp [9] D. Haussler, M. Kearns, N. Littlestone, M.K. Warmuth, Equivalence of models for polynomial learnability, Inform. Comput. 95 (2) (1991) [10] J. Jackson, On the efficiency of noise-tolerant PAC algorithms derived from statistical queries, in: Proc. 13th Annu. Conf. on Computational Learning Theory, 2000, pp [11] T. Joachims, Transductive inference for text classification using support vector machines, in: Proc. 16th Internat. Conf. on Machine Learning, 1999, pp [12] M. Kearns, Efficient noise-tolerant learning from statistical queries, in: Proc. 25th ACM Symp. on the Theory of Computing, 1993, pp [13] C.J. Merz, P.M. Murphy, UCI repository of machine learning databases, [14] T. Mitchell, Machine learning and data mining, Commun. ACM 42 (11) (1999) [15] K. Nigam, R. Ghani, Analyzing the applicability and effectiveness of co-training, in: Proc. 9th Internat. Conf. on Information and Knowledge Management, 2000, pp [16] K. Nigam, A.K. McCallum, S. Thrun, T.M. Mitchell, Text classification from labeled and unlabeled documents using EM, Machine Learning 39 (2/3) (2000) [17] J.R. Quinlan, C4.5: Programs for Machine Learning, Morgan Kaufmann, Los Altos, CA, [18] L.G. Valiant, A theory of the learnable, Commun. ACM 27 (11) (1984)
On the Sample Complexity of Noise-Tolerant Learning
 On the Sample Complexity of Noise-Tolerant Learning Javed A. Aslam Department of Computer Science Dartmouth College Hanover, NH 03755 Scott E. Decatur Laboratory for Computer Science Massachusetts Institute
On the Sample Complexity of Noise-Tolerant Learning Javed A. Aslam Department of Computer Science Dartmouth College Hanover, NH 03755 Scott E. Decatur Laboratory for Computer Science Massachusetts Institute
1 Differential Privacy and Statistical Query Learning
 10-806 Foundations of Machine Learning and Data Science Lecturer: Maria-Florina Balcan Lecture 5: December 07, 015 1 Differential Privacy and Statistical Query Learning 1.1 Differential Privacy Suppose
10-806 Foundations of Machine Learning and Data Science Lecturer: Maria-Florina Balcan Lecture 5: December 07, 015 1 Differential Privacy and Statistical Query Learning 1.1 Differential Privacy Suppose
Discriminative Learning can Succeed where Generative Learning Fails
 Discriminative Learning can Succeed where Generative Learning Fails Philip M. Long, a Rocco A. Servedio, b,,1 Hans Ulrich Simon c a Google, Mountain View, CA, USA b Columbia University, New York, New York,
Discriminative Learning can Succeed where Generative Learning Fails Philip M. Long, a Rocco A. Servedio, b,,1 Hans Ulrich Simon c a Google, Mountain View, CA, USA b Columbia University, New York, New York,
A Tutorial on Computational Learning Theory Presented at Genetic Programming 1997 Stanford University, July 1997
 A Tutorial on Computational Learning Theory Presented at Genetic Programming 1997 Stanford University, July 1997 Vasant Honavar Artificial Intelligence Research Laboratory Department of Computer Science
A Tutorial on Computational Learning Theory Presented at Genetic Programming 1997 Stanford University, July 1997 Vasant Honavar Artificial Intelligence Research Laboratory Department of Computer Science
Efficient Noise-Tolerant Learning from Statistical Queries
 Efficient Noise-Tolerant Learning from Statistical Queries MICHAEL KEARNS AT&T Laboratories Research, Florham Park, New Jersey Abstract. In this paper, we study the problem of learning in the presence
Efficient Noise-Tolerant Learning from Statistical Queries MICHAEL KEARNS AT&T Laboratories Research, Florham Park, New Jersey Abstract. In this paper, we study the problem of learning in the presence
MODULE -4 BAYEIAN LEARNING
 MODULE -4 BAYEIAN LEARNING CONTENT Introduction Bayes theorem Bayes theorem and concept learning Maximum likelihood and Least Squared Error Hypothesis Maximum likelihood Hypotheses for predicting probabilities
MODULE -4 BAYEIAN LEARNING CONTENT Introduction Bayes theorem Bayes theorem and concept learning Maximum likelihood and Least Squared Error Hypothesis Maximum likelihood Hypotheses for predicting probabilities
Learning Sparse Perceptrons
 Learning Sparse Perceptrons Jeffrey C. Jackson Mathematics & Computer Science Dept. Duquesne University 600 Forbes Ave Pittsburgh, PA 15282 jackson@mathcs.duq.edu Mark W. Craven Computer Sciences Dept.
Learning Sparse Perceptrons Jeffrey C. Jackson Mathematics & Computer Science Dept. Duquesne University 600 Forbes Ave Pittsburgh, PA 15282 jackson@mathcs.duq.edu Mark W. Craven Computer Sciences Dept.
Can PAC Learning Algorithms Tolerate. Random Attribute Noise? Sally A. Goldman. Department of Computer Science. Washington University
 Can PAC Learning Algorithms Tolerate Random Attribute Noise? Sally A. Goldman Department of Computer Science Washington University St. Louis, Missouri 63130 Robert H. Sloan y Dept. of Electrical Engineering
Can PAC Learning Algorithms Tolerate Random Attribute Noise? Sally A. Goldman Department of Computer Science Washington University St. Louis, Missouri 63130 Robert H. Sloan y Dept. of Electrical Engineering
CSCE 478/878 Lecture 6: Bayesian Learning
 Bayesian Methods Not all hypotheses are created equal (even if they are all consistent with the training data) Outline CSCE 478/878 Lecture 6: Bayesian Learning Stephen D. Scott (Adapted from Tom Mitchell
Bayesian Methods Not all hypotheses are created equal (even if they are all consistent with the training data) Outline CSCE 478/878 Lecture 6: Bayesian Learning Stephen D. Scott (Adapted from Tom Mitchell
Lecture 29: Computational Learning Theory
 CS 710: Complexity Theory 5/4/2010 Lecture 29: Computational Learning Theory Instructor: Dieter van Melkebeek Scribe: Dmitri Svetlov and Jake Rosin Today we will provide a brief introduction to computational
CS 710: Complexity Theory 5/4/2010 Lecture 29: Computational Learning Theory Instructor: Dieter van Melkebeek Scribe: Dmitri Svetlov and Jake Rosin Today we will provide a brief introduction to computational
Polynomial time Prediction Strategy with almost Optimal Mistake Probability
 Polynomial time Prediction Strategy with almost Optimal Mistake Probability Nader H. Bshouty Department of Computer Science Technion, 32000 Haifa, Israel bshouty@cs.technion.ac.il Abstract We give the
Polynomial time Prediction Strategy with almost Optimal Mistake Probability Nader H. Bshouty Department of Computer Science Technion, 32000 Haifa, Israel bshouty@cs.technion.ac.il Abstract We give the
Notes on Machine Learning for and
 Notes on Machine Learning for 16.410 and 16.413 (Notes adapted from Tom Mitchell and Andrew Moore.) Learning = improving with experience Improve over task T (e.g, Classification, control tasks) with respect
Notes on Machine Learning for 16.410 and 16.413 (Notes adapted from Tom Mitchell and Andrew Moore.) Learning = improving with experience Improve over task T (e.g, Classification, control tasks) with respect
Supervised Learning! Algorithm Implementations! Inferring Rudimentary Rules and Decision Trees!
 Supervised Learning! Algorithm Implementations! Inferring Rudimentary Rules and Decision Trees! Summary! Input Knowledge representation! Preparing data for learning! Input: Concept, Instances, Attributes"
Supervised Learning! Algorithm Implementations! Inferring Rudimentary Rules and Decision Trees! Summary! Input Knowledge representation! Preparing data for learning! Input: Concept, Instances, Attributes"
Empirical Risk Minimization, Model Selection, and Model Assessment
 Empirical Risk Minimization, Model Selection, and Model Assessment CS6780 Advanced Machine Learning Spring 2015 Thorsten Joachims Cornell University Reading: Murphy 5.7-5.7.2.4, 6.5-6.5.3.1 Dietterich,
Empirical Risk Minimization, Model Selection, and Model Assessment CS6780 Advanced Machine Learning Spring 2015 Thorsten Joachims Cornell University Reading: Murphy 5.7-5.7.2.4, 6.5-6.5.3.1 Dietterich,
PAC Generalization Bounds for Co-training
 PAC Generalization Bounds for Co-training Sanjoy Dasgupta AT&T Labs Research dasgupta@research.att.com Michael L. Littman AT&T Labs Research mlittman@research.att.com David McAllester AT&T Labs Research
PAC Generalization Bounds for Co-training Sanjoy Dasgupta AT&T Labs Research dasgupta@research.att.com Michael L. Littman AT&T Labs Research mlittman@research.att.com David McAllester AT&T Labs Research
On Learning µ-perceptron Networks with Binary Weights
 On Learning µ-perceptron Networks with Binary Weights Mostefa Golea Ottawa-Carleton Institute for Physics University of Ottawa Ottawa, Ont., Canada K1N 6N5 050287@acadvm1.uottawa.ca Mario Marchand Ottawa-Carleton
On Learning µ-perceptron Networks with Binary Weights Mostefa Golea Ottawa-Carleton Institute for Physics University of Ottawa Ottawa, Ont., Canada K1N 6N5 050287@acadvm1.uottawa.ca Mario Marchand Ottawa-Carleton
Ensembles of Classifiers.
 Ensembles of Classifiers www.biostat.wisc.edu/~dpage/cs760/ 1 Goals for the lecture you should understand the following concepts ensemble bootstrap sample bagging boosting random forests error correcting
Ensembles of Classifiers www.biostat.wisc.edu/~dpage/cs760/ 1 Goals for the lecture you should understand the following concepts ensemble bootstrap sample bagging boosting random forests error correcting
Computational Learning Theory. CS 486/686: Introduction to Artificial Intelligence Fall 2013
 Computational Learning Theory CS 486/686: Introduction to Artificial Intelligence Fall 2013 1 Overview Introduction to Computational Learning Theory PAC Learning Theory Thanks to T Mitchell 2 Introduction
Computational Learning Theory CS 486/686: Introduction to Artificial Intelligence Fall 2013 1 Overview Introduction to Computational Learning Theory PAC Learning Theory Thanks to T Mitchell 2 Introduction
FORMULATION OF THE LEARNING PROBLEM
 FORMULTION OF THE LERNING PROBLEM MIM RGINSKY Now that we have seen an informal statement of the learning problem, as well as acquired some technical tools in the form of concentration inequalities, we
FORMULTION OF THE LERNING PROBLEM MIM RGINSKY Now that we have seen an informal statement of the learning problem, as well as acquired some technical tools in the form of concentration inequalities, we
Classification Using Decision Trees
 Classification Using Decision Trees 1. Introduction Data mining term is mainly used for the specific set of six activities namely Classification, Estimation, Prediction, Affinity grouping or Association
Classification Using Decision Trees 1. Introduction Data mining term is mainly used for the specific set of six activities namely Classification, Estimation, Prediction, Affinity grouping or Association
Self bounding learning algorithms
 Self bounding learning algorithms Yoav Freund AT&T Labs 180 Park Avenue Florham Park, NJ 07932-0971 USA yoav@research.att.com January 17, 2000 Abstract Most of the work which attempts to give bounds on
Self bounding learning algorithms Yoav Freund AT&T Labs 180 Park Avenue Florham Park, NJ 07932-0971 USA yoav@research.att.com January 17, 2000 Abstract Most of the work which attempts to give bounds on
TTIC An Introduction to the Theory of Machine Learning. Learning from noisy data, intro to SQ model
 TTIC 325 An Introduction to the Theory of Machine Learning Learning from noisy data, intro to SQ model Avrim Blum 4/25/8 Learning when there is no perfect predictor Hoeffding/Chernoff bounds: minimizing
TTIC 325 An Introduction to the Theory of Machine Learning Learning from noisy data, intro to SQ model Avrim Blum 4/25/8 Learning when there is no perfect predictor Hoeffding/Chernoff bounds: minimizing
ML techniques. symbolic techniques different types of representation value attribute representation representation of the first order
 MACHINE LEARNING Definition 1: Learning is constructing or modifying representations of what is being experienced [Michalski 1986], p. 10 Definition 2: Learning denotes changes in the system That are adaptive
MACHINE LEARNING Definition 1: Learning is constructing or modifying representations of what is being experienced [Michalski 1986], p. 10 Definition 2: Learning denotes changes in the system That are adaptive
arxiv: v1 [cs.lg] 15 Aug 2017
![arxiv: v1 [cs.lg] 15 Aug 2017 arxiv: v1 [cs.lg] 15 Aug 2017](/thumbs/76/73518315.jpg) Theoretical Foundation of Co-Training and Disagreement-Based Algorithms arxiv:1708.04403v1 [cs.lg] 15 Aug 017 Abstract Wei Wang, Zhi-Hua Zhou National Key Laboratory for Novel Software Technology, Nanjing
Theoretical Foundation of Co-Training and Disagreement-Based Algorithms arxiv:1708.04403v1 [cs.lg] 15 Aug 017 Abstract Wei Wang, Zhi-Hua Zhou National Key Laboratory for Novel Software Technology, Nanjing
Induction of Decision Trees
 Induction of Decision Trees Peter Waiganjo Wagacha This notes are for ICS320 Foundations of Learning and Adaptive Systems Institute of Computer Science University of Nairobi PO Box 30197, 00200 Nairobi.
Induction of Decision Trees Peter Waiganjo Wagacha This notes are for ICS320 Foundations of Learning and Adaptive Systems Institute of Computer Science University of Nairobi PO Box 30197, 00200 Nairobi.
Boosting: Foundations and Algorithms. Rob Schapire
 Boosting: Foundations and Algorithms Rob Schapire Example: Spam Filtering problem: filter out spam (junk email) gather large collection of examples of spam and non-spam: From: yoav@ucsd.edu Rob, can you
Boosting: Foundations and Algorithms Rob Schapire Example: Spam Filtering problem: filter out spam (junk email) gather large collection of examples of spam and non-spam: From: yoav@ucsd.edu Rob, can you
Error Limiting Reductions Between Classification Tasks
 Error Limiting Reductions Between Classification Tasks Keywords: supervised learning, reductions, classification Abstract We introduce a reduction-based model for analyzing supervised learning tasks. We
Error Limiting Reductions Between Classification Tasks Keywords: supervised learning, reductions, classification Abstract We introduce a reduction-based model for analyzing supervised learning tasks. We
Decision Tree Learning
 Decision Tree Learning Berlin Chen Department of Computer Science & Information Engineering National Taiwan Normal University References: 1. Machine Learning, Chapter 3 2. Data Mining: Concepts, Models,
Decision Tree Learning Berlin Chen Department of Computer Science & Information Engineering National Taiwan Normal University References: 1. Machine Learning, Chapter 3 2. Data Mining: Concepts, Models,
Decision Tree Learning
 Decision Tree Learning Goals for the lecture you should understand the following concepts the decision tree representation the standard top-down approach to learning a tree Occam s razor entropy and information
Decision Tree Learning Goals for the lecture you should understand the following concepts the decision tree representation the standard top-down approach to learning a tree Occam s razor entropy and information
Machine Learning. Computational Learning Theory. Eric Xing , Fall Lecture 9, October 5, 2016
 Machine Learning 10-701, Fall 2016 Computational Learning Theory Eric Xing Lecture 9, October 5, 2016 Reading: Chap. 7 T.M book Eric Xing @ CMU, 2006-2016 1 Generalizability of Learning In machine learning
Machine Learning 10-701, Fall 2016 Computational Learning Theory Eric Xing Lecture 9, October 5, 2016 Reading: Chap. 7 T.M book Eric Xing @ CMU, 2006-2016 1 Generalizability of Learning In machine learning
Learning with multiple models. Boosting.
 CS 2750 Machine Learning Lecture 21 Learning with multiple models. Boosting. Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Learning with multiple models: Approach 2 Approach 2: use multiple models
CS 2750 Machine Learning Lecture 21 Learning with multiple models. Boosting. Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Learning with multiple models: Approach 2 Approach 2: use multiple models
Learning From Inconsistent and Noisy Data: The AQ18 Approach *
 Eleventh International Symposium on Methodologies for Intelligent Systems, Warsaw, pp. 411-419, 1999 Learning From Inconsistent and Noisy Data: The AQ18 Approach * Kenneth A. Kaufman and Ryszard S. Michalski*
Eleventh International Symposium on Methodologies for Intelligent Systems, Warsaw, pp. 411-419, 1999 Learning From Inconsistent and Noisy Data: The AQ18 Approach * Kenneth A. Kaufman and Ryszard S. Michalski*
The sample complexity of agnostic learning with deterministic labels
 The sample complexity of agnostic learning with deterministic labels Shai Ben-David Cheriton School of Computer Science University of Waterloo Waterloo, ON, N2L 3G CANADA shai@uwaterloo.ca Ruth Urner College
The sample complexity of agnostic learning with deterministic labels Shai Ben-David Cheriton School of Computer Science University of Waterloo Waterloo, ON, N2L 3G CANADA shai@uwaterloo.ca Ruth Urner College
Midterm, Fall 2003
 5-78 Midterm, Fall 2003 YOUR ANDREW USERID IN CAPITAL LETTERS: YOUR NAME: There are 9 questions. The ninth may be more time-consuming and is worth only three points, so do not attempt 9 unless you are
5-78 Midterm, Fall 2003 YOUR ANDREW USERID IN CAPITAL LETTERS: YOUR NAME: There are 9 questions. The ninth may be more time-consuming and is worth only three points, so do not attempt 9 unless you are
CSCI 5622 Machine Learning
 CSCI 5622 Machine Learning DATE READ DUE Mon, Aug 31 1, 2 & 3 Wed, Sept 2 3 & 5 Wed, Sept 9 TBA Prelim Proposal www.rodneynielsen.com/teaching/csci5622f09/ Instructor: Rodney Nielsen Assistant Professor
CSCI 5622 Machine Learning DATE READ DUE Mon, Aug 31 1, 2 & 3 Wed, Sept 2 3 & 5 Wed, Sept 9 TBA Prelim Proposal www.rodneynielsen.com/teaching/csci5622f09/ Instructor: Rodney Nielsen Assistant Professor
CS 6375: Machine Learning Computational Learning Theory
 CS 6375: Machine Learning Computational Learning Theory Vibhav Gogate The University of Texas at Dallas Many slides borrowed from Ray Mooney 1 Learning Theory Theoretical characterizations of Difficulty
CS 6375: Machine Learning Computational Learning Theory Vibhav Gogate The University of Texas at Dallas Many slides borrowed from Ray Mooney 1 Learning Theory Theoretical characterizations of Difficulty
M chi h n i e n L e L arni n n i g Decision Trees Mac a h c i h n i e n e L e L a e r a ni n ng
 1 Decision Trees 2 Instances Describable by Attribute-Value Pairs Target Function Is Discrete Valued Disjunctive Hypothesis May Be Required Possibly Noisy Training Data Examples Equipment or medical diagnosis
1 Decision Trees 2 Instances Describable by Attribute-Value Pairs Target Function Is Discrete Valued Disjunctive Hypothesis May Be Required Possibly Noisy Training Data Examples Equipment or medical diagnosis
Decision Trees.
 . Machine Learning Decision Trees Prof. Dr. Martin Riedmiller AG Maschinelles Lernen und Natürlichsprachliche Systeme Institut für Informatik Technische Fakultät Albert-Ludwigs-Universität Freiburg riedmiller@informatik.uni-freiburg.de
. Machine Learning Decision Trees Prof. Dr. Martin Riedmiller AG Maschinelles Lernen und Natürlichsprachliche Systeme Institut für Informatik Technische Fakultät Albert-Ludwigs-Universität Freiburg riedmiller@informatik.uni-freiburg.de
A Theoretical and Empirical Study of a Noise-Tolerant Algorithm to Learn Geometric Patterns
 Machine Learning, 37, 5 49 (1999) c 1999 Kluwer Academic Publishers. Manufactured in The Netherlands. A Theoretical and Empirical Study of a Noise-Tolerant Algorithm to Learn Geometric Patterns SALLY A.
Machine Learning, 37, 5 49 (1999) c 1999 Kluwer Academic Publishers. Manufactured in The Netherlands. A Theoretical and Empirical Study of a Noise-Tolerant Algorithm to Learn Geometric Patterns SALLY A.
Bayesian Learning Features of Bayesian learning methods:
 Bayesian Learning Features of Bayesian learning methods: Each observed training example can incrementally decrease or increase the estimated probability that a hypothesis is correct. This provides a more
Bayesian Learning Features of Bayesian learning methods: Each observed training example can incrementally decrease or increase the estimated probability that a hypothesis is correct. This provides a more
Bruits de classification constant et constant par morceaux: égalité des ensembles de classes de concepts apprenables
 Bruits de classification constant et constant par morceaux: égalité des ensembles de classes de concepts apprenables Liva Ralaivola, François Denis, Christophe N. Magnan Laboratoire d Informatique Fondamentale
Bruits de classification constant et constant par morceaux: égalité des ensembles de classes de concepts apprenables Liva Ralaivola, François Denis, Christophe N. Magnan Laboratoire d Informatique Fondamentale
SUPERVISED LEARNING: INTRODUCTION TO CLASSIFICATION
 SUPERVISED LEARNING: INTRODUCTION TO CLASSIFICATION 1 Outline Basic terminology Features Training and validation Model selection Error and loss measures Statistical comparison Evaluation measures 2 Terminology
SUPERVISED LEARNING: INTRODUCTION TO CLASSIFICATION 1 Outline Basic terminology Features Training and validation Model selection Error and loss measures Statistical comparison Evaluation measures 2 Terminology
Learning symmetric non-monotone submodular functions
 Learning symmetric non-monotone submodular functions Maria-Florina Balcan Georgia Institute of Technology ninamf@cc.gatech.edu Nicholas J. A. Harvey University of British Columbia nickhar@cs.ubc.ca Satoru
Learning symmetric non-monotone submodular functions Maria-Florina Balcan Georgia Institute of Technology ninamf@cc.gatech.edu Nicholas J. A. Harvey University of British Columbia nickhar@cs.ubc.ca Satoru
An Introduction to Statistical Theory of Learning. Nakul Verma Janelia, HHMI
 An Introduction to Statistical Theory of Learning Nakul Verma Janelia, HHMI Towards formalizing learning What does it mean to learn a concept? Gain knowledge or experience of the concept. The basic process
An Introduction to Statistical Theory of Learning Nakul Verma Janelia, HHMI Towards formalizing learning What does it mean to learn a concept? Gain knowledge or experience of the concept. The basic process
On the power and the limits of evolvability. Vitaly Feldman Almaden Research Center
 On the power and the limits of evolvability Vitaly Feldman Almaden Research Center Learning from examples vs evolvability Learnable from examples Evolvable Parity functions The core model: PAC [Valiant
On the power and the limits of evolvability Vitaly Feldman Almaden Research Center Learning from examples vs evolvability Learnable from examples Evolvable Parity functions The core model: PAC [Valiant
Data Mining Classification: Basic Concepts, Decision Trees, and Model Evaluation
 Data Mining Classification: Basic Concepts, Decision Trees, and Model Evaluation Lecture Notes for Chapter 4 Part I Introduction to Data Mining by Tan, Steinbach, Kumar Adapted by Qiang Yang (2010) Tan,Steinbach,
Data Mining Classification: Basic Concepts, Decision Trees, and Model Evaluation Lecture Notes for Chapter 4 Part I Introduction to Data Mining by Tan, Steinbach, Kumar Adapted by Qiang Yang (2010) Tan,Steinbach,
An Empirical Study of Building Compact Ensembles
 An Empirical Study of Building Compact Ensembles Huan Liu, Amit Mandvikar, and Jigar Mody Computer Science & Engineering Arizona State University Tempe, AZ 85281 {huan.liu,amitm,jigar.mody}@asu.edu Abstract.
An Empirical Study of Building Compact Ensembles Huan Liu, Amit Mandvikar, and Jigar Mody Computer Science & Engineering Arizona State University Tempe, AZ 85281 {huan.liu,amitm,jigar.mody}@asu.edu Abstract.
Introduction to ML. Two examples of Learners: Naïve Bayesian Classifiers Decision Trees
 Introduction to ML Two examples of Learners: Naïve Bayesian Classifiers Decision Trees Why Bayesian learning? Probabilistic learning: Calculate explicit probabilities for hypothesis, among the most practical
Introduction to ML Two examples of Learners: Naïve Bayesian Classifiers Decision Trees Why Bayesian learning? Probabilistic learning: Calculate explicit probabilities for hypothesis, among the most practical
CS 543 Page 1 John E. Boon, Jr.
 CS 543 Machine Learning Spring 2010 Lecture 05 Evaluating Hypotheses I. Overview A. Given observed accuracy of a hypothesis over a limited sample of data, how well does this estimate its accuracy over
CS 543 Machine Learning Spring 2010 Lecture 05 Evaluating Hypotheses I. Overview A. Given observed accuracy of a hypothesis over a limited sample of data, how well does this estimate its accuracy over
Rule Generation using Decision Trees
 Rule Generation using Decision Trees Dr. Rajni Jain 1. Introduction A DT is a classification scheme which generates a tree and a set of rules, representing the model of different classes, from a given
Rule Generation using Decision Trees Dr. Rajni Jain 1. Introduction A DT is a classification scheme which generates a tree and a set of rules, representing the model of different classes, from a given
Machine Learning
 Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 11, 2012 Today: Computational Learning Theory Probably Approximately Coorrect (PAC) learning theorem
Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 11, 2012 Today: Computational Learning Theory Probably Approximately Coorrect (PAC) learning theorem
COMP9444: Neural Networks. Vapnik Chervonenkis Dimension, PAC Learning and Structural Risk Minimization
 : Neural Networks Vapnik Chervonenkis Dimension, PAC Learning and Structural Risk Minimization 11s2 VC-dimension and PAC-learning 1 How good a classifier does a learner produce? Training error is the precentage
: Neural Networks Vapnik Chervonenkis Dimension, PAC Learning and Structural Risk Minimization 11s2 VC-dimension and PAC-learning 1 How good a classifier does a learner produce? Training error is the precentage
Machine Learning. Computational Learning Theory. Le Song. CSE6740/CS7641/ISYE6740, Fall 2012
 Machine Learning CSE6740/CS7641/ISYE6740, Fall 2012 Computational Learning Theory Le Song Lecture 11, September 20, 2012 Based on Slides from Eric Xing, CMU Reading: Chap. 7 T.M book 1 Complexity of Learning
Machine Learning CSE6740/CS7641/ISYE6740, Fall 2012 Computational Learning Theory Le Song Lecture 11, September 20, 2012 Based on Slides from Eric Xing, CMU Reading: Chap. 7 T.M book 1 Complexity of Learning
Statistical Machine Learning from Data
 Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Ensembles Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole Polytechnique Fédérale de Lausanne
Samy Bengio Statistical Machine Learning from Data 1 Statistical Machine Learning from Data Ensembles Samy Bengio IDIAP Research Institute, Martigny, Switzerland, and Ecole Polytechnique Fédérale de Lausanne
FINAL: CS 6375 (Machine Learning) Fall 2014
 FINAL: CS 6375 (Machine Learning) Fall 2014 The exam is closed book. You are allowed a one-page cheat sheet. Answer the questions in the spaces provided on the question sheets. If you run out of room for
FINAL: CS 6375 (Machine Learning) Fall 2014 The exam is closed book. You are allowed a one-page cheat sheet. Answer the questions in the spaces provided on the question sheets. If you run out of room for
10.1 The Formal Model
 67577 Intro. to Machine Learning Fall semester, 2008/9 Lecture 10: The Formal (PAC) Learning Model Lecturer: Amnon Shashua Scribe: Amnon Shashua 1 We have see so far algorithms that explicitly estimate
67577 Intro. to Machine Learning Fall semester, 2008/9 Lecture 10: The Formal (PAC) Learning Model Lecturer: Amnon Shashua Scribe: Amnon Shashua 1 We have see so far algorithms that explicitly estimate
Decision Tree Learning Lecture 2
 Machine Learning Coms-4771 Decision Tree Learning Lecture 2 January 28, 2008 Two Types of Supervised Learning Problems (recap) Feature (input) space X, label (output) space Y. Unknown distribution D over
Machine Learning Coms-4771 Decision Tree Learning Lecture 2 January 28, 2008 Two Types of Supervised Learning Problems (recap) Feature (input) space X, label (output) space Y. Unknown distribution D over
DECISION TREE LEARNING. [read Chapter 3] [recommended exercises 3.1, 3.4]
![DECISION TREE LEARNING. [read Chapter 3] [recommended exercises 3.1, 3.4] DECISION TREE LEARNING. [read Chapter 3] [recommended exercises 3.1, 3.4]](/thumbs/78/78784288.jpg) 1 DECISION TREE LEARNING [read Chapter 3] [recommended exercises 3.1, 3.4] Decision tree representation ID3 learning algorithm Entropy, Information gain Overfitting Decision Tree 2 Representation: Tree-structured
1 DECISION TREE LEARNING [read Chapter 3] [recommended exercises 3.1, 3.4] Decision tree representation ID3 learning algorithm Entropy, Information gain Overfitting Decision Tree 2 Representation: Tree-structured
Computational Learning Theory. CS534 - Machine Learning
 Computational Learning Theory CS534 Machine Learning Introduction Computational learning theory Provides a theoretical analysis of learning Shows when a learning algorithm can be expected to succeed Shows
Computational Learning Theory CS534 Machine Learning Introduction Computational learning theory Provides a theoretical analysis of learning Shows when a learning algorithm can be expected to succeed Shows
Selected Algorithms of Machine Learning from Examples
 Fundamenta Informaticae 18 (1993), 193 207 Selected Algorithms of Machine Learning from Examples Jerzy W. GRZYMALA-BUSSE Department of Computer Science, University of Kansas Lawrence, KS 66045, U. S. A.
Fundamenta Informaticae 18 (1993), 193 207 Selected Algorithms of Machine Learning from Examples Jerzy W. GRZYMALA-BUSSE Department of Computer Science, University of Kansas Lawrence, KS 66045, U. S. A.
Data Mining Classification: Basic Concepts and Techniques. Lecture Notes for Chapter 3. Introduction to Data Mining, 2nd Edition
 Data Mining Classification: Basic Concepts and Techniques Lecture Notes for Chapter 3 by Tan, Steinbach, Karpatne, Kumar 1 Classification: Definition Given a collection of records (training set ) Each
Data Mining Classification: Basic Concepts and Techniques Lecture Notes for Chapter 3 by Tan, Steinbach, Karpatne, Kumar 1 Classification: Definition Given a collection of records (training set ) Each
Testing Problems with Sub-Learning Sample Complexity
 Testing Problems with Sub-Learning Sample Complexity Michael Kearns AT&T Labs Research 180 Park Avenue Florham Park, NJ, 07932 mkearns@researchattcom Dana Ron Laboratory for Computer Science, MIT 545 Technology
Testing Problems with Sub-Learning Sample Complexity Michael Kearns AT&T Labs Research 180 Park Avenue Florham Park, NJ, 07932 mkearns@researchattcom Dana Ron Laboratory for Computer Science, MIT 545 Technology
COMS 4771 Introduction to Machine Learning. Nakul Verma
 COMS 4771 Introduction to Machine Learning Nakul Verma Announcements HW2 due now! Project proposal due on tomorrow Midterm next lecture! HW3 posted Last time Linear Regression Parametric vs Nonparametric
COMS 4771 Introduction to Machine Learning Nakul Verma Announcements HW2 due now! Project proposal due on tomorrow Midterm next lecture! HW3 posted Last time Linear Regression Parametric vs Nonparametric
A Bound on the Label Complexity of Agnostic Active Learning
 A Bound on the Label Complexity of Agnostic Active Learning Steve Hanneke March 2007 CMU-ML-07-103 School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 Machine Learning Department,
A Bound on the Label Complexity of Agnostic Active Learning Steve Hanneke March 2007 CMU-ML-07-103 School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 Machine Learning Department,
Hypothesis Evaluation
 Hypothesis Evaluation Machine Learning Hamid Beigy Sharif University of Technology Fall 1395 Hamid Beigy (Sharif University of Technology) Hypothesis Evaluation Fall 1395 1 / 31 Table of contents 1 Introduction
Hypothesis Evaluation Machine Learning Hamid Beigy Sharif University of Technology Fall 1395 Hamid Beigy (Sharif University of Technology) Hypothesis Evaluation Fall 1395 1 / 31 Table of contents 1 Introduction
Machine Learning
 Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 11, 2012 Today: Computational Learning Theory Probably Approximately Coorrect (PAC) learning theorem
Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 11, 2012 Today: Computational Learning Theory Probably Approximately Coorrect (PAC) learning theorem
CS6375: Machine Learning Gautam Kunapuli. Decision Trees
 Gautam Kunapuli Example: Restaurant Recommendation Example: Develop a model to recommend restaurants to users depending on their past dining experiences. Here, the features are cost (x ) and the user s
Gautam Kunapuli Example: Restaurant Recommendation Example: Develop a model to recommend restaurants to users depending on their past dining experiences. Here, the features are cost (x ) and the user s
Finite Mixture Model of Bounded Semi-naive Bayesian Networks Classifier
 Finite Mixture Model of Bounded Semi-naive Bayesian Networks Classifier Kaizhu Huang, Irwin King, and Michael R. Lyu Department of Computer Science and Engineering The Chinese University of Hong Kong Shatin,
Finite Mixture Model of Bounded Semi-naive Bayesian Networks Classifier Kaizhu Huang, Irwin King, and Michael R. Lyu Department of Computer Science and Engineering The Chinese University of Hong Kong Shatin,
1 Last time and today
 COMS 6253: Advanced Computational Learning Spring 2012 Theory Lecture 12: April 12, 2012 Lecturer: Rocco Servedio 1 Last time and today Scribe: Dean Alderucci Previously: Started the BKW algorithm for
COMS 6253: Advanced Computational Learning Spring 2012 Theory Lecture 12: April 12, 2012 Lecturer: Rocco Servedio 1 Last time and today Scribe: Dean Alderucci Previously: Started the BKW algorithm for
Machine Learning & Data Mining
 Group M L D Machine Learning M & Data Mining Chapter 7 Decision Trees Xin-Shun Xu @ SDU School of Computer Science and Technology, Shandong University Top 10 Algorithm in DM #1: C4.5 #2: K-Means #3: SVM
Group M L D Machine Learning M & Data Mining Chapter 7 Decision Trees Xin-Shun Xu @ SDU School of Computer Science and Technology, Shandong University Top 10 Algorithm in DM #1: C4.5 #2: K-Means #3: SVM
Introduction to Bayesian Learning. Machine Learning Fall 2018
 Introduction to Bayesian Learning Machine Learning Fall 2018 1 What we have seen so far What does it mean to learn? Mistake-driven learning Learning by counting (and bounding) number of mistakes PAC learnability
Introduction to Bayesian Learning Machine Learning Fall 2018 1 What we have seen so far What does it mean to learn? Mistake-driven learning Learning by counting (and bounding) number of mistakes PAC learnability
Unsupervised Learning with Permuted Data
 Unsupervised Learning with Permuted Data Sergey Kirshner skirshne@ics.uci.edu Sridevi Parise sparise@ics.uci.edu Padhraic Smyth smyth@ics.uci.edu School of Information and Computer Science, University
Unsupervised Learning with Permuted Data Sergey Kirshner skirshne@ics.uci.edu Sridevi Parise sparise@ics.uci.edu Padhraic Smyth smyth@ics.uci.edu School of Information and Computer Science, University
Lecture 3: Decision Trees
 Lecture 3: Decision Trees Cognitive Systems - Machine Learning Part I: Basic Approaches of Concept Learning ID3, Information Gain, Overfitting, Pruning last change November 26, 2014 Ute Schmid (CogSys,
Lecture 3: Decision Trees Cognitive Systems - Machine Learning Part I: Basic Approaches of Concept Learning ID3, Information Gain, Overfitting, Pruning last change November 26, 2014 Ute Schmid (CogSys,
Decision Trees.
 . Machine Learning Decision Trees Prof. Dr. Martin Riedmiller AG Maschinelles Lernen und Natürlichsprachliche Systeme Institut für Informatik Technische Fakultät Albert-Ludwigs-Universität Freiburg riedmiller@informatik.uni-freiburg.de
. Machine Learning Decision Trees Prof. Dr. Martin Riedmiller AG Maschinelles Lernen und Natürlichsprachliche Systeme Institut für Informatik Technische Fakultät Albert-Ludwigs-Universität Freiburg riedmiller@informatik.uni-freiburg.de
What Can We Learn Privately?
 What Can We Learn Privately? Sofya Raskhodnikova Penn State University Joint work with Shiva Kasiviswanathan Homin Lee Kobbi Nissim Adam Smith Los Alamos UT Austin Ben Gurion Penn State To appear in SICOMP
What Can We Learn Privately? Sofya Raskhodnikova Penn State University Joint work with Shiva Kasiviswanathan Homin Lee Kobbi Nissim Adam Smith Los Alamos UT Austin Ben Gurion Penn State To appear in SICOMP
Predicting with Distributions
 Proceedings of Machine Learning Research vol 65:1 28, 2017 Predicting with Distributions Michael Kearns MKEARNS@CIS.UPENN.EDU and Zhiwei Steven Wu WUZHIWEI@CIS.UPENN.EDU University of Pennsylvania Abstract
Proceedings of Machine Learning Research vol 65:1 28, 2017 Predicting with Distributions Michael Kearns MKEARNS@CIS.UPENN.EDU and Zhiwei Steven Wu WUZHIWEI@CIS.UPENN.EDU University of Pennsylvania Abstract
On the Efficiency of Noise-Tolerant PAC Algorithms Derived from Statistical Queries
 Annals of Mathematics and Artificial Intelligence 0 (2001)?? 1 On the Efficiency of Noise-Tolerant PAC Algorithms Derived from Statistical Queries Jeffrey Jackson Math. & Comp. Science Dept., Duquesne
Annals of Mathematics and Artificial Intelligence 0 (2001)?? 1 On the Efficiency of Noise-Tolerant PAC Algorithms Derived from Statistical Queries Jeffrey Jackson Math. & Comp. Science Dept., Duquesne
Question of the Day. Machine Learning 2D1431. Decision Tree for PlayTennis. Outline. Lecture 4: Decision Tree Learning
 Question of the Day Machine Learning 2D1431 How can you make the following equation true by drawing only one straight line? 5 + 5 + 5 = 550 Lecture 4: Decision Tree Learning Outline Decision Tree for PlayTennis
Question of the Day Machine Learning 2D1431 How can you make the following equation true by drawing only one straight line? 5 + 5 + 5 = 550 Lecture 4: Decision Tree Learning Outline Decision Tree for PlayTennis
Statistics and learning: Big Data
 Statistics and learning: Big Data Learning Decision Trees and an Introduction to Boosting Sébastien Gadat Toulouse School of Economics February 2017 S. Gadat (TSE) SAD 2013 1 / 30 Keywords Decision trees
Statistics and learning: Big Data Learning Decision Trees and an Introduction to Boosting Sébastien Gadat Toulouse School of Economics February 2017 S. Gadat (TSE) SAD 2013 1 / 30 Keywords Decision trees
Agnostic Learning of Disjunctions on Symmetric Distributions
 Agnostic Learning of Disjunctions on Symmetric Distributions Vitaly Feldman vitaly@post.harvard.edu Pravesh Kothari kothari@cs.utexas.edu May 26, 2014 Abstract We consider the problem of approximating
Agnostic Learning of Disjunctions on Symmetric Distributions Vitaly Feldman vitaly@post.harvard.edu Pravesh Kothari kothari@cs.utexas.edu May 26, 2014 Abstract We consider the problem of approximating
Learning with Rejection
 Learning with Rejection Corinna Cortes 1, Giulia DeSalvo 2, and Mehryar Mohri 2,1 1 Google Research, 111 8th Avenue, New York, NY 2 Courant Institute of Mathematical Sciences, 251 Mercer Street, New York,
Learning with Rejection Corinna Cortes 1, Giulia DeSalvo 2, and Mehryar Mohri 2,1 1 Google Research, 111 8th Avenue, New York, NY 2 Courant Institute of Mathematical Sciences, 251 Mercer Street, New York,
Computational Learning Theory
 CS 446 Machine Learning Fall 2016 OCT 11, 2016 Computational Learning Theory Professor: Dan Roth Scribe: Ben Zhou, C. Cervantes 1 PAC Learning We want to develop a theory to relate the probability of successful
CS 446 Machine Learning Fall 2016 OCT 11, 2016 Computational Learning Theory Professor: Dan Roth Scribe: Ben Zhou, C. Cervantes 1 PAC Learning We want to develop a theory to relate the probability of successful
CHAPTER-17. Decision Tree Induction
 CHAPTER-17 Decision Tree Induction 17.1 Introduction 17.2 Attribute selection measure 17.3 Tree Pruning 17.4 Extracting Classification Rules from Decision Trees 17.5 Bayesian Classification 17.6 Bayes
CHAPTER-17 Decision Tree Induction 17.1 Introduction 17.2 Attribute selection measure 17.3 Tree Pruning 17.4 Extracting Classification Rules from Decision Trees 17.5 Bayesian Classification 17.6 Bayes
Short Note: Naive Bayes Classifiers and Permanence of Ratios
 Short Note: Naive Bayes Classifiers and Permanence of Ratios Julián M. Ortiz (jmo1@ualberta.ca) Department of Civil & Environmental Engineering University of Alberta Abstract The assumption of permanence
Short Note: Naive Bayes Classifiers and Permanence of Ratios Julián M. Ortiz (jmo1@ualberta.ca) Department of Civil & Environmental Engineering University of Alberta Abstract The assumption of permanence
Learning the Semantic Correlation: An Alternative Way to Gain from Unlabeled Text
 Learning the Semantic Correlation: An Alternative Way to Gain from Unlabeled Text Yi Zhang Machine Learning Department Carnegie Mellon University yizhang1@cs.cmu.edu Jeff Schneider The Robotics Institute
Learning the Semantic Correlation: An Alternative Way to Gain from Unlabeled Text Yi Zhang Machine Learning Department Carnegie Mellon University yizhang1@cs.cmu.edu Jeff Schneider The Robotics Institute
Solving Classification Problems By Knowledge Sets
 Solving Classification Problems By Knowledge Sets Marcin Orchel a, a Department of Computer Science, AGH University of Science and Technology, Al. A. Mickiewicza 30, 30-059 Kraków, Poland Abstract We propose
Solving Classification Problems By Knowledge Sets Marcin Orchel a, a Department of Computer Science, AGH University of Science and Technology, Al. A. Mickiewicza 30, 30-059 Kraków, Poland Abstract We propose
Occam s Razor Just Got Sharper
 Occam s Razor Just Got Sharper Saher Esmeir and Shaul Markovitch Computer Science Department, Technion Israel Institute of Technology, Haifa 32000, Israel {esaher, shaulm}@cs.technion.ac.il Abstract Occam
Occam s Razor Just Got Sharper Saher Esmeir and Shaul Markovitch Computer Science Department, Technion Israel Institute of Technology, Haifa 32000, Israel {esaher, shaulm}@cs.technion.ac.il Abstract Occam
hsnim: Hyper Scalable Network Inference Machine for Scale-Free Protein-Protein Interaction Networks Inference
 CS 229 Project Report (TR# MSB2010) Submitted 12/10/2010 hsnim: Hyper Scalable Network Inference Machine for Scale-Free Protein-Protein Interaction Networks Inference Muhammad Shoaib Sehgal Computer Science
CS 229 Project Report (TR# MSB2010) Submitted 12/10/2010 hsnim: Hyper Scalable Network Inference Machine for Scale-Free Protein-Protein Interaction Networks Inference Muhammad Shoaib Sehgal Computer Science
Computational Learning Theory
 1 Computational Learning Theory 2 Computational learning theory Introduction Is it possible to identify classes of learning problems that are inherently easy or difficult? Can we characterize the number
1 Computational Learning Theory 2 Computational learning theory Introduction Is it possible to identify classes of learning problems that are inherently easy or difficult? Can we characterize the number
Understanding Generalization Error: Bounds and Decompositions
 CIS 520: Machine Learning Spring 2018: Lecture 11 Understanding Generalization Error: Bounds and Decompositions Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the
CIS 520: Machine Learning Spring 2018: Lecture 11 Understanding Generalization Error: Bounds and Decompositions Lecturer: Shivani Agarwal Disclaimer: These notes are designed to be a supplement to the
Generalization, Overfitting, and Model Selection
 Generalization, Overfitting, and Model Selection Sample Complexity Results for Supervised Classification Maria-Florina (Nina) Balcan 10/03/2016 Two Core Aspects of Machine Learning Algorithm Design. How
Generalization, Overfitting, and Model Selection Sample Complexity Results for Supervised Classification Maria-Florina (Nina) Balcan 10/03/2016 Two Core Aspects of Machine Learning Algorithm Design. How
Foundations of Machine Learning
 Introduction to ML Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu page 1 Logistics Prerequisites: basics in linear algebra, probability, and analysis of algorithms. Workload: about
Introduction to ML Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu page 1 Logistics Prerequisites: basics in linear algebra, probability, and analysis of algorithms. Workload: about
Confusion matrix. a = true positives b = false negatives c = false positives d = true negatives 1. F-measure combines Recall and Precision:
 Confusion matrix classifier-determined positive label classifier-determined negative label true positive a b label true negative c d label Accuracy = (a+d)/(a+b+c+d) a = true positives b = false negatives
Confusion matrix classifier-determined positive label classifier-determined negative label true positive a b label true negative c d label Accuracy = (a+d)/(a+b+c+d) a = true positives b = false negatives
Chapter 6: Classification
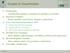 Chapter 6: Classification 1) Introduction Classification problem, evaluation of classifiers, prediction 2) Bayesian Classifiers Bayes classifier, naive Bayes classifier, applications 3) Linear discriminant
Chapter 6: Classification 1) Introduction Classification problem, evaluation of classifiers, prediction 2) Bayesian Classifiers Bayes classifier, naive Bayes classifier, applications 3) Linear discriminant
Decision Tree Learning
 Decision Tree Learning Goals for the lecture you should understand the following concepts the decision tree representation the standard top-down approach to learning a tree Occam s razor entropy and information
Decision Tree Learning Goals for the lecture you should understand the following concepts the decision tree representation the standard top-down approach to learning a tree Occam s razor entropy and information
Computational Learning Theory
 Computational Learning Theory Pardis Noorzad Department of Computer Engineering and IT Amirkabir University of Technology Ordibehesht 1390 Introduction For the analysis of data structures and algorithms
Computational Learning Theory Pardis Noorzad Department of Computer Engineering and IT Amirkabir University of Technology Ordibehesht 1390 Introduction For the analysis of data structures and algorithms
Decision Trees. CS57300 Data Mining Fall Instructor: Bruno Ribeiro
 Decision Trees CS57300 Data Mining Fall 2016 Instructor: Bruno Ribeiro Goal } Classification without Models Well, partially without a model } Today: Decision Trees 2015 Bruno Ribeiro 2 3 Why Trees? } interpretable/intuitive,
Decision Trees CS57300 Data Mining Fall 2016 Instructor: Bruno Ribeiro Goal } Classification without Models Well, partially without a model } Today: Decision Trees 2015 Bruno Ribeiro 2 3 Why Trees? } interpretable/intuitive,
Worst-Case Analysis of the Perceptron and Exponentiated Update Algorithms
 Worst-Case Analysis of the Perceptron and Exponentiated Update Algorithms Tom Bylander Division of Computer Science The University of Texas at San Antonio San Antonio, Texas 7849 bylander@cs.utsa.edu April
Worst-Case Analysis of the Perceptron and Exponentiated Update Algorithms Tom Bylander Division of Computer Science The University of Texas at San Antonio San Antonio, Texas 7849 bylander@cs.utsa.edu April
Lecture 9: Bayesian Learning
 Lecture 9: Bayesian Learning Cognitive Systems II - Machine Learning Part II: Special Aspects of Concept Learning Bayes Theorem, MAL / ML hypotheses, Brute-force MAP LEARNING, MDL principle, Bayes Optimal
Lecture 9: Bayesian Learning Cognitive Systems II - Machine Learning Part II: Special Aspects of Concept Learning Bayes Theorem, MAL / ML hypotheses, Brute-force MAP LEARNING, MDL principle, Bayes Optimal
Logistic Regression and Boosting for Labeled Bags of Instances
 Logistic Regression and Boosting for Labeled Bags of Instances Xin Xu and Eibe Frank Department of Computer Science University of Waikato Hamilton, New Zealand {xx5, eibe}@cs.waikato.ac.nz Abstract. In
Logistic Regression and Boosting for Labeled Bags of Instances Xin Xu and Eibe Frank Department of Computer Science University of Waikato Hamilton, New Zealand {xx5, eibe}@cs.waikato.ac.nz Abstract. In
