Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 2018 m. ruduo (1 semestras), X s db s, t 0.
|
|
|
- Tamsin White
- 5 years ago
- Views:
Transcription
1 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 218 m. ruduo (1 semestras), Prove the following: Proposition. If X t, t, is an Itô process and f C 3 (IR), then f ( ) ( ) t X t f X = f ( ) X s dxs. 2. Let X t, t, be a solution of the stochastic differential equation (SDE) X t = 1 + X s (1 X s ) ds + X s db s, t. It is known that X t >, t. Find any function f C 2 (, ) such that Y t = f(x t ), t, is a solution of an SDE with additive noise. Write this SDE. Reminder. An SDE is said to be an equation with additive noise if its diffusion coefficient is a nonzero constant. Answer: E.g., f(x) = ln x; Y t = ( 1 2 ey s ) ds + B t. 3. Find the limit X := L 2 - lim n 2n i=1 B 3( i )[ B 2( i ) n n and EX. Answer: X = 2 5 B B3 t dt, EX =. 4. Solve the SDE B 2( i 1 )] n dx t = X t (1 X t )(2 X t ) dt + X t (2 X t ) db t, X = x, when a) < x < 2; b) x = 2. Answer: a) X t = 2x/(x + (2 x)e 2B t ); b) X t = Can a diffusion process have a stationary density with infinitely many maximum points? (If yes, give an example; if not, argue why not.) Answer: Yes. Example: dx t = f(x t ) dt + db t with f(x) = sin 2 xe x2, x IR.
2 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM I kursas, 218 m. ruduo (1 semestras), Find the second moment EXt 2 and the covariance function C(t, s) := Cov(X t, X s ), t, s, of the stochastic integral X t = B2 u db u, t. Reminder. The covariance of random variables X and Y is Cov (X, Y ) := E(XY ) EXEY. 2. Find the limit and EX. X := L 2 - lim n 2n i=1 B 3( i )[ ( i ( i 1 )] B B n n) n
3 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 217 m. ruduo (1 semestras), Prove the integration-by-parts formulas for Itô processes X and Y : X s dy s = X t Y t X Y Y s dx s X, Y t, X s dy s = X t Y t X Y Y s dx s. 2. Find the covariance function C(t, s) := Cov(X t, X s ), t, s, of the stochastic integral X t = B2 u db u, t. Reminder. The covariance of random variables X and Y is Cov (X, Y ) := E(XY ) EXEY. Answer: (t s) Find the limit and EX. X := L 2 - lim n 4. Solve the SDE X t = 1 + 2n i=1 B 3( i )[ ( i ( i 1 )] B B n n) n X s (3 X s ) ds + 2 X s db s, t. Answer: X t = exp{3t + 2B t }/(1 + exp{3s + 2B s} ds). 5. Ar gali difuzinis procesas su multiplikatyviu triukšmu turėti toki pati stacionaru tanki kaip difuzinis procesas su adityviu triukšmu? (Jei taip, pateikite pavyzdi ; jei ne, pagri skite kodėl.) Can a diffusion process with multiplicative noise have the same stationary density as a diffusion process with additive noise has? (If yes, give an example; if not, argue why not.) Answer: Yes. Example: dx t = (X t Xt 3 ) dt + X t db t and dx t = X t dt + db t.
4 Stochastinės analizės egzaminas ERASMUS sudentams MIF magistrantūra, FDM, I kursas, 217 m. rudens semestras, Prove the integration-by-parts formulas for Itô processes X and Y : X s dy s = X t Y t X Y Y s dx s X, Y t, X s dy s = X t Y t X Y Y s dx s. 2. Find the stochastic integral Ats.: 1 3 e3b t ( 3 2 s s)e3b s ds. 3. Find the limit and EX. X := L 2 - lim 4. Solve the SDE X t = 1 + n n k=1 s 2 e 3B s db s. B 3( k )[ ( k B B n n) ( k 1 )] X s (2 X s ) ds + 3 X s db s, t. 5. Find the covariance function C(t, s) := Cov(X t, X s ) of the solution of the Langevin equation dx t = ax t dt + bdb t, X = x. Reminder. The covariance of random variables X and Y is Cov (X, Y ) := E(XY ) EXEY. n
5 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 217 m. rudens semestras, Raskite atsitiktinio proceso (geometrinio Brauno judesio), tenkinančio SDL X t = x + μ X s ds + σ X s db s, t, antra ji ir trečia ji momentus (EX 2 t ir EX 3 t ). Ats.: EX 2 t = x 2 e (2μ+σ2 )t, EX 3 t = x 3 e (3(μ+σ2 )t. 2. Raskite reguliaru Ito procesa A t, t, su kuriuo atsitiktinis procesas M t := yra martingalas. Ats.: A t = 9 B4 s ds. ( 2 Bt 3 3 B s ds) At, t, Find the second and third moments (EX 2 t and EX 3 t ) of the process (geometric Brownian motion) satisfying the SDE X t = x + μ X s ds + σ X s db s, t. 2. Find a regular Itô processs A t, t, such that the random process M t := is a martingale. ( 2 Bt 3 3 B s ds) At, t,
6 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 216 m. ruduo (1 semestras), Prove the following: Proposition. If X t, t, is an Itô process and f C 3 (IR), then f ( ) ( ) t X t f X = f ( ) X s dxs. 2. Let X t, t, be a solution of the stochastic differential equation (SDE) X t = 1 + X s (1 X s ) ds + X s db s, t. It is known that X t >, t. Find any function f C 2 (, ) such that Y t = f(x t ), t, is a solution of an SDE with additive noise. Write this SDE. Reminder. An SDE is said to be an equation with additive noise if its diffusion coefficient is a nonzero constant. Answer: f(x) = ln x; Y t = ( 1 2 ey s ) ds + B t. 3. Let X and Y be bounded adapted random processes, and M t = X s db s, t. Find a regular random processa t, t, such that the process ( ) 2 N t := Y s dm s At, t, is a martingale. Answer: A t = (X sy s ) 2 ds. 4. A random process X t, t, is a solution of the SDE dx t = μx t dt + σx t db t, X = x. Find EX n t, t, for all n IN. Answer: x n exp{(μn σ2 n(n 1))t}. 5. Solve the SDE dx t = 2X t (1 X t )(1 2X t ) dt + 2X t (1 X t ) db t, X = x, when a) < x < 1; b) x = 1. Answer: a) X t = x/(x + (1 x)e 2B t ); b) X t = 1.
7 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 216 m. ruduo (1 semestras), I rodykite teigini : Teiginys. Jei X t, t, Ito procesas ir f C 3 (IR), tai f ( ) ( ) t X t f X = f ( ) X s dxs. 2. Tarkime, kad X t, t, yra stochastinės diferencialinės lygties (SDL) X t = 1 + X s (1 X s ) ds + X s db s, t, sprendinys. Yra žinoma, kad X t >, t. Raskite kokia nors funkcija f C 2 (, ), su kuria procesas Y t = f(x t ), t, būtu SDL su adityviu triukšmu sprendinys. Parašykite ta lygti. Priminimas. Sakoma, kad SDL yra lygtis su adityviu triukšmu, jei jos difuzijos koeficientas yra nenulinė konstanta. Ats.: f(x) = ln x; Y t = ( 1 2 ey s ) ds + B t. 3. Tarkime, kad X ir Y yra aprėžti suderinti atsitiktiniai procesai, M t = X s db s, t. Raskite reguliaru atsitiktini procesa A t, t, su kuriuo procesas ( ) 2 N t := Y s dm s At, t, būtu martingalas. Ats.: A t = (X sy s ) 2 ds. 4. Atsitiktinis procesas X t, t, yra SDL dx t = μx t dt + σx t db t, X = x, sprendinys. Raskite EX n t, t, su bet kokiu n IN. Ats.: x n exp{(μn σ2 n(n 1))t}. 5. Išspre skite SDL dx t = 2X t (1 X t )(1 2X t ) dt + 2X t (1 X t ) db t, X = x, kai a) < x < 1; b) x = 1. Ats: a) X t = x/(x + (1 x)e 2B t ); b) X t = 1.
8 Stochastinės analizės egzaminas (R. Gylys) 1. Pažymėkime X x t, t, stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x, su koeficientais b ir σ, tenkinančiais Lipšico sa lyga, sprendini. I rodykite, kad X x t P X x t, kai x x, su visais t (tolydumas pradinės sa lygos atžvilgiu). 2. Tarkime, kad X t, t, yra stochastinės diferencialinės lygties (SDL) X t = 1 + b(x s ) ds + σ(x s ) db s, t, su Lipšico koeficientais b ir σ sprendinys ir f C 2 b (IR). Raskite reguliaru procesa A t, t, su kuriuo atsitiktinis procesas M t := f(x t ) A t, t, yra martingalas. 3. Išspre skite SDL X t = 1 + X s (1 X 2 s ) ds + X s db s, t. 4. Stochastinės diferencialinės lygties dx t = b(x t ) dt+σ(x t ) db t, X = x, aproksimacija {X h, h > } apibrėžiama lygybėmis X h = x, X h (k+1)h = Xh kh + b(x h kh)h + σ(x h kh) ξ k h, k =, 1, 2,... ; čia {ξ k } nepriklausomu tolygiai pasiskirsčiusiu intervale [ a, a] atsitiktiniu dydžiu seka. Parinkite parametro a reikšme, su kuria ši aproksimacija būtu pirmos eilės silpnoji aproksimacija.
9 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 216 m. rudens semestras, Let X t, t, be a solution of the stochastic differential equation (SDE) X t = 1 + X s (1 X s ) ds + X s db s, t, and let f C 2 b (IR). Find a regular process A t, t, such that the random process M t := f(x t ) A t, t, is a martingale. 2. Let X t, t, and Y t, t, be solutions of the SDEs and X t = x + a X s ds + b X s db s, t, Y t = y + c Y s ds + d Y s db s, t. Write an SDE satisfied by the random process Z t := X t Y t, t Tarkime, kad X t, t, yra stochastinės diferencialinės lygties (SDL) X t = 1 + X s (1 X s ) ds + X s db s, t, sprendinys ir f Cb 2(IR). Raskite reguliaru procesa procesas M t := f(x t ) A t, t, yra martingalas. A t, t, su kuriuo atsitiktinis 2. Tarkime, kad X t, t, ir Y t, t, yra SDL ir X t = x + a X s ds + b X s db s, t, Y t = y + c Y s ds + d Y s db s, t, sprendiniai. Parašykite SDL, kuria tenkina atsitiktinis procesas Z t := X t Y t, t.
10 Stochastinės analizės egzaminas (V. Jurgelevičius) 1. Ar gali Brauno judesio trajektorija (su teigiama tikimybe) tenkinti Lipšico sa lyga kokiame nors baigtiniame intervale? (Iš Brauno judesio trajektoriju nediferencijuojamumo neišplaukia, kad jos netenkina Lipšico sa lygos.) Priminimas. Funkcija f : [a, b] IR tenkina Lipšico sa lyga, jei egzistuoja tokia konstanta L, kad f(y) f(x) L y x, x, y [a, b]. 2. Raskite reguliaru Ito procesa A t, t, su kuriuo atsitiktinis procesas M t := (B 2 t t) 2 A t, t, yra martingalas. Raskite šio martingalo kvadratine variacija M t. Ats.: A t = 4 B2 s ds, M t = 16 B2 s(bs 2 s) 2 ds. 3. Išspre skite SDL X t = 1 + X s (1 X s ) ds + Ats.: X t = exp{t + B t }/(1 + exp{s + B s } ds). 4. Tarkime, kad X ir Y yra tiesiniu SDL ir X s db s, t. X t = x + a X s ds + b X s db s, t, Y t = y + c Y s ds + d Y s db s, t, sprendiniai. Parašykite tiesine SDL, kuria tenkina atsitiktinis procesas Z t := X t Y t, t. Ats.: Z t = xy + (a + c + bd) Z s ds + (b + d) Z s db s.
11 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 215 m. ruduo (1 semestras), I rodykite teigini : Teiginys. Jei X t, t, Ito procesas ir f C 3 (IR), tai f ( ) ( ) t X t f X = f ( ) X s dxs. ( ) Apskaičiuokite E se B s db s Ats.: 4( 1 e 2t (2t 2 2t + 1) 1 ). 3. Raskite reguliaru Ito procesa A t, t, su kuriuo atsitiktinis procesas M t := (B 2 t t) 2 A t, t, yra martingalas. Raskite šio martingalo kvadratine variacija M t. Ats.: A t = 4 B2 s ds, M t = 16 B2 s(bs 2 s) 2 ds. 4. Tarkime, kad X ir Y yra Stratonovičiaus SDL X t = X s ds + 3 X s db s ir Y t = Y s ds + 6 Y s db s sprendiniai. Parašykite Stratonovičiaus SDL, kuria tenkina atsitiktinis procesas Z t := X t Y t, t. Ats.: Z t = Z s ds + 9 Z s db s. 5. Ar gali difuzinis procesas su multiplikatyviu triukšmu turėti toki pati stacionaru tanki kaip difuzinis procesas su adityviu triukšmu? Jei ne, pagri skite kodėl; jei taip, pateikite pavyzdi. Ats.: Taip.
12 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 215 m. rudens semestras, Raskite stochastini integrala s 2 e 3B s db s. Ats.: 1 3 e3b t ( 3 2 s s)e3b s ds. 2. Raskite riba X := L 2 - lim n n k=1 B 2( k )[ n B 2( k n ) B 2( k 1 )] n ir EX. Ats.: X = B B2 t dt, EX = 5 2.
13 Stochastinės analizės egzaminas (G. Lileika), (Š. Dirmeikis) 1. Pažymėkime X x t, t, stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x, su koeficientais b ir σ, tenkinančiais Lipšico sa lyga, sprendini. I rodykite, kad Xt x pagal tikimybe, kai x x, su visais t (tolydumas pradinės sa lygos atžvilgiu). X x t 2. Raskite Lanževeno lygties dx t = ax t dt + bdb t, X = x, sprendinio kovariacine funkcija C(t, s) := Cov(X t, X s ). 3. Išspre skite SDL dx t = a 2 X 2 t (1 X t ) dt + ax t (1 X t ) db t, X = x (, 1). Čia a > konstanta. Patarimas. Atlikite pakeitima Y t = X t /(1 X t ). 4. Lygties dx t = rx t dt+σx t db t, X = x, sprendinys X t = x exp{(r σ2 2 )t+σb t} >, t, jei pradinė reikšmė x >. 1) I rodykite, kad jei σ 2 2r, tai šios lygties Milšteino aproksimacija taip pat teigiama su bet kokia pradine reikšme x >. 2) Tarkime, kad 2r < σ 2 < 4r. Sukonstruokite šios lygties Milšteino tipo 1-os eilės silpna ja aproksimacija {X h, h > }, kuri taip pat būtu teigiama su bet kokia pradine reikšme x >.
14 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 214 m. ruduo (1 semestras), Difuzinio proceso stacionariojo tankio apibrėžimas. Tiesioginė Kolmogorovo lygtis stacionariajam tankiui. (1 t.) Teiginys. Jei difuzinis procesas X, apibrėžiamas stochastine diferencialine lygtimi arba dx t = b(x t ) dt + σ(x t ) db t, dx t = b(x t ) dt + σ(x t ) db t, turi stacionaru ji tanki p intervale (a, b) ir σ(x) > su visais x (a, b), tai p turi pavidala p (x) = N { x σ ν (x) exp b(u) } 2 c σ 2 (u) du, x (a, b); čia (I) lygčiai ν = 2, (S) lygčiai ν = 1, c bet koks taškas i intervalo (a, b), N normuojanti konstanta, su kuria b a p (x) dx = 1. (4 t.) Pastaba. Čia laikoma, kad koeficientai b ir σ yra pakankamai,,geri, kad p tenkintu tiesiogine Kolmogorovo lygti. (I) (S) 2. Raskite proceso X t := B2 s ds, t, kovariacija C(t, s) = Cov (X t, X s ), t, s. Priminimas. Atsitiktiniu dydžiu X ir Y kovariacija Cov (X, Y ) := E[(X EX)(Y EY )] = E(XY ) EX EY. Ats.: s3 (2t s), t s Tarkime, kad atsitiktiniu procesu pora X ir Y tenkina lygtis X t = x X s ds 2 Y s db s, Y t = y Y s ds + 2 X s db s, t. Raskite atsitiktini procesa Z t := Xt 2 + Yt 2, t. Ats.: Z t = x 2 + y 2 e t, t. 4. Išspre skite SDL ( 1 ) dx t = 4 X t dt + X t db t, X = x >. t ). Patarimas. Atlikite pakeitima Y t = X t (yra žinoma, kad lygties sprendinys X t, Ats.: X t = e t ( x + es/2 db s ) 2, t. 5. Lygties dx t = μx t dt+σx t db t, X = x, sprendinys X t = x exp{(μ σ2 2 )t+σb t} >, t, jei pradinė reikšmė x >. 1) I rodykite, kad jei σ 2 2μ, tai šios lygties Milšteino aproksimacija taip pat teigiama su bet kokia pradine reikšme x >. 2) Tarkime, kad 2μ < σ 2 < 4μ. Sukonstruokite šios lygties Milšteino tipo 1-os eilės silpna ja aproksimacija {X h, h > }, kuri taip pat būtu teigiama su bet kokia pradine reikšme x >. Spr.: 1) a(x, s, y) = x + (μ σ2 2 2) a(x, s, y) := x + (μ σ2 4 )xs + σxy + σ2 2 xy2 = (μ σ2 2 )xs + x(1 + σ 2 y)2 + σ2 )xs + σxy + σ2 4 xy2 = (μ σ2 4 )xs + x(1 + σ 2 y)2 >. 4 xy2 >.
15 1. Raskite Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 214 m. rudens semestras, ( 2 ( E B s ds) 2, ir E Bs ds) 2 t. 2. Atsitiktinis procesas X t, t, yra stochastinės Verhulsto lygties X t = x + λ X s (μ X s ) ds + σ X s db s, t, sprendinys (x, λ, μ, σ > ). Yra žinoma, kad X t >, t. Pažymėkime Y t := ln X t. Prašykite stochastine diferencialine lygti, kuria tenkina atsitiktinis procesas Y.
16 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 213/14 m.m., rudens semestras, I rodykite teigini : Teiginys. Jei X t, t, Ito procesas ir f C 3 (IR), tai f ( ) ( ) t X t f X = f ( ) X s dxs. 2. Tarkime, kad B t, t, Brauno judesys ir X t Cov (X t, X s ), t s. := B u du, t. Raskite Ats.: t 2 ( s 2 t 6 ). 3. Tarkime, kad X t, t, yra Ito procesas, f C 2 (IR) ir Y t := f(x t ), t. I rodykite, kad Y taip pat yra Ito procesas ir raskite ju kvadratiniu variaciju Y t ir X t sa ryši. 4. Tarkime, kad X ir Y yra SDL X t = X s ds + 3 X s db s ir Y t = Y s ds + 6 Y s db s sprendiniai. Parašykite SDL, kuria tenkina atsitiktinis procesas Z t := X t Y t, t. Ats.: Z t = Z s ds + 9 Z s db s. 5. Nubrėžkite difuzinio proceso, apibrėžiamo SDL dx t = X t (X 2 t 1) dt + σdb t stacionariojo tankio grafiko eskiza. Kaip keičiasi grafikas didinant parametra σ >?
17 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 213 m. rudens semestras, Tarkime, kad B t, t, Brauno judesys ir X t := B t+1 B t, t. Raskite Cov (X t, X t+s ), t, s. Ats.: (1 s) +. Let B t, t, be a Brownian motion, and let X t := B t+1 B t, t. Find Cov (X t, X t+s ), t, s. 2. Atsitiktinis procesas X t = e at cos B t, t, yra martingalas. Raskite parametra a. Ats.: 1 2. The random process X t = e at cos B t, t, is a martingale. Find the value of the parameter a.
18 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 212/13 m.m., rudens semestras, perlaikymas, Ito ir Stratonovičiaus integralu Ito proceso atžvilgiu apibrėžimai. I rodykite šiu integralu sa ryši Y X = Y X X, Y. I rodykite šias šiu integralu savybes: W (Z X) = (W Z) X; W (Z X) = (W Z) X. 2. Raskite E(B t BsB 2 u ), t s u. Ats.: 3su. 3. Tarkime, kad Ito procesas X t = K s ds + H s db s =, t. I rodykite, kad K t = H t =, t. Patarimas. Pritaikykite Ito formule procesui Y t = e X2 t. 4. Tarkime, kad X ir Y yra SDL X t = X s ds + 3 X s db s ir Y t = Y s ds + Y s db s sprendiniai. Parašykite SDL, kuria tenkina atsitiktinis procesas Z t := X t Y t, t. Ats.: Z t = Z s ds + 4 Z s db s. 5. Raskite lim t + EX4 t, jei X t lygties X t = 1 2 X ds + 3B t sprendinys. Ats.: 3 5 /2 4.
19 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 212/13 m.m., rudens semestras, I rodykite integravimo dalimis formules Ito procesams X ir Y : X s dy s = X t Y t X Y Y s dx s X, Y t, X s dy s = X t Y t X Y Y s dx s. 2. Raskite E(B t B s B 2 u), t s u. Ats.: su + 2u Raskite atsitiktinio dydžio ξ N(a, σ 2 ) skirstinio Laplaso transformacija φ(λ) := E exp{λξ}, λ IR. Patarimas. Pasinaudokite tuo, kad ξ d == a + σb 1, ir Ito formule. Ats.: exp{λa + λ 2 σ 2 /2}. 4. Išspre skite SDL X t = 1 + X s (1 X s ) ds + Ats.: X t = exp{t + B t }/(1 + exp{s + B s } ds). X s db s, t. 5. Raskite Lanževeno lygties dx t = ax t dt + bdb t, X = x, sprendinio kovariacine funkcija C(t, s) := Cov(X t, X s ). Priminimas. Atsitiktiniu dydžiu X ir Y kovariacija Cov (X, Y ) := E(XY ) EXEY. Ats.: b 2 2a (e a(t s) e a(t+s) ).
20 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 212 m.m., rudens semestras, Pateikite toki SDL X t = x + b(x s) ds + σ(x s) db s netrivialu pavyzdi (σ ), kad su bet kokia pradine sa lyga x ( 1, 1) lygties sprendinys X t ( 1, 1), t. 2. Atsitiktinis tolydus aprėžtas procesas X t, t, yra toks, kad procesas M t = X s ds, t [, T ], yra martingalas. I rodykite, kad X t = su visais t [, T ].
21 Stochastinės analizės egzaminas doktorantūra, (R. Malukas) 1. I rodykite, kad P{B t, t [, T ]} = su bet kokiu T >. Čia B t, t, Brauno judesys. 2. Pažymėkime X x t, t, stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x, su koeficientais b ir σ, tenkinančiais Lipšico sa lyga, sprendini. I rodykite, kad Xt x pagal tikimybe, kai x x, su visais t (tolydumas pradinės sa lygos atžvilgiu). X x t 3. Tarkime, kad X t, t, tolydus aprėžtas suderintas (su Brauno judesiu) procesas, nelygus tapatingai nuliui, ir Y t := X u du, t. Ar gali procesas Y būti martingalas? 4. Raskite riba I := L 2 - lim n n k=1 ( k B n)[ B 2( k n ) B 2( k 1 )]. n
22 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 211/12 m.m., rudens semestras, perlaikymas, Teorema. Jei stochastinės diferencialinėa lygties X t = x + b(x s ) ds + σ(x s ) db s, t [, T ], koeficientai b ir σ tenkina Lipšico sa lyga, tai lygtis turi vieninteli sprendini X H 2 [, T ]. 2. Raskite Cov (Bt 2, B2 s ds), t. Priminimas. Atsitiktiniu dydžiu X ir Y kovariacija Cov (X, Y ) := E[(X EX)(Y EY )]. 3. Ar atsitiktinis procesas X t = B2 u db u B2 u du, t, yra martingalas? 4. Tarkime, kad X ir Y du Ito procesai. Apibrėžkime atgalini stochastini integrala T X s dy s := P- lim n X i+1 ΔY i ; i čia, kaip visada, Δ n = { = t n < t n 1 < < t n k n = T }, n IN, bet kokia intervalo [, T ] skaidiniu seka, su kuria Δ n := max i t n i+1 tn i, kai n ; X i = X(t n i ), ΔX i = X i+1 X i. I rodykite Ito formule tokiam integralui: jei X Ito procesas ir F C 3 (IR), tai F (X T ) F (X ) = T F (X s ) dx s 1 2 T Patarimas. Pasinaudokite jau žinomomis Ito formulėmis. 5. Išspre skite SDL X t = x + X s (1 X s )(2 X s ) ds + F (X s ) d X s. X s (2 X s ) db s.
23 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 211/12 m.m., rudens semestras, Teorema. Jei stochastinės diferencialinės lygties X t = x + b(x s ) ds + σ(x s ) db s, t [, T ], koeficientai b ir σ tenkina Lipšico sa lyga, tai lygtis turi vieninteli sprendini X H 2 [, T ]. 2. Raskite Cov (B t, B s ds), t. Priminimas. Atsitiktiniu dydžiu X ir Y kovariacija Cov (X, Y ) := E[(X EX)(Y EY )]. 3. Tarkime, kad X t, t, tolydus aprėžtas suderintas (su Brauno judesiu) procesas, nelygus tapatingai nuliui, ir Y t := X u du, t. Ar gali procesas Y būti martingalas? 4. Tarkime, kad X ir Y du Ito procesai. Apibrėžkime atgalini stochastini integrala T X s dy s := P- lim n X i+1 ΔY i ; i čia, kaip visada, Δ n = { = t n < t n 1 < < t n k n = T }, n IN, bet kokia intervalo [, T ] skaidiniu seka, su kuria Δ n := max i t n i+1 tn i, kai n ; X i = X(t n i ), ΔX i = X i+1 X i. I rodykite Ito formule tokiam integralui: jei X Ito procesas ir F C 3 (IR), tai F (X T ) F (X ) = T F (X s ) dx s 1 2 T Patarimas. Pasinaudokite jau žinomomis Ito formulėmis. 5. Išspre skite SDL X t = x + X s ( 1 2 X s kai a) < x < 1; b) x = 1. Ats: a) X t = x/(x + (1 x)e B t ); b) X t = 1. F (X s ) d X s. ) (1 X s ) ds + X s (1 X s ) db s,
24 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 211 m.m., rudens semestras, Lygties dx t = b(x t ) dt + σ(x t ) db t sprendinio trečiasis laipsnis M t = X 3 t, t, yra martingalas. a) Raskite b(x), x IR, jei σ(x) = x, x IR; b) Raskite koeficientu b ir σ sa ryši bendru atveju. 2. Lygties dx t = b(x t ) dt + σ(x t ) db t su pradine sa lyga X = 1 koeficientai b ir σ. Ar gali jos sprendinys būti teigiamas ir aprėžtas (neatsitiktine konstanta)? (Jei taip, pateikite pavyzdi ; jei ne, pagri skite).
25 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 21/11 m.m., rudens semestras, I rodykite teigini : Teiginys. Jei difuzinis procesas X, apibrėžiamas stochastine diferencialine lygtimi dx t = b(x t ) dt + σ(x t ) db t, (I) arba dx t = b(x t ) dt + σ(x t ) db t, (S) turi stacionaru ji tanki p intervale (a, b) ir σ(x) > su visais x (a, b), tai p turi pavidala p (x) = N { x σ ν (x) exp 2 c b(u) } σ 2 (u) du, x (a, b); ia (I) lygčiai ν = 2, (S) lygčiai ν = 1, c bet koks taškas i intervalo (a, b), N normuojanti konstanta, su kuria b a p (x) dx = 1. Pastaba. Čia laikoma, kad koeficientai b ir σ yra pakankamai,,geri, kad p tenkintu tiesiogine Kolmogorovo lygti. 2. Raskite proceso X t := Bt 4, t, kovariacija C(t, s) = Cov (X t, X s ), t, s. Priminimas. Atsitiktiniu dydžiu X ir Y kovariacija Cov (X, Y ) := E[(X EX)(Y EY )]. 3. Tarkime, kad Ito procesas X t = K s ds + H s db s =, t. I rodykite, kad K t = H t =, t. Patarimas. Pritaikykite Ito formule procesui Y t = e X2 t. 4. Išspre skite SDL dx t = a 2 X 2 t (1 X t ) dt + ax t (1 X t ) db t, X = x (, 1). Čia a > konstanta. Patarimas. Atlikite pakeitima Y t = X t /(1 X t ). 5. SDL dx t = μx t dt+σx t db t, X = x, sprendinys X t = x exp{(μ σ 2 /2)t+σB t } >, t, jei pradinė reikšmė x >. 1) I rodykite, kad jei σ 2 2μ, tai šios lygties Milšteino aproksimacija (bet ne Eulerio) taip pat teigiama su bet kokia pradine reikšme x >. 2) Tarkime, kad 2μ < σ 2 < 4μ. Sukonstruokite šios lygties Milšteino tipo 1-os eilės silpna ja aproksimacija {X h, h > }, kuri taip pat būtu teigiama su bet kokia pradine reikšme x >.
26 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 21/11 m.m., rudens semestras, Raskite mažėjančia funkcija f: IR (, ), su kuria procesas M t = f(b t + t), t, yra martingalas. 2. Atsitiktinis procesas X apibrėžtas intervale [, 1) lygybe X t := (1 t) db s 1 s, t < 1. Išveskite SDL šiam procesui. I rodykite, kad X t L 2 prasme, kai t 1.
27 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 29/1 m.m., rudens semestras, I rodykite teigini : Teiginys. Jei X t, t, Ito procesas ir f C 3 (IR), tai f ( ) ( ) t X t f X = f ( ) X s dxs. 2. Atsitiktinis procesas X t := B t tb 1, t [, 1], vadinamas Brauno tiltu. Raskite jo kovariacija C(t, s) = Cov (X t, X s ), t, s [, 1]. Priminimas. Atsitiktiniu dydžiu X ir Y kovariacija Cov (X, Y ) := E[(X EX)(Y EY )]. 3. Atsitiktinis procesas X t, t, yra stochastinės diferencialinės lygties X t = 1 + X s ds + X s db s sprendinys. Atsitiktinis dydis Y i gyja dvi reikšmes ir a su tikimybėmis atitinkamai p ir q. Raskite tokius a, p ir q, kad EY = EX 1 ir EY 2 = EX 2 1 (t.y. tokius, kad sutaptu atsitiktiniu dydžiu Y ir X 1 pirmieji du momentai). 4. Ar galima Stratonovičiaus stochastinėje diferencialinėje lygtyje dx t = X t dt + σ(x t ) db t parinkti toki griežtai teigiama koeficienta σ(x), x IR, kad lygties (su bet kokia pradine sa lyga) sprendinys būtu martingalas? (Jei taip, pateikite pavyzdi ; jei ne, pagri skite.) 5. Ar gali stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x (, 1), (σ() = σ(1) =, σ(x) >, x (, 1)) stacionarus tankis būti p (x) = 1, x (, 1) (t.y. tolygiojo intervale (,1) skirstinio tankis)? (Jei taip, pateikite pavyzdi ; jei ne, pagri skite.)
28 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 29/1 m.m., rudens semestras, Ito procesai X ir Y tenkina lygtis X t = x + Y s db s ir Y t = y X s db s, t. I rodykite, kad Z t := Xt 2 + Yt 2 = (x 2 + y 2 ) e t, t. 2. Sugalvokite toki Ito procesu sekos {X n } ir nereguliaraus Ito proceso X pavyzdi, kad: 1) X n X tolygiai intervale [, T ], t.y. beveik tikrai sup Xt n X t, n ; t [,T ] 2) X n T 1 2 X T.
29 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 28/9 m.m., rudens semestras, , perlaikymas 1. I rodykite teigini : Teiginys. Jei X t, t, Ito procesas ir f C 3 (IR), tai f ( ) ( ) t X t f X = f ( ) X s dxs. 2. Raskite reguliaru atsitiktini procesa A t, t, su kuriuo atsitiktinis procesas M t = tbt 2 A t, t, būtu martingalas. Ats.: A t = (B2 s + s) ds. 3. X t, t, stochastinės diferencialinės lygties dx t = X t dt + X t db t su pradine sa lyga X = x IR sprendinys. Raskite EXt 3, t. Ats.: EXt 3 = x 3, t. 4. Raskite lim t + EX5 t, jei X t lygties dx t = X t dt + db t su pradine sa lyga X = 1 sprendinys. Ats.:. 5. Stochastinės diferencialinės lygties dx t = b(x t ) dt + X t db t, X = x, silpnoji aproksimacija {X h, h > } apibrėžiama lygybėmis X h = x, X h (k+1)h = Xh kh + b(x h kh)h + ax h kh ξ k h, k =, 1, 2,... ; čia {ξ k } nepriklausomu tolygiai pasiskirsčiusiu intervale [ 1, 1] atsitiktiniu dydžiu seka. Parinkite parametro a reikšme, su kuria ši aproksimacija būtu pirmos eilės. Ats.: a = 1/ 3.
30 Stochastinės analizės egzaminas MIF magistrantūra, FDM I kursas, 28/9 m.m., rudens semestras, I rodykite teigini : Tarkime, kad b: [, ) IR IR, o funkcija σ = σ(s, x), (s, x) [, ) IR, yra dukart tolydiai diferencijuojama. Jei atsitiktinis procesas X t, t, yra Ito lygties X t = x + ( b + 1 ) 2 σσ x (s, X s ) ds + σ(s, X s ) db s, t, sprendinys, tai jis yra Stratonovičiaus lygties X t = x + sprendinys. b(s, X s ) ds + σ(s, X s ) db s, t, 2. Parinkite funkcija f(s), s, taip, kad atsitiktinis procesas X t = t 2 B t + f(s)b s ds, t, būtu martingalas. Ats.: f(s) = 2s. 3. X t, t, stochastinės diferencialinės (CIR) lygties dx t = (1 X t ) dt+ X t db t su pradine sa lyga X = x sprendinys. Raskite EX 2 t, t. Ats.: EX 2 t = (x 1)e t + (x 2 3x )e 2t. 4. Ar galima λ IR parinkti taip, kad difuzinio proceso, apibrėžto Ferhiulsto lygtimi dx t = (λ X t )X t dt + X t db t, X = x >, stacionarusis tankis sutaptu su difuzijos, apibrėžtos CIR lygtimi dx t = (1 X t ) dt + X t db t, X = x >, stacionariuoju tankiu? Ats.: Galima, λ = 3/2. 5. Nagrinėkime stochastinės diferencialinės lygties dx t = μx t dt + σx t db t, X = x, silpna sias aproksimacijas {X h, h > }, turinčias pavidala X h = x, X h (k+1)h = Xh kh μx h khh σx h khδb k + a(x h kh)δb 2 k, k =, 1, 2,.... Ar galima parinkti funkcija a(x), x IR, taip, kad aproksimacija būtu pirmos eilės? Pastaba. Čia ΔB k = B (k+1)h B kh. Ats.: Galima, a(x) = 2μx.
31 Stochastinės analizės 1/2 egzamino bandymas MIF magistrantūra, FDM, I kursas, 28 m.m., rudens semestras, f L 2 [, ), t.y. f : [, ) IR mati (neatsitiktinė) funkcija ir f 2 (t) dt < +. Nesinaudodami 3.8a teorema, i rodykite, kad ) E (B t f(s) db s = f(s) ds, t. 2. X t, t, stochastinės diferencialinės lygties dx t = X t db t su pradine sa lyga X = x sprendinys. Raskite EX 2 t ir EX 3 t, t.
32 Stochastinės analizės egzaminas MIF magistrantūra, I kursas, 27/8 m.m., rudens semestras, I rodykite teorema ir jos išvada : Teorema. Sakykime, X = {X x } homogeninis difuzinis procesas, apibrėžiamas lygtimi dx t = b(x t ) dt + σ(x t ) db t. Jei funkcija f Cb 2 (IR), tai f priklauso proceso X generatoriaus A apibrėžimo sričiai D A ir Af = bf σ2 f. Be to, su kiekviena tokia funkcija yra teisinga Dynkino formulė Ef(X x t ) = f(x) + E Af(X x s ) ds, t. Išvada. Sakykime, X = {X x } homogeninis difuzinis procesas su generatoriumi A ir f C 2 b (IR). Pažymėkime u(t, x) = T tf(x) = Ef(X x t ), (t, x) IR + IR. Tada funkcija u yra lygties dalinėmis išvestinėmis su pradine sa lyga u t = Au, u(, x) = f(x) sprendinys. Čia operatorius A taikomas funkcijos u = u(t, x) argumento x atžvilgiu. 2. Ar egzistuoja tokia parametro a IR reikšmė, su kuria atsitiktinis procesas X t = B 3 t + atb t, t, yra martingalas? Ats.: a = Kiekvienam atsitiktiniam laiptiniam procesui X S b [, T ] teisinga nelygybė ( T ) 4 ( T ) 2 E X s db s CE Xs 2 ds su C = 36 (3.5.5 teiginys). Kokia mažiausia galima C reikšmė šioje nelygybėje, kai X neatsitiktinė laiptinė funkcija? Ats.: C = Ar gali tikimybė { T P X s db s > T X s db s } būti lygi? 1? 1/2? (Atsakymus pagri skite.) Ats.: Galimi visi atvejai. 5. Nagrinėkime stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x, tokio pavidalo aproksimacija {X h, h > }: X h = x, X h (k+1)h = Xh kh + c k b(x h kh)h + d k σ(x h kh)δb k, k =, 1, 2,.... Kuriais iš šiu atveju ji yra yra pirmos eilės silpnoji aproksimacija: a) c k = 1, d k = 1; b) c k = 1, d k = 1; c) c k = 1, d k = 1; d) c k = 1, d k = 1; e) c k = 1, d k = ( 1) k? (Atsakymus pagri skite.) Ats.: a), b), e).
33 Stochastinės analizės 1/2 egzamino MIF magistrantūra, FDM, I kursas, 27/8 m.m., 1 semestras, Ar atsitiktinis procesas X t = B 3 t tb t, t, yra martingalas? 2. X t stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t su pradine sa lyga X = 1/2 sprendinys. Ar gali būti, kad P{ X t < 1} = 1 su visais t > ir kartu P{ X t > 1 ε} > su visais t > ir ε >? (Jei ne pagri skite, jei taip pateikite pavyzdi.)
34 Stochastinės analizės egzaminas MIF magistrantūra, I kursas, 26/7 m.m., 2 semestras, , perlaikymas 1. I rodykite teigini : Teiginys. Jei X t, t, Ito procesas ir f C 3 (IR), tai f ( ) ( ) t X t f X = f ( ) X s dxs. 2. Raskite stochastini integrala Bse 2 B s db s. 3. X t stochastinės diferencialinės lygties sprendinys. Ar gali būti, kad P{ X t < 1} = 1 visais t > ir kartu P{ X t > 1 ε} > visais t > ir ε >? 4. Raskite lygties dx t = b(x t ) dt 2X t db t poslinkio koeficienta b(x), jei žinoma, kad jos sprendinio trečiasis laipsnis M t = X 3 t, t, yra martingalas. 5. Parašykite Markovo proceso X t = arctg (1 + B t ), t, generatoriu.
35 Stochastinės analizės egzaminas MIF magistrantūra, I kursas, 26/7 m.m., 2 semestras, Ito ir Stratonovičiaus integralu Ito proceso atžvilgiu apibrėžimai. I rodykite šiu integralu sa ryši Y X = Y X X, Y. I rodykite šias šiu integralu savybes: W (Z X) = (W Z) X; W (Z X) = (W Z) X. 2. Raskite stochastini integrala B s e B s db s. 3. Atsitiktinis procesas X t, t, tenkina stochastine diferencialine lygti (SDL) X t = 1 2 Xs 3 ds + 4 X s db s, t. Parašykite SDL (integraliniu pavidalu), kuria tenkina atsitiktinis procesas Y t = X 2 t +1, t. 4. Raskite lygties dx t = b(x t ) dt + X t db t poslinkio koeficienta b(x), jei žinoma, kad jos sprendinio kvadratas M t = X 2 t, t, yra martingalas. 5. Ar gali difuzinio proceso stacionarusis tankis turėti daugiau kaip du lokaliuosius maksimumus? (Jei taip, pateikite toki procesa apibrėžiančios SDL pavyzdi ; jei ne, pagri skite)
36 Stochastinės analizės i skaita (1/2 egzamino) MIF magistrantūra, I kursas, 26/7 m.m., 1 semestras, Raskite stochastini integrala sin(b s + 2s) db s. 2. Atsitiktinis procesas X t, t, tenkina stochastine diferencialine lygti (SDL) X t = 2 + (1 X s ) ds + Xs db s, t. Parašykite SDL, kuria tenkina atsitiktinis procesas Y t = X t, t.
37 Stochastinės analizės egzaminas MIF magistrantūra, I kursas, 25/6 m.m., 2 semestras, , perlaikymas 1. I rodykite teigini : Teiginys. Jei X t, t, Ito procesas ir F C 3 (IR), tai F ( ) ( ) t X t F X = F ( ) X s dxs. 2. Remiantis Dūbo nelygybe (3.8.6 ), E sup t T B 2 t 4T. I rodykite, kad E sup t T B 2 t 2T. Patarimas. Jums gali praversti paprasta lygybė E sup t T B 2 t = max{(sup t T B t ) 2, (inf t T B t ) 2 }. 3. Parašykite stochastine diferencialine lygti (integraliniu pavidalu), kuria tenkina atsitiktinis procesas X t = arctg (1 + B t ), t. 4. Ar gali du skirtingi difuziniai procesai turėti ta pati stacionaru ji tanki? (Jei ne, pagri skite; jei taip, pateikite pavyzdi.) 5. Ar gali Eulerio aproksimacija būti kokios nors stochastinės diferencialinės lygties (SDL) stiprioji 1-os eilės aproksimacija? 2-ios eilės? (Jei ne, pagri skite; jei taip, pateikite tokios SDL pavyzdi (pavyzdžius).)
38 Stochastinės analizės egzaminas MIF magistrantūra, I kursas, 25/6 m.m., 2 semestras, Martingalo apibrėžimas. I rodykite, kad atsitiktinis procesas ( ) 2 N t := X s db s Xs 2 ds, t [, T ], yra martingalas, jei X H 2 [, T ]. 2. Ar gali stochastinis integralas T X t db t būti teigiamas (su tikimybe 1), jei a) X laiptinis procesas? b) bendru atveju? (Jei ne, pagri sti; jei taip, pateikti pavyzdi (pavyzdžius).) 3. Patikrinkite, kad atsitiktinis procesas X t := tg (π/4 + B t ), t, yra stochastinės diferencialinės lygties dx t = X t (1 + X 2 t ) dt + (1 + X 2 t ) db t su pradine sa lyga X = 1 sprendinys. 4. Išspre skite stochastine diferencialine lygti X t = x + cos X s sin 3 X s ds kai a) x =, b) x = π/2, c) x = 3π/2. sin 2 X s db s, t, 5. Stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x, silpnoji aproksimacija {X h, h > } apibrėžiama lygybėmis X h = x, X h (k+1)h = Xh kh + b(x h kh)h + σ(x h kh)ξ k h, k =, 1, 2,.... Čia {ξ k } nepriklausomu vienodai pasiskirsčiusiu atsitiktiniu dydžiu seka su P{ξ k = } = 1 2 ir P{ξ k = a} = P{ξ k = a} = 1 4. Raskite a >, su kuriuo ši aproksimacija yra pirmos eilės.
39 Stochastinės analizės i skaita (1/2 egzamino) MIF magistrantūra, I kursas, 25/6 m.m., 1 semestras, Sakykime, Δ n = { = t n < t n 1 < < t n k n = T }, n IN, bet kokia intervalo [, T ] skaidiniu seka, su kuria diametras Δ n := max i t n i+1 tn i, kai n. Raskite P lim n i (ΔX i ) 2 = P lim n jei X t = exp{2b t 3t}, t. k n 1 i= ( X(t n i+1 ) X(t n i ) ) 2, 2. X toks suderintas atsitiktinis procesas, kad E T X2 t dt >. Ar gali Ito procesas Y t := X s db s, t [, T ], būti aprėžtas intervale [, T ]? (Jei ne, pagri sti; jei taip, pateikti pavyzdi.)
40 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 24/5 m.m., 2 semestras, , perlaikymas 1. Bet kokiam Ito procesui Y su Y = pažymėkime E(Y ) t := exp{y t 1 2 Y t} (procesas E(Y ) vadinamas proceso Y stochastine eksponente). I rodykite šias stochastiniu eksponenčiu savybes: 1) jei Y yra Ito procesas, tai procesas X := E(Y ) yra lygties X t = 1 + X s dy s, t, sprendinys; 2) jei Y ir Z du Ito procesai, Y = Z =, tai E(Y )E(Z) = E(Y + Z + Y, Z ); 3) jei Y Ito procesas su Y =, tai E(Y ) 1 = E( Y + Y ). 2. Sakykime, Δ n = { = t n < t n 1 < < t n k n = T }, n IN, bet kokia intervalo [, T ] skaidiniu seka, su kuria diametras Δ n := max i t n i+1 tn i, kai n. Tarkime, kad X ir Y du Brauno judesiai (nebūtinai nepriklausomi). Ar gali sumos ΔX i ΔY i = i k n 1 i= ( X(t n i+1 ) X(t n i ) )( Y (t n i+1) Y (t n i ) ), kai n, konverguoti pagal tikimybe i a) T/2? b) T? (Jei ne, pagri skite; jei taip pateikte pavyzdi arba pavyzdžius) 3. Raskite ( ) 2, ( 3 E B s ds E B s ds) ir E(sin B t ), t. 4. Stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x, silpnoji aproksimacija {X h, h > } apibrėžiama lygybėmis X h = x, X h (k+1)h = Xh kh + b(x h kh)h + σ(x h kh)ξ k h, k =, 1, 2,.... Čia {ξ k } nepriklausomu tolygiai pasiskirsčiusiu intervale [ a, a] atsitiktiniu dydžiu seka. Raskite a >, su kuriuo ši aproksimacija yra pirmos eilės. 5. Parašykite stochastine diferencialine lygti, kuria tenkina Ito procesas X t = Φ 2 t, t. Čia Φ TSDL dφ t = a(t)φ t dt + b(t)φ t db t sprendinys su pradine sa lyga Φ = 1.
41 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 24/5 m.m., 2 semestras, Stratonovičiaus integralo apibrėžimas. I rodykite šias jo savybes: 1) Y X t = Y X t X, Y t; 2) Z (Y X) t = (ZY ) X t ; 3) Y X, Ỹ X t = (Y Ỹ ) X, X t. 2. Sakykime, Δ n = { = t n < t n 1 < < t n k n = T }, n IN, bet kokia intervalo [, T ] skaidiniu seka, su kuria diametras Δ n := max i t n i+1 tn i, kai n. Tarkime, kad X ir Y du nepriklausomi Brauno judesiai. I rodykite, kad ΔX i ΔY i = i k n 1 i= ( X(t n i+1 ) X(t n i ) )( Y (t n i+1) Y (t n i ) ) pagal tikimybe, kai n. (Kitaip tariant, dvieju nepriklausomu Brauno judesiu kovariacija lygi.) 3. Raskite E B s ds, ( 2 ( E B s ds) 3 ir E B s ds) t. 4. Tarkime, kad f i C[, ), i = 1, 2, 3, 4. I rodykite, kad stochastinė diferencialinė lygtis X t = x + turi vieninteli sprendini. (f 1 (t)x t + f 2 (t)) dt + (f 3 (t)x t + f 4 (t)) db t, t, 5. Stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x, silpnoji aproksimacija {X h, h > } apibrėžiama lygybėmis X h = x, X h (k+1)h = Xh kh + b(x h kh)h + σ(x h kh)ξ k h, k =, 1, 2,.... Čia {ξ k } nepriklausomu tolygiai pasiskirsčiusiu intervale [ a, a] atsitiktiniu dydžiu seka. Raskite a >, su kuriuo ši aproksimacija yra pirmos eilės.
42 Stochastinės analizės i skaita (1/2 egzamino) MIF magistrantūra, I kursas, 24/5 m.m., 1 semestras, I rodykite, kad P{B t, t [, T ]} = su bet kokiu T >. Čia B t, t, Brauno judesys. 2. Sugalvokite toki Ito procesu sekos {X n } ir Ito proceso X pavyzdi, kad: 1) X n X tolygiai baigtiniuose intervaluose, t.y. su visais T > beveik tikrai sup Xt n X t, n ; t [,T ] 2) X n X.
43 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 23/4 m.m., 2 semestras, I rodykite, kad jei f Cb 3 (IR), tai f(b t ) = f() + f (B s ) db s f (B s ) ds, t. 2. Parašykite stochastine diferencialine lygti (integraliniu pavidalu), kuria tenkina atsitiktinis procesas X t = 1/(2 + e 3B t ), t. 3. I rodykite, kad atsitiktinis procesas X t := B2 s ds, t, turi baigtine variacija kiekviename intervale [, T ]. Raskite jos vidurki. 4. X stochastinės diferencialinės lyties dx t = X 2 t db t X 2 t dt, t, su pradine sa lyga X = sprendinys, f(t) := EXt 3, t. I rodykite, kad sup f (t) < Atsitiktinis procesas X t, t, tenkina stochastine diferencialine lygti X t = X s ds + B t, t. Raskite X t pasiskirstymo tankio p t riba, kai t. t
44 Stochastinės analizės i skaita (1/2 egzamino) MIF magistrantūra, I kursas, 23/4 m.m., 1 semestras, Pateikite pavyzdi tokio tolydaus atsitiktinio proceso X t, t, kad d 1) X t == B t su visais t ; 2) proceso X trajektorijos kiekviename intervale [, T ] turi baigtine variacija. 2. Pažymėkime X x t, t, stochastinės diferencialinės lygties dx t = b(x t ) dt + σ(x t ) db t, X = x, su koeficientais b ir σ, tenkinančiais Lipšico sa lyga, sprendini. I rodykite, kad Xt x X x t pagal tikimybe, kai x x, su visais t (tolydumas pradinės sa lygos atžvilgiu). Pastaba. Abiejuose uždaviniuose B t, t, Brauno judesys.
45 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 22/3 m.m., 2 semestras, , 1 perlaikymas 1. I rodykite teorema ir jos išvada : Teorema. Sakykime, X = {X x } homogeninis difuzinis procesas, apibrėžiamas lygtimi dx t = b(x t ) dt + σ(x t ) db t. Jei funkcija f C 2 (IR) turi aprėžtas pirma ja ir antra ja išvestines, tai f priklauso proceso X generatoriaus A apibrėžimo sričiai D A ir Af = bf σ2 f. Be to, su kiekviena tokia funkcija yra teisinga Dynkino formulė Ef(X x t ) = f(x) + E Af(X x s ) ds, t. Išvada. Sakykime, X = {X x } homogeninis difuzinis procesas su generatoriumi A ir f C 2 b (IR). Pažymėkime u(t, x) = T tf(x) = Ef(X x t ), (t, x) IR + IR. Tada funkcija u yra lygties dalinėmis išvestinėmis su pradine sa lyga u t = Au, u(, x) = f(x) sprendinys. Čia operatorius A taikomas funkcijos u = u(t, x) argumento x atžvilgiu. 2. Raskite riba I := L 2 - lim n k=1 n [ 1 ( k 2 n) B + 2 ( k 1 )][ 3 B n B 2( k n ) B 2( k 1 )]. n 3. Pažymėkime τ := min{t : B t = 1}. I rodykite, kad Eτ = +. Patarimas. Pritaikykite stochastiniu integralu savybes integralui 1I [,τ] (t) db t. 4. Tarkime, kad X t, t, yra lygties X t = 2 + X s ds + X s db s sprendinys. Raskite ( ) E Xt 3 6 Xs 3 ds, t. 5. Sugalvokite stochastine diferencialine lygti ir jos sprendinio X aproksimacija X h, h >, kuri: 1) yra trečios eilės silpnoji aproksimacija intervale [, 1], t.y. su visomis f C b (IR) Ef(X h 1 ) Ef(X 1 ) = O(h 3 ), kai h ; 2) nėra jokios teigiamos eilės stiprioji aproksimacija intervale [, 1], tiksliau, su visais α > E X h 1 X 1 /h α +, kai h.
46 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 22/3 m.m., 2 semestras, I rodykite teigini : Teiginys. Jei X t, t, Ito procesas ir F C 2,3 ([, ) IR) (t.y. F = F (t, x), t, x IR, yra dukart tolydžiai diferencijuojama pagal pirma ji argumenta t ir triskart pagal antra ji x), tai F ( ) ( ) t t, X t F, X = F x( ) s, Xs dxs + F s( s, Xs ) ds. 2. Raskite riba I := L 2 - lim n n k=1 ( k B n)[ B 2( k n ) B 2( k 1 )]. n 3. Pažymėkime τ := min{t : B t = 1}. Tada B τ = 1 b.t. ir todėl EB τ = 1. Kita vertus, B τ = τ db t = 1I [,τ] (t) db t ir todėl EB τ = (3.8a arba 3.8b teorema). Kur klaida? 4. Tarkime, kad X t, t, stochastinės diferencialinės lygties dx t = X t dt + X t db t, X = 1, sprendinys. I rodykite, kad atsitiktinis procesas M t := X 3 t 6 yra martingalas. X 3 s ds, t, 5. Sugalvokite stochastine diferencialine lygti ir jos sprendinio X aproksimacija X h, h >, kuri: 1) yra antros eilės silpnoji aproksimacija, t.y. su visais T > ir visomis f C b (IR) Ef(X h T ) Ef(X T ) = O(h 2 ), kai h ; 2) nėra jokios teigiamos eilės stiprioji aproksimacija, tiksliau, su visais T > ir α > E X h T X T /h α +, kai h.
47 Stochastinės analizės i skaita MIF magistrantūra, I kursas, 22/3 m.m., 1 semestras, Raskite riba I := L 2 - lim n n k=1 B 2( k )[ ( k B B n n) ( k 1 n )]. 2. Išspre skite stochastine diferencialine lygti X t = 1 + (2X s 3Xs 4 ) ds + 5 X s db s. Pastaba. Abiejuose uždaviniuose B t, t, Brauno judesys.
48 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 21/2 m.m., 2 semestras, , 4 perlaikymas 1. I rodykite šias laiptiniu stochastiniu procesu stochastinio integralo Brauno judesio atžvilgiu savybes: 1) E T X t db t =. ( T ) 2 T 2) E X t db t = E Xt 2 dt. ( T T ) 3) E X t db t Y t db t = E T X t Y t dt. 2. Raskite E Bs 3 dy s, jei Y t = B 2 B t. 3. Tarkime, kad {B n } reguliariu ju procesu seka, konverguojanti i Brauno judesi B tolygiai kompaktiškuose intervaluose. Pažymėkime X n stochastinės diferencialinės lygties dx n t = X n t db n t X n t db t, X n = 1/2, sprendini. Raskite riba X t := lim n Xn t, t. 4. I rodykite, kad jei X, Y H 2 [, ) ir α, β IR, tai (αx t + βy t ) db t = α X t db t + β Y t db t. 5. Tarkime, kad X yra Ito procesas, Y ir Z yra lygčiu dy t = Y t dx t ir dz t = Z t dx t su pradinėmis sa lygomis Y = 2 ir Z = 1/2 sprendiniai. Parašykite stochastine diferencialine lygti, kuria tenkina atsitiktinis procesas W t := Y t Z t, t.
49 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 2 semestras, , 3 perlaikymas 1. I rodykite teigini : Teiginys. Jei b: [, ) IR IR, o funkcija σ = σ(s, x), (s, x) [, ) IR, yra dukart tolydžiai diferencijuojama, tai kiekvienas Stratonovičiaus lygties X t = x + b(s, X s ) ds + sprendinys yra Ito lygties X t = x + sprendinys. 2. Raskite σ(s, X s ) db s, t, ( b + 1 ) 2 σσ x (s, X s ) ds + σ(s, X s ) db s, t, B 2 s dy s, jei Y t = B 2 s db s. 3. Tarkime, kad {B n } reguliariu ju procesu seka, konverguojanti i Brauno judesi B tolygiai kompaktiškuose intervaluose. Pažymėkime X n lygties X n t = 1 + X n s db n s X n s db s sprendini. Raskite riba X t := lim n Xn t, t. 4. I rodykite nelygybe E B 2 s db s t 3/2, t. 5. Tarkime, kad X yra Ito procesas, Y ir Z yra lygčiu dy t = Y t dx t ir dz t = Z t dx t su pradinėmis sa lygomis Y = Z = 1 sprendiniai. I rodykite, kad W t := Y t Z t yra lygties dw t = W t d X t su pradine sa lyga W = 1 sprendinys.
50 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 2 semestras, , 2 perlaikymas 1. Bet kokiam Ito procesui Y su Y = pažymėkime E(Y ) t := exp{y t 1 2 Y t} (procesas E(Y ) vadinamas proceso Y stochastine eksponente). I rodykite šias stochastiniu eksponenčiu savybes: 1) jei Y yra Ito procesas, tai procesas X := E(Y ) yra lygties X t = 1 + X s dy s, t, sprendinys; 2) jei Y ir Z du Ito procesai, Y = Z =, tai E(Y )E(Z) = E(Y + Z + Y, Z ); 3) jei Y Ito procesas su Y =, tai E(Y ) 1 = E( Y + Y ). 2. Išspre skite lygti X t = B t + X s db s, t. 3. Tarkime, kad {B n } reguliariu ju procesu seka, konverguojanti i Brauno judesi B tolygiai kompaktiškuose intervaluose. Pažymėkime X n stochastinės diferencialinės lygties dxt n = Xt n d(b n B) t, X n = 1, sprendini. Raskite riba X t := lim n Xn t, t. 4. Raskite B (B B) t, t. 5. Parašykite Markovo proceso X t = e 2B t+3t, t, generatoriu.
51 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 2 semestras, , perlaikymas sesijos metu 1. Bet kokiam Ito procesui Y su Y = pažymėkime E(Y ) t := exp{y t 1 2 Y t} (procesas E(Y ) vadinamas proceso Y stochastine eksponente). I rodykite šias stochastiniu eksponenčiu savybes: 1). jei Y yra Ito procesas, tai procesas X := E(Y ) yra lygties X t = 1 + X s dy s, t, sprendinys; 2) jei Y ir Z du Ito procesai, Y = Z =, tai E(Y )E(Z) = E(Y + Z + Y, Z ); 3) jei Y Ito procesas su Y =, tai E(Y ) 1 = E( Y + Y ). 2. Raskite EX 3 t, t, jei X stochastinės diferencialinės lygties dx t = X t dt + db t, X = 1, sprendinys. 3. Tarkime, kad {B n } reguliariu ju procesu seka, konverguojanti i Brauno judesi B tolygiai kompaktiškuose intervaluose. Pažymėkime X n stochastinės diferencialinės lygties dx n t = X n t dt + X n t d(b B n ) t, X n = 1, sprendini. Raskite riba 4. Raskite X t := lim n Xn t, t. B 2 s db 2 s, t. 5. Parašykite Stratonovičiaus stochastine diferencialine lygti, kurios sprendinys yra atsitiktinis procesas X t = B 3 t, t. Ar tai vienintelis šios lygties sprendinys?
52 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 2 semestras, I rodykite teigini : Teiginys. Jei difuzinis procesas X, apibrėžiamas stochastine diferencialine lygtimi dx t = b(x t ) dt + σ(x t ) db t, (I) arba dx t = b(x t ) dt + σ(x t ) db t, (S) turi stacionaru ji tanki p intervale (a, b) ir σ(x) > su visais x (a, b), tai p turi pavidala p (x) = N { x σ ν (x) exp 2 c b(u) } σ 2 (u) du, x (a, b); čia (I) lygčiai ν = 2, (S) lygčiai ν = 1, c bet koks taškas iš intervalo (a, b), N normuojanti konstanta, su kuria b a p (x) dx = 1. Pastaba. Čia laikoma, kad koeficientai b ir σ yra pakankamai,,geri, kad p tenkintu tiesiogine Kolmogorovo lygti. 2. Raskite EX t, t, jei X stochastinės diferencialinės lygties dx t = (X t + 1) dt + sprendinys. X 2 t + 1 db t, X = 1, 3. Išspre skite Stratonovičiaus stochastine diferencialine lygti dx t = (2X t 3X 2 t ) dt + 4X t db t, X = X t := B s ds, Y t := s db s, t. Raskite E X s dy s. 5. Tarkime, kad X t, t, Ito procesas ir Y t := dx s 1 + X 2 s X s d X s (1 + X 2 s ) 2, t. I rodykite, kad E Y t < π, t.
53 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 2 semestras, , perlaikymas sesijos metu 1. I rodykite teigini : Teiginys. Jei b: [, ) IR IR, o funkcija σ = σ(s, x), (s, x) [, ) IR, yra dukart tolydžiai diferencijuojama, tai kiekvienas Stratonovičiaus lygties X t = x + b(s, X s ) ds + sprendinys yra Ito lygties X t = x + sprendinys. σ(s, X s ) db s, t, ( b + 1 ) 2 σσ x (s, X s ) ds + σ(s, X s ) db s, t, 2. Ar gali Brauno judesio trajektorija (su teigiama tikimybe) tenkinti Lipšico sa lyga kokiame nors baigtiniame intervale? (Iš Brauno judesio trajektoriju nediferencijuojamumo neišplaukia, kad jos netenkina Lipšico sa lygos.) Priminimas: sakoma, kad funkcija f : [a, b] IR tenkina Lipšico sa lyga (intervale [a, b]), jei egzistuoja konstanta C, su kuria f(t) f(s) C t s, t, s [a, b]. 3. Raskite cos B s db s ir cos B s db s, t. 4. Su bet kokia f C 2 b (IR) pažymėkime a(t, x) := Ef(xeB t t ), (t, x) [, ) IR. I rodykite, kad funkcija a tenkina diferencialine lygti 5. a t(t, x) = 1 2 xa x(t, x) x2 a xx(t, x).
54 Stochastinės analizės egzamino klausimai MIF magistrantūra, I kursas, 2 semestras, I rodykite teorema ir jos išvada : Teorema. Sakykime, X = {X x } homogeninis difuzinis procesas, apibrėžiamas lygtimi dx t = b(x t ) dt + σ(x t ) db t. Jei funkcija f C 2 (IR) turi aprėžtas pirma ja ir antra ja išvestines, tai f priklauso proceso X generatoriaus A apibrėžimo sričiai D A ir Af = bf σ2 f. Be to, su kiekviena tokia funkcija teisinga lygybė (Dynkino formulė) Ef(X x t ) = f(x) + E Af(X x s ) ds, t. Išvada. Sakykime, X = {X x } homogeninis difuzinis procesas su generatoriumi A ir f C 2 b (IR). Pažymėkime u(t, x) = T tf(x) = Ef(X x t ), (t, x) IR + IR. Tada funkcija u yra lygties dalinėmis išvestinėmis su pradine sa lyga u t = Au, u(, x) = f(x) sprendinys. Čia operatorius A taikomas funkcijos u = u(t, x) argumento x atžvilgiu. 2. Sakykime, Δ n = { = t n < t n 1 < < t n k n = T }, n IN, bet kokia intervalo [, T ] skaidiniu seka, su kuria diametras Δ n := max i t n i+1 tn i, kai n. Su bet kokiais Ito procesais X ir Y raskite riba k n 1 P- lim Y (t n i ) ( X(t n i+1) X(t n i ) ) 3. n i= 3. Raskite E B 4, B 2 t, t. 4. Patikrinkite, kad atsitiktinis procesas x exp{t + B t } X t := 1 + 2x, t, 2 t exp{2(s + B s)} ds yra stochastinės diferencialinės lygties X t = x + (X s X 3 s ) ds + sprendinys. 5. I rodykite, kad lygties dalinėmis išvestinėmis X s db s, t, 2 u(t, x) = x u(t, x) + x2 u(t, x), (t, x) [, ) IR, t x x2 su pradine sa lyga u(, x) = f(x) (f Cb 2 (IR)) sprendinys yra u(t, x) = 1 ( ) f xe y 2t e y2 /2 dy, (t, x) (, ) IR. 2π
Theoretical Tutorial Session 2
 1 / 36 Theoretical Tutorial Session 2 Xiaoming Song Department of Mathematics Drexel University July 27, 216 Outline 2 / 36 Itô s formula Martingale representation theorem Stochastic differential equations
1 / 36 Theoretical Tutorial Session 2 Xiaoming Song Department of Mathematics Drexel University July 27, 216 Outline 2 / 36 Itô s formula Martingale representation theorem Stochastic differential equations
I forgot to mention last time: in the Ito formula for two standard processes, putting
 I forgot to mention last time: in the Ito formula for two standard processes, putting dx t = a t dt + b t db t dy t = α t dt + β t db t, and taking f(x, y = xy, one has f x = y, f y = x, and f xx = f yy
I forgot to mention last time: in the Ito formula for two standard processes, putting dx t = a t dt + b t db t dy t = α t dt + β t db t, and taking f(x, y = xy, one has f x = y, f y = x, and f xx = f yy
Bernardo D Auria Stochastic Processes /10. Notes. Abril 13 th, 2010
 1 Stochastic Calculus Notes Abril 13 th, 1 As we have seen in previous lessons, the stochastic integral with respect to the Brownian motion shows a behavior different from the classical Riemann-Stieltjes
1 Stochastic Calculus Notes Abril 13 th, 1 As we have seen in previous lessons, the stochastic integral with respect to the Brownian motion shows a behavior different from the classical Riemann-Stieltjes
p 1 ( Y p dp) 1/p ( X p dp) 1 1 p
 Doob s inequality Let X(t) be a right continuous submartingale with respect to F(t), t 1 P(sup s t X(s) λ) 1 λ {sup s t X(s) λ} X + (t)dp 2 For 1 < p
Doob s inequality Let X(t) be a right continuous submartingale with respect to F(t), t 1 P(sup s t X(s) λ) 1 λ {sup s t X(s) λ} X + (t)dp 2 For 1 < p
The concentration of a drug in blood. Exponential decay. Different realizations. Exponential decay with noise. dc(t) dt.
 The concentration of a drug in blood Exponential decay C12 concentration 2 4 6 8 1 C12 concentration 2 4 6 8 1 dc(t) dt = µc(t) C(t) = C()e µt 2 4 6 8 1 12 time in minutes 2 4 6 8 1 12 time in minutes
The concentration of a drug in blood Exponential decay C12 concentration 2 4 6 8 1 C12 concentration 2 4 6 8 1 dc(t) dt = µc(t) C(t) = C()e µt 2 4 6 8 1 12 time in minutes 2 4 6 8 1 12 time in minutes
Stochastic Differential Equations
 CHAPTER 1 Stochastic Differential Equations Consider a stochastic process X t satisfying dx t = bt, X t,w t dt + σt, X t,w t dw t. 1.1 Question. 1 Can we obtain the existence and uniqueness theorem for
CHAPTER 1 Stochastic Differential Equations Consider a stochastic process X t satisfying dx t = bt, X t,w t dt + σt, X t,w t dw t. 1.1 Question. 1 Can we obtain the existence and uniqueness theorem for
Stochastic Calculus February 11, / 33
 Martingale Transform M n martingale with respect to F n, n =, 1, 2,... σ n F n (σ M) n = n 1 i= σ i(m i+1 M i ) is a Martingale E[(σ M) n F n 1 ] n 1 = E[ σ i (M i+1 M i ) F n 1 ] i= n 2 = σ i (M i+1 M
Martingale Transform M n martingale with respect to F n, n =, 1, 2,... σ n F n (σ M) n = n 1 i= σ i(m i+1 M i ) is a Martingale E[(σ M) n F n 1 ] n 1 = E[ σ i (M i+1 M i ) F n 1 ] i= n 2 = σ i (M i+1 M
Introduction to numerical simulations for Stochastic ODEs
 Introduction to numerical simulations for Stochastic ODEs Xingye Kan Illinois Institute of Technology Department of Applied Mathematics Chicago, IL 60616 August 9, 2010 Outline 1 Preliminaries 2 Numerical
Introduction to numerical simulations for Stochastic ODEs Xingye Kan Illinois Institute of Technology Department of Applied Mathematics Chicago, IL 60616 August 9, 2010 Outline 1 Preliminaries 2 Numerical
Turinys. Geometrinės diferencialinių lygčių teorijos savokos. Diferencialinės lygties sprendiniai. Pavyzdžiai. CIt, (- 00,0) C'It, (0, (0);
 Turinys In this chapter we illustrate the qualitative approach to differential equations and introduce some key ideas such as phase portraits and qualitative equivalence Geometrinės diferencialinių lygčių
Turinys In this chapter we illustrate the qualitative approach to differential equations and introduce some key ideas such as phase portraits and qualitative equivalence Geometrinės diferencialinių lygčių
Lecture 12: Diffusion Processes and Stochastic Differential Equations
 Lecture 12: Diffusion Processes and Stochastic Differential Equations 1. Diffusion Processes 1.1 Definition of a diffusion process 1.2 Examples 2. Stochastic Differential Equations SDE) 2.1 Stochastic
Lecture 12: Diffusion Processes and Stochastic Differential Equations 1. Diffusion Processes 1.1 Definition of a diffusion process 1.2 Examples 2. Stochastic Differential Equations SDE) 2.1 Stochastic
Stochastic Differential Equations.
 Chapter 3 Stochastic Differential Equations. 3.1 Existence and Uniqueness. One of the ways of constructing a Diffusion process is to solve the stochastic differential equation dx(t) = σ(t, x(t)) dβ(t)
Chapter 3 Stochastic Differential Equations. 3.1 Existence and Uniqueness. One of the ways of constructing a Diffusion process is to solve the stochastic differential equation dx(t) = σ(t, x(t)) dβ(t)
MA8109 Stochastic Processes in Systems Theory Autumn 2013
 Norwegian University of Science and Technology Department of Mathematical Sciences MA819 Stochastic Processes in Systems Theory Autumn 213 1 MA819 Exam 23, problem 3b This is a linear equation of the form
Norwegian University of Science and Technology Department of Mathematical Sciences MA819 Stochastic Processes in Systems Theory Autumn 213 1 MA819 Exam 23, problem 3b This is a linear equation of the form
Exercises. T 2T. e ita φ(t)dt.
 Exercises. Set #. Construct an example of a sequence of probability measures P n on R which converge weakly to a probability measure P but so that the first moments m,n = xdp n do not converge to m = xdp.
Exercises. Set #. Construct an example of a sequence of probability measures P n on R which converge weakly to a probability measure P but so that the first moments m,n = xdp n do not converge to m = xdp.
1. Stochastic Processes and filtrations
 1. Stochastic Processes and 1. Stoch. pr., A stochastic process (X t ) t T is a collection of random variables on (Ω, F) with values in a measurable space (S, S), i.e., for all t, In our case X t : Ω S
1. Stochastic Processes and 1. Stoch. pr., A stochastic process (X t ) t T is a collection of random variables on (Ω, F) with values in a measurable space (S, S), i.e., for all t, In our case X t : Ω S
Solution for Problem 7.1. We argue by contradiction. If the limit were not infinite, then since τ M (ω) is nondecreasing we would have
 362 Problem Hints and Solutions sup g n (ω, t) g(ω, t) sup g(ω, s) g(ω, t) µ n (ω). t T s,t: s t 1/n By the uniform continuity of t g(ω, t) on [, T], one has for each ω that µ n (ω) as n. Two applications
362 Problem Hints and Solutions sup g n (ω, t) g(ω, t) sup g(ω, s) g(ω, t) µ n (ω). t T s,t: s t 1/n By the uniform continuity of t g(ω, t) on [, T], one has for each ω that µ n (ω) as n. Two applications
MSH7 - APPLIED PROBABILITY AND STOCHASTIC CALCULUS. Contents
 MSH7 - APPLIED PROBABILITY AND STOCHASTIC CALCULUS ANDREW TULLOCH Contents 1. Lecture 1 - Tuesday 1 March 2 2. Lecture 2 - Thursday 3 March 2 2.1. Concepts of convergence 2 3. Lecture 3 - Tuesday 8 March
MSH7 - APPLIED PROBABILITY AND STOCHASTIC CALCULUS ANDREW TULLOCH Contents 1. Lecture 1 - Tuesday 1 March 2 2. Lecture 2 - Thursday 3 March 2 2.1. Concepts of convergence 2 3. Lecture 3 - Tuesday 8 March
Random Variables. Random variables. A numerically valued map X of an outcome ω from a sample space Ω to the real line R
 In probabilistic models, a random variable is a variable whose possible values are numerical outcomes of a random phenomenon. As a function or a map, it maps from an element (or an outcome) of a sample
In probabilistic models, a random variable is a variable whose possible values are numerical outcomes of a random phenomenon. As a function or a map, it maps from an element (or an outcome) of a sample
Bernardo D Auria Stochastic Processes /12. Notes. March 29 th, 2012
 1 Stochastic Calculus Notes March 9 th, 1 In 19, Bachelier proposed for the Paris stock exchange a model for the fluctuations affecting the price X(t) of an asset that was given by the Brownian motion.
1 Stochastic Calculus Notes March 9 th, 1 In 19, Bachelier proposed for the Paris stock exchange a model for the fluctuations affecting the price X(t) of an asset that was given by the Brownian motion.
Brownian Motion. 1 Definition Brownian Motion Wiener measure... 3
 Brownian Motion Contents 1 Definition 2 1.1 Brownian Motion................................. 2 1.2 Wiener measure.................................. 3 2 Construction 4 2.1 Gaussian process.................................
Brownian Motion Contents 1 Definition 2 1.1 Brownian Motion................................. 2 1.2 Wiener measure.................................. 3 2 Construction 4 2.1 Gaussian process.................................
Weak convergence and large deviation theory
 First Prev Next Go To Go Back Full Screen Close Quit 1 Weak convergence and large deviation theory Large deviation principle Convergence in distribution The Bryc-Varadhan theorem Tightness and Prohorov
First Prev Next Go To Go Back Full Screen Close Quit 1 Weak convergence and large deviation theory Large deviation principle Convergence in distribution The Bryc-Varadhan theorem Tightness and Prohorov
SDE Coefficients. March 4, 2008
 SDE Coefficients March 4, 2008 The following is a summary of GARD sections 3.3 and 6., mainly as an overview of the two main approaches to creating a SDE model. Stochastic Differential Equations (SDE)
SDE Coefficients March 4, 2008 The following is a summary of GARD sections 3.3 and 6., mainly as an overview of the two main approaches to creating a SDE model. Stochastic Differential Equations (SDE)
Stability of Stochastic Differential Equations
 Lyapunov stability theory for ODEs s Stability of Stochastic Differential Equations Part 1: Introduction Department of Mathematics and Statistics University of Strathclyde Glasgow, G1 1XH December 2010
Lyapunov stability theory for ODEs s Stability of Stochastic Differential Equations Part 1: Introduction Department of Mathematics and Statistics University of Strathclyde Glasgow, G1 1XH December 2010
Mathematical Methods for Neurosciences. ENS - Master MVA Paris 6 - Master Maths-Bio ( )
 Mathematical Methods for Neurosciences. ENS - Master MVA Paris 6 - Master Maths-Bio (2014-2015) Etienne Tanré - Olivier Faugeras INRIA - Team Tosca November 26th, 2014 E. Tanré (INRIA - Team Tosca) Mathematical
Mathematical Methods for Neurosciences. ENS - Master MVA Paris 6 - Master Maths-Bio (2014-2015) Etienne Tanré - Olivier Faugeras INRIA - Team Tosca November 26th, 2014 E. Tanré (INRIA - Team Tosca) Mathematical
Partial Differential Equations with Applications to Finance Seminar 1: Proving and applying Dynkin s formula
 Partial Differential Equations with Applications to Finance Seminar 1: Proving and applying Dynkin s formula Group 4: Bertan Yilmaz, Richard Oti-Aboagye and Di Liu May, 15 Chapter 1 Proving Dynkin s formula
Partial Differential Equations with Applications to Finance Seminar 1: Proving and applying Dynkin s formula Group 4: Bertan Yilmaz, Richard Oti-Aboagye and Di Liu May, 15 Chapter 1 Proving Dynkin s formula
An adaptive numerical scheme for fractional differential equations with explosions
 An adaptive numerical scheme for fractional differential equations with explosions Johanna Garzón Departamento de Matemáticas, Universidad Nacional de Colombia Seminario de procesos estocásticos Jointly
An adaptive numerical scheme for fractional differential equations with explosions Johanna Garzón Departamento de Matemáticas, Universidad Nacional de Colombia Seminario de procesos estocásticos Jointly
Infinite-dimensional methods for path-dependent equations
 Infinite-dimensional methods for path-dependent equations (Università di Pisa) 7th General AMaMeF and Swissquote Conference EPFL, Lausanne, 8 September 215 Based on Flandoli F., Zanco G. - An infinite-dimensional
Infinite-dimensional methods for path-dependent equations (Università di Pisa) 7th General AMaMeF and Swissquote Conference EPFL, Lausanne, 8 September 215 Based on Flandoli F., Zanco G. - An infinite-dimensional
Solutions to the Exercises in Stochastic Analysis
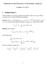 Solutions to the Exercises in Stochastic Analysis Lecturer: Xue-Mei Li 1 Problem Sheet 1 In these solution I avoid using conditional expectations. But do try to give alternative proofs once we learnt conditional
Solutions to the Exercises in Stochastic Analysis Lecturer: Xue-Mei Li 1 Problem Sheet 1 In these solution I avoid using conditional expectations. But do try to give alternative proofs once we learnt conditional
Harnack Inequalities and Applications for Stochastic Equations
 p. 1/32 Harnack Inequalities and Applications for Stochastic Equations PhD Thesis Defense Shun-Xiang Ouyang Under the Supervision of Prof. Michael Röckner & Prof. Feng-Yu Wang March 6, 29 p. 2/32 Outline
p. 1/32 Harnack Inequalities and Applications for Stochastic Equations PhD Thesis Defense Shun-Xiang Ouyang Under the Supervision of Prof. Michael Röckner & Prof. Feng-Yu Wang March 6, 29 p. 2/32 Outline
Verona Course April Lecture 1. Review of probability
 Verona Course April 215. Lecture 1. Review of probability Viorel Barbu Al.I. Cuza University of Iaşi and the Romanian Academy A probability space is a triple (Ω, F, P) where Ω is an abstract set, F is
Verona Course April 215. Lecture 1. Review of probability Viorel Barbu Al.I. Cuza University of Iaşi and the Romanian Academy A probability space is a triple (Ω, F, P) where Ω is an abstract set, F is
ODE Homework Solutions of Linear Homogeneous Equations; the Wronskian
 ODE Homework 3 3.. Solutions of Linear Homogeneous Equations; the Wronskian 1. Verify that the functions y 1 (t = e t and y (t = te t are solutions of the differential equation y y + y = 0 Do they constitute
ODE Homework 3 3.. Solutions of Linear Homogeneous Equations; the Wronskian 1. Verify that the functions y 1 (t = e t and y (t = te t are solutions of the differential equation y y + y = 0 Do they constitute
Brownian Motion. An Undergraduate Introduction to Financial Mathematics. J. Robert Buchanan. J. Robert Buchanan Brownian Motion
 Brownian Motion An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan 2010 Background We have already seen that the limiting behavior of a discrete random walk yields a derivation of
Brownian Motion An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan 2010 Background We have already seen that the limiting behavior of a discrete random walk yields a derivation of
A Class of Fractional Stochastic Differential Equations
 Vietnam Journal of Mathematics 36:38) 71 79 Vietnam Journal of MATHEMATICS VAST 8 A Class of Fractional Stochastic Differential Equations Nguyen Tien Dung Department of Mathematics, Vietnam National University,
Vietnam Journal of Mathematics 36:38) 71 79 Vietnam Journal of MATHEMATICS VAST 8 A Class of Fractional Stochastic Differential Equations Nguyen Tien Dung Department of Mathematics, Vietnam National University,
Errata for Stochastic Calculus for Finance II Continuous-Time Models September 2006
 1 Errata for Stochastic Calculus for Finance II Continuous-Time Models September 6 Page 6, lines 1, 3 and 7 from bottom. eplace A n,m by S n,m. Page 1, line 1. After Borel measurable. insert the sentence
1 Errata for Stochastic Calculus for Finance II Continuous-Time Models September 6 Page 6, lines 1, 3 and 7 from bottom. eplace A n,m by S n,m. Page 1, line 1. After Borel measurable. insert the sentence
Approximation of random dynamical systems with discrete time by stochastic differential equations: I. Theory
 Random Operators / Stochastic Eqs. 15 7, 5 c de Gruyter 7 DOI 1.1515 / ROSE.7.13 Approximation of random dynamical systems with discrete time by stochastic differential equations: I. Theory Yuri A. Godin
Random Operators / Stochastic Eqs. 15 7, 5 c de Gruyter 7 DOI 1.1515 / ROSE.7.13 Approximation of random dynamical systems with discrete time by stochastic differential equations: I. Theory Yuri A. Godin
MA 8101 Stokastiske metoder i systemteori
 MA 811 Stokastiske metoder i systemteori AUTUMN TRM 3 Suggested solution with some extra comments The exam had a list of useful formulae attached. This list has been added here as well. 1 Problem In this
MA 811 Stokastiske metoder i systemteori AUTUMN TRM 3 Suggested solution with some extra comments The exam had a list of useful formulae attached. This list has been added here as well. 1 Problem In this
Lecture two. January 17, 2019
 Lecture two January 17, 2019 We will learn how to solve rst-order linear equations in this lecture. Example 1. 1) Find all solutions satisfy the equation u x (x, y) = 0. 2) Find the solution if we know
Lecture two January 17, 2019 We will learn how to solve rst-order linear equations in this lecture. Example 1. 1) Find all solutions satisfy the equation u x (x, y) = 0. 2) Find the solution if we know
Mean-square Stability Analysis of an Extended Euler-Maruyama Method for a System of Stochastic Differential Equations
 Mean-square Stability Analysis of an Extended Euler-Maruyama Method for a System of Stochastic Differential Equations Ram Sharan Adhikari Assistant Professor Of Mathematics Rogers State University Mathematical
Mean-square Stability Analysis of an Extended Euler-Maruyama Method for a System of Stochastic Differential Equations Ram Sharan Adhikari Assistant Professor Of Mathematics Rogers State University Mathematical
A Concise Course on Stochastic Partial Differential Equations
 A Concise Course on Stochastic Partial Differential Equations Michael Röckner Reference: C. Prevot, M. Röckner: Springer LN in Math. 1905, Berlin (2007) And see the references therein for the original
A Concise Course on Stochastic Partial Differential Equations Michael Röckner Reference: C. Prevot, M. Röckner: Springer LN in Math. 1905, Berlin (2007) And see the references therein for the original
Some Properties of NSFDEs
 Chenggui Yuan (Swansea University) Some Properties of NSFDEs 1 / 41 Some Properties of NSFDEs Chenggui Yuan Swansea University Chenggui Yuan (Swansea University) Some Properties of NSFDEs 2 / 41 Outline
Chenggui Yuan (Swansea University) Some Properties of NSFDEs 1 / 41 Some Properties of NSFDEs Chenggui Yuan Swansea University Chenggui Yuan (Swansea University) Some Properties of NSFDEs 2 / 41 Outline
Bridging the Gap between Center and Tail for Multiscale Processes
 Bridging the Gap between Center and Tail for Multiscale Processes Matthew R. Morse Department of Mathematics and Statistics Boston University BU-Keio 2016, August 16 Matthew R. Morse (BU) Moderate Deviations
Bridging the Gap between Center and Tail for Multiscale Processes Matthew R. Morse Department of Mathematics and Statistics Boston University BU-Keio 2016, August 16 Matthew R. Morse (BU) Moderate Deviations
for all f satisfying E[ f(x) ] <.
![for all f satisfying E[ f(x) ] <. for all f satisfying E[ f(x) ] <.](/thumbs/86/94473244.jpg) . Let (Ω, F, P ) be a probability space and D be a sub-σ-algebra of F. An (H, H)-valued random variable X is independent of D if and only if P ({X Γ} D) = P {X Γ}P (D) for all Γ H and D D. Prove that if
. Let (Ω, F, P ) be a probability space and D be a sub-σ-algebra of F. An (H, H)-valued random variable X is independent of D if and only if P ({X Γ} D) = P {X Γ}P (D) for all Γ H and D D. Prove that if
LAN property for sde s with additive fractional noise and continuous time observation
 LAN property for sde s with additive fractional noise and continuous time observation Eulalia Nualart (Universitat Pompeu Fabra, Barcelona) joint work with Samy Tindel (Purdue University) Vlad s 6th birthday,
LAN property for sde s with additive fractional noise and continuous time observation Eulalia Nualart (Universitat Pompeu Fabra, Barcelona) joint work with Samy Tindel (Purdue University) Vlad s 6th birthday,
Branching Processes II: Convergence of critical branching to Feller s CSB
 Chapter 4 Branching Processes II: Convergence of critical branching to Feller s CSB Figure 4.1: Feller 4.1 Birth and Death Processes 4.1.1 Linear birth and death processes Branching processes can be studied
Chapter 4 Branching Processes II: Convergence of critical branching to Feller s CSB Figure 4.1: Feller 4.1 Birth and Death Processes 4.1.1 Linear birth and death processes Branching processes can be studied
Homogenization with stochastic differential equations
 Homogenization with stochastic differential equations Scott Hottovy shottovy@math.arizona.edu University of Arizona Program in Applied Mathematics October 12, 2011 Modeling with SDE Use SDE to model system
Homogenization with stochastic differential equations Scott Hottovy shottovy@math.arizona.edu University of Arizona Program in Applied Mathematics October 12, 2011 Modeling with SDE Use SDE to model system
Lecture 4: Ito s Stochastic Calculus and SDE. Seung Yeal Ha Dept of Mathematical Sciences Seoul National University
 Lecture 4: Ito s Stochastic Calculus and SDE Seung Yeal Ha Dept of Mathematical Sciences Seoul National University 1 Preliminaries What is Calculus? Integral, Differentiation. Differentiation 2 Integral
Lecture 4: Ito s Stochastic Calculus and SDE Seung Yeal Ha Dept of Mathematical Sciences Seoul National University 1 Preliminaries What is Calculus? Integral, Differentiation. Differentiation 2 Integral
lim n C1/n n := ρ. [f(y) f(x)], y x =1 [f(x) f(y)] [g(x) g(y)]. (x,y) E A E(f, f),
![lim n C1/n n := ρ. [f(y) f(x)], y x =1 [f(x) f(y)] [g(x) g(y)]. (x,y) E A E(f, f), lim n C1/n n := ρ. [f(y) f(x)], y x =1 [f(x) f(y)] [g(x) g(y)]. (x,y) E A E(f, f),](/thumbs/76/73980372.jpg) 1 Part I Exercise 1.1. Let C n denote the number of self-avoiding random walks starting at the origin in Z of length n. 1. Show that (Hint: Use C n+m C n C m.) lim n C1/n n = inf n C1/n n := ρ.. Show that
1 Part I Exercise 1.1. Let C n denote the number of self-avoiding random walks starting at the origin in Z of length n. 1. Show that (Hint: Use C n+m C n C m.) lim n C1/n n = inf n C1/n n := ρ.. Show that
Strong Markov property of determinantal processes associated with extended kernels
 Strong Markov property of determinantal processes associated with extended kernels Hideki Tanemura Chiba university (Chiba, Japan) (November 22, 2013) Hideki Tanemura (Chiba univ.) () Markov process (November
Strong Markov property of determinantal processes associated with extended kernels Hideki Tanemura Chiba university (Chiba, Japan) (November 22, 2013) Hideki Tanemura (Chiba univ.) () Markov process (November
Feller Processes and Semigroups
 Stat25B: Probability Theory (Spring 23) Lecture: 27 Feller Processes and Semigroups Lecturer: Rui Dong Scribe: Rui Dong ruidong@stat.berkeley.edu For convenience, we can have a look at the list of materials
Stat25B: Probability Theory (Spring 23) Lecture: 27 Feller Processes and Semigroups Lecturer: Rui Dong Scribe: Rui Dong ruidong@stat.berkeley.edu For convenience, we can have a look at the list of materials
Brownian motion. Samy Tindel. Purdue University. Probability Theory 2 - MA 539
 Brownian motion Samy Tindel Purdue University Probability Theory 2 - MA 539 Mostly taken from Brownian Motion and Stochastic Calculus by I. Karatzas and S. Shreve Samy T. Brownian motion Probability Theory
Brownian motion Samy Tindel Purdue University Probability Theory 2 - MA 539 Mostly taken from Brownian Motion and Stochastic Calculus by I. Karatzas and S. Shreve Samy T. Brownian motion Probability Theory
Problem 1. Construct a filtered probability space on which a Brownian motion W and an adapted process X are defined and such that
 Stochatic Calculu Example heet 4 - Lent 5 Michael Tehranchi Problem. Contruct a filtered probability pace on which a Brownian motion W and an adapted proce X are defined and uch that dx t = X t t dt +
Stochatic Calculu Example heet 4 - Lent 5 Michael Tehranchi Problem. Contruct a filtered probability pace on which a Brownian motion W and an adapted proce X are defined and uch that dx t = X t t dt +
Stochastic Processes. Monday, November 14, 11
 Stochastic Processes 1 Definition and Classification X(, t): stochastic process: X : T! R (, t) X(, t) where is a sample space and T is time. {X(, t) is a family of r.v. defined on {, A, P and indexed
Stochastic Processes 1 Definition and Classification X(, t): stochastic process: X : T! R (, t) X(, t) where is a sample space and T is time. {X(, t) is a family of r.v. defined on {, A, P and indexed
PROBABILITY: LIMIT THEOREMS II, SPRING HOMEWORK PROBLEMS
 PROBABILITY: LIMIT THEOREMS II, SPRING 218. HOMEWORK PROBLEMS PROF. YURI BAKHTIN Instructions. You are allowed to work on solutions in groups, but you are required to write up solutions on your own. Please
PROBABILITY: LIMIT THEOREMS II, SPRING 218. HOMEWORK PROBLEMS PROF. YURI BAKHTIN Instructions. You are allowed to work on solutions in groups, but you are required to write up solutions on your own. Please
Finite element approximation of the stochastic heat equation with additive noise
 p. 1/32 Finite element approximation of the stochastic heat equation with additive noise Stig Larsson p. 2/32 Outline Stochastic heat equation with additive noise du u dt = dw, x D, t > u =, x D, t > u()
p. 1/32 Finite element approximation of the stochastic heat equation with additive noise Stig Larsson p. 2/32 Outline Stochastic heat equation with additive noise du u dt = dw, x D, t > u =, x D, t > u()
A new approach for investment performance measurement. 3rd WCMF, Santa Barbara November 2009
 A new approach for investment performance measurement 3rd WCMF, Santa Barbara November 2009 Thaleia Zariphopoulou University of Oxford, Oxford-Man Institute and The University of Texas at Austin 1 Performance
A new approach for investment performance measurement 3rd WCMF, Santa Barbara November 2009 Thaleia Zariphopoulou University of Oxford, Oxford-Man Institute and The University of Texas at Austin 1 Performance
Random Variables. P(x) = P[X(e)] = P(e). (1)
![Random Variables. P(x) = P[X(e)] = P(e). (1) Random Variables. P(x) = P[X(e)] = P(e). (1)](/thumbs/86/94250597.jpg) Random Variables Random variable (discrete or continuous) is used to derive the output statistical properties of a system whose input is a random variable or random in nature. Definition Consider an experiment
Random Variables Random variable (discrete or continuous) is used to derive the output statistical properties of a system whose input is a random variable or random in nature. Definition Consider an experiment
Poisson Jumps in Credit Risk Modeling: a Partial Integro-differential Equation Formulation
 Poisson Jumps in Credit Risk Modeling: a Partial Integro-differential Equation Formulation Jingyi Zhu Department of Mathematics University of Utah zhu@math.utah.edu Collaborator: Marco Avellaneda (Courant
Poisson Jumps in Credit Risk Modeling: a Partial Integro-differential Equation Formulation Jingyi Zhu Department of Mathematics University of Utah zhu@math.utah.edu Collaborator: Marco Avellaneda (Courant
ECE 636: Systems identification
 ECE 636: Systems identification Lectures 3 4 Random variables/signals (continued) Random/stochastic vectors Random signals and linear systems Random signals in the frequency domain υ ε x S z + y Experimental
ECE 636: Systems identification Lectures 3 4 Random variables/signals (continued) Random/stochastic vectors Random signals and linear systems Random signals in the frequency domain υ ε x S z + y Experimental
For a stochastic process {Y t : t = 0, ±1, ±2, ±3, }, the mean function is defined by (2.2.1) ± 2..., γ t,
 CHAPTER 2 FUNDAMENTAL CONCEPTS This chapter describes the fundamental concepts in the theory of time series models. In particular, we introduce the concepts of stochastic processes, mean and covariance
CHAPTER 2 FUNDAMENTAL CONCEPTS This chapter describes the fundamental concepts in the theory of time series models. In particular, we introduce the concepts of stochastic processes, mean and covariance
Turinys. Kurso struktūra. 2 Diferencialinės lygtys. 4 Matematinių modelių pavyzdžiai
 Turins ir matematiniai modeliai 26 CHAPTER INTRODUCTION TO DIFFERENTIAL EQUATIONS paskaita Olga Štikonienė d Diferencialinių lgčių ir skaičiavimo matematikos d W. T katedra, MIF VU WHAT LIES AHEAD Throughout
Turins ir matematiniai modeliai 26 CHAPTER INTRODUCTION TO DIFFERENTIAL EQUATIONS paskaita Olga Štikonienė d Diferencialinių lgčių ir skaičiavimo matematikos d W. T katedra, MIF VU WHAT LIES AHEAD Throughout
BSDEs and PDEs with discontinuous coecients Applications to homogenization K. Bahlali, A. Elouain, E. Pardoux. Jena, March 2009
 BSDEs and PDEs with discontinuous coecients Applications to homogenization K. Bahlali, A. Elouain, E. Pardoux. Jena, 16-20 March 2009 1 1) L p viscosity solution to 2nd order semilinear parabolic PDEs
BSDEs and PDEs with discontinuous coecients Applications to homogenization K. Bahlali, A. Elouain, E. Pardoux. Jena, 16-20 March 2009 1 1) L p viscosity solution to 2nd order semilinear parabolic PDEs
Convoluted Brownian motions: a class of remarkable Gaussian processes
 Convoluted Brownian motions: a class of remarkable Gaussian processes Sylvie Roelly Random models with applications in the natural sciences Bogotá, December 11-15, 217 S. Roelly (Universität Potsdam) 1
Convoluted Brownian motions: a class of remarkable Gaussian processes Sylvie Roelly Random models with applications in the natural sciences Bogotá, December 11-15, 217 S. Roelly (Universität Potsdam) 1
Selected Exercises on Expectations and Some Probability Inequalities
 Selected Exercises on Expectations and Some Probability Inequalities # If E(X 2 ) = and E X a > 0, then P( X λa) ( λ) 2 a 2 for 0 < λ
Selected Exercises on Expectations and Some Probability Inequalities # If E(X 2 ) = and E X a > 0, then P( X λa) ( λ) 2 a 2 for 0 < λ
EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as
![EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as EEL 5544 Noise in Linear Systems Lecture 30. X (s) = E [ e sx] f X (x)e sx dx. Moments can be found from the Laplace transform as](/thumbs/85/92409620.jpg) L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
L30-1 EEL 5544 Noise in Linear Systems Lecture 30 OTHER TRANSFORMS For a continuous, nonnegative RV X, the Laplace transform of X is X (s) = E [ e sx] = 0 f X (x)e sx dx. For a nonnegative RV, the Laplace
Exercises in stochastic analysis
 Exercises in stochastic analysis Franco Flandoli, Mario Maurelli, Dario Trevisan The exercises with a P are those which have been done totally or partially) in the previous lectures; the exercises with
Exercises in stochastic analysis Franco Flandoli, Mario Maurelli, Dario Trevisan The exercises with a P are those which have been done totally or partially) in the previous lectures; the exercises with
Lecture # 37. Prof. John W. Sutherland. Nov. 28, 2005
 Lecture # 37 Prof. John W. Sutherland Nov. 28, 2005 Linear Regression 8 y 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 x Modeling To describe the data above, propose the model: y = B 0 + B 1 x + ε Fitted model will
Lecture # 37 Prof. John W. Sutherland Nov. 28, 2005 Linear Regression 8 y 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 x Modeling To describe the data above, propose the model: y = B 0 + B 1 x + ε Fitted model will
Formulas for probability theory and linear models SF2941
 Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
Formulas for probability theory and linear models SF2941 These pages + Appendix 2 of Gut) are permitted as assistance at the exam. 11 maj 2008 Selected formulae of probability Bivariate probability Transforms
1.1 Definition of BM and its finite-dimensional distributions
 1 Brownian motion Brownian motion as a physical phenomenon was discovered by botanist Robert Brown as he observed a chaotic motion of particles suspended in water. The rigorous mathematical model of BM
1 Brownian motion Brownian motion as a physical phenomenon was discovered by botanist Robert Brown as he observed a chaotic motion of particles suspended in water. The rigorous mathematical model of BM
Properties of Summation Operator
 Econ 325 Section 003/004 Notes on Variance, Covariance, and Summation Operator By Hiro Kasahara Properties of Summation Operator For a sequence of the values {x 1, x 2,..., x n, we write the sum of x 1,
Econ 325 Section 003/004 Notes on Variance, Covariance, and Summation Operator By Hiro Kasahara Properties of Summation Operator For a sequence of the values {x 1, x 2,..., x n, we write the sum of x 1,
Exact Simulation of Diffusions and Jump Diffusions
 Exact Simulation of Diffusions and Jump Diffusions A work by: Prof. Gareth O. Roberts Dr. Alexandros Beskos Dr. Omiros Papaspiliopoulos Dr. Bruno Casella 28 th May, 2008 Content 1 Exact Algorithm Construction
Exact Simulation of Diffusions and Jump Diffusions A work by: Prof. Gareth O. Roberts Dr. Alexandros Beskos Dr. Omiros Papaspiliopoulos Dr. Bruno Casella 28 th May, 2008 Content 1 Exact Algorithm Construction
(A n + B n + 1) A n + B n
 344 Problem Hints and Solutions Solution for Problem 2.10. To calculate E(M n+1 F n ), first note that M n+1 is equal to (A n +1)/(A n +B n +1) with probability M n = A n /(A n +B n ) and M n+1 equals
344 Problem Hints and Solutions Solution for Problem 2.10. To calculate E(M n+1 F n ), first note that M n+1 is equal to (A n +1)/(A n +B n +1) with probability M n = A n /(A n +B n ) and M n+1 equals
Optimization Theory. Linear Operators and Adjoints
 Optimization Theory Linear Operators and Adjoints A transformation T. : X Y y Linear Operators y T( x), x X, yy is the image of x under T The domain of T on which T can be defined : D X The range of T
Optimization Theory Linear Operators and Adjoints A transformation T. : X Y y Linear Operators y T( x), x X, yy is the image of x under T The domain of T on which T can be defined : D X The range of T
where r n = dn+1 x(t)
 Random Variables Overview Probability Random variables Transforms of pdfs Moments and cumulants Useful distributions Random vectors Linear transformations of random vectors The multivariate normal distribution
Random Variables Overview Probability Random variables Transforms of pdfs Moments and cumulants Useful distributions Random vectors Linear transformations of random vectors The multivariate normal distribution
Introduction to Random Diffusions
 Introduction to Random Diffusions The main reason to study random diffusions is that this class of processes combines two key features of modern probability theory. On the one hand they are semi-martingales
Introduction to Random Diffusions The main reason to study random diffusions is that this class of processes combines two key features of modern probability theory. On the one hand they are semi-martingales
ELEMENTS OF PROBABILITY THEORY
 ELEMENTS OF PROBABILITY THEORY Elements of Probability Theory A collection of subsets of a set Ω is called a σ algebra if it contains Ω and is closed under the operations of taking complements and countable
ELEMENTS OF PROBABILITY THEORY Elements of Probability Theory A collection of subsets of a set Ω is called a σ algebra if it contains Ω and is closed under the operations of taking complements and countable
Albert N. Shiryaev Steklov Mathematical Institute. On sharp maximal inequalities for stochastic processes
 Albert N. Shiryaev Steklov Mathematical Institute On sharp maximal inequalities for stochastic processes joint work with Yaroslav Lyulko, Higher School of Economics email: albertsh@mi.ras.ru 1 TOPIC I:
Albert N. Shiryaev Steklov Mathematical Institute On sharp maximal inequalities for stochastic processes joint work with Yaroslav Lyulko, Higher School of Economics email: albertsh@mi.ras.ru 1 TOPIC I:
Simulation of conditional diffusions via forward-reverse stochastic representations
 Weierstrass Institute for Applied Analysis and Stochastics Simulation of conditional diffusions via forward-reverse stochastic representations Christian Bayer and John Schoenmakers Numerical methods for
Weierstrass Institute for Applied Analysis and Stochastics Simulation of conditional diffusions via forward-reverse stochastic representations Christian Bayer and John Schoenmakers Numerical methods for
A Short Introduction to Diffusion Processes and Ito Calculus
 A Short Introduction to Diffusion Processes and Ito Calculus Cédric Archambeau University College, London Center for Computational Statistics and Machine Learning c.archambeau@cs.ucl.ac.uk January 24,
A Short Introduction to Diffusion Processes and Ito Calculus Cédric Archambeau University College, London Center for Computational Statistics and Machine Learning c.archambeau@cs.ucl.ac.uk January 24,
A Note on the Central Limit Theorem for a Class of Linear Systems 1
 A Note on the Central Limit Theorem for a Class of Linear Systems 1 Contents Yukio Nagahata Department of Mathematics, Graduate School of Engineering Science Osaka University, Toyonaka 560-8531, Japan.
A Note on the Central Limit Theorem for a Class of Linear Systems 1 Contents Yukio Nagahata Department of Mathematics, Graduate School of Engineering Science Osaka University, Toyonaka 560-8531, Japan.
Interest Rate Models:
 1/17 Interest Rate Models: from Parametric Statistics to Infinite Dimensional Stochastic Analysis René Carmona Bendheim Center for Finance ORFE & PACM, Princeton University email: rcarmna@princeton.edu
1/17 Interest Rate Models: from Parametric Statistics to Infinite Dimensional Stochastic Analysis René Carmona Bendheim Center for Finance ORFE & PACM, Princeton University email: rcarmna@princeton.edu
is well-defined, and is distributed according to a Cauchy law If t 0, compute P( X t Y ).
 MA 539 - PROBLEM LIST DISCRETE TIME PROCESSES AND BROWNIAN MOTION Problem 1. Let γ a,b be the function: 1. Gaussian vectors and CLT γ a,b (x) = 1 Γ(a)b a xa 1 e x/b 1 {x>}, where a, b > and Γ(x) = e t
MA 539 - PROBLEM LIST DISCRETE TIME PROCESSES AND BROWNIAN MOTION Problem 1. Let γ a,b be the function: 1. Gaussian vectors and CLT γ a,b (x) = 1 Γ(a)b a xa 1 e x/b 1 {x>}, where a, b > and Γ(x) = e t
Stochastic Viral Dynamics with Beddington-DeAngelis Functional Response
 Stochastic Viral Dynamics with Beddington-DeAngelis Functional Response Junyi Tu, Yuncheng You University of South Florida, USA you@mail.usf.edu IMA Workshop in Memory of George R. Sell June 016 Outline
Stochastic Viral Dynamics with Beddington-DeAngelis Functional Response Junyi Tu, Yuncheng You University of South Florida, USA you@mail.usf.edu IMA Workshop in Memory of George R. Sell June 016 Outline
Math 510 midterm 3 answers
 Math 51 midterm 3 answers Problem 1 (1 pts) Suppose X and Y are independent exponential random variables both with parameter λ 1. Find the probability that Y < 7X. P (Y < 7X) 7x 7x f(x, y) dy dx e x e
Math 51 midterm 3 answers Problem 1 (1 pts) Suppose X and Y are independent exponential random variables both with parameter λ 1. Find the probability that Y < 7X. P (Y < 7X) 7x 7x f(x, y) dy dx e x e
IEOR 4701: Stochastic Models in Financial Engineering. Summer 2007, Professor Whitt. SOLUTIONS to Homework Assignment 9: Brownian motion
 IEOR 471: Stochastic Models in Financial Engineering Summer 27, Professor Whitt SOLUTIONS to Homework Assignment 9: Brownian motion In Ross, read Sections 1.1-1.3 and 1.6. (The total required reading there
IEOR 471: Stochastic Models in Financial Engineering Summer 27, Professor Whitt SOLUTIONS to Homework Assignment 9: Brownian motion In Ross, read Sections 1.1-1.3 and 1.6. (The total required reading there
Controlled Diffusions and Hamilton-Jacobi Bellman Equations
 Controlled Diffusions and Hamilton-Jacobi Bellman Equations Emo Todorov Applied Mathematics and Computer Science & Engineering University of Washington Winter 2014 Emo Todorov (UW) AMATH/CSE 579, Winter
Controlled Diffusions and Hamilton-Jacobi Bellman Equations Emo Todorov Applied Mathematics and Computer Science & Engineering University of Washington Winter 2014 Emo Todorov (UW) AMATH/CSE 579, Winter
Second order weak Runge Kutta type methods for Itô equations
 Mathematics and Computers in Simulation 57 001 9 34 Second order weak Runge Kutta type methods for Itô equations Vigirdas Mackevičius, Jurgis Navikas Department of Mathematics and Informatics, Vilnius
Mathematics and Computers in Simulation 57 001 9 34 Second order weak Runge Kutta type methods for Itô equations Vigirdas Mackevičius, Jurgis Navikas Department of Mathematics and Informatics, Vilnius
Applications of Ito s Formula
 CHAPTER 4 Applications of Ito s Formula In this chapter, we discuss several basic theorems in stochastic analysis. Their proofs are good examples of applications of Itô s formula. 1. Lévy s martingale
CHAPTER 4 Applications of Ito s Formula In this chapter, we discuss several basic theorems in stochastic analysis. Their proofs are good examples of applications of Itô s formula. 1. Lévy s martingale
STOCHASTIC CALCULUS JASON MILLER AND VITTORIA SILVESTRI
 STOCHASTIC CALCULUS JASON MILLER AND VITTORIA SILVESTRI Contents Preface 1 1. Introduction 1 2. Preliminaries 4 3. Local martingales 1 4. The stochastic integral 16 5. Stochastic calculus 36 6. Applications
STOCHASTIC CALCULUS JASON MILLER AND VITTORIA SILVESTRI Contents Preface 1 1. Introduction 1 2. Preliminaries 4 3. Local martingales 1 4. The stochastic integral 16 5. Stochastic calculus 36 6. Applications
Derivation of Itô SDE and Relationship to ODE and CTMC Models
 Derivation of Itô SDE and Relationship to ODE and CTMC Models Biomathematics II April 23, 2015 Linda J. S. Allen Texas Tech University TTU 1 Euler-Maruyama Method for Numerical Solution of an Itô SDE dx(t)
Derivation of Itô SDE and Relationship to ODE and CTMC Models Biomathematics II April 23, 2015 Linda J. S. Allen Texas Tech University TTU 1 Euler-Maruyama Method for Numerical Solution of an Itô SDE dx(t)
Reflected Brownian Motion
 Chapter 6 Reflected Brownian Motion Often we encounter Diffusions in regions with boundary. If the process can reach the boundary from the interior in finite time with positive probability we need to decide
Chapter 6 Reflected Brownian Motion Often we encounter Diffusions in regions with boundary. If the process can reach the boundary from the interior in finite time with positive probability we need to decide
The multidimensional Ito Integral and the multidimensional Ito Formula. Eric Mu ller June 1, 2015 Seminar on Stochastic Geometry and its applications
 The multidimensional Ito Integral and the multidimensional Ito Formula Eric Mu ller June 1, 215 Seminar on Stochastic Geometry and its applications page 2 Seminar on Stochastic Geometry and its applications
The multidimensional Ito Integral and the multidimensional Ito Formula Eric Mu ller June 1, 215 Seminar on Stochastic Geometry and its applications page 2 Seminar on Stochastic Geometry and its applications
Solutions and Proofs: Optimizing Portfolios
 Solutions and Proofs: Optimizing Portfolios An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan Covariance Proof: Cov(X, Y) = E [XY Y E [X] XE [Y] + E [X] E [Y]] = E [XY] E [Y] E
Solutions and Proofs: Optimizing Portfolios An Undergraduate Introduction to Financial Mathematics J. Robert Buchanan Covariance Proof: Cov(X, Y) = E [XY Y E [X] XE [Y] + E [X] E [Y]] = E [XY] E [Y] E
Dynamical systems with Gaussian and Levy noise: analytical and stochastic approaches
 Dynamical systems with Gaussian and Levy noise: analytical and stochastic approaches Noise is often considered as some disturbing component of the system. In particular physical situations, noise becomes
Dynamical systems with Gaussian and Levy noise: analytical and stochastic approaches Noise is often considered as some disturbing component of the system. In particular physical situations, noise becomes
DISCRETE-TIME STOCHASTIC MODELS, SDEs, AND NUMERICAL METHODS. Ed Allen. NIMBioS Tutorial: Stochastic Models With Biological Applications
 DISCRETE-TIME STOCHASTIC MODELS, SDEs, AND NUMERICAL METHODS Ed Allen NIMBioS Tutorial: Stochastic Models With Biological Applications University of Tennessee, Knoxville March, 2011 ACKNOWLEDGEMENT I thank
DISCRETE-TIME STOCHASTIC MODELS, SDEs, AND NUMERICAL METHODS Ed Allen NIMBioS Tutorial: Stochastic Models With Biological Applications University of Tennessee, Knoxville March, 2011 ACKNOWLEDGEMENT I thank
On a class of stochastic differential equations in a financial network model
 1 On a class of stochastic differential equations in a financial network model Tomoyuki Ichiba Department of Statistics & Applied Probability, Center for Financial Mathematics and Actuarial Research, University
1 On a class of stochastic differential equations in a financial network model Tomoyuki Ichiba Department of Statistics & Applied Probability, Center for Financial Mathematics and Actuarial Research, University
Stochastic Calculus and Black-Scholes Theory MTH772P Exercises Sheet 1
 Stochastic Calculus and Black-Scholes Theory MTH772P Exercises Sheet. For ξ, ξ 2, i.i.d. with P(ξ i = ± = /2 define the discrete-time random walk W =, W n = ξ +... + ξ n. (i Formulate and prove the property
Stochastic Calculus and Black-Scholes Theory MTH772P Exercises Sheet. For ξ, ξ 2, i.i.d. with P(ξ i = ± = /2 define the discrete-time random walk W =, W n = ξ +... + ξ n. (i Formulate and prove the property
µ X (A) = P ( X 1 (A) )
 1 STOCHASTIC PROCESSES This appendix provides a very basic introduction to the language of probability theory and stochastic processes. We assume the reader is familiar with the general measure and integration
1 STOCHASTIC PROCESSES This appendix provides a very basic introduction to the language of probability theory and stochastic processes. We assume the reader is familiar with the general measure and integration
Multivariate Random Variable
 Multivariate Random Variable Author: Author: Andrés Hincapié and Linyi Cao This Version: August 7, 2016 Multivariate Random Variable 3 Now we consider models with more than one r.v. These are called multivariate
Multivariate Random Variable Author: Author: Andrés Hincapié and Linyi Cao This Version: August 7, 2016 Multivariate Random Variable 3 Now we consider models with more than one r.v. These are called multivariate
Gaussian processes for inference in stochastic differential equations
 Gaussian processes for inference in stochastic differential equations Manfred Opper, AI group, TU Berlin November 6, 2017 Manfred Opper, AI group, TU Berlin (TU Berlin) inference in SDE November 6, 2017
Gaussian processes for inference in stochastic differential equations Manfred Opper, AI group, TU Berlin November 6, 2017 Manfred Opper, AI group, TU Berlin (TU Berlin) inference in SDE November 6, 2017
Lecture 25: Review. Statistics 104. April 23, Colin Rundel
 Lecture 25: Review Statistics 104 Colin Rundel April 23, 2012 Joint CDF F (x, y) = P [X x, Y y] = P [(X, Y ) lies south-west of the point (x, y)] Y (x,y) X Statistics 104 (Colin Rundel) Lecture 25 April
Lecture 25: Review Statistics 104 Colin Rundel April 23, 2012 Joint CDF F (x, y) = P [X x, Y y] = P [(X, Y ) lies south-west of the point (x, y)] Y (x,y) X Statistics 104 (Colin Rundel) Lecture 25 April
Brownian Motion on Manifold
 Brownian Motion on Manifold QI FENG Purdue University feng71@purdue.edu August 31, 2014 QI FENG (Purdue University) Brownian Motion on Manifold August 31, 2014 1 / 26 Overview 1 Extrinsic construction
Brownian Motion on Manifold QI FENG Purdue University feng71@purdue.edu August 31, 2014 QI FENG (Purdue University) Brownian Motion on Manifold August 31, 2014 1 / 26 Overview 1 Extrinsic construction
