hal , version 1-30 Oct 2013
|
|
|
- Henry Lewis French
- 5 years ago
- Views:
Transcription
1 Noname manuscrp No. (wll be nsered by he edor) Adjon-based opmzaon on a newor of dscrezed scalar conservaon law PDEs wh applcaons o coordnaed ramp meerng ac Relly Wald Krchene Mara Laura Delle Monache Samha Samaranayae Paola Goan Alexandre M. Bayen Submed: Ocober 23, 2013 hal , verson 1-30 Oc 2013 Absrac The adjon mehod provdes a compuaonally effcen means of calculang he graden for applcaons n consraned opmzaon. In hs arcle, we consder a newor of scalar conservaon laws wh general opology, whose behavor s modfed by a se of conrol parameers n order o mnmze a gven objecve funcon. Afer dscrezng he correspondng paral dfferenal equaon models va he Godunov scheme, we deal he compuaon of he graden of he dscrezed sysem wh respec o he conrol parameers and show ha he complexy of s compuaon scales lnearly wh he number of dscree sae varables for newors of small verex degree. The mehod s appled o solve he problem of coordnaed ramp meerng on freeway newors. Numercal smulaons on he I15 freeway n Calforna demonsrae an mprovemen n performance and runnng me compared o exsng mehods. Keywords conrol of dscrezed PDEs, newor of hyperbolc conservaon laws, adjon based opmzaon, ransporaon engneerng, ramp meerng 1 Inroducon Newors of one-dmensonal conservaon laws, descrbed by sysems of nonlnear frs-order hyperbolc paral dfferenal equaons (PDEs), are an effcen framewor for modelng physcal phenomena, such as gas ppelne flow [1], supply chan [2], waer channels [3, 4], or freeway raffc evoluon [5, 6, 7]. Opmzaon and conrol of hese newors s an acve feld of research [8, 9, 10]. More generally, numerous echnques exs for he conrol of conservaon laws, such as, for example, bacseppng [11, 12], Lyapunov-based mehods [11], and opmal conrol mehods [13, 14, 15]. One such approach, nown as he adjon mehod, asusednopmalconrolandesmaonofpdeconsraned sysems, can be derved n varous ways dependng on he framewor of neres (PDE, dscrezaon of he PDE, or code mplemenng he dscrezaon of he PDE). The connuous adjon mehod [16, 8, 17, 18] operaes drecly on he PDE and a so-called adjon PDE sysem, whch when solved can be used o oban an explc expresson of he graden of he underlyng opmzaon problem. Conversely, he dscree adjon mehod [19, 8, 10] frs dscrezes a connuous-me PDE and hen requres he soluon of a se of lnear equaons o solve for he graden. Fnally, a hrd approach exss, whch uses auomac dfferenaon echnques o auomacally generae an adjon solver from he numercal represenaon of he forward sysem [20, 21]. Whle he connuous adjon formulaon resuls n a compac formulaon, beer nuon no he sysem s sensves wh respec o he objecve, and well-posedness of he conrol s soluon (when can be proved), s ofen dffcul o derve for sysems of hyperbolc nonlnear PDEs conrolled by boundary condons, when hese boundary condons have o be wren n he wea sense. Addonally, he connuous adjon mus evenually be dscrezed n order o produce numercal soluons for he opmzaon problem. Fnally, he dfferenaon of he forward PDE s somemes problemac due o he lac of regulary of he soluon [5, 6] whch maes he formal defnon of he adjon problem more dffcul. The dscree adjon approach derves he graden drecly from he dscrezed sysem, hus Unversy of Calforna, Bereley - Calforna, USA E-mal: jacdrellybereley.edu Inra Sopha Anpols - Méderranée, Sopha Anpols, France
2 hal , verson 1-30 Oc 2013 avodng worng drecly wh wea boundary condons n he connuous sysem [5, 6, 22]. Auomac dfferenaon echnques can smplfy he repeve seps of he dscree adjon dervaon, bu somemes a he cos of sub-opmal code mplemenaons wh respec o memory and CPU consumpon [23]. A more-dealed analyss of he rade-offs assocaed wh each mehod s gven n [23]. There exs many applcaons of he adjon mehod for conrol, opmzaon and esmaon of physcal sysems n engneerng. Shape opmzaon of arcraf [18, 24, 17] has appled he mehod effecvely o reduce he compuaonal cos n graden mehods assocaed wh he large number of opmzaon parameers. The echnque has also been appled n parameer denfcaon of bologcal sysems [25]. Sae esmaon problems can be phrased as opmal conrol problems by seng he unnown sae varables as conrol parameers and penalzng errors n resulng sae predcons from nown values. Ths approach has been appled o such problems as open waer sae esmaon [26, 27] and freeway raffc sae esmaon [28]. Snce conservaon laws may be nonlnear by naure and lead o non-convex or nonlnear formulaons of he correspondng opmzaon problem, fewer effcen opmzaon echnques exs for he dscrezed verson of hese problems han for convex problems for example. One approach s o approxmae he sysem wh a relaxed verson n order o use effcen lnear programmng echnques. In ransporaon, by relaxng he Godunov dscrezaon scheme, he lnearzaon approach was used n [29] for opmal ramp meerng, and n [30] for opmal roue assgnmen whch s exac when he relaxaon gap can be shown o be zero. The ramp meerng echnque n [31] uses an addonal conrol parameer (varable speed lms) o mmc he lnearzed freeway dynamcs. Whle he upsde of hese mehods s reduced compuaonal complexy and he guaranee of fndng a globally opmal soluon, he downsde s ha he model of he lnearzed physcal sysem may grealy dffer from he acual sysem o whch he conrol polces would be appled. Alernavely, nonlnear opmzaon echnques can be appled o he dscrezed sysem whou any modfcaon o he underlyng dynamcs. Ths approach leads o more expensve opmzaon algorhms, such as graden descen, and no guaranee of fndng a global opmum. One dffculy n hs approach comes n he compuaon of he graden, whch, f usng fne dfferences, requres a full forward-smulaon for each perurbaon of a conrol parameer. Ths approach s aen n [32, 33] o compue several ypes of decenralzed ramp meerng sraeges. The ncreased complexy of he fne dfferences approach for each addonal conrol parameer maes he mehod unsuable for real-me applcaon on moderaely-szed freeway newors. Ramp meerng s a common freeway conrol sraegy, provdng a means of dynamcally conrollng freeway hroughpu whou drecly mpedng manlne flow or mplemenng complex ollng sysems. Whle meerng sraeges have been developed usng mcroscopc models [34], mos sraeges are based off macroscopc sae parameers, such as vehcle densy and he densy s relaon o speed [35, 36, 37]. Reacve meerng sraeges [38, 39, 40] use feedbac from freeway loop deecors o arge a desred manlne densy, whle predcve meerng sraeges [33, 10, 29, 41] use a physcal model wh predced boundary flow daa o generae polces over a fne me horzon. Predcve mehods are ofen embedded whn a model predcve conrol loop o handle unceranes n he boundary daa and cumulave model errors [31]. Ths arcle develops a framewor for effcen conrol of dscrezed conservaon law PDE newors usng he adjon mehod [19, 42] va Godunov dscrezaon [43], whle dealng s applcaon o coordnaed ramp meerng on freeway newors. Noe ha he mehod can be exended whou sgnfcan dffculy o oher numercal schemes commonly used o dscreze hyperbolc PDEs. We show how he complexy of he graden compuaon n nonlnear opmal conrol problems can be grealy decreased by usng he dscree adjon mehod and explong he decouplng naure of he problem s newor srucure, leadng o effcen graden compuaon mehods. Afer gvng a general framewor for compung he graden over he class of scalar conservaon law newors, we show ha he sysem s paral dervaves have a sparsy srucure resulng n graden compuaon mes lnear n he number of sae and conrol varables for newors of small verex degree. The resuls are demonsraed by runnng a coordnaed ramp meerng sraegy on a 19 mle freeway srech n Calforna faser han real-me, whle gvng raffc performance superor o ha of sae of he ar praconers ools. The res of he arcle s organzed as follows. Secon 2 gves an overvew of scalar conservaon law newors and her dscrezaon va he Godunov mehod, whle nroducng he nonlnear, fne-horzon opmal conrol problem. Secon 3 deals he adjon mehod dervaon for hs class of problems and shows how can be used o compue he graden n lnear me n he number of dscree sae and conrol varables. Secon 4 shows how he adjon mehod can be appled o he problem of opmal coordnaed 2
3 ramp meerng, wh numercal resuls on a real freeway newor n Calforna shown n Secon 5. Fnally, some concludng remars are gven n Secon 6. 2 Prelmnares 2.1 Conservaon Law PDEs In hs paper we focus on scalar hyperbolc conservaon laws. In parcular, we consder he non-lnear ranspor equaon of he form: (, x)+ xf ( (, x)) = 0 (, x) 2 R + R (1) where = (, x) 2 R + s he scalar conserved quany and f : R +! R + s he flux funcon. Throughou he arcle we suppose ha f s a srcly concave funcon. The Cauchy problem o solve s hen + xf( ) =0, (, x) 2 R + R, (2) (0,x)= (x), x 2 R hal , verson 1-30 Oc 2013 where (x) s he nal condon. I can be shown ha here exss a unque wea enropy soluon for he Cauchy problem (2) as descrbed n Defnon 21. Defnon 21 A funcon 2 C 0 (R + ; L 1 loc\bv) s an admssble soluon o (2) f sasfes he Kružhov enropy condon [44] on (R + R),.e.,forevery 2 R and for all ' 2C 1 c (R 2 ; R + ), R + R ( ' +sgn( )(f( ) f())x')dxd + '(0,x)dx 0. (3) R For furher deals regardng he heory of hyperbolc conservaon laws we refer he reader o [5, 45]. Defnon 22 Remann Problem. A Remann problem s a Cauchy problem wh a pecewse-consan nal daum (called he Remann daa): (x) = ( x<0 + x 0 We denoe he correspondng self-smlar enropy wea soluons by W R 2.2 Newor of PDEs x ;, +. AneworsdefnedasaseofN lns I = {1,...,N}, wh juncons. Each juncon 2 s defned as he unon of wo non-empy ses: he se of n ncomng lns Inc () = 1,..., n Iand he se of m ougong lns Ou () = n +1,..., n +m I.Eachln 2Ihasanassocaedupsreamjuncon U 2 and downsream juncon D 2,andhasanassocaedspaaldoman(0,L ) over whch he evoluon of he sae on ln, (, x), solveshecauchyproblem: ( ( ) + f ( ) x =0 (0,x) = (x) where 2 BV \ L 1 loc (L ; R) s he nal condon on ln. Forsmplcyofnoaon,hssecon consders a sngle juncon 2 wh Inc () =(1,...,n) and Ou () =(n +1,...,n+ m). Remar 1 There s redundancy n he labelng of he juncons, f ln s drecly upsream of ln j, hen we have D = U j. See Fg. 2. Whle he dynamcs on each ln (, x) s deermned by (4), he dynamcs a juncons sll needs o be defned. (4) 3
4 Fg. 1: Soluon of boundary condons a juncon. The boundary condons (ˆ 1,...,ˆ 5) are produced by applyng he Remann solver o he nal condons, ( 1,..., 5). Defnon 23 Remann problem a juncons. A Remann problem a s a Cauchy problem correspondng o an nal daum ( 1,..., n+m) 2 R n+m whch s consan on each ln. Defnon 24 A Remann solver s a map ha assgns a soluon o each Remann nal daa. For each juncon s a funcon hal , verson 1-30 Oc 2013 RS : R m+n! R m+n ( 1,..., n+m) 7! RS ( 1,..., n+m) =(ˆ 1,...,ˆ n+m) where ˆ provdes he race for ln a he juncon for all me 0. For a ln 2 Inc (), hesoluon (, x) over s spaal doman x<0 s gven by he soluon o he followng Remann problem: 8 >< ( ) + f ( ) x =0 ( >: (0,x) = x<0 (5) ˆ x 0, The Remann problem for an ougong ln s defned smlarly, wh he excepon ha (0,x>0) = and (0,xapple 0) = ˆ. Fg. 1 gves a depcon of Remann soluon a he juncon. Noe ha he followng properes for he Remann Solver holds: All waves produced from he soluon o Remann problems on all lns, generaed by he boundary condons a a juncon, mus emanae ou from he juncon. Moreover, he soluon o he Remann problem on an ncomng ln mus produce waves wh negave speeds, whle he soluon on an ougong ln mus produce waves wh posve speed. The sum of all ncomng fluxes mus equal he sum of all ougong fluxes: X f (ˆ )= X f (ˆ j ). 2Inc() j2ou() Ths condon guaranees mass conservaon a juncons. The Remann solver mus produce self-smlar soluons,.e. RS (RS ( 1,..., n+m)) = RS ( 1,..., n+m) =(ˆ 1,...,ˆ n+m) The jusfcaon for hese condons can be found n [5]. 2.3 Godunov Dscrezaon In order o fnd approxmae soluons we use he classcal Godunov scheme [43]. We use he followng noaon: x j+ 1 are he cell nerfaces and = he me wh 2 N and j 2 Z. x j s he cener of he 2 cell, x = x j+ 1 x 2 j 1 he cell wdh, and s he me sep. 2 4
5 or or Fg. 2: Space dscrezaon for a ln 2I. Sep sze s unform x, whdscreevalue j represenng he sae beween x j 1 and x j. Godunov scheme for a sngle ln. The Godunov scheme s based on he soluons of exac Remann problems. The man dea of hs mehod s o approxmae he nal daum by a pecewse consan funcon, hen he correspondng Remann problems are solved exacly and a global soluon s found by pecng hem ogeher. Fnally one aes he mean on he cell and proceed by eraon. Gven (, x), he cell average of a me n he cell C j =]x j 1 2,x j+ 1 2 ] s gven by j = 1 x ˆ xj+ 1 2 x j 1 2 (,x)dx. (6) hal , verson 1-30 Oc 2013 Then we proceed as follows: 1. We solve he Remann problem a each cell nerface x j+ 1 wh nal daa ( j, j+1) Compue he cell average a me +1 n each compuaonal cell and oban +1 j. We remar ha waves n wo neghbourng cells do no nersec before f he followng Couran Fredrchs Lewy (CFL) condon holds, max apple x,where max =max f 0 (a) s he maxmum wave speed of he Remann soluon a he nerfaces. Godunov scheme can be expressed as follows: +1 j = j where g G s he Godunov numercal flux gven by g G : R R! R a x (gg ( j, j+1) g G ( j 1, j )), (7) j, j+1 7! g G j, j+1 = f(w R (0; j, j+1 )). Godunov scheme a juncons. The scheme jus dscussed apples o he case n whch a sngle cell s adjacen o anoher sngle cell. Ye, a juncons, a cell may share a boundary wh more han one cell. A more general Godunov flux can be derved for such cases. For ncomng lns near he juncon, we have: +1 L = L x (f(ˆ L ) g G ( L 1, L )), 2{1,...,n} where L are he number of cells for ln (see Fg. 2) and ˆ s he soluon of he Remann solver RS 1,..., n+m for ln a he juncon. The same can be done for he ougong lns: +1 1 = 1 x (gg ( 1, 2) f(ˆ 1)), 2{n +1,...,n+ m} Remar 2 Usng he Godunov scheme, each mesh grd a a gven can be seen as a node for a 1-o-1 juncon wh one ncomng and one ougong ln. I s herefore more convenen o consder ha every dscrezed cell s, raher, a ln wh boh an upsream and downsream juncon. Thus, we consder newors n whch he sae of each ln 2I a a me-sep 2{0,...,T 1} s represened by he sngle dscree value. 5
6 hal , verson 1-30 Oc 2013 Fg. 3: Self-smlar soluon for Remann problem wh nal daa j, j+1. The self-smlar soluon a x =0for he op dagram (.e. W R 0; j, j+1 ), gves he flux soluon o he dscrezed problem n he boom dagram. The prevous remar allows us o develop a generalzed updae sep for all dscree sae varables. We frs nroduce a defnon n order o reduce he cumbersome naure of he precedng noaon. Le he sae varables adjacen o a juncon 2 a a me-sep 2 {0,...,T 1} be represened as :=,..., 1 n +m.smlarly,welehesoluonofaremannsolverberepresenedasˆ := RS ( ). Then, for a ln 2Iwhupsreamanddownsream juncons, U and D,andme-sep 2{0,...,T 1}, heupdaesepbecomes: +1 = = f RS f RS x D U f ˆ x f ˆ D U where (s) s he h elemen of he uple s. ThsequaonshusageneralwayofwrngheGodunov scheme n a way whch apples everywhere, ncludng a juncons. (8) Worng drecly wh flux soluons a juncons. The equaons can be smplfed f we do no explcly represen he soluon of he Remann solver, ˆ, and, nsead, drecly calculae he flux soluon from he Remann daa. We denoe hs drec compuaon by g G, he Godunov flux soluon a a juncon: g G : R n +m! R n +m Ths gves a smplfed expressons for he updae sep: 7! f (RS ( )) = (f (ˆ 1),...,f(ˆ n+m)). (9) +1 = g G x D D g G U. (10) U Full dscree soluon mehod. We assume a dscree scalar hyperbolc newor of PDEs wh lns I and juncons,andanowndscreesaeame-sep, : 2I. The soluon mehod for advancng he dscree sysem forward one me-sep s gven n Algorhm (1), or alernavely Algorhm (2). 6
7 Algorhm 1 Remann solver updae procedure Inpu: nal sae a me =, : 2I Oupu: resulng sae a me =( +1)), +1 : 2I for juncon 2: # Apply Remann solver o ˆ = RS for ln 2I: # updae densy on ln wh juncon fluxes +1 = f ˆ x D f ˆ U Algorhm 1 aes as npu he sae a a me-sep for all lns : 2I and reurns he sae advanced by one me-sep +1 : 2I. The algorhm frs eraes over all juncons, calculangall he boundary condons, ˆ.Then,healgorhmeraesoveralllns 2Io compue he updaed sae +1 usng he prevously compued boundary condons, as n 8. hal , verson 1-30 Oc 2013 Algorhm 2 Godunov juncon flux updae procedure Inpu: nal sae a me =, : 2I Oupu: resulng sae a me =( +1)), +1 : 2I for ln 2I: # updae densy on ln wh drec Godonuv fluxes +1 = g G x D D g G U U Algorhm 2 s smlar o Algorhm 1, excep ha he boundary condons ˆ are no explcly compued, bu raher he Godunov flux soluon s used o updae he sae, as n 10. Algorhm 2 s more suable f a Godunov flux soluon s derved for solvng juncons, whle Algorhm 1 s more suable f one uses a Remann solver a juncons. 2.4 Sae, Conrol, and Governng Equaons The res of he arcle focuses on conrollng sysems of he form n Equaon (10) n whch some pars of he sae can be conrolled drecly (for example, n he form of boundary conrol). We wsh o solve he sysem n Algorhm 2 T me-seps forward,.e. we wsh o deermne he dscree sae values for all lns 2Iand all me-seps 2{0,...,T 1}. Furhermore,aeachme-sep, weassumeaseof conrol varables u 1,...,u M 2 R M ha nfluence he soluon of he Remann problems a juncons, where M s he number of conrolled values a each me-sep, and each conrol may be updaed a each me-sep. We assume ha a conrol may only nfluence a subse of juncons, whch s a reasonable assumpon f he conrols have some spaal localy. Thus, for a juncon 2,weassumewhoulossofgeneralyha asubseofheconrolparameers u j,...,u 1 j M 2 R M nfluence he soluon of he Remann solver. Smlar o he noaon developed for sae varables, for conrol varables, we defne u := u j,...,u 1 j M as he concaenaon of he conrol varables around he juncon. To accoun for he addon of conrols, we modfy he Remann problem a a juncon 2 a me-sep o be a funcon of he curren sae of connecng lns,andhecurrenconrolparameersu. Then usng he same noaon as before, we express he Remann solver as: RS : R n +m R M! R n +m, u 7! RS, u = ˆ. 7
8 We represen he enre sae of he solved sysem wh he vecor 2 R NT,wherefor 2Iand 2{0,...,T 1}, wehave N+ =.Smlarly,werepresenheenreconrolvecorbyu 2 R MT, where u M+j = u j. For each sae varable,wrehecorrespondngupdaeequaonh : h : R NT R MT! R (, u) 7! h (, u) =0. Ths aes he followng form: h (, u) = 1 + L f L f h 0 (, u) = 0 =0 (11) RS 1, u 1 D D D RS, u 1 U =08 2{2,...,T 1}, (12) 1 U U hal , verson 1-30 Oc 2013 or n erms of he Godunov juncon flux: h (, u) = 1 + x x g G D g G U D, u 1 D U, u 1 U for all lns 2I,where s he nal condon for ln. Thus,wecanconsrucasysemofNT governng equaons H (, u) =0,whereheh, s he equaon n H a ndex N +, dencalohe orderng of he correspondng dscree sae varable. 3AdjonBasedFlowOpmzaon 3.1 Opmal Conrol Problem Formulaon In addon o our governng equaons H (, u) =0, we also nroduce a cos funcon C, whchweassume o be n C 2 : (13) C : R NT R MT! R (, u) 7! C (, u) whch reurns a scalar ha serves as a merc of performance of he sae and conrol values of he sysem. We wsh o mnmze he quany C over he se of conrol parameers u, whleconsrannghesaeof he sysem o sasfy he governng equaons H (, u) =0,whch s,agan,he concaenaed verson of(12) or (13). We summarze hs wh he followng opmzaon problem: mn u C (, u) subjec o: H (, u) =0 (14) Boh he cos funcon and governng equaons may be non-convex n hs problem. 8
9 3.2 Calculang he Graden We wsh o use graden nformaon n order o fnd conrol values u ha gve locally opmal coss C = C ( (u ), u ). Snce here may exs many local mnma for hs opmzaon problem (14) (whch s nonconvex n general), graden mehods do no guaranee global opmaly of u. Sll, nonlnear opmzaon mehods such as neror pon opmzaon ulze graden nformaon o mprove performance [46]. In a descen algorhm, he opmzaon procedure wll have o descend a cos funcon, by couplng he graden, whch, a a nomnal pon 0, u 0 s gven by: d uc 0, u 0 = C(, u) d C(, u) +. (15) 0,u du u 0 0,u 0 The man dffculy s o compue he erm d du. Nex we ae advanage of he fac ha he dervave of H (, u) wh respec o u s equal o zero along rajecores of he sysem: d uh 0, u 0 = H(, u) d H(, u) + =0. (16) 0,u du u 0 0,u 0 hal , verson 1-30 Oc 2013 The paral dervave erms, H 2 R NT NT, H u 2 R NT MT, C 2 R NT,andC u 2 R MT,canallbe evaluaed (more deals provded n Secon 3.3) and hen reaed as consan marces. Thus, n order o evaluae d uc 0, u 0 2 R MT,wemussolveacoupledsysemofmarxequaons. Noe 1 In (16), H and H u mgh no necessarly be defned, eher because f self s no smooh (noe ha we oo f o be C 2 o avod hs problem), or because g G s no smooh. The dervaons below are vald when he parals H and H u can ndeed be aen. There are several sengs n whch he condons for dfferenably are sasfed, see n parcular [8, 47]. Forward sysem. If we solve for d du 2 RNT MT n (16), whch we call he forward sysem: H d du = hen we can subsue he solved value for d du no (15) o oban he full expresson for he graden. Secon 3.3 below gves deals on he nverbly of H, guaraneeng a soluon for d Adjon sysem. Insead of evaluang d du drecly, he adjon mehod solves he followng sysem, called he adjon sysem, for a new unnown varable 2 R NT (called he adjon varable): Then he expresson for he graden becomes: Hu, We defne D o be he maxmum juncon degree on he newor: du. H T = C T (17) d uc 0, u 0 = T H u + C u (18) D =max 2 (n + m ), (19) and also defne D u o be he maxmum number of consrans ha a sngle conrol varable appears n, whch s equvalen o: D u =max X u2u 2 :u2u (n + m ). (20) Noe ha u 2 u : 2 s a -dependen se. By convenon, juncons are eher acuaed or no, so here s no dependency on,.e.f9 s.. u 2 u,hen8, u 2 u. Usng hese defnons, we show laer n Secon 3.4 how he complexy of compung he graden s reduced from O(D NMT 2 ) o O(T (D N + D um)) by consderng he adjon mehod over he forward mehod. AgraphcaldepconofD and D u are gven n Fg. 4. Freeway newors are usually consdered o have opologes ha are nearly planar, leadng o juncons degrees whch ypcally do no exceed 3 or 4, 9
10 B E B E BB E A C F A C F AA C F F (a) D (b) D (c) D Fg. 4: Depcon of D and D v for an arbrary graph. Fg. 4a shows he underlyng graphcal srucure for an arbrary PDE newor. Some conrol parameer u 1 has nfluence over juncons A, B, andf,whle anoher conrol parameer u 2 has nfluence over only juncon C. Fg. 4b depcs he cener juncon havng he larges number of connecng edges, hus gvng D =5.Fg.4cshowshaconrolparameeru 1 nfluences hree juncons wh sum of juncons degrees equal o sx, whch s maxmal over he oher conrol parameer u 2.leadngoheresulD u =6. Noe ha n Fg. 4c, he ln gong from juncon A o juncon B s couned wce: once as an ougong ln AB and once as n ncomng ln BA. hal , verson 1-30 Oc 2013 regardless of he oal number of lns. Also, from he localy argumen for conrol varables n Secon (2.4), asngleconrolvarable snfluenceoversaevarableswllnogrowwhheszeofhenewor.snce he D and D u ypcally do no grow wh NT or MT for freeway newors, he complexy of evaluang he graden for such newors can be consdered lnear for he adjon mehod. 3.3 Evaluang he Paral Dervaves Whle no assumpons are made abou he sparsy of he cos funcon C, henewored-srucureofhe PDE sysem and he Godunov dscrezaon scheme allows us o say more abou he srucure and sparsy of H and H u. Paral dervave expressons. Gven ha he governng equaons requre he evaluaon of a Remann solver a each sep, we deal some of he necessary compuaonal seps n evaluang he H and H u marces. If we consder a parcular governng equaon h (, u) =0,henwemaydeermneheparalerm wh respec o l j 2 by applyng he chan rule: h l j = l j 1 l j + L f 0 RS D L f 0 RS U 1 D 1 U, u 1 D, u 1 U l j l j RS D RS U 1 D 1 U, u 1 D, u 1 U (21) or f we consder he composed Remann flux solver g G n (9): h l j = l j 1 l j + L l j g G D 1 D, u 1 D l j g G U 1 U!, u 1 U (22) AdagramofhesrucureofheH marx s gven n Fg. (5a). Smlarly for H u,weaeaconrol parameer u l j 2 u, andderveheexpresson: h u l j =+ L f 0 RS D L f 0 RS U 1 D 1 U, u 1 D, u 1 U u l j u l j RS D RS U 1 D 1 U, u 1 D, u 1 U (23) or for he composed Godunov juncon flux solver g G : 10
11 hal , verson 1-30 Oc 2013 (a) Orderng of he paral dervave erms. Consrans and sae varables are clusered frs by me, and hen by cell ndex. h u l j = L u l j Fg. 5: Srucure of he H marx. g G D 1 D, u 1 D (b) Sparsy srucure of he H marx. Besdes he dagonal blocs, whch are deny marces, blocs where l 6= 1 are zero. u l j g G U 1 U!, u 1. (24) u l j 1 U U Analyzng (21), he only paral erms ha are no rval o compue are RS l 1, u 1 j D D D and RS l 1, u 1. Smlarly for (23), he only nonrval erms are RS j U U U u l 1, u 1 j D D D and RS, u 1.Onceoneobanshesoluonsoheseparalerms,henonecancon- U sruc he full H and H u marces and use (17) and (18) o oban he graden value. As hese expressons are wren for a general scalar conservaon law, he only seps n compung he graden ha are specfc o a parcular conservaon law and Remann solver are compung he dervave of he flux funcon f and he paral dervave erms jus dscussed. These expressons are explcly calculaed for he problem of opmal ramp meerng n Secon (4). U 3.4 Complexy of Solvng Graden va Forward Mehod vs. Adjon Mehod Ths secon demosraes he followng proposon: Proposon 31 The oal complexy for he adjon mehod on a scalar hyperbolc newor of PDEs s O(T (D N + D um)). We can show he lower-rangular srucure and nverbly of H by examnng (11) and (12). For 2{1,...,T 1}, wehavehah s only a funcon of and of he sae varables from he prevous me-sep 1. Thus,basedonourorderngschemenSecon2.4oforderngvarablesbyncreasng me-sep and orderng consrans by correspondng varable, we now ha he dagonal erms of H are always 1 and all upper-rangular erms mus be zero (snce hose erms correspond o consrans wh a dependence of fuure values). These wo condons demonsrae boh ha H s lower-rangular and s nverble due o he ones along he dagonal. Addonally, f we consder ang paral dervaves wh respec o he varable l j,henwecan deduce from Equaon (12) ha all paral erms wll be zero excep for he dagonal erm, and hose erms nvolvng consrans a me j +1 wh lns connecng o he downsream and upsream juncons j D and j U respecvely. To summarze, H marces for sysems descrbed n Secon 2.4 wll be square, 11
12 Fg. 6: Freeway newor model. For a juncon 2 D 1 = 2( D 1) = 2 U a me-sep 2{0,...,T 1}, he upsream manlne densy are represened by 2( 1),hedownsreammanlnedensyby 2, heon-ramp densy by 2 1, andheoff-rampsplraoby 2( 1). hal , verson 1-30 Oc 2013 nverble, lower-rangular and each column wll have a maxmum cardnaly equal o D n (19). The sparsy srucure of H s depced n Fg. 5b. Usng he same lne of argumen for he maxmum cardnaly of H,wecanboundhemaxmum cardnaly of each column of H u.tangasngleconrolvarableu l j,hevarablecanonlyappearnhe consrans a me-sep j +1 ha correspond o a ln ha connecs o a juncon such ha u l j 2 u l+1. These condons gve us he expresson for D u n (20), or he maxmum cardnaly over all columns n H u. If we only consder he lower rangular form of H, hen he complexy of solvng for he graden usng he forward sysem s O((NT) 2 MT), where he domnang erm comes from solvng (15), whch requres he soluon of MT separae NT NT lower-rangular sysems. The lower-rangular sysem allows for forward subsuon, whch can be solved n O((NT) 2 ) seps, gvng he overall complexy O((NT) 2 MT). The complexy of compung he graden va he adjon mehod s O((NT) 2 +(NT)(MT)), whch s ceranly more effcen han he forward-mehod, as long as MT > 1. The effcency s ganed by consderng ha (17) only requres he soluon of a sngle NT NT upper-rangular sysem (va bacwardsubsuon), followed by he mulplcaon of T H v,annt NT and an NT MT marx n (18), wh acomplexyofo((nt) 2 +(NT)(MT)). For he adjon mehod, hs complexy can be mproved upon by consderng he sparsy of he H and H u marces, as dealed n Secon 3.4. For he bacward-subsuon sep, each enry n he vecor s solved by a mos D mulplcaons, and hus he complexy of solvng (17) s reduced o O(D NT). Smlarly, for he marx mulplcaon of T H v,whle s no necessarly sparse, we now ha each enry n he resulng vecor requres a mos D u mulplcaons, gvng a complexy of O(D umt). 4 Applcaons o Opmal Coordnaed Ramp Meerng on Freeways 4.1 Formulaon of he Newor Model And Explc Remann Solver Model. Consder a freeway secon wh lns I = {1,...,2N} wh a lnear sequence of manlne lns = {2, 4,...,2N} and connecng on-ramp lns = {1, 3,...,2N 1}. Adscreeme =, 0 apple apple T 1, manlne ln 2 2I, 2{1,...,N} has a downsream juncon 2 D = 2(+1) U and an upsream juncon 2 U = 2( D 1),whleon-ramp2 1 2I, 2{1,...,N} has a downsream juncon 2 D 1 = 2 U = 2( D 1) and an upsream juncon 2 U 1. The off-ramp drecly downsream of ln 2, 2{1,...,N} has, a me-sep, asplrao 2 represenng he rao of cars whch say on he freeway over he oal cars leavng he upsream manlne of juncon 2. D The model assumes ha all flux from on-ramp 2 1 eners downsream manlne 2. Snce2 U s he source of he newor, has no upsream manlne or off-ramp, and smlarly 2N D has no downsream manlne or on-ramp ( 2N =0). Each ln 2Ihas a dscrezed sae value 2 R a each me-sep 2{0,...,T 1}, harepresenshedensyofvehclesonheln.thesevaluesaredepcednfg.6. uncons ha have no on-ramps can be effecvely represened by addng an on-ramp wh no demand whle juncons wh no off-ramps can be represened by seng he spl rao o 1. The vehcle flow dynamcs on all lns (manlnes, on-ramps, and off-ramps) are modeled usng he conservaon law governng he densy evoluon (1), where s he densy sae, and f s he flux funcon (or fundamenal dagram) f ( ). In he conex of raffc, hs model s referred o as he Lghhll-Whham- Rchards (LWR) model [36, 35]. The fundamenal dagram f s ypcally assumed o be concave, and has a bounded doman [0, max ] and a maxmum flux value F max aaned a a crcal densy c : f ( c )=F max. We assume ha he fundamenal dagram has a rapezodal form as depced n Fg. 7. For he remander of 12
13 he arcle, we nsanae he conservaon law n (1) wh he LWR equaon as apples o raffc flow modelng. hal , verson 1-30 Oc 2013 As conrol npu, an on-ramp 2 1 2I, 2 {1,...,N} a me-sep 2{0,...,T 1} has a meerng rae u [0, 1] whch lms he flux of vehcles leavng he on-ramp. Inuvely, he meerng rae acs as a fraconal decrease n he flow leavng he on-ramp and enerng he manlne freeway. The doman of he meerng conrol s o force he conrol o neher mpose negave flows nor send more vehcles han presen n a queue. Is mahemacal model s expressed n (31). Fg. 7: Fundamenal dagram (he name of he flux For noaonal smplcy we defne he se of funcon n ransporaon leraure) wh free-flow denses of lns ncden o 2 U = D n 2(o 1) a speed v, congesonwavespeedw, maxfluxf max, me-sep as crcal densy c,andmaxdensy max =. 2 U 2( 1), 2 1, 2.The off-ramp s consdered o have nfne capacy, and hus has no bearng on he soluon of juncon problems. Inal condons are handled as n (11), whle for 2{1,...,T 1}, hemanlnedensy 2 usng he Godunov scheme from (12) s gven by: h 2(, u) = g G L D 2 2 g G L U D 2 1 U 2 = g 1 2,D g 1 2,U L 2,u 1 2+1,u (25) =0 (26) where we have nroduced some subsuons o reduce he noaonal burden of hs secon: g,d s he Godunov flux a me-sep exng a ln a he downsream boundary of he ln, and g,u s he Godunov flux enerng he ln a he upsream boundary. We also mae he assumpon ha on-ramps have nfne capacy and a free-flow velocy v 2 1 = L 2 1 o preven he ramp congeson from blocng demand from ever enerng he newor. Snce he on-ramp has no physcal lengh, he lengh s chosen arbrarly and he vrual velocy chosen above s chosen o replcae he dynamcs n [48]. We can hen smplfy he on-ramp updae equaon o be: h 2 1(, u) = = L 2 1 L 2 g G 2 U 1 U 2,u g 1 2 1,D D D (27) =0 (28) where D s he on-ramp flux demand, and he same noaonal smplfcaon has been used for he downsream flux. Ths formulaon resuls n srong boundary condons a he on-ramps whch guaranees all demand eners he newor. Deals on wea versus srong boundary condons can be found n [48, 22, 6]. The on-ramp model n (27) dffers from [48] n ha we model he on-ramp as a dscrezed PDE wh an nfne crcal densy, whle [48] models he on-ramp as an ODE buffer. Whle boh models mplemen srong boundary condons, he dscrezed PDE model maes he freeway newor more algned wh he PDE newor framewor presened n hs arcle. Remann solver. For he ramp meerng problem, here are many poenal Remann solvers ha sasfy he properes requred n Secon 2.2. Followng he model of [48], for each juncon U 2, weaddwomodelng decsons: 1. The flux soluon maxmzes he ougong manlne flux g 2,U. 13
14 (a) Case 1: Prory volaed due o lmed upsream manlne demand enerng downsream manlne. (b) Case 2: Prory volaed due o lmed on-ramp demand enerng downsream manlne. (c) Case 3: Prory rule sasfed due o suffcen demand from boh manlne and on-ramp. Fg. 8: Godunov juncon flux soluon for ramp meerng model a juncon 2. U Therecangularregon represens he feasble flux values for 2( 1)g 2( 1),D and g 2 1,D as deermned by he upsream demand, whle he lne wh slope represens feasble flux values as deermned by mass balance. The 1 2( 1) 2( 1)g 2( 1),D erm accouns for only he flux ou of ln 2( 1) ha says on he manlne. The flux soluon, represened by he red crcle, s he pon on he feasble regon ha mnmzes he dsance from he prory lne 2( 1)g 2( 1),D = p 2( 1) g 2 1,D. hal , verson 1-30 Oc Subjec o (1), he flux soluon aemps o sasfy g2( 1),D = p 2( 1)g2 1,D, wherep 2( 1) 2 R + s a mergng parameer for juncon 2( D 1). Snce (1) allows mulple flux soluons a he juncon, (2) s necessary o oban a unque soluon. Ths leads o he followng sysem of equaons ha gves he flux soluon of he Remann solver a me-sep 2{1,...,T 1} and juncon 2 U for 2{1,...,N}: 2( 1) =mn 2 =mn d 2 1 = u 2 1 mn v 2( 1) 2( 1),F max w 2 max 2 2 L ( 1),F max 2 1,F max 2 1 g2,u =mn 2( 1) 2( 1) + d 2 1, 8 >< g2( 1),D = g 2 >: 1,D = g 2,U 2( 1) g 2,U d 2 1 2( 1) p 2( 1) g 2,U (1+p 2( 1)) 2( 1) 2 p 2( 1) g 2,U 2( 1)(1+p 2( 1)) 2( 1) [Case 1] g 2,U 1+p 2( 1) d 2 1 [Case 2] oherwse [Case 3] (29) (30) (31) (32) (33) 2( 1)g 2( 1),D (34) where, for noaonal smplcy, a he edges of of he range for, anyundefnedsaevalues(e.g. 0)are assumed o be zero by convenon. Equaons (29) and (31) deermne he maxmum flux ha can ex ln 2( 1) and ln 2 1 respecvely. Equaon (30) gves he maxmum flux allowed no ln 2. The acual flux no ln 2, shown n (32), s gven as he mnmum of he demand from upsream lns and supply of he downsream ln. See [48] for more deals on he model for hs equaon. The flux ou of ln 2( 1) s spl no hree cases n (33). The soluons are depced n Fg. 8, whch demonsraes how he flux soluon depends upon he respecve demands and he mergng parameer p 2( 1).Fnally, Equaon (34) gves he flux ou of he on-ramp 2 1, whchshedfferencebeweenhefluxnoln2 and he flux ou of ln 2( 1) he remans on he manlne. For =0,heupdaeequaonsgvenbyapre-specfednalcondon,asn(11).Noehahe equaons can be solved sequenally va forward subsuon. Also, we do no nclude he flux resul for off-ramps explcly here snce s value has no bearng on furher calculaons, and we wll henceforh gnore s calculaon. To demonsrae ha ndeed he flux soluon sasfes he flux conservaon propery, he off-ramp flux s rvally deermned o be 2( 1) g 2( 1),D. 14
15 4.2 Formulaon of he Opmal Conrol Problem Opmal coordnaed ramp-meerng. Includng he nal condons as specfed n (11) wh (25) and (27) gves a complee descrpon of he sysem H (, u) =0, 2 R 2N, u 2 R, where: 2N+ := 1 apple apple 2N,0 apple apple T 1 u N+ := u 2 1 apple apple N,0 apple apple T 1 The objecve of he conrol s o mnmze he oal ravel me on he newor, expressed by he cos funcon C: C (, u) = TX 2NX =1 =1 L. The opmal coordnaed ramp-meerng problem can be formulaed as an opmzaon problem wh PDE-newor consrans: hal , verson 1-30 Oc 2013 mn u C (, u) (35) subjec o: H (, u) = 0 0 apple u apple 1 8u 2 u Snce he adjon mehod n Secon 3 only deals wh equaly consrans, we add barrer penales o he cos funcon [49, 9]: C (, u, )=C (, u) X log ((1 u)(u 0)). (36) u2u As 2 R + ends o zero, he soluon o (36) wll approach he soluon o he orgnal problem (35). Thus we can solve (35) by eravely solvng he augmened problem: mn u C (, u, ) (37) subjec o: H (, u) = 0 wh decreasng values of. Asaresul, C wll approach C as he number of eraons ncreases. Applyng he adjon mehod. To use he adjon mehod as descrbed n Secon 3, we need o compue he paral dervave marces H, H u, C and C u.compungheparaldervaveswhrespecohecos funcon s sragh forward: C C u 2 = L 1 apple apple 2N,0 apple apple T 1 = 1 1 u apple apple N,0 apple apple T 1 u 2 To compue he paral dervaves of H, we follow he procedure n Secon 3.2. For an upsream juncon 2 U 2 and me-sep 2{1,...,T 1}, weonlyneedocompueheparaldervavesofhe flux solver g G 2 U 2,u U 2 1 wh respec o he adjacen sae varables and ramp meerng conrol u. We calculae he paral dervaves of he funcons n (29)-(34) wh respec o eher a sae or conrol varables 2 [ u: 15
16 hal , verson 1-30 Oc ( 1) = s 2 s = d s = s g 2,U = s g 2( 1),D = s g 2 ( v 2( 1) s = 2( 1),v max 2( 1) apple F2( 1) 0 oherwse ( w 2 s = 2,w 2 max 2 2 apple F2 max 0 oherwse 8 >< u 2 1 s = 2 1, 2 1 apple F2 max 1 mn 2 1,F2 max 1 s = u 2 1 >: 0 oherwse 8 < : 8 >< >: 2( 1) 2 s 2( 1) s 1 2( 1) 1,D = s g 2,U 2( 1) s + d 2( 1) s p 2( 1) s g 2,U d 2 1 s 2( 1) 2( 1) + d 2 1 apple 2 oherwse g 2,U p 2( 1) 1+p 2( 1) 2( 1) 2( 1) g 2,U 1+p 2( 1) d 2( 1) 2( 1)(1+p 2( 1)) s g 2,U oherwse 2( 1) s g 2( These expressons fully quanfy he paral dervave values needed n (22) and (24). Thus we can consruc he H and H u marces. Wh hese marces and C and C u, we can solve for he adjon varable 2 R 2NT n (17) and subsue s value no (18) o oban he graden of he cos funcon C wh respec o he conrol parameer u. 5 Numercal Resuls for Model Predcve Conrol Implemenaons To demonsrae he effecveness of usng he adjon ramp meerng mehod o compue gradens, we mplemened he algorhm on praccal scenaros wh feld expermenal daa. The algorhm can hen be used as a graden compuaon subroune nsde any descen-mehod opmzaon solver ha aes advanage of frs-order graden nformaon. Our mplemenaon maes use of he open-source IpOp solver [46], an neror pon, nonlnear program opmzer. To serve as comparsons, wo oher case scenaros were run: 1. No conrol: he meerng rae s se o 1 on all on-ramps a all mes. 2. Alnea [38]: a well-adoped, feedbac-based ramp meerng algorhm commonly used n he praconer s communy. Alnea s compuaonally effcen and decenralzed, mang a popular choce for large newors, bu does no ae esmaed boundary flow daa as npu. Snce Alnea has a number of unng parameers, we perform a modfed grd-search echnque over he dfferen parameers ha scales lnearly wh he number of on-ramps, and selec he bes-performng parameers, n order o be far o hs framewor. A full grd-search approach scales exponenally wh he number of on-ramps, renderng nfeasble for moderae-sze freeway newors. All smulaons were run on a 2012 commercal lapop wh 8 GB of RAM and a dual-core 1.8 GHz Inel Core 5 processor. 1),D Noe 2 To demonsrae he reduced runnng me assocaed wh he adjon approach, we also mplemened a graden descen usng a fne dfferences approach smlar o [33, 32], whch requres an O(T 2 NM) compuaon for each sep n graden descen, bu proved o be compuaonally nfeasble for even small, synhec newors. Runnng ramp meerng on even a newor of 4 lns over 6 me-seps for 5 graden seps oo well over 4 mnues, renderng he mehod useless for real-me applcaons. The comparson of runnng mes of fne dfferences versus he adjon mehod s gven n Fg. 9. Due o he mpraccally large runnng mes assocaed wh fne dfferences, we do no consder he fne dfferences n furher resuls, whch only becomes worse as he problem scales o larger newors and me horzons. 16
17 Toal ravel me (veh-s) Fne dfferences Adjon Runnng me (ms) Fg. 9: Runnng me of ramp meerng algorhm usng IpOp wh and whou graden nformaon. Newor consss of 4 lns and 6 me-seps wh synhec boundary flux daa. The mehod usng graden nformaon va he adjon mehod converged well before he compleon of he frs sep of he fne dfferences descen mehod. hal , verson 1-30 Oc 2013 Fg. 10: Model of secon of I15 Souh n San Dego, Calforna. The freeway secon spannng 19.4 mles was spl no 125 lns wh 9 on-ramps. 5.1 Implemenaon of I15S n San Dego As npu no he opmzaon problem, we consruced a model of a 19.4 mle srech of he I15 Souh freeway n San Dego, Calforna beween San Marcos and Mra Mesa. The newor has N =125lns, and M =9on-ramps, wh boundary daa specfed for T =1800me-seps, for a me horzon of 120 mnues gven =4 seconds.theneworsshownnfg.10. Ln lengh daa was obaned usng he Scenaro Edor sofware developed as par of he Conneced Corrdors projec, a collaboraon beween UC Bereley and PATH research nsue n Bereley, Calforna. Fundamenal dagram parameers, spl raos, and boundary daa were also obaned usng calbraon echnques developed by Conneced Corrdors. Denses resulng n free-flow speeds were chosen as nal condons on he manlne and on-ramps. The daa used n calbraon was aen from PeMS sensor daa [50] durng a mornng rush hour perod, scaled o generae congesed condons. The npu daa was chosen o demonsrae he effecveness of he adjon ramp meerng mehod n a real-world seng. A profle of he manlne and on-ramps durng a forward-smulaon of he newor s shown n Fg. 11 under he descrbed boundary condons. 5.2 Fne-Horzon Opmal Conrol Expermenal Seup. The adjon ramp meerng algorhm s compared o he reacve Alnea scheme, for whch we assume ha perfec boundary condons and nal condons are avalable. The merc we use o compare he dfferen sraeges s reduced-congeson percenage, c 2 ( 1, 100], whchwedefneas: c c c =100 1 c nc where c c,c nc 2 R + are he congeson resulng from he conrol and no-conrol scenaros, respecvely. We use he merc for congeson as defned n [51]; for a gven secon of road S and me horzon T,he congeson s gven as c (S, T )= X (s2s, 2T ) apple max TTT (s, ) VMT (s, ) v s, 0 17
18 (a) Densy profle. The uns are he rao of a ln s vehcle densy o a ln s jam densy. (b) On-ramp queue profle n uns of vehcles. Fg. 11: Densy and queue profle of no-conrol freeway smulaon. In he frs 80 mnues, congeson poces form on he freeway and queues form on he on-ramps, hen evenually clear ou before 120 mnues. hal , verson 1-30 Oc 2013 (a) Densy dfference profle n uns of change n densy from he conrol scenaro o he no conrol scenaro over he jam densy of he ln. (b) Queue dfference profle n uns of vehcles. Fg. 12: Profle dfferences for manlne denses and on-ramp queues. Evdenced by he manly negave dfferences n he manlne denses and he manly posve dfferences n he on-ramp queue lenghs, he adjon ramp meerng algorhm effecvely lms on-ramp flows n order o reduce manly congeson. Vew n color. where v s s he free-flow velocy, VMT s oal vehcle mles raveled, and TTT s oal ravel me over he ln s and me-sep. Snce s nfeasble o compue he global opmum for all cases, a reduced congeson of 100% serves as an upper bound on he possble amoun of mprovemen. Resuls. Fg. 12 shows a dfference profle for boh densy and queue lenghs beween he no conrol smulaon and he smulaon applyng he ramp meerng polcy generaed from he adjon mehod. Negave dfferences n Fgs. 12a and 12b ndcae where he adjon mehod resuled n fewer vehcles for he specfc ln and me-sep. The adjon mehod was successful n appropraely decdng whch ramps should be meered n order o mprove hroughpu for he manlne. Runnng me analyss shows ha he adjon mehod can produce benefcal resuls n real-me applcaons. Fg. 13 deals he mprovemen of he adjon mehod as a funcon of he overall runnng me of he algorhm. Afer jus a few graden seps, he adjon mehod ouperforms he Alnea mehod. Gven ha he me horzon of wo hours s longer han he perod of me one can expec reasonably accurae boundary flow esmaes, more praccal smulaons wh shorer me horzons should perm more graden seps n a real-me seng. Whle he adjon mehod leads o queues wh a consderable number of cars n some on-ramps, hs can be addressed by nroducng barrer erms no he cos funcon ha lm he maxmum queue lengh. The Alnea mehod esed for he I15 newor had no prescrbed maxmum queue lenghs as well, bu was 18
19 3.5 Reduced Congeson (%) Adjon 0.5 Alnea Runnng me (seconds) Fg. 13: Reduced congeson versus smulaon me for freeway newor. The resuls ndcae ha he algorhm can run wh performance beer han Alnea f gven an updae me of less han a mnue. no able o produce sgnfcan mprovemens n oal ravel me reducon, whle he adjon mehod was more successful. 5.3 Model Predcve Conrol hal , verson 1-30 Oc 2013 To sudy he performance of he algorhm under nosy npu daa, we embed boh our adjon ramp meerng algorhm and he Alnea algorhm nsde of a model predcve conrol (MPC) loop. Expermenal Seup. The MPC loop begns a a me by esmang he nal condons of he raffc on he freeway newor and he predced boundary fluxes over a ceran me horzon T h.thesevalues are nosy, as exac esmaon of hese parameers s no possble on real freeway newors. The esmaed condons are hen passed o he ramp meerng algorhm o compue an opmal conrol polcy over he T h me perod. The sysem s hen forward-smulaed over an updae perod of T u apple T h,usnghe exac nal condons and boundary condons, as opposed o he nosy daa used o compue conrol parameers. The sae of he sysem and boundary condons a + T u are hen esmaed (wh nose) and he process s repeaed. Anon-negavenose facor, 2 R +, s used o sudy how he adjon mehod and Alnea perform as he qualy of esmaed daa decreases. If s he acual densy for a cell and me-sep, hen he densy passed o he conrol schemes s gven by: = (1 + R) where R s a unformly dsrbued random varable wh mean 0 and doman [ was appled o boh nal and boundary condons. Two dfferen expermens were conduced: 0.5, 0.5]. The nose facor 1. Real-me I15 Souh: MPC s run for he I15 Souh newor wh T h =80mnues and T u =26 mnues. A nose facor of 2% was chosen for he nal and boundary condons. The number of eraons was chosen n order o ensure ha each MPC eraon fnshed n he predeermned updae me T u. 2. Nose Robusness: MPC s for over a synhec newor wh lengh 12 mles and boundary condons over 75 mnues. The expermens are run over a profle of nose facors beween 1% and 8000%. Resuls. Real-Tme I15 Souh. The resuls are summarzed n Fg. 14a. The adjon mehod appled once o he enre horzon wh perfec boundary and nal condon nformaon serves as a baselne performance for he oher smulaons, whch had nosy npu daa and lmed nowledge of predced boundary condons. The adjon mehod sll performs well under he more realsc condons of he MPC loop wh nose, resulng n 2% reduced congeson or 40 car-hours n relaon o no conrol, as compared o he 3% reduced (60 car-hours) congeson acheved by he adjon mehod wh no nose and full me horzon (T h = T ). In comparson, he Alnea mehod was only able o acheve 1.5% reduced congeson (30 car-hours) for boh he nosy and no-nose scenaros. The resuls ndcae ha, under a realsc assumpon of a 2% nose facor n he sensor nformaon, he algorhm s ably o consder boundary condons resuls n an mprovemen upon srcly reacve polces, such as Alnea. 19
20 Reduced Congeson (%) Adjon Adjon w/ Nose Alnea Alnea w/ Nose (a) Reduced congeson Reduced Congeson (%) Adjon Alnea Nose facor (-) (b) Reduced congeson wh ncreasng sensor nose for newor wh synhec daa. Fg. 14: Summary of model predcve conrol smulaons. The resuls ndcae ha he adjon mehod has superor performance for moderae nose levels on he nal and boundary condons. hal , verson 1-30 Oc 2013 Robusness o Nose. Smulaon resuls on he synhec newor wh varyng levels of nose are shown n Fg. 14b. The adjon mehod s able o ouperform he Alnea mehod when he nose level s less han 80%, a reasonable assumpon for daa provded by well-mananed loop deecors. As he nal and boundary condon daa deeroraes, he adjon mehod becomes useless. Snce Alnea does no rely on boundary daa, s able o produce mprovemens, even wh severely nosy daa. The resuls ndcae ha he adjon mehod wll ouperform Alnea under reasonable nose levels n he sensor daa. 6Conclusons Ths arcle has dealed a smple framewor for fne-horzon opmal conrol mehods on a newor of scalar conservaon laws derved from frs dscrezng he newor va he Godunov mehod, hen applyng he dscree adjon o hs sysem. To alor he framewor o a specfc applcaon, one need only provde he paral dervaves of he Remann solver a a newor juncon as well as he paral dervaves of he objecve. Furhermore, we show ha for hs class of problems, he sparsy paern allows he problem o be mplemened wh only lnear memory and lnear compuaonal complexy wh respec o he number of sae and conrol parameers. We demonsrae he scalably of he approach by mplemenng a coordnaed ramp meerng algorhm usng he adjon mehod and applyng he algorhm o he I-15 Souh freeway n Calforna. The algorhm runs n a fracon of real-me and produces sgnfcan mprovemens over exsng algorhms. The ramp meerng algorhm has been fully mplemened whn Conneced Corrdors [52] sysem, a projec by UC Bereley and PATH for negraed corrdor managemen, as a componen of he raffc smulaor module. Fuure wor ncludes nvesgang decenralzed, coordnaed conrol schemes over physcal newors va he adjon mehod o allow raffc conrol sraeges o scale o regonal-scale newors. 7Acnowledgmens The auhors have been suppored by he Calforna Deparmen of Transporaon under he Conneced Corrdors program, CAREER gran CNS under he projec Lagrangan Sensng n Large Scale Cyber-Physcal Infrasrucure Sysems, he European Research Councl under he European Unon s Sevenh Framewor Program (FP/ ) / ERC Gran Agreemen n , he INRIA assocaed eam Opmal REroue Sraeges for Traffc managemen and he France-Bereley Fund under he projec Opmal Traffc Flow Managemen wh GPS Enabled Smarphones. References [1] B. Rohfarb e al. Opmal desgn of offshore naural-gas ppelne sysems. In: Operaons Research 18.6 (1970), pp
21 hal , verson 1-30 Oc 2013 [2] S. Brunnermeer and S. Marn. Ineroperably cos analyss of he US auomove supply chan: Fnal repor. Tech.rep.DIANEPublshng,1999. [3] T. S. Rabban e al. Feed-Forward Conrol of Open Channel Flow Usng Dfferenal Flaness. In: IEEE Transacons on Conrol Sysems Technology 18.1 (an. 2010), pp ssn: do: /TCST [4] X. Lrco and V. Fromon. Boundary conrol of hyperbolc conservaon laws usng a frequency doman approach. In: Auomaca 45.3 (2009), pp [5] M. Garavello and B. Pccol. Traffc flow on newors. Vol.1.Amercannsueofmahemacal scences Sprngfeld, MA, USA, sbn: [6] D. B. Wor e al. A raffc model for velocy daa assmlaon. In: Appled Mahemacs Research express (Apr. 2010), p. 1. ssn: do: /amrx/abq002. [7] E. Frazzol, M. A. Dahleh, and E. Feron. Real-me moon plannng for agle auonomous vehcles. In: ournal of Gudance, Conrol, and Dynamcs 25.1 (2002), pp [8] M. Guga e al. Opmal Conrol for Traffc Flow Newors. In: ournal of Opmzaon Theory and Applcaons (Sep. 2005), pp ssn: do: /s z. [9] A. Bayen, R. Raffard, and C. Tomln. Adjon-based conrol of a new euleran newor model of ar raffc flow. In: IEEE Transacons on Conrol Sysems Technology 14.5 (Sep. 2006), pp ssn: do: /TCST [10] A. Kosalos and M. Papageorgou. Nonlnear Opmal Conrol Appled o Coordnaed Ramp Meerng. In: IEEE Transacons on Conrol Sysems Technology 12.6 (Nov. 2004), pp ssn: do: /TCST [11].-M. Coron e al. Local Exponenal H 2 Sablzaon of a 2 X 2 Quaslnear Hyperbolc Sysem Usng Bacseppng. In: SIAM ournal on Conrol and Opmzaon 51.3 (2013), pp ssn: do: /CDC [12] O. Glass and S. Guerrero. On he unform conrollably of he Burgers equaon. In: SIAM ournal on Conrol and Opmzaon 46.4 (an. 2007), pp ssn: do: / [13] D. acque, M. Krsc, and C. C. de W. Opmal conrol of scalar one-dmensonal conservaon laws. In: Amercan Conrol Conference, IEEE.Ieee,2006,6 pp.sbn: do: /ACC [14] L. Blanchard e al. Shape Graden for Isogeomerc Srucural Desgn. In: ournal of Opmzaon Theory and Applcaons (Sep. 2013), pp ssn: do: /s [15] D. Keller. Opmal Conrol of a Nonlnear Sochasc Schrodnger Equaon. In: ournal of Opmzaon Theory and Applcaons (Sep. 2013). ssn: do: /s [16] D. acque, C. C. de W, and D. Koeng. Opmal Ramp Meerng Sraegy wh Exended LWR Model, Analyss and Compuaonal Mehods. In: Proceedngs of he 16h IFAC World Congress [17] P. Mon and T. Bewley. Feedbac Conrol of Turbulence. In: Appled Mechancs Revews 47.6S (1994), S3. ssn: do: / [18]. Reuher e al. Aerodynamc Shape Opmzaon of Complex Arcraf Confguraons va an Adjon Formulaon. Research Insue for Advanced Compuer Scence, NASA Ames Research Cener, [19] M. B. Gles and N. A. Perce. An nroducon o he adjon approach o desgn. In: Flow, Turbulence and Combuson (2000), pp [20].-D. Müller and P. Cusdn. On he performance of dscree adjon CFD codes usng auomac dfferenaon. In: Inernaonal journal for numercal mehods n fluds (2005), pp [21] R. Gerng and T. Kamns. Recpes for adjon code consrucon. In: ACM Transacons on Mahemacal Sofware (TOMS) 24.4 (1998), pp [22] I. S. Srub and A. M. Bayen. Wea formulaon of boundary condons for scalar conservaon laws: An applcaon o hghway raffc modellng. In: Inernaonal ournal of Robus and Nonlnear Conrol (2006), pp [23] M. B. Gles, D. Ghae, and M. C. Dua. Usng auomac dfferenaon for adjon CFD code developmen. In: (2005). [24] M. B. M. B. Gles and N. A. N. Perce. Adjon equaons n CFD : dualy, boundary condons and soluon behavour. In: AIAA paper (1997), pp [25] R. L. Raffard e al. An adjon-based parameer denfcaon algorhm appled o planar cell polary sgnalng. In: Auomac Conrol, IEEE Transacons on 53.Specal Issue (2008), pp
V.Abramov - FURTHER ANALYSIS OF CONFIDENCE INTERVALS FOR LARGE CLIENT/SERVER COMPUTER NETWORKS
 R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
FTCS Solution to the Heat Equation
 FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
Dynamic Team Decision Theory. EECS 558 Project Shrutivandana Sharma and David Shuman December 10, 2005
 Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Variants of Pegasos. December 11, 2009
 Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Volatility Interpolation
 Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
An introduction to Support Vector Machine
 An nroducon o Suppor Vecor Machne 報告者 : 黃立德 References: Smon Haykn, "Neural Neworks: a comprehensve foundaon, second edon, 999, Chaper 2,6 Nello Chrsann, John Shawe-Tayer, An Inroducon o Suppor Vecor Machnes,
An nroducon o Suppor Vecor Machne 報告者 : 黃立德 References: Smon Haykn, "Neural Neworks: a comprehensve foundaon, second edon, 999, Chaper 2,6 Nello Chrsann, John Shawe-Tayer, An Inroducon o Suppor Vecor Machnes,
Dual Approximate Dynamic Programming for Large Scale Hydro Valleys
 Dual Approxmae Dynamc Programmng for Large Scale Hydro Valleys Perre Carpener and Jean-Phlppe Chanceler 1 ENSTA ParsTech and ENPC ParsTech CMM Workshop, January 2016 1 Jon work wh J.-C. Alas, suppored
Dual Approxmae Dynamc Programmng for Large Scale Hydro Valleys Perre Carpener and Jean-Phlppe Chanceler 1 ENSTA ParsTech and ENPC ParsTech CMM Workshop, January 2016 1 Jon work wh J.-C. Alas, suppored
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Relative controllability of nonlinear systems with delays in control
 Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Outline. Probabilistic Model Learning. Probabilistic Model Learning. Probabilistic Model for Time-series Data: Hidden Markov Model
 Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon
Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon
EEL 6266 Power System Operation and Control. Chapter 5 Unit Commitment
 EEL 6266 Power Sysem Operaon and Conrol Chaper 5 Un Commmen Dynamc programmng chef advanage over enumeraon schemes s he reducon n he dmensonaly of he problem n a src prory order scheme, here are only N
EEL 6266 Power Sysem Operaon and Conrol Chaper 5 Un Commmen Dynamc programmng chef advanage over enumeraon schemes s he reducon n he dmensonaly of he problem n a src prory order scheme, here are only N
Robustness Experiments with Two Variance Components
 Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
( ) () we define the interaction representation by the unitary transformation () = ()
 Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
CH.3. COMPATIBILITY EQUATIONS. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
J i-1 i. J i i+1. Numerical integration of the diffusion equation (I) Finite difference method. Spatial Discretization. Internal nodes.
 umercal negraon of he dffuson equaon (I) Fne dfference mehod. Spaal screaon. Inernal nodes. R L V For hermal conducon le s dscree he spaal doman no small fne spans, =,,: Balance of parcles for an nernal
umercal negraon of he dffuson equaon (I) Fne dfference mehod. Spaal screaon. Inernal nodes. R L V For hermal conducon le s dscree he spaal doman no small fne spans, =,,: Balance of parcles for an nernal
WiH Wei He
 Sysem Idenfcaon of onlnear Sae-Space Space Baery odels WH We He wehe@calce.umd.edu Advsor: Dr. Chaochao Chen Deparmen of echancal Engneerng Unversy of aryland, College Par 1 Unversy of aryland Bacground
Sysem Idenfcaon of onlnear Sae-Space Space Baery odels WH We He wehe@calce.umd.edu Advsor: Dr. Chaochao Chen Deparmen of echancal Engneerng Unversy of aryland, College Par 1 Unversy of aryland Bacground
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 4
 CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5
![[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5 [ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5](/thumbs/85/92299540.jpg) TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL
 DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
Reactive Methods to Solve the Berth AllocationProblem with Stochastic Arrival and Handling Times
 Reacve Mehods o Solve he Berh AllocaonProblem wh Sochasc Arrval and Handlng Tmes Nsh Umang* Mchel Berlare* * TRANSP-OR, Ecole Polyechnque Fédérale de Lausanne Frs Workshop on Large Scale Opmzaon November
Reacve Mehods o Solve he Berh AllocaonProblem wh Sochasc Arrval and Handlng Tmes Nsh Umang* Mchel Berlare* * TRANSP-OR, Ecole Polyechnque Fédérale de Lausanne Frs Workshop on Large Scale Opmzaon November
Chapter 6: AC Circuits
 Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
On computing differential transform of nonlinear non-autonomous functions and its applications
 On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
Approximate Analytic Solution of (2+1) - Dimensional Zakharov-Kuznetsov(Zk) Equations Using Homotopy
 Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD
 Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
2.1 Constitutive Theory
 Secon.. Consuve Theory.. Consuve Equaons Governng Equaons The equaons governng he behavour of maerals are (n he spaal form) dρ v & ρ + ρdv v = + ρ = Conservaon of Mass (..a) d x σ j dv dvσ + b = ρ v& +
Secon.. Consuve Theory.. Consuve Equaons Governng Equaons The equaons governng he behavour of maerals are (n he spaal form) dρ v & ρ + ρdv v = + ρ = Conservaon of Mass (..a) d x σ j dv dvσ + b = ρ v& +
Math 128b Project. Jude Yuen
 Mah 8b Proec Jude Yuen . Inroducon Le { Z } be a sequence of observed ndependen vecor varables. If he elemens of Z have a on normal dsrbuon hen { Z } has a mean vecor Z and a varancecovarance marx z. Geomercally
Mah 8b Proec Jude Yuen . Inroducon Le { Z } be a sequence of observed ndependen vecor varables. If he elemens of Z have a on normal dsrbuon hen { Z } has a mean vecor Z and a varancecovarance marx z. Geomercally
Cubic Bezier Homotopy Function for Solving Exponential Equations
 Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Performance Analysis for a Network having Standby Redundant Unit with Waiting in Repair
 TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
THE PREDICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS
 THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
CS286.2 Lecture 14: Quantum de Finetti Theorems II
 CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Lecture 6: Learning for Control (Generalised Linear Regression)
 Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
John Geweke a and Gianni Amisano b a Departments of Economics and Statistics, University of Iowa, USA b European Central Bank, Frankfurt, Germany
 Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
P R = P 0. The system is shown on the next figure:
 TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
. The geometric multiplicity is dim[ker( λi. number of linearly independent eigenvectors associated with this eigenvalue.
 Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
In the complete model, these slopes are ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL. (! i+1 -! i ) + [(!") i+1,q - [(!
 ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
Li An-Ping. Beijing , P.R.China
 A New Type of Cpher: DICING_csb L An-Png Bejng 100085, P.R.Chna apl0001@sna.com Absrac: In hs paper, we wll propose a new ype of cpher named DICING_csb, whch s derved from our prevous sream cpher DICING.
A New Type of Cpher: DICING_csb L An-Png Bejng 100085, P.R.Chna apl0001@sna.com Absrac: In hs paper, we wll propose a new ype of cpher named DICING_csb, whch s derved from our prevous sream cpher DICING.
e-journal Reliability: Theory& Applications No 2 (Vol.2) Vyacheslav Abramov
 June 7 e-ournal Relably: Theory& Applcaons No (Vol. CONFIDENCE INTERVALS ASSOCIATED WITH PERFORMANCE ANALYSIS OF SYMMETRIC LARGE CLOSED CLIENT/SERVER COMPUTER NETWORKS Absrac Vyacheslav Abramov School
June 7 e-ournal Relably: Theory& Applcaons No (Vol. CONFIDENCE INTERVALS ASSOCIATED WITH PERFORMANCE ANALYSIS OF SYMMETRIC LARGE CLOSED CLIENT/SERVER COMPUTER NETWORKS Absrac Vyacheslav Abramov School
Comb Filters. Comb Filters
 The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
Appendix H: Rarefaction and extrapolation of Hill numbers for incidence data
 Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Modeling and Solving of Multi-Product Inventory Lot-Sizing with Supplier Selection under Quantity Discounts
 nernaonal ournal of Appled Engneerng Research SSN 0973-4562 Volume 13, Number 10 (2018) pp. 8708-8713 Modelng and Solvng of Mul-Produc nvenory Lo-Szng wh Suppler Selecon under Quany Dscouns Naapa anchanaruangrong
nernaonal ournal of Appled Engneerng Research SSN 0973-4562 Volume 13, Number 10 (2018) pp. 8708-8713 Modelng and Solvng of Mul-Produc nvenory Lo-Szng wh Suppler Selecon under Quany Dscouns Naapa anchanaruangrong
Tight results for Next Fit and Worst Fit with resource augmentation
 Tgh resuls for Nex F and Wors F wh resource augmenaon Joan Boyar Leah Epsen Asaf Levn Asrac I s well known ha he wo smple algorhms for he classc n packng prolem, NF and WF oh have an approxmaon rao of
Tgh resuls for Nex F and Wors F wh resource augmenaon Joan Boyar Leah Epsen Asaf Levn Asrac I s well known ha he wo smple algorhms for he classc n packng prolem, NF and WF oh have an approxmaon rao of
Single-loop System Reliability-Based Design & Topology Optimization (SRBDO/SRBTO): A Matrix-based System Reliability (MSR) Method
 10 h US Naonal Congress on Compuaonal Mechancs Columbus, Oho 16-19, 2009 Sngle-loop Sysem Relably-Based Desgn & Topology Opmzaon (SRBDO/SRBTO): A Marx-based Sysem Relably (MSR) Mehod Tam Nguyen, Junho
10 h US Naonal Congress on Compuaonal Mechancs Columbus, Oho 16-19, 2009 Sngle-loop Sysem Relably-Based Desgn & Topology Opmzaon (SRBDO/SRBTO): A Marx-based Sysem Relably (MSR) Mehod Tam Nguyen, Junho
Existence and Uniqueness Results for Random Impulsive Integro-Differential Equation
 Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS. Youngwoo Ahn and Kitae Kim
 Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.
![. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue. . The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.](/thumbs/78/77822798.jpg) Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Lecture VI Regression
 Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
Time-interval analysis of β decay. V. Horvat and J. C. Hardy
 Tme-nerval analyss of β decay V. Horva and J. C. Hardy Work on he even analyss of β decay [1] connued and resuled n he developmen of a novel mehod of bea-decay me-nerval analyss ha produces hghly accurae
Tme-nerval analyss of β decay V. Horva and J. C. Hardy Work on he even analyss of β decay [1] connued and resuled n he developmen of a novel mehod of bea-decay me-nerval analyss ha produces hghly accurae
Fall 2010 Graduate Course on Dynamic Learning
 Fall 200 Graduae Course on Dynamc Learnng Chaper 4: Parcle Flers Sepember 27, 200 Byoung-Tak Zhang School of Compuer Scence and Engneerng & Cognve Scence and Bran Scence Programs Seoul aonal Unversy hp://b.snu.ac.kr/~bzhang/
Fall 200 Graduae Course on Dynamc Learnng Chaper 4: Parcle Flers Sepember 27, 200 Byoung-Tak Zhang School of Compuer Scence and Engneerng & Cognve Scence and Bran Scence Programs Seoul aonal Unversy hp://b.snu.ac.kr/~bzhang/
CS 268: Packet Scheduling
 Pace Schedulng Decde when and wha pace o send on oupu ln - Usually mplemened a oupu nerface CS 68: Pace Schedulng flow Ion Soca March 9, 004 Classfer flow flow n Buffer managemen Scheduler soca@cs.bereley.edu
Pace Schedulng Decde when and wha pace o send on oupu ln - Usually mplemened a oupu nerface CS 68: Pace Schedulng flow Ion Soca March 9, 004 Classfer flow flow n Buffer managemen Scheduler soca@cs.bereley.edu
Testing a new idea to solve the P = NP problem with mathematical induction
 Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Solving the multi-period fixed cost transportation problem using LINGO solver
 Inernaonal Journal of Pure and Appled Mahemacs Volume 119 No. 12 2018, 2151-2157 ISSN: 1314-3395 (on-lne verson) url: hp://www.pam.eu Specal Issue pam.eu Solvng he mul-perod fxed cos ransporaon problem
Inernaonal Journal of Pure and Appled Mahemacs Volume 119 No. 12 2018, 2151-2157 ISSN: 1314-3395 (on-lne verson) url: hp://www.pam.eu Specal Issue pam.eu Solvng he mul-perod fxed cos ransporaon problem
Lecture 11 SVM cont
 Lecure SVM con. 0 008 Wha we have done so far We have esalshed ha we wan o fnd a lnear decson oundary whose margn s he larges We know how o measure he margn of a lnear decson oundary Tha s: he mnmum geomerc
Lecure SVM con. 0 008 Wha we have done so far We have esalshed ha we wan o fnd a lnear decson oundary whose margn s he larges We know how o measure he margn of a lnear decson oundary Tha s: he mnmum geomerc
A Simulation Based Optimal Control System For Water Resources
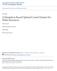 Cy Unversy of New York (CUNY) CUNY Academc Works Inernaonal Conference on Hydronformacs 8--4 A Smulaon Based Opmal Conrol Sysem For Waer Resources Aser acasa Maro Morales-Hernández Plar Brufau Plar García-Navarro
Cy Unversy of New York (CUNY) CUNY Academc Works Inernaonal Conference on Hydronformacs 8--4 A Smulaon Based Opmal Conrol Sysem For Waer Resources Aser acasa Maro Morales-Hernández Plar Brufau Plar García-Navarro
CHAPTER 10: LINEAR DISCRIMINATION
 CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g
CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g
A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION
 S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
Genetic Algorithm in Parameter Estimation of Nonlinear Dynamic Systems
 Genec Algorhm n Parameer Esmaon of Nonlnear Dynamc Sysems E. Paeraks manos@egnaa.ee.auh.gr V. Perds perds@vergna.eng.auh.gr Ah. ehagas kehagas@egnaa.ee.auh.gr hp://skron.conrol.ee.auh.gr/kehagas/ndex.hm
Genec Algorhm n Parameer Esmaon of Nonlnear Dynamc Sysems E. Paeraks manos@egnaa.ee.auh.gr V. Perds perds@vergna.eng.auh.gr Ah. ehagas kehagas@egnaa.ee.auh.gr hp://skron.conrol.ee.auh.gr/kehagas/ndex.hm
New M-Estimator Objective Function. in Simultaneous Equations Model. (A Comparative Study)
 Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
Graduate Macroeconomics 2 Problem set 5. - Solutions
 Graduae Macroeconomcs 2 Problem se. - Soluons Queson 1 To answer hs queson we need he frms frs order condons and he equaon ha deermnes he number of frms n equlbrum. The frms frs order condons are: F K
Graduae Macroeconomcs 2 Problem se. - Soluons Queson 1 To answer hs queson we need he frms frs order condons and he equaon ha deermnes he number of frms n equlbrum. The frms frs order condons are: F K
Notes on the stability of dynamic systems and the use of Eigen Values.
 Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
5th International Conference on Advanced Design and Manufacturing Engineering (ICADME 2015)
 5h Inernaonal onference on Advanced Desgn and Manufacurng Engneerng (IADME 5 The Falure Rae Expermenal Sudy of Specal N Machne Tool hunshan He, a, *, La Pan,b and Bng Hu 3,c,,3 ollege of Mechancal and
5h Inernaonal onference on Advanced Desgn and Manufacurng Engneerng (IADME 5 The Falure Rae Expermenal Sudy of Specal N Machne Tool hunshan He, a, *, La Pan,b and Bng Hu 3,c,,3 ollege of Mechancal and
Ordinary Differential Equations in Neuroscience with Matlab examples. Aim 1- Gain understanding of how to set up and solve ODE s
 Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Online Appendix for. Strategic safety stocks in supply chains with evolving forecasts
 Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
The Dynamic Programming Models for Inventory Control System with Time-varying Demand
 The Dynamc Programmng Models for Invenory Conrol Sysem wh Tme-varyng Demand Truong Hong Trnh (Correspondng auhor) The Unversy of Danang, Unversy of Economcs, Venam Tel: 84-236-352-5459 E-mal: rnh.h@due.edu.vn
The Dynamc Programmng Models for Invenory Conrol Sysem wh Tme-varyng Demand Truong Hong Trnh (Correspondng auhor) The Unversy of Danang, Unversy of Economcs, Venam Tel: 84-236-352-5459 E-mal: rnh.h@due.edu.vn
ON THE WEAK LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS
 ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
Method of upper lower solutions for nonlinear system of fractional differential equations and applications
 Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
3. OVERVIEW OF NUMERICAL METHODS
 3 OVERVIEW OF NUMERICAL METHODS 3 Inroducory remarks Ths chaper summarzes hose numercal echnques whose knowledge s ndspensable for he undersandng of he dfferen dscree elemen mehods: he Newon-Raphson-mehod,
3 OVERVIEW OF NUMERICAL METHODS 3 Inroducory remarks Ths chaper summarzes hose numercal echnques whose knowledge s ndspensable for he undersandng of he dfferen dscree elemen mehods: he Newon-Raphson-mehod,
Let s treat the problem of the response of a system to an applied external force. Again,
 Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Dynamic Team Decision Theory
 Dynamc Team Decson Theory EECS 558 Proec Repor Shruvandana Sharma and Davd Shuman December, 005 I. Inroducon Whle he sochasc conrol problem feaures one decson maker acng over me, many complex conrolled
Dynamc Team Decson Theory EECS 558 Proec Repor Shruvandana Sharma and Davd Shuman December, 005 I. Inroducon Whle he sochasc conrol problem feaures one decson maker acng over me, many complex conrolled
Epistemic Game Theory: Online Appendix
 Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
FI 3103 Quantum Physics
 /9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
/9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 2017 EXAMINATION
 INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
First-order piecewise-linear dynamic circuits
 Frs-order pecewse-lnear dynamc crcus. Fndng he soluon We wll sudy rs-order dynamc crcus composed o a nonlnear resse one-por, ermnaed eher by a lnear capacor or a lnear nducor (see Fg.. Nonlnear resse one-por
Frs-order pecewse-lnear dynamc crcus. Fndng he soluon We wll sudy rs-order dynamc crcus composed o a nonlnear resse one-por, ermnaed eher by a lnear capacor or a lnear nducor (see Fg.. Nonlnear resse one-por
12d Model. Civil and Surveying Software. Drainage Analysis Module Detention/Retention Basins. Owen Thornton BE (Mech), 12d Model Programmer
 d Model Cvl and Surveyng Soware Dranage Analyss Module Deenon/Reenon Basns Owen Thornon BE (Mech), d Model Programmer owen.hornon@d.com 4 January 007 Revsed: 04 Aprl 007 9 February 008 (8Cp) Ths documen
d Model Cvl and Surveyng Soware Dranage Analyss Module Deenon/Reenon Basns Owen Thornon BE (Mech), d Model Programmer owen.hornon@d.com 4 January 007 Revsed: 04 Aprl 007 9 February 008 (8Cp) Ths documen
TSS = SST + SSE An orthogonal partition of the total SS
 ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
M. Y. Adamu Mathematical Sciences Programme, AbubakarTafawaBalewa University, Bauchi, Nigeria
 IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
Political Economy of Institutions and Development: Problem Set 2 Due Date: Thursday, March 15, 2019.
 Polcal Economy of Insuons and Developmen: 14.773 Problem Se 2 Due Dae: Thursday, March 15, 2019. Please answer Quesons 1, 2 and 3. Queson 1 Consder an nfne-horzon dynamc game beween wo groups, an ele and
Polcal Economy of Insuons and Developmen: 14.773 Problem Se 2 Due Dae: Thursday, March 15, 2019. Please answer Quesons 1, 2 and 3. Queson 1 Consder an nfne-horzon dynamc game beween wo groups, an ele and
Motion of Wavepackets in Non-Hermitian. Quantum Mechanics
 Moon of Wavepaces n Non-Herman Quanum Mechancs Nmrod Moseyev Deparmen of Chemsry and Mnerva Cener for Non-lnear Physcs of Complex Sysems, Technon-Israel Insue of Technology www.echnon echnon.ac..ac.l\~nmrod
Moon of Wavepaces n Non-Herman Quanum Mechancs Nmrod Moseyev Deparmen of Chemsry and Mnerva Cener for Non-lnear Physcs of Complex Sysems, Technon-Israel Insue of Technology www.echnon echnon.ac..ac.l\~nmrod
Robust and Accurate Cancer Classification with Gene Expression Profiling
 Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Online Supplement for Dynamic Multi-Technology. Production-Inventory Problem with Emissions Trading
 Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Advanced Macroeconomics II: Exchange economy
 Advanced Macroeconomcs II: Exchange economy Krzyszof Makarsk 1 Smple deermnsc dynamc model. 1.1 Inroducon Inroducon Smple deermnsc dynamc model. Defnons of equlbrum: Arrow-Debreu Sequenal Recursve Equvalence
Advanced Macroeconomcs II: Exchange economy Krzyszof Makarsk 1 Smple deermnsc dynamc model. 1.1 Inroducon Inroducon Smple deermnsc dynamc model. Defnons of equlbrum: Arrow-Debreu Sequenal Recursve Equvalence
How about the more general "linear" scalar functions of scalars (i.e., a 1st degree polynomial of the following form with a constant term )?
 lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
Attribute Reduction Algorithm Based on Discernibility Matrix with Algebraic Method GAO Jing1,a, Ma Hui1, Han Zhidong2,b
 Inernaonal Indusral Informacs and Compuer Engneerng Conference (IIICEC 05) Arbue educon Algorhm Based on Dscernbly Marx wh Algebrac Mehod GAO Jng,a, Ma Hu, Han Zhdong,b Informaon School, Capal Unversy
Inernaonal Indusral Informacs and Compuer Engneerng Conference (IIICEC 05) Arbue educon Algorhm Based on Dscernbly Marx wh Algebrac Mehod GAO Jng,a, Ma Hu, Han Zhdong,b Informaon School, Capal Unversy
Department of Economics University of Toronto
 Deparmen of Economcs Unversy of Torono ECO408F M.A. Economercs Lecure Noes on Heeroskedascy Heeroskedascy o Ths lecure nvolves lookng a modfcaons we need o make o deal wh he regresson model when some of
Deparmen of Economcs Unversy of Torono ECO408F M.A. Economercs Lecure Noes on Heeroskedascy Heeroskedascy o Ths lecure nvolves lookng a modfcaons we need o make o deal wh he regresson model when some of
NATIONAL UNIVERSITY OF SINGAPORE PC5202 ADVANCED STATISTICAL MECHANICS. (Semester II: AY ) Time Allowed: 2 Hours
 NATONAL UNVERSTY OF SNGAPORE PC5 ADVANCED STATSTCAL MECHANCS (Semeser : AY 1-13) Tme Allowed: Hours NSTRUCTONS TO CANDDATES 1. Ths examnaon paper conans 5 quesons and comprses 4 prned pages.. Answer all
NATONAL UNVERSTY OF SNGAPORE PC5 ADVANCED STATSTCAL MECHANCS (Semeser : AY 1-13) Tme Allowed: Hours NSTRUCTONS TO CANDDATES 1. Ths examnaon paper conans 5 quesons and comprses 4 prned pages.. Answer all
APOC #232 Capacity Planning for Fault-Tolerant All-Optical Network
 APOC #232 Capacy Plannng for Faul-Toleran All-Opcal Nework Mchael Kwok-Shng Ho and Kwok-wa Cheung Deparmen of Informaon ngneerng The Chnese Unversy of Hong Kong Shan, N.T., Hong Kong SAR, Chna -mal: kwcheung@e.cuhk.edu.hk
APOC #232 Capacy Plannng for Faul-Toleran All-Opcal Nework Mchael Kwok-Shng Ho and Kwok-wa Cheung Deparmen of Informaon ngneerng The Chnese Unversy of Hong Kong Shan, N.T., Hong Kong SAR, Chna -mal: kwcheung@e.cuhk.edu.hk
Advanced Machine Learning & Perception
 Advanced Machne Learnng & Percepon Insrucor: Tony Jebara SVM Feaure & Kernel Selecon SVM Eensons Feaure Selecon (Flerng and Wrappng) SVM Feaure Selecon SVM Kernel Selecon SVM Eensons Classfcaon Feaure/Kernel
Advanced Machne Learnng & Percepon Insrucor: Tony Jebara SVM Feaure & Kernel Selecon SVM Eensons Feaure Selecon (Flerng and Wrappng) SVM Feaure Selecon SVM Kernel Selecon SVM Eensons Classfcaon Feaure/Kernel
Chapter Lagrangian Interpolation
 Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Including the ordinary differential of distance with time as velocity makes a system of ordinary differential equations.
 Soluons o Ordnary Derenal Equaons An ordnary derenal equaon has only one ndependen varable. A sysem o ordnary derenal equaons consss o several derenal equaons each wh he same ndependen varable. An eample
Soluons o Ordnary Derenal Equaons An ordnary derenal equaon has only one ndependen varable. A sysem o ordnary derenal equaons consss o several derenal equaons each wh he same ndependen varable. An eample
Bayes rule for a classification problem INF Discriminant functions for the normal density. Euclidean distance. Mahalanobis distance
 INF 43 3.. Repeon Anne Solberg (anne@f.uo.no Bayes rule for a classfcaon problem Suppose we have J, =,...J classes. s he class label for a pxel, and x s he observed feaure vecor. We can use Bayes rule
INF 43 3.. Repeon Anne Solberg (anne@f.uo.no Bayes rule for a classfcaon problem Suppose we have J, =,...J classes. s he class label for a pxel, and x s he observed feaure vecor. We can use Bayes rule
( t) Outline of program: BGC1: Survival and event history analysis Oslo, March-May Recapitulation. The additive regression model
 BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
Should Exact Index Numbers have Standard Errors? Theory and Application to Asian Growth
 Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
ISSN MIT Publications
 MIT Inernaonal Journal of Elecrcal and Insrumenaon Engneerng Vol. 1, No. 2, Aug 2011, pp 93-98 93 ISSN 2230-7656 MIT Publcaons A New Approach for Solvng Economc Load Dspach Problem Ansh Ahmad Dep. of Elecrcal
MIT Inernaonal Journal of Elecrcal and Insrumenaon Engneerng Vol. 1, No. 2, Aug 2011, pp 93-98 93 ISSN 2230-7656 MIT Publcaons A New Approach for Solvng Economc Load Dspach Problem Ansh Ahmad Dep. of Elecrcal
Machine Learning Linear Regression
 Machne Learnng Lnear Regresson Lesson 3 Lnear Regresson Bascs of Regresson Leas Squares esmaon Polynomal Regresson Bass funcons Regresson model Regularzed Regresson Sascal Regresson Mamum Lkelhood (ML)
Machne Learnng Lnear Regresson Lesson 3 Lnear Regresson Bascs of Regresson Leas Squares esmaon Polynomal Regresson Bass funcons Regresson model Regularzed Regresson Sascal Regresson Mamum Lkelhood (ML)
