Quantitative recurrence for beta expansion. Wang BaoWei
|
|
|
- Annis Clara Morrison
- 5 years ago
- Views:
Transcription
1 Introduction Further study Quantitative recurrence for beta expansion Huazhong University of Science and Technology July
2 Introduction Further study Contents 1 Introduction Background Beta expansion 2 Known results and our formulations Proofs 3 Further study
3 Introduction FurtherBackground study Beta expansion 1 Introduction Background Beta expansion 2 3 Further study
4 Introduction FurtherBackground study Background Beta expansion A well known theory on recurrence is Poincaré s recurrence theorem. Theorem (Poincaré s Recurrence Theorem) Let T : X X be a measurable transformation on a probability space (X, B, µ). Let B B with µ(b) > 0. Then for almost all points x B, the orbit {T n (x)} n 0 returns to B infinitely often.
5 Introduction FurtherBackground study Background Beta expansion A well known theory on recurrence is Poincaré s recurrence theorem. Theorem (Poincaré s Recurrence Theorem) Let T : X X be a measurable transformation on a probability space (X, B, µ). Let B B with µ(b) > 0. Then for almost all points x B, the orbit {T n (x)} n 0 returns to B infinitely often. However, this information is only of qualitative nature and it is only concerned with a fixed target B.
6 Introduction FurtherBackground study Problems Beta expansion Problem 1 With which frequency an orbit visits a given set of positive measure; and
7 Introduction FurtherBackground study Problems Beta expansion Problem 1 With which frequency an orbit visits a given set of positive measure; and Problem 2 With which rate a given point returns to an arbitrarily small neighborhood of itself.
8 Introduction FurtherBackground study Problems Beta expansion Problem 1 With which frequency an orbit visits a given set of positive measure; and Problem 2 With which rate a given point returns to an arbitrarily small neighborhood of itself. Problem 3 What happens if the ball B shrinks with time and more generally if the ball also moves around with time?
9 Introduction FurtherBackground study Beta expansion Beta expansion Let β > 1 be a real number. The beta transformation with respect to β is given as T β (x) = βx(mod 1). Hence, any x [0, 1) can be expanded uniquely as an finite or infinite series with the form x = ɛ 1(x, β) β + ɛ 2(x, β) β 2 +, where ɛ n (x, β) = [βt n 1 β (x)] are called the digits of x and the ( ) sequence ɛ 1 (x, β), ɛ 2 (x, β), is called the sequence of the beta expansion of x with respect to the base β.
10 Introduction FurtherBackground study Admissible sequence Beta expansion Definition An n-block (ɛ 1, ɛ 2,, ɛ n ) is called admissible in base β if there exists x [0, 1] such that ɛ k (x, β) = ɛ k for all 1 k n. An infinite sequence (ɛ 1, ɛ 2,, ɛ n, ) is admissible in base β if (ɛ 1, ɛ 2,, ɛ k ) is admissible in base β for all k 1.
11 Introduction FurtherBackground study Admissible sequence Beta expansion Definition An n-block (ɛ 1, ɛ 2,, ɛ n ) is called admissible in base β if there exists x [0, 1] such that ɛ k (x, β) = ɛ k for all 1 k n. An infinite sequence (ɛ 1, ɛ 2,, ɛ n, ) is admissible in base β if (ɛ 1, ɛ 2,, ɛ k ) is admissible in base β for all k 1. Denote by Σ β all infinite admissible sequence in the beta expansion with respect to the base β.
12 Introduction FurtherBackground study Beta expansion Characterizations on admissible sequence Theorem (W. Parry) Let β > 1 be a real number and ɛ(1, β) be the β-expansion of 1. We denote by w an infinite sequence of positive integer. (1) If ɛ(1, β) is infinite, w Σ β if and only if σ k (w) < lex ɛ(1, β), for all k 0. (2)If ɛ(1, β) is finite, i.e., ɛ(1, β) = (ɛ 1 (1, β),, ɛ n (1, β), 0 ) with ɛ n (1, β) 0. Then w Σ β if and only if σ k (w) < lex ɛ (1, β), for all k 0. where ɛ (1, β) = ( ɛ 1 (1, β), ɛ 2 (1, β),, ɛ n 1 (1, β), (ɛ n (1, β) 1)) is a purely periodic sequence.
13 Introduction FurtherKnown study results and our formulations Proof of the result 1 Introduction 2 Known results and our formulations Proofs 3 Further study
14 Introduction FurtherKnown study results and our formulations Known results Proof of the result Quantitative recurrence properties to general settings. Theorem (Boshernitzan) Let (X, µ, T, d) be a measure dynamical system with a metric d. Assume that, for some α > 0, the Hausdorff α-measure H α is σ- finite on the space X. Then for µ-almost all x X, lim inf n n 1 α d(t n x, x) <. If, moreover, H α (X) = 0, then for µ-almost all x X, lim inf n n 1 α d(t n x, x) = 0.
15 Introduction FurtherKnown study results and our formulations Proof of the result When applied to beta transformation, one has, almost surely, lim inf n nd(t n x, x) <.
16 Introduction FurtherKnown study results and our formulations Proof of the result Quantitative recurrence properties to beta transformations. Theorem (W. Philipp) Let φ be a positive function defined on natural numbers N. The set { } R β (φ) := x [0, 1] : Tβ n x B(x, φ(n) 1 ), infinitely often n N is a full or null set if and only if the series n 1 φ 1 (n) diverges or not.
17 Introduction FurtherKnown study results and our formulations Our formulations Proof of the result Given a general function φ : N R +, find the Hausdorff dimension of the set { } x [0, 1] : Tβ n x x < φ(n) 1, infinitely often n N.
18 Introduction FurtherKnown study results and our formulations Our formulations Proof of the result Given a general function φ : N R +, find the Hausdorff dimension of the set { } x [0, 1] : Tβ n x x < φ(n) 1, infinitely often n N. Theorem (Main result) For any β > 1, dim H R β (φ) = 1, where b = lim inf 1 + b n log β φ(n). n
19 Introduction FurtherKnown study results and our formulations Difficulties Proof of the result In studying the metric theory related to beta transformation, one of the big obstacle lies in estimating the length of a cylinder I β (ɛ 1,, ɛ n ) = {x [0, 1] : ɛ k (x, β) = ɛ k, 1 k n} for general β > 1.
20 Introduction FurtherKnown study results and our formulations Our strategy Proof of the result Principle As far as Haudorff dimension or metric theory is concerned, we can discard some bad points without affecting the final results.
21 Introduction FurtherKnown study results and our formulations Our strategy Proof of the result Principle As far as Haudorff dimension or metric theory is concerned, we can discard some bad points without affecting the final results. As a result, we confine our attention to good points: {x = (ɛ 1,, ɛ n, ) : (ɛ 1,, ɛ n, ) Σ βn }, where β N is defined as the solution to the equation 1 = ɛ 1(1, β) β N + ɛ 2(1, β) β 2 N + + ɛ N(1, β) βn N.
22 Introduction FurtherKnown study results and our formulations Proof of the result By the criterion for admissible sequence, one can know easy that Σ βn Σ β. More importantly, for any admissible block (ɛ 1,, ɛ n ) Σ βn, (ɛ 1,, ɛ n, 0 N, 1) Σ βn, so is in Σ β.
23 Introduction FurtherKnown study results and our formulations Proof of the result By the criterion for admissible sequence, one can know easy that Σ βn Σ β. More importantly, for any admissible block (ɛ 1,, ɛ n ) Σ βn, (ɛ 1,, ɛ n, 0 N, 1) Σ βn, so is in Σ β. As a consequence, Proposition For any admissible block (ɛ 1,, ɛ n ) Σ βn, then it holds the following length estimation I β (ɛ 1,, ɛ n ) 1 β n.
24 Introduction FurtherKnown study results and our formulations Cantor subset Proof of the result It is easy to see that if the β-expansion of T n x and that of x coincide in a long block from the very beginning, one can make sure that T n x and x are close enough. So, our Cantor subset is defined as follows.
25 Introduction FurtherKnown study results and our formulations Cantor subset Proof of the result It is easy to see that if the β-expansion of T n x and that of x coincide in a long block from the very beginning, one can make sure that T n x and x are close enough. So, our Cantor subset is defined as follows. Level 1. E 1 = I β ((ɛ 1,, ɛ n1 0 N ) w1+1 0 N ) ɛ 1,,ɛ n1 Σ n 1 β N where w 1 is some rational with w 1 (n 1 + N) N such that β (n 1+N)w 1 < φ(n 1 ) 1, but β (n 1+N)w 1 +1 φ(n 1 ) 1. Then it follows that, for any x I β ((ɛ 1,, ɛ n1 0 N ) w N ), T n 1 β x x < 1 φ(n 1 ). (2.1)
26 Introduction FurtherKnown study results and our formulations Proof of the result Level 2. Write m 1 = (w 1 + 1)(n 1 + N), t 2 = n 2 m 1. For each I β = I β (ɛ 1,, ɛ m1 ), set E 2 (I β ) = I β ((ɛ 1,, ɛ 0 N n2 ) w2+1 0 N ), ɛ m1 +1,,ɛ n2 Σ t 2 βn where w 2 is some rational with w 2 (n 2 + N) N such that β (n 2+N)w 2 < φ(n 1 2 ), but β (n 2+N)w 2 +1 φ(n 1 2 ).
27 Introduction FurtherKnown study results and our formulations Proof of the result Level 2. Write m 1 = (w 1 + 1)(n 1 + N), t 2 = n 2 m 1. For each I β = I β (ɛ 1,, ɛ m1 ), set E 2 (I β ) = I β ((ɛ 1,, ɛ 0 N n2 ) w2+1 0 N ), ɛ m1 +1,,ɛ n2 Σ t 2 βn where w 2 is some rational with w 2 (n 2 + N) N such that β (n 2+N)w 2 < φ(n 1 2 ), but β (n 2+N)w 2 +1 φ(n 1 2 ). Then finally, define E 2 = I β (ɛ 1,,ɛ m1 ) E 1 E 2 (I β (ɛ 1,, ɛ m1 )).
28 Introduction Further study 1 Introduction 2 3 Further study
29 Introduction Further study Further study Size of the level set defined by the Birkhoff ergodic related to beta expansion. Theorem (Fan, Feng, Wu) Let (Σ A, T ) be a topologically mixing subshift of finite type on an alphabet consisting of m symbols and let Φ : Σ A R d be a continuous function. For any possible limit of the ergodic limit α of lim n 1 n n 1 j=0 Φ(T j x), one has n 1 1 ) { h top (x Σ A : lim Φ(T j x) = α = sup h µ : n n j=0 } Φdµ = α where h µ denotes the entropy of µ and h top denotes the topological entropy.c d.
30 Introduction Further study If we relate above system with beta shift, it deals with the β with finite expansion of the unit 1. Then how about the case for general β. Question 1 Given β > 1. Denote by Σ β the collection of all infinite admissible sequence in the beta expansion in base β. Let Φ : Σ β R be a continuous function. How about the size of the set x [0, 1] : lim n n 1 1 n j=0 Φ(T j (ɛ(x, β))) = α, where ɛ(x, β) denotes the sequence of the β-expansion of x.
31 Introduction Further study Shrinking target problems for beta transformation. Question 2 Given β > 1 and x 0 [0, 1). Let Φ be a positive function defined on N. Find the Hausdorff dimension of the set { } x [0, 1] : T n x x 0 < Φ(n), for infinite many n N.
32 Introduction Further study Thanks THANK YOU!
Diophantine approximation of beta expansion in parameter space
 Diophantine approximation of beta expansion in parameter space Jun Wu Huazhong University of Science and Technology Advances on Fractals and Related Fields, France 19-25, September 2015 Outline 1 Background
Diophantine approximation of beta expansion in parameter space Jun Wu Huazhong University of Science and Technology Advances on Fractals and Related Fields, France 19-25, September 2015 Outline 1 Background
dynamical Diophantine approximation
 Dioph. Appro. Dynamical Dioph. Appro. in dynamical Diophantine approximation WANG Bao-Wei Huazhong University of Science and Technology Joint with Zhang Guo-Hua Central China Normal University 24-28 July
Dioph. Appro. Dynamical Dioph. Appro. in dynamical Diophantine approximation WANG Bao-Wei Huazhong University of Science and Technology Joint with Zhang Guo-Hua Central China Normal University 24-28 July
The dimensional theory of continued fractions
 Jun Wu Huazhong University of Science and Technology Advances on Fractals and Related Topics, Hong Kong, Dec. 10-14, 2012 Continued fraction : x [0, 1), 1 x = 1 a 1 (x) + 1 a 2 (x) + a 3 (x) + = [a 1 (x),
Jun Wu Huazhong University of Science and Technology Advances on Fractals and Related Topics, Hong Kong, Dec. 10-14, 2012 Continued fraction : x [0, 1), 1 x = 1 a 1 (x) + 1 a 2 (x) + a 3 (x) + = [a 1 (x),
Uniform Diophantine approximation related to b-ary and β-expansions
 Uniform Diophantine approximation related to b-ary and β-expansions Lingmin LIAO (joint work with Yann Bugeaud) Université Paris-Est Créteil (University Paris 12) Universidade Federal de Bahia April 8th
Uniform Diophantine approximation related to b-ary and β-expansions Lingmin LIAO (joint work with Yann Bugeaud) Université Paris-Est Créteil (University Paris 12) Universidade Federal de Bahia April 8th
PHY411 Lecture notes Part 5
 PHY411 Lecture notes Part 5 Alice Quillen January 27, 2016 Contents 0.1 Introduction.................................... 1 1 Symbolic Dynamics 2 1.1 The Shift map.................................. 3 1.2
PHY411 Lecture notes Part 5 Alice Quillen January 27, 2016 Contents 0.1 Introduction.................................... 1 1 Symbolic Dynamics 2 1.1 The Shift map.................................. 3 1.2
Rudiments of Ergodic Theory
 Rudiments of Ergodic Theory Zefeng Chen September 24, 203 Abstract In this note we intend to present basic ergodic theory. We begin with the notion of a measure preserving transformation. We then define
Rudiments of Ergodic Theory Zefeng Chen September 24, 203 Abstract In this note we intend to present basic ergodic theory. We begin with the notion of a measure preserving transformation. We then define
UNIVERSITY OF BRISTOL. Mock exam paper for examination for the Degrees of B.Sc. and M.Sci. (Level 3)
 UNIVERSITY OF BRISTOL Mock exam paper for examination for the Degrees of B.Sc. and M.Sci. (Level 3) DYNAMICAL SYSTEMS and ERGODIC THEORY MATH 36206 (Paper Code MATH-36206) 2 hours and 30 minutes This paper
UNIVERSITY OF BRISTOL Mock exam paper for examination for the Degrees of B.Sc. and M.Sci. (Level 3) DYNAMICAL SYSTEMS and ERGODIC THEORY MATH 36206 (Paper Code MATH-36206) 2 hours and 30 minutes This paper
Lecture Notes Introduction to Ergodic Theory
 Lecture Notes Introduction to Ergodic Theory Tiago Pereira Department of Mathematics Imperial College London Our course consists of five introductory lectures on probabilistic aspects of dynamical systems,
Lecture Notes Introduction to Ergodic Theory Tiago Pereira Department of Mathematics Imperial College London Our course consists of five introductory lectures on probabilistic aspects of dynamical systems,
Correlation dimension for self-similar Cantor sets with overlaps
 F U N D A M E N T A MATHEMATICAE 155 (1998) Correlation dimension for self-similar Cantor sets with overlaps by Károly S i m o n (Miskolc) and Boris S o l o m y a k (Seattle, Wash.) Abstract. We consider
F U N D A M E N T A MATHEMATICAE 155 (1998) Correlation dimension for self-similar Cantor sets with overlaps by Károly S i m o n (Miskolc) and Boris S o l o m y a k (Seattle, Wash.) Abstract. We consider
Three hours THE UNIVERSITY OF MANCHESTER. 31st May :00 17:00
 Three hours MATH41112 THE UNIVERSITY OF MANCHESTER ERGODIC THEORY 31st May 2016 14:00 17:00 Answer FOUR of the FIVE questions. If more than four questions are attempted, then credit will be given for the
Three hours MATH41112 THE UNIVERSITY OF MANCHESTER ERGODIC THEORY 31st May 2016 14:00 17:00 Answer FOUR of the FIVE questions. If more than four questions are attempted, then credit will be given for the
n=1 f(t n x)µ(n) = o(m), where µ is the Möbius function. We do this by showing that enough of the powers of T are pairwise disjoint.
 Möbius disjointness for interval exchange transformations on three intervals (with A. Eskin) We show that 3-IETs that satisfy a mild diophantine condition satisfy Sarnak s Möbius disjointness conjecture.
Möbius disjointness for interval exchange transformations on three intervals (with A. Eskin) We show that 3-IETs that satisfy a mild diophantine condition satisfy Sarnak s Möbius disjointness conjecture.
Proof: The coding of T (x) is the left shift of the coding of x. φ(t x) n = L if T n+1 (x) L
 Lecture 24: Defn: Topological conjugacy: Given Z + d (resp, Zd ), actions T, S a topological conjugacy from T to S is a homeomorphism φ : M N s.t. φ T = S φ i.e., φ T n = S n φ for all n Z + d (resp, Zd
Lecture 24: Defn: Topological conjugacy: Given Z + d (resp, Zd ), actions T, S a topological conjugacy from T to S is a homeomorphism φ : M N s.t. φ T = S φ i.e., φ T n = S n φ for all n Z + d (resp, Zd
DYADIC DIOPHANTINE APPROXIMATION AND KATOK S HORSESHOE APPROXIMATION
 DYADIC DIOPHANTINE APPROXIMATION AND KATOK S HORSESHOE APPROXIMATION TOMAS PERSSON AND JÖRG SCHMELING Preprints in Mathematical Sciences 2006:3 Centre for Mathematical Sciences Mathematics CENTRUM SCIENTIARUM
DYADIC DIOPHANTINE APPROXIMATION AND KATOK S HORSESHOE APPROXIMATION TOMAS PERSSON AND JÖRG SCHMELING Preprints in Mathematical Sciences 2006:3 Centre for Mathematical Sciences Mathematics CENTRUM SCIENTIARUM
Dynamical Borel-Cantelli lemmas for Gibbs measures
 Dynamical Borel-Cantelli lemmas for Gibbs measures N. Chernov and D. Kleinbock To appear in Israel J. Math. Abstract Let T : X X be a deterministic dynamical system preserving a probability measure µ.
Dynamical Borel-Cantelli lemmas for Gibbs measures N. Chernov and D. Kleinbock To appear in Israel J. Math. Abstract Let T : X X be a deterministic dynamical system preserving a probability measure µ.
(1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define
![(1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define](/thumbs/88/116259117.jpg) Homework, Real Analysis I, Fall, 2010. (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define ρ(f, g) = 1 0 f(x) g(x) dx. Show that
Homework, Real Analysis I, Fall, 2010. (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define ρ(f, g) = 1 0 f(x) g(x) dx. Show that
1. Theorem. (Archimedean Property) Let x be any real number. There exists a positive integer n greater than x.
 Advanced Calculus I, Dr. Block, Chapter 2 notes. Theorem. (Archimedean Property) Let x be any real number. There exists a positive integer n greater than x. 2. Definition. A sequence is a real-valued function
Advanced Calculus I, Dr. Block, Chapter 2 notes. Theorem. (Archimedean Property) Let x be any real number. There exists a positive integer n greater than x. 2. Definition. A sequence is a real-valued function
Lecture 4. Entropy and Markov Chains
 preliminary version : Not for diffusion Lecture 4. Entropy and Markov Chains The most important numerical invariant related to the orbit growth in topological dynamical systems is topological entropy.
preliminary version : Not for diffusion Lecture 4. Entropy and Markov Chains The most important numerical invariant related to the orbit growth in topological dynamical systems is topological entropy.
(x k ) sequence in F, lim x k = x x F. If F : R n R is a function, level sets and sublevel sets of F are any sets of the form (respectively);
 STABILITY OF EQUILIBRIA AND LIAPUNOV FUNCTIONS. By topological properties in general we mean qualitative geometric properties (of subsets of R n or of functions in R n ), that is, those that don t depend
STABILITY OF EQUILIBRIA AND LIAPUNOV FUNCTIONS. By topological properties in general we mean qualitative geometric properties (of subsets of R n or of functions in R n ), that is, those that don t depend
A quantitative approach to syndetic transitivity and topological ergodicity
 Available online at www.isr-publications.com/jnsa J. Nonlinear Sci. Appl., 10 (2017), 4680 4686 Research Article Journal Homepage: www.tjnsa.com - www.isr-publications.com/jnsa A quantitative approach
Available online at www.isr-publications.com/jnsa J. Nonlinear Sci. Appl., 10 (2017), 4680 4686 Research Article Journal Homepage: www.tjnsa.com - www.isr-publications.com/jnsa A quantitative approach
functions as above. There is a unique non-empty compact set, i=1
 1 Iterated function systems Many of the well known examples of fractals, including the middle third Cantor sets, the Siepiński gasket and certain Julia sets, can be defined as attractors of iterated function
1 Iterated function systems Many of the well known examples of fractals, including the middle third Cantor sets, the Siepiński gasket and certain Julia sets, can be defined as attractors of iterated function
25.1 Ergodicity and Metric Transitivity
 Chapter 25 Ergodicity This lecture explains what it means for a process to be ergodic or metrically transitive, gives a few characterizes of these properties (especially for AMS processes), and deduces
Chapter 25 Ergodicity This lecture explains what it means for a process to be ergodic or metrically transitive, gives a few characterizes of these properties (especially for AMS processes), and deduces
MAS3706 Topology. Revision Lectures, May I do not answer enquiries as to what material will be in the exam.
 MAS3706 Topology Revision Lectures, May 208 Z.A.Lykova It is essential that you read and try to understand the lecture notes from the beginning to the end. Many questions from the exam paper will be similar
MAS3706 Topology Revision Lectures, May 208 Z.A.Lykova It is essential that you read and try to understand the lecture notes from the beginning to the end. Many questions from the exam paper will be similar
Metric Spaces and Topology
 Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
Chapter 2 Metric Spaces and Topology From an engineering perspective, the most important way to construct a topology on a set is to define the topology in terms of a metric on the set. This approach underlies
NOTIONS OF DIMENSION
 NOTIONS OF DIENSION BENJAIN A. STEINHURST A quick overview of some basic notions of dimension for a summer REU program run at UConn in 200 with a view towards using dimension as a tool in attempting to
NOTIONS OF DIENSION BENJAIN A. STEINHURST A quick overview of some basic notions of dimension for a summer REU program run at UConn in 200 with a view towards using dimension as a tool in attempting to
Section 11.1 Sequences
 Math 152 c Lynch 1 of 8 Section 11.1 Sequences A sequence is a list of numbers written in a definite order: a 1, a 2, a 3,..., a n,... Notation. The sequence {a 1, a 2, a 3,...} can also be written {a
Math 152 c Lynch 1 of 8 Section 11.1 Sequences A sequence is a list of numbers written in a definite order: a 1, a 2, a 3,..., a n,... Notation. The sequence {a 1, a 2, a 3,...} can also be written {a
Thermodynamics for discontinuous maps and potentials
 Thermodynamics for discontinuous maps and potentials Vaughn Climenhaga University of Houston July 11, 2013 Plan of talk Dynamical system { X a complete separable metric space f : X X a measurable map Potential
Thermodynamics for discontinuous maps and potentials Vaughn Climenhaga University of Houston July 11, 2013 Plan of talk Dynamical system { X a complete separable metric space f : X X a measurable map Potential
Smooth flows with fractional entropy dimension
 Smooth flows with fractional entropy dimension Steve Hurder MCA Montreal, July 27, 2017 University of Illinois at Chicago www.math.uic.edu/ hurder Theorem (K. Kuperberg, 1994) Let M be a closed, orientable
Smooth flows with fractional entropy dimension Steve Hurder MCA Montreal, July 27, 2017 University of Illinois at Chicago www.math.uic.edu/ hurder Theorem (K. Kuperberg, 1994) Let M be a closed, orientable
MATH 614 Dynamical Systems and Chaos Lecture 6: Symbolic dynamics.
 MATH 614 Dynamical Systems and Chaos Lecture 6: Symbolic dynamics. Metric space Definition. Given a nonempty set X, a metric (or distance function) on X is a function d : X X R that satisfies the following
MATH 614 Dynamical Systems and Chaos Lecture 6: Symbolic dynamics. Metric space Definition. Given a nonempty set X, a metric (or distance function) on X is a function d : X X R that satisfies the following
Density of periodic points, invariant measures and almost equicontinuous points of Cellular Automata
 Density of periodic points, invariant measures and almost equicontinuous points of Cellular Automata Pierre Tisseur a a Department of Mathematics, Trent University, Peterborough, Ontario, Canada Abstract
Density of periodic points, invariant measures and almost equicontinuous points of Cellular Automata Pierre Tisseur a a Department of Mathematics, Trent University, Peterborough, Ontario, Canada Abstract
Entropy dimensions and a class of constructive examples
 Entropy dimensions and a class of constructive examples Sébastien Ferenczi Institut de Mathématiques de Luminy CNRS - UMR 6206 Case 907, 63 av. de Luminy F3288 Marseille Cedex 9 (France) and Fédération
Entropy dimensions and a class of constructive examples Sébastien Ferenczi Institut de Mathématiques de Luminy CNRS - UMR 6206 Case 907, 63 av. de Luminy F3288 Marseille Cedex 9 (France) and Fédération
Diophantine approximation of fractional parts of powers of real numbers
 Diophantine approximation of fractional parts of powers of real numbers Lingmin LIAO (joint work with Yann Bugeaud, and Micha l Rams) Université Paris-Est Créteil Huazhong University of Science and Technology,
Diophantine approximation of fractional parts of powers of real numbers Lingmin LIAO (joint work with Yann Bugeaud, and Micha l Rams) Université Paris-Est Créteil Huazhong University of Science and Technology,
Analysis III Theorems, Propositions & Lemmas... Oh My!
 Analysis III Theorems, Propositions & Lemmas... Oh My! Rob Gibson October 25, 2010 Proposition 1. If x = (x 1, x 2,...), y = (y 1, y 2,...), then is a distance. ( d(x, y) = x k y k p Proposition 2. In
Analysis III Theorems, Propositions & Lemmas... Oh My! Rob Gibson October 25, 2010 Proposition 1. If x = (x 1, x 2,...), y = (y 1, y 2,...), then is a distance. ( d(x, y) = x k y k p Proposition 2. In
Introduction to Hausdorff Measure and Dimension
 Introduction to Hausdorff Measure and Dimension Dynamics Learning Seminar, Liverpool) Poj Lertchoosakul 28 September 2012 1 Definition of Hausdorff Measure and Dimension Let X, d) be a metric space, let
Introduction to Hausdorff Measure and Dimension Dynamics Learning Seminar, Liverpool) Poj Lertchoosakul 28 September 2012 1 Definition of Hausdorff Measure and Dimension Let X, d) be a metric space, let
A non-uniform Bowen s equation and connections to multifractal analysis
 A non-uniform Bowen s equation and connections to multifractal analysis Vaughn Climenhaga Penn State November 1, 2009 1 Introduction and classical results Hausdorff dimension via local dimensional characteristics
A non-uniform Bowen s equation and connections to multifractal analysis Vaughn Climenhaga Penn State November 1, 2009 1 Introduction and classical results Hausdorff dimension via local dimensional characteristics
Symbolic extensions for partially hyperbolic diffeomorphisms
 for partially hyperbolic diffeomorphisms Todd Fisher tfisher@math.byu.edu Department of Mathematics Brigham Young University Workshop on Partial Hyperbolicity Entropy Topological entropy measures the exponential
for partially hyperbolic diffeomorphisms Todd Fisher tfisher@math.byu.edu Department of Mathematics Brigham Young University Workshop on Partial Hyperbolicity Entropy Topological entropy measures the exponential
Dirichlet uniformly well-approximated numbers
 Dirichlet uniformly well-approximated numbers Lingmin LIAO (joint work with Dong Han Kim) Université Paris-Est Créteil (University Paris 12) Hyperbolicity and Dimension CIRM, Luminy December 3rd 2013 Lingmin
Dirichlet uniformly well-approximated numbers Lingmin LIAO (joint work with Dong Han Kim) Université Paris-Est Créteil (University Paris 12) Hyperbolicity and Dimension CIRM, Luminy December 3rd 2013 Lingmin
ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY
 ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY AND ω-limit SETS CHRIS GOOD AND JONATHAN MEDDAUGH Abstract. Let f : X X be a continuous map on a compact metric space, let ω f be the collection of ω-limit
ORBITAL SHADOWING, INTERNAL CHAIN TRANSITIVITY AND ω-limit SETS CHRIS GOOD AND JONATHAN MEDDAUGH Abstract. Let f : X X be a continuous map on a compact metric space, let ω f be the collection of ω-limit
Segment Description of Turbulence
 Dynamics of PDE, Vol.4, No.3, 283-291, 2007 Segment Description of Turbulence Y. Charles Li Communicated by Y. Charles Li, received August 25, 2007. Abstract. We propose a segment description for turbulent
Dynamics of PDE, Vol.4, No.3, 283-291, 2007 Segment Description of Turbulence Y. Charles Li Communicated by Y. Charles Li, received August 25, 2007. Abstract. We propose a segment description for turbulent
DYNAMICAL SYSTEMS PROBLEMS. asgor/ (1) Which of the following maps are topologically transitive (minimal,
 DYNAMICAL SYSTEMS PROBLEMS http://www.math.uci.edu/ asgor/ (1) Which of the following maps are topologically transitive (minimal, topologically mixing)? identity map on a circle; irrational rotation of
DYNAMICAL SYSTEMS PROBLEMS http://www.math.uci.edu/ asgor/ (1) Which of the following maps are topologically transitive (minimal, topologically mixing)? identity map on a circle; irrational rotation of
Lecture 5: Oscillatory motions for the RPE3BP
 Lecture 5: Oscillatory motions for the RPE3BP Marcel Guardia Universitat Politècnica de Catalunya February 10, 2017 M. Guardia (UPC) Lecture 5 February 10, 2017 1 / 25 Outline Oscillatory motions for the
Lecture 5: Oscillatory motions for the RPE3BP Marcel Guardia Universitat Politècnica de Catalunya February 10, 2017 M. Guardia (UPC) Lecture 5 February 10, 2017 1 / 25 Outline Oscillatory motions for the
Dynamical Systems and Ergodic Theory PhD Exam Spring Topics: Topological Dynamics Definitions and basic results about the following for maps and
 Dynamical Systems and Ergodic Theory PhD Exam Spring 2012 Introduction: This is the first year for the Dynamical Systems and Ergodic Theory PhD exam. As such the material on the exam will conform fairly
Dynamical Systems and Ergodic Theory PhD Exam Spring 2012 Introduction: This is the first year for the Dynamical Systems and Ergodic Theory PhD exam. As such the material on the exam will conform fairly
INTRODUCTION TO FRACTAL GEOMETRY
 Every mathematical theory, however abstract, is inspired by some idea coming in our mind from the observation of nature, and has some application to our world, even if very unexpected ones and lying centuries
Every mathematical theory, however abstract, is inspired by some idea coming in our mind from the observation of nature, and has some application to our world, even if very unexpected ones and lying centuries
THE REAL NUMBERS Chapter #4
 FOUNDATIONS OF ANALYSIS FALL 2008 TRUE/FALSE QUESTIONS THE REAL NUMBERS Chapter #4 (1) Every element in a field has a multiplicative inverse. (2) In a field the additive inverse of 1 is 0. (3) In a field
FOUNDATIONS OF ANALYSIS FALL 2008 TRUE/FALSE QUESTIONS THE REAL NUMBERS Chapter #4 (1) Every element in a field has a multiplicative inverse. (2) In a field the additive inverse of 1 is 0. (3) In a field
New rotation sets in a family of toral homeomorphisms
 New rotation sets in a family of toral homeomorphisms Philip Boyland, André de Carvalho & Toby Hall Surfaces in São Paulo April, 2014 SP, 2014 p.1 Outline The rotation sets of torus homeomorphisms: general
New rotation sets in a family of toral homeomorphisms Philip Boyland, André de Carvalho & Toby Hall Surfaces in São Paulo April, 2014 SP, 2014 p.1 Outline The rotation sets of torus homeomorphisms: general
Week 2: Sequences and Series
 QF0: Quantitative Finance August 29, 207 Week 2: Sequences and Series Facilitator: Christopher Ting AY 207/208 Mathematicians have tried in vain to this day to discover some order in the sequence of prime
QF0: Quantitative Finance August 29, 207 Week 2: Sequences and Series Facilitator: Christopher Ting AY 207/208 Mathematicians have tried in vain to this day to discover some order in the sequence of prime
PERIODIC POINTS OF THE FAMILY OF TENT MAPS
 PERIODIC POINTS OF THE FAMILY OF TENT MAPS ROBERTO HASFURA-B. AND PHILLIP LYNCH 1. INTRODUCTION. Of interest in this article is the dynamical behavior of the one-parameter family of maps T (x) = (1/2 x
PERIODIC POINTS OF THE FAMILY OF TENT MAPS ROBERTO HASFURA-B. AND PHILLIP LYNCH 1. INTRODUCTION. Of interest in this article is the dynamical behavior of the one-parameter family of maps T (x) = (1/2 x
HAUSDORFF DIMENSION OF MEASURES VIA POINCARÉ RECURRENCE
 HAUSDORFF DIMENSION OF MEASURES VIA POINCARÉ RECURRENCE L. BARREIRA AND B. SAUSSOL Abstract. We study the quantitative behavior of Poincaré recurrence. In particular, for an equilibrium measure on a locally
HAUSDORFF DIMENSION OF MEASURES VIA POINCARÉ RECURRENCE L. BARREIRA AND B. SAUSSOL Abstract. We study the quantitative behavior of Poincaré recurrence. In particular, for an equilibrium measure on a locally
Je Lagarias, University of Michigan. Workshop on Discovery and Experimentation in Number Theory Fields Institute, Toronto (September 25, 2009)
 Ternary Expansions of Powers of 2 Je Lagarias, University of Michigan Workshop on Discovery and Experimentation in Number Theory Fields Institute, Toronto (September 25, 2009) Topics Covered Part I. Erdős
Ternary Expansions of Powers of 2 Je Lagarias, University of Michigan Workshop on Discovery and Experimentation in Number Theory Fields Institute, Toronto (September 25, 2009) Topics Covered Part I. Erdős
Dirichlet uniformly well-approximated numbers
 Dirichlet uniformly well-approximated numbers Lingmin LIAO (joint work with Dong Han Kim) Université Paris-Est Créteil (University Paris 12) Approximation and numeration Université Paris Diderot-Paris
Dirichlet uniformly well-approximated numbers Lingmin LIAO (joint work with Dong Han Kim) Université Paris-Est Créteil (University Paris 12) Approximation and numeration Université Paris Diderot-Paris
arxiv: v1 [math.ds] 1 Oct 2014
![arxiv: v1 [math.ds] 1 Oct 2014 arxiv: v1 [math.ds] 1 Oct 2014](/thumbs/71/66050382.jpg) A NOTE ON THE POINTS WITH DENSE ORBIT UNDER AND MAPS arxiv:1410.019v1 [math.ds] 1 Oct 014 AUTHOR ONE, AUTHOR TWO, AND AUTHOR THREE Abstract. It was conjectured by Furstenberg that for any x [0,1]\Q, dim
A NOTE ON THE POINTS WITH DENSE ORBIT UNDER AND MAPS arxiv:1410.019v1 [math.ds] 1 Oct 014 AUTHOR ONE, AUTHOR TWO, AND AUTHOR THREE Abstract. It was conjectured by Furstenberg that for any x [0,1]\Q, dim
Moreover, µ is monotone, that is for any A B which are both elements of A we have
 FRACTALS Contents. Algebras, sigma algebras, and measures 2.. Carathéodory s outer measures 5.2. Completeness 6.3. Homework: Measure theory basics 7 2. Completion of a measure, creating a measure from
FRACTALS Contents. Algebras, sigma algebras, and measures 2.. Carathéodory s outer measures 5.2. Completeness 6.3. Homework: Measure theory basics 7 2. Completion of a measure, creating a measure from
On negative bases.
 On negative bases Christiane Frougny 1 and Anna Chiara Lai 2 1 LIAFA, CNRS UMR 7089, case 7014, 75205 Paris Cedex 13, France, and University Paris 8, Christiane.Frougny@liafa.jussieu.fr 2 LIAFA, CNRS UMR
On negative bases Christiane Frougny 1 and Anna Chiara Lai 2 1 LIAFA, CNRS UMR 7089, case 7014, 75205 Paris Cedex 13, France, and University Paris 8, Christiane.Frougny@liafa.jussieu.fr 2 LIAFA, CNRS UMR
Lecture 5 - Hausdorff and Gromov-Hausdorff Distance
 Lecture 5 - Hausdorff and Gromov-Hausdorff Distance August 1, 2011 1 Definition and Basic Properties Given a metric space X, the set of closed sets of X supports a metric, the Hausdorff metric. If A is
Lecture 5 - Hausdorff and Gromov-Hausdorff Distance August 1, 2011 1 Definition and Basic Properties Given a metric space X, the set of closed sets of X supports a metric, the Hausdorff metric. If A is
Seminar In Topological Dynamics
 Bar Ilan University Department of Mathematics Seminar In Topological Dynamics EXAMPLES AND BASIC PROPERTIES Harari Ronen May, 2005 1 2 1. Basic functions 1.1. Examples. To set the stage, we begin with
Bar Ilan University Department of Mathematics Seminar In Topological Dynamics EXAMPLES AND BASIC PROPERTIES Harari Ronen May, 2005 1 2 1. Basic functions 1.1. Examples. To set the stage, we begin with
beta-numeration and Rauzy fractals for non-unit Pisot numbers
 beta-numeration and Rauzy fractals for non-unit Pisot numbers Anne Siegel (Irisa, CNRS, Rennes) Kanazawa, June 05 Overview β-expansion: expand a positive real number in a non-integer Pisot basis β Represent
beta-numeration and Rauzy fractals for non-unit Pisot numbers Anne Siegel (Irisa, CNRS, Rennes) Kanazawa, June 05 Overview β-expansion: expand a positive real number in a non-integer Pisot basis β Represent
Nonadditive Measure-theoretic Pressure and Applications to Dimensions of an Ergodic Measure
 Nonadditive Measure-theoretic Pressure and Applications to Dimensions of an Ergodic Measure Yongluo Cao, Huyi Hu and Yun Zhao, Department of Mathematics, Soochow University, Suzhou 25006, Jiangsu, P.R.China
Nonadditive Measure-theoretic Pressure and Applications to Dimensions of an Ergodic Measure Yongluo Cao, Huyi Hu and Yun Zhao, Department of Mathematics, Soochow University, Suzhou 25006, Jiangsu, P.R.China
An introduction to Geometric Measure Theory Part 2: Hausdorff measure
 An introduction to Geometric Measure Theory Part 2: Hausdorff measure Toby O Neil, 10 October 2016 TCON (Open University) An introduction to GMT, part 2 10 October 2016 1 / 40 Last week... Discussed several
An introduction to Geometric Measure Theory Part 2: Hausdorff measure Toby O Neil, 10 October 2016 TCON (Open University) An introduction to GMT, part 2 10 October 2016 1 / 40 Last week... Discussed several
Hausdorff dimension of weighted singular vectors in R 2
 Hausdorff dimension of weighted singular vectors in R 2 Lingmin LIAO (joint with Ronggang Shi, Omri N. Solan, and Nattalie Tamam) Université Paris-Est NCTS Workshop on Dynamical Systems August 15th 2016
Hausdorff dimension of weighted singular vectors in R 2 Lingmin LIAO (joint with Ronggang Shi, Omri N. Solan, and Nattalie Tamam) Université Paris-Est NCTS Workshop on Dynamical Systems August 15th 2016
On Periodic points of area preserving torus homeomorphisms
 On Periodic points of area preserving torus homeomorphisms Fábio Armando Tal and Salvador Addas-Zanata Instituto de Matemática e Estatística Universidade de São Paulo Rua do Matão 11, Cidade Universitária,
On Periodic points of area preserving torus homeomorphisms Fábio Armando Tal and Salvador Addas-Zanata Instituto de Matemática e Estatística Universidade de São Paulo Rua do Matão 11, Cidade Universitária,
Measure and Category. Marianna Csörnyei. ucahmcs
 Measure and Category Marianna Csörnyei mari@math.ucl.ac.uk http:/www.ucl.ac.uk/ ucahmcs 1 / 96 A (very short) Introduction to Cardinals The cardinality of a set A is equal to the cardinality of a set B,
Measure and Category Marianna Csörnyei mari@math.ucl.ac.uk http:/www.ucl.ac.uk/ ucahmcs 1 / 96 A (very short) Introduction to Cardinals The cardinality of a set A is equal to the cardinality of a set B,
1 Topology Definition of a topology Basis (Base) of a topology The subspace topology & the product topology on X Y 3
 Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
A Short Introduction to Ergodic Theory of Numbers. Karma Dajani
 A Short Introduction to Ergodic Theory of Numbers Karma Dajani June 3, 203 2 Contents Motivation and Examples 5 What is Ergodic Theory? 5 2 Number Theoretic Examples 6 2 Measure Preserving, Ergodicity
A Short Introduction to Ergodic Theory of Numbers Karma Dajani June 3, 203 2 Contents Motivation and Examples 5 What is Ergodic Theory? 5 2 Number Theoretic Examples 6 2 Measure Preserving, Ergodicity
Dynamical Systems 2, MA 761
 Dynamical Systems 2, MA 761 Topological Dynamics This material is based upon work supported by the National Science Foundation under Grant No. 9970363 1 Periodic Points 1 The main objects studied in the
Dynamical Systems 2, MA 761 Topological Dynamics This material is based upon work supported by the National Science Foundation under Grant No. 9970363 1 Periodic Points 1 The main objects studied in the
Problem Set 5. 2 n k. Then a nk (x) = 1+( 1)k
 Problem Set 5 1. (Folland 2.43) For x [, 1), let 1 a n (x)2 n (a n (x) = or 1) be the base-2 expansion of x. (If x is a dyadic rational, choose the expansion such that a n (x) = for large n.) Then the
Problem Set 5 1. (Folland 2.43) For x [, 1), let 1 a n (x)2 n (a n (x) = or 1) be the base-2 expansion of x. (If x is a dyadic rational, choose the expansion such that a n (x) = for large n.) Then the
MARKOV PARTITIONS FOR HYPERBOLIC SETS
 MARKOV PARTITIONS FOR HYPERBOLIC SETS TODD FISHER, HIMAL RATHNAKUMARA Abstract. We show that if f is a diffeomorphism of a manifold to itself, Λ is a mixing (or transitive) hyperbolic set, and V is a neighborhood
MARKOV PARTITIONS FOR HYPERBOLIC SETS TODD FISHER, HIMAL RATHNAKUMARA Abstract. We show that if f is a diffeomorphism of a manifold to itself, Λ is a mixing (or transitive) hyperbolic set, and V is a neighborhood
Economics 204 Fall 2011 Problem Set 2 Suggested Solutions
 Economics 24 Fall 211 Problem Set 2 Suggested Solutions 1. Determine whether the following sets are open, closed, both or neither under the topology induced by the usual metric. (Hint: think about limit
Economics 24 Fall 211 Problem Set 2 Suggested Solutions 1. Determine whether the following sets are open, closed, both or neither under the topology induced by the usual metric. (Hint: think about limit
4 Countability axioms
 4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
Multifractal analysis of Bernoulli convolutions associated with Salem numbers
 Multifractal analysis of Bernoulli convolutions associated with Salem numbers De-Jun Feng The Chinese University of Hong Kong Fractals and Related Fields II, Porquerolles - France, June 13th-17th 2011
Multifractal analysis of Bernoulli convolutions associated with Salem numbers De-Jun Feng The Chinese University of Hong Kong Fractals and Related Fields II, Porquerolles - France, June 13th-17th 2011
MTG 5316/4302 FALL 2018 REVIEW FINAL
 MTG 5316/4302 FALL 2018 REVIEW FINAL JAMES KEESLING Problem 1. Define open set in a metric space X. Define what it means for a set A X to be connected in a metric space X. Problem 2. Show that if a set
MTG 5316/4302 FALL 2018 REVIEW FINAL JAMES KEESLING Problem 1. Define open set in a metric space X. Define what it means for a set A X to be connected in a metric space X. Problem 2. Show that if a set
The Existence of Chaos in the Lorenz System
 The Existence of Chaos in the Lorenz System Sheldon E. Newhouse Mathematics Department Michigan State University E. Lansing, MI 48864 joint with M. Berz, K. Makino, A. Wittig Physics, MSU Y. Zou, Math,
The Existence of Chaos in the Lorenz System Sheldon E. Newhouse Mathematics Department Michigan State University E. Lansing, MI 48864 joint with M. Berz, K. Makino, A. Wittig Physics, MSU Y. Zou, Math,
MA651 Topology. Lecture 9. Compactness 2.
 MA651 Topology. Lecture 9. Compactness 2. This text is based on the following books: Topology by James Dugundgji Fundamental concepts of topology by Peter O Neil Elements of Mathematics: General Topology
MA651 Topology. Lecture 9. Compactness 2. This text is based on the following books: Topology by James Dugundgji Fundamental concepts of topology by Peter O Neil Elements of Mathematics: General Topology
On fuzzy entropy and topological entropy of fuzzy extensions of dynamical systems
 On fuzzy entropy and topological entropy of fuzzy extensions of dynamical systems Jose Cánovas, Jiří Kupka* *) Institute for Research and Applications of Fuzzy Modeling University of Ostrava Ostrava, Czech
On fuzzy entropy and topological entropy of fuzzy extensions of dynamical systems Jose Cánovas, Jiří Kupka* *) Institute for Research and Applications of Fuzzy Modeling University of Ostrava Ostrava, Czech
Now, the above series has all non-negative terms, and hence is an upper bound for any fixed term in the series. That is to say, for fixed n 0 N,
 l p IS COMPLETE Let 1 p, and recall the definition of the metric space l p : { } For 1 p
l p IS COMPLETE Let 1 p, and recall the definition of the metric space l p : { } For 1 p
Lecture 16 Symbolic dynamics.
 Lecture 16 Symbolic dynamics. 1 Symbolic dynamics. The full shift on two letters and the Baker s transformation. 2 Shifts of finite type. 3 Directed multigraphs. 4 The zeta function. 5 Topological entropy.
Lecture 16 Symbolic dynamics. 1 Symbolic dynamics. The full shift on two letters and the Baker s transformation. 2 Shifts of finite type. 3 Directed multigraphs. 4 The zeta function. 5 Topological entropy.
Kolmogorov Complexity and Diophantine Approximation
 Kolmogorov Complexity and Diophantine Approximation Jan Reimann Institut für Informatik Universität Heidelberg Kolmogorov Complexity and Diophantine Approximation p. 1/24 Algorithmic Information Theory
Kolmogorov Complexity and Diophantine Approximation Jan Reimann Institut für Informatik Universität Heidelberg Kolmogorov Complexity and Diophantine Approximation p. 1/24 Algorithmic Information Theory
Chapter 2: Introduction to Fractals. Topics
 ME597B/Math597G/Phy597C Spring 2015 Chapter 2: Introduction to Fractals Topics Fundamentals of Fractals Hausdorff Dimension Box Dimension Various Measures on Fractals Advanced Concepts of Fractals 1 C
ME597B/Math597G/Phy597C Spring 2015 Chapter 2: Introduction to Fractals Topics Fundamentals of Fractals Hausdorff Dimension Box Dimension Various Measures on Fractals Advanced Concepts of Fractals 1 C
Entropy for zero-temperature limits of Gibbs-equilibrium states for countable-alphabet subshifts of finite type
 Entropy for zero-temperature limits of Gibbs-equilibrium states for countable-alphabet subshifts of finite type I. D. Morris August 22, 2006 Abstract Let Σ A be a finitely primitive subshift of finite
Entropy for zero-temperature limits of Gibbs-equilibrium states for countable-alphabet subshifts of finite type I. D. Morris August 22, 2006 Abstract Let Σ A be a finitely primitive subshift of finite
Unique equilibrium states for geodesic flows in nonpositive curvature
 Unique equilibrium states for geodesic flows in nonpositive curvature Todd Fisher Department of Mathematics Brigham Young University Fractal Geometry, Hyperbolic Dynamics and Thermodynamical Formalism
Unique equilibrium states for geodesic flows in nonpositive curvature Todd Fisher Department of Mathematics Brigham Young University Fractal Geometry, Hyperbolic Dynamics and Thermodynamical Formalism
Contents Ordered Fields... 2 Ordered sets and fields... 2 Construction of the Reals 1: Dedekind Cuts... 2 Metric Spaces... 3
 Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Analysis Math Notes Study Guide Real Analysis Contents Ordered Fields 2 Ordered sets and fields 2 Construction of the Reals 1: Dedekind Cuts 2 Metric Spaces 3 Metric Spaces 3 Definitions 4 Separability
Dept of Math., SCU+USTC
 2015 s s Joint work with Xiaosheng Wu Dept of Math., SCU+USTC April, 2015 Outlineµ s 1 Background 2 A conjecture 3 Bohr 4 Main result 1. Background s Given a subset S = {s 1 < s 2 < } of natural numbers
2015 s s Joint work with Xiaosheng Wu Dept of Math., SCU+USTC April, 2015 Outlineµ s 1 Background 2 A conjecture 3 Bohr 4 Main result 1. Background s Given a subset S = {s 1 < s 2 < } of natural numbers
Topological Properties of Invariant Sets for Anosov Maps with Holes
 Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2011-11-10 Topological Properties of Invariant Sets for Anosov Maps with Holes Skyler C. Simmons Brigham Young University - Provo
Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2011-11-10 Topological Properties of Invariant Sets for Anosov Maps with Holes Skyler C. Simmons Brigham Young University - Provo
Solutions to Tutorial 8 (Week 9)
 The University of Sydney School of Mathematics and Statistics Solutions to Tutorial 8 (Week 9) MATH3961: Metric Spaces (Advanced) Semester 1, 2018 Web Page: http://www.maths.usyd.edu.au/u/ug/sm/math3961/
The University of Sydney School of Mathematics and Statistics Solutions to Tutorial 8 (Week 9) MATH3961: Metric Spaces (Advanced) Semester 1, 2018 Web Page: http://www.maths.usyd.edu.au/u/ug/sm/math3961/
COBHAM S THEOREM AND SUBSTITUTION SUBSHIFTS
 COBHAM S THEOREM AND SUBSTITUTION SUBSHIFTS FABIEN DURAND Abstract. This lecture intends to propose a first contact with subshift dynamical systems through the study of a well known family: the substitution
COBHAM S THEOREM AND SUBSTITUTION SUBSHIFTS FABIEN DURAND Abstract. This lecture intends to propose a first contact with subshift dynamical systems through the study of a well known family: the substitution
Li- Yorke Chaos in Product Dynamical Systems
 Advances in Dynamical Systems and Applications. ISSN 0973-5321, Volume 12, Number 1, (2017) pp. 81-88 Research India Publications http://www.ripublication.com Li- Yorke Chaos in Product Dynamical Systems
Advances in Dynamical Systems and Applications. ISSN 0973-5321, Volume 12, Number 1, (2017) pp. 81-88 Research India Publications http://www.ripublication.com Li- Yorke Chaos in Product Dynamical Systems
Waiting times, recurrence times, ergodicity and quasiperiodic dynamics
 Waiting times, recurrence times, ergodicity and quasiperiodic dynamics Dong Han Kim Department of Mathematics, The University of Suwon, Korea Scuola Normale Superiore, 22 Jan. 2009 Outline Dynamical Systems
Waiting times, recurrence times, ergodicity and quasiperiodic dynamics Dong Han Kim Department of Mathematics, The University of Suwon, Korea Scuola Normale Superiore, 22 Jan. 2009 Outline Dynamical Systems
Problem Set 2: Solutions Math 201A: Fall 2016
 Problem Set 2: s Math 201A: Fall 2016 Problem 1. (a) Prove that a closed subset of a complete metric space is complete. (b) Prove that a closed subset of a compact metric space is compact. (c) Prove that
Problem Set 2: s Math 201A: Fall 2016 Problem 1. (a) Prove that a closed subset of a complete metric space is complete. (b) Prove that a closed subset of a compact metric space is compact. (c) Prove that
Mid Term-1 : Practice problems
 Mid Term-1 : Practice problems These problems are meant only to provide practice; they do not necessarily reflect the difficulty level of the problems in the exam. The actual exam problems are likely to
Mid Term-1 : Practice problems These problems are meant only to provide practice; they do not necessarily reflect the difficulty level of the problems in the exam. The actual exam problems are likely to
Distribution of Prime Numbers Prime Constellations Diophantine Approximation. Prime Numbers. How Far Apart Are They? Stijn S.C. Hanson.
 Distribution of How Far Apart Are They? June 13, 2014 Distribution of 1 Distribution of Behaviour of π(x) Behaviour of π(x; a, q) 2 Distance Between Neighbouring Primes Beyond Bounded Gaps 3 Classical
Distribution of How Far Apart Are They? June 13, 2014 Distribution of 1 Distribution of Behaviour of π(x) Behaviour of π(x; a, q) 2 Distance Between Neighbouring Primes Beyond Bounded Gaps 3 Classical
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY. (τ + arg z) + 1
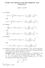 NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
NOTES AND ERRATA FOR RECURRENCE AND TOPOLOGY JOHN M. ALONGI p.11 Replace ρ(t, z) = ρ(t, z) = p.11 Replace sin 2 z e τ ] 2 (τ + arg z) + 1 1 + z (e τ dτ. sin 2 (τ + arg z) + 1 z 2 z e τ ] 2 1 + z (e τ dτ.
Part III. 10 Topological Space Basics. Topological Spaces
 Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
McGill University Math 354: Honors Analysis 3
 Practice problems McGill University Math 354: Honors Analysis 3 not for credit Problem 1. Determine whether the family of F = {f n } functions f n (x) = x n is uniformly equicontinuous. 1st Solution: The
Practice problems McGill University Math 354: Honors Analysis 3 not for credit Problem 1. Determine whether the family of F = {f n } functions f n (x) = x n is uniformly equicontinuous. 1st Solution: The
Problemas abiertos en dinámica de operadores
 Problemas abiertos en dinámica de operadores XIII Encuentro de la red de Análisis Funcional y Aplicaciones Cáceres, 6-11 de Marzo de 2017 Wikipedia Old version: In mathematics and physics, chaos theory
Problemas abiertos en dinámica de operadores XIII Encuentro de la red de Análisis Funcional y Aplicaciones Cáceres, 6-11 de Marzo de 2017 Wikipedia Old version: In mathematics and physics, chaos theory
A LITTLE REAL ANALYSIS AND TOPOLOGY
 A LITTLE REAL ANALYSIS AND TOPOLOGY 1. NOTATION Before we begin some notational definitions are useful. (1) Z = {, 3, 2, 1, 0, 1, 2, 3, }is the set of integers. (2) Q = { a b : aεz, bεz {0}} is the set
A LITTLE REAL ANALYSIS AND TOPOLOGY 1. NOTATION Before we begin some notational definitions are useful. (1) Z = {, 3, 2, 1, 0, 1, 2, 3, }is the set of integers. (2) Q = { a b : aεz, bεz {0}} is the set
Tiling Dynamical Systems as an Introduction to Smale Spaces
 Tiling Dynamical Systems as an Introduction to Smale Spaces Michael Whittaker (University of Wollongong) University of Otago Dunedin, New Zealand February 15, 2011 A Penrose Tiling Sir Roger Penrose Penrose
Tiling Dynamical Systems as an Introduction to Smale Spaces Michael Whittaker (University of Wollongong) University of Otago Dunedin, New Zealand February 15, 2011 A Penrose Tiling Sir Roger Penrose Penrose
ERGODIC THEORY OF PARABOLIC HORSESHOES
 ERGODIC THEORY OF PARABOLIC HORSESHOES MARIUSZ URBAŃSKI AND CHRISTIAN WOLF Abstract. In this paper we develop the ergodic theory for a horseshoe map f which is uniformly hyperbolic, except at one parabolic
ERGODIC THEORY OF PARABOLIC HORSESHOES MARIUSZ URBAŃSKI AND CHRISTIAN WOLF Abstract. In this paper we develop the ergodic theory for a horseshoe map f which is uniformly hyperbolic, except at one parabolic
VARIATIONAL PRINCIPLE FOR THE ENTROPY
 VARIATIONAL PRINCIPLE FOR THE ENTROPY LUCIAN RADU. Metric entropy Let (X, B, µ a measure space and I a countable family of indices. Definition. We say that ξ = {C i : i I} B is a measurable partition if:
VARIATIONAL PRINCIPLE FOR THE ENTROPY LUCIAN RADU. Metric entropy Let (X, B, µ a measure space and I a countable family of indices. Definition. We say that ξ = {C i : i I} B is a measurable partition if:
Solutions for B8b (Nonlinear Systems) Fake Past Exam (TT 10)
 Solutions for B8b (Nonlinear Systems) Fake Past Exam (TT 10) Mason A. Porter 15/05/2010 1 Question 1 i. (6 points) Define a saddle-node bifurcation and show that the first order system dx dt = r x e x
Solutions for B8b (Nonlinear Systems) Fake Past Exam (TT 10) Mason A. Porter 15/05/2010 1 Question 1 i. (6 points) Define a saddle-node bifurcation and show that the first order system dx dt = r x e x
A generic property of families of Lagrangian systems
 Annals of Mathematics, 167 (2008), 1099 1108 A generic property of families of Lagrangian systems By Patrick Bernard and Gonzalo Contreras * Abstract We prove that a generic Lagrangian has finitely many
Annals of Mathematics, 167 (2008), 1099 1108 A generic property of families of Lagrangian systems By Patrick Bernard and Gonzalo Contreras * Abstract We prove that a generic Lagrangian has finitely many
A construction of strictly ergodic subshifts having entropy dimension (joint with K. K. Park and J. Lee (Ajou Univ.))
 A construction of strictly ergodic subshifts having entropy dimension (joint with K. K. Park and J. Lee (Ajou Univ.)) Uijin Jung Ajou University, Suwon, South Korea Pingree Park Conference, July 5, 204
A construction of strictly ergodic subshifts having entropy dimension (joint with K. K. Park and J. Lee (Ajou Univ.)) Uijin Jung Ajou University, Suwon, South Korea Pingree Park Conference, July 5, 204
Differential equations: Dynamics and Chaos. Pierre Berger
 Differential equations: Dynamics and Chaos Pierre Berger 2 Contents 1 Introduction 5 1.1 What is a dynamical system?.............................. 5 1.2 Plan............................................
Differential equations: Dynamics and Chaos Pierre Berger 2 Contents 1 Introduction 5 1.1 What is a dynamical system?.............................. 5 1.2 Plan............................................
