Definition A transition system S is a pair of the form. where C is the set of configurations and T C C is a relation, the
|
|
|
- Samuel Thornton
- 5 years ago
- Views:
Transcription
1 Transition system Definition transition system S is a pair of the form = S T) (, where is the set of configurations and T is a relation, the transition relation. lgorithms and Data Structures hapter 1: Transition Systems 1
2 Sequences generated by a transition system Definition Let S = (, T) be a transition system. S generates a set of sequences, S(S), defined as follows: 1. the finite sequence c 0, c 1,...,c n (for n 0) belongs to S(S) if (ι) c 0 2 (ιι) for all i with» 1» i n: (c i 1, c i 2 T ) 2. the infinite sequence c 0, c 1,...,c n,... belongs to S(S) if (ι) c 0 2 (ιι) for all i 1: (c i 1, c i 2 T ) lgorithms and Data Structures hapter 1: Transition Systems 2
3 Processes generated by a transition system Definition Let S = (, T) be a transition system. The set of processes generated by S, written P (S), is the subset of S(S) containing 1. all infinite sequences of S(S) 2. all finite sequences c 0, c 1,...,c n (n 0) of S(S) for which it holds that there is no c 2 with (c n, c) 2 T. The final configuration of a finite process is called a dead configuration. lgorithms and Data Structures hapter 1: Transition Systems 3
4 Football Football b] j»» 2 Ng 2 + b]» b] + b]» b] +» + b] b] + b] +» b] b] b]» + b] b]» b] + + 1] b]» b] + 1] b]» + + b] b] Transition system onfigurations: f[t, X, a, 0 t 90, X f,, Rg, a, b [t,, a, [t 2,, a, if t 88 [t,, a, [t 2,, a 1, if t 88 [t,, a, [t 1,, a, if t 89 [t,, a, [t 1,, a 1, if t 89 [90,, a, [90, R, a, [t,, a, [t 2,, a, if t 88 [t,, a, [t 2,, a, b if t 88 [t,, a, [t 1,, a, if t 89 [t,, a, [t 1,, a, b if t 89 [90,, a, [90, R, a, lgorithms and Data Structures hapter 1: Transition Systems 4
5 Induction principle Induction principle Let P(0), P(1),...,P(n),... bestatements. If P(0) a) is true b) for all n 0 it holds P(n) that implies + P(n 1), P(n) then is true for all n 0. lgorithms and Data Structures hapter 1: Transition Systems 5
6 Invariance principle Invariance principle for transition systems Let S = (, T) be a transition system and let c 0 2 be a configuration. If I(c) is a statement about the configurations of the system, the following holds. If a) I(c 0 ) is true b) for all (c, c 0 ) 2 T it holds that I(c) implies I(c 0 ) then I(c) is true for any configuration c that occurs in a sequence starting with c 0. lgorithms and Data Structures hapter 1: Transition Systems 6
7 Termination principle Termination principle for transition systems Let S = (, T) be a transition system and let µ :! N be a function. If for all (c, c 0 ) 2 T it holds that µ(c) > µ(c 0 ) then all processes in P (S) are finite. lgorithms and Data Structures hapter 1: Transition Systems 7
8 Nim Nim g n] 2] n] 1] n] 2] 1] n] Transition system onfigurations: f, N [, [, n if n 2 [, [, n if n 1 [, [, n if n 2 [, [, n if n 1 lgorithms and Data Structures hapter 1: Transition Systems 8
9 Towers of Hanoi Transition system Hanoi(n) onfigurations: f[,, ] j f,, g a partition of f1,..., ngg [,,] [n frg,[ frg,] if (r = min ) ^ (r < min ) [,, ] [ n frg,, [ frg] if (r = min ) ^ (r < min ) [,, ] [ [ frg, n frg, ] if (r = min ) ^ (r < min ) [,, ] [, n frg, [ frg] if (r = min ) ^ (r < min ) [,, ] [ [ frg,, n frg] if (r = min ) ^ (r < min ) [,, ] [, [ frg, n frg] if (r = min ) ^ (r < min ) lgorithms and Data Structures hapter 1: Transition Systems 9
10 Euclid s algorithm Transition Euclid system onfigurations: n] j f[m, m, 1g n n] [m, [m n] n, if > m n [m, n] [m, n m] if m < n lgorithms and Data Structures hapter 1: Transition Systems 10
11 Expressions Transition Expressions system onfigurations: f0, 1, +, E, T, )g (, αeβ αtβ αeβ αt+eβ αtβ α0β αtβ α1β αtβ α(e)β lgorithms and Data Structures hapter 1: Transition Systems 11
12 Expressions (context-free) Transition Expressions system onfigurations: f0, 1, +, E, T, )g (, E T, T+E T 0, (E) 1, lgorithms and Data Structures hapter 1: Transition Systems 12
13 Graph coloring Transition Grapholoring system onfigurations: Danish graphs if there are no pink nodes lgorithms and Data Structures hapter 1: Transition Systems 13
14 Red-black tree Definition red-black tree is binary search tree in which all internal nodes are colored either red or black, in which the leaves are black, and Invariant I 2 Each red node has a black parent. Invariant I 3 There is the same number of black nodes on all paths from the root to a leaf lgorithms and Data Structures hapter 1: Transition Systems 14
15 Insertion Illegitimate red node: x Invariant I2 : Each legitimate red node has a black parent. 0 lgorithms and Data Structures hapter 1: Transition Systems 15
16 Insertion: transitions 1 and 2 The illegitimate node is the root of the tree: x x The illegitimate node has a black father: x 3 x lgorithms and Data Structures hapter 1: Transition Systems 16
17 Insertion: transitions 3.1 and 3.2 The illegitimate node has a red father and a red uncle: x x x x lgorithms and Data Structures hapter 1: Transition Systems 17
18 Insertion: transitions 4.1 and 4.2 The illegitimate node has a red father and a black uncle: x x x x lgorithms and Data Structures hapter 1: Transition Systems 18
19 Deletion Illegitimate black node: Invariant I 0 1 The tree satisfies I 1 if we remove the illegitimate node. Invariant I 0 2 Each red node has a legitimate black father. lgorithms and Data Structures hapter 1: Transition Systems 19
20 Deletion: transition 1 The illegitimate node is the root: lgorithms and Data Structures hapter 1: Transition Systems 20
21 Deletion: transitions 2 and 3 The illegitimate node has a red father and a red closer nephew: The illegitimate node has a red father and a black closer nephew: lgorithms and Data Structures hapter 1: Transition Systems 21
22 Deletion: transitions 4.1 and 4.2 The illegitimate node has a black father, a black sibling and one red nephew: lgorithms and Data Structures hapter 1: Transition Systems 22
23 Deletion: transition 5 The illegitimate node has a black father, a black sibling and two black nephews D D 5 lgorithms and Data Structures hapter 1: Transition Systems 23
24 Deletion: transition 6 The illegitimate node has a black father and a red sibling: lgorithms and Data Structures hapter 1: Transition Systems 24
Definition A transition system S is a pair of the form. where C is the set of configurations and T C C is a relation, the
 Transition system Definition 1.3.1 A transition system S is a pair of the form = S T) (C, where C is the set of configurations and T C C is a relation, the transition Λ relation. Algorithms and Data Structures
Transition system Definition 1.3.1 A transition system S is a pair of the form = S T) (C, where C is the set of configurations and T C C is a relation, the transition Λ relation. Algorithms and Data Structures
Department of Computer Science Aarhus University. Algorithms and Data Structures. Transition systems
 Department of Computer Science Aarhus University Algorithms and Data Structures Transition systems Mikkel Nygaard Erik Meineche Schmidt February 2014 Contents 1 Transition systems 1 1.1 Introduction............................
Department of Computer Science Aarhus University Algorithms and Data Structures Transition systems Mikkel Nygaard Erik Meineche Schmidt February 2014 Contents 1 Transition systems 1 1.1 Introduction............................
The null-pointers in a binary search tree are replaced by pointers to special null-vertices, that do not carry any object-data
 Definition 1 A red black tree is a balanced binary search tree in which each internal node has two children. Each internal node has a color, such that 1. The root is black. 2. All leaf nodes are black.
Definition 1 A red black tree is a balanced binary search tree in which each internal node has two children. Each internal node has a color, such that 1. The root is black. 2. All leaf nodes are black.
Inge Li Gørtz. Thank you to Kevin Wayne for inspiration to slides
 02110 Inge Li Gørtz Thank you to Kevin Wayne for inspiration to slides Welcome Inge Li Gørtz. Reverse teaching and discussion of exercises: 3 teaching assistants 8.00-9.15 Group work 9.15-9.45 Discussions
02110 Inge Li Gørtz Thank you to Kevin Wayne for inspiration to slides Welcome Inge Li Gørtz. Reverse teaching and discussion of exercises: 3 teaching assistants 8.00-9.15 Group work 9.15-9.45 Discussions
ICS141: Discrete Mathematics for Computer Science I
 ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
ICS141: Discrete Mathematics for Computer Science I Dept. Information & Computer Sci., Jan Stelovsky based on slides by Dr. Baek and Dr. Still Originals by Dr. M. P. Frank and Dr. J.L. Gross Provided by
CS213d Data Structures and Algorithms
 CS21d Data Structures and Algorithms Heaps and their Applications Milind Sohoni IIT Bombay and IIT Dharwad March 22, 2017 1 / 18 What did I see today? March 22, 2017 2 / 18 Heap-Trees A tree T of height
CS21d Data Structures and Algorithms Heaps and their Applications Milind Sohoni IIT Bombay and IIT Dharwad March 22, 2017 1 / 18 What did I see today? March 22, 2017 2 / 18 Heap-Trees A tree T of height
d(ν) = max{n N : ν dmn p n } N. p d(ν) (ν) = ρ.
 1. Trees; context free grammars. 1.1. Trees. Definition 1.1. By a tree we mean an ordered triple T = (N, ρ, p) (i) N is a finite set; (ii) ρ N ; (iii) p : N {ρ} N ; (iv) if n N + and ν dmn p n then p n
1. Trees; context free grammars. 1.1. Trees. Definition 1.1. By a tree we mean an ordered triple T = (N, ρ, p) (i) N is a finite set; (ii) ρ N ; (iii) p : N {ρ} N ; (iv) if n N + and ν dmn p n then p n
Administrivia. COMP9020 Lecture 7 Session 2, 2017 Induction and Recursion. Lecture 6 recap. Lecture 6 recap
 Administrivia COMP9020 Lecture 7 Session 2, 2017 Induction and Recursion Guidelines for good mathematical writing Assignment 1 Solutions now available; marks available soon Assignment 2 available on Saturday,
Administrivia COMP9020 Lecture 7 Session 2, 2017 Induction and Recursion Guidelines for good mathematical writing Assignment 1 Solutions now available; marks available soon Assignment 2 available on Saturday,
Algorithm Analysis Recurrence Relation. Chung-Ang University, Jaesung Lee
 Algorithm Analysis Recurrence Relation Chung-Ang University, Jaesung Lee Recursion 2 Recursion 3 Recursion in Real-world Fibonacci sequence = + Initial conditions: = 0 and = 1. = + = + = + 0, 1, 1, 2,
Algorithm Analysis Recurrence Relation Chung-Ang University, Jaesung Lee Recursion 2 Recursion 3 Recursion in Real-world Fibonacci sequence = + Initial conditions: = 0 and = 1. = + = + = + 0, 1, 1, 2,
Decision Trees. Lewis Fishgold. (Material in these slides adapted from Ray Mooney's slides on Decision Trees)
 Decision Trees Lewis Fishgold (Material in these slides adapted from Ray Mooney's slides on Decision Trees) Classification using Decision Trees Nodes test features, there is one branch for each value of
Decision Trees Lewis Fishgold (Material in these slides adapted from Ray Mooney's slides on Decision Trees) Classification using Decision Trees Nodes test features, there is one branch for each value of
7.11 A proof involving composition Variation in terminology... 88
 Contents Preface xi 1 Math review 1 1.1 Some sets............................. 1 1.2 Pairs of reals........................... 3 1.3 Exponentials and logs...................... 4 1.4 Some handy functions......................
Contents Preface xi 1 Math review 1 1.1 Some sets............................. 1 1.2 Pairs of reals........................... 3 1.3 Exponentials and logs...................... 4 1.4 Some handy functions......................
Models of Computation. by Costas Busch, LSU
 Models of Computation by Costas Busch, LSU 1 Computation CPU memory 2 temporary memory input memory CPU output memory Program memory 3 Example: f ( x) x 3 temporary memory input memory Program memory compute
Models of Computation by Costas Busch, LSU 1 Computation CPU memory 2 temporary memory input memory CPU output memory Program memory 3 Example: f ( x) x 3 temporary memory input memory Program memory compute
Discrete Mathematics
 Discrete Mathematics Trees H. Turgut Uyar Ayşegül Gençata Yayımlı Emre Harmancı 2001-2016 License You are free to: c 2001-2016 T. Uyar, A. Yayımlı, E. Harmancı Share copy and redistribute the material
Discrete Mathematics Trees H. Turgut Uyar Ayşegül Gençata Yayımlı Emre Harmancı 2001-2016 License You are free to: c 2001-2016 T. Uyar, A. Yayımlı, E. Harmancı Share copy and redistribute the material
Recursion and Induction
 Recursion and Induction Themes Recursion Recursive Definitions Recurrence Relations Induction (prove properties of recursive programs and objects defined recursively) Examples Tower of Hanoi Gray Codes
Recursion and Induction Themes Recursion Recursive Definitions Recurrence Relations Induction (prove properties of recursive programs and objects defined recursively) Examples Tower of Hanoi Gray Codes
Problem: Data base too big to fit memory Disk reads are slow. Example: 1,000,000 records on disk Binary search might take 20 disk reads
 B Trees Problem: Data base too big to fit memory Disk reads are slow Example: 1,000,000 records on disk Binary search might take 20 disk reads Disk reads are done in blocks Example: One block read can
B Trees Problem: Data base too big to fit memory Disk reads are slow Example: 1,000,000 records on disk Binary search might take 20 disk reads Disk reads are done in blocks Example: One block read can
Recursion and Induction
 Recursion and Induction Themes Recursion Recursive Definitions Recurrence Relations Induction (prove properties of recursive programs and objects defined recursively) Examples Tower of Hanoi Gray Codes
Recursion and Induction Themes Recursion Recursive Definitions Recurrence Relations Induction (prove properties of recursive programs and objects defined recursively) Examples Tower of Hanoi Gray Codes
Dictionary: an abstract data type
 2-3 Trees 1 Dictionary: an abstract data type A container that maps keys to values Dictionary operations Insert Search Delete Several possible implementations Balanced search trees Hash tables 2 2-3 trees
2-3 Trees 1 Dictionary: an abstract data type A container that maps keys to values Dictionary operations Insert Search Delete Several possible implementations Balanced search trees Hash tables 2 2-3 trees
2 GRAPH AND NETWORK OPTIMIZATION. E. Amaldi Introduction to Operations Research Politecnico Milano 1
 2 GRAPH AND NETWORK OPTIMIZATION E. Amaldi Introduction to Operations Research Politecnico Milano 1 A variety of decision-making problems can be formulated in terms of graphs and networks Examples: - transportation
2 GRAPH AND NETWORK OPTIMIZATION E. Amaldi Introduction to Operations Research Politecnico Milano 1 A variety of decision-making problems can be formulated in terms of graphs and networks Examples: - transportation
MIT Loop Optimizations. Martin Rinard
 MIT 6.035 Loop Optimizations Martin Rinard Loop Optimizations Important because lots of computation occurs in loops We will study two optimizations Loop-invariant code motion Induction variable elimination
MIT 6.035 Loop Optimizations Martin Rinard Loop Optimizations Important because lots of computation occurs in loops We will study two optimizations Loop-invariant code motion Induction variable elimination
Mathematical Induction. Rosen Chapter 4.1,4.2 (6 th edition) Rosen Ch. 5.1, 5.2 (7 th edition)
 Mathematical Induction Rosen Chapter 4.1,4.2 (6 th edition) Rosen Ch. 5.1, 5.2 (7 th edition) Motivation Suppose we want to prove that for every value of n: 1 + 2 + + n = n(n + 1)/2. Let P(n) be the predicate
Mathematical Induction Rosen Chapter 4.1,4.2 (6 th edition) Rosen Ch. 5.1, 5.2 (7 th edition) Motivation Suppose we want to prove that for every value of n: 1 + 2 + + n = n(n + 1)/2. Let P(n) be the predicate
Dictionary: an abstract data type
 2-3 Trees 1 Dictionary: an abstract data type A container that maps keys to values Dictionary operations Insert Search Delete Several possible implementations Balanced search trees Hash tables 2 2-3 trees
2-3 Trees 1 Dictionary: an abstract data type A container that maps keys to values Dictionary operations Insert Search Delete Several possible implementations Balanced search trees Hash tables 2 2-3 trees
Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set
 Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set P.N. Balister E. Győri R.H. Schelp April 28, 28 Abstract A graph G is strongly set colorable if V (G) E(G) can be assigned distinct nonempty
Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set P.N. Balister E. Győri R.H. Schelp April 28, 28 Abstract A graph G is strongly set colorable if V (G) E(G) can be assigned distinct nonempty
1. To be a grandfather. Objects of our consideration are people; a person a is associated with a person b if a is a grandfather of b.
 20 [161016-1020 ] 3.3 Binary relations In mathematics, as in everyday situations, we often speak about a relationship between objects, which means an idea of two objects being related or associated one
20 [161016-1020 ] 3.3 Binary relations In mathematics, as in everyday situations, we often speak about a relationship between objects, which means an idea of two objects being related or associated one
MATH 523: Primal-Dual Maximum Weight Matching Algorithm
 MATH 523: Primal-Dual Maximum Weight Matching Algorithm We start with a graph G = (V, E) with edge weights {c(e) : e E} Primal P: max {c(e)x(e) : e E} subject to {x(e) : e hits i} + yi = 1 for all i V
MATH 523: Primal-Dual Maximum Weight Matching Algorithm We start with a graph G = (V, E) with edge weights {c(e) : e E} Primal P: max {c(e)x(e) : e E} subject to {x(e) : e hits i} + yi = 1 for all i V
Tree-adjoined spaces and the Hawaiian earring
 Tree-adjoined spaces and the Hawaiian earring W. Hojka (TU Wien) Workshop on Fractals and Tilings 2009 July 6-10, 2009, Strobl (Austria) W. Hojka (TU Wien) () Tree-adjoined spaces and the Hawaiian earring
Tree-adjoined spaces and the Hawaiian earring W. Hojka (TU Wien) Workshop on Fractals and Tilings 2009 July 6-10, 2009, Strobl (Austria) W. Hojka (TU Wien) () Tree-adjoined spaces and the Hawaiian earring
Outline. Computer Science 331. Cost of Binary Search Tree Operations. Bounds on Height: Worst- and Average-Case
 Outline Computer Science Average Case Analysis: Binary Search Trees Mike Jacobson Department of Computer Science University of Calgary Lecture #7 Motivation and Objective Definition 4 Mike Jacobson (University
Outline Computer Science Average Case Analysis: Binary Search Trees Mike Jacobson Department of Computer Science University of Calgary Lecture #7 Motivation and Objective Definition 4 Mike Jacobson (University
Decision Trees / NLP Introduction
 Decision Trees / NLP Introduction Dr. Kevin Koidl School of Computer Science and Statistic Trinity College Dublin ADAPT Research Centre The ADAPT Centre is funded under the SFI Research Centres Programme
Decision Trees / NLP Introduction Dr. Kevin Koidl School of Computer Science and Statistic Trinity College Dublin ADAPT Research Centre The ADAPT Centre is funded under the SFI Research Centres Programme
Data Mining Classification: Basic Concepts and Techniques. Lecture Notes for Chapter 3. Introduction to Data Mining, 2nd Edition
 Data Mining Classification: Basic Concepts and Techniques Lecture Notes for Chapter 3 by Tan, Steinbach, Karpatne, Kumar 1 Classification: Definition Given a collection of records (training set ) Each
Data Mining Classification: Basic Concepts and Techniques Lecture Notes for Chapter 3 by Tan, Steinbach, Karpatne, Kumar 1 Classification: Definition Given a collection of records (training set ) Each
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Data Structures and Algorithms Spring 2017-2018 Outline 1 Sorting Algorithms (contd.) Outline Sorting Algorithms (contd.) 1 Sorting Algorithms (contd.) Analysis of Quicksort Time to sort array of length
Heaps and Priority Queues
 Heaps and Priority Queues Motivation Situations where one has to choose the next most important from a collection. Examples: patients in an emergency room, scheduling programs in a multi-tasking OS. Need
Heaps and Priority Queues Motivation Situations where one has to choose the next most important from a collection. Examples: patients in an emergency room, scheduling programs in a multi-tasking OS. Need
HW Graph Theory SOLUTIONS (hbovik) - Q
 1, Diestel 3.5: Deduce the k = 2 case of Menger s theorem (3.3.1) from Proposition 3.1.1. Let G be 2-connected, and let A and B be 2-sets. We handle some special cases (thus later in the induction if these
1, Diestel 3.5: Deduce the k = 2 case of Menger s theorem (3.3.1) from Proposition 3.1.1. Let G be 2-connected, and let A and B be 2-sets. We handle some special cases (thus later in the induction if these
On the minimum neighborhood of independent sets in the n-cube
 Matemática Contemporânea, Vol. 44, 1 10 c 2015, Sociedade Brasileira de Matemática On the minimum neighborhood of independent sets in the n-cube Moysés da S. Sampaio Júnior Fabiano de S. Oliveira Luérbio
Matemática Contemporânea, Vol. 44, 1 10 c 2015, Sociedade Brasileira de Matemática On the minimum neighborhood of independent sets in the n-cube Moysés da S. Sampaio Júnior Fabiano de S. Oliveira Luérbio
Data Structures and and Algorithm Xiaoqing Zheng
 Data Structures and Algorithm Xiaoqing Zheng zhengxq@fudan.edu.cn Trees (max heap) 1 16 2 3 14 10 4 5 6 7 8 7 9 3 8 9 10 2 4 1 PARENT(i) return i /2 LEFT(i) return 2i RIGHT(i) return 2i +1 16 14 10 8 7
Data Structures and Algorithm Xiaoqing Zheng zhengxq@fudan.edu.cn Trees (max heap) 1 16 2 3 14 10 4 5 6 7 8 7 9 3 8 9 10 2 4 1 PARENT(i) return i /2 LEFT(i) return 2i RIGHT(i) return 2i +1 16 14 10 8 7
Entropy as a measure of surprise
 Entropy as a measure of surprise Lecture 5: Sam Roweis September 26, 25 What does information do? It removes uncertainty. Information Conveyed = Uncertainty Removed = Surprise Yielded. How should we quantify
Entropy as a measure of surprise Lecture 5: Sam Roweis September 26, 25 What does information do? It removes uncertainty. Information Conveyed = Uncertainty Removed = Surprise Yielded. How should we quantify
Chapter 9: Relations Relations
 Chapter 9: Relations 9.1 - Relations Definition 1 (Relation). Let A and B be sets. A binary relation from A to B is a subset R A B, i.e., R is a set of ordered pairs where the first element from each pair
Chapter 9: Relations 9.1 - Relations Definition 1 (Relation). Let A and B be sets. A binary relation from A to B is a subset R A B, i.e., R is a set of ordered pairs where the first element from each pair
Phylogenetic Networks with Recombination
 Phylogenetic Networks with Recombination October 17 2012 Recombination All DNA is recombinant DNA... [The] natural process of recombination and mutation have acted throughout evolution... Genetic exchange
Phylogenetic Networks with Recombination October 17 2012 Recombination All DNA is recombinant DNA... [The] natural process of recombination and mutation have acted throughout evolution... Genetic exchange
Data Structures and Algorithms " Search Trees!!
 Data Structures and Algorithms " Search Trees!! Outline" Binary Search Trees! AVL Trees! (2,4) Trees! 2 Binary Search Trees! "! < 6 2 > 1 4 = 8 9 Ordered Dictionaries" Keys are assumed to come from a total
Data Structures and Algorithms " Search Trees!! Outline" Binary Search Trees! AVL Trees! (2,4) Trees! 2 Binary Search Trees! "! < 6 2 > 1 4 = 8 9 Ordered Dictionaries" Keys are assumed to come from a total
Definition: A binary relation R from a set A to a set B is a subset R A B. Example:
 Chapter 9 1 Binary Relations Definition: A binary relation R from a set A to a set B is a subset R A B. Example: Let A = {0,1,2} and B = {a,b} {(0, a), (0, b), (1,a), (2, b)} is a relation from A to B.
Chapter 9 1 Binary Relations Definition: A binary relation R from a set A to a set B is a subset R A B. Example: Let A = {0,1,2} and B = {a,b} {(0, a), (0, b), (1,a), (2, b)} is a relation from A to B.
F 99 Final Quiz Solutions
 Massachusetts Institute of Technology Handout 53 6.04J/18.06J: Mathematics for Computer Science May 11, 000 Professors David Karger and Nancy Lynch F 99 Final Quiz Solutions Problem 1 [18 points] Injections
Massachusetts Institute of Technology Handout 53 6.04J/18.06J: Mathematics for Computer Science May 11, 000 Professors David Karger and Nancy Lynch F 99 Final Quiz Solutions Problem 1 [18 points] Injections
Discrete Wiskunde II. Lecture 5: Shortest Paths & Spanning Trees
 , 2009 Lecture 5: Shortest Paths & Spanning Trees University of Twente m.uetz@utwente.nl wwwhome.math.utwente.nl/~uetzm/dw/ Shortest Path Problem "#$%&'%()*%"()$#+,&- Given directed "#$%&'()*+,%+('-*.#/'01234564'.*,'7+"-%/8',&'5"4'84%#3
, 2009 Lecture 5: Shortest Paths & Spanning Trees University of Twente m.uetz@utwente.nl wwwhome.math.utwente.nl/~uetzm/dw/ Shortest Path Problem "#$%&'%()*%"()$#+,&- Given directed "#$%&'()*+,%+('-*.#/'01234564'.*,'7+"-%/8',&'5"4'84%#3
Gap Embedding for Well-Quasi-Orderings 1
 WoLLIC 2003 Preliminary Version Gap Embedding for Well-Quasi-Orderings 1 Nachum Dershowitz 2 and Iddo Tzameret 3 School of Computer Science, Tel-Aviv University, Tel-Aviv 69978, Israel Abstract Given a
WoLLIC 2003 Preliminary Version Gap Embedding for Well-Quasi-Orderings 1 Nachum Dershowitz 2 and Iddo Tzameret 3 School of Computer Science, Tel-Aviv University, Tel-Aviv 69978, Israel Abstract Given a
Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set
 Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set P.N. Balister E. Győri R.H. Schelp November 8, 28 Abstract A graph G is strongly set colorable if V (G) E(G) can be assigned distinct
Coloring Vertices and Edges of a Path by Nonempty Subsets of a Set P.N. Balister E. Győri R.H. Schelp November 8, 28 Abstract A graph G is strongly set colorable if V (G) E(G) can be assigned distinct
4.8 Huffman Codes. These lecture slides are supplied by Mathijs de Weerd
 4.8 Huffman Codes These lecture slides are supplied by Mathijs de Weerd Data Compression Q. Given a text that uses 32 symbols (26 different letters, space, and some punctuation characters), how can we
4.8 Huffman Codes These lecture slides are supplied by Mathijs de Weerd Data Compression Q. Given a text that uses 32 symbols (26 different letters, space, and some punctuation characters), how can we
CSC 421: Algorithm Design & Analysis. Spring 2015
 CSC 421: Algorithm Design & Analysis Spring 2015 Complexity & lower bounds brute force decision trees adversary arguments problem reduction 1 Lower bounds on problems when studying a problem, may wish
CSC 421: Algorithm Design & Analysis Spring 2015 Complexity & lower bounds brute force decision trees adversary arguments problem reduction 1 Lower bounds on problems when studying a problem, may wish
Advanced Implementations of Tables: Balanced Search Trees and Hashing
 Advanced Implementations of Tables: Balanced Search Trees and Hashing Balanced Search Trees Binary search tree operations such as insert, delete, retrieve, etc. depend on the length of the path to the
Advanced Implementations of Tables: Balanced Search Trees and Hashing Balanced Search Trees Binary search tree operations such as insert, delete, retrieve, etc. depend on the length of the path to the
Chapter 7 Network Flow Problems, I
 Chapter 7 Network Flow Problems, I Network flow problems are the most frequently solved linear programming problems. They include as special cases, the assignment, transportation, maximum flow, and shortest
Chapter 7 Network Flow Problems, I Network flow problems are the most frequently solved linear programming problems. They include as special cases, the assignment, transportation, maximum flow, and shortest
Chapter ML:III. III. Decision Trees. Decision Trees Basics Impurity Functions Decision Tree Algorithms Decision Tree Pruning
 Chapter ML:III III. Decision Trees Decision Trees Basics Impurity Functions Decision Tree Algorithms Decision Tree Pruning ML:III-34 Decision Trees STEIN/LETTMANN 2005-2017 Splitting Let t be a leaf node
Chapter ML:III III. Decision Trees Decision Trees Basics Impurity Functions Decision Tree Algorithms Decision Tree Pruning ML:III-34 Decision Trees STEIN/LETTMANN 2005-2017 Splitting Let t be a leaf node
Search Trees. Chapter 10. CSE 2011 Prof. J. Elder Last Updated: :52 AM
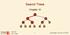 Search Trees Chapter 1 < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 3 - Binary Search Trees Ø A binary search
Search Trees Chapter 1 < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 3 - Binary Search Trees Ø A binary search
AVL trees. AVL trees
 Dnamic set DT dnamic set DT is a structure tat stores a set of elements. Eac element as a (unique) ke and satellite data. Te structure supports te following operations. Searc(S, k) Return te element wose
Dnamic set DT dnamic set DT is a structure tat stores a set of elements. Eac element as a (unique) ke and satellite data. Te structure supports te following operations. Searc(S, k) Return te element wose
On the Average Path Length of Complete m-ary Trees
 1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 17 2014, Article 14.6.3 On the Average Path Length of Complete m-ary Trees M. A. Nyblom School of Mathematics and Geospatial Science RMIT University
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 17 2014, Article 14.6.3 On the Average Path Length of Complete m-ary Trees M. A. Nyblom School of Mathematics and Geospatial Science RMIT University
CS6375: Machine Learning Gautam Kunapuli. Decision Trees
 Gautam Kunapuli Example: Restaurant Recommendation Example: Develop a model to recommend restaurants to users depending on their past dining experiences. Here, the features are cost (x ) and the user s
Gautam Kunapuli Example: Restaurant Recommendation Example: Develop a model to recommend restaurants to users depending on their past dining experiences. Here, the features are cost (x ) and the user s
Heaps Induction. Heaps. Heaps. Tirgul 6
 Tirgul 6 Induction A binary heap is a nearly complete binary tree stored in an array object In a max heap, the value of each node that of its children (In a min heap, the value of each node that of its
Tirgul 6 Induction A binary heap is a nearly complete binary tree stored in an array object In a max heap, the value of each node that of its children (In a min heap, the value of each node that of its
ASSIGNMENT 1 SOLUTIONS
 MATH 271 ASSIGNMENT 1 SOLUTIONS 1. (a) Let S be the statement For all integers n, if n is even then 3n 11 is odd. Is S true? Give a proof or counterexample. (b) Write out the contrapositive of statement
MATH 271 ASSIGNMENT 1 SOLUTIONS 1. (a) Let S be the statement For all integers n, if n is even then 3n 11 is odd. Is S true? Give a proof or counterexample. (b) Write out the contrapositive of statement
Section 7.1 Relations and Their Properties. Definition: A binary relation R from a set A to a set B is a subset R A B.
 Section 7.1 Relations and Their Properties Definition: A binary relation R from a set A to a set B is a subset R A B. Note: there are no constraints on relations as there are on functions. We have a common
Section 7.1 Relations and Their Properties Definition: A binary relation R from a set A to a set B is a subset R A B. Note: there are no constraints on relations as there are on functions. We have a common
Chapter 2: Finite Automata
 Chapter 2: Finite Automata Peter Cappello Department of Computer Science University of California, Santa Barbara Santa Barbara, CA 93106 cappello@cs.ucsb.edu Please read the corresponding chapter before
Chapter 2: Finite Automata Peter Cappello Department of Computer Science University of California, Santa Barbara Santa Barbara, CA 93106 cappello@cs.ucsb.edu Please read the corresponding chapter before
Dynamic Programming on Trees. Example: Independent Set on T = (V, E) rooted at r V.
 Dynamic Programming on Trees Example: Independent Set on T = (V, E) rooted at r V. For v V let T v denote the subtree rooted at v. Let f + (v) be the size of a maximum independent set for T v that contains
Dynamic Programming on Trees Example: Independent Set on T = (V, E) rooted at r V. For v V let T v denote the subtree rooted at v. Let f + (v) be the size of a maximum independent set for T v that contains
Informal Definition: Telling things apart
 9. Decision Trees Informal Definition: Telling things apart 2 Nominal data No numeric feature vector Just a list or properties: Banana: longish, yellow Apple: round, medium sized, different colors like
9. Decision Trees Informal Definition: Telling things apart 2 Nominal data No numeric feature vector Just a list or properties: Banana: longish, yellow Apple: round, medium sized, different colors like
1 Computational Problems
 Stanford University CS254: Computational Complexity Handout 2 Luca Trevisan March 31, 2010 Last revised 4/29/2010 In this lecture we define NP, we state the P versus NP problem, we prove that its formulation
Stanford University CS254: Computational Complexity Handout 2 Luca Trevisan March 31, 2010 Last revised 4/29/2010 In this lecture we define NP, we state the P versus NP problem, we prove that its formulation
Problem. Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26
 Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Binary Search Introduction Problem Problem Given a dictionary and a word. Which page (if any) contains the given word? 3 / 26 Strategy 1: Random Search Randomly select a page until the page containing
Massachusetts Institute of Technology 6.042J/18.062J, Fall 02: Mathematics for Computer Science Professor Albert Meyer and Dr.
 Massachusetts Institute of Technology 6.042J/18.062J, Fall 02: Mathematics for Computer Science Professor Albert Meyer and Dr. Radhika Nagpal Quiz 1 Appendix Appendix Contents 1 Induction 2 2 Relations
Massachusetts Institute of Technology 6.042J/18.062J, Fall 02: Mathematics for Computer Science Professor Albert Meyer and Dr. Radhika Nagpal Quiz 1 Appendix Appendix Contents 1 Induction 2 2 Relations
Advanced Analysis of Algorithms - Midterm (Solutions)
 Advanced Analysis of Algorithms - Midterm (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Solve the following recurrence using substitution:
Advanced Analysis of Algorithms - Midterm (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Solve the following recurrence using substitution:
1 Non-deterministic Turing Machine
 1 Non-deterministic Turing Machine A nondeterministic Turing machine is a generalization of the standard TM for which every configuration may yield none, or one or more than one next configurations. In
1 Non-deterministic Turing Machine A nondeterministic Turing machine is a generalization of the standard TM for which every configuration may yield none, or one or more than one next configurations. In
The Complexity of Constructing Evolutionary Trees Using Experiments
 The Complexity of Constructing Evolutionary Trees Using Experiments Gerth Stlting Brodal 1,, Rolf Fagerberg 1,, Christian N. S. Pedersen 1,, and Anna Östlin2, 1 BRICS, Department of Computer Science, University
The Complexity of Constructing Evolutionary Trees Using Experiments Gerth Stlting Brodal 1,, Rolf Fagerberg 1,, Christian N. S. Pedersen 1,, and Anna Östlin2, 1 BRICS, Department of Computer Science, University
25. Minimum Spanning Trees
 695 25. Minimum Spanning Trees Motivation, Greedy, Algorithm Kruskal, General Rules, ADT Union-Find, Algorithm Jarnik, Prim, Dijkstra, Fibonacci Heaps [Ottman/Widmayer, Kap. 9.6, 6.2, 6.1, Cormen et al,
695 25. Minimum Spanning Trees Motivation, Greedy, Algorithm Kruskal, General Rules, ADT Union-Find, Algorithm Jarnik, Prim, Dijkstra, Fibonacci Heaps [Ottman/Widmayer, Kap. 9.6, 6.2, 6.1, Cormen et al,
25. Minimum Spanning Trees
 Problem Given: Undirected, weighted, connected graph G = (V, E, c). 5. Minimum Spanning Trees Motivation, Greedy, Algorithm Kruskal, General Rules, ADT Union-Find, Algorithm Jarnik, Prim, Dijkstra, Fibonacci
Problem Given: Undirected, weighted, connected graph G = (V, E, c). 5. Minimum Spanning Trees Motivation, Greedy, Algorithm Kruskal, General Rules, ADT Union-Find, Algorithm Jarnik, Prim, Dijkstra, Fibonacci
Classification: Decision Trees
 Classification: Decision Trees Outline Top-Down Decision Tree Construction Choosing the Splitting Attribute Information Gain and Gain Ratio 2 DECISION TREE An internal node is a test on an attribute. A
Classification: Decision Trees Outline Top-Down Decision Tree Construction Choosing the Splitting Attribute Information Gain and Gain Ratio 2 DECISION TREE An internal node is a test on an attribute. A
Computing Static Single Assignment (SSA) Form
 Computing Static Single Assignment (SSA) Form Overview What is SSA? Advantages of SSA over use-def chains Flavors of SSA Dominance frontiers revisited Inserting φ-nodes Renaming the variables Translating
Computing Static Single Assignment (SSA) Form Overview What is SSA? Advantages of SSA over use-def chains Flavors of SSA Dominance frontiers revisited Inserting φ-nodes Renaming the variables Translating
On Ramsey s Theorem for Pairs
 On Ramsey s Theorem for Pairs Peter A. Cholak, Carl G. Jockusch Jr., and Theodore A. Slaman On the strength of Ramsey s theorem for pairs. J. Symbolic Logic, 66(1):1-55, 2001. www.nd.edu/~cholak Ramsey
On Ramsey s Theorem for Pairs Peter A. Cholak, Carl G. Jockusch Jr., and Theodore A. Slaman On the strength of Ramsey s theorem for pairs. J. Symbolic Logic, 66(1):1-55, 2001. www.nd.edu/~cholak Ramsey
What you learned in Math 28. Rosa C. Orellana
 What you learned in Math 28 Rosa C. Orellana Chapter 1 - Basic Counting Techniques Sum Principle If we have a partition of a finite set S, then the size of S is the sum of the sizes of the blocks of the
What you learned in Math 28 Rosa C. Orellana Chapter 1 - Basic Counting Techniques Sum Principle If we have a partition of a finite set S, then the size of S is the sum of the sizes of the blocks of the
CS 4407 Algorithms Lecture: Shortest Path Algorithms
 CS 440 Algorithms Lecture: Shortest Path Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Outline Shortest Path Problem General Lemmas and Theorems. Algorithms Bellman-Ford
CS 440 Algorithms Lecture: Shortest Path Algorithms Prof. Gregory Provan Department of Computer Science University College Cork 1 Outline Shortest Path Problem General Lemmas and Theorems. Algorithms Bellman-Ford
Each internal node v with d(v) children stores d 1 keys. k i 1 < key in i-th sub-tree k i, where we use k 0 = and k d =.
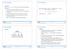 7.5 (a, b)-trees 7.5 (a, b)-trees Definition For b a an (a, b)-tree is a search tree with the following properties. all leaves have the same distance to the root. every internal non-root vertex v has at
7.5 (a, b)-trees 7.5 (a, b)-trees Definition For b a an (a, b)-tree is a search tree with the following properties. all leaves have the same distance to the root. every internal non-root vertex v has at
The Pure Parsimony Problem
 Haplotyping and Minimum Diversity Graphs Courtney Davis - University of Utah - Trinity University Some Genetics Mother Paired Gene Representation Physical Trait ABABBA AAABBB Physical Trait ABA AAA Mother
Haplotyping and Minimum Diversity Graphs Courtney Davis - University of Utah - Trinity University Some Genetics Mother Paired Gene Representation Physical Trait ABABBA AAABBB Physical Trait ABA AAA Mother
Lecture 6 January 15, 2014
 Advanced Graph Algorithms Jan-Apr 2014 Lecture 6 January 15, 2014 Lecturer: Saket Sourah Scrie: Prafullkumar P Tale 1 Overview In the last lecture we defined simple tree decomposition and stated that for
Advanced Graph Algorithms Jan-Apr 2014 Lecture 6 January 15, 2014 Lecturer: Saket Sourah Scrie: Prafullkumar P Tale 1 Overview In the last lecture we defined simple tree decomposition and stated that for
Tree sets. Reinhard Diestel
 1 Tree sets Reinhard Diestel Abstract We study an abstract notion of tree structure which generalizes treedecompositions of graphs and matroids. Unlike tree-decompositions, which are too closely linked
1 Tree sets Reinhard Diestel Abstract We study an abstract notion of tree structure which generalizes treedecompositions of graphs and matroids. Unlike tree-decompositions, which are too closely linked
Priority queues implemented via heaps
 Priority queues implemented via heaps Comp Sci 1575 Data s Outline 1 2 3 Outline 1 2 3 Priority queue: most important first Recall: queue is FIFO A normal queue data structure will not implement a priority
Priority queues implemented via heaps Comp Sci 1575 Data s Outline 1 2 3 Outline 1 2 3 Priority queue: most important first Recall: queue is FIFO A normal queue data structure will not implement a priority
Parikh s theorem. Håkan Lindqvist
 Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Notes for Lecture Notes 2
 Stanford University CS254: Computational Complexity Notes 2 Luca Trevisan January 11, 2012 Notes for Lecture Notes 2 In this lecture we define NP, we state the P versus NP problem, we prove that its formulation
Stanford University CS254: Computational Complexity Notes 2 Luca Trevisan January 11, 2012 Notes for Lecture Notes 2 In this lecture we define NP, we state the P versus NP problem, we prove that its formulation
Amortized analysis. Amortized analysis
 In amortized analysis the goal is to bound the worst case time of a sequence of operations on a data-structure. If n operations take T (n) time (worst case), the amortized cost of an operation is T (n)/n.
In amortized analysis the goal is to bound the worst case time of a sequence of operations on a data-structure. If n operations take T (n) time (worst case), the amortized cost of an operation is T (n)/n.
Complexity Theory VU , SS The Polynomial Hierarchy. Reinhard Pichler
 Complexity Theory Complexity Theory VU 181.142, SS 2018 6. The Polynomial Hierarchy Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität Wien 15 May, 2018 Reinhard
Complexity Theory Complexity Theory VU 181.142, SS 2018 6. The Polynomial Hierarchy Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität Wien 15 May, 2018 Reinhard
Outline. Complexity Theory EXACT TSP. The Class DP. Definition. Problem EXACT TSP. Complexity of EXACT TSP. Proposition VU 181.
 Complexity Theory Complexity Theory Outline Complexity Theory VU 181.142, SS 2018 6. The Polynomial Hierarchy Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität
Complexity Theory Complexity Theory Outline Complexity Theory VU 181.142, SS 2018 6. The Polynomial Hierarchy Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität
R-cross-sections of the semigroup of order-preserving transformations of a finite chain
 R-cross-sections of the semigroup of order-preserving transformations of a finite chain Eugenija A. Bondar Ural Federal University AAA9+NSAC 07 Novi Sad, Serbia, June -8 Bondar Е.А. R-cross-sections of
R-cross-sections of the semigroup of order-preserving transformations of a finite chain Eugenija A. Bondar Ural Federal University AAA9+NSAC 07 Novi Sad, Serbia, June -8 Bondar Е.А. R-cross-sections of
A class of heuristics for the constrained forest problem
 Discrete Applied Mathematics 154 (2006) 6 14 www.elsevier.com/locate/dam Communication A class of heuristics for the constrained forest problem Michael Laszlo, Sumitra Mukherjee Nova Southeastern University,
Discrete Applied Mathematics 154 (2006) 6 14 www.elsevier.com/locate/dam Communication A class of heuristics for the constrained forest problem Michael Laszlo, Sumitra Mukherjee Nova Southeastern University,
Induction on Decision Trees
 Séance «IDT» de l'ue «apprentissage automatique» Bruno Bouzy bruno.bouzy@parisdescartes.fr www.mi.parisdescartes.fr/~bouzy Outline Induction task ID3 Entropy (disorder) minimization Noise Unknown attribute
Séance «IDT» de l'ue «apprentissage automatique» Bruno Bouzy bruno.bouzy@parisdescartes.fr www.mi.parisdescartes.fr/~bouzy Outline Induction task ID3 Entropy (disorder) minimization Noise Unknown attribute
Binary Search Trees. Motivation
 Binary Search Trees Motivation Searching for a particular record in an unordered list takes O(n), too slow for large lists (databases) If the list is ordered, can use an array implementation and use binary
Binary Search Trees Motivation Searching for a particular record in an unordered list takes O(n), too slow for large lists (databases) If the list is ordered, can use an array implementation and use binary
Parametric euclidean algorithm
 Theoretical Mathematics & Applications, vol.3, no.3, 2013, 13-21 ISSN: 1792-9687 (print), 1792-9709 (online) Scienpress Ltd, 2013 Parametric euclidean algorithm Ali Ayad 1, Ali Fares 2 and Youssef Ayyad
Theoretical Mathematics & Applications, vol.3, no.3, 2013, 13-21 ISSN: 1792-9687 (print), 1792-9709 (online) Scienpress Ltd, 2013 Parametric euclidean algorithm Ali Ayad 1, Ali Fares 2 and Youssef Ayyad
3. Branching Algorithms
 3. Branching Algorithms COMP6741: Parameterized and Exact Computation Serge Gaspers Semester 2, 2015 Contents 1 Introduction 1 2 Maximum Independent Set 3 2.1 Simple Analysis................................................
3. Branching Algorithms COMP6741: Parameterized and Exact Computation Serge Gaspers Semester 2, 2015 Contents 1 Introduction 1 2 Maximum Independent Set 3 2.1 Simple Analysis................................................
SIGNAL COMPRESSION Lecture 7. Variable to Fix Encoding
 SIGNAL COMPRESSION Lecture 7 Variable to Fix Encoding 1. Tunstall codes 2. Petry codes 3. Generalized Tunstall codes for Markov sources (a presentation of the paper by I. Tabus, G. Korodi, J. Rissanen.
SIGNAL COMPRESSION Lecture 7 Variable to Fix Encoding 1. Tunstall codes 2. Petry codes 3. Generalized Tunstall codes for Markov sources (a presentation of the paper by I. Tabus, G. Korodi, J. Rissanen.
Tree Decompositions and Tree-Width
 Tree Decompositions and Tree-Width CS 511 Iowa State University December 6, 2010 CS 511 (Iowa State University) Tree Decompositions and Tree-Width December 6, 2010 1 / 15 Tree Decompositions Definition
Tree Decompositions and Tree-Width CS 511 Iowa State University December 6, 2010 CS 511 (Iowa State University) Tree Decompositions and Tree-Width December 6, 2010 1 / 15 Tree Decompositions Definition
Section Summary. Relations and Functions Properties of Relations. Combining Relations
 Chapter 9 Chapter Summary Relations and Their Properties n-ary Relations and Their Applications (not currently included in overheads) Representing Relations Closures of Relations (not currently included
Chapter 9 Chapter Summary Relations and Their Properties n-ary Relations and Their Applications (not currently included in overheads) Representing Relations Closures of Relations (not currently included
Realization Plans for Extensive Form Games without Perfect Recall
 Realization Plans for Extensive Form Games without Perfect Recall Richard E. Stearns Department of Computer Science University at Albany - SUNY Albany, NY 12222 April 13, 2015 Abstract Given a game in
Realization Plans for Extensive Form Games without Perfect Recall Richard E. Stearns Department of Computer Science University at Albany - SUNY Albany, NY 12222 April 13, 2015 Abstract Given a game in
Strong Mathematical Induction
 Strong Mathematical Induction Lecture 23 Section 5.4 Robb T. Koether Hampden-Sydney College Mon, Feb 24, 2014 Robb T. Koether (Hampden-Sydney College) Strong Mathematical Induction Mon, Feb 24, 2014 1
Strong Mathematical Induction Lecture 23 Section 5.4 Robb T. Koether Hampden-Sydney College Mon, Feb 24, 2014 Robb T. Koether (Hampden-Sydney College) Strong Mathematical Induction Mon, Feb 24, 2014 1
Information Theory and Statistics Lecture 2: Source coding
 Information Theory and Statistics Lecture 2: Source coding Łukasz Dębowski ldebowsk@ipipan.waw.pl Ph. D. Programme 2013/2014 Injections and codes Definition (injection) Function f is called an injection
Information Theory and Statistics Lecture 2: Source coding Łukasz Dębowski ldebowsk@ipipan.waw.pl Ph. D. Programme 2013/2014 Injections and codes Definition (injection) Function f is called an injection
Limitations of Algorithm Power
 Limitations of Algorithm Power Objectives We now move into the third and final major theme for this course. 1. Tools for analyzing algorithms. 2. Design strategies for designing algorithms. 3. Identifying
Limitations of Algorithm Power Objectives We now move into the third and final major theme for this course. 1. Tools for analyzing algorithms. 2. Design strategies for designing algorithms. 3. Identifying
Search Trees. EECS 2011 Prof. J. Elder Last Updated: 24 March 2015
 Search Trees < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Learning Outcomes Ø From this lecture, you should be able to: q Define the properties of a binary search
Search Trees < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Learning Outcomes Ø From this lecture, you should be able to: q Define the properties of a binary search
if the two intervals overlap at most at end
 Activity Selection Given a set of activities represented by intervals (s i f i ), i =1 ::: n. To select a maximum number of compatible intervals (activities). Two activities (s i f i ) and (s j f j ) are
Activity Selection Given a set of activities represented by intervals (s i f i ), i =1 ::: n. To select a maximum number of compatible intervals (activities). Two activities (s i f i ) and (s j f j ) are
Lecture 6 September 21, 2016
 ICS 643: Advanced Parallel Algorithms Fall 2016 Lecture 6 September 21, 2016 Prof. Nodari Sitchinava Scribe: Tiffany Eulalio 1 Overview In the last lecture, we wrote a non-recursive summation program and
ICS 643: Advanced Parallel Algorithms Fall 2016 Lecture 6 September 21, 2016 Prof. Nodari Sitchinava Scribe: Tiffany Eulalio 1 Overview In the last lecture, we wrote a non-recursive summation program and
Assignment 5: Solutions
 Comp 21: Algorithms and Data Structures Assignment : Solutions 1. Heaps. (a) First we remove the minimum key 1 (which we know is located at the root of the heap). We then replace it by the key in the position
Comp 21: Algorithms and Data Structures Assignment : Solutions 1. Heaps. (a) First we remove the minimum key 1 (which we know is located at the root of the heap). We then replace it by the key in the position
Learning Decision Trees
 Learning Decision Trees Machine Learning Fall 2018 Some slides from Tom Mitchell, Dan Roth and others 1 Key issues in machine learning Modeling How to formulate your problem as a machine learning problem?
Learning Decision Trees Machine Learning Fall 2018 Some slides from Tom Mitchell, Dan Roth and others 1 Key issues in machine learning Modeling How to formulate your problem as a machine learning problem?
Recursive Definitions. Recursive Definition A definition is called recursive if the object is defined in terms of itself.
 Recursion Recursive Definitions Recursive Definition A definition is called recursive if the object is defined in terms of itself. Base Case Recursive definitions require a base case at which to either
Recursion Recursive Definitions Recursive Definition A definition is called recursive if the object is defined in terms of itself. Base Case Recursive definitions require a base case at which to either
13 Dynamic Programming (3) Optimal Binary Search Trees Subset Sums & Knapsacks
 13 Dynamic Programming (3) Optimal Binary Search Trees Subset Sums & Knapsacks Average-case analysis Average-case analysis of algorithms and data structures: Input is generated according to a known probability
13 Dynamic Programming (3) Optimal Binary Search Trees Subset Sums & Knapsacks Average-case analysis Average-case analysis of algorithms and data structures: Input is generated according to a known probability
