BRUNN-MINKOWSKI INEQUALITIES IN PRODUCT METRIC MEASURE SPACES
|
|
|
- Harold Gregory
- 5 years ago
- Views:
Transcription
1 BRUNN-MINKOWSKI INEQUALITIES IN PRODUCT METRIC MEASURE SPACES MANUEL RITORÉ AND JESÚS YEPES NICOLÁS Abstract. Given one metric measure space satisfying a linear Brunn-Minkowski inequality, and a second one Y satisfying a Brunn-Minkowski inequality with exponent p 1, we prove that the product Y with the standard product distance and measure satisfies a Brunn-Minkowski inequality of order 1/1 + p 1 under mild conditions on the measures and the assumption that the distances are strictly intrinsic. The same result holds when we consider restricted classes of sets. We also prove that a linear Brunn-Minkowski inequality is obtained in Y when Y satisfies a Prékopa-Leindler inequality. In particular, we show that the classical Brunn-Minkowski inequality holds for any pair of weakly unconditional sets in R n i.e., those containing the projection of every point in the set onto every coordinate subspace when we consider the standard distance and the product measure of n one-dimensional real measures with positively decreasing densities. This yields an improvement of the class of sets satisfying the Gaussian Brunn-Minkowski inequality. Furthermore, associated isoperimetric inequalities as well as recently obtained Brunn-Minkowski s inequalities are derived from our results. 1. Introduction The n-dimensional volume of a set M in the n-dimensional Euclidean space R n i.e., its n-dimensional Lebesgue measure is denoted by volm, or vol n M if the distinction of the dimension is useful. The symbol B n stands for the n-dimensional closed unit ball with respect to the Euclidean norm. Relevant families of subsets of Euclidean space used in this work are those of unconditional and weakly unconditional sets: a subset A R n is said to be unconditional if for every x 1,..., x n A and every ɛ 1,..., ɛ n [ 1, 1] n one has ɛ 1 x 1,..., ɛ n x n A. In a similar way, we will say that A is weakly unconditional see Figure 1 if for every x 1,..., x n A and every ɛ 1,..., ɛ n {0, 1} n one has ɛ 1 x 1,..., ɛ n x n A. Weakly unconditional sets are those for which the projection of every point in the set onto any coordinate subspace is again contained in the set. Equivalently, Date: May 4, Mathematics Subject Classification. Primary 52A40, 28A35; Secondary 60G15, 52A20. Key words and phrases. Brunn-Minkowski inequality, metric measure space, product space, Gaussian measure, product measure, isoperimetric inequality. First author is supported by MICINN-FEDER grant MTM C2-1-P and Junta de Andalucía grants FQM-325 and P09-FQM Second author is partially supported by ICMAT Severo Ochoa project SEV MINECO and by Programa de Ayudas a Grupos de Excelencia de la Región de Murcia, Fundación Séneca, 19901/GERM/15.
2 2 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS a set A is weakly unconditional if and only if every non-empty 1-section of A, through parallel lines to the coordinate axes, contains the origin identifying the corresponding 1-dimensional affine subspace with its direction; cf. Figure 1. A 2 A = A A 1 A 2 {0} s A 0 0 l A 1 Figure 1. The weakly unconditional hull A of A. Every 1-section s of A, through a parallel line l to a coordinate axis, contains the origin 0 l. Given an arbitrary non-empty set B R n, B will denote its weakly unconditional hull i.e., the intersection of all weakly unconditional sets containing B, which is just the union of B with every projection of it onto any coordinate subspace. The unconditional hull of B is defined in a similar way, see Figure 2. y p 0 x Figure 2. The unconditional hull of the point p R 2 is the gray square, while the weakly unconditional hull of p consists of the four marked points It is worth mentioning that an unconditional set in R is an interval symmetric with respect to the origin, and that a weakly unconditional set in R is just a set containing the origin.
3 BRUNN-MINKOWSKI INEQUALITIES 3 Another notion used in this paper is that of positively decreasing function. We say that a non-negative function f : R R 0 is positively decreasing if the functions t ft, t f t are decreasing i.e., non-increasing on [0,. The Minkowski sum of two non-empty sets A, B R n denotes the classical vector addition of them: A + B = {a + b : a A, b B}. It is natural to wonder about the possibility of relating the volume of the Minkowski sum of two sets in terms of their volumes; this is the statement of the Brunn-Minkowski inequality. Indeed, taking λ 0, 1 and A and B two non-empty Lebesgue measurable subsets of R n such that their linear combination λa + λb = {1 λa + λb : a A, b B} is also measurable, then the Brunn-Minkowski inequality ensures that 1.2 vol 1 λa + λb 1/n 1 λvola 1/n + λvolb 1/n. The above inequality is sometimes introduced in a weaker form although they are actually equivalent because of the homogeneity of the volume, often referred to as its multiplicative or dimension free version: 1.3 vol 1 λa + λb vola 1 λ volb λ. The Brunn-Minkowski inequality admits an equivalent analytic version, the Prékopa-Leindler inequality, originally proved in [30] and [25], from where inequality 1.3 can be immediately obtained. Theorem A Prékopa-Leindler Inequality. Let λ 0, 1 and let f, g, h : R n R 0 be non-negative measurable functions such that, for any x, y R n, Then h 1 λx + λy fx 1 λ gy λ. 1 λ λ h dx f dx g dx. R n R n R n The Prékopa-Leindler inequality is naturally connected to log-concave functions i.e., functions of the form e u where u : R n R { } is convex. In other words, a non-negative function φ is log-concave if φ1 λx + λy φx 1 λ φy λ for any x, y R n and λ 0, 1. In the same way, f is quasi-concave if φ1 λx + λy min{φx, φy}, or equivalently if its superlevel sets are convex. In particular, if µ is a measure on R n such that dµx = φx dx, where φ is log-concave a measure like this will be called a log-concave measure then, by Theorem A, 1.4 µ 1 λa + λb µa 1 λ µb λ. for any A, B R n measurable such that 1 λa + λb is so, for λ 0, 1. However, although multiplicative Brunn-Minkowski type inequalities 1.4 may be easily obtained it is enough to consider log-concave measures, something very different occurs when dealing with the 1/n-form of the Brunn-Minkowski inequality 1.2. A relevant space where the general Brunn-Minkowski inequality does not hold for arbitrary sets is the so-called Gauss space: R n endowed with the standard n-dimensional Gaussian measure given by 1 x 2 dγ n x = e 2 dx. 2π n/2
4 4 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS Indeed, since 1/2π n/2 e x 2 2 is log-concave, γ n satisfies 1.4; however, it is easy to see that 1.5 γ n 1 λa + λb 1/n 1 λγn A 1/n + λγ n B 1/n does not hold in general, as it was pointed out in [16, Section 7] via A = B n and B = x + B n for x large enough. To this respect, since a condition on the position of the sets is clearly needed, the authors conjectured Question 7.1 the following. Conjecture 1.1 [16]. The Gaussian Brunn-Minkowski inequality 1.5 holds for any closed convex sets A, B such that 0 A B. In the same paper [16] the authors were able to verify this conjecture when both sets are coordinate boxes containing the origin and when one of them is a slab containing the origin: [ a 1, a 2 ] R n 1 for a 1, a 2 > 0 as well as when the sets are both dilates of the same centrally symmetric closed convex set. In [28], the authors showed that Conjecture 1.1 is in general not true: it is enough to consider 1.6 A = {x, y R 2 : y x tan α}, B = A + 0, ε, for ε > 0 small enough and α < π/2 sufficiently close to π/2. At this point, it is natural to ask for the weakest assumption in relation to the position of the sets needed to obtain Brunn-Minkowski s inequality 1.5. In a recent paper, [26, Theorem 1], the authors have proved in a very elegant way that 1.5 holds for the case of unconditional sets. More precisely, the authors show: Theorem B [26]. Let µ = µ 1 µ n be a product measure on R n such that µ i is the measure given by dµ i x = φ i x dx, where φ i : R R 0 is a positively decreasing even function, i = 1,..., n. Let λ 0, 1 and let = A, B R n be unconditional measurable sets so that 1 λa + λb is also measurable. Then µ1 λa + λb 1/n 1 λµa 1/n + λµb 1/n. In the same paper the authors pose the following: Question 1.2. Can one remove the assumption of unconditionality in the Gaussian Brunn-Minkowski inequality? Here we give a positive answer to this question by showing that it is enough to consider weakly unconditional sets. Furthermore, this may be regarded as a positive answer to the necessary slight reformulation of Conjecture 1.1, see Remark 4.1. We would like also to point out that a natural assumption for the validity of 1.5 is convexity and central symmetry see [16, Section 7]; this issue remains, to the best of our knowledge, still open. One of our main results reads, in the more general setting of product of measures with positively decreasing densities, as follows: Theorem 1.3. Let µ = µ 1 µ n be a product measure on R n such that µ i is the measure given by dµ i x = φ i x dx, where φ i : R R 0 is a positively decreasing function, i = 1,..., n. Let λ 0, 1 and let = A, B R n be weakly unconditional measurable sets such that 1 λa + λb is also measurable. Then 1.7 µ1 λa + λb 1/n 1 λµa 1/n + λµb 1/n.
5 BRUNN-MINKOWSKI INEQUALITIES 5 We would like to point out that, in contrast to Theorem B, not only the symmetry assumption on the sets may be removed but also that of the density functions involved in the product measure. Our approach is based on obtaining new Brunn-Minkowski inequalities from certain simpler spaces that satisfy some Brunn-Minkowski type inequality. To this end, we have the following definition. Definition 1.4. Let, d, µ be a metric measure space. We will say that it satisfies the Brunn-Minkowski inequality with respect to the parameter p R {± }, and we denote it by BMp for short, if 1.8 µc 1 λµa p + λµb p 1/p holds for all λ 0, 1 and any non-empty measurable sets A, B, C with µaµb > 0 such that C 1 λa d λb for a precise formulation of the operation d see Definition 2.2 in Subsection 2.1. If 1.8 holds for general non-empty measurable sets A, B, C such that C 1 λa d λb, without the restriction µaµb > 0, we say that, d, µ satisfies the general Brunn-Minkowski inequality with respect to the parameter p R {± }. We denote it by BMp for short. In the same way, we say that a certain family F P of measurable sets satisfies BMp resp. BMp if the above definition holds when dealing with sets A, B, C F. On the other hand, we will say that, d, µ satisfies the Prékopa-Leindler inequality, denoted by PL for short, if for any λ 0, 1 and non-negative µ- measurable functions f, g, h : R 0 such that hz fx 1 λ gy λ, for all x, y, and z 1 λ{x} d λ{y}, then 1 λ h dµ f dµ g dµ λ. In the same way, a function φ : R 0 will be said to be log-concave if φz φx 1 λ φy λ, for all x, y, z 1 λ{x} d λ{y}, and any λ 0, 1. With this notation we obtain our second main result: Theorem 1.5. Let, d, µ, Y, d Y, µ Y be metric measure spaces where µ is σ-finite, µ Y is locally finite and µ Y is a Radon measure. If, d, µ, Y, d Y, µ Y satisfy BM1 and BMp, respectively, for some p 1, then Y, d Y, µ Y satisfies BM 1/1 + p 1. In the statement of Theorem 1.5, we follow the usual convention of assuming that the quantity 1/1 + p 1 is equal to 0 when p = 0, and equal to 1 when p =. The distance d Y is the usual Euclidean product distance and µ Y the standard product measure, see Section 2. As pointed out to the authors by Luca Rizzi, Theorem 1.5 can be generalized when Y satisfies the weighted BM1/n, N/n Brunn-Minkowski inequality µc 1/n 1 λ N/n µa 1/n + λ N/n µb 1/n.
6 6 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS In this case the product Y satisfies the weighted Brunn-Minkowski inequality BM1/n + 1, N + 1/n + 1. See Theorem 3.3. This result yields, in the setting of product metric spaces, the same weighted Brunn-Minkowski inequality as the one in corank 1 Carnot groups obtained in [2]. The linear Brunn-Minkowski inequality BM1 plays a relevant role and becomes one of the main ingredients in this paper. Thus we also focus on this type of inequalities. To this aim, we have the following result in the setting of product metric spaces endowed with log-concave measures. Theorem 1.6. Let, d, µ, Y, d Y, µ Y be metric measure spaces which satisfy BM1 and PL, respectively. Let µ be the measure on Y given by dµx, y = φx, ydµ Y x, y where φ is a log-concave function. Assume that µ, µ Y are σ- finite. Let λ 0, 1 and let A, B Y be non-empty measurable sets such that 1 λa λb is also measurable and so that Then sup x Y χ A x, yφx, y dµ Y = sup x Y χ B x, yφx, y dµ Y. µ 1 λa λb 1 λµa + λ µb. The paper is organized as follows. Section 2 is devoted to collecting some definitions and preliminary considerations. In Section 3 we prove Theorems 1.5 and 1.6 in fact, a more general version of the latter as well as some related result in Theorem 3.1. Next, in Section 4, we particularize the results obtained in the precedent section to get some Brunn-Minkowski type inequalities for product measures on R n. Among others, we show Theorem 1.3 as well as we study its associated isoperimetric type inequality, Theorem 4.3. Finally, in Section 5, we present some other applications that can be derived from the results of Section Background material and auxiliary results Another equivalent version of the Brunn-Minkowski inequality that appears in the literature is the following: 2.1 vol 1 λa + λb min{vola, volb}. The equivalent expressions of the Brunn-Minkowski inequality, 1.2, 1.3, 2.1, can be rewritten in terms of the p-th mean of two non-negative numbers, where p is a parameter varying in R {± }. We recall this definition, for which we follow [6] regarding a general reference for p-th means of non-negative numbers, we refer also to the classic text of Hardy, Littlewood and Pólya [19], as well as to the excellent handbook about means by Bullen [7]. Consider first the case p R and p 0; given a, b 0 such that ab 0 and λ 0, 1, we define M p a, b, λ = 1 λa p + λb p 1/p. For p = 0 we set M 0 a, b, λ = a 1 λ b λ and, to complete the picture, for p = ± we define M a, b, λ = max{a, b} and M a, b, λ = min{a, b}. Finally, if ab = 0, we will define M p a, b, λ = 0 for all p R {± }. Note that M p a, b, λ = 0, if ab = 0, is redundant for all p 0, however it is relevant for p > 0 as we will briefly comment later on. Moreover,
7 BRUNN-MINKOWSKI INEQUALITIES 7 one can easily check that, for any p R {± }, M p a, b, λ = lim q p M q a, b, λ. Furthermore, for p 0, we will allow that a, b take the value and in that case, as usual, M p a, b, λ will be the value that is obtained by continuity. With this definition, inequalities 1.2, 1.3, 2.1 can be rephrased as 2.2 vol 1 λa + λb M p vola, volb, λ, where p takes the values 1/n, 0 and, respectively. We notice that, in the case p = 1/n, and with the above considered notation, we are only taking into account sets A, B such that volavolb > 0. This distinction is usual in the literature when dealing with Brunn-Minkowski type inequalities and we shall discuss about it later cf. Proposition 2.7 and the precedent paragraph. For this reason, we will maintain both notations, M p a, b, λ and 1 λa p +λb p 1/p, along the paper when p = 0, ±, the latter must be understood again as the values that are obtained by continuity. Here, we are interested in studying Brunn-Minkowski type inequalities in the context of a metric measure space i.e., a set endowed with a distance d and a measure µ. To this end, two elements playing a relevant role in the above family of inequalities 2.2 must be studied: the operation the Minkowski sum, +, in 2.2 and the measure the Lebesgue measure, vol, in 2.2 together with the appropriate p-th mean according to the geometry of the space The operation: the distance comes into play. Since we intend to study Brunn-Minkowski type inequalities in spaces without a linear structure, first we should interpret 1.1 in terms of the distance associated to the Euclidean norm. To this aim, we notice that, given x, y, z R n and λ 0, 1, the relation z = 1 λx + λy holds if and only if 2.3 z x = λ x y, z y = 1 λ x y. In other words, {1 λx + λy} = B x, λ x y B y, 1 λ x y here Ba, r denotes the n-dimensional closed Euclidean ball of radius r centered at a, i.e., Ba, r = a + rb n. The above intersection is non-empty in any normed space considering, as natural, balls with respect to the distance induced by the given norm since 1 λx + λy for x, y and λ 0, 1 always satisfies 2.3. However, it does not necessarily contain a unique point: consider, for instance, R n endowed with the infinity norm, or the Heisenberg group endowed with its standard Carnot-Carathéodory distance. This does not suppose a big inconvenient for us; the problem is when dealing with metric spaces for which the latter intersection may be empty. A trivial example of this would be Z n endowed with the Euclidean metric of R n restricted on Z n. Since this space is not path-connected this obstacle cannot be overcome, i.e., there does not exist an equivalent distance satisfying the above non-empty intersection condition for any pair of points and any λ [0, 1]. An example of a path-connected space for which a given distance has also the above-mentioned peculiarity is the unit circle S 1 in the plane with the restriction of the distance given by to S 1. Here the solution is to consider the intrinsic metric on S 1 associated to its length structure. These considerations lead us to the following definition we recommend the reader to [8, Chapter 2] for enlightening discussions on these topics.
8 8 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS Definition 2.1. Let, d be a metric space. We will say that d is a strictly intrinsic distance if for any x, y the closed balls B d x, r 1, B d y, r 2 have a non-empty intersection provided that r 1 + r 2 = dx, y. An interesting class of metric spaces with strictly intrinsic distances is the one of complete length spaces endowed with their associated distances. Following the proof of [8, Theorem ], one may show that a metric space, d, where d is a strictly intrinsic distance, needs to be path-connected. For the sake of brevity in our exposition, from now on a metric space will mean a set provided with a strictly intrinsic distance d. Under this consideration, we may extend 1.1 to the context of a metric space cf Definition 2.2. Let, d be a metric space. If λ 0, 1 and A, B are two nonempty subsets of, the d-convex combination 1 λa d λb of A and B will be the non-empty set given by λa d λb = { z : dz, a = λda, b, dz, b = 1 λda, b, a A, b B }. This notion of d-convex combination has already appeared in the literature. It can be found in [22, Definition 1.1] and, in the setting of Riemannian manifolds, denominated as the barycenter of two points, in [12, p. 29]. When the distance is clear, the index of d will be omitted and we shall write just 1 λa λb to denote 1 λa d λb. When the metric d is such that the intersection B d x, λdx, y Bd y, 1 λdx, y = {z} for any x, y and λ 0, 1, it allows us to define an operation on, + d : [0, 1], given by + d x, y, λ = z. For simplicity we write 1 λx + d λy = + d x, y, λ and further, for A, B, 1 λa + d λb = {1 λa + d λb : a A, b B} = 1 λa d λb. An easy way to construct such a metric space endowed with the above-mentioned operation + d is as follows. Example 2.3. Given an injective function φ : R n on a set, assume that dx, y = φx φy, x, y, is an strictly intrinsic distance on. Then the operation + d is well-defined and we have 1 λx + d λy = φ 1 1 λφx + λφy. When working with product spaces, the d-convex combination of two subsets cf. 2.4 might not be clear since there is not a sole distance d associated to the product metric space. So, it is convenient to clarify which distance will be fixed for the product space. To this aim, let, d and Y, d Y be metric spaces and consider the product space Y. One can define a distance d Y on Y whose induced topology agrees with the product topology as follows: d Y x1, x 2, y 1, y 2 = d x 1, y 1, d Y x 2, y 2 where is a norm in R 2. When taking the Euclidean norm, this distance is the so-called product metric, which will be denoted from now on as ρ.
9 BRUNN-MINKOWSKI INEQUALITIES 9 For our purposes cf. 2.2, amongst all the distances d on Y, we are interested in considering the smallest possible d-convex combination. First we notice that, from the definition of d Y, and for any non-empty A, B Y and λ 0, 1, we get λa d Y λb 1 λa λb, where 1 λa λb is the set given by 1 λa λb = { z =z 1, z 2 Y : d z 1, a 1 = λd a 1, b 1, d z 1, b 1 = 1 λd a 1, b 1, d Y z 2, a 2 = λd Y a 2, b 2, d Y z 2, b 2 = 1 λd Y a 2, b 2, for some a 1, a 2 A, b 1, b 2 B }. The following result shows that, in a sense, the most convenient distance on Y cf. 2.5 is the product metric ρ. Proposition 2.4. Let, d and Y, d Y be metric spaces and let ρ be the product metric on Y. If A, B are non-empty subsets of Y and λ 0, 1 then 1 λa ρ λb = 1 λa λb. Proof. For the sake of simplicity, we will write d 1 = d, d 2 = d Y. If we denote by A i = d i a i, b i, B i = d i z i, a i, C i = d i z i, b i, for i = 1, 2, and we put A = A 1, A 2, B = B 1, B 2, C = C 1, C 2 R 2 0, we have that the defining conditions of ρ are 2.6 B 2 = λ A 2, C 2 = 1 λ A 2. From the triangle inequality for d i we get 2.7 A i B i + C i, for i = 1, 2. By 2.7, the triangle inequality for 2 and 2.6, respectively, we have A 2 B + C 2 B 2 + C 2 = A 2. Thus, from the equality case of the triangle inequality for 2, we obtain C = rb where, by 2.6, r = 1 λ λ. Finally, from the equality case of 2.7, we get A i = B i + C i = 1 + rb i = 1 λ B i, for i = 1, 2. This, together with the already obtained C = rb, implies that B i C i = 1 λa i, i = 1, 2. The proof is concluded. = λa i and For simplicity, from now on unless we say explicitly the opposite, when working with product metric spaces, will stand for ρ i.e., = ρ = The role of the measure. As we have commented before, we intend to study Brunn-Minkowski type inequalities. Even considering R n endowed with the classical Minkowski addition +, it would be naive to try to generalize 2.2 when replacing the volume with an arbitrary measure µ. Indeed, if we consider R provided with the measure µ given by dµx = x 2 dx and we take A = [1, 2], B = A, then we clearly have µa = µb > µ[ 1/2, 1/2] = µ A + B/2, which prevents any possible Brunn-Minkowski type inequality cf Other examples of spaces where certain Brunn-Minkowski type inequalities do not hold in general although
10 10 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS the multiplicative Brunn-Minkowski inequality is immediately fulfilled by Theorem A are related to the so-called log-concave measures. Thus, since there arise some pathologies even when considering R n with the Minkowski addition and the most important probability measure in R n, in order to derive a certain Brunn-Minkowski inequality with respect to a fixed mean M p cf. 2.2, we should either impose some conditions on the measure or consider certain subfamilies of sets or sometimes, as commented above, both of them. For the sake of completeness, we collect some definitions and results that to be used throughout our discussion. Definition 2.5. A measure space is a pair, µ that is, we omit for simplicity the σ-algebra Σ which contains, by assumption, the σ-algebra of all Borel sets in, where µ is a measure on the metric space, d that is assumed to be complete. Such a measure is said to be Borel, whereas the triple, d, µ is called a metric measure space. When considering the product measure space associated to the measure spaces, µ and Y, µ Y, we often denote by µ Y, instead of µ µ Y, the completion of the usual product measure of µ and µ Y. Moreover, in this case,, µ and Y, µ Y are assumed to be measure spaces so that µ Y is also Borel. Regarding the measurability of the sets, it is worth noting that the assumption that A and B are measurable is not sufficient to guarantee that 1 λa λb is measurable, as happens with the Lebesgue measure in relation to the Minkowski addition see [15, Section 10]. The following results are classical and can be found in any book on measure theory e.g. [10]. Proposition C. Let, µ be a measure space. If A n n N is a decreasing sequence of µ-measurable sets such that µa n < + for some n N, then + µ A n = lim µa n. n n=1 Theorem D Fubini-Tonelli s theorem. Let, µ, Y, µ Y be σ-finite measure spaces and let f : Y R 0 be a non-negative measurable function. Then fx, y dµ Y x, y = fx, y dµ Y y dµ x Y Y = fx, y dµ x dµ Y y. Y Therefore, for any non-negative measurable function h : R 0, Cavalieri s Principle + hx dµ x = µ {x : hx t} dt holds. 0 In the following, when dealing with product spaces, we use the following notation: given C Y, for any t we denote by Ct = {y Y : t, y C}.
11 BRUNN-MINKOWSKI INEQUALITIES 11 Definition 2.6. Let, d, µ be a metric measure space. The measure µ is said to be locally finite if for every point x there exists r x > 0 such that µ B d x, r x <. We say that µ is inner regular if the measure of any set can be approximated from inside by compact subsets of : if for any measurable set A µa = sup{µk : K A, K compact} holds. If µ is both inner regular and locally finite, it is called a Radon measure. Finally, µ is said to be strictly positive if µ B d x, r > 0 for all r > 0 and any x. In the same way, we say that µ is strictly positive around x, if µ B d x, r > 0 for all r > 0. Regarding Definition 1.4, we note that, d, µ satisfies the Brunn-Minkowski inequality BMp if µc M p µa, µb, λ holds for all λ 0, 1 and any measurable sets A, B, C such that C 1 λa λb. We notice that for all p 0, a space satisfies BMp if and only if it also satisfies BMp. The following result shows that when dealing with some special spaces, both notions are also equivalent for p > 0. Before showing it, we would like to point out that this property is trivially fulfilled for p = 1/n in R n endowed with the Lebesgue measure vol cf. 1.2, as an easy consequence of both the translation invariance and the homogeneity of degree n of the volume. However, when considering a different measure µ, in principle, the case µaµb = 0 cannot be easily obtained. Proposition 2.7. Let, d, µ be a metric measure space, where, d is locally compact and µ is a strictly positive Radon measure. If, d, µ satisfies BMp with respect to the parameter p > 0 then it satisfies BMp. Proof. Since µ is Radon then it is inner regular and thus it is enough to show the statement of this result for arbitrary non-empty compact sets A and B. Moreover, we will consider the case in which one of the sets, say B, has measure zero whereas the other one, A, has positive measure it is immediate otherwise. Let b 0 B and consider, for any n N, B n = B B d b0, 1/n. On the one hand, B n n N is clearly a decreasing sequence and + + B n = B B d b 0, 1 = B {b 0 } = B. n n=1 n=1 Moreover, since is locally compact, we may assume, without loss of generality, that B d b0, 1 n is compact and then also Bn for all n N. Hence 1 λa λb n is compact and thus µ 1 λa λb n < + because µ is locally finite. So, from Proposition C, we have lim n µ + 1 λa λb n = µ 1 λa λbn. On the other hand, we may assume that µ B d b0, 1/n < + for all n N because µ is locally finite, and thus the same holds for µb n. Furthermore, since µ is strictly positive, µ B d b0, 1 n > 0 and hence µbn > 0. Therefore, by hypothesis, n=1 µ 1 λa λb n 1 λµa p + λµb n p 1/p,
12 12 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS and taking limits on both sides and using Proposition C we get lim n µ 1 λa λb n 1 λµa p + λµb p 1/p = 1 λ 1/p µa. So, we must just check that n N 1 λa λbn 1 λa λb furthermore, we have equality since the reverse inclusion is trivially fulfilled. To this aim, let z n N 1 λa λbn. Then, for each n N, there exist an A, b n B n such that 2.8 dz, a n = λda n, b n, dz, b n = 1 λda n, b n. Since B n n is decreasing and is locally compact, there exists n 0 N such that B n is compact for n n 0. As A is compact we may assume, taking subsequences if necessary, that a n n, b n n are convergent, with limits a A and b B n0, respectively. Repeating the argument with the tails of the sequence b n n, we get that b B n for all n n 0 and hence b B. Now, taking limits on 2.8, we may assert that z 1 λa λb. This concludes the proof. Now we collect some examples of spaces or families of sets satisfying linear Brunn- Minkowski inequalities, since these spaces/families will be very useful along this paper cf. Theorems 3.1 and 1.5. Example 2.8. Let = αi where I = [0, L] R for some L > 0 and α : I R n is an injective function. Let d be the distance defined, as in Definition 2.3, via α 1 by the equality dx, y = α 1 x α 1 y. Let µ be the pushforward of the one-dimensional Lebesgue measure vol 1 on R. Then, by the Brunn-Minkowski inequality in R cf. 1.2, we have µ1 λa λb = µ α 1 λα 1 A + λα 1 B = vol 1 1 λα 1 A + λα 1 B 1 λvol 1 α 1 A + λvol 1 α 1 B = 1 λµa + λµb. The following linear version of the Brunn-Minkowski inequality, due to Bonnesen, can be found in the literature e.g. [3, 17, 29]. From now on, L n n 1 will be the set of vectorial hyperplanes of R n, the orthogonal projection of a set A onto H will be denoted by A H, and by a convex body we will mean a non-empty compact convex set. Example 2.9. Let K, L R n be convex bodies for which there exists H L n n 1 such that either vol n 1 K H = vol n 1 L H or Then, for all λ 0, 1, max vol n 1 K x + H = max vol n 1 L x + H. x H x H vol 1 λk + λl 1 λvolk + λvoll. We notice that a positively decreasing function φ : R R 0 is quasi-concave and furthermore φ0 = sup x R φx. Thus, as a consequence of [11, Theorem 4.1] we get the following example, which will play a relevant role along this paper. Example Let µ be the measure on R given by dµx = φxdx, where φ : R R 0 is positively decreasing. Let λ 0, 1 and let A, B R be
13 BRUNN-MINKOWSKI INEQUALITIES 13 measurable sets containing the origin and such that 1 λa+λb is also measurable. Then BM1 holds: µ1 λa + λb 1 λµa + λµb. We recall that weakly unconditional sets in R are those containing the origin. Hence BM1 holds for weakly unconditional sets. On the other hand, if µ is a strictly positive finite measure, taking A = [ 1, 1], and B i = [i, i + 1] for all i N, we have lim i µ1 λa + λb i = lim i µb i = 0, and we conclude that BM1 cannot hold for A and B i when i is large. This shows the necessity of taking weakly unconditional sets to ensure the validity of BM1. The following result shows that, when dealing with measures µ on the real line given by dµx = φxdx, where φ is a continuous function, the converse is also true. That is, the fact that the linear Brunn-Minkowski inequality holds for any pair of measurable sets containing the origin characterizes the nature of φ. Proposition Let µ be the measure on R given by dµx = φxdx, where φ is a non-negative continuous function. If 2.9 µ1 λa + λb 1 λµa + λµb holds for any measurable sets A, B R containing the origin and all λ 0, 1, and so that 1 λa + λb is also measurable, then φ is positively decreasing. Proof. Let F : R R be the function given by F x = x 0 φt dt. Fix x, y > 0 and take A = [0, x] and B = [0, y]. Then, from 2.9, we get F 1 λx + λy 1 λf x + λf y. Since it is true for arbitrary x, y R >0 and λ 0, 1, we may assure that F is concave on R >0. In the same way, we obtain that F is convex on R <0. Moreover, since φ is continuous, by the fundamental theorem of calculus we get F x = φx for all x R. Now, the concavity of F on R >0 resp. the convexity of F on R <0 implies that φx = F x is decreasing on R >0 resp. φx = F x is increasing on R <0. The result is now concluded from the continuity of φ. Remark The condition that the sets A and B contain the origin in Proposition 2.11 is necessary but weak enough to allow a wide range of measures to satisfy BM1. Indeed, if we assume a more restrictive condition, such as BM1 holds for any pair of Euclidean balls in R, then the measure µ is a constant multiple of the Lebesgue measure vol 1 see [34, Theorem 1.2] and [4]. This shows once again the necessity of taking weakly unconditional sets to ensure BM1 when dealing with arbitrary measures. 3. Brunn-Minkowski inequalities in product measure spaces One of the best known proofs of the Brunn-Minkowski inequality 1.2 is a classical version due to Kneser and Süss [23], which is also reproduced in [3] and [33]. Hadwiger and Ohmann [18] gave a particularly beautiful proof for the compact setting, which is also reproduced in the survey by Gardner [15, Section 4] and in Burago and Zalgaller s monograph [9] see also the references therein. Knothe [24] gave a proof of the Brunn-Minkowski inequality using a volume-preserving map.
14 14 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS Both Kneser-Süss and Hadwiger-Ohmann s proofs have an inductive flavor; the first one in the dimension n whereas the second one in the number of boxes that determine the set the general case is then obtained by approximation. However, both the homogeneity and the translation invariance of the volume play a crucial role in these proofs. Thus, it is not possible to imitate these proofs in the context of metric measure spaces. Nevertheless, one may obtain Brunn-Minkowski inequalities in further spaces where the measure does not satisfy neither homogeneity nor translation invariance. To this aim, here we will exploit some classical analytic tools that are often used when dealing with some material relative to the Prékopa-Leindler inequality, Theorem A e.g. [4, 6, 13, 20]. First we will show a linear Brunn-Minkowski inequality on product metric spaces in the spirit of Bonnesen s inequality in Example 2.9. Theorem 3.1. Let, d, µ, Y, d Y, µ Y be metric measure spaces which satisfy BM1 and BMp, respectively, where p R {± } and µ, µ Y are σ-finite. Let λ 0, 1 and let A, B Y be non-empty measurable sets such that 1 λa λb is also measurable and so that 3.1 sup µ Y Ax = sup µ Y Bx. x x Then µ Y 1 λa λb 1 λµ Y A + λ µ Y B. Proof. Along this proof we will use the same symbol to denote the operation on any of the three spaces, Y and Y. We shall denote the product measure µ Y simply by µ. We set α = sup x µ Y Ax = sup x µ Y Bx R 0 {+ }. In case α = 0, Fubini-Tonelli s Theorem and 3.1 imply that µa = µb = 0 and the linear Brunn-Minkowski inequality holds trivially. Hence we may assume that α > 0. For any pair of points s, r such that µ Y Asµ Y Br > 0, the sets Ar and Bs are non-empty. Take a point t λ 1 λ{s} λ{r}. This implies that d t λ, s = λd s, r, d t λ, r = 1 λd s, r. From these equalities the inclusion 1 λa λb tλ 1 λas λbr follows immediately and, since BMp is satisfied on Y, we get 1 µ Y λa λb tλ µ Y 1 λas λbr 3.2 M p µ Y As, µ Y Br, λ. Consider now the non-negative functions f, g, h : R 0 defined by ft = µ Y At, gt = µ Y Bt, and ht = µ Y 1 λa λb t. We clearly have cf { x : fx t }, { x : gx t }, for all 0 t < α. From 3.3 and 3.2 we get {x : hx t} 1 λ{x : fx t} λ{x : gx t}
15 BRUNN-MINKOWSKI INEQUALITIES 15 for all 0 < t < α. Therefore, by the linear Brunn-Minkowski inequality in, we have µ {x : hx t} 1 λµ {x : fx t} + λµ {x : gx t} for all 0 < t < α. Finally, by the above inequality, and using Fubini-Tonelli s Theorem and Cavalieri s Principle, Theorem D, we get µ 1 λa λb = hx dµ x as desired. = + 0 α 0 α 0 µ {x : hx t} dt µ {x : hx t} dt 1 λµ {x : fx t} α + λµ {x : gx t} dt 0 = 1 λ fx dµ x + λ gx dµ x = 1 λµa + λ µb, As an immediate consequence of the proof of the above result we get the following corollary. Corollary 3.2. Let, d, µ, Y, d Y, µ Y be metric measure spaces for which there exist certain families F P, F Y PY that satisfy BM1 and BMp, respectively, where p R {± } and µ, µ Y are σ-finite. Let A, B Y be measurable sets such that 1 λa λb is also measurable and so that If moreover A, B satisfy: then i At, Bt F Y for all t, sup µ Y Ax = sup µ Y Bx. x x ii {x : µ Y Ax t}, {x : µ Y Bx t} F for all 0 < t < sup x µ Y Ax or a.e., µ Y 1 λa λb 1 λµ Y A + λ µ Y B. The above proof can be exploited to obtain a general Brunn-Minkowski inequality in the setting of product metric measure spaces. This is the content of Theorem 1.5. Proof of Theorem 1.5. Along this proof we will use the same symbol to denote the operation on any of the three spaces, Y and Y. We shall denote the product measure µ Y simply by µ.
16 16 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS Let A, B, C Y be measurable sets such that µaµb > 0 and C 1 λa λb. Since µ is a Radon measure we may assume, without loss of generality, that A and B are compact: to prove this, we choose two sequences of compact sets K i i and L i i with positive volume such that K i A, L i B for all i N, and µa = lim i µk i, µb = lim i µl i. Assuming that BM1/1 + p 1 holds for the pair K i, L i we clearly have µc µ1 λk i λl i M 1/1+p 1 µk i, µl i, λ. Taking limits on both sides, we get BM1/1 + p 1 for {A, B, C}. We take the non-negative functions f, g, h : R 0 given by where ft = µ Y At, gt = µ Y Bt, ht = µ Y Ct, µ Y A µ Y B C p C p = M p µy A, µ Y B, λ. We notice that the above functions are well-defined: denominators are positive since µaµb > 0, and they are finite because {y Y : x, y A for some x } and {y Y : x, y B for some x } are compact subsets of Y and µ Y is locally finite. Furthermore sup t ft = sup gt = 1. t We show that, for any pair of points s, r, and any t λ 1 λ{s} λ{r}, we have 3.4 ht λ min{fs, gr}. To check the validity of 3.4, it is enough to consider the case µ Y Asµ Y Br > 0. Hence, As, Br are non-empty, the inclusions trivially hold, and we have Ct λ 1 λa λb t λ 1 λas λbr C p ht λ = µ Y Ct λ M p µ Y As, µ Y Br, λ. Now, for p 0, +, we obtain M p µy As, µ Y Br, λ = 1 λµ Y As p + λµ Y Br p 1/p where θ = λ µ Y B p 0, 1. C p p For the case p = 0, we get = C p 1 θfs p + θgr p 1/p C p min{fs, gr}, M 0 µy As, µ Y Br, λ = µ Y As 1 λ µ Y Br λ = C 0 fs 1 λ gr λ C 0 min{fs, gr}.
17 BRUNN-MINKOWSKI INEQUALITIES 17 For p =, we clearly have M µy As, µ Y Br, λ = max{µ Y As, µ Y Br} C min{fs, gr}. Therefore, we have shown 3.4. The definition of f and g implies that the sets { x : fx t }, { x : gx t } are non-empty for any t [0, 1. Now, 3.4 trivially implies {x : hx t} 1 λ{x : fx t} λ{x : gx t} and, since satisfies BM1, we have µ {x : hx t} 1 λµ {x : fx t} + λµ {x : gx t} for any t [0, 1. Now, following similar steps to those described at the end of the proof of Theorem 3.1, we get µ 1 λa λb = C p hx dµ x C p 1 λ fx dµ x + λ gx dµ x µa µb = C p 1 λ + λ. µ Y A µ Y B The latter quantity is no smaller than M 1/1+p 1 µa, µb, λ. When p 0,, this follows from the reverse Hölder inequality, [7, Theorem 1, p. 178], 1 λa 1 b 1 + λa 2 b 2 1 λa p 1 + λa p 1/p 2 1 λb q 1 + 1/q λbq 2 where q = 1/1 + p 1 is the Hölder conjugate of p 1, just by taking a 1 = µ Y A 1, a 2 = µ Y B 1, b 1 = µa, b 2 = µb. The case p = 0 follows from the Arithmetic-Geometric mean inequality and the case p = is immediate. Regarding Definition 1.4, we could say that a metric measure space, d, µ satisfies the Brunn-Minkowski inequality with respect to the parameters p R {± } and q 1,, BMp, q for short, if µc 1 λ q µa p + λ q µb p 1/p holds for all λ 0, 1 and any non-empty measurable sets A, B, C with µaµb > 0 such that C 1 λa d λb. Analogously, if the above condition holds for general non-empty measurable sets A, B, C such that C 1 λa d λb, without the restriction µaµb > 0, we say that, d, µ satisfies BMp, q. This notion is sometimes useful e.g. [22], [1, Section 4], and the references therein when the classical Brunn-Minkowski inequality BMp does not hold. In particular, given n, N > 0, a metric measure space satisfies BM1/n, N/n if µc 1/n 1 λ N/n µa 1/n + λ N/n µb 1/n
18 18 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS holds for all measurable sets A, B, C with µaµb > 0 such that C 1 λa λb. Under the same initial assumptions of Theorem 1.5, and following its proof, we may assert that if, d, µ, Y, d Y, µ Y satisfy BM1, q and BMp, q, respectively, for some 0 p 1 and q 1,, then Y, d Y, µ Y satisfies BM 1/1 + p 1, q. We notice that, since 1 λ q + λ q 1, here the case p = 0 makes no sense. A not so trivial generalization of Theorem 1.5, pointed out to the authors by Luca Rizzi, is the following. Theorem 3.3. Let, d, µ, Y, d Y, µ Y be metric measure spaces where µ is σ-finite, µ Y is locally finite and µ Y is a Radon measure. Let n, N > 0. Assume that, d, µ, Y, d Y, µ Y satisfy BM1 and BM1/n, N/n, respectively. Then Y, d Y, µ Y satisfies BM 1/n + 1, N + 1/n + 1. Proof. The proof follows closely the one of Theorem 1.5. By similar arguments it is enough to show that the desired Brunn-Minkowski inequality holds for compact subsets A, B in Y. We shall denote the product measure µ Y simply by µ and let p = 1/n, q = N/n. We consider the non-negative functions f, g, h : R 0 given by where ft = µ At µ A, gt = µ Bt µ B, ht = µ Ct C p,q, C p,q = M p,q µ A, µ B, λ = 1 λ q µ A p + λq µ B p 1/p. The above functions are well-defined and sup t ft = sup gt = 1. t For any pair of points s, r, and any t λ 1 λ{s} λ{r}, we have 3.5 ht λ min{fs, gr}. To check the validity of 3.5 is enough to consider the case µ Asµ Br > 0. Hence As, Br are non-empty, the inclusion trivially holds, and we have Ct λ 1 λa λb t λ 1 λas λbr C p,q ht λ = µ Ct λ µ 1 λas λbr M p,q µ As, µ Br, λ C p,q min{fs, gr}. Hence 3.5 follows. The definition of f and g implies that the sets {f t} = { x : fx t }, {g t} = { x : gx t } are non-empty for any t [0, 1. Now 3.5 trivially implies {h t} 1 λ {f t} λ {g t}
19 BRUNN-MINKOWSKI INEQUALITIES 19 and, since satisfies BM1, we have µ {h t} 1 λµ {f t} + λµ {g t} for any t [0, 1. Following similar steps to those described at the end of the proof of Theorem 3.1, we get µc = C p,q hx dµ x C p,q 1 λ fx dµ x + λ µa µb = C p,q 1 λ + λ µ A µ B We apply the reverse Hölder inequality 1 λa 1 b 1 + λa 2 b 2 1 λa p 1 + λa p 2 gx dµ x 1/p 1 λb p. 1 + λbp 2 see [7, Theorem 1, p. 178], where p = 1/1 + p 1 = n and a 1 = 1 λ N n µ Y A 1, a 2 = 1 λ N n µ Y B 1, b 1 = 1 λ N n µa, b 2 = λ N n µb. 1/p, This implies µc M p,q µa, µb, λ and completes the proof. Theorem 3.3 can be applied to the product of one or several copies of the real line with a Carnot group. The validity of the above Brunn-Minkowski inequality for corank 1 Carnot groups has been recently established by Balogh et al., see Theorem 4.2 ii in [2]. From the proof of Theorem 1.5, we may obtain the following corollary, which will be very useful in order to obtain some Brunn-Minkowski inequalities for certain subfamilies of sets as, for instance, Theorem 1.3 shows. Corollary 3.4. Let, d, µ, Y, d Y, µ Y be metric measure spaces for which there exist certain families F P, F Y PY that satisfy BM1 and BMp, respectively, where p 1 and µ, µ Y are σ-finite. Let A, B Y be measurable sets such that 1 λa λb is so for λ 0, 1. If moreover A, B satisfy: then i The non-negative functions f, g : R 0 given by ft = µ Y At, gt = µ Y Bt µ Y A µ Y B are well-defined, i.e., 0 < µ Y A, µ Y B < +, ii At, Bt F Y for all t, iii {x : fx t}, {x : gx t} F for any 0 < t < 1 or a.e., µ Y 1 λa λb M1/1+p 1 µ Y A, µ Y B, λ
20 20 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS Remark 3.5. We would like to point out that, following the ideas of the proof of Theorem 1.5, we cannot expect to exchange the role of the linear Brunn-Minkowski inequality BM1 by a different one BMp, p 1. Indeed, if that was the case, it would be possible to get an enhanced version of the classical Brunn-Minkowski inequality when assuming a common maximal volume section through parallel planes of dimension smaller than n 1, a fact that is known to be not true see [21, Section 2]. From the proof of Theorem 1.5, we may also assert the following: Corollary 3.6. Let, d, µ, Y, d Y, µ Y be metric measure spaces where µ is σ-finite, µ Y is locally finite and µ Y is Radon. If the spaces, d, µ, Y, d Y, µ Y satisfy PL and BM0, respectively, then Y, d Y, µ Y satisfies BM0. In the same way as we use simple spaces that satisfy some Brunn-Minkowski inequality in order to obtain others on more involved ones, we will take advantage of spaces that satisfy the Prékopa-Leindler inequality, or more generally the socalled Borell-Brascamp-Lieb inequality, which is a generalization of Theorem A for p-th means see [6], [4] and also [15] for a detailed presentation. We collect it here for the sake of completeness. Theorem E Borell-Brascamp-Lieb inequality. Let λ 0, 1, 1/n p and let f, g, h : R n R 0 be non-negative measurable functions such that, for any x, y R n, Then h 1 λx + λy M p fx, gy, λ. h dx M p/np+1 f dx, g dx, λ. R n R n R n Now, in the spirit of Definition 1.4 and with the above-mentioned goal in mind, we give the following definition. Definition 3.7. We say that, d, µ satisfies the Borell-Brascamp-Lieb inequality with respect to m = m > 0 for the value p 1/m, BBLp, m for short, if for any λ 0, 1 and non-negative µ -measurable functions f, g, h : R 0 such that 3.6 hz M p fx, gy, λ, for all x, y, and z 1 λ{x} λ{y}, then h dµ M q f dµ, p mp+1. g dµ, λ, where q = qp, m = In the same way, a function φ : R 0 is said to be p-concave, for p R {± }, if 3.7 φz M p φx, φy, λ, for all x, y, z 1 λ{x} λ{y}, and any λ 0, 1.
21 BRUNN-MINKOWSKI INEQUALITIES 21 Taking a look at the result collected in Example 2.9 cf. also Theorem 3.1, at a first moment, one could think that 3.8 γ n 1 λk + λl 1 λγ n K + λγ n L holds for convex bodies K, L for which K H = L H or max x H γ n 1 K x + H = max x H γ n 1 L x + H, for a certain H L n n 1. Considering once again K = B n, L = x 0 + B n where x 0 is large enough, one may observe that the above linear version of the Gaussian Brunn-Minkowski inequality does not hold under these assumptions. However, if one replaces the condition on a common maximal n 1-dimensional Gaussian measure section with a common maximal n 1-dimensional marginal measure section, one can show that 3.8 holds. This is the content of the following theorem, in the more general setting of metric measure spaces for an analytic version of it in R n we refer the reader to [13, Theorem 3.2] and the references therein. As a particular case, for p = 0, Theorem 1.6 is obtained. Theorem 3.8. Let, d, µ, Y, d Y, µ Y be metric measure spaces which satisfy BM1 and BBLp, m, respectively, with some m > 0. Let µ be the measure on Y given by dµx, y = φx, ydµ Y where φ is a p-concave function, and µ, µ Y are σ-finite. Let λ 0, 1 and let A, B Y be non-empty measurable sets such that 1 λa λb is also measurable and so that sup x χ A x, yφx, y dµ Y = sup x χ B x, yφx, y dµ Y. Then Y µ 1 λa λb 1 λµa + λ µb. Proof. Let f, g, h : Y R 0 be the functions given by f = χ A φ, g = χ B φ and h = χ 1 λa λb φ. Given x 1, y 1 and z 1 1 λ{x 1 } λ{y 1 }, let f x1, g y1, h z1 : Y R 0 and F, G, H : R 0 given by f x1 = fx 1,, g y1 = gy 1,, h z1 = hz 1,, F x 1 = Y f x 1 dµ Y, Gy 1 = Y g y 1 dµ Y, Hz 1 = Y h z 1 dµ Y. From 3.7, we have h z1 z 2 M p f x1 x 2, g y1 y 2, λ, for all x 2, y 2 Y, and z 2 1 λ{x 2 } λ{y 2 }. Thus, by the BBL inequality in Y we obtain 3.9 Hz 1 M q F x 1, Gy 1, λ, p mp+1. where q = qp, m = By hypothesis sup x F x = sup x Gx =: α and, from 3.9, {x : Hx t} 1 λ{x : F x t} λ{x : Gx t} for all 0 < t < α. The proof now concludes as at the end of the proof of Theorem 3.1. As a consequence of the above result, and since the Gaussian density is logconcave, we have that 3.8 holds under the assumption of a common maximal marginal measure section. This fact will be collected in Theorem 4.7. Y
22 22 MANUEL RITORÉ AND JESÚS YEPES NICOLÁS We finish this section by collecting some results for product spaces in the spirit of the precedent ones, and which will be useful in order to derive some further inequalities, as it will be shown in Section 5. Theorem 3.9. Let m 1, m 2 > 0 and p 1/m 1 + m 2. If Y, d Y, µ Y satisfies BBLp, m 2 and, d, µ satisfies BBLq, m 1 where q = qp, m 2, then Y, d Y, µ Y satisfies BBLp, m 1 + m 2. Proof. Let λ 0, 1 and let f, g, h : Y R 0 be measurable functions satisfying 3.6 for all x, y Y, and z 1 λ{x} λ{y}. Arguing in the same way as in the above proof and using the same notation, by the BBL inequality in Y we notice that p 1/m 1 + m 2 1/m 2 we obtain Hz 1 M q F x 1, Gy 1, λ, where q = qp, m 2 = p m 1 2p+1 m 1. Now, from the BBL inequality in we get h dµ Y = H dµ M q F dµ, Y where q = qq, m 1 = q m 1q+1 = = M q Y f dµ Y, G dµ, λ g dµ Y, λ, Y p m 1+m 2p+1. It finishes the proof. As straightforward consequences of the above result we get the following corollaries. Corollary Let m > 0 and p 1/nm, where n Z >0. If, d, µ satisfies BBLp/rmp+1, m, for r = 0, 1,..., n 1, then n, d n, µ n satisfies BBLp, mn. Corollary Let, d, µ and Y, d Y, µ Y be metric measure spaces which satisfy PL. Then Y, d Y, µ Y also satisfies PL. In particular, the space n, d n, µ n satisfies PL. 4. Brunn-Minkowski inequalities for product measures on R n We start this section by showing Theorem 1.3 which, as mentioned in the introduction, allows us to assert that the Gaussian Brunn-Minkowski inequality 1.5 holds for the more general case of weakly unconditional sets. We present a simple proof of it, based on a direct application of Corollary 3.4 and Example Proof of Theorem 1.3. Without loss of generality, we may assume that µ is not the zero measure. Hence, since φ i is positively decreasing for i = 1,..., n, the measure µ i is strictly positive around the origin and locally finite, and we get that the product measure µ is a Radon measure. Thus, by the proof of Proposition 2.7, since 0 A B, we may assume that the sets A, B satisfy µaµb > 0. Furthermore, as at the beginning of the proof of Theorem 1.5, we may assume that A, B are compact. The theorem now follows from recursively applying Corollary 3.4 with = R and Y = R m, m = 1,..., n 1, taking the families of weakly unconditional sets F, F Y in R and R m. The one-dimensional case was proved in Example We notice that conditions ii and iii of Corollary 3.4 are satisfied because of the definition of weakly unconditional sets.
23 BRUNN-MINKOWSKI INEQUALITIES 23 Remark 4.1. We would like to point out some facts regarding the necessity of the conditions in Theorem 1.3 as well as the consequences of this result in relation to the Gaussian Brunn-Minkowski inequality 1.5. i Taking into account the above-mentioned negative result from [28] one may think that the weakly unconditional case is the strongest one that may be expected regarding Conjecture 1.1. Indeed, since both sets in 1.6 contain the origin and furthermore their projection onto the y-axis, the sole missing points which make them impossible for the sets to be weakly unconditional are those belonging to the x-axis; however, the Gaussian Brunn-Minkowski inequality is not true for such sets. ii The assumption on the measure in Theorem 1.3 of being a product measure is needed, as it is shown in [26, Example 1] via the density ϕx = 1 2 χ 2C x χ C x, where C is the square {x, y R 2 : x 1, y 1}. iii Furthermore, the assumption on the density functions in Theorem 1.3 of being positively decreasing is needed, as Proposition 2.11 shows. As a straightforward consequence of Theorem 1.3 together with the fact that r + sc = rc + sc for any convex set C R n and any r, s 0, we get the following result. Corollary 4.2. Let µ = µ 1 µ n be a product measure on R n such that µ i is the measure given by dµ i x = φ i x dx, where φ i : R R 0 is a positively decreasing function, i = 1,..., n. Let = A, B R n be weakly unconditional convex sets. Then the functions t µa + tb 1/n and t µta 1/n are concave on [0, +. As it occurs in the Euclidean setting, we can deduce an isoperimetric type inequality as a consequence of 1.7. To this aim, we will introduce some notation. Let W µ 1 A; B = Vµ A[n 1], B[1] = 1 µa + tb µa lim inf n t 0 + t be the first quermassintegral of A with respect to the set B associated to the measure µ. Here we are assuming that A and B are measurable sets such that A + tb is also measurable for all t 0. In a similar way we may define µ + A = lim inf t 0 + µa + tb n µa, t the surface area measure associated to µ. Clearly, µ + A = nw µ 1 A; B n. Moreover, and following the notation of [26], we will write t=1 M µ A = nµa d µta, dt provided that the pair A, µ is so that the above left derivative exists. Clearly, M vol A = 0 for any measurable set A and thus this functional does not appear in the classical isoperimetric inequality. For more information about the role of this functional in the literature, we refer the reader to [26] and the references therein. With this notation, we get an isoperimetric type inequality in Theorem 4.3. This result was previously obtained in [26, Corollary 4], without the equality case, in the setting of Theorem B. The main idea of the proof we present here goes back to the classical proof of the Minkowski first inequality that can be found in [33, Theorem 7.2.1].
Chapter 1. Measure Spaces. 1.1 Algebras and σ algebras of sets Notation and preliminaries
 Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
A glimpse into convex geometry. A glimpse into convex geometry
 A glimpse into convex geometry 5 \ þ ÏŒÆ Two basis reference: 1. Keith Ball, An elementary introduction to modern convex geometry 2. Chuanming Zong, What is known about unit cubes Convex geometry lies
A glimpse into convex geometry 5 \ þ ÏŒÆ Two basis reference: 1. Keith Ball, An elementary introduction to modern convex geometry 2. Chuanming Zong, What is known about unit cubes Convex geometry lies
ON A LINEAR REFINEMENT OF THE PRÉKOPA-LEINDLER INEQUALITY
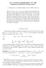 ON A LINEAR REFINEMENT OF TE PRÉKOPA-LEINDLER INEQUALITY A. COLESANTI, E. SAORÍN GÓMEZ, AND J. YEPES NICOLÁS Abstract. If f, g : R n R 0 are non-negative measurable functions, then the Prékopa-Leindler
ON A LINEAR REFINEMENT OF TE PRÉKOPA-LEINDLER INEQUALITY A. COLESANTI, E. SAORÍN GÓMEZ, AND J. YEPES NICOLÁS Abstract. If f, g : R n R 0 are non-negative measurable functions, then the Prékopa-Leindler
1 Lesson 1: Brunn Minkowski Inequality
 1 Lesson 1: Brunn Minkowski Inequality A set A R n is called convex if (1 λ)x + λy A for any x, y A and any λ [0, 1]. The Minkowski sum of two sets A, B R n is defined by A + B := {a + b : a A, b B}. One
1 Lesson 1: Brunn Minkowski Inequality A set A R n is called convex if (1 λ)x + λy A for any x, y A and any λ [0, 1]. The Minkowski sum of two sets A, B R n is defined by A + B := {a + b : a A, b B}. One
Math 341: Convex Geometry. Xi Chen
 Math 341: Convex Geometry Xi Chen 479 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca CHAPTER 1 Basics 1. Euclidean Geometry
Math 341: Convex Geometry Xi Chen 479 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca CHAPTER 1 Basics 1. Euclidean Geometry
MATHS 730 FC Lecture Notes March 5, Introduction
 1 INTRODUCTION MATHS 730 FC Lecture Notes March 5, 2014 1 Introduction Definition. If A, B are sets and there exists a bijection A B, they have the same cardinality, which we write as A, #A. If there exists
1 INTRODUCTION MATHS 730 FC Lecture Notes March 5, 2014 1 Introduction Definition. If A, B are sets and there exists a bijection A B, they have the same cardinality, which we write as A, #A. If there exists
Probabilistic Methods in Asymptotic Geometric Analysis.
 Probabilistic Methods in Asymptotic Geometric Analysis. C. Hugo Jiménez PUC-RIO, Brazil September 21st, 2016. Colmea. RJ 1 Origin 2 Normed Spaces 3 Distribution of volume of high dimensional convex bodies
Probabilistic Methods in Asymptotic Geometric Analysis. C. Hugo Jiménez PUC-RIO, Brazil September 21st, 2016. Colmea. RJ 1 Origin 2 Normed Spaces 3 Distribution of volume of high dimensional convex bodies
3 (Due ). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due ). Show that the open disk x 2 + y 2 < 1 is a countable union of planar elementary sets. Show that the closed disk x 2 + y 2 1 is a countable
n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1)
![n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1) n [ F (b j ) F (a j ) ], n j=1(a j, b j ] E (4.1)](/thumbs/81/82707553.jpg) 1.4. CONSTRUCTION OF LEBESGUE-STIELTJES MEASURES In this section we shall put to use the Carathéodory-Hahn theory, in order to construct measures with certain desirable properties first on the real line
1.4. CONSTRUCTION OF LEBESGUE-STIELTJES MEASURES In this section we shall put to use the Carathéodory-Hahn theory, in order to construct measures with certain desirable properties first on the real line
Around the Brunn-Minkowski inequality
 Around the Brunn-Minkowski inequality Andrea Colesanti Technische Universität Berlin - Institut für Mathematik January 28, 2015 Summary Summary The Brunn-Minkowski inequality Summary The Brunn-Minkowski
Around the Brunn-Minkowski inequality Andrea Colesanti Technische Universität Berlin - Institut für Mathematik January 28, 2015 Summary Summary The Brunn-Minkowski inequality Summary The Brunn-Minkowski
Course 212: Academic Year Section 1: Metric Spaces
 Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
Course 212: Academic Year 1991-2 Section 1: Metric Spaces D. R. Wilkins Contents 1 Metric Spaces 3 1.1 Distance Functions and Metric Spaces............. 3 1.2 Convergence and Continuity in Metric Spaces.........
2 (Bonus). Let A X consist of points (x, y) such that either x or y is a rational number. Is A measurable? What is its Lebesgue measure?
 MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
MA 645-4A (Real Analysis), Dr. Chernov Homework assignment 1 (Due 9/5). Prove that every countable set A is measurable and µ(a) = 0. 2 (Bonus). Let A consist of points (x, y) such that either x or y is
CHAPTER 6. Differentiation
 CHPTER 6 Differentiation The generalization from elementary calculus of differentiation in measure theory is less obvious than that of integration, and the methods of treating it are somewhat involved.
CHPTER 6 Differentiation The generalization from elementary calculus of differentiation in measure theory is less obvious than that of integration, and the methods of treating it are somewhat involved.
On isotropicity with respect to a measure
 On isotropicity with respect to a measure Liran Rotem Abstract A body is said to be isoptropic with respect to a measure µ if the function θ x, θ dµ(x) is constant on the unit sphere. In this note, we
On isotropicity with respect to a measure Liran Rotem Abstract A body is said to be isoptropic with respect to a measure µ if the function θ x, θ dµ(x) is constant on the unit sphere. In this note, we
Chapter 1 Preliminaries
 Chapter 1 Preliminaries 1.1 Conventions and Notations Throughout the book we use the following notations for standard sets of numbers: N the set {1, 2,...} of natural numbers Z the set of integers Q the
Chapter 1 Preliminaries 1.1 Conventions and Notations Throughout the book we use the following notations for standard sets of numbers: N the set {1, 2,...} of natural numbers Z the set of integers Q the
08a. Operators on Hilbert spaces. 1. Boundedness, continuity, operator norms
 (February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
(February 24, 2017) 08a. Operators on Hilbert spaces Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ [This document is http://www.math.umn.edu/ garrett/m/real/notes 2016-17/08a-ops
Tools from Lebesgue integration
 Tools from Lebesgue integration E.P. van den Ban Fall 2005 Introduction In these notes we describe some of the basic tools from the theory of Lebesgue integration. Definitions and results will be given
Tools from Lebesgue integration E.P. van den Ban Fall 2005 Introduction In these notes we describe some of the basic tools from the theory of Lebesgue integration. Definitions and results will be given
MA651 Topology. Lecture 10. Metric Spaces.
 MA65 Topology. Lecture 0. Metric Spaces. This text is based on the following books: Topology by James Dugundgji Fundamental concepts of topology by Peter O Neil Linear Algebra and Analysis by Marc Zamansky
MA65 Topology. Lecture 0. Metric Spaces. This text is based on the following books: Topology by James Dugundgji Fundamental concepts of topology by Peter O Neil Linear Algebra and Analysis by Marc Zamansky
THEOREMS, ETC., FOR MATH 516
 THEOREMS, ETC., FOR MATH 516 Results labeled Theorem Ea.b.c (or Proposition Ea.b.c, etc.) refer to Theorem c from section a.b of Evans book (Partial Differential Equations). Proposition 1 (=Proposition
THEOREMS, ETC., FOR MATH 516 Results labeled Theorem Ea.b.c (or Proposition Ea.b.c, etc.) refer to Theorem c from section a.b of Evans book (Partial Differential Equations). Proposition 1 (=Proposition
Mathematics for Economists
 Mathematics for Economists Victor Filipe Sao Paulo School of Economics FGV Metric Spaces: Basic Definitions Victor Filipe (EESP/FGV) Mathematics for Economists Jan.-Feb. 2017 1 / 34 Definitions and Examples
Mathematics for Economists Victor Filipe Sao Paulo School of Economics FGV Metric Spaces: Basic Definitions Victor Filipe (EESP/FGV) Mathematics for Economists Jan.-Feb. 2017 1 / 34 Definitions and Examples
Introduction to Topology
 Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Introduction to Topology Randall R. Holmes Auburn University Typeset by AMS-TEX Chapter 1. Metric Spaces 1. Definition and Examples. As the course progresses we will need to review some basic notions about
Exercises: Brunn, Minkowski and convex pie
 Lecture 1 Exercises: Brunn, Minkowski and convex pie Consider the following problem: 1.1 Playing a convex pie Consider the following game with two players - you and me. I am cooking a pie, which should
Lecture 1 Exercises: Brunn, Minkowski and convex pie Consider the following problem: 1.1 Playing a convex pie Consider the following game with two players - you and me. I am cooking a pie, which should
Reminder Notes for the Course on Measures on Topological Spaces
 Reminder Notes for the Course on Measures on Topological Spaces T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie
Reminder Notes for the Course on Measures on Topological Spaces T. C. Dorlas Dublin Institute for Advanced Studies School of Theoretical Physics 10 Burlington Road, Dublin 4, Ireland. Email: dorlas@stp.dias.ie
Chapter 2 Convex Analysis
 Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
Chapter 2 Convex Analysis The theory of nonsmooth analysis is based on convex analysis. Thus, we start this chapter by giving basic concepts and results of convexity (for further readings see also [202,
1.1. MEASURES AND INTEGRALS
 CHAPTER 1: MEASURE THEORY In this chapter we define the notion of measure µ on a space, construct integrals on this space, and establish their basic properties under limits. The measure µ(e) will be defined
CHAPTER 1: MEASURE THEORY In this chapter we define the notion of measure µ on a space, construct integrals on this space, and establish their basic properties under limits. The measure µ(e) will be defined
l(y j ) = 0 for all y j (1)
 Problem 1. The closed linear span of a subset {y j } of a normed vector space is defined as the intersection of all closed subspaces containing all y j and thus the smallest such subspace. 1 Show that
Problem 1. The closed linear span of a subset {y j } of a normed vector space is defined as the intersection of all closed subspaces containing all y j and thus the smallest such subspace. 1 Show that
Measure Theory on Topological Spaces. Course: Prof. Tony Dorlas 2010 Typset: Cathal Ormond
 Measure Theory on Topological Spaces Course: Prof. Tony Dorlas 2010 Typset: Cathal Ormond May 22, 2011 Contents 1 Introduction 2 1.1 The Riemann Integral........................................ 2 1.2 Measurable..............................................
Measure Theory on Topological Spaces Course: Prof. Tony Dorlas 2010 Typset: Cathal Ormond May 22, 2011 Contents 1 Introduction 2 1.1 The Riemann Integral........................................ 2 1.2 Measurable..............................................
Introduction to Real Analysis Alternative Chapter 1
 Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
On the Brunn-Minkowski inequality for general measures with applications to new isoperimetric-type inequalities
 On the Brunn-Minkowski inequality for general measures with applications to new isoperimetric-type inequalities Galyna Livshyts, Arnaud Marsiglietti, Piotr Nayar, Artem Zvavitch June 8, 2015 Abstract In
On the Brunn-Minkowski inequality for general measures with applications to new isoperimetric-type inequalities Galyna Livshyts, Arnaud Marsiglietti, Piotr Nayar, Artem Zvavitch June 8, 2015 Abstract In
Integral Jensen inequality
 Integral Jensen inequality Let us consider a convex set R d, and a convex function f : (, + ]. For any x,..., x n and λ,..., λ n with n λ i =, we have () f( n λ ix i ) n λ if(x i ). For a R d, let δ a
Integral Jensen inequality Let us consider a convex set R d, and a convex function f : (, + ]. For any x,..., x n and λ,..., λ n with n λ i =, we have () f( n λ ix i ) n λ if(x i ). For a R d, let δ a
The Caratheodory Construction of Measures
 Chapter 5 The Caratheodory Construction of Measures Recall how our construction of Lebesgue measure in Chapter 2 proceeded from an initial notion of the size of a very restricted class of subsets of R,
Chapter 5 The Caratheodory Construction of Measures Recall how our construction of Lebesgue measure in Chapter 2 proceeded from an initial notion of the size of a very restricted class of subsets of R,
An introduction to some aspects of functional analysis
 An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
An introduction to some aspects of functional analysis Stephen Semmes Rice University Abstract These informal notes deal with some very basic objects in functional analysis, including norms and seminorms
Functional Analysis. Franck Sueur Metric spaces Definitions Completeness Compactness Separability...
 Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Functional Analysis Franck Sueur 2018-2019 Contents 1 Metric spaces 1 1.1 Definitions........................................ 1 1.2 Completeness...................................... 3 1.3 Compactness......................................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University
 Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
Lecture Notes in Advanced Calculus 1 (80315) Raz Kupferman Institute of Mathematics The Hebrew University February 7, 2007 2 Contents 1 Metric Spaces 1 1.1 Basic definitions...........................
B. Appendix B. Topological vector spaces
 B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
B.1 B. Appendix B. Topological vector spaces B.1. Fréchet spaces. In this appendix we go through the definition of Fréchet spaces and their inductive limits, such as they are used for definitions of function
Integration on Measure Spaces
 Chapter 3 Integration on Measure Spaces In this chapter we introduce the general notion of a measure on a space X, define the class of measurable functions, and define the integral, first on a class of
Chapter 3 Integration on Measure Spaces In this chapter we introduce the general notion of a measure on a space X, define the class of measurable functions, and define the integral, first on a class of
NOTES ON THE REGULARITY OF QUASICONFORMAL HOMEOMORPHISMS
 NOTES ON THE REGULARITY OF QUASICONFORMAL HOMEOMORPHISMS CLARK BUTLER. Introduction The purpose of these notes is to give a self-contained proof of the following theorem, Theorem.. Let f : S n S n be a
NOTES ON THE REGULARITY OF QUASICONFORMAL HOMEOMORPHISMS CLARK BUTLER. Introduction The purpose of these notes is to give a self-contained proof of the following theorem, Theorem.. Let f : S n S n be a
Construction of a general measure structure
 Chapter 4 Construction of a general measure structure We turn to the development of general measure theory. The ingredients are a set describing the universe of points, a class of measurable subsets along
Chapter 4 Construction of a general measure structure We turn to the development of general measure theory. The ingredients are a set describing the universe of points, a class of measurable subsets along
(1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define
![(1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define](/thumbs/88/116259117.jpg) Homework, Real Analysis I, Fall, 2010. (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define ρ(f, g) = 1 0 f(x) g(x) dx. Show that
Homework, Real Analysis I, Fall, 2010. (1) Consider the space S consisting of all continuous real-valued functions on the closed interval [0, 1]. For f, g S, define ρ(f, g) = 1 0 f(x) g(x) dx. Show that
Appendix B Convex analysis
 This version: 28/02/2014 Appendix B Convex analysis In this appendix we review a few basic notions of convexity and related notions that will be important for us at various times. B.1 The Hausdorff distance
This version: 28/02/2014 Appendix B Convex analysis In this appendix we review a few basic notions of convexity and related notions that will be important for us at various times. B.1 The Hausdorff distance
Basic convexity. 1.1 Convex sets and combinations. λ + μ b (λ + μ)a;
 1 Basic convexity 1.1 Convex sets and combinations AsetA R n is convex if together with any two points x, y it contains the segment [x, y], thus if (1 λ)x + λy A for x, y A, 0 λ 1. Examples of convex sets
1 Basic convexity 1.1 Convex sets and combinations AsetA R n is convex if together with any two points x, y it contains the segment [x, y], thus if (1 λ)x + λy A for x, y A, 0 λ 1. Examples of convex sets
Set, functions and Euclidean space. Seungjin Han
 Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
Set, functions and Euclidean space Seungjin Han September, 2018 1 Some Basics LOGIC A is necessary for B : If B holds, then A holds. B A A B is the contraposition of B A. A is sufficient for B: If A holds,
Lecture 4 Lebesgue spaces and inequalities
 Lecture 4: Lebesgue spaces and inequalities 1 of 10 Course: Theory of Probability I Term: Fall 2013 Instructor: Gordan Zitkovic Lecture 4 Lebesgue spaces and inequalities Lebesgue spaces We have seen how
Lecture 4: Lebesgue spaces and inequalities 1 of 10 Course: Theory of Probability I Term: Fall 2013 Instructor: Gordan Zitkovic Lecture 4 Lebesgue spaces and inequalities Lebesgue spaces We have seen how
Probability and Measure
 Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 84 Paper 4, Section II 26J Let (X, A) be a measurable space. Let T : X X be a measurable map, and µ a probability
Part II Year 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2018 84 Paper 4, Section II 26J Let (X, A) be a measurable space. Let T : X X be a measurable map, and µ a probability
THEOREMS, ETC., FOR MATH 515
 THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
THEOREMS, ETC., FOR MATH 515 Proposition 1 (=comment on page 17). If A is an algebra, then any finite union or finite intersection of sets in A is also in A. Proposition 2 (=Proposition 1.1). For every
Murat Akman. The Brunn-Minkowski Inequality and a Minkowski Problem for Nonlinear Capacities. March 10
 The Brunn-Minkowski Inequality and a Minkowski Problem for Nonlinear Capacities Murat Akman March 10 Postdoc in HA Group and Postdoc at the University of Connecticut Minkowski Addition of Sets Let E 1
The Brunn-Minkowski Inequality and a Minkowski Problem for Nonlinear Capacities Murat Akman March 10 Postdoc in HA Group and Postdoc at the University of Connecticut Minkowski Addition of Sets Let E 1
Statistics 612: L p spaces, metrics on spaces of probabilites, and connections to estimation
 Statistics 62: L p spaces, metrics on spaces of probabilites, and connections to estimation Moulinath Banerjee December 6, 2006 L p spaces and Hilbert spaces We first formally define L p spaces. Consider
Statistics 62: L p spaces, metrics on spaces of probabilites, and connections to estimation Moulinath Banerjee December 6, 2006 L p spaces and Hilbert spaces We first formally define L p spaces. Consider
LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS. S. G. Bobkov and F. L. Nazarov. September 25, 2011
 LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS S. G. Bobkov and F. L. Nazarov September 25, 20 Abstract We study large deviations of linear functionals on an isotropic
LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS S. G. Bobkov and F. L. Nazarov September 25, 20 Abstract We study large deviations of linear functionals on an isotropic
The small ball property in Banach spaces (quantitative results)
 The small ball property in Banach spaces (quantitative results) Ehrhard Behrends Abstract A metric space (M, d) is said to have the small ball property (sbp) if for every ε 0 > 0 there exists a sequence
The small ball property in Banach spaces (quantitative results) Ehrhard Behrends Abstract A metric space (M, d) is said to have the small ball property (sbp) if for every ε 0 > 0 there exists a sequence
Convex Geometry. Otto-von-Guericke Universität Magdeburg. Applications of the Brascamp-Lieb and Barthe inequalities. Exercise 12.
 Applications of the Brascamp-Lieb and Barthe inequalities Exercise 12.1 Show that if m Ker M i {0} then both BL-I) and B-I) hold trivially. Exercise 12.2 Let λ 0, 1) and let f, g, h : R 0 R 0 be measurable
Applications of the Brascamp-Lieb and Barthe inequalities Exercise 12.1 Show that if m Ker M i {0} then both BL-I) and B-I) hold trivially. Exercise 12.2 Let λ 0, 1) and let f, g, h : R 0 R 0 be measurable
ON THE UNIQUENESS PROPERTY FOR PRODUCTS OF SYMMETRIC INVARIANT PROBABILITY MEASURES
 Georgian Mathematical Journal Volume 9 (2002), Number 1, 75 82 ON THE UNIQUENESS PROPERTY FOR PRODUCTS OF SYMMETRIC INVARIANT PROBABILITY MEASURES A. KHARAZISHVILI Abstract. Two symmetric invariant probability
Georgian Mathematical Journal Volume 9 (2002), Number 1, 75 82 ON THE UNIQUENESS PROPERTY FOR PRODUCTS OF SYMMETRIC INVARIANT PROBABILITY MEASURES A. KHARAZISHVILI Abstract. Two symmetric invariant probability
Review of measure theory
 209: Honors nalysis in R n Review of measure theory 1 Outer measure, measure, measurable sets Definition 1 Let X be a set. nonempty family R of subsets of X is a ring if, B R B R and, B R B R hold. bove,
209: Honors nalysis in R n Review of measure theory 1 Outer measure, measure, measurable sets Definition 1 Let X be a set. nonempty family R of subsets of X is a ring if, B R B R and, B R B R hold. bove,
Lebesgue Integration on R n
 Lebesgue Integration on R n The treatment here is based loosely on that of Jones, Lebesgue Integration on Euclidean Space We give an overview from the perspective of a user of the theory Riemann integration
Lebesgue Integration on R n The treatment here is based loosely on that of Jones, Lebesgue Integration on Euclidean Space We give an overview from the perspective of a user of the theory Riemann integration
2) Let X be a compact space. Prove that the space C(X) of continuous real-valued functions is a complete metric space.
 University of Bergen General Functional Analysis Problems with solutions 6 ) Prove that is unique in any normed space. Solution of ) Let us suppose that there are 2 zeros and 2. Then = + 2 = 2 + = 2. 2)
University of Bergen General Functional Analysis Problems with solutions 6 ) Prove that is unique in any normed space. Solution of ) Let us suppose that there are 2 zeros and 2. Then = + 2 = 2 + = 2. 2)
Steiner s formula and large deviations theory
 Steiner s formula and large deviations theory Venkat Anantharam EECS Department University of California, Berkeley May 19, 2015 Simons Conference on Networks and Stochastic Geometry Blanton Museum of Art
Steiner s formula and large deviations theory Venkat Anantharam EECS Department University of California, Berkeley May 19, 2015 Simons Conference on Networks and Stochastic Geometry Blanton Museum of Art
Topological properties of Z p and Q p and Euclidean models
 Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
Topological properties of Z p and Q p and Euclidean models Samuel Trautwein, Esther Röder, Giorgio Barozzi November 3, 20 Topology of Q p vs Topology of R Both R and Q p are normed fields and complete
BORELL S GENERALIZED PRÉKOPA-LEINDLER INEQUALITY: A SIMPLE PROOF. Arnaud Marsiglietti. IMA Preprint Series #2461. (December 2015)
 BORELL S GENERALIZED PRÉKOPA-LEINDLER INEQUALITY: A SIMPLE PROOF By Arnaud Marsiglietti IMA Preprint Series #2461 December 215 INSTITUTE FOR MATHEMATICS AND ITS APPLICATIONS UNIVERSITY OF MINNESOTA 4 Lind
BORELL S GENERALIZED PRÉKOPA-LEINDLER INEQUALITY: A SIMPLE PROOF By Arnaud Marsiglietti IMA Preprint Series #2461 December 215 INSTITUTE FOR MATHEMATICS AND ITS APPLICATIONS UNIVERSITY OF MINNESOTA 4 Lind
Measure and integration
 Chapter 5 Measure and integration In calculus you have learned how to calculate the size of different kinds of sets: the length of a curve, the area of a region or a surface, the volume or mass of a solid.
Chapter 5 Measure and integration In calculus you have learned how to calculate the size of different kinds of sets: the length of a curve, the area of a region or a surface, the volume or mass of a solid.
Banach Spaces V: A Closer Look at the w- and the w -Topologies
 BS V c Gabriel Nagy Banach Spaces V: A Closer Look at the w- and the w -Topologies Notes from the Functional Analysis Course (Fall 07 - Spring 08) In this section we discuss two important, but highly non-trivial,
BS V c Gabriel Nagy Banach Spaces V: A Closer Look at the w- and the w -Topologies Notes from the Functional Analysis Course (Fall 07 - Spring 08) In this section we discuss two important, but highly non-trivial,
consists of two disjoint copies of X n, each scaled down by 1,
 Homework 4 Solutions, Real Analysis I, Fall, 200. (4) Let be a topological space and M be a σ-algebra on which contains all Borel sets. Let m, µ be two positive measures on M. Assume there is a constant
Homework 4 Solutions, Real Analysis I, Fall, 200. (4) Let be a topological space and M be a σ-algebra on which contains all Borel sets. Let m, µ be two positive measures on M. Assume there is a constant
SOME MEASURABILITY AND CONTINUITY PROPERTIES OF ARBITRARY REAL FUNCTIONS
 LE MATEMATICHE Vol. LVII (2002) Fasc. I, pp. 6382 SOME MEASURABILITY AND CONTINUITY PROPERTIES OF ARBITRARY REAL FUNCTIONS VITTORINO PATA - ALFONSO VILLANI Given an arbitrary real function f, the set D
LE MATEMATICHE Vol. LVII (2002) Fasc. I, pp. 6382 SOME MEASURABILITY AND CONTINUITY PROPERTIES OF ARBITRARY REAL FUNCTIONS VITTORINO PATA - ALFONSO VILLANI Given an arbitrary real function f, the set D
Introduction and Preliminaries
 Chapter 1 Introduction and Preliminaries This chapter serves two purposes. The first purpose is to prepare the readers for the more systematic development in later chapters of methods of real analysis
Chapter 1 Introduction and Preliminaries This chapter serves two purposes. The first purpose is to prepare the readers for the more systematic development in later chapters of methods of real analysis
L p Spaces and Convexity
 L p Spaces and Convexity These notes largely follow the treatments in Royden, Real Analysis, and Rudin, Real & Complex Analysis. 1. Convex functions Let I R be an interval. For I open, we say a function
L p Spaces and Convexity These notes largely follow the treatments in Royden, Real Analysis, and Rudin, Real & Complex Analysis. 1. Convex functions Let I R be an interval. For I open, we say a function
Topology. Xiaolong Han. Department of Mathematics, California State University, Northridge, CA 91330, USA address:
 Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Topology Xiaolong Han Department of Mathematics, California State University, Northridge, CA 91330, USA E-mail address: Xiaolong.Han@csun.edu Remark. You are entitled to a reward of 1 point toward a homework
Part III. 10 Topological Space Basics. Topological Spaces
 Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
Part III 10 Topological Space Basics Topological Spaces Using the metric space results above as motivation we will axiomatize the notion of being an open set to more general settings. Definition 10.1.
Star bodies with completely symmetric sections
 Star bodies with completely symmetric sections Sergii Myroshnychenko, Dmitry Ryabogin, and Christos Saroglou Abstract We say that a star body is completely symmetric if it has centroid at the origin and
Star bodies with completely symmetric sections Sergii Myroshnychenko, Dmitry Ryabogin, and Christos Saroglou Abstract We say that a star body is completely symmetric if it has centroid at the origin and
Sobolev spaces. May 18
 Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Sobolev spaces May 18 2015 1 Weak derivatives The purpose of these notes is to give a very basic introduction to Sobolev spaces. More extensive treatments can e.g. be found in the classical references
Lebesgue Measure on R n
 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, Dedicated to Franco Giannessi and Diethard Pallaschke with great respect
 GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, 2018 BORIS S. MORDUKHOVICH 1 and NGUYEN MAU NAM 2 Dedicated to Franco Giannessi and Diethard Pallaschke with great respect Abstract. In
GEOMETRIC APPROACH TO CONVEX SUBDIFFERENTIAL CALCULUS October 10, 2018 BORIS S. MORDUKHOVICH 1 and NGUYEN MAU NAM 2 Dedicated to Franco Giannessi and Diethard Pallaschke with great respect Abstract. In
REAL AND COMPLEX ANALYSIS
 REAL AND COMPLE ANALYSIS Third Edition Walter Rudin Professor of Mathematics University of Wisconsin, Madison Version 1.1 No rights reserved. Any part of this work can be reproduced or transmitted in any
REAL AND COMPLE ANALYSIS Third Edition Walter Rudin Professor of Mathematics University of Wisconsin, Madison Version 1.1 No rights reserved. Any part of this work can be reproduced or transmitted in any
A note on the convex infimum convolution inequality
 A note on the convex infimum convolution inequality Naomi Feldheim, Arnaud Marsiglietti, Piotr Nayar, Jing Wang Abstract We characterize the symmetric measures which satisfy the one dimensional convex
A note on the convex infimum convolution inequality Naomi Feldheim, Arnaud Marsiglietti, Piotr Nayar, Jing Wang Abstract We characterize the symmetric measures which satisfy the one dimensional convex
INDISTINGUISHABILITY OF ABSOLUTELY CONTINUOUS AND SINGULAR DISTRIBUTIONS
 INDISTINGUISHABILITY OF ABSOLUTELY CONTINUOUS AND SINGULAR DISTRIBUTIONS STEVEN P. LALLEY AND ANDREW NOBEL Abstract. It is shown that there are no consistent decision rules for the hypothesis testing problem
INDISTINGUISHABILITY OF ABSOLUTELY CONTINUOUS AND SINGULAR DISTRIBUTIONS STEVEN P. LALLEY AND ANDREW NOBEL Abstract. It is shown that there are no consistent decision rules for the hypothesis testing problem
On the Brunn-Minkowski inequality for general measures with applications to new isoperimetric type-inequalities
 On the Brunn-Minkowski inequality for general measures with applications to new isoperimetric type-inequalities Galyna Livshyts, Arnaud Marsiglietti, Piotr Nayar, Artem Zvavitch April 24, 215 Abstract
On the Brunn-Minkowski inequality for general measures with applications to new isoperimetric type-inequalities Galyna Livshyts, Arnaud Marsiglietti, Piotr Nayar, Artem Zvavitch April 24, 215 Abstract
Part V. 17 Introduction: What are measures and why measurable sets. Lebesgue Integration Theory
 Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Part V 7 Introduction: What are measures and why measurable sets Lebesgue Integration Theory Definition 7. (Preliminary). A measure on a set is a function :2 [ ] such that. () = 2. If { } = is a finite
Measures and Measure Spaces
 Chapter 2 Measures and Measure Spaces In summarizing the flaws of the Riemann integral we can focus on two main points: 1) Many nice functions are not Riemann integrable. 2) The Riemann integral does not
Chapter 2 Measures and Measure Spaces In summarizing the flaws of the Riemann integral we can focus on two main points: 1) Many nice functions are not Riemann integrable. 2) The Riemann integral does not
Optimization Theory. A Concise Introduction. Jiongmin Yong
 October 11, 017 16:5 ws-book9x6 Book Title Optimization Theory 017-08-Lecture Notes page 1 1 Optimization Theory A Concise Introduction Jiongmin Yong Optimization Theory 017-08-Lecture Notes page Optimization
October 11, 017 16:5 ws-book9x6 Book Title Optimization Theory 017-08-Lecture Notes page 1 1 Optimization Theory A Concise Introduction Jiongmin Yong Optimization Theory 017-08-Lecture Notes page Optimization
Chapter 2 Metric Spaces
 Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
Chapter 2 Metric Spaces The purpose of this chapter is to present a summary of some basic properties of metric and topological spaces that play an important role in the main body of the book. 2.1 Metrics
MEASURE AND INTEGRATION. Dietmar A. Salamon ETH Zürich
 MEASURE AND INTEGRATION Dietmar A. Salamon ETH Zürich 9 September 2016 ii Preface This book is based on notes for the lecture course Measure and Integration held at ETH Zürich in the spring semester 2014.
MEASURE AND INTEGRATION Dietmar A. Salamon ETH Zürich 9 September 2016 ii Preface This book is based on notes for the lecture course Measure and Integration held at ETH Zürich in the spring semester 2014.
Some Background Material
 Chapter 1 Some Background Material In the first chapter, we present a quick review of elementary - but important - material as a way of dipping our toes in the water. This chapter also introduces important
Chapter 1 Some Background Material In the first chapter, we present a quick review of elementary - but important - material as a way of dipping our toes in the water. This chapter also introduces important
Analysis-3 lecture schemes
 Analysis-3 lecture schemes (with Homeworks) 1 Csörgő István November, 2015 1 A jegyzet az ELTE Informatikai Kar 2015. évi Jegyzetpályázatának támogatásával készült Contents 1. Lesson 1 4 1.1. The Space
Analysis-3 lecture schemes (with Homeworks) 1 Csörgő István November, 2015 1 A jegyzet az ELTE Informatikai Kar 2015. évi Jegyzetpályázatának támogatásával készült Contents 1. Lesson 1 4 1.1. The Space
Topological properties
 CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
MATH MEASURE THEORY AND FOURIER ANALYSIS. Contents
 MATH 3969 - MEASURE THEORY AND FOURIER ANALYSIS ANDREW TULLOCH Contents 1. Measure Theory 2 1.1. Properties of Measures 3 1.2. Constructing σ-algebras and measures 3 1.3. Properties of the Lebesgue measure
MATH 3969 - MEASURE THEORY AND FOURIER ANALYSIS ANDREW TULLOCH Contents 1. Measure Theory 2 1.1. Properties of Measures 3 1.2. Constructing σ-algebras and measures 3 1.3. Properties of the Lebesgue measure
Lebesgue Measure on R n
 8 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
8 CHAPTER 2 Lebesgue Measure on R n Our goal is to construct a notion of the volume, or Lebesgue measure, of rather general subsets of R n that reduces to the usual volume of elementary geometrical sets
Problem set 4, Real Analysis I, Spring, 2015.
 Problem set 4, Real Analysis I, Spring, 215. (18) Let f be a measurable finite-valued function on [, 1], and suppose f(x) f(y) is integrable on [, 1] [, 1]. Show that f is integrable on [, 1]. [Hint: Show
Problem set 4, Real Analysis I, Spring, 215. (18) Let f be a measurable finite-valued function on [, 1], and suppose f(x) f(y) is integrable on [, 1] [, 1]. Show that f is integrable on [, 1]. [Hint: Show
ON KRONECKER PRODUCTS OF CHARACTERS OF THE SYMMETRIC GROUPS WITH FEW COMPONENTS
 ON KRONECKER PRODUCTS OF CHARACTERS OF THE SYMMETRIC GROUPS WITH FEW COMPONENTS C. BESSENRODT AND S. VAN WILLIGENBURG Abstract. Confirming a conjecture made by Bessenrodt and Kleshchev in 1999, we classify
ON KRONECKER PRODUCTS OF CHARACTERS OF THE SYMMETRIC GROUPS WITH FEW COMPONENTS C. BESSENRODT AND S. VAN WILLIGENBURG Abstract. Confirming a conjecture made by Bessenrodt and Kleshchev in 1999, we classify
Filters in Analysis and Topology
 Filters in Analysis and Topology David MacIver July 1, 2004 Abstract The study of filters is a very natural way to talk about convergence in an arbitrary topological space, and carries over nicely into
Filters in Analysis and Topology David MacIver July 1, 2004 Abstract The study of filters is a very natural way to talk about convergence in an arbitrary topological space, and carries over nicely into
Linear Algebra I. Ronald van Luijk, 2015
 Linear Algebra I Ronald van Luijk, 2015 With many parts from Linear Algebra I by Michael Stoll, 2007 Contents Dependencies among sections 3 Chapter 1. Euclidean space: lines and hyperplanes 5 1.1. Definition
Linear Algebra I Ronald van Luijk, 2015 With many parts from Linear Algebra I by Michael Stoll, 2007 Contents Dependencies among sections 3 Chapter 1. Euclidean space: lines and hyperplanes 5 1.1. Definition
From the Brunn-Minkowski inequality to a class of Poincaré type inequalities
 arxiv:math/0703584v1 [math.fa] 20 Mar 2007 From the Brunn-Minkowski inequality to a class of Poincaré type inequalities Andrea Colesanti Abstract We present an argument which leads from the Brunn-Minkowski
arxiv:math/0703584v1 [math.fa] 20 Mar 2007 From the Brunn-Minkowski inequality to a class of Poincaré type inequalities Andrea Colesanti Abstract We present an argument which leads from the Brunn-Minkowski
212a1214Daniell s integration theory.
 212a1214 Daniell s integration theory. October 30, 2014 Daniell s idea was to take the axiomatic properties of the integral as the starting point and develop integration for broader and broader classes
212a1214 Daniell s integration theory. October 30, 2014 Daniell s idea was to take the axiomatic properties of the integral as the starting point and develop integration for broader and broader classes
Helly's Theorem and its Equivalences via Convex Analysis
 Portland State University PDXScholar University Honors Theses University Honors College 2014 Helly's Theorem and its Equivalences via Convex Analysis Adam Robinson Portland State University Let us know
Portland State University PDXScholar University Honors Theses University Honors College 2014 Helly's Theorem and its Equivalences via Convex Analysis Adam Robinson Portland State University Let us know
MATH41011/MATH61011: FOURIER SERIES AND LEBESGUE INTEGRATION. Extra Reading Material for Level 4 and Level 6
 MATH41011/MATH61011: FOURIER SERIES AND LEBESGUE INTEGRATION Extra Reading Material for Level 4 and Level 6 Part A: Construction of Lebesgue Measure The first part the extra material consists of the construction
MATH41011/MATH61011: FOURIER SERIES AND LEBESGUE INTEGRATION Extra Reading Material for Level 4 and Level 6 Part A: Construction of Lebesgue Measure The first part the extra material consists of the construction
Real Analysis Math 131AH Rudin, Chapter #1. Dominique Abdi
 Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS
 Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
Bendikov, A. and Saloff-Coste, L. Osaka J. Math. 4 (5), 677 7 ON THE REGULARITY OF SAMPLE PATHS OF SUB-ELLIPTIC DIFFUSIONS ON MANIFOLDS ALEXANDER BENDIKOV and LAURENT SALOFF-COSTE (Received March 4, 4)
Best approximations in normed vector spaces
 Best approximations in normed vector spaces Mike de Vries 5699703 a thesis submitted to the Department of Mathematics at Utrecht University in partial fulfillment of the requirements for the degree of
Best approximations in normed vector spaces Mike de Vries 5699703 a thesis submitted to the Department of Mathematics at Utrecht University in partial fulfillment of the requirements for the degree of
The Canonical Gaussian Measure on R
 The Canonical Gaussian Measure on R 1. Introduction The main goal of this course is to study Gaussian measures. The simplest example of a Gaussian measure is the canonical Gaussian measure P on R where
The Canonical Gaussian Measure on R 1. Introduction The main goal of this course is to study Gaussian measures. The simplest example of a Gaussian measure is the canonical Gaussian measure P on R where
High-dimensional distributions with convexity properties
 High-dimensional distributions with convexity properties Bo az Klartag Tel-Aviv University A conference in honor of Charles Fefferman, Princeton, May 2009 High-Dimensional Distributions We are concerned
High-dimensional distributions with convexity properties Bo az Klartag Tel-Aviv University A conference in honor of Charles Fefferman, Princeton, May 2009 High-Dimensional Distributions We are concerned
ON GENERALIZED-CONVEX CONSTRAINED MULTI-OBJECTIVE OPTIMIZATION
 ON GENERALIZED-CONVEX CONSTRAINED MULTI-OBJECTIVE OPTIMIZATION CHRISTIAN GÜNTHER AND CHRISTIANE TAMMER Abstract. In this paper, we consider multi-objective optimization problems involving not necessarily
ON GENERALIZED-CONVEX CONSTRAINED MULTI-OBJECTIVE OPTIMIZATION CHRISTIAN GÜNTHER AND CHRISTIANE TAMMER Abstract. In this paper, we consider multi-objective optimization problems involving not necessarily
1 An Elementary Introduction to Monotone Transportation
 An Elementary Introduction to Monotone Transportation after K. Ball [3] A summary written by Paata Ivanisvili Abstract We outline existence of the Brenier map. As an application we present simple proofs
An Elementary Introduction to Monotone Transportation after K. Ball [3] A summary written by Paata Ivanisvili Abstract We outline existence of the Brenier map. As an application we present simple proofs
4 Countability axioms
 4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
4 COUNTABILITY AXIOMS 4 Countability axioms Definition 4.1. Let X be a topological space X is said to be first countable if for any x X, there is a countable basis for the neighborhoods of x. X is said
Part II Probability and Measure
 Part II Probability and Measure Theorems Based on lectures by J. Miller Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
Part II Probability and Measure Theorems Based on lectures by J. Miller Notes taken by Dexter Chua Michaelmas 2016 These notes are not endorsed by the lecturers, and I have modified them (often significantly)
