Applications of the definite integral to calculating volume and length
|
|
|
- Noel Nichols
- 5 years ago
- Views:
Transcription
1 Chapter 5 Applications of the definite integral to calculating volume and length In this chapter we consider applications of the definite integral to calculating geometric quantities such as volumes. The idea will be to dissect the three dimensional objects into pieces that resemble disks or shells, whose volumes we can approximate with simple formulae. The volume of the entire object is obtained by summing up volumes of a stack of disks or a set of embedded shells, and considering the limit as the thickness of the dissection cuts gets thinner. In Figure 5. we first remind the reader of the volumes of some of the geometric shapes that will be used as elementary pieces into which our shapes will be carved. Recall that, from earlier discussion, we have r τ τ r h disk shell Figure 5.: The volumes of these simple 3D shapes are given by simple formulae. We use them as basic elements in computing more complicated volumes.. The volume of a cylinder of height h having circular base of radius r, is V cylinder = πr 2 h v December 2, 25
2 Math 3 Notes Chapter 5 2. The volume of a circular disk of thickness τ, and radius r (shown in Figure 5. a), as a special case of the above, is V disk = πr 2 τ. 3. The volume of a cylindrical shell of height h, with circular radius r and small thickness τ (shown in Figure 5. b) is V shell = 2πrhτ. (This approximation holds for τ << r.) 5. Surfaces of revolution In our first approach to volumes, we will restrict attention to surfaces of revolution, i.e. surfaces formed when some curve (described by a function such as y = f(x)) is rotated about one of the axes. In Figure 5.2(a) we show one such curve, and the surface it forms when it is revolved about the x axis. We note that if this surface is cut into slices along the x axis, the cross-sections look like circles. (The circle will have a radius that depends on the position of the cut.) In Figure 5.2(b) we show how a set of disks of various radii can approximately represent the shape of interest. The total (a) y=f(x) r (b) x Figure 5.2: (a) A surface of revolution, showing dissection into slices along its axis of rotation. (b) The same surface is approximated by a set of disks. Each disk has some radius r (that varies along the length of the object) and thickness x. Note that the thickness is in the direction of the x axis: this will remind us that we integrate with respect to x. volume of these disks is not the same, clearly, as the volume of the object, since some of these stick out beyond the surface. However, if we make the thickness of these disks very small, we will get a v December 2, 25 2
3 Math 3 Notes Chapter 5 good approximation of the desired volume. In the limit, as the thickness becomes infinitesimal, we arrive at the true volume. In most of the examples discussed in this chapter, the key step is to make careful observation of the way that the radius of a given disk depends on the function that generates the surface. (By this we mean the function that specifies the curve that forms the surface of revolution.) We also pay attention to the dimension that forms the disk thickness. Some of our examples will involve surfaces revolved about the x axis, and others will be revolved about the y axis. In setting up these examples, a diagram is usually quite helpful. Example : Volume of a sphere y f(x k) x k x x x Figure 5.3: When the semicircle (on the left) is rotated about the x axis, it generates a sphere. On the right, we show one disk generated by the revolution of the shaded rectangle. We can think of a sphere of radius R as a surface formed by rotating a semi-circle about its long axis. (See Figure 5.3.) A function that describe the semi-circle is y = f(x) = R 2 x 2. We show the sphere dissected into a set of disks, each of width x. The disks are lined up along the x axis with coordinates x k. These are just integer multiples of the slice thickness x, so for example, x k = k x. The radius of the disk depends on its position. Indeed, the radius of a disk through the x axis at a point x k is specified by the function r k = y k = f(x k ). The volume of the k th disk is V k = πr 2 k x. v December 2, 25 3
4 Math 3 Notes Chapter 5 By the above remarks, using the fact that the function actually determines the radius, we have The total volume of all the disks is V k = π(f(x k )) 2 x V k = π( R 2 x 2 k )2 x = π(r 2 x 2 k ) x. V = k V k = π(f(x k )) 2 x. as x, this sum becomes a definite integral, and represents the true volume. We must ascertain where to start and end the summation: i.e. the interval over which the disks are arranged. From the figure, we note that the semi-circle extends from x = R to x = R. Thus V sphere = R -R π(f(x k )) 2 dx = π R -R (R 2 x 2 ) dx We compute ) V sphere = π (R 2 x x3 R 3 -R We can also make the observation that this is twice the volume obtained for the interval < x < R, V sphere = 2π ) (R 2 x x3 R = 2π 3 After simplification, we arrive at the familiar formula ) (R 3 R3 3 V sphere = 4 3 πr3 Example 2: Volume of a paraboloid: disk method Consider the curve y = f(x) = x 2 If we rotate this curve about the y axis, we will get a paraboloid as shown in Figure 5.4. In this section we show how to compute the volume by dissecting into disks stacked up along the y axis. Solution The width of each disk is y and, when taken to be very small, will become dy in the integral below. The volume of each disk is V disk = πr 2 y where the radius, r is now in the direction parallel to the x axis. Thus we express radius as r = x = f(y). v December 2, 25 4
5 Math 3 Notes Chapter x Figure 5.4: The curve that generates the shape of a paraboloid (left) and the shape of the paraboloid (right). We must express the equation of the curve in the form x as a function of y. From y = x 2 we have x 2 = y so x = y. The shape extends from a smallest value of y = up to y =. Thus the volume is We compute V = π V = π [f(y)] 2 dy = π [ y] 2 dy ) ( y) dy = π (y y2 2 ( V = π ) = π 2 2. The above example was set up using disks. However, there are other options. Below, we show yet another method, comprised of cylindrical shells to compute the volume of a cone. In some cases, one method is preferable to another, but here either method works equally well. Example 3: Volume of cone: shell method We use the shell method to find the volume of the cone formed by rotating the curve y = x about the y axis. Solution We show the cone and its generating curve in Figure 5.5, together with a representative shell used in the calculation of total volume. The volume of a cylindrical shell of radius r, height h and thickness τ is V shell = 2πrhτ. v December 2, 25 5
6 Math 3 Notes Chapter x y y= x dx x Figure 5.5: Top: The curve that generates the cone (left) and the shape of the cone (right). Bottom: the cone showing one of the series of shells that are used in this example to calculate its volume. We will place these shells one inside the other so that their radii are parallel to the x axis (so r = x). Then the heights of the shells are determined by the y value (i.e. h = y = x = r). For the tallest shell r =, and for the flattest shell r =. The thickness of the shell is dr. Therefore, the volume of one shell is V shell = 2πr( r) dr. The volume of the whole set of shells is obtained by integrating over r, to obtain: We find that V = 2π r( r) dr = 2π (r r 2 ) dr. ( ) r 2 V = 2π 2 r3 ( = 2π 3 2 ) = π 3 3. v December 2, 25 6
7 Math 3 Notes Chapter 5 Example 3 Find the volume of the surface formed by rotating the curve y = f(x) = x < x < (a) about the x axis. (b) about the y axis. Solution (a) If we rotate this curve about the x axis, we obtain a bowl shape; dissecting this surface leads to disks stacked along the x axis, with thickness x dx, with radii in the y direction, i.e. r = y = f(x), and with x in the range < x <. The volume will thus be V = π [f(x)] 2 dx = π [ x] 2 dx = π x dx Thus V = π x2 2 = π 2. (b) When the curve is rotated about the y axis, it forms a surface with a sharp point at the origin. The disks are stacked along the y axis, with thickness y dy, and radii in the x direction. We must rewrite the function in the form x = g(y) = y 2. We now use the interval along the y axis, i.e. < y < The volume is then V = π [f(y)] 2 dy = π V = π y5 5 [y 2 ] 2 dy = π = π 5. y 4 dy. 5.2 Mass and density In the previous chapter, we the idea of density of one dimension. Underlying the integral we computed was the idea that the interval could be dissected into small parts (of width x), and a sum of pieces transformed into an integral. In the next examples, we consider similar ideas, but instead of dissecting the region into -dimensional intervals, we have slightly more interesting geometries. v December 2, 25 7
8 Math 3 Notes Chapter A glucose density gradient A cylindrical test-tube of radius r, and height h, contains a solution of glucose which has been prepared so that the concentration of glucose is greatest at the bottom and decreases gradually towards the top of the tube. (This is called a density gradient). Suppose that the concentration c as a function of the depth x is c(x) =. +.5x grams per centimeter 3. (x = at the top of the tube, and x = h at the bottom of the tube.) Determine the total amount of glucose in the tube (in gm). neglect the rounded lower portion of the tube: i.e. assume that it is a simple cylinder. In Figure 5.6 we show a rough version of what this gradient might look like. In reality, the transition between high and low concentration would be smoother than shown in this figure. x= r x x=h Figure 5.6: A test-tube of radius r containing a gradient of glucose. A disk-shaped slice of the tube with small thickness x has approximately constant density. Solution We assume a simple cylindrical tube and consider imaginary slices of this tube along its vertical axis. Suppose that the thickness of a slice is x. Then the volume of each of these (disk shaped) slices is πr 2 x. The amount of glucose in the slice is approximately equal to the concentration c(x) multiplied by the volume of the slice, i.e. the small slice contains an amount πr 2 xc(x) of glucose. In order to sum up the total amount over all slices, we use a definite integral. (We imagine x dx becoming infinitesimal as the number of slices increases.) The integral we want is h G = πr 2 c(x) dx. Even though the geometry of the test-tube may, at first glance, seem more complicated than the one-dimensional highway of the previous example, we observe here that the integral that computes the total amount is still a sum over a single spatial variable, x. (Note the resemblance between the integrals L h I = C(x) dx and G = πr 2 c(x) dx v December 2, 25 8
9 Math 3 Notes Chapter 5 here and in the previous problem.) We have neglected the complication of the rounded bottom portion of the test-tube, so that integration over its length (which is actually summation of disks shown in Figure 5.7) is a one-dimensional problem. In this case the amount is h ( ) G = πr 2 (. +.5x)dx = πr 2.x +.5x2 h 2 ( ) = πr 2.h +.5h2 2 Suppose that the height of the test-tube is h = cm and its radius is r = cm. Then the total mass of glucose in grams is ( G = π.() +.5() ) = π ( + 25) = 26π 2 In the next example, we consider a circular geometry, but the concept of dissecting and summing is the same. Our task is to determine how to set up the problem in terms of an integral, and, again, we must imagine which type of subdivision would lead to the summation (integration) needed to compute total amount A circular colony of bacteria Bacteria are growing in a circular colony with a radius of cm. At distance r from the center of the colony, the density of the bacteria, in units of one million cells per square centimeter, is observed to be b(r) = r 2 (Note: r is distance from the center in cm, so that r ). What is the total number of bacteria in the colony? Side view Top view (one ring) r r Figure 5.7: A colony of bacteria with circular symmetry. A ring of small thickness r has roughly constant density. Solution Figure 5.7 shows a rough sketch of a petri dish with a colony of bacteria growing inside. The density v December 2, 25 9
10 Math 3 Notes Chapter 5 b(r) b(r)= r 2 r Figure 5.8: Bacterial density as a function of radius as a function of distance from the center is given by b(r), whose graph looks like Figure 5.8. Note that the density of the bacteria is actually smooth, but to accentuate the strategy of dissecting the region, we have shown rings of constant density in Figure 5.7. One such ring is shown on the right from a top view: We see that this ring occupies the region between two circles, e.g. between a circle of radius r and a slightly bigger circle of radius r + r. The area of that ring would then be A ring = π(r + r) 2 πr 2 = π(2r r + ( r) 2 ). However, if we make the thickness of that ring really small ( r ), then the quadratic term is very very small so that A ring 2πr r. Consider all the bacteria that are found inside a ring of radius r and thickness r (see Figure 5.7.) The total number within such a ring is the product of the density, b(r) and the area of the ring, i.e. b(r) (2πr r) = 2πr( r 2 ) r. We will get the total number in the colony by summing up over all the rings from r = to r = and letting the thickness, r dr become very small. But, as with other examples, this is equivalent to calculating a definite integral, namely: B total = 2π We calculate the result as follows: ( r 2 )rdr = 2π ( ) r 2 B total = 2π 2 r4 = (πr 2 π r4 4 2 ) (r r 3 )dr = π π 2 = π 2. Thus the total number of bacteria in the entire colony is π/2 million which is approximately.57 million cells. v December 2, 25
11 Math 3 Notes Chapter 5 y l y x x Figure 5.9: 5.3 Length of a curve: Arc length The idea of dissection also applies to the problem of determining the length of a curve. Before we look in detail at this construction, we consider a simple example, shown in Figure 5.9. In the triangle shown, by the Pythagorean theorem we have the length of the sloped side given as follows: l 2 = x 2 + y 2 l = ( ) x 2 + y 2 = + y2 x = + x 2 We now consider a curve given by some function y = f(x) a < x < b, ( ) 2 y x. x as shown in Figure 5.(a). We will approximate this curve by a set of line segments, as shown in Figure 5.(b). To obtain these, we have selected some step size x along the x axis, and placed points on the curve at each of these x values. We connect the points with straight line segments, and determine the length of those segments. (The total length of the segments is only an approximation of the length of the curve, but as the subdivision gets finer and finer, we will arrive at the true total length of the curve by summing up the lengths of all the small line segments fit to it.) We show one such segment enlarged inthe circular inset in Figure 5.. Its slope, shown at right is given by y/ x. According to our remarks, above, the length of this segment is given by ( ) 2 y l == + x. x As the step size is made smaller and smaller x dx, y dy and ( ) 2 dy l + dx. dx We recognize the ratio in this root as the derivative, dy/dx. If our curve is given by a function y = f(x) then we can rewrite this as dl = + (f (x)) 2 dx. v December 2, 25
12 Math 3 Notes Chapter 5 Thus, the length of the entire curve is obtained from summing (i.e. adding up) these small pieces, i.e. b L = + (f (x)) 2 dx. a y y y=f(x) y=f(x) y x x y=f(x) x y x Figure 5.: Top: Given the graph of a function, y = f(x) (at left), we draw secant lines connecting points on its graph at values of x that are multiples of x (right). Bottom: a small part of this graph is shown, and then enlarged, to illustrate the relationship between the arc length and the length of the secant line segment. Example Find the length of a line whose slope is -2 given that the line extends from x = to x = 5. Solution We could find the equation of the line, but that is not necessary: we are given told that the slope f (x) is -2. The integral in question is L = 5 The constant 5 comes out, and we get L = (f (x)) 2 dx = + ( 2)2 dx. dx = 5x 5 = 5[5 ] = 4 5. v December 2, 25 2
13 Math 3 Notes Chapter 5 Example 2 Find an integral that represents the length of the curve that forms the graph of the function y = f(x) = x 3 < x < 2. Solution We find that Thus, the integral is L = 2 dy dx = f (x) = 3x 2 + (3x2 ) 2 dx = 2 + 9x4 dx. At this point, we will not attempt to find the actual length, as we must first develop techniques for finding the anti-derivative for functions such as + 9x 4. Using the spreadsheet to calculate arclength Most integrals for arclength contain squareroots and functions that are not easy to integrate, simply because their antiderivatives are difficult to determine. Some examples will be easier once we develop further integration techniques..5.5 Arc Length cumulative length L y = f(x) =-x^2 y = f(x) =-x^2.... length increment.. Figure 5.: The spreadsheet can be used to compute approximate values of integrals, and hence to calculate arclength. Shown here is the graph of the function y = f(x) = x 2 for x, together with the length increment and the cumulative arclength along that curve. v December 2, 25 3
14 Math 3 Notes Chapter 5 However, now that we know the idea behind determining the length of a curve, we can find a numerical value in a given situation. The spreadsheet gives a simple tool for doing the necessary summations, and we show one such example in this section. We show here how to calculate the length of the curve y = f(x) = x 2 using a simple numerical procedure implemented on the spreadsheet. We have chosen a step size of x =. along the x axis, for the interval < x <. We calculate the function, the slopes of the little segments (change in y divided by change in x), and from this, computer the length of each segment dl = + ( y/ x) 2 x and the accumulated length along the curve from left to right, L. The final value of L =.4782 represents the total length of the curve over the entire interval < x <. x y = f(x) y/ x dl L = dl In Figure 5.(a) we show the actual curve y = x 2. with points placed on it at each multiple of x. In Figure 5.(b), we show (in blue) how the lengths of the little straight-line segments connecting these points changes across the interval. (The segments on the left along the original curve are nearly flat, so their length is very close to x. The segments on the right part of the curve are much more slanted, and their lengths are thus bigger.) We also show (in red) how the total accumulated length L depends on the position x across the interval. This function represents the total arclength of the curve y = x How the alligator gets its smile The American alligator, Alligator mississippiensis has a set of teeth best viewed at some distance. The regular arrangement of these teeth, i.e. their spacing along the jaw is important in giving the reptile its famous bite. We will concern ourselves here with how that pattern of teeth is formed as the alligator develops from its embryonic stage to that of an adult. As is the case in humans, the teeth on an alligator do not form or sprout simultaneously. In the development of the baby alligator, there is a sequence of initiation of teeth, one after the other, at well-defined positions along the jaw. v December 2, 25 4
15 Math 3 Notes Chapter 5 Paul Kulesa, a former student of James D Muray, set out to understand the pattern of development of these teeth, based on data in the literature about what happens at distinct stages of embryonic growth. Of interest in his research were several questions, including what determines the positions and timing of initiation of individual teeth, and what mechanisms lead to this pattern of initiation. One theory proposed by this group was that chemical signals that diffuse along the jaw at an early stage of development give rise to instructions that are interpreted by jaw cells: where the signal is at a high level, a tooth will start to initiate. While we will not address the details of the mechanism of develpoment here, we will find a simple application of the ideas of arclength in the developmental sequence of teething. Shown in Figure 5.2 is a smiling baby alligator (no doubt thinking of some future tasty meal). A close up of its smile (at an earlier stage of development) reveals the shape of the jaw, together with the sites at which teeth are becoming evident. (One of these sites, called primordia, is shown enlarged in an inset in this figure.) Paul Kulesa found that the shape of the alligator s jaw can be described remarkably well by a parabola. A proper choice of coordinate system, and some experimentation leads to the equation of the best fit parabola y = f(x) = ax 2 + b where a =.256, and b = 7.28 (in units not specified). We show this curve in Figure 5.3(a). Also shown in this curve is a set of points at which teeth are found, labled by order of appearance. In Figure 5.3(b) we see the same curve, but we have here superimposed the function L(x) given by the arc length along the curve from the front of the jaw (i.e. the top of the parabola), i.e. L(x) = x + [f (s)] 2 ds. This curve measures distance along the jaw, from front to back. The distances of the teeth from one another, or along the curve of the jaw can be determined using this curve if we know the x coordinates of their positions. The table below gives the original data, courtesy of Dr. Kulesa, showing the order of the teeth, their (x, y) coordinates, and the value of L(x) obtained from the arclength formula. We see from this table that the teeth do not appear randomly, nor do they fill in the jaw in one sweep. Rather, they appear in several stages. In Figure 5.3(c), we show the pattern of appearance: Plotting the distance along the jaw of successive teeth reveals that the teeth appear in waves of nearly equally-spaced sites. (By equally spaced, we refer to distance along the parabolic jaw.) The first wave (teeth, 2, 3) are followed by a second wave (4, 5, 6, 7), and so on. Each wave forms a linear pattern of distance from the front, and each successive wave fills in the gaps in a similar, equaly spaced pattern. The true situation is a bit more complicated: the jaw grows as the teeth appear as shown in 5.3(c). This has not been taken into account in our simple treatment here, where we illustrate only the essential idea of arc length application. v December 2, 25 5
16 Math 3 Notes Chapter 5 Tooth number position distance along jaw x y L(x) v December 2, 25 6
17 Math 3 Notes Chapter 5 Figure 5.2: Alligator mississippiensis and its teeth v December 2, 25 7
18 Math 3 Notes Chapter 5 8. Alligator teeth 4. arc length L(x) along jaw 5 jaw y = f(x) (a) (b). Distance along jaw teeth in order of appearance. 3. (c) (d) Figure 5.3: (a) The parabolic shape of the jaw, showing positions of teeth and numerical order of emergence. (b) Arc length along the jaw from front to back. (c) Distance of successive teeth along the jaw. (d) Growth of the jaw. v December 2, 25 8
19 Math 3 Notes Chapter References. P.M. Kulesa and J.D. Murray (995). Modelling the Wave-like Initiation of Teeth Primordia in the Alligator. FORMA. Cover Article. Vol., No. 3, J.D. Murray and P.M. Kulesa (996). On A Dynamic Reaction-Diffusion Mechanism for the Spatial Patterning of Teeth Primordia in the Alligator. Journal of Chemical Physics. J. Chem. Soc., Faraday Trans., 92 (6), P.M. Kulesa, G.C. Cruywagen, S.R. Lubkin, M.W.J. Ferguson and J.D. Murray (996). Modelling the Spatial Patterning of Teeth Primordia in the Alligator. Acta Biotheoretica, 44, v December 2, 25 9
Applications of the definite integral to volume, mass, and length
 118 Chapter 5 Applications of the definite integral to volume, mass, and length 5.1 Introduction In this chapter, we consider applications of the definite integral to calculating geometric quantities such
118 Chapter 5 Applications of the definite integral to volume, mass, and length 5.1 Introduction In this chapter, we consider applications of the definite integral to calculating geometric quantities such
Integrals. D. DeTurck. January 1, University of Pennsylvania. D. DeTurck Math A: Integrals 1 / 61
 Integrals D. DeTurck University of Pennsylvania January 1, 2018 D. DeTurck Math 104 002 2018A: Integrals 1 / 61 Integrals Start with dx this means a little bit of x or a little change in x If we add up
Integrals D. DeTurck University of Pennsylvania January 1, 2018 D. DeTurck Math 104 002 2018A: Integrals 1 / 61 Integrals Start with dx this means a little bit of x or a little change in x If we add up
Technique 1: Volumes by Slicing
 Finding Volumes of Solids We have used integrals to find the areas of regions under curves; it may not seem obvious at first, but we can actually use similar methods to find volumes of certain types of
Finding Volumes of Solids We have used integrals to find the areas of regions under curves; it may not seem obvious at first, but we can actually use similar methods to find volumes of certain types of
Learning Objectives for Math 166
 Learning Objectives for Math 166 Chapter 6 Applications of Definite Integrals Section 6.1: Volumes Using Cross-Sections Draw and label both 2-dimensional perspectives and 3-dimensional sketches of the
Learning Objectives for Math 166 Chapter 6 Applications of Definite Integrals Section 6.1: Volumes Using Cross-Sections Draw and label both 2-dimensional perspectives and 3-dimensional sketches of the
Integration to Compute Volumes, Work. Goals: Volumes by Slicing Volumes by Cylindrical Shells Work
 Week #8: Integration to Compute Volumes, Work Goals: Volumes by Slicing Volumes by Cylindrical Shells Work 1 Volumes by Slicing - 1 Volumes by Slicing In the integration problems considered in this section
Week #8: Integration to Compute Volumes, Work Goals: Volumes by Slicing Volumes by Cylindrical Shells Work 1 Volumes by Slicing - 1 Volumes by Slicing In the integration problems considered in this section
MATH 18.01, FALL PROBLEM SET # 6 SOLUTIONS
 MATH 181, FALL 17 - PROBLEM SET # 6 SOLUTIONS Part II (5 points) 1 (Thurs, Oct 6; Second Fundamental Theorem; + + + + + = 16 points) Let sinc(x) denote the sinc function { 1 if x =, sinc(x) = sin x if
MATH 181, FALL 17 - PROBLEM SET # 6 SOLUTIONS Part II (5 points) 1 (Thurs, Oct 6; Second Fundamental Theorem; + + + + + = 16 points) Let sinc(x) denote the sinc function { 1 if x =, sinc(x) = sin x if
8.2 APPLICATIONS TO GEOMETRY
 8.2 APPLICATIONS TO GEOMETRY In Section 8.1, we calculated volumes using slicing and definite integrals. In this section, we use the same method to calculate the volumes of more complicated regions as
8.2 APPLICATIONS TO GEOMETRY In Section 8.1, we calculated volumes using slicing and definite integrals. In this section, we use the same method to calculate the volumes of more complicated regions as
Gauss s Law & Potential
 Gauss s Law & Potential Lecture 7: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Flux of an Electric Field : In this lecture we introduce Gauss s law which happens to
Gauss s Law & Potential Lecture 7: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Flux of an Electric Field : In this lecture we introduce Gauss s law which happens to
Volume: The Disk Method. Using the integral to find volume.
 Volume: The Disk Method Using the integral to find volume. If a region in a plane is revolved about a line, the resulting solid is a solid of revolution and the line is called the axis of revolution. y
Volume: The Disk Method Using the integral to find volume. If a region in a plane is revolved about a line, the resulting solid is a solid of revolution and the line is called the axis of revolution. y
MATH 280 Multivariate Calculus Fall Integration over a curve
 dr dr y MATH 28 Multivariate Calculus Fall 211 Integration over a curve Given a curve C in the plane or in space, we can (conceptually) break it into small pieces each of which has a length ds. In some
dr dr y MATH 28 Multivariate Calculus Fall 211 Integration over a curve Given a curve C in the plane or in space, we can (conceptually) break it into small pieces each of which has a length ds. In some
Chapter 2 Polynomial and Rational Functions
 SECTION.1 Linear and Quadratic Functions Chapter Polynomial and Rational Functions Section.1: Linear and Quadratic Functions Linear Functions Quadratic Functions Linear Functions Definition of a Linear
SECTION.1 Linear and Quadratic Functions Chapter Polynomial and Rational Functions Section.1: Linear and Quadratic Functions Linear Functions Quadratic Functions Linear Functions Definition of a Linear
Unit #13 - Integration to Find Areas and Volumes, Volumes of Revolution
 Unit #1 - Integration to Find Areas and Volumes, Volumes of Revolution Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Areas In Questions #1-8, find the area of one strip
Unit #1 - Integration to Find Areas and Volumes, Volumes of Revolution Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Areas In Questions #1-8, find the area of one strip
LESSON 14: VOLUME OF SOLIDS OF REVOLUTION SEPTEMBER 27, 2017
 LESSON 4: VOLUME OF SOLIDS OF REVOLUTION SEPTEMBER 27, 27 We continue to expand our understanding of solids of revolution. The key takeaway from today s lesson is that finding the volume of a solid of
LESSON 4: VOLUME OF SOLIDS OF REVOLUTION SEPTEMBER 27, 27 We continue to expand our understanding of solids of revolution. The key takeaway from today s lesson is that finding the volume of a solid of
Solutions to the Exercises of Chapter 5
 Solutions to the Eercises of Chapter 5 5A. Lines and Their Equations. The slope is 5 5. Since (, is a point on the line, y ( ( is an ( 6 8 8 equation of the line in point-slope form. This simplifies to
Solutions to the Eercises of Chapter 5 5A. Lines and Their Equations. The slope is 5 5. Since (, is a point on the line, y ( ( is an ( 6 8 8 equation of the line in point-slope form. This simplifies to
(Refer Slide Time: 2:08 min)
 Applied Mechanics Prof. R. K. Mittal Department of Applied Mechanics Indian Institute of Technology, Delhi Lecture No. 11 Properties of Surfaces (Contd.) Today we will take up lecture eleven which is a
Applied Mechanics Prof. R. K. Mittal Department of Applied Mechanics Indian Institute of Technology, Delhi Lecture No. 11 Properties of Surfaces (Contd.) Today we will take up lecture eleven which is a
Integral Calculus: Mathematics 103
 Integral Calculus: Mathematics 103 Notes by Leah Edelstein-Keshet: All rights reserved University of British Columbia January 2, 2010 ii Leah Edelstein-Keshet Contents Preface xvii 1 Areas, volumes and
Integral Calculus: Mathematics 103 Notes by Leah Edelstein-Keshet: All rights reserved University of British Columbia January 2, 2010 ii Leah Edelstein-Keshet Contents Preface xvii 1 Areas, volumes and
14.1. Multiple Integration. Iterated Integrals and Area in the Plane. Iterated Integrals. Iterated Integrals. MAC2313 Calculus III - Chapter 14
 14 Multiple Integration 14.1 Iterated Integrals and Area in the Plane Objectives Evaluate an iterated integral. Use an iterated integral to find the area of a plane region. Copyright Cengage Learning.
14 Multiple Integration 14.1 Iterated Integrals and Area in the Plane Objectives Evaluate an iterated integral. Use an iterated integral to find the area of a plane region. Copyright Cengage Learning.
Integrated Math II Performance Level Descriptors
 Limited Integrated Math II Performance Level Descriptors A student performing at the Limited Level demonstrates a minimal command of Ohio s Learning Standards for Integrated Math II. A student at this
Limited Integrated Math II Performance Level Descriptors A student performing at the Limited Level demonstrates a minimal command of Ohio s Learning Standards for Integrated Math II. A student at this
f x and the x axis on an interval from x a and
 Unit 6: Chapter 8 Areas and Volumes & Density Functions Part 1: Areas To find the area bounded by a function bwe use the integral: f d b a b 0 f d f d. a b a f and the ais on an interval from a and. This
Unit 6: Chapter 8 Areas and Volumes & Density Functions Part 1: Areas To find the area bounded by a function bwe use the integral: f d b a b 0 f d f d. a b a f and the ais on an interval from a and. This
Solutions to Homework 1
 Solutions to Homework 1 1. Let f(x) = x 2, a = 1, b = 2, and let x = a = 1, x 1 = 1.1, x 2 = 1.2, x 3 = 1.4, x 4 = b = 2. Let P = (x,..., x 4 ), so that P is a partition of the interval [1, 2]. List the
Solutions to Homework 1 1. Let f(x) = x 2, a = 1, b = 2, and let x = a = 1, x 1 = 1.1, x 2 = 1.2, x 3 = 1.4, x 4 = b = 2. Let P = (x,..., x 4 ), so that P is a partition of the interval [1, 2]. List the
Foundations of Calculus. November 18, 2014
 Foundations of Calculus November 18, 2014 Contents 1 Conic Sections 3 11 A review of the coordinate system 3 12 Conic Sections 4 121 Circle 4 122 Parabola 5 123 Ellipse 5 124 Hyperbola 6 2 Review of Functions
Foundations of Calculus November 18, 2014 Contents 1 Conic Sections 3 11 A review of the coordinate system 3 12 Conic Sections 4 121 Circle 4 122 Parabola 5 123 Ellipse 5 124 Hyperbola 6 2 Review of Functions
MTH301 Calculus II Glossary For Final Term Exam Preparation
 MTH301 Calculus II Glossary For Final Term Exam Preparation Glossary Absolute maximum : The output value of the highest point on a graph over a given input interval or over all possible input values. An
MTH301 Calculus II Glossary For Final Term Exam Preparation Glossary Absolute maximum : The output value of the highest point on a graph over a given input interval or over all possible input values. An
MTH101 Calculus And Analytical Geometry Lecture Wise Questions and Answers For Final Term Exam Preparation
 MTH101 Calculus And Analytical Geometry Lecture Wise Questions and Answers For Final Term Exam Preparation Lecture No 23 to 45 Complete and Important Question and answer 1. What is the difference between
MTH101 Calculus And Analytical Geometry Lecture Wise Questions and Answers For Final Term Exam Preparation Lecture No 23 to 45 Complete and Important Question and answer 1. What is the difference between
ENGI Parametric Vector Functions Page 5-01
 ENGI 3425 5. Parametric Vector Functions Page 5-01 5. Parametric Vector Functions Contents: 5.1 Arc Length (Cartesian parametric and plane polar) 5.2 Surfaces of Revolution 5.3 Area under a Parametric
ENGI 3425 5. Parametric Vector Functions Page 5-01 5. Parametric Vector Functions Contents: 5.1 Arc Length (Cartesian parametric and plane polar) 5.2 Surfaces of Revolution 5.3 Area under a Parametric
5.5 Volumes: Tubes. The Tube Method. = (2π [radius]) (height) ( x k ) = (2πc k ) f (c k ) x k. 5.5 volumes: tubes 435
![5.5 Volumes: Tubes. The Tube Method. = (2π [radius]) (height) ( x k ) = (2πc k ) f (c k ) x k. 5.5 volumes: tubes 435 5.5 Volumes: Tubes. The Tube Method. = (2π [radius]) (height) ( x k ) = (2πc k ) f (c k ) x k. 5.5 volumes: tubes 435](/thumbs/78/77255700.jpg) 5.5 volumes: tubes 45 5.5 Volumes: Tubes In Section 5., we devised the disk method to find the volume swept out when a region is revolved about a line. To find the volume swept out when revolving a region
5.5 volumes: tubes 45 5.5 Volumes: Tubes In Section 5., we devised the disk method to find the volume swept out when a region is revolved about a line. To find the volume swept out when revolving a region
Graphs of Polynomial Functions
 Graphs of Polynomial Functions By: OpenStaxCollege The revenue in millions of dollars for a fictional cable company from 2006 through 2013 is shown in [link]. Year 2006 2007 2008 2009 2010 2011 2012 2013
Graphs of Polynomial Functions By: OpenStaxCollege The revenue in millions of dollars for a fictional cable company from 2006 through 2013 is shown in [link]. Year 2006 2007 2008 2009 2010 2011 2012 2013
Calculating Moments of Inertia
 Calculating Moments of Inertia Lana Sheridan 1 Definitions The moment of inertia, I of an object for a particular axis is the constant that links the applied torque τ about that axis to the angular acceleration
Calculating Moments of Inertia Lana Sheridan 1 Definitions The moment of inertia, I of an object for a particular axis is the constant that links the applied torque τ about that axis to the angular acceleration
Introduction to Computer Graphics (Lecture No 07) Ellipse and Other Curves
 Introduction to Computer Graphics (Lecture No 07) Ellipse and Other Curves 7.1 Ellipse An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r1 and r from two fixed
Introduction to Computer Graphics (Lecture No 07) Ellipse and Other Curves 7.1 Ellipse An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r1 and r from two fixed
Solid of Revolution. IB Mathematic HL. International Baccalaureate Program. October 31, 2016
 1 Solid of Revolution IB Mathematic HL International Baccalaureate Program 2070 October 31, 2016 2 Introduction: Geometry is one of the areas of math that I feel passionate about, thereby I am inspired
1 Solid of Revolution IB Mathematic HL International Baccalaureate Program 2070 October 31, 2016 2 Introduction: Geometry is one of the areas of math that I feel passionate about, thereby I am inspired
18.01 Single Variable Calculus Fall 2006
 MIT OpenCourseWare http://ocw.mit.edu 8. Single Variable Calculus Fall 6 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Lecture 3 8. Fall 6 Lecture 3:
MIT OpenCourseWare http://ocw.mit.edu 8. Single Variable Calculus Fall 6 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Lecture 3 8. Fall 6 Lecture 3:
Review. The derivative of y = f(x) has four levels of meaning: Physical: If y is a quantity depending on x, the derivative dy
 Math 132 Area and Distance Stewart 4.1/I Review. The derivative of y = f(x) has four levels of meaning: Physical: If y is a quantity depending on x, the derivative dy dx x=a is the rate of change of y
Math 132 Area and Distance Stewart 4.1/I Review. The derivative of y = f(x) has four levels of meaning: Physical: If y is a quantity depending on x, the derivative dy dx x=a is the rate of change of y
MAT137 - Term 2, Week 4
 MAT137 - Term 2, Week 4 Reminders: Your Problem Set 6 is due tomorrow at 3pm. Test 3 is next Friday, February 3, at 4pm. See the course website for details. Today we will: Talk more about substitution.
MAT137 - Term 2, Week 4 Reminders: Your Problem Set 6 is due tomorrow at 3pm. Test 3 is next Friday, February 3, at 4pm. See the course website for details. Today we will: Talk more about substitution.
Functions and their Graphs
 Chapter One Due Monday, December 12 Functions and their Graphs Functions Domain and Range Composition and Inverses Calculator Input and Output Transformations Quadratics Functions A function yields a specific
Chapter One Due Monday, December 12 Functions and their Graphs Functions Domain and Range Composition and Inverses Calculator Input and Output Transformations Quadratics Functions A function yields a specific
Answers for Ch. 6 Review: Applications of the Integral
 Answers for Ch. 6 Review: Applications of the Integral. The formula for the average value of a function, which you must have stored in your magical mathematical brain, is b b a f d. a d / / 8 6 6 ( 8 )
Answers for Ch. 6 Review: Applications of the Integral. The formula for the average value of a function, which you must have stored in your magical mathematical brain, is b b a f d. a d / / 8 6 6 ( 8 )
Calculus III. Math 233 Spring Final exam May 3rd. Suggested solutions
 alculus III Math 33 pring 7 Final exam May 3rd. uggested solutions This exam contains twenty problems numbered 1 through. All problems are multiple choice problems, and each counts 5% of your total score.
alculus III Math 33 pring 7 Final exam May 3rd. uggested solutions This exam contains twenty problems numbered 1 through. All problems are multiple choice problems, and each counts 5% of your total score.
Practice Exam 1 Solutions
 Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
Figure 21:The polar and Cartesian coordinate systems.
 Figure 21:The polar and Cartesian coordinate systems. Coordinate systems in R There are three standard coordinate systems which are used to describe points in -dimensional space. These coordinate systems
Figure 21:The polar and Cartesian coordinate systems. Coordinate systems in R There are three standard coordinate systems which are used to describe points in -dimensional space. These coordinate systems
Math 122 Fall Handout 15: Review Problems for the Cumulative Final Exam
 Math 122 Fall 2008 Handout 15: Review Problems for the Cumulative Final Exam The topics that will be covered on Final Exam are as follows. Integration formulas. U-substitution. Integration by parts. Integration
Math 122 Fall 2008 Handout 15: Review Problems for the Cumulative Final Exam The topics that will be covered on Final Exam are as follows. Integration formulas. U-substitution. Integration by parts. Integration
Chapter 6 Some Applications of the Integral
 Chapter 6 Some Applications of the Integral Section 6.1 More on Area a. Representative Rectangle b. Vertical Separation c. Example d. Integration with Respect to y e. Example Section 6.2 Volume by Parallel
Chapter 6 Some Applications of the Integral Section 6.1 More on Area a. Representative Rectangle b. Vertical Separation c. Example d. Integration with Respect to y e. Example Section 6.2 Volume by Parallel
Since x + we get x² + 2x = 4, or simplifying it, x² = 4. Therefore, x² + = 4 2 = 2. Ans. (C)
 SAT II - Math Level 2 Test #01 Solution 1. x + = 2, then x² + = Since x + = 2, by squaring both side of the equation, (A) - (B) 0 (C) 2 (D) 4 (E) -2 we get x² + 2x 1 + 1 = 4, or simplifying it, x² + 2
SAT II - Math Level 2 Test #01 Solution 1. x + = 2, then x² + = Since x + = 2, by squaring both side of the equation, (A) - (B) 0 (C) 2 (D) 4 (E) -2 we get x² + 2x 1 + 1 = 4, or simplifying it, x² + 2
Calculus with Analytic Geometry 3 Fall 2018
 alculus with Analytic Geometry 3 Fall 218 Practice Exercises for the Final Exam I present here a number of exercises that could serve as practice for the final exam. Some are easy and straightforward;
alculus with Analytic Geometry 3 Fall 218 Practice Exercises for the Final Exam I present here a number of exercises that could serve as practice for the final exam. Some are easy and straightforward;
36. Double Integration over Non-Rectangular Regions of Type II
 36. Double Integration over Non-Rectangular Regions of Type II When establishing the bounds of a double integral, visualize an arrow initially in the positive x direction or the positive y direction. A
36. Double Integration over Non-Rectangular Regions of Type II When establishing the bounds of a double integral, visualize an arrow initially in the positive x direction or the positive y direction. A
1 Summation: Adding up the pieces
 1 Summation: Adding up the pieces 1.1 Answer the following questions: (a) What is the value of the fifth term of the sum S = 0 (5 + 3k)/k? (b) How many terms are there in total in the sum S = 17 e k? (c)
1 Summation: Adding up the pieces 1.1 Answer the following questions: (a) What is the value of the fifth term of the sum S = 0 (5 + 3k)/k? (b) How many terms are there in total in the sum S = 17 e k? (c)
Lecture 21. Section 6.1 More on Area Section 6.2 Volume by Parallel Cross Section. Jiwen He. Department of Mathematics, University of Houston
 Section 6.1 Section 6.2 Lecture 21 Section 6.1 More on Area Section 6.2 Volume by Parallel Cross Section Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math1431
Section 6.1 Section 6.2 Lecture 21 Section 6.1 More on Area Section 6.2 Volume by Parallel Cross Section Jiwen He Department of Mathematics, University of Houston jiwenhe@math.uh.edu math.uh.edu/ jiwenhe/math1431
MATH2321, Calculus III for Science and Engineering, Fall Name (Printed) Print your name, the date, and then sign the exam on the line
 MATH2321, Calculus III for Science and Engineering, Fall 218 1 Exam 2 Name (Printed) Date Signature Instructions STOP. above. Print your name, the date, and then sign the exam on the line This exam consists
MATH2321, Calculus III for Science and Engineering, Fall 218 1 Exam 2 Name (Printed) Date Signature Instructions STOP. above. Print your name, the date, and then sign the exam on the line This exam consists
New Rochelle High School Geometry Summer Assignment
 NAME - New Rochelle High School Geometry Summer Assignment To all Geometry students, This assignment will help you refresh some of the necessary math skills you will need to be successful in Geometry and
NAME - New Rochelle High School Geometry Summer Assignment To all Geometry students, This assignment will help you refresh some of the necessary math skills you will need to be successful in Geometry and
Chapter 1. Areas, volumes and simple sums. 1.1 Introduction. 1.2 Areas of simple shapes
 Chapter 1 Areas, volumes and simple sums 1.1 Introduction One of the main goals in this course will be calculating areas enclosed by curves in the plane and volumes of three dimensional shapes. We will
Chapter 1 Areas, volumes and simple sums 1.1 Introduction One of the main goals in this course will be calculating areas enclosed by curves in the plane and volumes of three dimensional shapes. We will
Problem. Set up the definite integral that gives the area of the region. y 1 = x 2 6x, y 2 = 0. dx = ( 2x 2 + 6x) dx.
 Wednesday, September 3, 5 Page Problem Problem. Set up the definite integral that gives the area of the region y x 6x, y Solution. The graphs intersect at x and x 6 and y is the uppermost function. So
Wednesday, September 3, 5 Page Problem Problem. Set up the definite integral that gives the area of the region y x 6x, y Solution. The graphs intersect at x and x 6 and y is the uppermost function. So
Math 2 Variable Manipulation Part 7 Absolute Value & Inequalities
 Math 2 Variable Manipulation Part 7 Absolute Value & Inequalities 1 MATH 1 REVIEW SOLVING AN ABSOLUTE VALUE EQUATION Absolute value is a measure of distance; how far a number is from zero. In practice,
Math 2 Variable Manipulation Part 7 Absolute Value & Inequalities 1 MATH 1 REVIEW SOLVING AN ABSOLUTE VALUE EQUATION Absolute value is a measure of distance; how far a number is from zero. In practice,
3. On the grid below, sketch and label graphs of the following functions: y = sin x, y = cos x, and y = sin(x π/2). π/2 π 3π/2 2π 5π/2
 AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
AP Physics C Calculus C.1 Name Trigonometric Functions 1. Consider the right triangle to the right. In terms of a, b, and c, write the expressions for the following: c a sin θ = cos θ = tan θ =. Using
Figure 25:Differentials of surface.
 2.5. Change of variables and Jacobians In the previous example we saw that, once we have identified the type of coordinates which is best to use for solving a particular problem, the next step is to do
2.5. Change of variables and Jacobians In the previous example we saw that, once we have identified the type of coordinates which is best to use for solving a particular problem, the next step is to do
Infinite series, improper integrals, and Taylor series
 Chapter Infinite series, improper integrals, and Taylor series. Determine which of the following sequences converge or diverge (a) {e n } (b) {2 n } (c) {ne 2n } (d) { 2 n } (e) {n } (f) {ln(n)} 2.2 Which
Chapter Infinite series, improper integrals, and Taylor series. Determine which of the following sequences converge or diverge (a) {e n } (b) {2 n } (c) {ne 2n } (d) { 2 n } (e) {n } (f) {ln(n)} 2.2 Which
Circle Theorems. Angles at the circumference are equal. The angle in a semi-circle is x The angle at the centre. Cyclic Quadrilateral
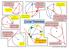 The angle in a semi-circle is 90 0 Angles at the circumference are equal. A B They must come from the same arc. Look out for a diameter. 2x Cyclic Quadrilateral Opposite angles add up to 180 0 A They must
The angle in a semi-circle is 90 0 Angles at the circumference are equal. A B They must come from the same arc. Look out for a diameter. 2x Cyclic Quadrilateral Opposite angles add up to 180 0 A They must
Math 221 Exam III (50 minutes) Friday April 19, 2002 Answers
 Math Exam III (5 minutes) Friday April 9, Answers I. ( points.) Fill in the boxes as to complete the following statement: A definite integral can be approximated by a Riemann sum. More precisely, if a
Math Exam III (5 minutes) Friday April 9, Answers I. ( points.) Fill in the boxes as to complete the following statement: A definite integral can be approximated by a Riemann sum. More precisely, if a
Final Exam 12/11/ (16 pts) Find derivatives for each of the following: (a) f(x) = 3 1+ x e + e π [Do not simplify your answer.
 Math 105 Final Exam 1/11/1 Name Read directions carefully and show all your work. Partial credit will be assigned based upon the correctness, completeness, and clarity of your answers. Correct answers
Math 105 Final Exam 1/11/1 Name Read directions carefully and show all your work. Partial credit will be assigned based upon the correctness, completeness, and clarity of your answers. Correct answers
6.1 Area Between Curves. Example 1: Calculate the area of the region between the parabola y = 1 x 2 and the line y = 1 x
 AP Calculus 6.1 Area Between Curves Name: Goal: Calculate the Area between curves Keys to Success: Top Curve Bottom Curve (integrate w/respect to x or dx) Right Curve Left Curve (integrate w/respect to
AP Calculus 6.1 Area Between Curves Name: Goal: Calculate the Area between curves Keys to Success: Top Curve Bottom Curve (integrate w/respect to x or dx) Right Curve Left Curve (integrate w/respect to
d` = 1+( dy , which is part of the cone.
 7.5 Surface area When we did areas, the basic slices were rectangles, with A = h x or h y. When we did volumes of revolution, the basic slices came from revolving rectangles around an axis. Depending on
7.5 Surface area When we did areas, the basic slices were rectangles, with A = h x or h y. When we did volumes of revolution, the basic slices came from revolving rectangles around an axis. Depending on
Radiation Heat Transfer Prof. J. Srinivasan Centre for Atmospheric and Oceanic Sciences Indian Institute of Science Bangalore
 Radiation Heat Transfer Prof. J. Srinivasan Centre for Atmospheric and Oceanic Sciences Indian Institute of Science Bangalore Lecture - 7 Evaluations of shape factors (Refer Slide Time: 00:18) The last
Radiation Heat Transfer Prof. J. Srinivasan Centre for Atmospheric and Oceanic Sciences Indian Institute of Science Bangalore Lecture - 7 Evaluations of shape factors (Refer Slide Time: 00:18) The last
Examples from Section 6.3: Volume by Cylindrical Shells Page 1
 Examples from Section 6.3: Volume by Cylindrical Shells Page 1 Questions Example Find the volume of the region which is created when we rotate the region below y = x x 3 and above < x < about the y-axis.
Examples from Section 6.3: Volume by Cylindrical Shells Page 1 Questions Example Find the volume of the region which is created when we rotate the region below y = x x 3 and above < x < about the y-axis.
7.1 Indefinite Integrals Calculus
 7.1 Indefinite Integrals Calculus Learning Objectives A student will be able to: Find antiderivatives of functions. Represent antiderivatives. Interpret the constant of integration graphically. Solve differential
7.1 Indefinite Integrals Calculus Learning Objectives A student will be able to: Find antiderivatives of functions. Represent antiderivatives. Interpret the constant of integration graphically. Solve differential
Applications of Differentiation
 MathsTrack (NOTE Feb 2013: This is the old version of MathsTrack. New books will be created during 2013 and 2014) Module9 7 Introduction Applications of to Matrices Differentiation y = x(x 1)(x 2) d 2
MathsTrack (NOTE Feb 2013: This is the old version of MathsTrack. New books will be created during 2013 and 2014) Module9 7 Introduction Applications of to Matrices Differentiation y = x(x 1)(x 2) d 2
Integration is the reverse of the process of differentiation. In the usual notation. k dx = kx + c. kx dx = 1 2 kx2 + c.
 PHYS122 - Electricity and Magnetism Integration Reminder Integration is the reverse of the process of differentiation. In the usual notation f (x)dx = f(x) + constant The derivative of the RHS gives you
PHYS122 - Electricity and Magnetism Integration Reminder Integration is the reverse of the process of differentiation. In the usual notation f (x)dx = f(x) + constant The derivative of the RHS gives you
Integral Calculus with Applications to the Life Sciences
 Integral Calculus with Applications to the Life Sciences Leah Edelstein-Keshet Mathematics Department, University of British Columbia, Vancouver November 2, 27 Course Notes for Mathematics 3 c Leah Keshet.
Integral Calculus with Applications to the Life Sciences Leah Edelstein-Keshet Mathematics Department, University of British Columbia, Vancouver November 2, 27 Course Notes for Mathematics 3 c Leah Keshet.
Applications of the definite integral to rates, velocities and densities
 Chapter 4 Applications of the definite integral to rates, velocities and densities 4.1 Displacement, velocity and acceleration Recall from our study of derivatives that for xt) the position of some particle
Chapter 4 Applications of the definite integral to rates, velocities and densities 4.1 Displacement, velocity and acceleration Recall from our study of derivatives that for xt) the position of some particle
PROFESSOR: WELCOME BACK TO THE LAST LECTURE OF THE SEMESTER. PLANNING TO DO TODAY WAS FINISH THE BOOK. FINISH SECTION 6.5
 1 MATH 16A LECTURE. DECEMBER 9, 2008. PROFESSOR: WELCOME BACK TO THE LAST LECTURE OF THE SEMESTER. I HOPE YOU ALL WILL MISS IT AS MUCH AS I DO. SO WHAT I WAS PLANNING TO DO TODAY WAS FINISH THE BOOK. FINISH
1 MATH 16A LECTURE. DECEMBER 9, 2008. PROFESSOR: WELCOME BACK TO THE LAST LECTURE OF THE SEMESTER. I HOPE YOU ALL WILL MISS IT AS MUCH AS I DO. SO WHAT I WAS PLANNING TO DO TODAY WAS FINISH THE BOOK. FINISH
(a) The best linear approximation of f at x = 2 is given by the formula. L(x) = f(2) + f (2)(x 2). f(2) = ln(2/2) = ln(1) = 0, f (2) = 1 2.
 Math 180 Written Homework Assignment #8 Due Tuesday, November 11th at the beginning of your discussion class. Directions. You are welcome to work on the following problems with other MATH 180 students,
Math 180 Written Homework Assignment #8 Due Tuesday, November 11th at the beginning of your discussion class. Directions. You are welcome to work on the following problems with other MATH 180 students,
MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS
 MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT100 is a fast-paced and thorough tour of precalculus mathematics, where the choice of topics is primarily motivated by the conceptual and technical knowledge
MAT100 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT100 is a fast-paced and thorough tour of precalculus mathematics, where the choice of topics is primarily motivated by the conceptual and technical knowledge
18.02SC Multivariable Calculus, Fall 2010 Transcript Recitation 34, Integration in Polar Coordinates
 18.02SC Multivariable Calculus, Fall 2010 Transcript Recitation 34, Integration in Polar Coordinates DAVID JORDAN: Hello, and welcome back to recitation. So today I want to practice doing some computings
18.02SC Multivariable Calculus, Fall 2010 Transcript Recitation 34, Integration in Polar Coordinates DAVID JORDAN: Hello, and welcome back to recitation. So today I want to practice doing some computings
May 2015 Timezone 2 IB Maths Standard Exam Worked Solutions
 May 015 Timezone IB Maths Standard Exam Worked Solutions 015, Steve Muench steve.muench@gmail.com @stevemuench Please feel free to share the link to these solutions http://bit.ly/ib-sl-maths-may-015-tz
May 015 Timezone IB Maths Standard Exam Worked Solutions 015, Steve Muench steve.muench@gmail.com @stevemuench Please feel free to share the link to these solutions http://bit.ly/ib-sl-maths-may-015-tz
5.2 LENGTHS OF CURVES & AREAS OF SURFACES OF REVOLUTION
 5.2 Arc Length & Surface Area Contemporary Calculus 1 5.2 LENGTHS OF CURVES & AREAS OF SURFACES OF REVOLUTION This section introduces two additional geometric applications of integration: finding the length
5.2 Arc Length & Surface Area Contemporary Calculus 1 5.2 LENGTHS OF CURVES & AREAS OF SURFACES OF REVOLUTION This section introduces two additional geometric applications of integration: finding the length
GRE Quantitative Reasoning Practice Questions
 GRE Quantitative Reasoning Practice Questions y O x 7. The figure above shows the graph of the function f in the xy-plane. What is the value of f (f( ))? A B C 0 D E Explanation Note that to find f (f(
GRE Quantitative Reasoning Practice Questions y O x 7. The figure above shows the graph of the function f in the xy-plane. What is the value of f (f( ))? A B C 0 D E Explanation Note that to find f (f(
( ) ) in 2 ( ) ) in 3
 Chapter 1 Test Review Question Answers 1. Find the total surface area and volume of a cube in which the diagonal measures yards. x + x ) = ) x = x x A T.S. = bh) = ) ) = 1 yd V = BH = bh)h = ) ) ) = yd.
Chapter 1 Test Review Question Answers 1. Find the total surface area and volume of a cube in which the diagonal measures yards. x + x ) = ) x = x x A T.S. = bh) = ) ) = 1 yd V = BH = bh)h = ) ) ) = yd.
Calculus II (Fall 2015) Practice Problems for Exam 1
 Calculus II (Fall 15) Practice Problems for Exam 1 Note: Section divisions and instructions below are the same as they will be on the exam, so you will have a better idea of what to expect, though I will
Calculus II (Fall 15) Practice Problems for Exam 1 Note: Section divisions and instructions below are the same as they will be on the exam, so you will have a better idea of what to expect, though I will
Lab 11: Numerical Integration Techniques. Figure 1. From the Fundamental Theorem of Calculus, we know that if we want to calculate f ( x)
 Lab 11: Numerical Integration Techniques Introduction The purpose of this laboratory experience is to develop fundamental methods for approximating the area under a curve for the definite integral. With
Lab 11: Numerical Integration Techniques Introduction The purpose of this laboratory experience is to develop fundamental methods for approximating the area under a curve for the definite integral. With
Electric Fields and Continuous Charge Distributions Challenge Problem Solutions
 Problem 1: Electric Fields and Continuous Charge Distributions Challenge Problem Solutions Two thin, semi-infinite rods lie in the same plane They make an angle of 45º with each other and they are joined
Problem 1: Electric Fields and Continuous Charge Distributions Challenge Problem Solutions Two thin, semi-infinite rods lie in the same plane They make an angle of 45º with each other and they are joined
Ohio s State Tests ITEM RELEASE SPRING 2018 INTEGRATED MATHEMATICS II
 Ohio s State Tests ITEM RELEASE SPRING 2018 INTEGRATED MATHEMATICS II Table of Contents Content Summary and Answer Key... iii Question 1: Question and Scoring Guidelines... 1 Question 1: Sample Responses...
Ohio s State Tests ITEM RELEASE SPRING 2018 INTEGRATED MATHEMATICS II Table of Contents Content Summary and Answer Key... iii Question 1: Question and Scoring Guidelines... 1 Question 1: Sample Responses...
9.1 Circles and Parabolas. Copyright Cengage Learning. All rights reserved.
 9.1 Circles and Parabolas Copyright Cengage Learning. All rights reserved. What You Should Learn Recognize a conic as the intersection of a plane and a double-napped cone. Write equations of circles in
9.1 Circles and Parabolas Copyright Cengage Learning. All rights reserved. What You Should Learn Recognize a conic as the intersection of a plane and a double-napped cone. Write equations of circles in
Note: Each problem is worth 14 points except numbers 5 and 6 which are 15 points. = 3 2
 Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
Math Prelim II Solutions Spring Note: Each problem is worth points except numbers 5 and 6 which are 5 points. x. Compute x da where is the region in the second quadrant between the + y circles x + y and
5 Integrals reviewed Basic facts U-substitution... 4
 Contents 5 Integrals reviewed 5. Basic facts............................... 5.5 U-substitution............................. 4 6 Integral Applications 0 6. Area between two curves.......................
Contents 5 Integrals reviewed 5. Basic facts............................... 5.5 U-substitution............................. 4 6 Integral Applications 0 6. Area between two curves.......................
In this lesson, students manipulate a paper cone
 NATIONAL MATH + SCIENCE INITIATIVE Mathematics G F E D C Cone Exploration and Optimization I H J K L M LEVEL Algebra 2, Math 3, Pre-Calculus, or Math 4 in a unit on polynomials MODULE/CONNECTION TO AP*
NATIONAL MATH + SCIENCE INITIATIVE Mathematics G F E D C Cone Exploration and Optimization I H J K L M LEVEL Algebra 2, Math 3, Pre-Calculus, or Math 4 in a unit on polynomials MODULE/CONNECTION TO AP*
MAC Calculus II Spring Homework #6 Some Solutions.
 MAC 2312-15931-Calculus II Spring 23 Homework #6 Some Solutions. 1. Find the centroid of the region bounded by the curves y = 2x 2 and y = 1 2x 2. Solution. It is obvious, by inspection, that the centroid
MAC 2312-15931-Calculus II Spring 23 Homework #6 Some Solutions. 1. Find the centroid of the region bounded by the curves y = 2x 2 and y = 1 2x 2. Solution. It is obvious, by inspection, that the centroid
Math 3 Variable Manipulation Part 7 Absolute Value & Inequalities
 Math 3 Variable Manipulation Part 7 Absolute Value & Inequalities 1 MATH 1 REVIEW SOLVING AN ABSOLUTE VALUE EQUATION Absolute value is a measure of distance; how far a number is from zero. In practice,
Math 3 Variable Manipulation Part 7 Absolute Value & Inequalities 1 MATH 1 REVIEW SOLVING AN ABSOLUTE VALUE EQUATION Absolute value is a measure of distance; how far a number is from zero. In practice,
1. If the line l has symmetric equations. = y 3 = z+2 find a vector equation for the line l that contains the point (2, 1, 3) and is parallel to l.
 . If the line l has symmetric equations MA 6 PRACTICE PROBLEMS x = y = z+ 7, find a vector equation for the line l that contains the point (,, ) and is parallel to l. r = ( + t) i t j + ( + 7t) k B. r
. If the line l has symmetric equations MA 6 PRACTICE PROBLEMS x = y = z+ 7, find a vector equation for the line l that contains the point (,, ) and is parallel to l. r = ( + t) i t j + ( + 7t) k B. r
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document
 Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Mathematics 1 Lecture Notes Chapter 1 Algebra Review
 Mathematics 1 Lecture Notes Chapter 1 Algebra Review c Trinity College 1 A note to the students from the lecturer: This course will be moving rather quickly, and it will be in your own best interests to
Mathematics 1 Lecture Notes Chapter 1 Algebra Review c Trinity College 1 A note to the students from the lecturer: This course will be moving rather quickly, and it will be in your own best interests to
Things You Should Know Coming Into Calc I
 Things You Should Know Coming Into Calc I Algebraic Rules, Properties, Formulas, Ideas and Processes: 1) Rules and Properties of Exponents. Let x and y be positive real numbers, let a and b represent real
Things You Should Know Coming Into Calc I Algebraic Rules, Properties, Formulas, Ideas and Processes: 1) Rules and Properties of Exponents. Let x and y be positive real numbers, let a and b represent real
Pre Calculus. Intro to Integrals.
 1 Pre Calculus Intro to Integrals 2015 03 24 www.njctl.org 2 Riemann Sums Trapezoid Rule Table of Contents click on the topic to go to that section Accumulation Function Antiderivatives & Definite Integrals
1 Pre Calculus Intro to Integrals 2015 03 24 www.njctl.org 2 Riemann Sums Trapezoid Rule Table of Contents click on the topic to go to that section Accumulation Function Antiderivatives & Definite Integrals
The Not-Formula Book for C2 Everything you need to know for Core 2 that won t be in the formula book Examination Board: AQA
 Not The Not-Formula Book for C Everything you need to know for Core that won t be in the formula book Examination Board: AQA Brief This document is intended as an aid for revision. Although it includes
Not The Not-Formula Book for C Everything you need to know for Core that won t be in the formula book Examination Board: AQA Brief This document is intended as an aid for revision. Although it includes
MATH II CCR MATH STANDARDS
 RELATIONSHIPS BETWEEN QUANTITIES M.2HS.1 M.2HS.2 M.2HS.3 M.2HS.4 M.2HS.5 M.2HS.6 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents
RELATIONSHIPS BETWEEN QUANTITIES M.2HS.1 M.2HS.2 M.2HS.3 M.2HS.4 M.2HS.5 M.2HS.6 Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents
Answer Explanations for: ACT June 2012, Form 70C
 Answer Explanations for: ACT June 2012, Form 70C Mathematics 1) C) A mean is a regular average and can be found using the following formula: (average of set) = (sum of items in set)/(number of items in
Answer Explanations for: ACT June 2012, Form 70C Mathematics 1) C) A mean is a regular average and can be found using the following formula: (average of set) = (sum of items in set)/(number of items in
Absolute Extrema and Constrained Optimization
 Calculus 1 Lia Vas Absolute Extrema and Constrained Optimization Recall that a function f (x) is said to have a relative maximum at x = c if f (c) f (x) for all values of x in some open interval containing
Calculus 1 Lia Vas Absolute Extrema and Constrained Optimization Recall that a function f (x) is said to have a relative maximum at x = c if f (c) f (x) for all values of x in some open interval containing
Double integrals using polar coordinates Let s look at a motivating example:
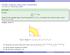 Double integrals using polar coordinates Let s look at a motivating example: Example Evaluate e x +y da where is the bounded region in the first quadrant (x 0, y 0) between the circles of radius 1 and
Double integrals using polar coordinates Let s look at a motivating example: Example Evaluate e x +y da where is the bounded region in the first quadrant (x 0, y 0) between the circles of radius 1 and
Prentice Hall Mathematics, Pre-Algebra 2007 Correlated to: Michigan Grade Level Content Expectations (Grades 8)
 NUMBER AND OPERATIONS Understand real number concepts N.ME.08.01 Understand the meaning SE/TE: Direct Instruction: 189 (Ex. 48), 588-591, of a square root of a number and its 593-596, 598-599, 603, 608,
NUMBER AND OPERATIONS Understand real number concepts N.ME.08.01 Understand the meaning SE/TE: Direct Instruction: 189 (Ex. 48), 588-591, of a square root of a number and its 593-596, 598-599, 603, 608,
Math 1A UCB, Fall 2010 A. Ogus Solutions 1 for Problem Set 4
 Math 1A UCB, Fall 010 A. Ogus Solutions 1 for Problem Set 4.5 #. Explain, using Theorems 4, 5, 7, and 9, why the function 3 x(1 + x 3 ) is continuous at every member of its domain. State its domain. By
Math 1A UCB, Fall 010 A. Ogus Solutions 1 for Problem Set 4.5 #. Explain, using Theorems 4, 5, 7, and 9, why the function 3 x(1 + x 3 ) is continuous at every member of its domain. State its domain. By
SOL Warm-Up Graphing Calculator Active
 A.2c (a) Factoring polynomials SOL Warm-Up 1. Which of the following represents 12x 2 + 6x + 3 in simplified form after factoring out the greatest common factor? A 12(x 2 + 2x + 4) B x(12x 2 + 6x + 3)
A.2c (a) Factoring polynomials SOL Warm-Up 1. Which of the following represents 12x 2 + 6x + 3 in simplified form after factoring out the greatest common factor? A 12(x 2 + 2x + 4) B x(12x 2 + 6x + 3)
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Free Response Questions Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom
 Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
Free Response Questions 1969-010 Compiled by Kaye Autrey for face-to-face student instruction in the AP Calculus classroom 1 AP Calculus Free-Response Questions 1969 AB 1 Consider the following functions
FINAL EXAM STUDY GUIDE
 FINAL EXAM STUDY GUIDE The Final Exam takes place on Wednesday, June 13, 2018, from 10:30 AM to 12:30 PM in 1100 Donald Bren Hall (not the usual lecture room!!!) NO books/notes/calculators/cheat sheets
FINAL EXAM STUDY GUIDE The Final Exam takes place on Wednesday, June 13, 2018, from 10:30 AM to 12:30 PM in 1100 Donald Bren Hall (not the usual lecture room!!!) NO books/notes/calculators/cheat sheets
4.4: Optimization. Problem 2 Find the radius of a cylindrical container with a volume of 2π m 3 that minimizes the surface area.
 4.4: Optimization Problem 1 Suppose you want to maximize a continuous function on a closed interval, but you find that it only has one local extremum on the interval which happens to be a local minimum.
4.4: Optimization Problem 1 Suppose you want to maximize a continuous function on a closed interval, but you find that it only has one local extremum on the interval which happens to be a local minimum.
Unit 3: Number, Algebra, Geometry 2
 Unit 3: Number, Algebra, Geometry 2 Number Use standard form, expressed in standard notation and on a calculator display Calculate with standard form Convert between ordinary and standard form representations
Unit 3: Number, Algebra, Geometry 2 Number Use standard form, expressed in standard notation and on a calculator display Calculate with standard form Convert between ordinary and standard form representations
