Lagrangian for RLC circuits using analogy with the classical mechanics concepts
|
|
|
- Beverly Rose
- 5 years ago
- Views:
Transcription
1 Lagrangian for RLC circuis using analogy wih h classical mchanics concps Albrus Hariwangsa Panuluh and Asan Damanik Dparmn of Physics Educaion, Sanaa Dharma Univrsiy Kampus III USD Paingan, Maguwoharjo, Slman, Yogyakara, Indonsia panuluh@usd.ac.id Absrac. W sudy and formula h Lagrangian for h LC, RC, RL, and RLC circuis by using h analogy concp wih h mchanical problm in classical mchanics formulaions. W found ha h Lagrangian for h LC and RLC circuis ar govrnd by wo rms i.. kinic nrgy-lik and ponial nrgy-lik rms. Th Lagrangian for h RC circui is only a conribuion from h ponial nrgy-lik rm and h Lagrangian for h RL circui is only from h kinic nrgy-lik rm.. Inroducion Lagrangian formalism is a powrful way o obain h quaion of moion of a physical sysm. Th Lagrangian formalism is urnd up o solv problms ha ar no simpl by using Nwonian Mchanics []. In Nwonian mchanics, w usually formula h mchanical problm (physical sysm) in h form of forc or vcor. Manwhil, in Lagrangian mchanics, w approach h mchanical problm in h form of nrgy which is a scalar. If w know h Lagrangian of a physical sysm, hn w can obain h quaion of moion of a physical sysm by using h Eulr-Lagrang quaion []. In h lcrical subjc, h RLC (Rsisanc-Inducanc-Capacianc) circui is commonly discussd in sudn physics xbooks as an xampl of h applicaion of lcronics principls o build an lcronic dvic [3]. In h mahmaical physics subjc, h RLC circui is commonly usd o show h applicaion of diffrnial quaion in h physical sysm [4]. Th knowldg of RLC circui is crainly of gra physical inrs boh from xprimnal (applid) and horical sids. Rcnly, h RLC circui and is physical propris o b an inrsing rsarch subjc du o h dvlopmn of msoscopic physics and nanophysics ha nd a quanum mchanics bcaus h msoscopic sysm and nanophysics ar no anymor a macroscopic sysm. Th analysis of RLC circui as a msoscopic sysm by using quanum mchanics basd on Cardirola-Kanai Hamilonian and quanum invarian mhod o solv h Schrödingr quaion for h RLC circui and o obain h corrsponding wav funcions in rm of a paricular soluion of Miln- Pnny quaion was rpord by Pdrosa and Pinhiro [5]. Th quanum mchanics ramn of h RLC circui wih discr charg and smiclassical considraion can b found in Urras-Diaz [6] ha obaind h approximaion of nrgy ignvalus in rm of a dimnsionlss paramr L C h ( is h lcron charg, and h is h Planck consan). In liraur, w found mos analysis of h RC, RL, LC, and RLC circuis, as a msoscopic sysm or nanophysics, ar commonly discussd and formulad by using h concp of quanum mchanics [7-0]. As w hav alrady known ha h
2 nrgy opraor in quanum mchanics is h Hamilonian which is dfind as h sum of nrgy kinic and nrgy ponial of h physical sysm. In classical mchanics, w also know ha w can formula h physical sysm in form of Lagrangian dfind as h kinic nrgy minus ponial nrgy of h physical sysm. Thus, i is also an inrsing problm o know h xplici form of h Lagrangian for RC, LC, RL, and RLC circuis and is phnomnological implicaions. In his papr, w formula h Lagrangian for LC, RC, RL, and RLC circuis by using h analogy wih h classical mchanics formulaion for a physical sysm. W also discuss h advanags of h lagrangian formulaion of LC, RC, RL, and RLC circuis compar o h o lcrical formulaion as on can find in h mos of h sudn xbooks. W organizd his papr as follow: in scion w driv h Lagrangian for LC circui; in scion 3 w driv h Lagrangian formulaion for h RC circui; in scion 4, w formula h lagrangian for RL circui; in scion 5 w driv h Lagrangian for RLC circui. Finally, in scion 6 w wri h conclusions.. Lagrangian for h LC Circui In his scion, w formula h Lagrangian for h LC circui. W bgin wih by wriing h diffrnial quaion of Kirchhoff s rul for LC circui wihou sourc as follow d q q 0. () d LC By analogy wih h harmonic oscillaor, w can pu h angular frquncy rgarding L and C as follow. () LC As w know from h mahmaical physics, h gnral soluion of Eq. () is givn by i -i q( ) k k (3) whr w can drmin h consans k and k from h appropria boundary valus. Mahmaically, hr is wo possibl iniial condiions for h capacior C. Firs, a im = 0 h capacior has zro chargs: q(0) = 0 and a im = h charg of h capacior rach a maximum valu ha is Q and his procss is known as charging procss. Scond, a im = 0 i is possibl ha h capacior C has iniial charg Q 0 and a im = h capacior has no charg which is known as discharging a capacior. If w pu h h iniial condiion q(0) = 0 ino Eq. (3), hn w hav 0 0 q(0) 0 k k (4) ha implis k k (5) By insring Eq. (5) ino Eq. (3), w obain i i q( ) k( ). (6) If w us Eulr s quaion, hn Eq. (6) rads q( ) ik sin( ). (7) I is clar from Eq. (7) ha h charg as a sin funcion. Th soluion of h diffrnial quaion of Eq. () wih h iniial condiion q(0) = 0 is no rlvan o h physical raliy alhough i is possibl from h mahmaics poin of viw. Thrfor w discard h charging procss wih h soluion in h form of sin funcion. If w pu h iniial condiion q(0) Q0 k k for discharging procss ino Eq. (3), hn w hav k Q0 k. (8) By insring h Eq. (8) ino h Eq. (3) and afr doing a lil algbra, h Eq. (3) bcom -i q( ) Q0 iksin( ). (9) Th scond rm of Eq. (9) dos no saisfy h iniial condiion ha = q = 0, so w drop h scond rm of Eq. (9) and finally, w hav h soluion for discharging capacior in h LC circui as follow
3 -i q( ) Q0. (0) Now, w ar in h posiion o formula h Lagrangian for LC circui. To formula h lagrangian of a physical sysm, w mus know h ponial nrgy and kinic nrgy of h sysm. Th ponial nrgy for h LC circui is givn by V ( q) q. C () By analogy wih h ponial nrgy of harmonic oscillaor, w can pu h corrsponding paramrs as follow m L, x q, k. C () By insring Eq. (0) ino Eq. (), hn w find h ponial nrgy of h LC circui as follow i VLC Q0, C (3) and h kinic nrgy of oscillaor harmonic sysm is Tho mx. (4) By using h analogy in Eq. () and ak drivaiv of Eq. (0), w hav h kinic nrgy of h LC circui as follow i TLC L Q0. (5) From Eqs. (3) and (5), w finally can wri h Lagrangian for h LC circui as follow i i LLC L Q0 Q0, C (6) which is composd of wo rms ha can b pu as kinic nrgy-lik and ponial nrgy-lik. 3. Lagrangian for h RC Circui In his scion, w formula h Lagrangian for h RC circui. Th diffrnial quaion of Kirchhoff s rul for RC circui wihou a sourc is givn by dq q R 0. (7) d C I has alrady known ha hr ar also wo procsss ha can b assignd o h RC circui i.. charging or discharging of h capacior C. By ingraing Eq. (7), and using h valus of q = 0 a im = 0 and q = q a h im =, w hn hav / q ( ) RC. (8) From Eq. (8) i is apparn ha h soluion is unaccpabl bcaus if w pu, hn h charg bcoms zro which is conrary o h physical procss as a charging procss. By ingraing Eq. (8), and using h valus of q = Q 0 a im = 0 and q = q a im =, hn w obain / q( ) Q0 RC. (9) which is rlvan o h physical procss as prviously sad. I is clar ha hr is no kinic nrgy rm for h RC circui. Th ponial nrgy in h RC circui as follows / RC VRC Q0. (0) C Bcaus hr is no kinic nrgy in h RC circui, hn h Lagrangian of RC circui as follows / RC LRC Q0. () C
4 4. Lagrangian for h RL Circui Th diffrnial quaion for h RL circui is givn by di L RI 0 d. () Th soluion of h Eq. () rad / I( ) I0 R L. (3) For h RL circui, w can mak an analogy wih h quaion of moion of a paricl wih h forc is vlociy dpndn as follow dv m kv 0, (4) d By puing L corrspond o mass m and h rsisanc R corrspond o fricion consan k, hn w can pu h currn I in Eq. (3) as a corrsponding vlociy in Eq. (4). To formula h kinic nrgy of h RL circui, w us h analogy concp by using h usual mchanical kinic nrgy ½ mv and lcric currn I corrspond wih vlociy v, and hn w hav R / L TRL LI0 (5) as h kinic nrgy rm for RL circui. For h RL circui, hr is no ponial nrgy rm. Thus, h lagrangian for h RL circui rad R / L LRL LI0. (6) 5. Lagrangian for h RLC Circui Th diffrnial quaion for h RLC circui as follows d q dq q L R 0 d d C or d q R dq q 0 (7) d L d LC By using analogy wih a dampd harmonic oscillaor, w hav R, 0 (8) L LC whr γ and ω 0 as damping facor and naural frquncy rspcivly. Th gnral soluion of Eq. (7) as follows ( ) ( ) q( ) C C (9) whr 0. (30) Thr ar hr possibl cass for h paramr i.. ovrdamping, criical damping and undrdamping. 5. Ovrdamping Ovrdamping will occur whn λ > 0 so h xponns in h firs and scond rm in Eq. (9) ar ral. If w insr h discharging capacior boundary condiion ino Eq. (9), hn w hav h soluion as follow ( ) q( ) Q0. (3) By using h sam procdur o formula h Lagrangian for LC circui, w hn hav h Lagrangian for ovrdamping RLC circui as follow
5 ( ) ( ) 0 ( ) 0 Q LRLCovr L Q. (3) C Afr doing a lil algbra ha is by xpanding and simplifying λ and γ, h Eq. (3) bcom R R 4 R R 4 L L LC R R R 4 L L LC Q0 Q 0 L C L LC C LRLCovr. (33) On can s ha h Lagrangian for ovrdamping RLC circui as shown in Eq. (33) is composd of wo rms i.. kinic nrgy-lik and ponial nrgy-lik. 5. Criical Damping Criical damping will occur whn λ = 0. As shown in [6], h Eq (9) bcoms q( ) C C. (34) By insring h discharging capacior boundary condiion hn Eq (34) bcoms q( ) Q0 (35) and by using h sam procdur as prviously, w find h Lagrangian for h criical damping RLC circui as follow R / L R R / L Q0 LRLCcri Q0, (36) 8 L C which is composd of wo rms i.. nrgy kinic lik and ponial nrgy-lik. 5.3 Undrdamping Th RLC circui will undrgo h undrdamping whn λ < 0, and h gnral soluion for h cas of undrdamping RLC circui can b rad in [6] q( ) Acos( d 0) (37) whr R 0. (38) LC 4L By insring h discharging capacior boundary condiion and w s h iniial phas angl θ 0 by 0 o, hn Eq (37) bcom q( ) Q0 cos( ) (39) and w obain h lagrangian for h undrdamping RLC circui as follow R /L R Q0 cos 0 cos 0 sin R LRLCund L Q Q (40) L LC 4L C By inspcing Eq. (4), w can s ha h firs rm is kinic nrgy-lik and h scond rm is ponial nrgy-lik. I is clar from Eqs. (33), (36), and (40) ha h Lagrangians for h RLC circui ar h sum of h kinic nrgy-lik and ponial nrgy-lik as wll as on can find in classical mchanics. I can b sad ha h Lagrangian rms of h RLC circui indpndn of h valu of λ qualiaivly. 6. Conclusions W hav sudid and valuad h Lagrangian for LC, RC, LR, and RLC circuis by using h analogy wih h classical mchanics concp o formula h lagrangian of a physical sysm. W find ha h lagrangian for LC and RLC circuis ar composd of rms ha can b assignd as kinic nrgy and ponial nrgy rms in corrsponding wih h Lagrangian of a physical sysm in classical mchanics. Manwhil, h Lagrangian for h RC circui is only from ponial nrgy-lik conribuion and h and h lagrangian for h LR circui is only kinic nrgy-lik conribuion. W
6 also find ha h conribuion rms o h Lagrangian of h LRC circui indpndn of h valu of λ qualiaivly. Rfrncs [] Arya A P 998 Inroducion o Classical Mchanics nd Ediion (Nw Jrsy: Prnic-Hall) [] Fowls R and Cassiday G L 005 Analyical Mchanics 7h Ediion (Conncicu: Thomson Larning Inc.) [3] Srway R A and Jw J W 008 Physics for Sciniss and Enginrs wih Modrn Physics 7h Ediion (Conncicu: Thomson Larning Inc.) [4] Boas M L 006 Mahmaical Mhods in h Physical Scincs 3rd Ediion (Nw Jrsy: John Wily&Sons) [5] Pdrosa I A and Pinhiro A P 0 On h quanizaion of h dissipaiv sysms Prog. Thor. Phys [6] Urras-Diaz C A 008 Discr charg quanum circuis and lcrical rsianc Phys. L. A [7] Buo F A 993 Msoscopic physics and nanolcronics: nanoscinc and nanochnology Phys. Rp [8] Li Y Q and Chn B 996 Quanum hory for msoscopic lcric circuis Phys. Rv. B [9] Lu T and Li Y Q 00 Msoscopic circui wih linar dissipaion Mod. Phys. L. B [0] Flors J C and Urraz-Diaz C A 00 Msoscopic circuis wih charg discrnss: Quanum currn magnificaion for muual inducancs Phys. Rv. B
General Article Application of differential equation in L-R and C-R circuit analysis by classical method. Abstract
 Applicaion of Diffrnial... Gnral Aricl Applicaion of diffrnial uaion in - and C- circui analysis by classical mhod. ajndra Prasad gmi curr, Dparmn of Mahmaics, P.N. Campus, Pokhara Email: rajndraprasadrgmi@yahoo.com
Applicaion of Diffrnial... Gnral Aricl Applicaion of diffrnial uaion in - and C- circui analysis by classical mhod. ajndra Prasad gmi curr, Dparmn of Mahmaics, P.N. Campus, Pokhara Email: rajndraprasadrgmi@yahoo.com
Charging of capacitor through inductor and resistor
 cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
cur 4&: R circui harging of capacior hrough inducor and rsisor us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R, an inducor of inducanc and a y K in sris.
On the Derivatives of Bessel and Modified Bessel Functions with Respect to the Order and the Argument
 Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn
Inrnaional Rsarch Journal of Applid Basic Scincs 03 Aailabl onlin a wwwirjabscom ISSN 5-838X / Vol 4 (): 47-433 Scinc Eplorr Publicaions On h Driais of Bssl Modifid Bssl Funcions wih Rspc o h Ordr h Argumn
Boyce/DiPrima 9 th ed, Ch 2.1: Linear Equations; Method of Integrating Factors
 Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Boc/DiPrima 9 h d, Ch.: Linar Equaions; Mhod of Ingraing Facors Elmnar Diffrnial Equaions and Boundar Valu Problms, 9 h diion, b William E. Boc and Richard C. DiPrima, 009 b John Wil & Sons, Inc. A linar
Lecture 2: Current in RC circuit D.K.Pandey
 Lcur 2: urrn in circui harging of apacior hrough Rsisr L us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R and a ky K in sris. Whn h ky K is swichd on, h charging
Lcur 2: urrn in circui harging of apacior hrough Rsisr L us considr a capacior of capacianc is conncd o a D sourc of.m.f. E hrough a rsisr of rsisanc R and a ky K in sris. Whn h ky K is swichd on, h charging
Transfer function and the Laplace transformation
 Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
Lab No PH-35 Porland Sa Univriy A. La Roa Tranfr funcion and h Laplac ranformaion. INTRODUTION. THE LAPLAE TRANSFORMATION L 3. TRANSFER FUNTIONS 4. ELETRIAL SYSTEMS Analyi of h hr baic paiv lmn R, and
CSE 245: Computer Aided Circuit Simulation and Verification
 CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
CSE 45: Compur Aidd Circui Simulaion and Vrificaion Fall 4, Sp 8 Lcur : Dynamic Linar Sysm Oulin Tim Domain Analysis Sa Equaions RLC Nwork Analysis by Taylor Expansion Impuls Rspons in im domain Frquncy
A HAMILTON-JACOBI TREATMENT OF DISSIPATIVE SYSTEMS
 Europan Scinific Journal Ocobr 13 diion vol9, No3 ISSN: 1857 7881 (Prin) - ISSN 1857-7431 A AMILTON-JACOBI TREATMENT OF DISSIPATIVE SYSTEMS Ola A Jarab'ah Tafila Tchnical Univrsiy, Tafila, Jordan Khald
Europan Scinific Journal Ocobr 13 diion vol9, No3 ISSN: 1857 7881 (Prin) - ISSN 1857-7431 A AMILTON-JACOBI TREATMENT OF DISSIPATIVE SYSTEMS Ola A Jarab'ah Tafila Tchnical Univrsiy, Tafila, Jordan Khald
Elementary Differential Equations and Boundary Value Problems
 Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
Elmnar Diffrnial Equaions and Boundar Valu Problms Boc. & DiPrima 9 h Ediion Chapr : Firs Ordr Diffrnial Equaions 00600 คณ ตศาสตร ว ศวกรรม สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา /55 ผศ.ดร.อร ญญา ผศ.ดร.สมศ
Wave Equation (2 Week)
 Rfrnc Wav quaion ( Wk 6.5 Tim-armonic filds 7. Ovrviw 7. Plan Wavs in Losslss Mdia 7.3 Plan Wavs in Loss Mdia 7.5 Flow of lcromagnic Powr and h Poning Vcor 7.6 Normal Incidnc of Plan Wavs a Plan Boundaris
Rfrnc Wav quaion ( Wk 6.5 Tim-armonic filds 7. Ovrviw 7. Plan Wavs in Losslss Mdia 7.3 Plan Wavs in Loss Mdia 7.5 Flow of lcromagnic Powr and h Poning Vcor 7.6 Normal Incidnc of Plan Wavs a Plan Boundaris
Midterm exam 2, April 7, 2009 (solutions)
 Univrsiy of Pnnsylvania Dparmn of Mahmaics Mah 26 Honors Calculus II Spring Smsr 29 Prof Grassi, TA Ashr Aul Midrm xam 2, April 7, 29 (soluions) 1 Wri a basis for h spac of pairs (u, v) of smooh funcions
Univrsiy of Pnnsylvania Dparmn of Mahmaics Mah 26 Honors Calculus II Spring Smsr 29 Prof Grassi, TA Ashr Aul Midrm xam 2, April 7, 29 (soluions) 1 Wri a basis for h spac of pairs (u, v) of smooh funcions
Spring 2006 Process Dynamics, Operations, and Control Lesson 2: Mathematics Review
 Spring 6 Procss Dynamics, Opraions, and Conrol.45 Lsson : Mahmaics Rviw. conx and dircion Imagin a sysm ha varis in im; w migh plo is oupu vs. im. A plo migh imply an quaion, and h quaion is usually an
Spring 6 Procss Dynamics, Opraions, and Conrol.45 Lsson : Mahmaics Rviw. conx and dircion Imagin a sysm ha varis in im; w migh plo is oupu vs. im. A plo migh imply an quaion, and h quaion is usually an
Voltage v(z) ~ E(z)D. We can actually get to this wave behavior by using circuit theory, w/o going into details of the EM fields!
 Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Lecture 1: Growth and decay of current in RL circuit. Growth of current in LR Circuit. D.K.Pandey
 cur : Growh and dcay of currn in circui Growh of currn in Circui us considr an inducor of slf inducanc is conncd o a DC sourc of.m.f. E hrough a rsisr of rsisanc and a ky K in sris. Whn h ky K is swichd
cur : Growh and dcay of currn in circui Growh of currn in Circui us considr an inducor of slf inducanc is conncd o a DC sourc of.m.f. E hrough a rsisr of rsisanc and a ky K in sris. Whn h ky K is swichd
whereby we can express the phase by any one of the formulas cos ( 3 whereby we can express the phase by any one of the formulas
 Third In-Class Exam Soluions Mah 6, Profssor David Lvrmor Tusday, 5 April 07 [0] Th vrical displacmn of an unforcd mass on a spring is givn by h 5 3 cos 3 sin a [] Is his sysm undampd, undr dampd, criically
Third In-Class Exam Soluions Mah 6, Profssor David Lvrmor Tusday, 5 April 07 [0] Th vrical displacmn of an unforcd mass on a spring is givn by h 5 3 cos 3 sin a [] Is his sysm undampd, undr dampd, criically
Physics 160 Lecture 3. R. Johnson April 6, 2015
 Physics 6 Lcur 3 R. Johnson April 6, 5 RC Circui (Low-Pass Filr This is h sam RC circui w lookd a arlir h im doma, bu hr w ar rsd h frquncy rspons. So w pu a s wav sad of a sp funcion. whr R C RC Complx
Physics 6 Lcur 3 R. Johnson April 6, 5 RC Circui (Low-Pass Filr This is h sam RC circui w lookd a arlir h im doma, bu hr w ar rsd h frquncy rspons. So w pu a s wav sad of a sp funcion. whr R C RC Complx
7.4 QUANTUM MECHANICAL TREATMENT OF FLUCTUATIONS *
 Andri Tokmakoff, MIT Dparmn of Chmisry, 5/19/5 7-11 7.4 QUANTUM MECANICAL TREATMENT OF FLUCTUATIONS * Inroducion and Prviw Now h origin of frquncy flucuaions is inracions of our molcul (or mor approprialy
Andri Tokmakoff, MIT Dparmn of Chmisry, 5/19/5 7-11 7.4 QUANTUM MECANICAL TREATMENT OF FLUCTUATIONS * Inroducion and Prviw Now h origin of frquncy flucuaions is inracions of our molcul (or mor approprialy
REPETITION before the exam PART 2, Transform Methods. Laplace transforms: τ dτ. L1. Derive the formulas : L2. Find the Laplace transform F(s) if.
 Tranform Mhod and Calculu of Svral Variabl H7, p Lcurr: Armin Halilovic KTH, Campu Haning E-mail: armin@dkh, wwwdkh/armin REPETITION bfor h am PART, Tranform Mhod Laplac ranform: L Driv h formula : a L[
Tranform Mhod and Calculu of Svral Variabl H7, p Lcurr: Armin Halilovic KTH, Campu Haning E-mail: armin@dkh, wwwdkh/armin REPETITION bfor h am PART, Tranform Mhod Laplac ranform: L Driv h formula : a L[
On the Speed of Heat Wave. Mihály Makai
 On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.
On h Spd of Ha Wa Mihály Maai maai@ra.bm.hu Conns Formulaion of h problm: infini spd? Local hrmal qulibrium (LTE hypohsis Balanc quaion Phnomnological balanc Spd of ha wa Applicaion in plasma ranspor 1.
An Indian Journal FULL PAPER. Trade Science Inc. A stage-structured model of a single-species with density-dependent and birth pulses ABSTRACT
 [Typ x] [Typ x] [Typ x] ISSN : 974-7435 Volum 1 Issu 24 BioTchnology 214 An Indian Journal FULL PAPE BTAIJ, 1(24), 214 [15197-1521] A sag-srucurd modl of a singl-spcis wih dnsiy-dpndn and birh pulss LI
[Typ x] [Typ x] [Typ x] ISSN : 974-7435 Volum 1 Issu 24 BioTchnology 214 An Indian Journal FULL PAPE BTAIJ, 1(24), 214 [15197-1521] A sag-srucurd modl of a singl-spcis wih dnsiy-dpndn and birh pulss LI
LaPlace Transform in Circuit Analysis
 LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz
LaPlac Tranform in Circui Analyi Obciv: Calcula h Laplac ranform of common funcion uing h dfiniion and h Laplac ranform abl Laplac-ranform a circui, including componn wih non-zro iniial condiion. Analyz
UNSTEADY FLOW OF A FLUID PARTICLE SUSPENSION BETWEEN TWO PARALLEL PLATES SUDDENLY SET IN MOTION WITH SAME SPEED
 006-0 Asian Rsarch Publishing work (ARP). All righs rsrvd. USTEADY FLOW OF A FLUID PARTICLE SUSPESIO BETWEE TWO PARALLEL PLATES SUDDELY SET I MOTIO WITH SAME SPEED M. suniha, B. Shankr and G. Shanha 3
006-0 Asian Rsarch Publishing work (ARP). All righs rsrvd. USTEADY FLOW OF A FLUID PARTICLE SUSPESIO BETWEE TWO PARALLEL PLATES SUDDELY SET I MOTIO WITH SAME SPEED M. suniha, B. Shankr and G. Shanha 3
Double Slits in Space and Time
 Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
Doubl Slis in Sac an Tim Gorg Jons As has bn ror rcnly in h mia, a am l by Grhar Paulus has monsra an inrsing chniqu for ionizing argon aoms by using ulra-shor lasr ulss. Each lasr uls is ffcivly on an
A MATHEMATICAL MODEL FOR NATURAL COOLING OF A CUP OF TEA
 MTHEMTICL MODEL FOR NTURL COOLING OF CUP OF TE 1 Mrs.D.Kalpana, 2 Mr.S.Dhvarajan 1 Snior Lcurr, Dparmn of Chmisry, PSB Polychnic Collg, Chnnai, India. 2 ssisan Profssor, Dparmn of Mahmaics, Dr.M.G.R Educaional
MTHEMTICL MODEL FOR NTURL COOLING OF CUP OF TE 1 Mrs.D.Kalpana, 2 Mr.S.Dhvarajan 1 Snior Lcurr, Dparmn of Chmisry, PSB Polychnic Collg, Chnnai, India. 2 ssisan Profssor, Dparmn of Mahmaics, Dr.M.G.R Educaional
Applied Statistics and Probability for Engineers, 6 th edition October 17, 2016
 Applid Saisics and robabiliy for Enginrs, 6 h diion Ocobr 7, 6 CHATER Scion - -. a d. 679.. b. d. 88 c d d d. 987 d. 98 f d.. Thn, = ln. =. g d.. Thn, = ln.9 =.. -7. a., by symmry. b.. d...6. 7.. c...
Applid Saisics and robabiliy for Enginrs, 6 h diion Ocobr 7, 6 CHATER Scion - -. a d. 679.. b. d. 88 c d d d. 987 d. 98 f d.. Thn, = ln. =. g d.. Thn, = ln.9 =.. -7. a., by symmry. b.. d...6. 7.. c...
Review Lecture 5. The source-free R-C/R-L circuit Step response of an RC/RL circuit. The time constant = RC The final capacitor voltage v( )
 Rviw Lcur 5 Firs-ordr circui Th sourc-fr R-C/R-L circui Sp rspons of an RC/RL circui v( ) v( ) [ v( 0) v( )] 0 Th i consan = RC Th final capacior volag v() Th iniial capacior volag v( 0 ) Volag/currn-division
Rviw Lcur 5 Firs-ordr circui Th sourc-fr R-C/R-L circui Sp rspons of an RC/RL circui v( ) v( ) [ v( 0) v( )] 0 Th i consan = RC Th final capacior volag v() Th iniial capacior volag v( 0 ) Volag/currn-division
H is equal to the surface current J S
 Chapr 6 Rflcion and Transmission of Wavs 6.1 Boundary Condiions A h boundary of wo diffrn mdium, lcromagnic fild hav o saisfy physical condiion, which is drmind by Maxwll s quaion. This is h boundary condiion
Chapr 6 Rflcion and Transmission of Wavs 6.1 Boundary Condiions A h boundary of wo diffrn mdium, lcromagnic fild hav o saisfy physical condiion, which is drmind by Maxwll s quaion. This is h boundary condiion
Boyce/DiPrima 9 th ed, Ch 7.8: Repeated Eigenvalues
 Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
Boy/DiPrima 9 h d Ch 7.8: Rpad Eignvalus Elmnary Diffrnial Equaions and Boundary Valu Problms 9 h diion by William E. Boy and Rihard C. DiPrima 9 by John Wily & Sons In. W onsidr again a homognous sysm
I) Title: Rational Expectations and Adaptive Learning. II) Contents: Introduction to Adaptive Learning
 I) Til: Raional Expcaions and Adapiv Larning II) Conns: Inroducion o Adapiv Larning III) Documnaion: - Basdvan, Olivir. (2003). Larning procss and raional xpcaions: an analysis using a small macroconomic
I) Til: Raional Expcaions and Adapiv Larning II) Conns: Inroducion o Adapiv Larning III) Documnaion: - Basdvan, Olivir. (2003). Larning procss and raional xpcaions: an analysis using a small macroconomic
C From Faraday's Law, the induced voltage is, C The effect of electromagnetic induction in the coil itself is called selfinduction.
 Inducors and Inducanc C For inducors, v() is proporional o h ra of chang of i(). Inducanc (con d) C Th proporionaliy consan is h inducanc, L, wih unis of Hnris. 1 Hnry = 1 Wb / A or 1 V sc / A. C L dpnds
Inducors and Inducanc C For inducors, v() is proporional o h ra of chang of i(). Inducanc (con d) C Th proporionaliy consan is h inducanc, L, wih unis of Hnris. 1 Hnry = 1 Wb / A or 1 V sc / A. C L dpnds
ECE 2100 Circuit Analysis
 ECE 1 Circui Analysis Lesson 35 Chaper 8: Second Order Circuis Daniel M. Liynski, Ph.D. ECE 1 Circui Analysis Lesson 3-34 Chaper 7: Firs Order Circuis (Naural response RC & RL circuis, Singulariy funcions,
ECE 1 Circui Analysis Lesson 35 Chaper 8: Second Order Circuis Daniel M. Liynski, Ph.D. ECE 1 Circui Analysis Lesson 3-34 Chaper 7: Firs Order Circuis (Naural response RC & RL circuis, Singulariy funcions,
Chapter 5 The Laplace Transform. x(t) input y(t) output Dynamic System
 EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +
EE 422G No: Chapr 5 Inrucor: Chung Chapr 5 Th Laplac Tranform 5- Inroducion () Sym analyi inpu oupu Dynamic Sym Linar Dynamic ym: A procor which proc h inpu ignal o produc h oupu dy ( n) ( n dy ( n) +
UNIT #5 EXPONENTIAL AND LOGARITHMIC FUNCTIONS
 Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Answr Ky Nam: Da: UNIT # EXPONENTIAL AND LOGARITHMIC FUNCTIONS Par I Qusions. Th prssion is quivaln o () () 6 6 6. Th ponnial funcion y 6 could rwrin as y () y y 6 () y y (). Th prssion a is quivaln o
Voltage v(z) ~ E(z)D. We can actually get to this wave behavior by using circuit theory, w/o going into details of the EM fields!
 Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Considr a pair of wirs idal wirs ngh >, say, infinily long olag along a cabl can vary! D olag v( E(D W can acually g o his wav bhavior by using circui hory, w/o going ino dails of h EM filds! Thr
Lecture 4: Laplace Transforms
 Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
Lur 4: Lapla Transforms Lapla and rlad ransformaions an b usd o solv diffrnial quaion and o rdu priodi nois in signals and imags. Basially, hy onvr h drivaiv opraions ino mulipliaion, diffrnial quaions
2.1. Differential Equations and Solutions #3, 4, 17, 20, 24, 35
 MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
MATH 5 PS # Summr 00.. Diffrnial Equaions and Soluions PS.# Show ha ()C #, 4, 7, 0, 4, 5 ( / ) is a gnral soluion of h diffrnial quaion. Us a compur or calculaor o skch h soluions for h givn valus of h
EXERCISE - 01 CHECK YOUR GRASP
 DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
DIFFERENTIAL EQUATION EXERCISE - CHECK YOUR GRASP 7. m hn D() m m, D () m m. hn givn D () m m D D D + m m m m m m + m m m m + ( m ) (m ) (m ) (m + ) m,, Hnc numbr of valus of mn will b. n ( ) + c sinc
Logistic equation of Human population growth (generalization to the case of reactive environment).
 Logisic quaion of Human populaion growh gnralizaion o h cas of raciv nvironmn. Srg V. Ershkov Insiu for Tim aur Exploraions M.V. Lomonosov's Moscow Sa Univrsi Lninski gor - Moscow 999 ussia -mail: srgj-rshkov@andx.ru
Logisic quaion of Human populaion growh gnralizaion o h cas of raciv nvironmn. Srg V. Ershkov Insiu for Tim aur Exploraions M.V. Lomonosov's Moscow Sa Univrsi Lninski gor - Moscow 999 ussia -mail: srgj-rshkov@andx.ru
Let s look again at the first order linear differential equation we are attempting to solve, in its standard form:
 Th Ingraing Facor Mhod In h prvious xampls of simpl firs ordr ODEs, w found h soluions by algbraically spara h dpndn variabl- and h indpndn variabl- rms, and wri h wo sids of a givn quaion as drivaivs,
Th Ingraing Facor Mhod In h prvious xampls of simpl firs ordr ODEs, w found h soluions by algbraically spara h dpndn variabl- and h indpndn variabl- rms, and wri h wo sids of a givn quaion as drivaivs,
Control System Engineering (EE301T) Assignment: 2
 Conrol Sysm Enginring (EE0T) Assignmn: PART-A (Tim Domain Analysis: Transin Rspons Analysis). Oain h rspons of a uniy fdack sysm whos opn-loop ransfr funcion is (s) s ( s 4) for a uni sp inpu and also
Conrol Sysm Enginring (EE0T) Assignmn: PART-A (Tim Domain Analysis: Transin Rspons Analysis). Oain h rspons of a uniy fdack sysm whos opn-loop ransfr funcion is (s) s ( s 4) for a uni sp inpu and also
fiziks Institute for NET/JRF, GATE, IIT JAM, JEST, TIFR and GRE in PHYSICAL SCIENCES MATEMATICAL PHYSICS SOLUTIONS are
 MTEMTICL PHYSICS SOLUTIONS GTE- Q. Considr an ani-symmric nsor P ij wih indics i and j running from o 5. Th numbr of indpndn componns of h nsor is 9 6 ns: Soluion: Th numbr of indpndn componns of h nsor
MTEMTICL PHYSICS SOLUTIONS GTE- Q. Considr an ani-symmric nsor P ij wih indics i and j running from o 5. Th numbr of indpndn componns of h nsor is 9 6 ns: Soluion: Th numbr of indpndn componns of h nsor
A Condition for Stability in an SIR Age Structured Disease Model with Decreasing Survival Rate
 A Condiion for abiliy in an I Ag rucurd Disas Modl wih Dcrasing urvival a A.K. upriana, Edy owono Dparmn of Mahmaics, Univrsias Padjadjaran, km Bandung-umng 45363, Indonsia fax: 6--7794696, mail: asupria@yahoo.com.au;
A Condiion for abiliy in an I Ag rucurd Disas Modl wih Dcrasing urvival a A.K. upriana, Edy owono Dparmn of Mahmaics, Univrsias Padjadjaran, km Bandung-umng 45363, Indonsia fax: 6--7794696, mail: asupria@yahoo.com.au;
Chapter 3: Fourier Representation of Signals and LTI Systems. Chih-Wei Liu
 Chapr 3: Fourir Rprsnaion of Signals and LTI Sysms Chih-Wi Liu Oulin Inroducion Complx Sinusoids and Frquncy Rspons Fourir Rprsnaions for Four Classs of Signals Discr-im Priodic Signals Fourir Sris Coninuous-im
Chapr 3: Fourir Rprsnaion of Signals and LTI Sysms Chih-Wi Liu Oulin Inroducion Complx Sinusoids and Frquncy Rspons Fourir Rprsnaions for Four Classs of Signals Discr-im Priodic Signals Fourir Sris Coninuous-im
S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]
![S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15] S.Y. B.Sc. (IT) : Sem. III. Applied Mathematics. Q.1 Attempt the following (any THREE) [15]](/thumbs/92/108666103.jpg) S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
S.Y. B.Sc. (IT) : Sm. III Applid Mahmaics Tim : ½ Hrs.] Prlim Qusion Papr Soluion [Marks : 75 Q. Amp h following (an THREE) 3 6 Q.(a) Rduc h mari o normal form and find is rank whr A 3 3 5 3 3 3 6 Ans.:
5. An object moving along an x-coordinate axis with its scale measured in meters has a velocity of 6t
 AP CALCULUS FINAL UNIT WORKSHEETS ACCELERATION, VELOCTIY AND POSITION In problms -, drmin h posiion funcion, (), from h givn informaion.. v (), () = 5. v ()5, () = b g. a (), v() =, () = -. a (), v() =
AP CALCULUS FINAL UNIT WORKSHEETS ACCELERATION, VELOCTIY AND POSITION In problms -, drmin h posiion funcion, (), from h givn informaion.. v (), () = 5. v ()5, () = b g. a (), v() =, () = -. a (), v() =
Circuit Transients time
 Circui Tranin A Solp 3/29/0, 9/29/04. Inroducion Tranin: A ranin i a raniion from on a o anohr. If h volag and currn in a circui do no chang wih im, w call ha a "ady a". In fac, a long a h volag and currn
Circui Tranin A Solp 3/29/0, 9/29/04. Inroducion Tranin: A ranin i a raniion from on a o anohr. If h volag and currn in a circui do no chang wih im, w call ha a "ady a". In fac, a long a h volag and currn
CHAPTER. Linear Systems of Differential Equations. 6.1 Theory of Linear DE Systems. ! Nullcline Sketching. Equilibrium (unstable) at (0, 0)
 CHATER 6 inar Sysms of Diffrnial Equaions 6 Thory of inar DE Sysms! ullclin Skching = y = y y υ -nullclin Equilibrium (unsabl) a (, ) h nullclin y = υ nullclin = h-nullclin (S figur) = + y y = y Equilibrium
CHATER 6 inar Sysms of Diffrnial Equaions 6 Thory of inar DE Sysms! ullclin Skching = y = y y υ -nullclin Equilibrium (unsabl) a (, ) h nullclin y = υ nullclin = h-nullclin (S figur) = + y y = y Equilibrium
Lecture 1: Numerical Integration The Trapezoidal and Simpson s Rule
 Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Lcur : Numrical ngraion Th Trapzoidal and Simpson s Rul A problm Th probabiliy of a normally disribud (man µ and sandard dviaion σ ) vn occurring bwn h valus a and b is B A P( a x b) d () π whr a µ b -
Chapter 12 Introduction To The Laplace Transform
 Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and
Chapr Inroducion To Th aplac Tranorm Diniion o h aplac Tranorm - Th Sp & Impul uncion aplac Tranorm o pciic uncion 5 Opraional Tranorm Applying h aplac Tranorm 7 Invr Tranorm o Raional uncion 8 Pol and
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS. Assoc. Prof. Dr. Burak Kelleci. Spring 2018
 DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion
DEPARTMENT OF ELECTRICAL &ELECTRONICS ENGINEERING SIGNALS AND SYSTEMS Aoc. Prof. Dr. Burak Kllci Spring 08 OUTLINE Th Laplac Tranform Rgion of convrgnc for Laplac ranform Invr Laplac ranform Gomric valuaion
Impulsive Differential Equations. by using the Euler Method
 Applid Mahmaical Scincs Vol. 4 1 no. 65 19 - Impulsiv Diffrnial Equaions by using h Eulr Mhod Nor Shamsidah B Amir Hamzah 1 Musafa bin Mama J. Kaviumar L Siaw Chong 4 and Noor ani B Ahmad 5 1 5 Dparmn
Applid Mahmaical Scincs Vol. 4 1 no. 65 19 - Impulsiv Diffrnial Equaions by using h Eulr Mhod Nor Shamsidah B Amir Hamzah 1 Musafa bin Mama J. Kaviumar L Siaw Chong 4 and Noor ani B Ahmad 5 1 5 Dparmn
Copyright 2012 Pearson Education, Inc. Publishing as Prentice Hall.
 Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
Chapr Rviw 0 6. ( a a ln a. This will qual a if an onl if ln a, or a. + k an (ln + c. Thrfor, a an valu of, whr h wo curvs inrsc, h wo angn lins will b prpnicular. 6. (a Sinc h lin passs hrough h origin
10. If p and q are the lengths of the perpendiculars from the origin on the tangent and the normal to the curve
 0. If p and q ar h lnghs of h prpndiculars from h origin on h angn and h normal o h curv + Mahmaics y = a, hn 4p + q = a a (C) a (D) 5a 6. Wha is h diffrnial quaion of h family of circls having hir cnrs
0. If p and q ar h lnghs of h prpndiculars from h origin on h angn and h normal o h curv + Mahmaics y = a, hn 4p + q = a a (C) a (D) 5a 6. Wha is h diffrnial quaion of h family of circls having hir cnrs
AR(1) Process. The first-order autoregressive process, AR(1) is. where e t is WN(0, σ 2 )
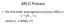 AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
AR() Procss Th firs-ordr auorgrssiv procss, AR() is whr is WN(0, σ ) Condiional Man and Varianc of AR() Condiional man: Condiional varianc: ) ( ) ( Ω Ω E E ) var( ) ) ( var( ) var( σ Ω Ω Ω Ω E Auocovarianc
A THREE COMPARTMENT MATHEMATICAL MODEL OF LIVER
 A THREE COPARTENT ATHEATICAL ODEL OF LIVER V. An N. Ch. Paabhi Ramacharyulu Faculy of ahmaics, R D collgs, Hanamonda, Warangal, India Dparmn of ahmaics, Naional Insiu of Tchnology, Warangal, India E-ail:
A THREE COPARTENT ATHEATICAL ODEL OF LIVER V. An N. Ch. Paabhi Ramacharyulu Faculy of ahmaics, R D collgs, Hanamonda, Warangal, India Dparmn of ahmaics, Naional Insiu of Tchnology, Warangal, India E-ail:
Phys463.nb Conductivity. Another equivalent definition of the Fermi velocity is
 39 Anohr quival dfiniion of h Fri vlociy is pf vf (6.4) If h rgy is a quadraic funcion of k H k L, hs wo dfiniions ar idical. If is NOT a quadraic funcion of k (which could happ as will b discussd in h
39 Anohr quival dfiniion of h Fri vlociy is pf vf (6.4) If h rgy is a quadraic funcion of k H k L, hs wo dfiniions ar idical. If is NOT a quadraic funcion of k (which could happ as will b discussd in h
Voltage/current relationship Stored Energy. RL / RC circuits Steady State / Transient response Natural / Step response
 Review Capaciors/Inducors Volage/curren relaionship Sored Energy s Order Circuis RL / RC circuis Seady Sae / Transien response Naural / Sep response EE4 Summer 5: Lecure 5 Insrucor: Ocavian Florescu Lecure
Review Capaciors/Inducors Volage/curren relaionship Sored Energy s Order Circuis RL / RC circuis Seady Sae / Transien response Naural / Sep response EE4 Summer 5: Lecure 5 Insrucor: Ocavian Florescu Lecure
Lecture 13 RC/RL Circuits, Time Dependent Op Amp Circuits
 Lecure 13 RC/RL Circuis, Time Dependen Op Amp Circuis RL Circuis The seps involved in solving simple circuis conaining dc sources, resisances, and one energy-sorage elemen (inducance or capaciance) are:
Lecure 13 RC/RL Circuis, Time Dependen Op Amp Circuis RL Circuis The seps involved in solving simple circuis conaining dc sources, resisances, and one energy-sorage elemen (inducance or capaciance) are:
Computational prediction of high ZT of n-type Mg 3 Sb 2 - based compounds with isotropic thermoelectric conduction performance
 Elcronic Supplnary Marial (ES for Physical Chisry Chical Physics. This journal is h Ownr Sociis 08 Supporing nforaion Copuaional prdicion of high ZT of n-yp Mg 3 Sb - basd copounds wih isoropic hrolcric
Elcronic Supplnary Marial (ES for Physical Chisry Chical Physics. This journal is h Ownr Sociis 08 Supporing nforaion Copuaional prdicion of high ZT of n-yp Mg 3 Sb - basd copounds wih isoropic hrolcric
Ministry of Education and Science of Ukraine National Technical University Ukraine "Igor Sikorsky Kiev Polytechnic Institute"
 Minisry of Educaion and Scinc of Ukrain Naional Tchnical Univrsiy Ukrain "Igor Sikorsky Kiv Polychnic Insiu" OPERATION CALCULATION Didacic marial for a modal rfrnc work on mahmaical analysis for sudns
Minisry of Educaion and Scinc of Ukrain Naional Tchnical Univrsiy Ukrain "Igor Sikorsky Kiv Polychnic Insiu" OPERATION CALCULATION Didacic marial for a modal rfrnc work on mahmaical analysis for sudns
EE 350 Signals and Systems Spring 2005 Sample Exam #2 - Solutions
 EE 35 Signals an Sysms Spring 5 Sampl Exam # - Soluions. For h following signal x( cos( sin(3 - cos(5 - T, /T x( j j 3 j 3 j j 5 j 5 j a -, a a -, a a - ½, a 3 /j-j -j/, a -3 -/jj j/, a 5 -½, a -5 -½,
EE 35 Signals an Sysms Spring 5 Sampl Exam # - Soluions. For h following signal x( cos( sin(3 - cos(5 - T, /T x( j j 3 j 3 j j 5 j 5 j a -, a a -, a a - ½, a 3 /j-j -j/, a -3 -/jj j/, a 5 -½, a -5 -½,
Section 5 Exercises, Problems, and Solutions. Exercises:
 Scion 5 Exrciss, Problms, and Soluions Exrciss: 1. Tim dpndn prurbaion hory provids an xprssion for h radiaiv lifim of an xcid lcronic sa, givn by τ R : τ h- R 4 c 4(E i - E f ) µ fi, whr i rfrs o h xcid
Scion 5 Exrciss, Problms, and Soluions Exrciss: 1. Tim dpndn prurbaion hory provids an xprssion for h radiaiv lifim of an xcid lcronic sa, givn by τ R : τ h- R 4 c 4(E i - E f ) µ fi, whr i rfrs o h xcid
CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees
![CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees CPSC 211 Data Structures & Implementations (c) Texas A&M University [ 259] B-Trees](/thumbs/74/70718364.jpg) CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs
CPSC 211 Daa Srucurs & Implmnaions (c) Txas A&M Univrsiy [ 259] B-Trs Th AVL r and rd-black r allowd som variaion in h lnghs of h diffrn roo-o-laf pahs. An alrnaiv ida is o mak sur ha all roo-o-laf pahs
Asymptotic Solutions of Fifth Order Critically Damped Nonlinear Systems with Pair Wise Equal Eigenvalues and another is Distinct
 Qus Journals Journal of Rsarch in Applid Mahmaics Volum ~ Issu (5 pp: -5 ISSN(Onlin : 94-74 ISSN (Prin:94-75 www.usjournals.org Rsarch Papr Asympoic Soluions of Fifh Ordr Criically Dampd Nonlinar Sysms
Qus Journals Journal of Rsarch in Applid Mahmaics Volum ~ Issu (5 pp: -5 ISSN(Onlin : 94-74 ISSN (Prin:94-75 www.usjournals.org Rsarch Papr Asympoic Soluions of Fifh Ordr Criically Dampd Nonlinar Sysms
Lab 10: RC, RL, and RLC Circuits
 Lab 10: RC, RL, and RLC Circuis In his experimen, we will invesigae he behavior of circuis conaining combinaions of resisors, capaciors, and inducors. We will sudy he way volages and currens change in
Lab 10: RC, RL, and RLC Circuis In his experimen, we will invesigae he behavior of circuis conaining combinaions of resisors, capaciors, and inducors. We will sudy he way volages and currens change in
Nonlocal Symmetries and Exact Solutions for PIB Equation
 Commun. Thor. Phys. 58 01 331 337 Vol. 58 No. 3 Spmbr 15 01 Nonlocal Symmris and Exac Soluions for PIB Equaion XIN Xiang-Png 1 MIAO Qian 1 and CHEN Yong í 1 1 Shanghai Ky Laboraory of Trusworhy Compuing
Commun. Thor. Phys. 58 01 331 337 Vol. 58 No. 3 Spmbr 15 01 Nonlocal Symmris and Exac Soluions for PIB Equaion XIN Xiang-Png 1 MIAO Qian 1 and CHEN Yong í 1 1 Shanghai Ky Laboraory of Trusworhy Compuing
Coherence and interactions in diffusive systems. Lecture 4. Diffusion + e-e interations
 Cohrnc and inracions in diffusiv sysms G. Monambaux cur 4 iffusion + - inraions nsiy of sas anomaly phasing du o lcron-lcron inracions - inracion andau Frmi liquid picur iffusion slows down lcrons ( )
Cohrnc and inracions in diffusiv sysms G. Monambaux cur 4 iffusion + - inraions nsiy of sas anomaly phasing du o lcron-lcron inracions - inracion andau Frmi liquid picur iffusion slows down lcrons ( )
MATH 308: Diff Eqs, BDP10 EXAMPLES [Belmonte, 2019] 1 Introduction 1.1 Basic Mathematical Models; Direction Fields
![MATH 308: Diff Eqs, BDP10 EXAMPLES [Belmonte, 2019] 1 Introduction 1.1 Basic Mathematical Models; Direction Fields MATH 308: Diff Eqs, BDP10 EXAMPLES [Belmonte, 2019] 1 Introduction 1.1 Basic Mathematical Models; Direction Fields](/thumbs/93/113091114.jpg) MATH 308: Diff Eqs, BDP0 EXAMPLES Blmon, 09 Mos problms ar from NSS9 Inroducion Basic Mahmaical Modls; Dircion Filds / Plo a dircion fild for dy/dx = 4x/y (a) Vrify ha h sraigh lins y = ±x ar soluions
MATH 308: Diff Eqs, BDP0 EXAMPLES Blmon, 09 Mos problms ar from NSS9 Inroducion Basic Mahmaical Modls; Dircion Filds / Plo a dircion fild for dy/dx = 4x/y (a) Vrify ha h sraigh lins y = ±x ar soluions
Wall. x(t) f(t) x(t = 0) = x 0, t=0. which describes the motion of the mass in absence of any external forcing.
 MECHANICS APPLICATIONS OF SECOND-ORDER ODES 7 Mechanics applicaions of second-order ODEs Second-order linear ODEs wih consan coefficiens arise in many physical applicaions. One physical sysems whose behaviour
MECHANICS APPLICATIONS OF SECOND-ORDER ODES 7 Mechanics applicaions of second-order ODEs Second-order linear ODEs wih consan coefficiens arise in many physical applicaions. One physical sysems whose behaviour
Coherence and interactions in diffusive systems. Cours 4. Diffusion + e-e interations
 Cohrnc and inracions in diffusiv sysms G. Monambaux Cours 4 iffusion + - inraions nsiy of sas anomaly phasing du o lcron-lcron inracions Why ar h flucuaions univrsal and wak localizaion is no? ΔG G cl
Cohrnc and inracions in diffusiv sysms G. Monambaux Cours 4 iffusion + - inraions nsiy of sas anomaly phasing du o lcron-lcron inracions Why ar h flucuaions univrsal and wak localizaion is no? ΔG G cl
3.4 Repeated Roots; Reduction of Order
 3.4 Rpd Roos; Rducion of Ordr Rcll our nd ordr linr homognous ODE b c 0 whr, b nd c r consns. Assuming n xponnil soluion lds o chrcrisic quion: r r br c 0 Qudric formul or fcoring ilds wo soluions, r &
3.4 Rpd Roos; Rducion of Ordr Rcll our nd ordr linr homognous ODE b c 0 whr, b nd c r consns. Assuming n xponnil soluion lds o chrcrisic quion: r r br c 0 Qudric formul or fcoring ilds wo soluions, r &
4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b
![4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b 4.1 The Uniform Distribution Def n: A c.r.v. X has a continuous uniform distribution on [a, b] when its pdf is = 1 a x b](/thumbs/71/65779443.jpg) 4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
4. Th Uniform Disribuion Df n: A c.r.v. has a coninuous uniform disribuion on [a, b] whn is pdf is f x a x b b a Also, b + a b a µ E and V Ex4. Suppos, h lvl of unblivabiliy a any poin in a Transformrs
The Optimal Timing of Transition to New Environmental Technology in Economic Growth
 h Opimal iming of ransiion o Nw Environmnal chnology in Economic Growh h IAEE Europan Confrnc 7- Spmbr, 29 Vinna, Ausria Akira AEDA and akiko NAGAYA yoo Univrsiy Background: Growh and h Environmn Naural
h Opimal iming of ransiion o Nw Environmnal chnology in Economic Growh h IAEE Europan Confrnc 7- Spmbr, 29 Vinna, Ausria Akira AEDA and akiko NAGAYA yoo Univrsiy Background: Growh and h Environmn Naural
Electrical Circuits. 1. Circuit Laws. Tools Used in Lab 13 Series Circuits Damped Vibrations: Energy Van der Pol Circuit
 V() R L C 513 Elecrical Circuis Tools Used in Lab 13 Series Circuis Damped Vibraions: Energy Van der Pol Circui A series circui wih an inducor, resisor, and capacior can be represened by Lq + Rq + 1, a
V() R L C 513 Elecrical Circuis Tools Used in Lab 13 Series Circuis Damped Vibraions: Energy Van der Pol Circui A series circui wih an inducor, resisor, and capacior can be represened by Lq + Rq + 1, a
RC, RL and RLC circuits
 Name Dae Time o Complee h m Parner Course/ Secion / Grade RC, RL and RLC circuis Inroducion In his experimen we will invesigae he behavior of circuis conaining combinaions of resisors, capaciors, and inducors.
Name Dae Time o Complee h m Parner Course/ Secion / Grade RC, RL and RLC circuis Inroducion In his experimen we will invesigae he behavior of circuis conaining combinaions of resisors, capaciors, and inducors.
On Ψ-Conditional Asymptotic Stability of First Order Non-Linear Matrix Lyapunov Systems
 In. J. Nonlinar Anal. Appl. 4 (213) No. 1, 7-2 ISSN: 28-6822 (lcronic) hp://www.ijnaa.smnan.ac.ir On Ψ-Condiional Asympoic Sabiliy of Firs Ordr Non-Linar Marix Lyapunov Sysms G. Sursh Kumar a, B. V. Appa
In. J. Nonlinar Anal. Appl. 4 (213) No. 1, 7-2 ISSN: 28-6822 (lcronic) hp://www.ijnaa.smnan.ac.ir On Ψ-Condiional Asympoic Sabiliy of Firs Ordr Non-Linar Marix Lyapunov Sysms G. Sursh Kumar a, B. V. Appa
( ) ( ) + = ( ) + ( )
 Mah 0 Homwork S 6 Soluions 0 oins. ( ps I ll lav i o you vrify ha h omplimnary soluion is : y ( os( sin ( Th guss for h pariular soluion and is drivaivs ar, +. ( os( sin ( ( os( ( sin ( Y ( D 6B os( +
Mah 0 Homwork S 6 Soluions 0 oins. ( ps I ll lav i o you vrify ha h omplimnary soluion is : y ( os( sin ( Th guss for h pariular soluion and is drivaivs ar, +. ( os( sin ( ( os( ( sin ( Y ( D 6B os( +
Arturo R. Samana* in collaboration with Carlos Bertulani*, & FranjoKrmpotic(UNLP-Argentina) *Department of Physics Texas A&M University -Commerce 07/
 Comparison of RPA-lik modls in Nurino-Nuclus Nuclus Procsss Aruro R. Samana* in collaboraion wih Carlos Brulani* & FranjoKrmpoicUNLP-Argnina *Dparmn of Physics Txas A&M Univrsiy -Commrc 07/ 0/008 Aomic
Comparison of RPA-lik modls in Nurino-Nuclus Nuclus Procsss Aruro R. Samana* in collaboraion wih Carlos Brulani* & FranjoKrmpoicUNLP-Argnina *Dparmn of Physics Txas A&M Univrsiy -Commrc 07/ 0/008 Aomic
Part I: Short Answer [50 points] For each of the following, give a short answer (2-3 sentences, or a formula). [5 points each]
![Part I: Short Answer [50 points] For each of the following, give a short answer (2-3 sentences, or a formula). [5 points each] Part I: Short Answer [50 points] For each of the following, give a short answer (2-3 sentences, or a formula). [5 points each]](/thumbs/92/109815505.jpg) Soluions o Midrm Exam Nam: Paricl Physics Fall 0 Ocobr 6 0 Par I: Shor Answr [50 poins] For ach of h following giv a shor answr (- snncs or a formula) [5 poins ach] Explain qualiaivly (a) how w acclra
Soluions o Midrm Exam Nam: Paricl Physics Fall 0 Ocobr 6 0 Par I: Shor Answr [50 poins] For ach of h following giv a shor answr (- snncs or a formula) [5 poins ach] Explain qualiaivly (a) how w acclra
MEM 355 Performance Enhancement of Dynamical Systems A First Control Problem - Cruise Control
 MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
MEM 355 Prformanc Enhancmn of Dynamical Sysms A Firs Conrol Problm - Cruis Conrol Harry G. Kwany Darmn of Mchanical Enginring & Mchanics Drxl Univrsiy Cruis Conrol ( ) mv = F mg sinθ cv v +.2v= u 9.8θ
3(8 ) (8 x x ) 3x x (8 )
 Scion - CHATER -. a d.. b. d.86 c d 8 d d.9997 f g 6. d. d. Thn, = ln. =. =.. d Thn, = ln.9 =.7 8 -. a d.6 6 6 6 6 8 8 8 b 9 d 6 6 6 8 c d.8 6 6 6 6 8 8 7 7 d 6 d.6 6 6 6 6 6 6 8 u u u u du.9 6 6 6 6 6
Scion - CHATER -. a d.. b. d.86 c d 8 d d.9997 f g 6. d. d. Thn, = ln. =. =.. d Thn, = ln.9 =.7 8 -. a d.6 6 6 6 6 8 8 8 b 9 d 6 6 6 8 c d.8 6 6 6 6 8 8 7 7 d 6 d.6 6 6 6 6 6 6 8 u u u u du.9 6 6 6 6 6
ECE 2100 Circuit Analysis
 ECE 1 Circui Analysis Lesson 37 Chaper 8: Second Order Circuis Discuss Exam Daniel M. Liynski, Ph.D. Exam CH 1-4: On Exam 1; Basis for work CH 5: Operaional Amplifiers CH 6: Capaciors and Inducor CH 7-8:
ECE 1 Circui Analysis Lesson 37 Chaper 8: Second Order Circuis Discuss Exam Daniel M. Liynski, Ph.D. Exam CH 1-4: On Exam 1; Basis for work CH 5: Operaional Amplifiers CH 6: Capaciors and Inducor CH 7-8:
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Introduction and Linear Systems
 FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Inroducion and Linar Sysms David Lvrmor Dparmn of Mahmaics Univrsiy of Maryland 9 Dcmbr 0 Bcaus h prsnaion of his marial in lcur will diffr from
FIRST-ORDER SYSTEMS OF ORDINARY DIFFERENTIAL EQUATIONS I: Inroducion and Linar Sysms David Lvrmor Dparmn of Mahmaics Univrsiy of Maryland 9 Dcmbr 0 Bcaus h prsnaion of his marial in lcur will diffr from
EE202 Circuit Theory II , Spring. Dr. Yılmaz KALKAN & Dr. Atilla DÖNÜK
 EE202 Circui Theory II 2018 2019, Spring Dr. Yılmaz KALKAN & Dr. Ailla DÖNÜK 1. Basic Conceps (Chaper 1 of Nilsson - 3 Hrs.) Inroducion, Curren and Volage, Power and Energy 2. Basic Laws (Chaper 2&3 of
EE202 Circui Theory II 2018 2019, Spring Dr. Yılmaz KALKAN & Dr. Ailla DÖNÜK 1. Basic Conceps (Chaper 1 of Nilsson - 3 Hrs.) Inroducion, Curren and Volage, Power and Energy 2. Basic Laws (Chaper 2&3 of
Chapter 7 Response of First-order RL and RC Circuits
 Chaper 7 Response of Firs-order RL and RC Circuis 7.- The Naural Response of RL and RC Circuis 7.3 The Sep Response of RL and RC Circuis 7.4 A General Soluion for Sep and Naural Responses 7.5 Sequenial
Chaper 7 Response of Firs-order RL and RC Circuis 7.- The Naural Response of RL and RC Circuis 7.3 The Sep Response of RL and RC Circuis 7.4 A General Soluion for Sep and Naural Responses 7.5 Sequenial
46. Let y = ln r. Then dy = dr, and so. = [ sin (ln r) cos (ln r)
 98 Scion 7.. L w. Thn dw d, so d dw w dw. sin d (sin w)( wdw) w sin w dw L u w dv sin w dw du dw v cos w w sin w dw w cos w + cos w dw w cos w+ sin w+ sin d wsin wdw w cos w+ sin w+ cos + sin +. L w +
98 Scion 7.. L w. Thn dw d, so d dw w dw. sin d (sin w)( wdw) w sin w dw L u w dv sin w dw du dw v cos w w sin w dw w cos w + cos w dw w cos w+ sin w+ sin d wsin wdw w cos w+ sin w+ cos + sin +. L w +
EE 434 Lecture 22. Bipolar Device Models
 EE 434 Lcur 22 Bipolar Dvic Modls Quiz 14 Th collcor currn of a BJT was masurd o b 20mA and h bas currn masurd o b 0.1mA. Wha is h fficincy of injcion of lcrons coming from h mir o h collcor? 1 And h numbr
EE 434 Lcur 22 Bipolar Dvic Modls Quiz 14 Th collcor currn of a BJT was masurd o b 20mA and h bas currn masurd o b 0.1mA. Wha is h fficincy of injcion of lcrons coming from h mir o h collcor? 1 And h numbr
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
FWM in One-dimensional Nonlinear Photonic Crystal and Theoretical Investigation of Parametric Down Conversion Efficiency (Steady State Analysis)
 Procdings of h Inrnaional MuliConfrnc of nginrs and Compur Sciniss 9 Vol II IMCS 9 March 8-9 Hong Kong FWM in On-dimnsional Nonlinar Phoonic Crysal and Thorical Invsigaion of Paramric Down Convrsion fficincy
Procdings of h Inrnaional MuliConfrnc of nginrs and Compur Sciniss 9 Vol II IMCS 9 March 8-9 Hong Kong FWM in On-dimnsional Nonlinar Phoonic Crysal and Thorical Invsigaion of Paramric Down Convrsion fficincy
( ) C R. υ in RC 1. cos. ,sin. ω ω υ + +
 Oscillaors. Thory of Oscillaions. Th lad circui, h lag circui and h lad-lag circui. Th Win Bridg oscillaor. Ohr usful oscillaors. Th 555 Timr. Basic Dscripion. Th S flip flop. Monosabl opraion of h 555
Oscillaors. Thory of Oscillaions. Th lad circui, h lag circui and h lad-lag circui. Th Win Bridg oscillaor. Ohr usful oscillaors. Th 555 Timr. Basic Dscripion. Th S flip flop. Monosabl opraion of h 555
Why Laplace transforms?
 MAE4 Linar ircui Why Lalac ranform? Firordr R cc v v v KVL S R inananou for ach Subiu lmn rlaion v S Ordinary diffrnial quaion in rm of caacior volag Lalac ranform Solv Invr LT V u, v Ri, i A R V A _ v
MAE4 Linar ircui Why Lalac ranform? Firordr R cc v v v KVL S R inananou for ach Subiu lmn rlaion v S Ordinary diffrnial quaion in rm of caacior volag Lalac ranform Solv Invr LT V u, v Ri, i A R V A _ v
DE Dr. M. Sakalli
 DE-0 Dr. M. Sakalli DE 55 M. Sakalli a n n 0 a Lh.: an Linar g Equaions Hr if g 0 homognous non-homognous ohrwis driving b a forc. You know h quaions blow alrad. A linar firs ordr ODE has h gnral form
DE-0 Dr. M. Sakalli DE 55 M. Sakalli a n n 0 a Lh.: an Linar g Equaions Hr if g 0 homognous non-homognous ohrwis driving b a forc. You know h quaions blow alrad. A linar firs ordr ODE has h gnral form
Direct Current Circuits. February 19, 2014 Physics for Scientists & Engineers 2, Chapter 26 1
 Direc Curren Circuis February 19, 2014 Physics for Scieniss & Engineers 2, Chaper 26 1 Ammeers and Volmeers! A device used o measure curren is called an ammeer! A device used o measure poenial difference
Direc Curren Circuis February 19, 2014 Physics for Scieniss & Engineers 2, Chaper 26 1 Ammeers and Volmeers! A device used o measure curren is called an ammeer! A device used o measure poenial difference
Harmonic oscillator in quantum mechanics
 Harmonic oscillaor in quanum mechanics PHYS400, Deparmen of Physics, Universiy of onnecicu hp://www.phys.uconn.edu/phys400/ Las modified: May, 05 Dimensionless Schrödinger s equaion in quanum mechanics
Harmonic oscillaor in quanum mechanics PHYS400, Deparmen of Physics, Universiy of onnecicu hp://www.phys.uconn.edu/phys400/ Las modified: May, 05 Dimensionless Schrödinger s equaion in quanum mechanics
SUPERCRITICAL BRANCHING DIFFUSIONS IN RANDOM ENVIRONMENT
 Elc. Comm. in Proa. 6 (), 78 79 ELECTRONIC COMMUNICATIONS in PROBABILITY SUPERCRITICAL BRANCHING DIFFUSIONS IN RANDOM ENVIRONMENT MARTIN HUTZENTHALER ETH Zürich, Dparmn of Mahmaics, Rämisrass, 89 Zürich.
Elc. Comm. in Proa. 6 (), 78 79 ELECTRONIC COMMUNICATIONS in PROBABILITY SUPERCRITICAL BRANCHING DIFFUSIONS IN RANDOM ENVIRONMENT MARTIN HUTZENTHALER ETH Zürich, Dparmn of Mahmaics, Rämisrass, 89 Zürich.
Section 3.8, Mechanical and Electrical Vibrations
 Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Consider a system of 2 simultaneous first order linear equations
 Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm
Soluon of sysms of frs ordr lnar quaons onsdr a sysm of smulanous frs ordr lnar quaons a b c d I has h alrna mar-vcor rprsnaon a b c d Or, n shorhand A, f A s alrady known from con W know ha h abov sysm
Feedback Control and Synchronization of Chaos for the Coupled Dynamos Dynamical System *
 ISSN 746-7659 England UK Jornal of Informaion and Comping Scinc Vol. No. 6 pp. 9- Fdbac Conrol and Snchroniaion of Chaos for h Copld Dnamos Dnamical Ssm * Xdi Wang Liin Tian Shmin Jiang Liqin Y Nonlinar
ISSN 746-7659 England UK Jornal of Informaion and Comping Scinc Vol. No. 6 pp. 9- Fdbac Conrol and Snchroniaion of Chaos for h Copld Dnamos Dnamical Ssm * Xdi Wang Liin Tian Shmin Jiang Liqin Y Nonlinar
ERROR ANALYSIS A.J. Pintar and D. Caspary Department of Chemical Engineering Michigan Technological University Houghton, MI September, 2012
 ERROR AALYSIS AJ Pinar and D Caspary Dparmn of Chmical Enginring Michigan Tchnological Univrsiy Houghon, MI 4993 Spmbr, 0 OVERVIEW Exprimnaion involvs h masurmn of raw daa in h laboraory or fild I is assumd
ERROR AALYSIS AJ Pinar and D Caspary Dparmn of Chmical Enginring Michigan Tchnological Univrsiy Houghon, MI 4993 Spmbr, 0 OVERVIEW Exprimnaion involvs h masurmn of raw daa in h laboraory or fild I is assumd
Math 3301 Homework Set 6 Solutions 10 Points. = +. The guess for the particular P ( ) ( ) ( ) ( ) ( ) ( ) ( ) cos 2 t : 4D= 2
 Mah 0 Homwork S 6 Soluions 0 oins. ( ps) I ll lav i o you o vrify ha y os sin = +. Th guss for h pariular soluion and is drivaivs is blow. Noi ha w ndd o add s ono h las wo rms sin hos ar xaly h omplimnary
Mah 0 Homwork S 6 Soluions 0 oins. ( ps) I ll lav i o you o vrify ha y os sin = +. Th guss for h pariular soluion and is drivaivs is blow. Noi ha w ndd o add s ono h las wo rms sin hos ar xaly h omplimnary
