Stability of Limit Cycles in Hybrid Systems

Transcription

1 Proceedings of the 34th Hawaii International Conference on Sstem Sciences - 21 Stabilit of Limit Ccles in Hbrid Sstems Ian A. Hiskens Department of Electrical and Computer Engineering Universit of Illinois at Urbana-Champaign Urbana IL USA hiskens@ece.uiuc.edu Abstract Limit ccles are common in hbrid sstems. However the nonsmooth dnamics of such sstems makes stabilit analsis difficult. This paper uses recent extensions of trajector sensitivit analsis to obtain the characteristic multipliers of nonsmooth limit ccles. The stabilit of a limit ccle is determined b its characteristic multipliers. The concepts are illustrated using a coupled tank sstem with on/offvalve switching. 1 Introduction Hbrid sstems are characterized b interactions between continuous (smooth) dnamics and discrete events. Such sstems are common across a diverse range of application areas. Examples include power sstems 1, robotics 2, manufacturing 3 and airtraffic control 4. In fact, an sstem where saturation limits are routinel encountered can be thought of as a hbrid sstem. The limits introduce discrete events which (often) have a significant influence on overall behaviour. Man hbrid sstems exhibit periodic behaviour. Discrete events, such as saturation limits, can act to trap the evolving sstem state within a constrained region of state space. Therefore even when the underling continuous dnamics are unstable, the discrete events can induce a stable limit set. Limit ccles (periodic behaviour) are often created in this wa. An example is presented in Section 4. Limit ccles can be stable (attracting), unstable (repelling) or non-stable (saddle). The stabilit of periodic behaviour is determined b characteristic (or Floquet) multipliers. Characteristic multipliers are a generalization of the eigenvalues at an equilibrium point. A periodic solution corresponds to a fixed point of a Poincaré map. Stabilit of the periodic solution is the same as the stabilit of the fixed point. The characteristic multipliers are the eigenvalues of the Poincaré map linearized about the fixed point. It is shown in Section 3 that this linearized map is given b trajector sensitivities. This paper uses a recent extension of trajector sensitivit analsis 5to determine the stabilit of limit ccles in hbrid sstems. A brief review of hbrid sstem modelling is given in Section 2. Stabilit analsis of limit ccles is presented in Section 3, and an example is considered in Section 4. Trajector sensitivit equations for hbrid sstems are provided in the appendix. 2 Model Deterministic hbrid sstems can be represented b a model that consists of differential, switched algebraic, and state-reset (DSAR) equations, i.e., ẋ = f(x,) (1) =g () (x,) (2) { g = (i ) (x,) d,i < g (i+) i =1,..., d (3) (x,) d,i > x + = h j (x, ) e,j = j {1,..., e (4) where x = x z, f = f, h j = x h j λ λ and x are the continuous dnamic states, z are discrete dnamic states, are algebraic states, and λ are parameters. The model can capture complex behaviour, from hsteresis and non-windup limits through to rule-based /1 $1. (c) 21 IEEE 1

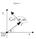
2 Proceedings of the 34th Hawaii International Conference on Sstem Sciences - 21 sstems 1. A more extensive presentation of this model is given in 5. In this model, the parameters λ form part of the extended state x. This allows a convenient development of trajector sensitivities. To ensure that parameters remain fixed at their initial values, the corresponding differential equations (1) are defined as λ =. Awa from events, sstem dnamics evolve smoothl according to the familiar differentialalgebraic model x * x P(x) Γ ẋ = f(x,) (5) = g(x,) (6) Σ where g is composed of g () together with appropriate choices of g (i ) or g (i+), depending on the signs of the corresponding elements of d. At switching events (3), some component equations of g change. To satisf the new g = equation, algebraic variables ma undergo a step change. Reset events (4) force a discrete change in elements of z. Algebraic variables ma also step at a reset event to ensure g = is satisfied with the altered values of z. The flows of x and are defined respectivel as x(t) = φ x (x,t) (7) (t) = φ (x,t) (8) where x(t) and (t) satisf (1)-(4), along with initial conditions, φ x (x,t )=x (9) g(x,φ (x,t )) =. (1) Trajector sensitivities Φ x,φ describe the sensitivit of the flows to perturbations in initial conditions x. These sensitivities underlie the linearization of the Poincaré map, and so pla a major role in determining the stabilit of periodic solutions. A summar of the variational equations governing the evolution of these sensitivities is given in the Appendix. 3 Limit Ccle Analsis Stabilit of limit ccles is determined using Poincaré maps. A Poincaré map effectivel samples the flow of a periodic sstem once ever period. The concept is illustrated in Figure 1. If the limit ccle is stable, oscillations approach the limit ccle over time. The samples provided b the corresponding Poincaré map approach a fixed point. A non-stable limit ccle results in divergent oscillations. The samples of the Poincaré mapdivergeforsuchacase. Figure 1: Poincaré map. To define a Poincaré map, consider the limit ccle Γ shown in Figure 1. Let Σ be a hperplane transversal to Γ at x. The trajector emanating from x will again encounter Σ at x after T seconds, where T is the minimum period of the limit ccle. Due to the continuit of the flow φ x with respect to initial conditions, trajectories starting on Σ in a neighbourhood of x will, in approximatel T seconds, intersect Σ in the vicinit of x. Hence φ x and Σ define a mapping x k+1 = P (x k ):=φ x (x k,τ r (x k )). (11) where τ r (x k ) T is the time taken for the trajector to return to Σ. Complete details can be found in 6, 7. Stabilit of the Poincaré map (11) is determined b linearizing P at the fixed point x, i.e., x k+1 = DP(x ) x k. (12) From the definition of P (x) given b (11), it follows that DP(x ) is closel related to the trajector sensitivities φ x(x,t ) x Φ x (x,t). In fact, it is shown in 6that DP(x )= (I f(x, )σ t ) f(x, ) t Φ x (x,t) (13) σ where σ is a vector normal to Σ. The matrix Φ x (x,t) x x (T )isexactlthetrajector sensitivit matrix after one period of the limit ccle, i.e., starting from x and returning to x.this matrix is called the Monodrom matrix. Itisshownin 6that one eigenvalue of Φ x (x,t)isalwas1,and the corresponding eigenvector lies along f(x, ). The remaining eigenvalues of Φ x (x,t) coincide with the eigenvalues of DP(x ),andareknownasthecharacteristic multipliers m i of the periodic solution. The /1 $1. (c) 21 IEEE 2

3 Proceedings of the 34th Hawaii International Conference on Sstem Sciences - 21 characteristic multipliers are independent of the choice of cross-section Σ. Therefore, for hbrid sstems, it is often convenient to choose Σ as a triggering hpersurface corresponding to a switching or reset event that occurs along the periodic solution. Because the characteristic multipliers m i are the eigenvalues of the linear map DP(x ), the determine the stabilit of the Poincaré mapp (x k ), and hence the stabilit of the periodic solution. Three cases are of importance: Q 1 Q A Q 1) All m i lie within the unit circle, i.e., m i < 1, i. The map is stable, so the periodic solution is stable. x 2 2) All m i lie outside the unit circle. The periodic solution is unstable. 3) Some m i lie outside the unit circle. The periodic solution is non-stable. Interestingl, there exists a particular cross-section Σ, such that DP(x )ζ =Φ x (x,t)ζ (14) where ζ Σ. This cross-section Σ is the hperplane spanned b the n 1 eigenvectors of Φ x (x,t)that are not aligned with f(x, ). Therefore the vector σ that is normal to Σ is the left eigenvector of Φ x (x,t) corresponding to the eigenvalue 1. The hperplane Σ is invariant under Φ x (x,t), i.e., Φ x (x,t)maps vectors ζ Σ back into Σ. 4 Example The two-tank sstem of Figure 2 can be used to illustrate limit ccles in hbrid sstems 8. The sstem consists of two tanks and two valves. The first valve adds to the inflow in tank 1, whilst the second valve is a drain valve from tank 2. There is also constant outflow from tank 2 caused b a pump. The sstem is linearized at a desired operating point. The objective is to keep the water levels in both tanks within limits using a discrete open/close switching strateg for the valves. The valve associated with tank 1 should open when the level of tank 1 falls to 1, and close when the level of tank 2 goes above 1. The tank 2 valve should open when the level of tank 2 rises to 1, and close when the tank 2 level falls to. Let the water levels of tanks 1 and 2 be given b and x 2 respectivel. The behaviour of is given b ẋ 1 = 2 ẋ 1 = + 3 when tank 1 valve is closed when tank 1 valve is open. Q 2 Q B Figure 2: Two-tank example. Likewise, x 2 is driven b ẋ 2 = when tank 2 valve is closed ẋ 2 = x 2 5 when tank 2 valve is open. This sstem can be modelled in the DSAR form as, ẋ 1 = + 1 ẋ 2 = + 2 = 1 3 = 3 x < = 1 +2 = > = 2 + x 2 +5 = 4 + x 4 < 2 = 2 = 4 + x >. The phase portrait of Figure 3 shows the behaviour of this sstem for various initial conditions. Trajectories are shown as thin lines. All trajectories approach a stable nonsmooth limit ccle, indicated b the darker line. The limit ccle is shown b itself in Figure 4. The limit ccle encounters a triggering hpersurface at = 1. (This event corresponds to the tank 1 valve opening.) This surface provides a convenient cross-section Σ for defining a Poincaré map. Consider the point x = t on the limit ccle immediatel after the switching event. Based on this choice for x, the trajector sensitivities after one period of the limit ccle give, Φ x (x,t)= /1 $1. (c) 21 IEEE 3

4 Proceedings of the 34th Hawaii International Conference on Sstem Sciences Tank 2 height, x Tank 2 height, x Tank 1 height, Figure 3: Phase portrait for example. which has eigenvalues of 1. and.113, and corresponding right eigenvectors ev 1 =, ev =..574 From the model, f(x, )= x1 +3 = 4 1 Notice that ev 1 =.2425f(x, ). Therefore, as anticipated, the eigenvector corresponding to the unit eigenvalue lies along f(x, ). The other eigenvalue,.113, is the characteristic multiplier for this limit ccle. Its magnitude is less than one, proving that the limit ccle is stable. We shall now confirm that.113 is reall an eigenvalue of DP(x ). For the chosen hpersurface = 1, the normal vector is σ =1 t. Therefore from (13), DP(x )= which has eigenvalues of and.113. When restricted to the hperplane Σ, the zero eigenvalue disappears, leaving the characteristic multiplier. Now consider the special cross-section Σ that is spanned b ev 2, i.e., the eigenvector of Φ x (x,t)that is not aligned with f(x, ). In this case σ = t and DP(x )= Tank 1 height, Figure 4: Limit ccle. which again has eigenvalues of and.113. Vectors ζ Σ satisf so DP(x )ζ = and = Φ x (x,t)ζ = = x 2 = x 2 = x Σ x Σ Notice that DP(x )ζ =Φ x (x,t)ζ for all ζ Σ. 5 Conclusions Hbrid sstems frequentl exhibit periodic behaviour. However the nonsmooth nature of such sstems complicates stabilit analsis. Those complications have been addressed in this paper through application of recent extensions to trajector sensitivit analsis. Deterministic hbrid sstems can be represented b a coupled set of differential, switched algebraic, and state-reset equations. The variational equations describing the evolution of trajector sensitivities for this model have recentl been developed, and are included as an appendix /1 $1. (c) 21 IEEE 4

5 Proceedings of the 34th Hawaii International Conference on Sstem Sciences - 21 Standard Poincaré map results extend naturall to hbrid sstems. The Monodrom matrix is obtained b evaluating trajector sensitivities over one period of the (possibl nonsmooth) cclical behaviour. One eigenvalue of this matrix is alwas unit. The remaining eigenvalues are the characteristic multipliers of the periodic solution. Stabilit is ensured if all multipliers lie inside the unit circle. Instabilit occurs if an multiplier lies outside the unit circle. Acknowledgements The author wishes to acknowledge the support of the Australian Research Council through the project grant Analsis and Assessment of Voltage Collapse, the EPRI/DoD Complex Interactive Networks/Sstems Initiative, and the Grainger Foundation. References 1I.A. Hiskens and M.A. Pai, Hbrid sstems view of power sstem modelling, in Proceedings of the IEEE International Smposium on Circuits and Sstems, Geneva, Switzerland, Ma 2. 2M.H. Raibert, Legged Robots That Balance, MIT Press, Cambridge, MA, S. Pettersson, Analsis and design of hbrid sstems, Ph.D. Thesis, Department of Signals and Sstems, Chalmers Universit of Technolog, Göteborg, Sweden, C. Tomlin, G. Pappas, and S. Sastr, Conflict resolution for air traffic management: A stud in multiagent hbrid sstems, IEEE Transactions on Automatic Control, vol. 43, no. 4, pp , April I.A. Hiskens and M.A. Pai, Trajector sensitivit analsis of hbrid sstems, IEEE Transactions on Circuits and Sstems I, vol. 47, no. 2, pp , Februar 2. 6T.S Parker and L.O. Chua, Practical Numerical Algorithms for Chaotic Sstems, Springer-Verlag, New York, NY, R. Sedel, Practical Bifurcation and Stabilit Analsis, Springer-Verlag, New York, 2nd edition, M. Rubensson, B. Lennartsson, and S. Pettersson, Convergence to limit ccles in hbrid sstems - an A example, in Preprints of 8th International Federation of Automatic Control Smposium on Large Scale Sstems: Theor & Applications, RioPatras, Greece, 1998, pp Trajector Sensitivit Equations The sensitivit of the flows φ x and φ to initial conditions x are obtained b linearizing (7),(8) about the nominal trajector, x(t) = φ x(x,t) x x (15) (t) = φ (x,t) x x. (16) The time-varing partial derivative matrices given in (15),(16) are known as trajector sensitivities, andcan be expressed in the alternative forms φ x (x,t) x x x (t) Φ x (x,t) (17) φ (x,t) x (t) Φ (x x,t). (18) The form x x, x enables a clearer development of the variational equations describing the evolution of the sensitivities. This development is summarized below. The alternative form Φ x (x,t), Φ (x,t) highlights the connection between the sensitivities and the underling flows. Awa from events, where sstem dnamics evolve smoothl, trajector sensitivities x x and x are obtained b differentiating (5),(6) with respect to x. This gives ẋ x = f x (t)x x + f (t) x (19) = g x (t)x x + g (t) x (2) where f x f/ x, and likewise for the other Jacobian matrices. Note that f x, f, g x, g are evaluated along the trajector, and hence are time varing matrices. It is shown in 5that the solution of this (potentiall high order) DA sstem can be obtained as a b-product of solving the original DA sstem (5),(6). Initial conditions for x x are obtained from (9) as x x (t )=I where I is the identit matrix. Initial conditions for x follow directl from (2), =g x (t )+g (t ) x (t ) /1 $1. (c) 21 IEEE 5

6 Proceedings of the 34th Hawaii International Conference on Sstem Sciences - 21 Equations (19),(2) describe the evolution of the sensitivities x x and x between events. However at an event, the sensitivities are generall discontinuous. It is necessar to calculate jump conditions describing the step change in x x and x. For clarit, consider a single switching/reset event, so the model (1)-(4) reduces to the form ẋ = f(x,) (21) { g = (x,) s(x,) < g + (22) (x,) s(x,) > x + = h(x, ) s(x,)=. (23) Let (x(τ),(τ)) be the point where the trajector encounters the hpersurface s(x,) =, i.e., the point where an event is triggered. This point is called the junction point and τ is the junction time. Just prior to event triggering, at time τ,wehave where x = x(τ ) = φ x (x,τ ) = (τ )=φ (x,τ ) g (x, )=. Similarl, x +, + are defined for time τ +,justafterthe event has occurred. It is shown in 5that the jump conditions for the sensitivities x x are given b ( x x (τ + )=h x x x (τ ) f + h x f ) τ x (24) where ( ) h x = h x h (g ) 1 gx τ ( ) s x s (g ) 1 g τ x x x (τ ) τ x = ( ) sx s (g ) 1 gx τ f f = f(x(τ ), (τ )) f + = f(x(τ + ), + (τ + )). The sensitivities x immediatel after the event are given b x (τ + )= ( g + (τ + ) ) 1 g + x (τ + )x x (τ + ). Following the event, i.e., for t>τ +, calculation of the sensitivities proceeds according to (19),(2), until the next event is encountered. The jump conditions provide the initial conditions for the post-event calculations. Hbrid sstems usuall involve man discrete events. The more general case follows naturall though, and is presented in /1 $1. (c) 21 IEEE 6