Πk=1. z e - z/2. 2 /e. e zk. 1-z. 1+ 2n. 1-z - 2. () z = -z( ) () z = e. = e. e - z 2 () z ( z/2) z is expressed by the Hadamard product as follows.
|
|
|
- Jeffrey Ernest Elliott
- 5 years ago
- Views:
Transcription
1 08 Factoriation of Completed Riemann Zeta 8. Hadamard product of Formula 8..0 ( Hadamard 893 ) When is Riemann eta function and the the eros are k k =,,3,, the following expression holds. /e () = ( -) k= - k e k n = n e - n Using this formula, we can easily obtain factoriation of a completed eta function. Formula 8.. ( Hadamard product of ) Let completed eta function be as follows. - - () = -( ) () When non-trivial eros of are k = x k iy k k =,,3, and is Euler-Mascheroni constant, is expressed by the Hadamard product as follows. () = e () = e log log -- log log -- k= n = - k From the Weierstrass expression on the gamma function, n = n e - n Substituting this for Formula 8..0, From this, - / e = ( /) /e e - / () = ( -) ( / ) k= = e k x n xn - e xn yn xn y n xn y n e log e - e - / - ( / ) k= = e ( -) ( /) - -( ) () = e - k - k log-- k= log-- k= - - e k e k - k - k e k e k (.0) (.)
2 Multiplying both sides by - i.e ( ) () = e = e () log log -- log -, = e k= log log k e k k= - k This formula means that the completed eta function is incompletely factored at the non-trivial eros. Now, let the non-trivial eros are k = x k iy k k =,,3,. Then, e k (.0) k= - k e k = n = = n = - xn iy n By using this, (.0) is expressed as follows. () = e log log -- e xn iyn - xn iy n x n xn - e xn yn xn y n xn y n n = x n xn - e xn yn xn y n xn y n e xn iyn (.) If x n = / n =,,3,, (.) becomes () = e log log -- n = - /4 yn /4 yn e /4 yn Althogh a general formula for generating eros whose real part is / is not known, Mathematica has a function y n = Im[ZetaZero [n ]] that generates this numerically. When both sides of (.') are drawn overlapping using known non-trivial,500 eros, it is as follows.. (.') - -
3 As a special value for (.), an important formula used in the next section is obtained. Formula 8.. ( Special value ) When non-trivial eros of Riemann eta function are x n iy n n =,,3,, the following expression holds. n = xn x n - - e xn yn xn y n = e log -log - = (.) Giving = to (.), From this, ( ) = e log log -- n = xn x n - - e xn yn xn y n n = xn x n - - e xn yn xn y n = e log -log - = (. ) = (.) If x n = / n =,,3,, (.) becomes r= From this, n = /- - ( /) y r /4 y n / e ( / ) y r r = = e /4 y r = e log -log - log = - log- = (.' ) As a special value for (.0), the following formulas is obtained. Formula 8..3 ( Special value ) When non-trivial eros of Riemann eta function are x k iy k k =,,3,, the following expression holds. - - = (.3) n = x n iy n x n iy n 3 Giving =-, to (.0) respectively, e - e log log -- log log -- k= k= - e k k - e k k = ( -) = 3 = ( ) = - 3 -
4 Multiplying both sides respectively, k= - k k = 3 Let k = x k iy k k =,,3,. Then, k= k= From these, k= Therefore, n = - k k - k = n = = n = k - x n iy n - xn iy n xn iy n = n = n = - xn iy n - xn iy n xn iy n - x n iy n - x n iy n xn iy n = 3 - x n iy n - xn iy n xn iy n (.3) Both sides of (.3 ) were computed using known non-trivial 0000 eros in an attempt. Both sides was equal up to 3 decimal places
5 8. Non-trivial eros whose real part is not / According to Theorem 7.4. in " 07 Completed Riemann Zeta ", if Riemann eta function has non-trivial ero whose real part is not /, the one set have to consist of the following four. / s i s, /- s i s 0< s </ In this section, we will consider how the formulas in the previous section are expressed when non-trivial eros whose real part is / and non-trivial eros whose real part is not / are mixed. Lemma 8.. Let be Euler-Mascheroni constant, non-trivial eros of Riemann eta function are x n iy n n =,,3,. Among them, eros whose real part is / are / iy r r =,,3, and eros whose real parts is not / are / s i s 0< s </ s =,,3,. Then Formual 8.. (.) is expressed as follows. () = e log log -- Formula 8.. (.) was as follows. () = e r= - /4 yr /4 yr e /4 yr s s= - e / s s / s s / s s s s s= - e / s s / s s / s s log log -- n = x n xn - e xn yn xn y n xn y n s Regarding non-trivial eros / iy r r =,,3, whose real part is /, a part of the right side is expressed as follows. r= - /4 yr /4 yr e /4 yr On the other hand, regarding non-trivial eros / s i s 0< s </ whose real part is not /, a part of the right side is expressed as follows. s= s= s - e / s s / s s / s s s s s - e / s s / s s / s s Multiplying these, we obtain the desired expression. (.) (.) - 5 -
6 Theorem 8.. Let be Euler-Mascheroni constant, non-trivial eros of Riemann eta function are x n iy n n =,,3,. Among them, eros whose real part is / are / iy r r =,,3, and eros whose real parts is not / are / s i s 0< s </ s =,,3,. Then the following expressions hold. n = n = n = x n - - xn y n x n x n y n = r = = (.) /4 y r s = s / s s s / s (.3) s x n log = x - log - = (.4) n y n Substituting = for Formula 8.. (.), ( ) = e log log -- n = Substituting = for Lemma 8.. (.), ( ) = e log log -- From these, n = xn e xn yn x n - - xn y n = e Here, conveniently, So, r = /4 y r s= xn x n - - e xn yn xn y n = (. ) s s / s s - / s s e r = /4 y r s s s = / s s / s s s s = - s= / s s / s s s s = / s s s / s s s s / s s - / s s s s s s = - - / s s / s s / s s / s s = = s s - / s s / s s s s / s s / s s (. ) - 6 -
7 n = n = x n - - xn y n x n x n y n = r = And, from (. ) and (.), = (.) /4 y r s = s / s s s / s (.3) s n = x n log = x - log - = (.4) n y n Although the story goes a little aside, using (.), we obtain the following special values. Formula 8..3 ( Special values ) When non-trivial eros of Riemann eta function are x k iy k k =,,3,, the following expressions hold. n = n = - xn iy n xn iy n - xn iy n xn iy n = (.5 ) = 3 From the proof of Formula 8..3 in the previous section, k= k= - k k = 3 k= From Theorem 8.., n = = n = = n = - k x n - - xn y n Substituting this for ( ), k= - k = n = - xn iy n xn iy n k - xn iy n xn iy n = n = = n = x n - - xn y n x n xn y n (.5 - ) = (.) - xn iy n Substituting this and ( - ) for ( 0 ) sequentially, = 3 k= k = n = xn iy n - xn iy n ( ) ( - ) ( 0 ) = (.5 ) xn iy n (.5 - ) (.5 ) and (.5 - ) were calculated using known non-trivial eros. It was as follows
8 Well, let us return to the subject. By using Theorem 8.., the very important following theorem is obtained. Theorem 8..4 Let non-trivial eros of Riemann eta function are x n iy n n =,,3, and be Euler-Mascheroni constant. If the following expression holds, non-trivial eros whose real parts is not / do not exist. r = /4 y r log = - log - = (. ' ) Although non-trivial eros / iy r r =,,3, exist in fact, assume non-trivial eros / s i s, /- s i s (0 < s </)exist in addition. Then, the following expression holds from Theorem 8.. (.3), (.4). r = /4 y r s = s s log = / s s / s - log - s Here, the following inequality holds for 0< s </ and arbitrary real number s, So, Thus, i.e. s / s s / s s s = r = r = s = / s s / s s / s s s s > 0 for 0< / s s / s s </ s /4 y r /4 y r log < - log - log - log - As the contrapositive to the above, this theorem holds. > 0 Note This theorem shows that the equation (. ' ) is equivalent to the Riemann hypothesis. However, for the proof of (.'), the imaginary part y r of the non-trivial eros / iy r r =,,3, have to be obtained as a formula
9 Both sides of (. ' ) were calculated with the formula manipulation software Mathematica using known nontrivial eros. Both sides coincided with four decimal places
10 8.3 Factoriation of ( ) Formula 8.. ( Hadamard product ) is what the completed eta function is incompletely factored at the non-trivial eros. However, using Theorem 8.., the compensation terms disappear and is completely factoried at the non-trivial eros. Theorem 8.3. ( Factoriation of ( )) Let Riemann eta function be, the non-trivial eros are n = x n iy n n =,,3, and completed eta function be as follows. - - () = -( ) Then, is factoried as follows. () = n = From Formula 8.. (.), () = e () x n - xn y (3.) n xn y n log log -- n = On the other hand, from Theorem 8.. (.4), n = From this, x n log = x - log - n y n xn n= xn e yn = e log - log- Substituting this for the right side of the above, () = e = n = log log -- In addition, this formula is known. n = x n n= - e xn y n xn y n x n - xn y n xn y n xn xn yn e log - log- x n - xn y (3.) n xn y n If x n = / n =,,3,, (3.) becomes () = n = - /4 yn /4 yn (3.') When both sides of (3.') are drawn overlapping using known non-trivial,500 eros, it is as follows.. This is exactly the same as the one in Formula 8.. (.')
11 - -
12 8.4 Factoriation of () By replacing with / in Theorem 8.3., completed eta function that is an even function is obtained. Theorem 8.4. ( Factoriation of () ) Let Riemann eta function be, the non-trivial eros are n = x n iy n n =,,3, and completed eta function be as follows. () = - Then, is factoried as follows. () = ( 0) n = Where, ( 0 ) = n = - - x n -/ - x n -/ y n x n -/ (4.) y n x n -/ y n x n y n = - 4 /4 4 = (4. 0 ) From Theorem 8.3., - - () = -( ) () = n = () x n - xn y (3.) n xn y n Replacing with / in the first expression, = - Substituting =0 for this, ( 0 ) = - /4 4 4 Replacing with / in (3.), = n = = n = = n = - - x n - xn y n x n - xn y n = xn y n /4 x n - xn y n xn y n xn y n x n -x n /4 y n x n - - x n y n xn y n xn y n xn y n = : () - -
13 i.e. = n = Since / = (), () = n = Substituting =0 for this, ( 0 ) = n = x n -/ y n x n y n x n y n x n -/ y n x n -/ y n x n y n Substituting this for the right side of (), we obtain (4.), x n -/ - x n -/ y n x n -/ y n x n -/ - x n -/ y n x n -/ y n Lemma 8.4. Among Theorem 8.4. (4.), the product h () of the factor whose real part x n is / is expressed as follows. h () = h () 0 r= yr (4.) Where, h () 0 = r= y r /4 y r (4. 0 ) Replacing a part of x n with / in Theorem 8.4., we obtain the desired expression immediately. Note It is the Riemann hypothesis that () = h () must be. Lemma Assume that the factor whose real part is not / exists among Theorem B8.4. (4.). Then, when two real s > /8, the product () of these factors is numbers are s, s expressed as follows. () = ( 0) s= s.t. 0< s </ & s s s - s s s Where, ( 0 ) = s= / s s 4 s (4.3) s s s /- s s < (4.3 0 ) If such a product of factors exists, according to Theorem 7.4. in " 07 Completed Riemann Zeta ", the one set have to consist of the following four
14 / s i s, /- s i s 0 < s < / So, replacing a part of x n, y n with / s, s respectively in Theorem 8.4., Last, 0 s= () =( ) = s () 0 s= s () 0 = s= - = s () 0 s= = s= s s s s - s s s s / s s s s / s s s - s s s s s s s s s s s s s s - s s s / s s /- s s s s / s s s s / s s 4 s (4.3) s = / s /- s / s s /- s 4 s s s - s = 6 s s s 4 s 4 (4.3 0 ) i.e. / s s /- s s s - s = 6 s s Here, if 0< s </ & s > /8, the following inequality holds. From this, Therefore, s > s - 8 s - s 6 > 0 / s s /- s s Since, both sides are positive, From this, / s s s s / s s /- s s s s /- s s < < > s s s s - 4 -
15 If there are a plurality of such sets, s s s= / s s s s /- s s < Note The conditional expression s > /8 is valid. It is because the ero of () does not exist in the domain 0< s </ & s /8. Theorem When Riemann eta function is and the non-trivial eros sre n = x n iy n n=,,3,, If the following expression holds, non-trivial eros whose real parts is not / do not exist. r= y r /4 y r = - 4 /4 4 = (4.4 0 ) Although non-trivial eros / iy r r =,,3, exist in fact, assume non-trivial eros / s i s, /- s i s (0 < s </ & s > /8) exist in addition. Then, the following expression holds from Theorem 8.4., Lemma 8.4. and Lemma () = h () () = ( ) 0 r= yr s= ( 0= ) h () 0 ( 0) = r= y r /4 y r s s s s s s s= / s s s - s s s /- s s And, according to Lemma 8.4.3, when 0< s </ & s > /8, s s s= / s s Then, form (4. 0 '), i.e. r= r= y r /4 y r y r /4 y r > - 4 /4 - s s /- s s /4 As the contrapositive to the above, this theorem holds. 4 = - 4 /4 (4.') 4 = (4. 0 ') < (4.3 0 ) =
16 Both sides of (4.4 0 ) were calculated with the formula manipulation software Mathematica using known nontrivial eros. Both sides coincided with five decimal places. cf. If the square root of (4.4 0 ) is taken, it is as follows. This is also equivalent to the Riemann hypothesis. r= y r = /4 y r /8-4 = (4.5) Each factor on the left side is an imaginary part when non-trivial ero r = / i y r is converted to polar coordinates. That is, sinr = r= /8-4 = (4.5) Added Sec Added Sec.4 (Renewed) Alien's Mathematics Kano. Kono - 6 -
z-1 r-1 (1.0) () z = - Re Im z, both the real part Re 1 z and the imaginary part Im 1 z 27 Zeros of Super Derivative of Riemann Zeta 27.
 27 Zeros of Super Derivative of Riemann Zeta 27.1 Zeros of ' z 27.1.0 Laurent Expansion of ' z Accordint to " 26 Higher and Super Calculus of Zeta Function etc " Formula 26.1.2h, when r is a Stieltjes
27 Zeros of Super Derivative of Riemann Zeta 27.1 Zeros of ' z 27.1.0 Laurent Expansion of ' z Accordint to " 26 Higher and Super Calculus of Zeta Function etc " Formula 26.1.2h, when r is a Stieltjes
z-1 r-1 (1.0) () z = - Re Im z, both the real part Re 1 z and the imaginary part Im 1 z 27 Zeros of Super Derivative of Riemann Zeta 27.
 27 Zeros of Super Derivative of Riemann Zeta 27.1 Zeros of ' z 27.1.0 Laurent Expansion of ' z Accordint to " 26 Higher and Super Calculus of Zeta Function etc " Formula 26.1.2h, when r is a Stieltjes
27 Zeros of Super Derivative of Riemann Zeta 27.1 Zeros of ' z 27.1.0 Laurent Expansion of ' z Accordint to " 26 Higher and Super Calculus of Zeta Function etc " Formula 26.1.2h, when r is a Stieltjes
6 Global definition of Riemann Zeta, and generalization of related coefficients. p + p >1 (1.1)
 6 Global definition of Riemann Zeta, and generalization of related coefficient 6. Patchy definition of Riemann Zeta Let' review the definition of Riemann Zeta. 6.. The definition by Euler The very beginning
6 Global definition of Riemann Zeta, and generalization of related coefficient 6. Patchy definition of Riemann Zeta Let' review the definition of Riemann Zeta. 6.. The definition by Euler The very beginning
is defined in the half plane Re ( z ) >0 as follows.
 0 Abolute Value of Dirichlet Eta Function. Dirichlet Eta Function.. Definition Dirichlet Eta Function ( z) i defined in the half plane Re( z ) >0 a follow. () z = r- r z Thi erie i analytically continued
0 Abolute Value of Dirichlet Eta Function. Dirichlet Eta Function.. Definition Dirichlet Eta Function ( z) i defined in the half plane Re( z ) >0 a follow. () z = r- r z Thi erie i analytically continued
SJÄLVSTÄNDIGA ARBETEN I MATEMATIK
 SJÄLVSTÄNDIGA ARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Gamma function related to Pic functions av Saad Abed 25 - No 4 MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET, 6 9
SJÄLVSTÄNDIGA ARBETEN I MATEMATIK MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET Gamma function related to Pic functions av Saad Abed 25 - No 4 MATEMATISKA INSTITUTIONEN, STOCKHOLMS UNIVERSITET, 6 9
B 2k. E 2k x 2k-p : collateral. 2k ( 2k-n -1)!
 13 Termwise Super Derivative In this chapter, for the function whose super derivatives are difficult to be expressed with easy formulas, we differentiate the series expansion of these functions non integer
13 Termwise Super Derivative In this chapter, for the function whose super derivatives are difficult to be expressed with easy formulas, we differentiate the series expansion of these functions non integer
The real primes and the Riemann hypothesis. Jamel Ghanouchi. Ecole Supérieure des Sciences et Techniques de Tunis.
 The real primes and the Riemann hypothesis Jamel Ghanouchi Ecole Supérieure des Sciences et Techniques de Tunis Jamel.ghanouchi@live.com bstract In this paper, we present the Riemann problem and define
The real primes and the Riemann hypothesis Jamel Ghanouchi Ecole Supérieure des Sciences et Techniques de Tunis Jamel.ghanouchi@live.com bstract In this paper, we present the Riemann problem and define
VII.8. The Riemann Zeta Function.
 VII.8. The Riemann Zeta Function VII.8. The Riemann Zeta Function. Note. In this section, we define the Riemann zeta function and discuss its history. We relate this meromorphic function with a simple
VII.8. The Riemann Zeta Function VII.8. The Riemann Zeta Function. Note. In this section, we define the Riemann zeta function and discuss its history. We relate this meromorphic function with a simple
Riemann Conjecture Proof and Disproof
 From the SelectedWorks of James T Struck Winter March 2, 2018 Riemann Conjecture Proof and Disproof James T Struck Available at: https://works.bepress.com/james_struck/72/ Disproving and Proving the Riemann
From the SelectedWorks of James T Struck Winter March 2, 2018 Riemann Conjecture Proof and Disproof James T Struck Available at: https://works.bepress.com/james_struck/72/ Disproving and Proving the Riemann
CHAPTER III THE PROOF OF INEQUALITIES
 CHAPTER III THE PROOF OF INEQUALITIES In this Chapter, the main purpose is to prove four theorems about Hardy-Littlewood- Pólya Inequality and then gives some examples of their application. We will begin
CHAPTER III THE PROOF OF INEQUALITIES In this Chapter, the main purpose is to prove four theorems about Hardy-Littlewood- Pólya Inequality and then gives some examples of their application. We will begin
,... We would like to compare this with the sequence y n = 1 n
 Example 2.0 Let (x n ) n= be the sequence given by x n = 2, i.e. n 2, 4, 8, 6,.... We would like to compare this with the sequence = n (which we know converges to zero). We claim that 2 n n, n N. Proof.
Example 2.0 Let (x n ) n= be the sequence given by x n = 2, i.e. n 2, 4, 8, 6,.... We would like to compare this with the sequence = n (which we know converges to zero). We claim that 2 n n, n N. Proof.
arxiv: v2 [math.gm] 24 May 2016
![arxiv: v2 [math.gm] 24 May 2016 arxiv: v2 [math.gm] 24 May 2016](/thumbs/79/78993821.jpg) arxiv:508.00533v [math.gm] 4 May 06 A PROOF OF THE RIEMANN HYPOTHESIS USING THE REMAINDER TERM OF THE DIRICHLET ETA FUNCTION. JEONWON KIM Abstract. The Dirichlet eta function can be divided into n-th partial
arxiv:508.00533v [math.gm] 4 May 06 A PROOF OF THE RIEMANN HYPOTHESIS USING THE REMAINDER TERM OF THE DIRICHLET ETA FUNCTION. JEONWON KIM Abstract. The Dirichlet eta function can be divided into n-th partial
Projection Theorem 1
 Projection Theorem 1 Cauchy-Schwarz Inequality Lemma. (Cauchy-Schwarz Inequality) For all x, y in an inner product space, [ xy, ] x y. Equality holds if and only if x y or y θ. Proof. If y θ, the inequality
Projection Theorem 1 Cauchy-Schwarz Inequality Lemma. (Cauchy-Schwarz Inequality) For all x, y in an inner product space, [ xy, ] x y. Equality holds if and only if x y or y θ. Proof. If y θ, the inequality
Σk=1. g r 3/2 z. 2 3-z. g 3 ( 3/2 ) g r 2. = 1 r = 0. () z = ( a ) + Σ. c n () a = ( a) 3-z -a. 3-z. z - + Σ. z 3, 5, 7, z ! = !
 09 Maclauin Seies of Completed Riemann Zeta 9. Maclauin Seies of Lemma 9.. ( Maclauin seies of gamma function ) When is the gamma function, n is the polygamma function and B n,kf, f, ae Bell polynomials,
09 Maclauin Seies of Completed Riemann Zeta 9. Maclauin Seies of Lemma 9.. ( Maclauin seies of gamma function ) When is the gamma function, n is the polygamma function and B n,kf, f, ae Bell polynomials,
A Proof of the Riemann Hypothesis and Determination of the Relationship Between Non- Trivial Zeros of Zeta Functions and Prime Numbers
 A Proof of the Riemann Hypothesis and Determination of the Relationship Between on- Trivial Zeros of Zeta Functions and Prime umbers ABSTRACT Murad Ahmed Abu Amr MSc Degree in Physics, Mutah University
A Proof of the Riemann Hypothesis and Determination of the Relationship Between on- Trivial Zeros of Zeta Functions and Prime umbers ABSTRACT Murad Ahmed Abu Amr MSc Degree in Physics, Mutah University
THE GAMMA FUNCTION AND THE ZETA FUNCTION
 THE GAMMA FUNCTION AND THE ZETA FUNCTION PAUL DUNCAN Abstract. The Gamma Function and the Riemann Zeta Function are two special functions that are critical to the study of many different fields of mathematics.
THE GAMMA FUNCTION AND THE ZETA FUNCTION PAUL DUNCAN Abstract. The Gamma Function and the Riemann Zeta Function are two special functions that are critical to the study of many different fields of mathematics.
NOTES ON RIEMANN S ZETA FUNCTION. Γ(z) = t z 1 e t dt
 NOTES ON RIEMANN S ZETA FUNCTION DRAGAN MILIČIĆ. Gamma function.. Definition of the Gamma function. The integral Γz = t z e t dt is well-defined and defines a holomorphic function in the right half-plane
NOTES ON RIEMANN S ZETA FUNCTION DRAGAN MILIČIĆ. Gamma function.. Definition of the Gamma function. The integral Γz = t z e t dt is well-defined and defines a holomorphic function in the right half-plane
Math 259: Introduction to Analytic Number Theory Functions of finite order: product formula and logarithmic derivative
 Math 259: Introduction to Analytic Number Theory Functions of finite order: product formula and logarithmic derivative This chapter is another review of standard material in complex analysis. See for instance
Math 259: Introduction to Analytic Number Theory Functions of finite order: product formula and logarithmic derivative This chapter is another review of standard material in complex analysis. See for instance
Multiple Solutions of Riemann-Type of Functional Equations. Cao-Huu T., Ghisa D., Muscutar F. A.
 1 Multiple Solutions of Riemann-Type of Functional Equations Cao-Huu T., Ghisa D., Muscutar F. A. 1 York University, Glendon College, Toronto, Canada York University, Glendon College, Toronto, Canada 3
1 Multiple Solutions of Riemann-Type of Functional Equations Cao-Huu T., Ghisa D., Muscutar F. A. 1 York University, Glendon College, Toronto, Canada York University, Glendon College, Toronto, Canada 3
5.4 Bessel s Equation. Bessel Functions
 SEC 54 Bessel s Equation Bessel Functions J (x) 87 # with y dy>dt, etc, constant A, B, C, D, K, and t 5 HYPERGEOMETRIC ODE At B (t t )(t t ), t t, can be reduced to the hypergeometric equation with independent
SEC 54 Bessel s Equation Bessel Functions J (x) 87 # with y dy>dt, etc, constant A, B, C, D, K, and t 5 HYPERGEOMETRIC ODE At B (t t )(t t ), t t, can be reduced to the hypergeometric equation with independent
Positive Series: Integral Test & p-series
 Positive Series: Integral Test & p-series Calculus II Josh Engwer TTU 3 March 204 Josh Engwer (TTU) Positive Series: Integral Test & p-series 3 March 204 / 8 Bad News about Summing a (Convergent) Series...
Positive Series: Integral Test & p-series Calculus II Josh Engwer TTU 3 March 204 Josh Engwer (TTU) Positive Series: Integral Test & p-series 3 March 204 / 8 Bad News about Summing a (Convergent) Series...
Riemann s Zeta Function and the Prime Number Theorem
 Riemann s Zeta Function and the Prime Number Theorem Dan Nichols nichols@math.umass.edu University of Massachusetts Dec. 7, 2016 Let s begin with the Basel problem, first posed in 1644 by Mengoli. Find
Riemann s Zeta Function and the Prime Number Theorem Dan Nichols nichols@math.umass.edu University of Massachusetts Dec. 7, 2016 Let s begin with the Basel problem, first posed in 1644 by Mengoli. Find
First, let me recall the formula I want to prove. Again, ψ is the function. ψ(x) = n<x
 8.785: Analytic Number heory, MI, spring 007 (K.S. Kedlaya) von Mangoldt s formula In this unit, we derive von Mangoldt s formula estimating ψ(x) x in terms of the critical zeroes of the Riemann zeta function.
8.785: Analytic Number heory, MI, spring 007 (K.S. Kedlaya) von Mangoldt s formula In this unit, we derive von Mangoldt s formula estimating ψ(x) x in terms of the critical zeroes of the Riemann zeta function.
A Simple Counterexample to Havil s Reformulation of the Riemann Hypothesis
 A Simple Counterexample to Havil s Reformulation of the Riemann Hypothesis Jonathan Sondow 209 West 97th Street New York, NY 0025 jsondow@alumni.princeton.edu The Riemann Hypothesis (RH) is the greatest
A Simple Counterexample to Havil s Reformulation of the Riemann Hypothesis Jonathan Sondow 209 West 97th Street New York, NY 0025 jsondow@alumni.princeton.edu The Riemann Hypothesis (RH) is the greatest
Two Articles Proving and Disproving the Riemann Conjecture
 From the SelectedWorks of James T Struck Spring May 30, 2018 Two Articles Proving and Disproving the Riemann Conjecture James T Struck Available at: https://works.bepress.com/james_struck/76/ Two Articles
From the SelectedWorks of James T Struck Spring May 30, 2018 Two Articles Proving and Disproving the Riemann Conjecture James T Struck Available at: https://works.bepress.com/james_struck/76/ Two Articles
Generalized Euler constants
 Math. Proc. Camb. Phil. Soc. 2008, 45, Printed in the United Kingdom c 2008 Cambridge Philosophical Society Generalized Euler constants BY Harold G. Diamond AND Kevin Ford Department of Mathematics, University
Math. Proc. Camb. Phil. Soc. 2008, 45, Printed in the United Kingdom c 2008 Cambridge Philosophical Society Generalized Euler constants BY Harold G. Diamond AND Kevin Ford Department of Mathematics, University
The Prime Unsolved Problem in Mathematics
 The Prime Unsolved Problem in Mathematics March, 0 Augustana Math Club 859: Bernard Riemann proposes the Riemann Hypothesis. 859: Bernard Riemann proposes the Riemann Hypothesis. 866: Riemann dies at age
The Prime Unsolved Problem in Mathematics March, 0 Augustana Math Club 859: Bernard Riemann proposes the Riemann Hypothesis. 859: Bernard Riemann proposes the Riemann Hypothesis. 866: Riemann dies at age
Riemann Zeta Function and Prime Number Distribution
 Riemann Zeta Function and Prime Number Distribution Mingrui Xu June 2, 24 Contents Introduction 2 2 Definition of zeta function and Functional Equation 2 2. Definition and Euler Product....................
Riemann Zeta Function and Prime Number Distribution Mingrui Xu June 2, 24 Contents Introduction 2 2 Definition of zeta function and Functional Equation 2 2. Definition and Euler Product....................
Math 495 Dr. Rick Kreminski Colorado State University Pueblo November 19, 2014 The Riemann Hypothesis: The #1 Problem in Mathematics
 Math 495 Dr. Rick Kreminski Colorado State University Pueblo November 19, 14 The Riemann Hypothesis: The #1 Problem in Mathematics Georg Friedrich Bernhard Riemann 1826-1866 One of 6 Million Dollar prize
Math 495 Dr. Rick Kreminski Colorado State University Pueblo November 19, 14 The Riemann Hypothesis: The #1 Problem in Mathematics Georg Friedrich Bernhard Riemann 1826-1866 One of 6 Million Dollar prize
ON THE SPEISER EQUIVALENT FOR THE RIEMANN HYPOTHESIS. Extended Selberg class, derivatives of zeta-functions, zeros of zeta-functions
 ON THE SPEISER EQUIVALENT FOR THE RIEMANN HYPOTHESIS RAIVYDAS ŠIMĖNAS Abstract. A. Speiser showed that the Riemann hypothesis is equivalent to the absence of non-trivial zeros of the derivative of the
ON THE SPEISER EQUIVALENT FOR THE RIEMANN HYPOTHESIS RAIVYDAS ŠIMĖNAS Abstract. A. Speiser showed that the Riemann hypothesis is equivalent to the absence of non-trivial zeros of the derivative of the
Continuity. Chapter 4
 Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
MA 1: PROBLEM SET NO. 7 SOLUTIONS
 MA 1: PROBLEM SET NO. 7 SOLUTIONS 1. (1) Obtain the number r = 15 3 as an approimation to the nonzero root of the equation 2 = sin() by using the cubic Taylor polynomial approimation to sin(). Proof. The
MA 1: PROBLEM SET NO. 7 SOLUTIONS 1. (1) Obtain the number r = 15 3 as an approimation to the nonzero root of the equation 2 = sin() by using the cubic Taylor polynomial approimation to sin(). Proof. The
Solutions Quiz 9 Nov. 8, Prove: If a, b, m are integers such that 2a + 3b 12m + 1, then a 3m + 1 or b 2m + 1.
 Solutions Quiz 9 Nov. 8, 2010 1. Prove: If a, b, m are integers such that 2a + 3b 12m + 1, then a 3m + 1 or b 2m + 1. Answer. We prove the contrapositive. Suppose a, b, m are integers such that a < 3m
Solutions Quiz 9 Nov. 8, 2010 1. Prove: If a, b, m are integers such that 2a + 3b 12m + 1, then a 3m + 1 or b 2m + 1. Answer. We prove the contrapositive. Suppose a, b, m are integers such that a < 3m
Ch 3.2: Direct proofs
 Math 299 Lectures 8 and 9: Chapter 3 0. Ch3.1 A trivial proof and a vacuous proof (Reading assignment) 1. Ch3.2 Direct proofs 2. Ch3.3 Proof by contrapositive 3. Ch3.4 Proof by cases 4. Ch3.5 Proof evaluations
Math 299 Lectures 8 and 9: Chapter 3 0. Ch3.1 A trivial proof and a vacuous proof (Reading assignment) 1. Ch3.2 Direct proofs 2. Ch3.3 Proof by contrapositive 3. Ch3.4 Proof by cases 4. Ch3.5 Proof evaluations
On the Natural Logarithm Function and its Applications
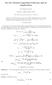 On the Natral Logarithm Fnction and its Applications By Edigles Gedes Febrary 4, 8 at March 7, 5 We love him, becase he rst loved s. - I John 4:9 Abstract. In present article, we create new integral representations
On the Natral Logarithm Fnction and its Applications By Edigles Gedes Febrary 4, 8 at March 7, 5 We love him, becase he rst loved s. - I John 4:9 Abstract. In present article, we create new integral representations
MATH 1014 Tutorial Notes 8
 MATH4 Calculus II (8 Spring) Topics covered in tutorial 8:. Numerical integration. Approximation integration What you need to know: Midpoint rule & its error Trapezoid rule & its error Simpson s rule &
MATH4 Calculus II (8 Spring) Topics covered in tutorial 8:. Numerical integration. Approximation integration What you need to know: Midpoint rule & its error Trapezoid rule & its error Simpson s rule &
Sums of Squares. Bianca Homberg and Minna Liu
 Sums of Squares Bianca Homberg and Minna Liu June 24, 2010 Abstract For our exploration topic, we researched the sums of squares. Certain properties of numbers that can be written as the sum of two squares
Sums of Squares Bianca Homberg and Minna Liu June 24, 2010 Abstract For our exploration topic, we researched the sums of squares. Certain properties of numbers that can be written as the sum of two squares
Introduction to Real Analysis Alternative Chapter 1
 Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
Christopher Heil Introduction to Real Analysis Alternative Chapter 1 A Primer on Norms and Banach Spaces Last Updated: March 10, 2018 c 2018 by Christopher Heil Chapter 1 A Primer on Norms and Banach Spaces
MATH 271 Summer 2016 Practice problem solutions Week 1
 Part I MATH 271 Summer 2016 Practice problem solutions Week 1 For each of the following statements, determine whether the statement is true or false. Prove the true statements. For the false statement,
Part I MATH 271 Summer 2016 Practice problem solutions Week 1 For each of the following statements, determine whether the statement is true or false. Prove the true statements. For the false statement,
1 + lim. n n+1. f(x) = x + 1, x 1. and we check that f is increasing, instead. Using the quotient rule, we easily find that. 1 (x + 1) 1 x (x + 1) 2 =
 Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
Chapter 5 Sequences and series 5. Sequences Definition 5. (Sequence). A sequence is a function which is defined on the set N of natural numbers. Since such a function is uniquely determined by its values
As usual Enoch Opeyemi Oluwole does not care about scientificness
 by Fausto Galetto ZETA Function_Enoch_O_O ignorance of Mathematical Basics From December 15 016 up to March 30 017 I have been reading papers uploaded in Academia.edu by Opeyemi Enoch; I wrote several
by Fausto Galetto ZETA Function_Enoch_O_O ignorance of Mathematical Basics From December 15 016 up to March 30 017 I have been reading papers uploaded in Academia.edu by Opeyemi Enoch; I wrote several
On the Nicolas inequality involving primorial numbers
 On the Nicolas inequality involving primorial numbers Tatenda Isaac Kubalalika March 4, 017 ABSTRACT. In 1983, J.L. Nicholas demonstrated that the Riemann Hypothesis (RH) is equivalent to the statement
On the Nicolas inequality involving primorial numbers Tatenda Isaac Kubalalika March 4, 017 ABSTRACT. In 1983, J.L. Nicholas demonstrated that the Riemann Hypothesis (RH) is equivalent to the statement
Synopsis of Complex Analysis. Ryan D. Reece
 Synopsis of Complex Analysis Ryan D. Reece December 7, 2006 Chapter Complex Numbers. The Parts of a Complex Number A complex number, z, is an ordered pair of real numbers similar to the points in the real
Synopsis of Complex Analysis Ryan D. Reece December 7, 2006 Chapter Complex Numbers. The Parts of a Complex Number A complex number, z, is an ordered pair of real numbers similar to the points in the real
The Continuing Story of Zeta
 The Continuing Story of Zeta Graham Everest, Christian Röttger and Tom Ward November 3, 2006. EULER S GHOST. We can only guess at the number of careers in mathematics which have been launched by the sheer
The Continuing Story of Zeta Graham Everest, Christian Röttger and Tom Ward November 3, 2006. EULER S GHOST. We can only guess at the number of careers in mathematics which have been launched by the sheer
Math 259: Introduction to Analytic Number Theory Functions of finite order: product formula and logarithmic derivative
 Math 259: Introduction to Analytic Number Theory Functions of finite order: product formula and logarithmic derivative This chapter is another review of standard material in complex analysis. See for instance
Math 259: Introduction to Analytic Number Theory Functions of finite order: product formula and logarithmic derivative This chapter is another review of standard material in complex analysis. See for instance
Modified Bessel functions : Iα, Kα
 Modified Bessel functions : Iα, Kα The Bessel functions are valid even for complex arguments x, and an important special case is that of a purely imaginary argument. In this case, the solutions to the
Modified Bessel functions : Iα, Kα The Bessel functions are valid even for complex arguments x, and an important special case is that of a purely imaginary argument. In this case, the solutions to the
Chapter 1. Complex Numbers. Dr. Pulak Sahoo
 Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistant Professor Department of Mathematics University Of Kalyani West Bengal, India E-mail : sahoopulak1@gmail.com 1 Module-1: Basic Ideas 1 Introduction
Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistant Professor Department of Mathematics University Of Kalyani West Bengal, India E-mail : sahoopulak1@gmail.com 1 Module-1: Basic Ideas 1 Introduction
1 Take-home exam and final exam study guide
 Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
Math 215 - Introduction to Advanced Mathematics Fall 2013 1 Take-home exam and final exam study guide 1.1 Problems The following are some problems, some of which will appear on the final exam. 1.1.1 Number
1 Topology Definition of a topology Basis (Base) of a topology The subspace topology & the product topology on X Y 3
 Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
Index Page 1 Topology 2 1.1 Definition of a topology 2 1.2 Basis (Base) of a topology 2 1.3 The subspace topology & the product topology on X Y 3 1.4 Basic topology concepts: limit points, closed sets,
BAIBEKOV S.N., DOSSAYEVA A.A. R&D center Kazakhstan engineering Astana c., Kazakhstan
 BAIBEKOV S.N., DOSSAYEVA A.A. R&D center Kazakhstan engineering Astana c., Kazakhstan DEVELOPMENT OF THE MATRIX OF PRIMES AND PROOF OF AN INFINITE NUMBER OF PRIMES -TWINS Abstract: This paper is devoted
BAIBEKOV S.N., DOSSAYEVA A.A. R&D center Kazakhstan engineering Astana c., Kazakhstan DEVELOPMENT OF THE MATRIX OF PRIMES AND PROOF OF AN INFINITE NUMBER OF PRIMES -TWINS Abstract: This paper is devoted
(z 0 ) = lim. = lim. = f. Similarly along a vertical line, we fix x = x 0 and vary y. Setting z = x 0 + iy, we get. = lim. = i f
 . Holomorphic Harmonic Functions Basic notation. Considering C as R, with coordinates x y, z = x + iy denotes the stard complex coordinate, in the usual way. Definition.1. Let f : U C be a complex valued
. Holomorphic Harmonic Functions Basic notation. Considering C as R, with coordinates x y, z = x + iy denotes the stard complex coordinate, in the usual way. Definition.1. Let f : U C be a complex valued
DOUBLE SERIES AND PRODUCTS OF SERIES
 DOUBLE SERIES AND PRODUCTS OF SERIES KENT MERRYFIELD. Various ways to add up a doubly-indexed series: Let be a sequence of numbers depending on the two variables j and k. I will assume that 0 j < and 0
DOUBLE SERIES AND PRODUCTS OF SERIES KENT MERRYFIELD. Various ways to add up a doubly-indexed series: Let be a sequence of numbers depending on the two variables j and k. I will assume that 0 j < and 0
MATH3500 The 6th Millennium Prize Problem. The 6th Millennium Prize Problem
 MATH3500 The 6th Millennium Prize Problem RH Some numbers have the special property that they cannot be expressed as the product of two smaller numbers, e.g., 2, 3, 5, 7, etc. Such numbers are called prime
MATH3500 The 6th Millennium Prize Problem RH Some numbers have the special property that they cannot be expressed as the product of two smaller numbers, e.g., 2, 3, 5, 7, etc. Such numbers are called prime
Hypergeometric series and the Riemann zeta function
 ACTA ARITHMETICA LXXXII.2 (997) Hypergeometric series and the Riemann zeta function by Wenchang Chu (Roma) For infinite series related to the Riemann zeta function, De Doelder [4] established numerous
ACTA ARITHMETICA LXXXII.2 (997) Hypergeometric series and the Riemann zeta function by Wenchang Chu (Roma) For infinite series related to the Riemann zeta function, De Doelder [4] established numerous
arxiv:chao-dyn/ v1 3 Jul 1995
 Chaotic Spectra of Classically Integrable Systems arxiv:chao-dyn/9506014v1 3 Jul 1995 P. Crehan Dept. of Mathematical Physics, University College Dublin, Belfield, Dublin 2, Ireland PCREH89@OLLAMH.UCD.IE
Chaotic Spectra of Classically Integrable Systems arxiv:chao-dyn/9506014v1 3 Jul 1995 P. Crehan Dept. of Mathematical Physics, University College Dublin, Belfield, Dublin 2, Ireland PCREH89@OLLAMH.UCD.IE
Explicit Bounds Concerning Non-trivial Zeros of the Riemann Zeta Function
 Explicit Bounds Concerning Non-trivial Zeros of the Riemann Zeta Function Mehdi Hassani Dedicated to Professor Hari M. Srivastava Abstract In this paper, we get explicit upper and lower bounds for n,where
Explicit Bounds Concerning Non-trivial Zeros of the Riemann Zeta Function Mehdi Hassani Dedicated to Professor Hari M. Srivastava Abstract In this paper, we get explicit upper and lower bounds for n,where
An iteration procedure for a two-term Machin-like formula for pi with small Lehmer s measure
 arxiv:706.08835v3 [math.gm] 6 Jul 07 An iteration procedure for a two-term Machin-like formula for pi with small Lehmer s measure S. M. Abrarov and B. M. Quine July 6, 07 Abstract In this paper we present
arxiv:706.08835v3 [math.gm] 6 Jul 07 An iteration procedure for a two-term Machin-like formula for pi with small Lehmer s measure S. M. Abrarov and B. M. Quine July 6, 07 Abstract In this paper we present
Hilbert Spaces. Hilbert space is a vector space with some extra structure. We start with formal (axiomatic) definition of a vector space.
 Hilbert Spaces Hilbert space is a vector space with some extra structure. We start with formal (axiomatic) definition of a vector space. Vector Space. Vector space, ν, over the field of complex numbers,
Hilbert Spaces Hilbert space is a vector space with some extra structure. We start with formal (axiomatic) definition of a vector space. Vector Space. Vector space, ν, over the field of complex numbers,
The natural numbers. Definition. Let X be any inductive set. We define the set of natural numbers as N = C(X).
 The natural numbers As mentioned earlier in the course, the natural numbers can be constructed using the axioms of set theory. In this note we want to discuss the necessary details of this construction.
The natural numbers As mentioned earlier in the course, the natural numbers can be constructed using the axioms of set theory. In this note we want to discuss the necessary details of this construction.
Real Numbers in the Neighborhood of Infinity
 Real Numbers in the Neighborhood of Infinity by Jonathan W. Tooker Abstract We demonstrate the existence of a broad class of real numbers which are not elements of any number field: those in the neighborhood
Real Numbers in the Neighborhood of Infinity by Jonathan W. Tooker Abstract We demonstrate the existence of a broad class of real numbers which are not elements of any number field: those in the neighborhood
Part 3.3 Differentiation Taylor Polynomials
 Part 3.3 Differentiation 3..3.1 Taylor Polynomials Definition 3.3.1 Taylor 1715 and Maclaurin 1742) If a is a fixed number, and f is a function whose first n derivatives exist at a then the Taylor polynomial
Part 3.3 Differentiation 3..3.1 Taylor Polynomials Definition 3.3.1 Taylor 1715 and Maclaurin 1742) If a is a fixed number, and f is a function whose first n derivatives exist at a then the Taylor polynomial
Proposed Proof of Riemann Hypothesis
 Proposed Proof of Riemann Hypothesis Aron Palmer Abstract Proposed proof of the Riemann hypothesis showing that positive decreasing continuous function which tends to zero as t goes to infinity can t have
Proposed Proof of Riemann Hypothesis Aron Palmer Abstract Proposed proof of the Riemann hypothesis showing that positive decreasing continuous function which tends to zero as t goes to infinity can t have
DIFFERENCE EQUATIONS
 Chapter 3 DIFFERENCE EQUATIONS 3.1 Introduction Differential equations are applicable for continuous systems and cannot be used for discrete variables. Difference equations are the discrete equivalent
Chapter 3 DIFFERENCE EQUATIONS 3.1 Introduction Differential equations are applicable for continuous systems and cannot be used for discrete variables. Difference equations are the discrete equivalent
e y [cos(x) + i sin(x)] e y [cos(x) i sin(x)] ] sin(x) + ey e y x = nπ for n = 0, ±1, ±2,... cos(nπ) = ey e y 0 = ey e y sin(z) = 0,
![e y [cos(x) + i sin(x)] e y [cos(x) i sin(x)] ] sin(x) + ey e y x = nπ for n = 0, ±1, ±2,... cos(nπ) = ey e y 0 = ey e y sin(z) = 0, e y [cos(x) + i sin(x)] e y [cos(x) i sin(x)] ] sin(x) + ey e y x = nπ for n = 0, ±1, ±2,... cos(nπ) = ey e y 0 = ey e y sin(z) = 0,](/thumbs/93/111506001.jpg) Worked Solutions 83 Chapter 3: Power Series Solutions II: Generalizations Theory 34 a Suppose that e z = 0 for some z = x + iy Then both the real imaginary parts of e z must be zero, e x cos(y) = 0 e x
Worked Solutions 83 Chapter 3: Power Series Solutions II: Generalizations Theory 34 a Suppose that e z = 0 for some z = x + iy Then both the real imaginary parts of e z must be zero, e x cos(y) = 0 e x
Mathematics 324 Riemann Zeta Function August 5, 2005
 Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Mathematics 324 Riemann Zeta Function August 5, 25 In this note we give an introduction to the Riemann zeta function, which connects the ideas of real analysis with the arithmetic of the integers. Define
Mahler measure and special values of L-functions
 Mahler measure and special values of L-functions Matilde N. Laĺın University of Alberta mlalin@math.ualberta.ca http://www.math.ualberta.ca/~mlalin October 24, 2008 Matilde N. Laĺın (U of A) Mahler measure
Mahler measure and special values of L-functions Matilde N. Laĺın University of Alberta mlalin@math.ualberta.ca http://www.math.ualberta.ca/~mlalin October 24, 2008 Matilde N. Laĺın (U of A) Mahler measure
CONSTRUCTION OF THE REAL NUMBERS.
 CONSTRUCTION OF THE REAL NUMBERS. IAN KIMING 1. Motivation. It will not come as a big surprise to anyone when I say that we need the real numbers in mathematics. More to the point, we need to be able to
CONSTRUCTION OF THE REAL NUMBERS. IAN KIMING 1. Motivation. It will not come as a big surprise to anyone when I say that we need the real numbers in mathematics. More to the point, we need to be able to
arxiv: v2 [math.nt] 28 Feb 2010
![arxiv: v2 [math.nt] 28 Feb 2010 arxiv: v2 [math.nt] 28 Feb 2010](/thumbs/94/120531494.jpg) arxiv:002.47v2 [math.nt] 28 Feb 200 Two arguments that the nontrivial zeros of the Riemann zeta function are irrational Marek Wolf e-mail:mwolf@ift.uni.wroc.pl Abstract We have used the first 2600 nontrivial
arxiv:002.47v2 [math.nt] 28 Feb 200 Two arguments that the nontrivial zeros of the Riemann zeta function are irrational Marek Wolf e-mail:mwolf@ift.uni.wroc.pl Abstract We have used the first 2600 nontrivial
(x 1, y 1 ) = (x 2, y 2 ) if and only if x 1 = x 2 and y 1 = y 2.
 1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall.
 .1 Limits of Sequences. CHAPTER.1.0. a) True. If converges, then there is an M > 0 such that M. Choose by Archimedes an N N such that N > M/ε. Then n N implies /n M/n M/N < ε. b) False. = n does not converge,
.1 Limits of Sequences. CHAPTER.1.0. a) True. If converges, then there is an M > 0 such that M. Choose by Archimedes an N N such that N > M/ε. Then n N implies /n M/n M/N < ε. b) False. = n does not converge,
Math 109 HW 9 Solutions
 Math 109 HW 9 Solutions Problems IV 18. Solve the linear diophantine equation 6m + 10n + 15p = 1 Solution: Let y = 10n + 15p. Since (10, 15) is 5, we must have that y = 5x for some integer x, and (as we
Math 109 HW 9 Solutions Problems IV 18. Solve the linear diophantine equation 6m + 10n + 15p = 1 Solution: Let y = 10n + 15p. Since (10, 15) is 5, we must have that y = 5x for some integer x, and (as we
Computing Bernoulli Numbers Quickly
 Computing Bernoulli Numbers Quickly Kevin J. McGown December 8, 2005 The Bernoulli numbers are defined via the coefficients of the power series expansion of t/(e t ). Namely, for integers m 0 we define
Computing Bernoulli Numbers Quickly Kevin J. McGown December 8, 2005 The Bernoulli numbers are defined via the coefficients of the power series expansion of t/(e t ). Namely, for integers m 0 we define
Understanding the Prime Number Theorem
 Understanding the Prime Number Theorem Misunderstood Monster or Beautiful Theorem? Liam Fowl September 5, 2014 Liam Fowl Understanding the Prime Number Theorem 1/20 Outline 1 Introduction 2 Complex Plane
Understanding the Prime Number Theorem Misunderstood Monster or Beautiful Theorem? Liam Fowl September 5, 2014 Liam Fowl Understanding the Prime Number Theorem 1/20 Outline 1 Introduction 2 Complex Plane
n! (k 1)!(n k)! = F (X) U(0, 1). (x, y) = n(n 1) ( F (y) F (x) ) n 2
 Order statistics Ex. 4. (*. Let independent variables X,..., X n have U(0, distribution. Show that for every x (0,, we have P ( X ( < x and P ( X (n > x as n. Ex. 4.2 (**. By using induction or otherwise,
Order statistics Ex. 4. (*. Let independent variables X,..., X n have U(0, distribution. Show that for every x (0,, we have P ( X ( < x and P ( X (n > x as n. Ex. 4.2 (**. By using induction or otherwise,
STATISTICS SYLLABUS UNIT I
 STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
STATISTICS SYLLABUS UNIT I (Probability Theory) Definition Classical and axiomatic approaches.laws of total and compound probability, conditional probability, Bayes Theorem. Random variable and its distribution
Exercise Solutions to Functional Analysis
 Exercise Solutions to Functional Analysis Note: References refer to M. Schechter, Principles of Functional Analysis Exersize that. Let φ,..., φ n be an orthonormal set in a Hilbert space H. Show n f n
Exercise Solutions to Functional Analysis Note: References refer to M. Schechter, Principles of Functional Analysis Exersize that. Let φ,..., φ n be an orthonormal set in a Hilbert space H. Show n f n
PROOF OF RIEMANN S HYPOTHESIS. MSC 2010 : 11A41; 11M06; 11M26 Keywords: Euler; Riemann; Hilbert; Polya; conjecture
 PROOF OF RIEMANN S HYPOTHESIS ROBERT DELOIN Abstract. Riemann s hypothesis (859) is the conjecture stating that: The real part of every non trivial zero of Riemann s zeta function is /. The main contribution
PROOF OF RIEMANN S HYPOTHESIS ROBERT DELOIN Abstract. Riemann s hypothesis (859) is the conjecture stating that: The real part of every non trivial zero of Riemann s zeta function is /. The main contribution
Chapter 7: The z-transform
 Chapter 7: The -Transform ECE352 1 The -Transform - definition Continuous-time systems: e st H(s) y(t) = e st H(s) e st is an eigenfunction of the LTI system h(t), and H(s) is the corresponding eigenvalue.
Chapter 7: The -Transform ECE352 1 The -Transform - definition Continuous-time systems: e st H(s) y(t) = e st H(s) e st is an eigenfunction of the LTI system h(t), and H(s) is the corresponding eigenvalue.
Continuity. Chapter 4
 Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Chapter 4 Continuity Throughout this chapter D is a nonempty subset of the real numbers. We recall the definition of a function. Definition 4.1. A function from D into R, denoted f : D R, is a subset of
Polyexponentials. Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH
 Polyexponentials Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH 45810 k-boyadzhiev@onu.edu 1. Introduction. The polylogarithmic function [15] (1.1) and the more general
Polyexponentials Khristo N. Boyadzhiev Ohio Northern University Departnment of Mathematics Ada, OH 45810 k-boyadzhiev@onu.edu 1. Introduction. The polylogarithmic function [15] (1.1) and the more general
The Riemann Hypothesis Project summary
 The Riemann Hypothesis Project summary The spectral theory of the vibrating string is applied to a proof of the Riemann hypothesis for the Hecke zeta functions in the theory of modular forms. A proof of
The Riemann Hypothesis Project summary The spectral theory of the vibrating string is applied to a proof of the Riemann hypothesis for the Hecke zeta functions in the theory of modular forms. A proof of
Zeros of ζ (s) & ζ (s) in σ< 1 2
 Turk J Math 4 (000, 89 08. c TÜBİTAK Zeros of (s & (s in σ< Cem Yalçın Yıldırım Abstract There is only one pair of non-real zeros of (s, and of (s, in the left halfplane. The Riemann Hypothesis implies
Turk J Math 4 (000, 89 08. c TÜBİTAK Zeros of (s & (s in σ< Cem Yalçın Yıldırım Abstract There is only one pair of non-real zeros of (s, and of (s, in the left halfplane. The Riemann Hypothesis implies
arxiv: v11 [math.gm] 30 Oct 2018
![arxiv: v11 [math.gm] 30 Oct 2018 arxiv: v11 [math.gm] 30 Oct 2018](/thumbs/88/116803036.jpg) Noname manuscript No. will be inserted by the editor) Proof of the Riemann Hypothesis Jinzhu Han arxiv:76.99v [math.gm] 3 Oct 8 Received: date / Accepted: date Abstract In this article, we get two methods
Noname manuscript No. will be inserted by the editor) Proof of the Riemann Hypothesis Jinzhu Han arxiv:76.99v [math.gm] 3 Oct 8 Received: date / Accepted: date Abstract In this article, we get two methods
The zeta function, L-functions, and irreducible polynomials
 The zeta function, L-functions, and irreducible polynomials Topics in Finite Fields Fall 203) Rutgers University Swastik Kopparty Last modified: Sunday 3 th October, 203 The zeta function and irreducible
The zeta function, L-functions, and irreducible polynomials Topics in Finite Fields Fall 203) Rutgers University Swastik Kopparty Last modified: Sunday 3 th October, 203 The zeta function and irreducible
On Exponential Decay and the Riemann Hypothesis
 On Exponential Decay and the Riemann Hypothesis JEFFREY N. COOK ABSTRACT. A Riemann operator is constructed in which sequential elements are removed from a decaying set by means of prime factorization,
On Exponential Decay and the Riemann Hypothesis JEFFREY N. COOK ABSTRACT. A Riemann operator is constructed in which sequential elements are removed from a decaying set by means of prime factorization,
Solution of the 8 th Homework
 Solution of the 8 th Homework Sangchul Lee December 8, 2014 1 Preinary 1.1 A simple remark on continuity The following is a very simple and trivial observation. But still this saves a lot of words in actual
Solution of the 8 th Homework Sangchul Lee December 8, 2014 1 Preinary 1.1 A simple remark on continuity The following is a very simple and trivial observation. But still this saves a lot of words in actual
Contents. Preface xi. vii
 Preface xi 1. Real Numbers and Monotone Sequences 1 1.1 Introduction; Real numbers 1 1.2 Increasing sequences 3 1.3 Limit of an increasing sequence 4 1.4 Example: the number e 5 1.5 Example: the harmonic
Preface xi 1. Real Numbers and Monotone Sequences 1 1.1 Introduction; Real numbers 1 1.2 Increasing sequences 3 1.3 Limit of an increasing sequence 4 1.4 Example: the number e 5 1.5 Example: the harmonic
An Introduction to the Riemann Hypothesis
 An Introduction to the Riemann Hypothesis Theodore J. Yoder May 7, Abstract Here we discuss the most famous unsolved problem in mathematics, the Riemann hypothesis. We construct the zeta function and its
An Introduction to the Riemann Hypothesis Theodore J. Yoder May 7, Abstract Here we discuss the most famous unsolved problem in mathematics, the Riemann hypothesis. We construct the zeta function and its
Z - Transform. It offers the techniques for digital filter design and frequency analysis of digital signals.
 Z - Transform The z-transform is a very important tool in describing and analyzing digital systems. It offers the techniques for digital filter design and frequency analysis of digital signals. Definition
Z - Transform The z-transform is a very important tool in describing and analyzing digital systems. It offers the techniques for digital filter design and frequency analysis of digital signals. Definition
MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS
 MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS ABDUL HASSEN AND HIEU D. NGUYEN Abstract. This paper investigates a generalization the classical Hurwitz zeta function. It is shown that many of the properties
MOMENTS OF HYPERGEOMETRIC HURWITZ ZETA FUNCTIONS ABDUL HASSEN AND HIEU D. NGUYEN Abstract. This paper investigates a generalization the classical Hurwitz zeta function. It is shown that many of the properties
The Limit Inferior and Limit Superior of a Sequence
 The Limit Inferior and Limit Superior of a Sequence James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University February 13, 2018 Outline The Limit Inferior
The Limit Inferior and Limit Superior of a Sequence James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University February 13, 2018 Outline The Limit Inferior
On Exponential Decay and the Riemann Hypothesis
 On Exponential Decay and the Riemann Hypothesis JEFFREY N. COOK ABSTRACT. A Riemann operator is constructed in which sequential elements are removed from a decaying set by means of prime factorization,
On Exponential Decay and the Riemann Hypothesis JEFFREY N. COOK ABSTRACT. A Riemann operator is constructed in which sequential elements are removed from a decaying set by means of prime factorization,
Final Exam - MATH 630: Solutions
 Final Exam - MATH 630: Solutions Problem. Find all x R satisfying e xeix e ix. Solution. Comparing the moduli of both parts, we obtain e x cos x, and therefore, x cos x 0, which is possible only if x 0
Final Exam - MATH 630: Solutions Problem. Find all x R satisfying e xeix e ix. Solution. Comparing the moduli of both parts, we obtain e x cos x, and therefore, x cos x 0, which is possible only if x 0
Hölder s and Minkowski s Inequality
 Hölder s and Minkowski s Inequality James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University September 1, 218 Outline Conjugate Exponents Hölder s
Hölder s and Minkowski s Inequality James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University September 1, 218 Outline Conjugate Exponents Hölder s
means is a subset of. So we say A B for sets A and B if x A we have x B holds. BY CONTRAST, a S means that a is a member of S.
 1 Notation For those unfamiliar, we have := means equal by definition, N := {0, 1,... } or {1, 2,... } depending on context. (i.e. N is the set or collection of counting numbers.) In addition, means for
1 Notation For those unfamiliar, we have := means equal by definition, N := {0, 1,... } or {1, 2,... } depending on context. (i.e. N is the set or collection of counting numbers.) In addition, means for
Estimating Prime Power Sums
 Estimating Prime Power Sums Francis Gerard Mentored By: Lawrence Washington, University of Maryland Personal Statement Number theory is a field that has, for me, always held a special kind of magic. There
Estimating Prime Power Sums Francis Gerard Mentored By: Lawrence Washington, University of Maryland Personal Statement Number theory is a field that has, for me, always held a special kind of magic. There
SPRING 2008: POLYNOMIAL IMAGES OF CIRCLES
 18.821 SPRING 28: POLYNOMIAL IMAGES OF CIRCLES JUSTIN CURRY, MICHAEL FORBES, MATTHEW GORDON Abstract. This paper considers the effect of complex polynomial maps on circles of various radii. Several phenomena
18.821 SPRING 28: POLYNOMIAL IMAGES OF CIRCLES JUSTIN CURRY, MICHAEL FORBES, MATTHEW GORDON Abstract. This paper considers the effect of complex polynomial maps on circles of various radii. Several phenomena
Math 229: Introduction to Analytic Number Theory The product formula for ξ(s) and ζ(s); vertical distribution of zeros
 Math 9: Introduction to Analytic Number Theory The product formula for ξs) and ζs); vertical distribution of zeros Behavior on vertical lines. We next show that s s)ξs) is an entire function of order ;
Math 9: Introduction to Analytic Number Theory The product formula for ξs) and ζs); vertical distribution of zeros Behavior on vertical lines. We next show that s s)ξs) is an entire function of order ;
It is the purpose of this chapter to establish procedures for efficiently determining the solution of a system of linear equations.
 Chapter 2. Linear Systems and their Solution It is the purpose of this chapter to establish procedures for efficiently determining the solution of a system of linear equations. We know that the data within
Chapter 2. Linear Systems and their Solution It is the purpose of this chapter to establish procedures for efficiently determining the solution of a system of linear equations. We know that the data within
THEOREM OF OSELEDETS. We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets [1].
![THEOREM OF OSELEDETS. We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets [1]. THEOREM OF OSELEDETS. We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets [1].](/thumbs/95/124190157.jpg) THEOREM OF OSELEDETS We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets []. 0.. Cocycles over maps. Let µ be a probability measure
THEOREM OF OSELEDETS We recall some basic facts and terminology relative to linear cocycles and the multiplicative ergodic theorem of Oseledets []. 0.. Cocycles over maps. Let µ be a probability measure
