Approximate Capacity Region of the MAC-IC-MAC
|
|
|
- Damian Rogers
- 5 years ago
- Views:
Transcription
1 1 Approximate Capacity Region of the MAC-IC-MAC Yimin Pang, Student Member, IEEE, and Mahesh Varanasi, Fellow, IEEE arxiv: v1 [cs.it] 8 Apr 2016 Abstract An approximate capacity region is established of a class of interfering multiple access channels consisting of two multiple-access channels (MACs), each with an arbitrary number of users, with interference from one of the transmitters of one MAC to the receiver of the other MAC, which we refer to henceforth as the MAC-IC-MAC. It is shown that, for the semi-deterministic MAC-IC-MAC, single-user coding at the non-interfering transmitters in each MAC and superposition coding at the interfering transmitter of each MAC achieves a rate region that is within a quantifiable gap of the capacity region, thereby generalizing the result by Telatar and Tse for the 2-user semi-deterministic interference channel. Next, with an explicit coding scheme, we establish an approximate capacity region that is within a one-bit gap of the capacity region for the Gaussian MAC-IC-MAC, thereby extending the work by Etkin et al for the two-user Gaussian interference channel. The symmetric generalized degrees of freedom (GDoF) of the symmetric Gaussian MAC-IC-MAC with more than one user per cell, which is a function of the interference strength (the ratio of INR to SNR at high SNR, both expressed in db) and the numbers of users in each cell, is V-shaped with flat shoulders. An analysis based on the deterministic method shows that, when interference is sufficiently weak or strong, the non-interfering transmitters are not mere sharers of the degrees of freedom with the interfering transmitters. They instead also utilize power levels that cannot be accessed by interfering transmitters (due to the restriction of superposition coding), thereby improving the symmetric sum GDoF to up to one degree of freedom per cell under a range of SINR exponent levels. Time sharing between interfering and non-interfering transmitters is suboptimal. Index Terms Approximate capacity, capacity region, constant gap, interference channel, interfering multiple access channel, MAC-IC-MAC, multiple access channel, generalized degrees of freedom. This work was supported in part by NSF Grant It was presented in part at the 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Yimin Pang is with the Department of Electrical, Computer and Energy Engineering, University of Colorado Boulder, Boulder, US, yipa5803@colorado.edu. Mahesh K. Varanasi is with the Department of Electrical, Computer and Energy Engineering, University of Colorado Boulder, Boulder, US, varanasi@colorado.edu.
2 2 I. INTRODUCTION Due to the rapid increase of data demands in recent years, wireless co-band communication has drawn significant interest in both theory and practice. Bluetooth and Wi-Fi have both been established on 2.4 GHz band, and more recently 3GPP introduced LTE Licensed Assisted Access (LAA) to offload LTE packets to unlicensed spectrum at 5 GHz, which causes Wi-Fi and LAA to coexist. Such emerging technologies motivate the study of co-band interference between cellular networks in network information theory. In this paper, we obtain an approximate capacity region for a class of mutually interfering two-cell networks in which there is interference from one of the transmitters of the MAC to the receiver of the other MAC. For brevity, we refer to this two-cell network as the MAC-IC-MAC. As shown in Fig. 1, the MAC-IC-MAC captures many practical communication scenarios. Fig. 1a shows an uplink cellular network where users a0 and b0 are located on the cell edge so that interference paths exist between the two cells as indicated by the dashed arrows, meanwhile users a1 and b1 do not cause interference to the neighboring cell due to their favorable access location in their own cell. Fig. 1b represents a femto cell network, where similar partial interference exists between the macro cell and femto cell. The study of the capacity region of MAC-IC-MAC could therefore provide an approach to increasing uplink throughput and cell edge spectrum efficiency for co-band networks. (a) A cellular network (b) A femto cell network Fig. 1. Examples of the MAC-IC-MAC The main results of this paper are: 1) An achievable rate region for discrete memoryless MAC-IC-MAC: the coding scheme we employ is what would be deemed the most natural for the MAC-IC-MAC: each of the two interfering transmitters employ rate-splitting and superposition coding (as in [1]) and the non-interfering transmitters in each MAC employ single-user random coding. An analysis of such a coding scheme results in an inner bound for the capacity region that is a polytope in a number of dimensions that is more than the total number of transmitters due to rate-splitting at the two interfering transmitters. Such a polytope is defined by an indeterminate number of sum-rate inequalities (indeed, exponentially many in the total number of transmitters) because there is no restriction on the number of users in each cell. Utilizing the particular structure of this polytope however, and using a form of structured Fourier-Motzkin elimination, the two split rates are projected out to obtain a closed-form description of the achievable rate region.
3 3 2) An outer bound on the capacity region of semi-deterministic MAC-IC-MAC: the proof of this outer bound uses genie-aided decoding arguments and it is shown that it is within a quantifiable gap to the capacity region, thereby extending the corresponding result for the two-user semi-deterministic interference channel obtained by Telatar and Tse [2]. 3) An inner bound for the Gaussian MAC-IC-MAC that is within a one-bit gap of the capacity region, thereby extending the same result for the Gaussian interference channel due to Etkin et al [3]. 4) The generalized degrees of freedom (GDoF) region for the Gaussian MAC-IC-MAC: the one bit gap capacity for Gaussian MAC-IC-MAC yields its GDoF region. In addition, the symmetric GDoF curve, which is a function of α, the interference strength (the ratio of INR to SNR at high SNR, both expressed in db) and the number of users in a cell, is V-shaped with flat shoulders on the two sides. The symmetric GDoF curve, which is plotted in Fig. 2, reveals that in a Gaussian MAC-IC-MAC with symmetric cell configuration and equal rate requirement, all transmitters can send information at an approximately interference-free rate in the high SNR regime when α = log INR log SNR [0, 1 1 K ] [1 + 1 K, ), where K is the number of users in each cell. As a byproduct, our result also says that the DoF of the K-user symmetric Gaussian MAC-IC-MAC is simply 1 K+1. In Section III.E, a few examples will be discussed to demonstrate the achievablity of GDoF region in various ranges of α using a deterministic analysis. It is shown that the non-interfering transmitters in the MAC-IC- MAC do not always share the DoF with the interfering transmitter in each cell (but when α = 1, they do). Using the deterministic approximation, we see that the rate-splitting and superposition coding scheme prevents interfering transmitters to use certain power levels, so that non-interfering transmitters occupy these unused levels, thereby improving the total DoF per cell. Consequently, merely time-sharing between interfering and non-interfering transmitters is suboptimal. Fig. 2. Symmetric GDoF of Gaussian MAC-IC-MAC Previous related works are summarized as follows. Multiple access channels are the best understood multi-terminal networks with the capacity region fully determined by Ahlswede [4] and Liao [5]. The key papers on interference channels are [2], [3], [6] [8]. For the interference channel, the Han-Kobayashi achievable scheme (H-K scheme) in [7] as well as its alternative superposition coding scheme of [1] (referred to henceforth as the CMG scheme) lead to the best inner bound to the capacity region known to date. Telatar and Tse [2] found an outer bound for the so-called semi-deterministic interference channel and quantified the gap to the CMG inner bound. For Gaussian
4 4 scalar and vector interference channels, Etkin et al [3] and Karmakar and Varanasi [9] characterized approximate capacity regions to within constant, channel coefficient- and SNR-independent gaps, respectively. For two cell interfering multiple access channel with an arbitrary number of transmitters in each cell, the work by [10] used interference alignment [11] to achieve interference-free degrees of freedom when the number of users in each cell goes to infinity. Perron et al. [12] defined a type of multiple-access interference channel with only four nodes, where one of the receivers must decode the messages from both transmitters. The capacity region within a quantifiable gap was obtained for the semi-deterministic case. Chaaban and Sezgin studied the fully-connected two-cell multiple access interference channel in which a two-user MAC interferes with a point-to-point link [13]. The capacity region is found for very strong and some cases of strong interference and upper and lower bounds on the sum-rate in the weak interference regime (with the lower bound achievable by treating interference as noise) are also obtained. Susbsequently, in [14], they showed that when the interference is weak, treating interference as noise in their model is sub-optimal. The cognitive radio version of that model was studied by the same authors in [15]. Buhler and Wunder [16] derived upper bounds on the sum rate and an achievable scheme for the linear deterministic version of the model in [13]. Fritschek and Wunder obtain a result on the reciprocity between the two-cell deterministic interfering MAC (IMAC) and the two-cell deterministic interfering broadcast channel (IBC) in [17], and obtain an achievable region under a weak interference condition for both those channels. In [18], the deterministic IMAC was revisited using the lower triangular deterministic model introduced by [19], and a constant gap sum capacity as well as the sum GDoF were obtained. For the Gaussian IMAC, Fritschek and Wunder [20] close the gap between the achievable sum rate regions for Gaussian IMAC and the deterministic IMAC. Their coding scheme employs signal scale alignment and lattice coding. Zhu et al. [21] studied the interference Z MAC, a special case of the channel in [13], where they obtained an achievable rate region based on superposition encoding and joint decoding. In the conference version of this paper [22], an approximate capacity region was presented for a special case of the MAC-IC-MAC with a two-user MAC in the first cell and a point-to-point link in the second cell 1 The notation used throughout the paper are summarized as follows. We use capital letters to denote random variables or sequences, such as X and X n, where X n = {X 1,, X n }. The underlying sample spaces are denoted by X and X n, and specific values of X and X n by x and x n. The t-th element of the random vector Xij n is denoted by Xn ij,t. Unless specified explicitly, we will use the usual short hand notation for (conditional) probability distributions where the lower case arguments also denote the random variables whose (conditional) distribution is being considered. For example, p(y x) denotes p Y X (y x). The j-th user in the i-th cell is indexed as ij, where i {a, b}, j Θ i {0,, (K i 1)} and K i is the user-number in cell-i. Hence the j-th transmitter in the i-th cell is denoted as Txij, whose message, input random variable, and rate are denoted as M ij, X ij and R ij, respectively. The signal-to-noise ration (SNR) and interference-to-noise ratio (INR) from Txij and Txi j to Rxi are written as SNR iji and INR i ji, respectively, where i, i {a, b} and i i. Similar notation is used for the 1 Since we are studying a more general channel model here than [22], the missing proofs in [22] can be completed by setting K a = 2 and K b = 1 in the results and proofs in Section III and Appendices. Typographical errors in [22] are also corrected in this version.
5 5 other cross-cell terms. The K i -tuples of messages, inputs and rates of cell i as denoted as M i, X i and R i. For example, the vector of inputs in cell-a (X a0,, X a(ka 1)) are denoted as X a, with similar abbreviation used for M a and R a. However, the Gaussian noise Z i, output Y i and random variables S i and T i are just single random variables. As defined later, we use Υ i to denote a subset of user indices in cell i that necessarily contain the interfering user i0, and Ω i to denote an arbitrary subset of users in cell i. The sets Ῡi and Ω i are defined as the complements of Υ i and Ω i. Again, the inputs of users in Υ i or Ω i are written as X Υi and X Ωi. But the same rule does not apply to R Υi and R Ωi, which denote ij Υ i R ij and ij Ω i R ij. We use C to denote the set of complex numbers, X CN (0, σ 2 ) to denote a complex random variable X whose distribution is the complex circularly symmetric zero-mean Gaussian distribution with variance σ 2, and to represent the magnitude of a complex number. To avoid writing out the rate regions explicitly all the time, we heavily rely on a generic region, which will be defined in Section II.D. The generic region is described by four set functions, each of which is a generic function of some subset Υ i or Ω i, and will be further defined in various concrete contexts whenever a region needs to be specified. The rest of the paper is organized as follows. Section II introduces the three channel models of MAC-IC-MAC and formulates the problem. Section III presents the five main results listed above; Section VI concludes the paper. Some detailed proofs are relegated to the appendices. II. CHANNEL MODELS AND PROBLEM FORMULATION In this section, we introduce in sequence the general discrete memoryless MAC-IC-MAC, the semi-deterministic MAC-IC-MAC and the Gaussian MAC-IC-MAC. We also define a generic region which we will use repeatedly in subsequent sections to describe inner and outer bounds on the capacity region of those three MAC-IC-MAC models. A. Discrete Memoryless MAC-IC-MAC (DM MAC-IC-MAC) In a DM MAC-IC-MAC, as shown in Fig. 3, there are two uplink communication cells: (Txa0 Txa(K a 1) Rxa) and (Txb0 Txb(K b 1) Rxb). Two interference links exist between these two cells which are governed by the marginal probability p Ya X b0 (y a x b0 ) and p Yb X a0 (y b x a0 ), respectively. The definition of DM MAC-IC-MAC is given below. (Please recall the notation system we have introduced in Section I, such as X i = {X i0,, X i(ki 1)} and etc.) Definition 1. A (K a, K b ) discrete memoryless MAC-IC-MAC is a (K a + K b )-transmitter-2-receiver network with transition probability satisfying p(y i x i, x i ) = p(y i x i, x i 0 ) (1) for i, i {a, b} and i i. The input and output random variables X ij and Y i are taken from discrete alphabet sets X ij and Y j respectively, where j {0,, K i }. Message M ij is generated from set M ij uniformly at random, and encoded at transmitters Txij. Receiver Rxi decodes M i as ˆM i.
6 6 Fig. 3. Discrete memoryless MAC-IC-MAC of Given the channel as defined in Definition 1, a (n, R a, R b, P e (n) ) coding scheme for a DM MAC-IC-MAC consists M ij, the message of transmitter ij, assumed to be uniformly distributed over M ij {1,, 2 nrij }; encoding functions f ij ( ) such that, decoding functions g i ( ) such that The probability of error P (n) e f ij ( ) : M ij X n ij, m ij x n ij(m ij ) g i ( ) : Y n i is defined to be P (n) e = P K i 1 j=0 M ij, y n i ˆm i { M i M } i : i {a, b} A K a + K b -tuple rate (R a, R b ) is said to be achievable if there exists a sequence of (n, R a, R b, P e (n) ) coding schemes for which P (n) e 0 as n. The capacity region of the MAC-IC-MAC, denoted as C, is the closure of achievable rate-tuples. An inner bound for C is obtained in Section III.A. Remark 2. The study of the MAC-IC-MAC at high SNR is also relevant to the fully-connected (K a + K b )- transmitter, 2-receiver, two-cell interference networks when the interference from all but one transmitter in each cell are sufficiently weak so that they are received at the unintended receiver at the noise level (and are therefore treated as noise). B. Semi-Deterministic MAC-IC-MAC The received interference in a semi-deterministic MAC-IC-MAC (as shown in Fig. 4) has a special structure as defined below. This structure includes specialization to Gaussian MAC-IC-MACs. Moreover, we will see that the genie-aided arguments of [2] for the 2-user IC can be extended to the semi-deterministic MAC-IC-MAC in obtaining outer bounds to the capacity region.
7 7 Fig. 4. Semi-deterministic MAC-IC-MAC Definition 3. Let S i be a random variable over the alphabet S i for i {a, b}. A MAC-IC-MAC is semi-deterministic if the outputs Y i satisfy Y i = Φ i (X i, S i ) (2) where for any fixed inputs x i, the mapping Φ i (x i, ) : S i Y i, s i y i is invertible. We use C SD to denote the capacity region of semi-deterministic MAC-IC-MAC. An outer bound will be obtained for C SD in Section III.B. C. Gaussian MAC-IC-MAC Consider an additive Gaussian MAC-IC-MAC, whose input-output relation can be written as Y a = Y b = K a 1 j=0 K b 1 j=0 h aj,a X aj + h b0,a X b0 + Z a (3) h bj,b X bj + h a0,b X a0 + Z b (4) where X ij and Y i are complex input and output random variables, h ij,i, h ij,i C are path attenuations from Txij to Rxi and Rxi, respectively, and Z i CN (0, 1) is the additive noise. The transmitted codeword x n ij (m ij) X n ij at Txij should meet the average per-codeword power constraints: 1 n n x ij,t (m ij ) 2 1 (5) t=1 The SNRs and INR at receiver Rxi are defined to be SNR ij,i = P ij h ij,i 2 (6) INR i 0,i = P i 0 h i 0,i 2 (7)
8 8 where P ij is the maximum average transmission power at Txij. We denote the capacity region of Gaussian MAC- IC-MAC by C G. The Gaussian MAC-IC-MAC is a special case of the semi-deterministic MAC-IC-MAC, as can be seen by choosing S i in (2) to be S i = h i 0,i X i 0 + Z i. In Section III.D, we will get an inner bound and an outer bound for C G. The inner bound will be derived based on an explicit coding scheme, and these two bounds will be within a one-bit gap. D. A Generic Region For brevity, we provide a definition of a generic region in this subsection in terms of which all key results are succinctly expressed later in the paper. Definition 4. For any sets Ω i {i0,, i(k i 1)}, Υ i {i1,, i(k i 1)} and Υ i = Υ i {i0}, where i {a, b}, let A Υi and E Υi be real-valued functions of set Υ i, and B Ωi and G Ωi be real-valued functions of the set Ω i. Define R(R a, R b, A, B, E, G) R Ka+K b + to be the region of (R a, R b ) such that for any Ω i and Υ i, R Ωa B Ωa (8) R Ωb B Ωb (9) R Υa + R Ωb A Υa + G Ωb (10) R Ωa + R Υb A Υb + G Ωa (11) R Υa + R Υb E Υa + E Υb (12) R Υa + R Ωa + R Υb A Υa + G Ωa + E Υb (13) R Υa + R Ωb + R Υb A Υb + G Ωb + E Υa (14) As will be observed in the later section, each set function represents a mutual information term for a certain set Ω i or Υ i. However, the exact mapping of these set functions are not given here. Instead, they will be assigned according to the channel model DM, semi-deterministic or Gaussian and as to whether the bound under consideration is an inner bound or an outer bound. When a concrete region needs to be shown, we will specialize each set function, and a rate region can be described by replacing the generic set functions in inequalities (8)-(14) with the specified ones. III. MAIN RESULTS In the previous section, we introduced several different models of MAC-IC-MAC. This section presents the main results of this paper, which are inner and/or outer bounds on the capacity regions for those models. Section III.A states an inner bound on the capacity region of general DM MAC-IC-MAC, supported by the random coding framework. Section III.B presents an outer bound for the semi-deterministic MAC-IC-MAC using a genie-aided decoding argument, and this outer bound will be proved, in Section III.C, to be within quantifiable gap to the inner bound derived in Section III.A. Section III.D focuses on the Gaussian MAC-IC-MAC, where we give a single
9 9 region inner bound (rather than a convex hull of a union of regions) of its capacity region based on the Etkin- Tse-Wang-type coding scheme [3], and a single region outer bound. These two bounds are within a one-bit gap. Finally, in Section III.E, the discussion on the GDoF of the Gaussian MAC-IC-MAC reveals how the non-interfering transmitters improve the symmetric sum GDoF under various interference strength parameter α, defined as the ratio of the INR to SNR, both expressed in db scale, at high SNR. A. Inner Bound on the Capacity Region of DM MAC-IC-MAC As being mentioned earlier, the H-K scheme (and its alternative CMG scheme) lead to the best inner bounds to date for the interference channel. In this section, we apply the CMG type scheme to the MAC-IC-MAC. More specifically, we employ superposition coding at Txi0 and use a single-user random codebook for transmitter Txij, j 0. Applying the joint-typicality decoding argument we derive a CMG-like inner bound for the DM MAC-IC- MAC as following. Definition 5. For any given jointly distributed random variables (Q, U a0, X a, U b0, X b ) with distribution p(q)p(u a0, x a q)p(u b0, x b q), let the non-negative real valued set functions A, B, E and G be and the region R in (Q, U a0, X a, U b0, X b ) R Ka+K b + to be A Υi I(X Υi ; Y i X Ῡi, U i0, U i 0, Q) (15) B Ωi I(X Ωi ; Y i X Ωi, U i 0, Q) (16) E Υi I(X Υi, U i 0 ; Y i X Ῡi, U i0, Q) (17) G Ωi I(X Ωi, U i 0 ; Y i X Ωi, Q) (18) R in (Q, U a0, X a, U b0, X b ) R(R a, R b, A, B, E, G) (19) Theorem 6. For a (K a, K b ) DM MAC-IC-MAC, R in R in (Q, U a0, X a, U b0, X b ) C (X a,u a0) Q (X b,u b0 ) Proof: The proof is done in two parts. With the interfering transmitters employing the CMG rate-splitting and superposition coding scheme as in the two-user interference channel in [1], and the non-interfering transmitters using independent random coding (as in a MAC), with each receiver decoding all its desired messages and the common sub-message of the interfering transmitter using simultaneous non-unique decoding, standard random analysis techniques lead to a intermediate rate region containing two auxiliary random variables which represent the common sub-message or cloud" codewords of interfering transmitters, and two auxiliary rates corresponding to these codebooks. This part of the proof extends the reliability analysis of the CMG coding scheme [1] to the MAC-IC-MAC. More specifically: 1) The non-interfering receiver Txij, j 0 sends information m n ij by some codeword x n ij (mn ij ) using a single-user random codebook; 2) the interfering transmitter Txi0 splits its message m i0
10 10 into common and private sub-messages m i0,c and m i0,p, respectively. The common information is first encoded into the cloud center codeword u n i0 (m i0,c), and then, based on the private sub-message m i0,p, the message m i0 is encoded into the codeword x n i0 (un i0 (m i0,c), m i0,p ) for transmission; 3) Rxi decodes all the information m n ij, j 0, and the public and private information m i0,c and m i0,p from all of its intended transmitters, and the common information m i 0,c from the non-intended transmitter Txi 0 (but non-uniquely). Second, we carry out Fourier-Motzkin elimination of the two auxiliary rates analytically to project the rate region onto R Ka+K b + of message rates, despite the numbers of users in both cells being arbitrary. In this step, the algebraic structure of the inequality system created in the first step is utilized, since a hand-crafted, brute-force Fourier-Motzkin elimination is not possible. The detailed proof is given in Appendix A. B. An Outer Bound for the Semi-Deterministic MAC-IC-MAC Next, we focus our attention on the semi-deterministic MAC-IC-MAC. The inner bound stated in the previous subsection automatically applies to the semi-deterministic MAC-IC-MAC. Besides, the semi-deterministic property given in (2) enables us to determine an outer bound. The key idea is to allow a genie to pass some channel side information about S i to help Rxi s decoding. Since providing side information to the receiver will not decrease the channel capacity, an outer bound can therefore be characterized. This idea was first introduced in the work of [2] for the two-user IC, and we show a similar argument that can be applied to semi-deterministic MAC-IC-MAC too. Definition 7. Given any set of random variables (Q, X a, T a, X b, T b ) with joint distribution p(q)p(x a, t a q)p(x b, t a q), let the set functions A, B, E and G be A Υi H(Y i X Ῡi, T i, X i 0, Q) H(S i X i, Q) (20) B Ωi H(Y i X Ωi, X i 0, Q) H(S i X i, Q) (21) E Υi H(Y i X Ῡi, T i, Q) H(S i X i, Q) (22) G Ωi H(Y i X Ωi, Q) H(S i X i, Q) (23) where the auxiliary random variable T i takes value from S i according to p Ti Q,X i,x i (t i q, x i, x i ) p Si X i0 (t i x i0 ) (24) and is conditionally independent of S i given X i. Define the region R SD out(q, T a, X a, T b, X b ) R Ka+K b + to be R(R a, R b, A, B, E, G). Remark 8. According to (24), a genie informs Rxi the distribution of the side information S i (refer to Fig. (4)), but not S i itself, since S i and T i are conditionally independent on X i. Therefore we have H(T i X i0 ) = H(S i X i0 ) and H(Ti n) = H(Sn i ). This observation plays an important role in the proof of the following theorem.
11 11 Theorem 9. For semi-deterministic MAC-IC-MAC, C SD R SD out (X a,t a) Q (X b,t b ) R SD out(q, T a, X a, T b, X b ) Proof: We first extend the genie-aided argument in [2] to upper bound the sum rates for a given user subset Υ i or Ω i. Then, linearly combining these bounds to cancel the genie random variables yields the theorem. Please refer to Appendix B for details. C. Quantifiable Gap Next, we show that for the semi-deterministic MAC-IC-MAC, the outer bound obtained in Theorem (9) is within a quantifiable gap of its capacity region. To prove this, we construct a sub-region inside the inner bound in Theorem 6 so the gap between this sub-region and the outer region can be bounded. Theorem 10. For any rate tuple (R a, R b ) R SD out, we have (R a I(X b0 ; S b T b )1 1 Ka, R b I(X a0 ; S a T a )1 1 Kb ) R in where 1 1 Ki is the all-one row vector of dimension K i. Proof: For some input distribution p(q)p(u a0, x a q)p(u b0, x b q), we first construct a sub-region of the inner region R SD in (Q, U a0, X a, U b0, X b ) R SD in (Q, U a0, X a, U b0, X b ), and then choose U i0 in R SD in (Q, U a0, X a, U b0, X b ) to be identically distributed to T i, and obtain a sub-region R SD in (Q, T a0, X a, T b0, X b ) R SD in (Q, U a0, X a, U b0, X b ). Finally, it can be shown that the gap between R SD in (Q, T a0, X a, T b0, X b ) and R SD out(q, T a0, X a, T b0, X b ) is quantifiable, so that the gap between R SD in C. and R SD out is also quantifiable. We relegate the complete proof to Appendix D. Approximate Capacity Region of Gaussian MAC-IC-MAC within One Bit The quantifiable gap on semi-deterministic MAC-IC-MAC capacity directly yields an approximation of the capacity region to within a constant-bit-gap for the Gaussian MAC-IC-MAC. The bounds in Theorem 6 and 9 are sufficient to provide an approximate capacity region for Gaussian MAC-IC-MAC, and according to Theorem (10), the gap between the inner and outer bounds will not exceed one bit. To verify the gap, choose T i = h i0,i X i0 + Z i and Z Z i i so that I(X i0 ; S i T i ) = h(h i0,i X i0 + Z i h i0,i X i0 + Z i ) h(h i0,i X i0 + Z i X i0, h i0,i X i0 + Z i ) h(z i Z i ) h(z i ) = 1 bit However, the inner bound for DM MAC-IC-MAC in Theorem 6 is a union of bounds, each of which corresponds to some choice of joint distribution p(q)p(u a, x a q)p(u b, x b q). A simple explicit coding scheme is preferred whose
12 12 achievable rate region is within a constant gap of the capacity region for Gaussian MAC-IC-MAC. Here, we will show that the Etkin-Tse-Wang type coding scheme [3] at the interfering transmitters and Gaussian codebooks (with maximum allowable power) at the non-interfering transmitters will lead to an inner bound within one bit gap to the capacity. The available power at the interfering transmitters is split between the common and private message in a manner such that the private message arrives at the unintended receiver at the noise level. Definition 11. Suppose C(P ) = log(1 + P ) for some P 0. Define the coefficient { } 1 µ i min 1,, (25) INR i 0,i set functions A, B, E and G be A Υi B Ωi ( µi SNR i0,i + ij Υ C SNR ) i\{i0} ij,i 1 + µ i INR i 0,i ( ) ij Ω C i SNR ij,i 1 + µ i INR i 0,i (26) (27) E Υi G Ωi C ( µi SNR i0,i + ij Υ i\{i0} SNR ij,i 1 + µ i INR i 0,i ) + (1 µ i )INR i 0,i 1 + µ i INR i 0,i ( ) ij Ω C i SNR ij,i + INR i 0,i 1 + µ i INR i 0,i (28) (29) and the region R G in R(R a, R b, A, B, E, G). Theorem 12. For the Gaussian MAC-IC-MAC, R G in CG. Proof: The result can be verified by computing the mutual information terms in Theorem 6 in the context of the proposed coding scheme. First, no time-sharing is adopted between any transmitters. Txij, j 0, uses single-user Gaussian codebook, while Txi0 employs Gaussian superposition coding in terms of splitting transmission power between each of their common and public messages P i0,c and P i0,p. If INR i 0,i < 1, the Gaussian noise dominates the interference at Rxi from Txi 0. Thus, Txi 0 allocates all the transmission power to its private message, and Rxi treats the interference from Txi as noise. When INR i 0,i 1, the transmission power at Txi0 needs to be split so that the power of the unintended private messages from Txi arrives at Rxi at unity (normalized to), i.e. P i0,p CN (0, 1 h i0,i 2 ) (30) Computing all the set functions in Theorem 6 in the context of this coding strategy, the Theorem is proved. Because the Gaussian MAC-IC-MAC is semi-deterministic (where S i = h i0,i X ij +Z i ), Theorem 9 is applicable, and an outer bound on the capacity region can be characterized accordingly.
13 13 Definition 13. Let the set functions A, B, E and G be, A Υi C SNR ij,i + SNR i0,i (31) 1 + INR ij Υ i0,i i\{i0} C (32) B Ωi E Υi G Ωi and define R G out R(R a, R b, A, B, E, G). ij Ω i SNR ij,i C SNR ij,i + SNR i0,i + INR 1 + INR ij Υ i0,i i 0,i (33) i\{i0} C SNR ij,i + INR i 0,i. (34) ij Ω i Theorem 14. For Gaussian MAC-IC-MAC, C G R G out. Proof: Refer to Appendix D. Next we show that the gap between R G in and RG out is within one bit, which implies an explicit coding scheme ensures an inner bound within one bit gap to the capacity. Theorem 15. There is no more than a one bit gap between R G in and RG out. Proof: It is enough to show the gap between each pattern is within one bit. We bound the gap between E Υi and E Υi for instance. E Υi = log 2 + µ i SNR i0,i + +(1 µ i )INR i 0,i log 2 + µ i SNR i0,i + ij Υ i\{i0} ) log ) +(1 µ i )INR i 0,i 1 = log ( 2 + min { 1, 1 + C Other gaps can be verified similarly. ij Υ i\{i0} = E Υi 1 ij Υ i\{i0} INR i0,i SNR ij,i min SNR ij,i ( 1 + µ i INR i 0,i ij Υ i\{i0} } SNR ij,i ) SNR i0,i + INR i 0,i } {INR i 0,i, 1 1 SNR i0,i SNR ij,i + + INR 1 + INR i0,i i 0,i 1
14 14 E. Generalized Degrees of Freedom Region of Gaussian MAC-IC-MAC The generalized degrees of freedom (GDoF) is an information-theoretic metric that characterizes the simultaneously accessible signal-level dimensions (per channel use) by the users of a network in the limit of high SNR, while the ratios of the SNRs and INRs relative to a reference SNR, each expressed in the db scale, are held constant, with each constant taken, in the most general case, to be arbitrary. In this section, we first compute the GDoF region of the Gaussian MAC-IC-MAC and then focus on the study of the symmetric GDoF curve. Given the Gaussian MAC-IC-MAC model as defined by (3) and (4), let ρ be a nominal value for SNR or INR, define ᾱ = (α a0,a,, α a(ka 1),a, α b0,b,, α b(kb 1),b, α a0b, α b0a ) as α ij,i = log(snrij,i) log ρ α i0,i = log(inr i0,i ) log ρ Remark 16. The GDoF of the Gaussian MAC-IC-MAC applies also to a fully connected (K a + K b )-transmitter-2- receiver interference network, when the interference from all but one transmitter in each cell is sufficiently weak to be at the noise level, i.e., the corresponding INR exponents of these links are equal to zero. Definition 17. The generalized degrees of freedom region of a (K a, K b ) Gaussian MAC-IC-MAC D(K a, K b, ᾱ) R Ka+K b + of the capacity region C G (K a, K b, ᾱ) is defined as R ij {(d a, d b ) :d ij = lim, i {a, b} ρ log ρ j {0,, K i 1}, and (R a, R b ) C G (K a, K b, ᾱ) } (35) Since we have the capacity region to within a one-bit gap for the Gaussian MAC-IC-MAC, computing GDoF region can be easily done by substituting SNR ij,i = ρ αij,i and INR ij,i = ρ α ij.i in (31)-(34), and computing the limits of the right hand side terms under ρ. Definition 18. For any two real numbers x and y, let (x y) + max{0, x y}. Define the set functions a, b, e and g as a Υi b Ωi e Υi g Ωi { } = max max α ij,i, (α i0,i α i0,i ) + ij Υ i\{i0} (36) = max α ij,i (37) ij Ω i { } = max max α ij,i, (α i0,i α i0,i ) +, α i 0i (38) ij Υ i\{i0} { } = max max α ij,i, α i 0i (39) ij Ω i Theorem 19. For (K a, K b ) Gaussian MAC-IC-MAC, the GDoF region D(K a, K b, ᾱ) is R(d a, d b, a, b, e, g). A Gaussian MAC-IC-MAC is symmetric if SNR ij,i = SNR and INR i 0,i = INR, i.e. all SNRs are identical and all INRs are identical. This does not mean the channel attenuation h ij,i s or h i 0,is are identical, since transmitters
15 15 may choose different transmission power. For arbitrary i and j, SNR and INR terms can thus be normalized as INR = SNR α = ρ α which implies α ij,i = 1 and α i0,i = α. For symmetric Gaussian MAC-IC-MAC, a simplified, yet instructive metric, the so-called symmetric GDoF, which is only a function of K and the interference strength parameter α, can be defined as follows. Definition 20. For a symmetric K-user Gaussian MAC-IC-MAC with GDoF region D G sym(k, ᾱ), the symmetric generalized degree-of-freedom d sym (K, α) is defined as the solution to the following equation d sym (K, α) max d=d a0= =d a(ka 1) =d b0 = =d b(kb 1) (d a,d b ) D(ᾱ) Given the GDoF region in Theorem 19, the symmetric GDoF of Gaussian MAC-IC-MAC can be derived according to the definition, which is stated below. d Theorem 21. Consider a symmetric K-user Gaussian MAC-IC-MAC where α ij,i = 1 and α i0,i symmetric GDoF d sym (K, α) for K 2 is given by = α 0, the 1 0 α < 1 1 K 1 K+1 d sym (K, α) = α + 2 K K α < 1 1 K+1 α 1 α < K 1 α K The symmetric GDoF curve for general K is plotted in Fig. 2 in Section I. In Fig. 5, we plot the numerical results of sum symmetric GDoF, i.e. Kd sym (K, α) for K equals 1, 2, 3 and 4. Sum symmetric GDoF offers us a straightforward way to observe the benefit of adding interference free transmitters to the entire cell GDoF, which is a measure of cell spectrum efficiency. When K = 1, we see the W curve which recovers the symmetric GDoF curve for 2-user IC given in [3], since the 2-user IC is a special case of Gaussian MAC-IC-MAC when we place only one (interfering) transmitter in each cell. When K 2, we get a V" curve with flat shoulders on both sides of the curve, which illustrates the benefit of adding non-interfering transmitters to the cell. Indeed, full GDoF (which is 1) can be achieved for α [0, 1 2 ] [ 3 K 2, ). When α = 1, the sum symmetric GDoF becomes K+1, approaching 1 for large K. As K increases, the width of the flat shoulder increases and the width of the dip around α = 1 decreases, leading to unit GDoF for an increasing range of α. Adding even just one non-interfering transmitter to the two-user IC improves GDoF significantly. This can be easily observed at α = 1 2 in Fig. 5. Because of interference, a two-user IC only allows each user to achieve 1 2 DoF, while a (K a = 2, K b = 2) MAC-IC-MAC could achieve full GDoF while providing 1 2 transmitters, a significant gain. DoF to each of the four We explain the benefit of the MAC-IC-MAC over the two-user IC using the deterministic method introduced in [23] by focusing on the achievability of the three key inflection points in the sum GDoF curve, namely, (1 1 K, 1),
16 Symmtric GDoF Symmetric GDoF curve of GS MAC-IC-MAC K=1 K=2 K=3 K= , Fig. 5. Sum Symmetric GDoF Kd sym(k, α) versus α for K = 1, 2, 3, 4 K (1, K+1 ) and (1 + 1 K, 1). In what follows, we pick K = 2 as an example. Fig. 6 shows the aligned received signals from Rxi s perspective for the three key values of α. The horizon line represents the noise floor. The transmitted power is partitioned into multiple levels, such that every power level could carry the same DoF. The shadowed signal levels in the figure are the signal levels being used to transmit information. When α = 1 2, the lower level of interference X i 0 will be under the noise floor, so it would be best to let Txi0 and Txi 0 use the lower power level, to get DoF 1 2 per transmitter and still leave DoF 1 2 to Txi1 and 1. The same principle for when α = 3 Txi 2, in which case the higher lever of X i 0 is above the intended received signal, and will be decoded as strong interference at Rxi. When α = 1, Rxi needs to decode the information from Txi0, Txi1 and Txi 0, which gives DoF 1 3 transmitter. to each X i ' 0 X i 1 X i 0 X i 1 X i 0 X i X i 1 X ' 0 i 0 X i ' 0 Fig. 6. Achieving symmetric GDoF when α = 1 2, α = 1 and α = 3 for (2, 2) Gaussian MAC-IC-MAC 2 Remark 22. Initially, the one bit gap result for Gaussian MAC-IC-MAC is obtained with the aid of the Etkin-Tse- Wang type coding scheme, which is different from the coding scheme being discussed here. It is not surprising that two different coding schemes end up with the same symmetric GDoF curve. However, the deterministic method clearly explains the role of the non-interfering transmitters. Apparently, the MAC-IC-MAC can be viewed as replacing each of the transmitters in a 2-user IC with a group of transmitters, one of which generates interference to the non-intended receiver. Mixing interfering and non-interfering transmitters certainly neutralizes the interference seen at the receivers, which increases the symmetric GDoF per cell. Going back to the example above, it would be interesting to re-explore the achievablity using time sharing
17 Sum Symmtric GDoF 17 scheme. Assume we perform time sharing between Txi0 and Txi1 in both cells. For some α, let d(1, α) be the symmetric DoF of the 2-user IC. To share the DoF evenly, Txi0 has to use 1 duration and leave the rest d(1,α) d(1,α)+1 portion to Txi1. This way we get sum GDoF 2d(1,α) d(1,α)+1 d(1,α)+1 portion of a uniform time which is less than the fundamental GDoF derived by the optimal coding scheme as shown in Fig. 7, except when α equals 0, 1 and 2. This illustrates the sub-optimality of time sharing in MAC-IC-MAC. The reason why superposition coding outperforms time sharing can be again observed from Fig. 6. Say α = 1 2, the role of Txi1 in the optimal scheme is to fill up the unused power levels after Txi0 instead of sharing DoF with Txi0. Time sharing can be performed in another way: let Txa0 and Txb1 send in the first half of unit time, and then Txa1 and Txb0, which is a time sharing scheme between two ZICs. It can be easily verified that this scheme has inferior performance compared to time sharing between non-interfering and interfering transmitters. The symmetric GDoF curve given in Fig. 2 points out the key idea that a linear combination of non-interfering and interfering transmitters does not yield linear combinations of their GDoFs. 1 Sum Symmetric GDoF curve of Gaussian MAC-IC-MAC K=1 K=2 with time sharing K= , Fig. 7. Superposition coding vs time sharing IV. CONCLUSIONS In this work, we extended the framework of Telatar and Tse [2] and Etkin et al [3] to a more general class of networks, namely the MAC-IC-MAC. We characterized the capacity region of semi-deterministic as well as Gaussian MAC-IC-MAC to within a bounded gap (independent of all channel parameters). In particular, it is shown that single-user coding at non-interfering transmitters and superposition coding at interfering transmitters leads to an inner bound within a quantifiable gap to the capacity region. For Gaussian MAC-IC-MAC, we show the Etkin- Tse-Wang type coding scheme achieves a one bit gap approximate capacity region, hence the GDoF region is fully characterized. The symmetric GDoF curve and example discussed reveal the role of non-interfering transmitters in improving the cell edge spectrum efficiency. The insights obtained here may also be relevant to fully-connected K-transmitter, 2-receiver interference networks when the interference from all but one transmitter in each cell are sufficiently weak to be at the noise level (and they are treated as noise).
18 18 APPENDIX A PROOF OF THEOREM 6 We prove the achievability through a random coding argument. We fix some p(q, u a0, x a, u b0, x b ), and obtain reliability conditions in the form of partial sum-rate restrictions, which gives an achievable region with respect to a specific joint distribution, with the overall inner region being the convex hull of the union over all choices of joint distributions. With a little abuse of the notation, we use B i0 to denote the rate of the public messages from transmitter Txi0 within this section. A. An Achievable Coding Scheme 1) Generate time sharing sequence q n according to p(q n ) = n t=1 p(q t); 2) Txij, j 0, generates 2 nrij sequences x n ij according to p(xn ij qn ) = n t=1 p(x ij,t q k ) and indexes them by l ij {1,, 2 nrij }; 3) Txi0 generates 2 nbi0 sequences u n i0 according to p(un i0 qn ) = n k=1 p(u i0k q k ) and indexes them by h i0 {1,, 2 nbi0 }. For each u n i0 (h i0), generate 2 Ri0 Bi0 sequences x n i0 according to p(xn i0 un i0 (h i0), q n ) = n k=1 p(x i0k u i0k (h i0 ), q k ) and index them by (h i0, l i0 ) {1,, 2 nbi0 } {1,, 2 n(ri0 Bi0) }; 4) Once the three codebooks are generated, they are fixed over time and revealed to receivers Rxa and Rxb; 5) A K i -tuple message (m i0,, m i(ki 1)) = ((h i0, l i0 ), l i1,, l i(ki 1))) is encoded to (x n i0 (h i0, l i0 ), x n i1 (l i1),, x n i(k (l i 1) i(k at Txi0-Txi(K i 1) and sent to the channel; 6) Upon receiving yi n, Rxi declares its decoded messages ( ˆm i0,, ˆm i(ki 1)) as the unique index pair ((ĥi0, ˆl i0 ), ˆl i1,, ˆl i(ki 1))) for which q n, x n i0 (ĥi0, ˆl i0 ), x n i1 (ˆl i1 ),, x n i(k i 1) (ˆl i(ki 1)), u n i 0 (ĥi 0 ) and yn i are jointly typical, for some ĥ i 0 {1,, 2nB i 0}. If such an index pair cannot be found, the decoder declares an error; 7) An error occurs if ( ˆM i0,, ˆM i(ki 1)) (M i0,, M i(ki 1)). For arbitraryω i and Υ i, any possible error events at Rxi falls into one of the four classes listed below: ĥi0 = 1, ˆl i0 1, ˆl Υi\{i0} 1, ˆl i 0 = 1; ˆl Ωi 1, ˆl i 0 = 1; ĥi0 = 1, ˆl i0 1, ˆl Υi\{i0} 1, ˆl i 0 1; ˆl Ωi 1, ˆl i 0 1. which can be bounded using set functions A, B, E and G as following, plus the non-negativity of B a0 and R a0 B a0, R Υa B a0 I(X Υa ; Y a X Ῡa, U a0, U b0, Q) = A Υa (40) R Ωa I(X Ωa ; Y a X Ωa, U b0, Q) = B Ωa (41) R Υa B a0 + B b0 I(X Υa, U b0 ; Y a X Ῡa, U a0, Q) = E Υa (42) R Ωa + B b0 I(X Ωa, U b0 ; Y a X Ωa, Q) = G Ωa (43) B a0 0 = C Ωa (44) B a0 R Υa 0 = D Υa (45)
19 19 R Υb B b0 I(X Υb ; Y b X Ῡb, U b0, U a0, Q) = A Υb (46) R Ωb I(X Ωb ; Y b X Ωb, U a0, Q) = B Ωb (47) R Υb B b0 + B a0 I(X Υb, U a0 ; Y b X Ῡb, U b0, Q) = E Υb (48) R Ωb + B a0 I(X Ωb, U a0 ; Y b X Ωb, Q) = G Ωb (49) B b0 0 = C Ωb (50) B b0 R Υb 0 = D Υb (51) B. Fourier Motzkin Elimination The elegant structure of the initial inequality system given above allows us to apply Fourier Motzkin elimination analytically. Without loss of generality, we first eliminate B a0. Note all the lower bounds in the system are contributed by A Υa, E Υa and C Ωa, and upper bounds by D Ωa, E Υb and G Ωb, therefore B a0 is eliminated when we exhaustively sum A Υa, E Υa and C Ωa with D Ωa, E Υb and G Ωb. The inequality system after eliminating B a0 becomes 0 A Υa + D Υa R Υa + R Υb B b0 A Υa + E Υb R Υa + R Ωb A Υa + G Ωb B b0 E Υa + D Υa R Υa + R Υb E Υa + E Υb R Υa + B b0 + R Ωb E Υa + G Ωb R Υa C Ωa + D Υa R Υb B b0 C Ωa + E Υb R Ωb C Ωa + G Ωb R Ωa + B b0 G Ωa R Υb B b0 A Υb B b0 C Ωb B b0 R Υb D Υb the starred inequalities are clearly redundant when it is taken into consideration that, by the chain rule of mutual information, A Υi E Υi and B Ωi G Ωi,. After removing these redundancies, we proceed to the elimination of B b0. New lower bounds are provided by C Ωb, A Υb and A Υa + E Υb, upper bounds are provided by D Ωb, E Υa, G Ωb
20 20 and E Υa + G Ωb. Eliminating B b0, a new system shows up as: 0 C Ωb + E Υa R Υb A Υb + E Υa R Υa + R Υb A Υa + E Υb + E Υa R Υb C Ωb + D Υb 0 A Υb + D Υb R Υa A Υa + E Υb + D Υb R Ωa C Ωb + G Ωa R Υb + R Ωa A Υb + G Ωa R Υa + R Υb + R Ωa A Υa + E Υb + G Ωa R Υa + R Ωb C Ωb + E Υa + G Ωb R Υb + R Υa + R Ωb A Υb + E Υa + G Ωb R Υa + R Υb + R Υa + R Ωb A Υa + E Υb + E Υa + G Ωb R Υa + R Ωb A Υa + G Ωb R Υa + R Υb E Υa + E Υb The starred inequalities can be identified as redundancies easily. Again, similar to the previous step, we obtain a region given as R Ωa B Ωa (52) R Υa A Υa + E Υb (53) R Ωb B Ωb (54) R Υb A Υb + E Υa (55) R Υa + R Ωb A Υa + G Ωb (56) R Υb + R Ωa A Υb + G Ωa (57) R Υa + R Υb E Υa + E Υb (58) R Υa + R Υb + R Ωa A Υa + E Υb + G Ωa (59) R Υb + R Υa + R Ωb A Υb + E Υa + G Ωb (60) It remains to show that inequalities (53) and (55) are redundant. Due to the symmetry of the channel, it is sufficient to show (53) is redundant.
21 21 Denote the region in Theorem 6 as R 0 for brevity, the region by inequalities (52)-(60) as R 1, R 2 = R 0 \R 1 and R 3 = {(R a, R b ) R 1 : U a0 = }. Since R 3 R 1, it is clear that R 2 R 3 = (61) Region R 3 can be obtained by setting U a0 = in initial system (40)-(51), and eliminating B b0, which is R Ωa I(X Ωa ; Y a X Ωa, U b0, Q) (62) R Ωb I(X Ωb ; Y b X Ωb, Q) (63) R Ωa + R Υb I(X Ωa, U b0 ; Y a X Ωa, Q) (64) + I(X Υb ; Y b X Ῡb, U b0, Q) Region R 2 is constituted by all the inequalities for region R 0 and R Υa A Υa + E Υb, here we explicitly write them as below R Ωa B Ωa (65) R Υa A Υa E Υb (66) R Ωb B Ωb (67) R Υa + R Ωb A Υa + G Ωb (68) R Υb + R Ωa A Υb + G Ωa (69) R Υa + R Υb E Υa + E Υb (70) R Υa + R Υb + R Ωa A Υa + E Υb + G Ωa (71) R Υb + R Υa + R Ωb A Υb + E Υa + G Ωb (72) From inequality (65), we know R Ωa B Ωa = I(X Ωa ; Y a X Ωa, U b0, Q) (73) adding inequalities (66) and (68), we have R Ωb G Ωb E Υb = I(X Ωb, U a0 ; Y b X Ωb, Q) I(X Υb, U a0 ; Y b X Ῡb, U b0, Q) = H(Y b X Ωb, Q) H(Y b X Ῡb, U b0, Q) H(Y b X Ωb, Q) H(Y b X Ῡb, X Υb, Q) = H(Y b X Ωb, Q) H(Y b X Ωb, X Ωb, Q) = I(X Ωb ; Y b X Ωb, Q) (74)
22 22 adding inequalities (66) and (71), we have R Υb + R Ωa G Ωa = I(X Ωa, U b0 ; Y a X Ωa, Q) I(X Ωa, U b0 ; Y a X Ωa, Q) (75) + I(X Υb ; Y b X Ῡb, U b0, Q) Note inequalities (62)-(64) are identical to (73)-(75), which means R 2 R 3 (76) it then contradicts (61). Hence, (53) and (55) are both redundancies, which completes the proof. APPENDIX B PROOF OF THEOREM 9 For some fixed p(q)p(t a, x a q)p(t b, x b q), applying Fano s inequality, chain rule, independence and Markov chain property, the sum rate R Ωa on any subset Ω a can be upper bounded by set functions B Ωa and G Ωa. To upper bound R Υa, we give genie information Ta n (as shown in Fig. 8) to help decoding at Rxa. Given that adding side information will not decrease the rate, as well as Ta n is independent of Sa n conditioning on Xa0, n R Υa can be upper bounded by A Υa and E Υa. Fig. 8. Genie aided semi-deterministic MAC-IC-MAC, where a genie provides information T a0 to Rxa0 and T b0 to Rxb0. nr Υa I(X n Υ a ; Y n a, X n Ῡ a, T n a, X n b0) + nɛ n = I(X n Υ a ; T n a X n Ῡ a, X n b0) + I(X n Υ a ; Y n a X n Ῡ a, T n a, X n b0) + nɛ n = I(X n Υ a ; T n a ) + I(X n Υ a ; Y n a X n Ῡ a, T n a, X n b0) + nɛ n = H(T n a ) H(T n a X n Υ a ) + H(Y n a X n Ῡ a, T n a, X n b0)
23 23 H(Y n a X n Υ a, X n Ῡ a, T n a, X n b0) + nɛ n = H(T n a ) H(T n a X n Υ a ) + H(Y n a X n Ῡ a, T n a, X n b0) H(Sb n Xb0) n + nɛ n n H(Ta n [ ) + H(Yat X Ῡat, T at, X b0,t ) t=1 H(T at X Υat) H(S bt X b0,t )] + nɛ n = A Υa H(S b X b0 ) + H(T n a ) + nɛ n (77) nr Ωa I(X n Ω a ; Y n a ) + nɛ n = I(X n Ω a ; Y n a X n Ωa, X n b0) + nɛ n = H(Y n a X n Ωi, X n b0) H(Y n i X n Ω a, X n Ωa, X n b0) + nɛ n = H(Ya n X n Ωa, Xb0) n H(Sb n Xb0) n + nɛ n n [ H(Yat X Ωat, X b0,t ) H(S bt X b0,t ) ] + nɛ n t=1 = B Ωa + nɛ n (78) nr Υa I(X n Υ a ; Y n a, X n Ῡ a, T n a ) + nɛ n = I(X n Υ a ; T n a X n Ῡ a ) + I(X n Υ a ; Y n a X n Ῡ a, T n a ) + nɛ n = I(X n Υ a ; T n a ) + I(X n Υ a ; Y n a X n Ῡ a, T n a ) + nɛ n = H(T n a ) H(T n a X n Υ a ) + H(Y n a X n Ῡ a, T n a ) H(Y n a X n Υ a, X n Ῡ a, T n a ) + nɛ n = H(T n a ) H(T n a X n Υ a ) + H(Y n a X n Ῡ a, T n a ) H(Sb n ) + nɛ n n [ H(Yat X Ῡat, T at ) H(T at X ] Υat) t=1 + H(T n a ) H(S n b ) + nɛ n = E Υa + H(T n a ) + nɛ n (79) nr Ωa I(X n Ω a ; Y n a ) + nɛ n = I(X n Ω a ; Y n a X n Ωa ) + nɛ n = H(Y n a X n Ωi ) H(Y n i X n Ω a, X n Ωa ) + nɛ n = H(Y n a X n Ωa ) H(S n b ) + nɛ n
24 24 n H(Y at X Ωat) H(Sb n ) + nɛ n t=1 = G Ωa + H(S b X b0 ) H(Sb n ) + nɛ n (80) Similarly, we could have 4 upper bounds on rate R b too, nr Υb A Υb H(S a X a0 ) + H(Tb n ) + nɛ n (81) nr Ωb B Ωb + nɛ n (82) nr Υb E Υb + H(Tb n ) + nɛ n (83) nr Ωb G Ωb + H(S a X a0 ) H(Sa n ) + nɛ n (84) The seven inequalities in Theorem 9 can be obtained by these linear combination of inequalities above: (78), (82), (77)+(80), (81)+(84), (79)+(83), (77)+(83)+(80) and (81)+(79)+(84). APPENDIX C PROOF OF THEOREM 10 For a semi-deterministic MAC-IC-MAC, the terms in Theorem 6 satisfy A Υi H(Y i X Ῡi, U i0, X i 0, Q) H(S i U i, Q) = A Υ i B Ωi H(Y 1 X 1b, X 2, Q) H(S 2 U 2, Q) = B Ω i E Υi = H(Y 1 U 1b, Q) H(S 2 U 2, Q) = E Υ i G Ωi = H(Y 1 Q) H(S 2 U 2, Q) = G Ω i because replacing U i0 with X i0 in the positive terms in Definition 6 would only reduce the corresponding conditional entropy. For some (Q, U a0, X a, U b0, X b ) with joint distribution p(q)p(u a0, x a q)p(u b0, x b q), define R in (Q, U a0, X a, U b0, X b ) to be R(R a, R b, A, B, E, G ). Next, we put a further restriction on U i0 in R in (Q, U a0, X a, U b0, X b ) such that p Ui0 X i0,q(u i0 x i0, q) = p Si X i0 (u i0 x i0 ) = p Ti X i0 (u i0 x i0 ) which results in another region R in (Q, T a, X a, T b, X b ), so that it can be concluded that R in Rin(Q, T a, X a, T b, X b ) On the other hand, we have Q,T a,x a T b,x b R in I(X i ; S i T i, Q) = H(S i T i, Q) H(S i X i, T i, Q) = H(S i T i, Q) H(S i X i, Q) Hence given any rate tuple (R a, R b ) R out, it is clear that (R a I(X b ; S b T b, Q)1 1 Ka, R b I(X a ; S a T a, Q)1 1 Kb ) R in R in, which proves the quantifiable gap.
On the Capacity and Degrees of Freedom Regions of MIMO Interference Channels with Limited Receiver Cooperation
 On the Capacity and Degrees of Freedom Regions of MIMO Interference Channels with Limited Receiver Cooperation Mehdi Ashraphijuo, Vaneet Aggarwal and Xiaodong Wang 1 arxiv:1308.3310v1 [cs.it] 15 Aug 2013
On the Capacity and Degrees of Freedom Regions of MIMO Interference Channels with Limited Receiver Cooperation Mehdi Ashraphijuo, Vaneet Aggarwal and Xiaodong Wang 1 arxiv:1308.3310v1 [cs.it] 15 Aug 2013
Superposition Encoding and Partial Decoding Is Optimal for a Class of Z-interference Channels
 Superposition Encoding and Partial Decoding Is Optimal for a Class of Z-interference Channels Nan Liu and Andrea Goldsmith Department of Electrical Engineering Stanford University, Stanford CA 94305 Email:
Superposition Encoding and Partial Decoding Is Optimal for a Class of Z-interference Channels Nan Liu and Andrea Goldsmith Department of Electrical Engineering Stanford University, Stanford CA 94305 Email:
On Network Interference Management
 On Network Interference Management Aleksandar Jovičić, Hua Wang and Pramod Viswanath March 3, 2008 Abstract We study two building-block models of interference-limited wireless networks, motivated by the
On Network Interference Management Aleksandar Jovičić, Hua Wang and Pramod Viswanath March 3, 2008 Abstract We study two building-block models of interference-limited wireless networks, motivated by the
Multicoding Schemes for Interference Channels
 Multicoding Schemes for Interference Channels 1 Ritesh Kolte, Ayfer Özgür, Haim Permuter Abstract arxiv:1502.04273v1 [cs.it] 15 Feb 2015 The best known inner bound for the 2-user discrete memoryless interference
Multicoding Schemes for Interference Channels 1 Ritesh Kolte, Ayfer Özgür, Haim Permuter Abstract arxiv:1502.04273v1 [cs.it] 15 Feb 2015 The best known inner bound for the 2-user discrete memoryless interference
Feedback Capacity of the Gaussian Interference Channel to Within Bits: the Symmetric Case
 1 arxiv:0901.3580v1 [cs.it] 23 Jan 2009 Feedback Capacity of the Gaussian Interference Channel to Within 1.7075 Bits: the Symmetric Case Changho Suh and David Tse Wireless Foundations in the Department
1 arxiv:0901.3580v1 [cs.it] 23 Jan 2009 Feedback Capacity of the Gaussian Interference Channel to Within 1.7075 Bits: the Symmetric Case Changho Suh and David Tse Wireless Foundations in the Department
A Comparison of Two Achievable Rate Regions for the Interference Channel
 A Comparison of Two Achievable Rate Regions for the Interference Channel Hon-Fah Chong, Mehul Motani, and Hari Krishna Garg Electrical & Computer Engineering National University of Singapore Email: {g030596,motani,eleghk}@nus.edu.sg
A Comparison of Two Achievable Rate Regions for the Interference Channel Hon-Fah Chong, Mehul Motani, and Hari Krishna Garg Electrical & Computer Engineering National University of Singapore Email: {g030596,motani,eleghk}@nus.edu.sg
An Achievable Rate Region for the 3-User-Pair Deterministic Interference Channel
 Forty-Ninth Annual Allerton Conference Allerton House, UIUC, Illinois, USA September 8-3, An Achievable Rate Region for the 3-User-Pair Deterministic Interference Channel Invited Paper Bernd Bandemer and
Forty-Ninth Annual Allerton Conference Allerton House, UIUC, Illinois, USA September 8-3, An Achievable Rate Region for the 3-User-Pair Deterministic Interference Channel Invited Paper Bernd Bandemer and
The Capacity Region of the Gaussian Cognitive Radio Channels at High SNR
 The Capacity Region of the Gaussian Cognitive Radio Channels at High SNR 1 Stefano Rini, Daniela Tuninetti and Natasha Devroye srini2, danielat, devroye @ece.uic.edu University of Illinois at Chicago Abstract
The Capacity Region of the Gaussian Cognitive Radio Channels at High SNR 1 Stefano Rini, Daniela Tuninetti and Natasha Devroye srini2, danielat, devroye @ece.uic.edu University of Illinois at Chicago Abstract
Simultaneous Nonunique Decoding Is Rate-Optimal
 Fiftieth Annual Allerton Conference Allerton House, UIUC, Illinois, USA October 1-5, 2012 Simultaneous Nonunique Decoding Is Rate-Optimal Bernd Bandemer University of California, San Diego La Jolla, CA
Fiftieth Annual Allerton Conference Allerton House, UIUC, Illinois, USA October 1-5, 2012 Simultaneous Nonunique Decoding Is Rate-Optimal Bernd Bandemer University of California, San Diego La Jolla, CA
Interference Channels with Source Cooperation
 Interference Channels with Source Cooperation arxiv:95.319v1 [cs.it] 19 May 29 Vinod Prabhakaran and Pramod Viswanath Coordinated Science Laboratory University of Illinois, Urbana-Champaign Urbana, IL
Interference Channels with Source Cooperation arxiv:95.319v1 [cs.it] 19 May 29 Vinod Prabhakaran and Pramod Viswanath Coordinated Science Laboratory University of Illinois, Urbana-Champaign Urbana, IL
Interference Channel aided by an Infrastructure Relay
 Interference Channel aided by an Infrastructure Relay Onur Sahin, Osvaldo Simeone, and Elza Erkip *Department of Electrical and Computer Engineering, Polytechnic Institute of New York University, Department
Interference Channel aided by an Infrastructure Relay Onur Sahin, Osvaldo Simeone, and Elza Erkip *Department of Electrical and Computer Engineering, Polytechnic Institute of New York University, Department
Approximately achieving the feedback interference channel capacity with point-to-point codes
 Approximately achieving the feedback interference channel capacity with point-to-point codes Joyson Sebastian*, Can Karakus*, Suhas Diggavi* Abstract Superposition codes with rate-splitting have been used
Approximately achieving the feedback interference channel capacity with point-to-point codes Joyson Sebastian*, Can Karakus*, Suhas Diggavi* Abstract Superposition codes with rate-splitting have been used
Survey of Interference Channel
 Survey of Interference Channel Alex Dytso Department of Electrical and Computer Engineering University of Illinois at Chicago, Chicago IL 60607, USA, Email: odytso2 @ uic.edu Abstract Interference Channel(IC)
Survey of Interference Channel Alex Dytso Department of Electrical and Computer Engineering University of Illinois at Chicago, Chicago IL 60607, USA, Email: odytso2 @ uic.edu Abstract Interference Channel(IC)
On the Capacity of the Interference Channel with a Relay
 On the Capacity of the Interference Channel with a Relay Ivana Marić, Ron Dabora and Andrea Goldsmith Stanford University, Stanford, CA {ivanam,ron,andrea}@wsl.stanford.edu Abstract Capacity gains due
On the Capacity of the Interference Channel with a Relay Ivana Marić, Ron Dabora and Andrea Goldsmith Stanford University, Stanford, CA {ivanam,ron,andrea}@wsl.stanford.edu Abstract Capacity gains due
Random Access: An Information-Theoretic Perspective
 Random Access: An Information-Theoretic Perspective Paolo Minero, Massimo Franceschetti, and David N. C. Tse Abstract This paper considers a random access system where each sender can be in two modes of
Random Access: An Information-Theoretic Perspective Paolo Minero, Massimo Franceschetti, and David N. C. Tse Abstract This paper considers a random access system where each sender can be in two modes of
Information Theory. Lecture 10. Network Information Theory (CT15); a focus on channel capacity results
 Information Theory Lecture 10 Network Information Theory (CT15); a focus on channel capacity results The (two-user) multiple access channel (15.3) The (two-user) broadcast channel (15.6) The relay channel
Information Theory Lecture 10 Network Information Theory (CT15); a focus on channel capacity results The (two-user) multiple access channel (15.3) The (two-user) broadcast channel (15.6) The relay channel
K User Interference Channel with Backhaul
 1 K User Interference Channel with Backhaul Cooperation: DoF vs. Backhaul Load Trade Off Borna Kananian,, Mohammad A. Maddah-Ali,, Babak H. Khalaj, Department of Electrical Engineering, Sharif University
1 K User Interference Channel with Backhaul Cooperation: DoF vs. Backhaul Load Trade Off Borna Kananian,, Mohammad A. Maddah-Ali,, Babak H. Khalaj, Department of Electrical Engineering, Sharif University
WIRELESS networks with multiple users are interference-limited
 4170 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 60, NO. 7, JULY 2014 On the Capacity and Degrees of Freedom Regions of Two-User MIMO Interference Channels With Limited Receiver Cooperation Mehdi Ashraphijuo,
4170 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 60, NO. 7, JULY 2014 On the Capacity and Degrees of Freedom Regions of Two-User MIMO Interference Channels With Limited Receiver Cooperation Mehdi Ashraphijuo,
Information Theory Meets Game Theory on The Interference Channel
 Information Theory Meets Game Theory on The Interference Channel Randall A. Berry Dept. of EECS Northwestern University e-mail: rberry@eecs.northwestern.edu David N. C. Tse Wireless Foundations University
Information Theory Meets Game Theory on The Interference Channel Randall A. Berry Dept. of EECS Northwestern University e-mail: rberry@eecs.northwestern.edu David N. C. Tse Wireless Foundations University
Approximate Capacity of Fast Fading Interference Channels with no CSIT
 Approximate Capacity of Fast Fading Interference Channels with no CSIT Joyson Sebastian, Can Karakus, Suhas Diggavi Abstract We develop a characterization of fading models, which assigns a number called
Approximate Capacity of Fast Fading Interference Channels with no CSIT Joyson Sebastian, Can Karakus, Suhas Diggavi Abstract We develop a characterization of fading models, which assigns a number called
Outer Bounds on the Secrecy Capacity Region of the 2-user Z Interference Channel With Unidirectional Transmitter Cooperation
 Outer Bounds on the Secrecy Capacity Region of the 2-user Z Interference Channel With Unidirectional Transmitter Cooperation Parthajit Mohapatra, Chandra R. Murthy, and Jemin Lee itrust, Centre for Research
Outer Bounds on the Secrecy Capacity Region of the 2-user Z Interference Channel With Unidirectional Transmitter Cooperation Parthajit Mohapatra, Chandra R. Murthy, and Jemin Lee itrust, Centre for Research
On the Duality between Multiple-Access Codes and Computation Codes
 On the Duality between Multiple-Access Codes and Computation Codes Jingge Zhu University of California, Berkeley jingge.zhu@berkeley.edu Sung Hoon Lim KIOST shlim@kiost.ac.kr Michael Gastpar EPFL michael.gastpar@epfl.ch
On the Duality between Multiple-Access Codes and Computation Codes Jingge Zhu University of California, Berkeley jingge.zhu@berkeley.edu Sung Hoon Lim KIOST shlim@kiost.ac.kr Michael Gastpar EPFL michael.gastpar@epfl.ch
Error Exponent Region for Gaussian Broadcast Channels
 Error Exponent Region for Gaussian Broadcast Channels Lihua Weng, S. Sandeep Pradhan, and Achilleas Anastasopoulos Electrical Engineering and Computer Science Dept. University of Michigan, Ann Arbor, MI
Error Exponent Region for Gaussian Broadcast Channels Lihua Weng, S. Sandeep Pradhan, and Achilleas Anastasopoulos Electrical Engineering and Computer Science Dept. University of Michigan, Ann Arbor, MI
Capacity bounds for multiple access-cognitive interference channel
 Mirmohseni et al. EURASIP Journal on Wireless Communications and Networking, :5 http://jwcn.eurasipjournals.com/content///5 RESEARCH Open Access Capacity bounds for multiple access-cognitive interference
Mirmohseni et al. EURASIP Journal on Wireless Communications and Networking, :5 http://jwcn.eurasipjournals.com/content///5 RESEARCH Open Access Capacity bounds for multiple access-cognitive interference
Multiaccess Channels with State Known to One Encoder: A Case of Degraded Message Sets
 Multiaccess Channels with State Known to One Encoder: A Case of Degraded Message Sets Shivaprasad Kotagiri and J. Nicholas Laneman Department of Electrical Engineering University of Notre Dame Notre Dame,
Multiaccess Channels with State Known to One Encoder: A Case of Degraded Message Sets Shivaprasad Kotagiri and J. Nicholas Laneman Department of Electrical Engineering University of Notre Dame Notre Dame,
Lecture 1: The Multiple Access Channel. Copyright G. Caire 12
 Lecture 1: The Multiple Access Channel Copyright G. Caire 12 Outline Two-user MAC. The Gaussian case. The K-user case. Polymatroid structure and resource allocation problems. Copyright G. Caire 13 Two-user
Lecture 1: The Multiple Access Channel Copyright G. Caire 12 Outline Two-user MAC. The Gaussian case. The K-user case. Polymatroid structure and resource allocation problems. Copyright G. Caire 13 Two-user
A Comparison of Superposition Coding Schemes
 A Comparison of Superposition Coding Schemes Lele Wang, Eren Şaşoğlu, Bernd Bandemer, and Young-Han Kim Department of Electrical and Computer Engineering University of California, San Diego La Jolla, CA
A Comparison of Superposition Coding Schemes Lele Wang, Eren Şaşoğlu, Bernd Bandemer, and Young-Han Kim Department of Electrical and Computer Engineering University of California, San Diego La Jolla, CA
820 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 2, FEBRUARY Stefano Rini, Daniela Tuninetti, and Natasha Devroye
 820 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 2, FEBRUARY 2012 Inner and Outer Bounds for the Gaussian Cognitive Interference Channel and New Capacity Results Stefano Rini, Daniela Tuninetti,
820 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 58, NO. 2, FEBRUARY 2012 Inner and Outer Bounds for the Gaussian Cognitive Interference Channel and New Capacity Results Stefano Rini, Daniela Tuninetti,
List of Figures. Acknowledgements. Abstract 1. 1 Introduction 2. 2 Preliminaries Superposition Coding Block Markov Encoding...
 Contents Contents i List of Figures iv Acknowledgements vi Abstract 1 1 Introduction 2 2 Preliminaries 7 2.1 Superposition Coding........................... 7 2.2 Block Markov Encoding.........................
Contents Contents i List of Figures iv Acknowledgements vi Abstract 1 1 Introduction 2 2 Preliminaries 7 2.1 Superposition Coding........................... 7 2.2 Block Markov Encoding.........................
Capacity of All Nine Models of Channel Output Feedback for the Two-user Interference Channel
 Capacity of All Nine Models of Channel Output Feedback for the Two-user Interference Channel Achaleshwar Sahai, Vaneet Aggarwal, Melda Yuksel and Ashutosh Sabharwal 1 Abstract arxiv:1104.4805v3 [cs.it]
Capacity of All Nine Models of Channel Output Feedback for the Two-user Interference Channel Achaleshwar Sahai, Vaneet Aggarwal, Melda Yuksel and Ashutosh Sabharwal 1 Abstract arxiv:1104.4805v3 [cs.it]
Diversity-Multiplexing Tradeoff of the Two-User Interference Channel
 Diversity-Multiplexing Tradeoff of the Two-User Interference Channel arxiv:0905.0385v2 [cs.it] 8 Sep 2009 Adnan Raja and Pramod Viswanath April 9, 2018 Abstract Diversity-Multiplexing tradeoff DMT) is
Diversity-Multiplexing Tradeoff of the Two-User Interference Channel arxiv:0905.0385v2 [cs.it] 8 Sep 2009 Adnan Raja and Pramod Viswanath April 9, 2018 Abstract Diversity-Multiplexing tradeoff DMT) is
The Capacity of the Semi-Deterministic Cognitive Interference Channel and its Application to Constant Gap Results for the Gaussian Channel
 The Capacity of the Semi-Deterministic Cognitive Interference Channel and its Application to Constant Gap Results for the Gaussian Channel Stefano Rini, Daniela Tuninetti, and Natasha Devroye Department
The Capacity of the Semi-Deterministic Cognitive Interference Channel and its Application to Constant Gap Results for the Gaussian Channel Stefano Rini, Daniela Tuninetti, and Natasha Devroye Department
Efficient Use of Joint Source-Destination Cooperation in the Gaussian Multiple Access Channel
 Efficient Use of Joint Source-Destination Cooperation in the Gaussian Multiple Access Channel Ahmad Abu Al Haija ECE Department, McGill University, Montreal, QC, Canada Email: ahmad.abualhaija@mail.mcgill.ca
Efficient Use of Joint Source-Destination Cooperation in the Gaussian Multiple Access Channel Ahmad Abu Al Haija ECE Department, McGill University, Montreal, QC, Canada Email: ahmad.abualhaija@mail.mcgill.ca
Cognitive Multiple Access Networks
 Cognitive Multiple Access Networks Natasha Devroye Email: ndevroye@deas.harvard.edu Patrick Mitran Email: mitran@deas.harvard.edu Vahid Tarokh Email: vahid@deas.harvard.edu Abstract A cognitive radio can
Cognitive Multiple Access Networks Natasha Devroye Email: ndevroye@deas.harvard.edu Patrick Mitran Email: mitran@deas.harvard.edu Vahid Tarokh Email: vahid@deas.harvard.edu Abstract A cognitive radio can
Primary Rate-Splitting Achieves Capacity for the Gaussian Cognitive Interference Channel
 Primary Rate-Splitting Achieves Capacity for the Gaussian Cognitive Interference Channel Stefano Rini, Ernest Kurniawan and Andrea Goldsmith Technische Universität München, Munich, Germany, Stanford University,
Primary Rate-Splitting Achieves Capacity for the Gaussian Cognitive Interference Channel Stefano Rini, Ernest Kurniawan and Andrea Goldsmith Technische Universität München, Munich, Germany, Stanford University,
i.i.d. Mixed Inputs and Treating Interference as Noise are gdof Optimal for the Symmetric Gaussian Two-user Interference Channel
 iid Mixed nputs and Treating nterference as Noise are gdof Optimal for the Symmetric Gaussian Two-user nterference Channel Alex Dytso Daniela Tuninetti and Natasha Devroye University of llinois at Chicago
iid Mixed nputs and Treating nterference as Noise are gdof Optimal for the Symmetric Gaussian Two-user nterference Channel Alex Dytso Daniela Tuninetti and Natasha Devroye University of llinois at Chicago
The Generalized Degrees of Freedom of the Interference Relay Channel with Strong Interference
 The Generalized Degrees of Freedom of the Interference Relay Channel with Strong Interference Soheyl Gherekhloo, Anas Chaaban, and Aydin Sezgin Chair of Communication Systems RUB, Germany Email: {soheyl.gherekhloo,
The Generalized Degrees of Freedom of the Interference Relay Channel with Strong Interference Soheyl Gherekhloo, Anas Chaaban, and Aydin Sezgin Chair of Communication Systems RUB, Germany Email: {soheyl.gherekhloo,
On the Capacity Region of the Gaussian Z-channel
 On the Capacity Region of the Gaussian Z-channel Nan Liu Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland, College Park, MD 74 nkancy@eng.umd.edu ulukus@eng.umd.edu
On the Capacity Region of the Gaussian Z-channel Nan Liu Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland, College Park, MD 74 nkancy@eng.umd.edu ulukus@eng.umd.edu
A Half-Duplex Cooperative Scheme with Partial Decode-Forward Relaying
 A Half-Duplex Cooperative Scheme with Partial Decode-Forward Relaying Ahmad Abu Al Haija, and Mai Vu, Department of Electrical and Computer Engineering McGill University Montreal, QC H3A A7 Emails: ahmadabualhaija@mailmcgillca,
A Half-Duplex Cooperative Scheme with Partial Decode-Forward Relaying Ahmad Abu Al Haija, and Mai Vu, Department of Electrical and Computer Engineering McGill University Montreal, QC H3A A7 Emails: ahmadabualhaija@mailmcgillca,
Lecture 10: Broadcast Channel and Superposition Coding
 Lecture 10: Broadcast Channel and Superposition Coding Scribed by: Zhe Yao 1 Broadcast channel M 0M 1M P{y 1 y x} M M 01 1 M M 0 The capacity of the broadcast channel depends only on the marginal conditional
Lecture 10: Broadcast Channel and Superposition Coding Scribed by: Zhe Yao 1 Broadcast channel M 0M 1M P{y 1 y x} M M 01 1 M M 0 The capacity of the broadcast channel depends only on the marginal conditional
Capacity Bounds for. the Gaussian Interference Channel
 Capacity Bounds for the Gaussian Interference Channel Abolfazl S. Motahari, Student Member, IEEE, and Amir K. Khandani, Member, IEEE Coding & Signal Transmission Laboratory www.cst.uwaterloo.ca {abolfazl,khandani}@cst.uwaterloo.ca
Capacity Bounds for the Gaussian Interference Channel Abolfazl S. Motahari, Student Member, IEEE, and Amir K. Khandani, Member, IEEE Coding & Signal Transmission Laboratory www.cst.uwaterloo.ca {abolfazl,khandani}@cst.uwaterloo.ca
ELEC546 Review of Information Theory
 ELEC546 Review of Information Theory Vincent Lau 1/1/004 1 Review of Information Theory Entropy: Measure of uncertainty of a random variable X. The entropy of X, H(X), is given by: If X is a discrete random
ELEC546 Review of Information Theory Vincent Lau 1/1/004 1 Review of Information Theory Entropy: Measure of uncertainty of a random variable X. The entropy of X, H(X), is given by: If X is a discrete random
arxiv: v1 [cs.it] 4 Jun 2018
![arxiv: v1 [cs.it] 4 Jun 2018 arxiv: v1 [cs.it] 4 Jun 2018](/thumbs/79/79490617.jpg) State-Dependent Interference Channel with Correlated States 1 Yunhao Sun, 2 Ruchen Duan, 3 Yingbin Liang, 4 Shlomo Shamai (Shitz) 5 Abstract arxiv:180600937v1 [csit] 4 Jun 2018 This paper investigates
State-Dependent Interference Channel with Correlated States 1 Yunhao Sun, 2 Ruchen Duan, 3 Yingbin Liang, 4 Shlomo Shamai (Shitz) 5 Abstract arxiv:180600937v1 [csit] 4 Jun 2018 This paper investigates
National University of Singapore Department of Electrical & Computer Engineering. Examination for
 National University of Singapore Department of Electrical & Computer Engineering Examination for EE5139R Information Theory for Communication Systems (Semester I, 2014/15) November/December 2014 Time Allowed:
National University of Singapore Department of Electrical & Computer Engineering Examination for EE5139R Information Theory for Communication Systems (Semester I, 2014/15) November/December 2014 Time Allowed:
On Multiple User Channels with State Information at the Transmitters
 On Multiple User Channels with State Information at the Transmitters Styrmir Sigurjónsson and Young-Han Kim* Information Systems Laboratory Stanford University Stanford, CA 94305, USA Email: {styrmir,yhk}@stanford.edu
On Multiple User Channels with State Information at the Transmitters Styrmir Sigurjónsson and Young-Han Kim* Information Systems Laboratory Stanford University Stanford, CA 94305, USA Email: {styrmir,yhk}@stanford.edu
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 61, NO. 3, MARCH
 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 6, NO., MARCH 05 57 On the Two-User Interference Channel With Lack of Knowledge of the Interference Codebook at One Receiver Alex Dytso, Daniela Tuninetti,
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 6, NO., MARCH 05 57 On the Two-User Interference Channel With Lack of Knowledge of the Interference Codebook at One Receiver Alex Dytso, Daniela Tuninetti,
Source-Channel Coding Theorems for the Multiple-Access Relay Channel
 Source-Channel Coding Theorems for the Multiple-Access Relay Channel Yonathan Murin, Ron Dabora, and Deniz Gündüz Abstract We study reliable transmission of arbitrarily correlated sources over multiple-access
Source-Channel Coding Theorems for the Multiple-Access Relay Channel Yonathan Murin, Ron Dabora, and Deniz Gündüz Abstract We study reliable transmission of arbitrarily correlated sources over multiple-access
On Gaussian MIMO Broadcast Channels with Common and Private Messages
 On Gaussian MIMO Broadcast Channels with Common and Private Messages Ersen Ekrem Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland, College Park, MD 20742 ersen@umd.edu
On Gaussian MIMO Broadcast Channels with Common and Private Messages Ersen Ekrem Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland, College Park, MD 20742 ersen@umd.edu
Source and Channel Coding for Correlated Sources Over Multiuser Channels
 Source and Channel Coding for Correlated Sources Over Multiuser Channels Deniz Gündüz, Elza Erkip, Andrea Goldsmith, H. Vincent Poor Abstract Source and channel coding over multiuser channels in which
Source and Channel Coding for Correlated Sources Over Multiuser Channels Deniz Gündüz, Elza Erkip, Andrea Goldsmith, H. Vincent Poor Abstract Source and channel coding over multiuser channels in which
Information Theory for Wireless Communications. Lecture 10 Discrete Memoryless Multiple Access Channel (DM-MAC): The Converse Theorem
 Information Theory for Wireless Communications. Lecture 0 Discrete Memoryless Multiple Access Channel (DM-MAC: The Converse Theorem Instructor: Dr. Saif Khan Mohammed Scribe: Antonios Pitarokoilis I. THE
Information Theory for Wireless Communications. Lecture 0 Discrete Memoryless Multiple Access Channel (DM-MAC: The Converse Theorem Instructor: Dr. Saif Khan Mohammed Scribe: Antonios Pitarokoilis I. THE
Mismatched Multi-letter Successive Decoding for the Multiple-Access Channel
 Mismatched Multi-letter Successive Decoding for the Multiple-Access Channel Jonathan Scarlett University of Cambridge jms265@cam.ac.uk Alfonso Martinez Universitat Pompeu Fabra alfonso.martinez@ieee.org
Mismatched Multi-letter Successive Decoding for the Multiple-Access Channel Jonathan Scarlett University of Cambridge jms265@cam.ac.uk Alfonso Martinez Universitat Pompeu Fabra alfonso.martinez@ieee.org
Joint Source-Channel Coding for the Multiple-Access Relay Channel
 Joint Source-Channel Coding for the Multiple-Access Relay Channel Yonathan Murin, Ron Dabora Department of Electrical and Computer Engineering Ben-Gurion University, Israel Email: moriny@bgu.ac.il, ron@ee.bgu.ac.il
Joint Source-Channel Coding for the Multiple-Access Relay Channel Yonathan Murin, Ron Dabora Department of Electrical and Computer Engineering Ben-Gurion University, Israel Email: moriny@bgu.ac.il, ron@ee.bgu.ac.il
X 1 : X Table 1: Y = X X 2
 ECE 534: Elements of Information Theory, Fall 200 Homework 3 Solutions (ALL DUE to Kenneth S. Palacio Baus) December, 200. Problem 5.20. Multiple access (a) Find the capacity region for the multiple-access
ECE 534: Elements of Information Theory, Fall 200 Homework 3 Solutions (ALL DUE to Kenneth S. Palacio Baus) December, 200. Problem 5.20. Multiple access (a) Find the capacity region for the multiple-access
Interference, Cooperation and Connectivity A Degrees of Freedom Perspective
 Interference, Cooperation and Connectivity A Degrees of Freedom Perspective Chenwei Wang, Syed A. Jafar, Shlomo Shamai (Shitz) and Michele Wigger EECS Dept., University of California Irvine, Irvine, CA,
Interference, Cooperation and Connectivity A Degrees of Freedom Perspective Chenwei Wang, Syed A. Jafar, Shlomo Shamai (Shitz) and Michele Wigger EECS Dept., University of California Irvine, Irvine, CA,
Shannon meets Wiener II: On MMSE estimation in successive decoding schemes
 Shannon meets Wiener II: On MMSE estimation in successive decoding schemes G. David Forney, Jr. MIT Cambridge, MA 0239 USA forneyd@comcast.net Abstract We continue to discuss why MMSE estimation arises
Shannon meets Wiener II: On MMSE estimation in successive decoding schemes G. David Forney, Jr. MIT Cambridge, MA 0239 USA forneyd@comcast.net Abstract We continue to discuss why MMSE estimation arises
Approximate Ergodic Capacity of a Class of Fading Networks
 Approximate Ergodic Capacity of a Class of Fading Networks Sang-Woon Jeon, Chien-Yi Wang, and Michael Gastpar School of Computer and Communication Sciences EPFL Lausanne, Switzerland {sangwoon.jeon, chien-yi.wang,
Approximate Ergodic Capacity of a Class of Fading Networks Sang-Woon Jeon, Chien-Yi Wang, and Michael Gastpar School of Computer and Communication Sciences EPFL Lausanne, Switzerland {sangwoon.jeon, chien-yi.wang,
The Unbounded Benefit of Encoder Cooperation for the k-user MAC
 The Unbounded Benefit of Encoder Cooperation for the k-user MAC Parham Noorzad, Student Member, IEEE, Michelle Effros, Fellow, IEEE, and Michael Langberg, Senior Member, IEEE arxiv:1601.06113v2 [cs.it]
The Unbounded Benefit of Encoder Cooperation for the k-user MAC Parham Noorzad, Student Member, IEEE, Michelle Effros, Fellow, IEEE, and Michael Langberg, Senior Member, IEEE arxiv:1601.06113v2 [cs.it]
Shannon s noisy-channel theorem
 Shannon s noisy-channel theorem Information theory Amon Elders Korteweg de Vries Institute for Mathematics University of Amsterdam. Tuesday, 26th of Januari Amon Elders (Korteweg de Vries Institute for
Shannon s noisy-channel theorem Information theory Amon Elders Korteweg de Vries Institute for Mathematics University of Amsterdam. Tuesday, 26th of Januari Amon Elders (Korteweg de Vries Institute for
Energy State Amplification in an Energy Harvesting Communication System
 Energy State Amplification in an Energy Harvesting Communication System Omur Ozel Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland College Park, MD 20742 omur@umd.edu
Energy State Amplification in an Energy Harvesting Communication System Omur Ozel Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland College Park, MD 20742 omur@umd.edu
Lecture 6 I. CHANNEL CODING. X n (m) P Y X
 6- Introduction to Information Theory Lecture 6 Lecturer: Haim Permuter Scribe: Yoav Eisenberg and Yakov Miron I. CHANNEL CODING We consider the following channel coding problem: m = {,2,..,2 nr} Encoder
6- Introduction to Information Theory Lecture 6 Lecturer: Haim Permuter Scribe: Yoav Eisenberg and Yakov Miron I. CHANNEL CODING We consider the following channel coding problem: m = {,2,..,2 nr} Encoder
The Capacity Region for Multi-source Multi-sink Network Coding
 The Capacity Region for Multi-source Multi-sink Network Coding Xijin Yan Dept. of Electrical Eng. - Systems University of Southern California Los Angeles, CA, U.S.A. xyan@usc.edu Raymond W. Yeung Dept.
The Capacity Region for Multi-source Multi-sink Network Coding Xijin Yan Dept. of Electrical Eng. - Systems University of Southern California Los Angeles, CA, U.S.A. xyan@usc.edu Raymond W. Yeung Dept.
Variable Length Codes for Degraded Broadcast Channels
 Variable Length Codes for Degraded Broadcast Channels Stéphane Musy School of Computer and Communication Sciences, EPFL CH-1015 Lausanne, Switzerland Email: stephane.musy@ep.ch Abstract This paper investigates
Variable Length Codes for Degraded Broadcast Channels Stéphane Musy School of Computer and Communication Sciences, EPFL CH-1015 Lausanne, Switzerland Email: stephane.musy@ep.ch Abstract This paper investigates
to be almost surely min{n 0, 3
 1 The DoF Region of the Three-Receiver MIMO Broadcast Channel with Side Information and Its Relation to Index Coding Capacity Behzad Asadi, Lawrence Ong, and Sarah J Johnson arxiv:160803377v1 [csit] 11
1 The DoF Region of the Three-Receiver MIMO Broadcast Channel with Side Information and Its Relation to Index Coding Capacity Behzad Asadi, Lawrence Ong, and Sarah J Johnson arxiv:160803377v1 [csit] 11
Secure Degrees of Freedom of the MIMO Multiple Access Wiretap Channel
 Secure Degrees of Freedom of the MIMO Multiple Access Wiretap Channel Pritam Mukherjee Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland, College Park, MD 074 pritamm@umd.edu
Secure Degrees of Freedom of the MIMO Multiple Access Wiretap Channel Pritam Mukherjee Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland, College Park, MD 074 pritamm@umd.edu
Sum Capacity of General Deterministic Interference Channel with Channel Output Feedback
 Sum Capacity of General Deterministic Interference Channel with Channel Output Feedback Achaleshwar Sahai Department of ECE, Rice University, Houston, TX 775. as27@rice.edu Vaneet Aggarwal Department of
Sum Capacity of General Deterministic Interference Channel with Channel Output Feedback Achaleshwar Sahai Department of ECE, Rice University, Houston, TX 775. as27@rice.edu Vaneet Aggarwal Department of
An Outer Bound for the Gaussian. Interference channel with a relay.
 An Outer Bound for the Gaussian Interference Channel with a Relay Ivana Marić Stanford University Stanford, CA ivanam@wsl.stanford.edu Ron Dabora Ben-Gurion University Be er-sheva, Israel ron@ee.bgu.ac.il
An Outer Bound for the Gaussian Interference Channel with a Relay Ivana Marić Stanford University Stanford, CA ivanam@wsl.stanford.edu Ron Dabora Ben-Gurion University Be er-sheva, Israel ron@ee.bgu.ac.il
A Proof of the Converse for the Capacity of Gaussian MIMO Broadcast Channels
 A Proof of the Converse for the Capacity of Gaussian MIMO Broadcast Channels Mehdi Mohseni Department of Electrical Engineering Stanford University Stanford, CA 94305, USA Email: mmohseni@stanford.edu
A Proof of the Converse for the Capacity of Gaussian MIMO Broadcast Channels Mehdi Mohseni Department of Electrical Engineering Stanford University Stanford, CA 94305, USA Email: mmohseni@stanford.edu
Degrees of Freedom Region of the Gaussian MIMO Broadcast Channel with Common and Private Messages
 Degrees of Freedom Region of the Gaussian MIMO Broadcast hannel with ommon and Private Messages Ersen Ekrem Sennur Ulukus Department of Electrical and omputer Engineering University of Maryland, ollege
Degrees of Freedom Region of the Gaussian MIMO Broadcast hannel with ommon and Private Messages Ersen Ekrem Sennur Ulukus Department of Electrical and omputer Engineering University of Maryland, ollege
Degrees-of-Freedom Robust Transmission for the K-user Distributed Broadcast Channel
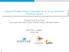 /33 Degrees-of-Freedom Robust Transmission for the K-user Distributed Broadcast Channel Presented by Paul de Kerret Joint work with Antonio Bazco, Nicolas Gresset, and David Gesbert ESIT 2017 in Madrid,
/33 Degrees-of-Freedom Robust Transmission for the K-user Distributed Broadcast Channel Presented by Paul de Kerret Joint work with Antonio Bazco, Nicolas Gresset, and David Gesbert ESIT 2017 in Madrid,
On the K-user Cognitive Interference Channel with Cumulative Message Sharing Sum-Capacity
 03 EEE nternational Symposium on nformation Theory On the K-user Cognitive nterference Channel with Cumulative Message Sharing Sum-Capacity Diana Maamari, Daniela Tuninetti and Natasha Devroye Department
03 EEE nternational Symposium on nformation Theory On the K-user Cognitive nterference Channel with Cumulative Message Sharing Sum-Capacity Diana Maamari, Daniela Tuninetti and Natasha Devroye Department
Fundamental Limits of Cloud and Cache-Aided Interference Management with Multi-Antenna Edge Nodes
 Fundamental Limits of Cloud and Cache-Aided Interference Management with Multi-Antenna Edge Nodes Jingjing Zhang and Osvaldo Simeone arxiv:72.04266v4 [cs.it] 2 Mar 208 Abstract In fog-aided cellular systems,
Fundamental Limits of Cloud and Cache-Aided Interference Management with Multi-Antenna Edge Nodes Jingjing Zhang and Osvaldo Simeone arxiv:72.04266v4 [cs.it] 2 Mar 208 Abstract In fog-aided cellular systems,
Secret Key Agreement Using Asymmetry in Channel State Knowledge
 Secret Key Agreement Using Asymmetry in Channel State Knowledge Ashish Khisti Deutsche Telekom Inc. R&D Lab USA Los Altos, CA, 94040 Email: ashish.khisti@telekom.com Suhas Diggavi LICOS, EFL Lausanne,
Secret Key Agreement Using Asymmetry in Channel State Knowledge Ashish Khisti Deutsche Telekom Inc. R&D Lab USA Los Altos, CA, 94040 Email: ashish.khisti@telekom.com Suhas Diggavi LICOS, EFL Lausanne,
L interférence dans les réseaux non filaires
 L interférence dans les réseaux non filaires Du contrôle de puissance au codage et alignement Jean-Claude Belfiore Télécom ParisTech 7 mars 2013 Séminaire Comelec Parts Part 1 Part 2 Part 3 Part 4 Part
L interférence dans les réseaux non filaires Du contrôle de puissance au codage et alignement Jean-Claude Belfiore Télécom ParisTech 7 mars 2013 Séminaire Comelec Parts Part 1 Part 2 Part 3 Part 4 Part
A digital interface for Gaussian relay and interference networks: Lifting codes from the discrete superposition model
 A digital interface for Gaussian relay and interference networks: Lifting codes from the discrete superposition model M. Anand, Student Member, IEEE, and P. R. Kumar, Fellow, IEEE Abstract For every Gaussian
A digital interface for Gaussian relay and interference networks: Lifting codes from the discrete superposition model M. Anand, Student Member, IEEE, and P. R. Kumar, Fellow, IEEE Abstract For every Gaussian
Lecture 2. Capacity of the Gaussian channel
 Spring, 207 5237S, Wireless Communications II 2. Lecture 2 Capacity of the Gaussian channel Review on basic concepts in inf. theory ( Cover&Thomas: Elements of Inf. Theory, Tse&Viswanath: Appendix B) AWGN
Spring, 207 5237S, Wireless Communications II 2. Lecture 2 Capacity of the Gaussian channel Review on basic concepts in inf. theory ( Cover&Thomas: Elements of Inf. Theory, Tse&Viswanath: Appendix B) AWGN
On Capacity Under Received-Signal Constraints
 On Capacity Under Received-Signal Constraints Michael Gastpar Dept. of EECS, University of California, Berkeley, CA 9470-770 gastpar@berkeley.edu Abstract In a world where different systems have to share
On Capacity Under Received-Signal Constraints Michael Gastpar Dept. of EECS, University of California, Berkeley, CA 9470-770 gastpar@berkeley.edu Abstract In a world where different systems have to share
On the Optimality of Treating Interference as Noise in Competitive Scenarios
 On the Optimality of Treating Interference as Noise in Competitive Scenarios A. DYTSO, D. TUNINETTI, N. DEVROYE WORK PARTIALLY FUNDED BY NSF UNDER AWARD 1017436 OUTLINE CHANNEL MODEL AND PAST WORK ADVANTAGES
On the Optimality of Treating Interference as Noise in Competitive Scenarios A. DYTSO, D. TUNINETTI, N. DEVROYE WORK PARTIALLY FUNDED BY NSF UNDER AWARD 1017436 OUTLINE CHANNEL MODEL AND PAST WORK ADVANTAGES
Lecture 4 Noisy Channel Coding
 Lecture 4 Noisy Channel Coding I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw October 9, 2015 1 / 56 I-Hsiang Wang IT Lecture 4 The Channel Coding Problem
Lecture 4 Noisy Channel Coding I-Hsiang Wang Department of Electrical Engineering National Taiwan University ihwang@ntu.edu.tw October 9, 2015 1 / 56 I-Hsiang Wang IT Lecture 4 The Channel Coding Problem
II. THE TWO-WAY TWO-RELAY CHANNEL
 An Achievable Rate Region for the Two-Way Two-Relay Channel Jonathan Ponniah Liang-Liang Xie Department of Electrical Computer Engineering, University of Waterloo, Canada Abstract We propose an achievable
An Achievable Rate Region for the Two-Way Two-Relay Channel Jonathan Ponniah Liang-Liang Xie Department of Electrical Computer Engineering, University of Waterloo, Canada Abstract We propose an achievable
Capacity Bounds for the K-User Gaussian Interference Channel
 Capacity Bounds for the K-User Gaussian Interference Channel Junyoung Nam Abstract arxiv:506.0339v3 [cs.it] 3 Jan 07 The capacity region of the K-user Gaussian interference channel GIC is a long-standing
Capacity Bounds for the K-User Gaussian Interference Channel Junyoung Nam Abstract arxiv:506.0339v3 [cs.it] 3 Jan 07 The capacity region of the K-user Gaussian interference channel GIC is a long-standing
The Capacity Region of the Cognitive Z-interference Channel with One Noiseless Component
 1 The Capacity Region of the Cognitive Z-interference Channel with One Noiseless Component Nan Liu, Ivana Marić, Andrea J. Goldsmith, Shlomo Shamai (Shitz) arxiv:0812.0617v1 [cs.it] 2 Dec 2008 Dept. of
1 The Capacity Region of the Cognitive Z-interference Channel with One Noiseless Component Nan Liu, Ivana Marić, Andrea J. Goldsmith, Shlomo Shamai (Shitz) arxiv:0812.0617v1 [cs.it] 2 Dec 2008 Dept. of
Cut-Set Bound and Dependence Balance Bound
 Cut-Set Bound and Dependence Balance Bound Lei Xiao lxiao@nd.edu 1 Date: 4 October, 2006 Reading: Elements of information theory by Cover and Thomas [1, Section 14.10], and the paper by Hekstra and Willems
Cut-Set Bound and Dependence Balance Bound Lei Xiao lxiao@nd.edu 1 Date: 4 October, 2006 Reading: Elements of information theory by Cover and Thomas [1, Section 14.10], and the paper by Hekstra and Willems
Secrecy in the 2-User Symmetric Interference Channel with Transmitter Cooperation: Deterministic View
 Secrecy in the 2-User Symmetric Interference Channel with Transmitter Cooperation: Deterministic View P. Mohapatra 9 th March 2013 Outline Motivation Problem statement Achievable scheme 1 Weak interference
Secrecy in the 2-User Symmetric Interference Channel with Transmitter Cooperation: Deterministic View P. Mohapatra 9 th March 2013 Outline Motivation Problem statement Achievable scheme 1 Weak interference
IT is well known (see, e.g., [2]-[10]) that the simple scheme. On the Optimality of Treating Interference as Noise: Compound Interference Networks
![IT is well known (see, e.g., [2]-[10]) that the simple scheme. On the Optimality of Treating Interference as Noise: Compound Interference Networks IT is well known (see, e.g., [2]-[10]) that the simple scheme. On the Optimality of Treating Interference as Noise: Compound Interference Networks](/thumbs/95/123045786.jpg) On the Optimality of Treating Interference as Noise: Compound Interference Networs Chunhua Geng, Student Member, IEEE, and Syed A. Jafar, Fellow, IEEE Abstract In a K-user Gaussian interference channel,
On the Optimality of Treating Interference as Noise: Compound Interference Networs Chunhua Geng, Student Member, IEEE, and Syed A. Jafar, Fellow, IEEE Abstract In a K-user Gaussian interference channel,
Interactive Decoding of a Broadcast Message
 In Proc. Allerton Conf. Commun., Contr., Computing, (Illinois), Oct. 2003 Interactive Decoding of a Broadcast Message Stark C. Draper Brendan J. Frey Frank R. Kschischang University of Toronto Toronto,
In Proc. Allerton Conf. Commun., Contr., Computing, (Illinois), Oct. 2003 Interactive Decoding of a Broadcast Message Stark C. Draper Brendan J. Frey Frank R. Kschischang University of Toronto Toronto,
THE practical bottleneck of today s communication networks
 1 Interference Channel with Generalized Feedback (a.k.a. with source cooperation: Part I: Achievable Region Shuang (Echo Yang and Daniela Tuninetti Abstract An Interference Channel with Generalized Feedback
1 Interference Channel with Generalized Feedback (a.k.a. with source cooperation: Part I: Achievable Region Shuang (Echo Yang and Daniela Tuninetti Abstract An Interference Channel with Generalized Feedback
Harnessing Interaction in Bursty Interference Networks
 215 IEEE Hong Kong-Taiwan Joint Workshop on Information Theory and Communications Harnessing Interaction in Bursty Interference Networks I-Hsiang Wang NIC Lab, NTU GICE 1/19, 215 Modern Wireless: Grand
215 IEEE Hong Kong-Taiwan Joint Workshop on Information Theory and Communications Harnessing Interaction in Bursty Interference Networks I-Hsiang Wang NIC Lab, NTU GICE 1/19, 215 Modern Wireless: Grand
Appendix B Information theory from first principles
 Appendix B Information theory from first principles This appendix discusses the information theory behind the capacity expressions used in the book. Section 8.3.4 is the only part of the book that supposes
Appendix B Information theory from first principles This appendix discusses the information theory behind the capacity expressions used in the book. Section 8.3.4 is the only part of the book that supposes
AN INTRODUCTION TO SECRECY CAPACITY. 1. Overview
 AN INTRODUCTION TO SECRECY CAPACITY BRIAN DUNN. Overview This paper introduces the reader to several information theoretic aspects of covert communications. In particular, it discusses fundamental limits
AN INTRODUCTION TO SECRECY CAPACITY BRIAN DUNN. Overview This paper introduces the reader to several information theoretic aspects of covert communications. In particular, it discusses fundamental limits
Lecture 5: Channel Capacity. Copyright G. Caire (Sample Lectures) 122
 Lecture 5: Channel Capacity Copyright G. Caire (Sample Lectures) 122 M Definitions and Problem Setup 2 X n Y n Encoder p(y x) Decoder ˆM Message Channel Estimate Definition 11. Discrete Memoryless Channel
Lecture 5: Channel Capacity Copyright G. Caire (Sample Lectures) 122 M Definitions and Problem Setup 2 X n Y n Encoder p(y x) Decoder ˆM Message Channel Estimate Definition 11. Discrete Memoryless Channel
5958 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 56, NO. 12, DECEMBER 2010
 5958 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 56, NO. 12, DECEMBER 2010 Capacity Theorems for Discrete, Finite-State Broadcast Channels With Feedback and Unidirectional Receiver Cooperation Ron Dabora
5958 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 56, NO. 12, DECEMBER 2010 Capacity Theorems for Discrete, Finite-State Broadcast Channels With Feedback and Unidirectional Receiver Cooperation Ron Dabora
ECE Information theory Final (Fall 2008)
 ECE 776 - Information theory Final (Fall 2008) Q.1. (1 point) Consider the following bursty transmission scheme for a Gaussian channel with noise power N and average power constraint P (i.e., 1/n X n i=1
ECE 776 - Information theory Final (Fall 2008) Q.1. (1 point) Consider the following bursty transmission scheme for a Gaussian channel with noise power N and average power constraint P (i.e., 1/n X n i=1
The Nash Equilibrium Region of the Linear Deterministic Interference Channel with Feedback
 The Nash Equilibrium Region of the Linear Deterministic Interference Channel with Feedback Samir M. Perlaza, Ravi Tandon, H. Vincent Poor and Zhu Han. Department of Electrical Engineering. Princeton University,
The Nash Equilibrium Region of the Linear Deterministic Interference Channel with Feedback Samir M. Perlaza, Ravi Tandon, H. Vincent Poor and Zhu Han. Department of Electrical Engineering. Princeton University,
On the Capacity of the Two-Hop Half-Duplex Relay Channel
 On the Capacity of the Two-Hop Half-Duplex Relay Channel Nikola Zlatanov, Vahid Jamali, and Robert Schober University of British Columbia, Vancouver, Canada, and Friedrich-Alexander-University Erlangen-Nürnberg,
On the Capacity of the Two-Hop Half-Duplex Relay Channel Nikola Zlatanov, Vahid Jamali, and Robert Schober University of British Columbia, Vancouver, Canada, and Friedrich-Alexander-University Erlangen-Nürnberg,
arxiv: v2 [cs.it] 28 May 2017
![arxiv: v2 [cs.it] 28 May 2017 arxiv: v2 [cs.it] 28 May 2017](/thumbs/90/104472980.jpg) Feedback and Partial Message Side-Information on the Semideterministic Broadcast Channel Annina Bracher and Michèle Wigger arxiv:1508.01880v2 [cs.it] 28 May 2017 May 30, 2017 Abstract The capacity of the
Feedback and Partial Message Side-Information on the Semideterministic Broadcast Channel Annina Bracher and Michèle Wigger arxiv:1508.01880v2 [cs.it] 28 May 2017 May 30, 2017 Abstract The capacity of the
Upper Bounds on the Capacity of Binary Intermittent Communication
 Upper Bounds on the Capacity of Binary Intermittent Communication Mostafa Khoshnevisan and J. Nicholas Laneman Department of Electrical Engineering University of Notre Dame Notre Dame, Indiana 46556 Email:{mhoshne,
Upper Bounds on the Capacity of Binary Intermittent Communication Mostafa Khoshnevisan and J. Nicholas Laneman Department of Electrical Engineering University of Notre Dame Notre Dame, Indiana 46556 Email:{mhoshne,
EE 4TM4: Digital Communications II. Channel Capacity
 EE 4TM4: Digital Communications II 1 Channel Capacity I. CHANNEL CODING THEOREM Definition 1: A rater is said to be achievable if there exists a sequence of(2 nr,n) codes such thatlim n P (n) e (C) = 0.
EE 4TM4: Digital Communications II 1 Channel Capacity I. CHANNEL CODING THEOREM Definition 1: A rater is said to be achievable if there exists a sequence of(2 nr,n) codes such thatlim n P (n) e (C) = 0.
Optimal Power Allocation for Parallel Gaussian Broadcast Channels with Independent and Common Information
 SUBMIED O IEEE INERNAIONAL SYMPOSIUM ON INFORMAION HEORY, DE. 23 1 Optimal Power Allocation for Parallel Gaussian Broadcast hannels with Independent and ommon Information Nihar Jindal and Andrea Goldsmith
SUBMIED O IEEE INERNAIONAL SYMPOSIUM ON INFORMAION HEORY, DE. 23 1 Optimal Power Allocation for Parallel Gaussian Broadcast hannels with Independent and ommon Information Nihar Jindal and Andrea Goldsmith
The Gallager Converse
 The Gallager Converse Abbas El Gamal Director, Information Systems Laboratory Department of Electrical Engineering Stanford University Gallager s 75th Birthday 1 Information Theoretic Limits Establishing
The Gallager Converse Abbas El Gamal Director, Information Systems Laboratory Department of Electrical Engineering Stanford University Gallager s 75th Birthday 1 Information Theoretic Limits Establishing
Intermittent Communication
 Intermittent Communication Mostafa Khoshnevisan, Student Member, IEEE, and J. Nicholas Laneman, Senior Member, IEEE arxiv:32.42v2 [cs.it] 7 Mar 207 Abstract We formulate a model for intermittent communication
Intermittent Communication Mostafa Khoshnevisan, Student Member, IEEE, and J. Nicholas Laneman, Senior Member, IEEE arxiv:32.42v2 [cs.it] 7 Mar 207 Abstract We formulate a model for intermittent communication
