COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS. Tensor perturbations in a universe with an elastic component
|
|
|
- Dwight Parker
- 5 years ago
- Views:
Transcription
1 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS Tensor perturbations in a universe with an elastic component Matej Škovran Bratislava 2011
2 Tensor perturbations in a universe with an elastic component WRITTEN PART OF DISSERTATION EXAM AND PROJECT OF DISSERTATION Matej Škovran COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS Department of Theoretical Physics and Didactics of Physics Study field: General Physics and Mathematical Physics Study programme: General Physics and Mathematical Physics Supervisor: Doc. RNDr. Vladimír Balek, CSc. BRATISLAVA 2011
3 Declaration I do hereby declare that this thesis has been composed by me and that the work described within is my own, unless stated otherwise. I certify it by my signature below. In Bratislava, March 29, 2011 Matej Škovran
4 Acknowledgement I would like to express my sincere gratitude to my supervisor doc. RNDr. Vladimír Balek, CSc. for the continuous support of my study and research as well as for his helpful hints, comments, opinions, and especially patience.
5 Contents Abstract Introduction I Written part of dissertation exam 9 1 Inflation Problems of non-inflationary scenario Horizon problem Flatness problem Monopole problem Mechanisms of inflation Old inflation New inflation Chaotic inflation Cosmological perturbations Relativistic theory of cosmological perturbations Gauge-invariant variables Choosing the gauge Evolution of cosmological perturbations Origin of primordial perturbations Spectrum of a perturbation Perturbation of a scalar field
6 2.3.3 Evolution of perturbations during inflationary era Spectrum of primordial perturbations Cosmic microwave background anisotropies Temperature anisotropy Sachs-Wolfe effect Gravitational waves Correlation function Primordial perturbations in the CMB Theory of relasticity Equations of motion Flat continuum Material characteristics Plane waves Modes Enhancement of tensor perturbations by shear stress Increase of tensor perturbations during the radiation dominated era Parametric space II Project of dissertation 63 6 Project of dissertation Current status of the problem Project objectives Bibliography
7 Abstract Author: ŠKOVRAN, Matej Title: Tensor perturbations in a universe with an elastic component [písomná práca k dizertačnej skúške] University: Comenius University in Bratislava Faculty: Faculty of Mathematics, Physics and Informatics Supervisor: Doc. RNDr. Vladimír Balek, CSc. of supervisor: vladimir.balek@fmph.uniba.sk Bratislava: FMFI UK, p. In this work, a summary of the theory studying cosmological perturbations is made. First, the concept of cosmological inflation is studied, since inflation is considered to be the source of perturbations. Then the theory describing cosmological perturbations is constructed and its basic observational consequences on the anisotropies of the cosmic microwave background radiation are derived. Finally, we propose a new mechanism which could enhance primordial gravitational waves so that they would be more likely to be observed in the near future. The mechanism is based on the interaction of perturbations with an elastic continuum filling the universe. Therefore, the theory describing such universe is studied, and then it is shown that this mechanism really works in a simple setting. Keywords: cosmological perturbations, inflation, relasticity 5
8 Abstrakt Autor: ŠKOVRAN, Matej Názov práce: Tenzorové perturbácie vo vesmíre s elastickou zložkou [písomná práca k dizertačnej skúške] Škola: Univerzita Komenského v Bratislave Fakulta: Fakulta matematiky, fyziky a informatiky Školiteľ: Doc. RNDr. Vladimír Balek, CSc. školiteľa: vladimir.balek@fmph.uniba.sk Bratislava: FMFI UK, s. V práci sme zhrnuli teóriu zaoberajúcu sa kozmologickými perturbáciami. Najprv študujeme koncept kozmologickej inflácie, ktorá je považovaná za zdroj perturbácií. Potom vybudujeme teóriu popisujúcu kozmologické perturbácie a odvodíme jej základné pozorovateľné dôsledky na anizotropie reliktného žiarenia. Nakoniec navrhneme nový mechanizmus, pomocou ktorého by bolo možné zosilnenie gravitačných vĺn, tak aby mohli byť s väčšou pravdepodobnosťou pozorované v blízkej budúcnosti. Tento mechanizmus je založený na interakcii perturbácií s elastickým kontínuom zapĺňajúcim vesmír. Z toho dôvodu študujeme teóriu popisujúcu takýto vesmír a potom v jednoduchom prípade ukazujeme, že tento mechanizmus naozaj funguje. Kľúčové slová: kozmologické perturbácie, inflácia, relasticita 6
9 Introduction In the most of the basic courses in cosmology, the universe is treated as isotropic and homogeneous, described by Robertson-Walker metric. This is just an approximation of a more interesting universe, with small departures from homogeneity and isotropy. Structures formed in the universe and anisotropies of the cosmic microwave background (CMB) are the main motivation for the study of these perturbations. We will focus on the theory of perturbations in the setting of inflation, the exponential expansion of the early universe after the Big Bang. According to the theory, quantum fluctuations are stretched during the inflationary era until their wavelength gets outside the Hubble horizon. Approximately at that moment, the perturbations start to behave as classical, which leads to the formation of structures and leaves an imprint on the cosmic microwave background as well. Anisotropies of CMB are a very important tool distinguishing between different scenarios of inflation, because each scenario predicts different spectrum of inhomogeneities. Recently, the space observatory Planck started to collect more precise data in comparison with those obtained from WMAP. These new data should provide enough information to eliminate at least some of existing models of inflation. One of the measurements with such potential is the observation of polarization of CMB [1]. Observation of the so called B-mode polarization would provide informations about tensor modes (gravitational waves) produced during inflation. The detection of the B-mode in the near future would be unfavourable to particle physics-motivated models, as primordial gravitational waves in such models are many orders smaller than observable values [12]. 7
10 This is the motivation for searching for a process which could enhance the amplitude of gravitational waves, or tensor perturbations. We propose a mechanism according to which these perturbations are amplified by interaction with an elastic component of the universe. The motivation for such study is that a network of cosmic strings or domain walls with elastic properties can be used to simulate the effect of dark energy [3]. The theory of elasticity in the setting of general relativity (also called relasticity) is necessary to describe the influence of the elastic continuum on the metric perturbations [18]. It is a theory developed to describe diametrically different phenomena, mainly solid crusts of neutron stars. However, we use it to show that it is possible to enhance the tensor perturbations for a proper choice of its parameters. 8
11 Part I Written part of dissertation exam 9
12 1 Inflation Cosmological inflation or just inflation is the exponential expansion of the early universe after the Big Bang. The idea of inflation was proposed in 1981 by Alan Guth. Guth noticed that scalar fields could get caught in a local minimum of the potential. The energy of empty space would then remain constant for a while as the universe expanded. It would produce a constant rate of expansion, meaning that scale parameter would grow exponentially. The scalar field responsible for inflation is called the inflaton. At the end of Guth s inflation, the inflaton field escapes by quantum tunneling from the local minimum to the global minimum of the potential, corresponding to the present universe. In the present one-inflaton scenarios, the inflaton field is not trapped in the local minimum of the potential, but rolls down the potential until it gets close to its global minimum. The energy of the inflaton field is then transferred to the radiation and the evolution of the universe continues as in the Friedmann model. 1.1 Problems of non-inflationary scenario Guth and others soon realized that the existence of an era of exponential expansion would solve some unsatisfactory aspects of the Hot Big Bang theory. The most important ones are the monopole problem, the flatness problem and the horizon problem. 10
13 1.1.1 Horizon problem If we consider chaotic distribution of matter after the Big Bang, the gravitational expansion does not give the early universe enough time to equilibrate, so that in the matter- or radiation-dominated universe the initial inhomogeneities could not have been smoothed out. On the other hand, the observed cosmic microwave background radiation (CMB) is very nearly isotropic. The light seen from all directions has almost the same temperature 2, 725K. That means the different regions of the universe have been in the thermal equilibrium at the time of recombination t re, when the photons have decoupled from matter and the universe became transparent. The time t re is also called the time of last scattering, because at recombination the photons scatter off the electrons for the last time. The problem is that while the observations of CMB suggest the universe was at the time t re at the thermal equilibrium, distant regions of the sky could not interact in any way in the noninflationary scenario. To show it let us define particle horizon t r h (t) = a(t) 0 cd t ) (1.1.1) a ( t as the maximum distance of causally connected regions at the time t after the Big Bang. The particle horizon has in radiation-dominated (a(t) t 1 2 ) as well as matter-dominated (a(t) t 2 3 ) universe the size of order t. The radius of the observable universe t 0 cd t r obs (t) = a(t) ) (1.1.2) a ( t is the radius at the time t of the comoving region of the universe which is observed today (at the time t 0 ). The horizons are the same (considered t re t 0 ) at the time t 0. If we neglect the effect of cosmological constant and extrapolate the dependence a t 2 3, valid for the universe filled with matter, to the time when the universe was radiation dominated, the ratio of 11 t re
14 the radius of the particle horizon to the radius of the observable region of the universe was proportional to t 1 3 since the time of last scattering, so that r obs (t re ) r h (t re ) = ( ) 1 tre t 0 3 = ( a(tre ) a(t 0 ) ) 1 2 (1.1.3) (considering the r h (t 0 ) and r obs (t 0 ) are the same as mentioned above). The fraction a(t re) a(t 0 can be computed from the temperature of the CMB and the ) temperature of radiation at the recombination. The temperature of the universe T depends on the scale factor as T (t) a 1 (t) and the temperature of CMB decreased approximately by the factor 1100 from the time of its emission at t re till the present time t 0. As a result, the particle horizon was smaller than the radius of observable universe by the factor 1100 at the time of recombination. Inflation provides an explanation. At the beginning of the inflationary era the observable part of the universe occupied a tiny space so that there was enough time for it to equilibrate. Now let us consider the exponential grow of the scale parameter starting at the time t i and ending at the time t I. The particle horizon at the time t I is r h (t I ) = e H It I t I t i e HI t cd t = c H I ( e N 1 ) (1.1.4) with H I being the constant expansion rate during the inflation era. The quantity N H I (t I t i ) denotes the number of e-foldings (time intervals in which the scale parameter increases by the factor e) during the inflation. Using (1.1.4) and (1.1.2) at the time t I we get the ratio r h (t I ) r obs (t I ) ( e N 1 ) a 0 H 0 a I H I, (1.1.5) where the lower index 0 denotes the present moment and the lower index I denotes the end of the inflation. To solve the horizon problem the particle horizon should be larger than the observable universe at the time t I. The 12
15 resulting condition (assuming e N 1) is e N > a IH I a 0 H 0, (1.1.6) where the term on the right side can be expressed in terms of energy densities (see [22]). The lower bound depends on the energy scale of the inflation. We need N > 62 for the energy scale GeV (Grand Unified Theory) and N > 68 for the energy scale GeV (Planck scale) Flatness problem The question of why the energy density in the early universe was so very close to the critical density and space was almost perfectly Euclidean on large scales is known as the flatness problem. The Friedmann equation can be rewritten as Ω tot (t) 1 = k a 2 H 2 (1.1.7) where Ω tot (t) ρ(t)/ρ crit (t) is the ratio between the energy density ρ(t) and critical density ρ crit (t) as a function of time t. If the universe possesses flat Euclidean geometry (k = 0), Ω tot (t) is precisely equal to one and remains so for all time. But in the case of non-euclidean geometry (k = 1 for closed and k = 1 for opened universe) Ω tot (t) changes in time. The observations tell us that the energy density of the universe is quite close to the critical density at the present. The interval of values cited in [19] is 0, 0081 < Ω tot (t 0 ) 1 < 0, (1.1.8) The parameter Ω tot (t) can be written as Ω tot (t) 1 1 Ω tot(t 0 ) Ω rad (t 0 ) [ ] 2 a(t) (1.1.9) a(t 0 ) in the limit t t 0 (see [19]), where Ω rad (t 0 ) ρ rad (t 0 )/ρ crit (t 0 ) refers to the radiation component of energy density and is of order Writing (1.1.9) at 13
16 the time t GUT of Grand Unified Theory (GUT) epoch, where a(t GUT )/a(t 0 ) 10 28, we get Ω tot (t GUT ) Ω tot (t 0 ) 1, (1.1.10) which means the energy density had to be very closely tuned to the critical density at the GUT epoch. There is no reason why the energy density should not have been so fine-tuned, but it seems unnatural for it to lie within a such a restrictive range out of all the possible values that it might have had. The inflation provides an explanation to this fine-tuning. The problem of non-inflationary scenario is that Ω tot (t) 1 always increases with time, forcing Ω tot away from one. The inflation on the other hand reverses this and drives Ω tot toward one rather than away from one. To put this quantitatively, let us suppose the universe began with a period of inflation followed by the evolution of scale parameter as in the Friedmann model. We assume that during inflation (starting at t i and ending at t I ) the scale parameter increases exponentially at the rate H I. Then the change of Ω tot (t) during the era of inflation can be calculated using (1.1.7). The result is Ω tot (t I ) 1 = e 2H I(t I t i ) Ω tot (t i ) 1. (1.1.11) Comparing this with the present value of Ω tot calculated from (1.1.7) and using N H I (t I t i ) we get ( ) 2 Ω tot (t 0 ) 1 = e 2N ai H I Ω tot(t i ) 1. (1.1.12) a 0 H 0 To estimate the number of e-foldings (N ) necessary to avoid flatness problem we assume that Ω tot (t i ) 1 is of order one. Then the same condition (1.1.6) which solves the horizon problem also solves the flatness problem Monopole problem Grand Unified Theories predict production of stable topological objects like magnetic monopoles with a high abundance at a very early stage of the evolution of the universe. They are predicted to be extraordinary mas- 14
17 sive, on the energy scale of GUT which is about GeV. The expected monopole relic density is at least one monopole per nucleon, but the search for monopoles shows that this is far in excess of the observational upper limits on the present density of monopoles. The GUT magnetic monopole was the relic particle initially considered, but there are now several other kinds of relict particles causing the same problem. The solution of the problem is that exponential expansion of the inflationary era is diminishing the monopole density below limits resulting from observations. In order that this works, a period of inflation is required to occur at a temperature below the GUT scale to avoid new thermal production of monopoles at the reheating. 1.2 Mechanisms of inflation Let us consider a homogeneous isotropic universe filled with scalar field φ (inflaton) and radiation. The matter and cosmological constant are not considered because the radiation term is dominant at very high energy scales expected at the start of inflation. At the start of inflation at the time t i, the energy density of scalar field freezes at the value ρ I ρ rad (t i ). Soon the radiation term proportional to a 4 and curvature term proportional to a 2 become also negligible and the evolution of scale parameter is governed by the Friedmann equation The solution of (1.2.1) is exponential expansion ȧ 2 (t) = 8πκ 3 ρ Ia 2 (t). (1.2.1) a(t) e H It, H I ( ) 1 8πκ 3 ρ 2 I (1.2.2) where H I is constant during the whole era of inflation. At the end of inflation the energy of scalar field is transferred to the particles produced thereby, which is called reheating. Although, as yet, there has been no direct observation of a fundamental 15
18 scalar particle (such as the Higgs boson), such particles play a vital role in inflationary cosmology. Various models of inflation including scalar fields were proposed Old inflation The original inflationary scenario proposed by Guth supposed that a scalar field was initially trapped in a local minimum of its potential. At the end of the inflation scalar field escaped the local minimum by quantum tunneling and jumped into the global minimum of the potential. Soon it was realized that transition from the initial false vacuum phase to the lower energy true vacuum phase could not have occurred everywhere simultaneously. Here and there small bubbles of true vacuum would be produced and consequently collisions of the walls of very large bubbles should lead to the generation of inhomogeneities that are considerably larger than those observed New inflation The second generation of inflationary models is also using scalar fields to provide the effective vacuum energy. The standard way to specify a particle theory is via its Lagrangian, from which the equations of motion can be derived. The Lagrangian of a scalar field is a sum of kinetic term 1 2 µφ µ φ and effective potential V (φ). The expressions (in the system of units in which c = ħ = 1) for the energy density and pressure of a homogeneous scalar field (φ φ(t)) are ρ = 1 2 φ2 + V (φ), p = 1 2 φ2 V (φ), (1.2.3) so the energy conservation equation ρ = 3H (ρ + p) takes the form φ + 3H φ + V (φ) = 0, (1.2.4) where H ȧ = [ 8πκ 1 a 3 2 φ2 + V (φ) ] during the period of scalar field dominance and the prime denotes differentiation with respect to the scalar field 16
19 φ. (See [12],[19] and [22].) The basis of the new inflation (also called slow-roll inflation) is the slowroll approximation φ 2 V (φ), φ H φ. (1.2.5) In this approximation, the equation (1.2.4) describing the evolution of scalar field becomes φ = V (φ) 3H = V (φ) 24πκV (φ). (1.2.6) According to (1.2.4), the scalar field rolls toward the minimum with the velocity (1.2.6) if the slow-roll condition is satisfied. The motivation of the slow-roll approximation is not clear at this point, but we will see that it leads to the exponential expansion of the universe. From the slow-roll approximation (1.2.6) and slow-roll conditions (1.2.5) the restrictions on the potential V (φ) V (φ) V (φ) 24πκ, V (φ) V (φ) 24πκ (1.2.7) can be derived. From these restrictions a possible form of the potential can be deduced. The potential V (φ) of new inflation (or slow-roll inflation) is characterized by a flat region for φ i < φ < φ I (the interval where the slow-roll approximation is valid) and then a sharp falloff to a minimum at φ 0. Inflation is assumed to start at a i with the field φ i far from the minimum, and then the field slowly rolls toward the minimum according to (1.2.6). In the interval where the potential is relatively flat we have a near perfect inflation, because H I ρ I V (φ) const. (1.2.8) for φ i < φ < φ I. At the end of the inflation, after the slow-roll conditions are violated, the field falls to the global minimum V (φ 0 ) and oscillates rapidly around the minimum, thereby transferring its energy to radiation and reheating the universe. 17
20 1.2.3 Chaotic inflation Chaotic inflation is a model of inflation proposed by Andrei Linde [13] to solve the problem of initial conditions in new one. Chaotic inflation does not depend on fine tuning of initial conditions as other models do, the only constraint on the potential being the slow-roll conditions. In particular, to satisfy slow-roll conditions for the power-law potential, the inflaton field scale must be initially substantially larger than the Planck energy. Otherwise the initial conditions are arbitrary, varying at random with position. In the regions of space where the inflaton field is distributed almost homogeneously and satisfies the slow-roll conditions, inflation occurred provided the region was sufficiently large. This is necessary, since otherwise the term a 2 φ, which appears on the left-hand side of equation (1.2.4) in case the field is nonuniform, would influence the previous slow-roll analysis [22]. A new feature of chaotic inflation is that, due to the vacuum fluctuations of the inflaton field, new inflating regions of space are produced all the time. A universe with this property is called self-reproducing. The mechanism of chaotic inflation leads to a universe highly inhomogeneous on scales much larger than the present horizon, with domains that seem to the observers deep inside them homogeneous and isotropic. Only such domains survive long enough for galaxies and stars, and the observer himself, to be able to appear in them. Thus, chaotic inflation explains why the universe is nearly homogeneous and isotropic from the very fact that we are present in it. This is a realization of a much discussed concept of contemporary cosmology called anthropic principle. 18
21 2 Cosmological perturbations Matter distribution in the universe can be considered homogeneous and isotropic on scales larger than a few hundred Mpc. This is consistent with the temperature fluctuations of the microwave background radiation, which show that the universe was extremely homogeneous and isotropic (with the accuracy of order 10 5 [19]) on all scales at the time of last scattering. On the other hand, a large scale structure is observed at the present time in the observable universe. Therefore, primordial inhomogeneities, serving as the seeds for structure formation, are an important part of the present cosmological models. 2.1 Relativistic theory of cosmological perturbations The Newtonian analysis of perturbations (see [16]) can be carried out, but for the large scale perturbations or in the case of relativistic matter the description within the setting of general relativity is needed. Unfortunately, the description is then more complicated and less illustrative, because of the freedom in the choice of coordinates used to describe perturbations. In the analysis of perturbations, we assume that the departure from homogeneity and isotropy is small, so that it can be treated within linearized theory. Because of the approximate homogeneity and isotropy of the universe and also negligible curvature at the present, we take Robertson-Walker metric with zero curvature as the unperturbed metric. 19
22 The total perturbed metric is defined as g g + δg, where g = dt dt a 2 (t)δ ij dx i dx j (2.1.1) is the unperturbed flat Robertson-Walker metric and δg is a small perturbation. We use the Einstein summation rule (Latin indices run from 1 to 3) and δ ij denotes Kronecker delta. To simplify the forthcoming calculations, we cast the perturbations to the metric into the form δg 00 = 2ϕ, (2.1.2) δg 0i = a(t) (B,i + S i ), (2.1.3) δg ij = a 2 (t) (2ψδ ij + 2E,ij + F i,j + F j,i + h ij ). (2.1.4) Perturbations ϕ, B, S i, ψ, E, F i and h ij = h ji (the notation is in consistency with [16], but perturbations are defined in cosmological rather than conformal time) are functions of x µ, satisfying the conditions F i,i = 0, S i,i = 0, (2.1.5) h ii = 0, h ij,i = 0. (2.1.6) The first two conditions say that F i and S i are 3-vectors with zero divergence, and the next two say that h ij is traceless and transverse 3-tensor. Considering these conditions we get ten independent functions, which coincides with the number of independent components of δg µν (Greek indices run from 0 to 3). Three decoupled modes of perturbations can be found scalar, vector and tensor perturbations. Scalar modes are described by the scalar functions ϕ, B, ψ, E. They are induced by energy density perturbations. Vector modes, characterized by vectors S i and F i, are related to the rotational motions of the fluid. The vector perturbations are generally ignored because of their quick decay, as well as because of the fact that there are just few known physical processes in which they can be generated. Tensor modes h ij describe gravitational waves with two polarizations 20
23 (usually denoted as and ) Gauge-invariant variables In a homogeneous and isotropic universe, the coordinates are chosen by the symmetry properties of the background, but there is no obvious choice of coordinates in the case of perturbed background. An illustrative example is given in [16], where homogeneous and isotropic energy density in one coordinate system transforms into a perturbed one in another coordinate system by a mere redefinition of the time coordinate. This means that by perturbing the coordinates, fictitious perturbations can be produced or physical perturbations can be removed. To distinguish physical from fictitious modes, it is helpful to find gauge-invariant variables, i.e. variables that do not depend on the choice of coordinates. In [16],[22] it is shown how the perturbations transform under an infinitesimal transformation of coordinates. Knowing that, gauge-invariant variables can be constructed. In [16], two gauge-invariant quantities describing scalar perturbations Φ = ϕ [ ( a B aė)]., (2.1.7) ( ) Ψ = ψ + ȧ B aė (2.1.8) are introduced. The dot denotes differentiation with respect to the cosmological time t. These quantities help us to distinguish physical perturbations from fictitious ones. If both Φ and Ψ are equal to zero, metric perturbations are fictitious and can be removed by a transformation of coordinates. On the other hand, there is an infinite number of gauge-invariant variables, because any combination of Φ and Ψ is also gauge-invariant. For vector perturbations only one gauge-invariant quantity V i = S i aėi (2.1.9) can be found. That means that only two of four independent functions (two 21
24 3-vectors obeying one constraint each) describe physical perturbations and the other two contain coordinate freedom. The case of tensor modes is the simplest. Perturbations h ij are gaugeinvariant by themselves, so that they already describe gravitational waves in a gauge-invariant manner Choosing the gauge The freedom of choice of coordinate system influences most importantly scalar perturbations. After finding gauge-invariant variables, some freedom still remains and can be used to fix two of the four scalars ϕ, B, ψ, E, since only two independent gauge-invariant variables can be constructed. Newtonian gauge. Newtonian gauge is defined by the conditions B = 0 and E = 0. These conditions give for the gauge-invariant variables Ψ = ψ, Φ = ϕ (2.1.10) and the part of the metric containing scalar perturbations takes the form g = (1 + 2Φ) dt dt (1 2Ψ) a 2 (t)δ ij dx i dx j. (2.1.11) If the spatial part of the stress-energy tensor is diagonal, we have Φ = Ψ [16], which leaves just one variable characterizing scalar perturbations. From the form of metric (2.1.11) it follows that this variable is a generalization of the Newtonian potential. Synchronous gauge. Synchronous gauge is defined by the conditions ϕ = 0 and B = 0, thus the part of the metric with the scalar perturbations takes the form g = dt dt a 2 (t) [(1 2ψ) δ ij 2E,ij ] dx i dx j. (2.1.12) 22
25 This gauge does not fix the coordinates uniquely. The freedom left is discussed in [16],[22]. Using the conditions ϕ = 0 and B = 0, the variables Φ and Ψ reduce to Φ = From these equations E and ψ can be expressed as ( a 2 Ė)., Ψ = ψ aȧ Ė. (2.1.13) ( 1 E = a 2 ψ = Ψ + ȧ a ) Φd t dt, (2.1.14) Φdt. (2.1.15) The integration constants appearing after the integration contain the residual coordinate freedom, which leads to a residual unphysical gauge mode. 2.2 Evolution of cosmological perturbations The dynamics of cosmological perturbations is described by Einstein equations G µ ν = 8πκT µ ν, (2.2.1) where T µ ν is the stress-energy tensor and G µ ν is the Einstein tensor. These equations take a very complicated form in a general case. Here, however, we assume only small perturbations to the background metric (2.1.1), and that means that the equations can be linearized. Einstein tensor can be split into the background term and the linear perturbation term, G µ. ν = G µ ν + δg µ ν and the stress-energy tensor can be written the same way, T ν µ. = T µ ν + δt ν µ. This leaves us with two sets of equations. One set describes the homogeneous and isotropic background and is known as the Friedmann equations [21], and the other set, describes the dynamics of the perturbations. Neither δg µ ν nor δt µ ν δg µ ν = 8πκδT µ ν, (2.2.2) are gauge-invariant. However, the construction of 23
26 gauge-invariant quantities (we will denote them as δg µ ν found in [16]. and δt µ ν) can be The direct calculation of δg µ ν for the scalar part of the perturbed metric leads to the equations ( 1 Ψ 3ȧ Ψ + ȧ ) a2 a a Φ = 4πκδT 0 0, (2.2.3) ( Ψ + ȧ ) a Φ = 4πκδT 0 i, (2.2.4),i [ Ψ + 3ȧ a Ψ + 1 ( ) a Φ + 2ä a + ȧ2 Φ + 1 ] (Φ Ψ) δ a 2 2a2 ij 1 (2.2.5) 2a (Φ Ψ) 2,ij = 4πκδTi j. The equations for the vector perturbations take the form V i = 16πκaδT (V ) 0 i, (2.2.6) (V i,j + V j,i ). + 2ȧ a (V i,j + V j,i ) = 16πκδT (V ) 0 i, (2.2.7) where δt (V ) 0 i is a divergenceless part of δg0 i. For the tensor perturbations we obtain ḧ ij + 3ȧ aḣij 1 a 2 h ij = 16πκδT (T ) i j, (2.2.8) where δt (T ) i j is traceless and transverse part of δgi j. Now, the only information about the perturbations that is still missing is the form of the perturbations to the stress-energy tensor. Let us consider the stress-energy tensor of a perfect fluid T µ ν = (ρ + p) u µ u ν pδ µ ν, (2.2.9) where ρ is the energy density, p is the pressure and u µ is the 4-velocity of the 24
27 fluid. Then the perturbations to this tensor can be written as δt 0 0 = δρ, δt 0 i = (ρ + p) ( δu,i + δu (V )i ), δt i j = δpδ i j, (2.2.10) where the 4-velocity is decomposed into the scalar part δu and the vector part δu (V )i (δu (V )i,i = 0) in the same way as the perturbation δg 0i to the metric, and the unperturbed quantities are denoted by the bar. With no anisotropic terms, we have δt (V ) 0 i = (ρ + p) δu (V ) i and δt (T ) i j = 0. In [22], also anisotropic terms of the perturbed stress-energy tensor (denoted as π S, π V i, π T ij) are introduced. We will include such terms into the theory in the next chapter, where the interpretation of these terms will be more clear. 2.3 Origin of primordial perturbations Before the idea of inflationary cosmology appeared, the initial perturbations were made to fit observational data by choosing the appropriate initial conditions for the universe. In this way the observed data about the large scale structure of the universe were explained. On the other hand, inflationary cosmology explains the origin of primordial inhomogeneities and predicts their spectrum, so that the testing of the theory by comparing its predictions with observations became possible after it has appeared Spectrum of a perturbation Let us consider a generic perturbation g(t, x), where t is cosmological time and x is a comoving coordinate of the background with Robertson-Walker metric. To describe the sample of perturbations observable at the present moment from the Earth one treats this perturbation as a random field. The perturbation is considered in a comoving cube of the comoving edge length L. The starting point of the theory is the Fourier expansion g(t, x) = k g k (t)e i k. x, (2.3.1) 25
28 where k is the comoving wave vector with the possible values k i = 2π L n i, n i Z. The expansion in a cube establishes an artificial periodicity, but this does not matter as long as the length L is much larger than any scale we are interested in. Fourier coefficients are complex functions g k = g kr + ig ki, satisfying the constraint g k = g k that results from the requirement that g(t, x) is real. As long as the perturbation is small, the time dependence of the coefficient g k (t) for the given k is determined by a linear differential equation, with no coupling between coefficients for different wavenumbers. Now, let us consider the statistical nature of perturbations. We have an ensemble of possible perturbations as realizations of a random process. Having an ensemble means having a set of universes, but the better interpretation is that averaging over the ensemble is equivalent to averaging over different volumes in an infinite universe. Fourier coefficients take different values in different realizations, and having a very large number of realizations, the probability distribution function can be defined as P (g kr, g ki ) = dp ( g kr, g ki ) dg kr dg ki, (2.3.2) where dp ( g k R, g k I) is the probability that the value of g kr lies in the interval ( g k R, g k R + dg kr ) and that of g ki lies in the interval ( g k I, g k I + dg ki ). The usual practice is to choose the Gaussian probability distribution P (g kr, g ki ) = P G (g kr )P G (g ki ) = g 2 kr e 2σ kr 2 2πσ 2 kr e g 2 ki 2σ ki 2 2πσ 2 ki (2.3.3) which greatly simplifies the discussion. Each real and imaginary part of Fourier coefficient has a Gaussian probability distribution P G, with no correlation between different coefficients except for the reality condition. The motivation for such choice of P is the fact that the perturbations generated by the vacuum fluctuations are Gaussian [12], and that this mechanism of producing cosmological perturbations is used in inflationary scenarios. An additional property of the perturbations generated in the course of the infla- 26
29 tion is that they are homogeneous and isotropic. This is included into the definition of P by letting the variance σ k depend only on k = k and making it independent of the position in space. Having chosen the probability distribution, one can calculate the ensemble average of g 2 (t, x). The result is g 2 (t, x) = k g k (t)e i k. x k g k (t)e i k. x = k, k g k g k e i ( k k ). x. (2.3.4) We have used the equality g k = g k in the second step. The expectation value of the product of Fourier coefficients is nonzero just in two cases: g k g k = g2 k = σ 2 kr σ 2 ki, (2.3.5) Knowing this, (2.3.4) can be reduced to g 2 (t, x) = k g k g k = g k 2 = σ 2 kr + σ 2 ki. (2.3.6) [ σkr 2 + σki 2 + ( ) σkr 2 σki 2 e i2k. x]. (2.3.7) As g(t, x) is a random field, also the phase of g k is considered random, with a uniform probability distribution. Therefore the variance of real and imaginary part is identical, and according to (2.3.6) it can be expressed in terms of g k as σk 2 = 1 g k 2 2. After inserting this into (2.3.7) we obtain g 2 (t, x) = 2 k σ 2 k = k g k 2. (2.3.8) In the continuous limit (the limit L ), the sum is replaced by the integral, ( ) 3 2π L k d 3 k, (2.3.9) 27
30 so that (2.3.8) becomes g 2 (t, x) = L3 2π 2 0 g k 2 k 2 dk = 0 P g dk k. (2.3.10) Here we have used the fact that g k 2 is a function of k only. In the last expression we have introduced the function P g (k), known as the spectrum of g: P g (k) = L3 2π 2 k3 g k 2. (2.3.11) Analogically to the g 2 (t, x), the two-point correlation function can be calculated [12]. The result is: g(t, x)g(t, x ) = d 3 k 4πk 3 P g(k)e i k.( x x ) = 0 P g (k) sin (kr) dk kr k, (2.3.12) where R = x x. From a finite cube with periodic boundary conditions and discrete k s we can pass to infinite space and continuous k s. In such formalism, we express g( x) as a Fourier integral, g( x) = g( k)e i k. x d3 k (2π) 3 2 (2.3.13) so that and if we use g 2 ( x) = g( k)g ( k ) e i( k k ). x d 3 kd 3 k (2π) 3, (2.3.14) g( k)g ( ( k ) = 2 σ 2 (k)δ k k ), (2.3.15) where σ(k) defines the root mean square of g( k) (a more detailed analysis shows that ist equals L 3 2 σ k ), we find g 2 ( x) = 2 σ 2 (k) d3 k (2π) 3 = 0 2 σ 2 (k) k2 dk 2π 2. (2.3.16) 28
31 By comparing this with (2.3.10) we obtain P g (k) = k3 2π 2 2 σ 2 (k) so that ( P g (k)δ k k ) = k3 2π g( k)g ( k ). (2.3.17) 2 This replaces equation (2.3.11) in the formalism with continuous k s Perturbation of a scalar field During inflation, classical physics predicts that the inflaton field ϕ becomes homogeneous and isotropic throughout the inflating region. However, as a consequence of the quantum theory one obtains vacuum fluctuations δϕ. Let us consider a scalar field φ with potential V (φ) filling the universe and let us introduce a small inhomogeneity δφ(t, x) to a homogeneous component φ(t). The total scalar field φ φ(t)+δφ(t, x) satisfies Klein-Gordon equation g φ + V,φ = 0, (2.3.18) where g 1 g µ ( gg µν ν ) is Laplace-Beltrami operator in curved spacetime. The equation follows from the action S = [ ] 1 2 gµν φ,µ φ,ν V (φ) ω g, (2.3.19) where ω g is the 4-form of volume defined by metric g (notation of structures introduced in differential geometry is consistent with [5]). A small perturbation δφ(t, x) induces only scalar perturbations (see [16]) so only perturbations ϕ, B, ψ and E have nonzero values in (2.1.2) (2.1.4). Using the unperturbed metric, we find that the Klein-Gordon equation for the homogeneous component reduces to φ + 3ȧ a φ + V,φ = 0. (2.3.20) The equation describing inhomogeneities in terms of gauge-invariant scalar field perturbation δφ δφ a φ(b aė) (see [16]) and scalar perturbations 29
32 Φ and Ψ, following from Klein-Gordon equation, takes the form ( δ φ + 3ȧ a δ φ δφ + V,φφδφ φ 3 Ψ + Φ ) + 2V,φ Φ = 0. (2.3.21) By varying the action (2.3.19) with respect to the metric g µν, we obtain the stress-energy tensor T µ ν = g µρ φ,ρ φ,ν (g ρσ φ,ρ φ,σ + V (φ)) δ µ ν. (2.3.22) The perturbed gauge-invariant components δt 0 i take the form δt 0 i = ( φδφ ),i (2.3.23) so that equation (2.2.4) yields Ψ + ȧ a Φ = 4πκ φδφ (2.3.24) From equation (2.2.5) it follows Φ = Ψ because of the fact that the nondiagonal spatial components δt µ ν are equal to zero, and the only solution consistent with Φ and Ψ being perturbations is Φ = Ψ Evolution of perturbations during inflationary era During the inflationary era the curvature scale H 1 (Hubble radius) is approximately fixed at a constant value H 1 I, where the expansion rate H I is defined in (1.2.2). On the other hand, the physical scale of perturbation, defined through the magnitude of the comoving wave vector k as λ phys = a 2π k, grows. We will solve (2.3.21) and (2.3.24) in the slow-roll approximation for two limiting cases: for short-wavelength perturbations with the physical wavelength λ phys much smaller than the curvature scale H 1, and for longwavelength perturbations with λ phys H 1. Short-wavelength perturbations. On the smallest scales a local inertial frame, in which the spacetime is approximated by the Minkowski metric, 30
33 can be always chosen. Therefore, the gravitational field is not substantial to the evolution of the short-wavelength perturbations. Omission of the perturbations of the space-time geometry caused by the inhomogeneity of the field produces only a small error [12]. Using this approximation and the slow-roll condition (1.2.7), and writing δφ in the form of Fourier expansion (2.3.13), we find that equation (2.3.21) reduces to δ φ k + 3Hδ φ k + k2 a 2 δφ k = 0, (2.3.25) where k is the comoving wavenumber. The resulting solution for δφ k in a small enough time interval during which H = ȧ a can be regarded constant, is δφ k. = C k k a e±i ah, (2.3.26) where C k is a constant which is determined by the initial conditions. The perturbation inside the Hubble horizon oscillates and its amplitude decreases as a 1. Long-wavelength perturbations. For large scale perturbation, the spatial derivative term φ in equation (2.3.21) can be neglected. To find the non-decaying slow-roll mode we omit terms proportional to δ φ and Φ (remind that Ψ = Φ). After finding the solution of the simplified equations one can check correctness of this step [16]. The approximation reduces equations (2.3.21) and (2.3.24) to 3Hδ φ + V,φφ δφ + 2V,φ Φ = 0, HΦ = 4πκ φδφ. (2.3.27) The result for the nondecaying mode of the scalar field perturbation is δφ k. = Ak V,φ V, (2.3.28) where we used H 2. = 8πκV during the slow-roll inflation and denoted the 3 integration constant by A k. The result for the scalar perturbation of metric 31
34 is Φ k = 4πκ φ H δφ k. = 1 2 A k ( V,φ In the second step we used approximation (1.2.6). V ) 2. (2.3.29) After horizon exit, the perturbation can be regarded as a classical quantity, with an almost constant value (in fact it slightly increases since V,φ /V grows towards the end of the inflation). slow-roll condition is violated and V,φ /V in units κ 1 2 Tensor perturbations. At the end of the inflation, the becomes of order unity. The case of tensor perturbations is simpler in comparison with scalar perturbations, as the tensor perturbations do not interact with the perturbed scalar field. In a universe filled by perfect fluid, i for which δt (T ) = 0, equation (2.2.8) simplifies to j ḧ ij + 3Hḣij a 2 h ij = 0. (2.3.30) We will rewrite the tensor perturbation as h ij (t, x i ) = d3 k h k (t)e ij ( k)e i k. x, (2.3.31) (2π) 3 2 where the polarization tensor e ij ( k) satisfies conditions e ii =e ij,i = 0 (summed over index i) and for the Fourier component of the perturbation h k (t) we have h k (t) = h (t) from reality condition. From equation (2.3.30) it follows that k the components h k satisfy equation ḧ k + 3Hḣk + k2 a 2 h k = 0, (2.3.32) which is of the same structure as equation (2.3.25). The same analysis as before gives for tensor perturbations in short-wavelength limit the expression h k. = Ck k a e±i ah, (2.3.33) where C k is integration constant. 32
35 In the long-wavelength limit (H k/a) the term proportional to k is negligible, so that ḧ k + 3Hḣk. = 0. (2.3.34) As a result, the nondecaying mode is approximately constant, h k. = Ã k. (2.3.35) Spectrum of primordial perturbations To find the spectrum of perturbations, we need to determine integration constants in (2.3.26), (2.3.28) for scalar perturbations and constants in (2.3.33), (2.3.35) for tensor perturbations. Until now, we treated perturbations as classical fields. However, the initial conditions are specified by vacuum fluctuations of the corresponding field, therefore it is necessary to treat perturbations as quantum fields (we use units in which ħ = 1). Scalar perturbations. In [16], a rough estimate for a typical amplitude of the minimal vacuum quantum fluctuations on a physical scale l is made, with the result δφ l l 1. Taking into account that δφ l δφ k k 3 2, where k a/l is the comoving wavenumber, we obtain δφ k k 1 2 a, (2.3.36) which implies C k k 1 2 (2.3.37) A more precise analysis, based on canonical commutation relations for a quantum field shows that C k = (2k) 1 2. The evolution of the mode according to (2.3.36) preserves the form of vacuum spectrum. The constant A k can be obtained by requiring that δφ k, which is already a classical field, has the minimal vacuum amplitude at the moment of horizon crossing; that is, we can find it by matching δφ k after horizon exit with δφ k we have estimated above. From equation (2.3.28) and estimate (2.3.36) it 33
36 follows A k [ k 1 2 a ( V V,φ ) ] k Ha, (2.3.38) where index k Ha fixes quantities at the moment of horizon crossing. Tensor perturbations. The action of tensor perturbations can be transformed into the action of canonically normalized real scalar fields. Thus, the same analysis as for scalar perturbations can be performed and up to a multiplication constant the results are same [16]. In particular, for the constant C k we have C k = 32πκC k. (2.3.39) The constant Ãk can be fixed by the same assumption as we made for A k. In this way we obtain where a k satisfies a k k/h. Spectrum. Ã k = C k a k, (2.3.40) The inflation smooths all pre-existing classical inhomogeneities by stretching them to very large scales, but it cannot remove quantum fluctuations. Always new fluctuations are created from vacuum, in place of already stretched ones. Because of this mechanism, fluctuations which would have been on the sub-planckian scale at the start of inflation can be observed at present. Having fixed the integration constants, the spectrum can be calculated. For a given wavenumber k, spectrum of the scalar field fluctuations at the moment of horizon crossing, k Ha, is P φ (k) = k3 2π 2 δφ k 2 = k3 2π 2 C k 2 a 2 k = ( ) 2 H. (2.3.41) 2π k Ha Here we have expressed the magnitude of the Fourier component of the field δφ as δφ k = 2 σ k and used the precise value C k = (2k) 1 2. Physically more interesting than the spectrum of the field φ is the spectrum of the scalar perturbation to the metric Φ, as Φ is more helpful for 34
37 computation of energy density perturbations in the post-inflationary era, after the energy of the inflaton field is transferred to radiation. At the end of inflation, the spectrum of scalar perturbations is ( P Φ (k) = k3 2π Φ k 2 k3 H 2 2π A k 2 κ 2 κ 2 2 2π V V,φ ) 2 k Ha We replaced the factor V,φ /V from equation (2.3.28) by κ 1 2. (2.3.42) as it becomes of that order at the end of inflation. In [16], it is shown that the amplitude of the metric perturbation in the radiation-dominated era differs from its amplitude at the end of inflation only by a numerical factor of order unity. The spectrum of tensor perturbations for a fixed wavenumber k is given by its value at the moment of horizon crossing, because according to (2.3.35) after horizon crossing the amplitude of tensor perturbations freezes to a constant value. The spectrum of tensor perturbations is up to a numerical factor the same as that of the scalar field, ( ) P h (k) = k3 2π h k 2 = k3 2 2 H Ã 2 2π 2 k = 32πκ, (2.3.43) 2π k Ha By comparing tensor perturbations to scalar ones we obtain tensor-toscalar ratio r P h(k) P Φ (k) 32π κ ( ) 2 V,φ V k Ha. (2.3.44) From the slow-roll condition (1.2.7) one finds just r 10 3, and from a more detailed analysis one obtains r 16 [22]. Values r 0.1, possibly observed in experiment Planck, still fit this constraint. However, according to [12], values r 0.1 require the energy scale of inflation well above the scale of Grand Unified Theory and, in addition to that, the corresponding scale of the inflaton field in the course of inflation must be comparable to Planck energy. For models of chaotic inflation these requirements are satisfied, but for the particle physics-motivated models they are not; therefore in such models one necessarily has r 1. 35
38 3 Cosmic microwave background anisotropies Primordial perturbations originated from quantum fluctuations. During the inflationary era, fluctuations were stretched to large scales with nearly unchanged amplitudes, and later, at the time of last scattering, they left their imprint on the cosmic microwave background that can be observed now. Thus, by observing the anisotropies of CMB the theoretical predictions about the creation and evolution of cosmological perturbations can be tested. 3.1 Temperature anisotropy The CMB radiation is described to a high accuracy by the blackbody distribution f(ω, T ) = 2 e ħω kt 1, (3.1.1) characterizing the number density in phase space. The factor of 2 represents two possible polarizations, ħω is the energy of the photon measured by the comoving observer and T is the effective temperature of the radiation. According to Liouville s theorem (see [5]) the phase volume of the Hamiltonian system is conserved along the trajectory of the particle. Since the particle number is conserved in the absence of interactions (this is satisfied after the time of last scattering), the distribution function is constant along the geodesics: df dt = 0 (3.1.2) 36
39 This equation is also called collisionless Boltzmann equation [12]. Now let us consider a universe filled with an almost homogeneous and isotropic thermal radiation. The effective temperature can be written as T (x µ, n) = T (t) + δt (x µ, n), (3.1.3) where x µ is the location of the observer and n is unit vector indicating the direction from which the radiation is arriving to the observer. Since the number density (3.1.1) is conserved, after the coordinate transformation x µ = x µ + ξ µ we obtain ω T (x µ ) = The frequency transforms as ω = ω (1 + a ξ ) i n i ξ µ and metric perturbations [16]. measured in new coordinates are ω T ( x µ ). (3.1.4) up to the terms linear in Therefore the temperature fluctuations δt = δt aṫ ξ0 + at ξ i n i. (3.1.5) We can observe the CMB radiation from one point only, thus the term independent from n (monopole component) is removed by redefining the background temperature. The n-dependent term (dipole component) of the temperature fluctuations depends on the motion of the observer with respect to the comoving coordinates as a result of Doppler effect. Because of that, only quadrupole and higher-order multipoles contain information about primordial perturbations Sachs-Wolfe effect The Sachs-Wolfe effect describes the influence of the gravitational potential on the CMB temperature fluctuations. To write it in terms of already defined scalar perturbations it is convenient to use Newtonian gauge, in which the metric takes the form (2.1.11) and scalar perturbation Φ is gravitational potential. 37
40 With the metric (2.1.11), geodesic can be computed and used in the Boltzmann equation (3.1.2). To the zeroth order in perturbations one obtains ( at ). = 0 (3.1.6) and to first order one obtains d dt ( ) δt T + Φ = 2 Φ t, (3.1.7) where d is total time derivative (see [16]). The first equation just tells us dt that the temperature of CMB is in unperturbed case proportional to a 1. After recombination, radiation is only a small fraction of total energy density, which means that the potential Φ is slowly varying in time. This allows us to neglect the last term in equation (3.1.7) and write δt T + Φ = const (3.1.8) along null geodesics. A photon emitted at the time of recombination t re and observed at the present time t 0 at the location x i 0 from the direction n propagates along the null geodesic, so that x i re(n i ) =. t 0 x i 0 n i t re dt a xi 0 n i r re, (3.1.9) where we have denoted by r re the radial coordinate of the surface of last scattering. Hence, from equation (3.1.8) it follows δt T (t 0, x i 0, n i ) = δt T (t re, n i r re ) + Φ(t re, n i r re ) Φ(t 0, x i 0). (3.1.10) The fractional temperature fluctuation observed from direction n is given by three terms. The first term describes initial temperature fluctuations on the surface of last scattering. The next two terms are the difference of gravitational potentials, coming from the gravitational redshift of radiation 38
41 on its way from the surface of last scattering to the observer. The last term contributes to the monopole component only, so as long as the coordinates x i 0 are fixed (to the Earth), this term can be ignored. Initial temperature perturbation on the surface of last scattering can be expressed in terms of the fractional perturbation to the photon energy density δ γ δε γ /ε γ, where δε γ is the perturbation to the unperturbed photon energy density ε γ. Spatial Fourier components of the initial temperature perturbation take the form (derivation is given in [16]) ( ) ( δt (t re, n i r re ) = 1 δ γ T k 4 k (t re ) + 3ia ) k. n k δ γ 2 k (t re ). (3.1.11) In case of long-wavelength perturbations at the time of recombination (λ phys (t re ) 2πa re /k H 1 (t re )), the fractional perturbation to the photon energy density satisfies (again see [16]) δ γ k (t re ). = 8 3 Φ k (t re ), δγ k (t re ). = 0, (3.1.12) which simplifies equation (3.1.10) to Gravitational waves δt T (t 0, x i 0, n i ) = 1 3 Φ(t re, n i r re ). (3.1.13) So far we have neglected tensor perturbations to the metric, but they are an important part of inflationary cosmology. The effect of gravitational waves on the anisotropies of CMB can be derived analogically to the Sachs-Wolfe effect. Let us consider tensor perturbations only. (This is possible, because in the linearized theory the contributions of various perturbations to the anisotropies of CMB are additive.) The metric takes the form g = dt dt a 2 (δ ij + h ij ) dx i dx j, (3.1.14) 39
42 where h ij satisfies conditions (2.1.6). The geodesics can be computed using this metric and the resulting formula can again be inserted into the Boltzmann equation (3.1.2). This procedure leads to the equation with the solution d δt dt T = 1 h ij 2 t ni n j, (3.1.15) δt T ( n) = 1 2 t 0 t re h ij t ni n j dt. (3.1.16) Generally, a term describing initial temperature perturbations on the surface of last scattering should appear on the right-hand side of this equation, but the tensor perturbations do not produce such kind of temperature fluctuations. 3.2 Correlation function To describe the anisotropies of CMB it is convenient to expand fractional perturbation of temperature into spherical harmonics Y lm ( n): δt T ( n) = l l=0 m= l a lm Y lm ( n). (3.2.1) We use the definition of spherical harmonics according to which Y lm = Y l m. Because of this and the reality of δt/t, the coefficients in (3.2.1) satisfy the condition a lm = a l m An important quantity describing CMB temperature fluctuations is the average of their product over the positions of the observer δt T ( n 1) δt T ( n 2) = lm C l Y lm ( n 1 )Y l m ( n 2 ) = l Here P l denotes Legendre polynomial and C l is defined as 2l + 1 4π C lp l ( n 1. n 2 ). (3.2.2) a lm a l m = δ ll δ mm C l, (3.2.3) 40
43 which means C l = a lm 2. (3.2.4) The average of two a lm coefficients takes such form because of the rotational invariance of the universe [22]. In reality, the observed quantity can not be averaged over position, it can be averaged only over m: C (obs) l 1 2l + 1 a lm a lm (3.2.5) The fractional difference between C l and C (obs) l is called cosmic variance. The mean square cosmic variance for Gaussian perturbations is [22] [ m ] C l C (obs) 2 l = 2 C l 2l + 1, (3.2.6) which means that variance is negligible for sufficiently large l but is substantial if one calculates low-order multipoles. Knowing this, we introduce a new quantity describing CMB temperature fluctuations, namely the two point correlation function C(θ) δt T ( n 1) δt T ( n 2), (3.2.7) where we take average over all directions n 1, n 2 satisfying n 1. n 2 = cos θ. It can be rewritten as a sum C(θ) = l 2l + 1 4π C(obs) l P l (cos θ), (3.2.8) Sometimes also the squared temperature difference averaged over the sky is computed, which is related to C(θ) by [δt ] 2 [T ] 2 T (θ) ( n1 ) T ( n 2 ) = 2 [C(0) C(θ)]. (3.2.9) T 41
44 3.3 Primordial perturbations in the CMB In order to compare measurements with theory, the last step remains to be taken. It is the computation of average (3.2.2), where the temperature fluctuations are given by (3.1.13) and (3.1.16) in terms of the primordial perturbations. Scalar perturbations. For scalar perturbations we have to compute δt T ( n 1) δt T ( n 2) = 1 9 Φ(t re, n 1 r re )Φ(t re, n 2 r re ). (3.3.1) Now we recall the expression (2.3.12) for the two-point correlation function of a generic perturbation. According to it, we get Φ(t re, n 1 r re )Φ(t re, n 2 r re ) = 0 P Φ (k) sin (kr) dk kr k, (3.3.2) where R = r re n 1 n 2 and P Φ (k) is the spectrum of primordial scalar perturbations at the time of recombination. The last step consists in using the expansion sin (kr re n 1 n 2 ) kr re n 1 n 2 = (2l + 1) jl 2 (kr re )P l ( n 1. n 2 ), (3.3.3) l=0 where j l are the spherical Bessel functions and P l are the Legendre polynomials of order l. After substituting (3.3.2) into (3.3.1) and comparing it with (3.2.2) one obtains the multipole moments C l = 4π 9 0 P Φ (k)j 2 l (kr re ) dk k. (3.3.4) 42
45 In the general case, considering the initial temperature perturbation given by (3.1.11) we get [16] C l = 2 π 0 ( Φ + δγ k 4 Tensor perturbations. ) j l (kr re ) δ γ 3a k 4k dj l (kr re ) d(kr re ) 2 t re k 2 dk. (3.3.5) In order to describe tensor perturbation as a random Gaussian perturbation, it is convenient to use expansion (2.3.31) where e ij ( k) will be random polarization tensor. The contribution of tensor perturbations to the correlation function according to relation (3.1.16) then takes form δt T ( n 1) δt T ( n 2) = 1 4 F ( n 1, n 2, k)ḣ k (t)ḣ k ( t)e i k.[ n 1 r(t) n 2 r( t)] dtd t d3 k (2π) 3 (3.3.6) where we have already used the fact that average over random polarization tensor is nonzero only for the same k. In addition to that, we have used the definitions F ( n 1, n 2, k) = e ij ( k)e mn ( t 0 k) n i 1n j 1n m 2 n n 2, r(t) = t dt a. (3.3.7) Tensor e ij ( k) is traceless and transversal, thus, with projection operator defined as P ij δ ij k i k j /k 2 it satisfies e ij ( k)e mn ( k) = P im P jn + P in P jm P ij P mn. (3.3.8) This allows us to compute F ( n 1, n 2, k). Then, after introducing the new variable x kr(t) instead of t, integration over the angular part of k gives [16] δt T ( n 1) δt T ( n 2) = 1 hk h k 4 x x ˆF [ sin ( n1 x n 1 x ) n 1 x n 1 x ] dxd x k2 dk 2π 2, (3.3.9) 43
46 where ˆF is operator ( ˆF 2 n 1. n 2 x ) 2 ) (1 + ( x x 2 x 2 ). (3.3.10) In order to obtain multipole moments C l corresponding to tensor perturbations, it remains to perform expansion (3.3.3) and use recurrence relations for spherical Bessel functions. The final expression for the multipole moments caused by tensor perturbations is [16] C l = (l 1) (l + 1) (l + 2) 2π 0 kr re 0 h k x j l (x) x 2 dx 2 k 2 dk. (3.3.11) 44
47 4 Theory of relasticity Einstein s theory of general relativity and mechanics of continuum are two well known theories. Both have important applications, but in different fields of physics. General relativity usually assumes matter to be in the form of ideal fluid in its cosmological and astronomical applications. On the other hand, mechanics of continuum is used in situations when Newtonian theory is valid. The development of the theory of relasticity (short name for relativistic elasticity) was motivated by the study of solid crusts of neutron stars. In this way the theory describing continua within the setting of general relativity has appeared. The simplest case is just one continuum extending over all spacetime, a 4-dimensional manifold M diffeomorphic to R 4 and equipped with metric tensor g. The signature ( + ++) of the spacetime metric is used, the same as in [18]. Properties of the continuum are defined on the 3-dimensional material manifold N diffeomorphic to R 3, whose points represent particles of which the continuum consists. Coordinates on spacetime manifold M are denoted x µ and coordinates on material manifold N are denoted X A (Greek indices run from 0 to 3 and Latin indices run from 1 to 3). The distribution of the points of the continuum in spacetime is described by the material mapping f that maps spacetime on the material manifold, specifying which particles are located at which worldpoints. In the coordinates X A, the material mapping f can be expressed through the coordinate component functions f A (x µ ). The material mapping is schematically depicted in figure
48 g f ρ x µ M R 4 f N R 3 ϵ f g ρ X A Figure 4.1: Material mapping f (maps spacetime M on the material manifold N ) Metric tensor g can be push-forwarded by the material mapping, providing the tensor ϵ f g on the material manifold interpreted as the strain tensor. After the strain tensor has been introduced, the quantity determining completely the dynamics of the continuum, the state function ρ, can be defined. State function ρ ρ(x A, ϵ(x A )) is a scalar function depending on the point of the material manifold and the strain tensor ϵ at that point. It is the energy density in the rest frame of the given particle, in the deformed continuum described by the strain tensor (see [17], [18]). 4.1 Equations of motion The dynamics of a spacetime containing relastic continuum is governed by the Einstein Hilbert action S = (L + R) ω g = ( ρ + R) ω g, (4.1.1) where R is scalar curvature, L is Lagrangian density of material fields equal to ρ (this gives the correct energy density component of the stress-energy tensor) and ω g is the 4-form of volume defined by metric g (see [5]). The same symbol ρ is used to denote the state function in the material manifold as well as the pulled-back state function in the spacetime manifold, but from the context it should be always clear which object is meant. The action (4.1.1) is written in a system of units in which c 4 /16πκ = 1. In these units, the Einstein equations take the form 2G µν = T µν. (4.1.2) 46
49 To calculate the variation of the action providing us with the equations of motion of the continuum it is necessary to pull-back the state function to the spacetime manifold. The state function appearing in the Einstein Hilbert action is a pull-back of the state function defined on the material manifold as a function of two arguments ρ(x A, ϵ(x A )). First of all, we need to express the components of the strain tensor ϵ. It is defined as push-forward of metric tensor g, therefore its components with respect to X A are H AB = g µν f A,µf B,ν. (4.1.3) This can be regarded as coordinates on the space of double contravariant tensors on the material manifold. Now, the pull-back of the state function can be made, giving f ρ = ρ(f A, H AB ). We now have everything ready for the variation of the action. The variation with respect to f A leads to the equation (the semicolon denotes covariant differentiation) ( ) ρ ρ f = 0, (4.1.4) A f,µ A ;µ and by varying the material part (Lagrangian term) of the action with respect to g µν we obtain the formula for the stress-energy tensor, T µν = 2 ρ H f,µf A B AB,ν ρg µν. (4.1.5) By the variation of scalar curvature with the respect to g µν, the Einstein tensor is acquired so that we obtain equations (4.1.2). 4.2 Flat continuum For simplicity, a homogeneous, isotropic and flat elastic continuum is chosen. This means that there exists a set of coordinates X A in the material manifold such that the state function is invariant with respect to Euclidean rotations and translations of X A. The consequence of this choice is that the partial derivatives of the state function with respect to X A are identically 47
50 zero. From now on, X A denotes this specific set of coordinates. Having fixed the coordinates X A on the material manifold, the material mapping f can be expressed in terms of the component functions f A. The spacetime is filled by one continuum, so it is possible to reduce the gauge freedom by requiring that f A (x µ ) = x A (x A are comoving coordinates). Then there remains only one free coordinate x 0. Further restriction can be g 00 = 1 (implying that x 0 equals the proper time t of the particles of the continuum), and the only freedom left is in the choice of the hypersurface x 0 = 0. Having completed the description of the continuum and the material mapping, we can specify the background metric. We assume that it is, just like the continuum, homogeneous, isotropic and flat. That means that it is equipped with the flat Robertson-Walker metric g = dt dt + a 2 (t)δ ij dx i dx j, (4.2.1) where a(t) is scale parameter and δ ij is the Kronecker delta. Such continuum could be called double-flat, because it has flat internal geometry and at the same time is embedded into a flat 3-dimensional space. With the metric (4.2.1), the Einstein tensor can be computed to obtain 2G 00 = 6ȧ2 a 2, 2G 0i = 0, 2G ij = ( 4äa + 2ȧ 2) δ ij, (4.2.2) and with the fixed material mapping f also the stress-energy tensor (4.1.5) can be evaluated, T 00 = ρ, T 0i = 0, T ij = 2 ρ H ij a2 ρδ ij. (4.2.3) The equations of motion are then contained in the Einstein equations (4.1.2). 4.3 Material characteristics In this section, the material characteristics of the continuum are introduced. First, Einstein s cosmological constant can be treated as the vacuum 48
51 energy ρ 0 contributing a constant term to ρ. The separation of the vacuum energy density is artificial, but such choice provides us with simpler formulae for other quantities to be defined. The remaining energy density can be written as a product of the particle density n and the energy per particle ε. In this way the general formula ρ = ρ 0 + nε (4.3.1) is obtained. As we will see, this can be written for the background metric (4.2.1) as ρ = ρ 0 + a 3 ε. In the double-flat continuum, the strain tensor of the background solution is H AB = a 2 δ AB, (4.3.2) and the invariance of ρ with respect to rotations ensures that the derivatives of ρ with respect to H AB are proportional to δ AB (the first derivatives) or equal to linear combinations of the products of δ AB (the higher derivatives). In [18], the particle density n is defined as n det H, (4.3.3) which gives the correct particle density for the background metric when (4.3.2) is used, n = 1 6 ε ACEε BDF H AB H CD H EF = a 3. (4.3.4) In the nonrelativistic theory, the elastic properties of a homogeneous and isotropic continuum are determined by two Lame coefficients λ and µ, and when the continuum is deformed in a homogeneous and isotropic way, its stress tensor is given by one scalar quantity the pressure σ. These quantities are defined analogically for a general relativistic homogeneous and isotropic continuum. The scalar σ is defined by the relation 2 ε H AB a2 σδ AB, (4.3.5) 49
52 and the scalars λ and µ are defined by the relation ( 2 2 ε H AB H CD + ) 2 ε a 4 [λδ H AB H DC AB δ CD + µ (δ AC δ BD + δ AD δ BC )]. (4.3.6) The true strain tensors are always symmetric, but for the purposes of differentiation we consider also nonsymmetric tensors. Then, to obtain correct results it is needed either to let ρ depend only on the symmetric part of H AB, or to symmetrize higher derivatives with respect to H AB s but the last and then insert symmetric values into the resulting expressions. We adopt the second procedure, therefore the left side of (4.3.6) is symmetrized. Using the quantities σ, λ and µ, the derivatives of the energy density ρ ρ 0 + nε can be written as and ( 2 2 ρ H AB H CD + 2 ρ H AB = a 1 (ε + σ) δ AB (4.3.7) ) 2 ρ = H AB H DC = a [(λ + 2σ + ε) δ AB δ CD + (µ ε) (δ AC δ BD + δ AD δ BC )]. (4.3.8) In (4.3.7) and (4.3.8), the derivative of particle density n with respect to H AB is used. This quantity can be expressed as n H = (n2 ) AB 1 2 H AB = 1 det H n 1 2 H = 1 AB 2 a3 a 4 δ AB = 1 2 a 1 δ AB, (4.3.9) where the definition n det H has been used. The above definition of λ and µ (motivated by the simple relation of these material characteristics to the second derivatives of ε in nonrelativistic elasticity) is not the only possible. It is more common to generalise Lame coefficients in such way that µ remains zero for ideal fluids under any pressure, so that it can be still called shear modulus as in ordinary elasticity [3]. In a theory with our definition of λ and µ, ideal fluids have µ + σ = 0 and the 50
53 shear modulus of an arbitrary elastic medium is [18] µ shear µ + σ. (4.3.10) The consequence of equation (4.3.2) is that the derivative with respect to a corresponds to the derivative with respect to H AB operator relation a3 2 according to the a = δab. (4.3.11) HAB Therefore, the scalars ε, σ, λ and µ as functions of a are not independent. The relations between them are and ε a = 3a 1 σ (4.3.12) σ a = a 1 (2σ + 3λ + 2µ). (4.3.13) Now, when we insert Einstein tensor (4.2.2) and stress-energy tensor (4.2.3) into Einstein equations (4.1.2), we are ready to write down the equations of motion in terms of the previously defined material characteristics. The (00) component of (4.1.2) yields the equation and (ij) components lead to the equation ȧ 2 a = 1 ( ρ0 + a 3 ε ) (4.3.14) 2 6 ä a ȧ2 a 2 = 1 4 a 3 (ε + σ). (4.3.15) The first equation is just the Friedmann equation describing flat universe containing dark energy with the density ρ 0 and an ideal fluid with the energy density a 3 ε and pressure a 3 σ. If we take into account the identity (4.3.12), we can see that the second equation is the time derivative of the first, thus contains no new information. 51
54 4.4 Plane waves In this section we introduce linear perturbations of the previously found background solution. The perturbations of the fields f and g are denoted by δf and δg. It is noteworthy that all perturbations are restricted by the dynamics and some perturbations correspond only to coordinate changes and therefore are not of physical interest. For simplicity we do not include the small perturbations to the Euclidean metric of the material manifold (introduced in [3]) into the theory. First, the gauge degrees of freedom are reduced in a way analogical to the fixation of the coordinates in the background solution. We require that the coordinates of the perturbed solutions are comoving in the same way as those of the background solution (f A (x µ ) = x A ), which implies δf A = 0. We fix δg 00 = 0, so the x 0 coordinate still measures the proper time of the particles (x 0 = ct). The last freedom is in the choice of the zero hypersurface, which we leave unfixed because the perturbed metric does not generally allow us to choose a certain nice hypersurface. To simplify the upcoming expressions, the perturbations are supposed to be complex. This is possible due to the fact that the dynamics of small perturbations is governed by linear equations and the solutions of a linear equation form a linear space; thus, it is sufficient to investigate some basis of them. The translation symmetry of the continuum offers an ansatz for such basis, the solutions of the form of complex plane waves depending on the space coordinates only through the multiplication factor e ik Ax A, where k A are the coordinate components of a constant wave covector on the material manifold, pulled-back by f to the spacetime. The rotational invariance of the background allows also for a further simplification. The coordinates can be rotated in such a way that x 1 becomes parallel to the wave covector, which means that the components of the wave covector become (k, 0, 0), where k k 1 is an arbitrary real number. In further computations we replace δg by more complicated expressions in order to obtain simpler looking results. 52
55 We define tensorial-looking, time-dependent quantities h 0i and h ij by putting δg 0i = ikh 0i (t)e ikx1, (4.4.1) and δg ij = a 2 (t)h ij (t)e ikx1. (4.4.2) Now everything is prepared for the variation. The variation of the equation of motion of the continuum (4.1.4) gives (ε + σ) ḣ01 = (2µ + 3λ + 5σ) ȧ a h 01 (µ + σ) h (λ + σ) h kk (4.4.3) (ε + σ) ḣ0α = (2µ + 3λ + 5σ) ȧ a h 0α (µ + σ) h 1α (4.4.4) where the index α assumes values 2 and 3. The variation of Einstein equations gives a set of equations, but as in the case of background solution, some of them are just time derivatives of the others. The final set of independent equations is (ḧ22 ḧ33) ( ) 2ȧ + k2 h aḣkk a 2 kk h 11 4ȧ a h 01 + ε + σ 2a h 3 kk = 0, (4.4.5) ḣ 11 ḣkk ε + σ h a 3 01 = 0, (4.4.6) ( k 2 ḣ 1α a + ε + σ ) h 2 a 3 0α = 0, (4.4.7) ( k 2 a + µ + σ ) (h 2 a 3 22 h 33 ) = 0, (4.4.8) ( k 2 a + µ + σ ) h 2 a 3 23 = 0. (4.4.9) + 3ȧ (ḣ22 ḣ33) + a ḧ ȧ aḣ23 + (See [18], and for the detailed expressions for the variations see [17].) 53
56 4.5 Modes The set of equations (4.4.3) to (4.4.9) can be divided into several subsets of coupled equations. Physically, it means that there are different modes of wave propagation. General relativity and nonrelativistic elasticity are two limiting cases of relasticity, therefore two modes of gravitational waves (as in general relativity) and two modes of transversal acoustic waves as well as one mode of longitudinal acoustic waves (as in nonrelativistic elasticity) are expected. In the terminology of the theory of cosmological perturbations the modes can be divided into tensor, vector and scalar ones. The freedom of choosing the zero hypersurface supplies one more mode, which makes the number of modes equal to the number of components of h 0i and h ij. First we have equations for h 22 h 33 and h 23. written in compact form as The equations can be ( k ḧ T ij + 3ȧ aḣt 2 ij + a + µ + σ ) h T 2 a 3 ij = 0 (4.5.1) where h T ij is the tensor part of h ij, a symmetric 3 3 matrix with nonzero components h T 22 = h T 33 = h 22 h 33, h T 23 = h 23. (4.5.2) 2 Equation (4.5.1) is a special case of equation (2.2.8), with the anisotropic i part of the perturbed stress-energy tensor δt (T ) coming from shear stress j in the elastic continuum. The equation describes (the h T 22 component) and (the h T 23 component) polarizations of gravitational waves [18]. In cosmological terms, it describes tensor perturbations. In the case µ + σ = 0 this equation coincides with the equation describing tensor perturbations in a universe filled with an ideal fluid (see [2],[11],[22]). Next we have a set of equations containing only h 0α and h 1α, ḣ 0α = 2µ + 3λ + 5σ ε + σ ȧ a h 0α µ σ ε + σ h 1α, (4.5.3) 54
57 ( k 2 ḣ 1α = a + ε + σ ) h 2 a 3 0α. (4.5.4) These modes can be recognized as transversal acoustic waves oscillating in the x α directions [18]. They describe vector perturbations. The remaining set of equations describes scalar cosmological perturbations, but includes also the remaining freedom of choosing the zero time hypersurface. In [18], the variables y 01, y 11 invariant with respect to the change of the hypersurface are defined by the relations h 01 = y 01 + y, h 11 = y ȧ a y, h kk = y ȧ y. (4.5.5) a In this way the physically relevant perturbations are identified. The choice of the zero time hypersurface is encoded in the variable y, satisfying the differential equation ẏ = a ε + σ y 4ȧ a (4.5.6) The equation itself is invariant, so that the whole freedom is in the choice of the initial condition for it. After eliminating y from the equations we get a pair of equations invariantly describing the propagation of a longitudinal acoustic wave, ( 2µ + 3λ + 5σ ẏ 01 = ε + σ ẏ 11 = ȧ a + a 4ȧ (2 k2 a ) ε + σ 2µ + λ + 3σ 1 y a 3 01 ε + σ 2 y 11, (4.5.7) ) ε + σ y a 3 01 a ε + σ y 4ȧ a (4.5.8) 55
58 5 Enhancement of tensor perturbations by shear stress Tensor perturbations as defects of metric produced during inflation could serve as an important tool for distinguishing between different types of inflationary models. In the most simple models of chaotic inflation tensor perturbations are large enough to be measured in near future. However, as we have seen at the end of section 2, in the particle physics-motivated inflationary models they are many orders smaller than the observable value. The open question is if it is possible to increase the amplitude of tensor perturbations after inflation, during the radiation dominated era. In [15] it is argued that this is impossible using the mechanism proposed earlier, with the suppression of scalar modes due to the decay of a homogeneous scalar field. Here we investigate another possible mechanism. We consider a universe containing, in addition to radiation, a component consisting of elastic matter. A motivation for that is that one can simulate the effect of dark energy by a network of cosmic strings or domain walls with elastic properties [3]. To describe a universe filled with an elastic continuum, and in particular tensor perturbations in it, the theory of relasticity (relativistic elasticity) must be used [3]. The evolution of gravitational waves (which are tensor perturbations), propagating in a universe that contains an elastic medium, is described by the equation (4.5.1). The evolution of tensor perturbations is usually considered within models that do not include shear stress (see [12],[22]). The equation then reduces to the equation describing evolution of 56
59 tensor perturbations in such models in the limit µ shear µ + σ 0. The shear modulus µ shear describes elastic properties of the continuum and depends on the scale parameter. The expression a 3 µ shear entering equation (4.5.1) depends on a in the same way as the energy density. In particular, for the network of cosmic strings it is proportional to a 2 and for domain walls to a 1 [3]. We aim to show that it is possible to increase tensor perturbations significantly during the radiation dominated era in models with negative shear modulus. (In [3] only the positive µ shear is admitted. Here we relax this restriction.) We consider perturbations whose wavelength is of order of horizon length at the end of inflation; i. e. they are by about 24 orders of magnitude smaller in size than the perturbations that enter horizon at recombination. Such perturbations are unobservable, both because of their small size (which excludes their indirect observation by means of CMB) and because of their small amplitude (which excludes their detection in LIGO-type experiments). Thus, we do not attempt any testable predictions here. We just want to demonstrate the effect we have mentioned above in a simple way, and we restrict ourselves to small-scale perturbations because we do not need to compute the power spectrum for them. To simplify the analysis even further, we use shear modulus of the form µ shear a 3 = µ 0 a 4, where µ 0 is a parameter of our model. Elastic media with such µ shear behave as radiation when expanding adiabatically through a sequence of partially relaxed states. A special case (stiff ultrarigid continuum) is considered as an example in [18]. 5.1 Increase of tensor perturbations during the radiation dominated era We analyzed the evolution of the tensor perturbations during the radiation dominated era; that means that we used the power-like dependence ( t 2 of the scale parameter on time a(t) = a rad. The constant a rad is t rad ) 1 the scale parameter at the moment t rad when inflation ended and radiation 57
60 dominated era started. The dependence a(t) t 1 2 is valid only for t > t rad and t t eq, where t eq is the time of matter-radiation equality. We analyzed how the amplitude of the gravitational wave depends on parameters k a µ 0. After substituting the scale parameter a(t) into the equation (4.5.1) we used numerical methods to find the solution. For that purpose we introduced the dimensionless time τ t t rad and the variable h(τ) defined by the relation h T ij(t rad τ) h(τ)h T ij(t rad ). The final form of the equation is h τ 1 h + ( C k τ 1 + C µ τ 2) h = 0, (5.1.1) where C k a C µ are defined as ( ) 2 ( ) 2 C k k 2 trad trad, C µ µ 0. (5.1.2) a rad a 2 rad We chose the initial conditions h(1) = 1 a h (1) = 0. The first condition results from the definition of h(τ) and the second condition is a simplification that does not influence the results. The dimensionless time τ is bounded from below by τ 1 and from above by τ teq t rad. The upper bound depends on the scale of inflation, and if we suppose that inflation takes place on the scale of Grand Unified Theory, it is of order The case µ 0 = 0. The case µ 0 = 0 reduces to the standard case in which the universe is filled with an ideal fluid. In this case equation (5.1.1) can be solved analytically. The solution is h(τ) = 1 [ {cos 2 ( ) ] C k τ [ τ 2 sin 2 ( ) ]} C k τ 1 C k (5.1.3) The tensor perturbations are oscillating with variable amplitude H 0 (τ) = ( ) C k τ 1 2. (From now on, we use capital letters to denote the amplitude of perturbations.) We recognize here the proportionality of tensor perturbations to a 1, which is just an effect of gravitational redshift [11]. 58
61 The case µ 0 0. We analyzed the influence of non-zero µ 0 on the amplitude of tensor perturbations. A typical time dependence of the perturbation, obtained by numerical solution of equation (5.1.1), is depicted in figure 5.1. h(τ) τ Figure 5.1: Tensor perturbations h(τ) and its amplitude H(τ) (C k = 5 a C µ = 100) Next we compared the amplitude H(τ) of tensor perturbations in the case of non-zero µ 0, with the amplitude H 0 (τ) introduced previously (in the case without µ 0 ). Both amplitudes decrease as τ 1 2 for large τ. We can easily see that this is the case from the form of equation (5.1.1): in the limit of infinite time τ, the term containing C µ is suppressed in comparison with the term containing C k, so that C µ = 0 effectively. Let us represent the function h(τ) as h(τ) = r(τ)h 0 (τ), where r(τ) (the ratio of the non-zero C µ perturbation to the H 0 (τ) amplitude) satisfies the equation r τ 1 r + ( C k τ 1 + C µ τ 2) r = 0, (5.1.4) ( ) 1 ( ) with the boundary conditions r(1) = C k and r (1) = C k. To compare the solutions we need to find the solution r(τ) of equation (5.1.4) and its amplitude denoted as R(τ) (the ratio of amplitudes of gravitational waves with and without the µ 0 -term). We are interested in such choice of parameters that the amplitude increases in comparison with the case without µ 0, but the amplitude can also relatively decrease as shown in figure
62 R(τ) a) c) b) τ Figure 5.2: a) Increasing amplitude (C k = 10 a C µ = 15) b) Decreasing amplitude (C k = 10 a C µ = 10) c) Case without shear modulus (C k = 10 a C µ = 0) As can be seen from the figure, the ratio of amplitudes R(τ) converges to a constant value, which is a consequence of the already mentioned fact that the C µ term in equation (5.1.1) is for large times negligible in comparison with C k term. After we found the numerical solution of equation (5.1.4), we computed the asymptotic value of the ratio of the two amplitudes H(τ) and H 0 (τ). It turns out that the ratio converges fast enough, so that it is possible to determine the asymptotic value (denoted as R ) with a sufficient precision in a reasonable time (we stopped the computation at the precision 10 4 percent). The moment when the solution becomes approximately constant depends on the choice of the parameters, but the main peak of amplitude is reached typically at the moment τ Cµ C k (the time when Ck and C µ terms are comparably large). The desired precision of the value of R was achieved at the times of order τ 10 7, which lie deep inside the interval of τ bounded from above by τ Parametric space The relative increase/decrease of the amplitude depends on the choice of the parameters C k and C µ. In this subsection we examine the parametric space (C k, C µ ) with the size of the step = 0.1 in both directions, and we 60
63 C µ ln(r ) C k Figure 5.3: The asymptotic value of the amplitude ratio R (µ 0 < 0) determine at each point how the amplitude evolves. We tried also a smaller size of step, but the figure did not change significantly. The dependence of the type of the solution on the choice of constants C k a C µ is shown in figure 5.3. The red colored areas are the areas where the amplitude decreases, and in the green areas the amplitude increases. The amplitude can increase also for positive µ 0, but less significantly than for the negative ones. The dependence is shown in figure 5.4. C µ ln(r ) C k Figure 5.4: The asymptotic value of the amplitude ratio R (µ 0 > 0) The dependence of the scale parameter on time, considered here, is valid 61
Introduction to Inflation
 Introduction to Inflation Miguel Campos MPI für Kernphysik & Heidelberg Universität September 23, 2014 Index (Brief) historic background The Cosmological Principle Big-bang puzzles Flatness Horizons Monopoles
Introduction to Inflation Miguel Campos MPI für Kernphysik & Heidelberg Universität September 23, 2014 Index (Brief) historic background The Cosmological Principle Big-bang puzzles Flatness Horizons Monopoles
INFLATION. - EARLY EXPONENTIAL PHASE OF GROWTH OF SCALE FACTOR (after T ~ TGUT ~ GeV)
 INFLATION - EARLY EXPONENTIAL PHASE OF GROWTH OF SCALE FACTOR (after T ~ TGUT ~ 10 15 GeV) -Phenomenologically similar to Universe with a dominant cosmological constant, however inflation needs to end
INFLATION - EARLY EXPONENTIAL PHASE OF GROWTH OF SCALE FACTOR (after T ~ TGUT ~ 10 15 GeV) -Phenomenologically similar to Universe with a dominant cosmological constant, however inflation needs to end
Structures in the early Universe. Particle Astrophysics chapter 8 Lecture 4
 Structures in the early Universe Particle Astrophysics chapter 8 Lecture 4 overview Part 1: problems in Standard Model of Cosmology: horizon and flatness problems presence of structures Part : Need for
Structures in the early Universe Particle Astrophysics chapter 8 Lecture 4 overview Part 1: problems in Standard Model of Cosmology: horizon and flatness problems presence of structures Part : Need for
Cosmology and particle physics
 Cosmology and particle physics Lecture notes Timm Wrase Lecture 9 Inflation - part I Having discussed the thermal history of our universe and in particular its evolution at times larger than 10 14 seconds
Cosmology and particle physics Lecture notes Timm Wrase Lecture 9 Inflation - part I Having discussed the thermal history of our universe and in particular its evolution at times larger than 10 14 seconds
PAPER 71 COSMOLOGY. Attempt THREE questions There are seven questions in total The questions carry equal weight
 MATHEMATICAL TRIPOS Part III Friday 31 May 00 9 to 1 PAPER 71 COSMOLOGY Attempt THREE questions There are seven questions in total The questions carry equal weight You may make free use of the information
MATHEMATICAL TRIPOS Part III Friday 31 May 00 9 to 1 PAPER 71 COSMOLOGY Attempt THREE questions There are seven questions in total The questions carry equal weight You may make free use of the information
COSMIC INFLATION AND THE REHEATING OF THE UNIVERSE
 COSMIC INFLATION AND THE REHEATING OF THE UNIVERSE Francisco Torrentí - IFT/UAM Valencia Students Seminars - December 2014 Contents 1. The Friedmann equations 2. Inflation 2.1. The problems of hot Big
COSMIC INFLATION AND THE REHEATING OF THE UNIVERSE Francisco Torrentí - IFT/UAM Valencia Students Seminars - December 2014 Contents 1. The Friedmann equations 2. Inflation 2.1. The problems of hot Big
XIII. The Very Early Universe and Inflation. ASTR378 Cosmology : XIII. The Very Early Universe and Inflation 171
 XIII. The Very Early Universe and Inflation ASTR378 Cosmology : XIII. The Very Early Universe and Inflation 171 Problems with the Big Bang The Flatness Problem The Horizon Problem The Monopole (Relic Particle)
XIII. The Very Early Universe and Inflation ASTR378 Cosmology : XIII. The Very Early Universe and Inflation 171 Problems with the Big Bang The Flatness Problem The Horizon Problem The Monopole (Relic Particle)
Gravitation et Cosmologie: le Modèle Standard Cours 8: 6 fevrier 2009
 Particules Élémentaires, Gravitation et Cosmologie Année 2008-09 Gravitation et Cosmologie: le Modèle Standard Cours 8: 6 fevrier 2009 Le paradigme inflationnaire Homogeneity and flatness problems in HBB
Particules Élémentaires, Gravitation et Cosmologie Année 2008-09 Gravitation et Cosmologie: le Modèle Standard Cours 8: 6 fevrier 2009 Le paradigme inflationnaire Homogeneity and flatness problems in HBB
Inflation and the Primordial Perturbation Spectrum
 PORTILLO 1 Inflation and the Primordial Perturbation Spectrum Stephen K N PORTILLO Introduction The theory of cosmic inflation is the leading hypothesis for the origin of structure in the universe. It
PORTILLO 1 Inflation and the Primordial Perturbation Spectrum Stephen K N PORTILLO Introduction The theory of cosmic inflation is the leading hypothesis for the origin of structure in the universe. It
Computational Physics and Astrophysics
 Cosmological Inflation Kostas Kokkotas University of Tübingen, Germany and Pablo Laguna Georgia Institute of Technology, USA Spring 2012 Our Universe Cosmic Expansion Co-moving coordinates expand at exactly
Cosmological Inflation Kostas Kokkotas University of Tübingen, Germany and Pablo Laguna Georgia Institute of Technology, USA Spring 2012 Our Universe Cosmic Expansion Co-moving coordinates expand at exactly
Lecture 12. Inflation. What causes inflation. Horizon problem Flatness problem Monopole problem. Physical Cosmology 2011/2012
 Lecture 1 Inflation Horizon problem Flatness problem Monopole problem What causes inflation Physical Cosmology 11/1 Inflation What is inflation good for? Inflation solves 1. horizon problem. flatness problem
Lecture 1 Inflation Horizon problem Flatness problem Monopole problem What causes inflation Physical Cosmology 11/1 Inflation What is inflation good for? Inflation solves 1. horizon problem. flatness problem
PROBLEM SET 10 (The Last!)
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe December 5, 2013 Prof. Alan Guth PROBLEM SET 10 (The Last!) DUE DATE: Tuesday, December 10, 2013, at 5:00 pm.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe December 5, 2013 Prof. Alan Guth PROBLEM SET 10 (The Last!) DUE DATE: Tuesday, December 10, 2013, at 5:00 pm.
Inflation. By The amazing sleeping man, Dan the Man and the Alices
 Inflation By The amazing sleeping man, Dan the Man and the Alices AIMS Introduction to basic inflationary cosmology. Solving the rate of expansion equation both analytically and numerically using different
Inflation By The amazing sleeping man, Dan the Man and the Alices AIMS Introduction to basic inflationary cosmology. Solving the rate of expansion equation both analytically and numerically using different
Astro 507 Lecture 28 April 2, 2014
 Astro 507 Lecture 28 April 2, 2014 Announcements: PS 5 due now Preflight 6 posted today last PF! 1 Last time: slow-roll inflation scalar field dynamics in an expanding universe slow roll conditions constrain
Astro 507 Lecture 28 April 2, 2014 Announcements: PS 5 due now Preflight 6 posted today last PF! 1 Last time: slow-roll inflation scalar field dynamics in an expanding universe slow roll conditions constrain
Oddities of the Universe
 Oddities of the Universe Koushik Dutta Theory Division, Saha Institute Physics Department, IISER, Kolkata 4th November, 2016 1 Outline - Basics of General Relativity - Expanding FRW Universe - Problems
Oddities of the Universe Koushik Dutta Theory Division, Saha Institute Physics Department, IISER, Kolkata 4th November, 2016 1 Outline - Basics of General Relativity - Expanding FRW Universe - Problems
Galaxies 626. Lecture 3: From the CMBR to the first star
 Galaxies 626 Lecture 3: From the CMBR to the first star Galaxies 626 Firstly, some very brief cosmology for background and notation: Summary: Foundations of Cosmology 1. Universe is homogenous and isotropic
Galaxies 626 Lecture 3: From the CMBR to the first star Galaxies 626 Firstly, some very brief cosmology for background and notation: Summary: Foundations of Cosmology 1. Universe is homogenous and isotropic
MATHEMATICAL TRIPOS Part III PAPER 53 COSMOLOGY
 MATHEMATICAL TRIPOS Part III Wednesday, 8 June, 2011 9:00 am to 12:00 pm PAPER 53 COSMOLOGY Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight. STATIONERY
MATHEMATICAL TRIPOS Part III Wednesday, 8 June, 2011 9:00 am to 12:00 pm PAPER 53 COSMOLOGY Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight. STATIONERY
From inflation to the CMB to today s universe. I - How it all begins
 From inflation to the CMB to today s universe I - How it all begins Raul Abramo Physics Institute - University of São Paulo abramo@fma.if.usp.br redshift Very brief cosmic history 10 9 200 s BBN 1 MeV
From inflation to the CMB to today s universe I - How it all begins Raul Abramo Physics Institute - University of São Paulo abramo@fma.if.usp.br redshift Very brief cosmic history 10 9 200 s BBN 1 MeV
Physics 133: Extragalactic Astronomy and Cosmology. Week 8
 Physics 133: Extragalactic Astronomy and Cosmology Week 8 Outline for Week 8 Primordial Nucleosynthesis Successes of the standard Big Bang model Olbers paradox/age of the Universe Hubble s law CMB Chemical/Physical
Physics 133: Extragalactic Astronomy and Cosmology Week 8 Outline for Week 8 Primordial Nucleosynthesis Successes of the standard Big Bang model Olbers paradox/age of the Universe Hubble s law CMB Chemical/Physical
4 Evolution of density perturbations
 Spring term 2014: Dark Matter lecture 3/9 Torsten Bringmann (torsten.bringmann@fys.uio.no) reading: Weinberg, chapters 5-8 4 Evolution of density perturbations 4.1 Statistical description The cosmological
Spring term 2014: Dark Matter lecture 3/9 Torsten Bringmann (torsten.bringmann@fys.uio.no) reading: Weinberg, chapters 5-8 4 Evolution of density perturbations 4.1 Statistical description The cosmological
MASAHIDE YAMAGUCHI. Quantum generation of density perturbations in the early Universe. (Tokyo Institute of Technology)
 Quantum generation of density perturbations in the early Universe MASAHIDE YAMAGUCHI (Tokyo Institute of Technology) 03/07/16@Symposium: New Generation Quantum Theory -Particle Physics, Cosmology, and
Quantum generation of density perturbations in the early Universe MASAHIDE YAMAGUCHI (Tokyo Institute of Technology) 03/07/16@Symposium: New Generation Quantum Theory -Particle Physics, Cosmology, and
PROBLEM SET 10 (The Last!)
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe December 8, 2016 Prof. Alan Guth PROBLEM SET 10 (The Last!) DUE DATE: Wednesday, December 14, 2016, at 4:00 pm.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe December 8, 2016 Prof. Alan Guth PROBLEM SET 10 (The Last!) DUE DATE: Wednesday, December 14, 2016, at 4:00 pm.
CHAPTER 4 INFLATIONARY MODEL BUILDING. 4.1 Canonical scalar field dynamics. Non-minimal coupling and f(r) theories
 CHAPTER 4 INFLATIONARY MODEL BUILDING Essentially, all models are wrong, but some are useful. George E. P. Box, 1987 As we learnt in the previous chapter, inflation is not a model, but rather a paradigm
CHAPTER 4 INFLATIONARY MODEL BUILDING Essentially, all models are wrong, but some are useful. George E. P. Box, 1987 As we learnt in the previous chapter, inflation is not a model, but rather a paradigm
Week 6: Inflation and the Cosmic Microwave Background
 Week 6: Inflation and the Cosmic Microwave Background January 9, 2012 1 Motivation The standard hot big-bang model with an (flat) FRW spacetime accounts correctly for the observed expansion, the CMB, BBN,
Week 6: Inflation and the Cosmic Microwave Background January 9, 2012 1 Motivation The standard hot big-bang model with an (flat) FRW spacetime accounts correctly for the observed expansion, the CMB, BBN,
Cosmological perturbations in a universe with an elastic component
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS Cosmological perturbations in a universe with an elastic component Dissertation thesis Study field: Study programme: Department:
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS Cosmological perturbations in a universe with an elastic component Dissertation thesis Study field: Study programme: Department:
Inflation. Jo van den Brand, Chris Van Den Broeck, Tjonnie Li Nikhef: April 23, 2010
 Inflation Jo van den Brand, Chris Van Den Broeck, Tjonnie Li Nikhef: April 23, 2010 Limitations of standard cosmology Horizon problem, flatness problem, missing exotic particles Horizon: largest distance
Inflation Jo van den Brand, Chris Van Den Broeck, Tjonnie Li Nikhef: April 23, 2010 Limitations of standard cosmology Horizon problem, flatness problem, missing exotic particles Horizon: largest distance
Structures in the early Universe. Particle Astrophysics chapter 8 Lecture 4
 Structures in the early Universe Particle Astrophysics chapter 8 Lecture 4 overview problems in Standard Model of Cosmology: horizon and flatness problems presence of structures Need for an exponential
Structures in the early Universe Particle Astrophysics chapter 8 Lecture 4 overview problems in Standard Model of Cosmology: horizon and flatness problems presence of structures Need for an exponential
Inflation. Week 9. ASTR/PHYS 4080: Introduction to Cosmology
 Inflation ASTR/PHYS 4080: Intro to Cosmology Week 9 1 Successes of the Hot Big Bang Model Consists of: General relativity Cosmological principle Known atomic/nuclear/particle physics Explains: dark night
Inflation ASTR/PHYS 4080: Intro to Cosmology Week 9 1 Successes of the Hot Big Bang Model Consists of: General relativity Cosmological principle Known atomic/nuclear/particle physics Explains: dark night
Inflationary Cosmology and Alternatives
 Inflationary Cosmology and Alternatives V.A. Rubakov Institute for Nuclear Research of the Russian Academy of Sciences, Moscow and Department of paricle Physics abd Cosmology Physics Faculty Moscow State
Inflationary Cosmology and Alternatives V.A. Rubakov Institute for Nuclear Research of the Russian Academy of Sciences, Moscow and Department of paricle Physics abd Cosmology Physics Faculty Moscow State
Gravitation: Cosmology
 An Introduction to General Relativity Center for Relativistic Astrophysics School of Physics Georgia Institute of Technology Notes based on textbook: Spacetime and Geometry by S.M. Carroll Spring 2013
An Introduction to General Relativity Center for Relativistic Astrophysics School of Physics Georgia Institute of Technology Notes based on textbook: Spacetime and Geometry by S.M. Carroll Spring 2013
Priming the BICEP. Wayne Hu Chicago, March BB
 Priming the BICEP 0.05 0.04 0.03 0.02 0.01 0 0.01 BB 0 50 100 150 200 250 300 Wayne Hu Chicago, March 2014 A BICEP Primer How do gravitational waves affect the CMB temperature and polarization spectrum?
Priming the BICEP 0.05 0.04 0.03 0.02 0.01 0 0.01 BB 0 50 100 150 200 250 300 Wayne Hu Chicago, March 2014 A BICEP Primer How do gravitational waves affect the CMB temperature and polarization spectrum?
The Expanding Universe
 Cosmology Expanding Universe History of the Universe Cosmic Background Radiation The Cosmological Principle Cosmology and General Relativity Dark Matter and Dark Energy Primitive Cosmology If the universe
Cosmology Expanding Universe History of the Universe Cosmic Background Radiation The Cosmological Principle Cosmology and General Relativity Dark Matter and Dark Energy Primitive Cosmology If the universe
Key: cosmological perturbations. With the LHC, we hope to be able to go up to temperatures T 100 GeV, age t second
 Lecture 3 With Big Bang nucleosynthesis theory and observations we are confident of the theory of the early Universe at temperatures up to T 1 MeV, age t 1 second With the LHC, we hope to be able to go
Lecture 3 With Big Bang nucleosynthesis theory and observations we are confident of the theory of the early Universe at temperatures up to T 1 MeV, age t 1 second With the LHC, we hope to be able to go
The early and late time acceleration of the Universe
 The early and late time acceleration of the Universe Tomo Takahashi (Saga University) March 7, 2016 New Generation Quantum Theory -Particle Physics, Cosmology, and Chemistry- @Kyoto University The early
The early and late time acceleration of the Universe Tomo Takahashi (Saga University) March 7, 2016 New Generation Quantum Theory -Particle Physics, Cosmology, and Chemistry- @Kyoto University The early
Contents. Part I The Big Bang and the Observable Universe
 Contents Part I The Big Bang and the Observable Universe 1 A Historical Overview 3 1.1 The Big Cosmic Questions 3 1.2 Origins of Scientific Cosmology 4 1.3 Cosmology Today 7 2 Newton s Universe 13 2.1
Contents Part I The Big Bang and the Observable Universe 1 A Historical Overview 3 1.1 The Big Cosmic Questions 3 1.2 Origins of Scientific Cosmology 4 1.3 Cosmology Today 7 2 Newton s Universe 13 2.1
Inflation and the cosmological constant problem
 Inflation and the cosmological constant problem Larissa Lorenz Sebastian Sapeta Krzyzowa 18. 8. September 00 Contents Standard model of cosmology and its problems The inflationary paradigm Review of the
Inflation and the cosmological constant problem Larissa Lorenz Sebastian Sapeta Krzyzowa 18. 8. September 00 Contents Standard model of cosmology and its problems The inflationary paradigm Review of the
Cosmological Issues. Consider the stress tensor of a fluid in the local orthonormal frame where the metric is η ab
 Cosmological Issues Radiation dominated Universe Consider the stress tensor of a fluid in the local orthonormal frame where the metric is η ab ρ 0 0 0 T ab = 0 p 0 0 0 0 p 0 () 0 0 0 p We do not often
Cosmological Issues Radiation dominated Universe Consider the stress tensor of a fluid in the local orthonormal frame where the metric is η ab ρ 0 0 0 T ab = 0 p 0 0 0 0 p 0 () 0 0 0 p We do not often
Triple unification of inflation, dark matter and dark energy
 Triple unification of inflation, dark matter and dark energy May 9, 2008 Leonard Susskind, The Anthropic Landscape of String Theory (2003) A. Liddle, A. Ureña-López, Inflation, dark matter and dark energy
Triple unification of inflation, dark matter and dark energy May 9, 2008 Leonard Susskind, The Anthropic Landscape of String Theory (2003) A. Liddle, A. Ureña-López, Inflation, dark matter and dark energy
Inflationary Massive Gravity
 New perspectives on cosmology APCTP, 15 Feb., 017 Inflationary Massive Gravity Misao Sasaki Yukawa Institute for Theoretical Physics, Kyoto University C. Lin & MS, PLB 75, 84 (016) [arxiv:1504.01373 ]
New perspectives on cosmology APCTP, 15 Feb., 017 Inflationary Massive Gravity Misao Sasaki Yukawa Institute for Theoretical Physics, Kyoto University C. Lin & MS, PLB 75, 84 (016) [arxiv:1504.01373 ]
Cosmology and the origin of structure
 1 Cosmology and the origin of structure ocy I: The universe observed ocy II: Perturbations ocy III: Inflation Primordial perturbations CB: a snapshot of the universe 38, AB correlations on scales 38, light
1 Cosmology and the origin of structure ocy I: The universe observed ocy II: Perturbations ocy III: Inflation Primordial perturbations CB: a snapshot of the universe 38, AB correlations on scales 38, light
POST-INFLATIONARY HIGGS RELAXATION AND THE ORIGIN OF MATTER- ANTIMATTER ASYMMETRY
 POST-INFLATIONARY HIGGS RELAXATION AND THE ORIGIN OF MATTER- ANTIMATTER ASYMMETRY LOUIS YANG ( 楊智軒 ) UNIVERSITY OF CALIFORNIA, LOS ANGELES (UCLA) DEC 27, 2016 NATIONAL TSING HUA UNIVERSITY OUTLINE Big
POST-INFLATIONARY HIGGS RELAXATION AND THE ORIGIN OF MATTER- ANTIMATTER ASYMMETRY LOUIS YANG ( 楊智軒 ) UNIVERSITY OF CALIFORNIA, LOS ANGELES (UCLA) DEC 27, 2016 NATIONAL TSING HUA UNIVERSITY OUTLINE Big
Inflation and the origin of structure in the Universe
 Phi in the Sky, Porto 0 th July 004 Inflation and the origin of structure in the Universe David Wands Institute of Cosmology and Gravitation University of Portsmouth outline! motivation! the Primordial
Phi in the Sky, Porto 0 th July 004 Inflation and the origin of structure in the Universe David Wands Institute of Cosmology and Gravitation University of Portsmouth outline! motivation! the Primordial
Relativity, Gravitation, and Cosmology
 Relativity, Gravitation, and Cosmology A basic introduction TA-PEI CHENG University of Missouri St. Louis OXFORD UNIVERSITY PRESS Contents Parti RELATIVITY Metric Description of Spacetime 1 Introduction
Relativity, Gravitation, and Cosmology A basic introduction TA-PEI CHENG University of Missouri St. Louis OXFORD UNIVERSITY PRESS Contents Parti RELATIVITY Metric Description of Spacetime 1 Introduction
VU lecture Introduction to Particle Physics. Thomas Gajdosik, FI & VU. Big Bang (model)
 Big Bang (model) What can be seen / measured? basically only light _ (and a few particles: e ±, p, p, ν x ) in different wave lengths: microwave to γ-rays in different intensities (measured in magnitudes)
Big Bang (model) What can be seen / measured? basically only light _ (and a few particles: e ±, p, p, ν x ) in different wave lengths: microwave to γ-rays in different intensities (measured in magnitudes)
Gravitational waves from the early Universe
 Gravitational waves from the early Universe Part 2 Sachiko Kuroyanagi (Nagoya University) 26 Aug 2017 Summer Institute 2017 GWs from inflation Inflation Accelerated expansion in the early Universe Solves
Gravitational waves from the early Universe Part 2 Sachiko Kuroyanagi (Nagoya University) 26 Aug 2017 Summer Institute 2017 GWs from inflation Inflation Accelerated expansion in the early Universe Solves
Lecture notes 20: Inflation
 Lecture notes 20: Inflation The observed galaxies, quasars and supernovae, as well as observations of intergalactic absorption lines, tell us about the state of the universe during the period where z
Lecture notes 20: Inflation The observed galaxies, quasars and supernovae, as well as observations of intergalactic absorption lines, tell us about the state of the universe during the period where z
2.1 Basics of the Relativistic Cosmology: Global Geometry and the Dynamics of the Universe Part I
 1 2.1 Basics of the Relativistic Cosmology: Global Geometry and the Dynamics of the Universe Part I 2 Special Relativity (1905) A fundamental change in viewing the physical space and time, now unified
1 2.1 Basics of the Relativistic Cosmology: Global Geometry and the Dynamics of the Universe Part I 2 Special Relativity (1905) A fundamental change in viewing the physical space and time, now unified
The Theory of Inflationary Perturbations
 The Theory of Inflationary Perturbations Jérôme Martin Institut d Astrophysique de Paris (IAP) Indian Institute of Technology, Chennai 03/02/2012 1 Introduction Outline A brief description of inflation
The Theory of Inflationary Perturbations Jérôme Martin Institut d Astrophysique de Paris (IAP) Indian Institute of Technology, Chennai 03/02/2012 1 Introduction Outline A brief description of inflation
Cosmology: An Introduction. Eung Jin Chun
 Cosmology: An Introduction Eung Jin Chun Cosmology Hot Big Bang + Inflation. Theory of the evolution of the Universe described by General relativity (spacetime) Thermodynamics, Particle/nuclear physics
Cosmology: An Introduction Eung Jin Chun Cosmology Hot Big Bang + Inflation. Theory of the evolution of the Universe described by General relativity (spacetime) Thermodynamics, Particle/nuclear physics
Cosmic Bubble Collisions
 Outline Background Expanding Universe: Einstein s Eqn with FRW metric Inflationary Cosmology: model with scalar field QFTà Bubble nucleationà Bubble collisions Bubble Collisions in Single Field Theory
Outline Background Expanding Universe: Einstein s Eqn with FRW metric Inflationary Cosmology: model with scalar field QFTà Bubble nucleationà Bubble collisions Bubble Collisions in Single Field Theory
Primordial Black Holes
 Primordial Black Holes In the reheating phase Juan Carlos Hidalgo. Instituto de Ciencias Físicas, UNAM INFLATION I: Primordial Fluctuations The Success of Inflation Explain the origin of our flatuniverse
Primordial Black Holes In the reheating phase Juan Carlos Hidalgo. Instituto de Ciencias Físicas, UNAM INFLATION I: Primordial Fluctuations The Success of Inflation Explain the origin of our flatuniverse
The Concept of Inflation
 The Concept of Inflation Introduced by Alan Guth, circa 1980, to provide answers to the following 5 enigmas: 1. horizon problem. How come the cosmic microwave background radiation is so uniform in very
The Concept of Inflation Introduced by Alan Guth, circa 1980, to provide answers to the following 5 enigmas: 1. horizon problem. How come the cosmic microwave background radiation is so uniform in very
Cosmic Inflation Lecture 16 - Monday Mar 10
 Physics 224 Spring 2008 Origin and Evolution of the Universe Cosmic Inflation Lecture 16 - Monday Mar 10 Joel Primack University of California, Santa Cruz Outline L15 L16 WMAP 5-year Data and Papers Released
Physics 224 Spring 2008 Origin and Evolution of the Universe Cosmic Inflation Lecture 16 - Monday Mar 10 Joel Primack University of California, Santa Cruz Outline L15 L16 WMAP 5-year Data and Papers Released
A873: Cosmology Course Notes. VII. Inflation
 Readings VII. Inflation Alan Guth s Inflationary Universe paper (Phys Rev D, Vol. 23, p. 347, 1981) is a classic, well worth reading. The basics are well covered by Ryden, Chapter 11. For more physics
Readings VII. Inflation Alan Guth s Inflationary Universe paper (Phys Rev D, Vol. 23, p. 347, 1981) is a classic, well worth reading. The basics are well covered by Ryden, Chapter 11. For more physics
Chapter 4. COSMOLOGICAL PERTURBATION THEORY
 Chapter 4. COSMOLOGICAL PERTURBATION THEORY 4.1. NEWTONIAN PERTURBATION THEORY Newtonian gravity is an adequate description on small scales (< H 1 ) and for non-relativistic matter (CDM + baryons after
Chapter 4. COSMOLOGICAL PERTURBATION THEORY 4.1. NEWTONIAN PERTURBATION THEORY Newtonian gravity is an adequate description on small scales (< H 1 ) and for non-relativistic matter (CDM + baryons after
Cosmological Issues. Consider the stress tensor of a fluid in the local orthonormal frame where the metric is η ab
 Cosmological Issues 1 Radiation dominated Universe Consider the stress tensor of a fluid in the local orthonormal frame where the metric is η ab ρ 0 0 0 T ab = 0 p 0 0 0 0 p 0 (1) 0 0 0 p We do not often
Cosmological Issues 1 Radiation dominated Universe Consider the stress tensor of a fluid in the local orthonormal frame where the metric is η ab ρ 0 0 0 T ab = 0 p 0 0 0 0 p 0 (1) 0 0 0 p We do not often
Zhong-Zhi Xianyu (CMSA Harvard) Tsinghua June 30, 2016
 Zhong-Zhi Xianyu (CMSA Harvard) Tsinghua June 30, 2016 We are directly observing the history of the universe as we look deeply into the sky. JUN 30, 2016 ZZXianyu (CMSA) 2 At ~10 4 yrs the universe becomes
Zhong-Zhi Xianyu (CMSA Harvard) Tsinghua June 30, 2016 We are directly observing the history of the universe as we look deeply into the sky. JUN 30, 2016 ZZXianyu (CMSA) 2 At ~10 4 yrs the universe becomes
The Cosmological Principle
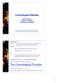 Cosmological Models John O Byrne School of Physics University of Sydney Using diagrams and pp slides from Seeds Foundations of Astronomy and the Supernova Cosmology Project http://www-supernova.lbl.gov
Cosmological Models John O Byrne School of Physics University of Sydney Using diagrams and pp slides from Seeds Foundations of Astronomy and the Supernova Cosmology Project http://www-supernova.lbl.gov
Cosmic Background Radiation
 Cosmic Background Radiation The Big Bang generated photons, which scattered frequently in the very early Universe, which was opaque. Once recombination happened the photons are scattered one final time
Cosmic Background Radiation The Big Bang generated photons, which scattered frequently in the very early Universe, which was opaque. Once recombination happened the photons are scattered one final time
Analyzing WMAP Observation by Quantum Gravity
 COSMO 07 Conference 21-25 August, 2007 Analyzing WMAP Observation by Quantum Gravity Ken-ji Hamada (KEK) with Shinichi Horata, Naoshi Sugiyama, and Tetsuyuki Yukawa arxiv:0705.3490[astro-ph], Phys. Rev.
COSMO 07 Conference 21-25 August, 2007 Analyzing WMAP Observation by Quantum Gravity Ken-ji Hamada (KEK) with Shinichi Horata, Naoshi Sugiyama, and Tetsuyuki Yukawa arxiv:0705.3490[astro-ph], Phys. Rev.
Archaeology of Our Universe YIFU CAI ( 蔡一夫 )
 Archaeology of Our Universe YIFU CAI ( 蔡一夫 ) 2013-11-05 Thermal History Primordial era 13.8 billion years by WMAP/NASA Large Scale Structure (LSS) by 2MASS Cosmic Microwave Background (CMB) by ESA/Planck
Archaeology of Our Universe YIFU CAI ( 蔡一夫 ) 2013-11-05 Thermal History Primordial era 13.8 billion years by WMAP/NASA Large Scale Structure (LSS) by 2MASS Cosmic Microwave Background (CMB) by ESA/Planck
Examining the Viability of Phantom Dark Energy
 Examining the Viability of Phantom Dark Energy Kevin J. Ludwick LaGrange College 11/12/16 Kevin J. Ludwick (LaGrange College) Examining the Viability of Phantom Dark Energy 11/12/16 1 / 28 Outline 1 Overview
Examining the Viability of Phantom Dark Energy Kevin J. Ludwick LaGrange College 11/12/16 Kevin J. Ludwick (LaGrange College) Examining the Viability of Phantom Dark Energy 11/12/16 1 / 28 Outline 1 Overview
Graceful exit from inflation for minimally coupled Bianchi A scalar field models
 Graceful exit from inflation for minimally coupled Bianchi A scalar field models Florian Beyer Reference: F.B. and Leon Escobar (2013), CQG, 30(19), p.195020. University of Otago, Dunedin, New Zealand
Graceful exit from inflation for minimally coupled Bianchi A scalar field models Florian Beyer Reference: F.B. and Leon Escobar (2013), CQG, 30(19), p.195020. University of Otago, Dunedin, New Zealand
Scale symmetry a link from quantum gravity to cosmology
 Scale symmetry a link from quantum gravity to cosmology scale symmetry fluctuations induce running couplings violation of scale symmetry well known in QCD or standard model Fixed Points Quantum scale symmetry
Scale symmetry a link from quantum gravity to cosmology scale symmetry fluctuations induce running couplings violation of scale symmetry well known in QCD or standard model Fixed Points Quantum scale symmetry
Fundamental Particles
 Fundamental Particles Standard Model of Particle Physics There are three different kinds of particles. Leptons - there are charged leptons (e -, μ -, τ - ) and uncharged leptons (νe, νμ, ντ) and their
Fundamental Particles Standard Model of Particle Physics There are three different kinds of particles. Leptons - there are charged leptons (e -, μ -, τ - ) and uncharged leptons (νe, νμ, ντ) and their
Reheating of the Universe and Gravitational Wave Production
 Imperial College London MSc Quantum Fields and Fundamental Forces Reheating of the Universe and Gravitational Wave Production Author: Luisa Lucie-Smith Supervisor: Prof. Arttu Rajantie Submitted in partial
Imperial College London MSc Quantum Fields and Fundamental Forces Reheating of the Universe and Gravitational Wave Production Author: Luisa Lucie-Smith Supervisor: Prof. Arttu Rajantie Submitted in partial
Astronomy 182: Origin and Evolution of the Universe
 Astronomy 182: Origin and Evolution of the Universe Prof. Josh Frieman Lecture 14 Dec. 2, 2015 Today The Inflationary Universe Origin of Density Perturbations Gravitational Waves Origin and Evolution of
Astronomy 182: Origin and Evolution of the Universe Prof. Josh Frieman Lecture 14 Dec. 2, 2015 Today The Inflationary Universe Origin of Density Perturbations Gravitational Waves Origin and Evolution of
Connecting Quarks to the Cosmos
 Connecting Quarks to the Cosmos Institute for Nuclear Theory 29 June to 10 July 2009 Inflationary Cosmology II Michael S. Turner Kavli Institute for Cosmological Physics The University of Chicago Michael
Connecting Quarks to the Cosmos Institute for Nuclear Theory 29 June to 10 July 2009 Inflationary Cosmology II Michael S. Turner Kavli Institute for Cosmological Physics The University of Chicago Michael
Examining the Viability of Phantom Dark Energy
 Examining the Viability of Phantom Dark Energy Kevin J. Ludwick LaGrange College 12/20/15 (11:00-11:30) Kevin J. Ludwick (LaGrange College) Examining the Viability of Phantom Dark Energy 12/20/15 (11:00-11:30)
Examining the Viability of Phantom Dark Energy Kevin J. Ludwick LaGrange College 12/20/15 (11:00-11:30) Kevin J. Ludwick (LaGrange College) Examining the Viability of Phantom Dark Energy 12/20/15 (11:00-11:30)
Extending classical big bang theory
 Chapter 21 Extending classical big bang theory The big bang is our standard model for the origin of the Universe and has been for almost half a century. This place in well earned. At a broader conceptual
Chapter 21 Extending classical big bang theory The big bang is our standard model for the origin of the Universe and has been for almost half a century. This place in well earned. At a broader conceptual
Origin of the Universe
 Origin of the Universe Shortcomings of the Big Bang Model There is tremendous evidence in favor of the Big Bang Cosmic Microwave Background Radiation Abundance of Deuterium, Helium, Lithium, all cooked
Origin of the Universe Shortcomings of the Big Bang Model There is tremendous evidence in favor of the Big Bang Cosmic Microwave Background Radiation Abundance of Deuterium, Helium, Lithium, all cooked
School Observational Cosmology Angra Terceira Açores 3 rd June Juan García-Bellido Física Teórica UAM Madrid, Spain
 School Observational Cosmology Angra Terceira Açores 3 rd June 2014 Juan García-Bellido Física Teórica UAM Madrid, Spain Outline Lecture 1 Shortcomings of the Hot Big Bang The Inflationary Paradigm Homogeneous
School Observational Cosmology Angra Terceira Açores 3 rd June 2014 Juan García-Bellido Física Teórica UAM Madrid, Spain Outline Lecture 1 Shortcomings of the Hot Big Bang The Inflationary Paradigm Homogeneous
Kinetic Theory of Dark Energy within General Relativity
 Kinetic Theory of Dark Energy within General Relativity Author: Nikola Perkovic* percestyler@gmail.com University of Novi Sad, Faculty of Sciences, Institute of Physics and Mathematics Abstract: This paper
Kinetic Theory of Dark Energy within General Relativity Author: Nikola Perkovic* percestyler@gmail.com University of Novi Sad, Faculty of Sciences, Institute of Physics and Mathematics Abstract: This paper
Closed Universes, de Sitter Space and Inflation
 Closed Universes, de Sitter Space and Inflation Chris Doran Cavendish Laboratory Based on astro-ph/0307311 by Lasenby and Doran The Cosmological Constant Dark energy responsible for around 70% of the total
Closed Universes, de Sitter Space and Inflation Chris Doran Cavendish Laboratory Based on astro-ph/0307311 by Lasenby and Doran The Cosmological Constant Dark energy responsible for around 70% of the total
Quantum Fluctuations During Inflation
 In any field, find the strangest thing and then explore it. (John Archibald Wheeler) Quantum Fluctuations During Inflation ( ) v k = e ikτ 1 i kτ Contents 1 Getting Started Cosmological Perturbation Theory.1
In any field, find the strangest thing and then explore it. (John Archibald Wheeler) Quantum Fluctuations During Inflation ( ) v k = e ikτ 1 i kτ Contents 1 Getting Started Cosmological Perturbation Theory.1
Ay1 Lecture 18. The Early Universe and the Cosmic Microwave Background
 Ay1 Lecture 18 The Early Universe and the Cosmic Microwave Background 18.1 Basic Ideas, and the Cosmic Microwave background The Key Ideas Pushing backward in time towards the Big Bang, the universe was
Ay1 Lecture 18 The Early Universe and the Cosmic Microwave Background 18.1 Basic Ideas, and the Cosmic Microwave background The Key Ideas Pushing backward in time towards the Big Bang, the universe was
Licia Verde. Introduction to cosmology. Lecture 4. Inflation
 Licia Verde Introduction to cosmology Lecture 4 Inflation Dividing line We see them like temperature On scales larger than a degree, fluctuations were outside the Hubble horizon at decoupling Potential
Licia Verde Introduction to cosmology Lecture 4 Inflation Dividing line We see them like temperature On scales larger than a degree, fluctuations were outside the Hubble horizon at decoupling Potential
MATHEMATICAL TRIPOS PAPER 67 COSMOLOGY
 MATHEMATICA TRIPOS Part III Wednesday 6 June 2001 9 to 11 PAPER 67 COSMOOGY Attempt THREE questions. The questions are of equal weight. Candidates may make free use of the information given on the accompanying
MATHEMATICA TRIPOS Part III Wednesday 6 June 2001 9 to 11 PAPER 67 COSMOOGY Attempt THREE questions. The questions are of equal weight. Candidates may make free use of the information given on the accompanying
i>clicker Quiz #14 Which of the following statements is TRUE?
 i>clicker Quiz #14 Which of the following statements is TRUE? A. Hubble s discovery that most distant galaxies are receding from us tells us that we are at the center of the Universe B. The Universe started
i>clicker Quiz #14 Which of the following statements is TRUE? A. Hubble s discovery that most distant galaxies are receding from us tells us that we are at the center of the Universe B. The Universe started
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe November 24, 2013 Prof. Alan Guth PROBLEM SET 9
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe November 24, 2013 Prof. Alan Guth PROBLEM SET 9 DUE DATE: Monday, December 2, 2013, at 5:00 pm. This is the last
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe November 24, 2013 Prof. Alan Guth PROBLEM SET 9 DUE DATE: Monday, December 2, 2013, at 5:00 pm. This is the last
About the format of the literature report
 About the format of the literature report Minimum 3 pages! Suggested structure: Introduction Main text Discussion Conclusion References Use bracket-number (e.g. [3]) or author-year (e.g. Zackrisson et
About the format of the literature report Minimum 3 pages! Suggested structure: Introduction Main text Discussion Conclusion References Use bracket-number (e.g. [3]) or author-year (e.g. Zackrisson et
The Effects of Inhomogeneities on the Universe Today. Antonio Riotto INFN, Padova
 The Effects of Inhomogeneities on the Universe Today Antonio Riotto INFN, Padova Frascati, November the 19th 2004 Plan of the talk Short introduction to Inflation Short introduction to cosmological perturbations
The Effects of Inhomogeneities on the Universe Today Antonio Riotto INFN, Padova Frascati, November the 19th 2004 Plan of the talk Short introduction to Inflation Short introduction to cosmological perturbations
Introduction to Cosmology
 Introduction to Cosmology Subir Sarkar CERN Summer training Programme, 22-28 July 2008 Seeing the edge of the Universe: From speculation to science Constructing the Universe: The history of the Universe:
Introduction to Cosmology Subir Sarkar CERN Summer training Programme, 22-28 July 2008 Seeing the edge of the Universe: From speculation to science Constructing the Universe: The history of the Universe:
PROBLEM SET 6 EXTRA CREDIT PROBLEM SET
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe May 3, 2004 Prof. Alan Guth PROBLEM SET 6 EXTRA CREDIT PROBLEM SET CAN BE HANDED IN THROUGH: Thursday, May 13,
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe May 3, 2004 Prof. Alan Guth PROBLEM SET 6 EXTRA CREDIT PROBLEM SET CAN BE HANDED IN THROUGH: Thursday, May 13,
Tuesday: Special epochs of the universe (recombination, nucleosynthesis, inflation) Wednesday: Structure formation
 Introduction to Cosmology Professor Barbara Ryden Department of Astronomy The Ohio State University ICTP Summer School on Cosmology 2016 June 6 Today: Observational evidence for the standard model of cosmology
Introduction to Cosmology Professor Barbara Ryden Department of Astronomy The Ohio State University ICTP Summer School on Cosmology 2016 June 6 Today: Observational evidence for the standard model of cosmology
Gravitational waves from the early Universe
 Gravitational waves from the early Universe Part 1 Sachiko Kuroyanagi (Nagoya University) 26 Aug 2017 Summer Institute 2017 What is a Gravitational Wave? What is a Gravitational Wave? 11 Feb 2016 We have
Gravitational waves from the early Universe Part 1 Sachiko Kuroyanagi (Nagoya University) 26 Aug 2017 Summer Institute 2017 What is a Gravitational Wave? What is a Gravitational Wave? 11 Feb 2016 We have
Dark Energy vs. Dark Matter: Towards a unifying scalar field?
 Dark Energy vs. Dark Matter: Towards a unifying scalar field? Alexandre ARBEY Centre de Recherche Astrophysique de Lyon Institut de Physique Nucléaire de Lyon, March 2nd, 2007. Introduction The Dark Stuff
Dark Energy vs. Dark Matter: Towards a unifying scalar field? Alexandre ARBEY Centre de Recherche Astrophysique de Lyon Institut de Physique Nucléaire de Lyon, March 2nd, 2007. Introduction The Dark Stuff
Classical Dynamics of Inflation
 Preprint typeset in JHEP style - HYPER VERSION Classical Dynamics of Inflation Daniel Baumann School of Natural Sciences, Institute for Advanced Study, Princeton, NJ 08540 http://www.sns.ias.edu/ dbaumann/
Preprint typeset in JHEP style - HYPER VERSION Classical Dynamics of Inflation Daniel Baumann School of Natural Sciences, Institute for Advanced Study, Princeton, NJ 08540 http://www.sns.ias.edu/ dbaumann/
New Insights in Hybrid Inflation
 Dr. Sébastien Clesse TU Munich, T70 group: Theoretical Physics of the Early Universe Excellence Cluster Universe Based on S.C., B. Garbrecht, Y. Zhu, Non-gaussianities and curvature perturbations in hybrid
Dr. Sébastien Clesse TU Munich, T70 group: Theoretical Physics of the Early Universe Excellence Cluster Universe Based on S.C., B. Garbrecht, Y. Zhu, Non-gaussianities and curvature perturbations in hybrid
CHAPTER 3 THE INFLATIONARY PARADIGM. 3.1 The hot Big Bang paradise Homogeneity and isotropy
 CHAPTER 3 THE INFLATIONARY PARADIGM Ubi materia, ibi geometria. Johannes Kepler 3.1 The hot Big Bang paradise In General Relativity, the Universe as a whole becomes a dynamical entity that can be modeled
CHAPTER 3 THE INFLATIONARY PARADIGM Ubi materia, ibi geometria. Johannes Kepler 3.1 The hot Big Bang paradise In General Relativity, the Universe as a whole becomes a dynamical entity that can be modeled
QUIZ 3. Quiz Date: December 7, 2016
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe December 21, 2016 Prof. Alan Guth QUIZ 3 Quiz Date: December 7, 2016 Reformatted to Remove Blank Pages Please
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.286: The Early Universe December 21, 2016 Prof. Alan Guth QUIZ 3 Quiz Date: December 7, 2016 Reformatted to Remove Blank Pages Please
MIT Exploring Black Holes
 THE UNIVERSE and Three Examples Alan Guth, MIT MIT 8.224 Exploring Black Holes EINSTEIN'S CONTRIBUTIONS March, 1916: The Foundation of the General Theory of Relativity Feb, 1917: Cosmological Considerations
THE UNIVERSE and Three Examples Alan Guth, MIT MIT 8.224 Exploring Black Holes EINSTEIN'S CONTRIBUTIONS March, 1916: The Foundation of the General Theory of Relativity Feb, 1917: Cosmological Considerations
Cosmology. Thermal history of the universe Primordial nucleosynthesis WIMPs as dark matter Recombination Horizon problem Flatness problem Inflation
 Cosmology Thermal history of the universe Primordial nucleosynthesis WIMPs as dark matter Recombination Horizon problem Flatness problem Inflation Energy density versus scale factor z=1/a-1 Early times,
Cosmology Thermal history of the universe Primordial nucleosynthesis WIMPs as dark matter Recombination Horizon problem Flatness problem Inflation Energy density versus scale factor z=1/a-1 Early times,
PAPER 310 COSMOLOGY. Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight.
 MATHEMATICAL TRIPOS Part III Wednesday, 1 June, 2016 9:00 am to 12:00 pm PAPER 310 COSMOLOGY Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight. STATIONERY
MATHEMATICAL TRIPOS Part III Wednesday, 1 June, 2016 9:00 am to 12:00 pm PAPER 310 COSMOLOGY Attempt no more than THREE questions. There are FOUR questions in total. The questions carry equal weight. STATIONERY
Second-order gauge-invariant cosmological perturbation theory: --- Recent development and problems ---
 Second-order gauge-invariant cosmological perturbation theory: --- Recent development and problems --- Kouji Nakamura (NAOJ) with Masa-Katsu Fujimoto (NAOJ) References : K.N. Prog. Theor. Phys., 110 (2003),
Second-order gauge-invariant cosmological perturbation theory: --- Recent development and problems --- Kouji Nakamura (NAOJ) with Masa-Katsu Fujimoto (NAOJ) References : K.N. Prog. Theor. Phys., 110 (2003),
The Once and Future CMB
 The Once and Future CMB DOE, Jan. 2002 Wayne Hu The On(c)e Ring Original Power Spectra of Maps 64º Band Filtered Ringing in the New Cosmology Gravitational Ringing Potential wells = inflationary seeds
The Once and Future CMB DOE, Jan. 2002 Wayne Hu The On(c)e Ring Original Power Spectra of Maps 64º Band Filtered Ringing in the New Cosmology Gravitational Ringing Potential wells = inflationary seeds
The History and Philosophy of Astronomy
 Astronomy 350L (Spring 2005) The History and Philosophy of Astronomy (Lecture 27: Modern Developments II: Inflation) Instructor: Volker Bromm TA: Amanda Bauer The University of Texas at Austin Big Bang
Astronomy 350L (Spring 2005) The History and Philosophy of Astronomy (Lecture 27: Modern Developments II: Inflation) Instructor: Volker Bromm TA: Amanda Bauer The University of Texas at Austin Big Bang
A100H Exploring the Universe: Big Bang Theory. Martin D. Weinberg UMass Astronomy
 A100H Exploring the : Martin D. Weinberg UMass Astronomy astron100h-mdw@courses.umass.edu April 21, 2016 Read: Chap 23 04/26/16 slide 1 Early Final Exam: Friday 29 Apr at 10:30 am 12:30 pm, here! Emphasizes
A100H Exploring the : Martin D. Weinberg UMass Astronomy astron100h-mdw@courses.umass.edu April 21, 2016 Read: Chap 23 04/26/16 slide 1 Early Final Exam: Friday 29 Apr at 10:30 am 12:30 pm, here! Emphasizes
Stephen Blaha, Ph.D. M PubHsMtw
 Quantum Big Bang Cosmology: Complex Space-time General Relativity, Quantum Coordinates,"Dodecahedral Universe, Inflation, and New Spin 0, 1 / 2,1 & 2 Tachyons & Imagyons Stephen Blaha, Ph.D. M PubHsMtw
Quantum Big Bang Cosmology: Complex Space-time General Relativity, Quantum Coordinates,"Dodecahedral Universe, Inflation, and New Spin 0, 1 / 2,1 & 2 Tachyons & Imagyons Stephen Blaha, Ph.D. M PubHsMtw
Quantum Mechanics in the de Sitter Spacetime and Inflationary Scenario
 J. Astrophys. Astr. (1985) 6, 239 246 Quantum Mechanics in the de Sitter Spacetime and Inflationary Scenario Τ. Padmanabhan Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400005 Received
J. Astrophys. Astr. (1985) 6, 239 246 Quantum Mechanics in the de Sitter Spacetime and Inflationary Scenario Τ. Padmanabhan Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400005 Received
