Localization Theorems for Matrices and Bounds for the Zeros of Polynomials over Quaternion Division Algebra
|
|
|
- Deirdre Butler
- 5 years ago
- Views:
Transcription
1 Floma 32:2 28) hps://doorg/2298/fil82553a Publshed by Faculy of Scences and Mahemacs Unversy of Nš Serba Avalable a: hp://wwwpmfnacrs/floma Localzaon Theorems for Marces and Bounds for he Zeros of Polynomals over Quaernon Dvson Algebra Sk Safue Ahmad a Iskhar Al a a Dscplne of Mahemacs School of Basc Scences Indan Insue of Technology Indore Smrol Indore Inda Absrac In hs paper we derve Osrowsk and Brauer ype heorems for he lef and rgh egenvalues of a uaernonc marx Generalzaons of Gerschgorn ype heorems are dscussed for he lef and he rgh egenvalues of a uaernonc marx Afer ha a suffcen condon for he sably of a uaernonc marx s gven ha generalzes he sably condon for a complex marx Fnally a characerzaon of bounds s derved for he zeros of uaernonc polynomals Inroducon Quaernons are exensvely used n he programmng of vdeo games compuer graphcs uanum physcs flgh dynamcs and conrol heory ec The soluons of lnear dfferenal euaons wh uaernon consan coeffcens lead o uaernonc polynomals So he sably analyss of such dfferenal euaons can be suded hrough localzaon heorems of uaernonc marces In recen pas fndng he zeros of uaernonc polynomals and fndng he bounds of zeros of uaernonc polynomals have ganed much aenon n he leraure Ths paper aemps o sudy he localzaon heorems for marces over a uaernon dvson algebra whch ncludes he Osrowsk Brauer and Gerschgorn ype of heorems Bounds for he zeros of uaernonc polynomals are also consdered Localzaon heorems for uaernonc marces have receved much aenon n he leraure due o her numerous applcaons n pure and appled scences; see e g and he references heren Unlke he case of marces over he feld of complex numbers localzaon heorems for uaernonc marces have been proposed for lef and rgh egenvalues separaely n Osrowsk and Brauer ype heorems for he rgh egenvalues of a uaernonc marx wh all real dagonal enres have been nroduced n 39 A Brauer ype heorem for he lef egenvalues of a uaernonc marx has been consdered n 6 Theorem 4 for he deleed absolue row sums whch s no same for he deleed absolue column sums of a uaernonc marx Smlar dfferences arse on he Gerschgorn and Osrowsk ype heorems for a uaernonc marx Therefore more research s reured o undersand he Osrowsk Gershgorn and Brauer ype heorems for marces over a uaernon dvson algebra Furhermore o nvesgang her applcaons n fndng varous bounds for he zeros of uaernonc polynomals and o 2 Mahemacs Subjec lassfcaon 2E5; 34L5; 5A8; 5A66 Keywords Skew feld; uaernonc marx; lef and rgh egenvalues; Gerschgorn ype heorems; Brauer ype heorem; uaernonc polynomals; uaernonc companon marces; sable uaernonc marx Receved: 27 January 27; Acceped: 9 Ocober 27 ommuncaed by Dragana vekovć Ilć orrespondng auhor: Sk Safue Ahmad The second auhor was funded by he SIR Gov of Inda Emal addresses: safue@acn safue@gmalcom Sk Safue Ahmad) skhara@acn Iskhar Al)
2 S S Ahmad I Al / Floma 32:2 28) analyze condons for he sably of a uaernonc marx one has o do furher research n hs drecon Therefore we have developed a general framework usng generalzed Holder neualy of uaernons o enhance our heory In he frs par of hs paper we provde a general framework for localzaon heorems for uaernonc marces Le M n H) be he space of all n n uaernonc marces Then for any A a j ) M n H) we prove a Osrowsk ype heorem whch saes ha all he lef egenvalues of A are locaed n he unon of n balls T A) : {z H : z a r A) γ c A) γ } where r A) : n j j a j and c A) : n j j a j γ From hs resul we deduce a suffcen condon for nverbly of a uaernonc marx We fnd ha he Brauer ype heorem proved n 6 Theorem 5 for he lef egenvalues n he case of deleed absolue column sums of a uaernonc marx s ncorrec and we prove a correced verson In fac n he case of he generalzed Hölder neualy over he skew feld of uaernons we show ha all he lef egenvalues of A a j ) M n H) are conaned n he unon of n generalzed balls: B A) : {z H : z a n ) γ r A) γ n p) A)) γ } where γ n p) A) : n j j a j p) p for any p ) wh p + Furher we prove ha all he rgh egenvalues of A M nh) wh all real dagonal enres are conaned n he unon of n generalzed balls B A) In he seuel we presen localzaon heorems for he rgh egenvalues of uaernonc marces In he second par of hs paper we provde bounds for he zeros of uaernonc polynomals usng he aforemenoned localzaon heorems Recall ha uaernonc polynomals n general are expressed n he followng forms z) : m z m + m z m + + z + ) p r z) : z m m + z m m + + z + 2) where j z H j m) The polynomals ) and 2) are called smple and monc f m Some recen developmens on he locaon and compuaon of zeros of uaernonc polynomals can be found n As a conseuence of he localzaon heorems for uaernonc marces we provde sharper bounds compared o he bound nroduced by G Opfer n 24 for he zeros of uaernonc polynomals Fnally we provde bounds for he zeros of uaernonc polynomals n erms of powers of he companon marces assocaed wh he uaernonc polynomals ) and 2) Some of our bounds are sharper han he bound from 24 The paper s organzed as follows: Secon 2 revews some exsng resuls from Secon 3 dscusses he Greshgorn ype Osrowsk ype and Brauer ype heorems for he lef and rgh egenvalues of a uaernonc marx Secon 4 explans bounds for he zeros of z) and p r z) omparsons are made wh he bound provded n 24 A suffcen condon for he sably of a uaernonc marx s also gven Secon 5 nroduces bounds for he zeros of he polynomals z) and p r z) n erms of powers of her companon marces Fnally Secon 6 summarzes hs work 2 Prelmnares Noaon: Throughou he paper R and denoe he felds of real and complex numbers respecvely The se of real uaernons s defned by H : { a + a + a 2 j + a 3 k : a a a 2 a 3 R } wh 2 j 2 k 2 jk The conjugae of H s : a a a 2 j a 3 k and he modulus of s : a 2 + a2 + a2 2 + a2 Ia) denoes he magnary par of a The real par of a uaernon 3 a + a + a 2 j + a 3 k s defned as R) a The collecon of all n-column vecors wh elemens n H s denoed by H n For x K n where K {R H} he ranspose of x s x T If x x x n T he conjugae of x s defned as x x x n T and he conjugae ranspose of x s defned as x H x x n For x y H n he nner produc s defned as x y : y H x and he norm of x s defned as x : x x The ses of m n real complex and uaernonc marces are denoed by M m n R) M m n ) and M m n H) respecvely
3 S S Ahmad I Al / Floma 32:2 28) When m n hese ses are denoed by M n K) K {R H} For A M m n K) he conjugae ranspose and conjugae ranspose of A are defned as A a j ) A T a j ) M n m H) and A H A) T M n m H) respecvely For z H n he vecor p-norm on H n s defned by z p : n z p ) /p where p < and z : { z } Defne R + : {α : α R α > } The se n : {r H : r ρ ρ f or all ρ H} s called an euvalence class of H Le x H n Then x can be unuely expressed as x x + x 2 j where x x 2 n Defne he funcon ψ : H n 2n by ψ x : x x 2 Ths funcon ψ s an njecve lnear ransformaon from H n o 2n Defnon 2 Le A M n H) Then A can be unuely expressed as A A + A 2 j where A A 2 M n ) Defne he funcon Ψ : M n H) M 2n ) by A A 2 Ψ A : A 2 A The marx Ψ A s called he complex adjon marx of A Defnon 22 Le A M n H) Then he lef rgh and he sandard egenvalues respecvely are gven by Λ l A) : { λ H : Ax λx for some nonzero x H n} Λ r A) : { λ H : Ax xλ for some nonzero x H n} and Λ s A) : { λ : Ax xλ for some nonzero x H n Iλ) } Defnon 23 Le A M n H) Then he marx A s sad o be sable f and only f Λ r A) H : { H : R) < } Defnon 24 Le A M n H) Then A s sad o be η-herman f A A η ) H where A η η H Aη and η { j k} Defnon 25 A marx A M n H) s sad o be nverble f here exss B M n H) such ha AB BA I n where I n s he n n deny marx We nex recall he followng resul necessary for he developmen of our heory Theorem Theorem 43 Le A M n H) Then he followng saemens are euvalen: a) A s nverble b) Ax has he unue soluon c) deψ A ) d) Ψ A s nverble e) A has no zero egenvalue Le A : a j ) M n H) and defne he absolue row and column sums of A as r A) : r A) + a and c A) : c A) + a n) 3 Dsrbuon of he lef and rgh egenvalues of uaernonc marces I s known from 29 orollary 32 ha a uaernonc marx A and s conjugae ranspose A H have he same rgh egenvalues However A and A H may no have he same lef egenvalues ake for example A and A j H We now presen he followng lemma for lef egenvalues of A and A j H Lemma 3 Le A M n H) and le λ H Then λ s a lef egenvalue of A f and only f λ s a lef egenvalue of A H
4 S S Ahmad I Al / Floma 32:2 28) Proof Le λ be a lef egenvalue of A Then here exss x ) H n such ha A λi n )x Ths can be wren as Ψ A λin )ψ x Hence follows ha λ s a lef egenvalue of A f and only f de Ψ A λin ) de Ψ H A λi n ) de ΨA λin ) H de ΨA H λi n ) Thus λ s a lef egenvalue of A H The Gerschgorn ype heorem s proved n 38 for he lef egenvalues usng deleed absolue row sums of a marx A M n H) However he Gerschgorn ype heorem for he lef egenvalues usng deleed absolue column sums of A has no ye been esablshed We now sae and prove he heorem Theorem 32 Le A : a j ) M n H) Then all he lef egenvalues of A are locaed n he unon of n Gerschgorn balls Ω A) : {z H : z a c A)} n ha s Λ l A) ΩA) : n Ω A) Proof Le λ be a lef egenvalue of A Then from Lemma 3 λ s a lef egenvalue of A H Then here exss some nonzero x H n such ha A H x λx Le x : x x n T H n and le x be an elemen of x such ha x x n Then x > From he -h euaon of A H x λx we have a j x j λx j Ths shows λ a a j : c A) j j We now have he followng localzaon heorem for he deleed absolue row and column sums of a marx A M n H) whch s known as Osrowsk ype heorem Theorem 33 Osrowsk ype heorem for he lef egenvalues) Le A : a j ) M n H) and le γ Then all he lef egenvalues of A are locaed n he unon of n balls T A) : {z H : z a r A) γ c A) γ } n ha s Λ l A) TA) : n T A) Proof Le γ ); as he cases γ and γ Gerschgorn ype heorems for column and row sums respecvely) can be obaned by akng lms We may assume ha all r A) > because we may perurb A by nserng a small nonzero enry ɛ > no any row n whch r A) ; he resulng marx has a ball ha s larger he ball for A and he resul follows n he lm as he perurbaon goes o zero Le λ be a lef egenvalue of A Then here exss some nonzero x H n such ha Ax λx Le x x x n T H n Then for each 2 n we have λ a x jj a j x j jj a j x j jj a j γ a j γ x j ) Applyng he generalzed Holder neualy wh p γ and γ we oban λ a x γ a j γ ) /γ jj jj a j γ jj a j γ x j ) γ jj a j x j γ γ γ r A) γ jj a j x j γ γ 3)
5 Snce r A) > hen from 3) we have Summng over all one obans ) λ γ a r A) γ x γ If S S Ahmad I Al / Floma 32:2 28) jj ) λ γ a r A) γ x γ a j x j jj γ a j x j γ c j A) x j γ 4) j ) λ γ a r A) γ > c A) for each such ha x hen 4) could no hold Hence we can conclude ha a leas one exss such as ) λ γ a r A) γ c A) ha s λ a r A) γ c A) γ Thus all he lef egenvalues of A are locaed n he unon of n balls T A) orollary 34 For any A : a j ) M n H) n 2 and for any γ Le us assume ha a > r A) γ r A) γ n 5) Then A s nverble Proof On he conrary suppose A s no nverble Then by Theorem 26 here s a lef egenvalue λ of A Now from Theorem 33 we oban a r A) γ c A) γ Ths conradcs our assumpon 5) Hence A s nverble The Brauer ype heorem s proved n 6 for he lef egenvalues n he case of deleed absolue column sums of a marx A M n H) Tha s f λ Λ l A) hen s conjugae λ les n he unon of nn ) 2 ovals of assn However hs s ncorrec as he followng example suggess: k Example 35 Le A Then by 6 Theorem 5 oval of assn s gven by { z H : z z j } j Here s a lef egenvalue of A and s conjugae s no conaned n he above oval of assn Accordng o 6 Theorem 5 f λ Λ l A) hen λ n j F j A) where j F j A) : { z H : z a z a jj c A)c j A) } j n j However hs resul s no necessarly rue as λ a λ a jj > c A)c j A) j n j whch follows from Example 35 Now we derve a correced verson of 6 Theorem 5 as follows: Theorem 36 Le A : a j ) M n H) Then all he lef egenvalues of A are locaed n he unon of nn ) 2 ovals of assn F j A) : { z H : z a z a jj c A)c j A) } j n j ha s Λ l A) FA) : n j F j A) j
6 S S Ahmad I Al / Floma 32:2 28) Proof Le λ be a lef egenvalue of A Then by Lemma 3 λ s a lef egenvalue of A H so ha here exss some nonzero x H n such ha A H x λx Le x : x x n T H n and le x s be an elemen of x such ha x s x n Then x s > learly f all he oher elemens of x are zero hen he reured resul holds Le x s and x be wo nonzero elemens of x such ha x s x x n s From he s-h euaon of A H x λx we have n j a jsx j λx s whch mples λ a ss )x s n j j s a jsx j Thus ) x λ a ss c s A) 6) x s Smlarly from A H x λx we oban ) xs λ a c A) x ombnng 6) and 7) we have λ a ss λ a c s A)c A) Hence all he lef egenvalues of A are locaed n he unon of nn ) 2 ovals of assn F j A) j n j For A : a j ) M n H) defne n p) A) : j j p a j p n p ) We are now ready o derve he followng localzaon heorem for lef egenvalues of a uaernonc marx Theorem 37 Le A : a j ) M n H) and le γ Then all he lef egenvalues of A are conaned n he unon of n generalzed balls } B A) : {z H : z a n ) γ r A) γ n p) A)) γ n 7) ha s for any p ) wh p + Λ l A) BA) : n B A) Proof Le µ be a lef egenvalue of A Then here exss some nonzero x H n such ha Ax µx Le x : x x n T H n and le x be an elemen of x such ha x x n Then from Ax µx we have a x + a j x j µx j j Ths mples µ a x j j a j x j j j Applyng he generalzed Hölder neualy o 8) we have µ a x a j p p x j j j a j x j 8) j j
7 S S Ahmad I Al / Floma 32:2 28) Snce x x for all n we have µ a x n p) A) n ) x ) ha s µ a n p) A) n ) Smlarly usng x x n) n 8) we ge µ a j j a j r A) 9) ) ombnng 9) and ) for γ we have ha s µ a γ n p) A)) γ n ) γ and µ a γ r A) γ ) µ a n ) γ Le us relae Theorem 37 o some exsng resuls: n p) A)) γ r A) γ Seng p 2 and γ mples ha he lef egenvalues of A : a j ) M n H) are conaned n he unon of n Greschgorn balls B A) : {z H : z a r A)} n ha s Ths resul can be found n 38 Theorem 6 Λ l A) BA) : n B A) Seng p 2 and γ mples ha he lef egenvalues of A : a j ) M n H) are conaned n he unon of n balls B A) : { z H : z a n ) 2 n 2) A) } n ha s Ths resul can be found n 36 Theorem Λ l A) BA) : n B A) We now presen a generalzaon of 38 Theorem 7 and 39 Theorem 3 by applyng he generalzed Hölder neualy over he skew feld of uaernons For a general marx A : a j ) M n H) all he rgh egenvalues may no le n he unon of n generalzed balls B A) n On he oher hand we show ha every conneced regon of he generalzed balls B A) n conans some rgh egenvalues of A Theorem 38 Le A : a j ) M n H) and le γ For every rgh egenvalue µ of A here exss a nonzero uaernon β such ha β µβ whch s also a rgh egenvalue) s conaned n he unon of n generalzed balls } B A) : {z H : z a n ) γ r A) γ n p) A)) γ n ha s { z µz : z H } n B A) where p ) wh p + Proof Le µ be a rgh egenvalue of A Then here exss some nonzero vecor x H n such ha Ax xµ Le x : x x n T H n and choose x from x as gven n Theorem 37 onsder ρ H such ha x µ ρx Then we have ρ a x a j x j a j x j 2) j j j j Usng he mehod from he proof of Theorem 37 we have ρ a n ) γ n p) A)) γ r A) γ Le us relae Theorem 38 o some exsng resuls:
8 Subsung p 2 and γ we oban Ths resul can be found n 38 Theorem 7 Subsung p 2 and γ we ge {z µz : z H} n Ths resul can be found n 39 Theorem 3 S S Ahmad I Al / Floma 32:2 28) {z µz : z H} n {z H : z a r A)} { z H : z a n n 2) A) } We nex presen a suffcen condon for he sably of a marx A M n H) Proposon 39 Le A : a j ) M n H) and le γ Assume ha Ra ) + n ) γ r A) γ n p) A)) γ < n 3) where p + wh p ) Then he marx A s sable Proof Le λ Λ r A) From Theorem 38 here exss ρ H such ha ρ λρ n B A) Whou loss of generaly we assume ρ λρ B l A) ha s ρ λρ a ll n ) γ r l A) γ n p) A)) γ l onsder λ : λ + λ 2 + λ 3 j + λ 4 k and a ll a l + b l + c l j + d l k Then from 3) we oban λ a l ) + ρ λ 2 ρ b l ) + ρ λ 3 jρ c l j) + ρ λ 4 kρ d l k) < Ra ll ) a l 4) The eualy 4) s possble when λ < ha s Rλ) < hence λ H Ths shows ha he marx A s sable When all he dagonal enres of a marx A M n H) are real we have he followng heorem Theorem 3 Le A : a j ) M n H) wh a R and le γ Then all he rgh egenvalues of A are conaned n he unon of n generalzed balls B A) : {z H : z a n ) γ r A) γ n p) A)) γ } n ha s Λ r A) BA) : n B A) where p ) wh p + Proof Le λ be a rgh egenvalue of A Then here exss some nonzero vecor x H n such ha Ax xλ Le x : x x n T H n and le x be an elemen of x such ha x x n Then x > Thus from Ax xλ we have a x + a j x j x λ j j snce a R so a x x a Then from he proof mehod of Theorem 37 we have λ a n ) γ n p) A)) γ r A) γ The above resul has grea sgnfcance as Herman and η-herman marces have all real dagonal enres In general η-herman marces arse wdely n applcaons To ha end we sae he followng proposon when all dagonal enres of A M n H) are real In parcular hs resul gves a suffcen condon for he sably of a marx A M n H)
9 S S Ahmad I Al / Floma 32:2 28) Proposon 3 Le A : a j ) M n H) wh a R and le γ Assume ha a + n ) γ r A) γ n p) A)) γ < n where p ) wh p + Then he marx A s sable From Theorem 3 all he complex rgh egenvalues of a marx A a j ) M n H) wh all real dagonal enres le n he unon of n-dscs D A) : {z : z a n ) γ r A) γ n p) A)) γ } n ha s Λ c A) DA) : n D A) However f dagonal enres are from \ R hen s no necessary ha all he complex rgh egenvalues of A are conaned n he unon of n-dscs D A) n as he followng examples sugges 2 j k Example 32 Le A : 2 The se of complex rgh egenvalues of A s k 3 + Λ c A) : {λ λ 2 λ 3 λ 4 λ 5 λ 6 } where λ λ λ λ 4 2 λ and λ For γ n 5) he dscs D A) D 2 A) and D 3 A) are as follows: D A) : {z : z + 2 2} D 2 A) : {z : z + 2 } and D 3 A) : {z : z 3 } From Fgure s clear ha λ λ 3 and λ 6 le ousde he dscs D A) D 2 A) and D 3 A) 5) 3 2 λ λ 3 D 3A) λ 5 Y axs D A) D 2A) λ 6 2 λ 2 λ Λ c A) X axs Fgure : Locaon of he complex rgh egenvalues of A from Example j + 2k j Example 33 Le A + j 2j k 2j + 2k In hs example here are sx complex rgh 3 + 2j 3k 8 egenvalues λ j j 6) whch are shown n Fgure 2 Subsung γ n 5) hen all he complex rgh egenvalues of he marx A are conaned n he unon of hree dscs D A) D 2 A) and D 3 A) where D A) : {z : z + 4 3} D 2 A) : {z : z } and D 3 A) : {z : z + 8 7}
10 S S Ahmad I Al / Floma 32:2 28) From Fgure 2 he sandard rgh egenvalues of A are λ λ 3 and λ 5 Then Λ r A) λ λ 3 λ 5 Also from Fgure 2 we observe ha Rλ ) H 3 5) Hence Rλ ) Rρ λ ρ) Rλ 2 ) Rτ λ 2 τ) and Rλ 3 ) Rν λ 3 ν) ρ τ ν H Thus he marx A s sable Y axs D 3 A) λ λ 2 D 2 A) λ 3 D A) λ 5 λ 6 λ Λ c A) X axs Fgure 2: Locaon of he complex rgh egenvalues of A from Example 33 In general smlar uaernonc marces may no have he same lef egenvalues see 38 Example 33 However he followng resul s rue Proposon 34 Le A M n H) and le W be any nverble real marx Then A and WAW have he same lef egenvalues Proof Le λ be a lef egenvalue of A Then here exss some nonzero vecor x H n such ha Ax λx Le W be an nverble real marx Then WAx Wλx λwx Now WAW Wx λwx Seng Wx y mples WAW y λy Le A : a j ) M n H) Suppose W dagw w 2 w n ) wh w R + n Then aj w ) W j AW and Λ l A) Λ l W AW) w Defne r W A) : j j a j w j w and c W A) : j j a j w w j n Applyng Theorem 33 o W AW we ge he followng heorem whch may be sharper han Theorem 33 dependng upon he choce of W Theorem 35 Le A : a j ) M n H) Then all he lef egenvalues of A are conaned n he unon of n balls T W A) : {z H : z a r W A)) γ c W A)) γ } n ha s Λ l A) Λ l W AW) T W A) : n TW A)
11 S S Ahmad I Al / Floma 32:2 28) Snce he above heorem holds for every W dagw w 2 w n ) where w R + we have Λ l A) Λ l W AW) W M n S) TW A) : T S A) where M n S) s a se of real dagonal marces wh non-negave enres Osrowsk ype se for he marx A Subsung γ n Theorem 35 we oban T S A) s called he mnmal Λ l A) Λ l W AW) η W A) : n ηw A) 6) where η W A) : { z H : z a r W A) } Therefore Λ l A) Λ l W AW) W M n S) ηw A) : η S A) where η S A) s called he frs mnmal Gerschgorn ype se for he marx A For γ n Theorem 35 we have Λ l A) Λ l W AW) Ω W A) : n ΩW A) 7) where Ω W A) : { z H : z a c W A) } Then Λ l A) Λ l W AW) W M n S) ΩW A) : Ω S A) where Ω S A) s called he second mnmal Gerschgorn ype se for he marx A 4 Bounds for he zeros of uaernonc polynomals In hs secon we derve bounds for he zeros of uaernonc polynomals by applyng he localzaon heorems for he lef egenvalues of a uaernonc marx Due o noncommuvy of uaernons we frs defne some basc facs on mulplcaon of uaernons For p H defne p : p For p H and H defne p : p : p p : p : p Recall he uaernonc polynomals z) and p r z) from ) and 2) Then he correspondng companon marces of he smple monc polynomals z) and p r z) are gven by pl : : m m m I pl m ) pl m 2 : m) and pr : T respecvely Le and defne smple monc reversal polynomals of z) and p r z) as follows: l z) : ) z m z m + z z m + + m z + r z) : z m p r z ) z m + z m + + z m + respecvely The correspondng companon marces of he smple monc reversal polynomals l z) and r z) are denoed by l and r respecvely We observe ha he zeros of l z) and r z) are he recprocal of zeros of z) and p r z) respecvely Now we need he followng resul:
12 S S Ahmad I Al / Floma 32:2 28) Proposon 4 32 Proposon Le λ H Then λ s a zero of he smple monc polynomal z) f and only f λ s a lef egenvalue of s correspondng companon marx pl In general a rgh egenvalue of pl s no necessarly a zero of he smple monc polynomal z) For example le a smple monc polynomal z) z 2 + jz + 2 Then s companon marx s gven by pl 2 j Here s a rgh egenvalue of pl However s no a zero of z) Analogous o Proposon 4 he followng resul s presened for p r z) Proposon 42 Le λ H Then λ s a zero of he smple monc polynomal p r z) f and only f λ s a lef egenvalue of s correspondng companon marx pr We now presen bounds for he zeros of z) as follows Theorem 43 Le z) be a smple monc polynomal over H of degree m Then every zero z of z) sasfes he followng neualy: r l ) γ c l ) γ)) z r ) γ c ) γ) m for every γ m Proof From Proposon 4 zeros of z) and lef egenvalues of pl are same Thus f z s a zero of z) hen z s a lef egenvalue of pl By applyng Theorem 33 Osrowsk ype heorem) o pl we oban z r ) γ c ) γ) m We use he respecve upper bounds for he zeros of he smple monc reversal polynomal l z) for he desred lower bounds for he zeros of z) orollary 44 Le z) be a smple monc polynomal over H of degree m Then every zero z of z) sasfes he followng neuales: { { } z + } + m ) 2 m ) { + m { } z m } Proof Subsung γ n Theorem 43 we oban he desred resuls Nex we derve he followng lemma whch gves a beer bound han Opfer s bound 24 Theorem 42 for { Lemma 45 Assume ha Then α T where α : + } and T : { m } m Proof ase : If hen α { + m } + m ase 2: If > hen α m ) { + } { + } and T : { m } m m { + } or m ) { + } and T : { m } { + m } + m Thus α T Ths complees he proof On he oher hand f < n Lemma 45 hen α T or α > T For example for a smple monc polynomal p l z) : z j + 2k)z 2 2kz + 5k we have α 4 and T 55 Hence α < T Furher f we consder p l z) z3 + 5jz j)z + 5 hen α 5 and T 36 Hence α > T Nex by applyng Theorem 33 o W pl W and W l W W s an nverble real dagonal marx) we oban dfferen and poenally sharper bounds
13 S S Ahmad I Al / Floma 32:2 28) Theorem 46 Le w R + m Then every zero z of he smple monc polynomal z) sasfes he followng neualy: m { r W l W ) γ c W l W ) γ} { z r W W ) γ c W W ) γ} m where W : dagw w 2 w m ) and γ Proof The companon marx of z) s gven by Then m m I pl m m W pl W m dag w w 2 w m w m w w m w 2 m By Proposon 34 pl and W pl W have he same lef egenvalues Res of he proof follows from he proof mehod of Theorem 43 orollary 47 Le z) be a smple monc polynomal over H of degree m Then every zero z of z) sasfes he followng neuales: { } w j + w m m j ) { } wj + w m j z where w j m d j+ j m w j+ m 2 w j w m w j m w m j m w j+ w + z j m w j+ w + Proof Subsung γ n Theorem 46 we ge he desred resuls Le w j w m j j m n he par ) of orollary 47 Then we oban { z 2 } j j m Ths s called he Kojma ype bound for he zeros of he smple monc polynomal z) For compuaon of bounds of he zeros of p r z) we defne he followng polynomal: z) : p r z) : j+ m j z j j H Now we dscuss he followng heorem whch shows relaon beween he zeros of p r z) and z) Theorem 48 Le λ H Then λ s a zero of he smple monc polynomal p r z) f and only f λ s a zero of he smple monc polynomal z) j w m ) Proof The correspondng companon marces of p r z) and z) are gven by pr : T and pl : H p r respecvely By Lemma 3 f λ s a lef egenvalue of pr hen λ s a lef egenvalue of H p r pl By Proposons 4 and 42 he lef egenvalues of pr and pl mply he zeros of p r z) and z) respecvely Hence f λ s a zero of p r z) hen λ s also a zero of z) Remark 49 Smlar resuls can be obaned for he uaernonc polynomal p r z) as well
14 S S Ahmad I Al / Floma 32:2 28) Bounds for he zeros of uaernonc polynomals by usng he powers of companon marces We presen some prelmnares resuls for he powers of companon marces pl and pr In general f λ s a lef egenvalue of a uaernonc marx A hen λ 2 s no necessarly a lef egenvalue of A 2 For example for a uaernonc marx A we have Λ l A) : { µ : µ α + βj + γk α 2 + β 2 + γ 2 } and A 2 So Λ l A 2 ) : {} Here j s a lef egenvalue of A bu j 2 s no a lef egenvalue of A 2 Proposon 5 If λ s a lef egenvalue of pl wh respec o he egenvecor x H n hen λ s a lef egenvalue of correspondng o he same egenvecor x H n Proof ase a): Le be a posve neger and le λ be a lef egenvalue of pl Then here exss x : λ λ 2 λ m T H n such ha pl x λx Therefore 2 x pl pl x) pl xλ xλ 2 x pl x) xλ xλ λ x Thus λ s a lef egenvalue of marx correspondng o he same egenvecor x H n ase b): Le be a negave neger From ase a) we have pl x xλ Ths mples x xλ Therefore 2 x x +) x) xλ xλ 2 x) +) xλ xλ λ x Thus λ s a lef egenvalue of wh respec o he same egenvecor x H n Nex we sae he followng resul for lef egenvalues of pr and p r s a nonzero neger) Proposon 52 If λ s a lef egenvalue of pr wh respec o he egenvecor x H n hen λ s a nonzero neger) s a lef egenvalue of p r correspondng o he same egenvecor x H n Proof ase a): Le be a posve neger and le λ be a lef egenvalue of pr Now from Lemma 3 λ s a lef egenvalue of H p r Then here exss x : λ λ) 2 λ) m H n such ha H p r x λx xλ Ths gves H pr ) 2 x H pr H p r x) H p r xλ xλ) 2 ) H pr x ) H pr H pr x) ) H p r xλ xλ) λ) x Thus λ) s a lef egenvalue of ) H p r Then by Lemma 3 λ s a lef egenvalue of p r ase b): Le be a negave neger From ase a) we have H p r x λx xλ Ths mples H p r ) x xλ) Thus H p r ) 2 x H p r ) { H p r ) x} H p r ) xλ) xλ) 2 H p r ) x H p r ) +) { H p r ) x} H p r ) +) xλ) xλ) λ) x
15 S S Ahmad I Al / Floma 32:2 28) Thus λ) s a lef egenvalue of H p r ) Then by Lemma 3 λ s a lef egenvalue of p r Furher we presen a framework o fnd he powers of he companon marx pl whch can be derved n a smple procedure as follows keepng n vew ha uaernons do no commue m m I Theorem 53 onsder pl pl m ) pl m 2 : m) a) If < m s a posve neger hen m m I D 8) b) f m hen where m ) m : m) m 2) m : m) m : m) m : m) m m m ) : m m) pl m ) m 2 : m) : 9) m : m ) + m m) pl m 2 : m) pl m : ) 2 m : ) : m : ) Noe ha pl k : m) denoes he k-h row of he marx pl pl m + : m) 2 m + : m) and D : m + : m) m m ) m I Proof Assumng 8) becomes pl where pl m ) pl m 2 : m) pl m ) : pl m 2 : m) : m Thus he heorem s rue for Now le us consder pl as m k k k A pl B m k D where A : pl : k : m k) B : pl k + : m m k + : m) : pl k + : m : m k) D : pl k + : m m k + : m) For k 3 we ge 3 2 m 2 m 2 I 2 D m A B m 2 D m 2 2 m 2 D 2 A + D B + DD Noe ha n each sep sze of he deny marx I reduces by order and he sze of marx ncreases by order Smlarly he marx D ncreases by row and decreases by column Fnally afer rearrangng
16 and separang and I marces we ge S S Ahmad I Al / Floma 32:2 28) m 2 m 2 I 2+ D where and D are of sze 3 3 and 3 m 3) respecvely Assumng ha he heorem s rue for k we have k+ k pl m k m k D k A + D B + DD k k+ m k m k I k+ D where he correspondng and D marces are gven n he saemen of he heorem The proof for m s smlar In he case of uaernonc marx pl T p r bu p r ) T for 2 Ths s llusraed by he followng example Example 54 onsder he followng smple monc polynomals over H : z) z 3 kz 2 + k j)z + + j) and p r z) z 3 z 2 k + zk j) + + j) The correspondng companon marces of z) and p r z) are gven by 2 2 I pl pl 3 ) pl 3 2 : 3) and pr T respecvely where pl 3 ) j and pl 3 2 : 3) : j k k Then j j 2 j j k k and 2 p r j k j j 2 j j k k j k Ths shows ha 2 p r 2 ) T Hence we can derve resuls analogous o Theorem 53 for he case of p r 2 m Theorem 55 onsder pr pr m) m I pr 2 : m m) a) If < m s a posve neger hen m p r m I D 2) b) f m hen where p r m ) p r : m m) m 2) p r : m m) p r : m m) p r : m m) m m : pr : m) 2 p r : m) p r : m) D : pr + : m m) 2 p r + : m m) p r + : m m) p r m) : pr m) p r m m) and p r 2 : m m) : p r : m m) + pr 2 : m m) m m) p r
17 S S Ahmad I Al / Floma 32:2 28) Proof The proof follows from he proof mehod of Theorem 53 Polynomals from Example 54 sasfy z) : p r z) z 3 + kz 2 + j k)z + j) and p r z) : z) z 3 + z 2 k + zj k) + j) Thus he companon marces correspondng o z) and p r z) are gven by pl pl and pr pr respecvely Nex + j j 2 + j j + k k and 2 p r j + k j j + j k j k j + k Then Now we have r 3 r )) / and 3 r )) /2 2 pr 2 )) /2 3 r 2 p r )) / and r 3 2 )) / r 2 p r )) /2 and 3 r )) /2 2 pr Furher we have he followng bounds for he zeros of z) and p r z) for γ r 3 2 )) /2 Theorem 56 Le z) and p r z) be he smple monc polynomals over H of degree m and le and p r 2) be he -h power of he companon marces pl and pr correspondng o z) and p r z) respecvely Then for γ bounds for every zero z of z) sasfy he followng neuales: m m r l )) γ/ c l )) γ)/ ) z m r )) γ/ )) γ)/ ) r c r z m r and bounds for every zero z of p r z) sasfy he followng neuales: m m r r r )) γ/ c l )) γ/ c r )) γ)/ ) z m l )) γ)/ ) z m )) γ/ )) γ)/ pl c pl 2) r )) γ/ )) γ)/ pr c pr 22) r r )) γ/ )) γ)/ pr c pr 23) )) γ/ )) γ)/ pl c 24) pl Proof Le λ be a lef egenvalue of pl Then by Proposon 5 λ 2 s posve neger) s a lef egenvalue of Hence by applyng Theorem 33 we ge 2) By Lemma 3 λ s a lef egenvalue of pr and by Proposon 52 λ) s a lef egenvalue of pr ) Then from Theorem 33 22) follows The proof of 23) and 24) are smlar Subsung 2 and γ n Theorem 56 we have he followng corollary orollary 57 Le z) and p r z) be he smple monc polynomals over H of degree m Then bounds for every zero z of z) sasfy he followng neuales: β z α and β 2 z α 2
18 S S Ahmad I Al / Floma 32:2 28) where /2 m /2 m α j m j j j j { α 2 + m ) /2 + m ) /2 + j + j m j ) } /2 2 j m m β β 2 2 j m j j /2 m m j j { + ) /2 + m j + m j m j+ ) /2 } m j+ /2 m + m ) /2 and bounds for every zero z of p r z) sasfy he followng neuales: where α 3 2 j m m α 4 j β 3 z α 3 and β 4 z α 4 { + m ) /2 + m ) /2 + j + j m j ) /2 } j /2 /2 m m j j j β 3 { + 2 j m ) /2 m + m ) /2 + m j + m j m j+ ) /2 m β 4 j j /2 m j m j m j+ Proof The proof follows from Theorem 56 and Appendx A Example 58 onsder he followng polynomals z) and p r z) over H: /2 m+ m z) z k)z j)z k)z j)z k)z + 6j 2) p r z) z 6 + z 5 + 3k) + z j) + z k) + z j) + z6 + 8k) + 6j 2) The zeros of z) are gven n 32 Moreover we fnd he zeros of p r z) by Nven s algorhm 23 Thus he zeros and bounds for he zeros of z) and p r z) are gven n he followng ables 6 oncluson In hs paper we have derved Osrowsk ype heorem for lef egenvalues of a uaernonc marx ha generalzes Osrowsk ype heorem for rgh egenvalues of a uaernonc marx when all he dagonal enres of a uaernonc marx are real We have derved a correced verson of he Brauer ype heorem for lef egenvalues for he deleed absolue column sums of a uaernonc marx Moreover we have exended localzaon heorems by applyng he generalzed Hölder neualy for lef as well as rgh egenvalues of a uaernonc marx Bounds for he zeros of uaernonc polynomals have derved As
19 S S Ahmad I Al / Floma 32:2 28) z z z 2 z 2 2k k k k Table : Zeros of z) and p r z) and her absolue values where z and z 2 are he se of zeros of z) and p r z) respecvely Example 58 lower bound upper bound orollary 44 ) orollary 44 2) Theorem 43 γ / Table 2: Lower and upper bounds for he zeros of z) and p r z) Example 54 lower bound lower bound orollary 57 a) orollary 57 b) orollary 57 2a) orollary 57 2b) Table 3: Lower and upper bounds for he zeros of z) and p r z) a conseuence we have shown ha some of our bounds are sharper han he bound gven n 24 Furher we have derved bounds va he powers of companon marces whch are always sharper han he bound gven n 24 Appendx A In hs appendx we sae formulas for he suares of uaernonc companon marces For 2 Theorem 53 mples 2 2 m 2 m 2 I 2 D where : pl m : 2) 2 m : 2) m m and pl m 3 : m) D m m 3 : m) m 2 m 3 m ) 2 m m 2 m 2 I 2 D where pl m : 2) 2 m : 2) m m and pl m 3 : m) D 2 m 3 : m) 2 3 m m 2 m 3 m ) 2 m 2 2 l 2 m 2 m 2 I 2 D where m m
20 S S Ahmad I Al / Floma 32:2 28) and and 2 l D m 2 m 2 m ) m 2 m 2 I 2 D where m m m 2 D m 2 m ) 2 2 For 2 Theorem 55 mples m p r where m 2 I D pr : 2 m) 2 p r : 2 m) m m and 2 p r m m 2 I D D pr 3 : m m) 2 p r 3 : m m) where m 2 2 m 3 3 m 2 m m m ) 2 m 2 and D 2 2 m 3 3 m 2 m ) 2 m m 2 m r where m 2 I D m m m 2 m 2 m and D )2 2 2 r m m m m 2 I D and D where m 2 m 2 m ) 2 2
21 S S Ahmad I Al / Floma 32:2 28) References S L Adler Quaernonc Quanum Mechancs and Quanum Felds Oxford Unversy Press New York A Baker Rgh egenvalues for uaernonc marces: a opologcal approach Lnear Algebra Appl ) A Brauer Lms for he characersc roos of a marx Duke Mah J 3946) J H onway D A Smh On Quaernons and Oconons: Ther Geomery Arhmec and Symmery A K Peers Nack 22 5 S Geršgorn Über de Abgrenzung der Egenwere ener arx Izv Akad Nauk SSSR Ser Ma 93) A Bunse-Gersner R Byers and V Mehrmann A uaernon QR algorhm Numer Mah 55989) B Gordon and T S Mozkn On he zeros of polynomals over dvson rngs Trans Amer Mah Soc 6965) T L Hankns Sr Wllam Rowan Hamlon The Johns Hopkns Unversy Press Balmore 98 9 M A Hassan Ineuales and bounds for he zeros of polynomals usng Perron-Frobenus and Gerschgorn heores Proceedngs of Amercan onrol onference Boson Massachuses Evanson IL: Amercan Auomac onrol ouncl 324) N J Hgham F Tsseur Bounds for egenvalues of marx polynomals Lnear Algebra Appl 35823) 5 22 R A Horn R Johnson Marx Analyss ambrdge Unversy Press New York R A Horn F Zhang A generalzaon of he complex auonne-akag facorzaon o uaernon marces Lnear and Mullnear Algebra 622) L Huang W So On lef egenvalues of a uaernonc marx Lnear Algebra Appl 3232) D Janovská and G Opfer The classfcaon and he compuaon of he zeros of uaernonc wo-sded polynomals Numer Mah 52) 8 5 D Janovská G Opfer A noe on he compuaon of all zeros of smple uaernonc polynomals SIAM J Numer Anal 48)2) W Junlang Z Lmn Xangpng and L Shengje The esmaon of egenvalues of sum dfference and ensor produc of marces over uaernon dvson algebra Lnear Algebra Appl 42828) G Kamberov P Norman F Ped and U Pnkall Quaernons Spnors and Surfaces onemporary Mahemacs vol 299 Amer Mah Soc Provnce 22 8 M Karow Self-adjon operaors and pars of Herman forms over he uaernons Lnear Algebra Appl ) 7 9 A Kaz ompuaonal Rgd Vehcle Dynamcs Kreger Publshng o 997) 2 J B Kupers Quaernons and roaon Seuences: a Prmer wh Applcaons o Orbs Aerospace and Vrual Realy Prnceon Unversy Press 22) 2 H Lee Egenvalues and canoncal forms of marces wh uaernon coeffcens Proc Roy Irsh Acad Sec 52A949) S D Leo G Duca and V Leonard Zeros of unlaeral uaernonc polnomals Elecron J Lnear Algebra 526) I Nven Euaons n uaernons Amer Mah Monhly 4894) G Opfer Polynomals and Vandermonde marces over he feld of uaernons Elecron Trans Numer Anal 3629) A M Osrowsk Über de deermnanen m uberwegender haupdagonale ommen Mah Helv 937) R Perera P Rocha On he deermnan of uaernonc polynomal marces and s applcaon o sysem sably Mah Mehods Appl Sc 328) R Perera P Rocha and P Veor Algebrac ools for he sudy of uaernonc behavoral sysems Lnear Algebra Appl 425) A Pogoru M Shapro On he srucure of he se of zeros of uaernonc polynomals omplex Var and Ellpc Func 4924) L Rodman Pars of herman and skew herman uaernonc marces canoncal forms and her applcaons Lnear Algebra Appl 42928) L Rodman Sably of nvaran subspaces of uaernon marces omplex Anal Oper Theory 65)22) L Rodman Topcs n Quaernon Lnear Algebra Prnceon Unversy Press Prnceon NJ) R Serôdo E Perera and J Vóra ompung he zeros of uaernon polynomals ompu Mah Appl 422) Took D P Mandc Augmened second-order sascs of uaernon random sgnals Sgnal Processng 92) Took D P Mandc and F Zhang On he unary dagonalsaon of a specal class of uaernon marces Appl Mah Le 242) R S Varga Geršgorn and H s rcles Sprnger Berln J L Wu Dsrbuon and esmaon for egenvalues of real uaernon marces ompu Mah Appl 5528) F Zhang Quaernons and marces of uaernons Lnear Algebra Appl 25997) F Zhang Geršgorn ype heorems for uaernonc marces Lnear Algebra Appl 42427) L Zou Y Jang and J Wu Locaon for he rgh egenvalues of uaernon marces J Appl Mah ompu 3822) 7 83
GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS. Youngwoo Ahn and Kitae Kim
 Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
. The geometric multiplicity is dim[ker( λi. number of linearly independent eigenvectors associated with this eigenvalue.
 Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.
![. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue. . The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.](/thumbs/78/77822798.jpg) Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
V.Abramov - FURTHER ANALYSIS OF CONFIDENCE INTERVALS FOR LARGE CLIENT/SERVER COMPUTER NETWORKS
 R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
Comparison of Differences between Power Means 1
 In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β
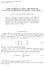 SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
Approximate Analytic Solution of (2+1) - Dimensional Zakharov-Kuznetsov(Zk) Equations Using Homotopy
 Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Relative controllability of nonlinear systems with delays in control
 Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Method of upper lower solutions for nonlinear system of fractional differential equations and applications
 Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
John Geweke a and Gianni Amisano b a Departments of Economics and Statistics, University of Iowa, USA b European Central Bank, Frankfurt, Germany
 Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
( ) () we define the interaction representation by the unitary transformation () = ()
 Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Notes on the stability of dynamic systems and the use of Eigen Values.
 Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
CS286.2 Lecture 14: Quantum de Finetti Theorems II
 CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
Existence and Uniqueness Results for Random Impulsive Integro-Differential Equation
 Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD
 Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
CH.3. COMPATIBILITY EQUATIONS. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
CH.3. COMPATIBILITY EQUATIONS Connuum Mechancs Course (MMC) - ETSECCPB - UPC Overvew Compably Condons Compably Equaons of a Poenal Vecor Feld Compably Condons for Infnesmal Srans Inegraon of he Infnesmal
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Online Supplement for Dynamic Multi-Technology. Production-Inventory Problem with Emissions Trading
 Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
In the complete model, these slopes are ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL. (! i+1 -! i ) + [(!") i+1,q - [(!
 ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
Epistemic Game Theory: Online Appendix
 Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Appendix H: Rarefaction and extrapolation of Hill numbers for incidence data
 Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
ON THE WEAK LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS
 ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5
![[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5 [ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5](/thumbs/85/92299540.jpg) TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
Dynamic Team Decision Theory. EECS 558 Project Shrutivandana Sharma and David Shuman December 10, 2005
 Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Ordinary Differential Equations in Neuroscience with Matlab examples. Aim 1- Gain understanding of how to set up and solve ODE s
 Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Testing a new idea to solve the P = NP problem with mathematical induction
 Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Department of Economics University of Toronto
 Deparmen of Economcs Unversy of Torono ECO408F M.A. Economercs Lecure Noes on Heeroskedascy Heeroskedascy o Ths lecure nvolves lookng a modfcaons we need o make o deal wh he regresson model when some of
Deparmen of Economcs Unversy of Torono ECO408F M.A. Economercs Lecure Noes on Heeroskedascy Heeroskedascy o Ths lecure nvolves lookng a modfcaons we need o make o deal wh he regresson model when some of
Comb Filters. Comb Filters
 The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
Survival Analysis and Reliability. A Note on the Mean Residual Life Function of a Parallel System
 Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
Cubic Bezier Homotopy Function for Solving Exponential Equations
 Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Lecture 18: The Laplace Transform (See Sections and 14.7 in Boas)
 Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
@FMI c Kyung Moon Sa Co.
 Annals of Fuzzy Mahemacs and Informacs Volume 8, No. 2, (Augus 2014), pp. 245 257 ISSN: 2093 9310 (prn verson) ISSN: 2287 6235 (elecronc verson) hp://www.afm.or.kr @FMI c Kyung Moon Sa Co. hp://www.kyungmoon.com
Annals of Fuzzy Mahemacs and Informacs Volume 8, No. 2, (Augus 2014), pp. 245 257 ISSN: 2093 9310 (prn verson) ISSN: 2287 6235 (elecronc verson) hp://www.afm.or.kr @FMI c Kyung Moon Sa Co. hp://www.kyungmoon.com
FI 3103 Quantum Physics
 /9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
/9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
On computing differential transform of nonlinear non-autonomous functions and its applications
 On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
Robust and Accurate Cancer Classification with Gene Expression Profiling
 Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
Robus and Accurae Cancer Classfcaon wh Gene Expresson Proflng (Compuaonal ysems Bology, 2005) Auhor: Hafeng L, Keshu Zhang, ao Jang Oulne Background LDA (lnear dscrmnan analyss) and small sample sze problem
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL
 DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
A Deza Frankl type theorem for set partitions
 A Deza Frankl ype heorem for se parons Cheng Yeaw Ku Deparmen of Mahemacs Naonal Unversy of Sngapore Sngapore 117543 makcy@nus.edu.sg Kok Bn Wong Insue of Mahemacal Scences Unversy of Malaya 50603 Kuala
A Deza Frankl ype heorem for se parons Cheng Yeaw Ku Deparmen of Mahemacs Naonal Unversy of Sngapore Sngapore 117543 makcy@nus.edu.sg Kok Bn Wong Insue of Mahemacal Scences Unversy of Malaya 50603 Kuala
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 4
 CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
Volatility Interpolation
 Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
Volaly Inerpolaon Prelmnary Verson March 00 Jesper Andreasen and Bran Huge Danse Mares, Copenhagen wan.daddy@danseban.com brno@danseban.com Elecronc copy avalable a: hp://ssrn.com/absrac=69497 Inro Local
A New Generalized Gronwall-Bellman Type Inequality
 22 Inernaonal Conference on Image, Vson and Comung (ICIVC 22) IPCSIT vol. 5 (22) (22) IACSIT Press, Sngaore DOI:.7763/IPCSIT.22.V5.46 A New Generalzed Gronwall-Bellman Tye Ineualy Qnghua Feng School of
22 Inernaonal Conference on Image, Vson and Comung (ICIVC 22) IPCSIT vol. 5 (22) (22) IACSIT Press, Sngaore DOI:.7763/IPCSIT.22.V5.46 A New Generalzed Gronwall-Bellman Tye Ineualy Qnghua Feng School of
Let s treat the problem of the response of a system to an applied external force. Again,
 Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Page 33 QUANTUM LNEAR RESPONSE FUNCTON Le s rea he problem of he response of a sysem o an appled exernal force. Agan, H() H f () A H + V () Exernal agen acng on nernal varable Hamlonan for equlbrum sysem
Tight results for Next Fit and Worst Fit with resource augmentation
 Tgh resuls for Nex F and Wors F wh resource augmenaon Joan Boyar Leah Epsen Asaf Levn Asrac I s well known ha he wo smple algorhms for he classc n packng prolem, NF and WF oh have an approxmaon rao of
Tgh resuls for Nex F and Wors F wh resource augmenaon Joan Boyar Leah Epsen Asaf Levn Asrac I s well known ha he wo smple algorhms for he classc n packng prolem, NF and WF oh have an approxmaon rao of
ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 45, Number 6, 2015 ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS DARIUSH KIANI AND MOHSEN MOLLAHAJIAGHAEI ABSTRACT. Le R be a fne commuave
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 45, Number 6, 2015 ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS DARIUSH KIANI AND MOHSEN MOLLAHAJIAGHAEI ABSTRACT. Le R be a fne commuave
( t) Outline of program: BGC1: Survival and event history analysis Oslo, March-May Recapitulation. The additive regression model
 BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
BGC1: Survval and even hsory analyss Oslo, March-May 212 Monday May 7h and Tuesday May 8h The addve regresson model Ørnulf Borgan Deparmen of Mahemacs Unversy of Oslo Oulne of program: Recapulaon Counng
Variants of Pegasos. December 11, 2009
 Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
3. OVERVIEW OF NUMERICAL METHODS
 3 OVERVIEW OF NUMERICAL METHODS 3 Inroducory remarks Ths chaper summarzes hose numercal echnques whose knowledge s ndspensable for he undersandng of he dfferen dscree elemen mehods: he Newon-Raphson-mehod,
3 OVERVIEW OF NUMERICAL METHODS 3 Inroducory remarks Ths chaper summarzes hose numercal echnques whose knowledge s ndspensable for he undersandng of he dfferen dscree elemen mehods: he Newon-Raphson-mehod,
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
Mechancs Physcs 5 Lecure 0 Canoncal Transformaons (Chaper 9) Wha We Dd Las Tme Hamlon s Prncple n he Hamlonan formalsm Dervaon was smple δi δ Addonal end-pon consrans pq H( q, p, ) d 0 δ q ( ) δq ( ) δ
( ) [ ] MAP Decision Rule
![( ) [ ] MAP Decision Rule ( ) [ ] MAP Decision Rule](/thumbs/82/84970741.jpg) Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
Announcemens Bayes Decson Theory wh Normal Dsrbuons HW0 due oday HW o be assgned soon Proec descrpon posed Bomercs CSE 90 Lecure 4 CSE90, Sprng 04 CSE90, Sprng 04 Key Probables 4 ω class label X feaure
This document is downloaded from DR-NTU, Nanyang Technological University Library, Singapore.
 Ths documen s downloaded from DR-NTU, Nanyang Technologcal Unversy Lbrary, Sngapore. Tle A smplfed verb machng algorhm for word paron n vsual speech processng( Acceped verson ) Auhor(s) Foo, Say We; Yong,
Ths documen s downloaded from DR-NTU, Nanyang Technologcal Unversy Lbrary, Sngapore. Tle A smplfed verb machng algorhm for word paron n vsual speech processng( Acceped verson ) Auhor(s) Foo, Say We; Yong,
F-Tests and Analysis of Variance (ANOVA) in the Simple Linear Regression Model. 1. Introduction
 ECOOMICS 35* -- OTE 9 ECO 35* -- OTE 9 F-Tess and Analyss of Varance (AOVA n he Smple Lnear Regresson Model Inroducon The smple lnear regresson model s gven by he followng populaon regresson equaon, or
ECOOMICS 35* -- OTE 9 ECO 35* -- OTE 9 F-Tess and Analyss of Varance (AOVA n he Smple Lnear Regresson Model Inroducon The smple lnear regresson model s gven by he followng populaon regresson equaon, or
5th International Conference on Advanced Design and Manufacturing Engineering (ICADME 2015)
 5h Inernaonal onference on Advanced Desgn and Manufacurng Engneerng (IADME 5 The Falure Rae Expermenal Sudy of Specal N Machne Tool hunshan He, a, *, La Pan,b and Bng Hu 3,c,,3 ollege of Mechancal and
5h Inernaonal onference on Advanced Desgn and Manufacurng Engneerng (IADME 5 The Falure Rae Expermenal Sudy of Specal N Machne Tool hunshan He, a, *, La Pan,b and Bng Hu 3,c,,3 ollege of Mechancal and
PHYS 705: Classical Mechanics. Canonical Transformation
 PHYS 705: Classcal Mechancs Canoncal Transformaon Canoncal Varables and Hamlonan Formalsm As we have seen, n he Hamlonan Formulaon of Mechancs,, are ndeenden varables n hase sace on eual foong The Hamlon
PHYS 705: Classcal Mechancs Canoncal Transformaon Canoncal Varables and Hamlonan Formalsm As we have seen, n he Hamlonan Formulaon of Mechancs,, are ndeenden varables n hase sace on eual foong The Hamlon
M. Y. Adamu Mathematical Sciences Programme, AbubakarTafawaBalewa University, Bauchi, Nigeria
 IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
IOSR Journal of Mahemacs (IOSR-JM e-issn: 78-578, p-issn: 9-765X. Volume 0, Issue 4 Ver. IV (Jul-Aug. 04, PP 40-44 Mulple SolonSoluons for a (+-dmensonalhroa-sasuma shallow waer wave equaon UsngPanlevé-Bӓclund
2/20/2013. EE 101 Midterm 2 Review
 //3 EE Mderm eew //3 Volage-mplfer Model The npu ressance s he equalen ressance see when lookng no he npu ermnals of he amplfer. o s he oupu ressance. I causes he oupu olage o decrease as he load ressance
//3 EE Mderm eew //3 Volage-mplfer Model The npu ressance s he equalen ressance see when lookng no he npu ermnals of he amplfer. o s he oupu ressance. I causes he oupu olage o decrease as he load ressance
A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION
 S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
S19 A NEW TECHNIQUE FOR SOLVING THE 1-D BURGERS EQUATION by Xaojun YANG a,b, Yugu YANG a*, Carlo CATTANI c, and Mngzheng ZHU b a Sae Key Laboraory for Geomechancs and Deep Underground Engneerng, Chna Unversy
Chapter Lagrangian Interpolation
 Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
NATIONAL UNIVERSITY OF SINGAPORE PC5202 ADVANCED STATISTICAL MECHANICS. (Semester II: AY ) Time Allowed: 2 Hours
 NATONAL UNVERSTY OF SNGAPORE PC5 ADVANCED STATSTCAL MECHANCS (Semeser : AY 1-13) Tme Allowed: Hours NSTRUCTONS TO CANDDATES 1. Ths examnaon paper conans 5 quesons and comprses 4 prned pages.. Answer all
NATONAL UNVERSTY OF SNGAPORE PC5 ADVANCED STATSTCAL MECHANCS (Semeser : AY 1-13) Tme Allowed: Hours NSTRUCTONS TO CANDDATES 1. Ths examnaon paper conans 5 quesons and comprses 4 prned pages.. Answer all
Robustness Experiments with Two Variance Components
 Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
Naonal Insue of Sandards and Technology (NIST) Informaon Technology Laboraory (ITL) Sascal Engneerng Dvson (SED) Robusness Expermens wh Two Varance Componens by Ana Ivelsse Avlés avles@ns.gov Conference
How about the more general "linear" scalar functions of scalars (i.e., a 1st degree polynomial of the following form with a constant term )?
 lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
lmcd Lnear ransformaon of a vecor he deas presened here are que general hey go beyond he radonal mar-vecor ype seen n lnear algebra Furhermore, hey do no deal wh bass and are equally vald for any se of
Track Properities of Normal Chain
 In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
On elements with index of the form 2 a 3 b in a parametric family of biquadratic elds
 On elemens wh ndex of he form a 3 b n a paramerc famly of bquadrac elds Bora JadrevĆ Absrac In hs paper we gve some resuls abou prmve negral elemens p(c p n he famly of bcyclc bquadrac elds L c = Q ) c;
On elemens wh ndex of he form a 3 b n a paramerc famly of bquadrac elds Bora JadrevĆ Absrac In hs paper we gve some resuls abou prmve negral elemens p(c p n he famly of bcyclc bquadrac elds L c = Q ) c;
Should Exact Index Numbers have Standard Errors? Theory and Application to Asian Growth
 Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Should Exac Index umbers have Sandard Errors? Theory and Applcaon o Asan Growh Rober C. Feensra Marshall B. Rensdorf ovember 003 Proof of Proposon APPEDIX () Frs, we wll derve he convenonal Sao-Vara prce
Performance Analysis for a Network having Standby Redundant Unit with Waiting in Repair
 TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
Scattering at an Interface: Oblique Incidence
 Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Existence of Time Periodic Solutions for the Ginzburg-Landau Equations. model of superconductivity
 Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Lecture 6: Learning for Control (Generalised Linear Regression)
 Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
Lecure 6: Learnng for Conrol (Generalsed Lnear Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure 6: RLSC - Prof. Sehu Vjayakumar Lnear Regresson
On the numerical treatment ofthenonlinear partial differentialequation of fractional order
 IOSR Journal of Mahemacs (IOSR-JM) e-iss: 2278-5728, p-iss: 239-765X. Volume 2, Issue 6 Ver. I (ov. - Dec.26), PP 28-37 www.osrjournals.org On he numercal reamen ofhenonlnear paral dfferenalequaon of fraconal
IOSR Journal of Mahemacs (IOSR-JM) e-iss: 2278-5728, p-iss: 239-765X. Volume 2, Issue 6 Ver. I (ov. - Dec.26), PP 28-37 www.osrjournals.org On he numercal reamen ofhenonlnear paral dfferenalequaon of fraconal
e-journal Reliability: Theory& Applications No 2 (Vol.2) Vyacheslav Abramov
 June 7 e-ournal Relably: Theory& Applcaons No (Vol. CONFIDENCE INTERVALS ASSOCIATED WITH PERFORMANCE ANALYSIS OF SYMMETRIC LARGE CLOSED CLIENT/SERVER COMPUTER NETWORKS Absrac Vyacheslav Abramov School
June 7 e-ournal Relably: Theory& Applcaons No (Vol. CONFIDENCE INTERVALS ASSOCIATED WITH PERFORMANCE ANALYSIS OF SYMMETRIC LARGE CLOSED CLIENT/SERVER COMPUTER NETWORKS Absrac Vyacheslav Abramov School
UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 2017 EXAMINATION
 INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
Li An-Ping. Beijing , P.R.China
 A New Type of Cpher: DICING_csb L An-Png Bejng 100085, P.R.Chna apl0001@sna.com Absrac: In hs paper, we wll propose a new ype of cpher named DICING_csb, whch s derved from our prevous sream cpher DICING.
A New Type of Cpher: DICING_csb L An-Png Bejng 100085, P.R.Chna apl0001@sna.com Absrac: In hs paper, we wll propose a new ype of cpher named DICING_csb, whch s derved from our prevous sream cpher DICING.
10. A.C CIRCUITS. Theoretically current grows to maximum value after infinite time. But practically it grows to maximum after 5τ. Decay of current :
 . A. IUITS Synopss : GOWTH OF UNT IN IUIT : d. When swch S s closed a =; = d. A me, curren = e 3. The consan / has dmensons of me and s called he nducve me consan ( τ ) of he crcu. 4. = τ; =.63, n one
. A. IUITS Synopss : GOWTH OF UNT IN IUIT : d. When swch S s closed a =; = d. A me, curren = e 3. The consan / has dmensons of me and s called he nducve me consan ( τ ) of he crcu. 4. = τ; =.63, n one
Online Appendix for. Strategic safety stocks in supply chains with evolving forecasts
 Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
FTCS Solution to the Heat Equation
 FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
FTCS Soluon o he Hea Equaon ME 448/548 Noes Gerald Reckenwald Porland Sae Unversy Deparmen of Mechancal Engneerng gerry@pdxedu ME 448/548: FTCS Soluon o he Hea Equaon Overvew Use he forward fne d erence
Part II CONTINUOUS TIME STOCHASTIC PROCESSES
 Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
Par II CONTINUOUS TIME STOCHASTIC PROCESSES 4 Chaper 4 For an advanced analyss of he properes of he Wener process, see: Revus D and Yor M: Connuous marngales and Brownan Moon Karazas I and Shreve S E:
New M-Estimator Objective Function. in Simultaneous Equations Model. (A Comparative Study)
 Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
Inernaonal Mahemacal Forum, Vol. 8, 3, no., 7 - HIKARI Ld, www.m-hkar.com hp://dx.do.org/.988/mf.3.3488 New M-Esmaor Objecve Funcon n Smulaneous Equaons Model (A Comparave Sudy) Ahmed H. Youssef Professor
Pendulum Dynamics. = Ft tangential direction (2) radial direction (1)
 Pendulum Dynams Consder a smple pendulum wh a massless arm of lengh L and a pon mass, m, a he end of he arm. Assumng ha he fron n he sysem s proporonal o he negave of he angenal veloy, Newon s seond law
Pendulum Dynams Consder a smple pendulum wh a massless arm of lengh L and a pon mass, m, a he end of he arm. Assumng ha he fron n he sysem s proporonal o he negave of he angenal veloy, Newon s seond law
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon Alernae approach o second order specra: ask abou x magnezaon nsead of energes and ranson probables. If we say wh one bass se, properes vary
THE PREDICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS
 THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
2.1 Constitutive Theory
 Secon.. Consuve Theory.. Consuve Equaons Governng Equaons The equaons governng he behavour of maerals are (n he spaal form) dρ v & ρ + ρdv v = + ρ = Conservaon of Mass (..a) d x σ j dv dvσ + b = ρ v& +
Secon.. Consuve Theory.. Consuve Equaons Governng Equaons The equaons governng he behavour of maerals are (n he spaal form) dρ v & ρ + ρdv v = + ρ = Conservaon of Mass (..a) d x σ j dv dvσ + b = ρ v& +
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
A DECOMPOSITION METHOD FOR SOLVING DIFFUSION EQUATIONS VIA LOCAL FRACTIONAL TIME DERIVATIVE
 S13 A DECOMPOSITION METHOD FOR SOLVING DIFFUSION EQUATIONS VIA LOCAL FRACTIONAL TIME DERIVATIVE by Hossen JAFARI a,b, Haleh TAJADODI c, and Sarah Jane JOHNSTON a a Deparen of Maheacal Scences, Unversy
S13 A DECOMPOSITION METHOD FOR SOLVING DIFFUSION EQUATIONS VIA LOCAL FRACTIONAL TIME DERIVATIVE by Hossen JAFARI a,b, Haleh TAJADODI c, and Sarah Jane JOHNSTON a a Deparen of Maheacal Scences, Unversy
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
TSS = SST + SSE An orthogonal partition of the total SS
 ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
ANOVA: Topc 4. Orhogonal conrass [ST&D p. 183] H 0 : µ 1 = µ =... = µ H 1 : The mean of a leas one reamen group s dfferen To es hs hypohess, a basc ANOVA allocaes he varaon among reamen means (SST) equally
arxiv: v1 [math.pr] 6 Mar 2019
![arxiv: v1 [math.pr] 6 Mar 2019 arxiv: v1 [math.pr] 6 Mar 2019](/thumbs/94/118755942.jpg) Local law and Tracy Wdom lm for sparse sochasc block models Jong Yun Hwang J Oon Lee Wooseok Yang arxv:1903.02179v1 mah.pr 6 Mar 2019 March 7, 2019 Absrac We consder he specral properes of sparse sochasc
Local law and Tracy Wdom lm for sparse sochasc block models Jong Yun Hwang J Oon Lee Wooseok Yang arxv:1903.02179v1 mah.pr 6 Mar 2019 March 7, 2019 Absrac We consder he specral properes of sparse sochasc
Lecture VI Regression
 Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
Lecure VI Regresson (Lnear Mehods for Regresson) Conens: Lnear Mehods for Regresson Leas Squares, Gauss Markov heorem Recursve Leas Squares Lecure VI: MLSC - Dr. Sehu Vjayakumar Lnear Regresson Model M
Lecture 2 M/G/1 queues. M/G/1-queue
 Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
Lecure M/G/ queues M/G/-queue Posson arrval process Arbrary servce me dsrbuon Sngle server To deermne he sae of he sysem a me, we mus now The number of cusomers n he sysems N() Tme ha he cusomer currenly
arxiv: v1 [math.co] 17 Aug 2009
![arxiv: v1 [math.co] 17 Aug 2009 arxiv: v1 [math.co] 17 Aug 2009](/thumbs/90/101395020.jpg) DESCENT POLYNOMIALS FOR PERMUTATIONS WITH BOUNDED DROP SIZE FAN CHUNG, ANDERS CLAESSON, MARK DUKES, AND RONALD GRAHAM arxv:0908.2456v1 [mah.co] 17 Aug 2009 Absrac. Movaed by ugglng sequences and bubble
DESCENT POLYNOMIALS FOR PERMUTATIONS WITH BOUNDED DROP SIZE FAN CHUNG, ANDERS CLAESSON, MARK DUKES, AND RONALD GRAHAM arxv:0908.2456v1 [mah.co] 17 Aug 2009 Absrac. Movaed by ugglng sequences and bubble
P R = P 0. The system is shown on the next figure:
 TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
TPG460 Reservor Smulaon 08 page of INTRODUCTION TO RESERVOIR SIMULATION Analycal and numercal soluons of smple one-dmensonal, one-phase flow equaons As an nroducon o reservor smulaon, we wll revew he smples
Density Matrix Description of NMR BCMB/CHEM 8190
 Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
Densy Marx Descrpon of NMR BCMBCHEM 89 Operaors n Marx Noaon If we say wh one bass se, properes vary only because of changes n he coeffcens weghng each bass se funcon x = h< Ix > - hs s how we calculae
2 Aggregate demand in partial equilibrium static framework
 Unversy of Mnnesoa 8107 Macroeconomc Theory, Sprng 2009, Mn 1 Fabrzo Perr Lecure 1. Aggregaon 1 Inroducon Probably so far n he macro sequence you have deal drecly wh represenave consumers and represenave
Unversy of Mnnesoa 8107 Macroeconomc Theory, Sprng 2009, Mn 1 Fabrzo Perr Lecure 1. Aggregaon 1 Inroducon Probably so far n he macro sequence you have deal drecly wh represenave consumers and represenave
Math 128b Project. Jude Yuen
 Mah 8b Proec Jude Yuen . Inroducon Le { Z } be a sequence of observed ndependen vecor varables. If he elemens of Z have a on normal dsrbuon hen { Z } has a mean vecor Z and a varancecovarance marx z. Geomercally
Mah 8b Proec Jude Yuen . Inroducon Le { Z } be a sequence of observed ndependen vecor varables. If he elemens of Z have a on normal dsrbuon hen { Z } has a mean vecor Z and a varancecovarance marx z. Geomercally
Outline. Probabilistic Model Learning. Probabilistic Model Learning. Probabilistic Model for Time-series Data: Hidden Markov Model
 Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon
Probablsc Model for Tme-seres Daa: Hdden Markov Model Hrosh Mamsuka Bonformacs Cener Kyoo Unversy Oulne Three Problems for probablsc models n machne learnng. Compung lkelhood 2. Learnng 3. Parsng (predcon
A moving horizon scheme for distributed state estimation
 . A movng horzon scheme for dsrbued sae esmaon arcello Farna, Gancarlo Ferrar-Trecae and Rccardo Scaoln The research of.f. and R.S. has receved fundng from European Communy hrough FP7/7-3 under gran agreemen
. A movng horzon scheme for dsrbued sae esmaon arcello Farna, Gancarlo Ferrar-Trecae and Rccardo Scaoln The research of.f. and R.S. has receved fundng from European Communy hrough FP7/7-3 under gran agreemen
RELATIONSHIP BETWEEN VOLATILITY AND TRADING VOLUME: THE CASE OF HSI STOCK RETURNS DATA
 RELATIONSHIP BETWEEN VOLATILITY AND TRADING VOLUME: THE CASE OF HSI STOCK RETURNS DATA Mchaela Chocholaá Unversy of Economcs Braslava, Slovaka Inroducon (1) one of he characersc feaures of sock reurns
RELATIONSHIP BETWEEN VOLATILITY AND TRADING VOLUME: THE CASE OF HSI STOCK RETURNS DATA Mchaela Chocholaá Unversy of Economcs Braslava, Slovaka Inroducon (1) one of he characersc feaures of sock reurns
CHAPTER 10: LINEAR DISCRIMINATION
 CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g
CHAPER : LINEAR DISCRIMINAION Dscrmnan-based Classfcaon 3 In classfcaon h K classes (C,C,, C k ) We defned dscrmnan funcon g j (), j=,,,k hen gven an es eample, e chose (predced) s class label as C f g
By HENRY H. KIM and KYU-HWAN LEE
 SPHERICAL HECKE ALGEBRAS OF SL OVER -DIMENSIONAL LOCAL FIELDS By HENRY H. KIM and KYU-HWAN LEE Absrac. In hs paper, we sudy sphercal Hece algebras of SL over wo dmensonal local felds. In order o defne
SPHERICAL HECKE ALGEBRAS OF SL OVER -DIMENSIONAL LOCAL FIELDS By HENRY H. KIM and KYU-HWAN LEE Absrac. In hs paper, we sudy sphercal Hece algebras of SL over wo dmensonal local felds. In order o defne
Motion of Wavepackets in Non-Hermitian. Quantum Mechanics
 Moon of Wavepaces n Non-Herman Quanum Mechancs Nmrod Moseyev Deparmen of Chemsry and Mnerva Cener for Non-lnear Physcs of Complex Sysems, Technon-Israel Insue of Technology www.echnon echnon.ac..ac.l\~nmrod
Moon of Wavepaces n Non-Herman Quanum Mechancs Nmrod Moseyev Deparmen of Chemsry and Mnerva Cener for Non-lnear Physcs of Complex Sysems, Technon-Israel Insue of Technology www.echnon echnon.ac..ac.l\~nmrod
MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES. Institute for Mathematical Research, Universiti Putra Malaysia, UPM Serdang, Selangor, Malaysia
 Malaysan Journal of Mahemacal Scences 9(2): 277-300 (2015) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Journal homeage: h://ensemumedumy/journal A Mehod for Deermnng -Adc Orders of Facorals 1* Rafka Zulkal,
Malaysan Journal of Mahemacal Scences 9(2): 277-300 (2015) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Journal homeage: h://ensemumedumy/journal A Mehod for Deermnng -Adc Orders of Facorals 1* Rafka Zulkal,
